专题16优化问题与导数的综合应用(课件)-2019年高考数学(理)名师揭秘之一轮总复习
高考数学导数专题专讲 专题16 导数中有关x与ex,lnx的组合函数问题(含答案)

专题16导数中有关x与e x,ln x的组合函数问题在函数的综合问题中,常以x与e x,ln x组合的函数为基础来命题,将基本初等函数的概念、图象与性质糅合在一起,发挥导数的工具作用,应用导数研究函数性质、证明相关不等式(或比较大小)、求参数的取值范围(或最值).着眼于知识点的巧妙组合,注重对函数与方程、转化与化归、分类讨论和数形结合等思想的灵活运用,突出对数学思维能力和数学核心素养的考查.六大经典超越函数的图象函数f(x)=x e x f(x)=e xxf(x)=xe x图象函数f(x)=x ln x f(x)=ln xxf(x)=xln x图象考点一x与ln x的组合函数问题(1)熟悉函数f(x)=h(x)ln x(h(x)=ax2+bx+c(a,b不能同时为0))的图象特征,做到对图(1)(2)中两个特殊函数的图象“有形可寻”.(2)熟悉函数f(x)=ln xh(x)(h(x)=ax2+bx+c(a,b不能同时为0),h(x)≠0)的图象特征,做到对图(3)(4)中两个特殊函数的图象“有形可寻”.【例题选讲】[例1]设函数f (x )=x ln x -ax 22+a -x (a ∈R ).(1)若函数f (x )有两个不同的极值点,求实数a 的取值范围;(2)若a =2,k ∈N ,g (x )=2-2x -x 2,且当x >2时不等式k (x -2)+g (x )<f (x )恒成立,试求k 的最大值.分析(1)将原问题转化为两个函数图象的交点问题,利用数形结合思想进行求解;(2)将不等式恒成立问题转化为函数的最值问题进行求解.解析(1)由题意知,函数f (x )的定义域为(0,+∞),f ′(x )=ln x +1-ax -1=ln x -ax ,令f ′(x )=0,可得a =ln x x,令h (x )=ln xx(x >0),则由题可知直线y =a 与函数h (x )的图象有两个不同的交点,h ′(x )=1-ln x x 2,令h ′(x )=0,得x =e ,可知h (x )在(0,e)上单调递增,在(e ,+∞)上单调递减,h (x )max =h (e)=1e ,当x →0时,h (x )→-∞,当x →+∞时,h (x )→0,故实数a (2)当a =2时,f (x )=x ln x -x 2+2-x ,k (x -2)+g (x )<f (x ),即k (x -2)+2-2x -x 2<x ln x -x 2+2-x ,整理得k (x -2)<x ln x +x ,因为x >2,所以k <x ln x +xx -2.设F (x )=x ln x +x x -2(x >2),则F ′(x )=x -4-2ln x (x -2)2.令m (x )=x -4-2ln x (x >2),则m ′(x )=1-2x >0,所以m (x )在(2,+∞)上单调递增,m (8)=4-2ln 8<4-2ln e 2=4-4=0,m (10)=6-2ln10>6-2ln e 3=6-6=0,所以函数m (x )在(8,10)上有唯一的零点x 0,即x 0-4-2ln x 0=0,故当2<x <x 0时,m (x )<0,即F ′(x )<0,当x >x 0时,F ′(x )>0,所以F (x )min =F (x 0)=x 0ln x 0+x 0x 0-2=0=x02,所以k <x 02,因为x 0∈(8,10),所以x02∈(4,5),故k 的最大值为4.点评1.极值点问题通常可转化为零点问题,且需要检验零点两侧导函数值的符号是否相反,若已知极值点求参数的取值范围,一定要对结果进行验证.解答任意性(恒成立)、存在性(有解)问题时通常有分离参变量、分拆函数等求解方法,可根据式子的结构特征,进行选择和调整,一般可转化为最值问题进行求解.2.对于有关x 与ln x 的组合函数为背景的试题,要求理解导数公式和导数的运算法则等基础知识,能够灵活利用导数研究函数的单调性,能够恰当地构造函数,并根据区间的不同进行分析、讨论,寻求合理的证明和解不等式的策略.【对点训练】1.若a =ln 22,b =ln 33,c =ln 66,则()A .a <b <cB .c <b <aC .c <a <bD .b <a <c1.答案C解析设f (x )=ln xx ,则f ′(x )=1-ln x x 2,所以f (x )在(0,e)上单调递增,在(e ,+∞)上单调递减,即有f (6)<f (4)<f (3),所以ln 66<ln 44=ln 22<ln 33,故c <a <b .2.已知a >b >0,a b =b a ,有如下四个结论:(1)b <e ;(2)b >e ;(3)存在a ,b 满足a ·b <e 2;(4)存在a ,b 满足a ·b >e 2,则正确结论的序号是()A .(1)(3)B .(2)(3)C .(1)(4)D .(2)(4)2.答案C解析由a b =b a 两边取对数得b ln a =a ln b ⇒ln a a =ln b b .对于y =ln xx,由图象易知当b <e<a 时,才可能满足题意.故(1)正确,(2)错误;另外,由a b =b a ,令a =4,b =2,则a >e ,b <e ,ab =8>e 2,故(4)正确,(3)错误.因此,选C .3.设x ,y ,z 为正数,且2x =3y =5z ,则()A .2x <3y <5zB .5z <2x <3yC .3y <5z <2xD .3y <2x <5z3.答案D解析令2x =3y =5z =t (t >1),两边取对数得x =log 2t =ln t ln 2,y =log 3t =ln t ln 3,z =log 5t =ln tln 5,从而2x =2ln 2ln t ,3y =3ln 3ln t ,5z =5ln 5ln t .由t >1知,要比较三者大小,只需比较2ln 2,3ln 3,5ln 5的大小.又2ln 2=4ln 4,e<3<4<5,由y =ln x x 在(e ,+∞)上单调递减可知,ln 33>ln 44>ln 55,从而3ln 3<4ln 4<5ln 5,3y <2x <5z ,故选D .4.下列四个命题:①ln 5<5ln 2;②ln π>πe;③<11;④3eln 2>42.其中真命题的个数是()A .1B .2C .3D .44.答案B解析构造函数f (x )=ln xx ,则f ′(x )=1-ln x x 2,当x ∈(0,e)时,f ′(x )>0,f (x )单调递增;当x∈(e ,+∞)时,f ′(x )<0,f (x )单调递减.①ln 5<5ln 2⇒2ln 5<5ln 2⇒ln 55<ln 22,又2<5<e ,故错误.②ln π>πe ⇒2ln π>πe ⇒ln ππ>12e=ln e e ,又e>π>e ,故正确.③<11⇒11ln 2<ln 11=2ln 11⇒ln 22=ln 44<ln 1111,又4>11>e ,故正确.④3eln 2>42⇒322eln 2>2×322⇒3232ln 22>ln e e ,显然错误.因此选B .5.已知函数f (x )=kx 2-ln x ,若f (x )>0在函数定义域内恒成立,则k 的取值范围是()ABC∞D5.答案D解析由题意得f (x )>0在函数定义域内恒成立,即kx 2-ln x >0在函数定义域内恒成立,即k >ln x x 2在函数定义域内恒成立,设g (x )=ln xx 2,则g ′(x )=x -2x ln x x 4=x (1-2ln x )x 4,当x ∈(0,e)时,g ′(x )>0,函数g (x )单调递增;当x ∈(e ,+∞)时,g ′(x )<0,函数g (x )单调递减,所以当x =e 时,函数g (x )取得最大值,此时最大值为g (e)=12e ,所以实数kD .6.已知0<x 1<x 2<1,则()A .ln x 1x 2>ln x 2x 1B .ln x 1x 2<ln x 2x 1C .x 2ln x 1>x 1ln x 2D .x 2ln x 1<x 1ln x 26.答案D解析设f (x )=x ln x ,则f ′(x )=ln x +1,由f ′(x )>0,得x >1e,所以函数f (x )调递增;由f ′(x )<0,得0<x <1e ,函数f (x )f (x )在(0,1)上不单调,所以f (x 1)与f (x 2)的大小无法确定,从而排除A ,B ;设g (x )=ln xx ,则g ′(x )=1-ln x x 2,由g ′(x )>0,得0<x <e ,即函数g (x )在(0,e)上单调递增,故函数g (x )在(0,1)上单调递增,所以g (x 1)<g (x 2),即ln x 1x 1<ln x 2x 2,所以x 2ln x 1<x 1ln x 2.故选D .7.已知函数f (x )=ax -ln xx,a ∈R .(1)若f (x )≥0,求a 的取值范围;(2)若y =f (x )的图象与直线y =a 相切,求a 的值.7.解析(1)由题易知,函数f (x )的定义域为(0,+∞).由f (x )≥0,得ax -ln xx ≥0,所以ax ≥ln x x ,又x >0,所以a ≥ln x x 2.令g (x )=ln xx 2,则g ′(x )=1-2ln x x 3.令g ′(x )>0,得0<x <e ,令g′(x )<0,得x >e .所以当0<x <e 时,g (x )单调递增,当x >e 时,g (x )单调递减.所以当x =e 时,g (x )取得最大值g (e)=12e ,所以a ≥12e,即a 的取值范围是12e ,+(2)设y =f (x )的图象与直线y =a 相切于点(t ,a )t )=a ,t )=0.因为f ′(x )=a -1-ln xx 2,所以-ln tt=a ,-1-ln t t 2=0,消去a 可得t -1-(2t -1)ln t =0.(*)令h (t )=t -1-(2t -1)ln t ,则h ′(t )=1t -2ln t -1,易知h ′(t )在(0,+∞)上单调递减,且h ′(1)=0,所以当0<t <1时,h ′(t )>0,h (t )单调递增,当t >1时,h ′(t )<0,h (t )单调递减.所以当且仅当t =1时,h (t )=0,即(*)式成立,所以a =1-ln 112=1.点评1.求解有关x 与e x ,x 与ln x 的组合函数问题,要把相关问题转化为熟悉易解的函数模型来处理;若函数最值不易求解时,可重新分拆、组合、构建新函数,然后借助导数研究函数的性质来求解.2.本例中(1)先将不等式f (x )≥0转化为a ≥ln xx 2,再构造函数g (x )=ln x x 2,求其最大值即可求得a 的取值范围;(2)先由y =f (x )的图象与直线y =a 相切,得到方程组,再构造新函数,通过研究新函数的单调性,求出a 的值.8.已知函数f (x )=x 3-a ln x (a ∈R ).(1)讨论函数f (x )的单调性;(2)若函数y =f (x )在区间(1,e]上存在两个不同零点,求实数a 的取值范围.8.解析(1)∵f ′(x )=3x 2-a x=3x 3-a x(x >0).①当a ≤0时,f ′(x )>0,此时函数在(0,+∞)上单调递增;②当a >0时,令f ′(x )=3x 3-ax=0,得x =3a 3,当xf′(x )<0,此时函数f (x )当xf ′(x )>0,此时函数f (x)(2)由题意知:a =x 3ln x在区间(1,e]上有两个不同实数解,即直线y =a 与函数g (x )=x 3ln x的图象在区间(1,e]上有两个不同的交点,因为g ′(x )=x 2(3ln x -1)(ln x )2,令g ′(x )=0,得x =3e ,所以当x ∈(1,3e)时,g ′(x )<0,函数在(1,3e)上单调递减;当x ∈(3e ,e]时,g ′(x )>0,函数在(3e ,e]上单调递增;则g (x )min =g (3e)=3e ,而g (e 127)=e19ln e 127=27e 19>27,且g (e)=e 3<27.所以要使直线y =a 与函数g (x )=x 3ln x 的图象在区间(1,e]上有两个不同的交点,则3e<a ≤e 3,所以a 的取值范围为(3e ,e 3].考点二x 与e x 的组合函数问题(1)熟悉函数f (x )=h (x )e g (x )(g (x )为一次函数,h (x )=ax 2+bx +c (a ,b 不能同时为0))的图象特征,做到对图(1)(2)中两个特殊函数的图象“有形可寻”.(2)熟悉函数f (x )=e xh (x )(h (x )=ax 2+bx +c (a ,b 不能同时为0),h (x )≠0)的图象特征,做到对图(3)(4)中两个特殊函数的图象“有形可寻”.【例题选讲】[例1]已知函数f (x )=a (x -1),g (x )=(ax -1)·e x ,a ∈R .(1)求证:存在唯一实数a ,使得直线y =f (x )和曲线y =g (x )相切;(2)若不等式f (x )>g (x )有且只有两个整数解,求a 的取值范围.分析(1)设切点的坐标为(x 0,y 0),然后由切点既在直线上又在曲线上得到关于x 0的方程,再构造函数,从而通过求导研究新函数的单调性使问题得证;(2)首先将问题转化为<1,然后令m (x )=x -x -1ex ,再通过求导研究函数m (x )的单调性,求得最小值,从而分a ≤0,0<a <1,a ≥1三种情况来讨论,进而求得a 的取值范围.解析(1)f ′(x )=a ,g ′(x )=(ax +a -1)e x .设直线y =f (x )和曲线y =g (x )的切点的坐标为(x 0,y 0),则y 0=a (x 0-1)=(ax 0-1)e x 0,得a (x 0e x 0-x 0+1)=e x 0,①又因为直线y =f (x )和曲线y =g (x )相切,所以a =g ′(x 0)=(ax 0+a -1)e x 0,整理得a (x 0e x 0+e x 0-1)=e x 0,②结合①②得x 0e x 0-x 0+1=x 0e x 0+e x 0-1,即e x 0+x 0-2=0,令h (x )=e x +x -2,则h ′(x )=e x +1>0,所以h (x )在R 上单调递增.又因为h (0)=-1<0,h (1)=e -1>0,所以存在唯一实数x 0,使得e x 0+x 0-2=0,且x 0∈(0,1),所以存在唯一实数a ,使①②两式成立,故存在唯一实数a ,使得直线y =f (x )与曲线y =g (x )相切.(2)令f (x )>g (x ),即a (x -1)>(ax -1)e x ,所以ax e x -ax +a <e x ,所以1,令m (x )=x -x -1e x ,则m ′(x )=e x +x -2ex,由(1)可得m (x )在(-∞,x 0)上单调递减,在(x 0,+∞)上单调递增,且x 0∈(0,1),故当x ≤0时,m (x )≥m (0)=1,当x ≥1时,m (x )≥m (1)=1,所以当x ∈Z 时,m (x )≥1恒成立.①当a ≤0时,am (x )<1恒成立,此时有无数个整数解,舍去;②当0<a <1时,m (x )<1a ,因为1a>1,m (0)=m (1)=1,所以两个整数解分别为0,1(2)≥1a,(-1)≥1a,解得a ≥e 22e 2-1,即a ∈e22e 2-1,+③当a ≥1时,m (x )<1a ,因为1a ≤1,m (x )在x ∈Z 时大于或等于1,所以m (x )<1a 无整数解,舍去.综上所述,a 的取值范围为e22e 2-1,+点评1.涉及函数的零点的个数问题、方程解的个数问题、函数图象的交点个数问题时,一般先通过导数研究函数的单调性、最大值、最小值等,再借助函数的大致图象判断零点、方程的根、函数图象的交点的情况,归根到底还是研究函数的性质,如单调性、极值等.2.在求解有关x 与e x 的组合函数综合题时要把握三点:(1)灵活运用复合函数的求导法则,由外向内,层层求导;(2)把相关问题转化为熟悉易解的函数模型来处理;(3)函数最值不易求解时,可重新组合、分拆,构建新函数,通过分类讨论新函数的单调性求最值.3.以形助数、数形沟通,实现数形结合,形象直观地得出结论,体现了直观想象等数学核心素养.考点三x 与e x ,ln x 的组合函数问题(1)熟悉函数f (x )=h (x )ln x ±e x (h (x )=ax 2+bx+c (a ,b 不能同时为0))的图形特征,做到对图(1)(2)(3)(4)所示的特殊函数的图象“有形可寻”.(2)熟悉函数f (x )=e xh (x )±ln x (其中h (x )=ax 2+bx +c (a ,b 不同时为0))的图形特征,做到对图(5)(6)所示的两个特殊函数的图象“有形可寻”.命题点1分离参数,设而不求【例题选讲】[例1]已知函数f (x )=ln x +m x ,g (x )=e xx(e =2.71828……为自然对数的底数),是否存在整数m ,使得对任意的x y =f (x )的图象在y =g (x )的图象下方?若存在,请求出整数m 的最大值;若不存在,请说明理由.解析假设存在整数m 满足题意,则不等式ln x +m x <e xx,对任意的x即m <e x -x ln x 对任意的x v (x )=e x -x ln x ,则v ′(x )=e x -ln x -1,令φ(x )=e x -ln x -1,则φ′(x )=e x -1x ,易知φ′(x )因为φe 12-2<0,φ′(1)=e -1>0且φ′(x )所以存在唯一的x 0φ′(x 0)=0,即e x 0-1x 0=0,则x 0=-ln x 0.当x x φ(x )单调递减;当x ∈(x 0,+∞)时,φ(x )单调递增.则φ(x )在x =x 0处取得最小值,且最小值为φ(x 0)=e x0-ln x 0-1=1x 0+x 0-1>2x 0·1x 0-1=1>0,所以v ′(x )>0,即v (x )m ≤e 12-12ln 12=e 12+12ln 2≈1.99529,故存在整数m 满足题意,且m 的最大值为1.点评1.对于恒成立或有解问题分离参数后,导函数的零点不可求,且不能借助图象或观察得到,常采用设而不求,整体代入的方法.2.本例通过虚设零点x 0得到x 0=-ln x 0,将e x 0-ln x 0-1转化为普通代数式1x 0+x 0-1,然后使用基本不等式求出最值,同时消掉x 0,即借助φ′(x 0)=0作整体代换,采取设而不求,达到化简求解的目的.命题点2分离ln x 与e x[例2]已知函数f (x )=ax 2-x ln x .(1)若函数f (x )在(0,+∞)上单调递增,求实数a 的取值范围;(2)若a =e ,证明:当x >0时,f (x )<x e x +1e .解析(1)由题意知,f ′(x )=2ax -ln x -1.因为函数f (x )在(0,+∞)上单调递增,所以当x >0时,f ′(x )≥0,即2a ≥ln x +1x在x >0时恒成立.令g (x )=ln x +1x(x >0),则g ′(x )=-ln xx 2,易知g (x )在(0,1)上单调递增,在(1,+∞)上单调递减,则g (x )max =g (1)=1,所以2a ≥1,即a ≥12.故实数a 的取值范围是12,+(2)证明若a =e ,要证f (x )<x e x +1e ,只需证e x -ln x <e x +1e x ,即e x -e x <ln x +1e x.令h (x )=ln x +1e x (x >0),则h ′(x )=e x -1e x 2,易知h (x )h (x )min =0,所以ln x +1e x≥0.再令φ(x )=e x -e x ,则φ′(x )=e -e x ,易知φ(x )在(0,1)上单调递增,在(1,+∞)上单调递减,则φ(x )max =φ(1)=0,所以e x -e x ≤0.因为h (x )与φ(x )不同时为0,所以e x -e x <ln x +1e x ,故原不等式成立.点评1.若直接求导比较复杂或无从下手时,可将待证式进行变形,构造两个都便于求导的函数,从而找到可以传递的中间量,达到证明的目标.2.本题第(2)小题中变形后再隔离分析构造函数,原不等式化为ln x +1e x>e x -e x (x >0)(分离ln x 与e x ),便于探求构造的函数h (x )=ln x +1e x 和φ(x )=e x -e x 的单调性,分别求出h (x )的最小值与φ(x )的最大值,借助“中间媒介”证明不等式.【对点训练】1.已知函数f (x )=ln x +ax(a >0).(1)若函数f (x )有零点,求实数a 的取值范围;(2)证明:当a ≥2e 时,ln x +a x -e -x >0.1.解析(1)由题意可知,函数f (x )的定义域为(0,+∞).由f (x )=ln x +ax=0有解,得a =-x ln x 有解,令g (x )=-x ln x ,则g ′(x )=-(ln x +1).∵当x g ′(x )>0,当x g ′(x )<0,∴函数g (x )g (x )max ==-1e ln 1e =1e .∵a =-x ln x 有解,且x >0,a >0,∴0<a ≤1e ,∴实数a ,1e .(2)要证当a ≥2e 时,ln x +a x -e -x >0,即证ln x +a x >e -x ,∵x >0,∴即证x ln x +a >x e -x ,即证(x ln x +a )min >(x e -x )max .令h (x )=x ln x +a ,则h ′(x )=ln x +1.当0<x <1e 时,f ′(x )<0;当x >1e 时,f ′(x )>0.∴函数h (x )∴h (x )min ==-1e +a ,故当a ≥2e 时,h (x )≥-1e +a ≥1e.①令φ(x )=x e -x ,则φ′(x )=e -x -x e -x =e -x (1-x ).当0<x <1时,φ′(x )>0;当x >1时,φ′(x )<0.∴函数φ(x )在(0,1)上单调递增,在(1,+∞)上单调递减,∴φ(x )max =φ(1)=1e .故当x >0时,φ(x )≤1e.②显然,不等式①②中的等号不能同时成立,故当a ≥2e 时,ln x +ax-e -x >0.。
高考数学专题复习《导数的综合应用》PPT课件

(1)∀x∈D,f(x)≤k⇔f(x)max≤k;∃x∈D,f(x)≤k⇔f(x)min≤k;
(2)∀x∈D,f(x)≤g(x) ⇔f(x)max≤g(x)min;∃x∈D,f(x)≤g(x) ⇔ f(x)min≤g(x)max.
4.含两个未知数的不等式(函数)问题的常见题型及具体转化策略
(+1)ln
H(x)=
,则
-1
1
=
--2ln
(-1)
2
,
2 -2+1
K'(x)= 2 >0,于是
K(x)在(1,+∞)上单调递增,
所以 K(x)>K(1)=0,于是 H'(x)>0,从而 H(x)在(1,+∞)上单调递增.由洛必达法
(x+1)x
则,可得 lim+
x-1
→1
取值范围是(-∞,2].
第三章
高考大题专项(一) 导数的综合应用
内
容
索
引
01
突破1
利用导数研究与不等式有关的问题
必备知识预案自诊
关键能力学案突破
02
突破2
利用导数研究与函数零点有关的问题
必备知识预案自诊
关键能力学案突破
【考情分析】
从近五年的高考试题来看,对导数在函数中的应用的考查常常是一大一小
两个题目,其中解答题的命题特点是:以三次函数、对数函数、指数函数及
(1)∀x1∈[a,b],x2∈[c,d],f(x1)>g(x2)⇔f(x)在[a,b]上的最小值>g(x)在[c,d]上的
最大值.
(2)∃x1∈[a,b],x2∈[c,d],f(x1)>g(x2)⇔f(x)在[a,b]上的最大值>g(x)在[c,d]上的
专题16 导数及其应用小题综合(学生卷)-十年(2015-2024)高考真题数学分项汇编(全国通用)
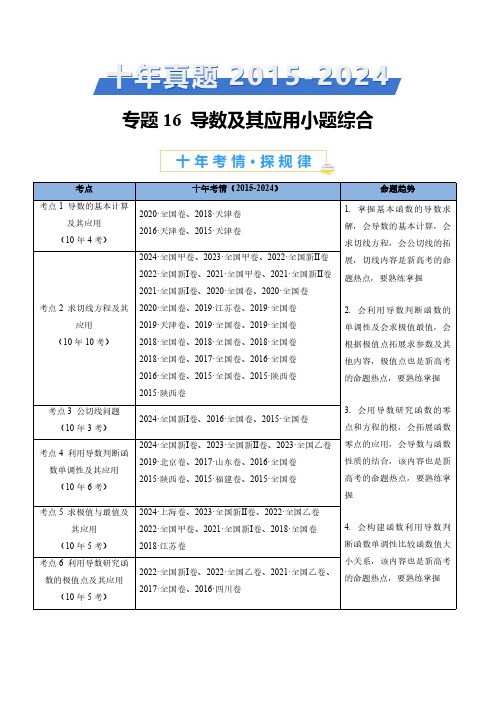
专题16导数及其应用小题综合考点十年考情(2015-2024)命题趋势考点1导数的基本计算及其应用(10年4考)2020·全国卷、2018·天津卷2016·天津卷、2015·天津卷1.掌握基本函数的导数求解,会导数的基本计算,会求切线方程,会公切线的拓展,切线内容是新高考的命题热点,要熟练掌握2.会利用导数判断函数的单调性及会求极值最值,会根据极值点拓展求参数及其他内容,极值点也是新高考的命题热点,要熟练掌握3.会用导数研究函数的零点和方程的根,会拓展函数零点的应用,会导数与函数性质的结合,该内容也是新高考的命题热点,要熟练掌握4.会构建函数利用导数判断函数单调性比较函数值大小关系,该内容也是新高考的命题热点,要熟练掌握考点2求切线方程及其应用(10年10考)2024·全国甲卷、2023·全国甲卷、2022·全国新Ⅱ卷2022·全国新Ⅰ卷、2021·全国甲卷、2021·全国新Ⅱ卷2021·全国新Ⅰ卷、2020·全国卷、2020·全国卷2020·全国卷、2019·江苏卷、2019·全国卷2019·天津卷、2019·全国卷、2019·全国卷2018·全国卷、2018·全国卷、2018·全国卷2018·全国卷、2017·全国卷、2016·全国卷2016·全国卷、2015·全国卷、2015·陕西卷2015·陕西卷考点3公切线问题(10年3考)2024·全国新Ⅰ卷、2016·全国卷、2015·全国卷考点4利用导数判断函数单调性及其应用(10年6考)2024·全国新Ⅰ卷、2023·全国新Ⅱ卷、2023·全国乙卷2019·北京卷、2017·山东卷、2016·全国卷2015·陕西卷、2015·福建卷、2015·全国卷考点5求极值与最值及其应用(10年5考)2024·上海卷、2023·全国新Ⅱ卷、2022·全国乙卷2022·全国甲卷、2021·全国新Ⅰ卷、2018·全国卷2018·江苏卷考点6利用导数研究函数的极值点及其应用(10年5考)2022·全国新Ⅰ卷、2022·全国乙卷、2021·全国乙卷、2017·全国卷、2016·四川卷5.要会导数及其性质的综合应用,加强复习考点7导数与函数的基本性质结合问题(10年6考)2024·全国新Ⅰ卷、2023·全国新Ⅰ卷、2022·全国新Ⅰ卷2021·全国新Ⅱ卷、2017·山东卷、2015·四川卷考点8利用导数研究函数的零点及其应用(10年6考)2024·全国新Ⅱ卷、2023·全国乙卷、2021·北京卷、2018·江苏卷、2017·全国卷、2015·陕西卷考点9利用导数研究方程的根及其应用(10年3考)2024·全国甲卷、2021·北京卷、2015·安徽卷2015·全国卷、2015·安徽卷考点10构建函数利用导数判断函数单调性比较函数值大小关系(10年3考)2022·全国甲卷、2022·全国新Ⅰ卷、2021·全国乙卷考点01导数的基本计算及其应用1.(2020·全国·高考真题)设函数e ()xf x x a=+.若(1)4e f '=,则a =.2.(2018·天津·高考真题)已知函数f (x )=exlnx ,()'f x 为f (x )的导函数,则()'1f 的值为.3.(2016·天津·高考真题)已知函数()(2+1)e ,()x f x x f x '=为()f x 的导函数,则(0)f '的值为.4.(2015·天津·高考真题)已知函数()()ln ,0,f x ax x x =∈+∞,其中a 为实数,()f x '为()f x 的导函数,若()13f '=,则a 的值为.考点02求切线方程及其应用1.(2024·全国甲卷·高考真题)设函数()2e 2sin 1x xf x x+=+,则曲线()y f x =在点()0,1处的切线与两坐标轴所围成的三角形的面积为()A .16B .13C .12D .232.(2023·全国甲卷·高考真题)曲线e 1xy x =+在点e 1,2⎛⎫ ⎪⎝⎭处的切线方程为()A .e4y x =B .e 2y x =C .e e 44y x =+D .e 3e24y x =+3.(2022·全国新Ⅱ卷·高考真题)曲线ln ||y x =过坐标原点的两条切线的方程为,.4.(2022·全国新Ⅰ卷·高考真题)若曲线()e x y x a =+有两条过坐标原点的切线,则a 的取值范围是.5.(2021·全国甲卷·高考真题)曲线2x 1y x 2-=+在点()1,3--处的切线方程为.6.(2021·全国新Ⅱ卷·高考真题)已知函数12()1,0,0x f x e x x <=>-,函数()f x 的图象在点()()11,A x f x 和点()()22,B x f x 的两条切线互相垂直,且分别交y 轴于M ,N 两点,则||||AM BN 取值范围是.7.(2021·全国新Ⅰ卷·高考真题)若过点(),a b 可以作曲线e x y =的两条切线,则()A .e b a <B .e a b <C .0e ba <<D .0e ab <<8.(2020·全国·高考真题)若直线l 与曲线yx 2+y 2=15都相切,则l 的方程为()A .y =2x +1B .y =2x +12C .y =12x +1D .y =12x +129.(2020·全国·高考真题)函数43()2f x x x =-的图像在点(1(1))f ,处的切线方程为()A .21y x =--B .21y x =-+C .23y x =-D .21y x =+10.(2020·全国·高考真题)曲线ln 1y x x =++的一条切线的斜率为2,则该切线的方程为.11.(2019·江苏·高考真题)在平面直角坐标系xOy 中,点A 在曲线y =ln x 上,且该曲线在点A 处的切线经过点(-e ,-1)(e 为自然对数的底数),则点A 的坐标是.12.(2019·全国·高考真题)已知曲线e ln x y a x x =+在点()1,ae 处的切线方程为2y x b =+,则A .,1a eb ==-B .,1a eb ==C .1,1a eb -==D .1,1a eb -==-13.(2019·天津·高考真题)曲线cos 2xy x =-在点()0,1处的切线方程为.14.(2019·全国·高考真题)曲线23()e x y x x =+在点(0,0)处的切线方程为.15.(2019·全国·高考真题)曲线y =2sin x +cos x 在点(π,–1)处的切线方程为A .10x y --π-=B .2210x y --π-=C .2210x y +-π+=D .10x y +-π+=16.(2018·全国·高考真题)设函数()()321f x x a x ax =+-+.若()f x 为奇函数,则曲线()y f x =在点()00,处的切线方程为()A .2y x=-B .y x=-C .2y x=D .y x=17.(2018·全国·高考真题)曲线()1e xy ax =+在点()01,处的切线的斜率为2-,则=a .18.(2018·全国·高考真题)曲线2ln y x =在点()1,0处的切线方程为.19.(2018·全国·高考真题)曲线2ln(1)y x =+在点(0,0)处的切线方程为.20.(2017·全国·高考真题)曲线21y x x=+在点(1,2)处的切线方程为.21.(2016·全国·高考真题)已知()f x 为偶函数,当0x ≤时,1()e x f x x --=-,则曲线()y f x =在点(1,2)处的切线方程是.22.(2016·全国·高考真题)已知()f x 为偶函数,当0x <时,()ln()3f x x x =-+,则曲线()y f x =在点(1,3)-处的切线方程是.23.(2015·全国·高考真题)已知函数()31f x ax x =++的图像在点()()1,1f 的处的切线过点()2,7,则=a .24.(2015·陕西·高考真题)设曲线x y e =在点(0,1)处的切线与曲线1(0)y x x=>上点P 处的切线垂直,则P 的坐标为.25.(2015·陕西·高考真题)函数x y xe =在其极值点处的切线方程为.考点03公切线问题1.(2024·全国新Ⅰ卷·高考真题)若曲线e x y x =+在点()0,1处的切线也是曲线ln(1)y x a =++的切线,则=a .2.(2016·全国·高考真题)若直线y kx b =+是曲线ln 2y x =+的切线,也是曲线ln(1)y x =+的切线,则b =.3.(2015·全国·高考真题)已知曲线ln y x x =+在点()1,1处的切线与曲线()221y ax a x =+++相切,则a=.考点04利用导数判断函数单调性及其应用1.(2024·全国新Ⅰ卷·高考真题)(多选)设函数2()(1)(4)f x x x =--,则()A .3x =是()f x 的极小值点B .当01x <<时,()2()f x f x <C .当12x <<时,4(21)0f x -<-<D .当10x -<<时,(2)()f x f x ->2.(2023·全国新Ⅱ卷·高考真题)已知函数()e ln xf x a x =-在区间()1,2上单调递增,则a 的最小值为().A .2eB .eC .1e -D .2e -3.(2023·全国乙卷·高考真题)设()0,1a ∈,若函数()()1xx f x a a =++在()0,∞+上单调递增,则a 的取值范围是.4.(2019·北京·高考真题)设函数f (x )=e x +a e −x (a 为常数).若f (x )为奇函数,则a =;若f (x )是R 上的增函数,则a 的取值范围是.5.(2017·山东·高考真题)若函数()e xf x (e=2.71828L ,是自然对数的底数)在()f x 的定义域上单调递增,则称函数()f x 具有M 性质,下列函数中具有M 性质的是A .()2xf x -=B .()2f x x=C .()-3xf x =D .()cos f x x=6.(2016·全国·高考真题)若函数()1sin 2sin 3f x x x a x =-+在R 上单调递增,则a 的取值范围是A .[]1,1-B .11,3⎡⎤-⎢⎥⎣⎦C .11,33⎡⎤-⎢⎥⎣⎦D .11,3⎡⎤--⎢⎣⎦7.(2015·陕西·高考真题)设()sin f x x x =-,则()f x =A .既是奇函数又是减函数B .既是奇函数又是增函数C .是有零点的减函数D .是没有零点的奇函数8.(2015·福建·高考真题)若定义在R 上的函数()f x 满足()01f =-,其导函数()f x '满足()1f x k '>>,则下列结论中一定错误的是()A .11f k k ⎛⎫<⎪⎝⎭B .111f k k ⎛⎫>⎪-⎝⎭C .1111f k k ⎛⎫<⎪--⎝⎭D .111k f k k ⎛⎫>⎪--⎝⎭9.(2015·全国·高考真题)设函数'()f x 是奇函数()f x (x R ∈)的导函数,(1)0f -=,当0x >时,'()()0xf x f x -<,则使得()0f x >成立的x 的取值范围是A .(,1)(0,1)-∞-B .(1,0)(1,)-È+¥C .(,1)(1,0)-∞-- D .(0,1)(1,)⋃+∞考点05求极值与最值及其应用1.(2024·上海·高考真题)已知函数()f x 的定义域为R ,定义集合()()(){}0000,,,M x x x x f x f x ∞=∈∈-<R ,在使得[]1,1M =-的所有()f x 中,下列成立的是()A .存在()f x 是偶函数B .存在()f x 在2x =处取最大值C .存在()f x 是严格增函数D .存在()f x 在=1x -处取到极小值2.(2023·全国新Ⅱ卷·高考真题)若函数()()2ln 0b cf x a x a x x =++≠既有极大值也有极小值,则().A .0bc >B .0ab >C .280b ac +>D .0ac <3.(2022·全国乙卷·高考真题)函数()()cos 1sin 1f x x x x =+++在区间[]0,2π的最小值、最大值分别为()A .ππ22-,B .3ππ22-,C .ππ222-+,D .3ππ222-+,4.(2022·全国甲卷·高考真题)当1x =时,函数()ln bf x a x x=+取得最大值2-,则(2)f '=()A .1-B .12-C .12D .15.(2021·全国新Ⅰ卷·高考真题)函数()212ln f x x x =--的最小值为.6.(2018·全国·高考真题)已知函数()2sin sin 2f x x x =+,则()f x 的最小值是.7.(2018·江苏·高考真题)若函数()()3221f x x ax a R =-+∈在()0,+∞内有且只有一个零点,则()f x 在[]1,1-上的最大值与最小值的和为.考点06利用导数研究函数的极值点及其应用1.(2022·全国新Ⅰ卷·高考真题)(多选)已知函数3()1f x x x =-+,则()A .()f x 有两个极值点B .()f x 有三个零点C .点(0,1)是曲线()y f x =的对称中心D .直线2y x =是曲线()y f x =的切线2.(2022·全国乙卷·高考真题)已知1x x =和2x x =分别是函数2()2e x f x a x =-(0a >且1a ≠)的极小值点和极大值点.若12x x <,则a 的取值范围是.3.(2021·全国乙卷·高考真题)设0a ≠,若a 为函数()()()2f x a x a x b =--的极大值点,则()A .a b<B .a b>C .2ab a <D .2ab a >4.(2017·全国·高考真题)若2x =-是函数21()(1)e x f x x ax -=+-的极值点,则()f x 的极小值为.A .1-B .32e --C .35e -D .15.(2016·四川·高考真题)已知a 为函数f (x )=x 3–12x 的极小值点,则a=A .–4B .–2C .4D .2考点07导数与函数的基本性质结合问题1.(2024·全国新Ⅰ卷·高考真题)(多选)设函数2()(1)(4)f x x x =--,则()A .3x =是()f x 的极小值点B .当01x <<时,()2()f x f x <C .当12x <<时,4(21)0f x -<-<D .当10x -<<时,(2)()f x f x ->2.(2023·全国新Ⅰ卷·高考真题)(多选)已知函数()f x 的定义域为R ,()()()22f xy y f x x f y =+,则().A .()00f =B .()10f =C .()f x 是偶函数D .0x =为()f x 的极小值点3.(2022·全国新Ⅰ卷·高考真题)(多选)已知函数()f x 及其导函数()f x '的定义域均为R ,记()()g x f x '=,若322f x ⎛⎫- ⎪⎝⎭,(2)g x +均为偶函数,则()A .(0)0f =B .102g ⎛⎫-= ⎪⎝⎭C .(1)(4)f f -=D .(1)(2)g g -=4.(2021·全国新Ⅱ卷·高考真题)写出一个同时具有下列性质①②③的函数():f x .①()()()1212f x x f x f x =;②当(0,)x ∈+∞时,()0f x '>;③()f x '是奇函数.5.(2017·山东·高考真题)若函数()x y e f x = 2.71828...e =(是自然对数的底数)在()f x 的定义域上单调递增,则称函数()f x 具有M 性质,下列函数中所有具有M 性质的函数的序号为①=2xf x -()②=3xf x -()③3=f x x ()④2=2f x x +()6.(2015·四川·高考真题)已知函数f (x )=2x ,g (x )=x 2+ax (其中a ∈R ).对于不相等的实数x 1,x 2,设m =1212()()f x f x x x --,n =1212()()g x g x x x --,现有如下命题:①对于任意不相等的实数x 1,x 2,都有m >0;②对于任意的a 及任意不相等的实数x 1,x 2,都有n >0;③对于任意的a ,存在不相等的实数x 1,x 2,使得m =n ;④对于任意的a ,存在不相等的实数x 1,x 2,使得m =-n.其中真命题有(写出所有真命题的序号).考点08利用导数研究函数的零点及其应用1.(2024·全国新Ⅱ卷·高考真题)(多选)设函数32()231f x x ax =-+,则()A .当1a >时,()f x 有三个零点B .当0a <时,0x =是()f x 的极大值点C .存在a ,b ,使得x b =为曲线()y f x =的对称轴D .存在a ,使得点()()1,1f 为曲线()y f x =的对称中心2.(2023·全国乙卷·高考真题)函数()32f x x ax =++存在3个零点,则a 的取值范围是()A .(),2-∞-B .(),3-∞-C .()4,1--D .()3,0-3.(2021·北京·高考真题)已知函数()lg 2f x x kx =--,给出下列四个结论:①若0k =,()f x 恰有2个零点;②存在负数k ,使得()f x 恰有1个零点;③存在负数k ,使得()f x 恰有3个零点;④存在正数k ,使得()f x 恰有3个零点.其中所有正确结论的序号是.4.(2018·江苏·高考真题)若函数()()3221f x x ax a R =-+∈在()0,+∞内有且只有一个零点,则()f x 在[]1,1-上的最大值与最小值的和为.5.(2017·全国·高考真题)已知函数211()2()x x f x x x a e e --+=-++有唯一零点,则=a A .12-B .13C .12D .16.(2015·陕西·高考真题)对二次函数2()f x ax bx c =++(a 为非零整数),四位同学分别给出下列结论,其中有且仅有一个结论是错误的,则错误的结论是A .1-是()f x 的零点B .1是()f x 的极值点C .3是()f x 的极值D .点(2,8)在曲线()y f x =上考点09利用导数研究方程的根及其应用1.(2024·全国甲卷·高考真题)曲线33y x x =-与()21y x a =--+在()0,∞+上有两个不同的交点,则a 的取值范围为.2.(2021·北京·高考真题)已知函数()lg 2f x x kx =--,给出下列四个结论:①若0k =,()f x 恰有2个零点;②存在负数k ,使得()f x 恰有1个零点;③存在负数k ,使得()f x 恰有3个零点;④存在正数k ,使得()f x 恰有3个零点.其中所有正确结论的序号是.3.(2015·安徽·高考真题)函数()32f x ax bx cx d =+++的图象如图所示,则下列结论成立的是()A .0a >,0b <,0c >,0d >B .0a >,0b <,0c <,0d >C .0a <,0b <,0c >,0d >D .0a >,0b >,0c >,0d <4.(2015·全国·高考真题)设函数()(21)x f xe x ax a =--+,其中1a <,若存在唯一的整数0x ,使得0()0f x <,则a 的取值范围是()A .3,12e ⎡⎫-⎪⎢⎣⎭B .33,2e 4⎡⎫-⎪⎢⎣⎭C .33,2e 4⎡⎫⎪⎢⎣⎭D .3,12e ⎡⎫⎪⎢⎣⎭5.(2015·安徽·高考真题)设30x ax b ++=,其中,a b 均为实数,下列条件中,使得该三次方程仅有一个实根的是.(写出所有正确条件的编号)①3,3a b =-=-;②3,2a b =-=;③3,2a b =->;④0,2a b ==;⑤1,2a b ==.考点10构建函数利用导数判断函数单调性比较函数值大小关系1.(2022·全国甲卷·高考真题)已知3111,cos ,4sin 3244a b c ===,则()A .c b a>>B .b a c>>C .a b c >>D .a c b>>2.(2022·全国新Ⅰ卷·高考真题)设0.110.1e ,ln 0.99a b c ===-,则()A .a b c <<B .c b a <<C .c<a<bD .a c b<<3.(2021·全国乙卷·高考真题)设2ln1.01a =,ln1.02b =,1c =-.则()A .a b c<<B .b<c<aC .b a c<<D .c<a<b。
高考数学专题突破教师版-导数的综合应用(考点讲析)

【解析】
(I) f (x) 的定义域为 (0, ) .当 a 4 时,
f (x) (x 1) ln x 4(x 1), f (x) ln x 1 3 , f (1) 2, f (1) 0. x
曲线 y f (x) 在 (1, f (1)) 处的切线方程为 2x y 2 0.
(II)当 x (1, ) 时, f (x) 0 等价于 ln x a(x 1) 0. x 1
数图象的交点横坐标.
【典例 1】(2019·全国高考真题(理))已知函数 f (x) sin x ln(1 x) , f (x) 为 f (x) 的导数.证明:
(1) f (x) 在区间 (1, ) 存在唯一极大值点; 2
(2) f (x) 有且仅有 2 个零点.
【答案】(1)见解析;(2)见解析
,
4
因为当 x
1 时, ln x
x 1,又 x1
x0
1,故 ex1x0
x02 (x1 1) x1 1
x02 ,
两边取对数,得 ln ex1x0 ln x02 ,
于是 x1 x0 2 ln x0 2(x0 1) ,整理得 3x0 x1 2 ,
【总结提升】 利用导数研究函数零点或方程根的方法 (1)通过最值(极值)判断零点个数的方法. 借助导数研究函数的单调性、极值后,通过极值的正负,函数单调性判断函数图象走势,从而判断零点个 数或者通过零点个数求参数范围. (2)数形结合法求解零点. 对于方程解的个数(或函数零点个数)问题,可利用函数的值域或最值,结合函数的单调性,画出草图数形 结合确定其中参数的范围. (3)构造函数法研究函数零点. ①根据条件构造某个函数,利用导数确定函数的单调区间及极值点,根据函数零点的个数寻找函数在给定 区间的极值以及区间端点的函数值与 0 的关系,从而求解. ②解决此类问题的关键是将函数零点、方程的根、曲线交点相互转化,突出导数的工具作用,体现转化与 化归的思想方法.
高三数学高考复习 《函数与导数》综合问题复习建议 课件(共31张PPT)

关于函数与导数
• 求解步骤(方法显性化,把握大方向)
– 分析问题:归类、联系
– 构建函数:确定研究对象,不要僵化,可能是局 部函数,也可能需要用化归的思想(将复杂的, 困难的问题转化为简单的,容易的,熟悉的问 题),也可能需要进行适当变形 – 研究函数:由性质得草图(比单纯描点效率高)
– 解决问题:看图说话,用形思考(但不能以图代 证),用数说理
《函数与导数》综合问题复习建议
内容提纲
1
关于《函数与导数》
2
举例说明
几点建议
3
关于函数与导数
• 为什么研究函数?
– 出于实际需要:生活中的变化无处不在,运动 是绝对的,静止是相对的,用函数来刻画变量 之间的依赖关系 – 数学建模的过程: 实际 情境 提出 问题 分析 问题
建立 模型
Hale Waihona Puke 确定 参数计算 求解
举例:“适当变形”选择研究对象
• 何时变形?
– 当研究对象的形式或问题的求解过程比较复杂 时:如需多于两次求导,或需分很多情况讨论
• 怎样变形?
– 变形以提取局部函数; – 分离变量(为避免讨论,但前提是方便分离且 分离后的函数方便研究性质); – 方程、不等式的等价转化
例 设函数 f ( x) x ln x . (1)若对任意 x (0, ) , 2 f ( x) x2 ax 3 恒成立,求 a 的取值范围.
(17 北京理)已知函数 f ( x) e x cos x x . (Ⅰ)求曲线 y f ( x ) 在点 (0, f (0)) 处的切线方程;
π (Ⅱ)求函数 f ( x ) 在区间 [0, ] 上的最大值和最小值. 2
关于函数与导数
19版高考数学一轮复习第二章函数、导数及其应用课时达标16导数与函数的综合问题理

课时达标 第16讲[解密考纲]本考点主要以基本初等函数为载体,综合应用函数、导数、方程、不等式等知识,常考查恒成立问题、存在性问题或者与实际问题相结合讨论最优解等问题,综合性较强,常作为压轴题出现.三种题型均有出现,以解答题为主,难度较大.1.已知函数f (x )=x 2-ax -a ln x (a ∈R ). (1)若函数f (x )在x =1处取得极值,求a 的值; (2)在(1)的条件下,求证:f (x )≥-x 33+5x 22-4x +116.解析 (1)f ′(x )=2x -a -ax,由题意可得f ′(1)=0,解得a =1.经检验,a =1时f (x )在x =1处取得极小值,所以a =1. (2)由(1)知,f (x )=x 2-x -ln x ,令g (x )=f (x )-⎝ ⎛⎭⎪⎫-x 33+5x22-4x +116=x 33-3x 22+3x -ln x -116,由g ′(x )=x 2-3x +3-1x =x 3-1x -3(x -1)= x -13x(x >0),可知g (x )在(0,1)上是减函数,在(1,+∞)上是增函数,∴g (x )min =g (1)=13-32+3-116=0,∴当x >0时,g (x )≥g (1)=0,于是f (x )≥-x 33+5x 22-4x +116.2.若函数f (x )=ax 3-bx +4,当x =2时,函数f (x )有极值-43.(1)求函数f (x )的解析式;(2)若方程f (x )=k 有3个不同的根,求实数k 的取值范围. 解析 (1)f ′(x )=3ax 2-b ,由题意得⎩⎪⎨⎪⎧f ′ 2 =12a -b =0,f 2 =8a -2b +4=-43,解得⎩⎪⎨⎪⎧a =13,b =4,故所求函数的解析式为f (x )=13x 3-4x +4.(2)由(1)得f ′(x )=x 2-4=(x +2)(x -2),令f ′(x )=0, 得x =2或x =-2.当x 变化时,f ′(x ),f (x )的变化情况如下表.因此,当x =-2时,f (x )有极大值3,当x =2时,f (x )有极小值-3,所以函数f (x )=13x 3-4x +4的图象大致如图所示.因为f (x )=k 有3个不同的根,所以直线y =k 与函数f (x )的图象有3个交点,所以-43<k <283. 3.(2018·河南新乡调研)已知函数f (x )=x -(a +1)ln x -a x (a ∈R ),g (x )=12x 2+ex-x e x.(1)当x ∈[1,e]时,求f (x )的最小值;(2)当a <1时,若存在x 1∈[e ,e 2],使得对任意的x 2∈[-2,0],f (x 1)<g (x 2)恒成立,求a 的取值范围.解析 (1)f (x )的定义域为(0,+∞),f ′(x )= x -1 x -ax2. ①当a ≤1时,x ∈[1,e],f ′(x )≥0,f (x )为增函数, 则f (x )min =f (1)=1-a .②当1<a <e 时,x ∈[1,a ]时,f ′(x )≤0,f (x )为减函数;x ∈[a ,e]时,f ′(x )≥0,f (x )为增函数,则f (x )min =f (a )=a -(a +1)ln a -1.③当a ≥e 时,x ∈[1,e]时,f ′(x )≤0,f (x )在[1,e]上为减函数, 则f (x )min =f (e)=e -(a +1)-ae .综上,当a ≤1时,f (x )min =1-a ; 当1<a <e 时,f (x )min =a -(a +1)ln a -1; 当a ≥e 时,f (x )min =e -(a +1)-ae.(2)由题意知,f (x )(x ∈[e ,e 2])的最小值小于g (x )(x ∈[-2,0])的最小值.由(1)知f (x )在[e ,e 2]上单调递增,f (x )min =f (e)=e -(a +1)-ae,g ′(x )=(1-e x )x .x ∈[-2,0]时,g ′(x )≤0,则g (x )为减函数.所以g (x )min =g (0)=1.所以e -(a +1)-ae <1,即a >e 2-2e e +1.所以a 的取值范围为⎝ ⎛⎭⎪⎫e 2-2e e +1,1.4.某商店经销一种奥运纪念品,每件产品成本为30元,且每卖出一件产品,需向税务部门上交a 元(a 为常数,2≤a ≤5)的税收,设每件产品的日售价为x 元(35≤x ≤41),根据市场调查,日销售量与e x(e 为自然对数的底数)成反比,已知每件产品的日售价为40元时,日销售量为10件.(1)求商店的日利润L (x )元与每件产品的日售价x 元的函数关系式; (2)当每件产品的日售价为多少元时该商店的日利润L (x )最大,说明理由. 解析 (1)设日销售量为k e x 件,则ke 40=10,∴k =10e 40. 则日销售量为10e40e x 件,每件利润为(x -30-a )元,则日利润L (x )=10e 40·x -30-aex(35≤x ≤41).(2)L ′(x )=10e 40·31+a -x ex(35≤x ≤41). ①当2≤a ≤4时,33≤31+a ≤35,L ′(x )≤0,L (x )在[35,41]上是减函数.∴当x =35时,L (x )的最大值为10(5-a )e 5.②当4<a ≤5时,35<31+a ≤36,由L ′(x )=0得x =a +31, 当x ∈(35,a +31)时,L ′(x )>0,L (x )在(35,a +31)上是增函数. 当x ∈(a +31,41]时,L ′(x )<0,L (x )在(a +31,41]上是减函数. ∴当x =a +31时,L (x )的最大值为10e9-a.综上可知,当2≤a ≤4时,日售价为35元可使日利润L (x )最大, 当4<a ≤5时,日售价为a +31元可使日利润L (x )最大. 5.(2018·辽宁五校联考)已知函数f (x )=(ax -1)ln x +x 22.(1)若a =2,求曲线y =f (x )在点(1,f (1))处的切线l 的方程;(2)设函数g (x )=f ′(x )有两个极值点,x 1,x 2,其中x 1∈(0,e],求g (x 1)-g (x 2)的最小值.解析 (1)当a =2时,f ′(x )=2ln x +x -1x+2,f ′(1)=2,f (1)=12,∴切线l 的方程为y -12=2(x -1),即4x -2y -3=0.(2)函数g (x )=a ln x +x -1x+a ,定义域为(0,+∞),g ′(x )=1+a x +1x 2=x 2+ax +1x2,令g ′(x )=0,得x 2+ax +1=0, ∴x 1+x 2=-a ,x 1x 2=1, 故x 2=1x 1,a =-⎝ ⎛⎭⎪⎫x 1+1x 1.g (x 1)-g (x 2)=g (x 1)-g ⎝ ⎛⎭⎪⎫1x 1=a ln x 1+x 1-1x 1+a -⎝ ⎛⎭⎪⎫a ln 1x 1+1x 1-x 1+a =2⎝ ⎛⎭⎪⎫x 1-1x 1+2a lnx 1=2⎝⎛⎭⎪⎫x 1-1x 1-2⎝ ⎛⎭⎪⎫x 1+1x 1ln x 1,令h (x )=2⎝⎛⎭⎪⎫x -1x -2⎝ ⎛⎭⎪⎫x +1x ln x ,x ∈(0,e].则[g (x 1)-g (x 2)]min =h (x )min ,h ′(x )=2 1+x 1-x ln x x2, 当x ∈(0,1]时,h ′(x )≤0,当x ∈(1,e]时,h ′(x )<0, 则当x ∈(0,e]时,h (x )单调递减, ∴h (x )min =h (e)=-4e ,故[g (x 1)-g (x 2)]min =-4e.6.已知函数f (x )=12ax 2-(2a +1)x +2ln x (a ∈R ).(1)当a =23时,求函数f (x )的单调区间;(2)当a >12时,设g (x )=(x 2-2x )e x,求证:对任意x 1∈(0,2],均存在x 2∈(0,2],使得f (x 1)<g (x 2)成立.解析 (1)由题知,定义域为x >0,f ′(x )=ax -(2a +1)+2x.当a =23时,f ′(x )=23x -73+2x = 2x -3 x -2 3x,令f ′(x )>0,解得0<x <32或x >2,令f ′(x )<0,解得32<x <2,则函数f (x )的单调递增区间为⎝ ⎛⎭⎪⎫0,32和(2,+∞),单调递减区间为⎝ ⎛⎭⎪⎫32,2. (2)若要命题成立,只需当x ∈(0,2]时,f (x )max <g (x )max由g ′(x )=(x 2-2)e x可知,当x ∈(0,2]时,函数g (x )在区间(0,2)上单调递减,在区间(2,2)上单调递增,g (0)=g (2)=0,故g (x )max =0,所以只需f (x )max <0.对函数f (x )来说,f ′(x )=ax -(2a +1)+2x = ax -1 x -2x.当a >12时,0<1a <2,则函数f (x )在区间⎝ ⎛⎭⎪⎫0,1a 上单调递增,在区间⎝ ⎛⎦⎥⎤1a ,2上单调递减,所以f (x )max =f ⎝ ⎛⎭⎪⎫1a =-2ln a -12a -2;当a ≥1时,显然小于0,满足题意;当12<a <1时,可令h (a )=-2ln a -12a -2,h ′(a )=1-4a2a, 可知函数h (a )在区间⎝ ⎛⎭⎪⎫12,1时单调递减,则h (a )<h ⎝ ⎛⎭⎪⎫12=2ln 2-3<0,满足题意;综上所述,当a >12时,对任意x 1∈(0,2],均存在x 2∈(0,2],使得f (x 1)<g (x 2)成立.。
2019年高考数学(理)一轮复习精品资料专题15导数的综合应用(教学案)含解析

2019年高考数学(理)一轮复习精品资料1.会求闭区间上函数的最大值、最小值(其中多项式函数一般不超过三次).2.会利用导数解决某些实际问题.1.利用导数解决生活中的优化问题的一般步骤(1)分析实际问题中各量之间的关系,列出实际问题的数学模型,写出实际问题中变量之间的函数关系式y =f (x );(2)求函数的导数f ′(x ),解方程f ′(x )=0;(3)比较函数在区间端点和f ′(x )=0的点的函数值的大小,最大(小)者为最大(小)值; (4)回归实际问题作答. 2.不等式问题(1)证明不等式时,可构造函数,将问题转化为函数的极值或最值问题.(2)求解不等式恒成立问题时,可以考虑将参数分离出来,将参数范围问题转化为研究新函数的值域问题. 3.方程解的个数问题构造函数,利用导数研究函数的单调性,极值和特殊点的函数值,根据函数性质结合草图推断方程解的个数.高频考点一 用导数解决与不等式有关的问题 例1、已知函数f (x )=ax +bx 2+1在点(-1,f (-1))处的切线方程为x +y +3=0. (1)求函数f (x )的解析式;(2)设g (x )=ln x ,求证:g (x )≥f (x )在[1,+∞)上恒成立; (3)若0<a <b ,求证:ln b -ln a b -a >2aa 2+b 2.(1)解 将x =-1代入切线方程得y =-2,所以f (-1)=b -a1+1=-2,化简得b -a =-4.①f ′(x )=a (x 2+1)-(ax +b )·2x(x 2+1)2, f ′(-1)=2a +2(b -a )4=-1.②联立①②,解得a =2,b =-2.所以f (x )=2x -2x 2+1.(3)证明 因为0<a <b ,所以b a>1,由(2)知ln b a >2·ba -2⎝ ⎛⎭⎪⎫b a 2+1,整理得ln b -ln a b -a >2aa 2+b 2,所以当0<a <b 时,ln b -ln a b -a >2aa 2+b 2.【方法规律】证明不等式通常需要构造函数,利用函数的最值、单调性证明.(1)证明不等式f (x )<g (x ),可构造函数F (x )=f (x )-g (x ),利用导数求F (x )的值域,得到F (x )<0即可; (2)对于证明含有两个变量a ,b 的不等式时,一种方法是通过变形构造成不等式f (a )>f (b ),然后利用函数f (x )的单调性证明,另一种方法是通过换元构造成单变量不等式,如本例令x =ba然后再利用已知关系证明即可.【变式探究】设函数f (x )=ln x -x +1. (1)讨论f (x )的单调性;(2)证明当x ∈(1,+∞)时,1<x -1ln x<x ;(3)设c >1,证明当x ∈(0,1)时,1+(c -1)x >c x. (1)解 依题意,f (x )的定义域为(0,+∞).f ′(x )=1x-1,令f ′(x )=0,得x =1,∴当0<x <1时,f ′(x )>0,f (x )单调递增. 当x >1时,f ′(x )<0,f (x )单调递减.(3)证明 由题设c >1,设g (x )=1+(c -1)x -c x, 则g ′(x )=c -1-c xln c .令g ′(x )=0,解得x 0=lnc -1ln cln c.当x <x 0时,g ′(x )>0,g (x )单调递增; 当x >x 0时,g ′(x )<0,g (x )单调递减.由(2)知1<c -1ln c<c ,故0<x 0<1.又g (0)=g (1)=0,故当0<x <1时,g (x )>0. 所以当x ∈(0,1)时,1+(c -1)x >c x. 高频考点二、不等式恒成立问题求参数的范围 例2、(2017·全国Ⅱ卷改编)设函数f (x )=(1-x 2)e x. (1)讨论f (x )的单调性;(2)当x ≥0时,f (x )≤ax +1,求正实数a 的取值范围. 解 (1)f ′(x )=-2x e x +(1-x 2)e x =(1-2x -x 2)e x. 令f ′(x )=0,得x 2+2x -1=0, 解得x 1=-2-1,x 2=2-1,令f ′(x )>0,则x ∈(-2-1,2-1),令f ′(x )<0,则x ∈(-∞,-2-1)∪(2-1,+∞). ∴f (x )在区间(-∞,-2-1),(2-1,+∞)上单调递减,在区间(-2-1,2-1)上单调递增. (2)f (x )=(1+x )(1-x )e x.当a ≥1时,设函数h (x )=(1-x )e x,h ′(x )=-x e x<0(x >0),因此h (x )在[0,+∞)上单调递减,又h (0)=1,故h (x )≤1,所以f (x )=(x +1)h (x )≤x +1≤ax +1. 当0<a <1时,设函数g (x )=e x -x -1,g ′(x )=e x-1>0(x >0), 所以g (x )在[0,+∞)上单调递增. 又g (0)=0,故e x≥x +1.当0<x <1时,f (x )=(1-x )(1+x )e x ≥(1-x )(1+x )2, 又(1-x )(1+x )2-(ax +1)=x (1-a -x -x 2), 取x 0=5-4a -12,则x 0∈(0,1), (1-x 0)(1+x 0)2-ax 0-1=0,故f (x 0)>ax 0+1. 综上可知,正实数a 的取值范围是[1,+∞). 【变式探究】已知函数f (x )=ax +ln x ,x ∈[1,e]. (1)若a =1,求f (x )的最大值;(2)若f (x )≤0恒成立,求实数a 的取值范围.(2)法一 ∵f (x )≤0即ax +ln x ≤0对x ∈[1,e]恒成立, ∴a ≤-ln xx,x ∈[1,e].令g (x )=-ln x x,x ∈[1,e],则g ′(x )=ln x -1x2, ∵x ∈[1,e],∴g ′(x )≤0, ∴g (x )在[1,e]上递减, ∴g (x )min =g (e)=-1e ,∴a ≤-1e.法二 要使x ∈[1,e],f (x )≤0恒成立,只需x ∈[1,e]时,f (x )max ≤0,显然当a ≥0时,f (x )=ax +ln x 在[1,e]上递增,∴f (x )max =f (e)=a e +1>0,不合题意; 当a <0时,f ′(x )=a +1x =ax +1x,令f ′(x )=0,x =-1a,当x <-1a 时,f ′(x )>0;当x >-1a时,f ′(x )<0.③当1<-1a <e 时,即-1<a <-1e时,f (x )在⎣⎢⎡⎦⎥⎤1,-1a 上递增,在⎣⎢⎡⎦⎥⎤-1a ,e 上递减,∴f (x )max =f ⎝ ⎛⎭⎪⎫-1a =-1+ln ⎝ ⎛⎭⎪⎫-1a ,∵1<-1a<e ,∴0<ln ⎝ ⎛⎭⎪⎫-1a <1,∴f ⎝ ⎛⎭⎪⎫-1a <0成立.由①②③可得a ≤-1e.【方法规律】由不等式恒(能)成立求参数的范围常有两种方法:(1)讨论最值:先构造函数,利用导数研究函数的单调性,求出含参函数的最值,进而得出相应的含参不等式求参数的取值范围;(2)分离参数:先分离参数变量,再构造函数,求出函数的最值,从而求出参数的取值范围.【变式探究】已知a 为实数,函数f (x )=a ln x +x 2-4x .(1)是否存在实数a ,使得f (x )在x =1处取得极值?证明你的结论;(2)设g (x )=(a -2)x ,若∃x 0∈⎣⎢⎡⎦⎥⎤1e ,e ,使得f (x 0)≤g (x 0)成立,求实数a 的取值范围. 解 (1)函数f (x )的定义域为(0,+∞),f ′(x )=a x +2x -4=2x 2-4x +ax.假设存在实数a ,使f (x )在x =1处取得极值,则f ′(1)=0,∴a =2,此时,f ′(x )=2(x -1)2x,当x >0时,f ′(x )≥0恒成立,∴f (x )在(0,+∞)上单调递增, ∴x =1不是f (x )的极值点.故不存在实数a ,使得f (x )在x =1处取得极值.∵x ∈⎣⎢⎡⎦⎥⎤1e ,e , ∴2-2ln x =2(1-ln x )≥0, ∴x -2ln x +2>0,∴x ∈⎝ ⎛⎭⎪⎫1e ,1时,G ′(x )<0,G (x )单调递减; x ∈(1,e)时,G ′(x )>0,G (x )单调递增,∴G (x )min =G (1)=-1. ∴a ≥G (x )min =-1.故实数a 的取值范围为[-1,+∞). 高频考点三、利用导数解决函数零点问题 例3、设函数f (x )=x 22-k ln x ,k >0.(1)求f (x )的单调区间和极值;(2)证明:若f (x )存在零点,则f (x )在区间(1,e]上仅有一个零点.(1)解 由f (x )=x 22-k ln x (k >0),得x >0且f ′(x )=x -k x =x 2-kx .由f ′(x )=0,解得x =k (负值舍去).f (x )与f ′(x )在区间(0,+∞)上的变化情况如下表:x (0,k ) k(k ,+∞) f ′(x )-+ f (x)k (1-ln k )2所以,f (x )的单调递减区间是(0,k ),单调递增区间是(k ,+∞).f (x )在x =k 处取得极小值f (k )=k (1-ln k )2.【方法技巧】函数零点问题通常可作以下适当转化来处理.函数y =f (x )的零点⇔方程f (x )=0的根⇔若f (x )=g (x )-h (x ),则f (x )的零点就是函数y =g (x )与y =h (x )图象交点的横坐标.【变式探究】设函数f (x )=x 3+ax 2+bx +c . (1)求曲线y =f (x )在点(0,f (0))处的切线方程;(2)设a =b =4,若函数f (x )有三个不同零点,求c 的取值范围.解 (1)由f (x )=x 3+ax 2+bx +c ,得f ′(x )=3x 2+2ax +b .因为f (0)=c ,f ′(0)=b ,所以曲线y =f (x )在点(0,f (0))处的切线方程为y =bx +c . (2)当a =b =4时,f (x )=x 3+4x 2+4x +c , 所以f ′(x )=3x 2+8x +4. 令f ′(x )=0,得3x 2+8x +4=0, 解得x =-2或x =-23.当x 变化时,f (x )与f ′(x )的变化情况如下:所以,当c >0且c -3227<0,存在x 1∈(-4,-2),x 2∈⎝ ⎛⎭⎪⎫-2,-23,x 3∈⎝ ⎛⎭⎪⎫-23,0,使得f (x 1)=f (x 2)=f (x 3)=0.由f (x )的单调性知,当且仅当c ∈⎝ ⎛⎭⎪⎫0,3227时,函数f (x )=x 3+4x 2+4x +c 有三个不同零点.高频考点四、利用导数解决生活中的优化问题例4、在某次水下科研考察活动中,需要潜水员潜入水深为60米的水底进行作业,根据以往经验,潜水员下潜的平均速度为v (米/单位时间),每单位时间的用氧量为⎝ ⎛⎭⎪⎫v 103+1(升),在水底作业10个单位时间,每单位时间用氧量为0.9(升),返回水面的平均速度为v2(米/单位时间),每单位时间用氧量为1.5(升),记该潜水员在此次考察活动中的总用氧量为y (升).(1)求y 关于v 的函数关系式;(2)若c ≤v ≤15(c >0),求当下潜速度v 取什么值时,总用氧量最少.(2)y ′=6v 50-240v 2=3(v 3-2 000)25v 2,令y ′=0得v =1032, 当0<v <1032时,y ′<0,函数单调递减; 当v >1032时,y ′>0,函数单调递增.若c <1032 ,函数在(c ,1032)上递减,在(1032,15)上递增, ∴当v =1032时,总用氧量最少. 若c ≥1032,则y 在[c ,15]上递增, ∴当v =c 时,这时总用氧量最少.【变式探究】某商场销售某种商品的经验表明,该商品每日的销售量y (单位:千克)与销售价格x (单位:元/千克)满足关系式y =ax -3+10(x -6)2,其中3<x <6,a 为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.(1)求a 的值;(2)若该商品的成本为3元/千克,试确定销售价格x 的值,使商场每日销售该商品所获得的利润最大. 解 (1)因为x =5时,y =11,所以a2+10=11,a =2.由上表可得,x =4时,函数f (x )取得极大值,也是最大值. 所以,当x =4时,函数f (x )取得最大值,且最大值等于42.答 当销售价格为4元/千克时,商场每日销售该商品所获得的利润最大.【感悟提升】在求实际问题中的最大值或最小值时,一般先设自变量、因变量、建立函数关系式,并确定其定义域,利用求函数最值的方法求解,注意结果应与实际情况相符合.用导数求实际问题中的最大(小)值,如果函数在区间内只有一个极值点,那么根据实际意义可知该极值点就是最值点.【变式探究】某品牌电动汽车的耗电量y 与速度x 之间有关系y =13x 3-392x 2-40x (x >0),为使耗电量最小,则速度应定为________.答案 40解析 由y ′=x 2-39x -40=0, 得x =-1或x =40, 由于0<x <40时,y ′<0;x >40时,y ′>0.所以当x =40时,y 有最小值.1. (2018年江苏卷)某农场有一块农田,如图所示,它的边界由圆O 的一段圆弧(P 为此圆弧的中点)和线段MN 构成.已知圆O 的半径为40米,点P 到MN 的距离为50米.现规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形ABCD ,大棚Ⅱ内的地块形状为,要求均在线段上,均在圆弧上.设OC 与MN 所成的角为.(1)用分别表示矩形和的面积,并确定的取值范围;(2)若大棚Ⅰ内种植甲种蔬菜,大棚Ⅱ内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为.求当为何值时,能使甲、乙两种蔬菜的年总产值最大.【答案】(1)矩形ABCD的面积为800(4sinθcosθ+cosθ)平方米,△CDP的面积为1600(cosθ–sinθcosθ),sinθ的取值范围是[,1).(2)当θ=时,能使甲、乙两种蔬菜的年总产值最大【解析】解:(1)连结PO并延长交MN于H,则PH⊥MN,所以OH=10.过O作OE⊥BC于E,则OE∥MN,所以∠COE=θ,故OE=40cosθ,EC=40sinθ,则矩形ABCD的面积为2×40cosθ(40sinθ+10)=800(4sinθcosθ+cosθ),△CDP的面积为×2×40cosθ(40–40sinθ)=1600(cosθ–sinθcosθ).过N作GN⊥MN,分别交圆弧和OE的延长线于G和K,则GK=KN=10.令∠GOK=θ0,则sinθ0=,θ0∈(0,).当θ∈[θ0,)时,才能作出满足条件的矩形ABCD,所以sinθ的取值范围是[,1).答:矩形ABCD的面积为800(4sinθcosθ+cosθ)平方米,△CDP的面积为1600(cosθ–sinθcosθ),sinθ的取值范围是[,1).答:当θ=时,能使甲、乙两种蔬菜的年总产值最大. 2.【2017课标1,理21】已知函数2()(2)xx f x ae a e x =+--.(1)讨论()f x 的单调性;(2)若()f x 有两个零点,求a 的取值范围. 【答案】(1)见解析;(2)()0,1.【解析】(1)()f x 的定义域为(),-∞+∞, ()()()()2221121x x x x f x ae a e ae e =+---'=+, (ⅰ)若0a ≤,则()0f x '<,所以()f x 在(),-∞+∞单调递减. (ⅱ)若0a >,则由()0f x '=得ln x a =-.当(),ln x a ∈-∞-时, ()0f x '<;当()ln ,x a ∈-+∞时, ()0f x '>,所以()f x 在(),ln a -∞-单调递减,在()ln ,a -+∞单调递增.3.【2017山东,理20】已知函数()22cos f x x x =+,()()cos sin 22x g x e x x x =-+-,其中 2.71828e =是自然对数的底数.(Ⅰ)求曲线()y f x =在点()(),f ππ处的切线方程;(Ⅱ)令()()()()h x g x af x a R =-∈,讨论()h x 的单调性并判断有无极值,有极值时求出极值. 【答案】(1)22ππ2y x =-- (2)见解析 【解析】(Ⅱ)由题意得 ()()()2cos sin 222cos x h x e x x x a x x =-+--+, 因为()()()()cos sin 22sin cos 222sin xx h x ex x x e x x a x x =-+-+--+--'()()2sin 2sin x e x x a x x =---()()2sin x e a x x =--,令()sin m x x x =- 则()1cos 0m x x ='-≥ 所以()m x 在R 上单调递增. 因为()00,m =所以 当0x >时, ()0,m x > 当0x <时, ()0m x <(1)当0a ≤时, xe a - 0>当0x <时, ()0h x '<, ()h x 单调递减, 当0x >时, ()0h x '>, ()h x 单调递增,所以 当0x =时()h x 取得极小值,极小值是 ()021h a =--;(2)当0a >时, ()()()ln 2sin x a h x e e x x '=--由 ()0h x '=得 1ln x a =, 2=0x ①当01a <<时, ln 0a <,当(),ln x a ∈-∞时, ()ln 0,0x a e e h x '-, ()h x 单调递增; 当()ln ,0x a ∈时, ()ln 0,0xae eh x -><', ()h x 单调递减; 当()0,x ∈+∞时, ()ln 0,0xae eh x ->>', ()h x 单调递增.所以 当ln x a =时()h x 取得极大值.极大值为()()()2ln ln 2ln sin ln cos ln 2h a a a a a a ⎡⎤=--+++⎣⎦,当0x =时()h x 取到极小值,极小值是 ()021h a =--; ②当1a =时, ln 0a =,所以 当(),x ∈-∞+∞时, ()0h x '≥,函数()h x 在(),-∞+∞上单调递增,无极值;综上所述:当0a ≤时, ()h x 在(),0-∞上单调递减,在()0,+∞上单调递增, 函数()h x 有极小值,极小值是()021h a =--;当01a <<时,函数()h x 在(),ln a -∞和()0,ln a 和()0,+∞上单调递增,在()ln ,0a 上单调递减,函数()h x 有极大值,也有极小值,极大值是()()()2ln ln 2ln sin ln cos ln 2h a a a a a a ⎡⎤=--+++⎣⎦极小值是()021h a =--;当1a =时,函数()h x 在(),-∞+∞上单调递增,无极值; 当1a >时,函数()h x 在(),0-∞和()ln ,a +∞上单调递增, 在()0,ln a 上单调递减,函数()h x 有极大值,也有极小值, 极大值是()021h a =--;极小值是()()()2ln ln 2ln sin ln cos ln 2h a a a a a a ⎡⎤=--+++⎣⎦.1.【2016高考江苏卷】(本小题满分16分) 已知函数()(0,0,1,1)xxf x a b a b a b =+>>≠≠. 设12,2a b ==. (1)求方程()2f x =的根;(2)若对任意x R ∈,不等式(2)f()6f x m x ≥-恒成立,求实数m 的最大值;(3)若01,1a b <<>,函数()()2g x f x =-有且只有1个零点,求ab 的值。
2019版高考数学理一轮课时达标16导数与函数的综合问题

课时达标 第16讲[解密考纲]本考点主要以基本初等函数为载体,综合应用函数、导数、方程、不等式等知识,常考查恒成立问题、存在性问题或者与实际问题相结合讨论最优解等问题,综合性较强,常作为压轴题出现.三种题型均有出现,以解答题为主,难度较大.1.已知函数f (x )=x 2-ax -a ln x (a ∈R ). (1)若函数f (x )在x =1处取得极值,求a 的值; (2)在(1)的条件下,求证:f (x )≥-x 33+5x 22-4x +116.解析 (1)f ′(x )=2x -a -ax ,由题意可得f ′(1)=0,解得a =1.经检验,a =1时f (x )在x =1处取得极小值,所以a =1. (2)由(1)知,f (x )=x 2-x -ln x ,令g (x )=f (x )-⎝⎛⎭⎫-x 33+5x 22-4x +116=x 33-3x 22+3x -ln x -116, 由g ′(x )=x 2-3x +3-1x =x 3-1x -3(x -1)=(x -1)3x(x >0),可知g (x )在(0,1)上是减函数,在(1,+∞)上是增函数,∴g (x )min =g (1)=13-32+3-116=0,∴当x >0时,g (x )≥g (1)=0,于是f (x )≥-x 33+5x 22-4x +116.2.若函数f (x )=ax 3-bx +4,当x =2时,函数f (x )有极值-43.(1)求函数f (x )的解析式;(2)若方程f (x )=k 有3个不同的根,求实数k 的取值范围. 解析 (1)f ′(x )=3ax 2-b ,由题意得⎩⎪⎨⎪⎧ f ′(2)=12a -b =0,f (2)=8a -2b +4=-43,解得⎩⎪⎨⎪⎧a =13,b =4, 故所求函数的解析式为f (x )=13x 3-4x +4.(2)由(1)得f ′(x )=x 2-4=(x +2)(x -2),令f ′(x )=0, 得x =2或x =-2.当x 变化时,f ′(x ),f (x )的变化情况如下表.因此,当x =-2时,f (x )有极大值283,当x =2时,f (x )有极小值-43,所以函数f (x )=13x 3-4x +4的图象大致如图所示.因为f (x )=k 有3个不同的根,所以直线y =k 与函数f (x )的图象有3个交点,所以-43<k <283.3.(2018·河南新乡调研)已知函数f (x )=x -(a +1)ln x -a x (a ∈R ),g (x )=12x 2+e x -x e x .(1)当x ∈[1,e]时,求f (x )的最小值;(2)当a <1时,若存在x 1∈[e ,e 2],使得对任意的x 2∈[-2,0],f (x 1)<g (x 2)恒成立,求a 的取值范围.解析 (1)f (x )的定义域为(0,+∞),f ′(x )=(x -1)(x -a )x 2.①当a ≤1时,x ∈[1,e],f ′(x )≥0,f (x )为增函数, 则f (x )min =f (1)=1-a .②当1<a <e 时,x ∈[1,a ]时,f ′(x )≤0,f (x )为减函数; x ∈[a ,e]时,f ′(x )≥0,f (x )为增函数, 则f (x )min =f (a )=a -(a +1)ln a -1.③当a ≥e 时,x ∈[1,e]时,f ′(x )≤0,f (x )在[1,e]上为减函数, 则f (x )min =f (e)=e -(a +1)-ae .综上,当a ≤1时,f (x )min =1-a ; 当1<a <e 时,f (x )min =a -(a +1)ln a -1; 当a ≥e 时,f (x )min =e -(a +1)-ae.(2)由题意知,f (x )(x ∈[e ,e 2])的最小值小于g (x )(x ∈[-2,0])的最小值.由(1)知f (x )在[e ,e 2]上单调递增,f (x )min =f (e)=e -(a +1)-ae ,g ′(x )=(1-e x )x .x ∈[-2,0]时,g ′(x )≤0,则g (x )为减函数.所以g (x )min =g (0)=1.所以e -(a +1)-ae <1,即a >e 2-2e e +1.所以a 的取值范围为⎝ ⎛⎭⎪⎫e 2-2e e +1,1.4.某商店经销一种奥运纪念品,每件产品成本为30元,且每卖出一件产品,需向税务部门上交a 元(a 为常数,2≤a ≤5)的税收,设每件产品的日售价为x 元(35≤x ≤41),根据市场调查,日销售量与e x (e 为自然对数的底数)成反比,已知每件产品的日售价为40元时,日销售量为10件.(1)求商店的日利润L (x )元与每件产品的日售价x 元的函数关系式; (2)当每件产品的日售价为多少元时该商店的日利润L (x )最大,说明理由. 解析 (1)设日销售量为k e x 件,则ke 40=10,∴k =10e 40.则日销售量为10e 40e x 件,每件利润为(x -30-a )元,则日利润L (x )=10e 40·x -30-ae x (35≤x ≤41).(2)L ′(x )=10e 40·31+a -xe x(35≤x ≤41).①当2≤a ≤4时,33≤31+a ≤35,L ′(x )≤0,L (x )在[35,41]上是减函数.∴当x =35时,L (x )的最大值为10(5-a )e 5.②当4<a ≤5时,35<31+a ≤36,由L ′(x )=0得x =a +31, 当x ∈(35,a +31)时,L ′(x )>0,L (x )在(35,a +31)上是增函数. 当x ∈(a +31,41]时,L ′(x )<0,L (x )在(a +31,41]上是减函数. ∴当x =a +31时,L (x )的最大值为10e 9-a .综上可知,当2≤a ≤4时,日售价为35元可使日利润L (x )最大, 当4<a ≤5时,日售价为a +31元可使日利润L (x )最大. 5.(2018·辽宁五校联考)已知函数f (x )=(ax -1)ln x +x 22.(1)若a =2,求曲线y =f (x )在点(1,f (1))处的切线l 的方程;(2)设函数g (x )=f ′(x )有两个极值点,x 1,x 2,其中x 1∈(0,e],求g (x 1)-g (x 2)的最小值. 解析 (1)当a =2时,f ′(x )=2ln x +x -1x +2,f ′(1)=2,f (1)=12,∴切线l 的方程为y -12=2(x -1),即4x -2y -3=0.(2)函数g (x )=a ln x +x -1x+a ,定义域为(0,+∞),g ′(x )=1+a x +1x 2=x 2+ax +1x2,令g ′(x )=0,得x 2+ax +1=0, ∴x 1+x 2=-a ,x 1x 2=1, 故x 2=1x 1,a =-⎝⎛⎭⎫x 1+1x 1. g (x 1)-g (x 2)=g (x 1)-g ⎝⎛⎭⎫1x 1=a ln x 1+x 1-1x 1+a -⎝⎛⎭⎫a ln 1x 1+1x 1-x 1+a =2⎝⎛⎭⎫x 1-1x 1+2a ln x 1=2⎝⎛⎭⎫x 1-1x 1-2⎝⎛⎭⎫x 1+1x 1ln x 1, 令h (x )=2⎝⎛⎭⎫x -1x -2⎝⎛⎭⎫x +1x ln x ,x ∈(0,e]. 则[g (x 1)-g (x 2)]min =h (x )min ,h ′(x )=2(1+x )(1-x )ln xx 2,当x ∈(0,1]时,h ′(x )≤0,当x ∈(1,e]时,h ′(x )<0, 则当x ∈(0,e]时,h (x )单调递减, ∴h (x )min =h (e)=-4e ,故[g (x 1)-g (x 2)]min =-4e.6.已知函数f (x )=12ax 2-(2a +1)x +2ln x (a ∈R ).(1)当a =23时,求函数f (x )的单调区间;(2)当a >12时,设g (x )=(x 2-2x )e x ,求证:对任意x 1∈(0,2],均存在x 2∈(0,2],使得f (x 1)<g (x 2)成立.解析 (1)由题知,定义域为x >0,f ′(x )=ax -(2a +1)+2x .当a =23时,f ′(x )=23x -73+2x =(2x -3)(x -2)3x,令f ′(x )>0,解得0<x <32或x >2,令f ′(x )<0,解得32<x <2,则函数f (x )的单调递增区间为⎝⎛⎭⎫0,32和(2,+∞),单调递减区间为⎝⎛⎭⎫32,2. (2)若要命题成立,只需当x ∈(0,2]时,f (x )max <g (x )max由g ′(x )=(x 2-2)e x 可知,当x ∈(0,2]时,函数g (x )在区间(0,2)上单调递减,在区间(2,2)上单调递增,g (0)=g (2)=0,故g (x )max =0,所以只需f (x )max <0.对函数f (x )来说,f ′(x )=ax -(2a +1)+2x =(ax -1)(x -2)x.当a >12时,0<1a <2,则函数f (x )在区间⎝⎛⎭⎫0,1a 上单调递增,在区间⎝⎛⎦⎤1a ,2上单调递减, 所以f (x )max =f ⎝⎛⎭⎫1a =-2ln a -12a -2; 当a ≥1时,显然小于0,满足题意;当12<a <1时,可令h (a )=-2ln a -12a -2,h ′(a )=1-4a 2a 2 , 可知函数h (a )在区间⎝⎛⎭⎫12,1时单调递减,则h (a )<h ⎝⎛⎭⎫12= 2ln 2-3<0,满足题意;综上所述,当a >12时,对任意x 1∈(0,2],均存在x 2∈(0,2],使得f (x 1)<g (x 2)成立.。
专题16 导数的综合应用与优化问题()-2019高考数学(文)名师揭秘之一轮

22
〔备选题〕例4已知函数 f(x)=x2-aln x 在(1,2] 上是增函数,g(x)=x-a x在(0,1)上为减函数.
(1)求实数 a 的值; (2)求证:当 x>0 时,方程 f(x)=g(x)+2 有唯一 解;
(3)当 b>-1 时,若 f(x)≥2bx-x12在 x∈(0,1]上 恒成立,求 b 的取值范围.
ห้องสมุดไป่ตู้
当 0<x<a 时,F′(x)<0,F(x)在区间(0,a)上单调
递减;
当 x>a 时,F′(x)>0,F(x)在区间(a,+∞)上单
调递增.
从而 F(x)min=F(a)=0. 因为 b>a,所以 f(a)+f(b)-2fa+2 b>0.
2019年8月10日
遇上你是缘分,愿您生活愉快,身体健 康,学业有成,金榜题名!
4
2.若 a>1e,则方程 ln x-ax=0 的实根的个数为
(A ) A.0 个 C.2 个
B.1 个 D.无穷多个
【解析】由于方程 ln x-ax=0 等价于lnxx=a.设 f(x)
=lnxx.∵f′(x)=1x·xx-2 ln x=1-xl2n x, 令 f′(x)=0,得 x=e,
∴f(x)在(0,e)上单调递增;在(e,+∞)上单调递减.∴f(x)
(2)求函数的导数f′(x),解方程f′(x)=0; (3)比较函数在区间端点和f′(x)=0的点处函数值 的大小,最大(小)者为最大(小)值; (4)回归实际问题作答.
2019年8月10日
遇上你是缘分,愿您生活愉快,身体健 康,学业有成,金榜题名!
14
二、恒成立问题求参数的取值范围
例2已知函数f(x)=(a+1)ln x+ax2+1. (1)讨论函数f(x)的单调性; (2)设a<-1,若对任意x1,x2∈(0,+∞),且x1 ≠x2,恒有|f(x1)-f(x2)|>4|x1-x2|,求a的取值范围.
2019年高考数学《优化指导》PPT教学课件第1篇 专题6 第2讲

2.绝对值不等式的成立问题的求解模型 (1)分离参数:根据不等式将参数分离化为a≥f(x)或a≤f(x)形式; (2) 转 化 最 值 : f(x)>a 恒 成 立 ⇔ f(x)min>a;f(x)<a 恒 成 立 ⇔ f(x)max<a;f(x)>a 有 解 ⇔f(x)max>a;f(x)<a有解⇔f(x)min<a;f(x)>a无解⇔f(x)max≤a;f(x)<a无解⇔f(x)min≥a; (3)得结论.
考向二 含绝对值的不等式的证明问题
1 1 【典例】 (2016· 全国卷Ⅱ)已知函数fx=|x-2|+|x+2|,M 为不等式 f(x)<2 的解 集. (1)求 M; (2)证明:当 a,b∈M 时,|a+b|<|1+ab|.
1 1 1 [ 规范解答] (1)当 x<-2时,f(x)=2-x-x-2=-2x❶<2, 1 解得-1<x<-2, 1 1 1 1 当-2≤x≤2时,f(x)=2-x+x+2=1❶<2 恒成立, 1 1 ❶ 当 x>2时,f(x)=2x<2 ,解得2<x<1, 综上可得,M={x|-1<x<1}. (2)当 a,b∈(-1,1)时,有(a2-1)(b2-1)>0❷, 即 a2b2+1>a2+b2, 则 a2b2+2ab+1>a2+2ab+b2❸, 则(ab+1)2>(a+b)2, 即|a+b|<|ab+1|.
不等式选讲是高考的选 考内容之一,考查的重 点是不等式的证明、绝 对值不等式的解法等, 命题的热点是绝对值不 等式的解法,以及绝对 值不等式与函数的综合 问题的求解.
02
典例感悟· 提能力
考向一 含绝对值的不等式的解法及应用
【典例】 (2017· 全国卷Ⅰ)已知函数 f(x)=-x2+ax+4,gx=|x+1|+|x-1|. (1)当 a=1 时,求不等式fx≥gx的解集; (2)若不等式fx≥gx的解集包含[-1,1],求 a 的取值范围.
2019年高考数学《优化指导》PPT教学课件第1篇 专题1 第1讲

( A )
B.|a|=|b| D.|a|>|b|
∵|a+b|=|a-b|,∴|a+b|2=|a-b|2.
3 → → 1 3 1 12.(2016· 全国卷Ⅲ)已知向量BA= , ,BC= , ,则∠ABC= ( A ) 2 2 2 2
A.30° C.60°
D
B.-6
所以a+b=(4,m-2).
因为(a+b)⊥b,所以(a+b)·b=0,所以12-2(m-2)=0,解得m=8.
方法二 因为(a+b)⊥b,所以(a+b)·b=0,即a·b+b2=3-2m+32+(-2)2=16- 2m=0,解得m=8.
11.(2017·全国卷Ⅱ)设非零向量a,b满足|a+b|=|a-b|,则
A.a⊥b C.a∥b
解析 方法一 ∴a2+b2+2a· b=a2+b2-2a· b. ∴a· b=0.∴a⊥b.故选 A. 方法二 利用向量加法的平行四边形法则. → → 在▱ ABCD 中,设AB=a,AD=b, → → 由|a+b|=|a-b|知|AC|=|DB|, 从而四边形 ABCD 为矩形,即 AB⊥AD,故 a⊥b.故选 A.
D项,i(1+i)=i+i2=-1+i,不是纯虚数. 故选C.
7.(2017·全国卷Ⅲ)复平面内表示复数z=i(-2+i)的点位于 A.第一象限 C.第三象限 解析 B.第二象限 D.第四象限
( C )
∵z=i(-2+i)=-1-2i,∴复数z=-1-2i所对应的复平面内的点为Z(-
1,-2),位于第三象限.故选C.
02
真题精选· 明考向
一、选择题
1.(2017·全国卷Ⅲ)已知集合A={1,2,3,4},B={2,4,6,8},则A∩B中元素的个数为 ( B ) A.1 C.3 ∴A∩B中元素的个数为2.故选B. B.2 D.4
2019年高考数学《优化指导》PPT教学课件第1篇 专题2

专题二
三角函数、解三角形
栏
目 导 航
02
解题通法· 短平快
01
考题通报· 明考情
01
年份
考题通报· 明考情
卷别 小题考查 大题考查 —
T8·同角三角函数的基本关系与三角函数的性质
全国卷Ⅰ T11·同角三角函数的基本关系与三角恒等变换 T16·正、余弦定理与三角形的面积公式 T7·三角恒等变换与余弦定理的应用 2018 全国卷Ⅱ T10·三角恒等变换与三角函数的性质 T15·利用三角恒等变换求值 T6·同角三角函数的基本关系、三角恒等变换与三角 全国卷Ⅲ 函数的性质 T11·三角形的面积公式及余弦定理的应用
1 3 3 π (2)由已知得2absin C= 2 .又 C=3,所以 ab=6. 由已知及余弦定理得 a2+b2-2abcos C=7, 故 a2+b2=13,从而(a+b)2=25,即 a+b=5. 所以△ABC 的周长为 5+ 7. ❶变式:利用正弦定理把已知等式中的边 a,b,c 变为 sin A,sin B,sin C. ❷变角:利用两角和的正弦公式及三角形的内角和定理把等式中 sin Acos B+sin Bcos A 变为 sin(A+B)再变为 sin C.
3 3 (2)若 c= 7,△ABC 的面积为 2 ,求△ABC 的周长. [ 解题示范] (1)由已知 2cos C(acos B+bcos A)=c 及正弦定理得 2cos C(sin Acos
B+sin Bcos A)=sin C,❶ 即 2cos Csin(A+B)=sin C, 故 2cos Csin C=sin C.❷ 1 π 可得 cos C=2,所以 C=3.
—
全国卷Ⅲ T6·三角恒等变换的求值问题
【配套K12】专题16 导数的综合应用与优化问题(检测)-2019年高考数学(文)名师揭秘之一轮总复

《2019年高考数学名师揭秘》之一轮总复习(文科)专题16导数的综合应用与优化问题本专题特别注意:1.导数与不等式证明2.极值点偏移问题3.导函数为0的替换作用4.导数与数列不等式的证明5.变形后求导6.讨论参数求参数7.与三角函数有关的含参数的求导问题 8.构造函数问题 9.恒成立求参数方法总结:1.有关超越型不等式的证明、方程根的探究等问题,构造函数应用导数推理求解是有效方法之一,也是近几年高考压轴题的常见命题方法之一.2.利用导数解决生活中的优化问题的思路是:阅读审题―――――→理解题意引入建模――――――――――――――→将实际问题抽象为数学问题解模――――――――――→应用导数解决模型回归实际.3.在解决生活中的优化问题时应注意: (1)实际问题的意义.(2)建立函数模型后还应根据实际问题情境确定函数的定义域.高考模拟:1.已知函数有两个零点,且,则下列结论错误的是()A. B. C. D.【答案】B【解析】分析:先通过函数有两个零点求出,再利用导数证明,即证明.因为函数f(x)有两个零点,所以又又令则所以函数g(x)在上为减函数,=0,又,又,∴,即.点睛:(1)本题主要考查利用导数求函数的单调区间、最值和零点问题,意在考查学生对这些知识的掌握能力和分析推理能力.(2)本题的解题关键是构造函数求函数的图像和性质.2.己知函数,若关于的方程恰有3个不同的实数解,则实数的取值范围是( )A. B. C. D.【答案】C【解析】分析:由题意,函数,得,得到函数的单调性与最大值,再又方程,解得或,结合图象,即可求解.详解:由题意,函数,可得,当时,,所以函数单调递增,当时,,所以函数单调递减,且,所以函数的最大值为,又方程,解得或,结合图象,可知只有一个实数解,要使得方程恰有三个不同的实数解,则,解得,故选C.点睛:本题主要考查了函数与方程的综合应用,其中解答中涉及到利用导数研究函数的单调性与最值,以及函数与方程等知识点的综合运用,把方程的解得个数转化为函数的图象的交点个数是解答的关键,着重考查了转化思想方法和数形结合思想的应用,试题有一定的难度,属于中档试题.3.已知函数(其中无理数),关于的方程有四个不等的实根,则实数的取值范围是()A. B. C. D.【答案】C详解:由题意可得函数的定义域为,且.令得或,则函数在,上单调递增;令得,则函数在上单调递减.∵∴函数的图象如图所示:令,则的增减性与相同,.∵关于的方程有四个不等的实根∴有四个不等的实根,即在和上分别有根.令,则.∴,即∴故选C.点睛:本题考查的是有关已知函数零点个数有关参数的取值范围问题,在求解的过程中,解题的思路是将函数零点个数问题转化为方程解的个数问题,将式子移项变形,转化为两条曲线交点的问题,画出函数的图象以及相应的直线,在直线移动的过程中,利用数形结合,求得相应的结果.4.已知是函数的零点,是函数的零点,且满足,则实数的最小值是()A. B. C. -2 D. -1【答案】D【解析】分析:利用导数研究函数的单调性可证明函数存在唯一零点,即,可得在有零点,由可得结果.①若,即,此时的零点为,显然符合题意;②(i)若,即或,若在只有一个零点,则;(ii)若在只有两个零点,则,解得,即的最小值为,故选D.点睛:对于一元二次方程根与系数的关系的题型常见解法有两个:一是对于未知量为不做限制的题型可以直接运用判别式解答(本题属于这种类型);二是未知量在区间上的题型,一般采取列不等式组(主要考虑判别式、对称轴、的符号)的方法解答.5.已知函数与的图像有4个不同的交点,则实数的取值范围是()A. B. C. D.【答案】C【解析】分析:函数与的图像有4个不同的交点,即有4个不同的实根,由可得,讨论其性质可得的取值范围.详解:函数与的图像有4个不同的交点,即有4个不同的实根,由可得,即其定义域为且,设(且),则则在上单调递增,在上单调递减,但且),故的值域为,设,则,此时此时,函数在上单调递减,在上单调递增,由图像可知,在上单调递减,在上单调递增,且当时,函数函数与的图像有4个不同的交点,则实数的取值范围为.故选C.点睛:本题考查利用导数眼函数零点问题,注意数形结合思想的应用,解题时注意函数的定义域,属难题.6.设函数是定义在上的可导函数,其导函数为,且有,则不等式的解集为A. B. C. D.【答案】B【解析】分析:根据题意,设g(x)=x2f(x),x<0,求出导数,分析可得g′(x)≤0,则函数g(x)在区间(﹣∞,0)上为减函数,结合函数g(x)的定义域分析可得:原不等式等价于,解可得x的取值范围,即可得答案.详解:根据题意,设g(x)=x2f(x),x<0,其导数g′(x)=[x2f(x)]′=2xf(x)+x2f′(x)=x(2f(x)+xf′(x)),又由2f(x)+xf′(x)>x2≥0,且x<0,则g′(x)≤0,则函数g(x)在区间(﹣∞,0)上为减函数,(x+2018)2f(x+2018)﹣4f(﹣2)>0⇒(x+2018)2f(x+2018)>(﹣2)2f(﹣2)⇒g(x+2018)>g(﹣2),又由函数g(x)在区间(﹣∞,0)上为减函数,则有,解可得:x<﹣2020,即不等式(x+2018)2f(x+2018)﹣4f(﹣2)>0的解集为(﹣∞,﹣2020);故选:B.点睛:利用导数解抽象函数不等式,实质是利用导数研究对应函数单调性,而对应函数需要构造. 构造辅助函数常根据导数法则进行:如构造,构造,构造,构造等7.已知,且,有且仅有一个整数解,则正数的取值范围是()A. B.C. D.【答案】A【解析】分析:构造函数,利用可得,结合可得,利用导数研究函数的单调性,由数形结合思想,列不等式求解即可详解:因为,所以,设,则,∴,即,又因为,∴,∴,,则在上为减函数,在上为增函数,曲线与都过点,当时,若有且仅有一个整数解,只能为,则,解之得,故选A.点睛:构造辅助函数是高中数学中一种常用的方法,解题中若遇到有关不等式、方程及最值之类问题,设法建立起目标函数,并确定变量的限制条件,通过研究函数的单调性、最值等问题,常可使问题变得明了,准确构造出符合题意的函数是解题的关键;解这类不等式的关键点也是难点就是构造合适的函数,构造函数时往往从两方面着手:①根据导函数的“形状”变换不等式“形状”;②若是选择题,可根据选项的共性归纳构造恰当的函数. 8.在平面直角坐标系内,如果两点满足条件:①都在函数的图象上;②关于原点对称,则称是函数的一对“奇点”(奇点与看作是同一奇点).已知函数恰有两对“奇点”,则实数的取值范围是()A. B. C. D.【答案】C【解析】分析:求出的一段图象关于原点对称的函数解析式,令与的另一段图象有2个交点即可.详解:当时,关于原点对称的函数为∵恰有两对“奇点”,与恰好有两个交点,显然设与恰好有1条公共切线,切点为,则,解得此时与轴交点为公切点.∴当 ,即时,有两对“奇点”.故选C.点睛:本题考查了函数交点个数的判断,考查对新定义的理解,属于中档题.9.已知是定义在上的函数,为的导函数,且满足,则下列结论中正确的是()A. 恒成立B. 恒成立C. D. 当时,;当时,【答案】A【解析】分析:先构造函数g(x)=(x-1)f(x),再利用导数得到函数的单调性和图像,从而得到恒成立.点睛:(1)本题主要考查导数的乘法运算,考查导数研究函数的单调性,意在考查学生对这些基础知识的掌握能力和分析推理能力、数形结合分析的能力. (2)解答本题有两个关键,其一是观察已知想到构造函数g(x)=(x-1)f(x),再求导,其二是得到函数g(x)的单调性后,分析出x>1时,g(x)>0,x<1时,g(x)<0.10.已知函数,当时,对于任意的实数,都有不等式成立,则实数的取值范围是A. B. C. D.【答案】D【解析】分析:求得f(x)的导数,可得f(x)的单调性,令g(x)=f(x)﹣f(1﹣x),可得g(x)的单调性,以及g(x)+g(1﹣x)=0,将原不等式转化,可得x1>1﹣sin2θ恒成立,由正弦函数的值域即可得到所求范围.详解:函数f (x )=e 2018x +mx 3﹣m (m >0), 导数为f′(x )=2018e 2018x +3mx 2, 可得m >0时,f (x )在R 上递增, 可令g (x )=f (x )﹣f (1﹣x ), 可得g (x )在R 上递增,且g (x )+g (1﹣x )=f (x )﹣f (1﹣x )+f (1﹣x )﹣f (x )=0, 由f (x 1)+f (sin 2θ)>f (x 2)+f (cos 2θ)成立, 可得f (x 1)﹣f (x 2)+f (sin 2θ)﹣f (cos 2θ)>0成立, 即为f (x 1)﹣f (1﹣x 1)+f (sin 2θ)﹣f (1﹣sin 2θ)>0, 即g (x 1)+g (sin 2θ)>0,可得g (x 1)>﹣g (sin 2θ)=g (1﹣sin 2θ), 即有x 1>1﹣sin 2θ恒成立,由于1﹣sin 2θ的最大值为1,可得x 1>1, 故选:D .点睛:处理抽象不等式的常用方法:般先利用函数的奇偶性得出区间上的单调性,再利用其单调性脱去函数的符号“f ”,转化为考查函数的单调性的问题或解不等式(组)的问题,若为偶函数,则,若函数是奇函数,则.11.已知函数()()()32,f x x ax bx c g x f x =+++=,曲线():C y g x =关于直线1x =对称,现给出如结论:①若0c >,则存在00x <,使0()0f x =;②若1c <-,则不等式()()g 1x g x +>的解集为12⎛⎫+∞ ⎪⎝⎭,;③若10c -<<,且y kx =是曲线():(0)C y g x x =< 的一条切线,则k 的取值范围是27,24⎛⎫-- ⎪⎝⎭. 其中正确结论的个数为( ) A. 0 B. 1 C. 2 D. 3 【答案】D【解析】由题意得()f x 过点()1,0,且()()()210,32,62,f f x x ax b f x x a ==++'=''+''所以10,6203,2a b c a a b c +++=+=∴=-=-,因此()()()()()()332321110f x x x c x c x c x f c =-+-+=--+-=,,①若0c >,则由()()()()311101,1f x x c x x x =--+-=⇒==±()0010,0.x f x =<=②若1c <-,则()()()()()3111g x f x x c x ==--+-,此时()()()23110f x x c =--+>',图像如图所示,因此不等式()()g 1x g x +> 等价于1122x x x +>-∴>,即不等式()()g 1x g x +>的解集为12⎛⎫+∞ ⎪⎝⎭,;③若10c -<<,且()()()231101f x x c x =--+=⇒=±'y kx =是曲线()()()()3111,(0)g x x c x x =--++-<的一条切线,设切点为()000,,(0)x y x <,则()()()()()220311311g x x c k x c =--++∴=--+'+,因为()()()300000111x c x yk x x --++-==,所以()()()()()()()32320000000111=3111131x c x x c c x x x x --++---++∴+=--+-()()()()()()223230000003113113121k x c x x x x x ∴=--++=----+-=-,由()()()()()3220000001101131=1210,1,02c c x x x x x x ⎛⎫-<<⇒+=--+--+∈⇒∈-⎪⎝⎭, 所以()3003271,1,21,224x k x ⎛⎫⎛⎫∴-∈--∴=-∈-- ⎪ ⎪⎝⎭⎝⎭, 综上,正确结论的个数为3,选D.点睛:求范围问题,一般利用条件转化为对应一元函数问题,即通过题意将多元问题转化为一元问题,再根据函数形式,选用方法求值域,如二次型利用对称轴与定义区间位置关系,分式型可以利用基本不等式,复杂性或复合型可以利用导数先研究单调性,再根据单调性确定值域. 12.已知函数()sin 2cos xf x x=+,如果0x >时,函数()f x 的图象恒在直线y kx =的下方,则k 的取值范围是( )A. 13⎡⎢⎣⎦B.1,3⎡⎫+∞⎪⎢⎣⎭ C. ⎫+∞⎪⎪⎣⎭ D. ⎡⎢⎣⎦【答案】B点睛:本题的解答过程是巧妙构造函数,先运用求导法则求出函数的导数,再运用分类整合思想分析推断不等式成立的条件,进而求得实数的取值范围,使得问题获解.13.若存在实常数k 和b ,使得函数()F x 和()G x 对其公共定义域上的任意实数x 都满足: ()F x kx b ≥+和()G x kx b ≤+恒成立,则称此直线y kx b =+为()F x 和()G x 的“隔离直线”,已知函数()()2f x x x R =∈,()()()10,2ln g x x h x e x x=<=,有下列命题:①()()()F x f x g x =-在x ⎛⎫∈ ⎪⎝⎭内单调递增; ②()f x 和()g x 之间存在“隔离直线”,且b 的最小值为-4;③()f x 和()g x 之间存在“隔离直线”,且k 的取值范围是](40 -,; ④()f x 和()h x之间存在唯一的“隔离直线”y e =. 其中真命题的个数有( )A. 1个B. 2个C. 3个D. 4个 【答案】C 【解析】①()()()()2211,,'20F x f x g x x x F x x x x ⎛⎫=-=-∴∈=+> ⎪⎝⎭,()()()F x f x g x ∴=-,在x ⎛⎫∈ ⎪⎝⎭内单调递增,故①正确;②,③设()(),f x g x 的隔离直线为y kx b =+,则2x kx b ≥+对一切实数x 成立,即有210,40k b ∆≤+≤,又1kx b x≤+对一切0x <成立,则210kx bx +-≤,即220,40,0,0b k k b ∆≤+≤≤≤,即有24k b ≤-且2424,1664,40b k k b k k ≤-≤≤--≤≤,同理421664,b k b ≤≤-可得40b -≤≤,故②正确,③错误,④函数()f x 和()h x的图象在x =此存在()f x 和()h x 的隔离直线,那么该直线过这个公共点,设隔离直线的斜率为k,则隔离直线方程为(y e k x -=,即y k x k =-,由()()f x kx e x R ≥-∈,可得20x kx e -+≥,当x R∈恒成立,则(20k ∆=-≤,只有k =y e =-,下面证明()h x e ≤-,令()()G x e h x =--2ln e e x =--, ()'x G x x=,当x =()'0G x =;当0x << ()'0G x <;当x > ()'0G x >;当x = ()'G x 取到极小值,极小值是0,也是最小值, ()()0G x e h x ∴=--≥,则()h x e ≤-, ∴函数()f x 和()h x存在唯一的隔离直线y e =-,故④正确,真命题的个数有三个,故选C.【方法点睛】本题考查利用导数研究函数的单调性与不等式恒成立问题、以及新定义问题,属于难题. 新定义题型的特点是:通过给出一个新概念,或约定一种新运算,或给出几个新模型来创设全新的问题情景,要求考生在阅读理解的基础上,依据题目提供的信息,联系所学的知识和方法,实现信息的迁移,达到灵活解题的目的.遇到新定义问题,应耐心读题,分析新定义的特点,弄清新定义的性质,按新定义的要求,“照章办事”,逐条分析、验证、运算,使问题得以解决.本题定义“隔离直线”达到考查导数在研究函数性质的应用的目的. 14.定义在R 上的偶函数()f x 的导函数为()f x ',且当()()0,20x xf x f x +'><.则( ) A.()()224f e f e>B. ()()931f f >C.()()239f e f e-<D.()()224f e f e-<【答案】D【解析】根据题意,设g (x )=x 2f (x ),其导数g′(x )=(x 2)′f (x )+x 2•f (x )=2xf (x )+x 2•f (x )=x[2f (x )+xf'(x )], 又由当x >0时,有2f (x )+xf'(x )<0成立,则数g′(x )=x[2f (x )+xf'(x )]<0, 则函数g (x )在(0,+∞)上为减函数,若g (x )=x 2f (x ),且f (x )为偶函数,则g (-x )=(-x )2f (-x )=x 2f (x )=g (x ), 即g (x )为偶函数,所以()()2g e g < 即()()224f e f e<因为()f x 为偶函数,所以()()2f 2f -=,所以()()224f e f e -<故选D点睛:本题考查函数的导数与函数单调性的关系,涉及函数的奇偶性与单调性的应用,关键是构造函数g (x )并分析g (x )的单调性与奇偶性.15.已知定义在R 上的函数()f x 的导函数为()f x ',且()()331fx f x '+>, ()116f =,则()11620x f x e--+≤的解集为( )A. [)1+∞,B. ()1+∞,C. (]1-∞, D. ()1-∞, 【答案】C点睛:本题考察导数中的构造函数技巧,本题的构造比较复杂,由条件()()33'1f x f x +>和问题()11620x f x e--+≤综合想到构造()()()131x g x e f x -=-,得到()g x 在R 上单调递增,将问题转化为()()1g x g ≤,得到答案。
高考数学一轮总复习 第三章 导数及其应用 第16讲 导数

所以∀x1,x2∈(-∞,0],都有 f(x1)-f(x2)≤f(x)
3.导数与不等式 (1)不等式的证明可以通过构造函数等价转换为 探究函数值的大小,然后应用导数讨论函数的单调性, 从而实现不等式的证明. (2)含参数不等式的恒成立问题,通过分离变量,
构造函数等价转换为函数最值问题,然后应用导数求 函数最值.
4.导数与方程 方程根的存在性问题等价转换为函数极值和单调 性问题研究,然后应用导数及数形结合确定方程根的 存在性和个数.
【解析】∵位移 s 与时间 t 的关系是 s=s(t)=3t -t2,
∴s′(t)=3-2t,∴s′(0)=3,故物体的初速度 是 3,故选 A.
2.定义域为 R 的可导函数 y=fx的导函数为 f′x,满足
fx>f′x,且 f0=1,则不等式fexx<1 的解集为( B )
A.-∞,0
B.0,+∞
设 y=t2-ln t(t>0).则由 y′=2t-1t =0 得:t= 22,当
t∈0, 22,y′<0,y>f 22,当 t∈ 22,+∞,y
′>0,y>f
22,所以当
MN
达到最小时
t
的值为
2 2.
4.要做一个底面为长方形的带盖的箱子,其体积为
72 cm3,其底面两邻边长之比为 1∶2,则它的宽为 __3_m _,长为 6 m ,高为 4 m 时,可使表面 积最小.
x (-∞,-2) -2 (-2,0) 0 (0,+∞)
f′(x)
+
0
-
0
+
f(x)
Z 极大 ]
极小 Z
当 x∈(-∞,0]时,f(x)最大值=f(-2)=e42,
导数与函数的综合问题 2019高考数学专项复习精讲

e
(2)由题意知f(x)(x∈[e,e2])的最小值小于g(x)(x∈[-2,0])的最小值. 当a<1时,由(1)知f(x)在[e,e2]上单调递增,
所以f(x)min=f(e)=e-(a+1)- a .
e
由题意知g'(x)=(1-ex)x.
考点突破
考点一 利用导数研究恒成立问题和存在性问题
命题角度一 恒成立问题
典例1 (2016陕西西北九校联考)已知函数f(x)=-ln x+t(x-1),t为实数.
(1)当t=1时,求函数f(x)的单调区间;
(2)当t= 1 时, k - 1 -f(x)<0在(1,+∞)上恒成立,求实数k的取值范围.
命题角度二 存在性问题
典例2 已知函数f(x)=x-(a+1)ln x- a (a∈R),g(x)= 1 x2+ex-xex.
x
2
(1)当x∈[1,e]时,求f(x)的最小值;
(2)当a<1时,若存在x1∈[e,e2],使得对任意的x2∈[-2,0], f(x1)<g(x2)恒成立, 求a的取值范围.
则h'(x)=f
'(x)-f
'(x0)= 1ex x
-
1
x0 e x0
=
(1
x)ex0 (1 e x x0
x0 )ex
.
设φ(x)=(1-x) ex0 -(1-x0)ex,则φ'(x)=- ex0 -(1-x0)ex,
∵x0<1,∴φ'(x)<0,∴φ(x)在R上单调递减,而φ(x0)=0,
2019年高考数学《优化指导》PPT教学课件第1篇 专题3 第1讲

所以其前 n 项和
1 1 1 1 1 1 n Tn=-1-2+3-4+…+n-n+1=-1-n+1=- , n+1
40 所以其前 40 项和为 T40=-41,故选 D.
2.(2018·齐齐哈尔二模)已知数列{an}的前n项和为Sn,且a2=4,S4=30,n≥2时,an+
2.等比数列的重要规律与推论 (1)an=a1qn 1=amqn m;p+q=m+n⇒ap· aq=am· an.
- -Байду номын сангаас
(2){an},{bn}成等比数列⇒{anbn}成等比数列. (3)连续 m 项的和(如 Sm,S2m-Sm,S3m-S2m,…)构成的数列是等比数列(注意: 这连续 m 项的和必须非零才能成立). S偶 (4)若等比数列有 2n 项, 公比为 q, 奇数项之和为 S 奇, 偶数项之和为 S 偶, 则 = S奇 q. (5)对于等比数列前 n 项和 Sn,有:
S1n=1, an= Sn-Sn-1n≥2.
1. (2018· 潍坊二模)设数列{an}的前 n 项和为 Sn, 若 Sn=-n 的前 40 项的和为 39 A.40 40 C.41 39 B.-40 40 D.-41
2
2 -n, 则数列 n+1a n
第一篇 二轮专题突破
专题三
第 1讲
数 列
小题考法——等差数列与等比数列
栏
目 导 航
02
对点自检· 熟生巧
01
基础备查· 快易通
01
基础备查· 快易通
一、主干知识要记牢 1.等差数列、等比数列 等差数列 通项公式 前n项 和公式 an=a1+(n-1)d na1+an Sn= 2 nn-1 =na1+ 2 d 等比数列 an=a1qn 1(q≠0)
