MATLAB实验四答案
实验四MATLAB数值计算与符号计算

实验四 MATLAB数值计算与符号计算一、实验目的1.掌握数据插值和曲线拟合的方法2.掌握求数值导数和数值积分的方法3.掌握代数方程数值求解的方法4.掌握常微分方程数值求解的方法5.掌握求解优化问题的方法6.掌握求符号极限、导数和积分的方法7.掌握代数方程符号求解的方法8.掌握常微分方程符号求解的方法二、实验原理1.数据插值a) 一维数据插值 Y1=interp1(X,Y,X1,’method’)b) 二维数据插值 Z1=interp2(X,Y,Z,X1,Y1,’method’)2.曲线拟合[P,S]=polyfit(X,Y,m)3.符号对象的建立(1)符号量名=sym(符号字符串):建立单个的符号变量或常量;(2)syms arg1 arg2,…,argn:建立n个符号变量或常量。
4.基本符号运算(1)基本四则运算:+,-,*,\,^(2)分子与分母的提取:[n,d]=numden(s)(3)因式分解与展开:factor(s),expand(s)(4)化简:simplify, simple(s)5.符号函数及其应用(1)求极限:limit(f,x,a)(2)求导数:diff(f,x,a);(3)求积分:int(f,v)三、实验内容1.按下表用3次样条方法插值计算0~900范围内整数点的正弦值和0~750范围内整数点的正切值,然后用5次多项式拟合方法计算相同的函数值,并将两种计算结果进行比较。
x2=0:75;y1=sin(pi.*x1./180);y2=tan(pi.*x2./180);;a=interp1(x1,y1,45,'cublic')b=interp1(x1,y1,45,'cublic')p1=polyfit(x1,y1,5)p2=polyfit(x2,y2,5)c1=polyval(p1,x1);c2=polyval(p2,x2);subplot(2,1,1);plot(x1,c1,':o',x1,y1,'r');subplot(2,1,2);plot(x2,c2,':o',x2,y2,'r');10203040506070802.(1)求函数33()sin cos f x x x =+在点,,,6432x ππππ=的数值导数。
MATLAB实验四_求微分方程的解

参数说明
[T,Y] = solver(odefun,tspan,y0)
odefun 为显式常微分方程,可以用命令 inline 定义,或 在函数文件中定义,然后通过函数句柄调用。
dy 2 2 y 2 x 2x 求初值问题 的数值解,求解范 例: dx 围为 [0,0.5] y( 0 ) 1
dsolve的输出个数只能为一个 或 与方程个数相等。
只有很少一部分微分方程(组)能求出解析解。 大部分微分方程(组)只能利用数值方法求数值解。
Matlab函数数值求解
[T,Y] = solver(odefun,tspan,y0)
其中 y0 为初值条件,tspan为求解区间;Matlab在数值求解 时自动对求解区间进行分割,T (列向量) 中返回的是分割点 的值(自变量),Y (数组) 中返回的是这些分割点上的近似解, 其列数等于因变量的个数。
数学实验
实验四
求微分方程的解
问题背景和实验目的
自牛顿发明微积分以来,微分方程在描述事物运 动规律上已发挥了重要的作用。实际应用问题通过 数学建模所得到的方程,绝大多数是微分方程。 由于实际应用的需要,人们必须求解微分方程。 然而能够求得解析解的微分方程十分有限,绝大多 数微分方程需要利用数值方法来近似求解。 本实验主要研究如何用 Matlab 来计算微分方程 (组)的数值解,并重点介绍一个求解微分方程的 基本数值解法--Euler折线法。
Runge-Kutta 方法
Euler 法与 R-K法误差比较
Matlab 解初值问题
用 Maltab自带函数 解初值问题 求解析解:dsolve 求数值解:
ode45、ode23、 ode113、ode23t、ode15s、 ode23s、ode23tb
MATLAB)课后实验答案

实验一 MATLAB 运算基础1、 先求下列表达式得值,然后显示MATLAB 工作空间得使用情况并保存全部变量。
(1) 0122sin 851z e =+(2) 21ln(2z x =+,其中2120.455i x +⎡⎤=⎢⎥-⎣⎦ (3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e a z a a --+=++=--L (4) 2242011122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪-+≤<⎩,其中t =0:0、5:2、5 解:4、 完成下列操作:(1) 求[100,999]之间能被21整除得数得个数。
(2) 建立一个字符串向量,删除其中得大写字母。
解:(1) 结果:(2)、 建立一个字符串向量 例如:ch='ABC123d4e56Fg9';则要求结果就是:实验二 MATLAB 矩阵分析与处理1、 设有分块矩阵33322322E R A O S ⨯⨯⨯⨯⎡⎤=⎢⎥⎣⎦,其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵与对角阵,试通过数值计算验证22E R RS A OS +⎡⎤=⎢⎥⎣⎦。
解: M 文件如下;5、 下面就是一个线性方程组:1231112340.951110.673450.52111456x x x ⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦(1) 求方程得解。
(2) 将方程右边向量元素b 3改为0、53再求解,并比较b 3得变化与解得相对变化。
(3) 计算系数矩阵A 得条件数并分析结论。
解: M 文件如下:实验三 选择结构程序设计1、 求分段函数得值。
2226035605231x x x x y x x x x x x x ⎧+-<≠-⎪=-+≤<≠≠⎨⎪--⎩且且及其他用if 语句实现,分别输出x=-5、0,-3、0,1、0,2、0,2、5,3、0,5、0时得y 值。
matlab实验4_循环结构程序设计_参考解答

高教社刘卫国《MATLAB 程序设计与应用》(第二版)实验参考解答
实验四:循环结构程序设计
clear all; close all; clc; y=0; n=1; while y<3
y=y+1/(2*n-1); n=n+1; end n=n-1; y=y-1/(2*n-1) n=n-1
运行结果:
y= 2.9944
x1=a/(b+x0); y=abs(x1-x0); x0=x1;
MATLAB 语言
3
WangChengyou © 山东大学威海分校
高教社刘卫国《MATLAB 程序设计与应用》(第二版)实验参考解答
实验四:循环结构程序设计
n=n+1; end x1 r1=(-b+sqrt(b^2+4*a))/2 r2=(-b-sqrt(b^2+4*a))/2
clear all; close all; clc; prime=[]; for n=2:49
x=n*(n+1)-1; signx=0; for k=2:sqrt(x)
MATLAB 语言
5
WangChengyou © 山东大学威海分校
高教社刘卫国《MATLAB 程序设计与应用》(第二版)实验参考解答
根据
π2 6
=1 12
+
1 22
+1 32
+"+
1 n2
,求 π 的近似值。当
n
分别取
100、1000、10000
时,
结果是多少?
要求:分别用循环结构和向量运算(使用 sum 函数)来实现。 答:程序设计:
(1) 循环结构
matlab实验内容答案

m a t l a b实验内容答案(总16页) -本页仅作为预览文档封面,使用时请删除本页-实验报告说明:matlab 课程实验需撰写8个实验报告,每个实验报告内容写每次实验内容中标号呈黑体大号字显示的题目。
第一次实验内容:实验一 MATLAB 运算基础一、实验目的1.熟悉启动和退出MATLAB 的方法。
2.熟悉MATLAB 命令窗口的组成。
3.掌握建立矩阵的方法。
4.掌握MATLAB 各种表达式的书写规则以及常用函数的使用。
二、实验内容1.先求下列表达式的值,然后显示MATLAB 工作空间的使用情况并保存全部变量。
(1)22sin8511z e ︒=+ (2)12ln(2z x =,其中2120.455i +⎡⎤=⎢⎥-⎣⎦(3)0.30.33sin(0.3), 3.0, 2.9, 2.8,,2.8,2.9,3.02a ae e z a a --=+=--- 提示:利用冒号表达式生成a 向量,求各点的函数值时用点乘运算。
(4)2220141122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪--≤<⎩,其中t =0::提示:用逻辑表达式求分段函数值。
2.已知12344347873657A -⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,131203327B -⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦求下列表达式的值:(1) A+6=B 和A-B+I(其中I 为单位矩阵)。
(2) A*B 和A.*B 。
(3) A^3和A^.3 。
(4) A/B 和B\A 。
(5)[A ,B]和[A([1,3],;);B^2] 。
3.设有矩阵A 和B12345678910111213141516171819202122232425A ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦, 30161769023497041311B ⎡⎤⎢⎥-⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎣⎦(1) 求它们的乘积C 。
(2) 将矩阵C 的右下角3×2子矩阵赋给D(3) 查看MATLAB 工作空间使用情况。
MATLAB)课后实验答案

实验一 MATLAB 运算基础1. 先求下列表达式的值,然后显示MATLAB 工作空间的使用情况并保存全部变量。
(1) 0122sin851z e =+ (2) 221ln(1)2z x x =++,其中2120.455i x +⎡⎤=⎢⎥-⎣⎦ (3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e a z a a --+=++=-- (4) 2242011122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪-+≤<⎩,其中t =0:0.5:2.5 解: M 文件:z1=2*sin(85*pi/180)/(1+exp(2))x=[2 1+2*i;-.45 5];z2=1/2*log(x+sqrt(1+x^2))a=-3.0:0.1:3.0;z3=(exp(0.3.*a)-exp(-0.3.*a))./2.*sin(a+0.3)+log((0.3+a)./2) t=0:0.5:2.5; z4=(t>=0&t<1).*(t.^2)+(t>=1&t<2).*(t.^2-1)+(t>=2&t<3) .*(t.^2-2*t+1)运算结果:z1=2*sin(85*pi/180)/(1+exp(2))x=[2 1+2*i;-.45 5];z2=1/2*log(x+sqrt(1+x^2))a=-3.0:0.1:3.0;z3=(exp(0.3.*a)-exp(-0.3.*a))./2.*sin(a+0.3)+log((0.3+a)./2)t=0:0.5:2.5;z4=(t>=0&t<1).*(t.^2)+(t>=1&t<2).*(t.^2-1)+(t>=2&t<3) .*(t.^2-2*t+1) z1 =0.2375z2 =0.7114 - 0.0253i 0.8968 + 0.3658i0.2139 + 0.9343i 1.1541 - 0.0044i2. 已知:1234413134787,2033657327A B --⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦求下列表达式的值:(1) A+6*B 和A-B+I (其中I 为单位矩阵)(2) A*B 和A.*B(3) A^3和A.^3(4) A/B 及B\A(5) [A,B]和[A([1,3],:);B^2]解: M 文件:A=[12 34 -4;34 7 87;3 65 7];B=[1 3 -1;2 0 3;3 -2 7]; A+6.*BA-B+eye(3)A*BA.*BA^3A.^3A/BB\A[A,B][A([1,3],:);B^2]运算结果:A=[12 34 -4;34 7 87;3 65 7];B=[1 3 -1;2 0 3;3 -2 7]; A+6.*BA-B+eye(3)A*BA.*BA^3A.^3A/BB\A[A,B][A([1,3],:);B^2]ans =18 52 -1046 7 10521 53 49ans =12 31 -332 8 840 67 1 ans =68 44 62309 -72 596154 -5 241 ans =12 102 468 0 2619 -130 49 ans =37226 233824 48604247370 149188 60076678688 454142 118820 ans =1728 39304 -6439304 343 65850327 274625 343 ans =16.4000 -13.6000 7.600035.8000 -76.2000 50.200067.0000 -134.0000 68.0000ans =109.4000 -131.2000 322.8000-53.0000 85.0000 -171.0000-61.6000 89.8000 -186.2000ans =12 34 -4 1 3 -134 7 87 2 0 33 65 7 3 -2 7 ans =12 34 -43 65 74 5 111 0 1920 -5 403. 设有矩阵A和B1234530166789101769,111213141502341617181920970212223242541311A B ⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦ (1) 求它们的乘积C 。
MATLAB程序的设计与应用(刘卫国编)课后实验答案

实验一 MATLAB 运算基础1. 先求下列表达式的值,然后显示MATLAB 工作空间的使用情况并保存全部变量。
(1) 0122sin851z e =+(2) 21ln(2z x =,其中2120.455i x +⎡⎤=⎢⎥-⎣⎦ (3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e a z a a --+=++=--L (4) 2242011122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪-+≤<⎩,其中t =0:0.5:2.5 解:2. 已知:1234413134787,2033657327A B --⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦求下列表达式的值:(1) A+6*B 和A-B+I (其中I 为单位矩阵)(2) A*B 和A.*B(3) A^3和A.^3(4) A/B 及B\A(5) [A,B]和[A([1,3],:);B^2]解:运算结果:3. 设有矩阵A 和B1234530166789101769,111213141502341617181920970212223242541311A B ⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦(1) 求它们的乘积C。
(2) 将矩阵C的右下角3×2子矩阵赋给D。
(3) 查看MATLAB工作空间的使用情况。
解:. 运算结果:4. 完成下列操作:(1) 求[100,999]之间能被21整除的数的个数。
(2) 建立一个字符串向量,删除其中的大写字母。
解:(1) 结果:(2). 建立一个字符串向量例如:ch='ABC123d4e56Fg9';则要求结果是:实验二 MATLAB 矩阵分析与处理1. 设有分块矩阵33322322E R A O S ⨯⨯⨯⨯⎡⎤=⎢⎥⎣⎦,其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对角阵,试通过数值计算验证22E R RS A O S +⎡⎤=⎢⎥⎣⎦。
(完整版)MATLAB)课后实验答案[1]
![(完整版)MATLAB)课后实验答案[1]](https://img.taocdn.com/s3/m/f6c08c5902d276a201292ece.png)
1 + e2 (2) z = 1 ln( x + 1 + x 2 ) ,其中 x = ⎡⎢ 2⎣-0.45 ⎦2 2 ⎪t 2 - 2t + 1 2 ≤ t <3 ⎨实验一MATLAB 运算基础1. 先求下列表达式的值,然后显示 MATLAB 工作空间的使用情况并保存全部变量。
(1) z = 2sin 8501221 + 2i ⎤5 ⎥(3) z = e 0.3a - e -0.3asin(a + 0.3) + ln 0.3 + a ,a = -3.0, - 2.9, L , 2.9, 3.03⎧t 2 0 ≤ t < 1 (4) z = ⎪t 2 - 11 ≤ t <2 ,其中 t=0:0.5:2.5 4⎩解:M 文件:z1=2*sin(85*pi/180)/(1+exp(2))x=[2 1+2*i;-.45 5];z2=1/2*log(x+sqrt(1+x^2))a=-3.0:0.1:3.0;3=(exp(0.3.*a)-exp(-0.3.*a))./2.*sin(a+0.3)+log((0.3+a)./2)t=0:0.5:2.5;z4=(t>=0&t<1).*(t.^2)+(t>=1&t<2).*(t.^2-1)+(t>=2&t<3) .*(t.^2-2*t+1)4.完成下列操作:(1)求[100,999]之间能被21整除的数的个数。
(2)建立一个字符串向量,删除其中的大写字母。
解:(1)结果:m=100:999;n=find(mod(m,21)==0);length(n)ans=43(2).建立一个字符串向量例如:ch='ABC123d4e56Fg9';则要求结果是:ch='ABC123d4e56Fg9';k=find(ch>='A'&ch<='Z');ch(k)=[]ch=⎣O2⨯3⎥,其中E、R、O、S分别为单位矩阵、随机矩阵、零矩S⎦阵和对角阵,试通过数值计算验证A=⎢⎥。
matlab实验指导答案详解(非常详细正确)

实验一MATLAB 工作环境熟悉及简单命令的执行一、实验目的:熟悉MATLAB 的工作环境,学会使用MATLAB 进行一些简单的运算。
二、实验内容:MATLAB 的启动和退出,熟悉MATLAB 的桌面(Desktop ),包括菜单(Menu )、工具条(Toolbar )、命令窗口(Command Window)、历史命令窗口、工作空间(Workspace)等;完成一些基本的矩阵操作;学习使用在线帮助系统。
三、实验步骤:1、启动MATLAB ,熟悉MATLAB 的桌面。
2、在命令窗口执行命令完成以下运算,观察workspace 的变化,记录运算结果。
(1)(365-52⨯2-70)÷3 >>(365-52*2-70)/3 ans = 63.6667(2)>>area=pi*2.5^2 area = 19.6350(3)已知x=3,y=4,在MATLAB 中求z :()232y x y x z -= >>x=3 >>y=4>>z = x ^2 * y ^3 / (x - y) ^2 z = 576(4)将下面的矩阵赋值给变量m1,在workspace 中察看m1在内存中占用的字节数。
m1=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡11514412679810115133216 执行以下命令>>m1 =[16 2 3 13 ; 5 11 10 8 ; 9 7 6 12 ; 4 14 15 1 ] >>m1( 2 , 3 ) ans = 10 >>m1( 11 ) ans = 6>>m1( : , 3 ) ans =3 10 6 15>>m1( 2 : 3 , 1 : 3 ) ans =5 11 10 9 7 6>>m1( 1 ,4 ) + m1( 2 ,3 ) + m1( 3 ,2 ) + m1( 4 ,1) ans = 34(5)执行命令>>help abs查看函数abs 的用法及用途,计算abs( 3 + 4i ) (6)执行命令>>x=0:0.1:6*pi; >>y=5*sin(x); >>plot(x,y)(6)运行MATLAB 的演示程序,>>demo ,以便对MATLAB 有一个总体了解。
MATLAB数学实验答案(全)

第一次练习教学要求:熟练掌握Matlab 软件的基本命令和操作,会作二维、三维几何图形,能够用Matlab 软件解决微积分、线性代数与解析几何中的计算问题。
补充命令vpa(x,n) 显示x 的n 位有效数字,教材102页fplot(‘f(x)’,[a,b]) 函数作图命令,画出f(x)在区间[a,b]上的图形 在下面的题目中m 为你的学号的后3位(1-9班)或4位(10班以上) 1.1 计算30sin limx mx mx x →-与3sin limx mx mxx →∞- syms xlimit((902*x-sin(902*x))/x^3) ans =366935404/3limit((902*x-sin(902*x))/x^3,inf)//inf 的意思 ans = 0 1.2 cos1000xmxy e =,求''y syms xdiff(exp(x)*cos(902*x/1000),2)//diff 及其后的2的意思 ans =(46599*cos((451*x)/500)*exp(x))/250000 - (451*sin((451*x)/500)*exp(x))/250 1.3 计算2211x y edxdy +⎰⎰dblquad(@(x,y) exp(x.^2+y.^2),0,1,0,1)//双重积分 ans = 2.13941.4 计算4224x dx m x +⎰ syms xint(x^4/(902^2+4*x^2))//不定积分 ans =(91733851*atan(x/451))/4 - (203401*x)/4 + x^3/12 1.5 (10)cos ,x y e mx y =求//高阶导数syms xdiff(exp(x)*cos(902*x),10) ans =-356485076957717053044344387763*cos(902*x)*exp(x)-3952323024277642494822005884*sin(902*x)*exp(x)1.6 0x =的泰勒展式(最高次幂为4).syms xtaylor(sqrt(902/1000+x),5,x)//泰勒展式 ans =-(9765625*451^(1/2)*500^(1/2)*x^4)/82743933602 +(15625*451^(1/2)*500^(1/2)*x^3)/91733851-(125*451^(1/2)*500^(1/2)*x^2)/406802 + (451^(1/2)*500^(1/2)*x)/902 +(451^(1/2)*500^(1/2))/500 1.7 Fibonacci 数列{}n x 的定义是121,1x x ==12,(3,4,)n n n x x x n --=+=用循环语句编程给出该数列的前20项(要求将结果用向量的形式给出)。
MATLAB相关的实验以及答案

y=zeros(size(x)); i=numel(x); for j=1:i if (x(j)>=0) y(j)=-3*x(j)^2+5; else y(j)=3*x(j)^2+5; end end x y
4. 编写一程序,求出 编写一程序,求出[100 1000]以内的全部素数。 以内的全部素数。 以内的全部素数 num=[ ]; i=1; for k1=100:1000 k2=fix(sqrt(k1)); sign=1; for k3=2:k2 if mod(k1,k3)==0 sign=0; break end end if sign==1 num(i)=k1; i=i+1; end end num
6. 建立函数count(x),其中x为一个班的学生成绩,统 建立函数 ,其中 为一个班的学生成绩, 为一个班的学生成绩 计该班学生成绩,其中优秀:成绩≥90,良好:80≤ 计该班学生成绩,其中优秀:成绩 ,良好: 成绩<90,中等:70≤成绩 成绩<80,及格:60≤成绩 成绩<70, 成绩 ,中等: 成绩 ,及格: 成绩 , 不及格:成绩<60,分别输出优秀、良好、中等、不 不及格:成绩 ,分别输出优秀、良好、中等、 及格的人数,要求有输入、输出提示语句。例如: 及格的人数,要求有输入、输出提示语句。例如: >> count 请输入该班学生成绩: %输出提示 请输入该班学生成绩: 输出提示 [34 67 98 89 78] %输入成绩 输入成绩 成绩优秀: %输出结果 成绩优秀:1 输出结果 成绩良好: 成绩良好:1 成绩中等: 成绩中等:1 成绩及格: 成绩及格:1 成绩不及格: 成绩不及格:1
2. 输入三角形的三条边,求三角形的面积。如果输入 输入三角形的三条边,求三角形的面积。 的三个数不能构成三角形,要求输出“ 的三个数不能构成三角形,要求输出“不能构成一个 三角形”这样的提示信息。 三角形”这样的提示信息。 提示: 提示: area = s(s −a)(s −b)(s −c) s = (a +b + c) / 2 a=input('a='); b=input('b='); c=input('c='); if (a+b>c)&(a+c>b)&(b+c>a) s=(a+b+c)/2; area=sqrt(s*(s-a)*(s-b)*(s-c)) else fprintf(‘不能构成一个三角形 不能构成一个三角形\n’) 不能构成一个三角形 end
MATLAB作业4参考答案

MATLAB作业4参考答案MATLAB作业四参考答案2yt,,sin(103)1、用在(0,3)区间内生成一组较稀疏的数据,并用一维数据插值的方法对给出的数据进行曲线拟合,并将结果与理论曲线相比较。
【求解】类似于上面的例子~可以用几乎一致的语句得出样本数据和插值效果。
>> t=0:0.2:3;y=sin(10*t.^2+3); plot(t,y,'o')ezplot('sin(10*t^2+3)',[0,3]); hold on x1=0:0.001:3;y1=interp1(t,y,x1,'spline'); plot(x1,y1)由于曲线本身变换太大~所以在目前选定的样本点下是不可能得出理想插值效果的~因为样本数据提供的信息量不够。
为了得到好的插值效果~必须增大样本数据的信息量~对本例来说~必须在快变化区域减小样本点的步长。
>> hold offt=[0:0.1:1,1.1:0.04:3]; y=sin(10*t.^2+3); plot(t,y,'o')ezplot('sin(10*t^2+3)',[0,3]); hold on x1=0:0.001:3;y1=interp1(t,y,x1,'spline'); plot(x1,y1)241,,xy22fxyexyxy,,(,)sin()2、用原型函数生成一组网络数据或随机数据,分别拟合出曲3xy,3面,并和原曲面进行比较。
【求解】由下面的语句可以直接生成一组网格数据~用下面语句还可以还绘制出给定样本点是三维表面图。
>> [x,y]=meshgrid(0.2:0.2:2);z=exp(-x.^2-y.^4).*sin(x.*y.^2+x.^2.*y)./(3*x.^3+y); surf(x,y,z) 选择新的密集网格~则可以通过二元插值得出插值曲面。
MATLAB全部实验及答案

MATLAB全部实验及答案MATLAB全部实验及答案实验一、MATLAB基本操作实验内容及步骤4、有关向量、矩阵或数组的一些运算(1)设A=15;B=20;求C=A+B与c=a+b?(2)设A=[1 2 3;4 5 6;7 8 9],B=[9 8 7;6 5 4;3 2 1];求A*B 与A.*B?A*B就是线代里面的矩阵相乘A.*B是对应位置的元素相乘(3)设a=10,b=20;求i=a/b=0.5与j=a\b=2?(4)设a=[1 -2 3;4 5 -4;5 -6 7]请设计出程序,分别找出小于0的矩阵元素及其位置(单下标、全下标的形式),并将其单下标转换成全下标。
clear,clca=[1 -2 3;4 5 -4;5 -6 7];[x,y]=find(a<0);c=[];for i=1:length(x)c(i,1)=a(x(i),y(i));c(i,2)=x(i);c(i,3)=y(i);c(i,4)=(y(i)-1)*size(a,2)+x(i);endc(5)在MATLAB命令行窗口运行A=[1,2;3,4]+i*[5,6;7,8];看结果如何?如果改成运行A=[1,2;3,4]+i[5,6;7,8],结果又如何?前面那个是虚数矩阵,后面那个出错(6)请写出完成下列计算的指令:a=[1 2 3;3 4 2;5 2 3],求a^2=?,a.^2=?a^2= 22 16 1625 26 2326 24 28a.^2=1 4 99 16 425 4 9(7)有一段指令如下,请思考并说明运行结果及其原因clearX=[1 2;8 9;3 6];X( : ) 转化为列向量(8)使用三元组方法,创建下列稀疏矩阵2 0 8 00 0 0 10 4 0 06 0 0 0方法一:clear,clcdata=[2 8 1 4 6];ir=[1 1 2 3 4 ];jc=[1 3 4 2 1];s=sparse(ir,jc,data,4,4);full(s)方法二:不用三元组法clear,clca=zeros(4,4);a(1,[1,3])=[2,8];a(2,4)=1;a(3,2)=4;a(4,1)=6;a(9)写出下列指令的运行结果>> A = [ 1 2 3 ]; B = [ 4 5 6 ];>> C = 3.^A>> D = A.^B5、已知+?=-334sin 234πt e y t 若需要计算t ∈[-1,1],取间隔为0.01,试计算出相对应的y 值。
数字图像处理及MATLAB实现实验四——图像变换

数字图像处理及MATLAB实现实验四——图像变换1.图像的傅⾥叶变换⼀(平移性质)傅⾥叶变换的平移性质表明了函数与⼀个指数项相乘等于将变换后的空域中⼼移到新的位置,并且平移不改变频谱的幅值。
I=imread('1.bmp');figure(1)imshow(real(I));I=I(:,:,3);fftI=fft2(I);sfftI=fftshift(fftI); %求离散傅⾥叶频谱%对原始图像进⾏⼆维离散傅⾥叶变换,并将其坐标原点移到频谱图中央位置RRfdp1=real(sfftI);IIfdp1=imag(sfftI);a=sqrt(RRfdp1.^2+IIfdp1.^2);a=(a-min(min(a)))/(max(max(a))-min(min(a)))*225;figure(2)imshow(real(a));I=imread('2.bmp');figure(1)imshow(real(I));I=I(:,:,3);fftI=fft2(I);sfftI=fftshift(fftI); %求离散傅⾥叶频谱%对原始图像进⾏⼆维离散傅⾥叶变换,并将其坐标原点移到频谱图中央位置RRfdp1=real(sfftI);IIfdp1=imag(sfftI);a=sqrt(RRfdp1.^2+IIfdp1.^2);a=(a-min(min(a)))/(max(max(a))-min(min(a)))*225;figure(2)imshow(real(a));I=imread('3.bmp');figure(1)imshow(real(I));I=I(:,:,3);fftI=fft2(I);sfftI=fftshift(fftI); %求离散傅⾥叶频谱%对原始图像进⾏⼆维离散傅⾥叶变换,并将其坐标原点移到频谱图中央位置RRfdp1=real(sfftI);IIfdp1=imag(sfftI);a=sqrt(RRfdp1.^2+IIfdp1.^2);a=(a-min(min(a)))/(max(max(a))-min(min(a)))*225;figure(2)imshow(real(a));实验结果符合傅⾥叶变换平移性质2.图像的傅⾥叶变换⼆(旋转性质)%构造原始图像I=zeros(256,256);I(88:168,124:132)=1; %图像范围是256*256,前⼀值是纵向⽐,后⼀值是横向⽐imshow(I)%求原始图像的傅⾥叶频谱J=fft2(I);F=abs(J);J1=fftshift(F);figureimshow(J1,[550])%对原始图像进⾏旋转J=imrotate(I,90,'bilinear','crop');figureimshow(J)%求旋转后图像的傅⾥叶频谱J=fft2(I);F=abs(J);J2=fftshift(F);figureimshow(J2,[550])3.图像的离散余弦变换⼀%对cameraman.tif⽂件计算⼆维DCT变换RGB=imread('cameraman.tif');figure(1)imshow(RGB)I=rgb2gray(RGB);%真彩⾊图像转换成灰度图像J=dct2(I);%计算⼆维DCT变换figure(2)imshow(log(abs(J)),[])%图像⼤部分能量集中在左上⾓处figure(3);J(abs(J)<10)=0;%把变换矩阵中⼩于10的值置换为0,然后⽤idct2重构图像K=idct2(J)/255;imshow(K)4.图像的离散余弦变换⼆% I=imread('1.bmp');% figure(1)% imshow(real(I));% I=I(:,:,3);% fftI=fft2(I);% sfftI=fftshift(fftI); %求离散傅⾥叶频谱% %对原始图像进⾏⼆维离散傅⾥叶变换,并将其坐标原点移到频谱图中央位置% RRfdp1=real(sfftI);% IIfdp1=imag(sfftI);% a=sqrt(RRfdp1.^2+IIfdp1.^2);% a=(a-min(min(a)))/(max(max(a))-min(min(a)))*225;% figure(2)% imshow(real(a));% I=imread('2.bmp');% figure(1)% imshow(real(I));% I=I(:,:,3);% fftI=fft2(I);% sfftI=fftshift(fftI); %求离散傅⾥叶频谱% %对原始图像进⾏⼆维离散傅⾥叶变换,并将其坐标原点移到频谱图中央位置% RRfdp1=real(sfftI);% IIfdp1=imag(sfftI);% a=sqrt(RRfdp1.^2+IIfdp1.^2);% a=(a-min(min(a)))/(max(max(a))-min(min(a)))*225;% figure(2)% imshow(real(a));% I=imread('3.bmp');% figure(1)% imshow(real(I));% I=I(:,:,3);% fftI=fft2(I);% sfftI=fftshift(fftI); %求离散傅⾥叶频谱% %对原始图像进⾏⼆维离散傅⾥叶变换,并将其坐标原点移到频谱图中央位置% RRfdp1=real(sfftI);% IIfdp1=imag(sfftI);% a=sqrt(RRfdp1.^2+IIfdp1.^2);% a=(a-min(min(a)))/(max(max(a))-min(min(a)))*225;% figure(2)% imshow(real(a));% %构造原始图像% I=zeros(256,256);% I(88:168,124:132)=1; %图像范围是256*256,前⼀值是纵向⽐,后⼀值是横向⽐% imshow(I)% %求原始图像的傅⾥叶频谱% J=fft2(I);% F=abs(J);% J1=fftshift(F);figure% imshow(J1,[550])% %对原始图像进⾏旋转% J=imrotate(I,90,'bilinear','crop');% figure% imshow(J)% %求旋转后图像的傅⾥叶频谱% J=fft2(I);% F=abs(J);% J2=fftshift(F);figure% imshow(J2,[550])% %对cameraman.tif⽂件计算⼆维DCT变换% RGB=imread('cameraman.tif');% figure(1)% imshow(RGB)% I=rgb2gray(RGB);% %真彩⾊图像转换成灰度图像% J=dct2(I);% %计算⼆维DCT变换% figure(2)% imshow(log(abs(J)),[])% %图像⼤部分能量集中在左上⾓处% figure(3);% J(abs(J)<10)=0;% %把变换矩阵中⼩于10的值置换为0,然后⽤idct2重构图像% K=idct2(J)/255;% imshow(K)RGB=imread('cameraman.tif');I=rgb2gray(RGB);I=im2double(I); %转换图像矩阵为双精度型T=dctmtx(8); %产⽣⼆维DCT变换矩阵%矩阵T及其转置T'是DCT函数P1*X*P2的参数B=blkproc(I,[88],'P1*x*P2',T,T');maxk1=[ 1111000011100000110000001000000000000000000000000000000000000000 ]; %⼆值掩模,⽤来压缩DCT系数B2=blkproc(B,[88],'P1.*x',mask1); %只保留DCT变换的10个系数I2=blkproc(B2,[88],'P1*x*P2',T',T); %重构图像figure,imshow(T);figure,imshow(B2);figure,imshow(I2);RGB=imread('cameraman.tif');I=rgb2gray(RGB);I=im2double(I); %转换图像矩阵为双精度型T=dctmtx(8); %产⽣⼆维DCT变换矩阵%矩阵T及其转置T'是DCT函数P1*X*P2的参数B=blkproc(I,[88],'P1*x*P2',T,T');maxk1=[ 1111000011100000100000000000000000000000000000000000000000000000 ]; %⼆值掩模,⽤来压缩DCT系数B2=blkproc(B,[88],'P1.*x',mask1); %只保留DCT变换的10个系数I2=blkproc(B2,[88],'P1*x*P2',T',T); %重构图像figure,imshow(T);figure,imshow(B2);figure,imshow(I2);5.图像的哈达玛变换cr=0.5;I=imread('cameraman.tif');I=im2double(I)/255; %将读⼊的unit8类型的RGB图像I转换为double类型的数据figure(1),imshow(I);%显⽰%求图像⼤⼩[m_I,n_I]=size(I); %提取矩阵I的⾏列数,m_I为I的⾏数,n_I为I的列数sizi=8;snum=64;%分块处理t=hadamard(sizi) %⽣成8*8的哈达码矩阵hdcoe=blkproc(I,[sizi sizi],'P1*x*P2',t,t');%将图⽚分成8*8像素块进⾏哈达码变换%重新排列系数CE=im2col(hdcoe,[sizi,sizi],'distinct');%将矩阵hdcode分为8*8互不重叠的⼦矩阵,再将每个⼦矩阵作为CE的⼀列[Y Ind]=sort(CE); %对CE进⾏升序排序%舍去⽅差较⼩的系数,保留原系数的⼆分之⼀,即32个系数[m,n]=size(CE);%提取矩阵CE的⾏列数,m为CE的⾏数,n为CE的列数snum=snum-snum*cr;for i=1:nCE(Ind(1:snum),i)=0;end%重建图像re_hdcoe=col2im(CE,[sizi,sizi],[m_I,n_I],'distinct');%将矩阵的列重新组织到块中re_I=blkproc(re_hdcoe,[sizi sizi],'P1*x*P2',t',t);%进⾏反哈达码变换,得到压缩后的图像re_I=double(re_I)/64; %转换为double类型的数据figure(2);imshow(re_I);%计算原始图像和压缩后图像的误差error=I.^2-re_I.^2;MSE=sum(error(:))/prod(size(re_I));。
实验4答案 Matlab程序设计1

实验4 Matlab 程序设计1实验目的:1、 掌握建立和执行M 文件的方法;2、 掌握实现选择结构的方法;3、 掌握实现循环结构的方法。
实验内容:1. 从键盘输入一个4位整数,按如下规则加密后输出。
加密规则:每位数字都加上7,然后用和除以10的余数取代该数字;再把第一位与第三位交换,第二位与第四位交换。
a = input('请输入一个四位整数:');a1 = fix(a/1000);a2 = rem(fix(a/100),10);a3 = rem(rem(fix(a/10),100),10);a4 = rem(a,10);a1 = rem(a1+7,10)a2 = rem(a2+7,10)a3 = rem(a3+7,10)a4 = rem(a4+7,10)b1 = a1;a1 = a3;a3 = b1;b2 = a2;a2 = a4;a4 = b2;b = a1*1000+a2*100+a3*10+a42. 求分段函数的值。
,x x x x y x x x x x x x ⎧+- <≠-⎪=-+ ≤<≠≠⎨⎪-- ⎩2226035605231且且及其他用if 语句实现,分别输出x=-5,-3,0,1,2,2.5,3,5时的y 值。
x = input(请输入X 的值:');if x <0 & x~=-3y = x.*x +x-6;elseif x>=0 & x<5 & x~=2 & x~=3y = x.*x-5*x+6;elsey = x.*x-x-1;endy3.输入一个百分制成绩,要求输出成绩等级A、B、C、D、E,其中90~100分为A,80~89分为B,70~79分为C,60~69分为D,60分以下为E。
要求:(1)分别用if语句和swich语句实现。
(2)输入百分制成绩后要判断该成绩的合理性,对不合理的成绩应输出出错信息。
MATLAB实验四:MATLAB程序设计 参考答案

function y=f(x) y=(x^3-2*x^2+x-6.3)/(x^2+0.05*x-3.14)
河南财经政法大学数学与信息科学学院
6
实验报告
f(1)*f(2)+f(3)
function f=f(a,b,c) f=g(a)*g(b)+g(c)^2; function g=g(x) g=(x^3-2*x^2+x-6.3)/(x^2+0.05*x-3.14);
a=rand(1,100); [b,c]=sort(a); index=c(1); i=1; while i<=7 if i==8 disp('You Lost!'); i=i+1; else d=input('please input the number you guess:'); if d>index disp('High'); elseif d<index disp('Low'); elseif d==index disp('You won!'); i=9;
syms i j k l n i=1;k=0; n=input('Input n:'); for j=1:n i=i*j; k=k+j; end fprintf('%d!=%d \n Sum(1,...,%d)=%d\n',n,i,n,k);
4、用 while-end 循环语句求不超过 1000 的偶数之和,并求显示出最大值。 s=0,n=0; while s<=1000 n=n+2; s=s+n; if s>1000 break end
数学实验4(程序设计)参考答案

实验4 MATLAB 程序设计一、实验目的:1.理解命令式M 文件和函数式M 文件的关系及各自的特点;2.掌握MATLAB 中关系运算和逻辑运算的正确使用方法;3.掌握MATLAB 中两种循环结构及选择结构的正确使用方法;4.能够编制简单的程序解决实际问题。
二、实验内容:1.满足条件01=a ,12=a ,…,n n n a a a +=++12(n=0,1,…)的数列称为Fibonacci 数列,(1)编写一个MATLAB 函数式M 文件fibo.m 来计算Fibonacci 数列的任意项的数值;(2)计算数列中第50项的数值并给出程序运行所用的时间;(3)编写一个MATLAB 命令式M 文件调用函数式M 文件fibo.m 来计算Fibonacci 数列的前n 项和的值;给出n=50时的结果。
(1)计算Fibonacci 数列的程序function x=fibo(n)if n<1|fix(n)~=ndisp('N must be a positive integer.');elseif n==1;x=0;elseif n==2x=[0,1];elsex=zeros(1,n);x(1)=0;x(2)=1;for k=3:nx(k)=x(k-1)+x(k-2);endend(2)计算数列中第50项的数值x= fibo(50);ticF=x(50)toc(3)Fibonacci 数列的前50项和的值x= fibo(50);FF=sum(x)2.利用下面的公式计算π的值14134171513114---++-+-=N N π,选择不同的N 值,比较结果的精确度。
function PI=hw2(n)if n<1|fix(n)~=ndisp('N must be a positive integer.');elsePI=0;for k=1:nx=1/(4*k-3)-1/(4*k-1);PI=PI+x;endendPI=4*PI;n N的最小正整数n。
matlab课后习题答案第四章(内容参考)
符号法在本例中,只求出一个极值点。其余很多极值点无法秋初,更不可能得到最小值。
16
〖目的〗
学习如何把高阶微分方程写成一阶微分方程组。
ode45解算器的导数函数如何采用匿名函数形式构成。
如何从ode45一组数值解点,求指定自变量对应的函数值。
18
〖目的〗
展示特征值分解可能存在的数值问题。
condeig是比较严谨的特征值分解指令。
Jordan分解的作用。
〖解答〗
(1)特征值分解
A=gallery(5)
[V,D]=eig(A);
diag(D)'%为紧凑地显示特征值而写
A =
-9 11 -21 63 -252
70 -69 141 -421 1684
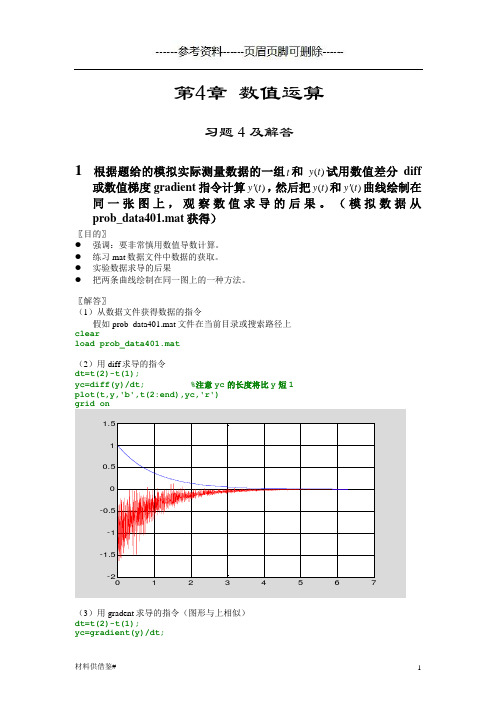
练习mat数据文件中数据的获取。
实验数据求导的后果
把两条曲线绘制在同一图上的一种方法。
〖解答〗
(1)从数据文件获得数据的指令
假如prob_data401.mat文件在当前目录或搜索路径上
clear
load prob_data401.mat
(2)用diff求导的指令
dt=t(2)-t(1);
yc=diff(y)/dt;%注意yc的长度将比y短1
求导会使数据中原有的噪声放大。
12
〖提示〗
指定区间内的积分函数可用cumtrapz指令给出。
在计算要求不太高的地方可用find指令算得。
〖目的〗
指定区间内的积分函数的数值计算法和cumtrapz指令。
find指令的应用。
〖解答〗
dt=1e-4;
t=0:dt:10;
