【浙教版初中数学】专项练习：函数y等于a(x减h)2的图象与性质

合集下载

4 课题：二次函数y=a(x-h)2的图象和性质-精选文档

课题：二次函数y ＝a (x －h )2的图象和性质【学习目标】1．使学生能利用描点法画出二次函数y ＝a(x －h)2的图象．2．让学生经历二次函数y ＝a(x －h)2性质探究的过程，理解函数y ＝a(x －h)2的性质，理解二次函数y ＝a(x －h)2的图象与二次函数y ＝ax 2的图象的关系．【学习重点】掌握二次函数y ＝a(x －h)2的图象和性质．【学习难点】二次函数y ＝a(x －h)2的图象和性质的运用．【导学流程】一、情景导入感受新知问题1：说说二次函数y ＝ax 2＋k 的图象的特征．问题2：二次函数y ＝x 2＋3的图象是一条抛物线，它的开口向上，对称轴是y 轴，顶点坐标是(0，3)；在对称轴的左侧，y 随x 的增大而减小，在对称轴的右侧，y 随x 的增大而增大；当x ＝__0时，y 取最小值．这节课我们继续探究二次函数y ＝a(x －h)2的图象．(板书课题)二、自学互研生成新知【自主探究】阅读教材P 33～P 35“思考”的内容，思考并填写课本中的问题，然后完成下列问题：①画出二次函数y ＝－12(x ＋1)2，y ＝－12(x －1)2的图象；在列表时，你会发现在0的两边等距离选取x 值时，对应的y 值不等，这样描出的点不对称，因此，需要修正x 的取值．请填写下表，然后对称性描点． x … －4 －3 －2 －1 0 1 2 3 4 …y ＝－12(x ＋1)2… －92 －2 －12 0 －12 －2 －92 －8 －252 … x … －4 －3 －2 －1 0 1 2 3 4 …y ＝－12(x －1)2… －252 －8 －92 －2 －12 0 －12 －2 －92 … ②观察图象，说出它们的开口方向、对称轴、顶点坐标(提示：把过(－1，0)且与x 轴垂直的直线记作直线x ＝－1)．y ＝－12(x ＋1)2的开口向下，对称轴为直线x ＝－1，顶点坐标为(－1，0)；y ＝－12(x －1)2的开口向下，对称轴为直线x ＝1，顶点坐标为(1，0)．【合作探究】抛物线y ＝a(x －h)2有怎样的性质？与y ＝ax 2有什么联系？归纳：1.二次函数y ＝a(x －h)2(a ≠0)的图象性质：开口方向：a>0时，开口向上，a<0时，开口向下，顶点(h ，0)，对称轴x ＝h ．最值：a>0时，有最小值y ＝0；a<0时，有最大值y ＝0，增减性：a>0且x>h 时，y 随x 的增大而增大，x<h 时，y 随x 的增大而减小；a<0且x>h 时，y 随x 的增大而减小，x<h 时，y 随x 的增大而增大．2．y ＝ax 2和y ＝a(x －h)2的图象有如下关系：y ＝ax 2――→h>0，向右平移h 个单位h<0，向左平移|h|个单位y ＝a(x －h)2. 3．由抛物线y ＝ax 2的图象通过平移得到y ＝a(x －h)2的图象左右平移的规律是(四字口诀)左加右减．4．对于二次函数的图象，只要|a|相等，则它们的形状相同，只是开口方向不同，且|a|越大，开口越小．师生活动：①明了学情：观察学生的图象的画法和阅读图象的能力．②差异指导：根据学情进行针对性指导．③生生互助：小组内相互交流研讨、修正结论，形成统一认识．三、典例剖析运用新知【合作探究】典例：抛物线y ＝15(x －4)2的开口向上，对称轴是直线x ＝4，顶点坐标是(4，0)，当x <4时，y 随x 的增大而减小；当x ＝4时，函数y 取得最小值，值为__0．变式1：把抛物线y ＝x 2向左平移2个单位，所得抛物线的函数表达式为( B )A ．y ＝x 2＋2B ．y ＝(x ＋2)2C ．y ＝x 2－2D ．y ＝(x －2)2变式2：已知二次函数y ＝3(x －a)2的图象上，当x>2时，y 随x 的增大而增大，则a 的取值范围是a ≤2．师生活动：①明了学情：了解学生对y ＝a(x －h)2(a ≠0)的图象和性质的掌握情况．②差异指导：根据学情适时个别或分类点拨．③生生互助：先独立思考完成，再小组内交流、讨论，互纠并找出原因．四、课堂小结回顾新知(1)抛物线y ＝a(x －h)2的开口方向、对称轴和顶点坐标．(2)图象的平移：抛物线y ＝ax 2――→h ＞0向右平移|h|个单位h ＜0向左平移|h|个单位抛物线y ＝a(x －h)2 五、检测反馈落实新知1．对于抛物线y ＝12(x －2)2，下列说法错误的是( D ) A ．开口向上B ．对称轴是直线x ＝2C ．最低点的坐标是(2，0)D ．当x>2时，y 随x 的增大而减小2．对于任何实数h ，抛物线y ＝x 2与抛物线y ＝(x －h)2( A )A ．形状与开口方向相同B ．对称轴相同C ．顶点相同D ．都有最高点3．抛物线y ＝3(x －2)2可以由抛物线y ＝3x 2向右平移2个单位得到．4．二次函数y ＝－2(x －1)2的图象开口方向向下，顶点坐标是(1，0)，对称轴是直线x ＝1．六、课后作业巩固新知(见学生用书)。

专项练习：函数y等于a(x减h)2的图象与性质(有答案)

函数()2h x a y -=的图象与性质
1、抛物线()232
1--=x y ，顶点坐标是 ,当x 时,y 随x 的增大而减小，函数有最值 .
2、试写出抛物线23x y =经过下列平移后得到的抛物线的解析式并写出对称轴和顶点坐标.
（1）右移2个单位；（2）左移3
2个单位；（3）先左移1个单位，再右移4个单位.
3、请你写出函数()2
1+=x y 和12+=x y 具有的共同性质（至少2个）.
4、二次函数()2h x a y -=的图象如图：已知2
1=a ，OA=OC ，试求该抛物线的解析式.
5、抛物线2)3(3-=x y 与x 轴交点为A ，与y 轴交点为B ，求A 、B 两点坐标及△AOB 的面积.
6、二次函数2)4(-=x a y ，当自变量x 由0增加到2时，函数值增加6.
（1）求出此函数关系式.（2）说明函数值y 随x 值的变化情况.
7、已知抛物线9)2(2++-=x k x y 的顶点在坐标轴上，求k 的值.
参考答案
1、（3，0），>3，大，y=0;
2、2)2(3-=x y ，2)3
2(3-=x y ，2)3(3-=x y ; 3、略；
4、2)2(2
1-=x y ； 5、（3，0），（0，27），40.5；
6、2)4(2
1--=x y ，当x<4时，y 随x 的增大而增大，当x>4时，y 随x 的增大而减小；
7、-8，-2，4.。

《二次函数y=a(x-h)2的图象和性质》教案、导学案、同步练习

《第2课时二次函数y＝a(x－h)2的图象和性质》教案【教学目标】1．会用描点法画出y＝a(x－h)2的图象．2．掌握形如y＝a(x－h)2的二次函数图象的性质，并会应用．3．理解二次函数y＝a(x－h)2与y＝ax2之间的联系．【教学过程】一、情境导入涵洞是指在公路工程建设中，为了使公路顺利通过水渠不妨碍交通，修筑于路面以下的排水孔道(过水通道)，通过这种结构可以让水从公路的下面流过．从如图所示的直角坐标系中，你能得到函数图象解析式吗？二、合作探究探究点：二次函数y＝a(x－h)2的图象和性质【类型一】y＝a(x－h)2的图象与性质的识别已知抛物线y＝a(x－h)2(a≠0)的顶点坐标是(－2，0)，且图象经过点(－4，2)，求a，h的值．解：∵抛物线y＝a(x－h)2(a≠0)的顶点坐标为(－2，0)，∴h＝－2.又∵抛物线y＝a(x＋2)2经过点(－4，2)，∴(－4＋2)2·a＝2，∴a＝1 2 .方法总结：抛物线y＝a(x－h)2的顶点坐标为(h，0)，对称轴是直线x＝h. 【类型二】二次函数y＝a(x－h)2增减性的判断对于二次函数y＝9(x－1)2，下列结论正确的是( )A．y随x的增大而增大B．当x＞0时，y随x的增大而增大C．当x＞－1时，y随x的增大而增大D ．当x ＞1时，y 随x 的增大而增大解析：由于a ＝9＞0，抛物线开口向上，而h ＝1，所以当x ＞1时，y 随x 的增大而增大．故选D.【类型三】确定y ＝a (x －h )2与y ＝ax 2的关系能否向左或向右平移函数y ＝－12x 2的图象，使得到的新的图象过点(－9，－8)？若能，请求出平移的方向和距离；若不能，请说明理由．解：能，设平移后的函数为y ＝－12(x －h )2，将x ＝－9，y ＝－8代入得－8＝－12(－9－h )2，所以h ＝－5或h ＝－13，所以平移后的函数为y ＝－12(x ＋5)2或y ＝－12(x ＋13)2.即抛物线的顶点为(－5，0)或(－13，0)，所以向左平移5或13个单位．方法总结：根据抛物线平移的规律，向右平移h 个单位后，a 不变，括号内变“减去h ”；若向左平移h 个单位，括号内应“加上h ”，即“左加右减”．【类型四】y ＝a (x －h )2的图象与几何图形的综合把函数y ＝12x 2的图象向右平移4个单位后，其顶点为C ，并与直线y ＝x分别相交于A 、B 两点(点A 在点B 的左边)，求△ABC 的面积．解析：利用二次函数平移规律先确定平移后抛物线解析式，确定C 点坐标，再解由得到的二次函数解析式与y ＝x 组成的方程组，确定A 、B 两点的坐标，最后求△ABC 的面积．解：平移后的函数为y ＝12(x －4)2，顶点C 的坐标为(4，0)，解方程组⎩⎨⎧y ＝12（x －4）2，y ＝x ，得⎩⎨⎧x ＝2，y ＝2，或⎩⎨⎧x ＝8，y ＝8.∵点A 在点B 的左边，∴A (2，2)，B (8，8)．∴S △ABC ＝S △OBC －S △OAC ＝12OC ×8－12OC ×2＝12.方法总结：两个函数交点的横纵坐标与两个解析式组成的方程组的解是一致的．三、板书设计【教学反思】教学过程中，强调学生自主探索和合作交流，在操作中探究二次函数y＝a(x －h)2的图象与性质，体会数学建模的数形结合思想方法.《第2课时二次函数y=a（x-h）2的图象和性质》导学案值。

二次函数y=a(x-h)2_的图象和性质

在同一坐标系中作出下列二次函数:
y 1 x 2 y 1 (x 2)2
2
2
y
1
6
(x
2)2
25
观察三条抛物线的 y 1 x 22
4
相互关系,并分别指 2
3
出它们的开口方向,
2
对称轴及顶点.
1
y 1 x2 2
y 1 x 22
2
-8
-6
-4
-2 B
2
4
6
y 1 (x 2)2 向左平移
2
2个单位
y 1 x2 2
向右-1 平移 y 1 (x 2)2
2个-2 单位
2
顶点(－2,0)
向左平移 2个单位
顶点(0,0)
向右-3 平移 2个-4 单位
顶点(2,0)
直线x=－2
向左平移对称轴:y轴向右平移 2个单位即直线: x=0 2个单位
直线x=2
y＝a(x-ｈ)2(a≠0)
a>0
（A）直线x=2 （B）直线x=-2
（C）y轴
（D）x轴
4、将抛物线 y 3x 2 向左平移3个单位所得的抛
物线的函数关系式为（ D ）
A、 y 3x2 3 B、5、抛物线 y (x 1)2 是由抛物线 y=-X2 向右平
顶点坐标
最值
增减性
在对称在对称轴右侧轴左侧
y=ax2
y=ax2+k
a＞0 a＜0 a＞0 a＜0
向上 y轴
向下 y轴向上 y轴向下 y轴
（0，0）（0,0）
（0,k）（0,k）
当x=0时， Y随x的增 Y随x的增 y最小值=0 大而减小大而增大

九年级数学二次函数y=a(x-h)2的图象与性质

二二次函数y=ax2的图象与y=a(x-h)2的图象的关系
想一想
抛物线 y 1 x 12，y 1 x 12 的图象与抛物线
2
2
y 1 x2 的图象有什么关系？
2
－4
y 1 x 12
2
－2 －2 －4
24
y 1 x 12
2
y 1 x 12
a,c的符号
a>0,c>0 a>0,c<0 a<0,c>0
a<0,c<0
图象
开口方向
向上
对称轴顶点坐标
y轴（直线x=0）（0,c）
函数的增减性最值
当x<0时，y随x增大而减小；当x>0时，y 随x增大而增大.
x=0时，y最小值=c
向下 y轴（直线x=0）
（0,c）
当x<0时，y随x增大而增大；当x>0时， y随x增大而减小.
解析：抛物线y＝－2x2的顶点坐标是(0，0)，抛物线y＝－2(x＋1)2的顶点坐标是(－1，0)．则由二次函数y＝－2x2的图象向左平移1个单位即可得到二次函数y＝－2(x＋1)2的图象．故选C.
当堂练习
1.把抛物线y=-x2沿着x轴方向平移3个单位长度，那么平移后抛物线的解析式是 y=-(x+3)2或y=-(x-3)2 . 2顶.二点次坐函标数是y_=_2(_(32_x,_-0_) 23__).2图象的对称轴是直线___x__32__，
解析：∵抛物线y＝3(x＋ 2 )2的对称轴为x＝－ 2，a＝ 3＞0，∴x＜－ 2时，y随x的增大而减小；x＞－ 2 时， y随x的增大而增大．∵点A的坐标为(－3 2，y1)，∴点 A在抛物线上的对称点A′的坐标为(3 2 ，y1)．∵－ 2＜ 1＜0＜3 2，∴y2＜y3＜y1.故答案为y2＜y3＜y1.

第2课时二次函数y=a(x-h)2的图象和性质

活动四：课堂总结反思【教学反思】 ①[授课流程反思]新课导入环节中, 引导学生在观察函数图象上下功夫, 同时给学生设置有悬念的问题, 使学生积极思考问题；在探究新知过程中, 让学生经历类比联想、归纳总结的过程, 应用由特殊到一般的思想, 增强学生的观察、分析、归纳和表达能力. ②[讲授效果反思] 引导学生注意三点: (1)明确记忆函数图象的开口方向、对称轴、顶点坐标；(2)函数图象的平移规律；(3)掌握函数的性质. ③[师生互动反思] 教学过程中, 教师对学生进行引导, 使他们能够积极投入到对数学知识的探索过程中来, 养成探索的好习惯. ④[习题反思]好题题号__________________________________________ 错题题号__________________________________________反思教学过程和教师表现, 进一步提升操作流程和自身素质. 一、知识回顾: 画出二次函数y ＝－ (x ＋1)2, y ＝－ (x －1)2的图象, 并考虑它们的开口方向、对称轴、顶点以及最值、函数值的变化情况．先列表：x … －4 －3 －2 －1 0 1 2 3 4 …y ＝－12(x ＋1)2… … y ＝－12(x －1)2……在坐标纸上描点并画图:(1)观察图象, 填开口方向顶点对称轴最值对称轴右侧的增(2)请在图上把抛物线y＝－x2也画上去(草图).①抛物线y＝－ (x＋1)2, y＝－ x2, y＝－ (x－1)2的形状大小________.②把抛物线y＝－ x2向______平移________个单位, 就得到抛物线y＝－ (x＋1)2；把抛物线y＝－ x2向______平移________个单位, 就得到抛物线y＝－ (x－1)2.(2)对于抛物线y＝a(x－h)2与y＝ax2的图象, 形状________, 位置__________.当h>0时, 抛物线y＝a(x－h)2的图象可由y＝ax2的图象向________平移________个单位得到；当h<0时, 抛物线y＝a(x－h)2的图象可由y＝ax2的图象向________平移________个单位得到．小试牛刀:2.抛物线y ＝4(x －2)2与y 轴的交点坐标是________, 与x 轴的交点坐标为________.3. (1)把抛物线y ＝3x2向右平移4个单位后, 得到的抛物线的表达式为________. (2)把抛物线y ＝3x2向左平移6个单位后, 得到的抛物线的表达式为________.4.(1)将抛物线y ＝－ (x －1)2向右平移2个单位后, 得到的抛物线表达式为__________． (2)将抛物线y ＝－13(x －4)2向________平移________个单位得到y ＝－13x 2.5. 写出一个顶点是(5, 0), 形状、开口方向与抛物线y ＝－2x2都相同的二次函数表达式__________.当堂巩固检测(1)二次函数y ＝2(x ＋5)2的图象是________, 开口________, 对称轴是________, 当x ＝____________时, y 有最________值, 是________.(2)二次函数y ＝－3(x －4)2的图象是由抛物线y ＝－3x2向________平移________个单位得到的；开口________, 对称轴是________, 当x ＝________时, y 有最__________值, 是__________.(3)将二次函数y ＝2x2的图象向右平移3个单位后得到函数________的图象, 其对称轴是________, 顶点是________, 当x________时, y 随x 的增大而增大；当x________时, y 随x 的增大而减小.(4)将二次函数y ＝－3(x －2)2的图象向左平移3个单位后得到函数____________的图象, 其顶点坐标是________, 对称轴是__________, 当x ＝________时, y 有最________值, 是________.(5)抛物线y ＝4(x －3)2的开口方向__________, 对称轴是__________, 顶点坐标是__________, 抛物线有最________点, 当x ＝__________时, y 有最________值, 其值为__________, 抛物线与x 轴的交点坐标为________, 与y 轴的交点坐标为________．三、课时小结1. 抛物线y ＝2(x ＋3)2的开口__________；顶点坐标为________；对称轴是________；当x ＞－3时, y 随x 的增大而__________；当x ＝－3时, y 有最________值是________. 2．抛物线y ＝m(x ＋n)2向左平移2个单位后, 得到的函数表达式是y ＝－4(x －4)2, 则m ＝________, n ＝________．3．二次函数y ＝a(x ＋h)2(a ≠0)的图象由y ＝ x2向右平移得到的, 且过点(1, 2), 试说明向右平移了几个单位？。

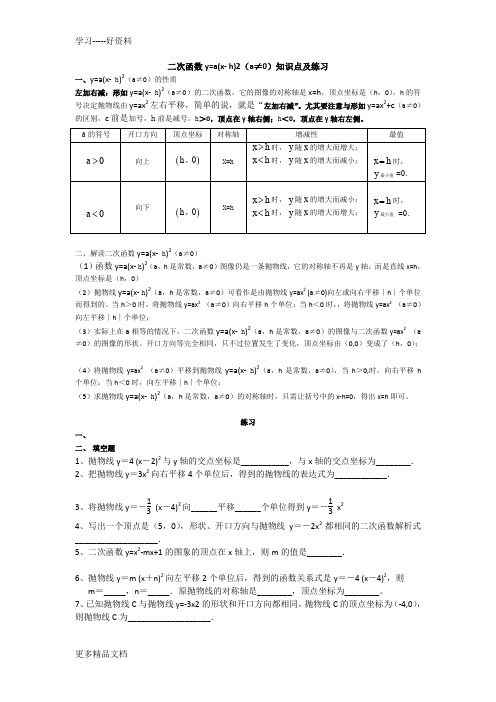
二次函数y=a(x-h)2知识点及练习

二次函数y=a(x-h)2（a≠0）知识点及练习一、y=a(x-h)2（a≠0）的性质左加右减：形如y=a(x-h)2（a≠0）的二次函数，它的图像的对称轴是x=h，顶点坐标是（h，0），h的符号决定抛物线由y=ax2左右平移，简单的说，就是“左加右减”。

尤其要注意与形如y=ax2+c（a ≠0）的区别，c前是加号，h前是减号。

h＞0，顶点在y轴右侧；h＜0，顶点在y轴右左侧。

a的符号开口方向顶点坐标对称轴增减性最值a>0向上(h，0)X=h x>h时，y随x的增大而增大；x=h时，x<h时，y随x的增大而减小；y最小值=0．a<0向下(h，0)X=h x>h时，y随x的增大而减小；x=h时，x<h时，y随x的增大而增大；y最大值=0．二、解读二次函数y=a(x-h)2（a≠0）（1）函数y=a(x-h)2（a，h是常数，a≠0）图像仍是一条抛物线，它的对称轴不再是y轴，而是直线x=h，顶点坐标是（h，0）（2）抛物线y=a(x-h)2（a，h是常数，a≠0）可看作是由抛物线y=ax2(a≠0)向左或向右平移∣h∣个单位而得到的。

当h＞0时，将抛物线y=ax2（a≠0）向右平移h个单位；当h＜0时，，将抛物线y=ax2（a≠0）向左平移∣h∣个单位；（3）实际上在a相等的情况下，二次函数y=a(x-h)2（a，h是常数，a≠0）的图像与二次函数y=ax2（a ≠0）的图像的形状、开口方向等完全相同，只不过位置发生了变化，顶点坐标由（0,0）变成了（h，0）；（4）将抛物线y=ax2（a≠0）平移到抛物线y=a(x-h)2（a，h是常数，a≠0），当h＞0,时，向右平移h个单位；当h＜0时，向左平移∣h∣个单位；（5）求抛物线y=a(x-h)2（a，h是常数，a≠0）的对称轴时，只需让括号中的x-h=0，得出x=h即可。

练习一、填空题1、抛物线y＝4(x－2)2与y轴的交点坐标是___________，与x轴的交点坐标为________．2、把抛物线y＝3x2向右平移4个单位后，得到的抛物线的表达式为____________．随意编辑113、将抛物线y＝－(x－4)2向______平移______个单位得到y＝－x2334、写出一个顶点是（5，0），形状、开口方向与抛物线y＝－2x2都相同的二次函数解析式___________________．5、二次函数y=x2-mx+1的图象的顶点在x轴上，则m的值是________．6、抛物线y＝m(x＋n)2向左平移2个单位后，得到的函数关系式是y＝－4(x－4)2，则m＝_____，n＝_____．原抛物线的对称轴是________，顶点坐标为________。

2.2 第3课时二次函数y=a(x-h)2的图象与性质1

2.2 二次函数的图象与性质第3课时二次函数y =a (x -h )2的图象与性质1．掌握二次函数y ＝ax 2与y ＝a (x －h )2(a ≠0)图象之间的联系；(重点)2．能灵活运用二次函数y ＝a (x －h )2(a ≠0)的知识解决简单的问题．(难点)一、情境导入二次函数y ＝ax 2＋c (a ≠0)的图象可以由y ＝ax 2(a ≠0)的图象平移得到：当c >0时，向上平移c 个单位长度；当c <0时，向下平移－c 个单位长度．问题：函数y ＝ (x －2)2的图象，能否也可以由函数y ＝ x 2平移得到？本节课我们就一起讨论．二、合作探究探究点：二次函数y ＝a (x －h )2的图象与性质【类型一】二次函数y ＝a (x －h )2的图象顶点为(－2，0)，开口方向、形状与函数y ＝－12x 2的图象相同的抛物线的解析式为( )A ．y ＝12(x －2)2B ．y ＝12(x ＋2)2C ．y ＝－12(x ＋2)2D ．y ＝－12(x －2)2解析：因为抛物线的顶点在x 轴上，所以可设该抛物线的解析式为y ＝a (x －h )2(a ≠0)，而二次函数y ＝a (x －h )2(a ≠0)与y ＝－12x 2的图象相同，所以a ＝－12，而抛物线的顶点为(－2，0)，所以h ＝2，把a ＝－12，h ＝2代入y ＝a (x －h )2得y ＝－12(x ＋2)2.故选C. 方法总结：决定抛物线形状的是二次项的系数，二次项系数相同的抛物线的形状完全相同．变式训练：见《学练优》本课时练习“课堂达标训练” 第5题【类型二】二次函数y ＝a(x －h )2的性质若抛物线y ＝3(x ＋2)2的图象上的三个点，A (－32，y 1)，B (－1，y 2)，C (0，y 3)，则y 1，y 2，y 3的大小关系为________________．解析：∵抛物线y ＝3(x ＋2)2的对称轴为x ＝－2，a ＝3＞0，∴x ＜－2时，y 随x 的增大而减小；x ＞－2时，y 随x 的增大而增大．∵点A 的坐标为(－32，y 1)，∴点A 在抛物线上的对称点A ′的坐标为(2，y 1)．∵－1＜0＜2，∴y 2＜y 3＜y 1.故答案为y 2＜y 3＜y 1.方法总结：函数图象上点的坐标满足解析式，即点在抛物线上．解决本题可采用代入求值方法，也可以利用二次函数的增减性解决．变式训练：见《学练优》本课时练习“课后巩固提升” 第4题【类型三】二次函数y ＝a (x －h )2的图象与y ＝ax 2的图象的关系将二次函数y ＝－2x 2的图象平移后，可得到二次函数y ＝－2(x ＋1)2的图象，平移的方法是( )A ．向上平移1个单位B ．向下平移1个单位C ．向左平移1个单位D ．向右平移1个单位解析：抛物线y ＝－2x 2的顶点坐标是(0，0)，抛物线y ＝－2(x ＋1)2的顶点坐标是(－1，0)．则由二次函数y ＝－2x 2的图象向左平移1个单位即可得到二次函数y ＝－2(x ＋1)2的图象．故选C.方法总结：解决本题要熟练掌握二次函数的平移规律．变式训练：见《学练优》本课时练习“课堂达标训练”第6题【类型四】二次函数y ＝a(x －h )2与三角形的综合如图，已知抛物线y ＝(x －2)2的顶点为C ，直线y ＝2x ＋4与抛物线交于A 、B 两点，试求S △ABC .解析：根据抛物线的解析式，易求得点C 的坐标；联立两函数的解析式，可求得A 、B 的坐标．画出草图后，发现△ABC 的面积无法直接求出，因此可将其转换为其他规则图形的面积求解．解：抛物线y ＝(x －2)2的顶点C 的坐标为(2，0)，联立两函数的解析式，得⎩⎪⎨⎪⎧y ＝2x ＋4，y ＝（x －2）2，解得⎩⎪⎨⎪⎧x 1＝0，y 1＝4，⎩⎪⎨⎪⎧x 2＝6，y 2＝16.所以点A的坐标为(6，16)，点B 的坐标为(0，4)．如图，过A 作AD ⊥x 轴，垂足为D ，则S △ABC ＝S梯形ABOD －S △ACD －S △BOC ＝12(OB ＋AD )·OD －12OC ·OB －12CD ·AD ＝12(4＋16)×6－12×2×4－12×4×16＝24.方法总结：解决本题要明确以下两点：(1)函数图象交点坐标为两函数解析式组成的方程组的解；(2)不规则图形的面积通常转化为规则图形的面积的和差．变式训练：见《学练优》本课时练习“课后巩固提升”第10题【类型五】二次函数y ＝a (x －h )2的探究性问题某抛物线是由抛物线y ＝－2x 2向左平移2个单位得到．(1)求抛物线的解析式，并画出此抛物线的大致图象；(2)设抛物线的顶点为A ，与y 轴的交点为B .①求线段AB 的长及直线AB 的解析式； ②在此抛物线的对称轴上是否存在点C ，使△ABC 为等腰三角形？若存在，求出这样的点C 的坐标；若不存在，请说明理由．解析：(1)抛物线y ＝－2x 2向左平移2个单位所得的抛物线的解析式是y ＝－2(x ＋2)2；(2)①根据(1)得出的抛物线的解析式，即可得出其顶点A 和B 点的坐标，然后根据A ，B 两点的坐标即可求出直线AB 的解析式；②本题要分三种情况进行讨论解答．解：(1)y ＝－2(x ＋2)2，图略；(2)①根据(1)得出的抛物线的解析式y ＝－2(x ＋2)2，可得A 点的坐标为(－2，0)，B 点的坐标为(0，－8)．因此在Rt △ABO 中，根据勾股定理可得AB ＝217.设直线AB 的解析式为y ＝kx －8，已知直线AB 过A 点，则有0＝－2k －8，k ＝－4，因此直线AB 的解析式为y ＝－4x －8；②本题要分三种情况进行讨论：当AB ＝AC 时，此时C 点的纵坐标的绝对值即为AB 的长，因此C 点的坐标为C 1(－2，217)，C 2(－2，－217)；当AB ＝BC 时，B 点位于AC 的垂直平分线上，所以C 点的纵坐标为B 点的纵坐标的2倍，因此C 点的坐标为C 3(－2，－16)；当AC ＝BC 时，此时C 为AB 垂直平分线与抛物线对称轴的交点．过B 作BD 垂直于抛物线的对称轴于D ，那么在直角三角形BDC 中，BD ＝2(A 点横坐标的绝对值)，CD ＝8－AC ，而BC ＝AC ，由此可根据勾股定理求出AC ＝174，因此这个C点的坐标为C 4(－2，174)．综上所述，存在四个点，C 1(－2，217)，C 2(－2，－217 )，C 3(－2，－16)，C 4(－2，－174)．方法总结：本题主要考查了二次函数图象的平移及等腰三角形的构成情况，主要涉及分类讨论、数形结合的数学思想方法的运用．变式训练：见《学练优》本课时练习“课后巩固提升”第10题三、板书设计二次函数y ＝a (x －h )2的图象与性质 1．二次函数y ＝a (x －h )2的图象与性质 2．二次函数y ＝a (x －h )2的图象与y ＝ax 2的图象的关系3．二次函数y ＝a (x －h)2的图象的应用本节课采用启发式、讨论式结合的教学方法，以问题的提出、问题的解决为主线，倡导学生主动参与教学实践活动，以独立思考和相互交流的形式，在教师的指导下发现、分析和解决问题，在引导分析时，给学生留出足够的思考时间和空间，让学生去联想、探索，从真正意义上完成对知识的自我建构. 另外，在教学过程中，采用多媒体辅助教学，直观呈现教学素材，从而更好地激发学生的学习兴趣，增大教学容量，提高教学效率.。

第4课时二次函数y=a(x-h)2的图象和性质

Page 12
的图象，
巩固提高
7.抛物线y=2x2﹣2 x+1与坐标轴的交点个数是（C ） A．0 B．1 C．2 D．3 8. 点P1（-1，y1），P2（3，y2），P3（5，y3）均在二次函数y=-（x+1）2的图象上，则y1，y2，y3 的大小关系是 y1＞y2＞y3 ．（用连“>”或“<” 表示）
Page 10
巩固提高
5.抛物线y=-2(x-1)2的顶点坐标和对称轴分别是 ( B) A．（-1，0），直线x=-1 B．(1，0)，直线x=1 C．(0，1)，直线x=-1 D．(0，1)，直线x=1
Page 11
巩固提高
6.关于函数下列说法正确的是 ( D ) A．顶点相同 B．顶点在直线y=-x上 C．最低点相同 D. 开口方向相同
Page 8
变式练习
3．抛物线y=m(x+n)2向左平移2个单位后，得到的函数关系式是y=-4(x-4)2，则m= -4 ，n= -6 .
Page 9
巩固提高
4. 将抛物线y=3x2向左平移2个单位，得到抛物线的解析式是 ( D ) A．y=3x2－2 B．y=3x2+2 C．y=3(x－2) 2 D．y=3(x+2) 2
4
．
（1）填空：抛物线的顶点坐标为（-1，0），对
称轴为直线x=-1 ，开口向下，在对称轴右侧，
y随x的增大而减小；在对称轴左侧，y随x的
增大而增大 .
Page 15
巩固提高
（2）画出函数图象. 列表：
x y
x −7 －5 −3 －1 1 3 5 y −9 －4 －1 0 1 －4 -9
第二十二章二次函数

22.1.3.2二次函数y=a(x-h)2的图像和性质.1.3.2二次函数y=a(x-h)2的图像和性质-----

板书设计：
教学反思：
重点：
难点：
重点：会用描点法画出二次函数y＝a(x－h)2的图象，理解二次函数y＝a(x－h)2的性质，理解二次函数y＝a(x－h)2的图象与二次函数y＝ax2的图象的关系是教学的重点。
难点：理解二次函数y＝a(x－h)2的性质，理解二次函数y＝a(x－h)2的图象与二次函数y＝ax2的图象的相互关系是教学的难点。
课题
22.1.3.1二次函数y=a（x-h）2
的图像和性质
课时
第四课时
主备教师
成员
教学目标
1．使学生能利用描点法画出二次函数y＝a(x—h)2的图象。
2．让学生经历二次函数y＝a(x－h)2性质探究的过程，理解函数y＝a(x－h)2的性质，理解二次函数y＝a(x－h)2的图象与二次函数y＝ax2的图象的关系。
问题7：在同一直角坐标系中，函数y＝－ (x＋2)2图象与函数y＝－ x 2的图象有何关系?
问题8：你能说出函数y＝－ (x＋2)2图象的开口方向、对称轴和顶点坐标吗?
问题9：你能得到函数y＝ (x＋2)2的性质吗?
四、课堂练习：P35练习。
五、小结：．谈谈本节课的收获和体会。
二次备课建议：
六、作业设置：同步学习32页4,5题
1．教师引导学生观察画出的两个函数图象．根据所画出的图象，完成以下填空：
开口方向
对称轴
顶点坐标
y＝2x2
y＝2(x－1)2
2．让学生分组讨论，交流合作，各组选派代表发表意见，达成共识：函数y＝2(x－1)2与y＝2x2的图象、开口方向相同、对称轴和顶点坐标不同；函数y＝2(x一1)2的图象可以看作是函数y＝2x2的图象向右平移1个单位得到的，它的对称轴是直线x＝数y＝2(x－1)2的性质吗?