一元二次方程根的判别式知识点
一元二次方程根的判别式

一元二次方程根的判别式一、重难点解析配方法解一元二次方程的一般形式导出公式法,分析判别式02=++c bx ax (0≠a )1.根的判别式(1) 当Δ=ac b 42->0时,原方程有两个不相等的实数根;(2) 当Δ=ac b 42-=0时,原方程有两个相等的实数根;(3) 当Δ=ac b 42-<0时,原方程没有实数根。
例:方程2210x x +-=的判别式等于8,故该方程有两个不相等的实数根;方程2230x x ++=的判别式等于-8,故该方程没有实数根。
二、典型题1.若关于x 的不等式12a x -<的解集为x <1,则关于x 的一元二次方程210x ax ++=根的情况是( ) A .有两个相等的实数根 B .有两个不相等的实数根C .无实数根D .无法确定 2.若关于x 的方程2230x x +-=与213x x a =+-有一个解相同,则a 的值为( ) A .1 B .1或﹣3C .﹣1D .﹣1或3 3.关于x 的一元二次方程()21320a x x -+-=有实数根,则a 的取值范围是( )A .18a >- B .18a ≥-C .18a >-且1a ≠D .18a ≥-且1a ≠ 4.关于x 的一元二次方程2(1)210m x x ---=有两个实数根,则实数m 的取值范围是( )A .m ≥0B .m >0C .m ≥0且m ≠1D .m >0且m ≠1 5.一元二次方程22(1)2(1)7x x +--=的根的情况是( )A .无实数根B .有一正根一负根C .有两个正根D .有两个负根6.关于x 的一元二次方程22(21)(1)0x k x k +-+-=无实数根,则k 的取值范围为 .7.关于x 的一元二次方程()23220x k x k -+++=.(1)求证:方程总有两个实数根;(2)若方程有一根小于1,求k 的取值范围.8.已知关于x 的一元二次方程0)(2)(2=-+++c a bx x c a ,其中c b a ,,分别为△ABC 三边的长。
一元二次方程的根的判别式

一元二次方程的根的判别式【学习目标】1.知道什么是一元二次方程的根的判别式.2.会用判别式判定根的情况.【主体知识归纳】1.一元二次方程的根的判别式:b2—4ac叫做一元二次方程ax2+bx+ c =0 (a^O)的根的判别式.通常用符号“△”来表示.2.对于一元二次方程ax2 + bx+ c= 0 (a z 0),当4> 0时,方程有两个不相等的实数根;当△ = 0时,方程有两个相等的实数根;当△< 0 时,方程没有实数根.反过来也成立.【基础知识讲解】1 .根的判别式是指△= b —4ac,而不是指△ =、、b2 4ac .2.根的判别式是在一元二次方程一般形式下得出的,因此,必须把所给的方程化为一般形式再判别根的情况.要注意方程中各项系数的符号.3.如果说一元二次方程有实根,那么应当包括有两个不相等的实数根和有两个相等的实数根两种情况,此时b2—4ac>0,不要丢掉等号.4.判别式有以下应用:(1)不解方程,判定一元二次方程根的情况;(2)根据一元二次方程根的情况,确定方程中未知系数的取值范围;(3)应用判别式进行有关的证明.例题精讲】例1 :不解方程,判别下列方程的根的情况:2(1)3x —2x —1 = 0;(2)y2= 2y—4;(3)(2k2+1) x2—2kx+1=0;( 4) 9x2—( p+7) x+p—3= 0.解:(1) •「△=( —2) —4 x 3x( —1 )= 4+ 12> 0,—原方程有两个不相等的实数根.(2)原方程就是 y —2y + 4 = 0.T △=( —2) —4x 1 x4 = 4 —16 v 0,二原方程无实数根.(3)v 2k2 + 1工0,二原方程为一元二次方程.又•/ △=( —2k) 2—4 (2k2 + 1)x 1 = —4k2—4v0,二原方程无实数根.(4)△=[—( p+ 7)]2—4x 9x( p—3)=( p—11) 2+ 36,v不论p取何实数,(p—11) 2均为非负数,•••(p—11)2 + 36>0, 即卩△ >0,•••原方程有两个不相等的实数根.说明:(1) 运用一元二次方程根的判别式判断方程根的情况时,要把不是一般形式的化为一般形式.(2)判别式的应用是以方程ax2 + bx+ c = 0中0为前提条件的,对于含字母系数的二次方程要特别注意这一点.⑶ 要判断含字母(代表实数)的二次式的正负等情况,配方是个有效的方法,如(4)小题.例2:已知关于x的一元二次方程(k —1)x2 + 2kx+ k + 3= 0. k取什么值时,(1)方程有两个不相等的实数根? (2)方程有两个相等的实数根? (3) 方程没有实数根?解:△= (2k)2—4 (k —1) (k+ 3)=—8k + 12.(1)当一8k + 12>0,且k —1工0, 即卩kv |且k工1时,方程有两个不相等的实数根;(2)当一8k + 12= 0,且k —1工0,即k= |时,方程有两个相等的实数根;(3)当一8k + 12v 0,且k —1工0,即k>1时,方程没有实数根.说明:当已知方程为一元二次方程时,要特别注意隐含的条件:二次项系数不等于零.例3:求证:不论a、b、c为何值,关于x的方程(b—x)2—4(a — x)( c —x) = 0必有实数根.剖析:此题考查运用一元二次方程根的判别式的能力,由于所给方程从形式上不能直接判断出方程的类型,因此应将方程进行整理,得-2 23x + (4 a + 4c —2b) x + b —4ac= 0,显然是关于x的一元二次方程,所以只要证明△》0即可.证明:略说明:判断一代数式的正、负时,通常的方法是将其进行恒等变形,配成完全平方式,再利用其非负性的特点进行证明.例4:如果关于x的方程x2 + 2x= 9没有实数根,试判断关于 y的方程y2+ my- 2n+ 5 = 0的根的情况.剖析:要判断y2 + my-2m+ 5= 0根的情况,只要判断△ 2= vm- 4(—2m+ 5) = m + 8m—20的取值情况即可.而x2 + 2x— m—9= 0没有实数根,可得△ i = 2—4( 一 m—9) = 4m+ 40v 0,即m v—10,而当n v—10时,吊+8m-20恒大于零,所以方程y2 + my—2m+ 5=0 有两个不等的实数根.说明:判定△的值用到了Z0所得的结论m v—10,这种条件和结论的相互转化在解综合性的题目中常常遇到.【同步达纲练习】1 .选择题(1)关于x的方程mf+ 4x + 1 = 0有两个不相等的实数根,则 m的取值范围是( )A.m v 4B. m K 4 且0C. mi> 4 且0D. m v 4 且0(2)关于 x 的方程 kx2+2x—1=0 无实数根,则 k 的取值范围是B. k v—1C. k K—1 ( )D. k=—1C. 1C.不论m 为何值,方程都没有实数根D.当一1v m< 1 A .无实数根 等的实数根C.有两个相等的实数根D .要根据a 、b 、 ⑶ 关于x 的一元二次方程(k — 1)x 2 + 2kx + k+ 3 = 0有两个不相等 的实数根,则k 的最大整数值是()A . 0B.— 1 D. 2 ⑷ 方程x 2+px+ q= 0有两个相等的实数根,则p 、q 之间的关系是 ()2 2A . p — 4q^0 B. p= 2、q C. p = 4qD. p 2> 4q(5) 关于x 的方程m i x 2 — 2mx^( mH 3)= 0的根的情况是()A .当m= 0时,方程有两个相等的实数根B .当m^ 0时,方程没有实数根时,方程有实数根(6) 设a 、b 、c 为三角形的三条边长,那么关于 x 的方程b 2x 2+(b 2+ c 2— a 2) x+c 2 = 0的根的情况是()B .有两个不相c的数值确定(7)已知a、b、c是厶ABC的三条边长,且关于x的方程(c— b) x2 + 2 (b— a) x+( a— b)= 0有两个相等的实数根,那么这个三角形是A.等边三角形B.等腰三角形C.不等边三角形D.直角三角形(8)已知方程x2— px+ vm= 0 (m存0)有两个相等的实数根,则方程 x2 + px— m=0的根的情况是()A.有两个不相等的实数根B.有两个相等的实数根C.没有实数根D.有无实数根,不能确定2.不解方程,判断下列方程根的情况:(1) y2—2y+ 1 = 0; (2) 4x2 + 5= 10x; ( 3) t2 = 7t - 15;(4) x2—2 .5 x = 3; 2(5) 0. 1x —0. 2x + 1 = 0; (6) 3x —(2 一 . 3 ) x + 1 = 0;3 .已知关于x的方程丄“- -(m—2) x + m= 0.4(1)有两个不相等的实数根,求 m的取值范围;(2)有两个相等的实数根,求 m的值,并求此时方程的根;(3)没有实数根,求m的最小整数值.2 2 24.求证:关于x的方程(a+ 1)x —2ax + (a+ 4) = 0没有实数根.5.已知关于x的方程x2—2mx- 3吊+ 8m—4= 0.(1)当m> 2时,试判断方程根的情况;(2)若方程的两个实数根一个小于5,另一个大于2,求m的取值范围.6.(1) k是什么正整数时,方程2x2—10x + 5k = 0有两个不相等的实数根?(2)k是什么负整数时,方程 x2—4x+ 2 — k = 0有两个不相等的实数根?(3)k是什么正数时,方程(2 + k) x2 + 6kx +4k+1 = 0有两个相等的实数根?7.已知△ ABC的三边分别是a、b、c,其中a、b的长是方程x2—4( .3 + 1)x + 16 .3 = 0的两个根,且a>b,关于x的一元二次方程a(1 — x2) + c(1 + x2) + 2bx= 0有两个相等的实数根,求△ ABC的三个内角的度数和三条边的长.。
一元二次方程根的判别式及根与系数的关系

一元二次方程根的判别式及根与系数的关系(一)一、知识归纳:1.一元二次方程ax 2+bx+c=0(a ≠0)的根的判别式是:△=b 2-4ac ,当△>0时;△=0;△<0时方程分别有两个不相等的实数根;有两个相等的实数根;没有实数根。
2.判别式“△”的应用:1)由“△”的符号判定方程根的情况;2)由“△”的符号,证明方程的根可能出现的情况;3)由方程的情况通过“△”的符号,确定方程中参数字母的取值范围。
例1. 关于x 的方程(m -1)x 2-2(m -3)x +m +2=0有实数根...,求m 的取值范围。
解:当m -1≠0时, 该方程为关于x 一元二次方程∵原方程有实数根 ∴0≥∆即Δ=[-2(m -3)]2-4(m -1)(m +2)=-28m +440≥即711≤m ,当m-1=0时,该方程变为4x+3=0,它是一元一次方程,有实数根34x =-练习:1.关于x 的方程m 2x 2+(2m+1)x+1=0有两个不相等的实数.........根.,求m 。
(注意二次项系数不为零)2.已知a ,b ,c 为一个三角形的三边,求证方程b 2x 2+(b 2+c 2-a 2)x+c 2=0无实数根。
3.已知方程x 2+2x=k-1没有实数根,求证方程x 2+kx=1-2k 必定有两个不相等的实数根。
4.已知x 1,x 2是关于x 的方程x 2+m 2x+n=0的两个实数根,y 1,y 2是关于y 的方程y 2+my+7=0两个实数根,且x 1-y 1=2, x 2-y 2=2,求m ,n 的值。
3.一般地,对于关于x 的一元二次方程ax 2+bx +c =0(a ≠0) 用求根公式求出它的两个根x 1、x 2 ,由一元二次方程ax 2+bx +c =0的求根公式知x 1=a ac b b 242-+-,x 2=aacb b 242---能得出以下结果:x 1+x 2= 即:两根之和等于x 1•x 2= 即:两根之积等于12x x +=a ac b b 242-+-+aacb b 242---=a acb b ac b b 24422----+- =12.x x =a ac b b 242-+-×aac b b 242---=2224)4)(4(a ac b b ac b b ----+- =2224)()(a -=由此得出,一元二次方程的根与系数之间存在得关系为 x 1+x 2=a b -, x 1x 2=ac 如果把方程ax 2+bx +c =0(a ≠0)的二次项系数化为1,则方程变形为 x 2+ x +ac=0(a ≠0), 则以x 1,x 2为根的一元二次方程(二次项系数为1)是: x 2-( )x +x 1x 2=0(a ≠0)3.一元二次方程ax 2+bx+c=0(a ≠0)的两根为x 1,x 2它的根与系数的关系是:例1:已知方程5x 2+k x -6=0的一个根为2,求它的另一个根及k 的值; 解:设方程的另一个根是x 1,那么5621-=x (为什么?)∴ x 1= 又x 1+2=5k-(为什么?)∴ k= 例2:利用根与系数的关系,求一元二次方程2x 2+3x -1=0的两个根的(1)平方和 (2)倒数和 解:设方程的两个根分别为x 1,x 2,那么x 1+x 2= , x 1x 2=(1)∵ (x 1+x 2)2= x 12+2 +x 22 ∴ x 12+x 22=(x 1+x 2)2-2 = (2)==+212111x x x x例3:求一个一元二次方程,使它的两个根是212313,- 解:所求的方程是x 2-(212313+-)x +( )212⋅=0 (为什么?) 即 x 2+ x- =0 或 6x 2+ x- =0。
一元二次方程根的判别式

17.3一元二次方程根的判别式【知识梳理】1.一元二次方程根的判别式我们把24b ac -叫做20(ax bx c a ++=≠0)的根的判别式,用符号∆来表示。
对于一元二次方程20(ax bx c a ++=≠0),其根的情况与判别式的关系是:当240b ac ∆=->时,方程有两个不相等的实数根;当240b ac ∆=-=时,方程有两个相等的实数根;当240b ac ∆=-<时,方程没有实数根.特别的:当240b ac ∆=-≥时,方程有两个实数根.上述判断反过来说,也是正确的。
即当方程有两个实数根时,240b ac ∆=->;当方程有两个相等的实数根时,240b ac ∆=-=;当方程没有实数根时,240b ac ∆=-<;2.一元二次方程的根的判别式的应用①不解方程判别方程根的情况,即先把方程化为一般形式,然后求出判别式24b ac ∆=-的值,最后根据∆的符号来确定根的情况;②根据一元二次方程根的情况确定方程中字母系数的取值范围,即先把方程化成一般形式并求出它的判别式,然后根据根的情况列出判别式的方程或不等式,最后解这个不等式或方程,但要去掉使方程二次项系数为零的字母的值。
若问题中没有这个限制条件,就要对二次项系数(含字母)是否为零进行讨论;③证明一元二次方程根的情况,可先把原方程化为一般形式,求出根的判别式,然后用配方法或因式分解法确定判别式的符号,并由此得出结论.3.利用根的判别式解题时的几点注意:①运用“∆”时必须把方程化为一般式;②不解方程判定方程的根的情况要由“∆”的符号判定;③运用判别式解题时,方程二次项系数一定不能为零;【典型例题】例1:不解方程,判别下列方程的根的情况(1)221150x x +-=(2)232x +=(3)(1)(2)8x x --=-【思路分析:一元二次方程根的情况是由根的判别式的符号决定的,所以在判别方程的根的情况时,要先把方程化为一般式,写出方程的a b c 、、,计算出∆的值,判断∆的符号】【答案:(1)221150x x +-=2,11,5a b c ===- 2241142(5)121401610b ac ∴∆=-=-⨯⨯-=+=>即∆>0∴方程有两个不相等的实数根.(2)232x +=将方程整理为一般式:2320x -+=3,2a b c ==-=224(4320b ac ∆=-=--⨯⨯=即0∆=∴方程有两个相等的实数根.(3)(1)(2)8x x --=-将方程化为一般式:23280x x -++=1,3,10a b c ==-=224(3)4110940310b ac ∆=-=--⨯⨯=-=-<即0∆<∴方程没有实数根】【小结:运用根的判别式判断方程的根的情况时,必须把方程化为一般式,然后正确地确定各项系数,再代入判别式进行计算,得出判别式的符号】课堂练习1:如果关于x 的一元二次方程22(21)10k x k x -++=有两个不相等的实数根,那么k 的取值范围是()A .k >14-B .k >14-且0k ≠C .k <14-D .14k ≥-且0k ≠课堂练习2:如果关于x 的方程:2320x x k -+=有实数根,那么k 的取值范围是_____.例2:求证方程2(1)310(0)m x mx m m -+++=≠必有两个不相等的实数根.【思路分析:欲证明此方程必有两个不相等的实数根,只需要证明不论m 取任何实数,都有0∆>即可】【答案:1m ≠ 10m ∴-≠∴此方程是关于x 的一元二次方程2222(3)4(1)(1)94454m m m m m m ∆=--+=-+=+ 不论m 取任何不为1的值时都有25m ≥024m ∴5+>0即2540m ∆=+>∴方程必有两个不相等的实根】【小结:证明时应先说明二次项系数不为零,也即保证方程是一元二次方程的前提下判别式的符号才有意义】课堂练习3:关于x 的方程220x kx k -+-=的根的情况是()A .有两个不相等的实数根B .有两个相等的实数根C .无实数根D .不能确定例3:当m 为何值时,关于x 的方程222(41)210x m m -++-=(1)有两个不相等的实根?(2)有两个相等的实根?(3)无实数根?【思路分析:根据一元二次方程根的情况,确定方程中字母系数的取值范围,是一元二次方程的根本判别式的另一类典型运用。
一元二次方程的根的判别式

一元二次方程的根的判别式Ting Bao was revised on January 6, 20021一元二次方程的根的判别式学习指导一、基本知识点:1.根的判别式:对于任何一个一元二次方程ax2+bx+c=0(a≠0)可以用配方法将其变形为:(x+)2=因为a≠0,所以4a2>0,这样一元二次方程ax2+bx+c=0的根的情况可由b2-4ac来判定。
我们把b2-4ac叫做一元二次方程ax2+bx+c=0的根的判别式,用希腊字母⊿来表示,即⊿=b2-4ac。
一元二次方程ax2+bx+c=0(a≠0),当⊿=b2-4ac>0时,有两个不相等的实数根;当⊿=b2-4ac=0时,有两个相等的实数根;当⊿=b2-4ac<0时,没有实数根。
上述性质反过来也成立。
2.判别式的应用(1)不解方程,判断方程的根的情况;(2)根据方程的根情况确定方程的待定系数的取值范围;(3)证明方程的根的性质;(4)运用于解综合题。
二、重点与难点一元二次方程的根的判别式的性质是初中数学中的一个重要内容,在高中数学中也有重要应用。
正确理解判别式的性质,熟练灵活地运用它,是本节的重点,同时也是难点。
三、例题解析例1不解方程,判断下列方程根的情况(1)2x2-5x+10=0(2)16x2-8x+3=0(3)(-)x2-x+=0(4)x2-2kx+4(k-1)=0(k为常数)(5)2x2-(4m-1)x+(m-1)=0(m为常数)(6)4x2+2nx+(n2-2n+5)=0(n为常数)解:(1)⊿=(-5)2-4×2×10=-55<0∴方程没有实数根(2)⊿=(-8)2-4×16×3=0∴方程有两个相等的实数根(3)⊿=(-)2-4(-)×=5-4+8>0∴方程有两个不相等实根(4)⊿=(-2k)2-4×1×4(k-1)=4k2-16k+16=4(k2-4k+4)=4(k-2)2≥0∴方程有实数根(5)⊿=〔-(4m-1)〕2-4×2×(m-1)=16m2-8m+1-8m+8=16m2-16m+9=4(2m-1)2+5>0∴方程有两个不相等实根(6)⊿=(2n)2-4×4(n2-2n+5)=4n2-16n2+32n-80=-12n2+32n-80=-12(n-)2-<0∴方程没有实数根说明:①解这类题目时,一般要先求出⊿=b2-4ac,然后对⊿=b2-4ac进行化简或变形,使⊿=b2-4ac的符号明朗化,进而说明⊿=b2-4ac的符号情况,得出结论。
中考数学知识点:一元二次方程根的判别式

中考数学知识点:一元二次方程根的判别式 新一轮的中考已经逐步进入复习中,小编为大家整理了一元二次方程根的判别式,让我们一起学习,一起进步吧!一元二次方程根的判别式1. 根的判别式念在一元二次方程ax2+bx+c=0(a≠0)中,代数b2-4ac起着重要的作用,我们把它叫做根的判别式,通常用记号△表示,即△=b2-4ac (注意不是△=)2. 根的判别式的应用(实际上就是定理)用三个定理来表示(我们通常把记号AB表示为A是命题的条件,B是命题的结论)于是有:定理1 ax2+bx+c=0(a≠0)中,△>0方程有两个不等实数根定理2 ax2+bx+c=0(a≠0)中,△=0方程有两个相等实数根定理3 ax2+bx+c=0(a≠0)中,△方程没有实数根注意:根据课本P27第8行的〝反过来也成立〞,得另三个定理,那就是定理4 ax2+bx+c=0(a≠0)中,方程有两个不等实数根△>0定理5 ax2+bx+c=0(a≠0)中,方程有两个相等实数根△=0定理6 ax2+bx+c=0(a≠0)中,方程没有实数根△(【答案】或提示:1.k>-1且k≠0; 2.无实数根)3.以下方程中,有两个相等实数根的方程是( )(A)7x2-x-1=0 (B)9x2=4(3x-1)(C)x2+7x+15=0 (D)#FormatImgID_1#x2-#FormatImgID_2#x+1=04.假设方程(k2-1)x2-6(3k-1)x+72=0 有两个不同的正整数根,那么整数k的值是( )。
5.假设a,b,c互不相等,那么方程(a2+b2+c2)x2+2(a+b+c)x+3=0( )(A)有两个相等的实数根 (B)有两个不相等的实数根(C)没有实数根 (D)根的情况不确定6.不解方程,判别以下方程的根的情况:(1)2x2+4x+35=0; (2)4m(m-1)+1=0; (3)0.2x2-5=#FormatImgID_3#x;(4)4(y2+0.09)=2.4y; (5) #FormatImgID_4#x2-#FormatImgID_5#=#FormatImgID_6#x;(6)2t=#FormatImgID_7#(t2+#FormatImgID_8#)7.关于x的方程x2+(2m+1)x+(m-2)2=0. m取什么值时,(1)方程有两个不相等的实数根? (2)方程有两个相等的实数根?(3)方程没有实数根?7.K取什么值时,方程4x2-(k+2)x+k-1=0有两个相等的实数根?并求出这时方程的根。
一元二次方程根的判别式及根与系数的关系—知识讲解(基础)

一元二次方程根的判别式及根与系数的关系—知识讲解(基础)责编:常春芳【学习目标】1. 会用一元二次方程根的判别式判别方程根的情况,由方程根的情况能确定方程中待定系数的取值范围;2. 掌握一元二次方程的根与系数的关系以及在各类问题中的运用.【要点梳理】知识点一、一元二次方程根的判别式1.一元二次方程根的判别式一元二次方程)0(02≠=++a c bx ax 中,ac b42-叫做一元二次方程)0(02≠=++a c bx ax 的根的判别式,通常用“∆”来表示,即ac b 42-=∆(1)当△>0时,一元二次方程有2个不相等的实数根;(2)当△=0时,一元二次方程有2个相等的实数根;(3)当△<0时,一元二次方程没有实数根.要点诠释:利用根的判别式判定一元二次方程根的情况的步骤:①把一元二次方程化为一般形式;②确定c b a .,的值;③计算ac b 42-的值;④根据ac b 42-的符号判定方程根的情况.2. 一元二次方程根的判别式的逆用在方程()002≠=++a c bx ax 中, (1)方程有两个不相等的实数根⇒ac b 42-﹥0; (2)方程有两个相等的实数根⇒ac b 42-=0; (3)方程没有实数根⇒ac b 42-﹤0.要点诠释: (1)逆用一元二次方程根的判别式求未知数的值或取值范围,但不能忽略二次项系数不为0这一条件;(2)若一元二次方程有两个实数根则 ac b 42-≥0.知识点二、一元二次方程的根与系数的关系1.一元二次方程的根与系数的关系如果一元二次方程)0(02≠=++a c bx ax 的两个实数根是21x x ,, 那么a b x x -=+21,ac x x =21. 注意它的使用条件为a ≠0, Δ≥0.也就是说,对于任何一个有实数根的一元二次方程,两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商.2.一元二次方程的根与系数的关系的应用(1)验根.不解方程,利用根与系数的关系可以检验两个数是不是一元二次方程的两个根;(2)已知方程的一个根,求方程的另一根及未知系数;(3)不解方程,可以利用根与系数的关系求关于x 1、x 2的对称式的值.此时,常常涉及代数式的一些重要变形;如:①222121212()2x x x x x x +=+-; ②12121211x x x x x x ++=; ③2212121212()x x x x x x x x +=+; ④2221121212x x x x x x x x ++=2121212()2x x x x x x +-=; ⑤22121212()()4x x x x x x -=+-;⑥12()()x k x k ++21212()x x k x x k =+++;⑦12||x x -== ⑧22212121222222121212()211()x x x x x x x x x x x x ++-+==;⑨12x x -==⑩12||||x x +===(4)已知方程的两根,求作一个一元二次方程;以两个数为根的一元二次方程是.(5)已知一元二次方程两根满足某种关系,确定方程中字母系数的值或取值范围;(6)利用一元二次方程根与系数的关系可以进一步讨论根的符号.设一元二次方程20(0)ax bx c a ++=≠的两根为1x 、2x ,则①当△≥0且120x x >时,两根同号.当△≥0且120x x >,120x x +>时,两根同为正数;当△≥0且120x x >,120x x +<时,两根同为负数.②当△>0且120x x <时,两根异号.当△>0且120x x <,120x x +>时,两根异号且正根的绝对值较大;当△>0且120x x <,120x x +<时,两根异号且负根的绝对值较大.要点诠释:(1)利用根与系数的关系求出一元二次方程中待定系数后,一定要验证方程的∆.一些考试中,往往利用这一点设置陷阱;(2)若有理系数一元二次方程有一根a +a a ,b 为有理数).【典型例题】类型一、一元二次方程根的判别式的应用1.不解方程,判断下列方程的根的情况:(1)???2x 2+3x-4=0 (2)ax 2+bx=0(a≠0)【答案与解析】(1) 2x 2+3x-4=0a=2, b=3, c=-4,? ∵Δ=b 2-4ac=32-4×2×(-4)=41>0? ∴方程有两个不相等的实数根.(2)∵a≠0, ∴方程是一元二次方程,此方程是缺少常数项的不完全的一元二次方程,将常数项视为零,? ∵Δ=b 2-4·a·0=b 2,? ∵无论b 取任何关数,b 2均为非负数,∴Δ≥0, 故方程有两个实数根.【总结升华】根据ac b42-的符号判定方程根的情况. 举一反三:【高清ID 号:388522 关联的位置名称(播放点名称):判别含字母系数的方程根的情况---例2(1)】【变式】不解方程,判别方程根的情况:2210x ax a -++= .【答案】无实根.2.(2015?本溪)关于x 的一元二次方程(k ﹣1)x 2﹣2x+1=0有两个不相等的实数根,则实数k 的取值范围是 .【思路点拨】此题要考虑两方面:判别式要大于0,二次项系数不等于0.【答案】k <2且k≠1; 【解析】解:∵关于x 的一元二次方程(k ﹣1)x 2﹣2x+1=0有两个不相等的实数根,∴k ﹣1≠0且△=(﹣2)2﹣4(k ﹣1)>0,解得:k <2且k ≠1.故答案为:k <2且k≠1.【总结升华】不能忽略二次项系数不为0这一条件.举一反三:【高清ID 号:388522 关联的位置名称(播放点名称):证明根的情况---例3】 【变式】m 为任意实数,试说明关于x 的方程x 2-(m-1)x-3(m+3)= 0恒有两个不相等的实数根.【答案】∵Δ=[-(m-1)]2-4×[-3(m+3)]=m 2+10m+37=(m+5)2+12>0,∴关于x 的方程x 2-(m-1)x-3(m+3)= 0恒有两个不相等的实数根. 类型二、一元二次方程的根与系数的关系的应用3.已知方程2560x kx +-=的一个根是2,求另一个根及k 的值.【思路点拨】根据方程解的意义,将x =2代入原方程,可求k 的值,再由根与系数的关系求出方程的另外一个根.【答案与解析】方法一:设方程另外一个根为x 1,则由一元二次方程根与系数的关系, 得125k x +=-,1625x =-,从而解得:135x =-,k =-7. 方法二:将x =2代入方程,得5×22+2k -6=0,从而k =-7. 设另外一根为x 1,则由一元二次方程根与系数的关系,得1725x +=,从而135x =-, 故方程的另一根为35-,k 的值为-7. 【总结升华】根据一元二次方程根与系数的关系12b x x a +=-,12c x x a=易得另一根及k 的值. 举一反三:【高清课堂:一元二次方程根的判别式及根与系数的关系(二)---例2】【变式】已知方程220x x c -+=的一个根是3,求它的另一根及c 的值.【答案】另一根为-1;c 的值为-3.4.(2015?咸宁)已知关于x 的一元二次方程mx 2﹣(m+2)x+2=0.(1)证明:不论m 为何值时,方程总有实数根;(2)m 为何整数时,方程有两个不相等的正整数根.【答案与解析】解:(1)△=(m+2)2﹣8m=m2﹣4m+4=(m﹣2)2,∵不论m为何值时,(m﹣2)2≥0,∴△≥0,∴方程总有实数根;(2)解方程得,x=,x1=2m,x2=1,∵方程有两个不相等的正整数根,∴m=1或2,m=2不合题意,∴m=1.【总结升华】本题考查的是一元二次方程根的判别式和求根公式的应用,此外要掌握整数根的意义及正确求解适合条件的整数根.。
4一元二次方程的根的判别式及根与系数的关系(名师总结)

一元二次方程的根的判别式及根与系数的关系【知识点1】一元二次方程的根的判别式概念:一元二次方程ax 2+bx +c=0 (a ≠0)的根的判别式为b 2-4ac ,通常用符号“△”来表示。
即△=b 2-4ac 一元二次方程ax 2+bx +c=0 (a ≠0)的根的情况是:①当△>0时,有两个不相等的实数根。
②当△=0时,有两个相等的实数根。
③当△<0时,没有实数根 ✪注:当△≧0时,方程有实数根。
【例1】已知a 、b 、c 分别是三角形的三边,则方程(a + b )x 2+ 2cx + (a + b )=0的根的情况是( ) A . 没有实数根B .可能有且只有一个实数根C .有两个相等的实数根D .有两个不相等的实数根【例2】如果关于x 的一元二次方程有两个不相等的实数根,那么的取值范围是( )A.>B >且C.<D.且【例3】已知关于的一元二次方程有两个不相同的实数根,则的取值范围是【例4】.已知关于x 的二次方程012)21(2=---x k x k 有实数根,则k 的取值范围是 。
【例5】已知a b ,是关于x 的方程2(21)(1)0x k x k k -+++=的两个实数根,则22a b +的最小值是【例6】关于x 的一元二次方程04)(2=-+++ca bx xb a 有两个相等的实数根,那么以a 、b 、c 为三边的三角形是 A 、以a 为斜边的直角三角形 B 、以c 为斜边的直角三角形 C 、以b 为底边的等腰三角形D 、以c 为底边的等腰三角形 【知识点2】一元二次方程根于系数的关系概念:若一元二次方程)0(02≠=++a c bx ax 有两个实数根21x x 和,那么=+21x x ,=∙21x x 。
这两个结论称为一元二次方程根与系数的关系,简称韦达定理。
【例1】在一元二次方程)0(02≠=++a c bx ax 中,有一根为0,则=c ;有一根为1,则=++c b a ;有一根为1-,则=+-c b a ;若两根互为倒数,则=c ;若两根互为相反数,则=b 。
一元二次方程的判别式及跟与系数的关系

一元二次方程的根的判别式及根与系数的关系要点一、一元二次方程的判别式1.定义:在一元二次方程()ax bx c a 2++=0≠0中,只有当系数a 、b 、c 满足条件△≥b ac 2=−40时才有实数根.这里b ac 2−4叫做一元二次方程根的判别式,记作△.2.判别式与根的关系:在实数范围内,一元二次方程()ax bx c a 2++=0≠0的根的情况由△b ac 2=−4确定. 设一元二次方程为()ax bx c a 2++=0≠0,其根的判别式为:△b ac 2=−4,则①△>0⇔方程()ax bx c a 2++=0≠0有两个不相等的实数根,x 12.②△=0⇔方程()ax bx c a 2++=0≠0有两个相等的实数根b x x a12==−2. ③△<0⇔方程()ax bx c a 2++=0≠0没有实数根. 特殊的:(1)若a ,b ,c 为有理数,且△为完全平方式,则方程的解为有理根;(2)若△为完全平方式,同时b −±2a 的整数倍,则方程的根为整数根.【例1】(1)不解方程,直接判断下列方程的解的情况: ①x x 27−−1=0 ②()x x 29=43−1 ③x x 2+7+15=0④()mx m x 2−+1+=02(m 为常数)(2)已知a 、b 、c 分别是三角形的三边,则方程()()a b x cx a b 2++2++=0的根的情况是( ) A .没有实数根B .可能有且只有一个实数根C .有两个相等的实数根D .有两个不相等的实数根【解析】(1)①△>0,有两个不等实根;②△=0,有两个相等实根; ③△<0,无实根;④△m 2=+1>0,方程有两个不等实根. (2)由题()()()()△c a b a b c c a b 22=2−4+=4++−−∵a b c ++>0,c a b −−<0,故方程没有实根.选A .【点评】这道题(1)主要考察判别式与根的关系,属于特别基础的题,锻炼孩子们的思维,(2)结合三角形三边关系来考察一元二次方程的判别式和根的个数的关系.【例2】(1)若关于x 的一元二次方程()k x x 21−1+−=04有实根,则k 的取值范围为______. 【解析】(1)≥k 0且≠k 1;【变式2-1】若关于x 的一元二次方程kx 2﹣4x+3=0有实数根,则k 的非负整数值是( ) A. 1 B. 0,1 C. 1,2 D. 1,2,3【答案】A.提示:根据题意得:△=16﹣12k≥0,且k≠0,解得:k≤,且k≠0. 则k 的非负整数值为1.【变式2-2】已知关于x 的一元二次方程有实数根,则m 的取值范围是________ 【答案】且m≠1 【解析】因为方程有实数根,所以,解得, 同时要特别注意一元二次方程的二次项系数不为0,即, ∴ m 的取值范围是且m≠1. 【总结升华】注意一元二次方程的二次项系数不为0,即,m≠1.【例3】已知:关于x 的方程有两个不相等的实数根,求k 的取值范围. 【答案】.【变式3-1】关于x的一元二次方程()k x 21−2−−1=0有两个不相等的实数根,则k 的取值范围______.≤k −1<2且k 1≠2, 由题意,得()()k k k k 4+1+41−2>0⎧⎪+1≥0⎨⎪1−2≠0⎩,解得≤k −1<2且k 1≠2;2(1)10m x x −++=54m ≤2(1)10m x x −++=214(1)450m m =−−=−+≥△54m ≤(1)0m −≠54m ≤(1)0m −≠2(1)04kkx k x +++=102k k ≠>-且【变式3-2】已知关于x 的方程x 2+2x+a ﹣2=0.(1)若该方程有两个不相等的实数根,求实数a 的取值范围; (2)当该方程的一个根为1时,求a 的值及方程的另一根. 【思路点拨】(1已知方程有两个不相等的实数根,即判别式△=b 2﹣4ac >0.即可得到关于a 的不等式,从而求得a 的范围.(2)设方程的另一根为x 1,根据根与系数的关系列出方程组,求出a 的值和方程的另一根. 【答案与解析】解:(1)∵b 2﹣4ac=(﹣2)2﹣4×1×(a ﹣2)=12﹣4a >0,解得:a <3.∴a 的取值范围是a <3;(2)设方程的另一根为x 1,由根与系数的关系得:,解得:,则a 的值是﹣1,该方程的另一根为﹣3.【变式3-2】关于x 的一元二次方程(k ﹣1)x 2﹣2x+1=0有两个不相等的实数根,则实数k 的取值范围是 .【思路点拨】此题要考虑两方面:判别式要大于0,二次项系数不等于0. 【答案】k <2且k≠1;【解析】解:∵关于x 的一元二次方程(k ﹣1)x 2﹣2x+1=0有两个不相等的实数根, ∴k ﹣1≠0且△=(﹣2)2﹣4(k ﹣1)>0, 解得:k <2且k≠1. 故答案为:k <2且k≠1.【总结升华】不能忽略二次项系数不为0这一条件.【例4】当a 、b 为何值时,方程()x a x a ab b 222+21++3+4+4+2=0有实根?(3)要使关于x 的一元二次方程()x a x a ab b 222+21++3+4+4+2=0有实根,则必有△≥0,即()()≥a a ab b 22241+−43+4+4+20,得()()a b a 22+2+−1≤0.又因为()()a b a 22+2+−1≥0,所以()()a b a 22+2+−1=0,得a =1,b 1=−2.【变式4-1】已知关于x 的一元二次方程()a x ax 213−1−+=04有两个相等的实数根,求代数式a a a21−2+1+的值.【解析】由题,一元二次方程()a x ax 213−1−+=04有两个相等的实数根, 所以a a 2−3+1=0.所以有a a a 2−2+1=,a a 2+1=3.代入a a a21−2+1+,得a a a a a a a a a 2211+13−2+1+=+===3.【点评】这道题主要是考察判别式与代数式的结合,难度不大.【变式4-2】m 为任意实数,试说明关于x 的方程x 2-(m-1)x-3(m+3)= 0恒有两个不相等的实数根. 【答案】∵Δ=[-(m-1)]2-4×[-3(m+3)]=m 2+10m+37=(m+5)2+12>0,∴关于x 的方程x 2-(m-1)x-3(m+3)= 0恒有两个不相等的实数根.【例5】在等腰△ABC 中,A ∠、B ∠、C ∠的对边分别为a 、b 、c ,已知a =3,b 和c 是关于x 的方程x mx m 21++2−=02的两个实数根,求△ABC 的周长.【解析】当b c =时,方程有两个相等的实数根,则=△m m 21⎛⎫−42−=0 ⎪2⎝⎭,∴m 1=−4,m 2=2.若m =−4,原方程化为x x 2−4+4=0, 则x x 12==2,即b c ==2, ∴△ABC 的周长为2+2+3=7. 若m =2,原方程化为x x 2+2+1=0, 则x x 12==−1,不合题意.当a b =或a c =时,x =3是方程的一个根, 则m m 19+3+2−=02,则m 22=−5,原方程化为x x 22221−+=055,解得x 1=3,x 27=5, ∴ABC △的周长为7373+3+=55.综上所述,ABC △的周长为7或375. 【点评】这道题主要考察学生们的分类讨论能力,应对多种情况是要理清思路.要点二、一元二次方程的根与系数关系(韦达定理)1.韦达定理:如果()ax bx c a 2++=0≠0的两根是x 1,x 2,则b x x a 12+=−,cx x a12=.(使用前提:△≥0)特别地,当一元二次方程的二次项系数为1时,设x 1,x 2是方程x px q 2++=0的两个根,则x x p 12+=−,x x q 12=. 2.韦达定理的逆定理:如果有两个数x 1,x 2满足b x x a 12+=−,cx x a12=,那么x 1,x 2必定是()ax bx c a 2++=0≠0的两个根.特别地,以两个数x 1、x 2为根的一元二次方程(二次项系数为1)是()x x x x x x 21212−++=0. 3.韦达定理与根的符号关系:在△≥b ac 2=−40的条件下,我们有如下结论: (1)当ca<0时,方程的两根必一正一负. ①若≥b a −0,则此方程的正根不小于负根的绝对值;②若ba−<0,则此方程的正根小于负根的绝对值.(2)当ca>0时,方程的两根同正或同负. ①若b a −>0,则此方程的两根均为正根;②若ba−<0,则此方程的两根均为负根.注意:(1)若ac <0,则方程()ax bx c a 2++=0≠0必有实数根.(2)若ac >0,方程()ax bx c a 2++=0≠0不一定有实数根.【例6】(1)已知一元二次方程ax ax c 2+2+=0的一根x 1=2,则方程的另一根______x 2=.(2)已知x 1,x 2是方程x x 2−3+1=0的两个实数根,则:①x x 2212+;②()()x x 12−2⋅−2;③x x x x 221122+⋅+;④x x x x 2112+;⑤x x 12−;⑥x x 2212−;⑦x x 1211−.【解析】(1)−4;(2)()x x x x x x 2222121212+=+−2⋅=3−2⨯1=7, ()()()x x x x x x 121212−2⋅−2=⋅−2++4=1−2⨯3+4=−1, ()x x x x x x x x 22211221212+⋅+=+−⋅=9−1=8,x x x x x x x x 2221211212+7+===7⋅1,()()x x x x x x 222121212−=+−4⋅=3−4⨯1=5,∴x x 12−=,∴()()(x x x x x x 22121212−=+−=3⨯=x x x x x x 21121211−−==.【点评】第三小题,主要是考察韦达定理的灵活运用,包含了各种变形情况.【例7】(1)已知关于x 的方程()x k x k 22+2−3+−3=0有两个实数根x 1,x 2,且x x x x 121211+=+,求k 值.(2)已知x 1,x 2是方程ax ax a 24−4++4=0的两实根,是否能适当选取a 的值,使得()()x x x x 1221−2−2的值等于54.【解析】(1)∵方程()x k x k 22+2−3+−3=0有两个实数根x 1,x 2,∴()()△≥k k k 22=2−3−4−3=21−120得:≤k 74. 由韦达定理得,()x x k x x k 12212+=−2−3⎧⎪⎨⋅=−3⎪⎩. ∵x x x x 121211+=+,∴x xx x x x 121212++=,x x 12+=0或x x 12=1,当x x 12+=0时,k 3−2=0,k 3=2,∵k 37=<24,所以k 3=2符合题意. 当x x 12=1时,k 2−3=1,k =±2,∵k 7≤4,∴k =2舍去.∴k 的值为32或−2. (2)显然a ≠0由()△a a a 2=16−16+4≥0得a <0, 由韦达定理知x x 12+=1,a x x a12+4=4, 所以()()()()()a x x x x x x x x x x x x a 2221221121212129+4−2−2=5−2+=9−2+=−24a a+36=4 若有()(),x x x x 12215−2−2=4则a a +365=44,∴a =9,这与0a <矛盾, 故不存在a ,使()()x x x x 12215−2⋅−2=4. 【点评】这道题主要锻炼孩子们的过程,以及有两个实根,解出来别忘了限制条件,这种类型的题比较常见,一定不要忽视∆的限定条件以及用韦达定理可得到的限定条件.【例8】(1)若m ,n 是方程x x 2+−1=0的两个实数根,则m m n 2+2+−1的值为________.(2)已知a ,b 是方程x x 2+2−5=0的两个实数根,则a ab a b 2−+3+的值为__________.(3)已知m 、n 是方程x x 2+2016+7=0的两个根,则()()m m n n 22+2015+6+2017+8= ________.【解析】(1)∵m ,n 是方程x x 2+−1=0的两个实数根,∴m n +=−1,m m 2+−1=0,则原式()()m m m n 2=+−1++=−1=−1,(2)∵a 是方程x x 2+2−5=0的实数根,∴a a 2+2−5=0,∴a a 2=5−2,∴a ab a b a ab a b a b ab 2−+3+=5−2−+3+=+−+5, ∵a ,b 是方程x x 2+2−5=0的两个实数根,∴a b +=−2,ab =−5,∴a ab a b 2−+3+=−2+5+5=8. 故答案为8.(3)∵m 、n 是方程x x 2+2016+7=0的两个根,∴m n +=−2016,mn =7;∴m m 2+2016+7=0,n n 2+2016+7=0,()()()()m m n n m m m n n n 2222+2015+6+2017+8=+2016+7−−1+2016+7++1()()()()m n mn m n =−+1+1=−+++1=−7−2016+1=2008故答案是:2008.【点评】这道题主要考查韦达定理根系关系的应用,进一步强化孩子对于韦达定理应用的理解.【例9】(1)已知一元二次方程()ax a x a 2+3−2+−1=0的两根都是负数,则k 的取值范围是_________.(2)已知二次方程342x x k 2−+−=0的两根都是非负数,则k 的取值范围是__________.【解析】(1)此方程两实根为,x x 12,由已知得a x x x x 1212≠0⎧⎪∆0⎪⎨+<0⎪⎪>0⎩≥,∴()()a a a a a a a a2≠0⎧⎪3−24−10⎪⎪2−3⎨<0⎪⎪−1⎪>0⎩-≥g ,即a 91<8≤.(2)此方程两实根为,x x 12,由已知得≥x x x x 1212∆≥0⎧⎪+≥0⎨⎪0⎩,得:∴2()43()k k ⎧⎪−4−⨯−2≥0⎪4⎪>0⎨3⎪−2⎪≥0⎪3⎩即k 102≤≤3. 【点评】这道题主要考查韦达定理和判别式结合不等式组的形式去判定根的具体情况,这类题是比较常见一类题,要将这种不等的思想传授给孩子.【课后作业】1.已知关于x 的一元二次方程()()k x k x 22−1+2+1+1=0有两个不相等的实数根,则k 的取值范围为_____________. A .k 1≥4 B .k 1>4且≠k 1 C .k 1<4且≠k 1 D .k 1≥4且≠k 1【解析】B .2.已知关于x 的一元二次方程x m 2−=0有两个不相等的实数根,则m 的取值范围__________.3.关于x 的方程()()m x m x 22−4+2+1+1=0有实根,则m 的取值范围__________.【解析】2.由题意可知,原方程的判别式(m m m 21∆=+4=1+3>0⇒>−3.又≥≤m m 1−0⇒1, 故≤m 1−<13.3.题设中的方程未指明是一元二次方程,还是一元一次方程,所以应分0m 2−4=和m 2−4≠0,两种情形讨论:当m 2−4=0即m =±2时,()m 2+1≠0,方程为一元一次方程,总有实根; 当m 2−4≠0即m ≠±2时,方程有根的条件是: [()]()≥m m m 22=2+1−4−4=8+20∆0,解得m 5≥−2.∴当m 5≥−2且m ≠±2时,方程有实根.综上所述:当m 5≥−2时,方程有实根.4.已知关于x 的方程()x k x k 2−+1+2−2=0. (1)求证:无论k 为何值,方程总有实根;(2)若等腰ABC △,底边a =3,另两边b 、c 恰好是此方程的两根,求ABC △的周长.【解析】(1)()()()≥△k k k 22=+1−42−2=−30,∴无论k 为何值,方程总有实根.(2)当a =3为底,b ,c 为腰时,b c =,∴方程有两个相等的实根,∴∆=0,即()k 2−3=0,k =3,此时方程为x x 2−4+4=0,解x x 12==2,∴ABC △的周长为3+2+2=7,当a =3为腰,则方程有一根为3,将x =3代入方程,得k =4,方程为x x 2−5+6=0,解得x 1=2,x 2=3,∴ABC △的周长为2+3+3=8,综上所述,ABC △的周长为7或8.5.关于x 的方程x kx 22+=10的一个根是−2,则方程的另一根是_______;k =________.6.已知a ,b ,c 为正数,若二次方程ax bx c 2++=0有两个实数根,那么方程a x b x c 2222++=0的根的情况是( ) A .有两个不相等的正实数根 B .有两个异号的实数根 C .有两个不相等的负实数根D .不一定有实数根7.设α,β是一元二次方程x x 2+3−7=0的两个根,则ααβ2+4+=________.【解析】5.设另一根为x ,由根与系数的关系可建立关于x 和k 的方程组,解之即得.x 5=2,k =−1. 6.a x b x c 2222++=0的()()D b a c b ac b ac 42222=−4=+2−2, ∵二次方程ax bx c 2++=0有两个实数根, ∴≥b ac 2−40, ∴b ac 2−2>0,∴()()△b a c b ac b ac 42222=−4=+2−2>0∴方程有两个不相等的实数根,而两根之和为负,两根之积为正. 故有两个负根.故选C .7.∵α,β是一元二次方程x x 2+3−7=0的两个根, ∴αβ+=−3,αα2+3−7=0, ∴αα2+3=7,∴ααβαααβ22+4+=+3++=7−3=4,故答案为:4.11 8.已知关于x 的方程()x m x m 22+2+2+−5=0有两个实数根,并且这两个根的平方和比这两个根的积大16,求m 的值.【解析】有实数根,则∆≥0,且x x x x 221212+−=16,联立解得m 的值.依题意有:()2()3()()x x m x x m x x x x m m 12212121222+=−2+2⎧⎪=−5⎪⎨+−=16⎪⎪∆=4+2−4−5≥0⎩,解得:m =−1或m =−15且m 9≥−4, ∴ m =−1.韦达定理说明了一元n 次方程中根和系数之间的关系。
(完整版)一元二次方程根的判别式知识点
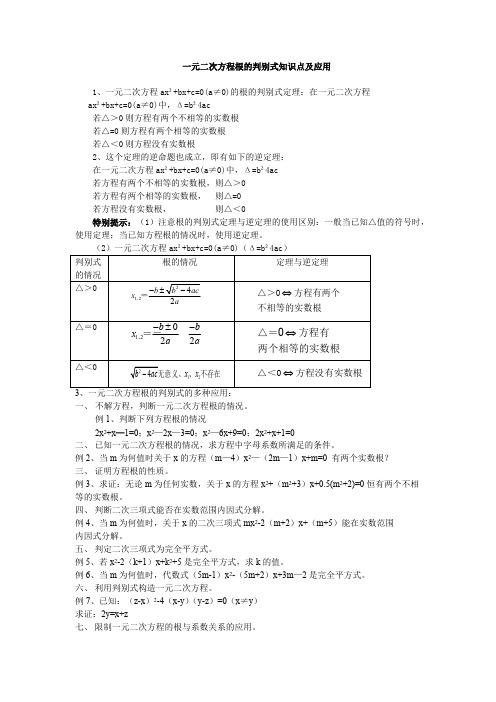
一元二次方程根的判别式知识点及应用1、一元二次方程ax²+bx+c=0(a≠0)的根的判别式定理:在一元二次方程ax²+bx+c=0(a≠0)中,Δ=b²4ac若△>0则方程有两个不相等的实数根若△=0则方程有两个相等的实数根若△<0则方程没有实数根2、这个定理的逆命题也成立,即有如下的逆定理:在一元二次方程ax²+bx+c=0(a≠0)中,Δ=b²4ac若方程有两个不相等的实数根,则△>0若方程有两个相等的实数根,则△=0若方程没有实数根,则△<0特别提示:(1)注意根的判别式定理与逆定理的使用区别:一般当已知△值的符号时,使用定理;当已知方程根的情况时,使用逆定理。
(2)一元二次方程ax²+bx+c=0(a≠0)(Δ=b²4ac)一、不解方程,判断一元二次方程根的情况。
例1、判断下列方程根的情况2x2+x━1=0;x2—2x—3=0;x2—6x+9=0;2x2+x+1=0二、已知一元二次方程根的情况,求方程中字母系数所满足的条件。
例2、当m为何值时关于x的方程(m—4)x2—(2m—1)x+m=0 有两个实数根?三、证明方程根的性质。
例3、求证:无论m为任何实数,关于x的方程x2+(m2+3)x+0.5(m2+2)=0恒有两个不相等的实数根。
四、判断二次三项式能否在实数范围内因式分解。
例4、当m为何值时,关于x的二次三项式mx2-2(m+2)x+(m+5)能在实数范围内因式分解。
五、判定二次三项式为完全平方式。
例5、若x2-2(k+1)x+k2+5是完全平方式,求k的值。
例6、当m为何值时,代数式(5m-1)x2-(5m+2)x+3m—2是完全平方式。
六、利用判别式构造一元二次方程。
例7、已知:(z-x)2-4(x-y)(y-z)=0(x≠y)求证:2y=x+z七、限制一元二次方程的根与系数关系的应用。
例8、已知关于x的方程x2-(k-1)x-3k-2=0的两个实数根的平方和为17,求k的值。
一元二次方程根的判别式知识点

一元二次方程根的判别式知识点
嘿,朋友们!今天咱来聊聊一元二次方程根的判别式这个超重要的知识点呀!你想想看,就好像是给一元二次方程这个“小家伙”做一个超级厉害的诊断!
比如说方程x² - 3x + 2 = 0 ,这里的判别式b² - 4ac 就开始发挥作用啦。
如果判别式大于零,那方程就有两个不一样的根,哎呀呀,就像你找到了两颗不一样的糖果一样惊喜呢!要是判别式等于零呢,那方程就只有一个根,就像是只有一颗独苗苗糖果咯。
可要是判别式小于零呢,嘿嘿,这方程就没根啦,就好像去糖果罐子找,结果啥都没找到,有点小失落呢!咱再看个例子,方程x² - 2x + 3 = 0 ,这里b² - 4ac 明显小于零呀,那不就没根嘛!
总之,一元二次方程根的判别式真的超级重要呀!它能让我们一下子就知道方程的根是啥情况,是不是很神奇呢?所以呀,一定要好好理解和掌握它哟!。
考点04 一元二次方程根的判别式以及根与系数的关系(解析版)

考点四一元二次方程根的判别式以及根与系数的关系知识点整合一、一元二次方程根的判别式及根与系数关系1.根的判别式一元二次方程2(0)0ax bx c a ++=≠是否有实数根,由24b ac -的符号来确定,我们把24b ac -叫做一元二次方程根的判别式.2.一元二次方程根的情况与判别式的关系(1)当240b ac ->时,方程2(0)0ax bx c a ++=≠有两个不相等的实数根;(2)当240b ac -=时,方程2(0)0ax bx c a ++=≠有1个(两个相等的)实数根;(3)当240b ac -<时,方程2(0)0ax bx c a ++=≠没有实数根.3.根与系数关系对于一元二次方程20ax bx c ++=(其中,,a b c 为常数,0a ≠),设其两根分别为1x ,2x ,则12b x x a +=-,12c x x a=.典例引领1.已知关于x 的一元二次方程()()22110x m x m m -+++=.(1)求证:无论m 取何值,方程总有两个不相等的实数根:(2)若该方程的一个根为1,求m 的值及另一个根.【答案】(1)证明见解析(2)当0m =时,方程的另一个根为0x =;当1m =时,方程的另一个根为2x =【分析】本题主要考查了一元二次方程根的判别式,解一元二次方程,一元二次方程的定义,熟练掌握一元二次方程的相关知识是解题的关键.(1)只需要证明()()221410m m m ∆=-+-+>⎡⎤⎣⎦恒成立即可;(2)把1x =代入原方程得到20m m -=,解方程求出m 的值,进而根据m 的值解方程求出方程的另一根即可.【详解】(1)证明:由题意得,()()22141m m m ∆=-+-+⎡⎤⎣⎦依题意有:215x -+=,21x k -⋅=,解得26x =,6k =-,故k 的值为6-,方程的另一个根为6x =.9.求证:对于任意实数m ,关于x 的方程22220x mx m -+-=总有两个不相等的实数根.【答案】见解析【分析】本题主要考查了一元二次方程()200ax bx c a ++=≠的根情况,判断其根的情况,完全取决于24b ac ∆=-的符号,当0> 时,方程有两个不相等的实数根;当Δ0=时,方程有两个相等的实数根;当Δ0<时,方程没有实数根.【详解】解:()24422m m =--△2488m m =-+()2414m =-+.()210m -≥,∴()241440m =-+≥>△.∴对于任意实数m ,关于x 的方程22220x mx m -+-=总有两个不相等的实数根.10.已知关于x 的一元二次方程()2320x m x m ++++=.(1)求证:不论实数m 取何值,方程总有实数根;(2)当m 取何值时,方程有两个相等的实数根?【答案】(1)见详解(2)1m =-【分析】本题考查了一元二次方程根的判别式,熟记“24b ac ∆=-”是解题关键.(1)方程有实数根时240b ac ∆=-≥,由此即可求解.(2)方程有两个相等的实数根即240b ac ∆=-=,由此即可求解.【详解】(1)证明:()()2243412b ac m m ∆=-=+-⨯⨯+26948m m m =++--221m m =++()21m =+(2)由题意得,222229k k ⨯+-=,整理得,245k k -=,根据()223122023342023k k k k -+=-+,计算求解即可.【详解】(1)解:∵2229x kx k +-=,∴22290x kx k -+-=,∴()()222419360k k ∆=--⨯⨯-=>,∴此方程有两个不相等的实数根;(2)解:由题意得,222229k k ⨯+-=,整理得,245k k -=,∴()2231220233420231520232038k k k k -+=-+=+=,∴23122023k k -+的值为2038.13.已知关于x 的方程22220x mx m ++-=.(1)试说明:无论m 取何值,方程总有两个不相等的实数根;(2)若方程有一个根为3,求22122043m m ++的值.【答案】(1)证明见解析(2)2029【分析】本题主要考查了一元二次方程根的判别式,一元二次方程的解,代数式求值;(1)根据一元二次方程根的判别式,进行证明即可;(2)根据方程有一个根为3,得出267m m +=-,然后整体代入求值即可.解题的关键是熟练掌握一元二次方程()200ax bx c a ++=≠的根与24b ac ∆=-有如下关系:当0∆>时,方程有两个不相等的实数根;当Δ0=时,方程有两个相等的实数根;当Δ0<时,方程无实数根.【详解】(1)证明:∵()()2222241244880m m m m ∆=-⨯⨯-=-+=>,∴无论m 取何值,方程总有两个不相等的实数根;(2)解:∵方程有一个根为3,∴223620m m ++-=,整理,得:267m m +=-,∴22122043m m ++()2262043m m =++()272043=⨯-+142043=-+2029=.14.已知关于x 的一元二次方程210x mx m -+-=.(1)若该方程有一个根是2,求该方程的另一个根;(2)求证:该方程总有两个实数根.【答案】(1)1(2)见解析【分析】本题主要考查了一元二次方程的解和根的判别式,(1)直接把2x =代入到原方程中得到关于m 的方程,再解方程即可得到答案;(2)根据一元二次方程根的判别式进行证明.掌握对于一元二次方程()200ax bx c a ++=≠,若240b ac ∆=->,则方程有两个不相等的实数根,若240b ac ∆=-=,则方程有两个相等的实数根,若24<0b ac ∆=-,则方程没有实数根;理解一元二次方程的解是使方程左右两边相等的未知数的值,是解决问题的关键.【详解】(1)解:当2x =时,4210m m -+-=3m ∴=,则原方程为:2320x x -+=,即:()()210x x --=,11x ∴=,22x =,∴另一个根1,(2)证明:()()2Δ411m m =--⨯⨯-244m m =-+()220m =-≥,∴该方程总有两个实数根;15.已知关于x 的一元二次方程()()25230x m x m +---=(1)求证:该方程总有两个实数根(2)如果该方程的两个实数根的差为4,求m 的值(2)“凤凰”方程必定有一个根是______;(3)已知方程20x mx n ++=是“凤凰”方程,且有两个相等的实数根,求mn 的值.【答案】(1)2230x x +-=(2)1(3)mn 2=-【分析】(1)本题主要考查一元二次方程根的情况,通过观察可以发现1x =是方程的根,直接写出一个根为1一元二次方程即可.(2)本题主要考查通过代数式观察,可以发现1x =是一元二次方程的一个根,直接求解即可.(3)本题主要考查由一元二次方程根的情况,推导出240b ac ∆=-=,可以得到一个方程,再由凤凰方程,又可以得到一个10m n ++=的方程,然后去求,m 和n 即可,最后求出mn 的值.【详解】(1)由题可知,要写出一个一元二次方程,并且满足一个根是1x =;即为:2230x x +-=.(2)关于x 的一元二次方程()200ax bx c a ++=≠,且满足0a b c ++=;∴1x =时,0a b c ++=;故凤凰”方程必定有一个根是1x =.(3)20x mx n ++= 是“凤凰”方程;10m n ∴++=,即1n m =--;方程20x mx n ++=有两个相等的实数根;240m n ∴∆=-=.将1n m =--代入,得()2410m m ---=;解得:2,1m n =-∴=;()212mn ∴=-⨯=-.19.已知关于x 的一元二次方程()23220x k x k ++++=.(1)求证:方程有两个实数根;(2)若方程的两个根分别为1x ,2x ,且1212217x x x x ++=,求k 的值.【答案】(1)见解析【分析】本题考查了一元二次方程根的判别式的意义,根与系数的关系,解一元二次方程;(1)求出0∆>即可证明;(2)根据根与系数的关系得出1221k x k x -=++,123x x +=,结合已知等式得出关于k 的一元二次方程,解方程可得答案.【详解】(1)证明:∵()()()2222234194444452140k k k k k k k ∆=---++=+--=-+=-+>,∴无论k 取何值,方程总有两个不相等的实数根;(2)解:∵方程22310x x k k ++--=有两个实数根1x ,2x ,∴1221k x k x -=++,123x x +=,又∵()()12113++=x x ,∴121213x x x x +++=,∴23131k k -+++=+,解得:12k =,21k =-.5.已知关于x 的一元二次方程220x x k ++=.(1)若方程有两个不相等的实数根,求k 的取值范围;(2)若m 是方程的根,且222m m +=,求k 的值.【答案】(1)1k <(2)2k =-【分析】本题主要考查了一元二次方程根的判别式与一元二次方程的解的含义,理解原理的应用是解本题的关键;(1)根据方程有两个不相等的实数根,可得240b ac ∆=->,求出k 的取值范围即可;(2)先由方程解的含义可得22m m k +=-,结合222m m +=即可求解.【详解】(1)解:∵关于x 的一元二次方程220x x k ++=有两个不相等的实数根,∴24440b ac k ∆=-=->,解得:1k <;(2)∵m 是方程220x x k ++=的根,∴220m m k ++=即22m m k +=-,∵222m m +=,∴2k -=,解得:2k =-.6.已知关于x 的一元二次方程2210(0)nx x n -+=≠有实数根.(1)求n 的取值范围;(2)当n 取最大值时,求方程2210(0)nx x n -+=≠的根.【答案】(1)1n ≤且0n ≠(2)121x x ==【分析】本题主要考查了一元二次方程的根的判别式以及解一元二次方程.(1)根据题意,可得240b ac ∆=-≥,即440n -≥,解不等式,并根据一元二次方程的定义确定n 的取值范围即可;(2)结合n 的取值范围确定n 的最大值,然后利用配方法解该方程即可.【详解】(1)解:根据题意,一元二次方程2210(0)nx x n -+=≠有实数根,则224(2)41440b ac n n ∆=-=--⨯⨯=-≥,解得1n ≤,又∵0n ≠,∴n 的取值范围是1n ≤且0n ≠;(2)由1n ≤且0n ≠得,n 的最大值为1,把1n =代入原方程得2210x x -+=,∴2(1)0x -=,解得121x x ==.7.己知一元二次方程2410x x m -+-=.(1)若方程有两个不相等的实数根,求实数m 的取值范围;(2)若方程有两个相等的实数根,求实数m 以及此时方程的根.【答案】(1)5m <(2)5m =,122x x ==【分析】本题考查了根的判别式,牢记“①当0∆>时,方程有两个不相等的实数根;②当Δ0=时,方程有两个相等的实数根;③当Δ0<时,方程无实数根.”(1)由方程有两个不相等的实数根结合根的判别式,即可得出关于m 的一元一次不等式,解之即可得出结论;(2)由方程有两个相等的实数根结合根的判别式,即可得出关于m 的一元一次方程,解之即可得出结论.【详解】(1)解:2(4)4(1)m ∆=---,方程有两个不相等的实数根,∴0∆>,解得5m <.(2) 方程有两个相等的实数根,∴Δ0=,即164(1)0m --=解得5m =(1)若所捂的部分为【详解】(1)解:∵方程有实数解是1x 和2x ,∴()22410k ∆=--≥,解得2k ≤,故k 的取值范围是2k ≤;(2)∵一元二次方程2210x x k ++-=的实数解是1x 和2x ,∴122x x +=-,121x x k ⋅=-,则()121221x x x x k +-=---,∵12121x x x x +-<-∴()211k ---<-,解得0k >,又由(1)知2k ≤,∴02k <≤,∵k 为整数,∴k 的值为1或2.13.已知关于x 的一元二次方程250x ax a ++-=.(1)若该方程的一个根为3,求a 的值及该方程的另一个根;(2)求证:不论a 为何值,该方程总有两个不相等的实数根.【答案】(1)方程的另一根为2-;(2)见解析【分析】本题主要考查一元二次方程根的判别式及根与系数的关系,(1)将方程的根代入可求得a 的值,再根据根与系数的关系可求得另一个根;(2)用a 表示出其判别式,利用配方可化为平方的形式,可判断判别式的符号,可得出结论;掌握一元二次方程根的判别式与根的个数的关系及根与系数的关系是解题的关键.【详解】(1)解:将3x =代入方程250x ax a ++-=可得:9350a a ++-=,解得1a =-;∴方程为260x x --=,设另一根为x ,则36x =-,。
一元二次方程根的判别式及根与系数的关系

一元二次方程根的判别式及根与系数的关系一、知识点:1.一元二次方程)0(02≠=++a c bx ax 根的判别式:2.一元二次方程根与系数的关系: (1)如果1x ,2x 是一元二次方程)0(02≠=++a c bx ax 的两个根,那么a b x x -=+21,ac x x =∙21 (2)如果1x ,2x 是方程02=++q px x 的两个根,那么p x x -=+21,q x x =∙21二、一元二次方程)0(02≠=++a c bx ax 根的判别式的应用:1. 不解方程,判断方程根的情况:(1);05432=--x x (2);01322=+-x x (3)26232-=+y y2. 证明方程根的情况:(1)已知关于x 的方程0)12(2)12(2=-++-k x k x .①求证:无论k 取什么实数值,这个方程总有实数根;②若等腰△ABC 中有两边的长恰好是这个方程的两个根,且这两边和为6,求△ABC 的周长.(2)小明说:“关于x 的方程)1.(0)1(4)1(222±≠=++-+m m mx x m 一定没有实数根”。
小明的说法对吗?说明你的理由.(3)求证:无论m 取何值,关于x 的方程01)32(2=++++m x m x 总有两个不相等的实数根。
(4)已知a ,b ,c 为△ABC 的三边,试判断关于x 的方程)(02)(2c b c b ax x c b ≠=-+--的根的情况.(5)已知a ,b ,c 为△ABC 的三边,且关于x 的方程0)()(2)(2=-+-+-b a x a b x b c 有两个相等的实数根,试判断△ABC 的形状.3. 已知方程根的情况,求字母系数的取值范围:(1)已知:关于x 的一元二次方程:0)1(22=+++k x k kx 有两个实数根,求k 的取值范围.(2)关于x 的一元二次方程06)4(22=+--x kx x 无实数根,求k 的最小整数值.(3)若关于x 的方程0122=--x kx 有实数根,求k 的取值范围.三、一元二次方程根与系数的关系的应用:1.已知方程一根,求方程另一根及字母系数的值:(1)已知32+是关于x 的方程042=+-c x x 的一个根,求方程的另一个根及c 的值.(2)已知方程:0422=--bx x 的一个根为1,求另一个根及b 的值.(3)已知关于x 的方程0252=++k kx x 的一个根是21,它的另一个根及k 的值.2. 已知方程两根之间的关系,求字母系数的值:(1)关于x 的方程0)1(22=+--m x m x 的两根互为相反数,求m 的值.(2)关于x 的方程02)1(2=+++-k x k x 的两个实数根的平方和等于6,求k 的值.(3)在Rt △ABC 中,∠C=90°, ∠A ,∠B ,∠C 的对边分别是a ,b ,c ,并且a ,b 是方程07822=+-x x 的两根. 求斜边c 的值.3. 不解方程,求代数式的值:(1)若1x ,2x 是方程01422=+-x x 的两个根,求下列代数式的值: ①2111x x +; ②2221x x + ③1221x x x x +;④221)x x -( ⑤)3)(3(21++x x(2)已知1x ,2x 是方程0132=+-x x 的两个根,求代数式21214x x x --的值.(3)如果实数a ,b 满足方程0172=+-a a ,0172=+-b b ,求代数式b a a b +的值.(4)关于x 的一元二次方程0122=++-k x x 的实数根是1x ,2x .(1)求k 的取值范围;(2)如果7)4)(4(21-=--x x ,求k 的值;(3)设k x x x x y 2)(22121----=,求y 的最大值.。
一元二次方程根的判别式及根与系数的关系—知识讲解

一元二次方程根的判别式及根与系数的关系—知识讲解
1.当Δ>0时,方程有两个不相等的实数根。
这是因为Δ大于0表示
判别式是一个正数,所以开方后可以得到一个实数。
这种情况下方程的根
可以通过求解下面的式子来得到:
x1=(-b+√Δ)/(2a)
x2=(-b-√Δ)/(2a)
2.当Δ=0时,方程有一个实数根。
这是因为Δ等于0表示判别式是
一个零,所以开方后可以得到同一个数字。
这种情况下方程的根可以通过
求解下面的式子来得到:
x=-b/(2a)
3.当Δ<0时,方程没有实数根。
这是因为Δ小于0表示判别式是一
个负数,所以开根号无法得到实数。
但是我们可以通过引入虚数单位i来
表示方程的根。
这种情况下方程的根可以通过求解下面的式子来得到:x1=(-b+√(-Δ)i)/(2a)
x2=(-b-√(-Δ)i)/(2a)
根据根与系数的关系
1.根与二次项系数a的关系:当a大于0时,方程开口向上,根的值
会随着a增大而增大;当a小于0时,方程开口向下,根的值会随着a减
小而增大。
2.根与一次项系数b的关系:根的值与b的正负有关,当b大于0时,根的值变大;当b小于0时,根的值变小。
3.根与常数项系数c的关系:根的值与c的正负有关,当c大于0时,根的值变小;当c小于0时,根的值变大。
这些关系可以帮助我们更好地理解和应用一元二次方程的根。
在实际
问题的解决中,根与系数的关系可以帮助我们分析方程的性质,例如方程
的图像形状和根的变化趋势,并在需要的时候做出合理的调整和判断。
15、一元二次方程根的判别式

一元二次方程知识点7、一元二次方程根的判别式1、一元二次方程有无解的判定:对于一元二次方程)0(02≠=++a c bx ax a c x a b x c x a b x a c bx ax -=+⇒-=+⇒-=+⇒222)(2222244)2()2(a ac b a b a c a b x a b x -=+-=++⇒22244)2(a ac b a b x -=+⇒0402≥⇒≠a a (1)当042≥-ac b 时:2244a ac b -≥0,有意义根据平方根的定义,有x +a b 2=±2244a ac b -即x =a ac b b 242-±-;(2)当042<-ac b 时:负数没有平方根在实数范围内x 的值不存在,所以方程没有实数根。
2、判别式的定义:把ac b 42-叫做一元二次方程)0(02≠=++a c bx ax 根的判别式,通常用符号“∆”来表示,即ac b 42-=∆。
3、判别式的作用:判定一元二次方程根有无情况和根的个数一般地,一元二次方程)0(02≠=++a c bx ax :①0>∆,方程有两个不相等的实数根;②0=∆,方程有两个相等的实数根;③0<∆,方程没有实数根。
例13、不解方程,直接判断方程根的情况例14、应用根的判别式确定系数中所含字母的取值范围例15、证明方程根的存在性问题例16、根的判别式在实际问题中的应用例17、一元二次方程判别式的综合探究题知识点8、一元二次方程根与系数关系1、韦达定理:若方程)0(02≠=++a c bx ax 的两根为21,x x ,则ac x x a b x x =⋅-=+2121;。
推论1.若方程02=++q px x 的两根为21,x x ,则q x x p x x =⋅-=+2121;;推论2.以两个数21,x x 为根的一元二次方程是0)(21212=++-x x x x x x 。
一元二次方程判别式以及根与系数关系

一元二次方程判别式以及根与系数关系知识总结1.一元二次方程的根的判别式(1)一元二次方程ax 2+bx +c =0(a ≠0)的根的情况由b 2-4ac 来确定.我们把b 2-4ac 叫做一元二次方程ax 2+bx +c =0(a ≠0)的根的判别式,通常用“Δ”来表示,即Δ=b 2-4ac .注意:要想利用根的判别式求解方程,首先要将方程化为一元二次方程的一般式ax 2+bx +c =0(a ≠0),以便确定a ,b ,c 并代入b 2-4ac 计算. (2)一元二次方程的根的情况与根的判别式的关系①利用根的判别式判定根的情况.一般地,方程ax 2+bx +c =0(a ≠0),当Δ>0时,有两个不相等的实数根;当Δ=0时,有两个相等的实数根;当Δ<0时,没有实数根.②根据方程根的情况,确定Δ的取值范围.当方程有两个不相等的实数根时,Δ>0;当方程有两个相等的实数根时,Δ=0;当方程没有实数根时,Δ<0.注意:①如果说一元二次方程有实数根,那么应该包括有两个不相等实数根或有两个相等的实数根两种情况,此时b 2-4ac ≥0,切勿丢掉等号.②当b 2-4ac <0时,方程在实数范围内无解(无实数根),但在复数范围内方程仍有两个解,这将在高中阶段学习.【例1】不解方程,判别下列方程的根的情况:(1)2x 2+3x -4=0;(2)3x 2+2=26x ;(3)ax 2+bx =0(a ≠0);(4)ax 2+c =0(a ≠0).(3)利用根的判别式确定方程中字母系数的取值范围若一元二次方程ax 2+bx +c =0(a ≠0)有两个不相等的实数根,则b 2-4ac >0;若一元二次方程ax 2+bx +c =0(a ≠0)有两个相等的实数根,则b 2-4ac =0.从而根据关于字母系数的方程或不等式求出字母系数的值或取值范围.在运用时应注意前提条件:必须是一元二次方程且符合其一般形式.【例2】已知关于x 的方程kx 2-4kx +k -5=0有两个相等的实数根,求k 的值,并解这个方程.【例3】当k 取何值时,关于x 的一元二次方程kx 2+9=12x ,(1)有两个不相等的实数根? (2)有两个相等的实数根? (3)没有实数根?2.一元二次方程的根与系数的关系(1)如果方程ax 2+bx +c =0(a ≠0)的两个根为x 1,x 2,那么x 1+x 2=-b a ,x 1·x 2=c a.这个关系通常称为韦达定理.(1)在实数范围内运用根与系数的关系时,必须注意两个条件: ①方程必须是一元二次方程,即二次项系数a ≠0;②方程有实数根,即Δ≥0.因此,解题时要注意分析题中隐含条件Δ≥0和a ≠0.(2)如果方程x 2+px +q =0的两根是x 1,x 2,这时韦达定理应是:x 1+x 2=-p ,x 1·x 2=q .【例4】不解方程,说明一元二次方程2x 2+4x =1必有实数根,并求出两根之和与两根之积.(2)利用根与系数的关系确定一元二次方程若x 1,x 2满足x 1+x 2=-b a ,x 1·x 2=c a,那么x 1,x 2是一元二次方程ax 2+bx +c =0的两根. 注意:(1)利用这一性质比较容易检验一元二次方程的解是否正确.(2)以x 1,x 2为根的一元二次方程(二次项系数为1)是x 2-(x 1+x 2)x +x 1x 2=0. 【例5】已知一个关于x 的一元二次方程,它的两根为2和6,请你写出这个一元二次方程.总结:已知两根求一元二次方程,其一般步骤是:①先根据两根分别求出两根之和与两根之积;②把两根之和、两根之积代入一元二次方程x 2-(x 1+x 2)x +x 1x 2=0,求出所要求的方程.【例6】求作一个一元二次方程,使它的两根分别是方程5x 2+2x -3=0各根的负倒数.(3)利用一元二次方程根与系数的关系求关于两根x 1,x 2的代数式的值已知一元二次方程ax 2+bx +c =0(a ≠0)的两根为x 1,x 2,则求含有x 1,x 2的代数式的值时,其方法是把含x 1,x 2的代数式通过转化,变为用x 1+x 2,x 1x 2的代数式进行表示,然后再整体代入求出代数式的值.解决此类问题时经常要运用到以下代数式及变形:①21x +22x =(x 1+x 2)2-2x 1x 2;②1x 1+1x 2=x 1+x 2x 1x 2;③(x 1+a )(x 2+a )=x 1x 2+a (x 1+x 2)+a 2;④|x 1-x 2|=(x 1-x 2)2=(x 1+x 2)2-4x 1x 2.【例7】已知方程2x 2+5x -6=0的两个根为x 1,x 2,求下列代数式的值.(1)(x 1-2)(x 2-2);(2)x 2x 1+x 1x 2.(4)已知含未知常数m 的一元二次方程两根关系式,求未知常数m 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一元二次方程根的判别
式知识点
集团档案编码:[YTTR-YTPT28-YTNTL98-UYTYNN08]
一元二次方程根的判别式知识点及应用
1、一元二次方程ax2+bx+c=0(a≠0)的根的判别式定理:在一元二次方程
ax2+bx+c=0(a≠0)中,Δ=b24ac
若△>0则方程有两个不相等的实数根
若△=0则方程有两个相等的实数根
若△<0则方程没有实数根
2、这个定理的逆命题也成立,即有如下的逆定理:
在一元二次方程ax2+bx+c=0(a≠0)中,Δ=b24ac
若方程有两个不相等的实数根,则△>0
若方程有两个相等的实数根,则△=0
若方程没有实数根,则△<0
特别提示:(1)注意根的判别式定理与逆定理的使用区别:一般当已知△值的符号时,使用定理;当已知方程根的情况时,使用逆定理。
一、不解方程,判断一元二次方程根的情况。
二、例1、判断下列方程根的情况
三、2x2+x━1=0;x2—2x—3=0;x2—6x+9=0;2x2+x+1=0
二、?已知一元二次方程根的情况,求方程中字母系数所满足的条件。
例2、当m为何值时关于x的方程(m—4)x2—(2m—1)x+m=0有两个实数根?
三、?证明方程根的性质。
例3、求证:无论m为任何实数,关于x的方程x2+(m2+3)x+0.5(m2+2)=0恒有两个不相等的实数根。
四、?判断二次三项式能否在实数范围内因式分解。
例4、当m为何值时,关于x的二次三项式mx2-2(m+2)x+(m+5)能在实数范围
内因式分解。
五、?判定二次三项式为完全平方式。
例5、若x2-2(k+1)x+k2+5是完全平方式,求k的值。
例6、当m为何值时,代数式(5m-1)x2-(5m+2)x+3m—2是
完全平方式。
六、?利用判别式构造一元二次方程。
例7、已知:(z-x)2-4(x-y)(y-z)=0(x≠y)
求证:2y=x+z
七、?限制一元二次方程的根与系数关系的应用。
例8、已知关于x的方程x2-(k-1)x-3k-2=0的两个实数根的平方和为17,求k的值。
八、?与几何知识相联系的问题。
例9、已知方程a(x2+1)-2bx+c(x2-1)=0有两个相等的实数根,a、b、c为一三角形的三条边,求此三角形的形状。
例10、已知a、b、c为直角三角形的三条边,c为斜边,求证:关于x的方程
x2-2(a+b)x+c2+ab=0有两个相等的实数根。
九、?判断其他类方程根的情况。
例12、分式方程无实数根,求m的取值范围。
例13、a、b、c为一三角形的三条边长,若方程ax-y+bc=0与方程x2-ax-y+b2=0只有一组公共的实数解,求次三角形的形状。
十、?解决二次函数的相关问题。
例14、若抛物线y=x2-ax+8的顶点在横轴上,求a值。
例15、求证:无论m为何值,二次函数y=x2-(m+4)x+2(m-1)总与横轴有两个交点。
例16、直线y=3x-3与y=x2-x+1有几个交点?
评析:二次函数与二次方程有密切的联系,抛物线与横轴交点个数由Δ决定,即Δ>0时,有两个交点;Δ=0时,有一个交点(或者说顶点在横轴上);Δ<0时没有交点(或者说当a>0时函数值恒为正,当a<0时函数值恒为负)。
十一、求最值问题。
例17、已知x为任意实数,求的最值。
十二、巧解方程(组)。
例18、求方程2x2-2xy+y2-2x+1=0的实数解。
