材料力学专项习题练习扭转
土木工程师-公共基础-材料力学-扭转
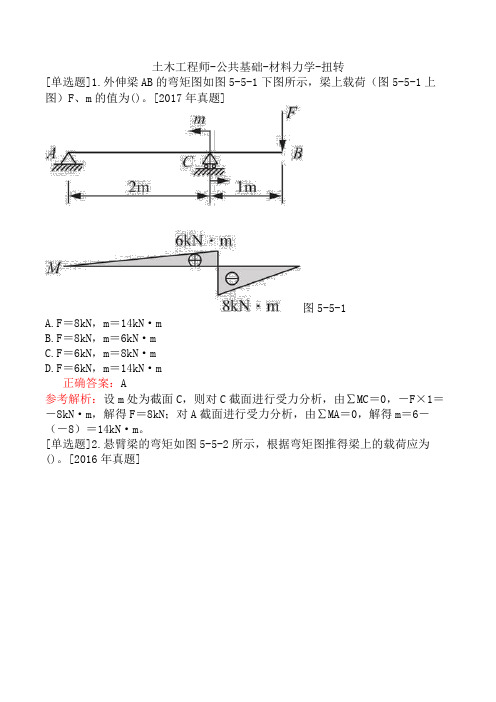
土木工程师-公共基础-材料力学-扭转[单选题]1.外伸梁AB的弯矩图如图5-5-1下图所示,梁上载荷(图5-5-1上图)F、m的值为()。
[2017年真题]图5-5-1A.F=8kN,m=14kN·mB.F=8kN,m=6kN·mC.F=6kN,m=8kN·mD.F=6kN,m=14kN·m正确答案:A参考解析:设m处为截面C,则对C截面进行受力分析,由∑MC=0,-F×1=-8kN·m,解得F=8kN;对A截面进行受力分析,由∑MA=0,解得m=6-(-8)=14kN·m。
[单选题]2.悬臂梁的弯矩如图5-5-2所示,根据弯矩图推得梁上的载荷应为()。
[2016年真题]图5-5-2A.F=10kN,m=10kN·mB.F=5kN,m=10kN·mC.F=10kN,m=5kN·mD.F=5kN,m=5kN·m正确答案:B参考解析:弯矩图在支座C处有一个突变,突变大小即为支座C处的弯矩值,m =10kN·m。
弯矩图的斜率值即为剪力值,显然BC段截面剪力为零,AB段截面剪力为+5kN(顺时针),因此根据B点截面处的竖向力平衡,可算得:F=5kN。
[单选题]3.简支梁AB的剪力图和弯矩图如图5-5-3所示,该梁正确的受力图是()。
[2016年真题]图5-5-3 A.B.C.D.正确答案:C参考解析:弯矩图在中间处突变,则构件中间有集中力偶大小为50kN·m;剪力图中间有突变,则说明构件中间有集中力,大小为100kN。
根据中间截面处的左右两侧剪力(顺时针为正)与集中荷载的平衡,则集中荷载竖直向下,C项正确。
[单选题]4.承受均布载荷的简支梁如图5-5-4(a)所示,现将两端的支座同时向梁中间移动l/8,如图(b)所示。
两根梁的中点(l/2处)弯矩之比Ma/Mb 为()。
[2013年真题]图5-5-4(a)图5-5-4(b)A.16B.4C.2D.1正确答案:C参考解析:支座未移动前中点处弯矩Ma=ql2/8,移动后中点处弯矩变为:Mb=(-ql/8)×(l/16)+q(l-2l/8)2/8=ql2/16,故Ma/Mb=2。
材料力学扭转练习题

材料力学扭转练习题基本概念题一、选择题1. 图示传动轴,主动轮A的输入功率为PA =0 kW,从动轮B,C,D,E的输出功率分别为PB =0 kW,PC = kW,PD = 10 kW,PE = 1kW。
则轴上最大扭矩T。
A.BA段 B.AC段 C.CD段 D.DE段max出现在题1图2. 图示单元体的应力状态中属正确的纯剪切状态的是。
题2图3. 上题图示单元体的应力状态中属正确的是。
4. 下列关于剪应力互等定理的论述中正确的是。
A.剪应力互等定理是由平衡B.剪应力互等定理仅适用于纯剪切的情况C.剪应力互等定理适用于各种受力杆件D.剪应力互等定理仅适用于弹性范围E.剪应力互等定理与材料的性能无关5. 图示受扭圆轴,其横截面上的剪应力分布图正确的是。
-12-题5图6. 实心圆轴,两端受扭转外力偶作用。
直径为D时,设轴内的最大剪应力为?,若轴的直径改为D2,其它条件不变,则轴内的最大剪应力变为。
A.8? B.?C.16? D.?7. 受扭空心圆轴,在横截面积相等的条件下,下列承载能力最大的轴是。
A.??0 B.??0.5C.??0. D.??0.88. 扭转应力公式T?的适用范围是。
IpA.各种等截面直杆 B.实心或空心圆截面直杆C.矩形截面直杆 D.弹性变形 E.弹性非弹性范围 9. 直径为D的实心圆轴,最大的容许扭矩为T,若将轴的横截面积增加一倍,则其最大容许扭矩为。
A.2TB.2T C.22TD.4T10. 材料相同的两根圆轴,一根为实心,直径为D1;另一根为空心,内径为d2,外径为D2d2D??。
若两轴横截面上的扭矩T,和最大剪应力?max均相同,则两轴外径之比1 D2D2为。
A.1??B.1?? C.343D.411. 阶梯圆轴及其受力如图所示,其中AB段的最大剪应力?max1与BC段的最大剪应力?max2的关系是。
A.?max1??max2B.?max1?313?max2C.?max1??max2D.?ma x1??max248-13-题12图题13图12. 在图示的圆轴中,AB段的相对扭转角?1和BC段的相对扭转角?2的关系是。
材料力学 扭转习题.

5 a =____________________ 。 4
扭转练习题
7.阶梯轴尺寸及受力如图所示,AB段的最大剪应力 max1 与BC段的最大剪应力
max 2 之比为 3:8
。
扭转练习题
二、选择
1.空心圆轴外径为D,内径为d,在计算最大剪应力时需要确定抗扭 截面系数Wt,以下正确的是( )。
答案: 剪应力互等,零。
)定理可
扭转练习题
5.现有两根材料、长度及扭矩相同的受扭圆轴,若两者直径之比为2:3。 则两者最大剪应力之比为_______________ 27:8 ,此时抗扭刚度之比为 16:81 _______________ 。
扭转练习题
6.内外径比值 d / D 0.8 的空心圆轴受扭时,若a点的剪应变 a 为已知,则b点的剪应变 b
扭转练习题
6.材料不同的两根扭转轴,其直径和长度相同,在扭矩相同的情况下,
它们的最大剪应力之间和扭转角之间的关系有四种答案: ( A ) ( B ) ( C )
1 2 , 1 2
1 2 , 1 2
1 2 , 1 2
( D ) 1 2 , 1 2
扭转练习题
一、填空
1.空心圆轴外径为D,内径为d=D/2,两端受扭转力偶 mx 作 max ( ), 用,则其横截面上剪应力呈( )分布,
min ( )。
答案:
256mx 线性, , 1/ 2 max。 3 15 D
2.圆截面杆扭转时,其变形特点是变形过程中横截面始 终保持( ),即符合( )。非圆截面杆扭转时,其 变形特点是变形过程中横截面发生( ),即不符合 ( )。 答案:平面,平面假设,翘曲,平面假设。
扭转习题

第三章 扭转习题一、单项选择题1、横截面都为圆的两个杆,直径分别为d 和D ,并且d=。
两杆横截面上扭矩相等两杆横截面上的最大切应力之比maxDmaxdττ为A 、2倍,B 、4倍,C 、8倍,D 、16倍。
二、1、扭转变形时,公式pTlGI τ=中的 表示单位长度的扭转角,公式中的T 表示横截面上的 ;G 表示杆材料的 弹性模量;I P 表示杆横截面对形心的 ;GI P 表示杆的抗扭 。
2、截面为圆的杆扭转变形时,所受外力偶的作用面与杆的轴线 .3、实心圆轴扭转时,横截面上的切应力分布是否均匀,横截面上离圆心愈远的点处切应力 ,圆心处的切应力为 ,圆周上切应力4、两根实心圆轴的直径d 和长度L 都相同,而材料不同,在相同扭矩作用下,它们横截面上的最大切应力是否相同 ,单位长度的扭转角是否相同 。
5、剪切虎克定律的表达式 G τγ=,式中的G 表示材料的 模量,式中的γ称为 。
6、根据切应力互等定理,单元体两互相垂直截面上在其相交处的切应力成对存在, 且 相等,而 现反。
三、 1、如图所示圆轴,一端固定。
圆轴横截面的直径D=100mm ,所受的外力偶矩M 1=6kN•m,M 2=4kN•m。
试求圆轴横截面上的最大扭矩和最大切应力。
答:圆轴横截面上的最大扭矩为 kN•m;圆轴横截面上的最大切应力为 Mpa 。
2、如图所示阶梯形圆轴,一端固定。
圆轴横截面的直径分别为外力偶矩M C =1200 N•m,M B =1800 N•m。
试求BC 段横截面上的扭矩和该阶梯轴的最 大切应力。
答:BC 段横截面上的扭矩为 N•m;该阶梯轴的最大切应力为 Mpa 。
3、如图所示圆轴,一端固定。
圆轴横截面的直径d=100mm ,所受的外力偶矩M 1=7000 N•mM 2=5000 N•m。
试求圆轴横截面上的最大扭矩和最大切应力。
答:最大扭矩为 N •m 。
最大切应力为 Mpa 。
4、某传动轴为实心圆轴,轴内的最大扭矩=1.5kN m T g,许用切应力[]=50MPa τ,试确定该轴的横截面直径。
(完整版)扭转练习题
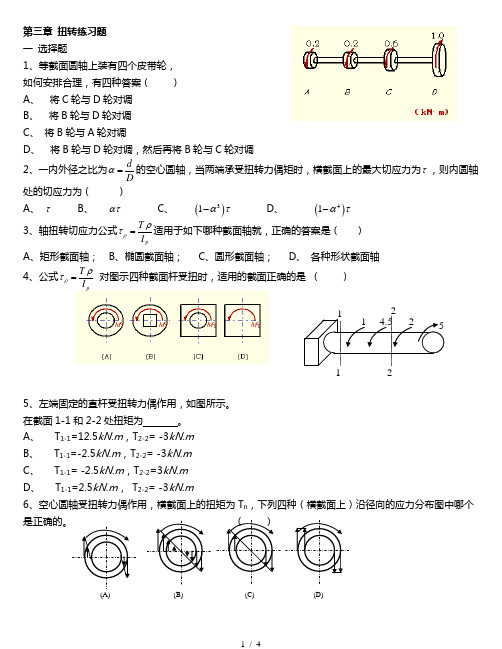
第三章 扭转练习题 一 选择题1、等截面圆轴上装有四个皮带轮, 如何安排合理,有四种答案( ) A 、 将C 轮与D 轮对调 B 、 将B 轮与D 轮对调 C 、 将B 轮与A 轮对调D 、 将B 轮与D 轮对调,然后再将B 轮与C 轮对调2、一内外径之比为dDα=的空心圆轴,当两端承受扭转力偶矩时,横截面上的最大切应力为τ,则内圆轴处的切应力为( )A 、 τB 、 ατC 、 ()31ατ-D 、 ()41ατ- 3、轴扭转切应力公式pT I ρρτ=适用于如下哪种截面轴就,正确的答案是( ) A 、矩形截面轴; B 、椭圆截面轴; C 、圆形截面轴; D 、 各种形状截面轴4、公式p T I ρρτ= 对图示四种截面杆受扭时,适用的截面正确的是 ( )5、左端固定的直杆受扭转力偶作用,如图所示。
在截面1-1和2-2处扭矩为 。
A 、 T 1-1=12.5kN.m ,T 2-2= -3kN.mB 、 T 1-1=-2.5kN.m ,T 2-2= -3kN.mC 、 T 1-1= -2.5kN.m ,T 2-2=3kN.mD 、 T 1-1=2.5kN.m , T 2-2= -3kN.m6、空心圆轴受扭转力偶作用,横截面上的扭矩为T n ,下列四种(横截面上)沿径向的应力分布图中哪个是正确的。
( )21 11 24.5 52(A)(B)(C)(D)7、图(1)、(2)所示两圆轴的材料、 长度均相同,扭转时两轴表面上 一点处的切应变相等γ1=γ2,则M e1与M e2的关系正确的是( )A 、 21e e M M =B 、 212e e M M =C 、 214e e M M =D 、 218e e M M = 8、一内、外直径分布为d 、D 的空心圆轴,其抗扭截面系数正确的是( )A 、 331616t D d W ππ=-; B 、333232t D d W ππ=- C 、 ()4416t W D d D π=- ; D 、 443232t D d W ππ=- 9、实心圆轴①和空心圆轴②,它们的横截面面积均相同,受相同扭矩作用,则其最大切应力正确的是( )A 、 max 2max1ττ>B 、 max 2max1ττ<C 、 max 2max1ττ=D 无法比较10 受扭圆轴,当横截面上的扭矩T 不变,而直径减小一半时,该横截面的最大切应力与原来的最大切应力之比正确的是( )A 、 2倍B 、 4倍C 、 6倍D 、 8倍 二、填空题1、当轴传递的功率一定时,轴的转速愈小,则轴受到的外力偶矩愈 ,当外力偶矩一定时,传递的功率愈大,则轴的转速愈 。
材料力学作业参考题解扭转

17.76MPa [ ]
(3)如图取坐标系,有:
T (x) m0 x
AB
l T (x) dx
m0
0 GI p
GI p
l
xdx
m0l 2
M 0l
0
2GI p 2GI p
32 389.9 40
0.064 [1
(5 /
6)4 ]
0.148弧度
8.48
3-16 如图所示,将空心圆杆(管)A套在实心圆杆B旳一端。两杆在同一横截面处有一直径 相同旳贯穿孔,但两孔旳中心线构成一β角,目前杆B上施加扭力偶使之扭转,将杆A和B旳 两孔对齐,装上销钉后卸去所施加旳扭力偶。试问两杆横截面上旳扭矩为多大?已知两杆旳 极惯性矩分别为 IpA和 IpB,且材料相同,切变模量为G。
620.7 16
0.043
49.4MPa [ ]
max 2
TDB W pDB
1432.4 16
0.073
21.3MPa [ ]
max
TAC GI pAC
180
80
32 620.7
109
180
0.044
1.77 / m [ ]
该轴满足强度与刚度要求
3-13 已知钻探机钻杆旳外径D=60mm,内径d=50mm,功率P=7.35kW,转速n=180r/min,钻 杆入土深度l=40m,材料旳G=80GPa,[ τ ]=40MPa。假设土壤对钻杆旳阻力沿长度均匀分布, 试求:(1)单位长度上土壤对钻杆旳阻力矩;(2)作钻杆旳扭矩图,并进行强度校核; (3)A、B两截面旳相对扭转角。
d 4
d 8
32 100 103
8 0.13
127MPa
材料力学专项习题练习扭转

扭 转1. 一直径为1D 的实心轴,另一内径为d , 外径为D , 内外径之比为22d D α=的空心轴,若两轴横截面上的扭矩和最大切应力均分别相等,则两轴的横截面面积之比12/A A 有四种答案:(A) 21α-; (B)(C); (D)。
2. 圆轴扭转时满足平衡条件,但切应力超过比例极限,有下述四种结论: (A) (B) (C) (D) 切应力互等定理: 成立 不成立 不成立 成立 剪切胡克定律: 成立 不成立 成立 不成立3. 一内外径之比为/d D α=的空心圆轴,当两端承受扭转力偶时,若横截面上的最大切应力为τ,则内圆周处的切应力有四种答案:(A) τ ; (B) ατ; (C) 3(1)ατ-; (D) 4(1)ατ-。
4. 长为l 、半径为r 、扭转刚度为p GI 的实心圆轴如图所示。
扭转时,表面的纵向线倾斜了γ角,在小变形情况下,此轴横截面上的扭矩T 及两端截面的相对扭转角ϕ有四种答案:7. 图示圆轴料的切变模量(A) 43π128d G a ϕ(C) 43π32d G a ϕ8. 一直径为D重量比21W W 9. 想弹塑性材料, 等直圆轴的极限扭矩是刚开始出现塑性变形时扭矩的 倍。
10. 矩形截面杆扭转变形的主要特征是 。
1-10题答案:1. D 2. D 3. B 4. C 5. B 6. C 7. B 8. 0.479. 横截面上的切应力都达到屈服极限时圆轴所能承担的扭矩;4/3 10. 横截面翘曲11. 已知一理想弹塑性材料的圆轴半径为R ,扭转加载到整个截面全部屈服,将扭矩卸掉所产生的残余应力如图所示,试证明图示残余应力所构成的扭矩为零。
证:截面切应力 4103s R R ρρττρ⎛⎫=-≤≤ ⎪⎝⎭截面扭矩 04d 12πd 03Rs s A T A R ρρτρτρρ⎛⎫==-⋅= ⎪⎝⎭⎰⎰ 证毕。
12. 图示直径为d 的实心圆轴,两端受扭转力偶e M 用1/m C τγ=表示,式中C ,m 为由实验测定的已知常数,试证明该轴的扭转切应力计算公式为:1/e (31)/2π()23m 1mm mM m d ρρτ+=+s /3证:几何方面 d d xρϕγρ= 物理方面 1/1/d d mmC C x ρϕτγρ⎛⎫== ⎪⎝⎭静力方面 1//21/e 0d d 2πd d md mAM T A C x ρϕρτρρρρ⎛⎫==⋅⋅=⋅⋅ ⎪⎝⎭⎰⎰1//221/0d 2πd d m d mC x ϕρρ+⎛⎫= ⎪⎝⎭⎰(31)/1/()d 22π(31)d m mmd C m x mϕ+⎛⎫= ⎪+⎝⎭1/e (31)/(31)d d 2π()2mm m M m d x Cm ϕ++⋅⎛⎫=⎪⎝⎭⋅ 所以 1/e (31)/2π()23m 1mm mM m d ρρτ+=+ 证毕。
电气工程师-公共基础-材料力学-扭转

电气工程师-公共基础-材料力学-扭转[单选题]1.已知实心圆轴按强度条件可承担的最大扭矩为T,若改变该轴的直径,使其横截面积增加1倍。
则可承担的最大扭矩为()。
[2019年真(江南博哥)题]A.B.2TC.D.4T正确答案:C参考解析:扭转剪应力公式为:。
式中,Wp为抗扭截面系数,且。
当横截面面积增加一倍时,直径变为原来的倍。
根据扭转剪应力公式,当最大剪应力不变时,直径变为原来的倍时,可承受的最大扭矩为。
[单选题]2.圆轴直径为d,剪切弹性模量为G,在外力作用下发生扭转变形,现测得单位长度扭转角为θ,圆轴的最大切应力是()。
[2013、2010年真题]A.τ=(16θG)/(πd3)B.τ=(θGπd3)/16C.τ=θGdD.τ=θGd/2正确答案:D参考解析:由公式θ=T/(GIp)得:T=θGIp。
其中,Ip=(d/2)·Wp。
则最大切应力τ=T/Wp=GθIp/Wp=θGd/2。
[单选题]3.在一套传动系统中,有多根圆轴,假设所有圆轴传递的功率相同,转速不同。
该系统的圆轴转速与其扭矩的关系是()。
[2016、2014年真题]A.转速快的轴扭矩大B.转速慢的轴扭矩大C.全部轴的扭矩相同D.无法确定正确答案:B参考解析:根据公式T=9550P/n可知,在功率相同的情况下转速慢的轴扭矩大。
式中,T为扭矩(N·m);P为功率(kW);n为转速(r/min);9550为常系数。
[单选题]4.图5-3-1所示两根圆轴,横截面面积相同,但分别为实心圆和空心圆。
在相同的扭矩T作用下,两轴最大切应力的关系是()。
[2013年真题]图5-3-1A.τa<τbB.τa=τbC.τa>τbD.不能确定正确答案:C参考解析:设d1为实心圆直径,D2为空心圆截面外径,d2为空心圆截面内径,α2=d2/D2。
由最大切应力公式τmax=T/WP,由两轴截面面积相等得:πd12/4=πD22(1-α22)/4,即:实心圆截面的抗扭截面系数WPa=πd13/16;空心圆截面的WPb=πD23(1-α24)/16,因此两轴的抗扭截面系数之比为:故τa>τb。
材料力学 扭转 题目+详解

3-2. 作出图示各杆的扭矩图。
解: (a)(1)用截面法求内力截面1-1eeXMT T Mm-=∴=--=∑110截面2-2eeeXMT T MMm20022-=∴=---=∑(2)画扭矩图(b )(1)用截面法求内力截面1-1eeXMT T Mm-=∴=+=∑110截面2-2(a)2xeeeXMT T MMm203 022=∴=+-=∑(2)画扭矩图(c )(1)用截面法求内力截面1-1kNT T mX30030 011-=∴=--=∑截面2-2kNT T mX1003020 012-=∴=--=∑截面3-3kNT T mX50302015 033=∴=--+=∑截面4-4kNT T mX15030201510 044=∴=--++=∑(2)画扭矩图T 4 4T(kNm)x3-8. 阶梯形圆轴直径分别为d 1=40mm ,d 2=70mm ,轴上装有三个皮带轮。
已知由轮3输入的功率为N 3=30kW,轮1输出的功率为N 1=13kW ,轴作匀速转动,转速n=200 r/min ,材料的许用剪应力[τ]=60MPa ,G=80GPa ,许用扭转角[θ]=2o /m 。
试校核轴的强度和刚度。
解:(1)计算外力扭矩NmnN MNmn N M4.143220030954995497.62020013954995493311=⨯===⨯==(2)计算内力扭矩NmMT Nm M T 4.14327.620332121====--(3)计算抗扭截面模量36322363111031.67161056.1216md πWm d πW t t --⨯==⨯==(4)强度校核MPaWT τMPaWT τt t 28.2142.492322max 1211max ====--强度足够。
(5)刚度校核][/77.1180211max θm πGIT θoop=⨯=-刚度足够。
2163d πR Md oo==3-19. 钻头简化成直径为20mm 的圆截面杆,在头部受均布阻抗扭矩m 的作用,许用剪应力为[τ]=70MPa 。
材料力学第3章扭转习题及答案

材料力学第3章扭转习题及答案第三章扭转一、判断题1.杆件受扭时,横截面上的最大切应力发生在距截面形心最远处。
(× ) 2.薄壁圆管和空心圆管的扭转切应力公式完全一样。
(× )3.圆杆扭转变形实质上是剪切变形。
(√ )4.非圆截面杆不能应用圆截面杆扭转切应力公式,是因为非圆截面杆扭转时“平截面假设”不能成立。
(√ )5.材料相同的圆杆,它们的剪切强度条件和扭转强度条件中,许用应力的意义相同,数值相等。
(× ) 6.切应力互等定理,仅适用于纯剪切情况。
(× ) 7.受扭杆件的扭矩,仅与杆件受到的转矩(外力偶矩)有关,而与杆件的材料及其横截面的大小、形状无关。
( √ ) 8.受扭圆轴在横截面上和包含轴的纵向截面上均无正应力。
(√ ) 9.受扭圆轴的最大切应力只出现在横截面上。
(× ) 10.因木材沿纤维方向的抗剪能力差,故若受扭木质圆杆的轴线与木材纤维方向平行,当扭矩达到某一极限值时,圆杆将沿轴线方向出现裂纹。
(√ )二、填空题1.一级减速箱中的齿轮直径大小不等,在满足相同的强度条件下,高速齿轮轴的直径要比低速齿轮轴的直径(小)。
2.当实心圆轴的直径增加1培时,其抗扭强度增加到原来的( 8 )倍,抗扭刚度增加到原来的( 16 )倍。
3.直径D=50mm 的圆轴,受扭矩T=2.15kn.m ,该圆轴横截面上距离圆心10mm 处的剪应力τ=(35.0 MPa ),最大剪应力τmax=(87.6 MPa )。
4.一根空心轴的内外径分别为d ,D ,当D=2d 时,其抗扭截面模量为(33256153215D d ππ或)。
5.直径和长度均相等的两根轴,在相同的扭矩作用下,而材料不同,它们的τmax 是(相)同的,扭转角φ是(不)同的。
6.等截面圆轴扭转时的单位长度相对扭转角为θ,若圆轴直径增大一倍,则单位长度扭转角将变为(16θ)。
三、选择题1.内、外径之比为α的空心圆轴,扭转时轴内的最大切应力为τ ,这时横截面上内边缘的切应力为( B )。
材料力学 扭转习题

IP2
T1 G1IP1 T2 G2IP2
2
1
扭转练习题
圆轴由两种材料组成,其剪切模量分别为G1和G2。设受扭时二者 之间无相对滑动,G1 2G2,则其横截面上的剪应力分布为( )。
T oG1 G2 d
G1 o G2
( A)
G1 o G2
(B)
D
答案: D
G1 o G2
(C )
处于线弹性、小变形状态,则(c)加载情况下的应力
与变形等于(a)和(b)两种情况的叠加。 ( )
m1
d l
m2
d l/2 l/2
m2 m1
d l/2 l/2
(a)
(b)
(c)
答案:
一内径为d、外径为D=2d的空心圆管与一直径为d的实
心圆杆结合成一组合圆轴,共同承受转矩Me。圆管与圆 杆的材料不同,其切变模量分别为G1和G2,且G1=G2/2, 假设两杆扭转变形时无相对转动,且均处于线弹性范围。
扭转练习题
一、填空
1.空心圆轴外径为D,内径为d=D/2,两端受扭转力偶 mx 作 用,则其横截面上剪应力呈( )分布, max ( ), min ( )。
答案:
线性,12556mDx3
,1
/
2
。
max
2.圆截面杆扭转时,其变形特点是变形过程中横截面始 终保持( ),即符合( )。非圆截面杆扭转时,其 变形特点是变形过程中横截面发生( ),即不符合 ( )。
试问两杆横截面上的最大切应力之比τ1/τ2为多大?并画 出沿半径方向的切应力变化规律。
因两杆扭转变形时无相对转动
Me 1 2
1 2
T1
D 2
材料力学扭转习题
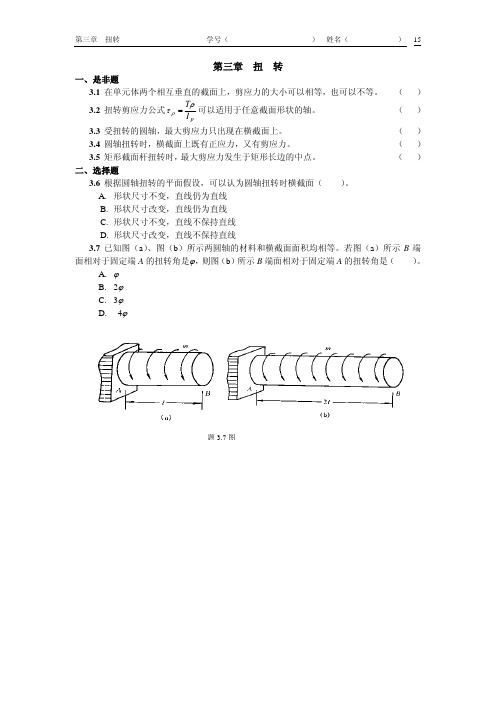
第三章 扭 转一、是非题3.1 在单元体两个相互垂直的截面上,剪应力的大小可以相等,也可以不等。
( )3.2 扭转剪应力公式pI T ρτρ=可以适用于任意截面形状的轴。
( ) 3.3 受扭转的圆轴,最大剪应力只出现在横截面上。
( )3.4 圆轴扭转时,横截面上既有正应力,又有剪应力。
( )3.5 矩形截面杆扭转时,最大剪应力发生于矩形长边的中点。
( )二、选择题3.6 根据圆轴扭转的平面假设,可以认为圆轴扭转时横截面( )。
A. 形状尺寸不变,直线仍为直线B. 形状尺寸改变,直线仍为直线C. 形状尺寸不变,直线不保持直线D. 形状尺寸改变,直线不保持直线3.7 已知图(a )、图(b )所示两圆轴的材料和横截面面积均相等。
若图(a )所示B 端面相对于固定端A 的扭转角是ϕ,则图(b )所示B 端面相对于固定端A 的扭转角是( )。
A.ϕ B.2ϕ C.3ϕ D. 4ϕ题3.7图三、计算题3.8作图示各杆的扭转图(图c中各量单位kN •m)。
101530m m m 3m20(a) (b) (c)题3.8图3.9T为圆杆横截面上的扭矩,试画出截面上与T对应的剪应力分布图。
(a) (b)(c)题3.9图3.10 发电量为15000kW 的水轮机主轴如图所示。
D = 550 mm ,d = 300 mm ,正常转速n = 250 r/min 。
材料的许用剪应力 [τ] = 50MPa 。
试校核水轮机主轴的强度。
3.11 阶梯形圆轴直径分别为d 1=40 mm ,d 2=70 mm ,轴上装有三个皮带轮,如图所示。
已知由轮3输入的功率为N 3=30 kW ,轮1输出的功率为N 1=13kW ,轴作匀速转动,转速n =200r/min ,材料的剪切许用应力[]τ=60 MPa ,G =80 GPa ,许用扭转角[]ϕ=2°/m 。
试校核轴的强度和刚度。
题3.10图 题3.11图3.12 实心轴和空心轴通过牙嵌式离合器连接在一起。
材料力学作业扭转

3、如图所示,截面积相等、材料相同的两轴,用牙嵌式 离 合 器 连 接 。 左 端 为 空 心 轴 , 外 径 d1=50mm, 内 径 d2=30mm,轴材料的〔τ〕=65MPa,工作时所受力偶 矩 M=1000N·m,试校核左、右两端轴的强度。如果 强度不够,轴径应增加到多少?
第四章扭转
班级(
A 1/4,1/16 B 1/8,1/16 C 1/8,1/64 D 8,16 3.下列结论中正确的是( ) 。 A.圆轴扭转时,横截面上有正应力,其大小与截面直径无关 B.圆轴扭转时,截面上有正应力,也有切应力,其大小均与截面直径无关 C.圆轴扭转时,横截面上只有切应力,其大小与到圆心的距离成正比 4.如图所示,圆轴扭转时,下列切应力分布图正确的是( ) 。
T 可以适用于任意截面形状的轴。 IP
(
3 受扭转的圆轴,最大切应力只出现在横截面上。 ( ) 4 圆轴扭转时,横截面上既有正应力,又有切应力。 ( ) 5 矩形截面杆扭转时,最大切应力发生于矩形长边的中点。 ( ) 二、选择或填空 1、 .图示的圆轴,用截面法求扭矩,无论取哪一段作为研究对象,其同一截面的扭矩大小与 符号( ) 。 a.完全相同 b.正好相反 c.不能确定 2、两根圆轴,材料相同,受力相同,而直径不同,当 d1=2d2 时,则两轴的最大切应力之比 τ1/τ2= ,单位扭转角 1 / 2 。
第四章扭转
班级(
)学号(
)姓名(
)
6、一密圈螺旋弹簧,承受轴向载荷 F=1kN 作用。设弹簧的平均直径 D=40mm,弹簧丝的直 径 d=7mm,许用应力〔τ〕受扭力矩作用。求支反力偶距。扭转刚度为已知常熟。
A
B
C
D
5.实心圆轴扭转时,横截面上的最小切应力( ) 。 A.一定为零 B.一定不为零 C.可能为零,也可能不为零 6.空心圆轴扭转时, 横截面上的最小切应力( ) 。 A.一定为零 B.一定不为零 C.可能为零,也可能不为零
材料力学习题扭转知识分享

材料力学习题扭转扭转基本概念题一、选择题(如果题目有5个备选答案,选出2~5个正确答案,有4个备选答案选出一个正确答案。
)1.图示传动轴,主动轮A的输入功率为P A = 50 kW,从动轮B,C,D,E 的输出功率分别为P B = 20 kW,P C = 5 kW,P D = 10 kW,P E = 15 kW。
则轴上T出现在( )。
最大扭矩maxA.BA段B.AC段C.CD段D.DE段题1图2.图示单元体的应力状态中属正确的纯剪切状态的是()。
题2图3.上题图示单元体的应力状态中属正确的是()。
4.下列关于剪应力互等定理的论述中正确的是()。
A.剪应力互等定理是由平衡B.剪应力互等定理仅适用于纯剪切的情况C . 剪应力互等定理适用于各种受力杆件D .剪应力互等定理仅适用于弹性范围E .剪应力互等定理与材料的性能无关 5. 图示受扭圆轴,其横截面上的剪应力分布图正确的是( )。
-12-题5图6. 实心圆轴,两端受扭转外力偶作用。
直径为D 时,设轴内的最大剪应力为τ,若轴的直径改为2D ,其它条件不变,则轴内的最大剪应力变为( )。
A .τ8B .τC .τ16D .16τ7. 受扭空心圆轴(D d =α),在横截面积相等的条件下,下列承载能力最大的轴是( )。
A .0=α(实心轴)B .5.0=αC .6.0=αD .8.0=α8. 扭转应力公式ρτρpI T =的适用范围是( )。
A .各种等截面直杆 B .实心或空心圆截面直杆C .矩形截面直杆D .弹性变形E .弹性非弹性范围9. 直径为D 的实心圆轴,最大的容许扭矩为T ,若将轴的横截面积增加一倍,则其最大容许扭矩为( )。
A .T 2B .T 2C .T 22D .T 410. 材料相同的两根圆轴,一根为实心,直径为1D ;另一根为空心,内径为2d ,外径为2D ,α=22D d 。
若两轴横截面上的扭矩T ,和最大剪应力m ax τ均相同,则两轴外径之比21D D 为( )。
材料力学习题册答案-第3章 扭转(完整资料).doc

此文档下载后即可编辑第三章扭转一、是非判断题1.圆杆受扭时,杆内各点处于纯剪切状态。
(×)2.杆件受扭时,横截面上的最大切应力发生在距截面形心最远处。
(×)3.薄壁圆管和空心圆管的扭转切应力公式完全一样。
(×)4.圆杆扭转变形实质上是剪切变形。
(×)5.非圆截面杆不能应用圆截面杆扭转切应力公式,是因为非圆截面杆扭转时“平截面假设”不能成立。
(√)6.材料相同的圆杆,他们的剪切强度条件和扭转强度条件中,许用应力的意义相同,数值相等。
(×)7.切应力互等定理仅适用于纯剪切情况。
(×)8.受扭杆件的扭矩,仅与杆件受到的转矩(外力偶矩)有关,而与杆件的材料及其横截面的大小、形状无关。
(√)9.受扭圆轴在横截面上和包含轴的纵向截面上均无正应力。
(√)10.受扭圆轴的最大切应力只出现在横截面上。
(×)11.受扭圆轴内最大拉应力的值和最大切应力的值相等。
(√ )12.因木材沿纤维方向的抗剪能力差,故若受扭木质圆杆的轴线与木材纤维方向平行,当扭距达到某一极限值时,圆杆将沿轴线方向出现裂纹。
( × )二、选择题1.内、外径之比为α的空心圆轴,扭转时轴内的最大切应力为τ,这时横截面上内边缘的切应力为 ( B )A τ;B ατ;C 零;D (1- 4α)τ 2.实心圆轴扭转时,不发生屈服的极限扭矩为T ,若将其横截面面积增加一倍,则极限扭矩为( C )A0 B 20T 0 D 40T 3.两根受扭圆轴的直径和长度均相同,但材料C 不同,在扭矩相同的情况下,它们的最大切应力τ、τ和扭转角ψ、ψ之间的关系为( B )A 1τ=τ2, φ1=φ2B 1τ=τ2, φ1≠φ2C 1τ≠τ2, φ1=φ2D 1τ≠τ2, φ1≠φ2 4.阶梯圆轴的最大切应力发生在( D )A 扭矩最大的截面;B 直径最小的截面;C 单位长度扭转角最大的截面;D 不能确定。
材料力学专项习题练习扭转

扭 转1. 一直径为1D 的实心轴,另一内径为d , 外径为D , 内外径之比为22d D α=的空心轴,若两轴横截面上的扭矩和最大切应力均分别相等,则两轴的横截面面积之比12/A A 有四种答案:(A) 21α-; (B)(C); (D)。
2. 圆轴扭转时满足平衡条件,但切应力超过比例极限,有下述四种结论: (A) (B) (C) (D) 切应力互等定理: 成立 不成立 不成立 成立 剪切胡克定律: 成立 不成立 成立 不成立3. 一内外径之比为/d D α=的空心圆轴,当两端承受扭转力偶时,若横截面上的最大切应力为τ,则内圆周处的切应力有四种答案:(A) τ ; (B) ατ; (C) 3(1)ατ-; (D) 4(1)ατ-。
4. 长为l 、半径为r 、扭转刚度为p GI 的实心圆轴如图所示。
扭转时,表面的纵向线倾斜了γ角,在小变形情况下,此轴横截面上的扭矩T 及两端截面的相对扭转角ϕ有四种答案:料的切变模量(A) 43π128d G a ϕ(C) 43π32d G a ϕ8. 一直径为D 重量比21W W 9. 10. 矩形截面杆扭转变形的主要特征是 。
1-10题答案:1. D 2. D 3. B 4. C 5. B 6. C 7. B 8. 0.479. 横截面上的切应力都达到屈服极限时圆轴所能承担的扭矩;4/3 10. 横截面翘曲11. 已知一理想弹塑性材料的圆轴半径为R ,扭转加载到整个截面全部屈服,将扭矩卸掉所产生的残余应力如图所示,试证明图示残余应力所构成的扭矩为零。
证:截面切应力 4103s R R ρρττρ⎛⎫=-≤≤ ⎪⎝⎭截面扭矩 04d 12πd 03Rs s A T A R ρρτρτρρ⎛⎫==-⋅= ⎪⎝⎭⎰⎰ 证毕。
12. 图示直径为d 的实心圆轴,两端受扭转力偶e M 用1/m C τγ=表示,式中C ,m 式为:证:几何方面 d d xρϕγρ=物理方面 1/1/d d mmC C x ρϕτγρ⎛⎫== ⎪⎝⎭静力方面 1//21/e 0d d 2πd d md mAM T A C x ρϕρτρρρρ⎛⎫==⋅⋅=⋅⋅ ⎪⎝⎭⎰⎰所以 1/e (31)/2π()23m 1mm mM m d ρρτ+=+ 证毕。
材料力学习题扭转

扭转基本概念题一、选择题(如果题目有5个备选答案,选出2~5个正确答案,有4个备选答案选出一个正确答案。
)1.图示传动轴,主动轮A的输入功率为P A = 50 kW,从动轮B,C,D,E的输出功率T出现在分别为P B = 20 kW,P C = 5 kW,P D = 10 kW,P E = 15 kW。
则轴上最大扭矩max ( )。
A.BA段B.AC段C.CD段D.DE段题1图2.图示单元体的应力状态中属正确的纯剪切状态的是()。
题2图3.上题图示单元体的应力状态中属正确的是()。
4.下列关于剪应力互等定理的论述中正确的是()。
A.剪应力互等定理是由平衡B.剪应力互等定理仅适用于纯剪切的情况C.剪应力互等定理适用于各种受力杆件D.剪应力互等定理仅适用于弹性范围E.剪应力互等定理与材料的性能无关5.图示受扭圆轴,其横截面上的剪应力分布图正确的是( )。
-12-题5图6. 实心圆轴,两端受扭转外力偶作用。
直径为D 时,设轴内的最大剪应力为τ,若轴的直径改为2D ,其它条件不变,则轴内的最大剪应力变为( )。
A .τ8B .8τC .τ16D .16τ7. 受扭空心圆轴(D d =α),在横截面积相等的条件下,下列承载能力最大的轴是( )。
A .0=α(实心轴)B .5.0=αC .6.0=αD .8.0=α8. 扭转应力公式ρτρpI T =的适用范围是( )。
A .各种等截面直杆 B .实心或空心圆截面直杆C .矩形截面直杆D .弹性变形E .弹性非弹性范围9. 直径为D 的实心圆轴,最大的容许扭矩为T ,若将轴的横截面积增加一倍,则 其最大容许扭矩为( )。
A .T 2B .T 2C .T 22D .T 410. 材料相同的两根圆轴,一根为实心,直径为1D ;另一根为空心,内径为2d ,外径为2D ,α=22D d 。
若两轴横截面上的扭矩T ,和最大剪应力m ax τ均相同,则两轴外径之比21D D 为( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
扭 转
1. 一直径为1D 的实心轴,另一内径为d , 外径为D , 内外径之比为22d D α=的空心轴,若两轴横截面上的扭矩和最大切应力均分别相等,则两轴的横截面面积之比12/A A 有四种答案:
(A) 2
1α-; (B)
(C)
; (D)。
2. 圆轴扭转时满足平衡条件,但切应力超过比例极限,有下述四种结论: (A) (B) (C) (D) 切应力互等定理: 成立 不成立 不成立 成立 剪切胡克定律: 成立 不成立 成立 不成立
3. 一内外径之比为/d D α=的空心圆轴,当两端承受扭转力偶时,若横截面上的最大切应力为τ,则内圆周处的切应力有四种答案:
(A) τ ; (B) ατ; (C) 3(1)ατ-; (D) 4(1)ατ-。
4. 长为l 、半径为r 、扭转刚度为p GI 的实心圆轴如图所示。
扭转时,表面的纵向线倾斜了γ角,在小变形情况下,此轴横截面上的扭矩T 及两端截面的相对扭转角ϕ有四种答案:
料的切变模量(A) 43π128d G a ϕ(C) 43π32d G a ϕ
8. 一直径为D 重量比21W W 9. 10. 矩形截面杆扭转变形的主要特征是 。
1-10题答案:1. D 2. D 3. B 4. C 5. B 6. C 7. B 8. 0.47
9. 横截面上的切应力都达到屈服极限时圆轴所能承担的扭矩;4/3 10. 横截面翘曲
11. 已知一理想弹塑性材料的圆轴半径为R ,扭转加载到整个截面全部屈服,将扭矩卸掉所产生的残余应力如图所示,试证明图示残余应力所构成的扭矩为零。
证:截面切应力 41
03s R R ρρττρ⎛⎫
=-≤≤ ⎪⎝⎭
截面扭矩 0
4d 12
πd 03R
s s A T A R ρρτρτρρ⎛⎫
==-⋅= ⎪⎝⎭⎰⎰ 证毕。
12. 图示直径为d 的实心圆轴,两端受扭转力偶e M 用1/m C τγ=表示,式中C ,m 式为:
证:几何方面 d d x
ρϕ
γρ=
物理方面 1/1/d d m
m
C C x ρϕτγ
ρ⎛⎫== ⎪
⎝⎭
静力方面 1//2
1/e 0
d d 2πd d m
d m
A
M T A C x ρϕρτρρ
ρρ⎛⎫==⋅⋅=
⋅⋅ ⎪⎝⎭
⎰⎰
所以 1/e (31)/2π()2
3m 1m
m m
M m d ρρτ+=+ 证毕。
13. 薄壁圆管扭转时的切应力公式为202πT
R τδ
=
(0R 为圆管的平均半径,δ为壁厚),试
证明,当010R δ≥时,该公式的最大误差不超过4.53%。
证:薄壁理论 202πT
R τδ
=
精确扭转理论:
误差 2
2max 0max max
41124R R δτττ
εδττ+
-==-=-
+
当010R δ≥时, 1
41001 4.53%145
ε+
≤-
=+ 证毕。
14. 在相同的强度条件下,用内外径之比0.5d D =的空心圆轴取代实心圆轴,可节省材料的百分比为多少?
解:设空心轴内外直径分别为22,d D ,实心轴直径为1d 节省材料
2212
22
1
1(1)121.7%A A D A d α--=-=
15. 一端固定的圆轴受集度为m 的均布力偶作用,发生扭转变形,已知材料的许用应力
][τ,若要求轴为等强度轴,试确定轴直径沿轴向变化的表达式()d x 。
解:取自由端为x 轴原点,x 轴沿轴线方向,则
扭矩方程 ()T x m x = 最大切应力 m a x 3p ()[]π()()16
T x m x
W x d x ττ=
==。
