2011年江苏省南京市中考数学试题(解析版)

合集下载

南京中考数学试题及答案word版

南京市2011年初中毕业生学业考试数学1．．一、选择题（本大题共6小题，每小题2分，共12分，在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确的选项的字母代号填涂在答．题卡相应位置．．．．．．上） 1A ．3B ．－3C ．±3D ．2．下列运算正确的是A ．a 2＋a 3=a 5B ．a 2•a 3=a 6C ．a 3÷a 2=aD ．(a 2)3=a 83．在第六次全国人口普查中，南京市常住人口约为800万人，其中65岁及以上人口占9.2%．则该市65岁及以上人口用科学记数法表示约为 A ．0.736×106人 B ．7.36×104人 C ．7.36×105人 D ．7.36×106 人 4．为了解某初中学校学生的视力情况，需要抽取部分学生进行调查，下列抽取学生的方法最合适的是A ．随机抽取该校一个班级的学生B ．随机抽取该校一个年级的学生C ．随机抽取该校一部分男生D ．分别从该校初一、初二、初三年级中各班随机抽取10%的学生 5．如图是一个三棱柱，下列图形中，能通过折叠围成一个三棱柱的是6．如图，在平面直角坐标系中，⊙P 的圆心是（2，a ）(a ＞2)，半径为2，函数y =x 的图象被⊙P 的弦AB的长为a 的值是 A．B．2+C．D．2二、填空题（本大题共10小题，每小题2分，共20分，不需要写出解答过程，请把答案直接填写在答题卡相应位置．．．．．．．上） 7．－2的相反数是________．8．如图，过正五边形ABCDE 的顶点A 作直线l ∥CD ，则∠1=____________．A ．BD ．(第5题)9．计算1)(2=_______________．10．等腰梯形的腰长为5㎝，它的周长是22㎝，则它的中位线长为___________㎝．11．如图，以O 为圆心，任意长为半径画弧，与射线OM 交于点A ，再以A 为圆心，AO 长为半径画弧，两弧交于点B ，画射线OB ，则cos ∠AOB 的值等于___________．12．如图，菱形ABCD 的连长是2㎝，E 是AB 中点，且DE ⊥AB ，则菱形ABCD 的面积为_________㎝2．13．如图，海边有两座灯塔A 、B ，暗礁分布在经过A 、B 两点的弓形（弓形的弧是⊙O 的一部分）区域内，∠AOB =80°，为了避免触礁，轮船P 与A 、B 的张角∠APB 的最大值为______°．14．如图，E 、F 分别是正方形ABCD 的边BC 、CD 上的点，BE =CF ，连接AE 、BF ，将△ABE 绕正方形的中心按逆时针方向转到△BCF ，旋转角为a （0°＜a ＜180°），则∠a =______． 15．设函数2y x =与1y x =-的图象的交战坐标为（a ，b ），则11a b-的值为__________． 16．甲、乙、丙、丁四位同学围成一圈依序循环报数，规定：①甲、乙、丙、丁首次报出的数依次为1、2、3、4，接着甲报5、乙报6……按此规律，后一位同学报出的数比前一位同学报出的数大1，当报到的数是50时，报数结束； ②若报出的数为3的倍数，则报该数的同学需拍手一次，在此过程中，甲同学需要拍手的次数为____________．三、解答题（本大题共12小题，共88分，请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）17．（6分）解不等式组523132x x x +⎧⎪+⎨⎪⎩≥＞，并写出不等式组的整数解．18．（6分）计算221()a b a b a b b a-÷-+-(第12题)(第8题)l (第11题)BA MO(第12题)A(第14题)ABCDF19．（6分）解方程x 2－4x ＋1=0 20．（7分）某校部分男生分3组进行引体向上训练，对训练前后的成绩进行统计分析，相应数据的统计图如下．⑴求训练后第一组平均成绩比训练前增长的百分数； ⑵小明在分析了图表后，声称他发现了一个错误：“训练后第二组男生引体向上个数没有变化的人数占该组人数的50%，所以第二组的平均数不可能提高3个这么多．”你同意小明的观点吗？请说明理由；⑶你认为哪一组的训练效果最好？请提出一个解释来支持你的观点．21．（7分）如图，将□ABCD 的边DC 延长到点E ，使CE =DC ，连接AE ，交BC 于点F ．⑴求证：△ABF ≌△ECF⑵若∠AFC =2∠D ，连接AC 、BE ．求证：四边形ABEC 是矩形．22．（7分）小颖和小亮上山游玩，小颖乘会缆车，小亮步行，两人相约在山顶的缆车终点会合．已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍，小颖在小亮出发后50 min 才乘上缆车，缆车的平均速度为180 m /min ．设小亮出发x min 后行走的路程为y m ．图中的折线表示小亮在整个行走过程中y 与x 的函数关系．⑴小亮行走的总路程是____________㎝，他途中休息了________min ． ⑵①当50≤x ≤80时，求y 与x 的函数关系式；②当小颖到达缆车终点为时，小亮离缆车终点的路程是多少？①训练前后各组平均成绩统计图训练后第二组男生引体向上增加个数分布统计图增加85个②(第20题)B D E (第21题)23．（7分）从3名男生和2名女生中随机抽取2014年南京青奥会志愿者．求下列事件的概率：⑴抽取1名，恰好是女生；⑵抽取2名，恰好是1名男生和1名女生．24．（7分）已知函数y =mx 2－6x ＋1（m 是常数）．⑴求证：不论m 为何值，该函数的图象都经过y 轴上的一个定点； ⑵若该函数的图象与x 轴只有一个交点，求m 的值．25．（7分）如图，某数学课外活动小组测量电视塔AB 的高度，他们借助一个高度为30m的建筑物CD 进行测量，在点C 处塔顶B 的仰角为45°，在点E 处测得B 的仰角为37°（B 、D 、E 三点在一条直线上）．求电视塔的高度h ．（参考数据：sin 37°≈0.60，cos 37°≈0.80，tan 37°≈0.75）26．（8分）如图，在Rt △ABC 中，∠ACB =90°，AC =6㎝，BC =8㎝，P 为BC 的中点．动点Q 从点P 出发，沿射线PC 方向以2㎝/s 的速度运动，以P 为圆心，PQ 长为半径作圆．设点Q 运动的时间为t s ．⑴当t =1.2时，判断直线AB 与⊙P 的位置关系，并说明理由； ⑵已知⊙O 为△ABC 的外接圆，若⊙P 与⊙O 相切，求t 的值．Bh (第25题)(第22题)27．（9分）如图①，P 为△ABC 内一点，连接P A 、PB 、PC ，在△P AB 、△PBC 和△P AC 中，如果存在一个三角形与△ABC 相似，那么就称P 为△ABC 的自相似点．⑴如图②，已知Rt △ABC 中，∠ACB =90°，∠ACB ＞∠A ，CD 是AB 上的中线，过点B 作BE ⊥CD ，垂足为E ，试说明E 是△ABC 的自相似点．⑵在△ABC 中，∠A ＜∠B ＜∠C ．①如图③，利用尺规作出△ABC 的自相似点P （写出作法并保留作图痕迹）； ②若△ABC 的内心P 是该三角形的自相似点，求该三角形三个内角的度数．28．（11分）问题情境已知矩形的面积为a （a 为常数，a ＞0），当该矩形的长为多少时，它的周长最小？最小值是多少？数学模型设该矩形的长为x ，周长为y ，则y 与x 的函数关系式为2()(0)a y x x x=+＞．探索研究⑴我们可以借鉴以前研究函数的经验，先探索函数1(0)y x x x=+＞的图象性质． ① 填写下表，画出函数的图象：(第26题)①②③(第27题)②观察图象，写出该函数两条不同类型的性质；③在求二次函数y =ax 2＋bx ＋c （a ≠0）的最大（小）值时，除了通过观察图象，还可以通过配方得到．请你通过配方求函数1y x x=+(x ＞0)的最小值．解决问题⑵用上述方法解决“问题情境”中的问题，直接写出答案．答案：一.选择题：ACCDBB 二.填空：7. 2 8. 36 9.10. 6 11.1212. 13. 40 14. 90 15. 12- 16. 4 17.解：解不等式①得：1x ≥- 解不等式②得：2x <所以，不等式组的解集是12x -≤<．不等式组的整数解是1-，0，1． 18.221)a ba b a b b a-÷-+-解：（()()()()a a b ba b a b a b a b b a⎡⎤-=-÷⎢⎥+-+--⎣⎦ ()()b b aa b a b b-=⋅+-1a b=-+ 19. 解法一：移项，得241x x -=-．配方，得24414x x -+=-+， 2(2)3x -=由此可得2x -=12x =22x =解法二：1,4, 1.a b c ==-=224(4)411120b ac -=--⨯⨯=>，422x ±==±12x =，22x =．20.解：⑴训练后第一组平均成绩比训练前增长的百分数是53100%3-⨯≈67%． ⑵不同意小明的观点，因为第二组的平均成绩增加8×10%+6×20%+5×20%+0×50%=3（个）．（3）本题答案不唯一，我认为第一组训练效果最好，因为训练后第一组平均成绩比训练前增长的百分数最大．21.证明：⑴∵四边形ABCD 是平行四边形，∴AB ∥CD,AB=CD ．∴∠ABF=∠ECF . ∵EC=DC , ∴AB=EC ．在△ABF 和△ECF 中，∵∠ABF=∠ECF ，∠AFB=∠EFC ，AB=EC ， ∴⊿ABF ≌⊿ECF ．（2）解法一：∵AB=EC ，AB ∥EC ，∴四边形ABEC 是平行四边形．∴AF=EF ， BF=CF ． ∵四边形ABCD 是平行四边形，∴∠ABC=∠D ，又∵∠AFC=2∠D ，∴∠AFC=2∠ABC ． ∵∠AFC=∠ABF+∠BAF ，∴∠ABF=∠BAF ．∴F A=FB ． ∴F A=FE=FB=FC , ∴AE=BC ．∴口ABEC 是矩形．解法二：∵AB=EC ，AB ∥EC ，∴四边形ABEC 是平行四边形． ∵四边形ABCD 是平行四边形，∴AD ∥BC ，∴∠D=∠BCE ．又∵∠AFC=2∠D ，∴∠AFC=2∠BCE ，∵∠AFC=∠FCE+∠FEC ，∴∠FCE=∠FEC ．∴∠D=∠FEC ．∴AE=AD ．又∵CE=DC ，∴AC ⊥DE ．即∠ACE=90°．∴口ABEC 是矩形． 22. 解⑴3600，20．⑵①当5080x ≤≤时，设y 与x 的函数关系式为y kx b =+．根据题意，当50x =时，1950y =；当80x =，3600y =．所以，y 与x 的函数关系式为55800y x =-．②缆车到山顶的路线长为3600÷2=1800（m ），缆车到达终点所需时间为1800÷180＝１0（min ）．小颖到达缆车终点时，小亮行走的时间为10＋50＝60（min ）．把60x =代入55800y x =-，得y=55×60—800=2500．所以，当小颖到达缆车终点时，小亮离缆车终点的路程是3600-2500=1100（m ）． 23. 解⑴抽取1名，恰好是女生的概率是25． ⑵分别用男1、男2、男3、女1、女2表示这五位同学，从中任意抽取2名，所有可能出现的结果有：（男1，男2），（男1，男3），（男1，女1），（男1，女2），（男2，男3），（男2，女1），（男2，女2），（男3，女1），（男3，女2），（女1，女2），共10种，它们出现的可能性相同，所有结果中，满足抽取2名，恰好是1名男生和1名女生（记为事件A ）的结果共6种，所以P （A ）=63105=． 24.解：⑴当x =0时，1y =．所以不论m 为何值，函数261y mx x =-+的图象经过y 轴上的一个定点（0，1）． ⑵①当0m =时，函数61y x =-+的图象与x 轴只有一个交点；②当0m ≠时，若函数261y mx x =-+的图象与x 轴只有一个交点，则方程2610mx x -+=有两个相等的实数根，所以2(6)40m --=，9m =．综上，若函数261y mx x =-+的图象与x 轴只有一个交点，则m 的值为0或9． 25.在Rt ECD ∆中，tan DEC ∠＝DCEC． ∴EC ＝tan DC DEC ∠≈30400.75=（m ）．在Rt BAC ∆中，∠BCA ＝45°，∴BA CA =在Rt BAE ∆中，tan BEA ∠＝BA EA ．∴0.7540hh =+．∴120h =（m ）．答：电视塔高度约为120m ． 26.解⑴直线AB 与⊙P 相切．如图，过点P 作PD ⊥AB , 垂足为D ．在Rt △A BC 中，∠ACB ＝90°，∵AC =6cm ，BC =8cm ，∴10AB cm =．∵P 为BC 的中点，∴PB =4cm ．∵∠P DB ＝∠ACB ＝90°，∠PBD ＝∠ABC ．∴△PBD ∽△ABC ． ∴PD PB AC AB =,即4610PD =，∴PD =2.4(cm) ．当 1.2t =时，2 2.4PQ t ==(cm)∴PD PQ =，即圆心P 到直线AB 的距离等于⊙P 的半径． ∴直线AB 与⊙P 相切．⑵ ∠ACB ＝90°，∴AB 为△ABC 的外切圆的直径．∴152OB AB cm ==．连接OP ．∵P 为BC 的中点，∴132OP AC cm ==． ∵点P 在⊙O 内部，∴⊙P 与⊙O 只能内切． ∴523t -=或253t -=，∴t =1或4． ∴⊙P 与⊙O 相切时，t 的值为1或4．27. 解⑴在Rt △ABC 中，∠ACB ＝90°，CD 是AB 上的中线，∴12CD AB =，∴CD =BD ．∴∠BCE ＝∠ABC ．∵BE ⊥CD ，∴∠BEC ＝90°，∴∠BEC ＝∠ACB ．∴△BCE ∽△ABC ． ∴E 是△ABC 的自相似点． ⑵①作图略．作法如下：（i ）在∠ABC 内，作∠CBD ＝∠A ；（ii ）在∠ACB 内，作∠BCE ＝∠ABC ；BD 交CE 于点P ．则P 为△ABC 的自相似点．②连接PB 、PC ．∵P 为△ABC 的内心，∴12PBC ABC ∠=∠，12PCB ACB ∠=∠． ∵P 为△ABC 的自相似点，∴△BCP ∽△ABC ．∴∠PBC ＝∠A ，∠BCP ＝∠ABC=2∠PBC =2∠A ， ∠ACB ＝2∠BCP=4∠A ．∵∠A +∠ABC+∠ACB ＝180°． ∴∠A +2∠A+4∠A ＝180°． ∴1807A ∠=．∴该三角形三个内角的度数分别为1807、3607、7207． 28. 解⑴①174，103，52，2，52，103，174．函数1y x x=+(0)x >的图象如图．②本题答案不唯一，下列解法供参考．当01x <<时，y 随x 增大而减小；当1x >时,y 随x 增大而增大；当1x =时函数1y x x =+(0)x >的最小值为2． ③1y x x =+=22+=22+-=22+，即1x =时，函数1y x x=+(0)x >的最小值为2．。

南京中考数学试题及答案word版收集资料

南京市2011年初中毕业生学业考试数学1．．一、选择题（本大题共6小题，每小题2分，共12分，在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确的选项的字母代号填涂在答题卡相应位置上）1A ．3B ．－3C ．±3D ．2．下列运算正确的是A ．a 2＋a 3=a 5B ．a 2•a 3=a 6C ．a 3÷a 2=aD ．(a 2)3=a 83．在第六次全国人口普查中，南京市常住人口约为800万人，其中65岁及以上人口占9.2%．则该市65岁及以上人口用科学记数法表示约为 A ．0.736×106人 B ．7.36×104人 C ．7.36×105人 D ．7.36×106 人 4．为了解某初中学校学生的视力情况，需要抽取部分学生进行调查，下列抽取学生的方法最合适的是A ．随机抽取该校一个班级的学生B ．随机抽取该校一个年级的学生C ．随机抽取该校一部分男生D ．分别从该校初一、初二、初三年级中各班随机抽取10%的学生 5．如图是一个三棱柱，下列图形中，能通过折叠围成一个三棱柱的是6．如图，在平面直角坐标系中，⊙P 的圆心是（2，a ）(a ＞2)，半径为2，函数y =x 的图象被⊙P 的弦AB的长为a 的值是 A．B．2+C．D．2二、填空题（本大题共10小题，每小题2分，共20分，不需要写出解答过程，请把答案直接填写在答题卡相应位置上）7．－2的相反数是________．8．如图，过正五边形ABCDE 的顶点A 作直线l ∥CD ，则∠1=____________．A ．B ．CD ．(第5题)㎝．11．如图，以O 为圆心，任意长为半径画弧，与射线OM 交于点A ，再以A 为圆心，AO 长为半径画弧，两弧交于点B ，画射线OB ，则cos ∠AOB 的值等于___________．12．如图，菱形ABCD 的连长是2㎝，E 是AB 中点，且DE ⊥AB ，则菱形ABCD 的面积为_________㎝2．13．如图，海边有两座灯塔A 、B ，暗礁分布在经过A 、B 两点的弓形（弓形的弧是⊙O 的一部分）区域内，∠AOB =80°，为了避免触礁，轮船P 与A 、B 的张角∠APB 的最大值为______°．14．如图，E 、F 分别是正方形ABCD 的边BC 、CD 上的点，BE =CF ，连接AE 、BF ，将△ABE 绕正方形的中心按逆时针方向转到△BCF ，旋转角为a （0°＜a ＜180°），则∠a =______． 15．设函数2y x =与1y x =-的图象的交战坐标为（a ，b ），则11a b-的值为__________． 16．甲、乙、丙、丁四位同学围成一圈依序循环报数，规定：①甲、乙、丙、丁首次报出的数依次为1、2、3、4，接着甲报5、乙报6……按此规律，后一位同学报出的数比前一位同学报出的数大1，当报到的数是50时，报数结束； ②若报出的数为3的倍数，则报该数的同学需拍手一次，在此过程中，甲同学需要拍手的次数为____________．三、解答题（本大题共12小题，共88分，请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）17．（6分）解不等式组523132x x x +⎧⎪+⎨⎪⎩≥＞，并写出不等式组的整数解．18．（6分）计算221()a ba b a b b a-÷-+- (第12题)(第14题)ABC DF19．（6分）解方程x 2－4x ＋1=0 20．（7分）某校部分男生分3组进行引体向上训练，对训练前后的成绩进行统计分析，相应数据的统计图如下．⑴求训练后第一组平均成绩比训练前增长的百分数； ⑵小明在分析了图表后，声称他发现了一个错误：“训练后第二组男生引体向上个数没有变化的人数占该组人数的50%，所以第二组的平均数不可能提高3个这么多．”你同意小明的观点吗？请说明理由；⑶你认为哪一组的训练效果最好？请提出一个解释来支持你的观点．21．（7分）如图，将□ABCD 的边DC 延长到点E ，使CE =DC ，连接AE ，交BC 于点F ．⑴求证：△ABF ≌△ECF⑵若∠AFC =2∠D ，连接AC 、BE ．求证：四边形ABEC 是矩形．22．（7分）小颖和小亮上山游玩，小颖乘会缆车，小亮步行，两人相约在山顶的缆车终点会合．已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍，小颖在小亮出发后50 min 才乘上缆车，缆车的平均速度为180 m /min ．设小亮出发x min 后行走的路程为y m ．图中的折线表示小亮在整个行走过程中y 与x 的函数关系．⑴小亮行走的总路程是____________㎝，他途中休息了________min ． ⑵①当50≤x ≤80时，求y 与x 的函数关系式；①训练前后各组平均成绩统计图训练后第二组男生引体向上增加个数分布统计图增加85个②(第20题)B D E (第21题)②当小颖到达缆车终点为时，小亮离缆车终点的路程是多少？23．（7分）从3名男生和2名女生中随机抽取2014年南京青奥会志愿者．求下列事件的概率：⑴抽取1名，恰好是女生；⑵抽取2名，恰好是1名男生和1名女生．24．（7分）已知函数y =mx 2－6x ＋1（m 是常数）．⑴求证：不论m 为何值，该函数的图象都经过y 轴上的一个定点； ⑵若该函数的图象与x 轴只有一个交点，求m 的值．25．（7分）如图，某数学课外活动小组测量电视塔AB 的高度，他们借助一个高度为30m的建筑物CD 进行测量，在点C 处塔顶B 的仰角为45°，在点E 处测得B 的仰角为37°（B 、D 、E 三点在一条直线上）．求电视塔的高度h ．（参考数据：sin 37°≈0.60，cos 37°≈0.80，tan 37°≈0.75）26．（8分）如图，在Rt △ABC 中，∠ACB =90°，AC =6㎝，BC =8㎝，P 为BC 的中点．动点Q 从点P 出发，沿射线PC 方向以2㎝/s 的速度运动，以P 为圆心，PQ 长为半径作圆．设点Q 运动的时间为t s ．⑴当t =1.2时，判断直线AB 与⊙P 的位置关系，并说明理由； ⑵已知⊙O 为△ABC 的外接圆，若⊙P 与⊙O 相切，求t 的值．Bh (第25题)(第22题)27．（9分）如图①，P 为△ABC 内一点，连接P A 、PB 、PC ，在△P AB 、△PBC 和△P AC 中，如果存在一个三角形与△ABC 相似，那么就称P 为△ABC 的自相似点．⑴如图②，已知Rt △ABC 中，∠ACB =90°，∠ACB ＞∠A ，CD 是AB 上的中线，过点B 作BE ⊥CD ，垂足为E ，试说明E 是△ABC 的自相似点．⑵在△ABC 中，∠A ＜∠B ＜∠C ．①如图③，利用尺规作出△ABC 的自相似点P （写出作法并保留作图痕迹）； ②若△ABC 的内心P 是该三角形的自相似点，求该三角形三个内角的度数．28．（11分）问题情境已知矩形的面积为a （a 为常数，a ＞0），当该矩形的长为多少时，它的周长最小？最小值是多少？数学模型设该矩形的长为x ，周长为y ，则y 与x 的函数关系式为2()(0)a y x x x=+＞．探索研究⑴我们可以借鉴以前研究函数的经验，先探索函数1(0)y x x x=+＞的图象性质． ① 填写下表，画出函数的图象：(第26题)①②③(第27题)②观察图象，写出该函数两条不同类型的性质；③在求二次函数y =ax 2＋bx ＋c （a ≠0）的最大（小）值时，除了通过观察图象，还可以通过配方得到．请你通过配方求函数1y x x=+(x ＞0)的最小值．解决问题⑵用上述方法解决“问题情境”中的问题，直接写出答案．答案：一.选择题：ACCDBB 二.填空：7. 2 8. 36 9.10. 6 11.1212. 13. 40 14. 90 15. 12- 16. 4 17.解：解不等式①得：1x ≥- 解不等式②得：2x <所以，不等式组的解集是12x -≤<．不等式组的整数解是1-，0，1． 18.221)a ba b a b b a-÷-+-解：（()()()()a a b ba b a b a b a b b a⎡⎤-=-÷⎢⎥+-+--⎣⎦ ()()b b aa b a b b-=⋅+-1a b=-+ 19. 解法一：移项，得241x x -=-．配方，得24414x x -+=-+， 2(2)3x -=由此可得2x -=12x =22x =解法二：1,4, 1.a b c ==-=224(4)411120b ac -=--⨯⨯=>，422x ±==±12x =，22x =．20.解：⑴训练后第一组平均成绩比训练前增长的百分数是53100%3-⨯≈67%． ⑵不同意小明的观点，因为第二组的平均成绩增加8×10%+6×20%+5×20%+0×50%=3（个）．（3）本题答案不唯一，我认为第一组训练效果最好，因为训练后第一组平均成绩比训练前增长的百分数最大．21.证明：⑴∵四边形ABCD 是平行四边形，∴AB ∥CD,AB=CD ．∴∠ABF=∠ECF . ∵EC=DC , ∴AB=EC ．在△ABF 和△ECF 中，∵∠ABF=∠ECF ，∠AFB=∠EFC ，AB=EC ， ∴⊿ABF ≌⊿ECF ．（2）解法一：∵AB=EC ，AB ∥EC ，∴四边形ABEC 是平行四边形．∴AF=EF ， BF=CF ． ∵四边形ABCD 是平行四边形，∴∠ABC=∠D ，又∵∠AFC=2∠D ，∴∠AFC=2∠ABC ． ∵∠AFC=∠ABF+∠BAF ，∴∠ABF=∠BAF ．∴F A=FB ． ∴F A=FE=FB=FC , ∴AE=BC ．∴口ABEC 是矩形．解法二：∵AB=EC ，AB ∥EC ，∴四边形ABEC 是平行四边形． ∵四边形ABCD 是平行四边形，∴AD ∥BC ，∴∠D=∠BCE ．又∵∠AFC=2∠D ，∴∠AFC=2∠BCE ，∵∠AFC=∠FCE+∠FEC ，∴∠FCE=∠FEC ．∴∠D=∠FEC ．∴AE=AD ．又∵CE=DC ，∴AC ⊥DE ．即∠ACE=90°．∴口ABEC 是矩形． 22. 解⑴3600，20．⑵①当5080x ≤≤时，设y 与x 的函数关系式为y kx b =+．根据题意，当50x =时，1950y =；当80x =，3600y =．所以，y 与x 的函数关系式为55800y x =-．②缆车到山顶的路线长为3600÷2=1800（m ），缆车到达终点所需时间为1800÷180＝１0（min ）．小颖到达缆车终点时，小亮行走的时间为10＋50＝60（min ）．把60x =代入55800y x =-，得y=55×60—800=2500．所以，当小颖到达缆车终点时，小亮离缆车终点的路程是3600-2500=1100（m ）． 23. 解⑴抽取1名，恰好是女生的概率是25． ⑵分别用男1、男2、男3、女1、女2表示这五位同学，从中任意抽取2名，所有可能出现的结果有：（男1，男2），（男1，男3），（男1，女1），（男1，女2），（男2，男3），（男2，女1），（男2，女2），（男3，女1），（男3，女2），（女1，女2），共10种，它们出现的可能性相同，所有结果中，满足抽取2名，恰好是1名男生和1名女生（记为事件A ）的结果共6种，所以P （A ）=63105=． 24.解：⑴当x =0时，1y =．所以不论m 为何值，函数261y mx x =-+的图象经过y 轴上的一个定点（0，1）． ⑵①当0m =时，函数61y x =-+的图象与x 轴只有一个交点；②当0m ≠时，若函数261y mx x =-+的图象与x 轴只有一个交点，则方程2610mx x -+=有两个相等的实数根，所以2(6)40m --=，9m =．综上，若函数261y mx x =-+的图象与x 轴只有一个交点，则m 的值为0或9． 25.在Rt ECD ∆中，tan DEC ∠＝DCEC． ∴EC ＝tan DC DEC ∠≈30400.75=（m ）．在Rt BAC ∆中，∠BCA ＝45°，∴BA CA =在Rt BAE ∆中，tan BEA ∠＝BA EA ．∴0.7540hh =+．∴120h =（m ）．答：电视塔高度约为120m ． 26.解⑴直线AB 与⊙P 相切．如图，过点P 作PD ⊥AB , 垂足为D ．在Rt △A BC 中，∠ACB ＝90°，∵AC =6cm ，BC =8cm ，∴10AB cm =．∵P 为BC 的中点，∴PB =4cm ．∵∠P DB ＝∠ACB ＝90°，∠PBD ＝∠ABC ．∴△PBD ∽△ABC ． ∴PD PB AC AB =,即4610PD =，∴PD =2.4(cm) ．当 1.2t =时，2 2.4PQ t ==(cm)∴PD PQ =，即圆心P 到直线AB 的距离等于⊙P 的半径． ∴直线AB 与⊙P 相切．⑵ ∠ACB ＝90°，∴AB 为△ABC 的外切圆的直径．∴152OB AB cm ==．连接OP ．∵P 为BC 的中点，∴132OP AC cm ==． ∵点P 在⊙O 内部，∴⊙P 与⊙O 只能内切． ∴523t -=或253t -=，∴t =1或4． ∴⊙P 与⊙O 相切时，t 的值为1或4．27. 解⑴在Rt △ABC 中，∠ACB ＝90°，CD 是AB 上的中线，∴12CD AB =，∴CD =BD ．∴∠BCE ＝∠ABC ．∵BE ⊥CD ，∴∠BEC ＝90°，∴∠BEC ＝∠ACB ．∴△BCE ∽△ABC ． ∴E 是△ABC 的自相似点． ⑵①作图略．作法如下：（i ）在∠ABC 内，作∠CBD ＝∠A ；（ii ）在∠ACB 内，作∠BCE ＝∠ABC ；BD 交CE 于点P ．则P 为△ABC 的自相似点．②连接PB 、PC ．∵P 为△ABC 的内心，∴12PBC ABC ∠=∠，12PCB ACB ∠=∠． ∵P 为△ABC 的自相似点，∴△BCP ∽△ABC ．∴∠PBC ＝∠A ，∠BCP ＝∠ABC=2∠PBC =2∠A ， ∠ACB ＝2∠BCP=4∠A ．∵∠A +∠ABC+∠ACB ＝180°． ∴∠A +2∠A+4∠A ＝180°． ∴1807A ∠=．∴该三角形三个内角的度数分别为1807、3607、7207． 28. 解⑴①174，103，52，2，52，103，174．函数1y x x=+(0)x >的图象如图．②本题答案不唯一，下列解法供参考．当01x <<时，y 随x 增大而减小；当1x >时,y 随x 增大而增大；当1x =时函数1y x x =+(0)x >的最小值为2． ③1y x x =+=22+=22+-=22+，即1x =时，函数1y x x=+(0)x >的最小值为2．。

2011年南京市中考数学试卷

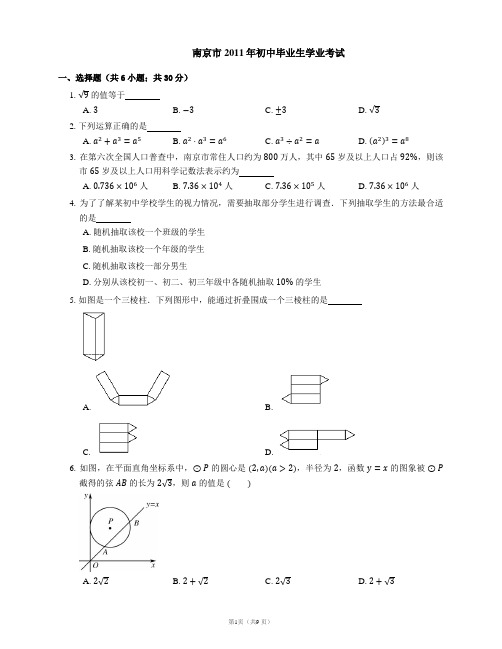
南京市2011年初中毕业生学业考试一、选择题（共6小题；共30分）1. 的值等于A. B. C. D.2. 下列运算正确的是A. B. C. D.3. 在第六次全国人口普查中，南京市常住人口约为万人，其中岁及以上人口占，则该市岁及以上人口用科学记数法表示约为A. 人B. 人C. 人D. 人4. 为了了解某初中学校学生的视力情况，需要抽取部分学生进行调查．下列抽取学生的方法最合适的是A. 随机抽取该校一个班级的学生B. 随机抽取该校一个年级的学生C. 随机抽取该校一部分男生D. 分别从该校初一、初二、初三年级中各随机抽取的学生5. 如图是一个三棱柱．下列图形中，能通过折叠围成一个三棱柱的是A. B.C. D.6. 如图，在平面直角坐标系中，的圆心是，半径为，函数的图象被截得的弦的长为，则的值是A. B. C. D.二、填空题（共10小题；共50分）7. 的相反数是．8. 如图，过正五边形的顶点作直线，则．9. 计算：．10. 等腰梯形的腰长为，它的周长是，则它的中位线长为．11. 如图，以为圆心，任意长为半径画弧，与射线交于点，再以为圆心，长为半径画弧，两弧交于点，画射线，则的值等于．12. 如图，菱形的边长是，是的中点，且，则菱形的面积为．13. 如图，海边立有两座灯塔，，暗礁分布在经过，两点的弓形（弓形的弧是的一部分）区域内，．为了避免触礁，轮船与，的张角的最大值为．14. 如图，，分别是正方形的边，上的点，，连接，．将绕正方形的中心按逆时针方向旋转到，旋转角为（），则．15. 设函数与的图象的交点坐标为，则的值为．16. 甲、乙、丙、丁四位同学围成一圈依序循环报数，规定：①甲、乙、丙、丁首次报出的数依次为，，，，接着甲报，乙报，按此规律，后一位同学报出的数比前一位同学报出的数大．当报到的数是时，报数结束；②若报出的数为的倍数，则报该数的同学需拍手一次．在此过程中，甲同学需拍手的次数为．三、解答题（共8小题；共104分）17. 解不等式组并写出不等式组的整数解．18. 计算：．19. 解方程．20. 某校部分男生分组进行引体向上训练．对训练前后的成绩进行统计分析，相应数据的统计图如下．（1）求训练后第一组平均成绩比训练前增长的百分数；（2）小明在分析了图表后，声称他发现了一个错误：“训练后第二组男生引体向上个数没有变化的人数占该组人数的，所以第二组的平均成绩不可能提高个这么多．”你同意小明的观点吗?请说明理由；（3）你认为哪一组的训练效果最好?请提供一个解释来支持你的观点．21. 从名男生和名女生中随机抽取 2014 年南京青奥会志愿者．求下列事件的概率：（1）抽取名，恰好是女生；（2）抽取名，恰好是名男生和名女生．22. 已知函数（是常数）．（1）求证：不论为何值，该函数的图象都经过轴上的一个定点；（2）若该函数的图象与轴只有一个交点，求的值．23. 如图，某数学课外活动小组测量电视塔的高度．他们借助一个高度为的建筑物进行测量，在点处测得塔顶的仰角为，在点处测得的仰角为（，，三点在一条直线上）．求电视塔的高度．（参考数据：，，）24. 如图1，为内一点，连接，，，在，和中，如果存在一个三角形与相似，那么就称为的自相似点．（1）如图2，已知中，，，是上的中线，过点作，垂足为．试说明是的自相似点；（2）在中，．（i）如图 3，利用尺规作出的自相似点（写出作法并保留作图痕迹）；（ii）若的内心是该三角形的自相似点，求该三角形三个内角的度数．答案第一部分1. A2. C3. C 【解析】因为万，所以首先确定为，再根据的位数为位可得，所以用科学记数法表示为．4. D 【解析】根据抽查的特点，对照每个选项的具体内容可得，答案选择D．这是因为分别从该校初一、初二、初三年级中各班随机抽取的学生，能够确保每位学生都有被抽到的可能，从而保证了抽查的全面性和随机性．5. B【解析】动手操作用纸片去折，看能不能折成三棱柱，观察就能得出答案选择 B．本题也可以直接发挥空间想象能力，通过观察所给四个选项中的展开图，得出答案．6. B 【解析】作，轴，垂足分别为，，交于点，连接．可得．根据勾股定理可得．因为的圆心是，所以，当时，，所以，所以，所以，所以，所以，所以，所以，所以．第二部分7.8.【解析】如图，连接．因为五边形是正五边形，所以，，所以．又因为，，所以，根据两直线平行，内错角相等可得．9.【解析】．10.11.【解析】根据作图过程可知，所以三角形是等边三角形，所以，所以．12.【解析】因为在菱形中，所以．因为是中点，所以．又因为，所以，所以菱形的面积为．13.【解析】首先根据题意确定张角的最大值的情况是点正好在圆周上．根据同弧所对的圆周角等于圆心角的一半，可得弧所对的圆周角为．再根据圆外角小于圆周角可得为了避免触礁，轮船与，的张角的最大值为．14.15.【解析】因为函数与的图象的交点坐标为，所以，，所以，．故．16.【解析】本题难度中等，考查学生探究数的规律的能力．根据①可知：甲报到的数除以余数为，即为，，，，．再根据②若报出的数为的倍数，则报该数的同学需拍手一次，所以甲同学需要拍手的次数为．第三部分17. 解不等式，得解不等式，得所以，不等式组的解集是．不等式组的整数解是，，．18.19. 移项，得配方，得由此可得20. （1）训练后第一组平均成绩比训练前增长的百分数是．（2）我不同意小明的观点，因为第二组的平均成绩增加（个）．（3）我认为第一组训练效果最好，因为训练后第一组平均成绩比训练前增长的百分数最大．21. （1）抽取名，恰好是女生的概率是．（2）分别用男、男、男、女、女表示这位同学．从中任意抽取名，所有可能出现的结果有（男，男），（男，男），（男，女），（男，女），（男，男），（男，女），（男，女），（男，女），（男，女），（女，女），共有种，它们出现的可能性相同．所有的结果中，满足抽取名，恰好是名男生和名女生（记为事件）的结果有种，所以．22. （1）当时，．所以不论为何值，函数的图象都经过轴上的一个定点．（2）（i）当时，函数的图象与轴只有一个交点；（ii）当时，若函数的图象与轴只有一个交点，则方程有两个相等的实数根．所以，．综上，若函数的图象与轴只有一个交点，则的值为或．23. 在中，，．在中，，．在中，，．．答：电视塔的高度约为．24. （1）在中，，是上的中线，．．．，．．．是的自相似点．（2）（i）如图所示，作法如下：①在内，作；②在内，作，交于点．则为的自相似点．（ii）连接，．是的内心，，．为的自相似点，．，，．，．．该三角形三个内角的度数分别为，，．。

2011年江苏省南京市中考数学试卷

2011年江苏省南京市中考数学试卷一、选择题（本大题共6小题，每小题2分，共12分,在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）1．（2分）的值等于（）A．3B．﹣3C．±3D．2．（2分）下列运算正确的是（）A．a2+a3=a5B．a2•a3=a6C．a3+a2=a D．（a2）3=a6 3．（2分）在第六次全国人口普查中，南京市常住人口约为800万人，其中65岁及以上人口占9.2%，则该市65岁及以上人口用科学记数法表示约为（）A．0.736×106人B．7.36×104人C．7.36×105人D．7.36×106人4．（2分）为了了解某初中学校学生的视力情况，需要抽取部分学生进行调查．下列抽取学生的方法最合适的是（）A．随机抽取该校一个班级的学生B．随机抽取该校一个年级的学生C．随机抽取该校一部分男生D．分别从该校初一、初二、初三年级中各随机抽取10%的学生5．（2分）如图是一个三棱柱．下列图形中，能通过折叠围成一个三棱柱的是（）A．B．C．D．6．（2分）如图，在平面直角坐标系中，⊙P的圆心是（2，a）（a＞2），半径为2，函数y=x的图象被⊙P截得的弦AB的长为，则a的值是（）A．2B．2+C．2D．2+二、填空题（本大题共10小题，每小题2分，共20分,不需写出解答过程，请把答案直接填写在答题卡相应位置上）7．（2分）﹣2的相反数是．8．（2分）如图，过正五边形ABCDE的顶点A作直线l∥CD，则∠1=．9．（2分）计算（+1）（2﹣）=．10．（2分）等腰梯形的腰长为5cm，它的周长是22cm，则它的中位线长为cm．11．（2分）如图所示，以O为圆心，任意长为半径画弧．与射线OM交于点A，再以A为圆心，AO为半径画弧，两弧交于点B，画射线OB，则cos∠AOB的值等于．12．（2分）如图，菱形ABCD的边长是2cm，E是AB的中点，且DE丄AB，则菱形ABCD的面积为cm2．13．（2分）如图，海边立有两座灯塔A、B，暗礁分布在经过A、B两点的弓形（弓形的弧是⊙O的一部分）区域内，∠AOB=80°．为了避免触礁，轮船P与A、B的张角∠APB的最大值为．14．（2分）如图，E、F分别是正方形ABCD的边BC、CD上的点，BE=CF，连接AE、BF．将△ABE绕正方形的中心按逆时针方向旋转到△BCF，旋转角为α（0°＜α＜180°），则∠α=．15．（2分）设函数y=与y=x﹣1的图象的交点坐标为（a，b），则﹣的值为．16．（2分）甲、乙、丙、丁四位同学围成一圈依序循环报数，规定：①甲、乙、丙、丁首次报出的数依次为1、2、3、4，接着甲报5，乙报6…按此规律，后一位同学报出的数比前一位同学报出的数大1．当报到的数是50时，报数结束；②若报出的数为3的倍数，则报该数的同学需拍手一次．在此过程中，甲同学需拍手的次数为．三、解答题（本大题共12小题，共88分，请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）17．（6分）解不等式组＞，并写出不等式组的整数解．18．（6分）计算（﹣）÷．19．（6分）解方程：x2﹣4x﹣1=0．20．（7分）某校部分男生分3组进行引体向上训练．对训练前后的成绩进行统计分析，相应数据的统计图如下．（1）求训练后第一组平均成绩比训练前增长的百分数；（2）小明在分析了图表后，声称他发现了一个错误：“训练后第二组男生引体向上个数没有变化的人数占该组人数的50%，所以第二组的平均成绩不可能提高3个这么多．”你同意小明的观点吗？请说明理由；（3）你认为哪一组的训练效果最好？请提供一个解释来支持你的观点．21．（7分）如图，将▱ABCD的边DC延长到点E，使CE=DC，连接AE，交BC于点F．（1）求证：△ABF≌△ECF；（2）若∠AFC=2∠D，连接AC、BE，求证：四边形ABEC是矩形．22．（7分）小颖和小亮上山游玩，小颖乘坐缆车，小亮步行，两人相约在山顶的缆车终点会合．已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍．小颖在小亮出发后50min 才乘上缆车，缆车的平均速度为180m/min．设小亮出发x min后行走的路程为y m，图中的折线表示小亮在整个行走过程中y与x的函数关系．（1）小亮行走的总路程是m，他途中休息了min；（2）①当50≤x≤80时，求y与x的函数关系式；②当小颖到达缆车终点时，小亮离缆车终点的路程是多少？23．（7分）从3名男生和2名女生中随机抽取2014年南京青奥会志愿者．求下列事件的概率：（1）抽取1名，恰好是女生；（2）抽取2名，恰好是1名男生和1名女生．24．（7分）已知函数y=mx2﹣6x+1（m是常数）．（1）求证：不论m为何值，该函数的图象都经过y轴上的一个定点；（2）若该函数的图象与x轴只有一个交点，求m的值．25．（7分）如图，某数学课外活动小组测量电视塔AB的高度．他们借助一个高度为30m的建筑物CD进行测量，在点C处测得塔顶B的仰角为45°，在点E 处测得B的仰角为37°（B、D、E三点在一条直线上）．求电视塔的高度h．（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）26．（8分）如图，在Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm．P为BC的中点，动点Q从点P出发，沿射线PC方向以2cm/s的速度运动，以P为圆心，PQ长为半径作圆．设点Q运动的时间为t s．（1）当t=1.2时，判断直线AB与⊙P的位置关系，并说明理由；（2）已知⊙O为△ABC的外接圆．若⊙P与⊙O相切，求t的值．27．（9分）如图①，P为△ABC内一点，连接PA、PB、PC，在△PAB、△PBC和△PAC中，如果存在一个三角形与△ABC相似，那么就称P为△ABC的自相似点．（1）如图②，已知Rt△ABC中，∠ACB=90°，∠ABC＞∠A，CD是AB上的中线，过点B作BE丄CD，垂足为E．试说明E是△ABC的自相似点；（2）在△ABC中，∠A＜∠B＜∠C．①如图③，利用尺规作出△ABC的自相似点P（写出作法并保留作图痕迹）；②若△ABC的内心P是该三角形的自相似点，求该三角形三个内角的度数．28．（11分）【问题情境】已知矩形的面积为a（a为常数，a＞0），当该矩形的长为多少时，它的周长最小？最小值是多少？【数学模型】设该矩形的长为x，周长为y，则y与x的函数关系式为y=2（x+）（x＞0）．【探索研究】（1）我们可以借鉴以前研究函数的经验，先探索函数y=x+（x＞0）的图象和性质．①填写下表，画出函数的图象；②观察图象，写出该函数两条不同类型的性质；③在求二次函数y=ax2+bx+c（a≠0）的最大（小）值时，除了通过观察图象，还可以通过配方得到．请你通过配方求函数y=x+（x＞0）的最小值．【解决问题】（2）用上述方法解决“问题情境”中的问题，直接写出答案．2011年江苏省南京市中考数学试卷参考答案与试题解析一、选择题（本大题共6小题，每小题2分，共12分,在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）1．（2分）的值等于（）A．3B．﹣3C．±3D．【解答】解：∵=3，故选：A．2．（2分）下列运算正确的是（）A．a2+a3=a5B．a2•a3=a6C．a3+a2=a D．（a2）3=a6【解答】解：A、a2与a3不是同类项，不能合并，故本选项错误；B、a2•a3=a2+3=a5≠a6，故本选项错误；C、a3与a2不是同类项，不能合并，故本选项错误；D、（a2）3=a2×3=a6，故本选项正确．故选：D．3．（2分）在第六次全国人口普查中，南京市常住人口约为800万人，其中65岁及以上人口占9.2%，则该市65岁及以上人口用科学记数法表示约为（）A．0.736×106人B．7.36×104人C．7.36×105人D．7.36×106人【解答】解：该市65岁及以上人口：8000000×9.2%=736000（人）将736 000人用科学记数法表示7.36×105人．故选：C．4．（2分）为了了解某初中学校学生的视力情况，需要抽取部分学生进行调查．下列抽取学生的方法最合适的是（）A．随机抽取该校一个班级的学生B．随机抽取该校一个年级的学生C．随机抽取该校一部分男生D．分别从该校初一、初二、初三年级中各随机抽取10%的学生【解答】解：因为要了解初中的视力情况范围较大、难度较大，所以应采取抽样调查的方法比较合适，本题考查的是调查方法的选择，正确选择调查方式要根据全面调查的优缺点再结合实际情况去分析，故只有D符合实际并具有普遍性，故选：D．5．（2分）如图是一个三棱柱．下列图形中，能通过折叠围成一个三棱柱的是（）A．B．C．D．【解答】解：A、折叠后有二个侧面重合，不能得到三棱柱；B、折叠后可得到三棱柱；C、折叠后有二个底面重合，不能得到三棱柱；D、多了一个底面，不能得到三棱柱．故选：B．6．（2分）如图，在平面直角坐标系中，⊙P的圆心是（2，a）（a＞2），半径为2，函数y=x的图象被⊙P截得的弦AB的长为，则a的值是（）A．2B．2+C．2D．2+【解答】解：过P点作PE⊥AB于E，过P点作PC⊥x轴于C，交AB于D，连接PA．∵PE⊥AB，AB=2，半径为2，∴AE=AB=，PA=2，根据勾股定理得：PE==1，∵点A在直线y=x上，∴∠AOC=45°，∵∠DCO=90°，∴∠ODC=45°，∴△OCD是等腰直角三角形，∴OC=CD=2，∴∠PDE=∠ODC=45°，∴∠DPE=∠PDE=45°，∴DE=PE=1，∴PD=．∵⊙P的圆心是（2，a），∴a=PD+DC=2+．故选：B．二、填空题（本大题共10小题，每小题2分，共20分,不需写出解答过程，请把答案直接填写在答题卡相应位置上）7．（2分）﹣2的相反数是2．【解答】解：﹣2的相反数是：﹣（﹣2）=2，故答案为：2．8．（2分）如图，过正五边形ABCDE的顶点A作直线l∥CD，则∠1=36°．【解答】解：∵多边形ABCDE是正五边形，∴∠BAE==108°，∠ABE=∠AEB，又∵∠2=∠ABE，∠1=∠AEB，∴∠1=∠2=（180°﹣∠BAE），即2∠1=180°﹣108°，∴∠1=36°．故答案为：36°．9．（2分）计算（+1）（2﹣）=．【解答】解：（+1）（2﹣），=2﹣×+1×2﹣1×，=2﹣2+2﹣，=．故答案为：．10．（2分）等腰梯形的腰长为5cm，它的周长是22cm，则它的中位线长为6 cm．【解答】解：∵等腰梯形的腰长为5cm，它的周长是22cm，∴AD+BC=22﹣5﹣5=12，∵EF为梯形的中位线，∴EF=（AD+BC）=6．故答案为：6．11．（2分）如图所示，以O为圆心，任意长为半径画弧．与射线OM交于点A，再以A为圆心，AO为半径画弧，两弧交于点B，画射线OB，则cos∠AOB的值等于．【解答】解：连接AB，由图可知：OA=0B，AO=AB∴OA=AB=OB，即三角形OAB为等边三角形，∴∠AOB=60°，∴cos∠AOB=cos60°=．故答案是：．12．（2分）如图，菱形ABCD的边长是2cm，E是AB的中点，且DE丄AB，则菱形ABCD的面积为2cm2．【解答】解：∵E是AB的中点，∴AE=1cm，∵DE丄AB，∴DE==cm．∴菱形的面积为：2×=2cm2．故答案为：2．13．（2分）如图，海边立有两座灯塔A、B，暗礁分布在经过A、B两点的弓形（弓形的弧是⊙O的一部分）区域内，∠AOB=80°．为了避免触礁，轮船P与A、B的张角∠APB的最大值为40°．【解答】解：∵海边立有两座灯塔A、B，暗礁分布在经过A、B两点的弓形（弓形的弧是⊙O的一部分）区域内，∠AOB=80°．∴当P点在圆上时，不进入经过A、B两点的弓形（弓形的弧是⊙O的一部分）区域内，轮船P与A、B的张角∠APB的最大，此时为∠AOB=80°的一半，为40°．故答案为：40°．14．（2分）如图，E、F分别是正方形ABCD的边BC、CD上的点，BE=CF，连接AE、BF．将△ABE绕正方形的中心按逆时针方向旋转到△BCF，旋转角为α（0°＜α＜180°），则∠α=90°．【解答】解：∵四边形ABCD是正方形．∴∠AOB=90°，故α=90°．故答案是：90°．15．（2分）设函数y=与y=x﹣1的图象的交点坐标为（a，b），则﹣的值为﹣．【解答】解：∵函数y=与y=x﹣1的图象的交点坐标为（a，b），∴b=，b=a﹣1，∴ab=2，b﹣a=﹣1，∴﹣==﹣．故答案为：﹣．16．（2分）甲、乙、丙、丁四位同学围成一圈依序循环报数，规定：①甲、乙、丙、丁首次报出的数依次为1、2、3、4，接着甲报5，乙报6…按此规律，后一位同学报出的数比前一位同学报出的数大1．当报到的数是50时，报数结束；②若报出的数为3的倍数，则报该数的同学需拍手一次．在此过程中，甲同学需拍手的次数为4．【解答】解：∵甲、乙、丙、丁首次报出的数依次为1、2、3、4，接着甲报5，乙报6…按此规律，后一位同学报出的数比前一位同学报出的数大1．当报到的数是50时，报数结束；∴50÷4=12余2，∴甲共报数13次，分别为1，5，9，13，17，21，25，29，33，37，41，45，49，∴报出的数为3的倍数，则报该数的同学需拍手一次．在此过程中，甲同学需报到：9，21，33，45这4个数时，应拍手4次．故答案为：4．三、解答题（本大题共12小题，共88分，请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）17．（6分）解不等式组＞，并写出不等式组的整数解．，【解答】解：＞由①得：x≥﹣1，由②得：x＜2，∴不等式组的解集为：﹣1≤x＜2，∴不等式组的整数解是：﹣1，0，1．18．（6分）计算（﹣）÷．【解答】解：原式=（﹣）•=（﹣）•（﹣），=﹣•，=﹣．19．（6分）解方程：x2﹣4x﹣1=0．【解答】解：∵x2﹣4x﹣1=0，∴x2﹣4x=1，∴x2﹣4x+4=1+4，∴（x﹣2）2=5，∴x=2±，∴x1=2+，x2=2﹣．20．（7分）某校部分男生分3组进行引体向上训练．对训练前后的成绩进行统计分析，相应数据的统计图如下．（1）求训练后第一组平均成绩比训练前增长的百分数；（2）小明在分析了图表后，声称他发现了一个错误：“训练后第二组男生引体向上个数没有变化的人数占该组人数的50%，所以第二组的平均成绩不可能提高3个这么多．”你同意小明的观点吗？请说明理由；（3）你认为哪一组的训练效果最好？请提供一个解释来支持你的观点．【解答】解：（1）训练后第一组平均成绩比训练前增长的百分数是×100%≈67%；（2）我不同意小明的观点，设第二组男生的人数为x人，第二组的平均成绩增加（8×10%•x+6×20%•x+5×20%•x+0×50%•x）÷x=3个．故不同意小明的观点；（3）本题答案不唯一，下列解法供参考．我认为第一组的训练效果最好；训练后每组的平均成绩比训练前增长的百分数分别为：第一组：×100%≈67%，第二组：×100%=50%，第三组：×100%≈22%，训练后第一组的平均成绩比训练前增长的百分数最大，所以第一组的训练效果最好．21．（7分）如图，将▱ABCD的边DC延长到点E，使CE=DC，连接AE，交BC于点F．（1）求证：△ABF≌△ECF；（2）若∠AFC=2∠D，连接AC、BE，求证：四边形ABEC是矩形．【解答】证明：（1）∵四边形ABCD是平行四边形，∴AB∥DC，AB=DC，∴∠ABF=∠ECF，∵EC=DC，∴AB=EC，在△ABF和△ECF中，∵∠ABF=∠ECF，∠AFB=∠EFC，AB=EC，∴△ABF≌△ECF（AAS）．（2）∵AB=EC，AB∥EC，∴四边形ABEC是平行四边形，∴FA=FE，FB=FC，∵四边形ABCD是平行四边形，∴∠ABC=∠D，又∵∠AFC=2∠D，∴∠AFC=2∠ABC，∵∠AFC=∠ABC+∠BAF，∴∠ABC=∠BAF，∴FA=FB，∴FA=FE=FB=FC，∴AE=BC，∴四边形ABEC是矩形．22．（7分）小颖和小亮上山游玩，小颖乘坐缆车，小亮步行，两人相约在山顶的缆车终点会合．已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍．小颖在小亮出发后50min 才乘上缆车，缆车的平均速度为180m/min．设小亮出发x min后行走的路程为y m，图中的折线表示小亮在整个行走过程中y与x的函数关系．（1）小亮行走的总路程是3600m，他途中休息了20min；（2）①当50≤x≤80时，求y与x的函数关系式；②当小颖到达缆车终点时，小亮离缆车终点的路程是多少？【解答】解：（1）3600，20；（2）①当50≤x≤80时，设y与x的函数关系式为y=kx+b，根据题意，当x=50时，y=1950；当x=80时，y=3600∴解得：∴函数关系式为：y=55x﹣800．②缆车到山顶的线路长为3600÷2=1800米，缆车到达终点所需时间为1800÷180=10分钟小颖到达缆车终点时，小亮行走的时间为10+50=60分钟，把x=60代入y=55x﹣800，得y=55×60﹣800=2500．∴当小颖到达缆车终点时，小亮离缆车终点的路程是3600﹣2500=1100米．23．（7分）从3名男生和2名女生中随机抽取2014年南京青奥会志愿者．求下列事件的概率：（1）抽取1名，恰好是女生；（2）抽取2名，恰好是1名男生和1名女生．【解答】解：（1）5名学生中有2名女生，所以抽取1名，恰好是女生的概率为；（2）由树形图可得出：共有20种情况，恰好是1名男生和1名女生的情况数有12种，所以概率为．24．（7分）已知函数y=mx2﹣6x+1（m是常数）．（1）求证：不论m为何值，该函数的图象都经过y轴上的一个定点；（2）若该函数的图象与x轴只有一个交点，求m的值．【解答】解：（1）当x=0时，y=1．所以不论m为何值，函数y=mx2﹣6x+1的图象都经过y轴上一个定点（0，1）；（2）①当m=0时，函数y=mx2﹣6x+1的图象与x轴只有一个交点；②当m≠0时，若函数y=mx2﹣6x+1的图象与x轴只有一个交点，则方程mx2﹣6x+1=0有两个相等的实数根，所以△=（﹣6）2﹣4m=0，m=9．综上，若函数y=mx2﹣6x+1的图象与x轴只有一个交点，则m的值为0或9．25．（7分）如图，某数学课外活动小组测量电视塔AB的高度．他们借助一个高度为30m的建筑物CD进行测量，在点C处测得塔顶B的仰角为45°，在点E 处测得B的仰角为37°（B、D、E三点在一条直线上）．求电视塔的高度h．（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）【解答】解：在Rt△ECD中，tan∠DEC=，∴EC=≈=40（m），在Rt△BAE中，tan∠BEA=，∴=0.75，∴h=120（m），答：电视塔的高度约为120m．26．（8分）如图，在Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm．P为BC的中点，动点Q从点P出发，沿射线PC方向以2cm/s的速度运动，以P为圆心，PQ长为半径作圆．设点Q运动的时间为t s．（1）当t=1.2时，判断直线AB与⊙P的位置关系，并说明理由；（2）已知⊙O为△ABC的外接圆．若⊙P与⊙O相切，求t的值．【解答】解：（1）直线AB与⊙P相切，如图，过P作PD⊥AB，垂足为D，在Rt△ABC中，∠ACB=90°，∵AC=6cm，BC=8cm，∴AB=10cm，∵P为BC中点，∴PB=4cm，∵∠PDB=∠ACB=90°，∠PBD=∠ABC，∴△PBD∽△ABC，∴，即，∴PD=2.4（cm），当t=1.2时，PQ=2t=2.4（cm），∴PD=PQ，即圆心P到直线AB的距离等于⊙P的半径，∴直线AB与⊙P相切；（2）∵∠ACB=90°，∴AB为△ABC的外接圆的直径，∴BO=AB=5cm，连接OP，∵P为BC中点，PO为△ABC的中位线，∴PO=AC=3cm，∵点P在⊙O内部，∴⊙P与⊙O只能内切，∴当⊙P在⊙O内部时：5﹣2t=3，当⊙O在⊙P内部时2t﹣5=3，∴t=1或4，∴⊙P与⊙O相切时，t的值为1或4．27．（9分）如图①，P为△ABC内一点，连接PA、PB、PC，在△PAB、△PBC和△PAC中，如果存在一个三角形与△ABC相似，那么就称P为△ABC的自相似点．（1）如图②，已知Rt△ABC中，∠ACB=90°，∠ABC＞∠A，CD是AB上的中线，过点B作BE丄CD，垂足为E．试说明E是△ABC的自相似点；（2）在△ABC中，∠A＜∠B＜∠C．①如图③，利用尺规作出△ABC的自相似点P（写出作法并保留作图痕迹）；②若△ABC的内心P是该三角形的自相似点，求该三角形三个内角的度数．【解答】解：（1）在Rt△ABC中，∠ACB=90°，CD是AB上的中线，∴CD=AB，∴CD=BD，∴∠BCE=∠ABC，∵BE⊥CD，∴∠BEC=90°，∴∠BEC=∠ACB，∴△BCE∽△ABC，∴E是△ABC的自相似点；（2）①如图所示，作法：①在∠ABC内，作∠CBD=∠A，②在∠ACB内，作∠BCE=∠ABC，BD交CE于点P，则P为△ABC的自相似点；②∵P是△ABC的内心，∴∠PBC=∠ABC，∠PCB=∠ACB，∵△ABC的内心P是该三角形的自相似点，∴∠PBC=∠A，∠BCP=∠ABC=2∠PBC=2∠A，∠ACB=2∠BCP=4∠A，∴∠A+2∠A+4∠A=180°，∴∠A=，∴该三角形三个内角度数为：，，．28．（11分）【问题情境】已知矩形的面积为a（a为常数，a＞0），当该矩形的长为多少时，它的周长最小？最小值是多少？【数学模型】设该矩形的长为x，周长为y，则y与x的函数关系式为y=2（x+）（x＞0）．【探索研究】（1）我们可以借鉴以前研究函数的经验，先探索函数y=x+（x＞0）的图象和性质．①填写下表，画出函数的图象；②观察图象，写出该函数两条不同类型的性质；③在求二次函数y=ax2+bx+c（a≠0）的最大（小）值时，除了通过观察图象，还可以通过配方得到．请你通过配方求函数y=x+（x＞0）的最小值．【解决问题】（2）用上述方法解决“问题情境”中的问题，直接写出答案．【解答】解：（1）①故答案为：，，，2，，，．函数y=x+的图象如图：②答：函数两条不同类型的性质是：当0＜x＜1时，y 随x的增大而减小，当x＞1时，y 随x的增大而增大；当x=1时，函数y=x+（x＞0）的最小值是2．③y=x+==+2=+2，∵x＞0，所以≥0，所以当x=1时，的最小值为0，∴函数y=x+（x＞0）的最小值是2．（2）答：矩形的面积为a（a为常数，a＞0），当该矩形的长为时，它的周长最小，最小值是4．。

南京中考数学试题及答案word版

南京市2011年初中毕业生学业考试数学1．．一、选择题（本大题共6小题，每小题2分，共12分，在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确的选项的字母代号填涂在答题卡相应位置上）1A ．3B ．－3C ．±3D ．2．下列运算正确的是A ．a 2＋a 3=a 5B ．a 2•a 3=a 6C ．a 3÷a 2=aD ．(a 2)3=a 83．在第六次全国人口普查中，南京市常住人口约为800万人，其中65岁及以上人口占9.2%．则该市65岁及以上人口用科学记数法表示约为 A ．0.736×106人 B ．7.36×104人 C ．7.36×105人 D ．7.36×106 人4．为了解某初中学校学生的视力情况，需要抽取部分学生进行调查，下列抽取学生的方法最合适的是A ．随机抽取该校一个班级的学生B ．随机抽取该校一个年级的学生C ．随机抽取该校一部分男生D ．分别从该校初一、初二、初三年级中各班随机抽取10%的学生5．如图是一个三棱柱，下列图形中，能通过折叠围成一个三棱柱的是6．如图，在平面直角坐标系中，⊙P 的圆心是（2，a ）(a ＞2)，半径为2，函数y =x 的图象被⊙P 的弦AB的长为a 的值是A．B．2+C．D．2二、填空题（本大题共10小题，每小题2分，共20分，不需要写出解答过程，请把答案直接填写在答题卡相应位置上）7．－2的相反数是________．A ．BD ．(第5题)8．如图，过正五边形ABCDE 的顶点A 作直线l ∥CD ，则∠1=____________．㎝．11．如图，以O 为圆心，任意长为半径画弧，与射线OM 交于点A ，再以A 为圆心，AO 长为半径画弧，两弧交于点B ，画射线OB ，则cos ∠AOB 的值等于___________．12．如图，菱形ABCD 的连长是2㎝，E 是AB 中点，且DE ⊥AB ，则菱形ABCD 的面积为_________㎝2．13．如图，海边有两座灯塔A 、B ，暗礁分布在经过A 、B 两点的弓形（弓形的弧是⊙O 的一部分）区域内，∠AOB =80°，为了避免触礁，轮船P 与A 、B 的张角∠APB 的最大值为______°．14．如图，E 、F 分别是正方形ABCD 的边BC 、CD 上的点，BE =CF ，连接AE 、BF ，将△ABE 绕正方形的中心按逆时针方向转到△BCF ，旋转角为a （0°＜a ＜180°），则∠a =______．15．设函数2y x =与1y x =-的图象的交战坐标为（a ，b ），则11a b-的值为__________．16．甲、乙、丙、丁四位同学围成一圈依序循环报数，规定：①甲、乙、丙、丁首次报出的数依次为1、2、3、4，接着甲报5、乙报6……按此规律，后一位同学报出的数比前一位同学报出的数大1，当报到的数是50时，报数结束；②若报出的数为3的倍数，则报该数的同学需拍手一次，在此过程中，甲同学需要拍手的次数为____________．三、解答题（本大题共12小题，共88分，请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）(第12题)(第14题)ABCDF17．（6分）解不等式组523132x x x +⎧⎪+⎨⎪⎩≥＞，并写出不等式组的整数解．18．（6分）计算221()a b a b a b b a-÷-+-19．（6分）解方程x 2－4x ＋1=0 20．（7分）某校部分男生分3组进行引体向上训练，对训练前后的成绩进行统计分析，相应数据的统计图如下．⑴求训练后第一组平均成绩比训练前增长的百分数；⑵小明在分析了图表后，声称他发现了一个错误：“训练后第二组男生引体向上个数没有变化的人数占该组人数的50%，所以第二组的平均数不可能提高3个这么多．”你同意小明的观点吗？请说明理由；⑶你认为哪一组的训练效果最好？请提出一个解释来支持你的观点．21．（7分）如图，将□ABCD 的边DC 延长到点E ，使CE =DC ，连接AE ，交BC 于点F ．⑴求证：△ABF ≌△ECF ⑵若∠AFC =2∠D ，连接AC 、BE ．求证：四边形ABEC 是矩形．①训练后第二组男生引体向上增加个数分布统计图增加85个②(第20题)BD22．（7分）小颖和小亮上山游玩，小颖乘会缆车，小亮步行，两人相约在山顶的缆车终点会合．已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍，小颖在小亮出发后50 min才乘上缆车，缆车的平均速度为180 m/min．设小亮出发x min后行走的路程为y m．图中的折线表示小亮在整个行走过程中y与x的函数关系．⑴小亮行走的总路程是____________㎝，他途中休息了________min．⑵①当50≤x≤80时，求y与x的函数关系式；②当小颖到达缆车终点为时，小亮离缆车终点的路程是多少？23．（7分）从3名男生和2名女生中随机抽取2014年南京青奥会志愿者．求下列事件的概率：⑴抽取1名，恰好是女生；⑵抽取2名，恰好是1名男生和1名女生．24．（7分）已知函数y=mx2－6x＋1（m是常数）．⑴求证：不论m为何值，该函数的图象都经过y轴上的一个定点；⑵若该函数的图象与x轴只有一个交点，求m的值．25．（7分）如图，某数学课外活动小组测量电视塔AB的高度，他们借助一个高度为30m 的建筑物CD进行测量，在点C处塔顶B的仰角为45°，在点E处测得B的仰角为37°（B、D、E三点在一条直线上）．求电视塔的高度h．（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）26．（8分）如图，在Rt △ABC 中，∠ACB =90°，AC =6㎝，BC =8㎝，P 为BC 的中点．动点Q 从点P 出发，沿射线PC 方向以2㎝/s 的速度运动，以P 为圆心，PQ 长为半径作圆．设点Q 运动的时间为t s ．⑴当t =1.2时，判断直线AB 与⊙P 的位置关系，并说明理由；⑵已知⊙O 为△ABC 的外接圆，若⊙P 与⊙O 相切，求t 的值．27．（9分）如图①，P 为△ABC 内一点，连接P A 、PB 、PC ，在△P AB 、△PBC 和△P AC 中，如果存在一个三角形与△ABC 相似，那么就称P 为△ABC 的自相似点．⑴如图②，已知Rt △ABC 中，∠ACB =90°，∠ACB ＞∠A ，CD 是AB 上的中线，过点B 作BE ⊥CD ，垂足为E ，试说明E 是△ABC 的自相似点．⑵在△ABC 中，∠A ＜∠B ＜∠C ． ①如图③，利用尺规作出△ABC 的自相似点P （写出作法并保留作图痕迹）；②若△ABC 的内心P 是该三角形的自相似点，求该三角形三个内角的度数．Bh (第25题)(第26题)BB B CC C①②③(第27题)28．（11分）问题情境已知矩形的面积为a （a 为常数，a ＞0），当该矩形的长为多少时，它的周长最小？最小值是多少？数学模型设该矩形的长为x ，周长为y ，则y 与x 的函数关系式为2()(0)ay x x x=+＞．探索研究⑴我们可以借鉴以前研究函数的经验，先探索函数1(0)y x x x=+＞的图象性质．① 填写下表，画出函数的图象：②观察图象，写出该函数两条不同类型的性质；③在求二次函数y =ax 2＋bx ＋c （a ≠0）的最大（小）值时，除了通过观察图象，还可以通过配方得到．请你通过配方求函数1y x x=+(x ＞0)的最小值．解决问题⑵用上述方法解决“问题情境”中的问题，直接写出答案．答案：一.选择题：ACCDBB二.填空：7. 2 8. 36 9.10. 6 11.1212. 13. 40 14. 90 15. 12- 16. 417.解：解不等式①得：1x ≥-解不等式②得：2x <所以，不等式组的解集是12x -≤<．不等式组的整数解是1-，0，1． 18.221)a b a b a b b a-÷-+-解：（()()()()a a b ba b a b a b a b b a ⎡⎤-=-÷⎢⎥+-+--⎣⎦()()b b aa b a b b-=⋅+-1a b=-+ 19. 解法一：移项，得241x x -=-．配方，得24414x x -+=-+，2(2)3x -=由此可得2x -=12x =22x =解法二：1,4, 1.a b c ==-=224(4)411120b ac -=--⨯⨯=>，2x ==±12x =，22x =．20.解：⑴训练后第一组平均成绩比训练前增长的百分数是53100%3-⨯≈67%．⑵不同意小明的观点，因为第二组的平均成绩增加8×10%+6×20%+5×20%+0×50%=3（个）．（3）本题答案不唯一，我认为第一组训练效果最好，因为训练后第一组平均成绩比训练前增长的百分数最大．21.证明：⑴∵四边形ABCD 是平行四边形，∴AB ∥CD,AB=CD ．∴∠ABF=∠ECF .∵EC=DC , ∴AB=EC ．在△ABF 和△ECF 中，∵∠ABF=∠ECF ，∠AFB=∠EFC ，AB=EC ， ∴⊿ABF ≌⊿ECF ．（2）解法一：∵AB=EC ，AB ∥EC ，∴四边形ABEC 是平行四边形．∴AF=EF ， BF=CF ．∵四边形ABCD 是平行四边形，∴∠ABC=∠D ，又∵∠AFC=2∠D ，∴∠AFC=2∠ABC ．∵∠AFC=∠ABF+∠BAF ，∴∠ABF=∠BAF ．∴F A=FB ．∴F A=FE=FB=FC , ∴AE=BC ．∴口ABEC 是矩形．解法二：∵AB=EC ，AB ∥EC ，∴四边形ABEC 是平行四边形．∵四边形ABCD 是平行四边形，∴AD ∥BC ，∴∠D=∠BCE ．又∵∠AFC=2∠D ，∴∠AFC=2∠BCE ， ∵∠AFC=∠FCE+∠FEC ，∴∠FCE=∠FEC ．∴∠D=∠FEC ．∴AE=AD ．又∵CE=DC ，∴AC ⊥DE ．即∠ACE=90°．∴口ABEC 是矩形．22. 解⑴3600，20．⑵①当5080x ≤≤时，设y 与x 的函数关系式为y kx b =+．根据题意，当50x =时，1950y =；当80x =，3600y =．所以，y 与x 的函数关系式为55800y x =-．②缆车到山顶的路线长为3600÷2=1800（m ），缆车到达终点所需时间为1800÷180＝１0（min ）．小颖到达缆车终点时，小亮行走的时间为10＋50＝60（min ）．把60x =代入55800y x =-，得y=55×60—800=2500．所以，当小颖到达缆车终点时，小亮离缆车终点的路程是3600-2500=1100（m ）．23. 解⑴抽取1名，恰好是女生的概率是25．⑵分别用男1、男2、男3、女1、女2表示这五位同学，从中任意抽取2名，所有可能出现的结果有：（男1，男2），（男1，男3），（男1，女1），（男1，女2），（男2，男3），（男2，女1），（男2，女2），（男3，女1），（男3，女2），（女1，女2），共10种，它们出现的可能性相同，所有结果中，满足抽取2名，恰好是1名男生和1名女生（记为事件A ）的结果共6种，所以P （A ）=63105=．24.解：⑴当x =0时，1y =．所以不论m 为何值，函数261y mx x =-+的图象经过y 轴上的一个定点（0，1）．⑵①当0m =时，函数61y x =-+的图象与x 轴只有一个交点；②当0m ≠时，若函数261y mx x =-+的图象与x 轴只有一个交点，则方程2610mx x -+=有两个相等的实数根，所以2(6)40m --=，9m =．综上，若函数261y mx x =-+的图象与x 轴只有一个交点，则m 的值为0或9．25.在Rt ECD ∆中，tan DEC ∠＝DCEC．∴EC ＝tan DC DEC ∠≈30400.75=（m ）．在Rt BAC ∆中，∠BCA ＝45°，∴BA CA =在Rt BAE ∆中，tan BEA ∠＝BA EA ．∴0.7540hh =+．∴120h =（m ）．答：电视塔高度约为120m ．26.解⑴直线AB 与⊙P 相切．如图，过点P 作PD ⊥AB , 垂足为D ．在Rt △A BC 中，∠ACB ＝90°，∵AC =6cm ，BC =8cm ，∴10AB cm =．∵P 为BC 的中点，∴PB =4cm ．∵∠P DB ＝∠ACB ＝90°，∠PBD ＝∠ABC ．∴△PBD ∽△ABC ．∴PD PB AC AB =,即4610PD =，∴PD =2.4(cm) ．当 1.2t =时，2 2.4PQ t ==(cm)∴PD PQ =，即圆心P 到直线AB 的距离等于⊙P 的半径．∴直线AB 与⊙P 相切．⑵ ∠ACB ＝90°，∴AB 为△ABC 的外切圆的直径．∴152OB AB cm ==．连接OP ．∵P 为BC 的中点，∴132OP AC cm ==．∵点P 在⊙O 内部，∴⊙P 与⊙O 只能内切．∴523t -=或253t -=，∴t =1或4．∴⊙P 与⊙O 相切时，t 的值为1或4．27. 解⑴在Rt △ABC 中，∠ACB ＝90°，CD 是AB 上的中线，∴12CD AB =，∴CD =BD ．∴∠BCE ＝∠ABC ．∵BE ⊥CD ，∴∠BEC ＝90°，∴∠BEC ＝∠ACB ．∴△BCE ∽△ABC ．∴E 是△ABC 的自相似点． ⑵①作图略．作法如下：（i ）在∠ABC 内，作∠CBD ＝∠A ；（ii ）在∠ACB 内，作∠BCE ＝∠ABC ；BD 交CE 于点P ．则P 为△ABC 的自相似点．②连接PB 、PC ．∵P 为△ABC 的内心，∴12PBC ABC ∠=∠，12PCB ACB ∠=∠．∵P 为△ABC 的自相似点，∴△BCP ∽△ABC ．∴∠PBC ＝∠A ，∠BCP ＝∠ABC=2∠PBC =2∠A ，∠ACB ＝2∠BCP=4∠A ．∵∠A +∠ABC+∠ACB ＝180°．∴∠A +2∠A+4∠A ＝180°．∴1807A ∠=．∴该三角形三个内角的度数分别为1807、3607、7207．28. 解⑴①174，103，52，2，52，103，174．函数1y x x=+(0)x >的图象如图．②本题答案不唯一，下列解法供参考．当01x <<时，y 随x 增大而减小；当1x >时,y 随x 增大而增大；当1x =时函数1y x x=+(0)x >的最小值为2．③1y xx=+=22+=22+-=22+，即1x=时，函数1y xx=+(0)x>的最小值为2．11。

2011年江苏省南京市中考数学试题(word版及答案)

南京市2011年初中毕业生学业考试数学数学注意事项：1．本试卷共6页，全卷满分120分，考试时间为120分钟，考生答题全部答在答题卡上，答在本试卷上无效．2．请认真核对监考教师在答题卡上所有粘贴条形码的姓名、考试证号是否与本人相符合，再将自己的姓名、准考证号用0.5毫米的黑色墨水签字笔填写在答题卡及本试卷上．3．答选择题必须用2B铅笔将答题卡上对应的答案标号涂黑．如需要改动，请用橡皮擦干净后，再选涂其他答案，答非选择题必须0.5毫米黑色墨水签字笔写在答题卡上指定位置，在其他位置答题一律无效．4．作图必须用2B铅笔作答，并请加黑加粗，描写清楚．一、选择题（本大题共6小题，每小题2分，共12分，在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确的选项的字母代号填涂在答．题卡相应位置．．．．．．上）1A．3B．－3C．±3D．2．下列运算正确的是A．a2＋a3=a5 B．a2•a3=a6C．a3÷a2=a D．(a2)3=a83．在第六次全国人口普查中，南京市常住人口约为800万人，其中65岁及以上人口占9.2%．则该市65岁及以上人口用科学记数法表示约为A．0.736×106人B．7.36×104人C．7.36×105人D．7.36×106 人4．为了解某初中学校学生的视力情况，需要抽取部分学生进行调查，下列抽取学生的方法最合适的是A．随机抽取该校一个班级的学生B．随机抽取该校一个年级的学生C．随机抽取该校一部分男生D．分别从该校初一、初二、初三年级中各班随机抽取10%的学生5．如图是一个三棱柱，下列图形中，能通过折叠围成一个三棱柱的是6．如图，在平面直角坐标系中，⊙P的圆心是（2，a）(a＞2)，半径为2，函数y=x的图象被⊙P的弦AB的长为a的值是A．B．2+C．D．2A．B．D．(第5题)二、填空题（本大题共10小题，每小题2分，共20分，不需要写出解答过程，请把答案直接填写在答题卡相应位置．．．．．．．上） 7．－2的相反数是________．8．如图，过正五边形ABCDE 的顶点A 作直线l ∥CD ，则∠1=____________．9．计算1)(2=_______________．10．等腰梯形的腰长为5㎝，它的周长是22㎝，则它的中位线长为___________㎝．11．如图，以O 为圆心，任意长为半径画弧，与射线OM 交于点A ，再以A 为圆心，AO 长为半径画弧，两弧交于点B ，画射线OB ，则cos ∠AOB 的值等于___________．12．如图，菱形ABCD 的连长是2㎝，E 是AB 中点，且DE ⊥AB ，则菱形ABCD 的面积为_________㎝2．13．如图，海边有两座灯塔A 、B ，暗礁分布在经过A 、B 两点的弓形（弓形的弧是⊙O 的一部分）区域内，∠AOB =80°，为了避免触礁，轮船P 与A 、B 的张角∠APB 的最大值为______°．14．如图，E 、F 分别是正方形ABCD 的边BC 、CD 上的点，BE =CF ，连接AE 、BF ，将△ABE 绕正方形的中心按逆时针方向转到△BCF ，旋转角为a （0°＜a ＜180°），则∠a =______． 15．设函数2y x =与1y x =-的图象的交战坐标为（a ，b ），则11a b-的值为__________． 16．甲、乙、丙、丁四位同学围成一圈依序循环报数，规定：①甲、乙、丙、丁首次报出的数依次为1、2、3、4，接着甲报5、乙报6……按此规律，后一位同学报出的数比前一位同学报出的数大1，当报到的数是50时，报数结束； ②若报出的数为3的倍数，则报该数的同学需拍手一次，在此过程中，甲同学需要拍手的次数为____________．三、解答题（本大题共12小题，共88分，请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）(第12题)(第8题)l(第11题)BA MO(第12题)A(第14题)ABCDF17．（6分）解不等式组523132x x x +⎧⎪+⎨⎪⎩≥＞，并写出不等式组的整数解．18．（6分）计算221()a b a b a b b a-÷-+-19．（6分）解方程x 2－4x ＋1=0 20．（7分）某校部分男生分3组进行引体向上训练，对训练前后的成绩进行统计分析，相应数据的统计图如下．⑴求训练后第一组平均成绩比训练前增长的百分数； ⑵小明在分析了图表后，声称他发现了一个错误：“训练后第二组男生引体向上个数没有变化的人数占该组人数的50%，所以第二组的平均数不可能提高3个这么多．”你同意小明的观点吗？请说明理由；⑶你认为哪一组的训练效果最好？请提出一个解释来支持你的观点．21．（7分）如图，将□ABCD 的边DC 延长到点E ，使CE =DC ，连接AE ，交BC 于点F ．⑴求证：△ABF ≌△ECF⑵若∠AFC =2∠D ，连接AC 、BE ．求证：四边形ABEC 是矩形．①训练后第二组男生引体向上增加个数分布统计图增加85个②(第20题)B D (第21题)22．（7分）小颖和小亮上山游玩，小颖乘会缆车，小亮步行，两人相约在山顶的缆车终点会合．已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍，小颖在小亮出发后50 min才乘上缆车，缆车的平均速度为180 m/min．设小亮出发x min后行走的路程为y m．图中的折线表示小亮在整个行走过程中y与x的函数关系．⑴小亮行走的总路程是____________㎝，他途中休息了________min．⑵①当50≤x≤80时，求y与x的函数关系式；②当小颖到达缆车终点为时，小亮离缆车终点的路程是多少？23．（7分）从3名男生和2名女生中随机抽取2014年南京青奥会志愿者．求下列事件的概率：⑴抽取1名，恰好是女生；⑵抽取2名，恰好是1名男生和1名女生．24．（7分）已知函数y=mx2－6x＋1（m是常数）．⑴求证：不论m为何值，该函数的图象都经过y轴上的一个定点；⑵若该函数的图象与x轴只有一个交点，求m的值．25．（7分）如图，某数学课外活动小组测量电视塔AB的高度，他们借助一个高度为30m 的建筑物CD进行测量，在点C处塔顶B的仰角为45°，在点E处测得B的仰角为37°（B、D、E三点在一条直线上）．求电视塔的高度h．（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）Bh (第25题)(第22题)26．（8分）如图，在Rt △ABC 中，∠ACB =90°，AC =6㎝，BC =8㎝，P 为BC 的中点．动点Q 从点P 出发，沿射线PC 方向以2㎝/s 的速度运动，以P 为圆心，PQ 长为半径作圆．设点Q 运动的时间为t s ．⑴当t =1.2时，判断直线AB 与⊙P 的位置关系，并说明理由； ⑵已知⊙O 为△ABC 的外接圆，若⊙P 与⊙O 相切，求t 的值．27．（9分）如图①，P 为△ABC 内一点，连接P A 、PB 、PC ，在△P AB 、△PBC 和△P AC 中，如果存在一个三角形与△ABC 相似，那么就称P 为△ABC 的自相似点．⑴如图②，已知Rt △ABC 中，∠ACB =90°，∠ACB ＞∠A ，CD 是AB 上的中线，过点B 作BE ⊥CD ，垂足为E ，试说明E 是△ABC 的自相似点．⑵在△ABC 中，∠A ＜∠B ＜∠C ．①如图③，利用尺规作出△ABC 的自相似点P （写出作法并保留作图痕迹）； ②若△ABC 的内心P 是该三角形的自相似点，求该三角形三个内角的度数．28．（11分）问题情境已知矩形的面积为a （a 为常数，a ＞0），当该矩形的长为多少时，它的周长最小？最小值是多少？数学模型设该矩形的长为x ，周长为y ，则y 与x 的函数关系式为2()(0)a y x x x=+＞．探索研究⑴我们可以借鉴以前研究函数的经验，先探索函(第26题)①②③(第27题)数1(0)y x x x=+＞的图象性质． ① 填写下表，画出函数的图象： ②②观察图象，写出该函数两条不同类型的性质；③在求二次函数y =ax 2＋bx ＋c （a ≠0）的最大（小）值时，除了通过观察图象，还可以通过配方得到．请你通过配方求函数1y x x=+(x ＞0)的最小值．解决问题⑵用上述方法解决“问题情境”中的问题，直接写出答案．答案：一.选择题：ACCDBB 二.填空：7. 2 8. 36 9.10. 6 11.1212. 13. 40 14. 90 15. 12-16. 4 17.解：解不等式①得：1x ≥- 解不等式②得：2x <所以，不等式组的解集是12x -≤<．不等式组的整数解是1-，0，1． 18.221)a ba b a b b a-÷-+-解：（()()()()a a b b a b a b a b a b b a ⎡⎤-=-÷⎢⎥+-+--⎣⎦()()b b aa b a b b -=⋅+- 1a b=-+ 19. 解法一：移项，得241x x -=-．配方，得24414x x -+=-+， 2(2)3x -=由此可得2x -=12x =22x =解法二：1,4, 1.a b c ==-=224(4)411120b ac -=--⨯⨯=>，2x ==±12x =，22x =．20.解：⑴训练后第一组平均成绩比训练前增长的百分数是53100%3-⨯≈67%． ⑵不同意小明的观点，因为第二组的平均成绩增加8×10%+6×20%+5×20%+0×50%=3（个）．（3）本题答案不唯一，我认为第一组训练效果最好，因为训练后第一组平均成绩比训练前增长的百分数最大．21.证明：⑴∵四边形ABCD 是平行四边形，∴AB ∥CD,AB=CD ．∴∠ABF=∠ECF . ∵EC=DC , ∴AB=EC ．在△ABF 和△ECF 中，∵∠ABF=∠ECF ，∠AFB=∠EFC ，AB=EC ， ∴⊿ABF ≌⊿ECF ．（2）解法一：∵AB=EC ，AB ∥EC ，∴四边形ABEC 是平行四边形．∴AF=EF ， BF=CF ． ∵四边形ABCD 是平行四边形，∴∠ABC=∠D ，又∵∠AFC=2∠D ，∴∠AFC=2∠ABC ． ∵∠AFC=∠ABF+∠BAF ，∴∠ABF=∠BAF ．∴F A=FB ． ∴F A=FE=FB=FC , ∴AE=BC ．∴口ABEC 是矩形．解法二：∵AB=EC ，AB ∥EC ，∴四边形ABEC 是平行四边形． ∵四边形ABCD 是平行四边形，∴AD ∥BC ，∴∠D=∠BCE ．又∵∠AFC=2∠D ，∴∠AFC=2∠BCE ，∵∠AFC=∠FCE+∠FEC ，∴∠FCE=∠FEC ．∴∠D=∠FEC ．∴AE=AD ．又∵CE=DC ，∴AC ⊥DE ．即∠ACE=90°．∴口ABEC 是矩形． 22. 解⑴3600，20．⑵①当5080x ≤≤时，设y 与x 的函数关系式为y kx b =+．根据题意，当50x =时，1950y =；当80x =，3600y =．所以，y 与x 的函数关系式为55800y x =-．②缆车到山顶的路线长为3600÷2=1800（m ），缆车到达终点所需时间为1800÷180＝１0（min ）．小颖到达缆车终点时，小亮行走的时间为10＋50＝60（min ）．把60x =代入55800y x =-，得y=55×60—800=2500．所以，当小颖到达缆车终点时，小亮离缆车终点的路程是3600-2500=1100（m ）． 23. 解⑴抽取1名，恰好是女生的概率是25． ⑵分别用男1、男2、男3、女1、女2表示这五位同学，从中任意抽取2名，所有可能出现的结果有：（男1，男2），（男1，男3），（男1，女1），（男1，女2），（男2，男3），（男2，女1），（男2，女2），（男3，女1），（男3，女2），（女1，女2），共10种，它们出现的可能性相同，所有结果中，满足抽取2名，恰好是1名男生和1名女生（记为事件A ）的结果共6种，所以P （A ）=63105=． 24.解：⑴当x =0时，1y =．所以不论m 为何值，函数261y mx x =-+的图象经过y 轴上的一个定点（0，1）． ⑵①当0m =时，函数61y x =-+的图象与x 轴只有一个交点；②当0m ≠时，若函数261y mx x =-+的图象与x 轴只有一个交点，则方程2610mx x -+=有两个相等的实数根，所以2(6)40m --=，9m =．综上，若函数261y mx x =-+的图象与x 轴只有一个交点，则m 的值为0或9． 25.在Rt ECD ∆中，tan DEC ∠＝DCEC． ∴EC ＝tan DC DEC ∠≈30400.75=（m ）．在Rt BAC ∆中，∠BCA ＝45°，∴BA CA =在Rt BAE ∆中，tan BEA ∠＝BA EA ．∴0.7540hh =+．∴120h =（m ）．答：电视塔高度约为120m ．26.解⑴直线AB 与⊙P 相切．如图，过点P 作PD ⊥AB , 垂足为D ．在Rt △A BC 中，∠ACB ＝90°，∵AC =6cm ，BC =8cm ，∴10AB cm ==．∵P 为BC 的中点，∴PB =4cm ．∵∠P DB ＝∠ACB ＝90°，∠PBD ＝∠ABC ．∴△PBD ∽△ABC ． ∴PD PB AC AB =,即4610PD =，∴PD =2.4(cm) ．当 1.2t =时，2 2.4PQ t ==(cm)∴PD PQ =，即圆心P 到直线AB 的距离等于⊙P 的半径． ∴直线AB 与⊙P 相切．⑵ ∠ACB ＝90°，∴AB 为△ABC 的外切圆的直径．∴152OB AB cm ==．连接OP ．∵P 为BC 的中点，∴132OP AC cm ==． ∵点P 在⊙O 内部，∴⊙P 与⊙O 只能内切． ∴523t -=或253t -=，∴t =1或4． ∴⊙P 与⊙O 相切时，t 的值为1或4．27. 解⑴在Rt △ABC 中，∠ACB ＝90°，CD 是AB 上的中线，∴12CD AB =，∴CD =BD ． ∴∠BCE ＝∠ABC ．∵BE ⊥CD ，∴∠BEC ＝90°，∴∠BEC ＝∠ACB ．∴△BCE ∽△ABC ． ∴E 是△ABC 的自相似点． ⑵①作图略．作法如下：（i ）在∠ABC 内，作∠CBD ＝∠A ；（ii ）在∠ACB 内，作∠BCE ＝∠ABC ；BD 交CE 于点P ．则P 为△ABC 的自相似点．②连接PB 、PC ．∵P 为△ABC 的内心，∴12PBC ABC ∠=∠，12PCB ACB ∠=∠． ∵P 为△ABC 的自相似点，∴△BCP ∽△ABC ．∴∠PBC ＝∠A ，∠BCP ＝∠ABC=2∠PBC =2∠A ， ∠ACB ＝2∠BCP=4∠A ．∵∠A +∠ABC+∠ACB ＝180°． ∴∠A +2∠A+4∠A ＝180°． ∴1807A ∠=．∴该三角形三个内角的度数分别为1807、3607、7207．28. 解⑴①174，103，52，2，52，103，174．函数1y x x=+(0)x >的图象如图．②本题答案不唯一，下列解法供参考．当01x <<时，y 随x 增大而减小；当1x >时,y 随x 增大而增大；当1x =时函数1y x x =+(0)x >的最小值为2． ③1y x x =+=22+=22+-=22+=0，即1x =时，函数1y x x =+(0)x >的最小值为2．。

2011年中考数学试题及答案解析江苏南京中考数学试卷试题

中考数学说明：本试卷共八大题，总分值120分，考试时间120分钟．请你认真审题，树立信心，沉着应答！一、填空题〔本大题10小题，每题２分，共20分〕1、计算：6-1= .2、在七巧板拼图中〔如图1〕，∠ABC ＝度 .3、“抛出的篮球会下落〞，这个事件是事件〔填“确定〞或“不确定〞〕.4、南宁国际会展中心是即将举办的中国—东盟博览会的会址，其总建筑面积为112100平方米，用科学记数法表示为________平方米〔保存三个有效数字〕.5、当x 时，分式x-13有意义. 6、如图2，D 、E 分别是⊙O 的半径OA 、OB 上的点，CD ⊥OA 、CE ⊥OB 、CD=CE ，那么AC 与CB 两弧长的大小关系是： .7、写出一个图象位于一、三角限的反比例函数表达式 8、顺次连接一个任意四边形四边的中点，得到一个___________四边形.图1 图2 图3 图49、图3是两张全等的图案，它们完全重合地叠放在一起，按住下面的图案不动，将上面图案绕点O 顺时针旋转，至少旋转______度角后，两张图案构成的图形是中心对称图形. 10、如图4，一个机器人从O 点出发，图3向正东方向走3米到达A 1点，再向正北方向走6米到达A 2点，再向正西方向走9米到达A 3点，再向正南方向走12米到达A 4点，再向正东方向走15米到达A 5点.按如此规律走下去，当机器人走到A 6点时，离O 点的距离是米.______________二、选择题〔本大题8小题，每题３分，共24分〕每题都给出代号为(A)、(B)、(C)、(D)的四个结论，其中只有一个是正确的．选择正确结论的代号填在括号内．11．以下运算正确的选项是〔〕 (A)224x x x += (B)22(1)1a a -=- (C)325x x xy +=(D)235a a a =得分评卷人得分评卷人ABCCABDEO·O北南东西O A 1 A 2A 3A 4A 5A 612．分式11a b+计算的结果是〔〕 (A)b a + (B)1a b + (C)2a b + (D)a bab+13．如图５，ABCD 是平行四边形，那么图中与DEF △相似的三角形共有〔〕 (A)１个 (B)２分(C)３个 (D)4个14．如图６，CD 是ABC Rt △斜边上的高，43AC BC ==，，那么 cos BCD ∠的值是〔〕(A)35(B)34(C)43(D)4515．中央电视台“开心辞典〞栏目有这么一道题：小兰从镜子中看到挂在她背后墙上的四个时钟如以下图所示，其中时间最接近四点钟的是〔〕 (A) (B) (C) (D)16．如图７，分别以等腰直角三角板的直角边、斜边为旋转轴旋转，所形成的旋转体的全面积依次记为12S S 、，那么12S S 与的大小关系为〔〕 (A)12S S > (B)12S S < (C)12S S =(D)无法判断17．函数2y ax a =-与(0)ay a=≠在同一直角坐标系中的图象可能是〔〕(A) (B) (C) (D) 18．观察图８寻找规律，在“？〞处填上的数字是〔〕 (A)128 (B)136(C)162 (D)188Ｂ E图５Ａ图６图72 2４ 8 14 26 48 88？图8三、〔本大题共2小题，每题８分，总分值16分〕19、〔此题总分值 8分〕计算：〔－2〕3＋21〔2004－3〕0－|－21|20、〔此题总分值 8分〕化简：4)223(2-÷+-+x xx x x x四、〔此题Ａ类题总分值７分，Ｂ类题总分值10分〕21．此题有Ａ、Ｂ两类题．Ａ类题总分值7分，Ｂ类题总分值10分．请你选择其中一类．．．．．．证明．〔Ａ类〕如图９，DE AB DF AC ⊥、⊥．垂足分别为E F 、．请你从下面三个条件中，再选出两个作为条件，另一个为结论，推出一个正确的命题〔只需写出一种情况〕． ①AB AC = ②BD CD = ③BE CF = ：DE AB DF AC ⊥、⊥，垂足分别为E F 、，＝，＝．求证：证明：B C 图９〔Ｂ类〕如图10，EG AF ∥，请你从下面三个条件中，再选两个作为条件，另一个为结论，推出一个正确的命题〔只需写出一种情况〕． ①AB AC = ②DE DF = ③BE CF = ：EG AF ∥，＝，＝．求证：证明：友情提醒：假设两题都做的同学，请你确认以哪类题记分，你的选择是类题．五、〔本大题共6小题，每题10分，共60分〕22、以下资料来源于2003年?南宁统计年鉴?□表示南宁市农民人均纯收入(元)〔1〕分别指出南宁市农民人均纯收相对于上一年哪年增长最快？Ｂ2000年 2001年 2002年 8796〔2〕据统计，2000年～2002年南宁市农民年人均纯收入的平均增长率为7.5%，城市居民年人均可支配收入的平均增长率为8.7%，假设年平均增长率不变，请你分别预计2004年南宁市农民人均纯收入和城市居民人均可支配收入各是多少？〔精确到1元〕〔3〕从城乡年人均收入增长率看，你有哪些积极的建议？〔写出一条建议〕23．如图11，石头A和石头B相距80cm，且关于竹竿l对称，一只电动青蛙在距竹竿30cm，距石头Ａ为60cm的1P处，按如下顺序循环跳跃：（１）请你画出青蛙跳跃的路径〔画图工具不作限制〕．（２）青蛙跳跃25次后停下，此时它与石头A相距cm，与竹竿l相距cm．Ｂ1Pl竹竿石头Ａ图1124、某饮料厂为了开发新产品，用A、B两种果汁原料各19千克、17.2千克，试制甲、乙两种新型饮料共50千克，下表是试验的相关数据：〔1〕假设甲种饮料需配制x千克，请你写出满足题意的不等式组，并求出其解集.〔2〕设甲种饮料每千克本钱为4元，乙种饮料每千克本钱为3元，这两种饮料的本钱总额为y元，请写出y与x的函数表达式.并根据〔1〕的运算结果，确定当甲种饮料配制多少千克时，甲、乙两种饮料的本钱总额最少？25、目前国内最大跨径的钢管混凝土拱桥——永和大桥，是南宁市又一标志性建筑，其拱形图形为抛物线的一局部〔如图11〕，在正常情况下，位于水面上的桥拱跨度为350米，拱高为85米.〔1〕在所给的直角坐标系中〔如图12〕，假设抛物线的表达式为y＝ax2＋b，请你根据上述数据求出a、b的值，并写出抛物线的表达式〔不要求写自变量的取值范围，a、b的值保存两个有效数字〕.85m图12〔2〕七月份汛期将要来临，当邕江水位上涨后，位于水面上的桥拱跨度将会减小 .当水位上涨 4 m 时，位于水面上的桥拱跨度有多大？〔结果保存整数〕.26．OABC 是一张放在平面直角坐标系中的矩形纸片，O 为原点，点A 在x 轴上，点C 在y 轴上，106OA OC ==，．（１）如图13，在AB 上取一点M ，使得CBM △沿CM 翻折后，点B 落在x 轴上，记作B '点．求B '点的坐标；（２）求折痕CM 所在直线的解析式；（３）作B G AB '∥交CM 于点G ，假设抛物线216y x m =+过点G ，求抛物线的解析式，并判断以原点O 为圆心，OG 为半径的圆与抛物线除交点G 外，是否图1325、如图14，点P 是圆上的一个动点，弦AB PC =是APB ∠的平分线，30BAC ∠=．（１）当PAC ∠等于多少度时，四边形PACB 有最大面积？最大面积是多少？（２）当PAC ∠等于多少度时，四边形PACB 是梯形？说明你的理由．ＣＣＰ图14。

2011年江苏省南京市中考数学试卷及答案

2011年江苏省南京市中考数学试卷一、选择题（本大题共6小题，每小题2分，共12分,在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）1、（2011•南京）的值等于（）A、3B、﹣3C、±3D、考点：算术平方根。

分析：此题考查的是9的算术平方根，需注意的是算术平方根必为非负数．解答：解：∵=3，故选A．点评：此题主要考查了算术平方根的定义，一个正数只有一个算术平方根，0的算术平方根是0．2、（2011•南京）下列运算正确的是（）A、a2+a3=a5B、a2•a3=a6C、a3+a2=aD、（a2）3=a6考点：幂的乘方与积的乘方；合并同类项；同底数幂的乘法。

专题：计算题。

分析：根据合并同类项法则、积的乘方和幂的乘方的法则运算．解答：解：A、a2与a3不是同类项，不能合并，故本选项错误；B、a2•a3=a2+3=a5≠a6，故本选项错误；C、a3与a2不是同类项，不能合并，故本选项错误；D、（a2）3=a2×3=a6，故本选项正确．故选D．点评：此题考查了幂的乘方与积的乘方、合并同类项等知识，属于基本题型．3、（2011•南京）在第六次全国人口普查中，南京市常住人口约为800万人，其中65岁及以上人口占9.2%，则该市65岁及以上人口用科学记数法表示约为2%，则该市65岁及以上人口用科学记数法表示约为（）A、0.736×106人B、7.36×104人C、7.36×105人D、7.36×106人考点：科学记数法—表示较大的数。

专题：计算题。

分析：先计算出该市65岁及以上人口数，然后用科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．解答：解：该市65岁及以上人口：8000000×9.2%=736000（人）将736 000人用科学记数法表示7.36×105人．故选C．点评：题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．4、（2011•南京）为了了解某初中学校学生的视力情况，需要抽取部分学生进行调查．下列抽取学生的方法最合适的是（）A、随机抽取该校一个班级的学生B、随机抽取该校一个年级的学生C、随机抽取该校一部分男生D、分别从该校初一、初二、初三年级中各随机抽取10%的学生考点：全面调查与抽样调查。

南京市中考数学试卷及答案.docx

B. <1南京市2011年初中毕业生学业考试注意事项：1. 本试卷共6页.全卷满分120分.考试时间为120分钟.考生答题全部答在答题卡上，答在本试卷上无效.2. 请认真核对监考教师在答题卡上所粘贴条形码的姓名、考试证号是否与本人相符合，再将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在答题卡及本试卷上.3. 答选择题必须用2B 铅笔将答题卡上对应的答案标号涂黑.如需改动，请用橡皮擦干净后，再选涂其他答案.答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡上的指定位置，在其他位置答题一律无效.4. 作图必须用2B 铅笔作答，并请加黑加粗，描写清楚.一、选择题（本大题共6小题，每小题2分，共12分.在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在等粵卡艰亩佟單上）1. V9的值等于A. 3B. -3C. ±3D.V3 2. 下列运算正确的是A. a 2+a 3=a sB. a 2 • a 3 =a eC. a 3-r-a 2=aD. （a 2）3=a 8 3. 在第六次全国人口普査中，南京市常住人口约为800万人，其中65岁及以上人口占9.2%, 则该市65岁及以上人口用科学记数法表示约为A. 0. 736 X106 人B. 7.36 X10* 人C. 7. 36X 105 人D. 7. 36X106 人 4. 为了了解某初中学校学生的视力情况,需要抽取部分学生进行调査.下列抽取学生的方法最合适的是 A. 随机抽取该校一个班级的学生B. 随机抽取该校一个年级的学生C. 随机抽取该校一部分男生D. 分别从该校初一、初二、初三年级中各随机抽取10%的学生5. 如图是一个三棱柱.下列图形中，能通过折叠围成一个三棱柱的是（第5题） D.13. 如图，海边立有两座灯塔A 、B,暗礁分布在经过A.B 两点的弓形（弓形的弧是OO 的一部分）区域内，ZAOB=80°.为了避免触礁，轮船P 与A 、B 的张角ZAPB 的最大值为 ▲ °, 14. 如图，E 、F 分别是正方形ABCD 的边BC 、CD 上的点,BE=CF,连接AE.BF.将AABE 绕正方形的中心按逆时针方向旋转到厶BCF,旋转角为a （0°<a<180°）,则Za= ▲6.如图，在平面直角坐标系中，OP 的圆心是（2,a ）（a>2）,半径为2,函数y=z 的图象被。

2011年江苏省南京中考数学试题及答案word版[1]

11．如图，以O为圆心，任意长为半径画弧，与射线OM交于点A，再以A为圆心，AO长为半径画弧，两弧交于点B，画射线OB，则cos∠AOB的值等于___________．
12．如图，菱形ABCD的连长是2㎝，E是AB中点，且DE⊥AB，则菱形ABCD的面积为_________㎝2．
13．如图，海边有两座灯塔A、B，暗礁分布在经过A、B两点的弓形（弓形的弧是⊙O的一部分）区域内，∠AOB=80°，为了避免触礁，轮船P与A、B的张角∠APB的最大值为______°．
27.解⑴在Rt △ABC中，∠ACB＝90°，CD是AB上的中线，∴ ，∴CD=BD．
∴∠BCE＝∠ABC．∵BE⊥CD，∴∠BEC＝90°，∴∠BEC＝∠ACB．∴△BCE∽△ABC．
∴E是△ABC的自相似点．
⑵①作图略．
作法如下：（i）在∠ABC内，作∠CBD＝∠A；
（ii）在∠ACB内，作∠BCE＝∠ABC；BD交CE于点P．
南京市2011年初中毕业生学业考试
数学
数学注意事项：
1．本试卷共6页，全卷满分120分，考试时间为120分钟，考生答题全部答在答题卡上，答在本试卷上无效．
2．请认真核对监考教师在答题卡上所有粘贴条形码的姓名、考试证号是否与本人相符合，再将自己的姓名、准考证号用0.5毫米的黑色墨水签字笔填写在答题卡及本试卷上．
⑵分别用男1、男2、男3、女1、女2表示这五位同学，从中任意抽取2名，所有可能出现的结果有：（男1，男2），（男1，男3），（男1，女1），（男1，女2），（男2，男3），（男2，女1），（男2，女2），（男3，女1），（男3，女2），（女1，女2），共10种，它们出现的可能性相同，所有结果中，满足抽取2名，恰好是1名男生和1名女生（记为事件A）的结果共6种，所以P（A）= ．

2011年南京中考数学试题及答案word版

南京市2011年初中毕业生学业考试数学数学注意事项：1．本试卷共6页，全卷满分120分，考试时间为120分钟，考生答题全部答在答题卡上，答在本试卷上无效．2．请认真核对监考教师在答题卡上所有粘贴条形码的姓名、考试证号是否与本人相符合，再将自己的姓名、准考证号用0.5毫米的黑色墨水签字笔填写在答题卡及本试卷上．3．答选择题必须用2B铅笔将答题卡上对应的答案标号涂黑．如需要改动，请用橡皮擦干净后，再选涂其他答案，答非选择题必须0.5毫米黑色墨水签字笔写在答题卡上指定位置，在其他位置答题一律无效．4．作图必须用2B铅笔作答，并请加黑加粗，描写清楚．一、选择题（本大题共6小题，每小题2分，共12分，在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确的选项的字母代号填涂在答题卡相应位置．．．．．．．上）1A．3B．－3C．±3D．2．下列运算正确的是A．a2＋a3=a5 B．a2•a3=a6C．a3÷a2=aD．(a2)3=a83．在第六次全国人口普查中，南京市常住人口约为800万人，其中65岁及以上人口占9.2%．则该市65岁及以上人口用科学记数法表示约为A ．0.736×106人B ．7.36×104人C ．7.36×105人D ．7.36×106人4．为了解某初中学校学生的视力情况，需要抽取部分学生进行调查，下列抽取学生的方法最合适的是A ．随机抽取该校一个班级的学生B ．随机抽取该校一个年级的学生C ．随机抽取该校一部分男生D ．分别从该校初一、初二、初三年级中各班随机抽取10%的学生5．如图是一个三棱柱，下列图形中，能通过折叠围成一个三棱柱的是6．如图，在平面直角坐标系中，⊙P 的圆心是（2，a ）(a＞2)，半径为2，函数y =x 的图象被⊙P 的弦AB的长为a 的值是AB．2+ C． D．2二、填空题（本大题共10小题，每小题2分，共20分，不需要写出解答过程，请把答案直接填写在答题卡相应位．．．．．．A ．B ．C D ．(第5题)置．上） 7．－2的相反数是________．8．如图，过正五边形ABCDE 的顶点A 作直线l ∥CD ，则∠1=____________．9．计算1)(2=_______________．10．等腰梯形的腰长为5㎝，它的周长是22㎝，则它的中位线长为___________㎝．11．如图，以O 为圆心，任意长为半径画弧，与射线OM 交于点A ，再以A 为圆心，AO 长为半径画弧，两弧交于点B ，画射线OB ，则cos ∠AOB 的值等于___________． 12．如图，菱形ABCD 的连长是2㎝，E 是AB 中点，且DE ⊥AB ，则菱形ABCD 的面积为_________㎝2．13．如图，海边有两座灯塔A 、B ，暗礁分布在经过A 、B 两点的弓形（弓形的弧是⊙O 的一部分）区域内，∠AOB =80°，为了避免触礁，轮船P 与A 、B 的张角∠APB(第12题)(第8题)l(第11题)BA MO(第12题)A(第14题)ABCDF的最大值为______°．14．如图，E 、F 分别是正方形ABCD 的边BC 、CD 上的点，BE =CF ，连接AE 、BF ，将△ABE 绕正方形的中心按逆时针方向转到△BCF ，旋转角为a （0°＜a ＜180°），则∠a =______．15．设函数2y x=与1y x =-的图象的交战坐标为（a ，b ），则11ab-的值为__________．16．甲、乙、丙、丁四位同学围成一圈依序循环报数，规定：①甲、乙、丙、丁首次报出的数依次为1、2、3、4，接着甲报5、乙报6……按此规律，后一位同学报出的数比前一位同学报出的数大1，当报到的数是50时，报数结束； ②若报出的数为3的倍数，则报该数的同学需拍手一次，在此过程中，甲同学需要拍手的次数为____________．三、解答题（本大题共12小题，共88分，请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）17．（6分）解不等式组523132x x x +⎧⎪+⎨⎪⎩≥＞，并写出不等式组的整数解． 18．（6分）计算221()a ba b a b b a-÷-+-19．（6分）解方程x 2－4x ＋1=020．（7分）某校部分男生分3组进行引体向上训练，对训练前后的成绩进行统计分析，相应数据的统计图如下．⑴求训练后第一组平均成绩比训练前增长的百分数； ⑵小明在分析了图表后，声称他发现了一个错误：“训练后第二组男生引体向上个数没有变化的人数占该组人数的50%，所以第二组的平均数不可能提高3个这么多．”你同意小明的观点吗？请说明理由；⑶你认为哪一组的训练效果最好？请提出一个解释来支持你的观点．21．（7分）如图，将□ABCD 的边DC①训练后第二组男生引体向上增加个数分布统计图增加85个②(第20题)BD延长到点E，使CE=DC，连接AE，交BC于点F．⑴求证：△ABF≌△ECF⑵若∠AFC=2∠D，连接AC、BE．求证：四边形ABEC是矩形．22．（7分）小颖和小亮上山游玩，小颖乘会缆车，小亮步行，两人相约在山顶的缆车终点会合．已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍，小颖在小亮出发后50 min才乘上缆车，缆车的平均速度为180 m/min．设小亮出发x min后行走的路程为y m．图中的折线表示小亮在整个行走过程中y与x的函数关系．⑴小亮行走的总路程是____________㎝，他途中休息了________min．⑵①当50≤x≤80时，求y与x的函数关系式；②当小颖到达缆车终点为时，小亮离缆车终点的路程是多少？(第22题)23．（7分）从3名男生和2名女生中随机抽取2014年南京青奥会志愿者．求下列事件的概率：⑴抽取1名，恰好是女生；⑵抽取2名，恰好是1名男生和1名女生．24．（7分）已知函数y=mx2－6x＋1（m是常数）．⑴求证：不论m为何值，该函数的图象都经过y轴上的一个定点；⑵若该函数的图象与x轴只有一个交点，求m的值．25．（7分）如图，某数学课外活动小组测量电视塔AB 的高度，他们借助一个高度为30m 的建筑物CD 进行测量，在点C 处塔顶B 的仰角为45°，在点E 处测得B 的仰角为37°（B 、D 、E 三点在一条直线上）．求电视塔的高度h ．（参考数据：sin 37°≈0.60，cos 37°≈0.80，tan 37°≈0.75）26．（8分）如图，在Rt △ABC 中，∠ACB =90°，AC =6㎝，BC =8㎝，P 为BC 的中点．动点Q 从点P 出发，沿射线PC 方向以2㎝/s 的速度运动，以P 为圆心，PQ 长为半径作圆．设点Q 运动的时间为t s ．⑴当t =1.2时，判断直线AB 与⊙P 的位置关系，并说明理由；⑵已知⊙O 为△ABC 的外接圆，若⊙P 与⊙O 相切，求t 的值．Bh (第25题)(第26题)27．（9分）如图①，P 为△ABC 内一点，连接PA 、PB 、PC ，在△PAB 、△PBC 和△PAC 中，如果存在一个三角形与△ABC 相似，那么就称P 为△ABC 的自相似点．⑴如图②，已知Rt △ABC 中，∠ACB =90°，∠ACB ＞∠A ，CD 是AB 上的中线，过点B 作BE ⊥CD ，垂足为E ，试说明E 是△ABC 的自相似点．⑵在△ABC 中，∠A ＜∠B ＜∠C ．①如图③，利用尺规作出△ABC 的自相似点P （写出作法并保留作图痕迹）；②若△ABC 的内心P 是该三角形的自相似点，求该三角形三个内角的度数．28．（11分）问题情境已知矩形的面积为a （a 为常数，a ＞0），当该矩形的长为多少时，它的周长最小？最小值是多少？①②③(第27题)数学模型设该矩形的长为x ，周长为y ，则y 与x 的函数关系式为2()(0)ay x x x=+＞．探索研究⑴我们可以借鉴以前研究函数的经验，先探索函数②观察图象，写出该函数两条不同类型的性质； ③在求二次函数y =ax 2＋bx ＋c （a ≠0）的最大（小）值时，除了通过观察图象，还可以通过配方得到．请你通过配方求函数1y x x=+(x ＞0)的最小值．解决问题⑵用上述方法解决“问题情境”中的问题，直接写出答案．答案：一.选择题：ACCDBB二.填空：7. 2 8. 36 9.10. 6 11. 1212.13. 40 14. 90 15. 12-16. 4 17.解：解不等式①得：1x≥-解不等式②得：2x<所以，不等式组的解集是12x-≤<．不等式组的整数解是1-，0，1．18.221)a ba b a b b a-÷-+-解：（()()()()a ab ba b a b a b a b b a⎡⎤-=-÷⎢⎥+-+--⎣⎦()()b b aa b a b b-=⋅+-1a b=-+19.解法一：移项，得241x x-=-．配方，得24414x x -+=-+，2(2)3x -= 由此可得2x -=12x =，22x =解法二：1,4, 1.a b c ==-=224(4)411120b ac -=--⨯⨯=>，2x ==±12x =，22x =．20.解：⑴训练后第一组平均成绩比训练前增长的百分数是53100%3-⨯≈67%． ⑵不同意小明的观点，因为第二组的平均成绩增加8×10%+6×20%+5×20%+0×50%=3（个）．（3）本题答案不唯一，我认为第一组训练效果最好，因为训练后第一组平均成绩比训练前增长的百分数最大．21.证明：⑴∵四边形ABCD 是平行四边形，∴AB ∥CD,AB=CD ．∴∠ABF=∠ECF.∵EC=DC , ∴AB=EC ．在△ABF 和△ECF 中，∵∠ABF=∠ECF ，∠AFB=∠EFC ，AB=EC ， ∴⊿ABF ≌⊿ECF ．（2）解法一：∵AB=EC ，AB ∥EC ，∴四边形ABEC 是平行四边形．∴AF=EF ， BF=CF ．∵四边形ABCD 是平行四边形，∴∠ABC=∠D ，又∵∠AFC=2∠D ，∴∠AFC=2∠ABC ．∵∠AFC=∠ABF+∠BAF ，∴∠ABF=∠BAF ．∴FA=FB ．∴FA=FE=FB=FC , ∴AE=BC ．∴口ABEC 是矩形．解法二：∵AB=EC ，AB ∥EC ，∴四边形ABEC 是平行四边形． ∵四边形ABCD 是平行四边形，∴AD ∥BC ，∴∠D=∠BCE ．又∵∠AFC=2∠D ，∴∠AFC=2∠BCE ，∵∠AFC=∠FCE+∠FEC ，∴∠FCE=∠FEC ．∴∠D=∠FEC ．∴AE=AD ．又∵CE=DC ，∴AC ⊥DE ．即∠ACE=90°．∴口ABEC 是矩形．22. 解⑴3600，20．⑵①当5080x ≤≤时，设y 与x 的函数关系式为y kx b =+．根据题意，当50x =时，1950y =；当80x =，3600y =．所以，y 与x 的函数关系式为55800y x =-．②缆车到山顶的路线长为3600÷2=1800（m ），缆车到达终点所需时间为1800÷180＝１0（min ）．小颖到达缆车终点时，小亮行走的时间为10＋50＝60（min ）．把60x =代入55800y x =-，得y=55×60—800=2500．所以，当小颖到达缆车终点时，小亮离缆车终点的路程是3600-2500=1100（m ）．23. 解⑴抽取1名，恰好是女生的概率是25． ⑵分别用男1、男2、男3、女1、女2表示这五位同学，从中任意抽取2名，所有可能出现的结果有：（男1，男2），（男1，男3），（男1，女1），（男1，女2），（男2，男3），（男2，女1），（男2，女2），（男3，女1），（男3，女2），（女1，女2），共10种，它们出现的可能性相同，所有结果中，满足抽取2名，恰好是1名男生和1名女生（记为事件A）的结果共6种，所以P（A）=63105=．24.解：⑴当x=0时，1y=．所以不论m为何值，函数261y mx x=-+的图象经过y轴上的一个定点（0，1）．⑵①当0m=时，函数61y x=-+的图象与x轴只有一个交点；②当0m≠时，若函数261y mx x=-+的图象与x轴只有一个交点，则方程2610mx x-+=有两个相等的实数根，所以2(6)40m--=，9m=．综上，若函数261y mx x=-+的图象与x轴只有一个交点，则m的值为0或9．25.在Rt ECD∆中，tan DEC∠＝DCEC．∴EC＝tan DCDEC∠≈30400.75=（m）．在Rt BAC∆中，∠BCA＝45°，∴BA CA=在Rt BAE∆中，tan BEA∠＝BAEA ．∴0.7540hh=+．∴120h=（m）．答：电视塔高度约为120m．26.解⑴直线AB与⊙P相切．如图，过点P 作PD ⊥AB , 垂足为D ．在Rt△A BC 中，∠ACB ＝90°，∵AC =6cm ，BC =8cm ， ∴10AB cm =．∵P 为BC 的中点，∴PB =4cm ．∵∠P DB ＝∠ACB ＝90°，∠PBD ＝∠ABC ．∴△PBD ∽△ABC ． ∴PD PB AC AB =,即4610PD =，∴PD =2.4(cm) ．当 1.2t =时，2 2.4PQ t ==(cm)∴PD PQ =，即圆心P 到直线AB 的距离等于⊙P 的半径． ∴直线AB 与⊙P 相切．⑵ ∠ACB ＝90°，∴AB 为△ABC 的外切圆的直径．∴152OB AB cm ==．连接OP ．∵P 为BC 的中点，∴132OP AC cm ==． ∵点P 在⊙O 内部，∴⊙P 与⊙O 只能内切．∴523t -=或253t -=，∴t =1或4．∴⊙P 与⊙O 相切时，t 的值为1或4．27. 解⑴在Rt △ABC 中，∠ACB ＝90°，CD 是AB 上的中线，∴12CD AB =，∴CD =BD ． ∴∠BCE ＝∠ABC ．∵BE ⊥CD ，∴∠BEC ＝90°，∴∠BEC ＝∠ACB ．∴△BCE ∽△ABC ．∴E 是△ABC 的自相似点．⑵①作图略．作法如下：（i ）在∠ABC 内，作∠CBD ＝∠A ；（ii ）在∠ACB 内，作∠BCE ＝∠ABC ；BD 交CE 于点P ．则P 为△ABC 的自相似点．②连接PB 、PC ．∵P 为△ABC 的内心，∴12PBC ABC ∠=∠，12PCB ACB ∠=∠． ∵P 为△ABC 的自相似点，∴△BCP ∽△ABC ．∴∠PBC ＝∠A ，∠BCP ＝∠ABC=2∠PBC =2∠A ，∠ACB ＝2∠BCP=4∠A ．∵∠A +∠ABC+∠ACB ＝180°． ∴∠A +2∠A+4∠A ＝180°． ∴1807A ∠=．∴该三角形三个内角的度数分别为1807、3607、7207．28. 解⑴①174，103，52，2，52，103，174．函数1y x x =+(0)x >的图象如图．②本题答案不唯一，下列解法供参考．当01x <<时，y 随x 增大而减小；当1x >时,y 随x 增大而增大；当1x =时函数1y x x =+(0)x >的最小值为2．③1y xx=+=22+=22+-=22+=0，即1x=时，函数1y xx=+(0)x>的最小值为2．。

2011南京数学中考试卷+答案

【考点】算术平方根。

【分析】利用算术平方根的定义，直接得出结果2．下列运算正确的是下列运算正确的是A．a2＋a3=a5 B．a2•a3=a6C．a3÷a2=a D．(a2)3=a8【答案】C．指数运算法则。

【考点】指数运算法则。

【分析】a3÷a2=a= a3-2= a 3．在第六次全国人口普查中，南京市常住人口约为800万人，其中65岁及以上人口占9.2%．则该市65岁及以上人口用科学记数法表示约为岁及以上人口用科学记数法表示约为A．0.736×106人B．7.36×104人C．7.36×105人D．7.36×106 人【答案】C．科学记数法。

【考点】科学记数法。

【分析】利用科学记数法的定义，直接得出结果:8000000×9.2%=736000=7.36×105. 4．为了解某初中学校学生的视力情况，需要抽取部分学生进行调查，下列抽取学生的方法最合适的是为了解某初中学校学生的视力情况，需要抽取部分学生进行调查，下列抽取学生的方法最合适的是 A．随机抽取该校一个班级的学生随机抽取该校一个班级的学生B．随机抽取该校一个年级的学生随机抽取该校一个年级的学生C．随机抽取该校一部分男生随机抽取该校一部分男生D．分别从该校初一、初二、初三年级中各班随机抽取10%的学生的学生【答案】D．随机抽样样本的抽取。

南京中考数学试题(word及答案)

南京市2011年初中毕业生学业考试数学数学注意事项：1. 本试卷共6页，全卷满分120分，考试时间为120分钟，考生答题全部答在答题卡上，答在本试卷上无效.2. 请认真核对监考教师在答题卡上所有粘贴条形码的姓名、考试证号是否与本人相符合，再将自己的姓名、准考证号用0.5毫米的黑色墨水签字笔填写在答题卡及本试卷上.3. 答选择题必须用2B铅笔将答题卡上对应的答案标号涂黑•如需要改动，请用橡皮擦干净后，再选涂其他答案，答非选择题必须0.5毫米黑色墨水签字笔写在答题卡上指定位置，在其他位置答题一律无效.4. 作图必须用2B铅笔作答，并请加黑加粗，描写清楚.一、选择题(本大题共6小题，每小题2分，共12分，在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确的选项的字母代号填涂在答题卡相应位置上)1. 、,9的值等于A. 3B. - 3C. ± 3D. -.32. 下列运算正确的是A. a2+ a3=a5B. a2?a3=a6C. a3* a2=a D . (a2)3=a83. 在第六次全国人口普查中，南京市常住人口约为800万人，其中65岁及以上人口占9.2% •则该市65岁及以上人口用科学记数法表示约为A. 0.736X 106人B. 7.36 X 104人C. 7.36X 105人 D . 7.36X 106人4. 为了解某初中学校学生的视力情况，需要抽取部分学生进行调查，下列抽取学生的方法最合适的是A. 随机抽取该校一个班级的学生B. 随机抽取该校一个年级的学生C .随机抽取该校一部分男生5.如图是一个三棱柱，下列图形中，能通过折叠围成一个三棱柱的是D .分别从该校初一、初二、初三年级中各班随机抽取10%的学生6.如图，在平面直角坐标系中，O 半径为2，函数y=x的图象被OA . 2、3B . 2 2、2 P的圆心是(2，a) (a>2)，P的弦AB的长为2.3，贝U a的值是C . 2 3 D . 2 3、填空题（本大题共10小题，每小题2分，共20分，不需要写出解答过程, 请把答案直接填写在答题卡相应位置上）9.计算（迈1）（213. __________ 如图，海边有两座灯塔 A 、B ，暗礁分布在经过 A 、B 两点的弓形（弓形的弧是O O的一部分）区域内，/ AOB=80。

2011年江苏省南京市中考数学试题(解析版)

南京中考数学试题及答案word版

南京中考数学试题及答案word版收集资料

2011年南京市中考数学试卷

2011年江苏省南京市中考数学试卷

南京中考数学试题及答案word版

2011年江苏省南京市中考数学试题(word版及答案)

2011年中考数学试题及答案解析江苏南京中考数学试卷试题

2011年江苏省南京市中考数学试卷及答案

南京市中考数学试卷及答案.docx

2011年江苏省南京中考数学试题及答案word版[1]

2011年南京中考数学试题及答案word版

最新中考数学试题及答案解析江苏南京中考数学试卷试题_试卷优秀名师资料

2011南京数学中考试卷+答案

南京中考数学试题(word及答案)