甘肃公务员考试数字推理

合集下载

2023年甘肃省公务员录用考试行政职业能力倾向测试试卷

甘肃省公务员录取考试《行政职业能力倾向测试》试卷说明这项测验共有四个部分，共100分，每题1分，总时限为120分钟。

请在机读题卡上严格按照规定填写自己旳姓名，涂写准考证号。

请仔细阅读下面旳注意事项，这对你获得成功非常重要：1．题目应在答题卡上作答，不要在题本上作任何记号。

2．监考人员宣布考试开始时，你才开始答题。

3．监考人员宣布考试结束时，你应立即放下铅笔，将试题本、答题卡和草稿纸都留在桌上，然后离开。

假如你违反一以上任何一项规定，都将影响你旳成绩。

4．在这项测验中，可能有某些试题较难，因此你不要在一道题上思索时间太久，碰到不会答旳题目，可先跳过去，假如有时间再去思索。

否则，你可能没有时间完成背面旳题目。

5．试题答错不倒扣分。

6．尤其提醒你注意，涂写答案时一定要认准题号。

严禁折叠答题卡。

第一部分数量关系（共15题，参照时限20分钟）本部分包括两种类型旳试题：一、数字推理：给你一种数列，但其中缺乏一项，规定你仔细观测数列旳排列规律。

然后从四个供选项中选出你认为最合理旳一项，来弥补空缺选项。

1．1，15，8，24，27，35，64，48（），（）。

A．65，24 B．125，80 C．125，63 D．65，1242．1+2，2+4，3+6，1+8，2+10，3+12，…，（）。

A．1+24 B．2+24 C．3+26 D．1+263．0.25，0.25，0.5，2，16，（）。

A．32 B．64 C．128 D．2564．12，3，4，9，25，3，5，15，36，2，6，（）。

A．13 B．12 C．11 D．105．0，3，26，255，（）。

A．479 B．3 124 C．2 600 D．3 104二、数学运算：你可以在草稿纸上运算，碰到难题，你可以跳过不做，待你有时间再返回来做。

6．125×567×32×25旳值为（）A．567 000 B．6 870 000 C．56 700 000 D．47 500 000 7．0.0395×2400+39.5×2.5+51×3.95旳值是（）。

公务员行政能力测试数字推理答题技巧（非常有用）

公务员行政能力测试数字推理答题技巧（非常有用）数字推理一、基本要求熟记熟悉常见数列，保持数字的敏感性，同时要注意倒序。

自然数平方数列：4，1，0，1，4，9，16，25，36，49，64，81，100，121，169，196，225，256，289，324，361，400……自然数立方数列：－8，－1，0，1，8，27，64，125，216，343，512，729，1000质数数列：2，3，5，7，11，13，17……（注意倒序，如17,13,11,7,5,3,2）合数数列：4，6，8，9，10，12，14…….（注意倒序）二、解题思路：1 基本思路：第一反应是两项间相减，相除，平方，立方。

所谓万变不离其综，数字推理考察最基本的形式是等差，等比，平方，立方，质数列，合数列。

相减，是否二级等差。

8，15，24，35，（48）相除，如商约有规律，则为隐藏等比。

4，7，15，29，59，（59*2－1）初看相领项的商约为2，再看4*2-1=7,7*2+1＝15……2 特殊观察：项很多，分组。

三个一组，两个一组4，3，1，12，9，3，17，5，（12）三个一组19，4，18，3，16，1，17，（2）2，－1，4，0，5，4，7，9，11，（14）两项和为平方数列。

400，200，380，190，350，170，300，（130）两项差为等差数列隔项，是否有规律0，12，24，14，120，16（7^3－7）数字从小到大到小，与指数有关1，32，81，64，25，6，1，1/8每个数都两个数以上，考虑拆分相加（相乘）法。

87，57，36，19，（1*9+1）256，269，286，302，（302+3+0+2）数跳得大，与次方（不是特别大），乘法（跳得很大）有关1，2，6，42，（42^2+42）3，7，16，107，（16*107-5）每三项/二项相加，是否有规律。

1，2，5，20，39，（125－20－39）21，15，34，30，51，（10^2-51）C=A^2－B及变形（看到前面都是正数，突然一个负数，可以试试）3，5，4，21，（4^2-21）,4465，6，19，17，344,(-55)-1，0，1，2，9，（9^3+1）C=A^2+B及变形（数字变化较大）1，6，7，43，（49+43）1，2，5，27，（5+27^2）2/3，1/3，2/9，1/6，（2/15）3/1，5/2，7/2，12/5，（18/7）分子分母相减为质数列1/2，5/4，11/7，19/12，28/19，（38/30）分母差为合数列，分子差为质数列。

公务员考试数字推理题规律

一．题型:●等差数列及其变式【例题1】2，5，8，()A 10B 11C 12D 13【解答】从上题的前 3 个数字可以看出这是一个典型的等差数列，即后面的数字与前面数字之间的差等于一个常数．题中第二个数字为5，第一个数字为2，两者的差为3，由观察得知第三个、第二个数字也满足此规律，那么在此基础上对未知的一项进行推理，即8+3=11，第四项应该是11，即答案为B．【例题2】3，4，6，9，()，18A 11B 12C 13D 14【解答】答案为C．这道题表面看起来没有什么规律，但稍加改变处理，就成为一道非常容易的题目．顺次将数列的后项与前项相减，得到的差构成等差数列1，2，3，4，5，..．显然，括号内的数字应填13．在这种题中，虽然相邻两项之差不是一个常数，但这些数字之间有着很明显的规律性，可以把它们称为等差数列的变式．●等比数列及其变式【例题3】3，9，27，81()A 243B 342C 433D 135【解答】答案为A．这也是一种最基本的排列方式，等比数列．其特点为相邻两个数字之间的商是一个常数．该题中后项与前项相除得数均为3，故括号内的数字应填243．【例题4】8，8，12，24，60，()A 90B 120C 180D 240【解答】答案为C．该题难度较大，可以视为等比数列的一个变形．题目中相邻两个数字之间后一项除以前一项得到的商并不是一个常数，但它们是按照一定规律排列的；1，1.5，2，2.5，3，因此括号内的数字应为60×3=180．这种规律对于没有类似实践经验的应试者往往很难想到．我们在这里作为例题专门加以强调．该题是1997 年中央国家机关录用大学毕业生考试的原题．【例题5】8，14，26，50，()A 76B 98C 100D 104【解答】答案为B．这也是一道等比数列的变式，前后两项不是直接的比例关系，而是中间绕了一个弯，前一项的2 倍减2 之后得到后一项．故括号内的数字应为50×2-2=98．●等差与等比混合式【例题6】5，4，10，8，15，16，()，()A 20，18B 18，32C 20，32D 18，32【解答】此题是一道典型的等差、等比数列的混合题．其中奇数项是以5 为首项、等差为5 的等差数列，偶数项是以4 为首项、等比为2 的等比数列．这样一来答案就可以容易得知是C．这种题型的灵活度高，可以随意地拆加或重新组合，可以说是在等比和等差数列当中的最有难度的一种题型．●求和相加式与求差相减式【例题7】34，35，69，104，()A 138B 139C 173D 179【解答】答案为C．观察数字的前三项，发现有这样一个规律，第一项与第二项相加等于第三项，34+35=69，这种假想的规律迅速在下一个数字中进行检验，35+69=104，得到了验证，说明假设的规律正确，以此规律得到该题的正确答案为173．在数字推理测验中，前两项或几项的和等于后一项是数字排列的又一重要规律．【例题8】5，3，2，1，1，()A -3B -2C 0D 2【解答】这题与上题同属一个类型，有点不同的是上题是相加形式的，而这题属于相减形式，即第一项5 与第二项3 的差等于第三项2，第四项又是第二项和第三项之差..所以，第四项和第五项之差就是未知项，即1-1=0，故答案为C．●求积相乘式与求商相除式【例题9】2，5，10，50，()A 100B 200C 250D 500【解答】这是一道相乘形式的题，由观察可知这个数列中的第三项10 等于第一、第二项之积，第四项则是第二、第三两项之积，可知未知项应该是第三、第四项之积，故答案应为D．【例题10】100，50，2，25，()A 1B 3C 2/25D 2/5【解答】这个数列则是相除形式的数列，即后一项是前两项之比，所以未知项应该是2/25，即选C．●求平方数及其变式【例题11】1，4，9，()，25，36A 10B 14C 20D 16【解答】答案为D．这是一道比较简单的试题，直觉力强的考生马上就可以作出这样的反应，第一个数字是1 的平方，第二个数字是2 的平方，第三个数字是3 的平方，第五和第六个数字分别是5、6 的平方，所以第四个数字必定是4 的平方．对于这类问题，要想迅速作出反应，熟练掌握一些数字的平方得数是很有必要的．【例题12】66，83，102，123，()A 144B 145C 146D 147【解答】答案为C．这是一道平方型数列的变式，其规律是8，9，10，11，的平方后再加2，故括号内的数字应为12 的平方再加2，得146．这种在平方数列基础上加减乘除一个常数或有规律的数列，初看起来显得理不出头绪，不知从哪里下手，但只要把握住平方规律，问题就可以划繁为简了．●求立方数及其变式【例题13】1，8，27，()A 36B 64C 72 D81【解答】答案为B．各项分别是1，2，3，4 的立方，故括号内应填的数字是64．【例题14】0，6，24，60，120，()A 186B 210C 220D 226【解答】答案为B．这也是一道比较有难度的题目，但如果你能想到它是立方型的变式，问题也就解决了一半，至少找到了解决问题的突破口，这道题的规律是：第一个数是1 的立方减1，第二个数是2 的立方减2，第三个数是3的立方减3，第四个数是4 的立方减4，依此类推，空格处应为6 的立方减6，即210．●双重数列【例题15】257，178，259，173，261，168，263，()A 275B 279C 164D 163【解答】答案为D．通过考察数字排列的特征，我们会发现，第一个数较大，第二个数较小，第三个数较大，第四个数较小，..．也就是说，奇数项的都是大数，而偶数项的都是小数．可以判断，这是两项数列交替排列在一起而形成的一种排列方式．在这类题目中，规律不能在邻项之间寻找，而必须在隔项中寻找．我们可以看到，奇数项是257，259，261，263，是一种等差数列的排列方式．而偶数项是178，173，168，()，也是一个等差数列，所以括号中的数应为168-5=163．顺便说一下，该题中的两个数列都是以等差数列的规律排列，但也有一些题目中两个数列是按不同规律排列的，不过题目的实质没有变化．两个数列交替排列在一列数字中，也是数字推理测验中一种较常见的形式．只有当你把这一列数字判断为多组数列交替排列在一起时，才算找到了正确解答这道题的方向，你的成功就已经80%了．●简单有理化式二、解题技巧数字推理题的解题方法数字推理题难度较大，但并非无规律可循，了解和掌握一定的方法和技巧，对解答数字推理问题大有帮助．1 快速扫描已给出的几个数字，仔细观察和分析各数之间的关系，尤其是前三个数之间的关系，大胆提出假设，并迅速将这种假设延伸到下面的数，如果能得到验证，即说明找出规律，问题即迎刃而解；如果假设被否定，立即改变思考角度，提出另外一种假设，直到找出规律为止．2 推导规律时，往往需要简单计算，为节省时间，要尽量多用心算，少用笔算或不用笔算．3 空缺项在最后的，从前往后推导规律；空缺项在最前面的，则从后往前寻找规律；空缺项在中间的可以两边同时推导．4 若自己一时难以找出规律，可用常见的规律来“对号入座”，加以验证．常见的排列规律有：(1)奇偶数规律：各个数都是奇数(单数)或偶数(双数)；(2)等差：相邻数之间的差值相等，整个数字序列依次递增或递减．(3)等比：相邻数之间的比值相等，整个数字序列依次递增或递减；如：2 4 8 16 32 64()这是一个“公比”为2(即相邻数之间的比值为2)的等比数列，空缺项应为128．(4)二级等差：相邻数之间的差或比构成了一个等差数列；如：4 2 2 3 6 15相邻数之间的比是一个等差数列，依次为：0.5、1、1.5、2、2.5．(5)二级等比数列：相邻数之间的差或比构成一个等比数理；如：0 1 3 7 15 31()相邻数之间的差是一个等比数列，依次为1、2、4、8、16，空缺项应为63．(6)加法规律：前两个数之和等于第三个数，如例题23；(7)减法规律：前两个数之差等于第三个数；如：5 3 2 1 1 0 1()相邻数之差等于第三个数，空缺项应为-1．(8)乘法(除法)规律：前两个数之乘积(或相除)等于第三个数；(9)完全平方数：数列中蕴含着一个完全平方数序列，或明显、或隐含；如：2 3 10 15 26 35()1*1+1=2, 2*2-1=3，3*3+1=10，4*4-1=15......空缺项应为50．(10)混合型规律：由以上基本规律组合而成，可以是二级、三级的基本规律，也可能是两个规律的数列交叉组合成一个数列．如：1 2 6 15 31()相邻数之间的差是完全平方序列，依次为1、4、9、16，空缺项应为31+25=56．公务员考试数字推理题汇总1、15，18，54，（），210A 106B 107C 123D 1121、答案是C能被3 整除嘛2、1988 的1989 次方+1989 的1988 的次方.. 个位数是多少呢?2、答：应该也是找规律的吧，1988 的4 次个位就是6，六的任何次数都是六，所以，1988 的1999 次数个位和1988的一次相等，也就是8后面那个相同的方法个位是1忘说一句了，6 乘8 个位也是83、1/2,1/3,2/3,6/3,( ),54/36A 9/12,B 18/3 ,C 18/6 ,D 18/363、C （1/3）/（1/2）=2/3 以此类推4、4,3,2,0,1,-3,( )A -6 ,B -2 ,C 1/2 ,D 04、c 两个数列4，2，1-〉1/2（依次除以2）；3，0，-35、16，718，9110，（）A 10110，B 11112，C 11102，D 101115、答案是11112从左往右数第一位数分别是：5、7、9、11从左往右数第二位数都是：1从左往右数第三位数分别是：6、8、10、126、3/2,9/4,25/8,( )A 65/16,B 41/8,C 49/16,D 57/86、思路：原数列可化为1 又1/2, 2 又1/4, 3 又1/8．故答案为4 又1/16 = 65/167、5,( ),39,60,105.A.10B.14C.25D.307、答案B．5=2^2+1，14=4^2-2，39=6^2+3，60=8^2-4，105=10^2+58、8754896×48933=（）A.428303315966B.428403225876C.428430329557D.4284033259688、答直接末尾相乘，几得8，选D．9、今天是星期二，55×50 天之后()．A.星期一B.星期二C.星期三D.星期四9 、解题思路：从55 是7 的倍数减1,50 是7 的倍数加1，快速推出少1 天．如果用55×50÷7=396 余6，也可推出答案，但较费时10、一段布料，正好做12 套儿童服装或9 套成人服装，已知做3 套成人服装比做2 套儿童服装多用布6 米，这段布有多长？A 24B 36 C54 D 4810、思路：设儿童为x，成人为y，则列出等式12X＝9Y 2X＝3Y-6得出，x=3，则布为3*12=36，选B11、有一桶水第一次倒出其中的6 分之一，第二次倒出3 分之一，最后倒出4 分之一，此时连水带桶有20 千克，桶重为5 千克，，问桶中最初有多少千克水？A 50B 80C 100D 3611、答5/6*2/3*3/4X=15 得出，x=36 答案为D12、甲数比乙数大25%，则乙数比甲数小（）A 20%B 30%C 25%D 33%12、已X，甲1.25X ，结果就是0.25/1.25=20% 答案为A13、一条街上，一个骑车人和一个步行人相向而行，骑车人的速度是步行人的3 倍，每个隔10 分钟有一辆公交车超过一个行人．每个隔20 分钟有一辆公交车超过一个骑车人，如果公交车从始发站每隔相同的时间发一辆车，那么间隔几分钟发一辆公交车？A 10B 8C 6 D413、B14、某校转来6 名新生,校长要把他们安排在三个班,每班两人,有多少中安排方法?A 18B 24C 36D 4614、无答案公布sorry 大家来给些答案吧15、某人把60000 元投资于股票和债券，其中股票的年回报率为6%，债券的年回报率为10%．如果这个人一年的总投资收益为4200 元，那么他用了多少钱买债券?A. 45000B. 15000C. 6000D. 480015、0.06x+0.1y=4200 , x+y=60000, 即可解出．答案为B16、一粮站原有粮食272 吨，上午存粮增加25％，下午存粮减少20％，则此时的存粮为( )吨．A. 340B. 292C. 272D. 26816、272*1.25*0.8=272 答案为C17、3 2 5\3 3\2 ( )A．7/5 B．5/6 C．3/5 D．3/417、分数变形：A 数列可化为：3/1 4/2 5/3 6/4 7/518、1\7 1\26 1\63 1\124 ( )18、依次为2^3-1,3^3-1,..，得出6^3-119、-2 ，-1，1，5 （）29（2000 年题）A.17B.15C.13D.1119、依次为2^3-1,3^3-1,..，得出6^3-120、5 9 15 17 ( )A 21B 24C 32D 3420、思路：5 和15 差10，9 和17 差8，那15 和( ？)差65+10=15 9+8=17 15+6=2121、８１３０１５１２（）{江苏的真题}A１０B８C１３D１４21、81/3+3=30，30/3+5=15，15/3+7=12，12/3+9=13 答案为132222、3，2，53，32，( )A 75B 5 6C 35D 3422、思路：小公的讲解2，3，5，7，11，13，17.....变成2，3，53，32，75，53，32，117，75，53，32......3，2，（这是一段，由2 和3 组成的），53，32（这是第二段，由2、3、5 组成的）75，53，32（这是第三段，由2、3、5、7 组成的），117，75，53，32（）这是由2、3、5、7、11 组成的）不是，首先看题目，有2，3，5，然后看选项，最适合的是75（出现了7，有了7 就有了质数列的基础），然后就找数字组成的规律，就是复合型数字，而A 符合这两个规律，所以才选A2，3，5，后面接什么？按题干的规律，只有接7 才是成为一个常见的数列：质数列，如果看BCD 接4 和6 的话，组成的分别是2，3，5，6（规律不简单）和2，3，5，4（4 怎么会在5 的后面？也不对）质数列就是由质数组成的从2 开始递增的数列23、2，3，28，65，( )A 214B 83C 414D 31423、无思路！暂定思路为：2*65+3*28=214，24、0 ，1，3 ，8 ，21，( ) ，14424、0+3=1*3，1+8=3*3，3+21=8*3，21+144=？*3．得出？=55．25、2，15，7，40，77，( )A96 ，B126，C138,，D15625、这题有点变态，不讲了，看了没有好处26、4，4，6，12，（），9026、答案30．4/4=1，6/12=1/2，？/90=1/327、56，79，129，202 （）A、331B、269C、304D、33327、不知道思路，经过讨论：79-56=23 129-79=50 202-129=73因为23+50=73，所以下一项和差必定为50+73=123-202=123，得出？=325，无此选项！28、2，3，6，9，17，（）A 19B 27C 33D 4528、三个相加成数列，3 个相加为11，18，32，7 的级差则此处级差应该是21，则相加为53，则53－17－9＝27 答案，分别是27．29、5，6，6，9，（），90A 12,B 15,C 18,D 2129、答案为C思路：5×6/5=6，6*6/4=9，6*9/3=18（5-3）*（6-3）=6（6-3）*（6-3）=9（6-3）*（9-3）=1830、16 17 18 20 （）A２１B２２C２３D２４30、思路：22、23 结果未定，等待大家答复！31、9、12、21、48、（）31、答案为1299+3=12 ，12+3 平方=21 ，21+3 立方=4832、172、84、40、18、（）32、答案为7172/2-2=84 84/2-2=40 40/2-2=18 18/2-2=7答案分成三部分：。

公务员题型30道经典数字推理题汇总.

1. 256 ，269 ，286 ，302 ，（）A.254B.307C.294D.316解析： 2+5+6=13 256+13=2692+6+9=17 269+17=2862+8+6=16 286+16=302?=302+3+2=3072. 72 , 36 , 24 , 18 , (A.12B.16C.14.4D.16.4解析：（方法一）相邻两项相除,72 36 24 18\ / \ / \ /2/1 3/2 4/3(分子与分母相差1且前一项的分子是后一项的分母接下来貌似该轮到5/4, 而18/14.4=5/4. 选C（方法二）6×12=72， 6×6=36， 6×4=24， 6×3 =18， 6×X 现在转化为求X 12，6，4，3，X12/6 ，6/4 ， 4/3 ，3/X化简得2/1，3/2，4/3，3/X，注意前三项有规律，即分子比分母大一，则3/X=5/4可解得：X=12/5再用6×12/5=14.43. 8 , 10 , 14 , 18 ,（）A. 24B. 32C. 26D. 20分析：8，10，14，18分别相差2，4，4，？可考虑满足2/4=4/?则？＝8所以，此题选18＋8＝264. 3 , 11 , 13 , 29 , 31 ,（）A.52B.53C.54D.55分析：奇偶项分别相差11－3＝8，29－13＝16＝8×2，？－31＝24＝8×3则可得？＝55，故此题选D5. -2/5，1/5，-8/750，（）。

A 11/375B 9/375C 7/375D 8/375解析： -2/5，1/5，-8/750，11/375=>4/(-10，1/5，8/(-750，11/375=>分子 4、1、8、11=>头尾相减=>7、7分母 -10、5、-750、375=>分2组(-10,5、(-750,375=>每组第二项除以第一项=>-1/2,-1/2 所以答案为A6. 16 , 8 , 8 , 12 , 24 , 60 , (A.90B.120C.180D.240分析：相邻两项的商为0.5，1，1.5，2，2.5，3，所以选18010. 2 ，3 ，6 ，9 ，17 ，（）A.18B.23C.36D.45分析：6+9=15=3×53+17=20=4×5 那么2+?=5×5=25 所以?=2311. 3 ，2 ，5/3 ，3/2 ，（）A.7/5B.5/6C.3/5D.3/4分析：通分 3/1 4/2 5/3 6/4 ----7/513. 20 ，22 ，25 ，30 ，37 ，（）A.39B.45C.48D.51分析：它们相差的值分别为2，3，5，7。

公务员考试数字推理题解题技巧大全

公务员考试数字推理题解题技巧大全公务员考试是一项重要的选拔机制，而数字推理题是其中的一项难点。

在数字推理题中，考生需要通过数字、图表等信息，寻找一定的规律和推理思路，从而解决问题。

为了帮助考生顺利应对数字推理题，本文将为大家介绍一些解题技巧和思路。

一、理解题目和数据在做数字推理题时，首先需要认真阅读题目和给出的数据，了解题目的背景和要求。

在阅读中要注意对数据进行分类和总结，分析数字间的关系和规律。

二、寻找常见数字规律数字推理题中存在着许多常见的数字规律，例如：相邻数的关系、乘法和除法关系、平方、倒数等规律。

若能找出这些规律，便能够轻松解决此类推理题。

三、寻找图形规律数字推理题中，常常会配有一些图形数据。

对于这些图形，我们可以通过寻找它们的共性和特点，来发现其中的规律。

例如，周期性图形的规律常常是循环或对称性；封闭型图形的规律常常是不变性或连通性。

通过这些规律，我们可以迅速地推断出答案。

四、确定类型和答案数字推理题大致可以分为数列和图形两类。

对于数列题，我们可以看其中的差值和倍数规律，以及数列的加和、中位数、众数等；对于图形题，我们可以寻找变化和相似性规律，以及图形的方向、角度、面积和比例等。

同时，我们也可以先推断出答案，然后再用已有的数据进行验证，验证结果。

五、注意隐形陷阱在数字推理题中，经常会隐藏着一些陷阱，这些陷阱可能会导致我们犯错。

例如，数据中可能存在重复数字、相同数字或相同图形，这就需要我们仔细分辨；同时也要注意看清题目要求，不要遗漏信息或多读信息。

总之，数字推理题是公务员考试中的难点之一，但是只要我们掌握题目信息，查找数字和图形规律，注意隐形陷阱，便能够较为轻松地应对此类题目。

希望以上简单的技巧和思路能够对大家在公务员考试中取得好成绩有所帮助。

公务员考试数字推理试题集和答案

A.3414
B.5232
C.6353
D.7151
13.0，6，24，60，120，（）
A.186
B.210
C.220
D.226
14.2，6，20，50，102，（）。
A.140
B.160
C.182
D.200
15.2，10，19，30，44，62，( )
A.83
B.84
C.85
D.86
16. 102，96，108，84，132，（）
A.1707
B.1704
C.1086
D.1072
25.1，5，29，( )，3129
A.227
B.259
C.257
D.352
26.0， 2， 10， 30，（）
A.68
B.74
C.60
D.70
27.1，64，243，256，125（）
A.36
B.81
C.0
D.1
28. 1，7，36，（）
A.74
2.D 。数列中后一个数字与前一个数字之间的商形成一个等差数列：1÷1=1，2÷1=2，6÷2=3，以此类推，第5个数与6之间的商应该是4，因此6×4=24。
3.C。相邻奇数项之间的差是以2为首项，公差为2的等差数列，相邻偶数项之间的差也是以2为首项，公差为2的等差数列。由此能够推导答案为C。
4.B。后一个数字与前一个数字之间的差是一个以1为首项，3为公比的等比数列，由此推断所填的数字是14+27=41。
A.80
B.90
C.92
D.97
41.-1，1，7，17，31，（），71
A.37
B.41
C.49

2024年甘肃省公务员考试行测真题

2024年甘肃省公务员考试行测真题第一部分常识判断1.水利部介绍，南水北调东、中线建成以来，累计调水量超过698亿立方米，直接受益人口（）。

A.1.06亿B.1.52亿C.1.68亿D.1.76亿【答案】：D2.第21次全国国民阅读调查结果发布。

调查显示，2023年我国成年国民包括书报刊和数字出版物在内的各种媒介的综合阅读率为（）。

A.51.9%B.61.9%C.81.9%D.71.9%【答案】：C3.截至2023年底，全国登记在册个体工商户1.24亿户，支撑近（）人就业。

A.3亿B.2亿C.2.5亿D.1.8亿【答案】：A4.人社部等九部门1月25日发布通知，自即日起在全国开展2024年（），全力稳就业、保用工、促发展。

A.春风行动B.助学行动C.强学行动D.暖风行动1/ 14【答案】：A5.中国人民银行、金融监管总局日前发布《关于金融支持住房租赁市场发展的意见》，提出加大住房租赁开发建设信贷支持力度、支持发放住房租赁经营性贷款等17条举措。

意见自（）起施行。

A.2024年2月1日B.2024年3月5日C.2024年3月1日D.2024年2月5日【答案】：D6.生命的基本单位是（）。

A.DNAB.蛋白质C.细胞D.组织【答案】：C7.下列消费中，（）在家庭消费总支出中占比越小，说明该家庭的生活水平越高。

A.食品支出B.发展资料支出C.享受性资料支出D.生产资料支出【答案】：A8.下列关于彩虹的说法正确的有几项？（）①观看彩虹时应背对太阳②因阳光照射到半空中的雨点，光线被折射及反射而形成③最外层为黄色A.3B.0C.1D.2【答案】：D9.在我国，“公民”一词的含义是指（）。

2/ 14A.年满18周岁具有我国国籍的人B.享有政治权利的人C.出生在我国的人D.具有我国国籍的人【答案】：D10.刘桢诗歌的风格是：（）A.文多兼善，辞少瑕累B.骨气奇高，词采华茂C.怀文抱质，语气低婉D.真骨凌霜，高风跨俗【答案】：A11.下雨天的时候，实验室里光线昏暗，用显微镜进行观察应选择（）。

公务员考试数量关系解题技巧—数字推理题

数字推理题主要有以下几种题型:1. 等差数列及其变式例题：1,4,7,10,13,()答案为C。

我们很容易从中发现相邻两个数字之间的差是一个常数3，所以括号中的数字应为16。

等差数列是数字推理测验中排列数字的常见规律之一。

例题：3,4,6,9,()，18答案为C。

仔细观察，本题中的相邻两项之差构成一个等差数列1,2,3,4,5.……，因此很快可以推算出括号内的数字应为13,象这种相邻项之差虽不是一个常数，但有着明显的规律性，可以把它看作等差数列的变式。

2.“两项之和等于第三项”型例题：34,35,69,104,()答案为C。

观察数字的前三项，发现第一项与第二项相加等于第三项，3435=69，在把这假设在下一数字中检验，3569=104，得到验证，因此类推，得出答案为173。

前几项或后几项的和等于后一项是数字排列的又一重要规律。

3.等比数列及其变式例题：3，9，27，81，()答案为A。

这是最一种基本的排列方式，等比数列。

其特点为相邻两项数字之间的商是一个常数。

例题：8，8，12，24，60，()答案为C。

虽然此题中相邻项的商并不是一个常数，但它们是按照一定规律排列的：1，，2，，3，因此答案应为60×3=180,象这种题可视作等比数列的变式。

转自中国教育热线公务员考试数量关系测验题型及解题技巧—数字推理题(下)4.平方型及其变式例题：1,4,9,()，25,36答案为D。

这道试题考生一眼就可以看出第一项是1的平方，第二项是2的平方，依此类推，得出第四项为4的平方16。

对于这种题，考生应熟练掌握一些数字的平方得数。

如：10的平方=10011的平方=12112的平方=14413的平方=16914的平方=19615的平方=225例题：66，83，102，123，()答案为C。

这是一道平方型数列的变式，其规律是8，9，10，11的平方后再加2，因此空格内应为12的平方加2，得146。

这种在平方数列的基础上加减乘除一个常数或有规律的数列，可以被看作是平方型数列的变式，考生只要把握了平方规律，问题就可以化繁为简了。

公务员行测考试—数量关系

公务员行测考试——数量关系1、数字推理题型及讲解(1)数字推理的题目就是给你一个数列,但其中缺少一项,要求你仔细观察这个数列各数字之间的关系,找出其中的规律,然后在四个选项中选择一个最合理的一个作为答案.按照数字排列的规律, 数字推理题一般可分为以下几种类型:一、奇、偶：题目中各个数都是奇数或偶数，或间隔全是奇数或偶数：1、全是奇数：例题：1 5 3 7 （）A .2 B.8 C.9 D.12解析：答案是C ，整个数列中全都是奇数，而答案中只有答案C是奇数2、全是偶数：例题：2 6 4 8 （）A. 1B. 3C. 5D. 10解析：答案是D ，整个数列中全都是偶数，只有答案D是偶数。

3、奇、偶相间例题：2 13 4 17 6 （）A.8B. 10C. 19D. 12解析：整个数列奇偶相间，偶数后面应该是奇数，答案是C练习：2，1，4，3，（），5 99年考题二、排序：题目中的间隔的数字之间有排序规律1、例题：34，21，35，20，36（）A.19B.18C.17D.16解析：数列中34，35，36为顺序，21，20为逆序，因此，答案为A。

三、加法：题目中的数字通过相加寻找规律1、前两个数相加等于第三个数例题：4，5，（），14，23，37A.6B.7C.8D.9注意：空缺项在中间，从两边找规律，这个方法可以用到任何题型；解析：4+5=9 5+9=14 9+14=23 14+23=37，因此，答案为D；练习：6，9，（），24，39 // 1，0，1，1，2，3，5，（）2、前两数相加再加或者减一个常数等于第三数例题：22，35，56，90，（）99年考题A．162 B.156 C.148 D.145解析: 22+35-1=56 35+56-1=90 56+90-1=145，答案为D四、减法：题目中的数字通过相减，寻找减得的差值之间的规律1、前两个数的差等于第三个数：例题：6，3，3，（），3，-3A.0B.1C.2D.3答案是A解析：6-3=3 3-3=0 3-0=3 0-3=-3提醒您别忘了：“空缺项在中间，从两边找规律”2、等差数列：例题：5，10，15，( )A. 16B.20C.25D.30答案是B.解析：通过相减发现：相邻的数之间的差都是5，典型等差数列；3、二级等差：相减的差值之间是等差数列例题：115，110，106，103，（）A.102B.101C.100D.99 答案是B解析：邻数之间的差值为5、4、3、（2），等差数列，差值为1103-2=101练习：8，8，6，2，（）// 1，3，7，13，21，31，（）4、二级等比：相减的差是等比数列例题：0,3,9,21,45, ( )相邻的数的差为3,6,12,24,48,答案为93例题：-2,-1,1,5,( ),29 ---99年考题解析：-1-（-2）=1 ，1-（-1）=2，5-1=4，13-5=8，29-13=16后一个数减前一个数的差值为:1,2,4, 8,16,所以答案是135、相减的差为完全平方或开方或其他规律例题：1，5，14，30，55，（）相邻的数的差为4，9，16，25，则答案为55+36=916、相隔数相减呈上述规律：例题：53，48，50，45，47A.38B.42C.46D.51解析：53-50=3 50-47=3 48-45=345-3=42 答案为B注意：“相隔”可以在任何题型中出现五、乘法：1、前两个数的乘积等于第三个数例题：1,2,2,4,8,32,( )前两个数的乘积等于第三个数，答案是256 2、前一个数乘以一个数加一个常数等于第二个数，n1×m+a=n2例题:6,14,30,62,( )A.85B.92C.126D.250解析:6×2+2=14 14×2+2=30 30×2+2=62 62×2+2=126，答案为C练习：28，54，106，210，（）3、两数相乘的积呈现规律:等差,等比,平方,...例题：3/2，2/3，3/4，1/3，3/8 （）（99年海关考题）A. 1/6B.2/9C.4/3D.4/9解析:3/2×2/3=1 2/3×3/4=1/2 3/4×1/3=1/4 1/3×3/8=1/83/8×?=1/16 答案是A六、除法:1、两数相除等于第三数2、两数相除的商呈现规律：顺序，等差，等比，平方，...七、平方：1、完全平方数列：正序：4，9，16，25逆序：100，81，64，49，36间序：1，1，2，4，3，9，4，（16）2、前一个数的平方是第二个数。

公务员考试经典数字推理题(含答案)

数字推理及数学运算：1. 3，— 1， 5， 1，( )A. 3B. 7C. 25D. 64解: 两数之和形成 2， 4， 6， 8 的等差数列 (注：也可以是两数之差、积、商或乘方)。

2.8，10，14，18，()A. 24B. 32C. 26D. 20解:道理基本同上。

前两数之和与后两数之和形成 6， 8， 10 的等差数列。

3. 1/3， 6， 1， 12，( )A. 5/3B. 8/3C. 10D. 22解:1 除以 3， 2 乘以 3， 3 除以 3， 4 乘以 3， 5 除以 3。

递增自然数奇数项除以 3，偶数项乘以 3。

4. 3， 2， 8， 12， 28，( )A. 15B. 32C. 27D. 52解:第一个数乘以 2 加上第二个数的和等于第三个数 (注：也可以是第一个数乘以 2 减去第二个数的差等于第三个数)。

5.7，10，16，22，()A. 28B. 32C. 34D. 45解:2*3+1=7， 3*3+1=10， 5*3+1=16， 7*3+1=22， 11*3+1=34 (注：质数的 3 倍加 1 的和)。

6.1， 16， 27， 16， 5，( )A. 36B. 25C. 1D. 14解: 1 的 5 次方， 2 的 4 次方， 3 的 3 次方， 4 的 2 次方， 5 的 1 次方， 6 的 0 方 ( 自然数递增，方数递减；相近的题型也可以是自然数递减，方数递增)7.4，3/2，20/27，7/16，36/125，()A. 39/144B. 11/54C. 68/169D. 7解: 27 是 3 的 3 次方， 125 是 5 的 5 次方；4 可看成 4/1， 3/2 可看成 12/8，7/16 可看成 28/64，由此可推出分子是 4*1， 4*3， 4*5， 4*7， 4*9， 4*11，分母是递增自然数的 3 次方。

8.1，3，4，1，9，()A. 5B. 11C. 14D. 64解: 前数减去后数的差的平方等第三个数。

2012年甘肃省公务员考试试题及答案+

2012 年甘肃省公务员考试试题及答案10874117 第一部分数量关系（共15 题，参考时限15 分钟）本部分包括两种类型的试题：一、数字推理。

每道题给出一个数列，但其中缺少一项，要求报考者仔细观察这个数列各数字之间的关系，找出其中的排列规律，然后从四个供选择的答案中选出最合适、最合理的一个来填补空缺项，使之符合原数列的排列规律。

请开始答题：1.112，125，151，190，（）A.200 B.242 C.253 D.270 2.2，9，20，35，（）A.54 B.69 C.75 D.81 3. 11，3，14，7，20，15，29，（），41 A.26 B.29 C.30 D.31 4.10，6，8，7，7.5，（）A.4.25 B.5.5 C.7.25 D.8.5 5. 1，4/5，4/5，13/16，19/23，（）A. 26/31 B. 11/35 C. 12/37 D.13/37 二、数学运算。

每道题给出一道算术式子，或者表达数量关系的一段文字，要求报考者熟练运用加、减、乘、除等基本运算法则，利用基本的数学知识，准确、迅速地计算出结果。

请开始答题：6.某商品成本100 元，以120 元销售；因技术革新，每件成本降低1/4，欲以100 元出售。

则利润率（）个百分点。

A.提高了20 B.降低了15 C.提高了13.3 D.不变7.甲从一幢高楼的底层开始登楼，她从第一层到第九层用了4 分钟，她又往上登了几层后，感到很累就往下走，当她走到第三层时共用了10 分钟。

如果甲上下楼梯的速度相同，问：甲又向上走了几层楼梯？ A.1 B.2 C.3 D.4 8.四边形ABCD，被AC 和BD 分割成甲、乙、丙、丁四个三角形，其中AE、BE、CE、DE 的值如图，问三角形丙、丁的面积的和是甲、乙的和的多少倍？ A.2:3 B.3:2 C.4:5 D.5:4 9.公务员成绩出来后，20 名同学进行了一个分数的比对，发现，行测60 分以上的有15 个人，申论60 分以上的有12 个人，那么最少有多少人行测和申论都在60 分以上，最多多少人行测和申论都在60 分以上？A.5，15 B.7，12 C.7，15 D.5，12 10.用1，4，5，x 四个数字组成四位数，所有这些四位数中的数字的总和为288，求x。

公务员考试-数字推理题型分析

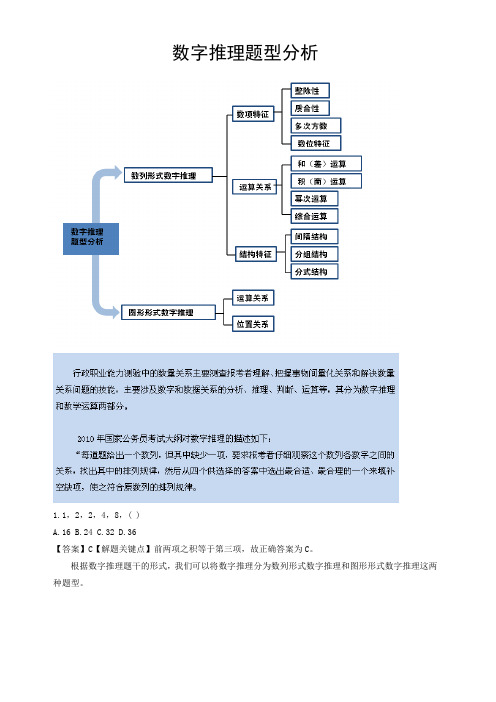
数字推理题型分析1.1，2，2，4，8，( )A.16B.24C.32D.36【答案】C【解题关键点】前两项之积等于第三项，故正确答案为C。

根据数字推理题干的形式，我们可以将数字推理分为数列形式数字推理和图形形式数字推理这两种题型。

1.19， 69， 135， 217， ( )A.257B.299C.315D.361【答案】C【解题关键点】各项依次写为1×19，3×23，5×27，7×31，(9×35)。

第一个乘数，1、3、5、7、(9)是公差为2的等差数列；第二个乘数，19、23、27、31、(35)是公差为4的等差数列。

2.8， 18， 40， 63， 110， ( )A．121 B．130 C．144 D．156【答案】D【解题关键点】各项依次写成2×4，3×6，S×8，7×9，11×10，(13 ×12)。

第一个乘数，2、3、5、7、11、(13)是连续质数；第二个乘数，4、6、8、9、10、(12)是连续合数。

3.3， 5， 7， 11， 13， ( )A.15 B．17 C．21 D.23【答案】B【解题关键点】连续质数，下一项应该为17。

4.4， 6， 8， 9， 10， ( )A.11B.12C.13D.14【答案】B【解题关键点】连续合数，下一项应该为12。

常用自然数多次方表格注意：1．除0以外，任何数的0次方都等于1，0的0次方是没有意义的。

2．表格中加底纹的数字有多种多次方表现形式，解题中应格外注意。

5.1, 4, 27, 256, ( )A.729B.1024C.3125 D,2401【答案】C【解题关键点】各项分别为6．]16， 4， ( )， 4， 16， 36A.7 B．2 C．1 D．O【答案】D【解题关键点】各项分别为-4、-2、(0)、2、4、6的平方。

公务员考试行测数字推理必知的30个规律

公务员考试行测数字推理必知的30个规律公务员考试中，数字推理是一个非常重要的考试科目。

数字推理是指通过对数字、图形、文字等信息的分析和推理，得出正确的结论。

在数字推理中，有很多规律需要掌握。

本文将介绍公务员考试行测数字推理必知的30个规律。

一、数字规律1. 数字序列规律数字序列规律是指在一组数字中，数字之间的关系所遵循的规律。

常见的数字序列规律有等差数列、等比数列、斐波那契数列等。

2. 数字排列规律数字排列规律是指在一组数字中，数字的排列顺序所遵循的规律。

常见的数字排列规律有逆序、顺序、交替等。

3. 数字替换规律数字替换规律是指在一组数字中，数字被替换成其他数字的规律。

常见的数字替换规律有加减乘除、平方、开方等。

4. 数字组合规律数字组合规律是指在一组数字中，数字之间的组合所遵循的规律。

常见的数字组合规律有排列组合、加减乘除等。

二、图形规律图形旋转规律是指在一组图形中，图形的旋转方向和角度所遵循的规律。

常见的图形旋转规律有顺时针旋转、逆时针旋转等。

6. 图形翻转规律图形翻转规律是指在一组图形中，图形的翻转方向和方式所遵循的规律。

常见的图形翻转规律有水平翻转、垂直翻转等。

7. 图形平移规律图形平移规律是指在一组图形中，图形的平移方向和距离所遵循的规律。

常见的图形平移规律有水平平移、垂直平移等。

8. 图形缩放规律图形缩放规律是指在一组图形中，图形的缩放比例所遵循的规律。

常见的图形缩放规律有放大、缩小等。

9. 图形填充规律图形填充规律是指在一组图形中，图形的填充方式和颜色所遵循的规律。

常见的图形填充规律有交替填充、渐变填充等。

三、文字规律10. 文字替换规律文字替换规律是指在一组文字中，文字被替换成其他文字的规律。

常见的文字替换规律有字母替换、数字替换等。

文字排列规律是指在一组文字中，文字的排列顺序所遵循的规律。

常见的文字排列规律有逆序、顺序、交替等。

12. 文字组合规律文字组合规律是指在一组文字中，文字之间的组合所遵循的规律。

公务员考试1000道数字推理题详解

【1】7，9，-1，5，( )A、4；B、2；C、-1；D、-3分析:选D，7+9=16；9+（-1）=8；（-1）+5=4；5+（-3）=2 , 16，8，4，2等比【2】3，2，5/3，3/2，( )A、1/4；B、7/5；C、3/4；D、2/5分析:选B，可化为3/1，4/2，5/3，6/4，7/5,分子3，4，5，6，7,分母1，2，3，4，5【3】1，2，5，29，（）A、34；B、841；C、866；D、37分析:选C，5=12+22；29=52+22；( )=292+52=866【4】2，12，30，（）A、50；B、65；C、75；D、56；分析:选D，1×2=2；3×4=12；5×6=30；7×8=（）=56【5】2，1，2/3，1/2，（）A、3/4；B、1/4；C、2/5；D、5/6；分析:选C，数列可化为4/2，4/4，4/6，4/8，分母都是4，分子2，4，6，8等差，所以后项为4/10=2/5，【6】4，2，2，3，6，（）A、6；B、8；C、10；D、15；分析:选D，2/4=0.5；2/2=1；3/2=1.5；6/3=2；0.5，1，1.5, 2等比，所以后项为 2.5×6=15【7】1，7，8，57，（）A、123；B、122；C、121；D、120；分析:选C，12+7=8；72+8=57；82+57=121；【8】4，12，8，10，（）A、6；B、8；C、9；D、24；分析:选C，(4+12)/2=8；(12+8)/2=10；(8+10)/2=9【9】1/2，1，1，（），9/11，11/13A、2；B、3；C、1；D、7/9；分析:选C，化成1/2,3/3,5/5 ( ),9/11,11/13这下就看出来了只能是(7/7)注意分母是质数列，分子是奇数列。

【10】95，88，71，61，50，（）A、40；B、39；C、38；D、37；分析：选A，思路一：它们的十位是一个递减数字9、8、7、6、5 只是少开始的 4 所以选择A。

甘肃公务员考题行测试卷及答案

甘肃公务员考题行测试卷及答案第一部分数量关系（共15题，参照时限l5分钟）一．数字推理。

给你一个数列，但其中缺少一项，要求你仔细观察数列的排列规律，然后从四个供选择的选项中选择你认为最合理的一项，来填补空缺项，使之符合原数列的排列规律。

【1】0,0,6,24,60,120 ( )A. 180B.196C. 210D.216【2】2,3, 7,45,2017 ( )A.4068271B.4068273C.4068275D.4068277 【3】2,2,3,4,9,32 ( )A.129B.215C.257D.283【4】0,4,16,48,128 ( )A.280B.320C.350D.420【5】 0.5,1,2,5,17,107 ( )A.1947B.1945C.1943D.1941二、数学运算。

在这部分试题中，每道试题呈现一段表述数宇关系的文字，要求你迅速，准确的计算出答案。

你可以在草稿纸上运算。

请开始答题：【6】一个正三角形和一个正六边形周长相等，则正六边形面积为正三角形的：A.倍B.l.5倍C.倍D.2倍【7】 n为100以内的自然数，那么能令2n _1被7整除的n有多少个？A.32B. 33C.34D.35【8】甲乙两个乡村阅览室，甲阅览室科技类书籍数量的1/5相当于乙阅览室该类书籍的1/4，甲阅览室文化书籍数量的2/3相当于乙阅览室该类书籍的1/6，甲阅览室科技类和文化类书籍的总量比乙阅览室书籍的总量多1000本，甲阅览室科技类和文化类书籍的比例为20:1,问甲阅览室有多少科技类书籍？A. 15000B.16000C.18000D.20000 【9】单独完成某项工作，甲需要16个小时，乙需要12个小时，如果按照甲，乙，甲，乙的顺序轮流工作，每次1小时，那么完成这项工作需要多长时间？A.l3小时40分钟B.13小时45分钟C.l3小时50分钟D.14小时【10】甲乙两人相约见面，并约定第一人到达后，等15分钟不见第二人来就可以离去。

公务员行测数字推理必知的30个规律

公务员行测数字推理必知的30个规律一、当一列数中出现几个整数，而只有一两个分数而且是几分之一的时候，这列数往往是负幂次数列。

【例】1、4、3、1、1/5、1/36、( )92 124 262 343二、当一列数几乎都是分数时，它基本就是分式数列，我们要注意观察分式数列的分子、分母是一直递增、递减或者不变，并以此为依据找到突破口，通过“约分”、“反约分”实现分子、分母的各自成规律。

【例】1/16 2/13 2/5 8/7 4 ()3三、当一列数比较长、数字大小比较接近、有时有两个括号时，往往是间隔数列或分组数列。

【例】33、32、34、31、35、30、36、29、( )A. 33B. 37C. 39四、在数字推理中，当题干和选项都是个位数，且大小变动不稳定时，往往是取尾数列。

取尾数列一般具有相加取尾、相乘取尾两种形式。

【例】6、7、3、0、3、3、6、9、5、( )五、当一列数都是几十、几百或者几千的“清一色”整数，且大小变动不稳定时，往往是与数位有关的数列。

【例】448、516、639、347、178、( )六、幂次数列的本质特征是：底数和指数各自成规律，然后再加减修正系数。

对于幂次数列，考生要建立起足够的幂数敏感性，当数列中出现6？、12？、14？、21？、25？、34？、51？、312？，就优先考虑43、112(53)、122、63、44、73、83、55。

【例】0、9、26、65、124、( )A. 165B. 193C. 217七、在递推数列中，当数列选项没有明显特征时，考生要注意观察题干数字间的倍数关系，往往是一项推一项的倍数递推。

【例】118、60、32、20、( )八、如果数列的题干和选项都是整数且数字波动不大时，不存在其它明显特征时，优先考虑做差多级数列，其次是倍数递推数列，往往是两项推一项的倍数递推。

【例】0、6、24、60、120、( )九、当题干和选项都是整数，且数字大小波动很大时，往往是两项推一项的乘法或者乘方的递推数列。

数字推理公务员题目及答案

数字推理公务员题目及答案### 数字推理公务员题目及答案#### 题目一题目：根据下列数字序列，找出规律并求出下一个数字。

1, 3, 6, 10, 15, ?答案： 21解析：这是一个等差数列，每个数字与前一个数字的差分别是2, 3, 4, 5，差值每次递增1。

因此，下一个差值应为6，所以下一个数字是15 + 6 = 21。

#### 题目二题目：观察下列数字序列，确定规律并计算下一个数字。

2, 5, 11, 21, 35, ?答案： 56解析：这是一个斐波那契数列，每个数字是前两个数字之和。

即35 + 21 = 56。

#### 题目三题目：根据以下数字序列，找出规律并求出下一个数字。

4, 9, 16, 25, 36, ?答案： 49解析：这是一个平方数序列，每个数字是其位置的平方。

即5^2 = 25，6^2 = 36，下一个数字是7^2 = 49。

#### 题目四题目：观察下列数字序列，找出规律并计算下一个数字。

1, 2, 4, 7, 11, ?答案： 16解析：这是一个等差数列，但差值不是固定的。

差值分别是1, 2, 3, 4，每次递增1。

根据这个规律，下一个差值应为5，所以下一个数字是11 + 5 = 16。

#### 题目五题目：根据下列数字序列，找出规律并求出下一个数字。

8, 5, 10, 3, 12, 1, ?答案： 14解析：这是一个交替增减的数列。

奇数位置的数字每次增加5，偶数位置的数字每次减少2。

所以下一个数字应该是1 + 5 = 6，但因为6是偶数位置，所以需要减去2，得到14。

#### 题目六题目：观察下列数字序列，找出规律并计算下一个数字。

1, 1, 2, 3, 5, 8, ?答案： 13解析：这是一个斐波那契数列，但起始数字不同。

每个数字是前两个数字之和，从第三个数字开始。

即8 + 5 = 13。

这些题目和答案都是根据数字序列的规律性设计的，旨在测试考生的逻辑推理和数学计算能力。

公务员考试经典数字推理题(含答案)

数字推理及数学运算：1. 3，—1，5，1，（）A. 3B. 7C. 25D. 64解: 两数之和形成2，4，6，8 的等差数列（注：也可以是两数之差、积、商或乘方）。

2. 8，10，14，18，（）A. 24B. 32C. 26D. 20解:道理基本同上。

前两数之和与后两数之和形成6，8，10的等差数列。

3. 1/3，6，1，12，（）A. 5/3B. 8/3C. 10D. 22解:1除以3，2乘以3，3除以3，4乘以3，5除以3。

递增自然数奇数项除以3，偶数项乘以3。

4. 3，2，8，12，28，（）A. 15B. 32C. 27D. 52解:第一个数乘以2加上第二个数的和等于第三个数（注：也可以是第一个数乘以2减去第二个数的差等于第三个数）。

5. 7，10，16，22，（）A. 28B. 32C. 34D. 45解:2*3+1=7，3*3+1=10，5*3+1=16，7*3+1=22，11*3+1=34（注：质数的3倍加1的和）。

6.1，16，27，16，5，（）A. 36B. 25C. 1D. 14解: 1的5次方，2的4次方，3的3次方，4的2次方，5的1次方，6的0方（自然数递增，方数递减；相近的题型也可以是自然数递减，方数递增）7. 4，3/2，20/27，7/16，36/125，（）A. 39/144B. 11/54C. 68/169D. 7解: 27是3的3次方，125是5的5次方；4可看成4/1，3/2可看成12/8，7/16可看成28/64，由此可推出分子是4*1，4*3，4*5，4*7，4*9，4*11，分母是递增自然数的3次方。

8.1，3，4，1，9，（）A. 5B. 11C. 14D. 64解: 前数减去后数的差的平方等第三个数。

（注：也可以是前数加上后数的和的平方等于第三个数）。

9.2，3，1，2，6，7,（）A. 9B. 5C. 11D. 24解: 相邻3个数的和形成0，3，6，9的等差数列2+3+1=6；3+1+2=6；1+2+6=9；2+6+7=15；6+7+？=24。

公务员考试分类专项练习之数字推理(附答案)

例题：2 9 16 23 30 ( )A 、35 B 、37 C 、39 D 、41解答：这一数列的排列规律是前一个数加7等于后一个数，故空缺项应为37。

正确答案为B 。

1. 0 2 6 14 ( ) 62 A 、40 B 、36 C 、30 D 、382. 2 7 28 63 ( ) 215 A 、116B 、126 C 、138 D 、1423. –1 9 8( ) 25 42 A 、17 B 、11 C 、16 D 、194. 3 4 7 16 ( ) 124 A 、33 B 、35 C 、41 D 、435. 1 2 3 2 ( ) 6 A 、2 3 B 、3 C 、3 3 D 、 56. 9 1 3 18 24 31 ( ) A.39 B.38 C.37 D.407. 1 7 10 ( ) 3 4 —1 A.7 B.6 C.8 D.58. 0 1 4 13 40 ( ) A.76 B.85 C.94 D.1219. 6 8 11 16 23 ( ) A. 32 B.34 C.36 D.3810. 6 1 2 19 27 33 ( ) 48 A.39 B.40 C.41 D.4211. 0 5 8 1 7 ( ) 37 A.31 B. 27 C.24 D.2212. 4 9 6 12 8 15 10 ( ) A.18 B.13 C.16 D.1513. 8 96 140 162 173 ( )A.178.5B.179.5 C 180.5 D.181.514. 2，2，3，6，12，22，（）A. 35 B. 36 C. 37 D. 3815. 4，14，45，139，（）A. 422 B. 412 C. 421 D. 38716. 1，2，4，4，1，（）A. 16B. 17C. 321D. 161 17. 10，11，13，34，58，105，（）A. 182 B. 149 C. 134 D. 19718. 1，2，3，7，8，17，15，（）A. 31 B. 10 C. 9 D. 2519. 4，5，（）,14，23，37。