七年级一元一次方程应用题常见数量关系[1] 2

合集下载

人教版初一数学一元一次方程应用题复习整理

一元一次方程复习第 1 页共 8 页
4 2
2
2 2
2
把一根半径为 2cm 的玻璃棒垂直插入水中后，问容器内的水将升高多少 cm？（圆柱的体积 =底面积×高）
分析：容器的底面积×容器中水的原来高度+玻璃棒的截面积×（容器中水的高度+水增加的高度） =容器的底面积×（容器中水原来的高度+水增加的高度）．解：设容器内的水将升高 x cm。 102 π•12+ 22 π（12+x）=102 π（12+x）解得：x=0.5．答：容器内的水将升高 0.5cm。甲行距+乙行距=原相距相向而行注意出发时间、地点
x x 3 3 2 3
解得：x=36 解法二解:设静水时轮船速度为 x 千米/时 2（x+3）=3（x-3）解得：x=15 则两码头之间的距离为 2（x+3）＝2×（15+3）＝36（千米） 2，一架飞机飞行在两个城市之间，风速为每小时 24 千米，顺风飞行需要 2 小时 50 分钟，逆风飞行需要 3 小时，求两城市间的距离。解:设两地距离为 x 千米，则有方程：
一元一次方程应用题复习整理
题中涉及的数量关系和差倍分问题等量关系增长量＝原有量×增长率现在量＝原有量＋增长量注意事项找出关键字，如： “大，小，多，少，增加，减少„„”
1，已知甲数是乙数的 3 倍多 12,甲乙两数的和是 60,求乙数. 解：设乙数为 x，那么甲数为３x+12 x+3x+12=60 解得：x=12 答：乙数是 12。 2，甲数是 20，先减少 10%，再增加 10%，现在的甲数是多少？ 20×（1-10%）×（1+10%） =20×90%×110% =19.8；答：现在的甲数是 19.8。 3，已知一个角的补角比这个角的余角的 3 倍大 10°，求这个角的度数。解：设这个角为∠α 。（180°﹣∠α ）﹣3（90°﹣∠α ）=10° 解得∠α =50° 则这个角的度数为 50°。等积问题 ①圆柱体的体积公式 V=底面积×高＝S·h＝π r2 h ②长方体的体积 V＝长×宽×高＝a b c 常见几何图形的面积、体积、周长计算公式，依据形虽变，但体积不变．要分清半径、直径等。

初一一元一次方程解应用题全部类型

1、和、差、倍、分问题；这类问题主要应搞清各量之间的关系，注意关键词语。

（1）倍数关系：通过关键词语“是几倍，增加几倍，增加到几倍，增加百分之几，增长率……”来体现。

（2）多少关系：通过关键词语“多少、和、差、不足、剩余……”来体现。

例1、某单位今年为灾区捐款2万5千元，比去年的2倍还多1000元，去年该单位为灾区捐款多少元？分析：相等关系是：今年捐款=去年捐款×2+1000。

解：设去年为灾区捐款x元，由题意得，2x+1000=250002x=24000∴ x=12000答：去年该单位为灾区捐款12000元。

例2、旅行社的一辆汽车在第一次旅程中用去油箱里汽油的25%，第二次旅程中用去剩余汽油的40%，这样油箱中剩的汽油比两次所用的汽油少1公斤，求油箱里原有汽油多少公斤？分析：等量关系为：油箱中剩余汽油+1=用去的汽油。

解：设油箱里原有汽油x公斤，由题意得，x(1-25%)(1-40%)+1=25%x+(1-25%)x×40%去分母整理得，9x+20=5x+6x∴ 2x=20∴ x=10答：油箱里原有汽油10公斤。

2、等积变形问题：“等积变形”是以形状改变而体积不变为前提。

常用等量关系为：原料体积=成品体积。

例3、现有直径为0.8米的圆柱形钢坯30米，可足够锻造直径为0.4米，长为3米的圆柱形机轴多少根？分析：等量关系为：机轴的体积和=钢坯的体积。

解：设可足够锻造x根机轴，由题意得，π()2×3x=π()2×30解这个方程得x=x=×10×==40答：可足够锻造直径为0.4米，长为3米的圆柱形机轴40根。

3、劳力调配问题：这类问题要搞清人数的变化，常见题型有（1）既有调入又有调出。

（2）只有调入没有调出，调入部分变化，其余不变；（3）只有调出没有调入，调出部分变化，其余不变。

例4、有两个工程队，甲队有285人，乙队有183人，若要求乙队人数是甲队人数的，应从乙队调多少人到甲队？分析：此问题中对乙队来说有调出，对甲队来说有调入。

初一数学上册一元一次方程的应用12种经典题型汇总

初一数学上册一元一次方程的应用12种经典题型汇总题型1：增长率问题某石油进口国这个月的石油进口量比上个月减少了5%,由于国际油价上涨,这个月进口石油的费用反而比上个月增加了14%.求这个月的石油价格相对上个月的增长率？解:设这个月的石油价格相对上个月的增长率为x.根据题意,得(1+x)x(1-5%)=1+14%解得x=0.2=20%答:这个月的石油价格相对上个月的增长率20%题型2：配套问题某服装厂要做一批某种型号的学生校服,已知某种布料每3m长可做2件上衣或3条裤子,一件上衣和一条裤子为一套,计划用600m长的这种布料做学生校服,应分别用多少米布料做上衣和裤子,才能恰好配套?解:设用x m布料做上衣,则用(600-x)m布料做裤子,则上衣共做2x/3件，裤子共做(600-x）条因为一件上衣配一条裤子,所以2x/3=600-x.解得x=360.所以600-360=240(m)答:应用360m布料做上衣,240m布料做裤子.题型3：销售问题某商品的进价是2000元,标价为3000元,商店将以利润率为5%的售价打折出售此商品,则该商店打几折出售此商品?解:设利润率为5%时售价为x元.根据题意（x-2000）/2000·100%=5%解得x=2100.所以2100/3000=7/10答:该商店打7折出售此商品.题型4：储蓄问题李明以两种方式储蓄了500元钱,一种方式储蓄的年利率是5%,另一种是4%,一年后共得利息23元5角,求两种储蓄各存了多少元钱？解:设年利率是5%的储蓄存了x元,则年利率是4%的储蓄存了(500-x)元.根据题意,得x·5%·1+(500-x)·4%·1=23.5解得x=350所以500-x=500-350=150答:年利率是5%和4%的储蓄分别存了350元和150元.题型5：等积变形问题用直径为4cm的圆钢,铸造3个直径为2cm,高为16cm的圆柱形零件,求需要截取多长的圆钢.解:设需要截取x cm长的圆钢.根据题意,得4·π·（4/2）^2=3·π·（2/2）^2·16解得x=12答:需要截取12cm长的圆钢。

七年级上册数学一元一次方程应用题知识点

七年级上册数学一元一次方程应用题的知识点主要包括以下几个方面：
1.方程的概念：了解方程的基本定义，即含有未知数的等式。

2.一元一次方程的解法：通过去分母、去括号、移项、合并同类项等步骤，将一元一
次方程化为标准形式，并求解。

3.方程的解与解集：理解方程的解是指使方程成立的未知数的值，而解集则是指所有
满足方程的未知数的值的集合。

4.实际问题的数学模型：能够将实际问题转化为数学问题，通过建立一元一次方程来
求解。

在应用题方面，通常会涉及到以下几种类型：
1.相遇问题：两个物体在某一点相遇，需要求出它们的速度和时间等参数。

2.追及问题：一个物体追赶另一个物体，需要求出追赶的速度和时间等参数。

3.利润与折扣问题：涉及到商品的利润和折扣计算，需要建立一元一次方程来求解。

4.工程的分配问题：需要分配一定量的工程任务给多个工人或机器，需要根据各自的
效率或能力进行分配，需要建立一元一次方程来求解。

总之，七年级上册数学一元一次方程应用题的知识点包括方程的概念、一元一次方程的解法、方程的解与解集以及实际问题的数学模型等。

通过掌握这些知识点，可以更好地解决实际问题。

【七年级数学代数培优竞赛专题】专题17 列一元一次方程解决实际问题【含答案】

专题17 列一元一次方程解决实际问题知识解读1.行程问题行程问题中的基本关系：路程=速度×时间.顺流、逆流问题中，顺流速度=船在静水中的速度+水速，逆流速度=船在静水中的速度－水速.2.销售问题销售问题中常见的数量关系：标价×折率=售价，售价一进价=利润，进价×利润率=利润。

3.分档问题现实生活中，有许多与费用有关的问题，其费用的计算方法会分成多个不同的档次.解题时要对照档次，认准计算方法，如果不能确定属于哪个档次时，要注意分类讨论.培优学案典例示范1.行程问题例1 甲、乙两列火车从A ，B 两地相向而行，乙车比甲车早出发1小时，甲车比乙车每小时快30千米，甲车发车2小时恰好与乙车相遇.相遇后为了错车，甲车放慢了速度，以它原来速度的倍23行驶，而乙车加快了速度，以它原来速度的倍行驶.结果2小时15分钟后，两车距离又等于A ，B 53两地之间的距离.求两车相遇前的速度及A ，B 两地之间的距离。

【提示】设乙车相遇前的速度为x 千米/小时，则甲车相遇前的速度为（x +30）千米/小时.分别用含x 的式子表示出相遇前两车的总行程和相遇后两车的总行程.【技巧点评】行程问题中基本的关系：路程=速度×时间.当问题较为复杂时，可借助表格来帮助分析：跟踪训练1甲、乙二人在一环形场地上从A点同时同向匀速跑步，甲的速度是乙的2.5倍，4分钟两人首次相遇，此时乙还需要跑300米才跑完第一圈，求甲、乙二人的速度及环形场地的周长.例2一条汽船在一条河上航行，若从A港到B港顺流航行需要3h，从B港到A港逆流航行需要4h，那么一根木棍从A港到B港顺水漂流需要多长时间？【提示】设汽船在静水中的速度为x千米/小时，水流的速度为y千米/小时.根据顺流汽船的行程和逆流汽船的行程都是A，B两港之间的距离可以列出方程，进而求出x与y的关系，而木棍漂流所用的时间等于A，B两港之间的距离除以水流速度。

初一数学一元一次方程应用题(完整版)

一元一次方程应用题归类列方程解应用题，是初中数学的重要内容之一。

许多实际问题都归结为解一种方程或方程组，所以列出方程或方程组解应用题是数学联系实际，解决实际问题的一个重要方面；下面老师就从以下几个方面分门别类的对常见的数学问题加以阐述，希望对同学们有所帮助.各题型一般模型：（1）倍数关系：通过关键词语“是几倍，增加几倍，增加到几倍，增加百分之几，增长率……”来体现。

（2）多少关系：通过关键词语“多、少、和、差、不足、剩余……”来体现。

根据2001年3月28日新华社公布的第五次人口普查统计数据，截止到2001年11月1日0时，全国每10万人中具有小学文化程度的人口为35701人，比1990年7月1日减少了3.66%，1990年6月底每10万人中约有多少人具有小学文化程度？分析：等量关系为：1、某石油进口国这个月的石油进口量比上个月减少了5%，由于国际油价上涨，这个月进口石油的费用反而比上个月增加了14%，求这个月的石油价格相对上个月的增长率。

2、某县城为鼓励居民节约用水，对自来水用户按分段计费方式收取水费：若每月用水不超过7m³，则按每立方米1元收费；若每月用水超过7m³，则超过部分按每立方米2元收费。

如果某居民今年5月缴纳了17元水费，那么这户居民今年5月的用水量为多少m³？3、芜湖供电公司分时电价执行时段分为平、谷两个时段，平段为8:00-22:00,14个小时；谷段为22:00-次日8:00，10个小时。

平段用电价格在原销售电价基础上每千瓦时上浮0.03元，谷段电价在原销售电价基础上每千瓦时下浮0.25元。

小明家5月份实用平段电量40千瓦时，谷段电量60千瓦时，按分时电价付费42.73元。

（1）问小明该月支付的平段、谷段电价每千瓦时各为多少元？（2）如不使用分时电价结算，5月份小明家将多支付电费多少元？4、某工厂食堂第三季度一共节煤7400斤，其中八月份比七月份多节约20%，九月份比八月份多节约25%，问该厂食堂九月份节约煤多少公斤？“等积变形”是以形状改变而体积不变为前提。

一元一次方程方程应用题总结归类

一元一次方程方程应用题总结归类列方程解应用题，是初中数学的重要内容之一。

许多实际问题都归结为解一种方程或方程组，所以列出方程或方程组解应用题是数学联系实际，解决实际问题的一个重要方面；下面老师就从以下几个方面分门别类的对常见的数学问题加以阐述，希望对同学们有所帮助.一行程问题：基本量、基本数量关系：路程=速度×时间，顺水速=静水速+水速，逆水速=静水速－水速，寻找相等关系的方法：抓住两码头之间的距离不变，水流速度，船在静水中的速度不变的特点来考虑。

（1）相向问题，寻找相等关系的方法：甲走的路程+乙走的路程=两地距离（2）追击问题：寻找相等关系的方法：第一，同地不同时出发：前者走的路程=追者走的路程；第二，同时不同地出发：前者走的路程+两地距离=追者所走的路程（3）航行问题：（4）飞行问题：1、火车提速后由天津到上海的时间缩短了7.42h，若天津到上海的路程为1326km，提速前火车的平均速度为xkm/h，提速后火车的平均速度为ykm/h，x、y应满足的关系式为：2、甲、乙骑自行车同时从相距65千米的两地相向而行，2小时相遇．甲比乙每小时多骑2.5千米，求乙的时速各是多少？3、一列客车长200米，一列货车长280米，在平行的轨道上相向行驶，从相遇到车尾离开经过18秒，客车及货车的速度比是5∶3，问两车每秒各行驶多少米？4、一架飞机在两城之间飞行，风速为24千米 /小时，顺风飞行需2小时50分，逆风飞行需要3小时。

（1）求无风时飞机的飞行速度（2）求两城之间的距离。

5、一条环行跑道长400米，甲每分钟行550米，乙每分钟行250米．（1）甲、乙两人同时同地反向出发，问多少分钟后他们再相遇？（2）甲、乙两人同时同地同向出发，问多少分钟后他们再相遇6、甲、乙两站相距480公里，一列慢车从甲站开出，每小时行90公里，一列快车从乙站开出，每小时行140公里。

（1）慢车先开出1小时，快车再开。

两车相向而行。

初一上册数学一元一次方程所有题型等量关系式

初一上册数学一元一次方程所有题型等量关系式
（1）等积类应用题的基本关系式：变形前的体积（容积）＝变形后的体积（容积）。

（2）调配类应用题的特点是：调配前的数量关系，调配后又有一种新的数量关系。

（3）利息类应用题的基本关系式：本金×利率＝利息，本金＋利息＝本息。

（4）商品利润率问题：商品的利润率，商品利润＝商品售价－商品进价。

（5）工程类应用题中的工作量并不是具体数量，因而常常把工作总量看作整体1，其中，工作效率＝工作总量÷工作时间。

（6）行程类应用题基本关系：路程＝速度×时间。

相遇问题：甲、乙相向而行，则：甲走的路程＋乙走的路程＝总路程。

追及问题：甲、乙同向不同地，则：追者走的路程＝前者走的路程＋两地间的距离。

环形跑道题：
①甲、乙两人在环形跑道上同时同地同向出发：快的必须多跑一圈才能追上慢的。

②甲、乙两人在环形跑道上同时同地反向出发：两人相遇时的总路程为环形跑道一圈的长度。

飞行问题、基本等量关系：①顺风速度＝无风速度＋风速②逆风速度＝无风速度－风速顺风速度－逆风速度＝2×风速航行问题，基本等量关系：①顺水速度＝静水速度＋水速②逆水速度＝静水速度－水速顺水速度－逆水速度＝2×水速（7）比例类应用题：若甲、乙的比为2：3，可设甲为2x，乙为3x。

（8）数字类应用题基本关系：若一个三位数，百位数字为a，十位数字为b，个位数字为c，则这三位数为：。

（9）浓度问题：溶质＝溶液×浓度（），溶液＝溶质＋溶剂。

1。

人教版初一数学一元一次方程与实际问题

人教版初一数学一元一次方程与实际问题本文涉及到的格式错误已经被删除。

一元一次方程解应用题（1）——路程问题教学目标：1.掌握行程问题，能够熟练地利用路程、速度、时间的关系列方程。

2.提高学生分析实际问题中数量关系的能力。

研究过程：基本等量关系：1.路程 = 速度 ×时间，时间 = 路程 ÷速度，速度 = 路程 ÷时间。

2.相向而行相遇时的等量关系：快者的路程 - 慢者的路程= 两人初相距的路程；同向而行追击时的等量关系：快者的路程 + 慢者的路程 = 两人初相距的路程。

新课探究：例1：甲、乙两站间的路程为360 km，一列慢车从甲站开出，每小时行驶48 km；一列快车从乙站开出，每小时行驶72 km。

⑴两列火车同时开出，相向而行，经过多少小时相遇？⑵快车先开25分钟，两车相向而行，慢车行驶了多少小时相遇？练一：1.甲、乙两人骑自行车同时从相距65 km的两地相向而行，2小时相遇，甲比乙每小时多骑2.5 km，求乙的速度？2.甲、乙两人在运动场上进行慢跑晨练，甲跑一圈3分钟，乙跑一圈2分钟，两人同时同地反向慢跑，求两人几分钟后第一次相遇？例2：一队学生去校外进行野外长跑训练。

他们以5 km/h 的速度行进，跑了18分钟的时候，学校要将一个紧急通知传给队长。

一名老师从学校出发，骑自行车以14 km/h的速度按原路追上去。

这名老师用多少时间可以追上学生队伍？练二：1.甲的步行速度是每小时5 km，乙的步行速度是每小时7.5 km，乙在甲的后面同时同向出发，120分钟后追上甲，那么开始时甲、乙两人相距多少千米？2.某班学生以每小时4 km的速度从学校步行到校办农场参加活动，走了1.5小时后，XXX奉命回学校取一件物品，他以每小时6 km的速度回校取了物品后，立即又以同样的速度追赶队伍，结果在距农场2 km处追上了队伍，求学校到农场的距离。

巩固练：1.在800米圆形跑道上有两人练中长跑，甲每分钟跑320米，乙每分钟跑280米。

七年级数学上册一元一次方程应用题常见的数量关系及题型归纳

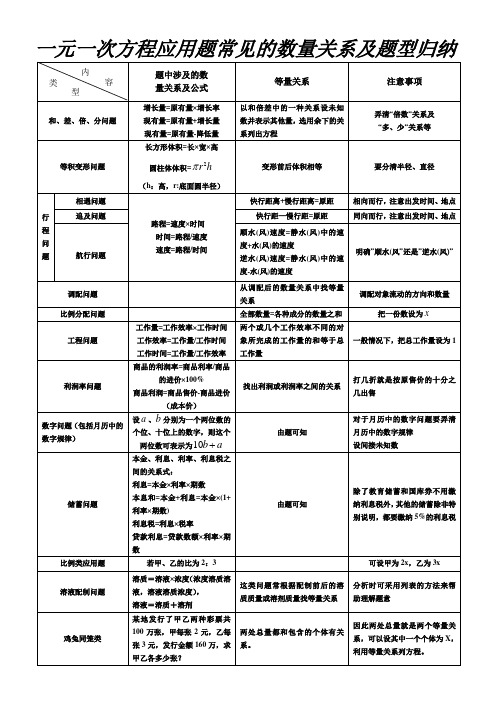
一元一次方程应用题常见的数量关系及题型归纳补充：1、数字问题一般可设个位数字为a，十位数字为b，百位数字为c．十位数可表示为10b+a，百位数可表示为100c+10b+a．然后抓住数字间或新数、原数之间的关系找等量关系列方程．2、市场经济问题（1）商品利润＝商品售价－商品成本价（2）商品利润率＝商品利润商品成本价×100%（3）商品销售额＝商品销售价×商品销售量（4）商品的销售利润＝（销售价－成本价）×销售量（5）商品打几折出售，就是按原标价的百分之几十出售，如商品打8折出售，即按原标价的80%出售．3、行程问题：路程＝速度×时间时间＝路程÷速度速度＝路程÷时间（1）相遇问题：快行距＋慢行距＝原距（2）追及问题：快行距－慢行距＝原距4、航行问题：顺水（风）速度＝静水（风）速度＋水流（风）速度逆水（风）速度＝静水（风）速度－水流（风）速度抓住两码头间距离不变，水流速和船速（静不速）不变的特点考虑相等关系．5、浓度问题溶质的重量＋溶剂的重量＝溶液的重量溶质的重量÷溶液的重量×100%＝浓度溶液的重量×浓度＝溶质的重量溶质的重量÷浓度＝溶液的重量6、增长率问题若平均增长（下降）数百分率为x，增长（或下降）前的是a,增长（或下降）n次后的量是b,则它们的数量关系可表示为：a(1+x)n=b7、加数＋加数＝和和－一个加数＝另一个加数被减数－减数＝差被减数－差＝减数差＋减数＝被减数因数×因数＝积积÷一个因数＝另一个因数被除数÷除数＝商被除数÷商＝除数商×除数＝被除数每份数×份数=总数总数÷每份数=份数总数÷份数=每份数8、工程问题公式（1）一般公式：工效×工时=工作总量；工作总量÷工时=工效；工作总量÷工效=工时。

七年级一元一次方程应用题分类大全

七年级一元一次方程应用题（一）1、匹配问题：例题2、某车间22名工人生产螺钉和螺母，每人每天平均生产螺钉1200个或螺母2000个，一个螺钉要配两个螺母。

为了使每天的产品刚好配套，应该分配多少名工人生产螺钉，多少名工人生产螺母？变式1：某车间每天能生产甲种零件120个，或乙种零件100个，甲、乙两种零件分别取3个、2个才能配成一套，现要在30天内生产最多的成套产品，问怎样安排生产甲、乙两种零件的天数？变式2：用白铁皮做罐头盒，每张铁片可制盒身10个或制盒底30个。

一个盒身与两个盒底配成一套罐头盒。

现有100张白铁皮，用多少张制盒身，多少张制盒底，可以既使做出的盒身和盒底配套，又能充分利用白铁皮？2、分配问题：例题1、把一些图书分给某班学生阅读，如果每人分3本，则剩余20本；如果每人分4本，则还缺25本.问这个班有多少学生？变式1：某水利工地派48人去挖土和运土，如果每人每天平均挖土5方或运土3方，那么应怎样安排人员，正好能使挖出的土及时运走？变式2：某校组织师生春游,如果只租用45座客车,刚好坐满;如果只租用60座客车,可少租一辆,且余30个座位.请问参加春游的师生共有多少人?3、利润问题(1)一件衣服的进价为x元,售价为60元,利润是______元,利润率是_______.变式：一件衣服的进价为x元,若要利润率是20%,应把售价定为________.(2)一件衣服的进价为x元,售价为80元,若按原价的8折出售,利润是______元,利润率是__________.变式1：一件衣服的进价为60元,若按原价的8折出售获利20元,则原价是______元,利润率是__________.变式2：一台电视售价为1100元,利润率为10%,则这台电视的进价为_____元.变式3：一件商品每件的进价为250元，按标价的九折销售时，利润为15.2%，这种商品每件标价是多少？变式4：一件夹克衫先按成本提高50%标价,再以八折(标价的80%)出售,结果获利28元,这件夹克衫的成本是多少元?变式5：一件商品按成本价提高20%标价,然后打九折出售,售价为270元.这种商品的成本价是多少?变式6：某商店在某一时间以每件60元的价格卖出两件衣服，其中一件盈利25%，另一件亏损25%，买这两件衣服总的是盈利还是亏损，或是不盈不亏？4、工程问题：（1）甲每天生产某种零件80个，3天能生产个零件。

七年级上册数学一元一次方程的应用题专题

课堂检测1．小亮用129元买了两种书，共10本，单价分别为15元、8元，问每种书各买了多少本？2．甲列车从A地开往B地，速度是60千米∕小时，乙列车同时从B地开往A地，速度是90千米∕小时.已知A,B两地相距200千米，两地相距的地方李A地多远？第 6 讲：一元一次方程的应用【考纲要求】本节课重点复习一元一次方程的应用，树立初步的方程思想.一元一次方程的应用非常广泛，不是人为分类固定模式,而是学会分析简单问题中的数量关系,建立方程解决问题;认识到利用方程解决问题的关键是寻找等量关系.主要利用：等积变形、行程、调配、销售以及与图表、图形等有关问题，达到提高我们能力的目的.要学习、解决这些问题，首先需把握以下几个基本量及基本数量关系：行程问题：(1)基本量:路程、时间、速度(2)基本数量关系: .销售问题：(1)基本量:商品进价、商品售价或标价、商品利润、商品利润率(2)基本数量关系:① .② .【教学重难点】等量关系发找方程解决应用题【本讲命题方向】填空题、选择题和应用题约3~5%【典型题例精讲】的正方形的长方体，求锻造后长方体的高为多少米？2.桌面上有甲、乙、丙三个圆柱形的杯子，杯深均为15公分，各装有10公分高的水，且表记录了甲、乙、丙三个杯子的底面积．今小明将甲、乙两杯内一些水倒入丙杯，过程中水没溢出，使得甲、乙、丙三杯内水的高度比变为3︰4︰5．若不计杯子厚度，则甲杯内水的高度变为多少公分？( )A．5.4 B．5.7 C．7.2 D．7.5【反思与小结】列方程解应用题的关键步骤是找出相等关系,在解决等积变形问题时利用的相等关系是 .（二）调配问题【例2】1.某车间有26名工人，每人每天可以生产800个螺钉或1000个螺母，1个螺钉需要配2个螺母，为使每天生产的螺钉和螺母刚好配套．设安排x名工人生产螺钉，则下面所列方程正确的是（）A．2×1000（26﹣x）=800x B．1000（13﹣x）=800xC．1000（26﹣x）=2×800x D．1000（26﹣x）=800x2.用正方形硬纸板做三棱柱盒子，每个盒子由3个矩形侧面和2个正三角形底面组成。

七年级一元一次方程应用题题型有哪些

七年级一元一次方程应用题题型有哪些
一、相遇问题
在这类题型中，通常会给出两个物体相遇的条件，例如两辆车从不同地方同时
出发相向而行，求它们相遇的时间。

利用一元一次方程可以很容易地解决这类问题。

二、零用钱问题
这类题型通常会描述一个人手中有一定数量的钱，先进行一系列购物后剩余的钱。

通过列方程的方式可以求解这些问题，帮助学生掌握方程在日常生活中的应用。

三、装订书籍问题
题目描述学校要为班级的学生装订几本数学书，每册装订费用若干元，需要求
解装订一定数量书籍需要的总费用。

这种类型的问题也可以用一元一次方程进行求解。

四、水果购买问题
问题描述某种水果的单价以及购买的重量，需要计算购买这些水果总共需要多
少钱。

同样，通过列方程可以快速解决这类问题。

五、人数问题
给定几组人员的总数及各组人数的关系，例如某场活动男女参与人数的比例等，需要通过方程求解各组的人数。

六、时间问题
描述物体的速度、时间和距离之间的关系，例如某物体以一定速度行驶一段距
离所需的时间等。

通过方程可以方便地解决这类实际问题。

结语
这些是七年级一元一次方程应用题常见的题型，通过解答这些问题，学生不仅
可以提升对方程的理解和运用能力，也能体会到数学在日常生活中的实际应用。

希望同学们多加练习，熟练掌握这些题型的解题方法。

七年级上册新人教版教材一元一次方程应用题带答案

【教材上出现的应用题】问题1 某校三年共购买计算机140台，去年购买数量是前年的2倍，今年购买数量又是去年的2倍.前年这个学校购买了多少台计算机？（P86）答案：解：设前年购买了x台，则x+2x+4x=140解得x=20答：前年购买了20台问题2 把一些图书分给某班学生阅读，如果每人分3本，则剩余20本；如果每人分4本，则还缺25本，这个班有多少学生？（P88）答案：解:(1)设这个班有x名学生．依题意有:3x+20=4x﹣25解得:x=45答:这个班有45名学生.例4 某制药厂制造一批药品，如用旧工艺，则废水排量要比环保限制的最大量还多200t；如用新工艺，则废水排量比环保限制的最大量少100t，新、旧工艺的废水排量之比为2:5，两种工艺的废水排量各是多少？（P90）答案：解:设新、旧工艺的废水排量分别为2xt、5xt，则依题意得5x-200=2x+100，解得 x=100．则2x=200，5x=500．答：新、旧工艺的废水排量分别为200t、500t．11.几个人共同种一批树苗，如果每人种10棵，则剩下6棵树苗未种；如果每人种12棵，则缺6棵树苗，求参与种树的人数.（P91）答案：解:设有x人种树,则树苗共有（10x+6）棵.12x-(10x+6)=6x=6答：参与种树人数为6人13.一个两位数的个位上的数的3倍加1是十位上的数，个位上的数与十位上的数的和等于9，这个两位数是多少？（P92）答案：解:设个位数为xx＋3x＋1＝9解得x＝2十位上的数：9―2＝7答：这个两位数是：7×10＋2＝72一艘船从甲码头到乙码头顺流而行，用了2h;从乙码头返回甲码头逆流而行，用了2.5h 。

已知水流的速度是3㎞/h ，求船在静水中的平均速度.（P94）答案：解：设船在静水中的速度为x 千米/时，则顺流的速度为（x+3）千米/时，逆流的速度为：（x-3）千米/时，由题意得：2（3+x ）=2.5（x-3），解得：x=27．答：船在静水中的平均速度为27千米/小时．10.王力骑自行车从A 地到B 地，陈平骑自行车从B 地到A 地，两人都沿同一公路匀速前进，已知两人在上午8时同时出发，到上午10时，两人还相距36km ，到中午12时，两人又相距36km ，求A 、B 两地间的路程。

《易错题》七年级数学上册第三单元《一元一次方程》-解答题专项经典题(含答案)

一、解答题1．列方程解应用题：为参加学校运动会，七年级一班和七年级二班准备购买运动服. 下面是某服装厂给出的运动服价格表：已知两班共有学生67人（每班学生人数都不超过60人），如果两班单独购买服装，每人只买一套，那么一共应付3650元. 问七年级一班和七年级二班各有学生多少人？解析：七年级一班有37人，七年级二班有30人；或者七年级一班有30人，七年级二班有37人.【分析】首先根据题中表格数据得出有一个班的人数大于35人，接着设大于35人的班有学生x 人，根据等量关系列出方程，求解即可.【详解】⨯=解：∵67604020>40203650∴所以一定有一个班的人数大于35人.设大于35人的班有学生x人，则另一班有学生（67-x）人，依题意得+-=x x5060(67)3650-=x6730答：七年级一班有37人，七年级二班有30人；或者七年级一班有30人，七年级二班有37人.【点睛】本题考查了一元一次方程的应用．解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系列出方程，再求解．2．全班同学去划船，如果减少一条船，每条船正好坐9个同学，如果增加一条船，每条船正好坐6个同学，问原有多少条船？解析：原有5条船．【分析】首先设原有x条船，根据“减少一条船，那么每条船正好坐9名同学；增加一条船，那么每条船正好坐6名同学”得出等式方程，求出即可．【详解】设原有x条船，如果减少一条船，即(x－1)条，则共坐9(x－1)人．如果增加一条船，则共坐6(x＋1)人，根据题意，得9(x －1)＝6(x ＋1)．去括号，得9x －9＝6x ＋6.移项，得9x －6x ＝6＋9.合并同类项，得3x ＝15.系数化为1，得x ＝5.答：原有5条船．【点睛】此题主要考查了一元一次方程的应用，根据题意利用全班人数列出等量关系式是完成本题的关键．3．已知16y x =-，227y x =+，解析下列问题：（1）当122y y =时，求x 的值；（2）当x 取何值时，1y 比2y 小3-．解析：（1）215x =；（2）18x 【分析】（1）根据题意列出等式，然后解一元一次方程即可；（2）根据题意得到213y y -=-，然后代入x ，解一元一次方程即可求解．【详解】（1）由题意得：62(27)x x -=+解得215x = 215x ∴=．（2）由题意得：27(6)3x x +--=-解得18x 18x ∴=．【点睛】本题考查了解一元一次方程，重点是熟练掌握移项、合并同类项、去括号、去分母的法则，细心求解即可．4．已知数轴上的A 、B 两点分别对应数字a 、b ，且a 、b 满足|4a-b|+（a-4）2=0（1）a= ，b= ，并在数轴上面出A 、B 两点；（2）若点P 从点A 出发，以每秒3个单位长度向x 轴正半轴运动，求运动时间为多少时，点P 到点A 的距离是点P 到点B 距离的2倍；（3）数轴上还有一点C 的坐标为30，若点P 和点Q 同时从点A 和点B 出发，分别以每秒3个单位长度和每秒1个单位长度的速度向C点运动，P点到达C点后，再立刻以同样的速度返回，运动到终点A．求点P和点Q运动多少秒时，P、Q两点之间的距离为4，并求此时点Q对应的数．解析：（1）4，16．画图见解析；（2）83或8秒；（3）点P和点Q运动4或8或9或11秒时，P，Q两点之间的距离为4．此时点Q表示的数为20，24，25，27．【分析】（1）根据非负数的性质求出a、b的值即可解决问题；（2）构建方程即可解决问题；（3）分四种情形构建方程即可解决问题.【详解】（1）∵a，b满足|4a-b|+（a-4）2≤0，∴a=4，b=16，故答案为4，16．点A、B的位置如图所示．（2）设运动时间为ts．由题意：3t=2（16-4-3t）或3t=2（4+3t-16），解得t=83或8，∴运动时间为83或8秒时，点P到点A的距离是点P到点B的距离的2倍；（3）设运动时间为ts．由题意：12+t-3t=4或3t-（12+t）=4或12+t+4+3t=52或12+t+3t-4=52，解得t=4或8或9或11，∴点P和点Q运动4或8或9或11秒时，P，Q两点之间的距离为4．此时点Q表示的数为20，24，25，27．【点睛】本题考查多项式、数轴、行程问题的应用等知识，具体的关键是学会构建方程解决问题，学会用分类讨论的思想思考问题．5．关于x的方程357644m x mx+=-的解比方程4(37)1935x x-=-的解大1，求m的值.解析：623 m=-【分析】分别求出两方程的解，根据题意列出关于m的方程，然后求解即可.【详解】解：357644m x m x +=-，整理得：2(310)321m x m x +=- 313x m =-解得：331m x =-， 4(37)1935x x -=-4747x =1x =由题意得：31131m --= 解得：623m =-【点睛】本题考查了一元二次方程的解和解方程，关键是能先用含有m 的式子表示x ，然后根据题意列出方程.6．如图，甲船逆水，静水速度为28海里/时；乙船顺水，静水速度为12海里/时，两船相距60海里.已知水流速度为3海里/时，两船同时相向而行.（1）两船同时航行1小时，求此时两船之间的距离；（2）再（1）的情况下，两船再继续航行1小时，求此时两船之间的距离；（3）求两船从开始航行到两船相距12海里，需要多长时间？解析：(1) 20海里;(2) 20海里;(3) 1.2小时或1.8小时.【分析】（1）根据1h 后甲、乙间的距离=两船相距-（甲船行驶的路程+乙船行驶的路程）即可得；（2）根据2h 后甲、乙间的距离=甲船行驶的路程-乙船行驶的路程即可得；（3）可分相遇前与相遇后两种情况讨论即可解答.【详解】解：根据题意可知甲船的行驶速度为28-3=25海里/时，乙船的行驶速度为12+3=15海里/时（1）1h 后甲、乙间的距离=60-25×1-15×1=20海里；（2）2h 后甲、乙间的距离=25×2-15×2=20海里；（3）相遇前，设两船从开始航行到两船相距12海里，需要t 小时则12=60-（25+15）t ，求得t=1.2小时相遇后，设两船从开始航行到两船相距12海里，需要t 1小时则12+60=（25+15）t 1，求得t 1=1.8小时故两船从开始航行到两船相距12海里，1.2小时或1.8小时.【点睛】本题主要考查列代数式与一元一次方程的实际应用，掌握船顺流航行时的速度与逆流航行的速度公式是解题的关键．7．图1为全体奇数排成的数表，用十字框任意框出5个数，记框内中间这个数为 a（如图2）．（1）请用含a的代数式表示框内的其余4个数；（2）框内的5个数之和能等于 2015，2020 吗?若不能，请说明理由；若能，请求出这5个数中最小的一个数，并写出最小的这个数在图1数表中的位置．（自上往下第几行，自左往右的第几个）解析：（1）详见解析；（2）详见解析.【分析】（1）上下相邻的数相差18，左右相邻的数相差是2，所以可用a表示；（2）根据等量关系：框内的5个数之和能等于2015，2020，分别列方程分析求解．【详解】（1）设中间的数是a，则a的上一个数为a−18，下一个数为a＋18，前一个数为a−2，后一个数为a＋2；（2）设中间的数是a，依题意有5a＝2015，a＝403，符合题意，这5个数中最小的一个数是a−18＝403−18＝385，2n−1＝385，解得n＝193，193÷9＝21…4，最小的这个数在图1数表中的位置第22排第4列．5a＝2020，a＝404，404是偶数，不合题意舍去；即十字框中的五数之和不能等于2020，能等于2015．【点睛】本题考查一元一次方程的应用，关键是看到表格中中间位置的数和四周数的关系，最后可列出方程求解．8．学校要购入两种记录本，预计花费460元，其中A种记录本每本3元，B种记录本每本2元，且购买A种记录本的数量比B种记录本的2倍还多20本．（1）求购买A和B两种记录本的数量；（2）某商店搞促销活动，A种记录本按8折销售，B种记录本按9折销售，则学校此次可以节省多少钱？解析：（1）购买A种记录本120本，B种记录本50本；（2）学校此次可以节省82元钱．【分析】根据两种记录本一共花费460元即可列出方程【详解】（1）设购买B种记录本x本，则购买A种记录表（2x+20）本，依题意，得：3（2x+20）+2x＝460，解得：x＝50，∴2x+20＝120．答：购买A种记录本120本，B种记录本50本．（2）460﹣3×120×0.8﹣2×50×0.9＝82（元）．答：学校此次可以节省82元钱．【点睛】根据题意中的等量关系列出方程是解决问题的关键9．某市居民生活用水实行“阶梯水价”收费，具体收费标准见下表：⨯+⨯-= (元).例：甲用户1月份用水25吨，应缴水费1.620 2.4(2520)44(1)若乙用户1月份用水10吨，则应缴水费________元；(2)若丙用户1月份应缴水费62.6元，则用水________吨；.(3)若丁用户1、2月份共用水60吨(1月份用水量超过了2月份)，设2月份用水a吨，求丁用户1、2月份各应缴水费多少元.(用含a的代数式表示)-元.当2月份用水量不超过20吨时，解析：(1)16；(2)32； (3) 1月份应缴水费(155 3.3)aa-元.应缴水费1.6a元；当2月份用水量超过20吨但不超过30吨时，应缴水费(2.416)【分析】（1）根据每户每月用水量不超过20时，水费价格为1.6元/吨，可知乙用户1月份用水10吨，则应缴水费：1.6×10，计算即可；（2）由于用水30吨时应缴水费为：1.6×20+2.4×10=56＜62.6，所以丙用户1月份用水超过30吨，列出方程，求解即可；（3）由丁用户1、2两个月共用水60吨，设2月份用水a吨，则1月份用水（60-a）吨，根据1月份用水量超过了2月份，得出1月份用水量超过了2月份，得出1月份用水量大于30吨，2月份用水量小于30吨，根据三级收费求出1月份应缴水费，分两种情况求出2月份应缴水费， ①当2月份用水量不超过20吨时；②当2月份用水量超过20吨但不超过30吨时；【详解】解：(1)依题意得：1.6×10=16；故答案为：16(2) 依题意得：由于用水30吨时应缴水费为：1.6×20+2.4×10=56＜62.6，所以丙用户1月份用水超过30吨，设用水为x 吨，依题意得：56(30) 3.362.6x +-⨯=解得：x=32故答案为：32；(3)因为1月份用水量超过了2月份，所以1月份用水量超过了30吨，2月份用水量少于30吨.1月份应缴水费20 1.610 2.4 3.3(6030)(155 3.3)a a ⨯+⨯+--=-元.①当2月份用水量不超过20吨时，应缴水费1.6a 元；②当2月份用水量超过20吨但不超过30吨时，应缴水费1.6202.4(20)(2.416)a a ⨯+-=-元.【点睛】本题主要考查了列代数式，代数式求值，掌握列代数式，代数式求值是解题的关键. 10．如图A 在数轴上所对应的数为﹣2．（1）点B 在点A 右边距A 点4个单位长度，求点B 所对应的数；（2）在（1）的条件下，点A 以每秒2个单位长度沿数轴向左运动，点B 以每秒2个单位长度沿数轴向右运动，当点A 运动到﹣6所在的点处时，求A ，B 两点间距离．（3）在（2）的条件下，现A 点静止不动，B 点沿数轴向左运动时，经过多长时间A ，B 两点相距4个单位长度．解析：（1）B 所对应的数为2；（2）A ，B 两点间距离是12个单位长度；（3）经过4秒或8秒长时间A ，B 两点相距4个单位长度．【分析】（1）根据左减右加可求点B 所对应的数；（2）先根据时间＝路程÷速度，求出运动时间，再根据路程＝速度×时间求解即可；（3）分两种情况：运动后的B 点在A 点右边4个单位长度；运动后的B 点在A 点左边4个单位长度；列出方程求解即可．【详解】解：（1）﹣2+4＝2．故点B 所对应的数为2；（2）（﹣2+6）÷2＝2（秒），4+（2+2）×2＝12（个单位长度）．故A ，B 两点间距离是12个单位长度．（3）运动后的B点在A点右边4个单位长度，设经过x秒长时间A，B两点相距4个单位长度，依题意有2x＝12﹣4，解得x＝4；运动后的B点在A点左边4个单位长度，设经过x秒长时间A，B两点相距4个单位长度，依题意有2x＝12+4，解得x＝8．故经过4秒或8秒长时间A，B两点相距4个单位长度．【点睛】本题考查了数轴，行程问题的数量关系的运用，解答时根据行程问题的数量关系列出方程是解决问题的关键．11．统计数据显示，在我国的664座城市中，按水资源情况可分为三类：暂不缺水城市、一般缺水城市和严重缺水城市．其中，暂不缺水城市数比严重缺水城市数的3倍多52座，一般缺水城市数是严重缺水城市数的2倍．求严重缺水城市有多少座？解析：102座．【分析】根据等量关系为：暂不缺水城市+一般缺水城市+严重缺水城市=664，据此列出方程，解可得答案．【详解】设严重缺水城市有x座，依题意得：（3x+52）+x+2x=664．解得：x=102．答：严重缺水城市有102座．【点睛】此题考查一元一次方程的应用，解题的关键在于找到合适的等量关系，列出方程求解．12．某市百货商店元月1日搞促销活动，购物不超200元不予优惠；购物超过200元而不足500元的按全价的90%优惠；超过500元，其中500元按9折优惠，超过部分按8折优惠，某人两次购物分别用了134元和466元．问：（1）列方程求出此人两次购物若其物品不打折共值多少钱？（2）若此人将这两次购物合为一次购买是否更节省？为什么？解析：（1）654元钱；（2）将这两次购物合为一次购买更节省，理由见解析.【分析】（1）根据“超过200元而不足500元的按9折优惠”可得：200×90%＝180元，由于第一次购物134元＜180元，故不享受任何优惠；由“超过500元，其中500元按9折优惠，超过部分8折优惠”可知500×90%＝450元，466＞450元，故此人购物享受“超过500元，其中500元按9折优惠，超过部分8折优惠”，设他所购价值x元的货物，首先享受500元钱时的9折优惠，再享受超过500元的8折优惠，把两次的花费加起来即可得出此人第二次购物不打折的花费，最后将两次购物不打折的花费相加即可；（2）计算出两次购物合为一次购买实际应付的费用，再与他两次购物所花的费用进行比较即可．【详解】解：（1）①因为134元＜200×90%＝180元，所以该人此次购物不享受优惠；②因为第二次付了466元＞500×90%＝450元，所以该人享受超过500元，其中500元按9折优惠，超过部分8折优惠．设他所购货物价值x元，则90%×500+（x﹣500）×80%＝466，解得x＝520，520+134＝654（元）．答：此人两次购物若其物品不打折共值654元钱；（2）500×90%+（654﹣500）×80%＝573.2（元），134+466＝600（元），∵573.2＜600，∴此人将这两次购物合为一次购买更节省．【点睛】此题主要考查了一元一次方程的应用，关键是分析清楚付款打折的情况，找出合适的等量关系列出方程．13．青岛、大连两个城市各有机床12台和6台，现将这些机床运往海南10台和厦门8台，每台费用如表一：问题1：如表二，假设从青岛运往海南x台机床，并且从青岛、大连运往海南机床共花费36万元，求青岛运往海南机床台数.问题2：在问题1的基础上，问从青岛、大连运往海南、厦门的总费用为多少万元？解析：问题1：青岛运往海南机床台数是4台；问题2：从青岛、大连运往海南、厦门的总费用为94万元.【分析】（1）假设从青岛运往海南x台机床，则从大连运往海南的就是10-x台，根据等量关系：“运往海南机床共花费36万元”，即可列出方程解决问题；（2）根据问题1中求出的分别从青岛和大连运出的台数，则它们剩下的台数都要运到厦门，由此利用乘法和加法的意义即可解答问题．【详解】（1）设从青岛运往海南x台机床，则从大连运往海南的就是10-x台，根据题意可得方程：4x+3（10-x）=36，4x+30-3x=36，x=6，则从大连运往海南的有：10-6=4（台）．答：从青岛运往海南6台，从大连运往海南4台．（2）根据上面计算结果可知：青岛剩下12-6=6（台）；大连剩下6-4=2（台），剩下的这些都要运往厦门，所以需要的费用是：6×8+2×5，=48+10，=58（万元），36+58=94（万元）．答：从青岛、大连运往海南、厦门的总费用为94万元．【点睛】观察表格，找出已知条件，和要求的问题，根据题干中的等量关系即可，此题条件稍微复杂，需要学生认真审题进行解答．14．解下列方程：（1）15(x＋15)＝1231-(x－7)．（2）2110121364x x x-++-=－1．解析：（1）x＝－516；（2）x＝16．【分析】（1）直接根据解一元一次方程的步骤进行即可；（2）直接根据解一元一次方程的步骤进行即可．【详解】解：（1）15(x＋15)＝1231-(x－7)．去分母，得6(x＋15)＝15－10(x－7)．去括号，得6x＋90＝15－10x＋70．移项及合并同类项，得16x＝－5．系数化为1，得x＝－5 16．（2）2110121 364x x x-++-=－1去分母，得4(2x－1)－2(10x＋1)＝3(2x＋1)－12．去括号，得8x－4－20x－2＝6x＋3－12．移项，得8x－20x－6x＝3－12＋4＋2．合并同类项，得－18x＝－3．系数化为1，得x ＝16．【点睛】此题主要考查解一元一次方程，熟练掌握解一元一次方程的步骤是解题关键．15．为了鼓励市民节约用水，某市水费实行分段计费制，每户每月用水量在规定用量及以下的部分收费标准相同，超出规定用量的部分收费标准相同.下表是小明家1至4月份水量和缴纳水费情况，根据表格提供的数据，回答：）规定用量内的收费标准是元吨，超过部分的收费标准是元/吨；（2）问该市每户每月用水规定量是多少吨？（3）若小明家六月份应缴水费50元，则六月份他们家的用水量是多少吨？解析：（1）2；3（2）规定用水量为10吨（3）六月份的用水量为20吨【分析】（1）由小明家1，2月份的用水情况，可求出规定用量内的收费标准；由小明家3，4月份的用水情况，可求出超过部分的收费标准；（2）设该市规定用水量为a 吨，由小明家3月份用水12吨缴纳26元，即可得出关于a 的一元一次方程，解之即可得出结论；（3）设小明家6月份的用水量是x 吨，根据应缴水费=2×10+3×超出10吨部分，即可得出关于x 的一元一次方程，解之即可得出结论．【详解】（1）由表可知，规定用量内的收费标准是2元/吨，超过部分的收费标准为3元/吨（2）设规定用水量为a 吨；则23(12)26a a +-=，解得：10a =，即规定用水量为10吨；（3）∵2102050⨯=<，∴六月份的用水量超过10吨，设用水量为x 吨，则2103(10)50x ⨯+-=，解得：20x， ∴六月份的用水量为20吨【点睛】本题考查了一元一次方程的应用以及有理数的混合运算，解题的关键是：通过分析小明家1-4月用水量和交费情况，找出结论；找准等量关系，正确列出一元一次方程．16．某商场投入13800元资金购进甲、乙两种矿泉水共500箱，矿泉水的成本价和销售价如表所示：类别/单价成本价销售价（元/箱）甲2436乙3348（1）该商场购进甲、乙两种矿泉水各多少箱？（2）全部售完500箱矿泉水，该商场共获得利润多少元？解析：（1）商场购进甲种矿泉水300箱，购进乙种矿泉水200箱（2）该商场共获得利润6600元【详解】（1）设商场购进甲种矿泉水x箱，购进乙种矿泉水y箱，由题意得：500{243313800 x yx y+=+=，解得：300 {200 xy==，答：商场购进甲种矿泉水300箱，购进乙种矿泉水200箱；（2）300×(36−24)+200×(48−33)=3600+3000=6600(元)，答：该商场共获得利润6600元．17．数学课上，某班同学用天平和一些物品（如图）探究了等式的基本性质.该班科技创新小组的同学提出问题：仅用一架天平和一个10克的砝码能否测量出乒乓球和一次性纸杯的质量？科技创新小组的同学找来足够多的乒乓球和某种一次性纸杯（假设每个乒乓球的质量相同，每个纸杯的质量也相同），经过多次试验得到以下记录：记录天平左边天平右边状态记录一6个乒乓球，1个10克的砝码14个一次性纸杯平衡记录二8个乒乓球7个一次性纸杯，1个10克的砝码平衡请算一算，一个乒乓球的质量是多少克？一个这种一次性纸杯的质量是多少克？解：（1）设一个乒乓球的质量是x 克，则一个这种一次性纸杯的质量是______克；（用含x 的代数式表示）（2）列一元一次方程求一个乒乓球的质量，并求出一个这种一次性纸杯的质量. 解析：（1）61014x +或8107x -；（2）一个乒乓球的质量是3克，一个这种一次性纸杯的质量是2克.【分析】(1)根据题意即可得出答案；（2）弄清题意，找到合适的等量关系，列出方程，解方程即可．【详解】解：（1）61014x +或8107x - （2）根据题意得，610810147x x +-= 6101620x x +=-6162010x x -=--1030x -=-3x =．当3x =时，610631021414x +⨯+==（克）．答：一个乒乓球的质量是3克，一个这种一次性纸杯的质量是2克．【点睛】本题考查了一元一次方程与实际问题，解题的关键是找到合适的等量关系，列出方程，解方程．18．检验下列方程后面小括号内的数是否为相应方程的解．(1)2x+5=10x-3（x=1）； (2)2(x-1)-12(x+1)=3(x+1)-13(x-1)（x=0）．解析：（1）是；（2）否．【分析】（1）先求出一元一次方程的解，然后进行判断即可；（2）先求出一元一次方程的解，然后进行判断即可；【详解】解：（1）25103x x +=-，∴88x -=-，∴1x =，∴括号内的数是方程的解；（2）112(1)(1)3(1)(1)23x x x x --+=+--， ∴77(1)(1)32x x -=+， ∴2233x x -=+，∴5x =-；∴括号内的数不是方程的解．【点睛】本题考查了解一元一次方程，解题的关键是掌握解一元一次方程的方法和步骤． 19．如果,a b 为定值，关于x 的方程2236kx a x bk +-=+无论k 为何值时，它的根总是1，求,a b 的值．解析：a=132,b=﹣4 【分析】先把方程化简，然后把x ＝1代入化简后的方程，因为无论k 为何值时，它的根总是1，就可求出a 、b 的值．【详解】解：方程两边同时乘以6得：4kx ＋2a ＝12＋x−bk ，（4k−1）x ＋2a ＋bk−12＝0①，∵无论为k 何值时，它的根总是1，∴把x ＝1代入①，4k−1＋2a ＋bk−12＝0，则当k ＝0，k ＝1时，可得方程组：12120412120a ab --⎧⎨--⎩＋＝＋＋＝，解得：a=132,b=﹣4 当a=132,b=﹣4时，无论为k 何值时，它的根总是1． ∴a=132,b=﹣4 【点睛】本题主要考查了一元一次方程的解，理解方程的解的定义，就是能够使方程左右两边相等的未知数的值．本题利用方程的解求未知数a 、b ．20．一项工程，由甲队独做需12个月完工，由乙队独做需15个月完工．现决定由两队合作，且为了加快进度，甲、乙两队都将提高工作效率．若甲队的工作效率提高40%，乙队的工作效率提高25%，，则两队合作，几个月可以完工？解析：5【分析】设两队合作x 个月完成，甲队原来的工作效率为112，将工作效率提高40%以后为112（1＋40%），乙队原来的工作效率为115，将工作效率提高25%以后为115（1＋25%），根据工作效率×工作时间＝工作总量1,列出方程，解方程即可【详解】解：设两队合作x 个月完成，由题意，得[112（1＋40%）＋115（1＋25%）]x ＝1，解得x ＝5．答：两队合作，5个月可以完工．【点睛】本题考查了一元一次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系列出方程．21．程大位是珠算发明家，他的名著《直指算法统宗》详述了传统的珠算规则，确立了算盘用书中有如下问题：一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚得几丁．意思是：有100个和尚分100个馒头，如果大和尚1人分3个，小和尚3人分1个，正好分完，大、小和尚各有多少人？解析：大和尚有25人，小和尚有75人【分析】设大和尚有x 人，则小和尚有（100x -）人，根据“3×大和尚人数+小和尚人数÷3=100”，即可得出关于x 的一元一次方程，此题得解．【详解】设大和尚有x 人，则小和尚有（100x -）人，根据题意得：10031003x x -+= 解得：25x =，则10075x -=，答：大和尚有25人，小和尚有75人．【点睛】本题考查了一元一次方程的应用，找准等量关系，正确列出一元一次方程是解题的关键． 22．松雷中学原计划加工一批校服，现有甲、乙两个工厂都想加工这批校服，已知甲工厂每天能加工这种校服16件，乙工厂每天能加工这种校服24件．且单独加工这批校服甲工厂比乙工厂要多用20天在加工过程中，学校每天需付甲工厂费用80元，乙工厂费用120元．（1）这批校服共有多少件？（2）在实际加工过程中，甲、乙两个工厂按原生产效率合作一段时间后，甲工厂停工了，乙工厂每天的生产效率提高25%，乙工厂单独完成剩余部分，且乙工厂的全部工作时间比甲工厂工作时间的2倍还多4天，则乙工厂共加工多少天？（3）经学校研究制定如下方案：方案一：由甲工厂单独完成；方案二：由乙工厂单独完成；方案三：按第（2）问方式完成并且每种方案在加工过程中，每个工厂需要一名工程师进行技术指导，并由学校提供每天10元的午餐补助费，请你通过计算帮学校选择一种既省时又省钱的加工方案．解析：（1）960件（2）28天（3）方案三【分析】（1）由题意设这批校服共有x 件，并根据题意建立一元一次方程进行求解即可；（2）根据题意设甲工厂加工a 天，则乙工厂共加工(24)a +天，并根据题意建立一元一次方程进行求解即可；（3）根据题意分别计算三种方案所需的时间与费用，并进行比较即可得出答案．【详解】解：（1）设这批校服共有x 件．由题意，得201624x x -=．解得960x =．答：这批校服共有960件．（2）设甲工厂加工a 天，则乙工厂共加工(24)a +天．依题意得 (1624)24(125%)(24)960a a a ++⨯++-=．解得12a =．2424428a +=+=．答：乙工厂共加工28天．（3）①方案一：需要耗时9601660÷=（天），费用为60(1080)5400⨯+=（元）； ②方案二：需要耗时9602440÷=（天），费用为40(12010)5200⨯+=（元）； ③方案三：甲工厂耗时12天，乙工厂耗时28天，故需要耗时28天，费用为12(1080)28(10120)4720⨯++⨯+=（元）．综上，方案三既省时又省钱．【点睛】本题考查一元一次方程的实际应用，读懂题干并依据题干条件建立一元一次方程求解是解题的关键．23．一位商人来到一座新城市，想租一套房子，A 家房东的条件是先交2000元，每月租金1200元；B 家房东的条件是每月租金1400元．（1）这位商人想在这座城市住半年，则租哪家的房子划算？（2）如果这位商人想住一年，租哪家的房子划算？（3）这位商人住多长时间时，租两家的房子租金一样？解析：（1）住半年时，租B 家的房子划算；（2）住一年时，租A 家的房子划算；（3）这位商人住10个月时，租两家的房子租金一样．【分析】（1）分别根据A 、B 两家租金的缴费方式计算A 、B 两家半年的租金，然后比较即得答案；（2）分别根据A 、B 两家租金的缴费方式计算A 、B 两家一年的租金，然后比较即得答案；（3）根据A 家租金（2000+1200×租的月数）=B 家租金（1400×租的月数）设未知数列方程解答即可．【详解】解：（1）如果住半年，交给A 家的租金是1200620009200⨯+=(元)，交给B 家的租金是140068400⨯=(元)，因为9200＞8400，所以住半年时，租B 家的房子划算．（2）如果住一年，交给A 家的租金是120012200016400⨯+=(元)，交给B 家的租金是14001216800⨯=(元)，因为16400＜16800，所以住一年时，租A 家的房子划算．（3）设这位商人住x 个月时，租两家的房子租金一样，根据题意，得120020001400x x +=．解方程，得10x =．答：这位商人住10个月时，租两家的房子租金一样．【点睛】本题考查了一元一次方程的应用，属于常考题型，正确理解题意、明确A 、B 两家租金的缴费方式是解题的关键．24．在我国明代数学家吴敬所著的《九章算法比类大全》中，有一道数学名题叫“宝塔装灯”，内容为“远望巍巍塔七层，灯光点点倍加增，共灯三百八十一，试问尖头几盏灯？”（“倍加增”指从塔的顶层到底层，每层灯的数量是上一层的2倍）那么，塔的顶层有几盏灯？解析：3盏【分析】根据题意列出方程求解即可．【详解】解：设塔的顶层有x 盏灯．根据题意，得248163264381x x x x x x x ++++++=．解得3x =．答：塔的顶层有3盏灯．【点睛】本题考查了一元一次方程的实际应用，掌握解一元一次方程的方法是解题的关键． 25．解方程：111(3)(3)1236x x x x ⎡⎤---=-+⎢⎥⎣⎦．解析：2x =【分析】。

列一元一次方程解应用题

列一元一次方程解应用题（一）和、差、倍、分问题：1、一群老人去赶集，集上买了一堆梨，一人1个多一个，一人2个少2个，几位老人几个梨？2、七年级二班有45人报名参加了文学社或书画社，已知参加文学社的人数比参加书画社的人数多5人，两个社都参加的有20人，问参加书画社的有多少人？3、一群割草人要把两片草地的草割完．两片草地一大一小，大的比小的大一倍，大家都先在大片草地上割了半天，午后分成两组，一半人继续在大片草地上割，到下午收工时恰好割完；另一半人到小片草地上割，到收工时还剩下一小块，这一小块次日由一个人去割，恰好需要一天工夫．问：这群割草者共有多少人?4、甲、乙、丙三人拿出同样多的钱，合伙订购同种规格的若干件商品，商品买来后，甲、乙分别比丙多拿了7、11件商品，最后结算时，甲付给丙14元，那么，乙应付给丙元。

（二）等积变形问题：1. 已知圆柱的底面直径是60毫米，高为100毫米，圆锥的底面直径是120毫米，且圆柱的体积比圆锥的体积多一半，求圆锥的高是多少？2、请根据图中给出的信息，列出正确的方程．小乌鸦，你飞到装有相同水量的小量筒，就可以喝到水了！x 58老乌鸦，我喝不到大量筒中的x3、如图是一块在电脑屏幕上出现的矩形块图，由6个颜色不同的正方形组成，设最小的一个正方形边长为1，求这个矩形块图的面积。

（三）调配问题：1、学校组织植树活动，已知在甲处植树的有27人，在乙处植树的有18人.如果要使在甲处植树的人数是乙处植树人数的2倍，需要从乙队调多少人到甲队？2、七年级三班学生参加义务劳动，原来每组8人，后来根据需要重新编组，每组14人，这样比原来减少3组。

问这个班共有学生多少人？3、某“希望学校”修建了一栋4层的教学大楼，每层楼有6间教室，进出这栋大楼共有3道门（两道大小相同的正门和一道侧门）. 安全检查中，对这3道门进行了测试：当同时开启一道正门和一道侧门时，2分钟内可以通过400名学生，若一道正门平均每分钟比一道侧门可多通过40名学生.（1）求平均每分钟一道正门和一道侧门各可以通过多少名学生？（2）检查中发现，紧急情况时因学生拥挤，出门的效率降低20%. 安全检查规定：在紧急情况下全大楼的学生应在5分钟内通过这3道门安全撤离. 假设这栋教学大楼每间教室最多有45名学生，问：建造的这3道门是否符合安全规定？为什么？4、甲、乙、丙三人在A、B两块地植树，其中甲在A地植树，丙在B地植树，乙先在A地植树，然后转到B地．已知甲、乙、丙每小时分别能植树8棵，6棵，10棵.若乙在A地植树10小时后立即转到B 地，则两块地同时开始同时结束；若要两块地同时开始，但A地比B地早9小时完成，则乙应在A地植树小时后立即转到B地．（四）行程问题。

一元一次方程应用题基本类型及解题所需等量关系

一元一次方程应用题基本类型及解题所需等量关系第一类、行程问题基本的数量关系：（1）路程＝速度×时间⑵速度＝路程÷时间⑶时间＝路程÷速度要特别注意：路程、速度、时间的对应关系（即在某段路程上所对应的速度和时间各是多少）常用的等量关系：1、甲、乙二人相向相遇问题⑴甲走的路程＋乙走的路程＝总路程⑵二人所用的时间相等或有提前量 (3)快行距＋慢行距＝原距2、甲、乙二人中，慢者所行路程或时间有提前量的同向追击问题⑴甲走的路程－乙走的路程＝提前量⑵二人所用的时间相等或有提前量(3)快行距－慢行距＝原距3、单人往返⑴各段路程和＝总路程⑵各段时间和＝总时间⑶匀速行驶时速度不变4、行船问题与飞机飞行问题(1)顺水（风）速度＝静水（风）速度＋水流（风）速度(2)逆水（风）速度＝静水（风）速度－水流（风）速度(3)水流速度=（顺水速度-逆水速度）÷2抓住两码头间距离不变，水流速和船速（静不速）不变的特点考虑相等关系．即顺水逆水问题常用等量关系：顺水路程=逆水路程5、考虑车长的过桥或通过山洞隧道问题将每辆车的车头或车尾看作一个人的行驶问题去分析，一切就一目了然。

6、时钟问题：⑴将时钟的时针、分针、秒针的尖端看作一个点来研究⑵通常将时钟问题看作以整时整分为起点的同向追击问题来分析。

常用数据：①°/分②分针的速度是6°/分③秒针的速度是6°/秒第二类：工程问题的基本关系：1．工程问题中的三个量及其关系为：工作总量＝工作效率×工作时间=工作总量工作效率工作时间=工作总量工作时间工作效率2．经常在题目中未给出工作总量时，设工作总量为单位1。

即完成某项任务的各工作量的和＝总工作量＝1．工程问题常用等量关系：先做的+后做的=完成量．第二类：商品利润问题（市场经济问题或利润赢亏问题(1)销售问题中常出现的量有：进价(或成本)、售价、标价（或定价）、利润等。

部编数学七年级上册专题07一元一次方程的应用(12大考点)专题讲练(解析版)含答案

专题07 一元一次方程的应用（12大考点）专题讲练一元一次方程的应用题属于人教版七年级上期期末必考题，需要完全掌握各个类型的应用题，该专题将应用题分为分段计费、行程问题、工程问题、方案优化选择、商品销售问题、比赛积分问题、日历问题（数字问题）、配套问题、调配问题、和差倍分问题（比例问题）、几何图形问题、动态问题等共进行方法总结与经典题型进行分类。

1、知识储备2、经典基础题考点1. 分段计费问题考点2. 行程问题考点3. 工程问题考点4. 方案优化问题考点5. 商品销售问题考点6. 比赛积分问题考点7. 配套问题考点8. 调配问题考点9. 数字与日历问题考点10．和、差、倍、分（比例）问题考点11. 几何问题（等积问题）考点12. 动态问题3、优选提升题1.用一元一次方程解决实际问题的一般步骤列方程解应用题的基本思路为：问题¾¾¾®分析抽象方程¾¾¾®求解检验解答．由此可得解决此类题的一般步骤为：审、设、列、解、检验、答． 2 .建立书写模型常见的数量关系1）公式形数量关系：生活中许多数学应用情景涉及如周长、面积、体积等公式。

在解决这类问题时，必须通过情景中的信息，准确联想有关的公式，利用有关公式直接建立等式方程。

长方形面积=长×宽长方形周长=2（长+宽）正方形面积=边长×边长正方形周长=4边长2）约定型数量关系：利息问题，利润问题，质量分数问题，比例尺问题等涉及的数量关系，像数学中的公式，但常常又不算数学公式。

我们称这类关系为约定型数量关系。

3）基本数量关系：在简单应用情景中，与其他数量关系没有什么差别，但在较复杂的应用情景中，应用方法就不同了。

我么把这类数量关系称为基本数量关系。

单价×数量=总价速度×时间=路程工作效率×时间=总工作量等。

3.分析数量关系的常用方法1）直译法分析数量关系：将题中关键性的数量关系的语句译成含有未知数的代数式，并找出没有公国的等量关系，翻译成含有未知数的等式。

一元一次方程火车过桥(隧道)问题—七年级数学上册

一元一次方程火车过桥（隧道）问题—七年级数学上册一列火车通过一座桥或者是钻过一个隧道，研究其车长、车速、桥长或隧道道长，过桥或钻隧道的时间等关系的一类应用题。

解答这类应用题，除了根据速度、时间、路程三量之间的关系进行计算外，还必须注意到车长，即通过的路程等于桥长或隧道长加车长。

【数量关系】火车过桥问题可以分为三种情况：(1)人与车相遇：路程和=火车车长速度和=车速+人速火车车长?(车速+人速)=相遇时间追及：路程差=火车车长速度差=车速人速火车车长?(车速人速)=追及时间(2)车与车相遇：路程和=甲车长+乙车长速度和=甲车速+乙车速(甲车长+乙车长)?(甲车速+乙车速)=相遇时间追及：路程差=快车长+慢车长速度差=快车速慢车速(快车长+慢车长)?(快车速慢车速)=追及时间(3)头对齐，尾对齐头对齐：路程差=快车车长速度差=快车速慢车速快车车长?(快车速慢车速)=错车时间尾对齐：路程差=慢车车长速度差=快车速慢车速，慢车车长?(快车速慢车速)=错车时间1、一列火车长150米，每秒钟行19米。

全车通过长800米的大桥，需要多少时间？分析：列车过桥，就是从车头上桥到车尾离桥止。

车尾经过的距离=车长+桥长，车尾行驶这段路程所用的时间用车长与桥长和除以车速。

解：（800+150）?19=50（秒）答：全车通过长800米的大桥，需要50秒。

2、一列火车长200米，以每秒8米的速度通过一条隧道，从车头进洞到车尾离洞，一共用了40秒。

这条隧道长多少米？分析：火车从车头进洞到车尾离洞，共走车长+隧道长。

这段路程是以每秒8米的速度行了40秒。

解：火车40秒所行路程：8?40=320（米）隧道长度：30=120（米）答：这条隧道长120米。

3、一列火车长119米，它以每秒15米的速度行驶，小华以每秒2米的速度从对面走来，经过几秒钟后火车从小华身边通过？解：火车与小华的速度和：15+2=17（米/秒）相距距离就是一个火车车长：119米经过时间：119?17=7（秒）答：经过7秒钟后火车从小华身边通过。