1第一章
人教版高中化学必修一第一章练习题及答案

必修1第一章《从实验学化学》测试题一、单项选择题(共10小题,每小题3分,共30分。
)1.下列实验基本操作(或实验注意事项)中,主要是出于实验安全考虑的是A.实验剩余的药品不能放回原试剂瓶C.气体实验装置在实验前进行气密性检查B.可燃性气体的验纯D.滴管不能交叉使用2.实验向容量瓶转移液体操作中用玻璃棒,其用玻璃棒的作用是A.搅拌 B.引流 C.加速反应 D.加快热量散失3.标准状况下的1mol H e 的体积为A.11.2LB.22.4LC.33.6LD.44.8L4.下列关于阿伏加德罗常数的说法正确的是A.阿伏加德罗常数是一个纯数,没有单位B.阿伏加德罗常数就是×1023C.阿伏加德罗常数是指1mol的任何粒子的粒子数 D.阿伏加德罗常数的近似值为:×1023mol-15. 16g某元素含有×10个原子,则该元素原子的相对原子质量为A.1B. 126.关于2molO2的叙述中,正确的是A.体积为44.8L B.质量为32g C.分子数为×10 D.含有4mol 原子7.在1mol H 2SO 4中,正确的是A.含有1mol H B.含有×10个氢原子C.含有×10个分子 D.含有×10个氧原子8.下列溶液中,溶质的物质的量浓度为L 的是A.1L 溶液中含有4g NaOH B.1L 水中溶解4gNaOH C.0.5L 溶液中含有 H 2SO 4 D.9.8g H 2SO 4溶于1L 水配成溶液9.1mol/L H2SO4的含义是()A、1L 水中含有1mol H2SO4B、1L 溶液中含有1mol H+C、将98gH2SO4溶于1L 水中配成的溶液D、该溶液c(H+)=2mol/L-232323232310.下列溶液中,Cl 的物质的量浓度与50mL 3mol/LNaCl 溶液中Cl-物质的量浓度相等是A.150mL 3mol/LKCl 溶液 B.150m L 1mol/LAlCl3溶液C.50mL3mol/LMgCl2溶液 D.75mL LMgCl2溶液11.下列溶液中,跟100mL L NaCl 溶液所含的Cl-物质的量浓度相同的是()A.100mL L MgCl 2溶液 B.200mL LCaCl 2溶液C.50ml 1mol/L NaCl 溶液 D.25ml LHCl 溶液12.配制一定物质的量浓度的NaOH 溶液时,造成实验结果偏低的是()A.定容时观察液面仰视 B.定容时观察液面俯视 C.有少量NaOH 溶液残留在烧杯中 D.容量瓶中原来有少量蒸馏水113.8g 无水硫酸铜配成L 的水溶液,下列说法正确的是()A.溶于500mL 水中 B.溶于1L 水中C.溶解后溶液的总体积为500mL D.溶解后溶液的总体积为1L 14、0.5L1mol/LFeCl 3溶液与0.2L1mol/L KCl 溶液中n(Cl—)之比为()A、1﹕1B、3﹕1C、15﹕2D、5﹕215、在1L 溶有和 MgCl 2的溶液中,c(Cl—)为()A、LB、LC、LD、L二、多项选择题(共6小题,每小题5分,共30分。
高一数学必修一 第一章综合 教学课件PPT

然表示同一个集合.
工具
必修1 第一章 集合与函数概念
栏目导引
2.解读集合表示的三种方法 集合常用的表示方法有三种,即列举法、描述法和 图示法,其中图示法包括 Venn 图法和数轴法两种. (1)列举法是把集合的元素Байду номын сангаас一列举出来,并用花括 号“{ }”括起来表示集合的方法. 使用列举法要注意:元素间用分隔号“,”且元素 不能重复. (2)描述法是用集合所含元素的共同特征表示集合 的方法. 使用描述法要注意:写清楚该集合中元素的代号(字 母或用字母表示的元素符号),准确说明该集合中元 素的特征.
工具
必修1 第一章 集合与函数概念
栏目导引
6.求函数定义域的注意点 (1)不对解析式化简变形,以免定义域变化. (2)求定义域的相关准则:①分式中分母不为零; ②偶次根式中被开方式非负;③x0 中 x≠0;④解 析式由几个式子构成时,定义域是使各式子有意 义的自变量的取值集合的交集.
(3)由实际问题建立的函数解析式,定义域要符合 实际.
课题导入
回顾所学知识
工具
必修1 第一章 集合与函数概念
栏目导引
第一章 综合复习课
工具
必修1 第一章 集合与函数概念
栏目导引
独立自学
1.第一章中我们主要学习了哪两块知识? 2.集合的性质有哪些?我们研究了函数
的哪些性质?
工具
必修1 第一章 集合与函数概念
栏目导引
引导探究一 知识点梳理
1.集合中元素特征的认识 确定性、互异性、无序性是集合中元素的三个特征. (1)确定性是指一个对象 a 和一个集合 A,a∈A 和 a∉A 必 居其一.它是确定一组对象能否构成集合的依据. (2)互异性是指同一个集合中的元素是互不相同的.相同 的对象归入同一集合时只能算作集合的一个元素.在解答 含参集合问题时,互异性是一个不可或缺的检验工具.
苏教版高中数学必修1:第一章集合_本章回顾_课件1

(1)求f(1); (2)求证:f(x)在(0,+∞)上是增函数; (3)判断f(x)在定义域内的奇偶性.
【思路点拨】 (1)赋值,x=y=1→f(1); (2)令 y=1x,用单调性定义证明; (3)令 x=-1,推得 f(-y)=f(y).
【解】 (1)令 x=y=1,得 f(1)=2f(1), 故 f(1)=0. (2)证明:令 y=1x,得 f(1)=f(x)+f1x=0, 故 f1x=-f(x). 任取 x1,x2∈(0,+∞),且 x1<x2,
【解】 设方程 x2-4ax+2a+6=0 有
实数根时 a 的取值范围是 U,令 Δ=(-
4a)2-4(2a+6)≥0,即(a+1)·(a-32)≥0,
解得
a≤ - 1
或
a≥
3 2
,
即
U=
aa≤-1或a≥32
.
若方程 x2-4ax+2a+6=0 的两根 x1,
x2 均非正,
a∈U,
补集思想的应用
补集思想为研究问题开辟了新的思路,在顺向 思维受阻或比较繁琐时,改用逆向思维,即采 用“正难则反”的方法.补集思想是转化思想 的又一种体现. 例2 已知集合A={x|x2-4ax+2a+6=0},B ={x|x>0},若A∩B≠∅,求实数a的取值范围. 【思路点拨】 先求A∩B=∅时的a的范围,利 用补集,可得A∩B≠∅的a的范围.
则x1+x2=4a≤0, x1x2=2a+6≥0.
所以-3≤a≤-1,此时 A∩B=∅.
因为{a|-3≤a≤-1}在 U 中的补集是
aa<-3或a≥32
,
所以当 A∩B≠∅时,实数 a 的取值范围
是aa<-3或a≥23 .
高中数学湘教版必修1:第一章 集合与函数 1.2.1

1.2 函数的概念和性质
1.2.1 对应、映射和函数
[学习目标]
1.能记住映射的定义,知道.会判断给出的对应是否是映射. 3.能记住函数的定义,知道什么是函数的定义域、值域. 4.能说出函数的三要素.
栏目索引
CONTENTS PAGE
所以只有当y≥-1时,它在A中才有原象, 而当y<-1时,它在A中就没有原象,
即集合B中小于-1的元素没有原象.
1.2.1 对应、映射和函数
15
规律方法 1.解答此类问题的关键: (1)分清原象和象; (2)搞清楚由原象到象的对应法则. 2.对A中元素,求象只需将原象代入对应法则即可,对于B中 元素求原象,可先设出它的原象,然后利用对应法则列出方 程(组)求解.
1.2.1 对应、映射和函数
5
(3)在函数y=f(x)(x∈A,y∈B)中,A叫作函数的 定义域 ,与 x∈A对应的数y叫x的 象 ,记作y=f(x),由所有x∈A的象组成 的集合叫作函数的 值域 .
(4)函数的三要素:① 对应法则 ;② 定义域 ;③ 值域 .
1.2.1 对应、映射和函数
6
课堂讲义
1.2.1 对应、映射和函数
16
跟踪演练 2
(1) 映射 f : A→B , A = { - 3 ,- 2 ,- 1,1,2,3,4} ,
对于任意 a∈A ,在集合 B 中和它对应的元素是 |a| ,则集合 B 中元素的最少个数是( D )
A.7
B.6
C.5
D.4
解析 由映射定义知,B中至少有元素1,2,3,4,
x≥0; x<0;
解
对于A中任意一个非负数都有唯一的元素1和它对应,对
于A中任意的一个负数都有唯一的元素0和它对应,∴是映射.
1 第一章 含能材料绪论

• 增塑剂含量高时在高温下容易变软,低温下脆性增大;对 表面钝感处理有限制。
• ③ 三基药:在双基药中加入硝基胍(NGU)、黑索今(RDX)、 奥克托今(HMX)等高能固体炸药,溶剂法挤压成型工艺。能 量高,但力学性能不好。
• ④ 低易损(不敏感)药:主要由70~85%的RDX或HMX 、 15~30%的粘合剂和其它附加物组成(不含硝酸酯)。力学 性能问题、能量与敏感性有矛盾。
火剂、起爆药等。 • 民用:民用爆破工业炸药、烟火剂等。用于开矿、土建、油
田、地质勘探、爆炸加工、烟花爆竹、影视拍摄等。 • ⑵ 组成:单组份和混合组份;特征基团(硝基、硝胺等)。 • ⑶ 结构体系:均质和非均质、单基和多基。 • ⑷ 其它:按性能特点:高能低烧蚀、高能低特征信号、低易
损性等;按制备工艺:浇铸、压装等。
• 借鉴固体推进剂经验,开始研究含能高分子化合物取代NC 作发射药的粘合剂。如BAMO(3,3-二叠氮甲基环氧丁烷) /AMMO(3-叠氮甲基-3-甲基环氧丁烷)共聚物、GAP(聚 叠氮缩水甘油醚)、NIMMO(聚3-硝氧甲基 -3-甲基氧杂环 丁烷)等。本身具有较高能量(有较大的正生成热)。
• ② 增塑剂
• 含能增塑剂:双基药(发射药、推进剂)
• 主 要 用 多 元 醇 硝 酸 酯 , 如 硝 化 甘 油 NG 、 硝 化 二 乙 二 醇 DEGN、硝化三乙二醇TEGN、丁三醇三硝酸酯BTTN等。 NG的能量、爆温、烧蚀、感度高。用DEGN或TEGN代替或 部分代替NG,可降低爆温,对高氮量NC的溶塑能力好。
高一数学必修1 数学 第一章 完整知识点梳理大全(最全)
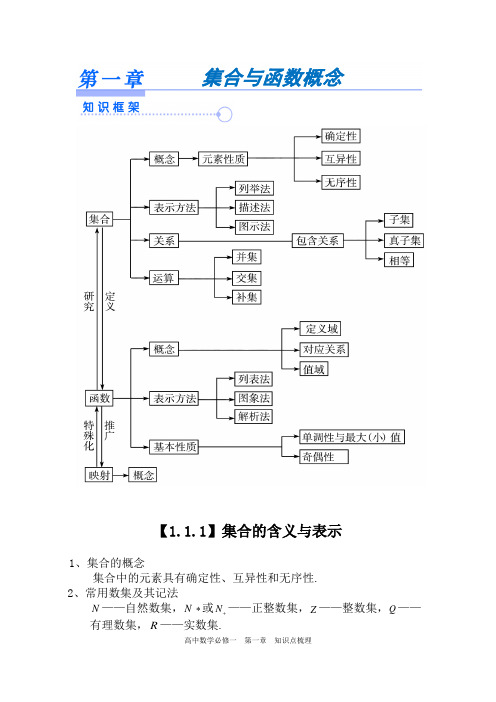
【1.1.1】集合的含义与表示1、集合的概念集合中的元素具有确定性、互异性和无序性. 2、常用数集及其记法N ——自然数集,N *或N +——正整数集,Z ——整数集,Q ——有理数集,R ——实数集.集合与函数概念3、集合与元素间的关系对象a 与集合M 的关系是a M ∈,或者a M ∉,两者必居其一. 4、集合的表示法①自然语言法:用文字叙述的形式来描述集合.②列举法:把集合中的元素一一列举出来,写在大括号内表示集合. ③描述法:{x |x 具有的性质},其中x 为集合的代表元素. ④图示法:用数轴或韦恩图来表示集合. 5、集合的分类①含有有限个元素的集合叫做有限集. ②含有无限个元素的集合叫做无限集.③不含有任何元素的集合叫做空集,记为∅.【1.1.2】集合间的基本关系6、子集、真子集、集合相等7、已知集合A 有(1)n n ≥个元素,则它有2n 个子集,它有21n -个真子集,它有21n -个非空子集,它有22n -非空真子集.【1.1.3】集合的基本运算8、交集、并集、补集)【补充知识】含绝对值的不等式与一元二次不等式的解法1、含绝对值的不等式的解法0)〖1.2〗函数及其表示【1.2.1】函数的概念1、函数的概念①设A 、B 是两个非空的数集,如果按照某种对应法则f ,对于集合A 中任何一个数x ,在集合B 中都有唯一确定的数()f x 和它对应,那么这样的对应(包括集合A ,B 以及A 到B 的对应法则f )叫做集合A 到B 的一个函数,记作:f A B →.②函数的三要素:定义域、值域和对应法则.③只有定义域相同,且对应法则也相同的两个函数才是同一函数. 2、区间的概念及表示法①设,a b 是两个实数,且a b <,满足a x b ≤≤的实数x 的集合叫做闭区间,记做[,]a b ;满足a x b <<的实数x 的集合叫做开区间,记做(,)a b ;满足a x b ≤<,或a x b <≤的实数x 的集合叫做半开半闭区间,分别记做[,)a b ,(,]a b ;满足,,,x a x a x b x b ≥>≤<的实数x 的集合分别记做[,),(,),(,],(,)a a b b +∞+∞-∞-∞.注意:对于集合{|}x a x b <<与区间(,)a b ,前者a ≥b ,而后者必须a b <.3、求函数的定义域时,一般遵循以下原则:①()f x 是整式时,定义域是全体实数.②()f x 是分式函数时,定义域是使分母不为零的一切实数. ③()f x 是偶次根式时,定义域是使被开方式为非负值时的实数的集合.④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1.(暂不讲)⑤tan y x =中,()2x k k Z ππ≠+∈.(暂不讲)⑥零(负)指数幂的底数不能为零.⑦若()f x 是由有限个基本初等函数的四则运算而合成的函数时,则其定义域一般是各基本初等函数的定义域的交集.⑧对于求复合函数定义域问题,一般步骤是:若已知()f x 的定义域为[,]a b ,其复合函数[()]f g x 的定义域应由不等式()a g x b ≤≤解出. ⑨对于含字母参数的函数,求其定义域,根据问题具体情况需对字母参数进行分类讨论.⑩由实际问题确定的函数,其定义域除使函数有意义外,还要符合问题的实际意义. 4、求函数的值域或最值求函数最值的常用方法和求函数值域的方法基本上是相同的. 事实上,如果在函数的值域中存在一个最小(大)数,这个数就是 函数的最小(大)值.因此求函数的最值与值域,其实质是相同的,只是提问的角度不同.求函数值域与最值的常用方法:①观察法:对于比较简单的函数,我们可以通过观察直接得到值域或最值.②配方法:将函数解析式化成含有自变量的平方式与常数的和,然后根据变量的取值范围确定函数的值域或最值. ③判别式法:若函数()y f x =可以化成一个系数含有y 的关于x 的二次方程2()()()0a y x b y x c y ++=,则在()0a y ≠时,由于,x y 为实数,故必须有2()4()()0b y a y c y ∆=-⋅≥,从而确定函数的值域或最值. ④不等式法:利用基本不等式确定函数的值域或最值.⑤换元法:通过变量代换达到化繁为简、化难为易的目的,三角代换可将代数函数的最值问题转化为三角函数的最值问题.⑥反函数法:利用函数和它的反函数的定义域与值域的互逆关系确定函数的值域或最值.⑦数形结合法:利用函数图象或几何方法确定函数的值域或最值.⑧函数的单调性法.【1.2.2】函数的表示法5、函数的表示方法表示函数的方法,常用的有解析法、列表法、图象法三种.解析法:就是用数学表达式表示两个变量之间的对应关系.列表法:就是列出表格来表示两个变量之间的对应关系.图象法:就是用图象表示两个变量之间的对应关系.6、映射的概念①设A、B是两个集合,如果按照某种对应法则f,对于集合A中任何一个元素,在集合B中都有唯一的元素和它对应,那么这样的对应(包括集合A,B以及A到B的对应法则f)叫做集合A到B的映射,记作:f A B→.②给定一个集合A到集合B的映射,且,∈∈.如果元素a和元a Ab B素b对应,那么我们把元素b叫做元素a的象,元素a叫做元素b的原象.〖1.3〗函数的基本性质【1.3.1】单调性与最大(小)值1、函数的单调性①定义及判定方法yxo②在公共定义域内,两个增函数的和是增函数,两个减函数的和是减函数,增函数减去一个减函数为增函数,减函数减去一个增函数为减函数.③对于复合函数[()]y f g x =,令()u g x =,若()y f u =为增,()u g x =为增,则[()]y f g x =为增;若()y f u =为减,()u g x =为减,则[()]y f g x =为增;若()y f u =为增,()u g x =为减,则[()]y f g x =为减;若()y f u =为减,()u g x =为增,则[()]y f g x =为减.简称:同增异减。
1 第一章 自然辩证法概述

哲学 普遍
具体应用 升华、抽象
自然辩证法 一般
理论指导 概括、总结
自然科学 特殊
(四)从发生的作用上看,自然辩证法是连结马克思主义哲 学和自然科学的中介和桥梁。
从两方面来理解:
一方面,自然辩证法是自然科学通向马克思主义哲学的中介。
这是从马克思主义哲学以自然科学为基础这一方面来理解的。 对自然科学的实证知识和材料,首先作出总结、概括的是自然辩证法。
毕达哥拉斯学派:“数”是宇宙的本原。 即使是到了近代,思辨方法对自然科学的影响也很大。
如牛顿,解决不了“行星运行的切线力”问题时,提出了“上 帝的第一推动力”,亚里士多德曾提出过“自身不动的第一推 动者”。
第三,从与自然科学的关系上看,自然哲学不承认自然科学 从其中分化出来,它认为能够包括自然科学,并且能代替自 然科学。
客体而自己成为主体?
四、自然辩证法的研究对象
从整体上讲,自然辩证法的研究对象是:
“人—科学技术—自然界”构成的整体系统
展开来看,它包括相互联系的三部分:
1.自然界的一般规律(自然界的辩证法) 2.人类认识自然、改造自然的一般规律(科学技术研究辩证法) 3.科学技术发展的一般规律(科学技术发展的辩证法)
一、自然辩证法的定义
自然辩证法是辩证唯物主义关于自然界和 科学技术发展的一般规律以及认识自然和 改造自然的一般方法的理论体系。
这一定义内在地包含了自然辩证法的核心、主 线、研究对象和研究内容。
二、自然辩证法的核心
核心:辩证唯物主义 (理论硬核,或理论内核)
自然辩证法是
辩证唯物主义关于自然界的一般规律的理论体系 辩证唯物主义关于科学技术体系
两者既有区别,又有联系。
1 第一章 绪论 生物分离工程.

原料液中常存在降解目标产物的杂质, 如可水解目标蛋白质的蛋白酶。
4 生物产品要求高质量
生物产物一般用作医药、食品和化妆品, 与人类生命息息相关。因此,要求分离纯 化过程必须除去原料液中含有的热原 (pyrogen)及具有免疫原性的异性蛋白等 有害人类健康的物质,并且防止这类物质 在操作过程中从外界混入。
分离,又称速度分离法。动力为压力差、电位梯度和磁场 梯度,如超滤、反渗析、电渗析、电泳和磁泳
扩散分离根据溶质在两相中分配平衡状态的差异实现分 离,又称平衡分离法。动力为偏离平衡态的浓度差,如蒸 馏、蒸发、吸收、萃取、结晶、吸附和离子交换等。
四、生物分离工程的一般步骤和单元操作
1、一般步骤
1) 发酵液的预处理与固液分离; 2) 初步纯化(或称产物的的提取); 3) 高度纯化(产物的精制); 4) 成品加工。
2、一般工艺过程:
发酵液
预处理
加热 调pH值 絮凝
碎片分离
离心分离 萃取 过滤 错流过滤
初步纯化
沉淀 吸附 萃取 超滤
细胞分离
沉降
离心分离 过滤
错流过滤
高度纯化
层析 亲和
离子交换 憎水
吸附 电泳
胞外产物
细胞破碎
匀化 研磨 溶胞
成品加工
无菌过滤 超虑 冷冻干燥 喷雾干燥
结晶
五、生物技术加工过程的选择标准
2 化学性质
化学热力学:化学平衡 反应动力学:反应速率 光化学性质:激光激发、离子化
3 生物学性质
分子识别:生物亲和力、生物学识别 传输性质:生物膜运输 反应、响应、控制:酶反应、免疫系统
机械分离:非均相 大小、密度差异,如过滤、重力沉淀、 离心沉淀
高一物理必修1 第一章 运动的描述

1 2 3
B C
速度
1.速度
速度v是指位移跟发生这段位移所用时间的 x 比值。用 v 表示.
t
(1) 速度是位移对时间的变化率。 (2) 速度是描述物体运动方向和快慢的物理量,或者是 描述物体位置变化快慢的物理量。
课堂练习
12.下列关于速度的说法中正确的是( C )
A. 速度是描述物体位置变化的物理量. B. 速度是描述物体位置变化大小的物理量. C. 速度是描述物体运动快慢的物理量. D. 速度是描述物体运动路程和时间关系的物理量.
15日09时0分“神州5号”飞船点火,经9小时40 分50秒,在15日18时40分50秒我国宇航员杨利伟 在太空中展示中国国旗和联合国国旗,再经11小 时42分10秒,于16日06时23分飞船在内蒙古中部 地区成功着陆。
位移和路程
1.位移
(1)位移是矢量 。 既有大小又有方向,位移并不一 定是物体运动的实际路径。
课堂练习
2. 在下列物体的运动中, 可视作质点的物体有: ( AC )
A. 研究一列火车从北京开往广州所需的时间; B. 研究转动的汽车轮胎; C. 研究绕地球运动时的航天飞机; D. 参加百米跑竞赛的运动员。
融会贯通
1、质点 用来代替物体的有质量的点。一个 物体能否看成质点是由具体的问题的性质 决定的。如物体自身体积和形状的大小并 不是判断物体能否看做质点的依据。同一 物体在不同的问题中,有时可看做质点有 时则不能,要具体问题具体分析。
A.甲车向东运动,乙车向西运动.
B.乙车向西运动,甲车不动.
C.甲车向西运动,乙车向东运动.
D.两车均向西运动,乙车速度大于甲车.
坐标系
1.意义 (1) 物理做机械运动时,其位置会随时间发生变化,为了定量地 描述物体的位置及其位置的变化,需要在参考系上建立适当的 坐标系。 (2) 物体的位置可认为就是质点在某时刻所在的空间的一点。
高中数学必修1_第一章_集合与函数概念_练习题

1.1集合练习题1、用列举法表示下列集合:(1){大于10而小于20的合数} ;(2)方程组2219x y x y +=⎧⎨-=⎩的解集 。
2.用描述法表示下列集合:(1)直角坐标平面内X 轴上的点的集合 ; (2)抛物线222y x x =-+的点组成的集合 ;(3)使216y x x =+-有意义的实数x 的集合 。
3.含两个元素的数集{}a a a -2,中,实数a 满足的条件是 。
4. 若{}2|60B x x x =+-=,则3 B ;若}{|23D x Z x =∈-<<,则1.5 D 。
5.下列关系中表述正确的是( )A.{}002=∈x B.(){}00,0∈C.0φ∈D.0N ∈6.对于关系:①∉{x x ∣≤Q ;③0∈N ; ④0∈∅,其中正确的个数是A 、4B 、3C 、2D 、 1 7.下列表示同一集合的是( ) A .{}M =(2,1),(3,2){}N =(1,2),(2,3)B .{}{}M N ==1,22,1C .{}2|1M y y x x R ==+∈,{}2|1N y y x x N ==+∈, D .{}2|1M x y y x x R ==-∈(,),{}2|1N y y x x N ==-∈,8.已知集合}{,,S a b c=中的三个元素是ABC ∆的三边长,那么ABC ∆一定不是 ( )A.锐角三角形B.直角三角形C.钝角三角形D.等腰三角形9.设a 、b 、c 为非0实数,则=M a b c a b ca b c a b c+++的所有值组成的集合为( )A 、{4}B 、{-4}C 、{0}D 、 {0,4,-4}10. 已知(){}{}2,1,,0|2--=∈=++R n m n mx x x ,求m ,n 的值.11.已知集合{}2|A x ax x x R =∈-3-4=0,(1)若A 中有两个元素,求实数a 的取值范围, (2)若A 中至多只有一个元素,求实数a 的取值范围。
人教版高一数学必修一-第一章-知识点与习题讲解

必修1第一章集合与函数基础知识点整理第1讲§1.1.1集合的含义与表示¤知识要点:1.把一些元素组成的总体叫作集合(set ),其元素具有三个特征,即确定性、互异性、无序性.2.集合的表示方法有两种:列举法,即把集合的元素一一列举出来,并用花括号“{}”括起来,基本形式为123{,,,,}n a a a a ⋅⋅⋅,适用于有限集或元素间存在规律的无限集.描述法,即用集合所含元素的共同特征来表示,基本形式为{|()x A P x ∈},既要关注代表元素x ,也要把握其属性()P x ,适用于无限集.3.通常用大写拉丁字母,,,A B C ⋅⋅⋅表示集合.要记住一些常见数集的表示,如自然数集N ,正整数集*N 或N +,整数集Z ,有理数集Q ,实数集R .∈、∉表(3){|}{|0}x y x x x==≠.点评:以上代表元素,分别是点、函数值、自变量.在解题中不能把点的坐标混淆为{1,4},也注意对比(2)与(3)中的两个集合,自变量的范围和函数值的范围,有着本质上不同,分析时一定要细心.*【例4】已知集合2{|1}2x aA a x +==-有唯一实数解,试用列举法表示集合A . 解:化方程212x ax +=-为:2(2)0x x a --+=.应分以下三种情况:⑴方程有等根且不是=0,得94a =-,此时的解为12x =,合.x 代入得a =1x =⑶方程有一解为:将x =a 1x =,合.综上可知,9{,4A =-.点评:运用分类讨论思想方法,研究出根的情况,从而列举法表示.注意分式方程易造成增根的现象.第2讲§1.1.2集合间的基本关系¤知识要点:1.一般地,对于两个集合A 、B ,如果集合A 中的任意一个元素都是集合B 中的元素,则说两个集合有包含关系,其中集合A 是集合B 的子集(subset ),记作A B ⊆(或B A ⊇),读作“A 含于B ”(或“B 包含A ”).A 与集合B ),.B A =,则B A =,则¤例题精讲:【例1】用适当的符号填空:){菱形}{;{等腰三角形)(). 元素,A =(ii )若0a ≠时,得1{}N a =.若N M ⊆,满足1123a a==-或,解得1123a a ==-或.故所求实数a 的值为0或12或13-.点评:在考察“A B ⊆”这一关系时,不要忘记“∅”,因为A =∅时存在A B ⊆.从而需要分情况讨论.题中讨论的主线是依据待定的元素进行.【例4】已知集合A ={a ,a +b ,a +2b },B ={a ,ax ,ax 2}.若A =B ,求实数x 的值.解:若22a b ax a b ax+=⎧⎨+=⎩⇒a +ax 2-2ax =0,所以a (x -1)2=0,即a =0或x =1.当a =0时,集合B 中的元素均为0,故舍去; 当x =1时,集合B 中的元素均相同,故舍去.若22a b ax a b ax⎧+=⎨+=⎩⇒2ax 2-ax -a =0. 因为a ≠0,所以2x 2-x -1=0,即(x -1)(2x +1)=0.又x ≠1,所以只有12x =-. 经检验,此时A =B 成立.综上所述12x =-.点评:抓住集合相等的定义,分情况进行讨论.融入方程组思想,结合元素的互异性确定集合.第3讲§1.1.3集合的基本运算(一)¤知识要点:集合的基本运算有三种,即交、并、补,学习时先理解概念,并掌握符号等,再结合解题的训B (读作“B (读作“,()U B A B ð. {|3B x =(){|U A B x =【例2】设A (1)()A BC ;(2()A A B C ð. {}6,5,4,1,0,1,2,3,4,5,6A =-----. )又{}3B C =,∴()A B C ={}3;)又{}1,2,3,4,5,6B C =, {})6,5,2,1,0B C =---. ()A A C B C {}6,3,2,1,0=-----.3】已知集合A =B A =,求实数:由A B A =,可得在数轴上表示集合A 由图形可知,m ≥研究不等式所表示的集合问题,关系,得到各端点之间的关系,特别要注意是否含端点的问题.【例4】已知全集*{|10,}U x x x N =<∈且,{2,4,5,8}A =,{1,3,5,8}B =,求()U C A B ,()U C A B ,()()U U C A C B ,()()U U C A C B ,并比较它们的关系.解:由{1,2,3,4,5,8}A B =,则(){6,7,9}U C A B =. 由{5,8}A B =,则(){1,2,3,4,6,7,9}U C A B = 由{1,3,6,7,9}U C A =,{2,4,6,7,9}U C B =, 则()(){6,7,9}U U C A C B =,-24mx BA 4mx A B-1 3 5()(){1,2,3,4,6,7,9}U U C A C B =.由计算结果可以知道,()()()U U U C A C B C A B =, ()()()U U U C A C B C A B =.另解:作出Venn 图,如右图所示,由图形可以直接观察出来结果. 点评:可用Venn 图研究()()()U U U C A C B C A B =与()()()U U U C A C B C A B =,在理解的基础记住此结论,有助于今后迅速解决一些集合问题.第4讲§1.1.3集合的基本运算(二)¤知识要点:1.含两个集合的Venn 图有四个区域,分别对应着这两个集合运算的结果.我们需通过Venn 图理解和掌握各区域的集合运算表示,解决一类可用列举法表示的集合运算.通过图形,我们还可以发现一些集合性质:()()()U U U C A B C A C B =,()()()U U U C A B C A C B =.维{}9A B =,求实数{}9A B =,则有:={9, 0, 4}-,不合题意,故舍去;不合题意,故舍去; B ,A B P 14B {1,3,4}A B =A B =∅;{1,3,4}A B ={1}A B =;{1,3,4}A B ={4}A B =;时,{3,}A a =,则{1,3,4,A B =B =∅.,需要对参数a 进行分情况讨论.罗列参数集合的性质和影响运算结果的可能而进行分析,不多不少是分类的原则|22(10x a ++=,a ∈B a 或{4,0}-.(i )若B =∅,则224(1)4(1)0a a ∆=+--<,解得a <1-; (ii )若0∈B ,代入得2a 1-=0⇒a =1或a =1-, 当a =1时,B =A ,符合题意;当a =1-时,B ={0}⊆A ,也符合题意.(iii )若-4∈B ,代入得2870a a -+=⇒a =7或a =1, 当a =1时,已经讨论,符合题意; 当a =7时,B ={-12,-4},不符合题意. 综上可得,a =1或a ≤1-. 点评:此题考查分类讨论的思想,以及集合间的关系的应用.通过深刻理解集合表示法的转换,及集合之间的关系,可以把相关问题化归为解方程的问题,这是数学中的化归思想,是重要数学思想方法.解该题时,特别容易出现的错误是遗漏了A =B 和B =∅的情形,从而造成错误.这需要在解题过程中要全方位、多角度审视问题.【例4】对集合A 与B ,若定义{|,}A B x x A x B -=∈∉且,当集合*{|8,}A x x x N=≤∈,集合{|(2)(5)(6)0}B x x x x x =---=时,有A B -=.(由教材P 12补集定义“集合A 相对于全集U 的补集为{|,}UC A x x x A =∈∉且”而拓展)解:根据题意可知,{1,2,3,4,5,6,7,8}A =,{0,2,5,6}B = 由定义{|,}A B x x A x B -=∈∉且,则 {1,3,4,7,8}A B -=.点评:运用新定义解题是学习能力的发展,也是一种创新思维的训练,关键是理解定义的实质性内涵,这里新定义的含义是从A 中排除B 的元素.如果再给定全集U ,则A B -也相当于()U A C B .第5讲§1.2.1函数的概念x ,(),与x a ,b )叫开.3)(3,1)(1,)---+∞. 3x ≥且9x ≠,(9,)+∞.】求下列函数的定义域与值域:)要使函数有意义,则54-05445445445444y x x x x ==⨯=⨯=-+≠-+=-----,所以值域为{|}4y y ≠-. (2)22192()24y x x x =-++=--+.所以原函数的定义域是R ,值域是9(,4-∞.【例3】已知函数1()1xf x x-=+.求:(1)(2)f 的值;(2)()f x 的表达式 解:(1)由121x x -=+,解得13x =-,所以1(2)3f =-.(2)设11x t x -=+,解得11t x t -=+,所以1()1t f t t -=+,即1()1xf x x-=+. 点评:此题解法中突出了换元法的思想.这类问题的函数式没有直接给出,称为抽象函数的研究,常常需要结合换元法、特值代入、方程思想等.【例4】已知函数22(),1x f x x R x =∈+.(1)求1()(f x f x+的值;(2)计算:111(1)(2)(3)(4)()()(234f f f f f f f ++++++.解:(1)由2222222221111()()1111111x x x x f x f x x x x x x ++=+=+==+++++. (2)原式11117(1)((2)())((3)(((4)())323422f f f f f f f =++++++=+=点评:对规律的发现,能使我们实施巧算.正确探索出前一问的结论,是解答后一问的关键..A 中的A 边函(1)|2|y x =-;(教材P 26练习题3) (2)|1||24|y x x =-++.解:(1)由绝对值的概念,有2,2|2|2,2x x y x x x -≥⎧=-=⎨-<⎩.所以,函数|2|y x =-的图象如右图所示.(2)33,1|1||24|5,2133,2x x y x x x x x x +>⎧⎪=-++=+-≤≤⎨⎪--<-⎩,所以,函数|1||24|y x x =-++的图象如右图所示.点评:含有绝对值的函数式,可以采用分零点讨论去绝对值的方法,将函数式化为分段函数,然后根据定义域的分段情况,选择相应的解析式作出函数图象.【例4】函数()[]f x x =的函数值表示不超过x 的最大整数,例如[ 3.5]4-=-,[2.1]2=,当(2.5,3]x ∈-时,写出()f x 的解析式,并作出函数的图象.解:3, 2.522,211,10()0,011,122,233,3x x x f x x x x x --<<-⎧⎪--≤<-⎪--≤<⎪=≤<⎨⎪≤<⎪≤<⎪=⎩.函数图象如右:域I 时,(说f 若0a <,当122b x x a <≤-时,有120x x -<,12bx x a+<-,即12()0a x x b ++>,从而12()()0f x f x -<,即12()()f x f x <,所以()f x 在(,2b a -∞-上单调递增.同理可得()f x 在[,)2ba-+∞上单调递减.【例3】求下列函数的单调区间:(1)|1||24|y x x =-++;(2)22||3y x x =-++.解:(1)33,1|1||24|5,2133,2x x y x x x x x x +>⎧⎪=-++=+-≤≤⎨⎪--<-⎩,其图象如右.由图可知,函数在[2,)-+∞上是增函数,在(,2]-∞-上是减函数.(2)22223,02||323,0x x x y x x x x x ⎧-++≥⎪=-++=⎨--+<⎪⎩,其图象如右.由图可知,函数在(,1]-∞-、[0,1]上是增函数,在[1,0]-、[1,)+∞上是减函数.点评:函数式中含有绝对值,可以采用分零点讨论去绝对值的方法,将函数式化为分段函数.第2小题也可以由偶函数的对称性,先作y 轴右侧的图象,并把y 轴右侧的图象对折到左侧,得到(||)f x 的图象.由图象研究单调性,关键在于正确作出函数图象.第8讲§1.3.1函数最大(小)值¤知识要点: 1.定义最大值:设函数()y f x =的定义域为I ,如果存在实数M 满足:对于任意的x ∈I ,都有()f x ≤M ;存在x 0∈I ,使得0()f x =M .那么,称M 是函数()y f x =的最大值(MaximumValue ).仿照最大值定义,可以给出最小值(MinimumValue )的定义.244ac b a-+再利用.现在他1010(10)x -件,所赚得的利润为 8)[10010(10)]x --.210280160010(x x +-=-360.所以,他将售出价定为14】求函数解法研究,也可以用换元法研究.【另解】令t =,则0t ≥,21x t =+,所以22115222()48y t t t =++=++,在0t ≥时是增函数,当0t =时,min 2y =,故函数的最小值为2.【例4】求下列函数的最大值和最小值:(1)25332,[,]22y x x x =--∈-;(2)|1||2|y x x =+--. 解:(1)二次函数232y x x =--的对称轴为2bx a=-,即1x =-.画出函数的图象,由图可知,当1x =-时,max 4y =;当32x =时,min 94y =-.所以函数25332,[,]22y x x x =--∈-的最大值为4,最小值为94-.(2) 3 (2)|1||2|2 1 (12)3 (1)x y x x x x x ≥⎧⎪=+--=--<<⎨⎪-≤-⎩.作出函数的图象,由图可知,[3,3]y ∈-.所以函数的最大值为3,最小值为-3.点评:二次函数在闭区间上的最大值或最小值,常根据闭区间与对称轴的关系,结合图象进行分析.含绝对值的函数,常分零点讨论去绝对值,转化为分段函数进行研究.分段函数的图象注意分段作出.()f x 叫偶()f x 叫于y ()f x -与(f x 则1()()1f x g x x ⎨⎪---=⎪-+⎩,即1()()1f x g x x ⎨⎪--=⎪-+⎩.两式相减,解得2()1x f x x =-;两式相加,解得21()1g x x =-.。
人教版高中物理必修1 第一章第1节《质点、参考系和坐标系》课件(共18张PPT)

牛顿第三定律的应用
汽车的前进
v
地面对车轮的摩擦力F'
车轮对地面的摩擦力 F
实例分析
如图所示,人站在木块上,通过滑轮拉动木块和人 一起匀速前进。
一
对
相
互
作
用 共同点
力
与 一 对
不 同
对象 时间
平 点 性质
衡
力
的
异
同
一对相互作用力
一对平衡力
等值、反向、共线
火箭与气体之间的相互作用
1.先放火箭 升空视频
F1
2.学生分析:
施力物体、
受力物体。
作用力和反
作用力
3.用气球模
拟发射过程。
F2
气体对火 箭的推力
火箭对气 体的推力
力是物体间的相互作用
牛 顿
内容:两个物体之间的作用力与反作用力总是
第
大小相等、方向相反、作用在一条直线上。
三
定
律
公式: F=—F’
注意:1、作用力和反作用力的关系: 异物、等值、反向、共线、同时、同性 2、一对相互作用力一对平衡力异同
异物
同物
一定同时 一定同性质
不一定同时 不一定同性质
【巩固练习3】
(多选)弹簧拉着木块在竖直平面内下降,弹簧拉木块的力与 木块拉弹簧的力是 ( BC ) A.一对平衡力 B.一对作用力反作用力 C.大小相等,方向相反,作用在一条直线上 D.大小相等,方向相反,作用在同一物体上
气体对 火箭的
推力
F1
16、在不违背原则的情况下,对别人要宽容,能帮就帮,千万不要把人逼绝了,给人留条后路,懂得从内心欣赏别人,虽然这很多时候很难 。
1 第一章 行政与政治

行政学原理
21世纪政治学系列教材
Tankertanker Design
第一节 行政与政治的内涵
二、行政与政治的制度性质
• 政治与行政都是建立在一定经济基础之上、为一 定经济基础服务的上层建筑。两者密切联系,又 互相区别。 • 政治制度是指在特定社会中,统治阶级通过组织 政权以实现其政治统治的原则和方式的总和。 • 行政制度即政府制度,是以一定的行政思想和观 念作指导的、由国家宪法和法律规定的有关国家 行政机关的产生、职能、权限、组织结构、领导 体制、活动规程等方面的准则体系以及政府体制 内各权力主体的关系形态。
行政学原理
21世纪政治学系列教材
Tankertanker Design
第一节 行政与政治的内涵
二、行政与政治的制度性质
行政制度具有四个基本特征和四种主要功能 , 即环境制约性、鲜明阶级性、效力强制性和形式多 样性以及规范行政权力运作、维护统治阶级利益、
促进社会经济发展和实现公共管理职能。
行政学原理
第三节 政党与政府的关系
• 作为一个社会主义国家的执政党,共产党是我国各项事业的 领导核心,无疑担负着调控政治与行政两者关系的角色。 • 当前我们政党与政府的关系错综复杂,存在一些需要抓紧解 决的问题,主要表现为:
1. 部分党委总揽全局、协调各方的作用发挥得不够;
2. 党侵蚀了政府的权力,政府的各项工作只以党委的个别领导 人意志为转移,无视现实生活中人民的利益与要求;
政治与行政二分法
行政与政治的关系
政党与政府的关系
行政学原理
21世纪政治学系列教材
Tankertanker Design
第一节 行政与政治的内涵
一、行政与政治的发展渊源 • 从发展渊源来看, • 先有政治现象,后有行政现象; • 先有政治学,后有行政学,行政学从政治学中分 离出来,作为一个独立的学科而存在; • 先有国家的政治功能出现,后有国家的行政功能 的出现,行政功能以执行政治功能为己任,是政 治功能的一个组成部分。
高一数学必修一-第一章-知识点与习题讲解

必修1第一章集合及函数根底学问点整理第1讲 §1.1.1 集合的含义及表示¤学习目的:通过实例,理解集合的含义,体会元素及集合的“属于”关系;能选择自然语言、图形语言、集合语言(列举法或描绘法)描绘不同的详细问题,感受集合语言的意义和作用;驾驭集合的表示方法、常用数集及其记法、集合元素的三个特征.¤学问要点:1. 把一些元素组成的总体叫作集合(set ),其元素具有三个特征,即确定性、互异性、无序性.2. 集合的表示方法有两种:列举法,即把集合的元素一一列举出来,并用花括号“{ }”括起来,根本形式为123{,,,,}n a a a a ⋅⋅⋅,适用于有限集或元素间存在规律的无限集. 描绘法,即用集合所含元素的共同特征来表示,根本形式为{|()x A P x ∈},既要关注代表元素x ,也要把握其属性()P x ,适用于无限集.3. 通常用大写拉丁字母,,,A B C ⋅⋅⋅表示集合. 要记住一些常见数集的表示,如自然数集N ,正整数集*N 或N +,整数集Z ,有理数集Q ,实数集R .4. 元素及集合之间的关系是属于(belong to )及不属于(not belong to ),分别用符号∈、∉表示,例如3N ∈,2N -∉.¤例题精讲:【例1】试分别用列举法和描绘法表示下列集合:(1)由方程2(23)0x x x --=的全部实数根组成的集合; (2)大于2且小于7的整数. 解:(1)用描绘法表示为:2{|(23)0}x R x x x ∈--=; 用列举法表示为{0,1,3}-.(2)用描绘法表示为:{|27}x Z x ∈<<; 用列举法表示为{3,4,5,6}.【例2】用适当的符号填空:已知{|32,}A x x k k Z ==+∈,{|61,}B x x m m Z ==-∈,则有:17 A ; -5 A ; 17 B . 解:由3217k +=,解得5k Z =∈,所以17A ∈;由325k +=-,解得73k Z =∉,所以5A -∉;由6117m -=,解得3m Z =∈,所以17B ∈.【例3】试选择适当的方法表示下列集合:(教材P 6 练习题2, P 13 A 组题4) (1)一次函数3y x =+及26y x =-+的图象的交点组成的集合; (2)二次函数24y x =-的函数值组成的集合; (3)反比例函数2y x =的自变量的值组成的集合.解:(1)3{(,)|}{(1,4)}26y x x y y x =+⎧=⎨=-+⎩.(2)2{|4}{|4}y y x y y =-=≥-. (3)2{|}{|0}x y x x x==≠.点评:以上代表元素,分别是点、函数值、自变量. 在解题中不能把点的坐标混淆为{1,4},也留意比照(2)及(3)中的两个集合,自变量的范围和函数值的范围,有着本质上不同,分析时肯定要细心.*【例4】已知集合2{|1}2x a A a x +==-有唯一实数解,试用列举法表示集合A .解:化方程212x a x +=-为:2(2)0x x a --+=.应分以下三种状况:⑴方程有等根且不是2±:由 △=0,得94a =-,此时的解为12x =,合.⑵方程有一解为2,而另一解不是2-:将2x =代入得2a =-,此时另一解12x =-,合.⑶方程有一解为2-,而另一解不是2:将2x =-代入得2a =,此时另一解为21x =+,合.综上可知,9{,2,2}4A =--.点评:运用分类探讨思想方法,探讨出根的状况,从而列举法表示. 留意分式方程易造成增根的现象.第2讲 §1.1.2 集合间的根本关系¤学习目的:理解集合之间包含及相等的含义,能识别给定集合的子集;在详细情境中,理解全集及空集的含义;能利用Venn 图表达集合间的关系.¤学问要点:1. 一般地,对于两个集合A 、B ,假如集合A 中的随意一个元素都是集合B 中的元素,则说两个集合有包含关系,其中集合A 是集合B 的子集(subset ),记作A B ⊆(或B A ⊇),读作“A 含于B ”(或“B 包含A ”).2. 假如集合A 是集合B 的子集(A B ⊆),且集合B 是集合A 的子集(B A ⊇),即集合A 及集合B 的元素是一样的,因此集合A 及集合B 相等,记作A B =.3. 假如集合A B ⊆,但存在元素x B ∈,且x A ∉,则称集合A 是集合B 的真子集(proper subset ),记作A ≠⊂B (或B ≠⊃A ). 4. 不含任何元素的集合叫作空集(empty set ),记作∅,并规定空集是任何集合的子集.5. 性质:A A ⊆;若A B ⊆,B C ⊆,则A C ⊆;若A B A =,则A B ⊆;若A B A =,则B A ⊆. ¤例题精讲:【例1】用适当的符号填空:(1){菱形} {平行四边形}; {等腰三角形} {等边三角形}.(2)∅ 2{|20}x R x ∈+=; 0 {0}; ∅ {0}; N {0}. 解:(1), ;(2)=, ∈, ,.A BBA AB A B A . B .C .D .【例2】设集合1,,}22{|,{|n n x n n A x x B x =∈=+∈==Z}Z ,则下列图形能表示A 及B关系的是( ).解:简洁列举两个集合的一些元素,3113{,1,,0,,1,,}2222A =⋅⋅⋅---⋅⋅⋅,3113{,,,,,}2222B =⋅⋅⋅--⋅⋅⋅,易知B ≠⊂A ,故答案选A .另解:由21,}2{|n x n B x +=∈=Z ,易知B ≠⊂A ,故答案选A . 【例3】若集合{}{}2|60,|10M x x x N x ax =+-==-=,且N M ⊆,务实数a 的值.解:由26023x x x +-=⇒=-或,因此,{}2,3M =-. (i )若0a =时,得N =∅,此时,N M ⊆;(ii )若0a ≠时,得1{}N a =. 若N M ⊆,满意1123a a ==-或,解得1123a a ==-或.故所务实数a 的值为0或12或13-.点评:在考察“A B ⊆”这一关系时,不要遗忘“∅” ,因为A =∅时存在A B ⊆.从而须要分状况探讨. 题中探讨的主线是根据待定的元素进展.【例4】已知集合A ={a ,a +b ,a +2b },B ={a ,ax ,ax 2}. 若A =B ,务实数x 的值. 解:若⇒a +ax 2-2ax =0, 所以a (x -1)2=0,即a =0或x =1. 当a =0时,集合B 中的元素均为0,故舍去; 当x =1时,集合B 中的元素均一样,故舍去. 若⇒2ax 2-ax -a =0.因为a ≠0,所以2x 2-x -1=0, 即(x -1)(2x +1)=0. 又x ≠1,所以只有12x =-.经检验,此时A =B 成立. 综上所述12x =-.点评:抓住集合相等的定义,分状况进展探讨. 融入方程组思想,结合元素的互异性确定集合.第3讲 §1.1.3 集合的根本运算(一)¤学习目的:理解两个集合的并集及交集的含义,会求两个简洁集合的并集及交集;理解在给定集合中一个子集的补集的含义,会求给定子集的补集;能运用Venn 图表达集合的关系及运算,体会直观图示对理解抽象概念的作用.¤学问要点:集合的根本运算有三种,即交、并、补,学习时先理解概念,并驾驭符号等,再念属于集合B 的元素所组成的集合,称为集合A 及B 的并集(union set )集合B 的元素所组成的集合,称为集合A 及B 的交集(intersection set )不属于集合A 的全部元素组成的集合,称为集合A 相对于全集U 的补集(complementary set )记号 A B (读作“A 并B ”) A B (读作“A 交B ”)UA (读作“A 的补集”)符号 {|,}AB x x A x B =∈∈或{|,}AB x x A x B =∈∈且{|,}UA x x U x A =∈∉且图形表示¤例题精讲:【例1】设集合,{|15},{|39},,()U R A x x B x x A B A B ==-≤≤=<<求. 解:在数轴上表示出集合A 、B ,如右图所示: {|35}A B x x =<≤,(){|1,9}U C A B x x x =<-≥或,【例2】设{|||6}A x Z x =∈≤,{}{}1,2,3,3,4,5,6B C ==,求: (1)()A B C ; (2)()A A B C . 解:{}6,5,4,3,2,1,0,1,2,3,4,5,6A =------. (1)又{}3B C =,∴()A B C ={}3; (2)又{}1,2,3,4,5,6B C =, 得{}()6,5,4,3,2,1,0A C B C =------.∴ ()A A C B C {}6,5,4,3,2,1,0=------.【例3】已知集合{|24}A x x =-<<,{|}B x x m =≤,且A B A =,务实数m 的取值范围.解:由A B A =,可得A B ⊆.在数轴上表示集合A 及集合B ,如右图所示:由图形可知,4m ≥.点评:探讨不等式所表示的集合问题,经常由集合之间的关系,得到各端点之间的关系,特殊要留意是否含端点的问题.【例4】已知全集*{|10,}U x x x N =<∈且,{2,4,5,8}A =,{1,3,5,8}B =,求()U C A B ,()U C A B ,()()U U C A C B , ()()U U C A C B ,并比拟它们的关系.解:由{1,2,3,4,5,8}A B =,则(){6,7,9}U C A B =. 由{5,8}A B =,则(){1,2,3,4,6,7,9}U C A B = 由{1,3,6,7,9}U C A =,{2,4,6,7,9}U C B =, 则()(){6,7,9}U U C A C B =, ()(){1,2,3,4,6,7,9}U U C A C B =.由计算结果可以知道,()()()U U U C A C B C A B =,UA-2 4 m x B A A BB A()()()U U U C A C B C AB =.另解:作出Venn 图,如右图所示,由图形可以干脆视察出来结果.点评:可用Venn 图探讨()()()U U U C A C B C A B =及()()()U U U C A C B C A B = ,在理解的根底记住此结论,有助于今后快速解决一些集合问题.第4讲 §1.1.3 集合的根本运算(二)¤学习目的:驾驭集合、交集、并集、补集的有关性质,运行性质解决一些简洁的问题;驾驭集合运算中的一些数学思想方法.¤学问要点:1. 含两个集合的Venn 图有四个区域,分别对应着这两个集合运算的结果. 我们需通过Venn 图理解和驾驭各区域的集合运算表示,解决一类可用列举法表示的集合运算. 通过图形,我们还可以发觉一些集合性质:()()()U U U C A B C A C B =,()()()U U U C A B C A C B =.2. 集合元素个数公式:()()()()n A B n A n B n A B =+-.3. 在探讨集合问题时,经常用到分类探讨思想、数形结合思想等. 也常由新的定义考察创新思维.¤例题精讲:【例1】设集合{}{}24,21,,9,5,1A a a B a a =--=--,若{}9A B =,务实数a 的值.解:由于{}{}24,21,,9,5,1A a a B a a =--=--,且{}9A B =,则有:当219 a -=时,解得5a =,此时={4, 9, 25}={9, 0, 4}A B -,-,不合题意,故舍去; 当29a =时,解得33a =或-.3 ={4,5,9} ={9,2,2}a A B =时,-,--,不合题意,故舍去; 3={4, 7 9}={9, 8, 4}a A B =-,--,,-,合题意. 所以,3a =-.【例2】设集合{|(3)()0,}A x x x a a R =--=∈,{|(4)(1)0}B x x x =--=,求A B , A B .(教材P 14 B 组题2)解:{1,4}B =.当3a =时,{3}A =,则{1,3,4}A B =,A B =∅; 当1a =时,{1,3}A =,则{1,3,4}A B =,{1}A B =; 当4a =时,{3,4}A =,则{1,3,4}A B =,{4}A B =;当3a ≠且1a ≠且4a ≠时,{3,}A a =,则{1,3,4,}A B a =,A B =∅.点评:集合A 含有参数a ,须要对参数a 进展分状况探讨. 罗列参数a 的各种状况时,需根据集合的性质和影响运算结果的可能而进展分析,不多不少是分类的原则.【例3】设集合A ={x |240x x +=}, B ={x |222(1)10x a x a +++-=,a R ∈},若A B =B ,务实数a 的值.解:先化简集合A ={4,0}-. 由A B =B ,则B ⊆A ,可知集合B 可为∅,或为{0},或{-4},或{4,0}-.(i )若B =∅,则224(1)4(1)0a a ∆=+--<,解得a <1-; (ii )若0∈B ,代入得2a 1-=0⇒a =1或a =1-, 当a =1时,B =A ,符合题意;当a =1-时,B ={0}⊆A ,也符合题意.(iii )若-4∈B ,代入得2870a a -+=⇒a =7或a =1, 当a =1时,已经探讨,符合题意;当a =7时,B ={-12,-4},不符合题意. 综上可得,a =1或a ≤1-.点评:此题考察分类探讨的思想,以及集合间的关系的应用. 通过深入理解集合表示法的转换,及集合之间的关系,可以把相关问题化归为解方程的问题,这是数学中的化归思想,是重要数学思想方法.解该题时,特殊简洁出现的错误是遗漏了A =B 和B =∅的情形,从而造成错误.这须要在解题过程中要全方位、多角度谛视问题.【例4】对集合A 及B ,若定义{|,}A B x x A x B -=∈∉且,当集合*{|8,}A x x x N =≤∈,集合{|(2)(5)(6)0}B x x x x x =---=时,有A B -= . (由教材P 12 补集定义“集合A 相对于全集U 的补集为{|,}U C A x x x A =∈∉且”而拓展)解:根据题意可知,{1,2,3,4,5,6,7,8}A =,{0,2,5,6}B = 由定义{|,}A B x x A x B -=∈∉且,则 {1,3,4,7,8}A B -=.点评:运用新定义解题是学习实力的开展,也是一种创新思维的训练,关键是理解定义的本质性内涵,这里新定义的含义是从A 中解除B 的元素. 假如再给定全集U ,则A B -也相当于()U A C B .第5讲 §1.2.1 函数的概念¤学习目的:通过丰富实例,进一步体会函数是描绘变量之间的依靠关系的重要数学模型,在此根底上学惯用集合及对应的语言来刻画函数,体会对应关系在刻画函数概念中的作用;理解构成函数的要素,会求一些简洁函数的定义域和值域.¤学问要点:1. 设A 、B 是非空的数集,假如按某个确定的对应关系f ,使对于集合A 中的随意一个数x ,在集合B 中都有唯一确定的数y 和它对应,那么就称f :A →B 为从集合A 到集合B 的一个函数(function ),记作y =()f x ,x A ∈.其中,x 叫自变量,x 的取值范围A 叫作定义域(domain ),及x 的值对应的y 值叫函数值,函数值的集合{()|}f x x A ∈叫值域(range ).2. 设a 、b 是两个实数,且a <b ,则:{x |a ≤x ≤b }=[a ,b ] 叫闭区间; {x |a <x <b }=(a ,b ) 叫开区间;{x |a ≤x <b }=[,)a b , {x |a <x ≤b }=(,]a b ,都叫半开半闭区间. 符号:“∞”读“无穷大”;“-∞”读“负无穷大”;“+∞”读“正无穷大”. 则 {|}(,)x x a a >=+∞,{|}[,)x x a a ≥=+∞,{|}(,)x x b b <=-∞,{|}(,]x x b b ≤=-∞,(,)R =-∞+∞. 3. 确定函数的三个要素是定义域、值域和对应法则. 当且仅当函数定义域、对应法则分别一样时,函数才是同一函数.¤例题精讲:【例1】求下列函数的定义域: (1);(2). 解:(1)由210x +-≠,解得1x ≠-且3x ≠-, 所以原函数定义域为(,3)(3,1)(1,)-∞----+∞. (2)由,解得3x ≥且9x ≠,所以原函数定义域为[3,9)(9,)+∞.【例2】求下列函数的定义域及值域:(1)3254x y x+=-; (2)22y x x =-++.解:(1)要使函数有意义,则540x -≠,解得54x ≠. 所以原函数的定义域是5{|}4x x ≠.32112813(45)233233305445445445444x x x y x x x x ++-+==⨯=⨯=-+≠-+=-----,所以值域为3{|}4y y ≠-.(2)22192()24y x x x =-++=--+. 所以原函数的定义域是R ,值域是9(,]4-∞.【例3】已知函数1()1x f x x-=+. 求:(1)(2)f 的值; (2)()f x 的表达式解:(1)由121x x -=+,解得13x =-,所以1(2)3f =-.(2)设11x t x -=+,解得11t x t -=+,所以1()1t f t t -=+,即1()1x f x x-=+.点评:此题解法中突出了换元法的思想. 这类问题的函数式没有干脆给出,称为抽象函数的探讨,经常须要结合换元法、特值代入、方程思想等.【例4】已知函数.(1)求1()()f x f x+的值;(2)计算:111(1)(2)(3)(4)()()()234f f f f f f f ++++++.解:(1)由2222222221111()()1111111x x x x f x f x x x x x x++=+=+==+++++. (2)原式11117(1)((2)())((3)())((4)())323422f f f f f f f =++++++=+=点评:对规律的发觉,能使我们施行巧算. 正确探究出前一问的结论,是解答后一问的关键.第6讲 §1.2.2 函数的表示法¤学习目的:在实际情境中,会根据不同的须要选择恰当的方法(图象法、列表法、解析法)表示函数;通过详细实例,理解简洁的分段函数,并能简洁应用;理解映射的概念.¤学问要点:1. 函数有三种表示方法:解析法(用数学表达式表示两个变量之间的对应关系,优点:简明,给自变量可求函数值);图象法(用图象表示两个变量的对应关系,优点:直观形象,反响改变趋势);列表法(列出表格表示两个变量之间的对应关系,优点:不需计算就可看出函数值).2. 分段函数的表示法及意义(一个函数,不同范围的x ,对应法则不同).3. 一般地,设A 、B 是两个非空的集合,假如按某一个确定的对应法则f ,使对于集合A 中的随意一个元素x ,在集合B 中都有唯一确定的元素y 及之对应,那么就称对应:f A B →为从集合A 到集合B 的一个映射(mapping ).记作“:f A B →”.判别一个对应是否映射的关键:A 中随意,B 中唯一;对应法则f . ¤例题精讲:【例1】如图,有一块边长为a 的正方形铁皮,将其四个角各截去一个边长为x 的小正方形,然后折成一个无盖的盒子,写出体积V 以x 为自变量的函数式是_____,这个函数的定义域为_______.解:盒子的高为x ,长、宽为2a x -,所以体积为V =2(2)x a x -.又由20a x >-,解得2a x <.所以,体积V 以x 为自变量的函数式是2(2)V x a x =-,定义域为{|0}2a x x <<.【例2】已知f (x )= ,求f [f (0)]的值. 解:∵ 0(,1)∈-∞, ∴ f (0)=32. 又 ∵ 32>1,∴ f (32)=(32)3+(32)-3=2+12=52,即f [f (0)]=52.【例3】画出下列函数的图象:(1)|2|y x =-; (教材P 26 练习题3) (2)|1||24|y x x =-++. 解:(1)由肯定值的概念,有.所以,函数|2|y x =-的图象如右图所示.(2)33,1|1||24|5,2133,2x x y x x x x x x +>⎧⎪=-++=+-≤≤⎨⎪--<-⎩,所以,函数|1||24|y x x =-++的图象如右图所示.点评:含有肯定值的函数式,可以采纳分零点探讨去肯定值的方法,将函数式化为分段函数,然后根据定义域的分段状况,选择相应的解析式作出函数图象.【例4】函数()[]f x x =的函数值表示不超过x 的最大整数,例如[ 3.5]4-=-,[2.1]2=,当( 2.5,3]x ∈-时,写出()f x 的解析式,并作出函数的图象.解:3, 2.522,211,10()0,011,122,233,3x x x f x x x x x --<<-⎧⎪--≤<-⎪--≤<⎪=≤<⎨⎪≤<⎪≤<⎪=⎩. 函数图象如右: 点评:解题关键是理解符号[]m 的概念,抓住分段函数的对应函数式.第7讲 §1.3.1 函数的单调性¤学习目的:通过已学过的函数特殊是二次函数,理解函数的单调性及其几何意义;学会运用函数图像理解和探讨函数的性质. 理解增区间、减区间等概念,驾驭增(减)函数的证明和判别.¤学问要点:1. 增函数:设函数y =f (x )的定义域为I ,假如对于定义域I 内的某个区间D 内的随意两个自变量x 1,x 2,当x 1<x 2时,都有f (x 1)<f (x 2),那么就说f (x )在区间D 上是增函数(increasing function ). 仿照增函数的定义可定义减函数.2. 假如函数f (x )在某个区间D 上是增函数或减函数,就说f (x )在这一区间上具有(严格的)单调性,区间D 叫f(x )的单调区间. 在单调区间上,增函数的图象是从左向右是上升的(如右图1),减函数的图象从左向右是下降的(如右图2). 由此,可以直观视察函数图象上升及下降的改变趋势,得到函数的单调区间及单调性.3. 推断单调性的步骤:设x 1、x 2∈给定区间,且x 1<x 2;→计算f (x 1)-f (x 2) →推断符号→下结论.¤例题精讲:【例1】试用函数单调性的定义推断函数2()1x f x x =-在区间(0,1)上的单调性. 解:任取12,x x ∈(0,1),且12x x <. 则1221121212222()()()11(1)(1)x x x x f x f x x x x x --=-=----. 由于1201x x <<<,110x -<,210x -<,210x x ->,故12()()0f x f x ->,即12()()f x f x >.所以,函数2()1x f x x =-在(0,1)上是减函数.【例2】求二次函数2()(0)f x ax bx c a =++<的单调区间及单调性.解:设随意12,x x R ∈,且12x x <. 则22121122()()()()f x f x ax bx c ax bx c -=++-++221212()()a x x b x x =-+-1212()[()]x x a x x b =-++. 若0a <,当122b x x a<≤-时,有120x x -<,12b x x a+<-,即12()0a x x b ++>,从而12()()0f x f x -<,即12()()f x f x <,所以()f x 在(,]2b a-∞-上单调递增. 同理可得()f x 在[,)2ba-+∞上单调递减. 【例3】求下列函数的单调区间: (1)|1||24|y x x =-++;(2)22||3y x x =-++.解:(1)33,1|1||24|5,2133,2x x y x x x x x x +>⎧⎪=-++=+-≤≤⎨⎪--<-⎩,其图象如右.由图可知,函数在[2,)-+∞上是增函数,在(,2]-∞-上是减函数.(2)22223,02||323,0x x x y x x x x x ⎧-++≥⎪=-++=⎨--+<⎪⎩,其图象如右.由图可知,函数在(,1]-∞-、[0,1]上是增函数,在[1,0]-、[1,)+∞上是减函数.点评:函数式中含有肯定值,可以采纳分零点探讨去肯定值的方法,将函数式化为分段函数. 第2小题也可以由偶函数的对称性,先作y 轴右侧的图象,并把y 轴右侧的图象对折到左侧,得到(||)f x 的图象. 由图象探讨单调性,关键在于正确作出函数图象.【例4】已知31()2x f x x +=+,指出()f x 的单调区间. 解:∵ 3(2)55()322x f x x x +--==+++, ∴ 把5()g x x-=的图象沿x 轴方向向左平移2个单位,再沿y 轴向上平移3个单位,得到()f x 的图象,如图所示.由图象得()f x 在(,2)-∞-单调递增,在(2,)-+∞上单调递增.点评:变形后结合平移学问,由平移变换得到一类分式函数的图象. 需知()f x a b ++平移变换规律.第8讲 §1.3.1 函数最大(小)值¤学习目的:通过已学过的函数特殊是二次函数,理解函数的最大(小)值及其几何意义;学会运用函数图像理解和探讨函数的性质. 能利用单调性求函数的最大(小)值.¤学问要点:1. 定义最大值:设函数()y f x =的定义域为I ,假如存在实数M 满意:对于随意的x ∈I ,都有()f x ≤M ;存在x 0∈I ,使得0()f x = M . 那么,称M 是函数()y f x =的最大值(Maximum Value ). 仿照最大值定义,可以给出最小值(Minimum Value )的定义.2. 配方法:探讨二次函数2(0)y ax bx c a =++≠的最大(小)值,先配方成后,当0a >时,函数取最小值为;当0a <时,函数取最大值.3. 单调法:一些函数的单调性,比拟简洁视察出来,或者可以先证明出函数的单调性,再利用函数的单调性求函数的最大值或最小值.4. 图象法:先作出其函数图象后,然后视察图象得到函数的最大值或最小值. ¤例题精讲:【例1】求函数261y x x =++的最大值.解:配方为,由2133()244x ++≥,得.所以函数的最大值为8.【例2】某商人假如将进货单价为8元的商品按每件10元售出时,每天可售出100件. 如今他采纳进步售出价,削减进货量的方法增加利润,已知这种商品每件提价1元,其销售量就要削减10件,问他将售出价定为多少元时,才能使每天所赚得的利润最大?并求出最大利润.解:设他将售出价定为x 元,则进步了(10)x -元,削减了10(10)x -件,所赚得的利润为(8)[10010(10)]y x x =---.即2210280160010(14)360y x x x =-+-=--+. 当14x =时,max 360y =. 所以,他将售出价定为14元时,才能使每天所赚得的利润最大, 最大利润为360元.【例3】求函数21y x x =+-的最小值.解:此函数的定义域为[)1,+∞,且函数在定义域上是增函数, 所以当1x =时,min 2112y =+-=,函数的最小值为2.点评:形如y ax b cx d =+±+的函数最大值或最小值,可以用单调性法探讨,也可以用换元法探讨.【另解】令1x t -=,则0t ≥,21x t =+,所以22115222()48y t t t =++=++,在0t ≥时是增函数,当0t =时,min 2y =,故函数的最小值为2.【例4】求下列函数的最大值和最小值:(1)25332,[,]22y x x x =--∈-; (2)|1||2|y x x =+--. 解:(1)二次函数232y x x =--的对称轴为2b x a=-,即1x =-. 画出函数的图象,由图可知,当1x =-时,max 4y =; 当32x =时,min 94y =-. 所以函数25332,[,]22y x x x =--∈-的最大值为4,最小值为94-. (2) 3 (2)|1||2|2 1 (12)3 (1)x y x x x x x ≥⎧⎪=+--=--<<⎨⎪-≤-⎩.作出函数的图象,由图可知,[3,3]y ∈-. 所以函数的最大值为3, 最小值为-3. 点评:二次函数在闭区间上的最大值或最小值,常根据闭区间及对称轴的关系,结合图象进展分析. 含肯定值的函数,常分零点探讨去肯定值,转化为分段函数进展探讨. 分段函数的图象留意分段作出.第9讲 §1.3.2 函数的奇偶性¤学习目的:结合详细函数,理解奇偶性的含义;学会运用函数图像理解和探讨函数的性质. 理解奇函数、偶函数的几何意义,能娴熟判别函数的奇偶性.¤学问要点:1. 定义:一般地,对于函数()f x 定义域内的随意一个x ,都有()()f x f x -=,那么函数()f x 叫偶函数(even function ). 假如对于函数定义域内的随意一个x ,都有()()f x f x -=-),那么函数()f x 叫奇函数(odd function ). 2. 具有奇偶性的函数其定义域关于原点对称,奇函数的图象关于原点中心对称,偶函数图象关于y 轴轴对称.3. 判别方法:先考察定义域是否关于原点对称,再用比拟法、计算和差、比商法等判别()f x -及()f x 的关系.¤例题精讲:【例1】判别下列函数的奇偶性:(1)31()f x x x=-; (2)()|1||1|f x x x =-++;(3)23()f x x x =-. 解:(1)原函数定义域为{|0}x x ≠,对于定义域的每一个x ,都有3311()()()()f x x x f x x x-=--=--=--, 所以为奇函数. (2)原函数定义域为R ,对于定义域的每一个x ,都有()|1||1||1||1|()f x x x x x f x -=--+-+=-++=,所以为偶函数.(3)由于23()()f x x x f x -=+≠±,所以原函数为非奇非偶函数.【例2】已知()f x 是奇函数,()g x 是偶函数,且1()()1f xg x x -=+,求()f x 、()g x . 解:∵ ()f x 是奇函数,()g x 是偶函数,∴ ()()f x f x -=-,()()g x g x -=.则,即.两式相减,解得2()1x f x x =-;两式相加,解得21()1g x x =-. 【例3】已知()f x 是偶函数,0x ≥时,2()24f x x x =-+,求0x <时()f x 的解析式.解:作出函数22242(1)2,0y x x x x =-+=--+≥的图象,其顶点为(1,2).∵ ()f x 是偶函数, ∴ 其图象关于y 轴对称.作出0x <时的图象,其顶点为(1,2)-,且及右侧形态一样,∴ 0x <时,22()2(1)224f x x x x =-++=--.点评:此题中的函数本质就是224||y x x =-+. 留意两抛物线形态一样,则二次项系数a 的肯定值一样. 此类问题,我们也可以干脆由函数奇偶性的定义来求,过程如下.【另解】当0x <时,0x ->,又由于()f x 是偶函数,则()()f x f x =-,所以,当0x <时,22()()2()4()24f x f x x x x x =-=--+-=--.【例4】设函数()f x 是定义在R 上的奇函数,且在区间(,0)-∞上是减函数,实数a 满意不等式22(33)(32)f a a f a a +-<-,务实数a 的取值范围.解:∵ ()f x 在区间(,0)-∞上是减函数, ∴ ()f x 的图象在y 轴左侧递减.又 ∵ ()f x 是奇函数,∴()f x 的图象关于原点中心对称,则在y 轴右侧同样递减.又 (0)(0)f f -=-,解得(0)0f =, 所以()f x 的图象在R 上递减.∵ 22(33)(32)f a a f a a +-<-,∴ 223332a a a a +->-,解得1a >.点评:定义在R 上的奇函数的图象肯定经过原点. 由图象对称性可以得到,奇函数在关于原点对称区间上单调性一样,偶函数在关于原点对称区间上的单调性相反.集合及函数根底测试一、选择题(共12小题,每题5分,四个选项中只有一个符合要求)1.函数y ==x 2-6x +10在区间(2,4)上是( )A .递减函数B .递增函数C .先递减再递增D .选递增再递减.2.方程组20{=+=-y x y x 的解构成的集合是 ( )A .)}1,1{(B .}1,1{C .(1,1)D .}1{3.已知集合A ={a ,b ,c },下列可以作为集合A 的子集的是 ( )A. aB. {a ,c }C. {a ,e }D.{a ,b ,c ,d }4.下列图形中,表示N M ⊆的是 ( )M N A M N B N M C M N D5.下列表述正确的是 ( )A.}0{=∅B. }0{⊆∅C. }0{⊇∅D. }0{∈∅6、设集合A ={x|x 参与自由泳的运发动},B ={x|x 参与蛙泳的运发动},对于“既参加自由泳又参与蛙泳的运发动”用集合运算表示为 ( )A.A∩BB.A ⊇BC.A∪BD.A ⊆B7.集合A={x Z k k x ∈=,2} ,B={Z k k x x ∈+=,12} ,C={Z k k x x ∈+=,14}又,,B b A a ∈∈则有( )A.(a+b )∈ AB. (a+b) ∈BC.(a+b) ∈ CD. (a+b) ∈ A 、B 、C 任一个8.函数f (x )=-x 2+2(a -1)x +2在(-∞,4)上是增函数,则a 的范围是( )A .a ≥5B .a ≥3C .a ≤3D .a ≤-59.满意条件{1,2,3}⊂≠M ⊂≠{1,2,3,4,5,6}的集合M 的个数是 ( )A. 8B. 7C. 6D. 510.全集U = {1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 }, A= {3 ,4 ,5 }, B= {1 ,3 ,6 },那么集合 { 2 ,7 ,8}是 ( )A. A BB. B AC. B C A C U UD. B C A C U U11.下列函数中为偶函数的是( )A .x y =B .x y =C .2x y =D .13+=x y12. 假如集合A={x |ax 2+2x +1=0}中只有一个元素,则a 的值是 ( )A .0B .0 或1C .1D .不能确定二、填空题(共4小题,每题4分,把答案填在题中横线上)13.函数f (x )=2×2-3|x |的单调减区间是___________.14.函数y =11+x 的单调区间为___________. 15.含有三个实数的集合既可表示成,又可表示成}0,,{2b a a +,则=+20042003b a .16.已知集合}33|{≤≤-=x x U ,}11|{<<-=x x M ,}20|{<<=x x N C U 那么集合=N ,=⋂)(N C M U ,=⋃N M .三、解答题(共4小题,共44分)17. 已知集合}04{2=-=x x A ,集合}02{=-=ax x B ,若A B ⊆,务实数a 的取值集合.18. 设f (x )是定义在R 上的增函数,f (xy )=f (x )+f (y ),f (3)=1,求解不等式f (x )+f (x -2)>1.19. 已知函数f (x )是奇函数,且当x >0时,f (x )=x 3+2x 2—1,求f (x )在R 上的表达式.20. 已知二次函数222)1(2)(m m x m x x f -+-+-=的图象关于y 轴对称,写出函数的解析表达式,并求出函数)(x f 的单调递增区间.必修1 第一章 集合测试集合测试参考答案:一、1~5 CABCB 6~10 ABACC 11~12 cB二、13 [0,43],(-∞,-43)14 (-∞,-1),(-1,+∞) 15 -1 16 03|{≤≤-=x x N 或}32≤≤x ;}10|{)(<<=⋂x x N C M U ;13|{<≤-=⋃x x N M 或}32≤≤x . 三、17 .{0.-1,1}; 18. 解:由条件可得f (x )+f (x -2)=f [x (x -2)],1=f (3).所以f [x (x -2)]>f (3),又f (x )是定义在R 上的增函数,所以有x (x -2)>3,可解得x >3或x <-1.答案:x >3或x <-1.19. .解析:本题主要是培育学生理解概念的实力.f (x )=x 3+2x 2-1.因f (x )为奇函数,∴f (0)=-1.当x <0时,-x >0,f (-x )=(-x )3+2(-x )2-1=-x 3+2x 2-1, ∴f (x )=x 3-2x 2+1.20. 二次函数222)1(2)(m m x m x x f -+-+-=的图象关于y 轴对称,∴1=m ,则1)(2+-=x x f ,函数)(x f 的单调递增区间为(]0,∞-..。
地理必修1 第一章 宇宙中的地球 知识点

太阳活动与地球
太阳活动 太阳黑子 (光球层)
约11年的周期性;太 阳活动高峰年,激烈 天气现象增加
耀斑和日珥 (色球层)
耀斑产生磁暴,影 响短波通信,威胁 宇航器的安全
太阳风 (日冕层)
太阳风,高纬地 区有极光现象
主要知识点
1、太阳活动最激烈的表现形式是耀斑 2、黑子大小和多少代表太阳活动的强 弱 3、太阳活动的主要标志是黑子和耀斑
自转线速度及公转线速度变化图
黄道交角示意图
太阳高度角计算图
在同一半球,所求地区太阳高度角=90°-(此地区纬度-太阳直射纬度) 在不同半球,所求地区太阳高度角=90°-(此地区纬度+太阳直射纬度) Nhomakorabea小结
1、地球公转的地理意义: (1)正午太阳高度的变化 (2)昼夜长短的变化 (3)四季的形成 (4)五带的形成
宇宙结构图
宇宙
不可见宇宙
可见宇宙=总星系 (半径约140亿光年)
河外星系
银河系
太阳系
其他行星系
其他恒星系
地月系
太阳系运行图
八大行星 运行结构 极其位置
类地 行星
巨行 星
远日 行星
太 阳
水星
金星
地球
火星
木星
土星
天王星
海王星
普通而特殊的行星——地球
普通性:外观和所处位置来看,地球是一颗普通的行星 特殊性: 1、外部条件:(1)安全稳定的宇宙环境(各行星各行其道) (2)稳定的光照(太阳没有发生太大变化) 2、内部条件:(1)适宜的温度(日地距离适中) (2)充足的液态水(日地距离适中水成液态) (3)比较厚的大气层(地球一定质量和体积)
总的来说:地球上存在生命
(二)太阳对地球的影响
物理必修一第一章习题及答案

蚁高一物理必修1第一章练习卷莆一、选择题莇1.下列说法中正确的是()蚂A .匀速运动就是匀速直线运动B .对于匀速直线运动来说,路程就是位移C .物体的位移越大,平均速度一定越大D .物体在某段时间内的平均速度越大,在其间任一时刻的瞬时速度也一定越大腿2.关于速度的说法正确的是()荿A .速度与位移成正比B .平均速率等于平均速度的大小C .匀速直线运动任何一段时间内的平均速度等于任一点的瞬时速度D .瞬时速度就是运动物体在一段较短时间内的平均速度蒆3.物体沿一条直线运动,下列说法正确的是()肃A .物体在某时刻的速度为3m/s ,则物体在1s 内一定走3m袁B .物体在某1s 内的平均速度是3m/s ,则物体在这1s 内的位移一定是3m 膈C .物体在某段时间内的平均速度是3m/s ,则物体在1s 内的位移一定是3m薆D .物体在发生某段位移过程中的平均速度是3m/s ,则物体在这段位移的一半时的速度一定是3m/s蒄4.关于平均速度的下列说法中,物理含义正确的是()艿A .汽车在出发后10s 内的平均速度是5m/s袇B .汽车在某段时间内的平均速度是5m/s ,表示汽车在这段时间的每1s 内的位移都是5m蚆C .汽车经过两路标之间的平均速度是5m/s蚁D .汽车在某段时间内的平均速度都等于它的初速度与末速度之和的一半肁5.火车以76km/h 的速度经过某一段路,子弹以600m /s 的速度从枪口射出,则()蚆A .76km/h 是平均速度B .76km/h 是瞬时速度C .600m/s 是瞬时速度D .600m/s 是平均速度螆6.某人沿直线做单方向运动,由A 到B 的速度为1v ,由B 到C 的速度为2v ,若BC AB ,则这全过程的平均速度是()A .2/)(21v v B .2/)(21v v C .)/()(2121v v v v D .)/(22121v v v v 肂7.如图是A 、B 两物体运动的速度图象,则下列说法正确的是()蒈A 物体A 的运动是以10m/s 的速度匀速运动虿B 物体B 的运动是先以5m /s 的速度与A 同方向袆C .物体B 在最初3s 内位移是10m 蒂D .物体B 在最初3s 内路程是10m膀8.有一质点从t =0开始由原点出发,其运动的速度—时间图象如图所示,则()蒇A .1t s 时,质点离原点的距离最大B .2t s 时,质点离原点的距离最大袆C .2ts 时,质点回到原点D .4ts 时,质点回到原袃9.如图所示,能正确表示物体做匀速直线运动的图象是()蚈芆10.质点做匀加速直线运动,加速度大小为2m/s 2,在质点做匀加速运动的过程中,下列说法正确的是()羆A .质点的未速度一定比初速度大2m/sB .质点在第三秒米速度比第2s 末速度大2m/s芄C .质点在任何一秒的未速度都比初速度大2m /sD .质点在任何一秒的末速度都比前一秒的初速度大2m /s莀11.关于加速度的概念,正确的是()艿A .加速度反映速度变化的快慢B .加速度反映速度变化的大小肅C .加速度为正值,表示物体速度一定是越来越大D .加速度为负值,表示速度一定是越来越小莁12.下列说法中正确的是()肂A .物体的加速度不为零,速度可能为零B .物体的速度大小保持不变时,可能加速度不为零肈C .速度变化越快,加速度一定越大D .加速度越小,速度一定越小膅13.一个做变速直线运动的物体,加速度逐渐减小,直至为零,那么该物体运动的情况可能是()螂A .速度不断增大,加速度为零时,速度最大B .速度不断减小,加速度为零时,速度最小薀C .速度的变化率越来越小D .速度肯定是越来越小的袇二、填空题芅14.如图所示为某一质点运动的速度图象,从图象可知:质点运动方向和第1s运动方向相同的是在______时间内,质点运动速度方向和第3s运动速度方向相同的是在______时间内。
高一数学必修第一章知识点总结

高一数学必修1第一章知识点总结一、集合有关概念1.集合的含义2.集合的中元素的三个特性:(1)元素的确定性,(2)元素的互异性,(3)元素的无序性,3.集合的表示:{ …} 如:{我校的篮球队员},{太平洋,大西洋,印度洋,北冰洋}(1)用拉丁字母表示集合:A={我校的篮球队员},B={1,2,3,4,5}(2)集合的表示方法:列举法与描述法。
注意:常用数集及其记法:非负整数集(即自然数集)记作:N正整数集N*或N+ 整数集Z 有理数集Q 实数集R 1)列举法:{a,b,c……}2)描述法:将集合中的元素的公共属性描述出来,写在大括号内表示集合的方法。
{x?R| x-3>2} ,{x| x-3>2} 3)语言描述法:例:{不是直角三角形的三角形} 4)Venn图:4、集合的分类:(1)有限集含有有限个元素的集合(2)无限集含有无限个元素的集合(3)空集不含任何元素的集合例:{x|x2=-5}二、集合间的基本关系1.“包含”关系—子集A⊆有两种可能(1)A是B的一部分,;(2)A与B是注意:B同一集合。
反之: 集合A不包含于集合B,或集合B不包含集合A,记作A⊆/B 或B⊇/A2.“相等”关系:A=B (5≥5,且5≤5,则5=5)实例:设A={x|x2-1=0} B={-1,1} “元素相同则两集合相等”即:①任何一个集合是它本身的子集。
A?A②真子集:如果A ?B,且A ? B 那就说集合A 是集合B 的真子集,记作A B(或B A)③如果 A ?B, B ?C ,那么 A ?C④ 如果A ?B 同时 B ?A 那么A=B3. 不含任何元素的集合叫做空集,记为Φ规定: 空集是任何集合的子集, 空集是任何非空集合的真子集。
有n 个元素的集合,含有2n 个子集,2n-1个真子集三、集合的运算 运算类型交 集 并 集 补 集 定 义 由所有属于A 且属于B 的元素所组成的集合,叫做A,B 的交集.记作A I B (读作‘A 交B ’),即A I B={x|x ∈A ,且x ∈B }. 由所有属于集合A 或属于集合B 的元素所组成的集合,叫做A,B 的并集.记作:A Y B (读作‘A 并B ’),即A Y B ={x|x ∈A ,或x ∈B}). 设S 是一个集合,A 是S 的一个子集,由S 中所有不属于A 的元素组成的集合,叫做S 中子集A 的补集(或余集) 记作A C S ,即C S A=},|{A x S x x ∉∈且韦 恩 图示 S A性 质 A I A=A A I Φ=Φ A I B=B I A A I B ⊆A A I B ⊆B A Y A=A A Y Φ=A A Y B=B Y A A Y B ⊇A A Y B ⊇B (C u A) I (C u B) = C u (A Y B)(C u A) Y (C u B) = C u (A I B) A Y (C u A)=UA I (C u A)= Φ.1.下列四组对象,能构成集合的是 ( )A 某班所有高个子的学生B 着名的艺术家C 一切很大的书D 倒数等于它自身的实数2.集合{a ,b ,c }的真子集共有 个3.若集合M={y|y=x 2-2x+1,x ∈R},N={x|x ≥0},则M 与N 的关系是 .4.设集合A=}{12x x <<,B=}{x x a <,若A ⊆B ,则a 的取值范围是5.50名学生做的物理、化学两种实验,已知物理实验做得正确得有40人,化学实验做得正确得有31人,两种实验都做错得有4人,则这两种实验都做对的有 人。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章
三、基本建设程序
(一) 基本建设程序的含义
(二) 基本建设程序的内容
第一章
三、基本建设程序
(一) 基本建设程序的含义
1.含义:
基本建设工作中必须按照一定的工作顺序,从决策、设计、施 工到竣工验收,有计划、有步骤、扎扎实实地工作,才能保证 工程建设的顺利进行。
就业去向:业主、造价咨询、设计、监理、施工 课程性质:专业选修 36个学时 2个学分
前言
前言
课程特点
1、土木工程概预算与清单计价是一门技术性、专业性、实践性、综合性和政 策性很强的课程。
2、不仅涉及土木工程技术、施工工艺、施工手段及方法,而且与社会性质、 国家的方针政策,分配制度有着密切的关系。
3、在研究的对象中,既有生产力方面的课题,也有生产关系方面的课题,既 有实际问题,又有方针政策问题。
3)内容:
市场供需研究、技术研究和经济研究。
比较重要的阶段
4)总论:
项目提出的背景、投资的必要性和经济意义以及研究工作 的依据和范围;需求预测和拟建规模;资源、原材料、燃 料及公共设施情况;建厂条件和方案选择,包括地理、气 象、水文、地质、地形条件和社会经济现状,交通运输及 水电气的现状和发展趋势;项目设计方案;环境保护,预 测对环境的影响;项目实施进度计划;投资估算和资金筹 措,主体工程和协作配套工程需要的投资、资金来源等; 财务和国民经济评价及评价结论。
• ①是建设项目进行材料、设备的安排、各种非标准设备的 制作的依据 • ②施工图预算编制的依据 • ③土建与安装工程施工的依据。
• 如果采用三阶段设计时,在初步设计和施工图设计之间增 加技术设计阶段,进一步确定初步设计中所采用工艺过程: 建筑和结构的重大技术问题,设备的选型和数量,并编制 修正概算。
是指原有企业或事业单位,由于各种原因迁到另外的地方建设 的项目。
第一章
二、基本建设项目分类
(三)按照规模分类
一般可分为大、中、小型项目,划分标准各行业和企 业不尽相同。
生产单一产品的企业 生产多种产品的企业 难以按生产能力划分 按产品的设计能力划分 按主要产品的设计能力划分 按全部投资额划分
第一章
编 制 设 计 任 务 书
设 计 阶 段
施 工 准 备 阶 段
组 织 施 工
竣 工 验 收
后 评 价 阶 段
施工预算
第一章
三、基本建设程序
1.项目建议书阶段
1)含义:
项目建议书是建设单位向国家提出要求建设某一具体项目 的建议文件。
2)作用:
推荐作用,是基本建设的最初级阶段,是投资决策前对拟 建项目的轮廓设想,主要是从拟建项目的必要性和可行性 进行考虑。
第一章
三、基本建设程序
1)施工图设计
• 施工图设计室根据批准的初步设计文件对工程建设方 案进一步具体化、明确化。其主要内容有:
• • • • ①建筑平立坡面图 ②建筑详图 ③结构布臵图和结构详图。 ④各种设备的标准型号、规格及非标准设备的施工图。
第一章
三、基本建设程序
1)施工图设计
• 施工图设计其作用
(1)固定资产再生产是固定资产消耗、补偿、更新、扩大过程, 是一个连续反复的过程。 (2)类型
简单再生产:更新和替换、维持原有规模、生产能力和功效。 扩大再生产:在原有基础上增添新的固定资产使生产能力和 工程效益增加。
注意:固定资产的再生产并不都是基本建设。
第一章
二、基本建设项目分类
基本建设项目是由基本建设工程项目组成,根 据工程项目的性质、用途和规模不同,可将建 设项目作如下分类:
1.实质:
形成新的固定资产的经济活动过程。
2.表现:
基本建设最终成果表现为固定资产的增加。
第一章
一、基本建设
3.实现和内容 ·基本建设是一种宏观的经济活动,它是通过建筑业的 勘察,它是通过建筑业的勘察设计和施工等活动,以 及其他有关部门的经济活动来实现。具体内容包括:
(1)资源开发规划工作:用以确定基本建设投资规模结构、建筑 布局、技术政策和技术结构、环境保护、项目决策等。 (2)建筑、生产准备竣工验收、联动试车
第一章
三、基本建设程序
4. 施工准备阶段
技术准备 征地拆迁 三通一平 五通一平 七通一平 水 电 路 场地平整 水 电 路 通讯 燃气 场地平整 水 排水 电力 道路 通讯 燃气 热力 场地平整 修建临时生产和生活设施 协调图纸和技术资料供应 落实地方材料和设备,制品的供应及施工测量等。 提高开工报告,按投资隶属关系报请基建主管部门核准。 银行会同建设、设计、施工单位做好通知会审,严格按计 划要求进行财政拨款或贷款。
第一章
第一章 建筑工程概预算总论
第一节 基本建设概论
第二节 基本建设工程项目和费用
第三节 基本建设概预算组成
第一章
第一节 基本建设概论
一、 基本建设的含义
二、 基本建设项目分类
三、 基本建设程序
第一章
一、基本建设
(一) 基本建设概念 ·基本建设是实现社会主义扩大再生产的重要手段,为 国民经济各部门的发展和人民物质文化生活水平的提 高建立物质基础。
2.特点:
1)多行业、多部门密切配合 2)综合性强、涉及面广、环节多
3.要求:
按照一定的顺序进行基本建设、妥善处理各个环节之间的关系, 才能保证工程建设的顺利进行。
第一章
三、基本建设程序
(二) 基本建设程序的内容
投资估算 概预算 合同价 工程结算 竣工决算
项 目 建 议 书
进 行 可 行 性 研 究
·具体指:建筑工程、安装工程、设备工器具的购买以
及其他基本建设工作。
第一章
一、基本建设
(二) 固定资产
·使用期限在一年以上,单位价值在规定数额以
上的主要劳动资料和非生产用房屋建筑。
1.特点:
(1)使用期限 (2)单位价值 (3)其转移过程特殊(价值)
第一章
一、基本建设
(二) 固定资产
2.固定资产再生产
5.迁建项目:是指原有企业或事业单位,由于各种原因迁到另
外的地方建设的项目。
第一章
二、基本建设项目分类
(二)按用途划分
1.生产性建设项目:
指直接用于物质生产或满足物质生产所需要的建设项目。具体 包括工业、建筑业、农业、林业、水利、气象、运输、邮电、 商业或物质供应、地质资源勘探等建设
2.非生产性建设项目:
前言
造价工程师
1. 经全国统一考试合格,取得《造价工程师执业资格证书》 并经注册登记,在建设工程中从事造价业务活动的专业技术人 员。 2. 由国家授予资格并准予注册后执业,专门接受某个部门或 某个单位的指定、委托或聘请,负责并协助其进行工程造价的 计价、定价及管理业务,以维护其合法权益的工程经济专业人 员。国家在工程造价领域实施造价工程师执业资格制度。凡从 事工程建设活动的建设、设计、施工、工程造价咨询、工程造 价管理等单位和部门,必须在计价、评估、审查(核)、控制 及管理等岗位配套有造价工程师执业资格的专业技术人员。 3. 1998年1月,人事部、建设部下发了《人事部、建设部关 于实施造价工程师执业资格考试有关问题的通知》(人发 „1998‟8号),并于当年在全国首次实施了造价工程师执业
建筑工程概预算
前言
前言
建筑工程概预算是介绍建设单位(业主)确定 建筑工程投入与建筑工程成本,施工企业(承 包商)确定工程收入的一门经济课程。
前言
前言
课程任务:
掌握工程造价的基本知识和定额基本原理; 计算建筑工程各阶段造价(重点施工图预算)思路和方法; 建立工程造价管理的思维观念和方法; 具有工程造价管理的初步能力。
第一章
三、基本建设程序
1)初步设计
• 就是对已经批准的可研报告所提的内容进行初步计算的概 括的计算,并作出初步决定,它由文字说明、图纸和总概 算三部分组成。 • 其作用就是作为主要设备订货、施工准备工作、土地征用、 控制基本建设投资、施工图设计或技术设计、编制施工组 织总设计和施工图预算的依据。 • 初步设计和总概算按其规模大小和规定的审批程序,报相 应的主管部门批准,经批准后方可进行技术设计或施工图 设计。
第一章
三、基本建设程序
4. 施工准备阶段
工程开工前对建设项目所需要的主要设备和材料 申请订货,并组织大型专业设备预安排和施工准 备,提出开工报告。 为保证施工顺利进行,在施工准备阶段,建设主 管部门应根据计划要求的建设进度,制定一个企 业或事业单位基建管理机构办理登记及拆迁,做 好施工沿线有关单位和部门的协调工作,抓紧配 套工程项目的落实,组织分工范围内的技术资料、 材料、设备的供应。
前言
报考条件
1.工程造价专业大专毕业,从事工程造价业务工作满5年;工程
或工程经济类大专毕业,从事工程造价业务工作满6年。
2.工程造价专业本科毕业,从事工程造价业务工作满4年;工程 或工程经济类本科毕业,从事工程造价业务工作满5年。 3.获上述专业第二学士学位或研究生班毕业和获硕士学位,从 事工程造价业务工作满3年。
第一章
二、基本建设项目分类
(一)按性质划分
1.新建项目:新开始建设的项目或对原有建设项目重新进行总
体设计,经扩大规模后,其新增固定资产价值超过原有固定资 产价值三倍以上的建设项目。
2.扩建项目:为扩大原有主要产品的生产能力或效益,增加新
产品生产能力,在原有固定资产的基础上,兴建一些主要车间 或其他固定资产的项目。
第一章
三、基本建设程序
5. 建筑实施阶段
是指按照计划、设计文件,编制施工组织设计进 行施工,将建设项目的设计变成可供人们进行生 产和生活的建筑物、构筑物等固定资产。
施工单位遵照施工程序合理组织施工,施工过程 中严格按照设计要求和施工规范,确保工程质量、 安全施工,推广应用新工艺、新技术,努力缩短 工期,降低造价。同时做好施工记录,建立技术 档案。
