2012年北京昌平二模数学理

合集下载

2012年北京市各区二模试题分类解析【数学理】(17)：几何证明选讲.pdf

二、[教学重点] 1．了解作者留学日本的情况、与藤野先生的交往和本文的写作背景。

2．把握课文的组织结构，理解课文的思想内容。

三、[教学难点] 掌握本文通过典型事例突出人物品质的写法五、[教学过程] 第一课时 [教学内容] 了解背景，学习词语，初读课文。

[教学环节] 一、导入新课学过了《从百草园到三味书屋》这篇散文，我们了解到三味书屋中的老先生虽然施行的是封建书塾教育，但思想还算开明，因此，鲁迅对他“很恭敬”。

虽是“很恭敬”，但并不是很有感情。

藤野先生是鲁迅在日本仙台学医时的一位日本医专的教授，他是一位怎样的老师呢？鲁迅对他的感情又是如何呢？让我们一起走访《藤野先生》吧！二、简介作者、藤野先生和作品的写作背景。

三、学生默读课文，疏通有关阅读障碍要求：1．标注出难字难词。

2．注意：文章变换了几个地点? 3．划分文章的段落层次，并说说各部分的大意。

学生默读后，讨论明确： 1．需要注意的字词列举如下：（多媒体展示）绯(fēi)红：鲜红。

会馆：旧时同乡或同业的人在京城、省会或大商埠设立的寄寓和机构。

流言：流传的毫无根据的坏话。

瞥(pīe)见：很快地看一下。

畸(jī)形：不正常的形状。

遗民：a．留下的在国外的人；b．改朝换代后仍效忠前一朝代的人；c．大乱后遗留下来的人民。

不逊(Xùn)：不客气；无礼貌；骄傲、蛮横。

美其名曰：(把不美的事物)美化它的名字叫。

四、学习课文第一部分 1．学生自由朗读第一部分内容。

2．思考：(1)请标出最能表现清国留学生丑态的词语和句子。

(2)对于这些清国留学生，“我”是持什么态度?哪些词语表明了“我”的态度? (3)从“我”的态度，可以看出作者的什么思想? 表达了作者对东京“清国留学生”的恶浊生活的憎恶、失望和不满，强有力地讽刺了这些顽固维护清王朝统治的“遗少”，强烈表达了作者对他们的极端憎恶的感情。

3．找出人物外貌、语言描写的语句，体现了人物什么特点。

2012年北京市各区高考二模试题分类解析【数学

一、集合（必修一）
1.（2012年朝阳二模文）设集合，则（ D ）
A．B．C．D．
2.（2012年丰台二模文9）已知集合A =｛x｜2x-x2>0｝，B =｛x｜x>1｝，则______．
答案：。

3.（2012年昌平二模文1）若集合,，则（ B ）
A.{}
B. {}
C. {}
D. {}
4.（2012年东城二模文1）若集合，且，则集合可能是（ A ）
A． B. C. D.
六、不等式（必修五）
1.（2012年西城二模文12）已知函数是上的偶函数，则实数
_____；不等式的解集为_____．
答案：，。

2.（2012年昌平二模文6）爬山是一种简单有趣的野外运动，有益于身心健康，但要注意安全，准备好必需物品，控制好速度.现有甲、乙两人相约爬山，若甲上山的速度为，下山的速度为（），乙上下山的速度都是（甲、乙两人中途不停歇），则甲、乙两人上下山所用的时间的关系为（ A ）
A． B. C. D. 不能确定
七、常用逻辑用语（选修2-1）
1.（2012年朝阳二模文3）如果命题“且”是假命题，“”也是假命题，则（ C ）
A．命题“或”是假命题B．命题“或”是假命题
C．命题“且”是真命题D．命题“且”是真命题
2.（2012年昌平二模文2）“” 是“垂直”的（ C ）
A. 充分而不必要条件 B必要而不充分条件 C. 充要条件 D.既不充分也不必要条件
3.（2012年海淀二模文2）已知命题：，. 则为（ D ）
A．， B. ，
C. ，
D. ，
温馨提示-专业文档供参考，请仔细阅读后下载，最好找专业人士审核后使用！。

2012昌平区中考数学二模

2012昌平区中考数学二模一、选择题（共8道小题，每小题4分，共32分）下列各题均有四个选项，其中只有一个是符合题意的．1．（4分）的倒数是（）A．﹣2 B．2 C．D．2．（4分）下列图形中，是中心对称图形，但不是轴对称图形的是（）A．B．C．D．3．（4分）如图，AB是⊙O的直径，C、D是⊙O上的两点，若∠ABC=70°，则∠BDC的度数为（）A．50°B．40°C．30°D．20°4．（4分）若|m+2|+（n﹣1）2=0，则m+2n的值为（）A．﹣4 B．﹣1 C．0 D．45．（4分）下列四个几何体中，主视图是三角形的是（）A．B．C．D．6．（4分）如图，用一个交叉卡钳（两条尺长AC和BD相等，OC=OD）量零件的内孔直径AB．若OC：OA=1：2，量得CD=10，则零件的内孔直径AB长为（）A．30 B．20 C．10 D．57．（4分）在1，2，3三个数中任取两个，组成一个两位数，则组成的两位数是偶数的概率为（）A．B．C．D．8．（4分）下图能折叠成的长方体是（）A．B．C．D．二、填空题（共4道小题，每小题4分，共16分）9．（4分）若分式的值为零，则x的值为．10．（4分）圆锥的母线长为3，底面半径为2，则它的侧面积为．11．（4分）已知一个菱形的周长是20，两条对角线的长的比是4：3，则这个菱形的面积是．12．（4分）如图的方格纸中，每个小方格都是边长为1的正方形，A、B两点是方格纸中的两个格点，在4×5的方格纸中，找出格点C，使△ABC的面积为1个平方单位，则满足条件的格点C的个数是．三、解答题（共6道小题，每小题5分，共30分）13．（5分）计算：2﹣1+sin45°﹣|﹣|+（﹣2012）0．14．（5分）解方程：15．（5分）已知，求代数式（x+1）2﹣4（x+1）+4的值．16．（5分）已知：如图，在等边三角形ABC中，点D、E分别是AB、BC延长线上的点，且BD=CE．求证：DC=AE．17．（5分）如图，已知：反比例函数（x＜0）的图象经过点A（﹣2，4）、B（m，2），过点A作AF⊥x轴于点F，过点B作BE⊥y轴于点E，交AF于点C，连接OA．（1）求反比例函数的解析式及m的值；（2）若直线l过点O且平分△AFO的面积，求直线l的解析式．18．（5分）列方程（组）解应用题：李明同学喜欢自行车和长跑两项运动，在某次训练中，他骑自行车的平均速度为每分钟600米，跑步的平均速度为每分钟200米，自行车路段和长跑路段共5000米，用时15分钟．求自行车路段和长跑路段的长度．四、解答题（共4道小题，每小题5分，共20分）19．（5分）在Rt△ABC中，∠ACB=90°，BC=4．过点A作AE⊥AB且AB=AE，过点E分别作EF⊥AC，ED⊥BC，分别交AC和BC的延长线与点F，D．若FC=5，求四边形ABDE的周长．20．（5分）如图，⊙O的半径OA与OB互相垂直，P是线段OB延长线上的一点，连接AP交⊙O于点D，点E在OP上且DE=EP．（1）求证：DE是⊙O的切线；（2）作DH⊥OP于点H，若HE=6，DE=4，求⊙O的半径的长．21．（5分）某学校为了了解学生本学期参加社会实践的情况，随机抽查了该校部分学生参加社会实践活动的天数，并用得到的数据绘制了下面两幅不完整的统计图：请你根据图中提供的信息，回答下列问题：（1）该校对多少名学生进行了抽样调查？（2）补全条形统计图和扇形统计图；（3）该校共有学生1000人，请你估计“活动时间不少于5天”的大约有多少人？22．（5分）类比学习：有这样一个命题：设x、y、z都是小于1的正数，求证：x（1﹣y）+y（1﹣z）+z（1﹣x）＜1．小明同学是这样证明的：如图，作边长为1的正三角形ABC，并分别在其边上截取AD=x，BE=z，CF=y，设△ADF、△CEF和△BDE的面积分别为S1、S2、S3，则，，．由S1+S2+S3＜S△ABC，得++＜．所以x（1﹣y）+y（1﹣z）+z（1﹣x）＜1．类比实践：已知正数a、b、c、d，x、y、z、t满足a+x=b+y=c+z=d+t=k．求证：ay+bz+ct+dx＜2k2．五、解答题（共3道小题，第23小题6分，第24，25小题各8分，共22分）23．（6分）已知m为整数，方程2x2+mx﹣1=0的两个根都大于﹣1且小于，当方程的两个根均为有理数时，求m 的值．24．（8分）如图所示，在平面直角坐标系xOy中，正方形OABC的边长为2cm，点A、C分别在y轴和x轴的正半轴上，抛物线y=ax2+bx+c经过点A、B和D（4，）．（1）求抛物线的解析式；（2）在抛物线的对称轴上找到点M，使得M到D、B的距离之和最小，求出点M的坐标；（3）如果点P由点A出发沿线段AB以2cm/s的速度向点B运动，同时点Q由点B出发沿线段BC以1cm/s的速度向点C运动，当其中一点到达终点时，另一点也随之停止运动．设S=PQ2（cm2）．①求出S与运动时间t之间的函数关系式，并写出t的取值范围；②当S=时，在抛物线上存在点R，使得以P、B、Q、R为顶点的四边形是平行四边形，求出点R的坐标．25．（8分）如图，在Rt△ABC中，∠ABC=90°，过点B作BD⊥AC于D，BE平分∠DBC，交AC于E，过点A作AF ⊥BE于G，交BC于F，交BD于H．（1）若∠BAC=45°，求证：①AF平分∠BAC；②FC=2HD．（2）若∠BAC=30°，请直接写出FC与HD的等量关系．参考答案与试题解析一、选择题（共8道小题，每小题4分，共32分）下列各题均有四个选项，其中只有一个是符合题意的．1．【解答】的倒数是﹣2，故选：A．2．【解答】A、不是轴对称图形，是中心对称图形．故此选项正确；B、是轴对称图形，也是中心对称图形．故此选项错误；C、是轴对称图形，不是中心对称图形．故此选项错误；D、是轴对称图形，不是中心对称图形．故此选项错误．故选：A．3．【解答】∵AB是⊙O的直径，∴∠ACB=90°，∵∠ABC=70°，∴∠BAC=90°﹣∠ABC=20°，∴∠BDC=∠BAC=20°．故选D．4．【解答】根据题意得，m+2=0，n﹣1=0，解得m=﹣2，n=1，∴m+2n=﹣2+2×1=0．故选C．5．【解答】主视图是三角形的一定是一个锥体，只有B是锥体．故选：B．6．【解答】∵两条尺长AC和BD相等，OC=OD∴OA=OB∵OC：OA=1：2∴OD：OB=OC：OA=1：2∵∠COD=∠AOB∴△AOB∽△COD∴CD：AB=OC：OA=1：2∵CD=10∴AB=20故选B．7．【解答】共有6种情况，是偶数的有2种情况，所以组成的两位数是偶数的概率为，故选A．8．【解答】根据各种符号的面的特点及位置可得，能折叠成的长方体是D．故选D．二、填空题（共4道小题，每小题4分，共16分）9．【解答】分式值为0，则2x﹣4=0，解得x=2，当x=2时，x+1=3≠0．故当x=2时，分式的值是0．10．【解答】圆锥的侧面积=2π×2×3÷2=6π．11．【解答】如图，菱形ABCD的周长是20，AC：BD=4：3，∵四边形ABCD是菱形，∴AB=BC=CD=AD=5，AC⊥BD，AC=2OA，BD=2OD，∴OA：OD=4：3，设OA=4x，OD=3x，在Rt△AOD中，AD==5x=5，∴x=1，∴OA=4，OD=3，∴AC=8，BD=6，∴∴S菱形ABCD=AC•BD=×8×6=24．故答案为：24．12．【解答】满足条件的C点有6个，如图平行于AB的直线上，与网格的所有交点就是．故答案为：6．三、解答题（共6道小题，每小题5分，共30分）13．【解答】原式=+﹣2+1=﹣．14．【解答】方程两边都乘以x（x﹣1），得x2+2（x﹣1）=x（x﹣1），解这个方程，得．经检验，是原方程的根．∴原方程的根是．15．【解答】原式=（x+1﹣2）2=（x﹣1）2，当时，原式==3．16．【解答】证明：∵△ABC是等边三角形，∴∠ABC=∠ACB=60°，BC=CA．∴∠DBC=∠ECA=180°﹣60°=120°．在△DBC与△ECA中，，∴△DBC≌△ECA．∴DC=AE．17．【解答】（1）把A（﹣2，4）代入y=得k=﹣2×4=﹣8，∴反比例函数的解析式为y=﹣，把B（m，2）代入y=﹣得，2m=﹣8，解得m=﹣4；（2）∵A点坐标为（﹣2，4）、B点坐标为（﹣4，2），而AF⊥x轴，BE⊥y轴，∴C点坐标为（﹣2，2），∴C点为AF的中点，∵直线l过点O且平分△AFO的面积，∴直线l过C点，设直线l的解析式为y=kx（k≠0），把C（﹣2，2）代入y=kx得2=﹣2k，解得k=﹣1，∴直线l的解析式为y=﹣x．18．【解答】：设自行车路段为x米根据题意得：，解得：x=3000，5000﹣x=2000米．答：自行车路段为3000米，长跑路段为2000米．四、解答题（共4道小题，每小题5分，共20分）19．【解答】∵∠ACB=90°，AE⊥AB，∴∠1+∠B=∠1+∠2=90°．∴∠B=∠2．∵EF⊥AC，∴∠4=∠5=90°．∴∠3=∠4．在△ABC和△EAF中，∵，∴△ABC≌△EAF（AAS）．∴BC=AF，AC=EF．∵BC=4，∴AF=4．∵FC=5，∴AC=EF=9．在Rt△ABC中，AB===．∴AE=．∵ED⊥BC，∴∠7=∠6=∠5=90°．∴四边形EFCD是矩形．∴CD=EF=9，ED=FC=5．∴四边形ABDE的周长=AB+BD+DE+EA=+4+9+5+=18+2．20．【解答】（1）证明：连接OD．∵OA=OD，∴∠A=∠1．∵DE=EP，∴∠2=∠P．∵OA⊥OB于O，∴∠A+∠P=90°．∴∠1+∠2=90°．∴∠ODE=90°．即OD⊥DE．∵OD是⊙O的半径，∴DE是⊙O的切线．（2）解：∵DH⊥OP于点H，∴∠DHE=90°．∵HE=6，DE=4，∴cos∠3===．∴∠3=30°∵在Rt△ODE中，tan∠3=，∴=．∴OD=4．即⊙O的半径为4．21．【解答】（1）总人数=20÷10%=200（名）；（2）实践6天的人数=200﹣20﹣30﹣60﹣40=50人，所占的比例==25%．补全图形如下：；（3）实践不少于5天的人数所占的比例=30%+25%+20%=75%，故可得“活动时间不少于5天”的人数大约为：（30%+25%+20%）×1000=750（名），答：“活动时间不少于5天”的大约有750人．22．【解答】证明：如图，作边长为k的正方形ABCD．并分别在各边上截取：AE=a，DH=b，CG=c，BF=d，∵a+x=b+y=c+z=d+t=k，∴BE=x，AH=y，DG=z，CF=t．∵∠A=∠B=∠C=∠D=90°，∴S1=ay，S2=dx，S3=ct，S4=bz．∵S1+S2+S3+S4＜S正方形ABCD，∴ay+dx+ct+bz＜k2．∴ay+bz+ct+dx＜2k2．五、解答题（共3道小题，第23小题6分，第24，25小题各8分，共22分）23．【解答】设y=2x2+mx﹣1．∵2x2+mx﹣1=0的两根都在﹣1和之间，∴当x=﹣1时，y＞0，即：2﹣m﹣1＞0．当x=时，y＞0，即：+m﹣1＞0．∴﹣2＜m＜1．∵m为整数，∴m=﹣2，﹣1，0；①当m=﹣2时，方程2x2﹣2x﹣1=0，△=4+8=12，∴此时方程的根为无理数，不合题意．②当m=﹣1时，方程2x2﹣x﹣1=0，x1=﹣，x2=1，符合题意．③当m=0时，方程2x2﹣1=0，x=±，不符合题意．综合①②③可知，m=﹣1．24．【解答】（1）据题意可知：A（0，2），B（2，2），C（2，0）．∵抛物线y=ax2+bx+c经过点A、B和D（4，），∴，∴，∴y=﹣x2+x+2；（2）点B关于抛物线的对称轴x=1的对称点为A．连接AD，与对称轴的交点即为M．∵A（0，2）、D（4，），∴直线AD的解析式为：y=﹣x+2，当x=1时，y=，则M（1，）；（3）①由图象知：PB=2﹣2t，BQ=t，AP=2t，∵在Rt△PBQ中，∠B=90°，∴S=PQ2=PB2+BQ2，∴=（2﹣2t）2+t2，即S=5t2﹣8t+4（0≤t≤1）．②当S=时，=5t2﹣8t+4即20t2﹣32t+11=0，解得：t=，t=＞1（舍）∴P（1，2），Q（2，）．∴PB=1．若R点存在，分情况讨论：（i）假设R在BQ的右边，如图所示，这时QR=PB，RQ∥PB，则R的横坐标为3，R的纵坐标为，即R（3，），代入y=﹣x2+x+2，左右两边相等，故这时存在R（3，）满足题意；（ii）假设R在PB的左边时，这时PR=QB，PR∥QB，则R（1，）代入y=﹣x2+x+2，左右两边不相等，则R不在抛物线上综上所述，存点一点R，以点P、B、Q、R为顶点的平行四边形只能是□PQRB．则R（3，）．此时，点R（3，）在抛物线=﹣x2+x+2上．25．【解答】（1）①∵BD⊥AC，AF⊥BE，∴∠ADH=∠HGB=90°．∵∠BHG=∠AHD，∴∠HBG=∠HAD．∵∠ABC=∠FGB=90°，∴∠BAF+∠AFB=90°，∠GBF+∠AFB=90°．∴∠GBF=∠BAF．∵BE平分∠DBC，∴∠GBF=∠HBG．∴∠HAD=∠BAF．即AF平分∠BAC．②∵在Rt△ABC中，∠ABC=90°，∠BAC=45°，∴∠C=∠BAC=45°，∴AB=BC．∵BD⊥AC，∴AD=DC=AC．过点D作KD∥FC交AF于K，∴==．∴FC=2KD，∵BE平分∠DBC，BE⊥AF，∴∠DBE=∠EBF，∠HGB=∠FGB=90°．∴∠BFH=∠BHF．∴∠BHF=∠DHK．∴∠BFH=∠DHK．∵KD∥BC，∴∠DKH=∠BFH．∴∠DKH=∠DHK．∴KD=HD．∴FC=2HD．（2）过点D作MD∥FC交AF于M，∵在Rt△ABC中，∠ABC=90°，∠BAC=30°，∴=，=，∴=，∵MD∥FC，∴==，∵BE平分∠DBC，BE⊥AF，∴∠DBE=∠EBF，∠HGB=∠FGB=90°．∴∠BFH=∠BHF．∵∠BHF=∠DHM．∴∠BFH=∠DHM．∵MD∥BC，∴∠DMH=∠BFH．∴∠DMH=∠DHM．∴MD=HD．∴=．∴FC=HD．。

2012年北京各区县二模试题分类几何综合解析版

2012年北京各区县二模试题分类几何综合解析版2012年北京市中考数学二模分类汇编——几何综合与中点有关的问题1.(昌平24) 如图，D 是△ABC 中AB 边的中点，△BCE 和△ACF 都是等边三角形，M 、N 别是CE 、CF 的中点. （1）求证：△DMN 是等边三角形；（2）连接EF ，Q 是EF 中点，CP ⊥EF 于点P .求证：DP ＝DQ . 同学们，如果你觉得解决本题有困难，可以阅读下面两位同学的解题思路作为参考：小聪同学发现此题条件中有较多的中点，因此考虑构造三角形的中位线，添加出了一些辅助线；小慧同学想到要证明线段相等，可通过证明三角形全等，如何构造出相应的三角形呢？她考虑将△NCM 绕顶点旋转到要证的对应线段的位置，由此猜想到了所需构造的三角形的位置.24. 证明：（1）取AC 的中点G ，连接NG 、DG .NME F C∴DG ＝21BC ，DG ∥BC ；△NGC 是等边三角形.∴NG = NC CM . …………………2分 ∵∠1 + ∠2 = 180º，∴∠NGD + ∠2 = 240º.∵∠2 + ∠3 = 240º，∴∠NGD =∠3.∴△NGD≌△NCM . ……………………3分 ∴ND = NM ，∠GND =∠CNM .∴∠DNM =∠GNC = 60º.∴△DMN 是等边三角形.………………………………4分（2）连接QN 、PM .∴QN=21CE= PM . ……………………5分Rt △CPE 中，PM =EM ，∴∠4= ∠5.∵MN ∥EF ，∴∠5= ∠6，∠7=∠8.67854P Q N M E C C 321G NM E F∵NQ ∥CE ，∴∠7= ∠4.∴∠6= ∠8.∴∠QND = ∠PMD . ………………………6分∴△QND ≌△PMD .∴DQ = DP . ……………………7分2.（丰台24）在△ABC 中，D 为BC 边的中点，在三角形内部取一点P ，使得∠ABP =∠ACP ．过点P 作PE ⊥AC 于点E ，PF ⊥AB 于点F ．（1）如图1，当AB =AC 时，判断的DE 与DF 的数量关系，直接写出你的结论；（2）如图2，当AB AC ，其它条件不变时，（1）中的结论是否发生改变？请说明理由．图1图224．解：（1）DE =DF ．……1分A E F PB DC E B A DF P（2）DE =DF 不发生改变． (2)分理由如下：分别取BP 、CP 的中点M 、N ，联结EM 、DM 、FN 、DN ．∵D 为BC 的中点，∴BP DN BP DN //,21=．……3分∵,AB PE ⊥∴BP BM EM 21==． ∴21,∠=∠=EM DN ．∴12213∠=∠+∠=∠．…4分同理,524,//DM FN MD PC =∠=∠．∴四边形MDNP 为平行四边形．……5分∴67∠=∠ ∵,41∠=∠∴35∠=∠． ∴EMD DNF ∠=∠．……6分∴△EMD ≌△DNF ． ∴DE =DF ．……7分3.(海淀25.)在矩形ABCD 中, 点F 在AD 延长线上，且DF = DC , M 为AB 边上一点, N 为MD 的中点, 点E 在直线CF 上（点E 、C 不重合）.（1）如图1, 若AB =BC , 点M 、A 重合, E为CF 的中点，试探究BN 与NE 的位置关系及BM CE 的值, 并证明你的结论;（2）如图2，且若AB =BC , 点M 、A 不重合,7654321N M C D B P F E ABN =NE ，你在（1）中得到的两个结论是否成立,若成立,加以证明; 若不成立, 请说明理由;（3）如图3，若点M 、A 不重合，BN =NE ，你在（1）中得到的结论两个是否成立, 请直接写出你的结论.图 1 图 2 图325. 解：（1）BN 与NE 的位置关系是BN ⊥NE ；CE BM 2 证明：如图，过点E 作EG ⊥AF 于G , 则∠EGN =90°．∵ 矩形ABCD 中, AB =BC ，∴ 矩形ABCD 为正方形.∴ AB =AD =CD , ∠A =∠ADC =∠DCB =90°．∴ EG//CD , ∠EGN =∠A , ∠CDF =90°．……………1分∵ E 为CF , F A ( M ) D N D A C E N M B F E C BF N M E C B∴ GF =DG =11.22DF CD = ∴ 1.2GE CD = ∵ N 为MD (AD )的中点，∴ AN =ND =11.22AD CD = ∴ GE =AN ,NG=ND+DG=ND+AN=AD=AB . ………2分∴ △NGE ≌△BAN ．∴ ∠1=∠2.∵ ∠2+∠3=90°，∴ ∠1+∠3=90°．∴ ∠BNE =90°.∴ BN ⊥NE ． ……………………………3分∵ ∠CDF =90°, CD =DF ,可得 ∠F =∠FCD =45°， 2.CF CD =. 于是122CF CE CE CE BM BA CD CD ==== …………4分（2）在（1）中得到的两个结论均成立.证明：如图，延长BN 交CD 的延长线于点G ，连结BE 、GE ，过E 作EH ⊥CE ，交CD 于点H ．H B C E M∵四边形ABCD是矩形，∴AB∥CG．∴∠MBN=∠DGN，∠BMN=∠GDN.∵N为MD的中点，∴MN=DN．∴△BMN≌△GDN．∴MB=DG，BN=GN.∵BN=NE，∴BN=NE=GN.∴∠BEG=90°． (5)分∵EH⊥CE，∴∠CEH =90°．∴∠BEG=∠CEH．∴∠BEC=∠GEH．由（1）得∠DCF =45°．∴∠CHE=∠HCE =45°．∴EC=EH,∠EHG =135°．∵∠ECB=∠DCB+∠HCE =135°，∴∠ECB =∠EHG．∴△ECB≌△EHG．∴EB=EG，CB=HG．∵BN=NG，∴BN⊥NE. ……………………6分∵BM =DG= HG-HD= BC-HD =CD-2CE，∴2. ……………………7分CEBM不一定等于（3）BN⊥NE；CEBM2. ……………………8分密云25．已知菱形ABCD的边长为1，60ADC∠=o，等边△AEF两边分别交DC、CB于点E、F．（1）特殊发现：如图1，若点E、F分别是边DC、CB的中点，求证：菱形ABCD对角线AC、BD的交点O即为等边△AEF的外心；（2）若点E、F始终分别在边DC、CB上移动，记等边△AEF的外心为P．①猜想验证：如图2，猜想△AEF的外心P落在哪一直线上，并加以证明；②拓展运用：如图3，当E 、F 分别是边DC 、CB 的中点时，过点P 任作一直线，分别交DA 边于点M ，BC 边于点G ，DC 边的延长线于点N ，请你直接写出11DM DN+的值．25．（本小题满分8分）证明：（1）如图1：分别连结OE 、OF ．∵四边形ABCD 是菱形，∴AD DC CB ==，AC BD ⊥，DO BO =，且112302ADC ∠=∠=∠=o ． ∴在Rt △AOD 中，有12AO AD =．又 E 、F 分别是边DC 、CB 的中点，∴1122EO CB DC OF ===．∴AO EO FO ==．∴点O 即为等边△AEF 的外心． ------------------------- 3分（2）①猜想：△AEF 的外心P 落在对角线DB 所在的直线上．证明：如图2：分别连结PE 、PA ，作PQ DC ⊥于Q ，PH AD⊥于H ．则90PQE PHD ∠=∠=o∵60ADC ∠=o， ∴在四边形QDHP 中，120QPH ∠=o．又 ∵点P 是等边△AEF 的外心，60EFA ∠=o，∴PE PA =，2260120EPA EFA ∠=∠=⨯=oo． ∴αβ∠=∠．∴△PQE ≌△PHA （AAS ）．∴PQ=PH ． ∴点P 在ADC ∠的角平分线上．∵菱形ABCD 的对角线DB 平分ADC ∠， ∴ 点P 落在对角线DB 所在直线上--- 6分 ②112DM DN+=． ---------------------- 8分旋转变换在几何证明应用延庆24. （1）如图1：在△ABC 中，AB=AC ，当∠ABD =∠ACD=60°时，猜想AB 与BD+CD 数量关系，请直接写出结果；（2）如图2：在△ABC 中，AB=AC ，当∠ABD =∠ACD=45°时，猜想AB 与BD+CD 数量关系并证明你的结论；（3）如图3：在△ABC 中，AB=AC ，当∠ABD =∠ACD=β（20°≤β≤70°）时，直接写出AB 与BD+CD 数量关系(用含β的式子表示)。

2012年北京市各区二模试题分类解析【数学理】(10)：平面向量.pdf

课题使用人编号07课型新授课课时1主备人石伟锋备课时间教学目标（一）情感、态度、价值观：树立正确的资源环境意识和对自然环境的忧患意识。

以保护环境为荣，以破坏环境为耻，树立人与自然和谐共处的人生价值。

有意识的控制人对自然的破坏行为。

（二）能力：能从自我做起，珍爱和保护大自然的一切生命。

提高保护自然、保护环境的能力。

（三）知识：了解人与大自然的不和谐之音的表现，懂得人与大自然和谐相处的重要性。

重点难点教学难点：自然景观遭到人为的破坏教具多媒体电子白板教法学法讨论、欣赏、感悟、体验历年考点展示交流自然物种在减少自然景观遭到人为破坏教师引导，PPT出示材料，阅读思考、讨论：大自然物种不断减少、甚至灭绝的原因是什么？如何保护物种，我们能做些什么？教师引导，PPT出示材料，这些自然景观为什么遭到人为破坏？如何去改变这种状况? 教师引导归纳总结结合本地实际，探讨如何保护自然景观学生先阅读课本和PPT材料 ⑴、思考讨论，学生畅所欲言 ⑵讨论：如何保护物种，我们能做些什么？分小组交流：结合本地实际，探讨如何保护自然景观 15教学过程环节知识点教师活动学生活动估时合作探究展示交流3、环境状况不容乐观教师：PPT出示，环境的一些恶化状况的图片，然后让学生谈谈所知道的情况在观察的基础上，让学生总结，什么是环境问题？有什么危害？并初步探讨如何解决这些问题？老师对一些有创意的观点和看法做法及时鼓励和表扬，激发学生探究和参与环保的热情，进行有效的情感教育和升华。

积极思考结合实际总结归纳建言献策 11强化应用形成能力巩固训练投放课堂练习限时规范训练巩固学习成果规范答题反馈补偿12 构建网络知识结构1、先由学生谈谈观点、收获、体会。

2、老师总结2教后反思初中学习网，资料共分享！我们负责传递知识！含义：是指人类不合理地开发利用自然资源所造成的环境污染与破坏。

2012昌平高三(二模)数学(理)

昌平区2011－2012学年度第二学期高三年级第二次统一练习数学试卷（理科）2012. 4第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.1. 已知全集U = R ，集合}{042≤-=x x |x A ，}2{<=x |x B ，则B A = A. {0≥x |x } B. {20<≤x |x } C. {42≤<x |x } D. {40≤≤x |x } 2. 在复平面内，与复数i+11对应的点位于A ．第一象限B ．第二象限C ．第三象限D ．第四象限3. “1=a ” 是“002=-=+y a x y x 和直线直线垂直”的A. 充分而不必要条件 B 必要而不充分条件 C. 充要条件 D.既不充分也不必要条件4. 已知直线l ：为参数）t t y t x (1⎩⎨⎧+==，圆C ：2cos ρθ=，则圆心C 到直线l 的距离是 A. 2 B.3 C.2 D. 15.已知空间几何体的三视图如图所示，则该几何体的各侧面图形中，是直角三角形的有 A. 0个 B. 1个C. 2个D. 3 个6. 某电视台曾在某时间段连续播放5个不同的商业广告，现在要在该时间段新增播一个商业广告与两个不同的公益宣传广告，且要求两个公益宣传广告既不能连续播放也不能在首尾播放，则在不改变原有5个不同的商业广告的相对播放顺序的前提下，不同的播放顺序共有 A. 60种 B. 120种 C. 144种 D. 300种 7．如图，在棱长为a 的正方体1111D C B A ABCD -中，P 为11D A 的中点，Q 为11B A 上任意一点，F E 、为CD 上任意两点，且EF 的长为定值，则下面的四个值中不为定值的是 A. 点P 到平面QEF 的距离B. 直线PQ 与平面PEF 所成的角C. 三棱锥QEF P -的体积D.二面角Q EF P --的大小C 1A 1C主视图左视图8. 设等差数列{}n a 的前n 项和为n S ，已知()37712012(1)1a a -+-=，()32006200612012(1)1a a -+-=-，则下列结论正确的是A ．20122012S =，20127a a <B ．20122012S =，20127a a >C ．20122012S =-，20127a a <D ．20122012S =-，20127a a >第二部分（非选择题共110分）二、填空题共6小题，每小题5分，共30分. 9．在∆ABC 中，4,2,2π===A b a 那么角C =_________.10.已知双曲线的方程为1422=-y x ，则其渐近线的方程为____________,若抛物线px y 22=的焦点与双曲线的右焦点重合，则_______p =.11. 如图给出了一个程序框图，其作用是输入x 的值，输出相应的y 值,若要使输入的x 值与输出的y 值相等，则这样的x 值有 ___________个.12. 如图，AB 是⊙O 的直径，CD 切⊙O 于点D ，CA 切⊙O 于点A ，CD 交AB 的延长线于点E .若3AC =，2ED =，则BE =_____;AO =_____.13. 若变量 x , y 满足约束条件⎪⎩⎪⎨⎧≤-≥≤400x y y x 表示平面区域M ，则当-42≤≤a 时，动直线a y x =+所经过的平面区域M 的面积为____________. 14. 若对于定义在R 上的函数f (x ) ,其图象是连续不断的，且存在常数λ(∈λR )使得 f (x +λ) +λf (x ) = 0对任意实数x 都成立，则称f (x ) 是一个“λ—伴随函数”. 有下列关于“λ—伴随函数”的结论：①f (x ) =0 是常数函数中唯一个“λ—伴随函数”；②f (x ) = x 不是“λ—伴随函数”；③f (x ) = x 2是一个“λ—伴随函数”； ④“21—伴随函数”至少有一个零点. 其中不正．．确．的序号是________________（填上所有不．正确．．的结论序号）．三、解答题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程.15．（本小题满分13分）已知向量a (cos ,sin ),θθ= b = (13-,), 22π≤θ≤π-. （Ⅰ）当b a ⊥时，求θ的值; （Ⅱ）求||b a +的取值范围.16．(本小题满分13分)某游乐场将要举行狙击移动靶比赛. 比赛规则是：每位选手可以选择在A 区射击3 次或选择在B 区射击2次，在A 区每射中一次得3分，射不中得0分; 在B 区每射中一次得2分，射不中得0分. 已知参赛选手甲在A 区和B 区每次射中移动靶的概率分别是41和)10(<<p p .(Ⅰ) 若选手甲在A 区射击，求选手甲至少得3分的概率； (Ⅱ) 我们把在A 、B 两区射击得分的数学期望高者作为选择射击区的标准，如果选手甲最终选择了在B 区射击，求p 的取值范围.17.（本小题满分14分）在正四棱柱1111ABCD A BC D -中, 122AA AB ==,E 为AD 中点,F 为1CC 中点.（Ⅰ）求证:1AD D F ⊥；（Ⅱ）求证://CE 平面1AD F ；(Ⅲ) 求平面1AD F 与底面ABCD 所成二面角的余弦值.18．（本小题满分13分）已知函数∈+--=a x a xax x f ,ln )1()(R . （Ⅰ）当1>a 时，求)(x f 的单调区间;（Ⅱ）若)(x f 在]1[e ,上的最小值为2-，求a 的值. 19．（本小题满分14分）如图，已知椭圆M :)0(12222>>=+b a b y a x ,离心率36=e ,椭圆与x 正半轴交于点A ，直线l 过椭圆中心O ，且与椭圆交于B 、C 两点，B (1,1).(Ⅰ) 求椭圆M 的方程；（Ⅱ）如果椭圆上有两点Q P 、,使PBQ ∠的角平分线垂直于AO ，问是否存在实数)0(≠λλ使得AC PQ λ=成立？20. (本小题满分13分)实数列 3210a ,a ,a ,a ，由下述等式定义123,0,1,2,3,.n n n a a n +=-=（Ⅰ）若0a 为常数，求123,,a a a 的值；（Ⅱ）求依赖于0a 和n 的n a 表达式；（Ⅲ）求0a 的值，使得对任何正整数n 总有1n n a a +>成立.昌平区2011－2012学年度第二学期高三年级第二次统一练习数学( 理科)试卷2012.4 参考答案一、选择题(本大题共8小题，每小题5分，共40分．)二、填空题(本大题共6小题，每小题5分，共30分．)9．127π 10. x y 21±= , 52 11. 3 12. 1 ， 2313． 7 14. ① ③三、解答题(本大题共6小题，共80分) 15．（本小题满分13分）解：（Ⅰ） a ⊥b ∴b a ⋅0sin cos 3=-=θθ ……… 2分得3tan =θ 又∵22π≤θ≤π-……… 4分即：θ=3π………6分（Ⅱ）||b a +=4)sin cos 3(21||2||22+-+=+⋅+θθb b a a )3sin(45π--=θ ……… 9分22π≤≤π-θ 6365π≤π-≤π-∴θ ……… 11分 21)3s i n (1≤π-≤-∴θ 4)3s i n (42≤π--≤-∴θ∴33≤+≤||b a ……… 13分16．（本小题满分13分)解：（Ⅰ）设“选手甲在A 区射击得0分”为事件M ,“选手甲在A 区射击至少得3分”为事件N ,则事件M 与事件N 为对立事件, 6427)411(41)(3003=-⋅⋅=)(C M P ………2分 6437642711=-=-=)M (P )N (P ………4分(Ⅱ) 设选手甲在A 区射击的得分为ξ,则ξ的可能取值为0，3，6,9.6427)41-(10)(3===ξP ;6427)411(41C 3)(213=-⋅⋅==ξP ; 649)411()41(6)(223=-==ξC P ; 641)41(9)(3===ξP所以ξ的分布列为49641964966427364270=⨯+⨯+⨯+⨯=ξ∴E 设选手甲在B 区射击的得分为η，则η的可能取值为0，2，4.2)-(10)(p P ==η；)1(2)1(C 2)(12p p p p P -=-⋅⋅==η;24)(p P ==η所以η的分布列为p p )p (p )p (E 441221022=⋅+-⋅+-⨯=η∴根据题意，有 ξηE E > ∴1169494<<∴>p ,p ……… 13分 17.（本小题满分14分）（Ⅰ）证明：在正四棱柱1111ABCD A BC D -中四边形ABCD 是正方形, AD CD ∴⊥1DD ABCD AD ABCD ⊥⊂ 平面，平面1AD DD ∴⊥ 1DD CD D = 11AD CDD C ∴⊥平面111D F CDDC ⊂ 平面 1A D D F∴⊥ ……… 4分（Ⅱ）证明：在正四棱柱1111ABCD A BC D -中,连结1A D ,交1AD 于点M ,连结,ME MF . M ∴为1AD 中点.E 为AD 中点，F 为1CC 中点. 111//2ME DD ME DD ∴=且……… 6分又1121DD CF DD //CF =且 ∴四边形CEMF 是平行四边形. MF //CE ∴ ……… 8分CE ⊄ 平面1AD F ,MF ⊂平面1AD F .//CE ∴平面1AD F .………9分(Ⅲ)解：以D 为坐标原点，分别以1,,DA DC DD 为,,x y z 轴建立空间直角坐标系如图. 则1(0,0,0),(1,0,0),(1,1,0),(0,1,0),(0,0,2),(0,1,1)D A B C D F……… 10分∴平面ABCD 的法向量为1(0,0,2)DD =………11分设平面1AD F 的法向量为(,,)x y z =n .1(1,1,1),(1,0,2)AF AD =-=-，分则有10,0.AF AD ⎧⋅=⎪⎨⋅=⎪⎩n n 所以 0,20.x y z x z -++=⎧⎨-+=⎩ 取1z =，得(2,1,1)=n .111cos ,6DD DD DD ⋅〈〉==n n n . ………13分平面F AD 1与平面所成二面角为锐角.所以平面1AD F 与底面ABCD 所成二面角的余弦值为618．（本小题满分13分）解：（Ⅰ）f (x )的定义域为｛x |0>x ｝……………1分.2222))(1()1(11)(x a x x x x a a x x a x a x f --=+-+=+-+='…………3分1>a 令0)(>'x f ，即a x x x a x x ><>--或得1,0))(1(2，∴)(x f 的增区间为（0，1），),(+∞a ……………4分令0)(<'x f ，即a x xa x x <<<--1,0))(1(2得， ∴)(x f 的减区间为),1(a ……………5分（Ⅱ）①当1≤a 时， 0)(≥'x f 在]1[e ,上恒成立， ∴)(x f 在]1[e ,恒为增函数. … 6分21)1()]([min -=-==∴a f x f ，得.(3舍去）=a ……… 7分②当e a <<1 时，令0)(='x f ，得1或a x =. 当a x <<1时，0)(<'x f ∴)(x f 在),1(a 上为减函数；当e x a <<时，0)(>'x f ∴)(x f 在),(e a 上为增函数；2)ln()1(1)()]([min -=+--==∴a a a a f x f ，得（舍）……… 10分③当e a >时，0)(≤'x f 在],1[e 上恒成立，此时)(x f 在],1[e 恒为减函数.2)1()()]([min -=+--==∴a eae ef x f ，得 .e a = ………12分综上可知 .e a = ……… 13分 19．（本小题满分14分）解：(Ⅰ)由题意可知2)(136abe -==,得 223b a = ……… 2分 )11(,B 点在椭圆上11122=+ba 解得：34422==b ,a ……… 4分故椭圆M 的方程为：143422=+y x ……… 4分（Ⅱ）由于PBQ ∠的平分线垂直于OA 即垂直于x 轴，故直线PB 的斜率存在设为k ，则QB 斜率为 - k ，因此PB 、QB 的直线方程分别为y = k (x -1)+1， y = -k (x -1) +1 ……… 6分由⎪⎩⎪⎨⎧=++-=14341)1(22y x x k y 得01631631222=--+--+k k x )k (k x )k (①由0>∆ ，得31-≠k ……… 8分点B 在椭圆上，x =1是方程①的一个根，设),(),,(Q Q p p y x Q y x P13163122+--=⋅∴k k k x P 即1316322+--=∴k k k x P ，同理1316322+-+=k k k x Q ………10分 ∴=PQk 311312213)13(22)(222=+--+-⋅=--+=--k k k k k k x x k x x k x x y y Q P Q P Q P Q P)1,1(),0,2(--C A 31=∴AC k 即：AC PQ k k =∴向量//，则总存在实数λ使λ=成立. ………13分20.（本小题满分13分）解：（Ⅰ）0131a a -=,0291a a +-=,03277a a -= ……… 2分（Ⅱ）由123,nn n a a +=-得1112(3)(3)(3)n n n n n n a a +++-=--- ……… 3分令(3)n n n a b =-，所以112(3)nn n n b b ++-=-所以121321()()()n n n b b b b b b b b -=+-+-++-23112342222(3)(3)(3)(3)n nb -=+++++---- 2111222()[()()()]3333n b -=+--+-++-1122()(1())133()31()3n b ----=+--- 1122(1()),153n b -=+-- ……… 6分所以1122(1())(3)3153n n n a a -=+---- ……… 7分所以1112(3)[(3)32]15n n n n a a --=⋅-+-+⋅ 1102(13)(3)[(3)32]15n n n a --=--+-+⋅101[2(1)3](1)35n n n n n a -=+-⋅+-⋅⋅ ……… 8分（Ⅲ）1111101[2(1)3](1)35n n n n n n n a a a +++++-=+-⋅+-⋅⋅101[2(1)3](1)35n n n n n a --+-⋅--⋅⋅ 0112(1)43()55n n n a =⋅+-⋅⋅- 所以101121()()(1)4()3535n nn n n a a a +-=+-⋅⋅- ……… 10分如果0105a ->，利用n 无限增大时，2()3n的值接近于零，对于非常大的奇数n ，有10n n a a +-<；如果0105a -<，对于非常大的偶数n ，10n n a a +-<，不满足题目要求.当015a =时，112,5n n n a a +-=⋅于是对于任何正整数n ，1n n a a +>，因此015a =即为所求. ……… 13分。

10.2012初三数学二模答案-昌平

昌平区 2011—2012 学年第二学期初三年级第二次统一练习
数学试卷参考答案及评分标准
一、选择题（共 8 个小题，每小题 4 分，共 32 分）
1
2
3
4
5
6
2012．6
7
8
B
C
D
C
B
B
A
D
二、填空题（共 4 个小题，每小题 4 分，共 16 分）
题号
9
10
11
12
答案
2
6π
24
三、解答题（共 6 道小题，每小题 5 分，共 30 分）
20
10
时间
3天 4天 5天 6天 7天及以上
各时间实践活动人数占抽样总人数百分比统计图
6天
5天
25 %
30%
7天及以上
4天
20%
15% 3天
10%
…………………………………………………… 3 分（ 3）（30%+25%+20% ）×1000=750（名）
答： “活动时间不少于 5 天 ”的大约有 750 人．
…………… 5 分
数学试卷答案第 2 页（共 6 页）
20．（1）证明：连结 OD． ∵ OA=OD ， ∴ ∠A=∠ 1． ∵ DE=EP ， ∴ ∠2=∠ P． ∵ OA OB 于 O， ∴ ∠A+∠ P=90°． ∴ ∠1+∠ 2=90°． ∴ ∠ODE =90°．即 OD DE ． ∵ OD 是⊙ O 的半径， ∴ DE 是⊙ O 的切线．
∵ ? A ? B ? C ? D 90 °,
1
1
1
1
∴
S1 = 2 ay ， S2 = 2 dx ， S3 = 2 ct ， S4 =

北京市2012年中考数学二模试题分类几何综合(教师版)

2012年市中考数学二模分类汇编——几何综合与中点有关的问题1.(昌平24) 如图，D 是△ABC 中AB 边的中点，△BCE 和△ACF 都是等边三角形，M 、N 分别是CE 、CF 的中点.（1）求证：△DMN 是等边三角形；（2）连接EF ，Q 是EF 中点，CP ⊥EF 于点P. 求证：DP ＝DQ.同学们，如果你觉得解决本题有困难，可以阅读下面两位同学的解题思路作为参考：小聪同学发现此题条件中有较多的中点，因此考虑构造三角形的中位线，添加出了一些辅助线；小慧同学想到要证明线段相等，可通过证明三角形全等，如何构造出相应的三角形呢？她考虑将△NCM 绕顶点旋转到要证的对应线段的位置，由此猜想到了所需构造的三角形的位置.24. 证明：（1）取AC 的中点G ，连接NG 、DG.∴DG ＝21BC ，DG ∥BC ；△NGC 是等边三角形.∴NG = NC ，DG = CM. …………………2分 ∵∠1 + ∠2 =180º， ∴∠NGD + ∠2 = 240º.∵∠2 + ∠3 = 240º，∴∠NGD =∠3.∴△NGD ≌△NCM .……………………3分 ∴ND = NM ，∠GND =∠M. ∴∠DNM =∠GNC= 60º.∴△DMN 是等边三角形.………………………………4分（2）连接QN 、PM.∴QN =21CE= PM. ……………………5分Rt △CPE 中，PM =EM ，∴∠4=∠5. ∵MN ∥EF ，∴∠5=∠6，∠7=∠8. ∵NQ ∥CE ，∴∠7=∠4. ∴∠6=∠8.∴∠QND=∠PMD. ………………………6分 ∴△QND ≌△PMD.∴DQ= DP. ……………………7分2.（丰台24）在△ABC 中，D 为BC 边的中点，在三角形内部取一点P ，使得∠ABP=∠ACP ．过点P 作PE ⊥AC 于点E ，PF ⊥AB 于点F ．（1）如图1，当AB=AC 时，判断的DE 与DF 的数量关系，直接写出你的结论；（2）如图2，当AB ≠AC ，其它条件不变时，（1）中的结论是否发生改变？请说明理由．图 1 图224．解：（1）DE=DF ．……1分（2）DE=DF 不发生改变．……2分理由如下：分别取BP 、CP 的中点M 、N ，联结EM 、DM 、FN 、DN ．∵D 为BC 的中点，∴BPDN BP DN //,21=．……3分∵,AB PE ⊥∴BP BM EM 21==．∴21,∠=∠=EM DN ．∴12213∠=∠+∠=∠．…4分AEFPBD CC E B AD FP 7654321NMCD BPFEA同理,524,//DM FN MD PC =∠=∠．∴四边形MDNP 为平行四边形．……5分 ∴67∠=∠∵,41∠=∠∴35∠=∠． ∴EMD DNF ∠=∠．……6分 ∴△EMD ≌△DNF ． ∴DE=DF ．……7分3.(海淀25.)在矩形ABCD 中, 点F 在AD 延长线上，且DF= DC, M 为AB 边上一点, N 为MD 的中点, 点E 在直线CF 上（点E 、C 不重合）.（1）如图1, 若AB=BC, 点M 、A 重合, E 为CF 的中点，试探究BN 与NE 的位置关系及BMCE的值, 并证明你的结论;（2）如图2，且若AB=BC, 点M 、A 不重合, BN=NE ，你在（1）中得到的两个结论是否成立, 若成立,加以证明; 若不成立, 请说明理由;（3）如图3，若点M 、A 不重合，BN=NE ，你在（1）中得到的结论两个是否成立, 请直接写出你的结论.图1 图2 图3 25. 解：（1）BN 与NE 的位置关系是BN ⊥NE ；CEBM证明：如图，过点E 作EG ⊥AF 于G, 则∠EGN=90°． ∵ 矩形ABCD 中, AB=BC ， ∴ 矩形ABCD 为正方形.∴ AB =AD =CD, ∠A=∠ADC =∠DCB=90°．∴ EG//CD, ∠EGN =∠A, ∠CDF=90°．……………1分 ∵ E 为CF 的中点，EG//CD, ∴ GF=DG =11.22DF CD =∴1.2GE CD =FA ( M ) DNDAACEDNM B FECB FNMECB321GFEA (M )CD NB∵ N 为MD(AD)的中点， ∴ AN=ND=11.22AD CD∴GE=AN, NG=ND+DG=ND+AN=AD=AB. ………2分 ∴△NGE ≌△BAN ． ∴∠1=∠2. ∵∠2+∠3=90°， ∴∠1+∠3=90°． ∴∠BNE=90°.∴ BN ⊥NE ． ……………………………3分 ∵∠CDF=90°, CD=DF, 可得 ∠F=∠FCD=45°， 2.CFCD.于是122.2CFCE CE CE BMBA CD CD …………4分（2）在（1）中得到的两个结论均成立.证明：如图，延长BN 交CD 的延长线于点G ，连结BE 、GE ，过E 作EH ⊥CE ，交CD 于点H ．∵ 四边形ABCD 是矩形，∴ AB ∥CG ．∴∠MBN=∠DGN ，∠BMN=∠GDN. ∵ N 为MD 的中点， ∴ MN=DN ． ∴△BMN ≌△GDN ． ∴ MB=DG ，BN=GN. ∵ BN=NE ，∴ BN=NE=GN. ∴∠BEG=90°． ……………5分HGABCDEM NF∵ EH ⊥CE ， ∴∠CEH=90°． ∴∠BEG=∠CEH ． ∴∠BEC=∠GEH ．由（1）得∠DCF=45°． ∴∠CHE=∠HCE=45°． ∴ EC=EH, ∠EHG=135°． ∵∠ECB=∠DCB+∠HCE=135°， ∴∠ECB=∠EHG ． ∴△ECB ≌△EHG ． ∴ EB=EG ，CB=HG ． ∵ BN=NG ，∴ BN ⊥NE. ……………………6分 ∵CE ， ∴CEBM. ……………………7分（3）BN ⊥NE ；CEBM. ……………………8分密云25．已知菱形ABCD 的边长为1，60ADC ∠=，等边△AEF 两边分别交DC 、CB 于点E 、F ．（1）特殊发现：如图1，若点E 、F 分别是边DC 、CB 的中点，求证：菱形ABCD 对角线AC 、BD 的交点O 即为等边△AEF 的外心；（2）若点E 、F 始终分别在边DC 、CB 上移动，记等边△AEF 的外心为P ． ①猜想验证：如图2，猜想△AEF 的外心P 落在哪一直线上，并加以证明；②拓展运用：如图3，当E 、F 分别是边DC 、CB 的中点时，过点P 任作一直线，分别交DA边于点M ，BC 边于点G ，DC 边的延长线于点N ，请你直接写出11DM DN +的值．25．（本小题满分8分）证明：（1）如图1：分别连结OE 、OF ． ∵四边形ABCD 是菱形，∴AD DC CB ==，AC BD ⊥，DO BO =，且112302ADC ∠=∠=∠=．∴在Rt △AOD 中，有12AO AD =．又 E 、F 分别是边DC 、CB 的中点，∴1122EO CB DC OF===．∴AO EO FO ==．∴点O 即为等边△AEF 的外心． ------------------------- 3分（2）①猜想：△AEF 的外心P 落在对角线DB 所在的直线上．证明：如图2：分别连结PE 、PA ，作PQ DC ⊥于Q ，PH AD ⊥于H ．则90PQEPHD ∠=∠=∵60ADC ∠=，∴在四边形QDHP 中，120QPH ∠=．又 ∵点P 是等边△AEF 的外心，60EFA ∠=，∴PE PA =，2260120EPA EFA ∠=∠=⨯=． ∴αβ∠=∠．∴△PQE ≌△PHA （AAS ）．∴PQ=PH ． ∴点P 在ADC ∠的角平分线上．∵菱形ABCD 的对角线DB 平分ADC ∠， ∴ 点P 落在对角线DB 所在直线上--- 6分 ②112DM DN +=． ---------------------- 8分旋转变换在几何证明应用延庆24. （1）如图1：在△ABC 中，AB=AC ，当∠ABD=∠ACD=60°时，猜想AB 与BD+CD 数量关系，请直接写出结果；（2）如图2：在△ABC 中，AB=AC ，当∠ABD=∠ACD=45°时，猜想AB 与BD+CD 数量关系并证明你的结论；（3）如图3：在△ABC 中，AB=AC ，当∠ABD=∠ACD=β（20°≤β≤70°）时，直接写出AB 与BD+CD 数量关系(用含β的式子表示)。

2012年北京市各区二模试题分类解析【数学理】(6)：数列.pdf

情感态度与价值观：正确认识发展与环保的矛盾，树立科学的发展观。

【教学重点】 1．了解那树的生命历程，把握树的价值、品格及其命运，理解作者的思想情感。

2．掌握托物寓意的表现手法，体会比喻、拟人等修辞的表达效果。

【教学难点】 1．揣摩关键语句，体味作者痛苦、悲悯、愤激的情感，感受老树命运的悲剧色彩。

2．正确理解蚂蚁王国的事情，体会作者的用意。

【教具准备】多媒体课件【教学方法】 1．朗读法 2．讨论点拨法 3．品读法 4．延伸拓展法【课时安排】一课时【教学过程】【教学目标】资料助读；朗读课文，整体感知；理清行文思路，把握树的生命历程；感知树的形象，体会作者的情感。

一、导语设计：大地上最悦目的颜色是绿色，大地上站立的最大的生命群体是森林，但是在今天，许多地方的绿色正逐渐被吞噬，他们在疾速奔驰的人类文明的车轮的碾压下，成片成片地消失了。

这不，就连街头那棵老树也未能幸免，就让我们一起拜读王鼎钧先生为那树写的“悼词”吧。

二、资料助读 1．关于作者王鼎钧，台湾著名的散文家。

主要的散文作品有《人生三书》(《开放的人生》《人生试金石》《我们现代人》)《人生观察》《长短调》《世事与棋》《情人眼》《碎玻璃》《灵感》等。

2.多媒体播放反映人类生存困境的若干画面，如水土流失、土壤沙化、沙漠蔓延、洪水肆虐、森林面积锐减、资源严重枯竭…… 三、朗读课文，整体感知 1．学生默读课文，积累生字生词，并交流。

多媒体显示；佝偻(gōu lóu)：脊背向前弯曲，文中指老树枝干弯曲。

倒坍(tān)：倒塌。

萌庇(yìn bì)：大树枝叶遮蔽阳光，宜于人们休息。

引颈受戮：伸长脖子接受杀戮。

踝骨(huái)：指树干靠近根的部位。

虬须(qiú)：卷曲的胡子。

这里指树根。

周道如砥(dī)这里形容公路的平坦，畅通无阻。

2．选朗读水平较高的学生范读课文，教师提醒学生注意把握感情分寸，应深沉，不宜强烈奔放。

2012年北京市各区二模试题分类解析【数学理】(1)：集合.pdf

1、认识生态环境破坏对我们将来生活的影响并提高环保意识。

2、学习报告文学写作手法的运用；并以此写作倡导书。

教学难点： 1、真正意义上认识到环保的重要性。

2、认识到环保是我们每个公民的职责；并制止环境破坏者的行为。

过程和方法：朗读课文后揣摩文章字里行间充盈的感情和中心的关系，体味文中所设置的悬念。

教学方法：诵读法与讨论法教学过程：一、导入：当我们眼见一个广阔、美丽、充满生机的地方变为荒漠；原本牛马成群，绿林环绕，河流清澈的生命绿洲，现在却是一片死寂，寸草不生，不见飞鸟，令人恐怖；我们会深思，这种生态的巨变，就发生在我们的身边，这就是我们今天要认识的一个地方——罗布泊。

二、初读课文：1、正确识读、理解文中生字：萧瑟（sè）和煦（xù）干涸（hé）吞噬（shì）裸露（luǒ）戈壁（gē）荡漾（yàng）娱乐（yú） 2、词语释义：萧瑟：①形容风吹树木的声音；②形容冷落，凄凉。

和煦：温暖，多指阳光、风等。

干涸：（河道、池塘等）没有水了。

吞噬：蚕食、并吞。

裸露：没有东西遮盖。

戈壁滩：蒙古或新疆人称沙漠地区，这种地区尽是沙子和石块，地面缺水，植物稀少。

沧海桑田：大海变成农田，农田变成大海。

比喻世事变化很大。

也说桑田沧海。

3、内容提要：要比较具体地把握课文内容，可以做一份内容提要，就下面几个问题画出要点：①今日罗布泊是怎样的一个地方？关键词是“沙漠”“神秘”。

②过去罗布泊是怎样的一个地方？关键词是“绿洲”“仙湖”。

③罗布泊为什么会消亡？关键词是“改道”“四盲”。

④同样的悲剧还有哪些？关键词是“青海湖”“月牙泉”。

全文充满了痛惜之情，为罗布泊生态环境的破坏而痛惜，为人们的盲目性造成的悲剧而痛惜。

生态意识，环保意识，可持续发展意识，是课文的基本理念。

课文又涉及西部大开发战略问题，用历史的教训，说明生态环境保护的重要。

2012年北京昌平中考二模数学

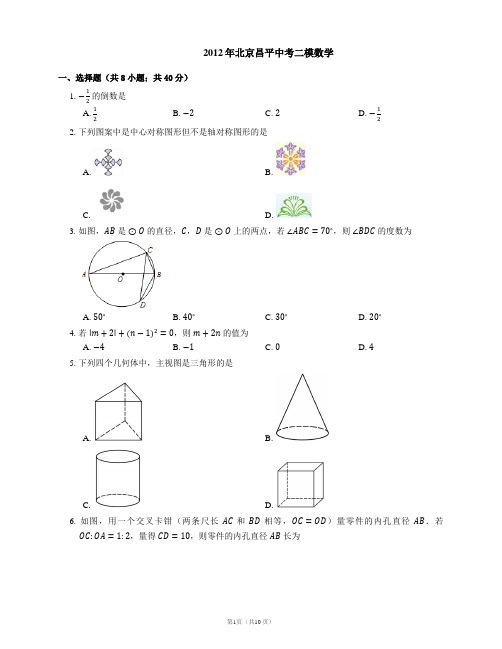
2012年北京昌平中考二模数学一、选择题（共8小题；共40分）1. 的倒数是______A. B. C. D.2. 下列图案中是中心对称图形但不是轴对称图形的是______A. B.C. D.3. 如图，是的直径，，是上的两点，若，则的度数为______A. B. C. D.4. 若，则的值为______A. B. C. D.5. 下列四个几何体中，主视图是三角形的是______A. B.C. D.6. 如图，用一个交叉卡钳（两条尺长和相等，）量零件的内孔直径．若，量得，则零件的内孔直径长为______A. B. C. D.7. 在，，三个数中任取两个，则这两个数之和是偶数的概率为______A. B. C. D.8. 下图能折叠成的长方体是______A. B.C. D.二、填空题（共4小题；共20分）9. 若分式的值为，则的值为______．10. 圆锥的母线长为，底面半径为，则它的侧面积为______．11. 已知一个菱形的周长是，两条对角线的长的比是，则这个菱形的面积是______．12. 如图的方格纸中，每个小方格都是边长为的正方形，，两点是方格纸中的两个格点，在的方格纸中，找出格点，使的面积为个平方单位，则满足条件的格点的个数是______．三、解答题（共13小题；共169分）13. 计算：．14. 解方程：．15. 已知，求代数式的值．16. 如图：已知在等边三角形中，点，分别是，延长线上的点，且．求证：．17. 如图，已知：反比例函数的图象经过点，，过点作轴于点，过点作轴于点，交于点，连接．（1）求反比例函数的解析式及的值；（2）若直线过点且平分的面积，求直线的解析式．18. 李明同学喜欢自行车和长跑两项运动，在某次训练中，他骑自行车的平均速度为每分钟米，跑步的平均速度为每分钟米，自行车路段和长跑路段共米，用时分钟．求自行车路段和长跑路段的长度．19. 在中，，．过点作且，过点分别作，，分别交和的延长线与点，．若，求四边形的周长．20. 如图，的半径与互相垂直，是线段延长线上的一点，连接交于点，点在上且．（1）求证：是的切线；（2）作于点，若，的半径的长．21. 某学校为了了解学生本学期参加社会实践的情况，随机抽查了该校部分学生参加社会实践活动的天数，并用得到的数据绘制了下面两幅不完整的统计图：请你根据图中提供的信息，回答下列问题：（1）该校对多少名学生进行了抽样调查?（2）补全条形统计图和扇形统计图；（3）该校共有学生人，请你估计“活动时间不少于天”的大约有多少人?22. 类比学习：有这样一个命题：设，，都是小于的正数，求证：．的正三角形，并分别在其边上截取，，，设，和的面积分别为，，，则，，．由，得．所以．类比实践：已知正数，，，，，，，满足．求证：．23. 已知为整数，方程的两个根都大于且小于，当方程的两个根均为有理数时，求的值．24. 如图所示，在平面直角坐标系中，正方形的边长为，点，分别在轴和轴的正半轴上，抛物线经过点，和．（1）求抛物线的解析式；（2）在抛物线的对称轴上找到点，使得到，的距离之和最小，求出点的坐标；（3）如果点由点出发沿线段以的速度向点运动，同时点由点出发沿线段以的速度向点运动，当其中一点到达终点时，另一点也随之停止运动．设．（i）求出与运动时间之间的函数关系式，并写出的取值范围；（ii）当时，在抛物线上存在点，使得以，，，为顶点的四边形是平行四边形，求出点的坐标．25. 如图，在中，，过点作于，平分，交于，过点作于，交于，交于．（1）若，求证：（i）平分；（ii）．（2）若，请直接写出与的等量关系．答案第一部分1. B2. C3. D4. C5. B6. B7. A8. D第二部分9.10.11.12.第三部分原式13.14. 去分母，得去括号，得合并同类项，得解得经检验，是原方程的解．原方程的解是．原式15.因为所以原式．16. 是等边三角形，，，．，，．17. （1）的图象经过点，，，，（2）直线过点，设直线的解析式为，其中．直线平分的面积，直线过的中点，，直线的解析式为．18. 设自行车路段为米，则解得．答：自行车路段为米，长跑路段为米．19. ，，．．，，．，，，．，．，．在中，．．，，四边形是矩形，，，四边形的周长为．20. （1）如图，连接．，．，．于，．．．即．是的半径，是的切线．（2）于点，．．．在中，，．，即的半径为．21. （1）（名）．答：该校对名学生进行了抽样调查．（2）补全统计图如图所示．（3）（名）答：“活动时间不少于天”的大约有人．22. 如图，作边长为的正方形．并分别在各边上截取：，，，．，，，，．，，，，．，正方形．．23. 设．的两根都在和之间，当时，，即．当时，，即．．为整数，．（i）当时，方程，，此时方程的根为无理数，不合题意．（ii）当时，方程，，，符合题意．（iii）当时，方程，，不符合题意．综合（i）（ii）（ii）可知，．24. （1）据题意，，，．抛物线经过点，和，．（2）点关于抛物线的对称轴的对称点为．如图，连接，与对称轴的交点即为．，，直线的解析式为．当时，，．（3），，．在中，，．．．（ii）当，．，（舍）．，．．根据分析，以点，，，为顶点的平行四边形只能是平行四边形．．此时，点在抛物线上．25. （1）（i），，．，．，，．．平分，．．即平分．（ii）在中，，，，．，．如图，过点作交于，．．平分，，，．．．．，．．．．（2）．。

昌平区2012-2013学年第二学期高三年级期第二次质量抽测数学试卷(理科)

侧视图俯视图2222正视图334昌平区2012－2013学年第二学期高三年级期第二次质量抽测数学试卷（理科）第Ⅰ卷（选择题共40分）一、选择题(本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．)（1）已知集合{|21}x A x =>，{|1}B x x =<，则A B =A. {|1}x x >B. {|0}x x >C. {|01}x x <<D. {|1}x x < （2）已知命题 :p x ∀∈R ，2x ≥，那么下列结论正确的是A. 命题:2p x x ⌝∀∈R ≤， B ．命题:2p x x ⌝∃∈<R ， C ．命题:2p x x ⌝∀∈-R ≤， D ．命题:2p x x ⌝∃∈<-R ， (3)圆22(2)1x y +-=的圆心到直线3,2x t y t =+⎧⎨=--⎩（t 为参数）的距离为A.22B.1C.2D. 22 (4)设0,x y x y +≥⎧⎨-≥⎩与抛物线24y x =-的准线围成的三角形区域（包含边界）为D ，),(y x P 为D 内的一个动点，则目标函数2z x y =-的最大值为A. 1-B. 0C. 2D. 3 (5) 在区间[]0,π上随机取一个数x ，则事件“1tan cos 2x x ≥g ”发生的概率为 A. 13 B. 12 C.23 D. 34(6) 已知四棱锥P ABCD -的三视图如图所示，则此四棱锥的四个侧面的面积中最大的是 A ．3 B ．25 C ．6 D ．8E D CBAOEDCBA（7）如图，在边长为2的菱形ABCD 中，60BAD ∠=，E 为CD 的中点，则AE BD ⋅的值为A ．1B ．3C ．5D ．7(8)设等比数列}{n a 的公比为q ，其前n 项的积为n T ，并且满足条件11a >，9910010a a ->，99100101a a -<-.给出下列结论：① 01q <<； ② 9910110a a ⋅->；③ 100T 的值是n T 中最大的；④ 使1n T >成立的最大自然数n 等于198. 其中正确的结论是A. ①③B. ①④C. ②③D. ②④第Ⅱ卷（非选择题共110分）一、填空题（本大题共6小题，每小题5分，共30分）（9）二项式51(2)x x+的展开式中3x 的系数为___________.（10）双曲线2221(0)y x b b-=>的一条渐近线方程为3y x =，则b = .（11）如图，AB 切圆O 于点A ,AC 为圆O 的直径，BC 交圆O 于点D ，E 为CD 的中点，且5,6,BD AC ==则CD =__________； AE =__________.（12）执行如图所示的程序框图，若①是6i <时，输出的S 值为；若①是2013i <时，输出的S 值为 .（13）已知函数241,(4)()log ,(04)x f x xx x ⎧+≥⎪=⎨⎪<<⎩ 开始10i S ,==12i i a π=+cosi S S a =+①输出S结束 1i i =+图1是否P FEDCB A若关于x 的方程()f x k =有两个不同的实根，则实数k 的取值范围是 .（14）曲线C 是平面内到直线1:1l x =-和直线2:1l y =的距离之积等于常数()20k k >的点的轨迹.给出下列四个结论：①曲线C 过点(1,1)-；②曲线C 关于点(1,1)-对称；③若点P 在曲线C 上，点,A B 分别在直线12,l l 上，则PA PB +不小于2.k④设0P 为曲线C 上任意一点，则点0P 关于直线1x =-、点(1,1)-及直线1y =对称的点分别为1P 、2P 、3P ，则四边形0123P PP P 的面积为定值24k .其中，所有正确结论的序号是 .三、解答题(本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤．) （15）（本小题满分13分）已知函数2()sin(2)23cos ,R f x x x x π=-+∈. （Ⅰ）求()6f π；（Ⅱ）求)(x f 的最小正周期及单调递增区间.（16）（本小题满分14分）如图,在四棱锥P ABCD -中,底面ABCD 是边长为2的正方形, 侧面PAD ⊥底面ABCD ，且22PA PD AD ==, E 、F 分别为PC 、BD 的中点． (Ⅰ) 求证：EF //平面PAD ； (Ⅱ) 求证：面PAB ⊥平面PDC ；(Ⅲ) 在线段AB 上是否存在点,G 使得二面角C PD G --的余弦值为13？说明理由.（17）（本小题满分13分）某市为了提升市民素质和城市文明程度，促进经济发展有大的提速，对市民进行了“生活满意”度的调查．现随机抽取40位市民，对他们的生活满意指数进行统计分析，得到如下分布表：满意级别非常满意满意一般不满意满意指数（分） 9060 30 0 人数（个）151762（I ）求这40位市民满意指数的平均值；（II ）以这40人为样本的满意指数来估计全市市民的总体满意指数，若从全市市民（人数很多）中任选3人，记ξ表示抽到满意级别为“非常满意或满意”的市民人数．求ξ的分布列；（III ）从这40位市民中，先随机选一个人，记他的满意指数为m ，然后再随机选另一个人，记他的满意指数为n ，求60n m ≥+的概率．（18）（本小题满分13分）已知函数21()ln (0).2f x x a x a =-> （Ⅰ）若2,a =求()f x 在(1,(1))f 处的切线方程；（Ⅱ）求()f x 在区间[1,e]上的最小值；（III ）若()f x 在区间(1,e)上恰有两个零点，求a 的取值范围.（19）（本小题满分13分）如图，已知椭圆22221(0)x y a b a b+=>>的长轴为AB ，过点B 的直线l 与x 轴垂直，椭圆的离心率32e =，F 为椭圆的左焦点，且1AF BF =g . （I ）求此椭圆的方程；（II ）设P 是此椭圆上异于,A B 的任意一点，PH x ⊥轴，H 为垂足，延长HP 到点Q 使得HP PQ =. 连接AQ 并延长交直线l 于点,M N 为MB 的中点，判定直线QN 与以AB 为直径的圆O 的位置关系．（20）（本小题满分14分）设数列{}n a 对任意*Nn ∈都有112()()2()n n kn b a a p a aa +++=++ (其中k 、b 、p 是常数) ．（I ）当0k =，3b =，4p =-时，求123n a a a a ++++ ；（II ）当1k =，0b =，0p =时，若33a =，915a =，求数列{}n a 的通项公式；（III ）若数列{}n a 中任意（不同）两项之和仍是该数列中的一项，则称该数列是“封闭数列”.当1k =，0b =，0p =时，设n S 是数列{}n a 的前n 项和，212a a -=，试问：是否存在这样的“封闭数列” {}n a ，使得对任意*N n ∈，都有0n S ≠，且12311111111218n S S S S <++++<．若存在，求数列{}n a 的首项1a 的所有取值；lyxNM QPHFOB A若不存在，说明理由．昌平区2012－2013学年第二学期高三年级期第二次质量抽测数学试卷参考答案（理科）一、选择题(本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．)题号（1）（2）（3）（4）（5）（6）（7）（8）答案CBADCCAB二、填空题（本大题共6小题，每小题5分，共30分．）（9）80 （10）3 （11）4 ；26 （12）5；2013 （13）(1, 2) （14） ②③④三、解答题(本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤．)（15）(本小题满分13分) 解：（Ⅰ）2()sin(2)23cos sin 23cos 232sin(2)33f x x x x x x ππ=-+=++=++..4分∴3()2sin()323236332f πππ=++=⨯+=..6分（Ⅱ）()2sin(2)33f x x π=++的最小正周期22T ππ==.…………………………8分又由5222(Z)2321212k x k k x k k πππππππππ-≤+≤+⇒-≤≤+∈可得函数)(x f 的单调递增区间为5,(Z)1212k k k ππππ⎡⎤-+∈⎢⎥⎣⎦.………13分（16）(本小题满分14分)(Ⅰ)证明：连结AC BD F = ，ABCD 为正方形，F 为AC 中点， E 为PC 中点.∴在CPA ∆中，EF //PA ．．．．．．．．．．．．．．．．．．..2分且PA ⊂平面PAD ，EF ⊄平面PAD ∴//EF PAD 平面．．．．．．．．．．．．．．．．．4分Gz yxO P FED C B A (Ⅱ)证明：因为平面PAD ⊥平面ABCD ，平面PAD 面ABCD AD =ABCD 为正方形，CD AD ⊥，CD ⊂平面ABCD 所以CD ⊥平面PAD .∴CD PA ⊥ ．．．．．．．．．．．．．．．．．．．．6分又22PA PD AD ==，所以PAD ∆是等腰直角三角形，且2APD π∠=即PA PD ⊥CD PD D = ，且CD 、PD ⊂面PDCPA ∴⊥面PDC又PA ⊂面PAB ，∴面PAB ⊥面PDC .…………..9分 (Ⅲ) 如图,取AD 的中点O , 连结OP ,OF . ∵PA PD =, ∴PO AD ⊥. ∵侧面PAD ⊥底面ABCD ,PAD ABCD AD ⋂=平面平面,∴PO ABCD ⊥平面,而,O F 分别为,AD BD 的中点,∴//OF AB , 又ABCD 是正方形,故OF AD ⊥. ∵22PA PD AD ==,∴PA PD ⊥,1OP OA ==. 以O 为原点,直线,,OA OF OP 分别为,,x y z 轴建立空间直角坐标系, 则有(1,0,0)A ,(0,1,0)F ,(1,0,0)D -,(0,0,1)P . 若在AB 上存在点,G 使得二面角C PD G --的余弦值为13，连结,.PG DG 设(1,,0)(02)G a a ≤≤.由(Ⅱ)知平面PDC 的法向量为(1,0,1)PA =-.设平面PGD 的法向量为(,,)n x y z = .∵(1,0,1),(2,,0)DP GD a ==--,∴由0,0n DP n GD ⋅=⋅= 可得00200x y z x a y z +⋅+=⎧⎨-⋅-⋅+⋅=⎩,令1x =,则2,1y z a =-=-,故2(1,,1)n a =-- ∴22221cos ,434222n PA n PA n PAaa ⋅<>====+⨯+, 解得，12a =. 所以，在线段AB 上存在点1(1,,0)2G ,使得二面角C PD G --的余弦值为13. .．．．．．．．．．．．．．14分（17）（本小题满分13分）解：（Ⅰ）记X 表示这40位市民满意指数的平均值，则1(9015601730602)63.7540X =⨯+⨯+⨯+⨯=（分）…………………2分（Ⅱ）ξ的可能取值为0、1、2、3.1251)51()54()0(3003===C P ξ12512)51()54()1(2113===C P ξ 12548)51()54()2(1223===C P ξ12564)51()54()3(0333===C P ξ ∴ξ的分布列为ξ0 1 2 3P125112512 12548 12564 ……………8分（Ⅲ）设所有满足条件60+≥m n 的事件为A①满足600==n m 且的事件数为：1121734A A = ②满足900==n m 且的事件数为：1121530A A = ③满足9030==n m 且的事件数为：1161590A A =24034309077()780P A A ++∴== 所以满足条件60+≥m n 的事件的概率为77780.……………………13分（18）（本小题满分13分）解：（I ）2,a =212()2ln ,'(),2f x x x f x x x=-=- 1'(1)1,(1),2f f =-=()f x 在(1,(1))f 处的切线方程为2230.x y +-=………………………..3分（Ⅱ）由2'().a x af x x x x-=-=由0a >及定义域为(0,)+∞，令'()0,.f x x a ==得①若1,01,a a ≤<≤即在(1,e)上，'()0f x >，)(x f 在[1,e]上单调递增，因此,()f x 在区间[1,e]的最小值为1(1)2f =. ②若21e,1e ,a a <<<<即在1,)a （上，'()0f x <，)(x f 单调递减；在,e)a （上，'()0f x >，)(x f 单调递增，因此()f x 在区间[1,e 上的最小值为1()(1ln ).2f a a a =- ③若2e,e ,a a ≥≥即在(1,e)上，'()0f x <，)(x f 在[1,e]上单调递减，因此,()f x 在区间[1,e]上的最小值为21(e)e 2f a =-. 综上，当01a <≤时，min 1()2f x =；当21e a <<时，min 1()(1ln )2f x a a =-；当2e a ≥时，2min 1()e 2f x a =-. ……………………………….9分 (III) 由（II ）可知当01a <≤或2e a ≥时，)(xf 在(1,e)上是单调递增或递减函数，不可能存在两个零点.当21e a <<时，要使()f x 在区间(1,e)上恰有两个零点，则∴21(1ln )0,21(1)0,21(e)e 0,2a a f f a ⎧-<⎪⎪⎪=>⎨⎪⎪=->⎪⎩即2e1e 2a a >⎧⎪⎨<⎪⎩，此时，21e e 2a <<.所以，a 的取值范围为21(e,e ).2…………………………………………………………..13分（19）（本小题满分13分）解：（Ⅰ）由题意可知，(,0)A a -, (,0)B a ，(,0)F c -， ()()1AF BF a c a c =+-=g2221a cb ∴-==又32e =， 22222222134c a b a e a a a --==== ，解得24a = 所求椭圆方程为2214x y +=…………………………5分（Ⅱ）设00(,)P x y ，则00(,2)Q x y 00(2,2)x x ≠≠-由(2,0),A -得0022AQ y k x =+ 所以直线AQ 方程002(2)2y y x x =++ 由(2,0),B -得直线l 2,x =的方程为008(2,)2y M x ∴+ 004(2,)2y N x ∴+ 由 0000200422224NQy y x x y k x x -+==--又点P 的坐标满足椭圆方程得到：2200+44x y = ，所以 220044x y -=- 000002200022442NQ x y x y x k x y y ===---∴直线NQ 的方程：00002()2x y y x x y -=-- 化简整理得到：220000244x x yy x y +=+= 即0024x x yy +=所以点O 到直线NQ 的距离220042+4d O x y ===圆的半径∴直线NQ 与AB 为直径的圆O 相切.……………………………………. 13分（20）（本小题满分14分）解：（I ）当0k =，3b =，4p =-时，1123()42()n n a a a a a +-=++ ， ①用1n +去代n 得，111213()42()n n n a a a a a a +++-=+++ ， ②②—①得，113()2n n n a a a ++-=，13n n a a +=，……………………………2分在①中令1n =得，11a =，则n a ≠0，∴13n na a +=， ∴数列{}n a 是以首项为1，公比为3的等比数列，∴123n a a a a ++++ =312n -………………………………………………….4分（II ）当1k =，0b =，0p =时，112()2()n n n a a a a a +=++ ， ③ 用1n +去代n 得，11121(1)()2()n n n n a a a a a a ++++=+++ ， ④④—③得， 11(1)0n n n a na a +--+=， ⑤.用1n +去代n 得，211(1)0n n na n a a ++-++=， ⑥⑥—⑤得，2120n n n na na na ++-+=，即211n n n n a a a a +++-=-，. ∴数列{}n a 是等差数列.∵33a =，915a =， ∴公差93293a a d -==-，∴23n a n =-…………………………………………9分（III ）由（II ）知数列{}n a 是等差数列，∵212a a -=，∴12(1)n a a n =+-. 又{}n a 是“封闭数列”，得：对任意*,N m n ∈，必存在*N p ∈使 1112(1)2(1)2(1)a n a m a p +-++-=+-，得12(1)a p m n =--+，故1a 是偶数， ············· 10分又由已知，111111218S <<，故1181211a <<.一方面，当1181211a <<时，1(1)n S n n a =+-0>，对任意*N n ∈，都有123111111112n S S S S S ++++≥> . 另一方面，当12a =时，(1)n S n n =+，1111n S n n =-+，则1231111111n S S S S n ++++=-+ ，取2n =，则1211121113318S S +=-=>，不合题意. 当14a =时，(3)n S n n =+，1111()33n S n n =-+，则 1231111111111()183123n S S S S n n n ++++=-+++++ 1118<，当16a ≥时，1(1)n S n n a =+-(3)n n >+，1111()33n S n n <-+， 123111*********()18312318n S S S S n n n ++++<-++<+++ ，又1181211a <<，∴14a =或16a =或18a =或110a =……………………….14分。

2012年北京市各区二模试题分类解析【数学理】(13)：排列、组合及二项式定理.pdf

4、背诵课文。

二、能力目标 1、复述课文，掌握作者求学的主要经历，理清行文思路，提高诵读能力。

2、理解本文对比手法的运用，体会其独特的表达效果。

三、情感目标学习作者克服困难、勤心求学的精神和意志，树立正确的苦乐观，珍惜现有的优越条件，努力学习，早日成才。

四、教学重点 1、翻译课文，背诵课文，理解本文作者执著的求学之志和殷殷劝勉之情。

2、把握寓理于事的写作方法和对比的表现手法，学习形象说理的技巧。

五、教学难点引导学生运用现代观念重新审视作品，理解文中作者的求学态度。

六、教学方法诵读法讨论点拨法复述法品读法延伸拓展法教学时间：二教时。

第一教时一、导入新课方法一：常言道：“自古雄才多磨难，从来纨绔少伟男。

”孟子也说：“夫天将降大任于斯人也，必先苦其心志，劳其筋骨，饿其体肤，空乏其身，行拂乱其所为。

” 这些都说明了苦难并非全是坏事。

只要我们善于化苦难为动力，则苦难就会成为成功的垫脚石。

今天我们来学习宋濂的《送东阳马生序》。

(板书课文标题) 方法二：同学们，在五单元前面几篇课文里，我们学习了几种古代不同体裁的文章，如吴均的书信体山水小品文——《与朱元思书》、陶渊明的自传体文章——《五柳先生传》、韩愈的议论性文章——《马说》，今天我们一起来学习一篇体裁为赠序的文章——《送东阳马生序》，看看作者是怎样用自己的切身体会勉励马生勤奋学习的。

二、作者简介：宋濂，明初文学家。

字景濂，号潜溪，浦江人（现渐江义乌人）。

他年少时受业于元末古文大家吴莱、柳贯、黄等。

元朝至正九年，召他为翰林院编修，因为身老不仕，隐居龙门山著书。

明初，征他作江南儒学提举，让他为太子讲经，修《元史》，官至翰林学士承旨、知制诰，朝廷的重要文书，大都由他参与撰写。

年老辞官，后因长孙宋慎犯罪，被流放到四川，途中病死。

他与刘基、高启为明初诗文三大家。

朱无璋称他为：开国文臣之首。

刘基称赞他为：当今文章第一。

四方学者称他为：太史公。

北京2012年昌平区高考二模试题

北京2012年昌平区高考二模试题学校班级__________姓名__________成绩注意事项：1．本试卷配有答题卡，请同学们将题答在答题卡上，填写在试题卷上的无效。

2．本试卷满分共300分，考试时间150分钟。

3．试卷答题时可能用到的相对原子质量：H—1，C—12，O—16，N—14，Na—23，，Cl—35.5，Ca—40第I卷（选择题，共126分）一、选择题：（本题包括13小题，每小题6分。

每小题只有一个选项符合题意）1．在人体的内环境中，可以发生的生理过程是A．血浆蛋白和血红蛋白的合成B．丙酮酸氧化分解，产生二氧化碳和水C．神经递质从突触前膜扩散到突触后膜D．食物中的淀粉经消化，最终形成葡萄糖2．下图表示光合作用与呼吸作用过程中物质变化的关系，下列说法不正确．．．的是A．1、3和4过程产生的[H]都能与氧结合产生水B．各种生物体（病毒除外）都能进行的过程是3C．能提供给绿色植物各种生命活动所需能量最多的过程是5D．2过程需多种酶参与，且需ATP供能3．下图表示人体和人体细胞内某些信息传递机制的模式图，图示中箭头表示信息传递方向。

下列有关的叙述中，正确的是A．如果该图表示一个完整的反射弧，则a 表示感受器，b 表示神经中枢，c表示效应器，且其中的信息以局部电流的形式由a 传到cB．如果该图中a 为下丘脑，b 为垂体，c 为甲状腺，则c 分泌的激素过多对于a 分泌d , b 分泌e 均具有抑制作用C．如果该图表示细胞中的遗传信息的表达过程，则d 过程只发生在细胞核中D．如果a 表示抗原，b 表示吞噬细胞和T 细胞，c 为B 细胞，则该过程表示体液免疫的反应阶段4．下面有关生物实验的叙述中，有几项说法是错误的①西瓜汁中含有丰富的葡萄糖和果糖，是还原糖的鉴定实验的理想材料②用显微镜观察根尖细胞有丝分裂时，看到的分生区细胞在右下方，为使观察目标移至视野中央，应该将装片向右下方移动③在层析法分离叶绿体中色素的结果中，蓝绿色色带最宽，表明叶绿素a 的含量最多④DNA 的粗提取实验中，向鸡血细胞溶液中加蒸馏水的目的是为了降低NaCI 溶液浓度至0 . 1 4mol/L ，此时DNA 溶解度最小，以便析出DNA⑤在探究温度对酶活性影响的实验中，用到了相互对照原则A．四项B．三项C．两项D．一项5．有关通过发酵工程生产谷氨酸的叙述中不正确的是A．发酵时所采用的培养基为液体培养基B．往往采用连续培养法来提高产量C．发酵时，要不断通入无菌空气，否则会生成乳酸或琥珀酸D．扩大培养、接种和生产谷氨酸时所用的培养基，其C：N=4：16．下列有关叙述中正确的是A．胶体产生丁达尔效应是由胶粒的大小决定的B．同一主族元素的氢化物，相对分子质量越大，它的沸点一定越高C．分子晶体溶于水时，一定不破坏共价键D．具有相同质子数和电子数的粒子中，可能是一种原子和一种离子7．一定条件下，充分燃烧一定量的丁烷放出热量161.9 KJ，经测定完全吸收生成的二氧化碳需消耗5mol/L的KOH溶液100mL，恰好生成正盐。

【VIP专享】2012年北京市昌平区初三数学二模题答案

3
B
4
C
11
2
……………………………………5 分
）（x+2）的值
16．证明：∵△ACB 和△ECD 都是等腰直角三角形，∠ACB=∠ECD=90°, A
∴EC=CD,AC=CB， …………………………2 分
∠ACB-∠ACD =∠ECD-∠ACD.
∴∠ACE=∠BCD. ………………………………………3 分 E
昌平区 2011-2012 学年第二学期初三年级第二次统一练习
数学试卷参考答案及评分标准 012.5
一、选择题（共 8 道小题，每小题 4 分，共 32 分）
题号
答案
1
B
2
A
二、填空题（共 4 道小题，每小题 4 分，共 16 分）
9
x≠1
10
m ≤ 9 且 m ≠0
4
三、解答题（共 6 道小题，每小题 5 分，共 30 分）
……………………………………1 分
∴AP=2. ……………………………………4 分 ∴P(1,0)或 P（-3,0） ∴m=1 或-3. ……………………………………5 分
18.解: 设每天应比原计划多加工 x 件衣服． …………………………………1 分
据题意，得 720 720 5 ．……………………………………………3 分 48 x 48
x 2 0 ，求（1
x
2
4
4
）
（x+2）
= x2 4 4 （x+2） ………………………2 分 (x 2)(x 2)
=
x2
x2
∵ x2 x 2 0 ，
…………………………3 分
∴ x2 x 2 . ………………………4 分

北京市2012届高三各区二模数学(理)试题分类汇编五、三角函数1(必修四)

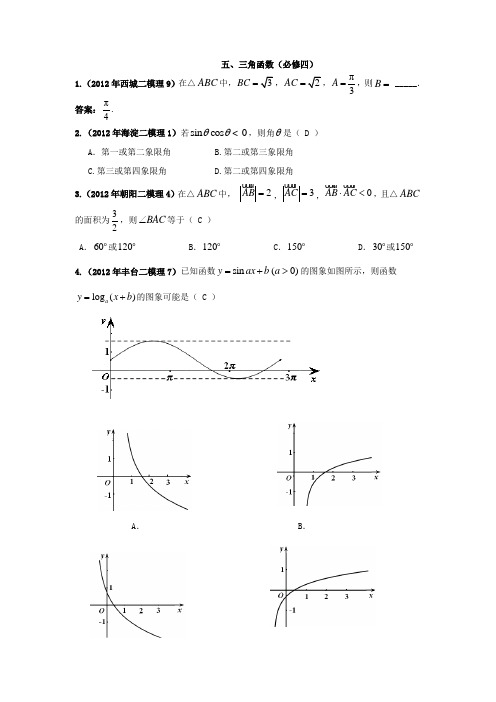
五、三角函数（必修四）1.（2012年西城二模理9）在△ABC 中，BC =，AC =，π3A =，则B = _____．答案：π4. 2.（2012年海淀二模理1）若sin cos 0θθ<，则角θ是（ D ） A ．第一或第二象限角 B.第二或第三象限角 C.第三或第四象限角 D.第二或第四象限角3.（2012年朝阳二模理4）在△ABC 中， 2AB = ，3AC = ，0AB AC ⋅<，且△ABC的面积为32，则BAC ∠等于（ C ） A ．60 或120 B ．120 C ．150 D ．30 或150 4.（2012年丰台二模理7）已知函数sin (0)y ax b a =+>的图象如图所示，则函数log ()a y x b =+的图象可能是（ C ）A ．B ．C ．D ．5.（2012年昌平二模理9）在∆ABC 中，4,2,2π===A b a 那么角C =_________.答案：127π。

6.（2012年东城二模理11）在平面直角坐标系xOy 中，将点A 绕原点O 逆时针旋转 90到点B ，那么点B 的坐标为____，若直线OB 的倾斜角为α，则sin2α的值为．7.（2012年海淀二模理11）在ABC ∆中，若120=∠A ，5c =，ABC ∆的面积为则a = .8.（2012年西城二模理15）已知函数22π()cos ()sin 6f x x x =--．（Ⅰ）求π()12f 的值；（Ⅱ）若对于任意的π[0,]2x ∈，都有()f x c ≤，求实数c 的取值范围．解：（Ⅰ）22ππππ()cos ()sin cos 12121262f =--==． ………………5分（Ⅱ） 1π1()[1cos(2)](1cos 2)232f x x x =+--- ………………7分1π13[cos(2)cos 2]2cos 2)2322x x x x =-+=+ ………………8分π)3x =+． ………………9分因为 π[0,]2x ∈，所以 ππ4π2[,]333x +∈， ………………10分所以当 ππ232x +=，即 π12x =时，()f x 取得最大值2． ………………11分所以 π[0,]2x ∀∈，()f x c ≤ 等价于2c ≤．故当 π[0,]2x ∀∈，()f x c ≤时，c的取值范围是)+∞． ………………13分 9.（2012年朝阳二模理15）已知函数()2cos cos f x x x x m =-+()R m ∈的图象过点π(,0)12M .（Ⅰ）求m 的值；（Ⅱ）在△ABC 中，角A ，B ，C 的对边分别是a ，b ，c .若cos +cos =2cos c B b C a B ，求()f A 的取值范围．解：（Ⅰ）由()12(cos 21)2f x x x m =-++π1sin(2)62x m =--+．…3分因为点π(,0)12M 在函数()f x 的图象上，所以ππ1sin(2)01262m ⋅--+=，解得12m =. …5分(Ⅱ) 因为cos +cos =2cos c B b C a B ，所以sin cos sin cos C B B C +=2sin cos A B ，所以sin(+)2sin cos B C A B =，即sin 2sin cos A A B =. ……7分又因为(0,A ∈π)，所以sin 0A ≠，所以1cos 2B =. ……8分又因为(0,B ∈π)，所以π3B =，2π3A C +=. ……10分所以2π03A <<， ππ7π2666A -<-<，所以πsin(2)6A -∈1(,1]2-.…12分所以()f A 的取值范围是1(,1]2-. ……13分10.（2012年丰台二模理15）已知函数()cos sin )f x x x x =-．（Ⅰ）求()3f π的值；（Ⅱ）求函数()y f x =在区间[0,]2π上的最小值，并求使()y f x =取得最小值时的x 的值．解：因为()cos sin )f x x x x =-2sin cos x x x -1cos 213()sin 222x x +-12sin 22x x -＝cos(2)6x π+-（Ⅰ）()cos(2)336f πππ=⨯+==7分（Ⅱ）因为 [0,]2x π∈，所以2666x ππ7π≤+≤．当 26x π+=π，即512x π=时，函数()y f x =有最小值是12--．当512x π=时，函数()y f x =有最小值是1-． …13分11.（2012年昌平二模理15）已知向量a (cos ,sin ),θθ= b = (13-,), 22π≤θ≤π-.（Ⅰ）当b a ⊥时，求θ的值;（Ⅱ）求||b a +的取值范围. 解：（Ⅰ） a ⊥b ∴b a ⋅0sin cos 3=-=θθ ……… 2分得3tan =θ 又∵22π≤θ≤π-……… 4分即：θ=3π……6分（Ⅱ）||b a +=4)sin cos 3(21||2||22+-+=+⋅+θθb b a a )3sin(45π--=θ ……… 9分22π≤≤π-θ 6365π≤π-≤π-∴θ … 11分 21)3sin(1≤π-≤-∴θ 4)3sin(42≤π--≤-∴θ∴33≤+≤||b a … 13分12.（2012年东城二模理15）已知函数()sin()f x A x =+ωϕ（其中∈R x ，0A >，ππ0,22ωϕ>-<<）的部分图象如图所示.（Ⅰ）求函数()f x 的解析式；（Ⅱ）已知在函数()f x 的图象上的三点,,M N P 的横坐标分别为-解：（Ⅰ）由图可知，1A =，最小正周期428T =⨯=.由2π8T ==ω，得4π=ω. ………3分又π(1)sin()14f ϕ=+= ，且ππ22ϕ-<<，所以ππ42+=ϕ，即4π=ϕ . ………5分所以π()sin()sin (1)444f x x x =+=+ππ. ………6分（Ⅱ）因为(1)0,(1)1,f f -==π(5)sin (51)1,4f =+=-所以(1,0),(1,1),(5,1)M N P --. …………7分所以MN PN MP ===.由余弦定理得3cos5MNP ∠==-. ………11分因为[)0,MNP ∠∈π，所以4sin 5MNP ∠=. ……13分。

2012年北京市各区二模试题分类解析【数学理】(4)：定积分.pdf

2．理解蕴含在两文中的作者的观点。

难点：1．两篇短文都采用“逐层深入论证”的结构，这是学习本文的一个难点。

教学过程：一、明确目标疏通第一章大意，理解寓含其中的作者的观点，学生畅谈各自看法，以加深理解。

二、整体感知《得道多助，失道寡助》选自《孟子·公孙丑》，标题是后来的编者加的。

此标题从内容上高度概括了本文的中心意即：凡讲仁义，行仁政的，就会得到广泛的支持与拥护；反之，就孤立，就会只有极少数人的支持与拥护。

孟子生活在各诸侯国互相攻伐，社会骚乱的战国时代。

因此，他提出“施仁政”，“行王道”的主张，反对武力兼并，这篇短论很能代表他的主张。

三、教学过程 1．投影习题，检测自学效果。

（1）下列句子朗读节奏划分有误的一句是（） A．夫／环而攻之。

B．是／天时不如地利也。

C．威天下／不以／兵革之利。

D．故君子／有不战，战／必胜矣（2）解释下句中加点词在文中的意思： ①池非不深也。

②域民不以封疆之界 2．讨论问题（1）本文作者从作战入手，设举了两个战例，从中可以看出，作者把决定战争胜负的客观因素归结为哪几个？作者认为它们之间的关系如何？（2）本文借论战，深入阐述了怎样的政治主张？这一主张是如何逐层推进论证的？（3）画出第3、4节中的排比句，诵读体会，议论文说理运用排比句式的表达作用。

练习：请你紧扣强调“青少年时期要努力学习”这一内容写一组排比句，加深体会。

《生于忧患，死于安乐》一章选自《孟子·告子》，文题同样是编者所加，该标题也恰好概括了本章的中心意思——忧患激励人奋起，使人生存发展；安逸享乐使人萎靡，必将导致灭亡，即逆境能成才。

表明了孟子关于人才要在困难环境中磨炼造就的观点。

文章摆事实，讲道理，举例典型，观点与材料紧密结合，说理透彻，令人信服。

1．指导朗读。

听录音范读，学生跟读，自由诵读。

（1）读准下列加点字的音：傅说忍性法家拂士曾益（2）正确划分下列句子的朗读节奏 ①必先/苦其/心志，劳其/筋骨，饿其/体肤，空乏/其身，行拂/乱其所为。