2006年福建泉州市中考试题及答案课改

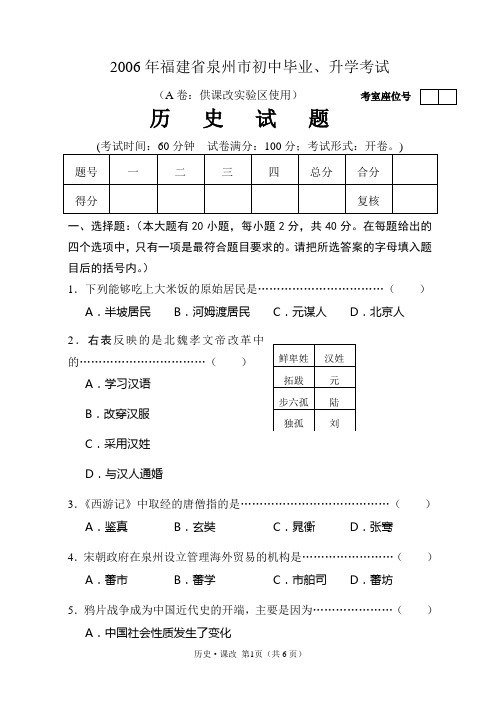
2006年福建省泉州市初中毕业、升学考试数 学 试 题一、填空题（每小题3分，共36分） 1．－2的相反数是 .2．分解因式：=+x x 32 .3．去年泉州市林业用地面积约为10 200 000亩，用科学记数法表示约为 亩. 4．甲、乙两人比赛射击，两人所得平均环数相同，其中甲所得环数的方差为12，乙所得环数的方差为8，那么成绩较为稳定的是 （填“甲”或“乙” ）. 5．某商品每件进价200元，现加价10%出售，则每件商品可获利润 元. 6．计算：=+++222x x x . 7．如图，△ABC 为⊙O 的内接三角形，AB 是直径，∠A =20°，则∠B = 度.8．函数x y 4=的图象经过原点、第一象限与第 象限. 9．抛掷一个质地均匀的正方体骰子，骰子的六个面上分别刻有1至6的点数，则掷得点数是2的概率是 . 10．只用同一种正多边形铺满地面，请你写出一种这样的正多边形： .11．如图，圆锥的高AO 与母线AB 的夹角20=α°，AB =2㎝，则该圆锥侧面展开扇形的弧长等于 ㎝.12．菱形ABCD 的一条对角线长为6，边AB 的长是方程01272=+-x x 的一个根，则菱形ABCD的周长为 .(满分：150分；考试时间：120分钟)(A 卷：供课改实验区使用)(第7题图)BB（第11题图）二、选择题（每小题4分，共24分）每小题有四个答案，其中有且只有一个答案是正确的，请把正确答案的代号写在题后的括号内，答对的得4分，答错、不答或答案超过一个的一律得0分. 13．计算：a 2·a 4的结果是（ ）A ．a 2；B ．a 6；C ．a 8；D ．a 16. 14．下列事件中，是必然事件的为（ ）A ．我市夏季的平均气温比冬季的平均气温高；B ．每周的星期日一定是晴天；C ．打开电视机，正在播放动画片；D ．掷一枚均匀硬币，正面一定朝上. 15．右边物体的正视图是（ ）16．已知两圆半径分别为1与5，圆心距为4，则这两圆的位置关系是（ ）A ．外离；B ．外切；C ．相交；D ．内切.17．某校篮球队五名主力队员的身高分别是174、179、180、174、178（单位：㎝），则这组数据的中位数是（ ）A ．174㎝；B ．177㎝；C ．178㎝；D ．180㎝. 18．如右图，在Rt △ABC 中，∠C=90°，AC=2，BC 的长为常数，点P 从起点C 出发，沿CB 向终点B 运动，设点P 所走过路程 CP 的长为x ，△APB 的面积为y ，则下列图象能大致反映y 与 x 之间的函数关系的是（ ）正面（第15题图）ABCDBCDA（第18题图）三、解答题（共90分）19．（8分）计算：|－3|＋2-1－20060.20．（8分）先化简下面的代数式，再求值：a (1－a )＋(a －1) (a ＋1)，其中13+=a .21．（8分）如图，在矩形ABCD 中，E 、F 分别是BC 、AD 上的点，且BE=DF .求证：△ABE ≌△CDF .B AEF DC22．（8分）《泉州晚报》2006年6月5日报道：去年我市空气质量状况总体良好.泉州市各县根据上图信息，解答下列问题：（1） 有哪些县（市、区）连续两年．．．．的空气质量API 指数小于或等于50？ （2） 哪个县（市、区）2005年比2004年空气质量API 指数下降最多？下降多少？23．（8分）如图，小王在操场上放风筝，已知风筝线AB 长100米，风筝线与水平线的夹角=α36°，小王拿风筝线的手离地面的高度AD 为1.5米，求风筝离地面的高度BE （精确到0.1米）.24．（8分）在两个布袋中分别装有三个小球，这三个小球的颜色分别为红色、白色、绿色，API 泉州市区 晋江市区 石狮市区 南安市区安溪县永春县 德化县 洛江区泉港区 惠安县 县（市、区）其他没有区别.把两袋小球都搅匀后，再分别从两袋中各取出一个小球，试求取出两个相同颜．．．色．小球的概率（要求用树状图个或列表方法求解）.25．（8分）在左图的方格纸中有一个Rt △ABC （A 、B 、C 三点均为格点），∠C=90°⑴请你画出将Rt △ABC 绕点C 顺时针旋转90°后所得到的Rt △C B A '''，其中A 、B 的对应点分别是A '、B '（不必写画法）；⑵设⑴中AB 的延长线与B A ''相交于D 点，方格纸中每一个小正方形的边长为1，试求BD 的长（精确到0.1）.26．（8分）某校的一间阶梯教室，第1排的座位数为a ，从第2排开始，每一排都比前一排增加b 个座位.⑴请你在下表的空格里填写一个适当的代数式：⑵已知第4排有18个座位，第15排座位数是第5排座位数的2倍，求第21排有多少个座位？27．（13分）一条隧道的截面如图所示，它的上部是一个以AD为直径的半圆O，下部是一个矩形ABCD.⑴当AD=4米时，求隧道截面上部半圆O的面积；⑵已知矩形ABCD相邻两边之和为8米，半圆O的半径为r米.①求隧道截面的面积S（米2）关于半径r（米）的函数关系式（不要求写出r的取值范围）；②若2米≤CD≤3米，利用函数图象求隧道截面的面积S的最大值（π取3.14，结果精确到0.1米）D28．（13分）如图，在直角坐标系中，O 为原点，A （4，12）为双曲线xky =（x>0）上的一点.⑴求k 的值；⑵过双曲线上的点P 作PB ⊥x 轴于B ，连接OP ，若Rt △OPB 两直角边的比值为41，试求点P 的坐标.⑶分别过双曲线上的两点P 1、P 2，作P 1B 1⊥x 轴于B 1，P 2B 2⊥x 轴于B 2，连结OP 1、OP 2.设Rt △OP 1B 1、Rt △OP 2B 2的周长分别为l 1、l 2，内切圆的半径分别为r 1、r 2,若221=l l ，试求21r r 的值.四、附加题（共10分）友情提示：请同学们做完上面考题后，再认真检查一遍，估计一下你的得分情况.如果你全卷得分低于90分（及格线），则本题的得分将计入全卷总分，但计入后全卷总分最多不超过90分；如果你全卷得分已经达到或超过90分，则本题的得分不计入全卷总分.1．（5分）将有理数1，－2，0按从小到大的顺序排列，用“<”号连接起来.2．（5分）如图，在△ABC 中，AB=AC ，∠B=50°，.求∠A 的度数.2006年福建省泉州市初中毕业、升学考试(A 卷：供课改实验区使用)数学试题参考答案及评分标准说 明：（一） 考生的正确解法与“参考答案”不同时，可参照“参考答案及评分标准”的精神进行评分.（二） 如解答的某一步出现错误，这一错误没有改变后续部分的考查目的，可酌情给分，但原则上不超过后面应得分数的二分之一；如属严重的概念性错误，就不给分. （三） 以下解答各行右端所注分数表示正确做完该步应得的累计分数. （四）评分最小单位是1分，得分或扣分都不出现小数. 一、填空题（每小题3分，共36分）1、2；2、)3(+x x ；3、1.02×107；4、乙；5、20；6、1；7、70；8、三；9、61；10、正三角形（或正四边形，正六边形）； 11、2π； 12、16.AB C二、选择题（每小题4分，共24分）13、B ； 14、A ； 15、B ； 16、D ； 17、C ； 18、C 三、解答题（共90分） 19．（本小题8分） 解：原式=3＋21－1 ……………………………………………………………………（6分） =212 …………………………………………………………………………（8分）20．（本小题8分）解：原式=122-+-a a a ………………………………………………………………（4分） =1-a …………………………………………………………………………（5分） 当13+=a 时原式=113-+ …………………………………………………………………………（7分）=3 ………………………………………………………………………………（8分） 21．（本小题8分）证明：∵四边形ABCD 是矩形∴AB=AD ，∠B=∠D=90° ………………（4分） 在△ABE 和△CDF 中AB=AD ∠B=∠D BE=DF∴△ABE ≌△CDF ………………………（8分）22．（本小题8分）解：（1）永春县和惠安县连续两年的空气质量API 指数小于或等于50 ……………（4分） （2）安溪县2005年比2004年空气质量API 指数下降最多，下降16. ……………（8分） 23．（本小题8分）解：在Rt △ABC 中，∠BAC=∠=α36°，AB=100米B AEFD∵sin =αABBC………………………………………（4分） ∴BC=AB ·sin =α100×sin36°≈100×0.5878=58.78（米） ………………………（6分） 又∵CE= AD=1.5米∴BE=BC ＋CE=58.78＋1.5=60.28≈60.3（米）答：风筝离地面的高度BE 约为60.3米……………（8分）24．（本小题8分） 解：（解法一）列举所有等可能结果，画树状图：布袋1红 白 绿布袋2 红白绿 红白绿 红白绿 由上图2可知，所有等可能结果共有9种，两个相同颜色小球的结果共3种， ∴P （相同颜色）=3193= …………………………………………………………………（8分）（解法二）列表如下：由上表可知，所有等可能结果共有9种，两个相同颜色小球的结果共3种， ∴P （相同颜色）=3193= …………………………………………………………………（8分）25．（本小题8分）4分）解：（1）方格纸中Rt △C B A ''为所画的三角形 …………（4分）（2）由（1）得∠A =∠A ' 又∵∠1=∠2∴△ABC ∽△BD A ' ……………………………（5分）∴B A AB BD BC ''= ……………………………………（6分） ∵1=BC ，2='B A ，22BC AC AB +=101322=+= ……………………………（7分）∴2101=BD 即102=BD ≈0.6 ∴BD 的长约为0.6 …………………………………（8分） 26．（本小题8分）解：（1）b a 3+ ……………………………………………………………………………（3分）（2）依题意得⎩⎨⎧+=+=+)4(214183b a b a b a …………………………………………………（5分）解得⎩⎨⎧==212b a ……………………………………………………………………（7分）∴12＋20×2=52答：第21排有52个座位. ………………………………………………………（8分） 27．（本小题13分）解：（1）当AD=4米时，S 半圆=22221221⨯=⨯ππ）（AD=2π（米2） …………………………………………（3分） （2）①∵AD=2r ，AD ＋CD=8∴CD=8－AD=8－2r ………………………………（4分）∴S =）（r r r CD AD r 282212122-+=⋅+ππ=r r 164212+-）（π ………………………………（8分）D②由①知r CD 28-= 又∵2米≤CD ≤3米 ∴2≤r 28-≤3∴2.5≤r ≤3 ………………………………………（9分）由①知S=r r 164212+-）（π≈r r 16414.3212+-⨯）（=－2.43r 2＋16r ………………………………………（10分） =43.26443.2843.22+--）（r ∵－2.43＜0，∴函数图象为开口向下的抛物线. ∵函数对称轴43.28=r ≈3.3 ………………………（11分） 又2.5≤r ≤3＜3.3由函数图象知，在对称轴左侧S 随r 的增大而增大， 故当r =3时，有S 最大值. ………………………（12分）31634212⨯+⨯-=）（最大值πS≈489414.321+⨯-⨯）（=26.13 ≈26.1（米2）答：隧道截面的面积S 的最大值约为26.1米2. …（13分）28．（本小题13分）解：（1）依题意得12=4k，k = 48 ………………………………………（3分） （2）由（1）得双曲线解析式为xy 48= ……………（4分）设P （m ，n ）∴mn 48= 即 48=mn ……………（5分）当41=PB OB 时，即41=n m 可设z m =，z n 4=. ∴z ·4z = 48，解得 32=z ∴32=m ，38=n∴P （32，38） …………………………………（7分） 当41=OB PB 时，同理可求得P （38，32）………（8分） （3）在Rt △OP 1B 1中，设OB 1=1a ，P 1B 1=1b ，OP 1=1c ，则P 1（1a ，1b ），由（2）得1a 1b =48； 在Rt △OP 2B 2中，设OB 2=2a ，P 2B 2=2b ，OP 2=2c ，则P 2（2a ，2b ），由（2）得2a 2b =48. ………………………………………………………………………………………………（9分）∵2421)21111111==⋅++b a r c b a （ 2421)21222222==⋅++b a r c b a （ ………………………………………………………（10分） ∴22221111)()(r c b a r c b a ⋅++=⋅++ ……………………………………………………（11分） 即1l ·1r =2l ·2r 故1221r r l l = ………………………………………………………………………………（12分） 又∵=21l l 2 ∴=12r r 2 即得=21r r 21…………………………………………………………（13分）四、附加题（共10分）1．解：－2 ＜ 0 ＜ 1 …………………………………………………………………（5分） 2． 解：∵AB=AC∴∠C=∠B=50°………………………………………（2分） ∴∠A=180°－∠C －∠BA B=180°－50°－50°=80°………………………………………………（5分）。