数值实验报告(迭代法) (1)
大学数学实验报告----迭代(一)——方程求解

Do M n , n, 2, 100
运行结果:
M n_Integer : Module y, k , m 2; k m ^ n 1 ;
x Mod k, n ;
Print n, " ", PrimeQ n , " ", x, "
", GCD m, n
Do M n , n, 2, 100
2 True 0 2 3 True 1 1 4 False 0 2 5 True 1 1 6 False 2 2 7 True 1 1 8 False 0 2 9 False 4 1 10 False 2 2 11 True 1 1 12 False 8 2 13 True 1 1 14 False 2 2 15 False 4 1 16 False 0 2 17 True 1 1 18 False 14 2 19 True 1 1 20 False 8 2 21 False 4 1 22 False 2 2 23 True 1 1 24 False 8 2 25 False 16 1 26 False 2 2 27 False 13 1 28 False 8 2 29 True 1 1 30 False 2 2 31 True 1 1 32 False 0 2 33 False 4 1 34 False 2 2 35 False 9 1 36 False 32 2 37 True 1 1 38 False 2 2 39 False 4 1 40 False 8 2
99 False 3 27 100 False 1 67 Null2
m=4 时
输入程序:
M n_Integer : Module y, k , m 4; k m ^ n 1 ; x Mod k, n ; Print n, " ", PrimeQ n , " ", GCD m, n , " ", x Do M n , n, 2, 100
数值分析迭代法数值分析实验报告jacobi迭代和seidel迭代分析

数值分析迭代法数值分析实验报告 jacobi迭代和seidel迭代分析导读:就爱阅读网友为您分享以下“数值分析实验报告jacobi迭代和seidel迭代分析”资讯,希望对您有所帮助,感谢您对的支持!数值分析实验报告一、实验目的1、了解熟悉jacobi迭代法和seidel迭代法的解法2、将原理与matlab语言结合起来,编程解决问题3、分析实验结果二、实验题目设线性方程组为2 2 31 201 31 x1 1 7 x801240 2 x 103 10 15 x 1 4考察用jacobi迭代法和seidel迭代法求解该线性方程组的收敛情况。
如果收敛,给出误差满足x(k) x(k 1)10 4的解。
三、实验原理将A 作如下分解A D L U这里a11D a22 0 a ,L 21 anna n100 a n2 0 0 a12 a1n 0 0 0 a2n ,0 00 0 JacobiU迭代矩阵为BJ D 1(L U)Seidel迭代矩阵为BS (D L) 1U它们的迭代格式都可化为x(k 1) Bx(k) g则迭代格式对任何初值都瘦脸的充要条件是迭代矩阵谱半径 (B) max k 1,其中, k是矩阵B的n个特征值,k 1,2 ,n 1 k nJacobi迭代矩阵的特征方程为det( I B J) 0Seidel迭代矩阵的特征方程为det( I B S) det( (D L) U) 0四、实验内容用matlab编写计算jacobi迭代矩程序,建立m文件如下:function[M]=BJ(A)D=diag(diag(A));L=tril(-A)+D;U=triu(-A)+D;M=inv(D)*(L+U);输入:>> A=[20 1 -3 -1;3 18 0 7;-1 2 40 -2;1 0 -1 5];>> [M]=BJ(A)M:M =0 -0.0500 0.1500 0.0500-0.1667 0 0 -0.38890.0250 -0.0500 0 0.0500-0.2000 0 0.2000 00 0.050.150.05 0.166700 0.3889 则jacobi迭代矩阵为:BJ 0.025 0.0500.05 0.2 00.20用matlab求jacobi迭代矩阵的特征根的算法如下:>> A=[0 -0.05 0.15 -0.05;-0.67 0 0 -0.39;0.025 -0.05 0 0.05;-0.2 0 0.2 0];[V,D]=eig(A)V =-0.1892 + 0.0450i -0.1892 - 0.0450i -0.3812 -0.5005-0.9467 -0.9467 0.8867 0.5461 -0.1528 - 0.1181i -0.1528 + 0.1181i -0.2099 -0.0466 -0.1056 + 0.1325i -0.1056 - 0.1325i 0.1561 0.6701D =-0.1774 + 0.0864i 0 0 0 0 -0.1774 - 0.0864i 0 0 0 0 0.2194 0 0 0 0 0.1355 则最大特征根为:0.2194 则(BJ) 0.2194 1,所以jacobi迭代法收敛用matlab编程jacobi迭代法求根的算法:function [n,x]=jacobi(A,b,X,nm,w)%用雅克比迭代法求解方程组Ax=b%输入:A为方程组的系数矩阵,b为方程组右端的列向量,X为迭代初值构成的列向量,nm为最大迭代次数,w 为误差精度%输出:x为求得的方程组的解构成的列向量,n为迭代次数n=1;m=length(A);D=diag(diag(A)); %令A=D-L-U,计算矩阵DL=tril(-A)+D; %令A=D-L-U,计算矩阵LU=triu(-A)+D; %令A=D-L-U,计算矩阵UM=inv(D)*(L+U); %计算迭代矩阵g=inv(D)*b; %计算迭代格式中的常数项%下面是迭代过程while n<=nmx=M*X+g; %用迭代格式进行迭代if norm(x-X,2)<wdisp(…迭代次数为‟);ndisp(…方程组的解为‟);xreturn;%上面:达到精度要求就结束程序,输出迭代次数和方程组的解endX=x;n=n+1;end%下面:如果达到最大迭代次数仍不收敛,输出警告语句及迭代的最终结果(并不是方程组的解)disp(…在最大迭代次数内不收敛!‟);输入数据:>> A=[20 1 -3 -1;3 18 0 7;-1 2 40 -2;1 0 -1 5];b=[1;2;10;-1];X=[0;0;0;0];>> nm=100;>> w=1e-4;>> [n,x]=jacobi1(A,b,X,nm,w)迭代次数为n =6方程组的解为x =0.06870.16450.2352-0.1667n =6x =0.06870.16450.2352-0.1667所以,满足精度的根为x = 0.0687 0.1645 0.2352用matlab编程计算seidel迭代矩阵算法为:function[M]=BS(A)D=diag(diag(A));L=tril(-A)+D;U=triu(-A)+D;M=inv(D-L)*U;输入:>> A=[20 1 -3 -1;3 18 0 7;-1 2 40 -2;1 0 -1 5]; >> [M]=BS(A)M =0 -0.0500 0.1500 0.0500 0 0.0083 -0.0250 -0.3972 -0.1667 迭代次数为6次0 -0.0017 0.0050 0.07110 0.0097 -0.0290 0.0042则seidel迭代矩阵为:0.150.05 0 0.05 00.0083 0.025 0.3972BS 0 0.00170.0050.0711 00.0097 0.0290.0042用matlab编程求得seidel矩阵的算法为:>> A=[0 -0.05 0.15 0.05;0 0.0083 -0.025 -0.3972;0 -0.0017 0.005 0.0711;0 0.0097 -0.029 0.0042];[V,D]=eig(A)V =1.0000 -0.1596 + 0.6750i -0.1596 - 0.6750i -0.91040 0.6965 0.6965 0.3924 0 -0.1250 + 0.0028i -0.1250 - 0.0028i 0.1313 0 0.0070 - 0.1348i 0.0070 + 0.1348i 0.0000D =0 0 0 0 0 0.0088 + 0.0768i 0 0 0 0 0.0088 - 0.0768i 0 0 0 0 -0.0001则特征根为 0 0.008+0.0768i 0.0088-0.0768i-0.0001则 (BS) 0.08 1,所以seidel迭代法收敛用seidel迭代法求根的算法为:function [n,x]=gaussseidel(A,b,X,nm,w)%用高斯-赛德尔迭代法求解方程组Ax=b%输入:A为方程组的系数矩阵,b为方程组右端的列向量,X为迭代初值构成的列向量,nm为最大迭代次数,w 为误差精度%输出:x为求得的方程组的解构成的列向量,n为迭代次数n=1;m=length(A);I=eye(m); %生成m*m阶的单位矩阵D=diag(diag(A)); %令A=D-L-U,计算矩阵DL=tril(-A)+D; %令A=D-L-U,计算矩阵LU=triu(-A)+D; %令A=D-L-U,计算矩阵U M=inv(D-L)*U; %计算迭代矩阵g=inv(I-inv(D)*L)*(inv(D)*b); %计算迭代格式中的常数项%下面是迭代过程while n<=nmx=M*X+g; %用迭代格式进行迭代if norm(x-X,2)<wdisp(…迭代次数为‟);ndisp(…方程组的解为‟);xreturn;%上面:达到精度要求就结束程序,输出迭代次数和方程组的解endX=x;n=n+1;end%下面:如果达到最大迭代次数仍不收敛,输出警告语句及迭代的最终结果(并不是方程组的解)disp(…在最大迭代次数内不收敛!‟);disp(…最大迭代次数后的结果为‟);x输入数据:>> A=[20 1 -3 -1;3 18 0 7;-1 2 40 -2;1 0 -1 5];b=[1;2;10;-1];X=[0;0;0;0];nm=100;w=1e-4;[n,x]=gaussseidel(A,b,X,nm,w) 迭代次数为n =5方程组的解为x =0.06870.16450.2352-0.1667n =5x =0.06870.16450.2352-0.166满足精度的根为x =0.0687 0.1645 0.2352 -0.1667 迭代次数为5次五、实验分析从实验过程可以看到求出满足精度的根,seidel迭代要比jacobi迭代快,这是因为在jacobi迭代计算中,计算向量x(k 1)时是按分量的角标由小到大依次计算的。
《数学实验》实验报告——迭代法

观察序列,并且判断极限。 Mathematica 程序如下:
当 x0=0.1,n=10 时,运行程序得
当 x0=0.5,n=10 时,运行程序得
当 x0=0.9,n=10 时,运行程序得
当 x0=1,n=10 时,运行程序得
实验结论:
10
由以上实验可得,函数 f(x)=x/2+1/x 的极限为 1.41421
《数学实验》实验报告
班级 实验 内容 **** 学号 **** 姓名 实验 类别 **** 成绩 实验 时间
迭代法
自选实验
2011.6.7
实验问题:
n 元线性方程组
a11 x1 a12 x 2 a1 n xn 0 a x a x a x 0 21 1 22 2 2n n am 1 x1 am 2 x 2 amn xn 0
其中,f[x_]:=为所求迭代函数,迭代n次产生相应是序列,并观察。
(3)线性方程组的迭代求解 对给定的矩阵 M、 数组 f 和初始向量 x0, 由 X^(n+1)=Mx^n+f,n=0,1,2,3……给定的结 果 其 Matheatica 程序如下:
2
实验过程:
1.迭代序列 ( 1 ) 给 定 的 实 数 域 上 光 滑 的 实 值 函 数 f(x) 以 及 初 值 x0, 定 义 数 列 x(n+1)=f(x0),n=0,1,2,3,……. 对函数 f(x)= (25*x - 85)/(x + 3)的迭代过程,可以形象地用蜘蛛网图像来直观地显示,运 行以下程序:
2.方程求根
用迭代序列求 g(x)=x^3-2*x+1 的根,其 matheatic 程序如下:
(精校版)迭代法解线性方程组数值分析实验报告

(完整word版)迭代法解线性方程组-数值分析实验报告编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整word版)迭代法解线性方程组-数值分析实验报告)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整word版)迭代法解线性方程组-数值分析实验报告的全部内容。
数学与计算科学学院《数值分析》课程设计题目:迭代法解线性方程组专业:信息与计算科学学号: 1309302—24姓名:谭孜指导教师:郭兵成绩:二零一六年六月二十日一、前言:(目的和意义)1.实验目的①掌握用迭代法求解线性方程组的基本思想和步骤.②了解雅可比迭代法,高斯—赛德尔法和松弛法在求解方程组过程中的优缺点。
2。
实验意义迭代法是用某种极限过程去逐步逼近线性方程组精确解的方法,它是解高阶稀疏方程组的重要方法。
迭代法的基本思想是用逐次逼近的方法求解线性方程组。
比较雅可比迭代法,高斯—赛德尔迭代方法和松弛法,举例子说明每种方法的试用范围和优缺点并进行比较.二、数学原理:设有方程组b Ax = …① 将其转化为等价的,便于迭代的形式f Bx x += …② (这种转化总能实现,如令b f A I B =-=,), 并由此构造迭代公式f Bx x k k +=+)()1( …③ 式中B 称为迭代矩阵,f 称为迭代向量。
对任意的初始向量)0(x ,由式③可求得向量序列∞0)(}{k x ,若*)(lim x x k k =∞→,则*x 就是方程①或方程②的解。
此时迭代公式②是收敛的,否则称为发散的。
构造的迭代公式③是否收敛,取决于迭代矩阵B 的性 1。
雅可比迭代法基本原理设有方程组),,3,2,1(1n i b x a j j nj ij ==∑= …①矩阵形式为b Ax =,设系数矩阵A 为非奇异矩阵,且),,3,2,1(,0n i a ii =≠从式①中第i 个方程中解出x,得其等价形式)(111j nj j ij ii i x a b a x ∑≠=-= …②取初始向量),,,()0()0(2)0(1)0(n x x x x =,对式②应用迭代法,可建立相应的迭代公式: )(111)()1(∑≠=++-=nj j i k j ij ii k ib x a a x…③ 也可记为矩阵形式:J x J k F B x k +==)()1( …④ 若将系数矩阵A 分解为A=D —L-U ,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=--=--00000000000000111211212211212222111211n n n nn n nn nn n n n n a a a a a a a a a a a a a a a a a a U L D A式中⎪⎪⎪⎪⎪⎭⎫⎝⎛=nn a a a D2211,⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=-0000121323121nn n n a a a a a a L ,⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=-0000122311312n n n n a a a a a a U 。
MATLAB计算方法迭代法牛顿法二分法实验报告

MATLAB计算方法迭代法牛顿法二分法实验报告实验报告一、引言计算方法是数学的一门重要应用学科,它研究如何用计算机来解决数学问题。
其中,迭代法、牛顿法和二分法是计算方法中常用的数值计算方法。
本实验通过使用MATLAB软件,对这三种方法进行实验研究,比较它们的收敛速度、计算精度等指标,以及它们在不同类型的问题中的适用性。
二、实验方法1.迭代法迭代法是通过不断逼近解的过程来求得方程的根。
在本实验中,我们选择一个一元方程f(x)=0来测试迭代法的效果。
首先,我们对给定的初始近似解x0进行计算,得到新的近似解x1,然后再以x1为初始近似解进行计算,得到新的近似解x2,以此类推。
直到两次计算得到的近似解之间的差值小于规定的误差阈值为止。
本实验将通过对复杂方程的迭代计算来评估迭代法的性能。
2.牛顿法牛顿法通过使用函数的一阶导数来逼近方程的根。
具体而言,对于给定的初始近似解x0,通过将f(x)在x0处展开成泰勒级数,并保留其中一阶导数的项,得到一个近似线性方程。
然后,通过求解这个近似线性方程的解x1,再以x1为初始近似解进行计算,得到新的近似解x2,以此类推,直到两次计算得到的近似解之间的差值小于规定的误差阈值为止。
本实验将通过对不同类型的方程进行牛顿法的求解,评估它的性能。
3.二分法二分法是通过将给定区间不断二分并判断根是否在区间内来求方程的根。
具体而言,对于给定的初始区间[a,b],首先计算区间[a,b]的中点c,并判断f(c)与0的大小关系。
如果f(c)大于0,说明解在区间[a,c]内,将新的区间定义为[a,c],再进行下一轮的计算。
如果f(c)小于0,说明解在区间[c,b]内,将新的区间定义为[c,b],再进行下一轮的计算。
直到新的区间的长度小于规定的误差阈值为止。
本实验将通过对复杂方程的二分计算来评估二分法的性能。
三、实验结果通过对一系列测试函数的计算,我们得到了迭代法、牛顿法和二分法的计算结果,并进行了比较。
数值分析实验报告 第一次

华中科技大学本科实验报告课程名称:数值分析姓名:姜福鑫学号:U201310044专业班级:应数1302指导老师:黄乘明实验题目:线性方程组的迭代解法日期:2015-4-9实验成绩:1.实验目的通过上机实验,理解利用计算机迭代求解线性方程组的整个过程,加深对所学计算方法的理论及算法特点的理解。
2.实验题目2.1利用算法2.1(Jacobi迭代法),编制MATLAB程序,求线性方程组。
(1)14x+42x+43x+44x=-414x+142x+43x+44x=1614x+42x+143x+44x=3614x+42x+43x+144x=561(2)10.9x+1.22x+2.13x+0.94x=-7.011.2x+11.22x+1.53x+2.54x=5.312.1x+1.52x+9.83x+1.34x=10.310.9x+2.52x+1.33x+12.34x=24.61的近似解,取初值x=T)0,0,0,0(2.2利用算法2.2(Gauss-Seidel迭代法),编制MATLAB程序,求线性方程组。
(1)6x-22x-3x-4x=-161-2x+122x-3x-4x=61-x-2x+63x-24x=81-x-2x-3x+124x=541(2)0.78x-0.022x-0.123x-0.144x=0.761-0.02x+0.862x-0.043x-0.064x=0.081-0.12x-0.042x+0.723x-0.084x=1.121-0.14x-0.062x-0.083x+0.744x=0.681的近似解,取初值x=T)0,0,0,0(2.3利用算法2.2(SOR法),编制MATLAB程序,求线性方程组。
(1)-4x+2x+3x+4x=11x-42x+3x+4x=11x+2x-43x+4x=11x+2x+3x-44x=11(2)x-0.253x-0.254x=0.51x-0.253x-0.254x=0.52-0.25x-0.252x+3x=0.51-0.25x-0.252x+4x=0.51的近似解,取初值x=T)0,0,0,0(3.程序文本function x=majacobi(A,b,x0,ep,N)n=length(b);if nargin<5,N=500;endif nargin<4,ep=1e-6;endif nargin<3,x0=zeros(n,1);endx=zeros(n,1);k=0;while k<Nfor i=1:nx(i)=(b(i)-A(i,[1:i-1,i+1:n])*x0([1:i-1,i+1:n]))/A(i,i);endif norm(x-x0,inf)<ep,break;endx0=x;k=k+1;endif k==N,Warning('已达到迭代次数上限');enddisp(['k=',num2str(k)])2.2function x=maseidel(A,b,x0,ep,N)n=length(b);if nargin<5,N=500;endif nargin<4,ep=1e-6;endif nargin<3,x0=zeros(n,1);endx=zeros(n,1);k=0;while k<Nfor i=1:nif i==1x(1)=(b(1)-A(1,2:n)*x0(2:n))/A(1,1);else if i==nx(n)=(b(n)-A(n,1:n-1)*x(1:n-1))/A(n,n);elsex(i)=(b(i)-A(i,1:i-1)*x(1:i-1)-A(i,i+1:n)*x0(i+1:n))/A(i,i);endendendif norm(x-x0,inf)<ep,break;endx0=x;k=k+1;endif k==N,Warning('已达到迭代次数上限');enddisp(['k=',num2str(k)])2.3function x=masor(A,b,omega,x0,ep,N)n=length(b);if nargin<6,N=500;endif nargin<5,ep=1e-6;endif nargin<4,x0=zeros(n,1);endif nargin<3,omega=1.5;endx=zeros(n,1);k=0;while k<Nfor i=1:nif i==1x1(1)=(b(1)-A(1,2:n)*x0(2:n))/A(1,1);else if i==nx1(n)=(b(n)-A(n,1:n-1)*x(1:n-1))/A(n,n);elsex1(i)=(b(i)-A(i,1:i-1)*x(1:i-1)-A(i,i+1:n)*x0(i+1:n))/A(i,i);endendx(i)=(1-omega)*x0(i)+omega*x1(i);endif norm(x-x0,inf)<ep,break;endx0=x;k=k+1;endif k==N,Warning('已达到迭代次数上限');enddisp(['k=',num2str(k)])4.运行结果与分析2.11.k=94x=-2.00000.00002.00004.00002.22.k=17x=-0.99860.00711.00321.96562.21.k=11 x=-1.07820.95532.88974.7306 2.22.k=8 x=1.55030.32321.99341.45392.31.k=21 x=-1.0000-1.0000-1.0000-1.0000 2.32.k=21 x= 1.00001.00001.00001.0000分析:对比三种方法,Jacobi迭代法次数较多才能到达精度要求,Gause-Seidel迭代法次数较少,SOR法次数处于两者之间。
第一次实验报告-迭代法
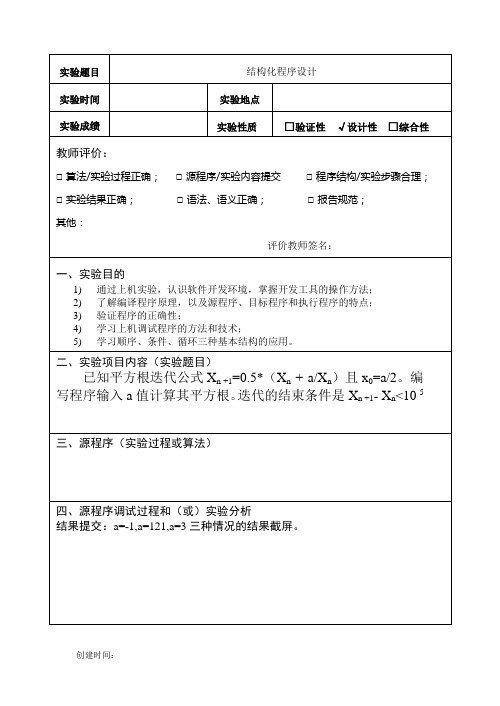
结果提交:a=-1,a=121,a=3三种情况的结果截屏。
实验题目
结构化程序设计
实验时间
实验地点
实验成绩
实验性质
□验证性√设计性□综合性
教师评价:
□算法/实验过程正确;□源程序/实验内容提交□程序结构/实验步骤合理;
□实验结果正确;□语法、语义正确;□报告规范;
其他:
评价教师签名:
一、实验目的
1)通过上机实验,认识软件开发环境,掌握开发工具的操作方法;
2)了解编译程序原理,以及源程序、目标程序和执行程序的特点;
3)验证程ห้องสมุดไป่ตู้的正确性;
4)学习上机调试程序的方法和技术;
5)学习顺序、条件、循环三种基本结构的应用。
二、实验项目内容(实验题目)
已知平方根迭代公式Xn +1=0.5*(Xn+ a/Xn)且x0=a/2。编写程序输入a值计算其平方根。迭代的结束条件是Xn +1- Xn<10-5
三、源程序(实验过程或算法)
数值分析上机实验报告

数值分析上机实验报告导言:本次上机实验主要是针对数值分析课程中的一些基本算法进行实验验证。
实验内容包括迭代法、插值法、数值积分和常微分方程的数值解等。
在实验过程中,我们将会使用MATLAB进行算法的实现,并对结果进行分析。
一、迭代法迭代法是解决函数零点、方程解等问题的常用方法。
我们将选择几个常见的函数进行迭代求根的实验。
(1)二分法二分法是一种简单而有效的迭代求根法。
通过函数在区间两个端点处的函数值异号来确定函数在区间内存在零点,并通过不断缩小区间来逼近零点。
(2)牛顿法牛顿法利用函数的一阶导数和二阶导数的信息来逼近零点。
通过不断迭代更新逼近值,可以较快地求得零点。
实验结果表明,对于简单的函数,这两种迭代法都具有很好的收敛性和稳定性。
但对于一些复杂的函数,可能会出现迭代失效或者收敛速度很慢的情况。
二、插值法插值法是在给定一些离散数据点的情况下,通过构造一个插值函数来逼近未知函数的值。
本实验我们将使用拉格朗日插值和牛顿插值两种方法进行实验。
(1)拉格朗日插值拉格朗日插值通过构造一个多项式函数来逼近未知函数的值。
该多项式经过离散数据点,并且是唯一的。
该方法简单易懂,但插值点越多,多项式次数越高,插值函数的精度也就越高。
(2)牛顿插值牛顿插值利用差商的概念,通过构造一个插值多项式来逼近未知函数的值。
与拉格朗日插值相比,牛顿插值的计算过程更加高效。
但同样要求插值点的选择要合理,否则可能出现插值函数不收敛的情况。
实验结果表明,这两种插值方法都能够很好地逼近未知函数的值。
插值点的选择对插值结果有很大的影响,过多或者过少的插值点都可能导致插值结果偏离真实函数的值。
三、数值积分数值积分是一种将定积分问题转化为数值求和的方法。
本实验我们将使用复合梯形求积法和复合辛普森求积法进行实验。
(1)复合梯形求积法复合梯形求积法将定积分区间等分为若干小区间,然后使用梯形公式对每个小区间进行近似求积,最后将结果相加得到整个定积分的近似值。
数值分析报告迭代法

数值分析报告一.Gauss_Seidel迭代法1.解题思路:输入矩阵A,右端项b,维数n,初始迭代向量想,容许误差e,容许最大迭代次数N;先对矩阵A进行判断:若det(A)~=0,则继续计算,否则输出失败信息;再对A进行收敛判断:p(M)<1,则继续计算,否则输出失败信息;计算出迭代矩阵,对x进行N次迭代,若x->x0,则输出x;否则输出失败。
2.Matlab程序:function [x,true]=Gauss_Seidel(A,b,x,n,e,N)if rank(A)==nDni=zeros(n,n);L=zeros(n,n);U=L;for i=1:nDni(i,i)=1/A(i,i);endB=eye(n,n)-Dni*A;g=Dni*b;for i=2:nfor j=1:i-1L(i,j)=B(i,j);U(j,i)=B(j,i);endendtrue=vrho(L+U);if(true<1)k=0;while k<Nt=x;m=U*x+g;x=(eye(n,n)-L)\m;k=k+1;endif max(x-t)>edisp('N is too small');returnendelsedisp('A is not convergent');returnendelsedisp('A is unavailable');returnend3.利用程序解决问题:1). A=[2,-1,0,0;-1,2,-1,0;0,-1,2,-1;0,0,-1,2];b=[1;0;1;0]; x=[1;0;1;0];[m,n]=Gauss_Seidel(A,b,x,4,0.00005,100)m =1.20001.40001.60000.8000n =0.80902). C=[10,4,4;4,10,8;4,8,10];d=[13;11;25]; x=[1;1;1]; [m,n]=Gauss_Seidel(C,d,x,3,0.00005,100)A is not convergentm =111n =1.0928二.Jacobi迭代法1.解题思路:输入矩阵A,右端项b,维数n,初始迭代向量想,容许误差e,容许最大迭代次数N;先对矩阵A进行判断:若det(A)~=0,则继续计算,否则输出失败信息;对x进行N次迭代,若x->x0,则输出x;否则输出失败。
【分析】数值分析迭代法

【关键字】分析数值分析实验报告(3)学院:信息学院班级:计算机0903班姓名:王明强学号:课题三线性方程组的迭代法一、问题提出1、设线性方程组=x= ( 1, -1, 0, 1, 2, 0, 3, 1, -1, 2 )2、设对称正定阵系数阵线方程组=x = ( 1, -1, 0, 2, 1, -1, 0, 2 )3、三对角形线性方程组=x= ( 2, 1, -3, 0, 1, -2, 3, 0, 1, -1 )试分别选用Jacobi 迭代法,Gauss-Seidol迭代法和SOR方法计算其解。
二、要求1、体会迭代法求解线性方程组,并能与消去法做以比较;2、分别对不同精度要求,如由迭代次数体会该迭代法的收敛快慢;3、对方程组2,3使用SOR方法时,选取松弛因子=0.8,0.9,1,1.1,1.2等,试看对算法收敛性的影响,并能找出你所选用的松弛因子的最佳者;4、给出各种算法的设计程序和计算结果。
三、目的和意义1、通过上机计算体会迭代法求解线性方程组的特点,并能和消去法比较;gauss消去法是一种规则化的加减消元法。
它的基本思想是:通过逐次消元计算把需要求求解的线性方程转化成上三角形方程组,也就是把线性方程组的系数矩阵转化为上三角矩阵,从而使一般线性方程组求解转化为等价(同解)的上三角方程组的求解。
消去法是直接方法的一种。
优点:对于简单的方程组可以很快得出结果,计算中如果没有舍入误差,在稳定的方程组中容易得到精确解,理论上可以求解任何可以求出解得方程组。
缺点:数值有的时候不稳定(可采用列主元gauss消去法),既要消去,又要回代,算法实现起来比较复杂,不适用于大规模方程组。
迭代法是从某一取定的初始向量x(0)出发,按照一个适当的迭代公式,逐次计算出向量x(1),x(2),......,使得向量序列{ x(k)}收敛于方程组的精确解,这样,对于适当大的k,可取x(k)作为方程组的近似解。
优点:算法简单,程序易于实现,特别适用求解庞大稀疏线性方程组。
数值分析迭代法范文

数值分析迭代法范文迭代法的基本思想是通过重复执行一些计算步骤,不断逼近问题的解。
该方法常用于求解无法通过解析方法求得解的问题,如非线性方程的根、方程组的解等。
在数值分析中,迭代法可用于求解各种数学问题,例如求解微分方程、积分、优化等。
在迭代法中,关键是选择一个适当的迭代函数和初始值。
迭代函数是一个映射,将当前的迭代结果映射到下一次迭代的结果。
迭代法通过重复应用迭代函数来不断逼近问题的解。
迭代法的步骤一般如下:1.选择一个初始值作为迭代的起点。
2.应用迭代函数计算下一次迭代的结果。
3.检查迭代的结果是否满足终止条件,如果满足则迭代结束,取得近似解;否则返回第二步继续迭代。
4.根据需要,可以设置最大迭代次数或迭代误差限制,以确保迭代的收敛性和计算效率。
迭代法的收敛性是评价其有效性的重要指标。
一个迭代法的收敛性是指当迭代次数趋于无穷大时,迭代结果是否与问题的解趋于一致。
常用的判断迭代法收敛性的方法是通过计算迭代序列的极限,判断序列是否收敛到所求解。
迭代法有很多的变种和改进方法,常用的有简单迭代法、牛顿迭代法、埃特金迭代法等。
每种迭代法有其适用的问题类型和求解效果,需要根据具体问题的特点进行选择。
例如,简单迭代法是一种基础的迭代算法,通过反复迭代计算近似解。
它适用于求解非线性方程的根,通过对原方程进行变形,找到满足一些条件的迭代函数,然后通过迭代计算逼近根的解。
牛顿迭代法是一种通过线性化原方程并应用牛顿法的迭代法。
它适用于求解非线性方程的根和优化问题。
该方法通过构造局部线性逼近来逐渐逼近所求解,具有较快的收敛速度。
埃特金迭代法是一种通过构造适当的迭代函数和近似解序列的加权平均值来提高迭代收敛速度的方法。
它适用于求解线性方程组和非线性方程的根等问题。
总而言之,数值分析迭代法是一种重要的数值计算方法。
通过选择适当的迭代函数和初始值,迭代法能够通过重复计算逼近复杂问题的解。
迭代法具有广泛的应用领域和多样化的改进方法,可以有效地解决科学和工程领域中的各种数学问题。
大学数学实验报告----迭代

数学实验报告综合实验迭代学院:数学与信息科学学院班级: 09级数学(4)班姓名:***学号:***综合实验——迭代给定实数域上光滑的实值函数()f x 以及初值0x 定义数列1(),0,1,n n x f x n +==⋅⋅⋅,n x ,0,1,n =⋅⋅⋅,称为()f x 的一个迭代数列.函数的迭代是数学研究中的一个非常重要的思想工具.哪怕是对一个相当简单的函数进行迭代,都可以产生异常复杂的行为,并由此而衍生了一些崭新的学科分支,如分型与混沌.同时,迭代在各种数值计算方法以及其他学科领域的诸多算法中处于核心的地位.我们将通过一系列实验介绍迭代在诸多领域的应用。
一、迭代(方程求解)二、迭代(分形)③按Shift 和Enter 键运行。
运行结果:redosierpinski ptlist_List : Blockt mp ,i,pnum Length ptlist3 ,For i 0,i pnum,i i 1,tmp Join t mp, ptlist3i 1,ptlist 3i 1 ptlist 3i 2 2, ptlist 3i 1 ptlist 3i 3 2, ptlist 3i 1 ptlist3i 2 2,ptlist 3i 2 ,ptlist 3i 2 ptlist 3i 3 2, ptlist 3i 1 ptlist 3i 3 2, ptlist3i 2ptlist3i 32,ptlist 3i 3 ;tmpshowsierpinski ptlist_List : Blockt mp ,i,pnum Length ptlist3 ,For i 0,i pnum,i i 1,AppendTo t mp,Polygonptlist3i 1,ptlist3i 2ptlist3i 3;Show G raphics t mp ,AspectRatio 1 GoldenRat po1 1,0 , 1,0 , 0,Sqrt 3;showsierpinski Nest r edosierpinski,po1,4三、复变函数迭代1.510.5-0.5-1-1.5-1.5-1-0.500.511.510.5-0.5-1-1.5-1.5-1-0.500.51 0.30.20.1-0.1-0.7-0.65-0.6-0.55-0.5-0.45四、迭代(混沌)五、迭代(几何形状的构造)。
迭代法实验报告

迭代法实验报告迭代法实验报告引言:迭代法是一种常见的数值计算方法,通过反复迭代逼近解的过程,来解决一些复杂的数学问题。
本实验旨在通过实际操作,深入理解迭代法的原理和应用,并通过实验数据验证其有效性。
一、实验目的本实验的主要目的有以下几点:1. 掌握迭代法的基本原理和步骤;2. 熟悉迭代法在数值计算中的应用;3. 理解迭代法的收敛性和稳定性;4. 验证迭代法在实际问题中的有效性。
二、实验原理迭代法是一种通过不断逼近解的方法,其基本原理可概括为以下几步:1. 选择一个初始值作为迭代的起点;2. 根据问题的特点和要求,构造一个递推公式;3. 通过不断迭代计算,逐步逼近解;4. 判断迭代过程是否收敛,并确定最终的解。
三、实验步骤1. 选择合适的初始值。
初始值的选择对迭代的结果有重要影响,通常需要根据问题的特点进行合理选取。
2. 构造递推公式。
根据问题的数学模型,建立递推公式,将问题转化为迭代求解的形式。
3. 进行迭代计算。
根据递推公式,进行迭代计算,直到满足收敛条件或达到预定的迭代次数。
4. 判断迭代结果。
根据实际问题的要求,判断迭代结果是否满足精度要求,并进行相应的调整和优化。
四、实验结果与分析通过实验操作,我们得到了一组迭代计算的结果。
根据实验数据,我们可以进行以下分析:1. 收敛性分析。
通过观察迭代过程中的数值变化,我们可以判断迭代法的收敛性。
如果数值逐渐趋于稳定,且与理论解的误差在可接受范围内,说明迭代法收敛。
2. 稳定性分析。
迭代法的稳定性是指在初始值变化时,迭代结果是否保持稳定。
通过改变初始值,我们可以观察迭代结果的变化情况,从而评估迭代法的稳定性。
3. 精度分析。
迭代法的精度取决于迭代过程中的误差累积情况。
通过与理论解的比较,我们可以评估迭代法的精度,并对迭代过程进行优化。
五、实验结论通过本次实验,我们深入了解了迭代法的原理和应用,通过实际操作验证了迭代法在数值计算中的有效性。
实验结果表明,迭代法在解决复杂数学问题中具有较高的准确性和稳定性,能够满足实际应用的需求。
数值分析实验报告--实验6--解线性方程组的迭代法

2/8
数值分析实验六:解线性方程组的迭代法
for k=1:1:n-1
3/8
数值分析实验六:解线性方程组的迭代法
张威震
if A(k,k)==0 error(['A(',num2str(k),',',num2str(k),')=0,Calculation
abort!']); end for ii=k+1:n m=A(ii,k)/A(k,k); A(ii,k:n)=A(ii,k:n)-m*A(k,k:n); end
的病态影响,其计算结果已经不可取。而 Gauss 列主元消去法的计算结果和精确解十分接 近。G-S 迭代法和 SOR 方法计算结果也比较准确,而 Jacobi 方法由于其迭代矩阵的谱半径 大于 1,已经不收敛,无法得出结果。总的来说,还是 Gauss 列主元消去法的结果最好。
1.3.2 增加系数矩阵 H 的维数
x* = 1, 1, 1, 1, 1, 1,
x1 = -1.6189e+03 5.2069e+04 -3.8477e+05 1.0716e+06 -1.2490e+06 5.1451e+05
x2 = 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000
x3 = NaN 谱半径 vrho(B)>1, 迭代法不收 敛,无法求 解。
数值分析实验报告之迭代法求非线性方程的根

数值分析实验报告之迭代法求非线性方程的根1.实验目的掌握迭代法求非线性方程根的基本原理和使用方法,加深对数值计算方法的理解与应用。
2.实验原理迭代法是一种通过不断逼近的方法求解非线性方程的根。
根据不同的函数特点和问题需求,可以选择不同的迭代公式进行计算,如牛顿迭代法、二分法、弦截法等。
3.实验内容本次实验使用牛顿迭代法求解非线性方程的根。
牛顿迭代法基于函数的局部线性逼近,通过不断迭代逼近零点,直至满足收敛条件。
具体步骤如下:Step 1:选择初始点X0。
Step 2:计算函数f(x)在X0处的导数f'(x0)。
Step 3:计算迭代公式Xn+1 = Xn - f(Xn) / f'(Xn)。
Step 4:判断收敛准则,若满足则迭代结束,输出解Xn;否则返回Step 2,继续迭代。
Step 5:根据实际情况判断迭代过程是否收敛,并输出结果。
4.实验步骤步骤一:选择初始点。
根据非线性方程的特点,选择恰当的初始点,以便迭代公式收敛。
步骤二:计算导数。
根据选择的非线性方程,计算函数f(x)的导数f'(x0),作为迭代公式的计算基础。
步骤三:迭代计算。
根据迭代公式Xn+1=Xn-f(Xn)/f'(Xn),计算下一个迭代点Xn+1步骤四:判断收敛。
判断迭代过程是否满足收敛条件,通常可以通过设置迭代次数上限、判断前后两次迭代结果的差值是否足够小等方式进行判断。
步骤五:输出结果。
根据实际情况,输出最终的迭代结果。
5.实验结果与分析以求解非线性方程f(x)=x^3-x-1为例,选择初始点X0=1进行迭代计算。
根据函数f(x)的导数计算公式,得到导数f'(x0)=3x0^2-1,即f'(1)=2根据迭代公式Xn+1=Xn-f(Xn)/f'(Xn),带入计算可得:X1=X0-(X0^3-X0-1)/(3X0^2-1)=1-(1-1-1)/(3-1)=1-0/2=1根据收敛准则,判断迭代结果是否满足收敛条件。
迭代数学实验

北京建筑工程学院理学院 实验报告课程名称 数学实验 实验名称 迭代(一)—方程求解 实验地点 基c425 日期 2015-7-1 姓名 周盈海 班级 信131 学号 201307010137 指导教师 高雁飞 成 绩 (1).利用迭代法求解方程(2).线性方程组的迭代求解【实验要求】1.(1).在同一直角坐标系中画出x y sin 2=及x y =的图像。
从图上观察,方程x x sin 2=的解的个数。
(2).利用迭代法,对x x sin 2=作迭代,取n x 极限,得到方程的解。
2. 利用迭代法,即f Mx x n n +=+1,M 是n 阶矩阵,f 是n 维列向量,对⎪⎪⎭⎫ ⎝⎛=5.0002.0M 作迭代,取n x 极限,得到线性方程组的解。
【实验内容】(主要包含问题分析、计算过程、实验结果等,按课程要求完成)问题的分析1.(1).在同一直角坐标系中画出x y sin 2=及x y =的图像。
由理论可知,方程x x sin 2=有3个解。
(2). 取初值为5.00=x ,对x x sin 2=作迭代,迭代序列应当收敛于0。
但对初值取不同的点,对x x sin 2=作迭代,迭代序列会出现不收敛的现象。
2. 给定实数域上光滑的实值函数f(x)以及初值x0定义数列,,1,0),(1 ==+n x f x n n ,1,0,=n x n 称为f(x)的一个迭代序列.给定迭代函数f(x)以及一个初值x0利用上式迭代得到数列 ,1,0,=n x n 如果数列n x 收敛于某个*x ,则有 )(**x f x =.即*x 是方程x=f(x)的解.由此启发我们用如下的方法求方程g(x)=0的近似解. 将方程g(x)=0改写为等价的方程 x=f(x),然后选取一初值利用上式做迭代.迭代数列n x 收敛的极限就是方程g(x)=0的解. 给定一个n 元线形方程组⎪⎩⎪⎨⎧=++=++n x nn n n n b x a x a b x a x a 1111111或写成矩阵的形式 Ax=b, 其中A=(ij a )是n 阶方阵,x=T n x x ),,(1 均为n 维列向量.任意给定初值向量0x ,由迭代f Mx xn n +=+1确定向量序列n x 收敛到向量*x ,则有f Mx x +=**即*x 是方程组的解。
数值分析实验1_求解方程迭代法

一 实验目的掌握方程迭代法思想,会用Aitken 法、牛顿法、弦截法求解方程。
二 实验内容1 用下列方法求方程201303==--x x x 在附近的根,要求准确到四位有效数字。
(1)牛顿法。
(2)单点弦截法(1、2班)。
(3)双点弦截法(3、4班)。
2 用Aitken 法求方程0123=--x x 在5.10=x 附近的根,精度要求为410-=ε。
三 实验步骤(算法)与结果1(1)算法流程图:程序代码(Python3.6):def newton(x0,N,e): %x0为初始点,N 为最大迭代次数,e 为精度值nit=0while nit<N:f=x0*x0*x0-3*x0-1df=3*x0*x0-3x1=x0-f/dfif abs(x1-x0)<e:breakx0=x1nit=nit+1print(nit,x1)print('迭代次数为',nit,'次时,','方程的根为',"%.4f" % x1)运行函数:>>> newton(2,5,0.00001) 输出:故应用牛顿迭代法,经过3次迭代,可得方程201303==--x x x 在附近的根为1.8794(2)算法流程图:程序代码(Python3.6): defxianjie(x1,x0,N,e): %x0,x1为初始点,N为最大迭代次数,e为精度值nit=0while nit<N:f0=x0*x0*x0-3*x0-1f1=x1*x1*x1-3*x1-1y=x1-f1/(f1-f0)*(x1-x0)if abs(y-x1)<e:breakx1=ynit=nit+1print(nit,x1)print('迭代次数为',nit,'次时,','方程的根为',"%.4f" % x1)运行函数:>>> xianjie(1,2,10,0.00001)输出:因此只需迭代5次,即可获得满足条件的根1.87942.算法流程图:程序代码(Python3.6):def aitken(x0,N,e): %x0为初始点,N为最大迭代次数,e为精度值nit=0while nit<N:y=pow((x0*x0*x0-1),0.5)z=pow((y*y*y-1),0.5)x1=x0-(y-x0)*(y-x0)/(z-2*y+x0)if abs(x1-x0)<e:breakx0=x1nit=nit+1print(nit,x0)print('迭代次数为',nit,'次时,','方程的根为',"%.4f" % x0)运行函数:>>> aitken(1.5,5,0.0001)输出:因此运用Aitken迭代加速法只需迭代2次即可得到满足精度要求的根,近似根为1.4656四实验收获与教师评语实验收获:掌握了运用Aitken法、牛顿法、弦截法求解方程的近似根的算法的基本流程,能够运用Python、MATLAB等语言实现并解出方程的近似根。
数值分析迭代法实验报告
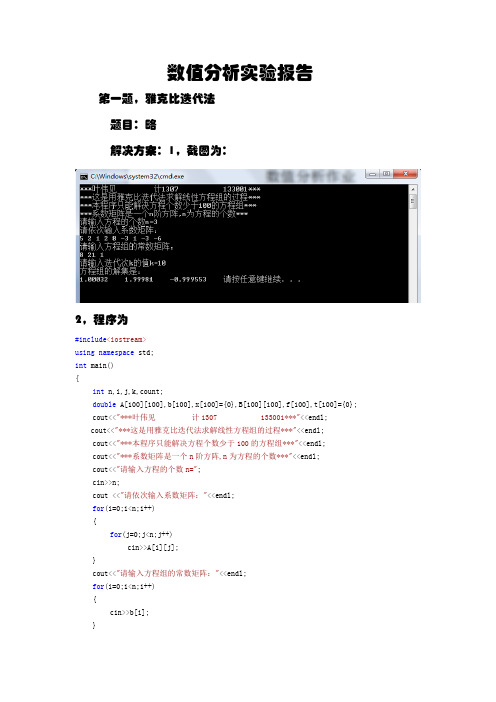
数值分析实验报告第一题,雅克比迭代法题目:略解决方案:1,截图为:2,程序为#include<iostream>using namespace std;int main(){int n,i,j,k,count;double A[100][100],b[100],x[100]={0},B[100][100],f[100],t[100]={0};cout<<"***叶伟见计1307 133001***"<<endl;cout<<"***这是用雅克比迭代法求解线性方程组的过程***"<<endl;cout<<"***本程序只能解决方程个数少于100的方程组***"<<endl;cout<<"***系数矩阵是一个n阶方阵,n为方程的个数***"<<endl;cout<<"请输入方程的个数n=";cin>>n;cout <<"请依次输入系数矩阵:"<<endl;for(i=0;i<n;i++){for(j=0;j<n;j++)cin>>A[i][j];}cout<<"请输入方程组的常数矩阵:"<<endl;for(i=0;i<n;i++){cin>>b[i];}cout<<"请输入迭代次k的值k=";cin>>k;for(i=0;i<n;i++){for(j=0;j<n;j++){if(i==j)B[i][j]=0;elseB[i][j]=-A[i][j]/A[i][i];}}for(i=0;i<n;i++){f[i]=b[i]/A[i][i];}for(count=1;count<=k;count++){for(i=0;i<n;i++){for(j=0;j<n;j++){t[i]=t[i]+B[i][j]*x[j];}t[i]=t[i]+f[i];}for(i=0;i<n;i++){x[i]=t[i];t[i]=0;}}cout<<"方程组的解集是:"<<endl;for(i=0;i<n;i++){cout<<x[i]<<" ";}return 0;}第二题,高斯赛德尔迭代法题目,略解决方案:1,截图2,程序#include<iostream>using namespace std;int main(){int n,i,j,k,count;double A[100][100],b[100],x[100]={0},B[100][100],f[100],t[100]={0}; cout<<"***这是用高斯赛德尔迭代法求解线性方程组的过程***"<<endl;cout<<"***本程序只能解决方程个数少于100的方程组***"<<endl;cout<<"***系数矩阵是一个n阶方阵,n为方程的个数***"<<endl;cout<<"请输入方程的个数n=";cin>>n;cout <<"请依次输入系数矩阵:"<<endl;for(i=0;i<n;i++){for(j=0;j<n;j++)cin>>A[i][j];}cout<<"请输入方程组的常数矩阵:"<<endl;for(i=0;i<n;i++){cin>>b[i];}cout<<"请输入迭代次k的值k=";cin>>k;for(i=0;i<n;i++){for(j=0;j<n;j++){if(i==j)B[i][j]=0;elseB[i][j]=-A[i][j]/A[i][i];}}for(i=0;i<n;i++){f[i]=b[i]/A[i][i];}for(count=1;count<=k;count++){for(i=0;i<n;i++){for(j=0;j<n;j++){t[i]=t[i]+B[i][j]*x[j];}x[i]=t[i]+f[i];t[i]=0;}}cout<<"方程组的解集是:"<<endl;for(i=0;i<n;i++){cout<<x[i]<<" ";}return 0;}第三题,用二分法求解方程的零点题目:用二分法求方程f(x)=4x*x*x+x*x-10 在区间[1,1.5]上的根,要求求出具有3位有效数的近似根解决方法:1程序:#include<iostream>#include<cmath>using namespace std;double f(double x){double f;f=x*x*x+4*x*x-10;return f;}int main(){double a=1,b=1.5;int m;cout<<"请输入零点值的有效位数:";cin>>m;while((b-a)>=0.5*pow(10,-m)){if(f((a+b)/2)==0)break;elseif(f(a)*f((a+b)/2)<0)b=(a+b)/2;elsea=(a+b)/2;}cout<<"f零点的值是:"<<(a+b)/2;return 0;}2,截图:。
数值分析实验四 方程组的迭代法1

数值分析实验四 方程组的迭代法组号 班级 学号 姓名 分数一:实验目的1、学会用Jacobi,Gauss-Seidel,SOR 方法计算方程组的数值解。
2、分析个算法的优劣。
二:实验内容及基本知识介绍1、迭代的原理:设线性方程组Ax=b,(3.13)这里,A=*()ij n n a 非奇异,1..0.n b b b ⎛⎫ ⎪ ⎪⎪=≠ ⎪ ⎪ ⎪⎝⎭,将式(3.13)变换成映射形式同解方程组x Gx f =+,(3.14)由此构造迭代格式()()f Gx x k k +=-1(3.15)对取定的初始向量()()0100...n x x x ⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭,得迭代序列()()()010...k n x x x ⎛⎫ ⎪ ⎪⎪= ⎪ ⎪ ⎪⎝⎭().,...2,1=k若()()()*1**...k n x xx x ⎛⎫⎪ ⎪⎪→= ⎪ ⎪ ⎪⎝⎭()*0,.k k x x →∞⎛⎫-→ ⎪⎝⎭等价于为某种向量范数,由式(3.15)取极限得f Gx x +=**从而*x 为式(3.14)的解,即式(3.13)的解.当k 充分大时,()*k x x≈ .2. Jacobi 迭代法和Gauss-Seide 迭代法对式(3.13)的系数矩阵做分解: A=L+D+U其中,L 为严格下三角矩阵,D 为对角阵,U 为严格上三角矩阵,即⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0002121n n a a a L ,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=nn a a a D 2211,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0002112 n n a a a U 代入式(3.13)得()()x U L b Dx b x U D L +-=⇒=++当D 可逆()0,1,...,ij a i n ≠=即时,有()[]()b D f U L D G f Gx x U L b D x 111,,---=+-=+=+-=对应迭代格式为()()f Gx x k k +=-1(3.16)其中,()U L D G +-=-1A D I 1--=,b D f 1-=称式(3.16)为Jacobi 迭代格式,它的分量形式为()()()n i x a b a x n i j j k j ii i iik i,...,11,11=⎥⎦⎤⎢⎣⎡-=∑≠=-迭代结束条件一般用()()1,k k xx εε--≤为精度要求,.为某种向量范数(常用∞-范数).Gauss-Seidel 迭代法选取分裂矩阵M 为A 的下三角部分,即选取M=D-L (下三角矩阵),A=M-N 于是得到解Ax=b 的Gauss-Seidel 迭代法()()()()01x 0,1,k k x Bx f k +⎧⎪⎨=+=⎪⎩ 初始向量 (2.7)其中()()()111,B I D LA D LU G f D L b ---=--=-≡=-称()1G D L U -=-为解A x b = 的Gauss-Seidel 迭代法的迭代阵下面给出Gauss-Seidel 迭代法的分量计算公式 记()()()()()1,,,,Tk k k k i nx x x x =由(2.7)式有()()()1k k D L x Ux b +-=+或()()()11k k k DxLx Ux b ++=++即()()()()111111,2,i nk k k ii ii ii jiijj j i a x b a x a x i n -++==+=--=∑∑于是解A x b =的Gauss-Seidel 迭代法计算公式为()()()()()()()()000111111,,/1,,;0,1,Tn i n k k k ii ii j ii j ii j j i x x x x b a x a x a i n k -++==+⎧=⎪⎪⎛⎫⎪=--⎨ ⎪⎝⎭⎪⎪==⎪⎩∑∑ 或()()()()()()()()()000111111,,/1,,;0,1,Tn k k i i i i n k k i i ii j ii j ii j j i x x x x x x x b a x a x a i n k +-+==+⎧=⎪⎪=+∆⎪⎪⎨⎛⎫⎪∆=-- ⎪⎪⎝⎭⎪==⎪⎩∑∑ 3、迭代加速——逐次超松弛法考虑Gauss-Seidel 迭代格式的加速算法 .方法是选取一个参数ω(称为超松弛因子),将Gauss-Seidel 迭代第k 步()()1111/i n k k i ii j ii jii j j i b a x a x a -+==+⎛⎫-- ⎪⎝⎭∑∑与第k+1步()1k i x -作适当加权平均得一新的迭代格式 ()()()()()111111/i n k k k k iiii i ii j ii j j j i x x a b a x a x ωω---==+⎛⎫=-+-- ⎪⎝⎭∑∑ (3.23)式(3.23)式称为主次超松弛迭代法(SOR )容易验证,式(3.23)定义合理,并可以证明其收敛的必要条件是0 2.1ωω<<=当时,SOR 法退化为Gauss-Seidel 迭代;当01ω<<时,称式(3.23)为低松弛法;当12ω<<时,称式(3.23)为超松弛法.SOR 法的加速效果依赖于松弛因子ω的选取三:实验问题及方法、步骤Jacobi 、Gauss-Seidel 和SOR 迭代算法都有向量和分量两种形式的表达形式,Jacobi 迭代算法见(3.16)和(3.17),Gauss-Seidel 迭代算法见(3.20)和(3.21),SOR 迭代算法见(3.23).这些迭代法都可能不收敛,对于这类大型稀疏线性方程组,可以考虑采用迭代法(主要用分量形式或稀疏存储)来进行计算,可以节省存储空间.1、程序1 解普通方程组的Gauss-Seidel 迭代 根据(3.21)编写 function x=nags(A,b,x0,e,N)%用途:用向量形式(普通存储格式)的Gauss-Seidel 迭代解线性方程组A %格式:x=nags(A,bx0,e,N) A 为系数矩阵,b 为右端向量,x 返回解向量,% x0为初值向量(默认原点),e 为精度(默认1e-4)设置迭代次数上限以防 % 发散(默认500) n=length(b);if nargin<5,N=500;end if nargin<4,e=1e-4;endif nargin<3,x0=zeros(n,1):end x=x0;x0=x+2*e;k=0;Al=tril(A);iAl=inv(Al); while norm(x0-x,inf)>e&k<n, k=k+1;x0=x;x=-iAl*(A-Al)*x0+iAl*b; disp(x') endif k==N,warning(‘已达迭代次数上限’); end2、 程序2 分量形式的SOR 迭代 根据式3.23编写 function x=nasor(A,b,omega,x0,e,N)%用途:用分量形式的SOR 迭代解线性方程组Ax=b%格式:x=nasor(A,b,omega,x0,e,N) A 为系数矩阵,b 未右端向量,x 返回解向量 %x0为初值向量(默认原点),e 为精度(默认1e-4),设置迭代次数上限以防发散 %(默认500),omega 是松弛因子,一般取1-2之间的数(默认1.5) n=length(b);if nargin<6,N=500;end if nargin<5,e=1e-4;endif nargin<4,x0=zeros(n,1):end x=x0;x0=x+2*e;k=o;L=tril(A ,-1);U=triu(A,l); while norm(x0-x,inf)>e&k<N, k=k+1 x0=x; fori=1:nx1(i)=(b(i)-L(I,1:i-1)*x(1:i-1,1)-U(I,i+1:n)*x0(i+1:n,...1))/A(i,i); x(i)=(1-omega)*x0(i)+omega*x1(i); end disp(x ’) endif k==N,warning(‘已达迭代次数上限’);end3、实验实验1分别用 Gauss-Seidel 迭代法与SOR 解线性方程组⎪⎩⎪⎨⎧=+---=-+-=--3322242024321321321x x x x x x x x x初值取()()()001231x x x === 松弛因子ω=1.45,取精度610-解:使用程序1,在MA TLAB 命令窗口执行: A=[4-2-1;-24-2;-1-23];b=[0-23]’; format long;x=nags(A,b,[1,1,1]’,1e-6)计算结果如下>> x=nags(A,b,[1 1 1]',1e-6)0.750000000000000 0.375000000000000 1.5000000000000000.562500000000000 0.531250000000000 1.5416666666666670.651041666666667 0.596354166666667 1.614583333333334 x =0.651041666666667 0.596354166666667 1.614583333333334使用程序2 在命令窗口执行 nasor(A,b,1.45,[1,1,1]’,1e-6) format short 计算结果如下>> nasor(A,b,1.45,[1,1,1]',1e-6) k =10.6375 0.0122 1.3199 k = 20.2004 0.3718 1.3123 k = 30.6550 0.5340 1.6923 k = 40.7058 0.7733 1.7772 k =50.8873 0.8587 1.9092 k = 60.9154 0.9364 1.9385 k =70.9697 0.9620 1.9763 k = 80.9775 0.9836 1.9840 k =90.9924 0.9903 1.9941 k =100.9942 0.9959 1.9959 k =110.9982 0.9976 1.9986k =120.9985 0.9990 1.9990 k =130.9996 0.9994 1.9997 k =140.9996 0.9998 1.9997 k = 150.9999 0.9998 1.9999 k =160.9999 0.9999 1.9999 k =171.0000 1.00002.0000 k =181.0000 1.00002.0000 k = 191.0000 1.00002.0000 k =201.0000 1.00002.0000 k =211.0000 1.00002.0000 k =221.0000 1.00002.0000 k =231.0000 1.00002.0000 k =241.0000 1.00002.0000 ans = 1.0000 1.0000 2.0000实验2、试用SOR 迭代计算线性方程组1231231235551241213613522474712x x x x x x x x x --+=⎧⎪+-=⎨⎪++=⎩取()()T0x0,0,0=,松弛因子分别选取为0.1t,1t 19ω=≤≤要求达到精度()()k 1k 4x x 10+--≤ 试通过数值计算得出不同的松弛因子所需要的迭代次数和收敛最快的松弛因子,并指出那些松弛因子使得迭代发散 解:编写程序如下:function[it,ws]=test61(A,b,w,maxit) if nargin<4, maxit=20000;if nargin<3, w=linspace(o.1,1.9,19);if nargin<2, b=[41 52 12]';if nargin<1,A=[-55 -5 12;21 36 -13;24 7 47];end;end;end;end;n=length(b);for k=1:length(w),xold=zeros(n,1);it(k)=0;convg=0;while ~convg,it(k)=it(k)+1;x=xold;for j=1:n,x(j)=x(j)+w(k)/A(j,j)*(b(j)-A(j,:)*x);endif norm(x-xold)<1e-4,convg=1;elsexold=x;endif it(k)>maxit,it(k)=inf;convg=1;xendendend[minit,ind]=min(it);ws=w(ind);在命令行上运行>> [it,ws]=test61x =-0.85102.07740.3804x =-0.85122.07800.3805x =-0.85132.07830.3805x =-0.85132.0783 0.3805 x =-0.8514 2.0784 0.3805 x =-0.8514 2.0784 0.3805 x =-0.8514 2.0785 0.3805 x =-0.8514 2.0785 0.3805 x =-0.8514 2.0785 0.3805 x =-0.8514 2.0785 0.3805 x =-0.8514 2.0785 0.3805 x =-0.8514 2.0785 0.3805 x =-0.8514 2.0785 0.3805 x =-0.8514 2.0785 0.3805 x =-0.85142.0785 0.3805 it =Columns 1 through 1693 49 33 24 19 15 12 10 8 6 6 11 20 44 556 InfColumns 17 through 19 Inf Inf Inf ws = 1.0000四计算结果分析实验1的结果可见SOR 法加速收敛效果非常明显 实验2可得到满足精度的近似解()0.8514,2.0785,0.3805T x =-()0.8514,2.0785,0.3805Tx =- 当0.1,1:19t t ω==时所需的迭代次数分别为93,49,33,24,19,15,12,10,8,6,6,11,20,44,556,∞,∞,∞,∞其中∞代表不收敛 可知, 1.0 1.1ωω==和时迭代最快, 1.6ω≥时迭代不收敛五思考与提高1、雅可比迭代法计算公式比较简单,每迭代一次只需计算一次矩阵和向量的乘法且计算过程中原始矩阵A 始终不变雅克比迭代法不使用变量的最新信息计算()1k ix +,而由高斯-赛德尔迭代公式可知,计算()1k x +的第i 个分量()1k i x +时,利用了已经计算出的最新分量()1k j x +()1,2,,1j i =-2、高斯-塞德尔迭代法可以看做比雅可比迭代法的一种改进,高斯-赛德尔迭代法比雅可比迭代法收敛较快,但这个结论只当A 满足一定条件时才是对的。
