理论力学桁架例题
理论力学4.4第4-4章平面简单桁架的内力计算

x y
0, F2 20 0 0, F1 0
解得: F1 0 F2 20kN
20kN
C
FAx F3 F4 FAy
10kN 10kN 10kN 10kN
F1
A
FBy
F2
FAx
解:(1) 取整体为研究对象
FAy
F1
(3) 取节点A为研究对象
F 0 , F F F cos 45 0 x Ax 4 3 F 0 , F F F sin 45 0 y Ay 1 3
F 0, F F 0, F M 0,
再以截面m-n左面部分为研究对象 MC 0
F3 A C FA F2 F4 F1
Fa F1b FA 2a 0 F1 4a F b
F
F
b
FB
例 题 4
C
求:桁架1、2杆的力。 解:(1) 取整体为研究对象
D a
M
解得:
a
B
0, P.2a FAy 3a 0
FAy 2P 3
α A E F FAC α α C α α
O α B C F G D FBC FGy FGx M
2M CG 2l cos 30 FBC 3l 参考受力图(b), 选x轴与FOB垂直。 ' O O F 0 , F . COS 30 F . COS 60 0 x BC AB
Fi Fix i Fiy j FR
i 1 i 1 i 1
n
n
n
《理论力学》第四章 静力学应用专题习题解
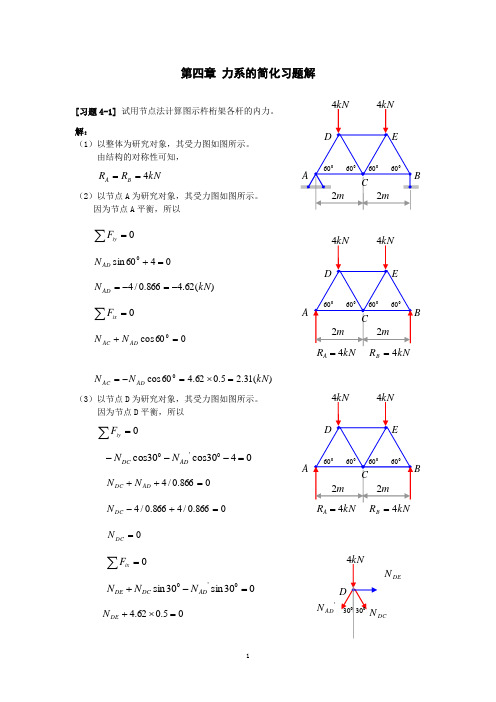
第四章 力系的简化习题解[习题4-1] 试用节点法计算图示杵桁架各杆的内力。
解:(1)以整体为研究对象,其受力图如图所示。
由结构的对称性可知, kN R R B A 4==(2)以节点A 为研究对象,其受力图如图所示。
因为节点A 平衡,所以0=∑iyF0460sin 0=+AD N)(62.4866.0/4kN N AD -=-=0=∑ixF060cos 0=+AD AC N N)(31.25.062.460cos 0kN N N AD AC =⨯=-= (3)以节点D 为研究对象,其受力图如图所示。
因为节点D 平衡,所以 0=∑iyF0430cos 30cos 0'0=---AD D C N N 0866.0/4=++AD D C N N 0866.0/4866.0/4=+-D C N0=DC N0=∑ixF030sin 30sin 0'0=-+AD D C D E N N N 05.062.4=⨯+DE NkN4)(akN4AB RkN 2AC23N A )(31.2kN N DE -=(4)根据对称性可写出其它杆件的内力如图所示。
[习题4-2] 用截面法求图示桁架指定杆件 的内力。
解:(a)(1)求支座反力以整体为研究对象,其受力图如图所示。
由对称性可知,kN R R B A 12==(2)截取左半部分为研究对象,其受力图 如图所示。
因为左半部分平衡,所以0)(=∑i CF M0612422843=⨯-⨯+⨯+⨯N 063243=⨯-++N )(123kN N =kN2AC23N A0=∑ixF0cos cos 321=++N N N αθ01252252421=+⋅+⋅N N012515221=+⋅+⋅N N0512221=++N N ……..(1) 0=∑iyF02812sin sin 21=--++αθN N025*******=+⋅+⋅N N02525121=+⋅+⋅N N052221=++N N0544221=++N N ……..(2) 05832=-N)(963.53/582kN N ==)(399.1652963.5252221kN N N -=-⨯-=--=解:(b )截取上半部分为研究对象,其受力图如图所示。
结构力学自测题(第三单元三铰拱、桁架、组合结构内力计算)

结构力学自测题(第三单元三铰拱、桁架、组合结构内力计算)姓名学号一、是非题(将判断结果填入括弧:以O 表示正确,以X 表示错误)1、图示拱在荷载作用下, N DE为30kN 。
()2、在相同跨度及竖向荷载下,拱脚等高的三铰拱,其水平推力随矢高减小而减小。
()3、图示结构链杆轴力为2kN(拉)。
()2m2m4、静定结构在荷载作用下产生的内力与杆件弹性常数、截面尺寸无关。
()5、图示桁架有:N1=N2=N3= 0。
()a a a a二、选择题(将选中答案的字母填入括弧内)1、在径向均布荷载作用下,三铰拱的合理轴线为:A.圆弧线;B.抛物线;C.悬链线;D.正弦曲线。
()2、图示桁架C 杆的内力是:A. P ;B. -P/2 ;C. P/2 ;D. 0 。
()3、图 示 桁 架 结 构 杆 1 的 轴 力 为 :A.2P ;B. -2PC.2P /2; D. -2P /2。
( )a a a a a a4、图 示 结 构 N DE ( 拉 ) 为:A. 70kN ;B. 80kN ;C. 75kN ;D. 64kN 。
( )4m 4m4m4m三 、填 充 题( 将 答 案 写 在 空 格 内 )1、图 示 带 拉 杆 拱 中 拉 杆 的 轴 力N a = 。
6m6m2、图 示 抛 物 线 三 铰 拱 , 矢 高 为 4m , 在 D 点 作 用力 偶 M = 80kN ·m ,M D 左 =_______,M D 右 =________。
8m 4m 4m3、图 示 半 圆 三 铰拱 , α 为 30°, V A = qa (↑), H A = qa /2 (→), K 截 面 的 ϕK =_______,Q K =________,Q K 的 计 算 式 为 __________________________________。
qAB Kαaa4、图 示 结 构 中 , AD 杆上 B 截 面 的 内 力M B =______ ,____面 受 拉 。
《理论力学》第五章-桁架与摩擦试题及答案
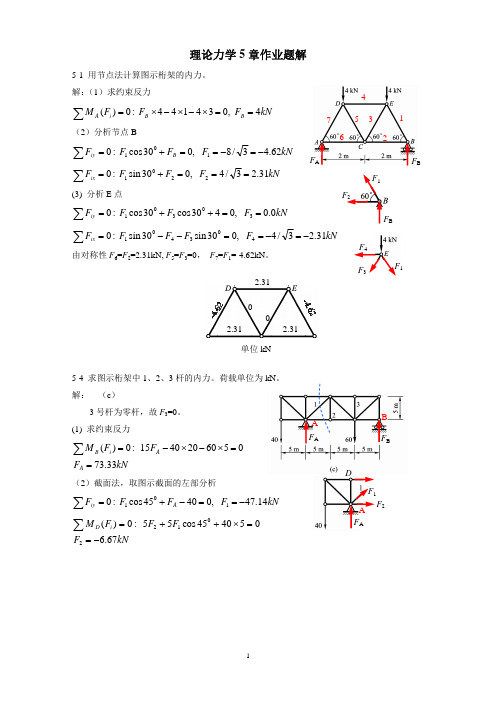
5-1 用节点法计算图示桁架的内力。
解:(1)求约束反力
r
å M A (Fi ) = 0 : FB ´ 4 - 4´1- 4´ 3 = 0, FB = 4kN
(2)分析节点 B
å Fiy = 0 : F1 cos300 + FB = 0, F1 = -8 / 3 = -4.62kN
F4 F3 F2 F1
δ δδδ FN4 FN3 FN2 FN1
附图(a)
FN4 δ F4
取脱离体钢管,示力图为(b),仅给出 4 号管的示力图。
r
å M D (Fi ) = 0 : FN 4 ´ 2d - F4 ´ 2r = 0 ⑶
同理对 3、2、1 号管可有:
FN3 ´ 2d - F3 ´ 2r = 0 ⑷ FN 2 ´ 2d - F2 ´ 2r = 0 ⑸ FN1 ´ 2d - F1 ´ 2r = 0 ⑹ 联合求得:W ´ 2d - F ´ 2r = 0 , F = 0.1kN 。
å Fix = 0 : F1 sin 300 + F2 = 0, F2 = 4 / 3 = 2.31kN
4
7
53
1
6
2
FA
FB
F1
(3) 分析 E 点
F2
å Fiy = 0 : F1 cos300 + F3 cos300 + 4 = 0, F3 = 0.0kN
FB
å Fix = 0 : F1 sin 300 - F4 - F3 sin 300 = 0, F4 = -4 / 3 = -2.31kN
木箱所需的水平力 F 。若不用钢管而使木箱直接在木板上移动,已知木箱与木板的摩擦因数
北京理工大学 理论力学 桁架

以各个节点为研究对象的求解方法
求 解 要 点
1. 逐个考虑各节点的平衡、画出它们 的受力图。 2. 应用平面汇交力系的平衡方程,根 据已知力求出各杆的未知内力。 3. 在受力图中,一般均假设杆的内力 为拉力,如果所得结果为负值,即 表示该杆受压。
节点法适用于求解全部杆件内力的情况
Theoretical Mechanics 返回首页
Theoretical Mechanics
返回首页
§6.6 刚体系统的平衡· 静定与超静定概念
桁架的基本假设
Theoretical Mechanics
返回首页
§6.6 刚体系统的平衡· 静定与超静定概念
桁架的工程应用
Theoretical Mechanics
返回首页
§6.6 刚体系统的平衡· 静定与超静定概念
轴向压缩内力
返回首页
§6.6 刚体系统的平衡· 静定与超静定概念
内力
理想桁架的内力特点: 1、内力是沿着杆轴线作用的;
2、同一杆件各横截面上的内力都相等。
Theoretical Mechanics
返回首页
§6.6 刚体系统的平衡· 静定与超静定概念
Theoretical Mechanics
返回首页
Theoretical Mechanics 返回首页
§6.6 刚体系统的平衡· 静定与超静定概念 课堂讨论: 如何计算杆 DG的内力?
B D G J
例题 例题
C
O
I
A
E
H
K Fp
L
Theoretical Mechanics
返回首页
§6.6 刚体系统的平衡· 静定与超静定概念 结果:
B D
桁架计算习题

取 D 结点为研究对象,得:
1 D 3 1 2 2 1
∑Y = 0
N12 y = −( N13 + 60) = −10kN
N12 = 11.31 × N12 y = −14.14 kN 8
N13 + N12 y + 60 = 0
N12 x = N12 y = −10kN
∑X =0
N 2 = N1 − N12 x = −90kN
0 3 1 G 9 4
N9 + N5 y − N6 y = 0
取 G 结点为研究对象,得:
∑Y = 0
N10 y = − N 9 = 30kN
N10 = 11.31 × N10 y = 42.43kN 8
N10 y + N 9 = 0
N10 x = N10 y = 30kN
0 6 0 3 0 3 5 4 0 6
= 3 4
C
=0
得
:
N ax × 6 + 100 × 4 − 150 × 12 = 0
N ax = 233.33kN
N ay N ax
N ay = 3 × 233.33 = 175kN 4
∴ Na
= 291.67kN
齐欣制作
西南交通大学结构力学教研室
13
西南交通大学结构力学教研室
b 0 a K
取 K 结点为研究对象,对称结构在对称荷载作用下:
F B 1 C F 2 A F D F
Ⅱ
b
Ⅱ
由 ∑ Y = 0 得, Rb = 0 5-14 解:根据支座特性及 L 型结点特N
N7 − F + 2N5x = 0
F F
N 7 = 2F
工程力学第5节 平面静定桁架的内力计算

F1 sin 30 G 0
n
Fiy 0
i1
F1 cos 30 F2 0
得 F1 40 kN(拉) F2 34.6 kN(压)
节点 B:
n
Fix 0
i1 n
Fiy 0
i1
F2 F6 0
得
F3 G 0
F6 34.6 kN(压) F3 20 kN(拉)
i1 n
Fiy 0
i1
FS1 sin 60 FS4 sin 60 0 FS1 cos 60 FS4 cos 60 FS3 0
解得
FS4 FS1 2F(压) 校核计算结果
将各杆内力计算结果列表如下
杆号
1
2
3
内 力 2F 1.73F 2F
半部分为研究对象进行受力分析,列平衡方程:
n
M E (Fi ) 0
FS1 1sin 60 FAy 1 0
i1
n
M D (Fi ) 0
i1 n
Fiy 0
i1
F1
1 2
FS3
1
sin
60
FAy
2 3
0
FAy FS2 sin 60 F1 0
• 因为只有三个独立平衡方程,因此作假想截面时, 一般每次最多只能截断三根杆件。
注意
• 由于平面汇交力系只能列出两个独立平衡方程,所 以应用节点法必须从只含两个未知力大小的节点开 始计算。
例2-15 平面桁架的受力及尺寸如图所示, 试求桁 架各杆的内力。
解 1)先求支座反力:以整体桁架为研究对象进行
理论力学试题

河北工程大学学年第学期期末考试试卷(1)卷一、(10分)已知力kjiF526+-=力的作用点坐标为M(-2,-4,1),求力F对三个坐标轴之矩以及对坐标原点的力矩。
=20 kN.m,q=10 kN/m , l=1m,求固定端支座A的约二、(10分)图示梁,已知m束力。
三、(20分)图示结构,已知AB=EC,BC=CD=ED=a,力P作用在AB中点,求支座A和E的约束力以及BD、BC杆的内力。
四、(20分)桁架受力如图所示,已知F1=10 kN,F2=F3=20 kN,。
试求桁架6,7,8,9杆的内力。
五、(10分)平面曲柄摆杆机构如图所示,曲柄OA的一端与滑块A用铰链连接。
当曲柄OA以匀角速度ω绕固定轴O转动时,滑块在摇杆O1B上滑动,并带动摇杆O1B绕固定轴O1摆动。
设曲柄长OA= r,两轴间距离OO1=l。
求当曲柄OA在水平位置时摇杆的角速度和角加速度。
六、(10分)图示四连杆机构,O1B=l, AB=1.5 l 且C点是AB 中点,OA 以角速度ω转动,在图示瞬时,求B、C 两点的速度和加速度,刚体AB 的角速度ABω七、(12分)质量为m长为l的均质杆OA,可绕O轴转动,图示为初始水平位置,由静止释放:1、计算杆初始瞬时的角加速度。
并求出该瞬时的惯性力。
2、计算杆初始瞬时O的支座约束力。
3、计算杆转动到铅垂位置时的角速度ω。
八、(8分)用虚位移原理求梁B支座的约束力。
kNmMkNFkNFkNF16201416321====第3题第2题第6题第5题河北工程大学 学年 第 学期 理论力学 期末考试 试卷(2 )参考答案一、(10分)解:()k j i F r F M o 281618++-=⨯=(4分)()18-=F M x ()16=F M y ()28=F M z (各2分)二、(10分)解:研究BC 杆,由()↓=⇒=∑kN N MC B100研究整体,由m kN M MA A.400=⇒=∑, 由00=⇒=∑A X X ,由()↑=⇒=∑kN Y Y A 300三、(20分)解:研究AB 杆,得05.05.0===BD BC A S P S P Y研究EC 杆,得Pa M P Y X E E E===5.00四、(20分)解:研究整体得:kN Y B 5.50=研究截面右半部分得: kN F S kN S kN S kN S 205.60S 5.245.502710698-=-=-====五、(10分)解:动点A ,动系O 1Bωr v v a A ==222221111222222221,sin ,sin l r r l r r lr AO vA O v l r r v v lr r e e a e +=+⋅+==∴⋅=+==∴+=ωωωωωϕϕ 又六、(10分) 解:利用瞬心法ωl v A 2=ωω32=AB (顺时针)ωωυl l AB B ==5.1七、(12分)解:1、lmg ml 21312=εl g 23=ε 0=gx R ()↑=mg l R gy 23mgl l g ml M g 2123312==(4分)2、0==O Cx X ma mg Y l l g m ma O Cy-=-=223 ()↑=mg Y O 41(4分)3、1212W T T =-20312122lmgml =-ωl g 3=ω(4分)八、(8分)解:解除B 支座的约束,给系统一组虚位移,列虚功方程,解得:kN Y B31=河北工程大学 学年 第 学期 期末考试试卷2一、(10分)如图所示简支梁,不计梁重。
理论力学06静力学专题_2桁架

第二节
一、桁架 桁架是工程中的一种 常见结构,其特点为
平面桁架的内力计算
直杆铰结而成
所有外力均作用于结 点上
各杆均为二力杆,即 各杆只承受轴力(拉力或压力)
本节主要任务就是计算桁架中各杆所受的轴力
说明: 在计算桁架内力时,规定拉为正压为负
1
二、节点法 节点法是计算桁架内力的一种基本方法 依次截取各个节点为研究对象,根据平面汇交力系平衡方程计算 各杆轴力 注意:所截取节点上的未知力一般不应超过 2 个
2
[例1] 试求图示平面桁架各杆件的内力。
解: 1)计算支座反力
选取桁架整体为研究对象
作受力图 由对称性,易得支座反力
FA FB 15 kN
2)用节点法计算各杆内力
为了方便计算,对桁架各 杆编号
12
8
4
1
13
11
7 9
5
6
3 2
10
3
先截取节点 B 为研究对象 作受力图,假设各杆轴力均 为拉力
17
[例4] 图示屋架,已知 F1 = 15 kN,F2 = 20 kN,l = 1 m,h = 3 m。 试求各杆轴力。 解:1)判断零杆 杆 EI、JG、GD、DJ、JO 均为零杆
18
2) 计算支座反力
选取桁架整体为研究对象 作受力图 取坐标轴,列平衡方程
Fix 0, FAx F1 sin 0
13
[例3] 试判断下列桁架中的零杆
F
C
1
3
A 30
2
D
4
l
30
B
5
结论: 杆 3 为零杆
14
F
F
理论力学桁架网络练习题

理论力学桁架网络练习题一、基本概念题1. 请简述桁架结构的特点。
2. 桁架中的杆件主要承受哪种类型的载荷?3. 什么是节点?桁架中的节点有哪些类型?4. 简述静定桁架与超静定桁架的区别。
5. 桁架结构中的零杆具有什么性质?二、计算题1. 已知一简单桁架,各杆件的长度和材料相同,求各杆件的内力。
2. 计算如下图所示桁架结构中各杆件的内力(图中已给出各杆件长度和载荷)。
3. 有一静定桁架,部分杆件长度和载荷已知,求剩余杆件的长度。
4. 已知一超静定桁架,求各杆件的内力。
5. 分析下图所示桁架结构,判断其是否为静定桁架,并说明理由。
三、分析题1. 分析桁架结构在不同载荷作用下的受力特点。
2. 论述桁架结构在工程中的应用及其优缺点。
3. 比较分析不同材料桁架的受力性能。
4. 针对一个实际桁架工程案例,分析其设计合理性。
5. 讨论桁架结构在地震作用下的稳定性问题。
四、作图题1. 根据给定条件,绘制一个静定桁架的受力图。
2. 绘制一个超静定桁架的受力图,并标明各杆件的内力。
3. 根据下图所示桁架结构,绘制其节点载荷图。
4. 绘制一个桁架结构的弯矩图和剪力图。
5. 请绘制一个简支桁架在均布载荷作用下的受力图。
五、综合题2. 分析一个实际桁架结构,提出改进措施,使其受力更加合理。
3. 针对一个超静定桁架,采用力法求解各杆件的内力。
4. 讨论桁架结构在温度变化影响下的受力特点。
5. 结合工程实际,论述桁架结构在施工过程中的注意事项。
六、判断题1. 桁架结构中的杆件只能承受轴向力。
()2. 所有桁架结构都必须是静定的。
()3. 在桁架结构中,节点载荷可以分解为各杆件的轴力。
()4. 超静定桁架的杆件内力可以通过静力平衡方程直接求出。
()5. 桁架结构的稳定性只与杆件长度有关。
()七、选择题A. 受拉杆件B. 受压杆件C. 零杆D. 弯曲杆件2. 桁架中的节点是:A. 杆件连接处B. 载荷作用点C. 支撑点D. 所有上述选项A. 杆件数量等于节点数减去支撑数B. 杆件数量等于节点数加上支撑数C. 载荷作用点等于节点数D. 支撑数等于节点数A. 力法B. 位移法C. 力矩分配法D. 直接平衡法5. 桁架结构的优化设计主要目的是:A. 减轻结构重量B. 提高结构稳定性C. 降低材料成本D. 所有上述选项八、填空题1. 桁架结构主要由______、______和______组成。
第3章例题-桁架-节点法

工 程 力 学 第 10 3 章 动 平 量 面 原 力 理 系 的 平 衡
例 jd-2 图示桁架受三铅垂力作用,且 F1 F2 F3 F , 杆长 AB=BD=DE=EH=a,求各杆的内力。 F2 F1 D F3
B A
FAx
1
30o
3
6
4
5
7
30o
E
8
9
30o
2
30o
C
H
FH
FAy
解 (2) 逐点求解(略)
方法二
F 0
i
FN3 FN4 cos 45 F3 cos 45 0
FN3 2F (拉杆)
FN1 F F F N2 F F N4 F 2F N5
y
F 0
i
FN5 FN4 cos 45 F3 cos 45 FN6 0
FN4
D
FN3 FN6 F3
FN5
x
FN6 2 2F (压杆)
!
版权所有 钟艳玲 张强
一个方程一个未知量,便于求解!
4
工 程 力 学 第 10 3 章 动 平 量 面 原 力 理 系 的 平 衡
例 jd-2 图示桁架受三铅垂力作用,且 F1 F2 F3 F , 杆长 AB=BD=DE=EH=a,求各杆的内力。 F2 F1 D F3
iy
ix
0
x
F2
F
0 FN5 2F (压杆)
y
FN5 cos 45 F2 0
(3) 节点 B
F
ix
0
F1
FN2 FN1 0
第二节平面桁架问题
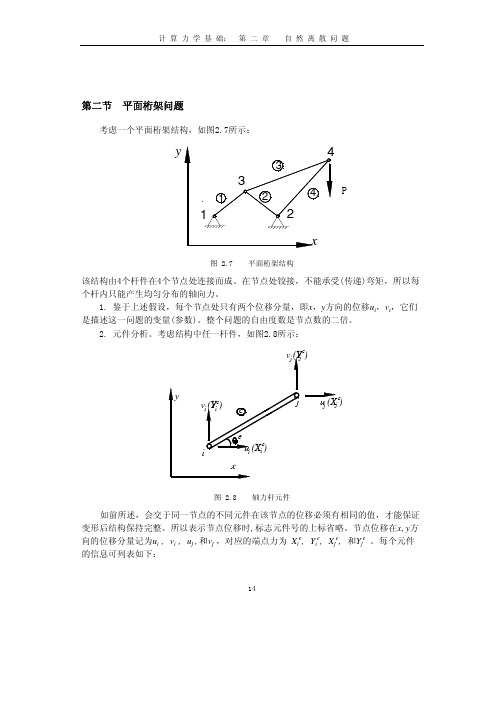
第二节 平面桁架问题考虑一个平面桁架结构,如图2.7所示:图 2.7 平面桁架结构该结构由4个杆件在4个节点处连接而成。
在节点处铰接,不能承受(传递)弯矩,所以每个杆内只能产生均匀分布的轴向力。
1. 鉴于上述假设,每个节点处只有两个位移分量,即x,y方向的位移u i,v i,它们1415元件号 节点号 节点坐标 弹性模量 横截面积 e i , j ( x i , y i );(x j , y j ) E e A e杆件的长度可由下式计算()()L x y x x y y e eej i j i =+=−+−∆∆2222()()ij i j e x x y y tg −−=θ其中e θ是杆件的轴向与x 轴正方向的夹角。
对于图2.8所示的结构,每个元件的节点号如下所示:424433322311j i e杆件产生节点位移u i ,v i ,u j ,v j 后,杆的长度变化为(以受拉为正,受压为负) ))sin cos (sin cos (e i e i e j e j e v u v u L θθθθ+−+=∆ 在节点 j 处的端点轴向力为ee ee e e e e eee jL L LA E L L A E F ∆=∆=∆=κ 其中e ee eLA E =κ 该力在x , y 方向的分量就是X j e 和Y j e ,其表达式为:ee e e e j e j L F X θκθcos cos ∆== j e e e j e e i e e e i e e v u v u θθκθκθθκθκsin cos cos cos sin cos 22++−−=e e e e e j e j L F Y θκθsin sin ∆== j e e j e e e i e e i e e e v u v u θκθθκθκθθκ22sin cos sin sin sin cos ++−−=由杆件本身的平衡得到 F i e = -F j e 即(2.11)(2.14a)(2.12)(2.14b)(2.13)16j eeej eei eeei eee je i v u v u X X θθκθκθθκθκsin cos cos cos sin cos 22−−+=−=j eej eeei eei eeeej e i v u v u Y Y θκθθκθκθθκ22sin cos sin sin sin cos −−+=−=把以上4式合并起来,写成矩阵形式如下⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡−−−−−−−−=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧j j i i e ee ee e e e e ee ee e e ee e e e e ee e e e j e j e i e i v u v u Y X Y X θθθθθθθθθθθθθθθθθθθθθθθθκ22222222sin cos sin sin cos sin cos sin cos cos sin cos sin cos sin sin cos sin cos sin cos cos sin cos 上式写成分块形式为F F k k k k d d i ej e ii eijejie jj e i j ⎧⎨⎪⎩⎪⎫⎬⎪⎭⎪=⎡⎣⎢⎢⎤⎦⎥⎥⎧⎨⎩⎫⎬⎭上式中各子矩阵,各子向量的意义是很明确的。
理论力学计算题及答案
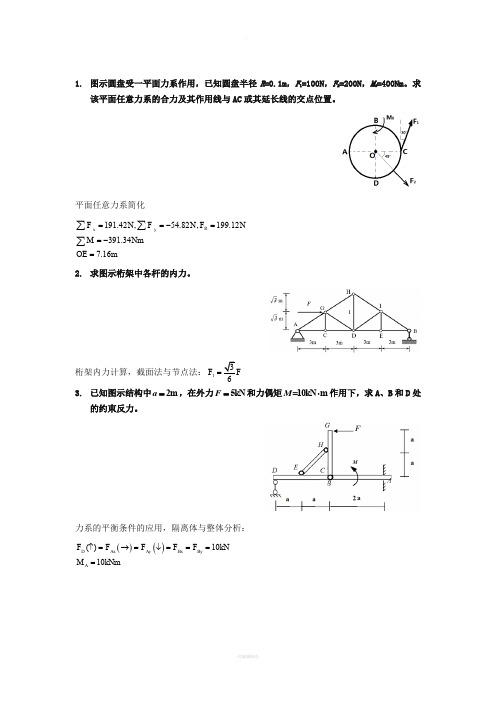
1. 图示圆盘受一平面力系作用,已知圆盘半径R =0.1m ,F 1=100N ,F 2=200N ,M 0=400Nm 。
求该平面任意力系的合力及其作用线与AC 或其延长线的交点位置。
平面任意力系简化191.42,54.82,199.12391.347.16R xyF N F N F NM NmOE m==-==-=∑∑∑2. 求图示桁架中各杆的内力。
桁架内力计算,截面法与节点法:136F F =3. 已知图示结构中2m a =,在外力5kN F =和力偶矩=10kN m M ⋅作用下,求A 、B 和D 处的约束反力。
力系的平衡条件的应用,隔离体与整体分析:()()()1010D Ax Ay Bx By A F F F F F kN M kNm↑=→=↓====4. 已知图示结构中1m =60,a οθ=,在外力10kN F =和力偶矩0=20kN m M ⋅作用下,求A 、C 处的约束反力。
同上()20,0,20,17.32Ax Ay A c F kN F M kNm F kN =→===5. 图示构件截面均一,图中小方形边长为b ,圆形半径均为R ,若右图中大方形和半圆形材料密度分别为12,ρρ,试计算确定两种情况下平面图形的质心位置。
以圆心为原点:()()3222c b x =-R b π→-左以方形下缘中点为原点:()()()12212123238c 2x =ρπρρρπρ++↑+右6. 斜坡上放置一矩形匀质物体,质量m=10kg ,其角点A 上作用一水平力F ,已知斜坡角度θ=30°,物体的宽高比b/h=0.3,物体与斜坡间的静摩擦系数s f =0.4。
试确定不致破坏平衡时F 的取值范围。
计算滑动和翻倒两种情况得到(1)滑动平衡范围14.12124.54N F N -≤≤,(2)翻倒平衡范围:8.6962.27N F N ≤≤7. 如图机构,折杆OBC 绕着O 轴作顺时针的匀速定轴转动,角速度为ω,试求此时扣环M的速度和加速度。
