SPSS15-生存分析
实战利用SPSS进行生存分析

实战利用SPSS进行生存分析生存分析(Survival Analysis)是一种用于分析个体在一定时间内发生其中一事件的概率的统计方法。
生存分析可以用于疾病的生存时间分析、产品寿命分析、客户流失分析等。
SPSS是一种常用的统计分析软件,可以进行生存分析的实证研究。
生存分析的基本概念包括:生存时间(Survival Time)、生存率(Survival Rate)、累积风险(Cumulative Hazard)以及生存函数(Survival Function)等。
生存时间是指个体从其中一起始点到发生其中一事件所经过的时间。
生存率是指个体在其中一时间点存活下来的概率,也称为存活函数。
累积风险是指个体在其中一时刻前发生其中一事件的风险累积值。
进行生存分析的步骤包括:导入数据、设置生存时间和事件变量、选择合适的生存分析方法、进行分析和结果解释。
首先,在SPSS中导入数据。
可以将数据以Excel格式保存,然后在SPSS中选择File->Open->Data,选择相应的文件导入。
选择合适的生存分析方法。
SPSS提供了多种生存分析方法,如Kaplan-Meier生存曲线、Cox回归模型等。
选择合适的方法可以根据研究目的和数据特点来确定。
例如,如果想了解不同因素对生存时间的影响,可以选择Cox回归模型。
在SPSS中,可以使用Analyze->Survival->Survival,然后选择合适的方法进行分析。
进行生存分析。
根据选择的方法,SPSS会输出相应的结果。
例如,对于Kaplan-Meier生存曲线分析,SPSS会生成生存曲线和相应的生存率表格;对于Cox回归模型,SPSS会输出回归系数、风险比率等统计结果。
可以通过点击Results窗口中的相应选项来查看结果。
结果解释。
根据生存分析结果,可以解读生存曲线、计算生存率、比较不同组别间的生存差异等。
对于Kaplan-Meier生存曲线,可以通过图形来比较不同组别的生存率;对于Cox回归模型,可以根据回归系数和风险比率来解释不同因素对生存时间的影响。
生存分析SPSS

生存分析SPSS生存分析是一种统计分析方法,用于研究个体在其中一种特定事件发生之前的生存时间或其持续时间。
生存数据通常是从健康、病理学或其他研究中收集到的,常见的应用有医学领域的生存率研究、产品的寿命分析等。
SPSS(Statistical Package for the Social Sciences)是一种常用的统计分析软件,它提供了强大的功能和易于使用的界面,可以进行生存分析和其他统计分析。
生存分析的目的是探讨事件发生的概率和时间。
与传统的统计分析方法不同,生存分析考虑了数据中的故障时间,即个体的生存时间。
生存时间可以是不同个体之间的差异,也可以是同一个体在不同时间点的变化。
在SPSS中进行生存分析,首先需要准备生存数据集。
生存数据集通常包括以下几个要素:个体的生存时间,事件是否发生,个体的特征变量等。
个体的生存时间可以是连续的,也可以是离散的。
事件是否发生通常用0表示未发生,1表示发生。
个体的特征变量可以是性别、年龄、治疗方式等。
在SPSS中进行生存分析,主要采用的方法是Kaplan-Meier生存曲线和Cox比例风险模型。
Kaplan-Meier生存曲线是一种非参数方法,用于估计生存时间和生存概率。
它将个体的生存时间按照事件是否发生进行分类,并计算每个时间点上的生存概率。
SPSS中可以通过选择“Analyze”菜单下的“Survival”子菜单中的“Nonparametric Tests”来进行Kaplan-Meier 生存曲线分析。
Cox比例风险模型是一种半参数方法,用于估计生存时间和危险因素对生存的影响。
它可以考虑多个危险因素,并通过估计每个危险因素的风险比来评估其对生存的影响。
SPSS中可以通过选择“Analyze”菜单下的“Survival”子菜单中的“Cox Regression”来进行Cox比例风险模型分析。
除了Kaplan-Meier生存曲线和Cox比例风险模型,SPSS还提供了其他生存分析方法,如Log-rank检验、Proportional Hazard模型等。
SPSS生存分析

SPSS生存分析生存分析(Survival Analysis)是一种统计方法,用于研究时间到达一些特定事件的概率。
该方法适用于各种学科领域,包括医学、社会科学、工程等,可以分析个体在不同时间点发生一些事件的风险。
生存分析的基本概念是生存函数和生存时间。
生存函数描述了在给定时间点之前没有发生事件的个体比例。
生存时间是指个体从起始时间点到达特定事件的时间。
生存分析的目标是估计生存函数,并比较不同因素对生存时间的影响。
SPSS(Statistical Package for the Social Sciences)是一种常用的统计分析软件,它提供了进行生存分析的功能。
以下将以SPSS进行生存分析为例,介绍生存分析的具体步骤。
首先,需要准备数据。
数据应包括个体的起始时间点和观察时间(或终止时间),以及是否发生特定事件的信息。
数据应按照个体的起始时间点排序。
在SPSS中,选择"Analyze"菜单下的"Survival"子菜单,然后选择"Kaplan-Meier"。
在弹出的窗口中,将起始时间点和观察时间字段分别拖放到"Time"和"Censored Time"框中,将事件发生与否的字段拖放到"Censoring Variable"框中。
点击"OK"按钮运行分析。
SPSS将输出生存函数曲线图和表格。
生存函数曲线图显示了在不同时间点的生存概率,曲线下降表示生存概率下降,即事件发生的风险增加。
生存函数表格列出了不同时间点的生存概率和标准误差。
通过观察曲线和表格,可以初步了解生存情况和影响生存的因素。
如果需要进一步比较不同因素对生存时间的影响,可以使用SPSS的"Analyze"菜单下的"Survival"子菜单中的其他功能,比如"Log-rank"检验、Cox回归模型等。
spss生存分析过程()

SPSS Survival(生存分析)菜单SPSS Survival菜单包括Life Tables过程、Kaplan-Meier 过程、Cox Regression过程、Cox w/Time-Dep Cov过程。
这里只介绍Life Tables过程和Kaplan-Meier过程。
Life Tables过程Life Tables过程用于:1、?估计某生存时间的生存率。
2、绘制各种曲线如生存函数、风险函数曲线等。
3、?对某一研究因素不同水平的生存时间分布进行比较,控制另一因素后对研究因素不同水平的生存时间分布进行比较,包括从总体上比较和不同水平之间进行两两比较。
一、建立数据文件定义两个列变量:时间变量:取名“time”,label标上“survival time(week)”。
生存状态变量:取名“status”,并赋值:0=“删失”,1=“死亡”。
二、操作过程从菜单选择1、Analyze==>Survival ==>Life Tables2、Time框:选入time3、Display Time Intervals框:在by前面的框内填入生存时间上限,本例填入20(此区间必须包括生存时间的最大值);在by 后面的框内填入生存时间的组距,本例填入5,以保证结果列出“15-”的组段。
4、Status框:选入status;击define events钮,在single value 框右边的空格中输入15、单击Option按钮,弹出对话框:✍Life Table(s) 输出寿命表,系统默认✍?Plots: 选Survival(累积生存函数曲线)击Continue6、单击OK钮附?:界面说明图1?? 寿命表主对话框【Time】框选入生存时间变量。
【Display Time Intervals】框欲输出生存时间范围及组距。
在by前面的框内填入生存时间上限,本例填入200(此区间必须包括生存时间的最大值);在by后面的框内填入生存时间的组距,本例填入20,以保证结果列出“100-”的组段。
利用spss做生存分析课程设计

利用spss做生存分析课程设计一、教学目标本课程的目标是使学生掌握生存分析的基本概念、方法和应用,能够熟练使用SPSS软件进行生存分析,并能够对生存数据分析结果进行解释和报告。
具体的学习目标包括:1.理解生存分析的基本概念,包括生存时间、事件发生时间和风险比等。
2.掌握生存分析的基本方法,包括Kaplan-Meier法、Cox比例风险模型等。
3.熟悉SPSS软件中进行生存分析的操作方法和步骤。
4.能够使用SPSS软件进行生存时间的收集和整理。
5.能够使用SPSS软件进行生存分析,包括Kaplan-Meier法和Cox比例风险模型。
6.能够对生存分析结果进行解释和报告,包括生存曲线、风险比、显著性检验等。
情感态度价值观目标:1.培养学生对生存数据分析的兴趣和主动性,提高学生对数据分析的敏感性和判断力。
2.培养学生对数据的尊重和诚实的态度,要求学生在数据分析中严谨、客观、公正。
二、教学内容本课程的教学内容主要包括生存分析的基本概念、方法和SPSS软件的应用。
具体的教学大纲如下:1.生存分析概述:介绍生存分析的基本概念、定义和应用领域。
2.Kaplan-Meier法:介绍Kaplan-Meier生存曲线及其计算方法,包括生存时间和事件发生时间的收集和整理。
3.Cox比例风险模型:介绍Cox比例风险模型的基本原理和计算方法,包括风险比、显著性检验等。
4.SPSS软件操作:介绍SPSS软件中进行生存分析的操作方法和步骤,包括数据输入、生存分析命令和结果输出。
三、教学方法本课程的教学方法采用讲授法、案例分析法和实验法相结合的方式。
具体方法如下:1.讲授法:通过教师的讲解和演示,向学生传授生存分析的基本概念、方法和SPSS软件的操作技巧。
2.案例分析法:通过分析具体的生存分析案例,使学生能够将理论知识与实际应用相结合,提高学生的分析能力和判断力。
3.实验法:通过实验操作,使学生能够亲自动手进行生存分析,培养学生的实践能力和操作技能。
SPSS生存分析过程

SPSS生存分析过程SPSS(Statistical Package for the Social Sciences)是一款常用的统计分析软件,它提供了许多功能强大的数据分析方法,其中包括生存分析(Survival Analysis)。
生存分析适用于研究时间至关重要的事件或结果的数据,例如疾病的存活时间、机械故障的发生时间等。
下面将介绍SPSS生存分析的具体过程。
一、数据准备在进行生存分析之前,首先需要准备好相关的数据。
常见的生存分析数据包括个体的生存时间(或称为观察时间)、生存状态(生存/死亡)、以及一些影响因素(如性别、年龄、治疗方式等)。
在SPSS中,可以将这些数据保存在一个数据集中,每一行代表一个个体,每一列代表一个变量。
二、加载数据集打开SPSS软件,选择“文件”-“打开”-“数据”,然后选择相应的数据文件进行加载。
三、生存曲线估计1.选择“分析”-“生存”-“生存曲线”菜单,打开生存曲线分析对话框。
2.将生存时间变量拖放到“时间”框中,将生存状态变量拖放到“事件”框中。
3. 选择评估生存函数类型,默认为“Kaplan-Meier”方法。
4.设置显著性水平,默认为0.055.点击“确定”按钮,即可生成生存曲线图。
生存曲线图显示了不同时间点上个体存活的比例。
根据生存曲线图,可以观察到存活时间的变化趋势,比较不同组别(如性别、年龄组别等)之间的存活差异。
四、生存分析模型除了生存曲线图,我们还可以进行更深入的生存分析,包括拟合生存分析模型和进行相关统计检验。
1. 选择“分析”-“生存”-“Cox 比例风险”菜单,打开Cox比例风险模型对话框。
2.将生存时间变量拖放到“时间”框中,将生存状态变量拖放到“事件”框中。
3.选择将影响因素拖放到“因素”框中,可以同时拖放多个因素进行分析。
选中的因素将出现在“选择项”列表中。
4.点击“方法”按钮,选择要使用的估计方法,如“法向向似然估计”。
5. 点击“确定”按钮,即可生成Cox比例风险模型的结果报告。
生存分析SPSS

生存分析SPSS生存分析是一种用于研究事件发生时间的统计方法,主要应用于医学研究领域,如生存时间、康复时间、心脏事件等的研究。
SPSS是一种常用的统计分析软件,可以用于进行生存分析。
生存分析的核心概念是生存函数和风险函数。
生存函数描述了一些时刻前存活的个体比例,而风险函数描述了在一些时刻内发生事件的个体比例。
通过生存函数和风险函数,可以得到不同因素对事件发生的影响程度。
生存分析常用的方法包括Kaplan-Meier法、Cox比例风险模型等。
使用SPSS进行生存分析的步骤如下:1.导入数据:在SPSS中,将数据导入到工作区,确保数据格式正确。
2.创建生存时间变量:根据研究需求,将事件发生的时间变量(如存活时间)输入到SPSS中。
3.创建事件变量:根据事件发生的情况,创建对应的事件变量(如生存状态),通常用1表示事件发生,0表示事件未发生。
4.进行生存函数分析:在SPSS的菜单栏中选择“分析”->“生存分析”->“生存函数”,将生存时间变量和事件变量输入到对应的框中,选择相应的统计量。
6.进行风险函数分析:在SPSS的菜单栏中选择“分析”->“生存分析”->“风险函数”,将生存时间变量和事件变量输入到对应的框中,选择相应的统计量。
7. 进行Cox比例风险模型分析:在SPSS的菜单栏中选择“分析”->“生存分析”->“Cox回归”,将生存时间变量和事件变量以及其他影响因素输入到对应的框中,进行模型拟合和参数估计。
8. 结果解读:分析结果会给出生存函数曲线、风险函数曲线以及Cox模型的参数估计和显著性检验结果。
根据研究问题进行合理解读,并绘制相应的图表和报告。
需要注意的是,进行生存分析时要选择适当的方法和模型,并考虑各种假设的合理性。
此外,对数据的质量和可靠性也要进行充分的检查和验证。
总结起来,SPSS是一种功能强大的统计分析软件,可以用于进行生存分析。
在使用SPSS进行生存分析时,需要导入数据、创建变量、选择适当的分析方法和模型,并对结果进行合理解读和报告。
SPSS教程第十五课生存分析

SPSS教程第十五课:生存分析信息来源:本站原创更新时间:2004-7-12 21:11:00在临床诊疗工作的评价中,慢性疾病的预后一般不适合用治愈率、病死率等指标来考核,因为其无法在短时间内明确判断预后情况,为此,只能对患者进行长期随访,统计一定时期后的生存或死亡情况以判断诊疗效果。
这就是生存分析。
第一节 Life Tables过程14.1.1主要功能调用此过程时,系统将采用即寿命表分析法,完成对病例随访资料在任意指定时点的生存状况评价。
14.1.2实例操作[例14-1]用中药+化疗(中药组,16例)和单纯化疗(对照组,10例)两种疗法治疗白血病患者后,随访记录存活情况如下所示,试比较两组的生存率。
14.1.2.1 数据准备激活数据管理窗口,定义变量名:随访月数的变量名为TIME,是否死亡的变量名为DEATH,分组(即中药组与对照组)的变量名为GROUP。
输入原始数据:随访月数按原数值;是否死亡的,是为1,否为0;分组的,中药组为1,对照组为2。
14.1.2.2 统计分析激活Statistics菜单选Survival中的Life Tables...项,弹出Life Tables 对话框(图14.1)。
从对话框左侧的变量列表中选time,点击 钮使之进入time框;在Display Time Intervals栏中定义需要显示生存率的时点,本例要求从0个月显示至48个月,间隔为2个月,故在0 through框中输入48,在by 框中输入2。
选death,点击 钮使之进入Status框,点击Define Event...钮弹出Life Tables:Define Event for Status Variable对话框,在Single value栏中输入1,表明death = 1为发生死亡事件者;点击Continue钮返回Life Tables 对话框。
选group,点击 钮使之进入Factor框,点击Define Range...钮,弹出Life Tables:Define Range for Factor Variable对话框,定义分组的范围,在Mininum框中输入1,在Maxinum框中输入2,点击Continue钮返回Life Tables对话框。
SPSS生存分析过程

SPSS Survival(生存分析)菜单SPSS Survival 菜单包括Life Tables 过程、Kaplan-Meier 过程、Cox Regression 过程、Cox w/Time-Dep Cov 过程。
这里只介绍Life Tables 过程和Kaplan-Meier 过程。
Life Tables 过程Life Tables 过程用于:1、估计某生存时间的生存率。
2、绘制各种曲线如生存函数、风险函数曲线等。
3、对某一研究因素不同水平的生存时间分布进行比较,控制另一因素后对研究因素不同水平的生存时间分布进行比较,包括从总体上比较和不同水平之间进行两两比较。
一、建立数据文件定义两个列变量:时间变量:取名“ time ”,label 标上“ survival time(week) 。
” 生存状态变量:取名“ status ”,并赋值:0=“删失”,1=“死亡”。
二、操作过程从菜单选择1、Analyze==>Survival ==>Life Tables2、Time 框:选入time3、Display Time Intervals 框:在by 前面的框内填入生存时间上限,本例填入20(此区间必须包括生存时间的最大值) ;在by 后面的框内填入生存时间的组距,本例填入5,以保证结果列出“15-”的组段。
4、 S tatus 框:选入 status ;击 define events 钮,在 single value 框右边的空 格中输入15、 单击Option 按钮,弹出对话框: Life Table(s)输出寿命表,系统默认 Plots:选Survival (累积生存函数曲线) 击 Continue6、单击0K 钮 附:界面说明, 4 Time :O 5Di epliy Tira s 020 Iz 5 SIatus: aarFactor:By Factor:2pti on^ .-图1寿命表主对话框【Time 】框 选入生存时间变量【Display Time Intervals 】框 欲输出生存时间范围及组距。
SPSS生存分析过程

SPSS Survival(生存分析)菜单SPSS Survival菜单包括Life Tables过程、Kaplan-Meier过程、Cox Regression过程、Cox w/Time-Dep Cov过程。
这里只介绍Life Tables过程和Kaplan-Meier过程。
Life Tables过程Life Tables过程用于:1、估计某生存时间的生存率。
2、绘制各种曲线如生存函数、风险函数曲线等。
3、对某一研究因素不同水平的生存时间分布进行比较,控制另一因素后对研究因素不同水平的生存时间分布进行比较,包括从总体上比较和不同水平之间进行两两比较。
一、建立数据文件定义两个列变量:时间变量:取名“time”,label标上“survival time(week)”。
生存状态变量:取名“status”,并赋值:0=“删失”,1=“死亡”。
二、操作过程从菜单选择1、Analyze==>Survival ==>Life Tables2、Time框:选入time3、Display Time Intervals框:在by前面的框内填入生存时间上限,本例填入20(此区间必须包括生存时间的最大值);在by后面的框内填入生存时间的组距,本例填入5,以保证结果列出“15-”的组段。
4、Status框:选入status;击define events钮,在single value框右边的空格中输入15、单击Option按钮,弹出对话框:●Life Table(s) 输出寿命表,系统默认● Plots: 选Survival(累积生存函数曲线)击Continue6、单击OK钮附:界面说明图1 寿命表主对话框【Time】框选入生存时间变量。
【Display Time Intervals】框欲输出生存时间范围及组距。
在by前面的框内填入生存时间上限,本例填入200(此区间必须包括生存时间的最大值);在by后面的框内填入生存时间的组距,本例填入20,以保证结果列出“100-”的组段。
spss-生存分析
如果是三组或多组且多组之间有差异,再做两两比较,如下:
试 例 估 : 计下 生表 存是 率对 ? 949 5 名 卵 巢 癌 病 人 的 随 访 结 果 , 时 间 均 为 年 ,
加权后
中位生存期为:3.2148
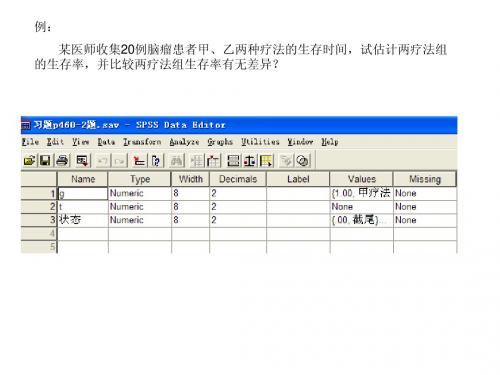
例:
某医师收集20例脑瘤患者甲、乙两种疗法的生存时间,试估计两疗法组 的生存率,并比较两疗法组生存率有无差异?
甲组 总共11人 存活8人 死亡3人 生存率27.3%
生存时间 状态 累积生存率 标准误 累计死亡例数 剩余存活例数
生存时间 标准误 95%CI(上限 下限)
中位生存时间 标准误 95%CI(上限 下限) 甲乙两种疗法log-Rank比较的卡方值 自由度 p值
SPSS数据分析—生存分析

SPSS数据分析—生存分析SPSS(统计分析软件)是一种常用的数据分析工具,可以进行各种统计分析,包括生存分析。
生存分析是一种用于研究时间相关性数据的统计方法,主要用于分析个体从其中一起始时间到其中一终止事件(通常是死亡或失效)的时间间隔。
生存分析的关键概念是生存函数和生存时间。
生存函数是一个描述个体在时间t下仍然存活的比例的函数,通常用S(t)表示。
生存时间是从个体入组(或开始)到终止事件发生的时间间隔。
SPSS可以进行生存分析的工作流程如下:1.导入数据:打开SPSS软件,导入包含所需数据的数据文件。
确保数据集包含需要的变量,如生存时间和事件状态(例如,是否死亡或失效)。
2.数据清理:检查数据集并进行必要的数据清理。
确保没有缺失值和异常值,以及确保数据是完整和准确的。
3. 运行生存分析:在SPSS软件中,选择适当的生存分析方法,如Kaplan-Meier(KM)法或Cox回归模型。
然后,输入所需的变量和参数,并运行生存分析。
- Kaplan-Meier(KM)法是一种非参数方法,用于估计生存函数。
它可以根据不同的参照组进行生存曲线的比较,并根据log-rank检验评估差异的统计显著性。
- Cox回归模型是一种半参数方法,用于估计生存时间与多个预测变量之间的关系。
它可以确定这些预测变量对生存时间的影响,并计算其风险比(hazard ratio)。
4.解释和报告结果:根据分析的结果,解释生存曲线和相关的统计显著性。
报告风险比和其统计显著性,并讨论其他发现和观察。
生存分析可以在许多领域中使用,如医学研究、流行病学、社会科学和金融研究。
它可以用于评估治疗方法的效果、分析因素对生存时间的影响、预测个体的生存概率等。
总之,SPSS是一种强大的工具,可以进行各种统计分析,包括生存分析。
使用SPSS进行生存分析,可以帮助研究人员从时间相关性数据中提取有关生存时间和生存概率的有用信息,并对数据进行进一步的解释和报告。
SPSS15-生存分析

时间分段
结果解释
将数据按时间分段,以便更好地捕捉时间 依赖性风险因素对生存时间的影响。
解释模型中时间依赖性变量的系数和风险 比,以评估其对生存时间的影响。
竞争风险模型的应用
竞争风险
竞争风险是指在生存分析中,由于其他原因导致死亡或失访的情况。
模型选择
选择适当的竞争风险模型,如Fine和Gray模型或Prentice、Williams和Peterson模型。
非参数模型
无模型假设
非参数模型不对数据分布作任何假设,适用于各种类 型的生存时间数据。
适用范围
适用于生存时间与协变量之间关系未知或非常复杂的 情形。
优点
灵活性高,能够捕捉数据的复杂关系,但计算量大, 解释性相对较弱。
04 生存分析案例解析
乳腺癌生存数据解析
乳腺癌生存数据
乳腺癌是一种常见的恶性肿瘤,生存分析在乳腺癌的研究中具有重要意义。通过对乳腺癌患者的生存时间、影响因素 和预后评估等方面进行分析,有助于为临床治疗和患者管理提供依据。
适用范围
适用于生存时间与协变量之间存在非线性关系的情形。
优点
能够同时处理生存时间和协变量之间的关系,提供更全面的分析。
参数模型
模型假设
参数模型对数据分布有严格的假设,如Weibull模型和 Exponential模型。
适用范围
适用于生存时间与协变量之间存在线性关系的情形。
优点
模型简单易用,能够提供准确的生存函数估计。
中的“右删失”或“截尾数据”的情况。
适用范围
02
适用于医学、生物学、经济学和社会科学等领域,用于研究个
体或系统的寿命、疾病进展、产品寿命等问题。
Байду номын сангаас
生存分析SPSS单因素和多因素对生存率的可能分析

(SPSS of Survival Analysis)
邹莉玲 预防医学教研室
生存分析的理论复习
1. 何为生存分析?
生存分析(survival analysis)是将事件的结果(终点事件)和 出现结果经历的时间结合起来分析的一种统计分析方法。
2. 生存分析的目的:
(1)描述生存过程:估计不同时间的总体生存率,计算中位生存期, 绘制生存函数曲线。统计方法包括Kaplan-Meier(K-M)法、 寿命表法。
6.001
a. 起始块编号 0,最初的对数似然函数:-2 倍对
b. 起始块编号 1. 方法 = 输入
结果提示: (1)对模型总体检验有显著意义(P=0.003),即至少 有1个自变量的总体回归系数不为0。
2-2.模型检验(逐步回归模型,Method=向前 法LR,自变量进入P≤0.05,剔除P>0.10 )
0
59 74 0 0 0 1 1
7
1
60 61 0 1 0 1 0 40
1
61 45 1 0 1 1 0 108
0
62 38 0 1 0 0 0 24
1
63 62 0 0 0 1 0 16
1
一、建立数据文件(data-03.sav) 二、操作过程
主菜单:分析Analyze生存SurvivalCox Regression
70
0
10 42
00
66
0
12 42
1 01 10
87
0
13 51
1 11 00
85
0
14 55 0 1 0 0 1 82 0
15 49
1 11 01
76
生存分析SPSS(单因素和多因素对生存率的可能分析)-文档资料

一、建立数据文件(data-01.sav)
定义5个变量: 生存时间变量:t,值标签“生存时间(月)” 生存状态变量 :status,取值“1=死亡,0=删失或存活” 频数变量:freq,值标签“人数” 分组变量:group,取值“1=甲组,2=乙组” 生存时间序号变量(可无):i
No X1 X2 X3 X4 X5 X6
实例分析
例2:(数据同例1)为了比较不同手术方法治疗肾上腺 肿瘤的疗效,某研究者随机将43例病人分成两组,甲组 23例、乙组20例的生存时间(月)如下所示:
其中有“+”者是删失数据,表示病人仍生存或失访,括号内为死亡人数。
(1)计算甲、乙两法各生存时间的生存率和标准误。 (2)估计两组的中位生存期。 (3)绘制各组生存函数曲线。 (4)比较两组的总体生存时间分布有无差别。
布的比较。 5. 对多组生存时间分布进行两两比较。 (比较总体生存时间分布采用wilcoxon检验)
实例分析
例1:为了比较不同手术方法治疗肾上腺肿瘤的疗效, 某研究者随机将43例病人分成两组,甲组23例、乙组20 例的生存时间(月)如下所示:
其中有“+”者是删失数据,表示病人仍生存或失访,括号内为死亡人数。
1)统计量: √生存分析表,系统默认。 √ 均值和中位生存时间,系统默认。
2)图: √生存函数 5. 单击比较因子Compare Factor按钮,弹出对话框:
1)检验统计量Test Statistics: 都用于检验时间分布是否相同。 √对数秩Log-rank:各时间点的权重一样。 Breslow:按各时间点的观察例数赋权。 Tarone-Ware:按各时间点观察例数的平方根赋权。
SPSS教程-生存分析

Survival Variable TIME
for GROUP = 1
Number Number Number Number
Cumul SE of SE of
Intrvl Entrng Wdrawn Exposd of Propn Propn Propn Proba- Cumul Proba- SE of
Start this During to Termnl Termi- Sur- Surv bility Hazard Sur- bility Hazard
Time Intrvl Intrvl Risk Events nating viving at End Densty Rate viving Densty Rate
14.1.2.3 结果解释
在结果输出窗又口口中将看到如下统计数据:
共有26个观察对象进入入分析。系统先显示示中药组(group = 1)的生生存状况寿命表,按用用户指 定,从0月月起,隔2个月月直至至42个月月(原指定从0—48个月月,但因42个月月后,生生存概率已为0, 故42个月月后至至48个月月的生生存状况不再显示示),分别显示示进入入该时点例数(Number Entrng this Intrvl)、从该时点失去的例数(Number Wdrawn Durong Intrvl)、该时点暴露于死亡危险的例 数(Number Exposd to Risk)、该时点死亡的例数(Number of Termnl Events)、该时点死亡概 率(Propn Terminating)、该时点生生存概率(Propn Surviving)、该时点末生生存率(Propn Surv at End)、单位时点的累积概率(Cumul Probability Densty)、该时点风险比比例(Hazard Rate)、 生生存率的标准误(SE of Cumul Surviving)、单位时点累积概率的标准误(SE of Probability Densty)、风险比比例的标准误(SE of Hazard Rate)。如本例,用用中药+化疗的方方式治疗白白血血病 患者,至至8个月月时,死亡率为17.39%,生生存概率为82.61%,生生存率为66.38%,风险比比例 为9.52%。至至42个月月时,生生存概率和生生存率均为0,此时风险比比例为100%。中药组的50%生生存率 在19.44个月月。
SPSS学习笔记之——生存分析的Cox回归模型(比例风险模型)

一、生存分析基本概念1、事件(Event)指研究中规定的生存研究的终点,在研究开始之前就已经制定好。
根据研究性质的不同,事件可以是患者的死亡、疾病的复发、仪器的故障,也可以是下岗工人的再就业等等。
2、生存时间(Survival time)指从某一起点到事件发生所经过的时间。
生存是一个广义的概念,不仅仅指医学中的存活,也可以是机器出故障前的正常运行时间,或者下岗工人再就业前的待业时间等等。
有的时候甚至不是通用意义上的时间,比如汽车在出故障前的行驶里程,也可以作为生存时间来考虑。
3、删失(Sensoring)指由于所关心的事件没有被观测到或者无法观测到,以至于生存时间无法记录的情况。
常由两种情况导致:(1)失访;(2)在研究终止时,所关心的事件还未发生。
4、生存函数(Survival distribution function)又叫累积生存率,表达式为S(t)=P(T>t),其中T为生存时间,该函数的意义是生存时间大于时间点t的概率。
t=0时S(t)=1,随着t的增加S(t)递减(严格的说是不增),1-S(t)为累积分布函数,表示生存时间T不超过t的概率。
二、生存分析的方法1、生存分析的主要目的是估计生存函数,常用的方法有Kaplan-Meier法和寿命表法。
对于分组数据,在不考虑其他混杂因素的情况下,可以用这两种方法对生存函数进行组间比较。
2、如果考虑其他影响生存时间分布的因素,可以使用Cox回归模型(也叫比例风险模型),利用数学模型拟合生存分布与影响因子之间的关系,评价影响因子对生存函数分布的影响程度。
这里的前体是影响因素的作用不随时间改变,如果不满足这个条件,则应使用含有时间依存协变量的Cox回归模型。
下面用一个例子来说明SPSS中Cox回归模型的操作方法。
例题要研究胰腺癌术中放疗对患者生存时间的影响,收集了下面所示的数据:操作步骤:SPSS变量视图菜单选择:点击进入Cox主对话框,如下,将time选入“时间”框,将代表删失的censor变量选入“状态”框,其余分析变量选入“协变量”框。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.data17-05文件收集63例病人的生存时间、结局及影响因 素。各变量的含义见下表。请用COX模型进行预后分析。
返回
第2题数据中的变量
返回
参考答案(第1题)
第1题:
生命表又称寿命表,是根据特定能够人群的年龄死亡编 制出来的一种统计表。它说明在特定人群年龄组死亡 率的条件下,人的生命过程或死亡过程。 Cox模型又称比例危险率回归模型,
h(t ) h0 (t ) e ( 1x1 2 x2 k xk )
当预后因素不止一个,危险率模式又难以估计时, Cox模型是一种方便的技术。
返回
参考答案(第2题操作)
返回
参考答案(第2题输出1)
第2题输出1
返回
参考答案(第2题输出2)
返回
第3题参考答案-操作
返回
进入方程变量的统计量
Step 5
a Variables not in the Equation
Step 5
未进入方程变量的统计量
age diagtime prior therapy
Score .424 .165 .248 1.650
df 1 1 1 1
Sig. .515 .684 .618 .199
第15章
生存分析
返回
目 录
基本概念
生存函数 Cox回归模型
生命表分析
生命表分析过程 生命表的实例分析
Kaplan-Meier分析
Kaplan-Meier分析过程 Kaplan-Meier实例分析
Cox Regression风险比例模型分析
Cox Regression分析过程 Cox Regression实例分析
各变量值分类编码
返回
Cox Regression实例分析输出3
Omnibus Tests of Model Coefficients -2 Log Likelihood 1011.768
b,c Omnibus Tests of Model Coefficients
Step 1a 5
-2 Log Likelihood 950.359 952.997
返回
参考答案(第3题输出2)
c,d Omnib us Tests of Model Coeffic ients
0 0 0 1
a. The (0,1) variable has been recoded, so its coefficients will not be the same as for indicator (0,1) coding. b. Indicator Parameter Coding c. Category variable: therapy (project) d. Category variable: cell (type) e. Category variable: prior
患者编号
年龄 诊断到治疗的 时间 生存时间 治疗前处理 治疗方案 病人状态 肺癌细胞组织 学分类 判断标准 0 1 0 1 ≤30 经过处理 标准方法 死亡 鳞癌 住院治疗 1 2 1 2 30~6 0 2 未经处理 实验方法 删失数据 小细胞肺 癌 住院和家 庭治 疗 30<kps<6 0 3 > 腺癌 家庭治 6 疗 0 kps>60 4 大细胞肺癌
Cox Regression
Total a. Dependent Variable: T
Block 0: Beginning Block
V a r i a b l e s n o t i n t h e E q u a t i oan X1 X2 X3 X4 X5 X6 Score df .354 11.300 3.063 13.040 4.634 6.018 a. Residual Chi Square 6 df Sig. = .001 Sig. 1 .552 1 .001 1 .080 1 .000 1 .031 1 .014 = 23.902 with
Cox Regression
返回
Cox 回归分析主对话框
返回
Cox模型定义分类协变量对话框
返回
Cox模型图形对话框
返回
Cox模型保存新变量对话框
返回
Cox模型选择项对话框
返回
数据文件中的变量
变量名 含 义 值 标 签 值 标 签 值 标 签 值 标 签
id
age diagtime time prior therapy status cell kps
K-M选择比较控制因素统计方法对话框
返回
K-M分析选择项对话框
返回
Kaplan-Meier实例分析输出1
不同分层及不同处理情况生存描述性统计量
返回
K-M实例分析输出2
不同分层及不同处理观测量删失情况
返回
K-M实例分析输出3
Log Rank检验统计量
返回
Cox Regression风险比例模型分析
a. Residual Chi Square = 2.675 with 4 df S ig. = .614
返回
Cox 回归实例分析输出6
Cov ariate Means
Correlation Matrix of Regression Coefficients cell(2) cell(3) kps cell(1) .570 .517 .159 cell(2) .471 .014 cell(3)
Hazard
0.06
0.04
0.02
0.00 0 50 100
生plan-Meier分析
返回
Kaplan-Meier分析主对话框
返回
K-M定义状态变量发生事件对话框
返回
K-M选择比较控制因素统计方法对话框
K-M选择比较控制因素统计方法对话框
返回
K-M分析保存新变量对话框
a. Variable(s) Entered at Step Number 1: age cell diagtime kps prior therapy b. Beginning Block Number 0, initial Log Likelihood function: -2 Log likelihood: 1011.768 c. Beginning Block Number 1. Method = Backward Stepwise (Wald)
Live Tables
返回
生命表分析主对话框
返回
定义状态变量对话框
定义状态变量所发生事件对话框
返回
定义控制变量范围对话框
返回
生存表选择项对话框
返回
生命表分析实例输出1
低脂肪食物老鼠生命表
返回
生命表分析实例输出2
比较食用不同食物老鼠生存时间的统计量
返回
生命表分析实例输出3
Density Function
参考答案(第3题输出1)
Case Process ing Summ ary N Cases available in analysis Cases dropped Eventa Censored Total Cases with missing values Cases with non-positive time Censored cases before the earliest event in a stratum Total 26 37 63 0 0 0 0 63 Percent 41.3% 58.7% 100.0% .0% .0% .0% .0% 100.0%
模型系数检验
返回
Cox 回归实例分析输出4
分析统计量
返回
Cox回归实例分析输出5
Variables in the Equation Step 1 age cell cell(1) cell(2) cell(3) diagtime kps prior therapy cell cell(1) cell(2) cell(3) kps B -.009 .856 1.188 .400 .000 -.033 -.072 -.290 .712 1.151 .325 -.031 SE .009 .275 .301 .283 .009 .006 .232 .207 .253 .293 .277 .005 Wald .844 17.916 9.687 15.610 1.999 .000 35.112 .097 1.958 17.080 7.939 15.441 1.381 35.612 df 1 3 1 1 1 1 1 1 1 3 1 1 1 1 Sig. .358 .000 .002 .000 .157 .992 .000 .755 .162 .001 .005 .000 .240 .000 Exp(B) .991 2.355 3.281 1.491 1.000 .968 .930 .748 2.038 3.161 1.384 .970
kps1
1
kps<=30
3
返回
Cox Regression分析实例输出1
Case P rocessing S ummary Cases available in analysis Cases dropped
a Event Censored Total Cases with missing values Cases with negative time Censored cases before the earliest event in a stratum Total
危险率函数
h(t ) lim
返回
Cox回归模型的有关公式
当生存时间是连续分布且预后变量间相互作用可被忽视时危险率h(t)为
h(t ) h0 (t )e( 1 x1+ 2 x2++ k xk )
