SPSS常用函数
spss函数大全解读资料

Spss 算术函数孙中友江苏ABS(numexpr 数值。
返回 numexpr (必须为数值的绝对值。
ARSIN(numexpr 数值。
返回 numexpr 的反正弦(以弧度为单位 ,求出的值必须为 -1 和 +1 之间的数字值。
ARTAN(numexpr 数值。
返回 numexpr 的反正切(以弧度为单位 , numexpr 必须为数字值。
COS(radians 数值。
返回 radians 的余弦(以弧度为单位 , radians 必须为数字值。
EXP(numexpr 数值。
返回 e 的 numexpr 次幂, 其中 e 是自然对数的底数, 而numexpr 是数值。
较大的 numexpr 值可能会产生超过机器性能的结果。
LN(numexpr 数值。
返回以 e 为底数的 numexpr 的对数, numexpr 必须为大于 0 的数值。
LNGAMMA(numexpr 数值。
返回 numexpr 的完全 Gamma 函数的对数, numexpr 必须为大于 0 的数值。
LG10(numexpr 数值。
返回以 10 为底数的 numexpr 的对数, numexpr 必须为大于 0 的数值。
MOD(numexpr,modulus 数值。
返回 numexpr 除以 modulus 所得到的余数。
两个参数都必须为数值,且 modulus 不得为 0。
RND(numexpr 数值。
返回对 numexpr 舍入后产生的整数, numexpr 必须为数值。
刚好以 .5 结尾的数值将舍去 0 以后的数值。
SIN(radians 数值。
返回 radians 的正弦(以弧度为单位 , radians 必须为数字值。
SQRT(numexpr 数值。
返回 numexpr 的正平方根, numexpr 必须为非负数。
TRUNC(numexpr 数值。
返回 numexpr 被截断为整数(向 0 的方向的值。
统计函数后缀 .n 可在所有统计函数中使用以指定有效参数的数目。
spss中的常用函数
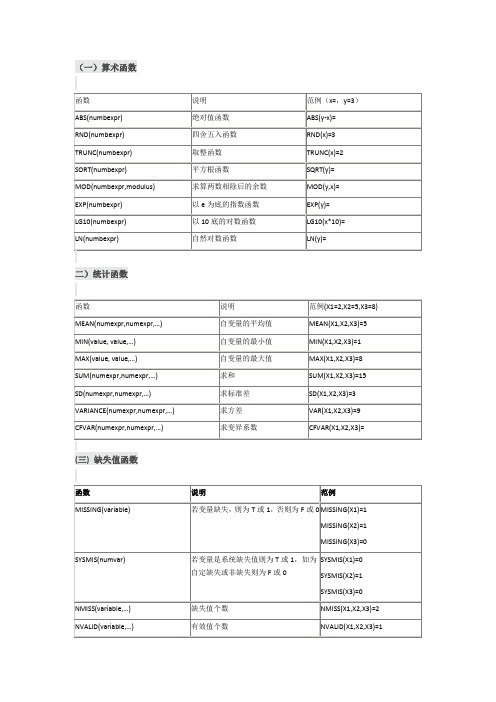
(一)算术函数
二)统计函数
注:X1为使用者界定缺失值,X2为系统缺失值,X3为非缺失值四)字符串型函数
五)时间日期函数
注:1 要正确显示以上函数值,必须先赋予其SPSS得日期型变量(DATA)格式,假设以上日期用mm/dd/yy格式显示,时间则用hh:mm:ss格式表示
2 1<=d<=31、1<=m<=12、1<=w<=52、1<=q<=4
六)其他函数
SPSS除了上述函数外,尚有日期和时间转换函数
(YOMODA\CTMIESDAYS\CTIMEHOURS\MDAYS等)、连续几率密度函数
(CDF\BINOM\CHISQ\CDF\EXP\LOGISTIC等),此外还有NORMAL(stddev)可产生平均数为0,标准差为stddev的正态分布随机数字。
UNIFORM(max)可产生平均数为0与max间呈均等分布的随机数字。
PS:还可以像EXCEL一样利用脚本编写自定义函数,目前SPSS支持python,Sax Basic(一种与VB兼容的编程语言)等语言,利用new--script可编写出自己需要的函数。
script界面如下:。
SPSS计算IC50

SPSS计算IC50IC50(half-maximal inhibitory concentration)是一种常用的药物治疗研究中的指标,用于衡量药物的抑制效果。
IC50值表示药物抑制治疗作用的浓度,即在该浓度下,药物能够抑制目标物理的活性达到50%。
在药物研究过程中,SPSS(Statistical Package for the Social Sciences)是一种常用的统计分析软件,可以用于处理实验数据和计算IC50值。
本文将介绍如何使用SPSS进行IC50计算。
首先,准备实验数据。
实验数据应包括不同药物浓度下的生物活性测定结果。
常见的生物活性测定结果包括细胞存活率、抑制率等。
假设我们的实验数据包括药物浓度(X值)和生物活性(Y值)两列数据。
接下来,在SPSS中导入实验数据。
打开SPSS软件,选择菜单中的“File”-“Open”选项,导入实验数据文件。
确保数据表中的药物浓度和生物活性数据对应的列已经正确标识。
接下来,进行IC50计算。
SPSS中没有内置的IC50计算函数,但可以通过使用SPSS的回归分析功能来估计IC50值。
在SPSS的统计菜单中,选择“Regression”-“Curve Estimation”选项。
在“Curve Fit”对话框中,选择适合的曲线拟合模型。
在药物研究中常见的曲线模型包括Logistic、Gompertz和Weibull等。
选择合适的模型后,点击“OK”进行计算。
计算完成后,SPSS会生成拟合曲线,并提供拟合参数的估计值。
其中,对于IC50计算,最关键的是估计药物浓度对应的生物活性50%的参数值。
通过查看拟合参数和拟合曲线,可以估算出IC50值。
最后,进行数据可视化和报告。
在SPSS中,可以使用图表功能对数据和结果进行可视化,以便更好地理解和传达研究结果。
例如,可以绘制药物浓度与生物活性的散点图,并添加拟合曲线。
另外,可以使用SPSS的报告功能,将结果导出为报告或表格,以便进一步分析和展示。
SPSS的常用的一些函数大全

算术函数ABS(numexpr) 数值。
返回numexpr(必须为数值)的绝对值。
ARSIN(numexpr) 数值。
返回numexpr 的反正弦(以弧度为单位),求出的值必须为-1 和+1 之间的数字值。
ARTAN(numexpr) 数值。
返回numexpr 的反正切(以弧度为单位),numexpr 必须为数字值。
COS(radians) 数值。
返回radians 的余弦(以弧度为单位),radians 必须为数字值。
EXP(numexpr) 数值。
返回e 的numexpr 次幂,其中e 是自然对数的底数,而numexpr 是数值。
较大的numexpr 值可能会产生超过机器性能的结果。
LN(numexpr) 数值。
返回以e 为底数的numexpr 的对数,numexpr 必须为大于0 的数值。
LNGAMMA(numexpr) 数值。
返回numexpr 的完全Gamma 函数的对数,numexpr 必须为大于0 的数值。
LG10(numexpr) 数值。
返回以10 为底数的numexpr 的对数,numexpr 必须为大于0 的数值。
MOD(numexpr,modulus) 数值。
返回numexpr 除以modulus 所得到的余数。
两个参数都必须为数值,且modulus 不得为0。
RND(numexpr) 数值。
返回对numexpr 舍入后产生的整数,numexpr 必须为数值。
刚好以 .5 结尾的数值将舍去0 以后的数值。
SIN(radians) 数值。
返回radians 的正弦(以弧度为单位),radians 必须为数字值。
SQRT(numexpr) 数值。
返回numexpr 的正平方根,numexpr 必须为非负数。
TRUNC(numexpr) 数值。
返回numexpr 被截断为整数(向0 的方向)的值。
统计函数后缀.n 可在所有统计函数中使用以指定有效参数的数目。
例如,仅当至少两个变量含有效值时,MEAN.2(A,B,C,D) 对变量A、B、C 和D 返回其有效值的均值。
用spss求函数参数

04
多元线性回归分析
多元线性回归模型简介
多元线性回归模型是一种统计学方法,用于研究多个自变量与因变量之间 的线性关系。
它通过建立数学模型来描述因变量如何受到多个自变量的影响,并估计每 个自变量的系数。
这些系数反映了自变量对因变量的影响程度和方向。
多元线性回归模型的适用条件
因变量与自变量之间存在 线性关系
SPSS软件简介
历史与发展
SPSS成立于1968年,最初是为社会科学领域的研究者提供统计分析工具。随着计算机技术的不断发展,SPSS的功能 和适用范围也不断扩展,成为全球众多研究者、学生和数据分析师的首选工具。
主要功能
SPSS提供了广泛的统计分析方法,包括描述性统计、回归分析、方差分析、非参数检验等多种功能,能够满足不同 领域的数据分析需求。
点击“确定”开始进行多元线性回归分析。
SPSS将输出回归结果,包括回归系数、标准误、显著 性水平等统计指标,以及模型摘要和方差分析表等。
05
非线性回归分析
非线性回归模型简介
非线性回归模型
非线性回归模型是一种用于描述因变量和自变量之间非线性关 系的统计模型。它扩展了线性回归模型,允许自变量和因变量
02 解读回归系数,了解自变量对因变量的影响程度 和方向。
03 根据需要,进行模型优化和调整,以提高预测精 度。
03
线性回归分析
线性回归模型简介
01
02
03
线性回归模型是一种预 测模型,用于描述因变 量与一个或多个自变量
之间的线性关系。
在线性回归模型中,因 变量是我们要预测的目 标变量,而自变量是我 们用来预测因变量的变
之间的关系是非线性的。
目的
通过非线性回归分析,我们可以探索和描述因变量与一个或多 个自变量之间的复杂关系,并估计这些关系中的参数。
SPSS操作方法:权重函数的选择08——【SPSS精品教程 资源池】

SPSS操作方法:权重变量的选择以书中例6.3为例,介绍权重变量的选择SPSS的操作方法。
由于原回归方程中有异方差性,故选择加权最小二乘法。
现以自变量X的幂函数为权重变量,通过Weight Estimation的方法选择最佳幂次。
1.单击Analyze→Regreessin→Weight Estimation,打开对话框如图1所示:从左边框中选择因变量Y进入Dependent 框内,选择一个或多个自变量进入Independent框内。
再选择拟作为权重变量的自变量进入Weight Variable 框中。
2.从Power range框内选择自变量的幂函数的幂值,系统默认从-2至2,也可以自行规定,从by框内选择步距,如选择0.2等。
系统默认为0.5。
(本例选择系统默认项)。
113.单击Options 按纽,打开Options 对话框,选择Save best weight as new variable ,可以保存权重变量在数据表中。
(本例选择)Display ANOVA and Estimates 表示输出加权最小二乘法的方差分析表、估计的摘要和回归系数表。
For best value 表示只输出最佳幂函数作为权重的统计分析表(系统默认)。
(本例选择系统默认项)所有选项完成后,返回主对话框,点击OK ,得输出结果。
加权最小二乘分析[DataSet2] E:\现代统计分析方法与应用(研究生)\现代统计分析方法与应用第二版数据\例6.3.sav幂摘要表1对数似然值b幂-2 -258.645-1.5 -243.464-1 -228.511-0.5 -213.8820 -199.7530.5 -186.4471 -175.1591.5 -172.183a2 -188.924a. 选择对应幂以用于进一步分析,因为它可以使对数似然函数最大化。
b. 因变量: y,源变量: x表1给出自变量所有幂值的对数似然函数值,其中最小的值对应的模型最佳。
使用SPSS软件进行因子分析和聚类分析的方法

使用SPSS软件进行因子分析和聚类分析的方法因子分析和聚类分析是一种常用的数据分析方法,可以用于数据降维和分组。
SPSS是一款常用的统计软件,提供了丰富的分析工具和函数,可以方便地进行因子分析和聚类分析。
一、因子分析:因子分析是一种多变量分析方法,可以将一组相关的变量转化为少数几个互相独立的综合变量,称为因子。
因子分析可以用于降低数据的维度,提取主要的因素,并分析因素之间的关系。
以下是使用SPSS软件进行因子分析的步骤:1.打开SPSS软件,并导入要进行因子分析的数据集。
2.菜单栏选择“分析”-“降维”-“因子”。
3.在弹出的因子分析对话框中,选择要进行因子分析的变量,将其添加到“因子”框中。
4.在“提取”选项中,选择提取的因子个数。
可以根据实际需求和经验进行选择。
5. 在“旋转”选项中,选择旋转方法。
常用的旋转方法有方差最大旋转(Varimax),斜交旋转(Oblique)等。
6.点击“确定”按钮,进行因子分析。
7.SPSS会生成因子载荷矩阵、解释方差表、因子得分等结果。
可以根据因子载荷矩阵和解释方差表来解释因子的含义和解释度。
8.根据具体需求和分析目的,可以进行因子得分的计算和因子分组的分析。
二、聚类分析:聚类分析是一种无监督学习方法,可以将一组样本数据自动分成若干互不相交的群组,称为簇。
聚类分析可以用于数据的分组和群体特征的分析。
以下是使用SPSS软件进行聚类分析的步骤:1.打开SPSS软件,并导入要进行聚类分析的数据集。
2.菜单栏选择“分析”-“分类”-“聚类”。
3.在弹出的聚类分析对话框中,选择要进行聚类分析的变量,将其添加到“变量”框中。
可以选择多个变量进行分析。
4.在“距离”选项中,选择计算样本间距离的方法。
常用的方法有欧几里得距离、曼哈顿距离等。
5. 在“聚类方法”选项中,选择聚类算法的方法。
常用的方法有层次聚类(Hierarchical Clustering)、K均值聚类(K-means)等。
SPSS生存分析

SPSS生存分析生存分析(Survival Analysis),也称为事件分析(Event Analysis)或持续时间分析(Duration Analysis),是一种统计方法,用于研究事件的发生和结束时间,如生命、疾病治愈、工作停留时间等。
生存分析的目的是研究一组对象的生命周期,并了解特定因素对事件发生和结束的影响。
在这种分析中,对象可以是个体、组织、产品等。
常见的应用包括生物医学研究、流失分析、医疗保险研究和个体退休研究等。
生存分析的关键概念是生存函数和风险函数。
生存函数是描述一个对象存活到给定时间的概率,通常用生存曲线表示。
风险函数描述了一个对象在给定时间点发生事件的风险,它可以用来比较不同组之间事件发生的差异。
在进行生存分析时,常用的统计模型包括Kaplan-Meier法、Cox比例风险模型和加速失效时间模型。
Kaplan-Meier法用于无偏估计生存函数,能够考虑有丢失数据和不完全随访的情况。
Cox比例风险模型可以用来估计各种相关因素对事件发生的相对风险,而加速失效时间模型可以考虑随时间变化的风险因素。
在使用SPSS进行生存分析时,首先需要导入数据并定义目标事件和截尾事件。
然后,可以使用Kaplan-Meier法绘制生存曲线,并进行生存函数的比较。
同时,也可以使用Cox比例风险模型来估计不同因素对事件发生的影响,并计算相对风险。
除了基本的生存分析方法外,SPSS还提供了许多扩展功能,如处理丢失数据、处理时间依赖变量和处理集群数据等。
这些功能可以帮助研究人员更好地分析和解释生存数据。
总之,生存分析是一种有力的统计方法,可以用于研究事件发生和结束的时间,并评估相关因素对事件的影响。
使用SPSS进行生存分析可以方便地进行数据处理、模型拟合和结果解释,使研究人员能够深入了解事件发生的模式和原因。
数据分析方法大全SPSS数据分析方法详解

数据分析方法大全SPSS数据分析方法详解SPSS(Statistical Package for the Social Sciences)是一种常用的数据分析软件,广泛应用于各个领域的研究和统计分析。
下面是一些常用的数据分析方法和技术,以及如何在SPSS中进行实施。
1.描述性统计分析:SPSS可以计算各种描述性统计指标,如平均数、中位数、标准差、百分位数等。
可以使用“统计”菜单下的“描述统计”选项完成。
2.相关分析:相关分析用于研究两个或多个变量之间的关系。
SPSS提供了许多方法来计算相关系数,如皮尔逊相关系数、斯皮尔曼等级相关系数等。
可以使用“分析”菜单下的“相关”选项进行分析。
3.回归分析:回归分析用于研究一个或多个自变量与因变量之间的关系。
SPSS提供了多种回归模型,如线性回归、多元回归、逐步回归等。
可以使用“分析”菜单下的“回归”选项进行分析。
4.方差分析:方差分析用于比较两个或多个组之间的平均值是否显著不同。
SPSS提供了单因素方差分析、二因素方差分析、协方差分析等多种方法。
可以使用“分析”菜单下的“方差”选项进行分析。
5.t检验和方差齐性检验:t检验用于比较两个样本平均值是否显著不同,而方差齐性检验用于检验两个样本方差是否相等。
SPSS提供了独立样本t检验、配对样本t检验、方差齐性检验等多种方法。
可以使用“分析”菜单下的“比较均值”选项进行分析。
6.散点图和箱线图:散点图用于可视化两个变量之间的关系,箱线图用于可视化不同组之间的差异。
可以使用“图表”菜单下的“散点图”和“箱线图”选项进行绘制。
7.因子分析和聚类分析:因子分析用于将多个变量归纳为较少的无关连的维度,聚类分析用于将相似的对象归为同一组。
SPSS提供了因子分析和聚类分析的功能,可以使用“分析”菜单下的“因子”和“聚类”选项进行分析。
8.生存分析:生存分析用于研究事件发生的时间和概率。
SPSS提供了生存分析的方法,如卡普兰-迈尔曲线、生存函数、风险比等。
函数对照表

数值型
返回一个来自柯西分布且具有指定位置 loc 和标 度参数 scale 的随机数
数值型
返回一个来自卡方分布且具有指定自由度 df 的随 机数
数值型
返回一个来自指数分布且具有指定形状参数 shape 的随机数
数值型
返回一个来自 F 分布且具有指定自由度的随机数
数值型
返回一个来自伽玛分布且具有指定形状参数 shape 和标度参数 scale 的随机数
返回自变量的变异系数(标准差/均值)。该函数 要求两个或两个以上自变量,且自变量必须为数 值型。
LAG(variable)
返回数据文件中前一个观测量所属变量的值。对 数 值 型 或 字 第一个观测量来说将返回缺失值(数值型变量) 符型
或空格(字符型变量)。
LAG(variable,ncases)
返回数据文件中前面第 数值型或字
NORMAL(stddev) RV.BERNOULLI(prob) RV.BETA(shape1,shape2) RV.BINOM(n,prob) RV.CAUCHY(loc,scale) RV.CHISQ(df) RV.EXP(shape) RV.F(df1,df2) RV.GAMMA(shape,scale) RV.GEOM(prob) RV.HYPER(total,sample,hits) PLACE(mean,scale) RV.LOGISTIC(mean,scale) RV.LNORMAL(a,b)
数值型
RV.WEIBULL(a,b)
数值型
UNIFORM(max)
数值型
返回一个来自负二项分布且具有指定临界值 theshold 和概率参数 prob 的随机数 返回一个来自正态分布且具有指定均值 mean 和 标度参数 stddev 的随机数 返回一个来自帕雷托分布且具有指定临界值 threshold 和形态参数 shape 的随机数 返回一个来自泊松分布且具有指定均值 mean 的 随机数 返回一个来自学生 T 分布且具有指定自由度 df 的随机数 返回一个来自均匀分布且具有指定最大值 max 和 最小值 min 的随机数 返回一个来自威布尔分布且具有指定参数的随机 数 返回一个来自均匀分布且介于 0 和指定参数 max 之间的随机数。Max 也可以是负数
spss 标准化

spss 标准化SPSS标准化。
在统计学中,标准化是一种常见的数据处理方法,它可以帮助我们消除不同变量之间的量纲差异,使得数据更具有可比性。
在SPSS软件中,标准化也是一个常用的操作步骤,下面我们将介绍如何在SPSS中进行标准化处理。
首先,打开SPSS软件并导入需要进行标准化处理的数据集。
在数据集导入后,选择“转换”菜单下的“变量计算”选项。
在弹出的对话框中,选择需要进行标准化处理的变量,并将其添加到右侧的“数值表达式”框中。
接下来,我们需要输入标准化的计算公式。
一般来说,标准化的计算公式为(X-μ)/σ,其中X为原始变量的取值,μ为原始变量的均值,σ为原始变量的标准差。
在SPSS中,我们可以通过内置的函数来计算均值和标准差,具体操作如下:在“数值表达式”框中输入“(变量名MEAN(变量名))/ STDDEV(变量名)”,其中“变量名”为需要进行标准化处理的变量名称。
然后点击“OK”按钮,SPSS将会自动计算标准化后的数值并添加到数据集中。
完成上述步骤后,我们就成功地对数据集中的变量进行了标准化处理。
标准化后的变量均值为0,标准差为1,从而消除了不同变量之间的量纲差异,使得它们更具有可比性。
需要注意的是,标准化处理并不会改变原始数据的分布形态,它只是改变了数据的尺度和位置,因此在进行标准化处理后,我们仍然可以使用原始数据的统计特征来进行分析和建模。
除了上述介绍的标准化方法外,SPSS软件还提供了其他一些标准化处理的选项,例如最小-最大标准化、范围标准化等。
这些方法可以根据具体的数据特点和分析需求来选择,以达到最佳的分析效果。
总之,标准化是数据分析中常用的一种数据处理方法,它可以帮助我们消除不同变量之间的量纲差异,使得数据更具有可比性。
在SPSS软件中,标准化处理也是非常简单和方便的,只需要几个简单的步骤就可以完成。
希望本文的介绍能够帮助大家更好地理解和应用SPSS中的标准化功能。
SPSS数据分析—生存分析

SPSS数据分析—生存分析SPSS(统计分析软件)是一种常用的数据分析工具,可以进行各种统计分析,包括生存分析。
生存分析是一种用于研究时间相关性数据的统计方法,主要用于分析个体从其中一起始时间到其中一终止事件(通常是死亡或失效)的时间间隔。
生存分析的关键概念是生存函数和生存时间。
生存函数是一个描述个体在时间t下仍然存活的比例的函数,通常用S(t)表示。
生存时间是从个体入组(或开始)到终止事件发生的时间间隔。
SPSS可以进行生存分析的工作流程如下:1.导入数据:打开SPSS软件,导入包含所需数据的数据文件。
确保数据集包含需要的变量,如生存时间和事件状态(例如,是否死亡或失效)。
2.数据清理:检查数据集并进行必要的数据清理。
确保没有缺失值和异常值,以及确保数据是完整和准确的。
3. 运行生存分析:在SPSS软件中,选择适当的生存分析方法,如Kaplan-Meier(KM)法或Cox回归模型。
然后,输入所需的变量和参数,并运行生存分析。
- Kaplan-Meier(KM)法是一种非参数方法,用于估计生存函数。
它可以根据不同的参照组进行生存曲线的比较,并根据log-rank检验评估差异的统计显著性。
- Cox回归模型是一种半参数方法,用于估计生存时间与多个预测变量之间的关系。
它可以确定这些预测变量对生存时间的影响,并计算其风险比(hazard ratio)。
4.解释和报告结果:根据分析的结果,解释生存曲线和相关的统计显著性。
报告风险比和其统计显著性,并讨论其他发现和观察。
生存分析可以在许多领域中使用,如医学研究、流行病学、社会科学和金融研究。
它可以用于评估治疗方法的效果、分析因素对生存时间的影响、预测个体的生存概率等。
总之,SPSS是一种强大的工具,可以进行各种统计分析,包括生存分析。
使用SPSS进行生存分析,可以帮助研究人员从时间相关性数据中提取有关生存时间和生存概率的有用信息,并对数据进行进一步的解释和报告。
SPSS Modeler常用函数简介

SPSS Modeler常用函数简介SPSS Modeler软件包含多种功能丰富的函数,几乎涵盖了我们日常工作的各种需要,主要有信息函数、转换函数、比较函数、逻辑函数、数值函数、三角函数、概率函数、位元整数运算、随机函数、字符串函数、日期和时间函数、序列函数、全局函数、空值和Null 值处理函数、特殊函数等15大类,本讲义将逐一介绍并说明其注意事项。
在本讲义中涉及到的函数,具体的字段格式按照如下约定表示:此外,本讲义中的函数以函数、结果类型(整数、字符串等)和说明(如果有)各占一列的形式一一列举说明。
例如,对函数rem的说明如下。
1. 信息函数信息函数用于深入了解特定字段的值。
它们通常用于派生标志字段。
例如,可以使用@BLANK函数来创建一个标志字段,以指示选定字段的值为空值的记录。
同样,可以使用存储类型函数(如is_string)来检查某个字段的存储类型。
2. 转换函数转换函数可用来构建新字段和转换现有文件的存储类型。
例如,可通过将字符串连接在一起或分拆字符串来形成新字符串。
若要连接两个字符串,请使用运算符“><”。
例如,字段Site的值为"BRAMLEY",则"xx"><Site将返回"xxBRAMLEY"。
即使参数不是字符串,“><”的结果也始终是字符串,因此,如果字段V1为3,字段V2为5,则V1><V2将返回"35"(字符串而非数值)。
请注意,转换函数及其他要求特定类型输入(如日期或时间值)的函数取决于“流选项”对话框中指定的当前格式。
例如,要将值为Jan2003、Feb2003等的字符串字段转换为日期存储格式,请选择MONYYYY作为流的默认日期格式。
3. 比较函数比较函数用于字段值的相互比较或与指定字符串进行比较。
例如,可以使用“=”来检查字符串是否相等。
Spss linest函数拟合

Spsslinest函数拟合
Spsslinest他的功能是通过使用“最小二乘法”计算最符合您的数据的直线来计算直线的统计值,并返回描述该直线的数组。
此函数的特点是,因为它返回数值数组,所以必须以数组公式的形式输入。
1.打开SPSS软件后先打开你需要分析的数据。
打开右上角的标识,选择你需要的文件,点击(打开),选择文件。
2.打开后如果你事先不知道两个变量之间是线性还是非线性,那就画散点图分析其趋势。
3.将相应的变量设置为x,y轴,点击(确定),接下来会自动在文档查看器中显示散点图,如果选取的样本多的话,有时候会连成曲线,不过不影响分析。
4.确定不是线性关系之后,用曲线拟合分析。
点击(分析)---(回归)---(曲线估计),进入到曲线估计面板里面设置。
5.在曲线估计框中设置好x,y轴,下面的11种模型中可以选择其中比较符合样本变化情况的,因为刚开始已经画出散点图了,所以这一步选择模型就比较容易,如果不知道选择那个,就多点几个。
6.然后找到和样本图像最为吻合和的图像,然后分析结果。
7.ANOVA那个表,也就是F检验,那个表代表的是对你进行回归的所有自变量的回归系数的一个总体检验,如果sig<0.05,说明至少有一个自变量能够有效预测因变量,这个在写数据分析结果时一般可以不报告。
8.然后看系数表,看标准化的回归系数是否显著,每个自变量都
有一个对应的回归系数以及显著性检验。
9.最后看模型汇总那个表,R方叫做决定系数,它是自变量可以解释的变异量占因变量总变异量的比例。
应用统计软件SPSS拟合生长曲线方程

应用统计软件SPSS拟合生长曲线方程应用统计软件SPSS拟合生长曲线方程生长曲线是描述生物个体或群体在时间维度下生长变化规律的数学模型。
在农林业、医学研究、环境科学等领域,对生长曲线进行研究和分析对于了解生物生长过程、规划生产和策划控制措施具有重要意义。
统计软件SPSS作为一种功能强大的数据分析工具,可以方便地拟合生长曲线方程,并对其进行参数估计和模型选择。
对于生物生长曲线的拟合,我们首先需要收集一定的生长数据。
例如,我们希望了解某种植物在不同时间段下的生长情况,我们可以定期测量其生长高度或重量。
收集到的数据可以是一个样本,也可以是多个样本的平均值。
在拟合曲线之前,我们需要对数据进行预处理,包括数据清洗、缺失数据的处理和异常值的处理等。
在SPSS中,我们可以使用数据编辑功能对数据进行操作。
接下来,我们可以利用SPSS的回归分析功能进行生长曲线的拟合。
根据生长曲线的特点,常见的拟合方程有指数曲线、对数曲线、多项式曲线等。
在SPSS中,我们可以选择合适的函数进行拟合。
以指数曲线为例,拟合方程通常为:Y = C × exp (a × X)其中Y为生长变量,X为时间变量,C、a为待估参数。
在SPSS的回归分析功能中,我们可以选择指数函数作为函数形式,并设置合适的因变量和自变量。
通过分析结果可以得到拟合曲线的公式及参数估计值。
在拟合过程中,我们还可以进行模型选择和比较。
SPSS提供了一系列的统计指标,如拟合度(R-squared)、残差标准差等,用于评估拟合模型的拟合程度和精度。
通常,较高的拟合度和较小的残差标准差表示模型的拟合效果较好。
通过比较不同模型的指标,我们可以选择最合适的模型,即拟合最精确的生长曲线。
除了拟合曲线,SPSS还提供了其他功能,如拟合优度检验、参数置信区间的估计、预测值的计算等。
这些功能可以进一步加强对生长曲线的分析和解释能力。
应用统计软件SPSS拟合生长曲线方程可以为生物研究和实际应用带来很多好处。
SPSS05日期时间函数及其应用(1)

返回
格利戈里历法很快在罗马天主教势力范围被 普遍接受,但是在英国却引起了一片喧嚣的反对 声,英国人仍然坚持朱利安历法,拒绝“抹掉10 天”。直到1752年,英国人才想通,理性终于占 了上风,不过从1582年到那时,历法又多出了1天, 所以英国议会在1752年作出决定,抹掉11天---1752年9月3日至13日,至此才接受了格利戈里的 改革。请注意,英国历史中,这11天什么也没有 发生。由此可以看到,一次历法改革是多么不容 易,对于一个聪明、合理的决定,仅仅因为看上 去有点怪就有人反对,竟然花了快二百年才接受!
常量格式示例2
格 式 q Q yyyy q Q yy mmm yyyy mmm yy ww WK yyyy ww WK yy Monday, Tuesday… Mon, Tue, Wed… January, February… Jan, Feb, Mar… 季度 Q 年(4位) 季度 Q 年(2位) 月份(英文)年(4位) 月份(英文)年(2位) 周数 “WK” 年(4位) 周数 “WK” 年(2位) 直接输入英文的星期几 直接输入星期几的英文缩写 直接输入英文月份 直接输入英文月份缩写 说 明 示 例 3Q1945,4Q1995 3Q45,4Q95 AUG1945 DEC1995 AUG45DEC95 33 WK 1945,52 WK 1995 33 WK 45,52 WK 95 Friday FRI August,December AUG,DEC 返回
常量格式示例3
格 式 dd-mmm-yyyy hh:mm dd-mmm-yyyy hh:mm:ss dd-mmm-yyyy hh:mm:ss.ss hh:mm hh:mm:ss hh:mm:ss.ss ddd hh:mm ddd hh:mm:ss ddd hh:mm:ss.ss 说 明 日(2位)-月(英文月份缩写)-年(4位) 时 (2位):分(2位) 日(2位)-月(英文月份缩写)-年(4位) 时 (2位):分(2位):秒(2位) 日(2位)-月(英文月份缩写)-年(4位) 时 (2位):分(2位):秒(2位).百分秒 时(2位):分(2位) 时(2位):分(2位):秒(2位) 时(2位):分(2位):秒(2位).百分秒 日数 时(2位):分(2位) 日数 时(2位):分(2位):秒(2位) 日数 时(2位):分(2位):秒(2位).百分秒 示 例 11-AUG-1945 11:10 11-AUG-1945 11:10:35 11-AUG-1945 11:10:35.30 11:30,08:50 11:08:05,08:15:25 11:08:05.80,08:15:25.45 128 08:50 128 08:50:30 128 08:50:30.78 返回
《SPSS统计分析》第05章 日期和时间函数及其运算

示例 3Q1945,4Q1995 3Q45,4Q95 AUG1945 DEC1995 AUG45DEC95 33 WK 1945,52 WK 1995 33 WK 45,52 WK 95 Friday FRI August,December AUG,DEC
返回
常量格式示例3
格式
dd-mmm-yyyy hh:mm
返回
日期时间型变量输入/输出格式-示例 1
返回
日期时间型变量输入/输出格式- 示例2
返回
日期时间函数
当前日期时间函数(Current Date/Time) 4个 日期的算术运算函数(Date Arithmetic) 2个 时间生成函数(Date Creation) 6个 日期提取函数(Date Extraction) 11个 时间间隔生成函数(Time duration creation )4个 时间间隔提取函数(Time duration Extraction) 8个 与日期时间有关的转换函数 1个
返回
格利戈里历法很快在罗马天主教势力范围被 普遍接受,但是在英国却引起了一片喧嚣的反对 声,英国人仍然坚持朱利安历法,拒绝“抹掉10 天”。直到1752年,英国人才想通,理性终于占 了上风,不过从1582年到那时,历法又多出了1天, 所以英国议会在1752年作出决定,抹掉11天---1752年9月3日至13日,至此才接受了格利戈里的 改革。请注意,英国历史中,这11天什么也没有 发生。由此可以看到,一次历法改革是多么不容 易,对于一个聪明、合理的决定,仅仅因为看上 去有点怪就有人反对,竟然花了快二百年才接受!
西方历法的第一次改革是罗马朱利乌斯·凯撒大帝于公 元前45年亲自引进的。当时采用的数字是一年365.25天, 于是朱利安历法成为最简单的历法:第一、二、三年都是 365天,三年余下的0.25天给第四年,第四年就有366天, 这就是闰年。于是重复365,365,365,366的周期,每年 都是整数。
spss二元指数函数拟合

spss二元指数函数拟合二元变量是数据统计中常用的一种变量,这种变量只有两个可能:是和否,对于这种变量来说,一般是很难进行直接的线性或非线性回归分析的。
这时要探究变量之间的关系,就需要用到二元回归分析。
接下来我们就通过一个简单的示例来介绍一下IBM SPSS Statistics中如何对二元变量进行回归分析。
一、概述1.样本数据这是一份肿瘤患者体内肿瘤情况的统计表,通过二元回归分析,我们可以拟合年龄、肿瘤大小和扩散等级这三个变量与“癌变部位的淋巴结是否含有癌细胞”的回归关系。
2.二元logistic回归在“分析”菜单下,可以打开“回归”中的“二元logistic回归”分析,这是SPSS提供的专门用于二元回归的一种分析方法。
二、操作指南1.变量设置将“癌变部位的淋巴结是否含有癌细胞”作为因变量,将剩余三个变量移入“协变量”窗口。
下面的方法设置的是协变量的输入方式,默认的“输入”就是将变量全部输入,其他的方法是根据一些特定的方法向前或向后剔除变量后再输入,我们这里使用“输入”即可。
选择变量是用来设置筛选变量的,本数据样本中变量较少,所以不使用这个功能。
2.分类设置分类窗口设置分类协变量,我们这里的分类变量是“肿瘤扩散等级”,选择“指示灯”对比方法,“最后一个”参考类别。
3.保存设置这是IBM SPSS Statistics分析中较为常见的一个分析保存对话框,用户可以在其中设置要保存的预测值、影响和残差,在需要保存的项目前勾选复选框即可。
勾选概率、组成员、杠杆值、标准化和协方差矩阵。
4.选项设置这个对话框设置统计图和步进概率,勾选分类图、霍斯默—莱梅肖拟合优度,在每个步骤输出。
步进概率中设置进入概率和删除概率,前者数值应小于后者,保持系统默认即可。
5.完成分析在输出日志中查看最终的分析结果,SPSS会为用户提供模型的相关参数,包括个案统计、显著性参数、模型拟合度参数等,本例中的显著性系数均较小,拟合参数较大,因此对于这三个自变量来说,因变量与它们的拟合效果并不明显。
spss计算标准差

spss计算标准差SPSS计算标准差。
标准差是统计学中常用的一种测度数据离散程度的指标,它能够反映一组数据的离散程度,是描述数据分布的重要统计量。
在SPSS软件中,计算标准差是非常常见的操作,下面我们将详细介绍如何在SPSS中进行标准差的计算。
首先,打开SPSS软件并导入需要进行标准差计算的数据文件。
在数据文件导入后,点击菜单栏中的“转换”选项,然后选择“计算变量”。
在弹出的对话框中,输入需要计算标准差的变量名称,并选择“标准差”作为计算的函数。
点击“箭头”将需要计算标准差的变量移入“数值变量”框中,然后点击“确定”按钮进行计算。
SPSS软件会自动计算所选变量的标准差,并将结果显示在数据文件中。
在结果中,标准差的数值将会显示在新生成的变量列中,我们可以通过查看这一列数据来获取标准差的计算结果。
需要注意的是,SPSS软件中的标准差计算默认使用的是总体标准差的计算公式,如果需要计算样本标准差,可以在计算变量对话框中选择“样本标准差”作为计算的函数。
除了通过计算变量功能进行标准差的计算外,SPSS软件还提供了更多灵活的计算方式。
用户可以通过编写语法或使用统计分析功能进行标准差的计算,这些方法可以更加灵活地满足用户的需求。
总之,在SPSS软件中计算标准差非常简单,用户只需要几步操作就可以得到所需的结果。
标准差作为描述数据离散程度的重要指标,在统计分析中具有非常重要的作用,因此掌握在SPSS中进行标准差计算的方法是非常有必要的。
希望通过本文的介绍,读者能够更加熟练地在SPSS中进行标准差的计算,从而更好地应用统计分析方法进行数据分析和研究。
当然,在实际操作中,读者还可以根据具体的需求和数据特点,灵活选择合适的计算方法,以便更好地理解和描述数据的离散程度。
总的来说,SPSS软件提供了丰富的功能和灵活的操作方式,使得标准差的计算变得非常简单和便捷。
通过学习和掌握SPSS中的标准差计算方法,相信读者可以更加轻松地进行数据分析和统计研究工作。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
SPSS常用函数
SPSS函数是一个常用程序,并且利用一个或多个自变量(参数)来执行。
每个SPSS函数均有一个关键名称,且绝不能写错。
通常,函数的格式为:函数名称(自变量,自变量,……),某些函数可能只含有一个自变量,而有些函数则可能含有多个自变量,当一个函数含有多个自变量时,各自变量间用逗号(,)隔开,而函数的自变量通常又可分为以下三种:
(1)常数,如SQRT(100);
(2)变量名称,如MEAN(VAR1,VAR2,VAR3);
(3)表达式,如MIN(30,SQRT(100))。
总之,SPSS函数和我们平时EXCEL里面函数格式规则并无差别。
SPSS提供了180多种函数,共可分为十多类(SPSS 17.0大小小分了18类)。
和EXCEL一样,我们也不可能记住所有函数,只要知道一些常用函数,至于其他函数要用的时候再去查找也不迟,下面将列举一些常用函数:
1.ArithmeticFunctions算术函数
算术函数是最常用的函数,可以满足对变量进行的一般运算,算术函数主要有:
﹡算术表达式也包括单值与变量名的情况。
2.StatisticalFunctions统计函数
统计函数也是统计分析中常用的函数之一,主要反映变量的数据特征,时间序列的滞后期变量等,具体函数有:。
