典型例题分析
材料力学典型例题与详解(经典题目)
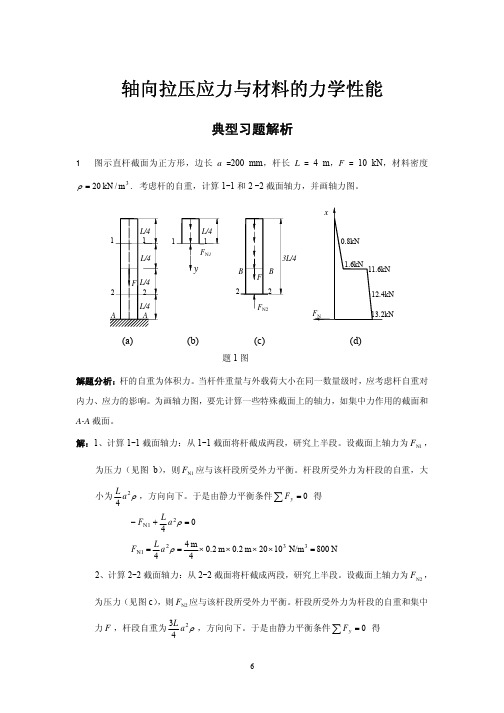
= 3.64
2、按挤压强度条件确定铆钉数:挤压面面积 A = δ d ,铆钉挤压强度条件为
σ bs
=
Fb Abs
=
F nδ d
≤ [σ
bs]
得
n
≥
δ
d
F [σ
bs
]
=
10
× 10 −3
m
×
160 ×103 20 ×10−3 m
N × 320
× 10 6
N/m 2
= 2.5
两者取大值,最后确定铆钉数 n = 4。
衡条件得 F 作用截面上侧轴力为
FNB +
=
L a2ρ 2
=
4 m × (0.2 m)2 2
× 20 × 103
N/m 3
= 1.6 × 103 N = 1.6 kN
然后将杆沿 F 作用截面(B-B)下侧截开,设截面上轴力为压力 FNB− ,研究上半部分
杆段。这时杆段受本身重量作用和集中力 F 作用,所以由静力平衡条件得 F 作用截面下侧 轴力为
FNB−
=
L a2ρ 2
+
F
=
4 m × (0.2 m)2 2
× 20 ×103
N/m 3
+ 10 ×103
N = 11.6 ×103 N = 11.6 kN
4、计算 A-A 截面轴力:从 A-A 截面将杆截开,设截面上轴力为压力 FNA ,则 FNA 应与该杆
上所有外力平衡。杆所受外力为杆的自重和集中力 F ,杆段自重为 La 2 ρ ,方向向下。于是
2 图示石柱桥墩,压力 F = 1000 kN,石料密度 ρ = 25 kN / m3 ,许用应力 [σ ] =1 MPa。试 比较下列三种情况下所需石料体积。(1)等截面石柱;(2)三段等长度的阶梯石柱;(3)等 强度石柱(柱的每个截面的应力都等于许用应力 [σ ] )。 解题分析:设计这样的桥墩时,要考虑桥墩自重对强度的影响。可以想象,在桥墩顶截面只 有压力 F 作用,轴力最小;在桥墩底截面,除压力 F 外,还承受桥墩本身重量,该处轴力 最大。当桥墩采用等截面石柱时,只要考虑底部截面的强度即可。如果采用阶梯型石柱,需 考虑每段的强度。如果要求各个截面强度相等,则需要对石柱的各截面进行特别设计。 解:1、采用等截面石柱
圆周运动典型例题及答案详解

“匀速圆周运动”的典型例题【例1】如图所示的传动装置中,A、B两轮同轴转动.A、B、C三轮的半径大小的关系是R A=R C=2R B.当皮带不打滑时,三轮的角速度之比、三轮边缘的线速度大小之比、三轮边缘的向心加速度大小之比分别为多少?【例2】一圆盘可绕一通过圆盘中心O且垂直于盘面的竖直轴转动.在圆盘上放置一木块,当圆盘匀速转动时,木块随圆盘一起运动(见图),那么[ ]A.木块受到圆盘对它的摩擦力,方向背离圆盘中心B.木块受到圆盘对它的摩擦力,方向指向圆盘中心C.因为木块随圆盘一起运动,所以木块受到圆盘对它的摩擦力,方向与木块的运动方向相同D.因为摩擦力总是阻碍物体运动,所以木块所受圆盘对它的摩擦力的方向与木块的运动方向相反E.因为二者是相对静止的,圆盘与木块之间无摩擦力【例3】在一个水平转台上放有A、B、C三个物体,它们跟台面间的摩擦因数相同.A的质量为2m,B、C各为m.A、B离转轴均为r,C为2r.则[ ]A.若A、B、C三物体随转台一起转动未发生滑动,A、C的向心加速度比B大B.若A、B、C三物体随转台一起转动未发生滑动,B所受的静摩擦力最小C.当转台转速增加时,C最先发生滑动D.当转台转速继续增加时,A比B先滑动【例4】如图,光滑的水平桌面上钉有两枚铁钉A、B,相距L0=0.1m.长L=1m 的柔软细线一端拴在A上,另一端拴住一个质量为500g的小球.小球的初始位置在AB连线上A的一侧.把细线拉直,给小球以2m/s的垂直细线方向的水平速度,使它做圆周运动.由于钉子B的存在,使细线逐步缠在A、B上.若细线能承受的最大张力T m=7N,则从开始运动到细线断裂历时多长?【说明】圆周运动的显著特点是它的周期性.通过对运动规律的研究,用递推法则写出解答结果的通式(一般表达式)有很重要的意义.对本题,还应该熟练掌握数列求和方法.如果题中的细线始终不会断裂,有兴趣的同学还可计算一下,从小球开始运动到细线完全绕在A、B两钉子上,共需多少时间?【例5】如图(a)所示,在光滑的圆锥顶用长为L的细线悬挂一质量为m的小球,圆锥顶角为2θ,当圆锥和球一起以角速度ω匀速转动时,球压紧锥面.此时绳的张力是多少?若要小球离开锥面,则小球的角速度至少为多少?【说明】本题是属于二维的牛顿第二定律问题,解题时,一般可以物体为坐标原点,建立xoy直角坐标,然后沿x轴和y轴两个方向,列出牛顿第二定律的方程,其中一个方程是向心力和向心加速度的关系,最后解联立方程即可。
(完整版)等差数列典型例题及分析

第四章 数列[例1]已知数列1,4,7,10,…,3n+7,其中后一项比前一项大3.(1)指出这个数列的通项公式;(2)指出1+4+…+(3n -5)是该数列的前几项之和.正解:(1)a n =3n -2;(2) 1+4+…+(3n -5)是该数列的前n -1项的和.[例2] 已知数列{}n a 的前n 项之和为① n n S n -=22 ② 12++=n n S n求数列{}n a 的通项公式。
正解: ①当1=n 时,111==S a 当2≥n 时,34)1()1(2222-=-+---=n n n n n a n 经检验 1=n 时 11=a 也适合,∴34-=n a n ②当1=n 时,311==S a 当2≥n 时,nn n n n a n 21)1()1(122=-----++= ∴ ⎩⎨⎧=n a n 23)2()1(≥=n n [例3] 已知等差数列{}n a 的前n 项之和记为S n ,S 10=10 ,S 30=70,则S 40等于 。
正解:由题意:⎪⎪⎩⎪⎪⎨⎧=⨯+=⨯+7022930301029101011d a d a 得152,521==d a 代入得S 40 =1204023940401=⨯⨯+d a 。
[例5]已知一个等差数列{}n a 的通项公式a n =25-5n ,求数列{}||n a 的前n 项和;正解: ⎪⎪⎩⎪⎪⎨⎧≥+--≤-6,502)5)(520(5,2)545(n n n n n n[例6]已知一个等差数列的前10项的和是310,前20项的和是1220,由此可以确定求其前n 项和的公式吗?[例7]已知:nn a -+=12lg 1024 (3010.02lg =)+∈N n (1) 问前多少项之和为最 大?(2)前多少项之和的绝对值最小? 解:(1) ⎩⎨⎧<-=≥-+=+02lg 102402lg )1(10241n a n a n n 3403340112lg 10242lg 1024<<⇒+≤<⇒n n∴3402=n (2) 0)2lg (2)1(1024=--+=n n n S n 当n n S S 或0=近于0时其和绝对值最小 令:0=n S 即 1024+0)2lg (2)1(=--n n 得:99.680412lg 2048≈+=n ∵ +∈N n ∴6805=n [例8]项数是n 2的等差数列,中间两项为1+n n a a 和是方程02=+-q px x 的两根,求证此数列的和n S 2是方程 0)lg (lg lg )lg (lg lg 2222=+++-p n x p n x 的根。
统计案例分析报告及典型例题

统计案例分析及典型例题§11.1 抽样方法1.为了了解所加工的一批零件的长度,抽取其中200个零件并测量了其长度,在这个问题中,总体的一个样本是 . 答案 200个零件的长度2.某城区有农民、工人、知识分子家庭共计2 004户,其中农民家庭1 600户,工人家庭303户,现要从中抽取容量为40的样本,则在整个抽样过程中,可以用到下列抽样方法:①简单随机抽样,②系统抽样,③分层抽样中的 . 答案 ①②③3.某企业共有职工150人,其中高级职称15人,中级职称45人,初级职称90人.现采用分层抽样抽取容量为30的样本,则抽取的各职称的人数分别为 . 答案 3,9,184.某工厂生产A 、B 、C 三种不同型号的产品,其相应产品数量之比为2∶3∶5,现用分层抽样方法抽出一个容量为n 的样本,样本中A 型号产品有16件,那么此样本的容量n= . 答案 80例1 某大学为了支援我国西部教育事业,决定从2007应届毕业生报名的18名志愿者中,选取6人组成志愿小组.请用抽签法和随机数表法设计抽样方案. 解 抽签法:第一步:将18名志愿者编号,编号为1,2,3, (18)第二步:将18个号码分别写在18张外形完全相同的纸条上,并揉成团,制成号签; 第三步:将18个号签放入一个不透明的盒子里,充分搅匀; 第四步:从盒子中逐个抽取6个号签,并记录上面的编号;基础自测第五步:所得号码对应的志愿者,就是志愿小组的成员. 随机数表法:第一步:将18名志愿者编号,编号为01,02,03, (18)第二步:在随机数表中任选一数作为开始,按任意方向读数,比如第8行第29列的数7开始,向右读;第三步:从数7开始,向右读,每次取两位,凡不在01—18中的数,或已读过的数,都跳过去不作记录,依次可得到12,07,15,13,02,09.第四步:找出以上号码对应的志愿者,就是志愿小组的成员.例2 某工厂有1 003名工人,从中抽取10人参加体检,试用系统抽样进行具体实施. 解 (1)将每个人随机编一个号由0001至1003. (2)利用随机数法找到3个号将这3名工人剔除. (3)将剩余的1 000名工人重新随机编号由0001至1000. (4)分段,取间隔k=100001=100将总体均分为10段,每段含100个工人.(5)从第一段即为0001号到0100号中随机抽取一个号l.(6)按编号将l ,100+l ,200+l,…,900+l 共10个号码选出,这10个号码所对应的工人组成样本. 例3 (14分)某一个地区共有5个乡镇,人口3万人,其中人口比例为3∶2∶5∶2∶3,从3万人中抽取一个300人的样本,分析某种疾病的发病率,已知这种疾病与不同的地理位置及水土有关,问应采取什么样的方法?并写出具体过程.解 应采取分层抽样的方法.3分过程如下:(1)将3万人分为五层,其中一个乡镇为一层.5分(2)按照样本容量的比例随机抽取各乡镇应抽取的样本. 300×153=60(人);300×152=40(人); 300×155=100(人);300×152=40(人); 300×153=60(人),10分因此各乡镇抽取人数分别为60人,40人,100人,40人,60人.12分(3)将300人组到一起即得到一个样本.14分练习:一、填空题1.(安庆模拟)某校高中生共有900人,其中高一年级300人,高二年级200人,高三年级400人,现分层抽取容量为45的样本,那么高一、高二、高三年级抽取的人数分别为 .答案15,10,202.某牛奶生产线上每隔30分钟抽取一袋进行检验,则该抽样方法为①;从某中学的30名数学爱好者中抽取3人了解学习负担情况,则该抽样方法为②.那么①,②分别为 .答案系统抽样,简单随机抽样3.下列抽样实验中,最适宜用系统抽样的是(填序号).①某市的4个区共有2 000名学生,且4个区的学生人数之比为3∶2∶8∶2,从中抽取200人入样②某厂生产的2 000个电子元件中随机抽取5个入样③从某厂生产的2 000个电子元件中随机抽取200个入样④从某厂生产的20个电子元件中随机抽取5个入样答案③4.(2013·重庆文)某校高三年级有男生500人,女生400人,为了解该年级学生的健康情况,从男生中任意抽取25人,从女生中任意抽取20人进行调查,这种抽样方法是 .答案分层抽样法5.某中学有高一学生400人,高二学生300人,高三学生200人,学校团委欲用分层抽样的方法抽取18名学生进行问卷调查,则下列判断不正确的是(填序号).①高一学生被抽到的概率最大②高三学生被抽到的概率最大③高三学生被抽到的概率最小④每名学生被抽到的概率相等答案①②③6.某商场有四类食品,其中粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20种,现从中抽取一个容量为20的样本进行食品安全检测,若采用分层抽样的方法抽取样本,则抽取的植物油类与果蔬类食品种数之和是 .答案 67.(天津文,11)一个单位共有职工200人,其中不超过45岁的有120人,超过45岁的有80人.为了调查职工的健康状况,用分层抽样的方法从全体职工中抽取一个容量为25的样本,应抽取超过45岁的职工 人. 答案 108.将参加数学竞赛的1 000名学生编号如下0001,0002,0003,…,1000,打算从中抽取一个容量为50的样本,按系统抽样的方法分成50个部分,如果第一部分编号为0001,0002,…,0020,从第一部分随机抽取一个号码为0015,则第40个号码为 . 答案 07959.某政府机关有在编人员100人,其中副处级以上干部10人,一般干部70人,工人20人,上级机关为了了解政府机构改革意见,要从中抽取一个容量为20的样本,试确定用何种方法抽取,如何抽取? 解 用分层抽样抽取. (1)∵20∶100=1∶5, ∴510=2,570=14,520=4∴从副处级以上干部中抽取2人,一般干部中抽取14人,从工人中抽取4人.(2)因副处级以上干部与工人人数较少,可用抽签法从中分别抽取2人和4人;对一般干部可用随机数表法抽取14人.(3)将2人、4人、14人编号汇合在一起就得到了容量为20的样本.10.某单位有工程师6人,技术员12人,技工18人,要从这些人中抽取一个容量为n 的样本.如果采用系统抽样法和分层抽样法抽取,不用剔除个体;如果样本容量增加一个,则在采用系统抽样时,需要在总体中先剔除1个个体,求样本容量n.解 总体容量为6+12+18=36.当样本容量是n 时,由题意知,系统抽样的间隔为n36,分层抽样的比例是36n ,抽取工程师36n ×6=6n (人),抽取技术人员36n ×12=3n (人),抽取技工36n×18=2n (人).所以n 应是6的倍数,36的约数即n=6,12,18,36.当样本容量为(n+1)时,在总体中剔除1人后还剩35人,系统抽样的间隔为135+n ,因为135+n 必须是整数,所以n 只能取6,即样本容量为6.总体分布的估计与总体特征数的估计1.一个容量为20的样本,已知某组的频率为0.25,则该组的频数为 . 答案 52.(2008·山东理)右图是根据《山东统计年鉴2007》中的资料作成的1997年至2006年我省城镇居民百户家庭人口数的茎叶图.图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的个位数字.从图中可以得到1997年至2006年我省城镇居民百户家庭人口数的平均数为 . 答案 303.63.在抽查产品的尺寸过程中,将其尺寸分成若干组,[a ,b )是其中的一组,抽查出的个体在该组上的频率为m,该组在频率分布直方图的高为h ,则|a-b|= . 答案 hm4.(2008·山东文,9)从某项综合能力测试中抽取100人的成绩,统计如表,则这100人成绩的标准差为 .答案 51025.为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁~18岁的男生体重(kg ),得到频率分布直方图如下:根据上图可得这100名学生中体重在[56.5,64.5)的学生人数是 . 答案 40基础自测典型例题:例1 在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交 作品的件数按5天一组分组统计,绘制了频率分布直方图(如图所示),已知从左到右各长方形高的比为2∶3∶4∶6∶4∶1,第三组的频数为12,请解答下列问题: (1)本次活动共有多少件作品参加评比? (2)哪组上交的作品数量最多?有多少件?(3)经过评比,第四组和第六组分别有10件、2件作品获奖,问这两组哪组获奖率高? 解 (1)第三组的频率为1464324+++++=51又因为第三组的频数为12,∴参评作品数为5112=60.(2)根据频率分布直方图,可以看出第四组上交的作品数量最多,共有60×1464326+++++=18(件).(3)第四组的获奖率是1810=95,第六组上交的作品数量为60×1464321+++++=3(件),∴第六组的获奖率为32=96,显然第六组的获奖率高.例4(14分)某化肥厂甲、乙两个车间包装肥料,在自动包装传送带上每隔30 min 抽取一包产品,称其重量,分别 记录抽查数据如下: 甲:102, 101, 99, 98, 103, 98,99;乙:110, 115, 90,85,75,115, 110.(1)这种抽样方法是哪一种? (2)将这两组数据用茎叶图表示;(3)将两组数据比较,说明哪个车间产品较稳定. 解 (1)因为间隔时间相同,故是系统抽样. 2分(2)茎叶图如下:5分(3)甲车间: 平均值:1x =71(102+101+99+98+103+98+99)=100,7分方差:s 12=71[(102-100)2+(101-100)2+…+(99-100)2]≈3.428 6.9分乙车间:平均值:2x =71(110+115+90+85+75+115+110)=100,11分方差:s 22=71[(110-100)2+(115-100)2+…+(110-100)2]≈228.571 4.13分∵1x =2x ,s 12<s 22,∴甲车间产品稳定.14分练习:1.为了了解小学生的体能情况,抽取了某小学同年级部分学生进行跳绳测试,将所得数据整理后,画出频率分布直方图如图所示,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数为5.(1)求第四小组的频率;(2)参加这次测试的学生人数是多少?(3)在这次测试中,学生跳绳次数的中位数落在第几小组内? 解 (1)第四小组的频率=1-(0.1+0.3+0.4)=0.2. (2)设参加这次测试的学生人数是n, 则有n=第一小组频率第一小组频数=5÷0.1=50(人).(3)因为0.1×50=5,0.3×50=15,0.4×50=20,0.2×50=10,即第一、第二、第三、第四小组的频数分别为5、15、20、10,所以学生跳绳次数的中位数落在第三小组内. 练习:一、填空题1.下列关于频率分布直方图的说法中不正确的是 . ①直方图的高表示取某数的频率②直方图的高表示该组上的个体在样本中出现的频率 ③直方图的高表示该组上的个体数与组距的比值④直方图的高表示该组上的个体在样本中出现的频率与组距的比值 答案 ①②③2.甲、乙两名新兵在同样条件下进行射击练习,每人打5发子弹,命中环数如下:甲:6,8,9,9,8;乙:10,7,7,7,9.则这两人的射击成绩 比 稳定. 答案 甲 乙4.某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果分成六组:右图是得到的频率分布直方图.设成绩小于17秒的学生人数占全班总人数的百分比为x,成绩大于等于15秒且小于17秒的学生人数为y ,则从频率分布直方图中可分析出x 和y 分别为 . 答案 0.9, 356.甲、乙两名同学在5次体育测试中的成绩统计的茎叶图如图所示,若甲、乙两人的平均成绩分别是x 甲、x 乙,则x 甲 x 乙, 比 稳定. 答案 < 乙 甲7.(上海,9)已知总体的各个体的值由小到大依次为2,3,3,7,a ,b ,12,13.7,18.3,20,且总体的中位数为10.5.若要使该总体的方差最小,则a 、b 的取值分别是 . 答案 10.5、10.5二、解答题10.为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小长方形面积之比为2∶4∶17∶15∶9∶3,第二小组频数为12.(1)第二小组的频率是多少?样本容量是多少?(2)若次数在110以上(含110次)为达标,试估计该学校全体高一学生的达标率是多少? (3)在这次测试中,学生跳绳次数的中位数落在哪个小组内?请说明理由. 解 (1)由于频率分布直方图以面积的形式反映了数据落在各小组内的频率大小, 因此第二小组的频率为:391517424+++++=0.08.又因为频率=样本容量第二小组频数, 所以样本容量=第二小组频率第二小组频数=08.012=150. (2)由图可估计该学校高一学生的达标率约为39151742391517++++++++×100%=88%.(3)由已知可得各小组的频数依次为6,12,51,45,27,9,所以前三组的频数之和为69,前四组的频数之和为114,所以跳绳次数的中位数落在第四小组内.线性回归方程1.下列关系中,是相关关系的为 (填序号). ①学生的学习态度与学习成绩之间的关系;基础自测②教师的执教水平与学生的学习成绩之间的关系;③学生的身高与学生的学习成绩之间的关系;④家庭的经济条件与学生的学习成绩之间的关系.答案①②2.为了考察两个变量x、y之间的线性相关关系,甲、乙两同学各自独立地做10次和15次试验,并利用最小二乘法求得回归直线分别为l1和l2.已知在两人的试验中发现变量x的观测数据的平均值恰好相等,都为s,变量y的观测数据的平均值也恰好相等,都为t,那么下列说法中正确的是(填序号).①直线l1,l2有交点(s,t)②直线l1,l2相交,但是交点未必是(s,t)③直线l1,l2由于斜率相等,所以必定平行④直线l1,l2必定重合答案①3.下列有关线性回归的说法,正确的是(填序号).①相关关系的两个变量不一定是因果关系②散点图能直观地反映数据的相关程度③回归直线最能代表线性相关的两个变量之间的关系④任一组数据都有回归直线方程答案①②③4.下列命题:①线性回归方法就是由样本点去寻找一条贴近这些样本点的直线的数学方法;②利用样本点的散点图可以直观判断两个变量的关系是否可以用线性关系表示;③通过回归直线yˆ=bˆx+aˆ及回归系数bˆ,可以估计和预测变量的取值和变化趋势. 其中正确命题的序号是 .答案①②③5.已知回归方程为yˆ=0.50x-0.81,则x=25时,yˆ的估计值为 .答案11.69例1下面是水稻产量与施化肥量的一组观测数据:施化肥量15 20 25 30 35 40 45水稻产量320 330 360 410 460 470 480(1)将上述数据制成散点图;(2)你能从散点图中发现施化肥量与水稻产量近似成什么关系吗?水稻产量会一直随施化肥量的增加而增长吗?解(1)散点图如下:(2)从图中可以发现施化肥量与水稻产量具有线性相关关系,当施化肥量由小到大变化时,水稻产量由小变大,图中的数据点大致分布在一条直线的附近,因此施化肥量和水稻产量近似成线性相关关系,但水稻产量只是在一定范围内随着化肥施用量的增加而增长.例2(14分)随着我国经济的快速发展,城乡居民的生活水平不断提高,为研究某市家庭平均收入与月平均生活支出的关系,该市统计部门随机调查了10个家庭,得数据如下:(1)判断家庭平均收入与月平均生活支出是否相关?(2)若二者线性相关,求回归直线方程.解(1)作出散点图:5分观察发现各个数据对应的点都在一条直线附近,所以二者呈线性相关关系. 7分(2)x =101 (0.8+1.1+1.3+1.5+1.5+1.8+2.0+2.2+2.4+2.8)=1.74,y=101(0.7+1.0+1.2+1.0+1.3+1.5+1.3+1.7+2.0+2.5)=1.42,9分bˆ=∑∑==-∙-ni ini i i x n xyx n y x 1221≈0.813 6,aˆ=1.42-1.74×0.813 6≈0.004 3,13分 ∴回归方程yˆ=0.813 6x+0.004 3.14分例3 下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y (吨)标准煤的几组对照数据.(1)请画出上表数据的散点图;(2)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程yˆ=b ˆx+a ˆ; (3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤? (参考数值:3×2.5+4×3+5×4+6×4.5=66.5) 解 (1)散点图如下图:(2)x =46543+++=4.5,y =45.4435.2+++=3.5∑=41i ii yx =3×2.5+4×3+4×5+6×4.5=66.5.∑=412i ix=32+42+52+62=86∴bˆ=24124144x x yx yx i i i ii -∙-∑∑===25.44865.45.345.66⨯-⨯⨯-=0.7aˆ =y -bˆx =3.5-0.7×4.5=0.35. ∴所求的线性回归方程为yˆ=0.7x+0.35. (3)现在生产100吨甲产品用煤 y=0.7×100+0.35=70.35,∴降低90-70.35=19.65(吨)标准煤.1.科研人员为了全面掌握棉花新品种的生产情况,查看了气象局对该地区年降雨量与年平均气温的统计数据(单位分别是mm,℃),并作了统计.(1)试画出散点图;(2)判断两个变量是否具有相关关系. 解 (1)作出散点图如图所示,(2)由散点图可知,各点并不在一条直线附近,所以两个变量是非线性相关关系.2.在研究硝酸钠的可溶性程度时,对于不同的温度观测它在水中的溶解度,得观测结果如下:由资料看y 与x 呈线性相关,试求回归方程. 解 x =30,y =50.1283.1120.850.767.66++++=93.6.bˆ=25125155x xyx yx i ii ii -∙-∑∑==≈0.880 9.aˆ=y -bˆx =93.6-0.880 9×30=67.173. ∴回归方程为yˆ=0.880 9x+67.173.3.某企业上半年产品产量与单位成本资料如下:(1)求出线性回归方程;(2)指出产量每增加1 000件时,单位成本平均变动多少? (3)假定产量为6 000件时,单位成本为多少元? 解 (1)n=6,∑=61i i x =21,∑=61i i y =426,x =3.5,y =71,∑=612i i x =79,∑=61i i i y x =1 481,bˆ=26126166x xyx yx i ii ii -∙-∑∑===25.3679715.364811⨯-⨯⨯-=-1.82.aˆ=y-bˆx=71+1.82×3.5=77.37.回归方程为yˆ=aˆ+bˆx=77.37-1.82x.(2)因为单位成本平均变动bˆ=-1.82<0,且产量x的计量单位是千件,所以根据回归系数b的意义有: 产量每增加一个单位即1 000件时,单位成本平均减少1.82元.(3)当产量为6 000件时,即x=6,代入回归方程:yˆ=77.37-1.82×6=66.45(元)当产量为6 000件时,单位成本为66.45元.一、填空题1.观察下列散点图,则①正相关;②负相关;③不相关.它们的排列顺序与图形对应顺序是 .答案a,c,b2.回归方程yˆ=1.5x-15,则下列说法正确的有个.①y=1.5x-15②15是回归系数a③1.5是回归系数a④x=10时,y=0答案 13.(2009.湛江模拟)某地区调查了2~9岁儿童的身高,由此建立的身高y(cm)与年龄x(岁)的回归模型为yˆ=8.25x+60.13,下列叙述正确的是 .①该地区一个10岁儿童的身高为142.63 cm②该地区2~9岁的儿童每年身高约增加8.25 cm③该地区9岁儿童的平均身高是134.38 cm④利用这个模型可以准确地预算该地区每个2~9岁儿童的身高答案 ②4.三点(3,10),(7,20),(11,24)的回归方程是 .答案 yˆ=1.75x+5.75 5.某人对一地区人均工资x(千元)与该地区人均消费y(千元)进行统计调查,y 与x 有相关关系,得到回归直线方程yˆ=0.66x+1.562.若该地区的人均消费水平为7.675千元,估计该地区的人均消费额占人均工资收入的百分比约为 . 答案 83%6.某化工厂为预测产品的回收率y,需要研究它和原料有效成分含量x 之间的相关关系,现取8对观测值,计算,得∑=81i i x =52, ∑=81i i y =228, ∑=812i i x =478, ∑=81i i i y x =1 849,则其线性回归方程为 .答案 yˆ=11.47+2.62x 7.有下列关系:①人的年龄与他(她)拥有的财富之间的关系;②曲线上的点与该点的坐标之间的关系;③苹果的产量与气候之间的关系;④森林中的同一种树木,其断面直径与高度之间的关系.其中,具有相关关系的是 . 答案 ①③④8.已知关于某设备的使用年限x 与所支出的维修费用y(万元),有如下统计资料:若y 对x 呈线性相关关系,则回归直线方程yˆ=b ˆx+a ˆ表示的直线一定过定点 . 答案 (4,5) 二、解答题9.期中考试结束后,记录了5名同学的数学和物理成绩,如下表:(1)数学成绩和物理成绩具有相关关系吗?(2)请你画出两科成绩的散点图,结合散点图,认识(1)的结论的特点. 解 (1)数学成绩和物理成绩具有相关关系.(2)以x 轴表示数学成绩,y 轴表示物理成绩,可得相应的散点图如下:由散点图可以看出,物理成绩和数学成绩对应的点不分散,大致分布在一条直线附近. 10.以下是某地搜集到的新房屋的销售价格y 和房屋的面积x 的数据:(1)画出数据对应的散点图;(2)求线性回归方程,并在散点图中加上回归直线. 解 (1)数据对应的散点图如图所示:(2)x =109,y =23.2,∑=512i i x =60 975,∑=51i iiy x=12 952,bˆ=25125155x xyx yx i ii ii -∙-∑∑==≈0.196 2aˆ=y -bˆx ≈1.814 2 ∴所求回归直线方程为yˆ=0.196 2x+1.814 2.11.某公司利润y 与销售总额x(单位:千万元)之间有如下对应数据:(1)画出散点图; (2)求回归直线方程;(3)估计销售总额为24千万元时的利润. 解 (1)散点图如图所示:(2)x =71(10+15+17+20+25+28+32)=21,y=71(1+1.3+1.8+2+2.6+2.7+3.3)=2.1,∑=712i ix=102+152+172+202+252+282+322=3 447,∑=71i iiy x=10×1+15×1.3+17×1.8+20×2+25×2.6+28×2.7+32×3.3=346.3,bˆ=27127177x x yx yx i i i ii -∙-∑∑===221744731.22173.346⨯-⨯⨯-≈0.104, aˆ=y -bˆx =2.1-0.104×21=-0.084, ∴yˆ=0.104x-0.084. (3)把x=24(千万元)代入方程得,yˆ=2.412(千万元).∴估计销售总额为24千万元时,利润为2.412千万元.12.某种产品的广告费支出x 与销售额y(单位:百万元)之间有如下对应数据:(1)画出散点图;(2)求回归直线方程;(3)试预测广告费支出为10百万元时,销售额多大? 解 (1)根据表中所列数据可得散点图如下:(2)列出下表,并用科学计算器进行有关计算:因此,x =525=5,y =5250 =50,∑=512i i x =145, ∑=512i i y =13 500, ∑=51i i i y x =1 380.于是可得:bˆ=25125155x xyx yx i ii ii -∙-∑∑===55514550553801⨯⨯-⨯⨯-=6.5;aˆ=y -bˆx =50-6.5×5=17.5. 因此,所求回归直线方程为:yˆ=6.5x+17.5. (3)根据上面求得的回归直线方程,当广告费支出为10百万元时,yˆ=6.5×10+17.5=82.5(百万元),即这种产品的销售收入大约为82.5百万元.§11.4 统计案例1.对有线性相关关系的两个变量建立的回归直线方程y ˆ=a ˆ+b ˆx 中,回归系数bˆ与0的大小关系为 .(填序号) ①大于或小于 ②大于 ③小于 ④不小于答案 ①2.如果有90%的把握说事件A 和B 有关系,那么具体计算出的数据 2 2.706.(用“>”,“<”,“=”填空) 答案 >3.对两个变量y 与x 进行回归分析,分别选择不同的模型,它们的相关系数r 如下,其中拟合效果最好的模型是 .①模型Ⅰ的相关系数r 为0.98 ②模型Ⅱ的相关系数r 为0.80 ③模型Ⅲ的相关系数r 为0.50 ④模型Ⅳ的相关系数r 为0.25 答案 ①4.下列说法中正确的有:①若r >0,则x 增大时,y 也相应增大;②若r <0,则x 增大时,y 也相应增大;③若r=1或r=-1,则x 与y 的关系完全对应(有函数关系),在散点图上各个点均在一条直线上 . 答案 ①③基础自测例1 (14分)调查339名50岁以上人的吸烟习惯与患慢性气管炎的情况,获数据如下:试问:(1)吸烟习惯与患慢性气管炎是否有关? (2)用假设检验的思想给予证明. (1)解 根据列联表的数据,得到χ2=))()()(()(2c d b d c a b a bc ad n ++++-2分 =13428356205)1316212143(3392⨯⨯⨯⨯-⨯⨯=7.469>6.6356分 所以有99%的把握认为“吸烟与患慢性气管炎有关”.9分(2)证明 假设“吸烟与患慢性气管炎之间没有关系”,由于事件A={χ2≥6.635}≈0.01,即A 为小概率事件,而小概率事件发生了,进而得假设错误,这种推断出错的可能性约有1%.14分例2 一台机器使用时间较长,但还可以使用.它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有 缺点零件的多少,随机器运转的速度而变化,下表为抽样试验结果:(1)对变量y 与x 进行相关性检验;(2)如果y 与x 有线性相关关系,求回归直线方程;(3)若实际生产中,允许每小时的产品中有缺点的零件最多为10个,那么,机器的运转速度应控制在什么范围内?解 (1)x =12.5,y =8.25,∑=41i iiy x=438,4x y =412.5,∑=412i i x =660,∑=412i i y =291,所以r=)4)(4(42412241241y yx xyx yx i ii ii ii --∙-∑∑∑====)25.272291()625660(5.412438-⨯--=25.6565.25≈62.2550.25≈0.995 4.因为r >r 0.05,所以y 与x 有很强的线性相关关系.(2)yˆ=0.728 6x-0.857 1. (3)要使yˆ≤10⇒0.728 6x-0.857 1≤10, 所以x ≤14.901 3.所以机器的转速应控制在14.901 3转/秒以下.例3 下表是某年美国旧轿车价格的调查资料,今以x 表示轿车的使用年数,y 表示相应的年均价格,求y 关于x 的回归 方程.解 作出散点图如图所示.可以发现,各点并不是基本处于一条直线附近,因此,y 与x 之间应是非线性相关关系.与已学函数图象比较,用y ˆ=e a x b ˆˆ来刻画题中模型更为合理,令zˆ=ln y ˆ,则z ˆ=b ˆx+a ˆ,题中数据变成如下表所示:相应的散点图如图所示,从图中可以看出,变换的样本点分布在一条直线附近,因此可以用线性回归方程拟合.由表中数据可得r ≈-0.996.|r|>r 0.05.认为x 与z之间具有线性相关关系,由表中数据得bˆ≈-0.298,a ˆ≈8.165,所以z ˆ=-0.298x+8.165,最后回代z ˆ=ln y ˆ,即y ˆ=e -0.298x+8.165为所求.1.某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关系?说明理由.解 (1)随机抽查这个班的一名学生,有50种不同的抽查方法,由于积极参加班级工作的学生有18+6=24人,所以有24种不同的抽法,因此由古典概型的计算公式可得抽到积极参加班级工作的学生的概率是P 1=5024=2512,又因为不太主动 参加班级工作且学习积极性一般的学生有19人,所以抽到不太主动参加班级工作且学习积极性一般的学生的概率是P 2=5019.(2)由2χ统计量的计算公式得2χ=25252624)761918(502⨯⨯⨯⨯-⨯⨯≈11.538,由于11.538>10.828,所以可以有99.9%的把握认为“学生的学习积极性与对待班级工作的态度有关系”.2.某个体服装店经营某种服装,一周内获纯利y (元)与该周每天销售这种服装的件数x 之间的一组数据如下:已知∑=712i i x =280, ∑=712i i y =45 309, ∑=71i i i y x =3 487,此时r 0.05=0.754.(1)求x ,y ;(2)判断一周内获纯利润y 与该周每天销售件数x 之间是否线性相关,如果线性相关,求出回归直线方程.解 (1)x =71(3+4+5+6+7+8+9)=6,y=71 (66+69+73+81+89+90+91)≈79.86.(2)根据已知∑=712i i x =280, ∑=712i i y =45 309, ∑=71i i i y x =3 487,得相关系数 r=)86.79730945)(67280(86.7967487322⨯-⨯-⨯⨯-≈0.973.由于0.973>0.754,所以纯利润y与每天销售件数x 之间具有显著线性相关关系. 利用已知数据可求得回归直线方程为yˆ=4.746x+51.386.3.某种书每册的成本费y (元)与印刷册数x (千册)有关,经统计得到数据如下:检验每册书的成本费y 与印刷册数的倒数x1之间是否具有线性相关关系,如有,求出y 对x 的回归方程.解 首先作变量置换,令u=x1,题目所给数据变成如下表所示的10对数据:然后作相关性检验.经计算得r ≈0.999 8>0.75,从而认为u 与y 之间具有线性相关关系.由公式得aˆ≈1.125,b ˆ≈8.973, 所以yˆ=1.125+8.973u, 最后回代u=x1,可得y ˆ=1.125+x973.8,这就是题目要求的y 对x 的回归曲线方程.回归曲线的图形如图所示,它是经过平移的反比例函数图象的一个分支.一、填空题1.对于独立性检验,下列说法中正确的是 . ①2χ的值越大,说明两事件相关程度越大 ②2χ的值越小,说明两事件相关程度越小 ③2χ≤2.706时,有90%的把握说事件A 与B 无关 ④2χ>6.635时,有99%的把握说事件A 与B 有关 答案 ①②④2.工人月工资y (元)依劳动生产率x(千元)变化的回归方程为y ˆ=50+80x ,下列判断正确的是 .①劳动生产率为1 000元时,工资为130元。
受力分析及物体平衡典型例题解析

受力分析及物体平衡典型例题解析在物理学中,受力分析和物体平衡是非常重要的基础知识。
通过对物体所受力的分析,我们可以了解物体的运动状态以及是否处于平衡状态。
本文将通过解析几个典型的例题,帮助读者更好地理解受力分析和物体平衡的概念。
例题一:垂直轴上的物体平衡将一个质量为10千克的木块悬挂在一根质量忽略不计的轻杆上,轻杆的一端固定在墙上,另一端与滑轮相连,滑轮距地面高度为2米。
现求木块上挂的重物的质量是多少?解析:首先,我们可以根据题目中给出的物体的质量和距离,得到所受到的重力,即10千克 * 9.8米/秒² = 98牛顿。
由于木块处于静止状态,根据角动量守恒定律,木块所受合力矩为零。
由于轻杆质量忽略不计,可以将滑轮视为质量忽略不计的点,即滑轮为定轴。
设木块上挂的重物的质量为M,根据力矩平衡公式有:2米 * 98牛顿 - 0米 * M = 0解得:M = 98千克所以,木块上挂的重物的质量为98千克。
例题二:倾斜面上的物体平衡一个质量为5千克的木箱被放置在一个倾角为30°的光滑斜面上,斜面上有一垂直向上的力F使木箱处于静止状态,求力F的大小。
解析:首先,我们可以根据题目中给出的物体的质量和斜面的倾角,得到物体所受到的重力,即5千克 * 9.8米/秒² = 49牛顿。
由于木箱处于静止状态,根据 Newton's第一定律,合力等于零。
这意味着斜面上的力F必须与斜面的竖直方向的分量相抵消。
设力F的大小为F1,根据受力分析,可以得到以下等式:F1 * cos30° = 49牛顿解得:F1 = 98牛顿所以,力F的大小为98牛顿。
例题三:悬挂物体和支撑力的分析一个质量为2千克的物体用绳子悬挂在天花板上,绳子的倾角为60°,求绳子的拉力和天花板对物体的支撑力。
解析:首先,根据题目中给出的物体的质量和绳子的倾角,可以得到物体所受到的重力,即2千克 * 9.8米/秒² = 19.6牛顿。
《用样本估计总体》典型例题及解析
《用样本估计总体》典型例题及解析1.校医务室从初中部三个年级各抽出100名学生进行视力调查,通过问卷调查,各年级100名学生中存在视力问题的人数如下:初一视力不良的男生有18人,女生有16人;初二视力不良的男生有20人,女生有22人;初三视力不良的男生有24人,女生有25人.根据调查结果整理出统计表,绘出视力不良率(视力不良人数占被调查人数的百分比)条形图,并说明根据调查结果得出的结论.解析:初中部学生视力调查统计表根据上述调查结果可以得到:(1)视力不良率随年级不同而呈上升趋势,初三学生的视力情况比初二学生差,而初二学生的视力情况又比初一学生差;(2)男女生的视力不良率没有明显的差异;(3)应积极采取措施,防止学生视力下降.例2.为估计某产品的使用寿命,对大量的产品进行抽样检验,100个样品的使用时间记录如下:579 585 402 355 203 488 362 397 355 413 316 303 278316 501 479 197 265 333 276 566 384 312 289 123 326432 357 476 357 432 326 123 316 266 317 540 364 335276 320 227 510 338 146 368 311 317 369 586 374 323338 364 407 305 133 365 188 316 366 524 504 290 248352 447 489 368 425 307 327 495 331 213 410 573 214167 246 337 343 512 319 447 503 198 283 401 357 344225 187 346 451 375 416 234 476 357 (单位:小时)根据抽样检验的100个样本的数据填写下表,作出条形图,并对这种产品的寿命进行估计.解析:(1)产品使用寿命统计表(2)产品使用寿命分布条形图(3)从抽样检验的情况分析,多数产品的使用寿命在200小时~500小时,约占全部样品的86%.半数以上的产品使用寿命在250小时~450小时.。
小学数学解方程应用题例题分析

小学数学解方程应用题例题分析1、甲有书的本数是乙有书的本数的3倍,甲、乙两人平均每人有82本书,求甲、乙两人各有书多少本。
解:设乙有书x本,则甲有书3x本X+3X=82×22、一只两层书架,上层放的书是下层的3倍,如果把上层的书搬60本到下层,那么两层的书一样多,求上、下层原来各有书多少本.解:设下层有书X本,则上层有书3X本3X-60=X+603、有甲、乙两缸金鱼,甲缸的金鱼条数是乙缸的一半,如从乙缸里取出9条金鱼放人甲缸,这样两缸鱼的条数相等,求甲缸原有金鱼多少条.解:设乙缸有X条,则甲缸有1/2X条X-9=1/2X+94、汽车从甲地到乙地,去时每小时行60千米,比计划时间早到1小时;返回时,每小时行40千米,比计划时间迟到1小时.求甲乙两地的距离.解:设计划时间为X小时60×(X-1)=40×(X+1)5、新河口小学的同学去种向日葵,五年级种的棵数比四年级种的3倍少10棵,五年级比四年级多种62棵,两个年级各种多少棵?解:设四年级种树X棵,则五年级种(3X-10)棵(3X-10)-X=626、熊猫电视机厂生产一批电视机,如果每天生产40台,要比原计划多生产6天,如果每天生产60台,可以比原计划提前4天完成,求原计划生产时间和这批电视机的总台数.解:设原计划生产时间为X天40×(X+6)=60×(X-4)7、甲仓存粮32吨,乙仓存粮57吨,以后甲仓每天存人4吨,乙仓每天存人9吨.几天后,乙仓存粮是甲仓的2倍?解:设X天后,乙仓存粮是甲仓的2倍(32+4X)×2=57+9X8、一把直尺和一把小刀共1.9元,4把直尺和6把小刀共9元,每把直尺和每把小刀各多少元?解:设直尺每把x元,小刀每把就是(1.9—x)元4X+6×(1.9—X)=99、甲、乙两个粮仓存粮数相等,从甲仓运出130吨、从乙仓运出230吨后,甲粮仓剩粮是乙粮仓剩粮的3倍,原来每个粮仓各存粮多少吨?解:设原来每个粮仓各存粮X吨X-130=(X-230)×310、师徒俩要加工同样多的零件,师傅每小时加工50个,比徒弟每小时多加工10个.工作中师傅停工5小时,因此徒弟比师傅提前1小时完成任务.求两人各加工多少个零件.解:设两人各加工X个零件X/(50-40)=X/50+5-111、买2.5千克苹果和2千克橘子共用去13.6元,已知每千克苹果比每千克橘子贵2.2元,这两种水果的单价各是每千克多少元?解:设橘子每千克X元,则苹果每千克(X+2.2)元2.5×(X+2.2)+2X=13.612、买4支钢笔和9支圆珠笔共付24元,已知买2支钢笔的钱可买3支圆珠笔,两种笔的价钱各是多少元?解:设钢笔每支X元,则圆珠笔每支2X/34X+9×2X/3=2413、一个两位数,个位上的数字是十位上数字的2倍,如果把十位上的数字与个位上的数字对调,那么得到的新两位数比原两位数大36.求原两位数.解:设十位上数字为X,则个位上的数字为2X,这个原两位数为(10X+2X)10×2X+X=(10X+2X)+3614、一个两位数,十位上的数字比个位上的数字小1,十位上的数字与个位上的数字的和是这个两位数的0.2倍.求这个两位数.解:设个位数字为X,则十位数字为(X-1)X+(X-1)=[X+10×(X-1)] ×0.215、有四只盒子,共装了45个小球.如变动一下,第一盒减少2个;第二盒增加2个;第三盒增加一倍;第四盒减少一半,那么这四只盒子里的球就一样多了.原来每只盒子中各有几个球?解:设现在每只盒子中各有x个球,原来各盒中球的个数分别为(x—2)个、(x+2)个、(x÷2)个、2x个(x—2)+ (x+2)+ (x÷2)+ 2x=4516、25除以一个数的2倍,商是3余1,求这个数.解:设这个数为X(25-1)÷2X=317、甲、乙分别从相距18千米的A、B两地同时同向而行,乙在前甲在后.当甲追上乙时行了1.5小时.乙车每小时行48千米,求甲车速度.解:设甲车速度为X小时/小时(X-48)×1.5=1818、甲、乙两车同时由A地到B地,甲车每小时行30千米,乙车每小时行45千米,甲车先出发2小时后乙车才出发,两车同时到达B地.求A、B两地的距离.解:设A、B两地的距离为X千米(X-30×2)/30=X/4519、师徒俩加工同一种零件,徒弟每小时加工12个,工作了3小时后,师傅开始工作,6小时后,两人加工的零件同样多,师傅每小时加工多少个零件.解:设师傅每小时加工X个零件6X=12×(3+6)20、有甲、乙两桶油,甲桶油再注入15升后,两桶油质量相等;如乙桶油再注人145升,则乙桶油的质量是甲桶油的3倍,求原来两桶油各有多少升?解:设甲桶原来有X升油,则乙桶原来有(X-15)升油X+15+145=3X21、一个工程队由6个粗木工和1个细木工组成.完成某项任务后,粗木工每人得200元,细木工每人工资比全队的平均工资多30元.求细木工每人得多少元.解:设细木工每人得X元(200×6+X)/(6+1)=X-30图片1、运送29.5吨煤,先用一辆载重4吨的汽车运3次,剩下的用一辆载重为2.5吨的货车运。
小学奥数浓度问题经典例题含解析

交叉相减求差: 30% 25% 5%; 25% 20% 5%;差的比值为:5% : 5% 1:1
所以质比量为1:1。 所以浓度为40%与浓度为10%的溶液混合液质量为300克。 所以质量比值为:2:1,原来浓度为40%的溶液有200克。 【评析】 除了两种溶液配比外,稀释和加溶质也可以用“十字交叉相减”法,如 果溶液加水,那么溶液就和0%的溶液来配比,如果单加溶质,就是溶液和100% 的溶液来配比.
设加入X克盐,
100 20% x (100 2x)30%, x 25
【2】★★两个杯子里分别装有浓度为40%与10%的盐水,将这两杯 盐水倒在一起混合后,盐水浓度变为30 % .若再加入300 克20%的 盐水,浓度变为25 % .请问:原有40%的盐水多少克?
【2】★★两个杯子里分别装有浓度为40%与10%的盐水,将这两杯 盐水倒在一起混合后,盐水浓度变为30 % .若再加入300 克20%的 盐水,浓度变为25 % .请问:原有40%的盐水多少克?
x=6(升), 第二次从乙容器倒人甲容器的混合液是6升.
【5】★★将25克白糖放人空杯中,倒人100克白开水充分搅拌后, 喝去一半糖水,又加人36克白开水,如果要使杯中的糖水和原来一 样甜,需要加人多少白糖?
【5】★★将25克白糖放人空杯中,倒人100克白开水充分搅拌后, 喝去一半糖水,又加人36克白开水,如果要使杯中的糖水和原来一 样甜,需要加人多少白糖?
【4】★★甲容器有纯酒精11升,乙容器有水15升.第一次将甲容器中的一 部分纯酒精倒人乙容器,使酒精和水混合.第二次将乙容器中的一部分混合 液倒入甲容器中,这样甲容器中的纯酒精含量为62.5% ,乙容器中的纯酒精 含量是25% ,那么,第二次从乙容器倒人甲容器的混合液是多少升?
光电效应经典例题解析

例题精选【典型例题1】已知LC振荡电路中电容器极板1上的电量随时间变化曲线如图所示,则:(A)a、c两时刻电路中电流最大,方向相同(B)a、c两时刻电路中电流最大,方向相反(C)b、d两时刻电路中电流最大,方向相同(D)b、d两时刻电路中电流最大,方向相反分析与解:应理解LC振荡电路电磁振荡时,电容两板电量最多时,是两板间电压最高,板间电场能最大的时刻,在放电结束(两极电量为零时)瞬间是线圈中电流最大,磁场能最大的时刻,b时刻是将要反向充电时刻,d时刻是将要正向充电时刻,因此选项D是正确的,在解题时不妨在电路上画出a时刻1极板带正电情况以帮助分析放电、充电的振荡电流方向情况.【典型例题2】要使LC振荡电路的周期增大一倍,可采用的办法是:(A)自感系数L和电容C都增大一倍.(B)自感系数L和电容C都减小一半.(C)自感系数L增大一倍,而电容C减小一半.(D)自感系数L减小一倍,而电容C增大一倍.分析与解:由于LC振荡电路频率一般较高,周期很短,用周期多少秒很不方便,因此在LC振荡电路中通常用频率公式而不象单摆振动用周期公式,这是应当注意区别的,此题问周期,则可将改写成进行讨论就方便了,显然正确答案应为A.【典型例题3】设是两种单色可见光1.2在真空中的波长,若,则这两种单色光相比(A)单色光频率较小(B)玻璃对单色光1折射率较大(C)在玻璃中,单色光1的传播速度较大(D)单色光1的能量较大分析与解:应掌握电磁波(光波)频率、波速、波长关系:(真空中),由题意及此式,可判断出,即单色光1频率较小.媒质折射率随频率增大而增大,因此说法B错误,值得注意的是光进入媒质后频率不变(颜色不变)但波速改变,由知,即频率越高,折射率越大、波速越小,说法C正确,光子能量,单色光1频率低,能量较小,因此说法D错误,此题正确答案应为A、C.【典型例题4】关于光谱,下面说法中正确的是(A)炽热的液体发射连续光谱(B)太阳光谱中的暗线说明太阳上缺少与这些暗线相应的元素(C)明线光谱和暗线光谱都可用于对物质成分进行分析(D)发射光谱一定是连续光谱分析与解:显然,这是一个考查对光谱知识了解情况的问题,考生在复习时,应知道的基本物理常识要重视,不能以为简单就可以不认真复习掌握了.正确答案应为A、C.【典型例题5】用绿光照射一光电管,能产生光电效应,欲使光电子从阴极逸出时的最大初动能增大,应(A)改用红光照射(B)增大绿光强度(C)增大光电管上的加速电压(D)改用紫光照射分析与解:此题也只是考查了光电效应实验中的实验规律及光子论解释,显然要增大光电子初动能,只能增大入射光子的频率,正确答案应为D.【典型例题6】使金属钠产生光电效应的光的最长波长是5000埃,因此,金属钠的逸出功J,现在用频率在Hz到Hz范围内的光照射钠,那么,使钠产生光电效应的频率范围是从__________Hz到__________Hz.(普朗克恒量J·s).分析与解:按照光子论对光电效应的解释,逸出功等于截止频率光子的能量,即由题给条件,可求出J,在给出频率范围中,只有大于截止频率的光,才能使金属钠产生光电效应,因Hz,故能使金属钠产生光电效应的频率范围为Hz到Hz,题目难度虽不大,但要求准确理解光电效应的有关知识,特别是应注意幂指数运算问题不要出错.【典型例题7】玻尔在他提出的原子模型中所做的假设有(A)原子处于称为定态的能量状态时,虽然电子做加速运动,但并不向外辐射能量.(B)原子的不同能量状态与电子沿不同的圆轨道绕核运动相对应,而电子的可能轨道的分布是不连续的.(C)电子从一个轨道跃迁到另一轨道时,辐射(或吸收)一定频率的光子.(D)电子跃迁时辐射的光子的频率等于电子绕核做圆周运动的频率.分析与解:本题检查学生是否知道玻尔模型的三个重要假设,正确答案为A、B、C.【典型例题8】Th(灶)经过一系列和衰变,变成Pb(铅)(A)铅核比钍核少8个质子(B)铅核比钍核少16个中子(C)共经过4次衰变和6次衰变(D)共经过6次衰变和4次衰变分析与解:应掌握原子核符号脚标意义,以及衰变时根据电量与质量守恒列出关系式,在多次衰变时,可设经历x次衰变与y次衰变,再列式就容易解答了,此题答案应为A、B、D.【典型例题9】在卢瑟福的粒子散射实验中,有极少数粒子发生大角度偏转,其原因(A)原子的正电荷和绝大部分质量集中在一个很小的核上(B)正电荷在原子中是均匀分布的(C)原子中存在着带负电的电子(D)原子只能处于一系列不连续的能量状态中分析与解:粒子散射实验是建立“原子核式结构”理论的重要实验,极少数粒子发生大角度偏转,说明粒子受到很大的库仑斥力,极“少数”意味着粒子接近核的机会很少,说明原子的正电荷和绝大部分质量集中在一个很小的粒子上.选项A正确.【典型例题10】右图中给出氢原子最低的四个能级.氢原子在这些能级之间跃迁所辐射的光子的频率最多有__________种,其中最小的频率等于__________赫.(保留两个数字)分析与解:氢原子中电子根据吸收光子能量不同,可以跃迁至任一较高能级,当氢原子处于较高能级时,也可能因释放光子能量不同,跃迁至不同较低能级,因而在题给四个较低能级间跃迁时,存在多种可能性.可以从最高能级逐级向下考虑:当时,有、、三种可能性;当时,有、二种可能性;当时,只有一种可能性.故有释放六种频率光子可能性.其中频率最小的光子相应能量也最小,即从跃迁至.由公式可求出最小频率为Hz.【典型例题11】裂变反应是目前核能利用中常用的反应.以原子核U为燃料的反应堆中,当U俘获一个慢中子后发生的裂变反应可以有多种方式,其中一种可表示为:U +n →Xe +Sr +n235.o439 1.0087 138.9178 93.9154反应方程下方的数字是中子及有关原子的静止质量(以原子质量单位u为单位).已知lu的质量对应的能量为MeV,此裂变反应释放出的能量是______________MeV.分析与解:重核裂变时有质量亏损,根据爱因斯坦质能方程,相应的质量亏损对应释放的能量.应先计算质量亏损:(u)由题给lu的质量对应的能量为MeV可得:MeV MeV【典型例题12】一束光从空气射向折射率的某种玻璃的表面,如图1所示,i代表入射角,则:(A)当时会发生全反射现象(B)无论入射角i是多大,折射角r都不会超过45°(C)欲使折射角,应以的角度入射(D)当入射角时,反射光线跟折射光线恰好互相垂直分析与解:此题综合检查了反射定律、折射定律、全反射现象等知识,难度不很大,但要求准确掌握有关知识,全反射发生条件是从媒质射向空气,因此说法A错误.根据折射定律:有,入射角最大不超过90°,因此,,即折射角不会超过45°,所以 B是正确的.当时,,故,说法C亦正确.为了分析说法D是否正确,应先画图分析一下,在图2中可以看出,如果反射光线跟折射光线恰好互相垂直,从几何关系可以得到,所以,代入折射定律公式有:因此,说法D正确,此题为多选题,正确答案为B.C、D.【典型例题13】为了观察门外的情况,有人在门上开了一个小圆孔,将一块圆柱形玻璃嵌入其中,圆柱体轴线与门面垂直,如图所示.从圆柱体底面中心看出去,可以看到门外入射光线与轴线间的最大夹角称做视场角.已知该玻璃的折射率为n,圆柱体长为l,底面半径为r,则视场角是A、 B、C、 D、分析与解:根据题意作出如图所示的光路示意图,其中视场角边缘的两条光线射到玻璃的左表面上,经折射后到玻璃右表面的中轴线O处,即到达眼睛所在处.图中角i即为视场角.根据光的折射定律,,由几何关系知:,因此 sin i=n sinβ,得:i=.本题的答案是B.【典型例题14】在双缝干涉实验中,以白光为光源,在屏幕上观察到了彩色干涉条纹.若在双缝中的一缝前放一红色滤光片(只能透过红光),另一缝前放一绿色滤光片(只能透过绿色),这时A、只有红色和绿色的双缝干涉条纹,其他颜色的双缝干涉条纹消失B、红色和绿色的双缝干涉条纹消失,其他颜色的双缝干涉条纹依然存在C、任何颜色的双缝干涉条纹都不存在,但屏上仍有光亮D、屏上无任何光亮分析与解:干涉现象是两列波长相等的光叠加而产生的现象,现在一条缝只能透过红色,另一条缝只能透过绿色,这两束光的波长不相等,不能发生干涉现象,因此任何双缝干涉条纹都不存在,但两缝分别透过了红色和绿色,屏上仍然有光亮.本题的正确答案是C.(本题考查对光的干涉现象及其产生的条件进行考查,对于平时学习只死记一些结论的考生,解答此题会出现一些困难,因为课本上没有讲过这类问题.但如果学习时能够真正理解干涉现象的产生条件,回答此题就不会有困难.)【典型例题15】图1中AB表示一直立的平面镜,是水平放置的米尺(有刻度的一面朝着平面镜,MN 是屏,三者互相平行.屏MN上的ab表示一条竖直的缝(即a、b之间是透光的).某人眼睛紧贴米尺上的小孔S(其位置见图),可通过平面镜看到米尺的一部分刻度.试在本题的图上用三角板作图求出可看到的部位,并在上把这部分涂以标志.分析与解:在分析人眼在确定位置可看到范围时,通常可运用光路可逆原理,设想人眼处有一点光源,该点光源发出光束能照射到的区间,也是能射入人眼光线的范围.本题中分析能观察到平面镜中尺子像的范围,有两种方法:一是作出尺子与障碍屏的像,考虑人眼处点光源发出光束能照射到镜中尺子的区间;二是作出人眼处点光源的像,考虑镜中人眼处点光源发出光束能照射到尺子的区间,分别如图2、图3所示,在作图时特别需要注意障碍屏缺口两端对光线的限制.【典型例题16】现有m=0.90kg的硝酸甘油(C3H5(NO3)3)被密封于体积V0=4.0×10-3m3的容器中,在某一时刻被引爆,瞬间发生激烈的化学反应,反应的产物全是氮、氧…等气体.假设:反应中每消耗1kg硝酸甘油释放能量U=6.00×106J/kg;反应产生的全部混合气体温度升高1K所需能量Q=1.00×103J/K;这些混合气体满足理想气体状态方程(恒量),其中恒量C=240J/K.已知在反应前硝酸甘油的温度T0=300K.若设想在化学反应后容器尚未破裂,且反应释放的能量全部用于升高气体的温度.求器壁受到的压强.分析与解:化学反应完成后,硝酸甘油释放的总能量:W=mU,设反应后气体的温度为T,根据题意,有W=Q(T-T0),器壁所受的压强:p=CT/V0.解以上三式并代入数据进行计算,得p=3.4×108Pa.(本题是比较典型的“信息题”,题目中涉及到了硝酸甘油爆炸的激烈的化学反应,但仔细读过此题后,可以看出解答这个题并不需要了解具体的化学反应过程,也不需要记住气体状态方程的具体形式(题目中给出了一定质量理想气体的状态方程的形式),但此题对考生的理解能力要求较高,其中“反应产生的全部混合气体温度升高1K所需能量Q=1.00×103J/K”这句话很重要,这里我们要联系物体温度升高吸收的热量的公式:Q吸=cmΔT,这里c是物质的比热、m是物质的质量,本题给出的Q值实际上是c、m的乘积,它称为“热容量”,把Q吸换成W,就得到W=Q(T-T0)的关系式.)。
计算机操作系统典型例题解析之三

计算机操作系统典型例题解析之三【例1】分配到必要的资源并获得处理机时的进程状态是(B)。
A、就绪状态B、执行状态C、阻塞状态D、新状态分析:进程有三种基本状态:就绪状态、执行状态和阻塞状态。
当进程已分配到除CPU以外的所有必要的资源后,只要能再获得处理机便可立即执行,这时的状态称为就绪状态;处于就绪状态的进程如果获得了处理机,其状态转换为执行状态;进程因发生某种事件(如I/O请求、申请缓冲空间等)而暂停执行时的状态,亦即进程的执行受到阻塞,故称这种状态为阻塞状态;而新状态是指创建了进程但尚未把它插入到就绪队列前的状态。
所以本题的答案是B。
【例2】挂起的进程被激活,应该使用(C)原语。
A、CreateB、SuspendC、ActiveD、Wakeup分析:在不少系统中,进程除了三种基本状态外,又增加了一些新的状态,其中最重要的是挂起状态。
“挂起”的实质是使进程不能继续执行,即使挂起后的进程处于就绪状态,它也不能参加对CPU的竞争,进程的挂起调用Suspend()原语。
因此,被挂起的进程处于静止状态,相反,没有挂起的进程则处于活动状态。
而且,处于静止状态的进程,只有通过“激活”动作,调用Active()原语,才能转换成活动状态,调入内存。
所以本题的答案是C。
【例3】任何时刻总是让具有最高优先数的进程占用处理器,此时采用的进程调度算法是(D)。
A非抢占式的优先数调度算法B、时间片轮转调度算法C、先来先服务调度算法D、抢占式的优先数调度算法分析:“让具有最高优先数的进程占用处理器”,我们可以知道,采用的进程调度算法是优先数调度算法,但是我们还要进一步分析是抢占式的还是非抢占式的。
“任何时刻总让”,通过这句话我们知道采用的是抢占式的,所以本题的答案是D。
【例4】若P、V操作的信号量S初值为2,当前值为-1,则表示有(B)等待进程。
A、0个B、1个C、2个D、3个分析:信号量的初始值表示系统中资源的数目,每次的Wait操作意味着进程请求一个单位的资源,信号量进行减1的操作,当信号量小于0时,表示资源已分配完毕,进程自我阻塞。
高中数学典型例题解析

任意角三角函数三、经典例题导讲[例1] 若A 、B 、C 是ABC ∆的三个内角,且)2(π≠<<C C B A ,则下列结论中正确的个数是( )①.C A sin sin < ②.C A cot cot < ③.C A tan tan < ④.C A cos cos < A .1 B.2 C.3 D.4错解:C A < ∴ C A sin sin <,C A tan tan <故选B错因:三角形中大角对大边定理不熟悉,对函数单调性理解不到位导致应用错误 正解:法1C A < 在ABC ∆中,在大角对大边,A C a c sin sin ,>∴>法2 考虑特殊情形,A 为锐角,C 为钝角,故排除B 、C 、D ,所以选A . [例2]已知βα,角的终边关于y 轴对称,则α与β的关系为 . 错解:∵βα,角的终边关于y 轴对称,∴22πβα=++πk 2,()z k ∈错因:把关于y 轴对称片认为关于y 轴的正半轴对称. 正解:∵βα,角的终边关于y 轴对称 ∴)(,22Z k k ∈+=+ππβα即)(,2z k k ∈+=+ππβα说明:(1)若βα,角的终边关于x 轴对称,则α与β的关系为)(,2Z k k ∈=+πβα(2)若βα,角的终边关于原点轴对称,则α与β的关系为)(,)12(Z k k ∈++=πβα (3)若βα,角的终边在同一条直线上,则α与β的关系为)(,Z k k ∈+=παβ[例3] 已知542cos ,532sin-==θθ,试确定θ的象限. 错解:∵0542cos ,0532sin <-=>=θθ,∴2θ是第二象限角,即.,222z k k k ∈+<<ππθπ从而.,244z k k k ∈+<<ππθπ故θ是第三象限角或第四象限角或是终边在y 轴负半轴上的角.错因:导出2θ是第二象限角是正确的,由0542cos ,0532sin <-=>=θθ即可确定, 而题中542cos ,532sin -==θθ不仅给出了符号,而且给出了具体的函数值,通过其值可进一步确定2θ的大小,即可进一步缩小2θ所在区间.正解:∵0542cos ,0532sin<-=>=θθ,∴2θ是第二象限角, 又由43sin 22532sinπθ=<=知z k k k ∈+<<+,22432ππθππ z k k k ∈+<<+,24234ππθππ,故θ是第四象限角. [例4]已知角α的终边经过)0)(3,4(≠-a a a P ,求ααααcot ,tan ,cos ,sin 的值. 错解:a y x r a y a x 5,3,422=+=∴=-=3434cot ,4343tan ,5454cos ,5353sin -=-=-=-=-=-===∴a a a a a a a a αααα错因:在求得r 的过程中误认为a >0正解:若0>a ,则a r 5=,且角α在第二象限3434cot ,4343tan ,5454cos ,5353sin -=-=-=-=-=-===∴a a a a a a a a αααα 若0<a ,则a r 5-=,且角α在第四象限3434cot ,4343tan ,5454cos ,5353sin -=-=-=-==--=-=-=∴a a a a a a a a αααα说明:(1)给出角的终边上一点的坐标,求角的某个三解函数值常用定义求解; (2)本题由于所给字母a 的符号不确定,故要对a 的正负进行讨论. [例5] (1)已知α为第三象限角,则2α是第 象限角,α2是第 象限角; (2)若4-=α,则α是第 象限角. 解:(1)α 是第三象限角,即Z k k k ∈+<<+,2322ππαππZ k k k ∈+<<+∴,4322ππαππ,Z k k k ∈+<<+,34224ππαππ当k 为偶数时,2α为第二象限角当k 为奇数时,2α为第四象限角而α2的终边落在第一、二象限或y 轴的非负半轴上.(2)因为ππ-<-<-423,所以α为第二象限角. 点评:α为第一、二象限角时,2α为第一、三象限角,α为第三、四象限角时,2α为第二、四象限角,但是它们在以象限角平分线为界的不同区域.[例6]一扇形的周长为20cm ,当扇形的圆心角α等于多少时,这个扇形的面积最大?最大面积是多少?解:设扇形的半径为rcm ,则扇形的弧长cm r l )220(-=扇形的面积25)5()220(212+--=⋅-=r r r S 所以当cm r 5=时,即2,10===rl cm l α时2max 25cm S =.点评:涉及到最大(小)值问题时,通常先建立函数关系,再应用函数求最值的方法确定最值的条件及相应的最值.[例7]已知α是第三象限角,化简ααααsin 1sin 1sin 1sin 1+---+。
归纳法典型例题

归纳法是一种重要的思维方法,它通过观察、比较、分析、综合等步骤,从个别事物或现象中概括出一般原理或规律。
下面是一些典型的归纳法例题,供您参考。
1. 案例分析题:研究动物行为的研究者发现,当食物短缺时,一些动物会表现出“领域行为”,即保护自己的领地不受侵犯。
请根据这一现象,归纳出一般原理:动物在食物短缺时往往会表现出保护自己的领域行为。
2. 论述题:通过对多篇关于新冠疫情的研究报告的阅读和分析,可以发现人们在面对疫情时的应对措施随着时间的变化而发生了变化。
请从这些变化中归纳出一般原理:面对疫情时,人们的应对措施会随着时间的推移而发生变化。
3. 填空题:根据以下例子,请归纳出一般原理:在自然环境中,生物的生存环境与其适应能力密切相关,适应能力强的生物更容易在自然环境中生存下来。
例子:在沙漠环境中,骆驼能够适应缺水的环境,因为它们有厚实的脂肪层和能够储存水的驼峰,这些特点使它们具有很强的适应能力。
因此,在沙漠环境中,骆驼更容易生存下来。
根据这个例子,可以得出一般原理:在______环境中,生物______能力强的生物更容易______下来。
4. 综合题:通过对过去十年内有关环保政策的研究,可以发现环保政策的实施对环境的影响是一个逐渐积累的过程。
请根据这一现象,归纳出一般原理:环保政策的实施需要长期坚持,才能对环境产生显著的影响。
以上这些例题涵盖了从具体现象到一般原理的归纳过程,通过分析个别实例,我们可以从中总结出普遍适用的原理或规律。
这种思维方法在科学研究中非常重要,因为它可以帮助我们更好地理解事物之间的联系,从而更好地预测和应对未来的变化。
初二物理压强典型例题解析

基础义务教育资料初二物理压强典型例题解析例1一块砖,平放、侧放、立放在水平地面上(如图1—4—1),关于砖对地面的压力和压强的说法中正确的是().图1—4—1A.平放时压力最大,压强最小B.侧放时压力最小,压强最大C.立放时压力最大,压强也最大D.三种放法压力一样大,立放压强最大讲解紧扣压强概念,当压力一定时(均为砖重G),则接触面积最小时(砖立放的情况),压强为最大.故正确答案为D.注意讨论此题型时要注意题目给出的条件,砖被放在水平面上,所以砖对水平地面的压力由重力产生,而砖的重力不因其放法的不同改变,所以砖对地面的压力不变,而对地面的压强,在压力一定的情况下与受力面积有关,立放时的接触面积比平放、侧放都小,所以立放压强最大.例2 如图1—4—2所示,烧瓶中的水停止沸腾后,若从烧瓶中往外抽气,会看到水又沸腾起来,这是由于().图1—4—2A .气压升高,水温升高B .气压降低,水温升高C .气压降低,水的沸点降低D .气压升高,水的沸点降低讲解 根据水的沸点与气压的关系,正确答案为C .注意 本题目只要搞清楚,从密闭烧瓶中往外抽气时可使瓶内气压降低,而沸点的高低与大气压有关,如果气压降低,沸点就降低,所以停止沸腾的水又重新沸腾.例3 已知图钉帽的面积是1厘米2,图钉尖的面积是5×10-4厘米2,手指对图钉帽的压力是20牛,那么图钉尖对墙的压强p 2是手对图钉帽的压强p 1的________倍. 讲解 由于p 1=1S F =2120厘米牛 p 2=1S F =2410520厘米牛-⨯ 所以p 1∶p 2=2410520厘米牛-⨯∶2120厘米牛=2000∶1 即p 2=2000 p 1填2000注意 该题说明两个问题:①图钉尖面积特别小,加在钉帽上一个较小的压力,就可以得到一个很大的压强;②固体可以大小不变地传递压力,而不一定能大小不变地传递压强,压强与受力面积有关.例4 一个棱长为0.2米,重为200牛顿的正方体物块,放在1米2的正方形水平桌面上,该正方体物块对桌面的压强是________帕.讲解 物块对桌面的压强p =1S F =物S G 所以p =22.02.0200米牛⨯=5×103帕 注意 本题主要考查了对压强的定义式的理解.物块放在水平桌面上,压力由重力产生,受力面积为接触面积,即物块的底面积,不能由桌面面积决定.例5 如图1—4—3所示,两长方体A 和B 叠放在水平地面上,A 受重力10牛,B 受重力30牛,已知A 对B 的压强与B 对地面的压强之比为3∶2,则A 与B 的底面积之比为________.图1—4—3讲解 由题意p A =A A S G =AS 牛10 p B =B B A S G G +=BS 牛10 所以S A ∶S B =A p 10∶Bp 40将p A ∶p B =3∶2代入 得S A ∶S B =1∶6注意 在求物体B 对地面压强时,当心别在压力FB 中漏掉物体A 的重力:F B =G B +G A .例6 图1—4—4是演示“液体内部的压强”的实验示意图,将图(a )和图(b )相比较,说明在液体内部:________________.(a)(b)(c)图1—4—4将图(a)和图(c)相比较,说明在液体内部:________________.讲解对比(a)图和(b)图得出同一深度处各个方向的压强都相等;对比(a)图和(c)图得出“压强随深度的增加而增大”.注意该实验题主要考查了学生的观察能力和分析能力.观察实验现象时,要兼顾金属盒上的橡皮膜的放法和U形管的高度差,才能分析出它所反映的物理规律.在做题时容易出现的问题是,学生观察到现象了,但不会叙述结论,而简单地答成(a)、(b)两图的高度差相同,(a)、(c)两图的高度差不同,这是现象而不是结论.所以明确物理现象,要正确地得出结论,表达也是很重要的.例7 在海拔几千米的高原上煮鸡蛋,水沸腾了很长时间,鸡蛋总是不熟,其原因是().A.大气压强小,水的沸点低B.高原上气压太低了C.炉火的温度低D.水沸腾的时间太长了讲解离地面越高,大气压强越小.一切液体的沸点,随气压减小而降低,气压增大而升高.大气压随着高度增加而减小,所以水的沸点随高度增加而降低.海拔1千米处约为97℃,3千米处约为91℃,6千米处约为80℃,9千米处约为70℃.在海拔8848米的珠穆朗玛峰顶大约在72℃水就沸腾了.所以选项A是正确的.注意大气压随高度的增加而减小,但减小的过程是不均匀的,越高,大气压随高度增加而减小得越慢;同一地点大气压强还随气象情况和季节不同而变化.晴天的大气压比阴天高一些,冬天的大气压比夏天高一些.例8用来测定大气压的仪器是().A.托里拆利实验B.气压计C.马德堡半球实验 D.无液气压计讲解用来测定大气压的仪器叫气压计.常用的气压计有水银气压计和金属盒气压计也叫无液气压计.托里拆利实验是测定大气压值的实验,马德堡半球的实验是证明大气压存在的实验.这道题选项B是正确的注意大气压的值并不是固定不变的,随着离地面高度的增加,大气压的值明显的降低.在海拔2 000米以内,我们可以近似地认为,每升高12米,大气压降低133帕(1毫米水银柱).利用大气压随高度变化的规律,在无液气压计的刻度盘上标上高度就构成了高度计,它是航空、登山必不可少的仪器.例9如图1—4—5所示为四个描述离心泵工作原理的示意图,其中正确的是().讲解水泵在起动前,先往泵壳里灌满水,起动后,叶轮在电动机带动下高速旋转,泵壳里的水也随着叶轮高速旋转,同时被甩入出水管中,这时叶轮附近压强减小,大气压迫使低处的水进入泵壳中而把水从低处抽到高处.所以选项D是正确的.A B C D图1—4—5注意 抽水机里的压强小于外面的大气压,大气压使低处的水进入抽水机,从而实现了利用大气压把水从低处抽到高处.例10 如图1—4—6所示,甲、乙、丙三个容器(容器重忽略不计)底面积都相同、高度也相同,如果三个容器都装有同种液体,求:图1—4—6(1)哪个容器受到液体的压强和压力最大?(2)哪个容器对桌面的压强和压力最大?讲解 (1)由于甲、乙、丙三个容器内装有同种液体,则甲ρ=乙ρ=丙ρ,如图所示容器装的液体深度相同h 甲=h 乙=h 丙.根据p =ρgh ,液体对容器底的压强相等即甲ρ=乙ρ=丙ρ .由于三个容器的底面积相同S 甲=S 乙=S 丙,根据p =S F ,得F =pS ,所以液体对容器底的压力相等F 甲=F 乙=F 丙.(2)容器对桌面的压力等于容器重力和容器内液体的重力之和.如图所示甲、乙、丙三个容器中装有的液体重G 甲<G 乙<G 丙,由题意可知容器对桌面的压力F ′=G ,所以丙容器对水平桌面的压力最大(F ′甲<F ′乙<F ′丙).由于三个容器的底面积相等S 甲=S 乙=S 丙,根据p =SF 得出丙容器对水平桌面的压强最大. 注意 在这道题的分析和解答中能够体会到液体的压强只与液体的密度和深长有关,与液体的总重、盛装液体容器的形状、大小等无关.而液体的压力则与液体的压强、受力面积有关,与容器内的液体重力无关.容器对桌面的压力和压强可以从容器的整体分析得出.例11如图1—4—7(a),物体A放在斜面上,画出A对斜面的压力示意图.精析此题考查学生是否明确压力的受力物体,考查压力大小并不总等于重力,还考查压力的方向.(a)(b)图1—4—7如图l—4—14(b),压力的作用点在斜面上,且方向垂直于斜面,在大小和方向上都与重力不同.注意:当物体放在水平面上,且处于静止状态时,压力大小F=G,这种情况是经常遇到的.但往墙上按图钉时,手对图钉的压力;擦黑板时,板擦对黑板的压力大小一般都不等于物体的重力.例12 (温州市中考试题)下列四个事例中,用于增大压强的是()A.推土机上安装两条履带B.铁轨铺在枕木上C.用滑雪板滑雪D.把刀刃磨薄精析在上述实例中,都是通过改变受力面积来改变压强题目要求找到增大压强的例子,而减小受力面积可以增大压所以,把刀刃磨薄增大了压强.答案 D例13如图1—4—8,指出各图中A、B、C、D四个点的深度.(a)(b)(c)图1—4—8精析只有正确找出液体中某点的深度,才能正确地计出压强.答案h A=(50—20)cm=30cmh B=40cmh C=(50—20)cm=30cmh D=50cm例14(北京市中考试题)如图1—4—9所示的试管内装有一定量的水,当试管竖直放置时,水对管底的压强为p1;当管倾斜放置时,水对管底的压强为p2,比较p1、p2的大小,则()图1—4—9(a)(b)A.p1>p2B.p1<p2C.p1=p2D.条件不足,无法判断精析此题考查深度变化对压强的影响.当管倾斜放置后,图(a)(b)比较,试管中液体的长度没有变化,但深度变为h2,h2<h l,根据ρ=ρ液gh,水的密度没变,水对管底压强减小.答案 A例15甲、乙两个等高的柱形容器,它们的底面积之比为2∶1,且都装满了水,若两个容器的水面上分别浮着质量比为1∶3的两个木块,则甲、乙两个容器底部受到的压强之比为()A.1∶2 B.1∶1 C.2∶3 D.1∶6精析容器中装满水,水的深度为h.容器的水面上漂浮木块后,容器中水的深度仍为装满水时的深度h.所以甲、乙两个容底部的压强之比为1∶1.答案 B例16 (重庆市中考试题)甲、乙两个长方体,由不同材料制成.其底面积分别为S甲=40cm2,S乙=30cm2,高度之比h甲∶h乙=3∶2,密度之比ρ甲∶ρ乙=3∶1.如图1—4—10所示,把甲放在水平桌面上,乙放在甲上,水平桌面受到的压强为7000Pa.把乙取下放在水平桌面上静止不动时,桌面对乙的支持力为多少牛?图1—4—10精析叠放体对水平桌面的压力为G甲+G乙.解设:水平桌面受到的压强为p甲对桌面压力F =pS 甲=7000Pa ×40×10-4m 2=28N F =G 甲+G 乙=28N 甲、乙重力之比 乙甲G G =g m gm 乙甲=乙乙甲甲V V ρρ=乙乙乙甲甲甲S h S h ρρ =230cm 3340cm 322⨯⨯⨯⨯=16 代入①式,解得G 甲=24N ,G 乙=4N乙单独放在水平桌面上,支持力N =G 乙=4N .答案 桌面对乙的支持力为4N例17 (北京市中考试题)如图1—4—11所示.将底面积为100cm 2,重为5N 的容器放在水平桌面上,容器内装有重45N ,深40cm 的水.求:(1)距容器底10cm 的A 处水的压强.(2)容器对水平桌面压强.(g 取10N/kg )图1—4—11精析 此题考查学生是否会利用液体压强公式进行计算,是否能区别液体对容器底面的压力和液体重力.已知:S =100cm 2=0.01cm 2,G 水=45N ,h 1=40cm =0.4m ,h 2=10cm =0.1m ,G 容器=5N求:p A 、p ′解 (1)p A =ρ水gh =ρ水gh (h 1-h 2)=1.0×103kg/m 3×10N/kg ×(0.4m -0.1m ) =3×103Pa(2)p ′=S F '=S G G 容器水+=20.01m5N 45N +=5×103Pa 答案 水中A 处压强为3×103Pa ,容器对桌面压强为5×103Pa例18 (北京市中考试题)如图1—4—12所示,甲、乙两个实心圆柱体放在水平地面上.它们对地面的压强相等,则下列判断正确的是 ( )甲乙图1—4—12A .甲的密度大,甲受到的重力小B .甲的密度小,甲受到的重力小C .甲的密度小,甲受到的重力大D .甲的密度大,甲受到的重力大 精析 柱体对水平地面的压强p =S F =S G =SgShρ=ρgh ,其中h 表示柱体高,ρ表示柱体.它们对地面的压强相等:p 甲=p 乙,ρ甲gh 甲=ρ乙gh 乙,∵ h 甲=h 乙 ∴ ρ甲>ρ乙.比较甲、乙的重力G 甲和G 乙.如果直接从G =ρgV 去分析,ρ甲>ρ乙,而V 甲>V乙.不易得到结论.∵从ρ甲=ρ乙,得甲甲S G =乙乙S G∵ S 甲>S 乙 ∴ G 甲>G 乙答案 A例19 (北京市中考试题)甲、乙两个正方体放在水平桌面上.它们对桌面的压强相等,压力之比为9∶4,则甲、乙的密度之比为 ( ) A .2∶3 B .3∶2 C .1∶1 D .4∶9 精析 物体对桌面的压强p =SF.对水平桌面的压力F =G ,而重力G =mg =ρgV ,通过几个公式,将压强、压力、重力、密度联系起来了.解法1 由p 甲=p 乙可写出甲甲S F =乙乙S F乙甲S S =乙甲F F =49 ∵ 正方体:乙甲S S =22ba =49∴ 甲、乙边长b a =23,甲、乙体积比:乙甲V V =33ba =827乙甲ρρ=乙甲甲甲V m V m //=乙甲G G ×甲乙V V =乙甲F F ×甲乙V V =49×278=32解法2 正方体对水平桌面压强p =SF=ρ固gh (h 为高,也是边长) 由ρ甲=ρ乙,可写出ρ甲gh 甲=ρ乙gh 乙乙甲ρρ=乙甲h h =b a =23(a 、b 分别为甲、乙边长) 答案 A例20 (北京西城区模拟题)如图1—4—13所示,A 和B 是用同一种材料制成的正方体,它们的边长分别为L A 和L B ,且L B =2L A .将物块A 放在物块B 的上面的中央.物块B 放在水平地面上.已知B 对地面的压强是9×103Pa ,则A 对B 的压强是 ( )图1—4—13A .1×103Pa B .1.8×103Pa C .4.5×103Pa D .4×103Pa精析 这道题实际上求A 对B 的压强p A 和B 对地面的压强p B 之比.要正确地求出压强,根据p =SF,先要求出压力比和受力面积S 之比. 解 已知:边长A B L L =12,同材料ρA =ρB =ρ 正方体的底面积之比:A B s s =22A B L L =14正方体的体积之比:A B V V =33AB L L =18B 和A 重力比:A B G G =A B gV gV ρρ=18A 对B 的压力和B 对地面的压力比:B A F F =B A A G G G +=811+=91A 对B 的压力和B 对地面的压强比:B A p p =B B A A S F S F //=B A F F ·A B s s =91×14=94 ∵ p B =9×103Pa ∴ p A =94×9×103 Pa =4×103Pa 答案 D例21 (北京市中考试题)有两个用同种材料制成的圆柱体A 和B ,A 的高度是B 的高度的3倍,将A 竖直放在水平地面上,B 竖直放在A 上,如图14-21(a )所示,这时A 对地面的压强与B 对A 的压强之比为3∶1.若将A 、B 倒置后,仍放在水平面上,如图1-4-21(b )所示,则A 对B 的压强与B 对水平面的压强之比是 ( )(a ) (b )图1—4—14A .1∶3B .1∶2C .4∶1D .1∶1精析 求叠加体的压强比,不要急于列综合算式,而应该先把压力比和受力面积比求出来.当压力和物重有关时,可以先把物体的重力比求出来. 解 A 和B 同材料:ρA =ρB =ρ,高度比B A h h =13图(a )中,B 对A 的压力为F B ,A 对地面的压力为F A ,则B A F F =B B B G G G +=AA AB S p S pB B B G G G +=A B p p =31可求得:A B G G =21∵A B G G =A B V V ρρ=A A B B h S h S =21 ∴AB s s =21×B A h h =21×13=23 图(b )中,A 对B 的压强p A ′和B 对地面的压强p B ′之比:''BA p p =BB A AF F S F ''=B A AG G G +×A B s s =122+×23=11答案 D例22 (北京市中考试题)甲、乙两支完全相同的试管,内装质量相等的液体,甲管竖直放置,乙管倾斜放置,两管液面相平,如图1—4—15所示.设液体对两管底的压强分别为p 甲和p 乙,则p 甲________ p 乙(填“大于”、“等于”或“小于”)图1—4—15精析 计算液体的压强应从公式p =ρ液gh 去分析.液体的密度和所求位置的液体深度是决定液体压强的两个关键量.解 比较甲、乙两试管底,液体的深度均为h .再比较液体的密度.从图中看V 甲<V乙,又因为m 甲=m 乙,所以根据ρ=Vm,得ρ甲>ρ乙. 又 ∴ p =ρ液gh ∴ p 甲>p 乙.答案 大于例23 如图1—4—16,甲和乙是底面积相同的容器,其中都装有深度相同的水, (1)比较水对容器底的压强 ( );(2)比较水对容器底面的压力 ( ); (3)比较其中所装水的重力 ( );(4)比较装水容器对桌面的压强 ( ).(不计容器重)甲乙图1—4—16精析 依据液体压强公式和F =pS 来比较压强和压强力. (1)p =ρ液gh ,甲、乙中ρ水和h 相同, ∴ p 甲=p 乙(2)水对容器底的压力:F =pS ,甲、乙中p 和S 相同, ∴ F 甲=F 乙(3)水的重力:G =mg =ρ水V g ,∵ V 甲>V 乙,G 甲>G 乙 注意 F 甲=pS =ρ液gh ·SG 甲=ρ水<V 甲S ∵ hS <V 甲 ∴ 分析得F 甲<G 甲, 图甲:F 甲<G 甲,图乙:F 甲=G 乙.∴ G 甲<G 乙. (4)对桌面压力为F ′=G 水+G 容器=G 水(不计容器重)对桌面压强p 甲′=SF '甲=SG 甲水p 乙′=SF '乙=SG 乙水∵ G 甲水>G 乙水∴ p 甲′>p 乙′例24 如图1—4—17所示,M 为固定在铁架台上两端开口的梯形管,N 为轻质塑料片,被水槽中水托住,并封住下端开口.若向M 几慢慢注入1kg 的水正好能将N 压掉;若不注入水,而是将质量是1kg 的金属块轻轻地放在N 上,则N 将________被压掉.(填“会”或“不会”)图1—4—17精析如图梯形管,装入1kg水,水的重力为G=mg=10N(g取10N/kg),而水对塑料片的压力F>10N,塑料片N刚好被压掉.若放上1kg金属块,对“N”的压力F′=10N<F∴N不会被压掉.答案不会例25 已知外界大气压为标准大气压,如图1—4—18所示的托里拆利实验装置中,管内水银上方为真空,则管内A点的压强为________,槽内B点的压强为________.强为________,槽内B点的压强为________.图1—4—18精析大气的压强仍可以从液体压强的公式进行分析.解管内水银面上方是真空,A点的压强是由A以上的水银柱产生的.∴p A=10cm Hg表示汞cm Hg也可以作为压强的单位.B点在水银槽下2cm深处,B处的压强是大气压和2cm水银柱共同产生的压强.答案A处压强为10cm Hg, B处压强78cm Hg例26如果有一个两端开口的玻璃管,在它的上端蒙上一层橡皮膜,灌水后,用手堵住开口端倒过来插入水槽中,如图l—4—19所示,放手后,橡皮膜形状是平的?凸起的还是凹进去的?图1—4—19精析从橡皮膜上、下表面受的压强去分析.解膜的下表面受到水对它向上的压强,大小为p1=p0— 水gh(p0为大气压,h为水柱高).膜的上表面受到天气对它向下的压强,大小为p0.比较p0和p1,可得p0>p1.橡皮膜从外向下凹进去.这个结果也可以通过实验检验.思考(1)此时若在管内与管外液面相平处划出一个小液片,液片是怎样达到平衡的?(2)橡皮膜凹进的程度跟管内液柱高有什么样的关系?例27 (北京)在水平面上竖直立着A、B两具实心圆柱体,它们的底面积之比是2∶3,对地面的压强分别为p A和p B,且p A∶p B=1∶3.把叠放在B上后,B对地面的压强为p B′,则p B与p B′之比是().A.11∶9 B.9∶11 C.2∶9 D.9∶2精析 因为在水平面上,所以F A =G A ,F B =G B ,根据p =SF,S A ∶S B =2∶3,B A G G =B A F F =B B A A S P S P =3321⨯⨯=92,G A =92G B ,当把A 叠放在B 上后,B 对地面的压力F B ′=G A +G B =92G B +G B =911G B ,则p B ∶p B ′=BB S F ∶B B S F '=F B ∶F B ′=G B ∶911G B =9∶11,选项B正确.注意 根据公式p =SF可知,压强p 是由压力的大小和受力面积的大小决定的,而压力是因物体间的相互作用而产生的,把A 叠放在B 上,则B 对地面的压力是A 对B 的压力和B 受到的重力的合力,即B 物体所受的向下的合力F 合B 产生的对水平地面的压力F B ′=F 合B =F A +G B =G A +G B .例28 (福建福州) 下表是某同学做“研究液体的压强”实验时所测得的部分数据记录.(1)实验次数l 、4、5说明:水的压强随________增加而增大;(2)实验次数1、2、3说明:在同一深度,水向各个方向的________.精析 由实验数据记录可以观察到,第1、4、5次实验,橡皮膜在液体内部的深度由3厘米、6厘米增加到9厘米,压强计的U形管两边的液面高度差由2.6厘米、5.4厘米增加到8.2厘米,即压强增大,所以水的压强随深度的增加而增大.由第1、2、3次实验,橡皮膜所在液体的深度都是3厘米处,可以得出:在同一深度,水向各个方向的压强相等.所以这道题的答案是:深度;压强相等.注意通过实验得出液体的压强特点:(1)液体对容器底和侧壁都有压强,液体内部向各个方向都有压强;(2)液体的压强随深度增加而增大;(3)在同一深度,液体向各个方向的压强相等;(4)不同的液体的压强还跟液体的密度有关系.例29 (内蒙古呼和浩特)如图1—4—20所示,容器中有液体,凸出的橡皮膜表明________________________.精析容器侧壁的孔是橡皮膜封住的,在没有倒入水的时候是平的,当向容器内倒进一定量的水时,橡皮膜向外凸出,凸出的橡皮膜表明水对容器的侧壁有压强.这道题的答案是:液体对容器侧壁有压强。
正弦定理边化角角化边公式例题类型

正弦定理边化角角化边公式例题类型典型例题分析1:已知a,b,c分别为△ABC内角A,B,C的对边,sin2B=2sinAsinC,且a>c,cosB=1/4,则a/c=()A.2B.1/2C.3D.1/3解:三角形ABC中,sin2B=2sinAsinC,由正弦定理:a/sinA=b/sinB=c/sinC=2R,得:b2=2ac,由余弦定理:b2=a2+c2﹣2accosB,即:a2+c2﹣5ac/2=0,等号两端同除以c2,得:(a/c)2-5/2·a/c+1=0,令a/c=t,∴2t2﹣5t+2=0,解得:t=2,t=1/2,a>c,∴t=2,则a/c=2,故答案选:A.考点分析;正弦定理.题干分析:由正弦定理将sin2B=2sinAsinC,转换成b2=2ac,根据余弦定理化简得:a2+c2﹣5ac/2=0,同除以c2,设c2=t,解得t的值,根据条件判断a/c的值.典型例题分析2:在△ABC中,BC=1,ccosA+acosC=2bcosB,△ABC 的面积S=√3,则AC等于()A.√13B.4C.3D.√15解:2bcosB=ccosA+acosC,由正弦定理,得2sinBcosB=sinCcosA+sinAcosC,∴2sinBcosB=sinB,又sinB≠0,∴cosB=1/2,∴B=π/3.∵△ABC的面积S=1/2ABBCsinB=1/2×AB×1×√3/2=√3,解得:AB=4,∴AC=√13.故选:A.考点分析:正弦定理.题干分析:利用正弦定理化边为角,可求导cosB,由此可得B,利用三角形面积公式可求AB,根据余弦定理即可求值得解.典型例题分析3:在△ABC中,角A,B,C所对的边分别是a,b,c,且acosB+bcosA=﹣2ccosC.(Ⅰ)求角C的大小;(Ⅱ)若c=√7,b=2,求△ABC的面积.解:(I)∵acosB+bcosA=﹣2ccosC,∴sinAcosB+sinBcosA=﹣2sinCcosC,即sinC=﹣2sinCcosC,∵sinC≠0,∴cosC=﹣1/2.∴C=2π/3.(II)由余弦定理得7=a2+4﹣2a×2×(-1/2),整理得a2+2a﹣3=0,解得a=1或a=﹣3(舍).∴S=1/2·absinC=1/2×1×2×√3/2=√3/2.考点分析:正弦定理;余弦定理.题干分析:(I)由正弦定理将边化角化简得出cosC;(II)使用余弦定理解出a,代入三角形的面积公式.典型例题分析4:如图,在△ABC中,D为线段AB上的点,且AB=3AD,AC=AD,CB=3CD,则sin2B/sinA=.考点分析:正弦定理.题干分析:设AC=x,CD=y,则AB=3x,BC=3y;利用余弦定理求出x2、y2的关系,再用二倍角化简sin2B/sinA,利用正弦、余弦定理即可求出结果.。
2-2 典型例题解析(1)

2-2 典型例题解析1.________是作业存在的唯一标志。
A.作业名B.进程控制块C.作业控制块D.程序名【分析】当一个作业开始由输入设备输入时,系统为其建立一个作业控制块JCB,并对其进行初始化。
初始化所需要的大部分信息取自作业控制说明书,如作业标识、用户名称、调度参数和资源需求等;其他一些信息由资源管理程序给出,如作业进入时间等。
作业控制块是批处理作业存在的标志,其中保存了系统对于作业进行管理所需要的全部信息,它们被保存在磁盘区域中。
【答案】C2.当作业进入完成状态________。
A.将删除该作业并收回其所占资源,同时输出结果B.将该作业的控制块从当前作业队列中删除,收回其所占资源,并输出结果C.将收回该作业所占资源并输出结果D.将输出结果并删除内存中的作业【分析】当作业运行结束或异常终止时,作业进入完成状态。
这时作业调度程序收回它占用的所有资源,做必要的善后处理。
具体包括:回收发给该进程的资源,包括外设、内存空间,进程运行时打开的文件等;释放该作业的JCB(作业控制块),将此作业注销,输出结果。
【答案】B3.当中央处理机处于管态时,它可以执行的指令是________。
A.计算机系统中的全部指令B.仅限于非特权指令C.仅限于访管指令D.仅限于特权指令【分析】为了防止用户使用特权指令,保证系统的正确操作,将中央处理机的工作状态划分成:管态和目态。
当中央处理机处于管态时可以执行包括特权指令在内的一切机器指令,当中央处理机处于目态时不允许执行特权指令。
【答案】A4.作业调度又称________,其主要功能是按照某种原则从后备队列中选取作业,并为作业做好运行前的准备工作和作业完成后的善后处理工作。
【分析】在操作系统中的调度分为三种:高级调度、中级调度和低级调度。
高级调度又称作业调度,作用是从后备队列中按照某种原则选取作业调入内存;低级调度又称进程调度,作用是从就绪队列中按照某种原则选取进程使之占用处理机来运行;中级调度是为了解决内存紧张的问题,把一些暂不运行的进程从内存移到外存,待有条件运行时再把它们调回内存运行,中级调度相当于存储管理中的对换功能。
《不等式的基本性质》典型例题及解析

《不等式的基本性质》典型例题及解析典型例题一例题01 根据不等式的基本性质,把下列不等式化成或的形式:(1);(2);(3);(4).解答(1)根据不等式的性质,不等式的两边都加5,不等号的方向不变,所以,∴.(2)根据不等式的性质,两边都减去,不等号的方向不变,所以,∴.(3)根据不等式的性质,两边都乘以4,不等号的方向不变,所以,∴.(4)根据不等式的性质,两边都除以-5,不等号的方向改变,所以,∴.例题02 若,用“<”或“>”来填空:(1);(2).分析由于,不等式两边都减去5,不等号的方向不变,不等式的两边都乘以-5,不等号的方向改变.解答(1)<,(2)>.例题03 用“”或“”号填空若且则:(1) _____;(2) _____;(3) _____;(4) _____;(5) _____;(6) _____;(7) _____;(8) _____.解答(1)因为,根据不等式的性质1,有;(2)因为,根据不等式的性质1,有;(3)因为,根据不等式的性质2,有;(4)因为,根据不等式的性质3,有,再由不等式性质1,有;(5)因为,由不等式的性质1,;(6)因为,由不等式的性质1,;(7)因为且,由不等式性质2知;(8)因为且,由不等式性质3,有说明解这类题应先观察不等号左右两边是由原来的不等式进行了什么样的变形得来的,弄清楚了,再对照不等式的性质,决定是否要改变不等号的方向.例题04 判断下列各题的结论是否正确,并说明理由.(1)如果,,那么;(2)如果,那么;(3)如果,那么;(4)如果,且,那么.解答(1)不正确.因为当或时,不成立;(2)正确.因为成立,必有且,根据不等式基本性质2,得;(3)正确.根据不等式基本性质1,由,两边都加上,得;(4)不正确.因为,那么有可能大于0,也有可能小于0,当时,根据不等式基本性质3,两边同除以得.说明①注意成立则隐含着这个条件且;②要注意(4)小题中的条件“”的讨论,因为代表有理数,所以可能取正,也可能取负数.例题05 根据不等式的基本性质,把下列不等式化成或的形式.(1);(2);(3);(4)解答(l)根据不等式基本性质1,不等式两边都加上5,不等号的方向不改变,所以,即(2)根据不等式基本性质1,不等式的两边都减去,不等式不改变方向,所以,即(3)根据不等式基本性质2,不等式两边同除以(或乘以),不等号不改变方,所以,即(4)根据不等式基本性质3,不等式两边同乘以-2(或除以-);不等号改变方向,所以,即说明在运用不等式基本性质3时,一定不要忘记改变不等号的方向.典型例题二1.有理数a,b在数轴上的位置如图,在下列各题中表示错误的是( )A.a−b>0 B.ab> 0 C.c−a<c−b D.>答案:D说明:不难看出a>b>0,所以A、B中表示的显然正确;由a>b可得−a<−b,两边同时加上c,则有c−a<c−b成立;只有D中的表示错误,因为a>b>0,所以将a>b两边同时除以ab,不等号方向不改变,即此时有>成立,所以答案为D.2.有理数a、b、c在数轴上的对应点的位置如图所示,下列式子中正确的有( )①b+c>0 ②a+b>a+c ③bc>ac ④ab>acA.1个 B.2个 C.3个 D.4个答案:C说明:由图中所给a、b、c三个数在数轴上点的位置,可以得到:①b>0,c<0且|b|<|c|,从而b+c<0;②b>c,不等式两边都加上a,得a+b>a+c;③a>b,不等式两边同乘以c(c<0),得ac<bc,即bc>ac;④b>c,不等式两边同乘以a(a>0),得ab>ac;所以②③④正确,答案为C.判断正误:①如果−a>−b,则a>b ( )错;−a>−b两边同乘以−1,不等号方向改变,得a<b②如果 2a>−2b,则a>−b ( )对; 2a>−2b两边同除以2,不等号方向不变,得a>−b③如果ab>ac,则b>c ( )错;当a≤0时,由ab>ac无法得出b>c④若x>,则x>1 ( )错;取x = −,则x>成立,但此时x>1不成立⑤若a−5>b−5,则a>b ( )对;a−5>b−5两边同加5即a>b⑥若a>b,则a2>b2 ( )错;取a = −1,b = −2,此时a>b成立,但a2<b2⑦若>,则a<b ( )错;取a = 1,b = −1,此时>成立,但a>b⑧若a>b,c>d,则ac>bd ( )错;取a = 1,b = 0,c = −1,d = −2,此时a>b,c>d都成立,但ac<bd。
数的性质 奇偶分析 奇偶分析

奇偶分析
主要学习内容
01 数的奇偶性 02 典型例题分析
一、数的奇偶性
一个自然数,要么是奇数,要么是偶数。这是自然数自身的 特性,称为数的奇偶性。利用自然数的奇偶性可以分析和解决很 多有趣的问题,我们把这种方法叫作奇偶分析法。
二、典型例题分析
【例1】 能不能在下式:1□2□3□4□5□6□7□8□9=10的每 个方框中,分别填入加号或减号,使等式成立? 解:在一个只有自然数加减法运算的式子中,如果把式子中减法 运算改成加法运算,那么所得结果的奇偶性不变。因此无论在给 出的式子每个方框中怎样添加减号,所得结果的奇偶性与在每个 方框中都填入加号所得结果的奇偶性一样。但是,每个方框中都 填入加号所得结果是45,是个奇数。而式子的右边是10,是个偶 数。也就是说从奇偶性上判断,要使题中式子成立是不可能的。
二、典型例题分析
【例2】桌上有7个杯子,开口全部向上,现在允许每次同时翻动其中6个, 能否经过若干次翻动使得所以杯子杯口全部向下?若可以,请指出最少 需要多少次,并给出具体的翻法。若不可以,请说明理由。 解:不可以。采用反证法。假设可以经过若干次翻动使得所有杯子杯口 全部向下,下面计算所有杯子被翻动的次数之和:
二、典型例题分析
【例3】在4×4的方格中填写1至16这16个数,将其中任意3个格子中的 数同时加1或减1称为一次操作。问能否经过若干次的这样的操作使得 16个方格中的数都是0。
解:不能。若最后16个方格中的数都为0,总和为0,是3的倍数,而 每次3个格同时加1或减1,加或减的都为3,所以刚开始16个数之和一 定得是3的倍数才行,而1+⋯+16=136,不是3的倍数,所以不能。
一方面,每个杯子从杯口向上变成杯口向下,需要翻动奇数次,一共 有7个杯子,7个奇数之和一定还是奇数,因此所有杯子被翻动的次数之 和是奇数;
(完整版)《抛物线》典型例题12例(含标准答案解析)

《抛物线》典型例题12 例典型例题一例 1 指出抛物线的焦点坐标、准线方程.22(1)x24 y (2)x ay2(a 0)分析:(1)先根据抛物线方程确定抛物线是四种中哪一种,求出p,再写出焦点坐标和准线方程.(2)先把方程化为标准方程形式,再对 a 进行讨论,确定是哪一种后,求p 及焦点坐标与准线方程.解:(1)p 2 ,∴焦点坐标是(0,1),准线方程是:y 12 1 1(2)原抛物线方程为:y2 1 x, 2 p 1 a a①当 a 0时,p 1,抛物线开口向右,2 4a11∴焦点坐标是(1 ,0),准线方程是:x 1.4a 4a②当a 0 时,p 1,抛物线开口向左,2 4a11∴焦点坐标是( ,0),准线方程是:x .4a 4a2 1 1 综合上述,当a 0时,抛物线x ay2的焦点坐标为(1 ,0),准线方程是:x14a 4a 典型例题二例 2 若直线y kx 2与抛物线y28x交于A、B两点,且AB中点的横坐标为2,求此直线方程.分析:由直线与抛物线相交利用韦达定理列出k 的方程求解.另由于已知与直线斜率及弦中点坐标有关,故也可利用“作差法”求 k .故所求直线方程为: y 2x 2 .则所求直线方程为: y 2x 2 .典型例题三例 3 求证:以抛物线的焦点弦为直径的圆心与抛物线的准线相切. 分析:可设抛物线方程为 y 2 2px(p 0).如图所示,只须证明 A 2B MM 1 ,解法一:设 A(x 1, y 1) 、 B(x 2, y 2 ) ,则由:y kx 22y 28x可得:k 2x 2 (4k 8)x 4 0.∵直线与抛物线相交, k 0 且 0, 则k1.∵AB 中点横坐标为: x 1 x 2 4k 82 k 22,解得: k 2 或 k 1舍去).解法二: 设A(x 1,y 1)、B(x 2,y 2) ,则有 y 1 28x 12y28x 2 .两式作差解: ( y 1 y 2)(y 1 y 2) 8(x 1 x 2) ,即y 1 y 2 x 1x28 y 1 y 2x 1 x 2 4 y 1y 2 kx 1 2 kx 2 2 k( x 1 x 2) 4 4k 4 ,k 4k 8 4 故 k2或 k 1 (舍去).1MM 1AB ,故以 AB 为直径的圆,必与抛物线的准线相切.12说明:类似有: 以椭圆焦点弦为直径的圆与相对应的准线相离, 以双曲线焦点弦为直径的圆与相应的准线相交.典型例题四例4(1)设抛物线 y 2 4x 被直线 y 2x k 截得的弦长为 3 5,求 k 值.为 9 时,求 P 点坐标.求 P 点坐标.k 2x 1 x 2 1 k, x 1 x 242 解:( 1)由 yy4x 2x 得: 4x 2 k2(4k 4)x k 2 0AB (1 22)( x 1 x 2)2 5( x 1 x 2)2 4x 1x 2 5 (1 k)2 k 2 5(1 2k)AB 3 5, 5(1 2k) 3 5 ,即 k 4 2)S 9 ,底边长为 3 5 ,∴三角形高 h 2 9 6 535 ∵点 P 在x 轴上,∴设 P 点坐标是 (x 0,0) 则点 P 到直线 y 2x 4的距离就等于 h ,即 0 2 2 22 12655x1或 x 0 5,即所求 P 点坐标是(- 1,0)或( 5,0).典型例题五MM 111 12( AA 1 BB 1) 12(AF2)以(1)中的弦为底边,以x 轴上的点 P 为顶点作三角形,当三角形的面积 分析:(1)题可利用弦长公式求 k ,(2)题可利用面积求高,再用点到直线距离设直线与抛物线交于 A (x 1,y 1)与B (x 2,y 2) 两点.则有:BF )范文 范例 指导 参考例5 已知定直线 l 及定点 A (A 不在 l 上),n 为过A 且垂直于 l 的直线,设 N 为 l 上任一点, AN 的垂直平分线交 n 于 B ,点 B 关于 AN 的对称点为 P ,求证 P 的轨迹为抛物线.分析:要证 P 的轨迹为抛物线, 有两个途径, 一个证明 P 点的轨迹符合抛物线的 定义,二是证明 P 的轨迹方程为抛物线的方程, 可先用第一种方法,由 A 为定点, l 为定直线,为我们提供了利用定义的信息,若能证明 PA PN 且 PN l 即可. 证明: 如图所示,连结 PA 、PN 、NB .由已知条件可知: PB 垂直平分 NA ,且 B 关于 AN 的对称点为 P . ∴ AN 也垂直平分 PB .则四边形 PABN 为菱形.即有 PA PN .AB l. PN l.则 P 点符合抛物线上点的条件:到定点 A 的距离与到定直线的距离相等,所以 P 点的轨迹为抛物线.典型例题六例6 若线段 P 1P 2为抛物线 C:y 2 2px(p 0)的一条 分析: 此题证的是距离问题,如果把它们用两点间 的距离表示出来,其计算量是很大的.我们可以用 抛物线的定义,巧妙运用韦达定理,也可以用抛物线的定义与平面几何知识,把结论证明出来.证法一:F(2p ,0),若过 F 的直线即线段 P 1P 2所在直线斜率不存在时,则有 P 1F P 2F p,111 1 2P 1F P 2F p p p焦点弦, F 为 C 的焦点,求证:1 12 P 1F P 2F p若线段P1P2 所在直线斜率存在时,设为k,则此直线为:y k(x 2p)(k 0) ,且设P1(x1,y1),P2(x2,y2) .k(x p )2得:k(x p )2 k2x2p(k22)xk2p24x 1 x22p(k 22)k2x 1 x 2根据抛物线定义有:P1 F x1 2p,P2F x12p , P1P2 x1 x2 p则 1 1 P1F P2F P1F P2 F P1F P2Fx1x2(x1 2p)(x2 2 )x2 p2p4x1x1x2 2p (x1 x2)1请将①②代入并化简得:112P1F P2F p证法二:如图所示,设P1、P2 、F点在C的准线l 上的射影分别是P1 、P2 、F ,且不妨设P2P2 n m P1P1 ,又设P2 点在FF P1P1 上的射影分别是A、B点,由抛物线定义知,P2 F n, P1F m, FF p又P2 AF ∽P2 BP1 ,AF P2 F BP1 P2P1p(m n ) 2mn 112 m n p即 AB 2psin 2故原命题成立.典型例题七例 7 设抛物线方程为 y 2 2px(p 0) ,过焦点 F 的弦 AB 的倾斜角为 焦点弦长为 AB 2 2p .sin分析: 此题做法跟上题类似,也可采用韦达定理与抛物线定义解决问题. 证法一: 抛物线 y 2 2px( p 0)的焦点为 (2p ,0), 过焦点的弦 AB 所在的直线方程为: y tan ( x 2p ) 由方程组 y tan (x 2p)消去 y 得: y 2 2 px2 2 2 2 24 x 2 tan 2 4 p(tan 2 ) p 2 tan 2,求证:x 1 x2设 A(x 1, y 1),B(x 2,y 2) ,则x1x2p(tan 22)tan 22p4p(1 2cot 2 )又 y 1 y 2 tan ( x 1 x 2 )AB (1 tan 2 )( x 1 x 2)2 (1 tan 2 ) (x 1 x 2) 2 4x 1x 2 (1 tan 2 ) p 2 (1 cot 2 ) 4 p4sec 2 4p 2 cot 2 (1 cot 2 )2p 2 sin1 4 sin证法二: 如图所示,分别作 AA 1、 BB 1垂直于准线 l .由抛物线定义有:AFAA 1 AF cos p BFBB 1pBF cos典型例题八例 8 已知圆锥曲线 C 经过定点 P (3,2 3) ,它的一个焦点为 F (1,0),对应于该 焦点的准线为 x 1,过焦点 F 任意作曲线 C 的弦 AB ,若弦 AB 的长度不超过 8, 且直线 AB 与椭圆 3x 2 2y 2 2 相交于不同的两点,求 ( 1) AB 的倾斜角 的取值范围.(2)设直线 AB 与椭圆相交于 C 、 D 两点,求 CD 中点 M 的轨迹方程. 分析:由已知条件可确定出圆锥曲线 C 为抛物线, AB 为抛物线的焦点弦,设其 斜率为 k ,弦 AB 与椭圆相交于不同的两点, 可求出 k 的取值范围, 从而可得 的 取值范围,求 CD 中点 M 的轨迹方程时,可设出 M 的坐标,利用韦达定理化简即 可.于是可得出:AFp1 cosBFp1 cosABAF BFpp1 cos1 cos2p21 cos2p2sin故原命题成立.解:(1)由已知得PF 4 .故P到x 1 的距离 d 4 ,从而PF d ∴曲线C是抛物线,其方程为y24x .设直线AB的斜率为k,若k 不存在,则直线AB与3x2∴k 存在.设AB的方程为y k ( x 1)4 x 2可得:ky24 y 4k 0 k( x 1)2 y22 无交点.2 由y2y设A、B坐标分别为(x1,y1)、(x2, y2),则:y1y2y1y2 4AB12 (1 k2 )(y1y2)2 1k k2 (y1 y2)2 k4(1 k2 )4y1 y2 k2∵弦AB的长度不超过8,24(1 k 2)k28即k2由y2k(x21)得:(2k23x22 y223)x24k 2x 2(k21)∵AB与椭圆相交于不同的两点,k2由k21和k2 3可得: 1 k故1 tan 3 或 3 tan又0 ,∴所求的取值范围是:3或232) 设CD中点M ( x, y) 、C( x3, y3 )、D(x4,y4)由y2k(x21)得:(2k23)x24k2x3x22 y222(k 21) 0典型例题九例 9 定长为 3的线段 AB 的端点 A 、 B 在抛物线 y 2 x 上移动,求 AB 的中点到 y 轴的距离的最小值,并求出此时 AB 中点的坐标.分析: 线段 AB 中点到 y 轴距离的最小值,就是其横坐标的最小值.这是中点坐 标问题,因此只要研究 A 、 B 两点的横坐标之和取什么最小值即可.解:如图,设 F 是y 2 x 的焦点, A 、 B 两点到准线的垂线分别是 AC 、BD , 又M 到准线的垂线为 MN , C 、 D 和N 是垂足,则x34k 22, x 3 x 12k 232 x3 x 42k 2 2k 2 3 1 232k 2 3 k 2 322k 23 9x42(k 2 1) 2k 2 3则2 51 2k 21 2223即25yx12k 2 2k 2322 y 2 2 (x 1)2 22 y 22 ( x 1) 2化简得: 3x 2 2 y 2 3x∴所求轨迹方程为: 3x 22y 23x 0( 2 x 2) 531 3 1 设M 点的横坐标为 x ,纵坐标为 y , MN x ,则 x 42 4等式成立的条件是 AB 过点 F .2 2 21(y 1 y 2) y 1 y 2 2y 1y 2 2x 2 2,y 1 y 2 2 , y5 2 5 所以 M(54, 22) ,此时 M 到y 轴的距离的最小值为 45 .说明:本题从分析图形性质出发, 把三角形的性质应用到解析几何中, 解法较简.典型例题十例 10 过抛物线 y 2 px 的焦点 F 作倾斜角为 的直线,交抛物线于 A 、B 两点, 求 AB 的最小值.分析:本题可分 2 和 2两种情况讨论.当 2 时,先写出 AB 的表达式, 再求范围.解:(1) 若 2 ,此时 AB 2p .11 12( AC BD) 21( AFBF)12AB当x 45时, y 1y 2 P 214,故MN1AB :y tan (x 2p ),即 x ta y n说明:(2) 若 2 ,因有两交点,所以 0.代入抛物线方程,有 ta 2 3n p y tan p 2 0 .故 ( y 2 y 1 ) 2 4 p 2tan 2 4p 2 4p 2 csc( x 2 x 1) 2 ( y 2 y 1)2tan 2 22 csc4 p 2 2tan 故 AB 22 4 p csc (1 12 ) 4p 2 csc 4 tan 2所以 AB 2p 2 sin 2p .因 2 ,所以这里不能取“=” 综合(1)(2) ,当 2 时, AB 最小值 2p .(1) 此题须对 分 2 和 2两种情况进行讨论;的大小以及判定直线与圆是否相切.解:①点 A 在抛物线上,由抛物线定义,则 AA ' AF 1 2, 又 AA ' // x 轴 1 3 . ∴ 2 3,同理 4 6 , 而 2 3 6 4 180 ,∴ 3 6 90 ,∴ A 'FB ' 90 .选 C .②过AB 中点 M 作MM ' l ,垂中为 M ',∴以 AB 为直径的圆与直线 l 相切,切点为 M ' .又 F ' 在圆的外部,∴ AF 'B 90 . 特别地,当 AB x 轴时, M '与 F '重合, AF 'B 90 .即 AF 'B 90 ,选 B .典型例题十二例 12 已知点 M(3,2), F 为抛物线 y 2 2x 的焦点,点 P 在该抛物线上移动, 当 PM PF 取最小值时,点 P 的坐标为 __________ .分析: 本题若建立目标函数来求 PM PF 的最小值是困难的,若巧妙地利用抛则 MM1(AA ' BB ' ) 2 1 12( AF BF ) 1 AB 2物线定义,结合图形则问题不难解决.1 由定义知PF PE ,故PM PF PF PM ME MN 3 .取等号时,M 、P、E三点共线,∴ P点纵坐标为2,代入方程,求出其横坐标为2,所以P点坐标为(2, 2) .。
典型例题分析

例题(175-11) 设相互独立的两个随机变量X,Y具有同分布 且,X的分布列为
X
0
1
P
1/2
1/2
则随机变量Z=max{ X ,Y }的分布列为 ?
例题 设随机变量X,Y相互独立,Y的概率密度为fY (y) X 是离散型随机变量,其分布规律为
X
1
2
3
P 0.2
0.3
0.5
求 Z=X+Y的概率密度
例题4 (P168-4) 设随机向量(X,Y)相互独立,下表列出了二维随机 向量(X,Y)的联合分布列及关于X,Y的边缘分布列的部分 数值,试将其余数值填入空白处
Y
X
y1
y2
y3
x1
1/24 1/8
1/12 1/4
x2
1/8
3/8
1/6
1/2
1/4 3/4 1/3 1
p. j
例题5(169-5)
补充作业 设随机变量(X,Y)的概率密度 1 0<x 1,0 y 2x
f ( x, y) 0 其他 (1)求边缘概率密度 (2)求条件概率密度f X|Y ( x | y), fY|X ( y | x) (3)Z 2X Y的概率密度 (4)求p{Y 1/ 2 | X 1/ 2} (5)求p{Y 1/ 2 | X =1/ 2}
练习题 设X~U(0,2),Y~U(0,1) U=1 X V=2Y 求(U,V)的联合密度函数
2
例题(P175-7) 一电子仪器由两部件组成,以X,Y分别表示 部件的寿命(单位:千小时),已知X和Y的联合分布函数
1 e0.5 x e0.5 y e0.5( x y) x 0, y 0
F(x, y) 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【典型例题分析】例1 (2008年四川卷)下图表示我国北方农牧交错带生产与生态定位。
读图,回答(1)-(2)题。
(1)北方农牧交错带农业发展方向是A .增大坡耕地面积,提高粮食产量B .大量开垦荒地,提高人均耕面积C .大规模机械化,建成商品粮基地D .退耕还林(草),发展舍饲养殖(2)北方农牧交错带的生态与生产功能是①东部农耕区的生态屏障和畜产品供应基地②东部农耕区的生态屏障和重要粮食供应基地③西部牧区的水源涵养带和饲草料供应基地④西部牧区的水源涵养带和重要粮食供应基地A .①③B .②③C .①④D .②④解析:农牧交错带生态环境脆弱,如果生产活动不合理,很容易产生荒漠化。
我国西北地区农牧地区由于过度发展种植业,沙漠化会不断地向东、向南发展。
答案:(1)D (2)A例2 (2008年江苏卷)图3为“我国江南丘陵某地地形结构和农业用地结构的饼状图”,对比分析回答(1)-(2)题。
(1)造成该地农业用地结构不合理的主要原因是A .过度开垦 D .过度放牧 C .过度围垦 D.过度养殖(2)该地实现农业可持续发展的出路在于A .缓坡退耕,发展大牧场放牧业B .修建梯田,扩大水稻种植面积 农 牧 交错 带草原牧区东部农耕区饲草料 农副产品 待育肥家畜深加工产品C.全面封山育林,改善生态环境 D.调整农业结构,发展立体农业解析:第10题:通过对比该地区地形百分比图和农业产业结构图可以明显地看出该地种植业比重过大.第11题:江南丘陵农业可持续发展的方向是充分利用气候资源优势、水资源优势,因地制宜地发展立体农业,有计划地实施封山育林,逐步改善农村能源问题。
答案:(1)A (2)D例3根据材料回答问题。
材料1:据报道,今年五一黄金周期间,两名越野赛车手在罗布泊地区失踪50多小时后获救。
材料2:见图11材料3:罗布泊地区位于塔里木盆地的东部,这里雅丹地貌发育。
雅丹地貌表现为垄、槽相间的形态(见图12),其发育与盛行风的吹蚀密切相关。
(1)罗布泊地区极端干旱环境形成的原因是。
(2)从图11中可知,在塔里木盆地(填写正确选项的字母)。
A.人类对于自然的适应能力减小,活动空间不断缩小B.历史上,人类活动的范围仅限于盆地周边的绿洲地区C.南缘河流流程缩短,是人类农业活动造成的D.人类活动范围的变化幅度,北缘较南缘地区小(3)赛车手在罗布泊地区迷路,可以通过雅丹地貌判断方向。
已知罗布泊地区经常吹东北风,可知雅丹地貌垄、槽的延伸方向为。
答案:(1)海陆位置与地形的影响(距海遥远,深居大陆内部,青藏高原及山地阻挡)(2)D (3)东北-西南例4 在8000年前,地球上大约有61亿公顷森林,近1/2的陆地被森林覆盖,目前,地球上仅存有39亿公顷森林和12亿公顷的稀疏林。
被破坏的世界森林面积估计每年在1000万顷以上,许多著名的“森林之国”(如泰国)已名存实亡。
早在1977年,泰国已从木材出口国变为木材进口国,泰国呵叻高原葱郁的森林已不复存在,裸露出砖红色的土壤,水土流失十分严重。
据此回答(1)~(2)题。
(1)关于上述材料的叙述正确的是()①世界上的森林面积在不断减少②世界上的森林面积没有什么变化③世界上森林面积减少造成了全球性的气候变化④世界上森林面积减少使水土流失现象十分严重A.①③ B.②④ C.③④ D.①④(2)在无林地区20cm厚的土层,只需40年就可以冲刷殆尽,而有林地区则需75年以上,这说明了森林具有的作用是()A.净化空气 B.保持水土 C.调节大气成分 D.含蓄水源【解析】(1)从材料中即可分析得出世界上的森林面积在不断减少并使得水土流失现象十分严重。
但并未涉及森林面积减少造成了全球性的气候变化问题。
(2)本题通过有林地区和无林地区土层的对比,说明森林具有保持水土的作用。
【答案】(1)D (2)B例5分析我国北方地区某地1970年和1980年有关统计资料,回答下列问题:(13分)统计项目耕地面积(万公顷)森林覆盖率(%)气温年较差(℃)年降水量(mm)河流含沙量(%)人口(万人)1970年 4 18 33 430 1.5 30 1980年 4.4 10 38 370 4.5 35 (1)该地区1970—1980年间,土地利用构成明显的变化是:耕地增加了_____%,森林覆盖率减少了_____%。
根据表格所示,森林减少的原因可能是____________________。
(2)该地区人均耕地是减少了还是增加了?__________。
相差了_____%。
(3)该地区的自然环境条件发生了怎样的改变?(4)分析上表,说说本地区环境发生变化的主要原因是什么?解析:本题主要考查了森林的作用。
答案:(1)10 8 毁林开荒(2)减少了 0.76(3)森林锐减;气候恶化(温差增大,降水减少);水土流失严重(河流含沙量增加了两倍)。
(4)①人口增加,为满足生存和生产的需要对资源进行掠夺式的开发;②滥伐林木,毁林开荒,导致森林锐减,森林调节气候、保持水土的作用大大减弱。
【针对训练】(2008年宁夏卷)读表1,完成1~2题。
表1某区域2000—2004年湿地的转化单位:hm2旱田城镇用地工矿用地草地其他转化来源湿地类型河渠489 -7 0 235 48海涂43 -155 -2027 0 17627水库坑塘25657 -33 -211 5694 926水田76 -793 -1053 0 0注:表中数据正值表示正向转化——湿地面积增加,负值表示逆向转化——湿地面积减少。
各类湿地面积变化幅度由小到大顺序为A、水库坑塘海涂水田河渠B、河渠水田海涂水库坑塘C、水田河渠水库坑塘海涂D、河渠水库坑塘海涂水田2、与2000年相比,2004年该区域A、物种多样性有所减少B、水鸟栖息地减少C、生态环境有所改善D、湿地面积减少近几年春季,受北方高压影响,我国北方多次发生大面积沙尘暴。
其中,河北怀来县的“天漠沙丘”向东南方向移了大约1000米。
据专家介绍,如果不控制这种局面,不出十年,沙漠就会逼近北京,根据以上材料及所学内容,完成3-5题:3.荒漠化的实质是()A.耕地退化B.草地退化C.土地退化D.林地退化4.我国风沙危害和荒漠化问题最为突出的地区是()A.东北地区B.西北地区C.华北地区D.西南地区5.导致荒漠化的自然因素有()①干旱②耕作技术落后,灌溉措施不当③过度放牧④气候异常A.①② B.②③ C.③④D.①④6.下图是公园(林草地)、操场(裸地)、足球场(草坪)三个典型地点的地面温度变化曲线图。
①、②、③三条曲线分别对应的地点是A.公园、操场、足球场 B.足球场、操场、公园C.操场、足球场、公园 D.公园、足球场、操场7.绿洲的面积大小关键取决于A.经济发展水平 B.土地开垦的规模C.水资源的多少 D.防护林带的规模.植树造林是治理风沙的有效措施。
右图表示某沙区生物治沙示意图,回答8~9题。
8.三幅图按治沙时间先后顺序排列为()A.A→B→C B.B→C→AC.B→A→C D.C→A→B9.在我国进行这项工作时,最适宜选种的植物是()A.杨树 B.桦树C.沙拐枣 D.柳树读我国西北部内陆两地景观示意图回答10~11题。
10.甲地以井为中心在草原上形成沙地,其原因可能是()A.由于过度开采地下水导致形成地下水漏斗区B.由于干旱地区地下水含盐量高,使植物不能生存C.由于风力侵蚀形成风蚀洼地D.水井周围地区农牧业活动较频繁而导致地表植被破坏11.在乙地区,可能反映该地区绿洲萎缩的现象有()A.沙尘暴频度减少B.土壤有机质增加,土壤紧实度下降C.土壤盐碱度升高D.生物生产能力提高下图为七省区某种植被面积占全国该种植被面积比例图,读图回答12~13题12.该植被可能是()A 沼泽B 温带落叶阔叶林C 荒漠D 草原13.该植被区最普遍的生态环境问题是()A 酸雨B 水土流失C 土地沙漠化D 沙尘暴新华社消息:中国科考队2004年8月23日结束了为期23天、行程近2000千米的科学探险考察,于27日返回北京,这是我国科学家首次对亚马孙地区进行的地理和生态环境综合科学考察。
阅读材料,回答 14-15 题:14. 亚马孙热带雨林分布面积比刚果盆地更大,原因是:①西高东低的地形②受暖流的影响大③受寒流的影响大④纬度低、热量充足⑤陆地面积大A.①③④ B.①②④ C.②④⑤ D.①②⑤15. 亚马孙热带雨林面积减少直接导致的后果是:A.海平面上升,淹没沿海地势较低的地区B.全球二氧化碳和氧气的平衡受到破坏,大气中二氧化碳的含量上升C.产生厄尔尼诺现象,亚马孙平原形成洪涝灾害D.中纬度地区降水增加,欧洲西部形成干旱少雨的气候湿地与森林、海洋被并称为全球三大生态系统,其在防洪、抗旱、调节气候、控制污染等方面具有其他生态系统所不可替代的功能和效益,被誉为地球之“肾”。
据此回答16—18题:16.下列地理事物中都属于湿地的是()①纳木错②滩涂③黄河④渤海⑤水稻田A.①②③④B.②③④⑤C.①③④⑤D.①②③⑤ 17.我国政府下令停止开垦三江平原上的沼泽地,主要原因是()A.三江平原的土壤十分贫瘠 B.开发的成本太高C.粮食过剩,价格下降 D.为了保护、改善生态环境18.长江下游湿地破坏严重,主要是因为该地区()A.用水增多,地表水减少 B.围湖造田,河湖淤废C.城市化进程加快,占用大量湿地 D.大片湿地改建为鱼塘19.(2008年江苏卷)下图为“1951—2000年我国部分省级行政区受沙尘暴影响强度比例统计图”。
读图回答下列问题。
(10分)(1)我国北部受沙尘暴影响强度的空间分布特点是。
(1分)(2)北京市受沙尘暴影响的强度总体上为度。
我国北部的沙尘暴多发生在季,主要因为该季节我国北部地区气候,植被稀少,且常有天气系统活动,风力强劲。
(4分)(3)首钢集团的搬迁使北京市的大气环境质量得到了明显改善。
首钢搬迁所运用的主要环境管理手段是(填选项字母)。
(2分)(4)贯彻“绿色奥运”理念,你认为进一步改善北京市的大气环境质量应采取哪些措施。
(3分)20.读我国北方某地区1965年和1975年的统计资料,回答下列问题:(4分)年1965 1975项目A森林覆盖率(%)20 3B耕地面积(公顷)24000 42000C年降水量(mm)450 380D气温年较差(℃)23 30E当年旱涝灾害次数 1 2F河流含沙量(%) 2 12G当年粮食亩产量(千克)250 125H当年粮食总产量(亿千克) 1 0.875(1)由A、B两个栏目可以看出,1965—1975年间,该地区耕地面积的增加,是靠__________等不合理的生产方式获得的。
(2)由C、D、E、F、G、H等栏目可以看出,由于森林资源遭到破坏,导致该地区__________恶化,__________加剧,最终使粮食产量逐年下降。
