高中数学人教A版必修5第三章二次函数与一元二次方程的关系课件
合集下载
二次函数与一元二次方程公开课 ppt课件

Δ=b2-4ac > 0 Δ=b2-4ac= 0 Δ=b2-4ac < 0
有两个相异的实数根 有两个相等的实数根
没有实数根
有两个交点 有一个交点 没有交点
例1.判断二次函数y=x2-2x-1与x轴的交点情况 解: a=1 b=-2 c=-1
∵ Δ=b2-4ac=(-2)2-4×1×(-1)=8>0
出这个公共点的坐标. • (3)当k取什么值时,抛物线与x轴没有公共点?
• 例3.已知:抛物线 yx2kxk2 • 求证:此抛物线与x轴必有两个不同交点.
即证明对应方程中的b2-4ac>0
联想:二次函数与x轴的交点个数可以借助
判别式解决,那么二次函数与一次 函数的交点个数又该怎么解决呢?
例如: 二次函数y=x2-2x-3和一次函数 y=x+2有交点吗?有几个?
4.一元二次方程 3 x2+x-10=0的两个根是x1=-2 ,
x是2=_(53-,_2,那_0么_)二_( 次_53 函_,数_0.y)= 3 x2+x-10与x轴的交点坐标
5.不与x轴相交的抛物线是( D )
A. y = 2x2 – 3 B. y=-2 x2 + 3
C. y= -x2 – 3x D. y=-2x2 - 4x - 5
6、如图,铅球运动员掷铅球的高度y(m)与水平
距离x(m)之间的函数关系式y=- 1 x2+ 2 x+ 5 ,则
12
3
3
该运动员此次掷铅球的成绩是___1_0_____。
7.如图,抛物线y=ax2+bx+c的对称轴是直线 x= - 1,
由图象知,关于x的方程ax2+bx+c=0的两个根分别是
二次函数与一元二次方程二次函数优秀ppt课件

7.一元二次方程 3 x2+x-10=0的两个根是x1=-
2 ,x2=5/3,那么二次函数 y= 3 x2+x-10与x轴的交
点坐标是_(-2_,_0_) _(5_/3,__0).
8.已知抛物线y = ax2+bx+c的图象如图,则关 于x的方程ax2 + bx + c-3 = 0根的情况是( A)
有 (2.5,0), (-1,0)
归纳:一元二次方程ax2+bx+c=0的两个根为 x1,x2 ,则抛物线 y=ax2+bx+c与x轴的交点坐标 是(x1,0),(x2,0)
随堂练习
1.不与x轴相交的抛物线是( D )
A. y = 2x2 – 3
B. y=-2 x2 + 3
C. y= -x2 – 3x D. y=-2(x+1)2 -3
一般地,当y取定值时,二次函数为一元 二次方程。
如:y=5时,则5=ax2+bx+c就 是一个一元二次方程。
从以上可以看出,
已知二次函数y的值为m,求相应自变量x的 值,就是求相应一元二次方程的解.
例如,已知二次函数y=-X2+4x的值为3,求自变 量x的值. 就是求方程3=-X2+4x的解,
例如,解方程X2-4x+3=0 就是已知二次函数y=X2-4x+3的值为0,求自变量 x的值.
考虑下列问题:(2)球的飞行高度能否达到 20 m? 若能,需要多少时间?
20 m
2s
(2)当 h = 20 时, 20 t – 5 t 2 = 20 t 2 - 4 t +4 = 0 t1=t2=2 当球飞行 2s 时,它的高度为 20m .
2 ,x2=5/3,那么二次函数 y= 3 x2+x-10与x轴的交
点坐标是_(-2_,_0_) _(5_/3,__0).
8.已知抛物线y = ax2+bx+c的图象如图,则关 于x的方程ax2 + bx + c-3 = 0根的情况是( A)
有 (2.5,0), (-1,0)
归纳:一元二次方程ax2+bx+c=0的两个根为 x1,x2 ,则抛物线 y=ax2+bx+c与x轴的交点坐标 是(x1,0),(x2,0)
随堂练习
1.不与x轴相交的抛物线是( D )
A. y = 2x2 – 3
B. y=-2 x2 + 3
C. y= -x2 – 3x D. y=-2(x+1)2 -3
一般地,当y取定值时,二次函数为一元 二次方程。
如:y=5时,则5=ax2+bx+c就 是一个一元二次方程。
从以上可以看出,
已知二次函数y的值为m,求相应自变量x的 值,就是求相应一元二次方程的解.
例如,已知二次函数y=-X2+4x的值为3,求自变 量x的值. 就是求方程3=-X2+4x的解,
例如,解方程X2-4x+3=0 就是已知二次函数y=X2-4x+3的值为0,求自变量 x的值.
考虑下列问题:(2)球的飞行高度能否达到 20 m? 若能,需要多少时间?
20 m
2s
(2)当 h = 20 时, 20 t – 5 t 2 = 20 t 2 - 4 t +4 = 0 t1=t2=2 当球飞行 2s 时,它的高度为 20m .
高中数学第3章3.2.1一元二次不等式及其解法课件新人教A必修5.ppt

变式训练1 解下列不等式:
(1)2+3x-2x2>0;
(2)x(3-x)≤x(x+2)-1.
解:(1)原不等式可化为 2x2-3x-2<0, ∴(2x+1)(x-2)<0. 故原不等式的解集是{x|-12<x<2}. (2)原不等式可化为 2x2-x-1≥0, ∴(2x+1)(x-1)≥0,
故原不等式的解集为{x|x≤-12或 x≥1}.
考点二 解含参数的一元二次不等式
解含参数的一元二次不等式时要注意对参数分类 讨论.讨论一般分为三个层次,第一层次是二次 项系数为零和不为零;第二层次是有没有实数根 的讨论,即判别式为Δ>0,Δ=0,Δ<0;第三层 次是根的大小的讨论.
例2 解关于x的不等式x2-ax-2a2<0. 【思路点拨】 解答本题通过因式分解,结合二 次函数图象分类讨论求解. 【解】 方程x2-ax-2a2=0的判别式Δ=a2+8a2 =9a2≥0,得方程两根x1=2a,x2=-a. (1)若a>0,则-a<x<2a, 此时不等式的解集为{x|-a<x<2a};
变式训练 2 已知不等式 ax2+bx+2>0 的解集为 {x|-12<x<13},求 2x2+bx+a<0 的解集. 解:∵ax2+bx+2>0 的解集为{x|-12<x<13}, ∴-12,13是方程 ax2+bx+2=0 的两实根.
由 根 与 系 数 的 关 系 得 -12+13=-ab -12×13=2a
2.二次函数 y=ax2+bx+c(a≠0)的图象的对称轴 方程是 x=-2ba,顶点坐标是(-2ba,4ac4-a b2).当 a>0 时,图象的开口方向向上;当 a<0 时,图象 的开口方向向下.
知新盖能
一元二次不等式的解法 一元二次不等式经过变形,可以化成以下两种标 准形式: (1)ax2+bx+c>0 (a>0); (2)ax2+bx+c<0 (a>0). 上述两种形式的一元二次不等式的解集,可通过 方程ax2+bx+c=0的根确定.设Δ=b2-4ac,则: ①Δ>0时,方程ax2+bx+c=0有两个_不__同__的解x1、 x_2_,_{x_设|_x_>x_x1_<2_或x_2_x,_<_则x_1}_不__等__式_,(1)不的等解式集(为2)的解集为 _{_x_|_x_1<_x_<_x_2_}____;
人教版高中数学必修五《二次函数与一元二次方程》

例题 5.方程 a(x+1)(x-3)=k(a>0)的根为 x1 和 x2, 且 x1<-1,x2>3,求 k 的取值范围
例题 6.已知抛物线 y=ax2+bx+c 与 y 轴交于点 C, 与 x 轴交于点 A(x1, 0)、 B(x2,0)(x 1<x2),顶点 M 的纵坐标为-4,若 x1、x2 是方程 x2-2(m-1)x+m2 2 -7=0 的两个根,且 x2 1+x2=10. (1)求 A、B 两点的坐标; (2)求抛物线的关系式及点 C 的坐标; (3)在抛物线上是否存在点 P,使△ABP 的面积等于四边形 ACMB 面积的 2 倍?若存在,求出所有符合条件的点的坐标 ;若不存在,请说明理由.
相关交点可以相互转化。
例题 1.如图所示, 你能直观看出哪些方程的 根?
是方程-x2+2x+3=m(m=4、3、0)的 根.以及方程-x2+2x+3=4x的一个根
例题 2.函数 y=(m+5)x +2(m+1)x+m 的图象全部在 x 轴的上方, 则
2
m 的取值范围是
。
例题 3. 1.抛物线 y=ax2+bx+c 与 x 轴的公共点是(-1,0)、(3,0),求 抛物线的对称轴是
二次函数与一元二次方程
回顾:一次函数与一元一次方程的关系
1.一元一次方程kx+b=0(k≠0)的根是 一次函数y=kx+b(k≠0)与x轴的交点
2. 反之,一次函数y=kx+b(≠0)与 x轴的交点是一元一次方程kx+b=0 (≠0)的根
3. 方程k1x+b1=k2x+b2(k1、k2≠0) 的根可以理解为一次函数y=k1x+b1 (k1≠0)与一次函数y=k2x+b2 (k2≠0) 的交点.反之也成立。
高中数学人教A版必修5第三章二次函数与一元二次方程的关系课件

4 、知识给人重量,成就给人光彩,大多数人只是看到了光彩,而不去称量重量。 8、没有人知道失败和成功间的差距是多么得小。它们之间只相差了一个词的距离,那就是胆怯。依靠坚持和信念必然可以让人从失败走向成 功。
17 、欲望以提升热忱,毅力以磨平高山。 13、光阴似箭,日月如梭,转眼间已经十二年了。这十二年里,我们都在成长着,心灵上,身体上,精神上,而爱,是这成长的养料。 18 、生活里,人们往往在笑话别人的时候特别起劲,幸灾乐祸的无所顾虑;却忽略了自己身上也有可笑之处,忽略了给他人带来的伤害。其实 ,人生舞台上人人都有可笑之处。
求证:不任m为何实数,抛物线与x轴都有两个不 同的交点,
四、小结
1、若一元二次方程ax2+bx+c=0的两个根是x1、 x2, 则抛物线y=ax2+bx+c与x轴的两个交点坐 标分别是A(x1,0 ), B( x2,0 )
2、若一元二次方程ax2+bx+c=0与二次三项式 ax2+bx+c及二次函数y=ax2+bx+c这三个“二次” 之间互相转化的关系。体现了数形结合的思想。
x
探究2、抛物线与X 轴的交点个数能不能用一元 二次方程的知识来说明呢?
Y b2-4ac<0
b2-4ac=0
b2-4ac>0
O
X
结论2:抛物线y=ax2+bx+c与x轴的交点个数可由
一元二次方程ax2+bx+c=0的根的情况说明:
1、 b2-4ac >0
有两个不等的实数根
一元二次方程ax2+bx+c=0 抛物线y=ax2+bx+c
(1)y=6x2-2x+1 (2)y=-15x2+14x+8
17 、欲望以提升热忱,毅力以磨平高山。 13、光阴似箭,日月如梭,转眼间已经十二年了。这十二年里,我们都在成长着,心灵上,身体上,精神上,而爱,是这成长的养料。 18 、生活里,人们往往在笑话别人的时候特别起劲,幸灾乐祸的无所顾虑;却忽略了自己身上也有可笑之处,忽略了给他人带来的伤害。其实 ,人生舞台上人人都有可笑之处。
求证:不任m为何实数,抛物线与x轴都有两个不 同的交点,
四、小结
1、若一元二次方程ax2+bx+c=0的两个根是x1、 x2, 则抛物线y=ax2+bx+c与x轴的两个交点坐 标分别是A(x1,0 ), B( x2,0 )
2、若一元二次方程ax2+bx+c=0与二次三项式 ax2+bx+c及二次函数y=ax2+bx+c这三个“二次” 之间互相转化的关系。体现了数形结合的思想。
x
探究2、抛物线与X 轴的交点个数能不能用一元 二次方程的知识来说明呢?
Y b2-4ac<0
b2-4ac=0
b2-4ac>0
O
X
结论2:抛物线y=ax2+bx+c与x轴的交点个数可由
一元二次方程ax2+bx+c=0的根的情况说明:
1、 b2-4ac >0
有两个不等的实数根
一元二次方程ax2+bx+c=0 抛物线y=ax2+bx+c
(1)y=6x2-2x+1 (2)y=-15x2+14x+8
《二次函数与一元二次方程的关系》ppt课件
结论和要点
通过本课件,我们了解到二次函数与一元二次方程之间的密切关系,以及它们在实际应用中的重 要性和用途。
密切关系
二次函数与一元二次方程存在密切的对应关系。
实际应用
二次函数与一元二次方程在建筑设计、汽车行驶路程、项目成本控制等实际应用中发挥重要 作用。
二次函数与一元二次方程的关系
二次函数与一元二次方程是密切相关的,通过二次函数的系数可以求解一元二次方程的根,反之亦然。
1
系数的求解
通过一元二次方程的系数可以确定二次函数的形式。
2
根的求解
通过二次函数的图像可以推导出一元二次方程的根。
3
相互转换
二次函数与一元二次方程可以相互转换,实现从函数到方程的求解和从方程到函数的绘 图。
如何由一元二次方程求解二次函数的 系数
通过一元二次方程的系数可以确定二次函数的形式,具体步骤包括:
1 步骤一
找出一元二次方程的a、b、c。
2 步骤二
将a、b、c代入二次函数的表达式。
3 步骤三
得到二次函数的形式。
如何由二次函数求解一元二次方程的 根
通过二次函数的图像可以推导出一元二次方程的根,具体步骤包括:
1 步骤一
观察二次函数的图像。2 Leabharlann 骤二根据图像找到方程的根。
实际应用中的例子
二次函数与一元二次方程在实际应用中有广泛的应用,例如:
建筑设计
二次函数的抛物线形状可以用于 建筑设计中的拱形结构。
汽车行驶路程
通过二次函数的图像可以预测汽 车行驶的路程。
项目成本控制
通过二次函数的图像可以进行项 目成本的控制和优化。
《二次函数与一元二次方 程的关系》
本课件将介绍二次函数与一元二次方程之间的关系,包括定义与图像、基本 形式、系数的求解、根的求解、实际应用的例子以及结论和要点。
《二次函数与一元二次方程的关系》ppt课件
解析 : 二次函数y=(m+1)x2 (m 1)x 1的
图象与x轴只有一个公共点, 方程(m+1)x2 (m 1)x 1 0有两 个相等的实数根,
2.若函数y (m 1)x2 (m 1)x 1 即 (m 1)2 4(m 1) 0
的图象与x轴只有一个公共点,求m 解之得m1 1,m2 3.
y=x2 -1
基础过关
1.在平面直角坐标系中,抛物线y=2x2 -x-3
与x轴的交点的个数是 ( B )
A.3 B.2 C.1 D.0 2.已知二次函数y=ax2 +bx+c(a 0) 的图象如图所示,则下列结论正确
的是 ( D )
A.a>0 B. c<0 C.b2 -4ac< D. a b c>0
•
3、越是没有本领的就越加自命不凡。 20.12.1 211:08: 1811:0 8Dec-20 12-Dec-20
•
4、越是无能的人,越喜欢挑剔别人的 错儿。 11:08:1 811:08: 1811:0 8Saturday, December 12, 2020
能力提升
5.已知二次函数 y kx2 6x 7 的图像与X轴
有两个不同的交点.
(1) 求k的取值范围
(2) 当k为何值时,这两个交点横坐标的平方和等
于50. 解:△= 36 28k
解:
x1 x2
6 k
,
x1
x2
7. k
x12 x22 (x1 x2 )2 2x1 x2 50,
∵ 36 28k >0
祝同学们学心进步!
共同进步!
欢迎批评指导!!
2019
ppt资料
16
•
1、有时候读书是一种巧妙地避开思考 的方法 。20.1 2.1220. 12.12Sa turday, December 12, 2020
人教A版高中数学必修5第三章 不等式3.2 一元二次不等式及其解法课件

2.高考对一元二次不等式解法的考查常有以下几个 命题角度:
(1)直接考查一元二次不等式的解法; (2)与函数的奇偶性等相结合,考查一元二次不等式 的解法; (3)已知一元二次不等式的解集求参数.
[例 1] 为( )
(1)(2014·全国高考)不等式组xx+2>0, 的解集 |x|<1
ax2+bx+c<0 对一切 x∈R 都成立的条件为a<0, Δ<0.
2.可用(x-a)(x-b)>0 的解集代替xx- -ab>0 的解集,你认为 如何求不等式xx- -ab<0,xx- -ab≥0 及xx- -ab≤0 的解集?
提示:xx--ab<0⇔(x-a)(x-b)<0; xx--ab≥0⇔xx--ba≠0x-;b≥0, xx--ab≤0⇔xx--ba≠0x-. b≤0,
考点二
一元二次不等式的恒成立问题
[例 2] 设函数 f(x)=mx2-mx-1. (1)若对于一切实数 x,f(x)<0 恒成立,求 m 的取值范 围; (2)若对于 x∈[1,3],f(x)<-m+5 恒成立,求 m 的取 值范围.
[自主解答] (1)要使 mx2-mx-1<0 恒成立,
若 m=0,显然-1<0;
xx≠-2ba
R
判别式 Δ=b2-4ac
Δ>0
ax2+bx+c<0
(a>0)的解集 {x|x<x1<x2}
Δ=0
∅
续表 Δ<0
∅
1.ax2+bx+c>0,ax2+bx+c<0(a≠0)对一切 x∈R 都成立 的条件是什么?
提示:ax2+bx+c>0 对一切 x∈R 都成立的条件为a>0, Δ<0.
(1)直接考查一元二次不等式的解法; (2)与函数的奇偶性等相结合,考查一元二次不等式 的解法; (3)已知一元二次不等式的解集求参数.
[例 1] 为( )
(1)(2014·全国高考)不等式组xx+2>0, 的解集 |x|<1
ax2+bx+c<0 对一切 x∈R 都成立的条件为a<0, Δ<0.
2.可用(x-a)(x-b)>0 的解集代替xx- -ab>0 的解集,你认为 如何求不等式xx- -ab<0,xx- -ab≥0 及xx- -ab≤0 的解集?
提示:xx--ab<0⇔(x-a)(x-b)<0; xx--ab≥0⇔xx--ba≠0x-;b≥0, xx--ab≤0⇔xx--ba≠0x-. b≤0,
考点二
一元二次不等式的恒成立问题
[例 2] 设函数 f(x)=mx2-mx-1. (1)若对于一切实数 x,f(x)<0 恒成立,求 m 的取值范 围; (2)若对于 x∈[1,3],f(x)<-m+5 恒成立,求 m 的取 值范围.
[自主解答] (1)要使 mx2-mx-1<0 恒成立,
若 m=0,显然-1<0;
xx≠-2ba
R
判别式 Δ=b2-4ac
Δ>0
ax2+bx+c<0
(a>0)的解集 {x|x<x1<x2}
Δ=0
∅
续表 Δ<0
∅
1.ax2+bx+c>0,ax2+bx+c<0(a≠0)对一切 x∈R 都成立 的条件是什么?
提示:ax2+bx+c>0 对一切 x∈R 都成立的条件为a>0, Δ<0.
二次函数与一元二次方程的关系课件

二次函数的对称性
二次函数的对称性是指二次函数图像关于某条直线对称的性 质。对于一般的二次函数$f(x) = ax^2 + bx + c$,其对称 轴的方程为$x = -frac{b}{2a}$。
二次函数的对称性对于理解函数的性质和解决实际问题具有 重要意义。例如,在解决几何问题时,可以利用二次函数的 对称性找到对称点或对称线。
一元二次方程的定义
总结词
只含有一个未知数且未知数的最高次 数为2的方程
详细描述
一元二次方程的一般形式为$ax^2 + bx + c = 0$,其中$a neq 0$。它是 一个方程,包含一个未知数$x$,且 $x$的最高次数为2。
二次函数与一元二次方程的关系
总结词:转化关系
详细描述:对于形如$f(x) = ax^2 + bx + c$的二次函数,如果我们将它等于0,即$ax^2 + bx + c = 0$,那么它就转化为 一元二次方程。此时,函数的图像与x轴的交点即为方程的根。
04
二次函数与一元二次方 程的解题技巧
如何解一元二次方程
因式分解法
如果一元二次方程可以写成两 个一次因式的乘积等于零的形 式,则可以通过因式分解法求
解。
配方法
将一元二次方程转化为一个完 全平方等于一个常数加一个线 性项的形式,然后求解。
公式法
对于一般形式的一元二次方程 ,可以使用求根公式求解。
十字相乘法
递增。
04
当 $a > 0$ 时,函数在区间 $(-infty, -frac{b}{2a}]$ 上单调递增,在区间 $[-frac{b}{2a}, +infty)$ 上单调 递减。
《二次函数与一元二次方程》课件

(-1,0),(-5,0),那么一元二次方程ax2+bx+c=
x1=-1,x2=-5
0的根为_________________.
2.抛物线y=x2+2x-3与y轴的交点坐标是_________,
(0,-3)
(1,0) (-3,0)
与x轴的交点坐标是________________.
3.抛物线y=-x2+bx+c的部分图象如下图所示,则
1.在平面直角坐标系内画出二次函数的图象;
2.观察图象,确定抛物线与 x 轴的公共点的坐标;
3.公共点的横坐标就是对应的一元二次方程的解.
当函数图象与 x 轴有两个公共点,且公共点的横坐标不
是整数时,可通过不断缩小根所在的范围估计一元二次
方程的解:
①观察函数图象与 x 轴的一个公共点的横坐标在哪两个
连续整数之间,从而确定这个公共点的横坐标的取值范
围.
②由①可确定方程 ax2+bx+c=0 的一个根在整数 m 和 n
(m<n)之间,再通过取平均数的方法不断缩小根所在的
范围,直到得出的根满足题目要求为止,具体过程如
下:取 m 和 n
+
的平均数
,计算出当
2
=
+
时的
2
函数值y2,将y2与自变量分别为 m 和 n 时的函数值ym,
量x的值时,二次函数问题就转化了一元二
次方程问题.
y=ax2+bx+c(a≠0)0
令y=m
m=ax2+bx+c(a≠0)0
二次函数
转化
思想
一元二次方程
新知探究
知识点1
y=ax2+bx+c(a≠0)0
x1=-1,x2=-5
0的根为_________________.
2.抛物线y=x2+2x-3与y轴的交点坐标是_________,
(0,-3)
(1,0) (-3,0)
与x轴的交点坐标是________________.
3.抛物线y=-x2+bx+c的部分图象如下图所示,则
1.在平面直角坐标系内画出二次函数的图象;
2.观察图象,确定抛物线与 x 轴的公共点的坐标;
3.公共点的横坐标就是对应的一元二次方程的解.
当函数图象与 x 轴有两个公共点,且公共点的横坐标不
是整数时,可通过不断缩小根所在的范围估计一元二次
方程的解:
①观察函数图象与 x 轴的一个公共点的横坐标在哪两个
连续整数之间,从而确定这个公共点的横坐标的取值范
围.
②由①可确定方程 ax2+bx+c=0 的一个根在整数 m 和 n
(m<n)之间,再通过取平均数的方法不断缩小根所在的
范围,直到得出的根满足题目要求为止,具体过程如
下:取 m 和 n
+
的平均数
,计算出当
2
=
+
时的
2
函数值y2,将y2与自变量分别为 m 和 n 时的函数值ym,
量x的值时,二次函数问题就转化了一元二
次方程问题.
y=ax2+bx+c(a≠0)0
令y=m
m=ax2+bx+c(a≠0)0
二次函数
转化
思想
一元二次方程
新知探究
知识点1
y=ax2+bx+c(a≠0)0
《二次函数与一元二次方程》ppt人教版5
(二1次)解函球数的:y=飞k行由x2高-抛度6x能+物否3的达线图到的象15与m表?x轴如达有果交能式点,,得需则要k多的2少取.飞1值行范时围-间是x?2(
6
)
x8
二次函数与一元二次方程的关系
10 10 5
即 A(.1)k<球3 的飞行高度能否x达B.2到k1<536m且x?k≠如0果5能,0需要多少飞行时间?
二次函数与一元二次方程关系密切.
二次函数与一元二次方程的关系
已知二次函数中因变量的值,求自变量的值 解一元二次方程
y - x2 6 x 8
若抛物线 y=ax2+bx+c 与 x 轴有交点,则
10 10 5
1m时,它离初始位置的水平距离是1m或5m.
5m时,它离初始位置的水平距离是3m.
即0秒时球地面飞出,4秒时球落回地面.
(2)y=x2-6x+9;
解得 x =1,x =5. 某学校初三年级的一场篮球比赛中,如图,队员甲正在投篮,已知球出手时距地面 米,与篮框中心的水平距离为7米,当球出手后水
平距离为4米时到达最大高度14米,设篮2 球运行轨迹为抛物线,篮框距地面3米.
1m时,它离初始位置的水平距离是1m或5m.
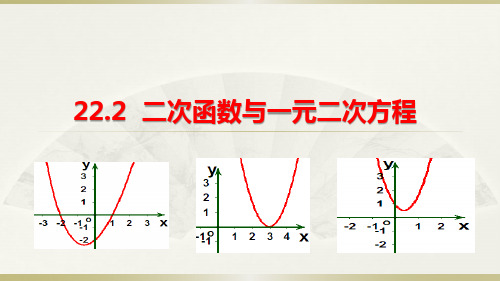
函数关系 h = 20t - 5t 2.
若一元二次方程
无实根,则抛物线
图象位于( )
即
h
1m时,它离初始位置的水平距离是1m或5m.
h=20t-5t2
5m,它离初始位置的水平距 离是多少?
A.k<3
B.k<3且k≠0
一解元:二由次抛方物程线的3x表2+达x-式1得0=0的两个根O是x1=-2 ,x2= ,那么二次函t 数 y= 3x2+x-10与x轴的交点坐标是
部优:《二次函数与一元二次方程的关系》课件

1. 当h取一些特殊值时,可以得到哪些关于t的 一元二次方程? 2. 如何求解这些一元二次方程的根?
一元二次方程20t-5t²=15有两个实数根1,3, 从函数解析式看,就是自变量取1,3时函数值为15; 从函数图象看,就是直线h=15与抛物线h=20t-5t²有两个 公共点(1,15),(3,15)
问题探究
如图,以40 m/s的速度将小球沿与地面成某一角度的方向击出时, 小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行 高度h(m)与飞行时间t(s)之间具有函数关系h=20t-5t². 请解答以下问题: (2)小球的飞行高度能否达到20 m? 如果能,需要多少飞行时间?
一元二次方程20t-5t²=20有两个相等的实数根2, 从函数解析式来看,就是自变量取2时函数值为20; 从函数图象看,就是直线h=20与抛物线h=20t-5t²有一个 公共点(2,20),此点也为图象的顶点.
2
2
4. 求一次函数y=2x+1与二次函数y=x²-4x+3图象的交点个数.
达标检测
5. 已知二次函数y=-x²+2x+m的部分图象如图所示,求关于x的一 元二次方程-x²+2x+m=0的解.
达标检测
1. 已知二次函数y=ax²+bx+c的部分图象如图所示,根据图象可得 关于x的一元二次方程ax²+bx+c=0的解为_______.
2. 已知二次函数y=ax²+bx+c,若ac<0,则其图象与x轴( ) A.有两个交点 B.有一个交点 C.没有交点 D.可能有一个交点
达标检测
3. 求二次函数 y - 1 x2 - 3x - 5抛物线y=ax²+bx+3的对称轴为直线x=1,如果关于x的 一元二次方程ax²+bx-8=0的一个根为4,那么该方程的另一个根
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在我的印象里,他一直努力而自知,每天从食堂吃饭后,他总是习惯性地回到办公室看厚厚的专业书不断提升和充实自己,他的身上有九零后少见的沉稳。同事们恭喜他,大多看 到了他的前程似锦,却很少有人懂得他曾经付出过什么。就像说的:“如果这世上真有奇迹,那只是努力的另一个名字,生命中最难的阶段,不是没有人懂你,而是你不懂自已。” 而他的奇迹,是努力给了挑选的机会。伊索寓言中,饥饿的狐狸想找一些可口的食物,但只找到了一个酸柠檬,它说,这只柠檬是甜的,正是我想吃的。这种只能得到柠檬,就说 柠檬是甜的自我安慰现象被称为:“甜柠檬效应”。一如很多人不甘平庸,却又大多安于现状,大多原因是不知该如何改变。看时,每个人都能从角色中看到自已。高冷孤独的安 迪,独立纠结的樊胜美,乐观自强的邱莹莹,文静内敛的关睢尔,古怪精灵的曲筱绡。她们努力地在城市里打拼,拥有幸或不幸。但她依然保持学习的习惯,这样无论什么事她都 有最准确的判断和认知;樊胜美虽然虚荣自私,但她努力做一个好HR,换了新工作后也是拼命争取业绩;小蚯蚓虽没有高学历,却为了多卖几包咖啡绞尽脑汁;关睢尔每一次出镜 几乎都是在房间里戴着耳机听课,处理文件;就连那个嬉皮的曲筱潇也会在新年之际为了一单生意飞到境外……其实她们有很多路可以走:嫁人,啃老,安于现状。但每个人都像 个负重的蜗牛一样缓缓前行,为了心中那丁点儿理想拼命努力。今天的努力或许不能决定明天的未来,但至少可以为明天积累,否则哪来那么多的厚积薄发和大器晚成?身边经常 有人抱怨生活不幸福,上司太刁,同事太蛮,公司格局又不大,但却不想改变。还说:“改变干嘛?这个年龄了谁还能再看书考试,混一天是一天吧。”一个“混”字就解释了他 的生活态度。前几天我联系一位朋友,质问为什么好久不联系我?她说自已每天累的像一条狗,我问她为什么那么拼?她笑:“如果不努力我就活得像一条狗了。”恩,新换的上 司,海归,虽然她有了磨合几任领导的经验,但这个给她带来了压力。她的英语不好,有时批阅文件全是大段大段的英文,她心里很怄火,埋怨好好的中国人,出了几天国门弄得 自己像个洋鬼子似的。上司也不舒服,流露出了嫌弃她的意思,甚至在一次交待完工作后建议她是否要调一个合适的部门?她的脸红到了脖子,想着自己怎么也算是老员工,由她 羞辱?两个人很不愉快。但她有一股子倔劲,不服输,将近40岁的人了,开始拿出发狠的学习态度,报了个英语培训班。回家后捧着英文书死啃,每天要求上中学的女儿和自己英 语对话,连看电影也是英文版的。功夫不负有心人,当听力渐渐能跟得上上司的语速,并流利回复,又拿出漂亮的英文版方案,新上司看她的眼光也从挑剔变柔和,某天悄悄放了 几本英文书在她桌上,心里突然发现上司并没那么讨厌。心态好了,她才发现新上司的优秀,自从她来了后,部门业绩翻了又翻,奖金也拿到手软,自己也感觉痛快。她说:这个 社会很功利,但也很公平。别人的傲慢一定有理由,如果想和平共处,需要同等的段位,而这个段位,自己可能需要更多精力,但唯有不断付出,才有可能和优秀的人比肩而立。 人为什么要努力?一位长者告诉我:“适者生存。”这个社会讲究适者生存,优胜劣汰。虽然也有潜规则,有套路和看不见的沟沟坎坎,但一直努力的人总会守得云开见月明。有 些人明明很成功了,但还是很拼。比如剧中的安迪,她光环笼罩,商场大鳄是她的男闺蜜,不离左右,富二代待她小心呵护,视若明珠,加上她走路带风,职场攻势凌历,优秀得 让身边人仰视。这样优秀的人,不管多忙,每天都要抽出两个小时来学习。她的学习不是目的,而是能量,能让未来的自己比过去更好一些。现实生活中,努力真的重要,它能改 变一个人的成长轨迹,甚至决定人生成败。有一句鸡汤:不着急,你想要的,岁月都会给你。其实,岁月只能给你风尘满面,而希望,唯有努力才能得到!9、懂得如何避开问题的 人,胜过知道怎样解决问题的人。在这个世界上,不知道怎么办的时候,就选择学习,也许是最佳选择。胜出者往往不是能力而是观念!在家里看到的永远是家,走出去看到的才 是世界。把钱放在眼前,看到的永远是钱,把钱放在有用的地方,看到的是金钱的世界。给人金钱是下策,给人能力是中策,给人观念是上策。财富买不来好观念,好观念能换来 亿万财富。世界上最大的市场,是在人的脑海里!要用行动控制情绪,不要让情绪控制行动;要让心灵启迪智慧,不能让耳朵支配心灵。人与人之间的差别,主要差在两耳之间的 那块地方!人无远虑,必有近忧。人好的时候要找一条备胎,人不好的时候要找一条退路;人得意的时候要找一条退路,人失意的时候要找一条出路!孩子贫穷是与父母的有一定 的关系,因为他小的时候,父母没给他足够正确的人生观。家长的观念是孩子人生的起跑线!有什么信念,就选择什么态度;有什么态度,就会有什么行为;有什么行为,就产生 什么结果。要想结果变得好,必须选择好的信念。播下一个行动,收获一种习惯;播下一种习惯,收获一种性格;播下一种性格,收获一种命运。思想会变成语言,语言会变成行
x
探究2、抛物线与X 轴的交点个数能不能用一元 二次方程的知识来说明呢?
Y b2-4ac<0
b2-4ac=0
b2-4ac>0
O
X
Байду номын сангаас
结论2:抛物线y=ax2+bx+c与x轴的交点个数可由
一元二次方程ax2+bx+c=0的根的情况说明:
1、 b2-4ac >0
有两个不等的实数根
一元二次方程ax2+bx+c=0 抛物线y=ax2+bx+c
a=
;若抛物线与x轴有两个交点,则a
的范围是
;若抛物线与坐标轴有两个
公共点,则a的范围是
;
2、已知抛物线y=x2-3x+a+1与x轴最多只有一
个交点,则a的范围是
。
3、已知抛物线y=x2+px+q与x轴的两个交点为 (-2,0),(3,0),则p= ,q= 。
4、判断下列各抛物线是否与x轴相交,如果 相交,求出交点的坐标。
与x轴有两个交点——相交。
2、 b2-4ac =0
有两个相等的实数根
一元二次方程ax2+bx+c=0 抛物线y=ax2+bx+c
与x轴有唯一公共点——相切(顶点)。
3、 b2-4ac <0
一元二次方程ax2+bx+c=0
没有实数根
抛物线y=ax2+bx+c
与x轴没有公共点——相离。
二、基础训练
1、已知抛物线y=x2-6x+a的顶点在x轴上,则
二次函数 与
一元二次方程的关系
一、探究
探究1、求二次函数图象y=x2-3x+2与x轴的交 点A、B的坐标。 解:∵A、B在轴上,
∴它们的纵坐标为0,
∴令y=0,则x2-3x+2=0
解得:x1=1,x2=2; ∴A(1,0) , B(2,0) 你发现方程 x2-3x+2=0 的解x1、x2与A、B的 坐标有什么联系?
3、已知是x1、x2方程x2-(k-3)x+k+4=0的两 个实根,A、B为抛物线y= x2-(k-3)x+k+4与 x轴的两个交点,P是y轴上异于原点的点,设 ∠PAB=α,∠PBA=β,问α、β能否相等?并说 明理由.
Y
P
α
β
AO B
X
4、已知抛物线y=x2-(m2+8)x+2(m2+6).
求证:不任m为何实数,抛物线与x轴都有两个不 同的交点,
四、小结
1、若一元二次方程ax2+bx+c=0的两个根是x1、 x2, 则抛物线y=ax2+bx+c与x轴的两个交点坐 标分别是A(x1,0 ), B( x2,0 )
2、若一元二次方程ax2+bx+c=0与二次三项式 ax2+bx+c及二次函数y=ax2+bx+c这三个“二次” 之间互相转化的关系。体现了数形结合的思想。
结论1:方程x2-3x+2=0的解就是抛物线y=x23x+2与x轴的两个交点的横坐标。因此,抛物 线与一元二次方程是有密切联系的。
即:若一元二次方程ax2+bx+c=0的两个根是
x1、x2, 则抛物线y=ax2+bx+c与轴的两个交
点坐标分别是A( y
x1,0),
B(x2,0)
x1 x2 OA B
1、已知二次函数y=x2-kx-2+k.
(1)求证:不论k取何值时,这个二次函数
y=x2-kx-2+k与x轴有两个不同的交点。 (2)如果二次函数y=x2-kx-2+k与轴两个交点为 A、B,设此抛物线与y轴的交点为C,当k为6 时,求S△ABC .
2、已知抛物线y=x2+2x+m+1。
(1)若抛物线与x轴只有一个交点,求m的值。 (2)若抛物线与直线y=x+2m只有一个交点, 求m的值。
(1)y=6x2-2x+1 (2)y=-15x2+14x+8
(3)y=x2-4x+4
6、抛物线y=ax2+bx+c(a≠0)的图象全部在 轴下方的条件是( D ) (A)a<0 b2-4ac≤0
(B)a<0 b2-4ac>0
(C)a>0 b2-4ac>0 (D)a<0 b2-4ac<0
三、例题推荐
