固体电子
合集下载
第五章 固体中电子的能量状态

反键态
导带
3p sp3
3s 成键态 价带
长春理工大学材料科学与工程学院教案
紧束缚近似对原子的内层电子是相当好的近似,它还可用来近似地 描述过渡金属的 d 带、类金刚石晶体以及惰性元素晶体的价带。紧 束缚近似是定量计算绝缘体、化合物及半导体特性的有效工具。 (10) 能带的三种图象
扩展布里渊区图象: 不同的能带在 k 空间中不同的布里渊区中给出。每一个布里渊区有 中一个能带,第 n 个能带在第 n 个布里渊区中。
长春理工大学材料科学与工程学院教案
由于认为 k 与 k+Gl 等价,因此可以认为 En(k)是以倒格矢 Gl 为周 期的周期函数,即对于同一能带 n,有
En (k) = En (k +Gl)
(11)能带的性质
¾ 能带具有周期性
E (k ) = E (k + n 2π ) a
电子波矢
k ' = k + n 2π a
长春理工大学材料科学与工程学院教案
—— 第一布里渊区和第二布里渊区能带的重叠
(9)原子能级与能带的对应 对于原子的内层电子,其电子轨道很小,因而形成的能带较 窄。这时原子能级与能带之间有简单的一一对应关系。
长春理工大学材料科学与工程学院教案
E
对于外层电子,由于其电子轨道较大,形成的能带就较宽。 这时,原子能级与能带之间比较复杂,不一定有简单的一一对应关 系。一个能带不一定与孤立原子的某个能级相对应,可能会出现能 带的重叠。 在某些情况下还可能出现不同原子态的相互作用。如:Si 的价带与 导带。
电子在运动过程中并不像自由电子那样完全不受任 何力 的作用,电子在运动过程中受到晶格中原子势 场的作用。
在一定的条件下根据布洛赫定理可知电子不再是完全被束 缚在某个原子周围,而是可以在整个固体中运动,称为共有 化电子。
固体电子学教程

课程基本内容
1、掌握晶体的基本结构以及晶体结合方式及其电子的运动特征(能带)。理解有效质量的意义。 2、理解施主、受主杂质能级的概念,深刻理解费米能级的意义。 3、理解非平衡载流子的注入与复合、寿命。掌握载流子的扩散、漂移运动以及连续性方程。 4、掌握 pn 结能带图、pn 结电流电压特性、pn 结电容。 5、理解表面电场效应及空间电荷层的电场、电势和电容。理解 MOS 结构的电容-电压特性。掌握 MOSFET 的结构、沟道形成原理、栅极阈值电压和工作特性,CMOS 反向器的构成和特点。 6、了解金属半导体的欧姆接触和肖特基接触,MESFET 的结构和工作特点。 7、了解微波高速器件的结构特点和性能特征,进一步加深对半导体中载流子运动规律的理解。 8、熟悉光电子器件对材料的要求、光电特性及相关的先进半导体工艺。 成绩:考核方式——闭卷;平时 20%,期末考试 80%
3
1.4 载流子的散射 载流子在运动过程中与晶体中的原子或杂质粒子碰撞,改变了原有的运动状态,做无规则的运动。 平均自由时间(驰豫时间)τ:载流子在两次受到散射的平均时间间隔。
1.5 载流子的输运
1.5.1 漂移运动、迁移率和电导率(参考书上 p38)
载流子在外电场的作用下沿一定方向作有规则的运动称为漂移运动。
直接带隙半导体:右图为砷化镓的动量-能量关系 曲线,其价带顶部与导带最低处发生在相同动量处(p= 0)。因此,当电子从价带转换到导带时,不需要动量转 换。这类半导体称为直接带隙半导体。 间接带隙半导体:
对硅而言,其动量-能量曲线中价带顶部发生在 p =0 时,但导带的最低处则发生在 p ≠ 0。因此当电子从 硅的价带顶部转换到导带最低点时,要保持能量和动量 守恒,不仅需要能量转换,也需要动量转换。这类半导 体称为间接带隙半导体。
1、掌握晶体的基本结构以及晶体结合方式及其电子的运动特征(能带)。理解有效质量的意义。 2、理解施主、受主杂质能级的概念,深刻理解费米能级的意义。 3、理解非平衡载流子的注入与复合、寿命。掌握载流子的扩散、漂移运动以及连续性方程。 4、掌握 pn 结能带图、pn 结电流电压特性、pn 结电容。 5、理解表面电场效应及空间电荷层的电场、电势和电容。理解 MOS 结构的电容-电压特性。掌握 MOSFET 的结构、沟道形成原理、栅极阈值电压和工作特性,CMOS 反向器的构成和特点。 6、了解金属半导体的欧姆接触和肖特基接触,MESFET 的结构和工作特点。 7、了解微波高速器件的结构特点和性能特征,进一步加深对半导体中载流子运动规律的理解。 8、熟悉光电子器件对材料的要求、光电特性及相关的先进半导体工艺。 成绩:考核方式——闭卷;平时 20%,期末考试 80%
3
1.4 载流子的散射 载流子在运动过程中与晶体中的原子或杂质粒子碰撞,改变了原有的运动状态,做无规则的运动。 平均自由时间(驰豫时间)τ:载流子在两次受到散射的平均时间间隔。
1.5 载流子的输运
1.5.1 漂移运动、迁移率和电导率(参考书上 p38)
载流子在外电场的作用下沿一定方向作有规则的运动称为漂移运动。
直接带隙半导体:右图为砷化镓的动量-能量关系 曲线,其价带顶部与导带最低处发生在相同动量处(p= 0)。因此,当电子从价带转换到导带时,不需要动量转 换。这类半导体称为直接带隙半导体。 间接带隙半导体:
对硅而言,其动量-能量曲线中价带顶部发生在 p =0 时,但导带的最低处则发生在 p ≠ 0。因此当电子从 硅的价带顶部转换到导带最低点时,要保持能量和动量 守恒,不仅需要能量转换,也需要动量转换。这类半导 体称为间接带隙半导体。
《固体电子论基础》课件

课件的编写目的和意义
课件的结构和内容安排
课件目的
掌握固体电子论的基本概念和原理 了解固体电子论在材料科学中的应用 掌握固体电子论的数学基础 了解固体电子论在物理、化学等领域的应用
适用人群
固体电子论专业本 科生
固体电子论爱好者
电子工程、材料科 学等领域的研究人 员
对固体电子论感兴 趣的其他人员
课件结构
固体电子论在器 件设计中的应用
半导体技术 太阳能电池 电子器件 磁学和光学应用
应用领域
固体电子结构与性质
固体电子结构
固体电子论的 概述
固体电子的能 级结构
固体电子的态 密度
固体电子的输 运性质
电子性质
电子的电荷与质 量
电子的能级与跃 迁
电子的波粒二象 性
电子在固体中的 行为
固体能带结构的定义
固体电子论概述
固体电子论的定义
定义与概念
固体电子论的研究对象
固体电子论的基本概念
固体电子论与量子力学、固体物理学的关系
固体电子论的起源
发展历程
固体电子论的发展阶段
固体电子论的应用领域
固体电子论的未来展望
研究内容
固体电子论的基 本概念和原理
固体电子论的研 究对象和方法
固体电子论在材 料科学中的应用
单击此处输入你的 项正文
电流方向:单向 导电
单击此处输入你的 项正文
伏安特性:正向和 反向伏安特调幅 信号解调为音频信
号
单击此处输入你的
项正文
开关电路:控制 电路的通断
单击此处输入你的 项正文
晶体管工作原理及应用
晶体管基本结构与工作原理 晶体管类型与特性 晶体管在电路中的应用 晶体管在固体电子器件中的重要性
固体中的电子态

边界上特征点: <100>*方向上X <111>*方向上L <110>*方向上K
§2.4 固体中电子态
5 电子态的表述 — 3维晶体中电子的能量与波矢关系
量化表达方式:波矢空间中特定方向 上能量与波矢的函数曲线——Cu
边界上特征点: <100>*方向上X <111>*方向上L <110>*方向上K
电子态的能带特征点 — 关键词:E(k)的能量突变点的特征、禁带的意义及原因
电子态的能带(允带) — 关键词:一个能带内的能态密度
电子在能带(允带)中的分布及特征 — 关键词:电子的分布情况与费米能级,与材料的关系
§2.4 固体中电子态
1. 电子态的表述 — 电子的能量与波矢关系
E(k ) 曲线具有平移对 2π
载流子体积密度
T=0K时载流子体积密度为零, 是绝缘体
T>0K下,电子由价带跃迁到导带 产生载流子,其体积密度随温度 升高呈指数规律增高,因此导电 性相应按指数规律增强
§2.4 固体中电子态
2-1 半导体的光吸收和发光问题
平移对称性的表现形式
§2.4 固体中电子态
2. 电子的“禁带”
各种表示图中,电子能量 -波矢关系的能量突变处
§2.4 固体中电子态
2. 电子的“禁带” 周期为a的势场—间距a的一维原子链
能量突变—电子波矢为π/a的整倍数处
能量与波矢中能量突变的原因
能量突变点处电子波长为2π/k=2a/n 这样的电子波在晶体中传播,相邻
正空间基矢 (a1, a2 , a3 )
倒易空间基矢 (g1 , g2 , g3 )
g1
=
2π
⋅
§2.4 固体中电子态
5 电子态的表述 — 3维晶体中电子的能量与波矢关系
量化表达方式:波矢空间中特定方向 上能量与波矢的函数曲线——Cu
边界上特征点: <100>*方向上X <111>*方向上L <110>*方向上K
电子态的能带特征点 — 关键词:E(k)的能量突变点的特征、禁带的意义及原因
电子态的能带(允带) — 关键词:一个能带内的能态密度
电子在能带(允带)中的分布及特征 — 关键词:电子的分布情况与费米能级,与材料的关系
§2.4 固体中电子态
1. 电子态的表述 — 电子的能量与波矢关系
E(k ) 曲线具有平移对 2π
载流子体积密度
T=0K时载流子体积密度为零, 是绝缘体
T>0K下,电子由价带跃迁到导带 产生载流子,其体积密度随温度 升高呈指数规律增高,因此导电 性相应按指数规律增强
§2.4 固体中电子态
2-1 半导体的光吸收和发光问题
平移对称性的表现形式
§2.4 固体中电子态
2. 电子的“禁带”
各种表示图中,电子能量 -波矢关系的能量突变处
§2.4 固体中电子态
2. 电子的“禁带” 周期为a的势场—间距a的一维原子链
能量突变—电子波矢为π/a的整倍数处
能量与波矢中能量突变的原因
能量突变点处电子波长为2π/k=2a/n 这样的电子波在晶体中传播,相邻
正空间基矢 (a1, a2 , a3 )
倒易空间基矢 (g1 , g2 , g3 )
g1
=
2π
⋅
固体电子学PPT

三维情况: a
2
a3 a1
三维原胞呈平行六面体,且每个原胞中仅有一个格点,原胞
的体积等Rn于每n个1a格1点在n空2a间2 占n据3的a3空间。
n1,n2,n3为包括零在内的任意整数
晶体中任一物理量沿基矢方向平移基矢的整数倍,保持性质不 变,体现了平移对称性。
2. 在波矢空间里——倒格子
晶体结构的周期性
补充:简并定态微扰
设Hˆ 0的 Ek 能级有f度简并,将f
个波函数记成 i (i=1,2,3…..),
f
0
k
Ci0 i
(1)
i 1
只考虑零级近似波函数与一级能量修正:
(Hˆ 0
Hˆ ) k(0)
(Ek (0)
Ek(1) )
(0) k
(2)
(1)式代入(2)式中, … …
f
f
f
f
Hˆ 0
Ci0i
Ci0Hˆ i
Ci0
Ek(
0) i
Ci0 Ek(1) i
i 1
i 1
i 1
i 1
f
f
Ci0Hˆ i Ci0Ek(1)i
i 1
i 1
两端左乘 m 并积分
f
f
Ci0
* m
Hˆ
i
d
Ci0
E (1) k
*
mi
d
i 1
i 1
f
f
Ci0H m i Ci0Ek(1) mi
i 1
11
2) 正、倒格子间的关系
I. ai b j 2 ij i, j 1, 2, 3
II. 倒格子原胞体积是正格子原胞体积的倒数的(2π )3倍。
固体电子论

+ + + + ++
与经典的相同点:正离子电场均匀,价电子不被原
+ + 子核束+缚。 + + +
考虑电子在一维金属丝(长为L)中的运动
一维无限深势阱 UU(x()x)
2 x2
2 y 2
2 z 2
(8 2m h2
)(E
U)
0
UU=0=0
2
x2
( 8h22m )E
3 eV
N (E)dE
2 eV
(2m3)1/ 2
23
3 eV
2 eV
EdE
(2m3)1/ 2
23
L
,ky
2ny
L
, kz
2nz
L
ky
每一个量子态都对应一个确定的 (nx , ny , nz )
2/L
kx • 在二维k空间量子化的示意图
在k空间中每一个点代表电子波矢分
量kx & ky 一个允许的结合
点:每个许可的状态可用一个点来代表
提问:kx轴相邻两点之间的距离是多少?
•
k
x
轴相邻的两个代表点间的间距为2 L
eikxL 1即:cos kx L i sin kx L 1
kx L 2nx
k
x
k y
2nx
L
2ny
L
k
z
2nz
L
• 电子波函数:
Ae Ae i k r
与经典的相同点:正离子电场均匀,价电子不被原
+ + 子核束+缚。 + + +
考虑电子在一维金属丝(长为L)中的运动
一维无限深势阱 UU(x()x)
2 x2
2 y 2
2 z 2
(8 2m h2
)(E
U)
0
UU=0=0
2
x2
( 8h22m )E
3 eV
N (E)dE
2 eV
(2m3)1/ 2
23
3 eV
2 eV
EdE
(2m3)1/ 2
23
L
,ky
2ny
L
, kz
2nz
L
ky
每一个量子态都对应一个确定的 (nx , ny , nz )
2/L
kx • 在二维k空间量子化的示意图
在k空间中每一个点代表电子波矢分
量kx & ky 一个允许的结合
点:每个许可的状态可用一个点来代表
提问:kx轴相邻两点之间的距离是多少?
•
k
x
轴相邻的两个代表点间的间距为2 L
eikxL 1即:cos kx L i sin kx L 1
kx L 2nx
k
x
k y
2nx
L
2ny
L
k
z
2nz
L
• 电子波函数:
Ae Ae i k r
固体电子5--能带结构

⎤ ⎥ ⎥⎦
⋅
ΔE
所以,能态密度g(E)为:
∫ N (E) = lim ΔZ = 2V dS
ΔE→0 ΔE (2π )3 ∇k E
<三维情况>
∫ N (E)
=
2S
(2π )2
dl ∇k E
<二维情况>
N(E) = 2L 2
2π dE / dk
<一维情况> 19
例:三维自由电子的能态密度
自由电子的E(k)∼k关系: E(k) = h2k 2 2m
只与k的模有关。
k空间等能面为球面,球面上:
为常数。
∇k E
=
h2k m
∫ ∫ 能态密度: N (E)
=
V
4π
3
dS = V ⋅ m
∇k E 4π 3 h2k
dS
=
Vm
h2π 2
k
=
V
2π
2
⎛⎜ ⎝
2m h2
⎞⎟3/ 2 E1/ 2 ⎠
N(E)和E呈抛物线关系。
20
自由电子和近自由电子
在第一布里渊区内离界面较远处,布洛赫电子的行 为近似于自由电子,在k空间的等能面为球面,近自由 电子与自由电子的能态密度非常相近。
11
能带结构
满带和空带、价带和导带 能带电子的导电性 导体、半导体和绝缘体的能带论解释。 能态密度
12
导体:除去完全充满的一系列能带外,还有部分被电子占据 的能带。后者起导电作用,称为导带。(a) 和(b)
绝缘体:电子恰好填满最低的一系列能带,再高的能带都是空 的。满带不导电。(c)
半导体: 能带结构类似绝缘体,但价带和导带之间的带隙较小, 杂质或者热激发会使导带有少部分电子或者价带缺少电子。(d)
固体电子学光电效应课件

固体电子学光电效应课件
所以光的波长越短,即频率越高,其光子的能量也越大; 反之,光的波长越长,其光子的能量也就越小。 在光线作用下,物体内的电子逸出物体表面向外发射的现象称为外光电效应。向外发射的电子叫光电子。基于外光电效应的光电器件有光电管、 光电倍增管等。 光照射物体,可以看成一连串具有一定能量的光子轰击物体,物体中电子吸收的入射光子能量超过逸出功A0时,电子就会逸出物体表面,产生光电子发射,超过部分的能量表现为逸出电子的动能。
固体电子学光电效应课件
Definition of laser
A laser is a device that generates light by a process called STIMULATED EMISSION. The acronym LASER stands for Light Amplification by Stimulated Emission of Radiation Semiconducting lasers are multilayer semiconductor devices that generates a coherent beam of monochromatic light by laser action. A coherent beam resulted which all of the photons are in phase.
法布里-珀罗 (F-P) 谐振腔
100%
90%
固体电子学光电效应课件
Diode Laser
固体电子学光电效应课件
Typical Application of Laser
The detection of the binary data stored in the form of pits on the compact disc is done with the use of a semiconductor laser. The laser is focused to a diameter of about 0.8 mm at the bottom of the disc, but is further focused to about 1.7 micrometers as it passes through the clear plastic substrate to strike the reflective layer. The reflected laser will be detected by a photodiode. Moral of the story: without optoelectronics there will no CD player!
所以光的波长越短,即频率越高,其光子的能量也越大; 反之,光的波长越长,其光子的能量也就越小。 在光线作用下,物体内的电子逸出物体表面向外发射的现象称为外光电效应。向外发射的电子叫光电子。基于外光电效应的光电器件有光电管、 光电倍增管等。 光照射物体,可以看成一连串具有一定能量的光子轰击物体,物体中电子吸收的入射光子能量超过逸出功A0时,电子就会逸出物体表面,产生光电子发射,超过部分的能量表现为逸出电子的动能。
固体电子学光电效应课件
Definition of laser
A laser is a device that generates light by a process called STIMULATED EMISSION. The acronym LASER stands for Light Amplification by Stimulated Emission of Radiation Semiconducting lasers are multilayer semiconductor devices that generates a coherent beam of monochromatic light by laser action. A coherent beam resulted which all of the photons are in phase.
法布里-珀罗 (F-P) 谐振腔
100%
90%
固体电子学光电效应课件
Diode Laser
固体电子学光电效应课件
Typical Application of Laser
The detection of the binary data stored in the form of pits on the compact disc is done with the use of a semiconductor laser. The laser is focused to a diameter of about 0.8 mm at the bottom of the disc, but is further focused to about 1.7 micrometers as it passes through the clear plastic substrate to strike the reflective layer. The reflected laser will be detected by a photodiode. Moral of the story: without optoelectronics there will no CD player!
第一章 固体中电子能量结构和状态 PPT

1.2.1 金属中自由电子的能级
一维情况,建立一维势阱模型
U(0) U(L)
边界条件 U( x) 0,U(0) U(L)
U(x) 0
电子能量
0
L
E
h2
2m2
2 2m
K2
代入一维薛定谔方程
d
2 ( x)
dx2
2mE 2
(x)
0
d
2 ( x)
dx 2
(
2
)2
(
x)
0
解得 Acos 2 x B sin 2 x
▪金属的费密(Fermi)-索末菲(Sommerfel)
电子理论
▪晶体能带理论
内容先后基本按照人类对电子行为认识的逐渐深入
1.1 .1电子的粒子性
霍尔效应(Hall effect) B
以金属导体为例:
I
金属中的电流就是自由
E
++_++ +_ ++_ ++_+++ Nhomakorabea+
_
+ +
_
+ +
_
+ +
_
+ +
d 2 ( x)
dx2
4 2
h2
p2 ( x)
因 P2 2mE (非相对论形式,E为经典粒子动能)
d
2 ( x)
dx2
2mE 2
(
x)
0
此为一维条件下自由电子的薛定谔方程
如电子是不自由的,其总能量是势能和动能之合 P2 2m(E U )
d
2 ( x)
固体物理晶体中的电子状态

波函数: uk reikr 布洛赫函数
能量:一个能级列变为一个能带。
单电子近似(准自由近似和紧束缚近似),又称为能带论
5.5晶体中电子的准经典运动
在量子力学中晶体中布洛赫电子的运动由波 包来描述。所谓波包由空间分布在r0附近的Δr 范围内,波矢取值在k0附近的Δk范围内的布洛 赫电子态组成,ΔrΔk必须满足不确定关系。一 般Δk必须小于第一布里渊区的线度,这样Δr 必须远大于晶体原胞的线度,只能在这个线度 内,布洛赫电子可以看作经典粒子。
净电流为0,不导电
施加外电场
k轴上各点均以完全相同的速度移动,电子在布里
渊区中不再分布对称,电流密度不能完全抵消。
净电流不为0,参与导电
不满带导电
F
不满带导电
三、导体和非导体模型
实际晶体中,电子从低到高填充能带,形成一系列 的满带。最外层价电子填充的能带,称为价带。
导体:价带是不满带。 非导体:价带也是满带。
三种近似方法:
1. 自由电子近似:(适用于金属晶体)
波函数: Aeikr 能量:E 2k 2 准连续
2m
2. 准自由电子近似:(适用于晶体中原子的外层电子)
波函数: uk reikr 布洛赫函数
能量:准连续的能量在布里渊区边界突变,分裂为能带。
3. 紧束缚近似:(适用于晶体中原子的内层电子)
有效质量大
k
x
kx
曲率愈小,有效质量愈大; 曲率愈大,有效质量愈小。
2. 有效质量有正、有负
能带底部,d 2E
dk 2
0,m*
0
能带顶部,d 2E 0,m* 0
dk 2
m*
m* 2
d2E dk 2
k
x
能量:一个能级列变为一个能带。
单电子近似(准自由近似和紧束缚近似),又称为能带论
5.5晶体中电子的准经典运动
在量子力学中晶体中布洛赫电子的运动由波 包来描述。所谓波包由空间分布在r0附近的Δr 范围内,波矢取值在k0附近的Δk范围内的布洛 赫电子态组成,ΔrΔk必须满足不确定关系。一 般Δk必须小于第一布里渊区的线度,这样Δr 必须远大于晶体原胞的线度,只能在这个线度 内,布洛赫电子可以看作经典粒子。
净电流为0,不导电
施加外电场
k轴上各点均以完全相同的速度移动,电子在布里
渊区中不再分布对称,电流密度不能完全抵消。
净电流不为0,参与导电
不满带导电
F
不满带导电
三、导体和非导体模型
实际晶体中,电子从低到高填充能带,形成一系列 的满带。最外层价电子填充的能带,称为价带。
导体:价带是不满带。 非导体:价带也是满带。
三种近似方法:
1. 自由电子近似:(适用于金属晶体)
波函数: Aeikr 能量:E 2k 2 准连续
2m
2. 准自由电子近似:(适用于晶体中原子的外层电子)
波函数: uk reikr 布洛赫函数
能量:准连续的能量在布里渊区边界突变,分裂为能带。
3. 紧束缚近似:(适用于晶体中原子的内层电子)
有效质量大
k
x
kx
曲率愈小,有效质量愈大; 曲率愈大,有效质量愈小。
2. 有效质量有正、有负
能带底部,d 2E
dk 2
0,m*
0
能带顶部,d 2E 0,m* 0
dk 2
m*
m* 2
d2E dk 2
k
x
电子的有效质量解释粒子性

电子的有效质量解释粒子性
电子的有效质量是指在固体中具有类似于自由电子的行为时所表现出来的等效质量。
在固体中,电子受到晶格周期性势场的影响,其运动受到了限制。
根据固体物理学中的能带理论,电子的运动可用一系列能量带或禁带来描述,其中包括导带和价带。
在电子靠近能带底部的情况下,由于其动能比较小,可以将其近似看作自由电子。
此时,电子的动量和能量之间满足自由电子动能关系,即E = (p^2) / (2m),这里的m是等效质量。
可以将电子的有效质量看作是电子在固体中的运动对外部施加的有效质量。
需要注意的是,电子的有效质量通常与外部条件和材料性质有关,不同材料中电子的有效质量可能不同。
对于半导体和绝缘体来说,电子的有效质量通常较大,而金属中的电子则通常具有较小的有效质量。
总之,电子的有效质量解释了在固体中电子的粒子性,即其在晶格约束下运动的行为。
第13章固体中的电子(12)

B
在氢原子的 L 壳层中,电子可能具有的量子数(n,l,ml, ms)是 (A)(1,0,0,-1/2)。 (B)(2,1,-1,1/2)。 (C)(2,0,1,-1/2)。 (D)(3,1,-1,-1/2)。 B
在原子的 L 壳层中,电子可能具有的四个量子数 (n,l,ml,ms)是 (1) (2,0,1,1/2)。 (2) (2,1,0,-1/2)。 (3) (2,1,1,1/2)。 (4) (2,1,-1,-1/2)。 以上四种取值中,哪些是正确的? (A) 只有 (1)、(2) 是正确的。 (B) 只有 (2)、(3) 是正确的。 (C) 只有 (2)、(3)、(4) 是正确的。 (D) 全部是正确的。
氩(Z = 18)原子基态的电子组态是: (A) 1s2 2s8 3p8。 (B) 1s2 2s22p6 3d8。 (C) 1s2 2s22p6 3s23p6。 (D) 1s2 2s22p6 3p43d2。
C
三、电子的总的角动量 J J L S 这一角动量的合成叫自旋轨道耦合
当 n 一定,l 可取 n 个值,
这个结果是因为:
现在知道,一切微观粒子都有自旋,按自旋分类: (1) 费米子:自旋为半整数,如 s = 1/2,3/2 如电子,中子,质子,中微子, 反西格玛负超子 Σ (王淦昌等,1959年) —— 服从泡利不相容原理。
(2) 玻色子:自旋为整数, 如 s = 0, 1 介子,光子等。 —— 不服从泡利不相容原理。
C
氢原子中处于 2p 状态的电子,描述其四个量子数 (n,l,ml,ms)可能取的值为 (A)(3,2,1,-1/2)。 (B)(2,0,0,1/2)。 (C)(2,1,-1,-1/2)。 (D)(1,0,0,1/2)。
固体物理 第五章 固体电子论基础2
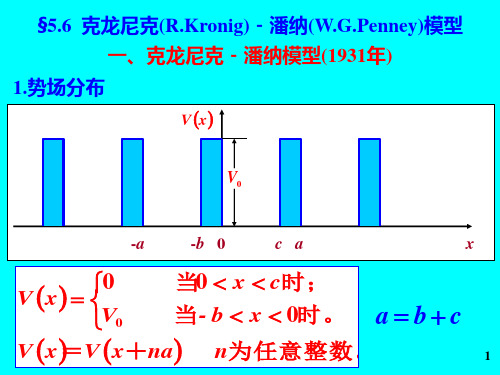
2
-a
-b 0
c a
d u du 2m 2 + ik 2 E - V - k u 0 2 2 dx dx
可得:
d 2u du 2 2 + ik - k u 0 2 2 dx dx
6
(2)特征方程为:
r 2 2ikr- 2 k 2 0 +
2.f(a)曲线
P f a sina cosa a
B0e
u x na Ane
i -k x na
Bne
-i k x na
9
u x 是周期函数
u x u x na
A0e
i -k x
B0e
-i k x -i k x na
ik e ik b
i -k e
i -k c
1
- i k e
-i k c
1
- -ik -e
- -ik b
- 1
ik
-e
ik b
- 1
0
i -k e i -k c -i k e-i k c - -ik e - -ik b
3 Vlim
b0
0
2ab
2
m m m lim 2 V0 - E ab lim 2 a bV0 - lim 2 abE V0 V0 V0 b 0 b 0 b0 m lim 2 a bV0 P bV0 保持有限值 V0 b 0
-ik x
D0e
- ik x
x 0
i -k A0 i k B0 -ik C0 ik D0 (2) - -
-a
-b 0
c a
d u du 2m 2 + ik 2 E - V - k u 0 2 2 dx dx
可得:
d 2u du 2 2 + ik - k u 0 2 2 dx dx
6
(2)特征方程为:
r 2 2ikr- 2 k 2 0 +
2.f(a)曲线
P f a sina cosa a
B0e
u x na Ane
i -k x na
Bne
-i k x na
9
u x 是周期函数
u x u x na
A0e
i -k x
B0e
-i k x -i k x na
ik e ik b
i -k e
i -k c
1
- i k e
-i k c
1
- -ik -e
- -ik b
- 1
ik
-e
ik b
- 1
0
i -k e i -k c -i k e-i k c - -ik e - -ik b
3 Vlim
b0
0
2ab
2
m m m lim 2 V0 - E ab lim 2 a bV0 - lim 2 abE V0 V0 V0 b 0 b 0 b0 m lim 2 a bV0 P bV0 保持有限值 V0 b 0
-ik x
D0e
- ik x
x 0
i -k A0 i k B0 -ik C0 ik D0 (2) - -
固体电子结构

BaO
2 2 135 140 3091 1923 3.3
3.2..3 离子极化
未极化的负离子
极化的负离子
离子的极化率(α): 描述离子本身变形性的物理量。 离子的极化力(f ): 描述一个离子对其他离子变形的影响能力。
1.离子的极化率(α ) 一般规律:
① 离子半径 r : r 愈大, α 愈大。
CsCl型
晶格:
简单立方
配位比: 8:8
(红球-Cs+ ,
绿球-Cl-)
晶胞中离子的个数: Cs Cl
:1个 -:8 1
1个
8
ZnS型(立方型)
晶格:面心立方
配位比:4:4 (红球-Zn2+ , 绿球-S2-) 晶胞中离子的个数: Zn2:4个
S2-:6 1 8 1 4个 28
r/pm 97
99
96
95
2.离子极化力(f ) 一般规律:
①离子半径 r :r 小者,极化力大。 ②离子电荷:电荷多者,极化力大。 ③离子的外层电子构型:
f :(18+2)e-,18e- > 9-17e- >8e当正负离子混合在一起时,着重考虑
正离子的极化力,负离子的极化率,但是 18e构型的正离子(Ag+, Cd2+ 等)也要考虑其 变形性。
上述数据代入上式求得:
△ rHm,6 =-689.1kJ·mol-1 则:U =689.1kJ·mol-1
2.Born-Lande公式
U KAZ1Z2 (1 1 )
R0
n
当 R0 以pm,U 以 kJ mol 1 为单位时,
U 138940 AZ1Z2 (1 1 ) kJ mol 1
固体电子论基础

• 边界条件:在势箱中运动的电子.
在 x 0 , 及 x L 处 , (1 x ) = 0 ( 驻 波 条 件 )
当 x 0 ,0 A x B x A x B x
当x
L,0
A x e ik x L
B e ik x L x
用 Ax B x代 入
0
A x e ik x L
A e ik x L x
A sin k x x sin k y y sin k z z
整理ppt
• 只剩下正弦项,余弦项为零.
• A为归一化常数,电子能量:
2
E
2m
(kx2
k
2 y
kz2 )(
h)
2
E
h2
8 2m
(nx2
ny2
nz2 )
2
L2
E
h2 8mL2
(nx2
ny2
nz2 )
粒子的状态由一组正整数(nx ,ny ,nz)来确定,
f(E) E1EF1,kB为 玻 尔 兹 曼 常 数 . ekBT
整理ppt
• E F 是费米能量,或者化学势. • 意义:体积不变的条件下,系统增加一个电子
所需要的自由能. • EF EF(T,N)是温度和电子数的函数. • 当 T0的时候,在EEF能级处,
1 f(EF)2
• 意义:表示在费米能级 E F ,被电子填充的几率 和不被电子填充的几率是相等的.
d Z 2 (2 L)3 d k 4 V C 3d k,L 3 V C :晶 体 体 积
整理ppt
• 自由电子能量:
E 2k 2 ,球 面 方 程 .微 分 得 : 2m
自由电子能量等于定植的球面半径
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
它与原坐标的关系: 哈密顿量可以消去交叉项:
2 2 1 2 H ( Pq q Qq ) 2 q
m iqna Qq (t ) ( t ) e n N n
该坐标体系下的总能量:
E(q )
1 (nq )q 2
以上结果说明:N个原子的集体振动可转化为N 个 独立的谐振子,谐振子的振动频率就是晶格的振动频 率。
§2.1 晶格振动和声子
首先考虑一维晶格的振动,然后把一些主要结论 和方法推广到三维晶格振动的分析和研究中去。
2.1.1 一维原子晶格的振动 1.运动方程
由一系列质量为 m的原子构成的一维原 子链,如图所示,其 平衡时原子间距为a。 用x n表示第n个原子 的位移,第n个原子和第n+1个原子的相对位移为
其解为
2n i q ( ) a t i qnat 2 Ae x2 n Ae 2n i q ( ) a qb t 2 i qnat Be x2 n 1 B ' e
上式代表角频率为ω 的简谐振动。其它各点的位 移按下列原则得出:
晶格振动波矢的数目=晶体原胞数
2.1.3 晶格振动量子化 声子
经典力学中,一维谐振子的 动能为: 势能为:
1 2 T mx 2
1 U m 2 x 2 2
在量子力学中,力学量 用算符表示,能量算符即 哈密顿算符。
解薛定谔方程 1 1 2 2 总能量为: E T U mx m x 可得到能量的本征值: 2 2 力学量连续取值
* 同种原子周围情况都相同,其振幅相同;原子不 同,其振幅不同。 * 相隔一个晶格常数a 的同种原子,位相差为qn。 把上式代入动力学方程,整理后得
B0 1 2 M A 1 2 e iqa 2 1 2 e A 1 2 m 0
在前面的讨论中没有考虑边界问题,认为一维晶体是无限的。但实 际晶体总是有限的,总存在边界,边界原子所处的情况与体内原子原子 不同,相应的振动状态也与体内原子不同。 设想一个有限晶体的长度为Na,对于一维有限的简单格子,第一个 原胞的原子核第N+1个原胞原子的振动情况相同,即
其中:
x 1 x N 1
1.5
晶体的结合
共价结合 金属性结合 范德华结合
பைடு நூலகம்
离子性结合
第二章
晶格振动和晶体的缺陷
在一般温度下,晶体内的粒子在各自平衡位置附 近振动。由于粒子间存在着相互作用力,因此,各 粒子的振动相互关联。 当振动很微弱时,粒子间非谐的相互作用可以忽 略,可近似地用简谐振动来处理,此时这些振动模 式是相互独立的。
按照上述方法,同样可以作出第二、第三、...布 里渊区。 布里渊区的边界由倒格 矢的垂直平分面构成。 第一布里渊区就是倒格 子原胞,其体积是一个倒 格点所占的体积,与倒格 子原胞的体积相等,即
b1 b 2 b 3
2
3
a1 a 2 a 3
2.1.2 周期性边界条件
1.氯化铯结构 2.氯化纳结构 3.金刚石结构 4.闪锌矿结构 5.密堆积结构
1.2晶列与晶面 倒格子
晶列指数(Index of Crystal Array)
晶面指数(Index of Lattice Plane)
1.2.3 倒格子
1.倒格子的定义
2.倒格矢与正格矢的关系
3.倒格矢与正格子晶面族的关系
d 2U dr 2 na
称为恢复力常数,或耦合常数。
除第n+1个原子外,原子n还受到第n-1个原子的 作用,其表达式为
f n,n 1 xn xn1
若仅考虑相邻原子的相互作用,则可以获得第 n 个原子所受到的总作用力,即
f n f n 1,n f n,n 1 ( xn 1 xn ) ( xn xn 1 ) ( xn 1 xn 1 2 xn )
例如:
热
格波在晶体中传播受到散射的过程可以理解为声子 同晶体中的原子的碰撞。
电
导电过程中电子遭受格波的散射,可以看作电子与声 子之间的碰撞。
光
光在晶体中的散射,很大程度上也可以看作是由于光 子与声子的相互作用乃至强烈的耦合。
§2.2 声学波与光学波
2.2.1 一维双原子晶格的振动
考虑由质量分别为M和m的两种不同原子所构成 的一维复式格子,如图所示。
这里的格波显然是平面简谐波, 如图所示。
格波的波长为 格波的波矢为
2 q
q
2
n
n是沿格波传播方向的单位矢量。
3. 色散关系
把上述解代入运动方程组中,可得
即
2
2 {1 cos(qa )} m
qa sin 2
一维晶格点阵的 第一布里渊区
xn1 xn
设在平衡位置 r na 时,两个原子间的相互作用势 能为 U (na), 产生相对位移后,相互作用势能变成 U (na ); 在平衡位置附近用泰勒级数展开,可得
1 d 2U 2 dU , U (na ) U (na) 2 dr na 2 dr na
相应的动力学方程为
d 2 x2 n 1 m 2 x2 n 2 x2 n 1 1 x2 n 1 x2 n 2 dt 2 M d x2 n x x x x 1 2 n 1 2n 2 2n 2 n 1 2 dt
式中第一项是常数,第二项为零(在平衡时势能取极 小值)。
当振动很微弱时,第n+1个原子对第n个原子的恢复 力近似为
dU d U f n1,n x x n 1 n 2 d dr na
2
这一近似成为简谐近似,式中
xm Ae
i ( qmat )
Ae
i ( qnat )
xn
即当第m个原子和第n个原子的距离满足时,
2s ma na q
原子因振动而产生的位移相等。 也就是说,原子震动随空间呈 周期性变化,空间周期λ=2π/q
晶体中所有原子共同参与的同一种频 率的振动,不同原子的振动位相随空间 呈周期性变化,这种振动以波的形式在 整个晶体中传播,称为格波。
b 设相邻两个不 同原子构成一个 B A a 分子,分子内两 原子平衡位置的间距为b,恢复力常数为β1 ;两分 子间两原子对应的恢复力常数为β2 。质量为 m 的 原子位于...2n-1,2n+1,2n+3...各点,质量为 M 的原子位于...2n-2,2n,2n+1...各点。
若只考虑相邻原子的相互作用,则第 2n+1 个原 子所受的恢复力为
1 2
2 m
如图所示,上式给出了 q和ω的色散关系,它说 明格波具有简正模式。
波矢具有简约的性质,可 将波矢限于一个周期范围。
q a a
4.布里渊区
从倒格子点阵的原点出发,作出它最近邻点的倒 格子点阵矢量,并作出每个矢量的垂直平分面,所 围成的具有最小体积的区域,称为第一布里渊区, 图所示。
晶格周期性条件决定了模式所取的能量值是分立 的。这些独立的、分立的振动模式,可以用一系列 独立的简谐振子——声子来描述。这样,晶格振动 的总体就可以看作是声子的系综。
晶格振动同晶体的许多宏观热学性质,如固体的 比热、热膨胀、热导等问题有密切的联系,对晶体 的电学、光学性质也有很大的影响。 在研究晶体的光学、电学等宏观性质时,由于晶 格振动对光子、电子和中子等都有散射作用,而引 入声子概念可以把上述散射当作声子与光子、电子 和中子的相互碰撞来处理。所以,在研究与晶格振 动有关的各种物理问题时,就变的非常形象直观。
可以用独立简谐振子的振动来表述格波的独立模 式,这就是声子的概念由来。
声子是晶格振动中的简谐振子的能量量子,声子 具有能量 、动量 q 。
声子只是反应晶体原子集体运动状态的激发单元, 它不能脱离固体而单独存在,不是一种粒子,是一种 准粒子。
引入声子概念,可使分析固体中的一系列微观过程 更加形象化。
(n=0,1,2…..)
即能量只能取一些分立值。
对于一维简单格子的情况,只考虑最紧邻粒子间的相互作用, 则晶体的势能为: 2 U (n 1 -n)
2
n
动能为:
1 n2 T m 2 n
势能函数包含有依赖于两原子坐标的交叉项,在处理多自由度的 振动问题时,往往引入新的坐标---正则坐标:
2 iqa
若A、B 有非零解,则其系数行列式必零,即
2 M 1 2
1 2 e iqa
1 2 e iqa
由此可以解得
0
2 m 1 2
1 2 1 2 16mM 1 2 2 2 2 qa sin m M m M 2 2mM 1 2 2
1.3晶体结构的对称性
晶系
1.3.1 物体的对称性与对称性操作 1.3.2 晶体的对称点群
1.3.3
晶系
1.三斜晶系 2.单斜晶系 3.正交晶系 4.四方晶系(又称正方晶系或四角晶系 ) 5.六方晶系 6.三角晶系 7.立方晶系
1.3.4 准晶系 1.4 确定晶体结构的方法
1.4.2 衍射方程 1.4.3反射公式 1.4.4 反射球
i ( qa t )
x1 A e
因此:
x N 1 A e
iqN a
i [ q ( n 1) a t ]
2 2 1 2 H ( Pq q Qq ) 2 q
m iqna Qq (t ) ( t ) e n N n
该坐标体系下的总能量:
E(q )
1 (nq )q 2
以上结果说明:N个原子的集体振动可转化为N 个 独立的谐振子,谐振子的振动频率就是晶格的振动频 率。
§2.1 晶格振动和声子
首先考虑一维晶格的振动,然后把一些主要结论 和方法推广到三维晶格振动的分析和研究中去。
2.1.1 一维原子晶格的振动 1.运动方程
由一系列质量为 m的原子构成的一维原 子链,如图所示,其 平衡时原子间距为a。 用x n表示第n个原子 的位移,第n个原子和第n+1个原子的相对位移为
其解为
2n i q ( ) a t i qnat 2 Ae x2 n Ae 2n i q ( ) a qb t 2 i qnat Be x2 n 1 B ' e
上式代表角频率为ω 的简谐振动。其它各点的位 移按下列原则得出:
晶格振动波矢的数目=晶体原胞数
2.1.3 晶格振动量子化 声子
经典力学中,一维谐振子的 动能为: 势能为:
1 2 T mx 2
1 U m 2 x 2 2
在量子力学中,力学量 用算符表示,能量算符即 哈密顿算符。
解薛定谔方程 1 1 2 2 总能量为: E T U mx m x 可得到能量的本征值: 2 2 力学量连续取值
* 同种原子周围情况都相同,其振幅相同;原子不 同,其振幅不同。 * 相隔一个晶格常数a 的同种原子,位相差为qn。 把上式代入动力学方程,整理后得
B0 1 2 M A 1 2 e iqa 2 1 2 e A 1 2 m 0
在前面的讨论中没有考虑边界问题,认为一维晶体是无限的。但实 际晶体总是有限的,总存在边界,边界原子所处的情况与体内原子原子 不同,相应的振动状态也与体内原子不同。 设想一个有限晶体的长度为Na,对于一维有限的简单格子,第一个 原胞的原子核第N+1个原胞原子的振动情况相同,即
其中:
x 1 x N 1
1.5
晶体的结合
共价结合 金属性结合 范德华结合
பைடு நூலகம்
离子性结合
第二章
晶格振动和晶体的缺陷
在一般温度下,晶体内的粒子在各自平衡位置附 近振动。由于粒子间存在着相互作用力,因此,各 粒子的振动相互关联。 当振动很微弱时,粒子间非谐的相互作用可以忽 略,可近似地用简谐振动来处理,此时这些振动模 式是相互独立的。
按照上述方法,同样可以作出第二、第三、...布 里渊区。 布里渊区的边界由倒格 矢的垂直平分面构成。 第一布里渊区就是倒格 子原胞,其体积是一个倒 格点所占的体积,与倒格 子原胞的体积相等,即
b1 b 2 b 3
2
3
a1 a 2 a 3
2.1.2 周期性边界条件
1.氯化铯结构 2.氯化纳结构 3.金刚石结构 4.闪锌矿结构 5.密堆积结构
1.2晶列与晶面 倒格子
晶列指数(Index of Crystal Array)
晶面指数(Index of Lattice Plane)
1.2.3 倒格子
1.倒格子的定义
2.倒格矢与正格矢的关系
3.倒格矢与正格子晶面族的关系
d 2U dr 2 na
称为恢复力常数,或耦合常数。
除第n+1个原子外,原子n还受到第n-1个原子的 作用,其表达式为
f n,n 1 xn xn1
若仅考虑相邻原子的相互作用,则可以获得第 n 个原子所受到的总作用力,即
f n f n 1,n f n,n 1 ( xn 1 xn ) ( xn xn 1 ) ( xn 1 xn 1 2 xn )
例如:
热
格波在晶体中传播受到散射的过程可以理解为声子 同晶体中的原子的碰撞。
电
导电过程中电子遭受格波的散射,可以看作电子与声 子之间的碰撞。
光
光在晶体中的散射,很大程度上也可以看作是由于光 子与声子的相互作用乃至强烈的耦合。
§2.2 声学波与光学波
2.2.1 一维双原子晶格的振动
考虑由质量分别为M和m的两种不同原子所构成 的一维复式格子,如图所示。
这里的格波显然是平面简谐波, 如图所示。
格波的波长为 格波的波矢为
2 q
q
2
n
n是沿格波传播方向的单位矢量。
3. 色散关系
把上述解代入运动方程组中,可得
即
2
2 {1 cos(qa )} m
qa sin 2
一维晶格点阵的 第一布里渊区
xn1 xn
设在平衡位置 r na 时,两个原子间的相互作用势 能为 U (na), 产生相对位移后,相互作用势能变成 U (na ); 在平衡位置附近用泰勒级数展开,可得
1 d 2U 2 dU , U (na ) U (na) 2 dr na 2 dr na
相应的动力学方程为
d 2 x2 n 1 m 2 x2 n 2 x2 n 1 1 x2 n 1 x2 n 2 dt 2 M d x2 n x x x x 1 2 n 1 2n 2 2n 2 n 1 2 dt
式中第一项是常数,第二项为零(在平衡时势能取极 小值)。
当振动很微弱时,第n+1个原子对第n个原子的恢复 力近似为
dU d U f n1,n x x n 1 n 2 d dr na
2
这一近似成为简谐近似,式中
xm Ae
i ( qmat )
Ae
i ( qnat )
xn
即当第m个原子和第n个原子的距离满足时,
2s ma na q
原子因振动而产生的位移相等。 也就是说,原子震动随空间呈 周期性变化,空间周期λ=2π/q
晶体中所有原子共同参与的同一种频 率的振动,不同原子的振动位相随空间 呈周期性变化,这种振动以波的形式在 整个晶体中传播,称为格波。
b 设相邻两个不 同原子构成一个 B A a 分子,分子内两 原子平衡位置的间距为b,恢复力常数为β1 ;两分 子间两原子对应的恢复力常数为β2 。质量为 m 的 原子位于...2n-1,2n+1,2n+3...各点,质量为 M 的原子位于...2n-2,2n,2n+1...各点。
若只考虑相邻原子的相互作用,则第 2n+1 个原 子所受的恢复力为
1 2
2 m
如图所示,上式给出了 q和ω的色散关系,它说 明格波具有简正模式。
波矢具有简约的性质,可 将波矢限于一个周期范围。
q a a
4.布里渊区
从倒格子点阵的原点出发,作出它最近邻点的倒 格子点阵矢量,并作出每个矢量的垂直平分面,所 围成的具有最小体积的区域,称为第一布里渊区, 图所示。
晶格周期性条件决定了模式所取的能量值是分立 的。这些独立的、分立的振动模式,可以用一系列 独立的简谐振子——声子来描述。这样,晶格振动 的总体就可以看作是声子的系综。
晶格振动同晶体的许多宏观热学性质,如固体的 比热、热膨胀、热导等问题有密切的联系,对晶体 的电学、光学性质也有很大的影响。 在研究晶体的光学、电学等宏观性质时,由于晶 格振动对光子、电子和中子等都有散射作用,而引 入声子概念可以把上述散射当作声子与光子、电子 和中子的相互碰撞来处理。所以,在研究与晶格振 动有关的各种物理问题时,就变的非常形象直观。
可以用独立简谐振子的振动来表述格波的独立模 式,这就是声子的概念由来。
声子是晶格振动中的简谐振子的能量量子,声子 具有能量 、动量 q 。
声子只是反应晶体原子集体运动状态的激发单元, 它不能脱离固体而单独存在,不是一种粒子,是一种 准粒子。
引入声子概念,可使分析固体中的一系列微观过程 更加形象化。
(n=0,1,2…..)
即能量只能取一些分立值。
对于一维简单格子的情况,只考虑最紧邻粒子间的相互作用, 则晶体的势能为: 2 U (n 1 -n)
2
n
动能为:
1 n2 T m 2 n
势能函数包含有依赖于两原子坐标的交叉项,在处理多自由度的 振动问题时,往往引入新的坐标---正则坐标:
2 iqa
若A、B 有非零解,则其系数行列式必零,即
2 M 1 2
1 2 e iqa
1 2 e iqa
由此可以解得
0
2 m 1 2
1 2 1 2 16mM 1 2 2 2 2 qa sin m M m M 2 2mM 1 2 2
1.3晶体结构的对称性
晶系
1.3.1 物体的对称性与对称性操作 1.3.2 晶体的对称点群
1.3.3
晶系
1.三斜晶系 2.单斜晶系 3.正交晶系 4.四方晶系(又称正方晶系或四角晶系 ) 5.六方晶系 6.三角晶系 7.立方晶系
1.3.4 准晶系 1.4 确定晶体结构的方法
1.4.2 衍射方程 1.4.3反射公式 1.4.4 反射球
i ( qa t )
x1 A e
因此:
x N 1 A e
iqN a
i [ q ( n 1) a t ]
