L16_17-能带论4
合集下载
能带理论——精选推荐
能带理论能带理论摘要阐述了能带理论提出的背景以及假设条件，在此基础上，主要给出了两个模型：近⾃由电⼦近似模型、紧束缚近似模型。
两者的假设不同，近⾃由近似模型认为价电⼦近似⾃由，晶体的周期性势场微扰很⼩；紧束缚近似模型认为电⼦受到原⼦核作⽤⽐较强，将其他原⼦的作⽤看做微扰。
两者共同基础是周期性势场中电⼦共有化运动，由两种模型研究电⼦的运动状态得出同⼀结论--能带。
在能带理论的基础上，定性的解释了绝缘体、半导体和导体。
Abstract This paper expounds the background and hypothesis of the theory of band theory,on the basis of it,two models are given:Near-free electron approximation model,tight-binding approximation model.Their assumptions are different,The near -free approximation model considers that the valence electrons are approximately free and the periodic potential of the crystal is very small;The tight-binding approximation model considers electrons are strongly affected by the nucleus,The role of other atoms as perturbation.The common basis of them is the electron co movement in the periodic potential field,It is concluded that the two models can be used to study the motion of electrons. On the basis of band theory, the properties of insulator, semiconductor and conductor are explained qualitatively.概述（背景、出发点）能带理论是讨论晶体（包括⾦属、绝缘体和半导体的晶体）中电⼦的状态及其运动的⼀种重要的近似理论。
能带理论
间的相互作用实现的。当 若干个原子相互靠近时，由于彼此之间的力的作用，原子 原有能级发生分裂，由一条变成多条。组成一条能带的众 多能级间隔很小，故可近似看成连续。 • 固体的导电性能由其能带结构决定。对一价金属，价带是 未满带，故能导电。对二价金属，价带是满带，但禁带宽 度为零，价带与较高的空带相交叠，满带中的电子能占据 空带，因而也能导电，绝缘体和半导体的能带结构相似， 价带为满带，价带与空带间存在禁带。半导体的禁带宽度 从0.1～4电子伏，绝缘体的禁带宽度从4～7电子伏。在任 何温度下，由于热运动，满带中的电子总会有一些具有足 够的能量激发到空带中，使之成为导带。由于绝缘体的禁 带宽度较大，常温下从满带激发到空带的电子数微不足道， 宏观上表现为导电性能差。半导体的禁带宽度较小，满带 中的电子只需较小能量就能激发到空带中，宏观上表现为 有较大的电导率。
•
形成简单分子时，便形成了分立的分子轨道，当原子形 成晶体时，便形成了分立的能带为阐明金属键的特性，化 学家们在MO（Molecular Orbit）理论的基础上，提出了 能带理论。现仅以金属Li为例定性讨论。 • Li原子核外电子为 1s2s。两个Li互相靠近形成Li2分 子。按照MO理论，Li分子应有四个MO。其中(σ1s)2与 (σ1s*)2的能量低，紧靠在Li是空着的(LUMO)。参与成键 的Li原子越多，由于晶格结点上不同距离的Li核对它们的 价电子有不同程度的作用力，导致电子能级发生分裂，而 且能级差也越来越小，能级越来越密，最终形成一个几乎 是连成一片的且具有一定的上、下限的能级，这就是能带。 对于N个Li原子的体系，由于1s与2s之间能量差异较大， 便出现了两条互不重叠或交盖的能带。这种具有未被占满 的MO的能带由于电子很容易从占有MO激发进入空的MO， 故而使Li呈现良好的导电性能。此种能带称为导带。在满 带与导带之间不再存在任何能级，是电子禁止区，称为禁 带。电子不易从满带逾越此空隙区进入导带。
•
形成简单分子时，便形成了分立的分子轨道，当原子形 成晶体时，便形成了分立的能带为阐明金属键的特性，化 学家们在MO（Molecular Orbit）理论的基础上，提出了 能带理论。现仅以金属Li为例定性讨论。 • Li原子核外电子为 1s2s。两个Li互相靠近形成Li2分 子。按照MO理论，Li分子应有四个MO。其中(σ1s)2与 (σ1s*)2的能量低，紧靠在Li是空着的(LUMO)。参与成键 的Li原子越多，由于晶格结点上不同距离的Li核对它们的 价电子有不同程度的作用力，导致电子能级发生分裂，而 且能级差也越来越小，能级越来越密，最终形成一个几乎 是连成一片的且具有一定的上、下限的能级，这就是能带。 对于N个Li原子的体系，由于1s与2s之间能量差异较大， 便出现了两条互不重叠或交盖的能带。这种具有未被占满 的MO的能带由于电子很容易从占有MO激发进入空的MO， 故而使Li呈现良好的导电性能。此种能带称为导带。在满 带与导带之间不再存在任何能级，是电子禁止区，称为禁 带。电子不易从满带逾越此空隙区进入导带。
SSP第4章能带论4_近自由近似-1
4.3 近自由电子近似
4.3.3 结果讨论
1、当波矢远离布里渊区边界时
k’= - k 2 即当 k ' k，且 k k ' nG -/a a 2 因 k k' n G， 有 H 'kk' H 'k 'k 0， a 因 k ' k， 有 E 0k E 0k '
G k
0
/a
k
波矢落在布 里渊区边界
因 k ' k， 有 E 0k E 0k ' 1 1 0 0 0 0 2 所以 E ( E k E k ' ) ((E k E k ' ) 4H 'kk' H 'k 'k ) 2 2 1 0 2 12 0 ( E k E k ) (4Vn ) 2 E 0 k Vn E E 0 k Vn 可见，在布里渊区边界 上能量发生劈裂， 0 E E k Vn 产生能隙 E， E E E 2Vn
E E 0 k Vn 0 E E k Vn 产生能隙 E E E E 2Vn
7
a
n，能量分成二支
4.3 近自由电子近似
4.3.5 能隙产生原因的解释
自由电子平面波在晶体中，如 X 射线传播；当波矢 k = n/a，即落 在布里渊区边界上，其波长 = 2/k = 2a/n，或 n = 2a，恰 为布拉格定律 (2d sin = n) 中 = 900 的全反射情形。 反射波和入射波干涉，形成驻 波，改变电子云分布；一 部分在离子实间区域，另 一部分在离子实周区域。
2
2Tn 2 2 Vn
2
)
4.3.3 结果讨论
1、当波矢远离布里渊区边界时
k’= - k 2 即当 k ' k，且 k k ' nG -/a a 2 因 k k' n G， 有 H 'kk' H 'k 'k 0， a 因 k ' k， 有 E 0k E 0k '
G k
0
/a
k
波矢落在布 里渊区边界
因 k ' k， 有 E 0k E 0k ' 1 1 0 0 0 0 2 所以 E ( E k E k ' ) ((E k E k ' ) 4H 'kk' H 'k 'k ) 2 2 1 0 2 12 0 ( E k E k ) (4Vn ) 2 E 0 k Vn E E 0 k Vn 可见，在布里渊区边界 上能量发生劈裂， 0 E E k Vn 产生能隙 E， E E E 2Vn
E E 0 k Vn 0 E E k Vn 产生能隙 E E E E 2Vn
7
a
n，能量分成二支
4.3 近自由电子近似
4.3.5 能隙产生原因的解释
自由电子平面波在晶体中，如 X 射线传播；当波矢 k = n/a，即落 在布里渊区边界上，其波长 = 2/k = 2a/n，或 n = 2a，恰 为布拉格定律 (2d sin = n) 中 = 900 的全反射情形。 反射波和入射波干涉，形成驻 波，改变电子云分布；一 部分在离子实间区域，另 一部分在离子实周区域。
2
2Tn 2 2 Vn
2
)
能带理论
(
K r
),
其中
K k 为电子波矢，
K Rn
=
K n1a1
+
K n2a2
+
K n3a3
是格矢。
根据布洛赫定理波函数写成如下形式：
ψ
K (r
)
=
eikK⋅rG
K u(r
),
G
其中u(r )具有与晶u格(rK一+样RK的n周) =期u性(rG，)即
首都师范大学物理系
ψ
K (r
K
u(r
)
=KeikK⋅rG
G
对于自由电子 hk为动量，但对于晶体中的布洛赫电子，hk 不
是真实动量。在研究晶体在外场作用下运动及电子与声子、
光子的相G互作用时, 它在形式上又好像起到动量的作用, 所 以又称 hk 为布洛赫电子的准动量或电子的晶体动量。
首都师范大学物理系
下面我们证明
ψ
G k
K (r )
=
ψ
G k+
K Kn
K (r )
N1 N2
K
K
N3
K
引入矢量 k = l 1 b 1 + l 2 b 2 + l 3 b 3
N1
N2
N3
首都师范大学物理系
式中
KKK b1、b2、b3为晶格三个倒格基矢，由于
K ai
⋅
K bj
= 2πδij
,
KK
λ ( Rn ) = eik⋅Rn
ψ
K (r
+
K Rn
)
=
KK
ψ eik ⋅Rn
K (r )
首都师范大学物理系
能带论计算方法简介
a
8
3、哈特利-福克近似
通过绝热近似，把电子的运动和原子核的运动分开，得到了多电子薛定谔方程：
引入哈特利波函数 ： 通过哈特利-福克自洽场近似方法，将多电子的薛定谔方程简化为单电子有效势方程：
在哈特利-福克近似中，已包含了电子与电子的交换相互作用，但自旋反平行电子间的排 斥相互作用没有被考虑：在 r 处已占据了一个电子，那么在r’处的电子数密度就不再是 p(r’) 而 应该减去一点；或者说，再加上一点带正电的关联空穴，即还需考虑电子关联相互作用。
在弱周期场近似中，波函数由平面波叠加而成，要使波函数在离子实附近有振荡的特 点，平面波的展开式中要有较多的频率成分，因而收敛很慢，所以平面波方法计算固体能 带实际计算难以进行。
1940年 Herring 提出了OPW方法，取波函数为平面波和紧束缚波函数的线性组合， 并要求与离子实不同壳层紧束缚波函数正交，从而自然地兼顾了波函数在离子实附近以及 在离子之间应有的特征，求解时，往往只需要取几个正交平 面波，结果就很好了。
a
9
4、交换关联泛函的简化
在 Hohenberg-Kohn-Sham 方程的框架下，多电子系统基态特性问题能在形式上转化成有效单 电子问题。该计算方案只有在找出交换关联势能泛函的准确的、便于表达的形式才有意义。
在具体计算中常用 W.Kohn 和 L.J.Sham 提出的交换关联泛函局域密度近似是一个简单可行而又 富有实效的近似。其基本思想是在局域密度近似中，可利用均匀电子气密度函数来得到非均匀电 子气的交换关联泛函。
方法上的简化使大分子系统的研究成可能，酶反应机制的理论计算就是其中典型的实例， 如今，密度泛函方法已经成为量子化学中应用最广泛的计算方法，因此沃尔特·科恩获得了 1998年诺贝奖。
能带理论基础
§2 Bloch定理
1、周期场模型 考虑一理想完整晶体，所有的原子实都周期性地静 止排列在其平衡位置上，每一个电子都处在除其自身外 其他电子的平均势场和原子实的势场中运动。按照周期 场近似，电子所感受到的势场具有周期性。这样的模型 称为周期场模型。
2、Bloch定理 ① 表述： 在周期场中，描述电子运动的Schrödinger方程为
晶体中电子： ψ k ( r ) = eik⋅r uk ( r ) 自由电子： 孤立原子：
ψ k ( r ) = Ae ik ⋅r
ψ ( r ) = Cu ( r )
可以看出，在晶体中运动电子的波函数介于自由电子 与孤立原子之间，是两者的组合。如果晶体中电子的 运动完全自由，则 uk ( r ) = A = const. ；若电子完全 被束缚在某个原子周围，则 eik⋅r = C = const. 。 但实际上晶体中的电子既不是完全自由的，也不是完 全被束缚在某个原子周围，因此，其波函数就具有 ψ k ( r ) = eik⋅r uk ( r ) 的形式。周期函数的性质 uk ( r ) 就反映了电子与晶格相互作用的强弱。
∴ψ ( r + Rl ) = eik⋅Rlψ ( r )
（4）定义一个新函数：
= exp ⎡ik ⋅ ( l1a1 + l 2 a2 + l 3a3 )⎤ψ ( r ) ⎣ ⎦
l1 l 2 l 3 1 2 3
l1 1
l2 2
l3 3
uk ( r ) = e
− ik ⋅r
ψ k (r )
uk ( r + Rl ) = e
− ik ⋅( r + Rl )
ψ k ( r + Rl )
=e
4能带理论
* i
2
r r j = env = σ E
• 以自由电子近似为例 • 将自由空间坐标转化为k空 间坐标 • 能量－动量关系 • 经典物理量的关系 • 基本物理量 能量，动量，力，速度， 有效质量
能带与导电特性
• 金属、绝缘体、半导体 • 倒格子周期性与热平衡两 种作用 • 满带电子不参与导电 • 不满带参与导电
• 赝势的选取
赝势选取不得改变离子实之间 的区域的波函数，也不改变能 量本征值。它反映离子实的吸 引作用和波函数正交要求。
• 赝势的计算结果
由赝势求出的波函数称为赝势 波函数。
锗能带图
三种计算方法比较
原子能级与晶体能带
h2k 2 Ek = V + 2m
r h r h r h r k = 1 b1 + 2 b2 + 3 b3 N1 N2 N3
ϕ k0 '
2
E k( 2 ) = r Gn
E k0 − E k0 ' r 1 r k + G n = 0 (? ) 2
k'
∑
k ' ∆V k
• 自由电子近似 势函数为常数 • 微扰理论应用 收敛要求 • 构建能带图
锗能带图
能带计算：紧束缚近似
1 ϕk =
∑
k'
k ' ∆V k E
k k
• 势函数也是周期函数 • 布洛赫波函数是平面波 与周期函数的乘积，晶 体周期性在波函数中的 反映 • 证明（略） • k 取值范围是由周期性 边界条件确定 • 周期条件体现在布里渊 区边界 • 波函数的形式是傅立叶 展开的形式，也可以认 为是平面波的叠加
能带计算：自由电子近似
2
r r j = env = σ E
• 以自由电子近似为例 • 将自由空间坐标转化为k空 间坐标 • 能量－动量关系 • 经典物理量的关系 • 基本物理量 能量，动量，力，速度， 有效质量
能带与导电特性
• 金属、绝缘体、半导体 • 倒格子周期性与热平衡两 种作用 • 满带电子不参与导电 • 不满带参与导电
• 赝势的选取
赝势选取不得改变离子实之间 的区域的波函数，也不改变能 量本征值。它反映离子实的吸 引作用和波函数正交要求。
• 赝势的计算结果
由赝势求出的波函数称为赝势 波函数。
锗能带图
三种计算方法比较
原子能级与晶体能带
h2k 2 Ek = V + 2m
r h r h r h r k = 1 b1 + 2 b2 + 3 b3 N1 N2 N3
ϕ k0 '
2
E k( 2 ) = r Gn
E k0 − E k0 ' r 1 r k + G n = 0 (? ) 2
k'
∑
k ' ∆V k
• 自由电子近似 势函数为常数 • 微扰理论应用 收敛要求 • 构建能带图
锗能带图
能带计算：紧束缚近似
1 ϕk =
∑
k'
k ' ∆V k E
k k
• 势函数也是周期函数 • 布洛赫波函数是平面波 与周期函数的乘积，晶 体周期性在波函数中的 反映 • 证明（略） • k 取值范围是由周期性 边界条件确定 • 周期条件体现在布里渊 区边界 • 波函数的形式是傅立叶 展开的形式，也可以认 为是平面波的叠加
能带计算：自由电子近似
第四章 能带理论
原子轨道线性组合法
（LCAO）
一、紧束缚近似处理方法
1 ）紧束缚近似方法的思想：电子在一个原子（格 点）附近时，主要受到该原子势场的作用，将其它 原子（格点）势场的作用看作微扰，并利用简并微 扰法，求出电子的原子能级与晶体中能带之间的相 互联系。 V(r－Rm)：Rm格点的原子势场， U(r)为晶体的周期性 势场，是所有原子的 势场之和。
第一部分：波数为k的行进平面波。 第二部分：该平面波受周期场的影响而产生的散射 波。
3. 几种晶格的布里渊区
1) 简单立方格子 —— 倒格子 简单立方格子 简单立方格子第一布里渊区为：原点和6 个 近邻格点的垂直平分面围成的立方体。
2) 体心立方格子 ——倒格子为面心立方格子
体心立方格子第一布里渊区为：原点和12 个近 邻格点连线的垂直平分面围成的正十二面体。
2 2 V r r E r 2m
V (r ) V (r Rn )
2
一、Bloch定理（1928年） 描述电子运动的Schrö dinger方程为
为周期性势场， R n 为任意格矢 V (r ) V (r Rn )
方程的解具有性质： r Rn eik Rn r
2 2 2m V r r E r
k为一矢量 Rn 时，波函数只增加了位 表明当平移晶格矢量 相因子 eik Rn 。 ——布洛赫定理
rRm
0
微扰以后电子的运动状态
微扰以后的状态用N 个简并态（原子轨道波函 数 i r Rm ）的线性组合构成晶体中电子共 有化运动的波函数： r ami r Rm
（LCAO）
一、紧束缚近似处理方法
1 ）紧束缚近似方法的思想：电子在一个原子（格 点）附近时，主要受到该原子势场的作用，将其它 原子（格点）势场的作用看作微扰，并利用简并微 扰法，求出电子的原子能级与晶体中能带之间的相 互联系。 V(r－Rm)：Rm格点的原子势场， U(r)为晶体的周期性 势场，是所有原子的 势场之和。
第一部分：波数为k的行进平面波。 第二部分：该平面波受周期场的影响而产生的散射 波。
3. 几种晶格的布里渊区
1) 简单立方格子 —— 倒格子 简单立方格子 简单立方格子第一布里渊区为：原点和6 个 近邻格点的垂直平分面围成的立方体。
2) 体心立方格子 ——倒格子为面心立方格子
体心立方格子第一布里渊区为：原点和12 个近 邻格点连线的垂直平分面围成的正十二面体。
2 2 V r r E r 2m
V (r ) V (r Rn )
2
一、Bloch定理（1928年） 描述电子运动的Schrö dinger方程为
为周期性势场， R n 为任意格矢 V (r ) V (r Rn )
方程的解具有性质： r Rn eik Rn r
2 2 2m V r r E r
k为一矢量 Rn 时，波函数只增加了位 表明当平移晶格矢量 相因子 eik Rn 。 ——布洛赫定理
rRm
0
微扰以后电子的运动状态
微扰以后的状态用N 个简并态（原子轨道波函 数 i r Rm ）的线性组合构成晶体中电子共 有化运动的波函数： r ami r Rm
能带论4
数）。所以赝势法的基本精神是适当地选取一种平滑势，波
函数用少数平面波展开，就可以使计算出的能带结构与实际 晶体接近，赝势方法除去在能带计算上（Be,Na,K,Ge,Si 等 金属和半导体的能带）取得很大成功外，也从理论上回答了 尽管在晶体中电子和离子的相互作用很强，近自由电子模型 在很多情形下仍十分成功的原因。
这是一个近似图，并不准确。
r0 a 0
原胞法示意图
根据Bloch定理，方程的解为： k r e
ik r
uk r
其中表征周期部分的函数 u(r) 应该在原胞的两个对称点上 例如 p1和 p2 点上取值相同。 为了方便地处理周期性的要求， Wigner和Seitz用相同体积的WS球代替实际原胞，原胞内的势 场也看成球对称的，因而可以数值求解，在 k＝0 点得到的波
1937年Slater 从原胞法结果中发现晶体离子之间的广大 区域里，晶体势几乎没有变化，因此采用了一种特殊的势重 新求解。“muffin-tin” （糕模势）在离子实处就是自由离子 势，在离子实外面严格是一个常数（见下页图）。因此波函
数为在
r r0
时是平面波： k
1 V
e
ik r
,
而在 r r0 时，为原子波函数。r0 是离子实半径。后者可 以通过求解自由原子的薛定谔方程得到，边界条件是在离子 实的表面 r0 处和平面波连续衔接。
现在假定电子处在 A 原胞中，求解运动方程时，可以认 为它只受到此原胞中离子势场的影响，其它原胞中离子势场 对A原胞中电子的影响可以忽略不计。
2 U r 2m
2 k
r
E k
k
r
只要求出一个原胞中的波函数就可以把整个晶体的问题解决 了（平均地说，每个原胞都被另一个传导电子所占据，这些电 子往往有屏蔽离子的作用，从而强烈地消弱了离子势场。）
第四章-能带理论-(Band-Theory)
1
与利用平面波描写零级近似状态的近自由电子 近似不同, 紧束缚近似中首先把电子看作所属原子 的电子, 晶体环境对电子的影响则作为微扰处理.
不考虑原子间相互作用, 简单晶格格点 Rm 原子的电子
将以原子束缚态的形式运动, 其波函数i r Rm 满足方程:
2
2m
2
V
r Rm
i
r Rm
根据能量函数的对称性, 可以得到如下推论: 简 约BZ可以分成若干等价的小区域. 以立方晶体为例, Oh点群有48个对称操作, 则简约BZ可以分割成48个 等价区域, 只需讨论其中一个就可以得到全部. 这 1/48的体积称为RBZ的不可约体积.
21
根据量子力学中的结论, 若 k 是 S-E 的解, 则其复共
imjnmnijrrrrdr??????????????????3minmiminmarrurvrrrrdrea?????????????????????????3inmimnmrrurvrrrrdrjrr??????????????设
能带理论 - 3 （Band Theory）
近自由电子适用于价电子束缚较弱的金属晶体, 采用赝 势方法后也可以用来研究半导体的价带和导带；对于价电子 束缚较强的半导体和绝缘体, 通常采用紧束缚近似 (TightBinding Approximation, TBA) 来讨论其电子结构.
若干分离能量值, 对应于不同的能带; 对于给定的 n, 能量 是 k 的连续函数. 这种能量函数的表示方法称为 RBZ 图像.
RBZ 实际上是倒空间的原胞, 以它的形状为单元周期重 复排列可以充满整个 k 空间, 这些单元是完全等价的. 因此
有 En k En k Gn .
23
除了RBZ和PBZ图像, 还有一种EBZ图像, 其差别 如下：
与利用平面波描写零级近似状态的近自由电子 近似不同, 紧束缚近似中首先把电子看作所属原子 的电子, 晶体环境对电子的影响则作为微扰处理.
不考虑原子间相互作用, 简单晶格格点 Rm 原子的电子
将以原子束缚态的形式运动, 其波函数i r Rm 满足方程:
2
2m
2
V
r Rm
i
r Rm
根据能量函数的对称性, 可以得到如下推论: 简 约BZ可以分成若干等价的小区域. 以立方晶体为例, Oh点群有48个对称操作, 则简约BZ可以分割成48个 等价区域, 只需讨论其中一个就可以得到全部. 这 1/48的体积称为RBZ的不可约体积.
21
根据量子力学中的结论, 若 k 是 S-E 的解, 则其复共
imjnmnijrrrrdr??????????????????3minmiminmarrurvrrrrdrea?????????????????????????3inmimnmrrurvrrrrdrjrr??????????????设
能带理论 - 3 （Band Theory）
近自由电子适用于价电子束缚较弱的金属晶体, 采用赝 势方法后也可以用来研究半导体的价带和导带；对于价电子 束缚较强的半导体和绝缘体, 通常采用紧束缚近似 (TightBinding Approximation, TBA) 来讨论其电子结构.
若干分离能量值, 对应于不同的能带; 对于给定的 n, 能量 是 k 的连续函数. 这种能量函数的表示方法称为 RBZ 图像.
RBZ 实际上是倒空间的原胞, 以它的形状为单元周期重 复排列可以充满整个 k 空间, 这些单元是完全等价的. 因此
有 En k En k Gn .
23
除了RBZ和PBZ图像, 还有一种EBZ图像, 其差别 如下：
L16_17-能带论4
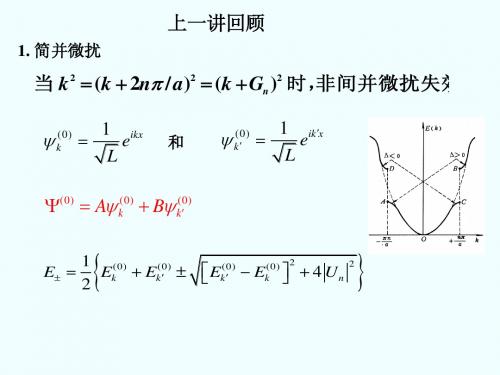
T H HT 0
若n,k(r)是晶体波动方程的解，那么，T() n,k(r) 也是方程的解，且n,k(r)与T() n,k(r)有相同的能量本 征值。
H n ,k
En k n ,k
T H n ,k
T En k n ,k
能带的平移对称性 En(k) 函 扩展布里渊区图象： 数 的 三 种 图 周期布里渊区图象： 象
En(k+G)=En(k)
简约布里渊区图象：
ⅢⅡ Ⅰ Ⅱ Ⅲ
k ( x) eikxuk ( x)
uk ( x) Bk Kh e
Kh
iKh x
, uk Km ( x) Bk Kh Km e
R s 近邻
交叠积分：
Rn R U V j d J R n R
j
例1：求简单立方晶体中由原子的s态所形成的能带 由于s态的原子波函数是球对称的，有
s J 0 2 J 1 cos k x a cos k y a cos k z a
能量的最高点和最低点？
在简单立方晶格的简约区中 点：k＝(0, 0, 0)
E s J 0 6 J1
X点：k＝(/a, 0, 0)
kz
R
M
E X s J 0 2 J1
将T()和H同时作用在任意函数f(r)上，
2 2 T Hf r T U r f r 2m r
半导体物理-能带论
能带论的三个基本假设
一、Born-Oppenheimer绝热近似 二、Hatree-Fock平均场近似 三、周期场近似（Periodic potential approximation）
Born-Oppenheimer绝热近似
绝热近似是考虑到轻粒子（电子）和 重粒子（离子）运动的差异。对于快速 运动的电子来说，离子的瞬间位置是重 要的。同时离子的运动不受电子的瞬间位置的影响 而只受它们的平均运动的影响。当应用于多电子的 原子时，这种论点就很容易理解。显然，由于离子 质量大，它不随电子的运动而运动，而只在整个电 子的平均场中运动。同时电子伴随着运动比较慢的 离子，从而原子保持完整。
关于Block 定理的几点讨论
k h h1 h b1 2 b2 3 b3 N1 N2 N3
若将k限制在简约区中取值，则称为简约波矢，若k在整 个k空间中取值，则称为广延波矢。由于h1，h2和h3为 整数，所以，k的取值不连续，在k空间中，k的取值构 成一个空间点阵，称为态空间点阵。每一个量子态k在k 空间中所占的体积为： 1 b 1 b 1 b b
N1
1
N2
2
N3
3
N
在k空间中，波矢k的分布密度为：
N va V k N 3 3 b 8 8
Born-Oppenheimer绝热近似
2 1 e / ˆ H 2 i , j 4 0 r i r j i 1 2m NZ 2 i NZ N 1 ( Ne) 2 Ze 2 / 2 M 2 i 1 i, j 4 0 R n R m i 1 n 1 4 0 r i R n N 2 n 2 2
关于Block 定理的几点讨论
对于k： eika ' 对于k’＝ k+Gn： eika eika eiGn a eika 这表明，这两个波矢量k和k’＝ k+Gn所描述的电子在晶 体中的运动状态相同。因此，为了使k和平移算符的本征 值一一对应， k必须限制在一定范围内，使之既能概括所 有不同的的取值，同时又没有两个波矢k相差一个倒格矢 Gn。与讨论晶格振动的情况相似，通常将k取在由各个倒 格矢的垂直平分面所围成的包含原点在内的最小封闭体积， 即简约区或第一布里渊区中。
能带理论
价带
∵由于能带少量重叠，
∴出现电子和空穴同时参与导电
又∵电子和空穴分属于不同的能带，它们具有不同的有效质量和速度
∴它们对电流的贡献不同
当空穴对电流的贡献起主要作用
导带
— 空穴导电型导体
空带
当电子对电流的贡献起主要作用
— 电子导电型导体
价带
形式3：Na,K,Cu,Al,Ag 金属的价带本来就没有被电子填满，同时价带又同邻近的空带重 叠 —— 形成一个更宽的导带 实际参与导电的是那些未被填满的价带中的电子 —— 电子导电型导体
En k G En k
* n,k G
r
n,k
r
（3）考虑晶体弱周期场的微扰，近自由电子能谱， 在布里渊区边界（即k =±π/a, ±2π/a , ±3π/a,… 处发生能量跳变，产生宽度分别为 2|V1|, 2|V2| , 2|V3|… 的禁带
E k 2 k 2 2m
, 的 自由电子动能为区边中心点
a
E
a
k
2k 2
2m
的二倍 ,0
a
Ec 2 k 2 2m
2 2m
2
2 a
EA
2k 2
2m
2
1
2
2m a
ky
Ec / EA 2
C , a a
空带
导带
例如: 当 Na 原子结合成晶体时，3s 能带只填满了一半电子，而 3p 能带与 3s 能带相交错。这样在被电子填满的能级上面有很多空着的能级，所以电 场很容易将价电子激发到较高的能级上，因此 Na 是良导体
第四章能带理论
T T f (r ) T f (r a ) f (r a a ) T T f (r )
T T T T
性质2： TαTβ= Tα+β
T f ( r ) f ( r a a ) T T f ( r ) f ( r a a ) T T T
15
性质3：平移算符Tα与H互相对易
2 2 H r V (r ) 2m
HT ( r ) H( r a ) 2 2 ( r V ( r )) ( r a ) 2m 2 2 ( r a V ( r a )) ( r a ) 2m H ( r a ) ( r a ) H ( r ) Ta
故晶体势场对电子运动的影 响看作微扰处理。 近自由电子近似
紧束缚近似
6
能带理论基本思想
理想晶体 具有周期性的晶格结构，因而等效势场V(r)也应具有周期性。 晶体中的电子 是在一个具有晶格周期性的等效势场中运动，其波动方 程为（即单电子薛定谔方程）：
2 2 V r E 2m 其 中V r V r Rn , Rn为 晶 格 平 移 矢 量 。
布洛赫定理
——1928 年布洛赫提出
一、定理内容：晶格具有平移对称性的单 电子哈密顿
2 2 H V (r ) 2m
的本征函数 ( r )可表示为
ik r (r ) e u(r )
其中
u(r ) u(r R) ，k 为简约波矢。
（2）定理证明。
13
（1）平移算符Tα及其性质
定义：平移算符Tα对于任意函数，都有：
T T T T
性质2： TαTβ= Tα+β
T f ( r ) f ( r a a ) T T f ( r ) f ( r a a ) T T T
15
性质3：平移算符Tα与H互相对易
2 2 H r V (r ) 2m
HT ( r ) H( r a ) 2 2 ( r V ( r )) ( r a ) 2m 2 2 ( r a V ( r a )) ( r a ) 2m H ( r a ) ( r a ) H ( r ) Ta
故晶体势场对电子运动的影 响看作微扰处理。 近自由电子近似
紧束缚近似
6
能带理论基本思想
理想晶体 具有周期性的晶格结构，因而等效势场V(r)也应具有周期性。 晶体中的电子 是在一个具有晶格周期性的等效势场中运动，其波动方 程为（即单电子薛定谔方程）：
2 2 V r E 2m 其 中V r V r Rn , Rn为 晶 格 平 移 矢 量 。
布洛赫定理
——1928 年布洛赫提出
一、定理内容：晶格具有平移对称性的单 电子哈密顿
2 2 H V (r ) 2m
的本征函数 ( r )可表示为
ik r (r ) e u(r )
其中
u(r ) u(r R) ，k 为简约波矢。
（2）定理证明。
13
（1）平移算符Tα及其性质
定义：平移算符Tα对于任意函数，都有：
2019星旅程l16-L17试题及答案
l16-171 . 在线值船有几个操作步骤（单选题）？C.4个正确2 . 皇家行前预订方式有哪些(多选题）？A.在线网站预订C.皇家微信公众号二维码D.电话预订正确3 . 大陆客人参加从香港出发的航次需要携带哪些有效证件（多选题）？A.有效的港澳通行证（含有效签注）B.香港过境来往另一个国家地区的中国护照（持有人）C.前往目的地的有效入境证件D.前往海外的续程车/船/机票正确4 . 建议携带轻便行李，重量上限为多少KG？（单选题）D.90KG正确5 . 到港登船流程，游客完成预定后最晚不得迟于登船日多少天完成？（单选题）A.3天前正确6 . 关于房间三/四人间的房间第三/四人的床是什么床？（单选题）B.沙发床正确7 . 游轮房卡（也成“船卡”）有哪些功能？（多选题）A.钥匙功能B.身份证明C.船上消费D.救生演习集合地点显示参加演习时出示房卡正确8 . 选项中，哪一项物品房间内不提供（单选题）？B.牙刷牙膏正确9 . 未成年人出行所需要的登船证明有哪些（多选题）？B.授权声明信C.随行监护人承诺D.未成年人出生证明影印本或户口本影印本正确10 . 下船离港流程，可优先下船有哪些类型的客人？（多选题）A.金色房卡套房贵宾D.坐轮椅游客与坐婴童车游客（均允许一名成年游客陪同）正确继续学习皇家加勒比国际游轮法律声明| 隐私政策| 邮轮业乘客权利法案| 上海工商皇家加勒比游轮船务（中国）有限公司版权所有限公司版权所有沪公网安备3102210201 . 哪一项不是包含在可订产品中？C.超凡住宿正确2 . 2019年“海洋光谱号”每个航次至登船日前多少小时均可进行预订?B.48正确3 . 请务必确保您的护照在航次结束后还有多少个月及以上的有效期?D.6正确4 . 登船凭证通过什么渠道打印纸质登船证?A.在线值船正确5 . APEC 商务旅行卡游客:是指持卡人凭有效护照和旅行卡在多少年内无须办理入境签证,可自由往来于,已批准入境的各APEC 经济体之间,以便利APEC 范围内各经济体的商务人员往来？C.3正确6 . 从港铁机场站乘机场快线到港铁哪个站，需时约30分钟，再转乘出租车，车程约20分钟即到达启德游轮码头。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
s J 0 2 J 1 cos k x a cos k y a cos k z a
能量的最高点和最低点？
在简单立方晶格的简约区中 点：k＝(0, 0, 0)
E s J 0 6 J1
X点：k＝(/a, 0, 0)
kz
R
M
E X s J 0 2 J1
J R s J1
Rs 近邻格矢
对于简单立方：
Rs＝(a, 0, 0), (0, a, 0), (0, 0, a)
a
a
ik a ik a E k s J 0 J 1 eikxa e ikxa e y e y eikza e ikza
上一讲回顾
1. 简并微扰
当 k 2 (k 2n / a)2 (k Gn )2 时， 非间并微扰失效
(0) k
1 ikx e L
和
(0) k
1 ik x e L
(0) A k(0) B k(0)
1 (0) (0) (0) (0) 2 E Ek Ek Ek Ek 4 U n 2
(a)
2 d 2 d [ ( 2 2ik k 2 ) V ( x )]u k ( x ) E (k )u k ( x ) (b) 2m d x dx
方程(a)和方程(b)中哈密顿量完全相同，因此其能量本征值 也相同，即En(k)=En(-k) ，能带具有反演对称性。同时还有
* * uk ( x) uk ( x), k ( x) k ( x)
T H HT 0
若n,k(r)是晶体波动方程的解，那么，T() n,k(r) 也是方程的解，且n,k(r)与T() n,k(r)有相同的能量本 征值。
H n ,k
En k n ,k
T H n ,k
T En k n ,k
i k r r T e un ,k r i k 1 r 1 e un ,k r ik r ' e u'n ,k ( r ) n ,k ( r ) n ,k ( r )
R s 近邻
交叠积分：
Rn R U V j d J R n R
j
例1：求简单立方晶体中由原子的s态所形成的能带 由于s态的原子波函数是球对称的，有
这表明，用T()作用在Bloch函数的结果只是将简约波矢k 变换到另一个简约波矢k。
HT ( ) n ,k ( r ) H n ,k ( r ) En (k ) n ,k ( r )
HT n ,k
E ( k ) (r ) En k T n ,k n n ,k
由于是正交变换，
由于 un ,k
1 k r k r
r 仍以格矢Rl为周期， 可以改写为
1
A B = A B
un , k
r
更准确和详细的推导参看PLA308,116(2003); PRB67,155114 (2003)
一、 En(k)函数的对称性
能带的点群对称性 En(αk)=En(k)
晶体点群对称操作的算符T()，物理意义：对于任意函 数f(r)，有
1 T f r f r
2
其中，－1是的逆操作，其定义为－1 r点经操作后变 换到r点。晶体中电子运动的哈密顿量为：
2 H U r 2m r
R点：k＝(/a, /a, /a) kx
X
ky
E R s J 0 6J1
由于s态波函数是偶宇称，s(r)= s(-r)， 所以，在 近邻重叠积分中波函数的贡献为正，即J1 > 0 。
点：能带底；R点：能带顶
能带宽度： E E R E 12J1
k ( x) eikxuk ( x) 由布洛赫定理：
取k态薛定谔方程的复共轭：
H [e ikxuk * ( x)] E (k )e ikxuk * ( x)
-k态的薛定谔方程：
H [e ikxu k ( x)] E (k )e ikxu k ( x)
2 d 2 d * * [ ( 2 2ik k 2 ) V ( x )]uk ( x ) E (k )uk ( x ) 2m d x dx
V ( x ) V ( x a ) V (Gn ) expiGn x
n
k ( x ) e ikx uk (Gn )e iG x
n
Gn
本征方程： Au 2u
Aln V '(Gl Gn ) (k Gn )2 l ,n
2
uk (G1 ) uk u (G ) k N
px k py k
C e
i k R i k R
p
x
{
C e
p p
y
kp C e
z
i k R
z
r R r R
r R
由于p轨道不是球对称的，因此，沿不同方向的近邻 重叠积分J(Rs)不完全相同。如 px ：电子主要集中在x轴
HT n ,k
En k T n ,k
在晶体中电子运动的本征态波函数为Bloch函数
n ,k
i k r r e un ,k r
n：能带标记，k：简约波矢，对应的能量本征值：En(k)
T n ,k
将T()和H同时作用在任意函数f(r)上，
2 2 T Hf r T U r f r 2m r
2 2 1 U r 2m 2 2 U r 2m r
在某些情况下还可能出现不同原子态的相互作用。如： Si的价带与导带。
反键态 3p sp3 3s 导带
成键态
价带
紧束缚近似对原子的内层电子是相当好的近似，它还可用 来近似地描述过渡金属的d带、类金刚石晶体以及惰性元
素晶体的价带。紧束缚近似是定量计算绝缘体、化合物及
半导体特性的有效工具。
§4.6 晶体能带的对称性
能带的平移对称性 En(k) 函 扩展布里渊区图象： 数 的 三 种 图 周期布里渊区图象： 象
En(k+G)=En(k)
简约布里渊区图象：
ⅢⅡ Ⅰ Ⅱ Ⅲ
k ( x) eikxuk ( x)
uk ( x) Bk Kh e
Kh
iKh x
, uk Km ( x) Bk Kh Km e
对于p电子、d电子等，这些状态都是简并的，因此，其 Bloch函数应是孤立原子的有关状态波函数的线性组合。
例2：求简单立方晶体由原子的p态所形成的能带
原子的p态为三重简并，其原子轨道可表为
{
p xf r
x
p yf r
y
p zf r
z
在简单立方晶体中，三个p轨道各自形成一个能带，其波 函数是各自原子轨道的线性组合。
s
J0
}
12J1
原子的一个s能级在晶体中展宽为一个相应的能带，能
带宽度取决于J1，即近邻原子波函数的重叠积分。
原子的内层电子轨道半径较小，所形成的能带校窄； 而外层电子的轨道半径较大，所形成的能带较宽。 以上讨论仅适用于原子能级非简并，且原子波函数重叠 很少的情况，即适用于原子内层 s电子所形成的能带。
原子的p态是奇宇称：
x
p x p x
x x
p 沿x轴方向的重叠积分J1 < 0，而J2 > 0。
y
E(k)
－＋ －＋
－ ＋ －＋ x
X
二、原子能级与能带的对应 对于原子的内层电子，其电子 E
轨道很小，因而形成的能带较
窄。这时，原子能级与能带之 间有简单的一一对应关系。 对于外层电子，由于其电子轨 道较大，形成的能带就较宽。 这时，原子能级与能带之间比较复杂，不一定有简单 的一一对应关系。一个能带不一定与孤立原子的某个 能级相对应，可能会出现能带的重叠。
方向，在六个近邻重叠积分中，沿x轴方向的重叠积分较
大，用J1表示；沿y方z
k p J 0 2 J1 cos k xa 2 J 2 cos k ya cos k za k p J 0 2 J 1 cos k ya 2 J 2 cos k za cos k xa k p J 0 2 J1 cos k za 2 J 2 cos k xa cos k ya
En k En k
上式对所有晶体点群的对称操作 都成立。 证明了在k空间中En(k)具有与晶体点群完全相同的对称性。
能带的反演对称性 En(k)=En(-k)
2 d 2 V ( x) 证明*： H 2 2m d x
k态的薛定谔方程：
H k ( x) E(k ) k ( x)
这里 2mE / , ' 2m( E U 0 ) /