【整理】重庆市中考第12、23题专题训练
重庆市2012年中考综合训练题二

A B OCDA BCD重庆市2012年中考综合训练题(二)一、选择题:(本大题10个小题,每题4分,共40分) 1.在-5,0,1,3这四个数中,最大的数是( )A .3 B.1 C.0 D. -5 2.计算22)3(xy -的结果是( )A.46xy B.429y x C.46xy - D.429y x - 3.由5个相同的正方体搭成的几何体如图所示,则它的左视图是( )4.如图,已知//AB ED ,65ECF ∠=,则BAC ∠的度数为( )A. 115B. 65C. 60D. 255. 我市三月份连续五天的日最高气温分别为23、20、20、21、24(单位:°C ),这组数据的极差是( )A. 1°CB. 2°CC.3°CD. 4°C 6.如图,⊙O 的直径CD ⊥AB ,∠AOC =50°,则∠CDB 大小为 ( )A .20° B.25° C.30° D.35°7.某家医院在元旦节那天出生了3个婴儿,假设生男生女的机会相同,那么这3个婴儿中,出现1个男婴、2个女婴的概率是( ) A.81 B. 83 C. 418.二次函数2(0)y ax bx c a =++≠图象如图,对称轴是直线1x =,) A .0c > B .20a b += C .240b ac -> D .a b c -+9.小亮同学骑车上学,路上要经过平路、下坡、上坡和平路(如图).分别为123v v v 、、,且123v v v <<,则小亮同学骑车上学时,离家的路程s 与所用时间t 的函数关系主视方向B EC FAD20题图10.如图①,将一个正六边形各边延长,构成一个正六角星形AFBDCE ,它的面积为1,取△ABC 和△DEF 各边中点,连接成正六角星形A 1F 1B 1D 1C 1E 1,如图②中阴影部分;取△A 1B 1C 1和△D 1E 1F 1各边中点,连接成正六角星形A 2F 2B 2D 2C 2E 2F 2,如图③中阴影部分;如此下去…,则正六角星形A 6F 6B 6D 6C 6E 6F 6的面积为(二、填空题:(本大题6个小题,每小题4分,共24分) 11.方程24x x =的解是_______________.12.已知ABC DEF △∽△,且ABC △的周长与DEF △的周长之比为1∶2,则ABC △的面积与DEF △的面积之比为_______________.13.据重庆商报报道:园博园开园仅仅一个月零几天,游客已突破百万,总接待人数1022500人次,此数用科学记数法表示是_______________.14.如图,BC 是⊙O 的直径,A 是CB 延长线上一点,AD 切⊙O 于点D ,如果AB=2,∠A=30°,那么AD 等于_________.15.将一枚六个面编号分别为1,2,3,4,5,6的质地均匀的正方体骰子先后投掷两次,记第一次掷出的点数为a ,第二次掷出的点数为b ,则使关于y x ,的方程组322ax by x y +=⎧⎨+=⎩只有正数解的概率为__________________.16.有甲、乙、丙三种矿石60克、60克、47克,含铁量分别为5%、8%、9%.现从三种矿石中各取一定量共计100克进行混合煅烧,使混合煅烧的矿石含铁量为7%,问甲种矿石最多取_______________克. 三、解答题:(本大题4个小题,每小题6分,共24分)解答时每小题必须给出必要的演算过程或推理步骤,请将解答书写在答题卡...中对应的位置上. 17.计算:()22012122(1)3π-⎛⎫-⨯-+-- ⎪⎝⎭解分式方程:1233x x x =+-- 19. 如图,已知四点B 、E 、C 、F 顺次在同一条直线上,A 、D 两点在直线BC 的同侧,BE =CF ,AB∥DE,∠ACB=∠DFE.求证:AC =DF .图① 图② 图③FEDCB A20.已知:在ΔABC 中,∠C=90º,BC=2,23sin =A 求∠B 和边AC 的大小. 四、解答题:(本大题4个小题,每小题10分,共40分)解答时每小题必须给出必要的演算过程或推理步骤,请将解答书写在答题卡...中对应的位置上. 21.先化简,再求值:222161816416x x x x x x ⎛⎫-+÷ ⎪++--⎝⎭,其中x 满足2210.x x --= 22.如图,一次函数的图象与反比例函数的图象相交于A 、B 两点.(1)求这两个函数的解析式;(2)连接AO 、BO,求AOB △的面积.23. 果农老张进行杨梅科学管理试验.把一片杨梅林分成甲、乙两部分,甲地块用新技术管理,乙地块用老方法管理,管理成本相同.在甲、乙两地块上各随机选取20棵杨梅树,根据每棵树产量把杨梅树划分成A ,B ,C ,D ,E 五个等级(甲、乙的等级划分标准相同,每组数据包括左端点不包括右端点).画出统计图如下:(1)补齐直方图,求a 的值及相应扇形的圆心角度数;(2)选择合适的统计量,比较甲乙两地块的产量水平,并说明试验结果;(3)若在甲地块随机抽查1棵杨梅树,求该杨梅树产量等级是B 的概率. 24. 已知:在直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,AD=2,AB=BC=3,EF 垂直平分CD(1)求CD 的长(2)求ta n ∠DEF 的值23题图五、解答题:(本大题2个小题,第25小题10分,第26小题12分,共22分)解答时每小题必须给出必要的演算过程或推理步骤,请将解答书写在答题卡...中对应的位置上.25. 一辆经营长途运输的货车在高速公路的A处加满油后,以每小时80千米的速度匀速行驶,前往与A处相距636千米的B地,下表记录的是货车一次加满油后油箱内余油量y(升)与行驶时间x(时)之间的关系:(1)请你认真分析上表中所给的数据,用你学过的一次函数、反比例函数和二次函数中的一种来表示y与x之间的变化规律,可直接写出它的函数表达式;(不要求写出自变量的取值范围)(2)按照(1)中的变化规律,货车从A处出发行驶4.2小时到达C处,求此时油箱内余油多少升?(3)在(2)的前提下,C处前方18千米的D处有一加油站,根据实际经验此货车在行驶中油箱内至少保证有10升油,如果货车的速度和每小时的耗油量不变,那么在D处至少加多少升油,才能使货车到达B地.(货车在D处加油过程中的时间和路程忽略不计)26.如图,在Rt△ABC中,∠C=90°,∠B=30°,BC=4.一等边三角形DEF的边EF在直线BC上,△DEF以每秒1个单位长度的速度沿直线CB向右匀速运动.开始时点E与点C重合,当点F与点B重合时停止运动.在运动过程中,直线DE、DF分别与直线AB相交于点G、H,当点F与点C 重合时,点D恰好在斜边AB上.(1)求△DEF的边长;(2)在整个运动过程中,设△DEF与△ABC重叠部分的面积为S,请直接写出S与t之间的函数关系式和相应的自变量t的取值范围;(3)在△DEF运动的过程中,图中是否存在与线段CF始终相等的线段?如果存在,请指出这条线段,并加以证明;如果不存在,请说明理由.参考答案一、选择题:1.A2.C3.D4.B5.D6. B7.B8.D9.C 10.C 二、填空题:11. 120,4x x == 12. 14 13. 61.022510⨯ 14. 23 15. 3613 16. 49 三、解答题: 17. 8- 18. 7x =19. ∵BE =CF ,∴BE+EC =CF+EC, ∴BC=EF; ∵AB∥DE,∴∠ABC=∠DEF ;又∵ ∠ACB=∠DFE,∴△ABC ≌△DEF,∴AC =DF . 20. 解:由23sin =A ,得∠A=60° 所以∠B=90º-∠A=90º-60°=30° 因为23sin ==AB BC A 所以232=AB ,解得AB=334. 21.解:()()()()()()()()()()22222444444444444481642216x x x x x x x x x x x x x x x x x x x x x x ⎡⎤+-=+⋅+-⎢⎥-+⎢⎥⎣⎦-⎛⎫=+⋅+- ⎪+-⎝⎭=-++=-+++=-+原式2221021=2116=18x x x x --=∴-=∴⨯+ 原式22.(1)y =0.5x +1,y =(2) 523. 解:(1)画直方图(略)a =10, 相应扇形的圆心角为:360°×10%=36°. (2)5.8020155365575685595=⨯+⨯+⨯+⨯+⨯=甲x ,7520255465975285395=⨯+⨯+⨯+⨯+⨯=乙x ,甲x >乙x ,由此说明通过新技术管理甲地块杨梅产量高于乙地块杨梅产量.(3)P =3.0206=. 24. 证明:延长BA ,CE 交于点F ,在ΔBEF 和ΔBEC 中,∵∠1=∠2,BE=BE ,∠BEF=∠BEC=90°, ∴ΔBEF ≌ΔBEC ,∴EF=EC ,从而CF=2CE 。
重庆中考数学23题专练

中考23题应用题专项练习1. 随着经济水平的不断提升,越来越多的人选择到电影院去观看电影,体验视觉盛宴,并且更多的人通过淘票票,猫眼等网上平台购票,快捷且享受更多优惠,电影票价格也越来越便宜. 2018年从网上平台购买5张电影票的费用比在现场购买3张电影票的费用少10元,从网上平台购买4张电影票的费用和现场购买2张电影票的费用共为190元.(1)请问2018年在网上平台购票和现场购票的每张电影票的价格各为多少元(2)2019年“元旦”当天,南坪上海城的“华谊兄弟影院”按照2018年在网上平台购票和现场购票的电影票的价格进行销售,当天网上和现场售出电影票总票数为600张. “元旦”假期刚过,观影人数出现下降,于是该影院决定将1月2日的现场购票的价格下调,网上购票价格保持不变,结果发现现场购票每张电影票的价格每降价元,则当天总票数比“元旦”当天总票数增加4张,经统计,1月2日的总票数中有53通过网上平台售出,其余均由电影院现场售出,且当天票房总收益为19800元,请问该电影院在1月2日当天现场购票每张电影票的价格下调了多少元2. 为了提高教学质量,促进学生全面发展,某中学计划投入99000元购进一批多媒体设备和电脑显示屏,且准备购进电脑显示屏的数量是多媒体设备数量的6倍现从商家了解到,一套多媒体设备和一个电脑显示屏的售价分别为3000元和600元(1)求最多能购进多媒体设备多少套(2)恰“315°次乐购时机,每套多媒体设备的售价下降a 53%,每个电脑显示屏的售价下降5a 元,决定多媒体设备和电脑显示屏的数量在(1)中购进最多量的基础上都增加a %,实际投入资金与计划投入资金相同,求a 的值3. 某商店经销甲、乙两种商品。
现有如下信息: 信息1:甲、乙两种商品的进货单价之和是3元; 信息2:甲商品零售单价比进货单价多1元,乙商品零售单价比进货单价的2倍少1元;信息3:按零售单价购买甲商品3件和乙商品2件,共付了12元请根据以上信息,解答下列问题: (1)求甲、乙两种商品的零售单价;(2)该商店平均每天卖出甲商品500件和乙商品1200件. 经调查发现,甲种商品零售单价每降元,甲种商品每天可多销售100件.商店决定把甲种商品的零售单价下降m(m>0)元,乙种商品的零售单价和销量都不变. 在不考虑其他因素的条件下,当m 为多少时,商店每天销售甲、乙两种商品获取的总利润为1700元4.幸福水果店计划用12 元/盒的进价购进一款水果礼盒以备销售。
2021年重庆年中考23题一元二次方程实际应用综合专题(重庆育才试题集)

2021年重庆年中考23题一元二次方程实际应用综合专题(重庆育才试题集)1(育才2021级初三上定时训练二)十九大以来,为全面推进新农村建设,积极改革农村产业结构,增加农民收入,致富村村委会多方努力,共获得流转耕地1000亩,全部用于种植纽橙和蔬菜,其中种植蔬菜的面积不少于种植纽橙面积的4倍.(1)求该村种植蔬菜的面积至少为多少亩?(2)今年村里按(1)中蔬菜种植面积的最小值种植蔬菜,纽橙和蔬菜上市后,纽橙每亩获利800元,蔬菜每亩获利600元;明年在保持纽橙种植面积不变的情况下,纽橙亩产量将上涨,预计每亩利润将增加3a%;同时利用新增流转耕地,使蔬菜种植面积扩大α%,并改良蔬菜种植结构,蔬菜每亩利润将增加a%这样,明年纽橙和蔬菜的总利润将比今年的总利润增加a%.求a的值.2(育才2020级初三下中考模拟5月份)为了准备科技节创意销售,宏帆初2018级某同学到批发市场购买了一些甲、乙两种型号的小元件,甲型小元件的单价是6元,乙型小元件的单价是3元,该同学的创意作品每件需要的乙型小元件的个数是甲型小元件的个数的2倍,同时,为了控制成本,该同学购买小元件的总费用不超过480元.(1)该同学最多可购买多少个甲型小元件?(2)在该同学购买甲型小元件最多的前提下,用所购买的甲、乙两种型号的小元件全部制作成创意作品,在制作中其他费用共花520元,销售当天,该同学在成本价(购买小元件的费用+其他费用)的基础上每件提高2a%(10<a<50)标价,但无人问津,于是该同学在标价的基础上降低a%出售,最终,在活动结束时作品全部卖完,这样,该同学在本次活动中赚了a%,求a的值.3(育才2020级初三下中考模拟二)为满足社区居民健身的需要,区政府准备采购若干套健身器材免费提供给社区,经考察,康乐公司有甲,乙两种型号的健身器材可供选择.(1)康乐公司2017年每套甲型健身器材的售价为2万元,经过连续两年降价,2019年每套售价为1.28万元,求每套甲型健身器材售价的年平均下降率n;(2)2019年市政府经过招标,决定年内采购并安装康乐公司甲,乙两种型号的健身器材共80套,采购专项经费总计不超过95万元,采购合同规定:每套甲型健身器材售价为1.28万元,每套乙型健身器材售价为1.4(1﹣n)万元.①甲型健身器材最多可购买多少套?②按照甲型健身器材购买最多的情况下,安装完成后,若每套甲型和乙型健身器材一年的养护费分别是购买价的8%和10%,区政府计划支出9万元进行养护,问该计划支出能否满足一年的养护需要?4(育才2020级初三下中考模拟三)随着夏季的到来,各类水果自然也成了大众喜爱的消费产品.已知某水果店第一次售出苹果和芒果共200千克,其中苹果的售价为24元/千克,芒果的售价为20元/千克,总销售额为4320元.(1)求水果店第一次售出苹果和芒果各多少千克;(2)通过最近的调查发现消费者更加青睐于购买芒果,经销售统计发现与第一次相比,芒果的售价每降低1元,销量就增加20千克,苹果的售价和销量均保持不变,如果第二次的苹果和芒果全部售完比第一次的总销售额多980元,求第二次芒果的售价.5(育才2019级初三下中考模拟一)某水果店以每千克6元的价格购进一批水果,由于销售状况良好,该店又购进一些同一种水果,第二次进货价格比第一次每千克便宜了1元,已知两次一共进货600千克.(1)若该水果店两次进货的总价格不超过3200元,求第一次至多购进水果多少千克?(2)在(1)的条件下,以第一次购进最大重量时的数量进货,在销售过程中,第一次购进的水果有3%的损耗,其售价比其进价多2a元,第二次购进的水果有5%的损耗,其售价比其进价多a元,该水果店希望售完两批水果后获利31.75%,求a的值.6(育才2020级初三下中考模拟二练习)每年的3月15日是“国际消费者权益日”,许多家居商城都会利用这个契机进行打折促销活动,甲卖家的A商品成本为600元,在标价1000元的基础上打8折销售(1)现在甲卖家欲继续降价吸引买主,问最多降价多少元,才能使利润率不低于20%?(2)据媒体爆料,有一些卖家先提高商品价格后再降价促销,存在欺诈行为,乙卖家也销售A商品,其成本、标价与甲卖家一致,以前每周可售出50件,现乙卖家先将标价提高2m%,再大幅降价24m元,使得A商品在3月15日那一天卖出的数量就比原来一周卖出的数量增加了m%后,这样一天的利润达到了20000元,求m的值7(双福育才2020级初三下中考模拟一)2020年初,武汉爆发了新型冠状病毒引起的肺炎,并迅速在全国蔓延。
重庆中考23题专题

重庆中考第23题专题题型一、条形图与扇形图结合1、为实施“农村留守儿童关爱计划”,某校结全校各班留守儿童的人数情况进行了统计,发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,并制成如下两幅不完整的统计图:(1)求该校平均每班有多少名留守儿童?并将该条形统计图补充完整;(2)某爱心人士决定从只有2名留守儿童的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名留守儿童来自同一个班级的概率。
2、在“传箴言”活动中,某班团支部对该班全体团员在一个月内所发箴言条数的情况进行了统计,并制成了如下两幅不完整的统计图:(1)求该班团员在这一个月内所发箴言的平均条数是多少?并将该条形统计图补充完整;(2)如果发了3条箴的同学中有两位同学,发了4条箴言的同学中有三位女同学.现要从发了3条箴和4条箴言的同学中分别选出一位参加该校团委组织的“箴言”活动总结会,请你用列表法或树状图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.3、2011年3月2日晚,重庆市公共租赁住房首次公开摇号配租在南坪国际会展中心举行,共有15281套、400万平方米公租房参与摇号配租.选中房源的申请人将从4月份开始,陆续住进公租房小区。
随着摇号配租,重庆成为近年来我国第一个配租公租房的城市.我校的一个数学兴趣小组在本校学生中开展主题为“公租房知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,分别记作A 、B 、C 、D ;并根据调查结果绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:(1)本次被调查的学生共有________人;在被调查者中“基本了解”的有 人. (2)将条形统计图和扇形统计图补充完整;(3)在“非常了解”的调查结果里,初三年级学生共有5人,其中3男2女,在这5人中,打算随机选出2位进行采访,请你用列表法或树状图的方法求出所选两位同学恰好都是男同学的概率?10%DAC30%BA B C D 等级A已入住公租房(套)图2A B C D40%20%35%各型号竣工公租房套数占已竣工的公租房套数的百分数图14、重庆市公租房倍受社会关注,2010年竣工的公租房有A 、B 、C 、D 四种型号共500套,B 型号公租房的 入住率为40%,A 、B 、C 、D 四种型号竣工的套数及入住的情况绘制了图1和图2两幅尚不完整的统计图. (1)2010年竣工的A 型号公租房套数是多少套; (2)请你将图1、图2的统计图补充完整;(3)在安置中,由于D 型号公租房很受欢迎,入住率很高,2010年竣工的D 型公租房中,仅有5套没有入住, 其中有两套在同一单元同一楼层,其余3套在不同的单元不同的楼层。
重庆中考数学第23题专题复习 三

2017重庆中考数学第23题专题复习三
1. (重庆南开(融侨)中学初2017届九年级(下)开学摸底考试)
为加强环境保护,从2014年起,某工厂决定经过设备改造等方式进行减排,此前该厂每年的废气排放量为450万立方米。
(1)若该厂要用五年的时间,将废气排放量减至不高于250万立方米且每年减少的废气排放量相同,那么每年至少要减少多少万立方米的废气排放量?
(2)2014、2015两年该厂的年废气减排量都恰好是(1)中的年废气减排量的最小值。
2016年地方更具体的环境保护措施出台后,该厂决定加大减排力度,决定用2016年、2017年两年时间刚好完成250万立方米的减排目标,且2016年的减排量在2015年的基础上增加%a ,2017年的减排量在2016年的基础上增加2%a 。
求a 的值。
(结果留根号)
2.(重庆八中初2017级九年级下周考(一)
重庆市第八中学校初2017级学生会准备购进笔记本和钢笔进行爱心义卖活动,并将义卖获得的利润全部用于购买图书,免费借阅给全校学生。
已知购进笔记本的单价为25元,共卖出120件,购进钢笔的单价是20元,共卖出150件。
每个笔记本的售价比每支钢笔的售价多20元,最后销售钢笔获利比销售笔记本获利少600元。
(1)求义卖的商品每件售价分别是多少元;
(2)为了让全校更多同学借阅到图书,初2017级学生会决定再进行一次义卖活动,此次义卖购进的商品单价为15元,此次商品的售价比钢笔上调了a%,卖出的件数比钢笔减少2a%,若这次获利4500元,求a 的值。
3.(重庆市巴蜀中学初2017级2016-2017学年度上期末)
4.(重庆市实验外国语学校初2017级2016-2017学年度上期末)。
2021年重庆年中考24题阅读材料题型综合专题练习(巴蜀试题集)

2021年重庆年中考24题阅读材料题型综合专题练习(巴蜀试题集)1(巴蜀2020级初三上自主训练四)一个正整数的各位数字都相同,我们称这样的数为“称心数”,如5,44,666,2222,…对任意一个三位数n,如果n满足各数位上的数字互不相同,且都不为零,那么称这个数为“相异数”.将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和记为S(n),如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和S(123)=213+321+132=666,是一个“称心数”.(1)计算:S(432),S(617),并判断是否为“称心数”;(2)若“相异数”n=100+10p+q(其中正整数p,q满足1≤p≤9,1≤q≤9),且S(n)为最大的三位“称心数”,求n的值.2(巴蜀2020级初三下定时训练一请阅读以下材料,并解决相应的问题:材料一:换元法是数学中的重要方法,利用换元法可以从形式上简化式子,在解某些特殊方程时,使用换元法常常可以达到转化与化归的目的,例如在求解一元四次方程x4﹣2x2+1=0时,令x2=t,则原方程可变为t2﹣2t+1=0,解得t=1,从而得到原方程的解为x=±1.村料二:杨辉三角形是中国数学史上的一个伟大成就,在中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现.它呈现了某些特定系数在三角形中的一种有规律的几何排列.如图为杨辉三角形:(1)利用换元法解方程:(x2+3x﹣1)2+2(x2+3x﹣1)=3(2)在杨辉三角形中,按照由上至下、从左到右的顺序观察,设a n是第n行的第2个数(其中n≥4),b n是第n行的第3个数,c n是第(n﹣1)行的第3个数.请利用换元法因式分解:4(b n﹣a n)•c n+13(巴蜀2020级初三下二诊考试)阅读以下材料:材料一:如果两个两位数ab ,cd ,将它们各自的十位数字和个位数字交换位置后得到两个完全不同的新数ba ,dc ,这两个两位数的乘积与交换后的两个两位数的乘积相等,则称这样的两个两位数为一对“有缘数对”. 例如:46×96=64×69=4416,所以,46和96是一对“有缘数对”,材料二:在进行一些数学式计算时,我们可以把某一单项式或多项式看作一个整体,运用整体换元,使得运算更简单.例如:计算(x 2+3x -1)(x 2+3x -8),令:(x 2+3x )=A ,原式=(A -1)(A -8)=A 2-9A +8=(x 2+3x )2-9(x 2+3x )+8=x 4+6x 3-27x +8 解决如下问题:(1)①请任写一对“有缘数对” 和 .②并探究“有缘数对”ab 和cd ,a ,b ,c ,d 之间满足怎样的等量关系.并写出证明过程.(2)若两个两位数(x 2+2x +3)(x 2-2x +4)与(x 2-2x +5)(x 2+2x +5)是一对“有缘数对”,请求出这两个两位数.4(巴蜀2020级初三下数学自主测试)对于平面内的∠MAN 及其内部的一点P ,设点 P 到直线 A M ,AN 的距离分别为 d 1,d 2,称12d d 和21d d 这两个数中较大的一个为点 P 关于∠MAN 的“偏率”.在平面直角坐标系 x Oy 中,(1)点 M ,N 分别为 x 轴正半轴,y 轴正半轴上的两个点. ①若点 P 的坐标为(1,5),则点 P 关于∠MON 的“偏率”为;②若第一象限内点 Q (a ,b )关于∠MON 的“偏率”为 1,则 a ,b 满足的关系为 ;(2)已知点 A (4,0),B (2,2),连接 O B ,AB ,点 C 是线段 A B 上一动点(点 C 不与点 A ,B 重合).若点C 关于∠AOB 的“偏率”为 2,求点 C 的坐标;(3)点 E ,F 分别为 x 轴正半轴,y 轴正半轴上的两个点,动点 T 的坐标为(t ,4),⊙T 是以点 T 为圆心,半径为 1,直 接写出 t 的取值范围 .5(巴蜀2020级初三下第三次模拟)阅读下列材料:已知实数m ,n 满足()()2222212180m n m n +++-=,试求222m n +的值.解:设222m n t +=,则原方程变为()()1180t t +-=,整理得2180t -=,281t =,9t ∴=± 因为2220m n +≥,所以2229m n +=.上面这种方法称为“换元法”,换元法是数学学习中最常用的一种思想方法,在结构较复杂的数和式的运算中,若把其中某些部分看成一个整体,并用新字母代替(即换元),则能使复杂的问题简单化.根据以上阅读材料内容,解决下列问题,并写出解答过程.(1)已知实数x ,y 满足222222322327()()x y x y +++-=,求22x y +的值.(2)若四个连续正整数的积为11880,求这四个连续正整数.6(巴蜀2020级初三下模拟考试一)数学不仅是一门科学,也是一种文化,即数学文化. 数学文化包括数学史、数学美 和数学应用等多方面. 古时候,在某个王国里有一位聪明的大臣,他发明了国际象棋, 献给了国王,国王从此迷上了下棋, 为了对聪明的大臣表示感谢,国王答应满足这位大 臣的一个要求.大臣说:“就在这个棋盘上放一些米粒吧. 第 1格放1粒米,第2格放2粒米,第3格放4粒米,然后是8粒、16粒、32粒····一直到第64格.” “你 真傻!就要这么一点米粒?”国王哈哈大笑.大臣说:“就怕您的国库里没有这么多米!” 国王的国库里有这么多米吗?题中问题就是求123631222...2+++++是多少?请同学们阅读以下解答过程就知道答案了.设2123631222?··2S =+++++ 则()2346323463642212222?··22222?··22S =++++++=++++++()()2346323463212222?··212222?··2S S ∴-=++++++-++++++即6421S =-事实上,按照这位大臣的要求,放满一个棋盘上的64个格子需要()2363641222?··221+++++=-粒米.那么64 21-到底多大呢?借助计算机中的计算器进行计算,可知 答案是一个20位数:18 446 744 073 709 551 615,这是一个非常大的数,所以国王是 不能满足大臣的要求.请用你学到的方法解决以下问题:()1我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增, 共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两 层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有多少盏灯?()2计算:13927?·····3n +++++. ()3某中学“数学社团”开发了一款应用软件,推出了“解数学题获取软件激活码”的 活动.这款软件的激活码为下面数学问题的答案:已知一列数 :1, 1, 2, 1, 2, 4, 1, 2, 4, 8, 1, 2, 4, 8, 16,?其中第一项是02,接下来的两项是012,2,再接下来的三项是0122,2,2?··,依此类推.求满足如下条件的所有正整数:10100N N <<, 且这一列数前N 项和为2的正整数幂.请直接写 出所有满足条件的软件激活码正整数N 的值7(巴蜀2020级初三上周测)阅读下列材料:材料一:所有正整数在进行某种规定步骤的运算后,会得到一个恒定不变的数,我们把这个恒定不变的数叫做稳定数。
2021重庆中考复习数学第12题专题训练三(含答案)

2021年重庆中考复习二次函数专题训练三1、已知二次函数2y ax bx c =++(a ≠0)的图象如图,则下列结论错误的是( C ) A .4a +2b +c >0B .abc <0C .b <a ﹣cD .3b >2 c2、如图所示,已知二次函数2y ax bx c =++的图象与x 轴交于A ,B 两点,与y 轴交于点C ,OA=OC ,对称轴为直线x =1,则下列结论:①abc <0;②11024a b c ++=;③ac+b+1=0;④2+c是关于x 的一元二次方程ax 2+bx +c =0的一个根.其中正确的有( B )A .1个B .2个C .3个D .4个3、二次函数2y ax bx c =++(a≠0)的图象如图所示,对称轴为x =1.给出下列结论:①ac >0;②24b ac >;③4a+2b+c >0;④3a+c >0.其中,正确的结论有( B )A .1个B .2个C .3个D .4个4、二次函数2y ax bx c =++的图象如图所示,对称轴是直线x =1.下列结论:①abc <0;②3a+c >0;③(a+c )2﹣b 2<0;④a+b≤m (am+b )(m 为实数).其中结论正确的个数为( C ) A .1个 B .2个 C .3个 D .4个5、如图,已知二次函数2y ax bx c =++的图象与x 轴分别交于A 、B 两点,与y 轴交于C 点,OA =OC .则由抛物线的特征写出如下结论:①abc >0;②240ac b ->;③a ﹣b+c >0;④ac+b+1=0.其中正确的个数是( B )A .4个 B .3个 C .2个 D .1个6、如图,二次函数y =ax 2+bx +c 的图象与x 轴交于点A (﹣1,0),与y 轴的交点B 在(0,2)与(0,3)之间(不包括这两点),对称轴为直线x =2.下列结论:①abc <0;②9a+3b+c >0;③若点M (,y 1),点N (,y 2)是函数图象上的两点,则y 1<y 2;④﹣<a <﹣.其中正确结论有( ) A .1个 B .2个C .3个D .4个解:①由开口可知:a <0,∴对称轴x =>0,∴b >0, 第1题图第2题图第3题图第4题图第5题图由抛物线与y轴的交点可知:c>0,∴abc<0,故①正确;②∵抛物线与x轴交于点A(﹣1,0),对称轴为x=2,∴抛物线与x轴的另外一个交点为(5,0),∴x=3时,y>0,∴9a+3b+c>0,故②正确;③由于<2,且(,y2)关于直线x=2的对称点的坐标为(,y2),∵,∴y1<y2,故③正确,④∵=2,∴b=﹣4a,∵x=﹣1,y=0,∴a﹣b+c=0,∴c=﹣5a,∵2<c<3,∴2<﹣5a<3,∴﹣<a <﹣,故④正确,故选:D.7、如图,已知二次函数y=ax2+bx+c的图象与x轴交于点A(﹣2,0),与y轴的交点B在(0,2)和(0,3)之间(不包括这两点),对称轴为直线x=2,下列结论:①abc>0,②9a+3b+c>0,③<a <,④4ac﹣b2<﹣14a,⑤b>c,其中正确的个数是()A.2个B.3个C.4个D.5个解:①∵抛物线开口向下,与y轴交于正半轴,对称轴为直线x=2,∴a<0,c>0,﹣=2,∴b=﹣4a>0,∴abc<0,结论①错误;②∵抛物线与x轴交于点A(﹣2,0),对称轴为直线x=2,∴抛物线与x轴另一交点坐标为(6,0),∴当x=3时,y>0,∴9a+3b+c>0,结论②正确;③∵抛物线与x轴交于点A(﹣2,0),对称轴为直线x=2,∴,∴12a=﹣c.∵抛物线与y轴的交点B在(0,2)和(0,3)之间,∴2<c<3,∴﹣3<12a<﹣2,∴﹣<a <﹣,结论③正确;④∵抛物线顶点的纵坐标大于3,∴>3.∵a<0,∴4ac﹣b2<12a<﹣14a,结论④正确;⑤∵12a=﹣c,b=﹣4a,∴﹣3b=﹣c,∴c=3b.∵c>0,∴b<c,结论⑤错误.故选:B.8、如图,已知二次函数y=ax2+bx+c(a≠0)图象过点(﹣1,0),顶点为(1,2),则结论:①abc<0;②x=1时,函数的最大值是2;③a+2b+4c>0;④2a=﹣b;⑤2c>3b.其中正确的结论有()A.4个B.3个C.2个D.1个解:①对称轴在y轴的右侧,则a、b异号,所以ab<0;由抛物线与y轴的交点位于y轴的正半轴则c>0,所以abc<0,故①正确;②∵抛物线的开口方向向下,顶点为(1,2),∴x=1时,函数的最大值是2,故②正确;③x =时,y>0,即a +b+c>0,∴a+2b+4c>0,故③正确;④∵抛物线的对称轴为直线x =﹣=1,∴2a=﹣b,故④正确;⑤∵抛物线过点(﹣1,0),∴a﹣b+c=0,而a =﹣b,∴﹣b﹣b+c=0,∴2c=3b,故⑤错误.综上所述,正确的结论有4个.故选:A.9、如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为直线x=1,点B坐标为(﹣1,0).则下面的四个结论:①2a+b=0;②8a+c<0;③abc>0;④当y<0时,x<﹣1或x>2,⑤对任意实数m,m(am+b)≤a+b.其中正确的结论有()个.A.2 B.3 C.4 D.5解:①对称轴﹣=1,∴2a+b=0,①正确;②x=﹣2时,y<0,∴4a﹣2b+c<0,由b=﹣2a,∴8a+c<0,②正确;③开口向下,a<0,对称轴在y轴右侧,b>0,与y轴交于正半轴,c>0,∴abc<0,③错误;④当x<﹣1或x>3时,y<0,④错误;⑤当x=1时,函数有最大值,∴am2+bm+c≤a+b+c,∴m(am+b)≤a+b,⑤正确.故选:B.10、(2018秋•西湖区校级期中)如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣2,0),与y轴的交点在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.有下列结论:①abc>0;②4a+2b+c>0;③;④b<c.其中正确的()A.①②B.①③C.①④D.③④解:①∵抛物线开口向上,对称轴为直线x=1,与y轴的交点在(0,﹣2)和(0,﹣1)之间,∴a>0,﹣=1,﹣2<c<﹣1,∴b<0,abc>0,结论①正确;②∵抛物线与x轴交于点A(﹣2,0),对称轴为直线x=1,∴抛物线与x轴的另一交点坐标为(4,0),∴当x=2时,y=4a+2b+c<0,结论②错误;③当x=﹣2时,y=4a﹣2b+c=0,∴4a﹣2b=﹣c.∵b=﹣2a,∴8a=﹣c.又∵﹣2<c<﹣1,∴<a <,结论③正确;④∵当x=﹣1时,y=a﹣b+c<0,a>0,∴﹣b+c<0,∴b>c,结论④错误.综上所述:正确的结论有①③.故选:B.11、(2019•惠城区校级一模)如图,二次函数y=ax2+bx+c(a≠0)图象与x轴交于A,B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0).则下面的四个结论:①abc>0;②8a+c <0;③b2﹣4ac>0;④当y<0时,x<﹣1或x>2.其中正确的有()A.4 个B.3 个C.2 个D.1 个解:①函数的对称轴在y轴右侧,则ab<0,而c>0,故abc<0,故原答案错误,不符合题意;②函数的对称轴为:x =﹣=1,故b=﹣2a,对称轴为x=1,点B坐标为(﹣1,0),则点A(3,0),故9a+3b+c=0,而b=﹣2a,即3a+c=0,a<0,故8a+c<0,正确,符合题意;③抛物线和x轴有两个交点,故b2﹣4ac>0正确,符合题意;④点B坐标为(﹣1,0),点A(3,0),则当y<0时,x<﹣1或x>3.故错误,不符合题意.故选:C.12、(2019秋•开福区校级月考)如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②16a+4b+c<0;③4ac﹣b2<8a;④;⑤b<c.其中正确结论有①③④.解:①∵函数开口方向向上,∴a>0;∵对称轴在y轴右侧∴ab异号,∵抛物线与y轴交点在y 轴负半轴,∴c<0,∴abc>0,故①正确;②当x=4时,y=16a+4b+c>0,故②错误;③∵二次函数y=ax2+bx+c的图象与y轴的交点在(0,﹣1)的下方,对称轴在y轴右侧,a>0,∴最小值:<﹣2,∵a>0,∴4ac﹣b2<﹣8a,∴4ac﹣b2<8a∴③正确;④∵图象与y轴的交点B在(0,﹣2)和(0,﹣1)之间,∴﹣2<c<﹣1,∴﹣2<﹣3a<﹣1,∴;故④正确;⑤∵二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),∴a﹣b+c=0,∴a=b﹣c,∵a>0,∴b﹣c>0,即b>c;故⑤错误;综上所述,正确的有①③④,13、如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B 在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0,②4a+2b+c>0,③4ac﹣b2<8a ,④<a <,⑤b>c.其中含所有正确结论的选项是()A.①③B.①③④C.②④⑤D.①③④⑤解:①∵函数开口方向向上,∴a>0;∵对称轴在y轴右侧∴ab异号,∵抛物线与y轴交点在y轴负半轴,∴c<0,∴abc>0,故①正确;②∵图象与x轴交于点A(﹣1,0),对称轴为直线x=1,∴图象与x轴的另一个交点为(3,0),∴当x=2时,y<0,∴4a+2b+c<0,故②错误;③∵图象与x轴交于点A(﹣1,0),∴当x=﹣1时,y=(﹣1)2a+b×(﹣1)+c=0,∴a﹣b+c=0,即a=b﹣c,c=b﹣a,∵对称轴为直线x=1∴=1,即b=﹣2a,∴c=b﹣a=(﹣2a)﹣a=﹣3a,∴4ac﹣b2=4•a•(﹣3a)﹣(﹣2a)2=﹣16a2<0∵8a>0∴4ac﹣b2<8a故③正确④∵图象与y轴的交点B在(0,﹣2)和(0,﹣1)之间,∴﹣2<c<﹣1,∴﹣2<﹣3a<﹣1,∴>a >;故④正确⑤∵a>0,∴b﹣c>0,即b>c;故⑤正确;故选:D.14、如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B 在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c >0;③4ac﹣b2<16a;④;⑤b>c.其中正确结论个数()A.2个B.3个C.4个D.5个解:①∵函数开口方向向上,∴a>0;∵对称轴在y轴右侧,∴a、b异号,b<0,∵抛物线与y轴交点在y轴负半轴,∴c<0,∴abc>0,故①正确;②∵图象与x轴交于点A(﹣1,0),对称轴为直线x=1,∴图象与x轴的另一个交点为(3,0),∴当x=2时,y<0,∴4a+2b+c<0,故②错误;③解法一:由图象知:抛物线与x轴有两个交点,∴b2﹣4ac>0,∴4ac﹣b2<0,∵16a>0,∴4ac﹣b2<16a;解法二:∵图象与x轴交于点A(﹣1,0),∴当x=﹣1时,y=(﹣1)2a+b×(﹣1)+c=0,∴a﹣b+c=0,即a=b﹣c,c=b﹣a,∵对称轴为直线x=1,∴﹣=1,即b=﹣2a,∴c=b﹣a=(﹣2a)﹣a=﹣3a,∴4ac﹣b2=4•a•(﹣3a)﹣(﹣2a)2=﹣16a2<0,∵16a>0,∴4ac﹣b2<16a,故③正确④∵图象与y轴的交点B在(0,﹣2)和(0,﹣1)之间,∴﹣2<c<﹣1∴﹣2<﹣3a<﹣1,∴<a <;故④正确⑤∵a>0,∴b﹣c>0,即b>c;故⑤正确;正确结论为:①③④⑤,有4个,故选:C.15、如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:①当x>3时,y <0;②a﹣b+c=0;③﹣1≤a≤﹣;④4a+2b+c<2;其中正确的结论是()A.①③④B.①②③C.①②④D.①②③④解:①由抛物线的对称性可求得抛物线与x轴令一个交点的坐标为(3,0),当x>3时,y<0,故①正确;②∵二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),∴当x=﹣1时,y=a﹣b+c=0,故②正确;③设抛物线的解析式为y=a(x+1)(x﹣3),则y=ax2﹣2ax﹣3a,令x=0得:y=﹣3a.∵抛物线与y轴的交点B在(0,2)和(0,3)之间,∴2≤﹣3a≤3.解得:﹣1≤a≤﹣,故③正确;④∵抛物线与x轴的交点为(﹣1,0)和(3,0),且开口向下,∴当x=2时,y=4a+2b+c>0,故④错误.故选:B.16、(2019•随县一模)如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与x轴交点的横坐标分别为x1、x2,其中﹣2<x1<﹣1,0<x2<1.下列结论:①4a﹣2b+c<0;②2a﹣b<0;③abc<0;④b2+8a<4ac.其中正确的结论有()A.1个B.2个C.3个D.4个解:由图知:抛物线的开口向下,则a<0;抛物线的对称轴x =﹣>﹣1,且c>0;①由图可得:当x=﹣2时,y<0,即4a﹣2b+c<0,故①正确;②已知x =﹣>﹣1,且a<0,所以2a﹣b<0,故②正确;③抛物线对称轴位于y轴的左侧,则a、b同号,又c>0,故abc>0,所以③不正确;④由于抛物线的对称轴大于﹣1,所以抛物线的顶点纵坐标应该大于2,即:>2,由于a<0,所以4ac﹣b2<8a,即b2+8a>4ac,故④错误;因此正确的结论是①②.故选:B.17、(2014•河东区一模)已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列结论:①abc>0;②2a﹣b>0;③20a<(4a+b)2;④0<a <.正确的个数为()A.1 B.2 C.3 D.4解:①由图象开口向上得到a>0,<0所以a和b同号,b>0,又因为图象和y轴交与负半轴,故c<0,所以abc<0,①不正确.②根据图象得﹣=﹣1,所以b=2a,即2a﹣b=0错误.③把(2,4)代入整理得,4a+2b+c=4,∴c=4﹣4a﹣2b ,由图象得,∴4ac﹣b2<﹣4a,即4a(4﹣4a﹣2b)﹣b2+4a<0,∴16a﹣16a2﹣8ab﹣b2+4a<0∴20a<16a2+8ab+b2,即20a<(4a+b)2,故正确.④c=4﹣4a﹣2b=4﹣8a,由图象得到﹣1<c<0,∴4﹣4a﹣2b>﹣1∴4a+2b<5,即2a+b <,又∵b=2ª,∴4a <即a又∵﹣1<4﹣8a<0,∴<a <.故错误.故选:A.。
重庆中考数学第12题专题练习_
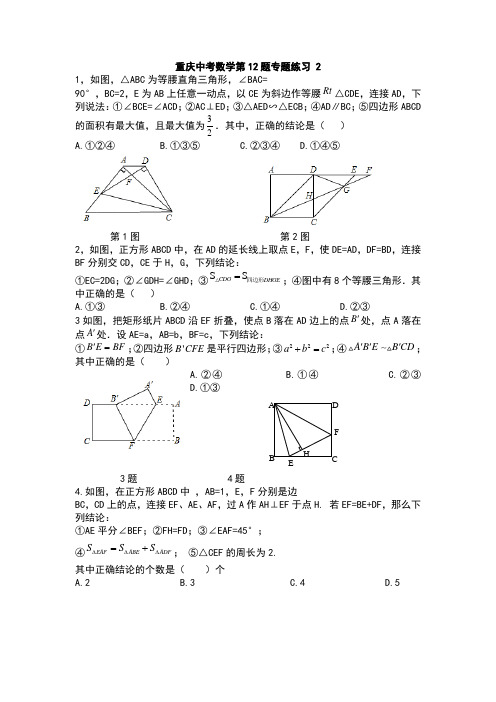
重庆中考数学第12题专题练习 21,如图,△ABC 为等腰直角三角形,∠BAC=90°,BC=2,E 为AB 上任意一动点,以CE 为斜边作等腰Rt △CDE ,连接AD ,下列说法:①∠BCE=∠ACD ;②AC ⊥ED ;③△AED ∽△ECB ;④AD ∥BC ;⑤四边形ABCD的面积有最大值,且最大值为32.其中,正确的结论是( )A.①②④B.①③⑤C.②③④D.①④⑤第1图 第2图2,如图,正方形ABCD 中,在AD 的延长线上取点E ,F ,使DE=AD ,DF=BD ,连接BF 分别交CD ,CE 于H ,G ,下列结论:①EC=2DG ;②∠GDH=∠GHD ;③S S CDG DHGE=四边形;④图中有8个等腰三角形.其中正确的是( )A.①③B.②④C.①④D.②③3如图,把矩形纸片ABCD 沿EF 折叠,使点B 落在AD 边上的点B '处,点A 落在点A '处.设AE=a ,AB=b ,BF=c ,下列结论: ①B E BF '=;②四边形'B CFE 是平行四边形;③222a b c +=;④A B E B CD ''';其中正确的是( )A.②④B.①④C.②③D.①③3题 4题4.如图,在正方形ABCD 中 ,AB=1,E ,F 分别是边BC ,CD 上的点,连接EF 、AE 、AF ,过A 作AH ⊥EF 于点H. 若EF=BE+DF ,那么下列结论:①AE 平分∠BEF ;②FH=FD ;③∠EAF=45°; ④EAF ABE ADF S S S ∆∆∆=+; ⑤△CEF 的周长为2. 其中正确结论的个数是( )个A.2B.3C.4D.5A D CB E FH5.如图,在正方形ABCD 中,点E 是AD 的中点,连接BE 、CE ,点F 是CE 的中点,连接DF 、BF ,点M 是BF 上一点且21=MF BM , 过点M 做BC MN ⊥于点N ,连接FN .下列结论中 ①CE BE =;②DFE BEF ∠=∠;③AB MN 61=;④61=∆EBNF FMN S S 四边形其中正确结论的个数是:()A .1个B .2个C .3个D .4个5题 6题6,如图,P 、Q 是矩形ABCD 的边BC 和CD 延长上的两点,AP 与CQ 相交 于点E ,且∠PAD =∠QAD。
2021年重庆中考数学第12题反比例函数专题训练

2021年重庆中考数学第12题反比例函数专题训练1.如图,矩形OABC的顶点A、C分别在x轴、y轴的正半轴上,点D在边OC上,且BD=OC,(k≠0)的图象以BD为边向下作矩形BDEF,使得点E在边OA上,反比例函数y=kx 经过边EF与AB的交点G.若DE=3,AG=2.25,则k的值为()A.10.8B. 9.6C. 3.2D. 32.在平面直角坐标系中,平行四边形ABCD的顶点A在y轴上,点C坐标为(−4,0),E(k<0,x<0)的图象上,为BC上靠近点C的三等分点,点B、E均在反比例函数y=kx,则k的值为()若tan∠OAD=12A.−2B. −2√5C. −6D. −4√2(k>0,x>0)上.若3.如图,正方形ABCD的顶点B在x轴上,点A、点C在双曲线y=kxx−2,则k的值为()直线BC的解析式为y=12A.24B. 12C. 6D. 44.如图,菱形ABCD的两个顶点B、D在反比例函数y=kx的图象上,对角线AC与BD的交点恰好是坐标原点O,已知点A(1,1),∠ABC=60°,则k的值是()A.−5B. −4C. −3D. −25.如图,在平行四边形ABCO中,过点B作BE//y轴,且E为OC的四等分点(OE>EC),D为AB中点,连接BE、DE、DC,反比例函数y=kx(k>0)的图象经过D、E两点,若△DEC的面积为3,则k的值为()A. 274B. 7 C. 272D. 2776.如图,在等腰△AOB中,AO=AB,顶点A为反比例函数y=kx(其中x>0)图象上的一点,点B在x轴正半轴上,过点B作BC⊥OB,交反比例函数y=kx的图象于点C,连接OC交AB于点D,若OB=8,OA=4√10,则△BCD的面积为()A.163B. 6B.245D. 57. 如图,平行四边形OABC 的顶点A 在x 轴的正半轴上,点D(3,2)在对角线OB 上,反比例函数y =kx (k >0,x >0)的图象经过C 、D 两点.已知平行四边形OABC 的面积是152,则点B 的坐标为( )A. (4,83)B. (92,3)C. (5,103)D. (245,165)8. 如图,在等腰△AOB 中,AO =AB ,顶点A 为反比例函数y =kx (其中x >0)图象上的一点,点B 在x 轴正半轴上,过点B 作BC ⊥OB ,交反比例函数y =kx 的图象于点C ,连接OC 交AB 于点D ,若△BCD 的面积为2,则k 的值为( ) A. 20B. 503 C. 16 D. 4039. 如图所示,四边形ABCD 的顶点都在坐标轴上,若AD//BC ,△ACD 与△BCD 的面积分别为20和40,若双曲线y =kx (k <0,x <0)恰好经过边AB 的四等分点E(BE <AE),则k 的值为( )A. −5B. −10C. −15D. −2010. 如图,双曲线y =kx (x >0)与矩形OBCD 的边BC 、CD 分别交于点E 、F ,且与矩形的对角线OC 交于点A ,连接EF ,与对角线OC 交于点H ,G 是对角线OC 上的一点,连接GF 、GE.若S △EFG =43,OG :GH :HC =3:1:2,sin∠COB =35,则点A 的坐标为( )A. (94,2716) B. (54√3,1516√3)C. (125,95)D. (43√3,√3)11. 如图,在平面直角坐标系中,正方形ABCD 的面积为20,顶点A 在y 轴上,顶点C 在x 轴上,顶点D 在双曲线y =kx (x >0)的图象上,边CD 交y 轴于点E ,若CE =ED ,则k 的值为( ) A. 52B. 3C. 72 D. 412.如图,等腰△ABC中,AB=AC,边AC过原点O,BC平行于x轴,AE⊥BC于点E,连接E点和AB边的中点D点,交x轴于点F.若D点在反比例函数y=kx(k≠0)的图象上,E点在反比例函数y=−2−kx(k≠0)的图象上,△ADE的面积是10,DF:EF=1:2,则k的值是()A. 7B. 385C. 8 D. 26313.如图,B,C是反比例函数y1=kx(x<0)图象上的两点,A(2,m)是反比例函数y2=−2x(x>0)图象上一点,连接AB,BC,AC,若∠BCA=90°,AC恰好经过原点,AB与y轴交于点D(0,5),则k的值为()A.−233B. −172C. −8D. −1014.如图,在平面直角坐标系中,△BCD为直角三角形,∠BCD=90°,其中B(0,4),tan∠OBC=12,点D在反比例函数y=kx(x>0)图象上,且CD=√5,以BC为边作平行四边形BCEF,其中点F在反比例函数y=kx(x>0)图象上,点E在x轴上,则点E的横坐标为()A. √5B. 52C. 3D. 7215.如图,在平面直角坐标系中,菱形ABCD的对角线AC,BD的交点与坐标原点O重合,AB与x轴交于点E,反比例函数y=kx(k>0,x>0)的图象经过点D.若点C(1,−2),E(−2,0),则k的值为()A.256B. 4 C. 167D. 32916.如图,已知直线y=13x−1与坐标轴交于A点和B点,与反比例函数y=kx(x>0)的图象交于点C,以AB为边向上作平行四边形ABED,D点刚好在反比例图象上,连接CE,CD,若CE//x轴,四边形BCDE面积为10,则k的值为()A. 10B. 283C. 9 D. 46517.如图:四边形ABCD为菱形,且对角线BD//x轴,A、C两点在y轴上,E点在BC上,且BE=2CE,双曲线y=kx(x>0)经过E、B两点,且S△EFB=8,则k的值为()C. 4D. 6A. 3B. 8318.已知:如图,在菱形OABC中,OC=8,∠AOC=60°,OA落在x轴正半轴上,点D是OC边上的一点(不与端点O,C重合),过点D作DE⊥AB于点E,若点D,E都在(x>0)图象上,则k的值为()反比例函数y=kxA.8√3B. 9C. 9√3D. 16。
2021年重庆年中考23题阅读材料题综合专题练习(11月中旬期中集合)(1)

重庆(1)若s ,t 都是“相异数”,其中s=100x+10y+1,210t x y =+-,(19,19,x y ≤≤≤≤x,y 都是正整数)且s 是完全平方数,规定:()()k F s F t =-,当()()20F s F t +≤时,求k 的最大值.2(南开2021级初三上期中测试)阅读下列材料,回答问题;材料一:在大于1的整数中,除了能被1和本身整除外,还能被其他数(0除外)整除的数,称为合数.材料二:若一个各个数位上的数字都不为零的四位数,其千位的数字与个位的数字相等,百位上的数字与十位上的数字相等,且该数前两位数字组成的两位数和后两位数字组成的两位数都是合数,则称该数为“对称合数”,如2552、6886都是“对称合数”.(1)最小的“对称合数”为 ;最大的“对称合数”为 ;(2)若“对称合数”的前两位数字组成的两位数和后两位数字组成的两位数之和四完全平方数,求满足条件的所有“对称合数”的个数,并把它们写出来.3(育才2020级初三上期中考试)任意一个三位正整数,如果它的前两位数能被2整除,它本身能被3整除,那么他们这样的数称为“夹心数”,例如:144前两位数12能被2整除,它本身能被3整除,所以144是一个“夹心数”.(1)判断324和425是不是“夹心数”?并说明理由;(2)若“夹心数”20010P x y =++(0,19x y y ≤≤≤≤,x,y 皆为整数),并且P 的各个数字之和为一个完全平方数,求满足添加的所有“夹心数”P ,并说明理由.4(一中共同体2021级初三上期中测试)若一个三位数abc t =(其中a 、b 、c 不全相等且都不为0),重新排列各数位上的数字必可得到一个最大数和一个最小数,此最大数和最小数的差叫做原数的差数,记为)(t T .例如,539的差数594359953)539(=-=T .(1)根据以上方法求出=)268(T __________,=)513(T __________;(2)已知三位数b a 1(其中1>>b a )的差数495)1(=b a T ,且各数位上的数字之和为3的倍数,求所有符合条件的三位数的值.5(巴蜀2021级初三上期中测试)我们把形如1aaa (19a ≤≤且a 为整数)的四位正整数叫做“三拖一”数,例如:2221,3331都是“三拖一”数.(1)最小的“三拖一”数为 ;最大的“三拖一”数为 ;(2)M ,N 是互不相同的“三拖一”数,且满足条件:M 与50的和的2倍与N 与75的和的3倍的和正好能被13整除,求满足条件的M 的值.6(八中2021级初三上期中测试)如果3个数位相同的自然数m 、n 、k 满足k n m =+,且k 各数位上的数字全部相同,则称数m 和数n 是一对“黄金搭档数”.例如:因为123,765,888都是三位数,123+765=888,所以123和765是一对“黄金搭档数".再如:因为26,29,55都是两位数,26+29=55,所以26和29是一对“黄金搭档数”.(1)若326与一个个位上的数字是3的数a 是一对 “黄金搭档数”,389与一个个位上的数字是8的数b 是一对“黄金搭档数”,直接写出a 和b 的值;(2)若s =10x +y (90,91≤≤≤≤y x ),t =10x +z (90,91≤≤≤≤z x )且y <z ,s 和t 是一对“黄金搭档数”,求这样的“黄金搭档数”一共有多少对?7(南开2021级初三上阶段测试二)材料一:若一个整数的个位数字截去,再用余下的数减去截去的个位数字的2倍,如果差是7的倍数,则原数能被7整除.如果差太大或心算不易看出是否7的倍数,就需要继续上述“截尾、倍大、相减、验差”的过程,直到能清楚判断为止.例如,判断133是否7的倍数的过程如下:13327-⨯=,所以133是7的倍数. 材料二:三位数M abc =(a ,b ,c 均不为0),若满足a b c <<且2a c b +=,则称M 为“递增教”. (1)请用上述方法判断6139是否为7的倍数?并说明理由.(2)若三位数N 既是“递增数”,又能被7整除,求所有符合条件的三位数N .8(十八中2021级初三上周测五)如果一个正整数的奇数数位上的数字之和与偶数数位上的数字之和的差(通常用大减小)是11的倍数,则这个正整数一定能被11整除,比如整数90827,奇数数位上数字之和为9+8+7=24,偶数数位上述职之和0+2-2,24-2=22,因为22为11的倍数,所以整数90827能被11整除;又比如143,奇数数位上数字之和为1+3=4,偶数数位上数字之和为4,4-4=0,因为0为11的倍数,所以143能被11整除;(1)直接写出能被11整除的最小的三位正整数为 ,能被11整除的最大的四位正整数为 ;(2)若四位正整数abcd 能被11整除,求证:正整数bcd a -也能被11整除;(3)若一个三位正整数abc 能被11整除(其中05,05a c <≤<≤),在这个三位数的首位数字前添上一个1后,得到的新的四位数1abc 还能被7整除,求原来这个三位数.9(八中2021级九上周测六)人和人之间讲友情,有趣的是,数与数之间也有相类似的关系,若两个不同的自然数的所有真因数(即除了自身外的正因数)之和相等,我们称这两个数位“亲和数”,例如:18的正因数有1、2、3、6、9、18,它的真因数之和为1+2+3+6+9=21,;51的正因数有1、3、17、51,它的真因数之和为1+3+17=21,所以称18和51为“亲和数”.数还可以与动物形象地联系起来,我们称一个两头(首位与末位)都是1的数为“两头蛇数”,例如:121,1351等.(1)8的真因数之和为 ;求证:一个四位的“两头蛇数”与它去掉两头后得到的两位数的3倍的差,能被7整除;(2)一个百位上的数为4的五位“两头蛇数”能被16的“亲和数”整除,若这个五位“两头蛇数”的千位上的数字小于十位上的数字,求满足条件的五位“两头蛇数”.10(八中2021级九上定时训练八)若在一个三位自然数中,百位上的数字恰好等于十位上数字与个位上的数字之和,则称这个三位数为“欢乐数”.例如:在自然数321中,3=2+1,则321是“欢乐数”;在自然数中,9=3+6,则称936是“欢乐数”.(1)请你直写出最小的“欢乐数”,并证明,任意一个“欢乐数”与其个位上数字的2倍之差一定能被11整除;(2)若将一个“欢乐数”加上其各数位上的数字之和,所得结果能被同时被4和9整除,求这样的“欢乐数”. 11(一中2021级初三上国庆作业一)阅读下列材料并解决问题:定义:对于任意一个实数R ,定义R 的干数m 是与R 最接近的两个整数中较小的一个整数,R 的支数n 是R 减去R 的干数m 之差,即n R m =-.例如:实数2.07,因为与2.07最接近的两个整数时2和3,且2小于3,所以2.07的干数m =2,2.07的支数n =2.07-2=0.07;实数 1.72-,因为与 1.72-最接近的两个整数是1-和2-,且2-小于1-,所以 1.72-的干数2m =-, 1.72-的支数1.72(2)0.28n =---=.相关结论:m 是一个整数,n 的取值范围是01n ≤<.(1)实数10.8的干数m = ,实数34-的支数n = ; (2)某实数的干数是x ,支数是y ,且30.5x y +=,求这个实数.12(一中2021级初三上入学测试)(一中2020级初三下定时训练七)中国古贤常说万物皆自然,而古希腊学者说万物皆数,我们最初接触的数就是自然数,在数的学习过程中,我们会对其中一些具有某种特征的自然数进行研究,我们研究了奇数、偶数、质数、合数等,现在我们来研究另一种特殊的自然数——“n 喜数”.定义:对于一个两位自然数,如果它的各个位和十位上的数字均不为零,且它正好等于其个位和十位上数字的和的n 倍(n 为正整数),我们就说这个自然数是一个“n 喜数”.例如:24是一个“4喜数”,因为244(24)=⨯+25不是一个“n 喜数”,因为25(25)n ≠+(1)判断44和72是否是“n 喜数”,请说明理由.(2)试讨论是否存在“7喜数”,若存在请求出“7喜数”,若不存在请说明理由.。
2018重庆市中考第12、23题专题训练.doc

x m x-11-xA. 8 (育)2018重庆市中考第12、23题专题训练• P <2' I 〕若数m 使关于x 的不蒔式组有且只有4个整数解.且使分式方;6x_/n20=3有整数解.则所有符合萸碗 的和为” •B. 9 ・ G ・・D. -923•“高新九龙毎烦山水城九龙坡区的创卫工作己进入最后阶段・某小区准备购 买-些清洁用品.改善小区清济提升小区品质,增强居民的归属感・现拟购买户 外垃圾桶和除草机共100件,且垃圾桶的数股不少于除草机的°倍・(1)该小区最多可以购买除草机多少个7 •⑵该小区计划以(D 中购买最多除車机的方案釆购清洁用品•某商场里・户外垃圾桶每个200元,除草机每台800元.该商场抓住商札与小区物管协商・将户外垃圾桶的单价降低了巾%(加>0).每台除草机的单价降低了 50元・于屯该小区购买垃圾桶的数疑将在原计划的基础上增加了 2加%・除草机的数见不饕总共用去3TOOO 元.求加的值.(九)12.如果关于x的方程ax2 +4X-2-0有两个不相等的实数根,且关于x的分式方程丄 +上匕=2有正数解,则符合条件的所有整数a的值的和是2-x x-2A.-lB. 0C. 1D. 2(九)23.九龙技区某社区开展全民读书活动,以丰富人们业余文化生活现计划筹资3000元用于购买科普书籍和文艺刊物(1)计划购买文艺刊物的资金不少于购买科普书籍资金的2倍,那么最少用多少资金购买文艺刊物?(2)经初步了解,有200户居民自愿参与集资,那么平均每户需集资150元.经筹委会进步宣传,自2愿参加的户数在200户的基础上增加了號(其屮a>50),如果每户平均集资在150元的基础上减少一a%,那么实际筹资将比计划筹资多6000元求Q的值。
12・若关干x的方程—x-3 x-3 3-x的解为整数.且不等式组2x-3>7x-a<0 无解,则所有满足条件的非负整数。
重庆市数学中考23题-应用题(1)

2015年数学中考预测-23题 应用题一、工程问题: 1.(13A 23.)随着铁路客运量的不断增长,重庆火车北站越来越拥挤,为了满足铁路交通的快速发展,该火车站从去年开始启动了扩建工程,其中某项工程,甲队单独完成所需时间比乙队单独完成所需时间多5个月,并且两队单独完成所需时间的乘积恰好等于两队单独完成所需时间之和的6倍.(1)求甲乙两队单独完成这项工程各需几个月?(2)若甲队每月的施工费为100万元,乙队每月的施工费比甲队多50万元。
在保证工程质量的前提下,为了缩短工期,拟安排甲乙两队分工合作完成这项工程。
在完成这项工程中,甲队施工时间是乙队施工时间的2倍,那么,甲队最多施工几个月才能使工程款不超过1500万元?(甲乙两队的施工时间按月取整数).2.(13B 23、)4.20雅安地震后,某商家为支援灾区人民,计划捐赠帐篷16800顶,该商家备有2辆大货车、8辆小车运送,计划大货车比小货车每辆每次多运帐篷200顶,大、小货车每天均运送一次,两天恰好运完.(1)求大、小货车原计划每辆每次各运送帐篷多少顶?(2)因地震导致路基受损,实际运送过程中,每辆大货车每次比原计划少运m 200顶,每辆小货车每次比原计划少运300顶.为了尽快将帐篷运送到灾区,大货车每天比原计划多跑m 21次,小货车每天比原计划多跑m 次,一天刚好运送了帐篷14400顶,求m 的值. 3.某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.(1)这项工程的规定时间是多少天?(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?4.“端午节”是我国的传统佳节,历来有吃“粽子”的习俗。
专题23 化学计算-2022年中考化学真题分项汇编(全国通用)(第01期)(解析版)

专题23 化学计算1.(2022年安徽省中考)荷叶中含有的荷叶碱(化学式为C19H21NO2)具有降脂、抑菌等作用。
下列有关荷叶碱的说法,正确的是()A.含有O2B.由四种非金属元素组成C.属于氧化物D.其中氢元素的质量分数最大【答案】B【解析】A. 荷叶碱由荷叶碱分子构成,是纯净物,不含其他物质,不含氧气。
错误。
B. 物质由元素组成,荷叶碱由碳、氢、氮、氧四种非金属元素组成。
正确。
C. 氧化物是由两种元素组成,其中一种是氧元素的化合物。
荷叶碱由四种元素组成,不是氧化物。
错误。
D. 荷叶碱中碳、氢、氮、氧元素的质量比为(12×19):(1×21):(14×1):(16×2),碳元素占比最大,所以碳元素的质量分数最大,错误。
故选:B。
2.(2022年四川省自贡市中考)4月28日我国化学家团队公布了最新研究成果:通过电催化结合生物合成的方式,将二氧化碳高效还原合成高浓度乙酸,进一步利用微生物可以合成葡萄糖(C6H12O6)和脂肪酸。
这项突破为人工和半人工合成“粮食”提供了新技术。
葡萄糖中碳、氢、氧的元素质量比为()A.1:1:1B.1:2:1C.6:1:6D.6:1:8【答案】D【解析】根据化合物中各元素质量比=各原子的相对原子质量×原子个数之比,进行分析判断。
葡萄糖中碳、氢、氧的元素质量比为(12×6):(1×12):(16×6)=6:1:8。
故选:D。
3.(2022年四川省南充市中考)人被有些蚊虫叮咬后,蚊虫在人的皮肤内分泌出蚁酸(化学式为HCOOH),使叮咬处痛痒。
下列有关蚁酸说法错误的是()A.蚁酸由碳、氢、氧三种元素组成B.蚁酸由5个原子构成C.蚁酸的相对分子质量为46D.蚁酸中氧元素的质量分数最大【答案】B【解析】A、由化学式可知,蚁酸是由碳、氢、氧三种元素组成的,故选项说法正确,不符合题意;B、蚁酸由蚁酸分子构成的,一个蚁酸分子由1个碳原子、2个氢原子和2个氧原子共5个原子构成的,故选项说法错误,符合题意;C 、蚁酸的相对分子质量为:12+1×2+16×2=46,故选项说法正确,不符合题意;D 、1个蚁酸分子是由1个碳原子、2个氢原子和2个氧原子构成的,蚁酸中碳、氢、氧三种元素的质量比为(12×1):(1×2):(16×2)=6:1:8,则蚁酸中氧元素的质量分数最大,故选项说法正确,不符合题意。
中考23题训练

中考23题训练1.(2013•乌鲁木齐)某公司销售一种进价为20元/个的计算机,其销售量y(万个)与销售(1)观察并分析表中的y与x之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出y(万个)与x(元/个)的函数解析式.(2)求出该公司销售这种计算器的净得利润z(万个)与销售价格x(元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?(3)该公司要求净得利润不能低于40万元,请写出销售价格x(元/个)的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元?2.(2013•铁岭)某商家独家销售具有地方特色的某种商品,每件进价为40元.经过市场调的函数关系式:y=﹣10x+1000(2)设一周的销售利润为S元,请求出S与x的函数关系式,并确定当销售单价在什么范围内变化时,一周的销售利润随着销售单价的增大而增大?(3)雅安地震牵动亿万人民的心,商家决定将商品一周的销售利润全部寄往灾区,在商家购进该商品的贷款不超过10000元情况下,请你求出该商家最大捐款数额是多少元?3.(2012•朝阳)某商家经销一种绿茶,用于装修门面已投资3000元,已知绿茶每千克成本50元,在第一个月的试销时间内发现,销量w(kg)随销售单价x(元/kg)的变化而变化,(1)请根据上表,写出w与x之间的函数关系式(不必写出自变量x的取值范围);(2)求y与x之间的函数关系式(不必写出自变量x的取值范围).并求出x为何值时,y 的值最大?(3)若在第一个月里,按使y获得最大值的销售单价进行销售后,在第二个月里受物价部门干预,销售单价不得高于90元,要想在全部收回投资的基础上使第二个月的利润达到1700元,那么第二个月里应该确定销售单价为多少元?4.(2012•菏泽)牡丹花会前夕,我市某工艺厂设计了一款成本为10元/件的工艺品投放市在下面的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式;(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价﹣成本总价)(3)菏泽市物价部门规定,该工艺品销售单价最高不能超过35元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?5.(2012•河北)某工厂生产一种合金薄板(其厚度忽略不计),这些薄板的形状均为正方形,边长在(单位:cm)在5~50之间.每张薄板的成本价(单位:元)与它的面积(单位:cm2)成正比例,每张薄板的出厂价(单位:元)有基础价和浮动价两部分组成,其中基础价与薄板的大小无关,是固定不变的.浮动价与薄板的边长成正比例.在营销过程中得到了(2)已知出厂一张边长为40cm的薄板,获得的利润为26元(利润=出厂价﹣成本价),①求一张薄板的利润与边长之间满足的函数关系式.②当边长为多少时,出厂一张薄板所获得的利润最大?最大利润是多少?参考公式:抛物线:y=ax2+bx+c(a≠0)的顶点坐标为(﹣,)6.(2012•西藏)为了落实国家的惠农政策,某地政府制定了农户投资购买收割机的补贴办(1)分别求出y1和y2的函数解析式;(2)旺叔准备投资10万元购买Ⅰ、Ⅱ两型收割机.请你设计一个能获得最大补贴金额的方案,并求出按此方案能获得的补贴金额.作业:7.(2012•青岛)在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y (个)与销售单价x(元/个)之间的对应关系如图所示:(1)试判断y与x之间的函数关系,并求出函数关系式;(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润w(元)与销售单价x(元/个)之间的函数关系式;(3)在(2)的条件下,若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.8.(2012•淮安)国家和地方政府为了提高农民种粮的积极性,每亩地每年发放种粮补贴120元.种粮大户老王今年种了150亩地,计划明年再承租50~150亩土地种粮以增加收入,考虑各种因素,预计明年每亩种粮成本y(元)与种粮面积x(亩)之间的函数关系如图所示:(1)今年老王种粮可获得补贴多少元?(2)根据图象,求y与x之间的函数关系式;(3)若明年每亩的售粮收入能达到2140元,求老王明年种粮总收入W(元)与种粮面积x (亩)之间的函数关系式.当种粮面积为多少亩时,总收入最高?并求出最高总收入.9.(2013•随州)某公司投资700万元购甲、乙两种产品的生产技术和设备后,进行这两种产品加工.已知生产甲种产品每件还需成本费30元,生产乙种产品每件还需成本费20元.经市场调研发现:甲种产品的销售单价为x(元),年销售量为y(万件),当35≤x<50时,y 与x之间的函数关系式为y=20﹣0.2x;当50≤x≤70时,y与x的函数关系式如图所示,乙种产品的销售单价,在25元(含)到45元(含)之间,且年销售量稳定在10万件.物价部门规定这两种产品的销售单价之和为90元.(1)当50≤x≤70时,求出甲种产品的年销售量y(万元)与x(元)之间的函数关系式.(2)若公司第一年的年销售量利润(年销售利润=年销售收入﹣生产成本)为W(万元),那么怎样定价,可使第一年的年销售利润最大?最大年销售利润是多少?(3)第二年公司可重新对产品进行定价,在(2)的条件下,并要求甲种产品的销售单价x (元)在50≤x≤70范围内,该公司希望到第二年年底,两年的总盈利(总盈利=两年的年销售利润之和﹣投资成本)不低于85万元.请直接写出第二年乙种产品的销售单价m(元)的范围.10.(2013•本溪)某蔬菜经销商到蔬菜种植基地采购一种蔬菜,经销商一次性采购蔬菜的采购单价y(元/千克)与采购量x(千克)之间的函数关系图象如图中折线AB﹣﹣BC﹣﹣CD 所示(不包括端点A).(1)当100<x<200时,直接写y与x之间的函数关系式:y=﹣0.02x+8.(2)蔬菜的种植成本为2元/千克,某经销商一次性采购蔬菜的采购量不超过200千克,当采购量是多少时,蔬菜种植基地获利最大,最大利润是多少元?(3)在(2)的条件下,求经销商一次性采购的蔬菜是多少千克时,蔬菜种植基地能获得418元的利润?11.(2013•朝阳)甲、乙两企业去年末都有利润积累,甲企业利润为300万元,甲企业认为:企业要可持续发展,必须进行自主创新和技术改造,由于投资更新等原因,甲企业的利润积累y甲(万元)与时间x(年)之间的函数图象呈抛物线(如图)乙企业的利润积累y乙(万元)每年增加50万元,预计第一年末(今年末)利润积累150万元.(1)乙企业去年末的利润积累是100万元,乙企业利润积累y乙(万元)与时间x(年)之间的函数关系式为y乙=100+50x(不必写出自变量x的取值范围).(2)到第几年末,甲企业的利润积累重新达到去年末与乙企业利润积累的倍数关系?(3)改造初期,甲企业的利润积累逐渐减少,甚至会低于乙企业的利润积累.随着甲企业进入改造成长期,甲企业的利润积累重新高于乙企业的利润积累,试问第几年(保留整数位.参考数据:≈3.6)甲企业开始进入改造成长期?5年后(含5年)甲企业进入改造成熟期,效益将显现出来.改造成熟期,甲企业的利润积累最少会高于乙企业的利润积累多少万元?12.(2011•恩施州)宜万铁路开通后,给恩施州带来了很大方便.恩施某工厂拟用一节容积是90立方米、最大载重量为50吨的火车皮运输购进的A、B两种材料共50箱.已知A种材料一箱的体积是1.8立方米、重量是0.4吨;B种材料一箱的体积是1立方米、重量是1.2吨;不计箱子之间的空隙,设A种材料进了x箱.(1)求厂家共有多少种进货方案(不要求列举方案)?(2)若工厂用这两种材料生产出来的产品的总利润y(万元)与x(箱)的函数关系大致如下表,请先根据下表画出简图,猜想函数类型,求出函数解析式(求函数解析式不取近似值),。
2024年重庆市中考数学真题试卷及答案解析(b卷)

2 (3)若点 D 在点 B 的右侧,连接 AD ,点 F 是 AD 的中点,且 AF AC .点 P 是直线 AC 上一动点,连 接 FP ,将 FP 绕点 F 逆时针旋转 60 得到 FQ ,连接 BQ ,点 R 是直线 AD 上一动点,连接 BR ,QR .在 点 P 的运动过程中,当 BQ 取得最小值时,在平面内将 BQR 沿直线 QR 翻折得到△TQR ,连接 FT .在
1
的解均为负整数,则所有满足条件的整数 a 的值之和是________.
17. 如图, AB 是 O 的直径, BC 是 O 的切线,点 B 为切点.连接 AC 交 O 于点 D ,点 E 是 O 上
一点,连接 BE ,DE ,过点 A 作 AF ∥ BE 交 BD 的延长线于点 F .若 BC 5 ,CD 3 ,F ADE ,
15. 如图,在 ABC 中, AB AC , A 36 , BD 平分 ABC 交 AC 于点 D .若 BC 2 ,则 AD 的
长度为________.
16.
若关于
x
的一元一次不等式组
2024年中考数学压轴题重难点知识剖析及训练—一线三等角相似、三垂直模型压轴题专题(含解析)

2024年中考数学压轴题重难点知识剖析及训练—一线三等角相似、三垂直模型压轴题专题(含解析)一线三等角概念“一线三等角”是一个常见的相似模型,指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。
不同地区对此有不同的称呼,“K形图”,“三垂直”,“弦图”等,以下称为“一线三等角”。
“一线三等角”的两种基本类型1.三等角都在直线的同侧2.三等角分居直线的两侧3.在初三各学校的考试和中考试题中,一线三等角的相似属于压轴题的热点题型之一,本专题从中考试题和初三各名校的试题中,精选一线三等角相似模型的经典好体,并根据角度区别把一线三等角模型细分为三类题型:三垂直模型、一线三锐角、一线三钝角,适合于初三学生进行压轴题专项突破时使用。
类型一:三垂直模型1.(雅礼)如图,点A 是双曲线()80y x x=<上一动点,连接OA ,作OB OA ⊥,使2OA OB =,当点A 在双曲线()80y x x =<上运动时,点B 在双曲线ky x=上移动,则k 的值为.【解答】解:过A 作AC ⊥y 轴于点C ,过B 作BD ⊥y 轴于点D ,∵点A 是反比例函数y =(x <0)上的一个动点,点B 在双曲线y =上移动,∴S △AOC =×|﹣8|=4,S △BOD =|k |,∵OB ⊥OA ,∴∠BOD +∠AOC =∠AOC +∠OAC =90°,∴∠BOD =∠OAC ,且∠BDO =∠ACO ,∴△AOC ∽△OBD ,∵OA =2OB ,∴=()2=,∴=,∴|k |=2.∴k <0,∴k =﹣2,故答案为:﹣2.2.(青竹湖)如图,︒=∠90AOB ,反比例函数()04<-=x xy 的图象过点()a A ,1-,反比例函数xky =()0,0>>x k 的图象过点B ,且x AB //轴,过点B 作OA MN //,交x 轴于点M ,交y 轴于点N ,交双曲线x ky =于另一点,则OBC ∆的面积为.【解答】解:∵反比例函数的图象过点A (﹣1,a ),∴a =﹣=4,∴A(﹣1,4),过A作AE⊥x轴于E,BF⊥x轴于F,∴AE=4,OE=1,∵AB∥x轴,∴BF=4,∵∠AOB=90°,∴∠EAO+∠AOE=∠AOE+∠BOF=90°,∴∠EAO=∠BOF,∴△AEO∽△OFB,∴=,∴OF=16,∴B(16,4),∴k=16×4=64,∵直线OA过A(﹣1,4),∴直线AO的解析式为y=﹣4x,∵MN∥OA,∴设直线MN的解析式为y=﹣4x+b,∴4=﹣4×16+b,∴b=68,∴直线MN的解析式为y=﹣4x+68,∵直线MN交x轴于点M,交y轴于点N,∴M(17,0),N(0,68),解得,或,∴C(1,64),﹣S△OCN﹣S△OBM=﹣﹣=510,∴△OBC的面积=S△OMN故答案为510.3.(广益)如图,点A,B在反比例函数y=(k>0)的图象上,点A的横坐标为2,点B的纵坐标为1,OA⊥AB,则k的值为.【解答】解:过点A作AM⊥x轴于点M,过点B作BN⊥AM于N,∵∠OAB=90°,∴∠OAM+∠BAN =90°,∵∠AOM+∠OAM=90°,∴∠BAN=∠AOM,∴△AOM∽△BAN,∴=,∵点A,B在反比例函数y=(k>0)的图象上,点A的横坐标为2,点B的纵坐标为1,∴A(2,),B(k,1),∴OM=2,AM=,AN=﹣1,BN=k﹣2,∴=,解得k1=2(舍去),k2=8,∴k的值为8,故答案为:8.4.(长沙中考2020)在矩形ABCD 中,E 为DC 上的一点,把ADE ∆沿AE 翻折,使点D 恰好落在BC 边上的点F .(1)求证:ABF FCE∆∆:(2)若23,4AB AD ==,求EC 的长;(3)若2AE DE EC -=,记,BAF FAE αβ∠=∠=,求tan tan αβ+的值.【详解】(1)证明:∵四边形ABCD 是矩形,∴∠B=∠C=∠D=90°,∴∠AFB+∠BAF=90°,∵△AFE 是△ADE 翻折得到的,∴∠AFE=∠D=90°,∴∠AFB+∠CFE=90°,∴∠BAF=∠CFE ,∴△ABF ∽△FCE .(2)解:∵△AFE 是△ADE 翻折得到的,∴AF=AD=4,∴()22224232AF AB --,∴CF=BC-BF=AD-BF=2,由(1)得△ABF ∽△FCE ,∴CE CF BF AB =,∴2223CE =,∴EC=233(3)解:由(1)得△ABF ∽△FCE ,∴∠CEF=∠BAF=α,∴tan α+tan β=BF EF CE EFAB AF CF AF+=+,设CE=1,DE=x ,∵2AE DE EC -=,∴AE=DE+2EC=x+2,AB=CD=x+1,2244AE DE x -=+∵△ABF ∽△FCE ,∴AB CF AF EF =2144x x x x -=+(211121x x x xx ++-+ ,∴112x x +=,∴1x x =-x 2-4x+4=0,解得x=2,∴CE=1,213x -=,EF=x=2,AF=2244AE DE x -=+=23tan α+tan β=CE EF CF AF +33323.5.(广益)矩形ABCD中,8AB=,12AD=,将矩形折叠,使点A落在点P处,折痕为DE.(1)如图1,若点P恰好在边BC上.①求证:△EBP∽△PCD;②求AE的长;(2)如图2,若E是AB的中点,EP的延长线交BC于点F,求BF的长.图1图2【解答】解:(1)①∵四边形ABCD是矩形,∴∠B=∠C=∠BAD=90°,∴∠BPE+∠BEP=90°,由折叠知,∠DPE=∠BAD=90°,∴∠BPE+∠CPD=90°,∴∠BEP=∠CPD,∵∠B=∠C=90°,∴△EBP∽△PCD;②∵四边形ABCD是矩形,∴∠B=∠C=90°,CD=AB=8,BC=AD=12,由折叠知,PE=AE,DP=AD=12,在Rt△DPC中,CP==4,∴BP=BC﹣CP=12﹣4,在Rt△PBE中,PE2﹣BE2=BP2,∴AE2﹣(8﹣AE)2=(12﹣4)2,∴AE=18﹣6;(2)如图,过点P作GH∥BC交AB于G,交CD于H.则四边形AGHD是矩形,设EG=x,则BG=4﹣x,∵∠A=∠EPD=90°,∠EGP=∠DHP=90°,∴∠EPG+∠DPH=90°,∠DPH+∠PDH=90°,∴∠EPG=∠PDH,∴△EGP∽△PHD,∴====,∴PH=3EG=3x,DH=AG=4+x,在Rt△PHD中,PH2+DH2=PD2,∴(3x)2+(4+x)2=122,解得x=(负值已经舍弃),∴BG=4﹣=,在Rt△EGP中,GP==,∵GH∥BC,∴△EGP∽△EBF,∴=,∴=,∴BF=3.6.(长郡)如图,在平面直角坐标系中,O 为原点,已知点Q 是射线OC 上一点,182OQ =,点P 是x 轴正半轴上一点,tan 1POC ∠=,连接PQ ,A 经过点O 且与QP 相切于点P ,与边OC 相交于另一点D .(1)若圆心A 在x 轴上,求A 的半径;(2)若圆心A 在x 轴的上方,且圆心A 到x 轴的距离为2,求A 的半径;(3)在(2)的条件下,若10OP <,点M 是经过点O ,D ,P 的抛物线上的一个动点,点F 为x 轴上的一个动点,若满足1tan 2OFM ∠=的点M 共有4个,求点F 的横坐标的取值范围.【解答】解:(1)∵圆心A 在x 轴上,⊙A 经过点O 且与QP 相切于点P ,∴PQ ⊥x 轴,OP 为直径,∵tan ∠POC =1,,∴PQ =OP ,∵在Rt △OPQ 中,.∴OP =18.∴⊙A 的半径为9;(2)如图所示,过点A 作AM ⊥x 轴于点M ,过点Q 作QB ⊥x 轴于B ,连接AP ,∵PQ是⊙A的切线,∴AP⊥PQ,则∠APQ=90°,∵AM⊥x轴,QB⊥x轴,∴∠AMP=∠PBC=90°,∴∠PAM=90°﹣∠APM=∠QPB,∴△APM∽△PBQ,∴,∵tan∠POC=1,QB=18,∴OB=QB=18,∵AM=2,设MP=MO=x,∴PB=18﹣2x,∴,解得x=3或x=6,∴MO=3或MO=x,∴A(3,2)或A(6,2),∴AP==或AP==2.∴半径为或2.(3)∵OP<10,∴BO=3,P(6,0),∴A(3,2),∵tan∠POC=1,设D(a,a),∵,∴(3﹣a)2+(2﹣a)2=13,解得:a=0或a=5,∴D(5,5),设抛物线解析式为y=ax2+bx,将点P(6,0),D(5,5)代入得,,解得:,∴y=﹣x2+6x,∵点F可能在点O的左边或点P的右边,,则|K FM|=,设直线MF:或,联立,,得或,当或,解得:或,∴直线MF:或,令y=0,解得:或,∴或.7.(麓山国际)有一边是另一边的倍的三角形叫做智慧三角形,这两边中较长边称为智慧边,这两边的夹角叫做智慧角.(1)已知Rt△ABC为智慧三角形,且Rt△ABC的一边长为,则该智慧三角形的面积为;(2)如图①,在△ABC中,∠C=105°,∠B=30°,求证:△ABC是智慧三角形;(3)如图②,△ABC是智慧三角形,BC为智慧边,∠B为智慧角,A(3,0),点B,C在函数y=上(x>0)的图象上,点C在点B的上方,且点B的纵坐标为.当△ABC是直角三角形时,求k的值.=AC•AB,【解答】解:(1)如图1,设∠A=90°,AC≤AB,S△ABC①若AC=,i)AB=AC=2,∴S=,ii)BC=AC=2,则AB=,∴S=,②若AB=,i)AB=AC,即AC=,∴S=,ii)BC=AB=2,则AC=∴S=,③若BC=,若AB=AC==1,∴S=,若AB=AC,AB=,,S=××=,故答案为:或1或或或.(2)证明:如图2,过点C作CD⊥AB于点D,∴∠ADC=∠BDC=90°,在Rt△BCD中,∠B=30°,∴BC=2CD,∠BCD=90°﹣∠B=60°,∵∠ACB=105°,∴∠ACD=∠ACB﹣∠BCD=45°,∴Rt△ACD中,AD=CD,∴AC=,∴,∴△ABC是智慧三角形.(3)∵△ABC是智慧三角形,BC为智慧边,∠B为智慧角,∴BC=AB,∵△ABC是直角三角形,∴AB不可能为斜边,即∠ACB≠90°∴∠ABC=90°或∠BAC=90°①当∠ABC=90°时,过B作BE⊥x轴于E,过C作CF⊥EB于F,过C作CG⊥x轴于G,如图3,∴∠AEB=∠F=∠ABC=90°,∴∠BCF+∠CBF=∠ABE+∠CBF=90°,∴∠BCF=∠ABE,∴△BCF∽△ABE,∴,设AE=a,则BF=AE=a,∵A(3,0),∴OE=OA+AE=3+a,∵B的纵坐标为,即BE=,∴CF=BE=2,CG=EF=BE+BF=,B(3+a,),∴OG=OE﹣GE=OE﹣CF=3+a﹣2=1+a,∴C(1+a,),∵点B、C在在函数y=上(x>0)的图象上,∴(3+a)=(1+a)(+a)=k解得:a1=﹣2(舍去),a2=1,∴k=,②当∠BAC=90°时,过C作CM⊥x轴于M,过B作BN⊥x轴于N,如图4,∴∠CMA=∠ANB=∠BAC=90°,∴∠MCA+∠MAC=∠MAC+∠NAB=90°,∴∠MCA=∠NAB,∴△MCA∽△NAB,∵BC=,∴2AB2=BC2=AB2+AC2,∴AC=AB,∴△MCA≌△NAB(AAS),∴AM=BN=,∴OM=OA﹣AM=3﹣,设CM =AN =b ,则ON =OA +AN =3+b ,∴C (3﹣,b ),B (3+b ,),∵点B 、C 在在函数y =上(x >0)的图象上,∴(3﹣)b =(3+b )=k解得:b =,∴k =18+15,综上所述,k 的值为或。
2023年重庆市中考英语试题(A卷,附答案)

2023年重庆市中考英语试题(A卷,附答案)第一部分听力(共四节,30分)第一节(共6小题,每小题1分,满分6分)听下面6个短对话,每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What will the woman probably do on Sunday?A. Visit a museum.B. Watch a movie.C. Go shopping.2. Where did the man find his wallet?A. On his desk.B. In his bag.C. Under his chair.3. What does the woman mean?A. The view is amazing.B. The pizza is delicious.C. The weather is terrible.4. How many children does the woman have?A. None.B. One.C. Two.5. What does the man think of the concert?A. It was too short.B. It was too loud.C. It was too expensive.6. What will the speakers do tonight?A. Go to a party.B. Watch a concert.C. Have dinner at home.第二节(共6小题,每小题1分,满分6分)听下面6个短对话,每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话读两遍。
中考数学专题复习《21~23题题型》测试卷-附带答案

中考数学专题复习《21~23题题型》测试卷-附带答案学校:___________班级:___________姓名:___________考号:___________1.市体育局对甲乙两运动队的某体育项目进行测试两队人数相等测试后统计队员的成绩分别为:7分8分9分10分(满分为10分).依据测试成绩绘制了如图所示尚不完整的统计图表:甲队成绩统计表成绩7分8分9分10分人数01m7请根据图表信息解答下列问题:(1)填空:α=__________︒m=_________(2)补齐乙队成绩条形统计图(3)①甲队成绩的中位数为_________ 乙队成绩的中位数为___________①分别计算甲乙两队成绩的平均数并从中位数和平均数的角度分析哪个运动队的成绩较好.2.某校在评选“劳动小能手”活动中随机调查了部分学生的周末家务劳动时间根据调查结果将劳动时长划分为A B C D四个组别并绘制成如下不完整统计图表学生周末家务劳动时长分组表组别A B C Dt(小时)0.5t<0.51t≤<1 1.5t≤< 1.5t≥请根据图表中的信息解答下列问题:(1)这次抽样调查共抽取______名学生条形统计图中的=a______ D组所在扇形的圆心角的度数是______(2)已知该校有900名学生根据调查结果请你估计该校周末家务劳动时长不低于1小时的学生共有多少人?(3)班级准备从周末家务劳动时间较长的三男一女四名学生中随机抽取两名学生参加“我劳动我快乐”的主题演讲活动 请用列表法或画树状图法求出恰好选中两名男生的概率.3..如图 ABC 内接于O AB 是O 的直径 BC BD = DE AC ⊥于点E DE 交BF 于点F 交AB 于点G 2BOD F ∠=∠ 连接BD .(1)求证:BF 是O 的切线(2)判断DGB 的形状 并说明理由(3)当2BD =时 求FG 的长.4.如图 AB 是O 的直径 点E C 在O 上 点C 是BE 的中点 AE 垂直于过C 点的直线DC 垂足为D AB 的延长线交直线DC 于点F .(1)求证:DC 是O 的切线(2)若2AE = 1sin 3AFD ∠= ①求O 的半径 ①求线段DE 的长.5.如图 在菱形ABCD 中 对角线,AC BD 相交于点,E O 经过,A D 两点 交对角线AC 于点F 连接OF 交AD 于点G 且AG GD =.(1)求证:AB 是O 的切线(2)已知O 的半径与菱形的边长之比为5:8 求tan ADB ∠的值.6.如图 在O 中 直径AB 垂直弦CD 于点E 连接,,AC AD BC 作CF AD ⊥于点F 交线段OB 于点G (不与点,O B 重合) 连接OF .(1)若1BE = 求GE 的长.(2)求证:2BC BG BO =⋅.(3)若FO FG = 猜想CAD ∠的度数 并证明你的结论.7. 我们可以通过中心投影的方法建立圆上的点与直线上点的对应关系 用直线上点的位置刻画圆上点的位置 如图 AB 是O 的直径 直线l 是O 的切线 B 为切点.P Q 是圆上两点(不与点A 重合 且在直径AB 的同侧) 分别作射线AP AQ 交直线l 于点C 点D .(1)如图1 当6AB = BP 的长为π时 求BC 的长.(2)如图2 当34AQ AB = BP PQ =时 求BC CD的值. (3)如图3 当6sin BAQ ∠=BC CD =时 连接BP PQ 直接写出PQ BP 的值.8.如图 一次函数1(0)y kx b k =+≠与函数为2(0)m y x x =>的图象交于1(4,1),,2A B a ⎛⎫ ⎪⎝⎭两点. (1)求这两个函数的解析式(2)根据图象 直接写出满足120y y ->时x 的取值范围(3)点P 在线段AB 上 过点P 作x 轴的垂线 垂足为M 交函数2y 的图象于点Q 若POQ △面积为3 求点P 的坐标.9..如图 在平面直角坐标系中 四边形OABC 是边长为2的正方形.点A C 在坐标轴上.反比例函数()0k y x x=>的图象经过点B . (1)求反比例函数的表达式(2)点D 在反比例函数图象上 且横坐标大于2 3OBD S =.求直线BD 的函数表达式.10.如图 点A 在反比例函数(0)k y k x=≠的图象上 点C 是点A 关于y 轴的对称点 OAC 的面积是8. (1)求反比例函数的解析式(2)当点A 的横坐标为2时 过点C 的直线2y x b =+与反比例函数的图象相交于点P 求交点P 的坐标.11.如图 点A 在反比例函数()0k y x x =>的图象上 AB y ⊥轴于点B 1tan 2AOB =∠ 2AB =. (1)求反比例函数的解析式(2)点C 在这个反比例函数图象上 连接AC 并延长交x 轴于点D 且45ADO ∠=︒ 求点C 的坐标.12.如图 一次函数2y x =的图象与反比例函数(0)ky x x=>的图象交于点()4,A n .将点A 沿x 轴正方向平移m 个单位长度得到点,B D 为x 轴正半轴上的点 点B 的横坐标大于点D 的横坐标 连接,BD BD 的中点C在反比例函数(0)k y x x =>的图象上. (1)求,n k 的值(2)当m 为何值时 AB OD ⋅的值最大?最大值是多少?13.如图 在平面直角坐标系xOy 中 直线y kx b =+与x 轴交于点()4,0A 与y 轴交于点()0,2B 与反比例函数m y x=在第四象限内的图象交于点()6,C a . (1)求反比例函数的表达式:(2)当m kx b x+>时 直接写出x 的取值范围 (3)在双曲线m y x=上是否存在点P 使ABP 是以点A 为直角顶点的直角三角形?若存在 求出点P 的坐标 若不存在 请说明理由.参考答案与解析1.【答案】(1)126,12m α=︒=(2)见解析(3)①9分 8分①=9.3x 甲 =8.3x 乙 中位数角度看甲队成绩较好 从平均数角度看甲队成绩较好【分析】(1)根据样本容量=频数÷所占百分比 结合圆心角的计算解答即可.(2)根据样本容量 求得7分的人数补图即可.(3)①根据有序数据的中间数据或中间两个数据的平均数为中位数计算即可.①根据加权平均数公式计算即可.【详解】(1)解:本次抽样调查的样本容量是72420360︒÷=︒(人) ①201712m =--=(人) 736012620α=⨯︒=︒故答案为:126 12.(2)①20-4-5-4=7(人)①补图如下:(3)①①甲队的第10个 11个数据都是9分①中位数是9+9=92(分)①乙队的第10个 11个数据都是8分①中位数是8+8=82(分)故答案为:9分 8分. ①①70+81+912+107==9.320x ⨯⨯⨯⨯甲(分)77+84+95+104==8.320x ⨯⨯⨯⨯乙(分)故从中位数角度看甲队成绩较好 从平均数角度看甲队成绩较好.【点睛】本题考查了中位数 条形统计图 扇形统计图 熟练掌握中位数 平均数 扇形统计图条形统计图的基本计算是解题的关键.2.【答案】(1)50 9 108︒(2)估计该校周末家务劳动时长不低于1小时的学生共有666人 (3)12【分析】(1)根据数据计算即可(2)根据(1)求出的D 组所占的比例计算结果(3)列出所有可能情况求概率.【详解】(1)解:这次抽样调查共抽取的人数有:224450÷=%(人)B 组的人数为:5018%9a =⨯=(人)D 组所占的比例为:18%18%44%30---=︒①D 组所在扇形的圆心角的度数是:36030%108︒⨯=︒(2)解:根据题意得 900(30%44%)666⨯+=(人)答:估计该校周末家务劳动时长不低于1小时的学生共有666人(3)解:列表如下: 男1 男2 男3 女男1 (男2 男1) (男3 男1) (女 男1)男2 (男1 男2) (男3 男2) (女 男2)男3 (男1 男3) (男2 男3) (女 男3)女 (男1 女) (男2 女) (男3 女)共有12中等可能结果 其中恰好选中两名男生的结果数为6①恰好选中两名男生的概率61122==. 【点睛】本题主要考查了统计的实际问题 涉及用样本估计总体的数量 求圆心角的度数 求概率等 属于基础题要认真读图.3.【答案】(1)见解析(2)DGB 是等腰三角形 理由见解析(3)4FG =【分析】(1)连接CO 根据圆周角定理得出2BOD BOC BAC ∠=∠=∠ 根据已知得出F BAC ∠=∠ 根据DE AC ⊥得出90AEG ∠=︒ 进而根据对等角相等 以及三角形内角和定理可得90FBG AEG ∠=∠=︒ 即可得证(2)根据题意得出AD AC = 则ABD ABC ∠=∠ 证明EF BC ∥ 得出AGE ABC ∠=∠ 等量代换得出FGB ABD ∠=∠ 即可得出结论(3)根据FGB ABD ∠=∠ AB BF ⊥ 设FGB ABD α∠=∠= 则90DBF F α∠=∠=︒- 等边对等角得出DB DF = 则224FG DG DB ===.【详解】(1)证明:如图所示 连接CO①BC BD = ①2BOD BOC BAC ∠=∠=∠①2BOD F ∠=∠ ①F BAC ∠=∠①DE AC ⊥ ①90AEG ∠=︒①AGE FGB ∠=∠①90FBG AEG ∠=∠=︒即AB BF ⊥ 又AB 是O 的直径 ①BF 是O 的切线(2)①BC BD = AB 是O 的直径 ①AD AC = BC AC ⊥ ①ABD ABC ∠=∠①DE AC ⊥ BC AC ⊥①EF BC ∥ ①AGE ABC ∠=∠又AGE FGB ∠=∠ ①FGB ABD ∠=∠ ①DGB 是等腰三角形(3)①FGB ABD ∠=∠ AB BF ⊥设FGB ABD α∠=∠= 则90DBF F α∠=∠=︒-①DB DF = ①224FG DG DB ===.【点睛】本题考查了切线的判定 等腰三角形的性质与判定 圆周角定理 熟练掌握以上知识是解题的关键.4.【答案】(1)证明见解析(2)①3 ①2【分析】(1)根据等弧所对的圆周角相等和等边对等角的性质 得到CAE ACO ∠=∠ 推出AD OC ∥ 进而得到OC DC ⊥ 再利用圆的切线的判定定理即可证明结论(2)①连接BE 根据直径所对的圆周角是直角和平行线的判定 得到BE DF ∥ 进而得到AFD ABE ∠=∠ 再利用锐角三角函数 求得6AB = 即可求出O 的半径①利用锐角三角函数 分别求出BF 和AD 的长 即可得到线段DE 的长.【详解】(1)证明:如图 连接OC 点C 是BE 的中点 CE CB ∴= CAE CAB ∴∠=∠OA OC = CAB ACO ∴∠=∠ CAE ACO ∴∠=∠AD OC ∴∥AD DC ⊥ OC DC ∴⊥ OC 是O 的半径 DC ∴是O 的切线(2)解:①如图 连接BEAB 是直径 90AEB ∴∠=︒ BE AD ∴⊥AD DF ⊥ BE DF ∴∥ AFD ABE ∠=∠∴ 1sin 3AFD ∠= 1sin 3AE ABE AB ∴∠== 2AE = 6AB ∴=∴O 的半径为3①由(1)可知 OC DF ⊥ 1sin 3OC AFD OF ∴∠== 3OC = 3OF OB BF BF =+=+ 3133BF ∴=+ 6BF ∴= 6612AF AB BF ∴=+=+= AD DF ⊥ 1sin 123AD AD AFD AF ∴∠=== 4AD ∴= 2AE = 422DE AD AE ∴=-=-=.【点睛】本题是圆和三角形综合题 考查了圆的切线的判定定理 圆的性质 等腰三角形的性质 锐角三角函数等知识 熟练掌握圆的相关性质 灵活运用正弦值求边长是解题关键.5.【答案】(1)见解析(2)tan 2ADB ∠=【分析】(1)利用垂径定理得OF AD ⊥ 利用菱形的性质得GAF BAF ∠=∠ 利用半径相等得OAF OFA ∠=∠ 即可证明90OAF BAF ∠+∠=︒ 据此即可证明结论成立(2)设4AG GD a == 由题意得:5:4OA AG = 求得5OA a = 由勾股定理得到3OG a = 求得2FG a = 利用菱形的性质求得ADB AFG ∠=∠ 据此求解即可.【详解】(1)证明:连接OA①AG GD = 由垂径定理知OF AD ⊥ ①90OGA FGA ∠=∠=︒①四边形ABCD 是菱形 ①GAF BAF ∠=∠ ①90GAF AFG BAF AFG ∠+∠=︒=∠+∠ ①OA OF = ①OAF OFA ∠=∠ ①90OAF BAF OAB ∠+∠=∠=︒ 又①OA 为O 的半径 ①AB 是O 的切线(2)解:①四边形ABCD 是菱形 AG GD = ①设4AG GD a == ①O 的半径与菱形的边长之比为5:8 ①在Rt OAG △中 :5:4OA AG = ①5OA a = 223OG OA AG a -= ①2FG OF OG a =-=①四边形ABCD 是菱形 ①BD AC ⊥ 即90DEA FGA ∠=︒=∠ ①ADB AFG ∠=∠ ①4tan tan 22AG aADB AFG FG a∠=∠===. 【点睛】本题考查了菱形的性质 垂径定理 切线的判定 求角的正切值 勾股定理 解答本题的关键是明确题意 找出所求问题需要的条件.6.【答案】(1)1(2)见解析【分析】(1)由垂径定理可得90AED ∠=︒ 结合CF AD ⊥可得DAE FCD ∠=∠ 根据圆周角定理可得DAE BCD ∠=∠ 进而可得BCD FCD ∠=∠ 通过证明BCE GCE ≌可得1GE BE == (2)证明ACB △CEB ∽ 根据对应边成比例可得2BC BA BE =⋅ 再根据2AB BO = 12BE BG =可证2BC BG BO =⋅【详解】(1)解:直径AB 垂直弦CD ∴90AED ∠=︒ ∴90DAE D ∠+∠=︒CF AD ⊥ ∴90FCD D ∠+∠=︒ ∴DAE FCD ∠=∠由圆周角定理得DAE BCD ∠=∠ ∴BCD FCD ∠=∠ 在BCE 和GCE 中BCE GCE CE CEBEC GEC ∠=∠⎧⎪=⎨⎪∠=∠⎩∴BCE GCE ≌()ASA∴1GE BE ==(2)证明:AB 是O 的直径 ∴90ACB ∠=︒在ACB △和CEB 中90ACB CEB ABC CBE ∠=∠=︒⎧⎨∠=∠⎩∴ACB △CEB ∽ ∴BC BABE BC= ∴2BC BA BE =⋅ 由(1)知GE BE = ∴12BE BG =又2AB BO =∴2122BC BA BE BO BG BG BO =⋅=⋅=⋅7.【答案】(1)3(2)34 10【分析】(1)根据扇形的弧长公式即可求出BOP ∠度数 利用切线的性质和解直角三角形即可求出BC 的长.(2)根据等弧所对圆周角相等推出BAC DAC ∠=∠ 再根据角平分线的性质定理推出CF CB = 利用直角三角形的性质即可求出FCD BAQ ∠=∠ 通过等量转化和余弦值可求出答案. (3)根据三角形相似的性质证明APQ ADC ∽△△和APB ABC ∽△△ 从而推出PQ APCDAD和BP AP BC AB = 利用已知条件将两个比例线段相除 根据正弦值即可求出答案 【详解】(1)解:如图1 连接OP 设BOP ∠的度数为n .=6AB BP 的长为ππ3π180n ⋅⋅∴=. 60n ∴= 即60BOP ∠=︒.1302BAP BOP ∴∠=∠=︒.直线l 是O 的切线90ABC ∴∠=︒.①233BC == (2)解:如图2 连接BQ 过点C 作CF AD ⊥于点FAB 为直径90BQA ∴∠=︒.3cos 4AQ BAQ AB ∴∠==. BP PQ = BAC DAC ∴∠=∠.CF AD ⊥ AB BC ⊥CF CB ∴=.90BAQ ADB ∠+∠=︒ 90FCD ADB ∠+∠=︒FCD BAQ ∴∠=∠.3cos cos 4BC FC FCD BAQ CD CD ∴==∠=∠=. (310理由如下: 如图3 连接BQAB BC ⊥ BQ AD ⊥90ABQ BAD ∴∠+∠=︒ 90ADB BAD ∠+∠=︒ ABQ ADC ∴∠=∠ABQ APQ ∠=∠ ∴APQ ADC ∠=∠. PAQ CAD ∠=∠ APQ ADC ∴∽△△PQ APCD AD.① BAP BAC ∠=∠ 90ABC APB ∠=∠=︒APB ABC ∴△∽△ BP APBC AB∴=.① BC CD = ÷①②得cos PQ ABBAQ BP AD ==∠. 6sin BAQ ∠=10cos BAQ ∴∠=.【点睛】本题是圆的综合题 考查了圆周角定理 相似三角形的判定与性质 解直角三角形以及三角函数 切线的性质定理 扇形的弧长公式 角平分线性质定理等 解题的关键在于熟练掌握相关性质定理和相关计算公式. 8.【答案】(1)129y x =-+ 24(0)y x x => (2)142x << (3)点P 的坐标为()2,5或5,42⎛⎫ ⎪⎝⎭【分析】(1)将(4,1)A 代入2(0)my x x=>可求反比例函数解析式 进而求出点B 坐标 再将(4,1)A 和点B 坐标代入1(0)y kx b k =+≠即可求出一次函数解析式(2)直线AB 在反比例函数图象上方部分对应的x 的值即为所求(3)设点P 的横坐标为p 代入一次函数解析式求出纵坐标 将x p =代入反比例函数求出点Q 的纵坐标 进而用含p 的代数式表示出PQ 再根据POQ △面积为3列方程求解即可. 【详解】(1)解:将(4,1)A 代入2(0)my x x => 可得14m = 解得4m =∴反比例函数解析式为24(0)y x x=>1,2B a ⎛⎫⎪⎝⎭在24(0)y x x =>图象上∴4812a == ∴1,82B ⎛⎫ ⎪⎝⎭将(4,1)A 1,82B ⎛⎫⎪⎝⎭代入1y kx b =+ 得:41182k b k b +=⎧⎪⎨+=⎪⎩ 解得29k b =-⎧⎨=⎩∴一次函数解析式为129y x =-+(2)解:142x << 理由如下: 由(1)可知1(4,1),,82A B ⎛⎫⎪⎝⎭当120y y ->时 12y y >此时直线AB 在反比例函数图象上方 此部分对应的x 的取值范围为142x <<即满足120y y ->时 x 的取值范围为142x <<(3)解:设点P 的横坐标为p将x p =代入129y x =-+ 可得129y p =-+ ∴(),29P p p -+.将x p =代入24(0)y x x=> 可得24y p =∴4,Q p p ⎛⎫⎪⎝⎭.∴429PQ p p=-+-∴11429322POQP SPQ x p p p ⎛⎫=⋅=⨯-+-⋅= ⎪⎝⎭整理得229100p p -+= 解得12p = 252p =当2p =时 292295p -+=-⨯+= 当52p =时 5292942p -+=-⨯+= ∴点P 的坐标为()2,5或5,42⎛⎫ ⎪⎝⎭.【点睛】本题属于一次函数与反比例函数的综合题 考查求一次函数解析式 反比例函数解析式 坐标系中求三角形面积 解一元二次方程等知识点 解题的关键是熟练运用数形结合思想.9.【答案】(1)4y x =(2)132y x =-+ 【分析】(1)根据四边形OABC 是边长为2的正方形求出点B 的坐标 代入ky x=求出k (2)设4,D a a ⎛⎫⎪⎝⎭过点D 作DH x ⊥轴 根据OBDOBHBHDODHSSSS=+-面积列方程 求出点D 坐标 再由待定系数法求出直线BD 的函数表达式.【详解】(1)解:四边形OABC 是边长为2的正方形 ∴4OABC S xy ==正方形 ∴4k =即反比例函数的表达式为4y x=. (2)解:设4,D a a ⎛⎫⎪⎝⎭过点D 作DH x ⊥轴点()2,2B 4,D a a ⎛⎫⎪⎝⎭(),0H a①12OBHS OH AB a =⋅= 1144(2)(2)222BHDa SDH AH a a a-=⋅=⋅⋅-= 122ODHSOH DH =⋅=3OBDOBHBHDODHSSSS=+-=∴4(2)232a a a-+-= 解得:14a = 21a =- 经检验4a = 是符合题意的根 即点()4,1D设直线BD 的函数解析式为y kx b =+ 得① 2241k b k b +=⎧⎨+=⎩ 解得:123k b ⎧=-⎪⎨⎪=⎩ 即:直线BD 的函数解析式为132y x =-+.【点睛】本题考查了反比例函数的几何意义和待定系数法求一次函数解析式 反比例函数ky x=图象上任意一点做x 轴 y 轴的垂线 组成的长方形的面积等于k 灵活运用几何意义是解题关键.10.【答案】(1)8y x=(2)(222,442P -++或(222,442P --- 【分析】(1)设,k A m m ⎛⎫ ⎪⎝⎭可得,k C m m ⎛⎫- ⎪⎝⎭ 结合OAC 的面积是8.可得()182k m m m += 从而可得答案(2)先求解()2,4A ()2,4C - 可得直线为28y x =+ 联立828y x y x ⎧=⎪⎨⎪=+⎩ 再解方程组即可. 【详解】(1)解:①点A 在反比例函数(0)ky k x=≠的图象上 ①设,k A m m ⎛⎫⎪⎝⎭①点C 是点A 关于y 轴的对称点 ①,k C m m⎛⎫- ⎪⎝⎭①OAC 的面积是8. ①()182km m m+= 解得:8k①反比例函数解析式为:8y x=(2)①点A 的横坐标为2时 ①842A y == 即()2,4A 则()2,4C -①直线2y x b =+过点C ①44b -+= ①8b =①直线为28y x =+ ①828y x y x ⎧=⎪⎨⎪=+⎩解得:22242x y ⎧=-+⎪⎨=+⎪⎩222442x y ⎧=--⎪⎨=-⎪⎩经检验 符合题意 ①(222,442P -++或(222,442P ---.【点睛】本题考查的是一次函数与反比例函数的综合应用 轴对称的性质 一元二次方程的解法 熟练的利用图形面积建立方程求解是解本题的关键.11.【答案】(1)8y x=(2)()4,2C 【分析】(1)利用正切值 求出4OB = 进而得到()2,4A 即可求出反比例函数的解析式(2)过点A 作AE x ⊥轴于点E 易证四边形ABOE 是矩形 得到2OE = 4AE = 再证明AED △是等腰直角三角形 得到4DE = 进而得到()6,0D 然后利用待定系数法求出直线AD 的解析式为6y x =-+ 联立反比例函数和一次函数 即可求出点C 的坐标. 【详解】(1)解:AB y ⊥轴90ABO ∴∠=︒1tan 2AOB =∠ 12AB OB ∴= 2AB =4OB ∴=()2,4A ∴点A 在反比例函数()0k y x x=>的图象上248k ∴=⨯=∴反比例函数的解析式为8y x=(2)解:如图 过点A 作AE x ⊥轴于点E90ABO BOE AEO ∠=∠=∠=︒∴四边形ABOE 是矩形2OE AB ∴== 4OB AE ==45ADO ∠=︒AED ∴是等腰直角三角形 4DE AE ∴== 246OD OE DE ∴=+=+= ()6,0D ∴设直线AD 的解析式为y kx b =+2460k b k b +=⎧∴⎨+=⎩ 解得:16k b =-⎧⎨=⎩∴直线AD 的解析式为6y x =-+点A C 是反比例函数8y x=和一次函数6y x =-+的交点 联立86y x y x ⎧=⎪⎨⎪=-+⎩ 解得:24x y =⎧⎨=⎩或42x y =⎧⎨=⎩ ()2,4A ()4,2C ∴.【点睛】本题是反比例函数综合题 考查了锐角三角函数值 矩形的判定和性质 待定系数法求函数解析式 反比例函数和一次函数交点问题等知识 求出直线AD 的解析式是解题关键. 12.【答案】(1)8n = 32k = (2)当6m =时 AB OD ⋅取得最大值 最大值为36【分析】(1)把点()4,A n 代入2y x = 得出8n = 把点()4,8A 代入(0)k y x x=> 即可求得32k = (2)过点C 作x 轴的垂线 分别交,AB x 轴于点,E F 证明ECB FCD △≌△ 得出,BE DF CE CF == 进而可得(8),4C 根据平移的性质得出,(48)B m + (12),0D m - 进而表示出AB OD ⋅ 根据二次函数的性质即可求解.【详解】(1)解:把点()4,A n 代入2y x = ①24n =⨯ 解得:8n =把点()4,8A 代入(0)k y x x=> 解得32k = (2)①点B 横坐标大于点D 的横坐标 ①点B 在点D 的右侧如图所示 过点C 作x 轴的垂线 分别交,AB x 轴于点,E F①AB DF ∥①B CDF ∠=∠在ECB 和FCD 中BCE DCF BC CDB CDF ∠=∠⎧⎪=⎨⎪∠=∠⎩①()ASA ECB FCD ≌①,BE DF CE CF ==①8A EF y ==①4CE CF ==①(8),4C①将点A 沿x 轴正方向平移m 个单位长度得到点B①,(48)B m +①4BE DF m ==-①(12),0D m -①12OD m =-①()()212636AB OD m m m ⋅=-=--+①当6m =时 AB OD ⋅取得最大值 最大值为36.【点睛】本题考查了一次函数与反比例函数综合 二次函数的性质 全等三角形的性质与判定 熟练掌握以上知识是解题的关键.13.【答案】(1)6y x =- (2)<2x -或06x << (3)()32-,或()16-, 【分析】(1)将()4,0A ()0,2B 代入y kx b =+,求得一次函数表达式 进而可得点C 的坐标 再将点C 的坐标代入反比例函数即可(2)将一次函数与反比例函数联立方程组 求得交点坐标即可得出结果(3)过点A 作AP BC ⊥交y 轴于点M 勾股定理得出点M 的坐标 在求出直线AP 的表达式 与反比例函数联立方程组即可.【详解】(1)解:把()4,0A ()0,2B 代入y kx b =+中得:402k b b +=⎧⎨=⎩ ①122k b ⎧=-⎪⎨⎪=⎩ ①直线y kx b =+的解析式为122y x =-+ 在122y x =-+中 当6x =时 1212y x =-+=- ①()61C -,把()61C -,代入m y x=中得:16m -= ①6m =-①反比例函数的表达式6y x=- (2)解:联立1226y x y x ⎧=-+⎪⎪⎨⎪=-⎪⎩解得61x y =⎧⎨=-⎩或23x y =-⎧⎨=⎩ ①一次函数与反比例函数的两个交点坐标分别为()()6123--,、, ①由函数图象可知 当<2x -或06x <<时 一次函数图象在反比例函数图象上方①当m kx b x+>时 <2x -或06x << (3)解:如图所示 设直线AP 交y 轴于点()0M m ,①()4,0A ()0,2B ①222244BM m m m =-=-+ 2222420AB 2222416AM m m =+=+①ABP 是以点A 为直角顶点的直角三角形①90BAM ∠=︒①222BM BA AM =+①22442016m m m -+=++解得8m =-①()08M -,同理可得直线AM 的解析式为28y x =- 联立286y x y x =-⎧⎪⎨=-⎪⎩解得32x y =⎧⎨=-⎩或16x y =⎧⎨=-⎩ ①点P 的坐标为()32-,或()16-,.【点睛】本题主要考查了反比例函数与一次函数综合 勾股定理 正确利用待定系数法求出对应的函数解析式是解题的关键.。
数学人教版九年级下册重庆中考第12题专题复习

重庆中考12题专题复习教学设计【教学目标】 知识与技能1、理解含参数不等式组有〔无〕解、有整数解和含参数分式方程有正数、整数、正整数解 等综合问题;2、能准确求出参数的取值范围 过程与方法经过“引、学、导、练〞等过程,总结出解决中考 12题的解题法宝情感态度价值观通过自主探究,总结归纳,感受了数形结合在数学中的实际运用, 增强了学生解决数学问题 的能力【教学重难点】重点:理解含参数不等式组有〔无〕解、有整数解和含参数分式方程有正数、整数、 正整数解等综合问题难点:通过不等式组和分式方程求参数取值范围 【教学过程】一、回忆考题 导入考点(2021年重庆中考第 12题〕从1a ,关3、1、、1、3这五个数字中,随机抽一个数,记为2于x 的不等式组1(2x7) 3x a 23无解,且使得关于x 的方程3 1xa 0x3x有整数解,那么这 5个数中所有满足条件的 a 的值之积〔 〕A 、-3B 、-2C 、213 D 、2考点?含参数不等式组有〔无〕解、有整数解和含参数分式方程有正数、整数、正整数解等综合问题二、师生合作探究考点探究1 含参数不等式组x 11、假设关于x的不等式组解集为x 1,那么m的取值范围_______x m12、假设关于x的不等式组有解,那么a的取值范围___________ x a变式1:将“有解〞变为“无解〞变式2:将“有解〞变为“有2个整数解〞点拔:含参数不等式组,先口诀,再等号或利用“数形结合〞,求出参数取值范围。
探究2 含参数分式方程假设关于x的方程2m11,那么m的值为____________x1点拔:含参数分式方程,将参数视常数,求出解后,正确理解“有负数解〞,不要忘了考虑增根。
三、例题讲解突破考点例1、(2021年重庆中考第12题〕从3、1,1、、1、3这五个数字中,随机抽一个数,记为a21(2x7)3x a21关于x的不等式组3无解,且使得关于x的方程33xx a0x有整数解,那么这5个数中所有满足条件的a的值之积〔〕A、-3B、-221 C、D、32例2、关于x的不等式组2(x1)4x1ax21x a 1有解,且关于x 的分式方程2x 2x有正整数解,那么整数 a 的个数为〔〕A 、3B 、2C 、1D 、0例2a ,关于x 的不等式组3:从-2、-1、 、0、1这五个数字中,随机抽取一个数,记为3x a 0ax 2的有非负解,那么这5个数3 2x恰有3个整数解,且使得关于x 的方程11x3中所有满足条件的 a 的个数〔〕A、1B、2C、3D、4方法提炼:1、将参数看作常数,求出解集和解;2、正确理解不等式组有解〔大小小大〕、无解〔大大小小〕、有几个整数解等,运用“口诀〞和“数形结合〞求出参数取值范围;切记不要忘了考虑等号是否成立;3、正确理解分式方程有正数解、有非负解等,如“有正整数解〞可分解为:有〔无增根〕、正〔大于 0〕、整数〔正整数、0、负整数〕四、跟踪训练稳固考点2(a x)x4如果关于x的不等式〔组〕3x4,解集x2,且关于x的分式方2x1程a31x有负分数解,那么符号条件的所有整数a的积是〔〕x1x1A、-3B、0C、3D、9五、归纳总结强化考点破解第12题法宝:一般是先将参数当成常数,正确求出含参不等式组的解集和分式方程的解,同时要正确理解有解、无解、有负整数解等关键词,灵活应用“口诀〞和“数形结合〞求出参数取值范围。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3000 元用于购买
(1) 计划购买文艺刊物的资金不少于购买科普书籍资金的
2 倍 , 那么最少用多少资金购买文
艺刊物 ?
(2) 经初步了解 , 有 200 户居民自愿参与集资 , 那么平均每户需集资 150 元 . 经筹委会进步宣传 , 自
愿参加的户数在 200 户的基础上增加了 a%(其中 a> 50), 如果每户平均集资在 150 元的基础上减少 2 5
)
2-x x- 2
A.1
B.2 C.3 D.4
23. 新年将至 , 腊肉和腊肠是川渝人的最爱 , “城口老腊肉”是汉族风味名菜 , 距今已有 500 多年的历
史, 在重庆市内外享有盛誉 . 某肉制品加工店每周购进一批新鲜猪肉用于制作腊肉和腊肠
, 每周均
全部售万 , 新鲜猪肉进价 24 元/ 千克 , 成品腊肉伤价 72 元 / 千克 , 成品腊肠售价 96 元/ 千克。
a%,那么实际筹资将比计划筹资多 6000 元 , 求 a 的值 。
2ቤተ መጻሕፍቲ ባይዱ
(八) 3
(八)
(八) 4
m - 4x>4
( 一)12. 如果关于 x 的不等式组 x - 11<3(x 1 ) 有且仅有三个整数解 , 且关于 x 的分式方程
2
2
2 - mx 6 -
1有非负数解 , 则符合条件的所有整数 m的个数是(
(1 ) 1 份份第一周售出腊肉、脂肠 140 千克 , 若第一周的销售额不低于 11520 元,则至少卖出腊肠 多少于克 ?
(2) 加工店发现消费者更偏爱腊肠 , 于是 1 月份的第二周 , 决定将腊肠价格上涨 a %,腊肉价裕下降 6
a %,并且在第一周腊肠最低销售量的基础上 3
, 腊肠销售量增加 a %,腊肉销售量不变 , 出于腊肉、腊 2
肠的制作过程需要将新鲜猪肉进行腌制、风干 , 在不考虑其他原材料的前提下,腊肠出品率为
60%,腊肉出品率为 50%,最终 1 月份第二周获利
( 出品率
成品量
100% )
所有新鲜猪肉量
5760 元,求 a 的值。
5
2018 重庆市中考第 12、23 题专题训练
( 育) (育)
1
(九) 12. 如果关于 x 的方程 ax 2 +4x-2=0 有两个不相等的实数根 , 且关于 x 的分式方程 1 1- ax 2 有 正 数解 , 则符合条件的所有整数 a 的值的和是
2 x x -2
A.-1 B.0
C.1
D.2
(九) 23. 九龙技区某社区开展全民读书活动 , 以丰富人们业余文化生活现计划筹资 科普书籍和文艺刊物
