高一数学函数的奇偶性1(20200806105116)

合集下载

数学专题复习_函数的奇偶性

高一数学专题复习：函数的奇偶性一、奇偶性的定义：定义：对于函数y＝f(x)的定义域内任意一个值x，若f(－x)＝f(x)恒成立，则函数y＝f(x)就叫做偶函数；若f(－x)＝－f(x)恒成立，则函数y＝f(x)就叫做奇函数.如果函数f(x)是奇函数或偶函数，那么我们就说函数f(x)具有奇偶性。

说明：(1)奇偶性是对整个定义域而言，是函数的整体性质。

定义中的等式f(－x)＝f(x)（或f(－x)＝－f(x)）对定义域里的任意x都要成立，若只对个别x值成立，则不能说这函数是偶函数（或奇函数）(2)其定义域关于原点对称。

等式f(－x)＝f(x)（或f(－x)＝－f(x)）成立，除了表明函数值相等（或互为相反数）外，首先表明对定义域中的任意x来说，-x也应在定义域之中，否则f(－x)无意义。

由此得结论：凡是定义域不关于原点对称的函数一定是非奇、非偶的函数.(3)奇函数若在0x=时有定义，则f(0)＝0．(4)偶函数f(x)有f(－x)＝f(x)＝f(|x|)(5)函数f(x)＝0既是奇函数也是偶函数，因为其定义域关于原点对称且既满足f(－x)＝f(x)也满足f(－x)＝－f(x)。

(6)四类函数：是奇函数不是偶函数，是偶函数不是奇函数，既是奇函数又是偶函数，既不是奇函数也不是偶函数。

(7)在公共定义域内，奇函数与奇函数的和为奇函数，偶函数与偶函数的和为偶函数，奇函数与奇函数的积为偶函数，偶函数与奇函数的和为奇函数。

二、奇偶函数图象的性质定理定理：①奇函数的图象关于原点对称，反过来，若一个函数的图象关于原点对称，则这个函数是奇函数；②偶函数的图象关于y轴对称，反过来，若一个函数的图象关于y轴对称，则这个函数是偶函数.即f(x)是奇函数⇔函数f(x)的图象关于原点对称；f(x)是偶函数⇔函数f(x)的图象关于y轴对称；三、函数奇偶性的判断方法判定函数的奇偶性的方法有：(1)定义法，先看定义域是否关于原点对称，如y=x2，x∈［－1，1)，既非奇又非偶函数.(2)特值法，起探路及判定否命题等作用，一方面，若f(－1)=f(1)〔f(－1)=－f(1)〕，则f(x)可能是偶(奇)函数.另一方面，若f(－1)≠f(1)〔f(－1)≠－f(1)〕，则f(x)一定不是偶(奇)函数.(3)和、差法，若f(x)+f(－x)=0，则f(x)为奇函数；若f(－x)－f(x)=0，则f(x)为偶函数.该方法应用的前提是用“特值法”先探路.(4)比值法，若f(x)／f(－x)=1(或－1)，则f(x)为偶(或奇)函数.(5)图象法，可直接根据图象的对称性来判定奇偶性.例：已知函数f(x)满足f(x+y)+ f(x－y)=2f(x)·f(y)(x、y∈R)，且f(0)≠0，试证f(x)是偶函数.证明：令x=y=0，有f(0)+f(0)=2f2(0).∵f(0)≠0，∴f(0)=1.令x=0，f(y)+f(－y)=2f(0)·f(y)=2f(y).∴f(－y)=f(y).∴f(x)是偶函数.1.若y =f (x )在x ∈［0，+∞)上的表达式为y =x (1－x )，且f (x )为奇函数，则x ∈(－∞，0］时f (x )等于（）A.－x (1－x )B.x (1+x )C.－x (1+x )D.x (x －1)2．已知奇函数f(x)在区间[3,7]上是增函数，且最小值是5，那么f(x)在区间[-7, -3]上是 ( )A.增函数且最小值是-5；B. 增函数且最大值是-5；C.减函数且最小值是-5；D. 减函数且最大值是-5.3．若)(),(x g x q 均为奇函数，),0(1)()()(+∞++=在x bg x aq x f 上有最大值5，则在)0,(-∞上)(x f 有（）A 、最小值-5B 、最小值-2C 、最小值-3D 、最大值-54．已知函数)(x f y =是偶函数，)2(-=x f y ，在[0，2]上是单调递减函数，则（）A 、)2()1()0(f f f <-<B 、)2()0()1(f f f <<-C 、)0()2()1(f f f <<-D 、)0()1()2(f f f <-<5．若函数)(x f y =是偶函数，R x ∈，在0<x 时，y 是增函数，对于||||,0,02121x x x x <><且，则（）A 、)()(21x f x f ->-B 、)()(21x f x f -<-C 、)()(21x f x f -=-D 、)()(21x f x f -≥-6．若f (x )= 121-x +a (x ∈R 且x ≠0)为奇函数，则a =_______________.7.已知f (x )=ax 2+bx +3a +b 是偶函数，且定义域为［a －1，2a ］，则a =_____________，b =____________.8．若f (x )是偶函数，当x ∈［0，+∞)时，f (x )=x －1，则f (x －1)＜0的解集是_______________.9．定义在[2,2]-上的偶函数()g x ，当0x ≥时，()g x 为减函数，若(1)()g m g m -<成立，求m 的取值范围。

高一数学《函数的奇偶性》教案设计

高一数学《函数的奇偶性》教案设计高一数学《函数的奇偶性》教案设计（精选5篇）教案是教师为顺利而有效地开展教学活动，根据教学大纲和教科书要求及学生的实际情况，以课时或课题为单位，对教学内容、教学步骤、教学方法等进行的具体设计和安排的一种实用性教学文书。

下面是小编整理的高一数学《函数的奇偶性》教案设计，希望对大家有帮助!高一数学《函数的奇偶性》教案设计篇1一、教学目标【知识与技能】理解函数的奇偶性及其几何意义【过程与方法】利用指数函数的图像和性质,及单调性来解决问题【情感态度与价值观】体会指数函数是一类重要的函数模型,激发学生学习数学的兴趣二、教学重难点【重点】函数的奇偶性及其几何意义【难点】判断函数的奇偶性的方法与格式三、教学过程(一)导入新课取一张纸，在其上画出平面直角坐标系，并在第一象限任画一可作为函数图象的图形，然后按如下操作并回答相应问题：1 以y轴为折痕将纸对折，并在纸的背面(即第二象限)画出第一象限内图形的痕迹，然后将纸展开，观察坐标系中的图形;问题：将第一象限和第二象限的图形看成一个整体，则这个图形可否作为某个函数y=f(x)的图象，若能请说出该图象具有什么特殊的性质?函数图象上相应的点的坐标有什么特殊的关系?答案：(1)可以作为某个函数y=f(x)的图象，并且它的图象关于y 轴对称;(2)若点(x，f(x))在函数图象上，则相应的点(-x，f(x))也在函数图象上，即函数图象上横坐标互为相反数的点，它们的纵坐标一定相等(二)新课教学1.函数的奇偶性定义像上面实践操作1中的图象关于y轴对称的函数即是偶函数，操作2中的图象关于原点对称的函数即是奇函数(1)偶函数(even function)一般地，对于函数f(x)的定义域内的任意一个x，都有f(-x)=f(x)，那么f(x)就叫做偶函数(学生活动)：仿照偶函数的定义给出奇函数的定义(2)奇函数(odd function)一般地，对于函数f(x)的定义域内的任意一个x，都有f(-x)=f(x)，那么f(x)就叫做奇函数注意：1 函数是奇函数或是偶函数称为函数的奇偶性，函数的奇偶性是函数的整体性质;2 由函数的奇偶性定义可知，函数具有奇偶性的一个必要条件是，对于定义域内的任意一个x，则-x也一定是定义域内的一个自变量(即定义域关于原点对称)2.具有奇偶性的函数的图象的特征偶函数的图象关于y轴对称;奇函数的图象关于原点对称3.典型例题(1)判断函数的奇偶性例1.(教材P36例3)应用函数奇偶性定义说明两个观察思考中的四个函数的奇偶性(本例由学生讨论，师生共同总结具体方法步骤) 解：(略)总结：利用定义判断函数奇偶性的格式步骤：1 首先确定函数的定义域，并判断其定义域是否关于原点对称;2 确定f(-x)与f(x)的关系;3 作出相应结论：若f(-x) = f(x) 或 f(-x)-f(x) = 0，则f(x)是偶函数;若f(-x) =-f(x) 或 f(-x)+f(x) = 0，则f(x)是奇函数(三)巩固提高1.教材P46习题1.3 B组每1题解：(略)说明：函数具有奇偶性的一个必要条件是，定义域关于原点对称，所以判断函数的奇偶性应应首先判断函数的定义域是否关于原点对称，若不是即可断定函数是非奇非偶函数2.利用函数的奇偶性补全函数的图象(教材P41思考题)规律：偶函数的图象关于y轴对称;奇函数的图象关于原点对称说明：这也可以作为判断函数奇偶性的依据(四)小结作业本节主要学习了函数的奇偶性，判断函数的奇偶性通常有两种方法，即定义法和图象法，用定义法判断函数的奇偶性时，必须注意首先判断函数的定义域是否关于原点对称，单调性与奇偶性的综合应用是本节的一个难点，需要学生结合函数的图象充分理解好单调性和奇偶性这两个性质课本P46 习题1.3(A组) 第9、10题， B组第2题四、板书设计函数的奇偶性一、偶函数：一般地，对于函数f(x)的定义域内的任意一个x，都有f(-x)=f(x)，那么f(x)就叫做偶函数二、奇函数：一般地，对于函数f(x)的定义域内的任意一个x，都有f(-x)=f(x)，那么f(x)就叫做奇函数三、规律：偶函数的图象关于y轴对称;奇函数的`图象关于原点对称高一数学《函数的奇偶性》教案设计篇2教学目标：了解奇偶性的含义，会判断函数的奇偶性。

高一必修一数学知识点：函数奇偶性

高一必修一数学学问点：函数奇偶性高一必修一数学学问点：函数奇偶性数学是学习和探讨现代科学技术必不行少的基本工具。

下面为大家带来了函数奇偶性的数学学问点，希望能够帮助到大家。

1．定义一般地，对于函数f(x)(1)假如对于函数定义域内的随意一个x，都有f(-x)=-f(x)，那么函数f(x)就叫做奇函数。

(2)假如对于函数定义域内的随意一个x，都有f(-x)=f(x)，那么函数f(x)就叫做偶函数。

(3)假如对于函数定义域内的随意一个x，f(-x)=-f(x)与f(-x)=f(x)同时成立，那么函数f(x)既是奇函数又是偶函数，称为既奇又偶函数。

(4)假如对于函数定义域内的随意一个x，f(-x)=-f(x)与f(-x)=f(x)都不能成立，那么函数f(x)既不是奇函数又不是偶函数，称为非奇非偶函数。

说明：①奇、偶性是函数的整体性质，对整个定义域而言②奇、偶函数的定义域肯定关于原点对称，假如一个函数的定义域不关于原点对称，则这个函数肯定不是奇(或偶)函数。

(分析：推断函数的奇偶性，首先是检验其定义域是否关于原点对称，然后再严格依据奇、偶性的定义经过化简、整理、再与f(x)比较得出结论)③推断或证明函数是否具有奇偶性的依据是定义2．奇偶函数图像的特征：定理奇函数的`图像关于原点成中心对称图表，偶函数的图象关于y轴或轴对称图形。

f(x)为奇函数《==》f(x)的图像关于原点对称点(x，y)→(-x，-y)奇函数在某一区间上单调递增，则在它的对称区间上也是单调递增。

偶函数在某一区间上单调递增，则在它的对称区间上单调递减。

3.奇偶函数运算(1).两个偶函数相加所得的和为偶函数.(2).两个奇函数相加所得的和为奇函数.(3).一个偶函数与一个奇函数相加所得的和为非奇函数与非偶函数.(4).两个偶函数相乘所得的积为偶函数.(5).两个奇函数相乘所得的积为偶函数.(6).一个偶函数与一个奇函数相乘所得的积为奇函数.。

函数的奇偶性(精辟讲解)

[难点正本疑点清源] 1．函数奇偶性的判断
判断函数的奇偶性主要根据定义：一般地，如果对于函数 f(x)的定义域内任意一个 x，都有 f(－x)＝f(x)(或 f(－x)＝－f(x))，那么函数 f(x)就叫做偶函数(或奇函数)．其中包含两个必备条件： ①定义域关于原点对称，这是函数具有奇偶性的必要不充分条件，所以首先考虑定义域有利于准确简捷地解决问题； ②判断 f(x)与 f(－x)是否具有等量关系．在判断奇偶性的运算中，可以转化为判断奇偶性的等价关系式 (f(x)＋f(－x)＝0(奇函数)或 f(x)－f(－x)＝0(偶函数)) 是否成立．
2．函数奇偶性的性质 (1)奇函数在关于原点对称的区间上若有单调性，则其单调性完全相同；偶函数在关于原点对称的区间上若有单调性，则其单调性恰恰相反． (2)若 f(x)为偶函数，则 f(－x)＝f(x)＝f(|x|)． (3)若奇函数 f(x)定义域中含有 0，则必有 f(0)＝0. f(0)＝0 是 f(x)为奇函数的既不充分也不必要条件． (4)定义在关于原点对称区间上的任意一个函数，都可表示成“一个奇函数与一个偶函数的和(或差)”． (5)复合函数的奇偶性特点是：“内偶则偶，内奇同外”． (6)既奇又偶的函数有无穷多个(如 f(x)＝0，定义域是关于原点对称的任意一个数集)．
∴f(x)为偶函数．
题型二函数的奇偶性与单调性
例 2 (1)已知 f(x)是 R 上的奇函数，且当 x>0 时，f(x) ＝x2－x－1，求 f(x)的解析式； (2)设 a>0，f(x)＝eax＋eax是 R 上的偶函数，求实数 a 的值；
(3)已知奇函数 f(x)的定义域为[－2,2]，且在区间 [－2,0]内递减，求满足 f(1－m)＋f(1－m2)<0 的实数 m 的取值范围．思维启迪 (1)f(x)是一个分段函数，当 x<0 时，转化为

高中数学函数的奇偶性(解析版)

1．函数的奇偶性(1)奇偶性的定高中数学函数的奇偶性(解析版)义奇偶性定义图象特点偶函数如果对于函数f (x )的定义域内任意一个x ，都有f (－x )＝f (x )，那么函数f (x )是偶函数关于y 轴对称奇函数如果对于函数f (x )的定义域内任意一个x ，都有f (－x )＝－f (x )，那么函数f (x )是奇函数关于原点对称(2)函数奇偶性常用结论结论1：如果函数f (x )是奇函数且在x ＝0处有意义，那么f (0)＝0．结论2：如果函数f (x )是偶函数，那么f (x )＝f (－x )＝f (|x |)．结论3：若函数y ＝f (x ＋b )是定义在R 上的奇函数，则函数y ＝f (x )关于点(b ，0)中心对称．结论4：若函数y ＝f (x ＋a )是定义在R 上的偶函数，则函数y ＝f (x )关于直线x ＝a 对称．结论5：已知函数f (x )是定义在区间D 上的奇函数，则对任意的x ∈D ，都有f (x )＋f (－x )＝0．特别地，若奇函数f (x )在D 上有最值，则f (x )max ＋f (x )min ＝0．推论1：若函数f (x )是奇函数，且g (x )＝f (x )＋c ，则必有g (－x )＋g (x )＝2c ．推论2：若函数f (x )是奇函数，且g (x )＝f (x )＋c ，则必有g (x )max ＋g (x )min ＝2c ．结论6：在公共定义域内有：奇±奇＝奇；偶±偶＝偶；奇±偶＝非奇非偶；奇)(÷⨯奇＝偶，偶)(÷⨯偶＝偶，奇)(÷⨯偶＝奇．结论7：若函数f (x )的定义域关于原点对称，则函数f (x )能表示成一个偶函数与一个奇函数的和的形式.记g (x )＝12[f (x )＋f (－x )]，h (x )＝12[f (x )－f (－x )]，则f (x )＝g (x )＋h (x )．结论8：奇函数在其定义域内关于原点对称的两个区间上具有相同的单调性；偶函数在其定义域内关于原点对称的两个区间上具有相反的单调性．结论9：偶函数在其定义域内关于原点对称的区间上有相同的最大(小)值，取最值时的自变量互为相反数；奇函数在其定义域内关于原点对称的区间上的最值互为相反数，取最值时的自变量也互为相反数．结论10：复合函数y ＝f [g (x )]的奇偶性：内偶则偶，两奇为奇．结论11：指数型函数的奇偶性(1)函数f (x )＝a x ＋a －x (a >0且a ≠1)是偶函数；(2)函数f (x )＝a x －a －x (a >0且a ≠1)是奇函数；(3)函数f (x )＝a x ＋1a x －1(a >0且a ≠1)是奇函数；(4)函数f (x )＝a x －a －x a x ＋a －x ＝a 2x ＋1a 2x－1(a >0且a ≠1)是奇函数；结论12：对数型函数的奇偶性(1)函数f (x )＝log a m －x m ＋x (a >0且a ≠1)是奇函数；函数f (x )＝log a m ＋xm －x (a >0且a ≠1)是奇函数；(2)函数f (x )＝log a x －m x ＋m (a >0且a ≠1)是奇函数；函数f (x )＝log a x ＋mx －m (a >0且a ≠1)是奇函数；(3)函数f (x )＝log a mx －b mx ＋b (a >0且a ≠1)是奇函数；函数f (x )＝log a mx ＋bmx －b(a >0且a ≠1)是奇函数；(4)函数f(x)＝log a(1＋m2x2±mx)(a>0且a≠1)是奇函数．2．函数的对称性(奇偶性的推广)(1)函数的轴对称定理1：如果函数y＝f(x)满足f(x＋a)＝f(b－x)，则函数y＝f(x)的图象关于直线x＝a＋b2对称．推论1：如果函数y＝f(x)满足f(a＋x)＝f(a－x)，则函数y＝f(x)的图象关于直线x＝a对称．推论2：如果函数y＝f(x)满足f(x)＝f(－x)，则函数y＝f(x)的图象关于直线x＝0（y轴）对称，就是偶函数的定义，它是上述定理1的简化．(2)函数的点对称定理2：如果函数y＝f(x)满足f(a＋x)＋f(a－x)＝2b，则函数y＝f(x)的图象关于点(a，b)对称．推论1：如果函数y＝f(x)满足f(a＋x)＋f(a－x)＝0，则函数y＝f(x)的图象关于点(a，0)对称．推论2：如果函数y＝f(x)满足f(x)＋f(－x)＝0，则函数y＝f(x)的图象关于原点(0，0)对称，就是奇函数的定义，它是上述定理2的简化．(3)两个等价关系若函数y＝f(x)关于直线x＝a轴对称，则以下三式成立且等价：f(a＋x)＝f(a－x)⇔f(2a－x)＝f(x)⇔f(2a＋x)＝f(－x)若函数y＝f(x)关于点(a，0)中心对称，则以下三式成立且等价：f(a＋x)＝－f(a－x)⇔f(2a－x)＝－f(x)⇔f(2a＋x)＝－f(－x)考点一判断函数的奇偶性【方法总结】判断函数的奇偶性：首先看函数的定义域是否关于原点对称；在定义域关于原点对称的条件下，再化简解析式，根据f(－x)与f(x)的关系作出判断．分段函数奇偶性的判断，要分别从x>0或x<0来寻找等式f(－x)＝f(x)或f(－x)＝－f(x)成立，只有当对称的两个区间上满足相同关系时，分段函数才具有确定的奇偶性．用函数奇偶性常用结论6或特值法可秒杀．【例题选讲】[例1](1)下列函数为偶函数的是()A．y＝B．y＝x2＋e|x|C．y＝x cos x D．y＝ln|x|－sin x答案B解析对于选项A，易知y＝tan B，设f(x)＝x2＋e|x|，则f(－x)＝(－x)2＋e|－x|＝x2＋e|x|＝f(x)，所以y＝x2＋e|x|为偶函数；对于选项C，设f(x)＝x cos x，则f(－x)＝－x cos(－x)＝－x cos x＝－f(x)，所以y＝x cos x为奇函数；对于选项D，设f(x)＝ln|x|－sin x，则f(2)＝ln2－sin 2，f(－2)＝ln2－sin(－2)＝ln2＋sin2≠f(2)，所以y＝ln|x|－sin x为非奇非偶函数，故选B．(2)下列函数中，既不是奇函数，也不是偶函数的是()A．y＝x＋sin2x B．y＝x2－cos x C．y＝2x＋12xD．y＝x2＋sin x 答案D解析对于A，定义域为R，f(－x)＝－x＋sin2(－x)＝－(x＋sin2x)＝－f(x)，为奇函数；对于B，定义域为R，f(－x)＝(－x)2－cos(－x)＝x2－cos x＝f(x)，为偶函数；对于C，定义域为R，f(－x)＝2－x＋12－x＝2x＋12x＝f(x)，为偶函数；对于D，y＝x2＋sin x既不是偶函数也不是奇函数．(3)设函数f(x)＝e x－e－x2，则下列结论错误的是()A．|f(x)|是偶函数B．－f(x)是奇函数C．f(x)|f(x)|是奇函数D．f(|x|)f(x)是偶函数答案D解析∵f(x)＝e x－e－x2，则f(－x)＝e－x－e x2＝－f(x)．∴f(x)是奇函数．∵f(|－x|)＝f(|x|)，∴f(|x|)是偶函数，∴f(|x|)f(x)是奇函数．(4)已知f(x)＝4－x2，g(x)＝|x－2|，则下列结论正确的是()A．h(x)＝f(x)＋g(x)是偶函数B．h(x)＝f(x)·g(x)是奇函数C．h(x)＝g(x)·f(x)2－x是偶函数D．h(x)＝f(x)2－g(x)是奇函数答案D解析h(x)＝f(x)＋g(x)＝4－x2＋|x－2|＝4－x2＋2－x，x∈[－2,2]．h(－x)＝4－x2＋2＋x≠h(x)，且h(－x)≠－h(x)，不满足函数奇偶性的定义，是非奇非偶函数．B．h(x)＝f(x)·g(x)＝4－x2|x－2|＝4－x2(2－x)，x∈[－2,2]．h(－x)＝4－x2(2＋x)≠h(x)，且h(－x)≠－h(x)，不满足函数奇偶性的定义，是非奇非偶函数．C．h(x)＝g(x)·f(x)2－x＝4－x2，x∈[－2，2)，定义域不关于原点对称，是非奇非偶函数．D．h(x)＝f(x)2－g(x)＝4－x2x，x∈[－2，0)∪(0，2]，是奇函数．(5)已知函数f(x)满足f(x＋1)＋f(－x＋1)＝2，则以下四个选项一定正确的是()A．f(x－1)＋1是偶函数B．f(x－1)－1是奇函数C．f(x＋1)＋1是偶函数D．f(x＋1)－1是奇函数答案－12解析法一：因为f(x＋1)＋f(－x＋1)＝2，所以f(x)＋f(2－x)＝2，所以函数y＝f(x)的图象关于点(1，1)中心对称，而函数y＝f(x＋1)－1的图象可看作是由y＝f(x)的图象先向左平移1个单位长度，再向下平移1个单位长度得到，所以函数y＝f(x＋1)－1的图象关于点(0，0)中心对称，所以函数y＝f(x＋1)－1是奇函数，故选D．法二：由f(x＋1)＋f(－x＋1)＝2，得f(x＋1)－1＋f(－x＋1)－1＝0，令F(x)＝f(x＋1)－1，则F(x)＋F(－x)＝0，所以F(x)为奇函数，即f(x＋1)－1为奇函数，故选D．【对点训练】1．下列函数为奇函数的是()A．f(x)＝x3＋1B．f(x)＝ln1－x1＋xC．f(x)＝e x D．f(x)＝x sin x1．答案B解析对于A，f(－x)＝－x3＋1≠－f(x)，所以其不是奇函数；对于B，f(－x)＝ln1＋x1－x＝－ln 1－x 1＋x＝－f(x)，所以其是奇函数；对于C，f(－x)＝e－x≠－f(x)，所以其不是奇函数；对于D，f(－x)＝－x sin(－x)＝x sin x＝f(x)，所以其不是奇函数．故选B．2．函数f(x)＝9x＋13x的图象()A．关于x轴对称B．关于y轴对称C．关于坐标原点对称D．关于直线y＝x对称2．答案B解析因为f(x)＝9x＋13x＝3x＋3－x，易知f(x)为偶函数，所以函数f(x)的图象关于y轴对称．3．下列函数中既不是奇函数也不是偶函数的是()A．y＝2|x|B．y＝lg(x＋x2＋1)C．y＝2x＋2－x D．y＝lg1x＋13．答案D解析对于D项，1x＋1>0，即x>－1，其定义域关于原点不对称，是非奇非偶函数．4．已知f(x)＝x2x－1，g(x)＝x2，则下列结论正确的是()A．f(x)＋g(x)是偶函数B．f(x)＋g(x)是奇函数C．f(x)g(x)是奇函数D．f(x)g(x)是偶函数4．答案A解析令h(x)＝f(x)＋g(x)，因为f(x)＝x2x－1，g(x)＝x2，所以h(x)＝x2x－1＋x2＝x·2x＋x2(2x－1)，定义域为(－∞，0)∪(0，＋∞)．因为h(－x)＝－x·2－x－x2(2－x－1)＝x(1＋2x)2(2x－1)＝h(x)，所以h(x)＝f(x)＋g(x)是偶函数，令F(x)＝f(x)g(x)＝x22(2x－1)，定义域为(－∞，0)∪(0，＋∞)．所以F(－x)＝(－x)22(2－x－1)＝x2·2x2(1－2x)，因为F(－x)≠F(x)且F(－x)≠－F(x)，所以F(x)＝g(x)f(x)既不是奇函数也不是偶函数．5．设f(x)＝e x＋e－x，g(x)＝e x－e－x，f(x)，g(x)的定义域均为R，下列结论错误的是() A．|g(x)|是偶函数B．f(x)g(x)是奇函数C．f(x)|g(x)|是偶函数D．f(x)＋g(x)是奇函数5．答案D解析f(－x)＝e－x＋e x＝f(x)，f(x)为偶函数．g(－x)＝e－x－e x＝－g(x)，g(x)为奇函数．|g(－x)|＝|－g(x)|＝|g(x)|，|g(x)|为偶函数，A正确；f(－x)g(－x)＝f(x)[－g(x)]＝－f(x)g(x)，所以f(x)g(x)为奇函数，B正确；f(－x)|g(－x)|＝f(x)|g(x)|，所以f(x)|g(x)|是偶函数，C正确；f(x)＋g(x)＝2e x，f(－x)＋g(－x)＝2e－x≠－(f(x)＋g(x))，且f(－x)＋g(－x)＝2e－x≠f(x)＋g(x)，所以f(x)＋g(x)既不是奇函数也不是偶函数，D错误，故选D．6．设函数f(x)，g(x)的定义域都为R，且f(x)是奇函数，g(x)是偶函数，则下列结论中正确的是() A．f(x)g(x)是偶函数B．|f(x)|g(x)是奇函数C．f(x)|g(x)|是奇函数D．|f(x)g(x)|是奇函数6．答案C解析对于A：令h(x)＝f(x)·g(x)，则h(－x)＝f(－x)·g(－x)＝－f(x)·g(x)＝－h(x)，∴h(x)是奇函数，A错．对于B：令h(x)＝|f(x)|g(x)，则h(－x)＝|f(－x)|g(－x)＝|－f(x)|·g(x)＝|f(x)|g(x)＝h(x)，∴h(x)是偶函数，B错．对于C：令h(x)＝f(x)|g(x)|，则h(－x)＝f(－x)|g(－x)|＝－f(x)·|g(x)|＝－h(x)，∴h(x)是奇函数，C正确．对于D：令h(x)＝|f(x)·g(x)|，则h(－x)＝|f(－x)·g(－x)|＝|－f(x)·g(x)|＝|f(x)·g(x)|＝h(x)，∴h(x)是偶函数，D错．考点二已知函数的奇偶性，求函数解析式中参数的值【方法总结】已知函数的奇偶性求函数解析式中参数的值：常常利用待定系数法，由f(x)±f(－x)＝0得到关于待求参数的恒等式，由系数的对等性得参数的值或对方程求解．对于选填题可用特值法进行秒杀．【例题选讲】[例2](1)若函数f(x)＝x ln(x＋a＋x2)为偶函数，则a＝________．答案1解析f(x)为偶函数，则y＝ln(x＋a＋x2)为奇函数，所以ln(x＋a＋x2)＋ln(－x＋a＋x2)＝0，则ln(a＋x2－x2)＝0，∴a＝1．(2)已知函数f(x)＝2×4x－a2x的图象关于原点对称，g(x)＝ln(ex＋1)－bx是偶函数，则log a b＝()A．1B．－1C．－12D．14答案B解析由题意得f(0)＝0，∴a＝2.∵g(1)＝g(－1)，∴ln(e＋1)－b＝ln(1e＋1)＋b，∴b＝12，∴log212＝－1．故选B．(3)若函数f(x)－1，0<x≤2，1，－2≤x≤0，g(x)＝f(x)＋ax，x∈[－2，2]为偶函数，则实数a＝答案－12解析因为f (x )－1，0<x ≤2，1，－2≤x ≤0，所以g (x )＝f (x )＋ax －1，－2≤x ≤0，1＋a )x －1，0<x ≤2，因为g (x )－1，－2≤x ≤0，＋a )x －1，0<x ≤2为偶函数，所以g (－1)＝g (1)，即－a －1＝1＋a －1＝a ，所以2a ＝－1，所以a ＝－12．(4)已知函数f (x )＝a －2e x ＋1(a ∈R )是奇函数，则函数f (x )的值域为()A ．(－1，1)B ．(－2，2)C ．(－3，3)D ．(－4，4)答案A解析法一：由f (x )是奇函数知f (－x )＝－f (x )，所以a －2e －x ＋1＝－a ＋2e x ＋1，得2a ＝2e x＋1＋2e －x ＋1，所以a ＝1e x ＋1＋e x e x ＋1＝1，所以f (x )＝1－2e x ＋1．因为e x ＋1>1，所以0<1e x ＋1<1，－1<1－2e x ＋1<1，所以函数f (x )的值域为(－1，1)．法二：函数f (x )的定义域为R ，且函数f (x )是奇函数，所以f (0)＝a －1＝0，即a ＝1，所以f (x )＝1－2e x ＋1．因为e x ＋1>1，所以0<1e x ＋1<1，－1<1－2e x ＋1<1，所以函数f (x )的值域为(－1，1)．(5)已知f (x )是奇函数，且当x ＜0时，f (x )＝－e ax ，若f (ln 2)＝8，则a ＝________．答案－3解析当x ＞0，－x ＜0，f (－x )＝－e－ax．因为f (x )是奇函数，所以当x ＞0时，f (x )＝－f (－x )＝e－ax，所以f (ln 2)＝e－a ln2＝(e ln 2)－a ＝2－a ＝8．解得a ＝－3．【对点训练】7．若f (x )＝ln(e 3x ＋1)＋ax 是偶函数，则a ＝________.7．答案－32解析函数f (x )＝ln(e 3x ＋1)＋ax 是偶函数，故f (－x )＝f (x )，即ln(e－3x＋1)－ax ＝ln(e 3x ＋1)＋ax ，化简得ln(1＋e 3x )－ln e 3x －ax ＝ln(e 3x ＋1)＋ax ，即－3x －ax ＝ax ，所以2ax ＋3x ＝0恒成立，所以a ＝－328．若函数f (x )＝x 3(12x －1＋a )为偶函数，则a 的值为________．8．答案12解析解法1：因为函数f (x )＝x 3(12x －1＋a )为偶函数，所以f (－x )＝f (x )，即(－x )3(12－x －1＋a )＝x 3(12x －1＋a )，所以2a ＝－(12－x －1＋12x －1)，所以2a ＝1，解得a ＝12.解法2：因为函数f (x )＝x 3(12x －1＋a )为偶函数，所以f (－1)＝f (1)，所以(－1)3×(12－1－1＋a )＝13×(121－1＋a )，解得a ＝12，经检验，当a ＝12时，函数f (x )为偶函数．9．函数f (x )＝(x ＋1)(x ＋a )x 3为奇函数，则a ＝________．9．答案－1解析由题意得f (－1)＋f (1)＝0，即2(a ＋1)＝0，解得a ＝－1，经检验，a ＝－1时，函数f (x )为奇函数．10．已知奇函数f (x )x ＋a ，x ＞0，－2－x，x ＜0，则实数a ＝________．10．答案－4解析因为函数f (x )为奇函数，则f (－x )＝－f (x )，f (－1)＝－f (1)，所以4－21＝－(21＋a )，解得a ＝－4．11．已知f (x )＝3ax 2＋bx －5a ＋b 是偶函数，且其定义域为[6a －1，a ]，则a ＋b ＝()A ．17B ．－1C ．1D ．711．答案A解析因为偶函数的定义域关于原点对称，所以6a －1＋a ＝0，所以a ＝17.又因为f (x )为偶函数，所以b ＝0，即a ＋b ＝17．故选A ．12．若函数f (x )＝ax ＋b ，x ∈[a －4，a ]的图象关于原点对称，则函数g (x )＝bx ＋ax ，x ∈[－4，－1]的值域为________．12．答案－2，－12解析由函数f (x )的图象关于原点对称，可得a －4＋a ＝0，即a ＝2，则函数f (x )＝2x ＋b ，其定义域为[－2，2]，所以f (0)＝0，所以b ＝0，所以g (x )＝2x ，易知g (x )在[－4，－1]上单调递减，故值域为[g (－1)，g (－4)]，即－2，－12．考点三已知函数的奇偶性，求函数的值【方法总结】已知函数的奇偶性求函数值：将待求值利用奇偶性转化为已知区间上的函数值求解．【例题选讲】[例3](1)已知函数f (x )是定义在R 上的奇函数，当x ∈(－∞，0)时，f (x )＝2x 3＋x 2，则f (2)＝____．答案12解析∵x ∈(－∞，0)时，f (x )＝2x 3＋x 2，且f (x )在R 上为奇函数，∴f (2)＝－f (－2)＝－[2×(－2)3＋(－2)2]＝12．(2)设f (x )是定义在R 上的奇函数，当x ≤0时，f (x )＝2x ＋2x ＋b (b 为常数)，则f (1)＝________．答案52解析由题意知f (0)＝20＋2×0＋b ＝0，解得b ＝－1．所以当x ≤0时，f (x )＝2x ＋2x －1，所以f (1)＝－f (－1)＝－[2－1＋2×(－1)－1]＝52(3)设函数f (x )是定义在R 上的奇函数，且f (x )3(x ＋1)，x ≥0，(x )，x <0，，则g (－8)＝()A ．－2B ．－3C ．2D ．3答案A解析法一当x <0时，－x >0，且f (x )为奇函数，则f (－x )＝log 3(1－x )，所以f (x )＝－log 3(1－x )．因此g (x )＝－log 3(1－x )，x <0，故g (－8)＝－log 39＝－2．法二由题意知，g (－8)＝f (－8)＝－f (8)＝－log 39＝－2．【对点训练】13．若函数f (x )是定义在R 上的奇函数，当x ≥0时，f (x )＝log 2(x ＋2)－1，则f (－6)＝()A ．2B ．4C ．－2D ．－413．答案C解析根据题意得f (－6)＝－f (6)＝1－log 2(6＋2)＝1－3＝－2．14．已知函数f (x )是偶函数，当x ＞0时，f (x )＝ln x ，则21(())f f e 的值为________．14．答案ln 2解析由已知可得21(f e ＝ln 1e 2＝－2，所以21((f f e＝f (－2)．又因为f (x )是偶函数，所以21(())f f e ＝f (－2)＝f (2)＝ln 2．15．已知f (x )是定义在R 上的奇函数，当x ≥0时，f (x )＝3x ＋m (m 为常数)，则f (－log 35)＝()A ．－6B ．6C ．4D ．－415．答案D解析因为f (x )是定义在R 上的奇函数，且当x ≥0时，f (x )＝3x ＋m ，所以f (0)＝1＋m ＝0⇒m ＝－1，则f (－log 35)＝－f (log 35)＝－(3log 35－1)＝－4．16．设函数f (x )是定义在R 上的奇函数，且f (x )3x ＋1，x ≥0，x ，x ＜0，则g (f (－8))＝()A ．－1B ．－2C ．1D ．216．答案A解析因为f (x )为奇函数，所以f (－8)＝－f (8)＝－log 39＝－2，所以g (f (－8))＝g (－2)＝f (－2)＝－f (2)＝－log 33＝－1．考点四已知函数的奇偶性，求函数的解析式【方法总结】已知函数的奇偶性求解析式：将待求区间上的自变量转化到已知区间上，再利用奇偶性求出，或充分利用奇偶性构造关于f (x )的方程(组)，从而得到f (x )的解析式．对于奇函数可在x 以及解析式前同时加负号，对于偶函数可在x 前加负号进行秒杀．【例题选讲】[例4](1)设f (x )为奇函数，且当x ≥0时，f (x )＝e x －1，则当x ＜0时，f (x )＝()A ．e －x －1B ．e －x ＋1C ．－e －x －1D ．－e －x ＋1答案D 解析通解：依题意得，当x <0时，f (x )＝－f (－x )＝－(e －x －1)＝－e －x ＋1，选D ．优解：依题意得，f (－1)＝－f (1)＝－(e 1－1)＝1－e ，结合选项知，选D ．(2)已知f (x )为偶函数，当x ≤0时，f (x )＝e －x －1－x ，则f (x )＝________．答案－x －1－x ，x ≤0x －1＋x ，x ＞0解析当x ＞0时，－x ＜0，则f (－x )＝e x －1＋x ，又f (－x )＝f (x )，因此f (x )＝e x －1＋x ．所以f (x )－x －1－x ，x ≤0x －1＋x ，x ＞0．(3)若定义在R 上的偶函数f (x )和奇函数g (x )满足f (x )＋g (x )＝e x ，则g (x )＝()A ．e x －e －xB ．12(e x ＋e －x )C ．12(e －x －e x )D ．12(e x －e －x )答案D解析因为f (x )＋g (x )＝e x ，所以f (－x )＋g (－x )＝f (x )－g (x )＝e －x ，所以g (x )＝12(e x －e －x )．【对点训练】17．已知f (x )是奇函数，且x ∈(0，＋∞)时的解析式是f (x )＝－x 2＋2x ，若x ∈(－∞，0)，则f (x )＝________．17．答案x 2＋2x解析由题意知f (x )是定义在R 上的奇函数，当x ∈(－∞，0)时，－x ∈(0，＋∞)，所以f (－x )＝－(－x )2＋2×(－x )＝－x 2－2x ＝－f (x )，所以f (x )＝x 2＋2x ．18．函数y ＝f (x )是R 上的奇函数，当x <0时，f (x )＝2x ，则当x >0时，f (x )＝()A ．－2xB ．2－xC ．－2－xD ．2x18．答案C解析当x >0时，－x <0，∵x <0时，f (x )＝2x ，∴当x >0时，f (－x )＝2－x ．∵f (x )是R 上的奇函数，∴当x >0时，f (x )＝－f (－x )＝－2－x ．19．已知f (x )是定义在R 上的奇函数，当x ＞0时，f (x )＝x 2－4x ，则f (x )＝________．19．答案2－4x ，x ＞0x 2－4x ，x ≤0解析∵f (x )是定义在R 上的奇函数，∴f (0)＝0．又当x ＜0时，－x ＞0，∴f (－x )＝x 2＋4x ．又f (x )为奇函数，∴f (－x )＝－f (x )，即f (x )＝－x 2－4x (x ＜0)，∴f (x )2－4x ，x ＞0，x 2－4x ，x ≤0.20．已知函数f (x )为奇函数，当x >0时，f (x )＝x 2－x ，则当x <0时，函数f (x )的最大值为________．20．答案14解析法一：当x <0时，－x >0，所以f (－x )＝x 2＋x ．又因为函数f (x )为奇函数，所以f (x )＝－f (－x )＝－x 2－x ＝＋14，所以当x <0时，函数f (x )的最大值为14．法二：当x >0时，f (x )＝x 2－x －14，最小值为－14，因为函数f (x )为奇函数，所以当x <0时，函数f (x )的最大值为14．考点五与奇函数相关的函数的求值【方法总结】对于可表示成奇函数加常数的函数，如果已知一个数的函数值，求它的相反数的函数值或求两个相反数的函数值的问题，可用奇函数的结论5的推论1：若函数f (x )是奇函数，且g (x )＝f (x )＋c ，则必有g (－x )＋g (x )＝2c ，如果是涉及到函数的最大值与最小值的问题则可用推论2：若函数f (x )是奇函数，且g (x )＝f (x )＋c ，则必有g (x )max ＋g (x )min ＝2c 进行秒杀．【例题选讲】[例5](1)已知函数f (x )＝ln(1＋9x 2－3x )＋1，则f (lg 2)＋1(lg )2f 等于()A ．－1B ．0C ．1D ．2答案D解析设g (x )＝ln(1＋9x 2－3x )＝f (x )－1，g (－x )＝ln(1＋9x 2＋3x )＝ln11＋9x 2－3x＝－g (x )．∴g (x )是奇函数，∴f (lg 2)－1＋1(lg 2f －1＝g (lg 2)＋1(lg )2g ＝0，因此f (lg 2)＋1(lg 2f ＝2．(2)已知函数f (x )＝ln(1＋x 2－x )＋1，f (a )＝4，则f (－a )＝________．若g (10)＝2019，则g (－10)的值为()A ．－2219B ．－2019C ．－1919D ．－1819答案D解析由题意，因为f (x ＋y )＝f (x )＋f (y )，∴f (0＋0)＝f (0)＋f (0)＝f (0)，即f (0)＝0，令y ＝－x ，则有f (x －x )＝f (x )＋f (－x )＝f (0)＝0，即f (－x )＝－f (x )，即f (x )是奇函数，若g (x )＝f (x )＋sin x ＋x 2，g (10)＝2019，则g (10)＝f (10)＋sin 10＋100＝2019，则g (－10)＝f (－10)－sin 10＋100＝－f (10)－sin 10＋100，两式相加得200＝2019＋g (－10)，得g (－10)＝200－2019＝－1819，故选D(4)已知函数f (x )＝a sin x ＋b ln 1－x1＋x＋t ，若1()2f ＋1()2f ＝6，则实数t ＝()A ．－2B ．－1C ．1D ．3答案D 解析令g (x )＝a sin x ＋b ln1－x1＋x ，则易知g (x )为奇函数，所以1(2g ＋1()2g -＝0，则由f (x )＝g (x )＋t ，得1()2f ＋1()2f -＝1()2g ＋1(2g -＋2t ＝2t ＝6，解得t ＝3．故选D ．(5)已知函数f (x )＝2|x |＋1＋x 3＋22|x |＋1的最大值为M ，最小值为m ，则M ＋m 等于()A ．0B ．2C ．4D ．8答案C解析易知f (x )的定义域为R ，f (x )＝2·(2|x |＋1)＋x 32|x |＋1＝2＋x 32|x |＋1，设g (x )＝x 32|x |＋1，则g (－x )＝－g (x )(x ∈R )，∴g (x )为奇函数，∴g (x )max ＋g (x )min ＝0．∵M ＝f (x )max ＝2＋g (x )max ，m ＝f (x )min ＝2＋g (x )min ，∴M ＋m ＝2＋g (x )max ＋2＋g (x )min ＝4，故选C ．【对点训练】21．已知函数f (x )＝x ＋1x－1，f (a )＝2，则f (－a )＝________．21．答案－4解析法一：因为f (x )＋1＝x ＋1x ，设g (x )＝f (x )＋1＝x ＋1x ，易判断g (x )＝x ＋1x故g (x )＋g (－x )＝x ＋1x －x －1x＝0，即f (x )＋1＋f (－x )＋1＝0，故f (x )＋f (－x )＝－2．所以f (a )＋f (－a )＝－2，故f (－a )＝－4．法二：由已知得f (a )＝a ＋1a －1＝2，即a ＋1a ＝3，所以f (－a )＝－a －1a －11＝－3－1＝－4．22．已知函数f (x )＝x 3＋sin x ＋1(x ∈R )，若f (a )＝2，则f (－a )的值为()A ．3B ．0C ．－1D ．－222．答案B解析设F (x )＝f (x )－1＝x 3＋sin x ，显然F (x )为奇函数，又F (a )＝f (a )－1＝1，所以F (－a )＝f (－a )－1＝－1，从而f (－a )＝0．故选B ．23．对于函数f (x )＝a sin x ＋bx 3＋cx ＋1(a ，b ，c ∈R )，选取a ，b ，c 的一组值计算f (1)，f (－1)，所得出的正确结果可能是()A ．2和1B ．2和0C ．2和－1D ．2和－223．答案B解析设g (x )＝a sin x ＋bx 3＋cx ，显然g (x )为定义域上的奇函数，所以g (1)＋g (－1)＝0，所以f (1)＋f (－1)＝g (1)＋g (－1)＋2＝2，只有B 选项中两个值的和为2．24．已知函数f (x )＝ax 3＋b sin x ＋4(a ，b ∈R )，f (lg(log 210))＝5，则f (lg(lg2))＝()A ．－5B ．－1C ．3D ．424．答案C解析设g (x )＝ax 3＋b sin x ，则f (x )＝g (x )＋4，且函数g (x )为奇函数．又lg(lg2)＋lg(log 210)＝lg(lg2·log 210)＝lg1＝0，所以f (lg(lg2))＋f (lg(log 210))＝2×4＝8，所以f (lg(lg2))＝3．故选C ．25．已知f (x )，g (x )分别是定义在R 上的偶函数和奇函数，且f (x )－g (x )＝x 3＋x 2＋1，则f (1)＋g (1)＝()A ．－3B ．－1C ．1D ．325．答案C解析用“－x ”代替“x ”，得f (－x )－g (－x )＝(－x )3＋(－x )2＋1，化简得f (x )＋g (x )＝－x 3＋x 2＋1，令x ＝1，得f (1)＋g (1)＝1．故选C ．26．设函数f (x )＝(x ＋1)2＋sin xx 2＋1的最大值为M ，最小值为m ，则M ＋m ＝________．26．答案2解析显然函数f (x )的定义域为R ，f (x )＝(x ＋1)2＋sin x x 2＋1＝1＋2x ＋sin x x 2＋1，设g (x )＝2x ＋sin xx 2＋1，则g (－x )＝－g (x )，∴g (x )为奇函数，由奇函数图象的对称性知g (x )max ＋g (x )min ＝0，∴M ＋m ＝[g (x )＋1]max＋[g(x)＋1]min＝2＋g(x)max＋g(x)min＝2．27．设函数f(x)＝(e x＋e－x)sin x＋t，x∈[－a，a]的最大值和最小值分别为M，N．若M＋N＝8，则t＝() A．0B．2C．4D．827．答案4解析设g(x)＝(e x＋e－x)sin x，x∈[－a，a]，因为g(x)是奇函数，所以g(x)max＋g(x)min＝0，所以M＋N＝g(x)max＋g(x)min＋2t＝2t＝8，所以t＝4．28．若定义在[－2020，2020]上的函数f(x)满足：对任意x1∈[－2020，2020]，x2∈[－2020，2020]都有f(x1＋x2)＝f(x1)＋f(x2)－2019，且x＞0时有f(x)＞2019，f(x)的最大值、最小值分别为M，N，则M＋N ＝()A．2019B．2020C．4040D．403828．答案D解析令x1＝x2＝0得f(0)＝2f(0)－2019，所以f(0)＝2019，令x1＝－x2得f(0)＝f(－x2)＋f(x2)－2019＝2019，所以f(－x2)＋f(x2)＝4038，令g(x)＝f(x)－2019，则g(x)max＝M－2019，g(x)min＝N －2019，因为g(－x)＋g(x)＝f(－x)＋f(x)－4038＝0，所以g(x)是奇函数，所以g(x)max＋g(x)min＝0，即M－2019＋N－2019＝0，所以M＋N＝4038．29．已知函数f(x)＝(x2－2x)·sin(x－1)＋x＋1在[－1，3]上的最大值为M，最小值为m，则M＋m＝() A．4B．2C．1D．029．答案A解析f(x)＝[(x－1)2－1]sin(x－1)＋x－1＋2，令t＝x－1，g(t)＝(t2－1)sin t＋t，则y＝f(x)＝g(t)＋2，t∈[－2，2]．显然M＝g(t)max＋2，m＝g(t)min＋2．又g(t)为奇函数，则g(t)max＋g(t)min＝0，所以M＋m＝4，故选A．30．若关于x的函数f(x)＋cos xt≠0)的最大值为a，最小值为b，且a＋b＝2，则t＝____．30．答案1解析f(x)＋cos x t＋t sin x＋x2x2＋cos x，设g(x)＝t sin x＋x2x2＋cos x，则g(x)为奇函数，g(x)max＝a－t，g(x)min＝b－t．∵g(x)max＋g(x)min＝0，∴a＋b－2t＝0，即2－2t＝0，解得t＝1．。

高一数学函数的奇偶性1

小结：
1. 奇偶性的概念 2. 判断奇偶性的步骤 3. 判断奇偶性时要注意的问题
； / 活性氧化铝球
bth19dwb
细的揣度。苏老太太曾赞宝音，一副水晶心肝，玲珑剔透，照人断事，巨细靡遗。宝音从前也自认有这般本事，如今想来，方知人心如海，其深叵测，怎是容易照得明、看得清的。就连生前相处共事最多的嘉颜，以表身份去面对，又发现作宝音时不曾发现的另一面。看来府中每个人，她都要重新审视了。幸而是苏明远行事，仍然被她料中。这位大少爷，人都说他天马行空、风流任性，她看来只不过是个孩子，竟不知为何人人敬他赞他、嗔他叹他。这孩子不久前为了某件要紧事，被家中长辈召回了罢？是违背他心意的事，他被家法所拘，不得不出力，闷得狠了，云深雷动时，看所有人都躲雨，他不耐烦，趁人都慌乱顾不得他，且一鞭下山来，去知己处排遣块垒。若给大老爷知道，要紧时候使这种贪顽任性，是要大怒的，所以一朵花去，也就能把他劝回了。丝丝缕缕心迹，一路算来，有何为难？他那件大事，很可能就与宝音之死有关，宝音安了心，要慢慢盘查出来。就已知线索去想，谢府在锦城是头挑的人家，再要有大事，而且秘不可宣，总跟宦途有关？谢二明诗如今在宫为贵人，杀宝音时尖声的人、金斗篷的人，完全陌生，莫非是宫中来的？宝音何以为变成宫中人要杀的对象……这却又不可解了。宝音叹口气，将府中所有人，在心底开成一份名单，从头想他们各自可能扮演什么角色。苏老太爷苏小横心底恰也在排一份名单，包括宝音想到的、也有宝音没想到的，名单上人物都揣摩过一遍，苏老太太已然回来。这场雨浇坏了锦城所有人家的登高兴致。苏府的人回到家中，如嘉颜所料，各各也都湿得差不多了。懂事的下人媳妇们说了很多吉祥话，以表示这雨实在是喜兆，主子们千万别恼。但不管怎么说，入夜的焰火是放不成了，雨小了些，但总不停。老太太体恤下人，吩咐连夜宵也不必再吃，各屋快回去换身干衣裳、早点歇憩，免得生病。她自己往苏小横这里来，苏小横慰问了两句，说正事道：“我那些孩儿们腿快的，已经打听回来，外头，没谁轻举妄动。”“我在山上见到梅家，他们倒也沉得住气。” 老太太皱着眉。她的眉毛当年是顶顶好看的，弯如新柳、秀如春月，如今上了年纪，稀疏些，皱起来，倒有了杀伐之气。她说的梅家，是二太太的娘家。“你哪，眼睛也别老盯着老二屋里的。”苏小横眯着眼睛，像要从空中看出一瓣梅花来，好让他在上面落笔赋新诗，“尘世间，镜花水月，镜中千重影、水上万般痕，凡事都不要看得太孤立了为好。”“可是我们二孙丫头，在宫里，不就在跟张家闺女斗吗？这玉坠不就为了扳倒张家闺女才藏出来吗？”老太太急了，急出些年少时的明朗泼辣样子，“张家和梅家是姻亲，梅家这些年一直态度含糊，骑着墙头草。我们家是娶了梅

高中数学公式大全函数的奇偶性与周期性的判定公式

高中数学公式大全函数的奇偶性与周期性的判定公式高中数学公式大全：函数的奇偶性与周期性的判定公式在高中数学中，函数的奇偶性和周期性是我们常常需要研究的性质之一。

通过判定函数的奇偶性和周期性，我们可以更好地了解函数的特点，解决问题。

本文将介绍函数的奇偶性和周期性的判定公式，帮助高中数学学习者更好地理解和应用这些概念。

一、函数的奇偶性判定公式函数的奇偶性是指函数在自变量取相反数时，函数值是否具有对称性的特点。

下面是函数奇偶性的判定公式：1. 若对任意的 x，有 f(-x) = f(x)，则函数 f(x) 为偶函数。

例如，f(x) = x^2 就是一个典型的偶函数，因为 f(-x) = (-x)^2 = x^2 = f(x)。

2. 若对任意的 x，有 f(-x) = -f(x)，则函数 f(x) 为奇函数。

例如，f(x) = x^3 就是一个典型的奇函数，因为 f(-x) = (-x)^3 = -x^3 = -f(x)。

通过奇偶性的判定公式，我们可以方便地判断一个函数是偶函数还是奇函数。

这在解题过程中具有重要的作用。

二、函数的周期性判定公式函数的周期性是指函数在某一区间内，其函数值具有重复的规律性。

下面是函数周期性的判定公式：1. 若存在正数 T，使得对于任意 x，有 f(x+T) = f(x)，则函数 f(x) 具有周期 T。

例如，f(x) = sin(x) 是一个周期为2π 的函数，因为sin(x+2π) =sin(x)。

2. 若函数 f(x) 的定义域为全体实数集合 R，且存在正数 T，使得对于任意 x，有 f(x+T) = f(x)，则函数 f(x) 具有周期 T。

例如，f(x) = tan(x) 是一个周期为π 的函数，因为tan(x+π) = tan(x)。

通过周期性的判定公式，我们可以快速确定函数是否具有周期，并且求出函数的周期值。

总结：函数的奇偶性和周期性是数学中重要的概念，对于我们理解和应用函数有着重要的帮助。

高一函数的奇偶性知识要点、例题讲解(数学)

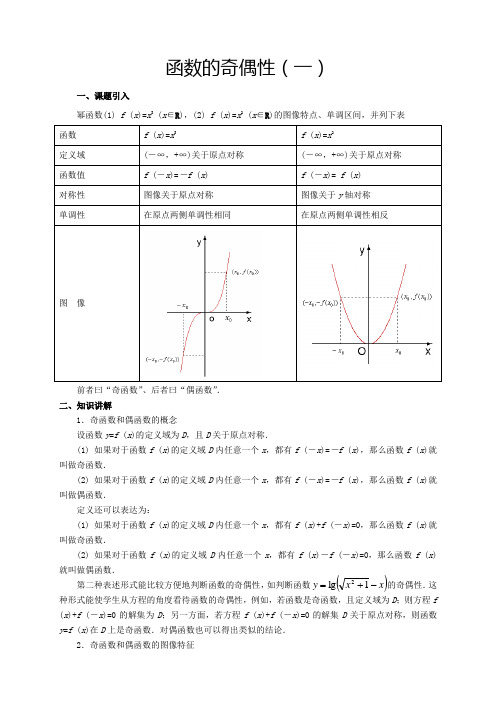
函数的奇偶性（一）一、课题引入幂函数(1) f (x )=x 3(x ∈R )，(2) f (x )=x 2(x ∈R )的图像特点、单调区间，并列下表函数 f (x )=x 3f (x )=x 2定义域 (－∞，+∞)关于原点对称(－∞，+∞)关于原点对称函数值 f (－x )=－f (x )f (－x )= f (x )对称性图像关于原点对称图像关于y 轴对称单调性在原点两侧单调性相同在原点两侧单调性相反图像前者曰“奇函数”、后者曰“偶函数”．二、知识讲解1．奇函数和偶函数的概念设函数y =f (x )的定义域为D ，且D 关于原点对称．(1) 如果对于函数f (x )的定义域D 内任意一个x ，都有f (－x )=－f (x )，那么函数f (x )就叫做奇函数．(2) 如果对于函数f (x )的定义域D 内任意一个x ，都有f (－x )=－f (x )，那么函数f (x )就叫做偶函数．定义还可以表达为：(1) 如果对于函数f (x )的定义域D 内任意一个x ，都有f (x )+f (－x )=0，那么函数f (x )就叫做奇函数．(2) 如果对于函数f (x )的定义域D 内任意一个x ，都有f (x )－f (－x )=0，那么函数f (x )就叫做偶函数．第二种表述形式能比较方便地判断函数的奇偶性，如判断函数()x xy -+=1lg2的奇偶性．这种形式能使学生从方程的角度看待函数的奇偶性，例如，若函数是奇函数，且定义域为D ；则方程f (x )+f (－x )=0的解集为D ；另一方面，若方程f (x )+f (－x )=0的解集D 关于原点对称，则函数y =f (x )在D 上是奇函数．对偶函数也可以得出类似的结论．2．奇函数和偶函数的图像特征(1) 奇函数的图像关于原点对称，反过来，图像关于原点对称的函数，必是奇函数． (2) 偶函数的图像关于y 轴对称，反过来，图像关于y 轴对称函数，必是偶函数．3．判断函数的奇偶性对于函数f (x )先求其定义域D ；并判别D 是否关于原点对称，然后再验证f (－x )=±f (x ) (或f (x )±f (x )=0，或()()1±=-x f x f 等)是否成立，最后作出正确结论．4．判断函数的奇偶性也可以用下列性质在公共定义域内，(1) 两个奇函数的和为奇函数；两个奇函数的积为偶函数． (2) 两个偶函数的和为偶函数；两个偶函数的积为偶函数． (3) 一个奇函数与一个偶函数的积为奇函数． (4) 函数f (x )与()x f 1同奇或同偶．以上结论，可在讲完出上一例：判断下列函数是否具有奇偶性：(1) f (x )=x 3；(2) f (x )=2x 4+3x 2；(3) ()313-+=xx x f ；(4) f (x )=x +1后，结合函数运算引出．直观引入后，可让学生在课后加以证明，这对学生加深对奇偶性的理解和用这一结论解题都是有帮助的．5．函数的奇偶性与单调性相结合，有以下两个结论： (1) 奇函数在原点两侧的对称区间上有相同的单调性． (2) 偶函数在原点两侧的对称区间上有相反的单调性．三、例题分析1．判断函数的奇偶性易犯的错误 (1) 因忽视定义域的特征致错例1．①()()11--=x x x x f ；②f (x )=x 2+(x +1)0错解：①()()x x x x x f =--=11，∴ f (x )是奇函数 ②∵ f (－x )=(－x )2+(－x +1)0=x 2+(x +1)0=f (x ) ∴ f (x )是偶函数．分析：一个函数是奇函数或偶函数的必要条件是定义域关于原点对称．正解：①定义域(－∞，1)∪(1，+∞)关于原点不对称，f (x )是非奇非偶函数．②定义域(－∞，－1)∪(－1，+∞)，∴ f (x )非奇非偶函数． (2) 因缺乏变形意识或方法致错．例2．判断()21151+-=x x f 的奇偶性．错解：∵ 5x－1≠0，∴ x ≠0．f (x )的定义域为(－∞，0)∪(0，+∞)，关于原点对称．∵ ()2151521151+-=+-=-xx x x f ， ∴ f (－x )≠f (x )，f (－x )≠－f (x )， ∴ f (x )是非奇非偶函数．分析：因演变过程不到位导致错误，所以要注意进行恒等变形．正解：()()1521521151-+=+-=xx x x f ，定义域为(－∞，0)∪(0，+∞)关于原点对称． ()()()()()x f x f xx x x x x -=-+-=-+=-+=--152155125115215 ∴ f (x )是奇函数．(3) 因忽视f (x )=0致错．例3．判断函数()2244x x x f -+-=的奇偶性．错解：由⎪⎩⎪⎨⎧≥-≥-040422x x 得x =±2，∴ f (x )的定义域为{－2，2}，关于原点对称．()()()()x f x x x x x f =-+-=--+--=-22224444，∴ f (x )为偶函数正解：f (x )的定义域为{－2，2}，此时，f (x )≡0，∴ f (x )既是奇函数又是偶函数．点评：函数f (x )=0 (x ≠0)是f (x )既是奇函数又是偶函数的一个必要条件，任何一个关于原点对称的区间都可以作为解析式为f (x )=0 (x ≠0)函数的定义域．注意：分段函数奇偶性的判定应注意两点：(1) 分段函数是一个函数，而不是几个函数； (2) 确定分段函数的奇偶性，要注意分类讨论． 2．函数的奇偶性的应用例4．已知f (x )是奇函数，且当x >0时，f (x )=x |x －2|，求f (x )<0时，f (x )的表达式．答：当x <0时，f (x )=x |x +2|．例5．已知f (x )=x 5+ax 3+bx －8，且f (－2)=10，则f (2)=_________ 解：令g (x )=f (x )+8=x 5+ax 3+bx ，则g (x )是奇函数∴ g (－2)+g (2)=0，即f (－2)+8+f (2)+8=0，∴ f (2)=－f (－2)－16=－26．例6．已知 f (x )、g (x )的定义域均为R ，f (x )为奇函数，g (x )为偶函数，且()()112+-=+x x x g x f ，求f (x )的解析式．答：()124++=x x xx f ．例7．已知函数y =f (x )是奇函数，在(0，+∞)上是减函数，且f (x )<0，判断()()x f x F 1=在区间(－∞，0)上是增函数还是减函数？并证明你的结论．答：F (x )在(－∞，0)是增函数．例8．定义在(－1，1)上的奇函数f (x )是减函数，且f (1－a )+f (1－a 2)<0，求实数a 的取值范围．答：a ∈(0，1)．点评：例8、9两题是函数的奇偶性与单调性的综合题．例9．已知f (x )是定义在R 上的奇函数，x >0时，f (x )=－x 2+2x －3．(1) 求f (x )的解析式； (2) 画出y =f (x )的图像； (3) 求出f (x )的单调区间．解：(1) ()()()⎪⎩⎪⎨⎧∞-∈++=∞+∈-+-=0320003222，，，，，x x x x x x x x f(2) 画图略．(3) 单调减区间为(]1-∞-，，[)∞+，1；单调增区间为[)01，-，(]10，．点评：本题是函数奇偶性、单调性、图像特征，画图等有关概念、性质、方法的综合运用的一道函数综合题．此题主要是考查学生综合、灵活运用所学知识解题的能力．四、习题1．已知f (x )是奇函数，且在x =0处有定义，你能确定f (0)的值吗？ 2．已知f (x )是偶函数，且在x =0处有定义，你能确定f (0)的值吗？3．函数()[)()⎩⎨⎧∞-∈-∞+∈=0101，，，，x x x f 是奇函数吗？答案1．f (0)=0 2．f (0)不定3．否五、引伸和提高定义域关于原点对称的任意一个函数f (x )都可以表示成一个偶函数与一个奇函数之和．即f (x )=21(F (x )+G (x ))其中F (x )= f (x )+f (－x )，G (x )=f (x )－f (－x ) (1) 利用这一结论可以很简捷地解决一些问题； (2) 在教学中，可根据学生的基础情况，适时引入．(3) 可以让学生自己证明，增强学生对抽象问题证明的能力，加深学生对奇、偶函数与一般函数关系的理解，使学生对构造法增加一次感性认识．六、思考题1．设，f (x )=kx +x6－4，(k ∈R )当x =2+3时，f (x )=0，求⎪⎪⎭⎫ ⎝⎛-231f 的值．答：32024231-=⎪⎪⎭⎫⎝⎛-f ．2．已知函数y =f (x )满足f (x +y )+f (x －y )=2f (x ) f (y ) (x ∈R ，y ∈R )，且f (0)≠0，那么f (x )是__________函数(填奇、偶)．答：偶函数函数的奇偶性（二）一般地，对于函数)(x f ，如果对于函数定义域内任意一个x ，都有)()(x f x f =-，那么函数)(x f 就叫做偶函数。

高一函数知识点总结奇偶性

高一函数知识点总结奇偶性函数是高中数学中的重要知识点之一，而函数的奇偶性则是函数理论中的一个重要概念。

在高一阶段，学生需要学习和掌握函数的奇偶性相关的知识，本文将对高一函数的奇偶性进行总结。

1. 函数的奇偶性概念函数的奇偶性是指函数在定义域内的奇偶性质。

如果对于在定义域内的任意x值，f(-x) = f(x)，那么这个函数就是偶函数；如果对于在定义域内的任意x值，f(-x) = -f(x)，那么这个函数就是奇函数；如果一个函数既不满足偶性质也不满足奇性质，那么这个函数就是既非偶函数也非奇函数。

2. 奇函数的性质奇函数的特点是关于原点对称，即图象关于原点对称。

此外，奇函数在坐标系的第一象限和第三象限的函数值相等，即f(x) = -f(-x)。

3. 偶函数的性质偶函数的特点是关于y轴对称，即图象关于y轴对称。

此外，偶函数在坐标系的第一象限和第二象限的函数值相等，即f(x) = f(-x)。

4. 奇偶函数的判定方法要判定一个函数是奇函数还是偶函数，可以通过以下方法：- 方法1：利用函数的定义，对于任意给定的x，计算f(-x)和f(x)的值是否相等或相反。

- 方法2：观察函数图象关于x轴的对称性。

如果函数的图象关于x 轴对称，则函数是偶函数；如果函数的图象关于原点对称，则函数是奇函数。

- 方法3：利用导函数的性质。

若函数的导函数是奇函数，则原函数是偶函数；若函数的导函数是偶函数，则原函数是奇函数。

5. 奇偶函数的性质应用奇偶函数在数学和物理中具有重要的应用。

在数学中，奇偶函数在积分计算时可以简化计算过程，同时在函数图象的对称性证明中也起到重要作用。

在物理中，奇函数和偶函数可用于描述对称和非对称的现象，如电荷分布的对称性、波函数的对称性等。

6. 奇偶函数的例子以下是一些常见的奇偶函数例子：- 正弦函数：sin(x)是奇函数，它在区间[-π, π]内关于原点对称。

- 余弦函数：cos(x)是偶函数，它在区间[-π, π]内关于y轴对称。

高中数学基础之函数的奇偶性与周期性

D.
考点二函数奇偶性的应用
【例 2】 (1)(2019·全国卷Ⅱ)设 f(x)为奇函数，且当 x≥0 时，f(x)＝ex－1，则
当 x<0 时，f(x)＝( D ) A．e－x－1
B．e－x＋1
C．－e－x－1
D．－e－x＋1
(2)(2020·长沙第一中学期末)若函数 f(x)＝xln(x＋ a＋x2)为偶函数，则 a＝ ___1_____.
又 x<0，∴－x>0. ∵x≥0 时，f(x)＝ex－1，∴－y＝e－x－1， ∴y＝－e－x＋1(x<0)，即 f(x)＝－e－x＋1(x<0)．解法三(赋值法)：∵f(x)是奇函数，且 x≥0 时，f(x)＝ex－1， ∴f(－1)＝－f(1)＝－(e1－1)＝1－e，即 f(－1)＝－e＋1，只有 D 符合． (2)因为 f(x)－f(－x)＝xln(x＋ a＋x2)＋xln(－x＋ a＋x2)＝xln(a＋x2－x2)＝xlna ＝0，所以 a＝1.
1．(2020·福州市高三期末)下列函数为偶函数的是( B )
A．y＝tan(x＋π4)
B．y＝x2＋e|x|
C．y＝xcosx
D．y＝ln|x|－sinx
[解析] 对于选项 A，易知 y＝tan(x＋π4)为非奇非偶函数；对于选项 B，设 f(x)
＝x2＋e|x|，则 f(－x)＝(－x)2＋e|－x|＝x2＋e|x|＝f(x)，所以 y＝x2＋e|x|为偶函数；对于选
ቤተ መጻሕፍቲ ባይዱ
B．最小正周期为 2π 的奇函数
C．最小正周期为 π 的偶函数
D．最小正周期为 2π 的偶函数
(2)(2020·河南南阳模拟)已知函数 f(x)是定义在 R 上的偶函数，并且满足 f(x＋

高一数学函数奇偶性知识点归纳

函数奇偶性知识点归纳考点分析配经典案例分析函数的奇偶性定义：1．偶函数：一般地，对于函数()f x 的定义域内的任意一个x ，都有()()f x f x -=，那么()f x 就叫做偶函数．2．奇函数：一般地，对于函数()f x 的定义域的任意一个x ，都有()()f x f x -=-，那么()f x 就叫做奇函数．二、函数的奇偶性的几个性质1、对称性：奇（偶）函数的定义域关于原点对称；2、整体性：奇偶性是函数的整体性质，对定义域内任意一个x 都必须成立；3、可逆性：)()(x f x f =-⇔)(x f 是偶函数；)()(x f x f -=-⇔)(x f 奇函数；4、等价性：)()(x f x f =-⇔0)()(=--x f x f (||)()f x f x ⇔=；)()(x f x f -=-⇔0)()(=+-x f x f ；5、奇函数的图像关于原点对称，偶函数的图像关于y 轴对称；6、可分性：根据函数奇偶性可将函数分类为四类：奇函数、偶函数、既是奇函数又是偶函数、非奇非偶函数。

7、判断或证明函数是否具有奇偶性的根据是定义。

8、如果一个奇函数f(x)在x=0处有意义，则这个函数在x=0处的函数值一定为0。

并且关于原点对称。

三、关于奇偶函数的图像特征一般地：奇函数的图像关于原点对称，反过来，如果一个函数的图像关于原点对称，那么这个函数是奇函数；即：f(x)为奇函数<=>f(x)的图像关于原点对称点（x,y ）→（-x,-y ）偶函数的图像关于y 轴对称，反过来，如果一个函数的图像关于y 轴对称，那么这个函数是偶函数。

即： f(x)为偶函数<=>f(x)的图像关于Y 轴对称点（x,y ）→（-x,y ）奇函数对称区间上的单调性相同（例：奇函数在某一区间上单调递增，则在它的对称区间上也是单调递增。

）偶函数对称区间上的单调性相反（例：偶函数在某一区间上单调递增，则在它的对称区间上单调递减）。

高一上册数学第一章4《函数的奇偶性》讲义

知识点一：函数奇偶性的定义1、函数奇偶性的定义（1）如果对于函数()f x 定义域内任意一个x ，都有()()f x f x -=，则函数()f x 就叫做偶函数；（2）如果对于函数()f x 定义域内任意一个x ，都有()()f x f x -=-，则函数()f x 就叫做奇函数；（3）如果函数()f x 是奇函数或偶函数，那么我们就说函数()f x 具有奇偶性。

2、具有奇偶性的函数图象特点：一般地，奇函数的图象关于原点对称，反过来，如果一个函数的图象关于原点对称，那么这个函数是奇函数；偶函数的图象关于y 轴对称，反过来，如果一个函数的图象关于y 轴对称，那么这个函数是偶函数。

【题型一】概念应用例1、已知函数2()3f x ax bx a b =+++为偶函数，其定义域为[2,1]a a -,则函数的值域为。

变式：已知函数()f x 为偶函数，且其图象与x 轴有四个交点，则方程()0f x =的所有实根之和为。

【题型二】判断奇偶性例2、下列函数是否具有奇偶性.(1) 3()35f x x x =- (2) 2()3||1f x x x =--(3) 22()22f x x x =-+-; (4) 2|2|2()1x f x x --=-(5) 22230()230x x x f x x x x ⎧++<=⎨-+->⎩ （6）1()(1)1x f x x x +=--例3、已知函数()y f x =是定义在R 上的奇函数，则下列函数中是奇函数的是 . ① ()||y f x =; ②()y f x =-; ③()·y x f x =; ④()y f x x =+.【题型三】利用奇偶性求值例4、若函数3()7f x ax bx =++,有(5)3f =,则(5)f -= 。

变式1：(),()f x g x 都是定义在R 上的奇函数，且()()()35g 2F x f x x =++,若()F a b =,则()F a -= 。

高一函数奇偶性知识点总结

高一函数奇偶性知识点总结在高中数学中，函数是一个非常重要的概念。

而函数的奇偶性是我们在学习和研究各类函数时需要了解和掌握的一项基本特性。

本文将从定义、性质和应用三个部分对高一函数的奇偶性知识点进行总结。

1.定义函数的奇偶性是指函数在定义域内某一点的改变是否与该点的自变量的改变符号相同。

具体来说，如果对于函数f(x)在定义域内的任意x值，有f(-x) = f(x)，则函数f(x)为偶函数；如果对于函数f(x)在定义域内的任意x值，有f(-x) = -f(x)，则函数f(x)为奇函数。

2.性质2.1 偶函数与奇函数的性质(1) 奇函数在原点对称，即关于原点中心对称；(2) 偶函数关于y轴对称，即关于y轴中心对称；(3) y = f(x)的图像关于原点对称时，则f(x)必为奇函数；(4) y = f(x)的图像关于y轴对称时，则f(x)必为偶函数；(5) 两个奇函数的和（或差）必为偶函数；(6) 两个偶函数的和必为偶函数，差必为偶函数或奇函数。

2.2 常见函数的奇偶性(1) 偶函数：常数函数f(x) = c；幂函数f(x) = x^2；三角函数f(x) = cos(x)等。

(2) 奇函数：零函数f(x) = 0；反比例函数f(x) = 1/x；正弦函数f(x) = sin(x)等。

3.应用3.1 约束条件的简化在解题过程中，函数的奇偶性可以用来简化约束条件。

例如，当一个函数满足奇函数的性质时，我们只需要在定义域的非负部分进行研究，即可以得到整个函数的性质。

3.2 函数图像的判断通过函数的奇偶性，我们可以推断函数图像在平面上的对称性质。

当函数为奇函数时，图像关于原点对称；当函数为偶函数时，图像关于y轴对称。

这样的判断可以帮助我们更直观地理解和绘制函数的图像。

3.3 积分计算中的应用在一些积分计算中，函数的奇偶性可以被用来简化积分式子。

根据奇偶函数的性质，我们可以将积分区间缩小一半，便于求解。

例如，当被积函数为奇函数时，可直接将积分区间由[-a,a]缩小为[0,a]，简化计算步骤。

高一数学函数的奇偶性1

1.3.2函数的奇偶性教学目标：理解函数的奇偶性教学重点：函数奇偶性的概念和判定教学过程：1、通过对函数xy 1=，2x y =的分析，引出函数奇偶性的定义2、函数奇偶性的几个性质：（1）奇偶函数的定义域关于原点对称；（2）奇偶性是函数的整体性质，对定义域内任意一个x 都必须成立；（3）)()()(x f x f x f ⇔=-是偶函数，)()()(x f x f x f ⇔-=-是奇函数；（4）0)()()()(=--⇔=-x f x f x f x f ,0)()()()(=-+⇔-=-x f x f x f x f ；（5）奇函数的图像关于原点对称，偶函数的图像关于y 轴对称；（6）根据奇偶性可将函数分为四类：奇函数、偶函数、既是奇函数又是偶函数、非奇非偶函数。

3、判断下列命题是否正确(1)函数的定义域关于原点对称，是函数为奇函数或偶函数的必要不充分条件。

此命题正确。

如果函数的定义域不关于原点对称，那么函数一定是非奇非偶函数，这一点可以由奇偶性定义直接得出。

(2)两个奇函数的和或差仍是奇函数；两个偶函数的和或差仍是偶函数。

此命题错误。

一方面，如果这两个函数的定义域的交集是空集，那么它们的和或差没有定义；另一方面，两个奇函数的差或两个偶函数的差可能既是奇函数又是偶函数，如,，可以看出函数与都是定义域上的函数，它们的差只在区间[－1，1]上有定义且，而在此区间上函数既是奇函数又是偶函数。

（3）是任意函数，那么与都是偶函数。

此命题错误。

一方面，对于函数，不能保证或；另一方面，对于一个任意函数而言，不能保证它的定义域关于原点对称。

如果所给函数的定义域关于原点对称，那么函数是偶函数。

（4）函数是偶函数，函数是奇函数。

此命题正确。

由函数奇偶性易证。

（5）已知函数是奇函数，且有定义，则。

此命题正确。

由奇函数的定义易证。

（6）已知是奇函数或偶函数，方程有实根，那么方程的所有实根之和为零；若是定义在实数集上的奇函数，则方程有奇数个实根。

高一数学函数的奇偶性1

小李补充：而且印度人的脑回路跟咱们根本不一样，咱觉得让人家吃牛粪是对他的侮辱，人家还觉得是赞扬呢！印度神牛嘛，牛粪也是神牛的一部分，吃神牛的粪便，是一种荣耀。当你碰到这种对手，又从哪里去赢？
大家哄堂大笑起来。
小李接着说，印度人吃饭，还真是不在乎色香味。印度人的饭菜，大部分看上去真是跟米田共一样。而且越是经过精心烹制，就越是神似。门口有家早点店，早晨的主食是萨摩撒：外面一层黄澄澄，里面一滩黄乎乎，咋看都像刚从厕所最浓处捞出来的。老葛劝我尝了一个，其实就是油炸的咖喱味的，豆馅大水饺，味道还算可以，只是不明白为什么外观要做得这么恶心。不止是萨摩撒，好些印度菜肴都是这种样子。
上次去参加当地一个有钱人家的宴会，自助的菜肴放在餐台上。走了一圈之后，感觉自己像掉进了大粪坑，满眼都是黄乎乎、半稠半稀的米田共。同去的美女小王，胃浅得很，看到当地人把黄汤子往嘴里送，扭头就跑到门外吐了起来。
想到一贯咋咋呼呼、罕遇对手的老牛吃瘪的样子，大家都笑起来。打水计算器
老张在那里总结：不要跟印对面辩论赢过印度人。印度有2300万神祇，每个人都是神的宠儿，对于有无数天神做靠山的人，你靠什么去赢？而且印度还有本书叫《辩经》，专门教人辩论，我们这些业余选手，如何是他们的对手？

高一数学函数的奇偶性1

Байду номын сангаас
他跟我说，加上我们这一批，今天是第四拨人了，从上一个凌晨一点到这一个凌晨一点，他总共只睡了两个来小时。我们这个公司已经有几百人在印度了，加上出差的、检查的、参观的、开会的，天天络绎不绝。而办事处只有两个人。接站、送行、洗衣、做饭、床品整理、房租电费、柴米油盐，，所有人的吃喝拉撒睡，哪一件事都不能马虎，因为每一个人都是他阿树的客人。
他一脸疲惫，而且是相当疲惫，两只眼睛里是通红的血丝。但只要有谁目光转向他，立刻就坐直了身子，向你报以愉快的微笑。我是第一次出国，兴奋是难免的，用磕磕巴巴的英语就跟他聊上了。词不达意、语法不通的问题，我自己都能觉得出来，可他居然全听懂了，而且热情地回应。他的英语吐字清晰，语速也较慢，词语基本上都是我学过的。看到自己第一次跟外国人打交道就能凑合个八九不离十，成就感油然而生。
阿树长着一张非常殷勤的脸，虽然第一次见面，可那双温润的眼睛像老朋友一样令人感到亲切，他的个头在一米八左右，一张典型的西孟加拉人的脸，棱角分明，眼窝深陷，卷卷的头发，黝黑的皮肤，脊背稍微有点弯，算不上帅气，但绝不会令人讨厌。一身西装显然是从地摊上买来的，因为太合身了，所以，只要一弯腰或者蹲下身来，就会箍到肋骨上。看到我们从海关大门口出来，老远就跑过来提行李，挨个人打招呼。清点好行李之后，先请我们每一个人都上车，然后他才与他的助手一起，一件一件把我们的行李轻拿轻放地提上车，堆放好，然后又清点一遍人数，这才开始开车。家乐棋牌

高一数学函数的奇偶性1(20200806105116)

款
[单选]某轮船速12kn，顶流顺风航行，流速2kn，风使船增速1kn，则1h后船舶对水航程为（）。A．10nmileB．11nmileC．12nmileD．13nmile [单选]单位力P=1沿图示桁架下弦移动，杆①内力影响线应为：（）A.B.C.D. [单选,A1型题]《医疗机构从业人员行为规范》的执行和实施情况，应列入（）A.医疗机构校验管理和医务人员年度考核B.定期考核和医德考评C.医疗机构等级评审D.医务人员职称晋升、评先评优的重要依据E.以上都对 [单选,A1型题]松子仁除润肠通便之功外，还具有的功效是（）A.利水消肿B.生津止渴C.润肺止咳D.养血安神E.益气健脾 [单选]对山西省某行政公署的具体行政行为不服申请的复议，由下列（）机关管辖。A.该行政公署B.该行政公署法制部门C.山西省人民政府D.山西省人民政府法制局 [单选,A1型题]诊断慢性支气管炎的主要依据是（）A.病史B.阳性体征C.胸部X线检查D.心电图改变E.肺功能检查 [名词解释]自燃 [单选]以下不易发生妊娠剧吐的因素是（）A.家庭经济条件较好B.葡萄胎C.多胎妊娠D.情绪不稳定E.精神紧张 [单选]关于外阴硬化性苔藓的描述错误的是()A．是一种以外阴及肛周皮肤萎缩变薄为主的皮肤病B．可发生包括幼女在内的任何年龄妇女C．主要症状为病损区皮肤发痒D．最后诊断的唯一方法是病理检查E．常采用外科疗法治疗 [单选]公安机关消防机构在消防监督检查中发现建筑消防设施不符合消防安全要求，存在影响公共安全的重大火灾隐患的，应当。（）A、口头报告本级人民政府B、书面报告本级人民政府C、书面报告本级公安机关D、书面报告上级公安机关消防机构 [单选]在五笔字型输入法中，属于“基本字根”的一项是（）。A、火B、氵C、吕D、里 [单选]以下哪种纤维属于化学纤维（）A.羊毛B.棉C.丝D.涤纶 [判断题]浮选过程中，应对细泥含量大及难浮选煤采用较小充气量，对易浮选煤采用较大充气量。A.正确B.错误 [填空题]若已知两点的坐标为A（100，100）和B（150，50），则直线AB的坐标方位角为（）。 [问答题,案例分析题]临床情景：张女士，33岁。因甲状腺腺瘤行右侧甲状腺次全切除术。术后第2天。要求：请为患者（医学模拟人或模具）切口换药。 [多选]根据织造方法不同，织物分为（）A.混纺织物B.机织物C.针织物D.非织造织物 [单选]进出第一肝门内的管道有（）A.门静脉、肝静脉、肝胆管B.肝动脉、门静脉、肝胆管C.肝动脉、肝静脉、门静脉D.肝总动脉、肝总管、门静脉E.肝动脉、肝胆管、肝静脉 [单选]某企业2009年12月31日“固定资产”科目余额为1000万元，“累计折旧”科目余额为300万元，“固定资产减值准备”科目余额为50万元。该企业2009年12月31日资产负债表“固定资产”的项目金额为()万元。A.650B.700C.950D.1000 [填空题]交流双速电梯当电梯制动减速时，则自动切断高速绕组电源，并将三相（）绕组接到电源上，电动机转入低速运行状态. [单选]中度以上支气管扩张病人适当而有效的治疗方案()A．病变局限于一肺段、一叶或多段者，可作肺段或肺叶切除B．应用抗生素治疗感染C．体位引流排除脓液D．一般支持疗法E．以上均不正确 [填空题]酒曲又称（），是用谷物制成的发酵剂、（）或（）。 [单选]既能化火，又能遏伤阳气的温邪是：（）.A．湿热B．温毒C．风热D．燥热 [单选]医疗机构发现突发公共卫生事件后，应当向当地卫生行政部门报告的时间要求为（）A.1小时内B.2小时内C.4小时内D.6小时内E.8小时内 [单选]关于脊柱的描述，正确的是()A．有8块颈椎B．有4块骶椎C．胸部运动最灵活D．腰曲凸向前E．颈曲凸向后 [单选]柜员名下尾箱为封存状态时，如果不准备卸载而是要继续使用，可以通过“（）”功能将封存中的尾箱恢复使用。A.0044尾箱管理-尾箱启用B.0043尾箱维护C.0060柜员日结D.0040柜员尾箱移交 [单选]海图底质注记中，缩写“M.S.”表示（）。A．分层底质，上层为沙，下层为泥B．分层底质，上层为泥，下层为沙C．沙的成分多于泥的成分的混合底质D．泥的成分多于沙的成分的混合底质 [单选]项目工程设计阶段，工程造价的计价形式是（）。A.项目投资估算B.设计概算和施工图预算C.竣工验收阶段的决策价D.招标投标阶段的工程合同价 [单选]将二维曲线的段进行等份加点用哪个命令：（）A．DivideB．AttachC．DeleteD．Weld [单选,A1型题]第一类精神药品每次处方（）A.不得超过1日常用量B.不得超过2日常用量C.不得超过3日常用量D.不得超过5日常用量E.不得超过7日常用量 [填空题]装卸汽轮机、燃机和压气机转子，应使用专用的（）或（）和专用的（），并应仔细检查（）的绑法是否合适，然后将转子（）。起吊时，禁止人站在转子上使起吊平衡。 [单选,A2型题,A1/A2型题]渗透压测定的原理是根据（）。A.比重高低B.黏度大小C.冰点下降D.沸点上升E.溶解度上升 [单选]中度侧脑室扩张指其测量值（）。A.1～3mmB.4～6mmC.7～10mmD.10～12mmE.>12mm [单选,A1型题]经产妇，30岁，足月妊娠在家自然分娩，胎儿娩出1小时后胎盘未娩出而入院。主诉产时顺利，娩出一个中等大小男婴，分娩至现在阴道出血量中等。前次妊娠有人工剥离胎盘史，检查宫底平脐，轮廓清晰，膀胱空虚，宫口可容3指，软产道完整，脐带外露，胎盘未娩出最常见的原 [单选]在企业有盈利，需要追加外部投资的情况下，下列有关外部融资需求的表述正确的是（）。A.销售增加，必然引起外部融资需求的增加B.销售净利率与外部融资需求成正比关系C.股利支付率与外部融资需求成正比关系D.资产周转率的提高必然引起外部融资额增加 [单选]医学人道主义最基本的思想是A.尊重病人生命B.同情病人C.帮助病人解除痛蕾D.为病人尽义务E.A和D [单选]下述哪项是肝硬化的典型病理改变A.纤维组织增生B.肝细胞变性坏死C.不同程度的炎性细胞浸润D.再生结节及假小叶形成E.呈小管样结构的新生细胞 [填空题]茄科有（）、（）、（）、（） [单选]校验供电系统保护装置灵敏度时，应使用（）运行方式下的短路电流数据。A.最小B.最大C.正常D.满载 [单选]一般住宅内，多层建筑中每层楼的消防栓（箱）内均配置（）瓶灭火器。A.1B.2C.3D.4 [单选]Afterconductinganabandonmentdrill，theMasterorpersoninchargeofashipshalllog（）.A.thenamesofcrewmemberswhoparticipatedinthedrillB.thelengthoftimethateachmotorpropelledlifeboatwasoperatedinthedrillC.thelengthoftimethelifeboatwasinthewaterD.thetimeittookt

高一数学函数的奇偶性1(20200806105116)

数学专题复习_函数的奇偶性

高一数学《函数的奇偶性》教案设计

高一必修一数学知识点：函数奇偶性

函数的奇偶性(精辟讲解)

高中数学函数的奇偶性(解析版)

高一数学函数的奇偶性1

高中数学公式大全函数的奇偶性与周期性的判定公式

高一函数的奇偶性知识要点、例题讲解(数学)

高一函数知识点总结奇偶性

高中数学基础之函数的奇偶性与周期性

高一数学 函数奇偶性知识点归纳

高一上册数学第一章4《函数的奇偶性》讲义

高一函数奇偶性知识点总结

高一数学函数的奇偶性1

高一数学函数的奇偶性1

高一数学函数的奇偶性1

高一数学函数的奇偶性1(20200806105116)

高一数学函数奇偶性知识点归纳