任意进制计数器构成以及时序逻辑电路设计
数电实验 计数器逻辑功能和设计

2.5 计数器逻辑功能和设计1.实验目的(1)熟悉四位二进制计数器的逻辑功能和使用方法。
(2)熟悉二-五-十进制计数器的逻辑功能和使用方法。
(3)熟悉中规模集成计数器设计任意进制计数器的方法。
(4)初步理解数字电路系统设计方法,以数字钟设计为例。
2.实验仪器设备(1)数字电路实验箱。
(2)数字万用表。
(3)数字集成电路:74161 4位二进制计数器74390 2二-五-十进制计数器7400 4与非门7408 4与门7432 4或门3.预习(1)复习实验所用芯片的逻辑功能及逻辑函数表达式。
(2)复习实验所用芯片的结构图、管脚图和功能表。
(3)复习实验所用的相关原理。
(4)按要求设计实验中的各电路。
4.实验原理(1)计数器是一个用以实现计数功能的时序逻辑部件,它不仅可以用来对脉冲进行计数,还常用做数字系统的定时、分频和执行数字运算以及其他特定的逻辑功能。
计数器的种类很多,按构成计数器中的各触发器是否使用一个时钟脉冲源来分,有同步计数器和异步计数器;根据计数进制的不同,分为二进制、十进制和任意进制计数器;根据计数的增减趋势分为加法、减法和可逆计数器;还有可预置数和可编程功能计数器等。
(2)利用集成计数器芯片构成任意(N)进制计数器方法。
①反馈归零法。
反馈归零法是利用计数器清零端的清零作用,截取计数过程中的某一个中间状态控制清零端,使计数器由此状态返回到零重新开始计数。
把模数大的计数器改成模数小的计数器,关键是清零信号的选择。
异步清零方式以N作为清零信号或反馈识别码,其有效循环状态为0~N-1;同步清零方式以N-1作为反馈识别码,其有效循环状态为0~N-1。
还要注意清零端的有效电平,以确定用与门还是与非门来引导。
②反馈置数法。
反馈置数法是利用具有置数功能的计数器,截取从Nb到Na 之间的N个有效状态构成N进制计数器。
其方法是当计数器的状态循环到Na时,由Na构成的反馈信号提供置数指令,由于事先将并行置数数据输入端置成了Nb 的状态,所以置数指令到来时,计数器输出端被置成Nb,再来计数脉冲,计数器在Nb基础上继续计数至Na,又进行新一轮置数、计数,其关键是反馈识别码的确定与芯片的置数方式有关。
时序逻辑电路的分析方法(新)

J1 = Q3Q2 ; J2 = Q1 ;
J3 = Q2Q1 ;
K1 = 1 K2 = Q3 Q1 K3 = Q2
Q1n+1 = J1Q1+K1Q1 =Q3Q2 Q1 =(Q3+Q2 ) Q1
3) 状态方程 Q2n+1 = J2Q2+K2Q2 =Q2Q1+Q3Q2Q1
Q3n+1 = J3Q3+K3Q3 =Q3Q2Q1+Q3Q2
置入
(Q3Q2Q1Q0 / Y)
(检查自启动情况略)
(二)M >N 的情况(用多片N进制计数器组合构成)
例1 试用两片74LS160构成百进制计数器。
1、连接线路
P.264.
图 5.3.39
Y
C Q3 Q2 Q1 Q0 EP
LD 74LS160(2)ET
RD D3 D2 D1 D0 CP
2、连接方式与特点
Q3 Q2 Q1 Q0 CP0 74LS290 CP1
R01R02 S91S92
三、任意进制计数器的构成方法
用 N 进制计数器,构成 M 进制计数器 (一) M<N 的情况
1、复位法(即清零法) 利用第M+1个状态译码, 使 RD=0 , 不等下一个CP到来,电路立即回到0000状态。 第M+1个状态为暂态,不等稳定,就已消失。 电路输出 M个稳定状态, 是M进制计数器。
5-3-2 计数器
计数器
同步
二进制 十进制 任意进制
异步
二进制 十进制 任意进制
加法,减法,可逆 加法,减法,可逆
加法计数器:随cp的输入,电路递增计数 减法计数器:随cp的输入,电路递减计数 可逆计数器:随cp的输入,电路可增可减计数
时序逻辑电路设计

时序逻辑电路设计1.以一个计数器74161为核心器件和少量门电路,设计一个带同步清0功能的5421BCD码计数器:电路有清0输入控制端R,当R=0时,同步清0;当R=1时,按5421BCD码规则同步计数,注意不能有过渡态。
5421BCD码编码规则:0~9分别为:0000、0001、0010、0011、0100、1000、1001、1010、1011、1100。
请写出设计过程。
2 试用JK触发器及与非门设计一个具有异步清零功能的2421BCD码十进制同步计数器,不要求自启动分析。
2421BCD码如下表所示:3.分析由移位计数器74194组成的时序,画出电路状态图?(排列次序:Q0 Q1 Q2 Q3功另外S1 S0=00,保持;S1 S0=01,右移;S1 S0=10,左移;S1 S0=11,置数。
)5 分析如图所示的电路功能,假设Q2Q1初态为00。
6.分析图中所示的时序电路,其中74283为四位加法器、74175为4D寄存器、14585为四位比较器,Y为输出。
画出状态转换图并说明电路功能。
7. 用JK触发器和门电路设计三位格雷码同步加法计数器,具有进位Y输出,要求:1、画出状态转换图;2、写出驱动(激励)方程、输出方程;3、画出逻辑电路图。
8. 试用两块十进制同步加法计数器74LS160及必要的其它器件实现可变模计数器,要求:①当A=0时,实现24进制计数器;当A=1时,实现60进制计数器;②不能有过渡状态;③写出设计过程,画出逻辑电路。
9. 试分析图5所示电路的功能(D IL 为左移数据输入), 按照(3210Q Q Q Q )画出状态图,并检查自启动。
10. 用D 触发器和必要的门电路设计一个序列信号发生器,使其输出信号Y 的周期为时钟CLK 周期的7倍,其输出波形如下图所示. 要求:1、画出状态转换图;2、写出驱动(激励)方程、输出方程;3、画出逻辑电路图.11. 图中为某时序的状态转换图,试用JK 触发器设计此同步时序电路,要求:(1)写出次态卡诺图、求出驱动方程; (2)画出逻辑电路图; (3)检查电路能否自启动。
实验六 任意进制计数器的构成
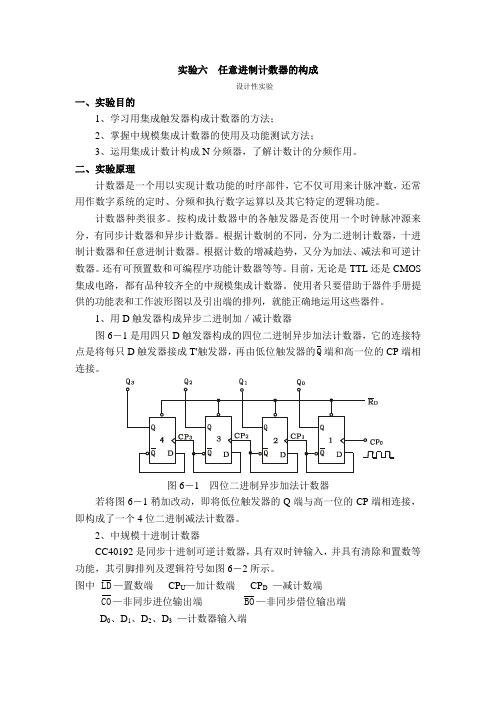
实验六任意进制计数器的构成设计性实验一、实验目的1、学习用集成触发器构成计数器的方法;2、掌握中规模集成计数器的使用及功能测试方法;3、运用集成计数计构成N分频器,了解计数计的分频作用。
二、实验原理计数器是一个用以实现计数功能的时序部件,它不仅可用来计脉冲数,还常用作数字系统的定时、分频和执行数字运算以及其它特定的逻辑功能。
计数器种类很多。
按构成计数器中的各触发器是否使用一个时钟脉冲源来分,有同步计数器和异步计数器。
根据计数制的不同,分为二进制计数器,十进制计数器和任意进制计数器。
根据计数的增减趋势,又分为加法、减法和可逆计数器。
还有可预置数和可编程序功能计数器等等。
目前,无论是TTL还是CMOS 集成电路,都有品种较齐全的中规模集成计数器。
使用者只要借助于器件手册提供的功能表和工作波形图以及引出端的排列,就能正确地运用这些器件。
1、用D触发器构成异步二进制加/减计数器图6-1是用四只D触发器构成的四位二进制异步加法计数器,它的连接特点是将每只D触发器接成T'触发器,再由低位触发器的Q端和高一位的CP端相连接。
图6-1 四位二进制异步加法计数器若将图6-1稍加改动,即将低位触发器的Q端与高一位的CP端相连接,即构成了一个4位二进制减法计数器。
2、中规模十进制计数器CC40192是同步十进制可逆计数器,具有双时钟输入,并具有清除和置数等功能,其引脚排列及逻辑符号如图6-2所示。
图中LD—置数端CP U—加计数端CP D—减计数端CO—非同步进位输出端BO—非同步借位输出端D0、D1、D2、D3—计数器输入端Q 0、Q 1、Q 2、Q 3 —数据输出端 CR图6-2 CC40192引脚排列及逻辑符号CC40192(同74LS192,二者可互换使用)的功能如表6-1,说明如下:当清除端CR 为高电平“1”时,计数器直接清零;CR 置低电平则执行其它功能。
当CR 为低电平,置数端LD 也为低电平时,数据直接从置数端D 0、D 1、D 2、D 3 置入计数器。
《数字电子技术》课程教学大纲

数字电子技术课程教学大纲(DIGITA1E1ECTRONICTECHNO1OGY)总学时数:56其中实验学时:0学分:3.5适用专业:电气工程与自动化专业一、课程的性质、目的和任务本课程是自动化专业的必修学科基础课程。
数字电子技术是电工、电子系列课程知识平台上的重要组成部分,是在电子技术方面入门性质的重要技术基础课。
其教学目的是使学生获得适应信息时代的电子技术方面的基本理论、基本知识和基本技能。
培养学生分析和解决问题的能力,为以后深入学习数字电子技术领域的相关内容和专业应用打好基础。
具体包括两方面:一是正确分析设计数字电路特别是集成电路的基础;二是进一步学习设计专用集成电路芯片的基础。
二、课程教学的基本要求在本课程学习中,要求学生掌握数字电子技术中的基本概念、基本原理和基本分析方法,其中包括:数字逻辑基础知识、逻辑门电路、组合逻辑电路的分析和设计、触发器时序逻辑电路的分析和设计、存储器和可编程逻辑器件、脉冲波形的产生和变换、数模和模数转换器的基本内容。
此外还应了解数字系统设计的一般方法。
三、课程的教学内容、重点和难点第一章数字逻辑概论(6学时)第一节数字逻辑电路概述(1)数字信号和数字电路的特点(2)数字电路的研究方法第二节数制(1)十进制数、二进制数、十六进制数的构成特点(2)非十进制数向十进制数转换及十六进制与二进制的相互转换的方法(3)十进制数向非十进制数转换的方法第三节二进制数的算术运算(1)无符号二进制数的算术运算(2)带符号二进制数的减法运算第四节编码(1)8421码内容及构成特点(2)2421码、5211码、循环码、余3循环码、ASC11码的构成特点及内容第五节基本逻辑运算第六节逻辑函数及其表示方法基本要求:(1)掌握数字信号与模拟信号的区别(2)掌握常用数制及其相互之间的转换(3)掌握原码、反码及补码的关系及转换(4)掌握8421码内容及构成特点;了解其它常用代码的构成特点重点难点:各种数制间相互转换,原码、反码及补码的概念及转换。
数字电子技术实验报告

实验报告课程名称数字电子技术实验项目门电路逻辑功能及测试、译码器及其应用、时序电路测试及研究、集成计数器及其应用项目一门电路逻辑功能及测试一、实验目的1、熟悉门电路的逻辑功能。
2、熟悉数字电路实验装置的结构、基本功能和使用方法。
二、实验原理用以实现基本逻辑运算和复合逻辑运算的单元电路通称为门电路。
常用的门电路在逻辑功能上有与门、或门、非门、与非门、或非门、与或非门、异或门等几种。
基本逻辑门可以分为分立器件电路和集成电路(Integrated Circuit,简称IC)两类。
用二极管、三极管和电阻等分立元器件组成的基本逻辑门电路即是分立器件电路。
随着集成电路制造工艺的日益完善,集成电路得到广泛应用。
集成基本逻辑门电路是最简单、最基本的数字集成元件,是构成各种复杂数字电路的基本逻辑单元,任何复杂的组合电路和时序电路都可用基本逻辑门通过适当的组合连接而成。
掌握各种基本逻辑门电路的逻辑功能、工作原理和电气特性,对于正确使用数字集成电路是十分必要的,是数字技术工作者所必备的基本功之一。
门电路的逻辑函数式分别为:与门Y =A·B或门Y =A+B非门Y =与非门Y =与非门Y =或非门Y =异或门Y =A⊕B与或非门Y =与门的逻辑功能为“有0 则0 ,全1 则1”;或门的逻辑功能为“有1则1 ,全0 则0”;非门的逻辑功能为输出与输入相反;与非门的逻辑功能为“有0 则1 ,全1 则0”;或非门的逻辑功能为“有1 则0 ,全0 则1”;异或门的逻辑功能为“不同则1 ,相同则0”。
三、实验内容及步骤实验前先检查实验箱电源是否正常。
然后选择实验用的集成电路连好线,特别注意Vcc 及地线不能接错。
线接好后经检查无误方可通电实验。
1、集成与非门74LS20的逻辑功能测试选用74LS20一只。
74LS20为双4输入与非门, 即在一块集成块内含有二个互相独立的与非门,每个与非门有4个输入端。
如图1-1(a)所示。
数字电路逻辑设计 第六章2

(一)反馈清零法
74160是模10计数器,要实现模853计数,须用三片74160级联。 ⑴先设计模1000计数器: M = M1×M2 ×M3=10 × 10 × 10=1000 ☆ 利用各片间进位信号快速传递方法,组成计数模值为1000计数器。 ⑵ 用异步清0法,使计数器计数脉冲输入到第853个脉冲时产整体置0 信号 使计数器返回到初始状态0000。 计数范围:
画出逻辑图如图
D2 D1 D0 CTT D3 CTP CTRDIV16 CO CT161 CR
LD
1
Q 3 Q2 Q 1 Q 0
0
0
&
O
0
(二)同步预置法
例:用四位同步二进制计数器74161设计余3BCD码计数器。
解:余3BCD码计数器的状态转移图如图所示
0011 1100
LD Q3Q2
画出逻辑图
&
1 CTP CR CTT 1
74161(1)
D0D1D2D3
Q0Q1Q2Q3 CO
CTP CTT
CR
74161(2)
D0D1D2D3
Q0Q1Q2Q3 CO
LD
LD
CP
(二)同步预置法
方法三、整体同步反馈置数: (利用进位输出作为置数译码信号) 计数范围196-255,当计数器计到255时,CO=1,使 两片74161置数控制端 /LD=0,下一个CP到来时置数。 预置输入=256-60=196 (196)10=(11000100)2 低位片预置数:0100 高位片预置数:1100
工作波形图: 5 6 7 8
9
10
6.5采用中规模集成器件设计任意进制计数器
1. M<N,N为单片计数器的最大计数值
计数器的原理

计数器的原理计数器是数字电路中广泛使用的逻辑部件,是时序逻辑电路中最重要的逻辑部件之一。
计数器除用于对输入脉冲的个数进行计数外,还可以用于分频、定时、产生节拍脉冲等。
计数器按计数脉冲的作用方式分类,有同步计数器和异步计数器;按功能分类,有加法计数器、减法计数器和既具有加法又有减法的可逆计数器;按计数进制的不同,又可分为二进制计数器、十进制计数器和任意进制计数器。
一、计数器的工作原理1、二进制计数器(1)异步二进制加法计数器图1所示为用JK触发器组成的4位异步二进制加法计数器逻辑图。
图中4个触发器F0~F3均处于计数工作状态。
计数脉冲从最低位触发器F0的CP端输入,每输入一个计数脉冲,F0的状态改变一次。
低位触发器的Q端与高位触发器的CP端相连。
每当低位触发器的状态由1变0时,即输出一负跳变脉冲时,高位触发器翻转。
各触发器置0端R D并联,作为清0端,清0后,使触发器初态为0000。
当第一个计数脉冲输入后,脉冲后沿使F0的Q0由0变1,F1、F2、F3均保持0态,计数器的状态为0001;当图1 4位异步二进制加法计数器第二个计数脉冲输入后,Q0由1变为0,但Q0的这个负跳变加至F1的CP端,使Q1由0变为1,而此时F3、F2仍保持0状态,计数器的状态为0010。
依此类推,对于F0来说,每来一个计数脉冲后沿,Q0的状态就改变,而对于F1、F2、F3来说,则要看前一位输出端Q是否从1跳到0,即后沿到来时,其输出端的状态才改变,否则Q1、Q2、Q3端的状态同前一个状态一样。
这样在第15个计数脉冲输入后,计数器的状态为1111,第16个计数脉冲输入,计数器恢复为0000。
由上述分析可知,一个4位二进制加法计数器有24=16种状态,每经过十六个计数脉冲,计数器的状态就循环一次。
通常把计数器的状态数称之为计数器的进制数(或称计数器的模),因此,4位二进制计数器也可称之为1位十六进制(模16)计数器。
表1所示为4位二进制加法计数器的状态表。
计数器原理图

计数器原理图计数器是数字电路中常用的一种逻辑电路,用于对输入脉冲进行计数。
计数器广泛应用于各种数字系统中,如计数器、频率分割器、时序控制等。
本文将介绍计数器的原理图及其工作原理。
计数器的原理图通常由触发器、门电路和时钟信号组成。
触发器是计数器的核心部件,它能够存储和传输信息。
门电路用于控制触发器的工作状态,而时钟信号则用于同步触发器的工作。
通过这些部件的组合,计数器能够实现对输入脉冲的计数。
在计数器的原理图中,常见的触发器包括RS触发器、D触发器、JK触发器和T触发器。
这些触发器都具有不同的特性和适用场景,可以根据具体的需求选择合适的触发器类型。
门电路通常由与门、或门、非门等组成,用于控制触发器的输入和输出。
时钟信号则用于同步各个触发器的工作,确保计数器能够按照预期的方式进行计数。
计数器的工作原理是通过触发器的状态变化来实现对输入脉冲的计数。
当输入脉冲到达时,触发器的状态会发生变化,从而实现对计数器的加一操作。
不同类型的计数器具有不同的计数方式,如二进制计数、BCD码计数等。
通过合理的设计和组合,计数器能够实现对输入脉冲的精确计数。
除了基本的计数器原理图外,还有一些特殊类型的计数器,如同步计数器、异步计数器、可逆计数器等。
这些计数器在特定的应用场景中具有特殊的优势,能够满足更复杂的计数需求。
总的来说,计数器是数字电路中非常重要的一种逻辑电路,它能够实现对输入脉冲的精确计数。
通过合理的设计和组合,计数器能够适应不同的应用场景,满足各种计数需求。
希望本文介绍的计数器原理图及其工作原理能够帮助读者更好地理解和应用计数器。
[数字电子技术基础期末考试题]数字电子技术基础第五版课后答案
![[数字电子技术基础期末考试题]数字电子技术基础第五版课后答案](https://img.taocdn.com/s3/m/1e560b70793e0912a21614791711cc7931b778c2.png)
[数字电子技术基础期末考试题]数字电子技术基础第五版课后答案一、单项选择题(每小题1分,共10分)1、以下描述一个逻辑函数的方法中,()只能唯一表示。
A。
表达式B。
逻辑图C。
真值表D。
波形图2、在不影响逻辑功能的情况下,CMOS与非门的多余输入端可()。
A。
接高电平B。
接低电平C。
悬空D。
通过电阻接地3、一个八位二进制减法计数器,初始状态为00000000,问经过268个输入脉冲后,此计数器的状态为()。
A。
11001111B。
11110100C。
11110010D。
111100114、若要将一异或非门当作反相器(非门)使用,则输入端A、B端的连接方式是()。
A。
A或B中有一个接“1”B。
A或B中有一个接“0”C。
A和B并联使用D。
不能实现5、在时序电路的状态转换表中,若状态数N=3,则状态变量数最少为()。
A。
16B。
4C。
8D。
26、下列几种TTL电路中,输出端可实现线与功能的门电路是()。
A。
或非门B。
与非门C。
异或门D。
OC门7、下列几种A、D转换器中,转换速度最快的是()。
A。
并行A、D转换器B。
计数型A、D转换器C。
逐次渐进型A、D转换器D。
双积分A、D转换器8、存储容量为8K8位的ROM存储器,其地址线为()条。
A。
8B。
12C。
13D。
149、4个触发器构成的8421BCD码计数器,共有()个无效状态。
A。
6B。
8C。
10D。
1210、以下哪一条不是消除竟争冒险的措施()。
A。
接入滤波电路B。
利用触发器C。
加入选通脉冲D。
修改逻辑设计二、填空题(每空1分,共20分)1、时序逻辑电路一般由()和()两分组成。
2、多谐振荡器是一种波形产生电路,它没有稳态,只有两个3、数字电路中的三极管一般工作于________区和________区。
4、四个逻辑变量的最小项最多有________个,任意两个最小项之积为________。
5、555定时器是一种用途很广泛的电路,除了能组成________触发器、________触发器和________三个基本单元电路以外,还可以接成各种实用电路。
第六章 时序逻辑电路计数器

EP ET
CLK Q0 Q1 Q2
C LD LD R D RD Q3
(b)功能表
图6.3.9 4注:74161和74LS161只是内部电路结构有些区别。74LS163 也是4位二进制加法计数器,但清零方式是同步清零
01
01
0
6.3.2 计数器
0 0 0 0 1 1 1 1
0 0 1 1 0 0 1 1
0 1 0 1 0 1 0 1
Ti Qi 1Qi 2 ...Q0 T0 1
T 触发器
1.定义: 凡在时钟信号作用下,具有表5.6.3所示功能的触 发器称为T 触发器 表5.6.3
在数字电路中,凡在 CP 时钟脉冲 控制下,根据输入信号T取值的不 同,具有保持和翻转功能的电路 ,即当 T=0 时能保持状态不变 , T=1 时一定翻转的电路,都称为 T 触发器。 2.特性方程: 由特性表可得
(a)逻辑图形符号 (b)功能表 图6.3.12 同步十六进制可逆计数器74LS193的图形符号及功能表
6.3.2 计数器
2. 同步十进制计数器:
①加法计数器 基本原理:在四位二 进制计数器基础上修 改,当计到1001时, 则下一个CLK电路状 态回到0000。
T1 Q0 Q0Q3
6.3.2 计数器
K1 & T3 J Q3 6 7 8 9 10 11 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 0 1 0 1 3 2 1 0 9 0 0 0 1 0
C K1
6.3.2 计数器
其逻辑电路如图6.3.15所示
驱动方程:
T0 1 (Q3 Q2 Q1 ) T1 Q0 Q0 (Q1 Q2 Q3 ) T2 Q1 Q1 Q0 T3 Q2
数电实验四——精选推荐

实验四:时序逻辑电路(集成寄存器和计数器)一、实验目的:1.熟悉中规模集成计数器的逻辑功能和使用方法;掌握用集成计数器组成任意模数为M的计数器。
2.加深理解移位寄存器的工作原理及逻辑功能描述;熟悉中规模集成移位寄存器的逻辑功能和使用方法;掌握用移位寄存器组成环形计数器的基本原理和设计方法。
二、知识点提示和实验原理:㈠计数器:计数器的应用十分广泛,不仅可用来计数,也可用于分频、定时和数字运算。
计数器种类繁多,根据计数体制不同,计数器可分为二进制计数器和非二进制计数器两大类。
在非二进制计数器中,最常用的是十进制计数器,其他的称为任意进制计数器。
根据计数器的增减趋势的不同,计数器可分为加法计数器和减法计数器。
根据计数脉冲引入方式不同,计数又可分为同步计数器和异步计数器。
在实际工程应用中,一般很少使用小规模的触发器组成计数器,而是直接选用中规模集成计数器。
用集成计数器实现任意M进制计数器:一般情况任意M进制计数器的结构分为3类,第一种是由集成二进制计数器构成,第二种为移位寄存器构成的移位寄存型计数器,第三种为集成触发器构成的简单专用计数器。
当M较小时通过对集成计数器的改造即可以实现,当M较大时,可通过多片计数器级联实现。
实现方法:(1)当所需计数器M值小于集成计数器本身二进制计数最大值时,用置数(清零)法构成任意进制计数器;⑵当所需计数器M值大于集成计数器本身二进制计数最大值时,可采用级联法构成任意进制计数器。
常用的中规模集成器件:4位二进制计数器74HC161,十进制计数器74HC160,加减计数器74HC191、74HC193,异步计数器74LS290。
所有芯片的电路、功能表见教材。
㈡寄存器:寄存器用来寄存二进制信息,将一些待运算的数据、代码或运算的中间结果暂时寄存起来。
按功能划分,寄存器可分为数码寄存器和移位寄存器两大类。
数码寄存器用来存放数码,一般具有接收数码、保持并清除原有数码等功能,电路结构和工作原理郡比较简单。
数字电路中的计数器和时序电路设计

数字电路中的计数器和时序电路设计数字电路中的计数器和时序电路设计是电子工程中非常重要的一部分。
通过设计和实现计数器和时序电路,我们能够实现各种数字计数和定时功能。
本文将介绍计数器和时序电路的基本原理,并讨论它们的设计过程和常见应用。
一、计数器的原理和设计计数器是一种能对输入脉冲进行计数的电路。
它由触发器、输入脉冲信号和控制电路组成。
计数器根据输入脉冲信号的数量来确定输出的状态,可以实现多种功能,如二进制计数、十进制计数、循环计数等。
1. 二进制计数器二进制计数器是最简单的计数器类型,它的输出状态按照二进制数进行变化。
例如,一个4位二进制计数器可以从0000计数到1111,然后重新开始。
设计二进制计数器时,我们可以使用触发器和逻辑门来构建。
2. 十进制计数器十进制计数器是一种特殊的计数器,它的输出状态按照十进制数进行变化。
一个4位的十进制计数器可以从0计数到9,然后重新开始。
设计十进制计数器时,可以使用二进制计数器和BCD(二进制编码十进制)转换器来实现。
3. 循环计数器循环计数器是一种特殊的计数器,它可以按照任意给定的计数序列进行循环计数。
例如,一个循环计数器可以按照1、2、3、1、2、3的序列进行计数。
设计循环计数器时,一种常见的方法是使用状态转换图来确定触发器和逻辑门的连接。
二、时序电路的原理和设计时序电路是一种能实现定时功能的电路。
它包括时钟信号源、触发器和控制电路。
时序电路可以用于各种应用,如定时器、频率分频器、状态机等。
1. 定时器定时器是一种能够按照给定的时间间隔产生定时脉冲信号的电路。
它通常由可编程的触发器和计数器组成。
定时器的设计需要确定计数器的初始值和触发器的工作模式,并设置适当的控制电路。
2. 频率分频器频率分频器是一种能够将输入信号的频率分频为较低频率的电路。
它通常使用计数器和触发器来实现。
频率分频器的设计要考虑到分频比例和触发器的连接方式。
3. 状态机状态机是一种能够根据特定的状态转换规则改变输出状态的电路。
实验八 时序逻辑电路设计实验

实验八时序逻辑电路设计实验一、实验概述本实验是使用74LS74双D触发器构成一个扭环形计数器,以及使用74LS112双JK触发器构成三进制加法计数器。
二、实验目的1、掌握简单的时序电路的设计方法2、掌握简单时序电路的调试方法三、实验预习要求1、查找74LS74、74LS112、74LS00芯片引脚图,并熟悉引脚功能2、复习教材中异步2n进制计数器构成方法及同步2n进制计数器构成方法的内容3、复习同步时序电路和异步时序电路的设计方法4、设计画出用74LS74构成异步四进制减法计数器的逻辑电路图5、设计画出用74LS112构成同步四进制加法计数器的逻辑电路图四、实验原理时序逻辑电路是数字逻辑电路的重要组成部分,时序逻辑电路又称时序电路,主要由存储电路和组合逻辑电路两部分组成。
它和我们熟悉的其他电路不同,其在任何一个时刻的输出状态由当时的输入信号和电路原来的状态共同决定,而它的状态主要是由存储电路来记忆和表示的。
同时时序逻辑电路在结构以及功能上的特殊性,相较其他种类的数字逻辑电路而言,往往具有难度大、电路复杂并且应用范围广的特点。
时序逻辑电路通常可以分为同步时序逻辑电路和异步时序逻辑电路两大类。
同步时序逻辑电路从构成方式来讲,同步时序电路所有操作都是在同一时钟严格的控制下步调一致地完成的。
从电路行为上,同步电路的时序电路公用同一个时钟,而所有的时钟变化都是在时钟的上升沿(或下降沿)完成的。
同步逻辑是时钟之间存在固定因果关系的逻辑,所有时序逻辑都是在同源时钟控制下运行。
注意,在用Verilog HDL实现时,并不要求是同一时钟,而是同源时钟。
所谓的同源时钟是指同一个时钟源衍生频率比值为2的幂次方,且初相位相同的时钟。
异步时序逻辑电路异步时序逻辑电路,顾名思义就是电路的工作节奏不一致,不存在单一的主控时钟,主要是用于产生地址译码七、FIFO和异步RAM的读写控制信号脉冲。
除可以使用带时钟的触发器外,还可以使用不带时钟的触发器和延迟元件作为存储元件;电路状态改变完全有外部输入的变化直接引起。
第六章 时序逻辑电路

6.2.时序逻辑电路的分析方法
一、状态转换表: 根据状态方程将所有的输入变量和电路初态的取 值,带入电路的状态方程和输出方程,得到电路次态 (新态)的输出值,列成表即为状态转换表
图6.2.1 此电路没有输入变量,属于穆尔型的时序逻辑电 路,输出端的状态只决定于电路的初态。
6.2.时序逻辑电路的分析方法
Q1* (Q2Q3 ) Q1 Q2 * Q1Q2 Q1Q3Q2 Q * Q Q Q Q Q 1 2 3 2 3 3
(3)输出方程:
Y Q2Q3
6.2.时序逻辑电路的分析方法
6.2.2时序逻辑电路的状态转换表、状态转换图、状态 机流程图和时序图
*
可得逻辑电路的状态方程:
J 0 K0 1 J Q , K 1 1 3 1 J 2 K2 1 J 3 Q1Q2 , K 3 1
Q * Q1 * Q2 Q * 3
* 0
Q0 Q3Q1 Q2 Q1Q2Q3
D1 Q1 D2 A Q1 Q2
(3) 输出方程:
Q1n 1 D1 Q1 n 1 Q2 D2 A Q1 Q2
图6.2.4
Y [( AQ1Q2 ) ( AQ1Q2 )] AQ1Q2 AQ1Q2
6.2.时序逻辑电路的分析方法
例6.2.1 试分析图6.2.1所示的时序逻辑电路的逻辑功能, 写出它的驱动方程、状态方程和输出方程,写出电路 的状态转换表,画出状态转换图和时序图。
图6.2.1
解:(1) 驱动方程: J1 (Q2Q3 ), K1 1 K 2 (Q1Q3 ) J 2 Q1 , J QQ , K 3 Q2 1 2 3
时序逻辑电路的分析方法和设计思路

时序逻辑电路
数字电路与逻辑设计
2. 异步时序逻辑电路的基本分析方法
以下图所示3个T′触发器构成的时序逻辑电路为例,我
们讨论其分析方法和步骤。
Q0
Q1
Q2
JQ
CP
C F0
KQ
JQ C F1 KQ
JQ C F2 KQ
“1”
RD
1
分析电路类型:
时序逻辑电路中如果除CP时钟脉冲外,无其它输入信 号,就属于莫尔型,若有其它输入信号时为米莱型;各位
为了能把在一系列时钟脉冲操作下的电路状态转换全过 程形象、直观地描述出来,常用的方法有状态转换真值表、 状态转换图、时序图和激励表等。这些方法我们将在对时 序逻辑电路的分析过程中,更加具体地加以阐明。
时序逻辑电路
数字电路与逻辑设计 1. 同步时序逻辑电路的基本分析方法
[例7.2.1] 分析如图7.2.2所示时序电路的逻辑功能
时序逻辑电路
数字电路与逻辑设计
1. 二进制计数器
当时序逻辑电路的触发器位数为n,电路状态按二进制数
的自然态序循环,经历2n个独立状态时,称此电路为二进
制计数器。
Q0
Q1
Q2
JQ
CP
C F0
KQ
JQ C F1 KQ
JQ C F2 KQ
“1”
RD
结构原理:三个JK触发器可构成一个“模8”二进制计数器。 触发器F0用时钟脉冲CP触发,F1用Q0触发,F2用Q1触发; 三位JK触发器均接成T′触发器—让输入端恒为高电平1; 计数器计数状态下清零端应悬空为“1”。(如上一节的分 析例题,就是一个三位触发器构成的二进制计数器。)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
故若由74LS161构成53进制计数器, 先要将53化成二进制数码, 再根据整体置数法或整体置零法实现53进制。
例:
(53)D=( 11 0101 )B
转换过程: 2 53 余 1 K0
2 26 余 0 K1
2 13 余 1 K2
2 6 余 0 K3
2 3 余 1 K4
(1)选定S0 0000000作 0 为初态
1
CLK 计数输入
EP D0 D1 D2 D3 C
ET
74160 LD
1 CLK
Q0
Q1
Q2
Q3 RD
EP D0 D1 D2 D3 C
ET
74160 LD
1 CLK
Q0
Q1
Q2
Q3 RD
进位输出
6.3.2 计数器
注意!
【例】试利用置零法和置数法由两片74LS161构成53进 制加法计数器。
解:用整体法先将两片74LS161构成256进制(16×16 进制),该256进制计数器实际为二进制计数器(28),
(1)整体置零法实现53进制。(M=53)
R DS 53 ( 000 11 1 ) B 01
利用整体置零法由74LS161构成53进制加法计数器如图
所示。
R DS53 ( 000 11 1 ) B 01
1010
1100
十进制数53对应的二进制数为0011 0101 实现从0000 0000到0011 0100的53进制计数器
1
CLK 计数输入
EP D0 D1 D2 D3 C
ET
74160 LD
1 CLK
Q0
Q1
Q2
Q3 RD
EP D0 D1 D2 D3 C
ET
74160 LD
1 CLK
Q0
Q1
Q2
Q3 RD
进位输 出CO
【例】用74160实现63进制计数器。
整体置零法 M=63,在SM=S63=0110 0011 处反馈清零。
【 】 内容 回顾
暂态
异步清零
a. 置零法(复位法)
【 】 内容 回顾
基本思想是:计数器从全0状态S0开始计数,计满M个
状态后产生清零信号,使计数器恢复到初态S0,然后
再重复上述过程。
异步清零
SM状态进行译码产生置 零信号并反馈到异步清
零端( RD),使计数器立
即返回S0状态。
10ns
左右
SM状态只在极短的瞬间 出现,通常称它为“过
为什么进位端要加一个反相器?不加会有什么结果? 1 2 3 4 5 6 7 8 9 10 11 12 131415 161718 19 20 21
CLK
C
C
【例】用74160实现24进制计数器。 整体置零法 M=24,在SM=S24=0010 0100 处反馈清零。
1
CLK 计数输入
EP D0 ET
渡态”。
暂态
利用异步复位端RD ,跳过多余状态,实现任意进制计数。
异步复位法①计数到M时,清0, (异步置零) ②写SM=( )2,全部Q为1的端相与非R→D
适用于异步清0的集 成计数器,当满足清0 条件时,立即清0。
【 】 内容 回顾
【例】用74160实现7进制计数器。
置零法,M=7,在SM=S7=0111处反馈清零。
RD(Q2Q1Q0)
1
EP D 0 D 1 D 2 D 3 C
1
ET
74160
LD
CLK 计数输入
CLK
R
Q0 Q1 Q2 Q3 D
进位输出
【例】用74161实现12进制计数器。 置零法,M=12,在SM=S12=1100处反馈清零。
RD(Q3Q2)
1
EP D 0 D 1 D 2 D 3 C
1
ET
1
CLK 计数输入
EP D0 D1 D2 D3 C
ET
74160 LD
1 CLK
Q0
Q1
Q2
Q3 RD
EP D0 D1 D2 D3 C
ET
74160 LD
1 CLK
Q0
Q1
Q2
Q3 RD
进位输 出CO
【例】用74160实现24进制计数器。 整体置数法 i=2, M=24,在Si+M-1=S25=0010 0101 处反馈置零。 1
74161
LD
CLK 计数输入
CLK
R
Q
0
QQQ
1
2
3
D
进位输出
6.3.2 计数器
注:由于清零信号随着计数器被清零而立即消失,其持续 的时间很短,有时触发器可能来不及动作(复位),清零 信号已经过时,导致电路误动作,故置零法的电路工作可 靠性低。为了改善电路的性能,在清零信号产生端和清零 信号输入端之间接一基本RS触发器,如图所示。
ET CLK
Q0
74160 Q1 Q2
LD R Q3 D
1
6.3(.以2 具计有数同器步预置数端 LD的集成计数器为例)
置数法的应用可以分三种情况: (现有N进制计数器,构成M进制)
取前M种状态 取后M种状态 取中间M种状态
取(i)2——(i+M-1)2 共M个状态
取中间M种状态
同步预置数法 :
处反馈置零。
1
CLK 计数输入
EP D0 D1 D2 D3 C
ET
74160 LD
1 CLK
Q0
Q1
Q2
Q3 RD
EP D0 D1 D2 D3 C
ET
74160 LD
1 CLK
Q0
Q1
Q2
Q3 RD
进位输出
【例】用74160实现63进制计数器。
整体置数法 1
i=6, M=63,在Si+M-1=S68=0110 1000 处反馈置零。
C
【例】用74160实现100进制计数器。 (2) 串行进位,M=100=10*10。
1
1
EP D0 D1 D2 D3 C
CLK
ET
74160 LD
CLK
Q0
Q1
Q2
Q3 RD
计数输入
1
EP D0 D1 D2 D3 C
ET
74160 LD
CLK
Q0
Q1
Q2
Q3 RD
1
?思考:为 不加什会么有进位什么端结要果加一?个反相器?
方法。
作业:
P349思考题和习题
6-12题、6-13题、6-14题、6-16题
2. M>N的情况
如果要求实现的进制M超过单片计数器的计数范围时, 必须将多片计数器级联,才能实现M进制计数器。
串行进位方式 并行进位方式
整体清0方式 整体置数方式
(1)M=M1•M2,即M分解为M1 ×M2 ,可采用串行进位方式/ 并行进位方式。(以两片级联为例)
6.3.2 计数器
1. M<N的情况
【 】 内容 回顾
在N进制计数器的顺序计数过程中,若设法使之跳 过(N-M)个状态,就可以得到M进制计数器了,其 方法有置零法(复位法)和置数法(置位法)。
置零法
置数法
6.3.2 计数器
a. 置零法:
置零法适用于有置 零(有异步和同步)输 入端的计数器,如异步 置零的有74LS160、161、 191、190、290,同步置 零的有74LS163、162, 其工作原理示意图如图 所示。
6.3.2 计数器 【例】试利用置零法和置数法由两片74LS161构 成53进制加法计数器。
解:若由74LS161构成53进制计数器,其构成的256进 制实际为二进制计数器(28),故先要将53化成二进制数码
(53)D=(110101)B =(0011 0101)B
(2)整体置数法实现53进制。(M=53)
6.3(.以2 具计有数同器步预置数端 LD的集成计数器为例)
置数法的应用可以分三种情况: (现有N进制计数器,构成M进制)
取前M种状态
置 零
取前M种状态
取0000——(M-1)2 个状态
【例】用74160实现7进制计数器(置数法)。
(1)置数法(取前M种状态), M=7,在SM-1=S6=0110处反馈置零。
串行进位方式 : 以低位片的进位输出信号作为高位片的时 钟输入信号。两片始终同时处于计数状态.
并行进位方式 : 以低位片的进位输出信号作为高位片的控 制信号(使能),两片的CLK同时接计数输入。
(2)当M为素数时,不能分解为M1和M2,采用整体 清0/整体置数方式。
首先将两片N进制计数器按串行进位方式或并行进 位方式联成N×N > M 进制计数器,再按照M<N的置零 法和置数法构成M进制计数器。此方法适合任何M进制 (可分解和不可分解)计数器的构成。
1
EP D0 D1 D2 D3 C
ET
74160 LD
1
CLK
CLK
Q0
Q1
Q2
Q3 RD
计数输入
EP D0 D1 D2 D3 C
ET
74160 LD
1
CLK
Q0
Q1
Q2
Q3 RD
进位输出
【例】用74160实现63进制计数器。 整体置数法 i=0, M=63,在Si+M-1=S62=0110 0010
00 0
1
0
0
1 0
1 01
6.3.2 计数器
b. 置数法: 有预置数功能的计数器可用此方法构成M进制计数
器。但注意74LS161(160)为同步预置数,74LS191(190) 为异步预置数。
