最新数学北师版初中九年级上册第四章综合精选习题
北师大版数学九年级上册第四章单元综合测试题附答案

北师大版数学九年级上册第四章单元综合测试题(图形的相似)一、选择题。
1.如图,D为△ABC边BC上一点,要使△ABD∽△CBA,应该具备下列条件中的()A.=B.=C.=D.=2.如图,在△ABC中,若DE∥BC,,DE=3cm,则BC的长为()A.3cm B.6cm C.9cm D.12cm3.如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是()A.B.C.D.4.如图,线段CD两个端点的坐标分别为C(3,3),D(4,1),以原点O为位似中心,在第一象限内将线段CD放大为原来的2倍后得到线段AB,则端点B 的坐标为()A.(6,6) B.(6,8) C.(8,6) D.(8,2)5.关于对位似图形的表述,下列命题正确的有()①相似图形一定是位似图形,位似图形一定是相似图形;②位似图形一定有位似中心;③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么这两个图形是位似图形;④位似图形上任意一组对应点P,P′与位似中心O的距离满足OP=k•OP′.A.①②③④B.②③④C.②③D.②④6.如图,A,B,C,D,E,G,H,M,N都是方格纸中的格点(即小正方形的顶点),要使△DEF与△ABC相似,则点F应是G,H,M,N四点中的()A.H或N B.G或H C.M或N D.G或M7.△ABC与△DEF的相似比为1:4,则△ABC与△DEF的周长比为()A.1:2 B.1:3 C.1:4 D.1:168.如图,在△ABC中,DE∥BC,若=,则=()A.B.C.D.9.在研究相似问题时,甲、乙同学的观点如下:甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的。
北师大版九年级上册第四章全章分课时习题精选(最新版)

北师大版九年级上册第四章全章分课时习题精选(最新版)4.1 成比例线段1.已知三条线的比如下,可以组成三角形的是( )A .5:20:30B .10:20:30 C.15:15:30 D.20:30: 30 2.下列四条线段中,不能成比例的是( ) A.. a =3,b =6,c =2,d =4 B. a =1,b =2,c =6,d =3 C. a =4,b =6,c =5,d =10D. a =2,b =5,c =15,d =233.在比例尺为1:n 的某市地图上,A ,B 两地相距5cm ,则A ,B 之间的实际距离为( ) A .51n cm B .251n2cm C .5ncm D.25n2cm4.若5x =7y,则y x 的值为( )A .75 B . 57 C .3:5 d.2 5.如果b a =b d成立,那么下列各式一定成立的是( )A .c a =b dB .bd ac =b cC .ba 1+ =d c 1+ D .b b a 2+=d dc 2+6.若a:b:c=3:5:7,且3a+2b-4c=9,则a+b+c 的值等于( )A .-3B .-5 C.-7 D.-157.已知M 是线段AB 延长线上一点,且AM :BM =5:2则AB :BM 为( )A.3:2 B .2:3 C .3:5 D .5:28.某班同学要测量学校升国旗的旗杆高度,在同一时刻,量得某同学的身高是1.5米,影长是1米,且旗杆的影长为8米,则旗杆的高度是( ) A.12米 B .11米 C .10米 D .9米9.若b b a -=74,则b a=____. 10.若b a =d c =52(b +d ≠0),则db c a ++=____.11.已知5922=-+b a b a ,则b a =____.12.如果两地相距250km ,那么在1: 10000000的地图上它们相距____cm 。
13.在Rt △ABC 中,斜边AB =205,409=BC AC ,试求AC ,BC 的值。
最新北师版九年级初三数学上册《第四章综合练习》同步练习题

第四章 图形的相似一、选择题1、【基础题】在比例尺为1:5000的地图上,量得甲,乙两地的距离为25 cm ,则甲、乙两地的实际距离是 ( )A. 1250千米B. 125千米C. 12.5千米D. 1.25千米2、【基础题】已知135=a b ,则ba ba +-的值是( ) ★A. 32B. 23C. 49D. 943、【基础题】如右图,在△ABC 中,看DE ∥BC ,12AD BD ,DE =4 cm ,则BC 的长为 ( ) A .8 cm B .12 cm C .11 cm D .10 cm 4、【基础题】如右图,DE 是ΔABC 的中位线,则ΔADE 与ΔABC 的面积之比是( ) A .1:1B .1:2C .1:3D .1:45、【基础题】如下图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC 相似的是( ) ★★★6、【基础题】下列结论不正确的是( ) ★ A. 所有的矩形都相似 B. 所有的正方形都相似 C. 所有的等腰直角三角形都相似 D. 所有的正八边形都相似7、【基础题】下列说法中正确的是( ) ★A. 位似图形可以通过平移而相互得到B. 位似图形的对应边平行且相等C. 位似图形的位似中心不只有一个D. 位似中心到对应点的距离之比都相等A8、【综合题Ⅰ】如左下图,ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件中,不能推出△ABP与△ECP相似的是()★★★A.∠APB=∠EPCB. ∠APE=90°C. P是BC的中点D. BP︰BC=2︰39、【综合题Ⅱ】如右上图,Rt△ABC中,AB⊥AC,AB=3,AC=4,P是BC边上一点,作PE⊥AB于E,PD⊥AC于D,设BP=x,则PD+PE=()A. 35x+ B. 45x- C.72D.21212525x x-10、【综合题Ⅲ】如图,在Rt ABC△内有边长分别为a,b,c的三个正方形.则a、b、c满足的关系式是()A. b a c=+B. b ac=C. 222b a c=+D. 22b a c==二、填空题11、【基础题】在同一时刻,高为1.5m的标杆的影长为2.5m,一古塔在地面上影长为50m,那么古塔的高为.12、【基础题】两个相似三角形面积比是9∶25,其中一个三角形的周长为36cm,则另一个三角形的周长是.13、【综合题Ⅰ】如左下图,在△ABC中,AB=5,D、E分别是边AC和AB上的点,且∠ADE=∠B,DE=2,那么AD·BC= . ★★★ABCDEP14、【基础题】如右上图,在△ABC 和△DEF 中,G 、H 分别是边BC 和EF 的中点,已知AB =2DE ,AC =2DF ,∠BAC =∠EDF . 那么AG :DH= ,△ABC 与△DEF的面积比是 . ★★★15、【基础题】把一个三角形改做成和它相似的三角形,如果面积缩小到原来的21倍,边长应缩小到原来的____倍.16、【综合Ⅱ】如左下图在Rt △ABC 中, ∠ACB =90°,CD ⊥AB 于D ,若AD =1,BD =4,则CD = . ★17、【基础题】如右上图,一人拿着一支厘米小尺,站在距电线杆约30米的地方,把手臂向前伸直,小尺竖直,看到尺上12厘米的长度恰好遮住电线杆,已知手臂长约60厘米,则电线杆的高为 . ★★★18、【基础题】已知一本书的宽与长之比为黄金比,且这本书的长是20 cm ,则它的宽为_____cm.(结果保留根号)19、【综合Ⅲ】顶角为36°的等腰三角形称为黄金三角形,如图,在△ABC 中,AB =AC =1,∠A =36°,BD 是三角形ABC 的角平分线,那么AD = . ★20、【提高题】如图,点1234A A A A ,,,在射线OA 上,点123B B B ,,在射线OB 上,且112233A B A B A B ∥∥,213243A B A B A B ∥∥.若212A B B △、323A B B △的面积分别为1、4,则图中三个阴影三角形面积之和为 .(第20题图)OA A A A AB B 1 B 2 B 3 1 4三、解答题 21、【基础题】如图,已知点E 是矩形ABCD 的边CD 上一点,BF ⊥AE 于点F ,求证△ABF ∽△EAD . 22、【综合Ⅰ】如图27-106所示,已知E 为ABCD 的边CD 延长线上的一点,连接BE 交AC 于O ,交AD 于F .求证BO 2=OF ·OE .23、如图,在平面直角坐标系中,已知OA=12 cm ,OB=6 cm ,点P 从O 点开始沿OA 边向点A 以1cm/s的速度移动,点Q 从点B 开始沿BO 边向点O 以1cm/s 的速度移动,如果P 、Q 同时出发,用t (单位:秒)表示移动的时间(06t ≤≤),那么:(1)当t 为何值时, △POQ 与△AOB 相似?(2)设△POQ 的面积为y ,求y 关于t 的函数解析式。
最新北师大版九年级数学上册第四章 图形的相似 综合题练习

北师大版九年级数学上册第四章图形的相似综合题练习1、在如图所示的一张矩形纸片ABCD(AD>AB)中,将纸片折叠一次,使点A与C重合,再展开,折痕EF交AD边于E,交BC边于F,分别连接AF和CE.(1)求证:四边形AFCE是菱形;(2)过E作EP⊥AD交AC于P,求证:2AE2=AC•AP;(3)若AE=8cm,△ABF的面积为9cm2,求△ABF的周长.2、如图,射线AM平行于射线BN,AB⊥BN,且AB=3,C是射线BN上的一个动点,连接AC,作CD⊥AC,且CD=AC,过C作CE⊥BN交AD于点E,设BC长为t.(1)AC长为,△ACD的面积为(用含有t的代数式表示);(2)求点D到射线BN的距离(用含有t的代数式表示);(3)是否存在点C,使△ACE为等腰三角形?若存在,请求出此时BC的长度;若不存在,请说明理由.3、已知:如图①,在Rt△ACB中,∠C=90°,AC=4 cm,BC=3 cm,点P由B出发沿BA 方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<2),解答下列问题:(1)当t为何值时,PQ∥BC;(2)设△AQP的面积为y(cm2),求y与t之间的函数关系式;(3)是否存在某一时刻t,使线段PQ恰好把Rt△ACB的周长和面积同时平分?若存在,求出此时t的值;若不存在,说明理由;(4)如图②,连接PC ,并把△PQC 沿QC 翻折,得到四边形PQP ′C ,那么是否存在某一时刻t ,使四边形PQP ′C 为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.4、在△ABC 中,∠C=Rt ∠,AC=4cm ,BC=5cm ,点D 在BC 上,并且CD=3cm ,现有两个动点P 、Q 分别从点A 和点B 同时出发,其中点P 以1cm/s 的速度,沿AC 向终点C 移动;点Q 以1.25cm/s 的速度沿BC 向终点C 移动.过点P 作PE ∥BC 交AD 于点E ,连接EQ ,设动点运动时间为x 秒.(1)用含x 的代数式表示AE 、DE 的长度;(2)当点Q 在BD (不包括点B 、D )上移动时,设△EDQ 的面积为y (cm 2),求y 与x 的函数关系式,并写出自变量x 的取值范围;(3)当x 为何值时,△EDQ 为直角三角形?5、如图,四边形OABC 是一张放在平面直角坐标系中的矩形纸片,点A 在x 轴上,点C 在Y 轴上,将边BC 折叠,使点B 落在边OA 的点D 处.已知折叠CE=55,且43 DA EA (1)判断OCD 与△ADE 是否相似?请说明理由;(2)求直线CE与x轴交点P的坐标;(3)是否存在过点D的直线L,使直线L、直线CE与x轴所围成的三角形和△CDE相似?如果存在,请直接写出其解析式并画出相应的直线;如果不存在,请说明理由.6、如图,已知直线l的函数表达式为483y x=-+,且l与x轴,y轴分别交于A B,两点,动点Q从B点开始在线段BA上以每秒2个单位长度的速度向点A移动,同时动点P从A点开始在线段AO上以每秒1个单位长度的速度向点O移动,设点Q P,移动的时间为t秒.(1)求出点A B,的坐标;(2)当t为何值时,APQ△与AOB△相似?(3)求出(2)中当APQ△与AOB△相似时,线段PQ所在直线的函数表达式.7、△ABC中,AB=AC=5,BC=6,点P从点B开始沿BC边以每秒1的速度向点C运动,点Q从点C开始沿CA边以每秒2的速度向点A运动,DE保持垂直平分PQ,且交PQ于点D,交BC于点E.点P,Q分别从B,C两点同时出发,当点Q运动到点A时,点Q、p停止运动,设它们运动的时间为x.1)当x=2秒时,射线DE经过点C;2)当点Q运动时,设四边形ABPQ的面积为y,求y与x的函数关系式;3)当点Q运动时,是否存在以P、Q、C为顶点的三角形与△PDE相似?若存在,求出x 的值;若不存在,请说明理由.8、等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P.(1)若AE=CF;①求证:AF=BE,并求∠APB的度数;②若AE=2,试求AP•AF的值;(2)若AF=BE,当点E从点A运动到点C时,试求点P经过的路径长.9、已知如图,▱ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线相交于G.(1)求证:AB=BH;(2)若GA=10,HE=2.求AB的值.10、已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P.(1)当点P在线段AB上时,求证:△AQP∽△ABC;(2)当△PQB为等腰三角形时,求AP的长.11、如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.(1)求证:△ADF∽△DEC;(2)若AB=8,AD=6,AF=4,求AE的长.12、如图,已知ED∥BC,∠EAB=∠BCF,(1)四边形ABCD为平行四边形;(2)求证:OB2=OE•OF;(3)连接OD,若∠OBC=∠ODC,求证:四边形ABCD为菱形.13、如图,菱形ABCD的边长为20cm,∠ABC=120°.动点P、Q同时从点A出发,其中P 以4cm/s的速度,沿A→B→C的路线向点C运动;Q以2cm/s的速度,沿A→C的路线向点C运动.当P、Q到达终点C时,整个运动随之结束,设运动时间为t秒.(1)在点P、Q运动过程中,请判断PQ与对角线AC的位置关系,并说明理由;(2)若点Q关于菱形ABCD的对角线交点O的对称点为M,过点P且垂直于AB的直线l交菱形ABCD的边AD(或CD)于点N.①当t为何值时,点P、M、N在一直线上?②当点P、M、N不在一直线上时,是否存在这样的t,使得△PMN是以PN为一直角边的直角三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.14、如图1,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C 以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).(1)直接用含t的代数式分别表示:QB=,PD=.(2)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q 的速度;(3)如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.15、如图△ABC中,AB=AC=10厘米,BC=12厘米,D是BC的中点,点P从B出发,以a厘米/秒(a>0)的速度沿BA匀速向点A运动,点Q同时以1厘米/秒的速度从D出发,沿DB匀速向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动,设它们运动的时间为t秒.(1)若a=2,△BPQ∽△BDA,求t的值;(2)设点M在AC上,四边形PQCM为平行四边形.①若a=,求PQ的长;②是否存在实数a,使得点P在∠ACB的平分线上?若存在,请求出a的值;若不存在,请说明理由.16、如图,∠C=90°,点A、B在∠C的两边上,CA=30,CB=20,连接AB.点P从点B出发,以每秒4个单位长度的速度沿BC的方向运动,到点C停止.当点P与B、C两点不重合时,作PD⊥BC交AB于点D,作DE⊥AC于点E.F为射线CB上一点,使得∠CEF=∠ABC.设点P运动的时间为x秒.(1)用含有x的代数式表示CE的长.(2)求点F与点B重合时x的值.(3)当点F在线段CB上时,设四边形DECP与四边形DEFB重叠部分图形的面积为y(平方单位).求y与x之间的函数关系式.17、已知:如图,矩形ABCD中,CH⊥BD于点H,P为AD上的一个动点(点P与点A、D不重合),CP与BD交于点E,若,DH:CD=5:13,设AP=x,四边形ABEP的面积为y.(1)求BD的长;(2)求y与x的函数关系式,并写出自变量x的取值范围;(3)当四边形ABEP的面积是△PED面积的5倍时,连接PB,判断△PAB与△PDC是否相似?如果相似,求出相似比;如果不相似,请说明理由.18、如图,在平面直角坐标系xOy中,直线AB与x轴交于点A,与y轴交于点B,且OA=3,AB=5.点P从点O出发沿OA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AO返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB﹣BO﹣OP 于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0).(1)求直线AB的解析式;(2)在点P从O向A运动的过程中,求△APQ的面积S与t之间的函数关系式(不必写出t的取值范围);(3)在点E从B向O运动的过程中,完成下面问题:①四边形QBED能否成为直角梯形?若能,请求出t的值;若不能,请说明理由;②当DE经过点O时,请你直接写出t的值.1、最困难的事就是认识自己。
北师大版九年级数学上册第四章测试题(附答案)

北师大版九年级数学上册第四章测试题(附答案)一、单选题(共12题;共24分)1.△ABC∽△A′B′C′,且∠A=68°,则∠A′=().A. 22°B. 44°C. 68°D. 80°2.对一个图形进行放缩时,下列说法中正确的是()A. 图形中线段的长度与角的大小都会改变B. 图形中线段的长度与角的大小都保持不变C. 图形中线段的长度保持不变、角的大小可以改变D. 图形中线段的长度可以改变、角的大小保持不变3.已知△ABC,以点A为位似中心,作出△ADE,使△ADE是△ABC放大2倍的图形,这样的图形可以作出()个A. 1个B. 2个C. 4个D. 无数个4.若,且3a-2b+c=3,则2a+4b-3c的值是()A. 14B. 42C. 7D.5.如图,AB是⊙O的直径,BC⊥AB,垂足为点B,连接CO并延长交⊙O于点D、E,连接AD并延长交BC 于点F.则下列结论正确的有()①∠CBD=∠CEB;② ;③点F是BC的中点;④若,则tanE= .A. ①②B. ③④C. ①②④D. ①②③6.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DF=50cm,EF=30cm,测得边DF离地面的高度AC=1.5m,CD=20m,则树高AB为()A. 12mB. 13.5mC. 15mD. 16.5m7.视力表对我们来说并不陌生.如图是视力表的一部分,其中开口向上的两个“E”之间的变换是()A. 平移B. 旋转C. 对称D. 位似8.如图,△ABC是⊙O的内接三角形,AD⊥BC于D点,且AC=5,CD=3,AB=4 ,则⊙O的直径等于()A. B. 3 C. 5 D. 79.如图,已知点是反比例函数在第一象限图像上的一个动点,连接,以为长,为宽作矩形,且点在第四象限,随着点的运动,点也随之运动,但点始终在反比例函数的图像上,则的值为()A. B. C. D.10.如图,正方形ABCD中,点E为对角线AC上一点,且AE CB,连接DE并延长交BC于点G,过点A 作AH⊥BE于点H,交BC于点F.以下结论:①BH HE;②∠BEG 45°;③△ABF ≌△DCG;④4BH2 BG·CD.其中正确结论的个数是( )A. 1个B. 2C. 3D. 411.如图,在矩形ABCD中,AD=AB.将矩形ABCD对折,得到折痕MN;沿着CM折叠,点D的对应点为E,ME与BC的交点为F;再沿着MP折叠,使得AM与EM重合,折痕为MP,此时点B的对应点为G.下列结论:①△CMP是直角三角形;②点C、E、G不在同一条直线上;③PC=MP;④BP=AB;⑤点F是△CMP外接圆的圆心.其中正确的个数为()A. 2个B. 3个C. 4个D. 5个12.如图,在边长为4的正方形ABCD中,E、F是AD边上的两个动点,且AE=FD,连接BE、CF、BD,CF 与BD交于点G,连接AG交BE于点H,连接DH,下列结论:①△ABG∽△FDG;②HD 平分∠EHG;③AG⊥BE;④S△HDG:S△HBG=tan∠DAG;⑤线段DH的最小值是.正确的个数有()A. 2个B. 3个C. 4个D. 5个二、填空题(共6题;共14分)13.两个相似多边形相似比为1:2,且它们的周长和为90,则这两个相似多边形的周长分别是________ ________ .14.如图,在▱ABCD中,AM= AD,BD与MC相交于点O,则S△MOD:S△COD=________.15.将一副三角板按图叠放,则△AOB与△DOC的面积之比等于________16.已知==≠0,则的值为 ________17.如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则等于________18.如图,直线l1∥l2∥l3,A,B,C分别为直线l1,l2,l3上的动点,连接AB,BC,AC,线段AC 交直线l2于点D.设直线l1,l2之间的距离为m,直线l2,l3之间的距离为n,若∠ABC=90°,BD=4,且则m+n的最大值为________.三、解答题(共3题;共24分)19.已知,如图,在平行四边形ABCD中,F为AD上一点,CF的延长线交BA延长线于点E.求证:.20.如图,在四边形ABCD中,AD∥BC,∠A=∠BDC.(1)求证:△ABD∽△DCB;(2)若AB=12,AD=8,CD=15,求DB的长.21.如图,AB是⊙O的直径,点C在⊙O上,CD与⊙O相切,BD∥AC.(1)图中∠OCD= °,理由是;(2)⊙O的半径为3,AC=4,求OD的长.四、作图题(共1题;共12分)22.如图(1)如图1,网格中每个小正方形的边长为1,点A,B均在格点上.则线段AB的长为________.请借助网格,仅用无刻度的直尺在AB上作出点P,使AP=.(2)⊙O为△ABC的外接圆,请仅用无刻度的直尺,依下列条件分别在图2,图3的圆中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法,请下结论注明你所画的弦).①如图2,AC=BC;②如图3,P为圆上一点,直线l⊥OP且l∥BC.五、综合题(共3题;共26分)23.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.(1)在图中找出一对相似三角形,并说明理由;(2)若AB=8,AD= ,AF= ,求AE的长.24.如图,双曲线经过的点顶,轴,OB交双曲线于点C,且(1)求k的值;(2)连接AC,求点C的坐标和的面积.25.(问题引入)如图(1),在中,,,过作则交延长线于点,则易得(直接应用)如图,已知等边的边长为,点, 分别在边, 上, , 为中点,为当上一动点,当在何处时,与相似,求的值.答案一、单选题1. C2. D3. B4. D5. C6. D7. D8. C9. A 10. D 11. B 12. C二、填空题13.30;60 14.2:3 15.1:3.16. 17.18.三、解答题19. 解:∵四边形ABCD为平行四边形,∴AB=CD,AD=BC,∠B=∠D,∵BE//CD,∴∠E=∠ECD,∴ΔDCF∽ΔBEC,∴,又∵AB=CD,AD=BC,∴20. (1)证明:∵AD∥BC,∴∠ADB=∠DBC.∵∠A=∠BDC,∴△ABD∽△DCB;(2)∵△ABD∽△DCB,AB=12,AD=8,CD=15,∴,即,解得DB=10,DB的长10.21. 解:(1)∵CD与⊙O相切,∴OC⊥CD,(圆的切线垂直于经过切点的半径)∴∠OCD=90°;故答案是:90,圆的切线垂直于经过切点的半径;(2)连接BC.∵BD∥AC,∴∠ACB=∠OCD=90°,∴在直角△ABC中,BC===2,∠A+∠ABC=90°,∵OC=OB,∴∠BCO=∠ABC,∴∠A+∠BCO=90°,又∵∠OCD=90°,即∠BCO+∠BCD=90°,∴∠BCD=∠A,又∵∠CBD=∠ACB,∴△ABC∽△CDB,∴=,∴=,解得:CD=3.由勾股定理可知,OD===3四、作图题22. (1)解:AB= 2 ,作图如图所示;所以,AP= 时AP:BP=2:1.点P如图所示.取格点M,N,连接MN交AB于P,则点P即为所求;(2)解:①如图1,CD即为所求;②如图2,CD即为所求.五、综合题23. (1)解:△ADF∽△DEC理由:∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,∴∠C+∠B=180°,∠ADF=∠DEC∵∠AFD+∠AFE=180°,∠AFE=∠B,∴∠AFD=∠C.在△ADF与△DEC中,,∴△ADF∽△DEC(2)解:∵四边形ABCD是平行四边形,∴CD=AB=8.由(1)知△ADF∽△DEC,∴,∴DE= .在Rt△ADE中,AE=24. (1)解:把代入得:,答:k的值为:6.(2)解:过点A、C、B分别作轴,轴,轴,垂足为F、D、E,,,,由∽得:,,把代入得:,,,,,.答:点C的坐标为,的面积为16.25. 解:设∵等边的边长为,,∵为中点,,① 和是对应边时, ,,即,整理得,解得,即的长为或;② 和是对应边时, ,,即,解得,即.综上所述,的值是或或.(拓展应用)已知在平行四边形中,,,,, ,求长.解:反向延长EF,与BA,BC的延长线相交于点N、M,∵四边形ABCD是平行四边形,∠A=60°,AB∥CD,∴∠D=120°,∴∠ANE=∠CMF=30°, ∠AEN=∠CFM=30°均为等腰三角形,∵AE=2,CF=3,易得,,将绕旋转到,,作,,又由旋转的性质得,BE=BG,∠ABE=∠GBC∵∠A=60°∴∠ABC=120°∵∠EBF=60°,∴∠ABE+∠CBF=60°,∴∠GBF=60°=∠EBF,又BF=BF ∴。
北师大版九年级上册数学第四章检测试题(附答案)

北师大版九年级上册数学第四章检测试题(附答案)一、单选题(共12题;共24分)1.在某次活动课中,甲、乙两个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:如图1,甲组测得一根直立于平地,长为80cm的竹竿的影长为60cm.如图2,乙组测得学校旗杆的影长为900cm.则旗杆的长为().A. 900cmB. 1000cmC. 1100cmD. 1200cm2.如图,已知△ABC∽△DEF,AB:DE=1:2,则下列等式一定成立的是()A. =B. =C. =D. =3.如图,在△ABC中,点D在边AB上,BD=2AD,DE∥BC交AC于点E,若线段DE=5,则线段BC的长为()A. 7.5B. 10C. 15D. 204.将两个长为a cm,宽为b cm的矩形铁片加工成一个长为c cm,宽为d cm的矩形铁片,有人就a,b,c,d的关系写出了如下四个等式,但是有一个写错了,它是( )A. B. C. D.5.应中共中央总书记胡锦涛的邀请,中国国民党主席连战先生、亲民党主席宋楚渝先生分别从台湾来大陆参观访问,先后来到西安,都参观了新建成的“大唐芙蓉园”,该园占地面积约为800000m2,若按比例尺1:2000缩小后,其面积大约相当于()A. 一个篮球场的面积;B. 一张乒乓球台台面的面积;C. 《重庆时报》的一个版面的面积;D. 数学课本封面的面积。
6.如图,AB是斜靠在墙上的一个梯子,梯脚B距墙1.4m,梯上点D距墙DE=1.2m,BD长0.5m,且△ADE∽△ABC ,则梯子的长为()A. 3.5mB. 3.85mC. 4mD. 4.2m7.下列叙述正确的是()A. 所有的矩形都相似B. 有一个锐角相等的直角三角形相似C. 边数相同的多边形一定相似D. 所有的等腰三角形相似8.如图,当小颖从路灯AB的底部A点走到C点时,发现自己在路灯B下的影子顶部落在正前方E处.若AC=4m,影子CE=2m,小颖身高为1.6m,则路灯AB的高为()A. 4.8米B. 4米C. 3.2米D. 2.4米9.如图,四边形ABCD∽四边形A1B1C1D1,AB=12,CD=15,A1B1=9,则边C1D1的长是()A. 10B. 12C.D.10.如图2,在□ABCD中,E是BC的中点,且∠AEC=∠DCE,则下列结论不正确的是()A. S△AFD=2S△EFBB. BF=DFC. 四边形AECD是等腰梯形D. ∠AEB=∠ADC11.一个三角形框架模型的三边长分别为20厘米、30厘米、40厘米,木工要以一根长为60厘米的木条为一边,做一个与模型三角形相似的三角形,那么另两条边的木条长度不符合条件的是()A. 30厘米、45厘米;B. 40厘米、80厘米;C. 80厘米、120厘米;D. 90厘米、120厘米12.如图,已知△ABC三个顶点的坐标分别为(1,2),(-2,3),(-1,0),把它们的横坐标和纵坐标都扩大到原来的2倍,得到点,,.下列说法正确的是()A. △与△ABC是位似图形,位似中心是点(1,0)B. △与△ABC是位似图形,位似中心是点(0,0) C. △与△ABC是相似图形,但不是位似图形 D. △与△ABC不是相似图形二、填空题(共6题;共12分)13.如图,AB∥DE,AE与BD相交于点C.若AC=4,BC=2,CD=1,则CE的长为________.14.如图,AB是⊙O的直径,AD是⊙O的切线,点C在⊙O上,BC∥OD,AB=2,OD=3,则BC的长为________.15.若两个相似多边形的周长的比是1:2,则它们的面积比为________16.如图,已知点A在反比例函数y= (x<0)上,作Rt△ABC,点D为斜边AC的中点,连DB并延长交y轴于点E.若△BCE的面积为8,则k=________.17.如图,线段AC与BD相交于点O,,若OA∶OC=4∶3,的面积是2,则的面积等于________.18.如图,点A(2,2 ),N(1,0), ∠AON=60°,点M为平面直角坐标系内一点,且MO=MA,则MN的最小值为________.三、解答题(共3题;共15分)19.如图,D为△ABC内一点,E为△ABC外一点,且∠1=∠2,∠3=∠4,找出图中的两对相似三角形并说明理由.20.“两个三角形相似,对应点连线经过同一点,那么这两个图形位似”是真命题吗?如果是,说出理由;如果不是,请举出反例.21.一条直线与三角形ABC的三边BC,CA,AB(或其延长线)分别交于D,E,F如图所示).求证:.四、作图题(共1题;共10分)22.如图,△ABC与△A´B´C´是位似图形,且相似比为.(1)在图中画出位似中心;(2)若,求的长.五、综合题(共4题;共59分)23.如图,在矩形ABCD中,AB=3,BC=4,将矩形ABCD绕点C按顺时针方向旋转α角,得到矩形A'B'C'D',B'C与AD交于点E,AD的延长线与A'D'交于点F.(1)如图①,当α=60°时,连接DD',求DD'和A'F的长;(2)如图②,当矩形A'B'CD'的顶点A'落在CD的延长线上时,求EF的长;(3)如图③,当AE=EF时,连接AC,CF,求AC•CF的值.24.小明利用灯光下自己的影子长度来测量路灯的高度.如图,CD和EF是两等高的路灯,相距27m,身高1.5m的小明(AB)站在两路灯之间(D、B、F共线),被两路灯同时照射留在地面的影长BQ=4m,BP=5m.(1)小明距离路灯多远?(2)求路灯高度.25.如图,已知Rt△ABC,∠C=90°,D为BC的中点,以AC为直径的⊙O交AB于点E.(1)求证:DE是⊙O的切线;(2)若AE:EB=1:2,BC=6,求AE的长.26.在等腰△ABC中,(1)如图1,若△ABC为等边三角形,D为线段BC中点,线段AD关于直线AB的对称线段为线段AE,连接DE,则∠BDE的度数为________;(2)若△ABC为等边三角形,点D为线段BC上一动点(不与B,C重合),连接AD并将线段AD绕点D逆时针旋转60°得到线段DE,连接BE.①根据题意在图2中补全图形;②小玉通过观察、验证,提出猜测:在点D运动的过程中,恒有CD=BE.经过与同学们的充分讨论,形成了几种证明的思路:思路1:要证明CD=BE,只需要连接AE,并证明△ADC≌△AEB;思路2:要证明CD=BE,只需要过点D作DF∥AB,交AC于F,证明△ADF≌△DEB;思路3:要证明CD=BE,只需要延长CB至点G,使得BG=CD,证明△ADC≌△DEG;…请参考以上思路,帮助小玉证明CD=BE.(只需要用一种方法证明即可)(3)小玉的发现启发了小明:如图3,若AB=AC=kBC,AD=kDE,且∠ADE=∠C,此时小明发现BE,BD,AC三者之间满足一定的数量关系,这个数量关系是________.(直接给出结论无须证明)答案一、单选题1. D2. D3. C4. B5. C6. A7. B8. A9. C 10. A 11.C 12. B二、填空题13. 2 14.15.1:4 16.16 17.18.三、解答题19. 解答:△ABD∽△CBE ,△ABC∽△DBE .∵∠1=∠2,∠3=∠4,∴△ABD∽△CBE ,∵∠1=∠2,∴∠ABC=∠DBE ,∴△ABC∽△DBE20.解:命题为真命题.因为两个三角形相似,对应点连线经过同一点,则利用相似三角形的性质可证明对应边平行或共线,所以那么这两个三角形位似.21.解:证明.证明:过B作BG∥EF,交AC于G.由平行线分线段成比例性质知= , = ,∴× × = × × =1四、作图题22. (1)解:如解图,连接,交于点,则点即为位似中心;(2)解:∵与是位似图形,且相似比为,,∴五、综合题23. (1)解:①如图①中,∵矩形ABCD绕点C按顺时针方向旋转α角,得到矩形A'B'C'D',∴A′D′=AD=B′C=BC=4,CD′=CD=A′B′=AB=3∠A′D′C=∠ADC=90°,∵α=60°,∴∠DCD′=60°,∴△CDD′是等边三角形,∴DD′=CD=3.②如图①中,连接CF.∵CD=CD′,CF=CF,∠CDF=∠CD′F=90°,∴△CDF≌△CD′F,∴∠DCF=∠D′CF= ∠DCD′=30°,在Rt△CD′F中,∵tan∠D′CF= ,∴D′F= ,∴A′F=A′D′﹣D′F=4﹣.(2)解:如图②中,在Rt△A′CD′中,∵∠D′=90°,∴A′C2=A′D′2+CD′2,∴A′C=5,A′D=2,∵∠DA′F=∠CA′D′,∠A′DF=∠D′=90°,∴△A′DF∽△A′D′C,∴= ,∴= ,∴DF= ,同理可得△CDE∽△CB′A′,∴= ,∴= ,∴ED= ,∴EF=ED+DF= .(3)解:如图③中,作FG⊥CB′于G.∵四边形A′B′CD′是矩形,∴GF=CD′=CD=3,∵S△CEF= •EF•DC= •CE•FG,∴CE=EF,∵AE=EF,∴AE=EF=CE,∴∠ACF=90°,∵∠ADC=∠ACF,∠CAD=∠FAC,∴△CAD∽△FAC,∴= ,∴AC2=AD•AF,∴AF= ,∵S△ACF= •AC•CF= •AF•CD,∴AC•CF=AF•CD= .24. (1)解:设DB=xm,∵AB∥CD ,∴∠QBA=∠QDC ,∠QAB=∠QCD ,∴△QAB∽△QCD∴同理可得∵CD=EF∴∴∴x=12即小明距离路灯12m(2)解:由得∴CD=6即路灯高6m 25. (1)证明:连接OE、EC,∵AC是⊙O的直径,∴∠AEC=∠BEC=90°,∵D为BC的中点,∴ED=DC=BD,∴∠1=∠2,∵OE=OC,∴∠3=∠4,∴∠1+∠3=∠2+∠4,即∠OED=∠ACB,∵∠ACB=90°,∴∠OED=90°,∴DE是⊙O的切线(2)解:由(1)知:∠BEC=90°,∵在Rt△BEC与Rt△BCA中,∠B=∠B,∠BEC=∠BCA,∴△BEC∽△BCA,∴= ,∴BC2=BE•BA,∵AE:EB=1:2,设AE=x,则BE=2x,BA=3x,∵BC=6,∴62=2x•3x,解得:x= ,即AE=26. (1)30°(2)①②思路1:如图2(a),连接AE,∵AD=DE,∠ADE=60°,∴△ADE是等边三角形,∵△ABC是等边三角形,∴AE=AD,AB=AC,∠EAD=∠BAD=60°,∴∠EAB=∠CAD,在△AEB△与ADC中,,∴△AEB≌△ADC,∴CD=BE;思路2:过点D作DF∥AB,交AC于F,∵△ABC是等边三角形,∴AC=BC,∠BAC=60°,∵DF∥AB,∴∠DFC=60°,∴△CDF是等边三角形,∴∠ADE=∠ACB=∠ABC=60°,∴∠DAF=∠EDB,在△ADF与△DEB中,,∴△ADF≌△DEB,∴DF=BE=CD;思路3:如图2(c),延长CB至G,使BG=CD,∵△ABC是等边三角形,∴AC=BC,∠BAC=60°,∵CD=BG,∴DG=AC,∴∠ADE=∠ACB=∠ABC=60°,∴∠DAF=∠EDB,在△ADC与△DEG中,,∴△ADC≌△DEG,∴CD=EG=BG=60°,∴BE=BG=CD;(3)k(BE+BD)=AC。
北师大版数学九年级上册第四章测试题及答案(共2套)

北师大版数学九年级上册第四章测试题(一)(图形的相似测试卷)一、选择题1.如图,A,B,C,D,E,G,H,M,N都是方格纸中的格点(即小正方形的顶点),要使△DEF与△ABC相似,则点F应是G,H,M,N四点中的()A.H或N B.G或H C.M或N D.G或M2.△ABC与△DEF的相似比为1:4,则△ABC与△DEF的周长比为()A.1:2 B.1:3 C.1:4 D.1:163.如图,在△ABC中,DE∥BC,若=,则=()A.B.C.D.4.在研究相似问题时,甲、乙同学的观点如下:甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.对于两人的观点,下列说法正确的是()A.两人都对B.两人都不对C.甲对,乙不对D.甲不对,乙对5.如图,△ABC中,P为AB上的一点,在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP•AB;④AB•CP=AP•CB,能满足△APC和△ACB相似的条件是()A.①②④B.①③④C.②③④D.①②③6.如图,在▱ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于()A.3:2 B.3:1 C.1:1 D.1:27.四边形ABCD与四边形A′B′C′D′位似,O为位似中心,若OA:OA′=1:3,则S四边形ABCD:S四边形A´B´C´D´=()A.1:9 B.1:3 C.1:4 D.1:58.小刚身高1.7m,测得他站立在阳光下的影长为0.85m,紧接着他把手臂竖直举起,测得影长为1.1m,那么小刚举起手臂超出头顶()A.0.5 m B.0.55 m C.0.6 m D.2.2 m9.如图,在△ABC中,DE∥BC,=,则下列结论中正确的是()A.= B.=C.= D.=10.如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,。
北师版九年级数学上册第四章达标测试卷含答案

北师版九年级数学上册第四章达标测试卷一、选择题(每题3分,共30分)1.下列四组图形中,不是相似图形的是( )2.【教材P 79随堂练习T 3改编】已知线段a ,b ,c ,d 是成比例线段,其中a=2 cm ,b =4 cm ,c =5 cm ,则d 等于( )A .1 cmB .10 cmC .52 cmD .85 cm 3.【教材P 119复习题T 3改编】如图,直线a ,b ,c 被直线l 1,l 2所截,交点分别为点A ,C ,E 和点B ,D ,F .已知a ∥b ∥c ,且AC =3,CE =4,则BDBF 的值是( )A .34B .43C .37D .474.【教材P 119复习题T 1(3)改编】若点C 是线段AB 的黄金分割点,AB =8 cm ,AC >BC ,则AC 的长为( )A .5-12 cm B .2(5-1)cm C .4(5-1)cm D .6(5-1)cm 5.在△ABC 和△DEF 中,AB =AC ,DE =DF ,根据下列条件,能判断△ABC和△DEF 相似的是( )A .AB DE =AC DF B .AB DE =BCEF C .∠A =∠E D .∠B =∠D 6.如图,为估算河的宽度(河两岸平行),在河对岸选定一个目标点A ,在近岸取点B ,C ,D ,使得AB ⊥BC ,CD ⊥BC ,点E 在BC 上,并且点A ,E ,D 在同一条直线上,若测得BE =20 m ,CE =10 m ,CD =20 m ,则河的宽度AB 等于( )A .60 mB .40 mC .30 mD .20 m7.【2021·兰州】如图,小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为5 m时,标准视力表中最大的“E”字高度为72.7 mm,当测试距离为3 m时,最大的“E”字高度为()A.4.36 mm B.29.08 mm C.43.62 mm D.121.17 mm8.【2020·云南】如图,平行四边形ABCD的对角线AC,BD相交于点O,E 是CD的中点,则△DEO与△BCD的面积的比等于()A.12B.14C.16D.189.【2020·河北】在如图所示的网格中,以点O为位似中心,四边形ABCD的位似图形是()A.四边形NPMQ B.四边形NPMRC.四边形NHMQ D.四边形NHMR10.【2020·牡丹江】如图,在矩形ABCD中,AB=3,BC=10,点E在BC 边上,DF⊥AE,垂足为F.若DF=6,则线段EF的长为()A.2 B.3 C.4 D.5二、填空题(每题3分,共24分)11.【教材P119复习题T1(2)改编】假期,爸爸带小明去A地旅游,小明想知道A地与他所居住的城市的距离,他在比例尺为1500 000的地图上测得所居住的城市距A地32 cm,则小明所居住的城市与A地的实际距离为________km.12.若a+bc=b+ca=c+ab=k(a+b+c≠0),则k=________.13.【2020·郴州】如图,在平面直角坐标系中,将△AOB以点O为位似中心,23为相似比作位似变换,得到△A1OB1,已知A(2,3),则点A1的坐标是__________.14.【2020·兰州】如图,四边形ABCD与四边形A′B′C′D′位似,位似中心为点O,OC=6,CC′=4,AB=3,则A′B′=________.15.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40 cm,EF=20 cm,测得边DF离地面的高度AC=1.5 m,CD=8 m,则树高AB=______m.16.【2021·南充】如图,在△ABC中,D为BC上一点,BC=3AB=3BD,则AD:AC的值为________.17.【2021·扬州】如图,在△ABC中,AC=BC,矩形DEFG的顶点D、E在AB上,点F,G分别在BC,AC上,若CF=4,BF=3,且DE=2EF,则EF的长为________.18.【2021·宿迁】如图,在△ABC中,AB=4,BC=5,点D,E分别在BC,AC上,CD=2BD,CE=2AE,BE交AD于点F,则△AFE面积的最大值是________.三、解答题(19,20,21,23题每题10分,其余每题13分,共66分) 19.(1)根据下列条件,判断△ABC与△A′B′C′是否相似,并说明理由.AB=4 cm,BC=6 cm,AC=8 cm.A′B′=12 cm,B′C′=18 cm,A′C′=21 cm.(2)若(1)中两三角形不相似,那么要使它们相似,不改变AC的长,A′C′的长应改为多少?20.如图,在▱ABCD中,AE:EB=2:3,DE交AC于点F.(1)求△AEF与△CDF的周长之比;(2)如果△CDF的面积为20 cm2,求△AEF的面积.21.如图,已知△ABC的三个顶点的坐标分别为A(0,-3),B(3,-2),C(2,-4).(正方形网格中每个小正方形的边长是1个单位长度)(1)画出△ABC向上平移6个单位长度后得到的△A1B1C1;(2)以点C为位似中心,在网格中画出△A2B2C,使△A2B2C与△ABC位似,且△A2B2C与△ABC的相似比为2:1,并直接写出点A2的坐标.22.【2020·苏州】如图,在矩形ABCD中,E是BC的中点,DF⊥AE,垂足为F.(1)求证:△ABE∽△DF A;(2)若AB=6,BC=4,求DF的长.23.如图,某水平地面上有一建筑物AB,在点D和点F处分别竖有2 m高的标杆CD和EF,两标杆相距52 m,并且建筑物AB,标杆CD和EF在同一竖直平面内,从标杆CD后退2 m到点G处,点G与建筑物顶端A 和标杆顶端C在同一条直线上;从标杆EF后退4 m到点H处,点H与建筑物顶端A和标杆顶端E在同一条直线上,求建筑物AB的高度.24.【2020·南京】如图,在△ABC和△A′B′C′中,D,D′分别是AB,A′B′上一点,ADAB=A′D′A′B′.(1)当CDC′D′=ACA′C′=ABA′B′时,求证:△ABC∽△A′B′C′.证明的途径可以用下面的框图表示,请填写其中的空格.(2)当CDC′D′=ACA′C′=BCB′C′时,判断△ABC与△A′B′C′是否相似,并说明理由.答案一、1.D 2.B 3.C 4.C 5.B 6.B 7.C 8.B 9.A10.B 点拨:易证△AFD ∽△EBA ,得AD EA =DFAB ,即10AE =63,则AE =5.由AD =10,DF =6,得AF =102-62=8. 故EF =AF -AE =8-5=3 .二、11.160 12.2 13.⎝ ⎛⎭⎪⎫43,2 14.5 15.5.5 16.33 17.12518.43 点拨:连接DE ,易证△CDE ∽△CBA ,得DE BA =CD CB =23,∠CED =∠CAB ,故DE ∥BA .易证△DFE ∽△AFB ,得DE AB =DF AF =23, 则S △AFE =35S △ADE .由CE =2AE ,得S △ADE =13S △ADC ,故S △AFE =15S △ADC . 由CD =2BD ,得S △ADC =23S △ABC ,故S △AFE =215S △ABC . 当AB ⊥BC 时,△ABC 面积最大,即△AFE 面积最大,计算得解.三、19.解:(1)△ABC 与△A ′B ′C ′不相似.理由如下:∵AB A ′B ′=412=13,BC B ′C ′=618=13,AC A ′C ′=821, ∴AB A ′B ′=BC B ′C ′≠AC A ′C ′. ∴△ABC 与△A ′B ′C ′不相似.(2)当A ′C ′=24 cm 时,两三角形相似.20.解:(1)∵四边形ABCD 是平行四边形,∴AB =CD ,AB ∥CD .∴∠EAF =∠DCF ,∠AEF =∠CDF . ∴△AEF ∽△CDF . ∵AE :EB =2:3,∴△AEF 的周长△CDF 的周长=AE CD =25.(2)∵△AEF∽△CDF,∴S△AEFS△CDF=⎝⎛⎭⎪⎫252=425.∵S△CDF=20 cm2,∴S△AEF=20×425=165(cm2).21.解:(1)如图,△A1B1C1就是所要画的三角形.(2)如图,△A2B2C就是所要画的三角形,点A2的坐标为(-2,-2).22.(1)证明:∵四边形ABCD是矩形,∴AD∥BC,∠B=90°.∴∠AEB=∠DAF.∵DF⊥AE,∴∠AFD=90°=∠B.∴△ABE∽△DFA.(2)解:∵E是BC的中点,BC=4,∴BE=2.∵AB=6,∠B=90°,∴AE=AB2+BE2=62+22=210.∵四边形ABCD是矩形,∴AD=BC=4.∵△ABE∽△DFA,∴ABDF=AEAD.∴DF=AB·ADAE=6×4210=6510.23.解:由题意得CD=DG=EF=2 m,DF=52 m,FH=4 m.∵AB⊥BH,CD⊥BH,EF⊥BH,∴∠ABH=∠CDG=∠EFH=90°.又∵∠CGD=∠AGB,∠EHF=∠AHB,∴△CDG∽△ABG,△EFH∽△ABH.∴CDAB=DGBG,EFAB=FHBH,即CDAB=DGDG+BD,EFAB=FHFH+DF+BD.∴2AB=22+BD,2AB=44+52+BD.∴22+BD=44+52+BD,解得BD=52 m.∴2AB=22+52,解得AB=54 m.答:建筑物AB的高度为54 m.24.解:(1)CDC′D′=ACA′C′=ADA′D′;∠A=∠A′(2)△ABC与△A′B′C′相似.理由如下:如图,过点D,D′分别作DE∥BC,D′E′∥B′C′,DE交AC于点E,D′E′交A′C′于点E′.∵DE∥BC,∴∠ADE=∠B,∠AED=∠ACB.∴△ADE∽△ABC.∴ADAB=DEBC=AEAC.同理,A′D′A′B′=D′E′B′C′=A′E′A′C′.∵ADAB=A′D′A′B′,∴DEBC=D′E′B′C′.∴DED′E′=BCB′C′.同理,AEAC=A′E′A′C′.∴AC-AEAC=A′C′-A′E′A′C′,即ECAC=E′C′A′C′.∴ECE′C′=ACA′C′.∵CDC′D′=ACA′C′=BCB′C′,∴CDC′D′=DED′E′=ECE′C′.∴△DCE∽△D′C′E′.∴∠CED=∠C′E′D′.∵DE∥BC,∴∠CED+∠ACB=180°.同理,∠C′E′D′+∠A′C′B′=180°.∴∠ACB=∠A′C′B′.AC A′C′=CBC′B′,∴△ABC∽△A′B′C′.又∵。
北师大版数学九年级上册第四章图形的相似单元综合练习含答案

北师大版数学九年级上册第四章图形的相似单元综合练习含答案1. 以下条件中,不能判定△ABC 与△A′B′C′相似的是( )A .∠A=45°,∠C=26°,∠A′=45°,∠B′=109°B .AB =2,AC =32,BC =2,A′B′=6,A′C′=9,B′C′=12 C .AB =1.5,AC =1514,∠A=36°,A′B′=2.1,A′C′=1.5,∠A′=36° D .AB =2,BC =1,∠C=90°,A′B′= 2,B′C′= 22,∠C′=90° 2. a b =52,那么以上等式中,不一定正确的选项是( ) A .2a =5b B.a 5=b 2 C .a +b =7 D.a +b b =723. 如图,在△ABC 中,点D 在边AB 上,BD =2AD ,DE ∥BC 交AC 于点E ,假定线段DE =5,那么线段BC 的长为( )A .7.5B .10C .15D .204. 如图,▱ABCD 中,G 是BC 延伸线上一点,AG 与BD 交于点E ,与DC 交于点F ,那么图中相似三角形共有( )A .3对B .4对C .5对D .6对5. 如图,△ABC 和△ADE 均为等边三角形,D 在BC 上,DE 与AC 相交于点F ,AB =9,BD =3,那么CF 等于( )A .1B .2C .3D .46. 如图,在△ABC 中,假设DE 与BC 不平行,那么以下条件中,不能判别△ADE ∽△ABC 的是( )A .∠ADE =∠CB .∠AED =∠B C.AD AB =DE BC D.AD AC =AE AB7. 小刚在打网球时,为使球恰恰能过网(网高为0.9 m),且落在对方区域离网5 m 的位置上,他击球的高度是2.25 m ,那么他应站在离网的( )A .15 m 处B .10 m 处C .8 m 处D .7.5 m 处8. 如图,D ,E 区分是△ABC 的边AB ,AC 上的一点,DE ∥BC ,AF ⊥BC 于点F ,交DE 于点G ,且AD ∶AB =5∶12,那么AG AF的值为( ) A.125 B.512 C.712 D.759. 两个相似三角形的相似比是1∶2,其中较小三角形的周长为6 cm ,那么较大的三角形的周长为( )A .3 cmB .6 cmC .9 cmD .12 cm10. 图中两个四边形是位似图形,它们的位似中心是( )A .点MB .点NC .点OD .点P11. 如图,在平面直角坐标系中,以原点O 为位似中心,将△ABO 扩展到原来的2倍,失掉△A′B′O.假定点A 的坐标是(1,2),那么点A′的坐标是( )A .(2,4)B .(-1,-2)C .(-2,-4)D .(-2,-1)12. 在比例尺为1∶2 000的地图上测得A ,B 两地间的图上距离为5 cm ,那么A ,B 两地间的实践距离为________m.13. 如图,直线AD ∥BE ∥CF ,BC =13AC ,DE =4,那么EF 的值是________. 14. 如图,在平行四边形ABCD 中,点E 是边BC 上的黄金联系点,且BE >CE ,AE 与BD 相交于点F ,那么BF ∶FD 的值为________.15. 如图,小明用长为3 m 的竹竿CD 做测量工具,测量学校旗杆AB 的高度,移动竹竿,使竹竿与旗杆的距离DB =12 m ,那么旗杆AB 的高为________m.16. △ABC ∽△DEF ,相似比为1∶2,且△ABC 的边AC 上的高为8,那么△DEF 的边DF 上的高为________.17. 如图,在△ABC 中,点D ,E 区分是AB ,AC 上的点,DE ∥BC ,且AD =AB ,△ADE 的周长为6 cm ,那么△ABC 的周长为________cm.18. 小华自制了一个简易的幻灯机,其任务状况如下图,幻灯片与屏幕平行,光源到幻灯片的距离是30 cm ,幻灯片到屏幕的距离是1.5 m ,幻灯片上小树的高度是10 cm ,那么屏幕上小树的高度是________cm.19. 如图,△OAB 与△OA ′B ′是相似比为1∶2的位似图形,点O 为位似中心,假定△OAB 内一点P (x ,y )与△OA ′B ′内一点P ′是一对对应点,那么点P ′的坐标是____________.20. x ∶y ∶z =2∶3∶4,求x +2y -z x -y +3z的值. 21. 如图,是小明设计用手电来测量古城墙高度的表示图,点P 处放一水平的平面镜,光线从点A 动身经平面镜反射后刚好射到古城墙CD 的顶端C 处,且测得AB =1.2 m ,BP =1.8 m ,PD =12 m ,求古城墙的高度CD.22. 如图,小明拿着一把厘米刻度尺,站在距电线杆约30 m 的中央,把手臂向前伸直,刻度尺竖直,刻度尺上18个刻度恰恰遮住电线杆,手臂长约60 cm ,小明能求出电线杆的高度吗?假定能,请你替小明写出求解进程.参考答案:1---11 BCCDB CDBDD C12. 10013. 214. 5-1215. 916. 1617. 1818. 6019. (-2x ,-2y)20. 解:设x =2k ,y =3k ,z =4k ,∴原式=2k +6k -4k 2k -3k +12k =4k 11k =411. 21. 解:由题意可得△PAB∽△PCD,∴PB PD =AB CD ,即1.812=1.2CD,解得CD =8,故古城墙的高度为8 m. 22. 解:可以求出电线杆的高度.过点A 作AN⊥EF 于N ,交BC 于M.∵BC∥EF,∴AM ⊥BC 于M ,∴△ABC ∽△AEF ,∴BC EF =AM AN,∵AM =0.6,AN =30,BC =0.18,∴EF =BC×AN AM =0.18×300.6=9 (m ).故电线杆的高度为9米.。
北师版九上数学教材习题课件-第四章复习题

19. 如图,在平面直角坐标系中,以原点为位似中心, 画出矩形OBCD的位似图形,要求它与矩形OBCD 的相似比为 1 . 你有几种方法? 2
解:作图略.(提示:将矩形OBCD
的横、纵坐标分别乘
1 2
或
1 2
,即可
得到所求作的2个位似图形)
20. 如图,AB和CD表示两根直立于地面的柱子,AD和BC 表示起固定作用的两根钢筋,AD与BC的交点为M. 已知 AB=10 m,CD=15 m,求点M离地面的高度MH. 解:由已知,AB⊥BD,MH⊥BD,CD⊥BD, ∴AB∥MH∥CD,∴∠A=∠MDC. 又∵∠AMB=∠DMC. ∴△ABM∽△DCM. ∴ BM AB 10 2. CM DC 15 3
8. 如图,AB与CD相交于点O,且AC∥BD. OA·OD=OC·OB 成立吗?为什么?
解:OA·OD=OC·OB成立. 理由如下:
∵AC∥BD,∴∠A=∠B,∠C=∠D.
∴△AOC∽△BOD.
OA ∴OB
=
OC OD
,即OA·OD=OC·OB.
9. 如图,在△ABC中,D,E分别是AB和AC上的点,且
23. 如图,△ABC的三边长分别a,b,c(a>b>c),
△A1B1C1的三边长分别为a1,b1,c1,
△ABC∽△A1B1C1,相似比为k(k>1).
(1)若c=a1,求证:a=kc; (1)证明:∵△ABC∽△A1B1C1,且相似比为k, ∴又∵aa1 c=ak,1,即∴aa==kkac1..
北师版
九(上)数学教材习题
第四章复习题
1. 判断正误:
(1)若线段a=5 cm,b=2 cm,则a∶b=5∶2; ( √)
(2)若A,B两地在地图上的距离为7 cm,地图的比
北师大版九年级数学上(新) 第四章检测题 (含答案)

初中数学试卷 金戈铁骑整理制作第四章检测题(时间:120分钟 满分:120分)一、选择题(每小题3分,共30分)1.下列说法正确的是( C )A .对应边都成比例的多边形相似B .对应角都相等的多边形相似C .边数相同的正多边形相似D .矩形都相似2.已知△ABC ∽△DEF ,相似比为3∶1,且△ABC 的周长为18,则△DEF 的周长为( C )A .2B .3C .6D .543.如图,已知BC ∥DE ,则下列说法不正确的是( C )A .两个三角形是位似图形B .点A 是两个三角形的位似中心C .AE ∶AD 是相似比 D .点B 与点E ,点C 与点D 是对应位似点4.如图,身高为1.6 m 的吴格霆想测量学校旗杆的高度,当她站在C 处时,她头顶端的影子正好与旗杆顶端的影子重合,并测得AC =2.0 m ,BC =8.0 m ,则旗杆的高度是( C )A .6.4 mB .7.0 mC .8.0 mD .9.0 m,第3题图),第4题图). ,第5题图),第6题图)5.如图,为估算某河的宽度,在河对岸选定一个目标点,在近岸取点B ,C ,D ,使得AB ⊥BC ,CD ⊥BC ,点E 在BC 上,并且点A ,E ,D 在同一条直线上.若测得BE =20 m ,CE =10 m ,CD =20 m ,则河的宽度AB 等于( B )A .60 mB .40 mC .30 mD .20 m6.“标准对数视力表”对我们来说并不陌生,如图是视力表的一部分,其中最上面较大的“E ”与下面四个较小“E ”中的哪一个是位似图形( B )A .左上B .左下C .右上D .右下7.如图,点A ,B ,C ,D 的坐标分别是(1,7),(1,1),(4,1),(6,1),以点C ,D ,E 为顶点的三角形与△ABC 相似,则点E 的坐标不可能是( B )A .(6,0)B .(6,3)C .(6,5)D .(4,2),第7题图) ,第8题图),第9题图) ,第10题图)8.如图,梯形ABCD 中,AD ∥BC ,∠B =∠ACD =90°,AB =2,DC =3,则△ABC 与△DCA 的面积比为( C )A .2∶3B .2∶5C .4∶9 D.2∶ 39.如图,在△ABC 中,∠A =36°,AB =AC ,AB 的垂直平分线OD 交AB 于点O ,交AC 于点D ,连接BD .下列结论错误的是( C )A .∠C =2∠AB .BD 平分∠ABCC .S △BCD =S △BOD D .点D 为线段AC 的黄金分割点10.如图,在直角梯形ABCD 中,AD ∥BC ,∠ABC =90°,AB =8,AD =3,BC =4,点P 为AB 边上一动点,若△P AD 与△PBC 是相似三角形,则满足条件的点P 的个数是( C )A .1个B .2个C .3个D .4个二、填空题(每小题3分,共18分)11.若x y =m n =45(y ≠n ),则x -m y -n=__45__. 12.如图是两个形状相同的红绿灯图案,则根据图中给出的部分数值,得到x 的值是__16__.13.如图,在△ABC 中,点P 是AC 上一点,连接BP .要使△ABP ∽△ACB ,则必须有∠ABP =__∠C __或∠APB =__∠ABC __或AB AP =__AC AB__.,第12题图) ,第13题图),第14题图) ,第15题图)14.如图,矩形ABCD 中,AB =2,BC =3,点E 是AD 的中点,CF ⊥BE 于点F ,则CF =__125__. 15.如图所示,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔50米有一根电线杆,小丽站在离南岸边15米的点P 处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为__22.5__米.16.劳技课上小敏拿出了一个腰长为8厘米,底边为6厘米的等腰三角形,她想用这个等腰三角形加工出一个边长比是1∶2的平行四边形,平行四边形的一个内角恰好是这个等腰三角形的底角,平行四边形的其他顶点均在三角形的边上,则这个平行四边形的较短的边长为__2.4_cm 或2411_cm __. 三、解答题(共72分) 17.(10分)如图,点D 是△ABC 的边AC 上的一点,连接BD ,已知∠ABD =∠C ,AB =6,AD =4,求线段CD 的长.解:在△ABD 和△ACB 中,∠ABD =∠C ,∠A =∠A ,∴△ABD ∽△ACB ,∴AB AC =AD AB ,∵AB =6,AD =4,∴AC =AB 2AD =364=9,则CD =AC -AD =9-4=518.(10分)一个钢筋三角架三边长分别是20厘米、50厘米、60厘米,现在再做一个与其相似的钢筋三角架,而只有长为30厘米和50厘米的两根钢筋,要求以其中一根为一边,从另一根上截下两段(允许有余料)作为两边,则不同的截法有多少种?写出你的设计方案,并说明理由.解:两种截法:①30厘米与60厘米的两根钢筋为对应边,把50厘米的钢筋按10厘米与25厘米两部分截,则有1020=2550=3060=12,从而两个三角形相似;②30厘米与50厘米长的两根钢筋为对应边,把50厘米分截出12厘米和36厘米两部分,则有2012=5030=6036=53,从而两三角形相似19.(10分)如图,在平面直角坐标系中,已知△ABC 三个顶点的坐标分别为A (-1,2),B (-3,4),C (-2,6).(1)画出△ABC 绕点A 顺时针旋转90°后得到的△A 1B 1C 1;(2)在网格内以原点O 为位似中心,画出将△A 1B 1C 1三条边放大为原来的2倍后的△A 2B 2C 2.解:20.(10分)如图,矩形ABCD 为台球桌面.AD =260 cm ,AB =130 cm.球目前在E 点位置,AE =60 cm.如果小丁瞄准了BC 边上的点F 将球打进去,经过反弹后,球刚好弹到D 点位置.(1)求证:△BEF ∽△CDF ;(2)求CF 的长.解:(1)证明:∵FG ⊥BC ,∠EFG =∠DFG ,∴∠BFE =∠CFD ,又∵∠B =∠C =90°,∴△BEF ∽△CDF(2)解:设CF =x ,则BF =260-x ,∵AB =130,AE =60,BE =70,由(1)得:△BEF∽△CDF ,∴BE CD =BF CF ,即70130=260-x x,∴x =169 cm ,即CF =169 cm21.(10分)已知,如图,△ABC 中,AD 是中线,且CD 2=BE ·BA .求证:ED ·AB =AD ·BD .证明:∵AD 是中线,∴BD =CD ,又CD 2=BE ·BA ,∴BD 2=BE ·BA ,即BE BD =BD AB,又∠B =∠B ,∴△BED ∽△BDA ,∴ED AD =BD AB,∴ED ·AB =AD ·BD22.(10分)如图,在平行四边形ABCD 中,过点A 作AE ⊥BC ,垂足为点E ,连接DE ,点F 为线段DE 上一点,且∠AFE =∠B .(1)求证:△ADF ∽△DEC ;(2)若AB =8,AD =63,AF =43,求AE 的长.解:(1)证明:∵四边形ABCD 是平行四边形,∴AB ∥CD ,AD ∥BC.∴∠C +∠B =180°,∠ADF =∠DEC.∵∠AFD +∠AFE =180°,∠AFE =∠B ,∴∠AFD =∠C.∴△ADF ∽△DEC (2)∵四边形ABCD 是平行四边形,∴CD =AB =8.由(1)知△ADF ∽△DEC ,∴AD DE =AF CD .∴DE =AD ·CD AF =63×843=12.在Rt △ADE 中,由勾股定理得AE =DE 2-AD 2=122-(63)2=623.(12分)将一副三角尺如图①摆放(在Rt △ABC 中,∠ACB =90°,∠B =60°;在Rt △DEF 中,∠EDF =90°,∠E =45°)点D 为AB 的中点,DE 交AC 于点P ,DF 经过点C .(1)求∠ADE 的度数;(2)如图②,将△DEF 绕点D 顺时针方向旋转角α(0°<α<60°),此时的等腰直角三角尺记为△DE ′F ′,DE ′交AC 于点M ,DF ′交BC 于点N ,试判断PM CN 的值是否随着α的变化而变化?如果不变,请求出PM CN的值;反之,请说明理由. 解:(1)由题意知:CD 是Rt △ABC 中斜边AB 上的中线,∴AD =BD =CD ,∵在△BCD 中,BD =CD 且∠B =60°,∴△BCD 是等边三角形,∴∠BCD =∠BDC =60°,∴∠ADE =180°-∠BDC -∠EDF =180°-60°-90°=30°(2)PM CN的值不会随着α的变化而变化,理由如下:∵△APD 的外角∠MPD =∠A +∠ADE =30°+30°=60°,∴∠MPD =∠BCD =60°,∵在△MPD 和△NCD 中,∠MPD=∠NCD =60°,∠PDM =∠CDN =α,∴△MPD ∽△NCD ,PM CN =PD CD ,又∵由(1)知AD=CD ,∴∠ACD =∠A =30°,即∠PCD =30°.在Rt △PCD 中,∠PCD =30°,∴PD CD =13=33,∴PM CN =PDCD =33。
北师版数学九年级上册第四章达标测试卷及答案

第四章达标测试卷一、选择题(每题3分,共30分)1.如图,已知l1∥l2∥l3,若AB=1,BC=2,DE=1.5,则EF的长为() A.1.5 B.2 C.2.5 D.32.下列说法正确的是()A.对应边都成比例的多边形相似B.对应角都相等的多边形相似C.边数相同的正多边形相似D.矩形都相似3.如图,在△ABC中,DE∥BC,ADDB=13,则DEBC等于()A.12 B.13 C.14 D.154.如图,四边形ABCD与四边形AEFG是位似图形,且AC∶AF=2∶3,则下列结论不正确的是()A.四边形ABCD与四边形AEFG是相似图形B.AD与AE的比是2∶3C.四边形ABCD与四边形AEFG的周长比是2∶3D.四边形ABCD与四边形AEFG的面积比是4∶95.已知△ABC如图所示,则下面4个三角形中与△ABC相似的是()6.如图,已知点C,D都是线段AB的黄金分割点,如果CD=4,那么AB的长度是()A.25-2 B.6-2 5 C.8+4 5 D.2+ 57.如图,在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD∶DB=3∶5,那么CF∶CB等于()A.5∶8 B.3∶8 C.3∶5 D.2∶58.如图,AB是斜靠在墙上的一个梯子,梯脚B距墙1.4 m,梯子上点D距墙1.2 m,BD长0.5 m,则梯子的长为()A.3.5 m B.3.85 m C.4 m D.4.2 m9.如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论:①DE BC=12;②S△DOES△COB=12;③ADAB=OEOB;④S△DOES△ADE=13.其中正确的个数是()A.1个B.2个C.3个D.4个10.如图,在△ABC中,AB=AC=18,BC=12,正方形DEFG的顶点E,F在△ABC内,顶点D,G分别在AB,AC上,AD=AG,DG=6,则点F到BC 的距离为()A.1 B.2 C.122-6 D.62-6二、填空题(每题3分,共24分)11.如图,线段AB BC=12,那么AC BC等于________.12.相邻两边长的比值是黄金比的矩形,叫做黄金矩形,从外形看,它最具美感.现在想要制作一张“黄金矩形”的贺年卡,如果较长的一条边长等于20 cm,那么与其相邻的一条边的长等于__________.13.若△ABC∽△A′B′C′,且对应中线之比为1∶2,则△ABC与△A′B′C′的面积之比为________.14.如图,在△ABC中,AB>AC,点D在AB上(点D与A,B不重合),若再增加一个条件就能使△ACD∽△ABC,则这个条件是________________(写出一个条件即可).15.如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3,4,x,那么x的值为________.16.如图,在平面直角坐标系中有两个点A(4,0),B(0,2),如果点C在x轴上(点C与点A不重合),当点C的坐标为__________________时,使得由点B,O,C组成的三角形与△AOB相似(不包括全等).17.为了测量校园水平地面上一棵树的高度,数学兴趣小组利用一组标杆、皮尺,设计了如图所示的测量方案.已知测量同学的眼睛A、标杆顶端F与树的顶端E在同一条直线上,此同学的眼睛距地面1.6 m,标杆长为3.3 m,且BC =1 m,CD=4 m,则ED=________.18.如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A落在矩形ABCD的边CD上,连接CE,则CE 的长是________.三、解答题(19,20题每题8分,21,22题每题9分,23,24题每题10分,25题12分,共66分)19.如图,已知∠ADC=∠BAC,BC=16 cm,AC=12 cm,求DC的长.20.如图,已知在▱ABCD中,AE∶EB=1∶2.(1)求△AEF与△CDF的周长之比;(2)如果S△AEF=6 cm2,求S△CDF的值.21.如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,6).(1)画出△ABC绕点A顺时针旋转90°后得到的△AB1C1;(2)在网格内以原点O为位似中心,画出将△AB1C1三条边放大为原来的2倍后的△A2B2C2.(3)△ABC与△A2B2C2的面积比为________.22.如图,在矩形ABCD中,E为BC上一点,DF⊥AE于F.(1)△ABE与△ADF相似吗?请说明理由.(2)若AB=6,AD=12,BE=8,求DF的长.23.如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶端A在同一直线上.已知DE=0.5 m,EF=0.25 m,目测点D到地面的距离DG=1.5 m,到旗杆的水平距离DC=20 m ,求旗杆的高度.24.如图,有一块面积等于1 200 cm2的三角形铁片ABC,已知底边与底边BC 上的高的和为100 cm(底边BC大于底边上的高),要把它加工成一块正方形铁片,使正方形的一边EF在边BC上,顶点D,G分别在边AB,AC上,求加工成的正方形铁片DEFG的边长.25.如图①,在等边三角形ABC中,线段AD为其内角平分线,过点D的直线B1C1⊥AC于点C1,交AB的延长线于点B1.(1)请你探究:ACAB=CDDB,AC1AB1=C1DDB1是否都成立?(2)请你继续探究:若△ABC为任意三角形,线段AD为其内角平分线,请问AC AB=CDDB仍然成立吗?并说明理由.(3)如图②,在Rt△ABC中,∠ACB=90°,AC=8,AB=403,E为AB上一点且AE=5,CE交其内角平分线AD于点F,试求DFAF的值.答案一、1.D 点拨:已知l 1∥l 2∥l 3,根据平行线分线段成比例,得EF DE =BCAB ,所以EF =3.2.C 3.C 4.B 5.A 6.C 7.A 8.A9.C 点拨:由中线BE ,CD 知,DE 为△ABC 的中位线,所以DE =12BC ,DE ∥BC ,所以DE BC =12,①正确;由DE ∥BC 易得△DOE ∽△COB ,则S △DOE S △COB =DEBC 2=14,②错误;由DE ∥BC 易得AD AB =DE BC ,DE BC =OE OB ,所以AD AB =OEOB ,③正确;由DE ∥BC 易知△ADE ∽△ABC ,则S △ADE S △ABC =DE BC 2=14,设△DOE 的边DE 上的高为h ,则△BOC 的边BC 上的高为2h ,△ABC 的边BC 上的高为6h ,则S △COBS △ABC =2h 6h =13,所以S △DOE S △ABC =112,所以S △DOE S △ADE =13,④正确.故选C.10.D 点拨:过点A 作AM ⊥BC 于点M ,交DG 于点N ,延长GF 交BC 于点H ,易证△ADG ∽△ABC ,∴∠ADG =∠B.∴DG ∥BC.∴AN ⊥DG .∵四边形DEFG 是正方形,∴FG ⊥DG .∴FH ⊥BC.∵AB =AC =18,BC =12,∴BM =12BC =6.由勾股定理可得AM =122.∴AN AM =DG BC ,即AN 122=612.∴AN =62.∴MN =AM -AN =62.∴FH =MN -GF =62-6. 二、11.32 12.(105-10) cm13.1∶414.∠ACD =∠ABC (答案不唯一)15.5或7 点拨:当6,8均为直角边时,x =5;当8为斜边时,x =7. 16.(-1,0)或(1,0) 17.10.1 m 18.3510三、19.解:∵∠ADC =∠BAC ,∠C =∠C , ∴△ADC ∽△BAC.∴ACBC=DCAC.∵BC=16 cm,AC=12 cm,∴DC=12×1216=9(cm).20.解:(1)∵四边形ABCD是平行四边形,∴AB=CD,DC∥AB.∴∠CAB=∠DCA,∠DEA=∠CDE.∴△AEF∽△CDF.∵AE∶EB=1∶2,∴AE∶AB=AE∶CD=1∶3.∴△AEF与△CDF的周长之比为1∶3.(2)∵△AEF∽△CDF,AE∶CD=1∶3,∴S△AEF∶S△CDF=1∶9.∵S△AEF=6 cm2,∴S△CDF=54 cm2.21.解:(1)如图,△AB1C1即为所求.(2)如图,△A2B2C2即为所求.(3)1∶422.解:(1)△ABE∽△DF A.理由如下:∵四边形ABCD是矩形,∴AD∥BC,∠B=90°.∴∠DAE=∠AEB.①又∵DF⊥AE,∴∠DF A=∠B=90°.②由①②知△DF A∽△ABE.(2)根据题意,得AE=10,由(1)可知DF AB=AD AE,∴DF=7.2.23.解:∵∠DEF=∠DCA,∠EDF=∠CDA,∴△DEF∽△DCA.∴DEDC=EFCA.∵DE=0.5 m,EF=0.25 m,DC=20 m,∴0.520=0.25CA.∴AC=10 m.又∵CB=DG=1.5 m,∴AB=AC+CB=10+1.5=11.5(m).答:旗杆的高度为11.5 m.24.解:作AM⊥BC于M,交DG于N,如图所示,由题易知AN⊥DG.设BC=a cm,BC边上的高为b cm,DG=DE=x cm,根据题意,得a+b=100,12ab=1 200,解得a=60,b=40,或a=40,b=60(不合题意,舍去),∴BC=60 cm,AM=40 cm.由题意知DG∥BC,∴∠ADG=∠B,∠AGD=∠C.∴△ADG∽△ABC.∴ANAM=DGBC,即40-x40=x60.解得x=24,即加工成的正方形铁片DEFG的边长为24 cm.25.解:(1)两个等式都成立.理由如下:∵△ABC为等边三角形,AD为角平分线,∴AD垂直平分BC,∠CAD=∠BAD=30°,AB=AC.∴DB=CD.∴ACAB=CDDB.∵B1C1⊥AC,∠C1AB1=60°,∴∠B1=30°.∴AB1=2AC1.∵∠DAB1=30°=∠B1,∴DA=DB1.又∵∠C1AD=30°,∠AC1D=90°,∴DA=2C1D.∴DB 1=2C 1 D.∴AC 1AB 1=C 1DDB 1.(2)结论仍然成立.理由如下:如图①,△ABC 为任意三角形,过B 点作BE ∥AC ,交AD 的延长线于点E ,∴∠E =∠CAD.又∵∠CAD =∠BAD ,∴∠E =∠BAD.∴BE =AB.由作图易证△EBD ∽△ACD ,∴AC EB =CDDB .又∵BE =AB ,∴对任意三角形,结论AC AB =CDDB 仍然成立.①②(第25题)(3)如图②,连接ED.∵AD 为△ABC 的内角平分线, ∴CD DB =AC AB =8403=35.∴BD BC =58.而BE AB =403-5403=58.∴BD BC =BE AB .又∵∠B =∠B ,∴△BDE ∽△BCA. ∴∠BDE =∠BCA.∴DE ∥AC. ∴∠FDE =∠CAF ,∠FED =∠ACF . ∴△DEF ∽△ACF . ∴DF AF =DE AC . 由(2)知AE =DE , ∴DF AF =DE AC =AE AC =58.。
九年级数学上册第4章精选《平行线分线段成比例》同步提升训练(北师大版)

《第二节 平行线分线段成比例》提升训练1.(教材P85习题T4变式)(上海中考)如图,在△ABC 中,点D ,E ,F 分别是边AB ,AC ,BC 上的点,DE ∥BC ,EF ∥AB ,且AD :DB =3:5,那么CF :CB 等于( )A .5:8B .3:8C .3:5D .2:52.(梧州中考)如图,AG :GD =4:1,BD :DC =2:3,则AE :EC 的值是( )A .3:2B .4:3C .6:5D .8:53.如图,直线1l ∥2l ∥3l ,AB =3,AD =2,DE =4,EF =7.5. 求BC ,BE 的长.4.如图,点F 是□ABCD 的边CD 上一点,连接BF 并延长交AD 的延长线于点E . 求证:DEDFAE DC .5.(南阳淅川县模拟)如图,在△ABC中,EF∥CD,DE∥BC.(1)求证:AF:FD=AD:DB;(2)若AB=15,AD:BD=2:1,求DF的长.链接河南中招6.(河南模拟)如图,在横格作业纸(横线等距)上一画条直线,与横格线交于A,B,C三点,则BC:AC等于( )A.2:3B.2:5C.3:4D.3:5微专题5作平行线转换线段的比【方法指导】求线段的比,通常利用平行线分线段成比例的基本事实及其推论得到比例线段,然后进行转化得到所求两条线段的比;遇到不能直接转化线段的比时,要联想到借助辅助线(作平行线)构造基本图形:A型与X型针对训练(郑州期中)如图,在△ABC中,AD是BC边上的中线,E在AC边上,且AE:EC=1:2,BE交AD于点P,则AP:PD等于( )A.1:1B.1:2C.2:3D.4:3【变式】如图,△ABC中,D在BC上,F是AD的中点,连接CF并延长交AB于点E,已知32CDBD=,则AEBE== .拔高题如图,△ABC中,AF:FD=1:3,BD=DC,求AE:EC的值.参考答案1.A2.D3.解:∵1l ∥2l ∥3l ,∴FB AB AD BE BC DE ==,即324BF BE BC ==.∴BC =6,BF =12BE . 又∵EF =BF +BE =7.5.∴12BE +BE =7.5. ∴BE =5. 4.证明:∵四边形ABCD 是平行四边形,∴CD ∥AB ,AD ∥BC . ∴DE EF AE EB =. 同理可得EF DF EB DC =.∴DE DF AE DC=. 5.解:(1)证明:∵EF ∥CD ,∴AF AE FD EC =. ∵DE ∥BC ,∴AD AE BD EC =. ∴AF AD FD BD=,即AF ∶FD =AD ∶DB . (2)103DF =6.C微专题 5针对训练 A变式 35拔高题解: 过点D 作DG ∥BE 交AC 于G ,则AF :FD =AE :EG =1:3,BD :CD =EG :CG = 1 :1,所以AE :EC =1:6.。
九年级数学上册第四章检测试题北师大版附答案

适用精选文件资料分享九年级数学上册第四章检测试题(北师大版附答案)第四章检测题 ( 时间:120 分钟满分:120分)一、选择题(每小题 3 分,共 30 分) 1.假如 mn=ab,那么以下比率式中错误的选项是====bn 2.( 贺州中考 ) 如图,在△ ABC中,点 D、E 分别为 AB、AC的中点,则△ ADE与四边形 BCED的面积比为 ( C ) A .1∶1 B.1∶2 C.1∶3 D.1∶4 3.如图,在△ ABC 中,∠ ACB=90°, CD⊥AB,DE⊥BC,那么与△ ABC 相似的三角形的个数有( D) A.1 个 B.2个 C.3 个D.4个 , 第 2题图),第 3 题图 ), 第 6 题图 ) 4.在中华经典美文阅读中,刘明同学发现自己的一本书的宽与长之比为黄金比.已知这本书的长为20cm,则它的宽约为 ( A ) A.12.36 cm B.13.6 cm C.32.36 cm D.7.64 cm 5.( 通辽中考 ) 某人要在报纸上刊登广告,一块 10cm×5cm的矩形版面要付广告费180 元,他要把该版面的边长都扩大为本来的 3 倍,在每平方厘米版面广告费同样的状况下,他对付广告费(C)A .540元 B .1080 元 C.1620 元 D.1800 元 6 .( 永州中考 ) 如图,在△ ABC 中,点 D是 AB边上的一点,若∠ ACD=∠ B, AD=1,AC=2,△ ADC 的面积为 1,则△ BCD的面积为 ( C ) A .1 B.2 C.3 D.4 7 .( 眉山中考 ) “今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获取,则井深为 ( B ) A.尺 B.57.5 尺 C.6.25 尺 D.56.5 尺 , 第 7 题图) , 第 8 题图) , 第 9 题图) , 第 10 题图) 8 .以以以下图,在矩形ABCD中,F 是 DC上一点, AE均分∠ BAF交 BC于点 E,且 DE⊥AF,垂足为点 M,BE=3,AE=26,则 MD的长是 ( C ) A.15 B.1510 C.1 D.1515 点拨:设 DM=a,证△ AEM≌△ AEB,△ ADM≌△ DEC,可得(a +3)2 =a2+(15)2 9 .如图,在△ ABC中, A、B两个极点在 x 轴的上方,点C的坐标是 ( -1,0) .以点 C为位似中心,在 x 轴的下方作△ ABC 的位似图形△ A′B′C,并把△ ABC的边长放大到本来的 2 倍.设点 B 的对应点 B′的横坐标是 a,则点 B的横坐标是 ( D ) A.- 12a B.- 12(a +1) C.-12(a -1) D.-12(a +3) 10.如图,在矩形 ABCD中,DE均分∠ ADC交 BC于点 E,点 F 是 CD边上一点 ( 不与点 D重合 ) .点P为 DE上一动点, PE<PD,将∠ DPF绕点 P 逆时针旋转 90°后,角的两边交射线 DA于 H,G两点,有以下结论:① DH= DE;② DP= DG;③DG+ DF= 2DP;④DP?DE=DH?DC,此中必定正确的选项是 ( D ) A.①②B.②③ C.①④ D.③④二、填空题 ( 每题 3 分,共 18 分) 11.若x∶y=1∶2,则 x-yx+y=__-13__.12 .若△ ABC∽△ A′B′C′,且 AB∶A′B′= 3∶4,△ ABC的周长为 12 cm,则△ A′B′C′的周长为 __16_cm__. 13.( 锦州中考 ) 如图, E 为?ABCD的边 AB延长线上的一点,且BE∶AB=2∶3,连接DE交BC于点F,则CF∶AD=__3∶5__., 第 13 题图), 第 14 题图), 第 15 题图),第 16 题图 ) 14.(阿坝州中考 ) 如图,在平面直角坐标系中,已知 A(1,0),D(3,0) ,△ABC与△ DEF位似,原点 O是位似中心.若 AB=1.5 ,则 DE=__4.5__ . 15 .如图,小明同学用自制的直角三角形纸板 DEF丈量树的高度 AB,他调整自己的地点,想法使斜边 DF保持水平,而且边 DE与点 B 在同向来线上,已知纸板的两条直角边 DE= 50 cm,EF=25 cm,测得边 DF离地面的高度 AC=1.6 m ,CD=10 m,则树高AB=__6.6__m. 16 .如图,在△ ABC中,分别以 AC,BC为边作等边△ACD和等边△ BCE.设△ ACD,△ BCE,△ ABC的面积分别是S1,S2,S3,现有以下结论:①S1∶S2=AC2∶BC2;②连接AE,BD,则△BCD≌△ ECA;③若 AC⊥BC,则 S1?S2=34S32.此中结论正确的序号是__①②③ __.三、解答题 ( 共 72 分) 17.(6 分) 如图,在△ ABC中,点D是边AB的四均分点,DE∥AC,DF∥BC,AC=8,BC=12,求四边形 DECF的周长.解:∵ DE∥AC,DF∥BC,∴四边形 DFCE是平行四边形,∴DE=FC,DF=EC,∵ DF∥BC,∴△ ADF∽△ ABC,∴ DFBC=AFAC=ADAB=14,∵ AC=8,BC=12,∴ AF=2,DF=3,∴ FC=AC-AF=8-2=6,∴ DE=FC=6,DF=EC=3,∴四边形 DECF的周长是DF+CF+CE+DE=3+6+3+6=18. 答:四边形 DECF的周长是 1818.(6 分)( 凉山州中考 ) 如图,在边长为 1 的正方形网格中建立平面直角坐标系,已知△ ABC三个极点分别为 A(-1,2) 、B(2,1) 、C(4,5). (1) 画出△ ABC关于 x 轴对称的△ A1B1C1; (2) 以原点 O为位似中心,在x 轴的上方画出△A2B2C2,使△A2B2C2与△ABC位似,且相似比为 2,并求出△ A2B2C2的面积.解:(1) 以以以下图,△A1B1C1就是所求三角形 (2) 以以以下图,△A2B2C2就是所求三角形.分别过点 A2、 C2作 y 轴的平行线,过点 B2 作 x 轴的平行线,交点分别为 E、F,∵ A(- 1,2) ,B(2 ,1) ,C(4 ,5) ,△A2B2C2与△ ABC位似,且相似比为 2,∴ A2(- 2,4) ,B2(4 ,2) ,C2(8,10) ,∴S△A2B2C2=8×10-12×6×2-12×4×8-12×6×10=2819.(6 分) 九年级 (1) 班课外活动小组利用标杆丈量学校旗杆的高度,以以以下图,已知标杆高度CD=3 m,标杆与旗杆的水平距离BD=15 m,人的眼睛与地面的高度 EF=1.6 m,人与标杆 CD的水平距离 DF=2 m,则旗杆 AB的高度.解:∵ CD⊥FB,∴ AB⊥FB,∴ CD∥AB,∴△ CGE∽△ AHE,∴ CGAH= EGEH,即: CD-EFAH=FDFD+BD,∴3-=22+15,∴ AH=11.9 ,∴AB=AH+HB=AH+EF=11.9 +=13.5(m)20.(7 分) 如图,在梯形 ABCD中, DC∥AB, AD=BC,E 是 DC延长线上的点,连接 AE,交 BC于点 F. (1) 求证:△ ABF∽△ ECF; (2) 假如AD=5 cm,AB=8 cm,CF=2 cm,求 CE的长. (1) 证明:∵ DC∥AB,∴∠ B=∠ ECF,∠ BAF=∠ E,∴△ ABF∽△ ECF(2) 解:∵ AD= BC,AD =5 cm,AB=8 cm,CF=2 cm,∴BF=3 cm. ∵由 (1) 知,△ABF∽△ ECF,∴BACE=BFCF,即 8CE=32. ∴CE= 163(cm) 21.(8 分) 如图,四边形 ABCD是矩形,E是 BD上的一点,∠BAE=∠B CE,∠AED=∠ CED,点 G是 BC、AE延长线的交点,AG与 CD订交于点 F. (1)求证:四边形 ABCD是正方形; (2) 当 AE=2EF时,判断 FG与 EF有何数目关系?并证明你的结论. (1) 证明:易证△ ABE≌△ CBE,∴AB=B C,∴四边形 ABCD是正方形 (2) 解:当 AE=2EF时, FG=3EF.证明以下:∵四边形 ABCD是正方形,∴ AB∥CD,AD∥BC,∴△ ABE∽△ FDE,△ ADE∽△ GBE. ∵AE= 2EF,∴ BE∶DE=AE∶EF=2.∴BG∶AD=BE∶DE= 2,即 BG=2AD. ∵ BC=AD,∴ CG=AD.易证△ADF∽△ GCF,∴ FG= AF,即 FG=AF=AE+EF=3EF22.(8 分)( 泰安中考 ) 如图,在四边形 ABCD中, AB=AC=AD,AC平分∠ BAD,点 P 是 AC延长线上一点,且 PD⊥AD. (1) 证明:∠ BDC=∠PDC; (2) 若AC与 BD订交于点 E,AB=1,CE∶CP=2∶3,求 AE 的长. (1) 证明:∵ AB=AD,AC均分∠ BAD,∴ AC⊥BD,∴∠ ACD+∠BDC=90°,∵AC=AD,∴∠ ACD=∠ADC,∴∠ ADC+∠ BDC=90°,∵PD⊥AD,∴∠ ADC+∠ PDC=90°,∴∠ BDC =∠ PDC (2) 解:过点 C作 CM⊥PD于点 M,∵∠ BDC=∠ PDC,∴ CE= CM,∵∠ CMP=∠ ADP=90°,∠ P=∠ P,∴△ CPM∽△ APD,∴ CMAD= PCPA,设 CM=CE=x,∵CE∶CP=2∶3,∴PC= 32x,∵AB= AD= AC=1,∴x1=32x32x+1,解得 x =13,故 AE=1-13=23 23 .(9 分) 晚餐后,小聪和小军在社区广场闲步,小聪问小军:“你有多高?”小军一时语塞.小聪思虑片晌,建议用广场照明灯下的影长及地砖长来丈量小军的身高.于是,两人在灯下沿直线 NQ挪动,如图,当小聪正好站在广场的 A 点( 距 N点 5 块地砖长 ) 时,其影长 AD恰好为 1 块地砖长;当小军正好站在广场的 B 点( 距 N点 9 块地砖长 ) 时,其影长 BF恰好为 2 块地砖长.已知广场所面由边长为 0.8 米的正方形地砖铺成,小聪的身高 AC为米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你依据以上信息,求出小军身高BE 的长. ( 结果精确到 0.01 米) 解:由题意得:∠ CAD=∠ MND=90°,∠CDA=∠ MDN,∴△ CAD∽△ MND,∴ CAMN= ADND,∴=1×(5+1)×0.8 ,∴MN=9.6 ,又∵∠EBF=∠MNF=90°,∠EFB=∠MFN,∴△ EFB∽△ MFN,∴ EBMN= BFNF,∴=2×0.8 ( 2+9)× 0.8 ,∴EB≈1.75 ,∴小军身高约为 1.75 米24.(10 分) 如图 (1) 是一种广场三联闲步机,其侧面表示图如图 (2) 所示,此中 AB=AC=120 cm,BC=80 cm,AD=30 cm,∠ DAC=90°. (1) 求点 A 到地面的距离; (2) 求点 D到地面的高度是多少?解:(1)过 A 作 AF⊥BC,垂足为 F,过点 D作 DH⊥AF,垂足为 H.∵AF⊥BC,垂足为 F,∴ BF=FC=12BC=40 cm.依据勾股定理,得 AF=AB2-BF2=1202-402=802(cm) (2) ∵∠ DHA=∠ DAC=∠ AFC=90°,∴∠ DAH +∠ FAC=90°,∠C+∠ FAC=90°,∴∠ DAH=∠ C,∴△DAH∽△ ACF,∴AHFC=ADAC,∴ AH40=30120,∴ AH=10 cm,∴ HF= (10 +802)cm.答: D到地面的高度为 (10 +802)cm25.(12 分) 从三角形 ( 不是等腰三角形 ) 一个极点引出一条射线与对边订交,极点与交点之间的线段把这个三角形切割成两个小三角形,假如分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的圆满切割线.(1) 如图 1,在△ABC中,CD为角均分线,∠A=40°,∠B=60°,求证:CD为△ABC的圆满切割线; (2) 在△ ABC中,∠ A=48°, CD是△ ABC的圆满分割线,且△ ACD为等腰三角形,求∠ ACB的度数. (3)如图 2,在△ ABC 中, AC=2,BC= 2,CD是△ ABC的圆满切割线,且△ ACD是以CD 为底边的等腰三角形,求圆满切割线 CD的长.解:(1) 如图 1 中,∵∠ A=40°,∠B=60°,∴∠ ACB=80°,∴△ ABC 不是等腰三角形,∵CD均分∠ ACB,∴∠ ACD=∠ BCD=12∠ACB=40°,∴∠ ACD=∠ A=40°,∴△ ACD为等腰三角形,∵∠ DCB=∠ A=40°,∠CBD=∠ ABC,∴△ BCD∽△ BAC,∴CD是△ ABC的圆满切割线 (2) ①当 AD=CD时,如图 3,∠ACD=∠ A=48°,∵△ BDC∽△ BCA,∴∠ BCD=∠ A=48°,∴∠ ACB=∠ ACD+∠ BCD=96° ②当 AD=AC时,如图4 中,∠ACD=∠ ADC=180°- 48°2=66°,∵△ BDC∽△ BCA,∴∠BCD =∠ A=48°,∴∠ ACB=∠ ACD+∠ BCD=114°;③当 AC=CD时,如图 5 中,∠ADC=∠ A=48°,∵△ BDC∽△ BCA,∴∠ BCD=∠ A=48°,∵∠ ADC>∠ BCD,矛盾,舍弃.∴∠ ACB=96°或 114° (3) 由已知AC=AD=2,∵△ BCD∽△ BAC,∴ BCBA= BDBC,设 BD=x,∴( 2)2=x(x +2) ,∵ x>0,∴ x= 3-1,∵△ BCD∽△ BAC,∴ CDAC=BDBC=3-1 2,∴ CD= 3-1 2×2= 6- 2。
2023年北师大版九年级上册数学第四章综合测试试卷及答案

( B)
A. 2
B.2
C.12
D.
3 3
-8-
第四章综合练习
8.在平面直角坐标系中,线段AB两个端点的坐标
分别为A(6,8),B(10,2),若以原点O为位似中心,
在第一象限内将线段AB缩短为原来的12后得到线段
CD,则点A的对应点C的坐标为( B )
A.(1,5)
B.(3,4)
C.(4,3)
D.(5,1)
OC于点G,则OGGC的值为
4 3
或
2 3
.
-15-
第四章综合练习
三、(本大题共2小题,每小题8分,满分16分) 15.已知△ABC与△DEF相似,相似比为1∶3.若 它们面积的和为40 cm2,求这两个三角形的面积. 解:△ABC的面积为4 cm2,△DEF的面积为36 cm2.
-16-
第四章综合练习
-6-
第四章综合练习
6.如图,在△ABC中,CD,BE分别是△ABC的
边AB,AC上的中线,则SS△△DBCEFF=( D )
A.25
B.12
C.13
D.14
-7-
第四章综合练习
7.已知△ABC的三边长分别为1, 3, 2,
△A'B'C'的两边长分别为 2, 6.
若△ABC∽△A'B'C',则△A'B'C'的第三边长为
=6,AC=9,A1B1=8,则线段B1C1的长为( C )
A.2
B.3
C.4
D.6
-3-
第四章综合练习
3.若点P是长度为10的线段上的黄金分割点,则
较短线段的长度为( B )
北师版九年级数学上册 第4章 图形的相似 综合测试卷(含答案)
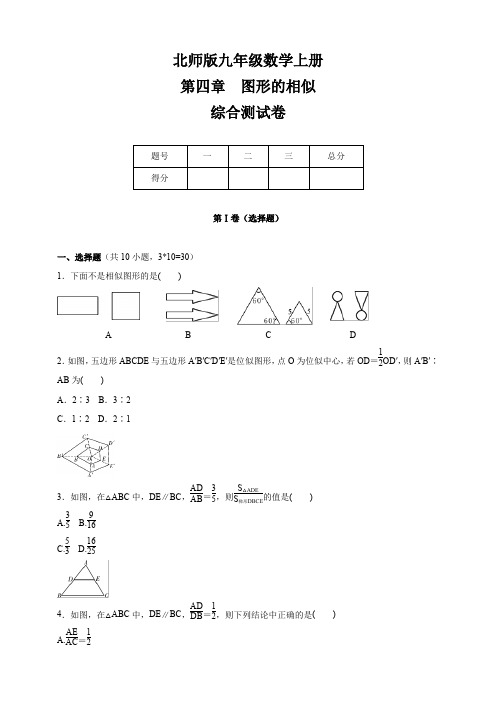
北师版九年级数学上册 第四章 图形的相似综合测试卷第Ⅰ卷(选择题)一、选择题(共10小题,3*10=30) 1.下面不是相似图形的是( )A B C D2.如图,五边形ABCDE 与五边形A′B′C′D′E′是位似图形,点O 为位似中心,若OD =12OD′,则A′B′∶AB 为( )A .2∶3B .3∶2C .1∶2D .2∶13.如图,在△ABC 中,DE ∥BC ,AD AB =35,则S △ADE S 梯形DBCE 的值是( ) A.35 B.916 C.53 D.16254.如图,在△ABC 中,DE ∥BC ,AD DB =12,则下列结论中正确的是( ) A.AE AC =12B.DE BC =12C.△ADE 的周长△ABC 的周长=13D.△ADE 的面积△ABC 的面积=135.点C 为线段AB 的黄金分割点,且AC>BC.下列说法中正确的有( ) ①AC =5-12AB ;②AC =3-52AB ;③AB ∶AC =AC ∶BC ;④AC≈0.618AB. A .1个 B .2个 C .3个 D .4个6.在平面直角坐标系中,点P(m ,n)是线段AB 上一点,以原点O 为位似中心把△AOB 放大到原来的两倍,则点P 的对应点的坐标为( ) A .(2m ,2n)B .(2m ,2n)或(-2m ,-2n)C .(12m ,12n)D .(12m ,12n)或(-12m ,-12n)7.如图,已知△ABC 和△ADE 均为等边三角形,D 在BC 上,DE 与AC 相交于点F ,AB =9,BD =3,则CF 等于( ) A .1 B .2 C .3 D .48.如图,在△ABC 中,D ,E 两点分别在边BC ,AD 上,且AD 为∠BAC 的平分线.若∠ABE =∠C ,AE ∶ED =2∶1,则△BDE 与△ABC 的面积比为( ) A .1∶6 B .1∶9 C .2∶13 D .2∶159.如图,点E ,F 分别在菱形ABCD 的边AB ,AD 上,且AE =DF ,BF 交DE 于点G ,延长BF 交CD 的延长线于点H ,若AF DF =2,则HFBG 的值为( ) A.23 B.712 C.12 D.51210.(2018·达州)如图,E ,F 是平行四边形ABCD 对角线AC 上两点,AE =CF =14AC.连接DE ,DF 并延长,分别交AB ,BC 于点G ,H ,连接GH ,则S △ADGS △BGH 的值为( ) A.12 B.23 C.34 D .1第Ⅱ卷(非选择题)二.填空题(共8小题,3*8=24)11.在△ABC 中,AB =12 cm ,BC =18 cm ,AC =24 cm ,另一个与它相似的△A′B′C′的周长为18 cm ,则△A′B′C′各边长分别为________cm ,________cm ,________cm. 12. 如图,已知AB ∥CD ,若AB CD =14,则OAOC=________.13.如图,在▱ABCD 中,E 为CD 上一点,连接AE ,BE ,BD ,且AE ,BD 交于点F ,已知S △DEF ∶S △ABF =4∶25,则DE ∶EC =________.14.如图,在平面直角坐标系中,已知A(1,0),D(3,0),△ABC 与△DEF 位似,原点O 是位似中心.若AB =1.5,则DE =________.15.如图,已知AB ⊥BD ,ED ⊥BD ,C 是线段BD 的中点,且AC ⊥CE ,ED =1,BD =4,那么AB =________.16.如图,阳光通过窗口AB 照到室内,在地面上留下一个亮区ED ,已知亮区一边到窗下的墙脚距离CE =2.7 m ,窗高AB =0.8 m ,窗口底边离地面的高度BC =1 m ,则亮区宽度ED =________.17.如图,梯形ABCD 中,AB ∥CD ,BE ∥AD ,且BE 交CD 于点E ,∠AEB =∠C.如果AB =3,CD =8,那么AD 的长是________.18.如图,在Rt △ABC 中,∠ABC =90°,AB =3,BC =4,在Rt △MPN 中,∠MPN =90°,点P 在AC 上,PM 交AB 于点E ,PN 交BC 于点F ,当PE =2PF 时,AP =________.三.解答题(共7小题, 46分)19.(6分) 如图,在△ABC 中,点D ,E 分别在边AB ,AC 上,∠AED =∠B ,射线AG 分别交线段DE ,BC 于点F ,G ,且AD AC =DF CG .(1)求证:△ADF ∽△ACG ;(2)若AD AC =12,求AFFG的值.20. (6分) 如图,点D是△ABC的边AC上的一点,连接BD,已知∠ABD=∠C,AB=6,AD=4,求线段CD的长.21. (6分) 如图,在△ABC中,AD是中线,且CD2=BE·BA.求证:ED·AB=AD·BD.22.(6分) ) 如图,在△ABC中,AB=AC,AD为BC边上的中线,DE⊥AB于点E.(1)求证:△BDE∽△CAD.(2)若AB=13,BC=10,求线段DE的长.23.(6分) 如图,在由边长为1个单位长度的小正方形组成的10×10网格中,已知点O,A,B均为网格线的交点.(1)在给定的网格中,以点O为位似中心,将线段AB放大为原来的2倍,得到线段A1B1(点A,B的对应点分别为A1,B1),画出线段A1B1;(2)将线段A1B1绕点B1逆时针旋转90°得到线段A2B1,画出线段A2B1;(3)以A,A1,B1,A2为顶点的四边形AA1B1A2的面积是20个平方单位.24.(8分) 如图,为测量山峰AB的高度,在相距50 m的D处和F处分别竖立高均为2 m的标杆DC 和FE,且AB,CD和EF在同一平面内,从标杆DC退后2 m到G处可以看到山峰A和标杆顶点C 在同一直线上,从标杆FE退后4 m到H处可以看到山峰A和标杆顶点E在同一直线上,求山峰AB 的高度及山峰与标杆CD之间的水平距离BD的长.25.(8分) 如图,在△ABC 中,点D 在边AB 上,点E 在线段CD 上,且∠ACD =∠B =∠BAE. (1)求证:AD BC =DEAC;(2)当点E 为CD 的中点时,求证:AE 2CE 2=ABCD.参考答案1-5 ADBCC 6-10 BBDBC 11. 4,6 ,8 12. 1413. 2∶3 14. 4.5 15. 4 16. 1.2m 17. 15 18. 319. 解:(1)证明:∵∠AED =∠B ,∠DAE =∠DAE ,∴∠ADF =∠C. 又∵AD AC =DFCG ,∴△ADF ∽△ACG(2)∵△ADF ∽△ACG ,∴AD AC =AFAG .又∵AD AC =12,∴AF AG =12,∴AF FG=120. 解:在△ABD 和△ACB 中,∠ABD =∠C ,∠A =∠A , ∴△ABD ∽△ACB ,∴AB AC =AD AB ,∵AB =6,AD =4,∴AC =AB 2AD =364=9,则CD =AC -AD =9-4=521. 证明:∵AD 是中线,∴BD =CD , 又CD 2=BE·BA ,∴BD 2=BE·BA , 即BE BD =BDAB, 又∠B =∠B ,∴△BED ∽△BDA , ∴ED AD =BDAB,∴ED·AB =AD·BD 22. 解:(1)∵AB =AC ,BD =CD ,∴AD ⊥BC ,∠B =∠C , ∵DE ⊥AB ,∴∠DEB =∠ADC ,∴△BDE ∽△CAD (2)∵AB =AC ,BD =CD ,∴AD ⊥BC , 在Rt △ADB 中,AD =AB 2-BD 2=12, ∵12AD·BD =12AB·DE ,∴DE =601323. 解:(1)如图所示,线段A 1B 1即为所求(2)如图所示,线段A 2B 1即为所求(3)由图可得,四边形AA 1B 1A 2为正方形,∴四边形AA 1B 1A 2的面积是(22+42)2=(20)2=20 24. 解:∵AB ⊥BH ,CD ⊥BH ,EF ⊥BH ,∴AB ∥CD ∥EF , ∴△CDG ∽△ABG ,△EFH ∽△ABH , ∴CD AB =DG DG +BD ,EF AB =FH FH +DF +BD. 又∵CD =DG =EF =2 m ,DF =50 m ,FH = 4 m , ∴2AB =22+BD ,2AB =450+4+BD , ∴22+BD =44+50+BD, 解得BD =50 m , ∴2AB =22+50, 解得AB =52 m25. 证明:(1)∵∠ACD =∠B =∠BAE ,∠BAC =∠BAE +∠CAE ,∠AED =∠ACD +∠CAE , ∴∠AED =△BAC.又∵∠DAE =∠B , ∴△AED ∽△BAC ,∴AD BC =DEAC(2)∵∠ADE =∠CDA ,∠DAE =∠ACD ,∴△DAE ∽△DCA ,∴AE AC =DEAD .又∵DE =EC ,∴AE CE =AC AD ,∴AE 2CE 2=AC 2AD 2.又∵∠DAC =∠BAC ,∠ACD =∠B , ∴△ACD ∽△ABC ,∴AC 2=AD·AB , ∴AE 2CE 2=AD·AB AD 2=ABAD。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 图形的相似
一、选择题
1、【基础题】在比例尺为1:5000的地图上,量得甲,乙两地的距离为25 c ,则甲、乙两地的实际距离是 ( )
A 1250千米
B 125千米 125千米 D 125千米
2、【基础题】已知135=
a
b ,则b
a b
a +-的值是( ) ★ A 32 B 23 49 D 9
4
3、【基础题】如右图,在△AB 中,看DE ∥B ,
1
2
AD BD ,DE =4 c ,则B 的长为 ( ) A .8 c B .12 c
.11 c D .10 c
4、【基础题】如右图,DE 是ΔAB 的中位线,则ΔADE 与ΔAB 的面积之比是( ) A .11 B .12 .13 D .14
5、【基础题】如下图,小正方形的边长均为1,则图中三角形(阴影部分)与△AB 相似的是( ) ★
★★
6、【基础题】下列结论不正确的是( ) ★ A 所有的矩形都相似 B 所有的正方形都相似 所有的等腰直角三角形都相似 D 所有的正八边形都相似
7、【基础题】下列说法中正确的是( ) ★
A 位似图形可以通过平移而相互得到
B 位似图形的对应边平行且相等 位似图形的位似中心不只有一个 D 位似中心到对应点的距离之比都相等 8、【综合题Ⅰ】如左下图,ABD 是正方形,E 是D 的中点,P 是B 边上的一点,下列条件中,
不能推出△ABP 与△EP 相似的是( ) ★★★
A. ∠APB =∠EP B ∠APE =90° P 是B 的中点 D BP ︰B =2︰3
9、【综合题Ⅱ】如右上图Rt △AB 中,AB ⊥A ,AB =3,A =4,P 是B 边上
一点,
作PE ⊥AB 于E ,PD ⊥A 于D ,设BP =,则PD+PE =( )
A
35
x + B 45
x -
72
D
212125
25
x x -
A
A B
C
D
E P
10、【综合题Ⅲ】如图,在
Rt ABC △内有
边长分别为a ,b ,c 的三个正方形.则a 、b 、c 满足的
关系式是( )
A b a c =+
B b ac =
222b a c =+ D 22b a c ==
二、填空题
11、【基础题】在同一时刻,高为15的标杆的影长为25,一古塔在地面上影长为50,那么古塔的高为 .
12、【基础题】两个相似三角形面积比是9∶25,其中一个三角形的周长为36c ,则另一个三角形的周长是 .
13、【综合题Ⅰ】如左下图,在△AB 中,AB =5,D 、E 分别是边A 和AB 上的点,且∠ADE =∠B ,DE =2,
那么AD ·B = ★★★
14、【基础题】如右上图,在△AB 和△DEF 中,G 、H 分别是边B 和EF 的中点,已知AB =2DE ,A =2DF ,
∠BA =∠EDF 那么AG :DH = ,△AB 与△DEF 的面积比是 ★★★
15、【基础题】把一个三角形改做成和它相似的三角形,如果面积缩小到原的2
1
倍,边长应缩小到原的____倍
16、【综合Ⅱ】如左下图在Rt△AB 中 ∠AB=90°D⊥AB 于D ,若AD =1,BD =4,则D = ★
17、【基础题】如右上图,一人拿着一支厘米小尺,站在距电线杆约30米的地方,把手臂向前伸直,小尺
竖直,
看到尺上12厘米的长度恰好遮住电线杆,已知手臂长约60厘米,则电线杆的高为 ★★★
18、【基础题】已知一本书的宽与长之比为黄金比,且这本书的长是20 c ,则它的宽为_____c (结果保留根号)
19、【综合Ⅲ】顶角为36°的等腰三角形称为黄金三角形,如图,在△AB
中,AB =A =1,∠A =36°,
BD 是三角形AB 的角平分线,那么AD = ★
20、【提高题】如图,点1234A A A A ,,,在射线OA 上,点123B B B ,,在射线OB 上,且
112233A B A B A B ∥∥,213243A B A B A B ∥∥.若212A B B △、323A B B △的面积分别为1、4,则图中三个
阴影三角形面积之和为 .
三、解答题
21、【基础题】如图,已知点E 是矩形ABD 的边D 上一点,BF ⊥AE 于点F ,求证△ABF ∽△EAD .
(第20题图)
O
B B
22、【综合Ⅰ】如图27-106所示,已知E 为ABD 的边D 延长线上的一点,连接BE 交A 于O ,交AD 于F .
求证BO 2
=OF ·OE .
23、如图,在平面直角坐标系中,已知OA=12 c ,OB=6 c ,点P 从O 点开始沿OA 边向点A 以1c/s 的速
度移动,点Q 从点B 开始沿BO 边向点O 以1c/s 的速度移动,如果P 、Q 同时出发,用t (单位:秒) 表示移动的时间(06t ≤≤),那么: (1)当t 为何值时, △POQ 与△AOB 相似?
(2)设△POQ 的面积为y ,求y 关于t 的函数解析式。
24、【综合Ⅱ】
一天,数学课外活动小组的同学们,带着皮尺去测量某河道因挖沙形成的“圆锥形坑”的深度,评估这些坑道对河道的影响,如图是同学们选择(确保测量过程中无安全隐患)的测量对象,测量方案如下:
①先测出沙坑坑沿的圆周长3454米;
②甲同学直立于沙坑坑沿的圆周所在的平面上,经过适当调整自己所处的位置,当他位于B时恰好他的视线经过沙坑坑沿圆周上一点A看到坑底S(甲同学的视线起点与点A、点S三点共线),经测量:AB=12米,B=16米
根据以上测量数据,求“圆锥形坑”的深度(圆锥的高),(π取314,结果精确到01米)
25、【综合Ⅱ】如图,在平面直角坐标系中,已知△AB
三个顶点的坐标分别为A(﹣1,2),
B(﹣3,4),(﹣2,6)
(1)画出△AB绕点A顺时针旋转90°后得到的△A1B11
(2)以原点O为位似中心,画出将△A1B11三条边放大为原的2倍后的△A2B22.
答案
一、选择题答案
1、【答案】 选D
2、【答案】 选D
3、【答案】 选B
4、【答案】 选D
5、【答案】 选B
6、【答案】 选A
7、【答案】 选D
8、【答案】 选
9、【答案】 选A 10、【答案】 选A 二、填空题答案
11、【答案】 30米 12、【答案】 60或
108
5
13、【答案】 AD ·B =AB ·DE =10 14、【答案】 2:1, 4:1 15、【答案】
2
2
倍 16、【答案】 2 17、【答案】 电线杆的高为6 米 18、【答案】 10(15-)
19、【答案】 AD =
2
1
5- 【提示】利用三角形相似的关系可以得到AC DC AD ⋅=2,设AD =x ,则D =1-x ,
可列方程x x -=
12,解得2
5
1±-=x ,∴AD =215-
20、【答案】 105 21、【答案】 略
22、【证明】在ABD 中,AB ∥E ,AD ∥B ,∴△AOF ∽△OB ,△AOB ∽△OE ,∴
AO OF OC OB =,AO OB
OC OE
=
, ∴
OF OB OB OE
=
,∴OB 2
=OF ·OE . 23、【答案】
(1)△POQ ∽△AOB 时①若
OQ OP OA OB =,即6612
t t
-=,122t t -=,∴4t =
②若OQ OP OB OA
=
,即6126t t -=,62t t -=,∴2t =∴当4t =或2t =时,△POQ 与△AOB 相似。
(2)∵OA=12OB=6由题意,得BQ=1·t=t ,OP=1·t=t ∴OQ=6-t
∴y=
21×OP ×OQ=21·t (6-t )=-2
1t 2
+3t (0≤t ≤6)
24、【答案】“圆锥形坑”的深度是73米 25、【答案】 如右图。
