五年级下册数学计算竞赛
人教数学五年级下册计算比赛(精品)

1、口算。
9×0.4=10×0.01=30.2-3.02= 4.3-0.25=1-0.82=9.6×0.3= 2.6÷0.01=20×25.4=4.8×0.4=5.4+4.62= 9-3.2= (1.5+2.4)×0.2= 3.6×0.6=9.5×0.1=7.2×0.8= 1.7+1.3×0.4= 5.4×0.6= 10×2.5=35×0.05= 8.5×0.5+0.6= 25分米50厘米=()米3角20分=()元2、解方程。
1.5x-10.8 =2.7 0.2x+2x=15.4 38.9-1.5a=5.44、简便计算。
36.54-1.76-4.54 0.85×199 2.5×2.5+4.6×2.5+2.5×2.9 1、口算。
12-3.8=8.1-0.05=0.64×0.4= 2.5×0.5= 0.24×0.3=0.2×0.5= 2.4×0.8= 0.1×0.01= 8.89+0.1= 2.5×3= 4×0.5= 4.4×(5×0.2)= 0.96×0.06= 7×1.3= 7×2.1= 13+0.7×0.7= 0.36×0.3= 0.35×0.7= 24×0.25= 4×1.7×0.25= 250平方米=( )公顷18分=( )小时15秒=( )分2、解方程。
0.5x+2x =27.5 1.5(3.2y+0.6)=10.5 1.2x+3.2×1.7=9.043、简便计算。
7.325-(5.325-1.7) 35×40.2 0.86×15.7-0.86×4.7-0.861、口算。
2019-2020学年人教版五年级下数学竞赛试卷及答案解析

参考答案与试题解析
一.计算题(共1小题,满分16分,每小题16分)
1.(16分)用递等式计算,能简算的要简算.
① +2 + +3
②(12.5×8﹣40)÷0.6
③3.4×2.77+0.23×3.4
④( + + )×72
⑤ + + +…+ +
⑥
【分析】①根据加法交换律和结合律进行简算;
A.108个B.110个C.119个D.128个
四.填空题(共4小题,满分20分,每小题5分)
6.(5分)在一个两位数的两个数字之间加上一个0,所得的新数是原数的9倍,原数是
7.(5分)图是由若干个棱长为1cm的小立方体搭成的,数一数它一共有个小立方体,从左面看可以看到个小正方形.
8.(5分)在信息时代,信息安全十分重要,往往需要对信息进行加密,若按照“叠3加1取个位”的方式逐位加密,明码“16”加密之后的密码为“49”,若某个四位明码按照上述加密方式,经过两次加密得到的密码是“2445”,则明码是
2019-2020学年人教版五年级下数学竞赛试卷
一.计算题(共1小题,满分16分,每小题16分)
1.(16分)用递等式计算,能简算的要简算.
① +2 + +3
②(12.5×8﹣40)÷0.6
③3.4×2.77+0.23×3.4
④( + + )×72
⑤ + + +…+ +
⑥
二.填空题(共2小题,满分10分,每小题5分)
2.(5分)如图所示,一个方格内每行、每列及对角线上的三个整数的和都相等,那么X=11.
五年级下册数学试题-2020年五年级数学竞赛模拟测试题(三)(解析版)全国通用

2020年五年级数学竞赛模拟测试题(三)1.计算:12 - 22 + 32 - 42 + ... - 20122 + 20132 =( )【分析】平方差公式原式 = 20132 - 20122 + ... + 52 - 42 + 32 - 22 +12 - 02= (2013 + 2012) ⨯ (2013 - 2012) + ... + (5 + 4) ⨯ (5 - 4) + (3 + 2) ⨯ (3 - 2) + (1 + 0) ⨯ (1 - 0)= 2013 + 2012 + ... + 5 + 4 + 3 + 2 +1 + 0= 20270912.可用三根管向容器中注入液体,采用第一根管注满容器的时间为10 小时。
采用第二根管和第三根管注满容器的时间分别为12 小时和15 小时。
由于压力降低,每根管的输入能力仅为原来的一半。
因此决定用三根管同时向容器中注入液体,问这时注满空容器需要( )小时。
【分析】工程问题。
设容器的总量为1,那么三根管子原来的工作效率分别为1,1和1;10 12 15压力减半之后一起开动,工效之和( 1+1+1) ÷ 2 =1,那么现在需要1÷1= 8 (小时)。
10 12 15 8 83.如右图,长方形ABCD 被其内部的一些直线划分成了若干块。
已知S△AMD =13 , S△BNC = 39 。
则图中阴影部分的面积是( )。
【分析】蝴蝶模型。
如图,连接 EF ,因为 AB / /CD ,所以 S∆A D M 所以阴影部分的面积是13 + 39 = 52 。
=S∆MEF, S∆NBC=S∆NEF;4.德国数学康托尔构造的这个图形叫分形,称做康托尔集.从长度为1 的线段开始,康托尔取走其中间三分之一而达到第一阶段;然后从每一个余下的三分之一线段中取走其中间三分之一而达到第二阶段。
无限量地重复这一过程,余下的无穷点集就称做康托尔集。
图中是康托尔集的最初几个阶段,当达到第六个阶段时,余下的所有线段的长度之和为()。
全国数学竞赛五年级试题精选B卷(1-11)

1.计算:3.14×67+8.2×31.4-90×0.3142.计算:12.65÷12.5÷0.83.计算:16.92÷[2.64×(5.6-2.1)+0.16]4.计算:(32×0.63×0.95)÷(1.6×21×1.9)5.用[a]表示不超过a的最大整数,{a}表示的a小数部分,即{a}=a—[a],定义一种运算“*”:a*b=(a+b)÷(b-1),求[4.1]+{2.6}*[3.5]的值。
6.数a的2倍加5,等于数b;数b的2倍加5,等于数c;数c的2倍加5,等于数d;数d的2倍加5,等于107.那么数a是几?7.如果计算符号*表示a*b = a-3b,则20*(6*2)的值是多少?8.算式(20122012+20132013)×20142014的得数的尾数是几?9.王乐乐每分钟吹一次肥皂泡,每次恰好吹出50个,肥皂泡吹出之后,经过一分钟有一半破了,经过两分钟还有110没有破,经过两分半钟肥皂泡全破了。
王乐乐在第30次吹出50个新的肥皂泡时,没有破的肥皂泡共有多少个?1.将1,2,3,···,n(n是自然数)排列成杨辉三角的形状(如图1所示),如果恰有100行则n是几?2.将分数513化成小数,求小数点后第1为到第1000位的所有数字的和。
3.在651后面添加一个三位数,得到的六位数能被595整除,求所添加的三位数。
4.在一个三位数中加上小数点,得到的小数与原来的三位数的和是201.3,求这个三位数。
5.有两位盲人,他们都各自买了三双黑袜和三双白袜,十二双袜子的布质、大小完全相同,而每双袜子都有一张商标纸连着,两位盲人不小心将12双袜子混在一起,他们怎样才能取回各自的黑袜和白袜呢?6有100个数排成一排:0,2,6,16,42,110,288,······,前两个数分别是0和2,从第二个数开始,每个数的3倍恰好是与他相邻的两个数之和,求最后一个数除以4的余数。
数学竞赛试卷五年级下册【含答案】

数学竞赛试卷五年级下册【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 下列哪个数是质数?A. 21B. 23C. 27D. 302. 一个等腰三角形的底边长为10厘米,腰长为12厘米,那么这个三角形的周长是多少厘米?A. 22厘米B. 32厘米C. 44厘米D. 52厘米3. 下列哪个数是偶数?A. 101B. 102C. 103D. 1044. 一个长方体的长、宽、高分别是8厘米、6厘米、4厘米,那么这个长方体的体积是多少立方厘米?A. 192立方厘米B. 200立方厘米C. 216立方厘米D. 224立方厘米5. 下列哪个分数是最简分数?A. 2/4B. 3/6C. 4/8D. 5/10二、判断题(每题1分,共5分)1. 0是最小的自然数。
()2. 任何两个奇数相加的和都是偶数。
()3. 任何两个偶数相加的和都是偶数。
()4. 一个正方形的周长等于它的面积。
()5. 1是任何非0自然数的因数。
()三、填空题(每题1分,共5分)1. 36的因数有:1、2、3、4、6、12、18、______。
2. 一个等边三角形的周长是18厘米,那么它的边长是______厘米。
3. 0.25小时等于______分钟。
4. 一个长方体的长是10厘米,宽是6厘米,高是4厘米,那么它的体积是______立方厘米。
5. 下列各数中,合数有:4、6、8、9、10、______。
四、简答题(每题2分,共10分)1. 请写出5个质数。
2. 请写出3个偶数。
3. 请写出3个奇数。
4. 请写出2个既是质数又是偶数的数。
5. 请写出2个既是奇数又是合数的数。
五、应用题(每题2分,共10分)1. 一个长方体的长是12厘米,宽是8厘米,高是6厘米,那么这个长方体的表面积是多少平方厘米?2. 一个等腰直角三角形的直角边长为10厘米,那么这个三角形的面积是多少平方厘米?3. 一个数加上它的2倍再加上它的3倍,结果是60,那么这个数是多少?4. 一个数的3倍减去它的2倍,结果是10,那么这个数是多少?5. 一个长方体的长、宽、高分别是10厘米、6厘米、4厘米,那么这个长方体的对角线长度是多少厘米?六、分析题(每题5分,共10分)1. 请分析一个长方体和一个正方体的相同点和不同点。
小学五年级下学期数学竞赛试题(含答案)

小学五年级下学期数学竞赛试题(含答案)一、拓展提优试题1.如果一个自然数的约数的个数是奇数,我们称这个自然数为“希望数”,那么,1000以内最大的“希望数”是.2.小松鼠储藏了一些松果过冬.小松鼠原计划每天吃6个松果,实际每天比原计划多吃2个,结果提前5天吃完了松果.小松鼠一共储藏了个松果.3.(8分)在长方形ABCD中,BE=5,EC=4,CF=4,FD=1,如图所示,那么△AEF的面积是;4.甲、乙两人进行射击比赛,约定每中一发得20分,脱靶一发扣12分,两人各打10分,共得208分,最后甲比乙多得64分,乙打中发.5.如图:平行四边形ABCD中,OE=EF=FD.平行四边形面积是240平方厘米,阴影部分的面积是平方厘米.6.(8分)有一种细胞,每隔1小时死亡2个细胞,余下的每个细胞分裂成2个.若经过5小时后细胞的个数记为164.最开始的时候有个细胞.7.如图中,A、B、C、D为正六边形四边的中点,六边形的面积是16,阴影部分的面积是.8.某数学竞赛有10道题,规定每答对一题得5分,答错或不答扣2分.A、B 两人各自答题,得分之和是58分,A比B多得14分,则A答对道题.9.如图,魔术师在一个转盘上的16个位置写下来了1﹣16共16个数,四名观众甲、乙、丙、丁参与魔术表演.魔术师闭上眼,然后甲从转盘中选一个数,乙、丙、丁按照顺时针方向依次选取下一个数,图示是一种可能的选取方式,魔术师睁开眼,说:“选到偶数的观众请举手.”,这时候,只有甲和丁举手,这时候魔术师就大喝一声:“我知道你们选的数了!”.你认为甲和丁选的数的乘积是.10.用一根34米长的绳子围成一个矩形,且矩形边长都是整数米,共有种不同的围法(边长相同的矩形算同一种围法).11.(8分)有一个特殊的计算器,当输入一个数后,计算器先将这个数乘以3,然后将其结果是数字逆序排列,接着再加2后显示最后的结果,小明输入了一个四位数后,显示结果是2015,那么小明输入的四位数是.12.(8分)小胖把这个月的工资都用来买了一支股票.第一天该股票价格上涨,第二天下跌,第三天上涨,第四天下跌,此时他的股票价值刚好5000元,那么小胖这个月的工资是元.13.如图是一个由26个相同的小正方体堆成的几何体,它的底层由5×4个小正方体构成,如果把它的外表面(包括底面)全部涂成红色,那么当这个几何体被拆开后,有3个面是红色的小正方体有块.14.同学们去春游,带水壶的有80人,带水果的有70人,两样都没带的有6人.若既带水壶又带水果的人数是所有参加春游人数的一半,则参加春游的同学共有人.15.某场考试共有7道题,每道题问的问题都只与这7道题的答案有关,且答案只能是1、2、3、4中的一个.已知题目如下:①有几道题的答案是4?②有几道题的答案不是2也不是3?③第⑤题和第⑥题的答案的平均数是多少?④第①题和第②题的答案的差是多少?⑤第①题和第⑦题的答案的和是多少?⑥第几题是第一个答案为2的?⑦有几种答案只是一道题的答案?那么,7道题的答案的总和是.【参考答案】一、拓展提优试题1.解:根据分析可得:1000以内最大的“希望数”就是1000以内最大的完全平方数,而已知1000以内最大的完全平方数是312=961,根据约数和定理可知,961的约数个数为:2+1=3(个),符合题意,答:1000以内的最大希望数是961.故答案为:961.2.解:(6+2)×[(5×6)÷2]=8×15,=120(个).答:小松鼠一共储藏了120个松果.故答案为:120.3.解:根据分析,AD=BE+EC=5+4=9,AB=1+4=5,S△EFC=×EC×FC=×4×4=8;S△ABE=×AB×BE=×5×5=12.5;S△ADF=×AD×DF=×9×1=4.5;S长方形ABCD=AB×AD=5×9=45,要求的△AEF的面积等于整体长方形的面积减去三个三角形的面积.S△AEF=S长方形ABCD﹣S△EFC﹣S△ABE﹣S△ADF=45﹣8﹣12.5﹣4.5=20.故答案是:20.4.解:假设全打中,乙得了:(208﹣64)÷2=72(分),乙脱靶:(20×10﹣72)÷(20+12),=128÷32,=4(发);打中:10﹣4=6(发);答:乙打中6发.故答案为:6.5.解:因为平行四边形ABCD中,AC和BD是对角线,把平行四边形ABCD 的面积平分4份,平行四边形面积是240平方厘米,所以S△DOC=240÷4=60(平方厘米),又因为△OCE、△ECF、△FCD和△DOC等高,OE=EF=FD,所以S△ECF=S△DOC=×60=20(平方厘米),所以阴影部分的面积是 20平方厘米.故答案为:20.6.解:第5小时开始时有:164÷2+2=84(个)第4小时开始时有:84÷2+2=44(个)第3小时开始时有:44÷2+2=24(个)第2小时开始时有:24÷2+2=14(个)第1小时开始时有:14÷2+2=9(个)答:最开始的时候有 9个细胞.故答案为:9.7.解:如图:连接正方形的一条对角线,延长DA,与最上边正六边形边的延长线交与一点,这样可得两个三角形①、②三角形①和三角形②是全等三角形,它们的面积相等,进而可得出阴影部分两侧的三角形可补到六边形的角上,这样就成了一个长方形,阴影部分的面积等于空白部分的面积,所以阴影部分的面积是正六边形面积的一半16÷2=8答:阴影部分的面积是8.故答案为:8.8.解:(58+14)÷2=72÷2=36(分)答错:(5×10﹣36)÷(2+5)=14÷7=2(道)答对:10﹣2=8道.故答案为:8.9.解:依题意可知:2个偶数中间间隔是2个奇数.发现只有数字10,11,9,12是符合条件的数字.乘积为10×12=120.故答案为:12010.解:设矩形的长为am,宽为bm,且a≥b,根据题意,a+b=17,由于a,b均为整数,因此(a,b)的取值有以下8种:(16,1),(15,2),(14,3),(13,4),(12,5),(11,6),(10,7),(9,8),故答案为8.11.解:依题意可知:经过了乘以3,再逆序排列,再加上2得到的数字是2015.那么要求原来的数字可以逆向思维求解.2015﹣2=2013,再逆序变成3102,再除以3得3102÷3=1034.故答案为:103412.解:5000÷(1﹣)÷(1+)÷(1﹣)÷(1+)=5000××××=5000(元)答:小胖这个月的工资是5000元.故答案为:5000.13.解:依题意可知:第一层的共有4个角满足条件.第二层的4个角是4面红色,去掉所有的角块其余的符合条件.分别是3+2+3+2=10(个);共10+4=14(个);故答案为:1414.解:设既带水壶又带水果的为x人,则参加春游的同学共有2x人,由题意可得:80+70﹣x+6=2x156﹣x=2x3x=156x=52则2x=2×52=104答:则参加春游的同学共有104人.故答案为:104.15.解:因为每道题的答案都是1、2、3、4的一个,所以①的答案不宜太大,不妨取1,此时②的答案其实就是7个答案中1和4的个数,显然只能取2、3、4中的一个,若取2,则意味着剩余的题目只能有一道题答案为1,这是④填1,⑦填2,⑤填3,⑥填2,而③无法填整数,与题意矛盾;所以②的答案取3,则剩余的题目答案为1和4各有1道,此时④填2,显然⑦只能填1,那么⑤填2,则4应该是⑥的答案,从而③填3,此时7道题的答案如表;它们的和是1+3+3+2+2+4+1=16.。
五年级下册数学竞赛题

一、仔细想,认真填(每空1分,共20分)1、===3628214( )÷12=( )(填小数)。
2、已知a 是非零自然数,且7a 是真分数,5a是假分数,那么a 的值可以是( )或( )。
3、426=-a 中,a 的值是( ),3÷a =( )。
4、数对(6,9)表示物体在第( )列,第( )行。
5、a =b+1(a 、b 是不为零的自然数),那么a 、b 的最大公因数是( ),最小公倍数是( )。
6、分母是8的最简真分数有( )个,它们的和是( )。
7、把5千克糖平均分给8个小朋友,每个小朋友分得5千克的( ),分得1千克的( )。
8、一个分数的分子与分母的和是56,约分后得31,原来这个分数是( )。
9、一根木头,锯成4段要付锯板费2.4元,如果锯成12段,要付( )元。
10、+⨯=72373 873⨯+= 二、小法官,我来当。
(每小题2分,共10分)1、b y x =-是方程。
( )2、3.14就是π。
( )3、一个数的倍数一定比它的因数大。
( )4、把一张饼分给4个小朋友,每人分得41。
( ) 三、对号入座,我来选。
(每小题2分,共16分)1、分母是7的真分数有( )个。
A. 6 B. 12C. 无数2、一个最简分数,分子与分母的和是12,这样的分数有( )个。
A. 1B. 2C. 3 3、如果a 是大于2的自然数,那么a a 1-( )是最简分数。
A. 一定B. 不一定C. 一定不 4、下面是方程的是( )。
A. 8917=-B. x -7>4C. 09=x 6、532⨯⨯=a ,52⨯=b ,那么a 、b 的最小公倍数是( )A. 15B. 30C. 607、a 与20的最小公倍数是60,那么a 应是( )A. 5B. 10C. 15四、认真计算,我最行。
(能简算的要简算)(每题4分,共20分)1、248.08.0÷=x2、749471095+++3、)6143(87-+ ( ) ( ) ( ) ( )4、)7492(98+-5、321161814121++++五、解决问题,我最棒!(共34分)1、刘老师买了2副羽毛球拍,付出80元钱,找回4元。
五年级下册数学试题-竞赛专题:第2讲-整除性(含答案)人教版

知识概述1.整除的概念:两个整数相除,余数为零(没有余数)我们就说被除数能被除数整除,即整数a 除以整数b(0b≠),除得的商正好是整数,我们就说a能被b整除(也可以说b能整除a),记为|b a,如15能被3整除,即为3|15。
2.整除的性质:(1)如果数a数b都能被数c整除,那么他们的和或差也能被c整除,即如果|c a,|c b,那么|()c a b±;(2)如果数a能被数b与数c的积整除,那么a也能被b或者c整除,即如果|bc a,那么|b a,|c a;(3)如果数a能被数b整除,也能被数c整除,且数b和数c互质,那么a一定能被b与c的乘积整除,即如果|b a,|c a,且(,)1b c=,那么|bc a。
(4)如果c能整除b,b能整除a,那么c能整除a。
即:如果|c b,|b a,那么|c a。
3.整除的特征:特征1:能被2整除的数为个位数字是0、2、4、6、8的整数。
“特征”包含两方面的意义:一方面,个位数字是偶数(包括0)的整数,必能被2整除,另一方面,能被2整除的数,其个位数字只能是偶数(包括0)。
(下同)特征2:能被5整除的数的个位是0或5。
特征3:能被3(或9)整除的数,各个数位数字之和能被3(或9)整除。
特征4:能被4(或25)整除的数其末两位数能被4(或25)整除。
特征5:能被8(或125)整除的数其末三位数能被8(或125)整除。
特征6:一个数奇数位上的数字和与偶数位上的数字和的差(大减小)能被11整除,这个数也能被11整除。
整除性请用数字9、7、2、5、1写出一个能被2整除的最大三位数。
【解析】这些数字组成的最大三位数是975,但是它不能被2整除,能被2整除的数末位数一定是“0、2、4、6、8”。
所以能被2整除的最大三位数为972。
在下面的数中,哪些能被2整除?哪些能被3整除?哪些能被5整除?234、79、775、885、378、864、63、75、26、40【解析】能被2整除的数有234、378、864、26、40;能被3整除的数有234、885、378、864、63、75;能被5整除的数有775、885、40。
苏教版五年级数学下学期应用题专项竞赛题
苏教版五年级数学下学期应用题专项竞赛题班级:__________ 姓名:__________1. 一辆汽车3.5小时行驶了266千米.照这样计算,要行驶1178千米,需要多少小时?2. 大桶油的质量是小桶油质量的1.5倍,若从大桶中取出2.5千克油放入小桶中,则大、小两桶油的质量相等。
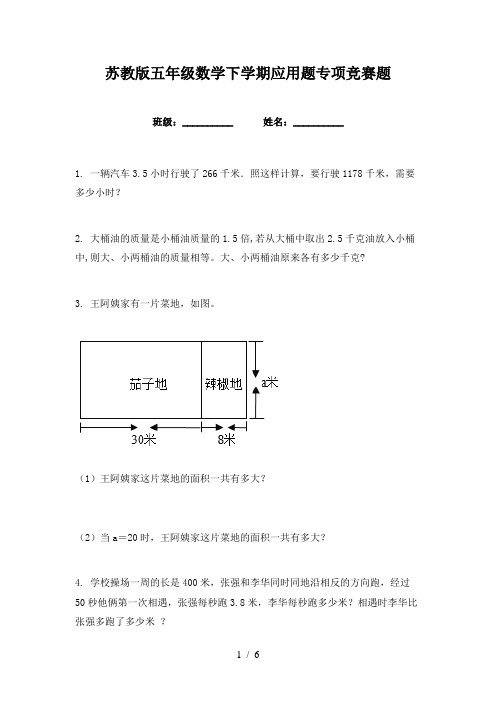
大、小两桶油原来各有多少千克?3. 王阿姨家有一片菜地,如图。
(1)王阿姨家这片菜地的面积一共有多大?(2)当a=20时,王阿姨家这片菜地的面积一共有多大?4. 学校操场一周的长是400米,张强和李华同时同地沿相反的方向跑,经过50秒他俩第一次相遇,张强每秒跑3.8米,李华每秒跑多少米?相遇时李华比张强多跑了多少米?5. 一辆快车和一辆慢车从相距660千米的两站同时相对开出,6小时后相遇。
已知慢车的速度比快车的多10千米,快车每小时行多少千米?(列方程解答)6. 粮店原有吨大米,卖吨后,又运进吨。
粮店现在有大米多少吨?7. 长方形中长a=16厘米,宽b=8厘米,根据公式s=ab,C=2(a+b)分别求长方形的周长和面积。
8. 甲、乙两地相距436km,一辆公汽和一辆货车从两地相向而行,货车每小时行42km,公汽每小时行46km。
货车开出2时后,公汽才出发,再经过几小时两车相遇?9. 挖一条长440m的水渠,甲、乙两队同时从两头开始挖,甲队每天挖24.5m,乙队每天挖30.5m。
经过多少天能完成挖渠任务?10. 北山小学书法教室的面积是a平方米,舞蹈教室的面积是书法教室的2.5倍。
(1)用式子表示舞蹈教室与书法教室的面积差。
(2)当a=50时,舞蹈教室比书法教室大多少平方米?11. 两个工程队共同修一条200千米的公路,各从一端相向施工,50天就完成了任务。
甲队平均每天修2.5千米,乙队平均每天修多少千米?(用方程解)12. A,B两地相距3500米,小红从A地骑自行车出发,每分钟行150米,2分钟后,兰兰从B地骑电动车出发,每分钟行350米,再经过几分钟两人相遇?13. 陈叔叔购置了一辆总价13.8万元的汽车,他采用分期付款的方式。
五年级数学竞赛初赛试题及答案 小学数学五年级下册 奥数试题及答案 人教版

五年级数学竞赛初赛试题及答案小学数学五年级下册奥数试题及答案人教版五年级数学竞赛初赛试题(满分120分)一、计算题(能用简便方法计算的,要用简便算法。
每题4分,共12分。
)2.77×13+255×999+510二、填空题(1~9题每空4分,10~12题每空3分,共54分。
)1.a=8.8+8.98+8.998+8.9998+8.99998,a的整数部分是____。
2.1995的约数共有____。
3.等式“学学×好好+数学=1994”,表示两个两位数的乘积,再加上一个两位数,所得的和是1994。
式中的“学、好、数”3个汉字各代表3个不同数字,其中“数”代表____。
4.如图1,“好、伙、伴、助、手、参、谋”这7个汉字代表1~7这7个数字。
已知3条直线上的3个数相加、2个圆圈上3个数相加所得的5个和都相等。
图中间的“好”代表____。
5.农民叔叔阿根想用20块长2米、宽1.2米的金属网建一个靠墙的长方形鸡窝(如图2)。
为了防止鸡飞出,所建鸡窝高度不得低于2米。
要使所建的鸡窝面积最大,BC的长应是米。
7.小胡和小涂计算甲、乙两个两位数的乘积,小胡看错了甲数的个位数字,计算结果为1274;小涂看错了甲数的十位数字,计算结果为819。
甲数是____。
8.1994年“世界杯”足球赛中,甲、乙、丙、丁4支队分在同一小组。
在小组赛中,这4支队中的每支队都要与另3支队比赛一场。
根据规定:每场比赛获胜的队可得3分;失败的队得0分;如果双方踢平,两队各得1分。
已知:(1)这4支队三场比赛的总得分为4个连续奇数;(2)乙队总得分排在第一;(3)丁队恰有两场同对方踢平,其中有一场是与丙队踢平的。
根据以上条件可以推断:总得分排在第四的是____队。
9.一块空地上堆放了216块砖(如图3),这个砖堆有两面靠墙。
现在把这个砖堆的表面涂满石灰,被涂上石灰的砖共有____块。
10.南方某城市的一家企业有90%的员工是股民,80%的员工是“万元户”,60%的员工是打工仔。
五年级下册数学试题-竞赛专题:第6讲-牛吃草问题(含答案)人教版

知识概述1.牛吃草问题类型:⎧⎧⎪⎨⎩⎪⎪⎧⎪⎨⎨⎩⎪⎪⎧⎪⎨⎪⎩⎩草增加简单牛吃草草减少牛的数量增加或减少牛吃草复杂牛吃草有多种动物的牛吃草抽水问题牛吃草变例入口问题牛吃草问题的难点在于草的总量有变化,因此要注意单位“1”的选取。
2.牛吃草问题解题步骤:第1步求出两个总量;第2步总量的差÷时间差=每天长草量=安排去吃新草的牛数;第3步每天长草量×天数=总共长出来的草;第4步草的总量-总共长出来的草=原有的草;第5步原有的草÷吃原有草的牛=能吃多少天。
牛吃草问题牛吃草问题是中环杯、小机灵杯等各大杯赛的常考点,这类问题的解题思路相对比较固定,常以牛吃草、检票、抽水机等题型出现。
只要我们掌握熟练牛吃草问题的解题思路,这类问题可轻松应对。
名师点题有一片牧场,草每天都在均匀地生长,如果在牧场上放养18头牛,那么10天能把草吃完;如果只放养24头牛,那么7天就把草吃完了。
请问:如果放养32头牛,多少天可以把草吃完?【解析】 设1头牛1天吃1份草。
18头牛10天吃的总草量:18×10=180; 24头牛7天吃的总草量:24×7=168;10-7=3天新长的草24*7=168(份)18*10=180(份)1天新生的草量:(180-168)÷(10-7)=4; 草地上原有草量:180-4×10=140;这片草地可供32头牛吃的天数:140÷(32-4)=5(天) 答:如果放养32头牛,5天可以把草吃完。
进入冬季后,有一片牧场上的草开始枯萎,因此草会均匀地减少。
现在开始在这片牧场上放牛,如果有38头牛,把草吃完需要25天;如果有30头牛,把草吃完需要30天。
如果有20头牛,这片牧场可以吃多少天?【解析】 设1头牛1天吃1份草。
38头牛25天吃的总草量:38×25=950; 30头牛30天吃的总草量:30×30=900; 1天减少的草量:(950-900)÷(30-25)=10; 草地上原有草量:900+10×30=1200;这片草地可供20头牛吃的天数:1200÷(20+10)=40(天) 答:如果有20头牛,这片牧场可以吃40天。
【竞赛题】人教版小学五年级下册数学第10讲《比例计算与列表分析》竞赛试题(含详解)

第十讲比例计算与列表分析比例是五年级的重要内容,之前我们已经学习过一些简单的比例问题,如按比例分配、化连比以及比例中的不变量.这一讲中,我们将继续比例的学习.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题1.学校组织体检,收费标准如下:老师每人3元,学生每人2元.已知老师和学生的人数比为2:9,共收得体检费3120元.那么老师、学生各有多少人?分析:老师、学生的人数比是多少?所有老师、所有学生支付的体检费之比又是多少?练习1.某高速公路收费站对于过往车辆每辆收费标准是:大客车10元,小客车6元.某日通过该收费站的大客车和小客车数量之比为5∶6,共收取过路费602元.求共有客车多少辆.例题2.徐福记的巧克力糖每6块包成一小袋,水果糖每15块包成一大袋.现有巧克力糖和水果糖各若干袋,而且巧克力糖比水果糖多30袋.如果巧克力糖的总块数与水果糖的总块数之比为7:10,那么它们各有多少块?分析:巧克力糖与水果糖比较,每袋的糖数之比是多少?题中还告诉我们,巧克力糖的总块数与水果糖的总块数之比为7:10,由此能求出两种糖的袋数之比吗?练习2.花店有玫瑰花和康乃馨,一束玫瑰花有9支,一束康乃馨有6支.已知玫瑰花比康乃馨少50束,且玫瑰花与康乃馨的总支数之比为3:7,问:花店共有多少支玫瑰花?- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -利用题目中的条件,我们可以将比例进行转化,比如例1中,题目告诉了我们人数比,然后我们要求出钱数之比;例2中,我们要通过块数比求出袋数的比.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题3.碧梨超市雇了一些卡车运输苹果、梨和香蕉,这三种水果的重量比是4:2:1.大型卡车专门运输苹果,中型卡车专门运输梨,小型卡车专门运输香蕉.这三种卡车的载重量之比是4:3:2.已知大型卡车比小型卡车多6辆,那么一共雇了多少辆卡车?分析:水果重量、卡车数量和卡车的载重量,这三个量之间有什么关系?练习3.三洋姥姥从超市买来了一些饮料有可乐、雪碧、冰红茶,三种饮料的瓶数比为4:5:9,大洋只喝可乐,二洋只喝雪碧,三洋只喝冰红茶,他们每人每天喝掉饮料的瓶数比是1:2:3,最终大洋比三洋晚10天就把自己的饮料喝完了,那么二洋的雪碧够他喝多少天?- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -当题目条件非常多的时候,列出表格来整理题中条件,能够使问题更为清晰明了,容易入手.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 例题4.某俱乐部男、女会员的人数之比是3:2,分为甲、乙、丙三组.已知甲、乙、丙三组的人数比是10:8:7,甲组中男、女会员的人数之比是3:1,乙组中男、女会员的人数之比是5:3.求丙组中男、女会员人数之比.分析:题中条件较多,不好处理,我们不妨设出其中一个量的“份数”来进行求解.设出哪个量的份数合适,以及设成多少份较好呢?我们所选取的数量最好是能与较多的其他数量关联在一起,同时所设出的份数最好能使得其余数量的份数也“比较整”,这样才最有助于我们的解题.Array练习4.有个工厂有三个分厂,全厂男、女职工人数的比是9:5,三个分厂人数比是8:9:11,第一分厂男、女职工人数比为3:1,第二分厂男、女职工人数比是5:4,第三分厂男职工比女职工多150人.这个厂共有职工多少人?例题5.有三个筐装有苹果和梨,已知苹果和梨的总数之比为4:3,第一个筐中苹果和梨个数比为6:5,第二个筐中苹果和梨个数比为3:5,且第一、第二、第三个筐的水果个数之比为11:16:9,求第三个筐中苹果和梨的个数比.分析:在填份数时,有时会出现除不尽的情况.这时只要适当扩倍就可以解决问题.例题6.某次数学竞赛设一、二、三等奖,已知:①甲、乙两校获一等奖人数比为1:2,且两校获奖总人数之比是5:4;②甲、乙两校获二等奖人数占两校获奖人数总和的14,其中乙校是甲校的3.5倍;③甲校三等奖获奖人数占该校获奖人数的45.请问:乙校获三等奖人数占该校获奖人数的几分之几?分析:本题中除了有比例的条件,还有分数的条件,倍数的条件.这些条件也都可以转化成比例的条件.比例尺地图上的比例尺,表示图上距离比实际距离缩小的程度,因此也叫缩尺.用公式表示为:/ 比例尺图上距离实际距离.比例尺通常有三种表示方法. (1)数字式,用数字的比例式或分数式表示比例尺的大小.例如地图上1厘米代表实地距离500千米,可写成:1:50000000,,或写成:五千万分之一.(2)线段式,在地图上画一条线段,并注明地图上1厘米所代表的实际距离.(3)文字式,在地图上用文字直接写出地图上1厘米代表实地距离多少千米,例如图上1厘米相当于地面距离10千米.三种表示方法可以互换. 根据地图上的比例尺,可以量算图上两地之间的实地距离;根据两地的实际距离和比例尺,可计算两地的图上距离;根据两地的图上距离和实际距离,可以计算比例尺.根据地图的用途,所表示地区范围的大小、图幅的大小和表示内容的详略等不同情况,制图选用的比例尺有大有小.地图比例尺中的分子通常为1,分母越大,比例尺就越小.通常比例尺大于二十万分之一的地图称为大比例尺地图;比例尺介于二十万分之一至一百万分之一之间的地图,称为中比例尺地图;比例尺小于一百万分之一的地图,称为小比例尺地图.在同样图幅上,比例尺越大,地图所表示的范围越小,图内表示的内容越详细,精度越高;比例尺越小,地图上所表示的范围越大,反映的内容越简略,精确度越低.1:2000000 1:4000001:100000 1:30000作业1. A 、B 两种商品的价格比是7:3.如果它们的价格分别上涨70元,它们的价格比就变成7:4.B 商品原来的价格是多少? 作业2. 某商店有桔子、苹果和梨出售.一斤桔子卖5元,一斤苹果卖4元,一斤梨卖3元,卡莉娅买了10斤水果,其中桔子和苹果的重量之比为5:9,苹果和梨的重量之比为3:2,那么她一共花了多少钱? 作业3. 某班同学去野外军训,他们在一起吃午餐,男生每人要吃3个馒头,女生每人要吃2个馒头,已知男生比女生多3人,且男生、女生吃的馒头总数之比为7:4,那么男生和女生各有多少人? 作业4. 碧丽小学的五年级有2个班,其中1班的男生和女生的人数比是2:3.全部五年级的学生中,男生和女生的人数比是3:4.又知道1班与2班的人数比是10:11,且1班的男生比2班的女生少10个.那么五年级一共有多少学生?作业5. 有两包糖,每包糖内都装有奶糖、水果糖和巧克力糖.已知:(1)第一包比第二包的奶糖少,且第一包与第二包糖的总数之比是1:2;(2)第一包和第二包中的水果糖总数占全部糖果总数的40%,其中第一包比第二包少; (3)第一包糖中巧克力糖与其它两种糖的总数之比为2:1. 那么,第一包与第二包的巧克力糖之比是多少?俗话说,兴趣是最好的老师。
五年级下册数学竞赛试题-第7讲 约数与倍数全国通用

第7讲约数与倍数内容概述掌握约数与倍数酌概念.学会约数个数与约数和的计算方法;掌握最大公约数、最小公倍数的常用计算方法;能够利用最大公约数和最小公倍数的性质解决相关的整数问题.典型问题兴趣篇1.(1)请写出105的所有约数;(2)请写出72的所有约数.2.(1) 20000的约数有多少个?(2) 720的约数有多少个?3.计算:(1) (28,72), [28,72]; (2) (28,44,260), [28, 44, 260].4.两个数的差是6,它们的最大公约数可能是多少?5.(1)求1085和1178的最大公约数和最小公倍数;(2)求3553,3910和1411的最大公约数.6.教师节到了,校工会买了320个苹果、240个桔子、200个香蕉来慰问退休老职工.请问:用这些水果最多可以分成多少份同样的礼物?在每份礼物中,苹果、桔子、香蕉各有多少个?7.一块长方形草地,长120米,宽90米,现在在它的四周种树,要求四个角和各边中点都要求种树,且相邻两棵树之间的距离都相等,请问:最少要种多少棵树?8.甲数和乙数的最大公约数是6,最小公倍数是90.如果甲数是18,那么乙数是多少?9.有甲、乙两个数,它们的最小公倍数是甲数的27倍.已知甲数是2、4、6、8、10、12、14、16的倍数,但不是18的倍数;乙数是两位数.乙数是多少?10.小悦、冬冬、阿奇在黑板上各写了一个自然数,这三个自然数的最大公约数是35,最小公倍数是70.这三个数的和可能是多少?拓展篇1.72共有多少个约数?其中有多少个约数是3的倍数?2.5400共有多少个约数?并求出所有约数乘积的质因数分解形式.3.两数乘积为2800,已知其中一个数的约数个数比另一个数的约数个数多1.这两个数分别是多少?4.计算:(1) (391, 357), [391, 357]; (2) (18, 24, 36), [18, 24, 36].5.1547、1573、1859这三个数的最大公约数是多少?最小公倍数是多少?6.张阿姨把225个苹果、350个梨和150个桔子平均分给小朋友们,最后剩下9个苹果、26个梨和6个桔子没分出去,请问:每个小朋友分了多少个苹果?7.一个数和16的最大公约数是8,最小公倍数是80.这个数是多少?8.两个自然数不成倍数关系,它们的最大公约数是18,最小公倍数是216.这两个数分别是多少?9.两个数的最大公约数是6,最小公倍数是420,如果这两个数相差18,那么较小的数是多少?10.有4个不同的正整数,它们的和是1111.请问:它们的最大公约数最大能是多少?11.甲、乙两个数的最小公倍数是90,乙、丙两个数的最小公倍数是105,甲、丙两个数的最小公倍数是126.请问:甲数是多少?12.甲、乙是两个不同的自然数,它们都只含有质因数2和3,并且都有12个约数,它们的最大公约数是12.请问:甲、乙两数之和是多少?超越篇1.360共有多少个奇约数?所有这些奇约数的和是多少?2.求出所有恰好含有10个约数的两位数,并求出每个数的所有约数之和.3.已知口与易的最大公约数是4,以与c 、易与c 的最小公倍数都是100,而且a ≤ b .满足条件的自然数a 、b 、c 共有多少组?4.所有70的倍数中,共有多少个数恰有70个约数?5.自然数n 是1,2,3,…,10的公倍数,而且它恰有72个约数,n 的最小值是多少?6.三条圆形跑道,圆心都在操场中的旗杆处.里圈跑道长51千米,中圈跑道长41千米,外圈跑道长83千米.甲、乙、丙三人分别在里圈、中圈、外圈沿同样的方向跑步,开始时,三人都在旗杆的正东方向,甲每小时跑321千米,乙每小时跑4千米,丙每小时跑5千米.他们同时出发.请问:几小时后,三人第一次同时回到出发点?7.如图11-1,在一个600×600的方格表ABCD 中,将AB 与线段CD 上除端点外的所有格点N 1,N 2,N 3,…,N 599分别相连,得到599条线段.请问,在这些线段中:(1)不会与其他格点相交的线段共有多少条?(2)经过格点最多的线段共经过多少个格点(不包括它的端点)?(3)除去端点,还恰好经过29个格点的直线有多少条?8.有些自然数等于自身约数个数的平方,例如l 和9都具有此性质,请问:是否还有其他自然数具有此性质?如果有,请举例;如果没有,请说明理由.。
【竞赛题】人教版小学五年级下册数学第09讲《立体几何》竞赛试题(含详解)

第九讲立体几何- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -首先,我们来学习一下长方体、正方体的体积与表面积的计算方法.练一练.1.一个正方体的棱长总和是72厘米,它的一个面是边长_______厘米的正方形,它的表面积是_______平方厘米,体积是_______立方厘米.2.一个长方体的长是5分米,宽是45厘米,高是24厘米,它的表面积是_______平方厘米,体积是_______立方厘米.3.做一个长8分米,宽4分米,高6分米的长方体玻璃鱼缸,至少需要_______平方分米的玻璃.4.有一块棱长是10厘米的正方体的铁块,现在要把它熔铸成一个横截面积是20平方厘米的长方体,这个长方体的长是_______厘米.如果要求这个长方体每条棱的长度都是整数厘米,它的表面积最小是_______平方厘米.相信同学们对于这些公式都很熟悉,但是对于较复杂的立体图形,往往我们并不能直接应用公式进行计算,这个时候又该怎么办呢?- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题1.有30个边长为1米的正方体,如图所示堆成一个四层的立体图形.请问:该立体图形的表面积等于多少平方米?分析:所谓表面积,就是立体图形露在外面的总面积.我们可以从上、下、左、右、前、后6个不同的方向去考虑这个立体图形,把每个方向露出的面积加在一起就行了.练习1.用14个棱长是1厘米的立方块拼成如右图所示的立体图形,问该图形的表面积是多少平方厘米?在观察物体的时候,我们往往可以从不同的角度进行观察.角度不同,看到的风景就会不同.比如:我们可以从正面看,上面看,左面看,看到的图形分别称为正视图,俯视图和左视图.并且容易发现:正面看和后面看,上面看和下面看,左面看和右面看得到的图形是相同的.对于较复杂的立体图形,通过三视图法往往可以很方便地计算出表面积.例题2.一个正方体被切成24个大小形状相同的小长方体(见下图),这些小长方体的表面积之和为162平方厘米,那么原正方体的体积是多少立方厘米?分析:我们先来分析一下切成小块的过程中,图形的表面积是如何变化的.同学们请看下图:一刀下去,正方体被一分为二.表面积和原来比,正好多出了A,B两个面.不难看出,这两个面的面积都等于原正方体6个面中1个面的面积.按这种方法,每切一刀,增加的都是两个面的面积.同学们可以计算一下,按如图的方式切了6刀后,表面积究竟增加了多少?练习2.一个正方体被切成36个大小形状相同的小长方体(见下图),这些小长方体的表面积之和为500平方厘米,那么原正方体的体积是多少立方厘米?例题3.如图,有一个边长为30厘米的大正方体,分别在它的角上、棱上、面上各挖掉一个大小相同的小正方体后,表面积变为5496平方厘米,那么挖掉的小正方体的棱长是多少厘米?分析:挖去小正方体后,表面积会发生变化.如果挖的位置,最终结果会有区别吗?练习3.一个正方体棱长10厘米,在它的表面上挖去一个棱长3厘米的小正方体.请求出剩下立体图形表面积的所有可能.除了长方体、正方体之外,圆柱和圆锥在我们的生活中也特别常见.如图,圆柱的两个圆面叫做底面;周围的面叫做侧面;两个底面之间的距离叫做高. 圆锥的圆面叫做底面;尖点叫做顶点;顶点到底面的距离叫做高,顶点到底面圆周上任意一点的连线叫做母线.关于圆锥的内容,我们不作深入的学习,同学们只需要学会如何计算它的体积即可.大家可以把圆柱想象成一个底面是圆形的柱子,那其他柱体也就是底面是其他图形的柱子.如图,所有“上下一般粗”的图形都称为柱体,图中的两个图形分别叫做三棱柱和四棱柱,它们的体积计算公式都是:V =⨯底面积高例题4.(1)如下左图,是长为8,宽为4的长方形,以长方形的长为轴旋转一周,求所形成的立体图形的体积和表面积是多少. (2)如下右图,是直角边分别为3和4的直角三角形,以边长为4的直角边为轴旋转一周,求所形成的立体图形的体积.分析:圆柱体的底面半径和高与长方形的长和高有什么关系?圆锥体呢?练习4.有一个圆柱和一个圆锥,它们的高和底面直径如图所示.圆柱体积及表面积分别是多少?圆锥的体积是多少?(π取3.14)6例题5.下图是一个棱长为4厘米的正方体,分别在前、后、左、右、上、下各面的中心位置挖去一个棱长1厘米的正方体,做成一种玩具.该玩具的表面积是多少平方厘米?如果把这些洞都打穿,表面积又变成了多少平方厘米?分析:打穿以后,表面积的计算有点复杂.想想都有哪些面是露在外面的?例题6.如图,一个底面长20分米,宽8分米,高15分米的长方形水池,存有三分之二池水.将一个高50分米,体积400立方分米的长方体竖直放入池中,那么长方体被水浸湿的部分有几分米高?分析:很明显长方体没有被水浸没,还有一部分在外面.水的体积没有变化过,但是形状发生了变化.原来是一个长方体,后来是什么样的形状?-正多面体正多面体,指各面都是全等的正多边形且每一个顶点所接的面数都是一样的凸多面体.一共有五种正多面体,分别是正四面体、正六面体(正方体)、正八面体、正十二面体和正二十面体.这些正多面体的作法都收录在了《几何原本》的第13卷中.柏拉图认为世界万物都是由火、气、水、土四元素构成的,其形状如正多面体中的四个.➢火的热令人感到尖锐和刺痛,好像小小的正四面体.➢空气是用正八面体制的,可以粗略感受到,它极细小的结合体十分顺滑.➢当水放到人的手上,它会自然流出,那它就应该是由很多小球所组成,好像正二十面体.➢土与其他的元素相异,因为它可以被堆栈,正如立方体.剩下没有用的正多面体——正十二面体,柏拉图以不清晰的语调写道:“神使用正十二面体以整理整个天空旳星座.”柏拉图的学生亚里士多德添加了第五个元素——以太,并认为天空是用此组成,但他没有将以太和正十二面体联系起来.约翰内斯·开普勒依随文艺复兴建立数学对应的传统,将五个正多面体对应五个行星——水星、金星、火星、木星和土星,同时它们本身亦对应了五个古典元素.在立体图形中,正多面体非常对称.除了正多面体之外,还有很多图形也具有非常漂亮的对称性.下面就是一些例子,不过要注意,它们可不是正多面体哦.作业1.如图所示,一个正方体被切成16个大小形状相同的小长方体,这些小长方体的表面积之和为256平方厘米,那么原正方体的体积是多少?作业2.一个正方体棱长8厘米,在它的表面上挖去一个棱长为2厘米的小正方体.则剩下的立体图形表面积可能是多少?作业3.如图,有一个边长为20厘米的大正方体,分别在它的角上、棱上、面上各挖掉一个大小相同的小正方体后,表面积变为2454平方厘米,那么挖掉的小正方体的边长是多少?作业4.图中的立体图形中,每个小正方形的边长都是1.那么这个立体图形的表面积和体积分别是多少?作业5.正方形的边长为4,按照图中所示的方式旋转,那么得到的旋转体的体积和表面积分别是多少?(π取3)俗话说,兴趣是最好的老师。
