rss20110602

合集下载

最需要转变的是思想观念

稿源：红网作者：王春芳
网页新闻
Powered By Google【‘我的2008’，中国有我一份力！】
相关热词搜索
留言板电话：010-82612286 保存全文浏览大中小打印关闭返回首页
Google提供的广告
SINA Corporation, All Rights Reserved
新浪公司版权所有
正确认识观念更新的重要意义
1.观念更新是企业创新发展的先导和前提。观念决定行动，思路决定出路。什么是观念？凡是人们对客观事物所形成的看法，凡是思维的结果都属观念之列，观念即认识，即思想，即观点，即看法。观念一旦形成，对人们的行为就会有驱动、导向和制约作用。观念就其本质来说，是属于主观世界的范畴，是一种意识和思维的过程，但是这种意识和思维与客观世界有着密切的关系。其一人们的观念来源于客观世界；其二人们的观念又指导社会实践；其三人们的观念产生于客观世界，指导着社会实践。同时，又在这一过程中不断地更新和发展。更新和发展的过程，实际上就是人们对客观世界认识不断深化的过程。因此，人类要想优化自身行为，就必须首先优化自己的观念。在社会进步、历史发展的浪潮推动下，观念的优化直接表现为观念的更新。
3、来源于社会劳动保障的改革滞后于经济改革，社会再就业观念和机制尚未完全形成。富余人员企业无力安排，个人又缺乏自谋职业的手段和能力，导致职工思想上反感，行动上抵触。
4、来源于社会腐败现象的存在。这类问题长时间得不到很好的解决，不仅影响人的工作积极性，而且容易使人丧失斗志，不求进取，对改革失去信心。
3更新观念是企业真正成为合格的市场竞争主体的先导和前提。在市场经济条件下，观念是一切变革的先导，是真正进入市场的前提。常言说得好：脑筋一变思路多，观念一转天地宽。这实际上就是说：观念是“无形资产”，观念是进入市场的第一道工序。观念背后是市场，观念背后是效益。市场竞争就是观念的竞争；结构调整就是思想观念的调整；观念的落后是最大的落后。更新观念，观念转变，不是一个新课题，我们已经说了好多年了பைடு நூலகம்党的十一届三中全会提出了“解放思想”的口号，解放思想其实就是要更新观念。“与时俱进”其实也是更新观念。观念落后可怕，更可怕的落后是我们根本不知道我们观念落后。没有一个人会说：我观念很落后，都以为观念落后，那是人家的事，不是我自己的事。实际上观念落后是每个人的事，包括我们自己，也包括各级领导干部。因为观念跟时代是紧紧相连的，但是为什么不敢承认自己观念落后？为什么总是认为观念落后是人家的事？就是因为观念看不见、摸不着，无形的，观念存在于每个人的头脑深处。“当局者迷，旁观者清”。

5月参阅信息

青岛振华路小学5月参阅信息他山之石北京市全面启动智能电表换装工作国家电网北京市电力公司9日启动北京市2013年智能电表换装工作，计划年内完成120万居民用户的换装工作。

随着人们生活水平不断提高，居民生活用电量不断攀升，2012年北京地区居民的户均生活用电量达到2100千瓦时。

国家电网北京公司自2011年开始逐步推广使用智能电表，两年来已免费为北京居民用户换装智能电表约190万具。

目前，北京市仍有约440万居民客户使用预付费卡表，大部分卡式电表已达到或接近使用寿命，根据《中华人民共和国计量法》等法律法规的相关要求需进行更换。

为了满足广大市民需求，进一步服务首都智慧城市建设，全面加快推进智能表换装工作，国家电网北京公司制定了三年智能表换装工作计划，自2013年至2015年，用三年时间完成全市范围内的智能电表换装工作。

智能电表作为新一代电能表，除了具备电能计量的基本功能外，还具有用电信息存储、远程采集、信息交互等功能。

与原有的卡式表和机械式表相比，智能电表能使客户切实享受到更加优质的电力服务。

据介绍，智能表客户购电渠道除了传统营业厅交费外，国家电网北京公司已联合工商银行、招商银行推出了网上银行购电。

2013年下半年还将推出智能表充值卡，通过拨打95598服务热线可以直接充值电费，同时购电金额不受限制，客户所购电费自动下发到电表内，免去了插卡环节，使用将更加便利。

同时，国家电网北京公司还将继续加强城区范围内“十分钟交费圈”建设，确保用电客户购电的便利性。

智能电表客户可通过拨打95598服务热线或登陆即将开通的95598互动网站（）就能随时查询自家用电信息。

同时增设了免费短信提醒服务，当电表内余额不足30元和10元时，会分两次发送短信提醒客户及时购电，避免突然停电给家庭生活带来不便。

社情民意青岛保障房获人居大奖成为全国范例日前，住房和城乡建设部公布了2012年中国人居环境奖获奖名单，青岛市保障性住房建设项目荣获“中国人居环境范例奖”，是全国唯一获此殊荣的保障性住房项目。

阿克苏增绿富民实现双赢

“我这一辈子，都要种树。

只要让我种树，我就知足了。

”83岁的毕可显，一生几乎都与林木为伴。

毕可显曾担任阿克苏地区林业处处长，是柯柯牙绿化工程的主导者之一。

柯柯牙一期绿化工程种树的成功，离不开这位老人的辛苦付出。

32年前，他敢于拍着胸脯向领导保障柯柯牙绿化工程树木的成活率，这底气来自于他在阿克苏地区实验林场30年植树造林摸索总结出来的荒漠盐碱地植树造林丰富经验。

毕可显曾担任过场长的阿克苏地区实验林场，被认为是柯柯牙绿化工程的发端，也是柯柯牙荒漠绿化工程二、三期的主战场。

从沙进绿退到绿进沙退阿克苏地区位于新疆天山南麓、塔克拉玛干大沙漠北缘。

历史上，这里沟壑纵横，沙砾密布，植被稀疏。

上世纪八十年代，阿克苏每年沙尘天气将近100天，大气总悬浮颗粒物超过国家大气环境质量二级标准的3.7倍。

更严峻的是，沙漠离城区只有6公里，还在以每年5米的速度逼近。

1986年，在严峻的现实面前，阿克苏地委作出了建设“柯柯牙”绿化工程的重大决策。

阿克苏人从此薪火相传，接续实施“柯柯牙”造林绿化工程，用心血和汗水在亘古荒原上建成了一道“绿色长城”，创造了荒漠变林海的人间奇迹。

阿克苏地委七任书记始终以改善生态、造福百姓为己任，亲自担任绿化工程总指挥，一届接着一届干，持之以恒、久久为功。

柯柯牙工程历时30多年、100余万人（次）参与，累计完成植树造林12万余亩，栽植各类树木千万余株，在戈壁荒滩上建成了南北长25公里，东西宽约2公里、面阿克苏增绿富民实现双赢文少宾Aksu Adds Green and Enriches the People to Achieve a Win-win Situation积110万亩的“绿色长城”，被联合国环境资源保护委员会列为“全球环境500佳”之一。

9月23日，当83岁的毕可显再次回到柯柯牙，回到实验林场，他完全被眼前一眼望不到头的绿色和挂满枝头的红枣震惊了。

“当年我们住在土块房，出门就是三尺厚的浮土。

SAP消息号

SAP消息号今天在查找一个消息号时，导出了一些相关的消息号，分享之……CO 0 ------------------------------------------------------------------------- CO 1 公司代码& 没有定义(检查输入项)CO 2 对公司代码& 你没有被授权CO 3 找不到工厂&，检查输入项CO 4 你对工厂& 无权CO 5 订单类型& 没有发现（检查输入项）CO 6 在工厂&中未发现MRP 控制器&（检查输入项）CO 7 对MRP 分组& 你没有被授权CO 8 对订单类型& 你没有被授权CO 9 物料& 没有发现CO 10 物料&未在工厂&中发现（检查输入项)CO 11 对交易& 你没有被授权CO 12 输入物料号或参照或科目确定CO 13 输入物料号或参照号或科目确定CO 14 计划订单& 没有发现（检查输入项）CO 15 在表TCO01 中的订单类型& 遗漏项CO 16 开始日期晚于"结束"日期(检查输入项)CO 17 未找到订单& (检查输入)CO 18 错误项合并(请核查输入项)CO 19 不完全项合并(完全输入项)CO 20 请输入工厂CO 21 输入MRP组CO 22 输入订单类型CO 23 在TC10中处理&没有有效的项(处理终止)CO 24 检查规则无法确定CO 25 物料没有BOMCO 26 工艺路线对于& 不能自动确定CO 27 前推式计划(输入起始日期)CO 28 倒排生产计划（输入结束日期）CO 29 无提前期计划（输入开始和完成时间）CO 30 开始日期不能迟于结束日期CO 31 & 不是工作日(下一工作日为：&)CO 32 日期& 迟于工厂日历有效期CO 33 日期& 早于工厂日历有效期限CO 34 工厂日历不在缓冲区(联系系统管理者)CO 35 日期& 非工作日（前一工作日：&）CO 36 输入订货数量CO 37 MAPL 记录未被选择CO 38 & 个MAPL 记录被选中CO 39 计划订单& 没有发现CO 40 计划订单& 已锁住CO 41 计划订单& 将不变换CO 42 在工厂& 对订单类型& 你没有被授权CO 43 在工厂& MRP 组& 中没有授权去转换计划订单CO 44 物料&未在工厂&中发现CO 45 物料类型& 未定义（检查输入项）CO 46 物料& 不能自行生产CO 47 已为外部采购计划物料&CO 48 物料& 打算自行生产CO 49 输入计划类型CO 50 为物料& 状态&不打算自制生产CO 51 订单/网络类型&没定义CO 52 输入计划类型CO 53 在工厂&3中物料&2的物料状态&1未定义CO 54 物料& 有状态&CO 55 输入有效的计划类型CO 56 日期& 无效（检查输入项）CO 57 未发现有效的物料单CO 58 没有BOM 未发现CO 59 有效的BOM项没有发现CO 60 &开始日期在过去CO 61 &交货日期在过去CO 62 订单&没有发现CO 63 订单& 仅能显示，因已取消CO 64 该状态的对象类型&不允许CO 65 状态对象已经存在CO 66 工序&是顺序&的参照工序(不能删除)CO 67 可用性日志不存在CO 68 物料& 的MRP 数据没有维护CO 69 物料& 的会计数据没有维护CO 70 物料&的工作计划数据没有被维护CO 71 物料& 的采购数据未被维护CO 72 虽分解估价但估价类型未输入CO 73 对估价类型& 没有维护估价数据CO 74 估价类型& 在自制生产中不允许CO 75 估价类型&未定义(检查输入项)CO 76 物料& 的会计数据没有维护CO 77 目标单位&不能转换为基本单位&CO 78 在转换单位&至&时溢出CO 79 输入有效选择IDCO 80 外部编号分配（输入有效订单号）CO 81 外部编号不在定义的编号间隔内CO 82 订单号& 已经存在(登录新编号)CO 83 订单类型&有内部编号分配（不需要输入）CO 84 订单&已在处理CO 85 订单& 在更新后将下达CO 86 订单已下达CO 87 当前的订单状态不允许部分订单下达CO 88 订单已锁住CO 89 订单开锁CO 90 检验激活- 标志自动设置CO 91 利润中心& 对整个订货提前期无效CO 92 利润中心& 找不到（检查输入项）CO 93 订单&已下达CO 94 订单&部分下达CO 95 在语言&工厂&中没有废品原因&的文本(检查输入项)CO 96 废品原因& 未在工厂& 中发现（检查输入项）CO 97 移动类型& 未定义（检查输入项）CO 98 输入单位和基本计量单位不能转换CO 99 更新不必要，因为没有修改CO 100 订单号& 已经保存CO 101 项目类别& 未定义（检查输入项)CO 102 项目类别& 未定义（检查输入项)CO 103 BOM & 未发现（检查输入项）CO 104 订单& 的当前状态不允许部分下达CO 105 没组件分配到工序&CO 106 选择一组件CO 107 你已到达最后的组件CO 108 你已到达第一个组件CO 109 订单类型&在工厂&没有定义工艺路线应用CO 110 输入订单类型CO 111 输入工厂CO 112 输入订单号CO 113 更改无法执行，因为订单& 被锁定CO 114 没有发现订单类型&的有效项CO 115 输入有效的下达期间码CO 116 期间，生产前/后的缓冲时间的下达将被复位CO 117 计划码将被忽略CO 118 不允许订单下达CO 119 废品数量不小于总订货数量CO 120 订单数量少于交货数量CO 121 订单&部分下达CO 122 ------------------------------------------------------------------------- CO 123 由于废品,订单数量& 增加&&CO 124 在工厂&没有为生成的工序定义参数CO 125 在工序层不能进行科目分配CO 126 维护所有数据CO 127 订单& 的当前状态不允许订单下达CO 128 计划订单不能被选择CO 129 * 130-150：与组件相关的消息CO 130 输入项目类别CO 131 项目类别& 未定义（检查输入项)CO 132 散装物料指示符不得再设置( 数量已经领取)CO 133 输入项目类别&的物料CO 134 不要为项目类别& 输入物料CO 135 物料类型& 不能使用项目类别&CO 136 对项目类别&，数量必须为正CO 137 对项目类别&，数量必须为负CO 138 因为StUn 不能转换为发货单位，数量单位& 没有定义CO 139 输入数量（不带小数位）CO 140 大量物件不允许用于成本核算相关项CO 141 在无约束的超量发货情况下，容差被忽略CO 142 维护工厂，订单类型和工序CO 143 输入检查规则CO 144 物料下达只可能通过工序下达CO 145 检查规则和/或物料下达已经重新设置CO 146 仓储地点&没有为物料&生成CO 147 鉴于批量因子&订货量增加到&CO 148 废品数量& 更新后被激活CO 149 低值大量物件和倒冲是相互排斥的CO 150 * 与打印相关的消息CO 151 输入一个打印类型CO 152 选择一种打印类型CO 153 选择一种打印模式CO 154 选择一种打印模式CO 155 输入有效工厂CO 156 用户& 未定义CO 157 选择模式eCO 158 选择模式CO 159 选择CO 160 选择一种处理类型CO 161 输入有效表，视图或透视表CO 162 字段&在结构&内没定义CO 163 输入有效字段名CO 164 订单&已标记后台打印CO 165 更新后，订单& 将标记为后台打印CO 166 维护编号范围对订单类型&CO 167 错误发生在为完成确认的编号分配中CO 168 错误发生在为对象&的编号分配中CO 169 报表控制当前正被处理（只显示）CO 170 订单&不能打印因为系统状态"删除"CO 171 订单&不能打印因为订单状态"技术性完成"CO 172 将打印订单& 的拷贝(初始清单已经打印)CO 173 你已经生成订单的打印需求CO 174 下一次更新后，订单将被打印出来CO 175 以显示模式原始－和部分打印输出不可能CO 176 无订单符合选择标准CO 177 无订单选择CO 178 将光标置于清单项CO 179 订单类型&没有定义参照文档类型CO 180 清单不能被选择对用户& 在工厂& 中CO 181 清单& 不存在格式(订单类型&，打印机&，工厂& )CO 182 对MRP 组& 工厂& 事务& 订单类型& 的事务控制丢失CO 183 没有为清单&(订单类型&，打印变式&)定义打印报表CO 184 订单&正在处理(打印不能运行)CO 185 后台打印请求生成CO 186 清单控制未为后台打印定义CO 187 选择打印不能在后台执行CO 188 输入有效MRP 分组CO 189 MRP 组& 未定义在每个工厂中。

RSS100N03中文资料

Transistor1/3Switching (30V, ±10A)RSS100N03z Features1) Low on-resistance.2) Built-in G-S Protection Diode.3) Small and Surface Mount Package (SOP8).z ApplicationsPower switching, DC/DC converter.z External dimensions (Unit : mm)z Structure•Silicon N-channel MOS FET z Equivalent circuitthe source terminals to protect the diode against static electricity when the product is in use. Use the protection circuit when the fixed voltages are exceeded.z Absolute maximum ratings (T a=25°C)∗1∗1∗2ParameterV V DSS Symbol 30V V GSS 20A I D ±10A I DP ±40A I S 1.6A I SP 6.4W P D 2°C Tch 150°CTstg −55 to +150Limits Unit Drain-source voltage Gate-source voltage Drain current Total power dissipatino Channel temperature Strage temperatureContinuous Pulsed Continuous Source current (Body diode)Pulsed∗1 Pw ≤10µs, Duty cycle ≤1%∗2 Mounted on a ceramic board.Transistor2/3z Thermal resistance (T a=25°C)°C / WRth (ch-a)62.5ParameterSymbol Limits Unit Channel to ambient∗ Mounted on a ceramic board.∗z Electrical characteristics (T a=25°C)z Body diode characteristics (Source-Drain Characteristics) (T a=25°C)Forward voltageV SD −− 1.2V I S=6.4A, V GS =0VParameterSymbol Min.Typ.Max.Unit Conditions∗Pulsed∗z Electrical characteristic curvesDRAIN-SOURCE VOLTAGE : V DS (V)C A P A C I T A N C E : C (p F )Fig.1 Typical Capacitancevs. Drain-Source VoltageDRAIN CURRENT : I D (A)S W I T C H I N G T I M E : t (n s )Fig.2 Switching CharacteristicsTOTAL GATE CHARGE : Qg (nC)G A T E -S O U R C E V O L T A G E : V G S (V )Fig.3 Dynamic Input CharacteristicsTransistor3/3GATE-SOURCE VOLTAGE : V GS (V)D R A I N C U R RE N T : I D (A )Fig.4 Typical Transfer CharacteristicsGATE-SOURCE VOLTAGE : V GS (V)S T A T I C D R A I N -S O U R C E O N -S T A T E R E S I S T A N C E : R D S (o n ) (m Ω)Fig.5 Static Drain-SourceOn-State Resistance vs. Gate-Source VoltageSOURCE-DRAIN VOLTAGE : V SD (V)S O U R C E C U R R E N T : I s (A )Fig.6 Source Current vs.Source-Drain VoltageDRAIN CURRENT : I D (A)1101001000S T A T I C D R A I N -S O U R C E O N -S T A T E R E S I S TA N C E : R D S (o n ) (m Ω)Fig.7 Static Drain-SourceOn-State Resistance vs. Drain Current (Ι)DRAIN CURRENT : I D (A)S T A T I C D R A I N -S O U R C E O N -S T A T E R E S I S T A N C E : R D S (o n ) (m Ω)Fig.8 Static Drain-SourceOn-State Resistance vs. Drain Current (ΙΙ)DRAIN CURRENT : I D (A)S T A T I C D R A I N -S O U R C E O N -S T A T E R E S I S T A N C E : R D S (o n ) (m Ω)Fig.9 Static Drain-SourceOn-State Resistance vs. Drain Current (ΙΙΙ)AppendixAbout Export Control Order in JapanProducts described herein are the objects of controlled goods in Annex 1 (Item 16) of Export Trade ControlOrder in Japan.In case of export from Japan, please confirm if it applies to "objective" criteria or an "informed" (by MITI clause)on the basis of "catch all controls for Non-Proliferation of Weapons of Mass Destruction.Appendix1-Rev1.0。

A nonparametric view of network models and

A nonparametric view of network models and Newman–Girvan and other modularitiesPeter J.Bickel a,1and Aiyou Chen baUniversity of California,Berkeley,CA 94720;and b Alcatel-Lucent Bell Labs,Murray Hill,NJ 07974Edited by Stephen E.Fienberg,Carnegie Mellon University,Pittsburgh,PA,and approved October 13,2009(received for review July 2,2009)Prompted by the increasing interest in networks in many ﬁelds,we present an attempt at unifying points of view and analyses of these objects coming from the social sciences,statistics,probability and physics communities.We apply our approach to the Newman–Girvan modularity,widely used for “community”detection,among others.Our analysis is asymptotic but we show by simulation and application to real examples that the theory is a reasonable guide to practice.modularity |proﬁle likelihood |ergodic model |spectral clusteringThe social sciences have investigated the structure of small networks since the 1970s,and have come up with elaborate modeling strategies,both deterministic,see Doreian et al.(1)for a view,and stochastic,see Airoldi et al.(2)for a view and recent work.During the same period,starting with the work of Erdös and Rényi (3),a rich literature has developed on the probabilistic properties of stochastic models for graphs.A major contribution to this work is Bollobás et al.(4).On the whole,the goals of the analyses of ref.4,such as emergence of the giant component,are not aimed at the statistical goals of the social science literature we have cited.Recently,there has been a surge of interest,particularly in the physics and computer science communities in the properties of networks of many kinds,including the Internet,mobile networks,the World Wide Web,citation networks,email networks,food webs,and social and biochemical networks.Identiﬁcation of “com-munity structure”has received particular attention:the vertices in networks are often found to cluster into small communities,where vertices within a community share the same densities of connect-ing with vertices in the their own community as well as different ones with other communities.The ability to detect such groups can be of signiﬁcant practical importance.For instance,groups within the worldwide Web may correspond to sets of web pages on related topics;groups within mobile networks may correspond to sets of friends or colleagues;groups in computer networks may corre-spond to users that are sharing ﬁles with peer-to-peer trafﬁc,or collections of compromised computers controlled by remote hack-ers,e.g.botnets (5).A recent algorithm proposed by Newman and Girvan (6),that maximizes a so-called “Newman–Girvan”mod-ularity function,has received particular attention because of its success in many applications in social and biological networks (7).Our ﬁrst goal is,by starting with a model somewhat less general than that of ref.4,to construct a nonparametric statistical frame-work,which we will then use in the analysis,both of modularities and parametric statistical models.Our analysis is asymptotic,let-ting the number of vertices go to ∞.We view,as usual,asymptotics as being appropriate insofar as they are a guide to what happens for ﬁnite n .Our models can,on the one hand,be viewed as special cases of those proposed by ref.4,and on the other,as encompass-ing most of the parametric and semiparametric models discussed in Airoldi et al.(2)from a statistical point of view and in Chung and Lu (8)for a probabilistic one.An advantage of our framework is the possibility of analyzing the properties of the Newman–Girvan modularity,and the reasons for its success and occasional fail-ures.Our approach suggests an alternative modularity which is,inprinciple,“fail-safe”for rich enough models.Moreover,our point of view has the virtue of enabling us to think in terms of “strength of relations”between individuals not necessarily clustering them into communities beforehand.We begin,using results of Aldous and Hoover (9),by introduc-ing what we view as the analogues of arbitrary inﬁnite population models on inﬁnite unlabeled graphs which are “ergodic”and from which a subgraph with n vertices can be viewed as a piece.This development of Aldous and Hoover can be viewed as a gener-alization of deFinetti’s famous characterization of exchangeable sequences as mixtures of i.i.d.ones.Thus,our approach can also be viewed as a ﬁrst step in the generalization of the classical construc-tion of complex statistical models out of i.i.d.ones using covariates,information about labels and relationships.It turns out that natural classes of parametric models which approximate the nonparametric models we introduce are the “blockmodels”introduced by Holland,Laskey and Leinhardt ref.10;see also refs.2and 11,which are generalizations of the Erdös–Rényi model.These can be described as follows.In a possibly (at least conceptually)inﬁnite population (of ver-tices)there are K unknown subcommunities.Unlabeled individ-uals (vertices)relate to each other through edges which for this paper we assume are undirected.This situation leads to the follow-ing set of probability models for undirected graphs or equivalently the corresponding adjacency matrices {A ij :i ,j ≥1},where A ij =1or 0according as there is or is not an edge between i and j .1.Individuals independently belong to community j withprobability πj ,1≤j ≤K ,K j =1πj =1.2.A symmetric K ×K matrix {P kl :1≤k ,l ≤K }of probabil-ities is given such that P ab is the probability that a speciﬁc individual i relates to individual j given that i ∈a ,j ∈b .The membership relations between individuals are estab-lished independently.Thus 1− 1≤a ,b ≤K πa πb P ab is the probability that there is no edge between i and j .The Erdös–Rényi model corresponds to K =1.We proceed to deﬁne Newman–Girvan modularity and an alter-native statistically motivated modularity.We give necessary and sufﬁcient conditions for consistency based on the parameters of the block model,properties of the modularities,and average degree of the graph.By consistency we mean that the modular-ities can identify the members of the block model communities perfectly.We also give examples of inconsistency when the con-ditions fail.We then study the validity of the asymptotics in a limited simulation and apply our approach to a classical small example,the Karate Club and a large set of Private Branch Exchange (PBX)data.We conclude with a discussion and some open problems.Author contributions:P .J.B.and A.C.performed research and analyzed data.The authors declare no conﬂict of interest.This article is a PNAS Direct Submission.1Towhom correspondence should be addressed.E-mail:bickel@.This article contains supporting information online at /cgi/content/full/0907096106/DCSupplemental.21068–21073PNASDecember 15,2009vol.106no.50 /cgi /doi /10.1073/pnas.0907096106S T A T I S T I C SRandom Graph ModelsConsider any probability distribution P on an inﬁnite undirected graph,or equivalently a probability distribution on the set of all matrices ||A ij :i ,j ≥1||where A ij =1or 0,A ij =A ji for all i ,j pairs,and A ii =0for all i ,thus excluding self relation.If the graph is unlabeled,it is natural to restrict attention to P such that ||A σi σj ||∼P for any permutation σof {1,2,3,...}.Hoover (see ref.9)has shown that all such probability distributions can be represented as,A ij =g (α,ξi ,ξj ,λij )where α,{ξi }and {λij }are i.i.d.U (0,1)variables andg (u ,v ,w ,z )=g (u ,w ,v ,z )for all u ,v ,w ,z .The variables ξcorrespond to latent variables,λbeing completely individual speciﬁc,ξgenerating relations between individuals and αa mixture variable which is unidenti-ﬁable even for an inﬁnite graph.Note that g is unidentiﬁable and the ξand λcould be put on another scale,e.g.Gaussian.We note that,this point of departure was also recently proposed by Hoff (12)but was followed to a different end.It is clear that the distributions representable as,A ij =g (ξi ,ξj ,λij )[1]where λij =λji ,are the extreme points of this set and play the same role as sequences of i.i.d.variables play in de Finetti’s theo-rem.Since given ξi and ξj ,the λij are i.i.d.,these distributions are naturally parametrized by the functionh (u ,v )≡P [A ij =1|ξi =u ,ξj =v ].As Diaconis and Janson (13)point out h (.,.)does not uniquely determine P but if h 1and h 2deﬁne the same P ,then there exists ϕ:[0,1]→[0,1]which is:measure preserving,i.e.such that ϕ(ξ1)has a U (0,1)distribution;and h 1(u ,v )=h 2(ϕ(u ),ϕ(v )).Given any h corresponding to P ,letP [X ij =1|ξi =u ]=g (u )=1h (u ,v )dv .It is well known (see section 10of ref.14)that there existsa measure preserving ϕg such that,g (ϕg (v ))is monotone non decreasing.Deﬁneh CAN (u ,v )=h (ϕg (u ),ϕg (v )).We claim thatg CAN (u )≡10h CAN (u ,v )dv =F −1(u )where F is the cdf of g CAN (ξi ),and h CAN is unique up to sets of measure 0.T o see this note that if h corresponds to P andg (u )≡ 10h (u ,v )dv is non decreasing,then since F is deter-mined by P only,g (u )=F −1(u ).But g (ϕg (u ))=g CAN (u )and ϕg (u )=g −1g CAN (u )=u .There is a reparametrization of h CAN (we drop the CAN sub-script in the future)which enables us to think of our model in terms more familiar to statisticians.Letρ=P (Edge)= 101h (u ,v )dudv .Then the conditional density of (ξi ,ξj )given that there is an edge between i and j is w (u ,v )=ρ−1h (u ,v ).This parametrization also permits us to decouple ρ∝E (Degree)of the graph from the inho-mogeneity structure.It is natural ﬁnally to let ρdepend on n butw (·,·)to be ﬁxed.If λn ≡E (Degree)→∞,we have what we maycall the “dense graph”limit.If λn =Ω(1),we are in the case most studied in probability theory where,for instance,λn =1is the threshold at which the so called “giant component”appears.This is the situation Bollobas et al.focus on.As we have noted,block models are of this type.Here we can think of the reparametrization as being ρ,π,||S ab ||=||ρ−1P ab ||,or ||W ab ||≡||ρ−1P ab πa πb ||.The models studied by Chung and others (8)given by,h (u ,v )∝a (u )a (v )[2]also fall under our description.The mixture model of Newman and Leicht (15)where,given communities 1,···,K ,P [X ij =1|i ∈s ,j ∈r ]=θri θsjis not of this type,since it is not invariant under permutations.It can be made invariant by summing over all permutations of {1,···,n },but is then generally not ergodic.Such models can be developed from our framework by permitting covariates Z i depending on vertex identity or Z ij depending on edge identity.Newman and Leicht’s example where the communities are WEB pages falls under this observation.From a statistical point of view,these models bear the same relation to our models as regression models do to single population models.Block models or models whereh (u ,v ,θ)∝K n k =1θk a k (u )a k (v )for known functions {a k }can be used to approximate general h .The latent eigenvalue model of Hoff (12)is of this type,but with a k which are extremely rough and unidentiﬁable since the a j (ξ)are independent,and for which no unique choice exists.We can think of the canonical version of the block model as corresponding to a labeling 1,···,K of the communities in the order W 1≤···≤W K where W j = k W jk ,which is proportional to the expected degree of a member of community j .The function h (·,·)then takes value P ab on the (a ,b )block of the product partition in which each axis is divided into consecutive intervals,of lengths π1,···,πK .Each corresponding vertical slice exhibits the relation pattern for that community with the diagonal block identifying the members of the community.The nonparametric h (·,·)gives the same intuitive picture on an arbitrarily ﬁne scale.We note that,as in nonpara-metric statistics,to estimate h or w ,regularization is needed.That is,we need to consider K n →∞at rates which depend on n and λn to obtain good estimates of h or w by using estimates of θabove or of block model parameters.We will discuss this further later.Newman–Girvan and Likelihood ModularitiesThe task of determining K communities corresponds to ﬁnd-ing a good assignment for the vertices e ≡{e 1,···,e n }where e j ∈{1,···,K }.There are K n such assignments.Suppose that the distribution of A follows a K block model with parame-ters π=(π1,···,πK )and P =||P ab ||K ×K .The observed A is a consequence of a realization c =(c 1,···,c n )of n indepen-dent Multinomial (1,π)variables.Evidently we can measure the adequacy of an assignment through the matrixR (c ,e )=||R ab ||K ×K ,where R ab =n −1n i =1I (c i =b ,e i =a ),the fraction of b mem-bers classiﬁed as a members if we use e .It is natural to ask for consistency of an assignment e ,that is,e =c ,i.e.R (c ,e )=diag (f (c ))Bickel and ChenPNASDecember 15,2009vol.106no.5021069where f a (e )=n −1n a (e )and n a (e )= ni =1I (e i =a ).The Newman–Girvan modularity Q NG (e ,A )is deﬁned as follows.Let {i :e i =k }denote e-community k ,i.e.as estimated by e .DeﬁneO kl (e ,A )=1≤i ,j ≤nA ij I (e i =k ,e j =l )to be the block sum of A .Obviously,O kk is twice the number of edges among nodes in the k -th e-community and for k =l ,O kl is the number of edges between nodes in the k -th e-community andnodes in the l -th e-community.Let D k (e ,A )= Kl =1O kl (e ,A ).It is easy to verify that D k is the sum of degrees for nodes inthe k -th e-community.Let L =K k =1D k be twice the number of edges among all nodes.Then the Newman–Girvan modularity is deﬁned byQ NG (e ,A )=K k =1O kk L−D k L2.The Newman–Girvan algorithm then searches for the member-ship assignment vector e that maximizes Q NG .Notice that if edges are randomly generated uniformly among all pairs of nodes with given node degrees,then the number of edges between the k th e-community and l th e-community is expected to be L −1D k D l .Therefore,the Newman–Girvan modularity measures the frac-tion of the edges on the graph that connect vertices of the same type (i.e.within-community edges)minus the expected value of the same quantity on a graph with the same community divisions but random connections between the vertices (6).Newman (16)contrasts and compares his modularity with spectral clustering,another common “community identiﬁcation”method which we will also compare to the likelihood modularity below.We seek conditions under which the ofﬁcial N-G assignmentˆc=arg max Q NG (e ,A )is consistent with probability tending to 1.Before doing so weconsider alternative modularities.For ﬁxed e ,the conditional,given {n k (e )}K 1,log-likelihood of A is 1 1≤a ,b ≤K (O ab log(P ab )+(n ab −O ab )log(1−P ab )),where n ab =n a n b if a =b ,n aa =n a (n a −1).If we maximize over P ,we obtain by letting τ(x )=x log x +(1−x )log(1−x ),Q LM (e ,A )=12 a ,bn ab τO abn abwhich we call the likelihood modularity.This is not a true like-lihood but a proﬁle likelihood where we treat e as an unknown parameter.We will argue below that the proﬁle likelihood is opti-mal in the usual parametric sense if λn→∞.But so are all other consistent modularities as deﬁned below.However,we expect that if λnlog nis bounded and certainly if λn =Ω(1),the most important case,this is false.We are deriving optimal and computationally implementable procedures for this case.We write general modularities in the form,Q (e ,A )=F nO μn ,L μn,f (e )where μn =E (L )=n (n −1)ρn and the matrix O (e ,A )isdeﬁned by its elements O ab (e ,A ),f (e )=(n 1(e )n ,···,n K (e )n )T ,and F n :M ×R +×G →R where M is the set of all nonnegative K ×K symmetric matrices and G is the K simplex.Note that both Q NGand Q LM can be written as such up to a proportionality constant.It is easy to see that if the K block model holds,E (O (e ,A )|c )E (L )=R (c ,e )SR T (c ,e )[3]where,by deﬁnition,R T 1=f (c ),R 1=f (e ),1=(1,···,1)T ,andS ab =ρ−1n P (A 12=1|c 1=a ,c 2=b ).Note that W ≡D (π)S D (π),where D (v )≡diag (v )for v K ×1.We deﬁne asymptotic consistency of a sequence of assignments ˆcby P [ˆc =c ]→1[4]as n →∞.We will assume that there exists a function F :M ×R +×G →R such that F n is approximated by F evaluated at the conditional expectation given c of the argument of F n .Suppose ﬁrst F n ≡F .It is intuitively clear from [3]that if ˆc→c ,then R (c ,ˆc )→D (π).Then,since f (c )→π,the following condition is natural.I.F (RSR T ,1,R 1)is uniquely maximized over R ={R :R ≥0,R T 1=π}by R =D (π),for all (π,S )in an open set Θ.This means c with f (c )=πis the right assignment for the limiting problem.Note that since F is not concave in R ,this is a strong condition.For (π,S )to be identiﬁable uniquely,we clearly also need that:II.S does not have two identical columns (T wo communi-ties cannot have identical probabilities of being related to other communities and within themselves)and πhas all entries positive (Each community has some members).We also need a few more technical conditions of a standard type.III.a)F is Lipschitz in its arguments.b)The directional deriv-atives ∂2F∂ 2(M 0+ (M 1−M 0),r 0+ (r 1−r 0),t 0+ (t −t 0))| =0+are continuous in (M 1,r 1,t )for all (M 0,r 0,t 0)in a neigh-borhood of (W ,1,π).c)Let G (R ,S )=F (RSR T ,1,R 1).Assume that on R ,∂G ((1− )D (π)+ R ,S∂| =0+<−C <0for all (π,S )∈Θ.Theorem 1.Suppose F ,S and πsatisfy I–III and ˆc is the maximizer of Q (e ,A ).Supposeλnlog n→∞.Then,for all (π,S )∈Θ,limit n →∞log P (ˆc=c )λn≤−s Q (π,S )<0.The proof is given in SI Appendix .We note that Snijders and Nowicki (11)established a related result,exponential convergence to 0of the mis-classiﬁcation prob-ability for λn =Ω(n )using node degree K-means clustering for K =2.Let F (c ,e )≡F (R (c ,e )SR T (c ,e ),f T (c )S f (c ),f (e )).In the gen-eral case it sufﬁces to show,limit n →∞Psup {|Q (e ,A )−F (c ,e )|:e }≤δΔnλn ≤−γ[5]for all δ>0,some γ>0,whereΔn =inf {|F (c ,e )−F (c ,c )|:|e −c |≥1}and |e −c |=n i =11(e i =c i ).We show in SI Appendix that Q NG and Q LM satisfy I and III and Eq.5for selected (π,S )for Q NG and all (π,S )for Q LM .An immediate consequence of the theorem is:21070 /cgi /doi /10.1073/pnas.0907096106Bickel andChenS T A T I S T I C SCorollary 1:If the conditions of Theorem 1hold and,ˆW≡L −1O (ˆc ,A ),ˆπ= 1n ni =1I (ˆci =a ):a =1,···,K ,then,√n (ˆπ−π)⇒N (0,D (π)−ππT ),√n (ˆW−W )⇒S ·(πηT +ηπT )−2(πT S η)W ,η=N (0,D (π)−ππT ),with A ·B denoting point-wise product.The limiting variances arewhat we would get for maximum likelihood estimates if ˆc=c ,i.e.we knew the assignment to begin with.So consistent modularities lead to efﬁcient estimates of the parameters.This follows since with probability tending to 1,ˆc=c .T o estimate w (·,·)in the nonparametric case we need K →∞,and w (·,·)and π(·)smooth.We approximate by W K ∼K −2||w (aK −1,bK −1)||,πK (a )∼K −1π(aK −1),where w (·,·),W K are canonical and the modularity deﬁning F K ,F K (·,·,·)is of order K −2.We have preliminary results in that direction but their formulation is complicated and we do not treat them further here.Consistency of N-G,L-MWe show in SI Appendix using the appropriate F NG ,F LM that the likelihood modularity is always consistent while the Newman–Girvan is not.This is perhaps not surprising since N-G focuses on the diagonal of O .In fact,we would hope that N-G is consis-tent under the submodel {(ρ,π,W ):W aa > b =a W ab for all a },which corresponds to Newman and Girvan’s motivation.We have shown this for K =2but it surprisingly fails for K >2.Here is a counterexample.Let K =3,π=(1/3,1/3,1/3)T andP =⎡⎣.06.040.04.12.040.04.66⎤⎦.As n →∞,with true labeling,Q NG approaches 0.033.How-ever,the maximum Q NG ,about 0.038,is achieved by merging the ﬁrst two communities.That is,two sparser communities are merged.This is consistent with an observation of Fortunato and Barthelemy (17).If for the proﬁle likelihood we maximize only over e such thatˆW aa (e )>b =a ˆW ab (e )for all a ,we obtain ˆcwhich is consis-tent under the submodel above,and in the Karate Club example performs like N-G.Computational IssuesComputation of optimal assignments using modularities is,in prin-ciple,NP hard.However,although the surface is multimodal,in the examples we have considered and generally when the signal is strong,optimization from several starting points using a label switching algorithm (19)works well.SimulationWe generate random matrices A and maximize Q NG ,Q LM to obtain node labels respectively,where Q LM is maximized using a label switching algorithm.T o make a fair comparison,the initial label-ing for Q NG and Q LM is to randomly choose 50%of the nodes with correct labels and the other 50%with random labels.For spectral clustering,we adopt the algorithm of (18)by using the ﬁrst K eigen-vectors of D (d )−1/2A D (d )−1/2,where d =(d 1,···,d n )T and d i is the degree of the i -th node.We generate the P matrix randomly by forcing symmetry and then add a constant to diagonalentriesFig.1.Empirical comparison of Newman–Girvan,likelihood modularities and spectral clustering (18),where K =3,the number of nodes n varies from 200to 1500,and the percent of correct labeling is computed from 100replicates of each simulation case.Here π,P are given in the text.such that I holds.The πis generated randomly from the simplex.T o be precise,the values for Fig.1are π=(.203,.286,.511)T andP =bn −1log n ·⎡⎣.43.06.13.06.34.17.13.17.40⎤⎦,where n varies from 200to 1,500and b varies from 10to 100.Obvi-ously,Fig.1says that the likelihood method exhibits much less incorrect labeling than Newman–Girvan and spectral clustering.This is consistent with theoretical comparison.Data ExamplesWe compare the L-M and N-G modularity algorithms below with applications to two real data sets.T o deal with the issue of non-convex optimization,we simply use many restarting points.Zachary’s “Karate Club”Network.We ﬁrst compare L-M and N-Gwith the famous “Karate Club”network of ref.20,from the social science literature,which has become something of a standard test for community detection algorithms.The network shows the pat-terns of friendship between the members of a karate club at a US university in the 1970s.The example is of particular interest because shortly after the observation and construction of the net-work,the club in question split into two components separated by the dashed line as shown in Figs.2and 3as a result of an internal dispute.Fig.2Left shows two communities identiﬁed by maximizing the likelihood modularity where the shapes of the ver-tices denote the membership of the corresponding individuals,and similarly the right panel shows communities identiﬁed by N-G.Obviously,the N-G communities match the two sub-divisions identiﬁed by the split save for one mis-classiﬁed individual.The L-M communities are quite different,and obviously one com-munity consists of ﬁve individuals with central importance that connect with many other nodes while the other community con-sists of the remaining individuals.Although not reﬂecting the split this corresponds to other plausible distinguishing characteristics of the individuals.However,if we force the constraint that within-community density is no less than the density of relationship to all other communities,the submodel we discussed,then we obtain two L-M communities that match the split perfectly.The same parti-tions as ours with and without constraint have also been reportedBickel and ChenPNASDecember 15,2009vol.106no.5021071Fig.2.Zachary’s karate club munities were identiﬁed by maximizing the likelihood modularity(Left)and by maximizing the Newman–Girvan modularity with K=2(Right),where the shapes of vertices indicate the membership of the corresponding individuals.The dashed line cuts the nodes into two groups which are the“known”communities that the club was split into.by Rosvall and Bergstrom using a data compression criterion(21), which is closely related to L-M.We note that,as is usual in cluster-ing,there is no ground truth,only features which can be validated ex post fact.It is interesting to note that,if instead of K=2,we put K=4,as in Fig.3,it is evident for both modularities that merg-ing the communities on either side of the eigenvector split,gives the“correct”Karate Club split.This suggests that the standard policy mentioned by Newman(16)of increasing the number of communities by splitting is not necessarily ideal since in this case the“misclassiﬁed”individual of Fig.2would never be“correctly”classiﬁed.Private Branch Exchange.Our second example is of a telephone communication network where connections are made among the internal telephones of a private business organization,a so called PBX.PBXs are differentiated from“key systems”in that users of key systems usually select their own outgoing lines,while PBXs select the outgoing line automatically.Our data contains621individuals.Fig.4Left shows the results of community detection by L-M,where the adjacency matrix is plotted but the nodes are sorted according to the membership of the corresponding individ-uals identiﬁed by maximizing the likelihood modularity.Similarly, the right panel of Fig.4shows the communities identiﬁed by N-G,where the maximum Newman–Girvan modularity is0.4217. Note that the identiﬁed communities by L-M have sizes323,81, 78,97,41,and1,respectively.The communities are ordered sim-ply by their average node degrees,essentially the order for h CAN. Interestingly,the last L-M community has only one node that communicates with almost everyone else,nodes in the second community only communicate with internal nodes,nodes in the fourth community and the sixth community,but not with others; Similarly,the third community only communicates with theﬁfth and sixth communities,and so on.In other words,communica-tion between communities is sparse.However,the communities identiﬁed by N-G are quite different with only theﬁfth commu-nity heavily overlapping with a community identiﬁed by L-M.This Fig.3.Zachary’s karate club munities were identiﬁed by maximizing the likelihood modularity(Left)and by maximizing the Newman–Girvanmodularity with K=4(Right),where the shapes of vertices indicate the membership of the corresponding individuals.The dashed line cuts the nodes intotwo groups which are the known communities that the club was split into./cgi/doi/10.1073/pnas.0907096106Bickel andChenS T A T I S T I CSFig.4.Private branch exchange data.(Left )The adjacency matrix where the nodes are sorted according to the membership of the corresponding individuals identiﬁed by maximizing L-M.(Right )Same as Left ,but with individuals identiﬁed by maximizing N-G with K =6.The colors on the within-community edges are used to differentiate the communities for both L-M and N-G.difference appears to be caused by the nodes in the 5th and 6th L-M communities which have many more between-community connections than within-community connections while N-G more or less maximizes within-community connections.We have ver-iﬁed that the group communicating with all others is a service group.Discussion1.As we noted,under our conditions the usual statistical goal of estimating the parameters πand P is trivial,since,once we have assigned individuals to the K communitiesconsistently,the natural estimates,ˆWand ˆπ,are not just consistent but efﬁcient.However,in the more realistic case where λn =Ω(1),or even just λn =Ω(log n ),this is no longer true.Elsewhere,we shall show that,indeed,estimation of parameters by maximum likelihood and Bayes classiﬁcation of individuals (no longer perfect)is optimal.2.A difﬁculty faced by all these methods,modularities or likelihoods,is that if K is large,searching over the space of classiﬁcations becomes prohibitively expensive.In sub-sequent work we intend to show that this difﬁculty maybe partly overcome by using the method of moments to ﬁrst estimate πand P ,and then study the likelihood in a neighborhood of the estimated values.Open Problems1.A fundamental difﬁculty not considered in the literature is the choice of K .From our nonparametric point of view,this can equally well be seen as,how to balance bias and variance in the estimation of w (·,·).We would like to argue that,as in nonparametric statistics,estimating w (·,·)with-out prior prejudices on its structure is as important an exploratory step in this context as,using histograms in ordinary statistics.2.The linking of this framework to covariates depending on vertice or edge identity is crucial,permitting relationship strength to be assessed as a function of vector variables.3.The links of our approach to spectral graph clustering and more generally clustering on the basis of similarities seem intriguing.ACKNOWLEDGMENTS.We thank Tin K Ho for help in obtaining the PBX data and for helpful discussions.We also thank the referees,whose references and comments improved this article immeasurably.1.Doreian P ,Batagelj V,Ferligoj A (2005)Generalized Blockmodeling (Cambridge UnivPress,Cambridge,UK).2.Airoldi EM,Blei DM,Fienberg SE,Xing XP (2008)Mixed-membership stochasticblockmodels.J Machine Learning Res 9:1981–2014.3.Erdös P ,Rényi A (1960)On the evolution of random graphs.Publ Math Inst HungarAcad Sci 5:17–61.4.Bollobas B,Janson S,Riordan O (2007)The phase transition in inhomogeneous randomgraphs.Random Struct Algorithms 31:3–122.5.Zhao Y ,et al.(2009)Botgraph:Large scale spamming botnet detection.Proceedingsof the 6th USENIX Symposium on Networked Systems Design and Implementation (USENIX,Berkeley,CA),pp 321–334.6.Newman MEJ,Girvan M (2004)Finding and evaluating community structure innetworks.Phys Rev E 69:026113.7.Guimera R,Amaral LAN (2005)Functional cartography of complex metabolic net-works.Nature 433:895–900.8.Chung FRK,Lu L (2006)Complex Graphs and Networks .CBMS Regional ConferenceSeries in Mathematics (Am Math Soc,Providence,RI).9.Kallenberg O (2005)Probabilistic symmetries and invariance principles.Probabilityand Its Application (Springer,New York).10.Holland PW,Laskey KB,Leinhardt S (1983)Stochastic blockmodels:First steps.SocNetworks 5:109–137.11.Snijders T,Nowicki K.(1997)Estimation and prediction for stochastic block-structuresfor graphs with latent block structure.J Classiﬁcation 14:75–100.12.Hoff PD (2008)Modeling homophily and stochastic equivalence in symmetric rela-tional data.Advances in Neural Information Processing Systems ,eds Platt J,Koller D,Roweis S (MIT Press,Cambridge,MA)Vol 20,pp 657–664.13.Diaconis P ,Janson S (2008)Graph limits and exchangeable random graphs.Rendicontidi Matematica 28:33–61.14.Hardy G,Littlewood J,Polya G (1988)Inequalities .(Cambridge Univ Press,Cambridge,UK),2nd Ed.15.Newman MEJ,Leicht EA (2007)Mixture models and exploratory analysis in networks.Proc Natl Acad Sci USA 104:9564–9569.16.Newman MEJ (2006)Finding community structure in networks using the eigenvectorsof matrices.Phys Rev E 74:036104.17.Fortunato S,Barthélemy M (2007)Resolution limit in community detection.Proc NatlAcad Sci USA 104:36–41.18.Ng AY ,Jordan MI,Weiss Y (2001)On spectral clustering:Analysis and an algorithm.Advances in Neural Information Processing Systems (MIT Press,Cambridge,MA)Vol 14,pp 849–856.19.Stephens M (2000)Dealing with label-switching in mixture models.J R Stat Soc B62:795–809.20.Zachary W (1977)An information ﬂow model for conﬂict and ﬁssion in small groups.J Anthropol Res 33:452–473.21.Rosvall M,Bergstrom C (2007)An information-theoretic framework for resolv-ing community structure in complex network.Proc Natl Acad Sci USA 104:7327–7331.Bickel and Chen PNAS December 15,2009vol.106no.5021073。

2022-2023学年粤教版(2019)必修2高一(下)综合信息技术试卷+答案解析(附后)

2022-2023学年粤教版（2019）必修2高一（下）综合信息技术试卷1. 2020年底，工信部特地为了老年人公布了首批适老化和无障碍改造App名单。

“适老版”的App的推出，是为了减少信息系统局限性中的（）A. 对外部环境有依赖性B. 本身具有安全隐患C. 由于技术门槛可能加剧数字鸿沟D. 数字化与网络化不够全面2. CNNIC发布的第48次《中国互联网络发展状况统计报告》显示网络直播与“吃住行游购娱”紧密结合，展现出了一种新的生活方式，这主要体现的信息社会特征是（）A. 数字生活B. 信息经济C. 在线政府D. 网络社会3. 下列关于信息系统和信息社会的说法，不正确的是（）A. 信息系统缩写APPB. 信息系统是人机交互系统C. 在信息系统中，数据一般存储在数据库里D. 信息社会指数越高表明信息社会发展水平越高4. Adobe Photoshop 属于（）A. 系统软件B. 杀毒软件C. 应用软件D. 教学软件5. 下列属于搭建信息系统的前期准备过程的是（）A. 需求分析→可行性分析→硬件选择→系统测试设计→详细设计B. 需求分析→可行性分析→开发模式选择→概要设计→详细设计C. 数据收集和输入→程序设计→硬件选择→详细设计→数据查询设计D. 数据收集和输入→数据存储→数据传输→数据加工处理→数据查询设计6. 共享单车大大方便了市民的出行，如图是共享单车系统的示意图，依据此图下列说法的正确的是（）A. 因无人监管，用户可以随意停车而不会被发现B. 在偏僻的地方为便于自己再次租车，可以用链条锁将车锁上C. 因没有管理员值班收费，用户可以偷逃费用而不被发现D. 用户可以通过软件实时了解周边的租车情况7. 下列关于信息社会的说法，不正确的是（）A. 信息社会是以人为本的B. 信息社会是可持续发展的C. 信息社会是以信息和知识作为重要资源的D. 信息社会最重要的竞争是高科技技术8. 在物流快递行业中，收件员使用移动智能终端，通过扫描快件条码的方式，将运单信息通过模块直接传输到后台服务器，同时可实现相关业务信息的查询等功能。

基于学术博客的知识交流研究.

收稿日期:2011-04-15㊀㊀㊀㊀修回日期:2011-05-23基金项目:国家大学生创新性实验资助项目 2010年华中师范大学大学生创新性实验重点项目(国家级) (编号:101051135)㊂作者简介:谢佳琳(1991-),女,本科,研究方向:电子商务;覃㊀鹤(1990-),女,本科,研究方向:电子商务㊂㊃知识管理㊃基于学术博客的知识交流研究谢佳琳㊀覃㊀鹤(华中师范大学信息管理系㊀武汉㊀430079)摘㊀要㊀以学术博客知识交流作为研究对象,阐述了学术博客的知识交流的整体过程及其主要步骤,包括知识转移㊁知识共享和知识创新㊂针对学术博客知识交流的特性重点分析它相对于传统知识交流方式的突破与缺陷,总结得出二者将长期保持互补共存㊁共同发展的关系,并为学术博客今后的发展提出相应的改进方向,促进知识在使用者之间的传播和交流㊂关键词㊀学术博客㊀知识交流㊀知识转移㊀知识共享中图分类号㊀G203㊀㊀㊀㊀㊀文献标识码㊀A㊀㊀㊀㊀㊀㊀文章编号㊀1002-1965(2011)08-0159-04Studies on the Knowledge Exchange Based on Academic BlogXIE Jialin ㊀QIN He(Department of Information Management ,Central China Normal University ,Wuhan ㊀430079)Abstract ㊀In order to further improve the academic communication between bloggers ,the paper chooses the knowledge exchange which is based on academic blog as the research object.First ,the overall process and main steps of knowledge exchange is given.Then ,focusing on the superiority and disadvantage comparing with the traditional way ,the paper concludes that the relationship of the traditional knowl-edge exchange mode and blog mode will be complementary and coexisting in a long -term ,and points out the corresponding improvement direction in the end.Keywords ㊀academic blog ㊀knowledge exchange ㊀knowledge transfer ㊀knowledge sharing0㊀引㊀言随着网络技术的发展,博客成为继E -mail ㊁BBS ㊁ICQ 之后出现的第四种网络交流方式,并以一种前所未有的速度渗透到社会的各个领域和角落㊂‘第26次中国互联网发展状况统计报告“显示,截至2010年6月,我国使用博客的用户规模扩大到2.31亿[1]㊂‘中国博客宣言“认为博客的出现,标志着以信息共享为特征的第一代门户之后,追求思想共享的第二代门户正在浮现,互联网开始真正凸显无穷的知识价值 [2]㊂博客具备链接㊁发布㊁评论㊁访问和订阅等功能,具有积极的知识价值,更有利于个人对于知识进行管理和交流㊂目前,一些论文已经将博客作为引用信息的来源,也有学者将博客作为发表学术观点的平台,也有图书馆通过博客提供参考服务㊂如此,学术博客作为新型的学术交流模型便应运而生㊂目前针对学术博客本身的研究相对较少,在国外的研究中,学术博客的概念还不清楚,相应的研究内容也比较含糊㊂总体上对学术博客的研究主要集中在学术博客的语言特征㊁学术质量㊁交流动机和链接分析上[3]㊂但关于学术博客的知识交流方式的研究更为少见,本文将从知识管理的角度,重点帮助了解学术博客的知识交流整体过程以及其中的具体交流步骤㊁评价基于学术博客的知识交流模式的优点和劣势㊂旨在通过对学术博客的知识交流方式的研究来明确学术博客对传统知识交流方式的延伸和发展,以及二者互补共存的关系,从而使学术博客能在知识交流过程中保持自身交流优势,与传统的知识交流方式相互补充以得到最大的发展㊂同时也为将来对学术博客改进的研究提供理论基础和方向㊂1㊀基于学术博客的知识交流过程从人类的交流历史看,非正式交流一直发挥着正式交流无法替代的作用,特别是网络信息交流过程中第30卷㊀第8期2011年8月㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀情㊀报㊀杂㊀志JOURNAL OF INTELLIGENCE ㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀Vol.30㊀No.8Aug.㊀2011传统信息交流和网络交流的融合,博客的出现正是人际交流在互联网上的一种延伸[4]㊂学术博客中的交流是一种自发性的交流,是利用网络时代新生的信息传递技术与其他博主进行的信息互动㊂整个学术博客的知识交流过程描述为,首先用户由于对知识的需求而受到驱动,引发用户诸如搜索㊁浏览和询问等信息搜寻行为,在这个过程中,发生了知识的转移[5]㊂知识来回转移的结果是形成了用户自己的知识库,同时由于这种不停的开发性存取达到知识的共享,最终目的是实现知识的再开发和创新㊂本文将引用和修改胡平昌教授在2008年发表的‘学术博客中的创新知识转移“中对用户行为实现过程的图示图1㊀学术博客中知识交流的过程基于学术博客的知识交流过程,这是一种交互的过程,这种过程主要体现在博客用户在知识的生产者和知识的消费者之间进行转换,也就是知识转移的过程㊂学术博客的博主可以邀请相关领域的专家学者针对某一问题进行讨论,通过这种双向交流沟通来完成知识的共享,博主获得知识,根据自己新获取的知识加以筛选㊁过滤和融合,使得知识库中的知识得到深加工,从而到达知识创新㊂下面将对学术博客知识交流过程中知识转移㊁知识共享和知识创新这三个主要步骤作进一步的分析㊂㊀1.1㊀知识转移㊀美国技术和创新管理学家Teece 于1977年最早提出: 通过技术的国际转移能够帮助企业积累有价值的知识并促进技术扩散,从而缩小地区之间的技术差距㊂ [6]知识转移应用到不同的研究领域,对于知识转移的定义也不尽相同,但是其内涵不乏相通之处㊂本文中将学术博客中的知识转移行为定义如下:知识接受者为了缩短与知识拥有者之间的知识差距,借助某种信息传播途径(例如超链接和内容搜图2㊀基于学术博客的知识转移索等),进行知识的获取㊁整理后存入其知识库的过程(如图2所示)㊂知识转移的主体有知识的接受者和知识的拥有者,知识转移的客体是知识内容,知识转移的过程需要借助某种途径进行,知识转移的目的是利用知识来指导行为㊁进行知识创新㊂通常转移的主体双方,知识接受者和知识拥有者之间的关系类似于委托人与代理人的关系,而且双方的这种委托-代理关系是不断转换的,但知识总是从在某一领域拥有知识较多的一方转移到拥有知识较少的一方㊂a.知识拥有者获取知识㊂拥有较多知识的博主因对知识存在新的需求而受到驱动,通过日常生活实践㊁㊂例如通过图书馆数据库的搜索引擎检索自己所需要的文献资料㊂b.知识拥有者发布知识㊂由于知识的拥有者所获得的知识可能是他人的隐性知识或者是零散无序的零次信息,这就需要知识的拥有者基于自己的思维方式和理论基础将获得的知识转化为显性知识,并进行有意识的筛选和过滤㊂最后将显性化的知识存入博主自己的知识库中并以博客的形式进行发布,供该博客圈或者其他博客圈的用户进行知识的获取㊂c.知识接受者获取知识拥有者的知识㊂知识接受者通过学术博客的推荐链接或是相关链接等检索到知识拥有者的博文,并顺利从其博文中获得所需的知识,同时知识接受者会对这部分知识进行选择性吸收㊂d.知识接受者发布知识:知识接受者将获取的知识以博文的形式添加到知识接受者自己的知识库当中,供其他的博主进行浏览,进而发生更多的知识转移㊂㊀1.2㊀知识的共享㊀与知识转移相同,对于知识共享的涵义到目前为止学界尚无统一的定义㊂较为普遍的观点认为知识共享是个过程,各个知识主体传播和交换信息㊁想法㊁经验等显性知识和隐性知识,并相互转化和反复提炼,以使其产生协同价值,从而提高知识个体的创新能力和适应能力[7]㊂Hendriks 曾指出,知识共享是一种沟通的过程,只是不像商品可以自由传送,向他人学习的时候,必须有重建的行为,必须具有知识去学习㊁共享他人的知识㊂知识共享包括两个过程:知识拥有者外化知识和知识需求者内化知识[8]㊂本文较为支持上述这种观点㊂在知识交流过程中,知识的积累㊁转移㊁共享和创新都是知识管理的基础,而只有知识共㊃061㊃㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀情㊀报㊀杂㊀志㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀第30卷享才能使知识创造价值[9]㊂学术博客的博主只有通过共享其观点和看法才能供其他浏览者阅读和评论进而发表自己的观点㊂学术博客的每一个用户都是一个开放的主体,个人不再是置身于互联网之外的个体,而是具有很强身份标识的网络节点,且允许这些个体将其内容进行公开㊂不同的开放主体在网络中互联,形成以人为中心的有不同主题的学术博客圈,在某个博客圈中,个体就某个主题分享信息资源,互相切磋学习心得,形成一种非正式制度下自发建立与协调的知识共享机制,这样一种机制使个体之间容易相互信任,从而形成鼓励共享的文化范围,提高了知识共享效率㊂㊀1.3㊀知识创新㊀基于学术博客的知识创新过程是指将既有知识库中的知识转化为目标知识的过程,是对知识的一种质的改善㊂知识以显性和隐性两种形式存在,隐性知识根植于个人的内心世界,它源于个人的经历,体现在其行为㊁世界观㊁价值观和情感之中,它是知识创新中最为基础性的,具有很强的抽象性和个性特征,并且往往很难被以某种方式表达出来,因此这种形态的知识很难被交流和传递㊂显性知识是在对待某个具体问题上所采用和体现出来的知识[10]㊂笔者认为,知识创新的本质就是通过隐性知识和显性知识之间螺旋向上的相互转化㊁往复循环的过程㊂知识创新在扩张个人知识数量的同时,也持续地改善个人的知识质量,最终将使个人的知识广度和知识深度获得可持续发展㊂2㊀学术博客对传统知识交流方式的突破传统的知识交流可以通过正式的和非正式两个渠道,相对而言正式交流渠道占有较大的分量㊂正式的交流渠道包括:同行专家评审的期刊论文㊁正规的学术会议,文摘索引等㊂整体上,传统的知识交流方式可以被描述为:作者创作作品,出版社根据市场的需求等因素对这些作品进行选择性印刷出版,然后通过书店得以在市场上传播和流通,图书馆等信息机构会对文献进行选择性收藏,读者可以从书店进行购买或者到图书馆进行借阅(如图3所示)㊂图3㊀传统的知识交流方式传统的知识交流方式是学术交流的一种重要途径,但是它的交流周期过长,知识传递效率较低,交流成本较高,并且有时间和空间的限制㊂学术博客所具有的知识交流特性在一定程度上弥补了传统知识交流方式的缺陷,同时它也是对传统知识交流方式的补充和突破㊂学术博客和传统知识交流方式相结合,共同发展将为学术交流的发展做出贡献㊂㊀2.1㊀知识交流的相对开放㊀传统的知识交流过程中,读者是通过到书店购买作品或者通过图书馆借阅作品来获得知识,即读者获得知识是要付出成本的,同时传统知识交流会受限于其繁琐㊁缓慢的交流环节,这样就限制了知识的传播范围和速度㊂但是学术博客交流的开放性打破了价格障碍,实现了博客的免费申请和信息的免费发布,这也是学术博客最显著的特点㊂绝大部分的博客都是向公众免费开放的,博主发布的信息或者资料可供其他用户免费浏览㊁复制和下载㊂这样极大的提高信息和知识的传播速度和影响范围,保证了知识共享的可行性㊂另一方面,学术博客用户在某一博客圈的地位很大程度上是由其对知识的奉献程度所决定的,由于这样一种利益驱动使得博主们愿意将自己所拥有的最有价值的知识贡献出来,所以对知识的隐藏概率越低,知识共享的障碍越小,学术知识传播也就更加自由㊂㊀2.2㊀从一对多到多对多的知识交流方式㊀传统的知识交流方式是一对多㊂从传统知识交流过程可知:作品从创作出来到被读者接收利用,要经过出版社出版发行㊁图书馆等文献收藏机构的收藏和组织㊂然而,这样的单向封闭的交流方式使得读者因为对作品的理解无法与作者进行面对面的交流而造成对作品误读,很大程度上影响了知识交流的丰富性㊂同时由于交流环节的繁杂和漫长,影响了学术资源的新颖性㊂学术博客是基于网络平台的,具有即时性,方便操作㊂用户将其文章进行发表,允许任何人进行自由阅读评论,以及由该文章主题所引起一系列与其相关知识领域的交流㊂在评论区经常出现对评论进行再评论的现象,例如博主对于读者评论的回复㊁读者对于其他读者的回复,这就是学术博客多对多的交流方式,这是博客传播能力和交流能力的延伸[11]㊂由于不同博客圈中的评论者对于同一问题关注重点是不同的,所以讨论的方向也会分为不同的小组㊂即博文在被读者评论后,将会引发更加激烈的,形成学术博客这种多对多的交流特性,这样就增强了学术博客的传播能力㊁丰富知识交流内容,以及启发学术灵感㊂3㊀思考与总结学术博客以其开放自由的交流环境㊁多对多的交互方式,以及链接㊁评论和订阅等强大的基本功能吸㊃161㊃㊀第8期㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀谢佳琳,等:基于学术博客的知识交流研究引了越来越多的学者参加,成为传统知识交流方式的重要补充,并与它共同发展㊂要引起注意的是,学术博客的这些特点为其带来优势的同时,也为其带来了不足与缺陷㊂例如,因为学术博客的版权很难在法律上进行界定,所以开放自由的发布和转载会很可能会引发知识产权问题;同时,频繁的互动交流也会造成信息的冗余㊁信息质量不高等问题㊂这些都需要我们在今后学术博客发展过程中对学术博客技术和互联网政策法规进行不断的完善㊂然而,传统的知识交流方式虽然存在交流周期过长㊁交流成本较高等缺点,但是其正规㊁严谨㊁力求真实的知识交流理念使它在人类知识交流历史上仍具有不可替代的重要作用㊂且传统的知识交流是基于传统的载体和媒介进行的,更有利于深层次的阅读和思考,满足知识交流对于内容的真实性和可靠性的要求,这是学术博客无法模仿的㊂在基于网络进行的知识交流方式盛行的今天,形成了一种以传统的知识交流方式为主,学术博客为辅的新型知识交流形态:传统的知识交流方式保证了知识交流内容的严谨和可靠,学术博客则弥补了传统知识交流方式的不足,使知识交流更加方便和快捷,保证了作品的新颖性以及读者对作品内容理解的准确性㊂通过这样一种新型的知识交流方式,人类对知识的需求获得更大程度满足的同时付出更少的成本㊂本文通过对学术博客的知识交流过程的研究,根据学术博客相对与传统知识交流方式存在的缺陷,我们提出从技术(如根据其交流特性确定其链接结构)和法律(如互联网著作权法)这两个方向同时进行改进,使得学术博客和传统知识交流模式更加契合,知识交流更加方便和高效㊂本文虽然指出了基于学术博客的知识交流的改进方向,但是并没有提出具体的解决方向㊂所以规范学术博客写作㊁妥善解决侵权风险等问题仍是目前学术博客知识交流过程中需要面临的问题㊂同时文章对于知识交流的具体步骤分析较为概括,并未对其进行深入的分析,有待改进㊂参考文献[1]㊀2010年7月CNNIC中国互联网发展统计报告[EB].http://[2]㊀李墨珺.博客质量的评价及其对学术交流的影响[J].情报资料工作,2008(2):61[3]㊀史新艳,肖仙桃.国外学术博客研究进展与趋势[J].情报资料工作,2010(2):107-108[4]㊀江㊀亮.学术博客的"无形学院"交流模式探析[J].情报科学,2006,24(2):276[5]㊀胡昌平,佘晶晶,等.学术博客中的创新知识转移[J].情报杂志,2008,27(5):3[6]㊀Teece D.Technonlogy Transfer by Multinational Firms:the Re-source Cost of Tansferring Technological Know-how[J].The E-conomic Journal,1997(87):242-261[7]㊀樊㊀斌.基于知识共享二维空间的隐性知识共享激励机制模型研究[A].第五届软科学国际研讨会论文集[C],2008:123 -124[8]㊀Hendriks P.Why Share Knowledge?The Influence of ICT on theMotivation for Knowledge Sharing[J].Knowledge and Process Management,1999(2):91-100[9]㊀燕㊀辉.知识博客与知识管理的差异探析[J].情报资料工作,2005(2):22[10]邱均平,段宇锋.论知识管理与知识创新[J].中国图书馆学报,1999(3):9-10[11]史新艳,肖仙桃.学术博客链接结构及其交流特性分析[J].图书情报知识,2009(5):81-83(责编:王平军)㊃261㊃㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀情㊀报㊀杂㊀志㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀第30卷。

Ch4 信号发送与信息甄别

26
4.3.1
工资与工龄正相关
即使在考虑了人力资本积累效应之后，工
资与工龄正相关现象依然存在
信息甄别：
工龄工资成为筛选有意长期工作者的信息甄别
机制
2014年7月31日8时17分
27
4.3.2 企业进入阻挠
在位者通过发送信号对潜在的进入加以阻
挠
在位者的生产效率（或单位成本）是私人信息通过发送高产量信号对潜在的进入构成阻挠
33
w 2 高能力者 C D
最高教育程度要求
高于
，那么高能力者将会放弃发送信号。
1
A
B
o
1
* s2
=2
s
2014年7月31日8时17分
10
4.1.3
分离均衡
与完全信息的情况作比较
高能力者需要花费一定数量的教育成本完全信息解显然要帕累托优于不完全信息下的
分离均衡解
与没有信号发送机制做比较
信息甄别机制中分离均衡是存在的
预期均衡（anticipatory equilibrium）
信息甄别机制下混同均衡也是可以成立的
2014年7月31日8时17分
25
4.3
应用
信号发送
劳动力市场经理人市场律师的市场
信息甄别
不同的劳动报酬机制汽车保险市场
2014年7月31日8时17分
高能力者接受足够的教育才能证明自己是高能力的，否则低能力者也会把自己伪装成高能力者
信号起作用的关键原因是高能力者能更轻
松地获得文凭
2014年7月31日8时17分
3
4.1.1 模型设定
劳动力选择受教育程度s 企业决定工资方案w(s) 在均衡状态下

参阅信息2011（25）

参阅信息2011（25）第一篇：参阅信息2011(25)参阅信息2011年第25期（总第319期）总经理工作部2011年7月29日【华能】1.华能集团将投60亿元建设“疆电东送”电源项目7月23日，华能集团公司总投资60亿元的哈密工业园2×66万千瓦电厂项目通过评审。

项目预计2012年4月开工，2014年10月投产后将成为“疆电东送”的主要支撑电源。

该项目将采用超临界燃煤空冷机组，比常规湿冷机组节水80%，采用哈密市污水处理厂的再生水作为生产水源。

项目投产后将通过直流外送至华中电网，在华中地区消纳。

2.2011年华能集团部门副主任级岗位公开竞聘考试阶段结束7月23日，2011年华能集团公司部门副主任级岗位公开竞聘面试圆满结束，标志着此次公开竞聘考试阶段工作已全部完成。

在两天半的时间内，62名考官组成24个考官组，分别对120名考生进行了面试。

每个岗位的面试考官由7人组成，其中集团公司考官3人、用人单位考官1人、系统内专家代表2人、外请专家1人。

考生在40分钟的面试时间内，进行了个人陈述、命题回答和自由提问回答等环节的测试，随后由考官在现场进行独立打分，华能集团公司监察部全过程参与监督。

【华电】1.华电“华衡166”轮命名暨交接仪式举行7月26日，华电煤业华远星海运有限公司首艘新建散货船“华衡166”轮命名暨交接仪式举行。

“华衡166”轮是华远星海运有限公司第一艘新造船舶，轮总长189.99米，型宽32.26 米，型深18米，载重量56841吨，于2010年7月7日开工建造，2011年3月16日顺利下水，6月13日成功试航。

“华衡166”1轮交付华远星公司后将立即投入商业运营，进一步提升华电集团下水煤运输和自产煤炭外运的保障能力。

2.华电云南石龙坝水电博物馆获准国家级注册博物馆近日，云南石龙坝电站获得云南省文物局批准，成为国有行业注册博物馆。

石龙坝电站是云南第一座水力发电站，同时也是中国大地上建成的第一个水力发电站，于1910年8月21日正式开工，到1912年5月28日建成发电，被称为“中国水电的鼻祖”。

6yue

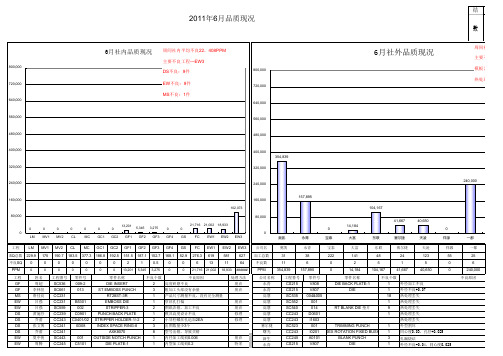
LATE-1
LATE-2
LATE-3
K PLATE-2 INSERT-1
E INSERT-3
NK DIE-2
NT DIE
OSS DIE
RING
OCK
K PLATE-6
PPER-1
22408 B5201
出图数量少3个 AXK8070 OUTSIDE NOTCH PUNCH DIE PLATE-1 DIE PLATE-2 DIE PLATE-3 DIE BACK PLATE-2 DIE PLATE INSERT-3 PUNCH INSERT-1 RT BLANK DIE-2 COUNT DIE EMBOSS DIE SPRING BLOCK UP BACK PLATE-6 STRIPPER-1 8 1 1 1 1 1 1 2 1 1 1 8 1 1 1 型号出错，导致买错内径加工线痕0.006 内型加工线痕0.2 SLOT DIE固定部内径+0.03~0.04 孔位置设计不良孔位置设计不良孔位置设计不良 EW孔位置不良开料时外型割坏穿丝孔打偏穿丝孔打偏弹簧型号放错高度尺寸磨小0.5 没有让位孔一个销钉加工+0.02
公司名称永青永青高慧高慧高慧高慧高慧赛尔捷曙光
工程番号 CS215 CS215 SC535 SC552 SC540 CC243 CC243 SC523 CC243
零件号 V808 V807 004&005 001 014 D0601 I1603 001
零件名称 DIE BACK PLATE-1 DIE
0
MV1 175 0
0
MV2 190.7 0
0
CL 183.5 0
0
MC 377.3 0

2024年上半年自考试00662新闻事业管理部分真题含解析

2024年上半年自考试00662新闻事业管理部分真题一、单项选择题1、评判品牌格言有三个标准，其中第一个标准是______。

A．表述简单B．表达明确C．富有启发D．富有激情2、资产是经济资源，首先要具有______。

A．排他性B．可估价性C．收益性D．资源性3、报纸因刊载虚假、失实报道而发表的更正或者答辩，应当自虛假、失实报道发现或者当事人要求之日起，发表在______。

A．随意一期报纸的版面上B．最近出版一期的报纸的随意版面上C．随意一期报纸的相同版面上D．最近出版一期的报纸的相同版面上4、菲利普·科特勒等认为，最优市场份额为______。

A．30%B．50%C．70%D．90%5、在新闻媒体成本控制的关键环节中，强调公开采购的环节是______。

A．预算环节B．生产环节C．财务环节D．评估环节6、假如用开车来形象概括人力资源管理的工作，则汽车的方向盘是______。

A．薪酬福利B．人力资源规划C．培训和开发D．绩效管理7、广播电视台的设立必须占用特定的______。

A．频率资源B．社会资源C．政府资源D．媒体资源8、1987年开始自办发行并引发了我国报刊发行“二渠道”现象的报纸是______。

A．《洛阳日报》B．《扬子晚报》C．《南方日报》D．《新民晚报》9、衡量媒体广告投放性价比的最常用指标是______。

A．十人成本B．百人成本C．千人成本D．万人成本10、电视台和广播电台运营模式表现为制播一体和______。

A．编采合一B．编采分离C．制播分离D．部版合一11、编辑选稿的主要依据是______。

A．行业惯例B．新闻价值C．媒体定位D．社会规范12、根据我国的有关规定，禁止外资进入的渠道经营是______。

A．报刊发行B．图书连锁经营C．电子出版物发行D．电视台经营13、分析财务报表，第一步应该分析报表的文字部分，其中首先应该阅读______。

A．财务报告摘要B．会计报表附注C．财务情况说明书D．注册会计师的审计报告14、我国广播电视业目前执行的是______。

今日舆情2011-6-10

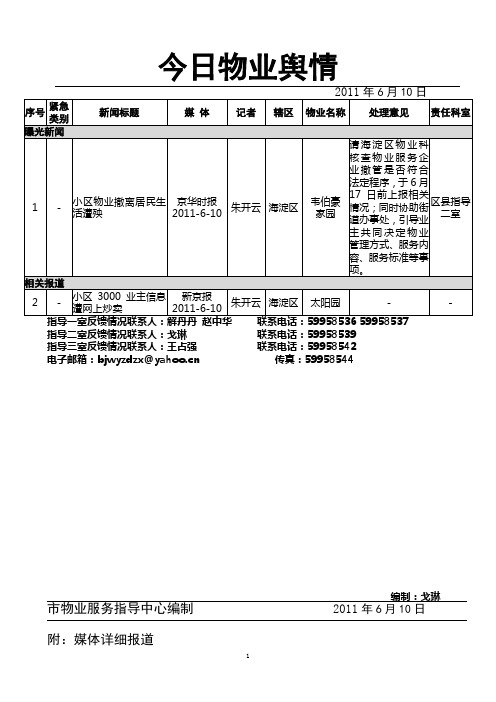
今日物业舆情2011年6月10日指导二室反馈情况联系人：戈琳联系电话：59958539指导三室反馈情况联系人：王占强联系电话：59958542电子邮箱：bjwyzdzx@ 传真：59958544编制：戈琳市物业服务指导中心编制 2011年6月10日附：媒体详细报道1.小区物业撤离居民生活遭殃京华时报海淀区“小区已经几天没热水了，垃圾也没人清扫，门口也没有保安。

”昨天，业主张女士无奈地说。

由于合同到期，6月5日晚24时，海淀区韦伯豪家园小区物业宣布撤离小区，致使小区混乱不堪。

昨天下午，记者在韦伯豪家园看到，小区门口堆了一大堆垃圾无人清扫，小区内塑料袋乱飞，楼道内阳台处也被垃圾占据。

居民称，从6月6日开始，小区的安保、保洁、热水等物业服务均陷入瘫痪状态。

在小区的公告栏处，张贴了物业撤出小区的通知。

通知称，物业公司决定2011年6月5日24时撤出物业服务。

物业经理胡女士称，物业撤出小区是无奈之举，物业服务合同已于2010年12月31日到期，按合同规定，在新物业没入驻之前，老物业需顺延3个月的物业服务。

但到现在新物业仍未入驻，胡经理称，他们一直在无合同保护的情况下为小区服务。

胡经理介绍，业委会已经向物业发出通知，决定不再与其续约。

胡经理说小区共有1009户，目前物业费、供暖费还有1069万未缴纳。

记者昨天下午来到小区业委会，大门紧锁，没有值班人员，业委会5人的电话均无法接通。

韦伯豪社区居委会主任表示，韦伯豪家园小区的真正业主不到一半，大多为租户，因此业主大会一直无法顺利召开。

因业主数额不够无法授权业委会，也就无法招标新的物业并签合同。

紫竹院街道居民科负责人表示，街道也一直在跟业委会和物业协商，并表示将实施临时应急措施，解决居民困境。

2.小区3000业主信息遭网上炒卖新京报海淀区昨日，一男子在赶集网千元叫卖海淀区太阳园3000户业主资料。

资料涉及业主手机号、房屋面积、车牌号等。

该男子称资料来源于他曾工作的物业。

河南省高中信息技术会考网络技术精选资料

选择试题集【第1题】下列叙述中，正确的是（C）。

A. 只要浏览网页就一定会感染病毒B. 计算机病毒不及时处理，可以危害人的身心健康C. 计算机病毒能够自我复制并具有传染性D. 只要电脑没有连入因特网，病毒就不会感染电脑【第2题】某台计算机的IP地址为202.168.9.36，子网掩码为255.255.255.0。

下列选项中，网络地址与其相同的是（D）A. IP地址为202.168.10.10，子网掩码为255.255.255.0B. IP地址为202.168.11.13，子网掩码为255.255.255.0C. IP地址为202.168.12.56，子网掩码为255.255.255.0D. IP地址为202.168.9.37，子网掩码为255.255.255.0【第3题】下列选项中，不属于网络连接设备的是（C）。

A. 集线器B. 交换机C. 同轴电缆D. 中继器【第4题】下列IP地址属于A类地址的是（A）。

A. 127.16.5.89B. 201.168.0.89C. 172.16.0.89D. 191.168.0.89【第5题】英文缩写DNS的中文意思是（A）。

A. 域名系统B. 统一资源定位器C. 调制解调器D. 中央处理器【第6题】在因特网中全文搜索引擎的工作过程如下，正确的顺序是（A）。

（1）返回查询结果给用户（2）从网上“抓取”网页（3）建立索引数据库（4）根据用户输入的条件在索引数据库中搜索排序A. （2）（3）（4）（1）B. （1）（2）（4）（3）C. （3）（2）（4）（1）D. （1）（2）（3）（4）【第7题】子网掩码是255.255.255.0的局域网，实际可用的IP地址数量是（A）。

A. 254B. 65534C. 128D. 1【第8题】某学校利用交换机和路由器将三个机房的计算机组成网络，这个网络属于（C）。

A. 家庭网B. 城域网C. 局域网D. 广域网【第9题】通过一台交换机连接的3台计算机组成的网络属于（B）。