第4章平面电磁波

合集下载

平面电磁波

例如铜：
f 1MHz, c 66106 m
f 30GHz, c 0.38106 m
4.4 电磁波的极化

本节要点
极化线极化圆极化椭圆极化

1. 极化(polarization)
金属导体金属导体
导体上的感应电动势等于零
导体上的感应电动势最大
无耗媒质中电场、磁场与功率流
4.2 无限大导电媒质中的平面电磁波
本节要点
复介电常数导电媒质中的平面波色散及其对通信的影响

1.复介电常数(complex permittivity)

无限大导电媒质中复介电常数
~ 1 j
实部代表位移电流的贡献，不会引起能量消耗。
+z轴方向传播的均匀平面波 -z轴方向传播的均匀平面波
4. 均匀平面波的基本概念

如果电介质区无限延伸，则电场矢量可一般地表示为 E ax E0e jkz 时域表达式为 Ex z, t E0 cost kz 0
下面，我们对平面波进行较为详细的分析。

代表场的波动状态，称为电磁波的相位。它由三部分构成:
~ 将无耗媒质的相位常数及波阻抗中的均以来取代，即得导电媒质中的复相位常数为

~ ~ k j
~ 1 j
2 1 1 1 2 1 2
~ 1 j

2
2.导体中均匀平面电磁波
导体中均匀平面波的电磁场及平均坡印廷矢量为
Ex E0ez e jz
Hy
E0e z e jz e j / 4

电磁场-平面电磁波

入射波电场垂直于入射面（即垂直极化）
注:入射面即y=0的平面，不是分界面
将 H 分解为界面的切线 t 向，上下边界应相等
• .
• 联解（1）（2）得到菲涅耳公式（设μ1 = μ2=μ）
• 考虑到
在介质1中合成波场的分量为：
讨论： 1）场的每一个分量都有因子向传播，相位沿x方向变化。
，表示合成波也沿x方
第四章平面电磁波
无线广播，通讯的载波，激光器发出的激光，都接近正弦电磁波，称谐和波或单色场。
• 通常正弦电流用复数表示：
称为电场的 x（或y, z）分量的复振幅，复振幅和幅角都是坐标的函数
.
• 利用复指数后，场量对时间的偏导数变得简单。
。将复数表达式代入正弦电磁场情况下的麦克斯韦方程组得：
时称为理想导体。
• （3）0.01 < < 100 称半导体， • 半导体材料对传导电流和位移电流都必须考虑。
• .注意: 某种材料是导体还是绝缘体或半导体，
• 不但与ζ 还与工作频率 ω有关。 • 例铜的电导率ζ =5 .7x 107 S/m , 在光频以下为良导体 • 对 x射线（设波长为0.1nm）, 铜却不是良导体。
电场瞬时值表达式：
为沿 -z 方向传播的平面波
电磁波的极化
• 平面电磁波是横波，它的 E矢量可以在垂直于传播方向（波矢 K 的方向）的任意方向振动，如果在垂直于传播方向的平面内，E 的振动限于某一固定的方向，则称为线偏振或平面偏振，E 的振动方向称为偏振方向或极化方向。 • 沿z轴方向传播的电磁波的电场矢量E 可以分解为两个互相正交的分量Ex , Ey 它们的振幅分别为 E1、 E2，相位差为φ=φ1-φ2
• .良导体的条件

在自由空间传播的均匀平面电磁波

在自由空间传播的均匀平面电磁波（空间中没有自由电荷，没有传导电流），电场和磁场都没有和波传播方向平行的分量，都和传播方向垂直。

此时，电矢量E，磁矢量H和传播方向k两两垂直。

只是在这种情况下，才可以说电磁波是横波。

沿一定途径（比如说波导）传播的电磁波为导行电磁波。

根据麦克斯韦方程，导行电磁波在传播方向上一般是有E和H分量的。

光的传播形态分类：根据传播方向上有无电场分量或磁场分量，可分为如下三类，任何光都可以这三种波的合成形式表示出来。

1、TEM波：在传播方向上没有电场和磁场分量，称为横电磁波。

若激光在谐振腔中的传播方向为z方向，那么激光的电场和磁场将没有ｚ方向的分量！实际的激光模式是准TEM模，即允许Ez、Hz分量的存在，但它们必须<<横向分量，因为较大的Ez意味着波矢方向偏离光轴较大，容易溢出腔外，所以损耗大，难于形成振荡。

2、TE波(即是物光里的s波)：在传播方向上有磁场分量但无电场分量，称为横电波。

在平面光波导(封闭腔结构)中，电磁场分量有Ey, Hx, Hz，传播方向为ｚ方向。

3、TM波(即是物光里的p波)：在传播方向上有电场分量而无磁场分量，称为横磁波。

在平面光波导(封闭腔结构)中，电磁场分量有Hy, Ex, Ez，传播方向为ｚ方向。

微波工程、电磁场理论等课程中有关于TEM、TE、TM模的更为详细的描述。

电动力学复习总结第四章电磁波的传播2012答案

第四章电磁波的传播一、填空题1、色散现象是指介质的( )是频率的函数. 答案：,εμ2、平面电磁波能流密度s 和能量密度w 的关系为( )。

答案：S wv =3、平面电磁波在导体中传播时,其振幅为( )。

答案：0x E e α-⋅ 。

6、 7、 9、的贡10、矩形波导中，能够传播的电磁波的截止频率=n m c ,,ω( )，当电磁波的频率ω满足( )时，该波不能在其中传播。

若b ＞a ，则最低截止频率为( )，该波的模式为( )。

答案： 22,,)()(b n a m n m c +=μεπω，ω＜n m c ,,ω，μεπb ，01TE11、全反射现象发生时,折射波沿( )方向传播.答案：平行于界面12、自然光从介质1(11με，)入射至介质2(22με，),当入射角等于( )时,反射波是完全偏振波.答案：201n i arctg n = 13、迅变电磁场中导体中的体电荷密度的变化规律是( ). 答案：0t e σερρ-= 1、）．均匀介质 B.真空中 C.导体内 D. A ．6、平面电磁波E 、B 、k 三个矢量的方向关系是（）A ．B E ⨯沿矢量k 方向 B. E B ⨯沿矢量k 方向C.B E ⨯的方向垂直于kD. k E ⨯的方向沿矢量B 的方向答案：A7、矩形波导管尺寸为b a ⨯ ,若b a >,则最低截止频率为（）A ．μεπa B. μεπb C. b a 11+μεπ D. a2μεπ 答案：A 8、亥姆霍兹方程220,(0)E k E E ∇+=∇⋅=对下列那种情况成立（） A ．真空中的一般电磁波 B. 自由空间中频率一定的电磁波C. 自由空间中频率一定的简谐电磁波D. 介质中的一般电磁波答案：C9、矩形波导管尺寸为b a ⨯ ,若b a >,则最低截止频率为（） 1、 21E E →∂-21B B →∂-表明：电场与磁场相互激发形成电磁波, 电磁波可以脱离场源而存在；222210E E B B v t ∂-⋅-⋅=∂ 一般随ω变化，存在色散（3）亥姆霍兹方程：(220,0E k E k E i B E ωεμω∇+==∇⋅==-∇⨯ 表示以一定频率按正弦规律变化的单色电磁波的基本方程，其每个解都代表一种可能存在的波模。

平面电磁波知识点

平面电磁波知识点电磁波是一种在空间中传播的波动现象，它由电场和磁场相互作用而产生。

平面电磁波作为电磁波的一种形式，具有特定的特性和应用。

本文将介绍平面电磁波的基本知识点，包括定义、特性、产生和传播、应用等内容。

一、平面电磁波的定义平面电磁波是指电场和磁场在空间中沿着一定方向传播的电磁波。

它的波动方向垂直于电场和磁场的传播方向，且电场和磁场的变化情况具有一定的关系。

平面电磁波包含了无线电波、微波、红外线、可见光、紫外线、X射线和γ射线等多个频段。

二、平面电磁波的特性1. 频率和波长：平面电磁波的频率和波长间存在确定的关系，即波长等于光速除以频率。

波长越短，频率越高，能量越大。

不同频段的电磁波对应着不同的波长和频率范围。

2. 周期和振幅：平面电磁波的周期指一个完整波形所经历的时间，振幅指波峰或波谷与波中心的距离。

波形的周期和振幅决定了平面电磁波的能量和强度。

3. 速度：平面电磁波在真空中的传播速度是一个恒定值，即真空中的光速。

它的数值约为299,792,458米每秒，通常记作c。

不同介质中的传播速度与光速有关，由该介质的折射率决定。

4. 方向性：平面电磁波的传播方向是垂直于电场和磁场方向的。

电场和磁场的方向彼此垂直，并且与传播方向形成右手定则。

三、平面电磁波的产生和传播1. 产生：平面电磁波可以通过加速带电粒子、振动电荷或电流等方式产生。

当带电粒子或电流经过加速、振动时，会产生电场和磁场的变化，从而产生平面电磁波。

2. 传播：平面电磁波的传播遵循麦克斯韦方程组。

根据这些方程，平面电磁波在真空中以光速传播，不受介质的影响。

当平面电磁波遇到介质时，会发生折射、反射或透射等现象，具体情况取决于介质的性质。

四、平面电磁波的应用1. 通信：平面电磁波广泛应用于无线通信领域。

不同频段的电磁波用于无线电、电视、手机、卫星通信等通信系统，实现声音、图像和数据的传输。

2. 医学：平面电磁波在医学诊断、治疗和影像技术中起到重要作用。

平面电磁波

1.正弦平面波在媒质分界面上的反射和折射规律
入射波
i
r
反射波
x
法 t 折射波线
1 1 2 2
z y
斯耐尔定律：
①入射线，反射线及折射线位于同一平面；
② 入射角 i 等于反射角 r ； ③ 折射角 t 与入射角 i 的关系为
sin i k2 sin t k1
k1 1 1
Ex Ex 0e jkz H y H y 0e jkz
写成瞬时形式为：
Ez ( z , t ) Ez 0 cos(t kz ) H y ( z , t ) H y 0 cos(t kz )
传播方向
理想介质中均匀平面波的电场和磁场
当 c 2 c1时，R<0，在分界面上电场为最小值，
磁场为最大值
三， ①导电媒质 (1，1，1 0) 对②导电煤
质 ( 2，2， 2 0) 的垂直入射
一区合成波：
E1 ex E (e
i x0
1z
Re )
1z
衰减
入射波，反射波在传播过程中都在衰减折射波在传播过程中也一样在衰减
则合成场强的大小为
E E E Em
2 x 2 y
合成场强的方向与x轴的夹角有如下关系:
tg Ey Ex sin(t kz y ) cos(t kz y ) tg (t kz y )
右旋圆极化：时间t越大，合成场强与x 轴的夹角越大，合成波矢量随着时间的旋转方向与
i x0
i x0
电磁波垂直入射到理想导体表面，电磁波产生全反射，第一煤质中的电磁波为驻波，具有驻波的性质！！
二，①为理想介质(1，1 ) ②为理想介质（ 2，2）

电动力学第四章电磁波的传播

第四章电磁波的传播讨论电磁场产生后在空间传播的情形和特性。

分三类情形讨论：一：平面电磁波在无界空间的传播问题二. 平面电磁波在分界面上的反射与透射问题；三.在有界空间传播 -导行电磁波第一部分平面电磁波在无界空间的传播问题讨论一般均匀平面电磁波和时谐电磁波在无界空间的传播问题1时变电磁场以电磁波的形式存在于时间和空间这个统一的物理世界。

2 研究某一具体情况下电磁波的激发和传播规律，从数学上讲就是求解在这具体条件下Maxwell equations 或 wave equations 的解。

3 在某些特定条件下，Maxwell equations或wave equations可以简化，从而导出简化的模型，如传输线模型、集中参数等效电路模型等等。

4最简单的电磁波是平面波。

等相面（波阵面）为无限大平面电磁波称为平面波。

如果平面波等相面上场强的幅度均匀不变，则称为均匀平面波。

5许多复杂的电磁波，如柱面波、球面波，可以分解为许多均匀平面波的叠加；反之亦然。

故均匀平面波是最简单最基本的电磁波模式，因此我们从均匀平面波开始电磁波的学习。

§4.1波动方程 (1)§4.2无界空间理想介质中的均匀平面电磁波 (4)§4.3 正弦均匀平面波在无限大均匀媒质中的传播 (7)4.1-4.3 总结 (13)§4.4电磁波的极化 (14)§4.5电磁波的色散与波速 (16)4.4-4.5 总结 (18)§4.1 波动方程本节主要容：研究各种介质情形下的电磁波波动方程。

学习要求： 1. 明确介质分类； 2. 理解和掌握波动方程推到思路 3. 分清楚、记清楚无界无源区理想介质和导电介质区波动方程和时谐场情形下理想介质和导电介质区波动方程4.1.1介质分类：电磁波在介质中传播，所以其波动方程一定要知道介质的电磁性质方程。

一般情况下，皆知的电磁性质方程很复杂，因为反应介质电磁性质的介电参数是量。

第四章电磁波的传播 §1. 平面电磁波§2. 电磁波在介质界面上的反射和折射§3. 有导体存在时电磁波的

知 H
E
较大，非铁磁
B
可取 = 0
(2) E k 在与 k 垂直平面上可将 E 分解成两个分量
(3) H k, 且 H E
(4)
nn ((EH22EH1)1
0 )0
即 Et E't E"t Ht H 't H"t
(5) ' ,
sin 2 sin " 1
(1 2 0 )
电磁波：迅变电磁场，导体内 = ？
电流：J
E
电荷：
E
/
,
J
E
J
0
t
t
J
,
d dt,
t
0e
t = 0 时，导体内 = 0 ，然后随 t 按指数衰减 t = 时，（ = / 特征时间） = 0 / e
导体内的自由电荷分布
t = 0 时，导体内 = 0 ，然后随 t 按指数衰减
o
y
x
平面电磁波的特性：（证明 see next page）
(1) 电磁波是横波， E k ， B k
(2) E B ， E B 沿 k 方向
(3) E 和 B同相，振幅比 E / B = v
平面电磁波
证明平面电磁波的特性
E 0
E
E0
ei
(
k
xt
)
E0
ei
( k xt
)i(k
E"
2 1 cos
2sin "cos
E 1 cos 2 cos" sin( ")
振幅关系 Fresnel 公式
(2) E || 入射面： (Ht H )

平面电磁波的能量传递

t V 2
2
(E H)dS
S
V Jc EdV
单位时间体积V中电磁能量的减少量
单位时间流出体积表面的电磁能量
欧姆功率损耗
可见：(E H) 为单位面积上的功率密度。
令： S E H ——坡印廷矢量：流出单位面积的功率密度。
3、坡印廷矢量
S E H ——流出单位面积的功率密度。
（1）瞬时坡印廷矢量
上式两边在给定的体积V内积分：
t
(1 E2 1 H 2)dV
V2
2
(E H)dV
V
V E JcdV
由高斯定律得： (E H)dV (E H) dS
V
S
(1E2 1 H2)dV
t V 2
2
(E H)dS
S
V E JcdV
——坡印廷定理
坡印廷定理：
(1 E2 1 H 2)dV
H 1.5cos(109t 5y)aˆ A/m x
H 1 . 5 e j5 y aˆ A / m x
(7) 媒质中的平均功率密度是
S av
1 2
Re[E
H *]
H * 1 . 5 e j 5 y aˆx
Sav
1 2
3771.5[aˆz
aˆx]
282.75aˆ
y
W/m2
A/m
小结：
6.4 平面电磁波的能量传递
1、平面波的能量 2、坡印廷定理 3、坡印廷矢量
1、均匀平面波的能量
电场能量密度:
we
1 2
E2
磁场能量密度:
wm
1 2
H 2
电磁场中任意体积V 内储存的总电磁能量为：
W

平面电磁波

第六章主平面电磁波要内容 9学时平面电磁波电磁波：变化的电磁场脱离场源后在空间的传播平面电磁波：等相位面为平面构成的电磁波均匀平面电磁波：等相位面上E、H 处处相等的电磁波若电磁波沿 x 轴方向传播，则H=H(x,t)，E=E(x,t) 平面电磁波知识结构框图电磁场基本方程组电磁波动方程均匀平面电磁波的传播特性平面电磁波的基本特性1. 理想介质中的均匀平面波 2. 损耗媒质中的均匀平面波 3. 均匀平面波的极化 4. 均匀平面波对平面边界的垂直入射 5. 均匀平面波对平面边界的斜入射 6. 各向异性媒质中的均匀平面波1-120 2-120理想介质中均匀平面波平面电磁波的极化导电媒质中均匀平面波平面电磁波的垂直入射平面电磁波的斜入射各向异性媒质中的均匀平面波x方向传播的一组均匀平面波3-120平面电磁波知识结构框图数的媒质， σ → ∞ 的媒质称为理想导体。

σ 介于两者之间的媒质称为有损耗媒质或导电媒质。

6.1 理想介质中的均匀平面波理想介质是指电导率 σ = 0 ，ε 、 μ 为实常6.1.1波动方程的解其通解为假设电磁场沿着 Z 轴方向传播，且电场仅有指向 X 轴的方向分量，则磁场必只有 Y 方向的分量，即：z z E x = f1 (t − ) + f 2 (t + ) v v ∂ 2 Ex + β 2 Ex = 0 ∂z 2对于时谐变电磁场：E = ex E x ( z, t )波动方程H = ey H y (z,t)其通解为则平面波是指波前面，即等相位面或者波前阵是平面的波。

均匀平面波是指波前面上场量振幅处处相等的波。

本节介绍最简单的情况，即介绍无源、均匀（homogeneous）（媒质参数与位置无关）、线性（linear）（媒质参数与场强大小无关）、各向同性（isotropic）（媒质参数与场强方向无关）的无限大理想介质中的时谐平面波。

4-120 5-120则∂E 2 =0 ∂t 2 ∂E 2 ∇ 2 E x − με 2x = 0 ∂t 2 ∂ E x 1 ∂E x2 − =0 ∂z 2 v 2 ∂t 2 ∇ 2 E − με其中： v =其中： β = ω μ εEx = Ex + e− jβ z + Ex − e+ jβ zE x = E x+ cos(ω t − β z ) + E x− cos(ω t + β z )对应的磁场为1∇ × E = −μ6-120με∂H ∂t∂H y ∂E x = −μ ∂z ∂t对应的磁场为∇ × E = −μ其通解为∂H ∂t∂H y ∂E x = −μ ∂z ∂t考察电场的一个分量，瞬时值表达式为：Ex ( z, t ) = Ex+ cos(ωt − β z + ϕx )其中Hy =β ⎡ E + cos(ω t − β z ) − E x− cos(ω t + β z ) ⎤ ⎦ ωμ ⎣ xωt 为时间相位， β z 为空间相位， ϕ x 是初始相位。

平面电磁波的性质要点

② 光波的分类（按矢量性）
自然光偏振光
部分偏振光各种光波电矢量振动示意图（时间平均意义上的）
1.3.3 电场波与磁场波的关系
由于 : k E k B k E 且 k k E B 1 c B B n
物理意义:
E和B之间的数值关系
① 电场的作用大于磁场的作用（讨论光与物质相互作用时）带电粒子受到的电场力：
Ex Ey Ex ( E ) z E y ' k x Ex ' k y x y x y
Ey
E k E
'
而(3)式右端的可写为：
' B k B t
'
B E t
(3)
得出: k E k B
I A' I A cos L I cos A A L与I , 有关系
入射光波接收面
同理，对于（4）式可以得出：
'
'
E B t
'
(5)
(4)
k B k E
k E k B
k B k E
(6)
(7)
(8)
证明： k , E , B 三个矢量是互相垂直，并组成右手坐标系。
对(5、６)式积分,并取积分的常数项为0，则有：
统计学的方法
I
1

0
E 20 x cos 2 (kz t 0 )dt
1 T E 20 x cos 2 (kz t 0 )dt T 0 1 E 20 x 2
物理意义：在均匀透明介质中，平面电磁波的强度（光强）正比于电场振幅的平方。

平面电磁波的性质要点

Div, Grad, Curl, and still more all The "Curl" of a vector function f : that
f f z f y f x f z f y f x , , y z z x x y
I S
1

② 光波的分类（按矢量性）
自然光偏振光
部分偏振光各种光波电矢量振动示意图（时间平均意义上的）
1.3.3 电场波与磁场波的关系
由于 : k E k B k E 且 k k E B 1 c B B n
物理意义:
E和B之间的数值关系
① 电场的作用大于磁场的作用（讨论光与物质相互作用时）带电粒子受到的电场力：
2
3
定义波印廷矢量S表示电磁波所传递的能流密度
定义: 单位时间内流过与波垂直的单位面积的能流量称为能流密度S。
S uV /( A Dt ) E 2 1

2 E
( J / s m2 )
能量流动具有方向性，所以定义了能流密度矢量：
1 S EB

V = A c Dt
Ex Ey Ex ( E ) z E y ' k x Ex ' k y x y x y
Ey
E k E
'
而(3)式右端的可写为：
' B k B t
'
B E t
(3)
得出: k E k B
1 1 2 3 u E D E ( J / m ) E 电场的能量密度 2 2 1 1 2 3 u H B B ( J / m ) 磁场的能量密度为 m 2 2

沿任意方向传播的平面电磁波

电磁波的重要性
电磁波在现代社会中发挥着至关重要的作用，它们是无线通信、卫星通信、导航、雷达和光谱分析等领域的基础。
电磁波的分类与特点
分类
传播速度
波动特性
能量与频率
穿透能力和吸收
电磁波可以根据频率、波长和传播方式等特征进行分类，如无线电波、微波、红外线、可见光、紫外线和X射线等。
电磁波在真空中的传播速度为光速，即每秒约 30万公里。
射角和反射角有关。
折射
当平面电磁波从一种介质进入另一种介质时，其传播方向会发生改变，这种现象称为折射。折射角与入射角和两种介质的折射率
有关。
散射
当平面电磁波遇到微小粒子或粗糙表面时，会向各个方向散射，这种现象称为散射。散射的程度取决于粒子的尺寸、形状和介质
的性质。
干涉与衍射现象
干涉
当两束或多束相干平面电磁波相遇时，它们会相互叠加，产生加强或减弱的现象，这种现象称为干涉。干涉是波动性质的一种表现，在通信、雷达和光学仪器等领域有广泛应用。
平面电磁波在电磁理论中占据重要地位，对于深入理解电磁波的传播特性、电磁场与物质的相互作用等基础问题具有重要意义。
应用领域
平面电磁波在通信、雷达、遥感、医学成像等领域具有广泛的应用，对于推动相关领域的技术进步和产业发展具有重要作用。
跨学科领域
平面电磁波的研究涉及到物理学、工程学、材料科学等多个学科领域，对于促进跨学科交流和合作具有积极意义。
04
平面波的传播特性
传播速度与介质关系
传播速度
平面电磁波在真空中的传播速度为光速，而在介质中的传播速度受介质折射率的影响，与介质折射率成反比。
介质影响
当平面电磁波从一种介质传播到另一种介质时，其传播方向会发生改变，这是因为不同介质的折射率不同。

电动力学第4章电磁波

x ex y e y z ez z ez .
（3.22）
显然，复波矢的实部和虚部一般不同向。
z x 这时导体中的平面电磁波的振幅函数为 E e E0e z , 0
可见，波的透射深度δ为导体中电磁波的相速度是
v 2 2 x z 2
导电流引起。如果引入“复电容率” i ,

（3.10）
式 H i E E 变为 H i E ,
这样，导体中的麦克斯韦方程组可改写为 E i H , E 0; H i E , H 0 .
2 2 1 1 z2 ( 2 2 sin 2 ) ( 2 2 sin 2 ) 2 2 2 2 . 2 c 2 c
。（其中使用了
k
(0)

c
）
（3.26）
讨论：电磁波正入射时θ=0，此时 , 均沿z方向，略去 z , z
如果引入复电容率变为311这样导体中的麦克斯韦方程组可改写为312这组方程和绝缘介质中的麦氏方程组的形式完全一样因此电磁波解的形式也和绝缘介质中电磁波解相同只是用一定频率下的平面电磁波解和本章第一小节作类比导体内电场应满足亥姆霍兹方程312其中313312的电磁波解必须满足的条件
第三节
平面电磁波在导体中的传播及其在导体表面的反射和折射
k表示导体内的波矢。设x z为入射面，
z轴指向导体内部的法线，由波矢的边值关系有 ( 0) kx k x x i x . （3.20）比较等式两边
(0) k
z

x
x 0, x kx , (0) 又 k 在zx平面内，那么有 (0) y y 0, ky k y y i y 0 那么 x ex y ez z ez sin ex z ez , （3.21） c

平面电磁波

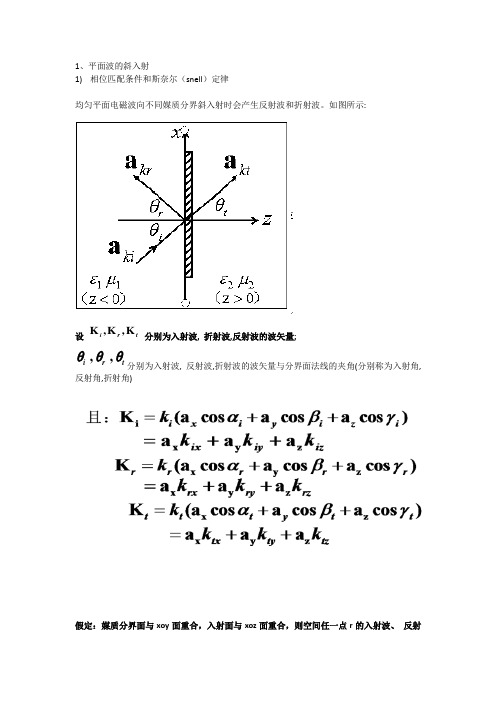
1、平面波的斜入射1) 相位匹配条件和斯奈尔（snell ）定律均匀平面电磁波向不同媒质分界斜入射时会产生反射波和折射波。

如图所示:设 K ,K ,K i r t 分别为入射波, 折射波,反射波的波矢量;,,i r t θθθ分别为入射波, 反射波,折射波的波矢量与分界面法线的夹角(分别称为入射角,反射角,折射角)假定：媒质分界面与xoy 面重合，入射面与xoz 面重合，则空间任一点r 的入射波、反射波、折射波的电场强度为：令：则有：所以：入射角等于反射角2）反射系数和折射系数斜入射的均匀平面波不论何种极化方式，都可以分解为两个正交的线极化波。

其中：极化方向与入射面垂直的称垂直极化波，与入射波平行的（或在入射面内的）称平行极化波，即：分别求出⊥E 和 ||E 的反射波和入射波，通过叠加就可以获得任意取向的入射波和折射波。

垂直极化波平行极化波3）合成电磁波(垂直极化)112sin sin sin i r t k k k θθθ==()0ix iz j k x k z i e -+=E 0i j i i e -⋅=K r E E (sin cos )0i i i jk x z i e θθ-+=E 0r j r r e -⋅=K r E E ()rx rz j k x k z e -+=r0E (sin cos )r r r jk x z e θθ--=r0E 0t j t t e -⋅=K r E E ()tx tz j k x k z t e -+=0E (sin cos )t t t jk x z t e θθ-+=0E 12;i r t k k k k k ===i r θθ=0E E ⊥=r0i R 2121cos cos cos cos i t i t ηθηθηθηθ-=＋0t E E ⊥=0i T 2212cos cos cos i i tηθηθηθ=+0110r i E R E =1212cos cos cos cos i t i t ηθηθηθηθ-=+0110t i E T E =2122cos cos cos i i t ηθηθηθ=+||E E E +=⊥a 、在媒质1中（z<0）b 、在媒质2中（z>0）2、平面电磁波对理想导体的斜入射1）垂直极化波a ）反射系数和折射系数将20η=代入一般公式，得： b ）合成场（z<0，媒质1区域）c ）合成电磁波的性质在(21)4cos n z k πθ-+=处为E1波腹点，H1x 的波节点。

平面电磁波的传播

(b) E iH (c) H 0
个独立。由旋度的散度为0可知， (b)(c)、(d)(a)。这是单色波E、B
(d ) H iE 表达式特点引起的。
2E 2E 0; 2B 2B 0 (2) 2E k2E 0; 2B k2B 0; k 2 2 (2)
k 称为波矢量，得到（齐次）亥姆霍兹(Helmholtz)方程(2)’。亥姆霍兹方程是一定频率下电磁波的基本方程，其解E(x)、B(x)代表电磁波场强在空间中的分布情况，每一种可能的形式称为一种波模。
(1)代入波动方程： 2E 2E 0; 2B 2B 0 (2)
(1)代入自由空间麦克斯韦方程：
D 0, E B ; B 0, H D
t
t
E 0, E iH , H 0, H iE
(a) E 0
注意：对于单色波，0时，麦克斯
韦方程的4个方程不相互独立，只有2
电磁波的传播
平面电磁波、电磁波的反射和折射、导体中的电磁波、谐振腔和波导
电磁波的基本知识
➢ 前两章讨论了静止电荷的静电场和恒定电流的磁场，其场强E或磁感强度B 在空间虽然可逐点变化，但在任一点不随时间变化；电场和磁场可单独地分别处理，它们之间不存在相互联系。 ➢ 本章进一步讨论随时间变化的电场与磁场，以及它们之间的相互联系、电磁场的传播。麦克斯韦在总结前人工作的基础上，提出了著名的电磁场理论（经典电磁场理论），指出变化电场和变化磁场形成了统一的电磁场，预言电磁场能以波动的形式在空间传播，称为电磁波；并得到电磁波在真空中传播的速度等于光速，从而断定光在本质上就是一种电磁波。后来，赫兹用振荡电路产生了电磁波，使麦克斯韦的学说得到了实验证明，为电学和光学奠定了统一的基础。因此，麦克斯韦的经典电磁场理论是人类对电磁规律的历史性总结，是19世纪物理学发展的最辉煌成就，是物理学发展史上一个重要的里程碑。

在自由空间传播的均匀平面电磁波

在自由空间传播的均匀平面电磁波（空间中没有自由电荷，没有传导电流），电场和磁场都没有和波传播方向平行的分量，都和传播方向垂直。

此时，电矢量E，磁矢量H和传播方向k两两垂直。

只是在这种情况下，才可以说电磁波是横波。

沿一定途径（比如说波导）传播的电磁波为导行电磁波。

根据麦克斯韦方程，导行电磁波在传播方向上一般是有E和H分量的。

光的传播形态分类：根据传播方向上有无电场分量或磁场分量，可分为如下三类，任何光都可以这三种波的合成形式表示出来。

1、TEM波：在传播方向上没有电场和磁场分量，称为横电磁波。

2、TE波(即是物光里的s波)：在传播方向上有磁场分量但无电场分量，称为横电波。

在平面光波导(封闭腔结构)中，电磁场分量有Ey, Hx, Hz，传播方向为ｚ方向。

3、TM波(即是物光里的p波)：在传播方向上有电场分量而无磁场分量，称为横磁波。

在平面光波导(封闭腔结构)中，电磁场分量有Hy, Ex, Ez，传播方向为ｚ方向。

微波工程、电磁场理论等课程中有关于TEM、TE、TM模的更为详细的描述。

第四章-平面波

第四章平面波本章从麦克斯韦方程及物质的本构关系出发，研究在均匀介质中平面波的传播及其主要特征。

首先讨论线性、均匀、各向同性介质中均匀平面波的传播，再推广到各向异性介质中的情况。

比平面波更复杂的电磁波也可用平面波展开，本章对此也作了讨论。

最后讨论平面波传播的传输线模型，为以后用传输线模型求解复杂的场问题打下基础。

4.1得出电场强度E 与磁场强度H 满足的波方程，4.2从波方程得到简单介质中的平面波解，4.3、4.4讨论平面波的极化特性以及平面波在有耗介质中的传播，4.5介绍色散与群速的基本概念，4.6与4.7分别研究电各向异性介质和磁各向异性介质中平面波的传播特征。

4.8讨论髙斯波束的平面波展开，4.9证明电磁波沿某一方向传播可与特定参数传输线上电压、电流波的传播等效，即电磁波传播的传输线模型。

4.1 波方程3.4已分析过，麦克斯韦方程组中两个旋度方程是独立的。

在两个旋度方程中电场强度E 与磁场强度H 耦合在一起。

从解方程角度看，先要将E 跟H “去耦”，即从两个旋度方程消去H （或E ），然后得到只关于E （或H ）的方程。

本节讨论无源、简单介质中麦克斯韦方程的解，所谓无源，就是指所研究的区域内不存在产生电磁场的源J 与ρv 。

对于简单介质，ε、μ是常量。

在这种特定情况下，将物质的本构关系（3.4.1）、（3.4.2）代入麦克斯韦方程（3.2.8）~（3.2.11），得到 ∇⨯E =–j ωμH （4.1.1） ∇⨯H = j ωεE （4.1.2） ∇⋅E = 0 （4.1.3） ∇⋅H = 0 （4.1.4）式（4.1.1）、（4.1.2）两个方程中，只有E 和H 两个独立的场量，但E 和H 耦合在一起。

为了从这两个方程得到只关于E 或H 的方程，对式（4.1.1）取旋度，并将式（4.1.2）代入，得到 ()()()E E H E μεωωεωμωμ2=-=⨯∇-=⨯∇⨯∇j j j利用恒等关系()()E E E 2∇-⋅∇∇=⨯∇⨯∇，而根据式（4.1.3），0=⋅∇E ，所以上式成为022=+∇E E μεω（4.1.5）同样对式（4.1.2）取旋度，将式（4.1.1）代入，并利用式（4.1.4）及上面的矢量运算恒等关系，得到022=+∇H H μεω（4.1.6）式（4.1.5）、（4.1.6）可合并写成 ()022=⎩⎨⎧+∇HEk（4.1.7）式中μεω22=k（4.1.8）在自由空间或真空中，μ = μ0，ε = ε0，k 记作k 000220εμω=k（4.1.9）式（4.1.5）、（4.1.6）或（4.1.7）叫做无源简单介质中的波方程，在这个方程中E 跟H 不再耦合在一起。

均匀平面电磁波的特性与特征参量

电磁波传播的相位速度仅与媒质特性相关。真空中电磁波的相位速度： p 0 v
1
=
11:43
1 f

vp f
0 0
3 108 (m / s) c(光速)
vp f
如果以 e n为表示波传播方向的单位矢量
对于均匀平面电磁波，有： H
同理可以推得：重要结论：
2
11:43
2 E k E 0 (k 2 2 )
考虑一种简单情况：
性质，知 E 只随z坐标变化。则方程可以简化为： 2 Ex k 2 Ex 0 z 2
解一元二次微分方程，可得上方程通解为：
均匀平面波电场矢量沿x方向，波沿z方向传播，则由均匀平面波
Ex E e jkz E e jkz
由电磁波的场量表达式可总结出波的传播特性均匀平面波的传播参数
角频率、频率和周期角频率ω ：表示单位时间内的相位变化，单位为rad /s
周期T ：时间相位变化 2π的时间间隔，即
Ex
o
T
Ex (0, t ) Emcost 的曲线
T 2π
T
2π
1 (Hz) 频率f ： f T 2π
22220e?ke?k????????????????????????22222220eeekexyz????22222222222222222?2222000xxxxyyyyzzzzeeekexeyezekexeyezekexyz????????????电场强度矢量的解05
理想介质中的均匀平面电磁波
0 0 0
4 107 120 377() 1 109 36
在自由空间中传播的电磁波，电场幅度与磁场幅度之比为377。

第4章 平面电磁波

平面电磁波

电磁场-平面电磁波

在自由空间传播的均匀平面电磁波

电动力学复习总结第四章 电磁波的传播2012答案

平面电磁波知识点

平面电磁波

电动力学第四章电磁波的传播

第四章 电磁波的传播 §1. 平面电磁波§2. 电磁波在介质界面上的反射和折射§3. 有导体存在时电磁波的

平面电磁波的能量传递

平面电磁波

平面电磁波的性质要点

平面电磁波的性质要点

沿任意方向传播的平面电磁波

电动力学 第4章 电磁波

平面电磁波

平面电磁波的传播

在自由空间传播的均匀平面电磁波

第四章-平面波

均匀平面电磁波的特性与特征参量

第4章平面电磁波

电动力学复习总结第四章电磁波的传播2012答案

第四章电磁波的传播 §1. 平面电磁波§2. 电磁波在介质界面上的反射和折射§3. 有导体存在时电磁波的

电动力学第4章电磁波