信号处理技术研讨课大作业参考模板 (2)

合集下载

信号与系统大作业模板

《信号与系统分析》大作业报告题目：基于Matlab的信号与系统分析仿真学号：课号：指导教师：2020 年12月26日一、设计思路：1.编写程序（函数），利用Matlab画出波形，并利用自变量替换方式实现信号的尺度变换、翻转和平移等运算；2.利用Matlab的impluse函数和step函数分别求解连续系统的冲激响应和阶跃响应，绘图并与理论值比较,利用卷积和函数conv计算连续时间信号的卷积，并绘图表示；3.利用函数quad和quadl求傅里叶变换，画出对应频谱，进行比较，验证尺度变换、时移、频移、卷积定理、对称性等性质；4.画出波形，利用quad函数或quadv函数求波形傅里叶级数，绘制单边幅度谱和单边相位谱，然后合成波形。

二、项目实现：1.信号的运算(1)编写程序（函数），画出图（a）所示波形f（t）(2)利用（1）中建立的函数，通过自变量替换的方式依次画出图（b）、（c）、（d）即f（2t）、f（-t）、f（t+5）的波形。

源代码：% Program ch1_1% f(t)t=-4:0.01:4;y=tripuls(t,6,0.8);subplot(211);plot(t,y);title('f(t)');xlabel('(a)');box off;% f(2t)y1=tripuls(2*t,6,0.8);subplot(234);plot(t,y1);title('f(2t)');xlabel('(b)');box off;% f(-t)t1=-t;y2=tripuls(-1*t1,6,0.8);subplot(235);plot(t1,y2);title('f(-t)');xlabel('(c)');box off;% f(t+5)t2=t-5;y3=tripuls(5+t2,6,0.8);subplot(236);plot(t2,y3);title('f(t+5)');xlabel('(d)');box off ;由图可知，Matlab 计算结果与理论值一致2.系统分析(1)已知一个因果LTI 系统的微分方程为y ”(t)+3y ’(t)+2y(t)=f(t),求系统的冲激响应和阶跃响应，绘图并与理论值比较。

(完整版)数字信号处理实验二

xlabel('时间序号n'); ylabel('振幅');
y = filter(num,den,x,ic);
yt = a*y1 + b*y2;
d = y - yt;
subplot(3,1,1)
stem(n,y);
ylabel('振幅');
title('加权输入: a \cdot x_{1}[n] + b \cdot x_{2}[n]的输出');
subplot(3,1,2)
%扫频信号通过2.1系统：
clf;
n = 0:100;
s1 = cos(2*pi*0.05*n);
s2 = cos(2*pi*0.47*n);
a = pi/2/100;
b = 0;
arg = a*n.*n + b*n;
x = cos(arg);
M = input('滤波器所需的长度=');
num = ones(1,M);
三、实验器材及软件
1.微型计算机1台
2. MATLAB 7.0软件
四、实验原理
1.三点平滑滤波器是一个线性时不变的有限冲激响应系统，将输出延时一个抽样周期，可得到三点平滑滤波器的因果表达式，生成的滤波器表示为
归纳上式可得
此式表示了一个因果M点平滑FIR滤波器。
2.对线性离散时间系统，若y1[n]和y2[n]分别是输入序列x1[n]和x2[n]的响应，则输入
plot(n, y);
axis([0, 100, -2, 2]);
xlabel('时间序号 n'); ylabel('振幅');

信号处理大作业

(4)分析特点：自相关的频谱分析与FFT分析类似，经过自变换的信号可以直接与原始信号进行对比分析，并能直观的看出其相似程度，且自相关图像在0点的值最大；之后变小，
若信号中有周期成分，则自相关函数也有周期性。例题中正弦信号的自相关函数为余弦函数。
FFT变换能有效降低时域信号的信噪比阀值，即具有良好的信号识别能力。能够看出信号幅值、相位的变化情况。而自相关变换却不可以。
s=s0+v;
subplot(2,1,1),plot(t,s),title('输入信号')
y=filtfilt(bz,az,s);
y1=filter(bz,az,s);
subplot(2,1,2),plot(t,y,t,y1,':'),title('输出信号'),xlabel('时间/s')
legend('filtfilt','filter')
bz =
1.0e-003 *
0.0604 0.3020 0.6039 0.6039 0.3020 0.0604
az =
1.0000 -3.9823 6.4281 -5.2458 2.1610 -0.3591
频率特性图像为2-1
图2-1数字滤波器的频率特性图形
Chebyschev滤波器源程序：
Fs=1000; %采样频率
string=['Boxcar,N=',num2str(N)];
h=hd.*(B)'; %得到FIR数字滤波器
[H,w]=freqz(h,[1],1024); %求其频率响应
db=20*log10(abs(H)+eps); %得到幅值

《数字信号处理》课程研究性学习报告数字滤波器设计专题研讨

《数字信号处理》课程研究性学习报告数字滤波器设计专题研讨《数字信号处理》课程研究性学习报告试点班专用姓名学号同组成员指导教师时间数字滤波器设计专题研讨【目的】 (1) 掌握IIR和FIR数字滤波器的设计方法及各自的特点。

(2) 掌握各种窗函数的时频特性及对滤波器设计的影响。

(3) 培养学生自主学习能力，以及发现问题、分析问题和解决问题的能力。

【研讨题目】基本题 1．IIR 数字滤波器设计设计一个IIR数字低通滤波器，其能取代下列指标的模拟低通滤波器(系统的抽样频率为44.1kHz) fp=2kHz， fs=10kHz , Ap=0.5dB, As=50dB (1) 分别用双线性变换和冲激响应不变法设计一个BW型数字低通滤波器，并进行比较。

(2) 用双线性变换分别设计Chebyshev I型Chebyshev I I 型和椭圆型数字低通滤波器，并进行比较。

【温磬提示】在数字滤波器的设计中，不管是用双线性变换法还是冲激响应不变法，其中的参数T的取值对设计结果没有影响。

但若所设计的数字滤波器要取代指定的模拟滤波器时，则抽样频率（或抽样间隔T）将对设计结果有影响。

模拟滤波器设计指标【设计步骤】数字低通滤波器模拟低通滤波器数字滤波器设计指标频率变换→ 双线性法冲击不变法【仿真结果】所设计滤波器的幅度响应和相位响应 BW型、Chebyshev I型、Chebyshev I I型和椭圆型滤波器的零极点分布【结果分析】双线性变换和冲激响应不变法所设计的滤波器的性能有什么不同。

BW型、Chebyshev I型、Chebyshev I I型和椭圆型滤波器的零极点分布各有什么特点。

答：双线性法得到的模拟频率与数字频率是非线性的，但是消除了频谱混叠的误差脉冲响应不变法的模拟频率域数字频率是线性的，但是有频谱混叠误差。

在极点图中，BW型极点离单位圆最远，椭圆极点离单位圆最近。

因而BW的稳定性最好，椭圆的稳定性最差。

【自主学习内容】极点图的做法【阅读文献】《信号与系统》【发现问题】 (专题研讨或相关知识点学习中发现的问题)：Cheby2型做的幅度响应在ws之后没有波动。

数字信号处理第二次讨论课

h(n)=h(N-1-n),N为偶数
同理，可得
H （ g ω）
M 1 n 0
2h(n) cos[ω (n τ )]
其中余弦函数关于过零点奇对称，关于w=0和2π偶对称。所以幅频特性关于w=0和2π偶对称。因此，情况2不能实现高通和带阻滤波器。
h1=[1,2,3,4,4,3,2,1]
h(n)=h(N-1-n),N为奇数
代入时域约束条件h(n)=h(N-1-n)和θ (ω ) ωτ N 1 和 jω jω jω jθ (ω ) H （ e ） h ( n ) e 、 H （ e ） H ( ω ) e g 得到：代入 n 0
H（ h(τ ) 2h(n) cos[ω (n τ )] g ω）
1、增大N 可以使主瓣变窄→过渡带变窄，同时旁瓣增多，震荡变密集→ 通带和阻带内震动加快，但并不能改变肩峰值和波动的相对大小（主瓣与旁瓣的相对比例）。
改进措施
2、改变窗函数的形状构造新的窗函数形状，使其谱函数的主瓣包含更多的能量，相应旁瓣幅度更小。旁边的减小可以使通带、阻带波动减小，从而加大阻带衰减。
n 0
N 1
jωn
H g (ω )e
j (πωτ )

n 0
N 1
h(n) cos[ω (n τ )] 0
如果要求单位脉冲响应h(n)、长度为N的FIR数字滤波器具有第二类线性相位特性，则h(n)应当关于 n=(N-1)/2点奇对称。
h(n)=-h(N-1-n) n从0到N-1
Part OLeabharlann e第一类线性相位特性：θ（ω） -τω

第二类线性相位特性：
满足群延时为常数即可称为线性相位。

2018-2019-数字信号处理》课程研究性学习报告,多速率信号处理专题研讨-范文模板 (9页)

本文部分内容来自网络整理，本司不为其真实性负责，如有异议或侵权请及时联系，本司将立即删除！== 本文为word格式，下载后可方便编辑和修改！ ==数字信号处理》课程研究性学习报告,多速率信号处理专题研讨篇一：北京交通大学数字信号处理04DSP研究性学习报告多速率信号处理《数字信号处理》课程研究性学习报告姓名学号同组成员指导教师时间多速率信号处理专题研讨【目的】(1) 掌握序列抽取运算与内插运算的频谱变化规律。

(2) 掌握确定抽取滤波器与内插滤波器的频率指标。

(3) 掌握有理数倍抽样率转换的原理及方法。

(4) 培养学生自主学习能力，以及发现问题、分析问题和解决问题的能力。

【研讨题目】基本题1．抽取、内插信号特征的时域/频域分析对于给定的单频模拟信号y(t)=sin(1000?t)，确定一个合适的采样频率fsam，获得离散信号y[k]，试进行以下问题的分析：(1) 对离散信号y[k]进行M=2倍抽取，对比分析y[k]和y[Mk]在时域/频域的关系；(2) 对离散信号y[k]进行L=2倍内插，对比分析y[k]和y[k/L]在时域/频域的关系。

【温磬提示】在多速率信号分析中，离散序列的抽取和内插是多速率系统的基本运算，抽取运算将降低信号的抽样频率，内插运算将提高信号的抽样频率。

两种运算的变换域描述中，抽取运算可能出现频谱线性混叠，而内插运算将出现镜像频谱。

【设计步骤】1、已知y(t)=sin(1000?t)频率为500Hz，周期为0.002s，可取时间范围T为0到0.004秒，两个周期，根据抽样定理取fsam?8000Hz，每个周期抽取16个点。

2、用函数xD=x(1:M:end)对离散信号进行M=2倍的抽取，用fft计算频谱。

3、用函数xL=zeros(1,L*length(x));xL(1:L:end)=x;对离散信号进行L=2的内插，用fft计算频谱。

【仿真结果】对离散信号y[k]抽取和内插的时域/频域对比分析结果。

现代信号处理大作业

现代信号处理大型作业一．试用奇阶互补法设计两带滤波器组(高、低通互补)，进而实现四带滤波器组；并画出其频响。

滤波器设计参数为：F p ＝1.7KHz , F r ＝2.3KHz , F s ＝8KHz , A rmin ≥70dB 。

（一）、分析与通常的滤波器相比，互补滤波器具有优良的结构特性和结构特性，具有较低的噪声能量和系数敏感性，其定义如下：一组滤波器H 12(),(),.......()Z H Z H Z n 如果满足下式：He Kjw k n(),==∑110<w<2π 则称这组滤波器为幅度互补滤波器;如果满足下式：He kjw k n()=∑=121, 0<w<2π则称这组滤波器为功率互补滤波器，同时互补滤波器还应该满足：Hz A z kk n()()=∑=1其中A(z)为全通函数，适当的选择全通函数，可以使两带函数具有所需要的低通和高通特性。

（二）、设计步骤(1) 对Fp 、Fr 进行预畸);();(''FsFrtg FsFptg r p ∏=Ω∏=Ω(2) 计算'''*r p c ΩΩ=Ω，判断'c Ω是否等于1，即该互补滤波器是否为互补镜像滤波器(3) 计算相关系数⎪⎩⎪⎨⎧-==+++=+-=-=ΩΩ=--=偶数)N 为(;21奇数)N 为 (;;lg /)16/1lg(;150152;1121;1;;])110)(110[(1213090500''02'''211－min1.0min1.0i i u q k N q q q q q k k q k k k k rp Ar Ap;)2cos()1(21))12(sin()1(21)1(21'2∑∑∞=∞=+-++-=Ωm mm m m m m i u Nm q u Nm q q ππ;42⎥⎦⎤⎢⎣⎡=N N;221N N N -⎥⎦⎤⎢⎣⎡=;)/1)(1(2'2'k k v i i i Ω-Ω-=12'1212,1;12N i v i i i =Ω+=--α 22'22,1;12N i v iii =Ω+=β (4) 互补镜像滤波器的数字实现;22i ii A αα+-=;22iii B ββ+-=1221,1;1)(N i ZA Z A Z H i i i =++=∏--22212,1;1)(N i ZB Z B Z Z H i i i =++=∏--- )];()([21)(21Z H Z H Z H L +=（三）、程序与结果 1．二带滤波器组（1）源程序： clear; clf;Fp=1700;Fr=2300;Fs=8000; Wp=tan(pi*Fp/Fs); Wr=tan(pi*Fr/Fs); Wc=sqrt(Wp*Wr); k=Wp/Wr;k1=sqrt(sqrt(1-k^2)); q0=0.5*(1-k1)/(1+k1);q=q0+2*q0^5+15*q0^9+150*q0^13; N=11;N2=fix(N/4); M=fix(N/2); N1=M-N2; for jj=1:M a=0;for m=0:5a=a+(-1)^m*q^(m*(m+1))*sin((2*m+1)*pi*jj/N);%N is odd, u=j end ab=0;for m=1:5b=b+(-1)^m*q^(m^2)*cos(2*m*pi*jj/N); end bW(jj)=2*q^0.25*a/(1+2*b);V(jj)=sqrt((1-k*W(jj)^2)*(1-W(jj)^2/k)); endfor i=1:N1alpha(i)=2*V(2*i-1)/(1+W(2*i-1)^2); endfor i=1:N2beta(i)=2*V(2*i)/(1+W(2*i)^2); endfor i=1:N1a(i)=(1-alpha(i)*Wc+Wc^2)/(1+alpha(i)*Wc+Wc^2); endfor i=1:N2b(i)=(1-beta(i)*Wc+Wc^2)/(1+beta(i)*Wc+Wc^2); endw=0:0.0001:0.5;LP=zeros(size(w));HP=zeros(size(w));for n=1:length(w)z=exp(j*w(n)*2*pi);H1=1;for i=1:N1H1=H1*(a(i)+z^(-2))/(1+a(i)*z^(-2)) ;endH2=1/z;for i=1:N2H2=H2*(b(i)+z^(-2))/(1+b(i)*z^(-2));endLP(n)=abs((H1+H2)/2);HP(n)=abs((H1-H2)/2);endplot(w,LP,'b',w,HP,'r');hold on;xlabel('digital frequency');ylabel('amptitude');（2）运行结果：见图1图1 二带数字滤波器组2．四带滤波器组（1）源程序：clf;Fp=1700;Fr=2300;Fs=8000;Wp=tan(pi*Fp/Fs);Wr=tan(pi*Fr/Fs);Wc=sqrt(Wp*Wr);k=Wp/Wr;k1=sqrt(sqrt(1-k^2));q0=0.5*(1-k1)/(1+k1);q=q0+2*q0^5+15*q0^9+150*q0^13;N=11;N2=fix(N/4);M=fix(N/2);N1=M-N2;for jj=1:Ma=0;for m=0:5a=a+(-1)^m*q^(m*(m+1))*sin((2*m+1)*pi*jj/N); % N is odd, u=jendb=0;for m=1:5b=b+(-1)^m*q^(m^2)*cos(2*m*pi*jj/N);endW(jj)=2*q^0.25*a/(1+2*b);V(jj)=sqrt((1-k*W(jj)^2)*(1-W(jj)^2/k));Endfor i=1:N1alpha(i)=2*V(2*i-1)/(1+W(2*i-1)^2);endfor i=1:N2beta(i)=2*V(2*i)/(1+W(2*i)^2);endfor i=1:N1a(i)=(1-alpha(i)*Wc+Wc^2)/(1+alpha(i)*Wc+Wc^2);endfor i=1:N2b(i)=(1-beta(i)*Wc+Wc^2)/(1+beta(i)*Wc+Wc^2);endw=0:0.0001:0.5;LLP=zeros(size(w));LHP=zeros(size(w));HLP=zeros(size(w));HHP=zeros(size(w));for n=1:length(w)z=exp(j*w(n)*2*pi);H1=1;for i=1:N1H1=H1*(a(i)+z^(-2))/(1+a(i)*z^(-2)) ;endH21=1;for i=1:N1H21=H21*(a(i)+z^(-4))/(1+a(i)*z^(-4)) ;H2=1/z;for i=1:N2H2=H2*(b(i)+z^(-2))/(1+b(i)*z^(-2));endH22=1/(z^2);for i=1:N2H22=H22*(b(i)+z^(-4))/(1+b(i)*z^(-4));endLP=((H1+H2)/2);HP=((H1-H2)/2);LLP(n)=abs((H21+H22)/2*LP);LHP(n)=abs((H21-H22)/2*LP);HHP(n)=abs((H21+H22)/2*HP);HLP(n)=abs((H21-H22)/2*HP);endplot(w,LLP,'b',w,LHP,'r',w,HLP,'k',w,HHP,'m')hold onxlabel('digital frequency');ylabel('amptitude');（2）运行结果：见图2图2 四带数字滤波器组二、根据《现代数字信号处理》第四章提供的数据，试用如下方法估计其功率谱，并画出不同参数情况下的功率谱曲线：1）Levison算法2）Burg算法3） ARMA 模型法 4） MUSIC 算法 1 Levinson 算法Levinson 算法用于求解Yule-Walker 方程，是一种按阶次进行递推的算法，即首先以AR （0）和AR （1）模型参数作为初始条件，计算AR （2）模型参数；然后根据这些参数计算AR （3）参数，等等，一直到计算出AR （p ）模型参数为止，需要的运算量数量级为2p ，其中p 为AR 模型的阶数。

信号处理结课论文与作业

数字信号处理技术在电力系统中的发展现状和趋势摘要：为了适应现代电力系统的要求，先进的数字信号处理技术被应用到电力系统中，充分发挥了其快速强大的运算和处理能力以及并行运行的能力，满足了电力系统监控的实时性和处理算法的复杂性等更高的要求。

本文首先简要介绍了电力系统和数字信号处理技术；然后详细阐述了数字信号处理技术在电力系统中的应用，包括傅里叶变换、小波变换、现代谱分析、相关分析、数学形态学，并介绍了数字信号处理技术在电力系统应用中的现状和趋势。

关键词：数字信号处理，电力系统Abstract: In order to meet the requirements of modern electric power system, theadvanced digital signal processing technology is applied to the electric power system.this technology has gave full play to its fast computation and processing capacity andthe ability to run in parallel, and it satisfies some higher requirements, such as the realtime monitoring of electric power system and the complexity of handle algorithm.This article first briefly introduced the electric power system and digital signalprocessing technology; And then expounds the application of digital signal processingtechnology in power system, including Fourier transform, wavelet transform, themodern spectrum analysis, correlation analysis and mathematical morphology, anddigital signal processing technology is introduced in the present situation and trend ofpower system applications.Keywords: digital signal processing, electric power system1、引言现代电力系统通过联网已经发展成供电区域辽阔和容量巨大的系统，作为国民经济发展的源动力，我国的电力系统正以空前的规模和速度扩大。

FFT spectrum analyzer数字信号处理第二次大作业

FFT spectrum analyzer based on MatlabN A M E ：XXXXXStudent ID ：00000000000Professor ：何岭松D a t e ：2013-10-08AbstractFourier transform is powerful method in signal process. It can transform the signal from time domain to frequency domain. In frequency domain some characteristic is more obvious than it in time domain. For the discrete signal, there is Discrete Fourier Transform (DFT). But the amount of calculation in DFT is large, to speed up in calculation, there is Fast Fourier Transform (FFT). For DFT and FFT, as the spectrum is discrete, and only the frequency sampling point is calculated, it caused the fence effect. And the energy leakage for cycle extension. To reduce the fence effect, window function is needed.In this project, FFT is used to analyze the spectrum of the signal. The signal can be generated in three ways, signal generator, read from wav files and input from the sound card. To reduce the fence effect, window function is supported.Keywords:FFT wav file sound card input window functionContent1. Introduction (1)2. Method (2)2.1 Signal spectrum analysis (2)2.1.1 Continuous Fourier Transform (2)2.1.2 Discrete Fourier Transform (DFT) (2)2.1.3 Fast Fourier Transform (FFT) (3)2.2 Window Function (3)2.3 Signal Source (4)2.4 Zoom spectrum (5)3. Results (5)3.1 Interface of the program (5)3.2 FFT the signal from signal generator (7)3.3 Read the wav file and spectrum analysis (9)3.4 Sound card input and spectrum analysis (10)3.5 Zoom FFT (10)3.6 Window function (10)4. Conclusions (13)5. References (13)1. IntroductionOne of the most commonly used method in signal processing is the spectrum analysis. It transform the signal from time domain to frequency domain. For some signal, the time domain analysis is very difficult, and some characteristics is hard to obtain from time domain analysis, such as if the signal has a cycle, the composition of the signal. Those characteristics is very clear in frequency domain.The method that transform the signal from time domain into frequency domain is Fourier Transform. For the continuous signal, integration is calculated. For the discrete signal, there is the Discrete Fourier Transform (DFT). The summation is instead the integration. As the summation is large calculation, especially when the sample point is large. A good way to speed up the calculation is the Fast Fourier Transform (FFT). FFT is much faster the DFT, especially when the sample point is large. For example, for a signal of 1024 points, the FFT is faster than the DFT 100 times.Generally, the signal is continuous, when we get the signal, we discrete the signal with a sample signal. For DFT or FFT, we discrete the spectrum, and only calculate the frequency sampling points. The frequency that we don’t sampled is ignored, which caused the Fence Effect. For the signal is long in time, it’s not possible to sample the whole signal. In fact, only a section of the signal is sampled, and then extend the signal with the cycle as sampled. The signal of cycle extension is different with the original. This caused the energy leakage. To reduce the fence effect, window function is used. In this project 5 window function is supported, they are rectangle window, triangle window, hanning window, hamming window and blackman window. User can select different window function by a group of radio button.The result of DFT or FFT is giving the whole spectrum. In some case, we just interest on a little range of the spectrum. For this case, zoom techniques of the spectrum is needed. In this project, it’s included.In this project, the source signal that to be analyze is generated in three ways,signal generator, read from wav file and record from sound card.2. Method2.1 Signal spectrum analysisThe spectrum analysis is one of the most commonly method in signal processing. For some characteristic of the signal is time domain is not easy to get, it transform the signal of time domain into frequency domain, and analyze the signal in frequency domain.2.1.1 Continuous Fourier TransformFor the continuous signal, the Fourier transform is show as2(f)(t)i t X x e df π∞--∞=⎰ (t)x is the signal in time domain. (f)X is the signal in frequency domain. For the signal is continuous, to calculate the form of the signal in frequency integration is needed.2.1.2 Discrete Fourier Transform (DFT)As digital signal is not continuous but discrete. It’s impossible to calculate all frequency points. To calculate the spectrum (f)X , it’s first to discrete the frequency:Fs f N∆= N is the size of sample point, and Fs is the sample frequency. Then, the frequency point is {0,f,2f,3f,......}∆∆∆ Finally, the spectrum of the signal is210(k f)(n)ei knN N H x t π--∆=∆∑ , k=0, 1, 2, ... , N-1 Where, N is the size of sample point, 1t Fs ∆=2.1.3 Fast Fourier Transform (FFT)From 2.1.2, we find that DFT can calculate the X(f), but if we extend it, we get this. 2101100(k f)(n)e2nk 2(n)cos()(n)sin()(1)iXR(2)i kn N N N N H x tnk x i x N N XR πππ----∆=∆⎡⎤=+⎢⎥⎣⎦=+∑∑∑ Where102nk 201211221(1)(n)cos()(0)cos()(1)cos()(2)cos()...N XR x x x x N N N Nππππ-⋅⋅⋅⋅⋅⋅==+++∑102nk 202212222(2)(n)sin()(0)cos()(1)cos()(2)cos()...N XR x x x x N N N Nππππ-⋅⋅⋅⋅⋅⋅==+++∑ From this, we can find that a large calculations of sine and cosine are repeat. If we reduce these repeat calculation, it will be much faster. That’s what FFT has done. As it’s name, FFT is faster than DFT, the larger the points are, the faster the FFT is compared with DFT. For a signal of 1024 points, the FFT is 100 times faster then DFT.2.2 Window FunctionAs DFT and FFT, spectrum is discrete, and only calculate the frequency sampling point, and other point is not. So Fence effect is caused, and some information of the spectrum is missed.The signal in time domain is l ong, even some are endless. It’s impossible tosample all the signal. In fact, the common method is sample a section as a cycle of the signal, and then extend the signal. As the signal of cycle extension is different with the original signal, Energy leakage is caused. From the mathematical point of view, this process can be described as(t)(t)w(t)y x =x(t) : Original signal.w(t) : Cutoff window functiony(t) : Extension signal.The energy leakage is not always bad for analysis. It reduced the fence effect, especially when a appropriate window function w(t) is chosen.There are 5 window function is supported in this project, they are Rectangle Window, Triangle Window, Hanning Window, Hamming Window and Blackman Window. The mathematic expression of the window functions are list in table 1.2.3 Signal SourceIn this project the signal generated in three ways. The first is from the signal generator based on Matlab, the second is read from wav files and the third is from computer’s sound card.For the signal generator, the program support 4 types, sine, cosine, square and triangle wave. The expression of the wave is list in table 2.In Matlab, there functions to read signal from wav file and record from the sound card. The function to read wav file is[Y, Fs, NBITS]=wavread(FILE);Y is the data read from the wav file, Fs is the sample rate, and NBITS is the number of bits per sample used to encode the data in the file.2.4 Zoom spectrumFor the normal FFT, it shows all the frequency. Sometimes, the characteristics focused only in a small range in frequency. From the spectrum from the normal FFT, it’s not convenient to observe the signal. Thus, zoom spectrum is needed.In the project, at first we make the signal a Z transform, and then analyze the signal. So the spectrum is in the range that we interested in.3. Results3.1 Interface of the programThe final interface of the program is show in fig. 3.1Fig.3.1 the final interface of the programAs shown in fig.3.1, the interface divide 6 parts. The first part is two axes. They show the signal in time domain and frequency domain respectively.The second part is the window function selection part. In this part, five window function are supported. They are Rectangle window, Triangle window, Hanning window, Hamming window and Blackman window. This part is shown in fig.3.2.The third part is the signal generator. It similar with project 1. It’s no more detail discussed here. It’s shown in fig. 3.3Fig3.2 window function selection fig.3.3 signal generatorThe forth part is the read wav file part. From the push button select wav file user can select the wav file. There two edit text box in this part, with which the user can set the sample section. This part is shown in fig 3.4.The fifth part is the record part. With this part, the user can input the sound from the computer’s sound card. There are 4 parameters should be set, they are sample point, sample Frequency, channel of the sound and the number of the data to encode. It’s show in fig 3.5 The sixth part is frequency spectrum refinement. With this part, user can zoom the interested frequency range. This part is shown in fig 3.6Fig 3.4 wav file read part fig3.5 sound card input partFig 3.6 Frequency spectrum refinement part3.2 FFT the signal from signal generatorThe signal that signal generator generated is the standard signal. They are sine wave, cosine wave, square wave and triangle wave. The time and frequency domain wave form is shown in fig 3.7 to fig.3.10.Fig.3.7 the sine wave generator (50,10,0===)f Hz AφFig.3.8 the cosine wave generator (50,10,0===)f Hz AφFig.3.9 the square wave (50,10,0===)f Hz AφFig.3.10 the triangle wave (50,10,0===)f Hz Aφ3.3 Read the wav file and spectrum analysisFig.3.11 The telephone dial tone simulation This fig is read a wav file and sample the 1 to 30720 points.3.4 Sound card input and spectrum analysisF ig 3.12 the wave form of the sound input from sound cardFig 3.12 shows the wave form input from the sound card. The number of sample point is 20480, sample frequency is 11025Hz, select the only 1 channel, and encode the data in 8 bits.3.5 Zoom FFTZoom the signal input from sound card in 3.4. To zoom the frequency from 0Hz to 800Hz to see more details. The zoomed spectrum is shown in fig 3.13. It shows more detail than in fig 3.12.Fig 3.13 spectrum after zoom FFT3.6 Window functionWindow function can reduce the fence effect. The effect of window function is shown in fig 3.14 to fig 3.18. The signal input is as 3.3, and zoom the 350 to 650Hz.Fig. 3.14 signal with rectangle window functionFig. 3.15 signal with triangle window functionFig 3.16 signal with hanning window functionFig 3.17 signal with hamming window functionFig 3.17 signal with Blackman window function From the figure above, we can find that the window function reduced the fence effect, and smoothed spectrum, especially the Blackman window function.4. ConclusionsFrom this project, I understand the DFT and FFT in theory, and use them to processing the signal. Besides, window function is used, and I also realized read signal from wav file and record the sound from the sound card. To observe the spectrum more convenient, zoom FFT is realized.Though I have learned a lot, but there still much work haven’t done yet. FFT function in Matlab is very fast, but there still many methods to speed up. I learned some, but haven’t add it into the project. I tried to read mp3, flac and other sound file, but failed.5. References[1] MATLAB® Creating Graphical User Interfaces User Guide. The MathWorks, Inc.2013.[2] Signal ProcessingToolbox™ User Guide.The mathworks,Inc.,2013.[3] Burrus.C.S, etc. Computer-based exercise for Signal Processing using MATLAB.Prentice-Hall,Inc. ,1994.[4]DIMITRIS G. MANOLAKIS, Applied Digital Signal Processing theory and practice Massachusetts Institute of Technology Lincoln Laboratory 2011。

数字信号处理大作业模板

数字信号处理作业设计报告一、目的1.增进对MATLAB的认识，加深对数字信号处理理论方面的理解。

2.掌握数字信号处理中IIR和FIR滤波器的设计。

3.了解和掌握用MATLAB实现IIR和FIR滤波器的设计方法、过程，为以后的设计打下良好基础。

二、数字信号处理课程设计1.IIR（无限脉冲响应）模拟滤波器设计（1）设计题目：巴特沃斯低通滤波器设计（2）设计要求：（通带最大衰减Rp=2，阻带最小衰减Rs=40，通带边界频率Wp=1500hz，阻带边界频率Ws=4200hz，滤波器类型：巴特沃斯低通滤波器）（3）设计原理：（4）Matlab源程序：（程序要有说明）（5）结果和仿真波形：（要有matlab图）2.IIR（无限脉冲响应）数字滤波器设计（1）设计题目：切比雪夫I型数字高通滤波器（2）设计要求：（通带最大衰减Rp=2db，阻带最小衰减Rs=30db，通带边界频率Wp=700hz，阻带边界频率Ws=500hz，采样频率fs=1khz，滤波器类型：切比雪夫I型数字高通滤波器）（3）设计原理：（4）Matlab源程序：（程序要有说明）（5）结果和仿真波形：（要有matlab图）3.FIR（有限脉冲响应）数字滤波器设计（1）设计题目：（2）设计要求：（通带最大衰减Rp，阻带最小衰减Rs，通带边界频率Wp，阻带边界频率Ws，窗函数类型等）（3）设计原理：（4）Matlab源程序：（程序要有说明）（5）结果和仿真波形：（要有matlab图）4、利用FFT进行频谱分析（1）设计要求：（满足条件的序列x(n)等）（2）设计原理：（3）Matlab源程序：（程序要有说明）（4）结果和仿真波形：（要有matlab图形和文字分析）三、总结（收获与体会）四、参考文献注：红字为说明，有错漏之处自行更正。

信号分析处理大作业报告+程序

1.设计方案如下①利用MATLAB中的wavread命令来读入语音信号，将它赋值给某一向量。

再将该向量看作一个普通的信号，对其进行FFT变换实现频谱分析，再依据实际情况对它进行滤波。

对于波形图与频谱图（包括滤波前后的对比图）都可以用MATLAB画出。

②由于音频信号是连续且长度未知，故可以采用N阶低通滤波器。

滤掉低频部分的噪音，剩下的就是原信号了。

③将去噪后的信号写成wav格式的文件可以使用wavwrite函数。

2. 步骤①录制一段歌曲，采用Matlab工具对此音频信号用FFT作谱分析。

②录制一段音频信号并命名为信xinhao1.wav存放在文件夹中。

③使用wavread函数读出此信号。

④用函数FFT进行傅里叶变换，得到波形图，幅值图，频谱图。

⑤加入一个随机高斯噪声，将原始信号与噪声叠加产生加噪之后的声音文件，得到xinhao2.wav文件。

⑥通过N阶低通滤波器对噪声语音滤波，在Matlab中，FIR 滤波器利用函数filter对信号进行滤波，得到xinhao3.wav文件。

首先通过MATLAB工具编程获取音频文件的原始信号波形，原信号幅值和原始信号频谱图如下：然后通过加一个高斯噪声对其分析可得加噪声后信号波形，加噪声后幅值和加噪声后信号频谱图如下：最后再通过N阶低通滤波器对噪声信号滤波，在Matlab中，FIR 滤波器利用函数filter对信号进行滤波，从而得到滤波后信号波形，滤波后幅值和滤波后信号频谱图：程序[x]=wavread('C:\Users\h\Desktop\xinhao1.wav');X=fft(x,2048);figure(1)fs=abs(X);plot(fs);xlabel('HZ');ylabel('|Y(d)|');subplot(2,2,1);plot(x);xlabel('HZ');ylabel('|Y(d)|');title('原始信号波形');subplot(2,2,2);plot(X);xlabel('HZ');ylabel('|Y(d)|');title('原始信号幅值');subplot(2,2,3);plot(fs);xlabel('HZ');ylabel('|Y(d)|');title('原始信号频谱');figure(2)N=length(x); %计算原始语音信号的长度y1=0.05*randn(N,1); %加上一个高斯随机噪声x1=x+y1;x2=fft(x1,2048);mt=abs(x1);plot(mt);xlabel('HZ');ylabel('|Y(d)|');subplot(2,2,1);plot(x1);xlabel('HZ');ylabel('|Y(d)|');title('加噪声后的波形');subplot(2,2,2);plot(x2);xlabel('HZ');ylabel('|Y(d)|');title('加噪声后的幅值');subplot(2,2,3);plot(mt);xlabel('HZ');ylabel('|Y(d)|');title('加噪声后的频谱');ht=43000;bits=16;wavwrite(x1,ht,bits,'C:\Users\wentao\h\xinhao2.wav');%将加噪声的信号保存figure(3)N=15;wc=0.3;[b,a]=butter(N,wc);x3=fft(x);fp=abs(x3);y2=filter(b,a,x);Y1=fft(y2);subplot(2,2,1);plot(y2);xlabel('HZ');ylabel('|Y(d)|');title('滤波后信号的波形');subplot(2,2,2);plot(Y1);xlabel('HZ');ylabel('|Y(d)|');title('滤波后信号的幅值');subplot(2,2,3);plot(fp);xlabel('HZ');ylabel('|Y(d)|');title('滤波后信号的频谱');wavwrite(y2,ht,bits,'C:\Users\h\Desktop\xinhao3.wav');%将滤波之后保存。

哈工大数字信号处理大作业 (2)(word文档良心出品)

数字信号处理上机实验报告学号：姓名:实验题目一1. 实验要求：序列卷积计算（1）编写序列基本运算函数，序列相加、相乘、翻转、求和；（2）使用自定义函数计算序列线性卷积，并与直接计算结果相比较。

两个序列分别为：() 1,05 0,others n nx n≤≤⎧=⎨⎩，()2,030,othersn nx n≤≤⎧=⎨⎩2. 实验过程和步骤：包含题目分析，实验程序和流程图（程序要有必要的注释）3. 实验结果和分析：包含程序运行结果图，结果分析和讨论(一)基本运算函数1.原序列2.序列相加序列相加程序function [y,n]=sigadd(x1,n1,x2,n2)%implements y(n)=x1(n)+x2(n)%---------------------------------------------% [y,n] = sigadd(x1,n1,x2,n2)% y = sum sequence over n, which includes n1 and n2% x1 = first sequence over n1% x2 = second sequence over n2 (n2 can be different from n1)%n=min(min(n1),min(n2)):max(max(n1),max(n2)); %duration of y(n) y1=zeros(1,length(n));y2=y1;y1(find((n>=min(n1))&(n<=max(n1))==1))=x1; %x1 with duration of y y2(find((n>=min(n2))&(n<=max(n2))==1))=x2; %x2 with duration of y y=y1+y2; %sequence addition3.序列相乘序列相乘程序function [y,n]=sigmult(x1,n1,x2,n2)%implements y(n)=x1(n)*x2(n)%---------------------------------------------% [y,n] = sigmult(x1,n1,x2,n2)% y = product sequence over n, which includes n1 and n2% x1 = first sequence over n1% x2 = second sequence over n2 (n2 can be different from n1)%n=min(min(n1),min(n2)):m(min(n1),min(n2)) %duration of y(n)y1=zeros(1,length(n));y2=y1;y1(find((n>=min(n1))&(n<=max(n1))==1))=x1; %x1 with duration of y y2(find((n>=min(n2))&(n<=max(n2))==1))=x2; %x2 with duration of y y=y1.*y2; %sequence multiplication4.序列翻转序列翻转程序function [y,n]=sigfold(x, n)%implements y(n)=x(-n)%--------------------------------------------- % [y,n] = sigfold(x,n)%y=fliplr(x);n=-fliplr(n);5.序列移位序列移位程序function [y,n]=sigshift(x,m,n0)%implements y(n)=x(n-n0)%--------------------------------------------- % [y,n] = sigshift(x,m,n0)%n=m+n0;y=x;主程序x1=[0:5];x2=[0,1,2,3];n1=0:5;n2=0:3;%N=n1+n2-1;figure(1)subplot(211)stem(x1)xlabel('x1')subplot(212)stem(x2)xlabel('x2')title('原序列')x= sigadd(x1,n1,x2,n2);figure(2)stem(x)xlabel('x1+x2')title('序列相加')figure(3)[x,n] = sigfold(x1,n1);stem(n,x)xlabel('x1(-n)')title('序列翻转')[x,n] = sigshift(x,n,2);figure(4)stem(n,x)xlabel('x1(-n+2)')title('序列移位')x= sigmult(x1,n1,x2,n2);figure(5)stem(x)title('序列相乘')xlabel('x1*x2')(二)自定义函数计算线性卷积1.题目分析使用上一题中的序列相乘、翻转和求和子函数计算线性卷积，并与这直接用conv 函数计算的线性卷积结果相比较。

西电数字信号处理大作业

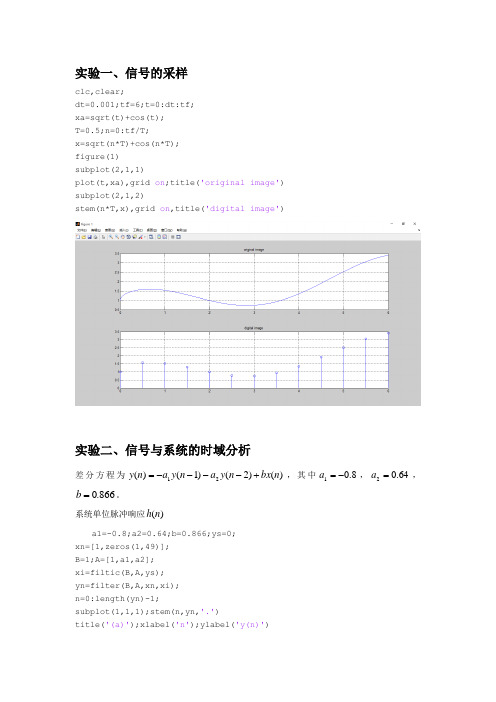
实验一、信号的采样clc,clear;dt=0.001;tf=6;t=0:dt:tf;xa=sqrt(t)+cos(t);T=0.5;n=0:tf/T;x=sqrt(n*T)+cos(n*T);figure(1)subplot(2,1,1)plot(t,xa),grid on ;title('original image')subplot(2,1,2)stem(n*T,x),grid on ,title('digital image')实验二、信号与系统的时域分析差分方程为)()2()1()(21n bx n y a n y a n y +----=，其中8.01-=a ，64.02=a ，866.0=b 。

系统单位脉冲响应)(n ha1=-0.8;a2=0.64;b=0.866;ys=0;xn=[1,zeros(1,49)];B=1;A=[1,a1,a2];xi=filtic(B,A,ys);yn=filter(B,A,xn,xi);n=0:length(yn)-1;subplot(1,1,1);stem(n,yn,'.')title('(a)');xlabel('n');ylabel('y(n)')输入x(n)=cos(n)T=0.1;z=cos(n*T);zn=conv(yn,z); figure(2);n1=1:99;stem(n1,zn,'.')实验三、系统的频域和Z域分析程序代码（画出dtft的幅度和频率谱）clc,clear;n=0:1:7;x=(0.9*exp(j*pi/3)).^n;w=0:pi/200:pi;X=x*exp(-j).^(n'*w);realX=real(X);imagX=imag(X);angX=angle(X);magX=abs(X);subplot(2,2,1);plot(w/pi,magX);grid xlabel('frequency in pi unit');title('magnitude part');subplot(2,2,2);plot(w/pi,realX);grid xlabel('frequency in pi unit');title('real part');subplot(2,2,3);plot(w/pi,imagX);grid xlabel('frequency in pi unit');title('imaginary part');subplot(2,2,4);plot(w/pi,angX);grid xlabel('frequency in pi unit');title('angel part');clc,clear;a=[1,-0.5,0.06];b=[1,1,0];m=0:length(b)-1;l=0:length(a)-1;w=0:pi/500:pi;num=b*exp(-j*m'*w);den=a*exp(-j*l'*w);H=num./den;magH=abs(H);angH=angle(H);H1=freqz(b,a,w);magH1=abs(H1);angH1=angle(H1);subplot(2,2,2);plot(w/pi,angH);grid;xlabel('w(frequency in pi units)');ylabel('ÏàÎ»rad/w');subplot(2,2,1);plot(w/pi,magH);grid;xlabel('w(frequency in pi units)');ylabel('·ù¶È|H|');subplot(2,2,3);plot(w/pi,magH1);grid;xlabel('w(frequency in pi units)');ylabel('·ù¶È|H1|');subplot(2,2,4);plot(w/pi,angH);grid;xlabel('w(frequency in pi units)');ylabel('ÏàÎ»rad/w');axis([0,1,-0.8,0]); figure(2);zplane(b,a);实验四、信号的频谱分析程序代码clc,clear;n=0:7;k=0:7;N=8;w=n*(2*pi)/8;x=(0.9*exp(j*pi/3)).^n;X1=[x zeros(1,8)];X2=[X1 zeros(1,16)];XK=x*exp(-j*k'*w);k1=0:15;n1=0:15;w1=n1*(2*pi)/16;XK1=X1*exp(-j*k1'*w1);k2=0:31;n2=0:31;w2=n2*(2*pi)/16;XK2=X2*exp(-j*k2'*w2);w3=0:pi/200:2*pi;X=x*exp(-j*n'*w3);magX=abs(X);angX=angle(X);magXK=abs(XK);angXK=angle(XK);magXK1=abs(XK1);angXK1=angle(XK1);magXK2=abs(XK2);angXK2=angle(XK2);subplot(4,2,1);plot(w3/pi,magX);xlabel('w/pi');ylabel('·ù¶È|X|');grid on;subplot(4,2,2);plot(w3/pi,angX);xlabel('w/pi');ylabel('ÏàÎ»rad/pi'); subplot(4,2,3);stem(n,magXK);xlabel('K');ylabel('·ù¶È|XK|');subplot(4,2,4);stem(n,magXK);xlabel('K');ylabel('ÏàÎ»rad/pi'); subplot(4,2,5);stem(n1,magXK1);xlabel('K1');ylabel('·ù¶È|XK1|'); subplot(4,2,6);stem(n1,magXK1);xlabel('K1');ylabel('ÏàÎ»rad/pi'); subplot(4,2,7);stem(n2,magXK2);xlabel('K2');ylabel('·ù¶È|XK2|'); subplot(4,2,8);stem(n2,magXK2);xlabel('K2');ylabel('ÏàÎ»rad/pi');实验五、IIR数字滤波器设计IIR汉宁窗低通高通低通巴特沃斯通带截止频率wp=0.2pi 通带最大衰减R=1dB阻带截止频率wp=0.35pi 阻带最大衰减R=10dBclc,clear;Wp=0.2;Ws=0.35;Rp=1;Rs=100;[N,Wc]=buttord(Wp,Ws,Rp,Rs);[Bz,Az]=butter(N,Wc)w=0:0.1:pi;[H,w1]=freqz(Bz,Az,w);;ang=angle(H);H=20*log10(abs(H))subplot(4,2,1); plot(w/pi,H) ;gridon ;xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB');title('µÍÍ¨ÂË²¨Æ÷')subplot(4,2,2);plot(w/pi,ang);gridon ;xlabel('\omega/\pi');ylabel('Phase/dB')[Bz1,Az1]=butter(N,Wc,'high')w=0:0.1:pi;[H1,w2]=freqz(Bz1,Az1,w);ang1=angle(H1);H1=20*log10(abs(H1))subplot(4,2,3); plot(w/pi,H1) ;gridon ;xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB');title('¸ßÍ¨ÂË²¨Æ÷')subplot(4,2,4);plot(w/pi,ang1);gridon ;xlabel('\omega/\pi');ylabel('Phase/dB')Wp1=[0.2 0.8];Ws1=[0.35 0.65];[N2,Wc1]=buttord(Wp1,Ws1,Rp,Rs);[Bz2,Az2]=butter(N2,Wc1,'stop')w=0:0.1:pi;[H2,w3]=freqz(Bz2,Az2,w);ang2=angle(H2);H2=20*log10(abs(H2))subplot(4,2,5); plot(w/pi,H2) ;gridon ;xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB');title('´ø×èÂË²¨Æ÷')subplot(4,2,6);plot(w/pi,ang2);gridon ;xlabel('\omega/\pi');ylabel('Phase/dB')Wp1=[0.2 0.8];Ws1=[0.35 0.65];[N2,Wc1]=buttord(Wp1,Ws1,Rp,Rs);[Bz3,Az3]=butter(N2,Wc1)w=0:0.1:pi;[H3,w4]=freqz(Bz3,Az3,w);ang3=angle(H3);H3=20*log10(abs(H3))subplot(4,2,7); plot(w/pi,H3) ;gridon ;xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB');title('´øÍ¨ÂË²¨Æ÷')subplot(4,2,8);plot(w/pi,ang3);gridon ;xlabel('\omega/\pi');ylabel('Phase/dB')切比雪夫1型通带截止频率wp=0.7pi 通带最大衰减R=1dB阻带截止频率wp=0.5pi 阻带最大衰减R=40dBclc,clear;Wp=0.7;Ws=0.5;Rp=1;Rs=40;[N,Wpo]=cheb1ord(Wp,Ws,Rp,Rs);[Bz,Az]=cheby1(N,Rp,Wpo)w=0:0.1:pi;[H,w1]=freqz(Bz,Az,w);ang=angle(H);H=20*log10(abs(H))subplot(4,2,1); plot(w/pi,H) ;gridon ;xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB');title('µÍÍ¨ÂË²¨Æ÷')subplot(4,2,2);plot(w/pi,ang);gridon ;xlabel('\omega/\pi');ylabel('Phase/dB')[Bz1,Az1]=cheby1(N,Rp,Wpo,'high');w=0:0.1:pi;[H1,w2]=freqz(Bz1,Az1,w);ang1=angle(H1);H1=20*log10(abs(H1))subplot(4,2,3); plot(w/pi,H1) ;gridon ;xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB');title('¸ßÍ¨ÂË²¨Æ÷')subplot(4,2,4);plot(w/pi,ang1);gridon ;xlabel('\omega/\pi');ylabel('Phase/dB')Wp1=[0.2 0.8];Ws1=[0.35 0.65];[N2,Wpo1]=cheb1ord(Wp1,Ws1,Rp,Rs);[Bz2,Az2]=cheby1(N2,Rp,Wpo1,'stop')w=0:0.1:pi;[H2,w3]=freqz(Bz2,Az2,w);ang2=angle(H2);H2=20*log10(abs(H2))subplot(4,2,5); plot(w/pi,H2) ;gridon ;xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB');title('´ø×èÂË²¨Æ÷')subplot(4,2,6);plot(w/pi,ang2);gridon ;xlabel('\omega/\pi');ylabel('Phase/dB')Wp1=[0.2 0.8];Ws1=[0.35 0.65];[N2,Wpo1]=cheb1ord(Wp1,Ws1,Rp,Rs);[Bz3,Az3]=cheby1(N2,Rp,Wpo1)w=0:0.1:pi;[H3,w4]=freqz(Bz3,Az3,w);ang3=angle(H3);H3=20*log10(abs(H3))subplot(4,2,7); plot(w/pi,H3) ;gridon ;xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB');title('´øÍ¨ÂË²¨Æ÷')subplot(4,2,8);plot(w/pi,ang3);gridon ;xlabel('\omega/\pi');ylabel('Phase/dB')实验六、FIR数字滤波器设计FIR汉宁窗低通高通低通% 采用Hamming窗设计一个带阻FIR滤波器阻带：0~0.5pi，阻带最小衰减Rs=40dB；通带：0.5~pi，通带最大衰减：Rp=1dB。

信号处理概述教案模板范文

教学目标：1. 理解信号处理的基本概念和重要性。

2. 掌握信号处理的基本类型和分类。

3. 了解信号处理的基本方法和技术。

4. 认识信号处理在实际应用中的重要性。

教学重点：1. 信号处理的基本概念和分类。

2. 信号处理的基本方法和技术。

教学难点：1. 信号处理在实际应用中的复杂性和多样性。

2. 信号处理方法的选择和应用。

教学时间：2课时教学过程：第一课时一、导入1. 通过展示生活中常见的信号（如电话、电视、雷达等），引导学生思考信号与信息的关系。

2. 引出信号处理的概念，说明信号处理的重要性。

二、新课导入1. 信号处理的基本概念：信号是携带信息的物理量，信号处理是对信号进行操作的过程，以提取、增强或改变信号中的有用信息。

2. 信号处理的分类：根据信号类型，可分为模拟信号处理和数字信号处理；根据处理方法，可分为滤波、调制、解调、压缩、扩展等。

三、信号处理的基本方法1. 滤波：通过滤波器对信号进行筛选，去除噪声或干扰。

2. 调制：将信息信号与载波信号进行叠加，以便于信号的传输。

3. 解调：将调制信号恢复为信息信号。

4. 压缩：减小信号的数据量，便于存储和传输。

5. 扩展：增加信号的数据量，提高信号的质量。

四、课堂小结1. 回顾本节课的主要内容，强调信号处理的基本概念、分类和方法。

2. 强调信号处理在实际应用中的重要性。

第二课时一、复习导入1. 复习上节课所学内容，提问学生信号处理的基本概念、分类和方法。

2. 针对学生的回答，进行补充和纠正。

二、信号处理的应用1. 介绍信号处理在各个领域的应用，如通信、雷达、图像处理、音频处理等。

2. 通过实际案例，展示信号处理在各个领域的应用效果。

三、信号处理的发展趋势1. 介绍信号处理技术的发展趋势，如人工智能、大数据、云计算等。

2. 分析信号处理技术在未来发展中的机遇和挑战。

四、课堂小结1. 回顾本节课的主要内容，强调信号处理在实际应用中的重要性。

2. 强调信号处理技术在未来的发展趋势。

信号分析与处理大作业

宁波理工学院信号分析与处理课程设计题目音频处理姓名胡蔡根专业班级电气131班指导教师崔家林学院信息学院完成日期 2015.12.20目录电器学原理课程报告 (3)1、概述部分............ 错误！未定义书签。

1.1、接触器基本概念.......................................................... 错误！未定义书签。

1.2、接触器分类............................................................. 错误！未定义书签。

1.2.1、根据控制线圈的电压不同，可分为：............................. 错误！未定义书签。

1.2.2、按操作机构分为：............................................................. 错误！未定义书签。

1.2.3、按动作方式分为：......................................................... 错误！未定义书签。

1、接触器工作原理. 错误！未定义书签。

2.1、接触器工作原理图：.................................................. 错误！未定义书签。

2.2、原理介绍...................................................................... 错误！未定义书签。

3、相关技术参数........ 错误！未定义书签。

3.2、额定电压...................................................................... 错误！未定义书签。

3.1.1、主触点上的额定电压......................................................... 错误！未定义书签。

北京交通大学数字信号处理第二次研讨

《数字信号处理》课程研究性学习报告数字信号处理第二次研讨【研讨题目】基本题3．已知一离散序列为x[k]=cos(Ω0k)+0.75cos(Ω1k), 0≤k≤ 63 其中Ω0=0.4π, Ω1=Ω0+π/64(1) 对x[k]做64点FFT, 画出此时信号的频谱。

(2) 如果(1)中显示的谱不能分辨两个谱峰，是否可对(1)中的64点信号补零而分辨出两个谱峰。

通过编程进行证实，并解释其原因。

(3) 给出一种能分辨出信号中两个谱峰的计算方案，并进行仿真实验。

（M2-4）【题目分析】分析影响谱峰分辨率的主要因数，进一步认识补零在在频谱计算中的作用。

【仿真结果】图1 不同点数FFT仿真结果【结果分析】（1）对x[k]64点FFT频谱如上图所示；（2）从图中可以看出，显示的谱不能分辨两个频谱；可以通过对(1)中的64点信号补零而分辨出两个谱峰，增加序列长度N，能使得谱峰显现出来。

（3）通过对序列进行补零，能改善显示分辨率，但是不能改善频谱分辨率。

因此可以适度对序列进行补零，增加频谱显示分辨率。

【自主学习内容】数字信号处理相关内容MATLAB函数用法【阅读文献】《数字信号处理》陈后金主编《matlab使用教程》百度文库【发现问题】(专题研讨或相关知识点学习中发现的问题)：熟练使用Matlab仿真程序很重要，不熟练会花费较多时间编程调试【问题探究】1.连续信号的频率是非周期的，离散信号的频谱是连续信号频谱的周期话，可能会出现频谱叠；2.窗函数的突然截断会导致频谱中出现多余的高频分量，增加信号的长度不能减少频谱泄露。

【仿真程序】图2 MA TLAB仿真程序实现MATLAB代码：function [ ] = H2 ( )w0=0.4*pi;dw=pi/64;w1=w0+dw;N_set=[64 128 256];L_set=[64 128 256 512];for N_index=1:length(N_set);N=N_set(N_index);k=0:N-1;x=cos(w0*k)+0.75*cos(w1*k);for L_index=1:length(L_set);L=L_set(L_index);if L<NcontinueendX=fft(x,L);m=(0:L-1)*2/L;subplot(length(L_set),length(N_set),(L_index-1)*length(N_set)+N_index );plot(m,abs(X));axis([0.38 0.44 0 100]);title(['N=' num2str(N) 'L=' num2str(L)]);hold on;fr1=[0.4 0.4];fr2=[0.4+1/64,0.4+1/64];y=[0 100];plot(fr1,y,'r',fr2,y,'g');endend。

数字信号处理实验课大作业

DSP 实验课大作业设计一实验目的在DSP 上实现线性调频信号的脉冲压缩、上实现线性调频信号的脉冲压缩、动目标显示（动目标显示（动目标显示（MTI MTI MTI）和动目标检测）和动目标检测）和动目标检测(MTD)(MTD)(MTD)，，并将结果与MATLAB 上的结果进行误差仿真。

上的结果进行误差仿真。

二实验内容1. MATLAB 仿真仿真设定带宽、脉宽、采样率、脉冲重复频率，用MATLAB 产生16个脉冲的LFM LFM，每个脉冲，每个脉冲有4个目标（静止，低速，高速），依次做：，依次做：1）脉冲压缩；脉冲压缩；2）相邻2脉冲做MTI MTI，产生，产生15个脉冲；个脉冲；3） 16个脉冲到齐后，做MTD MTD，输出，输出16个多普勒通道个多普勒通道4）改变PRF 后，利用两次PRF 下不同的速度结果，求不模糊速度下不同的速度结果，求不模糊速度2. DSP 实现实现将MATLAB 产生的信号，在visual dsp 中做频域脉压、中做频域脉压、MTI MTI MTI、、MTD MTD，将，将MTI 和MTD 结果导入Matlab ，并将其结果与MATLAB 的结果作比较。

三实验原理1.1. 频域脉冲压缩原理频域脉冲压缩原理一般通过匹配滤波实现脉冲压缩。

在接收机中设置一个与发射信号频率相匹配的压缩网络使经过调制的宽脉冲的发射信号（一般认为也是接受机输入端的回波信号）变成窄脉冲，使之得到良好的距离分辨力，这个过程就称为“脉冲压缩”。

而这个脉冲压缩网络实际上就是一个匹配滤波器网络。

络实际上就是一个匹配滤波器网络。

2.2. MTI 原理原理MTI MTI（（Moving Target Indication Indication）即动目标显示是利用运动目标带来的多普勒频）即动目标显示是利用运动目标带来的多普勒频移来消除静止杂波。

当雷达按照一定的周期辐射LFM 信号时，目标与雷达的距离不同会使得回波的相位有所不同。

信号处理基础实验部分课程设计 (2)

信号处理基础实验部分课程设计实验目的本实验的目的是通过搭建基本的信号处理系统，加深学生对信号处理知识的理解，培养学生的实验能力和解决问题的能力。

具体目标如下：1.掌握MATLAB/Simulink等工具在信号处理中的基本应用。

2.熟悉信号处理基本算法，理解各种滤波器的原理和实现方法。

3.学习信号的采样、重构等基本概念，并掌握在实际应用中的处理方法。

4.了解信号处理在实际应用中的基本流程和步骤，如通过FFT分析信号频谱、使用滤波器去除噪声等。

实验内容实验一：音频采集与重构对于一个给定的音频信号，要求你使用采集卡进行采集，并将其用DA输出。

然后，再通过重构来恢复原始信号，并计算其重构误差。

你需要研究并编写MATLAB程序完成此实验。

该实验的步骤如下：1.研究采集卡的使用方法。

2.使用MATLAB编写程序完成音频信号的采集。

3.将采集到的音频数据经过重构处理，并计算其误差。

4.对比音频信号采集数据和重构数据的差异，分析重构误差的来源。

实验二：信号滤波在这个实验中，你需要对一段信号进行滤波处理，并进行频域分析。

具体的，可以选择使用FIR或IIR滤波器。

你需要研究并编写MATLAB程序完成此实验。

该实验的步骤如下：1.选择合适的FIR或IIR滤波器。

2.根据选择的滤波器特性，计算其系数。

3.使用MATLAB将信号输入滤波器中，得到滤波后的信号。

4.对滤波后的信号进行频谱分析，比较滤波前后的信号频谱。

5.深入分析滤波器特性对滤波效果的影响。

实验三：信号噪声去除在这个实验中，你需要通过使用降噪算法，将一段含噪声的信号恢复为原始信号。

该实验的步骤如下：1.为原始信号添加噪声。

2.研究降噪算法，选择适当的算法。

3.根据选定算法及其参数，在MATLAB中实现该算法。

4.将加噪信号输入到算法中，得到去噪后信号。

5.对比去噪前后的信号，分析去噪算法的性能。

实验要求1.完成实验报告，说明实验原理、实验步骤、实验数据、实验分析和小结，体现实验思想和方法。

论文—手机传感器

信号处理技术研讨课大作业大作业成绩复核人题目：多种手机传感器的原理及应用学院：机电与信息工程学院专业：通信工程年级班级：2014级二班姓名：叶坤学号：201400800679任课教师：崔文韬，叶准学年学期：2014-2015学年第2学期多种手机传感器的原理及应用叶坤201400800679（山东大学（威海）机电与信息工程学院，山东威海264209）摘要：传感器的应用越来越广泛，现在的手机搭载了很多传感器，报告主要介绍了几种典型的传感器及其在手机中的应用，如重力感应器、光线传感器、距离感应器、心率感应器、气压感应器、三轴陀螺仪等。

这些传感器的应用为智能手机增加感知能力，使手机能够知道自己做什么，甚至做什么的动作。

关键词：重力感应器；光线感应器；距离感应器；气压感应器The principle and application of a variety of mobilephone sensorY ekun 201400800679(School of electrical and Information Engineering, Shandong University, Weihai 264209, China) Abstract: Sensor is more and more widely used, and now the mobile phone is equipped with many sensors，The report mainly introduces several typical sensor and its application in mobile phone, such as the gravity sensor, light sensor, proximity sensor, heart rate sensor, pressure sensor, three axis gyroscope. The application of sensors for intelligent mobile phone mobile phone to increase awareness, to know what to do,or do what action.Keywords: Gravity sensor, light sensor;; distance sensor; pressure sensor引言：传感器在生活中的应用越来越广泛，现在的智能手机上搭载了很多种类的传感器。