matlab实现Lagrange多项式插值观察龙格现象
拉格朗日插值龙格现象的matlab实现

拉格朗日插值法在实践中的应 用
在数值分析中的应用
单击此处添加标题
插值法:拉格朗日插值法是数值分析中常用的插值方法之一,具有简单易 行、计算量小等优点。
单击此处添加标题
数据拟合:拉格朗日插值法可以用于数据拟合,通过对已知数据进行插值, 得到未知数据的近似值。
单击此处添加标题
数值微积分:拉格朗日插值法在数值微积分中也有广泛应用,例如在求解 函数的导数、积分等运算时,可以利用拉格朗日插值法进行近似计算。
龙格现象
龙格现象的定义
定义:当插值多项式的阶数过高时, 插值结果可能变得不可预测或出现 剧烈振荡
解决方法:在实际应用中,应避免 使用过高的插值多项式阶数,而应 选择合适的阶数以保证插值结果的 稳定性和准确性
添加标题
添加标题
添加标题
添加标题
原因:由于高阶插值多项式对数据 点的敏感性增强,导致插值结果不 稳定
拉格朗日插值龙格现象的 Matlab实现
汇报人:XX
单击输入目录标题 拉格朗日插值法 龙格现象 拉格朗日插值法在Matlab中的实现 拉格朗日插值法的龙格现象分析 拉格朗日插值法在实践中的应用
添加章节标题
拉格朗日插值法
插值法的定义
插值法是一种数学方法,通过已知的离散数据点,构造一个多项式函数,使得该函数在 数据点处的取值等于已知的数据点值。
算法收敛性:在某些情况下,龙格现象可能导致算法收敛速度减慢,增加计算时间和计算成本。
实际应用限制:由于龙格现象的存在,某些数值方法在实际应用中可能受到限制,无法处理某些 复杂问题。
算法改进需求:为了克服龙格现象的影响,需要研究和发展新的数值方法和算法,提高数值计算 的稳定性和精度。
拉格朗日插值法在Matlab中的 实现
matlab实现拉格朗日插值,多项式插值,邻近插值,线性插值 程序

题 7:一维函数插值算法课题内容:课题 7:一维函数插值算法课题内容:对函数||e-y x=,取[-5,5]之间步长为 1 的值*10作为粗值,以步长0.1 作为细值,编写程序实现插值算法:最邻近插值算法,线性插值算法和三次多项式函数插值算法,并对比插值效果。
课题要求:1、设计良好的人机交互 GUI 界面。
2、自己编写实现插值算法。
3、在同一个图形窗口显示对比最后的插值效果。
附录一、界面设计二、图像结果三、程序设计1、线性插值function pushbutton1_Callback(hObject, eventdata, handles) x=-5:5;y=10*exp(-abs(x));f1=[];for x1=-5:0.1:5a=(x1-floor(x1));%请读者认真逐一带入推导if x1==floor(x1)f1=[f1,y(floor(x1)+6)];elsef1=[f1,y(floor(x1)+6)+a*(y(floor(x1)+7)-y(floor(x1)+6))]; endendm=-5:0.1:5plot(m,f1,'-r',x,y,'+')axis([-5 5 0 10])legend('liner插值','原函数');xlabel('X');ylabel('Y');title('liner插值与原函数的对比');grid2、多项式插值x0=-5:1:-3;y0=10*exp(-abs(x0));x=-5:0.1:-3;n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;endaxis([-5 5 0 10])plot(x,y,'m',x0,y0,'+')legend('三次多项式插值','原函数');xlabel('X');ylabel('Y');title('三次多项式插值与原函数的对比');gridhold onx0=-3:1:-1;y0=10*exp(-abs(x0));x=-3:0.1:-1;n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;endaxis([-5 5 0 10])plot(x,y,'m',x0,y0,'+')legend('三次多项式插值','原函数');xlabel('X');ylabel('Y');title('三次多项式插值与原函数的对比');gridhold onx0=-1:1:1;y0=10*exp(-abs(x0));x=-1:0.1:1;n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;endaxis([-5 5 0 10])plot(x,y,'m',x0,y0,'+')legend('三次多项式插值','原函数');xlabel('X');ylabel('Y');title('三次多项式插值与原函数的对比');gridhold onx0=1:1:3;y0=10*exp(-abs(x0));x=1:0.1:3;n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;endaxis([-5 5 0 10])plot(x,y,'m',x0,y0,'+')legend('三次多项式插值','原函数');xlabel('X');ylabel('Y');title('三次多项式插值与原函数的对比');gridhold onx0=3:1:5;y0=10*exp(-abs(x0));x=3:0.1:5;n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;endaxis([-5 5 0 10])plot(x,y,'m',x0,y0,'+')legend('三次多项式插值','原函数');xlabel('X');ylabel('Y');title('三次多项式插值与原函数的对比');grid3、最邻近插值function pushbutton3_Callback(hObject, eventdata, handles) x=-5:5;y=10*exp(-abs(x));f2=[];for x1=-5:0.1:5if abs(x1-floor(x1))<0.5f2=[f2,y(floor(x1)+6)];elsef2=[f2,y(floor(x1)+7)];endendm=[-5:0.1:5];f4=10*exp(-abs(m));plot(m,f2,'-r',x,y,'+')axis([-5 5 0 10])legend('nearest插值','原函数');xlabel('X');ylabel('Y');title('nearest插值与原函数的对比');grid。
MATLAB数值实验一(数据的插值运算及其应用完整版)

佛山科学技术学院实 验 报 告课程名称 数值分析 实验项目 插值法与数据拟合 专业班级 机械工程 姓 名 余红杰 学 号 10 指导教师 陈剑 成 绩 日 期 月 日一、实验目的1、学会Lagrange 插值、牛顿插值和三次样条插值等基本插值方法;2、讨论插值的Runge 现象3、学会Matlab 提供的插值函数的使用方法,会用这些函数解决实际问题。
二、实验原理1、拉格朗日插值多项式2、牛顿插值多项式3、三次样条插值 三、实验步骤1、用MATLAB 编写独立的拉格朗日插值多项式函数2、用MATLAB 编写独立的牛顿插值多项式函数3、用MATLAB 编写独立的三次样条函数(边界条件为第一、二种情形)4、已知函数在下列各点的值为:根据步骤1,2,3编好的程序,试分别用4次拉格朗日多项式4()L x 、牛顿插值多项式4()P x 以及三次样条函数()S x (自然边界条件)对数据进行插值,并用图给出 {(,),0.20.08,0,1,2,,10i i i x y x i i =+=},4()L x 、4()P x 和()S x 。
5、在区间[-1,1]上分别取10,20n =用两组等距节点对龙格函数21(),(11)125f x x x=-≤≤+作多项式插值,对不同n 值,分别画出插值函数及()f x 的图形。
6、下列数据点的插值可以得到平方根函数的近似,在区间[0,64]上作图。
(1)用这9个点作8次多项式插值8()L x 。
(2)用三次样条(第一边界条件)程序求()S x 。
7、对于给函数21()125f x x =+在区间[-1,1]上取10.2(0,1,,10)i x i i =-+=,试求3次曲线拟合,试画出拟合曲线并打印出方程,与第5题的结果比较。
四、实验过程与结果:1、Lagrange 插值多项式源代码:function ya=lag(x,y,xa) %x 所有已知插值点 %y 插值点对应函数值 %xa 所求点,自变量 %ya 所求点插值估计量 ya=0; mu=1; %初始化%循环方式求L 系数,并求和: for i = 1:length(y) for j = 1:length(x) if i ~= jmu = mu * (xa - x(j) ) / ( x(i) - x(j) ); else continue end endya = ya + y(i) * mu ; mu = 1; end2、Newton 源代码:function ya = newton(x,y,xa) %x 所有已知插值点 %y 插值点对应函数值 %xa 所求点,自变量 %ya 所求点插值估计量 %建立系数零矩阵D 及初始化:D = zeros(length(x)-1);ya = y(1);xi = 1;%求出矩阵D,该矩阵第一行为牛顿插值多项式系数:for i=1:(length(x)-1)D(i,1) = (y(i+1) -y(i))/(x(i+1) -x(i));endfor j=2:(length(x)-1)for i=1:(length(x)-j)D(i,j) = (D(i+1,j-1) - D(i,j-1)) / (x(i+j) - x(i)); endend%xi为单个多项式(x-x(1))(x-x(2))...的值for i=1:(length(x)-1)for j=1:ixi = xi*(xa - x(j));endya = ya + D(1,i)*xi;xi = 1;end3、三次样条插值多项式(1)(第一边界条件)源代码:function y=yt1(x0,y0,f_0,f_n,x) _____________(1)%第一类边界条件下三次样条插值;%xi 所求点;%yi 所求点函数值;%x 已知插值点;%y 已知插值点函数值;%f_0左端点一次导数值;%f_n右端点一次导数值;n = length(x0);z = length(y0);h = zeros(n-1,1);k=zeros(n-2,1);l=zeros(n-2,1);S=2*eye(n);for i=1:n-1h(i)= x0(i+1)-x0(i);endfor i=1:n-2k(i)= h(i+1)/(h(i+1)+h(i));l(i)= 1-k(i);end%对于第一种边界条件:k = [1;k]; _______________________(2)l = [l;1]; _______________________(3)%构建系数矩阵S:for i = 1:n-1S(i,i+1) = k(i);S(i+1,i) = l(i);end%建立均差表:F=zeros(n-1,2);for i = 1:n-1F(i,1) = (y0(i+1)-y0(i))/(x0(i+1)-x0(i));endD = zeros(n-2,1);for i = 1:n-2F(i,2) = (F(i+1,1)-F(i,1))/(x0(i+2)-x0(i));D(i,1) = 6 * F(i,2);end%构建函数D:d0 = 6*(F(1,2)-f_0)/h(1); ___________(4)dn = 6*(f_n-F(n-1,2))/h(n-1); ___________(5)D = [d0;D;dn]; ______________(6)m= S\D;%寻找x所在位置,并求出对应插值:for i = 1:length(x)for j = 1:n-1if (x(i)<=x0(j+1))&(x(i)>=x0(j))y(i) =( m(j)*(x0(j+1)-x(i))^3)/(6*h(j))+...(m(j+1)*(x(i)-x0(j))^3)/(6*h(j))+...(y0(j)-(m(j)*h(j)^2)/6)*(x0(j+1)-x(i))/h(j)+... (y0(j+1)-(m(j+1)*h(j)^2)/6)*(x(i)-x0(j))/h(j) ; break;else continue;endendend(2)(自然边界条件)源代码:仅仅需要对上面部分标注的位置做如下修改:__(1):function y=yt2(x0,y0,x)__(2):k=[0;k]__(3):l=[l;0]__(4)+(5):删除—(6):D=[0:D:0]4、——————————————PS:另建了一个f方程文件,后面有一题也有用到。
matlab与lagrange插值 英文版 数值分析课程设计

理学院School of Science数值分析课程设计报告学生姓刘永辉名:学生学******** 号:所在班******** 级:所在专*******业:指导教******** 师:实习场青岛理工大学所:实习时第五学期间:课程设计的题目:验证用chebyshev点的lagrange插值多项式逼近原函数比用等步长点的逼近好。
课程设计的目的:会用matlab编程进行lagrange插值并且分析插值结果。
实验项目的基本理论:lagrange插值法、matlab编程应用、chebyshev结点公式具体算法:1、在区间【-1,1】上取点,先按Chebyshev取点,即xk=cos((2k-1)pi/2/(n+1))取点,然后再进行拉格朗日插值,绘出图和插值点。
2、在区间【-1,1】进行均匀取点再拉格朗日插值,绘出图和插值点。
3、将两种插值结果进行比较。
程序代码和数值实验结果(包括必要的图表等):chebyshev结点的lagrange插值for a=1:10b=a+1;for c=1:bX(c)=cos((2*c-1)*pi/2/(a+1));Y(c)=1/(1+25*X(c)^2);x=-1:0.05:1;endm=length(x);for i=1:mz=x(i);s=0;for k=1:bL=1;for j=1:bif j~=kL=L*(z-X(j))/(X(k)-X(j));endends=s+L*Y(k);endy(i)=s;endfigure(1)plot(x,y,'r'); %注:红色线figure(2)plot(X,Y,'b*') %注:蓝色星型线end等步长节点的lagrange插值for a=2:2:10b=a+1;X=linspace(-1,1,b);Y=1./(1+25*X.^2);x=-1:0.05:1;m=length(x);for i=1:mz=x(i);s=0;for k=1:bL=1;for j=1:bif j~=kL=L*(z-X(j))/(X(k)-X(j)); endends=s+L*Y(k);endy(i)=s;endfigure(1)plot(x,y,'r');figure(2)plot(X,Y,'b*')end由上面几个图形初步分析可以知道:等步长结点插值时,当n比较大时,就会出现多项式插值的Runge现象,即当插值节点的个数n增加时,Lagrange插值多项式对原来函数的近似并非越来越好。
拉格朗日插值、牛顿插值的matlab代码

实验五多项式插值逼近信息与计算科学金融崔振威201002034031一、实验目的:拉格朗日插值和牛顿插值的数值实现二、实验内容:p171.1、p178.1、龙格现象数值实现三、实验要求:1、根据所给题目构造相应的插值多项式,2、编程实现两类插值多项式的计算3、试分析多项式插值造成龙格现象的原因主程序1、拉格朗日function [c,l]=lagran(x,y)%c为多项式函数输出的系数%l为矩阵的系数多项式%x为横坐标上的坐标向量%y为纵坐标上的坐标向量w=length(x);n=w-1;l=zeros(w,w);for k=1:n+1v=1;for j=1:n+1if k~=jv=conv(v,poly(x(j)))/(x(k)-x(j)) %对多项式做卷积运算endendl(k,:)=v;endc=y*l;牛顿插值多项式主程序function [p2,z]=newTon(x,y,t)%输入参数中x,y为元素个数相等的向量%t为插入的定点%p2为所求得的牛顿插值多项式%z为利用多项式所得的t的函数值。
n=length(x);chaS(1)=y(1);for i=2:nx1=x;y1=y;x1(i+1:n)=[];y1(i+1:n)=[];n1=length(x1);s1=0;for j=1:n1t1=1;for k=1:n1if k==j %如果相等则跳出循环continue;elset1=t1*(x1(j)-x1(k));endends1=s1+y1(j)/t1;endchaS(i)=s1;endb(1,:)=[zeros(1,n-1) chaS(1)];cl=cell(1,n-1); %cell定义了一个矩阵for i=2:nu1=1;for j=1:i-1u1=conv(u1,[1 -x(j)]); %conv()用于多项式乘法、矩阵乘法cl{i-1}=u1;endcl{i-1}=chaS(i)*cl{i-1};b(i,:)=[zeros(1,n-i),cl{i-1}];endp2=b(1,:);for j=2:np2=p2+b(j,:);endif length(t)==1rm=0;for i=1:nrm=rm+p2(i)*t^(n-i);endz=rm;elsek1=length(t);rm=zeros(1,k1);for j=1:k1for i=1:nrm(j)=rm(j)+p2(i)*t(j)^(n-i);endz=rm;endendplot(t,z,'y',x,y,'*r') %输出牛顿插值多项式的函数图p171.1(a)、f(x)=e x解:在matlab窗口中输入:>> x=[0 0.2 0.4 0.6 0.8 1];>> y=[exp(0) exp(0.2) exp(0.4) exp(0.6) exp(0.8) exp(1)]y =1.0000 1.2214 1.4918 1.82212.2255 2.7183>> [c,l]=lagran(x,y)可以得出输出结果为:c =0.0139 0.0349 0.1704 0.4991 1.0001 1.0000l =-26.0417 78.1250 -88.5417 46.8750 -11.4167 1.0000130.2083 -364.5833 369.7917 -160.4167 25.0000 0-260.4167 677.0833 -614.5833 222.9167 -25.0000 0260.4167 -625.0000 510.4167 -162.5000 16.6667 0-130.2083 286.4583 -213.5417 63.5417 -6.2500 026.0417 -52.0833 36.4583 -10.4167 1.0000 0由输出结果可以的出:P(x)的系数分别为:a0=0.0139 a1=0.0349 a2=0.1704 a3=0.4991 a4=1.0001 a5=1.0000(b)、f(x)=sin(x)解:在matlab窗口中输入:>> x=[0 0.2 0.4 0.6 0.8 1];>> y=[sin(0) sin(0.2) sin(0.4) sin(0.6) sin(0.8) sin(1)];>> [c,l]=lagran(x,y)可以得出输出结果为:c =0.0073 0.0016 -0.1676 0.0002 1.0000 0l =-26.0417 78.1250 -88.5417 46.8750 -11.4167 1.0000130.2083 -364.5833 369.7917 -160.4167 25.0000 0-260.4167 677.0833 -614.5833 222.9167 -25.0000 0260.4167 -625.0000 510.4167 -162.5000 16.6667 0-130.2083 286.4583 -213.5417 63.5417 -6.2500 026.0417 -52.0833 36.4583 -10.4167 1.0000 0由输出结果可以的出:P(x)的系数分别为:a0=0.0073 a1=0.0016 a2=-0.1676 a3=0.0002 a4=1.0000 a5=0(c)、f(x)=(x+1)x+1解:在matlab窗口中输入:>> x=[0 0.2 0.4 0.6 0.8 1];>> y=[1 1.2^1.2 1.4^1.4 1.6^1.6 1.8^1.8 2^2];>> [c,l]=lagran(x,y)可以得出输出结果为:c =0.3945 -0.0717 0.7304 0.9415 1.0052 1.0000l =-26.0417 78.1250 -88.5417 46.8750 -11.4167 1.0000130.2083 -364.5833 369.7917 -160.4167 25.0000 0-260.4167 677.0833 -614.5833 222.9167 -25.0000 0260.4167 -625.0000 510.4167 -162.5000 16.6667 0-130.2083 286.4583 -213.5417 63.5417 -6.2500 026.0417 -52.0833 36.4583 -10.4167 1.0000 0由输出结果可以的出:P(x)的系数分别为:a0=0.3945 a1=-0.0717 a2=0.7304 a3=0.9415 a4=1.0052 a5=1.0000P178.12、a0=5 a1=-2 a2=0.5 a3=-0.1 a4=0.003x0=0 x1=1 x2=2 x3=3 c=2.5解:在matlab窗口中输入:>> x=[5 -2 0.5 -0.1];>> y=[0 1 2 3];>> t=0:0.1:2.5;>> [u,v]=newTon(x,y,t)可得出输出结果:u =0.1896 -0.7843 -1.3928 2.8688v =2.8688 2.7218 2.5603 2.3855 2.1983 2.0000 1.7917 1.5745 1.3497 1.1182 0.8813 0.6401 0.3957 0.1493 -0.0980 -0.3451 -0.5908 -0.8340 -1.0735 -1.3082 -1.5370 -1.7588 -1.9723 -2.1765 -2.3702 -2.5523由此可以求出牛顿多项式为:f(x)=0.1896x^3--0.7843^x2--1.3928x+2.8688输出的图为:结果分析:利用牛顿插值多项式的函数,通过调用函数可以求得牛顿多项式与给定的点的值,并通过matlab做出函数图像。
拉格朗日插值法matlab程序

拉格朗日插值法matlab程序拉格朗日插值法是一种用于构造插值多项式的方法,它可以通过已知数据点来估计函数在其他位置的值。
在数值分析和工程应用中,拉格朗日插值法被广泛使用,尤其在数据处理和曲线拟合方面。
在本文中,我将为您介绍拉格朗日插值法的原理和应用,并共享一个用于实现该方法的简单matlab程序。
让我们来了解一下拉格朗日插值法的原理。
拉格朗日插值法是通过在已知数据点上构造一个插值多项式来实现的。
假设我们有n+1个不同的数据点(x0, y0), (x1, y1), ..., (xn, yn),我们希望通过这些数据点来估计函数在其他位置的值。
拉格朗日插值多项式的一般形式为:P(x) = Σ(yi * li(x))i=0 to n其中,li(x)是拉格朗日基础多项式,它的表达式为:li(x) = Π(x - xj) / (xi - xj)j=0 to n, j ≠ i通过以上公式,我们可以得到拉格朗日插值多项式P(x),从而实现对函数在其他位置的估计。
在matlab中,我们可以通过编写一个简单的程序来实现拉格朗日插值法。
下面是一个用于计算拉格朗日插值多项式的matlab程序:```matlabfunction [L, P] = lagrange_interp(x, y, xx)n = length(x);m = length(xx);L = zeros(n, m);for i = 1:nt = ones(1, m);for j = [1:i-1, i+1:n]t = t .* (xx - x(j)) / (x(i) - x(j));endL(i,:) = t;endP = y * L;end```在上面的程序中,x和y分别表示已知数据点的横纵坐标,xx表示我们希望估计函数值的位置。
程序返回的L矩阵存储了插值多项式的系数,P向量存储了估计函数值的结果。
通过这个简单的程序,我们就可以快速实现拉格朗日插值法的计算。
Lagrange插值多项式MATLAB编程实验报告

x0=sym('x');
lag=lag1(x,y,x0)
习题2.2:
x=[0.5,0.6,0.7];
y=[-0.693147,-0.510826,-0.356675];
x0=0.54;
lag=lag(x,y,x0)
一、结论:
(2)
(3)
(5)2.1:
2.2:
x0=-pi:pi;
plot(x,y,'r')
hold on
n=length(x0);
z=[];
for i=1:n
z(i)=lag(x,y,x0(i));
end
plot(x0,z,'b')
(4)
function [f]=lag1(x,y,x0) %建立n次多项式l(k)的表达函数(符号表达)
n=leቤተ መጻሕፍቲ ባይዱgth(x);
x0=sym('x');
f=0;
for k=1:n
l=1;
for i=1:n
if i~=k
l=l*(x0-x(i))/(x(k)-x(i));
else l=l*1;
end
end
L(k)=l;
end
for k=1:n
f=f+y(k)*L(k);
end
collect(f);
(5)
习题2.1:
x=[1,-1,2];
if i~=k
l=l*(x0-x(i))/(x(k)-x(i));
else l=l*1;
end
end
L(k)=l;
end
for k=1:n
f=f+y(k)*L(k);
Langrage和Newton插值法的matlab实现

仅供参考1.已知数据如下:(1)用MATLAB语言编写按Langrage插值法和Newton插值法计算插值的程序,对以上数据进行插值;(2)利用MATLAB在第一个图中画出离散数据及插值函数曲线。
(1.1)langrage插值法编程实现syms xx0=[0.2,0.4,0.6,0.8,1.0];y0=[0.98,0.92,0.81,0.64,0.38];for i=1:5a=1;for j=1:5if j~=ia=expand(a*(x-x0(j)));endendb=1;for k=1:5if k~=ib=b*(x0(i)-x0(k));endendA(i)=expand(a/b);endL=0;for p=1:5L=L+y0(p)*A(p);endLL =-25/48*x^4+5/6*x^3-53/48*x^2+23/120*x+49/50(1.2)Newton插值程序实现clear allclcsyms xx0=[0.2,0.4,0.6,0.8,1.0];y0=[0.98,0.92,0.81,0.64,0.38];for k=1:5for i=1:ka=1;b=0;for j=1:kif j~=ia=a*(x0(i)-x0(j));endendb=b+y0(i)/a;endA(k)=b;endB=[1,(x-x0(1)),(x-x0(1))*(x-x0(2)),(x-x0(1))*(x-x0(2))*(x-x0(3)),(x-x 0(1))*(x-x0(2))*(x-x0(3))*(x-x0(4))];L1=A.*B;l=0;for m=1:5l=l+L1(m);endL=expand(l)L =61/100+13/30*x+383/48*x^2-155/24*x^3+475/48*x^4(2)画图x0=[0.2,0.4,0.6,0.8,1.0];y0=[0.98,0.92,0.81,0.64,0.38];subplot(1,2,1);plot(x0(1),y0(1),'+r',x0(2),y0(2),'+r',x0(3),y0(3),'+r',x0(4),y0(4),' +r',x0(5),y0(5),'+r')x=0:0.05:1;y=-25/48.*x.^4+5/6.*x.^3-53/48.*x.^2+23/120.*x+49/50;subplot(1,2,2);plot(x,y)2.给定函数21(),[1,1]125f x x x ,利用上题编好的Langrage 插值程序(或Newton 插值程序),分别取3个,5个、9个、11个等距节点作多项式插值,分别画出插值函数及原函数()f x 的图形,以验证Runge 现象、分析插值多项式的收敛性。
数值分析课程设计-多项式插值的振荡现象matlab

数值分析课程设计多项式插值的振荡现象(姓名)(学号)指导教师学院名称专 业 名 称提交日期2012年6月一、 问题的提出考虑在一个固定区间上用插值逼近一个函数。
显然,Lagrange 插值中使用的节点越多,插值多项式的次数就越高。
我们自然关心插值多项式增加时,L n (x)是否也更加靠近被逼近的函数。
龙格(Runge)给出的一个例子是极著名并富有启发性的。
设区间[-1,1]上的函数21()125f x x=+ 考虑区间[-1,1]的一个等距划分,节点为21,0,1,2,,i i x i n n =-+=则拉格朗日插值多项式为201()()125nn i i i L x a x x ==+∑ 其中的a i (x),i=0,1,2,…,n 是n 次Lagrange 插值基函数。
二、 实验内容研究以下三个函数在各自区间上运用不同的划分1、21(),[1,1]125f x x x =∈-+ 2、4(),[5,5]1x h x x x=∈-+ 3、()arctan ,[5,5]g x x x =∈-运用在区间[-p,p]上等距划分(p>0),节点为2,0,1,2,,i i x p i n n =-+=以x 0,x 1,…,x n 为插值节点构造上述各函数的Lagrange 插值多项式。
运用区间[a,b]上切比雪夫(Chebychev)点的定义为(21)cos ,1,2,,1222(1)k b a b a k x k n n π⎛⎫+--=+=+ ⎪+⎝⎭以x 1,x 2,…,x n+1为插值节点构造上述各函数的Lagrange 插值多项式,比较其结果。
并分别比较两种划分方法,增加节点数,最大误差的变化。
三、 实验结果及分析(一) 等距划分 对于函数21(),[1,1]125f x x x =∈-+来说,使用等距划分其中绿色点线代表误差,红色划线代表Lagrange插值多项式,蓝色实线代表原函数。
可见对于等距划分来说节点数越多,最大误差越大,可是越靠近中间的误差越少。
Lagrange 插值多项式与Newton插值
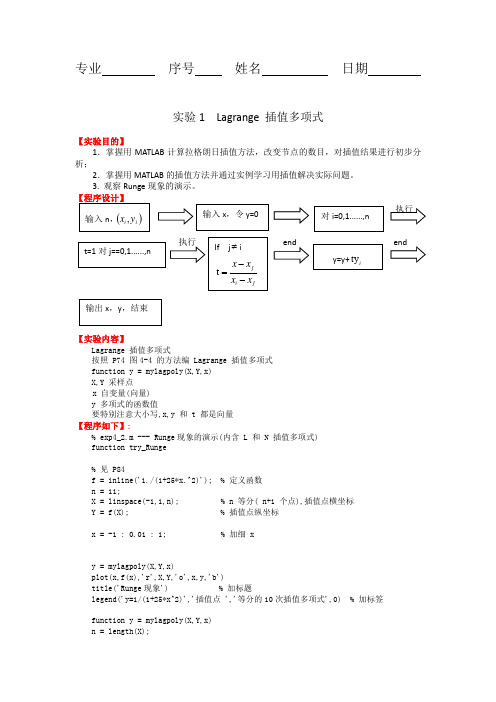
专业序号姓名日期实验1Lagrange 插值多项式【实验目的】1.掌握用MATLAB计算拉格朗日插值方法,改变节点的数目,对插值结果进行初步分析;2.掌握用MATLAB的插值方法并通过实例学习用插值解决实际问题。
3. 观察Runge现象的演示。
【实验内容】Lagrange 插值多项式按照 P74 图4-4 的方法编 Lagrange 插值多项式function y = mylagpoly(X,Y,x)X,Y 采样点x 自变量(向量)y 多项式的函数值要特别注意大小写,x,y 和 t 都是向量【程序如下】:% exp4_2.m --- Runge现象的演示(内含 L 和 N 插值多项式)function try_Runge% 见 P84f = inline('1./(1+25*x.^2)'); % 定义函数n = 11;X = linspace(-1,1,n); % n 等分( n+1 个点),插值点横坐标Y = f(X); % 插值点纵坐标x = -1 : 0.01 : 1; % 加细 xy = mylagpoly(X,Y,x)plot(x,f(x),'r',X,Y,'o',x,y,'b')title('Runge现象') % 加标题legend('y=1/(1+25*x^2)','插值点 ','等分的10次插值多项式',0) % 加标签function y = mylagpoly(X,Y,x)n = length(X);y = zeros(size(x));for i = 1:nt=1;for j = 1:nif j ~= it = t.*((x-X(j))/(X(i)-X(j))); % 注意这里是点乘,字母与书上不同,此时t变成向量了endendy=y+ t.*Y(i);end【运行结果如下】:【结果分析】:拉格朗日插值实验通过离散的点来构造一个函数来逼近原来的函数,理论上应该是点越多,构造函数应该会越来越逼近原函数,但是却发生了Range现象,所以在利用拉格朗日插值法来构造函数来逼近原函数时,应该选择适当的点来逼近原函数,但即使如此,依然不能有效的避免Range现象。
matlab实现Lagrange多项式插值观察龙格现象

Matlab进行Lagrange多项式插值拉格朗日插值法对函数y=1./(1+25*x.^2)在区间[-1,1]进行5次、10次、15次插值观察龙格现象主程序1.拉格朗日function [c,l]=lagran(x,y)%c为多项式函数输出的系数%l为矩阵的系数多项式%x为横坐标上的坐标向量%y为纵坐标上的坐标向量w=length(x);n=w-1;l=zeros(w,w);for k=1:n+1v=1;for j=1:n+1if k~=jv=conv(v,poly(x(j)))/(x(k)-x(j)) %对多项式做卷积运算endendl(k,:)=v;endc=y*l;2.在matlab窗口中输入:x=linspace(-1,1,6);y=1./(1+25*x.^2);lagran(x,y)回车可得结果:ans =-0.0000 1.2019 -0.0000 -1.7308 -0.0000 0.5673在matlab窗口中输入:x=linspace(-1,1,11);y=1./(1+25*x.^2);lagran(x,y)回车可得结果:ans =-220.9417 0.0000 494.9095 -0.0000 -381.4338 -0.0000 123.3597 0.0000 -16.8552 0.0000 1.0000在matlab窗口中输入:x=linspace(-1,1,16);y=1./(1+25*x.^2);lagran(x,y)回车可得结果:ans =1.0e+003 *Columns 1 through 140.0000 -1.5189 -0.0000 4.6511 -0.0000 -5.5700 0.0000 3.3477 0.0000 -1.0830 -0.0000 0.1901 -0.0000 -0.0180Columns 15 through 160.0000 0.00103.由以上结果可定义一下函数:function y=f1(x)y=1./(1+25*x.^2);function y=f2(x)y=1.2019*x.^4 -1.7308*x.^2+0.5673;function y=f3(x)y=-220.9417*x.^10+494.9095*x.^8-381.4338*x.^6+123.3597*x.^4-16.8552*x.^2+1;function y=f4(x)y=1*10^3*(-1.5189*x.^14+4.6511*x.^12-5.5700*x.^10+3.3477*x.^8-1.0830*x.^6+0.1901*x.^4-0.0180*x.^2+0.0010)4. 在matlab窗口中输入:s1=@f1;s2=@f2;s3=@f3;s4=@f4;fplot(s1,[-1 1],'r');hold on;fplot(s2,[-1 1],'k');hold on;fplot(s3,[-1 1],'g');hold on;fplot(s4,[-1 1],'b');xlabel('input');ylabel('output');title('龙格现象');legend('s1=f(x)','s2=L5(x)','s3=L10(x)','s4=L15(X)');grid on可以得到下图:。
拉格朗日插值matlab程序例题

拉格朗日插值是一种常用的数据拟合方法,它可以通过已知数据点来估计出未知数据点的值。
在数学和工程领域中,拉格朗日插值经常被用来进行数据的近似和预测。
在本文中,我们将深入探讨拉格朗日插值的原理和应用,并以Matlab程序例题来展示其实际运用。
1. 拉格朗日插值的原理拉格朗日插值是利用已知数据点来构造一个多项式,通过这个多项式来拟合数据并进行预测。
它的原理基于拉格朗日多项式的概念,即通过已知的n个点来构造一个n-1次的拉格朗日多项式,利用这个多项式来估计其他点的数值。
2. 拉格朗日插值的公式假设有n个已知的数据点(x1, y1), (x2, y2), …, (xn, yn),则拉格朗日插值多项式可以表示为:L(x) = Σ(yi * li(x)), i=1 to n其中li(x)是拉格朗日基函数,定义为:li(x) = Π((x - xj) / (xi - xj)), j=1 to n, j≠i利用这个公式,我们可以得到拉格朗日插值多项式,进而进行数据的拟合和预测。
3. 拉格朗日插值的Matlab程序实现下面我们将以一个具体的例题来展示如何使用Matlab来实现拉格朗日插值。
假设有如下数据点:y = [10, 5, 8, 3, 6];我们希望利用这些数据点来构造拉格朗日插值多项式,并使用这个多项式来估计x=3.5处的数值。
我们可以编写Matlab程序来实现拉格朗日插值。
代码如下:```matlabfunction result = lagrange_interpolation(x, y, xx)n = length(x);result = 0;for i = 1:ntemp = y(i);for j = 1:nif i ~= jtemp = temp * (xx - x(j)) / (x(i) - x(j));endendresult = result + temp;endend```我们可以调用这个函数来进行插值计算:```matlaby = [10, 5, 8, 3, 6];xx = 3.5;result = lagrange_interpolation(x, y, xx)disp(result);```通过这段程序,我们可以得到x=3.5处的插值结果为6.75。
拉格朗日插值龙格现象的matlab实现

拉格朗日插值龙格现象的MATLAB 实现姓名:袁宽 学号:2 专业:电气工程题目:对于函数211)(x x f +=,55≤≤-x 进行拉格朗日插值。
10=n ,按等距节点求分段线性插值,把)(x f 和插值多项式的曲线画在同一张图上进行比较。
观察Lagrange 插值及数值积分中的分段性插值。
f.m :function f= f( x )f=1./(1+x.^2);endLagrange.mfunction y=Lagrange(x0,y0,x);n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;End拉格朗日插值的曲线:x=[-5:1:5];y=1./(1+x.^2);x0=[-5:0.001:5];y0=Lagrange(x,y,x0);y1=1./(1+x0.^2);plot(x0,y0,'b')hold onplot(x0,y1,'r')使用龙格现象观察分段性插值的曲线:syms y x lx;y=1/(1+x^2);x0=-5:1:5;y0=zeros(1,length(x0));for i=1:11x=x0(i);y0(i)=eval(y);endM = -5:0.01:5;y1 = zeros(1,length(M));n = 1;for i=2:11for x=-5:0.01:5if x<x0(i) && x>=x0(i-1)lx(1)=y0(i-1)*(x-x0(i))/(x0(i-1)-x0(i));lx(2)=y0(i)*(x-x0(i-1))/(x0(i)-x0(i-1));y1(n) = lx(1)+lx(2);n = n+1;endendendezplot(y,[-5,5])hold onA =-5:0.01:5;plot(A,y1,'r');分别运行两个文件后的得到两个图形曲线:拉格朗日插值曲线分段插值曲线。
matlab 拉格朗日插值多项式

matlab 拉格朗日插值多项式
拉格朗日插值多项式是一种基于差商的插值方法,它可以用于生
成通过给定数据点的曲线。
该方法的实现依赖于 MATLAB 的插值函数。
以下是一个简单的分步骤的过程来解释如何使用 MATLAB 来使用拉格
朗日插值多项式进行插值。
第一步是定义数据点。
要使用拉格朗日插值多项式,需要有一组
完整的数据点。
可以使用 MATLAB 预定义的数据或手动定义自己的数据。
第二步是创建插值函数。
可以使用 MATLAB 的 interp1 函数来
定义插值函数。
该函数需要数据点和插值点作为输入,以及插值函数
类型(在此处选择拉格朗日插值多项式)。
第三步是绘制数据和插值曲线。
可以使用 plot 函数来对数据和
插值曲线进行绘图。
这使得您可以可视化数据点和插值过程,并检查
结果的准确性。
第四步是调整插值精度。
可以使用 MATLAB 的 interp1 函数来
调整插值的精度。
通常,较高的精度会导致更准确的结果,但也会增
加计算时间。
最后一步是验证和测试。
最后一步是验证和测试已生成的拉格朗
日插值多项式。
可以使用 MATLAB 的测试函数和可视化工具来检查曲
线的准确性和精度。
总之,使用 MATLAB 进行拉格朗日插值多项式插值是一种灵活、
快速、易用的方法。
使用该方法,可以快速生成插值曲线,使您能够
更好地理解数据,做出更明智的决策。
拉格朗日插值函数matlab例题

拉格朗日插值函数是一种常用的数学工具,它可以用于拟合数据、逼近函数和插值等多种数学问题。
在本文中,我将通过介绍拉格朗日插值函数的原理和应用,以及使用Matlab进行实例演示,帮助你更好地理解这一主题。
1. 拉格朗日插值函数的原理拉格朗日插值函数是通过拉格朗日插值多项式来实现插值的过程。
拉格朗日插值多项式是由一组互不相同的节点和函数值得到的,并且满足通过这些节点的所有函数值。
它的数学表达式如下所示:\[P(x) = \sum_{i=0}^{n} y_i l_i(x)\]其中 \(P(x)\) 是拉格朗日插值多项式,\(n\) 是节点数,\(y_i\) 是函数在节点 \(x_i\) 处的函数值,\(l_i(x)\) 是拉格朗日基函数。
2. 拉格朗日插值函数的应用拉格朗日插值函数广泛应用于各种领域,包括数值分析、数值计算和工程应用等。
它可以用于曲线拟合、图像处理、信号处理等多种领域,并且在实际问题中具有重要的作用。
3. 使用Matlab进行拉格朗日插值函数的实例演示接下来,我将使用Matlab进行一个简单的拉格朗日插值函数的实例演示,以便更直观地理解这一主题。
```matlab% 拉格朗日插值函数的实例演示x = [1, 2, 3, 4]; % 设定节点y = [1, 4, 9, 16]; % 对应的函数值xx = 1:0.1:4; % 生成插值点yy = zeros(size(xx)); % 初始化插值结果for i = 1:length(x)L = ones(size(xx));for j = 1:length(x)if j ~= iL = L.*(xx-x(j))/(x(i)-x(j));endendyy = yy + y(i)*L; % 计算插值结果endplot(x,y,'o',xx,yy,'-'); % 绘制插值结果xlabel('x'); ylabel('y');legend('节点','插值结果');```在这个实例中,我们首先定义了一组节点\(x\) 和对应的函数值\(y\),然后生成了插值点 \(xx\),利用拉格朗日插值多项式计算了插值结果\(yy\),最后使用Matlab进行了绘图展示。
用matlab编写拉格朗日插值算法的程序

用matlab编写拉格朗日插值算法的程序10[ 标签:matlab,插值算法,程序]用matlab编写拉格朗日插值算法的程序,并以下面给出的函数表为数据基础,在整个插值区间上采用拉格朗日插值法计算f(),写出程序源代码,输出计算结果xy匿名回答:1 人气:6 解决时间:2011-05-24 19:58满意答案好评率:83%做了一个测试,希望有所帮助。
代码:% 用matlab编写拉格朗日插值算法的程序,并以下面给出的函数表为数据基础,% 在整个插值区间上采用拉格朗日插值法计算f(),写出程序源代码,输出计算结果% x% yfunction main()clc;x = [ ]; y = [ ];x0 = ;f = Language(x,y,x0)function f = Language(x,y,x0)%求已知数据点的拉格朗日插值多项式%已知数据点的x坐标向量: x%已知数据点的y坐标向量: y%插值点的x坐标: x0%求得的拉格朗日插值多项式或在x0处的插值: f syms t l;if(length(x) == length(y))n = length(x);elsedisp('x和y的维数不相等!');return; %检错endh=sym(0);for (i=1:n)l=sym(y(i));for(j=1:i-1)l=l*(t-x(j))/(x(i)-x(j));end;for(j=i+1:n)l=l*(t-x(j))/(x(i)-x(j));end;h=h+l;endsimplify(h);if(nargin == 3)f = subs (h,'t',x0); %计算插值点的函数值elsef=collect(h);f = vpa(f,6); %将插值多项式的系数化成6位精度的小数end结果:f =>>如何用MATLAB编写的拉格朗日插值算法的程序、二阶龙格-库塔方法的程序和SOR迭代法的程序,要能运行的∮初夏戀雨¢回答:2 人气:29 解决时间:2009-12-08 19:04满意答案好评率:100%拉格朗日function y=lagrange(x0,y0,x) n=length(x0);m=length(x);for i=1:mz=x(i);s=;for k=1:np=;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j)); endends=p*y0(k)+s;endy(i)=s;endSOR迭代法的Matlab程序function [x]=SOR_iterative(A,b)% 用SOR迭代求解线性方程组,矩阵A是方阵x0=zeros(1,length(b)); % 赋初值tol=10^(-2); % 给定误差界N=1000; % 给定最大迭代次数[n,n]=size(A); % 确定矩阵A的阶w=1; % 给定松弛因子k=1;% 迭代过程while k<=Nx(1)=(b(1)-A(1,2:n)*x0(2:n)')/A(1,1);for i=2:nx(i)=(1-w)*x0(i)+w*(b(i)-A(i,1:i-1)*x(1:i-1)'-A(i,i+1:n)*x0(i+1:n)')/ A(i,i);endif max(abs(x-x0))<=tolfid = fopen('', 'wt');fprintf(fid,'\n********用SOR迭代求解线性方程组的输出结果********\n\n');fprintf(fid,'迭代次数: %d次\n\n',k);fprintf(fid,'x的值\n\n');fprintf(fid, '% \n', x);break;endk=k+1;x0=x;endif k==N+1fid = fopen('', 'wt');fprintf(fid,'\n********用SOR迭代求解线性方程组的输出结果********\n\n');fprintf(fid,'迭代次数: %d次\n\n',k);fprintf(fid,'超过最大迭代次数,求解失败!');fclose(fid);endMatlab中龙格-库塔(Runge-Kutta)方法原理及实现龙格-库塔(Runge-Kutta)方法是一种在工程上应用广泛的高精度单步算法。
Runge现象的演示(内含L和N插值多项式)

实验4_2 Runge现象的演示(内含L 和N 插值多项式)【实验目的】1、了解并掌握matlab软件的基本应用方法;2、初步了解matlab中部分函数,熟悉循环语句的使用;3、通过上机进一步掌握Lagrange插值多项式的建立。
【实验内容】(1)【实验一】 Lagrange 插值多项式(1)首先把本程序另存为一个不同的文件名;(2)把下面程序中开头的注释去掉,再把问号填写正确;.(2)【实验二】Newton 插值多项式对于Newton插值多项式,可以不计算差分表(矩阵),而直接计算差分表中的对角元(实际上只用到这些值),这样就能大大减少储存空间,P79 图4-5 就是这种方法, 请你证明图中y(k)就是差分表的对角元,并注意后半部分就是Horner 算法. 按此法编程【解】:手工分析怎样求解这题。
【计算机求解】:怎样设计程序?流程图?变量说明?能否将某算法设计成具有形式参数的函数形式?【实验一】Lagrange 插值多项式【程序如下】:function y=lagrange(X,Y,x);n=length(X);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:nt=1.0;for j=1:nif j~=kt=t*(z-X(j))/(X(k)-X(j));endends=t*Y(k)+s;endy(i)=s;endf = inline('1./(1+25*x.^2)');n = 30;X = linspace(-1,1,n);Y = f(X);x = -1 : 0.01 : 1;y=lagrange(X,Y,x);plot(x,f(x),'r',X,Y,'o',x,y,'b')title('Runge现象')legend('y=1/(1+25*x^2)','插值点','等分的30次插值多项式',0) 【运行结果如下】将n改为50次,得到下面图像:【结果分析】通过实验,可以更直观的将插值的结果展现出来,同时还能发现格式插值的弊端。
Lagrange插值MATLAB源程序

function y=lagrange(x0,y0,x); % x0自变量取值向量y0为对应x0的函数取值,x为要求插值点坐标n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j)); %插值基函数endends=p*y0(k)+s; %lagrange插值多项式endy(i)=s;end测试:x0=[0:2]y0=[2 3 5]Lagrange(x0,y0,x)x0=[0:2]y0=[2 3 5]x=[:2]Lagrange(x0,y0,x)function f=Newton(x,y,x0)syms t;n = length(x);c(1:n) = 0.0;f = y(1);y1 = 0;l = 1;for(i=1:n-1)for(j=i+1:n)y1(j) = (y(j)-y(i))/(x(j)-x(i));endc(i) = y1(i+1);l = l*(t-x(i));f = f + c(i)*l;simplify(f);y = y1;if(i==n-1)if(nargin == 3)f = subs(f,'t',x0);elsef = collect(f);endendendtest:x=[1 -1 2]y=[0 -3 4]x0=[-1:0.1:2]Newton(x,y,x0)function y = div_linear(x0,y0,x,n)for i = 1:n-1if (x >= x0(i)) && (x <= x0(i+1))y = (x - x0(i+1))/(x0(i) - x0(i+1))*y0(i) + ( x - x0(i))/(x0(i+1) -x0(i))*y0(i+1);elsecontinue;endendtest:〔例题3〕x0=[-1:0.2:1];y0= 1./(25*x0.^2+1);y=interp1(x0,y0,x0,'linear')plot(x0,y0,x0,y,'p');Newton插值MATLAB源程序(2)function [] = newton(x,y,v)x=input(“X数组=〞);y=input(“Y数组=〞);v=input(“插值点数值=〞);n=length(x);t=zeros(n,n);u=0;for i=1:nt(i,1)=y(i);endfor j=2:nfor i=2:nif i>=jt(i,j)=(t(i,j-1)-t(i-1,j-1))/(x(i)-x(i-j+1));endendendfor k=1:ns=1;m=1;for j=1:kif j<ks=s*(v-x(j));endendm=s*t(k,k);u=u+m;enddisp(“插值结果=〞);disp(u);end>>newtonNewton插值MATLAB源程序function yi=newton(x,y,xi)m=length(x);n=length(y);if m~=n error('x and y must same');endf=zeros(n+1,1);k=2;f(1)=y(1)while k~=n+1f(1)=y(k);k,x(k)for i=1:k-1if i~=k-1f(i+1)=(f(i)-y(i))/(x(k)-x(i));endendcs(i)=f(i+1);y(k)=f(k);k=k+1;endcfwh=0;for i=1:n-2w=1;for j=1:iw=w*(xi-x(j));endcfwh=cfwh+cs(i)*w;endyi=y(1)+cfwh;x=[0:2]y=[2 3 5]xi=newton(x,y,xi)Newton2))function f = Newton(x,y,x0)syms t;if(length(x) == length(y))n = length(x);c(1:n) = 0.0;elsedisp('x和y的维数不相等!');return;endf = y(1);y1 = 0;l = 1;for(i=1:n-1)for(j=i+1:n)y1(j) = (y(j)-y(i))/(x(j)-x(i));endc(i) = y1(i+1);l = l*(t-x(i));f = f + c(i)*l;simplify(f);y = y1;if(i==n-1)if(nargin == 3)f = subs(f,'t',x0);elsef = collect(f); %将插值多项式展开 f = vpa(f, 6); endendendx=[0:2]y=[2 3 5]x0Newton(x,y,x0)function [] = Newton(x,y,v)x=input('X数组=:');y=input('Y数组=:');v=input('插值点数值=:');n=length(x);t=zeros(n,n);u=0;for i=1:nt(i,1)=y(i);endfor j=2:nfor i=2:nif i>=jt(i,j)=(t(i,j-1)-t(i-1,j-1))/(x(i)-x(i-j+1)); endendendfor k=1:ns=1;m=1;for j=1:kif j<ks=s*(v-x(j));endendm=s*t(k,k);u=u+m;enddisp('插值结果=');disp(u);endx=[0:2]y=[2 3 5]vnewton(x,y,v)x0=[1 -1 2]y0=[0 -3 4]x=[-1:0.1:2]Lagrange(x0,y0,x)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Matlab进行Lagrange多项式插值
拉格朗日插值法对函数y=1./(1+25*x.^2)在区间[-1,1]进行5次、10次、15次插值观察龙格现象
主程序
1.拉格朗日
function [c,l]=lagran(x,y)
%c为多项式函数输出的系数
%l为矩阵的系数多项式
%x为横坐标上的坐标向量
%y为纵坐标上的坐标向量
w=length(x);
n=w-1;
l=zeros(w,w);
for k=1:n+1
v=1;
for j=1:n+1
if k~=j
v=conv(v,poly(x(j)))/(x(k)-x(j)) %对多项式做卷积运算
end
end
l(k,:)=v;
end
c=y*l;
2.在matlab窗口中输入:
x=linspace(-1,1,6);y=1./(1+25*x.^2);
lagran(x,y)
回车可得结果:
ans =
-0.0000 1.2019 -0.0000 -1.7308 -0.0000 0.5673
在matlab窗口中输入:
x=linspace(-1,1,11);y=1./(1+25*x.^2);
lagran(x,y)
回车可得结果:
ans =
-220.9417 0.0000 494.9095 -0.0000 -381.4338 -0.0000 123.3597 0.0000 -16.8552 0.0000 1.0000
在matlab窗口中输入:
x=linspace(-1,1,16);y=1./(1+25*x.^2);
lagran(x,y)
回车可得结果:
ans =
1.0e+003 *
Columns 1 through 14
0.0000 -1.5189 -0.0000 4.6511 -0.0000 -5.5700 0.0000 3.3477 0.0000 -1.0830 -0.0000 0.1901 -0.0000 -0.0180
Columns 15 through 16
0.0000 0.0010
3.由以上结果可定义一下函数:
function y=f1(x)
y=1./(1+25*x.^2);
function y=f2(x)
y=1.2019*x.^4 -1.7308*x.^2+0.5673;
function y=f3(x)
y=-220.9417*x.^10+494.9095*x.^8-381.4338*x.^6+123.3597*x.^4-16.8552*x.^2+1;
function y=f4(x)
y=1*10^3*(-1.5189*x.^14+4.6511*x.^12-5.5700*x.^10+3.3477*x.^8-1.0830*x.^6+0.1901*x.^4-0.0180*x.^2+0.0010)
4. 在matlab窗口中输入:
s1=@f1;s2=@f2;s3=@f3;s4=@f4;fplot(s1,[-1 1],'r');hold on;fplot(s2,[-1 1],'k');hold on;fplot(s3,[-1 1],'g');hold on;fplot(s4,[-1 1],'b');xlabel('input');ylabel('output');title('龙格现象');legend('s1=f(x)','s2=L5(x)','s3=L10(x)','s4=L15(X)');grid on
可以得到下图:。
