初一上册数学找规律练习题

合集下载

七年级数学上册有理数找规律题型专题练习

七年级数学上册有理数找规律题型专题练习一、等差型数列规律1. 有一组数：1，2，3，4，5，……，请观察这组数的构成规律，用你发现的规律确定第8个数为 , 第n个数为．2. 有一组数：2，5，8，11，14，…请观察这组数的构成规律，用你发现的规律确定第8个数为 , 第n个数为．3.有一组数：7，12，17，22，27，…请观察这组数的构成规律，用你发现的规律确定第8个数为 , 第n个数为．4.有一组数：4，7，10，13,…请观察这组数的构成规律，用你发现的规律确定第n个数为．5.有一组数：11，20，29，38，…请观察这组数的构成规律，用你发现的规律确定第n个数为．二、等比型数列规律1.有一组数：1，2，4，8，16，……，请观察这组数的构成规律，用你发现的规律确定第8个数为 , 第n个数为．2. 有一组数：1，4，16，64，……，请观察这组数的构成规律，用你发现的规律确定第n个数为．3. 有一组数：1，-1，1，-1，……，请观察这组数的构成规律，用你发现的规律确定第8个数为 , 第n个数为．4. 有一组数：27，9，3，1，……，请观察这组数的构成规律，用你发现的规律确定第8个数为 , 第n个数为．三、含n2型数列规律1.有一组数：1，4，9，16，25，……，请观察这组数的构成规律，用你发现的规律确定第8个数为 , 第n 个数为．2.有一组数：2，6，12，20，30，…请观察这组数的构成规律，用你发现的规律确定第8个数为 , 第n 个数为．3.有一组数：1，3，6，10，15，…请观察这组数的构成规律，用你发现的规律确定第8个数为 , 第n 个数为．4.有一组数：0，2，6，12，20，…请观察这组数的构成规律，用你发现的规律确定第8个数为 , 第n 个数为．四、其它数列规律列举1.有一组数：1，2，3，5，8，…请观察这组数的构成规律，用你发现的规律确定第7个数为 ,2.有一组数：-2，3，1，4，5，…请观察这组数的构成规律，用你发现的规律确定第7个数为 ,3. 观察下列面一列数：1，-2，3，-4，5，-6，…根据你发现的规律，第2013个数是___________4. 观察下列一组数：，，，，……　，它们是按一定规律排列的. 那么这一组21436587数的第k 个数是.5. 观察下列一组数：.,61,51,41,31,21,1它们是按一定规律排列的.那么这一组数的第2014个数是6.观察下列一组数：32，54，76，98，1110，……　，它们是按一定规律排列的，那么这一组数的第k 个数是五、循环型数列.1.已知221，422，32=8，42=16，25=32，……观察上面规律，试猜想20082的末位数是.2.已知21873,7293,2433,813,273,93,337654321…推测到203的个位数字是；3.若，，，…　；则的值为．1113a 2111a a 3211a a 2014a 六、算式型规律1. 已知22223322333388，，244441515，……，若288a a bb（a 、b 为正整数）则ab．2. 某数学活动小组的20位同学站成一列做报数游戏，规则是：从前面第一位同学开始，每位同学依次报自己顺序的倒数加1，第1位同学报111，第2位同学报121，…这样得到的20个数的积为_________________.3. 求1+2+22+23+...+22013的值，可令S=1+2+22+23+...+22013，则2S=2+22+23+24+ (22013)因此2S ﹣S=22013﹣１．仿照以上推理，计算出1+5+52+53+…+52013的值为：4. 研究下列算式，你会发现什么规律？1×3+1=22；2×4+1=32；3×5+1=42；4×6+1=52…………，（1）请用含n 的式子表示你发现的规律：___________________.（2）请你用发现的规律解决下面问题计算的值11111(1)(1)(1)(1)(1)13243546911七、数列阵型1.观察下列三行数：（课本P43页例4变式题）第一行：-1,2，-3,4，-5……第二行：1,4,9，16,25，……第三行：0,3,8,15,24，……(1)第一行数按什么规律排列？第1个图形第2个图形第3个图形第4个图形(2)第二行、第三行分别与第一行数有什么关系？(3)取每行的第10个数，计算这三个数的和．2.观察下面一列数：1，2，3，4，5，6，7，．．．将这列数排成下列形式：按照上述规律排下去，那么第10行从左边第4个数是：八、几何图形型1．观察下列图形：它们是按一定规律排列的，依照此规律，第16个图形共有个★．2.如图所示，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第个n 图形需要黑色棋子的个数是．3．如图，用同样大小的黑色棋子按图所示的方式摆图案，按照这样的规律摆下去，第100个图案需棋子枚．4．如图，每一幅图中有若干个大小不同的菱形，第1幅图中有1个，第2幅图中有3个，第3幅图中有5个，则第4幅图中有个，第n 幅图中共有个．图案1图案2图案3…………第1幅第2幅第3幅第n 幅5. 如图7-①，图7-②，图7-③，图7-④，…，是用围棋棋子按照某种规律摆成的一行“广”字，按n照这种规律，第5个“广”字中的棋子个数是______，第个“广”字中的棋子个数是________6.同样大小的黑色棋子按如图所示的规律摆放：第1第2第3第4（1）第5个图形有多少颗黑色棋子？（2）第几个图形有2013颗棋子？说明理由。

初一数学找规律练习题

初一数学找规律练习题一、数字规律1. 观察下列数列，找出规律，并写出下一个数：2, 4, 8, 16, 32, ____1, 3, 6, 10, 15, ____1, 4, 9, 16, 25, ____二、图形规律1. 观察下列图形，找出规律，并画出下一个图形：（图形：△ △△ △△△ △△△△）（图形：○□○□○□○□）3. 观察下列图形，找出规律，并画出下一个图形：（图形：□■□■■□■■■）三、数列与图形结合规律1. 观察下列数列与图形的结合，找出规律，并写出下一个数和画出对应的图形：数列：1, 2, 3, 4, 5图形：（△）（△△）（△△△）（△△△△）数列：1, 3, 6, 10, 15图形：（○）（□□）（△△△）（■■■■）四、应用题1. 小明发现一个有趣的现象，从1开始，连续几个自然数的和等于这几个自然数的个数乘以（个数加1）除以2。

请你找出这个规律，并计算1到100的和。

2. 小华在纸上画了一排正方形，每个正方形的边长分别为1cm、2cm、3cm、4cm……，请问这排正方形总面积是多少平方厘米？3. 一个数字三角形，第一行有1个数字，第二行有2个数字，以此类推，第n行有n个数字。

求这个数字三角形前10行的数字总和。

五、数表规律1 2 3 42 3 4 53 4 5 64 5 6 __1 3 6 102 5 9 143 7 12 184 __ __ __六、操作规律A → A + 1B → B + 2C → C + 3D → D + 4（初始值：A=1, B=2, C=3, D=4）A → A × 2B → B × 3C → C × 4D → D × 5（初始值：A=1, B=1, C=1, D=1）七、逻辑推理规律A > B,B > C,C > D那么 A > D 是否成立？如果 P 则 Q，如果 Q 则 R那么如果 P 则 R 是否成立？八、综合应用题1. 一个班级有50名学生，每名学生都有一个唯一的编号，编号从1到50。

(完整)初一找规律练习题

精心整理初一数学找规律一、数字排列规律题1、下面数列后两位应该填上什么数字呢？23581217 ___2、请填出下面横线上的数字。

112358 ____ 213、有一串数，它的排列规律是1、2、3、2、3、4、3、4、5、4、5、6、……聪明的你猜猜第100个数是什么？4、有一串数字36101521_ 第6个是什么数？|| 75、观察下列一组数的排列：1、2、3、4、3、2、1、2、3、4、3、2、1、…,吊门心八H I,1那么第2005个数是（）.A. 1 B . 2 C. 3 D . 46、100个数排成一行，其中任意三个相邻数中，中间一个数都等于它前后两个数的和，如果这100个数的前两个数依次为1 , 0，那么这100个数中“0”的个数为_________ .7、一组按规律排列的数：1, 3, 7, 13, 21,……请你推断第9个数是.4 9 16 25 36&已知下列等式：① 13= 12；② 13+ 23= 32;③ 13+ 23+ 33= 62;④13+ 23+ 33+ 43= 102; .... 由此规律知，第⑤个等式是.9、观察下列各式；①、12+1 = 1X2;②、22+2=2X 3;③、32+3=3X4; ....... 请把你猜想到的规律用自然数n表示出来。

10、观察下面的几个算式：①、1+2+仁4;②、1+2+3+2+仁9③、1+2+3+4+3+2+1 = 16 ④、1+2+3+4+5+4+3+2+1=25 ……根据你所发现的规律，请你直接写出第n个式子11、观察下列一组数的排列：1、2、3、4、3、2、1、2、3、4、3、2、1、…,精心整理那么第2005个数是()A. 1B. 2 C . 3 D. 412、把数字按如图所示排列起来，从上开始，依次为第一行、第二行、第三行、……，中间用虚线围的一列，从上至下依次为1、5、13、25、……，则第10个数为________ 。

七年级上册数学找规律试题

初一数学找规律：1 ．(2013山东滨州，18，4分)观察下列各式的计算过程：5×5=0×1×100+25，15×15=1×2×100+25，25×25=2×3×100+25，35×35=3×4×100+25，…… ……请猜测，第n 个算式(n 为正整数)应表示为____________________________．【答案】 [10(n －1)+5]×[10(n －1)+5]=100n(n －1)+25.2. （2013山东莱芜，17，4分）已知123456789101112…997998999是由连续整数1至999排列组成的一个数，在该数种从左往右数第2013位上的数字为 . 【答案】73．（3分）（2013•青岛）要把一个正方体分割成8个小正方体，至少需要切3刀，因为这8个小正方体都只有三个面是现成的．其他三个面必须用三刀切3次才能切出来．那么，要把一个正方体分割成27个小正方体，至少需用刀切 6 次；分割成64个小正方体，至少需要用刀切 9 次．4．（2013泰安）观察下列等式：31=3，32=9，33=27，34=81，35=243，36=729，37=2187…解答下列问题：3+32+33+34…+32013的末位数字是（）A ．0B ．1C ．3D ．7考点：尾数特征．分析：根据数字规律得出3+32+33+34…+32013的末位数字相当于：3+7+9+1+…+3进而得出末尾数字．解答：解：∵31=3，32=9，33=27，34=81，35=243，36=729，37=2187…∴末尾数，每4个一循环，∵2013÷4=503…1，∴3+32+33+34…+32013的末位数字相当于：3+7+9+1+…+3的末尾数为3，故选：C ．点评：此题主要考查了数字变化规律，根据已知得出数字变化规律是解题关键．5.对于实数x ，我们规定[]x 表示不大于x 的最大整数，例如[]12.1=，[]33=，[]35.2-=-，若5104=⎥⎦⎤⎢⎣⎡+x ，则x 的取值可以是（）.A.40B.45C.51D.56答案：C ．考点:新定义问题.点评:本题需要学生先通过阅读掌握新定义公式，再利用类似方法解决问题.考查了学生观察问题，分析问题，解决问题的能力.6.当白色小正方形个数n 等于1,2，3…时，由白色小正方形和和黑色小正方形组成的图形分别如图所示.则第n 个图形中白色小正方形和黑色小正方形的个数总和等于_____________.（用n 表示，n 是正整数）答案：n 2+4n考点：本题是一道规律探索题，考查了学生分析探索规律的能力．点评：解决此类问题是应先观察图案的变化趋势，然后从第一个图形进行分析，运用从特殊到一般的探索方式，分析归纳找出黑白正方形个数增加的变化规律，最后含有n 的代数式进行表示．7．（3分）（2013•烟台）将正方形图1作如下操作：第1次：分别连接各边中点如图2，得到5个正方形；第2次：将图2左上角正方形按上述方法再分割如图3，得到9个正方形…，以此类推，根据以上操作，若要得到2013个正方形，则需要操作的次数是（）A ． 502B ． 503C ． 504D ． 505考点：规律型：图形的变化类．分析：根据正方形的个数变化得出第n 次得到2013个正方形，则4n+1=2013，求出即可．解答：解：∵第1次：分别连接各边中点如图2，得到4+1=5个正方形；第2次：将图2左上角正方形按上述方法再分割如图3，得到4×2+1=9个正方形…，以此类推，根据以上操作，若第n 次得到2013个正方形，则4n+1=2013，解得：n=503．故选：B ．点评：此题主要考查了图形的变化类，根据已知得出正方形个数的变化规律是解题关键．8、（2013安徽）如图，观察每一个图中黑色正六边形的排列规律，则第10个图中黑色正六边形有个。

七年级上—找规律专题练习题

七年级上—找规律专题练习题1.七年级上—找规律专题练习题(1)-23,-18,-13,______,________； ; (2)2345,,,8163264--,_______,_________； 2．有一组数：1,2,5,10,17,26,.....,请观察这组数的构成规律,用你发现的规律确定第8个数为__________.3．观察下列算式：21=2,22 =4,23 =8,24＝16,25 =32,26=64,27＝128,通过观察,用你所发现的规律确定22011的个位数字是（）A. 2B. 4C. 6D. 84．一根lm 长的绳子,第一次剪去一半,第二次剪去剩下的一半,如此剪下去,第六次后剩下的绳子的长度为（）A.31()2m B. 51()2m C. 61()2m D. 121()2m5.下面一组按规律排列的数：1,2,4,8,16.......,第2011个数应是（）A. 22011B. 22011-1C.22010D ．以上答案不对 6．研究下列算式,你会发现什么规律？1×3＋1=4=22 2×4＋1 =9＝323×5＋1=16=42 4×6＋1 =25=52请你找出规律用公式表示出来：___________________7．观察下列三行数：第一行：-1,2,-3,4,-5…… 第二行：1,4,9,16,25,…… 第三行：0,3,8,15,24,……(1)第一行数按什么规律排列？__________________ _(2)第二行、第三行分别与第一行数有什么关系？___________________ (3)取每行的第10个数,计算这三个数的和．___________________8．有规律排列的一列数：2,4,6,8,10,12,……它的每一项可用式子2n(n 是正整数)表示．有规律排列的一列数：1,-2,3,-4,5,-6,7,-8...... (1)它的每一项你认为可用怎样的式子来表示？ (2)它的第100个数是多少？(3)2012是不是这列数中的数？如果是,是第几个数？9．如果对于任意非零有理数a,b 定义运算如下：a △b=ab ＋1,那么（-5)△（+4)△（-3）的值是多少？10．如果规定符号※的意义是a ※b=aba b+,求：2※（-3)※4的值．11．先完成下列计算：1×9＋2＝11；12×9＋3＝________；123×9 + 4=__________；……你能说出得数的规律吗？请你根据发现的算式的规律求出1234567×9 + 8的值．12．如果1+2-3-4+5+6-7-8 +9＋……,是从1开始的连续整数中依次两个取正, 两个取负写下去的一串数,则前2012个数的和是多少？依照以上各式成立的规律,使44a b a b +--=2成立,则a+b 的值为____________14．观察下列各式：12+1=1×2 22+2=2×3 32+3=3×4请把你猜想到的规律用自然数n 表示出来___________________15.观察下列各式：2×4=32-1,3×5 =42-1,4×6 =52-1,……把你发现的规律用含一个字母的等式表示_________ 16．观察下列各式找规律：12＋（1×2)2＋22＝（1×2＋1）2 22＋(2×3)2＋32 =（2×3＋1）232＋（3×4)2 +42＝(3×4＋1）2(1)写出第6个式子的值； (2）写出第n 个式子．17.（2011湖南益阳）观察下列算式：① 1 × 3 - 22= 3 - 4 = -1② 2 × 4 - 32= 8 - 9 = -1 ③ 3 × 5 - 42 = 15 - 16 = -1 ④ ……（1）请你按以上规律写出第4个算式；（2）把这个规律用含字母n 的式子表示出来；1. （2011浙江省）如图,下面是按照一定规律画出的“数形图”,经观察可以发现：图A 2比图A 1多出2个“树枝”,图A 3比图A 2多出4个“树枝”, 图A 4比图A 3多出8个“树枝”,……,照此规律,图A 6比图A 2多出“树枝”（） A.28 B.56 C.60 D. 124 2.（2011广东肇庆）如图5所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第n （n 是大于0的整数）个图形需要黑色棋子的个数是．3. （2011内蒙古乌兰察布）将一些半径相同的小圆按如图所示的规律摆放,请仔细观察,第 n 个图形有个小圆. （用含 n 的代数式表示）4. （2011湖南常德）先找规律,再填数：1111111111111111,,,,122342125633078456............111+_______.2011201220112012+-=+-=+-=+-=-=⨯则 5.（2011湖南益阳）观察下列算式：① 1 × 3 - 22= 3 - 4 = -1② 2 × 4 - 32= 8 - 9 = -1 ③ 3 × 5 - 42 = 15 - 16 = -1 ④ ……（1）请你按以上规律写出第4个算式；（2）把这个规律用含字母n 的式子表示出来；（3）你认为（2）中所写出的式子一定成立吗？并说明理由． 6.研究下列算式,你会发现什么规律？1×3+1=22； 2×4+1=32； 3×5+1=42； 4×6+1=52…………,第1个图形第 2 个图形第3个图形第 4 个图形（1）请用含n 的式子表示你发现的规律：___________________. （2）请你用发现的规律解决下面问题计算11111(1)(1)(1)(1)(1)13243546911+++++⨯⨯⨯⨯⨯的值一、数字找规律1．观察下列一组数：21,43,65,87,…… ,它们是按一定规律排列的. 那么这一组数的第k 个数是 .2.观察下面一列数,探求其规律： .,61,51,41,31,21,1 ---（1）写出这列数的第九个数；（2）第2008个数是什么数？如果这一列数无限排列下去,与哪个数越来越近？3．下列是有规律排列的一列数：325314385，，，，……其中从左至右第100个数是__________．4、有一组数：1,2,5,10,17,26,……,请观察这组数的构成规律,用你发现的规律确定第8个数为． 5. 已知221=,422=,32=8,42=16,25=32,……观察上面规律,试猜想20082的末位数是 .6、已知21873,7293,2433,813,273,93,337654321=======…推测到203的个位数字是； 7、观察下列等式：第一行 3=4－1 第二行 5=9－4 第三行 7=16－9 第四行 9=25－16 … …按照上述规律,第n 行的等式为____ ________ 8．已知下列等式： ① 13＝12； ② 13＋23＝32； ③ 13＋23＋33＝62； ④ 13＋23＋33＋43＝102； …… ……由此规律知,第⑤个等式是．9．观察下列各式：1×3=12+2×1,2×4=22+2×2, 3×5=32+2×3, … …请你将猜想到的规律用自然数n （n ≥1）表示出来： .10．观察下列顺序排列的等式：猜想：第n 个等式（n 为正整数）应为__ _________________。

七年级上数学规律题集锦

七年级上数学规律题集锦1、观察有趣的奇数的求和，并填空： 1=1×1=12； 1+3=22； 1+3+5=32； ……⑴ 1+3+5+7+…+17= ； ⑵ 1+3+5+7+…+ =172；⑶1+3+5+7+…+（2n-1）= 2、观察下列等式：211⨯=1-21，321⨯=21-31，431⨯=31-41，将以上三个等式两边分别相加得： 211⨯+321⨯+431⨯=1-21+21-31+31-41=1-41=43 ⑴ 猜想并写出：)1(1+⨯n n =⑵211⨯+321⨯+431⨯+…+100991⨯= ⑶ 计算：211⨯+321⨯+431⨯+…+)1(1+⨯n n3、已知：9×1+0=9，9×2+1=19， 9×3+2=29， 9×4+3=39， ……根据前面的式子的构成规律，写出第6个式子是什么？请用含n 的式子表示上面的规律。

4、给出依次排列的一列数：-1；2；-4；8；-16；32；…… ⑴ 写出32后面的三项数： ⑵ 按照规律，第n 个数为：5、已知：3；-6；9；-12；…；-2004；2007；-2010；完成下列问题： ⑴ 写出这一列数中第100个数； ⑵ 求这一列数的和；6、观察下列各数：⑴ 1；-2；3；-4；5；-6；7；…；第100个数为：；第2012个数是；⑵ 1；-21；32；-43；54；-65；76；…；其中第100个数为；第2012个数为：； 7、观察下面一列数，探求其规律；-1；21；-31；41；-51；61；…⑴ 写出第7、8、9三个数：，，。

⑵ 第2010个数是：，如果这一列数无限排列下去，与越来越接近。

8、观察下列各式：-1×21=-1+21；-21×31=-21+31；-31×41=-31+41；……⑴ 你发现的规律是：（用含n 的式子表示） ⑵ 用你发现的规律计算：（-1×21）+（-21×31）+ （-31×41）+ ……+（-20091×20101）+（-20101×20111）9、观察下列等式（式子中“！”是一种数学运算符号）：1！=1；2！=2×1；3！=3×2×1；4！=4×3×2×1；……则！！98100的值为：；10、你能比较两个数的20032004和20042003的大小吗？为了解决这个问题，我们应先把它抽象成一般的数学问题，写出它的一般形式，即比较n n+1和（n+1）n 的大小（n 为自然数，且n ≥1）,然后我们分析n=1,n=2,n=3, ……这些特殊数入手，从中发现规律，经过归纳猜想得出结论。

初一上册数学找规律练习题(同名7141)

找規律專題練習1、你喜歡吃拉麵嗎？拉麵館の師傅，用一根很粗の麵條，把兩頭捏合在一起拉伸，再捏合，再拉伸，反復幾次，就把這根很粗の麵條拉成了許多細の麵條，如下面草圖所示。

這樣捏合到第次後可拉出64根細麵條。

第一次捏合第二次捏合第三次捏合2、如下圖，將一張正方形紙片，剪成四個大小形狀一樣の小正方形，然後將其中の一個小正方形再按同樣の方法剪成四個小正方形，再將其中の一個小正方形剪成四個小正方形，如此迴圈進行下去；（1）填表：（2（3）如果剪了100次，共剪出多少個小正方形？（4）觀察圖形，你還能得出什麼規律？3、小明寫作業時不慎將墨水滴在數軸上，根據圖中の數值，判定墨蹟蓋住部分の整數の和是．（1）根據上表結果，描述所求得の一列數の變化規律（2）當x 非常大時，2100x の值接近於什麼數？ 5、現有黑色三角形“▲”和“△”共200個，按照一定規律排列如下： ▲ ▲△△▲△▲▲△△▲△▲▲……則黑色三角形有個，白色三角形有個。

6、仔細觀察下列圖形.當梯形の個數是n 時，圖形の周長是 .7、用火柴棒按如下方式搭三角形：(1) 填寫下表：(2) 照這樣の規律搭下去，搭n 個這樣の三角形需要______根火柴棒8、把編號為1，2，3，4，…の若干盆花按右圖所示擺放，花盆中の花按紅、黃、藍、紫の顏色依次迴圈排列，則第8行從左邊數第6盆花の顏色為___________色.9、已知一列數：1，―2，3，―4，5，―6，7，… 將這列數排成下列形式：第1行 1第2行－2 3第3行－4 5 －6第4行 7 －8 9 －10第5行 11 －12 13 －14 15 … …按照上述規律排下去，那麼第10行從左邊數第5個數等於．10、觀察下列算式：23451=+⨯ ，24462=+⨯，25473=+⨯，24846⨯+=，請你在察規律之後並用你得到の規律填空：250___________=+⨯, 第n 個式子呢? ___________________11、一張長方形桌子可坐6人，按下列方式講桌子拼在一起。

初一数学找规律练习题

初一数学找规律练习题初一数学找规律的练习题对于培养学生的观察力、分析力和推理能力非常重要。

以下是一些适合初一学生的数学找规律练习题：1. 观察数列，找出规律并填写缺失的数字：2, 4, 6, 8, __, 14, 162. 根据给出的数列，找出规律并完成数列：3, 6, 11, 18, __, 47, 763. 观察下列图形序列，找出规律并画出下一个图形：第一个图形：一个正方形第二个图形：两个正方形第三个图形：三个正方形，排成一行第四个图形：四个正方形，排成两行，每行两个第五个图形：______（请画出）4. 观察下列数列，找出规律并填写下一个数字：2, 5, 10, 17, 26, __5. 根据给出的图形序列，找出规律并完成下一个图形：第一个图形：一个圆形第二个图形：两个圆形，中间有一个正方形第三个图形：三个圆形，中间有一个正方形，正方形周围有四个三角形第四个图形：______（请画出）6. 观察下列数列，找出规律并计算第10个数字：1, 3, 6, 10, 15, ...7. 根据给出的图形序列，找出规律并画出第5个图形：第一个图形：一个三角形第二个图形：两个三角形，一个在另一个上面第三个图形：三个三角形，一个在另一个上面，最上面的三角形是倒立的第四个图形：四个三角形，最上面的三角形是倒立的，下面三个三角形依次排列第五个图形：______（请画出）8. 观察下列数列，找出规律并填写下一个数字：1, 4, 9, 16, 25, __9. 根据给出的图形序列，找出规律并完成下一个图形：第一个图形：一个圆形，里面有一个正方形第二个图形：一个圆形，里面有一个正方形和一个三角形第三个图形：一个圆形，里面有一个正方形，一个三角形和一个五边形第四个图形：______（请画出）10. 观察下列数列，找出规律并填写下一个数字：1, 1, 2, 3, 5, 8, ...答案提示：1. 102. 273. 五个正方形，排成两行，每行三个4. 375. 五个圆形，中间有一个正方形，正方形周围有五个三角形6. 1207. 五个三角形，最上面的三角形是倒立的，下面四个三角形依次排列，最下面的三角形也是倒立的8. 369. 一个圆形，里面有一个正方形，一个三角形，一个五边形和一个六边形10. 13这些练习题旨在帮助学生通过观察和分析来发现数字和图形的规律，从而提高他们的数学思维能力。

七年级上册找规律数学题

七年级上册找规律数学题一、数字规律题。

1. 观察下列数：1，4，9，16，25，…，按此规律，第n个数是（）- 解析：- 第1个数是1 = 1^2；- 第2个数是4=2^2；- 第3个数是9 = 3^2；- 第4个数是16=4^2；- 第5个数是25 = 5^2。

- 所以第n个数是n^2。

2. 有一组数：1, - 2,3,-4,5,-6,·s，按此规律，第n个数是（）- 解析：- 当n为奇数时，数为正数，即第n个数为n；- 当n为偶数时，数为负数，即第n个数为-n。

- 所以第n个数是( - 1)^n + 1n。

3. 观察数列：2,5,8,11,·s，则第n个数是（）- 解析：- 可以发现每一个数都比前一个数大3。

- 第1个数2 = 3×1 - 1；- 第2个数5=3×2 - 1；- 第3个数8 = 3×3-1；- 所以第n个数是3n - 1。

4. 数列1,(1)/(2),(1)/(3),(1)/(4),(1)/(5),·s，第n个数是（）- 解析：- 很明显，第n个数是(1)/(n)。

5. 找规律：0,3,8,15,24,·s，第n个数是（）- 解析：- 第1个数0 = 1^2-1；- 第2个数3=2^2-1；- 第3个数8 = 3^2-1；- 第4个数15=4^2-1；- 第5个数24 = 5^2-1；- 所以第n个数是n^2-1。

二、图形规律题。

6. 用火柴棒按下图的方式搭三角形：- 照这样的规律搭下去，搭n个这样的三角形需要多少根火柴棒？- 解析：- 搭1个三角形需要3根火柴棒；- 搭2个三角形需要3 + 2=5根火柴棒；- 搭3个三角形需要3+2×2 = 7根火柴棒；- 搭n个三角形需要3 + 2(n - 1)=2n + 1根火柴棒。

7. 观察下列图形的构成规律，根据此规律，第n个图形中有多少个圆？- 第1个图形有1个圆；- 第2个图形有1 + 2 = 3个圆；- 第3个图形有1+2 + 3=6个圆；- 第4个图形有1+2+3 + 4 = 10个圆；- 解析：- 第n个图形中圆的个数为1 + 2+3+·s+n=(n(n + 1))/(2)。

(完整)初一上册数学找规律练习题

(完整)初一上册数学找规律练习题找规律专题练习1、你喜欢吃拉面吗？拉面馆的师傅，用一根很粗的面条，把两头捏合在一起拉伸，再捏合，再拉伸，反复几次，就把这根很粗的面条拉出64根细面条。

第一次捏合第二次捏合第三次捏合2、如下图，将一张正方形纸片，剪成四个大小形状一样的小正方形，然后将其中的一个小正方形再按同样的方法剪成四个小正方形，再将其中的一个小正方形剪成四个小正方形，如此循环进行下去；（1）填表：（2）如果剪n次，共剪出多少个小正方形？（3）如果剪了100次，共剪出多少个小正方形？（4）观察图形，你还能得出什么规律？3、小明写作业时不慎将墨水滴在数轴上，根据图中的数值，判定墨迹盖住部分的整数的和是．（2）当x非常大时，2100x的值接近于什么数？5、现有黑色三角形“▲”和“△”共200个，按照一定规律排列如下：▲▲△△▲△▲▲△△▲△▲▲。

则黑色三角形有个，白色三角形有个。

6、仔细观察下列图形.当梯形的个数是n时，图形的周长是.7、用火柴棒按如下方式搭三角形：(1)填写下表：(2)照这样的规律搭下去，搭n个这样的三角形需要______12根火柴棒8、把编号为1，2，3，4，。

的若干盆花按右图所示摆放，花盆中的花按红、黄、蓝、紫的颜色依次循环排列，则第8行从左边数第6盆花的颜色为___________色.9、已知一列数：1，D2，3，D4，5，D6，7，。

将这列数排成下列形式：第1行1第2行－2 3第3行－4 5 －6第4行7 －8 9 －10第5行11 －12 13 －14 15 。

按照上述规律排下去，那么第10行从左边数第5个数等于．10、观察下列算式：23451=+? ，24462=+?，25473=+?，*****?+=，请你在察规律之后并用你得到的规律填空：250___________=+?, 第n 个式子呢? ___________________11、一张长方形桌子可坐6人，按下列方式讲桌子拼在一起。

七年级上册数学找规律试题

5.对于实数 x ，我们规定 [x ]表示不大于 x 的最大整数，例如 [1.2]= 1 ，[3]= 3 ，[- 2.5]= -3 ，若 ⎢⎥⎦ = 5 ，初一数学找规律：1 ．(2013 山东滨州，18，4 分)观察下列各式的计算过程：5×5=0×1×100+25， 15×15=1×2×100+25， 25×25=2×3×100+25， 35×35=3×4×100+25， …… ……请猜测，第 n 个算式(n 为正整数)应表示为____________________________．【答案】 [10(n －1)+5]×[10(n －1)+5]=100n(n －1)+25.2. （2013 山东莱芜，17，4 分）已知 123456789101112…997998999 是由连续整数 1 至 999 排列组成的一个数，在该数种从左往右数第 2013 位上的数字为 . 【答案】7 3．（3 分）（2013•青岛）要把一个正方体分割成 8 个小正方体，至少需要切 3 刀，因为这 8 个小正方体都只有三个面是现成的．其他三个面必须用三刀切 3 次才能切出来．那么，要把一个正方体分割成 27 个小正方体，至少需用刀切 6 次；分割成 64 个小正方体，至少需要用刀切 9 次． 4．（2013 泰安）观察下列等式：31=3，32=9，33=27，34=81，35=243，36=729，37=2187… 解答下列问题：3+32+33+34…+32013 的末位数字是（）A ．0B ．1C ．3D ．7 考点：尾数特征．分析：根据数字规律得出 3+32+33+34…+32013 的末位数字相当于：3+7+9+1+…+3 进而得出末尾数字．解答：解：∵31=3，32=9，33=27，34=81，35=243，36=729，37=2187… ∴末尾数，每 4 个一循环， ∵2013÷4=503…1，∴3+32+33+34…+32013 的末位数字相当于：3+7+9+1+…+3 的末尾数为 3，故选：C ．点评：此题主要考查了数字变化规律，根据已知得出数字变化规律是解题关键．⎡ x + 4 ⎤ ⎣10则 x 的取值可以是（）.A.40B.45C.51D.56答案：C ．考点:新定义问题.点评:本题需要学生先通过阅读掌握新定义公式，再利用类似方法解决问题.考查了学生观察问题，分析问题，解决问题的能力.6. 当白色小正方形个数 n 等于 1,2，3…时，由白色小正方形和和黑色小正方形组成的图形分别如图所示.则第 n 个图形中白色小正方形和黑色小正方形的个数总和等于_____________.（用 n 表示， n 是正整数）答案：n 2+4n考点：本题是一道规律探索题，考查了学生分析探索规律的能力．点评：解决此类问题是应先观察图案的变化趋势，然后从第一个图形进行分析，运用从特殊到一般的探索方式，分析归纳找出黑白正方形个数增加的变化规律，最后含有n 的代数式进行表示．A．87．（3分）（2013•烟台）将正方形图1作如下操作：第1次：分别连接各边中点如图2，得到5个正方形；第2次：将图2左上角正方形按上述方法再分割如图3，得到9个正方形…，以此类推，根据以上操作，若要得到2013个正方形，则需要操作的次数是（）A．502B．503C．504D．505考点：规律型：图形的变化类．分析：根据正方形的个数变化得出第n次得到2013个正方形，则4n+1=2013，求出即可．解答：解：∵第1次：分别连接各边中点如图2，得到4+1=5个正方形；第2次：将图2左上角正方形按上述方法再分割如图3，得到4×2+1=9个正方形…，以此类推，根据以上操作，若第n次得到2013个正方形，则4n+1=2013，解得：n=503．故选：B．点评：此题主要考查了图形的变化类，根据已知得出正方形个数的变化规律是解题关键．8、（2013安徽）如图，观察每一个图中黑色正六边形的排列规律，则第10个图中黑色正六边形有个。

七年级上册数学找规律试题

初一数学找规律:1 . （2013山东滨州，18, 4分）观察下列各式的计算过程: 5X5=0X1X100+25,15X15=1X2X100+25,25X25二2X3X100+25,35X35二3X4X100+25,请猜测，第n个算式（n为正整数）应表示为____________________________ .【答案】[10（n-1）+5] X [10（n-1） +5]=100n（n-1） +25.2.（2013山东莱芜，17, 4分）已知12-9是由连续整数1至999排列组成的一个数，在该数种从左往右数第2013位上的数字为 _______________ •【答案】73.（3分）（2013?青岛）要把一个正方体分割成8个小正方体，至少需要切3刀，因为这8个小正方体都只有三个面是现成的.英他三个而必须用三刀切3次才能切岀来.那么，要把一个正方体分割成27个小正方体，至少需用刀切6次:分割成64个小正方体，至少需要用刀切9次.4.（2013 泰安）观察下列等式：3'二3, 3==9, 3’二27, 3：二81, 3皂243, 3&二729, 3=2187…解答下列问题：彳+彳油帝‘…+彳曲的末位数字是（）A. 0B. 1C. 3D. 7考点：尾数特征.分析：根据数字规律得岀3+3：+3'+3「・+3曲的末位数字相当于：3+7+9+1+-+3进而得出末尾数字.解答：解：V3J=3, 3==9, 3'二27, 3：二81, 3皂243, 3*729, 3：二2187….••末尾数，每4个一循环，720134-4=503-1,.•.3+3订3'+3‘…+3曲的末位数字相当于:3+7+9+1+・・・+3的末尾数为3, 故选：C.点评：此题主要考查了数字变化规律，根据已知得岀数字变化规律是解题关键.Y 1 A5.对于实数% ,我们规定[x]表示不大于x的最大整数，例如[1.2] = 1 , [3] = 3 , [- 2.5] =-3，若—=5 ,则x的取值可以是（.45 C答案：C.考点:新定义问题.点评:本题需要学生先通过阅读掌握新左义公式，再利用类似方法解决问题•考查了学生观察问题，分析问题, 解决问题的能力.6.当白色小正方形个数“等于1,2, 3…时，由白色小正方形和和黑色小正方形组成的图形分别如图所示.则第“个图形中白色小正方形和黑色小正方形的个数总和等于 ______________ •（用"表示，兀是正整数）答案：n c+4n考点：本题是一道规律探索题，考査了学生分析探索规律的能力.点评：解决此类问题是应先观察图案的变化趋势，然后从第一个图形进行分析，运用从特殊到一般的探索方式，分析归纳找出黑白正方形个数增加的变化规律，最后含有"的代数式进行表示.I -0 n 三77・（3分）（2013?烟台）将正方形图1作如下操作：第1次：分別连接各边中点如图2,得到5个正方形：第2次：将图2左上角正方形按上述方法再分割如图3,得到9个正方形…，以此类推，根拯以上操作，若要得到2013个正方形，则需要操作的次数是（考点：规律型：图形的变化类.分析：根据正方形的个数变化得岀第n 次得到2013个正方形，则4n+l 二2013,求出即可. 解答：解：•••第1次：分别连接各边中点如图2,得到4+1二5个正方形；第2次：将图2左上角正方形按上述方法再分割如图3,得到4X2+1=9个正方形…, 以此类推，根据以上操作，若第n 次得到2013个正方形，则4n+l 二2013, 解得：n 二503・故选：B.点评：此题主要考查了图形的变化类，根据已知得出正方形个数的变化规律是解题关键.8、（2013安徽）如图，观察每一个图中黑色正六边形的排列规律，则第10个图中黑色正六边形有个。

初一数学找规律题及答案

初一数学找规律题及答案归纳法——找规律研究归纳法——找规律的具体方法和步骤是：（1）通过对几个特例的分析，寻找规律并归纳；（2）猜想符合规律的一般性结论；（3）验证或证明结论是否正确。

下面通过举例来说明这些问题。

一、数字排列规律题1、观察下列各算式：1+3=4=22，1+3+5=9=32，1+3+5+7=16=42按此规律1）猜想：1+3+5+7+…+2005+2007的值是多少？2）推广：1+3+5+7+9+…+（2n-1)+（2n+1)的和是多少？2、下面数列后两位应该填上什么数字呢？xxxxxxxx____3、请填出下面横线上的数字。

____214、有一串数，它的排列规律是1、2、3、2、3、4、3、4、5、4、5、6、……聪明的你猜猜第100个数是什么？5、有一串数字xxxxxxxx___第6个是什么数？6、观察下列一组数的排列：1、2、3、4、3、2、1、2、3、4、3、2、1、…，那么第2005个数是（）.A．1 B．2 C．3 D．47、100个数排成一行，其中任意三个相邻数中，中间一个数都等于它前后两个数的和，如果这100个数的前两个数依次为1.那么这100个数中“ ”的个数为_________个．二、几何图形变化规律题1、观察下列球的排列规律(其中●是实心球，○是空心球)：从第1个球起到第2004个球止，共有实心球个．2、观察下列图形排列规律（其中△是三角形，□是正方形，○是圆），□○△□□○△□○△□□○△□┅┅，若第一个图形是正方形，则第2008个图形是（填图形名称）.三、数、式计算规律题1、已知下列等式：①13＝12；②13＋23＝32；③13＋23＋33＝62；④13＋23＋33＋43＝102；由此规律知，第⑤个等式是．2、观察下面的几个算式：1+2+1=4。

1+2+3+2+1=9。

1+2+3+4+3+2+1=16。

1+2+3+4+5+4+3+2+1=25，…根据你所发现的规律，请你直接写出下面式子的结果：1+2+3+…+99+100+99+…+3+2+1=____.3、1+2+3+…+100＝？经过研究，这个问题的一般性结论是1+2+3+…+n1n n1，其中ｎ是正整数。

七年级上册数学找规律试题

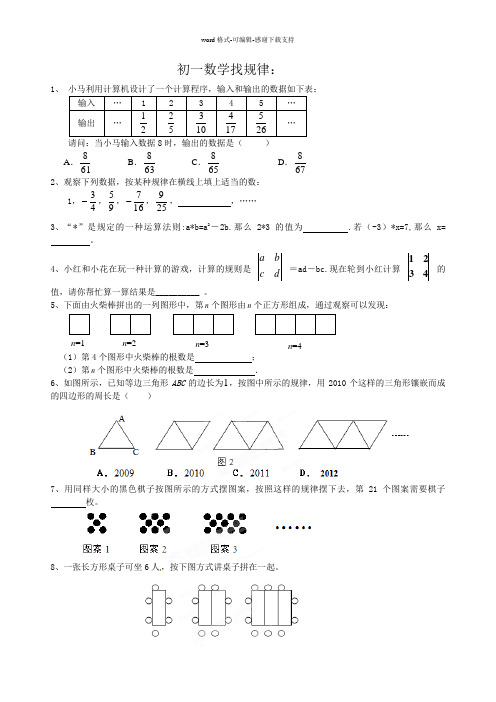
初一数学找规律：1、小马利用计算机设计了一个计算程序，输入和输出的数据如下表：输入 … 1 2 3 4 5 … 输出 … 21 52 103 174 265 … 请问：当小马输入数据8时，输出的数据是（）A ．618B ．638C ．658 D ．678 2、观察下列数据，按某种规律在横线上填上适当的数： 1，43-，95，167-，259，，…… 3、“*”是规定的一种运算法则:a*b=a 2－2b.那么2*3的值为 .若（-3）*x=7,那么x=。

4、小红和小花在玩一种计算的游戏，计算的规则是 d c b a ＝ad －bc.现在轮到小红计算 4321 的值，请你帮忙算一算结果是__________ 。

5、下面由火柴棒拼出的一列图形中，第n 个图形由n 个正方形组成，通过观察可以发现：（1）第4个图形中火柴棒的根数是；（2）第n 个图形中火柴棒的根数是．6、如图所示，已知等边三角形ABC 的边长为1，按图中所示的规律，用2010个这样的三角形镶嵌而成的四边形的周长是（）7、用同样大小的黑色棋子按图所示的方式摆图案，按照这样的规律摆下去，第21个图案需要棋子枚。

8、一张长方形桌子可坐6人，按下图方式讲桌子拼在一起。

n =1 n =2 n =3 n =4（1）2张桌子拼在一起可坐______人。

3张桌子拼在一起可坐____人，n 张桌子拼在一起可坐______人。

（2）一家餐厅有40张这样的长方形桌子，按照上图方式每5张桌子拼成1张大桌子，则40张桌子可拼成8张大桌子，共可坐______人。

9、如图，线段AB 上的点数与线段的总数有如下关系：如果线段AB 上有三个点时，线段总共有3条，如果线段AB 上有4个点时，线段总数有6条。

3=2+1 6=3+2+1 10=4+3+2+1（1）当线段AB 上有5个点时，线段总数共有条。

（2）当线段AB 上有6个点时，线段总数共有多少条？10、某城市大剧院地面的一部分为扇形，观众席的座位按下列方式设置：排数1 2 3 4 座位数 50 53 56 59按这种方式排下去，⑴第5、6排各有多少个座位？ ⑵第n 排有多少个座位？11、我国著名的数学家华罗庚曾说过：“数形结合百般好，割裂分家万事非”，如图6-2，在边长为1的正方形纸板上，依次贴上面积为21，41，81，…，n 21的长方形彩色纸片（n 为大于1的整数），请你用“数形结合”的思想，依数形变化的规律，计算+++814121…+n 21=_________. 12、计算91101415131412131-++-+-+-13、观察下列计算211211-=⨯，3121321-=⨯，4131431-=⨯，5141541-=⨯…… 从计算结果中找规律，利用规律计算201320121541431321211⨯++⨯+⨯+⨯+⨯ A C B A C D B A C D E B。

初一找规律经典题带答案

初一找规律经典题带答案一、数字排列1、观察下列各算式：1+3=4=22，1+3+5=9=32，1+3+5+7=16=42…按此规律（1）试猜想：1+3+5+7+…+2005+2007的值？（2）推广：1+3+5+7+9+…+（2n-1)+（2n+1)的和是多少？2、下面数列后两位应该填上什么数字呢？2 3 5 8 12 17 __ __3、请填出下面横线上的数字。

1 1 2 3 5 8 ____ 214、有一串数，它的排列规律是1、2、3、2、3、4、3、4、5、4、5、6、……聪明的你猜猜第100个（）二、几何图形变化1、观察下列球的排列规律(其中●是实心球，○是空心球)：●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●……从第1个球起到第2004个球止，共有实心球个．2、观察下列图形排列规律（其中△是三角形，□是正方形，○是圆），□○△□□○△□○△□□○△□┅┅，若第一个图形是正方形，则第2008个图形是（填图形名称）.三、数、式计算1、已知下列等式：①13＝12；②13＋23＝32；③13＋23＋33＝62；④13＋23＋33＋43＝102；由此纪律知，第⑤个等式是．2、观察下面的几个算式：1+2+1=4，1+2+3+2+1=9，1+2+3+4+3+2+1=16，1+2+3+4+5+4+3+2+1=25，…依照你所发现的纪律，请你间接写出下面式子的成效：1+2+3+…+99+100+99+…+3+2+1=____.3、已知：222，332，442，552，bb…，若10102符合前面式子的规律，则a baa纪律发现1．用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干个图案：第(4)个图案中有黑色地砖4块；那么第(n)个图案中有白色地砖块。

．．……2.我国著名数学家华罗庚曾说过：“数形结合百般好，隔裂分家万1事非。

”如图，在一个边长为1的正方形纸版上，顺次贴上面积为，第3题2111，，…，n的矩形彩色纸片（n为大于1的整数）。