导数的应用单元检测卷
章末检测3:第三章 导数及其应用

第三章 导数及其应用(时间:90分钟 满分:120分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.曲线y =12x 2-2x 在点⎝⎛⎭⎫1,-32处的切线的倾斜角为( ). A .-135° B .45° C .-45° D .135° 2.下列求导运算正确的是( ). A.⎝⎛⎭⎫x +3x ′=1+3x 2 B .(log 2x )′=1x ln 2C .(3x )′=3x log 3eD .(x 2cos x )′=-2x sin x3.函数y =x 4-2x 2+5的单调减区间为( ). A .(-∞,-1)及(0,1) B .(-1,0)及(1,+∞) C .(-1,1)D .(-∞,-1)及(1,+∞) 4.函数y =1+3x -x 3有( ). A .极小值-1,极大值1 B .极小值-2,极大值3 C .极小值-2,极大值2 D .极小值-1,极大值3 5.函数f (x )=x 2x -1( ).A .在(0,2)上单调递减B .在(-∞,0)和(2,+∞)上单调递增C .在(0,2)上单调递增D .在(-∞,0)和(2,+∞)上单调递减6.函数y =x 4-4x +3在区间[-2,3]上的最小值为( ). A .72 B .36 C .12 D .07.一个物体的运动方程为s =1-t +t 2(其中s 的单位是米,t 的单位是秒)那么物体在3秒末的瞬时速度是( ). A .7米/秒 B .6米/秒 C .5米/秒D .8米/秒8.已知f (x )=x 3+ax 2+(a +6)x +1有极大值和极小值,则a 的取值范围为( ). A .-1<a <2 B .-3<a <6 C .a <-1或a >2 D .a <-3或a >6 9.已知f (x )的导函数f ′(x )图象如右图所示, 那么f (x )的图象最有可能是图中的( ).10.如果圆柱的轴截面周长为定值4,则圆柱体积的最大值为( ). A.827π B.1627π C.89π D.169π 11.设曲线y =x n +1(n ∈N *)在(1,1)处的切线与x 轴的交点的横坐标为x n ,则log 2 010x 1+log 2010x 2+…+log 2 010x 2 009的值为().A .-log 2 0102 009B .-1C .(log 2 0102 009)-1D .112.设f (x )是定义在R 上的偶函数,当x >0时f (x )+xf ′(x )>0且f (1)=0,则不等式xf (x )>0的解集为( ). A .(-1,0)∪(1,+∞) B .(-1,0)∪(0,1) C .(-∞,-1)∪(1,+∞)D .(-∞,-1)∪(0,1)二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上) 13.若f (x )=x 3,f ′(x 0)=3,则x 0的值为________.14.曲线y =ln x 在点M (e ,1)处的切线的斜率是________,切线的方程为________. 15.函数y =x 3+x 2-5x -5的单调递增区间是________.16.设x =-2与x =4是函数f (x )=x 3+ax 2+bx 的两个极值点,则常数a -b 的值为________. 三、解答题(本大题共4小题,共40分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(10分)已知函数f (x )=x 3+ax 2+x +1,试讨论函数f (x )的单调区间.18.(10分)给定函数f (x )=x 33-ax 2+(a 2-1)x 和g (x )=x +a 2x.(1)求证:f (x )总有两个极值点;(2)若f (x )和g (x )有相同的极值点,求a 的值.19.(10分)已知函数f (x )=x 3+ax 2+bx +c 在x =-1与x =2处都取得极值. (1)求a ,b 的值及函数f (x )的单调区间;(2)若对x ∈[-2,3],不等式f (x )+32c <c 2恒成立,求c 的取值范围.20.(10分)若函数f (x )=ax 3-bx +4,当x =2时,函数f (x )有极值-43.(1)求函数的解析式.(2)若方程f (x )=k 有3个不同的根,求实数k 的取值范围. 答案:1.解析 y ′=x -2,所以斜率k =1-2=-1,因此,倾斜角为135°. 答案 D2.解析 ⎝⎛⎭⎫x +3x ′=1-3x 2,所以A 不正确;(3x )′=3x ln 3,所以C 不正确;(x 2cos x )′=2x cos x +x 2·(-sin x ),所以D 不正确;(log 2x )′=1x ln 2,所以B 正确.故选B. 答案 B3.解析 y ′=4x 3-4x =4x (x 2-1),令y ′<0得x 的范围为(-∞,-1),(0,1). 答案 A4.解析 y ′=-3x 2+3,令y ′=0得,x =1或x =-1, f (1)=3,f (-1)=-1. 答案 D5.解析 f ′(x )=2x (x -1)-x 2(x -1)2=x 2-2x (x -1)2=x (x -2)(x -1)2.令f ′(x )=0得x 1=0,x 2=2.∴x ∈(-∞,0)和(2,+∞)时,f ′(x )>0.x ∈(0,1)∪(1,2)时,f ′(x )<0. 答案 B6.解析 y ′=4x 3-4,令y ′=0,4x 3-4=0,x =1,当x <1时,y ′<0;当x >1时,y ′>0得y极小值=y |x =1=0,而端点的函数值y |x =-2=27,y |x =3=72,得y min =0.答案 D7.解析 s ′=2t -1,∴s ′|t =3=2×3-1=5. 答案 C8.解析 因为f (x )有极大值和极小值,所以导函数f ′(x )=3x 2+2ax +(a +6)有两个不等实根,所以Δ=4a 2-12(a +6)>0,得a <-3或a >6. 答案 D9.解析 ∵x ∈(-∞,-2)时,f ′(x )<0,∴f (x )为减函数;同理f (x )在(-2,0)上为增函数,(0,+∞)上为减函数. 答案 A10.解析 设圆柱的半径为R ,圆柱的高为h ,则2R +h =2.∵V =πR 2h =πR 2(2-2R )=2πR 2-2πR 3,∴V ′=2πR ·(2-3R )=0.令V ′=0,则R =0(舍)或R =23.经检验知,R =23时,圆柱体积最大,此时h =23,V max =π·49×23=827π.答案 A11.解析 ∵y ′|x =1=n +1,∴切线方程为y -1=(n +1)(x -1),令y =0,得x =1-1n +1=n n +1,即x n =nn +1.所以log 2 010x 1+log 2 010x 2+…+log 2 010x 2 009= log 2 010(x 1·x 2·…·x 2 009)=log 2 010⎝⎛⎭⎫12·23·…·2 0092 010=log 2 01012 010=-1. 答案 B12.解析 设F (x )=x ·f (x ),则F (x )是R 上的奇函数,且F (1)=0,由f (x )+xf ′(x )>0,(x >0)知F (x )在(0,+∞)上是增函数,∴F (x )>0的解集为(-1,0)∪(1,+∞). 答案 A13.解析 f ′(x 0)=3x 20=3,∴x 0=±1. 答案 ±114.解析 由于y ′=1x ,∴k =y ′|x =e =1e ,故切线的方程为y -1=1e (x -e),故y =1e x .答案 1ex -e y =015.解析 由y ′=3x 2+2x -5>0得x <-53,或x >1.答案 ⎝⎛⎭⎫-∞,-35,(1,+∞) 16.解析 ∵f ′(x )=3x 2+2ax +b ,∴⎩⎨⎧-2+4=-2a3,-2×4=b 3⇒⎩⎪⎨⎪⎧a =-3,b =-24.∴a -b =-3+24=21.答案 2117.解 f ′(x )=3x 2+2ax +1,Δ=(2a )2-4×3×1=4(a 2-3),①若Δ≤0即-3≤a ≤3,f ′(x )≥0恒成立, 此时f (x )的单调增区间为(-∞,+∞); ②若Δ>0即a <-3或a >3时, 令f ′(x )=0得x =-a ±a 2-33,f ′(x )>0得x <-a -a 2-33或x >-a +a 2-33,f ′(x )<0得-a -a 2-33<x <-a +a 2-33,∴此时f (x )的增区间为⎝ ⎛⎭⎪⎫-∞,-a +a 2-33和⎝ ⎛⎭⎪⎫-a +a 2-33,+∞,减区间为⎝ ⎛⎭⎪⎫-a +a 2-33,-a +a 2-33. 18.(1)证明 因为f ′(x )=x 2-2ax +(a 2-1)=[x -(a +1)]·[x -(a -1)], 令f ′(x )=0,解得x 1=a +1,x 2=a -1. 当x <a -1时,f ′(x )>0; 当a -1<x <a +1,f ′(x )<0.所以x =a -1为f (x )的一个极大值点. 同理可证x =a +1为f (x )的一个极小值点. 所以f (x )总有两个极值点.(2)解 因为g ′(x )=1-a 2x 2=(x -a )(x +a )x 2.令g ′(x )=0,则x 1=a ,x 2=-a . 因为f (x )和g (x )有相同的极值点,且x 1=a 和a +1,a -1不可能相等, 所以当-a =a +1时,a =-12;当-a =a -1时,a =12.经检验,当a =-12和a =12时,x 1=a ,x 2=-a 都是g (x )的极值点. 19.解 (1)f ′(x )=3x 2+2ax +b ,由题意得⎩⎪⎨⎪⎧f ′(-1)=0,f ′(2)=0,即⎩⎪⎨⎪⎧3-2a +b =0,12+4a +b =0,解得⎩⎪⎨⎪⎧a =-32,b =-6.∴f (x )=x 3-32x 2-6x +c ,f ′(x )=3x 2-3x -6.令f ′(x )<0,解得-1<x <2; 令f ′(x )>0,解得x <-1或x >2. ∴f (x )的减区间为(-1,2), 增区间为(-∞,-1),(2,+∞). (2)由(1)知,f (x )在(-∞,-1)上单调递增; 在(-1,2)上单调递减;在(2,+∞)上单调递增. ∴x ∈[-2,3]时,f (x )的最大值即为 f (-1)与f (3)中的较大者. f (-1)=72+c ,f (3)=-92+c .∴当x =-1时,f (x )取得最大值. 要使f (x )+32c <c 2,只需c 2>f (-1)+32c ,即2c 2>7+5c ,解得c <-1或c >72.∴c 的取值范围为(-∞,-1)∪⎝⎛⎭⎫72,+∞. 20.解 f ′(x )=3ax 2-b .(1)由题意得⎩⎪⎨⎪⎧f ′(2)=12a -b =0,f (2)=8a -2b +4=-43,解得⎩⎪⎨⎪⎧a =13,b =4, 故所求函数的解析式为f (x )=13x 3-4x +4.(2)由(1)可得f ′(x )=x 2-4=(x -2)(x +2), 令f ′(x )=0,得x =2或x =-2.当x 变化时,f ′(x ),f (x )的变化情况如下表:x (-∞,-2)-2 (-2,2) 2 (2,+∞)f ′(x ) + 0 -0 +f (x )283-43因此,当x =-2时,f (x )有极大值283,当x =2时,f (x )有极小值-43,所以函数f (x )=13x 3-4x +4的图象大致如图所示.若f (x )=k 有3个不同的根,则直线y =k 与函数f (x )的图象有3个交点,所以-43<k <283.。
导数单元测试题(含答案)

导数单元测试题(含答案)Derivative Unit Test ns (Experimental Class)I。
Multiple Choice ns1.The n of the tangent line to the curve y = -x + 3x at point (1,2) is ()A。
y = 3x-1 B。
y = -3x+5 C。
y = 3x+5 D。
y = 2x2.The maximum value of the n f(x) = x^2ex+1.x∈[-2,1] is ()A。
4e-1 B。
0 C。
e^2 D。
3e^23.If the n f(x) = (3/2)x^3+ax has three different zeros。
then the range of real number a is ()A。
(2,2) B。
2,2 C。
(0,1) D。
(1,)4.If the n f(x) = x^3+6bx^2+3b has a local minimum at (0,1)。
then the range of real number b is ()A。
(0,) B。
(,1) C。
(0,1) D。
(1,)5.If a>2.then the n f(x) = (3x-1)/(3ax^2+1) has exactly (。
) zeros in the interval (0,2).A。
1 B。
3 C。
2 D。
None6.The area of the triangle enclosed by the tangent line of the curve y=e^x at point (2,e) and the coordinate axes is ()A。
e B。
2e^2 C。
e^2 D。
e^2/27.The graph of the n f(x) is shown in the figure below。
人教版导数及其应用多选题单元达标检测试卷

人教版导数及其应用多选题单元达标检测试卷一、导数及其应用多选题1.已知偶函数()y f x =对于任意的0,2x π⎡⎫∈⎪⎢⎣⎭满足()()cos sin 0f x x f x x '+>(其中()f x '是函数()f x 的导函数),则下列不等式中不成立的是( )A34f ππ⎛⎫⎛⎫-< ⎪ ⎪⎝⎭⎝⎭B34f ππ⎛⎫⎛⎫-<- ⎪ ⎪⎝⎭⎝⎭C .()04f π⎛⎫>- ⎪⎝⎭ D.63f ππ⎛⎫⎛⎫<⎪ ⎪⎝⎭⎝⎭【答案】ABC 【分析】 构造函数()()cos f x g x x =,结合导数和对称性可知()g x 为偶函数且在0,2x π⎡⎫∈⎪⎢⎣⎭上单调递2643f f πππ⎛⎫⎛⎫⎛⎫<< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,从而可判断ABD 选项,由()04g g π⎛⎫< ⎪⎝⎭可判断C 选项.【详解】因为偶函数()y f x =对于任意的0,2x π⎡⎫∈⎪⎢⎣⎭满足()()cos sin 0f x x f x x '+>, 所以构造函数()()cos f x g x x =,则()()2cos sin ()0cos f x x f x x g x x'+'=>, ∴()g x 为偶函数且在0,2x π⎡⎫∈⎪⎢⎣⎭上单调递增,32333cos 3f g g f πππππ⎛⎫⎪⎛⎫⎛⎫⎛⎫⎝⎭∴-=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,4444cos 4f g g πππππ⎛⎫ ⎪⎛⎫⎛⎫⎛⎫⎝⎭-=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,666cos 6f g f ππππ⎛⎫ ⎪⎛⎫⎛⎫⎝⎭== ⎪ ⎪⎝⎭⎝⎭,由函数单调性可知643g g g πππ⎛⎫⎛⎫⎛⎫<< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭2643f f πππ⎛⎫⎛⎫⎛⎫<< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 对于AB,4343f f ππππ⎛⎫⎛⎫⎛⎫<=- ⎪ ⎪⎛⎫-= ⎪⎝⎭⎝⎭⎝ ⎪⎭⎭⎝,故AB 错误; 对于C ,()04g g π⎛⎫<⎪⎝⎭,()044f ππ⎛⎫⎛⎫<=- ⎪ ⎪⎝⎭⎝⎭,故C 错误;对于D 263f fππ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭,即63f ππ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭,故D 正确; 故选:ABC. 【点睛】关键点点睛:本题考查了利用导数研究函数的单调性,解题的关键是利用已知条件构造对应的新函数()()cos f x g x x=,利用导数研究函数的单调性,从而比较大小,考查学生的逻辑推理能力与转化思想,属于较难题.2.下列不等式正确的有( )A 2ln 3<B .ln π<C .15<D .3ln 2e <【答案】CD 【分析】构造函数()ln xf x x=,利用导数分析其单调性,然后由()2f f >、ff >、(4)f f >、()f f e <得出每个选项的正误.【详解】 令()ln x f x x =,则()21ln xf x x-'=,令()0f x '=得x e = 易得()f x 在()0,e 上单调递增,在(),e +∞上单调递减所以①()2f f>,即ln 22>22ln ln 3>=,故A 错误;②ff >>,所以可得ln π>B 错误;③(4)f f >ln 4ln 242>=,即ln152ln 2=>所以ln15ln >15<,故C 正确;④()f f e <ln e e <3ln 21e<,即3ln 22e <所以3eln 2<,故D 正确; 故选:CD 【点睛】关键点点睛:本题考查的是构造函数,利用导数判断函数的单调性,解题的关键是函数的构造和自变量的选择.3.已知函数()1ln f x x x x=-+,()()1ln x x x x g --=,则下列结论正确的是( ) A .()g x 存在唯一极值点0x ,且()01,2x ∈ B .()f x 恰有3个零点C .当1k <时,函数()g x 与()h x kx =的图象有两个交点D .若120x x >且()()120f x f x +=,则121=x x 【答案】ACD 【分析】根据导数求得函数()g x '在(0,)+∞上为单调递减函数,结合零点的存在性定,可判定A 正确;利用导数求得函数 ()f x 在(,0)-∞,(0,)+∞单调递减,进而得到函数 ()f x 只有2个零点,可判定B 不正确;由()g x kx =,转化为函数()()1ln x x x ϕ-=和 ()(1)m x k x =-的图象的交点个数,可判定C 正确;由()()120f x f x +=,化简得到 ()121()f x f x =,结合单调性,可判定D 正确. 【详解】由函数()()1ln x x x x g --=,可得 ()1ln ,0g x x x x '=-+>,则()2110g x x x''=--<,所以()g x '在(0,)+∞上为单调递减函数,又由 ()()110,12ln 202g g '=>=-+<, 所以函数()g x 在区间(1,2)内只有一个极值点,所以A 正确; 由函数()1ln f x x x x=-+, 当0x >时,()1ln f x x x x=-+,可得 ()221x x f x x -+-'=, 因为22131()024x x x -+-=---<,所以 ()0f x '<,函数()f x 在(0,)+∞单调递减;又由()10f =,所以函数在(0,)+∞上只有一个零点, 当0x <时,()1ln()f x x x x =--+,可得 ()221x x f x x -+-'=,因为22131()024x x x -+-=---<,所以 ()0f x '<,函数()f x 在(,0)-∞单调递减; 又由()10f -=,所以函数在(,0)-∞上只有一个零点, 综上可得函数()1ln f x x x x=-+在定义域内只有2个零点,所以B 不正确; 令()g x kx =,即()1ln x x x kx --=,即 ()1ln (1)x x k x -=-, 设()()1ln x x x ϕ-=, ()(1)m x k x =-,可得()1ln 1x x x ϕ'=+-,则 ()2110x x xϕ''=+>,所以函数()x ϕ'(0,)+∞单调递增, 又由()01ϕ'=,可得当(0,1)x ∈时, ()0x ϕ'<,函数()x ϕ单调递减, 当(1,)x ∈+∞时,()0x ϕ'>,函数 ()x ϕ单调递增, 当1x =时,函数()x ϕ取得最小值,最小值为()10ϕ=, 又由()(1)m x k x =-,因为1k <,则 10k ->,且过原点的直线,结合图象,即可得到函数()()1ln x x x ϕ-=和 ()(1)m x k x =-的图象有两个交点,所以C 正确;由120x x >,若120,0x x >>时,因为 ()()120f x f x +=,可得()()12222222211111ln ln 1f x f x x x f x x x x x ⎛⎫⎛⎫=-=--+=+-= ⎪ ⎪⎝⎭⎝⎭,即()121()f x f x =,因为()f x 在(0,)+∞单调递减,所以 121x x =,即121=x x , 同理可知,若120,0x x <<时,可得121=x x ,所以D 正确. 故选:ACD.【点睛】函数由零点求参数的取值范围的常用方法与策略:1、分类参数法:一般命题情境为给出区间,求满足函数零点个数的参数范围,通常解法为从()f x 中分离参数,然后利用求导的方法求出由参数构造的新函数的最值,根据题设条件构建关于参数的不等式,再通过解不等式确定参数的取值范围;2、分类讨论法:一般命题情境为没有固定的区间,求满足函数零点个数的参数范围,通常解法为结合函数的单调性,先确定参数分类标准,在每个小范围内研究零点的个数是否符合题意,将满足题意的参数的各个小范围并在一起,即可为所求参数的范围.4.设函数()ln f x x x =,()212g x x =,给定下列命题,其中正确的是( ) A .若方程()f x k =有两个不同的实数根,则1,0k e⎛⎫∈- ⎪⎝⎭;B .若方程()2kf x x =恰好只有一个实数根,则0k <;C .若120x x >>,总有()()()()1212m g x g x f x f x ->-⎡⎤⎣⎦恒成立,则m 1≥;D .若函数()()()2F x f x ag x =-有两个极值点,则实数10,2a ⎛⎫∈ ⎪⎝⎭. 【答案】ACD 【分析】利用导数研究函数的单调性和极值,且将题意转化为()y f x =与y k =有两个不同的交点,即可判断A 选项;易知1x =不是该方程的根,当1x ≠时,将条件等价于y k =和ln xy x=只有一个交点,利用导数研究函数的单调性和极值,从而可推出结果,即可判断B 选项;当120x x >>时,将条件等价于1122()()()()mg x f x mg x f x ->-恒成立,即函数()()y mg x f x =-在(0,)+∞上为增函数,通过构造新函数以及利用导数求出单调区间,即可求出m 的范围,即可判断C 选项;2()ln (0)F x x x ax x =->有两个不同极值点,根据导数的符号列出不等式并求解,即可判断D 选项. 【详解】解:对于A ,()f x 的定义域(0,)+∞,()ln 1f x x '=+, 令()0f x '>,有ln 1x >-,即1x e>, 可知()f x 在1(0,)e 单调递减,在1+e∞(,)单调递增,所以极小值等于最小值, min 11()()f x f e e∴==-,且当0x →时()0f x →,又(1)0f =,从而要使得方程()f x k =有两个不同的实根,即()y f x =与y k =有两个不同的交点,所以1(,0)k e∈-,故A 正确; 对于B ,易知1x =不是该方程的根,当1x ≠时,()0f x ≠,方程2()kf x x =有且只有一个实数根,等价于y k =和ln xy x=只有一个交点, 2ln 1(ln )-'=x y x ,又0x >且1x ≠, 令0y '>,即ln 1x >,有x e >, 知ln xy x=在0,1()和1e (,)单减,在+e ∞(,)上单增, 1x =是一条渐近线,极小值为e ,由ln xy x=大致图像可知0k <或=k e ,故B 错误;对于C ,当120x x >>时,[]1212()()()()m g x g x f x f x ->-恒成立, 等价于1122()()()()mg x f x mg x f x ->-恒成立, 即函数()()y mg x f x =-在(0,)+∞上为增函数, 即()()ln 10y mg x f x mx x =-''--'=≥恒成立,即ln 1+≥x m x在(0,)+∞上恒成立, 令ln 1()x r x x +=,则2ln ()xr x x -'=,令()0r x '>得ln 0x <,有01x <<,从而()r x 在(0,1)上单调递增,在(1,)+∞上单调递减, 则max ()(1)1r x r ==,于是m 1≥,故C 正确;对于D ,2()ln (0)F x x x ax x =->有两个不同极值点, 等价于()ln 120F x x ax +-'==有两个不同的正根, 即方程ln 12x a x+=有两个不同的正根, 由C 可知,021a <<,即102a <<,则D 正确. 故选:ACD.【点睛】关键点点睛:本题考查导数的应用,利用导数研究函数的单调性和极值,以及利用导数解决函数的零点问题和恒成立问题从而求参数范围,解题的关键在于将零点问题转化成两个函数的交点问题,解题时注意利用数形结合,考查转化思想和运算能力.5.设函数3()(,)f x x ax b a b R =++∈,下列条件中,使得()y f x =有且仅有一个零点的是( ) A .1,2a b == B .3,3a b =-=- C .0,2a b >< D .0,0a b <>【答案】ABC 【分析】求导2()3f x x a '=+,分0a ≥和0a <进行讨论,当0a ≥时,可知函数单调递增,有且只有一个零点;当0a <时,讨论函数的单调性,要使函数有一个零点,则需比较函数的极大值与极小值与0的关系,再验证选项即可得解. 【详解】3()f x x ax b =++,求导得2()3f x x a '=+当0a ≥时,()0f x '≥,()f x ∴单调递增,当x →-∞时,()f x →-∞;当x →+∞时,()f x →+∞;由零点存在性定理知,函数()f x 有且只有一个零点,故A ,C 满足题意;当0a <时,令()0f x '=,即230x a +=,解得13ax -=-,23a x -= 当x 变化时,()'f x ,()f x 的变化情况如下表:x,3a ⎛⎫--∞- ⎪ ⎪⎝⎭3a-- ,33a a ⎛⎫--- ⎪ ⎪⎝⎭3a- ,3a ⎛⎫-+∞ ⎪ ⎪⎝⎭()'f x+-+()f x极大值 极小值故当3ax -=-,函数()f x 取得极大值2333333a a a a a a f a b b ⎛⎫-----=-+=-+ ⎪ ⎪⎝⎭, 当3a x -=,函数()f x 取得极小值2333333a a a a a a f a b b ⎛⎫-----=++=+ ⎪ ⎪⎝⎭又当x →-∞时,()f x →-∞;当x →+∞时,()f x →+∞; 要使函数()f x 有且只有一个零点,作草图或则需0303a f a f ⎧⎛--<⎪ ⎪⎝⎨-⎪<⎪⎩,即20332033a a b a a b ⎧-<⎪⎪⎨-⎪<⎪⎩,即2033a ab -<<,B 选项,3,3a b =-=-,满足上式,故B 符合题意;则需00f f ⎧⎛>⎪ ⎪⎝⎨⎪>⎪⎩,即00b b ⎧>⎪⎪>,即0b >>,D 选项,0,0a b <>,不一定满足,故D 不符合题意; 故选:ABC 【点睛】思路点睛:本题考查函数的零点问题,如果函数()y f x =在区间[,]a b 上的图像是连续不断的一条曲线,并且有()()0f a f b <,那么,函数()y f x =在区间(),a b 内有零点,即存在(),c a b ∈,使得()0f c =,这个c 也就是方程()0f x =的根,考查学生的逻辑推理与运算能力,属于较难题.6.已知函数()21ln 2f x ax ax x =-+的图象在点()()11,x f x 处与点()()22,x f x 处的切线均平行于x 轴,则( )A .()f x 在1,上单调递增B .122x x +=C .()()121212x x x x f x f x ++++的取值范围是7,2ln 24⎛⎫-∞--⎪⎝⎭ D .若163a =,则()f x 只有一个零点 【答案】ACD 【分析】求导,根据题意进行等价转化,得到a 的取值范围;对于A ,利用导数即可得到()f x 在()1,+∞上的单调性;对于B ,利用根与系数的关系可得121x x =+;对于C ,化简()()121212x x x x f x f x ++++,构造函数,利用函数的单调性可得解;对于D ,将163a =代入()f x ',令()0f x '=,可得()f x 的单调性,进而求得()f x 的极大值小于0,再利用零点存在定理可得解. 【详解】 由题意可知,函数()f x 的定义域为()0,∞+,且()211ax ax ax a x x xf -+=-+=',则1x ,2x 是方程210ax ax -+=的两个不等正根,则212401a a x x a ⎧∆=->⎪⎨=>⎪⎩,解得4a >,当()1,x ∈+∞时,函数210y ax ax =-+>,此时()0f x '>, 所以()f x 在()1,+∞上单调递增,故A 正确;因为1x ,2x 是方程210ax ax -+=的两个不等正根,所以121x x =+,故B 错误; 因为()()221212121112221111ln ln 22x x x x f x f x x ax ax x ax ax a ++++=+++-++- 1112111ln 1ln 22a a a a a a a a⎛⎫=+++--=--+ ⎪⎝⎭, 易知函数()11ln 2h a a a a=--+在()4,+∞上是减函数, 则当4a >时,()()742ln 24h a h <=--,所以()()121212x x x x f x f x ++++的取值范围是7,2ln 24⎛⎫-∞-- ⎪⎝⎭,故C 正确;当163a =时,()1616133f x x x '=-+,令()0f x '=,得14x =或34, 则()f x 在10,4⎛⎫ ⎪⎝⎭上单调递增,在13,44⎛⎫⎪⎝⎭上单调递减,在3,4⎛⎫+∞ ⎪⎝⎭上单调递增, 所以()f x 在14x =取得极大值,且104f ⎛⎫< ⎪⎝⎭,()2ln 20f =>, 所以()f x 只有一个零点,故D 正确. 故选:ACD. 【点睛】关键点点睛:导数几何意义的应用主要抓住切点的三个特点: ①切点坐标满足原曲线方程; ②切点坐标满足切线方程;③切点的横坐标代入导函数可得切线的斜率.7.设函数()()1x af x a x a =->的定义域为()0,∞+,已知()f x 有且只有一个零点,下列结论正确的有( ) A .a e =B .()f x 在区间()1,e 单调递增C .1x =是()f x 的极大值点D .()f e 是()f x 的最小值【答案】ACD 【分析】()f x 只有一个零点,转化为方程0x a a x -=在(0,)+∞上只有一个根,即ln ln x ax a=只有一个正根.利用导数研究函数ln ()xh x x=的性质,可得a e =,判断A ,然后用导数研究函数()x e f x e x =-的性质,求出()'f x ,令()0f x '=,利用新函数确定()'f x 只有两个零点1和e ,并证明出()'f x 的正负,得()f x 的单调性,极值最值.判断BCD .【详解】()f x 只有一个零点,即方程0x a a x -=在(0,)+∞上只有一个根,x a a x =,取对数得ln ln x a a x =,即ln ln x ax a=只有一个正根. 设ln ()xh x x =,则21ln ()x h x x-'=,当0x e <<时,()0h x '>,()h x 递增,0x →时,()h x →-∞,x e >时,()0h x '<,()h x 递减,此时()0h x >,max 1()()h x h e e==. ∴要使方程ln ln x ax a =只有一个正根.则ln 1a a e =或ln 0a a<,解得a e =或0a <,又∵1a >,∴a e =.A 正确;()x e f x e x =-,1()x e f x e ex -'=-,1()0x e f x e ex -'=-=,11x e e x --=,取对数得1(1)ln x e x -=-,易知1x =和x e =是此方程的解.设()(1)ln 1p x e x x =--+,1()1e p x x-'=-,当01x e <<-时,()0p x '>,()p x 递增,1x e >-时,()0p x '<,()p x 递减,(1)p e -是极大值,又(1)()0p p e ==, 所以()p x 有且只有两个零点,01x <<或x e >时,()0p x <,即(1)ln 1e x x -<-,11e x x e --<,1e x ex e -<,()0f x '>,同理1x e <<时,()0f x '<,所以()f x 在(0,1)和(,)e +∞上递增,在(1,)e 上递减,所以极小值为()0f e =,极大值为(1)f ,又(0)1f =,所以()f e 是最小值.B 错,CD 正确. 故选:ACD . 【点睛】关键点点睛:本题考用导数研究函数的零点,极值,单调性.解题关键是确定()'f x 的零点时,利用零点定义解方程,1()0xe f x e ex-'=-=,11x e e x --=,取对数得1(1)ln x e x -=-,易知1x =和x e =是此方程的解.然后证明方程只有这两个解即可.8.在单位圆O :221x y +=上任取一点()P x y ,,圆O 与x 轴正向的交点是A ,将OA 绕原点O 旋转到OP 所成的角记为θ,若x ,y 关于θ的表达式分别为()x fθ=,()y g θ=,则下列说法正确的是( )A .()x f θ=是偶函数,()y g θ=是奇函数;B .()x f θ=在()0,π上为减函数,()y g θ=在()0,π上为增函数;C .()()1fg θθ+≥在02πθ⎛⎤∈⎥⎝⎦,上恒成立;D .函数()()22t f g θθ=+的最大值为2.【答案】ACD 【分析】依据三角函数的基本概念可知cos x θ=,sin y θ=,根据三角函数的奇偶性和单调性可判断A 、B ;根据辅助角公式知()()4f g πθθθ⎛⎫+=+ ⎪⎝⎭,再利用三角函数求值域可判断C ;对于D ,2cos sin2t θθ=+,先对函数t 求导,从而可知函数t 的单调性,进而可得当1sin 2θ=,cos 2θ=时,函数t 取得最大值,结合正弦的二倍角公式,代入进行运算即可得解. 【详解】由题意,根据三角函数的定义可知,x cos θ=,y sin θ=, 对于A ,函数()cos fθθ=是偶函数,()sin g θθ=是奇函数,故A 正确;对于B ,由正弦,余弦函数的基本性质可知,函数()cos f θθ=在()0,π上为减函数,函数()sin g θθ=在0,2π⎛⎫⎪⎝⎭为增函数,在,2ππ⎛⎫⎪⎝⎭为减函数,故B 错误; 对于C ,当0θπ⎛⎤∈ ⎥2⎝⎦,时,3,444πππθ⎛⎤+∈ ⎥⎝⎦()()cos sin 4f g πθθθθθ⎛⎫+=+=+∈ ⎪⎝⎭,故C 正确;对于D ,函数()()222cos sin2t fg θθθθ=+=+,求导22sin 2cos22sin 2(12sin )2(2sin 1)(sin 1)t θθθθθθ'=-+=-+-=--+, 令0t '>,则11sin 2θ-<<;令0t '<,则1sin 12θ<<, ∴函数t 在06,π⎡⎤⎢⎥⎣⎦和5,26ππ⎡⎤⎢⎥⎣⎦上单调递增,在5,66ππ⎛⎫⎪⎝⎭上单调递减,当6πθ=即1sin 2θ=,cos θ=时,函数取得极大值1222t =⨯=又当2θπ=即sin 0θ=,cos 1θ=时,212012t =⨯+⨯⨯=,所以函数()()22t f g θθ=+取得最大值2,故D 正确.故选:ACD. 【点睛】方法点睛:考查三角函数的值域时,常用的方法:(1)将函数化简整理为()()sin f x A x ωϕ=+,再利用三角函数性质求值域; (2)利用导数研究三角函数的单调区间,从而求出函数的最值.9.已知函数()e sin xf x a x =+,则下列说法正确的是( )A .当1a =-时,()f x 在0,单调递增B .当1a =-时,()f x 在()()0,0f 处的切线为x 轴C .当1a =时,()f x 在()π,0-存在唯一极小值点0x ,且()010f x -<<D .对任意0a >,()f x 在()π,-+∞一定存在零点 【答案】AC 【分析】结合函数的单调性、极值、最值及零点,分别对四个选项逐个分析,可选出答案. 【详解】对于A ,当1a =-时,()e sin x f x x =-,()e cos xf x x '=-, 因为()0,x ∈+∞时,e 1,cos 1xx >≤,即0fx,所以()f x 在0,上单调递增,故A 正确;对于B ,当1a =-时,()e sin xf x x =-,()e cos xf x x '=-,则()00e sin01f =-=,()00e cos00f '=-=,即切点为0,1,切线斜率为0,故切线方程为1y =,故B 错误;对于C ,当1a =时,()e sin x f x x =+,()e cos x f x x '+=,()e sin xf x x '=-', 当()π,0x ∈-时,sin 0x <,e 0x >,则()e sin 0xx f x -'=>'恒成立,即()e cos x f x x '+=在()π,0-上单调递增,又ππ22ππe cos e 220f --⎛⎫⎛⎫'-=-= ⎪ ⎪⎝⎭⎝⎭+>,3π3π443π3πe cos e442f --⎛⎫⎛⎫'-=-= ⎪ ⎪⎝⎭⎝-⎭+,因为123π3π421e e 2e ---⎛⎫=<⎪⎭< ⎝,所以3π43πe 024f -⎛⎫'-= ⎪-⎭<⎝,所以存在唯一03ππ,42x ⎛⎫∈-- ⎪⎝⎭,使得()00f x '=成立,所以()f x 在()0π,x -上单调递减,在()0,0x 上单调递增,即()f x 在()π,0-存在唯一极小值点0x ,由()000e cos 0xf x x +'==,可得()000000πe sin cos sin 4x f x x x x x ⎛⎫=+=-+=- ⎪⎝⎭,因为03ππ,42x ⎛⎫∈-- ⎪⎝⎭,所以0π3ππ,44x ⎛⎫-∈-- ⎪⎝⎭,则()00π4f x x ⎛⎫=- ⎪⎝⎭()1,0∈-,故C 正确;对于选项D ,()e sin xf x a x =+,()π,x ∈-+∞,令()e sin 0xf x a x =+=,得1sin ex xa -=, ()sin ex xg x =,()π,x ∈-+∞,则()πcos sin 4e e x xx x x g x ⎛⎫- ⎪-⎝⎭'==, 令0g x ,得πsin 04x ⎛⎫-= ⎪⎝⎭,则ππ4x k =+()1,k k ≥-∈Z ,令0g x,得πsin 04x ⎛⎫-> ⎪⎝⎭,则π5π2π,2π44x k k ⎛⎫∈++ ⎪⎝⎭()1,k k ≥-∈Z ,此时函数()g x 单调递减, 令0g x,得πsin 04x ⎛⎫-< ⎪⎝⎭,则5π9π2π,2π44x k k ⎛⎫∈++ ⎪⎝⎭()1,k k ≥-∈Z ,此时函数()g x 单调递增, 所以5π2π4x k =+()1,k k ≥-∈Z 时,()g x 取得极小值,极小值为5π5π2π2π445π5π2π5π4s 42in si πe e 4n k k g k k ++⎛⎫ ⎪⎛⎫⎝⎭== ⎪⎝⎭++()1,k k ≥-∈Z , 在()g x 的极小值中,3π4sin 3π45π5π42π4eg g -⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝+⎭-最小,当3ππ,4x ⎛⎫∈--⎪⎝⎭时,()g x 单调递减,所以函数()g x 的最小值为3π3π445πsin 3π144eg --⎛⎫-==- ⎪⎝⎭,当3π411a--<-时,即3π40a -<<时,函数()g x 与1=-y a无交点,即()f x 在()π,-+∞不存在零点,故D 错误.故选:AC. 【点睛】本题考查利用导数研究函数的极值、零点、最值,及切线方程的求法,考查学生的推理能力与计算求解能力,属于难题.10.函数()ln f x x x =、()()f x g x x'=,下列命题中正确的是( ).A .不等式()0g x >的解集为1,e ⎛⎫+∞ ⎪⎝⎭B .函数()f x 在()0,e 上单调递增,在(,)e +∞上单调递减C .若函数()()2F x f x ax =-有两个极值点,则()0,1a ∈D .若120x x >>时,总有()()()2212122m x x f x f x ->-恒成立,则m 1≥ 【答案】AD 【分析】对A ,根据()ln f x x x =,得到()()ln 1f x xg x x x'+==,然后用导数画出其图象判断;对B ,()1ln f x x '=+,当x e >时,()0f x '>,当0x e <<时,()0f x '<判断;对C ,将函数()()2F x f x ax =-有两个极值点,()ln 120x a x+=+∞在,有两根判断;对D ,将问题转化为22111222ln ln 22m m x x x x x x ->-恒成立,再构造函数()2ln 2m g x x x x =-,用导数研究单调性. 【详解】对A ,因为()()()ln 1ln f x x f x x x g x x x'+===、, ()2ln xg x x -'=, 令()0g x '>,得()0,1x ∈,故()g x 在该区间上单调递增;令()0g x '<,得()1x ∈+∞,,故()g x 在该区间上单调递减.又当1x >时,()0g x >,()10,11g g e ⎛⎫== ⎪⎝⎭, 故()g x 的图象如下所示:数形结合可知,()0g x >的解集为1,e ⎛⎫+∞ ⎪⎝⎭,故正确;对B ,()1ln f x x '=+,当x e >时,()0f x '>,当0x e <<时,()0f x '<,所以函数()f x 在()0,e 上单调递减,在(,)e +∞上单调递增,错误;对C ,若函数()()2F x f x ax =-有两个极值点,即()2ln F x x x ax =-有两个极值点,又()ln 21F x x ax '=-+,要满足题意,则需()ln 2100x ax -+=+∞在,有两根, 也即()ln 120x a x+=+∞在,有两根,也即直线()2y a y g x ==与的图象有两个交点. 数形结合则021a <<,解得102a <<. 故要满足题意,则102a <<,故错误; 对D ,若120x x >>时,总有()()()2212122m x x f x f x ->-恒成立, 即22111222ln ln 22m m x x x x x x ->-恒成立, 构造函数()2ln 2m g x x x x =-,()()12g x g x >,对任意的120x x >>恒成立,故()g x ()0+∞,单调递增,则()ln 10g x mx x '=--≥()0+∞, 恒成立, 也即ln 1x m x+≤,在区间()0,∞+恒成立,则()max 1g x m =≤,故正确. 故选:AD. 【点睛】本题主要考查导数在函数图象和性质中的综合应用,还考查了数形结合的思想、转化化归思想和运算求解的能力,属于较难题.。
高二数学《导数及其应用》单元检测题

高二数学《导数及其应用》单元检测题.选择题(每小题5分,共60 分)f(x) ax bx c f (1) 2 f ( 1)A . 4 B. 2 C.2 D.42. 函数f(x) lg x 11的零点所在的区间是xA.0,1 B. 1,2 C. 2,3 D. 3,10 3.已知函数f(x)在R上满足f(x) 2f (2 x) x2 8x 8,则曲线y= f (x)在点(1, f (1))处的切线方程是A. y 2x 1B. y xC. y 3x- 2D. y 2x 34.曲线y x3 3x2在点(1, 2)处的切线方程为A. y 3x 1B. y 3x+3C. y 3x 5D. y 2x5.设y 2,则y =A.2B. 2C.0D.以上都不是6.已知f(x) x(2014 ln x),若 f (x°) 2013 ,则X。
A . 1B . l n 2 C. 1 D . ee7.曲线y x2 11在点P (1, 12)处的切线与y轴交点的纵坐标是A.-9B.-3C.9D.158.函数f(x) c 32x ax ,若f⑵1,则aA.4B.-C.-4D. 14 49.函数f(x) 3 亠=ax + bx 在x= 1处有极值—2,,则a, b的值分别为A.1, —3B.1,3C. —1,3D.--1, —310.函数f(x) 3=x —3x(|x| v 1)A.有最大值,但无最小值B. 有最大值,也有最小值C.无最大值,也无最小值D. 无最大值,但有最小值2・ '11. y x sinx,贝y yA. 2xsinx B . x2 cosx2 2C. 2xcosx x cosx D . 2xsinx x cosxn12. 函数f (x) = x + 2cosx在[0 ,空]上取得最大值时x为n n nA.0B."6C. —D. —二.简答题(每小题5分,共20分)X13. 过原点作曲线y e的切线,则切线的方程为 __________________ .114. 设函数f(x) = x(ex + 1) + qx2,则函数f(x)的单调递增区间为_____________15. 若曲线y X 1(a€ R)在点(1,2)处的切线经过坐标原点,则a =。
高二下数学第一章导数及其应用单元检测(含答案)

阶段质量检测:导数及其应用(时间: 120分钟 满分:150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.以正弦曲线y =sin x 上一点P 为切点的切线为直线l ,则直线l 的倾斜角的范围是( ) A.⎣⎡⎦⎤0,π4∪⎣⎡⎭⎫3π4,π B .[0,π) C.⎣⎡⎦⎤π4,3π4 D.⎣⎡⎦⎤0,π4∪⎝⎛⎦⎤π2,3π4 2.函数f (x )=x +2cos x 在⎣⎡⎦⎤0, π2上的极大值点为( ) A .0 B.π6 C.π3 D.π23.函数f (x )的定义域为开区间(a ,b ),导函数f ′(x )在(a ,b )内的图象如图所示,则函数f (x )在开区间(a ,b )内有极小值点( )A .1个B .2个C .3个D .4个 4.若函数()ln f x x a x=+不是单调函数,则实数a 的取值范围是( ).A .[)0,+∞B .(],0-∞C .(),0-∞D .()0,+∞5.若e x ≥k +x 在R 上恒成立,则实数k 的取值范围为( ) A .(-∞,1] B .[1,+∞) C .(-∞,-1] D .[-1,+∞)6.若函数f (x )=x 33-a 2x 2+x +1在区间⎝⎛⎭⎫13,4上有极值点,则实数a 的取值范围是( ) A.⎝⎛⎭⎫2,103 B.⎣⎡⎭⎫2,103 C.⎝⎛⎭⎫103,174 D.⎝⎛⎭⎫2,174 7.函数f (x )=13ax 3+12ax 2-2ax +1的图象经过四个象限,则实数a 的取值范围是( )A.⎝⎛⎭⎫-310,67B.⎝⎛⎭⎫-85,-316C.⎝⎛⎭⎫-83,-116D.⎝⎛⎭⎫-∞,-310∪⎝⎛⎭⎫67,+∞ 8.已知函数f (x )的导函数f ′(x )=a (x -b )2+c 的图象如图所示,则函数f (x )的图象可能是( )9.某产品的销售收入y 1(万元)是产量x (千台)的函数:y 1=17x 2,生产成本y 2(万元)是产量x (千台)的函数:y 2=2x 3-x 2(x >0),为使利润最大,应生产( ) A .6千台 B .7千台 C .8千台D .9千台10..已知f (x )是定义在区间(0,+∞)内的函数,其导函数为f ′(x ),且不等式xf ′(x )<2f (x )恒成立,则( )A.4f (1)<f (2)B.4f (1)>f (2)C.f (1)<4f (2)D.f (1)>4f ′(2)11.已知y =f (x )是定义在R 上的奇函数,且当x <0时不等式f (x )+xf ′(x )<0成立,若a =30.3 ·f (30.3),b =log π3·f (log π3),c =log 319·f ⎝ ⎛⎭⎪⎫log 319,则a ,b ,c 的大小关系是( )A.a >b >cB.c >b >aC.a >c >bD.c >a >b12.若函数f (x )=sin xx ,且0<x 1<x 2<1,设a =21sin x x ,12sin b x x =,则a ,b 的大小关系是( )A .a >bB .a <bC .a =bD .a ,b 的大小不能确定二、填空题(本大题共4小题,每小题5分,满分20分.把答案填在题中的横线上) 13.若f (x )=13x 3-f ′(1)x 2+x +5,则f ′(1)=________.14.若函数f (x )=12x 2+(a -1)x -a ln x 存在唯一的极值,且此极值不小于1,则实数a 的取值范围为________.15.若函数f (x )=4xx 2+1在区间(m,2m +1)上单调递增,则实数m 的取值范围是__________.16.已知函数f (x )满足f (x )=f (π-x ),且当x ∈⎝⎛⎭⎫-π2,π2时,f (x )=x +sin x ,设a =f (1),b =f (2),c =f (3),则a ,b ,c 的大小关系是________.三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17. (本小题满分12分)若函数y =f (x )在x =x 0处取得极大值或极小值,则称x 0为函数y =f (x )的极值点.已知a ,b 是实数,1和-1是函数f (x )=x 3+ax 2+bx 的两个极值点. (1)求a 和b 的值;(2)设函数g (x )的导函数g ′(x )=f (x )+2,求g (x )的极值点.18. (2021·百师联盟考试)设函数f (x )=ln x +ax(a 为常数).(2)不等式f(x)≥1在x∈(0,1]上恒成立,求实数a的取值范围.19.(本小题满分12分)某个体户计划经销A,B两种商品,据调查统计,当投资额为x(x≥0)万元时,在经销A,B商品中所获得的收益分别为f(x)万元与g(x)万元,其中f(x)=a(x-1)+2,g(x)=6ln(x+b)(a>0,b>0).已知投资额为零时收益为零.(1)求a,b的值;(2)如果该个体户准备投入5万元经销这两种商品,请你帮他制定一个资金投入方案,使他能获得最大利润.20.(本小题满分12分) (2020·全国Ⅰ卷)已知函数f(x)=e x+ax2-x.(1)当a=1时,讨论f(x)的单调性;(2)当x≥0时,f(x)≥12x3+1,求a的取值范围.21.(本小题满分12分)已知函数f(x)=ln x+ax+1(a∈R).(2)若函数f (x )的图象与x 轴相切,求证:对于任意互不相等的正实数x 1,x 2,都有f (x 2)-f (x 1)x 2-x 1<1x 1+1x 2.22. (本小题满分12分) 已知函数f (x )=x 2-m ln x ,h (x )=x 2-x +a . (1)当a =0时,f (x )≥h (x )在(1,+∞)上恒成立,求实数m 的取值范围;(2)当m =2时,若函数k (x )=f (x )-h (x )在区间(1,3)上恰有两个不同零点,求实数a 的取值范围.参考答案1.【解析】选A y ′=cos x ,∵cos x ∈[-1,1],∴切线的斜率范围是[-1,1],∴倾斜角的范围是⎣⎡⎦⎤0,π4∪⎣⎡⎭⎫3π4,π. 2.答案:B3.【解析】选A 设极值点依次为x 1,x 2,x 3且a <x 1<x 2<x 3<b ,则f (x )在(a ,x 1),(x 2,x 3)上递增,在(x 1,x 2),(x 3,b )上递减,因此,x 1,x 3是极大值点,只有x 2是极小值点.4.【答案】C【解析】由题意知0x >,()1af x x'=+,要使函数()ln f x x a x =+不是单调函数,则需方程10ax+=在0x >上有解,即x a =-,所以0a <,故选C . 5.解析:选A 由e x ≥k +x ,得k ≤e x -x . 令f (x )=e x -x ,∴f ′(x )=e x -1. 当f ′(x )<0时,解得x <0,当f ′(x )>0时,解得x >0.∴f (x )在(-∞,0)上是减函数,在(0,+∞)上是增函数.∴f (x )min =f (0)=1. ∴实数k 的取值范围为(-∞,1].故选A.6.解析:选D 因为f (x )=x 33-a 2x 2+x +1,所以f ′(x )=x 2-ax +1.函数f (x )=x 33-a 2x 2+x +1在区间⎝⎛⎭⎫13,4上有极值点可化为f ′(x )=x 2-ax +1=0在区间⎝⎛⎭⎫13,4上有解, 即a =x +1x 在区间⎝⎛⎭⎫13,4上有解,设t (x )=x +1x ,则t ′(x )=1-1x 2, 令t ′(x )>0,得1<x <4,令t ′(x )<0,得13<x <1.所以t (x )在(1,4)上单调递增,在⎝⎛⎭⎫13,1上单调递减.所以t (x )min =t (1)=2,又t ⎝⎛⎭⎫13=103,t (4)=174,所以a ∈⎝⎛⎭⎫2,174. 7.【解析】选D f ′(x )=ax 2+ax -2a =a (x +2)(x -1),要使函数f (x )的图象经过四个象限,则f (-2)f (1)<0,即⎝⎛⎭⎫103a +1⎝⎛⎭⎫-76a +1<0,解得a <-310或a >67. 故选D. 8.【解析】选D 由导函数图象可知,当x <0时,函数f (x )递减,排除A 、B ;当0<x <x 1时,f ′(x )>0,函数f (x )递增.因此,当x =0时,f (x )取得极小值,故选D.9.【解析】选A 设利润为y ,则y =y 1-y 2=17x 2-(2x 3-x 2)=18x 2-2x 3,y ′=36x -6x 2,令y ′=0得x =6或x =0(舍),f (x )在(0,6)上是增函数,在(6,+∞)上是减函数,∴x =6时y 取得最大值.10.答案 B【解析】设函数g (x )=f (x )x 2(x >0),则g ′(x )=x 2f ′(x )-2xf (x )x 4=xf ′(x )-2f (x )x 3<0,所以函数g (x )在(0,+∞)上为减函数,因此g (1)>g (2), 即f (1)12>f (2)22,所以4f (1)>f (2). 11.答案 D【解析】 设g (x )=xf (x ),则g ′(x )=f (x )+xf ′(x ),又当x <0时,f (x )+xf ′(x )<0,∴x <0时,g ′(x )<0,g (x )在(-∞,0)上单调递减.由y =f (x )在R 上为奇函数, 知g (x )在R 上为偶函数,∴g (x )在(0,+∞)上是增函数, ∴c =g ⎝ ⎛⎭⎪⎫log 319=g (-2)=g (2),又0<log π3<1<30.3<3<2, ∴g (log π3)<g (30.3)<g (2),即b <a <c .12.【解析】选A f ′(x )=x cos x -sin xx 2,令g (x )=x cos x -sin x ,则g ′(x )=-x sin x +cos x-cos x =-x sin x .∵0<x <1,∴g ′(x )<0,即函数g (x )在(0,1)上是减函数,得g (x )<g (0)=0,故f ′(x )<0,函数f (x )在(0,1)上是减函数,由0<x 1<x 2<1得12211212sin sin ,sin sin x x x x x x x x >∴>,a >b ,故选A. 13.【解析】f ′(x )=x 2-2f ′(1)x +1,令x =1,得f ′(1)=23. 答案:2314.【解析】 对函数求导得f ′(x )=x -1+a ⎝⎛⎭⎫1-1x =(x +a )(x -1)x ,x >0,因为函数存在唯一的极值,所以导函数存在唯一的零点,且零点大于0,故x =1是唯一的极值点,此时-a ≤0,且f (1)=-12+a ≥1,所以a ≥32.答案 ⎣⎡⎭⎫32,+∞ 15.【解析】f ′(x )=4-4x 2(x 2+1)2,令f ′(x )>0,得-1<x <1,即函数f (x )的增区间为(-1,1).又f (x )在(m,2m +1)上单调递增,所以⎩⎪⎨⎪⎧m ≥-1,m <2m +1,2m +1≤1.解得-1<m ≤0.答案:(-1,0]16.【解析】f (2)=f (π-2),f (3)=f (π-3),因为f ′(x )=1+cos x≥0,故f (x )在⎝⎛⎭⎫-π2,π2上是增函数,∵π2>π-2>1>π-3>0,∴f (π-2)>f (1)>f (π-3),即c <a <b .答案:c <a <b17.【解析】(1)由题设知f ′(x )=3x 2+2ax +b ,且f ′(-1)=3-2a +b =0,f ′(1)=3+2a +b =0,解得a =0,b =-3.(2)由(1)知f (x )=x 3-3x .因为f (x )+2=(x -1)2(x +2),所以g ′(x )=0的根为x 1=x 2=1,x 3=-2,于是函数g (x )的极值点只可能是1或-2.当x <-2时,g ′(x )<0;当-2<x <1时, g ′(x )>0,故-2是g (x )的极值点.当-2<x <1或x >1时,g ′(x )>0, 故1不是g (x )的极值点.所以g (x )的极值点为-2. 18.【解析】 (1)函数f (x )的定义域为(0,+∞),f ′(x )=-a x 2+1x =x -ax 2,当a ≤0时,又x >0,∴x -a >0,∴f ′(x )>0, ∴f (x )在定义域(0,+∞)上单调递增;当a >0时,若x >a ,则f ′(x )>0,∴f (x )单调递增; 若0<x <a ,则f ′(x )<0,∴f (x )单调递减.综上可知:当a ≤0时,f (x )在(0,+∞)上是增函数;当a >0时,f (x )在区间(0,a )上是减函数,在区间(a ,+∞)上是增函数. (2)f (x )≥1⇔a x +ln x ≥1⇔ax ≥-ln x +1⇔a ≥ -x ln x +x 对任意x ∈(0,1]恒成立. 令g (x )=-x ln x +x ,x ∈(0,1].则g ′(x )=-ln x -x ·1x +1=-ln x ≥0,x ∈(0,1], ∴g (x )在(0,1]上单调递增,∴g (x )max =g (1)=1, ∴a ≥1,故a 的取值范围为[1,+∞).19.【解析】(1)由投资额为零时收益为零,可知f (0)=-a +2=0,g (0)=6ln b =0, 解得a =2,b =1.(2)由(1)可得f (x )=2x ,g (x )=6ln(x +1).设投入经销B 商品的资金为x 万元(0<x ≤5), 则投入经销A 商品的资金为(5-x )万元,设所获得的收益为S (x )万元, 则S (x )=2(5-x )+6ln(x +1)=6ln(x +1)-2x +10(0<x ≤5).S ′(x )=6x +1-2,令S ′(x )=0,得x =2.当0<x <2时,S ′(x )>0,函数S (x )单调递增;当2<x ≤5时,S ′(x )<0,函数S (x )单调递减.所以当x =2时,函数S (x )取得最大值, S (x )max =S (2)=6ln 3+6≈12.6万元.所以,当投入经销A 商品3万元,B 商品2万元时, 他可获得最大收益,收益的最大值约为12.6万元.20.解 (1)当a =1时,f (x )=e x +x 2-x ,x ∈R ,f ′(x )=e x +2x -1.故当x ∈(-∞,0)时,f ′(x )<0; 当x ∈(0,+∞)时,f ′(x )>0.所以f (x )在(-∞,0)单调递减,在(0,+∞)单调递增. (2)由f (x )≥12x 3+1得,e x +ax 2-x ≥12x 3+1,其中x ≥0, ①当x =0时,不等式为1≥1,显然成立,此时a ∈R .②当x >0时,分离参数a ,得a ≥-e x -12x 3-x -1x 2,记g (x )=-e x -12x 3-x -1x 2,g ′(x )=-(x -2)⎝ ⎛⎭⎪⎫e x -12x 2-x -1x 3.令h (x )=e x-12x 2-x -1(x >0), 则h ′(x )=e x -x -1,令H (x )=e x -x -1,H ′(x )=e x -1>0,故h ′(x )在(0,+∞)上是增函数,因此h ′(x )>h ′(0)=0,故函数h (x )在(0,+∞)上递增,∴h (x )>h (0)=0,即e x -12x 2-x -1>0恒成立,故当x ∈(0,2)时,g ′(x )>0,g (x )单调递增;当x ∈(2,+∞)时,g ′(x )<0,g (x )单调递减.因此,g (x )max =g (2)=7-e 24,综上可得,实数a 的取值范围是⎣⎢⎡⎭⎪⎫7-e 24,+∞. 21.【解析】(1) 函数f (x )的定义域为(0,+∞),f ′(x )=1x +a =ax +1x .当a ≥0时,f ′(x )>0,f (x )在(0,+∞)上单调递增; 当a <0时,由f ′(x )=0,得x =-1a .若x ∈⎝ ⎛⎭⎪⎫0,-1a ,f ′(x )>0,f (x )单调递增;若x ∈⎝ ⎛⎭⎪⎫-1a ,+∞,f ′(x )<0,f (x )单调递减.综上所述:当a ≥0时,f (x )在(0,+∞)上单调递增;当a <0时,f (x )在⎝ ⎛⎭⎪⎫0,-1a 单调递增,在⎝ ⎛⎭⎪⎫-1a ,+∞上单调递减.(2)证明 由(1)知,当a ≥0时,f (x )在(0,+∞)上单调递增,不满足条件. 所以a <0,此时f (x )的极大值为f ⎝ ⎛⎭⎪⎫-1a =-ln(-a ),由已知得-ln(-a )=0,故a =-1,此时f (x )=ln x -x +1.不妨设0<x 1<x 2,则f (x 2)-f (x 1)x 2-x 1<1x 1+1x 2等价于ln x 2x 1<x 2x 1-x 1x 2+x 2-x 1,即证:ln x 2x 1-x 2x 1+x 1x 2<x 2-x 1.令g (x )=ln x -x +1x (x >1),则g ′(x )=1x -1-1x 2=-⎝ ⎛⎭⎪⎫x -122+34x 2<0,故g (x )在(1,+∞)单调递减,所以g (x )<g (1)=0<x 2-x 1.所以对于任意互不相等的正实数x 1,x 2, 都有f (x 2)-f (x 1)x 2-x 1<1x 1+1x 2成立.22.【解析】(1)由f (x )≥h (x ),得m ≤xln x 在(1,+∞)上恒成立.令g (x )=xln x ,则g ′(x )=ln x -1(ln x )2,当x ∈(1,e)时,g ′(x )<0;当x ∈(e ,+∞)时,g ′(x )>0,所以g (x )在(1,e)上递减,在(e ,+∞)上递增. 故当x =e 时,g (x )的最小值为g (e)=e.所以m ≤e.即m 的取值范围是(-∞,e]. (2)由已知可得k (x )=x -2ln x -a .函数k (x )在(1,3)上恰有两个不同零点,相当于函数φ(x )=x -2ln x 与直线y =a 有两个不同的交点.φ′(x )=1-2x =x -2x ,当x ∈(1,2)时,φ′(x )<0,φ(x )递减,当x ∈(2,3)时,φ′(x )>0,φ(x )递增.又φ(1)=1,φ(2)=2-2ln 2,φ(3)=3-2ln 3,要使直线y =a 与函数φ(x )=x -2ln x 有两个交点,则2-2ln 2<a <3-2ln 3.即实数a 的取值范围是(2-2ln 2,3-2ln 3).。
2025版高考数学一轮总复习单元检测第三章一元函数的导数及其应用

单元检测一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 下列求导运算正确的是(C)A. B.C. D.解:对于,,故不正确.对于,,故不正确.对于,,故正确.对于,,故不正确.故选.2. 函数,则的单调递增区间是(B)A. B. C. D.解:函数的定义域为,求导得.由,解得.所以的单调递增区间是.故选.3. 曲线在,处的切线方程为(C)A. B. C. D.解:,.所以曲线在,处的切线方程为,即.故选.4. 函数的微小值点为(D)A. B. C. D.解:由题意,得的定义域为..令,得;令,得.所以在,上单调递减,在,上单调递增.所以函数在处取得微小值.故选.5. 在区间上有(B)A. 最大值B. 最大值C. 最小值D. 最小值解:,单调递增,在上有最小值,最大值 .故选.6. 如图为函数的图象,为函数的导函数,则不等式的解集为(D)A. B.C. D.解:由题图,可得函数的单调递增区间为,,单调递减区间为.所以当时,;当时,.由,可得或所以.故选.7. 已知函数,若,,,则,,的大小关系是(D)A. B. C. D.解:易知的定义域为,且,所以为偶函数.当时,,则,所以在上单调递增.又,,所以.所以,即.故选.8. 依据以往阅历,一超市中的某一商品每月的销售量(单位:件)与销售价格(单位:元/件)满足关系式,其中.已知该商品的成本为20元/件,则该超市每月销售该商品所获得利润的最大值为(B)A. 8 600元B. 8 060元C. 6 870元D. 4 060元解:设超市每月销售该商品所获得的利润为元.则,..令,得,则在上单调递增;令,得,则在上单调递减.所以.故选.二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9. 函数的定义域为,它的导函数的部分图象如图所示,则下列结论正确的是(AD)A. B. 是的微小值点C. 函数在上有极大值D. 是的极大值点解:由的图象,可知当时,,函数单调递增;当时,,函数单调递减.因此有,是的极大值点,所以选项,正确.当或时,,函数单调递增.因此函数在上没有极大值,且不是的微小值点,所以选项,错误.故选.10. 已知函数,则(ACD)A. 为其定义域上的增函数B. 为偶函数C. 的图象与直线相切D. 有唯一的零点解:的定义域为,,所以为上的增函数,正确.,故为奇函数,错误.,,故在原点处的切线方程为,正确.为上的增函数,,所以有唯一的零点,正确.故选.11. 已知三次函数的导函数的图象如图,且,,则(ABC)A. B.C. D.解:依据导函数的图象,可知.当时,,当时,,当时,.所以在上单调递增,在上单调递减,在上单调递增,故其大致图象如图所示.则有,所以,故正确.所以,故正确.由的图象,结合,知,,,所以,故正确.因为,所以.又在上单调递增,所以,故错误.故选.三、填空题:本题共3小题,每小题5分,共15分.12. [2024年全国Ⅲ卷]设函数.若,则1.解:,则,整理得,解得.故填1.13. 已知函数,,若这两个函数的图象在公共点处有相同的切线,则解:由题意,得,.因为,的图象在公共点处有相同的切线,所以即解得所以.故填.14. 已知函数,则的最小值为3.解:.当时,单调递增,.当时,,.当时,,单调递减;当时,,单调递增.所以.综上,.故填3.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15. (13分)求下列函数的导数:(1);解:.(2).[答案].16. (15分)已知函数.(1)若曲线在点处的切线与直线垂直,求的值;解:由题意,得,.因为曲线在点处的切线与直线垂直,所以,解得.(2)若函数在区间上单调递减,求的取值范围.[答案]因为函数在区间上单调递减,所以在区间上恒成立,故.当时,的最大值为.故的取值范围是.17. (15分)设函数.(1)求函数的解析式;解:,所以.(2)求函数的单调区间,极大值,微小值.[答案]令,解得或.因为,所以.当变更时,,变更状况如下.0 - 0极大值微小值所以的单调递增区间为,,单调递减区间为.的极大值为,微小值为.18. (17分)已知函数在处的极值为2,其中.(1)求,的值;解:,由题意,可得解得,.(2)证明:对随意的,.证明:.令,,则.令,则恒成立,所以在上单调递减,且,所以时,,所以,即证.19. (17分)已知函数.(1)求证:.解:证明:由题意,得.令,则.令,可得.当时,,函数单调递增;当时,,函数单调递减.所以,即.(2)设,若在区间内恒成立,求的最小值.[答案]若在区间内恒成立,则.令,可得.当时,,函数单调递增;当时,,函数单调递减.所以,因此.故的最小值为1.。
导数单元测试(含答案)

导数单元测试【检测试题】 一、选择题1. 设函数()y f x =可导,则0(1)(1)lim 3x f x f x∆→+∆-∆等于( ).A .'(1)fB .3'(1)fC .1'(1)3f D .以上都不对2. 已知函数f (x )=ax 2+c ,且(1)f '=2,则a 的值为( )B.2C.-1D. 03 .()f x 与()g x 是定义在R 上的两个可导函数,若()f x ,()g x 满足''()()f x g x =,则()f x 与()g x 满足( )A ()f x =2()g xB ()f x -()g x 为常数函数)C ()f x =()0g x =D ()f x +()g x 为常数函数4.三次函数x ax y +=3在()+∞∞-∈,x 内是增函数,则 ( )A . 0>aB .0<aC .1=aD .31=a 5.已知函数y =x 3-3x+c 的图像与x 恰有两个公共点,则c =( ) (A )-2或2 (B )-9或3 (C )-1或1 (D )-3或1 6.0'()f x =0是可导函数y =f(x)在点x =x 0处有极值的 ( )A .充分不必要条件B .必要不充分条件C .充要条件D .非充分非必要条件 7.曲线3()2f x x x在0p 处的切线平行于直线41y x ,则0p 点的坐标为( )A (1,0)B (2,8)C (1,0)和(1,4)--D (2,8)和(1,4)--·8.设函数()f x 在R 上可导,其导函数为,()f x ,且函数)(')1(x f x y -=的图像如题(8)图所示,则下列结论中一定成立的是( ) (A )函数()f x 有极大值(2)f 和极小值(1)f (B )函数()f x 有极大值(2)f -和极小值(1)f (C )函数()f x 有极大值(2)f 和极小值(2)f - (D )函数()f x 有极大值(2)f -和极小值(2)f9.已知函数()y f x =, ()y g x =的导函数的图象如下左图,那么()y f x =, ()y g x =的图象可能是( )10 . 抛物线22x y =上两点),(11y x A 、),(22y x B 关于直线m x y +=对称,且2121-=⋅x x ,则m 等于( )A .23 B .2 C .25D .3 [11. 设点P 在曲线12xy e =上,点Q 在曲线ln(2)y x =上,则PQ 最小值为( )()A 1ln 2- ()B2(1ln 2)- ()C 1ln 2+ ()D 2(1ln 2)+12. 已知函数()f x =3231ax x -+,若()f x 存在唯一的零点0x ,且0x >0,则a 的取值范围为( )A .(2,+∞)B .(-∞,-2)C .(1,+∞)D .(-∞,-1)二、填空题13.函数32y x x x =--的单调区间为_____________________________.14.已知函数3()f x x ax =+在R 上有两个极值点,则实数a 的取值范围是 .15.已知函数()ln f x ax x =-,若()1f x >在区间(1,)+∞内恒成立,则实数a 的范围为______________. 16. f (x )=ax 3-3x +1对x ∈[-1,1]总有f (x )≥0成立,则a = . [三、解答题:17.如图,一矩形铁皮的长为8cm ,宽为5cm ,在四个角上截去 四个相同的小正方形,制成一个无盖的小盒子,问小正方形的边长 为多少时,盒子容积最大[18.已知函数323()(2)632f x ax a x x =-++-(1)当2a >时,求函数()f x 极小值; (2)试讨论曲线()y f x =与x 轴公共点的个数。
人教版导数及其应用多选题单元综合模拟测评检测试卷

人教版导数及其应用多选题单元综合模拟测评检测试卷一、导数及其应用多选题1.已知:()f x 是奇函数,当0x >时,()'()1f x f x ->,(1)3f =,则( )A .(4)(3)f ef >B .2(4)(2)f e f ->-C .3(4)41f e >-D .2(4)41f e -<--【答案】ACD 【分析】由已知构造得'()+10x x e f ⎡⎤>⎢⎥⎣⎦,令()()+1x f x g x e =,判断出函数()g x 在0x >时单调递增,由此得()()4>3g g ,化简可判断A ;()()4>2g g ,化简并利用()f x 是奇函数,可判断B ;()()4>1g g ,化简可判断C ;由C 选项的分析得32(4)41>4+1f e e >-,可判断D.【详解】 因为当0x >时,()'()1fx f x ->,所以()'()10f x f x -->,即()[]'()+10xf x f e x ->,所以'()+10x x e f ⎡⎤>⎢⎥⎣⎦, 令()()+1xf xg x e=,则当0x >时,()'>0g x ,函数()g x 单调递增, 所以()()4>3g g ,即43(4)+1(3)+1>f f e e ,化简得(4)(3)1>(3)f f e e ef >+-,故A 正确;()()4>2g g ,即42(4)+1(2)+1>f f e e ,化简得222(4)(2)1>(2)f f e e e f >+-, 所以2(4)(2)e f f -<-,又()f x 是奇函数,所以2(4)(2)e f f -<-,故B 不正确;()()4>1g g ,即4(4)+1(1)+1>f f e e,又(1)3f =,化简得3(4)41f e >-,故C 正确; 由C 选项的分析得32(4)41>4+1f e e >-,所以2(4)41f e -<--,又()f x 是奇函数,所以2(4)41f e -<--,故D 正确, 故选:ACD. 【点睛】关键点点睛:解决本题中令有导函数的不等式,关键在于构造出某个函数的导函数,得出所构造的函数的单调性,从而可比较函数值的大小关系.2.在湖边,我们常看到成排的石柱子之间两两连以铁链,这就是悬链线(Catenary ),其形状因与悬在两端的绳子因均匀引力作用下掉下来之形相似而名.选择适当的坐标系后,悬链线的方程是一个双曲余弦函数()cosh 2xx aax e ef x a a a -+⎛⎫=⋅=⋅ ⎪⎝⎭,其中a 为非零常数,在此坐标平面上,过原点的直线与悬链线相切于点()()00,T x f x ,则0x a ⎡⎤⎢⎥⎣⎦的值可能为( )(注:[]x 表示不大于x 的最大整数)A .2-B .1-C .1D .2【答案】AC 【分析】求出导数,表示出切线,令0x t a=,可得()()110t tt e t e --++=,构造函数()()()11x x h x x e x e -=-++,可得()h x 是偶函数,利用导数求出单调性,结合零点存在性定理可得021x a -<<-或012xa<<,即可求出. 【详解】()2x xaae ef x a -+=⋅,()2x x aae ef x --'∴=,∴切线斜率002x x aae ek --=,()0002x x aae ef x a -+=⋅,则切线方程为()0000022x x x x aaaaee e ey a x x --+--⋅=-,直线过原点,()0000022x x x x aaa ae e e ea x --+-∴-⋅=⋅-令0x t a=,则可得()()110t tt e t e --++=, 令()()()11xxh x x e x e -=-++,则t 是()h x 的零点,()()()()11x x h x x e x e h x --=++-=,()h x ∴是偶函数,()()x x h x x e e -'=-+,当0x >时,()0h x '<,()h x 单调递减,()1120h e -=>,()22230h e e -=-+<,()h x ∴在()1,2存在零点t ,由于偶函数的对称性()h x 在()2,1--也存在零点,且根据单调性可得()h x 仅有这两个零点,021x a ∴-<<-或012xa<<, 02x a ⎡⎤∴=-⎢⎥⎣⎦或1. 故选:AC. 【点睛】本题考查利用导数求切线,利用导数研究函数的零点,解题的关键是将题目转化为令0x t a=,()()110t t t e t e --++=,求()()()11x xh x x e x e -=-++的零点问题.3.已知2()ln f x x x =,2()()f x g x x'=,()'f x 是()f x 的导函数,则下列结论正确的是( )A .()f x 在12e ,-⎛⎫+∞ ⎪⎝⎭上单调递增.B .()g x 在(0,)+∞上两个零点C .当120x x e <<< 时,221212()()()m x x f x f x -<-恒成立,则32m ≥D .若函数()()h x f x ax =-只有一个极值点,则实数0a ≥ 【答案】ACD 【分析】求出导函数()'f x ,由()0f x '>确定增区间,判断A ,然后可得()g x ,再利用导数确定()g x 的单调性与极值,结合零点存在定理得零点个数,判断B ,构造函数2()()x f x mx ϕ=-,由()ϕx 在(0,)e 上递减,求得m 范围,判断C ,利用导数研究()h x 的单调性与极值点,得a 的范围,判断D . 【详解】()(2ln 1)(0)f x x x x '=+>,令()0f x '>,得1212ln 10ln 2x x x e -+>⇒>-⇒>,故A 正确2ln 1()x g x x+=,212ln ()x g x x -'=,令()0g x '>得121ln 2x x e <⇒<,()0g x '<得120x e <<, 故()g x 在120,e ⎛⎫ ⎪⎝⎭上为减函数,在12e ⎛⎫+∞⎪⎝⎭上为增函数. 当x →时,()g x →-∞;当x →+∞时,()0g x →且g()0x >()g x ∴的大致图象为()g x ∴只有一个零点,故B 错.记2()()x f x mx ϕ=-,则()ϕx 在(0,)e 上为减函数,()(2ln 1)20x x x mx ϕ'∴=+-≤对(0,)x e ∈恒成立22ln 1m x ∴≥+对(0,)x e ∈恒成立 23m ∴≥32m ∴≥. 故C 正确.2()()ln h x f x ax x x ax =-=-,()(2ln 1)h x x x a =+'-,设()(2ln 1)H x x x =+,()h x 只有一个极值点, ()h x '0=只有一个解,即直线y a =与()y H x =的图象只有一个交点.()2(ln 1)12ln 3H x x x '=++=+,()H x '在(0,)+∞上为增函数,令()0H x '=,得32x e-=,当0(0,)x x ∈时,()0H x '<;当0(,)x x ∈+∞时,()0H x '>.()H x ∴在0(0,)x 上为减函数,在0(,)x +∞上为增函数,332203()21202H x e e --⎡⎤⎛⎫=⨯-+=-< ⎪⎢⎥⎝⎭⎣⎦,0(0,)x x ∈时,322ln 12ln 120x e -+<+=-<,即()0H x <,且0x →时,()0H x →,又x →+∞时,()H x →+∞,因此()H x 的大致图象如下(不含原点):直线y a =与它只有一个交点,则0a ≥.故D 正确. 故选:ACD . 【点睛】关键点点睛:本题考查用导数研究函数的性质,解题关键是由导数确定函数的单调性,得出函数的极值,对于零点问题,需要结合零点存在定理才能确定零点个数.注意数形结合思想的应用.4.阿基米德是伟大的物理学家,更是伟大的数学家,他曾经对高中教材中的抛物线做过系统而深入的研究,定义了抛物线阿基米德三角形:抛物线的弦与弦的端点处的两条切线围成的三角形称为抛物线阿基米德三角形.设抛物线C :2yx 上两个不同点,A B 横坐标分别为1x ,2x ,以,A B 为切点的切线交于P 点.则关于阿基米德三角形PAB 的说法正确的有( )A .若AB 过抛物线的焦点,则P 点一定在抛物线的准线上 B .若阿基米德三角形PAB 33C .若阿基米德三角形PAB 为直角三角形,则其面积有最小值14D .一般情况下,阿基米德三角形PAB 的面积212||4x x S -=【答案】ABC 【分析】设出直线AB 的斜截式方程、点,A B 的坐标,根据导数的几何意义求出切线,PA PB 的方程,进而求出点P 的坐标,将直线AB 的方程和抛物线方程联立,得到一元二次方程以及该方程两根的和、积的关系.A :把抛物线焦点的坐标代入直线AB 的斜截式方程中,根据抛物线的准线方程进行判断即可;B :根据正三角形的性质,结合正三角形的面积公式进行判断即可;C :根据直角三角形的性质,结合直角三角形的面积公式进行判断即可;D :根据点到直线距离公式、两点间距离公式进行求解判断即可.. 【详解】由题意可知:直线AB 一定存在斜率, 所以设直线AB 的方程为:y kx m =+,由题意可知:点221122(,),(,)A x x B x x ,不妨设120x x <<,由2'2yx y x ,所以直线切线,PA PB 的方程分别为:221112222(),2()y x x x x y x x x x -=--=-,两方程联立得:211122222()2()y x x x x y x x x x ⎧-=-⎨-=-⎩, 解得:12122x x x y x x +⎧=⎪⎨⎪=⎩,所以P 点坐标为:1212(,)2x x x x +,直线AB 的方程与抛物线方程联立得:2121220,y kx mx kx m x x k x x m y x=+⎧⇒--=⇒+==-⎨=⎩. A :抛物线C :2y x 的焦点坐标为1(0,)4,准线方程为 14y =-,因为AB 过抛物线的焦点,所以14m =,而1214x x m =-=-,显然P 点一定在抛物线的准线上,故本选项说法正确;B :因为阿基米德三角形PAB 为正三角形,所以有||||PA PB =,= 因为 12x x ≠,所以化简得:12x x =-,此时221111(,),(,)A x x B x x -, P 点坐标为:21(0,)x -,因为阿基米德三角形PAB 为正三角形,所以有||||PA AB =,112x x =-⇒=, 因此正三角形PAB, 所以正三角形PAB的面积为11sin 602224︒==, 故本选项说法正确;C :阿基米德三角形PAB 为直角三角形,当PA PB ⊥时, 所以1212121222121122122114PAPBx x x xx x kk x x x x x x x x ++--⋅=-⇒⋅=-⇒=---, 直线AB 的方程为:14y kx =+所以P 点坐标为:1(,)24k -,点 P 到直线AB 的距离为:=||AB ===,因为12121,4x x k x x +==-,所以21AB k =+, 因此直角PAB的面积为:2111(1)224k ⨯+=≥, 当且仅当0k =时,取等号,显然其面积有最小值14,故本说法正确; D :因为1212,x x k x x m +==-,所以1||AB x x ===-,点P 到直线AB 的距离为:212== 所以阿基米德三角形PAB的面积32121211224x x S x x -=⋅-=, 故本选项说法不正确. 故选:ABC【点睛】关键点睛:解决本题的关键就是一元二次方程根与系数关系的整体代换应用,本题重点考查了数学运算核心素养的应用.5.若存在常数k 和b ,使得函数()F x 和()G x 对其公共定义域上的任意实数x 都满足:()F x kx b ≥+和()G x kx b ≤+恒成立,则称此直线y kx b =+为()F x 和()G x 的“隔离直线”.已知函数()22x f x =(x ∈R ),()12g x x =(0x <),()ln h x e x =,(e 为自然对数的底数),则( )A .()()()m x f x g x =-在0x ⎛⎫∈ ⎪⎝⎭内单调递减 B .()f x 和()g x 之间存在“隔离直线”,且b 的最小值为2- C .()f x 和()g x 之间存在“隔离直线”,且k 的取值范围是[]2,1-D .()f x 和()g x 之间存在唯一的“隔离直线”,方程为2ey =-【答案】BD 【分析】对于A :令()()()m x f x g x =-,利用导数可确定()m x 单调性,进而作出判断; 对于B 和C :利用二次函数的性质以及不等式恒成立的知识求出b 、k 的范围,进而作出判断;对于选项D :根据隔离直线过()f x 和()h x 的公共点,可假设隔离直线为2e y kx =-;可得到222x ekx ≥-,再利用恒成立得出k 的值,最后尝试利用导数证明()2eh x ≤-,进而作出判断. 【详解】对于A ,()()()2122x m x f x g x x =-=-, ()322121022x m x x x x +'∴=+=>,当x ⎛⎫∈ ⎪⎝⎭时,()0m x '>,()m x ∴单调递增,故A 错误; 对于B ,C ,设()f x ,()g x 的隔离直线为y kx b =+,22x kx b ≥+对任意x ∈R 恒成立,即2220x kx b --≥对任意x ∈R 恒成立,所以21480k b ∆=+≤,所以0b ≤,又12kx b x ≤+对任意(),0x ∈-∞恒成立,即22210kx bx +-≤对任意(),0x ∈-∞恒成立,因为0b ≤,所以0k ≤且21480b k ∆=+≤,所以22k b ≤-且22b k ≤-,4248k b b ≤≤-,解得20k -≤≤,同理20b -≤≤, 所以b 的最小值为2-,k 的取值范围是[]2,0-, 故B 正确,C 错误; 对于D ,函数()f x 和()h x的图象在x =∴若存在()f x 和()h x 的隔离直线,那么该直线过这个公共点,设隔离直线的斜率为k,则隔离直线方程为(2e y k x -=,即2e y kx =-,则222x ekx ≥-(x ∈R),得2220x kx e -+≥对x ∈R 恒成立,则()24420k e ∆=-≤,解得k =,此时隔离直线方程为:2ey =-,下面证明()2e h x ≤-, 令()()ln 22e e G x h x e x =--=--(0x >),则()x G x x'=,当x =()0G x '=;当0x <<()0G x '<;当x >()0G x '>;∴当x =()G x 取到极小值,也是最小值,即()0min G x G==,()()02e G x h x ∴=--≥在()0,∞+上恒成立,即()2eh x ≤-,∴函数()f x 和()h x存在唯一的隔离直线2ey =-,D 正确. 故选:BD . 【点睛】关键点睛:本题考查导数中的新定义问题的求解;解题关键是能够充分理解“隔离直线”的定义,将问题转化为根据不等式恒成立求解参数范围或参数值、或不等式的证明问题,属于难题.6.设函数3()(,)f x x ax b a b R =++∈,下列条件中,使得()y f x =有且仅有一个零点的是( )A .1,2a b ==B .3,3a b =-=-C .0,2a b ><D .0,0a b <>【答案】ABC 【分析】求导2()3f x x a '=+,分0a ≥和0a <进行讨论,当0a ≥时,可知函数单调递增,有且只有一个零点;当0a <时,讨论函数的单调性,要使函数有一个零点,则需比较函数的极大值与极小值与0的关系,再验证选项即可得解. 【详解】3()f x x ax b =++,求导得2()3f x x a '=+当0a ≥时,()0f x '≥,()f x ∴单调递增,当x →-∞时,()f x →-∞;当x →+∞时,()f x →+∞;由零点存在性定理知,函数()f x 有且只有一个零点,故A ,C 满足题意;当0a <时,令()0f x '=,即230x a +=,解得13ax -=-,23a x -= 当x 变化时,()'f x ,()f x 的变化情况如下表:x,3a ⎛⎫--∞- ⎪ ⎪⎝⎭3a-- ,33a a ⎛⎫--- ⎪ ⎪⎝⎭3a- ,3a ⎛⎫-+∞ ⎪ ⎪⎝⎭()'f x+-+()f x极大值 极小值故当3ax -=-,函数()f x 取得极大值2333333a a a a a a f a b b ⎛⎫-----=-+=-+ ⎪ ⎪⎝⎭, 当3a x -=,函数()f x 取得极小值2333333a a a a a a f a b b ⎛⎫-----=++=+ ⎪ ⎪⎝⎭又当x →-∞时,()f x →-∞;当x →+∞时,()f x →+∞; 要使函数()f x 有且只有一个零点,作草图或则需00f f ⎧⎛<⎪ ⎪⎝⎨⎪<⎪⎩,即00b b ⎧<⎪⎪<,即0b <<,B 选项,3,3a b =-=-,满足上式,故B 符合题意;则需00f f ⎧⎛>⎪ ⎪⎝⎨⎪>⎪⎩,即00b b ⎧>⎪⎪>,即0b >>,D 选项,0,0a b <>,不一定满足,故D 不符合题意; 故选:ABC 【点睛】思路点睛:本题考查函数的零点问题,如果函数()y f x =在区间[,]a b 上的图像是连续不断的一条曲线,并且有()()0f a f b <,那么,函数()y f x =在区间(),a b 内有零点,即存在(),c a b ∈,使得()0f c =,这个c 也就是方程()0f x =的根,考查学生的逻辑推理与运算能力,属于较难题.7.关于函数()sin ,(,)x f e x x x π∈-=+∞+,下列结论正确的有( ) A .()f x 在(0,)+∞上是增函数 B .()f x 存在唯一极小值点0x C .()f x 在(,)π-+∞上有一个零点 D .()f x 在(,)π-+∞上有两个零点 【答案】ABD 【分析】根据函数()f x 求得()'f x 与()f x '',再根据()0f x ''>在(,)π-+∞恒成立,确定()'f x 在(,)π-+∞上单调递增,及(0,)x ∈+∞()0f x '>,且存在唯一实数03(,)42x ππ∈--,使0()=0f x ',从而判断A ,B 选项正确;再据此判断函数()f x 的单调性,从而判断零点个数.【详解】由已知()sin ,(,)x f e x x x π∈-=+∞+得()cos x f x e x '=+,()sin xf x e x ''=-,(,)x π∈-+∞,()0f x ''>恒成立,()'f x 在(,)π-+∞上单调递增,又3423()0,()0,(0)20422f e f e f ππππ--'''-=-<-=>=>(0,)x ∴∈+∞时()(0)0f x f ''>>,且存在唯一实数03(,)42x ππ∈--,使0()=0f x ',即00cos x e x =-,所以()f x 在(0,)+∞上是增函数,且()f x 存在唯一极小值点0x ,故A,B 选项正确. 且()f x 在0(,)x π-单调递减,0(,)x +∞单调递增,又()00f e ππ--=+>,000000()sin sin cos )04xf x e x x x x π=+=-=-<,(0)10=>f ,所以()f x 在(,)π-+∞上有两个零点,故D 选项正确,C 选项错误.故选:ABD. 【点睛】导数是研究函数的单调性、极值(最值)最有效的工具,而函数是高中数学中重要的知识点,对导数的应用的考查主要从以下几个角度进行: (1)考查导数的几何意义,往往与解析几何、微积分相联系. (2)利用导数求函数的单调区间,判断单调性;已知单调性,求参数. (3)利用导数求函数的最值(极值),解决生活中的优化问题. (4)考查数形结合思想的应用.8.已知函数()sin xf x x=,(]0,x π∈,则下列结论正确的有( ) A .()f x 在区间(]0,π上单调递减B .若120x x π<<≤,则1221sin sin x x x x ⋅>⋅C .()f x 在区间(]0,π上的值域为[)0,1 D .若函数()()cos g x xg x x '=+,且()1g π=-,()g x 在(]0,π上单调递减【答案】ACD 【分析】先求出函数的导数,然后对四个选项进行逐一分析解答即可,对于选项A :当0,2x π⎛⎫∈ ⎪⎝⎭时,可得()0f x '<,可得()f x 在区间0,2π⎛⎫⎪⎝⎭上单调递减;当,2x ππ⎡⎤∈⎢⎥⎣⎦,可得()0f x '<,可得()f x 在区间,2ππ⎡⎤⎢⎥⎣⎦上单调递减,最后作出判断; 对于选项B :由()f x 在区间(]0,π上单调递减可得()()12f x f x >,可得1212sin sin x x x x >,进而作出判断; 对于选项C :由三角函数线可知sin x x <,所以sin 1x x x x <=,sin ()0f πππ==,进而作出判断;对于选项D :()()()sin g x g x xg x x ''''=+-,可得()()sin xg x f x x''==,然后利用导数研究函数()g x '在区间(]0,π上的单调性,可得()()0g x g π''≤=,进而可得出函数()g x 在(]0,π上的单调性,最后作出判断.【详解】()2cos sin x x xf x x -'=, (]0,x π∈,当0,2x π⎛⎫∈ ⎪⎝⎭时,cos 0x >,由三角函数线可知tan x x <, 所以sin cos xx x<,即cos sin x x x <,所以cos sin 0x x x -<, 所以()0f x '<,所以()f x 在区间0,2π⎛⎫⎪⎝⎭上单调递减,当,2x ππ⎡⎤∈⎢⎥⎣⎦,cos 0x ≤,sin 0x ≥,所以cos sin 0x x x -<,()0f x '<, 所以()f x 在区间,2ππ⎡⎤⎢⎥⎣⎦上单调递减, 所以()f x 在区间(]0,π上单调递减,故选项A 正确; 当120x x π<<≤时,()()12f x f x >,所以1212sin sin x x x x >,即1221sin sin x x x x ⋅<⋅,故选项B 错误; 由三角函数线可知sin x x <,所以sin 1x x x x <=,sin ()0f πππ==, 所以当(]0,x π∈时,()[)0,1f x ∈,故选项C 正确;对()()cos g x xg x x '=+进行求导可得: 所以有()()()sin g x g x xg x x ''''=+-,所以()()sin xg x f x x''==,所以()g x ''在区间(]0,π上的值域为[)0,1, 所以()0g x ''≥,()g x '在区间(]0,π上单调递增,因为()0g π'=, 从而()()0g x g π''≤=,所以函数()g x 在(]0,π上单调递减,故选项D 正确. 故选:ACD. 【点睛】方法点睛:本题考查导数的综合应用,对于函数()sin xf x x=的性质,可先求出其导数,然后结合三角函数线的知识确定导数的符号,进而确定函数的单调性和极值,最后作出判断,考查逻辑思维能力和运算求解能力,属于中档题.9.已知函数()ln f x x mx =-有两个零点1x 、2x ,且12x x <,则下列结论不正确的是( ) A .10m e<<B .21x x -的值随m 的增大而减小C .101x <<D .2x e >【答案】C 【分析】由()0f x =得出ln xm x =,构造函数()ln x g x x=,利用导数分析函数()g x 的单调性与极值,数形结合可判断ACD 选项的正误;任取1m 、210,m e ⎛⎫∈ ⎪⎝⎭,且12m m <,设()()121g g m ξξ==,其中121e ξξ<<<;设()()122g g m ηη==,其中121e ηη<<<,利用函数()g x 的单调性结合不等式的基本性质得出2121ξξηη->-,可判断B 选项的正误. 【详解】令()0f x =,可得ln xm x =,构造函数()ln x g x x=,定义域为()0,∞+,()1ln xg x x-'=. 当0x e <<时, ()0g x '>,此时函数()g x 单调递增; 当x e >时,()0g x '<,此时函数()g x 单调递减. 所以,()()max 1g x g e e==,如下图所示:由图象可知,当10m e <<时,直线y m =与函数()ln x g x x=的图象有两个交点,A 选项正确;当1x >时,()0g x >,由图象可得11x e <<,2x e >,C 选项错误,D 选项正确;任取1m 、210,m e ⎛⎫∈ ⎪⎝⎭,且12m m <,设()()121g g m ξξ==,其中121e ξξ<<<;设()()122g g m ηη==,其中121e ηη<<<.由于函数()g x 在区间()1,e 上单调递增,且()()11g g ξη<,11ξη∴<; 函数()g x 在区间(),e +∞上单调递减,且()()22g g ξη<,22ξη∴>. 由不等式的基本性质可得1212ξξηη-<-,则2121ξξηη->-. 所以,21x x -的值随m 的增大而减小,B 选项正确. 故选:C. 【点睛】在利用导数研究函数的零点问题个数中,可转化为判定()m g x =有两个实根时实数m 应满足的条件,并注意()g x 的单调性、奇偶性、最值的灵活应用.另外还可作出函数()y g x =的大致图象,直观判定曲线交点个数,但应注意严谨性,进行必要的论证.10.函数()ln f x x x =、()()f x g x x'=,下列命题中正确的是( ).A .不等式()0g x >的解集为1,e ⎛⎫+∞ ⎪⎝⎭B .函数()f x 在()0,e 上单调递增,在(,)e +∞上单调递减C .若函数()()2F x f x ax =-有两个极值点,则()0,1a ∈D .若120x x >>时,总有()()()2212122m x x f x f x ->-恒成立,则m 1≥ 【答案】AD 【分析】对A ,根据()ln f x x x =,得到()()ln 1f x xg x x x'+==,然后用导数画出其图象判断;对B ,()1ln f x x '=+,当x e >时,()0f x '>,当0x e <<时,()0f x '<判断;对C ,将函数()()2F x f x ax =-有两个极值点,()ln 120x a x+=+∞在,有两根判断;对D ,将问题转化为22111222ln ln 22m m x x x x x x ->-恒成立,再构造函数()2ln 2m g x x x x =-,用导数研究单调性. 【详解】对A ,因为()()()ln 1ln f x x f x x x g x x x'+===、,()2ln xg x x -'=, 令()0g x '>,得()0,1x ∈,故()g x 在该区间上单调递增;令()0g x '<,得()1x ∈+∞,,故()g x 在该区间上单调递减. 又当1x >时,()0g x >,()10,11g g e ⎛⎫== ⎪⎝⎭, 故()g x 的图象如下所示:数形结合可知,()0g x >的解集为1,e ⎛⎫+∞ ⎪⎝⎭,故正确;对B ,()1ln f x x '=+,当x e >时,()0f x '>,当0x e <<时,()0f x '<,所以函数()f x 在()0,e 上单调递减,在(,)e +∞上单调递增,错误;对C ,若函数()()2F x f x ax =-有两个极值点,即()2ln F x x x ax =-有两个极值点,又()ln 21F x x ax '=-+,要满足题意,则需()ln 2100x ax -+=+∞在,有两根, 也即()ln 120x a x+=+∞在,有两根,也即直线()2y a y g x ==与的图象有两个交点. 数形结合则021a <<,解得102a <<. 故要满足题意,则102a <<,故错误;对D ,若120x x >>时,总有()()()2212122m x x f x f x ->-恒成立, 即22111222ln ln 22m m x x x x x x ->-恒成立, 构造函数()2ln 2m g x x x x =-,()()12g x g x >,对任意的120x x >>恒成立, 故()g x ()0+∞,单调递增,则()ln 10g x mx x '=--≥()0+∞, 恒成立, 也即ln 1x m x+≤,在区间()0,∞+恒成立,则()max 1g x m =≤,故正确. 故选:AD. 【点睛】本题主要考查导数在函数图象和性质中的综合应用,还考查了数形结合的思想、转化化归思想和运算求解的能力,属于较难题.。
(完整版)导数单元测试题(含答案)

导数单元测试题〔实验班用〕一、选择题1.曲线323y x x =-+在点(1,2)处的切线方程为( )A .31y x =-B .35y x =-+C .35y x =+D .2y x = 2.函数21()e x f x x +=⋅,[]1,2-∈x 的最大值为( ).A .14e -B . 0C .2eD . 23e 3.假设函数3()3f x x x a 有3个不同的零点,那么实数a 的取值范围是〔 〕A.(2,2)B.2,2C.(,1)D.(1,)4.假设函数3()63f x x bxb 在(0,1)内有极小值,那么实数b 的取值范围是〔 〕A.1(0,)2B. (,1)C. (0,)D. (0,1)5.假设2a >,那么函数321()13f x x ax 在区间(0,2)上恰好有( )A .0个零点B .3个零点C .2个零点D .1个零点6.曲线x y e =在点2(2)e ,处的切线与坐标轴所围三角形的面积为〔 〕A.294eB.22eC.2eD.22e7.函数()f x 的图象如下图,以下数值排序正确的选项是( ).A .(3)(2)0(2)(3)32f f f f -''<<<-B .(3)(2)0(3)(2)32f f f f -''<<<-C . (3)(2)0(3)(2)32f f f f -''<<<-D .(3)(2)0(2)(3)32f f f f -''<<<-8设(),()f x g x 分别是R 上的奇函数和偶函数, 当0x时,''()()()()0f x g x f x g x ,且(3)0g ,那么不等式()()0f x g x 解集是( )A .(3,0)(3,) B .(3,0)(0,3) C .(,3)(3,) D .(,3)(0,3)9.函数ln ln ()a x f x x+=在1,上为减函数,那么实数a 的取值范围是( )A .a eB .0a eC .a eD .10ea <<10.假设函数)(x f 的导数是)1()(+-='x x x f ,那么函数()(1)g x f x =--的单调减区间是( )A .(1,0)-B .(,1),(0,)-∞-+∞C .(2,1)--D .(,2),(1,)-∞--+∞ 11.二次函数2()f x ax bx c =++的导数为'()f x ,'(0)0f >,对于任意实数x 都有()0f x ≥,那么(1)'(0)f f 的最小值为〔 〕 A .3 B .52 C .2 D .3212.函数2()ln 22a f x x x x =--存在单调递减区间,那么a 的取值范围是〔 〕(A)[1,)-+∞ (B) (1,)-+∞ (C) (,1)-∞- (D) (,1]-∞- 二、填空题13.假设函数2()2ln f x x x =-在其定义域内的一个子区间(1,1)k k -+内不是单调函数,那么实数k 的取值范围是 . 14.点P 在曲线323+-=x x y 上移动,设在点P 处的切线的倾斜角为为α,那么α的取值范围是15.函数3()128f x x x =-+在区间[3,3]-上的最大值与最小值分别为,M m ,那么M m -=_________16.函数()f x 的定义域为[]15,-,局部对应值如下表,()f x 的导函数()y f x '=的图象如下图. 以下关于()f x 的命题: ①函数()f x 的极大值点为0,4; ②函数()f x 在[]02,上是减函数;③如果当[]1x ,t ∈-时,()f x 的最大值是2,那么t 的最大值为4; ④当12a <<时,函数()y f x a =-有4个零点; ⑤函数()y f x a =-的零点个数可能为0,1,2,3,4个. 其中正确命题的序号是 . 三、解答题17.函数)0()(23≠++=a cx bx ax x f ,当1-=x 时()f x 取得极值5,且11)1(-=f .〔1〕求()f x 的单调区间和极小值;〔2〕证明对任意12,x x )3,3(-∈,不等式32|)()(|21<-x f x f 恒成立. 18.函数)1ln(2)(2++=x ax x f ,其中a 为实数. 〔1〕假设()f x 在1=x 处有极值,求a 的值;(2) 假设()f x 在]32[,上是增函数,求a 的取值范围. 19.函数2()ln(1)()f x x ax a x a R =---∈. 〔1〕当1=a 时,求函数)(x f 的最值; 〔2〕求函数)(x f 的单调区间.20.某食品厂进行蘑菇的深加工,每公斤蘑菇的本钱20元,并且每公斤蘑菇的加工费为x -1 0 4 5 ()f x1221t 元〔t 为常数,且25)t ≤≤,设该食品厂每公斤蘑菇的出厂价为x 元〔2540x ≤≤〕,根据市场调查,日销售量q 与e x成反比,当每公斤蘑菇的出厂价为30元时,日销售量为100公斤.〔1〕求该工厂的每日利润y 元与每公斤蘑菇的出厂价x 元的函数关系式;〔2〕假设5=t ,当每公斤蘑菇的出厂价x 为多少元时,该工厂的利润y 最大,求最大值.21.函数1ln ()x f x x+=.〔1〕假设函数在区间1(,)2a a +(0)a >上存在极值,求实数a 的取值范围;〔2〕如果当1≥x 时,不等式()1≥k f x x +恒成立,求实数k 的取值范围.22.设函数2()(1)2ln(1).f x x x =+-+ 〔1〕求函数()f x 的单调区间;〔2〕当11,1xe e时,()f x m 不等式<恒成立,求实数m 的取值范围; 〔3〕假设关于x 的方程2()f x x x a =++在0,2上恰有两个相异实根,求实数a 的取值范围.导数单元测试题答案一、选择题 ACAAD DBDAA CB 二、填空题13.312k14.30,,2415.32 16. ①②⑤三、解答题17.解:〔1〕2()32(0)f x ax bx c a '=++≠,由题意得(1)11(1)5(1)0f f f =-⎧⎪-=⎨⎪'-=⎩ ,即115320a b c a b c a b c ++=-⎧⎪-+-=⎨⎪-+=⎩ ,解得139a b c =⎧⎪=-⎨⎪=-⎩,,.因此x x x x f 93)(23--=,2()3693(1)(3)f x x x x x '=--=+-.当 ),3()1,(+∞--∞∈ x 时,'()0f x >;当)3,1(-∈x 时,'()0f x <. 所以函数()f x 的单调增区间为)1,(--∞和),3(+∞;单调减区间为)3,1(-. 故函数()f x 在3=x 处取得极小值,()(3)27f x f ==-极小值.〔2〕由〔Ⅰ〕知32()39f x x x x =--在)1,3(--上递增,在)3,1(-上递减, 所以max ()(1)5f x f =-=;min ()(3)27f x f =±=-.所以,对任意12,x x )3,3(-∈恒有 12|()()||5(27)|32f x f x -<--=.18.解:〔1〕由得()f x 的定义域为)1(∞+-,. 又2()2,1f x ax x '=++ 因为()f x 在1=x 处有极值,(1)210f a '∴=+=,解之得 1.2a =-〔2〕依题意得()0≥f x '对[23]x ∀∈,恒成立, 即 201≥ax x 2++对[23]x ∀∈,恒成立. 221111()24a x x x ∴>=---++ 对[23]x ∀∈,恒成立.211[23]()24x x ∈∴-++,, [12,6],∈-- 41)21(12++-∴x 11[,],612∈-- 112≥a ∴-.19.解:〔1〕函数2()ln(1)()f x x ax a x a =---∈R 的定义域是(1,)+∞.当1a =时,32()12()2111x x f x x x x -'=--=--, 所以()f x 在3(1,)2为减函数在3(,)2+∞为增函数,所以函数()f x 的最小值为33()ln 224f =+.〔2〕22()2()211a x x a f x x a x x +-'=--=--, ①假设0a ≤时,那么22()221,()21a x x a f x x +-+=-≤>0在(1,)+∞恒成立, 所以()f x 的增区间为(1,)+∞.②假设20,12a a +>>则,故当2(1)2a x +∈,,22()2()01a x x f x x +-'=-≤; 当2[,)2a x +∈+∞时,22()2()01a x x f x x +-=-≥. 所以当0a >时,()f x 的减区间为2(1,)2a +,()f x 的增区间为2(,)2a ++∞.20.解:〔1〕设日销量3030,100,100e e e则x k k q k ==∴=, ………………2分所以日销量30100e e xq =.30100e (20)(2540)e x x t y x --∴=≤≤.………………7分〔2〕当5=t 时,30100e (25)exx y -=. ………………8分30100e (26)e xx y -'∴=. ………………9分026由得y x '≥≤,026由得,y x '≤≥[2526][2640]在,上单调递增,在,上单调递减.y ∴4max 26,100e 当时x y ∴==.………………11分当每公斤蘑菇的出厂价为26元时,该工厂的利润最大,最大值为4100e 元.……12分 21.解:〔Ⅰ〕因为1ln ()x f x x +=, x >0,那么2ln ()x f x x'=-,当01x <<时,()0f x '>;当1x >时,()0f x '<. 所以()f x 在〔0,1〕上单调递增;在(1,)+∞上单调递减, 所以函数()f x 在1x =处取得极大值. 因为函数()f x 在区间1(,)2a a +〔其中0a >〕上存在极值,所以1,11,2a a <⎧⎪⎨+>⎪⎩ 解得112a <<. 〔Ⅱ〕不等式(),1k f x x +≥即为(1)(1ln ),x x k x ++≥记(1)(1ln )(),x x g x x ++=那么min (), 1.k g x x ≤≥所以2[(1)(1ln )](1)(1ln )()x x x x x g x x '++-++'=2ln x xx-=. 令()ln h x x x =-,那么1()1h x x'=-,1x ≥,()0,h x '∴≥[()h x ∴在[1,)+∞上单调递增,min ()(1)10h x h ∴==>,从而()(1)0h x h >≥,所以()0g x '>,故()g x 在[1,)+∞上也单调递增, 所以min ()(1)2g x g ==. 所以2k ≤.22.解:〔2〕函数的定义域为。
《导数及其应用》单元测试题

《导数及其应用》单元测试题班别_________姓名_______ 学号______成绩______一、选择题(本大题共有10小题,每小题4,共40分)1. f(x)=x 3, 0'()f x =6,则x 0= ( )B. C.± D. ±12.若函数f(x)=2x 2+1,图象上P(1,3)及邻近上点Q(1+Δx,3+Δy), 则x y∆∆=( )A. 4B. 4ΔxC. 4+2Δx D . 2Δx3.若()()()k x f k x f x f k 2lim ,20000--='→则的值为 ( ) A .-2 B. 2 C.-1 D. 14.曲线y=x 3+x-2在点P 0处的切线平行于直线y=4x ,则点P 0的坐标是 ( )A .(0,1) B.(1,0) C.(-1,-4)或(1,0) D.(-1,-4)5.函数y=2x 3-3x 2-12x+5在[0,3]上的最大值与最小值分别是 ( )A .5 , -15 B.5 , 4 C.-4 , -15 D.5 , -166.设y=x-lnx ,则此函数在区间(0,1)内为 ( )A .单调递增B 、有增有减C 、单调递减D 、不确定7. 已知f(x)=3x ·sinx ,则f’(1)= ( ) A .31+cos1 B. 31sin1+cos1 C. 31sin1-cos1 D.sin1+cos18. 若函数()f x 在区间(,)a b 内函数的导数为正,且()0f b ≤,则函数()f x 在(,)a b 内有 ( )A. f(x) 〉0B. f(x)〈 0C. f(x) = 0D. 无法确定9. 抛物线y =(1-2x)2在点x =32处的切线方程为 ( )A. y=0 B .8x -y -8=0 C.x =1 D . y=0或者8x -y -8=010.函数()12ln 2+=x y 的导数是 ( ) A.1242+x xB. 1212+x C.()10ln 1242+x x D. ()e x x22log 124+二、填空题(每小题4分,共20分)11.若f(x)=x 3+3ax 2+3(a +2)x +1有极大值和极小值,则a 的取值范围是_________12.若函数a x x y +-=2323在[-1,1]上有最大值3,则该函数在[-1,1]上的最小值是______13.函数y=(1-sinx)2的导数是='y ________________14.函数()ln (0)f x x x x =>的单调递增区间是____.15.点P 在曲线323+-=x x y 上移动,设在点P 处的切线的倾斜角为为α,则α的取值范围是三、解答题:本大题5小题,共40分,解答写出文字说明、证明过程或演算步骤)。
第四单元_导数应用_单元质量评估_(北师大选修1-1)
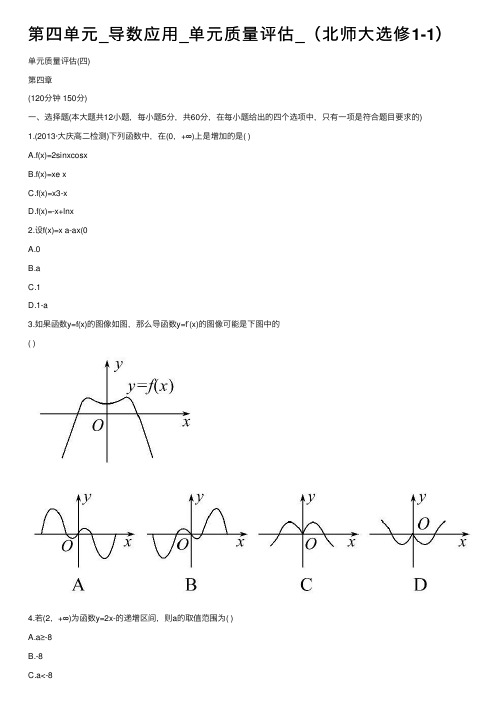
直平分AB,若∠BAO=θ(rad),则OA==,故 OB=, 又OP=10-10tanθ.
所以y=OA+OB+OP=++10-10tanθ, 所求函数关系式为y=+10(0<θ<).
②若OP=xkm,则OQ=10-x,所以OA=OB==, 所求函数关系式为y=x+2(0 (2)选择函数模型①, y′= =, 令y′=0得sinθ=,因为0<θ<,所以θ=, 当θ∈(0,)时,y′<0,y是减少的; 当θ∈(,)时,y′>0,y是增加的,所以当θ=时,y min=10+10. 这时点O位于线段AB的中垂线上,且距离AB边km处. 20.【解析】f(x)的定义域为(-1,1),易知函数f(x)是奇函数,故只需讨论函数在(0,1)内的单调性. 因为f′(x)=b·=-, 当00,(x2-1)2>0,所以-<0. 所以若b>0,则f′(x)<0,所以函数f(x)在(0,1)上是减少的;若b<0,则 f′(x)>0,所以函数f(x)在(0,1)上是增加的. 又函数f(x)是奇函数,而奇函数图像关于原点对称, 所以当b>0时,f(x)在(-1,1)上是减少的;当b<0时,f(x)在(-1,1)上是增加的. 21.【解题指南】(1)先求出切点处的导数,再代入点斜式方程求切线 方程. (2)转化为x-1>,再转化为求f(x)=x(x-1)-lnx,x>0的最小值问题. 【解析】(1)y'=,于是y'|x=1=1,因此l的方程为y=x-1. (2)只需要证明?x>0且x≠1,x-1>. 设f(x)=x(x-1)-lnx,x>0, 则f'(x)=2x-1-=, 当x∈(0,1)时,f'(x)<0;当x∈(1,+≦)时,f'(x)>0. 所以f(x)在(0,1)上单调递减,在(1,+≦)上单调递增. 所以f(x)在x=1处取得极小值,也是最小值. 所以f(x)>f(1)=0(x≠1). 因此,除切点(1,0)之外,曲线C在直线l的下方. 22.【解题指南】若m=2,则函数g(x)是一个具体的函数,可根据求最值的步骤来求函数g(x)在区间[1,]上的最大值;若函数 lo[f(x)+2]在区间[1,+≦)上是减少的,则f(x)+2在区间[1,+≦)上是增加的. 【解析】(1)当m=2时,g(x)=x+-lnx(x>0), 则g′(x)=1--=,由 g′(x)=<0,得x2-x-2<0. 又x>0,可解得0 (2)令h(x)=f(x)+2,则由条件得h(x)在区间[1,+≦)上是增加的,且h(x)>0在区间[1,+≦)恒成立,而h′(x)=f′(x)=1-≥0,则m ≤x2在区间[1,+≦)上恒成立,得m≤1.又f(x)+2>0在区间[1,+≦)恒成立,得f(1)+2>0, 即m>-3,所以实数m的取值范围是(-3,1]. 关闭Word文档返回原板块
(完整版)导数及其应用单元测试卷
《导数及其应用》单元测试卷一、 选择题1.已知物体的运动方程是23416441t t t s +-=(t 表示时间,s 表示位移),则瞬时速度为0的时刻是:( )A .0秒、2秒或4秒B .0秒、2秒或16秒C .2秒、8秒或16秒D .0秒、4秒或8秒2.下列求导运算正确的是( )A .211()1x x x '+=+B .21(log )ln 2x x '= C .3(3)3log x x e '= D .()2cos 2sin x x x '=- 3.曲线324y x x =-+在点(13),处的切线的倾斜角为( )A .30°B .45°C .60°D .120°4.函数y=2x 3-3x 2-12x+5在[0,3]上的最大值与最小值分别是( )A.5 , -15B.5 , 4C.-4 , -15D.5 , -165.汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程s 看作时间t 的函数,其图像可能是( )6.设函数1()21(0),f x x x x=+-< 则()f x ( ) A .有最大值 B .有最小值 C .是增函数 D .是减函数7.如果函数y=f (x )的图像如右图,那么导函数y=f (x )的图像可能是( )8.设()ln f x x x =,若0'()2f x =,则0x =( )A . 2eB . eC .ln 22 D . ln 2s O A . s O s O s O B . C . D .9.已知函数y=f(x)在区间(a,b)内可导,且x 0∈(a ,b )则000()()lim h f x h f x h h→+-- 的值为( ) A 、f’(x 0) B 、2 f’(x 0) C 、-2 f’(x 0) D 、010.设曲线11x y x +=-在点(32),处的切线与直线10ax y ++=垂直,则a =( ) A .2 B .12 C .12- D .2- 11.设a ∈R ,若函数3ax y e x =+,x ∈R 有大于零的极值点,则( )A .3a >-B .3a <-C .13a >- D .13a <- 12 f (x )与g(x )是定义在R 上的两个可导函数,若f (x ),g(x )满足f ′(x )=g ′(x ),则f (x )与g (x )满足A. f (x ) = g (x )B.f (x )-g (x )为常数函数C. f (x )=g (x )=0D.f (x )+g (x )为常数函数二 填空题13.直线12y x b =+是曲线()ln 0y x x =>的一条切线,则实数b = . 14.函数f(x)=(x 2-1) 3 +1有极_____值______.15.设曲线2ax y =在点(1,a )处的切线与直线062=--y x 平行,则=a .13.函数y=x+2cosx 在区间[0,2π]上的最大值是 三 解答题 17.已知函数32()f x x bx cx d =+++的图像过点P (0,2),且在点M (-1,)1(-f )处的切线方程为076=+-y x .①求函数)(x f y =的解析式;②求函数)(x f y =的单调区间.18.已知函数321()33f x x x x =+-,讨论函数()f x 的单调区间.19.设a ∈R ,函数233)(x ax x f -=,2=x 是函数)(x f y =的极值点. (Ⅰ)求a 的值;(Ⅱ)求函数233)(x ax x f -=在区间[]1,5-上的最值.20.某厂生产某种产品x 件的总成本32()120075c x x =+(元),已知产品单价的平方与产品件数x 成反比,生产100件这样的产品单价为50元,生产多少件产品时利润最大?21.已知过函数f (x )=123++ax x 的图象上一点B (1,b )的切线的斜率为-3.(1)求a 、b 的值;(2)求A 的取值范围,使不等式f (x )≤A -1987对于x ∈[-1,4]恒成立;22已知a 为实数,x=4是函数f (x)=a lnx +x2-12x 的一个极值点。
导数及其应用多选题单元达标综合模拟测评检测试卷

导数及其应用多选题单元达标综合模拟测评检测试卷一、导数及其应用多选题1.已知函数()sin sin f x ax a x =-,[]0,2x π∈,其中ln 1a a ->,则下列说法中正确的是( )A .若()f x 只有一个零点,则10,2a ⎛⎫∈ ⎪⎝⎭B .若()f x 只有一个零点,则()0f x ≥恒成立C .若()f x 只有两个零点,则31,2a ⎛⎫∈ ⎪⎝⎭D .若()f x 有且只有一个极值点0x ,则()01312a a f x π+--<⋅恒成立【答案】ABD 【分析】利用()00f =以及零点存在定理推导出当1a >时,函数()f x 在[]0,2π上至少有两个零点,结合图象可知当01a <<时,函数()f x 在()0,2π上有且只有一个极值点,利用导数分析函数()f x 在()0,2π上的单调性,可判断A 选项的正误;利用A 选项中的结论可判断B 选项的正误;取12a =,解方程()0f x =可判断C 选项的正误;分析出当()f x 在()0,2π上只有一个极值点时,01a <<,分13a =、103a <<、113a <<三种情况讨论,结合sin x x <可判断D 选项的正误. 【详解】构造函数()ln 1g x x x =--,其中0x >,则()111x g x x x-'=-=. 当01x <<时,()0g x '<,函数()g x 单调递减; 当1x >时,()0g x '>,此时,函数()g x 单调递增. 所以,()()min 10g x g ==.ln 1a a ->,0a ∴>且1a ≠.()sin sin f x ax a x =-,则()00f =.当1a >时,sin sin sin 02222a a f a a ππππ⎛⎫=-=-<⎪⎝⎭,3333sin sin sin 02222a a f a a ππππ⎛⎫=-=+> ⎪⎝⎭,由零点存在定理可知,函数()f x 在3,22ππ⎛⎫⎪⎝⎭内至少有一个零点, 所以,当1a >时,函数()f x 在区间[]0,2π上至少有两个零点, 所以,当函数()f x 在区间[]0,2π上只有一个零点时,01a <<.对于A 选项,当01a <<时,()()cos cos cos cos f x a ax a x a ax x '=-=-.01a <<,则022a ππ<<,022a ππ<<, cos 022a f a ππ⎛⎫'=> ⎪⎝⎭,()()()2cos2cos2cos210f a a a a ππππ'=-=-<, 由零点存在定理可知,函数()f x 在区间,22ππ⎛⎫⎪⎝⎭上至少有一个极值点, 令()0f x '=,可得cos cos ax x =,当()0,2x π∈时,02ax x π<<<,由()cos cos cos 2ax x x π==-,可得2ax x π=-,解得21x a π=+, 所以,函数()f x 在区间()0,2π上有且只有一个极值点21x a π=+. 作出函数1cos y ax =与函数2cos y x =在区间[]0,2π上的图象如下图所示:由图象可知,函数1cos y ax =与函数2cos y x =在区间()0,2π上的图象有且只有一个交点,记该交点的横坐标为0x ,当00x x <<时,cos cos ax x >,此时()0f x '>; 当02x x π<<时,cos cos ax x <,此时()0f x '<.所以,函数()f x 在区间()00,x 上单调递增,在区间()0,2x π上单调递减. 所以,()()()0max 00f x f x f =>=,又()2sin 2f a ππ=.若函数()f x 在区间[]0,2π上有且只有一个零点,则()2sin 20f a ππ=>.01a <<,则022a ππ<<,所以,02a ππ<<,解得102a <<,A 选项正确;对于B 选项,若函数()f x 在区间[]0,2π上有且只有一个零点时,由A 选项可知,函数()f x 在区间()00,x 上单调递增,在区间()0,2x π上单调递减.()00f =,()2sin 20f a ππ=>,所以,对任意的[]0,2x π∈,()0f x ≥,B 选项正确;对于C 选项,取12a =,则()1sin sin sin sin cos sin 1cos 2222222x x x x x x f x x ⎛⎫=-=-=- ⎪⎝⎭,02x π≤≤,则02x π≤≤,令()0f x =,可得sin 02x =或cos 12x=,可得02x =或2xπ=, 解得0x =或2x π=. 所以,当12a =时,函数()f x 有两个零点,C 选项错误; 对于D 选项,当1a >时,若02x π<<,则02ax a π<<,且22a ππ>,当()0,2x π∈时,令()0f x '=,可得出()()cos cos cos 2ax x k x k Z π==±∈,至少可得出2ax x π=-或2ax x π=+,即函数()f x 在区间()0,2π上至少有两个极值点,不合乎题意,所以,01a <<. 下面证明:当02x π<<时,sin x x <,构造函数()sin h x x x =-,其中02x π<<,则()1cos 0h x x '=->,所以,函数()sin h x x x =-在区间0,2π⎛⎫⎪⎝⎭上为增函数,所以,()()00h x h >=,即sin x x <.分以下三种情况来证明()01312a a f x π+--<⋅恒成立.()()000cos cos 0f x a ax x '=-=,可得00cos cos ax x =,0002ax x π<<<,由00cos cos ax x =可得出002ax x π=-,所以,021x a π=+. 则()000sin sin 2sin ax x x π=-=-. ①当13a =时,032x π=,则()1sin sin 33x f x x =-,31342sin sin 223233f ππππ⎛⎫=-=< ⎪⎝⎭,即()01312a a f x π+--<⋅成立;②当103a <<时,023,212x a πππ⎛⎫=∈ ⎪+⎝⎭, 则()()()0000002sin sin sin sin 1sin 1sin1f x ax a x x a x a x a a π=-=--=-+=-++ ()()()()22221sin 1sin 21sin 121111a a a a a a a a a a a ππππππ⎛⎫⎛⎫=+-=+-=+<+⋅= ⎪ ⎪++++⎝⎭⎝⎭ 1312a a π+--=⋅;③当113a <<时,023,12x a πππ⎛⎫=∈ ⎪+⎝⎭, ()()()()0000000sin sin sin sin 1sin 1sin f x ax a x x a x a x a x =-=--=-+=+-()()()()()()()01121sin 1sin 1sin 1111a a a x a a a a a a πππππ--⎛⎫=+-=+-=+<+⋅ ⎪+++⎝⎭()13112a a a ππ+--=-=.综上所述,当函数()f x 只有一个极值点0x 时,()01312a a f x π+--<恒成立. 故选:ABD. 【点睛】方法点睛:利用导数解决函数零点问题的方法:(1)直接法:先对函数求导,根据导数的方法求出函数的单调区间与极值,根据函数的基本性质作出图象,然后将问题转化为函数图象与x 轴的交点问题,突出导数的工具作用,体现了转化与化归思想、数形结合思想和分类讨论思想的应用; (2)构造新函数法:将问题转化为研究两函数图象的交点问题;(3)参变量分离法:由()0f x =分离变量得出()a g x =,将问题等价转化为直线y a =与函数()y g x =的图象的交点问题.2.函数()()320ax bx d a f x cx =+++≠有两个极值点1x 、()212x x x <,则下列结论正确的是( ) A .230b ac ->B .()f x 在区间()12,x x 上单调递减C .若()10af x <,则()f x 只有一个零点D .存在0x ,使得()()()1202f x f x f x +=【答案】ACD 【分析】利用极值点与导数的关系可判断A 选项的正误;取0a <,利用函数的单调性与导数的关系可判断B 选项的正误;分0a >、0a <两种情况讨论,分析函数()f x 的单调性,结合图象可判断C 选项的正误;计算出函数()f x 的图象关于点,33b b f a a ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭对称,可判断D 选项的正误. 【详解】()()320f x ax bx cx d a =+++≠,则()232f x ax bx c '=++.对于A 选项,由题意可知,关于x 的二次方程()23200ax bx c a ++=≠有两个不等的实根,则24120b ac ∆=->,可得230b ac ->,A 选项正确;对于B 选项,当0a <时,且当()12,x x x ∈时,()0f x '>,此时函数()f x 在区间()12,x x 上单调递增,B 选项错误;对于C 选项,当0a >时,由()0f x '>,可得1x x <或2x x >;由()0f x '<,可得12x x x <<.所以,函数()f x 的单调递增区间为()1,x -∞、()2,x +∞,单调递减区间为()12,x x , 由()10af x <,可得()10<f x ,此时,函数()f x 的极大值为()10<f x ,极小值为()2f x ,且()()210f x f x <<,如下图所示:由图可知,此时函数()f x 有且只有一个零点,且零点在区间()2,x +∞内; 当0a <时,由()0f x '<,可得1x x <或2x x >;由()0f x '>,可得12x x x <<. 所以,函数()f x 的单调递减区间为()1,x -∞、()2,x +∞,单调递增区间为()12,x x ,由()10af x <,可得()10f x >,此时,函数()f x 的极小值为()10f x >,极大值为()2f x ,且()()210f x f x >>,如下图所示:由图可知,此时函数()f x 有且只有一个零点,且零点在区间()2,x +∞内,C 选项正确; 对于D 选项,由题意可知,1x 、2x 是方程2320ax bx c ++=的两根, 由韦达定理可得1223bx x a +=-,123c x x a=, ()()()()()()()()3232f t x f t x a t x b t x c t x d a t x b t x c t x d ⎡⎤⎡⎤-++=-+-+-++++++++⎣⎦⎣⎦()()()()()(322322322322332332a t t x tx x b t tx x c t x d a t t x tx x b t tx x c ⎡⎤⎡=-+-+-++-+++++++++⎣⎦⎣()()322223222a t tx b t x ct d =+++++,取3bt a=-,则322223222333333b b b b b b f x f x a x b x c d a a a a a a ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫--+-+=-+⨯-+-++⋅-+⎢⎥⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦32222223333b b b b a b c d fa a a a ⎛⎫⎛⎫⎛⎫⎛⎫=-+⋅-+⋅-+=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,所以,函数()f x 的图象关于点,33b b f a a ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭对称, 1223bx x a+=-,()()1223b f x f x f a ⎛⎫∴+=- ⎪⎝⎭,D 选项正确. 故选:ACD. 【点睛】方法点睛:利用导数解决函数零点问题的方法:(1)直接法:先对函数求导,根据导数的方法求出函数的单调区间与极值,根据函数的基本性质作出图象,然后将问题转化为函数图象与x 轴的交点问题,突出导数的工具作用,体现了转化与化归思想、数形结合思想和分类讨论思想的应用; (2)构造新函数法:将问题转化为研究两函数图象的交点问题;(3)参变量分离法:由()0f x =分离变量得出()a g x =,将问题等价转化为直线y a =与函数()y g x =的图象的交点问题.3.已知函数()21ln 2f x ax ax x =-+的图象在点()()11,x f x 处与点()()22,x f x 处的切线均平行于x 轴,则( )A .()f x 在1,上单调递增B .122x x +=C .()()121212x x x x f x f x ++++的取值范围是7,2ln 24⎛⎫-∞-- ⎪⎝⎭D .若163a =,则()f x 只有一个零点 【答案】ACD 【分析】求导,根据题意进行等价转化,得到a 的取值范围;对于A ,利用导数即可得到()f x 在()1,+∞上的单调性;对于B ,利用根与系数的关系可得121x x =+;对于C ,化简()()121212x x x x f x f x ++++,构造函数,利用函数的单调性可得解;对于D ,将163a =代入()f x ',令()0f x '=,可得()f x 的单调性,进而求得()f x 的极大值小于0,再利用零点存在定理可得解. 【详解】 由题意可知,函数()f x 的定义域为()0,∞+,且()211ax ax ax a x x xf -+=-+=',则1x ,2x 是方程210ax ax -+=的两个不等正根,则2124010a a x x a ⎧∆=->⎪⎨=>⎪⎩,解得4a >, 当()1,x ∈+∞时,函数210y ax ax =-+>,此时()0f x '>,所以()f x 在()1,+∞上单调递增,故A 正确;因为1x ,2x 是方程210ax ax -+=的两个不等正根,所以121x x =+,故B 错误; 因为()()221212121112221111ln ln 22x x x x f x f x x ax ax x ax ax a ++++=+++-++- 1112111ln 1ln 22a a a a a a a a⎛⎫=+++--=--+ ⎪⎝⎭, 易知函数()11ln 2h a a a a=--+在()4,+∞上是减函数, 则当4a >时,()()742ln 24h a h <=--, 所以()()121212x x x x f x f x ++++的取值范围是7,2ln 24⎛⎫-∞--⎪⎝⎭,故C 正确; 当163a =时,()1616133f x x x '=-+,令()0f x '=,得14x =或34, 则()f x 在10,4⎛⎫ ⎪⎝⎭上单调递增,在13,44⎛⎫⎪⎝⎭上单调递减,在3,4⎛⎫+∞ ⎪⎝⎭上单调递增, 所以()f x 在14x =取得极大值,且104f ⎛⎫< ⎪⎝⎭,()2ln 20f =>, 所以()f x 只有一个零点,故D 正确. 故选:ACD. 【点睛】关键点点睛:导数几何意义的应用主要抓住切点的三个特点: ①切点坐标满足原曲线方程; ②切点坐标满足切线方程;③切点的横坐标代入导函数可得切线的斜率.4.(多选)已知函数()ln ()f x ax x a =-∈R ,则下列说法正确的是( ) A .若0a ≤,则函数()f x 没有极值 B .若0a >,则函数()f x 有极值C .若函数()f x 有且只有两个零点,则实数a 的取值范围是1,e ⎛⎫-∞ ⎪⎝⎭D .若函数()f x 有且只有一个零点,则实数a 的取值范围是1(,0]e ⎧⎫-∞⋃⎨⎬⎩⎭【答案】ABD 【分析】先对()f x 进行求导,再对a 进行分类讨论,根据极值的定义以及零点的定义即可判断. 【详解】解:由题意得,函数()f x 的定义域为(0,)+∞,且11()ax f x a x x'-=-=, 当0a ≤时,()0f x '<恒成立,此时()f x 单调递减,没有极值, 又当x 趋近于0时,()f x 趋近于+∞,当x 趋近于+∞时,()f x 趋近于-∞, ∴()f x 有且只有一个零点, 当0a >时,在10,a ⎛⎫⎪⎝⎭上,()0f x '<,()f x 单调递减, 在1,a ⎛⎫+∞⎪⎝⎭上,()0f x '>,()f x 单调递增, ∴当1x a=时,()f x 取得极小值,同时也是最小值, ∴min 1()1ln f x f a a ⎛⎫==+⎪⎝⎭, 当x 趋近于0时,ln x 趋近于-∞,()f x 趋近于+∞,当x 趋近于+∞时,()f x 趋近于+∞, 当1ln 0a +=,即1a e=时,()f x 有且只有一个零点; 当1ln 0a +<,即10a e<<时,()f x 有且仅有两个零点, 综上可知ABD 正确,C 错误. 故选:ABD . 【点睛】方法点睛:函数零点的求解与判断方法:(1)直接求零点:令()0f x =,如果能求出解,则有几个解就有几个零点; (2)零点存在性定理:利用定理不仅要函数在区间[]a b ,上是连续不断的曲线,且()()·0f a f b <,还必须结合函数的图象与性质(如单调性、奇偶性)才能确定函数有多少个零点;(3)利用图象交点的个数:将函数变形为两个函数的差,画两个函数的图象,看其交点的横坐标有几个不同的值,就有几个不同的零点.5.已知函数()1ln f x x x x=-+,给出下列四个结论,其中正确的是( ) A .曲线()y f x =在1x =-处的切线方程为10x y ++= B .()f x 恰有2个零点C .()f x 既有最大值,又有最小值D .若120x x >且()()120f x f x +=,则121=x x 【答案】BD 【分析】本题首先可根据()10f -=以及13f判断出A 错误,然后根据当0x >时的函数单调性、当0x <时的函数单调性、()10f -=以及()10f =判断出B 正确和C 错误,最后根据()()120f x f x +=得出()121f x f x ⎛⎫=⎪⎝⎭,根据函数单调性即可证得121=x x ,D 正确. 【详解】函数()1ln f x x x x=-+的定义域为()(),00,-∞⋃+∞, 当0x >时,()1ln f x x x x=-+,()2221111x x f x x x x -+-'=--=;当0x <时,1ln f x x x x,()2221111x x f x x x x -+-'=--=,A 项:1ln 1110f,22111131f,则曲线()y f x =在1x =-处的切线方程为031y x ,即33y x =--,A 错误;B 项:当0x >时,222215124x x x f xx x ,函数()f x 是减函数,当0x <时,222215124x x x f xx x ,函数()f x 是减函数,因为()10f -=,()10f =,所以函数()f x 恰有2个零点,B 正确; C 项:由函数()f x 的单调性易知,C 错误; D 项:当1>0x 、20x >时, 因为()()120f x f x +=, 所以1222222221111ln lnf x f x x x x fx x x x ,因为()f x 在()0,∞+上为减函数,所以121x x =,120x x >, 同理可证得当10x <、20x <时命题也成立,D 正确, 故选:BD. 【点睛】本题考查函数在某点处的切线求法以及函数单调性的应用,考查根据导函数求函数在某点处的切线以及函数单调性,导函数值即切线斜率,若导函数值大于0,则函数是增函数,若导函数值小于0,则函数是减函数,考查函数方程思想,考查运算能力,是难题.6.设函数()()1x af x a x a =->的定义域为()0,∞+,已知()f x 有且只有一个零点,下列结论正确的有( ) A .a e =B .()f x 在区间()1,e 单调递增C .1x =是()f x 的极大值点D .()f e 是()f x 的最小值【答案】ACD 【分析】()f x 只有一个零点,转化为方程0x a a x -=在(0,)+∞上只有一个根,即ln ln x ax a=只有一个正根.利用导数研究函数ln ()xh x x=的性质,可得a e =,判断A ,然后用导数研究函数()x e f x e x =-的性质,求出()'f x ,令()0f x '=,利用新函数确定()'f x 只有两个零点1和e ,并证明出()'f x 的正负,得()f x 的单调性,极值最值.判断BCD .【详解】()f x 只有一个零点,即方程0x a a x -=在(0,)+∞上只有一个根,x a a x =,取对数得ln ln x a a x =,即ln ln x ax a=只有一个正根. 设ln ()xh x x =,则21ln ()x h x x-'=,当0x e <<时,()0h x '>,()h x 递增,0x →时,()h x →-∞,x e >时,()0h x '<,()h x 递减,此时()0h x >,max 1()()h x h e e==. ∴要使方程ln ln x ax a =只有一个正根.则ln 1a a e =或ln 0a a<,解得a e =或0a <,又∵1a >,∴a e =.A 正确;()x e f x e x =-,1()x e f x e ex -'=-,1()0x e f x e ex -'=-=,11x e e x --=,取对数得1(1)ln x e x -=-,易知1x =和x e =是此方程的解.设()(1)ln 1p x e x x =--+,1()1e p x x-'=-,当01x e <<-时,()0p x '>,()p x 递增,1x e >-时,()0p x '<,()p x 递减,(1)p e -是极大值,又(1)()0p p e ==, 所以()p x 有且只有两个零点,01x <<或x e >时,()0p x <,即(1)ln 1e x x -<-,11e x x e --<,1e x ex e -<,()0f x '>,同理1x e <<时,()0f x '<,所以()f x 在(0,1)和(,)e +∞上递增,在(1,)e 上递减,所以极小值为()0f e =,极大值为(1)f ,又(0)1f =,所以()f e 是最小值.B 错,CD 正确. 故选:ACD . 【点睛】关键点点睛:本题考用导数研究函数的零点,极值,单调性.解题关键是确定()'f x 的零点时,利用零点定义解方程,1()0xe f x e ex-'=-=,11x e e x --=,取对数得1(1)ln x e x -=-,易知1x =和x e =是此方程的解.然后证明方程只有这两个解即可.7.已知函数()()2214sin 2x xe xf x e -=+,则下列说法正确的是( ) A .函数()y f x =是偶函数,且在(),-∞+∞上不单调 B .函数()y f x '=是奇函数,且在(),-∞+∞上不单调递增 C .函数()y f x =在π,02⎛⎫-⎪⎝⎭上单调递增 D .对任意m ∈R ,都有()()f m f m =,且()0f m ≥【答案】AD 【分析】由函数的奇偶性以及函数的单调性即可判断A 、B 、C 、D. 【详解】 解:对A ,()()222114sin =2cos 2x x xx e x e f x x e e-+=+-,定义域为R ,关于原点对称,()2211=2cos()2cos()()x x x xe ef x x x f x e e--++---=-=, ()y f x ∴=是偶函数,其图像关于y 轴对称,()f x ∴在(),-∞+∞上不单调,故A 正确;对B ,1()2sin xxf x e x e '=-+, 11()2sin()=(2sin )()x xx x f x e x e x f x e e--''-=-+---+=-, ()f x '∴是奇函数,令1()2sin xx g x e x e=-+, 则1()+2cos 2+2cos 0x x g x e x x e'=+≥≥, ()f x '∴在(),-∞+∞上单调递增,故B 错误;对C ,1()2sin x x f x e x e'=-+,且()'f x 在(),-∞+∞上单调递增, 又(0)0f '=,π,02x ⎛⎫∴∈- ⎪⎝⎭时,()0f x '<,()y f x ∴=在π,02⎛⎫- ⎪⎝⎭上单调递减,故C 错误;对D ,()y f x =是偶函数,且在(0,)+∞上单调递增,()()f m f m ∴=,且()(0)0f m f ≥=,故D 正确.故选:AD. 【点睛】用导数求函数的单调区间或判断函数的单调性问题时应注意如下几方面: (1)在利用导数讨论函数的单调区间时,首先要确定函数的定义域; (2)不能随意将函数的2个独立的单调递增(或递减)区间写成并集形式;(3)利用导数解决含参函数的单调性问题时,一般将其转化为不等式恒成立问题,解题过程中要注意分类讨论和数形结合思想的应用.8.对于函数2ln ()xf x x=,下列说法正确的是( )A .()f x 在x =12eB .()f x 有两个不同的零点C .fff <<D .若()21f x k x<-在()0,∞+上恒成立,则2e k >【答案】ACD 【分析】求得函数的导数312ln ()-'=xf x x ,根据导数的符号,求得函数的单调区间和极值,可判定A 正确;根据函数的单调性和()10f =,且x >()0f x >,可判定B 不正确;由函数的单调性,得到f f >,再结合作差比较,得到f f >,可判定C 正确;分离参数得到()221ln 1x k f x x x+>+=在()0,∞+上恒成立,令()2ln 1x g x x+=,利用导数求得函数()g x 的单调性与最值,可判定D 正确. 【详解】由题意,函数2ln ()x f x x =,可得312ln ()(0)xf x x x -'=>,令()0f x '=,即312ln 0xx-=,解得x =当0x <<()0f x '>,函数()f x 在上单调递增;当x >()0f x '<,函数()f x 在)+∞上单调递减,所以当x =()f x 取得极大值,极大值为12f e=,所以A 正确; 由当1x =时,()10f =,因为()f x 在上单调递增,所以函数()f x 在上只有一个零点,当x >()0f x >,所以函数在)+∞上没有零点,综上可得函数在(0,)+∞只有一个零点,所以B 不正确;由函数()f x 在)+∞上单调递减,可得f f >,由于ln ln 2ln ,242f f ππ====,则2ln ln 2ln ln 22444f f ππππππ-=-=-,因为22ππ>,所以0f f ->,即f f >,所以ff f <<,所以C 正确;由()21f x k x <-在()0,∞+上恒成立,即()221ln 1x k f x x x +>+=在()0,∞+上恒成立, 设()2ln 1x g x x +=,则()32ln 1x g x x --'=, 令()0g x '=,即32ln 10x x--=,解得x =所以当0x<<()0g x '>,函数()g x 在上单调递增; 当x>()0g x '<,函数()g x 在)+∞上单调递减, 所以当x=()g x 取得最大值,最大值为22e eg e =-=, 所以2ek >,所以D 正确. 故选:ACD. 【点睛】本题主要考查导数在函数中的综合应用,以及恒成立问题的求解,着重考查了转化与化归思想、逻辑推理能力与计算能力,对于恒成立问题,通常要构造新函数,利用导数研究函数的单调性,求出最值,从而求出参数的取值范围;也可分离变量,构造新函数,直接把问题转化为函数的最值问题.9.若方程()2110x m x -+-=和()120x m ex -+-=的根分别为()1212,x x x x <和3x ,()434x x x <,则下列判断正确的是( )A .3201x x <<<B .1310x x -<<C .(),1m ∈-∞-D .1112x ⎛⎫-∈- ⎪⎪⎝⎭【答案】ABD 【分析】根据题意将问题转化为,1x ,2x 和3x ,4x 分别是y m =与11y x x =--和12x xy e-=-交点的横坐标,再用导数研究函数11y x x =--和12x xy e-=-的单调性与取值情况,作出函数图象,数形结合即可解决问题. 【详解】解:由题,1x ,2x 和3x ,4x 分别是11m x x =--和12x xm e-=-的两个根, 即y m =与11y x x =--和12x xy e-=-交点的横坐标. 对于函数11y x x =--,定义域为{}0x x ≠,21'10y x=+>,所以函数在(),0-∞和()0,∞+上单调递增,且1x =时,1y =-;对于函数12x xy e-=-,11'x xy e--=,所以函数在(),1-∞上单调递增,在()1,+∞单调递减,且当,2x y →+∞→-,0x =时,2y =-,1x =时,1y =-; 故作出函数11y x x =--,12x xy e-=-的图像如图所示, 注意到:当()0,1x ∈时,11122x xx x x e---<-<-, 由图可知,3201x x <<<,()2,1m ∈--, 从而()11112,1x x --∈--,解得115,12x ⎛⎫--∈- ⎪ ⎪⎝⎭, 所以选项AD 正确,选项C 错误, 又121310x x x x -=<<. 故选:ABD .【点睛】本题考查利用导数研究函数的零点问题,考查化归转化思想与数形结合思想,是中档题.10.函数()ln f x x x =、()()f x g x x'=,下列命题中正确的是( ).A .不等式()0g x >的解集为1,e ⎛⎫+∞ ⎪⎝⎭B .函数()f x 在()0,e 上单调递增,在(,)e +∞上单调递减C .若函数()()2F x f x ax =-有两个极值点,则()0,1a ∈D .若120x x >>时,总有()()()2212122m x x f x f x ->-恒成立,则m 1≥ 【答案】AD 【分析】对A ,根据()ln f x x x =,得到()()ln 1f x xg x x x'+==,然后用导数画出其图象判断;对B ,()1ln f x x '=+,当x e >时,()0f x '>,当0x e <<时,()0f x '<判断;对C ,将函数()()2F x f x ax =-有两个极值点,()ln 120x a x+=+∞在,有两根判断;对D ,将问题转化为22111222ln ln 22m m x x x x x x ->-恒成立,再构造函数()2ln 2m g x x x x =-,用导数研究单调性. 【详解】对A ,因为()()()ln 1ln f x x f x x x g x x x'+===、, ()2ln xg x x-'=, 令()0g x '>,得()0,1x ∈,故()g x 在该区间上单调递增;令()0g x '<,得()1x ∈+∞,,故()g x 在该区间上单调递减. 又当1x >时,()0g x >,()10,11g g e ⎛⎫== ⎪⎝⎭, 故()g x 的图象如下所示:数形结合可知,()0g x >的解集为1,e ⎛⎫+∞ ⎪⎝⎭,故正确;对B ,()1ln f x x '=+,当x e >时,()0f x '>,当0x e <<时,()0f x '<,所以函数()f x 在()0,e 上单调递减,在(,)e +∞上单调递增,错误;对C ,若函数()()2F x f x ax =-有两个极值点,即()2ln F x x x ax =-有两个极值点,又()ln 21F x x ax '=-+,要满足题意,则需()ln 2100x ax -+=+∞在,有两根, 也即()ln 120x a x+=+∞在,有两根,也即直线()2y a y g x ==与的图象有两个交点. 数形结合则021a <<,解得102a <<. 故要满足题意,则102a <<,故错误; 对D ,若120x x >>时,总有()()()2212122m x x f x f x ->-恒成立, 即22111222ln ln 22m m x x x x x x ->-恒成立, 构造函数()2ln 2m g x x x x =-,()()12g x g x >,对任意的120x x >>恒成立, 故()g x ()0+∞,单调递增,则()ln 10g x mx x '=--≥()0+∞, 恒成立, 也即ln 1x m x+≤,在区间()0,∞+恒成立,则()max 1g x m =≤,故正确. 故选:AD. 【点睛】本题主要考查导数在函数图象和性质中的综合应用,还考查了数形结合的思想、转化化归思想和运算求解的能力,属于较难题.。
导数及其应用多选题单元达标测试综合卷学能测试试题

导数及其应用多选题单元达标测试综合卷学能测试试题一、导数及其应用多选题1.已知0a >,0b >,下列说法错误的是( )A .若1a b a b ⋅=,则2a b +≥B .若23a b e a e b +=+,则a b >C .()ln ln a a b a b -≥-恒成立D .2ln a a b be e-<恒成立 【答案】AD 【分析】对A 式化简,通过构造函数的方法,结合函数图象,说明A 错误;对B 不等式放缩22a b e a e b +>+,通过构造函数的方法,由函数的单调性,即可证明B 正确;对C 不等式等价变型()ln ln ln1-≥-⇔≥-a b a a b a b b a ,通过10,ln 1∀>>-x x x恒成立,可得C 正确;D 求出ln -a a b b e 的最大值,当且仅当11a b e =⎧⎪⎨=⎪⎩时取等号,故D 错误.【详解】A. 1ln ln 0⋅=⇔+=a b a b a a b b 设()ln f x x x =,()()0∴+=f a f b由图可知,当1+→b 时,存在0+→a ,使()()0f a f b += 此时1+→a b ,故A 错误. B. 232+=+>+a b b e a e b e b设()2xf x e x =+单调递增,a b ∴>,B 正确C. ()ln ln ln 1-≥-⇔≥-a ba ab a b b a又10,ln 1∀>>-x x x ,ln 1∴≥-a bb a,C 正确D. max 1=⇒=x x y y e e当且仅当1x =;min 1ln =⇒=-y x x y e 当且仅当1=x e;所以2ln -≤a a b b e e ,当且仅当11a b e =⎧⎪⎨=⎪⎩时取等号,D 错误.故选:AD 【点睛】本题考查了导数的综合应用,考查了运算求解能力和逻辑推理能力,转化的数学思想和数形结合的数学思想,属于难题.2.已知(0,1)x ∈,则下列正确的是( ) A .cos 2x x π+<B .22xx <C.sin 2x >D .1ln 1x x <- 【答案】ABC 【分析】构造函数()sin f x x x =-证明其在0,2π⎛⎫⎪⎝⎭单调递减,即可得sin 22x x ππ⎛⎫-<-⎪⎝⎭即可判断选项A ;作出2yx 和2x y =的函数图象可判断选项B ;作出()sin2xf x =,()h x =的图象可判断选项C ;构造函数()1ln 1x g x x =+-利用导数判断其在()0,1x ∈上的单调性即可判断选项D ,进而可得正确选项.【详解】对于选项A :因为()0,1x ∈,所以022x ππ<-<,令()sin f x x x =-,()cos 10f x x '=-≤,()sin f x x x =-在0,2π⎛⎫⎪⎝⎭单调递减,所以()()00f x f <=,即sin x x <,所以sin 22x x ππ⎛⎫-<- ⎪⎝⎭即cos 2x x π<-,可得cos 2x x π+<,故A 正确, 对于选项B :由图象可得()0,1x ∈,22x x <恒成立,故选项B 正确;对于选项C :要证22sin 24xx x >+ 令()sin 2x f x =,()224xh x x =+()()f x f x -=-,()sin2xf x =是奇函数, ()()h x h x -=,()224x h x x =+是偶函数, 令2224144x t x x ==-++ ,则y t = 因为24y x =+在()0,∞+单调递增,所以2414t x =-+在()0,∞+单调递增,而y t =调递增,由符合函数的单调性可知()224x h x x =+在()0,∞+单调递增, 其函数图象如图所示:由图知当()0,1x ∈时22sin 24xx x >+C 正确; 对于选项D :令()1ln 1x g x x =+-,()01x <<,()221110x g x x x x-'=-=<, 所以()1ln 1x g x x=+-在()0,1单调递减,所以()()1ln1110g x g >=+-=, 即1ln 10x x+->,可得1ln 1x x >-,故选项D 不正确.故选:ABC 【点睛】思路点睛:证明不等式恒成立(或能成立)一般可对不等式变形,分离参数,根据分离参数后的结果,构造函数,由导数的方法求出函数的最值,进而可求出结果;有时也可根据不等式,直接构成函数,根据导数的方法,利用分类讨论求函数的最值,即可得出结果.3.已知:()f x 是奇函数,当0x >时,()'()1f x f x ->,(1)3f =,则( )A .(4)(3)f ef >B .2(4)(2)f e f ->-C .3(4)41f e >-D .2(4)41f e -<--【答案】ACD 【分析】由已知构造得'()+10x x e f ⎡⎤>⎢⎥⎣⎦,令()()+1x f x g x e =,判断出函数()g x 在0x >时单调递增,由此得()()4>3g g ,化简可判断A ;()()4>2g g ,化简并利用()f x 是奇函数,可判断B ;()()4>1g g ,化简可判断C ;由C 选项的分析得32(4)41>4+1f e e >-,可判断D.【详解】因为当0x >时,()'()1fx f x ->,所以()'()10f x f x -->,即()[]'()+10xf x f e x ->,所以'()+10x x e f ⎡⎤>⎢⎥⎣⎦, 令()()+1xf xg x e=,则当0x >时,()'>0g x ,函数()g x 单调递增, 所以()()4>3g g ,即43(4)+1(3)+1>f f e e ,化简得(4)(3)1>(3)f f e e ef >+-,故A 正确;()()4>2g g ,即42(4)+1(2)+1>f f e e ,化简得222(4)(2)1>(2)f f e e e f >+-, 所以2(4)(2)e f f -<-,又()f x 是奇函数,所以2(4)(2)e f f -<-,故B 不正确;()()4>1g g ,即4(4)+1(1)+1>f f e e,又(1)3f =,化简得3(4)41f e >-,故C 正确; 由C 选项的分析得32(4)41>4+1f e e >-,所以2(4)41f e -<--,又()f x 是奇函数,所以2(4)41f e -<--,故D 正确, 故选:ACD. 【点睛】关键点点睛:解决本题中令有导函数的不等式,关键在于构造出某个函数的导函数,得出所构造的函数的单调性,从而可比较函数值的大小关系.4.已知函数()1ln f x x x x=-+,()()1ln x x x x g --=,则下列结论正确的是( ) A .()g x 存在唯一极值点0x ,且()01,2x ∈ B .()f x 恰有3个零点C .当1k <时,函数()g x 与()h x kx =的图象有两个交点D .若120x x >且()()120f x f x +=,则121=x x 【答案】ACD 【分析】根据导数求得函数()g x '在(0,)+∞上为单调递减函数,结合零点的存在性定,可判定A 正确;利用导数求得函数 ()f x 在(,0)-∞,(0,)+∞单调递减,进而得到函数 ()f x 只有2个零点,可判定B 不正确;由()g x kx =,转化为函数()()1ln x x x ϕ-=和 ()(1)m x k x =-的图象的交点个数,可判定C 正确;由()()120f x f x +=,化简得到 ()121()f x f x =,结合单调性,可判定D 正确. 【详解】由函数()()1ln x x x x g --=,可得 ()1ln ,0g x x x x '=-+>,则()2110g x x x''=--<,所以()g x '在(0,)+∞上为单调递减函数,又由 ()()110,12ln 202g g '=>=-+<, 所以函数()g x 在区间(1,2)内只有一个极值点,所以A 正确; 由函数()1ln f x x x x=-+, 当0x >时,()1ln f x x x x=-+,可得 ()221x x f x x -+-'=, 因为22131()024x x x -+-=---<,所以 ()0f x '<,函数()f x 在(0,)+∞单调递减;又由()10f =,所以函数在(0,)+∞上只有一个零点, 当0x <时,()1ln()f x x x x =--+,可得 ()221x x f x x -+-'=,因为22131()024x x x -+-=---<,所以 ()0f x '<,函数()f x 在(,0)-∞单调递减; 又由()10f -=,所以函数在(,0)-∞上只有一个零点, 综上可得函数()1ln f x x x x=-+在定义域内只有2个零点,所以B 不正确; 令()g x kx =,即()1ln x x x kx --=,即 ()1ln (1)x x k x -=-, 设()()1ln x x x ϕ-=, ()(1)m x k x =-, 可得()1ln 1x x x ϕ'=+-,则 ()2110x x xϕ''=+>,所以函数()x ϕ'(0,)+∞单调递增, 又由()01ϕ'=,可得当(0,1)x ∈时, ()0x ϕ'<,函数()x ϕ单调递减, 当(1,)x ∈+∞时,()0x ϕ'>,函数 ()x ϕ单调递增, 当1x =时,函数()x ϕ取得最小值,最小值为()10ϕ=, 又由()(1)m x k x =-,因为1k <,则 10k ->,且过原点的直线,结合图象,即可得到函数()()1ln x x x ϕ-=和 ()(1)m x k x =-的图象有两个交点,所以C 正确;由120x x >,若120,0x x >>时,因为 ()()120f x f x +=,可得()()12222222211111ln ln 1f x f x x x f x x x x x ⎛⎫⎛⎫=-=--+=+-= ⎪ ⎪⎝⎭⎝⎭,即()121()f x f x =,因为()f x 在(0,)+∞单调递减,所以 121x x =,即121=x x , 同理可知,若120,0x x <<时,可得121=x x ,所以D 正确.故选:ACD.【点睛】函数由零点求参数的取值范围的常用方法与策略:1、分类参数法:一般命题情境为给出区间,求满足函数零点个数的参数范围,通常解法为从()f x 中分离参数,然后利用求导的方法求出由参数构造的新函数的最值,根据题设条件构建关于参数的不等式,再通过解不等式确定参数的取值范围;2、分类讨论法:一般命题情境为没有固定的区间,求满足函数零点个数的参数范围,通常解法为结合函数的单调性,先确定参数分类标准,在每个小范围内研究零点的个数是否符合题意,将满足题意的参数的各个小范围并在一起,即可为所求参数的范围.5.已知2()ln f x x x =,2()()f x g x x'=,()'f x 是()f x 的导函数,则下列结论正确的是( )A .()f x 在12e ,-⎛⎫+∞ ⎪⎝⎭上单调递增.B .()g x 在(0,)+∞上两个零点C .当120x x e <<< 时,221212()()()m x x f x f x -<-恒成立,则32m ≥D .若函数()()h x f x ax =-只有一个极值点,则实数0a ≥ 【答案】ACD 【分析】求出导函数()'f x ,由()0f x '>确定增区间,判断A ,然后可得()g x ,再利用导数确定()g x 的单调性与极值,结合零点存在定理得零点个数,判断B ,构造函数2()()x f x mx ϕ=-,由()ϕx 在(0,)e 上递减,求得m 范围,判断C ,利用导数研究()h x 的单调性与极值点,得a 的范围,判断D . 【详解】()(2ln 1)(0)f x x x x '=+>,令()0f x '>,得1212ln 10ln 2x x x e -+>⇒>-⇒>,故A 正确2ln 1()x g x x+=, 212ln ()x g x x -'=,令()0g x '>得121ln 2x x e <⇒<,()0g x '<得120x e <<, 故()g x 在120,e ⎛⎫ ⎪⎝⎭上为减函数,在12e ⎛⎫+∞ ⎪⎝⎭上为增函数.当x →时,()g x →-∞;当x →+∞时,()0g x →且g()0x >()g x ∴的大致图象为()g x ∴只有一个零点,故B 错.记2()()x f x mx ϕ=-,则()ϕx 在(0,)e 上为减函数,()(2ln 1)20x x x mx ϕ'∴=+-≤对(0,)x e ∈恒成立22ln 1m x ∴≥+对(0,)x e ∈恒成立 23m ∴≥32m ∴≥. 故C 正确.2()()ln h x f x ax x x ax =-=-,()(2ln 1)h x x x a =+'-,设()(2ln 1)H x x x =+,()h x 只有一个极值点, ()h x '0=只有一个解,即直线y a =与()y H x =的图象只有一个交点.()2(ln 1)12ln 3H x x x '=++=+,()H x '在(0,)+∞上为增函数,令()0H x '=,得320x e -=,当0(0,)x x ∈时,()0H x '<;当0(,)x x ∈+∞时,()0H x '>.()H x ∴在0(0,)x 上为减函数,在0(,)x +∞上为增函数,332203()21202H x e e --⎡⎤⎛⎫=⨯-+=-< ⎪⎢⎥⎝⎭⎣⎦,0(0,)x x ∈时,322ln 12ln 120x e -+<+=-<,即()0H x <,且0x →时,()0H x →,又x →+∞时,()H x →+∞,因此()H x 的大致图象如下(不含原点):直线y a =与它只有一个交点,则0a ≥.故D 正确. 故选:ACD . 【点睛】关键点点睛:本题考查用导数研究函数的性质,解题关键是由导数确定函数的单调性,得出函数的极值,对于零点问题,需要结合零点存在定理才能确定零点个数.注意数形结合思想的应用.6.若存在常数k 和b ,使得函数()F x 和()G x 对其公共定义域上的任意实数x 都满足:()F x kx b ≥+和()G x kx b ≤+恒成立,则称此直线y kx b =+为()F x 和()G x 的“隔离直线”.已知函数()22x f x =(x ∈R ),()12g x x =(0x <),()ln h x e x =,(e 为自然对数的底数),则( )A .()()()m x f x g x =-在0x ⎛⎫∈ ⎪⎝⎭内单调递减 B .()f x 和()g x 之间存在“隔离直线”,且b 的最小值为2- C .()f x 和()g x 之间存在“隔离直线”,且k 的取值范围是[]2,1-D .()f x 和()g x 之间存在唯一的“隔离直线”,方程为2ey =-【答案】BD 【分析】对于A :令()()()m x f x g x =-,利用导数可确定()m x 单调性,进而作出判断; 对于B 和C :利用二次函数的性质以及不等式恒成立的知识求出b 、k 的范围,进而作出判断;对于选项D :根据隔离直线过()f x 和()h x 的公共点,可假设隔离直线为2e y kx =-;可得到222x ekx ≥-,再利用恒成立得出k 的值,最后尝试利用导数证明()2eh x ≤-,进而作出判断. 【详解】对于A ,()()()2122x m x f x g x x =-=-, ()322121022x m x x x x+'∴=+=>, 当x ⎛⎫∈ ⎪⎝⎭时,()0m x '>,()m x ∴单调递增,故A 错误; 对于B ,C ,设()f x ,()g x 的隔离直线为y kx b =+,22x kx b ≥+对任意x ∈R 恒成立,即2220x kx b --≥对任意x ∈R 恒成立, 所以21480k b ∆=+≤,所以0b ≤,又12kx b x ≤+对任意(),0x ∈-∞恒成立,即22210kx bx +-≤对任意(),0x ∈-∞恒成立,因为0b ≤,所以0k ≤且21480b k ∆=+≤,所以22k b ≤-且22b k ≤-,4248k b b ≤≤-,解得20k -≤≤,同理20b -≤≤, 所以b 的最小值为2-,k 的取值范围是[]2,0-, 故B 正确,C 错误;对于D ,函数()f x 和()h x 的图象在x =∴若存在()f x 和()h x 的隔离直线,那么该直线过这个公共点,设隔离直线的斜率为k,则隔离直线方程为(2ey k x -=,即2e y kx =-,则222x ekx ≥-(x ∈R),得2220x kx e -+≥对x ∈R 恒成立,则()24420k e ∆=-≤,解得k =,此时隔离直线方程为:2ey =-,下面证明()2e h x ≤-, 令()()ln 22e e G x h x e x =--=--(0x >),则()x G x x'=,当x =()0G x '=;当0x <<()0G x '<;当x >()0G x '>;∴当x =()G x 取到极小值,也是最小值,即()0min G x G==,()()02e G x h x ∴=--≥在()0,∞+上恒成立,即()2eh x ≤-,∴函数()f x 和()h x存在唯一的隔离直线2ey =-,D 正确. 故选:BD . 【点睛】关键点睛:本题考查导数中的新定义问题的求解;解题关键是能够充分理解“隔离直线”的定义,将问题转化为根据不等式恒成立求解参数范围或参数值、或不等式的证明问题,属于难题.7.(多选)已知函数()ln ()f x ax x a =-∈R ,则下列说法正确的是( ) A .若0a ≤,则函数()f x 没有极值 B .若0a >,则函数()f x 有极值C .若函数()f x 有且只有两个零点,则实数a 的取值范围是1,e ⎛⎫-∞ ⎪⎝⎭D .若函数()f x 有且只有一个零点,则实数a 的取值范围是1(,0]e ⎧⎫-∞⋃⎨⎬⎩⎭【答案】ABD 【分析】先对()f x 进行求导,再对a 进行分类讨论,根据极值的定义以及零点的定义即可判断. 【详解】解:由题意得,函数()f x 的定义域为(0,)+∞,且11()ax f x a x x'-=-=, 当0a ≤时,()0f x '<恒成立,此时()f x 单调递减,没有极值, 又当x 趋近于0时,()f x 趋近于+∞,当x 趋近于+∞时,()f x 趋近于-∞, ∴()f x 有且只有一个零点, 当0a >时,在10,a ⎛⎫⎪⎝⎭上,()0f x '<,()f x 单调递减, 在1,a ⎛⎫+∞⎪⎝⎭上,()0f x '>,()f x 单调递增, ∴当1x a=时,()f x 取得极小值,同时也是最小值, ∴min 1()1ln f x f a a ⎛⎫==+⎪⎝⎭, 当x 趋近于0时,ln x 趋近于-∞,()f x 趋近于+∞,当x 趋近于+∞时,()f x 趋近于+∞, 当1ln 0a +=,即1a e=时,()f x 有且只有一个零点; 当1ln 0a +<,即10a e<<时,()f x 有且仅有两个零点, 综上可知ABD 正确,C 错误. 故选:ABD . 【点睛】方法点睛:函数零点的求解与判断方法:(1)直接求零点:令()0f x =,如果能求出解,则有几个解就有几个零点; (2)零点存在性定理:利用定理不仅要函数在区间[]a b ,上是连续不断的曲线,且()()·0f a f b <,还必须结合函数的图象与性质(如单调性、奇偶性)才能确定函数有多少个零点;(3)利用图象交点的个数:将函数变形为两个函数的差,画两个函数的图象,看其交点的横坐标有几个不同的值,就有几个不同的零点.8.某同学对函数()sin e ex xxf x -=-进行研究后,得出以下结论,其中正确的是( ) A .函数()y f x =的图象关于原点对称B .对定义域中的任意实数x 的值,恒有()1f x <成立C .函数()y f x =的图象与x 轴有无穷多个交点,且每相邻两交点的距离相等D .对任意常数0m >,存在常数b a m >>,使函数()y f x =在[]a b ,上单调递减【分析】由函数奇偶性的定义即可判断选项A ;由函数的性质可知()sin 1xxx f x e e-=<-可得到sin x x x e e -<-,即sin 0x x e e x --->,构造函数()sin 0x x h x e e x x -=-->,求导判断单调性,进而求得最值即可判断选项B ;函数()y f x =的图象与x 轴的交点坐标为()0,πk (k Z ∈,且)0k ≠,可判断选项C ;求导分析()0f x '≤时成立的情况,即可判断选项D. 【详解】对于选项A :函数()sin e ex xxf x -=-的定义域为{}|0x x ≠,且 ()()sin sin x x x xx xf x f x e e e e----===--,所以()f x 为偶函数,即函数()y f x =的图象关于y 轴对称,故A 选项错误; 对于选项B :由A 选项可知()f x 为偶函数,所以当0x >时,0x x e e -->,所以()sin 1xxx f x e e-=<-,可得到sin x x x e e -<-,即sin 0x xe e x --->,可设()sin 0x x h x e e x x -=-->,,()cos x x h x e e x -'=+±,因为2x x e e -+>,所以()cos 0x x h x e e x -±'=+>,所以()h x 在()0+∞,上单调递增,所以()()00h x h >=,即()sin 1xxx f x e e-=<-恒成立,故选项B 正确;对于选项C :函数()y f x =的图象与x 轴的交点坐标为()()00k k Z k π∈≠,,且,交点()0π-,与()0π,间的距离为2π,其余任意相邻两点的距离为π,故C 选项错误; 对于选项D :()()()()2cos sin 0xx x x xxe e x e e xf x ee -----+-'=≤,可化为e x (cos x -sin x )()cos sin 0xex x --+≤,不等式两边同除以x e -得,()2cos sin cos sin x e x x x x -≤+,当()32244x k k k Z ππππ⎛⎫∈++∈⎪⎝⎭,,cos sin 0x x -<,cos sin 0x x +>,区间长度为12π>,所以对于任意常数m >0,存在常数b >a >m ,32244a b k k ππππ⎛⎫∈++⎪⎝⎭,,,()k Z ∈,使函数()y f x =在[]a b ,上单调递减,故D 选项正确;故选:BD思路点睛:利用导数研究函数()f x 的最值的步骤: ①写定义域,对函数()f x 求导()'f x ;②在定义域内,解不等式()0f x '>和()0f x '<得到单调性; ③利用单调性判断极值点,比较极值和端点值得到最值即可.9.已知函数()()2214sin 2xxex f x e -=+,则下列说法正确的是( ) A .函数()y f x =是偶函数,且在(),-∞+∞上不单调 B .函数()y f x '=是奇函数,且在(),-∞+∞上不单调递增 C .函数()y f x =在π,02⎛⎫- ⎪⎝⎭上单调递增D .对任意m ∈R ,都有()()f m f m =,且()0f m ≥【答案】AD 【分析】由函数的奇偶性以及函数的单调性即可判断A 、B 、C 、D. 【详解】 解:对A ,()()222114sin =2cos 2xx xx e x e f x x e e-+=+-,定义域为R ,关于原点对称,()2211=2cos()2cos()()x x x xe ef x x x f x e e --++---=-=,()y f x ∴=是偶函数,其图像关于y 轴对称,()f x ∴在(),-∞+∞上不单调,故A 正确;对B ,1()2sin xxf x e x e '=-+, 11()2sin()=(2sin )()x xx xf x e x e x f x e e --''-=-+---+=-, ()f x '∴是奇函数,令1()2sin xxg x e x e =-+, 则1()+2cos 2+2cos 0x xg x e x x e '=+≥≥, ()f x '∴在(),-∞+∞上单调递增,故B 错误;对C ,1()2sin x x f x e x e'=-+,且()'f x 在(),-∞+∞上单调递增,又(0)0f '=,π,02x ⎛⎫∴∈- ⎪⎝⎭时,()0f x '<,()y f x ∴=在π,02⎛⎫- ⎪⎝⎭上单调递减,故C 错误;对D ,()y f x =是偶函数,且在(0,)+∞上单调递增,()()f m f m ∴=,且()(0)0f m f ≥=,故D 正确.故选:AD. 【点睛】用导数求函数的单调区间或判断函数的单调性问题时应注意如下几方面: (1)在利用导数讨论函数的单调区间时,首先要确定函数的定义域; (2)不能随意将函数的2个独立的单调递增(或递减)区间写成并集形式;(3)利用导数解决含参函数的单调性问题时,一般将其转化为不等式恒成立问题,解题过程中要注意分类讨论和数形结合思想的应用.10.对于定义在1D 上的函数()f x 和定义在2D 上的函数()g x ,若直线y kx b =+(),k b R ∈同时满足:①1x D ∀∈,()f x kx b ≤+,②2x D ∀∈,()g x kx b ≥+,则称直线y kx b =+为()f x 与()g x 的“隔离直线”.若()ln xf x x=,()1x g x e -=,则下列为()f x 与()g x 的隔离直线的是( )A .y x =B .12y x =-C .3ex y =D .1122y x =- 【答案】AB 【分析】根据隔离直线的定义,函数()y f x =的图象总在隔离直线的下方,()y g x =的图象总在隔离直线的上方,并且可以有公共点,结合函数的图象和函数的单调性,以及直线的特征,逐项判定,即可求解. 【详解】根据隔离直线的定义,函数()y f x =的图象总在隔离直线的下方,()y g x =的图象总在隔离直线的上方,并且可以有公共点, 由函数()ln x f x x =,可得()21ln xf x x-'=, 所以函数()f x 在()0,e 上单调递增,在(),e +∞上单调递减,因为()10f =,()11f '=,此时函数()f x 的点(1,0)处的切线方程为1y x =-, 且函数()f x 的图象在直线1y x =-的下方;又由函数()1x g x e-=,可得()1e0x g x -'=>,()g x 单调递增,因为()()111g g '==,所以函数()g x 在点(1,1)处的切线方程为11y x -=-,即y x =, 此时函数()g x 的图象在直线y x =的上方,根据上述特征可以画出()y f x =和()y g x =的大致图象,如图所示,直线1y x =-和y x =分别是两条曲线的切线,这两条切线以及它们之间与直线y x =平行的直线都满足隔离直线的条件,所以A ,B 都符合; 设过原点的直线与函数()y f x =相切于点00(,)P x y , 根据导数的几何意义,可得切线的斜率为021ln x k x -=,又由斜002000ln 0y x k x x -==-,可得002100ln 1ln x x x x -=,解得0x e =, 所以21ln 12()e k e e -==,可得切线方程为2x y e =, 又由直线3xy e=与曲()y f x =相交,故C 不符合; 由直线1122y x =-过点()1,0,斜率为12,曲线()y f x =在点()1,0处的切线斜率为1,明显不满足,排除D. 故选:AB.【点睛】对于函数的新定义试题:(1)认真审题,正确理解函数的新定义,合理转化;(2)根据隔离直线的定义,转化为函数()y f x =的图象总在隔离直线的下方,()y g x =的图象总在隔离直线的上方.。
导数及其应用多选题单元达标综合模拟测评检测试题

导数及其应用多选题单元达标综合模拟测评检测试题一、导数及其应用多选题1.对于定义城为R 的函数()f x ,若满足:①(0)0f =;②当x ∈R ,且0x ≠时,都有()0xf x '>;③当120x x <<且12||||x x <时,都有12()()f x f x <,则称()f x 为“偏对称函数”.下列函数是“偏对称函数”的是( ) A .()321f x x x =-+B .()21xf x e x =--C .()3ln 1,0()2,0x x f x x x ⎧-+≤=⎨>⎩D .4()sin f x x x =【答案】BC 【分析】运用新定义,分别讨论四个函数是否满足三个条件,结合奇偶性和单调性,以及对称性,即可得到所求结论. 【详解】解:经验证,1()f x ,2()f x ,3()f x ,4()f x 都满足条件①;0()0()0x xf x f x >⎧'>⇔⎨'>⎩,或0()0x f x <⎧⎨'<⎩;当120x x <<且12||||x x <时,等价于21120x x x x -<<<-<,即条件②等价于函数()f x 在区间(,0)-∞上单调递减,在区间(0,)+∞上单调递增; A 中,()321f x x x =-+,()2132f x x x '=-+,则当0x ≠时,由()()321232230x x x x f x x =-+=-≤',得23x ≥,不符合条件②,故1()f x 不是“偏对称函数”;B 中,()21xf x e x =--,()21xf x e '=-,当0x >时,e 1x >,()20f x '>,当0x <时,01x e <<,()20f x '<,则当0x ≠时,都有()20xf x '>,符合条件②, ∴函数()21xf x e x =--在(),0-∞上单调递减,在()0,∞+上单调递增,由2()f x 的单调性知,当21120x x x x -<<<-<时,()2122()f x f x <-, ∴22212222222()()()()2x x f x f x f x f x e e x --<--=-++,令()2x x F x e e x -=-++,0x >,()220x x F x e e -'=--+≤-=, 当且仅当x x e e -=即0x =时,“=”成立,∴()F x 在[0,)+∞上是减函数,∴2()(0)0F x F <=,即2122()()f x f x <,符合条件③, 故2()f x 是“偏对称函数”; C 中,由函数()3ln 1,0()2,x x f x x x ⎧-+≤=⎨>⎩,当0x <时,31()01f x x =<-',当0x >时,3()20f x '=>,符合条件②,∴函数3()f x 在(),0-∞上单调递减,在()0,∞+上单调递增, 有单调性知,当21120x x x x -<<<-<时,()3132()f x f x <-, 设()ln(1)2F x x x =+-,0x >,则1()201F x x '=-<+, ()F x 在(0,)+∞上是减函数,可得()(0)0F x F <=,∴1222()()()()f x f x f x f x -<--()()222ln 1()0F x x f x =+-=<, 即12()()f x f x <,符合条件③,故3()f x 是“偏对称函数”;D 中,4()sin f x x x =,则()44()sin ()f x x x f x -=--=,则4()f x 是偶函数,而4()sin cos f x x x x '=+ ()x ϕ=+(tan x ϕ=),则根据三角函数的性质可知,当0x >时,4()f x '的符号有正有负,不符合条件②,故4()f x 不是“偏对称函数”; 故选:BC . 【点睛】本题主要考查在新定义下利用导数研究函数的单调性与最值,考查计算能力,考查转化与划归思想,属于难题.2.已知函数1(),()122x x f x e g x n ==+的图象与直线y =m 分别交于A 、B 两点,则( )A .f (x )图像上任一点与曲线g (x )上任一点连线线段的最小值为2+ln 2B .∃m 使得曲线g (x )在B 处的切线平行于曲线f (x )在A 处的切线C .函数f (x )-g (x )+m 不存在零点D .∃m 使得曲线g (x )在点B 处的切线也是曲线f (x )的切线 【答案】BCD 【分析】利用特值法,在f (x )与g (x )取两点求距离,即可判断出A 选项的正误;解方程12()(2)m f lnm g e-''=,可判断出B 选项的正误;利用导数判断函数()()y f x g x m =-+的单调性,结合极值的符号可判断出C 选项的正误;设切线与曲线()y g x =相切于点(C n ,())g n ,求出两切线的方程,得出方程组,判断方程组是否有公共解,即可判断出D 选项的正误.进而得出结论. 【详解】在函数1(),()122xx f x e g x n ==+上分别取点1(0,1),(2,)2P Q ,则||PQ =2ln 2<+(注ln 20.7≈),故A 选项不正确; ()x f x e =,1()22x g x ln =+,则()x f x e '=,1()g x x'=,曲线()y f x =在点A 处的切线斜率为()f lnm m '=, 曲线()y g x =在点B 处的切线斜率为12121(2)2m m g ee--'=,令12()(2)m f lnm g e-''=,即1212m m e-=,即1221m me -=,则12m =满足方程1221m me -=,m ∴∃使得曲线()y f x =在A 处的切线平行于曲线()y g x =在B 处的切线,B 选项正确;构造函数1()()()22xx F x f x g x m e ln m =-+=-+-,可得1()x F x e x'=-,函数1()xF x e x'=-在(0,)+∞上为增函数,由于1()20F e '<,F '(1)10e =->,则存在1(,1)2t ∈,使得1()0tF t e t'=-=,可得t lnt =-,当0x t <<时,()0F x '<;当x t >时,()0F x '>.∴11()()2222t t min t F x F t e ln m e lnt m ln ==-+-=-++-11132220222t m ln m ln ln m t =+++->+-=++>, ∴函数()()()F x f x g x m =-+没有零点,C 选项正确;设曲线()y f x =在点A 处的切线与曲线()y g x =相切于点(C n ,())g n ,则曲线()y f x =在点A 处的切线方程为()lnm y m e x lnm -=-,即(1)y mx m lnm =+-, 同理可得曲线()y g x =在点C 处的切线方程为1122n y x ln n =+-, ∴11(1)22m n n m lnm ln ⎧=⎪⎪⎨⎪-=-⎪⎩,消去n 得1(1)202m m lnm ln --++=,令1()(1)22G x x x lnx ln =--++,则11()1x G x lnx lnx x x-'=--=-, 函数()y G x '=在(0,)+∞上为减函数,G '(1)10=>,1(2)202G ln '=-<, 则存在(1,2)s ∈,使得1()0G s lns s'=-=,且1s s e =.当0x s <<时,()0G x '>,当x s >时,()0G x '<.∴函数()y G x =在(2,)+∞上为减函数,5(2)02G =>,17(8)20202G ln =-<, 由零点存 定理知,函数()y G x =在(2,)+∞上有零点, 即方程1(1)202m m lnm ln --++=有解.m ∴∃使得曲线()y f x =在点A 处的切线也是曲线()y g x =的切线.故选:BCD . 【点睛】本题考查导数的综合应用,涉及函数的最值、零点以及切线问题,计算量较大,考查了转化思想和数形结合思想,属难题.3.关于函数()2ln f x x x=+,下列判断正确的是( ) A .2x =是()f x 的极大值点 B .函数yf xx 有且只有1个零点C .存在正实数k ,使得()f x kx >恒成立D .对任意两个正实数1x ,2x ,且21x x >,若()()12f x f x =,则124x x +> 【答案】BD 【分析】对于A ,利用导数研究函数()f x 的极值点即可; 对于B ,利用导数判断函数y f xx 的单调性,再利用零点存在性定理即得结论;对于C ,参变分离得到22ln xk x x <+,构造函数()22ln x g x x x=+,利用导数判断函数()g x 的最小值的情况;对于D ,利用()f x 的单调性,由()()12f x f x =得到1202x x <<<,令()211x t t x =>,由()()12f x f x =得21222ln t x x t t-+=,所以要证124x x +>,即证2224ln 0t t t -->,构造函数即得. 【详解】A :函数()f x 的定义域为0,,()22212x f x x x x-'=-+=,当()0,2x ∈时,0f x,()f x 单调递减,当()2,x ∈+∞时,0fx,()f x 单调递增,所以2x =是()f x 的极小值点,故A 错误.B :()2ln y f x x x x x=-=+-,22221210x x y x x x -+'=-+-=-<,所以函数在0,上单调递减.又()112ln1110f -=+-=>,()221ln 22ln 210f -=+-=-<,所以函数yf xx 有且只有1个零点,故B 正确.C :若()f x kx >,即2ln x kx x +>,则22ln x k x x <+.令()22ln x g x x x=+,则()34ln x x xg x x-+-'=.令()4ln h x x x x =-+-,则()ln h x x '=-,当()0,1∈x 时,()0h x '>,()h x 单调递增,当()1,∈+∞x 时,()0h x '<,()h x 单调递减,所以()()130h x h ≤=-<,所以0g x,所以()22ln x g x x x=+在0,上单调递减,函数无最小值,所以不存在正实数k ,使得()f x kx >恒成立,故C 错误. D :因为()f x 在()0,2上单调递减,在2,上单调递增,∴2x =是()f x 的极小值点.∵对任意两个正实数1x ,2x ,且21x x >,若()()12f x f x =,则1202x x <<<. 令()211x t t x =>,则21x tx =,由()()12f x f x =,得121222ln ln x x x x +=+, ∴211222ln ln x x x x -=-,即()2121212ln x x x x x x -=,即()11121ln t x t x tx -=⋅,解得()121ln t x t t-=,()2121ln t t x tx t t-==,所以21222ln t x x t t-+=.故要证124x x +>,需证1240x x +->,需证22240ln t t t -->,需证2224ln 0ln t t tt t-->. ∵211x t x =>,则ln 0t t >, ∴证2224ln 0t t t -->.令()()2224ln 1H t t t t t =-->,()()44ln 41H t t t t '=-->,()()()414401t H t t t t-''=-=>>,所以()H t '在1,上是增函数.因为1t →时,()0H t '→,则()0H t '>,所以()H t 在1,上是增函数.因为1t →时,()0H t →,则()0H t >,所以2224ln 0ln t t tt t-->, ∴124x x +>,故D 正确. 故选:BD . 【点睛】关键点点睛:利用导数研究函数的单调性、极值点,结合零点存在性定理判断A 、B 的正误;应用参变分离,构造函数,并结合导数判断函数的最值;由函数单调性,应用换元法并构造函数,结合分析法、导数证明D 选项结论.4.对于函数()2ln 1f x x ax x a =+--+,其中a R ∈,下列4个命题中正确命题有( )A .该函数定有2个极值B .该函数的极小值一定不大于2C .该函数一定存在零点D .存在实数a ,使得该函数有2个零点【答案】BD【分析】求出导函数,利用导数确定极值,结合零点存在定理确定零点个数. 【详解】函数定义域是(0,)+∞,由已知2121()2x ax f x x a x x+-'=+-=,280a ∆=+>,2210x ax +-=有两个不等实根12,x x ,但12102x x =-<,12,x x 一正一负.由于定义域是(0,)+∞,因此()0f x '=只有一个实根,()f x 只有一个极值,A 错; 不妨设120x x <<,则20x x <<时,()0f x '<,()f x 递减,2x x >时,()0f x '>,()f x 递增.所以2()f x 是函数的极小值.222210x ax +-=,22212x a x -=,22222()ln 1f x x ax x a =+--+=222222222222212112ln 12ln 2x x x x x x x x x -+---+=-+--+,设21()2ln 2g x x x x x =-+--+,则22111()22(1)(2)g x x x x x x'=-+-+=-+, 01x <<时,()0g x '>,()g x 递增,1x >时,()0g x '<,()g x 递减,所以()g x 极大值=(1)2g =,即()2g x ≤,所以2()2f x ≤,B 正确; 由上可知当()f x 的极小值为正时,()f x 无零点.C 错;()f x 的极小值也是最小值为2222221()2ln 2f x x x x x =-+--+, 例如当23x =时,173a =-,2()0f x <,0x →时,()f x →+∞,又2422217171714()21()03333f e e e e e =--++=-+>(217()3e >, 所以()f x 在(0,3)和(3,)+∞上各有一个零点,D 正确. 故选:BD . 【点睛】思路点睛:本题考查用导数研究函数的极值,零点,解题方法是利用导数确定函数的单调性,极值,但要注意在函数定义域内求解,对零点个数问题,注意结合零点存在定理,否则不能确定零点的存在性.5.函数()()320ax bx d a f x cx =+++≠有两个极值点1x 、()212x x x <,则下列结论正确的是( ) A .230b ac ->B .()f x 在区间()12,x x 上单调递减C .若()10af x <,则()f x 只有一个零点D .存在0x ,使得()()()1202f x f x f x +=【答案】ACD 【分析】利用极值点与导数的关系可判断A 选项的正误;取0a <,利用函数的单调性与导数的关系可判断B 选项的正误;分0a >、0a <两种情况讨论,分析函数()f x 的单调性,结合图象可判断C 选项的正误;计算出函数()f x 的图象关于点,33b b f a a ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭对称,可判断D 选项的正误. 【详解】()()320f x ax bx cx d a =+++≠,则()232f x ax bx c '=++.对于A 选项,由题意可知,关于x 的二次方程()23200ax bx c a ++=≠有两个不等的实根,则24120b ac ∆=->,可得230b ac ->,A 选项正确;对于B 选项,当0a <时,且当()12,x x x ∈时,()0f x '>,此时函数()f x 在区间()12,x x 上单调递增,B 选项错误;对于C 选项,当0a >时,由()0f x '>,可得1x x <或2x x >;由()0f x '<,可得12x x x <<.所以,函数()f x 的单调递增区间为()1,x -∞、()2,x +∞,单调递减区间为()12,x x , 由()10af x <,可得()10<f x ,此时,函数()f x 的极大值为()10<f x ,极小值为()2f x ,且()()210f x f x <<,如下图所示:由图可知,此时函数()f x 有且只有一个零点,且零点在区间()2,x +∞内; 当0a <时,由()0f x '<,可得1x x <或2x x >;由()0f x '>,可得12x x x <<. 所以,函数()f x 的单调递减区间为()1,x -∞、()2,x +∞,单调递增区间为()12,x x , 由()10af x <,可得()10f x >,此时,函数()f x 的极小值为()10f x >,极大值为()2f x ,且()()210f x f x >>,如下图所示:由图可知,此时函数()f x 有且只有一个零点,且零点在区间()2,x +∞内,C 选项正确; 对于D 选项,由题意可知,1x 、2x 是方程2320ax bx c ++=的两根, 由韦达定理可得1223bx x a +=-,123c x x a=, ()()()()()()()()3232f t x f t x a t x b t x c t x d a t x b t x c t x d ⎡⎤⎡⎤-++=-+-+-++++++++⎣⎦⎣⎦()()()()()(322322322322332332a t t x tx x b t tx x c t x d a t t x tx x b t tx x c ⎡⎤⎡=-+-+-++-+++++++++⎣⎦⎣()()322223222a t tx b t x ct d =+++++,取3bt a=-,则322223222333333b b b b b b f x f x a x b x c d a a a a a a ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫--+-+=-+⨯-+-++⋅-+⎢⎥⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦32222223333b b b b a b c d fa a a a ⎛⎫⎛⎫⎛⎫⎛⎫=-+⋅-+⋅-+=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,所以,函数()f x 的图象关于点,33b b f a a ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭对称, 1223bx x a+=-,()()1223b f x f x f a ⎛⎫∴+=- ⎪⎝⎭,D 选项正确. 故选:ACD. 【点睛】方法点睛:利用导数解决函数零点问题的方法:(1)直接法:先对函数求导,根据导数的方法求出函数的单调区间与极值,根据函数的基本性质作出图象,然后将问题转化为函数图象与x 轴的交点问题,突出导数的工具作用,体现了转化与化归思想、数形结合思想和分类讨论思想的应用; (2)构造新函数法:将问题转化为研究两函数图象的交点问题;(3)参变量分离法:由()0f x =分离变量得出()a g x =,将问题等价转化为直线y a =与函数()y g x =的图象的交点问题.6.若函数()f x 满足对于任意1x ,2(0,1)x ∈,()()121222f x f x x x f ++⎛⎫≤⎪⎝⎭,则称函数()f x 为“中点凸函数”.则下列函数中为“中点凸函数”的是( )A .2()2f x x x =-B .()tan f x x =C .()sin cos f x x x =-D .()e ln x f x x =-【答案】ABD 【分析】 用计算()()121222f x f x x x f ++⎛⎫-⎪⎝⎭的正负值来解,运算量大,比较复杂.我们可分析“中点凸函数”的几何特征,结合图像作答.由已知“中点凸函数”的定义,可得“中点凸函数”的图象形状可能为:【详解】由“中点凸函数”定义知:定义域内12,x x 对应函数值的平均值大于或等于122x x +处的函数值,∴下凸函数:任意连接函数图象上不同的两点所得直线一定在图象上方或与图象重合.设()()11,Ax f x ,()()22,B x f x 为曲线()f x 在(0,1)上任意两点A 、B 、C 、D 选项对应的函数图象分别如下图示: ①2()2f x x x =-符合题意 ②()tan f x x =符合题意③()sin cos 2sin 4f x x x x π⎛⎫=-=- ⎪⎝⎭放大局部图像可见,在,14段,并不满足12,x x 对应函数值的平均值大于或等于122x x +处的函数值.不合题意④()e ln x f x x =-'1()e x f x x =-,''21()e 0x f x x+=>根据导函数作出图像如下符合题意. 故选:ABD 【点睛】本题主要考查了函数的新定义及其应用,其中解答中正确理解函数的新定义,以及结合函数的图象求解是解答的关键,学生可利用数形结合求解,需要较强的推理与运算能力.7.在数学中,布劳威尔不动点定理是拓扑学里一个非常重要的不动点定理,它得名于荷兰数学家鲁伊兹布劳威尔(L.E.Brouwer )简单的讲就是对于满足一定条件的连续函数()f x ,存在一个点0x ,使得()00f x x =,那么我们称该函数为“不动点”函数,而称0x 为该函数的一个不动点,依据不动点理论,下列说法正确的是( ) A .函数()sin f x x =有3个不动点B .函数2()(0)f x ax bx c a =++≠至多有两个不动点C .若定义在R 上的奇函数()f x ,其图像上存在有限个不动点,则不动点个数是奇数D .若函数()x f x e x a =+-[0,1]上存在不动点,则实数a 满足l a e ≤≤(e 为自然对数的底数)【分析】根据题目中的定义,结合导数、一元二次方程的性质、奇函数的性质进行判断即可. 【详解】令()sin g x x x =-,()1cos 0g x x '=-≥, 因此()g x 在R 上单调递增,而(0)0g =, 所以()g x 在R 有且仅有一个零点, 即()f x 有且仅有一个“不动点”,A 错误;0a ≠,20ax bx c x ∴++-=至多有两个实数根,所以()f x 至多有两个“不动点”,B 正确;()f x 为定义在R 上的奇函数,所以(0)0f =,函数()-y f x x =为定义在R 上的奇函数,显然0x =是()f x 的一个“不动点”,其它的“不动点”都关于原点对称,个数和为偶数, 因此()f x 一定有奇数个“不动点”,C 正确;因为()f x 在[0,1]存在“不动点”,则()f x x =在[0,1]有解,x =⇒2x a e x x =+-在[0,1]有解,令2()xm x e x x =+-,()12x m x e x '=+-,令()12x n x e x '=+-,()20x n x e '=-=,ln 2x =,()n x 在(0,ln 2)单调递减,在(ln 2,1)单调递增,∴min ()(ln 2)212ln 232ln 20n x n ==+-=->, ∴()0m x '>在[0,1]恒成立,∴()m x 在[0,1]单调递增,min ()(0)1m x m ==,max ()(1)m x m e ==,∴1a e ≤≤,D 正确,. 故选:BCD 【点睛】方法点睛:新定义题型的特点是:通过给出一个新概念,或约定一种新运算,或给出几个新模型来创设全新的问题情景,要求考生在阅读理解的基础上,依据题目提供的信息,联系所学的知识和方法,实现信息的迁移,达到灵活解题的目的.遇到新定义问题,应耐心读题,分析新定义的特点,弄清新定义的性质,按新定义的要求,“照章办事”,逐条分析、验证、运算,使问题得以解决.8.已知函数()1ln f x x x x=-+,给出下列四个结论,其中正确的是( ) A .曲线()y f x =在1x =-处的切线方程为10x y ++= B .()f x 恰有2个零点C .()f x 既有最大值,又有最小值D .若120x x >且()()120f x f x +=,则121=x x【分析】本题首先可根据()10f -=以及13f判断出A 错误,然后根据当0x >时的函数单调性、当0x <时的函数单调性、()10f -=以及()10f =判断出B 正确和C 错误,最后根据()()120f x f x +=得出()121f x f x ⎛⎫= ⎪⎝⎭,根据函数单调性即可证得121=x x ,D 正确.【详解】函数()1ln f x x x x=-+的定义域为()(),00,-∞⋃+∞, 当0x >时,()1ln f x x x x=-+,()2221111x x f x x x x -+-'=--=; 当0x <时,1ln f x x x x,()2221111x x f x x x x -+-'=--=,A 项:1ln 1110f,22111131f,则曲线()y f x =在1x =-处的切线方程为031y x ,即33y x =--,A 错误;B 项:当0x >时,222215124x xx f xx x ,函数()f x 是减函数,当0x <时,222215124x x x f xx x ,函数()f x 是减函数,因为()10f -=,()10f =,所以函数()f x 恰有2个零点,B 正确; C 项:由函数()f x 的单调性易知,C 错误; D 项:当1>0x 、20x >时, 因为()()120f x f x +=, 所以1222222221111ln lnf x f x x x x fx x x x , 因为()f x 在()0,∞+上为减函数,所以121x x =,120x x >, 同理可证得当10x <、20x <时命题也成立,D 正确, 故选:BD. 【点睛】本题考查函数在某点处的切线求法以及函数单调性的应用,考查根据导函数求函数在某点处的切线以及函数单调性,导函数值即切线斜率,若导函数值大于0,则函数是增函数,若导函数值小于0,则函数是减函数,考查函数方程思想,考查运算能力,是难题.9.已知函数()()2214sin 2x xe xf x e -=+,则下列说法正确的是( ) A .函数()y f x =是偶函数,且在(),-∞+∞上不单调 B .函数()y f x '=是奇函数,且在(),-∞+∞上不单调递增 C .函数()y f x =在π,02⎛⎫-⎪⎝⎭上单调递增 D .对任意m ∈R ,都有()()f m f m =,且()0f m ≥【答案】AD 【分析】由函数的奇偶性以及函数的单调性即可判断A 、B 、C 、D. 【详解】 解:对A ,()()222114sin =2cos 2x x xx e x e f x x e e-+=+-,定义域为R ,关于原点对称,()2211=2cos()2cos()()x x x xe ef x x x f x e e--++---=-=, ()y f x ∴=是偶函数,其图像关于y 轴对称,()f x ∴在(),-∞+∞上不单调,故A 正确;对B ,1()2sin xx f x e x e'=-+, 11()2sin()=(2sin )()x xx x f x e x e x f x e e--''-=-+---+=-, ()f x '∴是奇函数,令1()2sin xx g x e x e=-+, 则1()+2cos 2+2cos 0x x g x e x x e'=+≥≥, ()f x '∴在(),-∞+∞上单调递增,故B 错误;对C ,1()2sin x x f x e x e'=-+,且()'f x 在(),-∞+∞上单调递增, 又(0)0f '=,π,02x ⎛⎫∴∈- ⎪⎝⎭时,()0f x '<,()y f x ∴=在π,02⎛⎫- ⎪⎝⎭上单调递减,故C 错误;对D ,()y f x =是偶函数,且在(0,)+∞上单调递增,()()f m f m ∴=,且()(0)0f m f ≥=,故D 正确.故选:AD. 【点睛】用导数求函数的单调区间或判断函数的单调性问题时应注意如下几方面: (1)在利用导数讨论函数的单调区间时,首先要确定函数的定义域; (2)不能随意将函数的2个独立的单调递增(或递减)区间写成并集形式;(3)利用导数解决含参函数的单调性问题时,一般将其转化为不等式恒成立问题,解题过程中要注意分类讨论和数形结合思想的应用.10.在单位圆O :221x y +=上任取一点()P x y ,,圆O 与x 轴正向的交点是A ,将OA 绕原点O 旋转到OP 所成的角记为θ,若x ,y 关于θ的表达式分别为()x fθ=,()y g θ=,则下列说法正确的是( )A .()x f θ=是偶函数,()y g θ=是奇函数;B .()x f θ=在()0,π上为减函数,()y g θ=在()0,π上为增函数;C .()()1fg θθ+≥在02πθ⎛⎤∈⎥⎝⎦,上恒成立;D .函数()()22t f g θθ=+.【答案】ACD 【分析】依据三角函数的基本概念可知cos x θ=,sin y θ=,根据三角函数的奇偶性和单调性可判断A 、B ;根据辅助角公式知()()4f g πθθθ⎛⎫+=+ ⎪⎝⎭,再利用三角函数求值域可判断C ;对于D ,2cos sin2t θθ=+,先对函数t 求导,从而可知函数t 的单调性,进而可得当1sin 2θ=,cos θ=时,函数t 取得最大值,结合正弦的二倍角公式,代入进行运算即可得解. 【详解】由题意,根据三角函数的定义可知,x cos θ=,y sin θ=, 对于A ,函数()cos fθθ=是偶函数,()sin g θθ=是奇函数,故A 正确;对于B ,由正弦,余弦函数的基本性质可知,函数()cos fθθ=在()0,π上为减函数,函数()sin g θθ=在0,2π⎛⎫⎪⎝⎭为增函数,在,2ππ⎛⎫⎪⎝⎭为减函数,故B 错误; 对于C ,当0θπ⎛⎤∈ ⎥2⎝⎦,时,3,444πππθ⎛⎤+∈ ⎥⎝⎦()()cos sin 4f g πθθθθθ⎛⎫+=+=+∈ ⎪⎝⎭,故C 正确;对于D ,函数()()222cos sin2t fg θθθθ=+=+,求导22sin 2cos22sin 2(12sin )2(2sin 1)(sin 1)t θθθθθθ'=-+=-+-=--+, 令0t '>,则11sin 2θ-<<;令0t '<,则1sin 12θ<<, ∴函数t 在06,π⎡⎤⎢⎥⎣⎦和5,26ππ⎡⎤⎢⎥⎣⎦上单调递增,在5,66ππ⎛⎫⎪⎝⎭上单调递减,当6πθ=即1sin 2θ=,cos 2θ=时,函数取得极大值1222t =⨯=又当2θπ=即sin 0θ=,cos 1θ=时,212012t =⨯+⨯⨯=,所以函数()()22t f g θθ=+,故D 正确.故选:ACD. 【点睛】方法点睛:考查三角函数的值域时,常用的方法:(1)将函数化简整理为()()sin f x A x ωϕ=+,再利用三角函数性质求值域; (2)利用导数研究三角函数的单调区间,从而求出函数的最值.。
人教版导数及其应用多选题单元达标专项训练检测试卷

人教版导数及其应用多选题单元达标专项训练检测试卷一、导数及其应用多选题1.已知函数()32f x x ax x c =+-+(x ∈R ),则下列结论正确的是( ).A .函数()f x 一定存在极大值和极小值B .若函数()f x 在1()x -∞,、2()x ,+∞上是增函数,则21x x -≥ C .函数()f x 的图像是中心对称图形D .函数()f x 的图像在点00())(x f x ,(0x R ∈)处的切线与()f x 的图像必有两个不同的公共点 【答案】ABC 【分析】首先求函数的导数2()3210f x x ax =+-=',再根据极值点与导数的关系,判断AB 选项;证明()()2()333a a af x f x f -++--=-,判断选项C ;令0a c ==,求切线与()f x 的交点个数,判断D 选项.【详解】A 选项,2()3210f x x ax =+-='的24120a ∆=+>恒成立,故()0f x '=必有两个不等实根,不妨设为1x 、2x ,且12x x <,令()0f x '>,得1x x <或2x x >,令()0f x '<,得12x x x <<,∴函数()f x 在12()x x ,上单调递减,在1()x -∞,和2()x ,+∞上单调递增, ∴当1x x =时,函数()f x 取得极大值,当2x x =时,函数()f x 取得极小值,A 对, B 选项,令2()3210f x x ax =+-=',则1223ax x +=-,1213x x ⋅=-,易知12x x <,∴213x x -==≥,B 对, C 选项,易知两极值点的中点坐标为(())33a a f --,,又23()(1)()333a a a f x x x f -+=-+++-,∴()()2()333a a af x f x f -++--=-, ∴函数()f x 的图像关于点(())33aa f --,成中心对称,C 对,D 选项,令0a c ==得3()f x x x =-,()f x 在(0)0,处切线方程为y x =-,且3y x y x x =-⎧⎨=-⎩有唯一实数解, 即()f x 在(0)0,处切线与()f x 图像有唯一公共点,D 错, 故选:ABC . 【点睛】方法点睛:解决函数极值、最值综合问题的策略:1、求极值、最值时,要求步骤规范,含参数时,要讨论参数的大小;2、求函数最值时,不可想当然地认为极值点就是最值点,要通过比较才能下结论;3、函数在给定闭区间上存在极值,一般要将极值与端点值进行比较才能确定最值.2.若存在常数k 和b ,使得函数()F x 和()G x 对其公共定义域上的任意实数x 都满足:()F x kx b ≥+和()G x kx b ≤+恒成立,则称此直线y kx b =+为()F x 和()G x 的“隔离直线”.已知函数()22x f x =(x ∈R ),()12g x x =(0x <),()ln h x e x =,(e 为自然对数的底数),则( )A .()()()m x f x g x =-在0x ⎛⎫∈ ⎪⎝⎭内单调递减 B .()f x 和()g x 之间存在“隔离直线”,且b 的最小值为2- C .()f x 和()g x 之间存在“隔离直线”,且k 的取值范围是[]2,1-D .()f x 和()g x 之间存在唯一的“隔离直线”,方程为2ey =-【答案】BD 【分析】对于A :令()()()m x f x g x =-,利用导数可确定()m x 单调性,进而作出判断; 对于B 和C :利用二次函数的性质以及不等式恒成立的知识求出b 、k 的范围,进而作出判断;对于选项D :根据隔离直线过()f x 和()h x 的公共点,可假设隔离直线为2e y kx =-;可得到222x ekx ≥-,再利用恒成立得出k 的值,最后尝试利用导数证明()2eh x ≤-,进而作出判断. 【详解】对于A ,()()()2122x m x f x g x x =-=-, ()322121022x m x x x x +'∴=+=>,当x ⎛⎫∈ ⎪⎝⎭时,()0m x '>,()m x ∴单调递增,故A 错误; 对于B ,C ,设()f x ,()g x 的隔离直线为y kx b =+,22x kx b ≥+对任意x ∈R 恒成立,即2220x kx b --≥对任意x ∈R 恒成立, 所以21480k b ∆=+≤,所以0b ≤,又12kx b x ≤+对任意(),0x ∈-∞恒成立,即22210kx bx +-≤对任意(),0x ∈-∞恒成立,因为0b ≤,所以0k ≤且21480b k ∆=+≤,所以22k b ≤-且22b k ≤-,4248k b b ≤≤-,解得20k -≤≤,同理20b -≤≤, 所以b 的最小值为2-,k 的取值范围是[]2,0-, 故B 正确,C 错误; 对于D ,函数()f x 和()h x的图象在x =∴若存在()f x 和()h x 的隔离直线,那么该直线过这个公共点,设隔离直线的斜率为k,则隔离直线方程为(2e y k x -=,即2e y kx =-,则222x ekx ≥-(x ∈R),得2220x kx e -+≥对x ∈R 恒成立,则()24420k e ∆=-≤,解得k =,此时隔离直线方程为:2ey =-,下面证明()2e h x ≤-, 令()()ln 22e e G x h x e x =--=--(0x >),则()x G x x'=,当x =()0G x '=;当0x <<()0G x '<;当x >()0G x '>;∴当x =()G x 取到极小值,也是最小值,即()0min G x G==,()()02e G x h x ∴=--≥在()0,∞+上恒成立,即()2eh x ≤-,∴函数()f x 和()h x存在唯一的隔离直线2ey =-,D 正确. 故选:BD . 【点睛】关键点睛:本题考查导数中的新定义问题的求解;解题关键是能够充分理解“隔离直线”的定义,将问题转化为根据不等式恒成立求解参数范围或参数值、或不等式的证明问题,属于难题.3.关于函数()sin ,(,)x f e x x x π∈-=+∞+,下列结论正确的有( ) A .()f x 在(0,)+∞上是增函数 B .()f x 存在唯一极小值点0x C .()f x 在(,)π-+∞上有一个零点 D .()f x 在(,)π-+∞上有两个零点 【答案】ABD 【分析】根据函数()f x 求得()'f x 与()f x '',再根据()0f x ''>在(,)π-+∞恒成立,确定()'f x 在(,)π-+∞上单调递增,及(0,)x ∈+∞()0f x '>,且存在唯一实数03(,)42x ππ∈--,使0()=0f x ',从而判断A ,B 选项正确;再据此判断函数()f x 的单调性,从而判断零点个数.【详解】由已知()sin ,(,)x f e x x x π∈-=+∞+得()cos x f x e x '=+,()sin xf x e x ''=-,(,)x π∈-+∞,()0f x ''>恒成立,()'f x 在(,)π-+∞上单调递增,又3423()0,()0,(0)20422f e f e f ππππ--'''-=-<-=>=> (0,)x ∴∈+∞时()(0)0f x f ''>>,且存在唯一实数03(,)42x ππ∈--,使0()=0f x ',即00cos x e x =-,所以()f x 在(0,)+∞上是增函数,且()f x 存在唯一极小值点0x ,故A,B 选项正确. 且()f x 在0(,)x π-单调递减,0(,)x +∞单调递增,又()00f eππ--=+>,000000()sin sin cos )04x f x e x x x x π=+=-=-<,(0)10=>f ,所以()f x 在(,)π-+∞上有两个零点,故D 选项正确,C 选项错误.故选:ABD. 【点睛】导数是研究函数的单调性、极值(最值)最有效的工具,而函数是高中数学中重要的知识点,对导数的应用的考查主要从以下几个角度进行: (1)考查导数的几何意义,往往与解析几何、微积分相联系. (2)利用导数求函数的单调区间,判断单调性;已知单调性,求参数. (3)利用导数求函数的最值(极值),解决生活中的优化问题. (4)考查数形结合思想的应用.4.已知函数()1ln f x x x x=-+,给出下列四个结论,其中正确的是( ) A .曲线()y f x =在1x =-处的切线方程为10x y ++= B .()f x 恰有2个零点C .()f x 既有最大值,又有最小值D .若120x x >且()()120f x f x +=,则121=x x 【答案】BD 【分析】本题首先可根据()10f -=以及13f判断出A 错误,然后根据当0x >时的函数单调性、当0x <时的函数单调性、()10f -=以及()10f =判断出B 正确和C 错误,最后根据()()120f x f x +=得出()121f x f x ⎛⎫=⎪⎝⎭,根据函数单调性即可证得121=x x ,D 正确. 【详解】函数()1ln f x x x x=-+的定义域为()(),00,-∞⋃+∞, 当0x >时,()1ln f x x x x=-+,()2221111x x f x x x x -+-'=--=;当0x <时,1ln f x x x x,()2221111x x f x x x x -+-'=--=,A 项:1ln 1110f,22111131f,则曲线()y f x =在1x =-处的切线方程为031y x ,即33y x =--,A 错误;B 项:当0x >时,222215124x x x f xx x ,函数()f x 是减函数,当0x <时,222215124x x x f xx x ,函数()f x 是减函数,因为()10f -=,()10f =,所以函数()f x 恰有2个零点,B 正确; C 项:由函数()f x 的单调性易知,C 错误; D 项:当1>0x 、20x >时, 因为()()120f x f x +=, 所以1222222221111ln lnf x f x x x x fx x x x ,因为()f x 在()0,∞+上为减函数,所以121x x =,120x x >, 同理可证得当10x <、20x <时命题也成立,D 正确, 故选:BD. 【点睛】本题考查函数在某点处的切线求法以及函数单调性的应用,考查根据导函数求函数在某点处的切线以及函数单调性,导函数值即切线斜率,若导函数值大于0,则函数是增函数,若导函数值小于0,则函数是减函数,考查函数方程思想,考查运算能力,是难题.5.设函数()()1x af x a x a =->的定义域为()0,∞+,已知()f x 有且只有一个零点,下列结论正确的有( ) A .a e =B .()f x 在区间()1,e 单调递增C .1x =是()f x 的极大值点D .()f e 是()f x 的最小值【答案】ACD 【分析】()f x 只有一个零点,转化为方程0x a a x -=在(0,)+∞上只有一个根,即ln ln x ax a=只有一个正根.利用导数研究函数ln ()xh x x=的性质,可得a e =,判断A ,然后用导数研究函数()x e f x e x =-的性质,求出()'f x ,令()0f x '=,利用新函数确定()'f x 只有两个零点1和e ,并证明出()'f x 的正负,得()f x 的单调性,极值最值.判断BCD .【详解】()f x 只有一个零点,即方程0x a a x -=在(0,)+∞上只有一个根,x a a x =,取对数得ln ln x a a x =,即ln ln x ax a=只有一个正根. 设ln ()xh x x =,则21ln ()x h x x-'=,当0x e <<时,()0h x '>,()h x 递增,0x →时,()h x →-∞,x e >时,()0h x '<,()h x 递减,此时()0h x >,max 1()()h x h e e==. ∴要使方程ln ln x ax a =只有一个正根.则ln 1a a e =或ln 0a a<,解得a e =或0a <,又∵1a >,∴a e =.A 正确;()x e f x e x =-,1()x e f x e ex -'=-,1()0x e f x e ex -'=-=,11x e e x --=,取对数得1(1)ln x e x -=-,易知1x =和x e =是此方程的解.设()(1)ln 1p x e x x =--+,1()1e p x x-'=-,当01x e <<-时,()0p x '>,()p x 递增,1x e >-时,()0p x '<,()p x 递减,(1)p e -是极大值,又(1)()0p p e ==, 所以()p x 有且只有两个零点,01x <<或x e >时,()0p x <,即(1)ln 1e x x -<-,11e x x e --<,1e x ex e -<,()0f x '>,同理1x e <<时,()0f x '<,所以()f x 在(0,1)和(,)e +∞上递增,在(1,)e 上递减,所以极小值为()0f e =,极大值为(1)f ,又(0)1f =,所以()f e 是最小值.B 错,CD 正确. 故选:ACD . 【点睛】关键点点睛:本题考用导数研究函数的零点,极值,单调性.解题关键是确定()'f x 的零点时,利用零点定义解方程,1()0xe f x e ex-'=-=,11x e e x --=,取对数得1(1)ln x e x -=-,易知1x =和x e =是此方程的解.然后证明方程只有这两个解即可.6.已知函数()sin xf x x=,(]0,x π∈,则下列结论正确的有( ) A .()f x 在区间(]0,π上单调递减B .若120x x π<<≤,则1221sin sin x x x x ⋅>⋅C .()f x 在区间(]0,π上的值域为[)0,1 D .若函数()()cos g x xg x x '=+,且()1g π=-,()g x 在(]0,π上单调递减【答案】ACD 【分析】先求出函数的导数,然后对四个选项进行逐一分析解答即可, 对于选项A :当0,2x π⎛⎫∈ ⎪⎝⎭时,可得()0f x '<,可得()f x 在区间0,2π⎛⎫⎪⎝⎭上单调递减;当,2x ππ⎡⎤∈⎢⎥⎣⎦,可得()0f x '<,可得()f x 在区间,2ππ⎡⎤⎢⎥⎣⎦上单调递减,最后作出判断; 对于选项B :由()f x 在区间(]0,π上单调递减可得()()12f x f x >,可得1212sin sin x x x x >,进而作出判断; 对于选项C :由三角函数线可知sin x x <,所以sin 1x x x x <=,sin ()0f πππ==,进而作出判断;对于选项D :()()()sin g x g x xg x x ''''=+-,可得()()sin xg x f x x''==,然后利用导数研究函数()g x '在区间(]0,π上的单调性,可得()()0g x g π''≤=,进而可得出函数()g x 在(]0,π上的单调性,最后作出判断.【详解】()2cos sin x x xf x x -'=, (]0,x π∈,当0,2x π⎛⎫∈ ⎪⎝⎭时,cos 0x >,由三角函数线可知tan x x <, 所以sin cos xx x<,即cos sin x x x <,所以cos sin 0x x x -<, 所以()0f x '<,所以()f x 在区间0,2π⎛⎫⎪⎝⎭上单调递减,当,2x ππ⎡⎤∈⎢⎥⎣⎦,cos 0x ≤,sin 0x ≥,所以cos sin 0x x x -<,()0f x '<, 所以()f x 在区间,2ππ⎡⎤⎢⎥⎣⎦上单调递减, 所以()f x 在区间(]0,π上单调递减,故选项A 正确; 当120x x π<<≤时,()()12f x f x >,所以1212sin sin x x x x >,即1221sin sin x x x x ⋅<⋅,故选项B 错误; 由三角函数线可知sin x x <,所以sin 1x x x x <=,sin ()0f πππ==, 所以当(]0,x π∈时,()[)0,1f x ∈,故选项C 正确;对()()cos g x xg x x '=+进行求导可得: 所以有()()()sin g x g x xg x x ''''=+-,所以()()sin xg x f x x''==,所以()g x ''在区间(]0,π上的值域为[)0,1, 所以()0g x ''≥,()g x '在区间(]0,π上单调递增,因为()0g π'=, 从而()()0g x g π''≤=,所以函数()g x 在(]0,π上单调递减,故选项D 正确. 故选:ACD. 【点睛】方法点睛:本题考查导数的综合应用,对于函数()sin xf x x=的性质,可先求出其导数,然后结合三角函数线的知识确定导数的符号,进而确定函数的单调性和极值,最后作出判断,考查逻辑思维能力和运算求解能力,属于中档题.7.对于定义在1D 上的函数()f x 和定义在2D 上的函数()g x ,若直线y kx b =+(),k b R ∈同时满足:①1x D ∀∈,()f x kx b ≤+,②2x D ∀∈,()g x kx b ≥+,则称直线y kx b =+为()f x 与()g x 的“隔离直线”.若()ln xf x x=,()1x g x e -=,则下列为()f x 与()g x 的隔离直线的是( )A .y x =B .12y x =-C .3ex y =D .1122y x =- 【答案】AB 【分析】根据隔离直线的定义,函数()y f x =的图象总在隔离直线的下方,()y g x =的图象总在隔离直线的上方,并且可以有公共点,结合函数的图象和函数的单调性,以及直线的特征,逐项判定,即可求解. 【详解】根据隔离直线的定义,函数()y f x =的图象总在隔离直线的下方,()y g x =的图象总在隔离直线的上方,并且可以有公共点, 由函数()ln x f x x =,可得()21ln xf x x -'=, 所以函数()f x 在()0,e 上单调递增,在(),e +∞上单调递减,因为()10f =,()11f '=,此时函数()f x 的点(1,0)处的切线方程为1y x =-, 且函数()f x 的图象在直线1y x =-的下方; 又由函数()1x g x e-=,可得()1e0x g x -'=>,()g x 单调递增,因为()()111g g '==,所以函数()g x 在点(1,1)处的切线方程为11y x -=-,即y x =, 此时函数()g x 的图象在直线y x =的上方,根据上述特征可以画出()y f x =和()y g x =的大致图象,如图所示,直线1y x =-和y x =分别是两条曲线的切线,这两条切线以及它们之间与直线y x =平行的直线都满足隔离直线的条件,所以A ,B 都符合; 设过原点的直线与函数()y f x =相切于点00(,)P x y , 根据导数的几何意义,可得切线的斜率为021ln x k x -=, 又由斜002000ln 0y x k x x -==-,可得002100ln 1ln x x x x -=,解得0x =,所以21ln 12()e k e e -==,可得切线方程为2x y e =, 又由直线3xy e=与曲()y f x =相交,故C 不符合; 由直线1122y x =-过点()1,0,斜率为12,曲线()y f x =在点()1,0处的切线斜率为1,明显不满足,排除D. 故选:AB.【点睛】对于函数的新定义试题:(1)认真审题,正确理解函数的新定义,合理转化;(2)根据隔离直线的定义,转化为函数()y f x =的图象总在隔离直线的下方,()y g x =的图象总在隔离直线的上方.8.下列命题正确的有( ) A .已知0,0a b >>且1a b +=,则1222a b -<< B .3412a b ==2a bab+= C .323y x x x =--的极大值和极小值的和为6-D .过(1,0)A -的直线与函数3y x x =-有三个交点,则该直线斜率的取值范围是1(,2)(2,)4-+∞ 【答案】ACD 【分析】由等式关系、指数函数的性质可求2a b -的范围;利用指对数互化,结合对数的运算法求a b ab+;利用导数确定零点关系,结合原函数式计算极值之和即可;由直线与3y x x =-有三个交点,即可知2()h x x x k =--有两个零点且1x =-不是其零点即可求斜率范围. 【详解】A 选项,由条件知1b a =-且01a <<,所以21(1,1)a b a -=-∈-,即1222a b -<<;B 选项,34a b ==log a =4log b =1212112(log 3log 4)2a b ab a b+=+=+=; C 选项,2361y x x '=--中>0∆且开口向上,所以存在两个零点12,x x 且122x x +=、1213x x =-,即12,x x 为y 两个极值点,所以2212121212121212()[()3]3[()2]()6y y x x x x x x x x x x x x +=++--+--+=-;D 选项,令直线为(1)y k x =+与3y x x =-有三个交点,即2()()(1)g x x x k x =--+有三个零点,所以2()h x x x k =--有两个零点即可 ∴140(1)20k h k ∆=+>⎧⎨-=-≠⎩,解得1(,2)(2,)4k ∈-+∞故选:ACD 【点睛】本题考查了指对数的运算及指数函数性质,利用导数研究极值,由函数交点情况求参数范围,属于难题.9.已知函数()e sin xf x a x =+,则下列说法正确的是( )A .当1a =-时,()f x 在0,单调递增B .当1a =-时,()f x 在()()0,0f 处的切线为x 轴C .当1a =时,()f x 在()π,0-存在唯一极小值点0x ,且()010f x -<<D .对任意0a >,()f x 在()π,-+∞一定存在零点 【答案】AC 【分析】结合函数的单调性、极值、最值及零点,分别对四个选项逐个分析,可选出答案. 【详解】对于A ,当1a =-时,()e sin x f x x =-,()e cos xf x x '=-, 因为()0,x ∈+∞时,e 1,cos 1xx >≤,即0fx,所以()f x 在0,上单调递增,故A 正确;对于B ,当1a =-时,()e sin xf x x =-,()e cos xf x x '=-,则()00e sin01f =-=,()00e cos00f '=-=,即切点为0,1,切线斜率为0,故切线方程为1y =,故B 错误;对于C ,当1a =时,()e sin xf x x =+,()e cos xf x x '+=,()e sin xf x x '=-',当()π,0x ∈-时,sin 0x <,e 0x >,则()e sin 0xx f x -'=>'恒成立,即()e cos x f x x '+=在()π,0-上单调递增,又ππ22ππe cos e 220f --⎛⎫⎛⎫'-=-= ⎪ ⎪⎝⎭⎝⎭+>,3π3π443π3πe cos e 442f --⎛⎫⎛⎫'-=-= ⎪ ⎪⎝⎭⎝-⎭+,因为123π3π421e e 2e ---⎛⎫=<⎪⎭< ⎝,所以3π43πe 024f -⎛⎫'-= ⎪-⎭<⎝,所以存在唯一03ππ,42x ⎛⎫∈-- ⎪⎝⎭,使得()00f x '=成立,所以()f x 在()0π,x -上单调递减,在()0,0x 上单调递增,即()f x 在()π,0-存在唯一极小值点0x ,由()000e cos 0xf x x +'==,可得()000000πe sin cos sin 4x f x x x x x ⎛⎫=+=-+=- ⎪⎝⎭,因为03ππ,42x ⎛⎫∈-- ⎪⎝⎭,所以0π3ππ,44x ⎛⎫-∈-- ⎪⎝⎭,则()00π4f x x ⎛⎫=- ⎪⎝⎭()1,0∈-,故C 正确;对于选项D ,()e sin xf x a x =+,()π,x ∈-+∞,令()e sin 0xf x a x =+=,得1sin ex xa -=, ()sin ex xg x =,()π,x ∈-+∞,则()πcos sin 4e e x xx x x g x ⎛⎫- ⎪-⎝⎭'==, 令0g x ,得πsin 04x ⎛⎫-= ⎪⎝⎭,则ππ4x k =+()1,k k ≥-∈Z ,令0g x,得πsin 04x ⎛⎫-> ⎪⎝⎭,则π5π2π,2π44x k k ⎛⎫∈++ ⎪⎝⎭()1,k k ≥-∈Z ,此时函数()g x 单调递减, 令0g x,得πsin 04x ⎛⎫-< ⎪⎝⎭,则5π9π2π,2π44x k k ⎛⎫∈++ ⎪⎝⎭()1,k k ≥-∈Z ,此时函数()g x 单调递增, 所以5π2π4x k =+()1,k k ≥-∈Z 时,()g x 取得极小值,极小值为5π5π2π2π445π5π2π5π4s 42in si πe e 4n k k g k k ++⎛⎫ ⎪⎛⎫⎝⎭== ⎪⎝⎭++()1,k k ≥-∈Z , 在()g x 的极小值中,3π4sin 3π45π5π42π4eg g -⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝+⎭-最小,当3ππ,4x ⎛⎫∈--⎪⎝⎭时,()g x 单调递减,所以函数()g x的最小值为3π3π445πsin 3π144eg --⎛⎫-==- ⎪⎝⎭,当3π411a--<-时,即3π40a -<<时,函数()g x 与1=-y a无交点,即()f x 在()π,-+∞不存在零点,故D 错误.故选:AC. 【点睛】本题考查利用导数研究函数的极值、零点、最值,及切线方程的求法,考查学生的推理能力与计算求解能力,属于难题.10.当1x >时,()41ln ln 3k x x x x --<-+恒成立,则整数k 的取值可以是( ). A .2- B .1-C .0D .1【答案】ABC 【分析】将()41ln ln 3k x x x x --<-+,当1x >时,恒成立,转化为13ln ln 4x k x x x ⎛⎫<++ ⎪⎝⎭,.当1x >时,恒成立,令()()3ln ln 1xF x x x x x=++>,利用导数法研究其最小值即可. 【详解】因为当1x >时,()41ln ln 3k x x x x --<-+恒成立, 所以13ln ln 4x k x x x ⎛⎫<++ ⎪⎝⎭,当1x >时,恒成立, 令()()3ln ln 1xF x x x x x=++>, 则()222131ln 2ln x x x F x x x x x---'=-+=. 令()ln 2x x x ϕ=--,因为()10x x xϕ-'=>,所以()x ϕ在()1,+∞上单调递增. 因为()10ϕ<,所以()0F x '=在()1,+∞上有且仅有一个实数根0x , 于是()F x 在()01,x 上单调递减,在()0,x +∞上单调递增, 所以()()000min 00ln 3ln x F x F x x x x ==++.(*) 因为()1ln 3309F -'=<,()()21ln 22ln 4401616F --'==>,所以()03,4x ∈,且002ln 0x x --=, 将00ln 2x x =-代入(*)式, 得()()0000min 00023121x F x F x x x x x x -==-++=+-,()03,4x ∈. 因为0011t x x =+-在()3,4上为增函数, 所以713,34t ⎛⎫∈⎪⎝⎭,即()min 1713,41216F x ⎛⎫∈ ⎪⎝⎭.因为k 为整数,所以0k ≤. 故选:ABC 【点睛】本题主要考查函数与不等式恒成立问题,还考查了转化化归的思想和运算求解的能力,属于较难题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
导数的应用单元检测卷
一、选择题(本大题共12小题,每小题5分,共60分)
1.函数y =f (x )在x =x 0处的导数f ′(x 0) 的几何意义是( )
A .在点x =x 0处的函数值
B .在点(x 0,f (x 0))处的切线与x 轴所夹锐角的正切值
C .曲线y =f (x )在点(x 0,f (x 0))处的切线的斜率
D .点(x 0,f (x 0))与点(0,0)连线的斜率
2.下列导数运算正确的是( )
A.⎝⎛⎭⎫x +1x ′=1+1x 2 B .(2x )′=x 2x -1 C .(cos x )′=sin x D .(x ln x )′=ln x +1
3.函数f (x )=x 3+ax 2+3x -9在x =-3时取得极值,则a 等于( )
A .2
B .3
C .4
D .5
4.二次函数y =f (x )的图象过原点,且它的导函数y =f ′(x )的图象是过第一、二、三象限的一条直线,则函数y =f (x )的图象的顶点所在象限是( )
A .一
B .二
C .三
D .四
5.已知函数f (x )=-x 3+ax 2-x -1在(-∞,+∞)上是单调函数,则实数a 的取值范围是( )
A .(-∞,-3]∪[3,+∞)
B .[-3,3]
C .(-∞,-3]
D .[3,+∞)
6.已知函数y =f (x )的图象在点M (1,f (1))处的切线方程是y =12
x +2,则f (1)+f ′(1)的值等于( ) A .1 B.52
C .3
D .0 7.函数f (x )=ln x -x 在区间(0,e]上的最大值为( )
A .1-e
B .-1
C .-e
D .0
8.设f (x ),g (x )在[a ,b ]上可导,且f ′(x )>g ′(x ),则当a <x <b 时,有( )
A .f (x )>g (x )
B .f (x )<g (x )
C .f (x )+g (a )>g (x )+f (a )
D .f (x )+g (b )>g (x )+f (b )
9.若函数f (x )=12
x 2-a ln x 在(1,+∞)上为增函数,则实数a 的取值范围是( ) A .(1,+∞) B .[1,+∞) C .(-∞,1) D .(-∞,1]
10.若函数f (x )=x 3-3ax 2-2x +5在(0,1)内单调递减,则实数a 的取值范围是( )
A .a ≥16
B .a >16
C .a =16
D .0<a <16
11.设函数f (x )=13
x -ln x (x >0),则y =f (x )( ) A .在区间⎝⎛⎭⎫1e ,1,(1,e)内均有零点
B .在区间⎝⎛⎭⎫1e ,1,(1,e)内均无零点
C .在区间⎝⎛⎭⎫1e ,1内无零点,在区间(1,e)内有零点
D .在区间⎝⎛⎭⎫1e ,1内有零点,在区间(1,e)内无零点
12.函数f (x )=x sin x +cos x +1(x ∈[0,π])的最大值为( )
A.π2
+1 B .2 C .1 D .0
二、填空题(本大题共4小题,每小题5分,共20分)
13.在平面直角坐标系xOy 中,点P 在曲线C :y =x 3-10x +3上,且在第二象限内,已知曲线C 在点P 处的切线的斜率为2,则点P 的坐标为________.
14.若曲线y =ax 2-ln(x +1)在点(1,b )处的切线平行于x 轴,则a =________.
15.已知函数y =xf ′(x )的图象如图所示(其中f ′(x )是函数f (x )的导函数),给出以下说法:
①函数f (x )在区间(1,+∞)上是增函数;
②函数f (x )在区间(-1,1)上无单调性;
③函数f (x )在x =-12
处取得极大值; ④函数f (x )在x =1处取得极小值.
其中正确的说法有________.
16.设曲线y =x n +
1(n ∈N *)在(1,1)处的切线与x 轴的交点的横坐标为x n ,则log 2 019x 1+log 2 019x 2+…+log 2 019x 2 018的值为________.
三、解答题(本大题共6小题,共70分)
17.(10分) 已知函数f (x )=x 3+ax 2+bx +c ,曲线y =f (x )在点x =1处的切线为l :3x -y +1=0,若x =23
时,y =f (x )有极值.
(1)求a ,b ,c 的值;
(2)求y =f (x )在[-3,1]上的最大值和最小值.
.
18.(12分)设函数f (x )=ln x +ln(2-x )+ax (a >0).
(1)当a =1时,求f (x )的单调区间;
(2)若f (x )在(0,1]上的最大值为12
,求a 的值.
19.(12分)已知函数f (x )=(x +1)ln x -a (x -1).
(1)当a =4时,求曲线y =f (x )在(1,f (1))处的切线方程;
(2)若当x ∈(1,+∞)时,f (x )>0,求a 的取值范围.
20.(12分)经过多年的运作,“双十一”抢购活动已经演变成为整个电商行业的大型集体促销盛宴.为迎接2019年“双十一”网购狂欢节,某厂商拟投入适当的广告费,对网上所售产品进行促销.经调查测算,该促销产品在“双十一”的销售量P (万件)与促销费用x (万元)满足P =3-2x +1
(其中0≤x ≤a ,a 为正常数).已知生产该批产品P 万件还需投入成本(10+2P )万元(不含促销费用),产品的销售价格定为⎝⎛⎭
⎫4+20P 元/件,假定厂家的生产能力完全能满足市场的销售需求.
(1)将该产品的利润y (万元)表示为促销费用x (万元)的函数;
(2)促销费用投入多少万元时,厂家的利润最大?
21.(12分)已知函数f (x )=⎝⎛⎭⎫x 22-kx ln x +x 24
. (1)若f (x )在定义域内单调递增,求实数k 的值;
(2)若f (x )的极小值大于0,求实数k 的取值范围.
22.(12分) 已知函数 .
讨论 的单调性;
当 时,证明 .。
