冲南外内部资料5
南外仙林分校2017年一年级面试真题

禁止喧哗
禁止追逐打闹
垃圾入箱
禁止吸烟
请说出你刚才看到的禁止标志
本题16分,说出一个得2。
说出下面哪些是看书不文明现象
本题10分,指出一个得1分,说出理由1分。
小明想要借一本( joyful reading )
请跟老师说一遍,(
joyful reading ) 请再跟老师说一遍( joyful reading ) 现在你可以去借书了!你应该跟管理员怎么 说
3
2
1
10
5
9
7
8
6
4
你能再交换两次把它变成按从小到大的数字排列吗。
1
2
3
10
5
9
7
8
6
4
本题4分,10和4交换得2分
6和9交换得2分
一些小朋友已经坐到凳子上去了,已知2号、4号、6 号、、8号上面都坐上了小朋友
1
2
3
4
5
6
7
8
9
10
还有哪些凳子上可以坐呢?
1
2
3
4
5
6
7
8
9
10
本题10分,说出一个得2分,1、3、5、9、10号多一个倒扣2分
凳子都坐满了,可还有一些学生没有凳子坐,这时小 朋友们看到了地上有一块垫子,可这个垫子缺了一块, 请问是下面的哪一块?
本题4分。
突然有两个小朋友在图书馆打闹起来 这时小明提醒图书馆墙上有禁止标志
图书馆墙上有下面一些标志,请记住 这些标志,等会儿要考你们啊
禁止吃喝
禁止随地吐痰
禁止宠物入内
有序排队
南外仙林分校一年级面谈真题
2017年上午
广东深圳南山外国语学校(集团)2023-2024学年下学期九年级开学考数学试卷含参考答案

南山外国语学校(集团)2023-2024学年第二学期九年级开学考数学试卷一.选择题(每题3分,共30分)1.小明同学的微信钱包部分账单明细如图所示,10.5+表示收入10.5元,下列说法正确的是()A. 6.3−表示收入6.3元B. 6.3−表示支出 6.3−元C. 6.3−表示支出6.3元D.收支总和为16.8元2.国家级非物质文化遗产之一的东北大鼓是中国北方曲种,流行于辽宁、吉林、黑龙江3省,一度盛行于沈阳,故又称奉天大鼓、奉派大鼓、奉调大鼓、辽宁大鼓.如图是表演情景及乐器之一鼓的立体图形,该立体图形的主视图是()A.B.C.D.3.2021年8月52025年,我省林长制组织体系和目标责任体系更加完善,森林覆盖率超过31%,森林蓄积量达到2.9亿立方米.用科学记数法表示“2.9亿”,正确的是()A.92.910×B.82910×C.82.910×D.72910×4.下列事件中,属于随机事件的是()A.抛出的篮球会落下B.从装有红球、白球的袋中摸出黑球C.14人中至少有2人是同月出生D.经过有交通信号灯的路口,遇到绿灯5.如图,ABC∆中,90BAC∠=°,5AB=,10AC=,分别以点B和点C为圆心,大于12BC的长为半径作弧,两弧相交于D,E两点,连接DE交BC于点H,连接AH,则AH的长为()A.B C.D.56.一段加固后的护栏如图所示,该护栏竖直部分是由等距(任意相邻两根木条之间的距离相等)且平行的木条构成.已知50AC cm=,则BC的长度为()A.20cm B.25cm C.30cm D.1003cm7.翻花绳是中国民间流传的儿童游戏,在中国不同的地域,有不同的称法,如线翻花、翻花鼓、挑绷绷、解股等等,如图1是翻花绳的一种图案,可以抽象成右图,在矩形ABCD中,//IJ KL,//EF GH,1230∠=∠=°,3∠的度数为()A.30°B.45°C.50°D.60°8.下列说法不正确的是()A.方程23540x x+−=有两个不相等的实数根B.若△A B C′′′由ABC∆旋转得到,则它们的对应角、对应边以及对应边上的高都相等C.用尺规作图能完成:过一点作已知直线的垂线D.在同一平面内,若两个角的两边分别平行,则这两个角相等9.某市开发区在一项工程招标时,接到甲、乙两个工程队的投标书,工程领导小组根据甲、乙两队的投标书测算,共有三种施工方案:①甲队单独完成这项工程,刚好如期完工;②乙队单独完成此项工程要比规定工期多用5天;③,剩下的工程由乙队单独做,也正好如期完工.某同学设规定的工期为x 天,根据题意列出了方程:415xx x +=+,则方案③中被墨水污染的部分应该是( ) A .甲乙合作了4天 B .甲先做了4天 C .甲先做了工程的14D .甲乙合作了工程的1410.如图,AB 为圆O 的直径,C 为圆O 上一点,过点C 作圆O 的切线交AB 的延长线于点D ,13DB AD =,连接AC ,若8AB =,则AC 的长度为( )A .B .C .D .二.填空题(每题3分,共15分)11x 的取值范围是 .12.因式分解:2242ab ab a −+= .13.如图,在平面直角坐标系xOy 中,点A 在函数2(0)y x x=>的图象上,AC x ⊥轴于点C ,连接OA ,则OAC ∆面积为 .14.新定义:[a ,]b 为一次函数(0y ax b a =+≠,a ,b 为实数)的“关联数”.若“关联数”为[3,2]m −的一次函数是正比例函数,则点(1,1)m m −+在第 象限.15.如图,正方形ABCD 中,6AD =,点E 是对角线AC 上一点,连接DE ,过点E 作EF ED ⊥,交AB 于点F ,连接DF ,交AC 于点G ,将EFG ∆沿EF 翻折,得到EFM ∆,连接DM ,交EF 于点N ,若2AF =,则MN 的长为 .三.解答题(共55分)16.(5分)计算:201()(1)2sin602π−−−+°.17.(5分)先化简,再求值:2213()2(2)3x y x y −−+,其中2|1|(2)0x y −++=.18.(9分)下表是小明这一学期数学成绩测试记录,根据表格提供的信息,回答下列问题:(1)小明6次成绩的众数是 ,中位数是 ;(2)若把四次练习成绩的平均分89分作为平时成绩,按照学校规定,本学期的综合成绩的权重如图所示,请求出小明本学期的综合成绩;(3)若从四次练习成绩中随机抽取两次成绩作为平时成绩,则小明抽到两次成绩最好的练习的概率是多少?请用树状图或列表法示意.19.(8分)如图,ABC ∆中,AB AC =,点D 为BC 上一点,且AD DC =,过A ,B ,D 三点作O ,AE 是O 的直径,连接DE . (1)求证:AC 是O 的切线; (2)若4sin 5C =,6AC =,求O 的直径.20.(8分)某学校正在推进课堂信息化建设,希望通过采购一体机,提高学校硬件设备水平,更好的辅助教师教学.现有A ,B 两种型号64英寸8G 的教学一体机.若购买2台A 型一体机,6台B 型一体机需要10万元;3台A 型一体机,5台B 型一体机需要9.8万元. (1)请问每台A ,B 型一体机售价各是多少万元;(2)现需要采购一体机共100台,并且按照学校现有的设备匹配发现购进A 型一体机不超过35台,请问怎么安排采购方案,能使得本次采购费用最少.21.(11分)探究阅读题:【阅读】在大自然里,有很多数学的奥秘,一片美丽的心形叶片,一棵生长的幼苗都可以看作把一条抛物线的一部分沿直线折叠而形成.(如图1和图2) 【探究任务1】确定心形叶片的形状如图3建立平面直角坐标系,心形叶片下部轮廓线可以看作是二次函数24205y mx mx m =−−+图象的一部分,且过原点,求抛物线的解析式和顶点D 的坐标. 【探究任务2】研究心形叶片的尺寸如图3,心形叶片的对称轴直线2y x =+与坐标轴交于A 、B 两点,直线6x =分别交抛物线和直线AB 于点E 、F 点,点E 、E ′是叶片上的一对对称点,EE ′交直线AB 与点G ,求叶片此处的宽度EE ′.【探究任务3】研究幼苗叶片的生长小李同学在观察幼苗生长的过程中,发现幼苗叶片下方轮廓线都可以看作是二次函数24205y mx mx m =−−+图象的一部分.如图4,幼苗叶片下方轮廓线正好对应探究任务1中的二次函数,已知直线PD 与水平线的夹角为45°,三天后,点D 长到与点P 同一水平位置的点D ′时,叶尖Q 落在射线OP 上,如图5所示,求此时幼苗叶子的长度和最大宽度.22.(9分)综合与实践课上,老师让同学们以“线段的旋转”为主题开展数学活动.问题情境:在ABC ∆中,AB AC =,点D 在边BC 上,连接AD ,将AD 绕点A 逆时针旋转至AE 的位置,使得180DAE BAC ∠+∠=°. (1)操作判断当//AE BC 时,如图1,连接CE ,试判断四边形ADCE 的形状,并证明; (2)深入探究连接BE ,取BE 的中点G ,连接AG .善于思考的小东发现当点D 在BC 边上运动时,AGCD的值始终不变,请你利用图2求AGCD的值. (3)解决问题若60BAC ∠=°,6AB =,如图3,在(2)的探究中,当AD =时,直接写出C ,G 两点之间的距离.参考答案与试题解析一.选择题(共10小题)1.小明同学的微信钱包部分账单明细如图所示,10.5+表示收入10.5元,下列说法正确的是()A. 6.3−元−表示支出 6.3−表示收入6.3元B. 6.3C. 6.3−表示支出6.3元D.收支总和为16.8元【解答】解:根据10.5+表示收入10.5元,“收入”用正数表示,那么“支出”就用负数表示,−表示支出6.3元,6.3故选:C.2.国家级非物质文化遗产之一的东北大鼓是中国北方曲种,流行于辽宁、吉林、黑龙江3省,一度盛行于沈阳,故又称奉天大鼓、奉派大鼓、奉调大鼓、辽宁大鼓.如图是表演情景及乐器之一鼓的立体图形,该立体图形的主视图是()A.B.C.D.【解答】解:这个立体图形的主视图为:.故选:B.3.2021年8月5日,安徽省政府新闻办举办新闻发布会上获悉,到2025年,我省林长制组织体系和目标责任体系更加完善,森林覆盖率超过31%,森林蓄积量达到2.9亿立方米.用科学记数法表示“2.9亿”,正确的是()A.92.910×D.72910××C.829102.910×B.8【解答】解:2.9亿8==×,290000000 2.910故选:C.4.下列事件中,属于随机事件的是()A.抛出的篮球会落下B.从装有红球、白球的袋中摸出黑球C .14人中至少有2人是同月出生D .经过有交通信号灯的路口,遇到绿灯【解答】解:A 、抛出的篮球会落下,是必然事件,不符合题意; B 、从装有红球、白球的袋中摸出黑球,是不可能事件,不符合题意; C 、14人中至少有2人是同月出生,是必然事件,不符合题意;D 、经过有交通信号灯的路口,遇到绿灯,是随机事件,符合题意.故选:D .5.如图,ABC ∆中,90BAC ∠=°,5AB =,10AC =,分别以点B 和点C 为圆心,大于12BC 的长为半径作弧,两弧相交于D ,E 两点,连接DE 交BC 于点H ,连接AH ,则AH 的长为( )A .BC .D .5【解答】解:90BAC ∠=° ,5AB =,10AC =,BC ∴==,由作法得DE 垂直平分BC , BH CH ∴=, AH ∴为Rt ABC ∆斜边上的中线,12AH BC ∴==故选:B .6.一段加固后的护栏如图所示,该护栏竖直部分是由等距(任意相邻两根木条之间的距离相等)且平行的木条构成.已知50AC cm =,则BC 的长度为( )A .20cmB .25cmC .30cmD .1003cm【解答】解:过点C作CD AM⊥交AM于点D,交BN于点E,//BE AD,∴35 BC CEAC CD==,50AC cm=,30BC cm∴=.故选:C.7.翻花绳是中国民间流传的儿童游戏,在中国不同的地域,有不同的称法,如线翻花、翻花鼓、挑绷绷、解股等等,如图1是翻花绳的一种图案,可以抽象成右图,在矩形ABCD中,//IJ KL,//EF GH,1230∠=∠=°,3∠的度数为()A.30°B.45°C.50°D.60°【解答】解:如图:四边形ABCD是矩形,90C D∴∠=∠=°,190MJG∴∠+∠=°,290MGJ∠+∠=°,1230∠=∠=°,60MJG MGJ∴∠=∠=°,18060GMJ MJG MGJ∴∠=°−∠−∠=°,560∴∠=°,//IJ KL,//EF GH,∴四边形NPMO 是平行四边形,4560∴∠=∠=°, 3460∴∠=∠=°,故选:D .8.下列说法不正确的是( )A .方程23540x x +−=有两个不相等的实数根B .若△A BC ′′′由ABC ∆旋转得到,则它们的对应角、对应边以及对应边上的高都相等 C .用尺规作图能完成:过一点作已知直线的垂线D .在同一平面内,若两个角的两边分别平行,则这两个角相等 【解答】解:A 、方程23540x x +−=,△2543(4)730=−××−=>, ∴方程23540x x +−=有两个不相等的实数根,故本选项正确,不符合题意; B 、若△A B C ′′′由ABC ∆旋转得到,则它们的对应角、对应边以及对应边上的高都相等,正确,本选项不符合题意;C 、用尺规作图能完成:过一点作已知直线的垂线,正确,本选项不符合题意;D 、在同一平面内,若两个角的两边分别平行,则这两个角相等,错误这两个角也可能是互补,本选项符合题意. 故选:D .9标书测算,共有三种施工方案:①甲队单独完成这项工程,刚好如期完工;②乙队单独完成此项工程要比规定工期多用5天;③,剩下的工程由乙队单独做,也正好如期完工.某同学设规定的工期为x 天,根据题意列出了方程:415x x x +=+,则方案③中被墨水污染的部分应该是( ) A .甲乙合作了4天 B .甲先做了4天 C .甲先做了工程的14D .甲乙合作了工程的14【解答】解: 某同学设规定的工期为x 天,根据题意列出了方程:415xx x +=+, ∴甲工作了4天,乙工作了x 天,即甲乙合作了4天,剩下的工程由乙队单独做,也正好如期完工, ∴可知在③应填入的内容为:甲乙合作了4天,故选:A .10.如图,AB 为圆O 的直径,C 为圆O 上一点,过点C 作圆O 的切线交AB 的延长线于点D ,13DB AD =,连接AC,若8AB=,则AC的长度为()A.B.C.D.【解答】解:连接OC,BC,13DB AD=,AB为圆O的直径,OA OB DB∴==,90ACB∠=°,DC是圆O的切线,90OCD∴∠=°,OB DB=,CB OB∴=,8AB=,4BC∴=,在Rt ABC∆中,AC,故选:C.二.填空题(共5小题)11x的取值范围是3x>.【解答】解:30x∴−>,解得3x>.故答案为:3x>.12.因式分解:2242ab ab a −+= 22(1)a b − .【解答】解:原式22(21)a b b =−+22(1)a b −,故答案为:22(1)a b −.13.如图,在平面直角坐标系xOy 中,点A 在函数2(0)yx x=>的图象上,AC x ⊥轴于点C ,连接OA ,则OAC ∆面积为 1 .【解答】解: 函数2(0)yx x=>的图象经过点A ,AC x ⊥轴于点C , 1212S OAC ∴∆=×=, 故答案为1.14.新定义:[a ,]b 为一次函数(0y ax b a +≠,a ,b 为实数)的“关联数”.若“关联数”为[3,2]m −的一次函数是正比例函数,则点(1,1)m m −+在第 二 象限.【解答】解: “关联数”为[3,2]m −的一次函数是正比例函数,32y x m ∴+−是正比例函数,20m ∴−=,解得:2m =,则11m −=−,13m +=,故点(1,1)m m −+在第二象限.故答案为:二.15.如图,正方形ABCD 中,6AD =,点E 是对角线AC 上一点,连接DE ,过点E 作EF ED ⊥,交AB 于点F ,连接DF ,交AC 于点G ,将EFG ∆沿EF 翻折,得到EFM ∆,连接DM ,交EF 于点N ,若2AF =,则MN【解答】解:如图,取DF的中点K,连接AK,EK.连接GM交EF于H.四边形ACD是正方形,6AD AB∴==,90DAB∠=°,//AB CD,45DAC CAB∠=∠=°,DE EF⊥,90DEF DAF∴∠=∠=°,DK KF=,KA KD KF KE∴===,A∴,F,E,D四点共圆,45DFE DAE∴∠=∠=°,45EDF EFD∴∠=∠=°,DE EF∴=,2AF=,6AD=,DF∴DE DF∴==,//AF CD,∴13 FG AFDG DC==,FG FM∴==GM ∴==,FH GH HM ∴===, EF GM ⊥ ,GH HM ∴==EH EF FH ∴=−==, //MH DE ,∴14MH HN DE EN ==,15HN EH ∴==,MN ∴=. 三.解答题(共7小题)16.计算:201()(1)2sin602π−−−+°【解答】解:原式412=−+3=+ 17.先化简,再求值:2213()2(2)3x y x y −−+,其中2|1|(2)0x y −++=. 【解答】解:原式22342x y x y =−−−23x y =−−;2|1|(2)0x y −++= ,10x ∴−=,20y +=, 1x ∴=,2y =−,原式213(2)165=−−×−=−+=. 18.下表是小明这一学期数学成绩测试记录,根据表格提供的信息,回答下列问题:测试平时成绩 期中测试 期末测试 练习一 练习二 练习三 练习四成绩889290869096(1)小明6次成绩的众数是,中位数是;(2)若把四次练习成绩的平均分89分作为平时成绩,按照学校规定,本学期的综合成绩的权重如图所示,请求出小明本学期的综合成绩;(3)若从四次练习成绩中随机抽取两次成绩作为平时成绩,则小明抽到两次成绩最好的练习的概率是多少?请用树状图或列表法示意.【解答】解:(1)由题意知,小明6次成绩的众数是90,中位数是(9090)290+÷=,故答案为:90,90;(2)综合成绩为:8910%9660%9030%93.5×+×+×=(分),即小明本学期的综合成绩为93.5分.(3)画树状图如下:(练习一~四的成绩记为A,B,C,D)由树状图可知,共有12种等可能的结果,其中小明抽到两次成绩最好的练习B,C两组的有2种结果,∴概率为21 126=.19.如图,ABC∆中,AB AC=,点D为BC上一点,且AD DC=,过A,B,D三点作O,AE是O的直径,连接DE.(1)求证:AC是O的切线;(2)若4sin5C=,6AC=,求O的直径.【解答】(1)证明:AB AC = ,AD DC =,C B ∴∠=∠,1C ∠=∠,1B ∴∠=∠,又E B ∠=∠ ,1E ∴∠=∠,AE 是O 的直径,90ADE ∴∠=°,90E EAD ∴∠+∠=°,190EAD ∴∠+∠=°,即90EAC ∠=°,AE AC ∴⊥,AC ∴是O 的切线;(2)解:过点D 作DF AC ⊥于点F ,如图,DA DC = ,132CF AC ∴==, 在Rt CDF ∆中,4sin 5DF CDC == , 设4DF x =,5DC x =,3CF x ∴=,33x ∴=,解得1x =,5DC ∴=,5AD ∴=,90ADE DFC ∠=∠=° ,E C ∠=∠,ADE DFC ∴∆∆∽, ∴AE AD DC DF =,即554AE =,解得254AE =, 即O 的直径为254.20.某学校正在推进课堂信息化建设,希望通过采购一体机,提高学校硬件设备水平,更好的辅助教师教学.现有A ,B 两种型号64英寸8G 的教学一体机.若购买2台A 型一体机,6台B 型一体机需要10万元;3台A 型一体机,5台B 型一体机需要9.8万元.(1)请问每台A ,B 型一体机售价各是多少万元;(2)现需要采购一体机共100台,并且按照学校现有的设备匹配发现购进A 型一体机不超过35台,请问怎么安排采购方案,能使得本次采购费用最少.【解答】解:(1)设每台A 型一体机售价是x 万元,每台B 型一体机售价是y 万元,根据题意得:2610359.8x y x y += +=, 解得 1.11.3x y = =, 答:每台A 型一体机售价是1.1万元,每台B 型一体机售价是1.3万元;(2)设学校购进A 型一体机m 台,则购进B 型一体机(100)m −台,采购费用为w 元,根据题意得: 1.1 1.3(100)0.2130w m m m =+−=−+, 0.20−< ,35x ,∴当35x =时,w 有最小值,最小值为123,此时B 型一体机1003565−=(台),∴购买35台A 型一体机,65台B 型一体机时采购费用最少.21.探究阅读题:【阅读】在大自然里,有很多数学的奥秘,一片美丽的心形叶片,一棵生长的幼苗都可以看作把一条抛物线的一部分沿直线折叠而形成.(如图1和图2)【探究任务1】确定心形叶片的形状如图3建立平面直角坐标系,心形叶片下部轮廓线可以看作是二次函数24205y mx mx m =−−+图象的一部分,且过原点,求抛物线的解析式和顶点D 的坐标.【探究任务2】研究心形叶片的尺寸如图3,心形叶片的对称轴直线2y x =+与坐标轴交于A 、B 两点,直线6x =分别交抛物线和直线AB 于点E 、F 点,点E 、E ′是叶片上的一对对称点,EE ′交直线AB 与点G ,求叶片此处的宽度EE ′.【探究任务3】研究幼苗叶片的生长小李同学在观察幼苗生长的过程中,发现幼苗叶片下方轮廓线都可以看作是二次函数24205y mx mx m =−−+图象的一部分.如图4,幼苗叶片下方轮廓线正好对应探究任务1中的二次函数,已知直线PD 与水平线的夹角为45°,三天后,点D 长到与点P 同一水平位置的点D ′时,叶尖Q 落在射线OP 上,如图5所示,求此时幼苗叶子的长度和最大宽度.【解答】解:【探究任务1】:把(0,0)代入24205y mx mx m =−−+,得0205m =−+, 解得14m =, ∴抛物线解析式为2211(2)144y x x x =−=−−, ∴顶点D 的坐标为(2,1)−;【探究任务2】: 直线AB 的解析式为2y x =+,(2,0)A ∴−,(0,2)B ,2OA OB ∴==,45ABO ∴∠=°,在2y x =+中,当6x = 时,8y =, 在21(2)14y x =−−中, 当6x = 时,3y =,(6,8)F ∴,(6,3)E ,5EF ∴=.//EF OB ,45GFE ABO ∴∠=∠=°,E 、E ′是叶片上的一对对称点,2EE EG ′∴=,EG FG ⊥. EFG ∴∆是等腰直角三角形,∴EG =,∴2EE EG ′== 【探究任务3】: 直线PD 与x 轴成45°角,设直线PD 的解析式为y x b =−+,把点(2,1)D −代入得12b −=−+,解得1b =.∴直线PD 的解析式为1y x =−+, 联立2141y x x y x =− =−+ , 解得23x y =− =或21x y = =− , (2,3)P ∴−,同理可求出直线OP 的解析式为32y x =−, (2,3)D ∴′,把(2,3)D ′代入24205y mx mx =−−+,482053m m m ∴−−+=, 解得112m =, ∴抛物线解析式为211101233y x x =−+, 联立23211101233y x y x x =− =−+, 解得14x =−,210x =−,幼苗是越长越张开,210x ∴=−不合题意,舍去,(4,6)Q ∴−,作QH PD ′⊥交D P ′ 延长线于点H ,QD ∴′=设直线QD ′的解析式为2y kx b =+,把点(4,6)Q −和(2,3)D ′代入得224623k b k b −+= += , 解得2124k b =− = ,∴直线QD ′的解析式为142y x =−+, 作MN x ⊥轴交抛物线QD Q ′′和直线QD ′分别于点N ,M ,作NT QD ′⊥交曲线OD ′于N ′,2211110134()(1)21233124M N MN y y x x x x ∴=−=−+−−−+=−++, 34MN ∴=最大, //MN QH ,D QH NMT ∴∠′=∠,QHD MTN ′∠=∠ ,MNT ∴∆∽△QD H ′.::6:NT MN HD QD ∴=′′=∴NT =NN ′=, ∴叶片此时的长度为. 22.综合与实践课上,老师让同学们以“线段的旋转”为主题开展数学活动. 问题情境:在ABC ∆中,AB AC =,点D 在边BC 上,连接AD ,将AD 绕点A 逆时针旋转至AE 的位置,使得180DAE BAC ∠+∠=°.(1)操作判断当//AE BC时,如图1,连接CE,试判断四边形ADCE的形状,并证明;(2)深入探究连接BE,取BE的中点G,连接AG.善于思考的小东发现当点D在BC边上运动时,AGCD的值始终不变,请你利用图2求AGCD的值.(3)解决问题若60BAC∠=°,6AB=,如图3,在(2)的探究中,当AD=时,直接写出C,G两点之间的距离.【解答】解:(1)四边形ADCE是菱形,理由如下://AE BC,180DAE ADC∴∠+∠=°,又180DAE BAC∠+∠=°,BAC ADC∴∠=∠,180180DAC ADC ACD BAC ACD B∴∠=°−∠−∠=°−∠−∠=∠,AB AC=,B ACB∴∠=∠,DAC ACB∴∠=∠,AD CD∴=,又AD AE=,AE CD∴=,∴四边形ADCE是平行四边形,又AD AE=,∴四边形ADCE是菱形,(2)如图所示,延长BA至点F,使AF AB=,连接EF,G是BE的中点,∴12AG EF=,180 BAC DAE∠+∠=°,180BAC CAF∠+∠=°,DAE CAF∴∠=∠,DAE CAE CAF CAE∴∠−∠=∠−∠,DAC EAF∴∠=∠,又AD AE=,AC AB AF==,()ADC AEF SAS∴∆≅∆,CD EF∴=,∴12AG CD=,即12 AGCD=;(3)延长BA至点F,使AF=EF,过点A作AH BC⊥于点H,G是BE的中点,AG∴是三角形BEF是中位线//AG EF ∴,12AG EF=,BAG F∴∠=∠,180DAE BAC∠+∠=°,180BAC CAF∠+∠=°DAE CAF∴∠=∠,DAE CAE CAF CAE ∴∠−∠=∠−∠ 即DAC EAC ∠=∠,又AD AE = ,AC AB AF == ()ADC AEC SAS ∴∆≅∆, CD EF ∴=,C F ∠=∠ ∴12AG CD =,BAG C ∠=∠, 60BAC ∠=° ,AB AC =, ABC ∴∆是等边三角形, 60BAG C ∴∠=∠=°, G ∴点在AC 上,AH BC ⊥ , ∴132BH CH BC ===,∴AHAD =,∴2DH , 5CD CH DH ∴=+=或1CD CD CH =−=, ∴1522AG CD ==或12, ∴72CG AC AG =−=或112.。
南京外国语学校初中入学面测英文数学逻辑推理难点及突破技巧逐字稿
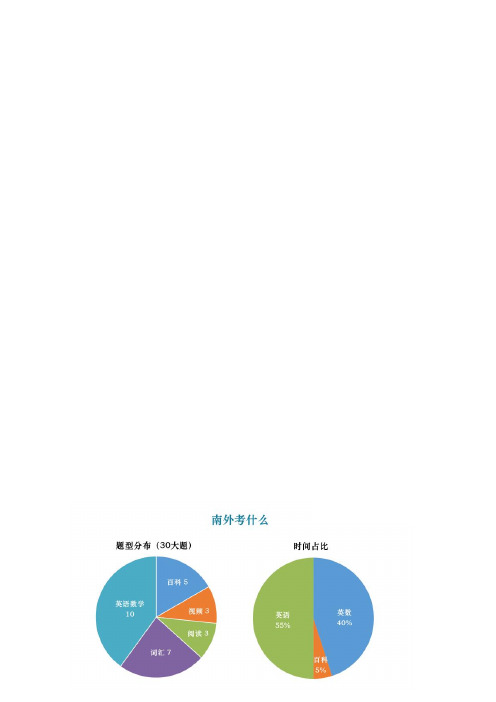
2019年南外面测情况1、内容:1小时,共有38个英语面测题。
正式开始前有5分钟的模拟面测,在形式、流程上高度仿真。
其中英数题目10道,分值占总体的40%.2、形式:采用PPT呈现面测题的形式,学生在答题纸上填写答案。
可以在草稿纸上进行适当的记录。
二、命题原则围绕外语学科核心素养,立足小学课本,结合学生的认知特点、思维发展规律和生活经历,着重通过“现学现评”的题型,选拔出学习能力强和学习潜力大的学生。
题目要求有科学性、原创性、趣味性、探究性和综合性。
从17年考试形式改为面测之后,题目的灵活性有了很大提高,尤其是进行了多个知识点的串联考察。
南外的考试的偏重点分析,17年难度比较简单,然后涉及的几何题目的占比和数论题目的占比大概是4:6,而18年开始数论题目的这个难度和数量都有很大程度的下降,但是几何题目的所占比例和难度都有了不小的提升。
究其原因:孩子们对于几何题目天生比较薄弱,导致了得分率会比较低。
从19年的题目来看数学的题目难度是较低的。
相应的做题的时间也相应的减少了,这样使得孩子们需要在短时间内获取一个正确的答案,对于孩子们来说总体的难度并没有下降。
们能做的只能是把所有的小学期间能够掌握的知识点都掌握踏实,并在这个基础上进行适当的拓展。
帮助孩子来更好的应对接下来可能面出现的题目挑战。
我们列举了南外从17~19的考点相比于几何题目一直保持在40%的比率,反观而逻辑推理题目每年都只有一道题,但是因为其相对简单的难度,如何能拿到这道题目的全分,变成了保证基础分值的重要因素。
所以尽可能快速高效的完成逻辑推理的题目是现在孩子想在南外面测中获得基础高分的一个关键因素。
逻辑推理就是根据已知条件进行推理,难度不是很高,但是要进行专项的训练。
逻辑思维能力的部分我推荐门萨系列的书,我自己就买了一套,里面的题目都非常有意思,孩子能感受到数学的趣味性,还能够提升自己的逻辑思维能力。
因为南外每年也都有考找规律的题目,这种类型很难说去找到相对应的题目进行训练,门萨里面就有挺多找规律的题目,而且角度都很新颖,可以开拓孩子的解题思维。
冲南外必须掌握的百科知识中英文版

(描述)a famous writer in the小学生百科知识大全(2015-2016中英文对照版)I Each of the following couplets(对联)describes an cie nt times (古代).Fill in the n ames.屈原杜甫诸葛亮李清照文天祥范仲淹欧阳修 (1)He is good at writi ng about huma n beings and ghosts;So it is true with his criticizing cruelty and corruptions.(写人写鬼咼人一等,刺贪刺虐入木二分。
)(2)A great poet, he suffers a lot from his misfort une; he is also good at writing about the life of the poor.(世上疮痍诗中圣哲,民间疾苦笔底波澜)(3)、Two memorials to the Ki ng are in return for three visits;The Lon gzh ong Pla n con tributes to a lege nd in history. (两表酬三顾,一对足千秋。
)(4)) Heroes from gen erati on to gen eratio n are fading away in history;Out of millions of millions of men of letters stands a female poet.(大河百代众浪齐奔淘尽万古英雄汗,词苑千载群芳竞秀盛开一枝女儿花。
) (5) 、 Starting off on a long journey, you are still homesick;Mean deri ng the mountains, you can rest un der the pavili ons. (翁去八百载,醉乡犹在;山行六七里,亭影不孤。
广东省深圳市南山外国语校2024届中考联考物理试题含解析

广东省深圳市南山外国语校2024届中考联考物理试题注意事项1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。
第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、单项选择题(本大题7小题,每题3分,共21分)1.下图的各现象中,可作为“物质质量与体积有关”事实依据的有()A.(1)与(2)B.(2)与(3)C.(2)与(4)D.(1)与(4)2.用四个相同的滑轮组成如图所示的两个滑轮组匀速提升重物甲、乙,不计绳重和摩擦,若绳自由端的拉力和移动的速度相同,则在相同时间内A.两图中做的额外功相同B.两图中做的有用功相同C.甲图中比乙图中的机械效率大D.甲图中比乙图中拉力做功的功率大3.有甲、乙两个溢水杯,甲溢水杯盛满酒精,乙溢水杯盛满某种液体,将一不吸水的小球轻轻放入甲溢水杯中,小球下沉到杯底,溢出酒精的质量是40g;将小球从甲溢水杯中取出擦干,轻轻放入乙溢水杯中,小球漂浮且有1/6 的体积露出液面,溢出液体的质量是50g.已知ρ酒精=0.8×103kg/m3,下列计算结果正确的是①液体的密度是1×103kg/m3②两种情境下小球受到的浮力之比为4:5③小球的密度1.2×103kg/m3④两种情境下小球排开液体的体积之比为6:5A.①②③B.①②④C.③④D.②④4.如图所示,电源电压保持6V 不变,电流表的量程为0 ~ 0.6A,电压表的量程为0 ~ 3V,定值电阻的规格为“100.5A”,滑动变阻器的规格为“201A”。
闭合开关,为了保证电路安全,在变阻器滑片移动过程中,下列说法正确的是A.电阻R1消耗功率允许的变化范围为0.4W~ 0.9WB.电流表示数允许的变化范围为0.2A~ 0.5AC.变阻器R2接入电路的阻值允许变化范围为2~ 20D.电路消耗总功率允许的变化范围为1.2W~ 3W5.如图为四冲程汽油机工作过程中某冲程的示意图,此冲程的名称及能量转化是A.此冲程为吸气冲程,内能转化为机械能B.此冲程为压缩冲程,机械能转化为内能C.此冲程为做功冲程,内能转化为机械能D.此冲程为排气冲程,机械能转化为内能6.在图所示的电路中,电源电压保持不变.闭合电键S,当滑动变阻器的滑片P向右移动时,不变的是()A.电流表A示数与电流表A1示数的差值B.电压表V示数与电流表A 示数的比值C.电压表V示数与电流表A 示数的乘积D.电压表V示数与电流表A1示数的乘积7.如图所示的各种做法中,符合安全用电原则的是A.用铜棒挑开通电的裸导线B.用湿布擦拭电灯C.在高压线附近放风筝D.保持电器外壳良好接地二、填空题(本大题7小题,共21分)8.民间艺人制作“糖画”时,先将糖化为糖浆,再用勺舀起糖浆在光滑的石板上绘制出蝴蝶、鱼等图案,等石板上的糖浆_________(选填“吸收”或“放出”)热量后就__________(填物态变化名称)成了如图所示的栩栩如生的“糖画”。
-冲南外奥数中英版第11期

1. The areas of the faces of a cuboid are 84 cm 2, 70 cm 2 and 30 cm2. Find the volume of thecuboid in cm 3.Answer :一个立方体的各个表面积是84平方厘米,70平方厘米和30厘米,这个立方体的体积是多少立方厘米?2. The fraction33311133113333++++++++can be wrritten in the formnmwhere the greatest common divisor of m and n is 1, Find m +n . Answer : 分数31331111113333++++++++可以写成n m,m 和n 最大的共同的除数是1,m +n 等于多少?3. At a local village gala, the entire population turned up, 500 people. The event raised £3,000.Tickets were priced as follows: £7.48 per man, £7.12 per woman and £0.45 per child. How many children were there? Answer :在一个本地的盛会上,所有的人口500人,筹集了3000元,票价为:男人每人7.48元,女人每人7.12元,儿童每人0.45元,有多少个儿童?4. Let two 8×12 rectangles share a common corner and overlap. The distance from the bottomright corner of one rectangle to the intersection point along the right edge of that rectangle is 7. What is the area of the shaded region?让两个8×12的长方形一个角重叠,从一个长方形底部右角到另一个长方形的右边交叉点的距离是7,阴影部分的面积是多少?5. A spy had to send the 4-digit code abcd to headquarters. For security reasons, hesent instead the 9 separate 4-digit codes shown. In each of the 9 codes, at least one of the digits a , b , c , and d occurs in its correct position. What is the value of abcd ? Answer :一个间谍发送一个四位数的密码,abcd 给总部,由于安全原因,他发送了9个不同的四位数密码(如图)来代替,这9个密码中, a,b,c,d,中至少有一个位置是正确的,abcd 的值是多少?6. In how many ways can one arrange the numbers 21, 31, 41, 51, 61, 71 and 81 such that thesum of every four consecutive numbers is divisible by 3? Answer :有多少种方法排列数字21, 31, 41, 51, 61, 71 和 81,使得每四个连续数字的和能被3整除?7. Given: ABCD is a trapezoid, AD ∥BC , AD :BC =1:2, :1:3AOF DOE S S ∆∆=, 224cm BEF S ∆=, Findthe area of AOF ∆. Answer :8. 已知ABCD 是一个梯形,AD ∥BC , AD :BC =1:2,:1:3AOF DOE S S ∆∆=, 224cm BEF S ∆=, 求AOF ∆的面积.9. In how many different ways can the seven empty circles inthe diagram on the right be filled in with the numbers 2 through 8 such that each number is used once, and each number is either greater than both its neighbors, or less than both its neighbors. Answer :用2-8填入右边图表中的七个空的圆圈中,每个数字只能使用一次,并且每个数字要大于它左右相邻的两个数字或者小于左右相邻的两个数字,有多少种填法?10. How many rectangles are there in the diagram on the right such that the sum of thenumbers within the rectangle is a multiple of 4? Answer :C B1 23 4 5 67 8 10 141115 129 1613在右边的图表中,有多少个长方形能使得长方形内的数字的和是4的倍数?11.What is the sum of the digits of the following product 9999×6666 ?Answer: ________9999×6666乘积各数位的和是多少?12.A digit is placed in each empty square in the grid to the right so that each row contains each of the digits 1, 2, 3, 4, 5 and each column contains each of the digits 1, 2, 3, 4, 5. What digit is placed in the square at the bottom right corner of the grid?Answer: ________一个数字放在右边格子的空四边形中,使得每一行包含1, 2, 3, 4, 5中的每一个数字,每一列也包含1, 2, 3, 4, 5中的每一个数字,在格子底部右下角的正方形中填什么数字?13.If you continue the given number pattern, in what row will the number 2009 be?7 -------------- row 114 21 -------------- row 228 35 42 -------------- row 349 56 63 70 -------------- row 4Answer: ________按下列数字的规则,数字2009将会有哪一排?14.There are 7 identical circles in the figure and each area is 10. Find the area of shaded region. Answer: ________在图表中有7个相同的圆,每个圆的面积是10,求阴影部分的面积。
2022-2023学年第二学期南山外国语学校(集团)【南外联考】初三数学答案

2022-2023学年第二学期南山外国语学校(集团)3月质量检测九年级数学试卷参考答案一、选择题(每小题3分,共30分)二、填空题(每小题3分,共15分)三、解答题(本题共7小题,其中第16题5分,第17题7分,第18题7分,第19题8分,第20题8分,第21题10分,第22题10分,共55分)16.(5分)解:原式===.当a=﹣1时,原式=..…………………….………………5分17.(7分)解:(1)本次接受调查的学生共有:(80+30+40+20)÷(1﹣15%)=200(人),∴m°=360°×=144°,n%=40÷200×100%=20%,∴m=144,n=20,故答案为:200,144,20;.…………………….………………3分(2)D的人数为:200×15%=30(人),补全条形统计图如下:.…………………….………………4分(3)根据题意画树状图如下:由树状图可知,共有20种等可能的结果,其中两次选中的既有八年级班级又有九年级班级的情况有12种情况,∴两次选中的既有八年级班级又有九年级班级的概率..…………………….………………7分18.(7分)解:(1)如图,过点A作AG⊥CF,垂足为F.由题意知:四边形AEFG是矩形.∴FG=AE=4米,∠EAG=∠AGC=∠AGF=90°.∵∠CAE=120°,∴∠CAG=∠CAE﹣∠EAG=30°.在Rt△AGC中,∵sin∠CAG=,AC的长度为24米,∴CG=AC×sin30°=24×=12(米).∴CF=CG+GF=4+12=16(米)答:云梯消防车最高点C距离地面的高度CF的长为16米;故答案为:16;.…………………….………………2分(2)如图,过点C作CH⊥AE,交EA的延长线于点H.当AC=30米,∠CAE=150°时,∠HAC=30°.在Rt△AHC中,∵cos∠HAC=,∴AH=cos∠HAC×AC=cos30°×30=×30=15≈1.7×15=25.5(米).∴HE=AE+AH=4+25.5=29.5(米).由题意知,四边形HEFC是矩形,∴CF=HE=29.5米,∵29.5>26,∴该消防车能够实施有效救援..…………………….………………7分19. (8分)解:(1)选择的两个条件是:①②,结论是③,这个命题是真命题,理由:连接OD,∵AB=BC,∴∠A=∠C,∵OA=OD,∴∠A=∠ADO,∴∠C=∠ADO,∴OD∥BC,∴∠ODE=∠DEC=90°,∵OD是圆O的半径,∴DE是⊙O的切线;故答案为:①②,③(答案不唯一);.…………………….………………4分(2)连接BD,∵AB为⊙O的直径,∴∠ADB=90°,∵AB=BC,∴AD=DC=5,∵∠ADB=∠DEC=90°,∠A=∠C,∴△CDE∽△ABD,∴=,∴=,∴AB=,∴⊙O的直径为:..…………………….………………8分20. (8分)解:(1)设该种商品每次降价的百分率为x,依题意,得:200(1﹣x)2=128,解得:x1=0.2=20%,x2=1.8(不合题意,舍去),答:该种商品每次降价的百分率为20%;.…………………….………………3分(2)设每件商品应降价x元,根据题意,得:(128﹣80﹣x)(20+5x)﹣100=1475,解方程得x1=41,x2=3,∵在降价幅度不超过10元的情况下,∴x=41不合题意舍去.答:每件商品应降价3元..…………………….………………8分21. (10分)解:(Ⅰ)列表(完成表格).…………………….………………2分(Ⅱ)描点并画图..…………………….………………3分(Ⅲ)(1)y=|x2﹣4x+3|的图象可由函数y1=x2﹣4x+3将x轴下方图象关于x轴对称,x轴上方图象不变得到;故答案为x轴下方图象关于x轴对称,x轴上方图象不变;.…………………….………………4分(2)结合图象,|x2﹣4x+3|>8时,y=|x2﹣4x+3|图象在y=8的上方,∴解集是x>5或x<﹣1;故答案为x>5或x<﹣1.…………………….………………5分(3)①令x=0,则y=|x2﹣4x+3|=3,令y=0,则y=|x2﹣4x+3|=0,解得x=1或3,∴A(1,0),B(3,0),C(0,3),∴设直线BC的解析式为y=kx+b(k≠0),则∴∴y=﹣x+3;.…………………….……………7分②直线BC过(0,3),(2,1)和(3,0)三个点,如图所示,此时,直线BC与y=|x2﹣4x+3|的图象只有3个交点,∴m=0.设直线BC向上平移后的直线为y=﹣x+3+m,∵平移后的直线与函数y=|x2﹣4x+3|的图象恰好有3个交点,∴直线BC只能向上平移,且直线y=﹣x+3+m和y=﹣x2+4x﹣3有且只有一个交点,则只有一个解,于是,消去y得x2﹣5x+6+m=0有两个相等的实数根,∴△=1﹣4m=0,∴m=.综上所述,m=0或m=时将直线BC沿y轴平移m个单位长度后与函数y=|x2﹣4x+3|的图象恰好有3个交点..…………………….………………10分22. (10分)解:(1)①证明:如图①中,过点E作ET⊥BC于点T.∵四边形ABCD是矩形,∴∠A=∠ADC=∠EDG=90°,在△AEF和△DEG中,,∴△AEF≌△DEG(ASA),∴EF=EG,∵△FGH是等腰直角三角形,∴HE=EF=EG,HE⊥FG,∵∠A=∠ABT=∠ETB=90°,∴四边形ABTE是矩形,∴∠AET=∠FEH=90°,∴∠AEF=∠TEH,在△EAF和△ETH中,,∴△EAF≌△ETH(AAS),∴EA=ET,∴四边形ABTE是正方形,∴AE=AB,∵AD=2AE,∴AD=2AB;.…………………….………………3分②解:如图①﹣1中,时FH交BE于点J.∵∠FJB=∠EJH,∠FBJ=∠EHJ=45°,∴∠BFH=∠BEH,∴tan∠BFH=tan∠BEH=2,∴=2,∵△EAF≌△ETH≌△EDG,∴AF=DG=TH=1,设AB=BT=x,则=2,∴x=3,∴BF=2,BH=4,在Rt△BFH中,FH===2,∴S△DGH=×2×2=10;.…………………….………………6分(2)解:如图②中,过点H作HQ⊥AB于点Q,过点E作ER⊥QH于点R,连接BH.同法可证,△EAF≌△ERH,∴EA=ER,AF=RH,∵AE=ED=2,∴ER=AE=2,∵四边形AQRE是正方形,∴AQ=AE=2,∴BQ=1,∴S△BCH=×4×1=2,设AF=RH=y,∴S△BFH=(3﹣y)•(2+y)=﹣(y﹣)2+,∵﹣<0,∴y=时,△BFH的面积最大,最大值为,∴四边形BCHF的面积的最大值=2+=..…………………….………………10分。
南京外国语学校高中招生考试数学冲刺试题(3)及答案

南京外国语学校高中招生考试数学冲刺试题(三)一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.用四舍五入法把0.06097精确到千分位后,所得近似值的有效数字是( ). A .0,6,0 B .0,6,1,0 C .6,0,9 D .6,1 2.下列等式正确的是( ).A .(-1)5 = 1B .(-2)3×(-2)2 = 26C .(-5)8 ÷(-5)2 =-56D .(-4)0 = 1 3.已知 x + y = x -1 + y -1≠0,则xy 的值为( ). A .-1B .0C .1D .24.如图,涪江河电站(青义)工程,需开挖土石方约53万m 3,要求34个月完成.施工队加班加点,提前两个月完工.施工队实际挖洞所用的时间t (月)与剩余土石方量M (万m 3)的函数关系图象大致是( ). A . B . C . D .5.已知等腰三角形的两边长分别为6 cm ,3 cm ,则该等腰三角形的周长是( ). A .9 cm B .12 cm 或15 cm C .12 cm D .15 cm 6.某次射击训练中,一小组的成绩如下表:已知该小组的平均成绩为8.1环,那么成绩为8环的人数是( ). A .5人 B .6人 C .4人 D .7人 7.若方程组⎩⎨⎧=-+=+3)1(,134y a ax y x 的解x 与y 相等,则a 的值等于( ).A .4B .10C .11D .12 8.如图,以点O 为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P 为切点,且AB = 4,OP = 2.连结OA 交小圆于点E ,则扇形OEP 的面积为( ). A .4π B .3π C .2π D .8π9.△ABC 中,A (-1,2),B (-3,1),C (0,-1).若将△ABC 绕点C 顺时针旋转180︒后得到△A ′B ′C ′,则A 点的对应点A ′ 的坐标是( ).A .(2,-3)B .(1,-3)C .(2,-4)D .(1,-4) 10.已知函数xy 21=,y 2 = x + 1,若y 1>y 2,则x 的取值范围是( ). A .x <-1 或 0<x <2 B .-1<x <0 或 x >2 C .-2<x <0 或 x >1 D .x <-2 或 0<x <1 11.设b >0,二次函数y = ax 2 + bx + a 2-1的图象为下列之一:则a 的值为( ). A .1B .-1C .251-- D .251+- 12.如图,l 1、l 2、l 3 是同一平面内的三条平行直线,l 1与l 2间的距离是1,l 2与l 3间的距离是2,正三角形ABC 的三顶点分别在l 1、l 2、l 3上,则△ABC 的边长a 是( ).A .32B .364C .4173 D .3212二、填空题:本大题共6个小题,每小题4分,共24分.将答案直接填写在题中横线上. 13.21-的倒数是 . 14.计算:(9a 2b -6ab 2)÷(3ab )= .15.代数式11-x 有意义时,字母x 的取值范围是 .16.如图,在等腰梯形ABCD 中,AD ∥BC ,AB = CD ,对角线AC 、BD 相交于点O BCAl 1l 2 l 3有四个结论:① 梯形ABCD 是轴对称图形; ② ∠DAC =∠DCA ; ③ △AOB ≌△DOC ; ④ △AOD ∽△BOC . 请把正确的结论的序号填在横线上: 17.如图,在直角三角形ABC 中,∠ACB = 90︒,CA = 4. 点P 是半圆弧AC 的中点,连接BP ,线段BP 把图形APCB 分成两部分,则这两部分面积之差的绝对值是 .18.口袋中有20个球,其中白球9个,红球5个,黑球6个.现从中任取10个球,使得白球不少于2个但不多于8个,红球不少于2个,黑球不多于3个,那么上述取法的种数是 .三、解答题:本大题共7个小题,共90分.解答应写出文字说明、证明过程或演算步骤.19.(本题共2个小题,每小题8分,共16分) (1)计算:︒+︒+︒30tan 160sin 160cos .(2)先化简,再求值:)2(2ab ab a a b a --÷-,其中a = 1 +3,b = 1.20.(本题满分12分)房屋交易会期间,某公司对参加本次房交会的消费者进行了随机问卷BDAOC调查.共发放1 000份调查问卷,并全部收回,根据调查问卷,将消费者年收入的情况整理后,制成表格如下:将消费者打算购买住房面积的情况调查后,做出部分频数分布直方图:注:每组包含最小值不包含最大值,且住房的面积取整数.请你根据以上信息,回答下列问题:(1)根据表格可得,被调查的消费者平均年收人为 万元;被调查的消费者年收入的中位数是 万元;在平均数、中位数这两个数中 更能反映被调查的消费者年收入的一般水平;(2)根据频数分布直方图可得,打算购买100-120平方米房子的人数为 人;打算购买住房面积小于100平方米的消费者人数与被调查人数的百分数是 面积/平方米;(3)在图中补全这个频数分布直方图.21.(本题满分12分)如图,请在下列四个等式中,选出两个作为条件,推出△AED 是等腰三角形,并予以证明.(写出一种即可) 等式:① AB = DC , ② BE = CE , ③ ∠B =∠C , ④∠BAE =∠CDE .22.(本题满分12分)平面直角坐标系中,点A 在第一象限,点B 的坐标为(3,0),OA = 2,∠AOB = 60 . (1)求点A 的坐标;(2)若直线AB 交y 轴于点C ,求△AOC 的面积.23.(本题满分12分)青年旅行社为吸引市民组团去香水湾风景区旅游,推出了如下收费标BADEC准:某单位组织员工去香水湾风景区旅游,共支付给青年旅行社旅游费用27000元,请问该单位这次共有多少员工去香水湾风景区旅游?24.(本题满分12分)如图,AB ,AC ,AD 是圆中的三条弦, 点E 在AD 上,且AB = AC = AE .请你说明以下各式成立的理由. (1)∠CAD = 2∠DBE ; (2)AD 2-AB 2 = BD · DC .25.(本题满分14分)设抛物线y = ax 2 + bx -2与x 轴交于两个不同的点如果人数不超过25人,人均旅游费用为1000元如果人数超过25人,每增加1人,人均旅游费用降低20元,但人均旅游费用不得低于700元DACE BA(-1,0)、B(m,0),与y轴交于点C.且∠ACB = 90°.Array(1)求m的值和抛物线的解析式;(2)已知点D(1,n)在抛物线上,过点A的直线y = x + 1交抛物线于另一点E.若点P在x轴上,以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标.参考答案一.1.D 2.D 3.C 4.A 5.D 6.A 7.C 8.C 9.D 10.D 11.B 12.D 二.13.—2 14. 3a -2b 15. x >1 16.①③④ 17.4 18.16三. 19.(1)原式=323121++=23321=++;(2)原式=ab ab a a b a 222+-÷-=b a b a b a -=--1)(2. 把a = 1 +3,b = 1代入,可得原式=33. 20.(1)2.39,1.8,中位数 (2)240,52% (3)如图(见前) 21.已知:①③(或①④,或②③,或②④) 证明:在△ABE 和△DCE 中,∵ ∠B =∠C ,∠BEA =∠CED ,AB = DC , ∴ △ABE ≌△DCE ,∴ AE = DE . △AED 是等腰三角形.22.(1)过点A 作x 轴的垂线,垂足为D . 在Rt △OAD 中,OA = 2,∠AOB = 60︒, ∴ ∠OAD = 30︒,OD =21OA = 1,于是 AD =3.A (1,3). (2)设直线AB 的解析式为y = kx + b , 把A (1,3),B (3,0)分别代入,得⎩⎨⎧+=+=,30,3b k b k 解得23-=k ,233=b . ∴ AB 的解析式为y =23-x +233.令 x = 0 得 y =233,则C (0,233). 所以,S △AOC =21OC ×1 =433. 23.设该单位这次共有x 名员工去香水湾风景区旅游,因为1000×25 = 25000<27000,所以员工人数一定超过25人.可得方程 x = 27000,整理,得 x 2-75x + 1350 = 0, 解得 x 1 = 45,x 2 = 30. 当x 1 = 45时,1000-20(x -25)= 600<700,故舍去x 1. 当x 2 = 30时,1000-20(x -25)= 900>700,符合题意. 答:该单位这次共有30名员工去香水湾风景区旅游. 24.(1)如图,连接BC ,∵ AB = AC = AE , ∴ ∠5 =∠2,∠2 +∠3 =∠6.又 ∠4 +∠5 =∠6 =∠2 +∠3, ∴ ∠4 =∠3.而 ∠1 =∠4 +∠3,∴ ∠1 = 2∠4,即 ∠CAD = 2∠DBE . (2)设BC 与AD 的交点为G . ∵ ∠2 = ∠5,∠BAG =∠DAB ,∴ △BAG ∽△DAB , ∴ AB 2 = AG · AD .∴ AD 2-AB 2 = AD 2-AG · AD = AD (AD -AG )= AD · DG . 又 ∵ ∠5 =∠ADC ,∠DBG =∠1,∴ △BDG ∽△ADC ,∴ DB : AD = DG :DC ,AG · AD = BD · DC . ∴ AD 2-AB 2 = BD · DC .25.(1)在y = ax 2 + bx -2中,令x = 0,得 y =-2, ∴ C (0,-2).∵ ∠ACB = 90°,CO ⊥AB ,∴ △AOC ∽△COB ,∴ OA ·OB = OC 2, ∴ OB = 4,即 m = 4.将A (-1,0),B (4,0)代入y = ax 2 + bx -2,解得21=a ,23-=b .∴ 抛物线的解析式为223212--=x x y . (2)D (1,n )代入223212--=x x y ,得 n =-3.由 y = x + 1和223212--=x x y 解得⎩⎨⎧=-=01y x 或 ⎩⎨⎧==76y x ∴ E (6,7).过E 作EH ⊥x 轴于H ,则H (6,0),∴ AH = EH = 7,∴ ∠EAH = 45°. 过D 作DF ⊥x 轴于F ,则F (1,0),∴ BF = DF = 3,∴ ∠DBF = 45°, ∴ ∠EAH =∠DBF = 45°.从而 ∠DBH = 135°,90°<∠EBA <135°, 则点P 只能在点B 的左侧:DA CE B124 5 63① 若△DBP 1∽△EAB ,则AEBD AB BP =1, ∴ 715272351=⨯=⋅=AE BD AB BP ,∴ 71371541=-=OP ,得 ),(07131P . ② 若△DBP 2∽△BAE ,则AB BD AE BP =2,∴ 542523272=⨯=⋅=AB BD AE BP , ∴ 52245422=-=OP , 得 ),(05222-P . 综合①、②,点P 的坐标为),(07131P 或),(05222-P .。
深圳南山外国语学校(集团)华侨城中学2023年九年级上学期月考数学试题(原卷版)

南山外国语学校(集团)华侨城中学2023-2024学年10月学情分析九年级数学试卷一、选择题(每题3分,共30分)1. 下列图形中既是中心对称图形又是轴对称图形的是( )A. B. C. D. 2. 如图,自由转动转盘,转盘上的指针(转盘被分成六等份)停在红色区域中的概率是( )A. 16B. 13C. 12 D. 13. 一元二次方程2430x x −+=的根的情况是( )A. 有两个相等实数根B. 有两个不相等的实数根C. 只有一个实数根D. 没有实数根 4. 矩形、菱形、正方形都具有的性质是( )A. 对角线互相垂直平分B. 对角线相等C. 对角线互相垂直D. 对角线互相平分 5. 用配方法解方程2430x x −−=,则配方正确的是( )A. 2(2)1x −=B. 2(2)1x +=C. 2(2)7x −=D. 2(2)7x += 6. 若29a b =,则a b a+的值为( ) A. 112 B. 79 C. 911 D. 727. 如图,四边形ABCD 是菱形,对角线AC 与BD 相交于点O ,DH BC ⊥于点H .若8AC =,6BD =,则DH 长度为( )的的A. 485B. 365C. 245D. 48. 如图,在长为54米、宽为38米的矩形草地上修同样宽的路,余下部分种植草坪.要使草坪的面积为1800平方米,设道路的宽为x 米,则可列方程为( )A. (54)(38)1800x x −−=B. 2(54)(38)1800x x x −−+=C. 543854381800x x ×−−=D. 54381800x x +=9. 如图,在矩形COED 中,点D 的坐标是()1,3,则CE 的长是( )A. 3B.C.D. 410. 如图,正方形ABCD 的边长为1,AC ,BD 是对角线.将△DCB 绕着点D 顺时针旋转45°得到△DGH ,HG 交AB 于点E ,连接DE 交AC 于点F ,连接FG ,则下列结论:①四边形AEGF 是菱形;②△AED ≌△GED ;③∠DFG =112.5°;④BC +FG =1.5.其中正确的结论是( )A. ①②③④B. ①②③C. ①②D. ②二、填空题(每题3分,共15分)11. 分解因式:228ab a −=______.12. 一个暗箱里放有a 个白球和3个红球,它们除颜色外完全相同.若每次将球搅匀后,任意摸出1个球记下颜色再放回暗箱.通过大量重复摸球试验后发现,摸到红球的频率稳定在20%附近,那么可以推算出a 的值大约是_____.13. 设m 是方程220230x x −+=的一个根,21m m −+的值为______.14. 在一次足球邀请赛中,参赛的每两个队之间都要比赛一场,共比赛28场,设共有x 个队参赛,根据题意,可列方程为______.15. 如图,在Rt △ABC 中,∠ACB=90º ,将△ABC 绕顶点C 逆时针旋转得到△A ′B ′C ,M 是BC 的中点,N 是A ′B ′的中点,连接MN ,若BC =2 cm,∠ABC =60°,则线段MN 的最大值为_____.三、解答题(共7小题,共55分)16. 解方程:(1)22350x x +−=.(2)24120x x −−=17. 先化简,再求值23224x x x x x x −÷ −+−.其中x 是﹣2、﹣1、0、2中的一个. 18. 为响应国家全面推进中小学校“社会主义核心价值观”教育活动,某校对全校学生进行了中期检测评价,检测结果分为A (优秀)、B (良好)、C (合格)、D (不合格)四个等级,并随机抽取若干名学生的检测结果作为样本进行数据处理,制作了如图所示不完整的统计表和统计图.(1)参加这次调查的学生总人数为 人;类别C 所对应扇形的圆心角度数为 °; (2)请补全条形统计图;(3)类别D 的4名学生中有3名男生和1名女生,班主任想从这4名学生中随机选取2名学生进行约谈,请用列举法(画树状图或列表)求所选取的2名学生恰好都是男生的概率.19. 如图,在ABCD 中,5AB =,4BC =,点F 是BC 上一点,若将DCF 沿DF 折叠,点C 恰好与AB 上的点E 重合,过点E 作EG BC ∥交DF 于点G ,连接CG .(1)求证:四边形EFCG 是菱形;(2)当A B ∠=∠时,求点B 到直线EF 的距离.20. 随着疫情防控形势稳步向好,“复工复产”成为主旋律.某生产无人机公司统计发现,公司今年2月份生产A 型无人机2000架,4月份生产A 型无人机达到12500架.(1)求该公司生长A 型无人机每月产量的平均增长率;(2)该公司还生产B 型无人机,已知生产1架A 型无人机的成本是200元,生产1架B 型无人机的成本是300元.现要生产AB 、两种型号的无人机共100架,其中A 型无人机数量不超过B 型无人机数量的3倍.公司生产A B 、两种型号无人机各多少架时才可使生产成本最少?21 阅读下列材料:解方程:42650x x −+=.这是一个一元四次方程,根据该方程的特点,它的解法通常是:.设2x y =,那么42x y =,于是原方程可变为2650y y −+= ①,解这个方程得:11y =,25y =.当11y =时,21x =.∴1x =±;当25y =时,25x =,∴x =以原方程有四个根:11x =,21x =−,3x =4x =.这个过程中,我们利用换元法达到降次的目的,体现了转化的数学思想.(1)用换元法解方程:()()2224120x x x x −−−−= (2)Rt ABC △三边是a ,b ,c ,若两直角边a ,b 满足()()7100a b a b ++−+=,斜边4c =,求Rt ABC △面积.22. 定义:对于一个四边形,我们把依次连接它的各边中点得到的新四边形叫做原四边形的“中点四边形”.如果原四边形的中点四边形是个正方形,我们把这个原四边形叫做“中方四边形”.概念理解】:(1)下列四边形中一定是“中方四边形”的是______.A .平行四边形B .矩形C .菱形D .正方形【性质探究】:(2)如图1,四边形ABCD 是“中方四边形”,观察图形,直接写出四边形ABCD 的对角线AC ,BD 的关系;【问题解决】:(3)如图2.以锐角ABC 的两边AB ,AC 为边长,分别向外侧作正方形ABDE 和正方形ACFG ,连接BE ,EG ,GC .求证:四边形BCGE 是“中方四边形”;【拓展应用】:如图3,已知四边形ABCD 是“中方四边形”,M ,N 分别是AB ,CD 的中点.(4)试探索AC 与MN 的数量关系,并说明理由.(5)若2AC =,求AB CD +的最小值.的【。
广东省深圳市南外集团大冲学校2023-2024学年九年级上学期月考数学试题
广东省深圳市南外集团大冲学校2023-2024学年九年级上学期月考数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题A .2π4.如下图,四边形ABCD 边形不一定为矩形的是(A ..C ..5.用配方法解一元二次方程的过程中,配方正确的是(A .2(22)x +=B .2(2)6x +=6.如图,在平面直角坐标系中,菱形的顶点D 在x 轴上,边A.(0,-8)C.(-5,0)=+ 7.已知一次函数y kx20++-=的根的情况是(x x k bA.没有实数根C.有两个相等的实数根8.已知m、n是一元二次方程值等于()A.2021B 9.如图,两个反比例函数在C1上,PA⊥x轴于点AA.4B.2 10.如图,点D,E,F分别在DF的中点,连接CM并延长交A .15B 二、填空题11.在一个不透明的袋子中放有每次把球充分搅匀后,任意摸出一球记下颜色后再放回袋子,通过大量重复试验后,发现摸到红球的频率稳定在12.如图,点D ,E 分别在4.5cm AC =,则CE 的长为13.如图,在矩形ABCD DC 于点H ,若8AB =14.如图,AOB 与CDB △CDB S =△.15.如图为边长为4的正方形ABCD三、解答题16.解方程:(1)2450x x +-=;(2)()()2323x x x -=-.17.本月深圳市提出了新一轮体育中考方案,某校对初一年级学生进行摸底测试,将目标效果测试中第三类选考项目中的三项(足球运球、篮球运球、排球垫球任选一项)情况进行统计,并将统计结果绘制成统计图,请你结合图中所给信息解答下列问题:各项目人数占比分布扇形统计图篮球运球成绩统计图(1)学校参加本次测试的人数有___________人,参加“排球垫球”测试的人数有___________人;(2)学校准备从“排球垫球”成绩较好的两男两女四名学生中,随机抽取两名学生为全校学生演示动作,请用列表法或画树状图法求恰好抽取到一名男生和一名女生的概率.18.如图,在四边形ABCD 中,AB ∥DC ,AB =AD ,对角线AC ,BD 交于点O ,AC 平分∠BAD ,过点C 作CE ⊥AB 交AB 的延长线于点F ,连接OE(1)求反比例函数的解析式,画出一次函数的图象;(2)请直接写出不等式0mkx b x+-<的解集;(3)求COD △的面积.21.设计货船通过双曲线桥的方案素材1一座曲线桥如图1所示,当水面宽16AB =米时,桥洞顶部离水面距离4CD =米.已知桥洞形如双曲①建立平面直角坐标系如图落在第一象限的角平分线上.甲说:点C可以在第一象限角平分线的任意位置.乙说:不对吧?当点C落在A的坐标为_______________曲线的函数表达式为_____________在双曲线的函数表达式为意.此时货船能通过该桥洞吗?若能,若不能,至少要增加多少吨货物?(提示:先求出桥洞所在双曲线的函数表达式),点G是AB的中点.菱形OB以及和点N分别是AB与1始终在线段BG上,两个菱形重叠部分的面积总等【类比探究】已知菱形ABCD 的对角线相交于点形ABCD 的边AB 、BC 相交于点(1)如图1,若等边PEF !的顶点(2)数学兴趣小组对上面的问题进行了拓展探究,如图平移至如图所示位置,若PAPC式子表示),并说明理由.(3)如图3,在(2)的条件下,延长GN PAk PN PC==,求k 的值.。
2024年4月深圳市南外+南二外集团初三联考数学答案

2023—2024学年第二学期期中检测参考答案一、选择题:本题共10小题,每小题3分,共30分。
在每小题给出的选项中,只有一项是符合题目要求的。
12345678910AABDBBCBCD二、填空题:本题共5小题,每小题3分,共15分。
11._2.8×105___________.12.m(m+5)(m-5).13.61.14.3233π-.15.三、解答题:本题共7小题,共55分。
第16题6分,第17题7分,第18、19、20题8分,第21、22题9分.解答应写出文字说明,证明过程或演算步骤。
16.(6分)()()23.143tan 6012π---︒+-11314=--+1141=-+74=-;17.(7分)解:2344111x x x x x -+⎛⎫--÷ ⎪--⎝⎭()2231121x x x x x x --++--=÷-()221412x x x x -⋅=---()()()222112x x x x x +--=⋅--22x x +=--,∵分式要有意义,∴()()210x x --≠,∴2x ≠且1x ≠,∴当x=3时,原式32532+=-=--.18.(8分)(1)解:如下图,线段AC 即为所求-----------------------------2分;(2)如图,作点A 关于直线3x =-的对称点D ,∵(0,4)A ,∴(6,4)D -,∴AD x ∥轴,即线段CD 即为所求-----------------------------4分;(3)由轴对称的性质可得,CD AC AB ==,又∵AD x ∥轴,∴四边形ABCD 为平行四边形,∵(0,4)A ,(3,0)C ,∴平行四边形ABCD 的中心G 坐标为3(,2)2-,将点3(,2)2G -代入直线y kx =,可得322k =-,解得43k =-,-----------------------------6分作直线OG ,则直线OG 可将四边形ABCD 的面积平分为相等的两部分-----------------------------8分.19.(8分)解(1)证明:连接OD ,OC OD = ,OCD ODC ∴∠=∠,-----------------------------1分2DOB OCD ODC BCD ∴∠=∠+∠=∠,12BCD BOD ∴∠=∠,12BCD A ∠=∠ ,BOD A ∴∠=∠,-----------------------------2分90ACB ∠=︒ ,90A B ∴∠+∠=︒,90BOD B ∴∠+∠=︒,-----------------------------3分90BDO ∴∠=︒,OD 是圆O 的半径,∴直线AB 与圆O 相切;-----------------------------4分(2)3sin 5OD B OB == ,3OD =,5OB ∴=,-----------------------------5分8BC OB OC ∴=+=,在Rt ACB △中,3sin 5AC B AB ==,∴设3AC x =,5AB x =,-----------------------------6分48BC x ∴==,2x ∴=,-----------------------------7分36AC x ∴==.-----------------------------8分其他解法酌情给分.20.(8分)解(1):设甲种烟花的进货单价为x 元,则乙种烟花的进货单价为()9x +元,-------------------1分由题意得:312042009x x =+,----------------------------2分解得:26x =,----------------------------3分经检验:26x =是原方程的解,且符合题意,则935x +=,(没检验扣一分)答:甲种烟花的进货单价为26元,则乙种烟花的进货单价为35元;----------------------------4分(2)设购进甲种烟花m 个,则乙种烟花()1000m -个,花费为y 元,由题意得:()26100035350009y m m m =+-⨯=-,----------------------------5分∵乙种烟花的购货数量不少于甲种烟花数量的3倍,∴10003m m -≥,解得:250m ≤,---------------------------6分∵90-<,则y 随m 的增大而减小,∴当250m =时,y 最小,最小为3500925032750y =-⨯=元,----------------------------7分则1000750m -=,答:购进甲种烟花250个,则乙种烟花750个,花费最少为32750元.----------------------------8分21.(9分)解(1)将30B (,),03C (,)代入2y x bx c =-++,得9303b c c -++=⎧⎨=⎩,解得23b c =⎧⎨=⎩,∴二次函数的解析式为223y x x =-++.----------------------------2分(2)设223P x x x ++(,-),直线BC 的解析式为y mx n =+,则303m n n +=⎧⎨=⎩,解得13m n =-⎧⎨=⎩,∴直线BC 的解析式为3y x =-+,----------------------------3分则3Q x x -+(,),∴()221133273322228CPB BPQ CPQ S S S QP OB x x x ⎛⎫=+=⋅=-+⨯=--+⎪⎝⎭ ----------------------------4分当32x =时,CPB △的面积最大,----------------------------5分此时,点P 的坐标为315,24⎛⎫⎪⎝⎭,CPB △的面积最大278.----------------------------6分(3)存在.如图,设点223P x x x ++(,-),PP '交CO 于点E ,若四边形POP C '是菱形,连接PP ',则32PE OC OE CE ⊥==,,∴23232x x -++=,----------------------------7分解得12102x =,22102x =----------------------------8分∴210362P ⎫+⎪⎪⎝⎭或P (23,2102-)----------------------------9分22.(9分)解(1)∵34AB AD BC DE ==,90ABC ADE ∠=∠=︒,∴ABC ADE △△∽,---------------------------1分∴BAC DAE ∠=∠,∴CAE BAD ∠=∠,∵43BC AB =,∴2253AC AB BC AB =+=,---------------------------2分同理,53AE AD =,∴35AB AD AC AE ==,CAE BAD ∽,∴35BD AD CE AE ==;--------------------------3分(2)如图,过点D 作DH BC ∥,交EF 的延长线于H ,作DN EF ⊥于N ,则BCF H ∠=∠∵△ABC 是等腰直角三角形,90ACB ∠=︒,6AB =,∴32AC BC ==由旋转知,AB AD =,AC AE =,60BAD CAE ∠=∠=︒,∴ABD △和ACE △都是等边三角形,---------------------------4分∴6AB BD ==,60ACE AEC ∠=∠=︒,∵90AED ACB ==︒∠∠,∴30BCF DEF ∠=∠=︒,∴30DEF H ∠=∠=︒,∴DH DE BC ===∴122DN DE ==,==NE ---------------------------5分∵BFC DFH ∠=∠,∴()AAS BCF DHF ≌,∴132===BF DF BD ,∴2FN =,∴EF EN FN =+---------------------------6分(3):过点N 作NH AC ⊥于点H ,如图所示:在等边△MNC 中,MC NC =,60MCN ∠=︒.在等边△ABC 中,60BCA ∠=︒,123DC BC ==,∴MCN BCA ∠=∠,∴MCN MCH BCA MCH ∠-∠=∠-∠,即MCD NCH ∠=∠.在MCD △和NCH △中,MDC NHC MCD NCH MC NC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AAS MCD NCH ≌,---------------------------7分∴MD NH =,1122CH CD BC AC ===,∴点N 总在NH 上,即NH 垂直平分AC ,∴点N 经过的路径为一条线段,起点为点M A 、重合时点N 的位置,终点为AC 的中点H ,---------------------------8分如图所示:在等边△MNC 中,点M A 、重合时,6MC AC ==,此时由等边三角形三线合一性得NH ===,。
广东省深圳市南山外国语学校(集团)2024-2025学年八年级上学期期中考试数学试卷

广东省深圳市南山外国语学校(集团)2024-2025学年八年级上学期期中考试数学试卷一、单选题1.2的平方根是()A .2B .4±CD .2.如图,围棋棋盘放在某平面直角坐标系内,已知黑棋(甲)的坐标为()2,2-,黑棋(乙)的坐标为()1,2--,则白棋(甲)的坐标为()A .()2,2-B .2,1C .()1,2D .()2,23.下列运算正确的是()A=B .3=C4=D =4.当x 从0开始逐渐增大时,对同一个x 值,下列函数中函数值先到达100的是()A .51y x =-B .5y x =C .2y x =D .22y x =+5.已知点()2,1A a a -+,点()23B ,,直线AB x ∥轴,则a 的值是()A .1B .2C .3D .46.某市出租车收费标准如下表:设行驶里程数为km x ,收费为y 元,则y 与x (3x ≥)之间的关系式为()里程数收费/元3km 以下(含3km )83km 以上每增加1km1.8A . 1.8y x =B . 1.88y x =+C .8y x =D . 1.82.6y x =+7.如图,在数轴上,点A,B表示的数分别为0,2,BC⊥AB于点B,且BC=1.连接AC,在AC上截取CD=BC,以点A为圆心,AD的长为半径画弧,交线段AB于点E,则点E表示的实数是()A.B+1C.2D1P,第2次碰弹,反弹时反射角等于入射角,当小球第1次碰到正方形的边时的点为1(2,0)P的坐标是()到正方形的边时的点为2P,…,第n次碰到正方形的边时的点为n P,则点2024A.(2,0)B.(4,3)C.(2,4)D.(4,1)二、填空题最接近的整数是.910.如图,阴影部分是两个正方形,其他三个图形是一个正方形和两个直角三角形,则阴影部分的面积之和为.=+的图象如图所示,则代数式7k b-的值为.11.直线y kx b12.“剪纸是一种用剪刀或刻刀在纸上剪刻花纹,用于装点生活或配合其他民俗活动的民间艺术.如图是一个正六边形剪纸,将其放在平面直角坐标系中,边OE 在x 轴上,若点E 的坐标为()4,0,则点A 的坐标为.13.在ABC V 中,6068ABC BC AC ∠=︒==,,,点D 、E 在AB AC 、边上,且=AD CE ,则CD BE +的最小值.三、解答题14.计算:+(2))211(4)15.如图,在平面直角坐标系xOy 中,ABC V 三个顶点的坐标分别为()0,2A ,()2,0B ,()5,3C .(1)画出ABC V 关于y 轴对称的111A B C △;(2)计算:ABC V 的面积是,AC 边上的高是.16.如图有一块等腰三角形菜地,其中13,10AC BC AB ===,点E 为AB 的中点.现需要开辟一块三角形的空地用于堆肥,已知4,3AF EF ==.(1)你能确定AEF △的形状吗,请说明理由.(2)计算阴影部分的面积.17.莲池区某学校门口道路中间的隔离护栏平面示意图如图所示,假如每根立柱宽为0.2米,立柱间距为3米.立柱根数12345护栏总长度(米)0.2 3.498.(1)根据如图所示,将表格补充完整;(2)设有x 根立柱,护栏总长度为y 米,则y 与x 之间的关系式是______.(3)求护栏总长度为93米时立柱的根数?18.阅读材料:像2)2)(0)a a ⨯-==≥,……这种两个含二次根式的代数式相乘,积不含二次根式,我们称这两个代数式互为有理化因式.在进行二次根式运算时,利用有理化因式可以化去分母中的根号.数学课上,老师出了一道题“已知a =求2361a a --的值.”聪明的小明同学根据上述材料,做了这样的解答:因为111a ==,所以1a -=所以2(1)2a -=,所以2212a a -+=.所以221a a -=,所以2363a a -=,所以23612a a --=.请你根据上述材料和小明的解答过程,解决如下问题:的有理化因式是;(2)比较大小:>,<,=,≥或≤中的一种);(3)若a =22123a a -++的值.19.【综合实践】新能源汽车多数采用电能作为动力来源,不需要燃烧汽油,这样就减少了二氧化碳等气体的排放,从而达到保护环境的目的.【实验操作】为了解汽车电池需要多久能充满,以及充满电量状态下电动汽车的最大行驶里程,某综合实践小组设计两组实验.实验Ⅰ:探究电池充电状态下电动汽车仪表盘增加的电量()%y 与时间t (分钟)的关系,数据记录如表1:电池充电状态时间t (分钟)0103060增加的电量()%y 0103060实验Ⅱ:探究充满电量状态下电动汽车行驶过程中仪表盘显示剩余电量()%e 与行驶里程s (千米)的关系,数据记录如表2:汽车行驶过程已行驶里程s (千米)0160200280显示剩余电量()%e 100605030【建立模型】(1)观察表1、表2发现都是一次函数模型,请结合表1、表2的数据,直接写出函数关系式(不写自变量的取值范围).y 关于t 的函数表达式为____________,e 关于s 的函数表达式为_____________;【解决问题】(2)某电动汽车在充满电量的状态下,从A 地出发前往距出发点480千米的B 地,在途中服务区进行一次充电后继续行驶,其已行驶里程数(s )和显示剩余电量(e )的函数关系如下图所示:①该车到达B 地时,显示剩余电量e 的值为____________;该车进入服务区充电前显示剩余电量e 的值为_____________.②该车中途充电用了多少分钟?③当汽车显示剩余电量e 的值为60时,该车距出发点A 地多少千米?20.如图,在平面直角坐标系中,直线26y x =+与x 轴,y 轴分别交于点A ,C ,经过点C 的另一直线与x 轴交于点()6,0B .(1)求直线BC 的解析式;(2)若点G 是直线BC 上一动点,过点G 作x 轴的垂线交x 轴于点M ,与直线26y x =+交于点H ,且满足12GH GM =,求点G 的横坐标;(3)若点G 是线段BC 上一动点,点N 在x 轴上,且满足45,OGN OG GN ∠=︒=,直接写出点G 和点N 的坐标.。
南京外国语学校高中招生考试数学冲刺试题(2)及答案

南京外国语学校高中招生考试数学冲刺试题(二)一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.-3的倒数是( ). A .3 B .-3C .31D .31-2.青藏高原是世界上海拔最高的高原,它的面积约为2 500 000平方千米.将2 500 000用科学记数法表示应为( ).A .0.25×107B .2.5×107C .2.5×106D .25×1053.在函数32+=x y 中,自变量x 的取值范围是( ). A .x ≠3B .x ≠0C .x >-3D .x ≠-34.如图,AD ∥BC ,点E 在BD 的延长线上, 若∠ADE = 155︒,则∠DBC 的度数为( ). A .155︒B .50︒C .45︒D .25︒5.小敏所在学习小组的同学们,响应“为祖国争光,为奥运添彩”的号召,主动到附近的7个社区帮助爷爷、奶奶们学习英语日常用语.他们记录的各社区参加其中一次活动的人数如下:33,32,32,31,28,26,32,那么这组数据的众数和中位数分别是( ). A .32,31B .32,32C .3,31D .3,326.若不等式ax + b >0的解集为abx -<,且a + b >0,则抛物线y = ax 2 + bx + c 的对称轴所在位置是( ).A .y 轴B .y 轴的右侧C .y 轴的左侧D .无法确定 7.如图,圆内接四边形ABCD 的对角线相交于E ,AB 、DC 的延长线相交于P ,则图中一定相似的三角形有( ). A .3对 B .4对 C .5对 D .6对 8.用圆心角为60°,半径为24 cm 的扇形做成一个圆锥的 侧面,那么这个圆锥底面圆的半径是( ).A .4π cmB .8π cmC .4 cmD .8 cm 9.以下四个命题:① 一组对边平行,一组对角相等的四边形是平行四边形;AD BCE C BEAD P② 一组对边平行且两条对角线相等的四边形是矩形; ③ 一组邻边相等且一条对角线平分一组对角的四边形是菱形; ④ 四条边相等的四边形是正方形. 其中真命题的个数为( ).A .1 个B .2 个C .3 个D .0个10.甲、乙、丙、丁四位同学参加校田径运动会4×100米接力跑比赛,如果任意安排四位同学的跑步顺序,那么恰好由甲将接力棒交给乙的概率是( ). A .41B .61 C .81 D .121 11.7条长度均为整数厘米的线段a 1,a 2,a 3,a 4,a 5,a 6,a 7,满足a 1<a 2<a 3<a 4<a 5<a 6<a 7,且这7条线段中的任意3条都不能构成三角形.若a 1 = 1厘米,a 7 = 21厘米,则a 6 =( ). A .18厘米B .13厘米C .8厘米D .5厘米12.方程组⎩⎨⎧=+=+6||,12||y x y x 的解的个数为( ).A .1B .2C .3D .4二、填空题:本大题共6个小题,每小题4分,共24分.将答案直接填写在题中横线上. 13.-5.9-(-6.1)= . 14.分解因式ab 2-9a ,得 .15.如图,△ABC 中,BD 平分∠ABC ,AD ⊥BD 于D , E 为AC 的中点,AB = 5,BC = 7,则DE = . 16.△ABC 中,∠A 和∠B 均为锐角,AC = 6,BC = 33,且33sin =A ,则cosB 的值为 .解 在△ABC 中作高CD .∵ AC = 6,33sin =A , ∴ 32sin =⋅=A AC CD , 15)32()33(22=-=DB , ∴ 353315cos ===BC DB B . 17.用“*”定义新运算:对于任意实数a ,b ,都有a * b = b 2 + 1.例如,7 * 4 = 42 + 1 = 17,那么 5 * 3 =;当m 为实数时,m * (m * 2)=_______.EDABC18.如图,在△ABC 中,AB = AC ,M ,N 分别是AB ,AC 的 中点,D ,E 为BC 上的点,连结DN ,EM .若AB = 13 cm ,BC = 10 cm ,DE = 5 cm ,则图中阴影部分的面积为cm 2.三、解答题:本大题共7个小题,共90分.解答应写出 文字说明、证明过程或演算步骤.19.(本题共2个小题,每小题8分,共16分)(1)计算:1212009|32|12-+---)()(.(2)解方程:21211=++-x x x .20.(本题满分12分)在平面直角坐标系xOy 中,直线y =-x 绕点O 顺时针旋转90︒得到C直线l .直线l 与反比例函数xky =的图象的一个交点为A (a ,3),试确定反比例函数的解析式.21.(本题满分12分)如图,梯形ABCD 中,AD ∥BC ,∠ABC = 90︒, ∠C = 45︒,BE ⊥CD 于点E ,AD = 1,CD = 22.求BE 的长.22.(本题满分12分)如图,⊙O 与Rt △ABC 的斜边AB 相切于点D A D B CE与直角边AC 相交于点E ,且DE ∥BC .已知AE =22,AC =23, BC = 6,求⊙O 的半径.23.(本题满分12分)某区九年级有3000名学生参加“科学发展观知识竞赛”活动.为了了解本次知识竞赛的成绩分布情况,从中抽取了200名学生的得分(得分取正整数,满分为100分)进行统计. 频率分布表:请你根据不完整的频率分布表,解答 下列问题:(1)补全频数分布直方图;(2)若将得分转化为等极,规定得分低于59.5分评为“D ”,59.5~69.5分评为“C ”,69.5~89.5分评为“B ”,89.5~100.5分评为“A ”.这次全区七年级参加竞赛的学生约有多少学生参赛成绩被评为“D ”?如果随机抽查一名参赛学生的成绩等级,则这名学生的成绩被评为“A ”,“B ”,“C ”,“D ”哪一个等极的可能性大?请说明理由.24.(本题满分12分)(1)如图,△ABC 中,∠ACB 是直角,∠B = 60 ,AD ,CE 分别是成绩49.5 59.5 69.5 79.5 89.5∠BAC ,∠ACB 的平分线,AD ,CE 相交于点F .请写出DF 与EF 之间的数量关系; (2)如图,△ABC 中,如果∠ACB 不是直角,而(1)中的其他条件不变,请问,在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.25.(本题满分14分)如图,在Rt △ABC 中,∠C = 90 ,BC = 8厘米,点D 在AC 上,CDFEBAD CEBAD C F= 3厘米.点P、Q分别由A、C两点同时出发,点P沿AC方向向点C匀速移动,速度为每秒k厘米,行完AC全程用时8秒;点Q沿CB方向向点B匀速移动,速度为每秒1厘米.设运动的时间为x秒(0<x<8),△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米.(1)求y1与x的函数关系,并在图中画出y1的图象;(2)如图2,y2的图象是抛物线的一部分,其顶点坐标是(4,12),求点P的速度及AC 的长;(3)在图2中,点G是x轴正半轴上一点(0<OG<8),过G作EF垂直于x轴,分别交y1、y2的图象于点E、F.①说出线段EF的长在图中所表示的实际意义;②当0<x<6时,求线段EF长的最大值.参考答案一.1.D 2.C 3.D 4.d 5.B 6.B 7.B 8.C 9.A 10.A 11.B 12.A 二.13.0.2 14.a (b + 3)(b -3) 15.1 16.3517.10,26 18.30 三.19.(1)原式=3232--1 + 2 = 1.(2)原方程可化为 (x + 1)+ 2x (x -1)= 2(x + 1)(x -1). 即 x + 1 + 2x 2-2x = 2x 2-2, ∴ x = 3. 经检验x = 3是原方程的解.20.依题意得,直线l 的解析式为y = x .因为A (a ,3)在直线y = x 上,则a = 3,即A (3,3). 又因为A (a ,3)在x k y =的图象上,可求得k = 9.所以反比例函数的解析式为xy 9=. 21.如图,过点D 作DF ∥AB 交BC 于F . ∵ AD ∥BC ,∠ABC = 90︒,∴ 四边形ABFD 是矩形,于是 BF = AD = 1. 在Rt △DFC 中,∠C = 45︒,CD = 22, 由CDCFC =cos ,得CF = 2, ∴ BC = BF + FC = 3. 在△BEC 中,∠BEC = 90︒,BC BE C =sin ,求得223=BE . 22.636)23(22=+=AB .∵ DE ∥BC , ∴ △AED ∽△ACB ,∴ AC AE CB ED =,423226=⨯=ED .过点O 作OF ⊥DE ,F 是垂足,连结OD ,则221==ED FD .由△OFD ∽△BCA ,得CAFDBA OD =,故所求半径3223263=⨯=OD . 23.(1)图见右.(2)由表知:评为“D ”的频率是20120010=. FAD BCE由此估计全区七年级参加竞赛的学生约有3000201⨯= 150(人)被评为“D ”. ∵ P (A )= 0.36,P (B )= 0.51, P (C )= 0.08,P (D )= 0.05,∴ P (B )>P (A )>P (C )>P (D ),∴ 随机抽查一名参赛学生的成绩等级,“B ”的可能性大. 24.(1)DF 与EF 之间的数量关系为 DF = EF . (2)(1)中的结论DF = EF 仍然成立.证明 过点F 分别作FG ⊥AB 于点G ,FH ⊥BC 于点H . ∵ ∠B = 60︒,且AD ,CE 分别是∠BAC ,∠ACB 的平分线, ∴ 可得∠GAF +∠HCF = 60︒,F 是△ABC 的内心. ∴ ∠GEF = 60︒ +∠EAF ,FG = FH .又 ∵ ∠HDF =∠B +∠EAF ,∴ ∠GEF =∠HDF , 因此,可得△GEF ≌△HDF ,∴ EF = DF . 证明二 如图,在AC 上截取AG = AE ,连结FG . ∵ ∠EAF =∠GAF ,AF 为公共边,∴ △EAF ≌△GAF .∴ ∠AFE =∠AFG ,EF = GF .由∠B = 60︒,AD ,CE 分别是∠BAC ,∠ACB 的平分线, 可得 ∠GAF +∠GCF = 60︒.进而得 ∠CFG = 60︒,△CFG ≌△CFD , ∴ GF = DF ,因此 DF = EF .25.(1)∵ CD CQ S DCQ ⋅⋅=∆21,CD = 3,CQ = x ,∴x y 231=.图象如图所示. (2)法一 CP CQ S PCQ ⋅⋅=∆21,CP = 8k -xk ,CQ = x ,∴ ()kx kx x kx k y 42182122+-=⋅-⨯=.∵ 抛物线顶点坐标是(4,12), ∴ 12444212=⋅+⋅-k k ,解得23=k .GF EBAD CHFEBAD CG成绩49.5 59.5 69.5 79.5 89.5则点P 的速度是每秒23厘米,AC = 12厘米. 法二 观察图象知,当x = 4时,△PCQ 面积为12. 此时 PC = AC -AP = 8k -4k = 4k ,CQ = 4.∴ 由CP CQ S PCQ ⋅⋅=∆21,得12244=⨯k ,解得23=k . 则点P 的速度每秒23厘米,AC = 12厘米.法三 设y 2的图象所在抛物线的解析式是y = ax 2 + bx + c . ∵ 图象过(0,0),(4,12),(8,0),∴ ⎪⎩⎪⎨⎧=++=++=,0864,12416,0c b a c b a c 解得 43-=a ,b = 6,c = 0, ∴ x x y 64322+-=. ①∵ CP CQ S PCQ ⋅⋅=∆21,CP = 8k -xk ,CQ = x , ∴ kx kx y 42122+-=. ② 比较①②,得23=k ,则点P 的速度每秒23厘米,AC = 12厘米.(3)① 观察图象,知线段EF = y 2-y 1,表示△PCQ 与△DCQ 的面积差(或△PDQ 面积).② ∵x x y 64322+-=,∴ EF = y 2-y 1 =x x x x x 29432364322+-=-+-, ∵ 二次项系数小于0,∴ 在0<x <6范围,当x = 3时,427=EF 最大.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
姓名:班级:
“英语万花筒”(五)
——六年级英语组
猜一猜
1. What’s found twice in any corner but only once in every room?
2. I am part of joys and sorrows(痛苦)and home would not be home without
me.
3. Why does B come before C?
4. What letter of the alphabet separates(分离) Spain from Africa?
5. Why is the letter F like Paris?
小小翻译家
1. Don’t believe him. What he tells you (他对你说的话)is all hot air.译:
2. He is worried and looks like a cat on the hot bricks. 译:
3. It is a red-letter day in the history of our factory. We’ll remember it for ever.
译:
4. The boy runs and runs until he is blue in the face. 译:
5. Don’t say. Look! It writes in black and white. 译:
数学小博士
1. A bottle of wine costs $10. If the wine is worth $9 more than the bottle, what is
the value of the bottle?
2.What is the next term is this series? 100 121 144 202 244 400
3.Can you find a number such that its double(双倍) is fourteen more than its
quarter(四分之一)?
福尔摩斯吧
After a recent marathon, the following was noted.
Alan finished after Simon. Ian finished after Kevin. Simon finished after Brian. Kevin finished before Alan. Brian finished after Kevin. Brian fishied before Alan. Simon finished before Ian. Alan finished before Ian.
Who finished where?
知识百花园
1. Which of these martial arts is no longer used fighting?
A. Boxing
B. Tai chi
C. Kung fu
D. backbones
2. Who invented air conditioning?
A. Dr Willis Carrier
B. Albert Einstein
C. Thomas Edison
3. Wei Qi is called in English.
A. Chinese chess
B. Go
C. bridge
D. Go Fish
4. Dr Bethune visited many countries in his life but he NEVER visited .
A. France
B. Germany
C. China
D. Spain
Lost years are worse than lost dollars. 一寸光阴一寸金,寸今难买寸光阴。
