粒子群聚类算法综述
粒子群算法聚类设计

(t 1) w (t ) r ( p (t ) z (t )) r ( p (t ) z (t ))
id id 1 1 id id 2 2 gd id
(3)
z (t 1) z (t ) v (t 1)
id id id
(4)
四.改进的粒子群优化算法
五.粒子群算法应用到模式分类
完整程序代码:
clc; clear all; format long; tic data=importdata(‘simulate_data.dat'); %--------参数设定----------N=70;%粒子数 c1=1.6;c2=1.6;%设定学习因子值(速度更新参数) wmax=0.9;wmin=0.4;%设定惯性权重初始及终止值 M=1600;%最大迭代数 K=4;%类别数 [S D]=size(data);%样本数和特征维数 %--------初始化---------------for i=1:N clmat(i,:)=randperm(S);%随机取整数 end clmat(clmat>K)=fix(rand*K+1);%取整函数
若加速系数、最大速度等参数太大,粒子群可能错过最优解,算法不能收
敛; 在收敛的情况下,由于所有的粒子都同时向最优解的方向飞去,所以粒子
趋向同一化( 失去了多样性 ) ,这样就使算法容易陷入局部最优解,即算法
收敛到一定精度时,无法继续优化。
四.改进的粒子群优化算法
2. 粒子群优化算法原理
粒子群优化算法具有进化计算和群智能的特点。与其他进化算法相类似, 粒子群算法也是通过个体间的协作与竞争,实现复杂空间中最优解的搜索。 粒子群算法可描述为:设粒子群在一个 n维空间中搜索,由m个粒子组成 种群 Z Z , Z ,...,Z ,其中的每个粒子所处的位置 Z Z , Z ,...,Z
粒子群算法粒子群算法简介
粒子群算法(1)----粒子群算法简介二、粒子群算法的具体表述上面罗嗦了半天,那些都是科研工作者写论文的语气,不过,PSO的历史就像上面说的那样。
下面通俗的解释PSO算法。
PSO算法就是模拟一群鸟寻找食物的过程,每个鸟就是PSO中的粒子,也就是我们需要求解问题的可能解,这些鸟在寻找食物的过程中,不停改变自己在空中飞行的位置与速度。
大家也可以观察一下,鸟群在寻找食物的过程中,开始鸟群比较分散,逐渐这些鸟就会聚成一群,这个群忽高忽低、忽左忽右,直到最后找到食物。
这个过程我们转化为一个数学问题。
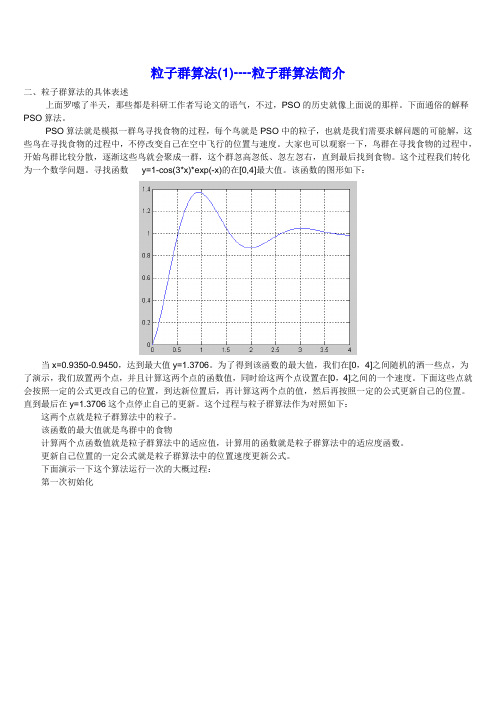
寻找函数y=1-cos(3*x)*exp(-x)的在[0,4]最大值。
该函数的图形如下:当x=0.9350-0.9450,达到最大值y=1.3706。
为了得到该函数的最大值,我们在[0,4]之间随机的洒一些点,为了演示,我们放置两个点,并且计算这两个点的函数值,同时给这两个点设置在[0,4]之间的一个速度。
下面这些点就会按照一定的公式更改自己的位置,到达新位置后,再计算这两个点的值,然后再按照一定的公式更新自己的位置。
直到最后在y=1.3706这个点停止自己的更新。
这个过程与粒子群算法作为对照如下:这两个点就是粒子群算法中的粒子。
该函数的最大值就是鸟群中的食物计算两个点函数值就是粒子群算法中的适应值,计算用的函数就是粒子群算法中的适应度函数。
更新自己位置的一定公式就是粒子群算法中的位置速度更新公式。
下面演示一下这个算法运行一次的大概过程:第一次初始化第一次更新位置第二次更新位置第21次更新最后的结果(30次迭代)最后所有的点都集中在最大值的地方。
粒子群算法(2)----标准的粒子群算法在上一节的叙述中,唯一没有给大家介绍的就是函数的这些随机的点(粒子)是如何运动的,只是说按照一定的公式更新。
这个公式就是粒子群算法中的位置速度更新公式。
下面就介绍这个公式是什么。
在上一节中我们求取函数y=1-cos(3*x)*exp(-x)的在[0,4]最大值。
粒子群算法简介

粒子群算法简介粒子群算法是一种常见的优化算法,它以鸟群捕食的过程为模型,通过模拟每个个体在搜索空间中的位置和速度变化,来寻找最优解。
本文将从算法流程、算法优势、应用领域等方面给出详细介绍。
一、算法流程1. 随机初始化群体中每个粒子的位置和速度;2. 评估每个粒子的适应度;3. 根据粒子历史最优位置和全局最优位置,更新粒子速度和位置;4. 重复步骤2、3直到满足停止条件。
粒子群算法的核心在于更新粒子速度和位置,其中位置表示搜索空间中的一个解,速度表示搜索方向和距离。
每个粒子具有自己的历史最优位置,同时全局最优位置则是所有粒子中适应度最优的解。
通过粒子之间的信息共享,使得整个群体能够从多个方向进行搜索,并最终收敛于全局最优解。
二、算法优势粒子群算法具有以下几个优势:1. 算法简单易于实现。
算法设计简单,无需求导和约束,易于编程实现。
2. 全局搜索能力强。
由于粒子之间的信息共享,整个群体具有多种搜索方向,可以有效避免局部最优解问题。
3. 收敛速度较快。
粒子搜索过程中,速度会受历史最优位置和全局最优位置的引导,使得整个群体能够较快向最优解方向靠近。
三、应用领域粒子群算法是一种通用的优化算法,广泛应用于各个领域,包括机器学习、智能控制、模式识别等。
具体应用场景如下:1. 遗传算法的优化问题,例如TSP问题等。
2. 数据挖掘中的聚类分析、神经网络训练等问题。
3. 工业控制、无人机路径规划等实际应用问题。
总之,粒子群算法是一种搜索优化方法,可以为我们解决各种实际应用问题提供帮助。
粒子群算法简介

4。基于Matlab的应用
• c.粒子速度更新 c.粒子速度更新
在这里 ,粒子速度更新算法基于式 (1) 与式 (3) 。在Matlab中 ,粒子速度更新伪码如 下: for dimIndex = 1 :dimSize w =最大加权因子 - (最大加权因子 - 最小加权因子)×当前世代数/总世代数; subtract1 = pBest - x(1 :dimSize) ; subtract2 = gBest - x(1 :dimSize) ; tempV =w×x (dimSize + dimIndex) + 2×subtract1 + 2×subtract2 ; if tempV > vMax x(dimSize + dimIndex) = vMax ; elseif tempV < - vMax x(dimSize + dimIndex) = - vMax ; else x(dimSize + dimIndex) = tempV; end end
其中 iter为当前迭代数 ,而 itermax是总的迭代次数。
3。算法介绍
• PSO框架图 PSO框架图
4。基于Matlab的应用
• a.参数编码 a.参数编码
在MATLAB环境中 ,种群中粒子及其速度我们都采用实数 编码。格式如下:dimSize 表示参数维度。
粒子群编码格式如下:popSize表示种群大小。
3。算法介绍
g.惯性权重g.惯性权重-w 惯性权重 粒子群算法在解空间内搜索时,在全局最优解附近出现“振 荡”的现象。从经验看,当Vmax<=2,使用接近于1的惯性权 重,当Vmax>=3,使用权重w=0.8较好,从理论上来说,为 了避免次问题发生,可以作如下改进:随着迭代进行,速度更新 公式中的加权因子w由最大加权因子wmax线性减小到最小加 权因子wmin。
讲座:粒子群算法介绍

其中,评价函数Eval完成以下任务: 1、根据公式计算该粒子所代表路径方案的行
驶成本Z,在计算中发货点任务的执行次序要 根据对应Xr值的大小顺序,由小到大执行。 2、将Xr按执行顺序进行重新整数序规范(guīfàn)。 例如,某粒子迭代一次后结果如下:
精品文档
VRP问题为整数规划问题,因此在算法实现过程中要作相应修 改。具体实现步骤如下:
Step1:初始化粒子群。
1.1 粒子群划分成若干个两两相互重叠的相邻子群; 1.2 每个粒子位置向量Xv的每一维随机取1~K(车辆数)之 间的整数,Xr的每一维随机取1~L(发货点任务数)之间的实
数;
1.3 每个速度向量Vv的每一维随机取-(K-1)~(K-1)(车辆数) 之间的整数,Vr的每一维随机取-(L-1)~(L-1)之间的实数; 1.4 用评价(píngjià)函数Eval评价(píngjià)所有粒子; 1.5 将初始评价值作为个体历史最优解Pi,并寻找各子群 内的最优解Pl和总群体内最优解Pg。
精品文档
带时间(shíjiān)窗车辆路径问题(续)
如何找到一个合适的表达方法,使粒子与解对 应,是实现算法的关键问题之一。构造一个 2L维的空间对应有L个发货点任务的VRP问 题,每个发货点任务对应两维:完成(wán 该 chéng) 任务车辆的编号k,该任务在k车行驶路径中 的次序r。为表达和计算方便,将每个粒子对 应的2L维向量X分成两个L维向量:Xv (表示 各任务对应的车辆)和Xr(表示各任务在对应的 车辆路径中的执行次序)。
精品文档
基本(jīběn)PSO算法(续)
PSO算法数学表示如下:
设搜索空间为D维,总粒子数为n。第i个粒子 位置表示为向量Xi=( xi1, xi2,…, xiD );第i个粒 子 “飞行”历史中的过去最优位置(即该位
基于粒子群算法的图像聚类研究与实现【文献综述】

毕业设计文献综述计算机科学与技术基于粒子群算法的图像聚类研究与实现一、前言1.写作目的图像聚类是数据挖掘中一项重要技术,图像聚类的好坏将直接影响后续图像处理与分析任务的质量。
图像聚类是指利用无监督的学习过程发现在图像中的隐藏的模式,它具有独立发现知识的能力。
粒子群算法属于进化算法的一种,它与遗传算法相似,也是从随机解出发,通过迭代寻找最优解,但它比遗传算法的规则更为简单,即没有交叉和变异操作,它通过追随当前搜索到的最优值来寻找全局最优。
粒子群算法由于实现容易、精度高、收敛快等优点在解决实际问题中具有优越性。
本课题主要研究的是基于粒子群算法的图像聚类方法,针对传统的基于K均值的图像聚类方法无法较好地对图像进行聚类,提出一种基于粒子群算法的图像聚类方法。
该方法通过从随机解出发,迭代寻找全局最优解。
提出的方法在图像数据集上进行仿真实验验证。
2.有关概念聚类分析是将具体或抽象的数据集划分为若干组或类的过程,聚类产生的每一组数据称为一个簇,簇中的每一数据称为一个对象。
聚类的目的是使同一簇中对象的特性尽可能相似,不同簇对象间的特性差异尽可能地大。
粒子群优化算法(panicle swarln optimization,PSO)是一种优化计算技术,是进化算法的一种,最早是由Kennedy与Eberhan于1995年提出的⋯。
源于对鸟群捕食的行为研究的PSO 算法是一种基于迭代的优化工具,概论简单、易于实现、参数较少、能有效解决复杂优化任务,目前已广泛应用于函数优化、神经网络训练、模糊系统控制以及其它遗传算法的应用领域。
[8]3.争论焦点由MacQueen提出的K均值算法是解决聚类分析问题的一种经典算法,广泛应用于数据挖掘和知识发现领域中。
它是一种爬山式的搜索算法,以其简单、快速和有效而被广泛使用。
但是,传统的K均值算法存在两个固有的缺点:(1)对于随机的初始值选取可能会导致不同的聚类结果,甚至存在着无解的情况;(2)该算法是基于目标函数的算法,通常采用梯度法求解极值,由于梯度法的搜索方向是沿着能量减少的方向进行,使得算法很容易陷入局部极值。
数据挖掘中的粒子群算法介绍

数据挖掘中的粒子群算法介绍随着信息时代的到来,数据的规模和复杂性不断增加,如何从海量数据中提取有用的信息成为了一项重要的任务。
数据挖掘作为一种有效的方法,被广泛应用于各个领域,如商业、医疗、金融等。
在数据挖掘中,粒子群算法是一种常用的优化算法,它模拟了鸟群或鱼群的行为,通过个体之间的合作和竞争来寻找最优解。
粒子群算法(Particle Swarm Optimization,简称PSO)是由Eberhart和Kennedy于1995年提出的一种基于群体智能的优化算法。
它通过模拟鸟群或鱼群的行为,将问题转化为一个粒子在解空间中搜索最优解的过程。
在粒子群算法中,每个粒子代表一个解,它通过不断更新自己的位置和速度来搜索最优解。
每个粒子都有一个适应度值,用于评估其解的质量。
粒子的速度和位置的更新是根据其个体最优解和群体最优解来进行的。
个体最优解是粒子自身曾经找到的最好解,而群体最优解是所有粒子曾经找到的最好解。
粒子群算法的基本思想是通过粒子之间的信息交流和协作来寻找全局最优解。
在搜索过程中,每个粒子根据自身的经验和群体的经验来更新自己的位置和速度。
具体来说,粒子的速度和位置的更新公式如下:v(t+1) = w * v(t) + c1 * rand() * (pbest - x(t)) + c2 * rand() * (gbest - x(t))x(t+1) = x(t) + v(t+1)其中,v(t)表示粒子在t时刻的速度,x(t)表示粒子在t时刻的位置,pbest表示粒子自身的最优解,gbest表示群体的最优解,w、c1和c2是控制因子,rand()表示一个0到1之间的随机数。
粒子群算法的优点是简单、易于实现,并且不需要求解导数等复杂的数学问题。
它具有全局搜索能力和较快的收敛速度,在解决复杂的优化问题时表现出了良好的性能。
在数据挖掘中,粒子群算法可以应用于多个任务,如聚类、分类、回归等。
在聚类任务中,粒子群算法可以帮助将相似的数据点分组,从而发现数据的内在结构。
粒子群综述-【精品文档】(完整版)

粒子群优化算法综述第一章概述粒子群优化算法(PSO)是近年来被广为关注和研究的一种智能优化算法,源于对鸟群捕食系统的模拟。
它收敛速度快、易实现并且仅有少量参数需要调整,因而一经提出就成为智能优化与进化计算领域的一个新的研究热点,目前己经被广泛应用于目标函数优化、动态环境优化、神经网络训练、模糊控制系统等许多领域[1]。
其中最具应用前景的领域包括多目标问题的优化、系统设计、分类、模式识别、生物系统建模、规划、信号处理、决策和模拟等。
粒子群优化算法的理论背景是“人工生命”。
人工生命(artificial life)是用来研究具有某些生命基本特征的人工系统,其中一个重要部分是利用生物技术来研究计算问题。
粒子群优化算法的诞生来源于一种生物一社会系统,该生物一社会系统的研究集中于简单个体组成的群落与环境之间的关系,以及个体之间的互动行为。
群居个体以集体的力量进行觅食、御敌,单个个体只能完成简单的任务,而由单个个体组成的群体却能完成复杂的任务,这种群体所表现出来的“智能”,就称之为群体智能(Swarm Intelligence,SI)[2]。
而从群居昆虫互相合作进行工作中得到启迪,研究其中的原理,并以此原理来设计新的求解问题的算法被称为群智算法。
在计算智能领域主要有两种基于群智能的算法,一种是蚁群算法(Ant Colony Optimization,ACO),它是对蚂蚁群落食物采集过程的模拟,己经成功运用在很多离散优化问题上[3];另一种是粒子群优化算法,最初由Jim Kennedy于1995年提出并成功的用于函数优化,后来又进行了有效的拓展[4]。
但是,PSO的发展历史尚短,在理论基础与应用推广上都还存在一些问题有待解决。
当PSO应用于高维复杂问题优化时,往往会早熟收敛(premature),也就是种群在还没有找到全局最优点时已经聚集到一点停滞不动。
这些早熟收敛点,有可能是局部极小点,也有可能是局部极小点邻域中的一个点。
粒子群算法简介优缺点及其应用

类似于人的“原动力”,如果原动力比较大,当达到某个目 标的时候,会继续向前实现更高的目标:如果原动力较小,到 达某个目标就停滞。
2024/2/19
第18页/共29页
17
Shi和Eberhart提出了一种随着算法迭代次数的增加惯性权重线 性下降的方法。
惯性权重的计算公式如下:
max
max min
kmax
kn
max和min分别表示权重的最大及最小值,kn为当前迭代次数, kmax表示最大迭代次数。
文献试验了将设置为从0.9到0.4的线性下降,使得PSO在开 始时探索较大的区域,较快地定位最优解的大致位置,随着 逐渐减小,粒子速度减慢,开始精细的局部搜索。该方法使 PSO更好地控制exploration和exploitation能力,加快了收敛速 度,提高了算法的性能,称之为权重线性下降的粒子群算法, 简记为LDW(Linearly Decreasing Inertia Weight)。
速度为 vi vi1, vi2,viN T
在找到两个最优解后,粒子即可根据下式来更新自己的速度和 位置:
vk 1 id
vikd
c1 rand1k
(Pbestikd
xikd ) c2
rand
k 2
(Gbest
k d
xikd
)
(1)
x k 1 id
xikd
v k 1 id
(2)
vikd :是粒子i在第k次迭代中第d维的速度;
公式(1)的第一项对应多样化(diversification)的特点,第二项、 第三项对应于搜索过程的集中化(intensification)特点,这三项之 间的相互平衡和制约决定了算法的主要性能。
直观理解粒子群算法

直观理解粒子群算法1.引言1.1 概述粒子群算法是一种模拟自然界群体行为的优化算法。
它最早由Eberhart和Kennedy于1995年提出,受到了鸟群觅食和鱼群游动行为的启发。
粒子群算法模拟了一个由许多粒子组成的群体,每个粒子代表一个潜在的解,并通过不断地调整自身的位置和速度来寻找最优解。
粒子群算法的基本原理是通过粒子之间的合作与竞争来达到全局最优解。
在算法开始时,每个粒子都会随机地在问题的解空间内选择一个初始位置和速度。
然后,根据粒子的当前位置和速度以及历史最优解的信息,每个粒子会更新自己的速度和位置。
更新的过程中,粒子会根据个体历史最优解和群体历史最优解两方面的信息进行权衡,从而平衡个体探索和群体协作的需求。
通过不断地迭代更新,粒子群算法能够逐渐收敛到全局最优解。
粒子群算法被广泛应用于优化问题的求解。
它在函数优化、组合优化、神经网络训练等领域取得了显著的成果。
由于其简单而直观的思想,粒子群算法易于理解和实现,同时具有较快的收敛速度和较好的全局搜索能力。
与其他优化算法相比,粒子群算法在处理高维、非线性、多模态等复杂问题时具有一定的优势。
综上所述,粒子群算法是一种基于群体行为的优化算法,通过模拟粒子之间的合作与竞争来寻找最优解。
它具有简单直观、易于实现和较好的全局搜索能力等优势。
在实际应用中,粒子群算法已经取得了一些显著的成果,并且有着较大的发展潜力。
文章结构部分的内容如下:文章结构部分旨在介绍本文的组织框架和内容安排,让读者能够清晰地了解整篇文章的结构和逻辑顺序。
本文分为三个主要部分:引言、正文和结论。
接下来将对每个部分的内容进行简要介绍。
首先是引言部分(Section 1),它主要用于引入本文的主题和背景。
在引言的第一部分(1.1 概述),我们将简要概括粒子群算法的基本概念和特点,为读者提供一个整体的认识。
接着,在第二部分(1.2 文章结构),我们将详细说明本文的组织结构和每个部分的内容安排,以便读者能够清晰地了解整个文章的构成。
粒子群算法研究综述

粒子群算法综述控制理论与控制工程09104046 吕坤一、粒子群算法的研究背景人工智能经过半个世纪的发展,经历了由传统人工智能、分布式人工智能到现场人工智能等阶段的发展。
到二十世纪九十年代,一些学者开始从各种活动和现象的交互入手,综合地由个体的行为模型开始分析社会结构和群体规律,于是90年代开始,就产生了模拟自然生物群体(swarm)行为的优化技术。
Dorigo等从生物进化的机理中受到启发, 通过模拟蚂蚁的寻径行为, 提出了蚁群优化方法;Eberhar 和Kennedy于1995年提出的粒子群优化算法是基于对鸟群、鱼群的模拟。
这些研究可以称为群体智能(swarm-intelligenee)。
通常单个自然生物并不是智能的,但是整个生物群体却表现出处理复杂问题的能力,群体智能就是这些团体行为在人工智能问题中的应用。
粒子群优化(Particle Swarm Optimization , PSC)最初是处理连续优化问题的, 目前其应用已扩展到组合优化问题。
由于其简单、有效的特点,PSC已经得到了众多学者的重视和研究。
二、粒子群算法的研究现状及研究方向粒子群算法(PSC)自提出以来,已经历了许多变形和改进,包括数学家、工程师、物理学家、生物学家以及心理学家在内的各类研究者对它进行了分析和实验,大量研究成果和经验为粒子群算法的发展提供了各许多合理的假设和可靠的基础,并为实际的工业应用指引了新的方向。
目前,PSC的研究也得到了国内研究者的重视,并已取得一定成果。
十多年来,PSC的研究方向得到发散和扩展,已不局限于优化方面研究。
PSC 算法按其研究方向分为四部分:算法的机制分析研究、算法性能改进研究、算法的应用研究及离散性PSC算法研究。
算法的机制分析主要是研究PSC算法的收敛性、复杂性及参数设置。
算法性能改进研究主要是对原始PSC算法的缺陷和不足进行改进,以提高原始PSC算法或标准PSC算法的一些方面的性能。
粒子群算法原文及解释

粒子群算法原文及解释粒子群优化算法(Particle Swarm Optimization,PSO)是一种模拟鸟群、鱼群等动物社会行为的优化算法。
通过模拟鸟群、鱼群等动物群体中的个体行为,粒子群优化算法能够有效地求解各种优化问题。
本文将从算法原理、算法流程、参数设置、优化问题、实现方式、改进策略、应用领域和性能评价等方面对粒子群优化算法进行详细的介绍。
一、算法原理粒子群优化算法基于群体智能理论,通过模拟鸟群、鱼群等动物群体中的个体行为来寻找最优解。
每个个体被称为一个粒子,它通过跟踪其自身的最优位置和群体的最优位置来更新自己的速度和位置。
粒子的速度和位置更新公式如下:v[i][j] = w * v[i][j] + c1 * rand() * (pbest[i][j] - x[i][j]) + c2 * rand() * (gbest - x[i][j])x[i][j] = x[i][j] + v[i][j]其中,v[i][j]表示粒子i在第j维上的速度,x[i][j]表示粒子i 在第j维上的位置,pbest[i][j]表示粒子i的个体最优位置,gbest 表示全局最优位置,w表示惯性权重,c1和c2表示加速因子,rand()表示随机函数。
二、算法流程粒子群优化算法的基本流程如下:1. 初始化粒子群,随机生成粒子的初始位置和初始速度。
2. 计算每个粒子的适应度值,记录粒子的个体最优位置和全局最优位置。
3. 根据粒子的适应度值更新粒子的速度和位置。
4. 重复步骤2和步骤3,直到满足终止条件(如达到预设的最大迭代次数或全局最优解的变化小于预设阈值)。
三、参数设置粒子群优化算法的参数包括惯性权重w、加速因子c1和c2等。
这些参数对算法的性能和收敛速度有着重要的影响,需要根据具体问题进行调整和优化。
通常需要通过实验来找到合适的参数设置。
四、优化问题粒子群优化算法适用于求解连续的、离散的优化问题。
对于不同的优化问题,需要根据问题的特性和要求来设计合适的粒子和适应度函数。
基于免疫进化粒子群优化的动态聚类算法

基于免疫进化粒子群优化的动态聚类算法基于免疫进化粒子群优化的动态聚类算法是一个新型的非参数聚类算法,用于在含有噪声和复杂度的数据集中实现聚类。
它利用了免疫进化粒子群算法(IEPSO),改进了聚类结果,以便更好地提取关键特征。
有效执行动态聚类训练过程,使用聚类中心来调整数据集,从而确保适当的划分。
在基于免疫进化粒子群优化的动态聚类算法中,IEPSO算法对聚类中心的位置进行优化,以便将每个数据项划分到最佳的聚类中心。
最近邻原则及欧几里得距离(Euclidean Distance)构成了该算法的基础。
此外,在IEPSO算法中,每个粒子的聚类中心代表了不同的聚类,每个粒子都是由所有样本(噪声和有用样本)组成的。
IEPSO算法在优化聚类中心位置时,首先使用最近邻原则进行聚类,以确定各个粒子所属的聚类中心,然后根据每个聚类中的实际噪声数量,以及距离每个样本的距离,调整聚类中心的位置,以便尝试使其贴近实际数据分布。
同时,IEPSO算法还添加了惯性因子,以及接受者因子和粒子间因子,用于提高聚类精度。
当IEPSO算法在动态聚类中执行完一次迭代之后,在更新聚类中心位置的同时,还会检测增加了噪声的数据,并将它们分配到新的聚类中心,以便识别新的噪声。
在更新数据集时,该算法还会使用粒子间各向同性的交叉变异原则,以加强其聚类性能。
基于免疫进化粒子群优化的动态聚类算法是一种有效的非参数聚类算法,使用IEPSO算法来优化聚类中心的位置,并使用进化的惯性系数和接受者因子来提升分类性能。
它可以有效地处理噪声和复杂度较高的数据集,提取关键特征,并可以动态地调整数据集,以检测到新添加的噪声数据。
粒子群算法综述

粒子群算法综述【摘要】:粒子群算法(pso)是一种新兴的基于群体智能的启发式全局搜索算法,具有易理解、易实现、全局搜索能力强等特点,倍受科学与工程领域的广泛关注,已得到广泛研究和应用。
为了进一步推广应用粒子群算法并为深入研究该算法提供相关资料,本文对目前国内外研究现状进行了全面分析,在论述粒子群算法基本思想的基础上,围绕pso的运算过程、特点、改进方式与应用等方面进行了全面综述,并给出了未来的研究方向展望。
【关键词】:粒子群算法优化综述优化理论的研究一直是一个非常活跃的研究领域。
它所研究的问题是在多方案中寻求最优方案。
人们关于优化问题的研究工作,随着历史的发展不断深入,对人类的发展起到了重要的推动作用。
但是,任何科学的进步都受到历史条件的限制,直到二十世纪中期,由于高速数字计算机日益广泛应用,使优化技术不仅成为迫切需要,而且有了求解的有力工具。
因此,优化理论和算法迅速发展起来,形成一门新的学科。
至今已出现线性规划、整数规划、非线性规划、几何规划、动态规划、随机规划、网络流等许多分支。
这些优化技术在诸多工程领域得到了迅速推广和应用,如系统控制、人工智能、生产调度等。
随着人类生存空间的扩大,以及认识世界和改造世界范围的拓宽,常规优化法如牛顿法、车辆梯度法、模式搜索法、单纯形法等已经无法处理人们所面的复杂问题,因此高效的优化算法成为科学工作者的研究目标之一。
1.粒子群算法的背景粒子群算法(particle swarm optimization,pso)是一种新兴的演化算法。
该算法是由j.kennedy和r.c.eberhart于1995年提出的一种基于群智能的随机优化算法。
这类算法的仿生基点是:群集动物(如蚂蚁、鸟、鱼等)通过群聚而有效的觅食和逃避追捕。
在这类群体的动物中,每个个体的行为是建立在群体行为的基础之上的,即在整个群体中信息是共享的,而且在个体之间存在着信息的交换与协作。
如在蚁群中,当每个个体发现食物之后,它将通过接触或化学信号来招募同伴,使整个群落找到食源;在鸟群的飞行中,每只鸟在初始状态下处于随机位置,且朝各个方向随机飞行,但随着时间推移,这些初始处于随机状态的鸟通过相互学习(相互跟踪)组织的聚集成一个个小的群落,并以相同的速度朝着相同的方向飞行,最终整个群落聚集在同一位置──食源。
基于改进粒子群算法的聚类算法

基于改进粒子群算法的聚类算法随着数据量的增加和数据种类的多样性,聚类算法成为了非常重要的数据分析工具。
传统的聚类算法包括K-means、层次聚类等。
但是,这些算法在实践中往往需要调参、对初始点的敏感度较高、容易陷入局部最优等问题。
因此,粒子群算法逐渐被应用到聚类算法的优化上。
1. 粒子群算法的基本思想粒子群算法(Particle Swarm Optimization,PSO)是一种基于群体智能的优化算法,在处理优化问题时,可以获取全局最优解。
PSO算法通过模拟‘鸟群找食’的过程,将优化问题看作是一个动态的‘粒子群’,在候选解空间中进行搜索,每个头痛‘粒子’是一种备选解,粒子的位置表示解的位置,速度表示解的变化率,群体通过学习,交流,协作完成搜索找到最优解的过程。
2. 基于改进粒子群算法的聚类算法原理基于改进粒子群算法的聚类算法(Particle Swarm Optimization Clustering,PSOC)在PSO的基础上,引入了距离计算公式、惯性权重、自适应策略等优化措施,在保证算法时间效率的情况下,能够更快、更精确地完成聚类任务。
3. PSOC 的优化措施3.1 PSOC 对距离的计算传统的粒子群算法只考虑到效用函数值的情况下进行收缩,产生很大的局限性。
PSOC算法在计算距离时,使用欧式距离公式,使得不同类别之间的距离更明显,不同于使用传统的算法失真的距离值,更加符合实际情况。
3.2 PSOC 对惯性权重的优化惯性权值的作用是在更新粒子位置和速度时,在进行平衡加速度和动量之间的重要作用。
传统的惯性权重在不同迭代过程中不同,会产生一定的影响,使psoc不稳定。
为了解决这个问题,智能算法引入了线性下降惯性权重策略,使得惯性权重值在逐渐递减的过程中,达到了平衡加速度和动量的效果。
3.3 PSOC 的自适应策略自适应策略指定算法参数细节的过程,自动完成。
通过PSOC算法中粒子的个数和最大迭代次数的优化来实现,可以减少调整算法时的耗费,提高算法效率。
粒子群优化算法及其相关研究综述【精品文档】(完整版)

粒子群优化算法及其相关研究综述摘要:粒子群优化是一种新兴的基于群体智能的启发式全局搜索算法,通过粒子间的竞争和协作以实现在复杂搜索空间中寻找全局最优点。
它具有易理解、易实现、全局搜索能力强等特点,倍受科学与工程领域的广泛关注,已经成为发展最快的智能优化算法之一。
本文围绕粒子群优化算法的原理、特点、改进与应用等方面进行全面综述,侧重于粒子群的改进算法,简短介绍了粒子群算法在典型理论问题中的应用,最后对其未来的研究提出了一些建议及研究方向的展望。
关键词:粒子群优化;PSO;群智能优化;智能算法Abstract: Particle swarm optimization is a new swarm intelligence-based heuristic global search algorithm, through competition and collaboration between the particles in order to achieve the advantages of looking at complex global search space. It has easy to understand, easy to implement, strong global search ability and other characteristics, much attention in the field of science and engineering, has become one of the fastest growing intelligent optimization algorithms. This paper focuses on aspects of the principle of particle swarm optimization, characteristics, improvement and application of a comprehensive review, focusing on improved PSO algorithm, a brief description of the particle swarm algorithm in a typical problem in the theory, and finally presented its future research Looking for some advice and research directions.Key Words: Particle Swarm optimization; PSO; Swarm intelligence optimization;Intelligent algorithm1 引言粒子群算法(Particle Swarm optimization,PSO)的基本概念源于对于鸟群捕食行为的简化社会模型的模拟,由Kenndy和Eberhart等人提出[1-2],1995年IEEE国际神经网络学术会议发表了题为“Particle Swarm Optimization”的论文,标志着PSO算法诞生。
粒子群聚类算法综述_李峻金

收稿日期:2009-04-02;修回日期:2009-06-13作者简介:李峻金(1985-),男,安徽阜阳人,硕士研究生,主要研究方向为人工智能与聚类分析(ts p ace1985@g m ai.l co m );向阳(1968-),女,湖南长沙人,副教授,硕士,主要研究方向为计算机与数据库安全;芦英明(1985-),男,陕西西安人,助理工程师,主要研究方向为装备系统工程;吴朔桐(1985-),女,内蒙古通辽人,助理工程师,主要研究方向为通信工程.粒子群聚类算法综述李峻金1,向 阳1,芦英明2,吴朔桐3(1.西安通信学院,西安710106;2.中国特种车辆研究所,北京100072;3.中国人民解放军61516部队,北京100094)摘 要:聚类分析是数据挖掘的重要技术之一,它能够通过无监督的学习过程发现隐藏的模式,具有独立发现知识的能力。
对现有文献中基于粒子群优化算法的聚类分析技术作了全面的介绍,对几种主要的粒子群聚类算法的基本原理及其特点进行了总结,并分析比较了它们的优点和不足,概述了粒子群聚类算法的常见应用领域;最后探讨了粒子群聚类算法进一步的研究方向。
关键词:聚类分析;群智能;粒子群优化算法中图分类号:TP301 文献标志码:A 文章编号:1001-3695(2009)12-4423-05do:i 10.3969/.j i ssn .1001-3695.2009.12.006Survey of parti cle s w arm cl usteri ng al gorit h m sL I Jun -ji n 1,X I ANG Y ang 1,LU Y i ng -m ing 2,W U Shuo -tong 3(1.X i .an Co mmun ic a tions Instit u te ,X i .an 710106,C hina;2.China .s Speci a l Vehicle R ese arc h In stit u t e ,Be i jing 100072,Ch i na;3.PLA 61516Un it ,Be i jing 100094,Ch i na )Abstract :C l ustering analysis i s one of t he m i portant datam i ning techn i ques t hat can d i scover h i dden m odes by unsupervi sed learn i ng and has t he ab ility of acquiri ng kno w ledge i ndependentl y .This paper presented an al-l around i n troduction of PSO-based cl ustering met hods i n existing literatures ,descri bed t he basic pri nci ples and the characteristics of t he existi ng popular particle s war m cl usteri ng al gorith m s ,and m ade the co m parison about theirm erits and de m erits .Then su mm arized the app lica -ti ons of particle s w ar m clusteri ng al gorith m s .F i nall y ,poi nted out t he future research d irections of parti cle s w ar m cl usteri ng a-l gorith m s .Key words :cl ustering analysis ;s w ar m i ntelli gence ;particl e s w ar m op tm i izati on(PS O)0 引言聚类(c l uste ri ng)是将一批现实或抽象的数据对象分组成为多个类或簇的过程[1]。
粒子群算法综述

粒子群优化算法粒子群优化算法又翻译为粒子群算法、微粒群算法、或微粒群优化算法。
定义粒子群优化算法(Particle Swarm optimization,PSO)又翻译为粒子群算法、微粒群算法、或微粒群优化算法。
是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法。
通常认为它是群集智能 (Swarm intelligence, SI) 的一种。
它可以被纳入多主体优化系统 (Multiagent Optimization System, MAOS). 粒子群优化算法是由Eberhart博士和kennedy博士发明。
PSO模拟鸟群的捕食行为PSO模拟鸟群的捕食行为。
一群鸟在随机搜索食物,在这个区域里只有一块食物。
所有的鸟都不知道食物在那里。
但是他们知道当前的位置离食物还有多远。
那么找到食物的最优策略是什么呢。
最简单有效的就是搜寻目前离食物最近的鸟的周围区域。
从模型中得到的启示PSO从这种模型中得到启示并用于解决优化问题。
PSO中,每个优化问题的解都是搜索空间中的一只鸟。
我们称之为“粒子”。
所有的粒子都有一个由被优化的函数决定的适应值(fitnessvalue),每个粒子还有一个速度决定他们飞翔的方向和距离。
然后粒子们就追随当前的最优粒子在解空间中搜索。
PSO初始化PSO初始化为一群随机粒子(随机解),然后通过叠代找到最优解,在每一次叠代中,粒子通过跟踪两个“极值”来更新自己。
第一个就是粒子本身所找到的最优解,这个解叫做个体极值pBest,另一个极值是整个种群目前找到的最优解,这个极值是全局极值gBest。
另外也可以不用整个种群而只是用其中一部分最优粒子的邻居,那么在所有邻居中的极值就是局部极值。
算法介绍在找到这两个最优值时, 粒子根据如下的公式来更新自己的速度和新的位置v[] = v[] + c1 * rand() * (pbest[] - present[]) + c2 * rand() * (gbest[] - present[]) (a)present[] = persent[] + v[] (b)v[] 是粒子的速度, persent[] 是当前粒子的位置. pbest[] and gbest[] 如前定义 rand () 是介于(0, 1)之间的随机数. c1, c2 是学习因子. 通常 c1 = c2 = 2.程序的伪代码如下For each particle____Initialize particleENDDo____For each particle________Calculate fitness value________If the fitness value is better than the best fitness value (pBest) in history____________set current value as the new pBest____End____Choose the particle with the best fitness value of all the particles as the gBest____For each particle________Calculate particle velocity according equation (a)________Update particle position according equation (b)____EndWhile maximum iterations or minimum error criteria is not attained在每一维粒子的速度都会被限制在一个最大速度Vmax,如果某一维更新后的速度超过用户设定的Vmax,那么这一维的速度就被限定为Vmax。
粒子群算法概述

“只有自我,没有社会” 完全没有信息的社会共享 导致算法收敛速度缓慢
粒子群算法的构成要素-权重因子 权重因子:惯性因子 、学习因子
k k-1 k 1 k 1 vid =wvid c1r1 ( pbestid xid ) c2r2 ( gbestd xid )
线性递减权值
run w wmax ( wmax wmin )* runmax
wmax最大惯性权重,wmin最小惯性权重,run当前迭代次 数,runmax为算法迭代总次数 较大的w有较好的全局收敛能力,较小的w则有较强的 局部收敛能力。因此,随着迭代次数的增加,惯性权重w 应不断减少,从而使得粒子群算法在初期具有较强的全局 收敛能力,而晚期具有较强的局部收敛能力。
k vid —第k次迭代粒子i飞行速度矢量的第d维分量 k xid —第k次迭代粒子i位置矢量的第d维分量
v =wv c1r1 ( pbestid x ) c2r2 ( gbestd x )
k id k-1 id
k 1 id
k 1 id
粒子速度更新公式包含三部分: 第一部分为粒子先前的速度 第二部分为“认知”部分,表示粒子本身的思考,可理解为 粒子i当前位置与自己最好位置之间的距离。 第三部分为“社会”部分,表示粒子间的信息共享与合作, 可理解为粒子i当前位置与群体最好位置之间的距离。
粒子群优化算法求最优解
D维空间中,有N个粒子;
粒子i位臵:xi=(xi1,xi2,…xiD),将xi代入适应函数f(xi)求适应值;
粒子i速度:vi=(vi1,vi2,…viD) 粒子i个体经历过的最好位臵:pbesti=(pi1,pi2,…piD)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
收稿日期:2009唱04唱02;修回日期:2009唱06唱13 作者简介:李峻金(1985唱),男,安徽阜阳人,硕士研究生,主要研究方向为人工智能与聚类分析(tspace1985@gmail.com);向阳(1968唱),女,湖南长沙人,副教授,硕士,主要研究方向为计算机与数据库安全;芦英明(1985唱),男,陕西西安人,助理工程师,主要研究方向为装备系统工程;吴朔桐(1985唱),女,内蒙古通辽人,助理工程师,主要研究方向为通信工程.粒子群聚类算法综述李峻金1,向 阳1,芦英明2,吴朔桐3(1.西安通信学院,西安710106;2.中国特种车辆研究所,北京100072;3.中国人民解放军61516部队,北京100094)摘 要:聚类分析是数据挖掘的重要技术之一,它能够通过无监督的学习过程发现隐藏的模式,具有独立发现知识的能力。
对现有文献中基于粒子群优化算法的聚类分析技术作了全面的介绍,对几种主要的粒子群聚类算法的基本原理及其特点进行了总结,并分析比较了它们的优点和不足,概述了粒子群聚类算法的常见应用领域;最后探讨了粒子群聚类算法进一步的研究方向。
关键词:聚类分析;群智能;粒子群优化算法中图分类号:TP301 文献标志码:A 文章编号:1001唱3695(2009)12唱4423唱05doi:10.3969/j.issn.1001唱3695.2009.12.006SurveyofparticleswarmclusteringalgorithmsLIJun唱jin1,XIANGYang1,LUYing唱ming2,WUShuo唱tong3(1.Xi’anCommunicationsInstitute,Xi’an710106,China;2.China’sSpecialVehicleResearchInstitute,Beijing100072,China;3.PLA61516Unit,Beijing100094,China)Abstract:Clusteringanalysisisoneoftheimportantdataminingtechniquesthatcandiscoverhiddenmodesbyunsupervisedlearningandhastheabilityofacquiringknowledgeindependently.Thispaperpresentedanall唱aroundintroductionofPSO唱basedclusteringmethodsinexistingliteratures,describedthebasicprinciplesandthecharacteristicsoftheexistingpopularparticleswarmclusteringalgorithms,andmadethecomparisonabouttheirmeritsanddemerits.Thensummarizedtheapplica唱tionsofparticleswarmclusteringalgorithms.Finally,pointedoutthefutureresearchdirectionsofparticleswarmclusteringal唱gorithms.Keywords:clusteringanalysis;swarmintelligence;particleswarmoptimization(PSO)0 引言聚类(clustering)是将一批现实或抽象的数据对象分组成为多个类或簇的过程[1]。
聚类分析源于数据挖掘、统计学、机器学习、模式识别等许多领域,是人们认识和探索事物之间内在联系的有效手段。
通过聚类,人们能够识别密集的和稀疏的区域,发现全局的分布模式以及数据属性之间有趣的相互关系。
此外,聚类分析也可以作为其他分析算法(如关联规则、分类等)的预处理步骤[2]。
在过去的几十年中,聚类分析在工程学、计算机科学、地球科学以及社会科学和经济学等许多领域起着越来越重要的作用。
随着计算机技术、网络技术和信息技术的迅速发展,一些规模巨大且结构复杂的数据在科学和工程应用领域不断出现。
如何处理这些数据并从中得到有益的信息,越来越引起人们的普遍关注。
大规模复杂数据集的出现对聚类分析技术提出了特殊的挑战,它要求聚类算法具有可伸缩性、处理不同类型数据、发现任意形状的簇、处理高维数据的能力等,并要求聚类结果对用户来说应该是可判断的、能理解的和可用的[2,3]。
面对这些问题与要求,传统的聚类分析方法已经显得无能为力。
为解决上述问题,研究者们开始尝试各种智能聚类方法。
群智能算法中的粒子群优化算法(PSO)逐渐引起人们的注意,并在聚类分析中取得了比传统方法更好的效果[4]。
PSO算法主要是在群体的集群行为和自组织原则指导下的随机搜索和优化技术,它强调分布式、相对简单主体之间直接或间接的交互作用,具有很强的适应性和鲁棒性。
PSO算法潜在的并行性和分布式特点使其能够处理以数据库形式存在的大量数据;另一方面,聚类可以被看成一个复杂的全局优化问题,因此PSO算法可以用于聚类分析。
1 传统聚类分析技术传统的聚类方法可以大致分为层次方法和划分方法两类,每一类又包含大量不同的算法。
层次方法是对给定的数据对象的集合进行层次的分界。
在层次聚类中,用一个“树”表示聚类的过程序列,根据层次分界的表示方式,层次方法又可以分为凝聚的和分裂的两种。
层次方法具有两个基本优点[5]:簇的数目不需要事先确定,它与第26卷第12期2009年12月 计算机应用研究ApplicationResearchofComputersVol.26No.12Dec.2009初始条件是相互独立的。
层次方法是一种静态的聚类方法,已做的合并或分裂操作不能返回,簇之间也不能交换数据对象,在某步没有选择好合并或分裂点的情况下,可能会导致低质量的聚类结果。
由于进行合并或分裂操作需要搜索和估算大量的对象或簇,使得层次方法的可伸缩性较差,同时由于缺乏关于全局状态或簇的规模等信息,该方法可能对有重叠的簇的划分失效[6]。
划分方法则通过评价函数某种簇的原型将数据集直接分解成若干个无关联的簇的集合。
它努力优化某种标准目标误差函数,该函数可能强调数据的全局或者局部结构。
划分方法主要有K唱均值(K唱means)和K唱中心点(K唱medoids)两种类型。
K唱均值算法对处理大数据集是相对可伸缩的和高效的,K唱中心点算法能在一定程度上消除K唱均值算法对孤立点的敏感性。
划分方法一般要求事先给定簇的个数,并且对初始值和噪声数据敏感。
由于划分方法基于对象间的距离和对某种标准的优化进行聚类,这种方法只能发现球状簇而不能发现任意形状的簇,同时算法极易陷入局部最优。
通过以上分析可以看出,层次方法和划分方法的优缺点交错对应,还没有一种方法能同时具有它们的优点。
2 基本粒子群聚类算法为了突破传统聚类方法的瓶颈,一些研究者尝试将粒子群智能算法用于聚类分析,通过将聚类视为一种优化问题,利用PSO算法的全局寻优能力来得到一个对数据集的近似最优划分。
2002年Omran等人[7]提出了一种基于粒子群优化的无指导图像分类算法。
这是最早提出的基于PSO的聚类算法,以后的粒子群聚类算法大都遵循其基本思想。
在他们的算法中,簇的个数由用户预先给定,粒子群中的每个粒子包含一个表示簇中心的数据向量,代表一种候选的划分,整个粒子群则代表了对数据集的多种划分。
算法首先将一组随机的簇中心赋值给各个粒子,对于每个粒子,按照最小距离原则对图像像素进行划分操作,随后根据给定的粒子适应度函数,按照PSO算法的步骤找到一个最优粒子,根据最优粒子的位置从而得到一个对数据集的近似最优划分。
他们将该算法应用在对合成图像、人脑的核磁共振图像以及Tahoe湖的(美国)地球资源(探测)卫星图像的聚类分析中。
结果显示,基于PSO的方法能得到较小的簇内距离和较大的簇间距离。
应用在由两种画笔生成的合成图像中,结果表明基于PSO的方法不会陷入局部最优。
在Omran等人工作的基础上,Merwe等人[8]提出了基本PSO聚类算法,用于对一般数据集进行聚类操作。
基本PSO聚类算法中粒子的适应性函数为Je。
Je=∑Ncj=1[∑橙zp∈Cjd(zp,mj)]/|Cj|Nc(1)mj=1nj∑橙zp∈Cjzp(2)d(zp,mj)=∑Nbk=1(zpk-mjk)2(3)其中:Nb为数据的维数;Nc为聚簇的个数;zp表示样本的数据向量;nj表示簇Cj中样本的个数;mj表示簇Cj中样本的均值(中心)。
基本PSO聚类算法的流程如下:算法1 基本PSO聚类算法begina)随机选择簇的中心并赋值给各个粒子,随机产生粒子的速度;repeatb)对每个粒子按照最小距离原则对数据进行划分,按照式(1)计算各个粒子的适应值,更新个体极值;c)根据各个粒子的个体极值,找出全局极值和全局极值位置;d)按粒子群优化算法的速度公式更新粒子的速度,并把它限制在vmax内;e)按粒子群优化算法的位置公式更新粒子的位置;until满足终止条件f)输出最优粒子的位置即最优的Nc个聚类中心end算法的终止条件可以是达到一定的循环次数、簇的中心变化很小或簇的成员不再改变。
基本PSO聚类算法提供了一条新的解决传统聚类问题的有效途径,从此各种基于粒子群思想的聚类算法被陆续提出并被应用在图像分割与识别、文本聚类、入侵检测等领域。
3 粒子群聚类研究现状已有的粒子群聚类算法大都是与传统聚类方法结合,将聚类视为一种优化问题,应用粒子群优化算法的全局寻优能力和分布式随机搜索特性解决传统聚类算法易陷入局部最优和对初值敏感问题。
一些混合算法通过改变PSO算法与传统聚类方法的结合方式以及应用改进的PSO算法有效提高了算法的收敛速度和全局寻优能力。
目前应用粒子群算法解决自动聚类问题的研究还较少。
3畅1 粒子群优化算法与K唱均值算法相结合继Omran等人[7]提出基本的PSO聚类算法并取得初步成功后,研究者借鉴其基本思路,开始将PSO算法与K唱means算法结合用于聚类分析,目的是采用PSO算法的连续优化形式,即利用PSO算法的全局搜索能力降低K唱means算法陷入局部最优的概率。
2003年Merwe等人[8]最早提出了一般形式下PSO与K唱means相结合的混合聚类方法。
该算法的基本思路是先用K唱means方法得到一组簇的中心,然后在粒子群初始化时将其赋值给某个粒子,其余粒子随机初始化,最后用基本PSO聚类算法即算法1完成聚类。
该算法采用K唱means+PSO的组合方式有效提高了收敛速度,并在一定程度上提高了聚类的有效性。
文献[9]对Omran于2002年提出的基于粒子群优化的图像聚类算法进行了更细致的研究,对适应度函数作了改进以达到同时最小化平均误差函数和簇内距离,以及最大化簇间距离的目标,同时讨论了PSO控制参数对算法性能的影响。
