长沙市南雅中学2019年春学期八年级数学下册第二次月考试卷附答案解析
精品解析:2019年湖南省长沙市中雅中学、南雅中学中考数学二模试卷(解析版)

2019年湖南省长沙市中雅中学、南雅中学中考数学二模试卷一、单项选择题(本大题共12个小题,每小题3分,共36分)1.下列实数为无理数的是( ) A. 4 B. 32 C. 2π D. 0【答案】C【解析】【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.【详解】解:A 、4=2是整数,是有理数,故选项不符合题意;B 、32是分数,是有理数,故选项不符合题意; C 、2π是无理数,故选项符合题意; D 、0是整数,是有理数,故选项不符合题意.故选:C .【点睛】此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.2.2019年“五一”小长假有四天假期,长沙市共接待游客356万人次,称为新晋“网红城市”,356万人用科学记数法表示为( )A. 3.56×106人B. 35.6×105人C. 3.6×105人D. 0.356×107人 【答案】A【解析】【分析】科学记数法的表示形式为a ×10n的形式,其中1≤|a |<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>10时,n是正数;当原数的绝对值<1时,n是负数.【详解】解:356万=56×106.故选:A.【点睛】此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.3.下列各式正确的是()A. (a2)3=a5B. 2a2+2a3=2a5C.433a bababD. (x﹣1)(x+1)=x2﹣1【答案】D【解析】【分析】各项计算得到结果,即可作出判断.【详解】解:A、原式=a6,不符合题意;B、原式不能合并,不符合题意;C、原式=a3,不符合题意;D、原式=x2﹣1,符合题意,故选:D.【点睛】此题考查了平方差公式,合并同类项,以及幂的乘方与积的乘方,熟练掌握公式及法则是解本题的关键.4.下列手机屏幕手势解锁图案中,是轴对称图形的是()A. B. C. D.【答案】A【解析】【分析】直接根据轴对称图形的概念求解.【详解】解:A、是轴对称图形,故此选项正确;B、不是轴对称图形,故此选项错误;C、不是轴对称图形,故此选项错误;D、不是轴对称图形,故此选项错误.故选:A.【点睛】此题主要考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.5.下列说法中不正确的是()A. 两条对角线互相垂直的矩形是正方形B. 两条对角线相等的菱形是正方形C. 两条对角线垂直且相等的平行四边形是正方形D. 两条对角线垂直且相等的四边形是正方形【答案】D【解析】【分析】根据既是矩形又是菱形的四边形是正方形进行判断.【详解】解:A、两条对角线互相垂直的矩形是正方形,故选项不符合题意;B、两条对角线相等的菱形是正方形,故选项不符合题意;C、两条对角线垂直且相等的平行四边形是正方形,故选项不符合题意;D、应是两条对角线垂直且相等的平行四边形是正方形,故选项符合题意.故选D【点睛】本题考查了正方形的判定,通过这道题可以掌握正方形和矩形,菱形的关系,熟练掌握性质是解题的关键.6.如图是一个由6个相同正方体组成的立体图形,它的主视图是()A.B.C.D.【答案】D【解析】【分析】主视图就是从正面看,看横和竖两个方向正方形的个数.【详解】解:从正面看第一层是3个小正方形,第二层右边2个小正方形,第三层右边2个小正方形,故选:D.【点睛】考核知识点:三视图.理解三视图的意义是关键.7.不等式组10114xx-<⎧⎪⎨≤⎪⎩的解集在数轴上表示正确的是()A.B.C.D.【答案】A【解析】【分析】先分别求出各不等式的解集,再在数轴上表示即可.【详解】解不等式组得:14xx<⎧⎨⎩…,∴在数轴上表示正确的是,故选:A.【点睛】把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.求不等式组的解集应遵循“同大取较大,同小取较小,小大大小中间找,大大小小解不了”的原则.8.已知一次函数y=(3﹣a)x+3,如果y随自变量x的增大而增大,那么a的取值范围为()A. a<3B. a>3C. a<﹣3D. a>﹣3.【答案】A【解析】【分析】根据题意一次函数y随自变量x的增大而增大,即可得出3﹣a>0,从而求得a的取值范围.【详解】∵一次函数y=(3﹣a)x+3,函数值y随自变量x的增大而增大∴3﹣a>0解得a<3故选:A.【点睛】本题考查了一次函数图像增减性问题,解决此类问题只要牢固掌握一次函数k>0,函数图像递增,k<0函数图像递减,反过来亦适用.9.将抛物线y=5x2先向右平移3个单位,再向上平移2个单位后,所得的抛物线的解析式为()A. y=5(x+3)2+2B. y=5(x+3)2﹣2C. y=5(x﹣3)2+2D. y=5(x﹣3)2﹣2【答案】C【解析】【分析】根据向右平移横坐标加,向上平移纵坐标加求出平移后的抛物线的顶点坐标,然后利用顶点式解析式写出即可.【详解】解:∵y=5x2先向右平移3个单位,再向上平移2个单位后的顶点坐标为(3,2),∴所得的抛物线的解析式为y=5(x﹣3)2+2.故选:C.【点睛】本题考查了二次函数图象与几何变换,利用顶点的变化确定函数解析式求解更简便.10.如图,已知CA、CB分别与⊙O相切于A、B两点,D是⊙O上的一点,连接AD、BD,若∠C=56°,则∠D等于()A. 72°B. 68°C. 64°D. 62°【答案】D【解析】【分析】连接OA,OB.根据圆周角定理和四边形内角和定理求解即可.详解】连接OA,OB,∵CA、CB切⊙O于点A、B,∴∠CAO=∠CBO=90°,∵∠C=56°,∴∠AOB=360°﹣∠CAO﹣∠CBO﹣∠C=360°﹣90°﹣90°﹣56°=124°.由圆周角定理知,∠D=12∠AOB=62°,故选:D.【点睛】本题考查了切线的性质、圆周角定理、以及四边形的内角和为360度.熟练掌握:圆心与切点的连线垂直切线;过圆心垂直于切线的直线必过切点;过圆外一点引圆的两条切线,切线长相等等知识是解题的关键.11.如图,考古队在A处测得古塔BC顶端C的仰角为45°,斜坡AD长10米,坡度i=3:4,BD长12米,请问古塔BC的高度为()米.A. 25.5B. 26C. 28.5D. 20.5【答案】B【解析】【分析】作AE⊥BC,AF⊥BD,由i=3:4,可设AF=3x,DF=4x,结合AD=10,利用勾股定理可求得x的值,解直角三角形即可得到结论.【详解】解:如图,过点A作AE⊥BC于点E,过点A作AF⊥BD,交BD延长线于点F,由i=3:4,可设AF=3x,DF=4x,∵AD=10,∴9x2+16x2=100,解得:x=2(负值舍去),则AF=BE=6,DF=8,∴AE=DF+BD=8+12=20,∵∠CAE=45°,∴CE=AE=20,则BC=CE+BE=20+6=26,故选:B.【点睛】本题考查了解直角三角形应用﹣坡度坡角问题,解题的关键是能根据题意构造直角三角形并结合图形利用三角函数解直角三角形.12.如图,在边长为1的正方形ABCD中,动点F、E分别以相同的速度从D、C两点同时出发向C、B运动(任何一个点到达即停止),BF、AE交于点P,连接CP,则线段CP的最小值为()A. 512-B.512+C. 51- D. 51+【答案】A【解析】【分析】首先判断出△ABE≌△BCF,即可判断出∠BAE=∠CBF,再根据∠BAE+∠BEA=90°,可得∠CBF+∠BEA =90°,所以∠APB=90°;然后根据点P在运动中保持∠APB=90°,可得点P的路径是一段以AB为直径的弧,设AB的中点为G,连接CG交弧于点P,此时CP的长度最小,最后在Rt△BCG中,根据勾股定理,求出CG的长度,再求出PG的长度,即可求出线段CP的最小值为多少.【详解】解:如图,∵动点F,E的速度相同,∴DF=CE,又∵CD=BC,∴CF=BE,在△ABE和△BCF中,AB BC1ABE BCF90 BE CF ︒==⎧⎪∠=∠=⎨⎪=⎩∴△ABE≌△BCF(SAS),∴∠BAE=∠CBF,∵∠BAE+∠BEA=90°,∴∠CBF+∠BEA=90°,∴∠APB=90°,∵点P在运动中保持∠APB=90°,∴点P的路径是一段以AB为直径的弧,设AB的中点为G,连接CG交弧于点P,此时CP的长度最小,在Rt△BCG中,CG=222215 BC BG122⎛⎫+=+=⎪⎝⎭,∵PG=1122 AB=,∴CP=CG﹣PG=5151 222--=,即线段CP的最小值为512-,故选:A.【点睛】此题还考查了全等三角形的判定和性质的应用,正方形的性质和应用,直角三角形的性质和应用,以及勾股定理的应用,解答此题的关键是判断出什么情况下,CP的长度最小.二、填空题(本大题共6个小题,每小题3分,共18分)13.分解因式:3a2﹣12=▲ .【答案】3(a+2)(a﹣2)【解析】要将一个多项式分解因式的一般步骤是首先看各项有没有公因式,若有公因式,则把它提取出来,之后再观察是否是完全平方式或平方差式,若是就考虑用公式法继续分解因式。
2018-2019湖南长沙南雅中学八年级下第二次月考数学试卷

x -2南雅中学初二年级第二次阶段性测试数学时量:120分钟满分:120分编辑:秋老师一、选择题(本题共12 小题,每小题3 分,共36 分)1.函数y =x -3中自变量x 的取值范围是()A.x > 2B.x ≥ 2C.x ≥ 2 且x ≠ 3D.x ≠ 32.下列方程是一元二次方程的是()A.x2 = 1B.x 2 +1+ 1 = 0xC.x2 +y -1 = 0D.x 3 - 2x2 = 13.若b > 0,则一次函数y =-x +b 的图象大致是()A B C D5.某种植物的主干长出若干数目的支干,每个支干又长出相同数目的小分支,主干、支干和小分支的总数是57 ,设每个支干长出x 个小分支,根据题意列出方程为()A. 1+x +x (1+x )=-1B. 1+x +x2 = 57C. x +x (1+x )= 57D. 1+ 2x2 = 576.某市高新区某厂今年新招聘一批员工,他们中不同文化程度的人数见下表:文化程度高中大专本科硕士博士人数9172095关于这组文化程度的人数数据,以下说法正确的是()A.众数是20B. 中位数是17C. 平均数是12D. 方差是268.若一元二次方程x2 - 2x +m = 0 有两个不相同的实数根,则实数m 的取值范围是()9.下列命题说法错误的是()B.一组对边平行且一组对角相等的四边形是平行四边形C.一条对角线平分一组对角的平行四边形是菱形D.对角线互相垂直的平行四边形是正方形E.四个角都相等的四边形是矩形10.已知实数m 、n 满足x2 - 7x + 2 = 0 ,则n +m的值是()m n11.如图,正方形ABCD中,点E、F分别在边BC、CD上,且AE=EF=FA,有下列结论:①∆ABE≅∆ADF;②CE =CF ;③∠AEB = 75︒;④ BE +DF =EF ;⑤S∆ABE+S∆SDF=S∆CEF;其中正确的有()个F.2G.3H.4I.512.如果关于x 的一元二次方程ax2 +bx +c = 0 (a ≠ 0)有下列说法:①若a +b +c = 0 ,则b2 - 4ac ≥ 0 ;②若方程两根为-1和2 ,则2a +c = 0 ;③若方程ax2 +c = 0有两个不相等的实根,则方程ax2 +bx +c = 0 必有两个不相等的实根;④若b = 2a + 3c ,则方程有两个不相等的实根,其中结论正确的是有()个A. 1B. 2C. 3D. 4二、填空题(本题共6 小题,每小题3 分,共18分)13. 方程(x-1)(x+ 2)= 2 (x + 2 )的根是;14.如果m 是关于x 的方程x2 + 2x - 3 = 0 的一个根,则2m2 + 4m =;15.如图,正方形ABCD 的边长为4 ,∆ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,使PD +PE 最小,则这个最小值为;第15 题图第16 题图16.如图,平行四边形ABCD 的对角线相交于点O ,且AD ≠CD ,过点O 作OM ⊥AC ,交AD 于点M ,如果∆CDM 的周长为8 ,那么平行四边形ABCD 的周长是;17. 股市规定:股票每天的涨、跌幅均不超过10% ,即当涨了原价的10% 后,便不能再涨,叫做涨停,即当跌了原价的10% 后,便不能再跌,叫做跌停,若一支股票某天跌停,之后两天又涨到原价,若这两天设股票股价平均增长率为 x ,则 x满足的方程是;于点 A 2 ,过点 A 2 作 y 轴的垂线交l 2 于点 A 3 ,过点 A 3 作 x 轴的垂线交l 1 于点 A 4 ,过点 A 4 作 y 轴的垂线交l 2 于点A 5 ,……,依次进行下去,则 A 2018 的横坐标为.三、解答题(本题共8 小题,第19 、20 、21每小题6 分,第 22 、23题每小题9 分,第 24 、25 、26 题每小题10 分,共66 分)18. 一块长为60 m ,宽为50 m 的矩形荒地,地方政府准备在此建一个综合性休闲广场,其中阴影部分为通道,通道的宽度均相等,中间的三个矩形(其中三个矩形的一边长均为 a m )区域将铺设塑胶地面作为运动场地. (1)设通道的宽度为 x m ,则 a ;(用含 x 的代数式表示) (2)若塑胶运动场地总的占地面积为2430 m 2,请问通道的宽度为多少?19.某养鸡场有2500只鸡准备对外出售,从中随机抽取了一部分鸡,根据它们的质量(单位:kg),绘制出如下的统计图1 和图2,请根据相关信息,解答下列问题:(1)图1 中m 的值为;(2)求统计的这组数据中的平均数、众数和中位数;(3)根据样本数据,估计这2500 只鸡中,质量为2.0 kg 的约有多少只?20.一商店销售某种商品,平均每天可售出20 件,每件盈利40 元,为了扩大销售,增加盈利,该店采取了降价措施,在每件盈利不少于25 元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2 件. (1)若降价3元,则平均每天销售数量为件;(2)当每件商品降价多少元时,该商店每天的销售利润为1200元.21.如图,在平面直角坐标系中xOy 中,A (4, 0),OA =OC ,∠AOC = 60︒,且CB / /OA ,OB 平分∠AOC ,点P 是四边形OABC 的内部的一点,且点P 到四边形OABC 的四条边的距离相等.(1)直接写出点P 的坐标是;(2)若一次函数y =x +b 的图象经过P 点,求b 的值;(3)若一次函数y =x +m 的图象与四边形OABC 有两个公共点时,直接写出m 的取值范围.23. 已知关于x 的方程x2 -(3k +1)x+ 2k 2 + 2k = 0(1)求证:无论k 取何值,方程总有实数根;(2)若等腰三角形ABC 的一边长a = 6 ,另两边长b 、c 恰好是这个方程的两根,求此三角形的周长.24.近段时间共享单车风靡全国,从而刺激了自行车生产厂家,某厂家准备生产A 、B 两种型号的共享单车,已知生产6 辆A 型单车与5辆B 型单车的成本相同,生产3辆A 型单车与2 辆B 型单车共需1080元.(1)求生产一辆A 型车和生产一辆B 型单车的成本各为多少元?(2)由于共享单车公司需求量加大,生产厂家需要再生产A 、B 两种型号的单车共10000 辆,恰逢原料商对基本原料的价格进行调整,调整后,A 型单车每辆成本价比原来降低10% ,B 型单车每辆的成本价不变,如果厂家准备投入的总成本不超过216 万元,那么至少要生产多少辆A 型单车?(3)在(2)的条件下,该生产厂家发现,销售过程中每辆A 型单车可获利100元,每辆B 型单车可获利120元,求全部销售完这批单车获得的利润z 与A 型单车辆数m 之间的函数关系式,并求获利最大的方案及最大利润.25.如果关于x 的一元二次方程ax2 +bx +c = 0 有两个实数根,且其中一个根为另一个根的2 倍,则称这样的方程为“倍根方程”,研究发现了此类方程的一般性结论:设其中一根为t ,则另一根为2t ,因此方程ax2 +bx +c = 0为倍根方程,下面我们根据此结论来解决问题:(1)方程①x2-x-2=0,方程②x2-6x+8=0这两个方程中,是被根方程的是(填序号即可);(2)若(x- 2)(mx +n )= 0 是倍根方程,求4m2 + 5mn +n2 的值;(3)若关于x 的一元二次方程x2 - 上,求此倍根方程的表达式. mx +2n = 0 (m ≥ 0)是倍根方程,且A (m, n )在一次函数y = 3x - 8 的图象326.(一)阅读思考通过解方程(组)使问题得到解决的思维方式就是方程思想,已学过的《勾股定理》及《一次函数》都与它有密切的联系,最近方程家族的《一元二次方程》我们也学习了它的求解方法和应用.(二)解决问题如图1,矩形ABCD 中,AB = 9 ,AD = 12 ,G 在CD 上,且DG = 5,点P 从点B 出发,以1个单位每秒的速度在BC 边上向点C 运动,设点P 的运动时间为x 秒.(1)∆APG 的面积为y ,求y 关于x 的函数关系式,并求出y = 34 时x 的值;(2)在点P 从点B 向C 运动的过程中,是否存在使AP ⊥GP 的时刻?若存在,求出x 的值,若不存在,请说明理由;(3)如图2,M 、N 分别是AP 、PG 的中点,在点P 从B 向C 运动的过程中,线段MN 扫过的图形是什么形状,并直接写出它的面积.。
八年级下第二次月考数学试卷+答案和解释

八年级下学期第二次月考数学试卷一.精心选一选,慧眼识金.(本大题共8小题,每小题3分,共24分)1.下列电视台的台标,是中心对称图形的是( )A.B.C.D.2.下列各式中,与是同类二次根式的是( )A.B.C.D.3.如果代数式有意义,那么x的取值范围是( )A.x≥0 B.x≠1 C.x>0 D.x≥0且x≠14.在一个不透明的盒子里有形状、大小相同的黄球2个、红球3个,从盒子里任意摸出1个球,摸到红球的概率是( )A.B.C.D.5.用配方法解方程x2+10x+9=0,配方正确的是( )A.(x+5)2=16 B.(x+5)2=34 C.(x﹣5)2=16 D.(x+5)2=256.如图,E、F分别是正方形ABCD的边AB、BC上的点,BE=CF,连接CE、DF.△CDF 可以看作是将△BCE绕正方形ABCD的中心O按逆时针方向旋转得到.则旋转角度为( )A.45°B.60°C.90°D.120°7.若关于x的分式方程=无解,则m的值为( )A.﹣1.5 B.1 C.﹣1.5或2 D.﹣0.5或﹣1.5 8.如图,反比例函数y1=和正比例函数y2=nx的图象交于A(﹣1,﹣3)、B两点,则﹣nx≥0的解集是( )A.﹣1<x<0 B.x<﹣1或0<x<1 C.x≤1或0<x≤1 D.﹣1<x<0或x≥1二.细心填一填,一锤定音.(本大题共10小题,每空格3分,共30分)9.调查某城市的空气质量,应选择__________.10.代数式在实数范围内有意义,则x的取值范围是__________.11.若反比例函数y=的图象过点A(1,﹣2),则k=__________.12.已知+=0,则﹣=__________.13.小丽与小刚一起玩“剪刀、石头、布”的游戏,小丽出“石头”的概率是__________.14.一个对角线长分别为6cm和8cm的菱形,顺次连接它的四边中点得到的四边形的面积是__________.15.若关于x的分式方程﹣2=有增根,则m的值为__________.16.函数y=与y=﹣x+2图象的交点坐标为(a,b),则的值为__________.17.如图,直线x=2与反比例函数和的图象分别交于A、B两点,若点P是y 轴上任意一点,则△PAB的面积是__________.18.如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线BD上有一点P,使PC+PE的和最小,则这个最小值为__________.三.耐心做一做,马到成功.(本大题共8个小题,共66分,解答时应写出文字说明、证明过程或演算步骤.)19.计算:(1)﹣﹣(﹣2)(2)(+﹣)(++)20.先化简,然后从1、、﹣1中选取一个你认为合适的数作为a的值代入求值.21.(16分)解方程:(1)=﹣3(2)﹣=(3)x2﹣9=0(4)x2+4x﹣5=0.22.某中学九①班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:(1)九①班的学生人数为__________,并把条形统计图补充完整;(2)扇形统计图中m=__________,n=__________,表示“足球”的扇形的圆心角是__________度.23.如图,O是菱形ABCD对角线AC与BD的交点,CD=5cm,OD=3cm;过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.(1)求OC的长;(2)求证:四边形OBEC为矩形;(3)求矩形OBEC的面积.24.某校为了创建书香校园,去年又购进了一批图书,经了解,科普书的单价比文学书的单价多4元,用1200元购进的科普书与用800元购进的文学书本数相等,求去年购进的文学书和科普书的单价各是多少元?25.我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线的一部分.请根据图中信息解答下列问题:(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?(2)求k的值;(3)当x=16时,大棚内的温度约为多少度?26.如图1,正方形ABCD中,C(﹣3,0),D(0,4).过A点作AF⊥y轴于F点,过B 点作x轴的垂线交过A点的反比例函数的图象于E点,交x轴于G点.(1)求证:△CDO≌△DAF;(2)求点E的坐标;(3)如图2,过点C作直线l∥AE,在直线l上是否存在一点P,使△PAC是等腰三角形?若存在,求P点坐标,不存在说明理由.八年级下学期第二次月考数学试卷一.精心选一选,慧眼识金.(本大题共8小题,每小题3分,共24分)1.下列电视台的台标,是中心对称图形的是( )A.B.C. D.考点:中心对称图形.分析:根据中心对称图形的概念对各选项分析判断后利用排除法求解.解答:解:A、不是中心对称图形,故A选项错误;B、不是中心对称图形,故B选项错误;C、不是中心对称图形,故C选项错误;D、是中心对称图形,故D选项正确.故选D.点评:本题考查了中心对称图形,掌握中心对称图形的概念:中心对称图形是要寻找对称中心,旋转180°后与原图重合是解题的关键.2.下列各式中,与是同类二次根式的是( )A.B.C.D.考点:同类二次根式.分析:先化简二次根式,再判定即可.解答:解:A、与不是同类二次根式,错误;B、与不是同类二次根式,错误;C、与不是同类二次根式,错误;D、与是同类二次根式,正确;故选D.点评:本题主要考查了同类二次根式,解题的关键是二次根式的化简.3.如果代数式有意义,那么x的取值范围是( )A.x≥0 B.x≠1 C.x>0 D.x≥0且x≠1考点:分式有意义的条件;二次根式有意义的条件.专题:计算题.分析:代数式有意义的条件为:x﹣1≠0,x≥0.即可求得x的范围.解答:解:根据题意得:x≥0且x﹣1≠0.解得:x≥0且x≠1.故选:D.点评:式子必须同时满足分式有意义和二次根式有意义两个条件.分式有意义的条件为:分母≠0;二次根式有意义的条件为:被开方数≥0.此类题的易错点是忽视了二次根式有意义的条件,导致漏解情况.4.在一个不透明的盒子里有形状、大小相同的黄球2个、红球3个,从盒子里任意摸出1个球,摸到红球的概率是( )A.B.C.D.考点:概率公式.分析:根据随机事件概率大小的求法,找准两点:①符合条件的情况数目;②全部情况的总数.二者的比值就是其发生的概率的大小.解答:解:∵共5个球中有3个红球,∴任取一个,是红球的概率是:,故选B.点评:本题考查概率的求法与运用,一般方法为:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=.5.用配方法解方程x2+10x+9=0,配方正确的是( )A.(x+5)2=16 B.(x+5)2=34 C.(x﹣5)2=16 D.(x+5)2=25考点:解一元二次方程-配方法.分析:移项,配方(方程两边都加上一次项系数的一半的平方),即可得出答案.解答:解:x2+10x+9=0,x2+10x=﹣9,x2+10x+52=﹣9+52,(x+5)2=16.故选A.点评:本题考查了用配方法解一元二次方程的应用,关键是能正确配方.6.如图,E、F分别是正方形A BCD的边AB、BC上的点,BE=CF,连接CE、DF.△CDF 可以看作是将△BCE绕正方形ABCD的中心O按逆时针方向旋转得到.则旋转角度为( )A.45°B.60°C.90°D.120°考点:旋转的性质.分析:据旋转性质得出旋转后C到D,只要根据正方形的性质和三角形的内角和定理求出∠COD即可.解答:解:将△CBE绕正方形的对角线交点O按逆时针方向旋转到△CDF时,C和D重合,即∠COD是旋转角,∵四边形ABCD是正方形,∴∠OCD=∠ODC=45°,∴∠COD=180°﹣45°﹣45°=90°,即旋转角是90°,故选C.点评:本题主要考查了旋转的性质,以及正多边形的性质,正确理解正多边形的性质以及旋转角(对应点与旋转中心所连线段的夹角等于旋转角)是解题的关键.7.若关于x的分式方程=无解,则m的值为( )A.﹣1.5 B.1 C.﹣1.5或2 D.﹣0.5或﹣1.5考点:分式方程的解.专题:压轴题.分析:先把方程两边乘以x(x﹣3)得到x(2m+x)﹣x(x﹣3)=2(x﹣3),整理得(2m+1)x=﹣6,由于关于x的分式方程=无解,则可能有x=3或x=0,然后分别把它们代入(2m+1)x=﹣6,即可得到m的值,然后再讨论方程(2m+1)x=﹣6无解得到m=﹣.解答:解:去分母得,x(2m+x)﹣x(x﹣3)=2(x﹣3),整理得,(2m+1)x=﹣6,∵关于x的分式方程=无解,∴x=3或x=0,把x=3代入(2m+1)x=﹣6得,(2m+1)×3=﹣6,解得m=﹣1.5;把x=0代入(2m+1)x=﹣6得,(2m+1)×0=﹣6,无解,又∵2m+1=0时,方程(2m+1)x=﹣6无解,∴m=﹣,所以m的值为﹣1.5或﹣0.5.故选:D.点评:本题考查了分式方程的解:把分式方程转化为整式方程,然后把整式方程的解代入原方程进行检验,若整式方程的解使分式方程的分母不为零,则这个整式方程的解是分式方程的解;若整式方程的解使分式方程的分母为零,则这个整式方程的解是分式方程的增根.8.如图,反比例函数y1=和正比例函数y2=nx的图象交于A(﹣1,﹣3)、B两点,则﹣nx≥0的解集是( )A.﹣1<x<0 B.x<﹣1或0<x<1 C.x≤1或0<x≤1 D.﹣1<x<0或x≥1考点:反比例函数与一次函数的交点问题.分析:求出≥nx,求出B的坐标,根据A、B的坐标结合图象得出即可.解答:解:∵﹣nx≥0,∴≥nx,∵反比例函数y1=和正比例函数y2=nx的图象交于A(﹣1,﹣3)、B两点,∴B点的坐标是(1,3),∴﹣nx≥0的解集是x<﹣1或0<x>1,故选B.点评:本题考查了一次函数与反比例函数的交点问题,函数的图象的应用,主要考查学生的理解能力和观察图象的能力.二.细心填一填,一锤定音.(本大题共10小题,每空格3分,共30分)9.调查某城市的空气质量,应选择抽样调查.考点:全面调查与抽样调查.专题:应用题.分析:根据全面调查和抽样调查的特点即可作出判断.解答:解:此题显然无法普查,必须采用抽样调查.点评:本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查;对于精确度要求高的调查,事关重大的调查往往选用普查.10.代数式在实数范围内有意义,则x的取值范围是x≥1.考点:二次根式有意义的条件.分析:先根据二次根式有意义的条件列出关于x的不等式,求出x的取值范围即可.解答:解:∵在实数范围内有意义,∴x﹣1≥0,解得x≥1.故答案为:x≥1.点评:本题考查的是二次根式有意义的条件,即被开方数大于等于0.11.若反比例函数y=的图象过点A(1,﹣2),则k=﹣2.考点:待定系数法求反比例函数解析式.专题:计算题;待定系数法.分析:此题只需将A(1,﹣2)代入反比例函数即可求得k的值.解答:解:将点(1,﹣2)代入y=得:,解得:k=﹣2.故答案为﹣2.点评:本题比较简单,考查的是用待定系数法求反比例函数的比例系数,是中学阶段的重点内容.12.已知+=0,则﹣=﹣.考点:二次根式的化简求值.专题:计算题.分析:利用非负数的性质求出a与b的值,代入原式计算即可得到结果.解答:解:∵+=0,∴2﹣a=0,b﹣3=0,解得:a=2,b=3,则原式=﹣=﹣.故答案为:﹣点评:此题考查了二次根式的.化简求值,熟练掌握运算法则是解本题的关键.13.小丽与小刚一起玩“剪刀、石头、布”的游戏,小丽出“石头”的概率是.考点:概率公式.分析:根据概率公式列式即可.解答:解:∵共有剪刀、石头、布三种情况,且每一种情况都具有等可能性,∴小丽出“石头”的概率是.故答案为:.点评:本题考查了概率公式,用到的知识点为:概率=所求情况数与总情况数之比.14.一个对角线长分别为6cm和8cm的菱形,顺次连接它的四边中点得到的四边形的面积是12cm2.考点:中点四边形.分析:根据顺次连接这个菱形各边中点所得的四边形是矩形,且矩形的边长分别是菱形对角线的一半,问题得解.解答:解:∵E、F、G、H分别为各边中点∴EF∥GH∥AC,EF=GH=AC,EH=FG=BD,EH∥FG∥BD∵DB⊥AC,∴EF⊥EH,∴四边形EFGH是矩形,∵EH=BD=3cm,EF=AC=4cm,∴矩形EFGH的面积=EH×EF=3×4=12cm2,故答案为:12cm2.点评:本题考查了菱形的性质,菱形的四边相等,对角线互相垂直,连接菱形各边的中点得到矩形,且矩形的边长是菱形对角线的一半.15.若关于x的分式方程﹣2=有增根,则m的值为3.考点:分式方程的增根.分析:增根是化为整式方程后产生的不适合分式方程的根.所以应先确定增根的可能值,让最简公分母x﹣3=0,得到x=3,然后代入化为整式方程的方程算出m的值.解答:解:方程两边都乘x﹣3,得x﹣2(x﹣3)=m∵原方程有增根,∴最简公分母x﹣3=0,解得x=3,当x=3时,m=3故m的值是3.故答案为:3.点评:本题考查了分式方程的增根.增根问题可按如下步骤进行:①让最简公分母为0确定增根;②化分式方程为整式方程;③把增根代入整式方程即可求得相关字母的值.16.函数y=与y=﹣x+2图象的交点坐标为(a,b),则的值为2.考点:反比例函数与一次函数的交点问题.专题:计算题.分析:根据反比例函数与一次函数的交点问题,解方程组可得到交点坐标,则得到a与b的值,然后把a、b的值代入中计算即可.解答:解:根据题意得,解得,所以函数y=与y=﹣x+2图象的交点坐标为(1,1),即a=1,b=1,所以=1+1=2.故答案为2.点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.17.如图,直线x=2与反比例函数和的图象分别交于A、B两点,若点P是y 轴上任意一点,则△PAB的面积是.考点:反比例函数系数k的几何意义.分析:先分别求出A、B两点的坐标,得到AB的长度,再根据三角形的面积公式即可得出△PAB的面积.解答:解:∵把x=2分别代入、,得y=1、y=﹣.∴A(2,1),B(2,﹣),∴AB=1﹣(﹣)=.∵P为y轴上的任意一点,∴点P到直线x=2的距离为2,∴△PAB的面积=AB×2=AB=.故答案是:.点评:此题考查了反比例函数图象上点的坐标特征及三角形的面积,求出AB的长度是解答本题的关键,难度一般.18.如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线BD上有一点P,使PC+PE的和最小,则这个最小值为4.考点:轴对称-最短路线问题;正方形的性质.分析:根据正方形的性质,推出C、A关于BD对称,推出CP=AP,推出EP+CP=AE,根据等边三角形性质推出AE=AB=EP+CP,根据正方形面积公式求出AB即可.解答:解:连接AC,∵正方形ABCD,∴AC⊥BD,OA=OC,∴C、A关于BD对称,即C关于BD的对称点是A,连接AE交BD于P,则此时EP+CP的值最小,∵C、A关于BD对称,∴CP=AP,∴EP+CP=AE,∵等边三角形ABE,∴EP+CP=AE=AB,∵正方形ABCD的面积为16,∴AB=4,∴EP+CP=4,故答案为:4.点评:本题考查了正方形的性质,轴对称﹣最短问题,等边三角形的性质等知识点的应用,解此题的关键是确定P的位置和求出EP+CP的最小值是AE,题目比较典型,但有一定的难度,主要培养学生分析问题和解决问题的能力.三.耐心做一做,马到成功.(本大题共8个小题,共66分,解答时应写出文字说明、证明过程或演算步骤.)19.计算:(1)﹣﹣(﹣2)(2)(+﹣)(++)考点:二次根式的混合运算.专题:计算题.分析:(1)先把各二次根式化为最简二次根式,然后去括号后合并即可;(2)先变形得到原式=[(+)﹣][(+)+],然后利用平方差公式和完全平方公式进行计算.解答:解:(1)原式=3﹣﹣2+10=13﹣;(2)原式=[(+)﹣][(+)+]=(+)2﹣()2=2+2+3﹣5=2.点评:本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.20.先化简,然后从1、、﹣1中选取一个你认为合适的数作为a的值代入求值.考点:分式的化简求值.专题:压轴题.分析:先把除法转化成乘法,再根据乘法的分配律分别进行计算,然后把所得的结果化简,最后选取一个合适的数代入即可.解答:解:=×=﹣==,由于a≠±1,所以当a=时,原式==.点评:此题考查了分式的化简求值,用到的知识点是乘法的分配律、约分,在计算时要注意把结果化到最简.21.(16分)解方程:(1)=﹣3(2)﹣=(3)x2﹣9=0(4)x2+4x﹣5=0.考点:解分式方程;解一元二次方程-直接开平方法;解一元二次方程-因式分解法.分析:(1)方程两边乘最简公分母(x﹣2),再把分式方程转化为整式方程求解;(2)方程两边乘最简公分母(x+2)(x﹣2),再把分式方程转化为整式方程求解;(3)先把方程变形为x2=9,然后利用直接开平方法其解;(4)把常数项﹣5移项后,应该在左右两边同时加上一次项系数4的一半的平方,然后直接开平方法求解;解答:解:(1)=﹣3,解:两边同乘以(x﹣2)得,1=x﹣1﹣3(x﹣2),解得:x=2,检验:当x=2时,x﹣2=0,∴原方程无解;(2)﹣=,解:两边同乘以(x+2)(x﹣2)得:(x﹣2)(x﹣2)﹣16=(x+2)(x+2),解得:x=﹣2,检验:当x=﹣2时,(x+2)(x﹣2)=0,∴原方程无解;(3)x2﹣9=0解:x2=9.两边直接开平方得:x=±3,∴方程的解为:x1=3,x2=﹣3,(4)x2+4x﹣5=0,解:由原方程移项,得x2+4x=5,方程两边同时加上一次项系数一半的平方,得到x2+4x+4=5+4,配方得(x+2)2=9.开方,得x+2=±3,解得x1=1,x2=﹣5.点评:本题考查了解分式方程,一元二次方程,熟练掌握解各类方程的方法是解题的关键.22.某中学九①班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:(1)九①班的学生人数为40,并把条形统计图补充完整;(2)扇形统计图中m=10,n=20,表示“足球”的扇形的圆心角是72度.考点:条形统计图;扇形统计图.分析:(1)根据喜欢篮球的有12人,占30%,即可求得总人数,利用总人数减去其它各组的人数,即可求得喜欢足球的人数;(2)利用百分比的计算公式,即可求得m、n的值,利用360°乘以对应的百分比,即可求得圆心角的度数.解答:解:(1)总人数是:12÷30%=40,则爱好足球的人数是:40﹣4﹣12﹣16=8.故答案是:40;(2)喜欢排球的人所占比例:×100%=10%,则m=10,喜欢足球的人所占的比例:×100%=20%,则n=20.示“足球”的扇形的圆心角是360°×20%=72°.故答案是:10,20,72.点评:本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.23.如图,O是菱形ABCD对角线AC与BD的交点,CD=5cm,OD=3cm;过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.(1)求OC的长;(2)求证:四边形OBEC为矩形;(3)求矩形OBEC的面积.考点:矩形的判定与性质;菱形的性质.专题:几何图形问题.分析:(1)在直角△OCD中,利用勾股定理即可求解;(2)利用矩形的定义即可证明;(3)利用矩形的面积公式即可直接求解.解答:解:(1)∵ABCD是菱形,∴AC⊥BD,∴直角△OCD中,OC===4cm;(2)∵CE∥DB,BE∥AC,∴四边形OBEC为平行四边形,又∵AC⊥BD,即∠COB=90°,∴平行四边形OBEC为矩形;(3)∵OB=0D,∴S矩形OBEC=OB•OC=4×3=12(cm2).点评:本题考查了菱形的性质以及矩形的判定,理解菱形的对角线的关系是关键.24.某校为了创建书香校园,去年又购进了一批图书,经了解,科普书的单价比文学书的单价多4元,用1200元购进的科普书与用800元购进的文学书本数相等,求去年购进的文学书和科普书的单价各是多少元?考点:分式方程的应用.分析:设文学书的单价是x元,则科普书的单价是(x+4)元,根据关键语句“用1200元购进的科普书与用800元购进的文学书本数相等”,可列方程求解.解答:解:设文学书的单价是x元,则科普书的单价是(x+4)元,根据题意,得=,解得x=8.经检验得:(x+4)x=12×8=96≠0,故x=8是方程的根,则x+4=12.答:去年购进的文学书的单价是8元,科普书的单价是12元.点评:本题主要考查了分式方程的应用,关键是正确理解题意,设出文学书的单价,表示出科普书的单价,根据购进的数量相等做为等量关系列方程求解.25.我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线的一部分.请根据图中信息解答下列问题:(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?(2)求k的值;(3)当x=16时,大棚内的温度约为多少度?考点:反比例函数的应用;一次函数的应用.分析:(1)根据图象直接得出大棚温度18℃的时间为12﹣2=10(小时);(2)利用待定系数法求反比例函数解析式即可;(3)将x=16代入函数解析式求出y的值即可.解答:解:(1)恒温系统在这天保持大棚温度18℃的时间为12﹣2=10小时.(2)∵点B(12,18)在双曲线y=上,∴18=,∴解得:k=216.(3)当x=16时,y==13.5,所以当x=16时,大棚内的温度约为13.5℃.点评:此题主要考查了反比例函数的应用,求出反比例函数解析式是解题关键.26.如图1,正方形ABCD中,C(﹣3,0),D(0,4).过A点作AF⊥y轴于F点,过B 点作x轴的垂线交过A点的反比例函数的图象于E点,交x轴于G点.(1)求证:△CDO≌△DAF;(2)求点E的坐标;(3)如图2,过点C作直线l∥AE,在直线l上是否存在一点P,使△PAC是等腰三角形?若存在,求P点坐标,不存在说明理由.考点:反比例函数综合题.专题:综合题.分析:(1)根据正方形的性质AD=CD,∠ADC=90°,再利用等角的余角相等得到∠DAF=∠CDO,于是可根据“AAS”证明△CDO≌△DAF;(2)由于△CDO≌△DAF,根据全等的性质得AF=OD=4,DF=OC=3,则A点坐标为(﹣4,7),再利用待定系数法可求出反比例函数解析式为y=﹣;与(1)中的方法一样可证明△CDO≌△BGC,得到CG=OD=4,则得到E点的横坐标为﹣7,然后利用反比例函数解析式可确定E点坐标;(3)如图2,作AH⊥x轴于H,在Rt△ACH中,根据勾股定理得到AC2=50,利用待定系数法求出直线AE的解析式为y=x+11,由于直线l∥AE,则直线l的解析式为设为y=x+b,把C(﹣3,0)代入可计算出b=3,则直线l的解析式为设为y=x+3,于是可设P点坐标为(t,t+3),然后利用两点间的距离公式得到AP2=(t+4)2+(t﹣4)2,CP2=(t+3)2+(t+3)2,接着进行分类讨论:当CP=CA时,即(t+3)2+(t+3)2=50;当AP=AC时,(t+4)2+(t﹣4)2=50;当PC=PA时,(t+3)2+(t+3)2=(t+4)2+(t﹣4)2,分别解方程求出t的值,从而可得到满足条件的P点坐标.解答:(1)证明:如图1,∵C(﹣3,0),D(0,4),∴OC=3,OD=4,∵四边形ABCD为正方形,∴AD=CD,∠ADC=90°,∴∠ADF+∠CDO=90°,∵AF⊥y轴,∴∠AFD=90°,∴∠ADF+∠DAF=90°,∴∠DAF=∠CDO,在△CDO和△DAF中,∴△CDO≌△DAF;(2)解:如图1,∵△CDO≌△DAF,∴AF=OD=4,DF=OC=3,∴OF=OD+DF=3+4=7,∴A点坐标为(﹣4,7),设反比例函数解析式为y=,把A(﹣4,7)代入y=得k=﹣4×7=﹣28,∴反比例函数解析式为y=﹣,与(1)中的方法一样可证明△CDO≌△BGC,∴CG=OD=4,∴OG=OC+CG=7,∴E点的横坐标为﹣7,把x=﹣7代入y=﹣得y=4,∴E点坐标为(﹣7,4);(3)解:存在.如图2,作AH⊥x轴于H,在Rt△ACH中,AH=7,CH=1,则AC2=72+12=50,设直线AE的解析式为y=mx+n,把A(﹣4,7)和E(﹣7,4)代入y=mx+n得,解得,∴直线AE的解析式为y=x+11,∵直线l∥AE,∴直线l的解析式为设为y=x+b,把C(﹣3,0)代入得﹣3+b=0,解得b=3,∴直线l的解析式为设为y=x+3,设P点坐标为(t,t+3),∴AP2=(t+4)2+(t﹣4)2,CP2=(t+3)2+(t+3)2,当CP=CA时,(t+3)2+(t+3)2=50,解得t1=2,t2=﹣8,此时P点坐标为(2,5)或(﹣8,﹣5);当AP=AC时,(t+4)2+(t﹣4)2=50,解得t1=3,t2=﹣3(舍去),此时P点坐标为(3,6);当PC=PA时,(t+3)2+(t+3)2=(t+4)2+(t﹣4)2,解得t=,此时P 点坐标为(,),综上所述,满足条件的P点坐标为(2,5)或(﹣8,﹣5)或(3,6)或(,).点评:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征、等腰三角形的性质、正方形的性质和三角形全等的判定与性质;会利用待定系数法求函数解析式和利用两点间的距离公式计算线段的长;理解坐标与图形的性质;会运用分类讨论的思想解决数学问题.第21 页共21 页。
八年级下第二次月考数学试卷+答案及解释

八年级(下)第二次月考数学试卷一.选择(共10题,每题3分,共30分)1.如果把分式中的x和y都扩大3倍,那么分式的值()A.扩大3倍B.缩小3倍C.缩小6倍D.不变2.已知反比例函数y=的图象经过点P(﹣1,2),则这个函数的图象位于()A.第二,三象限B.第一,三象限C.第三,四象限D.第二,四象限3.如果代数式有意义,那么x的取值范围是()A.x≥0 B.x≠1 C.x>0 D.x≥0且x≠14.计算的结果是()A.B.C.D.5.已知点A(﹣2,y1)、B(﹣1,y2)、C(3,y3)都在反比例函数y=的图象上,则()A.y1<y2<y3 B.y3<y2<y1 C.y3<y1<y2 D.y2<y1<y36.如图,过双曲线y=(k是常数,k>0,x>0)的图象上两点A,B分别作AC⊥x轴于C,BD⊥x轴于D,则△AOC的面积S1和△BOD的面积S2的大小关系为()A.S1>S2 B.S1=S2C.S1<S2 D.S1与S2无法确定7.解分式方程+=3时,去分母后变形为()A.2+(x+2)=3(x﹣1)B.2﹣x+2=3(x﹣1)C.2﹣(x+2)=3(1﹣x)D.2﹣(x+2)=3(x﹣1)8.若分式的值为0,则x的值为()A.﹣1 B.0 C.2 D.﹣1或29.在反比例函数y=,图象分布在一三象限,则m的取值范围是()A.m<0 B.m>0 C.m<D.m>10.函数y=kx+1与函数y=在同一坐标系中的大致图象是下图中的()A.B.C.D.二.填空(共8题,每题3分,共24分)11.若关于x的方程=+1无解,则a的值是.12.反比例函数y=的图象经过点(2,﹣1),则k的值为.13.的最简公分母是.14.若=2﹣x,则x的取值范围是.15.如图,矩形ABOC的面积为,反比例函数y=的图象过点A,则k=.16.计算:=.17.化简:a≥0,b≥0时,=.18.若实数a、b满足|a+2|,则=.三.解答题(共9题,共66分)19.计算:×(﹣1)2++﹣()﹣1.20.(a﹣)÷.21.先化简,再求值:1﹣÷,其中a=﹣1.22.解方程:﹣=1.23.已知,如图,矩形ABCD的对角线AC,BD相交于点O,BE∥AC,CE∥DB.求证:四边形OBEC是菱形.24.到离学校15千米的风景区去秋游,骑车的同学提前40分钟出发,其余的同学乘汽车出发,结果他们同时到达.已知汽车的速度是自行车的3倍,求自行车和汽车的速度.25.某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把1200m3的生活垃圾运走.(1)假如每天能运xm3,所需的时间为y天,写出y与x之间的函数关系式;(2)若每辆拖拉机一天能运12m3,则5辆这样的拖拉机要用多少天才能运完?26.y是x的反比例函数,且当x=4时,y=3.(1)写出y与x之间的函数表达式.(2)画出函数的图象,并根据图象说出当2≤x≤3时y的取值范围.27.(10分)(2015春•新沂市校级月考)如图,四边形ABCD为正方形,点A的坐标为(0,2),点B的坐标为(0,﹣3),反比例函数y1=的图象经过点C,一次函数y2=ax+b的图象经过点A、C.(1)求反比例函数和一次函数的表达式;(2)直接写出y2>y1时x的取值范围;(3)若点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求点P的坐标.八年级(下)第二次月考数学试卷参考答案与试题解析一.选择(共10题,每题3分,共30分)1.如果把分式中的x和y都扩大3倍,那么分式的值()A.扩大3倍B.缩小3倍C.缩小6倍D.不变考点:分式的基本性质.分析:要解此题,可以将x,y用3x,3y代入、化简,跟原式对比.解答:解:将x,y用3x,3y代入中可得=,∴分式的值不变.故选D.点评:此题考查的是对分式的性质的理解和运用.2.已知反比例函数y=的图象经过点P(﹣1,2),则这个函数的图象位于()A.第二,三象限B.第一,三象限C.第三,四象限D.第二,四象限考点:反比例函数的性质;待定系数法求反比例函数解析式.专题:待定系数法.分析:先把点代入函数解析式,求出k值,再根据反比例函数的性质求解即可.解答:解:由题意得,k=﹣1×2=﹣2<0,∴函数的图象位于第二,四象限.故选:D.点评:本题考查了反比例函数的图象的性质:k>0时,图象在第一、三象限,k<0时,图象在第二、四象限.3.如果代数式有意义,那么x的取值范围是()A.x≥0 B.x≠1 C.x>0 D.x≥0且x≠1考点:分式有意义的条件;二次根式有意义的条件.专题:计算题.分析:代数式有意义的条件为:x﹣1≠0,x≥0.即可求得x的范围.解答:解:根据题意得:x≥0且x﹣1≠0.解得:x≥0且x≠1.故选:D.点评:式子必须同时满足分式有意义和二次根式有意义两个条件.分式有意义的条件为:分母≠0;二次根式有意义的条件为:被开方数≥0.此类题的易错点是忽视了二次根式有意义的条件,导致漏解情况.4.计算的结果是()A.B.C.D.考点:分式的加减法.专题:计算题.分析:先通分,再根据同分母的分式相加减的法则进行计算即可.解答:解:原式=﹣==.故选B.点评:本题考查的是分式的加减法,异分母分式加减把分母不相同的几个分式化成分母相同的分式,再把分子相加减即可.5.已知点A(﹣2,y1)、B(﹣1,y2)、C(3,y3)都在反比例函数y=的图象上,则()A.y1<y2<y3 B.y3<y2<y1 C.y3<y1<y2 D.y2<y1<y3考点:反比例函数图象上点的坐标特征.分析:根据反比例函数图象上点的坐标特点解答即可.解答:解:∵k>0,函数图象在一,三象限,由题意可知,点A、B在第三象限,点C在第一象限,∵第三象限内点的纵坐标总小于第一象限内点的纵坐标,∴y3最大,∵在第三象限内,y随x的增大而减小,∴y2<y1.故选:D.点评:在反比函数中,已知各点的横坐标,比较纵坐标的大小,首先应区分各点是否在同一象限内.在同一象限内,按同一象限内点的特点来比较,不在同一象限内,按坐标系内点的特点来比较.6.如图,过双曲线y=(k是常数,k>0,x>0)的图象上两点A,B分别作AC⊥x轴于C,BD⊥x轴于D,则△AOC的面积S1和△BOD的面积S2的大小关系为()A.S1>S2 B.S1=S2C.S1<S2 D.S1与S2无法确定考点:反比例函数系数k的几何意义.专题:数形结合.分析:因为A,B都是双曲线y=(k是常数,k>0,x>0)的图象上的两点,根据过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值,即S=|k|,可知S1=S2.解答:解:依题意可知,△AOC的面积S1和△BOD的面积S2有S1=S2=|k|.故选B.点评:主要考查了反比例函数中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=|k|.7.解分式方程+=3时,去分母后变形为()A.2+(x+2)=3(x﹣1)B.2﹣x+2=3(x﹣1)C.2﹣(x+2)=3(1﹣x)D.2﹣(x+2)=3(x﹣1)考点:解分式方程.分析:本题考查对一个分式确定最简公分母,去分母得能力.观察式子x﹣1和1﹣x互为相反数,可得1﹣x=﹣(x﹣1),所以可得最简公分母为x﹣1,因为去分母时式子不能漏乘,所以方程中式子每一项都要乘最简公分母.解答:解:方程两边都乘以x﹣1,得:2﹣(x+2)=3(x﹣1).故选D.点评:考查了解分式方程,对一个分式方程而言,确定最简公分母后要注意不要漏乘,这正是本题考查点所在.切忌避免出现去分母后:2﹣(x+2)=3形式的出现.8.若分式的值为0,则x的值为()A.﹣1 B.0 C.2 D.﹣1或2考点:分式的值为零的条件.分析:根据分式值为零的条件可得x﹣2=0,再解方程即可.解答:解:由题意得:x﹣2=0,且x+1≠0,解得:x=2,故选:C.点评:此题主要考查了分式值为零的条件,关键是掌握分式值为零的条件是分子等于零且分母不等于零.注意:“分母不为零”这个条件不能少.9.在反比例函数y=,图象分布在一三象限,则m的取值范围是()A.m<0 B.m>0 C.m<D.m>考点:反比例函数的性质.分析:根据反比例函数图象所在象限可得1﹣2m>0,再解即可.解答:解:∵反比例函数y=,图象分布在一三象限,∴1﹣2m>0,解得:m,故选:C.点评:此题主要考查了反比例函数的性质,关键是掌握反比例函数(k≠0),(1)k>0,反比例函数图象在一、三象限;(2)k<0,反比例函数图象在第二、四象限内.10.函数y=kx+1与函数y=在同一坐标系中的大致图象是下图中的()A.B.C.D.考点:反比例函数的图象;一次函数的图象.分析:先根据一次函数的性质判断出k取值,再根据反比例函数的性质判断出k的取值,二者一致的即为正确答案.解答:解:A、由函数y=kx+1的图象可知k<0,由函数y=的图象可知k>0,相矛盾,故错误;B、由函数y=kx+1的图象可知k<0,由函数y=的图象可知k>0,正确;C、由函数y=kx+1的图象可知k<0,由函数y=的图象可知k<0,相矛盾,故错误;D、由函数y=kx+1的图象可知k>0,由函数y=的图象可知k<0,相矛盾,故错误.故选B.点评:本题主要考查了反比例函数的图象性质和一次函数的图象性质,要掌握它们的性质才能灵活解题.二.填空(共8题,每题3分,共24分)11.若关于x的方程=+1无解,则a的值是2或1.考点:分式方程的解.专题:压轴题.分析:把方程去分母得到一个整式方程,把方程的增根x=2代入即可求得a的值.解答:解:x﹣2=0,解得:x=2.方程去分母,得:ax=4+x﹣2,即(a﹣1)x=2当a﹣1≠0时,把x=2代入方程得:2a=4+2﹣2,解得:a=2.当a﹣1=0,即a=1时,原方程无解.故答案是:2或1.点评:首先根据题意写出a的新方程,然后解出a的值.12.反比例函数y=的图象经过点(2,﹣1),则k的值为﹣2.考点:待定系数法求反比例函数解析式.分析:将此点坐标代入函数解析式y=(k≠0)即可求得k的值.解答:解:将点(2,﹣1)代入解析式,可得k=2×(﹣1)=﹣2.故答案为:﹣2.点评:本题比较简单,考查的是用待定系数法求反比例函数的比例系数,是中学阶段的重点内容.13.的最简公分母是12x3yz.考点:最简公分母.分析:利用取各分母系数的最小公倍数与字母因式的最高次幂的积作公分母求解即可.解答:解:的最简公分母是12x3yz.故答案为:12x3yz.点评:本题主要考查了最简公分母,解题的关键是熟记最简公分母的定义.14.若=2﹣x,则x的取值范围是x≤2.考点:二次根式的性质与化简.分析:根据已知得出x﹣2≤0,求出不等式的解集即可.解答:解:∵=2﹣x,∴x﹣2≤0,x≤2则x的取值范围是x≤2故答案为:x≤2.点评:本题考查了二次根式的性质的应用,注意:当a≤0时,=﹣a.15.如图,矩形ABOC的面积为,反比例函数y=的图象过点A,则k=﹣.考点:反比例函数系数k的几何意义.分析:根据反比例函数中比例系数k的几何意义,得出等量关系|k|=,求出k的值.解答:解:依题意,有|k|=,∴k=±,又∵图象位于第二象限,∴k<0,∴k=﹣.故答案为:﹣.点评:反比例函数y=中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.16.计算:=3.考点:二次根式的混合运算.专题:计算题.分析:首先根据乘法分配律打开括号,然后合并同类根式即可求解.解答:解:,=﹣+3,=3.点评:此题主要考查了二次根式的混合运算,在加减的过程中,有同类二次根式的要合并;相乘的时候,被开方数简单的直接让被开方数相乘,再化简;较大的也可先化简,再相乘,灵活对待.17.化简:a≥0,b≥0时,=2ab.考点:二次根式的性质与化简.分析:利用二次根式的性质分别化简得出即可.解答:解:∵a≥0,b≥0,∴=2ab.故答案为:2ab.点评:此题主要考查了二次根式的性质与化简,正确掌握二次根式的性质是解题关键.18.若实数a、b满足|a+2|,则=1.考点:非负数的性质:算术平方根;非负数的性质:绝对值.分析:根据非负数的性质列出方程求出a、b的值,代入所求代数式计算即可.解答:解:根据题意得:,解得:,则原式==1.故答案是:1.点评:本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.三.解答题(共9题,共66分)19.计算:×(﹣1)2++﹣()﹣1.考点:二次根式的混合运算;负整数指数幂.专题:计算题.分析:根据完全平方公式和负整数指数幂的意义得到原式=×(3﹣2+1)++2﹣,然后合并即可.解答:解:原式=×(3﹣2+1)++2﹣=2﹣++2﹣=2+﹣.点评:本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了负整数指数幂.20.(a﹣)÷.考点:分式的乘除法.专题:计算题.分析:做乘法运算时要注意先把分子、分母能因式分解的先分解,然后约分,有括号的先算括号里面的.解答:解:原式=×=.点评:分式的乘除混合运算一般是统一为乘法运算,如果有括号,先算括号里面的,分子或分母是多项式时,通过分解因式,把分子分母中能够分解因式的部分,分解成乘积的形式,然后找到其中的公因式约去.21.先化简,再求值:1﹣÷,其中a=﹣1.考点:分式的化简求值.分析:先根据分式混合运算的法则把原式进行化简,再把a的值代入进行计算即可.解答:解:原式=1﹣×=1﹣==.当a=﹣1时,原式==1.点评:本题考查的是分式的化简求值,在解答此类题目时要注意通分及约分的灵活应用.22.解方程:﹣=1.考点:解分式方程.专题:计算题.分析:分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.解答:解:去分母得:x(x+2)﹣2=x2﹣4,去括号得:x2+2x﹣2=x2﹣4,解得:x=﹣1,经检验x=﹣1是分式方程的解.点评:此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.23.已知,如图,矩形ABCD的对角线AC,BD相交于点O,BE∥AC,CE∥DB.求证:四边形OBEC是菱形.考点:菱形的判定.专题:证明题.分析:先由已知条件证明四边形OBEC是平行四边形,再由矩形的性质得出OB=OC,由菱形的判定方法即可得出结论.解答:证明:∵BE∥AC,CE∥DB,∴四边形OBEC是平行四边形,∵四边形ABCD是矩形,∴OC=AC,OB=BD,AC=BD,∴OB=OC,∴四边形OBEC是菱形.点评:本题考查了矩形的性质、平行四边形的判定、菱形的判定;熟练掌握矩形的性质,并能进行推理论证是解决问题的关键.24.到离学校15千米的风景区去秋游,骑车的同学提前40分钟出发,其余的同学乘汽车出发,结果他们同时到达.已知汽车的速度是自行车的3倍,求自行车和汽车的速度.考点:分式方程的应用.分析:设骑自行车的速度是x千米/小时,根据一部分学生骑自行车先走,走了40分钟后,其余同学乘汽车出发,结果两者同时到达可列方程求解.解答:解:设自行车的速度为x千米/时,则﹣=解得x=15.经检验,x=15是原方程的根,3x=45.答:自行车的速度是15千米/时,汽车的速度是45千米/时.点评:本题考查了分式方程的应用,关键是知道他们同时到达,所以以时间做为等量关系可列方程求解.25.某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把1200m3的生活垃圾运走.(1)假如每天能运xm3,所需的时间为y天,写出y与x之间的函数关系式;(2)若每辆拖拉机一天能运12m3,则5辆这样的拖拉机要用多少天才能运完?考点:反比例函数的应用.分析:(1)根据每天能运xm3,所需时间为y天的积就是1200m3,即可写出函数关系式;(2)把x=5×12=60代入,即可求得天数;解答:解:(1)∵xy=1200,∴y=;(2)x=12×5=60,代入函数解析式得;y==20(天);点评:本题考查了反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用实际意义求解.26.y是x的反比例函数,且当x=4时,y=3.(1)写出y与x之间的函数表达式.(2)画出函数的图象,并根据图象说出当2≤x≤3时y的取值范围.考点:反比例函数的图象;待定系数法求反比例函数解析式.分析:(1)根据题意,设y=(k≠0),然后将x=3,y=4代入该函数式求得k的值;(2)利用描点法作出图象,根据图象回答问题.解答:解:(1)∵y是x的反比例函数,∴设y=(k≠0),又∵当x=3时,y=4,∴k=xy=3×4=12,∴该函数解析式为:y=;(2)函数y=的图象如图所示:当2≤x≤3时,4≤y≤6.点评:本题考查反比例函数的图象的作法与图象的运用,较为简单,容易掌握.27.(10分)(2015春•新沂市校级月考)如图,四边形ABCD为正方形,点A的坐标为(0,2),点B的坐标为(0,﹣3),反比例函数y1=的图象经过点C,一次函数y2=ax+b的图象经过点A、C.(1)求反比例函数和一次函数的表达式;(2)直接写出y2>y1时x的取值范围;(3)若点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求点P的坐标.考点:反比例函数与一次函数的交点问题.分析:(1)先根据正方形的性质求出点C的坐标为(5,﹣3),再将C点坐标代入反比例函数y1=中,运用待定系数法求出反比例函数的解析式;同理,将点A,C的坐标代入y=ax+b中,运用待定系数法求出一次函数函数的解析式;(2)求得反比例函数和一次函数的交点坐标,根据图象即可求得;(3)设P点的坐标为(x,y),先由△OAP的面积恰好等于正方形ABCD的面积,列出关于x的方程,解方程求出x的值,再将x的值代入y=﹣,即可求出P点的坐标.解答:解:(1)∵点A的坐标为(0,2),点B的坐标为(0,﹣3),∴AB=5,∵四边形ABCD为正方形,∴点C的坐标为(5,﹣3)∵反比例函数y1=的图象经过点C,∴﹣3=,解得k=﹣15,∴反比例函数的解析式为y1=﹣;∵一次函数y2=ax+b的图象经过点A,C,∴,解得,∴一次函数的解析式为y2=﹣x+2;(2)解得或,∴交点坐标为(5,﹣3),(﹣3,5),由图象知:当x<﹣3或0<x<5时,y2>y1;(3)设P点的坐标为(x,y),∵△OAP的面积恰好等于正方形ABCD的面积,∴×OA•|x|=52,∴×2|x|=25,解得x=±25.当x=25时,y=﹣=﹣,当x=﹣25时.y==,∴P点的坐标为(25,﹣)或(﹣25,).点评:本题考查了正方形的性质,反比例函数与一次函数的交点问题,运用待定系数法求反比例函数与一次函数的解析式,三角形的面积,难度适中.运用方程思想是解题的关键.。
八年级(下)学期 第二次月考数学试卷含解析
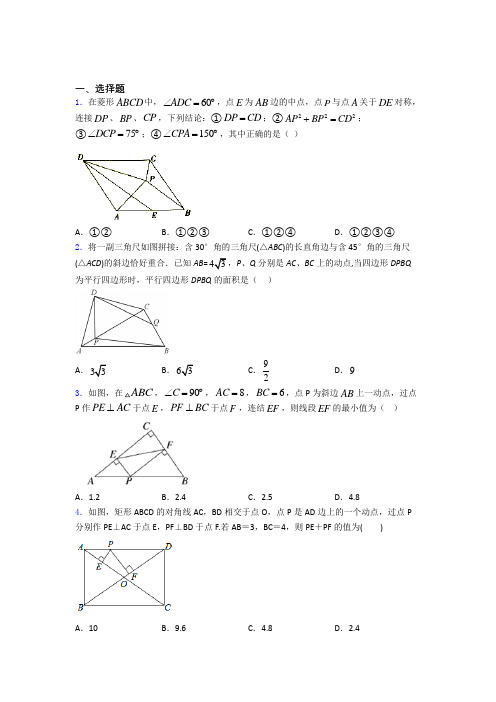
一、选择题1.在菱形ABCD 中,60ADC ∠=︒,点E 为AB 边的中点,点P 与点A 关于DE 对称,连接DP 、BP 、CP ,下列结论:①DP CD =;②222AP BP CD +=;③75DCP ∠=︒;④150CPA ∠=︒,其中正确的是( )A .①②B .①②③C .①②④D .①②③④2.将一副三角尺如图拼接:含30°角的三角尺(△ABC )的长直角边与含45°角的三角尺(△ACD )的斜边恰好重合.已知AB =43,P 、Q 分别是AC 、BC 上的动点,当四边形DPBQ 为平行四边形时,平行四边形DPBQ 的面积是( )A .33B .63C .92D .9 3.如图,在ABC ,90C ∠=︒,8AC =,6BC =,点P 为斜边AB 上一动点,过点P 作PE AC ⊥于点E ,PF BC ⊥于点F ,连结EF ,则线段EF 的最小值为( )A .1.2B .2.4C .2.5D .4.84.如图,矩形ABCD 的对角线AC ,BD 相交于点O ,点P 是AD 边上的一个动点,过点P 分别作PE ⊥AC 于点E ,PF ⊥BD 于点F.若AB =3,BC =4,则PE +PF 的值为( )A .10B .9.6C .4.8D .2.45.如图,长方形ABCD 中,点E 是边CD 的中点,将△ADE 沿AE 折叠得到△AFE ,且点F 在长方形ABCD 内,将AF 延长交边BC 于点G ,若BG=3CG ,则AD AB =( )A .54B .1C .52D .626.在ABCF 中,2BC AB =,CD AB ⊥于点D ,点E 为AF 的中点,若50ADE ∠=︒,则B 的度数是( )A .50︒B .60︒C .70︒D .80︒7.将矩形纸片ABCD 按如图所示的方式折叠,AE 、EF 为折痕,∠BAE =30°,AB =3 ,折叠后,点C 落在AD 边上的C 1处,并且点B 落在EC 1边上的B 1处.则BC 的长为( )A .3B .3C .2D .238.如图,在平行四边形ABCD 中,按以下步骤作图:①以A 为圆心,AB 长为半径画弧,交边AD 于点;②再分别以B ,F 为圆心画弧,两弧交于平行四边形ABCD 内部的点G 处;③连接AG 并延长交BC 于点E ,连接BF ,若BF =3,AB =2.5,则AE 的长为( )A .2B .4C .8D .59.如图,在ABCD 中,2,AB AD F =是CD 的中点,作BE AD ⊥于点E ,连接EF BF 、,下列结论:①CBF ABF ∠=∠;②FE FB =;③2EFB S S ∆=四边形DEBC ;④3BFE DEF ∠=∠;其中正确的个数是( )A .1B .2C .3D .410.如图,正方形ABCD 的边长为4,E 为BC 上一点,且BE =1,F 为AB 边上的一个动点,连接EF ,以EF 为边向右侧作等边△EFG ,连接CG ,则CG 的最小值为( )A .0.5B .2.5C .2D .1二、填空题11.如图,正方形ABCD 的边长为4,点E 为CD 边上的一个动点,以CE 为边向外作正方形ECFG ,连结BG ,点H 为BG 中点,连结EH ,则EH 的最小值为______12.在平行四边形ABCD 中,30,23,2A AD BD ∠=︒==,则平行四边形ABCD 的面积等于_____.13.如图,正方形ABCD 的对角线相交于点O ,对角线长为1cm ,过点O 任作一条直线分别交AD ,BC 于E ,F ,则阴影部分的面积是_____.14.如图,在正方形ABCD 中,点,E F 将对角线AC 三等分,且6AC =.点P 在正方形的边上,则满足5PE PF +=的点P 的个数是________个.15.如图,在△ABC 中,AB =3,AC =4,BC =5,P 为边BC 上一动点,PE ⊥AB 于E ,PF ⊥AC 于F ,则EF 的最小值为_____.16.如图,在矩形ABCD 中,AD =2AB ,∠BAD 的平分线交BC 于点E ,DH ⊥AE 于点H ,连接BH 并延长交CD 于点F ,连接DE 交BF 于点O ,下列结论:①∠AED =∠CED ;②OE =OD ;③BH =HF ;④BC ﹣CF =2HE ;⑤AB =HF ,其中正确的有_____.17.菱形OBCD 在平面直角坐标系中的位置如图所示,顶点B (23,0),∠DOB =60°,点P 是对角线OC 上一个动点,E (0,-1),则EP 十BP 的最小值为__________.18.如图,在矩形ABCD 中,16AB =,18BC =,点E 在边AB 上,点F 是边BC 上不与点B 、C 重合的一个动点,把EBF △沿EF 折叠,点B 落在点B '处.若3AE =,当CDB '是以DB '为腰的等腰三角形时,线段DB '的长为__________.19.已知:一组邻边分别为6cm 和10cm 的平行四边形ABCD ,DAB ∠和ABC ∠的平分线分别交CD 所在直线于点E ,F ,则线段EF 的长为________cm .20.如图,正方形ABCD 面积为1,延长DA 至点G ,使得AG AD =,以DG 为边在正方形另一侧作菱形DGFE ,其中45EFG ︒∠=,依次延长, , AB BC CD 类似以上操作再作三个形状大小都相同的菱形,形成风车状图形,依次连结点, , , ,F H M N 则四边形FHMN 的面积为___________.三、解答题21.如图,在正方形ABCD 中,点G 在对角线BD 上(不与点B ,D 重合),GE ⊥DC 于点E ,GF ⊥BC 于点F ,连结AG .(1)写出线段AG ,GE ,GF 长度之间的数量关系,并说明理由;(2)若正方形ABCD 的边长为1,∠AGF=105°,求线段BG 的长.22.如图, 平行四边形ABCD 中,3AB cm =,5BC cm =,60B ∠=, G 是CD 的中点,E 是边AD 上的动点,EG 的延长线与BC 的延长线交于点F ,连接CE ,DF . (1) 求证:四边形CEDF 是平行四边形;(2) ①当AE 的长为多少时, 四边形CEDF 是矩形;②当AE = cm 时, 四边形CEDF 是菱形, (直接写出答案, 不需要说明理由).23.如图,四边形OABC中,BC∥AO,A(4,0),B(3,4),C(0,4).点M从O出发以每秒2个单位长度的速度向A运动;点N从B同时出发,以每秒1个单位长度的速度向C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP垂直x 轴于点P,连结AC交NP于Q,连结MQ.(1)当t为何值时,四边形BNMP为平行四边形?(2)设四边形BNPA的面积为y,求y与t之间的函数关系式.(3)是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标;若不存在,请说明理由.24.如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.(1)求证:四边形BCEF是平行四边形;(2)若∠DEF=90°,DE=8,EF=6,当AF为时,四边形BCEF是菱形.25.如图,在平行四边形ABCD中,AB⊥AC,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转一个角度α(0°<α≤90°),分别交线段BC,AD于点E,F,连接BF.(1)如图1,在旋转的过程中,求证:OE=OF;(2)如图2,当旋转至90°时,判断四边形ABEF 的形状,并证明你的结论;(3)若AB =1,BC =5,且BF =DF ,求旋转角度α的大小.26.已知正方形,ABCD 点F 是射线DC 上一动点(不与,C D 重合).连接AF 并延长交直线BC 于点E ,交BD 于,H 连接CH .在EF 上取一点,G 使ECG DAH ∠=∠. (1)若点F 在边CD 上,如图1,①求证:CH CG ⊥.②求证:GFC 是等腰三角形.(2)取DF 中点,M 连接MG .若3MG =,正方形边长为4,则BE = .27.如图1,在OAB 中,OAB 90∠=,30AOB ∠=,8OB =,以OB 为边,在OAB Λ外作等边OBC Λ,D 是OB 的中点,连接AD 并延长交OC 于E .(1)求证:四边形ABCE 是平行四边形;(2)连接AC ,BE 交于点P ,求AP 的长及AP 边上的高BH ;(3)在(2)的条件下,将四边形OABC 置于如图所示的平面直角坐标系中,以E 为坐标原点,其余条件不变,以AP 为边向右上方作正方形APMN :①M 点的坐标为 .②直接写出正方形APMN 与四边形OABC 重叠部分的面积(图中阴影部分).28.如图,四边形ABCD 是边长为3的正方形,点E 在边AD 所在的直线上,连接CE ,以CE 为边,作正方形CEFG (点C 、E 、F 、G 按逆时针排列),连接BF.(1)如图1,当点E 与点D 重合时,BF 的长为 ;(2)如图2,当点E 在线段AD 上时,若AE=1,求BF 的长;(提示:过点F 作BC 的垂线,交BC 的延长线于点M ,交AD 的延长线于点N.)(3)当点E 在直线AD 上时,若AE=4,请直接写出BF 的长.29.在矩形ABCD 中,BE 平分∠ABC 交CD 边于点E .点F 在BC 边上,且FE⊥AE.(1)如图1,①∠BEC=_________°;②在图1已有的三角形中,找到一对全等的三角形,并证明你的结论;(2)如图2,FH∥CD 交AD 于点H ,交BE 于点M .NH∥BE,NB∥HE,连接NE .若AB=4,AH=2,求NE 的长.30.如图①,在ABC 中,AB AC =,过AB 上一点D 作//DE AC 交BC 于点E ,以E 为顶点,ED 为一边,作DEF A ∠=∠,另一边EF 交AC 于点F .(1)求证:四边形ADEF 为平行四边形;(2)当点D 为AB 中点时,ADEF 的形状为 ;(3)延长图①中的DE 到点,G 使,EG DE =连接,,,AE AG FG 得到图②,若,AD AG =判断四边形AEGF 的形状,并说明理由.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】如图,设DE交AP于0,根据菱形的性质、翻折不变性-判断即可解决问题;【详解】解:如图,设DE交AP于O.∵四边形ABCD是菱形∴DA=DC=AB∵A.P关于DE对称,∴DE⊥AP,OA=OP∴DA=DP∴DP=CD,故①正确∵AE=EB,AO=OP∴OE//PB,∴PB⊥PA∴∠APB=90°∴2222+==,故②正确PA PB AB CD若∠DCP=75°,则∠CDP=30°∵LADC=60°∴DP平分∠ADC,显然不符合题意,故③错误;∵∠ADC=60°,DA=DP=DC∴∠DAP=∠DPA,∠DCP=∠DPC,∠CPA=(360°-60°)=150°,故④正确.故选:C【点睛】本题考查菱形的性质、轴对称的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.2.D解析:D【解析】【分析】由于四边形DPBQ为平行四边形,则BC∥DP,即DP⊥AC,P为AC中点,作出平行四边形,再利用平行线的距离相等可知:PC就是□DPBQ的边PD所对应的高,代入面积公式求出面积即可.求得面积.【详解】当点P运动到边AC中点(如图),即CP=3时,以D,P,B,Q为顶点的平行四边形的顶点Q恰好在边BC上.∵四边形DPBQ为平行四边形,∴BC∥DP,∵∠ACB=90°,∴∠DPC=90°,即DP⊥AC.而在Rt△ABC中,AB3,BC3∴根据勾股定理得:AC=6,∵△DAC为等腰直角三角形,∴DP=CP=12AC=3,∵BC∥DP,∴PC是平行四边形DPBQ的高,∴S平行四边形DPBQ=DP•CP=33=9.故选D.【点睛】本题是四边形的综合题,考查了一副三角板所形成的四边形的边和角的关系;根据动点P 的运动路线确定其所形成的边和角的关系,利用三角函数和勾股定理求边和角的大小,得出结论.3.D解析:D【分析】连接PC ,当CP ⊥AB 时,PC 最小,利用三角形面积解答即可.【详解】解:连接PC ,∵PE ⊥AC ,PF ⊥BC ,∴∠PEC=∠PFC=∠C=90°,∴四边形ECFP 是矩形,∴EF=PC ,∴当PC 最小时,EF 也最小,即当CP ⊥AB 时,PC 最小,∵AC=8,BC=6,∴AB=10,∴PC 的最小值为:68 4.810AC BC PC AB ⋅⨯=== ∴线段EF 长的最小值为4.8.故选:D .【点睛】本题主要考查的是矩形的判定与性质,关键是根据矩形的性质和三角形的面积公式解答.4.D解析:D【分析】连接OP ,由矩形ABCD 的可求OA=OD=52 ,最后由S △AOD =S △AOP +S △DOP 即可解答. 【详解】解:如图:连接OP∵矩形ABCD ,AB =3,BC =4∴S 矩形ABCD =AB×BC=12, OA=OC,OB=OD,AC=BD,225AC =AB +BC ∴S △AOD =14S 矩形ABCD =3,OA=OD=52∴S △AOD =S △AOP +S △DOP =()111532222OA PE OD PF PE PF +=⨯+=∴PE+PF=2.4故答案为D.【点睛】本题考查了矩形的性质,正确的做出辅助线和运用数形结合思想是解答本题的关键.. 5.B解析:B【解析】【分析】根据中点定义得出DE=CE,再根据折叠的性质得出DE=EF,AF=AD,∠AFE=∠D=90°,从而得出CE=EF,连接EG,利用“HL”证明△ECG≌△EFG,根据全等三角形性质得出CG=FG,设CG=a,则BC=4a,根据长方形性质得出AD=BC=4a,再求出AF=4a,最后求出AG=AF+FG=5a,最后利用勾股定理求出AB,从而进一步得出答案即可.【详解】如图,连接EG,∵点E是CD中点,∴DE=EC,根据折叠性质可得:AD=AF,DE=EF,∠D=∠AFE=90°,∴CE=EF,在Rt△ECG与Rt△EFG中,∵EG=EG,EC=EF,∴Rt△ECG≌Rt△EFG(HL),∴CG=FG,设CG=a,∴BG=3CG=3a,∴BC=4a,∴AF=AD=BC=4a.∴AG=5a.在Rt △ABG 中, ∴224AB AG BG a =-=, ∴1AD AB=, 故选B.【点睛】本题主要考查了长方形与勾股定理及全等三角形判定和性质的综合运用,熟练掌握相关概念是解题关键,6.D解析:D【分析】连结CE ,并延长CE ,交BA 的延长线于点N ,根据已知条件和平行四边形的性质可证明△NAE ≌△CFE ,所以NE =CE ,NA =CF ,再由已知条件CD ⊥AB 于D ,∠ADE =50°,即可求出∠B 的度数.【详解】解:连结CE ,并延长CE ,交BA 的延长线于点N ,∵四边形ABCF 是平行四边形,∴AB ∥CF ,AB =CF ,∴∠NAE =∠F ,∵点E 是的AF 中点,∴AE =FE ,在△NAE 和△CFE 中,NAE F AE FEAEN FEC ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△NAE ≌△CFE (ASA ),∴NE =CE ,NA =CF ,∵AB =CF ,∴NA =AB ,即BN =2AB ,∵BC =2AB ,∴BC=BN,∠N=∠NCB,∵CD⊥AB于D,即∠NDC=90°且NE=CE,∴DE=12NC=NE,∴∠N=∠NDE=50°=∠NCB,∴∠B=80°.故选:D.【点睛】本题考查了平行四边形的性质,综合性较强,难度较大,解答本题的关键是正确作出辅助线,构造全等三角形,在利用等腰三角形的性质解答.7.B解析:B【解析】试题分析:由三角函数易得BE,AE长,根据翻折和对边平行可得△AEC1和△CEC1为等边三角形,那么就得到EC长,相加即可.解:连接CC1.在Rt△ABE中,∠BAE=30°,AB3∴BE=AB×tan30°=1,AE=2,∠AEB1=∠AEB=60°,∵四边形ABCD是矩形∴AD∥BC,∴∠C1AE=∠AEB=60°,∴△AEC1为等边三角形,同理△CC1E也为等边三角形,∴EC=EC1=AE=2,∴BC=BE+EC=3,故选B.8.B解析:B【分析】连接EF,先证AF=AB=BE,得四边形ABEF是菱形,据此知AE与BF互相垂直平分,继而得OB的长,由勾股定理求得OA的长,继而得出答案.【详解】由题意得:AF=AB,AE为∠BAD的角平分线,则∠BAE=∠FAE.又∵四边形ABCD是平行四边形,则AD∥BC,∠BAE=∠FAE=∠BEA,∴AF=AB=BE.连接EF,则四边形ABEF是菱形,∴AE与BF互相垂直平分,设AE与BF相交于点O,OB 2BF ==1.5.在Rt △AOB 中,OA 22222515AB OB =-=-=..2,则AE =2OA =4.故选B .【点睛】本题考查了作图﹣复杂作图,解题的关键是掌握菱形的性质与判定,平行四边形的性质,角平分线的尺规作图方法等. 9.C解析:C【分析】由平行四边形的性质结合AB=2AD ,CD=2CF 可得CF=CB ,从而可得∠CBF=∠CFB ,再根据CD ∥AB ,得∠CFB=∠ABF ,继而可得CBF ABF ∠=∠,可以判断①正确;延长EF 交BC 的延长线与M ,证明△DFE 与△CFM(AAS),继而得EF=FM=12EM ,证明∠CBE=∠AEB=90°,然后根据直角三角形斜边中线的性质即可判断②正确;由上可得S △BEF =S △BMF ,S △DFE =S △CFM ,继而可得S △EBF =S △BMF =S △EDF +S △FBC ,继而可得2EFB S S ∆=四边形DEBC ,可判断③正确;过点F 作FN ⊥BE ,垂足为N ,则∠FNE=90°,则可得AD//FN ,则有∠DEF=∠EFN ,根据等腰三角形的性质可得∠BFE=2∠EFN ,继而得∠BFE=2∠DEF ,判断④错误.【详解】∵四边形ABCD 是平行四边形,∴AD=BC ,AB=CD ,AD//BC ,∵AB=2AD ,CD=2CF ,∴CF=CB ,∴∠CBF=∠CFB ,∵CD ∥AB ,∴∠CFB=∠ABF ,∴CBF ABF ∠=∠,故①正确;延长EF 交BC 的延长线与M ,∵AD//BC ,∴∠DEF=∠M ,又∵∠DFE=∠CFM ,DF=CF ,∴△DFE 与△CFM(AAS),∴EF=FM=12EM ,∵BF ⊥AD ,∴∠AEB=90°,∵在平行四边形ABCD 中,AD ∥BC ,∴∠CBE=∠AEB=90°,∴BF=12EM , ∴BF=EF ,故②正确;∵EF=FM ,∴S △BEF =S △BMF ,∵△DFE ≌△CFM ,∴S △DFE =S △CFM ,∴S △EBF =S △BMF =S △EDF +S △FBC ,∴2EFB S S ∆=四边形DEBC ,故③正确;过点F 作FN ⊥BE ,垂足为N ,则∠FNE=90°,∴∠AEB=∠FEN ,∴AD//EF ,∴∠DEF=∠EFN ,又∵EF=FB ,∴∠BFE=2∠EFN ,∴∠BFE=2∠DEF ,故④错误,所以正确的有3个,故选C.【点睛】本题考查了平行四边形的性质,直角三角形斜边中线的性质,等腰三角形的判断与性质等,综合性较强,有一定的难度,正确添加辅助线,熟练掌握和灵活运用相关知识是解题的关键.10.B解析:B【分析】由题意分析可知,点F 为主动点,G 为从动点,所以以点E 为旋转中心构造全等关系,得到点G 的运动轨迹,之后通过垂线段最短构造直角三角形获得CG 最小值.【详解】由题意可知,点F 是主动点,点G 是从动点,点F 在线段上运动,点G 也一定在直线轨迹上运动,如图,将ΔEFB绕点E旋转60°,使EF与EG重合,得到ΔEFB≅ΔEHG,从而可知ΔEBH为等边三角形,点G在垂直于HE的直线HN上,如图,作CM⊥HN,则CM即为CG的最小值,作EP⊥CM,可知四边形HEPM为矩形,则1351=2.5222CM MP CP HE EC=+=+=+=.故选B.【点睛】本题考查了线段极值问题,构造图形计算,是极值问题中比较典型的类型.分清主动点和从动点,通过旋转构造全等,从而判断出点G的运动轨迹,是解本题的关键.二、填空题112【分析】过B点作HE的平行线交AC于O点,延长EG交AB于I点,得到BO=2HE,其中O点在线段AC上运动,再由点到直线的距离垂线段最短求出BO的长即可求解.【详解】解:过B点作HE的平行线交AC于O点,延长EG交AB于I点,如下图所示:∵H 是BG 的中点,且BO 与HE 平行,∴HE 为△BOG 的中位线,且BO=2HE ,故要使得HE 最短,只需要BO 最短即可,当E 点位于C 点时,则O 点与C 点重合,当E 点位于D 点时,则O 点与A 点重合,故E 点在CD 上运动时,O 点在AC 上运动,由点到直线的距离垂线段最短可知,当BO ⊥AC 时,此时BO 最短,∵四边形ABCD 是正方形,∴△BOC 为等腰直角三角形,且BC=4,、 ∴2222BO , ∴122HE BO ,2【点睛】本题考查了正方形的性质,等腰直角三角形的性质,点到直线的距离垂线段最短等知识点,本题的关键是要学会将要求的HE 线段长转移到线段BO 上.12.4323【分析】分情况讨论作出图形,通过解直角三角形得到平行四边形的底和高的长度,根据平行四边形的面积公式即可得到结论.【详解】解:过D 作DE AB ⊥于E ,在Rt ADE △中,30A ∠=︒,23AD = 132DE AD ∴==33AE AD ==, 在Rt BDE △中,2BD =,22222(3)1BE BD DE ∴=-=-=,如图1,4AB ∴=,∴平行四边形ABCD 的面积4343AB DE ==⨯=,如图2,2AB =,∴平行四边形ABCD 的面积2323AB DE ==⨯=,如图3,过B 作BE AD ⊥于E ,在Rt ABE △中,设AE x =,则23DE x =-,30A ∠=︒,3BE x =, 在Rt BDE △中,2BD =, 22232()(23)x x ∴=+-, 3x ∴=,23x =(不合题意舍去),1BE ∴=,∴平行四边形ABCD 的面积12323AD BE ==⨯=,如图4,当AD BD ⊥时,平行四边形ABCD 的面积43AD BD ==,故答案为:323【点睛】本题考查了平行四边形的性质,平行四边形的面积公式的运用、30度角的直角三角形的性质,根据题意作出图形是解题的关键.13.218cm 【分析】根据正方形的性质可以证明△AEO ≌CFO ,就可以得出S △AEO =S △CFO ,就可以求出△AOD 面积等于正方形面积的14,根据正方形的面积就可以求出结论. 【详解】解:如图:∵正方形ABCD 的对角线相交于点O ,∴△AEO 与△CFO 关于O 点成中心对称,∴△AEO ≌CFO ,∴S △AEO =S △CFO ,∴S △AOD =S △DEO +S △CFO ,∵对角线长为1cm ,∴S 正方形ABCD =1112⨯⨯=12cm 2, ∴S △AOD =18cm 2, ∴阴影部分的面积为18cm 2. 故答案为:18cm 2. 【点睛】 本题考查了正方形的性质的运用,全等三角形的判定及性质的运用正方形的面积及三角形的面积公式的运用,在解答时证明△AEO ≌CFO 是关键.14.8个【分析】作点F 关于BC 的对称点M ,连接FM 交BC 于点N ,连接EM ,交BC 于点H ,可得点H 到点E 和点F 的距离之和最小,可求最小值,即可求解.【详解】如图,作点F 关于BC 的对称点M ,连接FM 交BC 于点N ,连接EM ,交BC 于点H ,∵点E ,F 将对角线AC 三等分,且AC =6,∴EC =4,FC =2=AE ,∵点M 与点F 关于BC 对称,∴CF =CM =2,∠ACB =∠BCM =45°,∴∠ACM =90°,∴EM则在线段BC 存在点H 到点E 和点F 的距离之和最小为5,在点H 右侧,当点P 与点C 重合时,则PE +PF =4+2=6,∴点P 在CH 上时,PE +PF ≤6,在点H 左侧,当点P 与点B 重合时,∵FN ⊥BC ,∠ABC =90°,∴FN ∥AB ,∴△CFN ∽△CAB , ∴FN CN CF 1===AB CB CA 3,∵AB =BC =2AC =∴FN =13AB ,CN =13BC∴BN =BC -CN =,BF =,∵AB =BC ,CF =AE ,∠BAE =∠BCF ,∴△ABE ≌△CBF (SAS ),∴BE =BF ,∴PE +PF =∴点P 在BH 上时,PE +PF <∴在线段BC 上点H 的左右两边各有一个点P 使PE +PF =5,同理在线段AB ,AD ,CD 上都存在两个点使PE +PF =5.即共有8个点P 满足PE +PF =5,故答案为8.【点睛】本题考查了正方形的性质,最短路径问题,在BC 上找到点H ,使点H 到点E 和点F 的距离之和最小是本题的关键.15.4【分析】根据三个角都是直角的四边形是矩形,得四边形AEPF 是矩形,根据矩形的对角线相等,得EF =AP ,则EF 的最小值即为AP 的最小值,根据垂线段最短,知:AP 的最小值即等于直角三角形ABC 斜边上的高.【详解】解:连接AP ,∵在△ABC 中,AB =3,AC =4,BC =5,∴AB 2+AC 2=BC 2,即∠BAC =90°.又∵PE ⊥AB 于E ,PF ⊥AC 于F ,∴四边形AEPF 是矩形,∴EF =AP ,∵AP 的最小值即为直角三角形ABC 斜边上的高,设斜边上的高为h ,则S △ABC =1122BC h AB AC ⋅=⋅ ∴1153422h ⨯⋅=⨯⨯ ∴h=2.4,∴EF 的最小值为2.4,故答案为:2.4.【点睛】本题考查了矩形的性质和判定,勾股定理的逆定理,直角三角形的性质的应用,要能够把要求的线段的最小值转化为便于求的最小值得线段是解此题的关键.16.①②③④【分析】①根据角平分线的定义可得∠BAE =∠DAE =45°,可得出△ABE 是等腰直角三角形,根据等腰直角三角形的性质可得AE =,从而得到AE =AD ,然后利用“角角边”证明△ABE 和△AHD 全等,根据全等三角形对应边相等可得BE =DH ,再根据等腰三角形两底角相等求出∠ADE =∠AED =67.5°,根据平角等于180°求出∠CED =67.5°,从而判断出①正确; ②求出∠AHB =67.5°,∠DHO =∠ODH =22.5°,然后根据等角对等边可得OE =OD =OH ,判断出②正确;③求出∠EBH =∠OHD =22.5°,∠AEB =∠HDF =45°,然后利用“角边角”证明△BEH 和△HDF 全等,根据全等三角形对应边相等可得BH =HF ,判断出③正确;④根据全等三角形对应边相等可得DF =HE ,然后根据HE =AE ﹣AH =BC ﹣CD ,BC ﹣CF =BC ﹣(CD ﹣DF )=2HE ,判断出④正确;⑤判断出△ABH 不是等边三角形,从而得到AB ≠BH ,即AB ≠HF ,得到⑤错误.【详解】∵在矩形ABCD 中,AE 平分∠BAD ,∴∠BAE =∠DAE =45°,∴△ABE 是等腰直角三角形,∴AE =. ∵AD =,∴AE =AD .在△ABE 和△AHD 中,∵90BAE DAE ABE AHD AE AD ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩,∴△ABE ≌△AHD (AAS ),∴BE =DH ,∴AB =BE =AH =HD ,∴∠ADE =∠AED 12=(180°﹣45°)=67.5°,∴∠CED =180°﹣45°﹣67.5°=67.5°,∴∠AED =∠CED ,故①正确;∵∠AHB 12=(180°﹣45°)=67.5°,∠OHE =∠AHB (对顶角相等),∴∠OHE =∠AED ,∴OE =OH .∵∠DOH =90°﹣67.5°=22.5°,∠ODH =67.5°﹣45°=22.5°,∴∠DOH =∠ODH ,∴OH =OD ,∴OE =OD =OH ,故②正确;∵∠EBH =90°﹣67.5°=22.5°,∴∠EBH =∠OHD .在△BEH 和△HDF 中,∵EBH OHD BE DH AEB HDF ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△BEH ≌△HDF (ASA ),∴BH =HF ,HE =DF ,故③正确;由上述①、②、③可得CD =BE 、DF =EH =CE ,CF =CD ﹣DF ,∴BC ﹣CF =(CD +HE )﹣(CD ﹣HE )=2HE ,所以④正确;∵AB =AH ,∠BAE =45°,∴△ABH 不是等边三角形,∴AB ≠BH ,∴即AB ≠HF ,故⑤错误;综上所述:结论正确的是①②③④.故答案为①②③④.【点睛】本题考查了矩形的性质,全等三角形的判定与性质,角平分线的定义,等腰三角形的判定与性质,熟记各性质并仔细分析题目条件,根据相等的度数求出相等的角,从而得到三角形全等的条件或判断出等腰三角形是解题的关键,也是本题的难点.17【分析】先根据菱形的性质可得OC 垂直平分BD ,从而可得=DP BP ,再根据两点之间线段最短可得EP BP +的最小值为DE ,然后利用等边三角形的判定与性质求出点D 的坐标,最后利用两点之间的距离公式即可得.【详解】如图,连接BP 、DP 、EP 、DE 、BD ,过点D 作DA OB ⊥于点A , (23,0)B ,OB ∴=四边形ABCD 是菱形,OC ∴垂直平分BD ,OB OD ==点P 是对角线OC 上的点,DP BP ∴=,EP BP EP DP ∴+=+,由两点之间线段最短可知,EP DP +的最小值为DE ,即EP BP +的最小值为DE , ,60OB OD DOB =∠=︒,BOD ∴是等边三角形, DA OB ⊥,12OA OB ∴==3AD ===,D ∴,又(0,1)E -,DE ∴==即EP BP +【点睛】本题考查了菱形的性质、等边三角形的判定与性质、两点之间的距离公式等知识点,根据的最小值为DE是解题关键.两点之间线段最短得出EP BP18.16或10【分析】等腰三角形一般分情况讨论:(1)当DB'=DC=16;(2)当B'D=B'C时,作辅助线,构建平行四边形AGHD和直角三角形EGB',计算EG和B'G的长,根据勾股定理可得B'D的长;【详解】∵四边形ABCD是矩形,∴DC=AB=16,AD=BC=18.分两种情况讨论:(1)如图2,当DB'=DC=16时,即△CDB'是以DB'为腰的等腰三角形(2)如图3,当B'D=B'C时,过点B'作GH∥AD,分别交AB与CD于点G、H.∵四边形ABCD是矩形,∴AB∥CD,∠A=90°又GH∥AD,∴四边形AGHD是平行四边形,又∠A=90°,∴四边形AGHD是矩形,∴AG=DH,∠GHD=90°,即B'H⊥CD,又B'D=B'C,∴DH=HC=18CD=,AG=DH=8,3∵AE=3,∴BE=EB'=AB-AE=16-3=13,EG=AG-AE=8-3=5,在Rt△EGB'中,由勾股定理得:GB′12,∴B'H=GH×GB'=18-12=6,在Rt△B'HD中,由勾股定理得:B′D10=综上,DB'的长为16或10.故答案为: 16或10【点睛】本题是四边形的综合题,考查了矩形的性质,勾股定理,等腰三角形一般需要分类讨论.19.2或14【分析】利用当AB=10cm,AD=6cm,由于平行四边形的两组对边互相平行,又AE平分∠BAD,由此可以推出所以∠BAE=∠DAE,则DE=AD=6cm;同理可得:CF=CB=6cm,而EF=CF+DE-DC,由此可以求出EF长;同理可得:当AD=10cm,AB=6cm时,可以求出EF长【详解】解:如图1,当AB=10cm,AD=6cm∵AE平分∠BAD∴∠BAE=∠DAE,又∵AD∥CB∴∠EAB=∠DEA,∴∠DAE=∠AED,则AD=DE=6cm同理可得:CF=CB=6cm∵EF=DE+CF-DC=6+6-10=2(cm)如图2,当AD=10cm,AB=6cm,∵AE平分∠BAD,∴∠BAE=∠DAE又∵AD∥CB∴∠EAB=∠DEA,∴∠DAE=∠AED则AD=DE=10cm同理可得,CF=CB=10cm EF=DE+CF-DC=10+10-6=14(cm)故答案为:2或14.图1 图2【点睛】本题主要考查了角平分线的定义、平行四边形的性质、平行线的性质等知识,关键是平行四边形的不同可能性进行分类讨论.20.1382+【分析】如图所示,延长CD交FN于点P,过N作NK⊥CD于点K,延长FE交CD于点Q,交NS于点R,首先利用正方形性质结合题意求出AD=CD=AG=DQ=1,然后进一步根据菱形性质得出DE=EF=DG=2,再后通过证明四边形NKQR是矩形得出QR=NK=2,进一步可得2221382=+=+,再延长NS交ML于点Z,利用全等三角形性质与判定证FN FR NR明四边形FHMN为正方形,最后进一步求解即可.【详解】如图所示,延长CD交FN于点P,过N作NK⊥CD于点K,延长FE交CD于点Q,交NS于点R,∵ABCD为正方形,∴∠CDG=∠GDK=90°,∵正方形ABCD面积为1,∴AD=CD=AG=DQ=1,∴DG=CT=2,∵四边形DEFG为菱形,∴DE=EF=DG=2,同理可得:CT=TN=2,∵∠EFG=45°,∴∠EDG=∠SCT=∠NTK=45°,∵FE∥DG,CT∥SN,DG⊥CT,∴∠FQP=∠FRN=∠DQE=∠NKT=90°,∴FQ=FE+EQ=2+∵∠NKT=∠KQR=∠FRN=90°,∴四边形NKQR 是矩形,∴,∴FR=FQ+QR=2+,NR=KQ=DK −11=,∴22213FN FR NR =+=+再延长NS 交ML 于点Z ,易证得:△NMZ ≅△FNR(SAS),∴FN=MN ,∠NFR=∠MNZ ,∵∠NFR+∠FNR=90°,∴∠MNZ+∠FNR=90°,即∠FNM=90°,同理可得:∠NFH=∠FHM=90°,∴四边形FHMN 为正方形,∴正方形FHMN 的面积=213FN =+故答案为:13+【点睛】本题主要考查了正方形和矩形性质与判定及与全等三角形性质与判定的综合运用,熟练掌握相关方法是解题关键.三、解答题21.(1)AG 2=GE 2+GF 2,理由见解析;(2)6 【分析】(1)结论:AG 2=GE 2+GF 2.只要证明GA=GC ,四边形EGFC 是矩形,推出GE=CF ,在Rt △GFC 中,利用勾股定理即可证明;(2)作BN ⊥AG 于N ,在BN 上截取一点M ,使得AM=BM .设AN=x .易证AM=BM=2x ,,在Rt △ABN 中,根据AB 2=AN 2+BN 2,可得1=x 2+(x )2,解得x=4,推出BN=4,再根据BG=BN÷cos30°即可解决问题. 【详解】解:(1)结论:AG 2=GE 2+GF 2.理由:连接CG .∵四边形ABCD 是正方形,∴A 、C 关于对角线BD 对称,∵点G 在BD 上,∴GA=GC ,∵GE ⊥DC 于点E ,GF ⊥BC 于点F ,∴∠GEC=∠ECF=∠CFG=90°,∴四边形EGFC 是矩形,∴CF=GE ,在Rt △GFC 中,∵CG 2=GF 2+CF 2,∴AG 2=GF 2+GE 2.(2)作BN ⊥AG 于N ,在BN 上截取一点M ,使得AM=BM .设AN=x .∵∠AGF=105°,∠FBG=∠FGB=∠ABG=45°,∴∠AGB=60°,∠GBN=30°,∠ABM=∠MAB=15°,∴∠AMN=30°,∴AM=BM=2x ,MN=3x , 在Rt △ABN 中,∵AB 2=AN 2+BN 2,∴1=x 2+(2x+3x )2,解得x=62-, ∴BN=624+, ∴BG=BN÷cos30°=326+.【点睛】本题考查正方形的性质,矩形的判定和性质,勾股定理,直角三角形30度的性质.22.(1)证明见解析;(2)①当AE=3.5时,平行四边形CEDF 是矩形;②2【分析】(1)证明△FCG ≌△EDG (ASA ),得到FG=EG 即可得到结论;(2)①当AE=3.5时,平行四边形CEDF 是矩形.过A 作AM ⊥BC 于M ,求出BM=1.5,根据平行四边形的性质得到∠CDA=∠B=60°,DC=AB=3,BC=AD=5,求出DE=1.5=BM ,证明△MBA ≌△EDC(SAS),得到∠CED=∠AMB=90°,推出四边形CEDF 是矩形;②根据四边形CEDFCEDF 是菱形,得到CD ⊥EF ,DG=CG=1212CD=1.5,求出∠DEG=30°,得到DE=2DG=3,即可求出AE=AD-DE=5-3=2.【详解】(1)证明:∵ 四边形ABCD 是平行四边形,∴ CF ∥ED ,∴ ∠FCG =∠EDG ,∵ G 是CD 的中点,∴ CG =DG ,在△FCG 和△EDG 中,FCG EDG CG DG CGF DGE ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴ △FCG ≌△EDG (ASA ),∴ FG =EG ,∵ CG =DG ,∴ 四边形CEDF 是平行四边形;(2)解:①当AE=3.5时,平行四边形CEDF 是矩形, 理由是:过A 作AM ⊥BC 于M ,∵∠B=60°,∴∠BAM=30°,∵AB=3,∴BM=1.5,∵四边形ABCD 是平行四边形,∴∠CDA=∠B=60°,DC=AB=3,BC=AD=5, ∵AE=3.5,∴DE=1.5=BM ,在△MBA 和△EDC 中,BM DE B CDE AB CD =⎧⎪∠=∠⎨⎪=⎩,∴△MBA ≌△EDC(SAS),∴∠CED=∠AMB=90°,∵四边形CEDF 是平行四边形,∴四边形CEDF 是矩形;②∵四边形CEDFCEDF 是菱形,∴CD ⊥EF ,DG=CG=1212CD=1.5,∵∠CDE=∠B=60∘∠B=60∘,∴∠DEG=30°,∴DE=2DG=3,∴AE=AD-DE=5-3=2,故答案为:2.【点睛】此题考查了平行四边形的性质,矩形的判定定理,菱形的性质定理,直角三角形30度角所对的直角边等于斜边的一半,三角形全等的判定及性质定理,熟练掌握各定理并运用解答问题是解题的关键.23.(1)34;(2)y=4t+2;(3)存在,点M的坐标为(1,0)或(2,0).【分析】(1)因为BN∥MP,故当BN=MP时,四边形BNMP为平行四边形,此时点M在点P的左侧,求解即可;(2)y=12(BN+PA)•OC,即可求解;(3)①当∠MQA为直角时,则△MAQ为等腰直角三角形,则PA=PM,即可求解;②当∠QMA为直角时,则NB+OM=BC=3,即可求解.【详解】(1)∵BN∥MP,故当BN=MP时,四边形BNMP为平行四边形.此时点M在点P的左侧时,即0≤t<1时,MP=OP﹣OM=3﹣t﹣2t=3﹣3t,BN=t,即3﹣3t=t,解得:t=34;(2)由题意得:由点C的坐标知,OC=4,BN=t,NC=PO=3﹣t,PA=4﹣OP=4﹣(3﹣t)=t+1,则y=12(BN+PA)•OC=12(t+t+1)×4=4t+2;(3)由点A、C的坐标知,OA=OC=4,则△COA为等腰直角三角形,故∠OCA=∠OAC=45°,①当∠MQA为直角时,∵∠OAC=45°,故△MAQ为等腰直角三角形,则PA=PM,而PA=4﹣(3﹣t)=t+1,PM=OP﹣OM=(3﹣t)﹣2t=3﹣3t,故t+1=3﹣3t,解得:t=12,则OM=2t=1,故点M(1,0);②当∠QMA为直角时,则点M、P重合,则NB+OM=BC=3,即2t+t=3,解得:t=1,故OM =OP =2t =2,故点M (2,0);综上,点M 的坐标为(1,0)或(2,0).【点睛】本题是四边形综合题,涉及坐标与图形、平行四边形的性质、等腰直角三角形的判定和性质、图形的面积计算等,复杂度较高,难度较大,其中(3)要分类求解,避免遗漏.24.(1)详见解析;(2)145. 【分析】(1)由AB =DE ,∠A =∠D ,AF =DC ,易证得△ABC ≌DEF (SAS ),即可得BC =EF ,且BC ∥EF ,即可判定四边形BCEF 是平行四边形;(2)由四边形BCEF 是平行四边形,可得当BE ⊥CF 时,四边形BCEF 是菱形,所以连接BE ,交CF 与点G ,由三角形DEF 的面积求出EG 的长,根据勾股定理求出FG 的长,则可求出答案.【详解】(1)证明:∵AF =DC ,∴AC =DF ,在△ABC 和△DEF 中, AB DE A D AC DF =⎧⎪∠=∠⎨⎪=⎩,∴△ABC ≌△DEF (SAS ),∴BC =EF ,∠ACB =∠DFE ,∴BC ∥EF ,∴四边形BCEF 是平行四边形;(2)如图,连接BE ,交CF 于点G ,∵四边形BCEF 是平行四边形,∴当BE ⊥CF 时,四边形BCEF 是菱形,∵∠DEF =90°,DE =8,EF =6,∴DF 222286DE EF +=+10,∴S △DEF 11 22EG DF EF DE =⋅=⋅,。
八年级第二学期第二次月考数学试题含解析

一、选择题1.在菱形ABCD 中,60ADC ∠=︒,点E 为AB 边的中点,点P 与点A 关于DE 对称,连接DP 、BP 、CP ,下列结论:①DP CD =;②222AP BP CD +=;③75DCP ∠=︒;④150CPA ∠=︒,其中正确的是( )A .①②B .①②③C .①②④D .①②③④2.□ABCD 中,∠A=60°,点E 、F 分别在边AD 、DC 上,DE=DF ,且∠EBF=60°.若AE=2,FC=3,则EF 的长度为( )A .21B .25C .26D .53.如图,在正方形ABCD 中,E ,F 分别为BC ,DC 的中点,P 为对角线AC 上的一个动点,则下列线段的长等于BP EP +最小值的是( )A .AB B .CEC .ACD .AF4.如图,依次连结第一个菱形各边的中点得到一个矩形,再依次连结矩形各边的中点得到第二个菱形,按此方法继续下去.已知第一个菱形的面积为1,则第4个菱形的面积是( )A .14B .116C .132D .1645.如图,正方形ABCD 的边长为5,4AG CH ==,3BG DH ==,连接GH ,则线段GH 的长为( )A .435B .75 C .2 D .52-6.如图,在正方形ABCD 中,点E ,F 分别在BC 和CD 上,过点A 作GA AE ⊥,CD 的延长线交AG 于点G ,BE DF EF +=,若30DAF ∠=︒,则BAE ∠的度数为( )A .15°B .20°C .25°D .30°7.如图,点P ,Q 分别是菱形ABCD 的边AD ,BC 上的两个动点,若线段PQ 长的最大值为85 ,最小值为8,则菱形ABCD 的边长为( )A .6B .10C .12D .168.如图,在正方形ABCD 中,AB =4,E 是CD 的中点,将BCE 沿BE 翻折至BFE ,连接DF ,则DF 的长度是( )A .55B .255C .355D .4559.如图,正方形ABCD 的边长为10,AG=CH=8,BG=DH=6,连接GH ,则线段GH 的长为( )A .2.8B .22C .2.4D .3.510.如图,在菱形ABCD 中,AB=AC=1,点E 、F 分别为边AB 、BC 上的点,且AE=BF ,连接CE 、AF 交于点H ,连接DH 交AC 于点O ,则下列结论:①△ABF ≌△CAE ;②∠FHC=∠B ;③△ADO ≌△ACH ;④=3ABCD S 菱形;其中正确的结论个数是( )A .1个B .2个C .3个D .4个二、填空题11.如图,在矩形ABCD 中,∠BAD 的平分线交BC 于点E ,交DC 的延长线于点F ,点G 是EF 的中点,连接CG ,BG ,BD ,DG ,下列结论:①BC=DF ;②135DGF ︒∠=;③BG DG ⊥;④34AB AD =,则254BDG FDG S S =,正确的有__________________.12.如图,在正方形ABCD 中,点,E F 将对角线AC 三等分,且6AC =.点P 在正方形的边上,则满足5PE PF +=的点P 的个数是________个.13.如图,长方形纸片ABCD 中,AB =6 cm,BC =8 cm 点E 是BC 边上一点,连接AE 并将△AEB 沿AE 折叠, 得到△AEB′,以C ,E ,B′为顶点的三角形是直角三角形时,BE 的长为___________cm.14.如图,在矩形ABCD 中,AB =2,AD =3,E 为BC 边上一动点,作EF ⊥AE ,且EF =AE .连接DF ,AF .当DF ⊥EF 时,△ADF 的面积为_____.15.如图,有一张矩形纸条ABCD ,AB =10cm ,BC =3cm ,点M ,N 分别在边AB ,CD 上,CN =1cm .现将四边形BCNM 沿MN 折叠,使点B ,C 分别落在点B ',C '上.在点M 从点A 运动到点B 的过程中,若边MB '与边CD 交于点E ,则点E 相应运动的路径长为_____cm .16.如图,菱形ABCD 的边长是4,60ABC ∠=︒,点E ,F 分别是AB ,BC 边上的动点(不与点A ,B ,C 重合),且BE BF =,若//EG BC ,//FG AB ,EG 与FG 相交于点G ,当ADG 为等腰三角形时,BE 的长为________.17.如图,在菱形ABCD 中,AC 交BD 于P ,E 为BC 上一点,AE 交BD 于F ,若AB=AE ,EAD 2BAE ∠∠=,则下列结论:①AF=AP ;②AE=FD ;③BE=AF .正确的是______(填序号).18.定理:直角三角形斜边上的中线等于斜边的一半,即:如图1,在Rt △ABC 中,∠ACB =90°,若点D 是斜边AB 的中点,则CD =12AB ,运用:如图2,△ABC 中,∠BAC =90°,AB =2,AC =3,点D 是BC 的中点,将△ABD 沿AD 翻折得到△AED 连接BE ,CE ,DE ,则CE 的长为_____.19.如图,有一张长方形纸片ABCD ,4AB =,3AD =.先将长方形纸片ABCD 折叠,使边AD 落在边AB 上,点D 落在点E 处,折痕为AF ;再将AEF ∆沿EF 翻折,AF 与BC 相交于点G ,则FG 的长为___________.20.李刚和常明两人在数学活动课上进行折纸创编活动.李刚拿起一张准备好的长方形纸片对常明说:“我现在折叠纸片(图①),使点D 落在AB 边的点F 处,得折痕AE ,再折叠,使点C 落在AE 边的点G 处,此时折痕恰好经过点B ,如果AD=a ,那么AB 长是多少?”常明说;“简单,我会. AB 应该是_____”.常明回答完,又对李刚说:“你看我的创编(图②),与你一样折叠,可是第二次折叠时,折痕不经过点B ,而是经过了AB 边上的M 点,如果AD=a ,测得EC=3BM ,那么AB 长是多少?”李刚思考了一会,有点为难,聪明的你,你能帮忙解答吗?AB=_____.三、解答题21.如图,ABC ∆是等腰直角三角形,AB AC =,D 是斜边BC 的中点,,E F 分别是,AB AC 边上的点,且DE DF ⊥,若12BE =,5CF =,求线段EF 的长.22.在一次数学探究活动中,小明对对角线互相垂直的四边形进行了探究,得出了如下结论:如图1,四边形ABCD 的对角线AC 与BD 相交于点O ,AC BD ⊥,则2222AB CD AD BC +=+.(1)请帮助小明证明这一结论;(2)根据小明的探究,老师又给出了如下的问题:如图2,分别以Rt ACB 的直角边AC 和斜边AB 为边向外作正ACFG 和正方形ABDE ,连结CE 、BG 、GE .已知4AC =,5AB =,求GE 的长,请你帮助小明解决这一问题.23.如图,在Rt ABC ∆中,90ABC ∠=︒,30C ∠=︒,12AC cm =,点E 从点A 出发沿AB 以每秒1cm 的速度向点B 运动,同时点D 从点C 出发沿CA 以每秒2cm 的速度向点A 运动,运动时间为t 秒(06t <<),过点D 作DF BC ⊥于点F .(1)试用含t 的式子表示AE 、AD 、DF 的长;(2)如图①,连接EF ,求证四边形AEFD 是平行四边形;(3)如图②,连接DE ,当t 为何值时,四边形EBFD 是矩形?并说明理由.24.如下图1,在平面直角坐标系中xoy 中,将一个含30的直角三角板如图放置,直角顶点与原点重合,若点A 的坐标为()1,0-,30ABO ∠=︒.(1)旋转操作:如下图2,将此直角三角板绕点O 顺时针旋转30时,则点B 的坐标为 . (2)问题探究:在图2的基础上继续将直角三角板绕点O 顺时针60︒,如图3,在AB 边上的上方以AB 为边作等边ABC ,问:是否存在这样的点D ,使得以点A 、B 、C 、D 四点为顶点的四边形构成为菱形,若存在,请直接写出点D 所有可能的坐标;若不存在,请说明理由.(3)动点分析:在图3的基础上,过点O 作OP AB ⊥于点P ,如图4,若点F 是边OB 的中点,点M 是射线PF 上的一个动点,当OMB △为直角三角形时,求OM 的长.25.(1)如图①,在正方形ABCD 中,AEF ∆的顶点E ,F 分别在BC ,CD 边上,高AG 与正方形的边长相等,求EAF ∠的度数;(2)如图②,在Rt ABD ∆中,90,BAD AD AB ︒∠==,点M ,N 是BD 边上的任意两点,且45MAN ︒∠=,将ABM ∆绕点A 逆时针旋转90度至ADH ∆位置,连接NH ,试判断MN ,ND ,DH 之间的数量关系,并说明理由;(3)在图①中,连接BD 分别交AE ,AF 于点M ,N ,若正方形ABCD 的边长为12,GF=6,BM= 32,求EG ,MN 的长.26.如图,点A 、F 、C 、D 在同一直线上,点B 和点E 分别在直线AD 的两侧,且AB =DE ,∠A =∠D ,AF =DC .(1)求证:四边形BCEF 是平行四边形;(2)若∠DEF =90°,DE =8,EF =6,当AF 为 时,四边形BCEF 是菱形.27.如图,矩形ABCD 中,AB=4,AD=3,∠A 的角平分线交边CD 于点E .点P 从点A 出发沿射线AE 以每秒2个单位长度的速度运动,Q 为AP 的中点,过点Q 作QH ⊥AB 于点H ,在射线AE 的下方作平行四边形PQHM (点M 在点H 的右侧),设P 点运动时间为t 秒.(1)直接写出AQH 的面积(用含t 的代数式表示).(2)当点M 落在BC 边上时,求t 的值.(3)在运动过程中,整个图形中形成的三角形是否存在全等三角形?若存在,请写出所有全等三角形,并求出对应的t 的值;若不存在请说明理由(不能添加辅助线).28.已知四边形ABCD 是正方形,将线段CD 绕点C 逆时针旋转α(090α︒<<︒),得到线段CE ,联结BE 、CE 、DE . 过点B 作BF ⊥DE 交线段DE 的延长线于F .(1)如图,当BE =CE 时,求旋转角α的度数;(2)当旋转角α的大小发生变化时,BEF ∠的度数是否发生变化?如果变化,请用含α的代数式表示;如果不变,请求出BEF∠的度数;(3)联结AF,求证:2=.DE AF29.在正方形中,连接,为射线上的一个动点(与点不重合),连接,的垂直平分线交线段于点,连接,.提出问题:当点运动时,的度数是否发生改变?探究问题:(1)首先考察点的两个特殊位置:①当点与点重合时,如图1所示,____________②当时,如图2所示,①中的结论是否发生变化?直接写出你的结论:__________;(填“变化”或“不变化”)(2)然后考察点的一般位置:依题意补全图3,图4,通过观察、测量,发现:(1)中①的结论在一般情况下_________;(填“成立”或“不成立”)(3)证明猜想:若(1)中①的结论在一般情况下成立,请从图3和图4中任选一个进行证明;若不成立,请说明理由.30.已知:正方形ABCD和等腰直角三角形AEF,AE=AF(AE<AD),连接DE、BF,P是DE的中点,连接AP.将△AEF绕点A逆时针旋转.(1)如图①,当△AEF的顶点E、F恰好分别落在边AB、AD时,则线段AP与线段BF的位置关系为,数量关系为.(2)当△AEF绕点A逆时针旋转到如图②所示位置时,证明:第(1)问中的结论仍然成立.(3)若AB=3,AE=1,则线段AP的取值范围为.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】如图,设DE交AP于0,根据菱形的性质、翻折不变性-判断即可解决问题;【详解】解:如图,设DE交AP于O.∵四边形ABCD是菱形∴DA=DC=AB∵A.P关于DE对称,∴DE⊥AP,OA=OP∴DA=DP∴DP=CD,故①正确∵AE=EB,AO=OP∴OE//PB,∴PB⊥PA∴∠APB=90°∴2222PA PB AB CD+==,故②正确若∠DCP=75°,则∠CDP=30°∵LADC=60°∴DP平分∠ADC,显然不符合题意,故③错误;∵∠ADC=60°,DA=DP=DC∴∠DAP=∠DPA,∠DCP=∠DPC,∠CPA=(360°-60°)=150°,故④正确.故选:C【点睛】本题考查菱形的性质、轴对称的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.2.A解析:A【解析】【分析】由DE=DF,AE=2,FC=3可知AB-BC=1,过点E作EM⊥AB于M,根据30°角所对的直角等于斜边的一半可得AM=1,进而得出BM=BC,将△BEM顺时针旋转120°得△BEN,连接FN,可证△BEF≌△BFN,即可得出EF=FN,过点N作NG⊥DC交DC的延长线于点G,利用勾股定理即可求出答案.【详解】解:过点E作EM⊥AB于M,在Rt△AEM中,∠A=60°,∴∠AEM=30°,∴AM=12AE=1,∴3又∵DE=DF,AE=2,FC=3,∴DC-AD=1,即AB-BC=1,∴BM=BC,将△BEM顺时针旋转120°得△BEN,连接FN,则3BE=BN,∵∠EBF=60°,∠EBN=120°,∴∠NBF=60°,∴∠EBF=∠NBF又∵BE=BN,BF=BF,∴EF=FN ,过点N 作NG⊥DC 交DC 的延长线于点G ,∵∠GCN=180°-60°-90°=30°,∴NG=12NC=32∴CG=()2233322⎛⎫-= ⎪ ⎪⎝⎭ ∴FG=3+32=92∴FN=22932122⎛⎫⎛⎫+= ⎪ ⎪ ⎪⎝⎭⎝⎭∴EF=21故答案为21.【点睛】此题考查了平行四边形的性质、旋转的性质、勾股定理等知识,合理添加辅助线是解题关键.3.D解析:D【解析】【分析】连接DP ,当点D ,P ,E 在同一直线上时,由△PCF ≌△PCB 可得DP=BP ,BP EP + 的最小值为DE 长,依据△ADF ≌△DCE ,AF=DE,即可得到BP EP +最小值等于线段AF 的长.【详解】解:如图,连接DP ,∵PC=PC, ∠PCD=∠PCB=45°∴△PCF ≌△PCB∴BP=DP∴BP+PE =DP+PE∴当点D ,P ,E 在同一直线上时,BP EP +的最小值为DE 长,又∵AB=CD ,∠ADF=∠ECD ,DF=EC ,∴AF=DE,∴BP EP最小值等于线段AF的长,故选:D.【点睛】本题考查的是轴对称,最短路线问题,根据题意作出A关于BD的对称点C是解答此题的关键.4.D解析:D【分析】易得第二个菱形的面积为(12)2,第三个菱形的面积为(12)4,依此类推,第n个菱形的面积为(12)2n-2,把n=4代入即可.【详解】解:已知第一个菱形的面积为1;则第二个菱形的面积为原来的(12)2,第三个菱形的面积为(12)4,依此类推,第n个菱形的面积为(12)2n-2,当n=4时,则第4个菱形的面积为(12)2×4-2=(12)6=164.故选:D.【点睛】本题考查了三角形的中位线定理及矩形、菱形的性质,是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.5.C解析:C【分析】延长BG交CH于点E,根据正方形的性质证明△ABG≌△CDH≌△BCE,可得GE=BE-BG=1,HE=CH-CE=1,∠HEG=90°,由勾股定理可得GH的长.【详解】解:如图,延长BG交CH于点E,在△ABG 和△CDH 中,AB CD AG CH BG DH =⎧⎪=⎨⎪=⎩,∴△ABG ≌△CDH (SSS ),AG 2+BG 2=AB 2,∴∠1=∠5,∠2=∠6,∠AGB=∠CHD=90°,∴∠1+∠2=90°,∠5+∠6=90°,又∵∠2+∠3=90°,∠4+∠5=90°,∴∠1=∠3=∠5,∠2=∠4=∠6,在△ABG 和△BCE 中,1324AB BC ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ABG ≌△BCE (ASA ),∴BE=AG=4,CE=BG=3,∠BEC=∠AGB=90°,∴GE=BE -BG=4-3=1,同理可得:HE=1,在Rt △GHE 中,2222112GE EH +=+故选:C.【点睛】本题主要考查正方形的性质、全等三角形的判定与性质、勾股定理及其逆定理的综合运用,通过证三角形全等得出△GHE 为等腰直角三角形是解题的关键.6.A解析:A【分析】根据已知条件先证明△ABE ≌△ADG ,得到AE=AG ,再证明△AEF ≌△AGF ,得到EAF GAF ∠=∠,根据30DAF ∠=︒,设BAE ∠=x,利用GA AE ⊥得到方程求出x 即可求解.【详解】在正方形ABCD 中,AB=AD,90ABE ADG BAD ∠=∠=∠=︒∵GA AE ⊥∴90EAD DAG ∠+∠=︒又90EAD BAE ∠+∠=︒∴DAG BAE ∠∠=∴△ABE ≌△ADG (ASA )∴AE=AG ,BE=DG,∵BE DF EF +=∴BE DF DG DF EF +=+=∴EF=GF∴△AEF ≌△AGF (SSS )∴EAF GAF ∠=∠∵30DAF ∠=︒,设BAE ∠=x,∴EAF GAF ∠=∠=x+30°∵GA AE ⊥∴90EAF GAF ∠+∠=︒故x+30°+ x+30°=90°解得x=15°故选A .【点睛】此题主要考查全等三角形的判定与性质,解题的关键是熟知正方形的性质及全等三角形的判定定理.7.B解析:B【分析】当点P 和点A 重合时,当点C 和点Q 重合时,PQ 的值最大,当PQ ⊥BC 时,PQ 的值最小,利用这两组数据,在Rt△ABQ 中,可求得答案.【详解】当点P 和点A 重合时,当点C 和点Q 重合时,PQ 的值最大,85PQ =当PQ⊥BC时,PQ的值最小,∴PQ=8,∠Q=90°,在Rt△ACQ中,()2285816.CQ=-=在Rt△ABQ中,设AB=BC=x,则BQ=16-x,∴AQ2+BQ2=AB2即82+(16-x)2=x2解之:x=10.故答案为:B.【点睛】本题考查菱形的性质和勾股定理的运用,解题关键是根据菱形的性质,判断出PQ最大和最小的情况.8.D解析:D【分析】由勾股定理可求BE的长,由折叠的性质可得CE=EF=2,BE⊥CF,FH=CH,由面积法可求CH=45,由勾股定理可求EH的长,由三角形中位线定理可求DF=2EH=45.【详解】解:如图,连接CF,交BE于H,∵在正方形ABCD中,AB=4,E是CD的中点,∴BC=CD=4,CE=DE=2,∠BCD=90°,∴BE2216425BC CE+=+=∵将△BCE沿BE翻折至△BFE,∴CE=EF=2,BE⊥CF,FH=CH,∵S△BCE=12×BE×CH=12×BC×CE,∴CH=455,∴EH=221625 455CE CH-=-=,∵CE=DE,FH=CH,∴DF=2EH=45,故选:D.【点睛】本题考查了翻折变换,正方形的性质,全等三角形的判定与性质,掌握折叠的性质是本题的关键.9.B解析:B【分析】延长BG交CH于点E,根据正方形的性质证明△ABG≌△CDH≌△BCE,可得GE=BE-BG=2,HE=CH-CE=2,∠HEG=90°,从而由勾股定理可得GH的长.【详解】解:如图,延长BG交CH于点E,∵四边形ABCD是正方形,∴∠ABC=90°,AB=CD=10,∵AG=8,BG=6,∴AG2+BG2=AB2,∴∠AGB=90°,∴∠1+∠2=90°,又∵∠2+∠3=90°,∴∠1=∠3,同理:∠4=∠6,在△ABG和△CDH中,AB=CD=10AG=CH=8BG=DH=6∴△ABG≌△CDH(SSS),∴∠1=∠5,∠2=∠6,∴∠2=∠4,在△ABG和△BCE中,∵∠1=∠3,AB=BC,∠2=∠4,∴△ABG≌△BCE(ASA),∴BE=AG=8,CE=BG=6,∠BEC=∠AGB=90°,∴GE=BE-BG=8-6=2,同理可得HE=2,在Rt△GHE中,GH===故选:B.【点睛】本题主要考查正方形的性质、全等三角形的判定与性质、勾股定理及其逆定理的综合运用,通过证三角形全等得出△GHE为直角三角形且能够求出两条直角边的长是解题的关键.10.B解析:B【分析】根据菱形的性质,利用SAS证明即可判断①;根据△ABF≌△CAE得到∠BAF=∠ACE,再利用外角的性质以及菱形内角度数即可判断②;通过说明∠CAH≠∠DAO,判断△ADO≌△ACH不成立,可判断③;再利用菱形边长即可求出菱形面积,可判断④.【详解】解:∵在菱形ABCD中,AB=AC=1,∴△ABC为等边三角形,∴∠B=∠CAE=60°,又∵AE=BF,∴△ABF≌△CAE(SAS),故①正确;∴∠BAF=∠ACE,∴∠FHC=∠ACE+∠HAC=∠BAF+∠HAC=60°,故②正确;∵∠B=∠CAE=60°,则在△ADO和△ACH中,∠OAD=60°=∠CAB,∴∠CAH≠60°,即∠CAH≠∠DAO,∴△ADO≌△ACH不成立,故③错误;∵AB=AC=1,过点A作AG⊥BC,垂足为G,∴∠BAG=30°,BG=12,∴2,∴菱形ABCD 的面积为:BC AG ⨯=312⨯=32,故④错误; 故正确的结论有2个,故选B.【点睛】本题考查了全等三角形判定和性质,菱形的性质和面积,等边三角形的判定和性质,外角的性质,解题的关键是利用菱形的性质证明全等.二、填空题11.①③④【分析】由矩形的性质可得AB=CD ,AD=BC ,∠BAD=∠ABC=∠BCD=∠ADC=90°,AC=BD ,由角平分线的性质和余角的性质可得∠F=∠FAD=45°,可得AD=DF=BC ,可判断①;通过证明△DCG ≌△BEG ,可得∠BGE=∠DGC ,BG=DG ,即可判断②③;过点G 作GH ⊥CD 于H ,设AD=4x=DF ,AB=3x ,由勾股定理可求BD=5x ,由等腰直角三角形的性质可得HG=CH=FH=12x ,DG=GB=522x ,由三角形面积公式可求解,可判断④. 【详解】解:∵四边形ABCD 是矩形,∴AB=CD ,AD=BC ,∠BAD=∠ABC=∠BCD=∠ADC=90°,AC=BD ,∵AE 平分∠BAD ,∴∠BAE=∠DAE=45°,∴∠F=∠FAD ,∴AD=DF ,∴BC=DF ,故①正确;∵∠EAB=∠BEA=45°,∴AB=BE=CD ,∵∠CEF=∠AEB=45°,∠ECF=90°,∴△CEF 是等腰直角三角形,∵点G 为EF 的中点,∴CG=EG ,∠FCG=45°,CG ⊥AG ,∴∠BEG=∠DCG=135°,在△DCG 和△BEG 中,===BE CD BEG DCG CG EG ⎧⎪∠∠⎨⎪⎩,∴△DCG ≌△BEG (SAS ).∴∠BGE=∠DGC ,BG=DG ,∵∠BGE <∠AEB ,∴∠DGC=∠BGE <45°,∵∠CGF=90°,∴∠DGF <135°,故②错误;∵∠BGE=∠DGC ,∴∠BGE+∠DGA=∠DGC+∠DGA ,∴∠CGA=∠DGB=90°,∴BG ⊥DG ,故③正确;过点G 作GH ⊥CD 于H ,∵34AB AD =, ∴设AD=4x=DF ,AB=3x ,∴CF=CE=x ,22AB AD x +,∵△CFG ,△GBD 是等腰直角三角形,∴HG=CH=FH=12x ,52x , ∴S △DGF =12×DF×HG=x 2,S △BDG =12DG×GB=254x 2, ∴254BDG FDG S S =,故④正确;故答案为:①③④.【点睛】本题考查了矩形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质;熟练掌握矩形的性质,证明三角形全等和等腰直角三角形是解决问题的关键.12.8个【分析】作点F 关于BC 的对称点M ,连接FM 交BC 于点N ,连接EM ,交BC 于点H ,可得点H 到点E 和点F 的距离之和最小,可求最小值,即可求解.【详解】如图,作点F 关于BC 的对称点M ,连接FM 交BC 于点N ,连接EM ,交BC 于点H , ∵点E ,F 将对角线AC 三等分,且AC =6,∴EC =4,FC =2=AE ,∵点M 与点F 关于BC 对称,∴CF =CM =2,∠ACB =∠BCM =45°,∴∠ACM =90°,∴EM则在线段BC 存在点H 到点E 和点F 的距离之和最小为5,在点H 右侧,当点P 与点C 重合时,则PE +PF =4+2=6,∴点P 在CH 上时,PE +PF ≤6,在点H 左侧,当点P 与点B 重合时,∵FN ⊥BC ,∠ABC =90°,∴FN ∥AB ,∴△CFN ∽△CAB , ∴FN CN CF 1===AB CB CA 3,∵AB =BC AC =∴FN =13AB ,CN =13BC∴BN =BC -CN =,BF =,∵AB =BC ,CF =AE ,∠BAE =∠BCF ,∴△ABE ≌△CBF (SAS ),∴BE =BF ,∴PE +PF =∴点P 在BH 上时,PE +PF <∴在线段BC 上点H 的左右两边各有一个点P 使PE +PF =5,同理在线段AB ,AD ,CD 上都存在两个点使PE +PF =5.即共有8个点P 满足PE +PF =5,故答案为8.【点睛】本题考查了正方形的性质,最短路径问题,在BC上找到点H,使点H到点E和点F的距离之和最小是本题的关键.13.3或6【详解】①∠B′EC=90°时,如图1,∠BEB′=90°,由翻折的性质得∠AEB=∠AEB′=12×90°=45°,∴△ABE是等腰直角三角形,∴BE=AB=6cm;②∠EB′C=90°时,如图2,由翻折的性质∠AB′E=∠B=90°,∴A、B′、C在同一直线上,AB′=AB,BE=B′E,由勾股定理得,222268AB BC+=+,∴B′C=10-6=4cm,设BE=B′E=x,则EC=8-x,在Rt△B′EC中,B′E2+B′C2=EC2,即x2+42=(8-x)2,解得x=3,即BE=3cm,综上所述,BE的长为3或6cm.故答案为3或6.14.3﹣32 2【分析】作辅助线,构建全等三角形和矩形,利用面积法可得AE的长,根据勾股定理可得BE的长,设AE=x,证明△ABE≌△EQF(AAS),得FQ=BE=2,最后根据三角形面积公式可得结论.【详解】解:如图,过D作DH⊥AE于H,过E作EM⊥AD于M,连接DE,∵EF⊥AE,DF⊥EF,∴∠DHE=∠HEF=∠DFE=90°,∴四边形DHEF是矩形,∴DH=EF=AE,∵四边形ABCD是矩形,∴∠B=∠BAD=90°,∵∠AME=90°,∴四边形ABEM是矩形,∴EM=AB=2,设AE=x,则S△ADE=11AD EM AE DH 22⋅=⋅,∴3×2=x2,∴x6,∵x>0,∴x6,即AE6,由勾股定理得:BE22(6)2-2,过F作PQ∥CD,交AD的延长线于P,交BC的延长线于Q,∴∠Q=∠ECD=∠B=90°,∠P=∠ADC=90°,∵∠BAE+∠AEB=∠AEF=∠AEB+∠FEQ=90°,∴∠FEQ=∠BAE,∵AE=EF,∠B=∠Q=90°,∴△ABE ≌△EQF (AAS ),∴FQ =BE =2, ∴PF =2﹣2,∴S △ADF =1AD PF 2⋅=13(22)2⨯⨯-=3﹣322. 【点睛】 此题主要考查了矩形的性质,全等三角形的判定和性质,勾股定理,有难度,正确作辅助线构建全等三角形是关键,并用方程的思想解决问题. 15.101-【分析】探究点E 的运动轨迹,寻找特殊位置解决问题即可.【详解】如图1中,当点M 与A 重合时,AE =EN ,设AE =EN =xcm ,在Rt △ADE 中,则有x 2=32+(9﹣x )2,解得x =5,∴DE =10﹣1-5=4(cm ),如图2中,当点M 运动到MB ′⊥AB 时,DE ′的值最大,DE ′=10﹣1﹣3=6(cm ),如图3中,当点M 运动到点B ′落在CD 时,22221310NB C N C B ''''=++=DB ′(即DE ″)=10﹣110=(910)(cm ),∴点E的运动轨迹E→E′→E″,运动路径=EE′+E′B′=6﹣4+6﹣(9﹣10)=(101-)(cm).故答案为:101-.【点睛】本题考查翻折变换,矩形的性质,解直角三角形等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考填空题中的压轴题.16.83或4433-【分析】连接AC交BD于O,由菱形的性质可得AB=BC=4,∠ABD=30°,AC⊥BD,BO=DO,AO=CO,可证四边形BEGF是菱形,可得∠ABG=30°,可得点B,点G,点D三点共线,由直角三角形性质可求BD=43,AC=4,分两种情况讨论,利用等腰三角形的性质可求解.【详解】如图,连接AC交BD于O,∵菱形ABCD的边长是4,∠ABC=60°,∴AB=BC=4,∠ABD=30°,AC⊥BD,BO=DO,AO=CO,∵EG∥BC,FG∥AB,∴四边形BEGF是平行四边形,又∵BE=BF,∴四边形BEGF是菱形,∴∠ABG=30°,∴点B,点G,点D三点共线,∵AC⊥BD,∠ABD=30°,∴AO=12AB=2,22224223AB AO--=∴BD=AC=4,同理可求BE ,即, 若AD=DG'=4时,∴BG'=BD-DG'=4,∴BE'43==-; 若AG''=G''D 时,过点G''作G''H ⊥AD 于H ,∴AH=HD=2,∵∠ADB=30°,G''H ⊥AD ,∴DG''=2HG'',∵222HD HG''DG''+=,解得:HG''=,DG''=2HG''=∴BG''=BD-DG''=33-=, ∴BE''=83,综上所述:BE 为83或4- 【点睛】 本题考查了菱形的性质,含30度角的直角三角形的性质,勾股定理等知识,利用分类讨论思想解决问题是本题的关键.17.②③【分析】根据菱形的性质可知AC ⊥BD ,所以在Rt △AFP 中,AF 一定大于AP ,从而判断①;设∠BAE=x ,然后根据等腰三角形两底角相等表示出∠ABE ,再根据菱形的邻角互补求出∠ABE ,根据三角形内角和定理列出方程,求出x 的值,求出∠BFE 和∠BE 的度数,从而判断②③.【详解】解:在菱形ABCD 中,AC ⊥BD ,∴在Rt △AFP 中,AF 一定大于AP ,故①错误;∵四边形ABCD 是菱形,∴AD ∥BC ,∴∠ABE+∠BAE+∠EAD=180°,设∠BAE=x°,则∠EAD=2x°,∠ABE=180°-x°-2x°,∵AB=AE ,∠BAE=x°,∴∠ABE=∠AEB=180°-x°-2x°,由三角形内角和定理得:x+180-x-2x+180-x-2x=180,解得:x=36,即∠BAE=36°,∠BAE=180°-36°-2×36°=70°,∵四边形ABCD 是菱形,∴∠BAD=∠CBD=12∠ABE=36°, ∴∠BFE=∠ABD+∠BAE=36°+36°=72°,∴∠BEF=180°-36°-72°=72°,∴BE=BF=AF .故③正确∵∠AFD=∠BFE=72°,∠EAD=2x°=72°∴∠AFD=∠EAD∴AD=FD又∵AD=AB=AE∴AE=FD ,故②正确∴正确的有②③故答案为:②③【点睛】本题考查了菱形的性质,等腰三角形的性质,熟记各性质并列出关于∠BAE 的方程是解题的关键,注意:菱形的对边平行,菱形的对角线平分一组对角.18 【分析】根据12•BC •AH =12•AB •AC ,可得AH =13,根据 12AD •BO =12BD •AH ,得OB =13,再根据BE =2OB =13,运用勾股定理可得EC . 【详解】设BE 交AD 于O ,作AH ⊥BC 于H .在Rt △ABC 中,∠BAC =90°,AB =2,AC =3,由勾股定理得:BC∵点D 是BC 的中点,∴AD =DC =DB , ∵12•BC •AH =12•AB •AC ,∴AH =613, ∵AE =AB ,DE =DB ,∴点A 在BE 的垂直平分线上,点D 在BE 的垂直平分线上,∴AD 垂直平分线段BE ,∵12AD •BO =12BD •AH , ∴OB =613, ∴BE =2OB =121313, ∵DE =DB=CD , ∴∠DBE=∠DEB ,∠DEC=∠DCE ,∴∠DEB+∠DEC=12×180°=90°,即:∠BEC=90°, ∴在Rt △BCE 中,EC =22BC BE - =221213(13)()13-=51313. 故答案为:51313. 【点睛】本题主要考查直角三角形的性质,勾股定理以及翻折的性质,掌握“直角三角形斜边长的中线等于斜边的一半”以及面积法求三角形的高,是解题的关键.192【解析】【分析】根据折叠的性质可得∠DAF=∠BAF=45°,再由矩形性质可得FC=ED=1,然后由勾股定理求出FG 即可.【详解】由折叠的性质可知,∠DAF=∠BAF=45°,∴AE=AD=3,EB=AB-AD=1,∵四边形EFCB 为矩形,∴FC=BE=1,∵AB ∥FC ,∴∠GFC=∠DAF=45°,∴GC=FC=1,∴FG ===.【点睛】本题考查了折叠变换,矩形的性质是一种对称变换,理解折叠前后图形的大小不变,位置变化,对应边和对应角相等是解决此题的关键.2012a 【分析】(1)根据折叠的性质可得出,四边形AFED 为正方形,CE=GE=BF ,AEB GBE ABE EBC ∠∠∠∠+=+,即AEB ABE ∠∠=,得出AB=AE ,继而可得解;(2)结合(1)可知,AE AM ==,因为EC=3BM ,所以有1BM 2FM =,求出BM ,继而可得解.【详解】解:(1)由折叠的性质可得,CE=GE=BF ,AEB GBE ABE EBC ∠∠∠∠+=+,即AEB ABE ∠∠=, ∴AB=AE ,∵AE ==∴AB =.(2)结合(1)可知,AE AM ==,∴FM a =-,∵EC=3BM , ∴1BM 2FM =∴BM =∴1AB 22a a -=+=.;12a . 【点睛】本题是一道关于折叠的综合题目,主要考查折叠的性质,弄清题意,结合图形找出线段间的数量关系是解题的关键.三、解答题21.EF =13.【分析】首先连接AD ,由△ABC 是等腰直角三角形,AB=AC ,D 是斜边BC 的中点,可得:AD=DC ,∠EAD=∠C=45°,AD ⊥BC ,即∠CDF+∠ADF=90°,又DE ⊥DF ,可得:∠EDA+∠ADF=90°,故∠EDA=∠CDF ,从而可证:△AED ≌△CFD ;根据全等三角形的性质得到AE=CF=5,进而得出BE=AF=12.然后在Rt △AEF 中,运用勾股定理可将EF 的值求出;【详解】解:连接AD .∵△ABC 是等腰直角三角形,AB =AC ,D 是斜边BC 的中点,∴AD =DC =DB ,AD ⊥BC ,∴∠BAD =∠C =45°,∵∠EDA +∠ADF =90°,又∵∠CDF +∠ADF =90°,∴∠EDA =∠CDF .在△AED 与△CFD 中,EDA FDC AD CDEAD C ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△AED ≌△CFD (ASA ).∴AE =CF =5.∵AB =AC ,∴BE =AF =12.在Rt △AEF 中,∵∠EAF =90°,∴22222512169EF AE AF =+=+=,∴EF =13.【点睛】本题考查等腰直角三角形, 直角三角形斜边上的中线,掌握等腰三角形“三线合一”的性质、直角三角形斜边上的中线等于斜边的一半的性质为解题关键.22.(1)证明见解析;(273【分析】(1)由题意根据勾股定理分别表示出2222,AB CD AD BC ++进行分析求证即可;(2)根据题意连接CG 、BE ,证明△GAB ≌△CAE ,进而得BG ⊥CE ,再根据(1)的结论进行分析即可求出答案.【详解】解:(1)∵AC ⊥BD ,∴∠AOD=∠AOB=∠BOC=∠COD=90°,由勾股定理得,222222AD BC AO DO BO CO +=+++,222222AB CD AO BO CO DO +=+++,∴2222AD BC AB CD +=+;(2)连接CG 、BE ,如图2,∵∠CAG=∠BAE=90°,∴∠CAG+∠BAC=∠BAE+∠BAC ,即∠GAB=∠CAE ,在△GAB 和△CAE 中,AG AC GAB CAE AB AE =⎧⎪∠=∠⎨⎪=⎩,∴△GAB ≌△CAE (SAS ),∴∠ABG=∠AEC ,又∠AEC+∠AME=90°,∴∠ABG+∠AME=90°,即CE ⊥BG ,由(1)得,2222CG BE CB GE +=+,∵AC=4,AB=5,∴BC=3,2,2,∴222273GE CG BE CB =+-=,∴73【点睛】本题考查的是正方形的性质、全等三角形的判定和性质、垂直的定义、勾股定理的应用,熟练并正确理解全等三角形的判定和性质以及灵活运用勾股定理是解题的关键.23.(1)AE t =;122AD t =-;DF t =;(2)证明见解析;(3)3t =;理由见解析.【分析】(1)根据题意用含t 的式子表示AE 、CD ,结合图形表示出AD ,根据直角三角形的性质表示出DF ;(2)根据对边平行且相等的四边形是平行四边形证明;(3)根据矩形的定义列出方程,解方程即可.【详解】解:(1)由题意得,AE t =,2CD t =,则122AD AC CD t =-=-,∵DF BC ⊥,30C ∠=︒,∴12DF CD t == (2)∵90ABC ∠=︒,DF BC ⊥,∴AB DF , ∵AE t =,DF t =,∴AE DF =,∴四边形AEFD 是平行四边形;(3)当3t =时,四边形EBFD 是矩形,理由如下:∵90ABC ∠=︒,30C ∠=︒, ∴162BC AC cm ==, ∵BE DF ∥, ∴BE DF =时,四边形EBFD 是平行四边形,即6t t -=,解得,3t =,∵90ABC ∠=︒,∴四边形EBFD 是矩形,∴3t =时,四边形EBFD 是矩形.【点睛】本题考查的是直角三角形的性质、平行四边形的判定、矩形的判定,掌握平行四边形、矩形的判定定理是解题的关键.24.(1)(2,32);(2)存在,点D 的坐标为(0,3)或(1)或(0,-1);(3)OM=32或2 【分析】(1)过点B 作BD ⊥y 轴于D ,利用30°所对的直角边是斜边的一半和勾股定理求出OB ,再利用30°所对的直角边是斜边的一半和勾股定理求出BD 和OD 即可得出结论;(2)根据题意和等边三角形的性质分别求出点A 、B 、C 的坐标,然后根据菱形的顶点顺序分类讨论,分别画出对应的图形,根据菱形的对角线互相平分即可分别求出结论; (3)利用30°所对的直角边是斜边的一半和勾股定理求出OP 和BP ,然后根据直角三角形的直角顶点分类讨论,分别画出对应的图形,利用直角三角形斜边上的中线等于斜边的一半、平行四边形的判定及性质、等腰三角形的判定及性质求解即可.【详解】解:(1)如图2,过点B 作BD ⊥y 轴于D由图1中,点A 的坐标为()1,0-,30ABO ∠=︒,∠AOB=90°∴OA=1,AB=2OA=2由勾股定理可得OB=223AB OA -= ∵将此直角三角板绕点O 顺时针旋转30∴∠BOD=30°∴BD=132OB =∴OD=2232OB BD -=∴点B 的坐标为(3,32) 故答案为:(32,32); (2)在图2的基础上继续将直角三角板绕点O 顺时针60︒,此时点A 落在y 轴上,点B 落在x 轴上∴点A 的坐标为(0,1),点B 的坐标为(3,0)∵△ABC 为等边三角形∴∠ABC=60°,AB=BC=AC=2∴∠OBC=90°∴点C 的坐标为(3,2)设点D 的坐标为(a ,b )如图所示,若四边形ABCD 为菱形,连接BD ,与AC 交于点O∴点O既是AC的中点,也是BD的中点∴03322 12022ab⎧++=⎪⎪⎨++⎪=⎪⎩解得:3ab=⎧⎨=⎩∴此时点D的坐标为(0,3);当四边形ABDC为菱形时,连接AD,与BC交于点O∴点O既是AD的中点,也是BC的中点∴033212022ab⎧++=⎪⎪⎨++⎪=⎪⎩解得:231ab⎧=⎪⎨=⎪⎩∴此时点D的坐标为(23,1);当四边形ADBC为菱形时,连接CD,与AB交于点O∴点O既是AB的中点,也是CD的中点∴03310222ab++=⎨++⎪=⎪⎩解得:1ab=⎧⎨=-⎩∴此时点D的坐标为(0,-1);综上:点D的坐标为(0,3)或(23,1)或(0,-1);(3)∵OB=3,∠ABO=30°∴OP=12OB=32∴BP=223 2OB OP-=当∠OMB=90°时,如下图所示,连接BM∵F为OB的中点∴PF=12OB,MF=12OB,OF=BF∴PF=MF∴四边形OPBM为平行四边形∴OM=BP=32;当∠OBM=90°时,如下图所示,连接OM,∴∠PBM=∠PBO+∠OBM=120°∵点F为OB的中点∴FP=FB∴∠FPB=∠FBP=30°∴∠BMP=180°-∠PBM-∠FPB=30°∴∠BMP=∠BPM∴BM=BP=3 2在Rt △OBM 中,2=;综上:OM=32. 【点睛】 此题考查的是直角三角形的性质、菱形的性质、平行四边形的判定及性质、等边三角形的性质,掌握30°所对的直角边是斜边的一半、勾股定理、直角三角形斜边上的中线等于斜边的一半、菱形的性质、平行四边形的判定及性质、等边三角形的性质是解决此题的关键.25.(1)见解析;(2)MN 2=ND 2+DH 2,理由见解析;(3)EG=4,MN=【分析】(1)根据高AG 与正方形的边长相等,证明三角形全等,进而证明角相等,从而求出解. (2)用三角形全等和正方形的对角线平分每一组对角的知识可证明结论.(3)设EG=BE=x ,根据正方形的边长得出CE ,CF ,EF ,在Rt △CEF 中利用勾股定理得到方程,求出EG 的长,设MN=a ,根据MN 2=ND 2+BM 2解出a 值即可.【详解】解:(1)在Rt △ABE 和Rt △AGE 中,AB=AG ,AE=AE ,∴Rt △ABE ≌Rt △AGE (HL ).∴∠BAE=∠GAE .同理,∠GAF=∠DAF .∴∠EAF =12∠BAD =45°; (2)MN 2=ND 2+DH 2.∵∠BAM=∠DAH ,∠BAM+∠DAN=45°,∴∠HAN=∠DAH+∠DAN=45°.∴∠HAN=∠MAN ,又∵AM=AH ,AN=AN ,∴△AMN ≌△AHN (SAS ).∴MN=HN ,∵∠BAD=90°,AB=AD ,∴∠ABD=∠ADB=45°,∴∠HDN=∠HDA+∠ADB=90°,∴NH 2=ND 2+DH 2,∴MN 2=ND 2+DH 2;。
八年级下第二次月考数学试卷(有答案)

八年级(下)第二次月考数学试卷一、选择题:(共8个小题,每小题3分,共24分)1.下列各点中,位于第二象限的是()A.(8,﹣1)B.(8,0)C.(﹣,3)D.(0,﹣4)2.若分式的值为0,则x的值是()A.0B.﹣l C.5D.13.已知点(,6)在函数y=的图象上,则m的值是()A.﹣3B.﹣12C.1D.﹣14.下列计算中,正确的是()A.3﹣2=﹣6B.=C.a﹣1•a﹣2=a2D.=5.下列说法正确的是()A.平行四边形对角线相等B.矩形的对角线互相垂直C.菱形的四个角都相等D.菱形的对角线互相垂直平分且平分一组对角6.菱形ABCD的面积为120,对角线BD=24,则这个菱形的周长是()A.64B.60C.52D.507.如图,已知矩形ABCD,将△BCD沿对角线BD折叠,记点C的对应点为C′,若∠ADC′=20°,则∠BDC的度数为()A.55°B.45°C.60°D.65°8.如图,O是坐标原点,菱形OABC的顶点A的坐标为(﹣3,4),顶点C在x轴的负半轴上,函数y=(x<0)的图象经过顶点B,则k的值为()A.﹣12B.﹣27C.﹣32D.﹣36二、填空题:(本大题共8个小题,每小题3分,共24分).9.在函数y=中,自变量x的取值范围是.10.点P关于y轴的对称点P′的坐标是(﹣5,2),则点P的坐标是.11.分式方程的解是.12.造成宜宾雾霾天气的“元凶”是PM2.5,PM2.5是指大气中直径小于或等于0.00000025米的颗粒物,也称为可入肺颗粒物,它对空气质量和能见度等有重要的影响,会给人的健康带来严重危害.将0.00000025用科学记数法表示为.13.将直线y=7x﹣1向上平移8单位长度,得到的直线解析式为.14.如图,在平行四边形ABCD中,CE⊥AB,E为垂足.如果∠A=125°,则∠BCE=度.15.如图,在菱形ABCD中,点P是对角线AC上的一动点,PE⊥AB于点E.当P运动到一定位置时PE =4,则此时点P到AD的距离为.三、解答题:(本大题8个小题,共72分)解答应写出文字说明,证明过程或演算步骤.16.(12分)(1)计算:(﹣2018)0﹣+||﹣3﹣1;(2)解分式方程:=﹣2;17.(6分)先化简再求值:(+)÷,其中a=2.18.(8分)已知:如图,E、F是平行四边形ABCD的对角线BD上的两点,BE=DF.求证:(1)△ADF≌△CBE;(2)CE∥AF.19.(8分)如图,直线y=kx+b与双曲线y=交于A(2,n)、B(﹣3,﹣2)两点,与x轴,y轴分别交于C、D两点.(1)试求双曲线y=的解析式;(2)试求直线y=kx+b的解析式;(3)试求△AOB的面积.20.(8分)宜宾军分区帮助群众修建水渠抗旱减灾,原计划在规定时间内修建500m,由于加大了机械化作业程度,实际每天的进度是原来的1.5倍,结果不仅超额完成计划修建米数的20%,而且还比规定时间提前了5天.(1)设原计划的每天修建xm,利用工效、工作总量、时间之间的关系填写下表.(要求:填上适当的代数式,完成表格)速度(m/天)工作总量(m)所用时间(天)原计划x500实际(2)列出方程,并求原计划每天修建水渠的长度.21.(8分)宜宾绿源超市购进A、B两种白醋,已知每瓶B型白醋进价比A型贵0.50元,6瓶A型白醋与3瓶B型白醋进价共42元.两种白醋的销售价格如下表:品名A B售价(元) 6.58.0(1)求这两种型号的白醋每瓶的进价;(2)宜宾绿源超市打算购进这两种白醋共100瓶,进货总价不超过480元,全部售出后总利润不低于250元.设应购进A型白醋m瓶,总利润为w元.①求w与m之间的函数关系式;②求m的取值范围,并求出全部售出这批白醋后的最大利润.22.(10分)如图,过矩形ABCD的四个顶点作对角线AC,BD的平行线,分别相交于E,F,G,H四点,若AB=6,BC=8.(1)求证:四边形EFGH是菱形;(2)求图中阴影部分的面积.23.(12分)已知直线与x轴交于点A(﹣4,0),与y轴交于点B.(1)求b的值;(2)把△AOB绕原点O顺时针旋转90°后,点A落在y轴的A′处,点B若在x轴的B′处.①求直线A′B′的函数关系式;②设直线AB与直线A′B′交于点C,矩形PQMN是△AB′C的内接矩形,其中点P,Q在线段AB′上,点M在线段B′C上,点N在线段AC上.若矩形PQMN的两条邻边的比为1:2,试求矩形PQMN的周长.参考答案与试题解析一、选择题:(共8个小题,每小题3分,共24分)1.下列各点中,位于第二象限的是()A.(8,﹣1)B.(8,0)C.(﹣,3)D.(0,﹣4)【分析】依据位于第二象限的点的横坐标为负,纵坐标为正,即可得到结论.【解答】解:∵位于第二象限的点的横坐标为负,纵坐标为正,∴位于第二象限的是(﹣,3)故选:C.【点评】本题主要考查了点的坐标,解题时注意:位于第二象限的点的横坐标为负,纵坐标为正.2.若分式的值为0,则x的值是()A.0B.﹣l C.5D.1【分析】直接利用分式的值为零则分子为零进而得出答案.【解答】解:∵分式的值为0,∴x=1=0,解得:x=﹣1,故选:B.【点评】此题主要考查了分式的值为零的条件,正确把握定义是解题关键.3.已知点(,6)在函数y=的图象上,则m的值是()A.﹣3B.﹣12C.1D.﹣1【分析】根据点(,6)在函数y=的图象上,可以求得m的值,从而可以解答本题.【解答】解:∵点(,6)在函数y=的图象上,∴,解得,m=﹣3,故选:A.【点评】本题考查反比例函数图象上点的坐标特征,解答本题的关键是明确题意,利用反比例函数的性质解答.4.下列计算中,正确的是()A.3﹣2=﹣6B.=C.a﹣1•a﹣2=a2D.=【分析】利用负整数指数幂的意义对A、C进行判断;根据最简分式的定义对B进行判断;利用约分对D 进行判断.【解答】解:A、原式==,所以A选项错误;B、为最简分式,所以B选项错误;C、原式=•=,所以C选项错误;D、原式==,所以D选项正确.故选:D.【点评】本题考查了约分:约去分式的分子与分母的公因式,不改变分式的值,这样的分式变形叫做分式的约分.5.下列说法正确的是()A.平行四边形对角线相等B.矩形的对角线互相垂直C.菱形的四个角都相等D.菱形的对角线互相垂直平分且平分一组对角【分析】根据菱形的性质、矩形的性质、平行四边形的性质对各个命题分别判断,即可得出答案.【解答】解:A、平行四边形对角线互相平分,错误;B、矩形的对角线相等,错误;C、菱形的四条边都相等,错误;D、菱形的对角线互相垂直平分且平分一组对角,正确;故选:D.【点评】此题考查了命题与定理,解题的关键是掌握真命题与假命题的定义,能根据有关性质与判定对命题的真假进行判断是关键.6.菱形ABCD的面积为120,对角线BD=24,则这个菱形的周长是()A.64B.60C.52D.50【分析】菱形的面积可以根据对角线的长计算,已知菱形的面积,对角线BD的长即可计算AC的长,进而利用勾股定理解答即可.【解答】解:菱形ABCD的面积S=AC•BD=120,∵BD=24,∴AC==10,∴AB=,∴这个菱形的周长=13×4=52,故选:C.【点评】本题考查了根据对角线长计算菱形的面积的方法,本题中正确计算是解题的关键.7.如图,已知矩形ABCD,将△BCD沿对角线BD折叠,记点C的对应点为C′,若∠ADC′=20°,则∠BDC的度数为()A.55°B.45°C.60°D.65°【分析】由折叠的性质可知∠BDC=∠BDC′,故∠ADB=∠BDC′﹣∠ADC′=∠BDC﹣20°,根据∠ADB+∠BDC=90°,列方程求∠BDC.【解答】解:由折叠的性质,得∠BDC=∠BDC′,则∠ADB=∠BDC′﹣∠ADC′=∠BDC﹣20°,∵∠ADB+∠BDC=90°,∴∠BDC﹣20°+∠BDC=90°,解得∠BDC=55°.故选:A.【点评】本题考查了折叠的性质.关键是根据∠ADB+∠BDC=90°列方程求解.8.如图,O是坐标原点,菱形OABC的顶点A的坐标为(﹣3,4),顶点C在x轴的负半轴上,函数y=(x<0)的图象经过顶点B,则k的值为()A.﹣12B.﹣27C.﹣32D.﹣36【分析】根据点C的坐标以及菱形的性质求出点B的坐标,然后利用待定系数法求出k的值即可.【解答】解:∵A(﹣3,4),∴OA==5,∵四边形OABC是菱形,∴AO=CB=OC=AB=5,则点B的横坐标为﹣3﹣5=﹣8,故B的坐标为:(﹣8,4),将点B的坐标代入y=得,4=,解得:k=﹣32.故选:C.【点评】本题考查了菱形的性质以及利用待定系数法求反比例函数解析式,解答本题的关键是根据菱形的性质求出点B的坐标.二、填空题:(本大题共8个小题,每小题3分,共24分).9.在函数y=中,自变量x的取值范围是x≥.【分析】根据二次根式的性质,被开方数大于等于0可知:2x﹣1≥0,解得x的范围.【解答】解:根据题意得:2x﹣1≥0,解得,x≥.【点评】本题考查的是函数自变量取值范围的求法.函数自变量的范围一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数为非负数.10.点P关于y轴的对称点P′的坐标是(﹣5,2),则点P的坐标是(5,2).【分析】根据“关于y轴对称的点,纵坐标相同,横坐标互为相反数”解答.【解答】解:点P关于y轴的对称点P′的坐标是(﹣5,2),则点P的坐标是(5,2),故答案为:(5,2).【点评】本题主要考查关于x轴、y轴对称点的坐标,解决本题的关键是掌握好对称点的坐标规律:(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数;(3)关于原点对称的点,横坐标与纵坐标都互为相反数.11.分式方程的解是x=13.【分析】解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论.【解答】解:去分母,可得x﹣5=8,解得x=13,经检验:x=13是原方程的解.【点评】本题主要考查了解分式方程,解分式方程时,去分母后所得整式方程的解有可能使原方程中的分母为0,所以应检验.12.造成宜宾雾霾天气的“元凶”是PM2.5,PM2.5是指大气中直径小于或等于0.00000025米的颗粒物,也称为可入肺颗粒物,它对空气质量和能见度等有重要的影响,会给人的健康带来严重危害.将0.00000025用科学记数法表示为 2.5×10﹣7.【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【解答】解:0.00000025=2.5×10﹣7.故答案为:2.5×10﹣7.【点评】本题考查用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.13.将直线y=7x﹣1向上平移8单位长度,得到的直线解析式为y=7x+7.【分析】直接根据“上加下减”的原则进行解答即可.【解答】解:由“上加下减”的原则可知,把直线y=7x﹣1向上平移8个单位长度后所得直线的解析式为:y=7x﹣1+8,即y=7x+7.故答案为:y=7x+7.【点评】本题考查的是一次函数的图象与几何变换,熟知函数图象平移的法则是解答此题的关键.14.如图,在平行四边形ABCD中,CE⊥AB,E为垂足.如果∠A=125°,则∠BCE=35度.【分析】根据平行四边形的性质和已知,可求出∠B,再进一步利用直角三角形的性质求解即可.【解答】解:∵AD∥BC,∴∠A+∠B=180°,∴∠B=180°﹣125°=55°,∵CE⊥AB,∴在Rt△BCE中,∠BCE=90°﹣∠B=90°﹣55°=35°.故答案为:35.【点评】本题主要考查了平行四边形的性质,运用平行四边形对边平行的性质,得到邻角互补的结论,这是运用定义求四边形内角度数的常用方法.15.如图,在菱形ABCD中,点P是对角线AC上的一动点,PE⊥AB于点E.当P运动到一定位置时PE =4,则此时点P到AD的距离为4.【分析】作PF⊥AD于D,如图,根据菱形的性质得AC平分∠BAD,然后根据角平分线的性质得PF=PE=4.【解答】解:作PF⊥AD于D,如图,∵四边形ABCD为菱形,∴AC平分∠BAD,∵PE⊥AB,PF⊥AD,∴PF=PE=4,即点P到AD的距离为4.故答案为:4.【点评】本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.也考查了菱形的性质.三、解答题:(本大题8个小题,共72分)解答应写出文字说明,证明过程或演算步骤.16.(12分)(1)计算:(﹣2018)0﹣+||﹣3﹣1;(2)解分式方程:=﹣2;【分析】(1)原式利用零指数幂、负整数指数幂法则,以及算术平方根定义计算即可求出值;(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:(1)原式=1﹣6+﹣=﹣5;(2)去分母得:2x=3﹣4x+4,移项合并得:6x=7,解得:x=,经检验x=是分式方程的解.【点评】此题考查了解分式方程,以及实数的运算,熟练掌握运算法则是解本题的关键.17.(6分)先化简再求值:(+)÷,其中a=2.【分析】原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,把a的值代入计算即可求出值.【解答】解:原式=•=•=,当a=2时,原式=2.【点评】此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.18.(8分)已知:如图,E、F是平行四边形ABCD的对角线BD上的两点,BE=DF.求证:(1)△ADF≌△CBE;(2)CE∥AF.【分析】(1)根据平行四边形的性质得到AD=BC,∠DAF=∠BCE,利用SAS地理证明;(2)根据全等三角形的性质得到∠AFD=∠CEB,根据邻补角的定义得到∠AFB=∠CED,根据平行线的判定定理证明CE∥AF.【解答】证明:(1)∵四边形ABCD是平行四边形,∴AD=BC,∠DAF=∠BCE,在△ADF和△CBE中,,∴△ADF≌△CBE;(2)∵△ADF≌△CBE∴∠AFD=∠CEB,∴∠AFB=∠CED,∴CE∥AF.【点评】本题考查的是平行四边形的性质、全等三角形的判定和性质,掌握全等三角形的判定定理和性质定理是解题的关键.19.(8分)如图,直线y=kx+b与双曲线y=交于A(2,n)、B(﹣3,﹣2)两点,与x轴,y轴分别交于C、D两点.(1)试求双曲线y=的解析式;(2)试求直线y=kx+b的解析式;(3)试求△AOB的面积.【分析】用待定系数法求函数解析式,重点是确定关键点坐标.【解答】解:双曲线y=交于A(2,n)、B(﹣3,﹣2)两点(1)由B(﹣3,﹣2)坐标知:m=6,反比例函数的表达式为:y=,将A(2,n)代入上式,得n=3,答:反比例函数的表达式为:y=;(2)将A、B两点坐标A(2,3)、B(﹣3,﹣2)代入直线y=kx+b方程,易求直线表达式为:y=x+1,C点坐标为(﹣1,0),答:直线表达式为:y=x+1;(3)△AOB可以看成由底均为OC的△OCA、△OCB组成,△AOB的面积=•OC•(y A﹣y B)=×1×(3+2)=2.5.答:△AOB的面积为2.5.【点评】本题考查了反比例函数与一次函数的交点,通过求坐标,确定函数表达式,体现了方程思想.20.(8分)宜宾军分区帮助群众修建水渠抗旱减灾,原计划在规定时间内修建500m,由于加大了机械化作业程度,实际每天的进度是原来的1.5倍,结果不仅超额完成计划修建米数的20%,而且还比规定时间提前了5天.(1)设原计划的每天修建xm,利用工效、工作总量、时间之间的关系填写下表.(要求:填上适当的代数式,完成表格)速度(m/天)工作总量(m)所用时间(天)原计划x500实际 1.5x500(1+20%)(2)列出方程,并求原计划每天修建水渠的长度.【分析】(1)根据题意直接得出结论;(2)根据“比规定时间提前了5天”建立方程求解即可得出结论;【解答】解:(1)设原计划的每天修建xm,∵实际每天的进度是原来的1.5倍,∴实际每天修建为1.5xm,∵不仅超额完成计划修建米数的20%,∴实际完成了500(1+20%)m,即:所用时间为,故答案为:1.5x,500(1+20%),;(2)根据题意得,﹣=5,解得,x=20,经检验,x=20符合实际,即:原计划每天修建水渠的长度为20m.【点评】此题考查了分式方程的应用,审清题意,找到相等关系是解本题的关键.21.(8分)宜宾绿源超市购进A、B两种白醋,已知每瓶B型白醋进价比A型贵0.50元,6瓶A型白醋与3瓶B型白醋进价共42元.两种白醋的销售价格如下表:品名A B售价(元) 6.58.0(1)求这两种型号的白醋每瓶的进价;(2)宜宾绿源超市打算购进这两种白醋共100瓶,进货总价不超过480元,全部售出后总利润不低于250元.设应购进A型白醋m瓶,总利润为w元.①求w与m之间的函数关系式;②求m的取值范围,并求出全部售出这批白醋后的最大利润.【分析】(1)设A型白醋的进价为x元/瓶,B型白醋的进价为y元/瓶,根据“每瓶B型白醋进价比A型贵0.50元,6瓶A型白醋与3瓶B型白醋进价共42元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;(2)①设应购进A型白醋m瓶,总利润为w元,则购进B型白醋(100﹣m)瓶,根据总利润=单瓶利润×销售数量,即可找出w与m之间的函数关系式;②根据进货总价不超过480元结合全部售出后总利润不低于250元,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,再利用一次函数的性质即可解决最值问题.【解答】解:(1)设A型白醋的进价为x元/瓶,B型白醋的进价为y元/瓶,根据题意得:,解得:.答:A型白醋的进价为4.5元/瓶,B型白醋的进价为5元/瓶.(2)①设应购进A型白醋m瓶,总利润为w元,则购进B型白醋(100﹣m)瓶,根据题意得:w=(6.5﹣4.5)m+(8﹣5)(100﹣m)=﹣m+300.②根据题意得:,解得:40≤m≤50.∵w与m之间的函数关系式为一次函数,且k=﹣1<0,∴w随m的增大而减小,∴当m=40时,w取最大值,最大值为260.综上所述,m的取值范围为40≤m≤50,全部售出这批白醋后的最大利润为260元.【点评】本题考查了二元一次方程组的应用、一元一次不等式组的应用以及一次函数的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)①根据数量关系,找出w关于m的函数关系式;②根据各数量之间的关系,正确列出一元一次不等式组,根据一次函数的性质结合m的取值范围确定w的最大值.22.(10分)如图,过矩形ABCD的四个顶点作对角线AC,BD的平行线,分别相交于E,F,G,H四点,若AB=6,BC=8.(1)求证:四边形EFGH是菱形;(2)求图中阴影部分的面积.【分析】(1)由题意易得四边形EFGH是平行四边形,又因为矩形的对角线相等,可得EH=HG,所以平行四边形EFGH是菱形.(2)根据图可知阴影部分的面积等于矩形的面积解答即可.【解答】证明:(1)由题意知,HG∥EF∥AC,EH∥FG∥BD,HG=EF=AC,EH=FG=BD,∴四边形EFGH是平行四边形,∵矩形的对角线相等,∴AC=BD,∴EH=HG,∴平行四边形EFGH是菱形.(2)由图可知,阴影部分的面积等于矩形的面积=6×8=48.【点评】本题考查了矩形的性质及菱形的判定.注意掌握菱形的判定方法有三种:①定义:一组邻边相等的平行四边形是菱形;②四边相等;③对角线互相垂直平分的四边形是菱形.23.(12分)已知直线与x轴交于点A(﹣4,0),与y轴交于点B.(1)求b的值;(2)把△AOB绕原点O顺时针旋转90°后,点A落在y轴的A′处,点B若在x轴的B′处.①求直线A′B′的函数关系式;②设直线AB与直线A′B′交于点C,矩形PQMN是△AB′C的内接矩形,其中点P,Q在线段AB′上,点M在线段B′C上,点N在线段AC上.若矩形PQMN的两条邻边的比为1:2,试求矩形PQMN的周长.【分析】(1)点A在直线上,直接代入即可得b;(2)①根据旋转性质确定旋转后A′B′坐标,即可得解析式;②根据几何图形,确定P、Q、M、N四点的关系即可确定周长.【解答】解:(1)由题意得把A(﹣4,0)代入,得;(2)①由(1)得:,令x=0,得y=2,∴B(0,2)(4分)由旋转性质可知OA'=OA=4,OB'=OB=2∴A'(0,4),B'(2,0)(5分)设直线A'B'的解析式为y=ax+b,把A'、B'分别代入得:,解得∴直线A'B'的解析式为y=﹣2x+4;(7分)②∵点N在AC上∴可设N(x,)(﹣4<x<0)∵四边形PQMN为矩形∴NP=MQ=(8分)(ⅰ)当PN:PQ=1:2时PQ=2PN=∴Q(x+4+x,0)∴M(2x+4,)∵点M在B'C上∴解得此时,PQ=∴矩形PQMN的周长为(10分)(ⅱ)当PN:PQ=2:1时PQ=PN=∴Q(,0)M(,)∵点M在B'C上∴解得x=0此时PN=2,PQ=1∴矩形PQMN的周长为2(2+1)=6.(12分)综上所述,当PN:PQ=1:2时,矩形PQMN的周长为8.当PQ:PN=1:2时,矩形PQMN的周长为6.(13分)【点评】本题考查待定系数法求一次函数及其坐标特征,并综合几何旋转性质应用,是个综合性比较高的题,要求要熟练掌握函数图象性质.。
八年级(下)学期 第二次月考数学试卷含答案

一、选择题1.如图,在平行四边形ABCD 中,30, 6, 63,BCD BC CD E ︒∠===是AD 边上的中点,F 是AB 边上的一动点,将AEF ∆沿EF 所在直线翻折得到A EF '∆,连接A C ',则A C '的最小值为( )A .319B .313C .3193-D .632.如图,已知直线l //AB ,l 与AB 之间的距离为2.C 、D 是直线l 上两个动点(点C 在D 点的左侧),且AB =CD =5.连接AC 、BC 、BD ,将△ABC 沿BC 折叠得到△A ′BC .下列说法:①四边形ABDC 的面积始终为10;②当A ′与D 重合时,四边形ABDC 是菱形;③当A ′与D 不重合时,连接A ′、D ,则∠CA ′D +∠BC A′=180°;④若以A ′、C 、B 、D 为顶点的四边形为矩形,则此矩形相邻两边之和为35或7.其中正确的是( )A .①②③④B .①③④C .①②④D .①②③3.如图,矩形ABCD 中,AB =23,BC =6,P 为矩形内一点,连接PA ,PB ,PC ,则PA +PB +PC 的最小值是( )A .43+3B .221C .23+6D .454.如图,在平行四边形ABCD 中,120C ∠=︒,4=AD ,2AB =,点E 是折线BC CD DA --上的一个动点(不与A 、B 重合).则ABE △的面积的最大值是( )A 3B .1C .32D .235.如图,矩形ABCD 的对角线AC ,BD 相交于点O ,点P 是AD 边上的一个动点,过点P分别作PE ⊥AC 于点E ,PF ⊥BD 于点F.若AB =3,BC =4,则PE +PF 的值为( )A .10B .9.6C .4.8D .2.46.如图所示,在Rt ABC ∆中,90ABC ︒∠=,30BAC ︒∠=,分别以直角边AB 、斜边AC 为边,向外作等边ABD ∆和等边ACE ∆,F 为AC 的中点,DE 与AC 交于点O ,DF 与AB 交于点G .给出如下结论:①四边形ADFE 为菱形;②DF AB ⊥;③14AO AE =;④4CE FG =;其中正确的是( )A .①②③B .①②④C .①③④D .②③④ 7. 如图,点P 是正方形ABCD 的对角线BD 上一点,PE ⊥BC 于点E ,PF ⊥CD 于点F ,连接EF 给出下列五个结论:①AP=EF ;②AP ⊥EF ;③△APD 一定是等腰三角形;④∠PFE=∠BAP ;⑤PD=2EC .其中正确结论的番号是( )A .①②④⑤B .①②③④⑤C .①②④D .①④8.如图,已知△ABC 的面积为24,点D 在线段AC 上,点F 在线段BC 的延长线上,且BF =4CF ,四边形DCFE 是平行四边形,则图中阴影部分的面积为( )A .3B .4C .6D .89.如图,在ABC 中,ACB 90∠=︒,2AC BC ==,D 是AB 的中点,点E 在AC 上,点F 在BC 上,且AE CF =,给出以下四个结论:(1)DE DF =;(2)DEF 是等腰直角三角形;(3)四边形CEDF 面积ABC 1S 2=△;(4)2EF 的最小值为2.其中正确的有( ).A .4个B .3个C .2个D .1个10.如图,△ABC 中,AB =24,BC =26,CA =14.顺次连接△ABC 各边中点,得到△A 1B 1C 1;再顺次连接△A 1B 1C 1各边中点,得到△A 2B 2C 2…如此进行下去,得到n n n A B C ,则△A 8B 8C 8的周长为( )A .1B .12C .14D .18二、填空题11.如图,动点E F 、分别在正方形ABCD 的边AD BC 、上,AE CF =,过点C 作CG EF ⊥,垂足为G ,连接BG ,若4AB =,则线段BG 长的最小值为_________.12.如图,在平行四边形ABCD 中,AD=2AB .F 是AD 的中点,作CE ⊥AB, 垂足E 在线段AB 上,连接EF 、CF ,则下列结论:(1)∠DCF+12∠D =90°;(2)∠AEF+∠ECF =90°;(3)BEC S =2CEF S ; (4)若∠B=80︒,则∠AEF=50°.其中一定成立的是______ (把所有正确结论的字号都填在横线上).13.在锐角三角形ABC 中,AH 是边BC 的高,分别以AB ,AC 为边向外作正方形ABDE 和正方形ACFG ,连接CE ,BG 和EG ,EG 与HA 的延长线交于点M ,下列结论:①BG=CE ;②BG ⊥CE ;③AM 是△AEG 的中线;④∠EAM=∠ABC .其中正确的是_________.14.在ABCD 中,5AD =,BAD ∠的平分线交CD 于点E ,∠ABC 的平分线交CD 于点F ,若线段EF=2,则AB 的长为__________.15.如图,菱形ABCD 的边长是4,60ABC ∠=︒,点E ,F 分别是AB ,BC 边上的动点(不与点A ,B ,C 重合),且BE BF =,若//EG BC ,//FG AB ,EG 与FG 相交于点G ,当ADG 为等腰三角形时,BE 的长为________.16.如图,在正方形ABCD 中,点F 为CD 上一点,BF 与AC 交于点E ,若∠CBF=20°,则∠AED 等于__度.17.已知:如图,在ABC 中,AD BC ⊥,垂足为点D ,BE AC ⊥,垂足为点E ,M 为AB 边的中点,连结ME 、MD 、ED ,设4AB =,30DAC ∠=︒则EM =______;EDM 的面积为______,18.如图,在△ABC中,AB=AC,E,F分别是BC,AC的中点,以AC为斜边作Rt△ADC,若∠CAD=∠BAC=45°,则下列结论:①CD∥EF;②EF=DF;③DE平分∠CDF;④∠DEC=30°;⑤AB=2CD;其中正确的是_____(填序号)19.如图,在□ABCD中,对角线AC、BD相交于点O,AB=OB,E为AC上一点,BE平分∠ABO,EF⊥BC于点F,∠CAD=45°,EF交BD于点P,BP=5,则BC的长为_______.20.如图所示,已知AB=6,点C,D在线段AB上,AC =DB =1,P是线段CD上的动点,分别以AP,PB为边在线段AB的同侧作等边△AEP和等边△PFB,连接EF,设EF的中点为G,当点P从点C运动到点D时,则点G移动路径的长是_________.三、解答题=,对角线AC,BD交于点O,21.如图,在四边形ABCD中,AB∥DC,AB ADAC平分BAD⊥交AB的延长线于点E,连接OE.∠,过点C作CE AB(1)求证:四边形ABCD 是菱形;(2)若5AE =,3OE =,求线段CE 的长.22.如图,四边形OABC 中,BC ∥AO ,A (4,0),B (3,4),C (0,4).点M 从O 出发以每秒2个单位长度的速度向A 运动;点N 从B 同时出发,以每秒1个单位长度的速度向C 运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N 作NP 垂直x 轴于点P ,连结AC 交NP 于Q ,连结MQ .(1)当t 为何值时,四边形BNMP 为平行四边形?(2)设四边形BNPA 的面积为y ,求y 与t 之间的函数关系式.(3)是否存在点M ,使得△AQM 为直角三角形?若存在,求出点M 的坐标;若不存在,请说明理由.23.如图,在矩形ABCD 中,E 是AD 的中点,将ABE ∆沿BE 折叠,点A 的对应点为点G .图1 图2(1)填空:如图1,当点G 恰好在BC 边上时,四边形ABGE 的形状是________; (2)如图2,当点G 在矩形ABCD 内部时,延长BG 交DC 边于点F .①求证:BF AB DF =+. ②若3AD =,试探索线段DF 与FC 的数量关系.24.如图,在边长为1的正方形ABCD 中,E 是边CD 的中点,点P 是边AD 上一点(与点A D 、不重合),射线PE 与BC 的延长线交于点Q .(1)求证:PDE QCE ∆≅∆;(2)若PB PQ =,点F 是BP 的中点,连结EF AF 、,①求证:四边形AFEP 是平行四边形;②求PE 的长.25.已知:在ABC 中,∠BAC=90°,AB=AC ,点D 为直线BC 上一动点(点D 不与B 、C 重合).以AD 为边作正方形ADEF ,连接CF .(1)如图1,当点D 在线段BC 上时,BD 与CF 的位置关系为__________;CF 、BC 、CD 三条线段之间的数量关系____________________.(2)如图2,当点D 在线段BC 的延长线上时,其它条件不变,请你写出CF 、BC 、CD 三条线段之间的数量关系并加以证明;(3)如图3,当点D 在线段BC 的反向延长线上时,且点A 、F 分别在直线BC 的两侧,其它条件不变:①请直接写出CF 、BC 、CD 三条线段之间的关系.②若连接正方形对角线AE 、DF ,交点为O ,连接OC ,探究AOC △的形状,并说明理由.26.如图,在平面直角坐标系中,已知▱OABC 的顶点A (10,0)、C (2,4),点D 是OA 的中点,点P 在BC 上由点B 向点C 运动.(1)求点B 的坐标;(2)若点P 运动速度为每秒2个单位长度,点P 运动的时间为t 秒,当四边形PCDA 是平行四边形时,求t 的值;(3)当△ODP 是等腰三角形时,直接写出点P 的坐标.27.如图平行四边形ABCD,E,F分别是AD,BC上的点,且AE=CF,EF与AC交于点O.(1)如图①.求证:OE=OF;(2)如图②,将平行四边形ABCD(纸片沿直线EF折叠,点A落在A1处,点B落在点B1处,设FB交CD于点G.A1B分别交CD,DE于点H,P.请在折叠后的图形中找一条线段,使它与EP相等,并加以证明;(3)如图③,若△ABO是等边三角形,AB=4,点F在BC边上,且BF=4.则CF OF=(直接填结果).28.如图,矩形ABCD中,AB=4,AD=3,∠A的角平分线交边CD于点E.点P从点A出发沿射线AE以每秒2个单位长度的速度运动,Q为AP的中点,过点Q作QH⊥AB于点H,在射线AE的下方作平行四边形PQHM(点M在点H的右侧),设P点运动时间为t秒.(1)直接写出AQH的面积(用含t的代数式表示).(2)当点M落在BC边上时,求t的值.(3)在运动过程中,整个图形中形成的三角形是否存在全等三角形?若存在,请写出所有全等三角形,并求出对应的t的值;若不存在请说明理由(不能添加辅助线).29.在矩形ABCD中,BE平分∠ABC交CD边于点E.点F在BC边上,且FE⊥AE.(1)如图1,①∠BEC=_________°;②在图1已有的三角形中,找到一对全等的三角形,并证明你的结论;(2)如图2,FH∥CD交AD于点H,交BE于点M.NH∥BE,NB∥HE,连接NE.若AB=4,AH=2,求NE的长.30.已知:如图,在ABC中,直线PQ垂直平分AC,与边AB交于点E,连接CE,CF BA交PQ于点F,连接AF.过点C作//(1)求证:四边形AECF是菱形;AC ,AE=5,则求菱形AECF的面积.(2)若8【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】如图,先作辅助线,首先根据垂直条件,求出线段ME、DE长度,然后运用勾股定理求出DE的长度,再根据翻折的性质,当折线'EA,'AC与线段CE重合时,线段'AC长度最短,可以求出最小值.【详解】如图,连接EC,过点E 作EM ⊥CD 交CD 的延长线于点M.四边形ABCD 是平行四边形,6AD BC AD BC ∴==,,E 为AD 的中点,30BCD ∠=︒,330DE EA MDE BCD ∴==∠=∠=︒,,又 EM CD ⊥,133322ME DE DM ∴===, 3315363CM CD DM ∴=+== 根据勾股定理得: 22223153319.22CE ME CM ⎛⎫⎛⎫=+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭根据翻折的性质,可得'3EA EA ==,当折线'EA ,'AC 与线段CE 重合时,线段'AC 长度最短,此时'AC = 3193. 【点睛】本题是平行四边形翻折问题,主要考查直角三角形勾股定理,根据题意作出辅助线是解题的关键.2.A解析:A【解析】【分析】①根据平行四边形的判定方法可得到四边形ABCD 为平行四边形,然后根据平行四边形的面积公式计算;②根据折叠的性质得到AC=CD ,然后根据菱形的判定方法可判断四边形ABDC 是菱形; ③连结A′D ,根据折叠性质和平行四边形的性质得到CA′=CA=BD ,AB=CD=A′B ,∠1=∠CBA=∠2,可证明△A′CD ≌△A′BD ,则∠3=∠4,然后利用三角形内角和定理得到得到∠1=∠4,则根据平行线的判定得到A′D ∥BC ;④讨论:当∠CBD=90°,则∠BCA=90°,由于S △A1CB =S △ABC =5,则S 矩形A′CBD =10,根据勾股定理和完全平方公式进行计算;当∠BCD=90°,则∠CBA=90°,易得BC=2,而CD=5,于是得到结论.【详解】①∵AB=CD=5,AB ∥CD ,∴四边形ABCD 为平行四边形,∴四边形ABDC 的面积=2×5=10;故①正确;②∵四边形ABDC 是平行四边形,∵A′与D 重合时,∴AC=CD ,∵四边形ABDC 是平行四边形,∴四边形ABDC 是菱形;故②正确;③连结A′D ,如图,∵△ABC 沿BC 折叠得到△A′BC ,∴CA′=CA=BD ,AB=CD=A′B ,在△A′CD 和△A′BD 中CA BD CD BA A D A D ==='⎧⎪'⎨⎪''⎩,∴△A′CD ≌△A′BD (SSS ),∴∠3=∠4,又∵∠1=∠CBA=∠2,∴∠1+∠2=∠3+∠4,∴∠1=∠4,∴A′D ∥BC ,∴∠CA′D+∠BCA′=180°;故③正确;④设矩形的边长分别为a ,b ,当∠CBD=90°,∵四边形ABDC 是平行四边形,∴∠BCA=90°,∴S △A′CB =S △ABC =12×2×5=5, ∴S 矩形A′CBD =10,即ab=10,而BA′=BA=5,∴a 2+b 2=25,∴(a+b )2=a 2+b 2+2ab=45,∴5当∠BCD=90°时,∵四边形ABDC是平行四边形,∴∠CBA=90°,∴BC=3,而CD=5,∴(a+b)2=(2+5)2=49,∴a+b=7,∴此矩形相邻两边之和为35或7.故④正确.故选A.【点睛】本题考查了四边形综合题:熟练掌握平四边形的判定与性质以及特殊平行四边形的判定与性质;会运用折叠的性质确定相等的线段和角.3.B解析:B【解析】【分析】将△BPC绕点C逆时针旋转60°,得到△EFC,连接PF、AE、AC,则AE的长即为所求.【详解】解:将△BPC绕点C逆时针旋转60°,得到△EFC,连接PF、AE、AC,则AE的长即为所求.由旋转的性质可知:△PFC是等边三角形,∴PC=PF,∵PB=EF,∴PA+PB+PC=PA+PF+EF,∴当A、P、F、E共线时,PA+PB+PC的值最小,∵四边形ABCD是矩形,∴∠ABC=90°,∴tan∠ACB=ABBC3,∴∠ACB=30°,AC=2AB=43∵∠BCE=60°,∴∠ACE=90°,∴AE=22(43)6=221.故选B.【点睛】本题考查轴对称—最短问题、矩形的性质、旋转变换等知识,解题的关键是学会添加常用辅助线,学会用转化的思想思考问题,属于中考常考题型.4.D解析:D【分析】分三种情况讨论:①当点E在BC上时,高一定,底边BE最大时面积最大;②当E在CD 上时,△ABE的面积不变;③当E在AD上时,E与D重合时,△ABE的面积最大,根据三角形的面积公式可得结论.【详解】解:分三种情况:①当点E在BC上时,E与C重合时,△ABE的面积最大,如图1,过A作AF⊥BC于F,∵四边形ABCD是平行四边形,∴AB∥CD,∴∠C+∠B=180°,∵∠C=120°,∴∠B=60°,Rt△ABF中,∠BAF=30°,∴BF=12AB=1,AF=3,∴此时△ABE的最大面积为:12×4×3=23;②当E在CD上时,如图2,此时,△ABE的面积=12S▱ABCD=12×4×3=23;③当E 在AD 上时,E 与D 重合时,△ABE 的面积最大,此时,△ABE 的面积=23, 综上,△ABE 的面积的最大值是23;故选:D .【点睛】本题考查平行四边形的性质,三角形的面积,含30°的直角三角形的性质以及勾股定理等知识,解题的关键是学会添加常用辅助线,并运用分类讨论的思想解决问题.5.D解析:D【分析】连接OP ,由矩形ABCD 的可求OA=OD=52 ,最后由S △AOD =S △AOP +S △DOP 即可解答. 【详解】解:如图:连接OP∵矩形ABCD ,AB =3,BC =4∴S 矩形ABCD =AB×BC=12, OA=OC,OB=OD,AC=BD,225AC =AB +BC = ∴S △AOD =14S 矩形ABCD =3,OA=OD=52∴S △AOD =S △AOP +S △DOP =()111532222OA PE OD PF PE PF +=⨯+= ∴PE+PF=2.4故答案为D .【点睛】本题考查了矩形的性质,正确的做出辅助线和运用数形结合思想是解答本题的关键..6.D解析:D【分析】由题意得出条件证明△ABC ≌△DAF,根据对应角相等可推出②正确;由F 是AB 中点根据边长转换可以推出④正确;先推出△ECF ≌△DFA 得出对应边相等推出ADFE 为平行四边形且有组临边不等得出①错误;再由以上全等即可得出④正确.【详解】∵△ABD 是等边三角形,∴∠BAD=60°,AB=AD ,∵∠BAC=30°,知∴∠FAD=∠ABC=90°,AC=2BC,∵F为AC的中点道,∴AC=2AF,∴BC=AF,∴△ABC≌△DAF,∴FD=AC,∴∠ADF=∠BAC=30°,∴DF⊥AB,故②正确,∵EF⊥AC,∠ACB=90°,∴FG∥BC,∵F是AB的中点,∴GF=12 BC,∵BC=12AC,AC=CE,∴GF=14CE,故④说法正确;∵AE=CE,CF=AF,∴∠EFC=90°,∠CEF=30°,∵∠FAD=∠CAB+∠BAD=90°,∴∠EFC=∠DAF,∵DF⊥AB,∴∠ADF=30°,∴∠CEF=∠ADF,∴△ECF≌△DFA(AAS),∴AD=EF,∵FD=AC,∴四边形属ADFE为平行四边形,∵AD≠DF,∴四边形ADFE不是菱形;故①说法不正确;∴AO=12 AF,∴AO=12 AC,∵AE=AC,则AE=4AO,故③说法正确,故选D.【点睛】本体主要考查平行四边形的判定,等边三角形,三角形全等的判定,关键在于熟练掌握基础知识,根据图形结合知识点进行推导.7.A解析:A【分析】过P作PG⊥AB于点G,根据正方形对角线的性质及题中的已知条件,证明△AGP≌△FPE 后即可证明①AP=EF;④∠PFE=∠BAP;在此基础上,根据正方形的对角线平分对角的性质,在Rt△DPF中,DP2=DF2+PF2=EC2+EC2=2EC2,求得⑤DP=2EC.【详解】证明:过P作PG⊥AB于点G,∵点P是正方形ABCD的对角线BD上一点,∴GP=EP,在△GPB中,∠GBP=45°,∴∠GPB=45°,∴GB=GP,同理,得PE=BE,∵AB=BC=GF,∴AG=AB-GB,FP=GF-GP=AB-GB,∴AG=PF,∴△AGP≌△FPE,①∴AP=EF;∠PFE=∠GAP∴④∠PFE=∠BAP,②延长AP到EF上于一点H,∴∠PAG=∠PFH,∵∠APG=∠FPH,∴∠PHF=∠PGA=90°,即AP⊥EF;③∵点P是正方形ABCD的对角线BD上任意一点,∠ADP=45度,∴当∠PAD=45度或67.5度或90度时,△APD是等腰三角形,除此之外,△APD不是等腰三角形,故③错误.∵GF∥BC,∴∠DPF=∠DBC,又∵∠DPF=∠DBC=45°,∴∠PDF=∠DPF=45°,∴PF=EC,∴在Rt△DPF中,DP2=DF2+PF2=EC2+EC2=2EC2,∴EC.∴其中正确结论的序号是①②④⑤.故选:A.【点睛】本题考查了正方形的性质,全等三角形的判定及性质,垂直的判定,等腰三角形的性质,勾股定理的运用.本题难度较大,综合性较强,在解答时要认真审题.8.D解析:D【分析】连接EC,过A作AM∥BC交FE的延长线于M,求出平行四边形ACFM,根据等底等高的三角形面积相等得出△BDE的面积和△CDE的面积相等,△ADE的面积和△AME的面积相等,推出阴影部分的面积等于平行四边形ACFM的面积的一半,求出CF×h CF的值即可.【详解】连接DE、EC,过A作AM∥BC交FE的延长线于M,∵四边形CDEF是平行四边形,∴DE∥CF,EF∥CD,∴AM∥DE∥CF,AC∥FM,∴四边形ACFM是平行四边形,∵△BDE边DE上的高和△CDE的边DE上的高相同,∴△BDE的面积和△CDE的面积相等,同理△ADE的面积和△AME的面积相等,即阴影部分的面积等于平行四边形ACFM的面积的一半,是12×CF×h CF,∵△ABC的面积是24,BC=3CF∴12BC×h BC=12×3CF×h CF=24,∴CF×h CF=16,∴阴影部分的面积是12×16=8,故选:D.【点睛】此题考查平行四边形的判定及性质,同底等高三角形面积的关系,解题中注意阴影部分面积的求法,根据图形的特点选择正确的求法是解题的关键.9.A解析:A【分析】根据等腰三角形的性质,可得到:CD AB ⊥,从而证明ADE ≌CDF 且ADC 90∠=︒,即证明DE DF =和DEF 是等腰直角三角形,以及四边形CEDF 面积ABC 1S 2=△;再根据勾股定理求得EF ,即可得到答案. 【详解】∵ACB 90∠=︒,2AC BC == ∴22AB 222=+=∴A B 45∠=∠=︒∵点D 是AB 的中点∴CD AB ⊥,且1AD BD CD AB 22====∴DCB 45∠=︒∴A DCF ∠∠=,在ADE 和CDF 中 AD CD A DCF AE CF =⎧⎪∠=∠⎨⎪=⎩∴ADE ≌()CDF SAS∴DE DF =,ADE CDF ∠∠=∵CD AB ⊥∴ADC 90∠=︒∴EDF EDC CDF EDC ADE ADC 90∠∠∠∠∠∠=+=+==︒∴DEF 是等腰直角三角形∵ADE ≌CDF∴ADE 和CDF 的面积相等∵D 为AB 中点∴ADC 的面积1ABC 2=的面积 ∴四边形CEDF 面积EDC CDF EDC ADE ADC ABC 1S S S S S S 2=+=+==;当DE AC ⊥,DF BC ⊥时,2EF 值最小根据勾股定理得:222EF DE DF =+此时四边形CEDF 是正方形即EF CD ==∴22EF 2==∴正确的个数是4个故选:A .【点睛】本题考察了等腰三角形、全等三角形、正方形、直角三角形、勾股定理的知识;解题的关键是熟练掌握等腰三角形、全等三角形、正方形、直角三角形的性质,从而完成求解.10.C解析:C【分析】根据三角形中位线定理求出△A 1B 1C 1的周长,根据计算总结规律,根据规律解答.【详解】根据三角形中位线定理求出△A 1B 1C 1的周长,根据计算结果总结规律,根据规律解答. 解:∵A 1、C 1分别为AB 、AC 的中点,∴A 1C 1=BC =13,同理,A 1B 1=12AC =7,B 1C 1=12AB =12, ∴△A 1B 1C 1的周长=7+12+13=32, ∴△A 1B 1C 1的周长=△ABC 的周长×12, 则△A 2B 2C 2的周长=△A 1B 1C 1的周长×12=△ABC 的周长×(12)2, …… ∴△A 8B 8C 8的周长=△ABC 的周长×(12)8=64×1256=14, 故选:C .【点睛】本题考查三角形中位线定理,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.二、填空题11.102-【分析】连结AC,取OC中点M,连结 MB,MG,则MB,MG为定长,利用两点之间线段最短解决问题即可.【详解】连接AC,交EF于O,∵AD∥BC,∴∠EAO=∠FCO,∠AEO=∠CFO,∵AE=CF,∴△AEO≌△CFO(ASA),∴OA=OC,∴O是正方形的中心,∵AB=BC=4,∴AC=2OC=2,取OC中点M,连结 MB,MG,过点M作MH⊥BC于H,∵MC=12OC2,∴MH=CH=1,∴BH=4−1=3,由勾股定理可得MB2231+10在Rt△GOC中,M是OC的中点,则MG=12OC2∵BG≥BM−MG102,当B,M,G三点共线时,BG102,102.【点睛】本题主要考查了正方形的性质,根据正方形的性质得出当E,F运动到AD,BC的中点时,MG最小是解决本题的关键.12.(1) (2) (4)【分析】由平行四边形的性质和等腰三角形的性质得出(1)正确;由ASA证明△AEF≌△DMF,得出EF=MF,∠AEF=∠M,由直角三角形斜边上的中线性质得出CF=1 2EM=EF,由等腰三角形的性质得出∠FEC=∠ECF,得出(2)正确;证出S△EFC=S△CFM,由MC>BE,得出S△BEC<2S△EFC,得出(3)错误;由平行线的性质和互余两角的关系得出(4)正确;即可得出结论.【详解】(1)∵F是AD的中点,∴AF=FD,∵在▱ABCD中,AD=2AB,∴AF=FD=CD=AB,∴∠DFC=∠DCF,∵AD∥BC,∴∠DFC=∠FCB,∠BCD+∠D=180°,∴∠DCF=∠BCF,∴∠DCF=12∠BCD,∴∠DCF+12∠D=90°,故(1)正确;(2)延长EF,交CD延长线于M,如图所示:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠A=∠MDF,∵F为AD中点,∴AF=FD,在△AEF和△DMF中,A FDMAF DFAFE DFM∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△AEF≌△DMF(ASA),∴EF=MF,∠AEF=∠M,∵CE⊥AB,∴∠AEC=90°,∴∠AEC=∠ECD=90°,∵FM=EF,∴CF=12EM=EF,∴∠FEC=∠ECF,∴∠AEF+∠ECF=∠AEF+∠FEC=∠AEC=90°,故(2)正确;(3)∵EF=FM,∴S△EFC=S△CFM,∵MC>BE,∴S△BEC<2S△EFC,故(3)错误;(4)∵∠B=80°,∴∠BCE=90°-80°=10°,∵AB∥CD,∴∠BCD=180°-80°=100°,∴∠BCF=12∠BCD=50°,∴∠FEC=∠ECF=50°-10°=40°,∴∠AEF=90°-40°=50°,故(4)正确.故答案为:(1)(2)(4).【点睛】本题主要考查了平行四边形的性质、等腰三角形的性质和判定、全等三角形的判定与性质、直角三角形斜边上的中线性质等知识;本题综合性强,有一定难度,证明△AEF≌△DMF是解题关键.13.①②③④【分析】根据正方形的性质和SAS可证明△ABG≌△AEC,然后根据全等三角形的性质即可判断①;设BG、CE相交于点N,AC、BG相交于点K,如图1,根据全等三角形对应角相等可得∠ACE=∠AGB,然后根据三角形的内角和定理可得∠CNG=∠CAG=90°,于是可判断②;过点E作EP⊥HA的延长线于P,过点G作GQ⊥AM于Q,如图2,根据余角的性质即可判断④;利用AAS即可证明△ABH≌△EAP,可得EP=AH,同理可证GQ=AH,从而得到EP =GQ,再利用AAS可证明△EPM≌△GQM,可得EM=GM,从而可判断③,于是可得答案.【详解】解:在正方形ABDE和ACFG中,AB=AE,AC=AG,∠BAE=∠CAG=90°,∴∠BAE+∠BAC=∠CAG+∠BAC,即∠CAE=∠BAG,∴△ABG≌△AEC(SAS),∴BG=CE,故①正确;设BG、CE相交于点N,AC、BG相交于点K,如图1,∵△ABG ≌△AEC ,∴∠ACE =∠AGB ,∵∠AKG =∠NKC ,∴∠CNG =∠CAG =90°,∴BG ⊥CE ,故②正确;过点E 作EP ⊥HA 的延长线于P ,过点G 作GQ ⊥AM 于Q ,如图2,∵AH ⊥BC ,∴∠ABH +∠BAH =90°,∵∠BAE =90°,∴∠EAP +∠BAH =90°,∴∠ABH =∠EAP ,即∠EAM =∠ABC ,故④正确;∵∠AHB =∠P =90°,AB =AE ,∴△ABH ≌△EAP (AAS ),∴EP =AH ,同理可得GQ =AH ,∴EP =GQ ,∵在△EPM 和△GQM 中,90P MQG EMP GMQ EP GQ ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,∴△EPM ≌△GQM (AAS ),∴EM =GM ,∴AM 是△AEG 的中线,故③正确.综上所述,①②③④结论都正确.故答案为:①②③④.【点睛】本题考查了正方形的性质、三角形的内角和定理以及全等三角形的判定和性质,作辅助线构造出全等三角形是难点,熟练掌握全等三角形的判定和性质是关键.14.8或12【分析】根据平行四边形的性质得到BC=AD=5,∠BAE=∠DEA,∠ABF=∠BFC,根据角平分线的性质得到DE=AD=5,CF=BC=5,即可求出答案.【详解】在ABCD中,AB∥CD,BC=AD=5,∴∠BAE=∠DEA,∠ABF=∠BFC,∵BAD∠的平分线交CD于点E,∴∠BAE=∠DAE,∴∠DAE=∠DEA,∴DE=AD=5,同理:CF=BC=5,∴AB=CD=DE+CF-EF=5+5-2=8或AB=DE+CF+EF=5+5+2=12,故答案为:8或12.【点睛】此题考查平行四边形的性质,角平分线的性质,等腰三角形的等角对等边的判定,解题中注意分类思想的运用,避免漏解.15.83或4433【分析】连接AC交BD于O,由菱形的性质可得AB=BC=4,∠ABD=30°,AC⊥BD,BO=DO,AO=CO,可证四边形BEGF是菱形,可得∠ABG=30°,可得点B,点G,点D三点共线,由直角三角形性质可求3AC=4,分两种情况讨论,利用等腰三角形的性质可求解.【详解】如图,连接AC交BD于O,∵菱形ABCD 的边长是4,∠ABC=60°,∴AB=BC=4,∠ABD=30°,AC ⊥BD ,BO=DO ,AO=CO ,∵EG ∥BC ,FG ∥AB ,∴四边形BEGF 是平行四边形,又∵BE=BF ,∴四边形BEGF 是菱形,∴∠ABG=30°,∴点B ,点G ,点D 三点共线,∵AC ⊥BD ,∠ABD=30°,∴AO=12AB=2,22224223AB AO --= ∴BD=3AC=4,同理可求3BE ,即3, 若AD=DG'=4时,∴BG'=BD-DG'=434,∴BE'4344343-==; 若AG''=G''D 时,过点G''作G''H ⊥AD 于H ,∴AH=HD=2,∵∠ADB=30°,G''H ⊥AD ,∴DG''=2HG'',∵222HD HG''DG''+=,解得:HG''33=,DG''=2HG''433=, ∴BG''=BD-DG''=438343-= ∴BE''=83, 综上所述:BE 为83或434- 【点睛】本题考查了菱形的性质,含30度角的直角三角形的性质,勾股定理等知识,利用分类讨论思想解决问题是本题的关键.16.65【分析】先由正方形的性质得到∠ABF 的角度,从而得到∠AEB 的大小,再证△AEB ≌△AED ,得到∠AED 的大小【详解】∵四边形ABCD 是正方形∴∠ACB=∠ACD=∠BAC=∠CAD=45°,∠ABC=90°,AB=AD∵∠FBC=20°,∴ABF=70°∴在△ABE 中,∠AEB=65°在△ABE 与△ADE 中45AB AD BAE EAD AE AE =⎧⎪∠=∠=︒⎨⎪=⎩∴△ABE≌△ADE∴∠AED=∠AEB=65°故答案为:65°【点睛】本题考查正方形的性质和三角形全等的证明,解题关键是利用正方形的性质,推导出∠AEB 的大小.17.2【分析】根据EM 是Rt ABE △斜边上的中线,利用直角三角形斜边上的中线等于斜边的一半即可求出EM 的长;根据已知条件推导出DME 是等边三角形,且边长为2,进一步计算即可得解.【详解】解:∵AD BC ⊥,M 为AB 边的中点,4AB =∴在Rt ABD △中,114222DM AM AB ===⨯= 同理,在Rt ABE △中,114222EM AM AB ===⨯= ∴MDA MAD ∠=∠,MEA MAE ∠=∠∵2BME MEA MAE MAE ∠=∠+∠=∠,2BMD MDA MAD MAD ∠=∠+∠=∠ ∴DME BME BMD ∠=∠-∠ 22MAE MAD =∠-∠()2MAE MAD =∠-∠2DAC =∠60=︒∵=DM EM∴DME 是等边三角形,且边长为2∴122EDM S =⨯=故答案是:2【点睛】本题考查了直角三角形斜边上的中线的性质、三角形的外角定理、角的和差以及等边三角形的判定和性质,熟练掌握相关知识点是进行推理论证的前提.18.①②③⑤【分析】根据三角形中位线定理得到EF =12AB ,EF ∥AB ,根据直角三角形的性质得到DF =12AC ,根据三角形内角和定理、勾股定理计算即可判断.【详解】 ∵E ,F 分别是BC ,AC 的中点,∴EF =12AB ,EF ∥AB , ∵∠ADC =90°,∠CAD =45°,∴∠ACD =45°,∴∠BAC =∠ACD ,∴AB ∥CD ,∴EF ∥CD ,故①正确;∵∠ADC =90°,F 是AC 的中点,∴DF =CF=12AC , ∵AB=AC ,EF =12AB , ∴EF =DF ,故②正确;∵∠CAD=∠ACD=45°,点F 是AC 中点,∴△ACD 是等腰直角三角形,DF ⊥AC ,∠FDC=45°,∴∠DFC=90°,∵EF//AB ,∴∠EFC=∠BAC=45°,∠FEC=∠B=67.5°,∴∠EFD=∠EFC+∠DFC=135°,∴∠FED =∠FDE =22.5°,∵∠FDC =45°,∴∠CDE=∠FDC-∠FDE=22.5°,∴∠FDE=∠CDE ,∴DE平分∠FDC,故③正确;∵AB=AC,∠CAB=45°,∴∠B=∠ACB=67.5°,∴∠DEC=∠FEC﹣∠FED=45°,故④错误;∵△ACD是等腰直角三角形,∴AC2=2CD2,∴CD,∵AB=AC,∴AB CD,故⑤正确;故答案为:①②③⑤.【点睛】本题考查的是三角形中位线定理,等腰三角形的判定与性质,直角三角形的性质,平行线的性质,勾股定理等知识.掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.19.4【分析】过点E作EM∥AD,由△ABO是等腰三角形,根据三线合一可知点E是AO的中点,可证得EM=12AD=12BC,根据已知可求得∠CEF=∠ECF=45°,从而得∠BEF=45°,△BEF为等腰直角三角形,可得BF=EF=FC=12BC,因此可证明△BFP≌△MEP(AAS),则EP=FP=12FC,在Rt△BFP中,利用勾股定理可求得x,即得答案.【详解】过点E作EM∥AD,交BD于M,设EM=x,∵AB=OB,BE平分∠ABO,∴△ABO是等腰三角形,点E是AO的中点,BE⊥AO,∠BEO=90°,∴EM是△AOD的中位线,又∵ABCD是平行四边形,∴BC=AD=2EM=2x,∵EF⊥BC,∠CAD=45°,AD∥BC,∴∠BCA=∠CAD=45°,∠EFC=90°,∴△EFC为等腰直角三角形,∴EF=FC,∠FEC=45°,∴∠BEF=90°-∠FEC=45°,则△BEF为等腰直角三角形,∴BF=EF=FC=12BC=x,∵EM∥BF,∴∠EMP=∠FBP,∠PEM=∠PFB=90°,EM=BF,则△BFP ≌△MEP (ASA ),∴EP=FP=12EF=12FC=12x , ∴在Rt △BFP 中,222BP BF PF =+,即:2221(5)()2x x =+,解得:2x =,∴BC=2x =4,故答案为:4.【点睛】考查了平行四边形的性质,等腰三角形的性质,三线合一的应用,平行线的性质,全等三角形的判定和性质,利用勾股定理求三角形边长,熟记图形的性质定理是解题的关键. 20.2【分析】分别延长AE ,BF 交于点H ,易证四边形EPFH 为平行四边形,得出点G 为PH 的中点,则G 的运动轨迹为△HCD 的中位线MN ,再求出CD 的长度,运用中位线的性质求出MN 的长度即可.【详解】解:如图,分别延长AE ,BF 交于点H ,∵∠A=∠FPB=60°,∴AH ∥PF ,∵∠B=∠EPA=60°,∴BH ∥PE∴四边形EPFH 为平行四边形,∴EF 与HP 互相平分,∵点G 为EF 的中点,∴点G 为PH 的中点,即在P 运动的过程中,G 始终为PH 的中点,∴G 的运动轨迹为△HCD 的中位线MN ,∵CD=6-1-1=4,∴MN=12CD =2,∴点G移动路径的长是2,故答案为:2.【点睛】本题考查了等边三角形及中位线的性质,以及动点的问题,是中考热点,解题的关键是得出G的运动轨迹为△HCD的中位线MN.三、解答题21.(1)见解析;(2)11【分析】(1)根据题意先证明四边形ABCD是平行四边形,再由AB=AD可得平行四边形ABCD是菱形;(2)根据菱形的性质得出OA的长,根据直角三角形斜边中线定理得出OE=12AC,在Rt ACE∆应用勾股定理即可解答.【详解】(1)证明:∵AB CD∥,∴OAB DCA∠=∠,∵AC为DAB∠的平分线,∴OAB DAC∠=∠,∴DCA DAC∠=∠,∴CD AD AB==,∵AB CD∥,∴四边形ABCD是平行四边形,∵AD AB=,∴ABCD是菱形;(2)∵四边形ABCD 是菱形∴AO CO =∵CE AB ⊥∴90AEC ∠=︒∴26AC OE ==在Rt ACE ∆中,CE故答案为(2.【点睛】本题主要考查了菱形的判定和性质,平行四边形的判定和性质,角平分线的定义,勾股定理,熟练掌握菱形的判定与性质是解题的关键.22.(1)34;(2)y =4t +2;(3)存在,点M 的坐标为(1,0)或(2,0). 【分析】(1)因为BN ∥MP ,故当BN=MP 时,四边形BNMP 为平行四边形,此时点M 在点P 的左侧,求解即可;(2)y =12(BN +PA )•OC ,即可求解; (3)①当∠MQA 为直角时,则△MAQ 为等腰直角三角形,则PA =PM ,即可求解;②当∠QMA 为直角时,则NB +OM =BC =3,即可求解.【详解】(1)∵BN ∥MP ,故当BN =MP 时,四边形BNMP 为平行四边形.此时点M 在点P 的左侧时,即0≤t <1时,MP =OP ﹣OM =3﹣t ﹣2t =3﹣3t ,BN =t ,即3﹣3t =t ,解得:t =34; (2)由题意得:由点C 的坐标知,OC =4,BN =t ,NC =PO =3﹣t ,PA =4﹣OP =4﹣(3﹣t )=t +1,则y =12(BN +PA )•OC =12(t +t +1)×4=4t +2; (3)由点A 、C 的坐标知,OA =OC =4,则△COA 为等腰直角三角形,故∠OCA =∠OAC =45°,①当∠MQA 为直角时,∵∠OAC =45°,故△MAQ 为等腰直角三角形,则PA =PM ,而PA =4﹣(3﹣t )=t +1,PM =OP ﹣OM =(3﹣t )﹣2t =3﹣3t ,故t +1=3﹣3t ,解得:t =12,则OM =2t =1, 故点M (1,0);②当∠QMA 为直角时,则点M 、P 重合,则NB +OM =BC =3,即2t +t =3,解得:t =1,故OM =OP =2t =2,故点M (2,0);综上,点M 的坐标为(1,0)或(2,0).【点睛】本题是四边形综合题,涉及坐标与图形、平行四边形的性质、等腰直角三角形的判定和性质、图形的面积计算等,复杂度较高,难度较大,其中(3)要分类求解,避免遗漏.23.(1)四边形ABGE 的形状是正方形;(2)①详见解析;②DF=3CF【分析】(1)由四边形ABCD 是矩形,可得90A ABC ︒∠=∠=,由折叠得:90BGE A ︒∠=∠=,根据三个内角是直角可判断四边形ABGE 为矩形,由折叠得:AB=BG ,根据一组邻边相等的矩形是正方形可判断矩形ABGE 为正方形;(2)①如图,连结EF ,在矩形ABCD 中,AB=DC ,AD=BC ,∠A=∠C=∠D=90°,由△ABE 沿BE 折叠后得到△GBE ,可得BG=AB ,EG=AE=ED ,∠A=∠BGE=90°,故∠EGF=∠D=90°,由HL 可判断Rt △EGF ≌Rt △EDF ,得到DF=FG ,问题得证;②设AB=DC=a ,则AD=BC=3a ,另设CF=x ,则DF=DC-CF=a-x ,由①得BF=AB+DF =2a-x ,在Rt △BCF 中,由勾股定理得:BF 2=BC 2+CF 2,代入数据运算可得:x=14a ,即CF=14a ,DF=a-x=34a ,进而可得DF 与CF 关系. 【详解】 (1)四边形ABGE 的形状是正方形.理由是:∵四边形ABCD 是矩形,∴90A ABC ︒∠=∠=,由折叠得:90BGE A ︒∠=∠=,∴四边形ABGE 为矩形,由折叠得:AB=BG ,∴矩形ABGE 为正方形;故答案为:正方形.(2)①如图,连结EF ,在矩形ABCD 中,AB=DC ,AD=BC ,∠A=∠C=∠D=90°,。
八年级第二学期第二次月考数学试卷含解析

一、选择题1.如图,正方形ABCD 的边长为定值,E 是边CD 上的动点(不与点C ,D 重合),AE 交对角线BD 于点F , FG AE ⊥交BC 于点G ,GH BD ⊥于点H ,连结AG 交BD 于点N .现给出下列命题:① AF FG =;②DF DE =;③FH 的长度为定值;④GE BG DE =+;⑤222BN DF NF +=.真命题有( )A .2个B .3个C .4个D .5个2.七巧板是一种古老的中国传统智力玩具.如图,在正方形纸板ABCD 中,BD 为对角线,E 、F 分别为BC 、CD 的中点,AP ⊥EF 分别交BD 、EF 于O 、P 两点,M 、N 分别为BO 、DO 的中点,连接MP 、NF ,沿图中实线剪开即可得到一副七巧板.若AB =1,则四边形BMPE 的面积是( )A .17B .18C .19D .1103.如图,在四边形ABCD 中,AB ∥CD ,∠BCD=90°,AB=AD=10cm ,BC=8cm ,点P 从点A 出发,以每秒3cm 的速度沿折线A-B-C-D 方向运动,点Q 从点D 出发,以每秒2cm 的速度沿线段DC 方向向点C 运动、已知动点P ,Q 同时出发,当点Q 运动到点C 时,点P ,Q 停止运动,设运动时间为t 秒,在这个运动过程中,若△BPQ 的面积为20cm 2 , 则满足条件的t 的值有( )A .1个B .2个C .3个D .4个4.将个边长都为1cm 的正方形按如图所示的方法摆放,点分别是正方形对角线的交点,则2019个正方形重叠形成的重叠部分的面积和为( )A .B .C .D .5.如图,菱形ABCD 的边长为4,∠DAB =60°,E 为BC 的中点,在对角线AC 上存在一点P ,使△PBE 的周长最小,则△PBE 的周长的最小值为 ( )A .23B .4C .232+D .423+6.如图,矩形ABCD 中,O 为AC 中点,过点O 的直线分别与AB ,CD 交于点E ,F ,连结BF ,交AC 于点M ,连结DE ,BO .若60BOC ∠=︒,FO FC =,则下列结论:①AE CF =;②BF 垂直平分线段OC ;③EOB CMB ∆∆≌;④四边形是BFDE 菱形.其中正确结论的个数是( )A .1个B .2个C .3个D .4个7.如图,在菱形ABCD 中,2AB =,,E F 分别是AB ,BC 的中点,将CDF 沿着DF 折叠得到DFC '△,若C '恰好落在EF 上,则菱形ABCD 的面积为( )A .3B 37C 36D .228.如图,正方形纸片ABCD ,P 为正方形AD 边上的一点(不与点A ,点D 重合).将正方形纸片折叠,使点B 落在点P 处,点C 落在点G 处,PG 交DC 于点H ,折痕为EF ,连接,,BP BH BH 交EF 于点M ,连接PM .下列结论:①BE PE =;②BP EF =;③PB 平分APG ∠;④PH AP HC =+;⑤MH MF =,其中正确结论的个数是( )A .5B .4C .3D .2 9.如图,正方形ABCD 的边长为10,AG=CH=8,BG=DH=6,连接GH ,则线段GH 的长为( )A .2.8B .22C .2.4D .3.510.如图,正方形ABCD 中,延长CB 至E 使2CB EB =,以EB 为边作正方形EFGB ,延长FG 交DC 于M ,连接AM ,AF ,H 为AD 的中点,连接FH 分别与AB ,AM 交于点,N K .则下列说法:①ANH GNF △≌△;②DAM NFG ∠=∠;③2FN NK =;④:2:7AFN DMKH S S =△四边形.其中正确的有( )A .4个B .3个C .2个D .1个二、填空题11.如图,菱形ABCD 的BC 边在x 轴上,顶点C 坐标为(3,0)-,顶点D 坐标为(0,4),点E 在y 轴上,线段//EF x 轴,且点F 坐标为(8,6),若菱形ABCD 沿x 轴左右运动,连接AE 、DF ,则运动过程中,四边形ADFE 周长的最小值是_______.12.如图所示,菱形ABCD ,在边AB 上有一动点E ,过菱形对角线交点O 作射线EO 与CD 边交于点F ,线段EF 的垂直平分线分别交BC 、AD 边于点G 、H ,得到四边形EGFH ,点E 在运动过程中,有如下结论:①可以得到无数个平行四边形EGFH ;②可以得到无数个矩形EGFH ;③可以得到无数个菱形EGFH ;④至少得到一个正方形EGFH .所有正确结论的序号是__.13.如图正方形 ABCD 中,E 是 BC 边的中点,将△ABE 沿 AE 对折至△AFE ,延长 EF 交 CD 于 G ,接 CF ,AG .下列结论:① AE ∥FC ; ②∠EAG = 45°,且BE + DG = EG ;③ABCD 19CEF S S ∆=正方形;④ AD = 3DG ,正确是_______ (填序号).14.如图,Rt ABE ∆中,90,B AB BE ︒∠==, 将ABE ∆绕点A 逆时针旋转45︒,得到,AHD ∆过D 作DC BE ⊥交BE 的延长线于点C ,连接BH 并延长交DC 于点F ,连接DE 交BF 于点O .下列结论:①DE 平分HDC ∠;②DO OE =; ③CD HF =; ④2BC CF CE -=; ⑤H 是BF 的中点,其中正确的是___________15.如图,在平行四边形ABCD ,AD =2AB ,F 是AD 的中点,作CE ⊥AB ,垂足E 在线段AB 上,连接EF 、CF ,则下列结论:①∠BCD =2∠DCF ;②EF =CF ;③S △CDF =S △CEF ;④∠DFE =3∠AEF ,-定成立的是_________.(把所有正确结论的序号都填在横线上)16.在ABC 中,AB=12,AC=10,BC=9,AD 是BC 边上的高.将ABC 按如图所示的方式折叠,使点A 与点D 重合,折痕为EF ,则DEF 的周长为______.17.菱形ABCD 的周长为24,∠ABC=60°,以AB 为腰在菱形外作底角为45°的等腰△ABE ,连结AC ,CE ,则△ACE 的面积为___________.18.在平面直角坐标系xOy 中,点A 、B 分别在x 轴、y 轴的正半轴上运动,点M 为线段AB 的中点.点D 、E 分别在x 轴、y 轴的负半轴上运动,且DE =AB =10.以DE 为边在第三象限内作正方形DGFE ,则线段MG 长度的最大值为_____.19.如图,长方形ABCD 中,26AD =,12AB =,点Q 是BC 的中点,点P 在AD 边上运动,当BPQ 是以QP 为腰的等腰三角形时,AP 的长为______,20.如图,在四边形ABCD 中, //,5,18,AD BC AD BC E ==是BC 的中点.点P 以每秒1个单位长度的速度从点A 出发,沿AD 向点D 运动;点Q 同时以每秒3个单位长度的速度从点C 出发,沿CB 向点B 运动.点P 停止运动时,点Q 也随之停止运动,当运动时间为t 秒时,以点,,,P Q E D 为顶点的四边形是平行四边形,则t 的值等于_______.三、解答题21.如图,在Rt ABC ∆中,090BAC ∠=,D 是BC 的中点,E 是AD 的中点,过点A 作//BC AF 交BE 的延长线于点F(1)求证:四边形ADCF 是菱形(2)若4,5AC AB ==,求菱形ADCF 的面积22.如图,在Rt ABC 中,90ACB ∠=︒,过点C 的直线//MN AB ,D 为AB 边上一点,过点D 作DE BC ⊥,交直线MN 于E ,垂足为F ,连接CD 、BE(1)当D 在AB 中点时,四边形BECD 是什么特殊四边形?说明你的理由; (2)当D 为AB 中点时,A ∠等于 度时,四边形BECD 是正方形.23.如图,在正方形ABCD 中,点G 在对角线BD 上(不与点B ,D 重合),GE ⊥DC 于点E ,GF ⊥BC 于点F ,连结AG .(1)写出线段AG ,GE ,GF 长度之间的数量关系,并说明理由;(2)若正方形ABCD 的边长为1,∠AGF=105°,求线段BG 的长.24.在数学的学习中,有很多典型的基本图形.(1)如图①,ABC 中,90BAC ∠=︒,AB AC =,直线l 经过点A ,BD ⊥直线l ,CE ⊥直线l ,垂足分别为D 、E .试说明ABD CAE ≌;(2)如图②,ABC 中,90BAC ∠=︒,AB AC =,点D 、A 、F 在同一条直线上,BD DF ⊥,3AD =,4BD =.则菱形AEFC 面积为______.(3)如图③,分别以Rt ABC 的直角边AC 、AB 向外作正方形ACDE 和正方形ABFG ,连接EG ,AH 是ABC 的高,延长HA 交EG 于点I ,若6AB =,8AC =,求AI 的长度.25.如图,在Rt ABC 中,∠B =90°,AC =60cm ,∠A =60°,点D 从点C 出发沿CA 方向以4cm/s 的速度向点A 匀速运动.同时点E 从点A 出发沿AB 方向以2cm/秒的速度向点B 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D 、E 运动的时间是ts (0<t≤15).过点D 作DF ⊥BC 于点F ,连接DE ,EF .(1)求证:AE =DF ;(2)四边形AEFD 能够成为菱形吗?如果能,求出相应的t 值,如果不能,说明理由; (3)当t 为何值时,DEF 为直角三角形?请说明理由.26.如图1,在正方形ABCD 和正方形BEFG 中,点,,A B E 在同一条直线上,P 是线段DF 的中点,连接,PG PC .(1)求证:,PG PC PG PC ⊥=.简析:由Р是线段DF 的中点,//DC CF ,不妨延长GP 交DC 于点M ,从而构造出一对全等的三角形,即_______≅________.由全等三角形的性质,易证CMG 是_______三角形,进而得出结论;(2)如图2,将原问题中的正方形ABCD 和正方形BEFG 换成菱形ABCD 和菱形BEFG ,且60ABC BEF ∠=∠=︒,探究PG 与PC 的位置关系及PG PC的值,写出你的猜想并加以证明;(3)当6,2AB BE ==时,菱形ABCD 和菱形BEFG 的顶点都按逆时针排列,且60ABC BEF ∠=∠=︒.若点A B E 、、在一条直线上,如图2,则CP =________;若点A B G 、、在一条直线上,如图3,则CP =________.27.如图,在Rt ABC ∆中,90,40,60B AC cm A ∠=︒=∠=︒,点D 从点C 出发沿CA 方向以4/cm 秒的速度向点A 匀速运动,同时点E 从点A 出发沿AB 方向以2/cm 秒的速度向点B 匀速运动,当其中一个点到达终点时,另一个地点也随之停止运动.设点,D E 运动的时间是t 秒(010t <≤).过点D 作DF BC ⊥于点F ,连接,DE EF .(1)试问四边形AEFD 能够成为菱形吗?如果能,求出相应的t 值;如果不能,请说明理由;(2)当t 为何值时,90FDE ∠=︒?请说明理由.28.如图,锐角ABC ∆,AB AC =,点D 是边BC 上的一点,以AD 为边作ADE ∆,使AE AD =,EAD BAC ∠=∠.(1)过点E 作//EF DC 交AB 于点F ,连接CF (如图①)①请直接写出EAB ∠与DAC ∠的数量关系;②试判断四边形CDEF 的形状,并证明;(2)若60BAC ∠=,过点C 作//CF DE 交AB 于点F ,连接EF (如图②),那么(1)②中的结论是否任然成立?若成立,请给出证明,若不成立,请说明理由.29.已知:在矩形ABCD 中,点F 为AD 中点,点E 为AB 边上一点,连接CE 、EF 、CF ,EF 平分∠AEC .(1)如图1,求证:CF ⊥EF;(2)如图2,延长CE 、DA 交于点K, 过点F 作FG ∥AB 交CE 于点G 若,点H 为FG 上一点,连接CH,若∠CHG=∠BCE, 求证:CH=FK;(3)如图3, 过点H 作HN ⊥CH 交AB 于点N,若EN=11,FH-GH=1,求GK 长.30.如图,在矩形ABCD 中,AB a ,BC b =,点F 在DC 的延长线上,点E 在AD 上,且有12CBE ABF ∠=∠.(1)如图1,当a b =时,若60CBE ∠=︒,求证:BE BF =;(2)如图2,当32b a =时, ①请直接写出ABE ∠与BFC ∠的数量关系:_________; ②当点E 是AD 中点时,求证:2CF BF a +=;③在②的条件下,请直接写出:BCF ABCD S S ∆矩形的值.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】根据题意,连接CF ,由正方形的性质,可以得到△ABF ≌△CBF ,则AF=CF ,∠BAF=∠BCF ,由∠BAF=∠FGC=∠BCF ,得到AF=CF=FG ,故①正确;连接AC ,与BD 相交于点O ,由正方形性质和等腰直角三角形性质,证明△AOF ≌△FHG ,即可得到EH=AO ,则③正确;把△ADE 顺时针旋转90°,得到△ABM ,则证明△MAG ≌△EAG ,得到MG=EG ,即可得到EG=DE+BG ,故④正确;②无法证明成立,即可得到答案.【详解】解:连接CF ,在正方形ABCD 中,AB=BC ,∠ABF=∠CBF=45°,在△ABF 和△CBF 中,45AB BC ABF CBF BF BF =⎧⎪∠=∠=︒⎨⎪=⎩, ∴△ABF ≌△CBF (SAS ), ∴AF=CF ,∠BAF=∠BCF , ∵FG ⊥AE ,∴在四边形ABGF 中,∠BAF+∠BGF=360°-90°-90°=180°, 又∵∠BGF+∠CGF=180°, ∴∠BAF=∠CGF , ∴∠CGF=∠BCF ∴CF=FG , ∴AF=FG ;①正确; 连接AC 交BD 于O .∵四边形ABCD 是正方形,HG ⊥BD , ∴∠AOF=∠FHG=90°,∵∠OAF+∠AFO=90°,∠GFH+∠AFO=90°, ∴∠OAF=∠GFH , ∵FA=FG , ∴△AOF ≌△FHG , ∴FH=OA=定值,③正确;如图,把△ADE 顺时针旋转90°,得到△ABM ,∴AM=AE ,BM=DE ,∠BAM=∠DAE ,∵AF=FG ,AF ⊥FG , ∴△AFG 是等腰直角三角形, ∴∠FAG=45°,∴∠MAG=∠BAG+∠DAE=45°, ∴∠MAG=∠FAG , 在△AMG 和△AEG 中,45AM AE EAG MAG AG AG =⎧⎪∠=∠=︒⎨⎪=⎩, ∴△AMG ≌△AEG , ∴MG=EG ,∵MG=MB+BG=DE+BG , ∴GE= DE+BG ,故④正确;如图,△ADE 顺时针旋转90°,得到△ABM ,记F 的对应点为P ,连接BP 、PN , 则有BP=DF ,∠ABP=∠ADB=45°, ∵∠ABD=45°, ∴∠PBN=90°, ∴BP 2+BN 2=PN 2,由上可知△AFG 是等腰直角三角形,∠FAG=45°, ∴∠MAG=∠BAG+∠DAE=45°, ∴∠MAG=∠FAG , 在△ANP 和△ANF 中,45AP AF EAG MAG AN AN =⎧⎪∠=∠=︒⎨⎪=⎩, ∴△ANP ≌△ANF , ∴PN=NF , ∴BP 2+BN 2=NF 2, 即DF 2+BN 2=NF 2, 故⑤正确;根据题意,无法证明②正确, ∴真命题有四个, 故选C. 【点睛】本题考查了正方形的性质,全等三角形的判定与性质等知识,解题的关键是作辅助线构造出等腰三角形和全等三角形.2.B解析:B 【分析】根据三角形的中位线的性质得到EF ∥BD ,EF=12BD ,推出点P 在AC 上,得到PE=12EF ,得到四边形BMPE 平行四边形,过M 作MF ⊥BC 于F ,根据平行四边形的面积公式即可得到结论. 【详解】∵E ,F 分别为BC ,CD 的中点, ∴EF ∥BD ,EF=12BD , ∵四边形ABCD 是正方形,且AB=BC=1,∴, ∵AP ⊥EF , ∴AP ⊥BD , ∴BO=OD , ∴点P 在AC 上, ∴PE=12EF , ∴PE=BM ,∴四边形BMPE 是平行四边形, ∴BO=12BD , ∵M 为BO 的中点,∴BM=14, ∵E 为BC 的中点, ∴BE=12BC=12, 过M 作MF ⊥BC 于F ,∴MF=22BM=14,∴四边形BMPE 的面积=BE•MF=18, 故选B . 【点睛】本题考查了七巧板,正方形的性质,平行四边形的判定和性质,三角形的中位线的性质,正确的识别图形是解题的关键.3.B解析:B 【解析】 【分析】过A 作AH ⊥DC ,由勾股定理求出DH 的长.然后分三种情况进行讨论:即①当点P 在线段AB 上,②当点P 在线段BC 上,③当点P 在线段CD 上,根据三种情况点的位置,可以确定t 的值. 【详解】解:过A 作AH ⊥DC ,∴AH =BC =8cm ,DH =22AD AH - =10064-=6.i )当P 在AB 上时,即1003t ≤≤时,如图,1110382022BPQS BP BC t =⋅=-⨯=(),解得:53t =;ii )当P 在BC 上时,即103<t ≤6时,BP =3t -10,CQ =16-2t ,113101622022BPQSBP CQ t t =⋅=-⨯-=()(),化简得:3t 2-34t +100=0,△=-44<0,∴方程无实数解.iii)当P在线段CD上时,若点P在线段CD上,若点P在Q的右侧,即6≤t≤345,则有PQ=34-5t,13458202BPQS t=-⨯=(),295t=<6(舍去);若点P在Q的左侧时,即3485t≤<,则有PQ=5t-34,15348202BPQS t=-⨯=();t=7.8.综上所述:满足条件的t存在,其值分别为15 3t=,t2=7.8.故选B.【点睛】本题是平行四边形中的动点问题,解决问题时,一定要变动为静,将其转化为常见的几何问题,再进行解答.4.B解析:B【解析】【分析】根据题意可得,阴影部分的面积是正方形的面积的,已知两个正方形可得到一个阴影部分,则n个这样的正方形重叠部分即为n-1阴影部分的和.由此即可解答.【详解】由题意可得一个阴影部分面积等于正方形面积的,即一个阴影部分的面积为如图,5个这样的正方形重叠部分(阴影部分)的面积和为×4,∴n个这样的正方形重叠部分(阴影部分)的面积和为×(n-1),∴2019个正方形重叠形成的重叠部分的面积和为×(2019-1)=.故选B.【点睛】本题考查了正方形的性质,解决本题的关键是得到n个这样的正方形重叠部分(阴影部分)的面积和的计算方法,难点是求得一个阴影部分的面积.5.C解析:C 【分析】如下图,△BEP 的周长=BE+BP+EP ,其中BE 是定值,只需要BP+PE 为最小值即可,过点E 作AC 的对称点F ,连接FB ,则FB 就是BP+PE 的最小值. 【详解】如下图,过点E 作AC 的对称点F ,连接FB ,FE ,过点B 作FE 的垂线,交FE 的延长线于点G∵菱形ABCD 的边长为4,点E 是BC 的中点 ∴BE=2∵∠DAB=60°,∴∠FCE=60° ∵点F 是点E 关于AC 的对称点∴根据菱形的对称性可知,点F 在DC 的中点上 则CF=CE=2∴△CFE 是等边三角形,∴∠FEC=60°,EF=2 ∴∠BEG=60°∴在Rt △BEG 中,EG=1,3 ∴FG=1+2=3∴在Rt △BFG 中,()2233+3根据分析可知,BF=PB+PE ∴△PBE 的周长32 故选:C 【点睛】本题考查菱形的性质和利用对称性求最值问题,解题关键是利用对称性,将BP+PE 的长转化为FB 的长.6.C解析:C 【分析】通过证△AEO ≌CFO 可判断①;利用矩形的性质证△OCB 是正三角形,可得②;因OB≠MB ,得到③错误;通过证△EOB ≌△FCB 得到EB=FB ,从而证④. 【详解】∵四边形ABCD 是矩形 ∴AB ∥DC,AO=OC∴∠AEO=∠CFO,∠EAO=∠FCO ∴△AEO ≌CFO(AAS) ∴AE=FC ,①正确 ∵四边形ABCD 是矩形 ∴OC=OB ∵∠BOC=60°∴△OCB 是正三角形,∴OB=OC ∵FO=FC∴FB 是线段OC 的垂直平分线,②正确 ∵BM ⊥OC ,∴△OMB 是直角三角形,∴OB >BM ∴EOB CMB ∆∆≌是错误的,即③错误 ∵四边形ABCD 是矩形 ∴EB ∥DF ,AB=DC ∵AE=FC ∴EB=DF∴四边形EBFD 是平行四边形∵△AEO ≌△CFO ,OF=FC ,∴AE=EO=OF=FC ∵△OBC 是正三角形,∴∠BOC=60°=∠BCO ,BC=BO ∴∠FCO=30°,∴∠FOC=30° ∴∠FOB=30°+60°=90° ∴∠EOB=90°=∠FCB ∴△EOB ≌△FCB(SAS) ∴EB=FB∴平行四边形EBFD 是菱形,④正确 故选:C 【点睛】本题考查矩形的性质和证明,解题关键是证明△AOE ≌△COF 和证明△BOC 是正三角形.7.B解析:B 【分析】连接AC 、BD ,设交于点O ,延长DA 、FE ,设交于点G ,如图所示,先根据菱形的性质和平行线的性质得出∠G =∠BFE ,∠GAB =∠ABF ,进而可根据AAS 证明△AEG ≌△BEF ,可得GE=EF ,AG=BF ,由此可求出DG 的长,然后根据折叠的性质和平行线的性质可得∠ADF =∠DFE ,于是可得GF=GD ,则GF 可得,再根据三角形的中位线定理和等量代换可得AC 的长,进而可得AO 的长,然后根据勾股定理可求出DO 的长,即得BD 的长,再根据菱形的面积求解即可.【详解】解:连接AC、BD,设交于点O,延长DA、FE,设交于点G,如图所示,∵四边形ABCD是菱形,∴AD∥BC,AC⊥BD,BO=DO,AO=CO,∴∠G=∠BFE,∠GAB=∠ABF,∵,E F分别是AB,BC的中点,菱形的边长为2,∴AE=BE,BF=CF=1,12EF AC=,∴△AEG≌△BEF(AAS),∴GE=EF,AG=BF=1,∵AD=2,∴DG=3,∵将CDF沿着DF折叠得到DFC'△,若C'恰好落在EF上,∴∠CFD=∠DFE,∵AD∥BC,∴∠ADF=∠DFC,∴∠ADF=∠DFE,∴GF=GD=3,∵12EF AC=,12EF GF=,∴AC=FG=3,∴AO=13 22 AC=,在Rt△AOD中,由勾股定理得:22223722DO AD AO⎛⎫=-=-=⎪⎝⎭,∴BD=7,∴菱形ABCD的面积=11373722AC BD⋅=⨯⨯=.故选:B.【点睛】本题考查了菱形的性质、折叠的性质、全等三角形的判定和性质、菱形的面积、三角形的中位线定理以及勾股定理等知识,属于常考题型,具有一定的难度,正确作出辅助线、熟练掌握上述知识是解题的关键.8.B解析:B【分析】①③利用正方形的性质、翻折不变性即可解决问题;②构造全等三角形即可解决问题;④如图2,过B作BQ⊥PH,垂足为Q.证明△ABP≌△QBP(AAS),以及△BCH≌△BQH 即可判断;⑤利用特殊位置,判定结论即可;【详解】解:根据翻折不变性可知:PE=BE,故①正确;∴∠EBP=∠EPB.又∵∠EPH=∠EBC=90°,∴∠EPH−∠EPB=∠EBC−∠EBP.即∠PBC=∠BPH.又∵AD∥BC,∴∠APB=∠PBC.,故③正确;∴∠APB=∠BPH,即PB平分APG如图1中,作FK⊥AB于K.设EF交BP于O.∵∠FKB=∠KBC=∠C=90°,∴四边形BCFK是矩形,∴KF=BC=AB,∵EF⊥PB,∴∠BOE=90°,∵∠ABP+∠BEO=90°,∠BEO+∠EFK=90°,∴∠ABP=∠EFK,∵∠A=∠EKF=90°,∴△ABP≌△KFE(ASA),∴EF=BP,故②正确,如图2,过B作BQ⊥PH,垂足为Q.由(1)知∠APB=∠BPH,在△ABP和△QBP中,∠APB=∠BPH,∠A=∠BQP,BP=BP,∴△ABP≌△QBP(AAS).∴AP=QP,AB=BQ.又∵AB=BC,∴BC=BQ.又∵∠C=∠BQH=90°,BH=BH,∴△BCH≌△BQH(HL)∴QH=HC,∴PH=PQ+QH=AP+HC,故④正确;当点P与A重合时,显然MH>MF,故⑤错误,故选:B.【点睛】本题考查正方形的性质、翻折变换、全等三角形的判定和性质、等腰直角三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题属于中考选择题中的压轴题.9.B解析:B【分析】延长BG交CH于点E,根据正方形的性质证明△ABG≌△CDH≌△BCE,可得GE=BE-BG=2,HE=CH-CE=2,∠HEG=90°,从而由勾股定理可得GH的长.【详解】解:如图,延长BG交CH于点E,∵四边形ABCD是正方形,∴∠ABC=90°,AB=CD=10,∵AG=8,BG=6,∴AG2+BG2=AB2,∴∠AGB=90°,∴∠1+∠2=90°,又∵∠2+∠3=90°,∴∠1=∠3,同理:∠4=∠6,在△ABG和△CDH中,AB=CD=10AG=CH=8BG=DH=6∴△ABG≌△CDH(SSS),∴∠1=∠5,∠2=∠6,∴∠2=∠4,在△ABG和△BCE中,∵∠1=∠3,AB=BC,∠2=∠4,∴△ABG≌△BCE(ASA),∴BE=AG=8,CE=BG=6,∠BEC=∠AGB=90°,∴GE=BE-BG=8-6=2,同理可得HE=2,在Rt△GHE中,2222=+=+=GH GE HE2222故选:B.本题主要考查正方形的性质、全等三角形的判定与性质、勾股定理及其逆定理的综合运用,通过证三角形全等得出△GHE 为直角三角形且能够求出两条直角边的长是解题的关键.10.A解析:A【分析】根据正方形的性质,以及中点的性质可得△FGN ≌△HAN ,即证①;利用角度之间的等量关系的转换可以判断②;根据△AKH ∽△MKF ,进而利用相似三角形的性质即可判断③;设AN=12AG=x ,则AH=2x ,FM=6x ,根据△AKH ∽△MKF 得出2163AH x MF x ==,再利用三角形的面积公式求出△AFN 的面积,再利用DHKM ADM AKH S SS =-即可求出四边形DHKM的面积,作比即可判断④.【详解】 ∵四边形EFGB 是正方形,CE=2EB ,四边形ABCD 是正方形∴G 为AB 中点,∠FGN=∠HAN=90°,AD=AB即FG=AG=GB=12AB 又H 是AD 的中点 AH=12AD ∴FG=HA又∠FNG=∠HNA∴△FGN ≌△HAN ,故①正确;∵∠DAM+∠GAM=90°又∠NFG+∠FNG=90°即∠FNG=∠GAM∵∠FNG+∠NFG+90°=180°∠AMD+∠DAM+90°=180°∠FNG=∠GAM=∠AMD∴DAM NFG ∠=∠,故②正确;由图可得:MF=FG+MG=3EB△AKH ∽△MKF ∴13KH AH KF MF == ∴KF=3KH又∵NH=NF 且FH=KF+KH=4KH=NH+NF∴NH=NF=2KH∴FN=2NK ,故③正确;∵AN=GN 且AN+GN=AG∴可设AN=12AG=x ,则AH=2x ,FM=6x 由题意可得:△AKH ∽△MKF 且相似比为:2163AH x MF x == ∴△AKH 以AH 为底边的高为:11242x x ⨯= ∴212AFN S AN FG x =⨯⨯= 112225DHKM ADM AKH S S S AD DM AH x =-=⨯⨯-⨯⨯ 211172422222x x x x x =⨯⨯-⨯⨯= ∴2:7AFN DHKM S S =,故④正确; 故答案选择A .【点睛】本题考查了矩形、全等三角形的判定与性质以及相似三角形的判定与性质,难度较大,需要熟练掌握相关基础知识.二、填空题11.18【分析】由题意可知AD 、EF 是定值,要使四边形ADFE 周长的最小,AE +DF 的和应是最小的,运用“将军饮马”模型作点E 关于AD 的对称点E 1,同时作DF ∥AF 1,此时AE +DF 的和即为E 1F 1,再求四边形ADFE 周长的最小值.【详解】在Rt △COD 中,OC =3,OD =4,CD ,∵ABCD 是菱形,∴AD =CD =5,∵F 坐标为(8,6),点E 在y 轴上,∴EF =8,作点E 关于AD 的对称点E 1,同时作DF ∥AF 1,则E 1(0,2),F 1(3,6),则E 1F 1即为所求线段和的最小值,在Rt △AE 1F 1中,E 1F 1=22211EE +EF =-+(8-5)=52(62), ∴四边形ADFE 周长的最小值=AD +EF +AE +DF = AD +EF + E 1F 1=5+8+5=18.【点睛】本题考查菱形的性质、“将军饮马”作对称点求线段和的最小值,比较综合,难度较大.12.①③④【分析】由“AAS ”可证△AOE ≌△COF ,△AHO ≌△CGO ,可得OE =OF ,HO =GO ,可证四边形EGFH 是平行四边形,由EF ⊥GH ,可得四边形EGFH 是菱形,可判断①③正确,若四边形ABCD 是正方形,由“ASA ”可证△BOG ≌△COF ,可得OG =OF ,可证四边形EGFH 是正方形,可判断④正确,即可求解.【详解】解:如图,∵四边形ABCD 是菱形,∴AO =CO ,AD ∥BC ,AB ∥CD ,∴∠BAO =∠DCO ,∠AEO =∠CFO ,∴△AOE ≌△COF (AAS ),∴OE =OF ,∵线段EF 的垂直平分线分别交BC 、AD 边于点G 、H ,∴GH 过点O ,GH ⊥EF ,∵AD∥BC,∴∠DAO=∠BCO,∠AHO=∠CGO,∴△AHO≌△CGO(AAS),∴HO=GO,∴四边形EGFH是平行四边形,∵EF⊥GH,∴四边形EGFH是菱形,∵点E是AB上的一个动点,∴随着点E的移动可以得到无数个平行四边形EGFH,随着点E的移动可以得到无数个菱形EGFH,故①③正确;若四边形ABCD是正方形,∴∠BOC=90°,∠GBO=∠FCO=45°,OB=OC;∵EF⊥GH,∴∠GOF=90°;∠BOG+∠BOF=∠COF+∠BOF=90°,∴∠BOG=∠COF;在△BOG和△COF中,∵BOG COF BO COGBO FCO ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△BOG≌△COF(ASA);∴OG=OF,同理可得:EO=OH,∴GH=EF;∴四边形EGFH是正方形,∵点E是AB上的一个动点,∴至少得到一个正方形EGFH,故④正确,故答案为:①③④.【点睛】本题考查了菱形的判定和性质,平行四边形的判定,正方形的判定,全等三角形的判定和性质等知识,灵活运用这些性质进行推理是关键.13.①②④【分析】①根据折叠得△ABE ≌△AFE ,证明△EFC 是等腰三角形,得到∠EFC=∠ECF ,根据∠BEF=∠EFC+∠FEC ,得出∠BEA=∠AEF=∠EFC=∠ECF ,即可证明AE ∥FC ,故①正确;②根据四边形ABCD 是正方形,且△ABE ≌△AFE ,证明Rt △AFG ≌Rt △ADG ,得出∠FAG=∠GAD ,根据∠BAF+∠FAD=90°,推出∠EAF+∠FAG=45°,可得∠EAG=45°,根据全等得:BE=FE ,DG=FG ,即可得BE+DG=EF+GF=EG ,故②正确;③先求出S △ECG ,根据EF :FG=2a :3a =3:2,得出S △EFC :S △FCG =3:2,即S △EFC =2110a ,再根据S ABCD =a 2,得出S △CEF :S △ABCD =2110a :2a ,即S △CEF =110S ABCD ,故③错误;④设正方形的边长为a ,根据勾股定理得2a ,设DG=x ,则CG=a-x ,FG=x ,EG=2a +x ,再根据勾股定理求出x ,即可得出结论,故④正确.【详解】解:①由折叠可得△ABE ≌△AFE ,∴∠BEA=∠AEF ,BE=EF ,∵E 是BC 中点,∴BE=CE=EF ,∴△EFC 是等腰三角形,∴∠EFC=∠ECF ,∵∠BEF=∠EFC+∠FEC ,∴∠BEA=∠AEF=∠EFC=∠ECF ,∴AE ∥FC ,故①正确;②∵四边形ABCD 是正方形,且△ABE ≌△AFE ,∴AB=AF=AD ,∠B=∠D=∠AFG ,∴△AFG 和△ADG 是直角三角形,∴在Rt △AFG 和Rt △ADG 中AF AD AG AG ==⎧⎨⎩, ∴Rt △AFG ≌Rt △ADG (HL ),∴∠FAG=∠GAD ,又∵∠BAF+∠FAD=90°,∴2∠EAF+2∠FAG=90°,即∠EAF+∠FAG=45°,∴∠EAG=45°,由全等得:BE=FE ,DG=FG ,∴BE+DG=EF+GF=EG ,故②正确;③对于Rt △ECG ,S △ECG =12×EC ×CG=12×2a ×23a =216a , ∵EF :FG=2a :3a =3:2, 则S △EFC :S △FCG =3:2,即S △EFC =2110a , 又∵S ABCD =a 2,则S △CEF :S △ABCD =2110a :2a ,即S △CEF =110S ABCD ,故③错误; ④设正方形的边长为a , ∴AB=AD=AF=a ,BE=EF=2a =EC ,由勾股定理得, 设DG=x ,则CG=a-x ,FG=x , EG=2a +x , ∴EG 2=EC 2+CG 2,即(2a +x )2=(2a )2+(a-x )2, 解得x=3a ,CG=23a , 即AD=3DG 成立,故④正确.【点睛】本题考查了正方形的折叠问题,等腰三角形的判定和性质,平行线的判定,全等三角形的判定和性质,勾股定理,掌握这些知识点灵活运用是解题关键.14.①②④⑤【分析】根据∠B=90°,AB=BE ,△ABE 绕点A 逆时针旋转45°,得到△AHD ,可得△ABE ≅△AHD ,并且△ABE 和△AHD 都是等腰直角三角形,可证AD//BC ,根据DC ⊥BC ,可得∠HDE=∠CDE ,根据三角形的内角和可得∠HDE=∠CDE ,即DE 平分∠HDC ,所以①正确;利用∠DAB=∠ABC=∠BCD=90°,得到四边形ABCD 是矩形,有∠ADC=90°,∠HDC=45°,由①有DE 平分∠HDC ,得∠HDO=22.5°,可得∠AHB=67.5°,∠DHO=22.5°,可证OD=OH ,利用 AE=AD 易证∠OHE=∠HEO=67.5°,则有OE=OH ,OD=OE ,所以②正确;利用AAS 证明ΔDHE ≅ΔDCE ,则有DH=DC ,∠HDE=∠CDE=22.5°,易的∠DHF=22.5°,∠DFH=112.5°,则△DHF 不是直角三角形,并DH≠HF ,即有:CD≠HF ,所以③错误;根据△ABE 是等腰直角三角形,JH ⊥JE ,∵J 是BC 的中点,H 是BF 的中点,得到2JH=CF ,2JC=BC ,JC=JE+CE ,易证BC−CF=2CE ,所以④正确;过H 作HJ ⊥BC 于J ,并延长HJ 交AD 于点I ,得IJ ⊥AD ,I 是AD 的中点,J 是BC 的中点,H 是BF 的中点,所以⑤正确;【详解】∵Rt △ABE 中,∠B=90°,AB=BE ,∴∠BAE=∠BEA=45°,又∵将△ABE 绕点A 逆时针旋转45°,得到△AHD ,∴△ABE ≅△AHD ,并且△ABE 和△AHD 都是等腰直角三角形,∴∠EAD=45°,AE=AD ,∠AHD=90°,∴∠ADE=∠AED ,∴∠BAD=∠BAE+∠EAD=45°+45°=90°,∴AD//BC ,∴∠ADE=∠DEC ,∴∠AED=∠DEC ,又∵DC ⊥BC ,∴∠DCE=∠DHE=90°∴由三角形的内角和可得∠HDE=∠CDE ,即:DE 平分∠HDC ,所以①正确;∵∠DAB=∠ABC=∠BCD=90°,∴四边形ABCD 是矩形,∴∠ADC=90°,∴∠HDC=45°,由①有DE 平分∠HDC ,∴∠HDO=12∠HDC=12×45°=22.5°, ∵∠BAE=45°,AB=AH , ∴∠OHE=∠AHB=12 (180°−∠BAE)= 12×(180°−45°)=67.5°, ∴∠DHO=∠DHE−∠FHE=∠DHE−∠AHB=90°−67.5°=22.5°,∴OD=OH ,在△AED 中,AE=AD ,∴∠AED=12(180°−∠EAD)=12×(180°−45°)=67.5°, ∴∠OHE=∠HEO=67.5°,∴OE=OH ,∴OD=OE ,所以②正确;在△DHE 和△DCE 中,DHE DCE HDE CDE DE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴ΔDHE ≅ΔDCE(AAS),∴DH=DC ,∠HDE=∠CDE=12×45°=22.5°, ∵OD=OH ,∴∠DHF=22.5°, ∴∠DFH=180°−∠HDF−∠DHF=180°−45°−22.5°=112.5°,∴△DHF 不是直角三角形,并DH≠HF ,即有:CD≠HF ,所以③不正确;如图,过H 作HJ ⊥BC 于J ,并延长HJ 交AD 于点I ,∵△ABE 是等腰直角三角形,JH ⊥JE ,∴JH=JE ,又∵J 是BC 的中点,H 是BF 的中点,∴2JH=CF ,2JC=BC ,JC=JE+CE ,∴2JC=2JE+2CE=2JH+2CE=CF+2CE=BC ,即有:BC−C F=2CE ,所以④正确;∵AD//BC ,∴IJ ⊥AD ,又∵△AHD 是等腰直角三角形,∴I 是AD 的中点,∵四边形ABCD 是矩形,HJ ⊥BC ,∴J 是BC 的中点,∴H 是BF 的中点,所以⑤正确;综上所述,正确的有①②④⑤,故答案为:①②④⑤.【点睛】本题考查了全等三角形的判定与性质、旋转的性质、矩形的性质、角平分线的性质以及等腰直角三角形的判定与性质;证明三角形全等和等腰直角三角形是解决问题的关键.15.①②④【分析】①根据平行四边形的性质和等腰三角形的性质即可判断;②延长EF ,交CD 延长线于点M ,首先根据平行四边形的性质证明AEFDFM ≅△△,得出,FE MF AEF M =∠=∠,进而得出90ECD AEC ∠=∠=︒,从而利用直角三角形斜边中线的性质即可判断;③由FE MF =,得出EFC CFM SS =,从而可判断正误; ④设FEC x ∠= ,利用三角形内角和定理分别表示出∠DFE 和∠AEF ,从而判断正误. 【详解】①∵点F 是AD 的中点,∴AF FD = .∵在平行四边形ABCD 中,AD =2AB , //,AD BC AF FD CD ∴==,,DFC FCB DFC DCF ∴∠=∠∠=∠ , FCB DCF ∴∠=∠,∴∠BCD =2∠DCF ,故①正确; ②延长EF ,交CD 延长线于点M ,∵四边形ABCD 是平行四边形, //AB CD ∴,A MDF ∴∠=∠,∵点F 是AD 的中点,∴AF FD = .在AEF 和DFM 中,A FDM AF DFAFE DFM ∠=∠⎧⎪=⎨⎪∠=∠⎩()AEF DFM ASA ∴≅△△ ,FE MF AEF M ∴=∠=∠. CE AB ⊥ ,90AEC ∴∠=︒,90ECD AEC ∴∠=∠=︒,12CF EM EF ∴==,故②正确; ③∵FE MF =,∴EFC CFM S S = .CFM CDF MDF S S S =+△△△CDF EFC S S ∴<△△,故③错误;④设FEC x ∠= ,则FCE x ∠=,90DCF DFC x ∴∠=∠=︒- ,1802EFC x ∴∠=︒-,9018022703EFD x x x ∴∠=︒-+︒-=︒- .90AEF x ∠=︒- ,3DFE AEF ∴∠=∠,故④正确;综上所述,正确的有①②④,故答案为 :①②④.【点睛】本题主要考查平行四边形的性质,全等三角形的判定及性质,三角形内角和定理,掌握这些性质和定理是解题的关键.16.15.5【分析】先根据折叠的性质可得,AE DE EAD EDA =∠=∠,再根据垂直的定义、直角三角形的性质可得B BDE ∠=∠,又根据等腰三角形的性质可得BE DE =,从而可得6DE AE BE ===,同理可得出5DF AF CF ===,然后根据三角形中位线定理可得1 4.52EF BC ==,最后根据三角形的周长公式即可得. 【详解】由折叠的性质得:,AE DE EAD EDA =∠=∠AD 是BC 边上的高,即AD BC ⊥90B EAD ∴∠+∠=︒,90BDE EDA ∠+∠=︒B BDE ∴∠=∠BE DE ∴=1112622DE AE BE AB ∴====⨯= 同理可得:1110522DF AF CF AC ====⨯= 又,AE BE AF CF ==∴点E 是AB 的中点,点F 是AC 的中点EF ∴是ABC 的中位线119 4.522EF BC ∴==⨯= 则DEF 的周长为65 4.515.5DE DF EF ++=++=故答案为:15.5.【点睛】本题考查了折叠的性质、等腰三角形的性质、三角形中位线定理、直角三角形的性质等知识点,利用折叠的性质和等腰三角形的性质得出BE DE =是解题关键.17.9或9(31)+.【分析】分两种情况画图,利用等腰直角三角形的性质和勾股定理矩形计算即可.【详解】解:①如图1,延长EA交DC于点F,∵菱形ABCD的周长为24,∴AB=BC=6,∵∠ABC=60°,∴三角形ABC是等边三角形,∴∠BAC=60°,当EA⊥BA时,△ABE是等腰直角三角形,∴AE=AB=AC=6,∠EAC=90°+60°=150°,∴∠FAC=30°,∵∠ACD=60°,∴∠AFC=90°,∴CF=12AC=3,则△ACE的面积为:12AE×CF=12×6×3=9;②如图2,过点A作AF⊥EC于点F,由①可知:∠EBC=∠EBA+∠ABC=90°+60°=150°,∵AB=BE=BC=6,∴∠BEC=∠BCE=15°,∴∠AEF=45°-15°=30°,∠ACE=60°-15°=45°,∴AF=12AE,2AC=32∵AB=BE=6,∴AE=2∴2236AE AF-=∴EC=EF+FC=3632则△ACE的面积为:12EC×AF=1(3632)329(31)2⨯+⨯=+.故答案为:9或9(31)+.【点睛】本题考查了菱形的性质、等腰三角形的性质、等边三角形的判定与性质,解决本题的关键是掌握菱形的性质.18.10+55【分析】取DE的中点N,连结ON、NG、OM.根据勾股定理可得55NG=.在点M与G之间总有MG≤MO+ON+NG(如图1),M、O、N、G四点共线,此时等号成立(如图2).可得线段MG的最大值.【详解】如图1,取DE的中点N,连结ON、NG、OM.∵∠AOB=90°,∴OM=12AB=5.同理ON=5.∵正方形DGFE,N为DE中点,DE=10,∴222210555NG DN DG++===.在点M与G之间总有MG≤MO+ON+NG(如图1),如图2,由于∠DNG的大小为定值,只要∠DON=12∠DNG,且M、N关于点O中心对称时,M、O、N、G四点共线,此时等号成立,∴线段MG 取最大值10+55.故答案为:10+55.【点睛】此题考查了直角三角形的性质,勾股定理,四点共线的最值问题,得出M 、O 、N 、G 四点共线,则线段MG 长度的最大是解题关键.19.6.5或8或18【分析】根据题意分BP QP =、BQ QP =两种情况分别讨论,再结合勾股定理求解即可.【详解】解:∵四边形ABCD 是矩形,26AD =,点Q 是BC 的中点∴13BQ =∴①当BP QP =时,过点P 作PM BQ ⊥交BQ 于点M ,如图,则 6.5BM MQ ==,且四边形ABMP 为矩形∴ 6.5AP BM ==②当BQ QP =时,以点Q 为圆心,BQ 为半径作圆,与AD 交于P '、P ''两点,如图,。
八年级下册第二次月考数学试卷+解析

八年级下册第二次月考数学试卷一.选择题(每小题3分,共30分)1.函数y=,自变量x的取值范围是()A.x>2 B.x<2 C.x≥2 D.x≤22.直角三角形两直角边边长分别为6和8,则连结这两条直角边中点的线段长为()A.3 B.4 C.5 D.103.一次函数y=2x﹣3的图象不经过的象限是()A.第一象限B.第二象限C.第三象限D.第四象限4.在下列命题中,正确的是()A.一组对边平行的四边形是平行四边形B.有一个角是直角的四边形是矩形C.有一组邻边相等的平行四边形是菱形D.对角线互相垂直平分的四边形是正方形5.已知函数y=(m﹣3)x+2,若函数值y随x的增大而减小,则m的取值范围是()A.m>3 B.m<3 C.m≥3 D.m≤36.已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是()A. B.C.D.7.将直线y=4x的图象向下平移3个单位长度,所得直线的函数解析式是()A.y=4x+3 B.y=4x﹣3 C.y=4(x+3)D.y=4(x﹣3)8.若顺次连接四边形ABCD各边的中点所得四边形是菱形,则四边形ABCD一定是()A.菱形B.对角线互相垂直的四边形C.矩形D.对角线相等的四边形9.已知点(﹣4,y1),(2,y2)都在直线y=﹣x+2上,则y1,y2大小关系是()A.y1>y2B.y1=y2C.y1<y2D.不能比较10.如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2014OA2015的最小边长为()A.22013B.22014C.()2013D.()2014二、填空题(每小题2分,共14分)11.计算:+=.12.已知菱形的两条对角线长分别是6和8,则这个菱形的面积为.13.如图,阴影部分是一个正方形,此正方形的面积为cm2.14.已知矩形ABCD,当满足条件时,它成为正方形(填一个你认为正确的条件即可).15.如图,矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为.16.在▱ABCD中,AB=5,AD=2,∠DAB=120°,若以点A为原点,直线AB为x轴,如图建立直角坐标系,则C的坐标是.17.某公司市场营销部的个人月收入与其每月的销售量成一次函数关系,其图象如图所示,由图中给出的信息可知,营销人员没有销售时的收入是.三.解答题(8大题,共56分)18.先化简,再求值:(1﹣)÷,其中a=+1.19.如图,在菱形ABCD中,E,F分别是BC,CD上的一点,且BE=DF.求证:AE=AF.20.已知y与x+2成正比例,且当x=1时,y=6.(1)求y与x之间的函数关系式;(2)若点(m,1)在这个函数图象上,求m.21.如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫格点,以格点为顶点分别按下列要求画三角形和平行四边形.(1)使三角形三边长为3,,;(2)使平行四边形有一锐角为45°,且面积为4.22.电力资源丰富,并且得到了较好的开发.某地区一家供电公司为了鼓励居民用电,采用分段计费的方法来计算电费.月用电量x(度)与相应电费y(元)之间的函数图象如图.(1)月用电量为100度时,应交电费元;(2)当x≥100时,求y与x之间的函数关系式;(3)月用电量为250度时,应交电费多少元?23.已知直线y=﹣2x+6与x轴交于点A,与y轴交于点B.(1)点A的坐标为,点B的坐标为;(2)求出△AOB的面积;(3)直线AB上是否存在一点C(C与B不重合),使△AOC的面积等于△AOB的面积?若存在,求出点C的坐标;若不存在请说明理由.24.如图所示,四边形ABCD是正方形,M是AB延长线上一点.直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A、B重合),另一直角边与∠CBM 的平分线BF相交于点F.(1)如图1,当点E在AB边得中点位置时:①通过测量DE、EF的长度,猜想DE与EF满足的数量关系是.②连接点E与AD边的中点N,猜想NE与BF满足的数量关系是,请证明你的猜想.(2)如图2,当点E在AB边上的任意位置时,猜想此时DE与EF有怎样的数量关系,并证明你的猜想.25.如图,已知正方形ABCD的边长为8cm,有一动点P以1cm/s的速度沿A﹣B﹣C﹣D 的路径运动,设P点运动的时间为t(s)(0<t<24),△ADP的面积为S cm2.(1)当△ADP是等腰直角三角形时,直接写出t的值.答:t=;(2)求S与t的函数关系式并写出自变量t的取值范围;(3)当t为何值时,△ADP的面积为12cm2.八年级(下)第二次月考数学试卷参考答案与试题解析一.选择题(每小题3分,共30分)1.函数y=,自变量x的取值范围是()A.x>2 B.x<2 C.x≥2 D.x≤2考点:函数自变量的取值范围.分析:根据被开方数大于等于0列式计算即可得解.解答:解:由题意得,x﹣2≥0,解得x≥2.故选:C.点评:本题考查函数自变量的取值范围,解决本题的关键是二次根式的被开方数是非负数.2.直角三角形两直角边边长分别为6和8,则连结这两条直角边中点的线段长为()A.3 B.4 C.5 D.10考点:三角形中位线定理;勾股定理.分析:利用勾股定理列式求出斜边的长,再根据三角形的中位线平行于第三边并且等于第三边的一半解答.解答:解:如图,∵两条直角边长分别为6和8,∴斜边==10,∴两条直角边中点线段的长=×10=5.故选:C.点评:本题考查了三角形的中位线平行于第三边并且等于第三边的一半,以及勾股定理,熟记定理是解题的关键,作出图形更形象直观.3.一次函数y=2x﹣3的图象不经过的象限是()A.第一象限B.第二象限C.第三象限D.第四象限考点:一次函数的图象.分析:根据一次函数y=ax+b(a≠0)的a、b的符号判定该一次函数所经过的象限即可.解答:解:∵一次函数y=2x﹣3的k=2>0,b=﹣3<0,∴一次函数y=2x﹣3经过第一、三、四象限,即一次函数y=2x﹣3不经过第二象限.故选:B.点评:本题考查了一次函数的图象,即直线y=kx+b所在的位置与k、b的符号有直接的关系.k>0时,直线必经过一、三象限.k<0时,直线必经过二、四象限.b>0时,直线与y轴正半轴相交.b=0时,直线过原点;b<0时,直线与y轴负半轴相交.4.在下列命题中,正确的是()A.一组对边平行的四边形是平行四边形B.有一个角是直角的四边形是矩形C.有一组邻边相等的平行四边形是菱形D.对角线互相垂直平分的四边形是正方形考点:命题与定理.专题:综合题.分析:要找出正确命题,可运用相关基础知识分析找出正确选项,也可以通过举反例排除不正确选项,从而得出正确选项.两组对边平行的四边形是平行四边形;有一个角是直角的四边形是矩形、直角梯形、总之,只要有一个角是直角即可;有一组邻边相等的平行四边形是菱形;对角线互相垂直平分且相等的四边形是正方形.解答:解:A、应为两组对边平行的四边形是平行四边形;B、有一个角是直角的四边形是矩形、直角梯形、总之,只要有一个角是直角即可;C、符合菱形定义;D、应为对角线互相垂直平分且相等的四边形是正方形.故选:C.点评:本题考查平行四边形、矩形和菱形及正方形的判定与命题的真假区别.5.已知函数y=(m﹣3)x+2,若函数值y随x的增大而减小,则m的取值范围是()A.m>3 B.m<3 C.m≥3 D.m≤3考点:一次函数图象与系数的关系.分析:由一次函数y随x的增大而减小,得到该一次函数为减函数,得到m﹣3小于0,求出不等式的解集即可得到m的范围.解答:解:∵一次函数y=(m﹣3)x+2,y随x的增大而减小,∴一次函数为减函数,即m﹣3<0,解得:m<3,则m的取值范围是m<3.故选B.点评:此题考查了一次函数图象与系数的关系,一次函数y=kx+b(k≠0),当k>0时,y随x的增大而增大;当k<0时,y随x的减小而减小.6.已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是()A. B.C.D.考点:一次函数图象与系数的关系.分析:利用一次函数的性质进行判断.解答:解:∵一次函数y=kx+b,y随着x的增大而减小∴k<0又∵kb<0∴b>0∴此一次函数图形过第一,二,四象限.故选A.点评:熟练掌握一次函数的性质.k>0,图象过第1,3象限;k<0,图象过第2,4象限.b >o,图象与y轴正半轴相交;b=0,图象过原点;b<0,图象与y轴负半轴相交.7.将直线y=4x的图象向下平移3个单位长度,所得直线的函数解析式是()A.y=4x+3 B.y=4x﹣3 C.y=4(x+3)D.y=4(x﹣3)考点:一次函数图象与几何变换.分析:只向下平移,让比例系数不变,常数项减去平移的单位即可.解答:解:将直线y=4x的图象向下平移3个单位长度,所得直线的函数解析式是y=4x﹣3,故选B点评:此题考查一次函数与几何变换问题,关键是根据求直线平移后的解析式时要注意平移时k的值不变,只有b发生变化.上下平移时只需让b的值加减即可.8.若顺次连接四边形ABCD各边的中点所得四边形是菱形,则四边形ABCD一定是()A.菱形B.对角线互相垂直的四边形C.矩形D.对角线相等的四边形考点:三角形中位线定理;菱形的判定.分析:根据三角形的中位线定理得到EH∥FG,EF=FG,EF=BD,要是四边形为菱形,得出EF=EH,即可得到答案.解答:解:∵E,F,G,H分别是边AD,DC,CB,AB的中点,∴EH=AC,EH∥AC,FG=AC,FG∥AC,EF=BD,∴EH∥FG,EF=FG,∴四边形EFGH是平行四边形,假设AC=BD,∵EH=AC,EF=BD,则EF=EH,∴平行四边形EFGH是菱形,即只有具备AC=BD即可推出四边形是菱形,故选:D.点评:本题主要考查对菱形的判定,三角形的中位线定理,平行四边形的判定等知识点的理解和掌握,灵活运用性质进行推理是解此题的关键.9.已知点(﹣4,y1),(2,y2)都在直线y=﹣x+2上,则y1,y2大小关系是()A.y1>y2B.y1=y2C.y1<y2D.不能比较考点:一次函数图象上点的坐标特征.分析:先根据一次函数的解析式判断出函数的增减性,再根据两点横坐标的大小即可得出结论.解答:解:∵k=﹣<0,∴y随x的增大而减小.∵﹣4<2,∴y1>y2.故选:A.点评:本题考查的是一次函数图象上点的坐标特点,先根据题意判断出一次函数的增减性是解答此题的关键.10.如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2014OA2015的最小边长为()A.22013B.22014C.()2013D.()2014考点:勾股定理;含30度角的直角三角形.专题:规律型.分析:在直角三角形OA1A2中,利用30°所对的直角边等于斜边的一半得到OA2=2A1A2,由A1A2的长求出OA2的长,在直角三角形OA2A3中,利用锐角三角函数定义得到tan∠A2OA3等于A2A3与OA2的比值,求出A2A3的长,再利用30°所对的直角边等于斜边的一半求出OA3的长,同理求出A3A4的长,以此类推得到直角三角形△A2014OA2015的最小边长A2014A2015即可.解答:解:在Rt△OA1A2中,A1A2=1,∠OA1A2=90°,∠A1OA2=30°,∴OA2=2A1A2=2,在Rt△OA2A3中,OA2=2,∠OA2A3=90°,∠A2OA3=30°,∴A2A3=OA2tan∠A2OA3=2×=,OA3=2A2A3=,在Rt△OA3A4中,OA3=,∠OA3A4=90°,∠A3OA4=30°,∴A3A4=OA3tan∠A3OA4=×=()2,以此类推,Rt△A2014OA2015的最小边长A2014A2015=()2013.故选C.点评:此题考查了勾股定理以及含30°角的直角三角形的性质,锐角三角函数定义,属于规律型试题,利用了转化的思想,锻炼了学生归纳总结的能力.二、填空题(每小题2分,共14分)11.计算:+=3.考点:二次根式的加减法.分析:本题考查了二次根式的加减运算,应先化为最简二次根式,再合并同类二次根式.解答:解:原式=2+=3.点评:同类二次根式是指几个二次根式化简成最简二次根式后,被开方数相同的二次根式.二次根式的加减运算,先化为最简二次根式,再将被开方数相同的二次根式进行合并.合并同类二次根式的实质是合并同类二次根式的系数,根指数与被开方数不变.12.已知菱形的两条对角线长分别是6和8,则这个菱形的面积为24.考点:菱形的性质.专题:计算题.分析:因为菱形的面积为两条对角线积的一半,所以这个菱形的面积为24.解答:解:∵菱形的两条对角线长分别是6和8,∴这个菱形的面积为6×8÷2=24故答案为24点评:此题考查了菱形面积的求解方法:①底乘以高,②对角线积的一半.13.如图,阴影部分是一个正方形,此正方形的面积为64cm2.考点:勾股定理的应用.分析:由勾股定理和正方形的面积公式解答.解答:解:由图可知正方形的边长为=8cm,正方形的面积为8×8=64cm2.点评:此题很简单,只要熟知勾股定理和正方形的面积公式即可解答.14.已知矩形ABCD,当满足条件AB=BC时,它成为正方形(填一个你认为正确的条件即可).考点:正方形的判定.分析:根据有一组邻边相等或对角线互相垂直的矩形是正方形添加条件.解答:解:根据有一组邻边相等或对角线互相垂直的矩形是正方形,得到应该添加的条件为:AB=BC或BC=CD或CD=DA或DA=AB或AC⊥BD.故答案为:AB=BC.点评:本题是考查正方形的判别方法,判别一个四边形为正方形主要根据正方形的概念,途经有两种:①先说明它是矩形,再说明有一组邻边相等;②先说明它是菱形,再说明它有一个角为直角.15.如图,矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为6.考点:翻折变换(折叠问题).分析:先根据矩形的特点求出BC的长,再由翻折变换的性质得出△CEF是直角三角形,利用勾股定理即可求出CF的长,再在△ABC中利用勾股定理即可求出AB的长.解答:解:∵四边形ABCD是矩形,AD=8,∴BC=8,∵△AEF是△AEB翻折而成,∴BE=EF=3,AB=AF,△CEF是直角三角形,∴CE=8﹣3=5,在Rt△CEF中,CF===4,设AB=x,在Rt△ABC中,AC2=AB2+BC2,即(x+4)2=x2+82,解得x=6,则AB=6.故答案为:6.点评:本题考查了翻折变换及勾股定理,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解答此题的关键.16.在▱ABCD中,AB=5,AD=2,∠DAB=120°,若以点A为原点,直线AB为x轴,如图建立直角坐标系,则C的坐标是(4,).考点:平行四边形的性质;坐标与图形性质.分析:过点D作DE⊥x轴于点E,在Rt△ADE中求出AE、DE,继而可得出点D的坐标,由平行四边形的性质可得点C的坐标.解答:解:点B的坐标为(5,0),过点D作DE⊥x轴于点E,在Rt△ADE中,∠DAE=60°,AD=2,∴AE=1,DE=,故可得点D的坐标为(﹣1,),又∵四边形ABCD是平行四边形,CD=AB=5,∴点C的坐标为(4,),故答案为:(4,).点评:本题考查了平行四边形的性质及勾股定理的知识,属于基础题,熟知并掌握平行四边形的对边平行且相等是解题关键.17.某公司市场营销部的个人月收入与其每月的销售量成一次函数关系,其图象如图所示,由图中给出的信息可知,营销人员没有销售时的收入是300元.考点:一次函数的应用.分析:由图象是一条直线,知收入与销售量是一次函数关系,又由图象上的两点(1,800)和(2,1300),利用待定系数法确定函数关系,再求销售量为0时的函数值即可.解答:解:设y=kx+b,由图知,直线过(1,800)(2,1300),代入得:,解之得:∴y=500x+300,当x=0时,y=300.即营销人员没有销售时的收入是300元.故答案为:300元.点评:此题主要考查了一次函数的应用,由图象过两点利用待定系数法即可确定函数关系式,没有销售即销售量为0,求对应的函数值,把图象与题意结合起来考虑.三.解答题(8大题,共56分)18.先化简,再求值:(1﹣)÷,其中a=+1.考点:分式的化简求值.分析:先根据分式混合运算的法则把原式进行化简,再把a的值代入进行计算即可.解答:解:原式=•=,当a=+1时,原式===.点评:本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.19.如图,在菱形ABCD中,E,F分别是BC,CD上的一点,且BE=DF.求证:AE=AF.考点:全等三角形的判定与性质;菱形的性质.专题:证明题.分析:要求证AE=AF,只要证明△ABE≌△ADF即可.解答:证明:∵四边形ABCD是菱形,∴AB=AD,∠B=∠D.又∵BE=DF,∴△ABE≌△ADF(SAS),(5分)∴AE=AF.(6分)点评:证明线段相等的问题,最常用的方法是证明三角形全等.本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.20.已知y与x+2成正比例,且当x=1时,y=6.(1)求y与x之间的函数关系式;(2)若点(m,1)在这个函数图象上,求m.考点:待定系数法求一次函数解析式;一次函数图象上点的坐标特征.分析:(1)根据题意设出函数解析式,把当x=3时,y=6代入解析式,便可求出未知数的值,从而求出其解析式;(2)将点(m,1)代入函数的解析式中,即可求得m的值;解答:解:(1)解:∵y与x+2成正比例,∴设y=k(x+2),∵x=1时,y=6,∴6=k(1+2),解得:k=2,∴y与x的关系式为:y=2x+4;(4)把点(m,1)代入y=2x+4中,得1=2m+4,解得:m=﹣.点评:本题考查了待定系数法求一次函数的解析式,熟练掌握待定系数法是解题的关键.21.如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫格点,以格点为顶点分别按下列要求画三角形和平行四边形.(1)使三角形三边长为3,,;(2)使平行四边形有一锐角为45°,且面积为4.考点:勾股定理;平行四边形的性质.专题:作图题.分析:(1)根据勾股定理逆定理,所作三角形是以,为斜边的直角三角形,第三边为3,作三角形即可;(2)根据网格结构,作45°锐角,且使平行四边形的底边是2,高是2即可.解答:解:(1)(2)如图所示:(1)中△ABC即为所求作的三角形;(2)中,▱ABCD即为所求作的平行四边形.点评:本题考查了应用与设计作图,(1)根据勾股定理逆定理判断出所求作的三角形是直角三角形是解题的关键,解答此类题目熟练掌握并灵活运用网格结构非常重要.22.电力资源丰富,并且得到了较好的开发.某地区一家供电公司为了鼓励居民用电,采用分段计费的方法来计算电费.月用电量x(度)与相应电费y(元)之间的函数图象如图.(1)月用电量为100度时,应交电费60元;(2)当x≥100时,求y与x之间的函数关系式;(3)月用电量为250度时,应交电费多少元?考点:一次函数的应用.分析:(1)根据函数图象,当x=100时,可直接从函数图象上读出y的值;(2)设一次函数为:y=kx+b,将(100,60),(200,110)两点代入进行求解即可;(3)将x=250代入(2)式所求的函数关系式进行求解可得出应交付的电费.解答:解:(1)根据函数图象,知:当x=100时,y=60,故当月用电量为100时,应交付电费60元;故答案为:60(2)设一次函数为y=kx+b,当x=100时,y=60;当x=200时,y=110∴,解得:,所求的函数关系式为:y=0.5x+10(x≥100)(3)当x=250时,y=0.5×250+10=135,∴月用量为250度时,应交电费135元.点评:本题主要考查用待定系数法求一次函数关系式,并会用一次函数研究实际问题,具备在直角坐标系中的读图能力.注意自变量的取值范围不能遗漏.23.已知直线y=﹣2x+6与x轴交于点A,与y轴交于点B.(1)点A的坐标为(3,0),点B的坐标为(0,6);(2)求出△AOB的面积;(3)直线AB上是否存在一点C(C与B不重合),使△AOC的面积等于△AOB的面积?若存在,求出点C的坐标;若不存在请说明理由.考点:一次函数图象上点的坐标特征;三角形的面积.专题:计算题.分析:(1)根据坐标轴上点的坐标特征求A点和B点坐标;(2)根据三角形面积公式求解;(3)根据一次函数图象上点的坐标特征,设C(t,﹣2t+6),则利用三角形面积公式得到•3•|﹣2t+6|=9,然后解绝对值方程求出t的值即可得到C点坐标.解答:解:(1)当y=0时,﹣2x+6=0,解得x=3,则A(3,0);当x=0时,y=﹣2x+6=6,则B(0,6);故答案为(3,0),(0,6);(2)S△OAB=×3×6=9;(3)存在.设C(t,﹣2t+6),∵△AOC的面积等于△AOB的面积,∴•3•|﹣2t+6|=9,解得t1=6,t2=0(舍去),∴C点坐标为(6,﹣6).点评:本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(﹣,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.也考查了三角形面积公式.24.如图所示,四边形ABCD是正方形,M是AB延长线上一点.直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A、B重合),另一直角边与∠CBM 的平分线BF相交于点F.(1)如图1,当点E在AB边得中点位置时:①通过测量DE、EF的长度,猜想DE与EF满足的数量关系是DE=EF.②连接点E与AD边的中点N,猜想NE与BF满足的数量关系是NE=BF,请证明你的猜想.(2)如图2,当点E在AB边上的任意位置时,猜想此时DE与EF有怎样的数量关系,并证明你的猜想.考点:全等三角形的判定与性质;正方形的性质.分析:(1)①根据图形可以得到DE=EF,NE=BF,②要证明这两个关系,只要证明△DNE ≌△EBF即可.(2)DE=EF,连接NE,在DA边上截取DN=EB,证出△DNE≌△EBF即可得出答案.解答:解:(1)①DE=EF;②NE=BF;理由如下:∵四边形ABCD为正方形,∴AD=AB,∠DAB=∠ABC=90°,∵N,E分别为AD,AB中点,∴AN=DN=AD,AE=EB=AB,∴DN=BE,AN=AE,∵∠DEF=90°,∴∠AED+∠FEB=90°,又∵∠ADE+∠AED=90°,∴∠FEB=∠ADE,又∵AN=AE,∴∠ANE=∠AEN,又∵∠A=90°,∴∠ANE=45°,∴∠DNE=180°﹣∠ANE=135°,又∵∠CBM=90°,BF平分∠CBM,∴∠CBF=45°,∠EBF=135°,在△DNE和△EBF中,∴△DNE≌△EBF(ASA),∴DE=EF,NE=BF.(2)DE=EF,理由如下:连接NE,在DA边上截取DN=EB,∵四边形ABCD是正方形,DN=EB,∴AN=AE,∴△AEN为等腰直角三角形,∴∠ANE=45°,∴∠DNE=180°﹣45°=135°,∵BF平分∠CBM,AN=AE,∴∠EBF=90°+45°=135°,∴∠DNE=∠EBF,∵∠NDE+∠DEA=90°,∠BEF+∠DEA=90°,∴∠NDE=∠BEF,在△DNE和△EBF中,∴△DNE≌△EBF(ASA),∴DE=EF.点评:此题主要考查了正方形的性质以及全等三角形的判定与性质等知识,解决本题的关键就是求证△DNE≌△EBF.25.如图,已知正方形ABCD的边长为8cm,有一动点P以1cm/s的速度沿A﹣B﹣C﹣D 的路径运动,设P点运动的时间为t(s)(0<t<24),△ADP的面积为S cm2.(1)当△ADP是等腰直角三角形时,直接写出t的值.答:t=8s或16s;(2)求S与t的函数关系式并写出自变量t的取值范围;(3)当t为何值时,△ADP的面积为12cm2.考点:正方形的性质;动点问题的函数图象.专题:计算题.分析:(1)当点P运动到B点和C点时,△ADP是等腰直角三角形,然后写出对应的t 的值;(2)分类讨论:当点P在AB上运动或点P在BC上运动或点P在CD上运动时,分别写出对应的t的取值范围,然后根据三角形面积公式求出对应的S;(3)利用(2)中S与t的函数关系式,求函数值为12时所对应的t的值即可.解答:解:(1)当t=8s或16s时,△ADP是等腰直角三角形;故答案为8s或16s;(2)当0<t≤8时,如图1,S=•t•8=4t;当8<t≤16时,如图2,S=•8•8=32;当16<t<24时,如图3,S=•(24﹣t)•8=﹣4t+96;(3)当4t=12时,解得t=3(s);当﹣4t+96=12时,解得t=21(s),所以当t为3s或21s时,△ADP的面积为12cm2.点评:本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.也考查了分类讨论的思想.。
2019-2020年八年级下学期第二次月考数学试题(解析版)

2015年春期八年级第二次月考数学试题 一、选择题(每小题3分,共计24分) D. 当x >0时,y 1、y 2都随x 的增大而增大 6.如图,过x 轴正半轴任意一点P 作x 轴的垂线,分别与反比例函数y 1y 2A 和点B.若点C 是y 轴上任意一点,连结AC 、BC ,则△ABC 的面积为( ) A .1B .2C .3D .4 7.顺次连接菱形各边中点所得的四边形一定是 ( ) A.等腰梯形 B.正方形 C.平行四边形 D.矩形 8.若x<0) A .0 B .—2 C .0或—2 D .2 二、填空题(每小题3分,共计24分) 9.已知平行四边形ABCD ,请补充一个条件,使它成为矩形ABCD .你补充的条件是 . 10.分式26+-x x ,当x=_____________时,值为零;当x=_____________时,无意义.11.矩形的两条对角线的一个交角为60o ,两条对角线的和为8cm ,则这个矩形的一条较短边为 cm .班级姓名考号··································装························订线姓12当______m 时,其图象的两个分支在第一、三象限内;当______m 时,其图象在每个象限内y 随x 的增大而增大;13.已知空气的单位体积质量为0.00124克/厘米³,将0.00124克/厘米³用科学计数法表示为14.在函数y2,y 1),(-1,y 2)y 3),则y 1、y 2、y 3的大小关系为__________________(用“<”连接).15.如图,正方形ABCD 中,点E 、F 分别在边BC 、CD 上,且AE =EF =FA .你能得出的结论:① ② ③16. 如图,一次函数y=mx 与反比例函数y=xk 的图象交于A 、B 两点,过点A 作AM ⊥x 轴,垂足为M ,连结BM,若ABM S ∆=3,则k 的值是 .三、计算题(每小题6分,共计12分)17.先化简24x 4x 4x x x ++⎛⎫-÷ ⎪⎝⎭再从-3<x<2中,选择一个你喜欢的值代入求值。
八年级第二学期 第二次月考数学试卷含解析

一、选择题1.如图,E 、F 、G 、H 分别是BD 、BC 、AC 、AD 的中点,且AB =CD .结论:①EG ⊥FH ;②四边形EFGH 是矩形;③HF 平分∠EHG ;④EG 12=BC ;⑤四边形EFGH 的周长等于2AB .其中正确的个数是( )A .1B .2C .3D .42.在边长为2的正方形ABCD 中,P 为AB 上的一动点,E 为AD 中点,PE 交CD 延长线于Q ,过E 作EF PQ ⊥交BC 的延长线于F ,则下列结论:①APE DQE ∆≅∆;②PQ EF =;③当P 为AB 中点时,2CF =;④若H 为QC 的中点,当P 从A 移动到B 时,线段EH 扫过的面积为12,其中正确的是( )A .①②B .①②④C .②③④D .①②③3.如图,在正方形ABCD 中,CE =MN ,∠MCE =35°,那么∠ANM 等于( )A .45°B .50°C .55°D .60°4.如图,正方形ABCD 的边长为4,点E 在边AB 上,AE =1,若点P 为对角线BD 上的一个动点,则△PAE 周长的最小值是( )A .3B .4C .5D .65.如图,点O (0,0),B (0,1)是正方形OBB 1C 的两个顶点,以它的对角线OB 1为一边作正方形OB 1B 2C 1,以正方形OB 1B 2C 1的对角线OB 2为一边作正方形OB 2B 3C 2,再以正方形OB 2B 3C 2的对角线OB 3为一边作正方形OB 3B 4C 3,…,依次进行下去,则点B 6的坐标是( )A .(42,0)B .(42,0)-C .(8,0)-D .(0,8)-6.如图,把正方形ABCD 沿对边中点所在的直线对折后展开,折痕为,MN 再过点B 折叠纸片,使点A 格在MN 上的点F 处,折痕为,BE 若AB 长为2,则EN 的长为(( )A .33B .322-C 2D .237.如图,点O (0,0),A (0,1)是正方形1OAA B 的两个顶点,以1OA 对角线为边作正方形121OA A B ,再以正方形的对角线2OA 作正方形121OA A B ,…,依此规律,则点8A 的坐标是( )A .(-8,0)B .(0,8)C .(0,82)D .(0,16)8.如图,在菱形ABCD 中,5AB cm =,120ADC =∠︒,点E 、F 同时由A 、C 两点出发,分别沿AB 、CB 方向向点B 匀速移动(到点B 为止),点E 的速度为1/cm s ,点F 的速度为2/cm s ,经过t 秒DEF ∆为等边三角形,则t 的值为( )A .34B .43C .32D .539.如图,ABCD 的对角线,AC BD 交于点,O DE 平分ADC ∠交BC 于点,60,E BCD ∠=︒2,AD AB =连接OE .下列结论:ABCD S AB BD =⋅①;DB ②平分ADE ∠;AB DE =③;CDE BOC S S =④,其中正确的有( )A .1个B .2个C .3个D .4个10.如图,在ABC 中,AB=5,AC=12,BC=13,P 为边BC 上一动点,PE ⊥AB 于E ,PF ⊥AC 于F ,M 为EF 中点,则AM 的最小值为( )A .6013B .3013C .2413D .1213二、填空题11.在平行四边形ABCD 中, BC 边上的高为4 ,AB =5 ,25AC = ,则平行四边形ABCD 的周长等于______________ .12.如图,在平行四边形ABCD 中,对角线AC ,BD 相交于点O ,AB =OB ,点E ,F 分别是OA ,OD 的中点,连接EF ,EM ⊥BC 于点M ,EM 交BD 于点N ,若∠CEF =45°,FN =5,则线段BC 的长为_____.13.如图,在平行四边形ABCD 中,AD=2AB .F 是AD 的中点,作CE ⊥AB, 垂足E 在线段AB 上,连接EF 、CF ,则下列结论:(1)∠DCF+12∠D =90°;(2)∠AEF+∠ECF =90°;(3)BEC S =2CEF S ; (4)若∠B=80︒,则∠AEF=50°.其中一定成立的是______ (把所有正确结论的字号都填在横线上).14.如图,在矩形ABCD 中,∠ACB =30°,BC =23,点E 是边BC 上一动点(点E 不与B ,C 重合),连接AE ,AE 的中垂线FG 分别交AE 于点F ,交AC 于点G ,连接DG ,GE .设AG =a ,则点G 到BC 边的距离为_____(用含a 的代数式表示),ADG 的面积的最小值为_____.15.菱形ABCD 的周长为24,∠ABC=60°,以AB 为腰在菱形外作底角为45°的等腰△ABE ,连结AC ,CE ,则△ACE 的面积为___________.16.如图,在平面直角坐标系中,直线112y x =+与x 轴、y 轴分别交于A ,B 两点,以AB 为边在第二象限内作正方形ABCD ,则D 点坐标是_______;在y 轴上有一个动点M ,当MDC △的周长值最小时,则这个最小值是_______.17.在平行四边形 ABCD 中,AE 平分∠BAD 交边 BC 于 E ,DF 平分∠ADC 交边 BC 于 F ,若 AD=11,EF=5,则 AB= ___.18.已知:如图,在ABC 中,AD BC ⊥,垂足为点D ,BE AC ⊥,垂足为点E ,M 为AB 边的中点,连结ME 、MD 、ED ,设4AB =,30DAC ∠=︒则EM =______;EDM 的面积为______,19.如图,长方形ABCD 中AB =2,BC =4,正方形AEFG 的边长为1.正方形AEFG 绕点A 旋转的过程中,线段CF 的长的最小值为_____.20.如图,在△ABC 中,AB =AC ,E ,F 分别是BC ,AC 的中点,以AC 为斜边作Rt △ADC ,若∠CAD =∠BAC =45°,则下列结论:①CD ∥EF ;②EF =DF ;③DE 平分∠CDF ;④∠DEC =30°;⑤AB =2CD ;其中正确的是_____(填序号)三、解答题21.在四边形ABCD 中,AD ∥BC ,AB=8cm ,AD=16cm ,BC=22cm ,∠ABC=90°.点P 从点A 出发,以1cm/s 的速度向点D 运动,点Q 从点C 同时出发,以3cm/s 的速度向点B 运动,其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t 秒.(1)当t= 时,四边形ABQP 成为矩形?(2)当t= 时,以点P 、Q 与点A 、B 、C 、D 中的任意两个点为顶点的四边形为平行四边形?(3)四边形PBQD 是否能成为菱形?若能,求出t 的值;若不能,请说明理由,并探究如何改变Q 点的速度(匀速运动),使四边形PBQD 在某一时刻为菱形,求点Q 的速度.22.如图1,在正方形ABCD 中,点M 、N 分别在边BC 、CD 上,AM 、AN 分别交BD 于点P 、Q ,连接CQ 、MQ .且CQ MQ =.(1)求证:QAB QMC ∠=∠(2)求证:90AQM ∠=︒(3)如图2,连接MN ,当2BM =,3CN =,求AMN 的面积图1 图223.正方形ABCD 中,对角线AC 与BD 交于点O ,点P 是正方形ABCD 对角线BD 上的一个动点(点P 不与点B ,O ,D 重合),连接CP 并延长,分别过点D ,B 向射线作垂线,垂足分别为点M ,N .(1)补全图形,并求证:DM =CN ;(2)连接OM ,ON ,判断OMN 的形状并证明.24.(1)如图①,在正方形ABCD 中,AEF ∆的顶点E ,F 分别在BC ,CD 边上,高AG 与正方形的边长相等,求EAF ∠的度数;(2)如图②,在Rt ABD ∆中,90,BAD AD AB ︒∠==,点M ,N 是BD 边上的任意两点,且45MAN ︒∠=,将ABM ∆绕点A 逆时针旋转90度至ADH ∆位置,连接NH ,试判断MN ,ND ,DH 之间的数量关系,并说明理由;(3)在图①中,连接BD 分别交AE ,AF 于点M ,N ,若正方形ABCD 的边长为12,GF=6,BM= 32,求EG ,MN 的长.25.已知正方形,ABCD 点F 是射线DC 上一动点(不与,C D 重合).连接AF 并延长交直线BC 于点E ,交BD 于,H 连接CH .在EF 上取一点,G 使ECG DAH ∠=∠. (1)若点F 在边CD 上,如图1,①求证:CH CG ⊥.②求证:GFC 是等腰三角形.(2)取DF 中点,M 连接MG .若3MG =,正方形边长为4,则BE = .26.已知如图1,四边形ABCD 是正方形,45EAF ︒∠= .()1如图1,若点,E F 分别在边BC CD 、上,延长线段CB 至G ,使得BG DF =,若3,2BE BG ==,求EF 的长;()2如图2,若点,E F 分别在边CB DC 、延长线上时,求证: .EF DF BE =-()3如图3,如果四边形ABCD 不是正方形,但满足,90,45,AB AD BAD BCD EAF ︒︒=∠=∠=∠=且7, 13,5BC DC CF ===,请你直接写出BE 的长.27.如图,四边形ABCD 为矩形,C 点在x 轴上,A 点在y 轴上,D(0,0),B(3,4),矩形ABCD 沿直线EF 折叠,点B 落在AD 边上的G 处,E 、F 分别在BC 、AB 边上且F(1,4).(1)求G 点坐标(2)求直线EF 解析式(3)点N 在坐标轴上,直线EF 上是否存在点M ,使以M 、N 、F 、G 为顶点的四边形是平行四边形?若存在,直接写出M 点坐标;若不存在,请说明理由28.如图,ABCD 中,60ABC ∠=︒,连结BD ,E 是BC 边上一点,连结AE 交BD 于点F .(1)如图1,连结AC ,若6AB AE ==,:5:2BC CE =,求ACE △的面积; (2)如图2,延长AE 至点G ,连结AG 、DG ,点H 在BD 上,且BF DH =,AF AH =,过A 作AM DG ⊥于点M .若180ABG ADG ∠+∠=︒,求证:3BG GD AG +=.29.如图,ABC ∆是边长为3的等边三角形,点D 是射线BC 上的一个动点(点D 不与点B 、C 重合),ADE ∆是以AD 为边的等边三角形,过点E 作BC 的平行线,交直线AC 于点F ,连接BE .(1)判断四边形BCFE 的形状,并说明理由;(2)当DE AB ⊥时,求四边形BCFE 的周长;(3)四边形BCFE 能否是菱形?若可为菱形,请求出BD 的长,若不可能为菱形,请说明理由.30.如图①,在等腰Rt ABC 中,90BAC ∠=,点E 在AC 上(且不与点A 、C 重合),在ABC 的外部作等腰Rt CED ,使90CED ∠=,连接AD ,分别以AB ,AD 为邻边作平行四边形ABFD ,连接AF .()1请直接写出线段AF ,AE 的数量关系; ()2①将CED 绕点C 逆时针旋转,当点E 在线段BC 上时,如图②,连接AE ,请判断线段AF ,AE 的数量关系,并证明你的结论;②若25AB =2CE =,在图②的基础上将CED 绕点C 继续逆时针旋转一周的过程中,当平行四边形ABFD 为菱形时,直接写出线段AE 的长度.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【解析】【分析】根据三角形的中位线平行于第三边并且等于第三边的一半与AB=CD可得四边形EFGH是菱形,然后根据菱形的对角线互相垂直平分,并且平分每一组对角的性质对各小题进行判断即可得答案.【详解】∵E、F、G、H分别是BD、BC、AC、AD的中点,∴EF=12CD,FG=12AB,GH=12CD,HE=12AB,∵AB=CD,∴EF=FG=GH=HE,∴四边形EFGH是菱形,故②错误,∴EG⊥FH,HF平分∠EHG;故①③正确,∴四边形EFGH的周长= EF=FG=GH=HE =2AB,故⑤正确,没有条件可证明EG=12BC,故④错误,∴正确的结论有:①③⑤,共3个,故选C.【点睛】本题考查了三角形中位线定理与菱形的判定与菱形的性质,根据三角形的中位线定理与AB=CD判定四边形EFGH是菱形并熟练掌握菱形的性质是解答本题的关键.2.B解析:B【分析】利用正方形的性质、全等三角形的性质、勾股定理等知识依次判断即可;【详解】解:①∵四边形ABCD是正方形,∴AB=BC=CD=AD,∠A=∠B=90°,∵∠A=∠EDQ,∠AEP=∠QED,AE=ED,∴△AEP≌△DEQ,故①正确,②作PG⊥CD于G,EM⊥BC于M,∴∠PGQ=∠EMF=90°,∵EF⊥PQ,∴∠PEF=90°,∴∠PEN+∠NEF=90°,∵∠NPE+∠NEP=90°,∴∠NPE=∠NEF,∵PG=EM,∴△EFM≌△PQG,∴EF=PQ,故②正确,③连接QF.则QF=PF,PB2+BF2=QC2+CF2,设CF=x,则(2+x)2+12=32+x2,∴x=1,故③错误,④当P在A点时,Q与D重合,QC的中点H在DC的中点S处,当P运动到B时,QC的中点H与D重合,故EH扫过的面积为△ESD的面积=12,故④正确,则正确的是①②④,故选B.【点睛】本题考查正方形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,难度较大.3.C解析:C【分析】过B 作BF ∥MN 交AD 于F ,则∠AFB =∠ANM ,根据正方形的性质得出∠A =∠EBC =90°,AB =BC ,AD ∥BC ,推出四边形BFNM 是平行四边形,得出BF =MN =CE ,证Rt △ABF ≌Rt △BCE ,推出∠AFB =∠ECB 即可.【详解】解:过B 作BF ∥MN 交AD 于F ,则∠AFB =∠ANM ,∵四边形ABCD 是正方形,∴∠A =∠EBC =90°,AB =BC ,AD ∥BC ,∴FN ∥BM ,BF ∥MN ,∴四边形BFNM 是平行四边形,∴BF =MN ,∵CE =MN ,∴CE =BF ,在Rt △ABF 和Rt △BCE 中BF CE AB BC =⎧⎨=⎩∴Rt △ABF ≌Rt △BCE (HL ),∴∠ABF =∠MCE =35°,∴∠ANM =∠AFB =55°,故选:C .【点睛】本题考查了直角三角形全等的判定即性质,还涉及正方形的性质以及平行四边形的判定与性质,构造全等三角形是解题关键.4.D解析:D【分析】连接AC 、CE ,CE 交BD 于P ,此时AP +PE 的值最小,求出CE 长,即可求出答案.【详解】解:连接AC 、CE ,CE 交BD 于P ,连接AP 、PE ,∵四边形ABCD 是正方形,∴OA =OC ,AC ⊥BD ,即A 和C 关于BD 对称,∴AP =CP ,即AP +PE =CE ,此时AP +PE 的值最小,所以此时△PAE 周长的值最小,∵正方形ABCD 的边长为4,点E 在边AB 上,AE =1,∴∠ABC =90°,BE =4﹣1=3,由勾股定理得:CE =5,∴△PAE 的周长的最小值是AP +PE +AE =CE +AE =5+1=6,故选D .【点睛】本题考查了正方形的性质与轴对称——最短路径问题,知识点比较综合,属于较难题型.5.C解析:C【解析】【分析】根据已知条件如图可得到B 12 ,B 2所在的正方形的对角线长为2(2),B 3所在的正方形的对角线长为3(2),依据规律可得B 6所在的正方形的对角线长为62)=8,再根据B 6在x 轴的负半轴,就可得到B 6的坐标。
八年级数学下学期第二次月考测试卷含解析

一、选择题1.如图,在Rt △ABC 中,∠A=30°,BC=2,点D ,E 分别是直角边BC ,AC 的中点,则DE 的长为( )A .2B .3C .4D .232.如图,在平面直角坐标系中,正方形ABCD 的顶点A 落在y 轴上,点C 落在x 轴上,随着顶点C 由原点O 向x 轴正半轴方向运动,顶点A 沿y 轴负半轴方向运动到终点O ,在运动过程中OD 的长度变化情况是( )A .一直增大B .一直减小C .先减小后增大D .先增大后减少3.如图,在Rt ABC 中,90ACB ∠=︒,若CD ,CM 分别是斜边AB 上的高和中线,则下列结论中错误的是( )A .MCB MCA ∠=∠ B .MCB ACD ∠=∠C .B ACD ∠=∠D .MCA BCD ∠=∠4.如图,平行四边形ABCD 的对角线AC ,BD 相交于点O ,CE 平分DCB ∠交BD 于点F ,且60ABC ∠=︒,2AB BC =,连接OE ,下列结论:①30ACD ∠=︒;②·ABCDSAC BC =;③:1:4OE AC =.其中正确的有( )A .0个B .1个C .2个D .3个5.如图,正方形ABCD 中,点E 是AD 边的中点,BD 、CE 交于点H ,BE 、AH 交于点G ,则下列结论:①AG ⊥BE ;②5:2;③S △BHE =S △CHD ;④∠AHB=∠EHD .其中正确的个数是A .1B .2C .3D .46.已知,在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点1B 在y 轴上,点1C 、1E 、2E 、2C 、3E 、4E 、3C 均在x 轴正半轴上,若已知正方形1111D C B A 的边长为1,1160B C O ︒∠=,且112233////B C B C B C ,则点3A 的坐标是( )A .331(3,)++B .333(3,)2++C .331(3,)2++D .333(3,)++ 7.如图,平行四边形ABCD 中,对角线AC 、BD 相交于点O ,AD =12AC ,M 、N 、P 分别是OA 、OB 、CD 的中点,下列结论: ①CN ⊥BD ; ②MN =NP ;③四边形MNCP 是菱形; ④ND 平分∠PNM . 其中正确的有( )A .1 个B .2 个C .3 个D .4 个8.如图,矩形ABCD 中,O 为AC 中点,过点O 的直线分别与AB ,CD 交于点E ,F ,连接BF 交AC 于点M ,连接DE ,BO .若60COB ∠=,FO FC =,则下列结论:①FB OC ⊥,OM CM =; ②EOB CMB ≅; ③四边形EBFD 是菱形; ④:3:2MB OE =.其中正确结论的个数是( )A .1B .2C .3D .49.如图,在边长为2的等边三角形ABC 中,D 为边BC 上一点,且12BD CD =.点E ,F 分别在边,AB AC 上,且90,EDF M ︒∠=为边EF 的中点,连接CM 交DF于点N .若//DF AB ,则CM 的长为( )A .233B .334C .536D .310.如图,点P 是正方形ABCD 的对角线BD 上一点,PE ⊥BC 于点E ,PF ⊥CD 于点F ,连接EF 给出下列五个结论:①AP=EF ;②△APD 一定是等腰三角形;③AP ⊥EF ;④2PD=EF .其中正确结论的番号是( )A .①③④B .①②③C .①③D .①②④二、填空题11.如图,在矩形ABCD 中,4AB =,2AD =,E 为边CD 的中点,点P 在线段AB 上运动,F 是CP 的中点,则CEF ∆的周长的最小值是____________.12.如图,长方形纸片ABCD 中,AB =6 cm,BC =8 cm 点E 是BC 边上一点,连接AE 并将△AEB 沿AE 折叠, 得到△AEB′,以C ,E ,B′为顶点的三角形是直角三角形时,BE 的长为___________cm.13.如图,Rt ABE ∆中,90,B AB BE ︒∠==, 将ABE ∆绕点A 逆时针旋转45︒,得到,AHD ∆过D 作DC BE ⊥交BE 的延长线于点C ,连接BH 并延长交DC 于点F ,连接DE 交BF 于点O .下列结论:①DE 平分HDC ∠;②DO OE =; ③CD HF =; ④2BC CF CE -=; ⑤H 是BF 的中点,其中正确的是___________14.在ABCD 中,5AD =,BAD ∠的平分线交CD 于点E ,∠ABC 的平分线交CD 于点F ,若线段EF=2,则AB 的长为__________.15.如图,在菱形ABCD 中,AC 交BD 于P ,E 为BC 上一点,AE 交BD 于F ,若AB=AE ,EAD 2BAE ∠∠=,则下列结论:①AF=AP ;②AE=FD ;③BE=AF .正确的是______(填序号).16.如图,在矩形ABCD 中,16AB =,18BC =,点E 在边AB 上,点F 是边BC 上不与点B 、C 重合的一个动点,把EBF △沿EF 折叠,点B 落在点B '处.若3AE =,当CDB '是以DB '为腰的等腰三角形时,线段DB '的长为__________.17.如图,四边形ABCP是边长为4的正方形,点E在边CP上,PE=1;作EF∥BC,分别交AC、AB于点G、F,M、N分别是AG、BE的中点,则MN的长是_________.18.如图,在□ABCD中,对角线AC、BD相交于点O,AB=OB,E为AC上一点,BE平分∠ABO,EF⊥BC于点F,∠CAD=45°,EF交BD于点P,BP=5,则BC的长为_______.19.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点D为平面内动点,且满足AD =4,连接BD,取BD的中点E,连接CE,则CE的最大值为_____.20.李刚和常明两人在数学活动课上进行折纸创编活动.李刚拿起一张准备好的长方形纸片对常明说:“我现在折叠纸片(图①),使点D落在AB边的点F处,得折痕AE,再折叠,使点C落在AE边的点G处,此时折痕恰好经过点B,如果AD=a,那么AB长是多少?”常明说;“简单,我会. AB应该是_____”.常明回答完,又对李刚说:“你看我的创编(图②),与你一样折叠,可是第二次折叠时,折痕不经过点B,而是经过了AB边上的M点,如果AD=a,测得EC=3BM,那么AB长是多少?”李刚思考了一会,有点为难,聪明的你,你能帮忙解答吗?AB=_____.三、解答题21.如图,在四边形ABCD 中,AB ∥DC ,AB AD =,对角线AC ,BD 交于点O ,AC 平分BAD ∠,过点C 作CE AB ⊥交AB 的延长线于点E ,连接OE .(1)求证:四边形ABCD 是菱形; (2)若5AE =,3OE =,求线段CE 的长.22.在四边形ABCD 中,90A B C D ∠∠∠∠====,10AB CD ==,8BC AD ==.()1P 为边BC 上一点,将ABP 沿直线AP 翻折至AEP 的位置(点B 落在点E 处)①如图1,当点E 落在CD 边上时,利用尺规作图,在图1中作出满足条件的图形(不写作法,保留作图痕迹,用2B 铅笔加粗加黑).并直接写出此时DE =______;②如图2,若点P 为BC 边的中点,连接CE ,则CE 与AP 有何位置关系?请说明理由;()2点Q 为射线DC 上的一个动点,将ADQ 沿AQ 翻折,点D 恰好落在直线BQ 上的点'D 处,则DQ =______;23.如图,在菱形ABCD 中,AB =2cm ,∠ADC =120°.动点E 、F 分别从点B 、D 同时出发,都以0.5cm/s 的速度向点A 、C 运动,连接AF 、CE ,分别取AF 、CE 的中点G 、H .设运动的时间为ts (0<t <4). (1)求证:AF ∥CE ;(2)当t 为何值时,△ADF 32; (3)连接GE 、FH .当t 为何值时,四边形EHFG 为菱形.24.已知正方形ABCD .(1)点P 为正方形ABCD 外一点,且点P 在AB 的左侧,45APB ∠=︒. ①如图(1),若点P 在DA 的延长线上时,求证:四边形APBC 为平行四边形. ②如图(2),若点P 在直线AD 和BC 之间,以AP ,AD 为邻边作APQD □,连结AQ .求∠PAQ 的度数.(2)如图(3),点F 在正方形ABCD 内且满足BC=CF ,连接BF 并延长交AD 边于点E ,过点E 作EH ⊥AD 交CF 于点H ,若EH=3,FH=1,当13AE CF =时.请直接写出HC 的长________.25.如图平行四边形ABCD ,E ,F 分别是AD ,BC 上的点,且AE =CF ,EF 与AC 交于点O . (1)如图①.求证:OE =OF ;(2)如图②,将平行四边形ABCD (纸片沿直线EF 折叠,点A 落在A 1处,点B 落在点B 1处,设FB 交CD 于点G .A 1B 分别交CD ,DE 于点H ,P .请在折叠后的图形中找一条线段,使它与EP 相等,并加以证明;(3)如图③,若△ABO 是等边三角形,AB =4,点F 在BC 边上,且BF =4.则CFOF= (直接填结果).26.如图①,已知正方形ABCD 的边长为3,点Q 是AD 边上的一个动点,点A 关于直线BQ 的对称点是点P ,连接QP 、DP 、CP 、BP ,设AQ =x . (1)BP +DP 的最小值是_______,此时x 的值是_______; (2)如图②,若QP 的延长线交CD 边于点M ,并且∠CPD =90°.①求证:点M是CD的中点;②求x的值.(3)若点Q是射线AD上的一个动点,请直接写出当△CDP为等腰三角形时x的值.27.如图1,在正方形ABCD(正方形四边相等,四个角均为直角)中,AB=8,P为线段BC上一点,连接AP,过点B作BQ⊥AP,交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交AD于点N.(1)求证:BP=CQ;(2)若BP=13PC,求AN的长;(3)如图2,延长QN交BA的延长线于点M,若BP=x(0<x<8),△BMC'的面积为S,求S与x之间的函数关系式.28.在矩形ABCD中,BE平分∠ABC交CD边于点E.点F在BC边上,且FE⊥AE.(1)如图1,①∠BEC=_________°;②在图1已有的三角形中,找到一对全等的三角形,并证明你的结论;(2)如图2,FH∥CD交AD于点H,交BE于点M.NH∥BE,NB∥HE,连接NE.若AB=4,AH=2,求NE的长.29.如图,在长方形ABCD 中,AB =CD =6cm ,BC =10cm ,点P 从点B 出发,以2cm /秒的速度沿BC 向点C 运动,设点P 的运动时间为t 秒: (1)PC = cm .(用t 的代数式表示) (2)当t 为何值时,△ABP ≌△DCP ?(3)当点P 从点B 开始运动,同时,点Q 从点C 出发,以vcm /秒的速度沿CD 向点D 运动,是否存在这样v 的值,使得△ABP 与△PQC 全等?若存在,请求出v 的值;若不存在,请说明理由.30.如图,在平行四边形ABCD 中,BAD ∠的平分线交BC 于点E ,交DC 的延长线于F ,以EC CF 、为邻边作平行四边形ECFG 。
2018-2019年八年级下第二次月考数学试题(含答案)

初二年级第二学期第二次月考数学试卷一、 选择题(每小题2分,共30分)1. 下列式子中,属于最简二次根式的是( )A.9B.7 C. 20D.312. 在菱形AB C D 中,∠A :∠B :∠C :∠D 的值可以是( )A. 1:2:3:4B. 1:2:2:1 C . 1:2:1:2 D. 1:1:2:2 3. 三角形的三边长分别为6,8,10,它的最短边上的高为( )A. 6B. 4.5C. 2.4D. 84. 矩形的面积为12cm 2,周长为14cm ,则它的对角线长为( )A. 5cmB. 6cmC.26 cmD. 33cm5. 如图,EF 过矩形AB C D 对角线的交点O ,且分别交AB 、C D 于E 、F ,那么阴影部分的面积是矩形AB C D 的面积的( )A.51 B.41 C. 31 D.1036. 直角三角形的两直角边分别为5cm ,12cm ,其中斜边上的高为( )A. 6cmB. 8.5cmC. 1330cmD. 1360cm7. 下列计算正确的是( )A. 12)3(4916)9)(16(=-⨯-=-⋅=--B.10)10(2-=-C.13585822=+=+D.749)2425)(2425(242522==-+=-8. 如图:在△AB C 中,∠C =90°,AB =13,B C =5,则以A C 为直径的半圆面积为( )A. 6πB. 12πC. 36πD. 18π 9. 下列命题中,真命题是( )A. 两条对角线相等的四边形是矩形B. 两条对角线互相垂直的四边形是菱形C . 两条对角线互相垂直且相等的四边形是矩形 D. 两条对角线互相平分的四边形是平行四边形10. 如图,将一个边长分别为4、8的长方形纸片AB C D 折叠,使C点和A 点重合,则EB 的长是( )A. 3B. 4C.5D. 511. 如图,在直角坐标系中,将长方形OAB C 沿OB 对折,使点A 落在A 1处,已知OA =3,AB =1,则点A 1的坐标是( )A. (23,23) B. (23,3) C.(23,23) D. (21,23) 12. 如图,在△AB C 中,AB =A C =5,D 是B C 上的点,DE ∥AB 于点F ,那么四边形AFDE 的周长是( ) A. 5 B. 10 C. 15 D. 2013. 若顺次连结四边形AB C D 各边中点所得四边形是矩形,则四边形AB C D 必定是( ) A. 菱形 B. 对角线相互垂直的四边形 C. 正方形 D. 对角线相等的四边形14. 直角三角形中一直角边的长为10,另两边长为连续偶数,则直角三角形的周长为( ) A. 49 B. 17 C. 60 D. 不能确定15. 如图所示,正方形AB C D 的面积为12,△ABE 是等边三角形,点E在正方形AB C D 内,在对角线A C 上有一点P ,使PD +PE 的和最小,则这个最小值为( )A. 32B. 62C. 3D.6二、 填空题(每小题3分,共12分)16. 若x 31-在实数范围内有意义,则x 的取值范围是___________________。
八年级第二学期 第二次月考检测数学试卷含答案
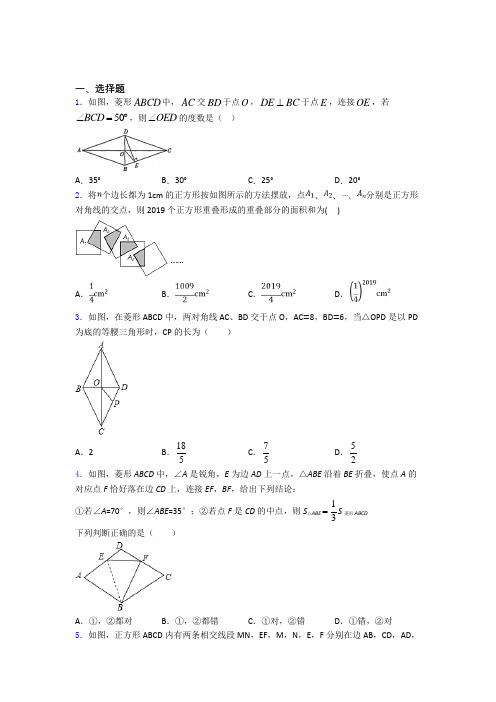
一、选择题1.如图,菱形ABCD中,AC交BD于点O,DE BC⊥于点E,连接OE,若50BCD∠=︒,则OED∠的度数是()A.35°B.30°C.25°D.20°2.将个边长都为1cm的正方形按如图所示的方法摆放,点分别是正方形对角线的交点,则2019个正方形重叠形成的重叠部分的面积和为( )A.B.C.D.3.如图,在菱形ABCD中,两对角线AC、BD交于点O,AC=8,BD=6,当△OPD是以PD 为底的等腰三角形时,CP的长为()A.2 B.185C.75D.524.如图,菱形ABCD中,∠A是锐角,E为边AD上一点,△ABE沿着BE折叠,使点A的对应点F恰好落在边CD上,连接EF,BF,给出下列结论:①若∠A=70°,则∠ABE=35°;②若点F是CD的中点,则S△ABE13=S菱形ABCD下列判断正确的是()A.①,②都对B.①,②都错C.①对,②错D.①错,②对5.如图,正方形ABCD内有两条相交线段MN,EF,M,N,E,F分别在边AB,CD,AD,BC 上.小明认为:若MN =EF ,则MN ⊥EF ;小亮认为:若MN ⊥EF ,则MN =EF ,你认为( )A .仅小明对B .仅小亮对C .两人都对D .两人都不对6.已知,在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点1B 在y 轴上,点1C 、1E 、2E 、2C 、3E 、4E 、3C 均在x 轴正半轴上,若已知正方形1111D C B A 的边长为1,1160B C O ︒∠=,且112233////B C B C B C ,则点3A 的坐标是( )A .331(3,)++B .333(3,)2++C .331(3,)2++D .333(3,)++ 7.如图,正方形ABCD (四边相等、四内角相等)中,AD =5,点E 、F 是正方形ABCD 内的两点,且AE =FC =4,BE =DF =3,则EF 的平方为( )A .2B .125C .3D .48.如图,点O (0,0),A (0,1)是正方形1OAA B 的两个顶点,以1OA 对角线为边作正方形121OA A B ,再以正方形的对角线2OA 作正方形121OA A B ,…,依此规律,则点8A 的坐标是( )A .(-8,0)B .(0,8)C .(0,82)D .(0,16)9.如图,90MON ∠=︒,矩形ABCD 在MON ∠的内部,顶点A ,B 分别在射线OM ,ON 上,4AB =,2BC =,则点D 到点O 的最大距离是( )A .222-B .222+C .252-D .22+10.如图,在平行四边形ABCD 中,按以下步骤作图:①以A 为圆心,AB 长为半径画弧,交边AD 于点;②再分别以B ,F 为圆心画弧,两弧交于平行四边形ABCD 内部的点G 处;③连接AG 并延长交BC 于点E ,连接BF ,若BF =3,AB =2.5,则AE 的长为( )A .2B .4C .8D .5二、填空题11.如图,在平面直角坐标系中,矩形ABCO 的边CO 、OA 分别在x 轴、y 轴上,点E 在边BC 上,将该矩形沿AE 折叠,点B 恰好落在边OC 上的F 处.若OA =8,CF =4,则点E 的坐标是_____.12.如图,ABC ∆是边长为1的等边三角形,取BC 边中点E ,作//ED AB ,//EF AC ,得到四边形EDAF ,它的周长记作1C ;取BE 中点1E ,作11//E D FB ,11//E F EF ,得到四边形111E D FF ,它的周长记作2C .照此规律作下去,则2020C =______.13.如图,在正方形ABCD 中,点,E F 将对角线AC 三等分,且6AC =.点P 在正方形的边上,则满足5PE PF +=的点P 的个数是________个.14.在锐角三角形ABC 中,AH 是边BC 的高,分别以AB ,AC 为边向外作正方形ABDE 和正方形ACFG ,连接CE ,BG 和EG ,EG 与HA 的延长线交于点M ,下列结论:①BG=CE ;②BG ⊥CE ;③AM 是△AEG 的中线;④∠EAM=∠ABC .其中正确的是_________.15.如图,菱形ABCD 的边长是4,60ABC ∠=︒,点E ,F 分别是AB ,BC 边上的动点(不与点A ,B ,C 重合),且BE BF =,若//EG BC ,//FG AB ,EG 与FG 相交于点G ,当ADG 为等腰三角形时,BE 的长为________.16.如图,在平面直角坐标系中,直线112y x =+与x 轴、y 轴分别交于A ,B 两点,以AB 为边在第二象限内作正方形ABCD ,则D 点坐标是_______;在y 轴上有一个动点M ,当MDC △的周长值最小时,则这个最小值是_______.17.如图,在平行四边形ABCD 中,AC ⊥AB ,AC 与BD 相交于点O ,在同一平面内将△ABC 沿AC 翻折,得到△AB’C ,若四边形ABCD 的面积为24cm 2,则翻折后重叠部分(即S △ACE ) 的面积为________cm 2.18.如图,在矩形ABCD 中,16AB =,18BC =,点E 在边AB 上,点F 是边BC 上不与点B 、C 重合的一个动点,把EBF △沿EF 折叠,点B 落在点B '处.若3AE =,当CDB '是以DB '为腰的等腰三角形时,线段DB '的长为__________.19.在平面直角坐标系xOy 中,点A 、B 分别在x 轴、y 轴的正半轴上运动,点M 为线段AB 的中点.点D 、E 分别在x 轴、y 轴的负半轴上运动,且DE =AB =10.以DE 为边在第三象限内作正方形DGFE ,则线段MG 长度的最大值为_____.20.定理:直角三角形斜边上的中线等于斜边的一半,即:如图1,在Rt △ABC 中,∠ACB =90°,若点D 是斜边AB 的中点,则CD =12AB ,运用:如图2,△ABC 中,∠BAC =90°,AB =2,AC =3,点D 是BC 的中点,将△ABD 沿AD 翻折得到△AED 连接BE ,CE ,DE ,则CE 的长为_____.三、解答题21.综合与实践.问题情境:如图①,在纸片ABCD □中,5AD =,15ABCD S =,过点A 作AE BC ⊥,垂足为点E ,沿AE 剪下ABE △,将它平移至DCE '的位置,拼成四边形AEE D '.独立思考:(1)试探究四边形AEE D '的形状.深入探究:(2)如图②,在(1)中的四边形纸片AEE D '中,在EE '.上取一点F ,使4EF =,剪下AEF ,将它平移至DE F ''的位置,拼成四边形AFF D ',试探究四边形AFF D '的形状;拓展延伸:(3)在(2)的条件下,求出四边形AFF D '的两条对角线长;(4)若四边形ABCD 为正方形,请仿照上述操作,进行一次平移,在图③中画出图形,标明字母,你能发现什么结论,直接写出你的结论.22.如图,平行四边形ABCD 的对角线AC BD 、交于点O ,分别过点C D 、作//,//CF BD DF AC ,连接BF 交AC 于点E .(1)求证: FCE BOE ≌;(2)当ADC ∠等于多少度时,四边形OCFD 为菱形?请说明理由.23.如图,点E 为▱ABCD 的边AD 上的一点,连接EB 并延长,使BF =BE ,连接EC 并延长,使CG =CE ,连接FG .H 为FG 的中点,连接DH ,AF .(1)若∠BAE =70°,∠DCE =20°,求∠DEC 的度数;(2)求证:四边形AFHD 为平行四边形;(3)连接EH ,交BC 于点O ,若OC =OH ,求证:EF ⊥EG .24.如下图1,在平面直角坐标系中xoy 中,将一个含30的直角三角板如图放置,直角顶点与原点重合,若点A 的坐标为()1,0-,30ABO ∠=︒.(1)旋转操作:如下图2,将此直角三角板绕点O 顺时针旋转30时,则点B 的坐标为 . (2)问题探究:在图2的基础上继续将直角三角板绕点O 顺时针60︒,如图3,在AB 边上的上方以AB 为边作等边ABC ,问:是否存在这样的点D ,使得以点A 、B 、C 、D 四点为顶点的四边形构成为菱形,若存在,请直接写出点D 所有可能的坐标;若不存在,请说明理由.(3)动点分析:在图3的基础上,过点O 作OP AB ⊥于点P ,如图4,若点F 是边OB 的中点,点M 是射线PF 上的一个动点,当OMB △为直角三角形时,求OM 的长.25.如图,在平行四边形ABCD 中,BAD ∠的平分线交BC 于点E ,交DC 的延长线于F ,以EC 、CF 为邻边作平行四边形ECFG .(1)求证:四边形ECFG 是菱形;(2)连结BD 、CG ,若120ABC ∠=︒,则BDG ∆是等边三角形吗?为什么? (3)若90ABC ∠=︒,10AB =,24AD =,M 是EF 的中点,求DM 的长.26.探究:如图①,△ABC 是等边三角形,在边AB 、BC 的延长线上截取BM =CN ,连结MC 、AN ,延长MC 交AN 于点P .(1)求证:△ACN ≌△CBM ;(2)∠CPN = °;(给出求解过程)(3)应用:将图①的△ABC 分别改为正方形ABCD 和正五边形ABCDE ,如图②、③,在边AB 、BC 的延长线上截取BM =CN ,连结MC 、DN ,延长MC 交DN 于点P ,则图②中∠CPN = °;(直接写出答案)(4)图③中∠CPN = °;(直接写出答案)(5)拓展:若将图①的△ABC 改为正n 边形,其它条件不变,则∠CPN = °(用含n 的代数式表示,直接写出答案).27.如图,ABCD 中,60ABC ∠=︒,连结BD ,E 是BC 边上一点,连结AE 交BD 于点F .(1)如图1,连结AC ,若6AB AE ==,:5:2BC CE =,求ACE △的面积; (2)如图2,延长AE 至点G ,连结AG 、DG ,点H 在BD 上,且BF DH =,AF AH =,过A 作AM DG ⊥于点M .若180ABG ADG ∠+∠=︒,求证:3BG GD +=.28.如图①,在等腰Rt ABC 中,90BAC ∠=,点E 在AC 上(且不与点A 、C 重合),在ABC 的外部作等腰Rt CED ,使90CED ∠=,连接AD ,分别以AB ,AD 为邻边作平行四边形ABFD ,连接AF .()1请直接写出线段AF ,AE 的数量关系;()2①将CED 绕点C 逆时针旋转,当点E 在线段BC 上时,如图②,连接AE ,请判断线段AF ,AE 的数量关系,并证明你的结论;②若25AB =,2CE =,在图②的基础上将CED 绕点C 继续逆时针旋转一周的过程中,当平行四边形ABFD 为菱形时,直接写出线段AE 的长度.29.已知,矩形ABCD 中,4,8AB cm BC cm ==,AC 的垂直平分EF 线分别交AD BC 、于点E F 、,垂足为O .(1)如图1,连接AF CE 、,求证:四边形AFCE 为菱形;(2)如图2,动点P Q 、分别从A C 、两点同时出发,沿AFB △和CDE △各边匀速运动一周,即点P 自A F B A →→→停止,点O 自C D E C →→→停止.在运动过程中,①已知点P 的速度为每秒5cm ,点Q 的速度为每秒4cm ,运动时间为t 秒,当A C P Q 、、、四点为顶点的四边形是平行四边形时,则t =____________.②若点P Q 、的运动路程分别为a b 、 (单位:,0cm ab ≠),已知AC P Q 、、、四点为顶点的四边形是平行四边形,则a 与b 满足的数量关系式为____________.30.已知三角形纸片ABC 的面积为48,BC 的长为8.按下列步骤将三角形纸片ABC 进行裁剪和拼图:第一步:如图1,沿三角形ABC 的中位线DE 将纸片剪成两部分.在线段DE 上任意..取一点F ,在线段BC 上任意..取一点H ,沿FH 将四边形纸片DBCE 剪成两部分; 第二步:如图2,将FH 左侧纸片绕点D 旋转180°,使线段DB 与DA 重合;将FH 右侧纸片绕点E 旋转180°,使线段EC 与EA 重合,再与三角形纸片ADE 拼成一个与三角形纸片ABC面积相等的四边形纸片.图1 图2(1)当点F ,H 在如图2所示的位置时,请按照第二步的要求,在图2中补全拼接成的四边形;(2)在按以上步骤拼成的所有四边形纸片中,其周长的最小值为_________.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【解析】【分析】根据直角三角形的斜边中线性质可得OE BE OD ==,根据菱形性质可得1652DBE ABC ︒∠=∠=,从而得到OEB ∠度数,再依据90OED OEB ︒∠=-∠即可. 【详解】 解:∵四边形ABCD 是菱形,50BCD ︒∠=,∵O 为BD 中点,1652DBE ABC ︒∠=∠=. DE BC ⊥,∴在 Rt BDE ∆中,OE BE OD ==,65OEB OBE ︒∴∠=∠=.906525OED ︒︒︒∴∠=-=.故选:C .【点睛】本题主要考查了菱形的性质、直角三角形斜边中线的性质,解决这类问题的方法是四边形转化为三角形.2.B解析:B【解析】【分析】 根据题意可得,阴影部分的面积是正方形的面积的,已知两个正方形可得到一个阴影部分,则n 个这样的正方形重叠部分即为n-1阴影部分的和.由此即可解答.【详解】 由题意可得一个阴影部分面积等于正方形面积的 , 即一个阴影部分的面积为如图,5个这样的正方形重叠部分(阴影部分)的面积和为×4, ∴n 个这样的正方形重叠部分(阴影部分)的面积和为×(n-1), ∴2019个正方形重叠形成的重叠部分的面积和为×(2019-1)=. 故选B .【点睛】本题考查了正方形的性质,解决本题的关键是得到n 个这样的正方形重叠部分(阴影部分)的面积和的计算方法,难点是求得一个阴影部分的面积. 3.C解析:C【解析】【分析】过O 作OE ⊥CD 于E .根据菱形的对角线互相垂直平分得出OB ,OC 的长,AC ⊥BD ,再利用勾股定理列式求出CD ,然后根据三角形的面积公式求出OE .在Rt △OED 中,利用勾股定理求出ED .根据等腰三角形三线合一的性质得出PE ,利用CP =CD -PD 即可得出结论.【详解】过O 作OE ⊥CD 于E .∵菱形ABCD 的对角线AC 、BD 相交于点O ,∴OB 12=BD 12=⨯6=3,OA =OC 12=AC 12=⨯8=4,AC ⊥BD ,由勾股定理得:CD 2222OD OC 34=+=+=5. ∵12OC ×OD =12CD ×OE ,∴12=5OE ,∴OE =2.4.在Rt △ODE 中,DE 22OD OE -223 2.4-=1.8.∵OD =OP ,∴PE =ED =1.8,∴CP =CD -PD =5-1.8-1.8=1.4=75.故选C .【点睛】本题考查了菱形的性质,等腰三角形的性质,勾股定理,求出OE 的长是解题的关键.4.A解析:A【解析】【分析】只要证明BF BC =,可得ABF BFC C 70∠∠∠===,即可得出ABE 35∠=;延长EF 交BC 的延长线于M ,只要证明DEF ≌CMF ,推出EF FM =,可得EMB BCDE S S =四边形,BEF MBE 1S S 2=,推出ABE ABCD 1S S 3菱形=. 【详解】 ①∵四边形ABCD 是菱形,∴AB ∥CD ,∠C=∠A=70°.∵BA=BF=BC ,∴∠BFC=∠C=70°,∴∠ABF=∠BFC=70°,∴∠ABE 12=∠ABF=35°,故①正确;②如图,延长EF 交BC 的延长线于M ,∵四边形ABCD 是菱形,F 是CD 中点,∴DF=CF ,∠D=∠FCM ,∠EFD=∠MFC ,∴△DEF ≌△CMF ,∴EF=FM ,∴S 四边形BCDE =S △EMB ,S △BEF 12=S △MBE ,∴S △BEF 12=S 四边形BCDE ,∴S △ABE 13=S 菱形ABCD .故②正确, 故选A .【点睛】本题考查了菱形的性质、等腰三角形的判定和性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.5.C解析:C【分析】分别过点E 作EG ⊥BC 于点G ,过点M 作MP ⊥CD 于点P ,设EF 与MN 相交于点O ,MP 与EF 相交于点Q ,根据正方形的性质可得EG=MP ;对于小明的说法,先利用“HL ”证明Rt △EFG ≌Rt △MNP ,根据全等三角形对应角相等可得∠MNP=∠EFG ,再根据角的关系推出∠EQM=∠MNP ,然后根据∠MNP+∠NMP=90°得到∠NMP+∠EQM=90°,从而得到∠MOQ=90°,根据垂直的定义即可证得MN ⊥EF ;对于小亮的说法,先推出∠EQM=∠EFG ,∠EQM=∠MNP ,然后得到∠EFG=∠MNP ,然后利用“角角边”证明△EFG ≌△MNP ,根据全等三角形对应边相等可得EF=MN .【详解】如图,过点E 作EG ⊥BC 于点G ,过点M 作MP ⊥CD 于点P ,设EF 与MN 相交于点O ,MP 与EF 相交于点Q ,∵四边形ABCD 是正方形,∴EG=MP ,对于小明的说法:在Rt △EFG 和Rt △MNP 中,MN EF EG MP ⎧⎨⎩==, ∴Rt △EFG ≌Rt △MNP (HL ),∴∠MNP=∠EFG ,∵MP ⊥CD ,∠C=90°,∴MP ∥BC ,∴∠EQM=∠EFG=∠MNP ,又∵∠MNP+∠NMP=90°,∴∠EQM+∠NMP=90°,在△MOQ 中,∠MOQ=180°-(∠EQM+∠NMP )=180°-90°=90°,∴MN ⊥EF ,故甲正确.对小亮的说法:∵MP ⊥CD ,∠C=90°,∴MP ∥BC ,∴∠EQM=∠EFG ,∵MN ⊥EF ,∴∠NMP+∠EQM=90°,又∵MP ⊥CD ,∴∠NMP+∠MNP=90°,∴∠EQM=∠MNP ,∴∠EFG=∠MNP ,在△EFG 和△MNP 中,90EFG MNP EGF MPN EG MP ∠∠⎧⎪∠∠︒⎨⎪⎩==== , ∴△EFG ≌△MNP (AAS ),∴MN=EF ,故小亮的说法正确,综上所述,两个人的说法都正确.故选C .【点睛】本题考查了正方形的性质、全等三角形的判定与性质、同角的余角相等的性质,作出辅助线,构造出全等三角形是解题的关键,通常情况下,求两边相等,或已知两边相等,都是想法把这两条线段转化为全等三角形的对应边进行求解.6.C解析:C【分析】根据两直线平行,同位角相等可得∠B 3C 3O=∠B 2C 2O=∠B 1C 1O=60°,然后利用三角形全等可得B 2E 2=E 1E 2=D 1E 1=E 3C 2,E 2C 2=E 3E 4=B 3E 4,解直角三角形求出OC 1、C 1E 、E 1E 2、E 2C 2、C 2E 3、E 3E 4、E 4C 3,再求出B 3C 3,过点A 3延长正方形的边交x 轴于M ,过点A 3作A 3N ⊥x 轴于N ,先求出A 3M ,再解直角三角形求出A 3N 、C 3N ,然后求出ON ,再根据点A 3在第一象限写出坐标即可.【详解】解∵B 1C 1∥B 2C 2∥B 3C 3,∴∠B 3C 3O =∠B 2C 2O =∠B 1C 1O =60°,∵正方形A 1B 1C 1D 1的边长为1,B 1C 1=C 1D 1,∠B 1C 1D 1=90°,∴∠C 1B 1O=∠D 1C 1E 1=30°,∴△C 1B 1O ≌△D 1C 1E 1;∴B 1O=C 1E 1,OC 1=D 1E 1,同理可得B 2E 2=E 1E 2=D 1E 1=E 3C 2;E 2C 2=E 3E 4=B 3E 4;111122223111111222OC D E E E B E C E B C ∴======⨯=11111222C E D C ===2234342231333236E C E E B E B E ====⨯= 433433316E C B E ==⨯= 3343112263B C E C ∴==⨯= 过点A 3延长正方形的边交x 轴于M ,过点A 3作A 3N ⊥x 轴于N ,则3323233333311333333339A M A D C DBC B C +=+=+=+⨯= 33333331A N A M ++===3313313329218C M A M +=== 34313333123C N E M C M ⎛⎫+-∴=-=-= ⎪ ⎪⎝⎭111122223343ON OC C E E E E C C E E E C N =++++++13131313133222626662'=+++++++= ∵点A 3在第一象限,∴点A 3的坐标是33132+⎭. 故选C.【点睛】本题考查正方形的性质,坐标与图形性质,全等三角形的判定与性质,30°角的直角三角形.熟练掌握有30°角的直角三角形各边之间的数量关系是解决本题的关键.7.A解析:A【分析】根据AB=5,AE=4,BE=3,可以确定△ABE 为直角三角形,延长BE 构建出直角三角形,在利用勾股定理求出EF的平方即可.【详解】∵四边形ABCD是正方形,∴AB=BC=CD=AD=5,如图,延长BE交CF于点G,∵AB=5,AE=4,BE=3,∴AE2+BE2=AB2,∴△ABE是直角三角形,同理可得△DFC是直角三角形,∵AE=FC=4,BE=DF=3,AB=CD=5,∴△ABE≌△CDF,∴∠BAE=∠DCF,∵∠ABC=∠AEB=902,∴∠CBG=∠BAE,同理可得,∠BCG=∠CDF=∠ABE,△ABE≌△BCG,∴CG=BE=3,BG=AE=4,∴EG=4-3=1,GF=4-3=1,∴EF2=EG2+GF2=1+1=2故选择:A【点睛】此题考查三角形的判定,勾股定理的运用,根据已知条件构建直角三角形求值是解题的关键.8.D解析:D【分析】根据题意和图形可看出每经过一次变化,都顺时针旋转45°2,可求出从A 到A3变化后的坐标,再求出A1、A2、A3、A4、A5,继而得出A8坐标即可.【详解】解:根据题意和图形可看出每经过一次变化,都顺时针旋转45°2∵从A到3A经过了3次变化,∵45°×3=135°,1×32=2,∴点3A 所在的正方形的边长为22,点3A 位置在第四象限,∴点3A 的坐标是(2,-2),可得出:1A 点坐标为(1,1),2A 点坐标为(0,2),3A 点坐标为(2,-2),4A 点坐标为(0,-4),5A 点坐标为(-4,-4),6A (-8,0),A 7(-8,8),8A (0,16),故选D.【点睛】本题考查了规律题,点的坐标,观察出每一次的变化特征是解答本题的关键.9.B解析:B【分析】取DC 的中点E ,连接OE 、DE 、OD ,根据三角形的任意两边之和大于第三边可知当O 、E 、D 三点共线时,点D 到点O 的距离最大,再根据勾股定理求出DE 的长,根据直角三角形斜边上的中线等于斜边的一半求出OE 的长,两者相加即可得解.【详解】取AB 中点E ,连接OE 、DE 、OD ,90MON ∠=︒,122OE AB ∴==. 在Rt DAE ∆中,利用勾股定理可得22DE =.在ODE ∆中,根据三角形三边关系可知DE OE OD +>,∴当O 、E 、D 三点共线时,OD 最大为222OE DE +=+.故选B .【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半得到性质,三角形的三边关系,矩形的性质,勾股定理,根据三角形的三边关系判断出点O 、E 、D 三点共线时,点D 到点O 的距离最大是解题的关键.10.B解析:B【分析】连接EF ,先证AF =AB =BE ,得四边形ABEF 是菱形,据此知AE 与BF 互相垂直平分,继而得OB 的长,由勾股定理求得OA 的长,继而得出答案.【详解】由题意得:AF =AB ,AE 为∠BAD 的角平分线,则∠BAE =∠FAE .又∵四边形ABCD 是平行四边形,则AD ∥BC ,∠BAE =∠FAE =∠BEA ,∴AF =AB =BE . 连接EF ,则四边形ABEF 是菱形,∴AE 与BF 互相垂直平分,设AE 与BF 相交于点O ,OB 2BF ==1.5.在Rt △AOB 中,OA 22222515AB OB =-=-=..2,则AE =2OA =4.故选B .【点睛】本题考查了作图﹣复杂作图,解题的关键是掌握菱形的性质与判定,平行四边形的性质,角平分线的尺规作图方法等.二、填空题11.(-10,3)【解析】试题分析:根据题意可知△CEF∽△OFA,可根据相似三角形的性质对应边成比例,可求得OF=2CE ,设CE=x ,则BE=8-x ,然后根据折叠的性质,可得EF=8-x ,根据勾股定理可得2224(8)x x +=-,解得x =3,则OF=6,所以OC=10,由此可得点E 的坐标为(-10,3). 故答案为:(-10,3)12.201812【分析】 根据几何图形特征,先求出1C 、2C 、3C ,根据求出的结果,找出规律,从而得出2020C .【详解】∵点E 是BC 的中点,ED ∥AB ,EF ∥AC∴DE 、EF 是△ABC 的中位线∵等边△ABC 的边长为1∴AD=DE=EF=AF =12 则1C =1422⨯= 同理可求得:2C =1,3C =12发现规律:规律为依次缩小为原来的12 ∴2020C =201812 故答案为:201812.【点睛】 本题考查找规律和中位线的性质,解题关键是求解出几组数据,根据求解的数据寻找规律.13.8个【分析】作点F 关于BC 的对称点M ,连接FM 交BC 于点N ,连接EM ,交BC 于点H ,可得点H 到点E 和点F 的距离之和最小,可求最小值,即可求解.【详解】如图,作点F 关于BC 的对称点M ,连接FM 交BC 于点N ,连接EM ,交BC 于点H , ∵点E ,F 将对角线AC 三等分,且AC =6,∴EC =4,FC =2=AE ,∵点M 与点F 关于BC 对称,∴CF =CM =2,∠ACB =∠BCM =45°,∴∠ACM =90°,∴EM则在线段BC 存在点H 到点E 和点F 的距离之和最小为5,在点H 右侧,当点P 与点C 重合时,则PE +PF =4+2=6,∴点P 在CH 上时,PE +PF ≤6,在点H 左侧,当点P 与点B 重合时,∵FN ⊥BC ,∠ABC =90°,∴FN ∥AB ,∴△CFN ∽△CAB , ∴FN CN CF 1===AB CB CA 3,∵AB =BC =2AC =∴FN =13AB ,CN =13BC∴BN =BC -CN =,BF =,∵AB=BC,CF=AE,∠BAE=∠BCF,∴△ABE≌△CBF(SAS),∴BE=BF=10,∴PE+PF=210,∴点P在BH上时,25<PE+PF<210,∴在线段BC上点H的左右两边各有一个点P使PE+PF=5,同理在线段AB,AD,CD上都存在两个点使PE+PF=5.即共有8个点P满足PE+PF=5,故答案为8.【点睛】本题考查了正方形的性质,最短路径问题,在BC上找到点H,使点H到点E和点F的距离之和最小是本题的关键.14.①②③④【分析】根据正方形的性质和SAS可证明△ABG≌△AEC,然后根据全等三角形的性质即可判断①;设BG、CE相交于点N,AC、BG相交于点K,如图1,根据全等三角形对应角相等可得∠ACE=∠AGB,然后根据三角形的内角和定理可得∠CNG=∠CAG=90°,于是可判断②;过点E作EP⊥HA的延长线于P,过点G作GQ⊥AM于Q,如图2,根据余角的性质即可判断④;利用AAS即可证明△ABH≌△EAP,可得EP=AH,同理可证GQ=AH,从而得到EP =GQ,再利用AAS可证明△EPM≌△GQM,可得EM=GM,从而可判断③,于是可得答案.【详解】解:在正方形ABDE和ACFG中,AB=AE,AC=AG,∠BAE=∠CAG=90°,∴∠BAE+∠BAC=∠CAG+∠BAC,即∠CAE=∠BAG,∴△ABG≌△AEC(SAS),∴BG=CE,故①正确;设BG、CE相交于点N,AC、BG相交于点K,如图1,∵△ABG ≌△AEC ,∴∠ACE =∠AGB ,∵∠AKG =∠NKC ,∴∠CNG =∠CAG =90°,∴BG ⊥CE ,故②正确;过点E 作EP ⊥HA 的延长线于P ,过点G 作GQ ⊥AM 于Q ,如图2,∵AH ⊥BC ,∴∠ABH +∠BAH =90°,∵∠BAE =90°,∴∠EAP +∠BAH =90°,∴∠ABH =∠EAP ,即∠EAM =∠ABC ,故④正确;∵∠AHB =∠P =90°,AB =AE ,∴△ABH ≌△EAP (AAS ),∴EP =AH ,同理可得GQ =AH ,∴EP =GQ ,∵在△EPM 和△GQM 中,90P MQG EMP GMQ EP GQ ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,∴△EPM ≌△GQM (AAS ),∴EM =GM ,∴AM 是△AEG 的中线,故③正确.综上所述,①②③④结论都正确.故答案为:①②③④.【点睛】本题考查了正方形的性质、三角形的内角和定理以及全等三角形的判定和性质,作辅助线构造出全等三角形是难点,熟练掌握全等三角形的判定和性质是关键.15.83或4433-【分析】连接AC交BD于O,由菱形的性质可得AB=BC=4,∠ABD=30°,AC⊥BD,BO=DO,AO=CO,可证四边形BEGF是菱形,可得∠ABG=30°,可得点B,点G,点D三点共线,由直角三角形性质可求BD=43,AC=4,分两种情况讨论,利用等腰三角形的性质可求解.【详解】如图,连接AC交BD于O,∵菱形ABCD的边长是4,∠ABC=60°,∴AB=BC=4,∠ABD=30°,AC⊥BD,BO=DO,AO=CO,∵EG∥BC,FG∥AB,∴四边形BEGF是平行四边形,又∵BE=BF,∴四边形BEGF是菱形,∴∠ABG=30°,∴点B,点G,点D三点共线,∵AC⊥BD,∠ABD=30°,∴AO=12AB=2,22224223AB AO--=∴BD=3AC=4,同理可求3BE,即3,若AD=DG'=4时,∴BG'=BD-DG'=434,∴BE'4344343-==;若AG''=G''D时,过点G''作G''H⊥AD于H,∴AH=HD=2,∵∠ADB=30°,G''H ⊥AD ,∴DG''=2HG'',∵222HD HG''DG''+=,解得:HG''=,DG''=2HG''=∴BG''=BD-DG''=33-=, ∴BE''=83,综上所述:BE 为83或4- 【点睛】本题考查了菱形的性质,含30度角的直角三角形的性质,勾股定理等知识,利用分类讨论思想解决问题是本题的关键.16.(3,2)-【分析】如图(见解析),先根据一次函数的解析式可得点A 、B 的坐标,从而可得OA 、OB 、AB 的长,再根据正方形的性质可得90BAD ∠=︒,DA AB =,然后根据三角形全等的判定定理与性质可得,AE OB DE OA ==,由此即可得出点D 的坐标;同样的方法可求出点C 的坐标,再根据轴对称的性质可得点C '的坐标,然后根据轴对称的性质和两点之间线段最短得出MDC △的周长值最小时,点M 的位置,最后利用两点之间的距离公式、三角形的周长公式即可得.【详解】如图,过点D 作DE x ⊥轴于点E ,作点C 关于y 轴的对称点C ',交y 轴于点F ,连接C D ',交y 轴于点M ',连接C M ',则CF y ⊥轴 对于112y x =+ 当0y =时,1102x +=,解得2x =-,则点A 的坐标为(2,0)A - 当0x =时,1y =,则点B 的坐标为(0,1)B2,1,OA OB AB ∴====四边形ABCD 是正方形90BAD ∴∠=︒,CD DA AB ===90DAE OAB ABO OAB ∴∠+∠=∠+∠=︒DAE ABO ∴∠=∠在ADE 和BAO 中,90AED BOA DAE ABO DA AB ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩()ADE BAO AAS ∴≅1,2AE OB DE OA ∴====213OE OA AE ∴=+=+=则点D 的坐标为(3,2)D -同理可证:CBF BAO ≅1,2CF OB BF OA ∴====123OF OB BF ∴=+=+=则点C 的坐标为(1,3)C -由轴对称的性质得:点C '的坐标为(1,3)C ',且CM C M '=MDC ∴△的周长为5CD DM CM DM C M'++=++由两点之间线段最短得:当点M 与点M '重合时,DM C M '+取得最小值DC ' (3,2),(1,3)D C '-22(31)(23)17DC '∴=--+-=则MDC △的周长的最小值为5517DC '+=+故答案为:(3,2)-,517+.【点睛】本题是一道较难的综合题,考查了正方形的性质、三角形全等的判定定理与性质、轴对称的性质等知识点,正确找出MDC △的周长最小时,点M 的位置是解题关键. 17.6【分析】由折叠的性质可得∠BAC=∠B'AC=90°,AB=AB',S △ABC =S △AB'C =12cm 2,可证点B ,点A ,点B'三点共线,通过证明四边形ACDB'是平行四边形,可得B'E=CE ,即可求解.【详解】解:∵四边形ABCD 是平行四边形,∴AB∥CD,S△ABC=1242=12cm2,∵在同一平面内将△ABC沿AC翻折,得到△AB′C,∴∠BAC=∠B'AC=90°,AB=AB',S△ABC=S△AB'C=12cm2,∴∠BAB'=180°,∴点B,点A,点B'三点共线,∵AB∥CD,AB'∥CD,∴四边形ACDB'是平行四边形,∴B'E=CE,∴S△ACE=12S△AB'C=6cm2,故答案为:6.【点睛】本题考查了翻折变换,平行四边形的判定和性质,证明点B,点A,点B'三点共线是本题的关键.18.16或10【分析】等腰三角形一般分情况讨论:(1)当DB'=DC=16;(2)当B'D=B'C时,作辅助线,构建平行四边形AGHD和直角三角形EGB',计算EG和B'G的长,根据勾股定理可得B'D的长;【详解】∵四边形ABCD是矩形,∴DC=AB=16,AD=BC=18.分两种情况讨论:(1)如图2,当DB'=DC=16时,即△CDB'是以DB'为腰的等腰三角形(2)如图3,当B'D=B'C时,过点B'作GH∥AD,分别交AB与CD于点G、H.∵四边形ABCD是矩形,∴AB∥CD,∠A=90°又GH∥AD,∴四边形AGHD是平行四边形,又∠A=90°,∴四边形AGHD是矩形,∴AG=DH,∠GHD=90°,即B'H⊥CD,又B'D=B'C,∴DH=HC=183CD=,AG=DH=8,∵AE=3,∴BE=EB'=AB-AE=16-3=13,EG=AG-AE=8-3=5,在Rt△EGB'中,由勾股定理得:GB′=2213512,∴B'H=GH×GB'=18-12=6,在Rt△B'HD中,由勾股定理得:B′D=226810+=综上,DB'的长为16或10.故答案为: 16或10【点睛】本题是四边形的综合题,考查了矩形的性质,勾股定理,等腰三角形一般需要分类讨论.19.10+55【分析】取DE的中点N,连结ON、NG、OM.根据勾股定理可得55NG=.在点M与G之间总有MG≤MO+ON+NG(如图1),M、O、N、G四点共线,此时等号成立(如图2).可得线段MG的最大值.【详解】如图1,取DE的中点N,连结ON、NG、OM.∵∠AOB=90°,∴OM=12AB=5.同理ON=5.∵正方形DGFE,N为DE中点,DE=10,∴222210555NG DN DG++===.在点M与G之间总有MG≤MO+ON+NG(如图1),如图2,由于∠DNG的大小为定值,只要∠DON=12∠DNG,且M、N关于点O中心对称时,M、O、N、G四点共线,此时等号成立,∴线段MG取最大值5故答案为:5【点睛】此题考查了直角三角形的性质,勾股定理,四点共线的最值问题,得出M、O、N、G四点共线,则线段MG长度的最大是解题关键.20.51313【分析】根据12•BC•AH=12•AB•AC,可得AH613,根据12AD•BO=12BD•AH,得OB=613,再根据BE=2OB 1213EC.【详解】设BE交AD于O,作AH⊥BC于H.在Rt△ABC中,∠BAC=90°,AB=2,AC=3,由勾股定理得:BC13∵点D是BC的中点,∴AD=DC=DB=132,∵12•BC•AH=12•AB•AC,∴AH=13 13,∵AE =AB ,DE =DB ,∴点A 在BE 的垂直平分线上,点D 在BE 的垂直平分线上,∴AD 垂直平分线段BE , ∵12AD •BO =12BD •AH , ∴OB =613, ∴BE =2OB =121313, ∵DE =DB=CD , ∴∠DBE=∠DEB ,∠DEC=∠DCE ,∴∠DEB+∠DEC=12×180°=90°,即:∠BEC=90°, ∴在Rt △BCE 中,EC =22BC BE - =221213(13)()13-=51313. 故答案为:513. 【点睛】本题主要考查直角三角形的性质,勾股定理以及翻折的性质,掌握“直角三角形斜边长的中线等于斜边的一半”以及面积法求三角形的高,是解题的关键.三、解答题21.(1)矩形;(2)菱形;(3)3104)见解析【分析】(1)由平移推出AD EE '=,即可证得四边形AEE D '是平行四边形,再根据AE BC ⊥,得到90AEE '∠=︒即可得到结论;(2)由平移推出AD FF '=,证得四边形AFF D '是平行四边形,根据AE EF ⊥得到90AEE '∠=︒,再根据勾股定理求出AF=5=AD ,即可证得四边形AFF D '是菱形; (3)先利用勾股定理求出22221310DF E F E D ''+=+=,再根据菱形的面积求出F A ';(4)在BC 边上取点E ,连接AE ,平移△ABE 得到△DCF ,可得四边形AEFD 是平行四边形.【详解】(1)四边形AEE D '是矩形,在ABCD □中,//AD BC ,AD BC =,由平移可知:BE CE ''=,∴BC EE '=,∴AD EE '=,∴四边形AEE D '是平行四边形,∵AE BC ⊥,∴90AEE '∠=︒,∴四边形AEE D '是矩形;(2)四边形AFF D '是菱形,在矩形AEE D '中,//AD EE ' ,AD EE '=,由平移可知:EF E F ='',∴EE FF ''=,∴AD FF '=,∴四边形AFF D '是平行四边形,∵AE EF ⊥,∴90AEE '∠=︒,在Rt AEF ,2222345AF AE EF =+=+=, ∴AF AD =,∴四边形AFF D '是菱形;(3)连接F A ',在Rt DFE '△中,22221310DF E F E D ''=+=+=,15ABCD AFF D S S '==平行四边形菱形,∴·30F A FD '=,∴310F A '=;(4)在BC 上取一点E ,连接AE ,平移△ABE 得到△DCF ,可得四边形AEFD 是平行四边形.【点睛】此题考查了平行四边形的性质,矩形的判定定理,菱形的判定及性质,平移的性质的应用,勾股定理.22.(1)见解析;(2)当ADC 满足90ADC ∠=︒时,四边形OCFD 为菱形,证明详见解析【分析】(1)证明四边形OCFD 是平行四边形,得出OD=CF ,证出OB=CF ,再证明全等即可(2)证出四边形ABCD 是矩形,由矩形的性质得出OC=OD ,即可得出四边形OCFD 为菱形.【详解】(1)证明:∵//,//CF BD DF AC ,∴四边形OCFD 是平行四边形, OBE CFE ∠=∠,∴OD CF =,∵四边形ABCD 是平行四边形,∴OB OD =,∴OB CF =,在FCE △和BOE △中, OBE CFE BEO FEC OB CF ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()FCE BOE AAS ≌.(2)当ADC 满足90ADC ∠=︒时,四边形OCFD 为菱形.理由如下:∵90ADC ∠=︒,四边形ABCD 是平行四边形,∴四边形ABCD 是矩形∴,,,OA OC OB OD AC BD ===∴OC OD =,∴四边形OCFD 为菱形【点睛】本题考查全等三角形判定与性质,平行四边形和菱形的判定与性质等知识,熟练掌握平行四边形的判定和性质和菱形的判定是解题的关键.23.(1)50°;(2)见解析;(3)见解析【分析】(1)由平行四边形的性质和平行线的判定和性质得出答案即可;(2)由平行四边形的性质得出AD =BC ,AD ∥BC ;证明BC 是△EFG 的中位线,得出BC ∥FG ,BC =12FG ,证出AD ∥FH ,AD ∥FH ,由平行四边形的判定方法即可得出结论; (3)连接EH ,CH ,根据三角形的中位线定理以及平行四边形的判定和性质即可得到结论.【详解】明:(1)∵四边形ABCD 是平行四边形,∴∠BAE =∠BCD =70°,AD ∥BC ,∵∠DCE =20°,∵AB ∥CD ,∴∠CDE =180°﹣∠BAE =110°,∴∠DEC =180°﹣∠DCE ﹣∠CDE =50°;。
长沙市八年级下学期数学第二次月考试卷

长沙市八年级下学期数学第二次月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分)下列各式:(1﹣x),,,,其中分式共有()A . 1个B . 2个C . 3个D . 4个2. (2分)(2019·禅城模拟) 如图,已知圆周角∠A=50°,则∠OBC的大小是()A . 50°B . 40°C . 130°D . 80°3. (2分) (2019八上·洪山期末) 下列各多项式从左到右变形是因式分解,并分解正确的是()A . (a﹣b)3﹣b(b﹣a)2=(b﹣a)2(a﹣2b)B . (x+2)(x+3)=x2+5x+6C . 4a2﹣9b2=(4a﹣9b)(4a+9b)D . m2﹣n2+2=(m+n)(m﹣n)+24. (2分) (2019七下·北京期中) 若a>b ,则下列不等式中错误的是().A . a-1>b-1B . a+1>b+1C . 2a>2bD . -2a>-2b5. (2分)已知不等式x﹣1≥0,此不等式的解集在数轴上表示为()A .B .C .D .6. (2分) (2019九上·新兴期中) 用配方法解一元二次方程x2+6x-3=0,原方程可变形为()A . (x+3)2=9B . (x+3)2=12C . (x+3)2=15D . (x+3)2=397. (2分)如图所示,一次函数y=kx+b(k、b为常数,且k≠0)与正比例函数y=ax(a为常数,且a≠0)相交于点P,则不等式kx+b>ax的解集是()A . x>1B . x<1C . x>2D . x<28. (2分)计算﹣的结果为()A . ﹣B . ﹣C . ﹣D . ﹣n9. (2分) (2017七下·杭州月考) 计算的结果是()A . ﹣m2﹣2m﹣1B . 2(m﹣1)2C . 2m2﹣4m﹣2D . ﹣2m2+4m﹣210. (2分)下列命题:①正多边形都是轴对称图形;②通过对足球迷健康状况的调查可以了解我国公民的健康状况;③方程的解是x=0;④如果一个角的两边与另一个角的两边分别平行,那么这两个角相等.其中真命题的个数有()A . 1个B . 2个C . 3个D . 4个二、填空题 (共7题;共8分)11. (1分) (2017九上·哈尔滨期中) 把多项式分解因式的结果是________.12. (1分) (2019八下·泰兴期中) 计算: = ________ .13. (2分) (2015八下·伊宁期中) 已知菱形的两条对角线长为8cm和6cm,那么这个菱形的周长是________ cm,面积是________ cm2 .14. (1分)如图,DE是三角形ABC的边AB的垂直平分线,分别交AB、BC于D、E,AE平分∠BAC,若∠B=30度,则∠C=________度.15. (1分)如图,在同一平面直角坐标系中作出相应的两个一次函数的图象,则不等式组的解为________16. (1分) (2015八上·江苏开学考) 已知:如图,AD=AC,BD=BC,O为AB上一点,那么,图中共有________对全等三角形.17. (1分)已知a2+a+1=0,则a4+2a3﹣3a2﹣4a+3的值是________.三、解答题 (共3题;共15分)18. (5分)(2017·平南模拟) 计算下面各题(1)计算:| ﹣2|+20150﹣()+3tan30°;(2)解不等式组:,并将不等式组的解集在所给数轴上表示出来.19. (5分)(2017·盘锦模拟) 计算:(1)先化简,再求值:(﹣)• ,其中x= ﹣2.(2)计算:|﹣4|+()﹣2﹣(﹣1)0﹣cos45°.20. (5分) (2016八上·萧山期中) 已知:线段a,m,h (m≥h), 求作:△ABC,使BC=a,AB=h,边BC上的中线等于m.四、解答题二 (共5题;共40分)21. (11分)(2017·宜春模拟) 如图(1),A1B1和A2B2是水面上相邻的两条赛道(看成两条互相平行的线段).甲是一名游泳运动健将,乙是一名游泳爱好者,甲在赛道A1B1上从A1处出发,到达B1后,以同样的速度返回A1处,然后重复上述过程;乙在赛道A2B2上以1.5m/s的速度从B2处出发,到达A2后以相同的速度回到B2处,然后重复上述过程(不考虑每次折返时的减速和转向时间).若甲、乙两人同时出发,设离开池边B1B2的距离为y (m),运动时间为t(s),甲游动时,y(m)与t(s)的函数图象如图2所示.(1)赛道的长度是________ m,甲的速度是________ m/s;当t=________s时,甲、乙两人第一次相遇,当t=________s时,甲、乙两人第二次相遇?(2)第三次相遇时,两人距池边B1B2多少米.22. (2分) (2015九上·宁波月考) 已知AB为⊙O的直径,C为⊙O上一点,AD与过C点的切线垂直,垂足为D,AD交⊙O于点E,∠CAB=30°(1)如图①,求∠DAC的大小;(2)如图②,若⊙O的半径为4,求DE的长.23. (2分) (2017七下·江都期末) 在“五•一”期间,某公司组织员工到扬州西湖旅游,如果租用甲种客车2辆,乙种客车3辆,则可载180人,如果租用甲种客车3辆,乙种客车1辆,则可载165人.(1)请问甲、乙两种客车每辆分别能载客多少人?(2)若该公司有303名员工,旅行社承诺每辆车安排一名导游,导游也需一个座位.①现打算同时租甲、乙两种客车共8辆,请帮助旅行社设计租车方案.②旅行前,旅行社的一名导游由于有特殊情况,旅行社只能安排7名导游,为保证所租的每辆车均有一名导游,租车方案调整为:同时租65座、45座和30座的大小三种客车,出发时,所租的三种客车的座位恰好坐满,请问旅行社的租车方案如何安排?24. (15分)甲、乙两人先后从A地出发,甲去B地,乙经过B地去C地,AB两地距离为80千米,AC两地距离为150千米,他们离A地的路程随时间变化的图象如图1所示,求:(1)甲的速度为________千米/时;乙从A地到C地所用的时间为________小时;(2)乙离开A地的路程s关于时间t的函数解析式.(3)设甲乙两人相距的路程为y,在图2中补全函数y随着时间t变化的图象.25. (10分) (2020八上·吴兴期末) 等腰Rt△ABC,点D为斜边AB上的中点,点E在线段BD上,连结CD,CE,作AH⊥CE,垂足为H,交CD于点G,AH的延长线交BC于点F.(1)求证:△ADG≌△CDE.(2)若点H恰好为CE的中点,求证:∠CGF=∠CFG.参考答案一、单选题 (共10题;共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共7题;共8分)11-1、12-1、13-1、14-1、15-1、16-1、17-1、三、解答题 (共3题;共15分)18-1、18-2、19-1、19-2、20-1、四、解答题二 (共5题;共40分)21-1、21-2、22-1、22-2、23-1、23-2、24-1、24-2、24-3、25-1、25-2、。
