2015学年概率与统计A卷

合集下载

2017-2018概率论与数理统计期末试题(A)答案

第1页(共3页)中国矿业大学(北京) 2017-2018 学年第1 学期《概率论与数理统计》试卷（ A 卷）答案和评分标准一、填空题（每小题3分，共30分）1、设,A B 为两个事件，()0.4,()0.8,()0.5P A P B P AB ===，则(|)P B A =____0.75__________ 2、设随机变量X 在(3,3)-上服从均匀分布，关于t 的方程24420t Xt X +++=有实根的概率为______21_________ 3、设随机变量X 的概率密度函数为)(x f X ，则随机变量X e Y 3=的概率密度函数为=)(y f Y _____⎪⎩⎪⎨⎧+∞<<⎪⎭⎫ ⎝⎛其他,00,13ln y y y f X ___________4、如果随机变量X 在)10,0(上服从均匀分布，现在对X 进行4次独立重复观测，至少有3次观测值大于5的概率为____516__________ 5、设随机变量X 服从参数为(0)λλ>的泊松分布，且[(1)(2)]1E X X --=，则λ=______1_________6、设随机变量,X Y 相互独立，且都服从参数2θ=的指数分布，则{max{,}2}P X Y ≤=_____12(1)e --_________7、设随机变量X 的方差为2.5，由切比雪夫不等式估计概率{|()|7.5P X E X -≥≤____245_______ 8、设总体2~(,)X N μσ，12,,,n X X X 是该总体X 的一个样本，1211()n i i i c X X -+=-∑为2σ的无偏估计，则c =_______)1(21-n ___________9、设随机变量X 和Y 相互独立，且都服从正态分布2(0,3)N ，而129,,X X X 和129,,,Y Y Y 分别来自正态总体X 和Y 的简单随机样本，则统计量Y服从____)9(t ________分布10、设总体),(~2σμN X ，抽取容量16n =的样本n x x x ,,,21 ，经计算得均值,2.5=x 样本标准方差2=s ,则未知参数μ的置信度为0.95的置信区间为_____)266.6,134.4(____________二、(10分)设工厂A 和工厂B 的产品次品率分别为1%和2%．现从A 和B 的产品分别占60%和40%的一批产品中随机抽取一件，发现是次品，求该次品属于工厂A 生产的概率．解：设事件A 表示产品来自工厂A ，事件B 表示产品来自工厂B ，事件C 表示抽取到的产品是次品，则%1)|(=A C P ，%2)|(=B C P ，%60)(=A P ，%40)(=B P 5分从而73%2%40%1%60%1%60)|()()|()()|()()|(=∙+∙∙=+=B C P B P A C P A P A C P A P C A P 5分第2页(共3页)三、(12分)学生完成一道作业的时间X 是一个随机变量，单位为小时．它的概率密度函数为21,0()20,cx x x f x ⎧+≤≤⎪=⎨⎪⎩其他（1）确定常数c ；（2）写出X 的分布函数；（3）试求出在20分钟以内完成一道作业的概率．解：（1）由概率密度函数的性质()122011()248c f x dx cx x dx +∞-∞==+=+⎰⎰ 解得21c = 4分（2）由2121,0()20,x x x f x ⎧+≤≤⎪=⎨⎪⎩其他，则()2230001()()217022112xxx x F x f t dt t t dt x x x -∞⎧<⎪⎪⎪==+=+≤≤⎨⎪⎪>⎪⎩⎰⎰ 4分（3）1117()()3354P X F ≤==4分四、(10分)设,X Y 是两个相互独立的随机变量，其概率密度函数分别是1,01()0,X x f x ≤≤⎧=⎨⎩其他 ,0()0,y Y e y f y -⎧>=⎨⎩其他求随机变量Z X Y =+的概率密度函数．解：由卷积公式()()()X Y X Y f z f x f z x dx +∞+-∞=-⎰3分易知仅当010x z x ≤≤⎧⎨->⎩ 即 01x x z≤≤⎧⎨<⎩时被积函数不为零 2分()01()00,0()011zz x X Y z x z f z e dx z e dx z --+--⎧<⎪⎪=≤<⎨⎪⎪≥⎩⎰⎰ 3分即0,0()101(1)1zX Y z z f z ez e e z -+-<⎧⎪=-≤<⎨⎪-≥⎩2分五、(10分)设(Y X ,)具有概率密度为26,01,01(,),0,xy x y f x y ⎧<<<<=⎨⎩其它（1）求边缘概率密度(),()X Y f x f y ，并判断,X Y 是否独立；（2）求条件概率密度)(y x f YX．解：（1）1206201()(,)0X xy dy x x f x f x y dy +∞-∞⎧=<<⎪==⎨⎪⎩⎰⎰其他12206301()(,)0Y xy dx y y f y f x y dx +∞-∞⎧=<<⎪==⎨⎪⎩⎰⎰其他显然，(,)()()X Y f x y f x f y =，所以,X Y 相互独立 6分（2）当10<<y 时，⎩⎨⎧<<==取其他值x x x y f y x f y x f Y Y X ,010,2)(),()( 4分第3页(共3页)六、(10分)设二维随机变量),(Y X 的联合概率密度函数为⎩⎨⎧<<<=其他,010,3),(x y x y x f （1）求随机变量),(Y X 的协方差cov(,)X Y ；（2）求随机变量),(Y X 的相关系数．解：（1）⎰⎰⎰⎰⎰+∞∞-+∞∞-====103233),()(1040210dx x ydy x dx dxdy y x xyf XY E x4333),()(1030210====⎰⎰⎰⎰⎰+∞∞-+∞∞-dx x dy x dx dy y x xf dx X E x83233),()(103010====⎰⎰⎰⎰⎰+∞∞-+∞∞-dx x dy xy dx dy y x yf dx Y E x则3cov(,)=()()()160X Y E XY E X E Y -= 5分（2）5333),()(104031022====⎰⎰⎰⎰⎰+∞∞-+∞∞-dx x dy x dx dy y x f x dx X E x513),()(104021022====⎰⎰⎰⎰⎰+∞∞-+∞∞-dx x dy xy dx dy y x f y dx Y E x8034353)()()(222=⎪⎭⎫ ⎝⎛-=-=X E X E X D320198351)()()(222=⎪⎭⎫ ⎝⎛-=-=Y E Y E Y D 193)()(),(==Y D X D Y X Cov ρ 5分七、(8分)一个复杂的系统由100个相互独立起作用的部件所组成，在整个运行期间每个部件损坏的概率为0.10，为了使整个系统起作用，至少必须84个部件正常工作，求整个系统起作用的概率．解：设X 表示正常工作的部件个数，则~(100,0.9)X B ，由棣莫弗-拉普拉斯定理，近似服从(0,1)N 分布， 4分则()()908490(84)1(84)11220.977233X P X P X P --⎛⎫≥=-<=-<≈-Φ-=Φ= ⎪⎝⎭4分八、(10分)设总体X 的概率密度函数为23,0,(,)0,.x e x f x x θθθ-⎧>⎪=⎨⎪⎩其他其中θ为未知参数且大于零，12,,,n X X X 为来自总体X 的简单随机样本，（1）求θ的矩估计量；（2）求θ的最大似然估计量．解：（1）由于22320()xxx E X xe dx e dx e d x x x θθθθθθθθ---+∞+∞+∞⎛⎫===-= ⎪⎝⎭⎰⎰⎰，令X θ=，解得θ的矩估计量为11=ni i X X n θ==∑ 5分（2）似然函数为2311,0(1,2,,)()(,)0,.i n xni i i ii e x i n L f x x θθθθ-==⎧>=⎪==⎨⎪⎩∏∏其他当0(1,2,,)i x i n >=时，()L θ=231inx i iexθθ-=∏，两边取对数31ln ()2ln ln ni i i L x x θθθ=⎡⎤=--⎢⎥⎣⎦∑令11ln ()21210n n i i i i d L n d x x θθθθ==⎡⎤=-=-=⎢⎥⎣⎦∑∑，解得θ的最大似然估计量为12=1ni inX θ=∑ 5分第4页(共3页)。

2017~2018(一)概率统计试卷(理工类)A卷(答案)

X2
...
X 100

1 } （用中心极限定理）
100
3
解： EX

1
xf (x)dx

1
x 2xdx

1
2 x 2 dx
2
0
0
0
3
EX 2 1 x 2 2xdx 1 2x3dx 1 , DX EX 2 (EX )2 1
0
0
2
18
P{ X1
M (M 1)
3.在 H0 为原假设, H1 为备择假设的假设检验中,若显著性水平为 ,则（ C ）。（A） P （接受 H0 H0 成立）= ；（B） P （接受 H1 H1 成立）= ；（C） P （接受 H1 H0 成立）= ；（D） P （接受 H0 H1 成立）= 。
4. 设随机变量 X 和Y ，若 E( XY ) E( X )E(Y ) ，则下列结论一定成立的是（B ）。
f
(x,
y)

Axe y
,0

x

1,0

y

x
2

0,
其他
求：（1）常数 A；（2）求 X 与 Y 的边缘概率密度 f X (x) 和 fY ( y) ；（3）判断 X 与 Y 的独立
性。
解：（1） f (x, y)dxdy 1
D
f (x, y)dxdy
U W ，拒绝 H 0 ,认为元器件的平均寿命有显著变化。
（八）（6）
已知 X 1 和 X 2 的概率分布律：
1
X1
~

1
0 1

概率论2015春A卷答案

(B) 1 2
(C) 1 2
(D) 1 2
X 9 相互独立， EX i 1, DX i 1
i 1,2,
9
9 ,则对任意给定的 0 ，
9 (A)P X i 1 1 2 i 1 9 (C)P X i 9 1 2 i 1
1 (B)P 9
X
i 1
i
1 1 2
9 (D)P X i 9 1 9 2 i 1
三、(10 分）甲、乙两人轮流投篮，甲先投。一般来说，甲、乙两人独立投篮的命中率分别为 0.7 和 0.6。但由于心理因素的影响，如果对方在前一次投篮中投中，紧跟在后面投篮的这一方的命中率就会有所下降，甲、乙的命中率分别变为 0.4 和 0.5。求：（1）乙在第一次投篮中投中的概率；（2）甲在第二次投篮中投中的概率。解：令
Y
2 2 X 12 X 2 X 10 服从 F (10,5) 2 2 2 2( X 11 X 12 X 15 )
分布.
《概率论与数理统计》试卷第 1 页共 8 页
5、设随机变量 X 的概率密度为 f ( x)
2x 0 x 1 其它
0
，以 Y 表示对 X 的三次独立重复观
座位号
题号得分
一
二
三
四
五
六
七
八
总分
专业
注意： (1.65) 0.95 (1.96) 0.975 (1.45) 0.926
1.40 0.92
_____________ ________ 学院
t0.99 (7) 2.998 , t0.95 (7) 1.895 , t0.99 (6) 3.143, t0.95 (6) 1.943

概率试卷A12-13-2本科评分标准

2012－2013学年第2学期概率论与数理统计A 卷评分标准一、单项选择题（本大题共5小题，每小题3分，共15分）. 1. 事件,A B 独立，且0()1P A <<，则下列选项不正确的是（A ）(|)()P B A P B =；（B ）(|)()P B A P A =；（C ）(|)()P B A P B =；（D ）(|)()P B A P B =.答：（B ）2. 已知离散型随机变量X 的分布律为4567125522a a a a ⎛⎫ ⎪ ⎪ ⎪⎝⎭，则概率(6)P X ≥等于（A ）516；（B ）58；（C ）78；（D ）1.答：（B ） 3. 设随机变量X 的概率密度函数为(),f x x R ∈，若2Y X =-，则Y 的概率密度函数为（A ）1,22y f y R ⎛⎫-∈ ⎪⎝⎭；（B ）,2y f y R ⎛⎫-∈ ⎪⎝⎭；（C ）2(2),f y y R -∈；（D ）(2),f y y R -∈.答：（A ）4. 已知随机变量X 服从正态分布2(,6)N μ，Y 服从正态分布2(,8)N μ，记1(6)p P X μ=≤-,2(8)p P Y μ=≥+，则（A ）12p p <；（B ）12p p >；（C ）12p p =；（D ）无法判断12,p p 的大小.答：（C ）5. 设12,,,n X X X L 为来自总体2(0,)N σ的简单样本，X 为样本均值，则下列选项不正确的是（A ）22211()nii Xn χσ=∑:；（B ）22211()(1)nii XX n χσ=--∑:；（C）(0,1)N σ:；（D ）2122(1,1)nii X F n X=-∑:.答：（D ）二、填空题（本大题共5小题，每小题3分，共15分）.6. 某人有10把外形相同的钥匙, 其中只有一把能打开门. 他随意地试用这些钥匙开门（用后不放回）, 则此人试了3次就把门打开的概率为110.7. 已知随机变量X 的概率密度函数为22,0()0,0x ae x f x x -⎧>=⎨≤⎩，则常系数a =1.8. 某餐厅每天接待300名顾客,据以往经验每位顾客的消费额(单位：元)服从区间[20,80]上的均匀分布, 若顾客的消费额是相互独立的,则该餐厅每天营业额的期望值为15000元.9. 设,X Y 为两个独立随机变量，若25,4DX DY ==,则(21)D X Y ++=41.10. 用机器包装牛肉罐头, 已知罐头重量（单位：kg ）服从正态分布2(,0.05)N μ,随机抽取25个罐头测其重量, 算得样本均值 1.01x =, 则μ的置信度为95%的置信区间为(0.9904,1.0296) (备用数据：0.025 1.96z =，0.05 1.65z =). 三、解答题（本大题共6小题，每小题10分，共60分）.11.某仪器上装有大、小2个不同功率的灯泡.已知当2个灯泡都完好时,仪器发生故障的概率为1%；当只有1个灯泡烧坏时,仪器发生故障的概率为20%；当2个灯泡都烧坏时,仪器发生故障的概率为85%.设这两个灯泡被烧坏与否互不影响,并且它们被烧坏的概率分别为0.1,0.2,若仪器发生了故障，求此时两个灯泡都烧坏的概率. 解：设A 表示仪器发生故障；i B 表示烧坏了i 个灯泡，0,1,2i =，则所求概率为222220()(|)()(|).........................................(6')()(|)()85%(0.10.2)....(9')1%(0.90.8)20%(0.10.80.20.9)85%(0.10.2)85. (381)i i i P AB P A B P B P B A P A P A B P B ===⨯⨯=⨯⨯+⨯⨯+⨯+⨯⨯=∑.................................................................(10')12．已知随机变量X 的概率密度函数为 0,0()2(1),012,1x x x f x e x x e x --≤⎧⎪=+-<<⎨⎪≥⎩,求：（1）{02}P X <<；（2）()X E e -. 解：（1）由密度函数的性质21212{02}().............................................(2')2(1)2.....................................(4')12...........................................................x x P X f x dx e x dx e dx e ---<<==+-+=-⎰⎰⎰............(5')（2）由题意111()()....................................................(7')2(1)2.................(9')12.. (X)x x xx x E ee f x dx e e x dx e e dx e +∞---∞+∞-----==+-+=-⎰⎰⎰.(10')13.设二维随机变量(,)X Y 的联合概率密度函数为6(1),01,0(,)0,x x y xf x y -<<<<⎧=⎨⎩其它，（1）求概率{12}P X Y +≤；（2）求出(,)X Y 关于X 的边缘概率密度函数()X f x ，进一步求出在14X =的条件下，Y 关于X 的条件概率密度函数|1(|)4Y X f y .解：（1）由题意{(,):12}14120{12}(,)..................(2')6(1)..............................................(4')9 (32)x y x y y yP X Y f x y dxdy dy x dx +≤-+≤==-=⎰⎰⎰⎰.......(5')（2）由边缘密度函数的定义0()(,)................................................................(6')6(1),016(1),01.........(8')0,0,X x f x f x y dy x x x x dy x +∞-∞=⎧-<<-<<⎧⎪==⎨⎨⎩⎪⎩⎰⎰其它其它故|4,0141(14,)(|)..............................(10')0,4(14)Y X X y f y f y f <<⎧==⎨⎩其它14．已知连续型随机变量X 的分布函数为(1),0(),011,1x x Ae x F x B x Ae x --⎧<⎪=≤<⎨⎪-≥⎩，（1）确定常系数,A B ；（2）求{122}P X <<；（3）求X 的概率密度函数()f x . 解：（1）由分布函数的性质(0)(0).......................................................(1')F F A B -+=⇒= (1)(1)1...................................................(2')F F B A -+=⇒=-因此可得12,12............................................................(3')A B == （2）由分布函数的性质(21)1{122}(2)(12).................................................(5')1111(1)......................................................(7')222P X F F e e ---<<=-=--=- （3）由密度函数定义可得(1)1,021(), 1......................................(10')20,xx e x f x e x --⎧<⎪⎪⎪=>⎨⎪⎪⎪⎩其它15. 设二维离散型随机变量(,)X Y 的联合分布律为已知0.2EX =-，且,X Y 的协方差(,)0.18Cov X Y =, 求,,a b c 的值.解：由题意，可得(,)X Y 关于X 的边缘分布律为1010.10.2a b c -⎛⎫ ⎪++⎝⎭，故0.10.2EX c a =-+=-，即0.3....................................................(2')a c -=又(,)X Y 关于Y 的边缘分布律为100.3a c b -⎛⎫ ⎪++⎝⎭,XY 的分布律为1010.3c b a -⎛⎫ ⎪+⎝⎭,故有(,)()()0.2()0.18Cov X Y E XY EXEY a c a c =-=--+=即0.6..................................................................................................(6')a c += 又111{,}1i j P X i Y j =-=-===∑∑，可得0.7.......................................(8')a b c ++=故0.45,0.1,0.15..........................................................................(10')a b c ===16．设总体X的概率密度函数为21(ln )2,0()0,0x x f x x μ--⎧>=≤⎩,其中μ是未知参数. 若12,,,n X X X L 是来自该总体的一个容量为n 的简单样本，求μ的最大似然估计量µμ.解：21(ln )21()......................................(3')i nx i L μμ--==似然函数为对数似然函数2111ln[()])(ln ).......................(5')2nni i i i L x μμ===---∑∑1ln[()]0(ln )0.......................................................(8')ni i d L x d μμμ==⇒-=∑令故^1ln ..................................................(10')ni i X n μμ==∑的最大似然估计量四、证明题（本大题共1个小题，5分）.17.设,X Y 为两个随机变量，若22(),()E X E Y 存在且至少有一个不为0，证明：222[()]()()E XY E X E Y ≤.证明：不防假定2()0E X ≠，对于任意实数t ，有2222[()]()2()()0.............(2')E tX Y t E X tE XY E Y +=++≥因此判别式222222[2()]4()()4[()]4()()0...............................(4')E XY E X E Y E XY E X E Y ∆=-=-≤此即 222[()]()()........................................(5')E XY E X E Y ≤ 五、应用题（本大题共1个小题，5分）.18. 某幼儿园准备举行一次六一文艺汇演，为了做好准备工作，学校现要统计来参加此次汇演的家长人数. 设各学生来参加汇演的家长数相互独立，且每个学生无家长，有1名家长或2名家长来参加此次汇演的概率约为0.05,0.8,0.15.已知此幼儿园共有400名学生，用中心极限定理估计来参加此次汇演的家长数超过450的概率（备用数据:4.36=，(1.15)0.8749Φ=）.解：设i X 表示第i 个学生来参加文艺汇演的家长数，1,2,,400i =L .由题意，{,1,2,,400}i X i =L 独立同分布，且分布律为0120.050.80.15⎛⎫ ⎪⎝⎭. 由中心极限定理,4001ii X=∑近似服从正态分布(440,76).......................................................(3')N因此所求概率为4004001440450...........................(4')i i i X P X P =⎧⎫-⎪⎪⎧⎫>=>⎨⎬⎩⎭⎪⎪⎩⎭∑∑(()11 1.1510.87490.1251...........................(5')≈-Φ≈-Φ≈-=。

2015年高考数学真题分类概率与统计

概率与统计（2015北京理科）16.（本小题13分）A，B两组各有7位病人，他们服用某种药物后的康复时间（单位：天）记录如下：A组：10，11，12，13，14，15，16B组：12，13，15，16，17，14，a假设所有病人的康复时间互相独立，从A，B两组随机各选1人，A组选出的人记为甲，B 组选出的人记为乙．(Ⅰ) 求甲的康复时间不少于14天的概率；(Ⅱ) 如果25a=，求甲的康复时间比乙的康复时间长的概率；(Ⅲ) 当a为何值时，A，B两组病人康复时间的方差相等？（结论不要求证明）【答案】（1）37，（2）1049，（3）11a=或18广东理科4．袋中共有15个除了颜色外完全相同的球，其中有10个白球，5个红球。

从袋中任取2个球，所取的2个球中恰有1个白球，1个红球的概率为A ．1 B. C. D.【答案】．【解析】从袋中任取个球共有种，其中恰好个白球个红球共有种，所以恰好个白球个红球的概率为，故选．（湖北理科）7．在区间上随机取两个数，记为事件“”的概率，为事件“”的概率，为事件“”的概率，则（）A ．B ．C ．D ．【答案】B（1）（2）（3）（湖南理科）12.在一次马拉松比赛中，35名运动员的成绩（单位：分钟）的茎叶图如图4所示. 若将运动员按成绩由好到差编为号，再用系统抽样方法从中抽取7人，则其中成绩在区间[139,151]上的运动员人数是 .21112110215B 2215105C =111110550C C =115010=10521B [0,1],x y 1p 12x y +≥2p 1||2x y -≤3p 12xy ≤123p p p <<231p p p <<312p p p <<321p p p <<135【答案】. 【解析】试题分析：由茎叶图可知，在区间的人数为，再由系统抽样的性质可知人数为人. （全国1卷）（19）某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x （单位：千元）对年销售量y （单位：t ）和年利润z （单位：千元）的影响，对近8年的年宣传费x1和年销售量y1（i=1,2，···，8）数据作了初步处理，得到下面的散点图及一些统计量的值。

《概率论与数理统计 (A)

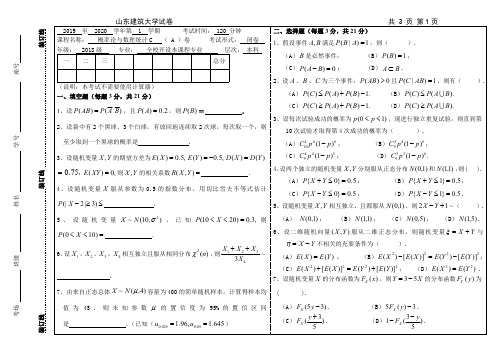
山东建筑大学试卷共3页第1页2019至2020学年第1学期考试时间：120分钟课程名称：概率论与数理统计C （A ）卷考试形式：闭卷年级：2018级专业：全校开设本课程专业层次：本科一二三总分（说明：本考试不需要使用计算器）一、填空题（每题3分，共21分）1、设()( )P AB P A B =，且()0.2P A =，则()P B ＝.2、设袋中有2个黑球、3个白球，有放回地连续取2次球，每次取一个，则至少取到一个黑球的概率是.3、设随机变量Y X ,的期望方差为,5.0)(=X E ,5.0)(-=Y E )()(Y D X D =，75.0=,0)(=XY E 则Y X ,的相关系数=),(Y X R ．4、设随机变量X 服从参数为0.5的指数分布，用切比雪夫不等式估计≤≥-)3|2(|X P .5、设随机变量),10(~2σN X ，已知,3.0)2010(=<<X P 则=<<)100(X P ．6、设1X ，2X ，3X ，4X 相互独立且服从相同分布2()n χ，则1234~3X X X X ++.7、由来自正态总体)4,(~μN X 容量为400的简单随机样本，计算得样本均值为45，则未知参数μ的置信度为95%的置信区间二、选择题（每题3分，共21分）1、假设事件,A B 满足(|)1P B A =，则（）.（A）B 是必然事件；（B）()1P B =；（C）()0P A B -=；（D）A B ⊂.2、设A 、B 、C 为三个事件，()0P AB >且(|)1P C AB =，则有（）.（A）()()() 1.P C P A P B ≤+-（B）()().P C P A B ≤ （C）()()() 1.P C P A P B ≥+-（D）()().P C P A B ≥ 3、设每次试验成功的概率为(01)p p <<，现进行独立重复试验，则直到第10次试验才取得第4次成功的概率为（）.（A）44610(1)C p p -；（B）3469(1)C p p -；（C）4459(1)C p p -；（D）3369(1).C p p -4、设两个独立的随机变量Y X ,分别服从正态分布)1,0(N 和)1,1(N ，则().（A）5.0}0{=≤+Y X P ；（B）5.0}1{=≤+Y X P ；（C）5.0}0{=≤-Y X P ；（D）5.0}1{=≤-Y X P .5、设随机变量Y X ,相互独立，且都服从)1,0(N ，则~12+-Y X （）.（A）)1,0(N ；（B）)1,1(N ；（C）)5,0(N ；（D）)5,1(N .6、设二维随机向量),(Y X 服从二维正态分布，则随机变量Y X +=ξ与Y X -=η不相关的充要条件为（）.（A）)()(Y E X E =；（B）2222)]([)()]([)(Y E Y E X E X E -=-；（C）2222)]([)()]([)(Y E Y E X E X E +=+；（D）)()(22Y E X E =.7、设随机变量X 的分布函数为()X F x ，则35Y X =-的分布函数()Y F y 为().（A）(53)X F y -.（B）5()3X F y -.（C）3()y F +.（D）31()yF --.考场班级姓名学号座号线装订线装订线山东建筑大学试卷共3页第2页三、计算应用题（共58分）1、（8分）装有10件某产品（其中一等品5件，二等品3件，三等品2件）的箱子中丢失一件产品，但不知是几等品，今从箱中任取2件产品，结果都是一等品，求丢失的也是一等品的概率.2、（12分）设随机变量X 的概率密度为)()(||+∞<<-∞=-x Aex f x ，求：（1）系数A ；（2）X 的分布函数；（3）)(X D .3、（8分）设),1,0(~N X 求||X Y =的概率密度.姓名学号线装订线装订线山东建筑大学试卷共3页第3页4、（10分）设二维随机变量），Y X (的联合概率密度为：⎩⎨⎧=0),(2Axy y x f 其他10 ,20<<<<y x 求：（1）参数A ；（2）X 和Y 的边缘概率密度并判断X 和Y 是否独立；（3）)5.0,1(≤≥Y X P .5、（12分）设随机变量X 和Y 的联合分布在点（0，1），（1，0）及（1，1）为顶点的三角形区域G 上服从均匀分布，试求),(Y X Cov .6、（8分）设总体X 的概率密度为101,,(;).0,x x f x θθθ-<<⎧=⎨⎩其它(0).θ>12,,,n x x x 是X 的简单样本观测值，试求（1）参数θ的矩估计值；（2）参数θ的极大似然估计值.姓名学号线装订线装订线。

2015级《概率论与数理统计》A卷及解答(精品文档)_共4页

x
s n
t
(n
1)

56.93

0.93 20
1.729

56.570
第4页共4页
步骤）
1.试卷中有一道选择题，共有 4 个答案可供选择，其中只有 1 个答案是正确的.任一考生如
果会解这道题，则一定能选出正确答案；如果不会解这道题，则不妨任选 1 个答案。设考
生会解这道题的概率是 0.8。
（1）求考生选出正确答案的概率；
（2）已知某考生所选答案是正确的，求他确实会解这道题的概率。
（2）设考试成绩至少高于 m 分， PX m 0.3333
因为 PX m 1 m 75 0.3333 ， m 75 0.6667
15
15
于是 m 75 0.431 ， m 81.465 15
故考试成绩至少高于 81 分能排名前 33.33%。
2
4
4.设(X,Y)为二维随机变量，且 D (X)>0，D (Y)>0，则下列等式成立的是
（A）（B）
(A) E( XY ) E( X ) E(Y ) (C) D( X Y ) D( X ) D(Y )
(B) Cov(X,Y) XY D( X ) D(Y ) (D) Cov(2X ,2Y ) 2Cov( X ,Y )
=0.09(i=1，2，…)，则
lim
P

n

i 1
X
i－
0.1n

0.6
=
n
n

2
1
t2
e 2 dt (2)
2
5.设总体

2007—2008学年概率论第一学期期终考试及参考答案

¯ ∼ N (0, 1), X ¯ − 1 ∼ N (−1, 1). (2) X 7. (1) E (X ) =
θ , θ +1
ˆ MM = θ
¯ X ¯; 1−X n i =1
(2) ln L(θ) = n ln θ + (θ − 1)
ln Xi , θ MLE = −
n i=1
n . ln Xi
1
上
专业
海
班级
海
事
姓名
大
学
学号
试
卷
得分
概率论与数理统计(卷A): 20080114
本试卷共8大题(第1, 2, 5, 6题每题10分, 第3, 4, 7, 8题每题15分) 可能用到的分位点表如下: z0.05 = 1.645 z0.0025 = 1.960 t0.025 (27) = 2.0518 t0.05 (27) = 1.7033 t0.025 (28) = 2.0484 t0.025 (29) = 2.0452 t0.05 (29) = 1.6991 t0.05 (13) = 1.7709 F0.025 (11, 16) = 211) = 3.28 F0.025 (7, 6) = 5.70 F0.025 (6, 7) = 5.12 1. 设A, B为两事件, 已知P(A) = 0.3, P( B) = 0.5, 计算: (1) 若A, B相互独立, 求P(A ∪ B); ¯ ). (2) 若P(A| B) = 0.4, 求P(A| B
3 8. 某厂利用两条自动化流水线灌装番茄酱, 从两条自动化流水线上分别抽取样本(X1 , · · · , X12 )与(Y1 , · · · , Y17 ), 观测后算得 x ¯ = 10.6(g), y ¯ = 9.5(g), s2 1 = 2.4, 2 s2 = 4.7, 假设这两条流水线上灌装的番茄酱的重量分别服从正态分 2 2 2 布N (µ1 , σ2 1 )与 N (µ2 , σ2 ), 且相互独立. µ1 , σ1 , µ2 , σ2 均未知. 求:

2013-2014学年《概率论与数理统计》期末考试试卷-(A)答案

1． 0.5 ；0.58 2． 2/5 3．4． 0.3 ；0.5 5． 10 ；8 6． 21 7． 8/9 8． )41.05,41.05(025.0025.0z z +-《概率论与数理统计》期末考试试卷 (A)一、填空题（每小题4分，共32分）.1．设 A 、B 为随机事件, P (A ) = 0.3, P (B ) = 0.4, 若 P (A |B ) =0.5, 则 P (A ⋃B ) = __0.5_____; 若 A 与 B 相互独立, 则 P (A ⋃B ) = ____0.58____.2．设随机变量 X 在区间 [1, 6] 上服从均匀分布, 则 P { 1 < X < 3} = _____2/5_________.3．设随机变量 X 的分布函数为,2,1 21 ,6.011 ,3.01,0 )(⎪⎪⎩⎪⎪⎨⎧≥<≤<≤--<=x x x x x F 则 X 的分布律为___________________________ .4．若离散型随机变量 X 的分布律为则常数 a = _0.3________; 又 Y = 2X + 3, 则 P {Y > 5} = _0.5________ .5．设随机变量 X 服从二项分布 b (50, 0.2), 则 E (X ) = ___10_____, D (X ) = _8__________.6．设随机变量 X ~ N (0, 1), Y ~ N (1, 3), 且X 和 Y 相互独立, 则D (3X - 2Y ) =___21______.7．设随机变量 X 的数学期望 E (X ) = μ, 方差 D (X ) = σ 2, 则由切比雪夫不等式有 P {|X - μ | < 3σ } ≥ _________________.8．从正态总体 N (μ, 0.1 2) 随机抽取的容量为 16 的简单随机样本, 测得样本均值5=x ，则未知参数 μ 的置信度为0.95的置信区间是 ____________________________. (用抽样分布的上侧分位点表示). 1. D 2. A 3. C 4. B 5. D 6. C详解：2.因为⎰∞-=xt t f x F d )()( 故⎰-∞-=-at t f a F d )()( 令u =-t ⎰∞+--=-a u u f a F d )()(⎰+∞=au u f d )(⎰+∞=at t f d )(⎰-=a t t f 0d )(21 (21d )(0=⎰+∞t t f )详解：4.因为X ~)1,0(N ,Y ~)1,1(N 所以 1)(=+Y X E ，2)(=+Y X D 故)()(Y X D Y X E Y X ++-+21-+=Y X ~)1,0(N 所以21}021{=≤-+Y X P 即 21}01{=≤-+Y X P 21}01{=≤-+Y X P二、选择题（只有一个正确答案，每小题3分，共18分）1．设A , B , C 是三个随机变量，则事件“A , B , C 不多于一个发生” 的逆事件为( D ).(A) A , B , C 都发生 (B) A , B , C 至少有一个发生 (C) A , B , C 都不发生 (D) A , B , C 至少有两个发生2．设随机变量 X 的概率密度为 f (x ), 且满足 f (x ) = f (-x ), F (x ) 为 X 的分布函数, 则对任意实数 a , 下列式子中成立的是 ( A ). (A) 错误!未找到引用源。

《概率统计D》试题(A卷答案)

海南大学2012-2013学年度第2学期试卷科目：《概率统计D 》试题(A 卷)姓名：学号：学院：专业班级：时限： 120 分钟考试形式：闭卷笔试,不用计算器注意：选择题、填空题、判断题答案就写在试卷纸上，计算题和应用题的答案必须写在后面的空白纸上！！！！！！！！！！！最后一张纸是稿纸，交卷时不用上交。

一、选择题(每题3分，共15分) :答案就填写在括号内.1、设A,B,C 是同一个试验E 的三个事件，则下列选项正确的是（4 ）（1）若A B CB =，则A=C ；（2）若A-B=C-B ，则A=C ；（3）若AB=CB ，则A=C ；（4）若AB=,A B Φ=Ω，则A B =。

3、一个随机变量的数学期望和方差都是1，则这个随机变量不可能服从（ 1 ）（1）二项分布；（2）泊松分布；（3）指数分布；（4）正态分布。

4、下列哪一个随机变量不服从泊松分布（ 4 ）（1）随机变量X 表示某校长的手机一天内收到的骚扰短信条数；（2）随机变量Y 表示某老师编写的教材一页上出现的印刷错误个数；（3）随机变量Z 表示海大一学期被退学的学生人数；（4）随机变量R 表示你到学校某办公室办事需要等待的时间。

5、某随机变量的分布函数为30,x 0F(x)x ,0x 11,x 1<⎧⎪=≤<⎨⎪≥⎩，则X 的数学期望E(X)=( 2 )（1）140x dx ⎰；（2）1303x dx ⎰；（3）1203x dx ⎰；（4）1401x dx xdx +∞+⎰⎰。

《概率论与数理统计》期末考试(A)卷答案与评分标准

海南师范大学物理、电子、自动化、地理、城规、计算机专业《概率论与数理统计》 2009—2010学年度第一学期期末考试（A ）卷答案与评分标准注意事项：1. 考前请将密封线内填写清楚 2. 所有答案请直接答在试卷上 3．考试形式：闭卷 4. 本试卷共五大题，满分100分，考试时间100分钟一、单项选择题（本题共六小题，每小题3分，共18分。

在每小题列出的四个选项中只有一个是符合题目要求的，请将其代码填在题后的括号内。

错选或未选均无分）1、设B A ,为随机事件, 若4.0)(,6.0)(==B P A P , 则有（ D ）. A ：1)(=B A P ； B ：24.0)(=AB P ； C ：6.0)(≤B A P ； D: 4.0)(≤AB P .2、设随机变量X 服从正态分布)1 ,0(N , )(x Φ为其分布函数，则}4{2<X P =（ A ） . A ：1)2(2-Φ ； B ：1)4(2-Φ ； C ： )2(21Φ-； D ：)2(1Φ-.3、己知二维随机变量),(Y X 具有分布函数),(y x F ，则（ D ）. A ：}{),(x X P x F <=+∞； B ：1),(=+∞x F ； C ：1),(=+∞-∞F ； D ：0),(=-∞x F .4、己知随机变量X 服从二项分布)2.0 ,5(B , 则=)(2X E （ C ）. A ：1； B ：0.8； C ：1.8； D ：0.2.5、设n X X X ,,,21 是来自总体) ,(2σμN 的简单随机样本，则∑==n i i X n X 11服从正态分布（ A ）. A ：) ,(2n N σμ； B ：) ,(2σn n N ； C ：) ,(2σμN ； D ：)1 ,0(N .6、设n X X X ,,,21 是来自总体) ,(2σμN 的简单随机样本，2 σ未知，检验假设 00μμ=：H ，对01μμ≠：H 时，需用到检验统计量是（ B ）. A ：n X Z σμ0-=； B ：n S X T 0μ-=； C ：222)1(σχS n -=； D ：n S X T n 0μ-=. 二、填空题（将答案直接填入栝号内，本题共六小题，每小题3分，共18分） 1、设事件B A 与相互独立,7.0)(,5.0)(==B A P A P ，则=)(B P ( 0.4 ) 第1页（共6页）第2页（共6页）2、设随机变量X 的概率密度函数为⎩⎨⎧≤≤=其它，,0,10,3)(2x x x f X 的概率分布函数为)(x F ，则=)5.0(F （ 0.125 ）.3、已知随机变量Y X 与的联合分布律为则概率==}1),{max(Y X P （ 0.6 ）；4、设随机变量X 的概率密度函数为⎩⎨⎧≤>=-，0,0,0,)(x x e x f x则X e Y 3-=的数学期望=)(Y E （ 41）.5、己知随机变量X 的期望,20)(=X E 方差,8)(=X D ,则≤≥-}620{X P ( 92);.6、设n X X X ,,,21 是来自总体),(2σμN 的简单随机样本，2σ未知，X 是样本均值, 2S 是样本均值,则μ的置信度为1-α的单侧置信下限为（）三、解答题（本题共 4小题，每小题8分，共32分）1、9.0)(,7.0)(,5.0)(===B A P B P A P ,试计算：)(AB P ,)(B A P -及)(B A A P 的值。

2018~2019(二)概率统计试卷(理工类)A卷答案

�� − ��
U=
~��(0,1)
��/√��
�� − �� W = {u|U > �� } = u �� > 1.64
√��
代入样本值
33.85 − 32 1.85
u=
=
= 1.83
√102/√100 √1.02
标准答案
(2)L(x, θ) = ∏
=( )
�� = min(�� , �� , … , �� )
（六）（10）设随机变量 X~B（100，0.2）（二项分布），用中心极限定理求 P（X>10）。
解： P(X > 10) = P 0. .99989
>
= 1−Φ
()
()
= 1 − Φ(−2.5) = Φ(2.5) =
3�� − 6�� + 3， 0 < �� < 1
�� (��) =
0,
其它
同理：
�� (��) = ��(��, ��)�� = 6(1 − ��)�� = 6(1 − ��)��
（2）D(X) = E(X − ��) = ��(�� − + − ��) = ��(�� − ) + 2�� −
− �� +
��( − ��) = ��(�� − ) + − �� − + ( − ��)

统计学原理试卷A及答案

浙经济职业技术学院成人大专2015学年第一学期统计学原理试卷A （闭卷）一、填空题（每空分，共 分）、研究某市居民生活状况，该市全部居民便构成了♉♉♉♉♉♉♉♉♉♉♉♉♉，每一家庭的收入是♉♉♉♉♉♉♉♉♉♉♉∙。

、普查的对象主要是♉♉♉♉♉♉♉♉♉♉♉∙∙现象，因而要求统一规定调查资料所属的。

、变量数列中各组标志值出现的次数称♉♉♉♉♉♉♉♉♉♉♉∙∙，各组单位数占单位总数的比重称♉♉♉♉♉♉♉♉♉♉♉。

∙ 、加权算术平均数的大小受♉♉♉♉♉♉♉♉♉♉♉∙和♉♉♉♉♉♉♉♉♉♉♉∙两大因素的影响。

、结构相对指标是♉♉♉♉♉♉♉♉♉♉♉∙∙与♉♉♉♉♉♉♉♉♉♉♉∙∙之比。

二、判断题（每小题分，共 分）、某一职工的文化程度在标志的分类上属于品质标志，职工的平均工资在指标的分类上属于质量指标。

☎ ✆ 、普查一般用来调查属于一定时点上社会经济现象的数量，它并不排斥对属专业班级姓名学号于时期现象的项目的调查。

☎ ✆、分组以后，各组的频数越大，则组的标志值对于全体标志水平所起的作用也越大；而各组的频率越大，则组的标志值对全体标志水平所起的作用越小。

☎ ✆、标志变异指标数值越大，说明总体中各单位标志值的变异程度越大，则平均指标的代表性越小。

☎ ✆、同一个总体，时期指标值的大小与时期长短成正比，时点指标值的大小与时点间隔成反比。

☎ ✆∙三、单选题（每小题分，共 分）、构成统计总体的个别事物称为（）✌、调查单位 、标志值 、品质标志 、总体单位、对一批商品进行质量检验，最适宜采用的方法是（）。

✌、全面调查 、抽样调查 、典型调查 、重点调查、下列分组中属于按品质标志分组的是（）。

✌、学生按考试分数分组 、产品按品种分组、企业按计划完成程度分组∙ 、家庭按年收入分组、某单位的生产小组工人工资资料如下： 元、 元、 元、 元、 元、 元、 元，计算结果均值为128X元，标准差为（）＝✌、⇔＝  、⇔＝  、⇔＝  、⇔＝ 、在销售量综合指数中 ∙ 表示（）。

暨南大学2015-2016年概率论与数理统计考试试卷A卷(无答案)

内A内A 第 1 页共 8 页暨南大学考试试卷说明：答题前请先填写首页上方及每页右上角的姓名、学号等信息（首页有两处）,（共10小题，每小题2分，共20分,请将12345678910题号答案1．设A 、B 、C 为三个事件，则事件“A 、B 、C 三个事件同时不发生”可表示为（）.(A ) A B C ⋂⋂; (B ) ABC ABC ABC ⋃+; (C ) ABC ; (D ) A B C ⋃⋃. 2.某人打靶的命中率为0.8，现独立地射击5次，则击中2次的概率为（）.（A ） 28.0; （B ）322.08.0; （C )32252.08.0C ; （D )32258.02.0C .3．如果 1)()(>+B P A P ，则A 与B 必定（）. )(A 独立； )(B 不独立； )(C 互斥； )(D 不互斥.2015-2016(2)概率论与数理统计内招A 卷学号：姓名：内A 第 2 页共 8 页4.关于连续型随机变量X ，它的分布函数和密度函数分别为()()F x f x 和，则表述正确的是（）.（A ） P(=)=()X x f x ; （B ） -()=()d x F x f t t ;（C ） ()0P X =x ; （D ） lim ()=0xF x .5.设二维随机向量(X ,Y )的概率密度函数为：(6)01,02(,)0a x y x y f x y --≤≤≤≤⎧=⎨⎩其他则常数a =( )，以下那个结论是正确的？(A ) 1/3； (B ) 1/9； (C ) 1/12； (D ) 1/15. 6.设随机变量x X ~f (x )e ,(x 0)λλ-=>，已知()1/2E X =，若Y λ服从参数为的泊松分布，则下列计算正确的是（）.(A ) ()2,()4E Y Var Y ==; （B ）(22)6Var Y --=-; （C ）2()4E Y =; （D ）2(+1)11E Y =. 7.设123456X ,X ,X ,X ,X ,X 是来自正态总体N (0,1)的样本，则统计量222222123456X X X X X X +++++服从（）分布.(A ) 正态分布; (B ) t 分布; (C ) F 分布; (D ) 2χ分布.8.设总体为[]0,θ上的均匀分布，则参数θ的矩估计为（）. (A ) 2X ; （B ）1X +; （C ）1X; （D ）2X . 9.设n X X X ,,21是来自总体()2,σμN 的样本，2,μσ均未知，则下列函数中是统计量的是（）.（A ） ∑=n i i X n 11 （B ） ()∑=-ni iX X1221σ（C ） ()∑=-n i i X n 121μ （D ） ()221σS n -.10.设321,,X X X 是来自(,1)N μ的样本,下面μ的无偏估计量中最有效的是（）.内A 第 3 页共 8 页)(A 3211313131ˆX X X ++=μ； )(B 3212949231ˆX X X ++=μ； )(C 3213216131ˆX X X ++=μ； )(D 32141254131ˆX X X ++=μ．二、填空题（共10小题, 每空2分, 共20分, 请将答案写在答题框内）12345678910题号答案1．某班共有30名学生，其中3名来自海南。

2015年高考数学(新课标Ⅱ版)分项汇编专题12概率和统计(含解析)理

专题12 概率和统计一．基础题组1. 【2014新课标，理5】某地区空气质量监测资料表明，一天的空气质量为优良的概率是0. 75，连续两天为优良的概率是0.6，已知某天的空气质量为优良，则随后一天的空气质量为优良的概率是（）A. 0.8B. 0.75C. 0.6D. 0.45 【答案】A()0.6(|)0.8()0.75P A B P B A P A ⋂===，故选A.2. 【2011新课标，理4】有3个兴趣小组，甲、乙两位同学各自参加其中一个小组，每位同学参加各个小组的可能性相同，则这两位同学参加同一个兴趣小组的概率为( ) A ．13B ．12C ．23D ．34【答案】A 【解析】3. 【2005全国3，理5】=+--+-→)342231(lim 221x x x x n（） A ．21-B ．21C ．61-D ．61【答案】C 【解析】4. 【2006全国2，理16】一个社会调查机构就某地居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如下图).为了分析居民的收入与年龄,学历,职业等方面的关系,要从这10 000人中再用分层抽样方法抽出100人作进一步调查,则在［2 500,3 000)(元)月收入段应抽出人.【答案】:255. 【2014全国2，理19】某地区2007年至2013年农村居民家庭纯收入y（单位：千元）的数据如下表：（Ⅰ）求y关于t的线性回归方程；（Ⅱ）利用（Ⅰ）中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入. 附：回归直线的斜率和截距的最小二乘法估计公式分别为：()()()121niii ni i t t y y b t t ∧==--=-∑∑，ˆˆay bt =- 6. 【2011新课标，理19】某种产品的质量以其质量指标值衡量，质量指标值越大表明质量越好，且质量指标值大于或等于102的产品为优质品．现用两种新配方(分别称为A 配方和B 配方)做试验，各生产了100件这种产品，并测量了每件产品的质量指标值，得到下面试验结果：A 配方的频数分布表(2)(理)已知用B 配方生产的一件产品的利润y (单位：元)与其质量指标值t 的关系式为2,942,941024,102t y t t -<⎧⎪=≤≤⎨⎪≥⎩从用B 配方生产的产品中任取一件，其利润记为X (单位：元)，求X 的分布列及数学期望．(以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率) 【解析】：(1)由试验结果知，用A 配方生产的产品中优质品的频率为2280.3100+=，所以用A 配方生产的产品的优质品率的估计值为0.3.由试验结果知，用B配方生产的产品中优质品的频率为32100.42100+=，所以用B配方生产的产品的优质品率的估计值为0.42.(2)用B配方生产的100件产品中，其质量指标值落入区间[90，94)，[94，102)，[102，110]的频率分别为0.04，0.54，0.42，因此P(X＝－2)＝0.04，P(X＝2)＝0.54，P(X＝4)＝0.42，即X的分布列为X的数学期望E(X)＝－2×0.04＋2×0.54＋4×0.42＝2.68.7. 【2006全国2，理18】某批产品成箱包装,每箱5件.一用户在购进该批产品前先取出3箱,再从每箱中任意抽取2件产品进行检验.设取出的第一,二,三箱中分别有0件,1件,2件二等品,其余为一等品.(1)用ξ表示抽检的6件产品中二等品的件数,求ξ的分布列及ξ的数学期望;(文19(1))求抽检的6件产品中恰有一件二等品的概率;(2)若抽检的6件产品中有2件或2件以上二等品,用户就拒绝购买这批产品,求这批产品被用户拒绝购买的概率.8. 【2005全国3，理17】(本小题满分12分)设甲、乙、丙三台机器是否需要照顾相互之间没有影响.已知在某一小时内，甲、乙都需要照顾的概率为0.05，甲、丙都需要照顾的概率为0.1，乙、丙都需要照顾的概率为0.125，（Ⅰ）求甲、乙、丙每台机器在这个小时内需要照顾的概率分别是多少；（Ⅱ）计算这个小时内至少有一台需要照顾的概率.9. 【2005全国2，理19】(本小题满分12分)甲、乙两队进行一场排球比赛，根据以往经验，单局比赛甲队胜乙队的概率为0.6．本场比赛采用五局三胜制，即先胜三局的队获胜，比赛结束．设各局比赛相互间没有影响．令x 为本场比赛的局数，求x 的概率分布和数学期望．(精确到0.001)3456.0)4.06.04.06.04.06.0()5(222224=⨯⨯+⨯⨯==c p ξ所以ξ的概率分布表如下所以ξ10．【2015高考新课标2，理3】根据下面给出的2004年至2013年我国二氧化硫排放量（单位：万吨）柱形图。

李志从概率论与数理统计14-15(1)试卷A

河北科技大学2014--2015学年第一学期《概率论与数理统计》期末考试试卷（A ）学院班级姓名学号一．单选题（每小题3分，共24分）1. 设A ，B 为随机事件，P （AB ）=1，则（）A ．A ，B 均是必然事件 B. P (A )= P (B )=1C ．AB 是必然事件 D. A 与B 不独立 2．设随机变量X 的密度函数为)1(1)(2x x f +=π，则X e Y 2=的密度函数为（） A ．21(4ln )y y π+ B ．22(4ln )y y π+ C ．22(4ln )y π+ D ． 22(14ln )y y π+3. 设随机变量X ，Y 不相关，2()()0,D X D Y σ==≠ 则下列命题错误的是（）A. Cov(X,Y)=0B. 2(2)5D X Y σ-=C. X ，Y 相互独立D. E (XY )=E (X )E (Y )4. 对正态总体的数学期望进行假设检验时，如果在显著性水平0.01α=下接受00H :μμ=，则在显著性水平0.05α=下，正确的是（）A ．必接受0HB ．可能接受，也可能拒绝0HC ．必拒绝0HD ．不接受，也不拒绝0H5. 12,X X 是来自正态总体2(0,)N σ的一组样本，下列结论中正确的是（）A ． 212/X X ～t(1) B ． 212212()()X X X X -+～ F （2,2） C ． 12X X -～2(0,)2N σ D ．221221()X X σ+～2(2)χ 6. 设()x Φ为标准正态分布函数，{,1001,2,i X A 1A 0,i Λ==　发生；，事件不发生；事件，且P(A)=0.2，X 1，X 2，…，X 100相互独立。

令∑==1001i i X Y ，则由中心极限定理知Y 的分布函数F （y ）近似于（）A .)420-(y Φ B ．)480(-Φy C ．)1620-(y Φ D ．)1680-(y Φ 7. 设随机变量X ，Y 均服从正态分布，且它们不相关，则( ).A ． X 与Y 一定相互独立;B ． X 与Y 未必独立;C ．（X, Y ）服从二维正态分布;D ． X+Y 服从一维正态分布.8. 设12,,,n X X X L 为正态总体(,4)N μ的一个样本，X 表示样本均值，则μ的置信度为1α- 的置信区间为（） A．/2/2(X z X z αα-+ B．/2/2(((X t n X t n αα--+- C ．/2/2(X z X z αα-+ D ．(X z X z αα-+ 二．填空题（每空3分，共36分）1．设A ，B ，C 是随机事件，P （AB ）=21，P （C ）=41，且B 与C 互不相容，则P （AB |C ）＝__________.2．已知)2(~E X ，~(2)Y π, 且X 与Y 不相关，则D(X -3Y )= .3．设总体~(100,30)X N ，1215(,,,)X X X K 和125(,,,)Y Y Y K 是其两个独立的样本，则D （X ）＝______________，~X Y - . 4. 连续四次掷一枚硬币，已知至少出现一次反面的概率为8165，则每次掷硬币时出现正面的概率为__________.5．设E (X )=E (Y )=2，D (X )=2，D (Y )=8, 3/4XY ρ=，则由切比雪夫不等式{||3}P X Y -≥≤ .6. 设二维随机向量（X ，Y ）的联合分布律为则当α= ， β = 时，X 与Y 相互独立.7. 设,01()0,ax b x f x +<<⎧=⎨⎩其它是连续型随机变量X 的概率密度函数，且13EX =，则a = ，b = .8．设1234,,,X X X X 是来自参数为θ的泊松分布总体的样本．现有θ的三个估计量11234()4T X X X X =+++，2123411()()63T X X X X =+++，31234(234)5T X X X X =+++，其中两个估计量是无偏的.9. 若X 服从自由度为n 的t 分布，则2X 服从分布.三．计算题（第一小题1分，其余各小题3分，共16分）设随机变量X和Y的联合分布在以点（0,0）、（0,1）、（1,1）为顶点的三角形区域上服从均匀分布，试求：（1）联合概率密度函数(,)f x y；（2）；{1}P X Y+≥（3）边缘概率密度函数()Xf x；；（4）条件概率密度函数|(|)Y Xf y x；（5）11 {|)}42 P Y X≥=（6）Z X Y =+,求Z 的概率密度函数(z)Z f四．计算题（8分）设总体X 的密度函数为()+1,01()0,x x f x θθ⎧<<⎪=⎨⎪⎩其他，(1)-θθ>为未知参数，12,,,n X X X L 为总体X 的样本，（1）求θ的矩估计量．（2）求θ的最大似然估计量．五．计算题（8分）在做单选题时（4个备选答案中只有一个正确答案），若一个学生不知道正确答案，他就作随机选择。

2015年高考数学真题概率和统计答案

2015年高考数学真题分类汇编专题11 概率和统计文20.【2015高考安徽，文17】某企业为了解下属某部门对本企业职工的服务情况，随机访问50名职工，根据这50名职工对该部门的评分，绘制频率分布直方图（如图所示），其中样本数据分组区间为[40,50],[50,60],,[80,90],[90,100]（Ⅰ）求频率分布图中a 的值；（Ⅱ）估计该企业的职工对该部门评分不低于80的概率；（Ⅲ）从评分在[40,60]的受访职工中，随机抽取2人，求此2人评分都在[40,50]的概率.【答案】（Ⅰ）0.006；（Ⅱ）0.4；（Ⅲ）110【解析】（Ⅰ）因为110)028.02022.00018.0004.0(=⨯+⨯+++a ，所以006.0=a（Ⅱ）由所给频率分布直方图知，50名受访职工评分不低于80的频率为4.010)018.0022.0(=⨯+，所以该企业职工对该部门评分不低于80的概率的估计值为0.4.（Ⅲ）受访职工评分在[50,60)的有：50×0.006×10＝3（人），即为321,,A A A ; 受访职工评分在[40,50)的有： 50×0.004×40＝2（人），即为21,B B .从这5名受访职工中随机抽取2人，所有可能的结果共有10种，它们是{}{}{}{},,,,,,,,21113121B A B A A A A A{}{}{}{}{}{},,,,,,,,,,,,2123132212312B B B A B A B A B A A A 又因为所抽取2人的评分都在[40,50)的结果有1种，即{}21,B B ，故所求的概率为101=p . 【考点定位】本题主要考查了频率分布直方图、概率和频率的关系、古典概型等基础知识.【名师点睛】利用频率分布直方图解题的时，注意其表达的意义，同时要理解频率是概率的估计值这一基础知识；在利用古典概型解题时，要注意列出所有的基本事件，千万不可出现重、漏的情况.21.【2015高考北京，文17】（本小题满分13分）某超市随机选取1000位顾客，记录了他们购买甲、乙、丙、丁四种商品的情况，整理成如下统计表，其中“√”表示购买，“×”表示未购买．（I ）估计顾客同时购买乙和丙的概率；（II ）估计顾客在甲、乙、丙、丁中同时购买3中商品的概率；（III ）如果顾客购买了甲，则该顾客同时购买乙、丙、丁中那种商品的可能性最大？【答案】（I ）0.2；（II ）0.3；（III ）同时购买丙的可能性最大. 【解析】试题分析：本题主要考查统计表、概率等基础知识，考查学生的分析问题解决问题的能力、转化能力、计算能力.（I ）由统计表读出顾客同时购买乙和丙的人数200，计算出概率；（II ）先由统计表读出顾客在甲、乙、丙、丁中同时购买3中商品的人数100200+，再计算概率；（III ）由统计表读出顾客同时购买甲和乙的人数为200，顾客同时购买甲和丙的人数为100200300++，顾客同时购买甲和丁的人数为100，分别计算出概率，再通过比较大小得出结论.试题解析：（Ⅰ）从统计表可以看出，在这1000位顾客中，有200位顾客同时购买了乙和丙，所以顾客同时购买乙和丙的概率可以估计为2000.21000=. （Ⅱ）从统计表可以看出，在在这1000位顾客中，有100位顾客同时购买了甲、丙、丁，另有200位顾客同时购买了甲、乙、丙，其他顾客最多购买了2种商品.所以顾客在甲、乙、丙、丁中同时购买3种商品的概率可以估计为1002000.31000+=.（Ⅲ）与（Ⅰ）同理，可得：顾客同时购买甲和乙的概率可以估计为2000.21000=，顾客同时购买甲和丙的概率可以估计为1002003000.61000++=，顾客同时购买甲和丁的概率可以估计为1000.11000=，所以，如果顾客购买了甲，则该顾客同时购买丙的可能性最大. 考点：统计表、概率.【名师点晴】本题主要考查的是统计表和古典概型，属于中档题．解题时一定要抓住重要字眼“估计”和“最大”，否则很容易失分．解此类统计表的试题一定要理解透彻题意，提取必要的信息．解本题需要掌握的知识点是古典概型概率公式，即()A P A =包含的基本事件的个数基本事件的总数．22.【2015高考福建，文18】全网传播的融合指数是衡量电视媒体在中国网民中影响了的综合指标．根据相关报道提供的全网传播2015年某全国性大型活动的“省级卫视新闻台”融合指数的数据，对名列前20名的“省级卫视新闻台”的融合指数进行分组统计，结果如表所示．（Ⅰ）现从融合指数在[4,5)和[]7,8内的“省级卫视新闻台”中随机抽取2家进行调研，求至少有1家的融合指数在[]7,8的概率；（Ⅱ）根据分组统计表求这20家“省级卫视新闻台”的融合指数的平均数．【答案】（Ⅰ）910；（Ⅱ）6.05．【解析】解法一：（I ）融合指数在[]7,8内的“省级卫视新闻台”记为1A ，2A ，3A ；融合指数在[)4,5内的“省级卫视新闻台”记为1B ，2B ．从融合指数在[)4,5和[]7,8内的“省级卫视新闻台”中随机抽取2家的所有基本事件是：{}12,A A ，{}13,A A ，{}23,A A ，{}11,A B ，{}12,A B ，{}21,A B ，{}22,A B ，{}31,A B ，{}32,A B ，{}12,B B ，共10个．其中，至少有1家融合指数在[]7,8内的基本事件是：{}12,A A ，{}13,A A ，{}23,A A ，{}11,A B ，{}12,A B ，{}21,A B ，{}22,A B ，{}31,A B ，{}32,A B ，共9个．所以所求的概率910P =．（II ）这20家“省级卫视新闻台”的融合指数平均数等于28734.5 5.5 6.57.5 6.0520202020⨯+⨯+⨯+⨯=．解法二：（I ）融合指数在[]7,8内的“省级卫视新闻台”记为1A ，2A ，3A ；融合指数在[)4,5内的“省级卫视新闻台”记为1B ，2B ．从融合指数在[)4,5和[]7,8内的“省级卫视新闻台”中随机抽取2家的所有基本事件是：{}12,A A ，{}13,A A ，{}23,A A ，{}11,A B ，{}12,A B ，{}21,A B ，{}22,A B ，{}31,A B ，{}32,A B ，{}12,B B ，共10个．其中，没有1家融合指数在[]7,8内的基本事件是：{}12,B B ，共1个．所以所求的概率1911010P =-=．（II ）同解法一．【考点定位】1、古典概型；2、平均值．【名师点睛】本题考差古典概型和平均数，利用古典概型的“等可能”“有限”性的特点，能方便的求出概率．由实际意义构造古典概型，首先确定试验的样本空间结构并计算它所含样本点总数，然后再求出事件A 所含基本事件个数，代入古典概型的概率计算公式；根据频率分布表求平均数，对于每组的若干个数可以采取区间中点值作为该组数据的数值，再求平均数．23.【2015高考广东，文17】（本小题满分12分）某城市100户居民的月平均用电量（单位：度），以[)160,180，[)180,200，[)200,220，[)220,240，[)240,260，[)260,280，[]280,300分组的频率分布直方图如图2．（1）求直方图中x 的值；（2）求月平均用电量的众数和中位数；（3）在月平均用电量为[)220,240，[)240,260，[)260,280，[]280,300的四组用户中，用分层抽样的方法抽取11户居民，则月平均用电量在[)220,240的用户中应抽取多少户？【答案】（1）0.0075；（2）230，224；（3）5．【解析】试题分析：（1）由频率之和等于1可得x 的值；（2）由最高矩形的横坐标中点可得众数，由频率之和等于0.5可得中位数；（3）先计算出月平均用电量为[)220,240，[)240,260，[)260,280，[]280,300的用户的户数，再计算抽取比例，进而可得月平均用电量在[)220,240的用户中应抽取的户数．试题解析：（1）由()0.0020.00950.0110.01250.0050.0025201x ++++++⨯=得：0.0075x =，所以直方图中x 的值是0.0075 （2）月平均用电量的众数是2202402302+= 因为()0.0020.00950.011200.450.5++⨯=<，所以月平均用电量的中位数在[)220,240内，设中位数为a ，由()()0.0020.00950.011200.01252200.5a ++⨯+⨯-=得：224a =，所以月平均用电量的中位数是224（3）月平均用电量为[)220,240的用户有0.01252010025⨯⨯=户，月平均用电量为[)240,260的用户有0.00752010015⨯⨯=户，月平均用电量为[)260,280的用户有0.0052010010⨯⨯=户，月平均用电量为[]280,300的用户有0.0025201005⨯⨯=户，抽取比例11125151055==+++，所以月平均用电量在[)220,240的用户中应抽取12555⨯=户考点：1、频率分布直方图；2、样本的数字特征（众数、中位数）；3、分层抽样.【名师点晴】本题主要考查的是频率分布直方图、样本的数字特征（众数、中位数）和分层抽样，属于中档题．解题时一定要注意频率分布直方图的纵轴是频率组距，否则很容易出现错误．解本题需要掌握的知识点是频率分布直方图、样本的数字特征（众数、中位数）和分层抽样，即在频率分布直方图中，各小长方形的面积的总和等于1，众数是最高矩形的横坐标中点，中位数左边和右边的直方图的面积相等，=⨯频率频率组距组距，=样本容量抽取比例总体容量．24.【2015高考湖南，文16】（本小题满分12分）某商场举行有奖促销活动，顾客购买一定金额的商品后即可抽奖，抽奖方法是：从装有2个红球12,A A 和1个白球B 的甲箱与装有2个红球12,a a 和2个白球12,b b 的乙箱中，各随机摸出1个球，若摸出的2个球都是红球则中奖，否则不中奖。

概率论与数理统计考试试卷与答案

05——06一.填空题（每空题2分，共计60分）1、A 、B 是两个随机事件，已知0.3)B (p ,5.0)(,4.0)A (p ===A B P ，则=)B A (p 0.6 ,=)B -A (p 0.1 ，)(B A P ⋅= 0.4 , =)B A (p 0.6。

2、一个袋子中有大小相同的红球6只、黑球4只。

（1）从中不放回地任取2只，则第一次、第二次取红色球的概率为： 1/3 。

（2）若有放回地任取2只，则第一次、第二次取红色球的概率为： 9/25 。

（3）若第一次取一只球观查球颜色后，追加一只与其颜色相同的球一并放入袋中后，再取第二只，则第一次、第二次取红色球的概率为： 21/55 。

3、设随机变量X 服从B （2，0.5）的二项分布，则{}=≥1X p 0.75, Y 服从二项分布B(98, 0.5), X 与Y 相互独立, 则X+Y 服从 B(100,0.5)，E(X+Y)= 50 ，方差D(X+Y)= 25 。

4、甲、乙两个工厂生产同一种零件，设甲厂、乙厂的次品率分别为0.1、0.15．现从由甲厂、乙厂的产品分别占60%、40%的一批产品中随机抽取一件。

（1）抽到次品的概率为： 0.12 。

（2）若发现该件是次品，则该次品为甲厂生产的概率为： 0.5 ． 5、设二维随机向量),(Y X 的分布律如右，则=a 0.1,=)(X E 0.4，Y X 与的协方差为: - 0.2 ，2Y X Z +=的分布律为:6、若随机变量X ~)4 ,2(N 且8413.0)1(=Φ，9772.0)2(=Φ,则=<<-}42{X P 0.815 ，(~,12N Y X Y 则+= 5 ， 16 ）。

7、随机变量X 、Y 的数学期望E(X)= -1，E(Y)=2, 方差D(X)=1，D(Y)=2, 且X 、Y 相互独立，则：=-)2(Y X E - 4 ，=-)2(Y X D 6 。

8、设2),(125===Y X Cov Y D X D ，）（，）（，则=+）（Y X D 309、设261,,X X 是总体)16,8(N 的容量为26的样本，X 为样本均值，2S 为样本方差。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

《概率论与数理统计》试卷
考试单位：汽车与电子工程学院学年学期：2015—2016学年第2学期考试对象：汽车服务工程专业2014年级1班试卷编号：A 卷命题教师（或单位）：胡鹏教研室主任：
一、选择题：(每小题3分，共15分)
1. 以A 表示事件“甲种产品畅销，乙种产品滞销”，则其对立事件A 为（A ）“甲种产品滞销，乙种产品畅销”；（B ）“甲、乙两种产品均畅销” （C ）“甲种产品滞销”；（D ）“甲种产品滞销或乙种产品畅销”
2.3个人独立地破译一个密码，他们能破译的概率分别为111
,,543求此密码被破译的概
率为
（A ）1/5 （B ）2/5 （C ）3/5 （D ）4/5 3. 设X ～2(,)N μσ,那么当σ增大时，{}P X μσ-<= (A ）增大 (B ）减少 (C ）不变 (D ）增减不定
4. 已知二维随机变量密度函数为22,1
(,)0,,cx y x y f x y ⎧≤≤=⎨⎩其他
，求常数c 的值为（）
(A ）214 (B ）204 (C ）224 (D ）无法确定
5．下列二元函数中，可以作为连续型随机变量的联合概率密度。

（A ）f(x,y)=cos x,0,⎧⎨⎩x ,0y 1
22
ππ
-≤≤≤≤其他（B) g(x,y)=cos x,0,⎧⎨⎩1x ,0y 222ππ-≤≤≤≤
其他
__________________学院__________级_______________________专业姓名____________ 学号____________
………………………………………………（密）………………………………（封）………………………………（线）…………………………………………
（C) ϕ(x,y)=cos x,0,
⎧⎨⎩0x ,0y 1
π≤≤≤≤其他
（D) h(x,y)=cos x,0,⎧⎨⎩1
0x ,0y 2π≤≤≤≤
其他
二、判断题：(每小题2分，共10分)
6.n μ为n 重贝努力试验中事件A 发生的次数，而p 为事件A 每次实验发生的概率则
n
n
μ收敛于p .( ) 7.若,ξη相互独立则()()()D D D ξηξη+=+.( ) 8.事件,A B 互斥则,A B 一定为不相容事件.( ) 9.等式()()()P A B P A P B +=+任何情况均成立. ( )
10.已知()F x 为随机变量ξ的分布函数则，12x x ∀<均有12()()F x F x
≤( ) 三、填空题：(每小题3分，共15分)
11．设X ～(5,0.3)B ,且{24}P x <<=______ .
12．若随机变量ξ在（1，4）上服从均匀分布，则方程210x x ξ++=有实根的概率是 .
13．设12,,,n X X X ⋅⋅⋅是独立的随机变量序列,且i EX μ=，2i DX σ=(1,2,)i =⋅⋅⋅设
1n
i i X X ==∑则i EX =
14．二维随机变量密度函数为1
sin(),0,(,)220,,x y x y f x y π⎧+≤≤
⎪=⎨⎪⎩其他
则协方差
cov(,)X Y =
15. 设~(0,1),x X N Y e =，则x Y e =的概率密度为
四、计算题：(每小题10分，共30分)
16. 设随机变量函数X 的分布函数为,0
()0,0x A Be x F x x λ-⎧+≥=⎨<⎩
（1）求常数,A B （2）求(2)P x ≤
（3）求概率密度函数()f x
17.在圆222x y R +≤内均匀投点(,)X Y 求（1）关于,X Y 的边际密度
（2）22R R P X Y ⎛⎫
<> ⎪⎝⎭
18．把一枚均匀的硬币连抛三次，以X表示出现正面的次数，Y表示正、反两面次数差的绝对值，求)
X的联合分布律与边缘分布
,
(Y
五、应用题：(每小题10分，共30分)
19. 一本50页的书，共有6个错别字，每个错字出现在哪一页的概率是相等的，求以下概率
（1）1～20页恰好有2个错字
(2)1～20页出现错字不少于2个？
20. 一箱产品，A，B两厂生产分别个占60％，40％，其次品率分别为1％，2％。

现在从中任取一件为次品，问此时该产品是哪个厂生产的可能性最大？
21.某商店年末进行有奖销售，通过抽取奖券确定奖品等级，奖品分为特等奖，一等奖，二等奖，三等奖，参与奖，每种奖项对应奖金为10000元，1000元，100元，10元，1元，每种奖券所占比率分别为0.01%,0.15%,1.34%,10%,88.5%，求奖金X的数学期望.。