2013届高考考前题型回顾复习
2013届高考生物二轮复习全攻略:1-1-3《细胞的生命历程》

b、c中表示染色体的是________,图甲中④产生的子细胞
内,a、b、c的数量分别为________。 (3)图甲⑤中存在的等位基因是________,造成这一结果 的可能原因有________。图甲⑥代表的个体中最多(不考 虑交叉互换)能产生________种染色体组合不同的配子。
减数第 二次分 裂
常考点6
有同 源染 色体
无同 源染 色体
常考点7 阅考人考前“叮嘱” 随堂精练
上页 下页 返回
(2)减数分裂中根据细胞质分裂情况判断细胞名称
常考点6
常考点7
阅考人考前“叮嘱”
随堂精练
上页 下页 返回
3.染色体、DNA数量变化曲线及判断 (1)有丝分裂、减数分裂与受精过程中三曲线变化
大小形态不同。 5.细胞分裂与变异类型的关系
常考点6 常考点7 阅考人考前“叮嘱” 随堂精练
上页 下页 返回
分裂方式 无丝分裂 有丝分裂 减数分裂
变异类型 基因突变 基因突变、染色体变异 基因突变、基因重组、染色体变异
题形式出现过。
常考点6
常考点7
阅考人考前“叮嘱”
随堂精练
上页 下页 返回
命题猜想
细胞分裂图像分析类试题
【押题1】 下列图甲、乙、丙分别是一些二倍体生物细胞的
染色体组成和分裂过程中物质或结构变化的相关模式 图。请分析回答下列问题。
常考点6
常考点7
阅考人考前“叮嘱”
随堂精练
上页 下页 返回
7江海中学2013届高三高考考前辅导化学试题

高三化学考前辅导材料江海中学高三化学备课组一、考前的心理准备心态调整:化学是高考的最后一门。
之前的考试,你可能是一路上顺风顺水;你也可能是磕磕绊绊,还在那捶胸顿足,有点后悔、有点郁闷、有点不爽。
但此时不是庆功的时候,也不是泄气、怨天尤人的时候,考好的四门,已是煮熟的鸭子(用我们的专业术语讲是不可逆的),所以让往考随风而去,收拾好心情轻装上路,打响最后一战,打好最后一战。
我难人亦难我不怕难我易人亦易我不大意心理状态好七分本事得十分心理状态差十分本事得七分若要化学夺高分心态平衡是根本心态平衡不怕不慌不骄不躁沉着冷静果断仔细二、考试争分策略容易题全得分,中难题少失分,较难题能争分。
与其难题多争一分,不如易题少失5分。
熟题不一定易,生题不一定难。
新题不会难大题不会深。
不要怕难题怪题,不要耗在难题上。
重Ⅰ卷,保证拿足基本分。
攻Ⅱ卷,规范表达夺高分。
争取急中生智,避免忙中出乱。
该得的分一定要得到,不该失的分一分都不失。
先做Ⅰ卷,且做完后马上涂卡;接着找“选做题”,选做“物质结构模块题”。
试想:此时不已把40+12=52分收入囊中了吗?心里踏实啦,后面就能势如破竹!再后的解题顺序就根据各人的具体情况了。
三、明确高考评分的要求及评分时坚持的原则1.化学专用名词中出现错别字(甚至白字)都要参照标准扣分。
如:催.化剂;加成.反应;苯.;油脂.;酯.化;金刚.石;容量瓶;坩埚..(钳);铵.盐、氨.气等等。
2.化学方程式、离子方程式未配平、条件错误或不全的,都不给分(包括反应物或生成物的系数有倍数(非最小公倍数),分数等均视为不规范而不给分。
“△”、“↑”、“↓”、“→”、“”、反应条件等均应正确使用。
3.凡是辨别不清的,皆为“0”分。
所以答题时,字不一定很漂亮,但须十分清晰。
即首先不能过分潦草,而且要十分清晰,易于辨认。
四、明确高考评分的要求及评卷中的有关规范的问题(1)结构式:苯环、双键、羧基、醛基等均应按教材的规范要求规范写出,许多官能团连在链的左边和右边写法不一样,例如:硝基(O2N- -NO2)、氨基(H2N- -NH2)、羟基(HO- -OH)、羧基(HOOC- -COOH)、醛基( OHC- -CHO)等,若不规范,则一律扣分,有时甚至定为“0”分。
3 东南中学2013届高三高考考前辅导英语试题

启东市东南中学2013届高三英语考前辅导材料2013届高三学子们:高考的钟声即将敲响!经过较为系统且全面的复习,你们在英语方面已取得了很大的进步。
其实,复习到现在,你们已经准备得相当充分了,只要你充满信心走进考场,胜利就在向你招手。
下面请跟随我进入模块复习的指导。
第一部分:听力(善于抓住要素)(1)听力部分的特点:1.语速:听力部分的朗读速度约为每分钟130--150个单词,低于或相当于高中英语教学大纲中规定的语速。
2.语音:在高考英语的考试说明中,并没有对听力部分的语音做出任何规定。
这两年高考英语听力试题一般都是美音。
但是语言学习一定要体现出其真实性、交际性和实用性。
所以,以后的听力部分肯定也会出现英音,澳大利亚式英语发音,甚至还会有背景音。
3.内容:源于生活,体现生活,和日常生活有密切联系。
具体涉及到的话题有:问路,购物,助人,询问时间,问候,新闻,约会,打电话等等。
话题的内容基本上都是在教大纲规定的高中生英语知识与能力要求的范围内。
答题前,一定要有足够的时间去阅读试题。
(在进行听力测试前,最好不要做其它题目)(2)审好试题:在听的过程中,要抓住与问题相关的关键词(如but,however, so, nevertheless等),要特别注意情景、说话者的角色和简单的数量关系等,其余主要是细节问题了。
答题时,相当一些试题与同义词或反义词的转换有关,如录音中是dear,选择项中可能是expensive或not cheap了。
做题思路:快读---预测---精听---巧记---细选。
在播放试音部分时,不要力求完全听懂,只要求迅速适应播音者的语音语速即可。
在进入考试后,可以说开始的5分钟是最重要的。
根据历年经验,考生在前五个听力小题上失分过多。
真正的原因在于,这些题只读一遍,考生心神不定,第1个听不清,稍作迟疑,第2个又过去了。
因此,最好的办法是,听清一个....做一个,不在听不清处纠缠,要学会及时放弃....................;不求全部拿下,但求能拿下的全部拿下。
2013届高考历史总复习 精典例题+详细解析 考前保温训练二

考前保温训练(二)(限时:45分钟满分:100分)一、选择题(本大题共12小题,每小题5分,共60分)1.(2012·汕头模拟)到了秦、汉统一,由封建转为郡县,古人称“化家为国”,一切贵族家庭都倒下了,只有一个家却变成了国家。
这里“化家为国”指的是( )A.分封制的瓦解B.郡县制的实行C.封建制度的确立D.郡国并行制的实施解析:选B 考查秦朝中央集权制度的建立。
“从封建转为郡县”“一切贵族家庭都倒下了,只有一个家变成国家”体现出随着郡县制取代封国制,天下逐渐变为皇帝一姓之家。
2.(2012·沈阳质监)《说文解字》关于家的解释:“从宀,豭(jiā)省声。
周伯温曰:豕居之圈曰家,故从宀从豕。
”材料反映出我国古代农耕文明的特点是( )A.种植业为主,家畜饲养业为辅B.以家庭为单位,“男耕女织”C.精耕细作的农业生产模式D.以农业为主,畜牧业为辅解析:选A 考查知识的再认再现和材料解读能力。
宀本意为房屋,豕指猪,豕居之圈曰家,说明重视家畜饲养业,故选A项。
3.(2012·南京二模)黄宗羲评价某先贤说:“先生之学,……出入于佛、老者久之。
及至居夷处困,动心忍性,因念圣人处此,更有何道?忽悟‘格物致知’之旨,圣人之道,吾性自足,不假外求。
”该先贤是( )A.程颢B.朱熹C.王阳明D.李贽解析:选C 本题考查对历史概念的把握和材料解读能力。
从材料中“圣人之道,吾性自足,不假外求”可知该思想家主张内心反省,不必外求,这是王阳明“心学”思想。
故选C项。
4.(2012·朝阳区模拟)下列各项中代表着中国经济与近代世界接轨,并开始踏入新的经济时代的是( )A.海陆丝绸之路的开通B.美洲作物普遍推广C.机器工业的逐步引进D.列强资本输入中国解析:选C 鸦片战争后中国被迫开放。
为了巩固清政府的统治,洋务派开始引进西方的机器,兴办近代军事和民用工业,客观上适应了西方工业文明扩展的趋势。
2013高考复习全攻略知识点全集一模题库二模题库三模题库高考真题

2013高考复习全攻略知识点全集一模题库二模题库三模题库高考真题答案 D A C B D C B C D C二、填空题(本大题共5小题,每小题5分. 共25分)11. 6 12. 11 13. 1214. 222, (4(1), (4tt为偶数)为奇数) 15. A.14 B.ttt5三、解答题(本大题共6小题,共75分)16.解:(1)13()(1cos2)sin222fxxx………………………2分1sin(2)26x,…………………………3分因为()fx最小正周期为π,所以22ππω,解得1ω ,…………………………4分所以1()sin(2)62πfxx, ………………………… 5分所以21()32πf. …………………………6分(2)分别由222,()262kxkkZ,3222,()262kxkkZ可得,()36kxkkZ,2,().63kxkkZ………………8分所以,函数()fx的单调增区间为[,],()3 6kkkZ;()fx的单调减区间为2[,],().63kkkZ………………………10分由2,(62ππxkπkZ)得,()26kπxπkZ.所以,()fx图象的对称轴方程为 ()26kπxπkZ.…………………………12分17.解:(1) 设4位乘客中至少有一名乘客在第2层下电梯的事件为A, …………………………1分由题意可得每位乘客在第2层下电梯的概率都是1 3,……………………………3分则4265()1()1381PAPA. ……………………………6分(2) X的可能取值为0,1,2,3,4, …………………………7分由题意可得每个人在第4层下电梯的概率均为13,且每个人下电梯互不影响,所以,1(4,)3XB .……………………………9分X 0 1234P168132812481881181………………………………11分 14()433EX.………………………………12分18.(1)证明:设F为DC的中点,连接BF,则DFAB ∵ABAD ,ABAD ,//ABDC,∴四边形ABFD为正方形,∵O为BD的中点,∴O为,AFBD的交点,∵2PDPB ,∴POBD ,………………………………..2分∵22BDADAB22 ,∴22POPBBO2,122AOBD,在三角形PAO中,2224POA OPA ,∴POAO ,……………………………3分∵AOBDO ,∴PO 平面ABCD;……………………………4分 (2)方法1:连接PF,∵O为AF的中点,E 为PA中点,∴//OEPF,∵OE 平面PDC,PF 平面PDC,∴//OE平面PDC. ……………………………8分方法2:由(Ⅰ)知PO 平面ABCD,又ABAD ,所以过O分别做,ADAB的平行线,以它们做,xy轴,以OP为z轴建立如图所示的空间直角坐标系,由已知得:(1,1,0)A ,(1,1,0)B ,(1,1,0)D (1,1,0)F,(1,3,0)C,(0,0,2)P,112(,,)222E,则112(,,)222OE,(1,3,2)PC .A,(1,1,2)PD,(1,1,2)PFDOCPBEFADOCPBEFxy∴12OEPF来源:www.shulihua.ne][∴//OEPF∵OE 平面PDC,PF 平面PDC,∴//OE平面PDC;…………………………………8分 (3) 设平面PDC的法向量为111(,,)nxyz,直线CB与平面PDC所成角θ,则00nPCnPD,即11111132020,解得111xyzxyz02yxz,令11z ,则平面PDC的一个法向量为(2,0,1)n,又(2,2,0)CB则223sincos,3θnCB,∴直线CB与平面PDC所成角的正弦值为33. ………………………………………12分[来源:www.shulihua.ne]19.解:(1)由题意可得OPOM ,……………………………2分所以0OPOM,即(,)(,4)0xyx ………………………………4分即240xy ,即动点P的轨迹W 的方程为24xy ……………5分(2)设直线l的方程为4ykx ,1122(,),(,)AxyBxy,则11'(,)Axy .由244ykxxy消y整理得24160xkx ,………………………………6分则216640k ,即||2k .………………………………7分12124,16xxkxx .…………………………………9分直线212221':()yyAByyxxxx212221222212212222121222112()1()4()41444y44yyyxxyxxxxyxxxxxxxxxxyxxxxxxx……………………………………12分即2144xxyx所以,直线'AB恒过定点(0,4). ……………………………………12分20.解:(Ⅰ)解法一:由nnSna21 ①可得当2 n时,12)1( n nSan②,由①-②可得,nnnnnaSSanna2)(2)1(11 ,所以nnanna)1(1 ,即当2 n时,nnaann11 ,所以1,,45,34,231453423n naaaaaaaann ,将上面各式两边分别相乘得,22naan ,即22anan (3 n),又222112 aSa,所以nan (3 n),此结果也满足21,aa,故nan 对任意 Nn都成立。
2013届高考历史总复习 精典例题+详细解析 考前保温训练一

考前保温训练(一)(限时:45分钟满分:100分)一、选择题(本大题共12小题,每小题5分,共60分)1.“任天者定,任人者争;定之以天,争乃不生。
”这句话充分说明了西周宗法制度的精神。
其中的“天”是指( )A.确定继统人选的天子B.决定嫡庶身份的天命C.辨别是非善恶的天理D.表现自然主义的天道解析:选B 题干材料的意思是宗法制下按嫡庶身份的规定决定继承关系就不会出现争斗,如果由人决定则会发生争斗。
由此可知答案为B项。
2.(2012·无锡一模)有学者指出,古代小农的供给行为具有双重性,即在满足自我家庭消费的同时,又积极向市场提供剩余农产品和主动以市场为导向安排生产活动。
对上述观点理解准确的是( ) A.古代小农生产具有多种经营的特点B.市场需求是影响古代小农生产的决定性因素C.古代小农具有强烈的商品生产意识D.古代小农主要通过市场交换获得生活必需品解析:选A 材料认为小农经济在自给自足的同时,并不排斥商品生产。
说明古代小农经济具有多种经营的特点。
3.有人认为董仲舒的“天人感应”学说继承了儒家思想的“仁政”思想。
这一观点主要是看到了董仲舒( )A.主张“民为贵,社稷次之,君为轻”B.提出“君者舟也,庶人者水也;水则载舟,水则覆舟”C.认为天子受命于天,地位不可动摇D.认为人君要爱护百姓,如果残暴,天将降灾祸于他解析:选D 本题只有C、D两项符合董仲舒的思想,其中D项体现董仲舒“天人感应”思想继承了儒家“仁政”思想。
4.(2012·湛江模拟)右图是清末上海《神州画报》上的漫画《此之谓中国之独立》,其中场景最早可能出现在( )A.《南京条约》之后B.《北京条约》之后C.《马关条约》之后D.《辛丑条约》之后解析:选C 本题考查《马关条约》的影响。
《马关条约》的签订,大大刺激了列强侵略中国的野心,随后列强掀起瓜分中国的狂潮,与图的寓意吻合,故选C项。
5.(2012·广东六校第二次联考)下表是小王同学在学习了“近代前期中国人民反侵略、求民主的斗争”之后的一个小结。
2013届高考历史二轮复习回扣课件:回扣1 考前必记的70个核心知识提炼

回扣一
(2)西周宗法制:目的:加强分封制形成的统治秩序,解决 贵族之间在权力、财产和土地继承上的矛盾。内容:划分 宗族内的嫡庶系统,形成相对独立的大宗和小宗。特点: 由嫡长子继承, 利用父系血缘关系的亲疏来维系政治等级。 作用:保证了各级贵族在政治上的垄断和特权地位;有利 于统治集团内部的稳定和团结。
回扣一
[古代西方政治] 6.雅典民主制度 (1)发展阶段 梭伦改革:动摇了旧氏族贵族世袭特权,为雅典奴隶制民 主政治奠定了基础。 克利斯提尼改革:铲除了旧氏族贵族的政治特权,雅典民 主政治确立起来。 伯利克里改革:使雅典民主政治发展到顶峰。 (2)主要内容:通过设立公民大会、五百人议事会、民众法 庭等机构,保证民主制度的正常运作;创造出法治基础上 的差额选举制、任期制、议会制、比例代表制等民主运作 的方式。
回扣一
回扣一 考前必记的 70 个核心知识提炼
[古代中国政治] 1.分封制和宗法制 (1)西周分封制: 目的: 巩固奴隶制国家政权的统治。 对象: 王族、功臣、古代帝王的后代。内容:周王授予诸侯土地 和人民,诸侯有服从命令、镇守疆土、随从作战、交纳贡 赋和朝觐述职的义务。诸侯在自己的封疆内,对卿大夫有 实行再分封的权利。特点:层层分封,等级森严;周天子 具有至尊权威,诸侯在自己的领地内享有相,开发边远地区, 形成众星捧月般的政治格局。瓦解:原因:受封的诸侯国 实力强大,王权衰弱。表现:出现春秋争霸、战国兼并的 混乱局面。
回扣一
18.“一国两制” (1)含义 世界上只有一个中国,大陆和台湾同属于一个中国,中国 的主权和领土完整不容分割。 在祖国统一的前提下,国家的主体坚持社会主义制度,同 时在台湾、香港和澳门保持原有的资本主义和生活方式长 期不变。 在中国国内两种社会制度长期并存,共同发展。
启东市汇龙中学2013届高三高考考前辅导数学试题

汇龙中学2013届高三数学考前辅导第一篇考前指导 5.23随着高考临近,高三将停课调整。
习惯于在老师引导下进行高考复习的同学,此时常会感到手足无措,失去再提高的机会。
在停课调整阶段,如何科学地、合理地、高效率地安排好数学复习,对高考成绩将起到很大作用。
现提出如不建议:一、停课期做什么?1.梳理知识,形成网络,注意覆盖面,不能有死角。
分清哪些内容只要一般理解,哪些内容应重点掌握,哪些知识又要求灵活运用和综合运用,把知识点从整体上再理一遍。
(用A 4纸一张,正反两面)分清哪些是主干知识,每条主线又有若干支线,一条支线又可分为若干分线,形成概念、公式网络图。
各线上应该注意什么?公式变形情况,计算方法,表述要求,证明步骤。
(用A 4纸一张,正反两面)2.梳理方法,形成体系,重解题建模,同类用同法。
分清哪些方法只适用于填空题,哪些用基本元法,哪些用性质法,哪些用特殊法,哪些用不完全归纳法。
(用A 4纸一张,正反两面,立出各方法中的注意点,各举一例,也许你所举例子恰是高考题)分清哪些方法是高考常用的方法,三角与解三角形的常用方法,立几中的证明与计算常用的方法,解几中的求轨迹方程与证明和计算常用的方法,函数与导数中证明和计算常用的方法,数列与不等式中证明和计算常用的方法,应用题中常用的分析方法。
(用A 4纸二张,正反两面,立出各方法中的注意点,各举一例,也许你所举方法恰是高考题的解法)3.理性思考,清醒做题,一追到底,会而不失分思考解题前的审题与解题表述的时间比,能否做到慢审题快解题,数学题中的字是“一字值千金”清醒做题是思路清晰,目标明确,框架凸显,层次分清,表述有序。
一追到底是运算到底,“看了就过,不一定能过得去”中较多的学友就是运算过不去。
解 题审 题 表 述 划出显性条件 分出几段完成 语言转为符号分析隐性条件 格 式 步 骤 段 落 计 算 第一步(细心) 第二步(依据) 第三步(规范)会而不失分是目前争分的关键,保证会做的不错,即使不完全会做,也要理解多少做多少,以增加得分机会。
2013届高三物理二轮复习 一、考前再记物理学史,不因送分题失分而遗憾课件(全国通用)

[解析]
惯性是物体保持原来运动状态不变的性质,故A
对;根据惯性定律可知没有力的作用,物体将保持原来的状 态,即静止状态或者匀速直线运动状态,故B错;行星在圆轨
道上的运动是变速运动,是在万有引力作用下的运动,所以
C错;运动物体如果不受力作用,将保持原来的运动状态, 即继续以同一速度沿着同一直线运动,D对。 [答案] AD
果与某一个力产生的效果相同,用这个力代替那几个力,这
个力叫做那几个力的合力,这种方法叫做等效法; 为计算弹 簧弹力做的功,把拉伸弹簧的过程分为很多小段,拉力在每 小段可以认为是恒力,用各小段做功的代数和代表弹力在整 个过程中做的功,这种研究方法叫做“微元法”; 在探究加速 度与力、质量之间的关系时,先保持质量不变探究加速度与 力的关系,再保持力不变探究加速度与质量的关系,这种研 究方法叫做控制变量法。 [答案] C
C.为计算弹簧弹力做的功,把拉伸弹簧的过程分为很 多小段,拉力在每小段可以认为是恒力,用各小段做功的代
数和代表弹力在整个过程中做的功
D.在探究加速度与力、质量之间的关系时,先保持质 量不变探究加速度与力的关系,再保持力不变探ຫໍສະໝຸດ 加速度与 质量的关系[解析]
在不需要考虑物体本身的大小和形状对所研究
问题的影响时,用有质量的点来代替物体,即质点,这种方 法叫做理想模型法;一个物体受到几个力共同作用产生的效
[题型特点]
物理学史与物理方法是近几年高考命题的
热点,题型为选择题,分值4~6分,主要考查对物理方法
的理解及物理学发展史的正误判断。
[力学部分] (1)1638年,意大利物理学家伽利略在《两种新科学的对话》 中用科学推理论证重物体和轻物体下落一样快;并在比萨斜塔做 了两个不同质量的小球下落的实验,证明了他的观点是正确的, 推翻了古希腊学者亚里士多德的观点(即:质量大的小球下落快是 错误的)。 (2)1654年,德国的马德堡市做了一个轰动一时的实验——马 德堡半球实验。 (3)1687年,英国科学家牛顿在《自然哲学的数学原理》著作 中提出了三条运动定律(即牛顿三大运动定律)。
2013届高三复习备考总结(桂如才)

2013届高三复习备考总结历史组:桂如才 2013年6月一年一度的高考牵动着千百万考生、教师和家长的心。
有人把高考比作独木桥,原因之一是是千千万万学子都想通过它到达自己的理想彼岸。
然而,桥窄人多,只有智者、有准备者才有望通过。
虽然知识的积累、掌握不是一朝一夕所能完成的,但考前的集中、系列化的训练,重要性不言而喻。
因此,做好备考工作,打好来年的一仗,是本学年的重中之重。
须知,高三,学子十二年的苦读,系于此间,教师的责任,便是做他们的助推器,给他们最大的帮助。
匆忙一学年即将过去,先将本学年工作小结如下:一、制定备考计划,构建合理序列凡事预则立,不预则废。
复习开始前,首先对高三学年的复习内容全面把握,整体安排复习计划,并详尽制定阶段复习计划。
并指导学生在班级整体计划的基础上,针对自己的具体情况制定一套相应的计划。
使学生能从教师的计划安排中明确复习的目标、做法和安排,同时从中发现自己的缺漏并有意识地进行补救,在自己的计划中引出教师未复习到的知识死角和问题所在,并安排出时间进行专题复习和难点的各个击破。
二、细心谋划,抓好“双基”抓好基础知识(历史基础的识记与历史知识体系)和基本技能(包括读阅读材料能力,更应该是学习的能力,学习的潜在能力,如理解能力、筛选信息的能力、综合分析的能力、判断的能力、思辨的能力、评价历史材料的能力等等)训练,提高学生的历史人文素养,是最主要、最根本的东西。
抓好“双基”,才可以在高考中以“不变”来“应万变”。
三、踏踏实实,抓好课本的复习历史教材是学生学习历史知识、培养历史能力。
历史高考试题是“题在课外,功在课内”。
如果把课本这个载体丢了,那么,它所负载的东西就很有可能被丢失,历史基础知识的学习和历史基本能力的培养也就很有可能落空,由课内到课外的拓展延伸也就谈不上了。
因此,虽然是高三,仍然以极其严肃的态度对待历史课本,不急功近利,认认真真地上好每一堂课,踏踏实实地教好每一节课程。
不仅“教好课本”,而且“用课本教”。
2013高考试题及答案

2013高考试题及答案2013年的高考是我国教育史上的重要里程碑,它关乎千万考生的未来,也引起了广泛的关注和讨论。
本文将全面回顾2013年高考试题,并附有解答,帮助读者更好地理解和回顾这一历史性的考试。
第一部分语文一、阅读理解(共两节,30分)第一节(共15小题;每小题2分,满分30分)阅读下面的短文,从每题所给的A、B、C和D项中,选出最佳选项,并在答题卡上将该项涂黑。
Passage 1(1)What is most important in a book? Many people would say the story is most important. However, many other people would say "The way it is written" is most important.(2)A good writer puts a lot of thought into the way he or she writes. In fact, a good writer doesn't just write; he or she "crafts" the book. A writer sometimes says that a book didn't "work" and that it needed to be "fixed". This is because the writer is like a craftsman. He or she works and works on a book until it is perfect.(3)Being a good writer is hard work. For a writer, writing takes a lot of time and effort. A writer might have to rewrite the same pages manytimes before he or she is happy with them. A writer may throw out several "first drafts" and may have to start all over again.(4)A good story is important. But readers can't enjoy a good story if they can't understand it. To make a story understandable, a writer must make it clear and easy to follow. The writing must flow smoothly. The writer must also make sure to put the right words in the right places.1. According to the passage, which of the following is most important ina book?A. The story.B. The characters.C. The writing style.D. The setting.答案:C2. What does a writer mean when he or she says a book needed to be "fixed"?A. The story has a mistake.B. The book was torn.C. The writer didn't like the book.D. The book needed some changes.答案:D......第二部分数学一、选择题1. x-2/x=13,那么x-3/x值是?A. 15B. 16C. 17D. 18答案:B2. 设90°<A<180°,且sinA = cos2A,则tan2A的值是?A. 1B. 2C. 3D. 4答案:C......第三部分英语一、单项填空1. — Do you know if Susan saw a doctor yesterday?— She _____ to see one, but I'm not sure if she did.A. wentB. had goneC. would goD. would have gone答案:A2. We decided to go hiking _____ it rained heavily.A. althoughB. ifC. unlessD. because答案:A......第四部分物理一、选择题1. 当光通过空气、水和玻璃的界面传播时,改变光传播方向的主要原因是:A. 自转B. 光非均匀传播C. 反射D. 折射答案:D2. 从理论上讲,有用的能量是指:A. 纳什B. 分子内的热运动C. 宏观上可转换成其他形式的能量D. 原子内的电子运动答案:C......通过以上试题的回顾和解答,我们能够看到2013年高考试题在科目设置、题型设计以及考查内容等方面的特点。
2013届高考数学二轮复习精选考前小题狂练4(苏教)

小题狂练(四)1.已知集合M ={1,2,3},N ={2,3,4},则M ∩N =________.2.已知复数z 满足(z -2)i =1+i(i 为虚数单位),则z 的模为________.3.为了分析某篮球运动员在比赛中发挥的稳定程度,统计了该运动员在6场比赛中的得分,用茎叶图表示如图所示,则该组数据的方差为________.4.在△ABC 中,a =8,B =60°,C =45°,则b =________.5.若过正三角形ABC 的顶点A 任作一条直线l ,则l 与线段BC 相交的概率为________.6.已知函数y =a n x 2(a n ≠0,n ∈N *)的图象在x =1处的切线斜率为2a n -1+1(n ≥2),且当n =1时其图象过点(2,8),则a 7的值为________.7.已知函数y =sin(ωx +φ)⎝ ⎛⎭⎪⎫ω>0,0<φ≤π2的部分图象如图,则φ的值为________.8.在平面直角坐标系xOy 中,直线3x +4y -5=0与圆x 2+y 2=4相交于A ,B 两点,则弦AB 的长等于________.9.如图是一个算法的流程图,则最后输出的S =________.10.设l 是一条直线,α,β,γ是不同的平面,则在下列命题中,假命题是________.①如果α⊥β,那么α内一定存在直线平行于β②如果α不垂直于β,那么α内一定不存在直线垂直于β③如果α⊥γ,β⊥γ,α∩β=l ,那么l ⊥γ④如果α⊥β,l 与α,β都相交,那么l 与α,β所成的角互余11.已知函数f (x )=x 33+ax 22+2bx +c 在区间(0,1)内取极大值,在区间(1,2)内取极小值,则z =(a +3)2+b 2的取值范围为________.12.平面向量a ,b 满足|a +2b |=5,且a +2b 平行于直线y =2x +1,若b =(2,-1),则a =________.13.(2012·南师大附中阶段测试)已知函数f (x )=|x 2+2x -1|,若a <b <-1,且f (a )=f (b ),则ab +a +b 的取值范围是________.14.定义在实数集上的偶函数f (x )满足f (x +2)=f (x ),且f (x )在[-3,-2]上单调递减,又α,β是锐角三角形的两内角,则f (sin α)与f (cos β)的大小关系是________.参考答案小题狂练(四)1.解析 M ∩N ={1,2,3}∩{2,3,4}={2,3}.答案 M ∩N ={2,3}2.解析 由(z -2)i =1+i ,得z =1+i i +2=3-i ,所以|z |=10.答案 103.解析 平均数x =14+17+18+18+20+216=18,故方差s 2=16(42+12+02+02+22+32)=5. 答案 54.解析 由正弦定理得b sin B =c sin C ,∴b =8sin 60°sin 45°=4 6.答案 4 65.解析 ∠BAC =60°,故所求的概率60°360°=16.答案 166.解析 因为y =a n x 2在x =1处的切线斜率为2a n ,所以2a n =2a n -1+1(n ≥2),即a n =a n -1+12(n ≥2),又8=4a 1⇒a 1=2,所以a 7=a 1+6×12=5.答案 57.解析 由三角函数图象可得周期T =2⎝ ⎛⎭⎪⎫5π6-π3=π=2πω,解得ω=2.由函数图象过点⎝ ⎛⎭⎪⎫π3,0,所以sin ⎝ ⎛⎭⎪⎫2×π3+φ=0⇒φ=π3+2k π,k ∈Z ,且0<φ≤π2,所以φ=π3.答案 π38.解析 圆x 2+y 2=4的圆心O (0,0)到直线3x +4y -5=0的距离d =|-5|5=1,弦AB 的长|AB |=2r 2-d 2=2 3.答案 2 39.解析 这是一个典型的当型循环结构,当n =1,3,5,7,9,11时满足条件,执行下面的语句,S =1+3+5+7+9+11=36,当n =13时不满足条件,退出循环,执行输出S =36.答案 3610.解析 如果α⊥β,那么α内一定存在直线平行于β,即命题①正确;如果α不垂直于β,那么α内一定不存在直线垂直于β,即命题②正确;如果α⊥γ,β⊥γ,α∩β=l ,那么l ⊥γ,即命题③正确;如果α⊥β,l 与α,β都相交,那么l 与α,β所成的角不一定互余,即命题④不正确.答案 ④11.解析 因为函数f (x )在区间(0,1)内取极大值,在区间(1,2)内取极小值,所以⎩⎨⎧ f ′(0)>0,f ′(1)<0,f ′(2)>0,即⎩⎨⎧ b <0,1+a +2b <0,a +b +2>0,对应可行域如图,目标函数z =(a +3)2+b 2的几何意义是可行域上的点(a ,b )到定点P (-3,0)的距离的平方,点P 到边界a +b +2=0的距离的平方为⎝ ⎛⎭⎪⎫122=12,到点(-1,0)的距离的平方为4,因为可行域不含边界,所以z 的取值范围是⎝ ⎛⎭⎪⎫12,4. 答案 ⎝ ⎛⎭⎪⎫12,4 12.解析 因为a +2b 平行于直线y =2x +1,所以可设a +2b =(m,2m ),所以|a +2b |2=5 m 2=5,解得m =1或-1,a +2b =(1,2)或(-1,-2),所以a =(1,2)-(4-2)=(-3,4)或(-1,-2)-(4,-2)=(-5,0).答案 (-3,4)或(-5,0)13.解析 作出函数图象可知若a <b <-1,且f (a )=f (b ),即为a 2+2a -1=-(b 2+2b -1),整理得(a +1)2+(b +1)2=4,设⎩⎨⎧a =-1+2cos θ,b =-1+2sin θ,θ∈⎝ ⎛⎭⎪⎫π,5π4∪⎝ ⎛⎭⎪⎫5π4,3π2,所以ab +a +b =-1+2sin 2θ∈(-1,1).答案 (-1,1)14.解析 因为f (x +2)=f (x )⇒f (x )的周期为2,所以f (x ),x ∈[-1,0]的单调性与[-3,-2]一致,单调递减,又f (x )是偶函数,所以在[0,1]上单调递增.又α,β是锐角三角形的两个内角,所以π2<α+β<π⇒0<π2-β<α<π2⇒1>sin α>sin ⎝ ⎛⎭⎪⎫π2-β=cos β>0⇒f (sin α)>f (cos β).答案 f (sin α)>f (cos β)。
2013届高考数学二轮复习精选考前小题狂练2(苏教)
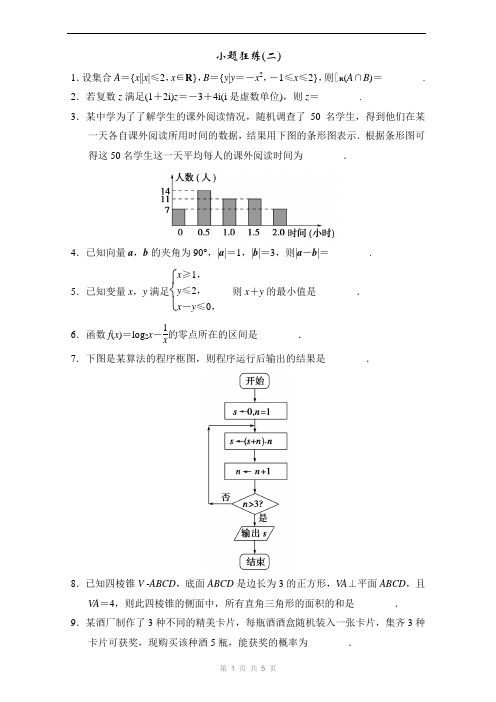
小题狂练(二)1.设集合A ={x ||x |≤2,x ∈R },B ={y |y =-x 2,-1≤x ≤2},则∁R (A ∩B )=________.2.若复数z 满足(1+2i)z =-3+4i(i 是虚数单位),则z =________.3.某中学为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,结果用下图的条形图表示.根据条形图可得这50名学生这一天平均每人的课外阅读时间为________.4.已知向量a ,b 的夹角为90°,|a |=1,|b |=3,则|a -b |=________.5.已知变量x ,y 满足⎩⎨⎧ x ≥1,y ≤2,x -y ≤0,则x +y 的最小值是________.6.函数f (x )=log 2x -1x 的零点所在的区间是________.7.下图是某算法的程序框图,则程序运行后输出的结果是________.8.已知四棱锥V -ABCD ,底面ABCD 是边长为3的正方形,VA ⊥平面ABCD ,且VA =4,则此四棱锥的侧面中,所有直角三角形的面积的和是________.9.某酒厂制作了3种不同的精美卡片,每瓶酒酒盒随机装入一张卡片,集齐3种卡片可获奖,现购买该种酒5瓶,能获奖的概率为________.10.在△ABC 中,三个内角A 、B 、C 的对边分别为a ,b ,c ,若b =25,∠B =π4,sin C =55,则c =________,a =________.11.已知sin ⎝ ⎛⎭⎪⎫α+π12=14,则sin ⎝ ⎛⎭⎪⎫5π12-α=________. 12.已知双曲线C :x 2a 2-y 2b 2=1的焦距为10,点P (2,1)在C 的渐近线上,则C 的方程为________.13.已知函数y =f (x )(x ∈R )上任一点(x 0,f (x 0))处的切线斜率k =(x 0-3)(x 0+1)2,则该函数的单调递减区间为________.14.如图是见证魔术师“论证”64=65飞神奇.对这个乍看起来颇为神秘的现象,我们运用数学知识不难发现其中的谬误.另外,我们可以更换图中的数据,就能构造出许多更加直观与“令人信服”的“论证”.请你用数列知识归纳:(1)这些图中的数所构成的数列:________;(2)写出与这个魔术关联的一个数列递推关系式:________.参考答案小题狂练(二)1.解析 由已知条件可得A =[-2,2],B =[-4,0],∴∁R (A ∩B )=(-∞,-2)∪(0,+∞). 答案 (-∞,-2)∪(0,+∞)2.解析 ∵(1+2i)z =-3+4i ,∴z =-3+4i 1+2i =(-3+4i )(1-2i )(1+2i )(1-2i )=5+10i 5=1+2i. 答案 1+2i3.解析 一天平均每人的课外阅读时间应为一天的总阅读时间与学生的比,即 0×7+0.5×14+1.0×11+1.5×11+2.0×750=0.97(小时). 答案 0.97小时4.解析 利用数量积的运算性质求解.由a ,b 的夹角是90°可得a·b =0,所以|a-b |=(a -b )2=1+9=10. 答案 105.解析 先由不等式组确定平面区域,再平移目标函数得最小值.作出不等式组对应的平面区域如图,当目标函数x +y 经过点(1,1)时,取得最小值2.答案 26.解析 利用零点存在定理求解.因为f (1)f (2)=(-1)⎝ ⎛⎭⎪⎫1-12<0,所以由零点存在定理可知零点所在的区间是(1,2).答案 (1,2)7.解析 由框图的顺序,s =0,n =1,s =(s +n )n =(0+1)×1=1,n =n +1=2,依次循环s =(1+2)×2=6,n =3,注意此刻3>3仍然否,所以还要循环一次s =(6+3)×3=27,n =4,此刻输出s =27.答案 278.解析 可证四个侧面都是直角三角形,其面积S =2×12×3×4+2×12×3×5=27.答案 279.解析 P =35-(3×25-3)35=5081. 答案 508110.解析 由正弦定理得b sin B =c sin C ,所以c =b sin C sin B =25×5522=2 2.由c <b 得C <B ,故C 为锐角,所以cos C =255,sin A =sin(B +C )=sin B cos C +cos B sin C =31010,由正弦定理得b sin B =a sin A ,所以a =b sin A sin B =25×3101022=6. 答案 22 611.解析 由sin ⎝ ⎛⎭⎪⎫α+π12=14,得cos ⎝ ⎛⎭⎪⎫α+π12=±154,所以sin ⎝ ⎛⎭⎪⎫5π12-α=cos ⎝ ⎛⎭⎪⎫α+π12=±154. 答案 ±15412.解析 由焦距为10知,c =5,即a 2+b 2=25,根据双曲线方程可知,渐近线方程为y =±b ax ,带入点P 的坐标得,a =2b ,联立方程组可解得a 2=20,b 2=5,所以双曲线方程x 220-y 25=1.答案 x 220-y 25=113.解析 由导数的几何意义可知,f ′(x 0)=(x 0-3)(x 0+1)2≤0,解得x 0≤3,即该函数的单调递减区间是(-∞,3].答案 (-∞,3]14.解析 利用推理知识求解.由图形可知,图中的数构成裴波纳契数列,所以(1)a n+2=a n +1+a n ,a 1=1,a 2=1;(2)题右图中间实质上有一个面积是1的平行四边形,有时空着,有时重合,所以与魔术有关的数列递推关系式可能是a n +2·a n-a 2n +1=(-1)n -1和a n a n +1≈0.618.答案 (1)a n +2=a n +1+a n ,a 1=1,a 2=1,(2)a n +2·a n -a 2n +1=(-1)n -1和a n a n +1≈0.618.。
2013届高考历史二轮复习回扣课件:回扣3 考前必记的五类不同思维类型的答题用语

回扣三
(3)中国传统科技重实用,西方近代科技重理论:中国传 统科技大多是生产经验的总结,实用性强,缺乏逻辑方 法进行理论概括和分析;西方近代科技属于理论科学, 大都属于对事物规律和本质的探索,主要采取观察和实 验的方法。
回扣三
12.程朱理学与陆王心学的比较 比较项 对世界本原 的具体认识 不同点 的途径 程朱理学 陆王心学 世界的本原 世界的本原 是 外 在 的 是 内 在 的 “理” 用“格物致 把握“理” 知 ” 的 方 法 去认识和把 握“理” “心” 进行内心的 反省,克服私 欲,恢复良知
回扣三
3.战后世界格局由两极格局向多极化方向发展的原因 (1)随着西欧由经济联合走向政治联合,实力越来越大,在 各个领域与美国和日本展开竞争。在外交上逐渐做到了 “用一个声音说话”,执行独立自主的外交政策,不再唯 美国马首是瞻。 (2)战后日本抓住机遇,经济高速发展,20 世纪 80 年代中 期成为在经济上唯一能与美国相抗衡的国家,经济上形成 了美、日、西欧鼎立的局面。日本以自己强大的经济实力 为基础,谋求政治大国地位,其国际影响力越来越大。
经验主义, 科学和技 科 学 与 生 产 紧 密
回扣三
生产组织 经济思想
资本主 义工厂制建 大企业时代(垄断 立 自由主义盛行 组织形成) 自由主义开始向 凯恩斯主义过渡 时代”
对人类进 人类进 入“蒸汽时 人 类 进 入 “ 电 气 程的影响 代”
回扣三
8.战时共产主义政策与新经济政策不同点之比较 (1)目的方面:前者是集中力量应付战争,后来借此直接向 社会主义过渡;后者是恢复发展生产,在此基础上逐步过 渡到社会主义。 (2)内容方面:前者取消商品和货币,按照共产主义原则分 配产品;后者是利用商品货币关系,实行国家资本主义, 以此发展和壮大社会主义经济。 (3)成效方面:前者有利于集中力量战胜敌人,但在战争结 束后引起了社会动乱;后者促进了经济的恢复发展,巩固 了工农联盟,稳定了社会秩序,进一步巩固了苏维埃政权。 (4)事实证明:前者不是向社会主义过渡的正确途径;后者 是向社会主义过渡的正确途径。
2013年高考数学总复习资料

2013年高考数学总复习资料2013数学总复习资料高三数学第三轮总复习分类讨论押题针对训练复习目标:1.掌握分类讨论必须遵循的原则 2.能够合理,正确地求解有关问题 命题分析:分类讨论是一种重要的逻辑方法,也是一种常用的数学方法,这可以培养学生思维的条理性和概括性,以及认识问题的全面性和深刻性,提高学生分析问题,解决问题的能力.因此分类讨论是历年数学高考的重点与热点.而且也是高考的一个难点.这次的一模考试中,尤其是西城与海淀都设置了解答题来考察学生对分类讨论问题的掌握情况.重点题型分析:例1.解关于x 的不等式:)()(232R a x a a a x ∈+<+解:原不等式可分解因式为:(x-a)(x-a 2)<0 (下面按两个根的大小关系分类)(1)当a>a 2⇒a 2-a<0即 0<a<1时,不等式的解为 x ∈(a 2, a).(2)当a<a 2⇒a 2-a>0即a<0或a>1时,不等式的解为:x ∈(a, a 2)(3)当a=a 2⇒a 2-a=0 即 a=0或 a=1时,不等式为x 2<0或(x-1)2<0不等式的解为 x ∈∅.综上,当 0<a<1时,x ∈(a 2, a)当a<0或a>1时,x ∈(a,a 2) 当a=0或a=1时,x ∈∅.评述:抓住分类的转折点,此题分解因式后,之所以不能马上写出解集,主要是不知两根谁大谁小,那么就按两个根之间的大小关系来分类.例2.解关于x 的不等式 ax 2+2ax+1>0(a ∈R) 解:此题应按a 是否为0来分类.(1)当a=0时,不等式为1>0, 解集为R. (2)a ≠0时分为a>0 与a<0两类①10)1(00440002>⇒⎩⎨⎧>->⇒⎪⎩⎪⎨⎧>->⇒⎩⎨⎧>>a a a a a a a a ∆时,方程ax 2+2ax+1=0有两根aa a aaaa a a a a x )1(12442222,1-±-=-±-=-±-=.则原不等式的解为),)1(1())1(1,(+∞-+-----∞aa a aa a . ②101000440002<<⇒⎩⎨⎧<<>⇒⎪⎩⎪⎨⎧<->⇒⎩⎨⎧<>a a a a a a a ∆时,方程ax 2+2ax+1=0没有实根,此时为开口向上的抛物线,则不等式的解为(-∞,+∞).③ 11000440002=⇒⎩⎨⎧==>⇒⎪⎩⎪⎨⎧=->⇒⎩⎨⎧=>a a a a a a a a 或∆时, 方程ax 2+2ax+1=0只有一根为x=-1,则原不等式的解为(-∞,-1)∪(-1,+∞).④01000440002<⇒⎩⎨⎧><<⇒⎪⎩⎪⎨⎧>-<⇒⎩⎨⎧><a a a a a a a a 或∆时, 方程ax 2+2ax+1=0有两根,aa a aa a a x )1(12)1(22,1-±-=-±-=当⎪⎩⎪⎨⎧-><120a a ,即a<-2时,不等式解为]2,1[a -.当⎪⎩⎪⎨⎧-=<120aa ,即a=-2时,不等式解为x=-1.综上:a=0时,x ∈(-∞,-1).a>0时,x ∈),2[]1,(+∞--∞a .-2<a<0时,x ∈]1,2[-a . a<-2时,x ∈]2,1[a -.a=-2时,x ∈{x|x=-1}.评述:通过上面三个例题的分析与解答,可以概括出分类讨论问题的基本原则为:10:能不分则不分; 20:若不分则无法确定任何一个结果; 30:若分的话,则按谁碍事就分谁.例4.已知函数f(x)=cos 2x+asinx-a 2+2a+5.有最大值2,求实数a 的取值.解:f(x)=1-sin 2x+asinx-a 2+2a+5.6243)2(sin 22++---=a a a x 令sinx=t, t ∈[-1,1].则6243)2()(22++---=a a a t t f (t ∈[-1,1]). (1)当12>a即a>2时,t=1,2533max=++-=a a y解方程得:22132213-=+=a a 或(舍). (2)当121≤≤-a 时,即-2≤a ≤2时,2a t =,262432max=++-=a a y,解方程为:34-=a 或a=4(舍). (3)当12-<a即a<-2时, t=-1时,y max =-a 2+a+5=2即 a 2-a-3=0 ∴ 2131±=a , ∵ a<-2, ∴ 2131±-=a 全都舍去.综上,当342213-=+=a a 或时,能使函数f(x)的最大值为2.例5.设{a n }是由正数组成的等比数列,S n是其前n 项和,证明:15.025.05.0log 2log log ++>+n n n S S S .证明:(1)当q=1时,S n =na 1从而 0)1()2(2121211212<-=+-+⋅=-⋅++a a n a n na S S S n n n(2)当q ≠1时,qq a S nn--=1)1(1, 从而.0)1()1()1)(1(2122121221212<-=-----=-⋅++++nn n n n n n q a q q a q q a S S S由(1)(2)得:212++<⋅n n nS S S .∵ 函数xy 5.0log =为单调递减函数.∴ 15.025.05.0log 2log log ++>+n n n S SS . 例6.设一双曲线的两条渐近线方程为2x-y+1=0, 2x+y-5=0,求此双曲线的离心率.分析:由双曲线的渐近线方程,不能确定其焦点位置,所以应分两种情况求解.解:(1)当双曲线的焦点在直线y=3时,双曲线的方程可改为1)3()1(222=---by a x ,一条渐近线的斜率为2=ab , ∴ b=2.∴555222==+==a aa b a c e .(2)当双曲线的焦点在直线x=1时,仿(1)知双曲线的一条渐近线的斜率为2=b a,此时25=e .综上(1)(2)可知,双曲线的离心率等于255或.评述:例5,例6,的分类讨论是由公式的限制条件与图形的不确定性所引起的,而例1-4是对于含有参数的问题而对参数的允许值进行的全面讨论.例7.解关于x 的不等式 1512)1(<+--x x a . 解:原不等式 012)1(55<⇔+--x x a 0)]2()1)[(2(022)1(012)1(<----⇔<--+-⇔<+--⇔a x a x x a x a x x a⎪⎩⎪⎨⎧>----<-⎪⎩⎪⎨⎧<---->-⎩⎨⎧<--=-⇔0)12)(2(01)3(0)12)(2(01)2(0)21)(2(01)1(a ax x a a a x x a x a 或或由(1) a=1时,x-2>0, 即 x ∈(2,+∞). 由(2)a<1时,012>--a a,下面分为三种情况.①⎩⎨⎧<<⇒⎪⎩⎪⎨⎧>--<012121a a aa a 即a<1时,解为)12,2(aa--.②0012121=⇒⎩⎨⎧=<⇒⎪⎩⎪⎨⎧=--<a a a aa a 时,解为∅.③ ⎪⎩⎪⎨⎧<--<2121a aa ⇒ ⎩⎨⎧><01a a 即0<a<1时,原不等式解为:)2,12(aa --.由(3)a>1时,aa --12的符号不确定,也分为3种情况.①⎩⎨⎧≤>⇒⎪⎩⎪⎨⎧≥-->012121a a a aa ⇒ a 不存在. ② ⇒⎩⎨⎧>>⇒⎪⎩⎪⎨⎧<-->012121a a a a a 当a>1时,原不等式的解为:),2()12,(+∞---∞ aa .综上:a=1时,x ∈(2,+∞).a<1时,x ∈)12,2(a a-- a=0时,x ∈∅.0<a<1时,x ∈)2,12(aa-- a>1时,x ∈),2()12,(+∞---∞ aa . 评述:对于分类讨论的解题程序可大致分为以下几个步骤:10:明确讨论的对象,确定对象的全体; 20:确定分类标准,正确分类,不重不漏; 30:逐步进行讨论,获得结段性结记; 40:归纳总结,综合结记. 课后练习:1.解不等式2)385(log 2>+-x x x2.解不等式1|)3(log ||log |3121≤-+x x3.已知关于x 的不等式052<--ax ax 的解集为M. (1)当a=4时,求集合M:(2)若3∈M ,求实数a 的取值范围.4.在x0y 平面上给定曲线y 2=2x, 设点A 坐标为(a,0), a ∈R ,求曲线上点到点A 距离的最小值d ,并写成d=f(a)的函数表达式.参考答案:1. ),(),(∞+235321 2.]4943[, 3. (1) M 为),(),(2452 ∞- (2)),9()35,(+∞-∞∈ a 4. ⎪⎩⎪⎨⎧<≥-==时当时当1||112)(a a a a a f d .2006年高三数学第三轮总复习函数押题针对训练复习重点:函数问题专题,主要帮助学生整理函数基本知识,解决函数问题的基本方法体系,函数问题中的易错点,并提高学生灵活解决综合函数问题的能力。
2013届高考数学考前归纳总结复习题4

圆锥曲线中的取值范围问题一、常见基本题型:对于求曲线方程中参数范围问题,应根据题设条件及曲线的几何性质构造参数满足的不等式,通过解不等式求得参数的范围;或建立为12 ∴122212223x x x x x x+=-⎧⎨=-⎩. 消去2x ,得212123()40x x xx ++=,2222213()4022km m k k --∴+=++ 整理得22224220k m m k +--=214m =时,上式不成立; 214m ≠时,2222241m k m -=-,∴22222041m k m -=≥-,∴211-<≤-m 或121≤<m把2222241m k m -=-代入(*)得211-<<-m 或121<<m∴211-<<-m 或121<<m若,所以点P 的轨迹C 是椭圆,C 的方程为134=+y x .(Ⅱ)由题意知,直线l 的斜率必存在,不妨设过N 的直线l 的方程为(1)y k x =-, 设A ,B 两点的坐标分别为11(, )A x y ,22(, )B x y .由22(1),143y k x x y =-⎧⎪⎨+=⎪⎩消去y 得2222(43)84120k x k x k +-+-=. 因为N 在椭圆内,所以0∆>.所以212228,34412.k x x k k x x ⎧+=⎪⎪+⎨-⎪= 则222(3)(3)6186x y x y xy xy +=++=+的取值范围是[0,36].3x y +的取值范围是[-6,6].∴36AP AQ x y ⋅=+-的取值范围是[-12,0]. 二、针对性练习1.已知椭圆的一个顶点为(0,1)A -,焦点在x 轴上.若右焦点到直线0x y -+=的距 离为3.(1)求椭圆的方程.(2)设直线(0)y kx m k =+≠与椭圆相交于不同的两点,MN .当||||AM AN =时,求m 的 取值范围.解:(1)依题意可设椭圆方程为2221x y a+=,则右焦点)F由②得22103m k -=>,解得12m >.综上求得m 的取值范围是122m <<.2. 如图所示,已知圆M A y x C ),0,1(,8)1(:22定点=++为圆上一动点,点P 在AM 上,点N 在CM 上,且满足N 点,0,2=⋅=的轨迹为曲线E .(I )求曲线E 的方程;(II )若过定点F (0,2)的直线交曲线E 于不同的两点,G H (点G 在点,F H 之间),且满足λ=, 求λ的取值范围.. λλλλλ2122221222122121)1(.,)1(,x x x x x x x x x x x x x ==++∴=+=+∴=∴, λλλλ222222)1()121(316,213)1()214(+=++=++-∴kk k k 整理得.331.316214.316323164,2322<<<++<∴<+<∴>λλλ解得k k .131,10<<∴<<λλ 又 又当直线GH 斜率不存在,方程为.31,31,0===λFH x)1,31[,131的取值范围是即所求λλ<≤∴3241)2(0200-+-=-x x x t . ∵20≠x∴23411)2(4100-=---=x x t .∵220<<-x , ∴ 12-<<-t .∴t 的取值范围为)1,2(--.4.已知椭圆2222:1x y C a b +=(0)a b >>,以原点为圆心,椭圆的短半轴长 为半径的圆与直线0x y -=相切.(Ⅰ)求椭圆C 的方程;(Ⅱ)若过点M (2,0)的直线与椭圆C 相交于两点,A B ,设P 为1212214[()4](12)y y ky k x x k t t t k +-==+-=+. ∵点P 在椭圆上,∴222222222(8)(4)22(12)(12)k k t k t k -+=++,∴22216(12)k t k =+.-12x -<∴22121220(1)[()4]9k x x x x ++-<∴422222648220(1)[4](12)129k k k k k -+-<++ , ∴22(41)(1413)0k k -+>,∴214k >.∴211k <<,∵22216(12)k t k =+,∴221688k t ==-,。
2013年高考语用题复习备考的思考 高考复习(高三)

在高考语文试题的各个组成板块中,语言文字综合运用类的题目是最富活力、最贴近生活、最能突出对语文素养的考查、最能体现课改精神的一个部分,因而,每年的高考语文试卷中,这一部分的题目总是异彩纷呈,佳作频现。
各省市的高考命题专家都把这一块当作试验田,努力创新,勇于尝试,为我们语文教学改革指明了方向,探索了道路,为高考语文试卷增添了亮点,但同时也给我们的复习备考提出了严峻挑战。
为了搞好2013届的语用题的复习备考,我们有必要对2012年的16套(上海除外)高考语文试题中的语用题做一个详细的梳理,从里面找出一些共性的东西,再结合我们教学的实际,恰当安排复习内容,努力提高复习备考的针对性、实效性。
2012年高考语用题的梳理2012年各省市高考试卷中的语用题形式多样,分值、在试卷上的位置也各不相同,为了便于比对,在这里按实用文体写作、图文转换、仿写、信息提取及句式变换、压缩与衔接过渡、文段修改、事件现象点评、情景拟写等几个方面进行梳理。
1、实用文体写作类(共7题)公关文体拟写广东卷22题,改写招聘启事,6分。
湖南卷3题,选出表达通顺、得体的“遗失启事”,3分;拟写推介语、宣传语、祝福语湖北卷20题,拟写书籍宣传语,4分;天津卷23题,对特定对象拟写表示敬意与祝福的一段话,4分;广东卷23题,拟写摄影作品展的前言,6分。
对联对偶类湖北卷21题,用对偶句描述宝黛初会的情景,4分;四川卷19题,补写有关节日的对联,5分。
2、图文转换类(共4题)漫画题福建卷16题,(1)为讽刺性漫画选标题(成语);湖北卷22题,为漫画配文或题诗;江苏卷4题,揭示漫画寓意。
图表类天津卷24题,根据统计表说明调查结果,概括统计对象的特点并略作说明。
3、仿写类(共6题)全国新课标卷17题,5分;重庆卷20题(2),2分;辽宁卷17题,6分;四川卷20题,6分;山东卷16题,4分;全国大纲卷20题,6分。
4、信息提取及句式变换类(共5题)下定义浙江卷5题,选取信息给“食品添加剂”下定义,3分;安徽卷18题,筛选整合信息给“年画”下定义,5分;辽宁卷16题,根据5个句子的信息,写一段介绍“飞行板”的文字。
2013年高考题整理

2013年全国高考题(大纲版)物理部分二、选择题:(本大题共8小题,在每小题给出的四个选项中,有的只有一项是符合题目要求,有的有多选项符合题目要求。
全部选对得6分,选对但不全得3分,有选错或不答的得0分)14.下列现象中,属于光的衍射现象的是( )A .雨后天空出现彩虹B .通过一个狭缝观察日光灯可看到彩色条纹C .海市蜃楼现象D .日光照射在肥皂泡上出现彩色条纹15.根据热力学第一定律,下列说法正确的是( )A .电冰箱的工作过程表明,热量可以从低温物体向高温物体传递B .空调机在制冷过程中,从室内吸收的热量少于向室外放出的热量C .科技的进步可以使内燃机成为单一热源的热机D .对能源的过度消耗将使自然界得能量不断减少,形成能源危机16.放射性元素氡(22286Rn )经α衰变成为钋21884Po ,半衰期为3.8天;但勘测表明,经过漫长的地质年代后,目前地壳中仍存在天然的含有放射性元素22286Rn 的矿石,其原因是( ) A .目前地壳中的22286Rn 主要来自于其它放射元素的衰变 B .在地球形成的初期,地壳中元素22286Rn 的含量足够高 C .当衰变产物21884Po 积累到一定量以后,21884Po 的增加会减慢22286Rn 的衰变进程 D .22286Rn 主要存在于地球深处的矿石中,温度和压力改变了它的半衰期17.纸面内两个半径均为R 的圆相切于O 点,两圆形区域内分别存在垂直纸面的匀强磁场,磁感应强度大小相等、方向相反,且不随时间变化。
一长为2R 的导体杆OA 绕过O 点且垂直于纸面的轴顺时针匀速旋转,角速度为ω,t =0时,OA 恰好位于两圆的公切线上,如图所示。
若选取从O 指向A 的电动势为正,下列描述导体杆中感应电动势随时间变化的图像可能正确的是( )18.“嫦娥一号”是我国首次发射的探月卫星,它在距月球表面高度为200 km 的圆形轨道上运行,运行周期为127分钟。
赏析含义

2013年高考考前回扣学案—赏析与含意区分一、考题回顾1.《长河》21.结合全文,谈谈你对最后两段使用的一连串问句作用的理解。
(4分) 答案:引发读者思考,强烈地表达了作者对于田河以及那里的人、事、物、景的回忆,对昔日生活的思恋与怀想。
2.《秋韵写意》20.解释下列两句话在文中的含意。
(4分)(1)当阳光初升,便信步朝回走,脚下的片片树叶像翩翩起舞的蝴蝶,小心翼翼地迈步,不要惊动那些失意的生命,这是一种悲悯情怀。
(2)其实,秋的味道是苦涩的,只有那些饮过苦药的病人才能真正感知秋的深层意蕴。
答案:20.(1)这句话体现了作者独自一人赏秋时闲适和惬意的心境;“不要惊动了失意的生命”,则表达出对生命的呵护与敬畏之情。
(2)秋天,恰如人之中年,是生命中最艰辛之处。
那些经历了病痛煎熬、坎坷磨砺的人,才会体悟到人生诸多况味,才对秋之意蕴的感知更进一层。
3.《绝盗》下面的文字,对刻画人物形象有什么作用?(4分)⑴蹬车的是个老头子,骨瘦肉紧,皮黑牙黄,小腿肚子赛两个铁球,一望便知是个长年蹬车的车夫。
⑵这不孝的禽兽,不管爹娘,跑到这儿造他妈宫殿来了。
小二、小三,给我把门砸开!答案:(1)运用肖像描写,写出了老头子的老辣凶悍。
(2)运用语言描写,表现了老头子的演技高超。
4.《布鞋,渐行渐远的温情之舟》请结合文意,赏析文中画线的句子。
(4分)(1)这些小舟遵循着天时与人命,白天漂浮在黄土海面之上,吆喝了大鱼小鱼般的牛羊群去放牧,夜晚时,它们则停泊在主人的梦乡边。
(2)布鞋成了围墙,女人们把流沿在血液里的天性和欢欣全部移植在了这围墙的两畦花圃中。
答案:(1)运用比喻、拟人手法,将布鞋比作浩瀚如海的高原上的小舟,赋予他们人的情态动作,生动形象,充满生活温情。
(2)运用比喻手法,将布鞋比作围墙,将鞋垫比作花圃,生动形象地写出了女人们爱美的天性,和对欢乐生活的追求。
5.《最深的夜最亮的灯》简要赏析文中画线的句子。
(4分)(1)舞台上的女子,一袭红裙,纤细的双手捂住耳朵,身体缓缓向后仰,向后仰,静默,静默,然后又一点、一点挺起了身子。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013届高考考前题型回顾复习填空题1、对于△ABC ,有如下四个命题:①若sin 2A =sin 2B ,则△ABC 为等腰三角形; ②若sin B =cos A ,则△ABC 是直角三角形; ③若sin 2A +sin 2B >sin 2C ,则△ABC 是钝角三角形; ④若a cos A 2=b cos B 2=c cos C 2,则△ABC 是等边三角形.其中正确的命题个数是________.解析 ①不对,可能2A +2B =π;②不对,如B =120°,A =30°;③不对,仅能说明C 为锐角;④对,由正弦定理可得sin A 2=sin B 2=sin C2,即A =B =C . 答案 1 变式训练:有四个关于三角函数的命题:p 1:∃x ∈R ,sin 2x 2+cos 2x 2=12;p 2:∃x ,y ∈R ,sin(x -y )=sin x -sin y ; p 3:∀x ∈[0,π],1-cos 2x2=sin x ; p 4:sin x =cos y ⇒x +y =π2.其中假命题的是________.解析 p 1:∃x ∈R ,sin 2x 2+cos 2x 2=12是假命题;p 2是真命题,如x =y =0时成立;p 3是真命题,∵∀x ∈[0,π],sin x ≥0,∴1-cos 2x 2=sin 2x =|sin x |=sin x ;p 4是假命题,如x =π2,y =2π时,sin x =cos y ,但x +y ≠π2.答案 p 1,p 4 2、已知a ∈R ,则“a >2”是“a 2>2a ”成立的______条件解析 a >2可以推出a 2>2a ;a 2>2a 可以推出a >2或a <0不一定推出a >2. 所以“a >2”是“a 2>2a ”的充分不必要条件.答案 充分不必要 3、设正四棱锥的侧棱长为1,则其体积的最大值为________.解析 法一 设正四棱锥的底面边长为x ,则体积V =13x 21-x 22=26x 4(2-x 2),记y =t 2(2-t ),t >0,利用导数可求得当t =43时,y max =3227,此时V max =4327;法二 设正四棱锥的侧棱与底面所成角为θ,则V =13×2cos 2θ×sin θ=23(1-sin 2θ)×sin θ,0<θ<π2,记y =(1-t 2)t,0<t<1,利用导数可求得当t =33时,y max =239,此时V max =4327. 4、若cos αcos(α+β)+sin αsin(α+β)=-35,β是第二象限的角,则tan 2β=________.cos(α+β-α)=cos β=-35,且β是第二象解析 ∵cos αcos(α+β)+sin αsin(α+β)=限的角,∴sin β=45,tan β=-43,所以tan 2β=2tan β1-tan 2β=247. 5、如图所示为函数f (x )=2sin(ωx +φ)(ω>0,π2≤φ≤π)的部分图象,其中A ,B 两点之间的距离为3,那么f (-1)=________.解析 由函数图象求解析式,再求函数值.由A ,B 两点之间的距离为3得T 2=3⇒T =6=2πω⇒ω=π3,又f (0)=2sin φ=1,且π2≤φ≤π,所以φ=56π,所以f (x )=2sin ⎝⎛⎭⎫π3x +5π6,故f (-1)=2sin ⎝⎛⎭⎫-π3+5π6=2sin π2=2.答案 2 6、若函数f (x )满足f (x +1)=f (x -1),且当x ∈[-1,1]时,f (x )=x 2,则函数F (x )=f (x )-|log 4x |的零点个数为________.解析 根据条件作出函数f (x ),y =|log 4x |,x >0的图象,由两个函数图象的交点个数确定函数零点个数.因为f (x +1)=f (x -1),所以函数,f (x )的周期为2,且x ∈[-1,1]时,f (x )=x 2,在同一坐标系中作出函数f (x ),y =|log 4x |,x >0的图象如图,由图象可知,交点个数是4,即F (x )的零点个数为4.7、设奇函数f (x )在(0,+∞)上为单调递减函数,且f (2)=0,则不等式3f (-x )-2f (x )5x≤0的解集为________.解析 由奇函数的定义化简解析式,再利用分类讨论的方法解不等式.因为函数f (x )是奇函数,所以3f (-x )-2f (x )5x=-3f (x )-2f (x )5x =-f (x )x ≤0,⇔⎩⎪⎨⎪⎧ x >0,f (x )≥0或⎩⎪⎨⎪⎧x <0,f (x )≤0,又奇函数f (x )在(0,+∞)上递减,f (2)=0,所以在(-∞,0)上递减,f (-2)=0,作出函数f (x )的大致示意图可得原不等式的解集为[-2,0)∪(0,2].8、定义在R 上的偶函数f (x )满足f (x +1)=-f (x ),且在[-1,0]上是增函数,给出下列关于f (x )的判断:①f (x )是周期函数;②f (x )关于直线x =1对称;③f (x )是[0,1]上的增函数;④f (x )在[1,2]上是减函数;⑤f (2)=f (0).以上命题中正确的是________.(写出所有正确命题的编号)解析 由f (x +1)=-f (x )=f (x -1),得函数f (x )是周期为2的周期函数,故①正确;因为f (2-x )=f (1+1-x )=-f (1-x )=f (-x )=f (x ),所以f (x )关于x =1对称,故②正确;因为f (x )是偶函数,且[-1,0]递增,周期是2,所以在[0,1]上递减,在[1,2]上递增,故③④均错误,⑤正确,故正确的是①②⑤.9、已知M 是曲线y =ln x +12x 2+(1-a )x 上任意一点,若曲线在M 点处的切线的倾斜角是均不小于π4的锐角,则实数a 的取值范围是________.解析 设M (x ,y )(x >0),因为在M 点处切线的倾斜角的范围是⎣⎡⎭⎫π4,π2,所以切线的斜率是[1,+∞),即y ′=1x +x +1-a ≥1,x ∈(0,+∞)恒成立,分离参数得a ≤1x +x ,x ∈(0,+∞)恒成立,所以a ≤⎝⎛⎭⎫1x +x min ,x ∈(0,+∞)时,由基本不等式得1x+x ≥2,所以a ≤2.答案 (-∞,2]10、如图,在直角梯形ABCD 中,已知BC ∥AD ,AB ⊥AD ,AB =4,BC =2,AD =4,若P 为CD 的中点,则P A →·PB →的值为________.解析 建立坐标系,应用坐标运算求数量积.以点A 为坐标原点,AD 、AB 所在直线为4),C (2,4),D (4,0),P (3,2),所以P A →·PB →=(-3,x 、y 轴建立平面直角坐标系,则A (0,0),B (0,-2)·(-3,2)=5.答案 5变式训练:(南京一中模拟试题)如图在△ABC 中,∠BAC =120︒,AB =1,AC =2,D 为BC 边上一点→DC =λ→BD ,则→AD ·→BC的取值范围是 .答案:(-2,5]解法简析:建立坐标系,标出A ,B ,C 的坐标, 写出BC 的方程,注意→DC =λ→BD 条件的具体含义,D 点的横坐标的范围是[-1,1).11、等差数列{a n }的公差d ∈(0,1),且sin 2a 3-sin 2a 7sin (a 3+a 7)=-1,当n =10时,数列{a n }的前n 项和S n 取得最小值,则首项a 1的取值范围为________.解析 因为{a n }是等差数列,所以sin 2a 3-sin 2a 7sin (a 3+a 7)=(sin a 3+sin a 7)(sin a 3-sin a 7)sin 2a 5=2sin a 5cos 2d (-2cos a 5sin 2d )sin 2a 5=-sin 4d =-1,得d =π8+k π2,k ∈Z ,又d∈(0,1),所以k =0,即d =π8.又由S 10是{S n }中的最小项,所以⎩⎨⎧a 10=a 1+9π8≤0,a11=a 1+5π4≥0,解得-54π≤a 1≤-98π.答案 ⎣⎡⎦⎤-54π,-98π 12、定义:F (x ,y )=y x (x >0,y >0),设数列{a n }满足a n =F (n ,1)F (2,n ),设S n 为数列{}a n a n +1的前n 项和,则S n ________1(填“>”、“=”、“<”).解析 由题意可得a n =1n 2,所以a n a n +1=1n (n +1)=1n -1n +1,其前n 项和S n =⎝⎛⎭⎫1-12+⎝⎛⎭⎫12-13+…+⎝⎛⎭⎫1n -1n +1=1-1n +1<1.答案 <13、已知双曲线的顶点到渐近线的距离为2,焦点到渐近线的距离为6,则该双曲线的离心率为________.ABD C解析 如图,A 、F 分别为顶点、焦点,则|OF ||OA |=|FC ||AB |,即c a =62=3.答案 3解答题1、已知△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且2a cos B =c cos B +b cos C . (1)求角B 的大小;(2)设向量m =(cos A ,cos 2A ),n =(12,-5),求当m·n 取最大值时,tan C 的值.解 (1)由题意,2sin A cos B =sin C cos B +cos C sin B , (2分)所以2sin A cos B =sin(B +C )=sin(π-A )=sin A .(3分) 因为0<A <π,所以sin A ≠0. 所以cos B =22.(5分)因为0<B <π,所以B =π4.(6分) (2)因为m·n =12cos A -5cos 2A ,(8分)所以m·n =-10cos 2A +12cos A +5=-10⎝ ⎛⎭⎪⎫cos A -352+435.(10分)所以当cos A =35时,m·n 取最大值. 此时sin A =45(0<A <π2),于是tan A =43.(12分)所以tan C =-tan(A +B )=-tan A +tan B1-tan A tan B=7.(14分)2、如图,在四棱锥P -ABCD 中,P A ⊥底面ABCD ,PC ⊥AD ,底面ABCD 为梯形,AB ∥DC ,AB ⊥BC ,P A =AB =BC ,点E 在棱PB 上,且PE =2EB . (1)求证:平面P AB ⊥平面PCB ;(2)求证:PD ∥平面EAC .解 (1)∵P A ⊥底面ABCD ,∴P A ⊥BC , 又AB ⊥BC ,P A ∩AB =A ,∴BC ⊥平面P AB . (3分) 又BC ⊂平面PCB , ∴平面P AB ⊥平面PCB . (6分)(2)∵P A ⊥底面ABCD ,又AD ⊂平面ABCD , ∴P A ⊥AD .又∵PC ⊥AD ,又PC ∩P A =P ,∴AD ⊥平面P AC ,又AC ⊂平面P AC , ∴AC ⊥AD . 在梯形ABCD 中,由AB ⊥BC ,AB =BC ,得∠BAC =π4,∴∠DCA =∠BAC =π4.又AC ⊥AD ,故△DAC 为等腰直角三角形. (4分) ∴DC =2AC =2(2AB )=2AB .连接BD ,交AC 于点M ,则DM MB =DCAB =2.在△BPD 中,PE EB =DMMB =2,∴PD ∥EM又PD ⊄平面EAC ,EM ⊂平面EAC ,∴PD ∥平面EAC .(14分)3、如图,某园林单位准备绿化一块直径为BC 的半圆形空地,△ABC 外的地方种草,△ABC 的内接正方形PQRS为一水池,其余的地方种花,若BC =a ,∠ABC =θ,设△ABC 的面积为S 1,正方形的PQRS 面积为S 2. (1)用a ,θ表示S 1和S 2;(2)当a 固定,θ变化时,求S 1S 2的最小值.解 (1)S 1=12a sin θ·a cos θ=14a 2sin 2θ, 设正方形边长为x ,则BQ =xtan θ,RC =x tan θ,∴x tan θ+x tan θ+x =a ,∴x =a 1tan θ+tan θ+1=a sin 2θ2+sin 2θ,(4分)S 2=⎝ ⎛⎭⎪⎫a sin 2θ2+sin 2θ2=a 2sin 22θ4+sin 22θ+4sin 2θ,(6分)(2)当a 固定,θ变化时,S 1S 2=14⎝ ⎛⎭⎪⎫4sin 2θ+sin 2θ+4,令sin 2θ=t ,则S 1S 2=14⎝ ⎛⎭⎪⎫4t +t +4(0<t ≤1),利用单调性求得t =1时,⎝ ⎛⎭⎪⎫S 1S 2min =94.(14分)4、已知椭圆C :x 2a 2+y 2b2=1(a >b >0)上任一点P 到两个焦点的距离的和为23,P 与椭圆长轴两顶点连线的斜率之积为-23.设直线l 过椭圆C 的右焦点F ,交椭圆C 于两点A (x 1,y 1),B (x 2,y 2). (1)若OA →·OB →=4tan ∠AOB(O 为坐标原点),求|y 1-y 2|的值;(2)当直线l 与两坐标轴都不垂直时,在x 轴上是否总存在点Q ,使得直线QA ,QB 的倾斜角互为补角?若存在,求出点Q 坐标;若不存在,请说明理由. 解 (1)由椭圆的定义知a =3,设P (x ,y ), 则有y x +3·y x -3=-23,则y 2x 2-3=-23,又点P 在椭圆上,则(3-x 2)b 23(x 2-3)=-b 23=-23,∴b 2=2,∴椭圆C 的方程是x 23+y 22=1.(3分)∵OA →·OB→=4tan ∠AOB,∴|OA →|·|OB→|cos ∠AOB =4tan ∠AOB,∴|OA →|·|OB →|sin ∠AOB =4, ∴S △AOB =12|OA →|·|OB →|sin ∠AOB =2, 又S △AOB =12|y 1-y 2|×1,故|y 1-y 2|=4.(7分)(2)假设存在一点Q (m,0),使得直线QA ,QB 的倾斜角互为补角, 依题意可知直线l 斜率存在且不为零,直线l 的方程为y =k (x -1)(k ≠0),由⎩⎪⎨⎪⎧y =k (x -1),x 23+y 22=1消去y 得(3k 2+2)x 2-6k 2x +3k 2-6=0,(9分)设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=6k 23k 2+2,x 1·x 2=3k 2-63k 2+2.∵直线QA ,QB 的倾斜角互为补角, ∴k QA +k QB =0,即y 1x 1-m +y 2x 2-m=0,(13分) 又y 1=k (x 1-1),y 2=k (x 2-1),代入上式可得2x 1x 2+2m -(m +1)(x 1+x 2)=0,∴2×3k 2-63k 2+2+2m -(m +1)×6k 23k 2+2=0,即2m -6=0,∴m =3,∴存在Q (3,0)使得直线QA ,QB 的倾斜角互为补角.(16分)附加题1、如图所示,在正方体ABCD -A 1B 1C 1D 1中,E 是棱DD 1的中点. (1)求直线BE 和平面ABB 1A 1所成的角的正弦值;(2)在棱C 1D 1上是否存在一点F ,使B 1F ∥平面A 1BE ?证明你的结论.解 设正方体的棱长为1.如图所示,以AB →,AD →,AA 1→为单位正交基底建立空间直角坐标系.(1)依题意,得B (1,0,0),E ⎝⎛⎭⎫0,1,12,A (0,0,0),D (0,1,0),所以BE →=⎝⎛⎭⎫-1,1,12,AD →=(0,1,0). 在正方体ABCD -A 1B 1C 1D 1中,因为AD ⊥平面ABB 1A 1, 所以AD →是平面ABB 1A 1的一个法向量. 设直线BE 和平面ABB 1A 1所成的角为θ, 则sin θ=|BE →·AD →||BE →||AD →|=132×1=23.即直线BE 和平面ABB 1A 1所成的角的正弦值为23.(2)依题意,得A 1(0,0,1),BA 1→=(-1,0,1),BE →=⎝⎛⎭⎫-1,1,12.设n =(x ,y ,z )是平面A 1BE 的一个法向量, 则由n ·BA 1→=0,n ·BE →=0,得⎩⎪⎨⎪⎧-x +z =0,-x +y +12z =0. 所以x =z ,y =12z .取z =2,得n =(2,1,2).设F 是棱C 1D 1上的点,则F (t,1,1)(0≤t ≤1). 又B 1(1,0,1),所以B 1F →=(t -1,1,0).而B 1F ⊄平面A 1BE ,于是B 1F ∥平面A 1BE ⇔B 1F →·n =0⇔(t -1,1,0)·(2,1,2)=0⇔2(t -1)+1=0⇔t =12⇔F 为C 1D 1的中点.这说明在棱C 1D 1上存在点F (C 1D 1的中点),使B 1F ∥平面A 1BE .2、已知多项式f (n )=15n 5+12n 4+13n 3-130n .(1)求f (-1)及f (2)的值;(2)试探求对一切整数n ,f (n )是否一定是整数?并证明你的结论. 解 (1)f (-1)=0,f (2)=17(2)先用数学归纳法证明,对一切正整数n ,f (n )是整数. ①当n =1时,f (1)=1,结论成立.②假设当n =k (k ≥1,k ∈N)时,结论成立,即f (k )=15k 5+12k 4+13k 3-130k 是整数,则当n =k +1时,f (k +1)=15(k +1)5+12(k +1)4+13(k +1)3-130(k +1)=C 05k 5+C 15k 4+C 25k 3+C 35k 2+C 45k +C 555+C 04k 4+C 14k 3+C 24k 2+C 14k +C 442+C 03k 3+C 13k 2+C 23k +C 333-130(k +1)=f (k )+k 4+4k 3+6k 2+4k +1. 根据假设f (k )是整数,而k 4+4k 3+6k 2+4k +1显然是整数. ∴f (k +1)是整数,从而当n =k +1时,结论也成立. 由①、②可知对一切正整数n ,f (n )是整数. (Ⅰ)当n =0时,f (0)=0是整数(Ⅱ)当n 为负整数时,令n =-m ,则m 是正整数,由(Ⅰ)知f (m )是整数, 所以f (n )=f (-m )=15(-m )5+12(-m )4+13(-m )3-130(-m )=-15m 5+12m 4-13m 3+130m =-f (m )+m 4是整数.综上,对一切整数n ,f (n )一定是整数.3、已知抛物线x y 22=及定点A (1,1),B (-1,0),M 是抛物线上的点,设直线AM ,BM 与抛物线的另一交点分别为21,M M .求证:当点M 在抛物线上变动时(只要21,M M 存在且1M 与2M 是不同两点),直线21M M 恒过一定点,并求出定点的坐标. 解:设M (2t 2,2t )若2t 2=1时,则点M 处的切线方程恰好过点B,则BM 与抛物线无交点M 1,舍去;若2t 2≠1时,则直线AM 的方程为)1(121212---=-x t t y ,联立)1222,)12()1(2(2)1(1212122122----⇒⎪⎩⎪⎨⎧=---=-t t t t M x y x t t y , 直线BM 的方程为)1(1222++=x t ty ,联立)1,21(2)1(1222222t t M x y x t t y ⇒⎪⎩⎪⎨⎧=++=, ∴M 1M 2的方程为)21(21)12()1(21122212222t x tt t t t t t y -------=-,即 12)1(21224222--+--=t t x t t t y ,化简得,02)22()24(2=-+-+-y t x t y x 对于任意的t 恒成立, ∴⎩⎨⎧==⇒⎪⎩⎪⎨⎧=-=-=-2102022024y x y x y x ,∴直线M 1M 2恒过定点(1,2)。
