数值计算课程设计报告(非线性方程求根)
数值分析实验五 非线性方程的求根1

数值分析实验五 非线性方程的求根组号 班级 学号 姓名 分数一:实验目的1、掌握用二分法解非线性方程的方法。
2、掌握用迭代法解非线性方程的方法。
3、掌握用牛顿法解非线性方程的方法。
4、学会运用Matlab 语言解决提供的函数求解实际问题。
二:实验内容所需的基本知识二分法的原理:设)(x f 在],[b a 上连续,且0)()(<⋅b f a f 。
则],[b a 为方程区间(设只有唯一根)。
取中点)(210b a x +=,检查)(a f 与)(0x f 是否同号,若同号,说明根*x 与b 之间,此时b b x a ==101,;若异号,说明根*x 在a 与0x 之间,此时011,x b a a ==,得新区间],[11b a 为原区间的一半。
对],[11b a 进行上述过程,取中点)(21111b a x +=,检查)(1a f 与)(1x f 是否同号,如此反复二分下去,即可得出一系列有根区间⊃⊃⊃],[],[],[2211b a b a b a …⊃⊃],[k k b a …,其中每个区间都是前一个区间的一半,因此],[k k b a 的长度k k k a b a b 2)(-=-,当∞→k 时趋于零,就是说,如果二分过程无限地继续下去,这些区间最终必收缩于一点*x ,该点显然就是所求的根。
迭代法原理:首先给定一个粗糙的初始值,然而用一个迭代公式反复校正这个初值,将已有近似根逐步精确化,一直到满足精度要求为止。
具体地,把方程0)(=x f 改写成x 的等价表达式)(x x ϕ=,若)(**x x ϕ=,称*x 为)(x ϕ的一个不动点,求)(x f 的零点就等价于求)(x ϕ的不动点。
任取一点0x 代入)(x ϕ求得 )(01x x ϕ= 又将1x 代入)(x ϕ求得)(12x x ϕ= 如此反复迭代下去一般地 )(1k k x x ϕ=+ k=0,1,2,………)(x ϕ称为迭代函数,)(x x ϕ=称为迭代公式。
数值分析实验报告之迭代法求非线性方程的根
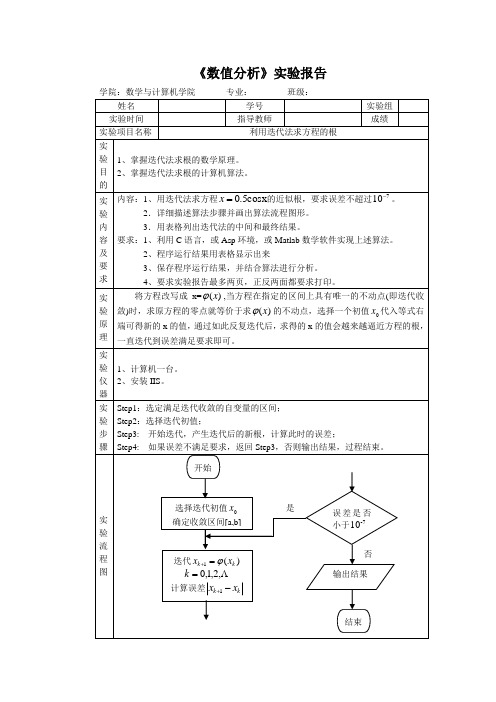
《数值分析》实验报告学院:数学与计算机学院专业:班级:姓名学号实验组实验时间指导教师成绩实验项目名称利用迭代法求方程的根实验目的1、掌握迭代法求根的数学原理。
2、掌握迭代法求根的计算机算法。
实验内容及要求内容:1、用迭代法求方程cosx5.0=x的近似根,要求误差不超过710-。
2.详细描述算法步骤并画出算法流程图形。
3.用表格列出迭代法的中间和最终结果。
要求:1、利用C语言,或Asp环境,或Matlab数学软件实现上述算法。
2、程序运行结果用表格显示出来3、保存程序运行结果,并结合算法进行分析。
4、要求实验报告最多两页,正反两面都要求打印。
实验原理将方程改写成x=)(xϕ,当方程在指定的区间上具有唯一的不动点(即迭代收敛)时,求原方程的零点就等价于求)(xϕ的不动点,选择一个初值x代入等式右端可得新的x的值,通过如此反复迭代后,求得的x的值会越来越逼近方程的根,一直迭代到误差满足要求即可。
实验仪器1、计算机一台。
2、安装IIS。
实验步骤Step1:选定满足迭代收敛的自变量的区间;Step2:选择迭代初值;Step3: 开始迭代,产生迭代后的新根,计算此时的误差;Step4: 如果误差不满足要求,返回Step3,否则输出结果,过程结束。
实验流程图开始选择迭代初值x确定收敛区间[a,b]迭代)(1kkxxϕ=+,2,1,0=k计算误差kkxx-+1结束误差是否小于7-10输出结果是否实验结果实验总结通过本次实验,我对迭代法求方程的根有了更深的认识,对其所用到的数学原理通过编程理解的更加清晰。
我是用Asp完成本次实验的,因为这样可以将结果很方便的用表格显示出来,让结果看起来比较清楚、明白和友好。
同时,我也用C语言编程实现过,结果是一样的,这也说明实验结果的正确性。
因为所给迭代方程是收敛的,不需要收敛性的验证,只要迭代达到误差的要求即可。
实验中遇到的一个问题是如何将结果中的小数点前的0补上去,让显示的更完整,通过网上查询,了解到可以根据对结果的判断将0加上去已达到完整显示,最终解决了这个问题。
第二次实验报告(非线性方程求根)

数学实验报告实验五学院:数学与统计学院班级:数学与统计学院(2)班姓名:石紫雲学号:0234非线性方程的数值解法实验1实验目的1)进一步熟练掌握求解非线性方程的牛顿迭代法和弦截法。
2)根据牛顿迭代法和弦截法的原理,编写程序求解非线性方程,提高编程解决问题的能力。
2 实验内容(1)用牛顿法和割线法求下列方程的根x^2-e^x=0;x*e^x-1=0;(23实验原理(1)牛顿迭代公式:1()/'()k k k k x x f x f x +=- 双点弦法公式:111()()()()k k k k k k k f x x x x x f x f x +--=--- (2)令2()f x x A =-,再用牛顿法求根。
4实验步骤1)根据牛顿迭代法,双点弦法的算法编写相应的求根函数;2)用牛顿迭代法和双点弦法分别对方程进行求解;5 程序设计牛顿迭代法x0=;N=100;k=0;eps=5e-6;delta=1e-6;while(1)x1=x0-fc1(x0)/fc2(x0);k=k+1;if k>Ndisp('Newton method failed')breakendif(abs(x1-x0)<delta || abs(fc1(x1))<delta) break;endx0=x1;endfprintf('%f',x0)fprintf('%f',abs(fc1(x1)))双点弦法function cutline(x0,x1)N=100;k=0;delta=5e-8;while(1)(abs(x1-x0)>=delta)c=x1;x1=cutnext(x0,x1);x0=c;k=k+1;if k>Ndisp('Cutline method failed')break;endif(abs(x1-x0)<delta || abs(fc1(x1))<delta) break;endendfprintf('%10f\n',x1);function y=cutnext(a,b)y=b-fc(b)/(fc(b)-fc(a))*(b-a);1)原函数function fc1=fc1(x)fc1=x^2-exp(x);end导函数function fc2=fc2(x)fc2=2*x-exp(x);end2)原函数function fc1=fc1(x) fc1=x*exp(x)-1;end导函数function fc2=fc2(x)fc2=1*exp(x)+x*exp(x);end3)原函数function fc1=fc1(x)fc1=x^2-5;end导函数function fc2=fc2(x)fc2=2*x;end6实验结果及分析注:牛顿迭代法由于设置delta=1e-6,所以算出的误差e<*10^-6;割线法由于设置delta=5e-8,所以误差e<*10^-8.7总结。
实验一 非线性方程求根

石家庄经济学院2014/2015学年第一学期数值分析实验报告班级: 5141090301学号: 514109030105姓名:张倩指导教师: 张敬敏实验一非线性方程求根一、实验题目1. 求方程f(x)=3x2-e x=0一个正根,并使误差不大于10-5。
(p22第3题)2. 计算√5,结果具有5位有效数字。
3. 求方程f(x)=x3-x-1=0在区间[1.0,1.5]内的一个实根,误差不大于10-5。
(选做)二、程序功能1. 使用迭代法求方程f(x)=3x2-e x=0一个正根,并使误差不大于10-5。
2. 用牛顿法计算√5,结果具有5位有效数字。
3. 利用二分法求方程f(x)=x3-x-1=0在区间[1.0,1.5]内的一个实根,精度为10-5。
三、算法算法1. 使用迭代法求方程f(x)=3x2-e x=0一个正根,并使误差不大于10-5。
算法2. 用牛顿法计算√5,结果具有5位有效数字。
for k=2,3,4….N do1)compute x:x g(x)四、重要标识符说明程序1. 重要标识符说明程序2. 重要标识符说明Error确定有效位数,abs取绝对值,for 迭代次数五、程序运行实例在matlab 6.5环境中,运行程序1,结果如图1所示。
图1 程序1运行结果在matlab 6.5环境中,运行程序2,结果如图2所示。
图2 程序2运行结果六、源程序程序1源程序:程序2源程序:Error=1e-5;x=2;for k=2:10xk=x;x=x/2+5/(2*x);if (abs(xk - x)<=Error)break;endend七、实验总结(不少于100字)。
数值分析实验报告——非线性方程求根

数值分析实验报告——非线性方程求根一、实验目的:1.掌握求解非线性方程的常用方法;2.了解非线性方程求根问题的数值解法;3.熟悉使用数值分析软件进行非线性方程求根的实现。
二、实验原理:非线性方程指的是形如f(x)=0的方程,其中f(x)是一个非线性函数。
非线性方程求根的常用方法包括二分法、割线法和牛顿法等。
其中,二分法是通过不断缩小区间范围来逼近方程的解;割线法是通过使用割线来逼近方程的解;牛顿法则是通过使用切线来逼近方程的解。
对于给定的非线性方程,可以根据实际情况选择合适的方法进行求根。
三、实验内容:1.编写求解非线性方程的函数,包括二分法、割线法和牛顿法;2.使用编写的函数求解给定的非线性方程,比较各个方法的收敛速度和精确程度;3.根据实际情况分析和选择合适的方法进行求根。
四、实验步骤:1.针对给定的非线性方程,编写二分法的函数实现:(1)首先确定方程的解存在的区间;(2)根据方程的解存在的区间,使用二分法逐步缩小区间范围;(3)根据设定的精度要求,不断循环迭代,直至满足要求或达到迭代次数限制;2.针对给定的非线性方程,编写割线法的函数实现:(1)首先需要确定方程的解存在的初始点;(2)根据方程的解存在的初始点,根据割线的定义进行迭代;(3)设定迭代的精度要求和限制次数,结束迭代;3.针对给定的非线性方程,编写牛顿法的函数实现:(1)首先需要确定方程的解存在的初始点;(2)根据方程的解存在的初始点,根据牛顿法的定义进行迭代;(3)设定迭代的精度要求和限制次数,结束迭代;4.根据给定的非线性方程,分别使用二分法、割线法和牛顿法进行求解,并比较各个方法的收敛速度和精确程度;5.分析实际情况,选择合适的方法进行求解。
五、实验结果:4.通过比较,发现割线法和牛顿法的收敛速度较快,精确程度较高,因此选择割线法进行求解。
六、实验总结:通过本次实验,我掌握了求解非线性方程的常用方法,并使用数值分析软件实现了二分法、割线法和牛顿法。
数值分析实验报告——非线性方程求根

数值分析实验报告——非线性方程求根二分法一、题目用二分法求方程=的所有根x.13要求每个根的误差小于-x+0.001..21二、方法二分法三、程序1、Jiangerfen.M的程序function[c,yc]=jiangerfen(f,a,b,tol1,tol2)if nargin<4 tol1=1e-3;tol2=1e-3;end%nargin<4表示若赋的值个数小于4,则tol1和tol2取默认值。
ya=feval('f',a);%令x=a代入到方程f中,ya即f(a)。
yb=feval('f',b);if ya*yb>0,disp('(a,b)不是有根区间');return,endmax=1+round((log(b -a)-log(tol2))/log(2));%round函数是将数据取整,使数据等于其最接近的整数。
for k=1:maxc=(a+b)/2;yc=feval('f',c);if((b-a)/2<tol2)|(abs(yc)<tol1),break,endif yb*yc<0a=c;ya=yc;elseb=c;yb=yc;endendk,c=(a+b)/2,yc=feval('f',c)2、f.M的程序function y=f(x);y=x^3-2*x-1;四、结果>> format compact>> fplot('[x^3-2*x-1,0]',[-1.5,2]);>> jiangerfen('f',-1.5,-0.8);k =8c =-0.9996yc =3.9017e-004>> jiangerfen('f',-0.8,-0.3);k =8c =-0.6184yc =2.7772e-004>> jiangerfen('f',1.3,2);k =10c =1.6179yc =-9.5348e-004>> jiangerfen('f',2,3);(a,b)不是有根区间方程f(x)=x^3-2*x-1的所有根为-0.9996,-0.6184 ,1.6179 。
数值计算课程设计报告(非线性方程求根)

数值计算方法课程设计报告课程设计名称:数值计算方法课程设计题目:非线性方程求根年级专业:组员姓名学号:指导教师:完成时间:非线性方程求根一、问题提出随着科学技术,生产力经济的发展,在科学与工程计算中存在着大量方程求根问题,例如贷款购房问题,工厂的最佳订货问题等都需要求解一类非线性方程的根,首先根据实际问题列出数学模型,确定变量,给出各个条件及相关函数;然后对建立的模型进行具体分析和研究,选择合适的求解方法;编写函数的程序,用计算机求出方程的解,通过所求解分析具体情况.求解非线性方程的问题有以下几种基本方法。
二分法简单易行,但收敛较慢,仅有线性收敛速度。
而且该方法不能用于求偶数重根或复根,但可以用来确定迭代法的初始值。
牛顿法是方程求根中常用的一种迭代方法,它除了具有简单迭代法的优点外,还具有二阶收敛速度(在单根邻近处)的特点,但牛顿法对初始值选取比较苛刻(必须充分靠近方程的根),否则牛顿法可能不收敛。
弦截法是牛顿法的一种修改,虽然比牛顿法收敛慢,但因它不需计算函数的导数,故有时宁可用弦截法而不用牛顿法,弦截法也要求初始值必须选取得充分靠近方程的根,否则也可能不收敛。
二、背景分析代数方程的求根问题是一个古老的数学问题。
理论上,n次代数方程在复数域内一定有 n个根(考虑重数)。
早在16世纪就找到了三次、四次方程的求根公式,但直到19世纪才证明大于等于5次的一般代数方程式不能用代数公式求解,而对于超越方程就复杂的多,如果有解,其解可能是一个或几个,也可能是无穷多个。
一般也不存在根的解析表达式。
因此需要研究数值方法求得满足一定精度要求的根的近似解。
牛顿迭代法是牛顿在17世纪提出的一种求解方程.多数方程不存在求根公式,从而求精确根非常困难,甚至不可能,从而寻找方程的近似根就显得特别重要.而在各种科学和工程计算中往往要用到非线性方程组的求解,而牛顿法又是最基础的迭代法,在各种计算力学、控制工程等领域中发挥了不可代替的作用.而在数值计算中,非线性方程组的求解同样具有重要意义.随着计算机技术的成熟和高速发展,对于非线性方程求根问题出现了大量的数学软件(如MATLAB,SAS,SPSSD等),计算机已经成为工程师应用数学解决工程问题的主要运算工具.同时,工程专业的学生对数学教育的需求重点正在从手工演绎和运算能力的培养转变到结合计算机软件进行建模、求解和论证能力的培养.我们采用Matlab数学软件平台,通过实例比较了二分法、牛顿迭代法、弦截法三种基本方法的优缺点。
数值计算课程设计报告-非线性方程求根(经典报告)

数值计算方法课程设计报告课程设计名称:数值计算方法课程设计题目:非线性方程求根年级专业:组员姓名学号:指导教师:非线性方程求根一、问题提出随着科学技术,生产力经济的发展,在科学与工程计算中存在着大量方程求根问题,例如贷款购房问题,工厂的最佳订货问题等都需要求解一类非线性方程的根,首先根据实际问题列出数学模型,确定变量,给出各个条件及相关函数;然后对建立的模型进行具体分析和研究,选择合适的求解方法;编写函数的程序,用计算机求出方程的解,通过所求解分析具体情况.求解非线性方程的问题有以下几种基本方法。
二分法简单易行,但收敛较慢,仅有线性收敛速度。
而且该方法不能用于求偶数重根或复根,但可以用来确定迭代法的初始值。
牛顿法是方程求根中常用的一种迭代方法,它除了具有简单迭代法的优点外,还具有二阶收敛速度(在单根邻近处)的特点,但牛顿法对初始值选取比较苛刻(必须充分靠近方程的根),否则牛顿法可能不收敛。
弦截法是牛顿法的一种修改,虽然比牛顿法收敛慢,但因它不需计算函数的导数,故有时宁可用弦截法而不用牛顿法,弦截法也要求初始值必须选取得充分靠近方程的根,否则也可能不收敛。
二、背景分析代数方程的求根问题是一个古老的数学问题。
理论上,n次代数方程在复数域内一定有 n个根(考虑重数)。
早在16世纪就找到了三次、四次方程的求根公式,但直到19世纪才证明大于等于5次的一般代数方程式不能用代数公式求解,而对于超越方程就复杂的多,如果有解,其解可能是一个或几个,也可能是无穷多个。
一般也不存在根的解析表达式。
因此需要研究数值方法求得满足一定精度要求的根的近似解。
牛顿迭代法是牛顿在17世纪提出的一种求解方程.多数方程不存在求根公式,从而求精确根非常困难,甚至不可能,从而寻找方程的近似根就显得特别重要.而在各种科学和工程计算中往往要用到非线性方程组的求解,而牛顿法又是最基础的迭代法,在各种计算力学、控制工程等领域中发挥了不可代替的作用.而在数值计算中,非线性方程组的求解同样具有重要意义.随着计算机技术的成熟和高速发展,对于非线性方程求根问题出现了大量的数学软件(如MATLAB,SAS,SPSSD等),计算机已经成为工程师应用数学解决工程问题的主要运算工具.同时,工程专业的学生对数学教育的需求重点正在从手工演绎和运算能力的培养转变到结合计算机软件进行建模、求解和论证能力的培养.我们采用Matlab数学软件平台,通过实例比较了二分法、牛顿迭代法、弦截法三种基本方法的优缺点。
数值分析非线性方程求根实验

实验报告一、实验目的1.迭代函数对收敛性的影响。
2.初值的选择对收敛性的影响。
二、实验题目1.用简单迭代法求方程01)(3=--=x x x f 的根。
分别化方程为如下等价方程: 31+=x x ;13-=x x ;x x 11+=;213-+=x x x 取初值5.10=x ,精度为410-,最大迭代次数为500,观察其计算结果并加以分析。
2.①用牛顿法求方程01)(3=-+=x x x f 在0.5附近的根,分别取初值1000,100,2,1,5.0,5.0,1,2,100,10000-----=x观察并比较计算结果,并加以分析。
②用牛顿法求方程0)(3=-=x x x f 所有根。
三、实验原理简单迭代法程序,牛顿迭代法程序。
四、实验内容及结果fun=inline('x^3-x-1');dfun=inline('3*x^2-1');-1000,x1=manewton(fun,dfun,-1000,1e-4) -100,x2=manewton(fun,dfun,-100,1e-4)-2,x3=manewton(fun,dfun,-2,1e-4)-1,x4=manewton(fun,dfun,-1,1e-4)-0.5,x5=manewton(fun,dfun,-0.5,1e-4) 0.5,x6=manewton(fun,dfun,0.5,1e-4)1,x7=manewton(fun,dfun,1,1e-4)2,x8=manewton(fun,dfun,2,1e-4)100,x9=manewton(fun,dfun,100,1e-4) 1000,x10=manewton(fun,dfun,1000,1e-4)3)在MA TLAB的主程序窗口输出以下结果:ans =-1000k=21x1 =0.682327804075895ans =-100k=16x2 =0.682327803903413ans =-2k=6x3 =0.682327803828020ans =-1k=5x4 =0.682327803828020ans =-0.500000000000000k=4x5 =0.682327803903932ans =0.500000000000000k=3x6 =0.682327803828347五、实验结果分析(1)实验1中用简单迭代法求方程01)(3=--=x x x f 的根:取初始值5.10=x 的时候,等价方程2和4是不收敛的。
数值分析实验报告 实验五 非线性方程求根

实验类别:数值分析专业:信息与计算科学班级:学号:姓名:中北大学理学院实验五 非线性方程求根【实验内容】设方程013)(3=--=x x x f 有三个实根8793.1*1=x ,*20.34729x =-, *3 1.532088x =-现采用下面四种不同计算格式,求0)(=x f 的根。
【实验方法与步骤】1、 213x x x +=用于求*3x 。
#include "math.h"#include "stdio.h"double f ( double x ){return((3*x+1) /x/x );}main(){double eps = 1e-10;double x1, x2 =-3;do{x1 = x2;x2 = f( x1 );printf( "\nx=%20.16lf \n", x2 ); }while( fabs( x2 - x1 ) >= eps ); scanf("%f",&x2);}2、 313-=x x 用于求*2x 。
#include "math.h"#include "stdio.h"double f ( double x ){return(( x*x*x-1) /3 );}main(){double eps = 1e-10;double x1, x2 =1.3;do{x1 = x2;x2 = f( x1 );printf( "\nx=%20.16lf\n", x2 );}while( fabs( x2 - x1 ) >= eps ); scanf("%f",&x2); }3、 313+=x x ,用于求*1x ,*3x 。
#include "math.h"#include "stdio.h"double f ( double x ){return(pow((3*x+1),1.0/3.0) ); }main(){double eps = 1e-10; double x1,x2 =1;do{x1 = x2;x2 = f( x1 );printf( "\nx=%20.16lf\n", x2 ); }while( fabs( x2 - x1 ) >= eps ); scanf("%f",&x2);}4、 x x 13+=用于求*1x 。
数值分析实验五 非线性方程的求根6

数值分析实验五 非线性方程的求根组号 班级 学号 姓名 分数一:实验目的1、 掌握用MA TLAB 软件求解非线性方程的基本用法。
2、 熟练运用不动点迭代法和牛顿法求解非线性方程的根。
二:实验内容及基本知识介绍不动点迭代法基本思路:首先给定一个粗糙的初始值,然而用一个迭代公式,反复校对这个初值,将已有近似值逐步精确化,一直到满足精度为止。
具体的,把方程()0f x =改写成x 的表达式()x x ϕ= ⑴ ,若()**x x ϕ=称*x 为()*x ϕ的一个不动点,求()f x 的零点等价于求()x ϕ的不动点。
在[],a b 上任取一点0x 代入()x ϕ求得()10x x ϕ=,又将1x 代入()x ϕ求得()21x x ϕ=,如此反复下去,一般地得()10,1,2,k k x x k ϕ+== ⑵。
()x ϕ称为迭代函数,()x x ϕ=为迭代公式。
牛顿法基本思想:将非线性方程()0f x =逐步转化为某种线性方程来求解。
设()0f x =的一个近似根0x ,则函数()f x 在点0x 附近可以用一阶泰勒公式()()()()0000f x f x f x x x '≈+-=来近似。
若()00f x '≠,解得()()000f x x x f x =-',将此根为原方程的近似根1x ,然后按上式迭代计算,使形成一种新的迭代公式()()10,1,2,k k k k f x x x k f x +=-=' 称为牛顿法。
三:实验问题及方法、步骤1.用MATLAB 函数求解方程3()310f x x x =--=在02x =附近的根。
首先建立如下的函数文件,Function y=f(x)y=x*x*x-3*x-1;然后在命令窗口中键入:fzero(@f,2),ans =1.87942.用不动点迭代法求()32410f x x x =+-在[1,1.5]上的一个根。
计算方法非线性方程求根实验

f (a ) ⋅ f (b) < 0 ;又设 f ( x) 的一个零点 x* ∈ (a, b) 的近似值 (设f ′( x0 ) ≠ 0) 。用过曲
计算方法非线性方程求根实验报告

实验报告一.MATLAB程序代码(1)function x=agui_bisect(fname,a,b,e)fa=feval(fname,a);fb=feval(fname,b);if fa*fb>0 error('两端函数值为同号');endk=0x=(a+b)/2while(b-a)>(2*e)fx=feval(fname,x);if fa*fx<0b=x;fb=fx;elsea=x;fa=fx;endk=k+1x=(a+b)/2end(2)function x=agui_diedai(fname,x0,e)N=100;x=x0;x0=x+2*e;k=0;while abs(x0-x)>e&k<Nk=k+1x0=x;x=feval(fname,x0);disp(x)endif k==N warning('已达到最大迭代次数');end(3)function x=agui_newton(fname,dfname,x0,e)N=100;x=x0;x0=x+2*e;k=0;while abs(x0-x)>e&k<Nk=k+1x0=x;x=x0-feval(fname,x0)/feval(dfname,x0);disp(x)endif k==N warning('已达最大迭代次数');end二. 实验结果及分析实验结果(1)x11=0.0903 (2)x5=0.0903 (3)x2=0.0903实验分析由三个结果对比可知,牛顿迭代法的迭代次数较少,且比较简单可靠。
可见牛顿迭代法要比二分法和迭代法的收敛速度快的多。
但是对函数有一定的要求。
牛顿迭代要求函数能求导。
数值分析实验报告之迭代法求非线性方程的根

数值分析实验报告之迭代法求非线性方程的根1.实验目的掌握迭代法求非线性方程根的基本原理和使用方法,加深对数值计算方法的理解与应用。
2.实验原理迭代法是一种通过不断逼近的方法求解非线性方程的根。
根据不同的函数特点和问题需求,可以选择不同的迭代公式进行计算,如牛顿迭代法、二分法、弦截法等。
3.实验内容本次实验使用牛顿迭代法求解非线性方程的根。
牛顿迭代法基于函数的局部线性逼近,通过不断迭代逼近零点,直至满足收敛条件。
具体步骤如下:Step 1:选择初始点X0。
Step 2:计算函数f(x)在X0处的导数f'(x0)。
Step 3:计算迭代公式Xn+1 = Xn - f(Xn) / f'(Xn)。
Step 4:判断收敛准则,若满足则迭代结束,输出解Xn;否则返回Step 2,继续迭代。
Step 5:根据实际情况判断迭代过程是否收敛,并输出结果。
4.实验步骤步骤一:选择初始点。
根据非线性方程的特点,选择恰当的初始点,以便迭代公式收敛。
步骤二:计算导数。
根据选择的非线性方程,计算函数f(x)的导数f'(x0),作为迭代公式的计算基础。
步骤三:迭代计算。
根据迭代公式Xn+1=Xn-f(Xn)/f'(Xn),计算下一个迭代点Xn+1步骤四:判断收敛。
判断迭代过程是否满足收敛条件,通常可以通过设置迭代次数上限、判断前后两次迭代结果的差值是否足够小等方式进行判断。
步骤五:输出结果。
根据实际情况,输出最终的迭代结果。
5.实验结果与分析以求解非线性方程f(x)=x^3-x-1为例,选择初始点X0=1进行迭代计算。
根据函数f(x)的导数计算公式,得到导数f'(x0)=3x0^2-1,即f'(1)=2根据迭代公式Xn+1=Xn-f(Xn)/f'(Xn),带入计算可得:X1=X0-(X0^3-X0-1)/(3X0^2-1)=1-(1-1-1)/(3-1)=1-0/2=1根据收敛准则,判断迭代结果是否满足收敛条件。
数值分析实验一非线性方程组求解

// MainFrm.cpp : implementation of the CMainFrame class // #include "stdafx.h"
实 验 源 代 码
#include "20141501069 于童实验一.h" #include "math.h" #include "MainFrm.h" #ifdef _DEBUG #define new DEBUG_NEW #undef THIS_FILE static char THIS_FILE[] = __FILE__; #endif
算法思想: 选定初始值 x0 , x1 ,并计算 f ( x0 ) 和 f ( x1 ) ;
弦 位 法
f ( x ) x n ( x x ) n 1 n n n 1 用迭代公式 x 计算 x2 ,再求 f ( x2 ) ; f ( x ) f ( x ) n n 1
0 x ,f ( x )) x , f( x )) 判别:如果 f (x 则迭代停止;否则,用 ( 和( 分别代替 2) 2 2 1 1
ReleaseDC(pDC); } void CMainFrame::Ondd() { // TODO: Add your command handler code here CDC*pDC=GetDC(); pDC->Rectangle(0,0,10000,10000); pDC->TextOut(10,30,"迭代法:方程 X^3-3X-1=0,迭代方程为:Xn+1=(3*Xn+1)^1/3"); double a=2; double b=pow(3*a+1,1.0/3); inti=0; intss=0; int s=0; int t=0; CString date; pDC->TextOut(20+20,50,"x0 : 2.000000"); while (fabs(a-b)>=0.00001) { i+=20; t++; ss++; if (t>=10) s=-10; pDC->TextOut(40+s,50+i,"x"); date.Format("%d",ss); pDC->TextOut(50+s+10,50+i,date); pDC->TextOut(60+10,50+i,":"); date.Format("%lf",b); pDC->TextOut(70+10,50+i,date); double temp=b-(b*b*b-3*b-1)/(3*b*b-3); a=b; b=temp; } } void CMainFrame::Onxw() { // TODO: Add your command handler code here CDC*pDC=GetDC(); pDC->Rectangle(0,0,10000,10000);
数值分析实验之非线性方程求根(Python现)

数值分析实验之⾮线性⽅程求根(Python现)详细实验指导见上⼀篇,此处只写内容啦实验内容:1. ⽤⼆分法求⽅程x3-3x-1=0在的所有根.要求每个根的误差⼩于0.001.提⽰与要求: (1) 利⽤精度找到迭代次数;(2) 由f(x)=3(x2-1)可取隔根区间[-2,-1].[-1,1].[1,2]);(3) ⽤程序求各隔根区间内的根.2. ⽤不动点迭代求: (1)x3+2x2+10x-20=0的所有根.或: (2)9x2-sinx-1=0在[0,1]上的⼀个根.3. ⽤Newton迭代法求解下列之⼀,准确到10-5:(1) x3-x-1=0的所有根;(2) e x+2-x+2cosx-6=0位于[0,2]上的根.实验代码:• ⽜顿迭代法1import math2 x=0.53 n = 14while n ==1 or abs(x-x1)>1e-5:5 x1 = x6def F(x1):7return 2**-x+2*math.cos(x)+math.exp(x)-68def F1(x1):9return math.exp(x)-math.log(2)*(2**-x)-2*math.sin(x)10 x = x1 - F(x1)/F1(x1)11print ('迭代步数:',n,'X1计算值=',x1,'X计算值=',x)12 n = n+113else:14print('⽅程的根=',(x))运⾏结果:• 不动点法1import numpy as np23def f(x):4return 9*x**2 - np.sin(x) - 156def g1(x):7return ((np.sin(x)+1)/9)**0.589def g2(x):10 result = (abs(2 * x + 1))**(1 / 5)11if (2 * x - 1) < 0:12return -result13return result1415def getEpsilon(x, epsilon):16 maxY = minY = x[0]17for each in x:18 maxY = max(f(each), maxY)19 minY = min((f(each), minY))20 epsilon = (maxY - minY) * epsilon21return epsilon2223def getInitialVal(x, N, step, epsilon):24 initalVal = []25for i in range(N + 1):26 y1, y2, y3 = f(x - step), f(x), f(x + step)27if (y1 * y2 < 0) and (i != 0):28 initalVal.append((x + x - step) / 2)29if ((y2 - y1) * (y3 - y2) < 0) and (abs(y2) < epsilon):30 initalVal.append(x)31 x += step3233return initalVal3435def findFixedPoint(initalVal, delta,epsilon):36 points = []37for each in initalVal:38if (abs(g1(each)) < 1):39 points.append(iteration(each, g1, delta,epsilon)) 40else:41 points.append(iteration(each, g2, delta,epsilon)) 42return points4344def iteration(p1, g, delta,epsilon):45while True:46 p2 = g(p1)47 err =abs(p2-p1)48 relerr = err/(abs(p2)+epsilon)49if err<delta or relerr<delta:50return p251 p1 = p25253def main():54 a, b, c = input().split('')55 a = float(a)56 b = float(b)57 c = int(c)58 delta = 10 ** (-c)59 N = 860 epsilon = 0.0161 step = (b - a) / N62 x = np.arange(a, b + epsilon, epsilon)6364 epsilon2 = getEpsilon(x,epsilon)65 initalVal = getInitialVal(a, N, step, epsilon2)66 ans = findFixedPoint(initalVal, delta,epsilon)6768for each in ans:69print('⽅程的根为:%.6f' % each)7071if__name__ == '__main__':72 main()运⾏结果:。
数值计算课程设计报告材料非线性方程求根

数值计算方法课程设计报告课程设计名称:数值计算方法课程设计题目:非线性方程求根年级专业:组员姓名学号:指导教师:完成时间:非线性方程求根一、问题提出随着科学技术,生产力经济的发展,在科学与工程计算中存在着大量方程求根问题,例如贷款购房问题,工厂的最佳订货问题等都需要求解一类非线性方程的根,首先根据实际问题列出数学模型,确定变量,给出各个条件及相关函数;然后对建立的模型进行具体分析和研究,选择合适的求解方法;编写函数的程序,用计算机求出方程的解,通过所求解分析具体情况.求解非线性方程的问题有以下几种基本方法。
二分法简单易行,但收敛较慢,仅有线性收敛速度。
而且该方法不能用于求偶数重根或复根,但可以用来确定迭代法的初始值。
牛顿法是方程求根中常用的一种迭代方法,它除了具有简单迭代法的优点外,还具有二阶收敛速度(在单根邻近处)的特点,但牛顿法对初始值选取比较苛刻(必须充分靠近方程的根),否则牛顿法可能不收敛。
弦截法是牛顿法的一种修改,虽然比牛顿法收敛慢,但因它不需计算函数的导数,故有时宁可用弦截法而不用牛顿法,弦截法也要求初始值必须选取得充分靠近方程的根,否则也可能不收敛。
二、背景分析代数方程的求根问题是一个古老的数学问题。
理论上,n次代数方程在复数域内一定有 n个根(考虑重数)。
早在16世纪就找到了三次、四次方程的求根公式,但直到19世纪才证明大于等于5次的一般代数方程式不能用代数公式求解,而对于超越方程就复杂的多,如果有解,其解可能是一个或几个,也可能是无穷多个。
一般也不存在根的解析表达式。
因此需要研究数值方法求得满足一定精度要求的根的近似解。
牛顿迭代法是牛顿在17世纪提出的一种求解方程.多数方程不存在求根公式,从而求精确根非常困难,甚至不可能,从而寻找方程的近似根就显得特别重要.而在各种科学和工程计算中往往要用到非线性方程组的求解,而牛顿法又是最基础的迭代法,在各种计算力学、控制工程等领域中发挥了不可代替的作用.而在数值计算中,非线性方程组的求解同样具有重要意义.随着计算机技术的成熟和高速发展,对于非线性方程求根问题出现了大量的数学软件(如MATLAB,SAS,SPSSD等),计算机已经成为工程师应用数学解决工程问题的主要运算工具.同时,工程专业的学生对数学教育的需求重点正在从手工演绎和运算能力的培养转变到结合计算机软件进行建模、求解和论证能力的培养.我们采用Matlab数学软件平台,通过实例比较了二分法、牛顿迭代法、弦截法三种基本方法的优缺点。
计算方法实验二非线性方程求根实验报告

实验报告学院:电子信息工程实验课程:计算方法学生姓名:学号:专业班级:通信工程实验二非线性方程求根1 目的与要求(1)进一步熟练掌握求解非线性方程的二分法与Newton迭代法。
(2)掌握二分法与Newton迭代法的算法,能运用程序设计语言和此方法编制软件求出任意指定一元三次方程在给定点附近的根。
2 实验内容用二分法和Newton迭代法求方程310x x--=在1.5 附近的根,精确到310-,输出每次的迭代结果并统计所用的迭代次数。
3 实验原理(1)二分法实验原理取[a,b]区间二等分的中点x1 =(a+b)/2(1)若f(x1)=0,则x1是f(x)=0的实根。
(2)若f(a)f(x1)<0 成立,则x* 必在区间(a, x1)内,取a1=a,b1= x1;否则x*必在区间(x1,b)内,则取a1= x1,b1=b,这样,得到新区间[a1,b1],其长度为[a,b]的一半。
(3)如此继续下去,进行n次等分(2)Newton迭代法实验原理4 程序设计(1)流程图二分法程序流程图Newton迭代法程序流程图(2)程序代码①二分法求非线性方程根#include<stdio.h>#include<math.h>double fun1(double x){return x*x*x-x-1;}double fun2(double x1,double x2){return (x1+x2)/2;}main(){int n=1;float a,b,c;printf("二分法求非线性方程的根\n"); scanf("a=%f,b=%f",&a,&b);if (fun1(a)*fun1(b)<0){while(fabs(b-a)>1e-3){c=fun2(a,b);if (fun1(a)*fun1(c)<0){b=c;}else if (fun1(c)*fun1(b)<0){a=c;}else{break;}printf("当前计算次数为%d 计算结果为%lf\n",n,fun2(a,b));n++;}}else{printf("不符合二分法使用条件,请重新输入:\n"); }}②Newton迭代法#include<stdio.h>#include<math.h>double fun1(double x){return x*x*x-x-1;}double fun2(double x){return 3*x*x-1;}double root(double num){double x1,x0;int n=1;x0=num;if (fun2(x0)==0){printf("Algorithm failed. Exit !"); }else{x1=x0-fun1(x0)/fun2(x0);printf("Newton迭代法求根\n");}while (fabs(x1-x0)>1e-3){printf("当前计算次数为%d 计算结果为%lf\n",n,x1); x0=x1;x1=x0-fun1(x0)/fun2(x0);n++;}}main(){root(1.5);}5 实验结果与分析(1)二分法求根结果界面(2)Newton迭代法求根结果界面分析:(1)本次试验两种算法均采用了while循环及if-else判断语句,编程函数并由主函数调用,较简单的实现了二分法与Newton迭代法的编程任务。
实验四非线性方程求根

《数值分析》课程设计实验报告实验四 非线性方程求根一、问题提出设方程3()310f x x x =--=有三个实根**121.8793,0.34727,x x ==- *3 1.53209x =-现采用下面六种不同计算格式,求 f(x)=0的根*1x 或*2x 1、 231x x x+= 2、 313x x -=3、 x =4、 213x x =-5、 x =6、 32131()31x x x x x --=-- 二、实验步骤#include "stdio.h"#include<math.h>main(){float x0=1.8793;printf("初值是%f\n",x0);/*输出x0*/float x1,x2,x3;x1=x0;int i;for(i=1;i<21;i++){x2=(3*x1+1)/(x1*x1);//第一种迭代方式 //x2=(x1*x1*x1-1)/3;//第二种迭代方式//x2=pow(3*x1+1,1.0/3);//第三种迭代方式//x2=1/(x1*x1-3);//第四种迭代方式//x2=sqrt(3+1/x1);//第五种迭代方式//x2=x1-(1/3.0)*((x1*x1*x1-3*x1-1)/(x1*x1-1));//第六种迭代方式x3=x2-x1;printf("第%d 次迭代值为%f,相邻两次迭代值差值为%f\n",i,x2,x3);/*输出x2*/x1=x2;if(x3<0)x3=-x3;if(x3<0.000001)//误差精度break;} } 当迭代格式为231x x x +=时,实验结果为由相邻两次迭代值差值结果可知,迭代过程处于发散状态。
当迭代格式为313x x -=,实验结果为由相邻两次迭代值差值结果可知,迭代过程前8次处于发散状态,第8次之后处于收敛状态,并且经过16次迭代,得到非线性方程的一个根。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数值计算方法课程设计报告课程设计名称:数值计算方法课程设计题目:非线性方程求根年级专业:组员姓名学号:指导教师:完成时间:非线性方程求根一、问题提出随着科学技术,生产力经济的发展,在科学与工程计算中存在着大量方程求根问题,例如贷款购房问题,工厂的最佳订货问题等都需要求解一类非线性方程的根,首先根据实际问题列出数学模型,确定变量,给出各个条件及相关函数;然后对建立的模型进行具体分析和研究,选择合适的求解方法;编写函数的程序,用计算机求出方程的解,通过所求解分析具体情况.求解非线性方程的问题有以下几种基本方法。
二分法简单易行,但收敛较慢,仅有线性收敛速度。
而且该方法不能用于求偶数重根或复根,但可以用来确定迭代法的初始值。
牛顿法是方程求根中常用的一种迭代方法,它除了具有简单迭代法的优点外,还具有二阶收敛速度(在单根邻近处)的特点,但牛顿法对初始值选取比较苛刻(必须充分靠近方程的根),否则牛顿法可能不收敛。
弦截法是牛顿法的一种修改,虽然比牛顿法收敛慢,但因它不需计算函数的导数,故有时宁可用弦截法而不用牛顿法,弦截法也要求初始值必须选取得充分靠近方程的根,否则也可能不收敛。
二、背景分析代数方程的求根问题是一个古老的数学问题。
理论上,n次代数方程在复数域内一定有 n个根(考虑重数)。
早在16世纪就找到了三次、四次方程的求根公式,但直到19世纪才证明大于等于5次的一般代数方程式不能用代数公式求解,而对于超越方程就复杂的多,如果有解,其解可能是一个或几个,也可能是无穷多个。
一般也不存在根的解析表达式。
因此需要研究数值方法求得满足一定精度要求的根的近似解。
牛顿迭代法是牛顿在17世纪提出的一种求解方程.多数方程不存在求根公式,从而求精确根非常困难,甚至不可能,从而寻找方程的近似根就显得特别重要.而在各种科学和工程计算中往往要用到非线性方程组的求解,而牛顿法又是最基础的迭代法,在各种计算力学、控制工程等领域中发挥了不可代替的作用.而在数值计算中,非线性方程组的求解同样具有重要意义.随着计算机技术的成熟和高速发展,对于非线性方程求根问题出现了大量的数学软件(如MATLAB,SAS,SPSSD等),计算机已经成为工程师应用数学解决工程问题的主要运算工具.同时,工程专业的学生对数学教育的需求重点正在从手工演绎和运算能力的培养转变到结合计算机软件进行建模、求解和论证能力的培养.我们采用Matlab数学软件平台,通过实例比较了二分法、牛顿迭代法、弦截法三种基本方法的优缺点。
三、 基本算法思想与实现 (1)二分法单变量函数方程:f (x )=0其中,f(x)在闭区间[a ,b]上连续、单调,且f(a)*f(b)<0,则有函数的介值定理可知,方程f (x )=0在(a ,b )区间内有且只有一个解*x ,二分法是通过函数在区间端点的符号来确定*x 所在区域,将有根区间缩小到充分小,从而可以求出满足给定精度的根*x 的近似值。
下面研究二分法的几何意义: 设1a =1,1b =b, 区间[]11,b a ,中点1x =211b a +及()1x f ,若()1x f =0,则*x =1x ,若 f(1a )*f(1x )<0,令2a =1a ,2b =1x ,则根*x ∈ [2a ,2b ]中,这样就得到长度缩小一半的有根区间[2a ,2b ],若 f(1b )*f(1x )<0,令2a =1x ,2b =1b ,则根*x ∈ [2a ,2b ]中,这样就得到长度缩小一半的有根区间[2a ,2b ],即f(2a )f(2b )<0,此时2b -2a =211a b -,对有根区间[2a ,2b ]重复上述步骤,即分半求中点,判断中电处符号,则可得长度有缩小一半的有根区间[2a ,2b ], 如图所示:重复上述过程,第n 步就得到根*x 的近似序列{}n x 及包含*x 的区间套,如下:(1)...],....[],[],[2211⊃⊃⊃n n b a b a b a(2)],[,0)()(*n n n n b a x b f a f ∈<(3)n a -nb =)(1121---n n b a =…=12--n ab (4) ,2n n n b a x +=且|*x -n x |≤12--n ab (n=1,2,3…..) 显然lim n x ,且n x 以等比数列的收敛速度收敛于*x ,因此用二分法求f (x )=0的实根*x 可以达到任意指定精度。
(2)牛顿迭代法设方程f(x)=0在其根*x 的某个领域U(*x ,δ)内有一阶连续导数,且f ’(*x ) ≠0。
求f(x)=0的根*x ,首先要将f(x)=0转化为等价形式()x x ϕ=,并使ϕ (x)满足不动点迭代的一般理论。
于是我们令ϕ (x)=x+h(x)f(x),可由ϕ ‘(1x )=0来确定h(x)的结构,根据ϕ’(x)=1+h ’(*x )f(*x )+h(*x )f ’(x1)=1+h(*x )f ’(*x )=0可得h(*x )=-1/f ’(*x ) ,由于f ’(x) ≠0,且f ’(x) 连续,因此当h(x)=-1/f ’(x) 时, h ’(x1)=0,即令ϕ (x)=x-f(x)/f ‘(x),从而有迭代格式1+k x = )(')(k k k x f x f x -(k=0,1,2,…..) 由于1x ,2x , 3x …….都在U 领域里,从而当B 比较小时,可用f ’(0x )可近似代替f ’(k x ),1+k x = k x -)()(0x f x f k ,此方法称为牛顿迭代法 下面研究牛顿法的几何意义:设r 是方程f (x )=0的根,选取0x 作为的r 初始近似值,经过(0x ,f(0x ))做曲线y=f(x)的切线的方程:y=f(0x )+f ’(0x )(x-0x ),求出L 与x 的交点的横坐标1x =0x -f(0x )/f ’(0x ),称1x 为r 的一次近似值经过点(1x ,f(1x ))做切线y=f(x)的切线,并求出该切线与x 轴的交点横坐标:2x =1x -f(1x )/f ’(1x ),2x 称为r 的二次近似值,重复以上操作可以得到r 的近似值序列。
下述三个定理分别讨论了牛顿法的收敛性质:定理1:对于方程f(x)=0,设f (x )在[a ,b]上有二阶连续导数且满足下述条件:(1)f(a)f(b)<0;(2)f ’(x)≠0, )(x f ''≠0,对任意的x ∈[a,b];(3)存在x ∈[a,b],使f (x ))(0x f ''>0,则由牛顿法产生的迭代序列{}n x 收敛于f(x)=0的根*x ,且)(2)()(**2**1lim x f x f x x x x k k k '''=--+∞→定理2:对于方程f(x)=0,设f (x )在[a ,b]上有二阶连续导数且满足下述条件:(1)f(a)f(b)<0;(2)对任意的x ∈[a,b], f ’(x)≠0, )(x f ''≠0(3))()(a f a f '<b-a, )()(b f b f '<b-a则对于任何0x ∈[a,b],由牛顿法产生的迭代序列{}n x 收敛于f(x)=0的根*x定理 3:设*x 是方程f(x)=0的根,在*x 的某个开区间内)(x f ''连续且f ’(x)≠0,则存在δ>0,当0x ∈【*xδ-,*x +δ】时,由牛顿迭代法1+k x =)(')(k k k x f x f x -(k=0,1,2,…..)式产生的序列{}n x 是以不低于二阶的收敛速度收敛到*x .(3)弦截法设k x ,1-k x 为方程f(x)=0的两个近似根。
用差商得:f(kx )-f(1-k x )/k x -1-k x ,代替牛顿迭代公式中的导数 f ’(kx ),于是得到如下的迭代公式:1+k x =k x -)()()()(11----k k k k k x x x f x f x f 。
下面研究割弦法的几何意义:经过点(kx ,f(kx ))及点(1-k x ,f(1-k x ))两点作割线,其点斜式方程为:Y=f (k x )-)()()(11k k k k k x x x x x f x f -----,其零点为X=k x - )()()()(11----k k k k k x x x f x f x f 把X 用1+k x 表示即得到迭代格式,它又称为双点弦割法,需要两个初值此割线与 X 轴交点的横坐标就是新的近似值1-k x ,所以弦截法又称为割线法,如图所示。
下面三个定理为弦割法收敛定理:定理1:设f (x )在其零点*x 的邻域U (*x ,δ)= [*x -δ,*x +δ] ( δ>0)内有二阶连续导数,0)(*≠'x f ,则当0x ∈U (*x ,δ)时,由割弦法式产生的序列{}n x 收敛于*x ,且收敛的阶为1.618。
定理2:设)(x f ''在区间[a,b] 上连续,且满足下述三点(1)f(a)f(b)<0;(2)对任意的x ∈[a,b],有f ’(x)≠0, )(x f ''≠0(3))()(a f a f '≤b-a, )()(b f b f '≤b-a则对于任意初始x ,1x ∈[a,b],由弦割法产生的迭代序列{}n x 收敛于f(x)=0唯一的根*x定理 3:设在其零点*x 的邻域U(*x ,δ)=[*x -δ,*x +δ](δ>0)内有二阶连续导数,f ’(x)≠0则当0x ∈ U(*x ,δ)时,由弦割1+k x =k x -)()()()(11----k k k k k x x x f x f x f式产生的序列{}n x 收敛于*x ,且收敛的阶为1.618。
四、 具体应用实例分析求解033)(23=--+=x x x x f 在5.1附近的根。
(1)二分法 建立erfen -M 文件:function [k,x,wuca,yx]=erfen(a,b,abtol) a(1)=a; b(1)=b;ya=fun(a(1));yb=fun(b(1)); %程序中调用的fun.m 为函数 if ya* yb>0,disp('注意:ya*yb>0,请重新调整区间端点a 和b.'), retur n endmax1=-1+ceil((log(b-a)- log(abtol))/ log(2)); % ceil 是向∞+方向取整 for k=1: max1+1 a;ya=fun(a); b;yb=fun(b); x=(a+b)/2; yx=fun(x); wuca=abs(b-a)/2; k=k-1;[k,a,b,x,wuca,ya,yb,yx]If yx==0a=x;b=x;elseif yb*yx>0b=x;yb=yx;elsea=x;ya=yx;endif b-a<abtol , retur n,endendk=max1; x; wuca; yx=fun(x);建立FUN函数文件:functiony=fun(x) y=x.^3+x.^2-3*x-3; 画图:>> x=[-10:0.1:10]; >> y=fun(x);>>plot(x,y);由图,我们选取区间[-6,6]输入程序:[k,x,wuca,yx]=erfen(-6,6,0.001)运行结果:k =13;x =1.7322;wuca =7.3242e-004;yx =0.0012(2)牛顿迭代法建立newtonqx -M文件:function[k,xk,yk,piancha,xdpiancha]=newtonqx(x0,tol,ftol,gxmax) x(1)=x0;for i=1: gxmaxx(i+1)=x(i)-fnq(x(i))/(dfnq(x(i))+eps); piancha=abs(x(i+1)-x(i));xdpiancha= piancha/( abs(x(i+1))+eps);i=i+1;xk=x(i);yk=fnq(x(i)); [(i-1) xkykpianchaxdpiancha]if (abs(yk)<ftol)&((piancha<tol)|(xdpiancha<tol))k=i-1;xk=x(i);[(i-1) xkykpianchaxdpiancha]return;endendif i>gxmaxdisp('请注意:迭代次数超过给定的最大值gxmax。
