第八届国际工业与应用数学大会
数学家的资料:智慧的证明——盘点数学界的大奖

数学家的资料:智慧的证明——盘点数学界的大奖
数学家的资料:很多同学都觉得数学是一门较难的科目,那幺能获得数学奖项的想必都是天才。
今天极客数学帮就来盘点下数学界天才的证明——数学大奖有哪些。
菲尔兹奖
菲尔兹奖(Fields Medal,全名:The
International Medals for Outstanding Discoveries in Mathematics),是一个在国际数学联盟(IMU)的国际数学家大会(ICM)上颁发的奖项。
它每四年颁奖一次,颁给二至四名有卓越贡献的年轻数学家。
得奖者须在该年元旦前未满四十岁。
菲尔兹奖是据加拿大数学家约翰·查尔斯·菲尔兹的要求设立的,被视为数学界的诺贝尔奖(诺贝尔奖未设数学奖)。
第八届全国高校出版社优秀畅销书一等奖(225种)

《新编基础会计(第四版)》
曲洪山等主编
大连理工大学出版社
《世纪商务英语函电与单证(第二版)》
刘杰英主编
大连理工大学出版社
《新版商务谈判日语》
刁鹂鹏编著
大连理工大学出版社
《成本会计习题与解答(第二版)》
鲁亮升主编
东北财经大学出版社
《经济法概论》
华本良主编
东北财经大学出版社
《新天地高职高专英语规划教材》(12册)听说教程1-4读写教程1-4综合教程1-4
《政治经济学(第三版)》
程恩富等主编
高等教育出版社
《知荣明耻从我做起(小学生读本)》
赵国柱等主编
人民教育出版社
《会计学基础》
韩辉主编
人民教育出版社.
《会计学基础实验教程》
张凯等编著
人民教育出版社
《教育新理念(修订版)》
袁振国主编
教育科学出版社
《为思维而教(修订版)》
郅庭瑾著
教育科学出版社
《教学论》
裴娣娜主编
杨怀定著
南京大学出版社
《高等数学(基础)》
冯宁主编
南京大学出版社
《管理学原理》
周三多等编著
南京大学出版社
《中小学班主任培训教材——小学班主任》
高谦民等主编
南京师范大学出版社
《供电企业典型诉讼案例评析》
周建海主编
河海大学出版社
《测量学(第四版)》
高井祥主编
中国矿业大学出版社
《煤矿重大安全生产隐患认定办法图解》
彭吉象著
北京大学出版社
《政治学基础(第二版)》
王浦劬等著
北京大学出版社
《公共行政学(第三版)》
ICIAM颁发的五大奖项中国数学会

究领域
他是本世纪最有影响力的工业与应 偏 微 分
用数学家之一在许多领域做出开创 方 程 ;
性贡献,例如,他系统地使用泛函 奇 异 摄
分析和弱解解决椭圆和抛物线微分 动等。
方程组;建立多种理论方法和数值
方法,解决问题非线性问题;深入
研究偏微分方程组的控制问题,最
优控制问题,推出了现在的标准希
尔伯特唯一方法;他在奇异摄动领
影响。
在偏微分方程求解及其应用做出重 非 齐 次
要贡献
边值问
题与应
用,偏
微分方
程
他是著名的应用数学家,他的工作 应 用 数
深刻影响现代应用数学的发展。他 学 , 数
Hale Waihona Puke 的工作对科学、工程、纯粹数学产 学 物
生重要影响。他提出了衍射的几何 理 , 力
理论,首次系统地描述了障碍物周 学
围和棱角处的波传播,在处理很多
澳大利亚悉尼
2007 年 瑞士苏黎世
2011 年 加拿大温哥华 2015 年 中国北京
Felix Otto
Emmanuel J. Candès Annalisa Buffa
裔
德国
美国,法 裔 美国
诸多方向均有重要的发现和 凝 聚 态 物
贡献;他的研究将数学模型、 理学,他的
分析和计算美妙地结合起 研究领域
ICIAM 科拉兹奖从 1999 年开始颁发,由德国工业与应用数学学 会资助设立。它奖励国际公认的在工业与应用数学中做出杰出工作的 42 岁以下的年青数学家。
ICIAM 拉格朗日奖从 1999 年开始颁发,由法国、意大利和西班 牙工业与应用数学学会共同资助设立。它对国际公认的一生为工业与 应用数学做出杰出贡献的数学家进行奖励。
数学的发展历史

开创写下了不可磨灭的一章
阿基米德的墓碑上刻的图
此后是千余年的停滞
• 随着希腊科学的终结,在欧洲出现了科学萧条,数学 发展的中心移到了印度、中亚细亚和阿拉伯国 家.在这些地方从5世纪到15世纪的一千年中间, 数学主要由于计算的需要而发展.印度人发明了 现代记数法 后来传到阿拉伯,从发掘出的材料看, 中国是使用十进制最早的国家 ,引进了负数.
的大小关系,平行线理论,三角形和多角形等积 面积相等 的条件,第一卷最 后两个命题是 毕达哥拉斯定理的正逆定理;
第二卷:几何与代数。讲如何把三角形变成等积的正方形;其中12、 13命题相当于余弦定理。
第三卷:本卷阐述圆,弦,切线,割线,圆心角,圆周角的一些定理。 第四卷:讨论圆内接和外切多边形的做法和性质; 第五卷:讨论比例理论,多数是继承自欧多克斯的比例理论,被认为 是"最重要的数学杰作之一" 第六卷:讲相似多边形理论,并以此阐述了比例的性质。 第五、第七、第八、第九、第十卷:讲述比例和算术的理论;第十 卷是篇幅最大的一卷,主要讨论无理量 与给定的量不可通约的量 ,其中第 一命题是极限思想的雏形。 第十一卷、十二、十三卷:最后讲述立体几何的内容.
学的内容,年代可以追溯到公元前2000年,其中甚至有“整勾 股数”及二次方程求解的记录。
莱茵德纸草书 1650 B.C.
莫斯科纸草书 vh(a2 abb2)
3
古巴比伦的“记事泥板”中关于 “整勾股数”的记载”
约公元前1000年
马其顿,1988年
20世纪在两河流域有约50万块泥版文 书出土,其中300多块与数学有关
秦九韶的《数书九章》 卷一“大衍总数术”
“贾宪三角”, 也称“杨辉三角”
中国现代科学家简介 2

中国现代科学家简介1、林巧稚(1901——1983),著名妇产科专家。
福建厦门人。
1929年毕业于协和医学院,获医学博士学位,并被聘为协和医学院妇产科医师。
后任妇产科主任兼教授。
1932年和1940年曾两次出国,在英国伦敦医学院、曼彻斯特医学院和美国芝加哥大学医学院进修。
回国后,历任协和医院、友谊医院妇产科主任兼教授、中国医学科学院副院长、北京市妇产科医院名誉院长、全国妇联副主席等职,她是中国科学院第一位女学部委员。
2、张钰哲(1902——1983),著名天文学家。
福建闽候人。
1919年考入清华大学。
1923年赴美留学。
1928年获芝加哥大学博士学位。
同年回国,曾任中央研究院天文研究所特约研究员、天文研究所所长。
1946年再次赴美,从事天文研究活动。
1948年回国。
担任中国科学院紫金山天文台台长、中国科学院数理化学部委员、中国天文学会理事长。
3、侯德榜(1890——1974),著名化学家。
福建闽候人。
1913年赴美留学。
先后在麻省理工学院、普拉特学院和哥伦比亚大学攻读化学。
1920年获哥伦比亚大学化学工程博士。
1921年回国,曾任塘沽永利碱厂总工程师、南京永利硫酸铵厂厂长、永利化学公司总经理。
新中国成立后,任重工业部化学局顾问、化工部副部长、中国化工学会副理事长、中国科学院技术科学部委员、全国科协副主席。
他是美国机械工程师协会、美国化工学会和英国皇家学会的名誉会员。
4、丁颖(1888——1964),著名农业科学家、水稻专家。
广东茂名人。
1912年毕业于广东高等师范。
1913年赴日本留学,攻读农业科学。
1924年回国,任中山大学农学院教授。
新中国成立后,历任华南农学院院长、全国科协副主席、中国农业科学院院长。
他是中国科学院生物学部委员,并曾被授予民主德国农科院通讯院士、全苏列宁农科院通讯院士等称号。
5、熊庆来(1893——1969),云南弥勒人。
1906年考入云南高等学堂。
1913年赴比利时留学,后转赴法国,先后就读于格伦诺勃尔大学、巴黎大学、蒙柏里大学和马赛大学,于1920年获理学硕士学位。
重邮科技处对于论文期刊级别的认定文件

部
6
法学
7
政治学
中国法学 中外法学
世界经济与政治
中国法学会 北京大学法学院 中国社会科学院世界经济与政治研
究所
— 59 —
序号 学科名称
8
社会学
9
民族学
10
教育学
11
心理学
12
语言学
13
文学
14 外国语言文学
29 INFORMS (管理科学与运筹学国际会议)
30 ICIS(International Conference on Information Systems,信息系统国际会议) IEEE/SMC(IEEE Conference on Systems, Man and Cybernetics,系统工程
31 国际会议)
32 IFORS(运筹学世界大会)
33 AOM(Academy of Management,美国管理学会国际会议) 34 AAA(American Accounting Association Conference,美国会计年会)
三峡大学2018年度学科竞赛计划统计表
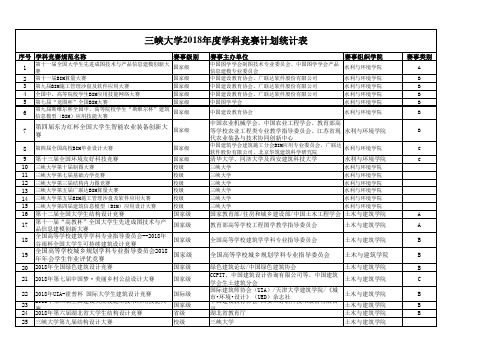
旅游信息化创新应用大赛 第二届“尖烽时刻”酒店管理模拟全国大赛 湖北省酒店管理沙盘模拟大赛
国家级 国家级 国家级 省级
教育部、商务部 教育部
教育部旅游教指委
湖北省旅游教指委
A C B
序号 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99
三峡大学 三峡大学 三峡大学
赛事组织学院
电气与新能源学院 电气与新能源学院 计算机与信息学院 计算机与信息学院 计算机与信息学院 计算机与信息学院 计算机与信息学院 计算机与信息学院 计算机与信息学院 计算机与信息学院 计算机与信息学院
赛事类别
A A A A B B
中国人力资源开发研究会
经济与管理学院 经济与管理学院 经济与管理学院 经济与管理学院
国家级 国家级 国家级
国家教育部/住房和城乡建设部/中国土木工程学会 土木与建筑学院 教育部高等学校工程图学教学指导委员会 全国高等学校建筑学学科专业指导委员会 土木与建筑学院 土木与建筑学院
A
A B B B C B
B B
全国高等学校城乡规划学科专业指导委员会2018 国家级 年年会学生作业评优竞赛
序号 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48
学科竞赛规范名称
三峡大学第五届理想空间设计竞赛
三峡大学第四届工程测量技能竞赛 三峡大学第四届地质技能竞赛 三峡大学第三届先进成图技术与产品信息建模创 校级 新大赛(土建类)
64 65 2018年第十二届“西门子杯”中国智能制造挑战赛 校内选拔赛 2018年蓝桥杯全国软件和信息技术专业人才大赛 2018年中国大学生计算机设计大赛 ACM-ICPC国际大学生程序设计竞赛 2018年全国大学生物联网设计竞赛 第十届高等学校信息技术创新与实践活动 2018年全国计算机仿真大奖赛 2018年三峡大学程序设计竞赛 2018年三峡大学FPGA应用设计竞赛 2018年三峡大学单片机应用设计竞赛 第三届全国大学生人力资源管理知识技能竞赛(精 创教育杯)
第8届国际工业与应用数学大会情况介绍

ICIAM Liaison
Industrial Promotion
执行委员会
大会主席:郭雷院士
执行委员会:
主 席: 郭雷院士
副主席: 袁
秘书长:
驷,清华大学
王跃飞,中科院数学与系统科学研究院 高小山,中科院数学与系统科学研究院 巩馥洲,中科院数学与系统科学研究院
副秘书长:闫桂英,中科院数学与系统科学研究院
会议日程
ICIAM奖项及获奖报告
• • • • • ICIAM Collatz Prize ICIAM Lagrange Prize ICIAM Maxwell Prize ICIAM Pioneer Prize ICIAM Su Buchin Prize
ICIAM历史上首 次加入这五个奖 项的获奖报告
会议历史
第一届:法国巴黎(1987) 第二届:美国华盛顿(1991) 第三届:德国汉堡(1995) 第四届:英国爱丁堡(1999) 第五届:澳大利亚悉尼(2003)
第六届:瑞士苏黎世(2007)
第七届:加拿大温哥华(2011) 第八届:中国北京(2015) 第九届:西班牙瓦伦西亚(2019)
会议组织
中科院数学院 国家数学交叉中心 北京大学 首都师范大学 上海交通大学 西安交通大学 南开大学 东北师范大学 湘潭大学 云南财经大学 河北师范大学
天津大学应用数学中心 武汉大学
清华大学
复旦大学 中国科技大学
浙江大学
四川大学
吉林大学
华中师范大学
竭诚欢迎更多学校成为ICIAM 2015大会的合办单位! 请联络大会秘书处咨询详情!
学术子委员会工作组
Minisymposium:
Lead by Yunqing HUANG , Xiangtan University
清华大学 各院系(学科)重要国际学术会议目录

清华大学各院系(学科)重要国际学术会议目录研究生院汇编二○○七年三月目录1. 建筑学院 (1)2. 土木工程系 (3)3. 建设管理系 (6)4. 水利水电工程系 (7)5. 环境科学与工程系 (9)6. 机械工程系 (11)7. 精密仪器系(机械工程) (13)8. 精密仪器系(仪器科学与技术) (15)9. 精密仪器系(光学工程) (17)10. 热能工程系 (18)11. 汽车工程系 (21)12. 工业工程系 (23)13. 电机系 (25)14. 电子工程系(电子科学与技术) (28)15. 电子工程系(信息与通信工程) (30)16. 计算机科学与技术系 (32)17. 自动化系 (34)18. 航天航空学院(工程热物理) (37)19. 航天航空学院(力学) (38)20. 工物系、核研院 (40)21. 化学工程系 (43)22. 材料科学与工程 (45)23. 数学系 (47)24. 物理系 (49)25. 化学系 (51)26. 生物系 (53)27. 经济管理学院(管理科学与工程) (56)28. 经济管理学院(工商管理、数量经济学) (57)29. 公共管理学院(公共管理) (59)30. 公共管理学院(管理科学与工程) (61)31. 人文学院 (62)32. 人文学院(外语系) (63)33. 法学院 (64)34. 新闻与传播学院 (65)35. 微纳电子学系 (66)36. 医学院 (68)建筑学院重要国际学术会议一、A类会议二、B类会议土木水利学院土木工程系重要国际学术会议一、A类会议二、B类会议土木水利学院建设管理系重要国际学术会议一、A类会议二、B类会议土木水利学院水利水电工程系重要国际学术会议一、A类会议二、B类会议环境科学与工程系重要国际学术会议一、A类会议二、B类会议机械工程系重要国际学术会议一、A类会议二、B类会议精仪系机械工程学科重要国际学术会议一、A类会议二、B类会议精仪系仪器科学与技术学科重要国际学术会议一、A类会议二、B类会议精仪系光学工程学科重要国际学术会议一、A类会议二、B类会议热能工程系重要国际学术会议一、A类会议二、B类会议汽车工程系重要国际学术会议一、A类会议二、B类会议工业工程系重要国际学术会议一、A类会议2006 年11 月08 日二、B类会议2006 年11 月08 日电机系重要国际学术会议电子系(电子科学与技术)重要国际学术会议目录(2007年1月11日)一、A类会议(序号不表示优先顺序)电子系(信息与通信工程)重要国际学术会议目录(2007年1月11日)一、A类会议(序号不表示优先顺序)二、B类会议(序号不表示优先顺序)计算机科学与技术系重要国际学术会议一、A类会议二、B类会议自动化系重要国际学术会议航天航空学院(工程热物理)重要国际学术会议一、A类会议二、B类会议航天航空学院(力学)重要国际学术会议一、A类会议二、B类会议工物系核研院核科学与技术学科重要国际学术会议一、A类会议二、B类会议化学工程系重要国际学术会议一、A类会议二、B类会议材料科学与工程系重要国际学术会议一、A类会议二、B类会议。
一位数学院士的两个40年—复旦教授李大潜

一位数学院士的两个40年: 复旦教授李大潜人物小传李大潜1937年生于江苏南通,复旦大学数学科学学院教授,研究领域为偏微分方程、控制理论、工业应用数学。
曾获国家自然科学奖二等奖,何梁何利基金科学与技术进步奖,华罗庚数学奖,上海市科技功臣奖,法兰西国家荣誉军团骑士勋章及法国巴黎十二大名誉博士称号等。
今年是改革开放40周年,也是我国改革事业承前启后、继往开来的关键节点。
本版今起推出系列访谈,以各行各业亲历者的视角,追溯历史,致敬时代,在回望中前瞻,在振奋中前行。
李大潜说,自己刚刚年逾八旬的人生差不多是以1978年为界,分为前后两个40年的。
在那一年的年底,党的十一届三中全会召开,改革开放昭苏万物的春风吹来,李大潜成为“文革”后第一批公派出国的访问学者之一。
如果说他人生的前40年是“埋头苦干”的话,那么这次走出国门的经历则是他日后成为享誉世界的数学家的重要转折。
改革开放40年,也是中国科学蓬勃发展与知识分子改变命运的40年。
今天,李大潜已是“五院院士”(中国科学院院士、发展中国家科学院院士、欧洲科学院院士、法国科学院外籍院士、葡萄牙科学院外籍院士)。
回首来路,他说:“个人的前途、命运总是和国家的前途、命运联系在一起的。
这不是唱高调,而应该是一个基本的觉悟。
”前40年我学会了4个字:“贵在坚持”一张师生签名的贺卡,一束鲜花,一场座谈会——8个月前,李大潜在复旦度过了自己执教一甲子的纪念日。
没有隆重的场面,省去了繁琐的仪式,取而代之的,是简单朴实的真情流露,正如李大潜一以贯之的行事风格。
在他看来,这样的风格来源于复旦数学薪火的代代相传。
1953年,高中时就对数学产生浓厚兴趣的李大潜考入了复旦大学数学系,年仅15岁的他是那届学生中年龄最小的。
4年后,李大潜以各科全优的成绩毕业,由于他在数学方面扎实的基础和超高悟性,受到一代数学大师苏步青的青睐,亲自提名他留校任教。
李大潜在学术上继承了苏步青、谷超豪两位大师的衣钵,并将之发扬创新。
自动化赛事

自动化专业可以参加的赛事1、全国大学生“飞思卡尔”杯智能汽车竞赛简介:全国大学生“飞思卡尔”杯智能汽车竞赛起源于韩国,是韩国汉阳大学汽车控制实验室在飞思卡尔半导体公司资助下举办的以HCS12单片机为核心的大学生课外科技竞赛。
组委会提供一个标准的汽车模型、直流电机和可充电式电池,参赛队伍要制作一个能够自主识别路径的智能车,在专门设计的跑道上自动识别道路行驶,最快跑完全程而没有冲出跑道并且技术报告评分较高为获胜者。
其设计内容涵盖了控制、模式识别、传感技术、汽车电子、电气、计算机、机械、能源等多个学科的知识,对学生的知识融合和实践动手能力的培养,具有良好的推动作用。
承办学校及全国总决赛特等奖学校第一届(2006年):承办:清华大学特等奖:清华大学第二届(2007年):承办:上海交通大学特等奖:上海交通大学第三届(2008年):承办:东北大学摄像头组冠、亚、季军:东北大学、北京科技大学、上海交通大学光电组冠、亚、季军:武汉科技大学、北京科技大学、东北大学第四届(2009年):承办:北京科技大学摄像头组冠、亚、季军:北京科技大学、上海交通大学、上海大学光电组冠、亚、季军:北京科技大学、清华大学、杭州电子科技大学第五届(2010年):承办:杭州电子科技大学摄像头组冠、亚、季军:北京科技大学、杭州电子科技大学信息工程学院、南京师范大学光电组冠、亚、季军:杭州电子科技大学、杭州电子科技大学信息工程学院、乐山师范学院电磁组冠、亚、季军:广东技术师范学院、清华大学、杭州电子科技大学第六届(2011年):承办:西北工业大学摄像头组冠、亚、季军:湖南大学、北京科技大学、山东大学光电组冠、亚、季军:西北工业大学、电子科技大学、乐山师范学院电磁组冠、亚、季军:杭州电子科技大学、北京科技大学、西北工业大学第七届(2012年):承办:南京师范大学摄像头组冠、亚、季军:北京科技大学、常熟理工学院、电子科技大学光电组冠、亚、季军:北京科技大学、山东大学、乐山师范学院电磁组冠、亚、季军:中南民族大学、浙江大学、华中科技大学第八届(2013年):承办:哈尔滨工业大学摄像头组冠、亚、季军:北京科技大学、武汉科技大学、西安交通大学光电组冠、亚、季军:北京科技大学、厦门大学、厦门大学嘉庚学院电磁组冠、亚、季军:电子科技大学、北京科技大学、东北大学秦皇岛分校2、大学生iCAN物联网创新创业大赛中国大学生iCAN物联网创新创业大赛,是教育部计算机教学指导委员会、全球华人微纳米分子系统学会联合主办的一项全国性物联网技术的年度创新赛事,是教育部质量工程支持项目之一,同时也是国际大学生物联网创新创业大赛(International Contest of Applications in Network of Things,简称iCAN)的中国选拔赛。
中国矿业大学大学生课外科技竞赛项目分类分级汇总表

竞赛分类 科技创新类 科技创新类 科技创新类 科技创新类 课程学习类 科技创新类 科技创新类 专业技能类 就业创业类 专业技能类 科技创新类 科技创新类 科技创新类 科技创新类 科技创新类 科技创新类 课程学习类 科技创新类 课程学习类 专业技能类 科技创新类 科技创新类 科技创新类 科技创新类 科技创新类 课程学习类 课程学习类 其他类 科技创新类 课程学习类 科技创新类
附件3:中国矿业大学大学生课外科技竞赛项目分类分级汇总表 序号 竞赛名称 1 挑战杯全国大学生课外学术科技作品竞赛和创业计划大赛 2 全国大学生数学建模比赛 3 全国大学生电子设计大赛 4 全国大学生结构设计大赛 5 全国大学生机械创新设计大赛 6 全国周培源大学生力学竞赛 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 飞思卡尔杯智能汽车竞赛 ACM国际大学生程序设计竞赛(亚洲区赛) 国际数学建模比赛 全国大学生节能减排社会实践与科技竞赛 中国室内设计大赛 全国大学生交通科技大赛 全国软件人才开发设计与创业大赛 英特尔杯大学生电子设计竞赛嵌入式系统专题邀请赛 全国大学生信息安全大赛 中国机器人大赛暨RoboCup公开赛 全国水利创新设计大赛 全国大学生嵌入式设计大赛 全国大学生地质技能竞赛 全国大学生电子商务“创新、创意及创业”挑战赛 全国大学生设计大师奖设计大赛 全国大学生英语竞赛 全国大学生广告艺术大赛 “外研社杯”全国大学生英语辩论赛 “外研社杯”全国英语演讲比赛 亚太(全国)大学生机器人大赛 国际机器人足球联盟(FIRA)世界杯机器人足球大赛 “高教杯”全国大学生先进图形技能与创新大赛 全国高校城市规划专业本科生设计作业评优竞赛
序号 86 87 88 89 90 91 92 93 94
华罗庚简介资料_华罗庚个人资料介绍

华罗庚简介资料_华罗庚个人资料介绍你了解华罗庚么?华罗庚,数学家,中国科学院院士,中国第一至第六届全国人大会委员,下面就是小编整理的华罗庚简介资料_华罗庚个人资料介绍,希望大家喜欢。
目录华罗庚简介华罗庚(1910.11.12—1985.6.12),出生于江苏常州金坛区,祖籍江苏丹阳。
数学家,中国科学院院士,美国国家科学院外籍院士,第三世界科学院院士,联邦德国巴伐利亚科学院院士。
中国第一至第六届全国人大会委员。
他是中国解析数论、矩阵几何学、典型群、自守函数论与多元复变函数论等多方面研究的创始人和开拓者,并被列为芝加哥科学技术博物馆中当今世界88位数学伟人之一。
国际上以华氏命名的数学科研成果有“华氏定理”、“华氏不等式”、“华—王方法”等。
华罗庚人物生平成长历程1910年11月12日出生于江苏常州金坛区,他幼时爱动脑筋,因思考问题过于专心常被同伴们戏称为“罗呆子”。
1922年,12岁从县城仁劬小学毕业后,进入金坛县立初中,王维克老师发现其数学才能,并尽力予以培养。
1925年,初中毕业后,就读上海中华职业学校,因拿不出学费而中途退学,退学回家帮助父亲料理杂货铺,故一生只有初中毕业文凭。
此后,他用5年时间自学完了高中和大学低年级的全部数学课程。
1927年秋,和吴筱元结婚。
1929年冬,他不幸染上伤寒病,落下左腿终身残疾,走路要借助手杖。
1929年,华罗庚受雇为金坛中学庶务员,并开始在上海《科学》等杂志上发表论文。
1930年春,华罗庚在上海《科学》杂志上发表《苏家驹之代数的五次方程式解法不能成立之理由》轰动数学界。
同年,清华大学数学系主任熊庆来,了解到华罗庚的自学经历和数学才华后,打破常规,让华罗庚进入清华大学图书馆担任馆员。
1931年,在清华大学数学系担任助理。
他自学了英、法、德文、日文,在国外杂志上发表了3篇论文。
1933年,被破格提升为助教。
1934年9月,被提升为讲师。
出国求学1935年,数学家诺伯特·维纳(Norbert Wiener)访问中国,他注意到华罗庚的潜质,向当时英国著名数学家哈代极力推荐。
中国优秀科技期刊办刊模式调查与发展路径分析——以第一届至第三届全国“百强科技期刊”为例

素是内容,因此内容是否精彩,是否有价值和吸引力是市场竞争中的重要因素,一言以蔽之——内容为王。
此类期刊应该在广泛市场调研的基础上对自己进行准确定位,优化和细分自身的栏目和选题,突出自身特色。
同时,应该更加重视开拓新的传播渠道,借助新的移动阅读终端,例如手机、电子阅读器等,实现更广泛地传播自身内容的目的。
二是时尚消费类女性期刊应该摒弃依靠国际期刊版权、搬运时尚潮流资讯的老套路,引领立足于本土的时尚文化。
此类杂志和期刊可以具有国际视野,但一定要具有本土意识,只有立足本土和当下,才能真正引领符合时代和地域特点的时尚潮流,形成具有原创性的时尚消费主张,传递具有中国品质的美学和理念,也才能真正引领中国审美潮流和消费理念,成为引领中国时尚潮流的旗帜。
三是特定人群期刊的改革与期刊整体体制改革以及各地妇联职能和工作形式的变化相联系,改革起来难度较大,但是在期刊内容、发布形式方面还是存在改进的空间,需要与边远地区的妇女工作结合起来,切实关注妇女需求,更好地服务当地。
同时可以借鉴体制外一些女性期刊的内容和发布形式,使自身成为该地区女性的精神家园和妇女援助的重要指引手册。
四是学术类期刊具有研究和引领的功能,女性期刊的主流阵地不能全部被家庭、时尚以及爱情所占据。
作为研究女性的学术期刊,具有增强性别平等意识、倡导正确的性别观念、引领先进性别文化的重要作用。
在关注全球女性研究理论前沿和动态的同时,也要更多地关注女性社会热点问题,例如女性教育、女性权益保护、女性参政问题等,站在理论和学术前沿的角度,站在时代的前沿,为推动男女平等和女性发展进行正确的引领和导航。
(作者单位:中华女子学院图书馆;本文摘自《中华女子学院学报》2019年第6期)中国优秀科技期刊办刊模式调查与发展路径分析——以第一届至第三届全国“百强科技期刊”为例赵燕萍 章 诚 林本兰科技期刊在学术交流、推动科技进步等方面具有重要作用,是一个国家科技水平与文化软实力的重要体现,与我国科技强国发展具有紧密联系。
大学本科专业(数学类-数学与应用数学)

大学本科专业(数学类-数学与应用数学),该专业所学具体内容、发展方向以及就业前景大纲:一、数学与应用数学专业概述A. 专业背景B. 专业定位C. 专业特点二、数学与应用数学专业课程设置A. 基础课程B. 专业核心课程C. 选修课程三、数学与应用数学专业发展方向A. 学术研究方向B. 应用领域发展方向C. 视野拓展方向四、数学与应用数学专业就业前景A. 学术领域就业前景B. 应用领域就业前景C. 竞争激烈的就业市场五、数学与应用数学专业个人发展建议A. 提高数学建模技能B. 多学习计算机科学知识C. 发展多元化的技能和兴趣摘要:摘要本文主要讨论大学本科数学与应用数学专业的具体内容、发展方向以及就业前景。
首先,我们将介绍该专业的基本课程和学习内容。
然后,我们将详细阐述该专业的发展方向,并探讨相关工作领域的就业前景。
最后,我们将分析该专业在整个国民经济和社会发展中的重要性,并提出一些具体的建议和措施来促进该专业的发展。
第一部分:数学与应用数学专业的基本课程和学习内容大学本科数学与应用数学专业是一种理工科学科,主要涵盖了数学基础理论和应用数学的知识领域。
该专业的主要课程包括微积分、线性代数、数学分析、概率论与数理统计、数值计算、离散数学、常微分方程等。
此外,大学本科数学与应用数学专业还会涉及物理、经济学、金融学、计算机科学等领域的课程。
学生们需要通过这些基础课程的学习掌握数学基本概念、数学主要工具和数学基本理论,同时也需掌握实际应用的技术和方法。
在学生们完成了基础课程的学习之后,他们可以开始学习更高级别的课程。
例如,实分析、泛函分析、复分析、拓扑学、代数学、微分几何等课程,这些课程可以使学生更加深入地学习数学的理论和应用。
此外,学生们还可以选择学习一些与数学相关的应用科学领域的课程,如计算机科学、物理学、工程学、经济学等,从而更加广泛地掌握应用领域的知识和技能。
第二部分:数学与应用数学专业的发展方向数学与应用数学专业的发展方向主要涉及三个方面:学术研究、应用创新和教育培训。
数学模型在地质学中的应用

数学模型在地质学中的应用一、绪论数学模型是一门新兴学科,是数学理论与实际问题相结合的一门科学.数学模型就是通过研究观察到的现象及实践经验,将其归结成一套反映其内部因素数量关系的数学公式、逻辑准则和具体算法,用以描述和研究客观现象的运动规律.它将现实问题归结为相应的数学问题,并在此基础上利用数学的概念、理论和方法进行深入的分析和研究,从定性或定量的角度描述实际问题,并为解决现实问题提供精确的数据和可靠的指导.数学建模是指建立数学模型,是运用数学的语言和方法,通过抽象、简化等方法来建立能够近似描述和解决实际问题的一种强有力的数学手段.数学模型的应用相当广泛,在分析与设计、预报与决策、控制与优化、规划与管理等方面都发挥了巨大的作用,取得了良好的社会效益和经济效益,为世人所瞩目,成为知识经济的推动力.同样,在广泛的地质学领域中,数学建模也处处存在,数学建模的存在,将地质学的发展推向了一个新的浪潮,可能有希望将地质学从一门定性科学转换成为一门定量科学[1].如今,在地质学的众多分支学科中,数学模型都得到了极其广泛的应用.本文主要运用数学模型来分析地质学中的一些实际问题,并把两者有机的结合起来,拓宽数学模型的发展领域,增加其对实践的指导意义,并为地质学的研究与发展提供新的方法.二、数学模型在矿产资源评价中的应用在矿产资源评价中,地质模型和数学模型的结合点是按有效的成矿理论建立区域成矿模式,然后用数学模型逼近,确定成矿地质条件与矿产资源量之间的关系,建立定量评价模型.简言之,矿产资源定量评价模型是用数学语言阐明地质条件与矿产资源量之间的关系[2].矿产资源评价中的数学模型是实现定量评价的工具,在矿产资源评价的实际工作中使用的数学模型可以是概率统计模型,也可以是确定性模型.1973年,D.P.Harris确定了矿产资源量(R)与地质条件(g1、g2、……、g n)之间的数学关系:R= f(g1、g2、……、g n)+ e + μ(1)式中,f为g1、g2、……、g n的函数,在一般情况下指评价使用的数学模型;e为函数f(g1、g2、……、g n)的估计误差;μ与g1、g2、……、g n以外的地质变量有关.公式(1)表明了地质模型转化为数学模型的基本原理,同时也表明了可以用数学模型来沟通矿产资源量与地质环境.从中也可以看到采用合理的数学模型描述矿产资源与地质条件之间关系是矿产资源评价实践的关键.随着数学模型的引进,矿产资源的评价进入了新的时代,用数学模型评价矿产资源,用经济指标圈定矿体成为主流.对于用经济指标圈定矿体,一种指标代替多种指标,不仅方便快捷,而且是经济合理的.下面介绍评价矿产资源的几个常用模型.矿产资源经济指数计算公式:σt=[(P0+△P t)/P0]/[(Q0+△Q t)/Q0]=αt/βt (2)式中,σt为矿产资源经济指数;P0、αt分别为基准年和t年矿产资源工业储量潜在价值及指数;Q0、βt分别为基准年和t年沿海地区工业总产值及指数;△P t、△Q t 分别为矿产潜在价值增量与工业总产值增量.矿山资产评估模型(此处为期权定价的Black-Sholes模型):C=e-r T [FN(d1)-XN(d2)](3)其中d1=[ln(F/X)- (σ2/2)T]/ σ[(T)1/2],d2= d1-σ[(T)1/2].式中,C为欧式看涨期权的价格;X为执行价格;T为一年表示的权利期间的长短;r为瞬间的无风险利率;N为累积正态分布函数;F为商品期货价格;σ为标准的资产价格的波动性.这些模型在矿山开发利用方面发挥了巨大的作用,有利于资源的有序开发与保护.三、数学模型在褶皱分类中的应用根据褶皱在沿垂直于褶皱轴向的剖面上的几何形态,可把褶皱归为两种基本的形态:半波褶曲(背形或向形),完整褶皱即谐波褶皱(背形连向形)[3].两者可以分别表达为:Z=ax2 (抛物线型)(4)Z= b×sin(nx + c)(谐波型)(5)式中,a、b、c、n均为实参数.此数学抽象基于两点考虑:一是单性原则,即基本的褶曲形态作为参与褶皱叠加的几何元素,应具有简单性,以便讨论问题;其二是完备性原则,即起码在数学的意义上可用(4)和(5)式给出其它复杂褶皱形态足够好的逼近.其实用傅立叶分析的方法来分析褶皱形状已是广泛讨论过的课题,该方法的实质便是用一系列三角函数来逼近任意形状的曲线(面).对一个褶皱分析,往往只需要傅里叶展开式的前几项就可以满足地质精度了.此处建立的上述对褶皱叠加元素的数学抽象,使千变万化的褶皱叠加现象,有了统一的数学基础,从而简化了对褶皱叠加的讨论.从褶皱叠加演化序列上分析,叠加褶皱实际上是递进变形过程,或后期对前期褶皱干涉的结果.当两期褶皱的干涉作用发生于空间的不同方位时,其结果较为复杂.此处只列举两种特定方位即两期褶皱轴向平行或垂直的叠加褶皱的数学表达式.Z=a1x2与Z=a2x2或Z=b1sin(n1x+c1)与Z=b2sin(n2x+c2)的叠加.写成数学表达式就是:Z=(a1+a2)x2(6)Z= b1sin(n1x+c1)+ b2sin(n2x+c2)(7)(6)式表示的褶皱仍是抛物线型的,但比原褶曲更为舒缓(a1a2<0)或更为拱起(a1a2>0).(7)式表示的叠加褶皱仍是谐波型的:当n1/n2为有理数时形成的叠加褶皱在空间上具有周期性,否则具准周期性.四、数学模型在矿山断层构造研究中的应用由于对矿山小断层构造认识不清楚,探测力度不够,构造预测准确性差,给矿山生产和建设带来很多困难.同时,因对小断层构造认识不清而导致底板突水,淹没工作面,甚至淹没矿井的现象也时有发生.所以,必须对矿山的小断层进行探查预测,并尽量提高预测的准确性.利用数学地质中统计分析的方法,通过对已被揭露的小断层构造的分析研究,经过数学计算,建立一种数学模型,用它来拟合矿井小断层构造的出现和展布规律,从而达到对矿山小断层构造既定性又定量的认识[4].矿山小断层构造的出现和展布规律,受到多种地质因素的影响.因此想要判断、预测矿山小断层,需要研究多个地质变量间的相关关系.数学模型的建立需要多元回归分析的方法来解决.通过对大量矿山小断层的解剖分析,从诸多影响因素中,选出了一些对因变量起主要作用的自变量,并将其引入回归方程,作重点分析,而把其次要作用的自变量除去,既避免了过分繁琐的数学计算,又使得到的回归方程具有较高的精度.所选用的主要因素有:(1)断层的断距;(2)断层的走向延展长度;(3)井下揭露断层地点的标高.预测矿山小断层的数学模型,其推导重点是应用数理统计中回归分析的方法,应用最小二乘法原理确定回归平面.设变量Y依赖于k个自变量X1,X2,X3,……,X k,根据实际观测资料得到如下的数据(表1):表1 自变量X 观测数据X 1X 2 …… X i …… X k Y X 11X 21 …… X i1 …… X k1 Y 1 X 12X 22 …… X i2 …… X k2 Y 2 :: : : : : : X 1JX 2J : X iJ : X kJ Y J :: : : : : : X 1n X 2n …… X in …… X kn Y n 表中:X iJ 表示第J 组数据、第i 个自变量的数值,其中i=1、2、3、……、k ,J=1、2、3、……、n .为了反映自变量X i 与因变量Y 之间的关系,首先配一个回归平面:Y=b 0+b 1X 1+b 2X 2+……+b k X k (8) 使实际观测值y i 与平面(1)上的相应y i 之间的偏差平方和21()n j j j y y ω∧==-∑ (9)为最小.为了满足上述条件,利用最小二乘法原理和微分学知识,构造k 元一次方程组,可以解出回归系数b 0、b 1、b 2、……、b k ,将其代入(8)式可得所要求的回归平面方程.然后,应用F 检验法.取统计量:n-k-=k F S 回偏(1)S (10) 根据给定的信度α,查F 分布表,找出临界值F α,比较F 与F α的大小,对回归方程进行显著性检验.①若F ≥F α,回归方程显著;②若F <F α,回归方程不显著.五、数学模型在矿山水文地质中的应用矿坑涌水量是确定矿床水文地质类型,矿床水文地质条件复杂程度和评价矿床开发经济技术条件的重要指标之一.矿坑涌水量预测是随着矿床地质勘探程度的深入和对矿床水文地质条件的深化而逐渐完成的,可以分为三个步骤:第一步:建立水文地质(概化)模型.其要求是:(1)概化已知状态下矿区水文地质条件;(2)给出未来开采井巷的内部边界条件;(3)预测未来开采条件下的外部边界.第二步:选择计算方法,建立相应的数学模型.第三步:求解数学模型,评价预测结果.矿山设计中,矿坑涌水量是水文地质设计中的最重要的环节之一.在各种水文地质资料收集齐全的情况下,选择合理的数学模型计算矿坑涌水量是重中之重[5].数学模型是工具,是用来对水文地质概化模型进行数学描述的[6].即使概化模型正确,还有赖于建立一个适合于概化模型的数学模型,才能获得满意的预测涌水值[7].六、数学模型在三维地质建模中的应用地质体作为一种复杂地质现象的表现,很早就为人们所重视,为人类社会的发展做出了巨大贡献,解决了生产资料问题,但一直停留在人们思维推理加现场验证,费时费力,无法进行现场模拟,无法进行现实再现.现在有了数学建模和计算机进入地学领域,一切问题迎刃而解[8].在石油和天然气的勘探和开发中,三维建模可谓大放异彩,用地震法等获得数据,通过一定的数学模型,可以生成油藏的三维位置图,可谓真实再现.它还可以结合钻井资料,并结合地震解释层面、断面模型、剥蚀面及切断面关系之间的数学关系,生成石油储层模型,为计算油藏体积和经济开发服务.在这方面,不规则三角网(图1)和棱柱模型为三维建模提供了可能,使能源开发定量化.除了资源,在工程地质上,三维地质建模也发挥了巨大作用.基于离散数据集的曲面插值拟合方法,精确通过工程勘察数据点,获得光滑的地质界面的数学模型,可以用于表达地形、地下水位面、岩层面、构造面等各种地质界面和岩土体物理力学参数的空间分布,为安全而精确的地下施工提供了依据.它主要利用了拟合函数,插值函数和权重函数等,生成一幅符合实际的三维施工图.最常见的三维显示模型如下:依据三维坐标转换可以导出三维点(x,y,z)和鸟瞰显示的平面二维坐标(u,v)之间的数学变换公式:u=(xcosα-ysinε+l)/(xsinαsinP+ycosαsinP+zcosP+n) (11) v=[(xsinαcosP+ycosαcosP-zsinP+m)D]/(xsinαsinP+ycosαsinP+zcosP-n) (12) 式中(l,m,n)为坐标之间的平移量(视点坐标和三维坐标位置坐标系之间的原点平移量);α为投影(鸟瞰方向)的方位角;P为投影(鸟瞰方向)的俯仰角;D为二维投影平面(进行三维显示的平面)到视点的距离.图1 不规则三角网及其生成过程七、数学模型在地球物理中的应用地球物理作为地球科学的一门重要学科,数学模型在其中发挥了巨大的作用,特别是在地球物理勘探方面,出现很多有用的数学模型,为电磁法和地震法等方法的解译提供了很好的数学基础.在石油勘探方面,地震法发挥巨大作用;在铁矿找矿方面,磁法功不可没.这都是数学模型在反演计算中发挥巨大作用的结果,使结果更加准确可靠.对于电法,常用的数学模型有,二维构造条件下的MT(大地电磁法)数学模型[9],以及CSAMT二维正演数学模型.八、数学模型在地球化学中的应用地球化学在寻找资源方面发挥了巨大作用,根据统计得出地球各元素的含量,建立起一个地球元素含量数学模型,然后在一些地方进行化学勘探,把得出的元素含量结果,输入数学模型,得出异常图,便可以找出异常地区的矿体.这其中要用到一些权重函数和插值函数,外加当地的各种因素,用这些函数进行权重比较和成图,得出需要的结果.目前,在前沿的缓变型地球化学灾害的研究中,数学模型发挥很大作用[10].所谓缓变地球化学灾害是指通过长期积累而存在于土壤或沉积物中的包括重金属和有机污染物在内的环境污染物,因环境物理化学条件(例如温度、PH值、湿度、有机质含量等)的改变减小了环境容量,某种或某些形态的污染物大量地被重新活化和突然释放出来并造成严重生态和环境损害的灾害现象.这种灾害具有明显的特征,其定量数学模型可较完整地概括出环境系统从“干净”到“污染”再到“灾害”的整个过程,可用于灾害的风险评估、预测、灾害爆发轨迹等方面的研究,为土壤污染防治和灾害预警提供了定量研究工具和可供实际采用的基本手段,可为当前的生态环境地球化学评价提供指导.其中,提出了一个著名的爆发时间公式,如下:t=[m(c BCP-c)]/v式中,m表示一个质量为m的土壤系统,且假定污染物输入后在系统均匀分布;c 表示当前污染物的浓度;c BCP表示爆发临界点的值;v表示污染物的输入速度;t表示缓变型地球化学灾害所需的时间.九、展望人类正进入信息社会时代,面临许多发展与对策问题.应用数学也同步进入一个新的发展阶段,国际间已多次举行过有关数学等方面的学术性会议,并且应用数学在科学、技术、生产、管理方面的应用也越来越广泛、深入,在航天,医学、生物学,地质学,图形处理等领域的前沿阵地上都发挥着重要作用.一种科学只有在成功地运用数学时,才算达到了真正完善的地步.陈述彭院士说过:“没有数学模型,人们辛勤获取的大量观测数据,就像一盘散沙,找不出其中哪些是璀璨的金粒,哪些能够显示出本质性的规律,从中提取有效的信息,升华为科学知识.”作为地学和遥感领域的专家,陈先生一句话点明了数学建模在地学中的巨大作用.上述只是介绍了数学模型在地质学一些领域内的应用,另外在地质学的其它方面,数学模型也发挥了巨大的作用,例如在遥感地质学、沉积地质学、矿物学、地质灾害预测等领域都有着不可替代的重要作用.随着现代科学技术从定性研究转向定量研究的发展趋势,在一切学科中,无论是高技术领域,还是描述密集性的学科,数学都将发挥着关键性的作用.参考文献1.翦知湣.地学发现中的数学模型方法,同济大学学报,1992,3(1):109-114. 2.朱裕生,余金生,李裕伟. 矿产资源评价中的数学模型,矿床地质研究所所刊,1986,1:57-88.3.刘德良,杨晓勇,陈增兵. 复合褶皱数学模型的应用,安徽地质,1995,5(4):74-79. 4.冯兆安,张树国,张兆强.矿山小断层构造预测中数学模型的建立及应用,山东煤炭科技,2001,3:43-45.5.吴志刚.浅谈数学模型在矿山水文地质中的应用,化工矿物与加工,2004,2:33-34. 6.胡琏. 试论水文地质数学模型及其应用. 水文地质工程地质,1986(5):11-15.7.涂国强,杨立中,贺玉龙等. 地质灾害预测数学模型研究,四川师范大学学报,2001,24(6):637-639.8.曾钱帮,何小萍.三维地质建模的数学模型与显示方法,工程地质计算机应用,2006,43(3):1-8.9.胡建德.电法勘探中的数学模型,数学实践与认识,2004,34(2):27-31.10.陈明,冯流,周国华.缓变型地球化学灾害:特征、模型和应用,地质通报,2005,24(10):916-921.附录最初接触数学模型时,以为数学模型是一门高深的课程,没有扎实的数学基础是很难掌握的,由于专业的限制,自己拥有的数学知识很有限,仅限于初高中及大学中的高等数学,概率论及线性代数,所以一直不敢参与数学建模竞赛之类的活动中.然而,通过对数学模型的学习,我发现之前对数学模型的理解都是不准确的.数学模型并非遥不可及,反而很贴近我们的生活,因为它解决的是现实生活中的问题,它源于实践,是对现实的模拟.数学建模不需要深奥的数学知识,一个恰当的公式或许就可以成就一个伟大的模型.我也意识到自己就曾经多次用数学方法来解决生活中出现的问题,终于明白了数学是一种必备工具,离开了数学,生活中的许多问题都会无法解决.通过学习我意识到数学模型需要人们有丰富的想象力和洞察力,外加那么一点灵感,才能把模型建立起来,而以前已经学过的微积分、线性代数等都成了求解所建模型的一种工具.通过韩老师的讲解下我才对数学模型有了全面认识.在上课期间感觉到老师渊博的学识与灵活的教学方式.老师在数学模型这门课的讲解中把理论与实例紧密的结合,不仅增加了课程的实用性同时在提高学生学习兴趣方面都大有裨益.另外老师严谨的学风,兢兢业业的治学态度,缜密的思维方式,以及对学生谦逊和蔼的教学态度都让我受益匪浅.因为学习的过程不单单是传授知识,更多的是良好思维习惯的培养与个人能力的提升,非常感谢韩老师将这一点很好的融会到教学实践过程中传授给我们.在写此篇论文过程中,我搜集并查阅了大量的文献资料,了解到数学模型在我的专业——地质领域中有着广泛的应用,数学模型的建立为解决实际地质问题提供了一个经济有效的方法,大大提高了解决实际问题的便捷性.数学建模有重要的价值和实际意义,必将会在现实得到更普遍的应用,为解决实际问题发挥其独特的作用.。
《均匀设计与分析》PPT课件

(1.1.1)
The SAS System • • • • • • • • • • • • • • • • • • • • • • • • • •
23:13 Tuesday, October 26, 2004 1
The GLM Procedure Number of observations 7 The SAS System 23:13 Tuesday, October 26, 2004 2 The GLM Procedure Dependent Variable: y Sum of Source DF Squares Mean Square F Value Pr > F Model 3 0.04877010 0.01625670 3.29 0.1773 Error 3 0.01483761 0.00494587 Corrected Total 6 0.06360771 R-Square Coeff Var Root MSE y Mean 0.766732 18.87608 0.070327 0.372571 Source DF Type I SS Mean Square F Value Pr > F x1 1 0.01045289 0.01045289 2.11 0.2420 x2 1 0.00032411 0.00032411 0.07 0.8145 x3 1 0.03799310 0.03799310 7.68 0.0695 Source DF Type III SS Mean Square F Value Pr > F x1 1 0.00454233 0.00454233 0.92 0.4086 x2 1 0.00219572 0.00219572 0.44 0.5529 x3 1 0.03799310 0.03799310 7.68 0.0695 Standard Parameter Estimate Error t Value Pr > |t| Intercept 0.2023641775 0.09932934 2.04 0.1344 x1 0.0371834416 0.03880000 0.96 0.4086 x2 -.0034469697 0.00517333 -0.67 0.5529 x3 0.0769480519 0.02776302 2.77 0.0695
11讲国际数学家大会

国际数学家大会编辑国际数学家大会ICM是由国际数学联盟IMU主办的,是数学家们为了数学交流,展示、研讨数学的发展,会见老朋、结交新朋友的国际性会议,是国际数学界的盛会。
大会每四年举行一次,首届大会1897年在瑞士苏黎士举行,至今已有百余年的历史。
它是全球性数学科学学术会议,被誉为数学界的奥林匹克盛会。
国际数学家大会国际数际数学家大会(International Congress of Mathematicians),是数学家们为了数学交流,展示、研讨数学的发展,会见老朋友、结交新朋友的国际性会议,是国际数学界的盛会。
四年举行一次,首届大会1897年在瑞士苏黎士举行,至2010年底共举行了26届。
1900年巴黎大会之后,除两次世界大战期间外,未曾中断过,它已成为高水平的全球性数学科学学术会议。
出席大会的数学家的人数,最少的一次是208人,最多的一次是4000多人。
每次大会一般都邀请一批杰出数学家分别在大会上作一小时的学术报告和学科组的分组会上作45分钟学术报告,凡是出席大会的数学家都可以申请在分组会上作10分钟的学术报告,或将自己的论文在会上散发。
其中学科组一般分为20个左右。
每次国际数学家大会的开幕式上,由国际数学联合会领导人宣布该届菲尔兹奖获奖者名单,颁发金质奖章和奖金,并由他人分别在大会上报告获奖者的工作。
从1983年召开的国际数学家大会开始,同时颁发奖励信息科学方面的奈望林纳奖。
2大会组织者2006年国际数学家大会明信片国际数学联盟(IMU)成立于1950年的国际数学家大会,目前共有65个成员国。
它的主要任务是:1.促进数学方面的国际交流;2.组织召开国际数学家大会,以及两届大会之间各种数学方面的国际性专门会议;3.颁发奖励,主要是菲尔兹(Fields)奖。
国际数学联盟的执委会在其最高权力机构——国际数学联盟成员国代表大会上选举产生。
国际数学联盟的参加国因国家大小及数学方面的发展情况不同,分为Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ五类,其有投票权的代表人数相应为1、2、3、4、5。
国防、军事领域渴求应用数学人才

2021年6月 科学中国人 29China Forum中国论坛国防、军事领域渴求应用数学人才文 张平文把核心技术牢牢掌握在自己手中,必须瞄准世界科技前沿,实现前瞻性基础研究、引领性原创成果的重大突破。
这就必须重视数学的作用。
应用数学作为数学的一个分支,具有强调“应用”的特点。
它的研究方向与很多科研、工程、管理问题相关,而这些问题又普遍存在于经济社会不同领域,利用应用数学解决实际问题将会带来显著效益。
当我们走自主创新道路、追求原创成果时,会对应用数学研究产生极大的需求。
但当前我国应用数学在成果落地方面,与国家期望还有较大差距。
应用数学在服务企业创新和产业变革方面,还有很大提升空间。
什么在驱动应用数学应用数学的价值观多元,可分为理论、交叉和落地三个不同层面,我称之为简洁与美、科学意义和经济社会价值。
应用数学也是数学,所以它非常关注简洁与美,这是我称之为“理论”的部分;应用数学也很关心科学意义,就是我们要运用数学去解决其他学科的问题,比如材料学、生命科学的问题,即“交叉”,这时,它的价值观就跟这些学科的价值观一致,我称之为科学意义;此外,应用数学还有一个重要价值观是“落地”,即经济与社会价值。
总的来说,应用数学着重于利用数学知识及计算机等工具去解决经济社会各领域的实际问题,并对解决问题中出现的关键数学问题进行归纳总结和分析研究。
驱动应用数学发展的因素主要有三个:一是国防建设。
第二次世界大战时,战争需要促使应用数学进入飞速发展阶段。
在研制原子弹、设计高性能飞机、破译敌方密码及调配军用物资等过程中,应用数学成为极为关键的手段,计算、运筹、优化等诸多应用数学分支由此蓬勃发展起来。
随着现代战争朝着数字化、智能化方向发展,利用算法来攻击敌方的交通、电力、网络等重要基础设施,将变得越发有效和重要。
未来算法的效率、精度、稳定性和可靠性还将提升,并与兵棋推演、人工智能和指挥控制系统相融合,成为战前预演、战时感知与决策、战后评估的关键。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
各位同学:
第八届国际工业与应用数学大会(ICIAM 2015)将于2015年8月10日至14日在北京召开。
会议的相关信息请见网站(英文):
/index.html
另,为方便大家了解相关情况,附ICIAM 2015的相关中文介绍以及ICIAM 2014 召开的相关情况:
********************************************************
*第八届国际工业与应用数学大会(ICIAM 2015)将在中国召开*
********************************************************
第八届国际工业与应用数学大会(ICIAM 2015)将于2015年8月10-14日在北京召开。
本次会议由中国工业与应用数学学会牵头,联合中国数学会、中国计算数学会、中国运筹学会、中国现场统计学会、中国系统工程学会等共同主办,得到了教育部、科技部、中国科学院、国家自然科学基金委员会的大力支持与指导。
国际工业与应用数学大会(ICIAM)每四年举办一次,是国际工业与应用数学领域水平最高、规模最大、影响最广的盛会,也是在数学界与国际数学家大会齐名的大会。
本次大会是首次在亚洲以及在发展中国家召开,预计参加人数超过3000名。
ICIAM 2015 将在坐落于北京奥林匹克公园的国家会议中心举办。
国家会议中心紧邻2008年奥运会主会场鸟巢和水立方,是目前中国条件最好的会议中心之一。
为扩大会议的影响,将出版论文集,收录会议主要信息与大会邀请报告。
Springer将编辑出版Intelligencer,介绍中国的工业与应用数学与北京的生活交通指南等。
ICIAM 2015会议议程包括授奖典礼与获奖人报告、邀请报告、minisymposium、论文报告、展板报告、卫星会议等。
它不仅将对我国数学特别是应用数学的发展产生巨大深远的影响,极大地促进数学与科学技术及国民经济的密切结合与相互推动,而且将在国际同行及朋友面前更好地展示我国改革开放以来的飞速发展和精神面貌。
目前ICIAM 2015的前期准备工作进展顺利。
由马志明教授任组长的Scientific Program Committee(SPC)已经于2012年开始工作,将按计划于2013年4月产生ICIAM 2015邀请报告人的初步名单。
大会组委会主席(Congress Director)由CSIAM理事长郭雷教授担任,组委会下设的Academic,Exhibition,Finance,Fundraising,ICIAM Liaison,Industry and Promotion,Local Arrangements,Publication,Publicity等九个工作组已经开始工作。
中国数学界的相关学术组织也都将参与到本次会议的组织。
会议由China Society for Industrial and Applied Mathematics (CSIAM)为牵头组织者;由Chinese Mathematical Society
(CMS),The Operations Research Society of China (ORSC),Chinese Computational Mathematical Society (CCMS),中国现场统计学会等作为协同组织者。
中国国家自然科学基金委员会已经为大会组织提供了部分经费支持。
做为大会秘书处的挂靠单位,国家数学与交叉科学中心(/)也为大会提供了人力与经费等方面的部分支持。
“ICIAM2015也得到了多个国家学术组织的支持。
SIAM表示将取消2015年的年会,积极参与ICIAM2015的组织。
East Asian Siam表示将其2015年会作为ICIAM2015的卫星会议。
Association for Women in Mathematics(AWM) will have its Noether Lecture delivered at ICIAM2015.
值此契机,为了展示我国工业与应用数学的发展以及所取得的成果,促进我国应用数学的进一步发展,我们热烈欢迎广大从事工业与应用数学研究的学者、工程师、同学,以及对这门学科感兴趣的朋友积极关注和参与。
让我们共同努力,将ICAM 2015办成最成功的一届国际工业与应用数学大会。
有关会议的更多信息请登录大会网站:
********************************************************
*第七届国际工业与应用数学大会(ICIAM 2011)在温哥华闭幕*
********************************************************
2011年7月22日,为期五天的第七届国际工业与应用数学大会(ICIAM2011)在加拿大温哥华闭幕。
来自超过70个国家和地区的近3000位应用数学工作者聚集一堂,共同探讨和交流国际应用数学的最新进展,及其在自然科学、工程技术和社会经济等领域中的广泛应用。
在大会闭幕式上,郭雷院士介绍了北京地区与应用数学相关的科研和教育等情况,并代表大会组委会热情邀请各国代表参加2015年在北京举行的下一届ICIAM大会,随后放映了专门为本次大会精心制作的北京宣传片。
本届大会主席 A. Gupta教授将象征着主办权的Talking Stick移交给郭雷院士。
ICIAM每四年举办一次,是国际工业与应用数学最高水平与最大规模的盛会,参加人员包括国际著名或资深学者,决策者,工业界代表以及年轻学者和研究生,对国际工业与应用数学的发展起着非常重要的推动作用。
在本次大会公布并颁发了ICIAM设立的5个重要奖项。
斯坦福大学的E.J. Candes、加州大学伯克利分校的A.J. Chorin、耶鲁大学的V. Rokhlin、加州大学伯克利分校的J.A. Sethian 与博茨瓦纳的E. Lungu分别获得ICIAM Colatz奖、ICIAM拉格朗日奖、ICIAM麦克斯韦奖、ICIAM先驱奖、ICIAM苏步青奖。
其中,苏步青应用数学奖由中国工业与应用数学学会于2003年提议设立,主要用于奖励从事应用数学研究并对新兴经济与人文发展, 特别是对发展中国家经济与文化,做出杰出贡献的数学家。
北京大学张平文教授和耿直教授分别在本次会
议上作了Phase Behavior of Complex Fluids和Causal Evaluation and Discovery的邀请报告。
除了传统的邀请报告、专题研讨、张贴论文、公众报告外,这次会议的创新点之一是遴选了17个“主题研讨会”,强调由重要新兴应用领域导致的数学问题和方法,包括癌症的数学方法、分子模拟中的量子方法、随机微分方程的数值解、带摩擦的金融市场、疾病动力学的数学理论、Cloaking与元材料、可控性与反问题、延迟网络动力系统、齐次化方法及其应用、数学流体动力学、复杂系统、数学物理前沿问题、小波在天气预报与石油勘探中的应用、液态晶体、非线性特征值问题等。
