c++英文字母统计,哈夫曼存盘(源码)
霍夫曼编码PPT课件

对于各值(码值)的代码(码字)就是从根节点出发到底层节点所经历 的分支序列。如a4的代码(码字)为00,a6的码字为111... ...通常a4和 a6等称为码值,00和111等称为码字。所有码值和码字对应关系如下表 所示:
Your company slogan
(三)霍夫曼表
将所有码值和码字的关系整理成一张表,为了整字 节输出码字,表中还含有各码字的长度。这种表就称 为霍夫曼表。本例霍夫曼表如表所示:
Your company slogan
进行压缩编码时,只要将码值用码字代替即可。所 以源符a1 a1 a2 a2 a3 a3 a3 a4 a4 a4 a4 a5 a5 a5 a6 a6 a6 a7 a7 a8编码为: 01001001101110110110100000000110110 11010000100001001。
Your company slogan
四、霍夫曼编码
(一)霍夫曼编码过程
设信息源空间为[A*P]:{A:a1 a2 ……an}{P(A):P(a1) P(a2)P(a3)……P(an)}其中∑ P(ak)=1,先用r个码的号码符 号集X:{x1,x2,……xr}对信源A中的每一个符号ak进行编码。 编码过程如下: 把信源符号ai按其出现的概率的大小顺序排列起来; 把最末两个具有最小概率的元素之概率加起来; 把该概率之和同其余概率由大到小排队,然后再把两个最 小概率加起来,再排队; 重复步骤 (2) 、 (3), 直到概率和达到 1 为止 ; 在每次合并消息时,将被合并的消息赋以1和0或0和1; 寻找从每个信源符号到概率为1处的路径,记录下路径上 的1和0; 对每个符号写出"1"、"0"序列(从码数的根到终节点)。 创建霍夫曼表。 压缩编码时,将码值用码字代替。
数据结构课程设计可选题目

数据结构课程设计可选题目一、课程设计的目的学习数据结构与算法的最终目的是解决实际的应用问题,特别是非数值计算类型的应用问题。
课程设计要求同学独立完成一个较为完整的应用需求分析,在完成设计和编程大型作业的过程中,深化对数据结构与算法课程中基本概念、理论和方法的理解;训练综合运用所学知识处理实际问题的能力,强化面向对象的程序设计理念;使同学的程序设计与调试水平有一个明显的提高。
二、数据结构课程设计可选题目1. 运动会分数统计(限1 人完成)任务:参加运动会有n个学校,学校编号为1……n。
比赛分成m个男子项目,和w个女子项目。
项目编号为男子1……m,女子m+1……m+w。
不同的项目取前五名或前三名积分;取前五名的积分分别为:7、5、3、2、1,前三名的积分分别为:5、3、2;哪些取前五名或前三名由学生自己设定。
(m<=20,n<=20)功能要求:1) 可以输入各个项目的前三名或前五名的成绩;2) 能统计各学校总分,3) 可以按学校编号或名称、学校总分、男女团体总分排序输出;4) 可以按学校编号查询学校某个项目的情况;可以按项目编号查询取得前三或前五名的学校;5) 数据存入文件并能随时查询;6) 规定:①输入数据形式和范围:可以输入学校的名称,运动项目的名称;②输出形式:有中文提示,各学校分数为整形;③界面要求:有合理的提示,每个功能可以设立菜单,根据提示,可以完成相关的功能要求。
④存储结构:学生自己根据系统功能要求自己设计,但是要求运动会的相关数据要存储在数据文件中。
(数据文件的数据读写方法等相关内容在c语言程序设计的书上)请在最后的上交资料中指明你用到的存储结构;⑤测试数据:要求使用a.全部合法数据;b.整体非法数据;c.局部非法数据进行程序测试,以保证程序的稳定。
测试数据及测试结果请在上交的资料中写明。
2. 飞机订票系统任务:通过此系统可以实现如下功能:⑴录入:可以录入航班情况(数据可以存储在一个数据文件中,数据结构、具体数据自定)⑵查询:可以查询某个航线的情况(如,输入航班号,查询起降时间,起飞抵达城市,航班票价,票价折扣,确定航班是否满仓);⑶可以输入起飞抵达城市,查询飞机航班情况;⑷订票:(订票情况可以存在一个数据文件中,结构自己设定)可以订票,如果该航班已经无票,可以提供相关可选择航班;⑸退票:可退票,退票后修改相关数据文件;⑹客户资料有姓名,证件号,订票数量及航班情况,订单要有编号。
Huffman霍夫曼编码

霍夫曼编码的局限性
利用霍夫曼编码,每个符号的编码长度只能 为整数,所以如果源符号集的概率分布不是 2负n次方的形式,则无法达到熵极限。 输入符号数受限于可实现的码表尺寸 译码复杂 需要实现知道输入符号集的概率分布 没有错误保护功能
尾码为DIFF的B位
原码,若DIFF0 反码,若DIFF0
按此规则,当DIFF0时,尾码的最高位是“1”; 而当DIFF0时则为“0”。解码时则可借此来判断 DIFF的正负。 书中例4—9
自适应霍夫曼编码提出的目的和意义:
在静态霍夫曼编码中,要构造编码树必须提前统计 被编码对象中的符号出现概率,因此必须对输入符 号流进行两遍扫描,第一遍统计符号出现概率并构 造编码树,第二遍进行编码,这在很多实际应用的 场合中之不能接受的。其次,在存储和传送霍夫曼
i 1 i
n
单位:以2为底的对数时是比特/符号(bit/symbol); 以e为底的对数时是奈特/符号(nat/symbol); 以10为底的对数时是哈特/符号( hart/symbol) 其中 I(xi)=-logp(xi) 表示某个事件xi的信息量。
平均码长 编码效率
例:现有一个由5个不同符号组成的30个符号的字 符串:BABACACADADABBCBABEBEDDABEEEBB 计算 (1) 该字符串的霍夫曼码 (2) 该字符串的熵 (3) 该字符串的平均码长
霍夫曼(Huffman)编码是一种统计编码。 属于无损(lossless)压缩编码。 以霍夫曼树─即最优二叉树,带权路径长 度最小的二叉树,经常应用于数据压缩。 根据给定数据集中各元素所出现的频率来 压缩数据的一种统计压缩编码方法。这些 元素(如字母)出现的次数越多,其编码的 位数就越少。 广泛用在JPEG, MPEG, H.2X等各种信息编 码标准中。
哈夫曼编码译码器数据结构C语言模板

一、需求分析目前,进行快速远距离通信的主要手段是电报,即将需传送的文字转化成由二级制的字符组成的字符串。
例如,假设需传送的电文为“ABACCDA ”,它只有4种字符,只需两个字符的串,便可以分辨。
假设A 、B 、C 、D 、的编码分别为00,01,10和11,则上述7个字符的电文便为“00010010101100”,总长14位,对方接受时,可按二位一分进行译码。
当然,在传送电文时,希望总长尽可能地短。
如果对每个字符设计长度不等的编码,且让电文中出现次数较多的字符采用尽可能短的编码,则传送电文的总长便可减少。
如果设计A 、B 、C 、D 的编码分别为0,00,1,01,则上述7个字符的电文可转换成总长为9的字符串“000011010”。
但是,这样的电文无法翻译,例如传送过去的字符串中前4个字符的字串“0000”就可以有很多种译法,或是“AAAA ”或者“BB ”,或者“ABA ”等。
因此,若要设计长短不等的编码,则必须是任一字符的编码都不是另一个字符的编码的前缀,这种编码称作前缀编码。
然而,如何进行前缀编码就是利用哈夫曼树来做,也就有了现在的哈夫曼编码和译码。
二、概要设计利用哈夫曼树编/译码 (一)、建立哈夫曼树 (二)、对哈夫曼树进行编码 (三)、输出对应字符的编码 (四)、译码过程主要代码实现: struct code //结构体的定义 { char a; int w; int parent; int lchild; int rchild; };void creation(code *p,int n,int m); //建立哈夫曼树 void coding(code *p,int n); //编码 void display(code *p,int n,int m); //输出函数 void translate(char **hc,code *p,int n); //译码三、 详细设计(一)、建立哈夫曼树a b c d1 2 3 4 5 * * * 6 7 a b * c *ab*c *d * 序号: 字符: 权值: 1 2 3 4 3 6 10 a b * 1 2 1 2 3 3 1 2 3 3 6 4 103 6 图3-1 图3-2 图3-3(二)、对哈夫曼树进行编码 主要代码实现:for(c=i,f=p[i].parent;f!=0;c=f,f=p[f].parent) { if(p[f].lchild==c) //左孩子编码为'0'{ cd[--start]='0'; } else //右孩子编码为'1'{ cd[--start]='1'; } }(三)、输出对应字符的码字符 编码 a 110 b 111 c 10 d(四)、译码过程 主要代码实现:if(strcmp(a,hc[i])==0) //比较两个字符串是否相等,相等则输出0 { for(c=2*n-1,j=0;a[j]!='\0';j++) //从根出发,按字符'0'或'1'确定找左孩子或右孩子 { if(a[j]=='0') //左孩子 {c=p[c].lchild;}else {c=p[c].rchild; //右孩子 }}ab* c* d*1 1 0 1 0 图3-4表3-1从叶子到根逆向求编码a b*c *d *0 1 1 1 从跟到叶子顺向求字符 图3-5四、 调试分析(一)、数字的输入判断(二)、字母的输入判断(三)、程序是否继续进行的判断五、 用户手册(一)、首先根据提示输入初始化数据,提示输入一个数字,请输入一个数a ,0<a<9999;提示输入一个字母,则请输入一个字母(a~z)或者(A~Z)中的一个字符;请勿在输入一个数字后再输入一个字符,或者在输入一个字符后再输入一个数字。
(完整word版)数据结构哈夫曼编码与译码

《数据结构》课程设计说明书题目哈夫曼编码与译码学号1267159206姓名张燕斌指导教师康懿日期2014.01。
02任务书目录第一章需求分析 (5)第二章总体设计 (6)第三章抽象数据类型定义 (7)3。
1 LinkList抽象数据类型的设计 (7)3.2 HuffmanTree抽象数据的设计 (7)第四章详细设计..。
...。
..。
....。
.....。
.。
.。
..。
.。
....。
.。
..。
..。
.。
.。
.。
.。
..。
....。
....。
.。
..。
...。
...。
7第五章测试 (10)第六章总结 (11)附录:程序代码 (12)第一章需求分析哈夫曼编码是一种编码方式,以哈夫曼树—即最优二叉树,带权路径长度最小的二叉树,经常应用于数据压缩。
哈弗曼编码使用一张特殊的编码表将源字符(例如某文件中的一个符号)进行编码。
这张编码表的特殊之处在于,它是根据每一个源字符出现的估算概率而建立起来的(出现概率高的字符使用较短的编码,反之出现概率低的则使用较长的编码,这便使编码之后的字符串的平均期望长度降低,从而达到无损压缩数据的目的)。
赫夫曼编码的应用很广泛,利用赫夫曼树求得的用于通信的二进制编码称为赫夫曼编码。
树中从根到每个叶子都有一条路径,对路径上的各分支约定:指向左子树的分支表示“0”码,指向右子树的分支表示“1”码,取每条路径上的“0”或“1”的序列作为和各个叶子对应的字符的编码,这就是赫夫曼编码。
哈弗曼译码输入字符串可以把它编译成二进制代码,输入二进制代码时可以编译成字符串。
第二章总体设计(1)输入一个字符串用结构体链表存储字符串中出现的不同字符及其出现的次数。
(2)定义赫夫曼数的结点结构体,把不同的字符及其在字符串中出现的次数作为叶子结点的元素及其权值,统计叶子结点的个数n,开辟可以存储2*n个结点的顺序表,来赫夫曼树的各个结点,然后按照一定的规则构造赫夫曼树。
(3)开辟一个可以存储叶子结点元素及指向存储其赫夫曼编码链表的指针的顺序表,然后从叶子结点开始向上访问,是左孩子的把“0”接进链表是右孩子的把“1”接进链表,直到根结点,然后把叶子结点的元素及存储其赫夫曼链表的头指针读入顺序表,直到把所有的叶子结点的元素及指向存储其赫夫曼编码链表的头指针读入顺序表,这样得到的赫夫曼编码是倒序的。
哈夫曼编码1952年Huffma...

第三章多媒体数据压缩3.1 数据压缩的基本原理和方法3.1 数据压缩的基本原理和方法•压缩的必要性音频、视频的数据量很大,如果不进行处理,计算机系统几乎无法对它进行存取和交换。
例如,一幅具有中等分辨率(640×480)的真彩色图像(24b/像素),它的数据量约为7.37Mb/帧,一个100MB(Byte)的硬盘只能存放约100帧图像。
若要达到每秒25帧的全动态显示要求,每秒所需的数据量为184Mb,而且要求系统的数据传输率必须达到184Mb/s。
对于声音也是如此,若采用16b样值的PCM编码,采样速率选为44.1kHZ ,则双声道立体声声音每秒将有176KB的数据量。
3.1 数据压缩的基本原理和方法•视频、图像、声音有很大的压缩潜力信息论认为:若信源编码的熵大于信源的实际熵,该信源中一定存在冗余度。
原始信源的数据存在着很多冗余度:空间冗余、时间冗余、视觉冗余、听觉冗余等。
3.1.1 数据冗余的类型•空间冗余:在同一幅图像中,规则物体和规则背景的表面物理特性具有相关性,这些相关性的光成像结果在数字化图像中就表现为数据冗余。
–一幅图象中同一种颜色不止一个象素点,若相邻的象素点的值相同,象素点间(水平、垂直)有冗余。
–当图象的一部分包含占主要地位的垂直的源对象时,相邻线间存在冗余。
3.1.1 数据冗余的类型•时间冗余:时间冗余反映在图像序列中就是相邻帧图像之间有较大的相关性,一帧图像中的某物体或场景可以由其它帧图像中的物体或场景重构出来。
–音频的前后样值之间也同样有时间冗余。
–若图象稳定或只有轻微的改变,运动序列帧间存在冗余。
3.1.1 数据冗余的类型•信息熵冗余:信源编码时,当分配给第i 个码元类的比特数b (y i )=-log p i ,才能使编码后单位数据量等于其信源熵,即达到其压缩极限。
但实际中各码元类的先验概率很难预知,比特分配不能达到最佳。
实际单位数据量d>H (S ),即存在信息冗余熵。
已知四个字符abcd的哈夫曼编码

《深度探讨:已知四个字符abcd的哈夫曼编码》在计算机科学中,哈夫曼编码是一种用于数据压缩的算法,通过对频率较高的字符赋予较短的编码,从而实现对数据的高效压缩。
在本文中,我们将深入探讨已知四个字符abcd的哈夫曼编码,分析其原理和实际应用,以及对该编码方式的个人观点和理解。
1. 哈夫曼编码的原理哈夫曼编码的核心思想是根据字符出现的频率来确定唯一的编码,使得频率较高的字符拥有较短的编码,而频率较低的字符拥有较长的编码。
在已知四个字符abcd的情况下,我们可以使用哈夫曼树来构建它们的编码方式。
我们需要计算每个字符出现的频率,并将它们按照频率从小到大进行排序。
我们选择频率最小的两个字符作为叶子节点,构建一个新的内部节点,其权重为两个叶子节点的权重之和。
依次类推,直到所有的字符都被合并成一个根节点,构成了哈夫曼树。
我们可以通过从根节点到叶子节点的路径来确定每个字符的哈夫曼编码。
2. 已知四个字符abcd的哈夫曼编码假设字符a、b、c、d的频率分别为4、3、2、1,那么我们可以按照上述原理来构建它们的哈夫曼编码。
我们将这四个字符按频率从小到大进行排序,得到d(1)、c(2)、b(3)、a(4)。
我们可以依次构建哈夫曼树,最终得到每个字符的哈夫曼编码为:a-0、b-10、c-110、d-111。
这样,我们就成功地为已知的四个字符abcd构建了哈夫曼编码。
3. 实际应用与个人观点哈夫曼编码在数据压缩领域有着广泛的应用,尤其在无损压缩中发挥着重要作用。
通过将频率较高的字符用较短的编码表示,可以大大减小数据的存储空间,提高数据传输的效率。
然而,哈夫曼编码也存在着一定的局限性,特别是在需要频繁更新编码表的场景下,会导致存储和传输的开销增加。
在实际应用中需要权衡其优缺点,并选择合适的压缩算法。
在个人看来,哈夫曼编码是一种非常精巧的算法,通过充分利用字符的频率信息来实现高效的数据压缩。
它不仅具有良好的压缩效果,而且在编解码的过程中也能够保持数据的完整性。
哈夫曼编码算法

《算法设计与分析》上机报告姓名:学号:日期:上机题目:哈夫曼编码算法实验环境:CPU: ; 内存: 6G ; 操作系统:Win7 64位;软件平台:Visual Studio2008 ;一、算法设计与分析:题目:哈夫曼编码是广泛地用于数据文件压缩的十分有效的编码方法。
其压缩率通常在20%~90%之间。
哈夫曼编码算法用字符在文件中出现的频率表来建立一个用0,1串表示各字符的最优表示方式。
一个包含100,000个字符的文件,各字符出现频率不同,如下表所示。
有多种方式表示文件中的信息,若用0,1码表示字符的方法,即每个字符用唯一的一个0,1串表示。
若采用定长编码表示,则需要3位表示一个字符,整个文件编码需要300,000位;若采用变长编码表示,给频率高的字符较短的编码;频率低的字符较长的编码,达到整体编码减少的目的,则整个文件编码需要(45×1+13×3+12×3+16×3+9×4+5×4)×1000=224,000位,由此可见,变长码比定长码方案好,总码长减小约25%。
哈夫曼编码步骤:一、对给定的n个权值{W1,W2,W3,...,Wi,...,Wn}构成n棵二叉树的初始集合F={T1,T2,T3,...,Ti,...,Tn},其中每棵二叉树Ti中只有一个权值为Wi的根结点,它的左右子树均为空。
(为方便在计算机上实现算法,一般还要求以Ti的权值Wi的升序排列。
)二、在F中选取两棵根结点权值最小的树作为新构造的二叉树的左右子树,新二叉树的根结点的权值为其左右子树的根结点的权值之和。
三、从F中删除这两棵树,并把这棵新的二叉树同样以升序排列加入到集合F中。
四、重复二和三两步,直到集合F中只有一棵二叉树为止。
二、核心代码:node* huffman(node C[],int n){BuildMaxHeap(C,n);for(int i=1;i<n;i++){node* z = new node;z->left = extract_min(C,n-i+1);z->right = extract_min(C,n - i);z->freq = z->left->freq + z->right->freq;C[n - i] = *z;MaxHeapify(C,n - i,n - i);}return &C[1];}三、结果与分析:其中“?”表示该结点没有字符最优性:二叉树T表示字符集C的一个最优前缀码,x和y是树T中的两个叶子且为兄弟,z 是它们的父亲。
哈夫曼编码算法与分析

算法与分析1.哈夫曼编码是广泛地用于数据文件压缩的十分有效的编码方法。
给出文件中各个字符出现的频率,求各个字符的哈夫曼编码方案。
2.给定带权有向图G =(V,E),其中每条边的权是非负实数。
另外,还给定V中的一个顶点,称为源。
现在要计算从源到所有其他各顶点的最短路长度。
这里路的长度是指路上各边权之和。
3.设G =(V,E)是无向连通带权图,即一个网络。
E中每条边(v,w)的权为c[v][w]。
如果G的子图G’是一棵包含G的所有顶点的树,则称G’为G的生成树。
生成树上各边权的总和称为该生成树的耗费。
在G的所有生成树中,耗费最小的生成树称为G的最小生成树。
求G的最小生成树。
求解问题的算法原理:1.最优装载哈夫曼编码1.1前缀码对每一个字符规定一个0,1串作为其代码,并要求任一字符的代码都不是其它字符代码的前缀,这种编码称为前缀码。
编码的前缀性质可以使译码方法非常简单。
表示最优前缀码的二叉树总是一棵完全二叉树,即树中任一结点都有2个儿子结点。
平均码长定义为:B(T)=∑∈CcTcdcf)()(f(c):c的码长,dt(c):c的深度使平均码长达到最小的前缀码编码方案称为给定编码字符集C的最优前缀码。
1.2构造哈夫曼编码哈夫曼提出构造最优前缀码的贪心算法,由此产生的编码方案称为哈夫曼编码。
哈夫曼算法以自底向上的方式构造表示最优前缀码的二叉树T。
算法以|C|个叶结点开始,执行|C|-1次的“合并”运算后产生最终所要求的树T。
编码字符集中每一字符c的频率是f(c)。
以f为键值的优先队列Q用在贪心选择时有效地确定算法当前要合并的2棵具有最小频率的树。
一旦2棵具有最小频率的树合并后,产生一棵新的树,其频率为合并的2棵树的频率之和,并将新树插入优先队列Q。
经过n-1次的合并后,优先队列中只剩下一棵树,即所要求的树T。
可用最小堆实现优先队列Q。
2.单源最短路径Dijkstra算法是解单源最短路径问题的贪心算法。
其基本思想是,设置顶点集合S并不断地作贪心选择来扩充这个集合。
霍夫曼编码的实验报告(3篇)

第1篇一、实验目的1. 理解霍夫曼编码的基本原理和实现方法。
2. 掌握霍夫曼编码在数据压缩中的应用。
3. 通过实验,加深对数据压缩技术的理解。
二、实验环境1. 操作系统:Windows 102. 编程语言:C++3. 开发环境:Visual Studio 20194. 数据源:文本文件三、实验原理霍夫曼编码是一种常用的数据压缩算法,适用于无损数据压缩。
它通过使用变长编码表对数据进行编码,频率高的数据项使用短编码,频率低的数据项使用长编码。
霍夫曼编码的核心是构建一棵霍夫曼树,该树是一种最优二叉树,用于表示编码规则。
霍夫曼编码的步骤如下:1. 统计数据源中每个字符的出现频率。
2. 根据字符频率构建一棵最优二叉树,频率高的字符位于树的上层,频率低的字符位于树下层。
3. 根据最优二叉树生成编码规则,频率高的字符分配较短的编码,频率低的字符分配较长的编码。
4. 使用编码规则对数据进行编码,生成压缩后的数据。
5. 在解码过程中,根据编码规则恢复原始数据。
四、实验步骤1. 读取文本文件,统计每个字符的出现频率。
2. 根据字符频率构建最优二叉树。
3. 根据最优二叉树生成编码规则。
4. 使用编码规则对数据进行编码,生成压缩后的数据。
5. 将压缩后的数据写入文件。
6. 读取压缩后的数据,根据编码规则进行解码,恢复原始数据。
7. 比较原始数据和恢复后的数据,验证压缩和解码的正确性。
五、实验结果与分析1. 实验数据实验中,我们使用了一个包含10000个字符的文本文件作为数据源。
在统计字符频率时,我们发现字符“e”的出现频率最高,为2621次,而字符“z”的出现频率最低,为4次。
2. 实验结果根据实验数据,我们构建了最优二叉树,并生成了编码规则。
使用编码规则对数据源进行编码,压缩后的数据长度为7800个字符。
将压缩后的数据写入文件,文件大小为78KB。
接下来,我们读取压缩后的数据,根据编码规则进行解码,恢复原始数据。
比较原始数据和恢复后的数据,发现两者完全一致,验证了压缩和解码的正确性。
26个英文字母和空格的赫夫曼码表

赫夫曼编码是一种基于频率的编码方法,通过根据字符出现的频率来构建独特的编码,以达到减少数据传输量的目的。
在这种编码方法中,出现频率较高的字符被赋予较短的编码,而出现频率较低的字符则被赋予较长的编码,这样就可以有效地减少数据的传输量和存储空间。
在这个主题中,我们将探讨26个英文字母和空格的赫夫曼码表,即每个字符对应的赫夫曼编码。
这个码表对于数据压缩和编码领域具有重要意义,因此我们有必要深入了解这个码表的构造和应用。
我们需要了解赫夫曼编码的原理和构造方法。
赫夫曼编码是由大卫·赫夫曼于1952年提出的,它是一种变长编码,在构造过程中通过建立霍夫曼树来确定字符的编码。
这种编码方法的特点是没有编码是其他编码的前缀,即它是一种前缀编码。
在赫夫曼编码中,字符的频率决定了编码的长度,频率较高的字符被赋予较短的编码,频率较低的字符则被赋予较长的编码,以实现数据的高效传输和存储。
赫夫曼编码是一种无损数据压缩的重要手段。
接下来,我们要具体探讨26个英文字母和空格的赫夫曼码表。
在这个码表中,每个英文字母和空格都有对应的赫夫曼编码,它们的编码长度根据它们在文本中出现的频率而定。
举个例子,英文字母“e”通常在英语文本中出现的频率较高,因此它的赫夫曼编码通常较短,而英文字母“z”的出现频率较低,因此它的赫夫曼编码通常较长。
通过构建赫夫曼树和确定每个字符的编码,就可以得到26个英文字母和空格的赫夫曼码表。
在实际应用中,26个英文字母和空格的赫夫曼码表可以被广泛应用于数据传输和存储领域。
在通信领域,赫夫曼编码可以用于无线通信和数据传输,通过减少数据的传输量来提高通信效率;在存储领域,赫夫曼编码可以用于数据压缩,减少文件的存储空间。
了解和应用26个英文字母和空格的赫夫曼码表对于提高数据传输效率和节省存储空间具有重要意义。
26个英文字母和空格的赫夫曼码表是赫夫曼编码在具体应用中的重要体现,它可以通过根据字符的频率构建独特的编码,从而实现数据的高效传输和存储。
哈夫曼编码详解(C语言实现)

哈夫曼编码详解(C语言实现)哈夫曼编码是一种常见的前缀编码方式,被广泛应用于数据压缩和传输中。
它是由大卫·哈夫曼(David A. Huffman)于1952年提出的,用于通过将不同的字符映射到不同长度的二进制码来实现数据的高效编码和解码。
1.统计字符频率:遍历待编码的文本,记录每个字符出现的频率。
2.构建哈夫曼树:根据字符频率构建哈夫曼树,其中出现频率越高的字符位于树的较低层,频率越低的字符位于树的较高层。
3.生成编码表:从哈夫曼树的根节点开始,遍历哈夫曼树的每个节点,为每个字符生成对应的编码。
在遍历过程中,从根节点到叶子节点的路径上的“0”表示向左,路径上的“1”表示向右。
4.进行编码:根据生成的编码表,将待编码的文本中的每个字符替换为对应的编码。
5.进行解码:根据生成的编码表和编码结果,将编码替换为原始字符。
下面是一个用C语言实现的简单哈夫曼编码示例:```c#include <stdio.h>#include <stdlib.h>#include <string.h>//定义哈夫曼树的节点结构体typedef struct HuffmanNodechar data; // 字符数据int freq; // 字符出现的频率struct HuffmanNode *left; // 左子节点struct HuffmanNode *right; // 右子节点} HuffmanNode;//定义编码表typedef structchar data; // 字符数据char *code; // 字符对应的编码} HuffmanCode;//统计字符频率int *countFrequency(char *text)int *frequency = (int *)calloc(256, sizeof(int)); int len = strlen(text);for (int i = 0; i < len; i++)frequency[(int)text[i]]++;}return frequency;//创建哈夫曼树HuffmanNode *createHuffmanTree(int *frequency)//初始化叶子节点HuffmanNode **leaves = (HuffmanNode **)malloc(256 * sizeof(HuffmanNode *));for (int i = 0; i < 256; i++)if (frequency[i] > 0)HuffmanNode *leaf = (HuffmanNode*)malloc(sizeof(HuffmanNode));leaf->data = (char)i;leaf->freq = frequency[i];leaf->left = NULL;leaf->right = NULL;leaves[i] = leaf;} elseleaves[i] = NULL;}}//构建哈夫曼树while (1)int min1 = -1, min2 = -1;for (int i = 0; i < 256; i++)if (leaves[i] != NULL)if (min1 == -1 , leaves[i]->freq < leaves[min1]->freq) min2 = min1;min1 = i;} else if (min2 == -1 , leaves[i]->freq < leaves[min2]->freq)min2 = i;}}}if (min2 == -1)break;}HuffmanNode *parent = (HuffmanNode*)malloc(sizeof(HuffmanNode));parent->data = 0;parent->freq = leaves[min1]->freq + leaves[min2]->freq;parent->left = leaves[min1];parent->right = leaves[min2];leaves[min1] = parent;leaves[min2] = NULL;}HuffmanNode *root = leaves[min1];free(leaves);return root;//生成编码表void generateHuffmanCode(HuffmanNode *root, HuffmanCode *huffmanCode, char *code, int depth)if (root->left == NULL && root->right == NULL)code[depth] = '\0';huffmanCode[root->data].data = root->data;huffmanCode[root->data].code = strdup(code);return;}if (root->left != NULL)code[depth] = '0';generateHuffmanCode(root->left, huffmanCode, code, depth + 1);}if (root->right != NULL)code[depth] = '1';generateHuffmanCode(root->right, huffmanCode, code, depth + 1);}//进行编码char *encodeText(char *text, HuffmanCode *huffmanCode)int len = strlen(text);int codeLen = 0;char *code = (char *)malloc(len * 8 * sizeof(char));for (int i = 0; i < len; i++)strcat(code + codeLen, huffmanCode[(int)text[i]].code);codeLen += strlen(huffmanCode[(int)text[i]].code);}return code;//进行解码char* decodeText(char* code, HuffmanNode* root) int len = strlen(code);char* text = (char*)malloc(len * sizeof(char)); int textLen = 0;HuffmanNode* node = root;for (int i = 0; i < len; i++)if (code[i] == '0')node = node->left;} elsenode = node->right;}if (node->left == NULL && node->right == NULL) text[textLen] = node->data;textLen++;node = root;}}text[textLen] = '\0';return text;int maichar *text = "Hello, World!";int *frequency = countFrequency(text);HuffmanNode *root = createHuffmanTree(frequency);HuffmanCode *huffmanCode = (HuffmanCode *)malloc(256 * sizeof(HuffmanCode));char code[256];generateHuffmanCode(root, huffmanCode, code, 0);char *encodedText = encodeText(text, huffmanCode);char *decodedText = decodeText(encodedText, root);printf("Original Text: %s\n", text);printf("Encoded Text: %s\n", encodedText);printf("Decoded Text: %s\n", decodedText);//释放内存free(frequency);free(root);for (int i = 0; i < 256; i++)if (huffmanCode[i].code != NULL)free(huffmanCode[i].code);}}free(huffmanCode);free(encodedText);free(decodedText);return 0;```上述的示例代码实现了一个简单的哈夫曼编码和解码过程。
数据结构---C语言描述-(耿国华)-课后习题答案

第一章习题答案2、××√3、(1)包含改变量定义的最小范围(2)数据抽象、信息隐蔽(3)数据对象、对象间的关系、一组处理数据的操作(4)指针类型(5)集合结构、线性结构、树形结构、图状结构(6)顺序存储、非顺序存储(7)一对一、一对多、多对多(8)一系列的操作(9)有限性、输入、可行性4、(1)A(2)C(3)C5、语句频度为1+(1+2)+(1+2+3)+…+(1+2+3+…+n)第二章习题答案1、(1)一半,插入、删除的位置(2)顺序和链式,显示,隐式(3)一定,不一定(4)头指针,头结点的指针域,其前驱的指针域2、(1)A(2)A:E、AB:H、L、I、E、AC:F、MD:L、J、A、G或J、A、G(3)D(4)D(5)C(6)A、C3、头指针:指向整个链表首地址的指针,标示着整个单链表的开始。
头结点:为了操作方便,可以在单链表的第一个结点之前附设一个结点,该结点的数据域可以存储一些关于线性表长度的附加信息,也可以什么都不存。
首元素结点:线性表中的第一个结点成为首元素结点。
4、算法如下:int Linser(SeqList *L,int X){ int i=0,k;if(L->last>=MAXSIZE-1){ printf(“表已满无法插入”);return(0);}while(i<=L->last&&L->elem[i]<X)i++;for(k=L->last;k>=I;k--)L->elem[k+1]=L->elem[k];L->elem[i]=X;L->last++;return(1);}5、算法如下:#define OK 1#define ERROR 0Int LDel(Seqlist *L,int i,int k){ int j;if(i<1||(i+k)>(L->last+2)){ printf(“输入的i,k值不合法”);return ERROR;}if((i+k)==(L->last+2)){ L->last=i-2;ruturn OK;}else{for(j=i+k-1;j<=L->last;j++)elem[j-k]=elem[j];L->last=L->last-k;return OK;}}6、算法如下:#define OK 1#define ERROR 0Int Delet(LInkList L,int mink,int maxk){ Node *p,*q;p=L;while(p->next!=NULL)p=p->next;if(mink<maxk||(L->next->data>=mink)||(p->data<=maxk)) { printf(“参数不合法”);return ERROR;}else{ p=L;while(p->next-data<=mink)p=p->next;while(q->data<maxk){ p->next=q->next;free(q);q=p->next;}return OK;}}9、算法如下:int Dele(Node *S){ Node *p;P=s->next;If(p= =s){printf(“只有一个结点,不删除”);return 0;}else{if((p->next= =s){s->next=s;free(p);return 1;}Else{ while(p->next->next!=s)P=p->next;P->next=s;Free(p);return 1;}}}第三章习题答案2、(1)3、栈有顺序栈和链栈两种存储结构。
lzw和霍夫曼编码

lzw和霍夫曼编码LZW(Lempel-Ziv-Welch)编码和Huffman编码是常见的无损数据压缩算法。
它们可以将数据以更高效的方式表示,并减少数据所占用的存储空间。
虽然两种编码算法有一些相似之处,但它们的工作原理和实施方法略有不同。
1.LZW编码:LZW编码是一种基于字典的压缩算法,广泛应用于文本和图像等数据的压缩。
它的工作原理是根据已有的字典和输入数据,将连续出现的字符序列转换为对应的索引,从而减少数据的存储空间。
LZW编码的过程如下:•初始化字典,将所有可能的字符作为初始词条。
•从输入数据中读取字符序列,并检查字典中是否已有当前序列。
•如果字典中存在当前序列,则继续读取下一个字符,将该序列与下一个字符连接成一个长序列。
•如果字典中不存在当前序列,则将当前序列添加到字典中,并输出该序列在字典中的索引。
•重复以上步骤,直到输入数据全部编码完成。
LZW编码的优点是可以根据实际数据动态更新字典,适用于压缩包含重复模式的数据。
2.霍夫曼编码:霍夫曼编码是一种基于频率的前缀编码方法。
它根据字符出现的频率构建一个最优二叉树(霍夫曼树),将出现频率较高的字符用较短的二进制码表示,出现频率较低的字符用较长的二进制码表示。
霍夫曼编码的过程如下:•统计输入数据中各个字符的频率。
•使用字符频率构建霍夫曼树,频率较高的字符在树的较低层,频率较低的字符在树的较高层。
•根据霍夫曼树,为每个字符分配唯一的二进制码,保持没有一个字符的编码是另一个字符编码的前缀。
•将输入数据中的每个字符替换为相应的霍夫曼编码。
•输出霍夫曼编码后的数据。
霍夫曼编码的优点是可以根据字符频率进行编码,使高频字符的编码更短,适用于压缩频率差异较大的数据。
总的来说,LZW编码和霍夫曼编码都是常见的无损数据压缩算法,用于减少数据的存储空间。
它们的选择取决于具体的场景、数据特点和应用需求。
数据结构课程设计题目

数据结构课程设计题目题目一:工资管理程序功能简介:完成员工工资信息管理,如员工工资信息的新建、存储、显示、修改和删除等功能(系统功能可充分自由发挥),最好用文件系统存储数据信息。
题目二:物品库存管理程序功能简介:实现物品库存管理,如进库、出库、浏览、修改等功能(系统功能可充分自由发挥),最好用文件系统存储数据信息。
题目三:个人财政支出管理程序功能简介:个人财政支出管理程序,如完成收入、支出、赢余的记录和管理等功能(系统功能可充分自由发挥),最好用文件系统存储数据信息。
题目四:电话簿管理程序功能简介:一个基本的电话簿管理程序,如插入、删除、显示、修改和查询联系人电话号码等功能(系统功能可充分自由发挥),最好用文件系统存储数据信息。
题目五:股票交易系统程序功能简介:股票交易系统的管理,如增加新股票、删除旧股票、挂起股票、住手交易、修改股票的名称、代码、股票买卖等功能(系统功能可充分自由发挥),最好用文件系统存储数据信息。
题目六:学生信息管理程序功能简介:完成学生基本的管理,如学生基本信息的新建、存储、显示、修改和删除等功能(系统功能可充分自由发挥),最好用文件系统存储数据信息。
题目七:学生成绩管理程序功能简介:完成学生成绩管理,如学生成绩信息的录入、显示、修改和浏览等功能(系统功能可充分自由发挥),最好用文件系统存储数据信息。
题目八:运动会分数统计任务:参加运动会有 n 个学校,学校编号为1……n。
比赛分成 m 个男子项目,和 w 个女子项目。
项目编号为男子1……m,女子m+1……m+w。
不同的项目取前五名或者前三名积分;取前五名的积分分别为:7、5、3、2、1,前三名的积分分别为:5、3、2;哪些取前五名或者前三名由学生自己设定。
(m<=20,n<=20)功能要求:可以输入各个项目的前三名或者前五名的成绩 ;能统计各学校总分,可以按学校编号或者名称、学校总分、男女团体总分排序输出 ;可以按学校编号查询学校某个项目的情况;可以按项目编号查询取得前三或者前五名的学校。
哈夫曼编码(Huffman Coding)

哈夫曼编码哈夫曼编码(Huffman Coding)是一种编码方式,哈夫曼编码是可变字长编码(VL C)的一种。
Huffman于1952年提出一种编码方法,该方法完全依据字符出现概率来构造异字头的平均长度最短的码字,有时称之为最佳编码,一般就叫作Huffman 编码。
以哈夫曼树─即最优二叉树,带权路径长度最小的二叉树,经常应用于数据压缩。
在计算机信息处理中,“哈夫曼编码”是一种一致性编码法(又称"熵编码法"),用于数据的无损耗压缩。
这一术语是指使用一张特殊的编码表将源字符(例如某文件中的一个符号)进行编码。
这张编码表的特殊之处在于,它是根据每一个源字符出现的估算概率而建立起来的(出现概率高的字符使用较短的编码,反之出现概率低的则使用较长的编码,这便使编码之后的字符串的平均期望长度降低,从而达到无损压缩数据的目的)。
这种方法是由David.A.Huffman发展起来的。
例如,在英文中,e的出现概率很高,而z的出现概率则最低。
当利用哈夫曼编码对一篇英文进行压缩时,e极有可能用一个位(bit)来表示,而z则可能花去25个位(不是26)。
用普通的表示方法时,每个英文字母均占用一个字节(byte),即8个位。
二者相比,e使用了一般编码的1/8的长度,z则使用了3倍多。
倘若我们能实现对于英文中各个字母出现概率的较准确的估算,就可以大幅度提高无损压缩的比例。
本文描述在网上能够找到的最简单,最快速的哈夫曼编码。
本方法不使用任何扩展动态库,比如STL或者组件。
只使用简单的C函数,比如:memset,memmove,qsort,malloc,realloc和memcpy。
因此,大家都会发现,理解甚至修改这个编码都是很容易的。
背景哈夫曼压缩是个无损的压缩算法,一般用来压缩文本和程序文件。
哈夫曼压缩属于可变代码长度算法一族。
意思是个体符号(例如,文本文件中的字符)用一个特定长度的位序列替代。
因此,在文件中出现频率高的符号,使用短的位序列,而那些很少出现的符号,则用较长的位序列。
哈夫曼编码
例2:假设用于通信的电文仅由8个字母
{a, b, c, d, e, f, g, h} 构成,它们在电文中出现的概率分别为{ 0.07, 0.19, 0.02, 0.06, 0.32, 0.03, 0.21, 0.10} ,试为这8个字母设计 哈夫曼编码。如果用0~7的二进制编码方案又如何?
解:先将概率放大100倍,以方便构造哈夫曼树。 权值集合 w={7, 19, 2, 6, 32, 3, 21, 10}, 按哈夫曼树构造规则(合并、删除、替换),可得到哈夫曼树。
14
采用顺序表实现对Huffman编码的存储 //---------------Huffman编码存储结构-----------------typedef struct { char ch; int start; char bits[n+1]; }HuffmanCode; typedef HuffmanCode HCode[n]; ch存放对应的字符,start存放Huffman编码在字符 数组bits[]中开始的位置。
17
FileExtract(void) 初始条件:压缩结果文件Code.txt和tail.txt存在。 操作结果: 将code.txt和tail.txt中的字符写成编码的二进制字符形式, 写进file00.txt。 FileTrans(HTree T,HCode H,int N) 初始条件: 已生成File00,txt并已求得各个字符的Huffman编码, Huffman树已建立。 操作结果:将Huffman编码翻译成原文件,写入translated.txt。 }ADT 还需要包含调用若干库文件:stdio.h, malloc.h, string.h。
13
概要分析
采用顺序表实现对Huffman树的存储 //---------------Huffman树存储结 构-----------------typedef struct { int weight; int lchild, rchild, parent; }HuffmanTree; typedef HuffmanTree HTree[m]; weight域存有该节点字符的权值,lchild、 rchild、parent分别存放该节点的左孩子、 右孩子和双亲节点在顺序表中的位置。
6.6哈夫曼编码

如何编程实现Huffman编码?
建议1:Huffman树中结点的结构可设计成5分量形式:
char weight parent lchild rchild
建议2: Huffman树的存储结构可采用顺序存储结构: 将整个Huffman树的结点存储在一个数组HT[1..n..m]中; 各叶子结点的编码存储在另一“复合”数组HC[1..n]中。
频度高的信息 用短码,反之 用长码,传输 效率肯定高!
令d=0;i=10,a=110,n=111,则: WPL2=1bit×7+2bit×5+3bit×(2+4)=35 明确:要实现Huffman编码,就要先构造Huffman树
例:假设字符A,B,C,D,E的出现概率为42, 28, 15, 10, 5。求电文的总长度最短的一种编码?
中序遍历的非递归算法或称迭代算法或称迭代算法见教材见教材p131p131设高度为h的二叉树上只有度为0的结点和度为2的结点则此类二叉树所包含的结点数至少为至多为已知某二叉树的后序遍历序列是dabec中序遍历序列是debac则它的前序遍历序列是已知某二叉树的前序遍历序列是abdgcefh中序遍历序列是dgbaechf则其后序遍历序列是某二叉树的前序序列为stuwv中序序列为uwtvs则其后序序列为任何一棵二叉树的叶结点在先序中序和后序遍历序列中的相对次序实现任意二叉树的后序遍历的非递归算法而不使用栈结构最佳方案是二叉树采用存储结构线索二叉树是一种结构一棵二叉树的结点的数据结构采用顺序存储见数组t则其二叉链表表示形式为
想一想:对它中序遍历之后是什么效果?
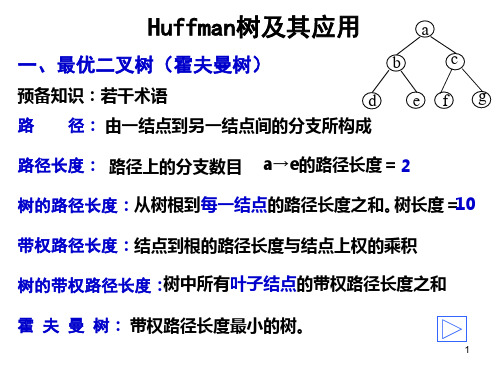
什么是带权树?
即路径带有权值。例如:
7
5
2
4
霍夫曼编码证明

霍夫曼编码证明霍夫曼编码的正确性可以通过数学归纳法来证明。
首先我们需要知道霍夫曼编码的特性:它是一种最佳的前缀编码,即没有任何一个编码是另一个编码的前缀。
我们使用数学归纳法证明霍夫曼编码的正确性:1. 首先考虑只有两个字符的情况。
假设字符A的出现概率为p,字符B的出现概率为q,且p >= q。
那么两个字符的霍夫曼编码应该满足以下条件:- 字符A编码的长度应该小于等于字符B编码的长度(因为p >= q)- 字符A编码的长度应该小于等于字符B编码的长度加1(因为前缀编码不能产生歧义)假设字符A的编码长度为k,字符B的编码长度为k或k+1。
那么字符A的出现概率为p,字符B的出现概率为q,用霍夫曼编码表示字符A的开销为p * k,表示字符B的开销为q * k + q * (k + 1) = q * (2k + 1)。
如果我们把字符A和字符B相互交换,字符A的概率变为q,字符B的概率变为p。
那么用霍夫曼编码表示字符A的开销为q * k,表示字符B的开销为p* k + p * (k + 1) = p * (2k + 1)。
由于p >= q,所以p * (2k +1) >= q * (2k + 1)。
因此,当只有两个字符时,霍夫曼编码的开销最小。
2. 假设在有n个字符的情况下,霍夫曼编码是最佳的前缀编码。
现在考虑有n+1个字符的情况。
我们将概率最小的两个字符合并成一个字符,并将其出现概率设置为合并前两个字符的出现概率之和。
这样我们就得到了n个字符,根据归纳假设,我们可以得到霍夫曼编码是最佳的前缀编码。
由于我们已经证明了有两个字符和n个字符时霍夫曼编码是最佳的前缀编码,而任意数量的字符都可以通过不断地合并概率最小的两个字符得到,因此我们可以得出结论:霍夫曼编码是最佳的前缀编码。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实习报告题目编号:系部:二系专业方向:计算机科学与技术班级:0422学生:高鹏程指导教师:章晓莉一、需求分析1、选题任务:编程实现txt文件(其中内容为英文文章)内容中26个字母、标点符号使用频率的统计,对文章进行Huffman编码存盘,并比较Huffman编码文件与原txt文件长度大小。
分析:选题所给出的要求实际就是通过统计某文章中字母出现的频率,并对频率值构造一棵Huffman树,利用Huffman树的特点构造文章中字母的Huffman编码,再按Huffman编码存储文件,实现文件数据的压缩目的。
设计方案:构造Huffman树首先要知道各个节点的权值,在这里,用约定俗成的方法对各个字母在文章中出现的次数计算出显得频率,以作为字母也就是各个节点的权值。
并以此来构造一棵Huffman树,运用Huffman的特点求出各个字母的前缀编码。
中间(这个词在此用的非常不合适,没有阐述清楚问题)用文件的一些操作实现对文章的读取和压缩后生成新文件。
程序接受的数据来自一个内容为英文文章的文本文件,将里面的各个字母转化为Huffman 编码(前缀编码)再以后缀为.huf的文件输出。
测试的数据主要是一些接连重复的字母和标点组合。
根据来判断转化后的Huffman是否相同来判断转化的是否正确。
二、程序设计:1、程序中用到的所有数据类型的定义:⑴、以下用到的结构体定义typedef struct {unsigned int weight;unsigned int parent, lchild, rchild;}HTNode;typedef HTNode HuffmanTree;typedef struct {int weight;int lchild, rchild, parent;}HTNode,HuffmanTree[m+1];⑵全局变量int num;⑶子函数定义void select(HuffmanTree T,int k,int &s1,int &s2);int Frq(char *s,int cnt[],char str[]);void ChuffmanTree(HuffmanTree HT, HuffmanCode HC,int cnt[],char str[]);void HuffmanEnCreathuf(HuffmanTree HT,HuffmanCode HC);2、主程序流程图:建立一个对应所有英文文章中可能出现的字母或标点符号的结构体数组——读入名为English.txt的文章,并计算其中出现的字母和标点符号出现的频率——建立一棵Huffman树——利用Huffman的特点求出出现过的字母和标点符号的Huffman 编码——利用循环把生成的Huffman(前缀编码)写入生成的后缀.huf文件3、各子程序间的调用关系:二、调试分析:⑴、遇到的问题:①遇到LNK2001错误:经仔细检查以后发现是因为有一个函数传入的参数和定义的不同。
②写入文件时的错误:对于文件写入函数了解的不充分,不能随意使用一个写入函数就期待实现全部写入。
③建立Huffman树时的错误主要是不理解建立的内在机制,总是产生非前缀代码,理解之后又借助老师的帮助终于产生了正确的前缀代码。
⑵算法的时间复杂度:O(n)算法的空间复杂度:254由于本人能力有限,时间也有限,未能找出改进的算法。
三、使用说明:在English.txt文件中输入要转化的英文文章,运行该程序即可得到名为English.huf 的文件。
五、测试结果:hello world!00100010101100111100101011111110以上的第二行为把English_huf.txt以记事本方式打开后的内容。
程序测试发现,错误的输入文件名依然有结果输出。
对某种类型文件的组织缺少研究,使得获得的压缩文件没有实际意义。
结果得分:中批改老师:章小莉2006.9.27六、其他注释源程序代码:#include <stdio.h>#include<string.h>#define n 100#define m 2*n-1typedef struct {char ch;char bits[9];int len;}CodeNode,HuffmanCode[n+1];/*定义一个结构体存放字符的前缀代码*/typedef struct {int weight;int lchild, rchild, parent;}HTNode,HuffmanTree[m+1];/*定义一个结构体存放Huffman树的结点信息*/void select(HuffmanTree T,int k,int &s1,int &s2);/*从Huffman树的结点中选出两个权值最小的结点*/int Frq(char *s,int cnt[],char str[]);/*计算s在文章中出现的频率*/void ChuffmanTree(HuffmanTree HT, HuffmanCode HC,int cnt[],char str[]);/*建立Huffman树*/void HuffmanEnCreathuf(HuffmanTree HT,HuffmanCode HC);/*运用Huffman树求出字符的前缀代码*/int num;void main(){char st[254],str[96],a;int cn[96];HuffmanTree HT;HuffmanCode HC;FILE *f_txt;if((f_txt = fopen("English.txt","rb")) == NULL){printf("can not open file English.txt\n");}fgets(st,254,f_txt);/*给数组st赋值*/printf("Press Enter to creat English.huf\n");scanf("%c",&a);num = Frq(st,cn,str);/*求出字符在文章中出现的频率*/ChuffmanTree(HT,HC,cn,str);/*建立Huffman树*/HuffmanEnCreathuf(HT,HC);/*求出前缀代码*/printf("English.huf creat ended!\n");printf("************Thanks for using!************\n");fclose(f_txt);}void select (HuffmanTree T,int k,int &s1,int &s2){/*利用两次for循环找出两个权值最小的结点*/int i,j;int min = 101;for(i = 1;i <= k;i++)if(T[i].weight < min && T[i].parent == 0){j = i;min = T[i].weight;/*将最小的权值赋予min*/}s1 = j;/*找出权值最小的结点*/min = 32767;for(i = 1;i <= k;i++)if(T[i].weight < min && T[i].parent == 0 && i != s1){j = i;min = T[i].weight;/*将第二小的权值赋予min*/}s2 = j;/*找出权值第二小的结点*/}int Frq (char *s,int cnt[],char str[]){char *p;int i, j, k;int temp[96];for(i = 1;i <= 95;i++)temp[i] = 0;for(p = s;*p != '\0';p++){if (*p >= '!' && *p <= '~'){k = *p - 32;/*转化为ASCII码*/temp[k]++;}/*判断p是否为字符*/}for(i = 1,j = 0;i <= 95;i++)if(temp[i] != 0){ j++;str[j] = i+32;cnt[j] = temp[i];}/*求出p出现的频率*/return j;}void ChuffmanTree(HuffmanTree HT,HuffmanCode HC,int cnt[],char str[]){/*建立Huffman树,根据字符出现的频率确定权值,作为Huffman树上各结点的权值*/int i,s1, s2;for(i = 1;i <= 2 * num - 1;i++){HT[i].lchild = 0;HT[i].rchild = 0;HT[i].parent = 0;HT[i].weight = 0;}/*初始化HT数组*/for(i = 1;i <= num;i++)HT[i].weight = cnt[i];/*转入各结点的权值*/for(i = num + 1;i <= 2 * num - 1;i++){select(HT,i-1,s1,s2);HT[s1].parent = i;HT[s2].parent = i;HT[i].lchild = s1;HT[i].rchild = s2;HT[i].weight = HT[s1].weight + HT[s2].weight;}/*建立Huffman树,用select依次找出两个权值最小的结点*/for(i = 0;i <= num;i++)HC[i].ch = str[i];i = 1;while(i <= num)printf("字符%c, 次}void HuffmanEnCreathuf(HuffmanTree HT,HuffmanCode HC){/*利用建立好的Huffman树求出前缀代码,放在HC数组中*/int c,p,i;char cd[n];int start;cd[num] = '\0';for(i = 1;i <= num;i++){start = num;c = i;while((p = HT[c].parent) > 0){cd[--start] = (HT[p].lchild == c) ? '0' : '1';c = p;}strcpy(HC[i].bits,&cd[start]);HC[i].len = num - start;}。
