高一10月份考试题
高一10月份月考(生物)试题含答案

高一10月份月考(生物)(考试总分:100 分)一、单选题(本题共计25小题,总分50分)1.(2分)下列关于细胞的叙述,正确的是A.细胞骨架由磷脂构成,对细胞起到了支撑、保护等作用B.细胞膜成分的更新一定伴随着分泌蛋白的分泌C.发菜和小球藻都是能将二氧化碳转化成糖类的原核生物D.当植物细胞处于质壁分离状态时,仍可能从外界吸收矿质元素2.(2分)研究发现,剧烈运动过程中肌细胞会增加分泌鸢尾素(一种多肽类激素),鸢尾素能促进胰岛素的释放,下列相关分析错误的是A.细胞利用氨基酸为原料合成鸢尾素B.剧烈运动时体内的胰岛素水平上升C.鸢尾素通过神经运送至胰岛B细胞D.胰岛素促进肌细胞对葡萄糖的摄取3.(2分)下列有关细胞的结构和功能的叙述,正确的是A.一个动物细胞中只含有一个中心体,高等植物中没有中心体B.用胰蛋白酶处理生物膜,生物膜的组成成分及通透性都会发生改变C.线粒体是有氧呼吸的主要场所,外膜上有运输葡萄糖和氧气的载体蛋白D.溶酶体内含有多种呼吸氧化酶,能分解衰老、损伤的细胞器4.(2分)下列有关细胞生命历程的叙述,错误的是A.生物体中被病原体感染的细胞的清除是由基因调控的B.细胞衰老的过程中,细胞的体积变小,细胞核体积增大C.细胞癌变的过程中,一定会发生染色体上基因排列顺序的变化D.高度分化的植物细胞只有处于离体状态时才有可能表现出全能性5.(2分)关于细胞中的化合物说法正确的是A.多糖是细胞生命活动所需的主要能源物质,常被称为"生命的燃料"B.二糖必须水解成单糖才能被细胞吸收,二糖水解时需要结合水的参与C.淀粉与糖原结构不同的根本原因是催化二者形成的酶的类型不同D.等量的脂肪比糖类含能量多,却不是生物体利用的主要能源物质6.(2分)线粒体外膜上的蛋白A可与蛋白B结合,细胞产生的活性氧核素可导致蛋白A 释放与之结合的蛋白B接着还会发生一系列的变化,使蛋白B与细胞中其他物质结合形成一种复合物.该复合物可活化蛋白酶,分解细胞中的蛋白质,最后导致细胞被吞噬细胞清除.下列相关叙述不正确的是A.题中描述的过程属于细胞编程性死亡B.癌细胞的细胞凋亡过程可能被抑制C.活化的蛋白酶可水解多种蛋白质,不具有酶的专一性D.接受某种信号,阻止蛋白B的表达后,细胞可能抗凋亡7.(2分)生物大分子是构成生命的基础物质,下列有关叙述正确的是A.T2噬菌体、染色体只由DNA和蛋白质组成B.蛋白质的营养价值与氨基酸的种类密切相关C.解旋酶可提供DNA双链解开所需的活化能D.T2噬菌体的核酸彻底水解产生4种有机小分子8.(2分)研究表明某些肿瘤细胞中MDR基因(多耐药基因1)高度表达后,会使这些癌细胞对化疗药物的抗性增强.MDR的表达产物是p糖蛋白(P-gp),该蛋白有ATP依赖性跨膜转运活性,可将药物转运至细胞外,使细胞获得耐药性.而P-gp转运蛋白低水平表达的癌细胞内,某些化疗药物的浓度明显升高.结合上述信息,分析下列叙述正确的是A.P-gp转运蛋白转运物质的方式属于协助扩散B.P-gp转运蛋白可将各种化疗药物转运出癌细胞C.化疗药物可提高P-gp转运蛋白基因高度表达的癌细胞比例D.提高癌细胞P-gp转运蛋白的活性为癌症治疗开辟了新途径9.(2分)如图表示人工无蛋白质的脂双层膜对不同物质的通透性,下列据图分析正确的是A.葡萄糖跨膜运输离不开蛋白质和能量B.部分水分子跨膜运输可能需要借助蛋白质C.由图可知,极性分子更易通过该脂双层膜D.温度不会改变气体透过该脂双层膜的速率10.(2分)果蝇的"生物钟"同时受某些细胞中X染色体上的Per基因和2号染色体上的Tim基因调控.研究发现,夜间Per蛋白积累,而过多的Per蛋白与Tim蛋白结合能进入细胞核抑制Per基因的活性,使白天Per蛋白水平降低,实现昼夜节律.下列分析错误的是A."生物钟"的形成过程存在反馈调节B."生物钟"的形成与基因的选择性表达有关C.Tim基因表达障碍时,Per蛋白会发生持续性积累D.Per基因和Tim基因遵循基因的自由组合定律,表达时互不干扰11.(2分)叶色变异是由体细胞突变引起的芽变现象.红叶杨由绿叶杨芽变后选育形成,其叶绿体基粒类囊体减少,光合速率减小,液泡中花青素含量增加.下列叙述正确的是A.红叶杨染色体上的基因突变位点可用普通光学显微镜观察识别B.两种杨树叶绿体基粒类囊体的差异可用普通光学显微镜观察C.两种杨树叶光合速率可通过"探究光照强弱对光合作用强度的影响"实验作比较D.红叶杨细胞中花青素绝对含量可通过"植物细胞的吸水和失水"实验测定12.(2分)假设图示为某动物(2n=4)体内一个分裂细胞的局部示意图,其中另一极的结构未绘出.已知该动物的基因型为GgX E Y,下列叙述正确的是A.图示细胞经过分裂能得到2种或4种配子B.图示完整细胞内应有6条染色单体C.图示细胞为初级精母细胞,应进行均等分裂D.图示未绘出的一极一定存在G、g两种基因13.(2分)科学家运用同位素示踪技术,巧妙地设计实验证实了DNA的半保留复制方式.下列实验方法组合正确的是①先用含有15N标记的NH4C1培养液连续培养大肠杆菌②先用含有14N的NH4Cl标记大肠杆菌DNA③将大肠杆菌转移到含14N的培养液中,在不同时刻收集大肠杆菌并提取DNA④加入解旋酶、DNA聚合酶以及一定量的脱氧核苷酸⑤亲代和子代DNA经密度梯度离心后,记录并比较不同密度条带的DNAA.①③④B.②④⑤C.①③⑤D.③④⑤14.(2分)如图为某同学在学习DNA的结构后画的含有两个碱基对的DNA片段(圆圈表示磷酸基团),下列为几位同学对此图的评价,其中正确的是A.甲说:"物质组成和结构上没有错误"B.乙说:"只有一处错误,就是U应改为T"C.丙说:"至少有三处错误,其中核糖应改为脱氧核糖"D.丁说:"如果说他画的是RNA双链则该图应是正确的"15.(2分)下列关于控制无关变量的实验操作,错误的是A.验证光合作用能产生淀粉的实验中,首先将实验植物作饥饿处理B.探究唾液淀粉酶的最适pH的实验中,将每一组温度控制在37℃C.探究唾液淀粉酶的最适温度的实验中,每一组都加入等量的淀粉D.验证光合作用需要光照的实验中,将叶片的一半用黑纸包住16.(2分)1880年美国生物学家恩格尔曼设计了一个实验研究光合作用的光谱.他将棱镜产生的光谱投射到丝状水绵体上,并在水绵悬液中放入好氧细菌,观察细菌的聚集情况(如下图).他得出光合作用在红光区和蓝光区最强的结论.下列叙述正确的是a bA.细菌的聚集情况说明细菌所含色素主要吸收红光和蓝紫光B.这个实验的巧妙之处在于选用具有椭圆形叶绿体的丝状水绵体,便于实验结果的观察C.这个实验的结论得出的依据是好氧细菌聚集多的地方,02浓度高,水绵光合作用强D.这个实验的自变量是不同的光强度,因变量是好氧细菌集中的部位17.(2分)假设D 、e 代表碗豆的优良基因,这两种基因是独立遗传的.现有DDEE 、ddee 两个品种,为培养出培育出优良品种DDee,可采用以下两种方法,下列叙述正确的是 方法一: DDEE×dd ee→F 1→F 2……→DDee 植株方法二: DDEE×dd ee→F 1−−−−→−花药离体培养F 2−−−−→−秋水仙素处理DDee 植株A.方法一育种过程中要对F 1去雄,从F 2开始筛选B.方法一操作简便,育种过程中不会发生基因突变C.方法二中花药离体培养得到的幼苗细胞不能形成四分体D.方法二中秋水仙素作用于F 2幼苗细胞减数分裂的前期18.(2分)为研究高浓度CO 2处理对某种植物的影响,研究人员将对照组植物以大气CO 2浓度处理150天、实验组植物以高浓度CO 2处理相同时间,随即将两组植物均转移至大气CO 2浓度条件进行恢复实验30天,结果如下图所示,相关分析不正确的是A.高浓度CO 2处理结束植物净光合速率明显提高B.气孔开放度下降导致植物净光合速率一定下降C.推测恢复初始时的实验组净光合速率低于结束时D.气孔开放度下降是植物对高浓度CO 2环境的适应19.(2分)植物受病原菌感染后,特异的蛋白水解酶被激活,从而诱导植物细胞编程性死亡,同时病原菌被消灭.激活蛋白水解酶有两条途径:①由钙离子进入细胞后启动;②由位于线粒体内膜上参与细胞呼吸的细胞色素c 含量增加启动,下列叙述正确的是A.蛋白水解酶能使磷酸二酯键断开B.钙离子通过自由扩散进入植物细胞C.细胞色素c 与有氧呼吸第一阶段有关D.细胞编程性死亡避免了病原菌对邻近细胞的进一步感染20.(2分)下列有关实验的叙述,正确的是A.用盐酸处理口腔上皮细胞可以加快健那绿染液对线粒体的染色速度B.在T 2噬菌体侵染细菌的实验中需要用未标记的T 2噬菌体作为对照组C.盐酸和酒精混合液(1:1)处理能使植物细胞相互分离,因而它可用于根尖解离D.用洋葱鳞片叶内表皮细胞作为实验材料观察细胞内的线粒体和叶绿体21.(2分)下列有关遗传分子的叙述,正确的是A.用含35S的完全培养基培养T2噬菌体,可以获得35S标记的噬菌体B.原核细胞内,转录的同时核糖体进入细胞核启动遗传信息的翻译C.DNA分子边解旋边复制,新合成的两条子链形成1个新的DNA分子D.一对等位基因的碱基序列一定不同,但在同源染色体上的位置一般相同22.(2分)下列有关孟德尔定律的叙述中,正确的是A.F1高茎豌豆自交所得F2中出现了高茎和矮茎,这是基因重组的结果B.孟德尔通过测交实验的结果推测出F1产生配子的种类及数量,从而验证其假说正确与否C.孟德尔利用山柳菊做杂交实验失败的原因是山柳菊有时为无性生殖D.孟德尔对分离现象及自由组合现象的解释是基于对减数分裂的研究而提出的假说23.(2分)红绿色盲为伴X染色体隐性遗传病,一个家庭中父母色觉正常,生了一个性染色体为XXY的孩子.不考虑基因突变,下列说法正确的是A.若孩子色觉正常,则出现的异常配子不会来自父亲B.若孩子色觉正常,则出现的异常配子不会来自母亲C.若孩子患红绿色盲,则出现的异常配子不会来自父亲D.若孩子患红绿色盲,则出现的异常配子不会来自母亲24.(2分)麦瓶草(XY)属于雌雄异株植物,其花色有红花和黄花两种类型,由一对等位基因控制用纯种品系进行杂交实验如下实验1:红花♀X黄花♂→子代50%红花雌株,50%红花雄株实验2:黄花♀κ红花♂→子代50%红花雌株,50%黄花雄株根据以上实验下列分析错误的是A.实验2子代雌雄株杂交的后代不出现雌性黄花植株B.实验1子代雌维株杂交的后代不出现雌性黄花植株C.两组实验子代中的雌性植株基因型相同D.两组实验正反交结果不同推测控制花色基因位于X染色体上25.(2分)下列关于细胞增殖和DNA复制的叙述,错误的是A.高等植物的体细胞增殖的方式是有丝分裂和无丝分裂B.基因型为X a Y的个体产生了基因型为X a Y的配子,原因是减数第一次分裂时同源染色体未分离C.T2噬菌体增殖时,需宿主细胞提供解旋酶作用于磷酸二酯键D.将一个DMA分子(第1代)的一条链用N标记转移到含15N的环境中复制到第n代则第n代中只含14N的DNA分子数为2n-1-1二、填空题(本题共计4小题,总分50分)26.(12分)学校科硏小组在晴朗的白天对某湖泊进行了研究:取6个透明玻璃瓶编号为1~6号,分别从同一取样点水深为1米处取水样后密封,测其溶氧量如图甲所示;另取一透明玻璃瓶(编号7),从该取样点某深度水层取水样后密封,每间隔2小时(h)测其CO2浓度如图乙所示.假如环境温度不变,细胞呼吸强度恒定.请据图回答:图甲图乙(1)经鉴定,1~6号瓶中均含有绿藻和蓝藻.与绿藻相比,蓝藻不含叶绿体,它能够进行光合作用的原因是__________________________________.(2)请分析出图甲测定结果的主要原因是_____________________________.(3)图乙中4~6h与8~10h时间段内,水样中C02浓度各自保持稳定,原因是_____________,分析这两个时间段7号瓶所处环境条件发生的变化是:后者比前者_____________.(4)若夜晚在该取样点的水深6米处取样,水样中生物种类与6号瓶相比_________(填"增多"、"减少"或"基本不变"),原因是__________________.27.(11分)某种多年生木本花卉花色为红色.研究小组尝试培育其他花色的新品种.已知该种植物为雌雄异株,性别决定方式为XY型,花色遗传受两对基因控制.其中一对位于X 染色体上(用A,a表示),另一对(用B,b表示)位置未确定.研究小组对纯合红花品系用射线多次处理后,经过杂交筛选最终获得一株白花雄株(甲).利用这株白花植株进行了杂交实验,结果如下表(不考虑致死和XY同源区段),请回答相关问题(1)B/b基因位于_______染色体上,判断的依据是______________________.(2)白花雄株(甲)的基因型是__________,F1雌株的基因型是______________.(3)请用上表中F1和F2为材料,仅选择一对雌雄亲本,采用一次杂交实验培育获得白花雌株,请简述培育过程,并推测子代雌株中白花所占的比例._______________________________.28.(12分)鹦鹉羽毛的颜色有蓝色、绿色、黄色和白色四种,由两对独立遗传的等位基因控制,其中B、b这对等位基因位于Z染色体上,其遗传机理如图.现有多组绿色雄鹦鹉与白色雌鹦鹉杂交(正交),后代雌、雄鹦鹉的羽毛均为绿色:反交后代中,雄鹦鹉羽毛均为绿色,雌鹦鹉羽毛均为蓝色.回答下列问题.(1)由鹦鹉羽毛颜色的遗传机理可知,基因与生物性状的关系是___________________.(2)控制羽毛颜色的基因型共有______种,正交亲本中绿色雄鹦鹉和白色雌鹦鹉的基因型分别是___________________,若某鹦鹉蓝色羽毛出现白色斑点,是由于_______________________.(3)养鸟专家在配制鹦鹉饲料时,发现含某微量元素的3号饲料会抑制黄色物质的合成,使黄羽变为白羽.现有3号饲料长期饲喂的一只蓝色雄鹦鹉和正常饲料喂养的各种雌鹦鹉,请设计杂交实验,确定该蓝色雄鹦鹉为纯合子还是杂合子.实验思路:__________________________________________________.预测结果及结论:______________________________________________________.29.(15分)科研人员从青藏高原祁连山地区的土壤中分离筛选出一株高效耐低温原油降解菌YF28-1(8),应用该菌能够提高高寒地区石油等烃类污染物的分解效率,为我国的环境保护事业做出贡献.请回答相关问题:(1)选择青藏高京祁连山地区进行筛选,其原因是________________________.(2)筛选原油降解茵的培养基中应加入作为唯一碳源.从功能上看,该种培养基称为_____培养基.(3)用平板划线法纯化该细菌时,第2次划线及其以后划线总是从上次划线的末端开始的原因是_______________________________________________________.(4)研究人员设计实验探究该菌降解原油的最适温度.实验分为5组,下图A-E为各组培养一段时间后菌落的生长情况.本实验所使用的接种方法是_____________接种操作时应特别注意控制的无关变量是__________.A-E组控制的不同条件是____________若要确定更准确的最适温度,应该在______组和_______组所对应的温度范围内设置更小的温度梯度,进一步实验.A B C D E答案一、单选题(本题共计25小题,总分50分)1.(2分)【答案】D2.(2分)【答案】C3.(2分)【答案】B4.(2分)【答案】C5.(2分)【答案】D6.(2分)【答案】C7.(2分)【答案】B8.(2分)【答案】C9.(2分)【答案】B10.(2分)【答案】D11.(2分)【答案】C12.(2分)【答案】C13.(2分)【答案】C14.(2分)【答案】C15.(2分)【答案】D16.(2分)【答案】C17.(2分)【答案】C18.(2分)【答案】B19.(2分)【答案】D20.(2分)【答案】C21.(2分)【答案】D22.(2分)【答案】C23.(2分)【答案】C24.(2分)【答案】A25.(2分)【答案】C二、填空题(本题共计4小题,总分50分)26.(12分)【答案】(1)含有光合(作用)色素和相应的酶(2)随着水深增大,光照强度逐渐减弱,藻类(绿藻和蓝藻)的数量减少(光合作用强度减弱)(3)两时间段内水样中生物细胞呼吸产生的CO2与藻类光合作用消耗的C02相等光照强度增大(4)减少白天水深6米处溶氧量几乎为零,而夜晚不能进行光合作用,没有了氧气供应,该处的好氧生物会转移27.(11分)【答案】(1)常F2出现8:7:1的分离比,说明这两点基因是自由组合的,因为Aa位于X染色体,所以B,b位于常染色体上.(2) bbX a Y BbX A X a.(3)选择F1中红花雌株和F2中白花雄株杂交,从后代中选出白花雌株个体,后代雌株中白花所占比例为1/428.(12分)【答案】(1)基因通过控制酶的合成控制代谢过程,进而控制生物性状;一种性状可由两个基因控制(2)15 AAZ B Z B、aaZ b W 体细胞发生了基因突变或染色体缺失(3)用该蓝色雄鹦鹉与多只白色雌鹦鹉杂交,子代用正常饲料喂养,观察并统计子代表现型及比例若子代雌雄鹦鹉的羽毛都为绿色或者都为蓝色,则该个体为纯合子;否则为杂合子29.(15分)【答案】(1)该地区的微生物更耐低温(2)原油选择(3)将聚集的菌体逐渐稀释以便获得单个菌落(4)稀释涂布平板法接种的菌液量(或涂布器的灭菌情况) 温度 B D。
黑龙江省龙东联盟2024-2025学年高一上学期10月份月考英语试卷

黑龙江省龙东联盟2024-2025学年高一上学期10月份月考英语试卷一、听力选择题1.What will the man do tonight?A.Buy some shoes.B.Go to the bank.C.Book a hotel room. 2.What time is it now?A.4: 10.B.4: 20.C.4: 30.3.What kind of music does the woman like best?A.Classical music.B.Light music.C.Pop music.4.What does the woman mean?A.The water there is not clean.B.The water is getting clearer.C.They can swim in the water there.5.Where does the conversation most probably take place?A.In a reading room.B.In a publishing house.C.In a bookstore.听下面一段对话,回答以下小题。
6.What will the woman do this weekend?A.Go to a concert with the man.B.Have dinner with her friend.C.Practise playing football.7.When will the speakers meet outside the Kent Theater?A.At eight this Thursday.B.At six this Saturday.C.At seven next Tuesday.听下面一段对话,回答以下小题。
8.What does the man offer to do?A.Lend his umbrella to the woman.B.Get the woman’s umbrella for her.C.Do the presentation for the woman.9.What is the woman probably going to do right away?A.Go for the presentation.B.Wait for the man.C.Study in the library.听下面一段对话,回答以下小题。
山东省实验中学2024-2025学年高一(上)月考数学试卷(10月份)(含答案)

2024-2025学年山东省实验中学高一(上)月考数学试卷(10月份)一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.已知U=R,A={x|−1<x<3},B={x|x≤2},则∁U(A∪B)=( )A. (−∞,−1]∪(2,+∞)B. (−∞,−1)∪[2,+∞)C. [3,+∞)D. (3,+∞)2.已知命题p:“∀x≥0,x2−x+1≥0”,则它的否定为( )A. ∀x<0,x2−x+1<0B. ∃x<0,x2−x+1<0C. ∀x≥0,x2−x+1<0D. ∃x≥0,x2−x+1<03.已知a,b是实数,则“a>1且b>1”是“ab+1>a+b”的( )A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件4.关于x的一元二次方程x2+2mx+m2+m=0的两个实数根的平方和为12,则m的值为( )A. m=−2B. m=3C. n=3或m=−2D. m=−3或m=25.设A={x|x2−8x+15=0},B={x|ax−1=0},若A∩B=B,则实数a的值不可以为( )A. 15B. 0 C. 3 D. 136.设a,b∈R+,且a+b=3,则2a+bab的最小值为( )A. 22B. 2+23C. 1+223D. 2+227.已知函数f(x)=2mx2−2(4−m)x+1,g(x)=mx,若对于任一实数x,f(x)与g(x)至少有一个为正数,则实数m的取值范围是( )A. (0,2)B. (0,8)C. (2,8)D. (−∞,0)8.高斯是德国著名的数学家,享有“数学王子”的称号,用其名字命名的“高斯函数”为:设x∈R,用[x]表示不超过x的最大整数,则y=[x]称为高斯函数,例如:[−2.1]=−3,[3.1]=3,已知函数f(x)=(x+1)2 x2+1−12,则函数y=[f(x)]的值域是( )A. {0,1}B. {0,1,2}C. {−1,0,1}D. {−1,0,1,2}二、多选题:本题共3小题,共18分。
2024-2025学年重庆市西南大学附中高一(上)月考数学试卷(10月份)(一)(含答案)

2024-2025学年重庆市西南大学附中高一(上)月考数学试卷(一)(10月份)一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.集合M={x|−2<x≤4},N={x||x|−3<0},那么集合M∩N=( )A. {x|−3<x<3}B. {x|−2<x≤4}C. {x|−3<x≤4}D. {x|−2<x<3}2.命题“∃x≥2,x2<5”的否定是( )A. ∃x≥2,x2≥5B. ∃x<2,x2≥5C. ∀x≥2,x2≥5D. ∀x<2,x2≥53.若“x>a”是“x2−2x−3<0”的必要不充分条件,则实数a的取值范围是( )A. (−∞,−1)B. (−∞,−1]C. (−1,+∞)D. [−1,+∞)4.不等式(x−2)(x−1)2x+3≤0的解集为( )A. {x|x≤−3或1≤x≤2}B. {x|x<−3或1≤x≤2}C. {x|−3≤x≤2}D. {x|−3<x≤2}5.下面命题正确的是( )A. 使x2<9成立的一个充分不必要条件是x<3B. “(x−1)2+(y−2)2=0”是“(x−1)(y−2)=0”的充要条件C. 已知x∈R,则“x>2”是“1x <12”的充要条件D. 已知a,b∈R,则“a−2b=0”是“ab=2”的必要不充分条件6.已知关于x的不等式ax2+bx+c<0(a,b,c∈R)的解集为(−3,2),则c2+4a+b的取值范围为( )A. [12,+∞)B. (−∞,12)C. (12,+∞)D. (−∞,12]7.若将有理数集Q分成两个非空的子集M与N,且满足M∪N=Q,M∩N=⌀,M中的每一个元素都小于N 中的每一个元素,则称(M,N)为有理数集的一个分割.试判断,对于有理数集的任一分割(M,N),下列选项中,不可能成立的是( )A. M没有最大元素,N有一个最小元素B. M没有最大元素,N也没有最小元素C. M有一个最大元素,N有一个最小元素D. M有一个最大元素,N没有最小元素8.已知x>2y>0,则x+8x+2y +2x−2y的最小值为( )A. 2B. 4C. 6D. 8二、多选题:本题共3小题,共18分。
2024-2025学年山东省济南市部分学校高一(上)质检数学试卷(10月份)(含答案)

2024-2025学年山东省济南市部分学校高一(上)质检数学试卷(10月份)一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合M ={−1,1,2,3},N ={−1,1},则M ∪N =( )A. {−1,1,2,3}B. {−1,1}C. {2,3}D. {1,2,3}2.“∀x ∈(2,+∞),x 2−2x >0”的否定是( )A. ∃x 0∈(−∞,2],x 20−2x 0≤0B. ∀x ∈(2,+∞),x 2−2x ≤0C. ∃x 0∈(2,+∞),x 20−2x 0≤0D. ∀x ∈(−∞,2],x 2−2x >03.不等式1−x 4+x ≥0的解集为( )A. {x|−4≤x ≤1}B. {x|x <−4或x ≥1}C. {x|−4<x ≤1}D. {x|x ≤−4或x ≥1}4.已知a ,b 均为正实数,且a +b =1,则下列选项错误的是( )A. a + b 的最大值为 2 B. 3a +4+a b 的最小值为7+2 14C. (a +1)(b +1)的最大值为94D. a 2a +3+b 2b +2的最小值为165.已知函数f(x +2)的定义域为(−3,4),则函数g(x)=f(x +1)3x−1的定义域为( )A. (−4,3) B. (−2,5) C. (13,3) D. (13,5)6.函数f(x)={x 2−(a +4)x +5,x <2(2a−3)x +1,x ≥2满足对∀x 1,x 2∈R 且x 1≠x 2,都有[f(x 1)−f(x 2)](x 1−x 2)<0,则实数a 的取值范围是( )A. (0,32)B. [0,32)C. (0,1)D. [0,1]7.已知函数f(x)的定义域为R ,f(x)−1为奇函数,f(x +2)为偶函数,则f(1)+f(2)+⋯+f(16)=( )A. 0B. 16C. 22D. 328.如果函数f(x)的定义域为[a,b],且值域为[f(a),f(b)],则称f(x)为“Ω函数.已知函数f(x)={5x,0≤x ≤2x 2−4x +m,2<x ≤4是“Ω函数,则m 的取值范围是( )A. [4,10] B. [4,14] C. [10,14] D. [14,+∞)二、多选题:本题共3小题,共18分。
辽宁省大连市滨城高中联盟2024-2025学年高一上学期10月份考试数学试卷

辽宁省大连市滨城高中联盟2024-2025学年高一上学期10月份考试数学试卷一、单选题1.已知集合{}2,1,1,3,5A =--,集合{}250,B x x x =-+>∈Z ,则图中阴影部分所表示的集合为( )A .{}2,1,1--B .{}0,3,5C .{}0,1D .{}0,22.若a <0,b <0,则p =2b a +2a b与q =a +b 的大小关系为( )A .p <qB .p ≤qC .p >qD .p ≥q3.命题“2R,10x x ax ∃∈-+<”为假命题的一个必要不充分条件是( ) A .[2,2]a ∈- B .(2,1)a ∈- C .[2,3]a ∈-D .(2,3)a ∈-4.下列不等式正确的是( )A .已知14a b ≤+≤,12a b -≤-≤,则42a b -的取值范围是[]2,10-B .若11a b>,则a b < C .若22ac bc ≥,则a b ≥ D .若0a >,0b >,且a b <,则a m ab m b+>+ 5.若关于x 、y 的方程组2204210y kx y x y --=⎧⎨--+=⎩的解集中只有一个元素,则实数k 的值为( )A .1B .0或1C .1-D .0或1-6.当一个非空数集G 满足“如果,a b G ∈,则a b +,a b -,ab G ∈,且0b ≠时,aG b∈”时,我们称G 就是一个数域,以下四个数域的命题:①0是任何数域的元素:②若数域G 有非零元素,则2024G ∈;③集合{}3,Z P xx k k ==∈∣是一个数域 ④有理数集是一个数域 其中真命题的个数为( ) A .1B .2C .3D .47.已知关于x 的不等式210ax bx -+>的解集为()2,,m m ⎛⎫-∞⋃+∞ ⎪⎝⎭,其中0m >,则1b m +的最小值为( )A .4B .C .2D .18.对于问题“已知关于x 的不等式20ax bx c ++>的解集为()2,4-,解关于x 的不等式20ax bx c -+>”,给出一种解法:由20ax bx c ++>的解集为()2,4-,得()()2a xb xc -+-+>的解集为()4,2-,即关于x 的不等式20ax bx c -+>的解集为()4,2-,类比上述解法,若关于x 的不等式320ax bx cxd +++>的解集为()()1,48,+∞U ,则关于x 的不等式320842a b cd x x x-+-+>的解集为( ) A .()(),168,2-∞---U B .()(),42,1-∞---U C .111,,2816⎛⎫⎛⎫-∞--- ⎪ ⎪⎝⎭⎝⎭UD .111,,02816⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭U二、多选题9.已知正数x ,y 满足2x y +=,则下列选项正确的是( ) A .11x y+的最小值是2B .xy 的最小值是1C .22x y +的最小值是4D .()1x y +的最大值是9410.下面命题正确的是( )A .对任意的x ∈R ,2214x a x a -+-+≥恒成立,则1a ≤-或3a ≥B 2的最小值是2C .已知a ,b ,(),0c ∈-∞,则1a b +,4b c +,9c a +至少有一个不大于4-D .设a ,b ∈R ,则“0a ≠”是“0ab ≠”的必要不充分条件11.设非空集合}{S x m x n =≤≤满足:当x ∈S 时,有x 2∈S .给出如下命题,其中真命题是( )A .若m =1,则{}|1S x x =≥B .若12m =-,则14≤n ≤1C .若12n =,则0m ≤ D .若n =1,则10m -≤≤三、填空题12.命题“1x ∀≤,20x x ->”的否定是.13.关于x 的一元二次方程()2640x ax a -+-=的两个正实数根分别为12,x x ,且1228x x +=,则a 的值是.14.若1a b >>,且35a b +=,则141a b b +--的最小值为,2ab b a b --+的最大值为.四、解答题15.已知集合4110A xx ⎧⎫=≤-⎨⎬-⎩⎭,{}221B x a x a =+<<+. (1)当3a =时,求A B ⋂;(2)若A B A =U ,求实数a 的取值范围.16.已知a ,b 为正实数,且满足216ab a b ++=. (1)求ab 的最大值; (2)求a b +的最小值; (3)写出1112+++a b 的最小值(直接写出结果即可). 17.(1)已知[]0,2a ∀∈时,不等式()231102ax a x a +++-<恒成立,求x 的取值范围.(2)已知存在[]2,2x ∈-,使不等式2320x mx m ++-≤成立,求m 的取值范围. 18.若实数x 、y 、m 满足x m y m -<-,则称x 比y 接近m , (1)2x 比0接近1,求x 的取值范围;(2)判断:“x 比y 接近0”是“22x yy x+>-”的什么条件(充分不必要条件,必要不充分条件,充要条件,既不充分又不必要条件),并加以证明.19.已知函数()222,R y ax a x a =-++∈(1)求不等式0y ≥的解集;(2)若存在0m >使关于x 的方程()21221ax a x m m-++=++有4个不同的实根,求实数a 的取值范围。
2024-2025学年四川省成都市成都七中高一(上)月考数学试卷(10月份)(含答案)

2024-2025学年四川省成都七中高一(上)月考数学试卷(10月份)一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合A ={1,2},B ={1,3,4},则A ∪B =( )A. {1}B. {1,3,4}C. {1,2}D. {1,2,3,4}2.已知0<x <3,0<y <5,则3x−2y 的取值范围是( )A. (−1,0)B. (−10,9)C. (0,4)D. (0,9)3.对于实数x ,“2+x 2−x ≥0”是“|x|≤2”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件4.下列命题中真命题的个数是( )①命题“∀x ∈R ,|x|+x 2≥0”的否定为“∃x ∈R ,|x|+x 2<0”;②“a 2+(b−1)2=0”是“a(b−1)=0”的充要条件;③集合A ={y|y = x 2+1},B ={x|y = x 2+1}表示同一集合.A. 0B. 1C. 2D. 35.已知实数x ,y 满足4x 2+4xy +y +6=0,则y 的取值范围是( )A. {y|−3≤y ≤2}B. {y|−2≤y ≤3}C. {y|y ≤−2}∪{y|y ≥3}D. {y|y ≤−3}∪{y|y ≥2}6.已知正实数a ,b 满足2a +b =1,则5a +b a 2+ab 的最小值为( )A. 3B. 9C. 4D. 87.关于x 的不等式(ax−1)2<x 2恰有2个整数解,则实数a 的取值范围是( )A. (−32,−43]∪(43,32]B. (−32,−43]∪[43,32)C. [−32,−43)∪(43,32]D. [−32,−43)∪[43,32)8.已知函数f(x)={4x 2−2x +3,x ≤122x +1x ,x >12,设a ∈R ,若关于x 的不等式f(x)≥|x−a 2|在R 上恒成立,则a 的取值范围是( )A. [−398,478]B. [−4,478]C. [−4,4 3]D. [−398,4 3]二、多选题:本题共3小题,共18分。
2024-2025学年四川省泸州市泸县五中高一(上)月考数学试卷(10月份)(含答案)

2024-2025学年四川省泸州市泸县五中高一(上)月考数学试卷(10月份)一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.下列集合与集合A={2,3}相等的是( )A. {(2,3)}B. {(x,y})|x=2,y=3}C. {x|x2−5x+6=0}D. {x=2,y=3}2.命题“∀x∈R都有x2+x+1>0”的否定是( )A. 不存在x∈R,x2+x+1>0B. 存在x0∈R,x20+x0+1≤0C. 存在x0∈R,x20+x0+1>0D. 对任意的x∈R,x2+x+1≤03.集合M满足{1,2}⫋M⊆{1,2,3,4,5},则集合⫋M的个数为( )A. 3B. 6C. 7D. 84.设全集U为实数集R,已知集合M={x|x2−4>0},N={x|x2−4x+3<0},则图中阴影部分所表示的集合为( )A. {x|x<−2}B. {x|x>3}C. {x|1≤x≤2}D. {x|x≥3,或x<−2}5.已知m∈R,则“m>14”是“方程x2+x+m=0有实数根”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分又不必要条件6.若m>0,n>0,且3m+2n−1=0,则3m +2n的最小值为( )A. 20B. 12C. 16D. 257.实数a,b,c满足a2=2a+c−b−1且a+b2+1=0,则下列关系成立的是( )A. b>a≥cB. c>a>bC. b>c≥aD. c>b>a8.已知集合A={x|x2−x−2≤0},B={x|2a<x<a+3},若A∩B=⌀,则实数a的取值范围是( )A. (−∞,−4)∪(3,+∞)B. (−∞,−4]∪[3,+∞)C. (−∞,−4)∪(1,+∞)D. (−∞,−4]∪[1,+∞)二、多选题:本题共3小题,共18分。
高一10月份月考(地理)试题含答案
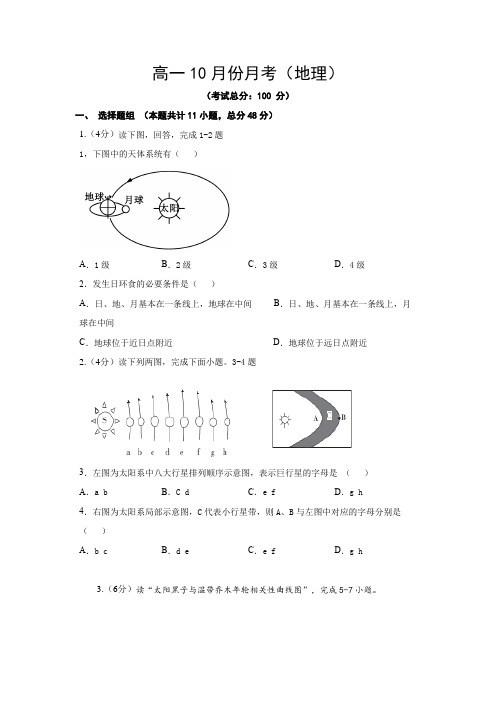
高一10月份月考(地理)(考试总分:100 分)一、选择题组(本题共计11小题,总分48分)1.(4分)读下图,回答,完成1-2题1,下图中的天体系统有()A.1级B.2级C.3级D.4级2.发生日环食的必要条件是()A.日、地、月基本在一条线上,地球在中间B.日、地、月基本在一条线上,月球在中间C.地球位于近日点附近D.地球位于远日点附近2.(4分)读下列两图,完成下面小题。
3-4题3.左图为太阳系中八大行星排列顺序示意图,表示巨行星的字母是()A.a b B.C d C.e f D.g h4.右图为太阳系局部示意图,C代表小行星带,则A、B与左图中对应的字母分别是()A.b c B.d e C.e f D.g h3.(6分)读“太阳黑子与温带乔木年轮相关性曲线图”,完成5-7小题。
5.图中年轮宽度与太阳黑子相对数之间的关系是()A.正相关B.负相关C.成反比D.没有相关性6.此图所反映的问题是()A.太阳活动能影响地球气候B.太阳活动发射的电磁波能扰动地球的电离层C.太阳活动时,抛出的带电粒子流扰动地球磁场,产生“磁暴”现象D.太阳活动时,太阳风使两极地区出现极光,从而影响中高纬度地区树木的生长7.太阳活动的周期大约是()A.5年B.11年C.37年D.76年4.(4分)下图为地质时期(局部)全球气温、降水量变化示意图。
据此完成8-9小题。
8.裸子植物繁盛时期全球气候特征是()A.总体比较湿润B.总体比较寒冷C.冷暖干湿交替D.温暖干旱明显9.在图示甲时期()A.被子开始出现B.是铁、金等矿藏重要的成矿时期C.大陆冰川覆盖面积广D.地壳运动剧烈,联合古陆开始解体5.(4分)北京时间2016年11月25日22时24分在新疆克孜勒苏州阿克陶发生6.7级地震,震中位于北纬39.27度,东经70.04度,震源深度10千米,地震已造成人员伤亡。
据此完成10-11小题。
10.此次地震岩层的断裂处位于()A.地壳中B.上地幔中C.下地幔中D.地核中11.这次地震震中的在家看电视的人们感到()A.先上下颠簸,后水平晃动B.只有水平晃动,没有上下颠簸C.先水平晃动,后上下颠簸D.只有上下颠簸,没有水平晃动6.(4分)读“联合古陆示意图”,回答13~14题。
辽宁省大连市滨城联盟2024-2025学年高一上学期10月月考英语试题

滨城高中联盟2024-2025学年度上学期高一10月份考试英语试卷第一部分听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A. £19.15.B. £9.18.C. £9.15.答案是C。
1. 【此处可播放相关音频,请去附件查看】What are the speakers talking about?A. What cake to make.B. What gift to buy.C. What event to celebrate.2. 【此处可播放相关音频,请去附件查看】What will the woman do tonight?A. Go to the theater.B. Get a ticket.C. Study for a test.3. 【此处可播放相关音频,请去附件查看】What does the man advise the woman to do?A. Apply for the position first.B. Pay a visit to the company.C. Call her workmates.4. 【此处可播放相关音频,请去附件查看】Why is the man late?A. He got lost.B. He had to get changed.C. He was trapped in heavy traffic.5. 【此处可播放相关音频,请去附件查看】What are the speakers going to do?A. Catch a bus.B. Wait for Janie.C. Eat at a restaurant.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
福建省福州市2024-2025学年高一上学期10月份第一次月考数学模拟试卷(解析版)

2024-2025学年福州市高一上学期第一次月考数学模拟试卷总分150分;考试时间120分钟;一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列各组对象中不能组成集合的是( ).A .2023年男篮世界杯参赛队伍B .中国古典长篇小说四大名著C .高中数学中的难题D .我国的直辖市【答案】C【分析】根据组成集合的要素之确定性即可得解.【详解】A ,B ,D 所表示的对象都能确定,能组成集合,选项C 高中数学中的难题,怎样算难题不能确定,不能组成集合,故选:C .2. 已知M,N 都是U 的子集,则图中的阴影部分表示( )A. M ∪NB. ∁U (M ∪N)C. (∁U M)∩ND. ∁U (M∩N)【答案】B【分析】观察图形可知,图中非阴影部分所表示的集合是A B ∪,从而得出图中阴影部分所表示的集合.【详解】由题意,图中非阴影部分所表示的集合是A B ∪,所以图中阴影部分所表示的集合为A B ∪的 补集,即图中阴影部分所表示的集合为()U C A B ,故选B.【点睛】本题主要考查集合的venn 图的表示及应用,其中venn 图既可以表示一个独立的集合,也可以表示集合与集合之间的关系,熟记venn 图的含义是解答的关键.3.若集合{}1,2,3A =,(){},|40,,Bx y x y x y A =+−>∈,则集合B 的真子集个数为( ) A .5B .6C .7D .8 【答案】C 【分析】先用列举法求出集合B ,在根据真子集的公式21n −求解.【详解】由题意可知()()(){}2,3,3,2,3,3B =,所以集合B 的真子集个数为3217−=个.故选:C4.已知集合{}12A x x =−<<,{}01B x x =<<,则( ) A .A B >B .A ⊆BC .B ⊆AD .A B = 【答案】C【分析】根据子集包含关系得到答案. 【详解】{}{}0112x x x x <<⊆−<<,故B ⊆A .故选:C5.已知命题3:0,p x x x ∀≥>,命题2:0,10q x x ∃<+>,则( )A .p 和q 均为真命题B .p ¬和q 均为真命题C .p 和q ¬均为真命题D .p ¬和q ¬均为真命题 【答案】B【分析】直接判断命题的真假,再根据命题的否定可判断.【详解】对于命题p ,当1x =时,3x x =,所以p 为假命题,则p ¬为真命题;对于命题q ,当1x =−时,210x ,所以q 为真命题.综上,p ¬和q 均为真命题.故选:B.6.设,a b ∈R ,则“1a <且1b <”是“2a b +<”的( ).A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【答案】A【分析】根据题意结合充分、必要条件分析判断.【详解】若1a <且1b <,则2a b +<,即充分性成立;若2a b +<,例如1,0a b ==,满足2a b +<,但不满足1a <且1b <,即必要性不成立;综上所述:“1a <且1b <”是“2a b +<”的充分不必要条件.故选:A.7.227x x +的最小值为( )A .B .C .D .【答案】B 【分析】利用基本不等式即可得解.【详解】由题意知0x ≠,所以2270,0x x >>,所以227x x +≥当且仅当227x x =,即2x 时,等号成立. 故选:B.8.若关于x 的方程()2210mx m x m +−+=有两个不相等的实数根,则实数m 的取值范围是( ).A .14m <B .14m >C .14m <且0m ≠ D .14m >且0m ≠ 【答案】C 【分析】根据给定条件,列出不等式组并求解即得.【详解】由方程()2210mx m x m +−+=有两个不相等的实数根,得()220Δ2140m m m ≠ −−> , 即410m −+>,解得14m <,因此14m <且0m ≠, 所以实数m 的取值范围是14m <且0m ≠. 故选:C二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.下列说法正确的是( )A .“11a b>”是“a b >”的充分不必要条件B .“A =∅”是“A B ∩=∅”的充分不必要条件C .若,,R a b c ∈,则“22ab cb >”的充要条件是“a c >”D .若,R a b ∈,则“220a b +≠”是“0a b +≠”的充要条件【答案】BD【分析】根据已知条件及特殊值法,结合充分条件必要条件的定义即可求解.【详解】对于A 选项,当2,3a b ==时, 11;23a b ><,当1,2a b =−=−时, 11212−>−−>−,,所以两者既不充分也不必要,故A 错误;对于B 选项,当A B ∩=∅时,可取}{}{1,2A B ==,但A ≠∅,当A =∅时,A B ∩=∅,故 B 正确; 对于C 选项,当 22ab cb >时, 20b >,从而a c >,反之,a c >时,若0b =,则 22ab cb =,所以两者不是充要条件,故 C 错误;对于D 选项,220,0a b a +≠≠且00b a b ≠⇔+≠,故D 正确,故选:BD .10.下列命题中,是真命题的有( )A .集合{}1,2的所有真子集为{}{}1,2B .若{}{}1,2,a b =(其中,a b ∈R ),则3a b +=C .{x x 是等边三角形}⊆}D .{}{}3,6,x x k k x x z z =∈⊆=∈N N【答案】BC【分析】根据真子集的定义即可判断A ;根据等集的定义即可判断B ;根据子集的定义即可判断CD.【详解】集合{}1,2真子集是∅,{}{}1,2共3个,所以A 为假命题;由{}{}1,2,a b =,知2a =,1b =,则3a b +=,则B 为真命题; 等边三角形是特殊的等腰三角形,所以C 为真命题;{}623,x x z z z ==×∈N ,所以{}{}6,3,x x z z x x k k =∈⊆=∈N N ,所以D 为假命题.故选:BC.11.若关于x 的一元二次不等式()20,,R ax bx c a b c ++>∈的解集为{}23x x −<<,则( )A .0a >B .0bc >C .0a b +=D .0a b c −+>【答案】BCD 【分析】抓住一元二次方程、一元二次不等式和一元二次函数“三个二次”的关系分析,结合图象即可一一判断.【详解】对于A ,由题意,结合二次函数2y ax bx c ++的图象知,抛物线开口应向下,则a<0,故A 错误;对于B ,依题意,a<0,且一元二次方程20ax bx c ++=的两根为2−和3, 由韦达定理,2323b a c a −+=− −×=,故0b a =−>,60c a =−>,即0bc >,故B 正确; 对于C ,由上分析可得0a b +=,故C 正确; 对于D ,由上分析可得()(6)40a b c a a a a −+=−−+−=−>,故D 正确.故选:BCD.12. 对于非空数集M ,定义()f M 表示该集合中所有元素的和.给定集合 1,2,3,4S ,定义集合(){},T f A A S A ⊆≠∅,则下列说法正确的是( )A. 7T ∈B. 8T ∉C. 集合T 中有10个元素D. 集合T 中有11个元素 【答案】AC【分析】列举出集合A ,求出对应的()f A 的值,可得出集合T ,即可得出合适的选项.【详解】A S ⊆ 且A ≠∅.①当A 为单元素集合时,集合A 可取{}1、{}2、{}3、{}4,()f A 可取1、2、3、4;②当A 中的元素个数为2时,集合A 可取{}1,2、{}1,3、{}1,4、{}2,3、{}2,4、{}3,4,()f A 可取3、4、5、6、7;③当A 中的元素个数为3时,集合A 可取{}1,2,3、{}1,2,4、{}1,3,4、{}2,3,4,()f A 可取6、7、8、9;④当A S =时,()10f A =.综上所述,{}1,2,3,4,5,6,7,8,9,10T =,AC 选项正确,BD 选项错误.故选:AC.三、填空题:本大题共4小题,每小题5分.13. 命题“x ∀∈R ,240x x −+≥”的否定为______.【答案】x ∃∈R ,240x x −+<【分析】利用全称量词命题的否定求解.【详解】由于全称量词命题的否定是存在量词命题,所以命题“x ∀∈R ,240x x −+≥”的否定为“x ∃∈R ,240x x −+<”.故答案为:x ∃∈R ,240x x −+<14.集合{}2|40A x x =−=的子集个数是 .【答案】4【分析】首先求集合,然后再求集合的子集个数.【详解】由x 2-4=0,解得:x =±2,故A ={2,-2},故子集的个数是22=4个.故答案为:4.【点睛】本题考查空集和子集个数,属于基础题.15. 已知0a >,则91a a ++的最小值是______. 【答案】5【分析】构造基本不等式求出最小值即可.【详解】由题意可得,99111511a a a a +=++−≥=++,当且仅当911a a +=+,即2a =时,等号成立.故答案为:5.16.不等式2320x x −++>的解集为 .【答案】2,13 −【分析】利用十字相乘法因式分解,即可解得;【详解】解:由2320x x −++>得232(1)(32)0x x x x −−=−+<,解得213x −<< 所以不等式2320x x −++>的解集为2,13 −. 故答案为:2,13 −.【点睛】本题考查一元二次不等式的解法,属于基础题.四、解答题:本大题共6个大题,共70分.解答应写出文字说明、证明过程或演算步骤. 17. 已知关于x 不等式:()23130ax a x −++<. (1)当2a =−时,解此不等式;(2)当0a >时,解此不等式.【答案】(1)1{|2x x <−或}3x > (2)当13a =时,解集为∅;当103a <<时,解集为1{|3}x x a<<;当13a >时,解集为1{|3}x x a << 【分析】(1)利用一元二次不等式的解法解出即可; (2)不等式可变形为(x -3)(x -1a )<0,然后分a =13、0<a <13、a >13三种情况讨论即可. 【小问1详解】当a =-2时,不等式-2x 2+5x +3<0整理得(2x +1)(x -3)>0,解得x <-12或x >3,当a =-2时,原不等式解集为{x |x <-12或x >3}.【小问2详解】当a >0时,不等式ax 2-(3a +1)x +<0整理得:(x -3)(x -1a )<0, 当a =13时,1a =3,此时不等式无解; 当0<a <13时,1a >3,解得3<x <1a ; 当a >13时,1a <3,解得1a <x <3; 综上:当a =13时,解集为∅; 当0<a <13时,解集为{x |3<x <1a }; 当a >13时,解集为{x |1a <x <3}. 18. 已知集合{}{}25,123A x x B x m x m =−≤≤=−≤≤+.(1)若4m =,求A B ∪;的(2)若A B B = ,求实数m 的取值范围.【答案】(1){}|211x x −(2)()[],41,1−∞−−【分析】(1)4m =时,求出集合B ,由此能求出A B ∪;(2)由A B B = 可得B A ⊆,当B =∅时,123m m −>+,当B ≠∅时,12312235m m m m −+ −− +,由此能求出实数m 的取值范围.【小问1详解】解:4m =时,集合{}|25A x x =− ,{}|311B x x = ,{}|211A B x x ∴=− .【小问2详解】解:A B B = ,B A ∴⊆,∴当B =∅时,123m m −>+,解得4m <−,当B ≠∅时,12312235m m m m −+ −− +,解得11m − , ∴实数m 的取值范围是()[],41,1−∞−− .19. 已知实数a >0,b >0,a +2b =2(1)求12a b+的最小值; (2)求a 2+4b 2+5ab 的最大值.【答案】(1)92; (2)92. 【分析】(1)利用12112(2)2a b a b a b +=++ 转化为用基本不等式求解; (2)22245(2)4a b ab a b ab ab ++=++=+,根据a +2b =2利用基本不等式求出ab 范围即可.【小问1详解】12112122(2)522b a a b a b a b a b +=++=++∵0,0a b >>,∴1221955222b a a b ++≥+= , 当且仅当22b a a b=,即23a b ==时,等号成立. ∴12a b +的最小值为92; 【小问2详解】∵22245(2)4a b ab a b ab ab ++=++=+,又22a b +=≥12≤ab ,故224219452a b ab ++≤+=, 当且仅当2a b =,即11,2a b ==时,等号成立. 故2245a b ab ++取得最大值92. 20. 某公司建造一间背面靠墙的房屋,地面面积为248m ,房屋正面每平方米的造价为1200元,房屋侧面每平方米的造价为8005800元,如果墙高为3m ,且不计房屋背面和地面的费用,那么怎样设计房屋能使总造价最低?最低总造价是多少?【答案】当房屋的正面边长为8m ,侧面边长为6m 时,房屋总造价最低,为63400元.【分析】设房屋的正面边长为xm ,侧面边长为y m ,总造价为z 元,由题意得出48xy =,然后根据题意得出z 关于x 的函数表达式,利用基本不等式可求出z 的最小值,利用等号求出对应的x 值,综合可得出结论.【详解】设房屋正面边长为xm ,侧面边长为y m ,总造价为z 元,则48xy =,即48y x=,5760043120068005800360058005800z x y x x ×=⋅+⋅+=++≥63400=. 当5760043600x x×=时,即当8x =时,z 有最小值,最低总造价为63400元. 答:当房屋的正面边长为8m ,侧面边长为6m 时,房屋总造价最低,为63400元.【点睛】本题考查基本不等式的应用,在利用基本不等式时,要注意等号成立的条件,考查计算能力,属的于基础题.21. 已知命题:p x ∃∈R ,240x x m −+=为假命题. (1)求实数m 的取值集合B ;(2)设{}34A x a x a =<<+,若x B ∈是x A ∈的必要不充分条件,求实数a 的取值范围.【答案】(1){}4Bm m => (2)43a a≥【分析】(1)由题意可得Δ0<,即可求得集合B ; (2)分析可知A B ,分A =∅、A ≠∅两种情况讨论,可得出关于实数a 的不等式(组),综合可得出实数a 的取值范围.【小问1详解】 解:由题意可得1640m ∆=−<,解得4m >,故{}4B m m =>.【小问2详解】解:由题意可知A B . 当A =∅时,则34a a ≥+,解得2a ≥,此时A B 成立; 当A ≠∅时,则3434a a a <+ ≥ ,解得423a ≤<. 综上所述,实数a 的取值范围是43a a≥. 22. 已知集合2{|320,R,R}A x ax x x a =−+=∈∈. (1)若A 是空集,求a 的取值范围;(2)若A 中只有一个元素,求a 的值,并求集合A ; (3)若A 中至多有一个元素,求a 的取值范围【答案】(1)9,8 +∞(2)a 的值为0或98,当0a =时23A = ,当98a =时43A =第11页/共11页(3)9{0},8∞ ∪+【分析】(1)A 是空集,则方程为二次方程,且方程无实根;(2)A 中只有一个元素,则方程为一次方程,或方程为二次方程且方程有两个相同的根; (3)A 中至多有一个元素,则方程为一次方程,或方程为二次方程且至多一个实根.【小问1详解】A 是空集,0a ∴≠且Δ0<,980a ∴−<,解得98a >, a ∴的取值范围为:98+∞(,); 【小问2详解】当0a =时,集合2{|320}3A x x=−+==, 当0a ≠时,Δ0=,980a ∴−=,解得98a =,此时集合43A =, 综上所求,a 的值为0或98,当0a =时,集合23A = ,当98a =时,集合43A =; 【小问3详解】 由12(),()可知,当A 中至多有一个元素时,98a ≥或0a =, a ∴的取值范围为:{}90[8+∞ ,).。
2021届高一上学期 第一学期10月月考(10月份月考)(word含答案版)

高一上学期第一学期10月月考第Ⅰ卷(选择题共40分)本卷共20小题,每小题2分。
在每小题列出的四个选项中,选出符合题目答案的一项。
可能用到的相对原子质量:Na 23 H 1 O 16 C 121. (2020·福建惠安中学月考)用下图表示的一些物质或概念间的从属关系不正确的是( )2.在①化合反应②分解反应③置换反应④复分解反应四种基本反应类型中,可以生成水的是( )A.只有②③B.只有①④C.只有①②④D.①②③④3.(2020·武汉期末)磁流体是电子材料的新秀,它既具有固体的磁性,又具有液体的流动性。
磁流体的分散质粒子直径在5.5~36nm之间。
下列说法正确的是( )A.所得的分散系属于悬浊液B.该分散系能产生丁达尔效应C.所得的分散系中水是分散质D.将所得分散系过滤,在滤纸上能得到分散质4.下列离子能大量共存的是( )A.使无色酚酞溶液呈红色的溶液中:Na+、K+、SO2-4、CO2-3B.无色透明的溶液中:Cu2+、K+、SO2-4、NO-3C.含有大量Ba(NO3)2的溶液中:Mg2+、NH+4、SO2-4、Cl-D.使紫色石蕊溶液呈红色的溶液中:Na+、K+、CO2-3、NO-35.下列离子方程式正确的是( )A.二氧化碳与足量澄清石灰水反应:CO2+2OH-===CO2-3+H2OB.将稀硫酸滴在铜片上:Cu+2H+===Cu2++H2↑C.碳酸氢钠溶液与稀H2SO4反应:CO2-3+2H+===H2O+CO2↑D.氯化镁溶液与氢氧化钠溶液反应:Mg2++2OH-===Mg(OH)2↓6.对四组无色透明溶液进行离子检验,四位同学各鉴定一组,他们的实验报告的结论如下,其中可能正确的是( )A.MnO-4、K+、S2-、Na+B.Mg2+、NO-3、OH-、Cl-C.K+、H+、Cl-、CO2-3D.Na+、OH-、Cl-、NO-37.按照物质的组成和性质进行分类,HNO3应属于①酸②氧化物③无氧酸④挥发性酸⑤化合物⑥混合物⑦纯净物⑧一元酸A.③④⑤⑦ B.②③④⑤ C.①④⑤⑦⑧ D.②⑤⑥⑦⑧8.下列化学反应中,不.属于氧化还原反应的是A.Cl2+H2O == HCl+HClO B.C +2H2SO4(浓)∆==CO2↑+ 2SO2↑+ 2H2OC.NH4Cl ∆== NH3↑+ HCl↑ D.2Al + Fe2O3高温==== 2Fe + Al2O39. 下列操作过程中一定有氧化还原反应发生的是10. 下列基本反应类型中,一定是氧化还原反应的是A. 复分解反应B.分解反应C.化合反应D. 置换反应11.右图为反应Fe + CuSO4 === Cu + FeSO4中电子转移的关系图,则图中的元素甲、乙分别表示A.Fe,SB.Fe,CuC.Fe,OD.Cu,S12.下列关于分散系的说法正确的是A. 稀硫酸、盐酸、空气和水等都是分散系B. 区分溶液和浊液一般用丁达尔现象C. 分散系中分散质粒子直径由大到小的顺序是:浊液、胶体、溶液D. 按稳定性由弱到强的顺序排列的是溶液、胶体、浊液(以水为分散剂时)13. 某一化学兴趣小组的同学在家中进行实验,按照图示连接好线路,发现图B中的灯泡亮了。
2024-2025学年福建省福州市福建师大附中高一(上)月考数学试卷(10月份)(含答案)

2024-2025学年福建师大附中高一(上)月考数学试卷(10月份)一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合A ={0,1},B ={1,2},则A ∪B 中元素的个数为( )A. 1B. 2C. 3D. 42.设集合M ={x|x 2−x ≥0},N ={x|x <2},则M ∩N =( )A. {x|x ≤0}B. {x|1≤x <2}C. {x|x ≤0或1≤x <2}D. {x|0≤x ≤1}3.函数f(x)= 3x −9的定义域为( )A. [−3,+∞) B. [−2,+∞) C. [2,+∞) D. [4,+∞)4.已知函数f(x)=ln x−ax 2+ax 恰有两个零点,则实数a 的取值范围为( )A. (−∞,0)B. (0,+∞)C. (0,1)∪(1,+∞)D. (−∞,0)∪{1}5.偶函数f(x)在区间[0,a](a >0)是单调函数,且满足f(0)⋅f(a)<0,则函数f(x)在区间[−a,a]内零点的个数是( )A. 1B. 2C. 3D. 46.已知函数f(x)={|log 3x|,x >0x 2+4x +1,x ≤0,函数F(x)=f(x)−b 有四个不同的零点x 1,x 2,x 3,x 4,且满足:x 1<x 2<x 3<x 4,则x 4x 3−x 1x 23+x 2x 232的取值范围是( )A. [2 2,+∞) B. (3,839] C. [3,+∞) D. [2 2,839]7.定义域R 的函数f(x)满足f(x +2)=3f(x),当x ∈[0,2]时,f(x)=x 2−2x ,若x ∈[−4,−2]时,f(x)≥118(3t −t)恒成立,则实数t 的取值范围是( )A. (−∞,−1]∪(0,3]B. (−∞,− 3]∪(0, 3]C. [−1,0)∪[3,+∞)D. [− 3,0)∪[ 3,+∞)8.设函数f(x)的定义域为R ,且f(x)=13f(x +1),当x ∈(−1,0]时,f(x)=x(x +1),若对任意x ∈(−∞,m],都有f(x)≥−8116,则实数m 的取值范围是( )A. (−∞,73]B. (−∞,114]C. (−∞,94]D. (−∞,3]二、多选题:本题共3小题,共18分。
2025-届高一年级10-月份教学质量检测物理

2025届高一年级10月份教学质量检测物理考试时间 75 分钟 姓名:___________班级:___________一、单选题(本大题共8 小题,每题4 分,共32 分,每道题仅有一个选项正确)1.下列关于运动的描述中,叙述正确的是()A .“太阳东升西落”,是以太阳为参考系的B .“明月松间照,清泉石上流”,是以明月为参考系的C .物体运动的轨迹是直线还是曲线,与参考系的选取有关D .诗句“卧看满天云不动,不知云与我俱东”中“云与我俱东”是以船为参考系的2.著名电动车制造商特斯拉预计今年年底推出新的自动驾驶系统“Autopilot ”。
该系统允许汽车在更复杂路况中使用定速巡航。
在某次测试中,测试车辆以时速120公里行驶了1200公里。
其中“时速120公里”、“行驶1200公里”分别是指()A.速度、位移 B.速度、路程 C.速率、位移 D.速率、路程3.一质点做单向直线运动,在前13路程内平均速率为v ,后23路程内平均速率为2v ,则该质点在全程的平均速度大小为()A .v B .32v C .43v D .65v 4.关于速度、速度的变化量和加速度的关系,以下说法正确的是()A.当速度的变化量的方向为正方向时,加速度的方向可能为负方向B.物体的加速度不断减小,速度一定越来越小C.速度不为零时,加速度一定不为零D.加速度不断增加,而速度可能越来越小5.一质点做直线运动的频闪照片如图所示,由此可以断定该质点的()A.加速度向左B.加速度向右C.速度向左D.速度向右6.汽车以15m/s 的速度在马路上匀速行驶,驾驶员发现正前方21m 处的斑马线上有行人,于是匀减速刹车礼让,汽车恰好停在斑马线前,假设驾驶员反应时间为0.4s 。
则汽车的加速度大小为()A.215m/s B.210m/s C.27.5m/s D.25m/s7.从地面以初速度0v 竖直向上抛出一小球A ,与此同时,在该小球上抛能到达的最高处有另外一个小球B 以初速度02v 竖直向下抛出。
山西省运城市2023-2024学年高一上学期10月月考试题 化学含解析

山西2023~2024年度教育发展联盟高一10月份调研测试化学(答案在最后)考生注意:1.本试卷满分100分,考试时间75分钟。
2.答题前,考生务必用直径0.5毫米,黑色,墨水签字笔将密封线内项目填写清楚。
3.考生作答时,请将答案答在答题卡上。
选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;非选择题请用直径0.5毫米,黑色,墨水签字笔在答题卡上各题的答题区域内作答,超出答题区域书写的答案无效,在试题卷、草稿纸上作答无效。
4.本卷命题范围:必修第一册第一章第1节到第3节结束。
5.可能用到的相对原子质量:H-1C-12O-16Na-23Cl-35.5一、单项选择题(本题共9小题,每小题3分,共27分。
在每小题给出的四个选项中只有一项是符合题目要求的)1.中华文化博大精深,下列诗文中隐含化学变化的是A.花气袭人知骤暖,鹊声穿树喜新晴B.千淘万漉虽辛苦,吹尽狂沙始到金C.炉火照天地,红星乱紫烟D.日照香炉生紫烟,遥看瀑布挂前川2.下列关于物质的分类正确的是分类碱酸碱性氧化物酸性氧化物纯净物A CH3CH2OH H2SO4Na2O CO氯水B Na2CO3HCl CuO SO3液氯C NaOH CH3COOH Mn2O7SO2盐酸D KOH HNO3CaO CO2胆矾A.AB.BC.CD.D3.下列有关胶体的说法正确的是A.有色玻璃属于固溶胶,分散剂为玻璃B.Fe(OH)3胶体制备的方程式为FeCl3+3H2O=Fe(OH)3↓+3HClC.德尔塔新冠病毒有可能在空气中以气溶胶的形式传播,气溶胶不属于胶体D.胶体区别于其他分散系的本质特征是能产生丁达尔效应4.在焊接铜器时常用NH4Cl溶液除去铜器表面的氧化铜,其反应为CuO+NH4Cl→Cu+CuCl2+N2+H2O(未配平)。
下列说法正确的是A.该反应中NH4Cl被氧化,发生还原反应B.该反应中氧化剂和还原剂的个数之比为2:1C.该反应中产生1个氮气分子时,转移3个电子D.该反应中被还原的CuO占参与反应的CuO的3 45.下列工业生产过程中,必需加入氧化剂才能实现的是A.由H2O2制备O2B.由Cl-制备Cl2C.由Na2CO3制备BaCl2D.由Fe3+制备Fe2+6.常温下,下列各组离子在指定溶液中一定能大量共存的是A.澄清透明的溶液中:H+、Fe2+、SO24-、Cl-B.使石莣变红的溶液中:Ca2+、NH4+、CO23-、SO24-C.BaCl2溶液中:K+、Na+、OH-、Ag+D.使pH试纸变蓝的溶液中:NH4+、HCO3-、Cl-、K+7.下列说法或者有关化学用语的描述正确的是A.氨水能导电,所以氨水是电解质B.固态氯化氢不导电,液态氯化氢可以导电C.NaHSO4在水中的电离方程式为NaHSO4=Na++H++SO24-D.电解质溶于水形成的溶液一定能导电,非电解质溶于水形成的溶液一定不能导电8.下列离子组加入相应试剂后,发生反应的离子方程式正确的是选项离子组加入试剂离子方程式A Mg2+、SO24-Ba(OH)2溶液SO24-+Ba2+=BaSO4↓B H+、Cl-足量石灰乳2H++2OH-=2H2OC K+、HCO3-NaHSO4溶液CO23-+2H+=H2O+CO2↑D Na+、H+、SO24-少量CuO CuO+2H+=Cu2++H2OA.AB.BC.CD.D9.下列化学方程式中,表示电子转移的方向和数目都正确的是A.B.C.D.二、不定项选择题(本题共4小题,每小题4分,共16分。
湖南省长沙市2024-2025学年高一上学期10月月考数学试题含答案

2024年下学期10月份考试试卷高一数学(答案在最后)时量:120分钟分值:150分命题人:一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列表示集合6N N A x x ++⎧⎫=∈∈⎨⎬⎩⎭和(){}22536B x x x=+=关系的Venn 图中正确的是()A.B.C.D.【答案】A 【解析】【分析】依题意可求得集合,A B ,根据集合中的元素可判断两集合之间的关系.【详解】根据题意由6N ,N x x++∈∈可得1,2,3,6x =,即{}1,2,3,6A =;解方程()22536x x+=可得256x x +=或256x x +=-,解得1x =或6x =-或2x =-或3x =-,即可得{}1,2,3,6B =---;因此可得集合,A B 有交集,但没有包含关系.故选:A2.如果对于任意实数x ,[]x 表示不超过x 的最大整数,例如[]π3=,[]0.60=,[]1.62-=-,那么“1x y -<”是“[][]x y =”的().A.充分条件B.必要条件C.充分必要条件D.既不充分也不必要条件【答案】B 【解析】【分析】举出反例得到充分性不成立,再设[][]x y k ==,得到1k x k ≤<+,1k y k ≤<+,故1x y -<,必要性成立,得到答案.【详解】不妨设 1.6, 2.5x y ==,满足1x y -<,但[][]1,21.6 2.5==,不满足[][]x y =,充分性不成立,若[][]x y =,不妨设[][]x y k ==,则1k x k ≤<+,1k y k ≤<+,故1x y -<,必要性成立,故“1x y -<”是“[][]x y =”的必要条件.故选:B3.已知命题p :x ∀∈R ,01xx >-,则p ⌝为().A.x ∀∈R ,01xx ≤- B.x ∃∈R ,01xx ≤-C.x ∀∈R ,01xx ≤-或10x -= D.x ∃∈R ,01xx ≤-或10x -=【答案】D 【解析】【分析】利用全称命题的否定求解即可.【详解】由全称命题的否定是特称命题知:原命题的否定为x ∃∈R ,01xx ≤-或10x -=.故选:D4.若正实数x ,y 满足40x y xy +-=,则t xy =的取值范围为()A.{|04}t t <≤B.{|2}t t ≥C.{|4}t t ≥D.{|16}t t ≥【答案】D 【解析】【分析】由基本不等式得到4x y +≥,求出答案.【详解】正实数x ,y 满足40x y xy +-=,则4x y +≥,当且仅当x y =时取等号,所以t xy =,即xy ≥,即t ≥,两边平方,结合0t >,解的16t ≥.故选:D.5.已知命题2:,230p x ax x ∀∈++>R 为真命题,则实数a 的取值范围是()A.1|02a a ⎧⎫<≤⎨⎩⎭B.1|03a a ⎧⎫<<⎨⎬⎩⎭C.1|3a a ⎧⎫≥⎨⎬⎩⎭D.1|3a a ⎧⎫>⎨⎬⎩⎭【答案】D 【解析】【分析】问题转化为不等式2230ax x ++>的解集为R ,根据一元二次不等式解集的形式求参数的值.【详解】因为命题2:,230p x ax x ∀∈++>R 为真命题,所以不等式2230ax x ++>的解集为R .所以:若0a =,则不等式2230ax x ++>可化为230x +>⇒32x >-,不等式解集不是R ;若0a ≠,则根据一元二次不等式解集的形式可知:20Δ2120a a >⎧⎨=-<⎩⇒13a >.综上可知:13a >故选:D6.若实数αβ,满足1312αβ-<<<-,则αβ-的取值范围是()A.1312αβ-<-<-B.250αβ-<-<C.10αβ-<-<D.11αβ-<-<【答案】C 【解析】【分析】根据不等式的性质及题中条件即可得到结果.【详解】因为αβ<,所以0αβ-<,又1312α-<<-,1312β-<<-,所以1213β<-<所以11αβ-<-<,故10αβ-<-<,故选:C7.关于x 的一元二次不等式()()()2120x a x a --+->⎡⎤⎣⎦,当01a <<时,该不等式的解集为()A.2|21a x x x a -⎧⎫><⎨⎬-⎩⎭或 B.2|21a x x a -⎧⎫<<⎨⎬-⎩⎭C.2|21a x x x a -⎧⎫<>⎨⎬-⎩⎭或 D.2|21a x x a -⎧⎫<<⎨⎬-⎩⎭【答案】B 【解析】【分析】由01a <<,知10a -<,原不等式等价于()2201a x x a -⎛⎫--< ⎪-⎝⎭,再确定相应二次方程的根的大小得不等式的解集.【详解】由01a <<,则10a -<,原不等式等价于不等式()2201a x x a -⎛⎫--< ⎪-⎝⎭的解集,又由01a <<,则方程()2201a x x a -⎛⎫--= ⎪-⎝⎭的两根分别为1222,1a x x a -==-,当01a <<时,221a a -<-,故原不等式的解集为2|21a x x a -⎧⎫<<⎨⎬-⎩⎭.故选:B8.已知长为a ,宽为b 的长方形,如果该长方形的面积与边长为1k 的正方形面积相等;该长方形周长与边长为2k 的正方形周长相等;该长方形的对角线与边长为3k 的正方形对角线相等;该长方形的面积和周长的比与边长为4k 的正方形面积和周长的比相等,那么1k 、2k 、3k 、4k 大小关系为()A.1423k k k k ≤≤≤B.3124k k k k ≤≤≤C.4132k k k k ≤≤≤D.4123k k k k ≤≤≤【答案】D 【解析】【分析】先求出21ab k =,22a b k +=3=,2442k aba b k =+,然后利用基本不等式比较大小即可.【详解】由题意可得,21ab k=①,22a b k +=3=③,2442k aba b k =+④,且,0a b >,由基本不等式的关系可知,a b +≥a b =时等号成立,由①②得,2122k k ≥,所以21k k ≥⑤,因为()22222()22+=++≤+a b a b ab a b,所以222()2a b a b ++≥,当且仅当a b =时等号成立,由②③得,2223422k k ≥,所以32k k ≥⑥,又2ab aba b ≤=+,当且仅当a b =时等号成立,由①④得,241422k kk ≤,所以41k k ≤⑦,综合⑤⑥⑦可得,4123k k k k ≤≤≤.故选:D .二、多项选择题:本大题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求.全部选对得6分,部分选对得部分分,有选错的得0分.9.下列说法不正确的是()A.“a b <”是“11a b>”的必要不充分条件B.若1x y +=,则xy 的最大值为2C.若不等式20ax bx c ++>的解集为{|13}x x <<,则230a b c ++<D.命题“R x ∃∈,使得210x +=.”的否定为“R x ∀∉,使得210x +≠.”【答案】ABD 【解析】【分析】根据充分条件和必要条件的定义判断A ,消元,根据二次函数性质判断B ,根据一元二次不等式的解集与二次方程的关系求,,a b c 的关系,由此判断23a b c ++的正负,判断C ,根据含量词的命题的否定方法判断D.【详解】对于A ,取1a =-,1b =,则a b <,但11a b<,取1a =,1b =-,则11a b>,但a b >,所以“a b <”是“11a b>”的既不充分也不必要条件,A 错误;对于B ,因为1x y +=,所以()2211124xy x x x x x ⎛⎫=-=-+=--+ ⎪⎝⎭,所以xy 的最大值为14,B 错误;因为不等式20ax bx c ++>的解集为{|13}x x <<,所以0a <,且1,3为方程20ax bx c ++=的根,所以13b a +=-,13c a⨯=,所以4b a =-,3c a =,所以238920a b c a a a a ++=-+=<,C 正确;命题“R x ∃∈,使得210x +=.”的否定为“R x ∀∈,使得210x +≠.”D 错误;故选:ABD.10.已知正数a ,b 满足238a b +=,则下列说法正确的是()A.83ab ≤ B.227a b +>C.224932a b +≥ D.11126436a b a b +≥++【答案】ACD 【解析】【分析】由已知条件结合基本不等式及相关结论检验选项A,C,D ,举出反例检验选项B ,即可判断.【详解】对于A ,因为823a b =+≥,故83ab ≤,当且仅当23,238a b a b =+=,即42,3a b ==时等号成立,故A 正确;对于B ,当2,1b a ==时,2267a b +=<,B 显然错误;对于C ,因为22249(23)12641232a b a b ab ab +=+-=-≥,当且仅当42,3a b ==时等号成立,故C 正确;对于D ,由238a b +=可得()6932324a b a b +=+=,即()264324a b a b +++=,所以111264326432643242643a b a b a b a b a b a b a b a b ++++++⎛⎫+=+ ⎪++++⎝⎭143261122242643246a b a b a b a b ⎛++⎛⎫=++≥+= ⎪ ++⎝⎭⎝当且仅当2643a b a b +=+,即42,3a b ==时等号成立,故D 正确.故选:ACD.11.对于一个非空集合B ,如果满足以下四个条件:①(){},,B a b a A b A ⊆∈∈,②(),,a A a a B ∀∈∈,③,a b A ∀∈,若(),a b B ∈且(),b a B ∈,则a b =,④,,a b c A ∀∈,若(),a b B ∈且(),b c B ∈,则(),a c B ∈,就称集合B 为集合A 的一个“偏序关系”,以下说法正确的是()A.设{}1,2A =,则满足是集合A 的一个“偏序关系”的集合B 共有3个B.设{}1,2,3A =,则集合()()()()(){}1,1,1,2,2,1,2,2,3,3B =是集合A 的一个“偏序关系”C.设{}1,2,3A =,则含有四个元素且是集合A 的“偏序关系”的集合B 共有6个D.(){},R,R,R a b a b a b =∈'∈≤是实数集R 的一个“偏序关系”【答案】ACD 【解析】【分析】A 选项,分析出()()1,1,2,2B ∈,分析③可知,()1,2和()2,1只能二选一,或两者均不能在B 中,从而得到足是集合A 的一个“偏序关系”的集合B 共有3个;B 选项,()1,2B ∈且()2,1B ∈,但12≠,B 错误;C 选项,分析出()()()1,1,2,2,3,3B ∈,再添加一个元素即可,从而得到答案;D 选项,通过分析均满足四个条件,D 正确.【详解】A 选项,{}1,2A =,则(){}()()()(){},,1,1,1,2,2,1,2,2a b a A b A ∈∈=,通过分析②可知,()()1,1,2,2B ∈,分析③可知,()1,2和()2,1只能二选一,或两者均不能在B 中,取()(){}1,1,2,2B =,或()()(){}1,1,2,2,1,2B =,或()()(){}1,1,2,2,2,1B =,故满足是集合A 的一个“偏序关系”的集合B 共有3个,A 正确;B 选项,集合()()()()(){}1,1,1,2,2,1,2,2,3,3B =,()1,2B ∈且()2,1B ∈,但12≠,故②不成立,故BC 选项,{}1,2,3A =,通过分析②可知,()()()1,1,2,2,3,3B ∈,结合③和④,可再添加一个元素,即()()()()()()1,2,2,1,1,3,3,1,2,3,3,2中任选一个,即取()()()(){}1,1,2,2,3,3,1,2B =,或()()()(){}1,1,2,2,3,3,1,3B =,或()()()(){}1,1,2,2,3,3,2,3B =,或()()()(){}11,1,2,2,3,3,,2B =,或()()()(){}11,1,2,2,3,3,,3B =,或()()()(){}21,1,2,2,3,3,,3B =,共6个,C 正确;D 选项,(){},R,R,R a b a b a b =∈'∈≤是R 的子集,满足①,且当a b =时,()R,,a a a R '∀∈∈,满足②,当a b =时,满足③,,,R a b c ∀∈,若(),a b R '∈且(),b c R '∈,则,a b b c ≤≤,所以a c ≤,则(),a c R ∈',满足④,故(){},R,R,R a b a b a b =∈'∈≤是实数集R 的一个“偏序关系,D 正确.故选:ACD三、填空题:本题共3小题,每小题5分,共15分.12.设,a b ∈R ,集合{}1,,0,b a b a a ⎧⎫+⊇⎨⎬⎩⎭,则a b +=______【答案】0【解析】【分析】根据ba可知0a ≠,故0a b +=.【详解】由ba可知0a ≠,又{}1,,0,b a b a a ⎧⎫+⊇⎨⎬⎩⎭,故0a b +=.故答案为:013.已知条件:30p x ⌝-<<,条件:q x a ⌝>,且q 是p 的充分不必要条件,则a 的取值范围是_________.【答案】(],3-∞-.【分析】根据充分、必要条件的定义及命题的否定形式计算参数范围即可.【详解】由题设得:0p x ≥或3x ≤-,设P ={0x x ≥或3x ≤-},同理可得:q x a £,设{}Q x x a =≤,因为q 是p 的充分不必要条件,所以Q P ⊆,因此3a ≤-.故答案为:(],3-∞-.14.出入相补是指一个平面(或立体)图形被分割成若干部分后面积(或体积)的总和保持不变,我国汉代数学家构造弦图,利用出入相补原理证明了勾股定理,我国清代的梅文鼎、李锐、华蘅芳、何梦瑶等都通过出入相补原理创造了不同的面积证法证明了勾股定理.在下面两个图中,若AC b =,()BC a b a =≥,AB c =,图中两个阴影三角形的周长分别为1l ,2l ,则12l l a b++的最小值为________.【答案】12+【解析】【分析】根据图形中的相似关系先表示出12l l +,然后利用基本不等式求解出最小值.【详解】如图1,易知BDE V ∽ACB △,且BD CD BC b a =-=-,所以1l BD b a AC b a b c -==++,所以()1b al a b c b-=⨯++;如图2,易知GFH ∽ACB △,且FG a =,所以2l FG a AC b a b c ==++,所以()2al a b c b=⨯++,所以22221222112l l a b c a b a b a b a b a b a b ab+++++==+=++++++221121ab a b =+++,又因为222a b ab +≥,所以2221ab a b +≤,当且仅当a b =时取等号,所以121211112l l a b +≥+=+++,所以最小值为212+,故答案为:212+.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.已知{|23}A x x =-≤≤,{|53}B x a x a =-<<,全集R U =.(1)若12a =,求A B ,A B ⋂;(2)若()U B A B =ðI ;求实数a 的取值范围.【答案】(1)9|32A B x x ⎧⎫⋃=-<≤⎨⎬⎩⎭,3|22A B x x ⎧⎫⋂=-≤<⎨⎬⎩⎭,(2)283a a a ⎧⎫≤-≥⎨⎬⎩⎭或【解析】【分析】(1)由条件根据集合运算法则求A B ,A B ⋂即可;(2)由条件可得U B A ⊆ð,根据集合包含关系列不等式可求a 的取值范围.【小问1详解】因为12a =,所以93{|53}|22B x a x a x x ⎧⎫=-<<=-<<⎨⎬⎩⎭,又{|23}A x x =-≤≤,所以9|32A x x B ⎧⎫-<≤=⎨⎬⎩⎭ ,3|22A B x x ⎧⎫=-≤<⎨⎬⎩⎭ ,【小问2详解】因为()U B A B =ðI ,所以U B A ⊆ð,因为{|23}A x x =-≤≤,所以{2U A x x =<-ð或}3x >,又{|53}B x a x a =-<<,当B =∅时,U B A ⊆ð,此时35a a ≤-,接的52a ≤-,当B ≠∅时,由U B A ⊆ð,可得3532a a a >-⎧⎨≤-⎩或3553a a a >-⎧⎨-≥⎩,所以5223a -<≤-或8a ≥,综上23a ≤-或8a ≥.所以a 的取值范围23a a ⎧≤-⎨⎩或}8a ≥.16.(1)设a b c d ,,,均为正数,且a b c d +=+,证明:若ab cd >>(2)已知,,a b c 为正数,且满足1abc =,证明:222111a b c a b c ++≤++.【答案】(1)证明见解析(2)证明见解析【解析】【分析】(1)先对(2)利用基本不等式结合1abc =可证得结论【详解】(1)因为222a b c d =++=++又因为,0a b c d ab cd +=+>>,,,a b c d >为正数,所以22>,>(2)因为2222222,2,2a b ab b c bc c a ac +≥+≥+≥,当且仅当a b c ==时,取等号,又1abc =,故有222111ab bc ca a b c ab bc ca abc a b c++++≥++==++.所以222111a b c a b c ++≤++,当且仅当1a b c ===时取等号.17.已知p :2280x x +-≤,q :()22210x m x m m -+++≤.(1)若q 是p 的充分不必要条件,求实数m 的取值范围;(2)若q 是p 的既不充分也不必要条件,求实数m 的取值范围.【答案】(1)41m -≤≤(2)1m >或4m <-【解析】【分析】(1)解不等式化简命题,p q ,由充分不必要条件列出不等式求解;(2)根据命题,p q 的关系,可得对应集合互不包含,列出不等式求解.【小问1详解】由2280x x +-≤,可得42x -≤≤,则p :42x -≤≤,又由()22210x m x m m -+++≤,可得1m x m +≤≤,则q :1m x m +≤≤,若q 是p 的充分不必要条件,可得[],1m m +是[]4,2-的真子集,有412m m ≥-⎧⎨+≤⎩,解可得41m -≤≤;【小问2详解】若q 是p 的既不充分也不必要条件,则[],1m m +和[]4,2-互不包含,可得12m +>或4m <-,解得1m >或4m <-.18.某蛋糕店推出两款新品蛋糕,分别为薄脆百香果蛋糕和朱古力蜂果蛋糕,已知薄脆百香果蛋糕单价为x 元,朱古力蜂果蛋糕单位为y 元,现有两种购买方案:方案一:薄脆百香果蛋糕购买数量为a 个,朱古力蜂果蛋糕购买数量为b 个,花费记为1S ;方案二:薄脆百香果蛋糕购买数量为b 个,朱古力蜂果蛋糕购买数量为a 个,花费记为2S .(其中4,4y x b a >>>>)(1)试问哪种购买方案花费更少?请说明理由;(2)若a ,b ,x ,y 同时满足关系4224y x b a a =-=+-,求这两种购买方案花费的差值S 最小值(注:差值S =花费较大值-花费较小值).【答案】(1)采用方案二;理由见解析(2)24【解析】【分析】(1)列出两种方案的总费用的表达式,作差比较,即可求解;(2)根据题意,得到214((4S S x a a -=-⋅+-,利用换元法和基本不等式,即可求解.【小问1详解】解:方案一的总费用为1S ax by =+(元);方案二的总费用为2S bx ay =+(元),由21()()()()()S S bx ay ax by a y x b x y y x a b -=+-+=-+-=--,因为4,4y x b a >>>>,可得0,0y x a b ->-<,所以()()0y x a b --<,即210S S -<,所以21S S <,所以采用方案二,花费更少.【小问2详解】解:由(1)可知()()(1244S S y x b a x a a ⎛⎫-=--=-⋅+⎪-⎝⎭,令t =,则24x t =+,所以2224(1)33x t t t -=-+=-+≥,当1t =时,即5x =时,等号成立,又因为4a >,可得40a ->,所以44(4)44844a a a a +=-++≥=--,当且仅当444a a -=-时,即6,14a b ==时,等号成立,所以差S 的最小值为2483=⨯,当且仅当5,8,6,14x y a b ====时,等号成立,所以两种方案花费的差值S 最小为24元.19.已知集合{}()*1,2,3,,2N ,4n S n n n =∈≥ ,对于集合n S 的非空子集A ,若n S 中存在三个互不相同的元素,,a b c ,使得,,+++a b b c c a 均属于A ,则称集合A 是集合n S 的“期待子集”.(1)试判断集合{}{}123,4,5,3,5,7A A ==是否为集合4S 的“期待子集”;(直接写出答案,不必说明理由)(2)如果一个集合中含有三个元素,,x y z ,同时满足①x y z <<,②x y z +>,③x y z ++为偶数.那么称该集合具有性质P .对于集合n S 的非空子集A ,证明:集合A 是集合n S 的“期待子集”的充要条件是集合A 具有性质P .【答案】(1)1A 是集合4S 的“期待子集”,2A 不是集合4S 的“期待子集”(2)证明见解析【解析】【分析】(1)根据所给定义判断即可.(2)先证明必要性,再证明充分性,结合所给“期待子集”的定义及性质P 的定义证明即可;【小问1详解】因为{}41,2,3,4,5,6,7,8S =,对于集合{}13,4,5A =,令345a b b c c a +=⎧⎪+=⎨⎪+=⎩,解得213a b c =⎧⎪=⎨⎪=⎩,显然41S ∈,42S ∈,43S ∈所以1A 是集合4S 的“期待子集”;对于集合2{3,5,7}A =,令111111357a b b c c a +=⎧⎪+=⎨⎪+=⎩,则111152a b c ++=,因为4111,,a b c S ∈,即111N *a b c ++∈,故矛盾,所以2A 不是集合4S 的“期待子集”【小问2详解】先证明必要性:当集合A 是集合n S 的“期待子集”时,由题意,存在互不相同的,,n a b c S ∈,使得,,a b b c c a A +++∈,不妨设a b c <<,令x a b =+,y a c =+,z b c =+,则x y z <<,即条件P 中的①成立;又()()()20x y z a b c a b c a +-=+++-+=>,所以x y z +>,即条件P 中的②成立;因为()()()()2x y z a b c a b c a b c ++=+++++=++,所以x y z ++为偶数,即条件P 中的③成立;所以集合A 满足条件P .再证明充分性:当集合A 满足条件P 时,有存在A ∈x,y,z ,满足①x y z <<,②x y z +>,③x y z ++为偶数,记2x y z a z ++=-,2x y z b y ++=-,2x y z c x ++=-,由③得,,Z a b c ∈,由①得a b c z <<<,由②得02x y z a z ++=->,所以,,n a b c S ∈,因为a b x +=,a c y +=,b c z +=,所以a b +,b c +,c a +均属于A ,即集合A 是集合n S 的“期待子集”【点睛】关键点睛:涉及集合新定义问题,关键是正确理解给出的定义,然后合理利用定义,结合相关的其它知识,分类讨论,进行推理判断解决.。
辽宁省县域重点高中协作体2024-2025学年高一上学期10月份质量监测数学试卷(含解析)

辽宁省县域重点高中协作体高一10月份质量监测数学本试卷满分150分,考试时间120分钟.注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.2.答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.答非选择题时,将答案写在答题卡上.写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列关系正确的是( )A. B. C. D.2.命题“,”的否定为( )A.,B.,C.,D.,3.已知集合,,若,则m 的取值范围为( )A. B. C. D.4.已知,,则( )A. B. C. D.5.“”是“”的( )A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件6.已知关于x 的不等式的解集为,则m 的取值范围为( )A. B. C. D.7.公园的绿化率是指绿化面积与公园的面积之比.已知某公园的面积为,绿化面积为,现对该公园再扩建面积,其中绿化面积为,则扩建后公园的绿化率与原来公园的绿化率相比( )A.变大B.变小C.当时,变大D.当时,变大2π∈Q0∉N 4-∉Z 2024-∈R 0x ∃>210x ->0x ∀>210x -≤0x ∀≤210x -≤0x ∀≤210x ->0x ∃≤210x -≤{}A x x m =<()5,7B =-B A ⊆()5,-+∞[)5,-+∞()7,+∞[)7,+∞a c >b d >ab cd>a c b d >a b c d +>+a b c d ->-2x <311,240x x x +>+⎧⎨-<⎩240mx x m -+≥R (),2-∞(],2-∞()2,+∞[)2,+∞2m a ()2m0b b a <<22m x 22m x 2a b >2a b <8.已知某班有50名同学,据统计发现同学们喜爱的第33届巴黎奥运会的比赛项目都集中在乒乓球、跳水、射击这三个比赛项目.13名同学只喜欢乒乓球比赛,10名同学只喜欢跳水比赛,8名同学只喜欢射击比赛,同时喜欢乒乓球与跳水比赛的同学有14名,喜欢乒乓球与射击比赛的同学有11名,喜欢跳水与射击比赛的同学有10名,则该班同时喜欢乒乓球、跳水、射击比赛的同学有( )A.8人B.7人C.6人D.5人二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.9.下列命题为真命题的是( )A.,B.,C.,D.,10.已知全集,,,则( )A. B.C. D.11.已知,,关于x 的不等式在上恒成立,则( )A. B.C.不等式的解集为(0,1) D.不等式的解集为三、填空题:本题共3小题,每小题5分,共15分.12.已知非零实数x ,y ,z 满足,则_______.13.已知集合,,且,则__________;__________.14.记表示x ,y 中较大的数,已知x ,y 均为正数,则的最小值为_______.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(13分)已知集合,,.(1)用列举法表示集合U ;(2)求.16.(15分)按要求完成下面问题:(1)已知,,求的取值范围;0x ∃>3x x=0x ∀>2x x >x ∀∈R 2570x x -+>0x ∃<20x x -<U =R {}32A x x =-<<{}14B x x =<<()3,4A B =- (][)U ,14,B =-∞+∞ ð()()[)U ,24,A B =-∞+∞ ð()()(][)U U ,34,A B =-∞-+∞ ðða ∈R 0b >()()22320x x x a b ----≥R 2a =02b <<2bx a -<02x b ax -≥-()[),14,-∞+∞ 20,0,x y x z -=⎧⎨-=⎩2x z y z -=+{}1,4A ={}20B x x mx n =++=A B A B = m =n ={}max ,x y 4max ,x y y x ⎧⎫⎨⎬⎩⎭{}3126U x x =∈-≤N {}2,4,6,8B ={}3,C x x k k ==∈Z ()U B C ð14a <<21b -<<-2a b +(2)已知,证明:“”是“”的充要条件.17.(15分)已知集合,,甲、乙求解时,甲因看错a ,求出,乙因看错b ,求出,且甲、乙计算过程正确.(1)求a ,b 的值;(2)已知,求.18.(17分)已知全集,集合.(1)求集合M ;(2)若,,求m 的最大值(3)若关于x 的不等式的解集为N ,且“”是”的充分不必要条件,求a 的取值范围.19.(17分)已知,.(1)若,证明:;(2)若,求的最小值;(3)若恒成立,求x 的取值范围.0a bc ++=2220a b c ++=0ab bc ac ++=(){},23M x y x ay =-=(){},1N x y bx y =+=M N (){}2,5M N =- (){}1,5M N =-- (){}22,5Q x y x y =-=-N Q U =R {}2U 2320M x x x =-->ð[]2,1A m m =-+()U A M =R ð()2220x a x a -++≤x N ∈x M ∈0a >0b >22a b +=12ab ≤02a <<142a a+-(()0b x a b +-+≤参考答案及解析一、选择题1.D 【解析】因为是无理数,所以也是无理数,所以,A 项错误自然数集包含元素0,所以,B 项错误;表示整数集,所以,C 项错误;-2024是实数,所以,D 项正确.故选D 项.2.A 【解析】存在量词命题的否定为全称量词命题,所以“,”的否定为,.故选A 项.3.D 【解析】如图所示,由,得.故选D 项.4.C 【解析】当,,,时,,,此时,A 项错误;当,,,时,,,此时,B 项错误;根据不等式的性质及,,可知,C 项正确;当,,,时,,,此时,D 项错误.故选C 项.5.B 【解析】由得,由“”推不出“”,充分性不成立;由“”可推出“”,必要性成立.综上,“是”的必要不充分条件.故选B 项.6.D 【解析】当时,,解得,不合题意;当时,解得.故选D 项.7.C 【解析】原来公园的绿化率为,扩建后公园的绿化率为,则,所以扩建后公园的绿化率与原来公园的绿化率相比的变化情况与,的大小有关,A ,B 项错误;π2π2π∉Q N 0∈N Z 4-∈Z 2024-∈R 0x ∃>210x ->0x ∀>210x -≤B A ⊆7m ≥1a =-2c =-1b =-2d =-1ab =4cd =ab cd <2a =1c =2b =1d =1a b =1c d =a c b d=a c >b d >a b c d +>+2a =1c =2b =1d =0a b -=0c d -=a b c d -=-311,240,x x x +>+⎧⎨-<⎩02x <<2x <02x <<02x <<2x <2x <311,240x x x +>+⎧⎨-<⎩0m =40x -≥0x ≤0m ≠()20,440,m m m >⎧⎪⎨--⨯⨯≤⎪⎩2m ≥b a 2b x a x++()()()()()22222a b x b a x a b x b x b a x a a a x a a x +-+-+-==+++a 2b当时,,则扩建后公园的绿化率与原来公园的绿化率相比变大,C 项正确;当时,,则扩建后公园的绿化率与原来公园的绿化率相比变小,D 项错误.故选C 项.8.A 【解析】如图,设该班同时喜欢乒乓球、跳水、射击比赛的同学有x 人,由图可知,解得.故选A 项.二、选择题9.AC 【解析】当时,,,使得成立,所以命题“,”为真命题,A 项正确;当时,,,则,所以命题“,”为假命题,B 项错误;因为,所以命题“,”为真命题,C 项正确;当时,,,所以,则命题“,”为假命题,D 项错误.故选AC 项.10.BCD 【解析】因为,,所以,A 项错误;因为,,所以,B 项正确;又,所以,C 项正确;因为,所以,D 项正确.故选BCD 项.11.ACD 【解析】由,解得或,由,解得,2a b >02b x b a x a+->+2a b <02b x b a x a +-<+(14)(11)(10)5010138x x x x -+-+-+=---8x =1x =3311x ==1x =3x x =0x ∃>3x x =12x =214x =12x =2x x <0x ∀>2x x >225357024x x x ⎛⎫-+=-+> ⎪⎝⎭x ∀∈R 2570x x -+>0x <20x >0x ->20x x ->0x ∃<20x x -<{}32A x x =-<<{}14B x x =<<()1,2A B = U =R {}14B x x =<<(][)U ,14,B =-∞+∞ ð{}32A x x =-<<()()[)U ,24,A B =-∞+∞ ð(][)U ,32,A =-∞-+∞ ð()()(][)U U ,34,A B =-∞-+∞ ðð2230x x --≥1x ≤-3x ≥2230x x --≤13x -≤≤由,解得或,由,解得,要满足题意,则解得,,A 项正确,B 项错误;不等式化为,则,解得,所以不等式的解集为(0,1),C 项正确;不等式化为,即解得或,所以不等式的解集为,D 项正确.故选ACD 项.三、填空题12.【解析】由得,,所以.13.-5 4【解析】由可知,则解得,.14.2【解析】设,中较大的数为M ,则,,所以,则,当且仅当,即时取得等号.四、解答题15.解:(1).(2)由,,得,又,所以.16.(1)解:因为,所以,又,所以,20x a b --≥2a b x -≤2a b x +≥20x a b --≤22a b a b x -+≤≤1,23,2a b a b -⎧=-⎪⎪⎨+⎪=⎪⎩2a =4b =2bx a -<211x -<1211x -<-<01x <<2bx a -<02x b ax -≥-4022x x -≥-()()2240,220,x x x ⎧--≥⎨-≠⎩1x <4x ≥02x b ax -≥-()[),14,-∞+∞ 13-20,0,x y x z -=⎧⎨-=⎩2y x =z x =22123x z x x y z x x --==-++A B A B = A B =14,14,m n +=-⎧⎨⨯=⎩5m =-4n =x y 4y x x M y≤4y M x ≤424x y M y x ≥+≥=2M ≥224x y =2x y ={}{}{}312690,1,2,3,4,5,6,7,8,9U x x x x =∈-≤=∈≤=N N {}0,1,2,3,4,5,6,7,8,9U ={}2,4,6,8B ={}U 0,1,3,5,7,9B =ð{}{}3,,3,0,3,6,9,12,C x x k k ==∈=⋅⋅⋅-⋅⋅⋅Z (){}U 0,3,9B C = ð14a <<228a <<21b -<<-027a b <+<故的取值范围为(0,7).(2)证明:先证充分性:因为,所以,所以,,,故.再证必要性:因为,所以,因为,所以,即,所以.综上,“”是“”的充要条件.17.解:(1)由题意可知解得,.(2)由(1)可知,由整理得,解得,,将其代入中,得,,故.18.解:(1)由,解得或,所以,故.(2)由(1)可知,又,,2a b +2220a b c ++=0a b c ===0ab =0bc =0ac =0ab bc ac ++=0ab bc ac ++=2220ab bc ac ++=0a b c ++=()20a b c ++=2222220a b c ab bc ac +++++=2220a b c ++=2220a b c ++=0ab bc ac ++=251,2(1)53,b a -+=⎧⎨⨯-+=⎩1a =2b =(){},21N x y x y =+=225,21,x y x y ⎧-=-⎨+=⎩23440x x --=123x =-22x =21x y +=173y =23y =-()27,,2,333N Q ⎧⎫⎛⎫=--⎨⎬ ⎪⎝⎭⎩⎭22320x x -->12x <-2x >U 122M x x x ⎧⎫=<->⎨⎬⎩⎭或ð122M x x ⎧⎫=-≤≤⎨⎬⎩⎭U 122M x x x ⎧⎫=<->⎨⎬⎩⎭或ð[]2,1A m m =-+()U A M =R ð所以解得,故m 的最大值为.(3)由“”是“”的充分不必要条件,可知.由,得.当时,,显然不满足;当时,,显然满足;当时,,要满足,则,所以.综上,的取值范围为.19.(1)证明:因为,,所以,故,当且仅当,即,时取等号.(2)解:因为,所以,则,当且仅当,即时取得等号,故的最小值为.(3)解:因为,,所以,则可化为恒成立.12,212,m m ⎧-≤-⎪⎨⎪+≥⎩312m ≤≤32x N ∈x M ∈N M Þ()2220x a x a -++≤()()20x a x --≤2a >{}2N x x a =≤≤N M Þ2a ={}2N =N M Þ2a <{}2N x a x =≤≤N M Þ12a >-122a -<<a 1,22⎛⎤- ⎥⎝⎦0a >0b >22a b =+≥≤12ab ≤2a b =1a =12b =02a <<20a ->()141142222a a a a a a ⎛⎫+=++-⎡⎤ ⎪⎣⎦--⎝⎭()124119555422222a a a a ⎛-⎛⎫=++≥+=⨯+= ⎪ -⎝⎭⎝242a a a a -=-23a =142a a +-920a >0b >0b +>(()0b x a b +-+≤x ≤又,当且仅当时取得等号,,则,故的取值范围为.()22b b a b a b +≤++=+2a b =()122a b a b +≥=+12x ≤x 1,2⎛⎤-∞ ⎥⎝⎦。
2024-2025学年江苏省盐城市五校联盟高一(上)第一次学情调研数学试卷(10月份)(含答案)

2024-2025学年江苏省盐城市五校联盟高一(上)第一次学情调研数学试卷(10月份)一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.集合M ={x|−1<x <1},N ={x|0≤x <2},则M ∩N =( )A. {x|−1<x <2}B. {x|0≤x <1}C. {x|0<x <1}D. {x|−1<x <0}2.不等式(x−1)(x−3)≤0的解集是( )A. (−∞,1)∪(3,+∞)B. (−∞,1]∪[3,+∞)C. (1,3)D. [1,3]3.命题p :∀x >2,x 2−1>0,则¬p 是( )A. ∀x >2,x 2−1≤0B. ∀x ≤2,x 2−1>0C. ∃x >2,x 2−1≤0D. ∃x ≤2,x 2−1≤04.若a ∈R ,则a =2是(a−1)(a−2)=0的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件5.下列结论正确的是( )A. 若a >b >0,则ac 2>bc 2B. 若ab >0,a >b ,则1a <1bC. 若a >b ,c >d ,则a−c >b−dD. 若a >b ,m >0,则b +m a +m >b a 6.已知t >0,则函数y =t 2−4t +1t 的最小值为( )A. −4 B. −2 C. 0 D. 27.设集合A ={x|2a <x <a +2},B ={x|x <−3或x >5},若A ∩B =⌀,则实数a 的取值范围为( )A. [−32,+∞)B. (−32,+∞)C. (−∞,−32]D. (−∞,−32)8.若两个正实数x ,y 满足4x +y =xy 且存在这样的x ,y 使不等式x +y 4<m 2+3m 有解,则实数m 的取值范围是( )A. (−1,4)B. (−4,1)C. (−∞,−4)∪(1,+∞)D. (−∞,−3)∪(0,+∞)二、多选题:本题共3小题,共18分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013年12月庄河第四高级中学阶段性检测题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间100分钟.
第Ⅰ卷(选择题,共60分) 一、选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知全集(}.7,5,3,1{},6,4,2{},7.6,5,4,3,2,1{ A B A U 则===B C U )等于( )
A .{2,4,6}
B .{1,3,5}
C .{2,4,5}
D .{2,5}
2.集合{}0,1,2A =的真子集的个数是( )
A. 16
B. 8
C. 7
D.4
3.下列图形中,不可能是函数y=f(x)图像的是 ( )
4.给出下列四个对应,其中构成映射的是 ( )
x y
x x
x
y
y
y
A B
C
D
1 2 3
4 5
1
2 3 4
5 6
1 2
3 4 5
1 2 3 4
5 6 7 8
B.只有①④ ② ③
④
A.只有①② ①
5.下列四组函数中,表示同一个函数的是 ( ) A.2()||,()f x x g t t ==
B. 22()()()f x x g x x ==,
C.21()()11x f x g x x x -=
=+-, D. 0
()()1f x x g x ==,
6.下列函数中,y 随x 的增大而增大的是 ( )
A. 4y x =-
B. 104
x y =- C. 13y x =-- D.
13y x = 7.2
,2,
()(4)],2,
x x f x f x x -≤⎧=-=⎨>⎩设则f[ ( ) A. 4 B. 16 C. -4 D. -16 8.1
(
)34,()2
x f x f x +=+已知则的解析式是() A.()51f x x =+ B. ()32f x x =+ C. ()61f x x =+ D.
9.
14)(2
+-=mx x x f ,当2-≥x 时y 随着x 的增大而增大 ,当2-≤x 时y 随着x 的增大而减小,则)1(f 的值等于( )
A. 13
B. 1
C. 21
D. 3- 10.已知函数y f x =+()
1定义域是[]-23,,则()y f x =的定义域是( ) A []05
2
, B []-14, C []-55, D []-37,
11.用集合语言表示图中阴影部分正确的是( )
A. ()()U A B C A B
B. U C B A
C. ()
U C A B A D.()()U C A B A B
C.只有①②④
D.只有③④
U
A B
12.已知22(1)()(12)2(2)x x f x x x x x +≤-⎧⎪
=-<<⎨⎪≥⎩
,若()3f x =,则x 的值是( )
A 1
B 1或
32 C 1,3
2
或3± D 3 第Ⅱ卷(非选择题 共90分)
二、填空题:本大题4小题,每小题5分,共20分. 把正确答案填在答题卡上。
13. 已知一一映射:(,)(,),f x y x y x y →+-则(3,5)的原象是____________ 14. 已知函数[]()34-10,5f x x =-的值域为,则其定义域为__________________ 15.已知2()1,(31)f x x f x =++则的解析式是_________________________
16.2
()f x x bx c =++对于任意的实数x,都有f(1+x)=f(-x),问
(2),(2),(0)f f f -的大小关系为____________________________
三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.
17.(本小题10分)
已知二次函数的图象经过(1,0),(0,-2),(3,0)三点,求其解析式。
18.(本小题12分)
设集合{}{}
2
1,3,a ,1,1,,A B a a B A a ≠
==-+⊂且求的值。
19.(本小题12分)下列不等式的解集
2
2(1
260,(2)3100
x x x x --≥-++>)
20.(本小题12分)已知二次函数
222y x x =-+
[]
[)(1).(2).3,0(3).3,3x x ∈∈-∈-当x R 时,求f(x)的值域?
当时,求f(x)的值域?当时,求f(x)的值域?
21.(本小题12分)
21,3,21,x y x --⎧⎪
=⎨⎪+⎩画出2,-21,1,x x x ≤-<<≥的图象,并用图象说出它的值域。
22.(本小题12分)出租汽车收费办法是:行驶里程在3千米以内(含3千米)按7元收费;超过3千米,在5千米(含5千米)以内,每千米按1.8元加收;超过5千米,每千米按2.4元加收。
列出分段函数方程式
2013年10月庄河第四高级中学阶段性检测题答案
一.选择题
1 2 3 4 5 6 7 8 9 10 11 12 A C D B A D B C C B A D
二.填空题
13____(4,-1)__________ 14______[-2,3]____________
15_2
(31)962f x x x +=++_ 16_(2)(2)(0)f f f ->>_____
三.解答题
17.(本小题10分)
12=()()()(0,2)()(01)(03)2
2
(632)
()3
f x f x f x f x a a f x ∴=-∴=--=-=-=-解法一:设f(x)a(x-x )(x-x ).................2分过(1,0),(3,0)a(x-1)(x-3)又
过分
22(1)(3)
28
() 2 (233)
=.........................................2()(1,0),(0,2),(3,0)02..................930x x f x x x ax bx c f x a b c c a b c --=-+-++-++=⎧⎪
∴=-⎨⎪++=⎩
整理得:分
解法二:设f(x)分过三点
2............................................2238.. (43228)
() 2 (33)
a b c f x x x ⎧=-⎪⎪
⎪
⇒=⎨⎪
=-⎪⎪⎩
∴=-+-分分
...........2分
18.(本小题12分)
{}{}{}{}{}2222
1311321
213,2,13-113,-1,132113,1()
21B A
a a a a a a a a a a B B A
a B B A
a a a a a B A
≠
≠
≠
≠
⊂∴-+=-+=-+===-==⊂==⊂-+=∴==-⊂解:或1)当时或当时,A=,,满足当时,A=,,满足)当时a=1
当a=1时,A=,与集合中元素互异性矛盾a=1舍综上所述,当或时
19.(本小题12分)
222603
(,][2,)
2
(2)31003100(35)(2)05
(,2)
3
x x x x x x x x x --≥≥∴∈-∞-+∞-++>--<+-<∴∈-(1)2x 解(2x+3)(x-2)0解:
20.(本小题12分)
22
min 2
2
max min 4412(2)1
441
[1,)
b 2(2)=-1221b 4-=24(3)2(3)21702a
c b a y x a ac b a a
x -⨯⨯--===⨯∴∈+∞-=-=⨯-∈=--⨯-+===∈对解:(1)由题意:a=1,b=-2,c=2a>0,开口向上,二次函数有最小值。
y 由题意:顶点坐标(,)(1,1)
如图,当x [-3,0]时,在x=-3时取最大值,y 当时取最小值,y 即:当x [-3,0]min max [2,17](3)1317[1,17)
y x y ∈∈==-=∈∈时,如图,当x [-3,3)时,在x=1时取最大值,y 当时取最小值,y 即:当x [-3,3)时,
21.(本小题12分)
[3,)y ∈+∞
-3 -2 -1 0 1 2 3
1
-2 -1 0 1 2
3
-1
x
y
22.(本小题12分)
y 解:设汽车行驶的里程为x 千米,则出租汽车收费为元7,
1.6 1.8,
2.4 1.4,x x ⎧⎪
+⎨⎪-⎩
由题意:y=3355x x x ≤<≤>。
