五年级上《不规则图形的面积》练习题及答案
五年级奥数题解第二讲《不规则图形面积的计算(二)》[1]
![五年级奥数题解第二讲《不规则图形面积的计算(二)》[1]](https://img.taocdn.com/s3/m/a6f6887aa26925c52cc5bf54.png)
第二讲不规则图形面积的计算(二)不规则图形的另外一种情况,就是由圆、扇形、弓形与三角形、正方形、长方形等规则图形组合而成的,这是一类更为复杂的不规则图形,为了计算它的面积,常常要变动图形的位置或对图形进行适当的分割、拼补、旋转等手段使之转化为规则图形的和、差关系,同时还常要和“容斥原理”合并使用才能解决。
例1:如下图(1),在一个正方形内,以正方形的三条边为直径向内作三个半圆,求阴影部分的面积。
(1)(2)解法一:把上图靠下边的半圆换成(面积与它相等)右边的半圆,得到图(2)。
这时,右图中阴影部分与不含阴影部分的大小形状完全一样,因此它们的面积相等。
所以上图中阴影部分的面积等于正方形面积的一半。
解法二:将上半个“弧边三角形”从中间切开,分别补贴在下半圆的上侧边上,如图(3)所示。
阴影部分的面积是正方形面积的一半。
(3)(4)解法三:将下面的半圆从中间切开,分别贴补在上面弧边三角形的两侧,如图(4)所示。
阴影部分的面积是正方形的一半。
例2:如下图,正方形ABCD的边长为4厘米,分别以B、D为圆心以4厘米为半径在正方形内画圆,求阴影部分面积。
解:由容斥原理,S阴影=S扇形ACB+S扇形ACD-S正方形ABCD=4π×AB2×2-AB2=4π×42×2-42=16×(2π-1)≈16×2214.3-=9.12(平方厘米)。
例3:如下图,矩形ABCD中,AB=6厘米,BC=4厘米,扇形ABE半径AE=6厘米,扇形CBF的半径CB=4厘米。
求阴影部分的面积。
EB解:S阴景=S扇形ABE+S扇形CBF-S矩形ABCD=41×π×62+41×π×42-6×4=41×π(36+16)-24=13π-24=15(平方厘米)(取π=3)例4:如下图,直角三角形ABC中,AB是圆的直径,且AB=20厘米,如果阴影(1)的面积比阴影(2)的面积大7平方厘米,求BC长。
五年级上册数学一课一练-第6单元第4课时《组合图形的面积及不规则图形的面积》

第6单元第4课时《组合图形的面积及不规则图形的面积》同步练习一、选择题。
1、如图是一个直角梯形,图中阴影部分面积是100平方厘米,空白部分面积是()平方厘米.A.140 B.120 C.100 D.702、下面三个完全一样的直角梯形中,阴影部分的面积().A.甲最大B.乙最大 C.丙最大 D.一样大3、如图的长方形的面积是96,空白部分的面积().A.24 B.32 C.484、如图,平行四边形的面积是24cm2,则阴影部分的面积是().A.2cm2B.4cm2C.10cm2D.12cm25、如图所示,正方形的边长6厘米,计算阴影部分的面积,方法正确的是().A.6×6﹣×3×3 B.6×6﹣×6×6÷2C.×3×3×2 D.3×3×÷46、图中阴影部分的面积是()平方厘米.A.24 B.28 C.327、如图阴影部分的面积是().A.36cm2B.42cm2C.48cm2D.56cm28、如图中,阴影部分的面积是()平方厘米.A.400 B.200 C.314 D.1579、估算方格纸中不规则图形的面积时,下列说法不正确的是().A、可以采用数方格的方法。
B、可以把它看成近似规则图形进行估算。
C、方格纸中每个方格的边长表示的长度越长,估算的结果也就越准确。
10、如图A、B分别是长方形长和宽的中点,阴影部分面积是长方形的().A. B. C. D.二、填一填。
1、如图,四边形ABCD是一个梯形,由三个直角三角形拼成,它的面积是平方厘米.2、如图,边长相等的两个正方形中,画了甲、乙两个三角形(用阴影表示),它们的面积相比 .3、如图中阴影部分的面积是60平方厘米,空白部分的面积是平方厘米.4、(1)亮亮刚出生时脚印的面积约 cm²(假设每个小方格的面积是1cm²)(2)亮亮5岁时脚印的面积约是 cm²。
【小学】五年级上册数学一课一练 5.4不规则图形的的面积(含答案)

五年级上册数学一课一练不规则图形的的面积一、单选题1 图形与其余2个的面积不一样大。
A B C2右图涂色部分的面积是 cm2。
A 2B 4C 63某正方形园地是由边长为1米的四个小正方形组成的,现要在园地上建一个花坛(阴影部分)使花坛面积是园地面积的一半,以下图中设计不合要求的是()A B C D4如图中阴影部分的面积是()平方厘米.(单位:厘米)A 132BC 289 D二、判断题5判断,正确的填“正确”,错误的填“错误”.两个面积相等的梯形,上底、下底和高一定相等.6下面两图中阴影部分的面积相等。
每个小方格的边长表示1cm7任何一个梯形都可以分成两个等高的三角形。
三、填空题8图中直角三角形的面积是2021厘米,阴影部分的面积是________平方厘米.(用小数表示)9按要求解答.求下面图形的面积是________ 已知条件如图中所示,单位:cm.10如图是由6个面积是1平方厘米的正方形组成的,三角形C的面积是________平方厘米,三角形A,B,C的面积和是________平方厘米,空白部分的面积是________平方厘米.11如图所示,正六边形ABCDEF的面积是36平方厘米,AG= AB,CH= CD,则四边形BCHG的面积是________平方厘米.四、解答题12计算组合图形的面积。
单位:cm13求如图图形的面积。
(合多少公顷)五、综合题14列式计算:(1)6除的商,加上3,在乘3,积是多少?(2)与的和除以它们的差的2倍,商是多少?(3)如图:三角形ABC为直角三角形,BC为圆的直径,BC=2021,S1、S2阴影部分的面积,且S1=S2,求三角形ABC的面积?六、应用题15求下面图形中阴影部分的面积.(先在图中量出并标出计算时需要的数据)参考答案一、单选题1【答案】B【解析】【解答】观察图形可知,C图形中的凸出部分可以剪拼到凹进去的部分,组成一个长方形,与A 图形的面积相等,B图形的面积与其余2个的面积不一样大故答案为:B【分析】比较图形面积的大小,可以用剪拼、平移等方法将图形进行分割与组合,然后判断大小2【答案】B【解析】【解答】解:2×2=4cm²故答案为:B【分析】把上面的半圆移动到下面,阴影部分的面积就是一个边长2cm的正方形的面积,根据正方形面积公式计算即可3【答案】B【解析】【解答】解:A、阴影部分是一个三角形,三角形的底和高都与正方形的边长相等,所以三角形面积是正方形面积的一半;符合要求;B、阴影部分的面积和是个小正方形的面积,大于大正方形面积的一半,不符合要求;C、阴影部分的面积之和相当于2个小正方形的面积,是大正方形面积的一半,符合要求;D、阴影部分重新组合后相当于两个小正方形的面积,是大正方形面积的一半,符合要求故答案为:B【分析】根据大正方形平均分的份数结合阴影部分的大小判断出阴影部分的面积相当于几个小正方形的面积即可做出选择4【答案】B【解析】【解答】解:10÷2=5(厘米)×52÷2=×25÷2=(平方厘米)10×5÷2=25(平方厘米)﹣25=(平方厘米)答:阴影部分的面积是平方厘米.故选:B.【分析】根据图可知,半圆面积﹣三角形面积=阴影面积.于是应先求出半圆面积和三角形面积,半圆的直径是10厘米,半径可求出,面积即可求得;三角形的底为10厘米,高就是圆的半径,运用三角形面积公式即可求得.进而解决问题.二、判断题5【答案】错误【解析】【解答】解答:两个面积相等的梯形,上底、下底和高不一定相等.梯形的面积相等,是用上底+下底×高÷2这个公式计算后所得的结果相等.【分析】上底、下底和高不相等的梯形,面积可能相等.6【答案】正确【解析】【解答】根据分析,作图如下:(1)2×2÷2×2=4÷2×2=4(cm2)(2)2×12×2÷2=24÷2=22=4(cm2)两图中阴影部分的面积相等,原题说法正确故答案为:正确【分析】(1)第一个图的阴影部分可以分成两个底为2厘米,高为2厘米的相等三角形,据此利用三角形的面积公式计算即可;(2)第二个图的阴影部分可以分成一个长为2厘米,宽为1厘米的长方形与一个底是2厘米,高是2厘米的三角形,将两个图形的面积相加即可得到阴影部分的面积,然后比较两个图的阴影部分的面积大小即可7【答案】正确【解析】【解答】根据梯形的定义可知,有一组对边平行的四边形叫平行四边形。
小学数学人教版(2014秋)五年级上册第六单元 多边形的面积不规则图形的面积-章节测试习题

章节测试题1.【答题】如图所示,它是由18个边长为1厘米的小正方形组成的长方形,图中阴影部分的面积是()平方厘米.A.12B.18C.5D.20【答案】C【分析】如图所示,阴影部分由①、②、③三个三角形组成,分别求出三个三角形的面积,即可得解.【解答】三角形①的面积=1×2÷2=1(平方厘米);三角形②的面积=3×2÷2=3(平方厘米);三角形③的面积=2×1÷2=1(平方厘米).阴影部分的面积=1+3+1=5(平方厘米),选C.2.【答题】下面两个图形的面积相比,()。
A.①>②B.①<②C.①=②【答案】B【分析】因为两图形都在45的网格中,哪个图形所占的格数多,哪个的面积就大,由此得出结论。
【解答】图形①在45的网格中占据9格,图形②在45的网格中占据12格;所以面积大小①<②。
3.【答题】图中整格的有______个,半格的有______个,面积约是______平方厘米.【答案】24,20,34【分析】本题考查估计不规则图形的面积.用方格纸估算不规则图形的面积,先数整格的,再数不满整格的,不满整格的按半格计算.【解答】由图可知,图中整格的有24个,半格的有20个,1个整格的面积是:1×1=1(平方厘米),24+20÷2=34(格),所以不规则图形的面积约是:34×1=34(平方厘米).故本题答案为24,20,34.4.【答题】写出下面图形的面积。
(1)______平方厘米(2)______平方厘米【答案】16,21【分析】本题考查不规则图形面积的计算。
【解答】(1)由图可知,每个小正方形的边长是1cm,则一个小正方形的面积是:1×1=1(cm²);如下图所示:将这个不规则图形分成上、下两部分,每一部分是形状相同的梯形,梯形的上底是2cm,下底是6cm,高是2cm,则梯形的面积是:(2+6)×2÷2=8×2÷2=16÷2=8(cm²);不规则图形的面积是:8×2=16(cm²);(2)图中不规则图形共占了21个小正方形,所以面积是21cm²。
《不规则立体图形的表面积和体积(一)》配套练习题

《不规则立体图形的表面积和体积(一)》配套练习题一、解答题1、如右图,在一个棱长为10的立方体上截取一个长为8,宽为3,高为2的小长方体,那么新的几何体的表面积是多少?2、在一个棱长为50厘米的正方体木块,在它的八个角上各挖去一个棱长为5厘米的小正方体,问剩下的立体图形的表面积是多少?3、从一个棱长为10厘米的正方形木块中挖去一个长10厘米、宽2厘米、高2厘米的小长方体,剩下部分的表面积是多少?(写出符合要求的全部答案)4、如图,在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体,求这个立体图形的表面积.5、如图,棱长分别为1厘米、2厘米、3厘米、5厘米的四个正方体紧贴在一起,则所得到的多面体的表面积是_______平方厘米.6、用棱长是1厘米的立方块拼成如右图所示的立体图形,问该图形的表面积是多少平方厘米?7、有30个边长为1米的正方体,在地面上摆成如图的形状,然后把露出的表面涂成红色.求被涂成红色的表面积.8、右图是一个零件的直观图.下部是一个棱长为40cm的正方体,上部是圆柱体的一半.求这个零件的表面积和体积(π=3.14).9、用铁皮做一个如图(单位:cm)所示的管道工件,需用铁皮多少平方厘米(π=3.14)?10、如图所示,三个圆柱堆放在一起,求这个立体图形的表面积和体积(单位:米)(π=3.14).答案部分一、解答题1、【正确答案】600【答案解析】我们从三个方向(前后、左右、上下)考虑,新几何体的表面积仍为原立方体的表面积:10×10×6=600.【答疑编号10296776】2、【正确答案】15000【答案解析】对于和长方体相关的立体图形表面积,一般从上下、左右、前后3个方向考虑.变化前后的表面积不变:50×50×6=15000(平方厘米).【答疑编号10296777】3、【正确答案】592平方厘米;632平方厘米;648平方厘米;672平方厘米【答案解析】按图1所示沿一条棱挖,为592平方厘米;按图2所示在某一面上挖,为632平方厘米;按图3所示在某面上斜着挖,为648平方厘米;按图4所示挖通两个对面,为672平方厘米.【答疑编号10296778】4、【正确答案】214平方分米【答案解析】我们把上面的小正方体想象成是可以向下“压缩”的,“压缩”后我们发现:小正方体的上面与大正方体上面中的阴影部分合在一起,正好是大正方体的上面.这样这个立体图形的表面积就可以分成这样两部分:上下方向:大正方体的两个底面;四周方向(左右、前后方向):小正方体的四个侧面,大正方体的四个侧面.上下方向:5×5×2=50(平方分米);侧面:5×5×4=100(平方分米),4×4×4=64(平方分米).这个立体图形的表面积为:50+100+64=214(平方分米).【答疑编号10296779】5、【正确答案】194【答案解析】(法1)四个正方体的表面积之和为:(12+22+32+52)×6=39×6=234(平方厘米),重叠部分的面积为:12×3+(22×2+12)+(32+22+12)+(32+22+12)=3+9+14+14=40(平方厘米),所以,所得到的多面体的表面积为:234-40=194(平方厘米).(法2)三视图法.从前后面观察到的面积为52+32+22=38平方厘米,从左右两个面观察到的面积为52+32=34平方厘米,从上下能观察到的面积为52=25平方厘米.表面积为(38+34+25)×2=194(平方厘米).【答疑编号10296780】6、【正确答案】46【答案解析】该图形的上、左、前三个方向的表面分别由9、7、7块正方形组成.该图形的表面积等于(9+7+7)×2=46个小正方形的面积,所以该图形表面积为46平方厘米.【答疑编号10296781】7、【正确答案】56【答案解析】4×4+(1+2+3+4)×4=56(平方米).【答疑编号10296782】8、【正确答案】11768cm2,89120cm3【答案解析】表面积=40×40×5+3.14×40×40÷2+3.14×(40÷2)2÷2×2=8000+2512+1256=11768cm2,体积=40×40×40+3.14×(40÷2)2×40÷2=64000+25120=89120cm3.【答疑编号10296783】9、【正确答案】2355cm2【答案解析】将两个同样的工件可拼成下图的圆柱体,所以一个工件需铁皮3.14×15×(46+54)÷2=2355(cm2)【答疑编号10296784】10、【正确答案】262.19平方米;240.995立方米【答案解析】表面积:[3.14×(5÷2)2×2+3.14×5×10]+3.14×3×5+3.14×2×3 =3.14×12.5+3.14×50+3.14×15+3.14×6=3.14×83.5=262.19(平方米)体积:3.14×(5÷2)2×10+3.14×(3÷2)2×5+3.14×(2÷2)2×3=3.14×62.5+3.14×11.25+3.14×3=3.14×76.75=240.995(立方米)【答疑编号10296785】。
五年级上册图形面积练习题及答案

5.1 平行四边形的面积1. 一个平行四边形的底是12厘米,高是6厘米,面积是多少平方厘米?2. 一块平行四边形的瓜地,底长16米,高13.6米,如果平均每平方米栽瓜苗35棵,共栽多少棵?3.求下面图形的面积。
4. 长方形的面积等于平行四边形的面积。
()5. 把一个长方形的框架拉成平行四边形,它的面积和周长都不变。
( )5.2 三角形的面积1. 等底等高的两个三角形面积相等。
()2.求下面图形的面积,单位分米。
3. 一个三角形的底是9厘米,高是6厘米,面积是()。
4. 两个三角形的底和高都相等,那么它们的面积相等。
()5.3 梯形的面积1. 一堆钢管,每相邻两层都相差1根,最上层2根,最下层8根,这堆钢管共()根。
2. 判断:梯形的高越长,面积就越大。
()3. 计算下列图形的面积。
(单位:米)4.利用一面墙,用篱笆围一块梯形菜地,已知篱笆全长35米,求菜地的面积是多少平方米?5.4 不规则图形的面积1. 下面图形的面积是( )平方厘米。
2. 整格()个,不满格()个,面积大约()cm2(每个小方格的面积是1 cm2)。
3. 下面图形的面积是()平方米。
4.下图中是一块不规则的土地,估一估它的面积。
1答案1. 12×6 =72(平方厘米)2. 16×13.6×35=7616(棵)3.4×2.5=10(平方厘米)2答案1. √2.8.2×7÷2=28.7(平方分米)3.27平方厘米4. √3答案1. 352. ×3. (8+12)×10÷2=100(平方米)4. 35-8=27(米) 27×8÷2=108(平方米)4答案1. 162. 18 12 223. 26004. 126平方米。
西师大版小学数学五年级上册第五单元第四课《不规则图形的面积》说课课件附板书含反思及课堂练习和答案

六、说教学过程
(一)、导入新课 1.师:同学们,我们已经学习了平行四边形、三角形、梯形面积的计算 方法,谁能说说这些图形的面积计算公式是如何推导出来的?
引导学生回顾后回答:运用转化的方法,把平行四边形、三角形、梯 形转化成我们学过的图形。 2.师:想一想,平行四边形、三角形、梯形的面积计算公式是怎样的, 并举手回答。 ①平行四边形的面积=底×高 ②三角形的面积=底×高÷2 ③梯形的面积=(上底+下底)×高÷2
(2)提问:39格与63格之间相差很大,同学们觉得这样得 出的面积数准确吗?引导学生分析得出:只按整格数,结果比
实际面积小了;把不完整的都算作整个方格数,结果比实际面 积大了。(3)追问:不满一格的应该怎样处理呢?学生讨论后 回答。学生回答预测:有的不完整的方格比半格大,有的比半 格小,所以可以把不完整的方格看作半格,这样比较合理。
本课不足的地方就是孩子们的估计值与准确数值之间还存在着一定的误差, 如何有效缩小误差的范围,还有待进一步加强。
我的说课完毕,谢谢各位老师!
七、课堂练习
1.基本图形的面积
(1)长方形的面积=( )×( )
(2)正方形的面积=( )×( )
(3)三角形的面积=( )×( )÷( )
(4)平行四边形的面积=( )×( )
(5)梯形的面积=(
)
2.实验田大约有多大?(每个方格表示1m2)分析与解答:
实验田的形状是一块不规则图形,要求出它的面积,需要把它变成规则图形来解 决,或者把实验田图纸放在透明的方格纸下,数方格。一般情况下,不完整的方 格看作半格。实验田大约占( )个方格,即( )m2。
一、说教材
大家好,今天我说课的内容是西师大版小学数学五年级上册第五单元 第四课《 不规则图形的面积 》。本节课主要内容是 让学生学习估计、计 算不规则图形的面积,对不规则图形的面积计算非常陌生,因此,教材在 编排上,主要采用让学生数方格的方法来解决不规则图形的面积估算方法。 学生在利用方格估计面积时,要让学生明确不满一格的按半格算,这样学 生有了统一的标准,估算出来的误差就会缩小。教师在教学中还要注意引 导学生尝试猜测,自主探索,主动与他人交流,从中体会出解决一些数学 活动问题的经验。
苏教版数学五年级上:《不规则图形的面积》

2m
3m
3m 3m (方法四) 3m
3m
一块长方形草坪,中间有一条小路, 求草坪的面积。
2m 40m 60m
2m
3m
3m 3m 3m
3m
方法一:
把组合图形分割成一个长方形加一个梯形
2m 3m
3m
3m
3m
3m
方法二:
把组合图形添补成一个长方形减去一个梯形
2m
3m 3m 3m
3m
3m
方法三:
把组合图形分解成一个三角形加一个长方形
2m
3m
3m
3m
3m
3m
(方法三)
方法四:
把组合图形分解成一个三角形加一个梯形
图三
不规则图形面积怎样计算?
这个图形是由哪些简单图形组成的?同学 们分组讨论,四人一组。
中队旗面积 = 梯形面积 + 梯形面积
中队旗面积 = 长方形面积 + 三角形面积 × 2
分割法
中队旗面积 = 梯形面积 + 三角形面积
添补法
中队旗面积 = 长方形面积 — 三角形面积
老师家新买了住房,计划在 客厅铺地板。至少要买多大面积 的地板呢?
3m 3m
3m
7m 四
4m 3m
4m
4m
6m 3m
6m 3m
6m 3m 7m
7m
7m
分割法
4m 3m 3m
6m 3m
添补法
7m
}
转化
一.下面各个图形可以分成哪些已经学 过的图形?
怎么计算组合图形的面积?
1、分图形:用分割法或添补法把不规 则图形分成我们会计算的简单图形。 2、找条件:分别计算简单图形的面积。 3、算面积:最后求和或差。
2022年五年级上册数学同步练习 不规则图形的面积 3

五年级上册数学一课一练不规则图形的面积一、单选题1.( )图形与其余2个的面积不一样大。
A. B. C.2.如图,图1是由6个相同的正方形拼成,从图1中拿走1个正方形变成图2,那么()。
A. 面积变小,周长变大B. 面积和周长都变小C. 面积变小,周长不变D. 无法判断3.观察图,下列选项正确的是()。
A. 甲周长<乙周长B. 甲面积=乙面积C. 甲周长=乙周长D. 甲面积>乙面积4.下图中甲、乙两部分的()。
A. 周长相等,面积不相等B. 周长和面积都相等C. 周长不相等,面积相等二、判断题5.用4个边长1cm的小正方形拼成两个不同的图形,这两个图形的周长不同,面积也不同。
6.右图中的阴影部分面积占长方形的。
7.如图所示,阴影部分面积是10×10÷2÷2=25平方单位.三、填空题8.估一估下列图形的面积。
(每个小方格的边长表示1cm)面积约为________cm2;面积约为________cm29.下图表示的是一间房子侧面墙的形状.它的面积是________平方米.10.如图,圆的半径是3分米,阴影部分的面积是________平方分米.11.求阴影部分的面积.________12.下列方格中,哪个图形面积大四、解答题13.计算组合图形的面积。
(单位:米)14.求阴影部分的面积。
(单位:厘米)五、应用题15.如图所示,正方形ABCD的面积为2平方厘米,它的对角线长AC=2厘米,扇形ACD是以D为圆心,以AD为半径的圆面积的一部分,那么,阴影部分的面积是多少平方厘米?(π取)16.如图,已知BO=2DO,CO=5AO,阴影部分的面积和为22平方厘米,求四边形ABCD的面积.参考答案一、单选题1.【答案】B【解析】【解答】观察图形可知,C图形中的凸出部分可以剪拼到凹进去的部分,组成一个长方形,与A 图形的面积相等,B图形的面积与其余2个的面积不一样大.故答案为:B.【分析】比较图形面积的大小,可以用剪拼、平移等方法将图形进行分割与组合,然后判断大小.2.【答案】A【解析】【解答】解:图1的周长是10个正方形边长,图2的周长是12个正方形边长,周长变大;图1的面积是6个小正方形,图2的面积是5个小正方形,面积变小。
2022年五年级上册数学同步练习 不规则图形的面积 (含解析)
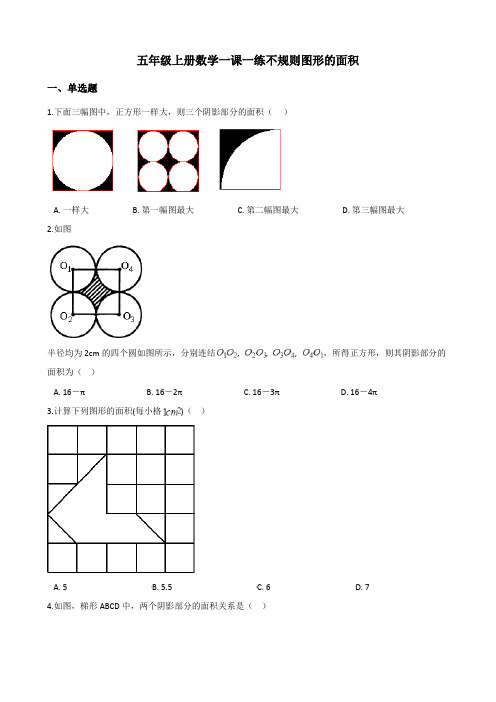
五年级上册数学一课一练不规则图形的面积一、单选题1.下面三幅图中,正方形一样大,则三个阴影部分的面积()A. 一样大B. 第一幅图最大C. 第二幅图最大D. 第三幅图最大2.如图半径均为2cm的四个圆如图所示,分别连结, , , ,所得正方形,则其阴影部分的面积为()A. 16-πB. 16-2πC. 16-3πD. 16-4π3.计算下列图形的面积(每小格)()A. 5B. 5.5C. 6D. 74.如图,梯形ABCD中,两个阴影部分的面积关系是()A. S1=S2B. S1>S2C. S1<S2二、判断题5.计算组合图形的面积也要用到基本图形的面积公式。
6.用8个1立方厘米的小方块拼成一个正方体.如果拿去一个小方块,它的表面积不变.7.如图是我国珍贵的历史文化遗产《易经》中的一个主要图形﹣﹣﹣太极图,它是数形结合的光辉典范.图中阴阳(即圈内黑白)两部分的面积相等.(判断对错)三、填空题8.求下面图形的面积。
(每个小方格的边长表示1cm)________ cm2________cm29.如图所示,O1、O2分别是所在圆的圆心.如果两圆半径均为2厘米,且图中两块阴影部分的面积相等,那么EF的长度是________厘米.10.下图是一个矩形,长为10厘米,宽为5厘米,则阴影部分面积为________平方厘米.11.计算阴影部分面积(p 取3.14)________ .12.小明已经算出了下面这个六角星每个星角的面积是28cm2,还想计算出整个六角星的面积.于是又测量了以下几个数据,你能帮小明解决问题吗?整个六角星的面积是________13.看图计算(单位:厘米)平行四边形AFEB的面积S=________平方厘米平行四边形CFED的面积S=________平方厘米四、解答题14.如图,正方形的边长是4厘米,求阴影部分的周长和面积.五、综合题16.计算下面图形中阴影部分的面积。
(单位:分米) (1)(2)六、应用题17.如图,圆O直径是10厘米,求阴影部分的面积.参考答案一、单选题1.【答案】A【解析】【解答】假设正方形的边长是4,第一个图形:4×4-3.14×(4÷2)²=16-3.14×4第二个图形:4×4-3.14×(4÷4)²×4=16-3.14×4第三个图形:4×4-3.14×4²÷4=16-3.14×4所以三个阴影部分的面积一样大.故答案为:A【分析】三个阴影部分的面积都是正方形面积减去内部空白部分的面积,假设出正方形的边长,然后根据正方形和圆面积公式分别计算阴影部分的面积并作出判断即可.2.【答案】D【解析】【解答】解:正方形边长:2×2=4(cm)阴影部分的面积:4×4-π×22=16-4π故答案为:D【分析】阴影部分的面积是正方形面积减去四个扇形面积,这四个扇形面积刚好是一个半径2cm的圆面积,由此计算即可.3.【答案】A【解析】【解答】解:整格的有3格,是3平方厘米;半格的有4格,是2平方厘米,共3+2=5(平方厘米) 故答案为:A【分析】采用数方格的方法,先数出整格的,然后数出半格的,把两个半格组成一个整格,这样就能计算4.【答案】A【解析】【解答】解:如图:根据长方形和平行四边形面积公式可知:S1+S3=S2+S3所以:S1=S2。
不规则图形面积的计算(练习题)及详细讲解

第一讲不规则图形面积得计算(一)习题一(及详细答案)一、填空题(求下列各图中阴影部分得面积):二、解答题:1、如右图,ABCD为长方形,AB=10厘米,BC=6厘米,E、F分别为AB、AD中点,且FG=2GE、求阴影部分面积。
2、如右图,正方形ABCD与正方形DEFG得边长分别为12厘米与6厘米、求四边形CMGN (阴影部分)得面积、3、如右图,正方形ABCD得边长为5厘米,△CEF得面积比△ADF得面积大5平方厘米、求CE得长。
4、如右图,已知CF=2DF,DE=EA,三角形BCF得面积为2,四边形BEDF得面积为4、求三角形ABE得面积、5、如右图,直角梯形ABCD得上底BC=10厘米,下底AD=14厘米,高CD=5厘米、又三角形ABF、三角形BCE与四边形BEDF得面积相等。
求三角形DEF得面积、6、如右图,四个一样大得长方形与一个小得正方形拼成一个大正方形,其中大、小正方形得面积分别就就是64平方米与9平方米、求长方形得长、宽各就就是多少?7、如右图,有一三角形纸片沿虚线折叠得到右下图,它得面积与原三角形面积之比为2:3,已知阴影部分得面积为5平方厘米、求原三角形面积、8、如右图,ABCD得边长BC=10,直角三角形BCE得直角边EC长8,已知阴影部分得面积比△EFG得面积大10、求CF得长、习题一解答一、填空题:二、解答题:ﻫﻫ3、CE=7厘米、ﻫ可求出BE=12、所以CE=BE-5=7厘米、4、3、提示:加辅助线BD∴CE=4,DE=CD-CE=5-4=1。
同理AF=8,DF=AD-AF=14-8=6,6、如右图,大正方形边长等于长方形得长与宽得与、中间小正方形得边长等于长方形得长与宽得差、而大、小正方形得边长分别就就是8米与3米,所以长方形得宽为(8-3)÷2=2、5(米),长方形得长为8-2、5=5、5(米)、7、15平方厘米、解:如右图,设折叠后重合部分得面积为x平方厘米,ﻫx=5、所以原三角形得面积为2×5+5=15平方厘米、∴阴影部分面积就就是:10x-40+S△GEF由题意:S△GEF+10=阴影部分面积,∴10x-40=10,x=5(厘米)、。
五年级上册图形面积练习题及答案

5.1 平行四边形的面积1. 一个平行四边形的底是12厘米,高是6厘米,面积是多少平方厘米?2. 一块平行四边形的瓜地,底长16米,高13.6米,如果平均每平方米栽瓜苗35棵,共栽多少棵?3.求下面图形的面积。
4. 长方形的面积等于平行四边形的面积。
()5. 把一个长方形的框架拉成平行四边形,它的面积和周长都不变。
( )5.2 三角形的面积1. 等底等高的两个三角形面积相等。
()2.求下面图形的面积,单位分米。
3. 一个三角形的底是9厘米,高是6厘米,面积是()。
4. 两个三角形的底和高都相等,那么它们的面积相等。
()5.3 梯形的面积1. 一堆钢管,每相邻两层都相差1根,最上层2根,最下层8根,这堆钢管共()根。
2. 判断:梯形的高越长,面积就越大。
()3. 计算下列图形的面积。
(单位:米)4.利用一面墙,用篱笆围一块梯形菜地,已知篱笆全长35米,求菜地的面积是多少平方米?5.4 不规则图形的面积1. 下面图形的面积是( )平方厘米。
2. 整格()个,不满格()个,面积大约()cm2(每个小方格的面积是1 cm2)。
3. 下面图形的面积是()平方米。
4.下图中是一块不规则的土地,估一估它的面积。
1答案1. 12×6 =72(平方厘米)2. 16×13.6×35=7616(棵)3.4×2.5=10(平方厘米)2答案1. √2.8.2×7÷2=28.7(平方分米)3.27平方厘米4. √3答案1. 352. ×3. (8+12)×10÷2=100(平方米)4. 35-8=27(米) 27×8÷2=108(平方米)4答案1. 162. 18 12 223. 26004. 126平方米。
小学奥数全国推荐最新五年级奥数通用学案附带练习题解析答案37不规则图形的面积(一)

年 级 五年级学 科 奥数版 本通用版课程标题 不规则图形的面积(一)我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形,一般称为基本图形或规则图形,它们的面积及周长都可由相应的公式直接计算。
实际问题中,有些图形是由一些基本图形组合、拼凑成的,它们的面积及周长可能无法应用公式直接计算。
我们一般称这样的图形为不规则图形。
组合的形式分为两种:一是拼接组合,二是重叠组合。
由于组合图形具有条件相等的特点,往往使得问题的解决无从下手。
那么,怎样去计算不规则图形的面积及周长呢?我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系,这样问题就能解决了。
本节课主要用公式法、求和差法、分割法、等量代换法解答不规则图形的面积问题。
1. 常见图形的面积公式:名称 图形面积公式长方形ab正方形 2a三角形 ah 21 平行四边形ah梯形h b a ⋅+)(212. 几个重要结论:(1)如果两个三角形的底和高分别相等,那么这两个三角形的面积相等。
(2)如果两个三角形的底(或高)相等,那么它们的面积之比等于它们的高(或底)之比。
例1 如图所示,大正方形和小正方形的边长分别为4和2,求阴影部分的面积。
分析与解:如题图,欲求阴影部分的面积,通过分析发现它是一个底是2、高是4的三角形,可以直接利用三角形的面积公式求得阴影部分的面积为2×4÷2=4。
本题是利用公式直接求解,这种方法是根据已知条件,从整体出发观察组合图形的特征,并与熟悉的基本图形产生联想。
例2正方形甲的边长是5厘米,正方形乙的边长是4厘米,阴影部分的面积是多少?分析与解:两个正方形的面积和:+=41(平方厘米);三个空白三角形的面积和:(5+4)×5÷2+4×4÷2+5×(5-4)÷2=33(平方厘米);阴影部分的面积:41-33=8(平方厘米)。
部编人教版五年级数学上册不规则图形的面积例5

-- 不规则图形的面积例5
学习目标:
1.初步掌握“把不规则地图形 转化为近 似的多边形 来求图形的面积”。 2.用数格子方法 和转化近似的图形求面 积法 估测不规则图形的面积。
不规则图形的面积
2.估计一片树叶面积的大小.
3.估计一片树叶面积的大致范围 4、如何更精确的来估计该怎么办?
教师组织研讨3
方法3: 我是用转化的方法,将叶子的图形近似转化成 长方形,然后求出长方形的面积大约是30cm2,因 此,叶子的面积大约是3则的图形,我们可以怎样 估算它的
面积呢?
1)用数方格的方法估算不规则的图形的面
积。先数出满格的面积,再估出不是满格的面 积,最后再加起来;
方法1: 在叶子上画出所有的方格线; 先数满格的有18格,所以它的面积一定大于18cm2; 再数不是满格的也有18格,把不满一格的都按半格计算 大约有9cm2; 所以:这片叶子的面积大约有: ( )+ ( )=( )cm2。
教师组织研讨2:
方法2:
我是用转化的方法,先将叶子的图形近似 转化成平行四边形,后求出平行四边形的面 积大约是(列式). . . 请问:你还有其它的办法吗?
2)用转化的方法把不规则的图形转化为 学过的图形进行估算。
二、练习
图中每个小方格的面积为1m2, 请你估计这个池塘的面积。
又快又对的奖
三、课堂小结
回顾一下,今天我们是如何 学习求不规则图形面积的,还有 什么问题吗?
四、布置作业
又快又对的奖
作业:第102页练习二十二,
第7题、8,9,第10题。
一、合作探究
1.情境:
图中每个小方格的面积是1cm2 ,请你 估计 这片形状不规则叶子的面积。 问:说一说你观察图后发现了 一些什么情况?
《不规则立体图形的表面积和体积(二)》配套练习题
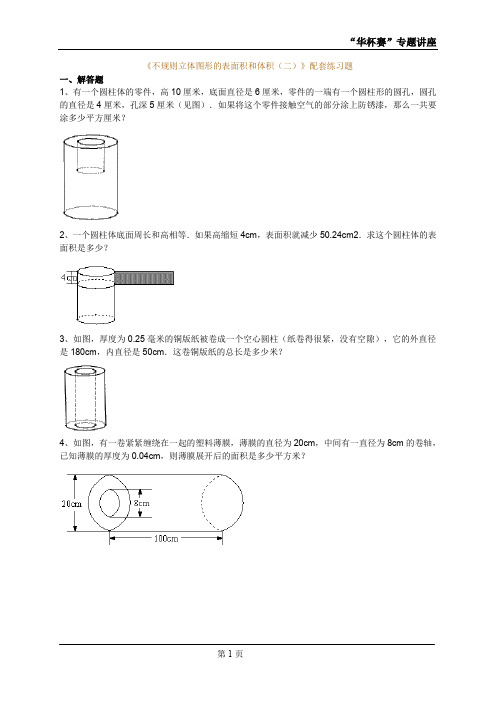
《不规则立体图形的表面积和体积(二)》配套练习题一、解答题1、有一个圆柱体的零件,高10厘米,底面直径是6厘米,零件的一端有一个圆柱形的圆孔,圆孔的直径是4厘米,孔深5厘米(见图).如果将这个零件接触空气的部分涂上防锈漆,那么一共要涂多少平方厘米?2、一个圆柱体底面周长和高相等.如果高缩短4cm,表面积就减少50.24cm2.求这个圆柱体的表面积是多少?3、如图,厚度为0.25毫米的铜版纸被卷成一个空心圆柱(纸卷得很紧,没有空隙),它的外直径是180cm,内直径是50cm.这卷铜版纸的总长是多少米?4、如图,有一卷紧紧缠绕在一起的塑料薄膜,薄膜的直径为20cm,中间有一直径为8cm的卷轴,已知薄膜的厚度为0.04cm,则薄膜展开后的面积是多少平方米?5、一个盖着瓶盖的瓶子里面装着一些水,瓶底面积为10平方厘米,(如下图所示),请你根据图中标明的数据,计算瓶子的容积是多少立方厘米?6、一个酒精瓶,它的瓶身呈圆柱形(不包括瓶颈),如图.已知它的容积为26.4π立方厘米.当瓶子正放时,瓶内的酒精的液面高为6厘米.瓶子倒放时,空余部分的高为2厘米.问:瓶内酒精的体积是多少立方厘米?合多少升?7、铁路油罐车由两个半球面和一个圆柱面钢板焊接而成,尺寸如图所示.问:该油罐车的容积是多少立方米?(π=3.14)8、如图所示,一个5×5×5的立方体,在一个方向上开有1×1×5的孔,在另一个方向上开有2×1×5的孔,在第三个方向上开有3×1×5的孔,剩余部分的体积是多少?表面积为多少?9、如图,原来的大正方体是由125个小正方体所构成的.其中有些小正方体已经被挖除,图中涂黑色的部分就是贯穿整个大正方体的挖除部分.请问剩下的部分共有多少个小正方体?10、如图,ABCD是矩形,BC=6cm,AB=10cm,对角线AC、BD相交O.E、F分别是AD与BC的中点,图中的阴影部分以EF为轴旋转一周,则白色部分扫出的立体图形的体积是多少立方厘米?(π取3)答案部分一、解答题1、【正确答案】307.72【答案解析】涂漆的面积等于大圆柱表面积与小圆柱侧面积之和,为6π×10+π×(6÷2)2×2+4π×5=60π+18π+20π=98π=307.72(平方厘米).【答疑编号10299065】2、【正确答案】182.8736【答案解析】圆柱体底面周长和高相等,说明圆柱体侧面展开是一个正方形.高缩短4cm,表面积就减少50.24cm2.阴影部分的面积为圆柱体表面积减少部分,值是50.24cm2,所以底面周长是50.24÷4=12.56(cm),侧面积是:12.56×12.56=157.7536(cm2),两个底面积是:3.14×(12.56÷3.14÷2)2×2=25.12(cm2).所以表面积为:157.7536+25.12=182.8736(cm2).【答疑编号10299073】3、【正确答案】9388.6【答案解析】卷在一起时铜版纸的横截面的面积为(cm2),如果将其展开,展开后横截面的面积不变,形状为一个长方形,宽为0.25mm(即0.025cm),所以长为7475π÷0.025=938860cm=9388.6m.所以这卷铜版纸的总长是9388.6米.【答疑编号10299080】4、【正确答案】65.94【答案解析】缠绕在一起时塑料薄膜的体积为:[π×(20÷2)2-π×(8÷2)2]×100=8400π(cm3)薄膜展开后为一个长方体,体积保持不变,而厚度为0.04cm,所以薄膜展开后的面积为:8400π÷0.04=659400cm2=65.94平方米【答疑编号10299082】5、【正确答案】60【答案解析】由已知条件知,第二个图上部空白部分的高为7-5=2cm,从而水与空着的部分的比为4∶2=2∶1,由左图知水的体积为10×4,所以总的容积为40÷2×(2+1)=60立方厘米.【答疑编号10299088】6、【正确答案】62.172;0.062172【答案解析】6÷2=326.4π÷(3+1)×3=62.172(立方厘米)62.172立方厘米=62.172毫升=0.062172升.答:酒精的体积是62.172立方厘米,合0.062172升.【答疑编号10299090】7、【正确答案】41.9【答案解析】(立方米)【答疑编号10299093】8、【正确答案】100;204【答案解析】求体积:开了3×1×5的孔,挖去3×1×5=15,开了1×1×5的孔,挖去1×1×5-1=4;开了2×1×5的孔,挖去2×1×5-(2+2)=6,剩余部分的体积是:5×5×5-(15+4+6)=100.(另解)将整个图形切片,如果切面平行于纸面,那么五个切片分别如图:得到总体积为:22×4+12=100.求表面积:表面积可以看成外部和内部两部分.外部的表面积为5×5×6-12=138,内部的面积可以分为前后、左右、上下三个方向,面积分别为2×(2×5+1×5-1×2-1×3)=202×(1×5+3×5-1×3-1)=322×(1×5+1×5-1×1-2)=14所以总的表面积为:138+20+32+14=204.【答疑编号10299104】9、【正确答案】72【答案解析】对于这一类从立体图形中间挖掉一部分后再求体积(或小正方体数目)的题目一般可以采用“切片法”来做,所谓“切片法”,就是把整个立体图形切成一片一片的(或一层一层的),然后分别计算每一片或每一层的体积或小正方体数目,最后再把它们相加.采用切片法,俯视第一层到第五层的图形依次如下,其中黑色部分表示挖除掉的部分.从图中可以看出,第1、2、3、4、5层剩下的小正方体分别有22个、11个、11个、6个、22个,所以总共还剩下22+11+11+6+22=72(个)小正方体.【答疑编号10299107】10、【正确答案】180【答案解析】扫出的图形如图所示,白色部分实际上是一个圆柱减去两个圆锥后所形成的图形.两个圆锥的体积之和为(立方厘米);圆柱的体积为π×32×10=270(立方厘米),所以白色部分扫出的体积为270-90=180(立方厘米).【答疑编号10299110】。
小升初小学数学几何图形应用题专题练习《不规则立体图形的表面积》答案详解

几何图形—专题11《不规则立体图形的表面积》一.选择题1.(2019春•南山区期末)将棱长为1厘米的小正方体按如图方式摆方在地上,露在外面的面的积是()平方厘米.A.18 B.21 C.24 D.27【解答】解:露在外面的总面数:126624++=(个)一个正方形面的面积:114⨯=(平方厘米)立体图形的总面积:12424⨯=(平方厘米)答:露在外面的面积是24平方厘米.故选:C.2.(2019•郾城区)如图是一个长3厘米、宽与高都是2厘米的长方体.将它挖掉一个棱长1厘米的小正方体,它的表面积()A.比原来大B.比原来小C.不变【解答】解:据题意和图可知,挖掉一个棱长1厘米的小正方体后,它的表面积去掉了2个面,也就是减少了2平方厘米;但是它的表面同时增加了4个面,也就是增加了4平方厘米;所以它的表面积增加了2平方厘米.故选:A.3.(2014•天津)如图,桌面上的模型由20个棱长为a的小正方体组成,现将该模型露在外面的部分涂上涂料,则涂上涂料部分的总面积为()A.250a40a D.220a B.230a C.2【解答】解:从正面看,有10个面露在外面,从左面看,有10个面露在外面,从右面看,有10个面露在外面,从后面看,有10个面露在外面,从上面看,有10个面露在外面,所以涂上涂料部分的总面积为:22⨯++++=.(1010101010)50a a50a.答:涂上涂料部分的总面积为2故选:D.4.(2009春•旅顺口区期末)把9个棱长是10厘米的正方体堆放在墙角(如图),露在外面的面积是()厘米2.A.1500 B.1600 C.1700 D.1800⨯⨯++,【解答】解:(1010)(656)=⨯,10017=(厘米2),1700答:露在外面的面积是1700厘米2.故选:C.5.从由8个棱长是1厘米的小正方体拼成的大正方体中,拿走一个小正方体,如图,这时它的表面积是( )平方厘米.A.增加了B.减小了C.不变【解答】解:观察图形可知,拿走一个小正方体减少了3个面,又增加了3个面,则表面积不变.故选:C.二.填空题6.(2019•北京模拟)21个棱长为1厘米的小正方体组成一个立方体如图,它的表面积是56平方厘米.【解答】解:(9712)2(11)++⨯⨯⨯=⨯⨯⨯28211=(平方厘米)56答:它的表面积是56平方厘米.故答案为:56.7.(2019•益阳模拟)图形是由棱长为1厘米的正方体拼成的,它的表面积是18平方厘米;至少还需要个这样的小正方体才能拼成一个大正方体.【解答】解:根据题干分析可得:(1)表面积为:⨯⨯⨯-⨯⨯,1164116=-,246=(平方厘米),18-=(个),(2)844答:它的表面积是18平方厘米;至少还需要4个这样的小正方体才能拼成一个大正方体.故答案为:18;4.8.(2018•海门市)如图,5个棱长为2分米的正方体硬纸箱堆放在墙角,体积一共是40立方分米,露在外面的硬纸面积是平方分米.⨯⨯⨯=(立方分米)【解答】解:(1)体积是:222540⨯⨯++(2)露在外部的面积是:22(433)=⨯410=(平方分米)40答:体积一共是40立方分米,露在外面的硬纸面积是40平方分米.故答案为:40,40.9.(2017春•宝安区期末)如图是同样大小的小方块堆积起来的,每个小方块的棱长是1cm,这堆小方块露在外面的面积是15平方厘米【解答】解:根据题干分析可得:⨯⨯++11(465)=⨯115=(平方厘米),15答:这堆小方块露在外面的面积是15平方厘米.故答案为:15平方厘米.10.(2015春•汉源县校级期末)计算下面图形的表面积和体积.(单位:分米)⨯+⨯+⨯⨯【解答】解:表面积:(868262)2=++⨯(481612)2=⨯762=(平方分米)152⨯⨯-⨯⨯体积:862421=-968=(立方分米)88答:图形的表面积是152平方分米,体积是88立方分米.11.(2019•益阳模拟)下图是由棱长为2厘米的小正方体搭成的,它的体积是72立方厘米,表面积是平方厘米.⨯⨯⨯=(立方厘米)【解答】解:222972⨯⨯++⨯22(844)2=⨯⨯⨯22162=(平方厘米)128答:它的体积是72立方厘米,表面积是128平方厘米.故答案为:72;128.12.(2019•芜湖模拟)如图的立体图形是由棱长1厘米的小正方体组成的,它的表面积是18平方厘米,至少还需要个这样的小正方体才能拼一个正方体.【解答】解:根据题干分析可得:(1)表面积为:⨯⨯⨯-⨯⨯1164116246=-=(平方厘米)18-=(个)(2)844答:它的表面积是18平方厘米;至少还需要4个这样的小正方体才能拼成一个大正方体.故答案为:18;4.13.(2017•长沙)如图所示,图中所示的立体图形由8个棱长为1cm的立方体块组成,这个立体图形表面积为302cm【解答】解:从前、后、左、右、上、下方向,看到的面的个数分别为:6、6、4、4、5、5.表面积是:⨯⨯+++++11(664455)=⨯1302=30()cm30cm.答:这个立体图形的表面积是2故答案为:30.14.(2014春•相城区校级期末)如图是由棱长1厘米的正方体拼搭成的,放在桌面上的面的大小是4平方厘米,它的表面积是平方厘米,体积是立方厘米.在这个基础上至少添个这样的正方体,就能搭成一个长方体.⨯⨯=(平方厘米)【解答】解:(1)1144⨯⨯⨯+⨯+⨯(2)(11)(425242)=⨯12626=(平方厘米)⨯⨯⨯=(立方厘米)(3)11164⨯⨯-(4)3236=-186=(个)12答:放在桌面上的面的大小是4平方厘米,它的表面积是26平方厘米,体积是6立方厘米.在这个基础上至少添12个这样的正方体,就能搭成一个长方体.故答案为:4,26,6,12.15.将棱长是1cm的小正方体靠墙角摆成如图所示的几何体,摆这个几何体一共用了20个小正方体,要把露在外面的面涂上颜色,那么涂色面的面积之和是平方厘米.+++=(个)【解答】解:(1)1063120答:摆这个几何体一共用了20个小正方体.(2)从正面、上面和右面看,都有10个小正方形,所以涂色的小正方形一共有:⨯=(个)10330⨯⨯=(平方厘米)113030答:涂色面的面积之和是30平方厘米.故答案为:20;30.三.判断题16.(2010秋•零陵区期末)把体积是31m.错误.(判断对错)1m的石块放在地上,石块的占地面积是2【解答】解:由于石块是不规则立体图形,所以不能确定它的底面的形状和面积的具体数量,因此,“把体积是31m.”这种说法是错误的.1m的石块放在地上,石块的占地面积是2故答案为:错误.四.应用题17.如图,把棱长为2cm的小正方体堆成如图所示的形状,求这个立体图形的表面积和体积.【解答】解:(1)图中几何体露出的面有:10416272⨯+⨯=(个)所以这个几何体的表面积是:2272288⨯⨯=(平方厘米)(2)这个几何体共有4层组成,所以共有小正方体的个数为:1491630+++=(个)所以这个几何体的体积为:22230240⨯⨯⨯=(立方厘米)答:这个立体图形的表面积是288平方厘米,体积是240立方厘米.五.解答题18.(2015秋•射阳县校级期末)动手操作:如图,用若干个棱长为1厘米的正方体重叠成如图所示的形状,求这个立体图形的表面积和体积.【解答】解:(1)图中几何体露出的面有:⨯+⨯+⨯927282=++18141648=(个),所以这个几何体的表面积是:114848⨯⨯=(平方厘米);(2)这个几何体共有3层组成,所以共有小正方体的个数为:25916++=(个),所以这个几何体的体积为:1111616⨯⨯⨯=(立方厘米).答:这个立体图形的表面积是48平方厘米,体积是16立方厘米.19.(2014•台湾模拟)用1立方公分的立方块组成下图,求总表面积?【解答】解:[162162(1622)]1⨯+⨯+⨯+⨯=++⨯(323234)1=⨯981=(平方公分).98答:总表面积是98平方公分.20.李丽家装修,决定安装一个滑道,为了安装方便,需要在一个长方体铁块上截去一个长、宽、高分别为6分米、2分米、1分米的小长方体,已知粉刷1平方分米需花费2.75元,那么粉刷这个零件与截去之前的零件相比相差多少元?⨯+⨯+⨯⨯-⨯+⨯【解答】解:62612126261=-2218=(平方分米)4⨯=(元)2.75411答:粉刷这个零件与截去之前的零件相比相差11元.21.如图是由18个边长为1厘米的正方体拼搭成的立体图形,它的表面积是多少平方厘米?+=(个【解答】解:上、下共:9918+=(个)左、右共:7714+=(个)前、后共:8816⨯⨯++表面积:(11)(181416)148=⨯=(平方厘米)48答:这个图形的表面积是48平方厘米.22.3个棱长都是20厘米的正方体堆放在墙角处(如图),露在外面的面积是多少?【解答】解:2020(322)⨯⨯++4007=⨯2800=(平方厘米)答:露在外面的面积是2800平方厘米.23.求图形的表面积与体积(1)(2)【解答】解:(1)556(16516252)2552⨯⨯+⨯+⨯+⨯⨯-⨯⨯150(803210)250=+++⨯-150122250=+⨯-15024450=+-344=(平方厘米)5551652⨯⨯+⨯⨯125160=+285=(立方厘米)答:它的表面积是344平方厘米,体积是285立方厘米.(2)2[3.142040 3.14(202)2]2(204020254025)2040⨯⨯+⨯÷⨯÷+⨯+⨯+⨯-⨯[2512 3.141002]2(8005001000)2800 =+⨯⨯÷+++⨯-3140223002800=÷+⨯-=+-157********=-6170800=(平方分米)53702⨯÷⨯÷+⨯⨯3.14(202)402204025=⨯⨯÷+3.1410040220000=÷+12560220000=+628020000=(立方分米)26280答:它的表面积是5370平方分米,体积是26280立方分米.24.有一个长方体形状的零件,中间挖去一个正方体的孔,你能算出它的表面积吗?(单位:分米)⨯+⨯+⨯⨯+⨯⨯【解答】解:(868565)2224=⨯+11821623616=+=(平方分米)252答:它的表面积是252平方分米.25.(2012春•嘉兴期末)如图是由棱长为5cm的正方体搭成的,它的体积是多少立方厘米?它的表面积是多少平方厘米?⨯⨯⨯,【解答】解:(1)5559=⨯,12591125=(立方厘米);⨯⨯⨯+⨯⨯⨯+⨯⨯⨯,(2)554255525572=++,200250350=(平方厘米);800答:图形的体积是1125立方厘米,表面积是800平方厘米.26.(2012•射洪县)把若干个边长2厘米的正方体重叠起来堆成如图所示的立体图形,这个立体图形的表面积是224平方厘米.⨯+⨯⨯⨯,【解答】解:(94102)(22)=⨯,564=(平方厘米);224答:这个立方体的表面积是224平方厘米.故答案为:224.27.(2012春•吴中区校级期末)在一个棱长为5厘米的正方体上剜去一块长5厘米,宽和高都是1厘米的小长方体,剩下部分的表面积是多少?(1)(2)(3)【解答】解:根据题干分析可得:⨯⨯-⨯⨯,(1)556112=-,1502=(平方厘米),148答:这个立体图形的表面积是148平方厘米.⨯⨯+⨯⨯-⨯⨯,(2)556512112=+-,150102=(平方厘米),158答:这个立体图形的表面积为158平方厘米.⨯⨯+⨯⨯-⨯⨯,(3)556514112=+-,150202=(平方厘米),168答:这个立体图形的表面积是168平方厘米.28.(2009•金华)如图,这座领奖台由四个相同的长方体拼合而成,把它的前后面和②、③两侧面涂上白色油漆,踏板和①的侧面铺上红地毯.(单位:厘米)(1)需要油漆部分的面积是多少?(2)这个领奖台所占的空间有多大?⨯⨯⨯+⨯⨯【解答】解:(1)60204230202=+,96001200=(平方厘米)10800答:需要油漆部分的面积是10800平方厘米.⨯⨯⨯=(立方厘米)(2)6030204144000答:这个领奖台所占的空间有144000立方厘米大.29.将15个棱长为1的正方体堆放在桌面上(如图),喷上红色后再将它们分开.没有涂上红色的部分,面积是几平方厘米?⨯⨯⨯-⨯⨯⨯+⨯+【解答】解:1161511(726210)=-⨯90136=-9036=(平方厘米)54答:面积是54平方厘米.30.如图由19个棱长是2厘米的小正方体重叠而成.求这个立体图形的表面积.⨯⨯⨯⨯【解答】解:(23)(23)6=⨯⨯666=(平方厘米)216答:这个立体图形的表面积是216平方厘米.31.计算立体图形的表面积和体积.【解答】解:(1)(1251210510)25(128)2⨯+⨯+⨯⨯-⨯-⨯ (6012050)2542=++⨯-⨯⨯2302202=⨯-⨯46040=-2420()cm =(2)125105(128)5⨯⨯-⨯-⨯6010545=⨯-⨯⨯600100=-3500()cm =答:不规则图形的表面积是2420cm ,体积是3500cm .。
28不规则图形的面积计算

如何利用规律实现更好记忆呢?
认识图形(二) 认识平面图形
超级记忆法-记 忆规律 第四个
记忆周 期是 1天 第五个 记忆周 期是 2天 第六个 记忆周 期是 4天
第 记七 忆个 周如何利用规律实现更好记忆呢?
期是 7天 第八个
认识图形(二) 认识平面图形
超级记忆法-场景法
例1
想一想,
怎样把这个图形 转化成已学过的图 形?小组合作,你 们怎样分的,在图
这些方法 有什么相 同点和不 同点?
上画出来,一种方
法画一张图。
12 345
返回
不规则图形的面积计算
方法一:分成一个长方形和一个梯形。
12m 4m
10m 10-4=6(m)
15m
12×4+(12+15)×6÷2=129(㎡) 答:这块草坪的面积是129㎡。
人教版七年级上册Unit4 Where‘s my backpack?
认识图形(二) 认识平面图形
超级记忆法-记 忆方法 TIP1:在使用场景记忆法时,我们可以多使用自己熟悉的场景(如日常自己的
卧室、平时上课的教室等等),这样记忆起来更加轻松;
TIP2:在场景中记忆时,可以适当采用一些顺序,比如上面例子中从上到下、 从左到右、从远到近等顺序记忆会比杂乱无序乱记效果更好。
苏教版 数学 五年级 上册
2 多边形的面积
不规则图形的面积计算
情景导入
探究新知
课堂练习
课堂小结
课后作业
不规则图形的面积计算
情景导入
华丰小学校园里有一块草坪 (如下图),它的面积是多少 平方米?
你准备怎 样算?与同 学交流。
