数理经济学茹少峰课后题及答案
数理经济学_茹少峰_第1章课后题及答案
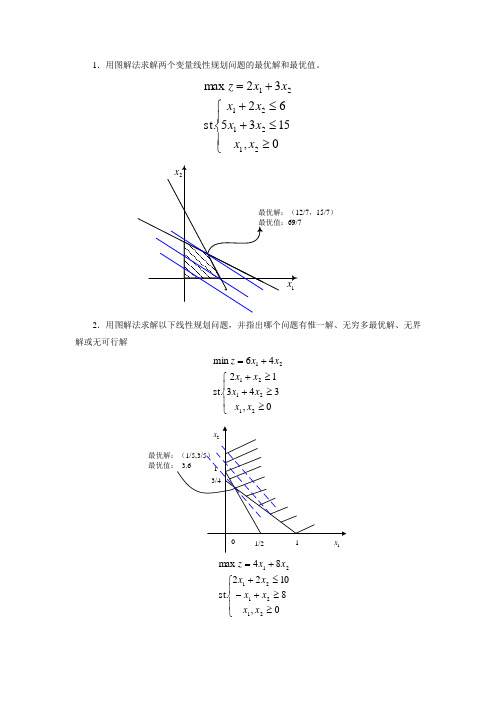
第1章习题答案1．什么是数理经济学？解：什么是数理经济学尚无统一的定义，以下是几种代表性的定义。
美国经济学家Kenneth J. Arrow（阿罗）等人在《数理经济学手册》一书中指出：数理经济学是包括数学概念和方法在经济学，特别是在经济理论中的各种应用。
Alpha C. Chiang（蒋中一）、Kevin Wainwright（凯尔文·温赖特）在《数理经济学的基本方法》一书中指出：数理经济学是一种经济分析方法，是经济学家利用数学符号描述经济问题，运用已知的数学定理进行推理的一种方法。
就分析的具体对象而言，它可以是微观或宏观经济理论，也可以是公共财政、城市经济学或其他学科方面的理论。
路甬祥、杜瑞芝分别在《现代科学技术大众百科—科技与社会卷》和《数学史辞典》指出：数理经济学是运用数学符号、数学方法和数学图形表述和论证经济现象及其相互依存关系的一门综合性边缘学科，研究经济活动中的数量关系并从中寻找规律。
杨小凯在《数理经济学基础》中指出：数理经济学主要是进行定性分析的理论经济学，它研究最优经济效果、利益协调和最优价格的确定这些经济学基本理论问题，为经济计量学、管理科学、经济控制论提供模型框架、结构和基础理论，它实在是经济学的基础之基础。
由以上定义可以看出：数理经济学主要是介绍数学方法如何应用到经济分析中，如经济问题如何用数学模型表示，一个变量的变化如何影响另一变量的变化等问题。
因此，数理经济学与其说是一门经济学分支学科，不如说它是一种经济学分析方法。
2．数理经济学是如何诞生的？简述其发展过程。
解：数理经济学的诞生和发展是数学在经济学中应用的过程，也是经济学发展的必然结果。
因为经济学家不仅仅要关心现实生活中的许多经济现象，更要对经济现象的数量，如价格、产量、收入、就业、失业、CPI、GDP等进行度量，要和数量打交道，便要研究数量之间的变化与关系，以此来把握经济运行规律，故数学就必然进入经济学的领域。
数理金融初步 Ross 第三版 中文答案
数理金融初步 Ross 第三版中文答案1. 引言数理金融是研究金融市场中与数学、统计学和经济学有关的问题的学科。
其中，Ross的《数理金融初步第三版》是该领域的经典教材，本文将提供该教材的中文答案。
本文将为读者提供一些重要章节的练习题和问题的解答，并以Markdown 文本格式输出。
2. 第一章 - 投资者行为与资本市场2.1 投资者效用最大化问题练习题 1问题：假设投资者对风险有所厌恶，并且资本市场上仅有一个无风险资产和一个风险资产。
请问投资者在这种情况下会如何分配其投资组合？答案：在这种情况下，投资者会将部分资金投资于无风险资产，以确保资金的安全性。
同时，为了获取更高的回报，他们也会将一部分资金投资于风险资产。
投资者的投资组合将根据其风险厌恶程度确定，较为保守的投资者会分配更多的资金投资于无风险资产，而较为激进的投资者则会分配更多的资金投资于风险资产。
练习题 2问题：在现实中，投资者往往不是对风险完全厌恶或完全喜爱，而是在二者之间存在一种权衡。
这种权衡的概念是什么？答案：这种权衡的概念称为风险偏好。
风险偏好是指投资者愿意承担的风险与预期回报之间的关系。
不同的投资者具有不同的风险偏好，一些投资者更喜欢高回报但也更高风险的投资，而另一些投资者则更愿意选择较低风险但也较低回报的投资。
2.2 资本市场均衡练习题 1问题：什么是资本市场的均衡？答案：资本市场的均衡是指在资产供给和需求相等的情况下，资本市场达到一种稳定状态的状态。
在这种情况下，投资者无法通过买入或卖出资产来获取额外的利润。
资本市场均衡通常是由各类投资者在市场上的交互行为决定的。
问题：资本市场均衡是否意味着所有投资者都将获得相同的回报？答案：不是。
尽管资本市场均衡确保了投资者无法通过买入或卖出资产来获取额外的利润，但不同投资者的投资组合可能会在回报上有所不同。
这是因为投资者的投资组合选择取决于他们的风险厌恶程度以及对不同资产的预期回报和风险的评估。
数理经济学课后题第2节
第二章 习题答案1．假设教材《数理经济学》的需求集为：{}6000|),(2==q p q p D ，其中，q 为需求量（万册），p 为价格（元）。
如果价格从20元提高为21元，则需求量将作如何变动？ 解：2220206000212160001513.61p q p q q q ======当时，，得；当时，，得 所以，价格从20元提高为21元，则需求量从15万册下降到13.61万册。
2．设某厂商的成本函数为323151500)(q q q q C +-+=，证明，其边际成本总是正的。
证明：因为边际成本函数，()()22C'156331120q q q q =-+=-+>所以，其边际成本总是正的。
3．设某厂商的成本函数为q q q q C +++=1201000)(，求边际成本函数。
解：边际成本函数为()C'20q =++4．设某一商品的需求函数为：18000)(2+==p p q q D，其中：q 为需求量，p 为价格。
若价格从9下降为8.50，问需求量将作如何变动？ 解：2280008000997.568.5109.22918.51p q p q ======++当时，；当时， 所以，价格从9下降为8.5时，需求量将从97.56上升为109.22.5．若某人的效用函数取下述形式：322121)3()2(),(++=x x x x u ，其中：u 为总效用函数，1x ，2x 为所消费商品的数量，要求计算：（1）每一商品的边际效用函数；（2）当消费的每种商品均为3个单位时，第一种商品的边际效用值。
解：（1）商品1的边际效用函数：()()3112223MU x x =++商品2的边际效用函数：()()22212323MU x x =++（2）123x x ==当时，()()31232332160MU =++= 6．假定某厂商的生产函数为：αα-=1),(L AK L K Q ，其中：0>A 及10<<α。
数理经济学第6章课后题解答
数理经济学第6章课后题解答第六章习题答案1．考虑如下最优化问题≥≤+=0,1..max 2121211x x x x t s x y 用图解法解此题。
并检验均衡解点是否满足（1）约束规格；（2）库恩—塔克极大化条件解：可行域为OAB利用图解法求的均衡点为)0,1(B ，1max =y对于)0,1(B 来说，有112221≤=+x x ，因此该约束规格是紧的。
构建拉格朗日函数 )1(),,(2221121-++=x x x x x L λλ≥-+≥=-+==??=+=??01,00)1(020212221222122211x x x x x x L x x x Lλλλ?)0,1(B 符合T K -条件2．考虑如下最优化问题≥≥-=0,0..min 212211x x x x t s x y用图解法解此题。
并检验均衡解点是否满足（1）约束规格；（2）库恩—塔克极大化条件解：利用图解法求的均衡点为)0,0(o ，0min =y求法同上，可知约束规范是紧的构建拉格朗日函数 )(),,(221121x x x x x L -+=λλ≥-≥=-==??=+=??0,00)(0021221221211x x x x xL x x Lλλλλ?)0,0(o 符合T K -条件3. 考虑如下最优化问题≥≥-=00..min 22311x x x t s x y检验均衡解点是否满足（1）约束规格；（2）库恩—塔克极大化条件解：利用图解法求的均衡点为)0,0(o ，0min =y求法同上，可知约束规范是紧的构建拉格朗日函数 )(),,(231121x x x x x L -+=λλ≥-≥=-==??=+=??0,00)(00312312312211x x x x x L x x L λλλλ?)0,0(o 不符合T K -条件4．写出下面优化问题的一阶必要条件>≤++--=0,,2..),,(max 222z y x z y x t s z y x z y x f 解：)2(),,(22221-++---=z y x z y x x x L λλ一阶必要条件为：=-++≥=+-=??=+-=??=-=??0)2(,0021021021222z y x z z Ly y L x xL λλλλλ5．求解下面最优化问题（1）??≥≤+++0,122..4max 22y x y x t s y x x （2）≥≥-≥--≥-+=0,160..min 212212121x x x x x x x t s x x y（3）≥≥+≥+++=0,,302105..10540min 3213121321x x x x x x x t s x x x y （4）>>≤+-=0,04..),(max 21222122121x x x x t s x x x x f（5）≥≤+=0,16..max 212121x x x x t s x x y 解：（1）2 2(,,)4(221)L x y x x y x y λλ=++-+-一阶必要条件为：2120820(221)00,221Lx x L y y x y x y λλλλ??=+-==-=+-=??≥+≤?解得314,,1055x y λ=== （2）图解法可行域为314,,1055x y λ===，均衡解点(1,1) min 2A y = (3) 12312123112213(,,,,)40510(105)(302)L x x x x x x x x x x λλλλ=+++--+--一阶必要条件为：12112231122131212134052050100(105)0(3023)0,0,510230Lx L x L x x x x x x x x x λλλλλλλλ??=--≥=-≥=-≥--=??--=??≥+≥?+≥? (4) 222121212(,,)(4)L x x x x x x λλ=--+- 一阶必要条件为：1122222122212120220(4)00,4Lx x L x x x x x x x λλλλ??=-==--=????+-=?≥+≤? 解得1212,0,4x x λ===(5) 121212(,,)(16)L x x x x x x λλ=-+- 一阶必要条件为：2112121200(16)00,16Lx x L x x x x x x λλλλ??=-==-=???+-=?≥+≤? 解得128x x λ===6．考虑如下最优化模型≥≥---=0,0)1(..m a x 213121x x x x t s x y 证明：（1）均衡解()()12,1,0x x **=不满足库恩-塔克条件；（2）当引进新乘数00≥λ，把拉格朗日函数修改成如下形式()()[]n i i mi i n x x x g r x x x f Z ,,,,,,2112100 -+=∑=λλ，则在点()0,1处满足库恩-塔克条件。
数理经济学第5章课后题答案
第五章 习题答案1．求下面等式约束最优化问题可能的极值点，要求写出一阶必要条件并求解由一阶必要条件构成的方程组。
（1）164..),(max 212121=+=x x t s x x x x f ，（2）32..),(min max 222122121=+=x x t s x x x x f or（3）11..),(min max 22=+=+=y x y x t s xy y x f or 和解：（1）首先写出拉格朗日函数：121212(,,)(164)L x x x x x x λλ=+--将L 对1x ，2x 和λ分别求偏导数可得：1221120401640x x L x L x L x x λλλ=-=⎧⎪=-=⎨⎪=--=⎩ 解得128, 2x x **==，2λ*=，此时16f =。
则点(8,2)为目标函数的驻点，且在该点处约束条件满足约束规格。
（2）首先写出拉格朗日函数：222121212(,,)(32)L x x x x x x λλ=+--\将L 对1x ，2x 和λ分别求偏导数可得：12121212221224020320x x L x x x L x x L x x λλλ=-=⎧⎪=-=⎨⎪=--=⎩ 解得121, 1x x **==，12λ*=，此时1f =；或者121, 1x x **==-，12λ*=-，此时1f =-；或者121, 1x x **=-=，12λ*=，此时1f =；或者121, 1x x **=-=-，12λ*=-，此时1f =-。
则点(1,1)、(1,1)-、(1,1)-和(1,1)--为目标函数的驻点，且在这些点处约束条件满足约束规格。
（3）首先写出拉格朗日函数：221212(,,,)(1)(1)L x y xy x y x y λλλλ=+--+--将L 对x ，y ，1λ和2λ分别求偏导数可得：1212122220201010x yL y x L x y L x y L x y λλλλλλ=--=⎧⎪=--=⎪⎨=--=⎪⎪=--=⎩ 解得111,0,2x y λ***===-2,1λ*=，此时0f =；或者110,1,2x y λ***===- ，21λ*=，此时0f =。
数理经济学茹少峰课后题及答案
1.求下列函数的极值。
解得，(x, y) (2a b,2b a)为可能的极值点根据充分条件，函数f (x, y)的二阶导师组成的Hessian 矩阵为H 3 0，因此(2a b,2b a)为f (x, y)的严格极小值点，极值为3a 2 5ab(2) 根据一元函数极值的必要条件，可得因此该函数在其定义域内为单调递增函数，极值不存在。
(3) 根据一元函数极值的必要条件，可得求得极值点为x 1。
由充分条件知y 6x 6。
当x 1时y '' 0，所以该函数极值不存在2 2(1) y x xy y 3ax 3by(3) y x 1 316解：(1)根据二元函数极值的必要条件，可得(2) y(4) y2x y 3a 0， f y2x 1 2x In x -- x xx 2y 3b 03b 2。
(4) 根据一元函数极值的必要条件，可得求的极值点为x e解：根据二元函数极值的必要条件，可得由充分条件知y2x In x 43x- 0当X e时，y0 ,因此该函数存在极大值为-e2. 讨论函数f x , yxy x 2y21的极值。
(x, y) 1 1(0,0),(x ，y )(-，2)，(x ， 1 1(2, 2),(x,y) 1 1(2,2)，(x ，y)(昇为可能的极值点根据充分条件，函数 f (x, y)的二阶导师组成的Hessian 矩阵为(x,y) (0,0)时，H 1 0,因此函数在该点无极值;3 (x,y)(［丄)时，H 22 2 -2值为1;81 1 z(x,y)(-,-)时，H2 21-22 0,海赛矩阵为正定矩阵，因此函数在该点有严格极小2 -22 0，海赛矩阵为正定矩阵，因此函数在该点有严格极2阵，因此函数在该点有严格极大值为8；阵，因此函数在该点有严格极大值为所以函数的Hessian 矩阵为证明：(1)同上，可求得函数的 Hessian 矩阵为5. 某完全竞争厂商由单一可变投入L (劳动)，每期工资率为W 0。
茹少锋教授管理运筹学课后答案
试用单纯形法求其满意解，若有多个满意解，求出其中两个。
解：将原模型转化为
A = b=
选d-i=（i=1，2，3）取为基变量， =(0,P1, P2)
B-1b= B-1A-C=
检验数行 按 形成：
单纯形表
1
0
1
0
0
-1
0
0
6
(2)
-1
0
1
0
0
-1
0
2
2
-3
0
0
1
0
0
-1
6
p0
0
180
0
6
0+180
140+0
280+0
280
2
7
0+180
140+180
280+0
320
1
8
0+360
140+180
280+0
360
0
9
0+360
140+180
280+0
420+0
420
3
10
0+360
140+180
280+180
420+0
460
2
k=1时，S1=10，u1=0，1，2，3，4，5
当 时取到最大值， =
k=3时，
当 时取到最大值，
k=2时
当 时有最大值，
k=1时
当 时有最大值，
故最优策略集为
2．某工厂生产三种产品，运送各种产品的重量与利润关系如下表所示。现将三种产品运往市场销售。运输能力总量不超过10吨，问如何安排运输使得总利润最大？
数理经济学第5章课后题答案
页脚内容1第五章 习题答案1．求下面等式约束最优化问题可能的极值点，要求写出一阶必要条件并求解由一阶必要条件构成的方程组。
（1）164..),(max 212121=+=x x t s x x x x f ，（2）32..),(min max 222122121=+=x x t s x x x x f or（3）11..),(min max 22=+=+=y x y x t s xy y x f or 和解：（1）首先写出拉格朗日函数：121212(,,)(164)L x x x x x x λλ=+-- 将L 对1x ，2x 和 λ分别求偏导数可得：1221120401640x x L x L x L x x λλλ=-=⎧⎪=-=⎨⎪=--=⎩ 解得128, 2x x **==，2λ*=，此时16f =。
则点(8,2)为目标函数的驻点，且在该点处约束条件满足约束规格。
（2）首先写出拉格朗日函数：222121212(,,)(32)L x x x x x x λλ=+--将L 对1x ，2x 和 λ分别求偏导数可得：12121212221224020320x x L x x x L x x L x x λλλ=-=⎧⎪=-=⎨⎪=--=⎩页脚内容2解得121, 1x x **==，12λ*=，此时1f =；或者121, 1x x **==-，12λ*=-，此时1f =-；或者121, 1x x **=-=，12λ*=，此时1f =；或者121, 1x x **=-=-，12λ*=-，此时1f =-。
则点(1,1)、(1,1)-、(1,1)-和(1,1)--为目标函数的驻点，且在这些点处约束条件满足约束规格。
（3）首先写出拉格朗日函数：221212(,,,)(1)(1)L x y xy x y x y λλλλ=+--+--将L 对x ，y ，1λ和2λ分别求偏导数可得：1212122220201010x yL y x L x y L x y L x y λλλλλλ=--=⎧⎪=--=⎪⎨=--=⎪⎪=--=⎩ 解得111,0,2x y λ***===-2,1λ*=，此时0f =；或者110,1,2x y λ***===- ，21λ*=，此时0f =。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第四章 习题答案1.求下列函数的极值。
（1）by ax y xy x y 3322--++= （2）x xy 212-=（3）()1613+-=x y （4）()1ln >=x xxy 解：（1）根据二元函数极值的必要条件，可得032=-+=a y x f x ，032=-+=b y x f y解得，)2,2(),(a b b a y x --=为可能的极值点。
根据充分条件，函数),(y x f 的二阶导师组成的Hessian 矩阵为03>=H ，因此)2,2(a b b a --为),(y x f 的严格极小值点，极值为22353b ab a ---。
（2）根据一元函数极值的必要条件，可得因此该函数在其定义域内为单调递增函数，极值不存在。
（3）根据一元函数极值的必要条件，可得求得极值点为1=x 。
由充分条件知66''-=x y 。
当1=x 时0''=y ，所以该函数极值不存在。
（4）根据一元函数极值的必要条件，可得求的极值点为e x =。
由充分条件知4''3ln 2xxx x y -=。
当e x =时，013''<-=ey ，因此该函数存在极大值为e 1。
2. 讨论函数()()122-+=y x xy y x f ，的极值。
解：根据二元函数极值的必要条件，可得)21,21(),(),21,21(),(),21,21(),(),21,21(),(),0,0(),(--=-=-===y x y x y x y x y x 为可能的极值点。
根据充分条件，函数),(y x f 的二阶导师组成的Hessian 矩阵为)0,0(),(=y x 时，01<-=H ，因此函数在该点无极值；)21,21(),(=y x 时，0223212123>==H ，海赛矩阵为正定矩阵，因此函数在该点有严格极小值为81-；)21,21(),(--=y x 时，0223212123>==H ，海赛矩阵为正定矩阵，因此函数在该点有严格极小值为81-；)21,21(),(-=y x 时，0223212123>=--=H ，0)1(,0)1(221>->-A A ，则海赛矩阵为负定矩阵，因此函数在该点有严格极大值为81；)21,21(),(-=y x 时，0223212123>=--=H ，0)1(,0)1(221>->-A A ，则海赛矩阵为负定矩阵，因此函数在该点有严格极大值为813. 试说明对于任意的0>βα，，生产函数βαL AK x f =)(是凹函数。
证明：βαL KA f K 1-∂=,11--∂=ββαL K A f KL βααL K A f KK 2)1(-∂-=,2)1(--=βαββL K A f LL所以函数的Hessian 矩阵为因为10,10<<<<βα，所以0),(>L K H ;且0)1(,0)1(221>->-A A ,Hessian 是 负定的，因此生产函数是严格凹函数。
4. 考虑生产函数βαK L y =。
如果11010<+<<<<βαβα，，，试说明该生产函数对于L 和K 的任意取值都是严格凹函数。
如果1=+βα，该函数是什么形状？证明：（1）同上，可求得函数的Hessian 矩阵为Hessian 是负定的，该函数对于K 、L 任意取值都是严格凹函数。
5. 某完全竞争厂商由单一可变投入L （劳动），每期工资率为0W 。
若该厂商每期的固定成本为F ，产品的价格为0P ，要求：（1） 写出厂商的生产函数、收益函数、成本函数和利润函数；（2） 何为利润最大化的一阶条件？解释此条件的经济意义；（3） 什么样的经济环境才能保证利润最大化而不是最小？解:（1）生产函数为：)(L f Q =收益函数为：)(L f P Q P R ⋅=⋅=成本函数为：F W L C +⋅=0利润函数为：)()(0F LW L Pf C R +-=-=π（2）利润最大化的一阶条件为：0)(0=-=∂∂W LL df P L π，即P W L L df 0)(=。
该条件的经济含义为：在利润最大化时，单个要素的边际产量等于要素单位成本与产品价格的比值。
（3）要满足利润最大化而不是最小，则要满足利润最大化的二阶充分条件：因为0>P ，所以0)(22<Ld L df ，也就是说，在边际产出递减规律的经济条件下才能实现利润最大化.6. 某厂商有如下的总成本函数C 与总需求函数Q ：，Q Q -Q C 5011173123++= P Q -=100.请回答下列问题：（1） 确定总收益函数R 与总利润函数π。
（2） 确定利润最大化的产出水平及最大利润。
解：（1）)100(Q Q PQ R -==(2)利润最大化的一阶必要条件为：解得，11,1==**Q Q 。
利润最大化的二阶充分条件为：1222+-=∂∂Q Qπ， 当1=Q 时，02>∂∂Qπ，函数取得极小值为-55.33； 当11=Q 时，02<∂∂Qπ，函数取得极大值为111.33； 所以，在产出水平为11时，利润最大为111.33。
7. 设有二次利润函数()，k jQ hQ ++=2Q π试确定系数所满足的约束，使下列命题成立：（1） 证明若什么也不生产，由于固定成本的关系，利润将为负；（2） 证明利润函数为严格凹函数；（3） 求在正的产出水平Q 下的最大化利润。
解：（1）由题可知，当0=Q 时，k =π。
由于固定成本存在的关系，利润为负，因此系数必须满足的条件为0<k 。
（2）因为利润函数为严格凹函数，其一阶必要条件为02=+=∂∂j hQ Qπ， 求得hjQ 2-=；二阶充分条件为h Q 22=∂∂π。
函数为严格凹函数满足的充要条件：0)(''<x f ，即02<∂∂Qπ, 因此，0<h 。
(3)在正的产出水平下，02>-=hjQ ，因此0>j 。
8. 假设有一个垄断市场环境下的两产品厂商，产品的价格分别为1P 和2P ，产品的需求函数Q 及成本函数C 为：211240-P P -Q =，21235-P -P Q =，102221++=Q Q C ，求利润最大化的价格水平。
解：利润函数2835185270837212122212211-++---=-+=P P P P P P C Q P Q P π利润最大化的一阶必要条件为：027*******=+--=∂∂P P P π,018568212=+--=∂∂P P P π解得，,5.21,721==**P P又020,06,01421222112211>=-<-=<-=πππππ所以，在利润最大化是价格水平为,5.21,721==P P9. 假设有一个完全竞争条件下的两产品厂商，产品的价格分别为1P 和2P ，单位时间内i 产品的产出水平为i Q ，厂商成本函数为22212122Q Q Q Q C ++=，求：（1） 利润最大化的产出水平；（2） 若总成本函数为222122Q Q C +=，两产品的生产是否存在技术相关性，1Q 与2Q 的新最优水平是多少？（3） 对参变量1P 和2P 进行比较静态分析。
解:（1）)22(2221212211Q Q Q QQ P Q P ++-+=π4211=--=∂∂Q Q P Q π,041222=--=∂∂Q Q P Q π可得,34211P P Q -=,3413212P P Q --= （2）)22(22212211Q QQ P Q P +-+=π04111=-=∂∂Q P Q π，04211=-=∂∂Q P Q π， 可得，1141P Q =,2241P Q = 而0212=∂∂Q Q π,即在最优产量下，21,Q Q 不存在技术相关性。
（3）由（1）问中的最优产量,34211P P Q -=,3413212P P Q --= 3411=∂∂P Q ,3121-=∂∂P Q ,31312-=∂∂P Q ,3422-=∂∂P Q 即，产品1价格上升1单位，产量上升34，价格下降313； 产品1价格上升1单位，产量下降31，价格下降34；10.一个公司有严格凹的生产函数()L K Q ,。
给定=P 产品价格，=r 资本的利用率，=ω工资。
要求：（1） 对利润达到最大化的投入要素K 与L 进行比较静态分析，并作简要的分析说明；（2） 假定生产函数是规模报酬递减的Coob-Douglas 函数，做同样的比较静态分析。
解：（1）wL rK L K PQ --=),(π利润最大化时，最优解为),,(w r P K K *=，),,(w r P L L *=******--=wL rK L K PQ ),(π为最优值函数。
r 变化对最大利润的影响为：**********-∂∂-∂∂∂∂+∂∂-∂∂∂∂=∂∂K r L w r L L Q P r K r r K K Q P r π 利润最大化时有0=-∂∂**r K Q P ,0=-∂∂**w LQ P则r K r ∂∂=-=∂∂**ππ，wL w ∂∂=-=∂∂**ππ 即当资本利用率或工资提高时，利润率随之下降，当产品价格上涨时，最大利润率随之上升。
（2）wL rK L PK --=βαπ利润最大化时，最优解为),,(w r P K K *=，),,(w r P L L *=******--=wL rK L K PQ ),(π为最优值函数。
r K r ∂∂=-=∂∂**ππ，w L w ∂∂=-=∂∂**ππ,βαπ)()(***=∂∂L K P11. 考虑参数为a 的极大化问题函数()()043;22>++-=a a ax x a x f ：（1） 利用包络定理求函数()a x f ;的最大值关于参数a 的导数；（2） 分析参数a 对目标函数的最大值的影响。
解：（1）假设最优解为)(a x x *=，（2）一阶条件为0)),((=∂∂*xa a x f ，即03)(2=+-*a a x 所以，参数a 与木匾函数的最大值同向变动。
12. 考虑参数最优化问题()1323,m ax 2343+-+-=x e x x a a x f a （a 为参数）：（1） 求目标函数的极大值关于参数a 的导数；（2） 分析参数a 对目标函数的极大值的影响（假设这个问题的最优解()0≠*a x ）。
解：（1）假设最优解)(a x x *=利用包络定理（2）0)(≠*a x ，由（1）中结果，0),(<*daa x df，所以参数a 对目标函数极值的影响是同增同减的。