《高二数学抽样方法》PPT课件
合集下载
高中数学抽样方法 ppt

样可以证明(证明从略),个体a第1次未
1 被抽到、而第2次被抽到的概率也是 6
.
由于个体a第1次被抽到与第2次被抽到是
互斥事件,根据互斥事件的概率加法公式,
在先后抽取2个个体的过程中,个体a被抽到
1 1 1 的概率P= . 6 6 3
又由于个体a的任意性,说明在抽样过程
中每个个体被抽到的概率相等,都是
抽签法简便易行,当总体的个体数不多时,
适宜采用这种方法.
(2)随机数表法
本章后面的附表1是一个随机数表.表中共 随机出现0,1,2,……,9这十个数字,确 切地说,在表中每个位置上出现各个数字的 概率都是相等的.因此在制作一个随机数表 时,必须保证表中每个位置上的数字是等概 率出现的.下面举例说明如何用随机数表来 抽取样本.
注:将总体中的N个个体编号时可以从0开 始.例如 N=100时,编号可以是00,01, 02,……,99,这样总体中的所有个体均可 用两位数字号码表示,便于运用随机数表. 当随机地选定开始读数的数后,读数的方 向可以向右,也可以向左、向上、向下等等.
在上面每两位、每两位地读数过程中,得到一串
两位数字号码,在去掉其中不合要求和与前面重 复的号码后,其中依次出现的号码可以看成是依 次从总体中抽取的各个个体的号码.由于随机数 表中每个位置上出现哪一个数字是等概率的,每 次读到哪一个两位数字号码,即从总体中抽到哪 一个个体的号码也是等概率的,因而利用随机数 表抽取样本保证了各个个体被抽取的概率相等.
为了检验某种产品的质量,决定从40件
产品中抽取10件进行检查.在利用随机数 表抽取这个样本时,可以按下面的步骤进 行: 第一步,先将40件产品编号,可以编为00, 01,02,…,38,39。
《高中数学抽样方法》课件

05
抽样调查的实施步骤与注意事项
实施步骤
明确调查目的
首先需要明确调查的目的和目标,确定调查 的范围和对象。
制定调查计划
根据调查目的制定详细的调查计划,包括调查 方法、调查内容、调查时间等。
选择合适的抽样方法
根据实际情况选择合适的抽样方法,如简单随机 抽样、分层抽样等。
实施调查
按照调查计划进行调查,收集数据。
分层随机抽样
定义
先将总体分成若干层次或类别,然后从各层次或 类别中随机抽取一定数量的样本。
特点
能够提高样本的代表性,减小抽样误差。
适用范围
总体存在明显的层次或类别。
整群随机抽样
定义
先将总体分成若干群或组,然后从各群或组中随机抽取一定数量 的样本。
特点
便于组织,节省经费。
适用范围
总体群或组特征明显,且群或组间差异不大。
总结词
针对性、准确性、可靠性
详细描述
该案例通过抽样调查的方法,对某品牌手机的市场占有率进行调查,旨在了解该品牌手机在市场中的销售情况和 竞争力。在抽样过程中,确保了样本的针对性和准确性,同时也注重了样本的可靠性,以确保调查结果的可信度 和说服力。
案例三:某高校大学生消费情况的抽样调查
总结词
客观性、科学性、可行性
详细描述
该案例通过抽样调查的方法,对某高校大学生的消费情况进行调查,旨在了解大学生的消费习惯和消 费水平。在抽样过程中,确保了样本的客观性和科学性,同时也注重了样本的可行性,以方便调查的 实施和数据的收集。
THANKS
感谢观看
样本容量的影响因素
01
02
03
04
总体规模
总体规模越大,需要的样 本容量也越大,以保持相 同的置信水平和误差范围 。
高二数学抽样方法

朋友曾经问我做不做嗨团,这期间,我因为上班忙就搁置了,6号那天,她一问我,我就问她,我不大会网上操作,我行吗?她说,你肯定行,你那么善良,对人那么实诚,人缘又好!我说,那一 天能挣一碗牛肉面钱吗?她哈哈大笑说:一碗牛肉面钱随便挣了。我说,我干。从朋友和我视频,我做出决定,不超过一分钟时间。
我坐在理发店建群。从她群里转发素材,挑选了一款纸巾给老板看,理发店老板很爽快,快速下单,一会,朋友说,呀,你已经开张了!这么快,你挣了半碗牛肉面钱了。一碗牛肉面六元,一包纸 巾利润三元,我那时不懂,看不来我挣了多少钱!只知道开张了!所以,到如今,我很感激我的第一位爽快的客人,热情善良的孙先生。随后,闺蜜又团了纸巾,生命中,关键时刻,总有几个人会为你 鼓劲加油,不离不弃,这都是人生值得骄傲和感动的事情!往后几天,朋友,家人、同事,陆续来团东西,给予我大力支持,让我更有信心!
朋友自去年五月份内养后就开始做嗨团,她开始做的时候,我看她团里东西这么便宜,又联想到实体店老板说的网上东西哪里有好的!常言说:便宜没好货,好货不便宜。我是不大网购的。但是想 帮助朋友,就去团东西,第一次团了竹筒粽子,价格超便宜,回来特别好吃,从此一发不可收拾,经常在她群里团、团、团!也邀请了身边亲朋好友进去一起团,心里,就接受
我坐在理发店建群。从她群里转发素材,挑选了一款纸巾给老板看,理发店老板很爽快,快速下单,一会,朋友说,呀,你已经开张了!这么快,你挣了半碗牛肉面钱了。一碗牛肉面六元,一包纸 巾利润三元,我那时不懂,看不来我挣了多少钱!只知道开张了!所以,到如今,我很感激我的第一位爽快的客人,热情善良的孙先生。随后,闺蜜又团了纸巾,生命中,关键时刻,总有几个人会为你 鼓劲加油,不离不弃,这都是人生值得骄傲和感动的事情!往后几天,朋友,家人、同事,陆续来团东西,给予我大力支持,让我更有信心!
朋友自去年五月份内养后就开始做嗨团,她开始做的时候,我看她团里东西这么便宜,又联想到实体店老板说的网上东西哪里有好的!常言说:便宜没好货,好货不便宜。我是不大网购的。但是想 帮助朋友,就去团东西,第一次团了竹筒粽子,价格超便宜,回来特别好吃,从此一发不可收拾,经常在她群里团、团、团!也邀请了身边亲朋好友进去一起团,心里,就接受
抽样方法培训课件(PPT 50张)

简介
• 在上述四个问题中,已包含了研究方法论的基本概念。第一
个问题涉及研究的总体(population),第二个问题涉及样 本(sample)与抽样方法(method of sampling),第三个 问题涉及样本大小(sample size),第四个问题涉及取样 的误差(sampling error)与偏差(sampling bias)。
恰当的抽样框架对于精确的抽样是至关重要的。
抽样术语 (6)
抽样术语 (7)
样本(sample):我们通过抽样方法所获得的一组(9)
参数(parameter):关于总体中某一变量的综合描 述。例如,全中国20至30岁男性的平均身高,就是一 个参数值。
• 如果使用这些术语来说明,那么选取研究对象的程序是:
(1)界定研究的总体,(2)选取研究样本,(3)决定样 本大小,与(4)避免抽样误差。
抽样的基本思想 (1)
当我们从事一项研究时,都期望研究结果具有相当程 度的普遍性,而能解释某一个“特定群体”的情形。 这个“特定群体”就是研究的全部对象,称为“总 体”(population)。
抽样术语 (3)
目标总体(target population or theoretical population):在理论上明确界定的个体的集合体, 它必须受几个方面的限定:内容、单位、范围、时间。
目标总体是在理论上明确定义的整体,但在实际中很 难做到使符合这一定义的一切个体均能有机会被选入 样本。
经典例子 (3)
《文摘》能准确预测之前总统选举是因为高收入和低 收入的选民在投票上并无差异。 此外,在大萧条之前,很多低收入的人能负担得起电 话和汽车。
经典例子 (4)
两个教训: 首先,抽样框架至关重要。
高二数学抽样方法

何申的审美视角也始终关注他所在的“热河”城,先后创作了许多“热河系列”小说,曾经的官员、会首,以及大兵、闲人、地摊商贩、下岗平民等在他的笔下构成了一幅热河众生相,生动表现了 热河人民勤劳质朴、古道热肠、多才多艺、与世无争的性格。这些作品尽情展示了热河这座塞外古城的风土人情、世态习俗,有力地弘扬了山庄文化,具有较高的审美价值和文化传承价值。
何申之所以被称为河北的“赵树理”,不仅在于他的作品深得赵树理的精髓,也在于多年来,他与赵树理一样,始终坚持“写人民,为人民而写”的创作方向,与人民休戚相关、血脉相连,积极反 映农民的心声和时代的脉动,创作出了接地气、得民心、顺民意的人民群众所喜闻乐见的作品。他经历了由下乡知青到县级领导的人生历程,从普通农民到县级干部都是他的审美对象,并重点塑造了农 民和农村干部的群体形象,开创了“乡镇干部系列”和“农民系列”。他一方面专注描绘这些人的生活状况,表现他们在社会转型期的热望和追求、苦闷和忧虑、艰辛和无奈,写出他们庸常人生的生命 本相、生存困顿;另一方面,他又追求人物性格的复杂性和多样性,力图在人物的独特命运、丰富内心世界的展示中融注丰富深邃的社会历史意蕴,所以在这些人物的身上既有质朴善良、忍辱负重、坚 韧不拔的传统美德,也有伴随着农村改革开放形成的开拓进取、刚柔相济、灵活善变的新质。这些人物个性突出、鲜明活脱,是有着深刻社会价值和高度审美价值的完满而富有生气的性格整体。六福
何申之所以被称为河北的“赵树理”,不仅在于他的作品深得赵树理的精髓,也在于多年来,他与赵树理一样,始终坚持“写人民,为人民而写”的创作方向,与人民休戚相关、血脉相连,积极反 映农民的心声和时代的脉动,创作出了接地气、得民心、顺民意的人民群众所喜闻乐见的作品。他经历了由下乡知青到县级领导的人生历程,从普通农民到县级干部都是他的审美对象,并重点塑造了农 民和农村干部的群体形象,开创了“乡镇干部系列”和“农民系列”。他一方面专注描绘这些人的生活状况,表现他们在社会转型期的热望和追求、苦闷和忧虑、艰辛和无奈,写出他们庸常人生的生命 本相、生存困顿;另一方面,他又追求人物性格的复杂性和多样性,力图在人物的独特命运、丰富内心世界的展示中融注丰富深邃的社会历史意蕴,所以在这些人物的身上既有质朴善良、忍辱负重、坚 韧不拔的传统美德,也有伴随着农村改革开放形成的开拓进取、刚柔相济、灵活善变的新质。这些人物个性突出、鲜明活脱,是有着深刻社会价值和高度审美价值的完满而富有生气的性格整体。六福
抽样方法(PPT41页)

样本容量与总体个数的比例为 1:100,则高中 应抽取人数为 2400*1/100=24 人,初中应抽取人数 为 10800*1/100=108 人 , 小 学 应 抽 取 人 数 为 11100*1/100=111 人.
知识探究(三):分层抽样的基本思想
思考 2:具体在三类学生中抽取样本时(如在 10800 名初中生中抽取 108 人),可以用哪种抽 样方法进行抽样?
3. 将锅里的汤“搅拌均匀”,品尝一小勺就知道 汤的味道,这是一个简单随机抽样问题,对这种 抽样方法,我们从理论上作些分析.
知识探究(一):简单随机抽样的基本思想
实例. 食品卫生工作人员,要对校园食品店的一 批小包装饼干进行卫生达标检验,打算从中抽取 一定数量的饼干作为检验的样本.其抽样方法是, 将这批小包装饼干放在一个麻袋中搅拌均匀,然 后逐个不放回抽取若干包,这种抽样方法就是简 单随机抽样.那么简单随机抽样的含义如何?
知识探究(一):简单随机抽样的基本思想
思考:
6. 在 1936 年美国总统选举前,一份颇有名气的杂 志的工作人员对兰顿和罗斯福两位候选人做了一 次民意测验.调查者通过电话簿和车辆登记簿上的 名Байду номын сангаас给一大批人发了调查表.调查结果表明,兰顿当 选的可能性大(57%),但实际选举结果正好相反, 最后罗斯福当选(62%).你认为预测结果出错的原 因是什么?
用分层抽样,抽取教学人员 12 人,管 理人员 1 人,后勤服务人员 2 人.
理论迁移
例 3 某公司在甲、乙、丙、丁四个地区分别有 150 个、120 个、180 个、150 个销售点,公司 为了调查产品的销售情况,需从这 600 个销售 点中抽取一个容量为 100 的样本,记这项调查 为①;在丙地区中有 20 个特大型销售点,要从 中抽取 7 个调查其销售收入和售后服务等情 况,记这项调查为②,完成这两项调查宜分别 采用什么方法?
知识探究(三):分层抽样的基本思想
思考 2:具体在三类学生中抽取样本时(如在 10800 名初中生中抽取 108 人),可以用哪种抽 样方法进行抽样?
3. 将锅里的汤“搅拌均匀”,品尝一小勺就知道 汤的味道,这是一个简单随机抽样问题,对这种 抽样方法,我们从理论上作些分析.
知识探究(一):简单随机抽样的基本思想
实例. 食品卫生工作人员,要对校园食品店的一 批小包装饼干进行卫生达标检验,打算从中抽取 一定数量的饼干作为检验的样本.其抽样方法是, 将这批小包装饼干放在一个麻袋中搅拌均匀,然 后逐个不放回抽取若干包,这种抽样方法就是简 单随机抽样.那么简单随机抽样的含义如何?
知识探究(一):简单随机抽样的基本思想
思考:
6. 在 1936 年美国总统选举前,一份颇有名气的杂 志的工作人员对兰顿和罗斯福两位候选人做了一 次民意测验.调查者通过电话簿和车辆登记簿上的 名Байду номын сангаас给一大批人发了调查表.调查结果表明,兰顿当 选的可能性大(57%),但实际选举结果正好相反, 最后罗斯福当选(62%).你认为预测结果出错的原 因是什么?
用分层抽样,抽取教学人员 12 人,管 理人员 1 人,后勤服务人员 2 人.
理论迁移
例 3 某公司在甲、乙、丙、丁四个地区分别有 150 个、120 个、180 个、150 个销售点,公司 为了调查产品的销售情况,需从这 600 个销售 点中抽取一个容量为 100 的样本,记这项调查 为①;在丙地区中有 20 个特大型销售点,要从 中抽取 7 个调查其销售收入和售后服务等情 况,记这项调查为②,完成这两项调查宜分别 采用什么方法?
抽样方法PPT教学课件

联围 系
简单 ①抽样 在起 总体中 从总体中
随 过程中 始 的个 逐个抽
机 每个个 部 体数 取
抽 体被抽 分 较少
样 到的概 抽
系统 抽
率相等 ②抽样 过程都
样 总体中 将总体均 时 的个 分成几 采
类
共同
别点
分 ①抽样过 层 程中每 抽 个个体 样 被抽到 的概率 相等② 抽样过
相互 联 系
每层 抽 样 时 采 用 简
• 【思路点拨】 布估计总体分布
【自主解答】 (1)频率分布表如下:
分组
频数 频率
[1.30,1.34)
4
0.04
[1.34,1.38)
25 0.25
[1.38,1.42)
30 0.30
[1.42,1.46)
29 0.29
[1.46,1.50)
10 0.10
[1.50,1.54) 合计
2
0.02
• (1)求极差; • (2)频率分布表; • (4)画出频率分布直方图.
• 1.观察下面频率
分布表 分组
频数 频率
[3.95,4.35) 2
[4.35,4.75) 4
[4.75,5.15) 14
[5.15,5.55) 25
[5.55,5.95) 45
[5.95,6.35) 46
[教师选讲](2009 年海南三亚 3 月)100 人中, 青年人 45,中年人 25 人,老年人 30 人, 从中抽取一个容量为 20 的样本. 试分析,随机抽样,系统抽样,分层抽样
方法下每个人被抽到的概率.
【解析】 (1)用简单随机抽样法:每个个体被抽 到的概率为12000=15. (2)用系统抽样法:将 100 人均匀分成 20 组,每组 5 人,每组取一个,每个个体被抽到的概率为15. (3)用分层抽样法:老、中、青人数之比为 6∶5∶9, 老年人占130,从老年人中取 20×130=6 人,每个老 年人被抽到的概率为360=15,同理可得中年人、青 年人被抽到的概率为15.
简单 ①抽样 在起 总体中 从总体中
随 过程中 始 的个 逐个抽
机 每个个 部 体数 取
抽 体被抽 分 较少
样 到的概 抽
系统 抽
率相等 ②抽样 过程都
样 总体中 将总体均 时 的个 分成几 采
类
共同
别点
分 ①抽样过 层 程中每 抽 个个体 样 被抽到 的概率 相等② 抽样过
相互 联 系
每层 抽 样 时 采 用 简
• 【思路点拨】 布估计总体分布
【自主解答】 (1)频率分布表如下:
分组
频数 频率
[1.30,1.34)
4
0.04
[1.34,1.38)
25 0.25
[1.38,1.42)
30 0.30
[1.42,1.46)
29 0.29
[1.46,1.50)
10 0.10
[1.50,1.54) 合计
2
0.02
• (1)求极差; • (2)频率分布表; • (4)画出频率分布直方图.
• 1.观察下面频率
分布表 分组
频数 频率
[3.95,4.35) 2
[4.35,4.75) 4
[4.75,5.15) 14
[5.15,5.55) 25
[5.55,5.95) 45
[5.95,6.35) 46
[教师选讲](2009 年海南三亚 3 月)100 人中, 青年人 45,中年人 25 人,老年人 30 人, 从中抽取一个容量为 20 的样本. 试分析,随机抽样,系统抽样,分层抽样
方法下每个人被抽到的概率.
【解析】 (1)用简单随机抽样法:每个个体被抽 到的概率为12000=15. (2)用系统抽样法:将 100 人均匀分成 20 组,每组 5 人,每组取一个,每个个体被抽到的概率为15. (3)用分层抽样法:老、中、青人数之比为 6∶5∶9, 老年人占130,从老年人中取 20×130=6 人,每个老 年人被抽到的概率为360=15,同理可得中年人、青 年人被抽到的概率为15.
《高二数学抽样方法》课件

抽样误差是不可避免的,但可以 通过增大样本容量、改进抽样方 法等方式减小抽样误差。
应用实例的启示
抽样方法在不同领域具有广泛应 用,为我们提供了解世界、发现 规律的重要手段。
3
系统抽样
4
按照一定的系统规则从总体中选取样本, 如每隔k个个体选取一个样本。
简单随机抽样
从总体中随机地选取个体,确保每个个 体被选中的概率相等。
整群抽样
将总体划分为互不相交的群体,从每个 群体中抽取全部个体作为样本。
抽样误差
抽样误差是由于样本选择的随机性而引起的估计值与总体参数之间的差异。 可通过增加样本容量、提高抽样方式等方法减小抽样误差。
《高二数学抽样方法》 PPT课件
高二数学抽样方法PPT课件是为了帮助学生更好地理解数学抽样方法而设计的。 本课件内容详实,涵盖了抽样的定义、分类、方法、误差以及应用实例等方 面的知识。
什么是抽样?
抽样是从总体中选取部分个体进行观察和研究的方法。通过抽样,我们可以 从大量的数据中获取有代表性的样本,从而进行有效的分析和推断。
应用实例
市场调研
通过抽样方法了解消费者需求 和市场趋势,为企业决策提供 依据。
社会调查
利用抽样方法收集和分析社会 问题的数据,为社会决策提供 支持。
医学研究
通过抽样方法研究人群的健康 状况和疾病发生规律,为医学 实践提供参考。
总结
抽样方法的优缺点比较
抽样误差及其减小方法
不同抽样方法各有优势和局限性, 选择适合的抽样方法是确保研究 结果可靠的关键。
抽样分类
简单随ห้องสมุดไป่ตู้抽样
随机选择个体,每个个体被选中的概率相等。
整群抽样
将总体划分为若干互不相交的群体,从每个群体 中抽取样本。
高二上学期数学必修教学课件第章抽样方法

简单随机抽样方法简单易行,能够保证每个个体被选中的概率相等,从
而得到具有代表性的样本。
02
缺点
当总体中个体差异较大时,简单随机抽样可能导致样本的代表性不足。
此外,在某些情况下,获取总体的完整名单可能较为困难。
03
适用范围
简单随机抽样适用于总体中个体差异较小且容易获取完整名单的情况。
例如,在市场调研、社会调查等领域中,可以采用简单随机抽样方法从
• 结果分析:通过对不同年级学生的数学成绩进行评估,可以了解各年级学生的 数学水平及差异情况,为学校制定针对性的教学措施提供参考依据。
优缺点及适用范围讨论
优点
分层抽样能够充分考虑总体内部的结构差异,使得抽取的样本更具代表性;同时可以根据 各层的特征灵活调整抽样策略,提高抽样的效率。
缺点
分层抽样需要对总体进行分层处理,如果分层不当或者分层变量选择不合理,可能会导致 抽样的偏差;此外,当总体内部差异较大时,分层抽样可能需要较大的样本量才能达到预 期的精度要求。
06
按照抽样间隔等距抽取其余样本。
实例:生产线产品质量检测
生产线产品质量检测背景:在生产线 中,为了保证产品质量,需要对产品
进行抽样检测。
系统抽样应用
确定总体容量(生产线上的产品总数 )和样本容量(需要检测的产品数量 );
计算抽样间隔,即生产线上的产品总 数除以需要检测的产品数量;
在第一个抽样间隔内随机抽取一个产 品进行检测;
总体与样本关系
样本是总体的一个子集, 通过样本可以推断总体的 特征。
抽样误差与置信水平介绍
抽样误差
抽样误差与置信水平关系
由于抽样而产生的样本统计量与总体 参数之间的差异。
置信水平越高,抽样误差越小,样本 统计量推断总体参数的可靠性越高。
抽样方法-PPT课件

将总体分 成几层, 按比例分 层抽取
用简单随 机抽样或 系统抽样 对各层抽 样
总体中 的个体 数较少
总体中 的个体 数较多
总体由 差异明 显的几 部分组 成
例 3 某高级中学有学生 270 人,其中一年级 108 人,二、三年级
各 81 人,现要利用抽样方法抽取 10 人参加某项调查,考虑选
用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随
机抽样和分层抽样时,将学生按一、二、三年级依次统一编号
为 1,2,…,270;使用系统抽样时,将学生统一随机编号 1,2,…,
270,并将整个编号依次分为 10 段.如果抽得号码有下列四
种情况:
①7,34,61,88,115,142,169,196,223,250;
②5,9,100,107,111,121,180,195,200,265;
____5_0___.
பைடு நூலகம்
2.某单位有职工 750 人,其中青年职工 350 人,中年职工 250
人,老年职工 150 人,为了了解该单位职工的健康情况,用
分层抽样的方法从中抽取样本.若样本中的青年职工为 7 人,
则样本容量为
(B )
A.7
B.15
C.25
D.35
3.一支田径队有男运动员 48 人,女运动员 36 人,若用分层
“等距”的,①③符合,②④不符合,所以①③都可能为
系统抽样,②④都不能为系统抽样.
答案 D
小结:
1、抽样方法:简单随机抽样、系统抽样、 分层抽样,
2、简单随机抽样:逐一抽取; 分层抽样:按比例进行分配; 系统抽样:平均分段
3、简单随机抽样是基础,系统抽样与分层抽样 是补充和发展,三者相辅相成,对立统一.
高中数学抽样方法.ppt
当nn不是整数时通过从总体中剔除一些个体使剩下的总体中个体的个数n?能被n整除这时4按照事先确定的规则抽取样本通常是将l加上间隔k得到第2个编号lk第3个编号l2k这样继续下去直到获取整个样本
2.1 抽样方法
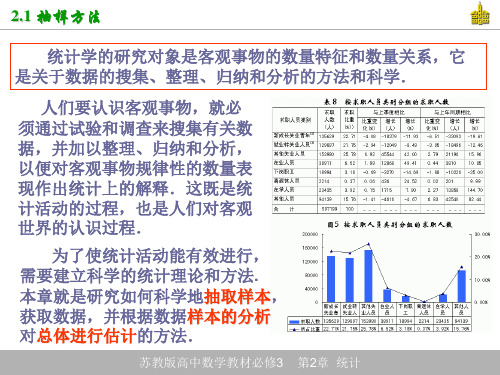
统计学的研究对象是客观事物的数量特征和数量关系,它 是关于数据的搜集、整理、归纳和分析的方法和科学.
2.1 抽样方法
系统抽样的步骤:
(1)采用随机的方式将总体中的个体编号。为简便起见, 有时可直接采用个体所带有的号码,如考生的准考证号、 街道上各户的门牌号,等等;
(2)整个的编号分段(即分成几个部分),要确定分段的 间隔k.当N/n(N为总体中的个体的个数,n为样本容量) 是整数时,k=N/n;当N/n不是整数时,通过从总体中剔除 一些个体使剩下的总体中个体的个数N'能被n整除,这时 k=N'/n;
苏教版高中数学教材必修3 第2章 统计
2.1 抽样方法 如果问题6中,学生人数是1003,如何进行系统抽样?
解:(1)随机将这1003个个体进行编号1,2,3,……1003; (2)利用简单随机抽样,先从总体中剔除3个个体(可以随
机数表法),将剩下的个体重新编号然后按系统抽样的方法进 行.
苏教版高中数学教材必修3 第2章 统计
第二步,在附录1随机数表中任选一个数作为开始.
第三步,获取样本号码.
为了保证所选定数字的随机性,应在面对 随机数表之前就指出开始数字的纵横位置
苏教版高中数学教材必修3 第2章 统计
2.1 抽样方法 问题4.为了检验某种产品的质量,决定从40件产品中抽取10件 进行检查,如何抽样? 例如选取第8行第9列开始.
方案:通常将各班同学平均分成5组,再在第一组用抽签法确 定一个学号的学生,按每组逐次加10的原则抽取5名代表, 例:抽取学号为02,12,22,32,42等5位代表.
2.1 抽样方法
统计学的研究对象是客观事物的数量特征和数量关系,它 是关于数据的搜集、整理、归纳和分析的方法和科学.
2.1 抽样方法
系统抽样的步骤:
(1)采用随机的方式将总体中的个体编号。为简便起见, 有时可直接采用个体所带有的号码,如考生的准考证号、 街道上各户的门牌号,等等;
(2)整个的编号分段(即分成几个部分),要确定分段的 间隔k.当N/n(N为总体中的个体的个数,n为样本容量) 是整数时,k=N/n;当N/n不是整数时,通过从总体中剔除 一些个体使剩下的总体中个体的个数N'能被n整除,这时 k=N'/n;
苏教版高中数学教材必修3 第2章 统计
2.1 抽样方法 如果问题6中,学生人数是1003,如何进行系统抽样?
解:(1)随机将这1003个个体进行编号1,2,3,……1003; (2)利用简单随机抽样,先从总体中剔除3个个体(可以随
机数表法),将剩下的个体重新编号然后按系统抽样的方法进 行.
苏教版高中数学教材必修3 第2章 统计
第二步,在附录1随机数表中任选一个数作为开始.
第三步,获取样本号码.
为了保证所选定数字的随机性,应在面对 随机数表之前就指出开始数字的纵横位置
苏教版高中数学教材必修3 第2章 统计
2.1 抽样方法 问题4.为了检验某种产品的质量,决定从40件产品中抽取10件 进行检查,如何抽样? 例如选取第8行第9列开始.
方案:通常将各班同学平均分成5组,再在第一组用抽签法确 定一个学号的学生,按每组逐次加10的原则抽取5名代表, 例:抽取学号为02,12,22,32,42等5位代表.
1.2.抽样方法ppt课件

(4)抽取:按照事先确定的规则抽取样本(通常是将l加上 间隔k,得到第2个编号l+k,第3个编号l+2k,这样继续下去 ,直到获取整个样本).
例:某装订厂平均每小时大约装订图书362册,要求检验员
每小时抽取40册图书,检查其质量状况,请你设计一个调查 方案
解:我们可以采用系统抽样,按照下面的步骤设计方案
1. 一个田径队,有男运动员 56 人,女运动员 42 人,比赛后,立即用分 层抽样的方法,从全体队员中抽出一个容量为 28 的样本进行尿 样兴奋剂检查,其中男运动员应抽_________人.
2. 高二年级 12 个班共有 580 人,要采用分层抽样的方法从高二年 级的全体学生中抽取一个容量为 60 的样本,已知某班有 58 名学 生,那么从该班抽取的学生数是
第二步,在随机数表中任选一个数作为开始. 第三步,从选定的数(如第8行第9列的数5 )开始向 右读下去,得到一个两位数字号码59,由于59>39, 将它去掉;继续向右读,得到16,将它取出;继续读 下去,又得到19,10,12,07,39,38,33,21,随 后的两位数字号码是12,由于它在前面已经取出,将 它去掉,再继续下去,得到34.
下抽问盒质件从量抽你①②③问从题子量进8检取列样 认总逐每台题 无里检行验)23抽?为体个一电:限1有验检(。:取为 判中不次脑多,测假8的放抽样什 断中0个个在后设个回取,个本么 简零抽,8数 地 时不台体的?单件样再为抽,放电中方随,时把有取每回脑抽法机从,它限;个地已取是抽中从放个个随编1选中回0否样;体机好0出任盒个属的等抽号5意 子个于 依可个取,拿里体能简 据零对2台出;作地件编有单进一为被进号哪随行个样抽行随些机质零本到机?;。
(2)分段(即分成几个部分),要确定分段的间隔k.当N/n (N为总体中的个体的个数,n为样本容量)是整数时, k=N/n;当N/n不是整数时,通过从总体中剔除一些个体使 剩下的总体中个体的个数N'能被n整除,这时k=N'/n;
例:某装订厂平均每小时大约装订图书362册,要求检验员
每小时抽取40册图书,检查其质量状况,请你设计一个调查 方案
解:我们可以采用系统抽样,按照下面的步骤设计方案
1. 一个田径队,有男运动员 56 人,女运动员 42 人,比赛后,立即用分 层抽样的方法,从全体队员中抽出一个容量为 28 的样本进行尿 样兴奋剂检查,其中男运动员应抽_________人.
2. 高二年级 12 个班共有 580 人,要采用分层抽样的方法从高二年 级的全体学生中抽取一个容量为 60 的样本,已知某班有 58 名学 生,那么从该班抽取的学生数是
第二步,在随机数表中任选一个数作为开始. 第三步,从选定的数(如第8行第9列的数5 )开始向 右读下去,得到一个两位数字号码59,由于59>39, 将它去掉;继续向右读,得到16,将它取出;继续读 下去,又得到19,10,12,07,39,38,33,21,随 后的两位数字号码是12,由于它在前面已经取出,将 它去掉,再继续下去,得到34.
下抽问盒质件从量抽你①②③问从题子量进8检取列样 认总逐每台题 无里检行验)23抽?为体个一电:限1有验检(。:取为 判中不次脑多,测假8的放抽样什 断中0个个在后设个回取,个本么 简零抽,8数 地 时不台体的?单件样再为抽,放电中方随,时把有取每回脑抽法机从,它限;个地已取是抽中从放个个随编1选中回0否样;体机好0出任盒个属的等抽号5意 子个于 依可个取,拿里体能简 据零对2台出;作地件编有单进一为被进号哪随行个样抽行随些机质零本到机?;。
(2)分段(即分成几个部分),要确定分段的间隔k.当N/n (N为总体中的个体的个数,n为样本容量)是整数时, k=N/n;当N/n不是整数时,通过从总体中剔除一些个体使 剩下的总体中个体的个数N'能被n整除,这时k=N'/n;
抽样方法PPT课件

例:在一项有关二战士兵的经典研究中,研究人员从名册 中每隔10个士兵抽出一个来进行研究。然而士兵的名册是 以下列组织方式来编排的:首先是中士,接着是下士,其 后才是二等兵;用一班一班的方式进行编排,每班10个人。 因此名册中每隔10个就是中士。如此系统抽样可能会得到 一个完全是中士的样本,也可能会得到一个完全不含中士 的样本。
将总体按编号顺序 平均分成50部分, 可得抽样间距为: K=1000/50=20,每 部分包含20个个 体。
1
2
随 机 将 这 1000 名 学生编号为1,2, 3 , …… , 1000 (比如可以利用准
考证号)。
以18为起始号,每
间隔20抽取一个号
码,这样就得到一
个容量为50的样本:
18,38,58, …… ,
举例:某大学共有100
个班,每班都是30名同学,总共3000名学生,现在 要抽取300名。先从100个班中抽取10个班,则这10
个班的全部学生就构成了样本。
四、整群抽样
3.优缺点:
1)优点:简便易行、节省费用。
例:研究某市10万户家庭生活状况,抽取1000户。若 要获得全市家庭的抽样框几乎是不可能的,因此无法进 行简单随机抽样和系统抽样。但整群抽样则轻而易举。 假设全市有200个居委会,每个居委会有500户左右家 庭。我们只要有这200个居委会的名单,按上述两种方 法之一,抽取两个居委会,然后该两个居委会的所有家 庭构成样本。
•有些情况又不宜采用比例抽样。在总体类型或 层次的单位数目太少时,往往采取不按比例抽 样的方法,以便于对不同层次的子总体进行专 门研究或进行比较。 比如:从500男工中抽取30人,从100女工中 抽取30人,则可以对两类进行比较,不会影响 推论统计时的条件。
将总体按编号顺序 平均分成50部分, 可得抽样间距为: K=1000/50=20,每 部分包含20个个 体。
1
2
随 机 将 这 1000 名 学生编号为1,2, 3 , …… , 1000 (比如可以利用准
考证号)。
以18为起始号,每
间隔20抽取一个号
码,这样就得到一
个容量为50的样本:
18,38,58, …… ,
举例:某大学共有100
个班,每班都是30名同学,总共3000名学生,现在 要抽取300名。先从100个班中抽取10个班,则这10
个班的全部学生就构成了样本。
四、整群抽样
3.优缺点:
1)优点:简便易行、节省费用。
例:研究某市10万户家庭生活状况,抽取1000户。若 要获得全市家庭的抽样框几乎是不可能的,因此无法进 行简单随机抽样和系统抽样。但整群抽样则轻而易举。 假设全市有200个居委会,每个居委会有500户左右家 庭。我们只要有这200个居委会的名单,按上述两种方 法之一,抽取两个居委会,然后该两个居委会的所有家 庭构成样本。
•有些情况又不宜采用比例抽样。在总体类型或 层次的单位数目太少时,往往采取不按比例抽 样的方法,以便于对不同层次的子总体进行专 门研究或进行比较。 比如:从500男工中抽取30人,从100女工中 抽取30人,则可以对两类进行比较,不会影响 推论统计时的条件。
抽样方法PPT优秀课件6

应用举例
问题:为了了解参加某种知识竞赛的1000名学生的成 绩,应采用什么样的抽样方法恰当? 解:适宜选用系统抽样,抽样过程如下:
⑴ 随机将这1000名学生编号为1,2,3,……, 1000(比如可以利用准考证号). ⑵ 将总体按编号顺序平均分成50部分,每部分包 含20个个体 . ⑶ 在第一部分的个体编号1,2,……,20中,利 用简单随机抽样抽取一个号码,比如是18 .
分层抽样
按20:160=1:8 的比例,从业务人员中抽取12人,从 管理人员中抽取5人从后勤服务人员中抽取3人,都 用抽签法从各类人员中抽取所需的人数,最后合在 一起
练习:为了对流水线上的产品质量进行检验,质检人员 每隔5分钟抽一件产品进行检验,这种抽样方法是 系统抽。样
练习:某单位有老年人28人,中年人54人,青年人81人,为
应用举例
例:一个单位有职工160人,其中业务人员96人,管 理人员40人,后勤服务人员24人,现要从中抽取容 量为20的一个样本,请简述三种抽样方法的过程?
简单随机抽样 (抽签法)
将160人从1至160编上号,然后作出160个号签放入 箱中拌匀,从中抽取20个签,与签号相同的20个人 被选出
系统抽样
94.对一个适度工作的人而言,快乐来自于工作,有如花朵结果前拥有彩色的花瓣。――[约翰·拉斯金] 95.没有比时间更容易浪费的,同时没有比时间更珍贵的了,因为没有时间我们几乎无法做任何事。――[威廉·班] 96.人生真正的欢欣,就是在于你自认正在为一个伟大目标运用自己;而不是源于独自发光.自私渺小的忧烦躯壳,只知抱怨世界无法带给你快乐。――[萧伯纳]
97.有三个人是我的朋友爱我的人.恨我的人.以及对我冷漠的人。 爱我的人教我温柔;恨我的人教我谨慎;对我冷漠的人教我自立。――[J·E·丁格] 98.过去的事已经一去不复返。聪明的人是考虑现在和未来,根本无暇去想过去的事。――[英国哲学家培根] 99.真正的发现之旅不只是为了寻找全新的景色,也为了拥有全新的眼光。――[马塞尔·普劳斯特] 100.这个世界总是充满美好的事物,然而能看到这些美好事物的人,事实上是少之又少。――[罗丹] 101.称赞不但对人的感情,而且对人的理智也发生巨大的作用,在这种令人愉快的影响之下,我觉得更加聪明了,各种想法,以异常的速度接连涌入我的脑际。――[托尔斯泰] 102.人生过程的景观一直在变化,向前跨进,就看到与初始不同的景观,再上前去,又是另一番新的气候――。[叔本华] 103.为何我们如此汲汲于名利,如果一个人和他的同伴保持不一样的速度,或许他耳中听到的是不同的旋律,让他随他所听到的旋律走,无论快慢或远近。――[梭罗] 104.我们最容易不吝惜的是时间,而我们应该最担心的也是时间;因为没有时间的话,我们在世界上什么也不能做。――[威廉·彭] 105.人类的悲剧,就是想延长自己的寿命。我们往往只憧憬地平线那端的神奇【违禁词,被屏蔽】,而忘了去欣赏今天窗外正在盛开的玫瑰花。――[戴尔·卡内基] 106.休息并非无所事事,夏日炎炎时躺在树底下的草地,听着潺潺的水声,看着飘过的白云,亦非浪费时间。――[约翰·罗伯克] 107.没有人会只因年龄而衰老,我们是因放弃我们的理想而衰老。年龄会使皮肤老化,而放弃热情却会使灵魂老化。――[撒母耳·厄尔曼] 108.快乐和智能的区别在于:自认最快乐的人实际上就是最快乐的,但自认为最明智的人一般而言却是最愚蠢的。――[卡雷贝·C·科尔顿] 109.每个人皆有连自己都不清楚的潜在能力。无论是谁,在千钧一发之际,往往能轻易解决从前认为极不可能解决的事。――[戴尔·卡内基] 110.每天安静地坐十五分钟·倾听你的气息,感觉它,感觉你自己,并且试着什么都不想。――[艾瑞克·佛洛姆] 111.你知道何谓沮丧---就是你用一辈子工夫,在公司或任何领域里往上攀爬,却在抵达最高处的同时,发现自己爬错了墙头。--[坎伯] 112.「伟大」这个名词未必非出现在规模很大的事情不可;生活中微小之处,照样可以伟大。――[布鲁克斯] 113.人生的目的有二:先是获得你想要的;然后是享受你所获得的。只有最明智的人类做到第二点。――[罗根·皮沙尔·史密斯] 114.要经常听.时常想.时时学习,才是真正的生活方式。对任何事既不抱希望,也不肯学习的人,没有生存的资格。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
随机数表的方法抽出剔除的个体; (3)系统抽样适用于总体容量较大的情况; (4)系统抽样是等可能抽样.
2020/12/14
h
19
2020/12/14h源自10练习:用随机表法,求解问题3.
问题3:对本班同学对看足球比赛的喜爱程度(很喜爱、喜爱、 一般、不喜爱、很不喜爱)进行调查.
2020/12/14
h
11
一般地,设一个总体的个体数为N,如果通过逐个抽 取的方法从中抽取一个样本,且每次抽取时各个个体被 抽到的概率相等,就称这样的抽样为简单随机抽样.
抽签法
2020/12/14
h
5
抽签法的一般步 骤:
(1)将总体中所有个体编号(对已经有编号的个体, 可以省略编号的过程);
(2)制作与个体编号相同的号签; (3)将号签放在一个箱子中搅匀; (4)按要求随机抽取号签,并记录; (5)将编号与号签一致的个体抽出.
抽签法的适用范 围:
抽签法简单易行,适用于总体中个体数不多的情形.
2020/12/14
h
1
统计学的研究对象是客观事物的数量特征和数量关系,它 是关于数据的搜集、整理、归纳和分析的方法和科学.
人们要认识客观事物,就必 须通过试验和调查来搜集有关数 据,并加以整理、归纳和分析, 以便对客观事物规律性的数量表 现作出统计上的解释.这既是统 计活动的过程,也是人们对客观 世界的认识过程.
2020/12/14
h
14
将总体分成均衡的几个部分,然后按照预先定出的规则, 从每一部分抽取一个个体,得到所需要的样本,这种抽样叫做 系统抽样(也称为等距抽样).
2020/12/14
h
15
问题6 :为了了解参加某种知识竞赛的1000名学生的成 绩,应采用什么样的抽样方法恰当?
解:抽样过程如下: (1)随机将这1000名学生编号为1,2,3,……,1000(比 如可以利用准考证号); (2)将总体按编号顺序平均分成50部分,每部分包含20个 个体. (3)在第一部分的个体编号1,2,……,20中,利用简单 随机抽样抽取一个号码,比如是18; (4)以18为起始号,每间隔20抽取一个号码,这样就得到 一个容量为50的样本:18,38,58,……,978,998.
h
8
问题4.为了检验某种产品的质量,决定从40件产品中抽取10件 进行检查,如何抽样? 例如选取第8行第9列开始.
6行: 16 22 77 94 39 49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64 7行: 84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 8行: 63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79 9行: 33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54 10行: 57 60 86 32 44 09 47 27 96 54 49 17 46 09 62 90 52 84 77 27 08 02 73 43 28
2020/12/14
h
6
抽签法的制签比较麻 烦,如何简化制签过程?
随机数表法
制作一个表,其中 每个数都是用随机方法产生 的,这样的表称为随机数表.
如何用随机数表来抽取样本?
2020/12/14
h
7
问题4.为了检验某种产品的质量,决定从40件产品中抽取10件
进行检查,如何抽样?
由于需要编号,如果总体中的个体数太多, 采用随机表法进行抽样就显得不太方便了
第一步,先将40件产品编号,可以编为00,01,02,,38,39.
所谓编号,实际上是编数字号码.不 要编号成:0,1,2,…,39
第二步,在附录1随机数表中任选一个数作为开始.
第三步,获取样本号码.
为了保证所选定数字的随机性,应在面对 随机数表之前就指出开始数字的纵横位置
2020/12/14
16 19 10 12 07 39 38 33 21 34
2020/12/14
h
9
注:当随机地选定开始读数的数后,读数的方向可以向右,也 可以向左、向上、向下等等.
在上面每两位、每两位地读数过程中,得到一串两位数字
号码,在去掉其中不合要求和与前面重复的号码后,其中依次 出现的号码可以看成是依次从总体中抽取的各个个体的号 码.由于随机数表中每个位置上出现哪一个数字是等概率的, 每次读到哪一个两位数字号码,即从总体中抽到哪一个个体的 号码也是等概率的.因而利用随机数表抽取样本保证了各个个 体被抽取的概率相等.
(3)在第一段用简单随机抽样确定起始的个体编号;
(4)按照事先确定的规则抽取样本(通常是将l加上间隔k, 得到第2个编号l+k,第3个编号l+2k,这样继续下去,直到 获取整个样本).
2020/12/14
h
18
注意以下4点:
(1)系统抽样称为等距抽样; (2)注意当N/n不是整数时,要去掉一些个体,可以再用
2020/12/14
h
4
问题3:对本班同学对看足球比赛的喜爱程度(很喜爱、喜爱、 一般、不喜爱、很不喜爱)进行调查.
方案:将全班同学按学号编号,制作相应的卡片号签,放入同一 个箱子里均匀搅拌,从中抽出15个号签,就相应的15名学生对 看足球比赛的喜爱程度(很喜爱、喜爱、一般、不喜爱、很不 喜爱)进行调查.
2020/12/14
h
16
如果问题6中,学生人数是1003,如何进行系统抽样?
解:(1)随机将这1003个个体进行编号1,2,3,……1003; (2)利用简单随机抽样,先从总体中剔除3个个体(可以随
机数表法),将剩下的个体重新编号然后按系统抽样的方法进 行.
2020/12/14
h
17
系统抽样的步骤:
普查
全面、准确,但可行性差;
抽样调查
样本要具有代表性、广泛性等特点.
所要解决的问题是如何根据样本来推断总体-样本估计 总体的思想.
2020/12/14
h
3
总体:所要考察对象的全体. 个体:总体中的每一个考察对象. 样本:从总体中抽取的一部分个体叫做这个总体的一个样本. 样本容量:样本中个体的数目.
为了使统计活动能有效进行, 需要建立科学的统计理论和方法. 本章就是研究如何科学地抽取样本, 获取数据,并根据数据样本的分析 对总体进行估计的方法.
2020/12/14
h
2
问题 1. 2008高考考试中,某地有考生有2 万名,如果为了了解这些考生数学的主观题的 得分情况,我们应该怎样做?
问题2. 今有某灯泡厂生产的灯泡10000只, 怎样才能了解到这批灯泡的使用寿命呢?
(1)采用随机的方式将总体中的个体编号。为简便起见, 有时可直接采用个体所带有的号码,如考生的准考证号、 街道上各户的门牌号,等等;
(2)整个的编号分段(即分成几个部分),要确定分段的 间隔k.当N/n(N为总体中的个体的个数,n为样本容量) 是整数时,k=N/n;当N/n不是整数时,通过从总体中剔除 一些个体使剩下的总体中个体的个数N'能被n整除,这时 k=N'/n;
总体的个数较多,采用简单随机抽样较为费事.
2020/12/14
h
13
问题5:为了了解高一年级15个班的同 学(每班50名)的视力情况,从这15个 班中抽取一个容量为75的样本进行检查, 应如何抽取样本?
方案:通常将各班同学平均分成5组,再在第一组用抽签法确 定一个学号的学生,按每组逐次加10的原则抽取5名代表, 例:抽取学号为02,12,22,32,42等5位代表.
注意以下四点:
(1)它要求被抽取样本的总体的个体数有限; (2)它是从总体中逐个进行抽取; (3)它是一种不放回抽样; (4)它是一种等概率抽样.
2020/12/14
h
12
问题 1. 2008高考考试中,某地有考生有2 万名,如果为了了解这些考生数学的主观题的 得分情况,我们应该怎样做?
问题2. 今有某灯泡厂生产的灯泡10000只, 怎样才能了解到这批灯泡的使用寿命呢?
2020/12/14
h
19
2020/12/14h源自10练习:用随机表法,求解问题3.
问题3:对本班同学对看足球比赛的喜爱程度(很喜爱、喜爱、 一般、不喜爱、很不喜爱)进行调查.
2020/12/14
h
11
一般地,设一个总体的个体数为N,如果通过逐个抽 取的方法从中抽取一个样本,且每次抽取时各个个体被 抽到的概率相等,就称这样的抽样为简单随机抽样.
抽签法
2020/12/14
h
5
抽签法的一般步 骤:
(1)将总体中所有个体编号(对已经有编号的个体, 可以省略编号的过程);
(2)制作与个体编号相同的号签; (3)将号签放在一个箱子中搅匀; (4)按要求随机抽取号签,并记录; (5)将编号与号签一致的个体抽出.
抽签法的适用范 围:
抽签法简单易行,适用于总体中个体数不多的情形.
2020/12/14
h
1
统计学的研究对象是客观事物的数量特征和数量关系,它 是关于数据的搜集、整理、归纳和分析的方法和科学.
人们要认识客观事物,就必 须通过试验和调查来搜集有关数 据,并加以整理、归纳和分析, 以便对客观事物规律性的数量表 现作出统计上的解释.这既是统 计活动的过程,也是人们对客观 世界的认识过程.
2020/12/14
h
14
将总体分成均衡的几个部分,然后按照预先定出的规则, 从每一部分抽取一个个体,得到所需要的样本,这种抽样叫做 系统抽样(也称为等距抽样).
2020/12/14
h
15
问题6 :为了了解参加某种知识竞赛的1000名学生的成 绩,应采用什么样的抽样方法恰当?
解:抽样过程如下: (1)随机将这1000名学生编号为1,2,3,……,1000(比 如可以利用准考证号); (2)将总体按编号顺序平均分成50部分,每部分包含20个 个体. (3)在第一部分的个体编号1,2,……,20中,利用简单 随机抽样抽取一个号码,比如是18; (4)以18为起始号,每间隔20抽取一个号码,这样就得到 一个容量为50的样本:18,38,58,……,978,998.
h
8
问题4.为了检验某种产品的质量,决定从40件产品中抽取10件 进行检查,如何抽样? 例如选取第8行第9列开始.
6行: 16 22 77 94 39 49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64 7行: 84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 8行: 63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79 9行: 33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54 10行: 57 60 86 32 44 09 47 27 96 54 49 17 46 09 62 90 52 84 77 27 08 02 73 43 28
2020/12/14
h
6
抽签法的制签比较麻 烦,如何简化制签过程?
随机数表法
制作一个表,其中 每个数都是用随机方法产生 的,这样的表称为随机数表.
如何用随机数表来抽取样本?
2020/12/14
h
7
问题4.为了检验某种产品的质量,决定从40件产品中抽取10件
进行检查,如何抽样?
由于需要编号,如果总体中的个体数太多, 采用随机表法进行抽样就显得不太方便了
第一步,先将40件产品编号,可以编为00,01,02,,38,39.
所谓编号,实际上是编数字号码.不 要编号成:0,1,2,…,39
第二步,在附录1随机数表中任选一个数作为开始.
第三步,获取样本号码.
为了保证所选定数字的随机性,应在面对 随机数表之前就指出开始数字的纵横位置
2020/12/14
16 19 10 12 07 39 38 33 21 34
2020/12/14
h
9
注:当随机地选定开始读数的数后,读数的方向可以向右,也 可以向左、向上、向下等等.
在上面每两位、每两位地读数过程中,得到一串两位数字
号码,在去掉其中不合要求和与前面重复的号码后,其中依次 出现的号码可以看成是依次从总体中抽取的各个个体的号 码.由于随机数表中每个位置上出现哪一个数字是等概率的, 每次读到哪一个两位数字号码,即从总体中抽到哪一个个体的 号码也是等概率的.因而利用随机数表抽取样本保证了各个个 体被抽取的概率相等.
(3)在第一段用简单随机抽样确定起始的个体编号;
(4)按照事先确定的规则抽取样本(通常是将l加上间隔k, 得到第2个编号l+k,第3个编号l+2k,这样继续下去,直到 获取整个样本).
2020/12/14
h
18
注意以下4点:
(1)系统抽样称为等距抽样; (2)注意当N/n不是整数时,要去掉一些个体,可以再用
2020/12/14
h
4
问题3:对本班同学对看足球比赛的喜爱程度(很喜爱、喜爱、 一般、不喜爱、很不喜爱)进行调查.
方案:将全班同学按学号编号,制作相应的卡片号签,放入同一 个箱子里均匀搅拌,从中抽出15个号签,就相应的15名学生对 看足球比赛的喜爱程度(很喜爱、喜爱、一般、不喜爱、很不 喜爱)进行调查.
2020/12/14
h
16
如果问题6中,学生人数是1003,如何进行系统抽样?
解:(1)随机将这1003个个体进行编号1,2,3,……1003; (2)利用简单随机抽样,先从总体中剔除3个个体(可以随
机数表法),将剩下的个体重新编号然后按系统抽样的方法进 行.
2020/12/14
h
17
系统抽样的步骤:
普查
全面、准确,但可行性差;
抽样调查
样本要具有代表性、广泛性等特点.
所要解决的问题是如何根据样本来推断总体-样本估计 总体的思想.
2020/12/14
h
3
总体:所要考察对象的全体. 个体:总体中的每一个考察对象. 样本:从总体中抽取的一部分个体叫做这个总体的一个样本. 样本容量:样本中个体的数目.
为了使统计活动能有效进行, 需要建立科学的统计理论和方法. 本章就是研究如何科学地抽取样本, 获取数据,并根据数据样本的分析 对总体进行估计的方法.
2020/12/14
h
2
问题 1. 2008高考考试中,某地有考生有2 万名,如果为了了解这些考生数学的主观题的 得分情况,我们应该怎样做?
问题2. 今有某灯泡厂生产的灯泡10000只, 怎样才能了解到这批灯泡的使用寿命呢?
(1)采用随机的方式将总体中的个体编号。为简便起见, 有时可直接采用个体所带有的号码,如考生的准考证号、 街道上各户的门牌号,等等;
(2)整个的编号分段(即分成几个部分),要确定分段的 间隔k.当N/n(N为总体中的个体的个数,n为样本容量) 是整数时,k=N/n;当N/n不是整数时,通过从总体中剔除 一些个体使剩下的总体中个体的个数N'能被n整除,这时 k=N'/n;
总体的个数较多,采用简单随机抽样较为费事.
2020/12/14
h
13
问题5:为了了解高一年级15个班的同 学(每班50名)的视力情况,从这15个 班中抽取一个容量为75的样本进行检查, 应如何抽取样本?
方案:通常将各班同学平均分成5组,再在第一组用抽签法确 定一个学号的学生,按每组逐次加10的原则抽取5名代表, 例:抽取学号为02,12,22,32,42等5位代表.
注意以下四点:
(1)它要求被抽取样本的总体的个体数有限; (2)它是从总体中逐个进行抽取; (3)它是一种不放回抽样; (4)它是一种等概率抽样.
2020/12/14
h
12
问题 1. 2008高考考试中,某地有考生有2 万名,如果为了了解这些考生数学的主观题的 得分情况,我们应该怎样做?
问题2. 今有某灯泡厂生产的灯泡10000只, 怎样才能了解到这批灯泡的使用寿命呢?
