第六章数据的代表单元测试题
北师大版八年级数学上册 第六章 数据的分析 单元测试题
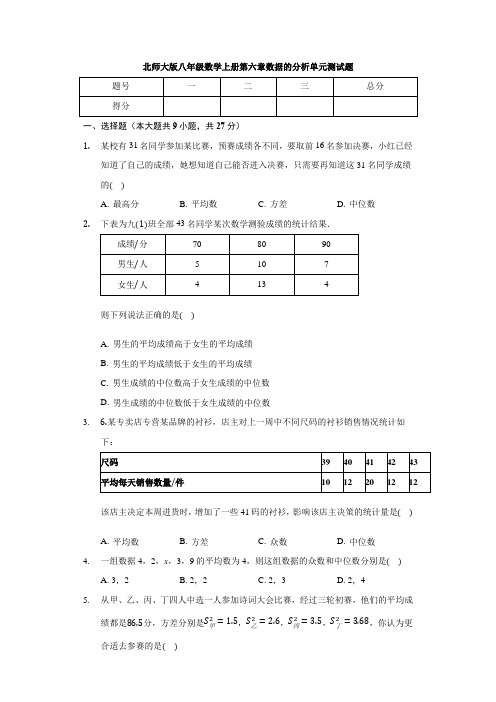
北师大版八年级数学上册第六章数据的分析单元测试题一、选择题(本大题共9小题,共27分)1.某校有31名同学参加某比赛,预赛成绩各不同,要取前16名参加决赛,小红已经知道了自己的成绩,她想知道自己能否进入决赛,只需要再知道这31名同学成绩的()A. 最高分B. 平均数C. 方差D. 中位数2.下表为九(1)班全部43名同学某次数学测验成绩的统计结果.则下列说法正确的是()A. 男生的平均成绩高于女生的平均成绩B. 男生的平均成绩低于女生的平均成绩C. 男生成绩的中位数高于女生成绩的中位数D. 男生成绩的中位数低于女生成绩的中位数3. 6.某专卖店专营某品牌的衬衫,店主对上一周中不同尺码的衬衫销售情况统计如下:该店主决定本周进货时,增加了一些41码的衬衫,影响该店主决策的统计量是()A. 平均数B. 方差C. 众数D. 中位数4.一组数据4,2,x,3,9的平均数为4,则这组数据的众数和中位数分别是()A. 3,2B. 2,2C. 2,3D. 2,45.从甲、乙、丙、丁四人中选一人参加诗词大会比赛,经过三轮初赛,他们的平均成绩都是86.5分,方差分别是S甲2=1.5,S乙2=2.6,S丙2=3.5,S丁2=3.68,你认为更合适去参赛的是()A. 甲B. 乙C. 丙D. 丁6.测试五位学生的“一分钟跳绳”成绩,得到五个各不相同的数据,在统计时,出现了一处错误:将最高成绩写得更高了,计算结果不受影响的是()A. 方差B. 标准差C. 中位数D. 平均数7.在“经典诵读”比赛活动中,某校10名学生参赛成绩如图所示,对于这10名学生的参赛成绩,下列说法正确的是()A. 众数是90分B. 中位数是95分C. 平均数是95分D. 方差是158.甲、乙、丙、丁四名射击运动员在选拔赛中,每人射击了10次,甲、乙两人的成绩如表所示,丙、丁两人的成绩如图所示.欲选一名运动员参赛,从平均数与方差两个因素分析,应选()甲乙平均数/环 9 8方差/环 1 1A. 甲B. 乙C. 丙D. 丁9.小明在五天投掷铅球训练中,每天训练的最好成绩(单位:m)分别为10.1,10.4,10.6,10.5,10.4,关于这组数据,下列说法错误的是()A. 平均数是10.4B. 中位数是10.6C. 众数是10.4D. 方差是0.028二、填空题(本大题共7小题,共21分)10.某餐厅供应单价分别为10元、18元、25元三种价格的抓饭,如图是该餐厅某月销售抓饭情况的扇形统计图,根据该统计图可算得该餐厅销售抓饭的平均单价为__________元.第2页,共17页11.已知一组数据6,x,3,3,5,1的众数是3和5,则这组数据的中位数是______.12.一组数据2,4,a,6,7,7的中位数是5,则方差S2=______.13.某校初一共有四个班参加语文考试,甲班共有a人,平均得x分;乙班共有b人,平均得y分;丙班共有c人,平均得z分;丁班共有d人,平均得w分,则该校初一年级语文平均得分为___________________.14.已知一组从小到大排列的数据:1,x,y,2x,6,10的平均数与中位数都是5,则这组数据的众数是______.15.如图是甲、乙两射击运动员10次射击成绩的折线统计图,则这10次射击成绩更稳定的运动员是______.16.已知一组数据−3,−1,0,a,3的平均数是0,则这组数据的方差是__________.三、解答题(本大题共5小题,共52分)17.某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%,面试占40%计算候选人的综合成绩(满分为100分).他们的各项成绩如下表所示:候选人笔试成绩/分面试成绩/分甲90 88乙84 92丙x90丁88 86(1)直接写出这四名候选人面试成绩的中位数;(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.18.甲、乙两名队员参加射击训练,成绩分别被制成如图的两个统计图:根据以上信息,整理分析数据如表所示:平均成绩(环)中位数(环)众数(环)方差甲a7 7 1.2乙7 b8 c(1)请分别计算表格中a,b,c的值;(2)若选派其中一名参赛,你认为应选哪名队员?请说明理由。
2020-2021学年北师大版小学四年级数学下册《第六章 数据的表示和分析》单元测试题(有答案)

2020-2021学年北师大版小学四年级数学下册《第六章数据的表示和分析》单元测试题一.选择题(共8小题)1.如图,()可以表示下面哪种情况的统计.A.4个学生期末数学考试成绩B.四年级喜欢各项运动的男女生人数C.小明1﹣﹣8岁的身高D.蛋糕店的草莓蛋糕和芒果蛋糕最近5天的销售情况2.如图是小明每天上学走的路程统计图,那么他从家到学校需要走()千米.A.5B.2.5C.103.下面说法中错误的是()A.在研究平均数问题时可以用移多补少的方法B.我们在研究小数的意义时运用了数形结合的思想方法C.28+374+26 此题进行简便运算,我们头脑里可以想a﹣b﹣c=a﹣(b+c)这一运算律4.游泳池平均水深130厘米,小红身高1.35米,她在游泳池里一定不会有危险.这句话对吗?()A.对B.不对C.不知道5.淘气从家去书城,中途休息了几分钟,到书城买完书后直接回家.下面正确描述淘气这一过程的图象是()A.B.C.D.6.下面三幅图是4名学生一分钟内投篮投进个数情况统计图,图()中虚线所指的位置表示平均每人投进的个数.A.B.C.7.淘气家的热水器中有60L水,晚上,爸爸先洗了10min澡,用了一半的水.5min后,淘气也去洗澡,他洗了15min,把热水器中的水刚好用完了.下面能描述热水器中水的体积随时间变化的情况的是()A.B.C.D.8.下面是育英小学和西门小学四、五、六年级学生回收电池统计图.根据统计情况估计一下,哪个学校的学生回收的电池更多?()A.西门小学B.育英小学C.两个学校一样多二.填空题(共8小题)9.下面是某学校五(1)班学生拥有课外读物情况,五(1)班共有学生人,平均每人拥有课外读物本.性别人数平均每人拥有课外读物/本男生1625女生243010.刘小兵折的纸飞机前4次飞行的距离如表:第1次第2次第3次第4次飞行距离/米18122117(1)这架纸飞机前4次飞行的平均距离是米.(2)如果再飞一次,并使平均飞行距离达到18米,第5次飞行的距离至少要达到米.11.看图回答问题.如图是小军从家去图书馆借书的行程图.①小军家到图书馆距离千米.②小军在图书馆待了分钟.③小军去的途中停了分钟.④小军去的时候平均每小时行千米.12.如图是打国际长途电话所需付的电话费与通话时间之间的关系图.(1)打2分钟需要元电话费,3分钟以上每分钟元.(2)打6分钟需要元,10.4元打了分钟.13.五(1)一班有男生20人,平均身高158cm;有女生16人,平均身高140cm,全班学生的平均身高是cm.14.在一幅条形统计图中,用3.5厘米长的直条表示21人,用厘米的直条表示42人.15.如图是希望小学四年级一周内向“我爱祖国”主题活动投稿情况统计图.请根据条形图回答问题.(1)每格代表篇.(2)这一周内,周投稿篇数最多,周投稿篇数最少.(3)周四比周二多投稿篇.(4)这一周一共投稿篇.16.一个长方体容器(如图1)现在以每分钟25升的速度向这个容器注水,容器的底面有一块隔板(垂直于底面,不考虑厚度),将容器隔为A,B部分,B部分的底有一个洞,水按每分钟10升的速度往下漏.(如图2)表示从注水开始A部分水的高度变化情况,观察并思考回答下面的问题:(1)隔板的高度是分米.(2)注水36分钟共漏出水升.(3)如果不让B部分的洞漏水,只要分就能使水箱A部分的水位到达5分米.三.判断题(共5小题)17.四一班的数学平均分是92分,四一班没有不及格的.(判断对错)18.在一幅条形统计图中,用2厘米长的直条表示600吨,那么表示1800吨的直条应画6厘米..(判断对错)19.折线统计图便于直观了解数据的大小及不同数据的差异.(判断对错)20.游泳池平均水深110厘米,小强身高130厘米,下水游泳一定没有危险。
北师大版四年级下册数学第六单元 数据的表示和分析单元测试卷及答案

北师大版四年级下册数学第六单元数据的表示和分析单元测试卷及答案一、选择题(共5题,共计20分)1、甲、乙两位同班同学是邻居,甲中午回家吃午饭,乙在班级吃午饭。
下面()图描述的是乙一天的情况.A. B. C.D.2、在“书香校园”活动中,我校同学平均每人捐了5本书。
()A.全校每个同学一定都捐了5本。
B.可能有人捐了10本书。
3、学科检测中,小红语文得了86分,英语得了92分,她三门科目的平均分是91分,数学得了()分。
A.91B.93C.95D.974、某小学六(1)班环保小组的5名同学记录了自己家中一周内丢弃塑料袋的数量,结果如下(单位:个):32,25,27,26,25.如果该班有45名同学,根据提供的数据估计本周全班同学各家共丢弃塑料袋大约()A.900B.1080C.12155、梅梅做跳绳练习,第一次跳了69下,第二次跳了75下。
她要想三次的平均成绩达到80下,第三次至少要跳()。
A.80下B.96下C.90下D.75下二、填空题(共8题,共计24分)6、从一箱桃子中随意取出5个,分别重88克、98克、80克、95克、89克,平均每个重________克。
这箱桃子共有50个,估一估,这箱桃子大约重________克。
7、18、19、20、21、22这五个数的平均数是________。
8、统计表用________呈现数据,条形统计图用________呈现数据。
统计过程中,记录调查结果和整理数据,常用画________字的方法。
9、如图是六年级两个班同学8~12月参加社会实践活动的人数统计图,六(1)班8~12月平均每月参加社会实践活动的有________人.10、下面是星球商场第一季度销售电视机数量统计表:2月份销售的台数被弄污了,请你帮忙算出2月份销售________台电视机。
11、下图________是单式统计图.________是复式条形统计图.12、在一个10千米的越野赛中,小刚的参赛方法是:前半程以20千米/时的速度前进,后半段路以15千米/时的速度到达终点,那么在整个过程中,小刚的平均速度是________千米/时.13、学校气象小组一天中测得气温如下:14度、16度、20度、21度、14度,这一天的平均气温是________度。
四年级数学下册 第六单元《数据的表示和分析》单元测评必刷卷(解析版)(北师大版)

北师大版四年级下册数学单元测评必刷卷第6章《数据的表示和分析》测试时间:90分钟满分:100分+30分题号一二三四五B卷总分得分A 卷基础训练(100 分)一、选择题(每题2分,共20分)1.(2021·辽宁四年级期中)某人骑车沿直线旅行,先前进了akm休息了一段时间,又原路返回了bkm(b<a)。
再前进ckm,则此人离起点的距离s与时间t的关系示意图是()。
A.B.C.D.【答案】B【分析】应根据时间的不断变化,来反映离家的远近,特别是“休息了一段时间后又按原路返回bkm”,要通过图象反映出来。
【详解】因为他休息了一段时间,那么在这段时间内,时间在增长,路程没有变化,应排除第一个;又按原路返回bkm,说明随着时间的增长,他离出发点近了点,排除第四个;C选项虽然离出发点近了,但时间没有增长,应排除第三个;故答案为:B。
【点睛】本题主要考查了s-t图象,解题应首先看清横轴和纵轴表示的量,然后根据实际情况采用排除法求解。
2.(2020·陕西四年级期末)乐乐语、数、英三科的平均分是90分,其中数学是89分,语文是88分,英语是()分。
A.88 B.90 C.93【答案】C【分析】三科的平均分乘3等于三科的总分,再减去数学和语文的分数,即等于英语的分数。
【详解】90×3-89-88=270-89-88=181-88=93(分)故答案为:C。
【点睛】本题主要考查学生对平均数知识的掌握和灵活运用。
3.(2021·北京五年级期末)五(1)班女生有19人,平均身高1.52米,男生有22人,平均身高1.48米。
下面说法错误的是()。
A.五(1)班男生平均身高比女生平均身高低B.五(1)班同学平均身高在1.48米~1.52米之间C.张丽是女生,她的身高一定是1.52米D.王山是男生,他的身高可能是1.52米【答案】C【分析】要想比较五(1)班男生平均身高比女生平均身高的高低,直接比较1.52和1.48的大小即可;要想求五(1)班同学平均身高,用身高总和除以总人数即可;张丽是女生,她的身高可能比平均数高,也可能比平均数低;王山是男生,他的身高可能是平均数1.52米。
四年级下册数学单元测试-6.数据的表示和分析+北师大版(含答案)

四年级下册数学单元测试-6。
数据的表示和分析一、单选题1.要想清楚地反映某地区近年来经济发展变化情况,用()统计图更合适。
A. 条形B. 折线C. 扇形D. 复式2.折线统计图表示()。
A. 数量关系的多少和增减变化情况B. 数量的多少C. 部分与总数的关系3.只表示数量多少的统计图是()。
A. 条形统计图B. 折线统计图C. 扇形统计图4.要统计小红身高的变化情况应选用()统计图。
A. 折线B. 扇形C. 条形二、判断题5. 条形统计图能直观反映初三三班身高各档的人数情况。
()6.在制作条形统计图时,一格可以代表一、十、几十,或更多个单位。
()7.心电图的图形是折线统计图。
()8.同一个条形统计图中的每一小格代表的数量可以不相等。
()三、填空题9.小明从早上8时到下午18时每隔两小时记录一次室外的温度,他想要看一下这10个小时中温度的变化,需要用________统计图。
10.在读书比赛中,小朱读了6本,小明读了4本,小华读了3本,小军读了7本,平均每人读________本课外书。
11.三个连续奇数的和是177,这三个数的平均数是________,其中最大的数是________。
四、解答题12.下面是新新工厂三名技术人员的年龄情况统计表。
王宁张震吕志广32岁 30岁 34岁这三名技术人员的平均年龄是多少岁?13.下面是光明小学四年级学生体育达标等级情况统计表。
等级优良合格不合格人数(人) 120 90 60 15(1)图中1格代表________人。
(2)请根据表格中的数据,完成上面的条形统计图。
(3)体育达标等级中得________的人数最多,得良的人数是不及格的________倍。
(4)根据上面统计图,你想说点什么?14.下面是小明家去年上半年电费统计表。
月份1月 2月 3月 4月 5月 6月电费/元35 45 38 50 42 48(1)根据统计表中的数据绘制完成统计图。
(2)小明家________月份电费开支最大,________月份电费开支最小。
北师大版八年级数学上册《第六章数据的分析》章节检测卷-带答案

北师大版八年级数学上册《第六章数据的分析》章节检测卷-带答案学校:___________班级:___________姓名:___________考号:___________1 平均数算术平均数、加权平均数A.基础夯实1. 有一组数据:2 4 5 6 8 这组数据的平均数为()A. 3B. 4C. 5D. 62. 2012年5月某日我国部分城市的最高气温统计如下表所示.城市武汉成都北京上海海南南京拉萨深圳气温(℃)27 27 24 25 28 28 23 26则这组数据的平均数是()A. 24B. 25C. 26D. 273. 若a,b,c的平均数为7,则a+1、b+2、c+3的平均数为()A. 7B. 8C. 9D. 104. 如果一组数据−3−20 1 x 6 9 12的平均数为3 则x为()A. 2B. 3C. −1D. 15. 某学校在开展“生活垃圾分类星级家庭”评选活动中,从八年级任选出10名同学汇报了各自家庭1天生活垃圾收集情况,将有关数据整理如下表.生活垃圾收集量(单位:kg)0.5 1 1.5 2同学数 2 3 4 1请你计算每名同学家庭平均1天生活垃圾收集量是()A. 0.9kgB. 1kgC. 1.2kgD. 1.8kg6. [2023·梅州期末]某校体育期末考核“仰卧起坐”和“800米”两项,并按3:7的比例算出期末成绩.已知小林这两项的考试成绩分别为80分,90分,则小林的体育期末成绩为分.7. 七年级一班某次英语测验后,现以80分为基准,超出的记为正数,不足的记为负数,抽查了4名同学,记录结果如下:+8−2+6−4.那么这4名同学的平均成绩是多少分?B.能力提升8. 若1 4 m7 8的平均数是5 则1 4 m+107 8的平均数是()A. 5B. 6C. 7D. 89. 某校招聘教师,规定综合成绩由笔试成绩和面试成绩构成,其中笔试占60%,面试占40%,有一名应聘者的综合成绩为78分,笔试成绩是80分,则面试成绩为分. 10. 评定学生的学科期末成绩由考试分数,作业分数,课堂参与分数三部分组成,并按3:2:5的比例确定,已知小明的数学考试分数为80分,作业分数为95分,课堂参与分数为82分求小明的数学期末成绩为多少.C.拓展思维11. 某农户在承包的荒山上共种植了44棵樱桃树2020年采摘时先随意采摘5棵树上的樱桃称得每棵树上的樱桃质量(单位:kg)如下:35 35 34 39 37.(1)根据以上数据估计该农户2020年樱桃的产量是多少千克;(2)已知该农户的这44棵树在2019年共收获樱桃1440kg若近几年的产量的年增长率相同依照(1)中估计的2020年的产量预计2021年该农户可收获樱桃多少千克?12. 小青在本学期的数学成绩如下表所示(成绩均取整数).测验类别平时期中考试期末考试测验1 测验2 测验3 课题学习成绩88 70 96 86 85 x(1)计算小青本学期平时的平均成绩;(2)如果学期的总评成绩是根据如图所示的权重计算那么本学期小青的期末考试成绩x至少为多少分才能保证达到总评成绩90分的最低目标?2 中位数与众数A.基础夯实1. 某学习小组7位同学为玉树地震灾区捐款捐款金额分别为5元6元6元6元7元8元9元则这组数据的中位数与众数分别为()A. 6元6元B. 7元6元C. 7元8元D. 6元8元2. 为切实落实“双减”丰富课后服务活动形式某校开展学生的绘画书法散文诗等艺术作品征集活动从八年级7个班收集到的作品数量(单位:件)分别为50 45 4246 50 44 52 则这组数据的中位数和平均数分别是()A. 46 47B. 45 47C. 50 46D. 42 463. 为了了解某种小麦的长势随机抽取了50株麦苗进行测量测量结果如表.苗高(cm)10 11 12 13 14株数(株)7 12 10 14 7则麦苗高的中位数是()A. 10B. 11C. 12D. 134. [2023·深圳校考]某校男子篮球队10名队员进行定点投篮练习每人投篮10次他们投中的次数统计如表.投中次数 3 5 6 7 9人数 1 3 2 2 2则这些队员投中次数的众数中位数分别为()A. 6 6B. 5 5C. 5 6D. 3 65. 为调动学生参与体育锻炼的积极性某校组织了一分钟跳绳比赛活动体育老师随机抽取了10名参赛学生的成绩将这组数据整理后制成统计表.一分钟跳绳个数181 184 185 186学生人数 2 5 1 2则这组数据的中位数是;众数是.B.能力提升6. 已知一组数据分别为3 8 4 5 x这组数据的众数是8 则这组数据的中位数是()A. 3B. 4C. 5D. 87. 一组数据1 x 5 7有唯一众数且中位数是6 则平均数是.8. 2022年11月5日第二十三届深圳读书月盛大开幕本届读书月以“读时代新篇创文明典范”为年度主题2300余场文化活动“阅”动全城.春海学校积极响应深圳读书月的号召在校内推广课外阅读活动.为了解七八年级学生每周课外阅读的情况分别从两个年级随机抽取了10名学生进行调查并对调查数据进行整理分析.现将参与调查的每个学生每周课外阅读的时间用x(小时)表示并将两个年级的调查数据分成四组:A.0≤x<4 B.4≤x<8 C.8≤x<12 D.12≤x≤16.以下是相关的数据信息:七年级学生调查数据:3 14 8 9 9 11 8 11 16 11.八年级学生调查数据位于C组中的是9 10 10 10.七八年级抽取的学生每周课外阅读时间统计表平均数众数中位数七年级10 a b八年级9 10 c根据以上信息解答下列问题:(1)分别求出上述图表中a b c的值:a=b=c=;(2)若七八年级共有1 000名学生请你估计该校七八年级学生每周课外阅读时间不少于12小时的共有多少人.C.拓展思维9. 某校积极响应“弘扬传统文化”的号召开展经典诗词背诵活动并在活动之后举办经典诗词大赛.为了解本次系列活动的持续效果学校在活动初期随机抽取部分学生调查“一周诗词背诵数量”并根据调查结果绘制成不完整的条形扇形统计图如图所示.诗词大赛结束后一个月再次调查这部分学生“一周诗词背诵数量”绘制成统计表.大赛后学生“一周诗词诵背数量”统计表一周诗词诵背数量3首4首5首6首7首8首人数9 11 15 42 23 20请根据上述调查的信息分析:(1)活动启动之初学生“一周诗词背诵数量”的中位数为首;(2)估计大赛结束后一个月该校学生(总数1 200人)“一周诗词背诵数量”不少于6首的人数;(3)选择适当的统计量从两个不同的角度分析两次调查的相关数据评价该校经典诗词背诵系列活动的效果.4 数据的离散程度极差方差标准差A.基础夯实1. 某中学在备考2023中考体育的过程中抽取该校九年级20名男生进行立定跳远测试成绩如下表所示则下列叙述正确的是()成绩(单位:m) 2.10 2.20 2.25 2.30 2.35 2.40 2.45 2.50人数 2 3 2 4 5 2 1 1A. 这些男生成绩的众数是5B. 这些男生成绩的中位数是2.30C. 这些男生的平均成绩是2.25D. 这些男生成绩的极差是0.352. [2023·深圳期末]南山区博物馆五位小讲解员的年龄分别为10 12 12 13 15(单位:岁)则三年后这五位小讲解员的年龄数据中一定不会改变的是()A. 方差B. 众数C. 中位数D. 平均数3. 方差是刻画数据波动程度的量.对于一组数据x1,x2,x3,⋯,x15可用如下算式计算方差:s2=1[(x1−5)2+(x2−5)2+(x3−5)2+⋯+(x15−5)2]则这组数据的平均数是15()A. 5B. 10C. 15D. 1154. 小林爸爸想了解他在学校的数学学习情况于是询问得知了他本学期的近5次数学单元测验成绩(单位:分)分别为88 91 89 92 90 试求小林这5次测验成绩的方差以便帮助小林分析他的数学成绩是否相对稳定.B.能力提升5. 某校九年级参加了“维护小区周边环境”“维护繁华街道卫生”“义务指路”等志愿者活动如图是根据该校九年级六个班的同学某天“义务指路”总人次所绘制的折线统计图则关于这六个数据下列说法正确的是()A. 极差是40B. 众数是58C. 中位数是51.5D. 平均数是606. 某班有40人一次体能测试后老师对测试成绩进行了统计.由于小亮没有参加本次集体测试因此计算其他39人的平均分为90分方差s2=41.后来小亮进行了补测成绩为90分关于该班40人的测试成绩下列说法正确的是()A. 平均分不变方差变大B. 平均分不变方差变小C. 平均分和方差都不变D. 平均分和方差都改变7. 在对一组样本数据进行分析时小华列出了方差的计算公式:s2=(2−x)2+(3−x)2+(3−x)2+(4−x)2请根据此公式提供的信息试求数据2+x0,3+x0,3+x0,4+x0的n标准差.C.拓展思维8. 已知一组数据1 2 3 4 x的方差与另一组数据2020202120222023 2024的方差相等请尝试求x的值.9. 为了解某校八年级暑期参加义工活动的时间某研究小组随机采访了该校八年级的20位同学得到这20位同学暑假参加义工活动的天数的统计如下:天数(天)0 2 3 5 6 8 10人数 1 2 4 8 2 2 1(1)这20位同学暑期参加义工活动的天数的中位数是天众数是天极差是天;(2)若小明同学把天数中的数据“8”看成了“7”那么中位数众数方差极差四个指标中受影响的是;(3)若该校有500位八年级学生试用这20位同学的样本数据去估计该校八年级学生暑期参加义工活动的总天数.章末复习A.基础夯实1. 某校规定英语竞赛成绩85分以上为优秀老师将85分记为0 并将一组5名同学的成绩简记为−3+140 +5−6这5名同学的平均成绩是()A. 83分B. 87分C. 82分D. 84分2. [2023·翠园初级中学校考]某校开展安全知识竞赛进入决赛的有6名同学他们的成绩(单位:分)分别是100 99 90 99 88 97.这6名同学的决赛成绩的中位数和众数分别是()A. 99 99B. 90 98C. 98 99D. 94.5993. [2023·清远期中]班长统计去年1~8月“书香校园”活动中全班的课外书阅读数量(单位:本)绘制了折线统计图(如图).下列说法中正确的是()A. 这组数据的极差是47B. 这组数据的众数是42C. 这组数据的中位数是58D. 月阅读数量超过40本的有5个月4. 某校5个小组在一次植树活动中植树株数的统计图如图所示则平均每组植树株.5. 如果一组数据2 4 x 3 5的众数是4 那么该组数据的平均数是.6. 一组数据是6 8 10 8 这组数据的方差是 .B.能力提升7. 小明同学随机调查七(2)班6名同学每天食堂午饭消费金额 制作如下统计表:类别 同学1 同学2 同学3 同学4 同学5 同学6 金额(元)565668则这组消费金额的( ) A. 平均数为5B. 中位数为5C. 众数为6D. 方差为68. 每年的6月6日是全国爱眼日 就在手机充斥着人们生活 占用大部分时间的同时 其蓝光危害以及用眼过度带来的影响也在悄然威胁着人们的视力健康 某班为了解全班学生的视力情况 随机抽取了10名学生进行调查 将抽取学生的视力统计结果如下表.下列说法错误的是( )视力 4.5 4.6 4.7 4.8 4.9 5.0 人数112 312A. 平均数为4.7B. 中位数为4.8C. 众数为4.8D. 方差为0.02369. 某射击运动员练习射击 5次成绩分别是8 9 7 8 x (单位:环) 下列说法中正确的是 (填序号). ①若这5次成绩的平均数是8 则x =8; ②若这5次成绩的中位数为8 则x =8; ③若这5次成绩的众数为8 则x =8; ④若这5次成绩的方差为8 则x =8.C.拓展思维10. 设x −是x 1,x 2,⋯ ,x n 的平均数 即x −=x 1+x 2+⋯+x nn则方差s 2=1n×[(x 1−x −)2+(x 2−x −)2+⋯+(x n −x −)2] 它反映了这组数据的波动性.(1) 求证:对任意实数a x 1−a x 2−a ⋯ x n −a 与x 1 x 2 ⋯ x n 方差相同;[x12+x22+⋯+x n2]−x2;(2)求证:s2=1n(3)以下是我校初三(1)班10位同学的身高(单位:cm):169 172 163 173 175 168 170 167 170 171 计算这组数据的方差.参考答案1 平均数算术平均数加权平均数A.基础夯实1.【答案】C2.【答案】C3.【答案】C4.【答案】D5.【答案】C6.【答案】877.【答案】解:这4名同学的平均成绩是80+14×(8−2+6−4)=80+14×8=82(分)。
四年级数学北师大版下册《第六单元 数据的分析和表示》单元测试01(含答案)

答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的小朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!北师大版四年级数学下册《第六单元数据的分析和表示》单元测试一、填空题。
1.四年级各班植树情况如下:(1)四个班中()班植树的棵数最多,是()棵;()班植树的棵数最少,是()棵。
(2)平均每个班植()棵树。
2.下面是一架模型飞机的飞行情况统计图。
(1)这个统计图纵轴上每格表示()米(2)这架模型飞机一共飞行了()秒,飞行高度最高是()米。
它前()秒是上升的,后()秒是下降的。
(3)估计这架模型飞机在第15秒时的飞行高度大约是()米。
二、选择题1.要反映一位病人24小时内心跳次数的变化情况,护士需要把病人心跳数据制成()。
A.统计表B.条形统计图C.折线统计图2.某次射击训练中,一小组的成绩如下表所示:已知该小组的平均成绩为8.1环,那么成绩为8环的人数是()。
北师版八年级数学上册 第六章 数据的分析(单元综合测试卷)

第六章数据的分析(单元重点综合测试)班级___________姓名___________学号____________分数____________考试范围:全章的内容;考试时间:120分钟;总分:120分一、单选题(本大题共10小题,每小题3分,共30分)1.已知一组数据:4,1,2,3,4,这组数据的中位数和众数分别是()A .4,4B .3.5,4C .3,4D .2,42.在“我的阅读生活”校园演讲比赛中,有11名学生参加比赛,他们决赛的最终成绩各不相同,其中一名学生想知道自己能否进入前6名,除了要了解自己的成绩外,还要了解这11名学生成绩的()A .众数B .方差C .平均数D .中位数3.已知数据3,x ,7,1,10的平均数为5,则x 的值是()A .3B .4C .5D .64.甲、乙、丙、丁四人参加射击训练,经过三组练习,他们的平均成绩都是9.5环,方差分别是20.45s =甲,20.55s =乙,20.4s =丙,20.35s =丁,你认为谁的成绩更稳定()A .甲B .乙C .丙D .丁5.在“双减”政策下,某学校规定,学生的学期学业成绩由三部分组成:平时成绩占20%,期中成绩占30%,期末成绩占50%,小颖的平时、期中、期末成绩分别为80分,90分,92分,则小颖本学期的学业成绩为()A .92分B .90分C .89分D .85分6.在第60届国际数学奥林匹克比赛中,中国队荣获团体总分第一名.我国参赛选手比赛成绩的方差计算公式为:()()()222212613838386s x x x ⎡⎤=-+-++-⎣⎦ ,下列说法错误的是().A .我国一共派出了6名选手B .我国参赛选手的平均成绩为38分C .我国选手比赛成绩的中位数为38D .我国选手比赛成绩的团体总分为228分7.我校开展了“好书伴我成长”读书活动,为了解5月份九年级学生的读书情况,随机调查了九年级50名学生读书的册数,统计数据如下表所示,下列说法正确的是()册数01234人数41216171A.众数是17B.中位数是2C.平均数是2D.方差是28.某聊天软件规定:若任意连续5天,好友双方的每日聊天记录的条数不低于100,则双方可以获得“星形”标识.甲、乙两位好友连续5天在该软件上聊天,下面是这5天日聊天记录条数的统计量,一定能判断甲、乙获得“星形”标识的是()A.中位数为110条,极差为20条B.中位数为110条,众数为112条C.中位数为106条,平均数为102条D.平均数为110条,方差为10条29.某商场招聘员工一名,现有甲、乙、丙三人竞聘,通过计算机、语言和商品知识三项测试,他们各自成绩(百分制)如下表所示,若商场需要招聘负责将商品拆装上架的人员,对计算机、语言和商品知识分别赋权2,3,5,那么从成绩看,应该录取()应试者计算机语言商品知识甲607080乙807060丙708060A.甲B.乙C.丙D.任意一人都可10.某排球队6名场上队员的身高(单位:cm)是:180,184,188,190,192,194.现用一名身高为188cm 的队员换下场上身高为194cm的队员,与换人前相比,场上队员的身高()A.平均数变小,方差变小B.平均数变小,方差变大C.平均数变大,方差变小D.平均数变大,方差变大二、填空题(本大题共8小题,每小题3分,共24分)11.数据1,8,8,4,6,4的中位数为.12.我国是世界上严重缺水的国家之一.为了倡导“节约用水从我做起”,小刚在他所在班的50名同学中,随机调查了10名同学家庭中一年的月均用水量(单位:t),并将调查结果绘成了如下的条形统计图,则这10个样本数据的平均数是,众数是,中位数是.13.已知一组数据3,a ,4,6,7,它们的平均数是5,则这组数据的方差是.14.新冠疫情期间,小李同学连续两周居家健康检测,如下图是小李记录的体温情况折线统计图,记第一周体温的方差为21s ,第二周体温的方差为22s ,试判断两者之间的大小关系21s 22s (用“>”、“=”、“<”填空).小李连续两周居家体温测量折线统计图15.开学前,根据学校防疫要求,小芸同学连续14天进行了体温测量,结果统计如表:体温(℃)36.336.436.536.636.736.8天数(天)233411这14天中,小芸体温的中位数和众数分别是℃.16.宁城有机苹果园引进了甲、乙、丙、丁四个品种的苹果树.为了了解每种苹果树的产量情况,从每个品种中随机抽取10棵进行采摘,经统计每种苹果树10棵产量的平均数x 和方差2s 如下表:甲乙丙丁平均数()kg x 194194188188方差2s 9.28.68.99.7若从这四个品种中选出一种产量既高又稳定的苹果树进行种植,应选的品种为.17.将5个整数从大到小排列,中位数是4;如果这个样本中的唯一众数是6,则这5个整数可能的最大的和是.18.一组数据1x 、2x 、…、n x 的方差是0.8,则另一组数据11x +、21x +、…、1n x +的方差是.三、解答题(本大题共9小题,共66分)19.甲、乙两人在相同的情况下各打靶6次,每次打靶的成绩依次如下(单位:环):甲:9,6,7,6,7,7乙:4,5,8,7,8,10(1)计算两人打靶成绩的方差;(2)请推荐一人参加比赛,并说明理由.20.某公司要在甲、乙两人中招聘一名职员,对两人的学历、能力、经验这三项进行了测试,各项满分均为10分,成绩高者被录用.图1是甲、乙两人测试成绩的条形统计图.(1)分别计算甲、乙两人三项成绩之和,则会被录用;(2)若将甲、乙两人的三项测试成绩,分别按照扇形统计图(图2)各项所占之比进行计算,甲成绩为分,乙成绩为分,则会被录用.21.某调查小组采用随机抽样方法,对某市部分中小学生一天中阳光体育运动时间进行了抽样调查,并把所得数据整理后绘制成如下不完整的统计图.(1)填空:本次调查的中位数为________小时;(2)通过计算补全条形统计图;(3)请估计该市中小学生一天中阳光体育运动的平均时间.22.某药店有3000枚口罩准备出售,从中随机抽取了一部分口罩,根据它们的价格(单位:元),绘制出如图的统计图,请根据相关信息,解答下列问题:(1)图①中的m值为________;此次抽样随机抽取了口罩_______枚;(2)求统计的这些数据的平均数、众数和中位数;(3)根据样本数据,估计这3000枚口罩中,价格为1.8元的口罩约有多少枚?23.某校七年级一班和二班各派出10名学生参加一分钟跳绳比赛,成绩如下表:跳绳成绩(个)132133134135136137一班人数(人)120232二班人数(人)014122(1)两个班级跳绳比赛成绩的众数、中位数、平均数、方差如下表:众数中位数平均数方差一班136135.5135 2.8二班134a135b表中数据a=,b=;(2)请用所学的统计知识,从两个不同角度比较两个班跳绳比赛的成绩.24.为鼓励学生积极加入中国共青团组织,某学校团委在八、九年级各抽取50名学生开展团知识竞赛,为便于统计成绩,制定了取整数的计分方式,满分10分.竞赛成绩如图所示.平均数众数中位数方差八年级87b 1.88九年级8a8c请根据图表中的信息,解答下列问题:(1)填空:a =______,b =______,c =________;(2)现要给成绩突出的年级颁奖,如果分别从众数和方差两个角度来分析,你认为应该给哪个年级颁奖?25.为了了解学生对党的二十大精神的学习领会情况,某校团委从七、八年级各随机抽取20名学生进行测试,获得了他们的测试成绩(百分制),并对数据(测试成绩)进行整理、描述和分析.下面给出了部分信息.a .八年级学生测试成绩的频数分布直方图如下,(数据分为4组:6070x ≤<,7080x ≤<,8090x ≤<,90100x ≤≤).b .八年级学生测试成绩在8090x ≤<这一组的是:81838484848689c .七、八年级学生测试成绩的平均数、中位数、众数如下:年级平均数中位数众数七83.18889八83.5m根据以上信息,回答下列问题:(1)表中m 的值为______,八年级学生测试成绩在8090x ≤<这一组的众数是______;(2)七年级学生小亮和八年级学生小宇的成绩都是86分,这两名学生在本年级成绩排名更靠前的是______(填“小亮”或“小宇”);(3)成绩不低于80分的学生可获得优秀奖,假设该校八年级300名学生都参加测试,估计八年级获得优秀奖的学生人数.26.今年是五四运动100周年,也是中华人民共和国成立70周年,为缅怀五四先驱崇高的爱国情怀和革命精神,巴蜀中学开展了“青春心向党,建功新时代”为主题的系列纪念活动.历史教研组也组织了近代史知识竞赛,七、八年级各有300名学生参加竞赛.为了解这两个年级参加竞赛学生的成绩情况,从中各随机抽取20名学生的成绩,并对数据进行了整理和分析(成绩得分用x 表示,数据分为6组:7075A x ≤<;:7589B x <<;:8085C x ≤<;:8590D x ≤<;:9095E x ≤<;:95100F x ≤≤)绘制了如下统计图表:年级平均数中位数众数极差七年级85.8mn26八年级86.286.58718七年级测试成绩在C 、D 两组的是:8183838383868788888989根据以上信息,解答下列问题(1)上表中m =_______,n =_______.(2)记成绩90分及90分以上为优秀,则估计七年级参加此次知识竞赛成绩为优秀的学生有多少名?(3)此次竞赛中,七、八两个年级学生近代史知识掌握更好的是________(填“七”或“八“)年级,并说明理由?27.某市民用水拟实行阶梯水价,每人每月用水量中不超过w 吨的部分按4元/吨收费,超出w 吨的部分按10元/吨收费,该市随机调查居民,获得了他们3月份的每人用水量数据,绘制出如图不完整的两张统计图表:请根据以下图表提供的信息,解答下列问题:表1组别月用水量x 吨/人频数频率第一组0.51x <≤1000.1第二组1 1.5x <≤n第三组 1.52x <≤2000.2第四组2 2.5x <≤m 0.25第五组 2.53x <≤1500.15第六组3 3.5x <≤500.05第七组 3.54x <≤500.05第八组4 4.5x <≤500.05合计1(1)观察表1可知这次抽样调查的中位数落在第_______组,表1中m 的值为_________,n 的值为_______;表2扇形统计图中“用水量2.5 3.5x <≤”部分的的圆心角为___________.(2)如果w 为整数,那么根据此次调查,为使80%以上居民在3月份的每人用水价格为4元/吨,w 至少定为多少吨?(3)利用(2)的结论和表1中的数据,假设表1中同组中的每个数据用该组区间的右端点值代替,估计该市居民3月份的人均水费.第六章数据的分析(单元重点综合测试)班级___________姓名___________学号____________分数____________考试范围:全章的内容;考试时间:120分钟;总分:120分一、单选题(本大题共10小题,每小题3分,共30分)1.已知一组数据:4,1,2,3,4,这组数据的中位数和众数分别是()A.4,4B.3.5,4C.3,4D.2,4【答案】C【分析】根据中位数和众数的定义分别进行解答即可.【解析】解:把这组数据从小到大排列:1,2,3,4,4,最中间的数是3,则这组数据的中位数是3;4出现了2次,出现的次数最多,则众数是4;故选:C.【点睛】此题考查了中位数和众数,将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数)叫做这组数据的中位数;众数是一组数据中出现次数最多的数.2.在“我的阅读生活”校园演讲比赛中,有11名学生参加比赛,他们决赛的最终成绩各不相同,其中一名学生想知道自己能否进入前6名,除了要了解自己的成绩外,还要了解这11名学生成绩的()A.众数B.方差C.平均数D.中位数【答案】D【分析】此题主要考查统计中的中位数、理解中位数的定义是解题的关键.11人成绩的中位数是第6名的成绩.参赛选手要想知道自己是否能进入前6名,只需要了解自己的成绩以及全部成绩的中位数,比较即可.【解析】解:由于总共有11个人,且他们的分数互不相同,第6的成绩是中位数,要判断是否进入前6名,故应知道中位数的多少.故选:D.3.已知数据3,x,7,1,10的平均数为5,则x的值是()A.3B.4C.5D.6【答案】B【分析】本题考查算术平均数,解题的关键是根据平均数的计算方法列方程求解.【解析】解: 数据3,x ,7,1,10的平均数为5,3711055x ∴++++=⨯,解得4x =,故选:B .4.甲、乙、丙、丁四人参加射击训练,经过三组练习,他们的平均成绩都是9.5环,方差分别是20.45s =甲,20.55s =乙,20.4s =丙,20.35s =丁,你认为谁的成绩更稳定()A .甲B .乙C .丙D .丁【答案】D【分析】本题考查了根据方差判断稳定性,根据方差越小数据越稳定,即可解答.【解析】解:∵2222s s s s <<<丁丙甲乙,∴丁的成绩更稳定,故选:D .5.在“双减”政策下,某学校规定,学生的学期学业成绩由三部分组成:平时成绩占20%,期中成绩占30%,期末成绩占50%,小颖的平时、期中、期末成绩分别为80分,90分,92分,则小颖本学期的学业成绩为()A .92分B .90分C .89分D .85分【答案】C【分析】本题主要考查加权平均数,根据加权平均数的计算方法计算即可.熟练掌握加权平均数的意义是解题的关键.【解析】解:小颖本学期的学业成绩为:20%8030%9050%9289⨯+⨯+⨯=(分).故选:C .6.在第60届国际数学奥林匹克比赛中,中国队荣获团体总分第一名.我国参赛选手比赛成绩的方差计算公式为:()()()222212613838386s x x x ⎡⎤=-+-++-⎣⎦ ,下列说法错误的是().A .我国一共派出了6名选手B .我国参赛选手的平均成绩为38分C .我国选手比赛成绩的中位数为38D .我国选手比赛成绩的团体总分为228分【答案】C7.我校开展了“好书伴我成长”读书活动,为了解5月份九年级学生的读书情况,随机调查了九年级50名学生读书的册数,统计数据如下表所示,下列说法正确的是()册数01234人数41216171A.众数是17B.中位数是2C.平均数是2D.方差是28.某聊天软件规定:若任意连续5天,好友双方的每日聊天记录的条数不低于100,则双方可以获得“星形”标识.甲、乙两位好友连续5天在该软件上聊天,下面是这5天日聊天记录条数的统计量,一定能判断甲、乙获得“星形”标识的是()A.中位数为110条,极差为20条B.中位数为110条,众数为112条C.中位数为106条,平均数为102条D.平均数为110条,方差为10条29.某商场招聘员工一名,现有甲、乙、丙三人竞聘,通过计算机、语言和商品知识三项测试,他们各自成绩(百分制)如下表所示,若商场需要招聘负责将商品拆装上架的人员,对计算机、语言和商品知识分别赋权2,3,5,那么从成绩看,应该录取()应试者计算机语言商品知识甲607080乙807060丙708060A.甲B.乙C.丙D.任意一人都可10.某排球队6名场上队员的身高(单位:cm)是:180,184,188,190,192,194.现用一名身高为188cm 的队员换下场上身高为194cm的队员,与换人前相比,场上队员的身高()A.平均数变小,方差变小B.平均数变小,方差变大C.平均数变大,方差变小D.平均数变大,方差变大二、填空题(本大题共8小题,每小题3分,共24分)11.数据1,8,8,4,6,4的中位数为.12.我国是世界上严重缺水的国家之一.为了倡导“节约用水从我做起”,小刚在他所在班的50名同学中,随机调查了10名同学家庭中一年的月均用水量(单位:t),并将调查结果绘成了如下的条形统计图,则这10个样本数据的平均数是,众数是,中位数是.【答案】 6.8 6.5 6.5【分析】根据条形统计图,即可知道每一名同学家庭中一年的月均用水量.再根据加权平均数的计算方法、中位数和众数的概念进行求解;13.已知一组数据3,a,4,6,7,它们的平均数是5,则这组数据的方差是.14.新冠疫情期间,小李同学连续两周居家健康检测,如下图是小李记录的体温情况折线统计图,记第一周体温的方差为21s,第二周体温的方差为22s,试判断两者之间的大小关系21s22s(用“>”、“=”、“<”填空).小李连续两周居家体温测量折线统计图【答案】<【分析】方差反应是数据的波动程度,方差越大,波动性越大,结合折线图可得小丽第一周居家体温在36.6C ~36.8C ︒︒之间,第二周居家体温在36.4C ~37.2C ︒︒之间,从最大值与最小值的差可以得到答案.【解析】解:根据折线统计图很容易看出小丽第一周居家体温在36.6C ~36.8C ︒︒之间,第二周居家体温在36.4C ~37.2C ︒︒之间,小丽第一周居家体温数值波动小于其第二周居家体温数值波动,2212s s ∴<.故答案为:<.【点睛】本题考查的是折线统计图,数据的波动性即方差,理解方差的含义是解题的关键.15.开学前,根据学校防疫要求,小芸同学连续14天进行了体温测量,结果统计如表:体温(℃)36.336.436.536.636.736.8天数(天)233411这14天中,小芸体温的中位数和众数分别是℃.【答案】36.5,36.6【分析】根据中位数的定义:一组数据从小到大(或从大到小)排列,若数据有奇数个,则最中间的数为中位数,若数据有偶数个,则最中间两数的平均数为中位数,根据众数的定义:一组数据出现次数最多的数,即可判断.【解析】 共有14个数据,其中第7、8个数据均为36.5,∴这组数据的中位数为36.5;其中36.6出现了4次,出现次数最多,∴众数为36.6.【点睛】本题考查了中位数和众数,理解中位数和众数的定义是解题的关键.16.宁城有机苹果园引进了甲、乙、丙、丁四个品种的苹果树.为了了解每种苹果树的产量情况,从每个品种中随机抽取10棵进行采摘,经统计每种苹果树10棵产量的平均数x 和方差2s 如下表:甲乙丙丁平均数()kg x 194194188188方差2s 9.28.68.99.7若从这四个品种中选出一种产量既高又稳定的苹果树进行种植,应选的品种为.【答案】乙【分析】本题考查了方差:一组数据中各数据与它们的平均数的差的平方的平均数,叫做这组数据的方差.方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.先比较平均数得到甲组和乙组的产量较好,然后比较方差得到乙品种既高产又稳定.【解析】解:因为丙、丁的平均数比甲、乙的平均数小,而乙的方差比甲的小,所以乙的产量既高产又稳定,所以产量既高又稳定的苹果树进行种植,应选的品种是乙;故答案为:乙.17.将5个整数从大到小排列,中位数是4;如果这个样本中的唯一众数是6,则这5个整数可能的最大的和是.【答案】21【分析】根据中位数为4,可得第三个数是4,再由这组数据的唯一众数是6,可得6应该是4后面的两个数字,4前面两个数字最大的时候是3,2,即可求解.【解析】∵这组数据共5个,且中位数为4,∴第三个数是4;又∵这组数据的唯一众数是6,∴6应该是4后面的两个数字,且4前面两个数字都小于4,且都不相等,∴4前面两个数字最大的时候是3,2,∴其和为2346621++++=,∴这组数据可能的最大的和为21.故答案为21.【点睛】主要考查了根据一组数据的中位数来确定数据的能力.将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.注意:找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求.如果是偶数个则找中间两位数的平均数.18.一组数据1x 、2x 、…、n x 的方差是0.8,则另一组数据11x +、21x +、…、1n x +的方差是.三、解答题(本大题共9小题,共66分)19.甲、乙两人在相同的情况下各打靶6次,每次打靶的成绩依次如下(单位:环):甲:9,6,7,6,7,7乙:4,5,8,7,8,10(1)计算两人打靶成绩的方差;(2)请推荐一人参加比赛,并说明理由.(或推荐乙.在甲、乙平均成绩相同的前提下,乙一直处于上升趋势,有潜力.【点睛】本题考查了方差的概念,利用方差做决策,结合生活实际理解数学概念是本题的亮点.20.某公司要在甲、乙两人中招聘一名职员,对两人的学历、能力、经验这三项进行了测试,各项满分均为10分,成绩高者被录用.图1是甲、乙两人测试成绩的条形统计图.(1)分别计算甲、乙两人三项成绩之和,则会被录用;(2)若将甲、乙两人的三项测试成绩,分别按照扇形统计图(图2)各项所占之比进行计算,甲成绩为分,乙成绩为分,则会被录用.21.某调查小组采用随机抽样方法,对某市部分中小学生一天中阳光体育运动时间进行了抽样调查,并把所得数据整理后绘制成如下不完整的统计图.(1)填空:本次调查的中位数为________小时;(2)通过计算补全条形统计图;(3)请估计该市中小学生一天中阳光体育运动的平均时间.【答案】(1)1(2)见解析(3)1.18小时.【分析】此题主要考查了条形统计图以及扇形统计图的应用,根据统计图得出正确信息是解题关键.(1)利用0.5小时的人数为100人,所占比例为20%,即可求出样本容量;(2)先可求出1.5小时的人数,画图即可;(3)计算出该市中小学生一天中阳光体育运动的平均时间即可.【解析】(1)解:由题意可得:0.5小时的人数为:100人,所占比例为:20%,10020%500÷=,∴本次调查共抽样了500名学生;∴第250名学生的运动时间为1小时,第251名学生的运动时间为1小时,(3)根据题意得:1000.52001120100200120⨯+⨯+++即该市中小学生一天中阳光体育运动的平均时间约22.某药店有3000枚口罩准备出售,从中随机抽取了一部分口罩,根据它们的价格(单位:元),绘制出如图的统计图,请根据相关信息,解答下列问题:(1)图①中的m值为________;此次抽样随机抽取了口罩_______枚;(2)求统计的这些数据的平均数、众数和中位数;(3)根据样本数据,估计这3000枚口罩中,价格为1.8元的口罩约有多少枚?【答案】(1)28,50(2)1.52元,1.8元,1.5元(3)960枚23.某校七年级一班和二班各派出10名学生参加一分钟跳绳比赛,成绩如下表:跳绳成绩(个)132133134135136137一班人数(人)120232二班人数(人)014122(1)两个班级跳绳比赛成绩的众数、中位数、平均数、方差如下表:众数中位数平均数方差一班136135.5135 2.8二班134a135b表中数据a=,b=;(2)请用所学的统计知识,从两个不同角度比较两个班跳绳比赛的成绩.【答案】(1)134.5,1.8;(2)①两个班级的平均成绩相同,二班的方差比一班的方差小,所以二班成绩比)(2137+-24.为鼓励学生积极加入中国共青团组织,某学校团委在八、九年级各抽取50名学生开展团知识竞赛,为便于统计成绩,制定了取整数的计分方式,满分10分.竞赛成绩如图所示.平均数众数中位数方差八年级87b 1.88九年级8a 8c请根据图表中的信息,解答下列问题:(1)填空:a =______,b =______,c =________;(2)现要给成绩突出的年级颁奖,如果分别从众数和方差两个角度来分析,你认为应该给哪个年级颁奖?25.为了了解学生对党的二十大精神的学习领会情况,某校团委从七、八年级各随机抽取20名学生进行测试,获得了他们的测试成绩(百分制),并对数据(测试成绩)进行整理、描述和分析.下面给出了部分信息.a .八年级学生测试成绩的频数分布直方图如下,(数据分为4组:6070x ≤<,7080x ≤<,8090x ≤<,90100x ≤≤).b.八年级学生测试成绩在8090x≤<这一组的是:81838484848689c.七、八年级学生测试成绩的平均数、中位数、众数如下:年级平均数中位数众数七83.18889八83.5m根据以上信息,回答下列问题:(1)表中m的值为______,八年级学生测试成绩在8090x≤<这一组的众数是______;(2)七年级学生小亮和八年级学生小宇的成绩都是86分,这两名学生在本年级成绩排名更靠前的是______(填“小亮”或“小宇”);(3)成绩不低于80分的学生可获得优秀奖,假设该校八年级300名学生都参加测试,估计八年级获得优秀奖的学生人数.【答案】(1)83.5,84(2)小宇(3)180【分析】本题考查频数分布直方图,平均数,中位数,众数的意义和用样本估计总体,准确理解这些概念是的关键.(1)结合题意,根据中位数和众数的意义解答即可,(2)根据中位数的意义,比较七、八年级的中位数即可得出答案,(3)先算出样本中成绩不低于80分的百分比,再乘以300即可得到答案.【解析】(1)解:八年级一共有20名同学,中位数是成绩数据由小到大排列后第10,11个数据分别为83、84,26.今年是五四运动100周年,也是中华人民共和国成立70周年,为缅怀五四先驱崇高的爱国情怀和革命精神,巴蜀中学开展了“青春心向党,建功新时代”为主题的系列纪念活动.历史教研组也组织了近代史知识竞赛,七、八年级各有300名学生参加竞赛.为了解这两个年级参加竞赛学生的成绩情况,从中各随机抽取20名学生的成绩,并对数据进行了整理和分析(成绩得分用x 表示,数据分为6组:7075A x ≤<;:7589B x <<;:8085C x ≤<;:8590D x ≤<;:9095E x ≤<;:95100F x ≤≤)绘制了如下统计图表:年级平均数中位数众数极差七年级85.8m n 26八年级86.286.58718七年级测试成绩在C、D两组的是:8183838383868788888989根据以上信息,解答下列问题(1)上表中m=_______,n=_______.(2)记成绩90分及90分以上为优秀,则估计七年级参加此次知识竞赛成绩为优秀的学生有多少名?(3)此次竞赛中,七、八两个年级学生近代史知识掌握更好的是________(填“七”或“八“)年级,并说明理由?。
四年级下册数学单元测试-第6单元数据的表示和分析(含答案)
第6单元数据的表示和分析一.选择题1.条形统计图可以通过条形的()看出数量的多和少.A.长短B.宽窄C.颜色2.根据统计结果,你认为a选项的数值大约是()比较合理.A.10 B.12 C.16 D.243.三个数的平均数是15.7,加上第四个数后平均数是16,第四个数是()A.15.85 B.18 C.16.9 D.17.24.父亲节,学校“文苑”专栏登出了某同学回忆父亲的诗:“同辞家门赴车站,别时叮咛语千万,学子满载信心去,老父怀抱希望还。
”如果用纵轴y表示父亲和学生在行进中离家的距离,横轴t表示离家的时间,那么下面与上述诗意大致相吻合的图象是()A.B.C.D.5.某市规定每户每月用水量不超过6吨,每吨价格为2.5元,当用水量超过6吨时,超过部分每吨水价格为3元,下图中能表示每月水费与用水量关系的示意图是()A.B.C.D.6.要求某商店2019年平均每月销售冰箱多少台,正确的算式是()某商店2019年冰箱销售情况统计表时间/季度一二三四数量/台106208370280 A.(106+208+370+180)÷4B.(106+208+370+180)÷12C.(106+208+370+180)÷24D.(106+208+370+180)÷3657.四位同学在跳绳比赛中成绩如下,求哪位同学跳的最接近四人的平均数。
正确的选项是()。
A.张莉B.王红C.李超D.赵冬8.如图,()可以表示下面哪种情况的统计.A.4个学生期末数学考试成绩B.四年级喜欢各项运动的男女生人数C.小明1﹣﹣8岁的身高D.蛋糕店的草莓蛋糕和芒果蛋糕最近5天的销售情况二.填空题9.在一幅条形统计图中,用0.8厘米表示200吨,要表示750吨的数量,直条应当画厘米.10.要观察病人的体温,用统计图表示比较合适.11.图中每格代表人,四(2)班一共有名同学.其中,喜欢的人数最少,喜欢羽毛球的人数是喜欢人数的倍.12.根据统计图填空:第组做的好事最多,比最少的小组多做件,全班共做了件.13.“五一”假期,淘气一家自驾游去外地,按计划准点到达目的地,他们选择早上6:00出发,匀速行驶一段时间后,因途中出现故障耽搁了一段时间,故障排除后,他们加快速度仍匀速前进,结果恰好准点到达,如果他们的行驶路程(m)与所用时间(h)的部分关系如图所示,则他们原计划准点到达的时刻是.14.淘气身高142厘米,爸爸身高178厘米.爸爸和淘气的平均身高是厘米.15.小明参加期中测试,语文、数学、英语三科的平均成绩是87分,如果数学成绩不算在内,平均成绩是83分,小明数学得了分。
北师大版八年级上册数学 第六章 数据的分析 单元测试(含解析)

第六章数据的分析单元测试一.选择题1.某校5个环保小队参加植树活动,平均每组植树10棵,已知第一、二、三、五组分别植树9棵、12棵、9棵、8棵,则第四小组植树()A.7棵B.9棵C.10棵D.12棵2.一组数据2,x,﹣2,1,3的平均数是0.8,则x的值是()A.﹣3.2B.﹣1C.0D.13.甲乙丙丁4位同学的平均身高1.65米,而甲乙丙3位同学的平均身高1.63米,下列说法一定正确的是()A.4人丁最高B.丁身高1.71米C.4人身高中位数1.63D.4人甲最高4.在某市举办的主题为“英雄武汉”的网络演讲比赛中,七位选手的得分分别为:88,84,87,90,86,92,94,则这组数据的中位数是()A.86B.88C.90D.925.九九重阳节期间,某班学生积极参加向敬老院孤寡老人献爱心活动,该班50名学生的捐款统计情况如表:金额/元5102050100人数6171485则他们捐款金额的众数和中位数分别是()A.100,10B.10,20C.17,10D.17,206.某中学为了解“停课不停学”期间学生在家的学习情况,随机抽查了40名学生每天做家庭作业的时间,并将调查结果统计如表所示,则这40名学生每天做家庭作业的时间的众数和中位数分别为()60708090100110120每天做家庭作业的时间(分钟)人数(名)2459875 A.90,90B.100,95C.90,95D.100,1007.为了解学生体育锻炼的用时情况,陈老师对本班50名学生一天的锻炼时间进行调查,并将结果绘制成如图统计图,那么一天锻炼时间为1小时的人数占全班人数的()A.14%B.16%C.20%D.50%8.甲、乙、丙、丁四位同学五次数学测验的成绩的平均数相同,五次测验的方差如表.如果从四位同学中选出一位状态稳定的同学参加全国数学联赛,那么应选择()甲乙丙丁方差425519 A.甲B.乙C.丙D.丁9.某公司的生产量在1﹣7月份的增长变化情况如图所示,从图上看,下列结论正确的是()A.这七个月中,每月的生产量不断增加B.1月份生产量最大C.2﹣6月生产量逐月减少D.这七个月中,生产量有增加有减少10.某班级开展“好书伴成长”读书活动,统计了1至7月份该班同学每月阅读课外书的数量,绘制了折线统计图,下列说法正确的是()A.每月阅读课外书本数的众数是45B.每月阅读课外书本数的中位数是58C.从2到6月份阅读课外书的本数逐月下降D.从1到7月份每月阅读课外书本数的最大值比最小值多45二.填空题11.学校将平时成绩、期中成绩和期末成绩按3:3:4计算学生的学期平均成绩.若某同学的数学平时成绩、期中成绩和期末成绩分别是90分、85分、90分,则该同学数学学期平均成绩是分.12.若5个正数a1,a2,a3,a4,a5的平均数是a,则a1,a2,0,a3,a4,a5的平均数是.13.为了解学生暑期在家的阅读情况,随机调查了30名学生某一天的阅读小时数,具体统计如下:阅读时间(小时)2 2.53 3.54学生人数(名)128163则关于这30名学生阅读小时的众数是.14.在从小到大排列的五个整数中,中位数是2,唯一的众数是4,则这五个数和的最大值是.15.在某校举行的数学竞赛中,某班10名学生的成绩统计如图所示,则这10名学生成绩的众数是分.16.某市5月1~7日的平均气温如图所示,则这七日平均气温的中位数是.17.甲、乙两人各打靶5次,已知甲所中的环数是8,7,9,7,9,乙所中的环数的平均数是8,方差是0.5,那么的射击成绩比较稳定.18.已知一组数据x1,x2,…x n的方差是2,则另一组数据x1﹣a,x2﹣a,…,x n﹣a的方差是.19.为保证中小学生每天锻炼一小时,某校开展了形式多样的体育活动项目,小明对某班同学参加锻炼的情况进行了统计,并绘制了如图的统计图(1)和图(2),则扇形统计图(2)中表示“足球”项目扇形的圆心角的度数为.20.有一学校为了解九年级学生某次体育测试成绩,现对这次体育测试成绩进行随机抽样调查,结果统计如下,其中扇形统计图(如图)中C等级所在扇形的圆心角为36°.被抽取的体育测试成绩频数分布表等级成绩(分)频数(人数)A36<x≤4019B32<x≤36bC28<x≤325D24<x≤284E20<x≤242合计a 请你根据以上图表提供的信息,解答下列问题:(1)a=,b=.(2)A等级的频率是.(3)在扇形统计图中,B等级所对应的圆心角是度.三.解答题21.某中学在“书香校园”读书活动中,为了解学生的课外读书情况,学校从各年级随机抽样调查了部分学生在一周内的课外阅读时间,绘制了如图的统计图.请根据图中信息,解答下列问题:(1)被抽查学生课外阅读时间的众数为(h),中位数为(h);(2)若该学校共有1200名学生,请你估算该校学生一周内课外阅读时间不少于3h的学生人数.22.某校为了解七年级学生对“预防新冠病毒知识”的掌握情况,从七年级随机抽取了50名学生进行测试,并对测试成绩(百分制)进行整理、描述和分析,部分信息如下:a.测试成绩频数分布表分数50≤x<6060≤x<7070≤x<8080≤x<9090≤x<100频数6101115m b.成绩在70≤x<80这一组的是:70 72 74 75 76 76 77 77 77 78 79根据以上信息,回答下列问题:(1)表中m=;(2)这50名学生测试成绩的中位数是,众数落在80≤x<90范围内(填“一定”或“不一定”);(3)该校七年级学生有500人,假设全部参加此次测试,请估计成绩不低于75分的人数.23.习总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气”巴川量子中学响应号召,鼓励师生利用课余时间广泛阅读,学校文学社为了解学生课外阅读情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:(一)数据收集:从全校随机抽取20名学生,进行每周用于课外阅读时间的调查,数据如下(单位:min):306081504411013014690100 6080120140758110308192(二)整理数据:按如下分段整理样本数据:0≤x<4040≤x<8080≤x<120120≤x<160课外阅读时间(min)等级D C B A人数3584(三)分析数据:补全下列表格中的统计量:平均数中位数众数80a b (四)得出结论(1)表格中的数据a=,b=.(2)如果学校现有学生1000人,估计全校等级为“B”的学生人数;(3)假设平均阅读一本课外书的时间为320分钟,请你用样本平均数估计该校学生每人一年(按52周计算)平均阅读课外书的数量.24.如图是我国某市200年9月1﹣7日甲型H1N1流感病例数资料,请根据此图回答问题:(1)2009年9月1﹣7日甲型H1N1流感病例总数是多少?(2)发病最高日人数是发病最低日人数的几倍?(3)在9月3﹣5日发病的人数占这段时间病例总数的几分之几?25.甲、乙两名同学本学期的五次数学测试成绩如下(单位:分):第1次第2次第3次第4次第5次甲8683908086乙7882848992(1)完成下表:中位数平均数方差甲85乙848524.8(2)请运用所学的统计知识,从两个不同角度评价甲、乙两人的数学成绩.26.在新的教学改革的推动下,某中学初一年级积极推进未来小班教学.为了了解一段时间以来的数学小班教学的学习效果,年级组织了多次定时测试,现随机选取甲、乙两个班,从中各抽取20名同学在某一次定时测试中的数学成绩,过程如下,请补充完整.收集数据:甲班的20名同学的数学成绩统计(单位:分)86 90 60 76 92 83 56 76 85 7096 96 90 68 78 80 68 96 85 81乙班的20名同学的数学成绩统计(单位:分)78 96 75 76 82 87 60 54 87 72100 82 78 86 70 92 76 80 98 78整理数据:(成绩得分用x表示)数量分数/班级0≤x<6060≤x<7070≤x<8080≤x<9090≤x≤100甲班(人数)13466乙班(人数)11864分析数据,请回答下列问题:(1)完成下表:平均分中位数众数甲班80.6a=96乙班80.3579b=(2)在甲班成绩得分的扇形图中,成绩在60≤x<70的扇形所对的圆心角α的度数为,c=.(3)根据以上数据,你认为班(填“甲”或“乙”)的同学的学习效果更好一些,你的理由是;(4)若此次数学成绩不低于80分为优秀,请估计全年级1000人中优秀人数为多少?参考答案1.解:设第四小组植树x株,由题意得:9+12+9+x+8=10×5,解得,x=12,则第四小组植树12棵;故选:D.2.解:∵数据2,x,﹣2,1,3的平均数是0.8,∴2+x﹣2+1+3=5×0.8,解得x=0,故选:C.3.解:丁同学的身高为:1.65×4﹣1.63×3=1.71(米);故选:B.4.解:将这组数据从小到大的顺序排列为:84,86,87,88,90,92,94,处于中间位置的是88,则这组数据的中位数是88.故选:B.5.解:根据题意可知捐款10元的人数有17人,人数最多,即10元是捐款金额的众数,把50名同学捐款从小到大排列,最中间的两个数是20,20,中位数是20元.故选:B.6.解:由图表可得:∵某中学40名学生每天做家庭作业的时间为90分钟的有9人,最多,∴这40名学生每天做家庭作业的时间的众数为:90分;∵40个数据中,第20,21个数据的平均数是中位数,而第20,21个数据分别是90,100,∴中位数为:95分.故选:C.7.解:由题意可得,25÷50×100%=0.5×100%。
北师大版八年级数学上册《第六章 数据的分析》单元检测卷-带答案

北师大版八年级数学上册《第六章数据的分析》单元检测卷-带答案核心考点整合考点1 平均数1.下表是小红参加一次“阳光体育”活动比赛的得分情况:项目跑步花样跳绳跳绳得分90 80 70评总分时,按跑步占50%,花样跳绳占30%,跳绳占20%考评,则小红的最终得分为分.2. 某新能源车销售网点2023 年7月至12月的销售数量如图所示,则这半年来平均每月的销售量为辆(结果保留整数).考点2 中位数3.2024 年4 月24 日是我国第九个“中国航天日”,某校开展了一次航天知识竞赛,共选拔5名选手参加总决赛,他们的决赛成绩(单位:分)分别是92,93,94,90,96.则这5名选手决赛成绩的中位数是.4.已知一组数据:7,6,8,x,3,它们的平均数是6,则这组数据的中位数是( )A.2B.6C.8D.7考点3 众数5.为了解某班学生参加体育锻炼的情况,从该班学生中随机抽取5名同学进行调查.经统计,他们这天的体育锻炼时间(单位;分钟)分别为65,60,75,60,80.这组数据的众数为( )A.65B.60C.75D.80考点4 方差,由公式提供的信息判断:①样本容量为3;②样本中6.某组数据的方差计算公式为s2=2(2−x̅)2+3(3−x̅)2+2(5−x̅)2n位数为3;③样本众数为3;④样本平均数为10₃.其说法正确的( )3A.①②④B.②④C.②③D.③④考点5 极差7.在杭州亚运会的跳水比赛中,对某运动员的第一个动作,8位裁判的打分如下(单位:分):9,8.5,7.5,8.5,8.5, 7.5,7,8,这组数据的极差是.考点6 标准差8.对于一次函数y=3x+4,自变量分别取值x₁,x₂,…,xₙ,若这组数据的方差为5,则对应的函数值为y ₁,y₂,…, yn 这组数据的标准差为.考点7 平均数、众数、中位数的应用9.某公司为提高服务质量,对其某个部门开展了客户满意度问卷调查,客户满意度以分数呈现,满意度从低到高为1分,2分,3分,4分,5分,共5档.公司规定:若客户所评分数的平均数或中位数低于3.5分,则该部门需要对服务质量进行整改.工作人员从收回的问卷中随机抽取了20份,如图是根据这20 份问卷中的客户所评分数绘制的统计图.(1)求客户所评分数的中位数、平均数,并判断该部门是否需要整改.(2)工作人员从余下的问卷中又随机抽取了1份,与之前的20份合在一起,重新计算后,发现客户所评分数的平均数大于3.55分,求工作人员抽取的问卷所评分数为几分? 与(1)相比,中位数是否发生变化?考点8 方差的应用10.超市货架上有一批大小不一的鸡蛋,某顾客从中选购了部分大小均匀的鸡蛋,设货架上原有鸡蛋的质量(单位:g)平均数和方差分别为x,s²,i该顾客选购的鸡蛋的质量平均数和方差分别为x₁,s²,则下列结论一定成立的是( )A.x̅<x̅1B.x̅>x̅1C.s2>s12D.s2<s1211.某篮球队对队员进行定点投篮测试,每人每天投篮10次,现对甲、乙两名队员在五天中投进球的个数统计如下表:(1)求甲、乙两名队员投进球个数的平均数;(2)如果从甲、乙两名队员中选出一人去参加定点投篮比赛,应选哪名队员? 请说明理由.思想方法整合思想1 整体思想12.已知一组数据a₁,a₂,a₃,a₄,a₅的平均数为8,则另一组数据a₁+10,a₂−10,a₃+10,a₄−10,a₅+10的平均数为( )A.6B.8C.10D.12思想2 方程思想13.8名学生在一次数学测试中的成绩(单位:分)为80,82,79,69,74,78,x,81,这组成绩的平均数是77 分,则x的值为( )A.76B.75C.74D.73参考答案1 832 470 3.93分4. B 5. B 6. C 7.28. √5【点拨】因为这组数据x₁,x₂,…,x₀的方差为5所以函数值y₁,y₁,…,yₙ这组数据的方差是:3²×5 =45,所以这组数据的标准差为√45=3√5,【解】(1)由统计图可知,第10个数据是3分,第11个数据是4分,所以中位数为3.5分,由统计图可得平均数为1×1+3×2+6×3+5×4+5×5=3.5(分),所以客户所评分数的平均数和中位数都不低于3.5分20所以该部门不需要整改.>3.55,解得x>4.55(2) 设工作人员抽取的问卷所评分数为x 分,则有 3.5×20+x20+1因为满意度从低到高为1分,2分,3分,4分,5分,共5档.所以工作人员抽取的问卷所评分数为5分所以加入这个数据,客户所评分数按从小到大排列后,第11 个数据是4 分,即加入这个数据后,中位数是4 分所以与(1)相比,中位数发生了变化,由3.5分变成4 分。
第六单元 数据的表示和分析(单元测试)(含答案)四年级下册数学北师大版

第六单元数据的表示和分析(单元测试)四年级下册数学北师大版一、单选题1.下面哪一个事件最合适用右图表示。
( )A.小红最近五次语文考试的成绩变化情况B.杭州一到五月平均气温变化情况C.某超市5月份5种不同饼干销售情况D.小红五次身高测量的变化情况2.某小学四年级四个班的学生做“爱心卡”送给福利院的小朋友,图中虚线所在的位置能反映出平均每班制作“爱心卡”的张数的是( )。
A.B.C.D.3.甲、乙两位同班同学是邻居,甲中午回家吃午饭,乙在班级吃午饭。
下面( )图描述的是乙一天的情况.A.B.C.D.4.六(1)班50名学生一分钟跳绳的平均成绩是156下,小明、小强、小芳都是六(1)班的学生,他们的成绩各不相同,下面说法正确的是( )。
A.小明的成绩是三人中最低的,他的成绩一定少于156下B.小明、小强、小芳三人中一定有一人的成绩是156下C.这三位同学的平均成绩一定是156下D.小强的成绩全班最高,他的成绩多于156下5.下面四幅图中,虚线所指的位置能表示小亮这五天投篮平均成绩的是( )A.B.C.D.二、判断题6.某公园规定,身高在140厘米及以下的儿童免票入园,四年级(1)班同学的平均身高是138厘米,所以全班同学都可以免票。
( )7.星期天早上,小红和爸爸、妈妈吃早餐共花15元,那么每人肯定都花了5元。
( )8.学校篮球队队员的平均身高是160厘米,学校篮球队中可能有身高超过160厘米的队员。
()9.六年级为结对学校捐款,男生平均每人捐9元,女生平均每人捐11元,全年级平均每人捐10元。
( )10.小张语文、数学的平均分是96分,如果语文是94分,那么数学一定是98分。
( )三、填空题11.四(2) 班参加阅读节朗诵比赛,得分情况如下:评委123456分数92 分96 分94 分88 分93 分95 分四(2) 班的平均得分是 分。
12.在一幅条形统计图中,用1.5 厘米的直条表示 10吨, 厘米的直条表示 40吨,用9厘米的直条表示 吨。
第6章数据与分析单元测试(原卷版)

第六章数据与分析(单元测试)一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.某商场对上周末某品牌运动服的销售情况进行了统计,如下表所示:经理决定本周进货时多进一些红色的,可用来解释这一现象的统计知识是()颜色黄色绿色白色紫色红色数量(件)120 150 230 75 430A.平均数B.中位数C.众数D.平均数与中位数2.在某市举办的主题为“英雄武汉”的网络演讲比赛中,七位选手的得分分别为:88,84,87,90,86,92,94,则这组数据的中位数是()A.86 B.88 C.90 D.923.小颖八年级第一学期的数学成绩分别为:平时90分,期中86分,期末95分.若按如图所显示的权重要求计算,则小颖该学期总评成绩为()A.88分B.91.8分C.92.8分D.93分4.八年级某班五个合作学习小组人数如下:5,7,6,x,7.已知这组数据的平均数是6,则x的值为()A.7 B.6 C.5 D.45.某企业为了解员工给灾区“爱心捐款”的情况,随机抽取部分员工的捐款金额整理绘制成如图所示的直方图,根据图中信息,下列结论错误的是()A.样本中位数是200元B .样本容量是20C .该企业员工捐款金额的极差是450元D .该企业员工最大捐款金额是500元6.甲、乙、丙、丁四位同学五次数学测验的成绩的平均数相同,五次测验的方差如表.如果从四位同学中选出一位状态稳定的同学参加全国数学联赛,那么应选择( )甲 乙 丙 丁 方差4 2 55 19A .甲B .乙C .丙D .丁7.今年某市7月1日到7日的每一天最高气温变化如折线图所示,则关于这组数据的描述正确的是( )A .最小值是32B .众数是33C .中位数是34D .平均数是348.某校合唱团有90名成员,下表是合唱团成员的年龄分布统计表: 年龄(单位:岁) 13 14 15 16 17 频数(单位:名)1729x26﹣x18对于不同的x ,下列关于年龄的统计量不会发生改变的是( ) A .平均数、中位数 B .平均数、方差C .众数、中位数D .众数、方差9.已知数据1x ,2x ,3x 的平均数 5x =,方差23S =,则数据12x ,22x ,32x 的平均数和方差分别为( ) A .5,12B .5,6C .10,12D .10,610.某聊天软件规定:若任意连续5天,好友双方的每日聊天记录的条数不低于100,则双方可以获得“星形”标识.甲、乙两位好友连续 5 天在该软件上聊天,下面是这 5天日聊天记录条数的统计量,一定能判断甲、乙获得“星形”标识的是( ) A .中位数为 110 条,极差为 20 条 B .中位数为 110 条,众数为 112 条 C .中位数为 106 条,平均数为 102 条D .平均数为 110 条,方差为 10 条2二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上11.甲、乙两篮球队队员身高的平均数都为2.08米,方差分别是S甲2、S乙2,且S甲2>S乙2,则队员身高比较整齐的球队是.12.如果一组数据中有3个6、4个1-,2个2-、1个0和3个x,其平均数为x,那么x=______.13.如图是马丽的妈妈前三次购买苹果单价的统计图,第四次又买的苹果单价是a元/千克,发现这四个单价的众数恰好也是中位数,则a=____________ .14.若一组数据3,x,4,2的众数和中位数相等,则x的值为________.15.某次射击训练中,一小组的成绩如下表所示:已知该小组的平均成绩为8环,那么成绩为7环的人数是______人.环数7 8 9人数 4 316.某校在“爱护地球,绿化祖国”的活动中,组织同学开展植树造林活动,为了了解同学的植树情况,学校抽查了初一年级所有同学的植树情况(初一年级共有两个班),并将调查数据整理绘制成如图所示的部分数据尚不完整的统计图表,下面有四个推断:初一年级植树情况统计表棵树/棵 1 2 3 4 5人数7 33 a12 3①a的值为20;②初一年级共有80人;③一班植树棵树的众数是3;④二班植树棵树的中位数是2.其中合理的是.17.我们知道,方差是度量数据波动程度的量.此外,统计中还常用标准差来度量数据的波动程度,其中标准差s=√(x1−x)2+(x2−x)2+?+(xn−x)2n,已知一组数据x1,x2,x3,x4,x5的方差是3,则另一组新数据2x1+1,2x2+1,2x3+1,2x4+1,2x5+1的标准差为.18.为丰富体育课堂,学校决定开设“A:踢毽子,B:篮球,C:跳绳,D:乒乓球”(如图)四项运动项目(每位同学必须选择一项),为了解学生最喜欢哪一项运动项目,随机抽取了一部分学生进行调査,并将调査结果绘制成如图的统计图,则参加调査的学生中最喜欢眺绳运动项目的学生人数为40人.三、解答题(本大题共8小题,共66分.解答时应写出文字说明、证明过程或演算步骤)19.(6分)某公司欲招聘一名工作人员,对甲、乙两位候选人进行了听、说、读、写的测试.他们的成绩如表所示:候选人听说读写甲8 9 8 7乙9 8 6 8①如果听、说、读、写同样重要,应录取谁?②如果听、说、读、写按4:2:1:3来计算,应录取谁?20.(6分)某中学在“书香校园”读书活动中,为了解学生的课外读书情况,学校从各年级随机抽样调查了部分学生在一周内的课外阅读时间,绘制了如图的统计图.请根据图中信息,解答下列问题:(1)被抽查学生课外阅读时间的众数为(h),中位数为(h);(2)若该学校共有1200名学生,请你估算该校学生一周内课外阅读时间不少于3h的学生人数.21.(6分)为响应学校提出的“每天锻炼一小时,健康幸福一辈子”的号召,八年级一班举办了踢毽子比赛,体育委员统计了全班每个同学60秒踢毽子的次数.若次数用x表示,列出了以下频数分布表:次数15≤x<30 30≤x<45 45≤x<60 60≤x<75 75≤x<90 90≤x<105 105≤x<120频数 2 4 10 22 8 3 1根据以上信息,回答下列问题:(1)踢毽子次数在60≤x<90范围内的人数占全班人数的百分比为;(2)此频数分布表的组距是,组数是;(3)你如何评价这个班学生踢毽子的成绩?22.(6分)某校七年级甲班、乙班举行一分钟投篮比赛,每班派10名学生参赛,在规定时间内进球数不少于8个为优秀学生.比赛数据的统计图表如下(数据不完整):甲班乙班1分钟投篮测试成绩统计表甲班乙班平均数 6.5 a中位数b 6方差 3.45 4.65优秀率30% c根据以上信息,解答下列问题:(1)直接写出a,b,c的值.(2)你认为哪个班的比赛成绩要好一些?请简要说明理由.23.(8分)某商场招聘员工一名,现有甲、乙两人竞聘.通过计算机、语言和商品知识三项测试,他们各自成绩(百分制)如下表所示:应试者计算机语言商品知识甲70 50 80乙50 60 85(1)若商场需要招聘负责将商品拆装上架的人员,对计算机、语言和商品知识分别赋权2,3,5,计算这两名应试者的平均成绩.从成绩看,应该录取谁?(2)若商场需要招聘电脑收银员,计算机、语言、商品知识成绩分别占50%,30%,20%,计算这两名应试者的平均成绩.从成绩看,应该录取谁?24.(10分)某校九年级在“停课不停学”期间,为促进学生身体健康,布置了“云键身”任务,为了解学生完成情况,体育教师随机抽取一班与二班各10名学生进行网上视频跳绳测试,他的测试结果与分析过程如下:(1)收集数据:两班学生每分钟跳绳个数分别记录如下(二班一个数据不小心被墨水遮盖):一班:100 94 86 86 84 94 76 69 59 94二班:99 96 ■ 82 96 79 65 96 55 96(2)整理,描述数据:根据上面得到的两组数据,分别绘制了频数分布直方图如下:(3)分析数据:两组样本数据的平均数、众数.中位数、方差如下表所示:班级平均数众数中位数方差一班①94 86 147.76二班83.7 96 ②215.21根据以上数据填出表格中①,②两处的数据并补全二班的频数分布直方图;(4)得出结论:根据以上信息,判断哪班完成情况较好?说明理由(至少从两个不同角度说明判断的合理性).25.(12分)某校举行了“珍爱生命,预防溺水”主题知识竞赛活动,八(1)、八(2)班各选取五名选手参赛.两班参赛选手成绩依次如下:(单位:分)甲:8,8,7,8,9乙:5,9,7,10,9学校根据两班的成绩绘制了如下不完整的统计图表:根据以上信息,请解答下面的问题:(1)a= ,b= ,c= ;(2)学校根据这些学生的成绩,确定八(1)班为获胜班级,请问学校评定的依据是什么?(3)若八(2)班又有一名学生参赛,考试成绩是8分,则八(2)班这6名选手成绩的平均数与5名选手成绩的平均数相比会.(选填“变大”“变小”或“不变”)26.(12分)某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同,小宇根据他们的成绩绘制了如下尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业). 甲、乙两人射箭成绩统计表(1)a =______,x =乙_____;(2)请完成图中表示乙成绩变化情况的折线;(3)①观察折线图,可看出______的成绩比较稳定(填“甲”或“乙”).参照小宇的计算方法,计算乙成绩的方差,并验证你的判断.②请你从平均数和方差的角度分析,谁将被选中.第1次 第2次 第3次 第4次 第5次 甲成绩 9 4 7 4 6 乙成绩757a7。
北师大版八年级上册数学第六章 数据的分析 单元测试卷(含答案解析)

北师大版八年级上册数学第六章数据的分析单元测试卷一、单选题1.一组数据6,7,8,9,10,这组数据的平均数是()A.6B.7C.8D.92.“魅力凉都”六盘水某周连续7天的最高气温(单位℃)是18,22,22,23,24,25,26,则这组数据的中位数是()A.18B.22C.23D.243.小张五次数学考试成绩分别为:86分、78分、80分、85分、92分,李老师想了解小张数学成绩波动情况,则李老师最关注小张数学成绩的()A.方差B.众数C.中位数D.平均数4.一组数据1,2,3,5,3,4,10的极差、众数分别是()A.3,3B.9,3C.5,4D.6,10 5.甲、乙、丙、丁四人参加训练,近期的10次百米测试平均成绩都是13.2秒,方差如下表所示则这四人中发挥最稳定的是()A.甲B.乙C.丙D.丁6.某球员参加一场篮球比赛,比赛分4节进行,该球员每节得分如折线统计图所示,则该球员平均每节得分为()A.7分B.8分C.9分D.10分7.一组数据的算术平均数是40,将这组数据中的每一个数据都减去5后,所得的新的一组数据的平均数是()A.40B.35C.25D.58.某电脑公司销售部为了定制下个月的销售计划,对20位销售人员本月的销售量(单位:台)进行了统计,绘制成如图所示的统计图,则这20位销售人员本月销售量的中位数、众数分别是()A.20台,14台B.19台,20台C.20台,20台D.25台,20台9.某青年排球队12名队员的年龄情况如下:则这个队队员年龄的众数和中位数是()A.19,19B.19,20C.19,20.5D.20,1910.若一组数据2,3,4,5,x的方差与另一组数据5,6,7,8,9的方差相等,则x 的值为().A.1B.6C.1或6D.5或611.如图是某单元楼居民六月份的用电(单位:度)情况,则关于用电量描述不正确的是()A.众数为30B.中位数为30C.平均数为24D.方差为84 12.某次期中考试,小明、小亮的语文、数学、英语三科的分数如下:如果将语文、数学、英语这三科的权重比由3:5:2变成5:3:2,那么分数变化情况是()A.小明增加的分数多B.小亮增加的分数多C .两人增加的分数一样多D .两人的分数都减少了13.如图是成都市某周内日最高气温的折线统计图,关于这7天的日最高气温的说法正确的是( )A .极差是8℃B .众数是28℃C .中位数是24℃D .平均数是26℃14.若一组数据1a ,2a ,3a 的平均数为4,方差为3,那么数据12a +,22a +,32a +的平均数和方差分别是( ) A .4, 3B .6, 3C .3, 4D .6 515.A 、B 、C 、D 、E 五名射击运动员在一次比赛中的平均成绩是80环,而A 、B 、C 三人的平均成绩是78环,那么下列说法中一定正确的是( ) A .D 、E 的成绩比其他三人好 B .B 、E 两人的平均成绩是83环 C .最高分得主不是A 、B 、CD .D 、E 中至少有1人的成绩不少于83环。
数学四年级下册第六单元《数据的表示和分析》单元测试卷

数学四年级下册第六单元《数据的表示和分析》单元测试卷
姓名:________ 班级:________ 成绩:________
同学们,经过一段时间的学习,你一定长进不少,让我们好好检验一下自己吧!
一、解答题
1 . 据报道4月22日~27日一种传染病的发病人数如下图:
(1)从________日至________日发病人数在逐渐下降?
(2)从________日至________日发病人数在逐日上升?
(3)你对预防传染病有什么好的建议?
2 . 小强家原来平均每月用电156.9度,使用节能电器后,原来一年用的电现在可以多用3个月。
现在平均每个月用电多少度?
3 . 班主任要为运动员准备一些水果,他对班里的运动员们最喜欢的水果情况进行了统计。
水果苹果橘子桃子西瓜
人数621189
请你把统计表中的数据在下图中涂色表示出来。
4 . 小明期中考试语文、外语、常识的平均分是82分,数学成绩公布后,他的平均成绩提高了4分,小明期中考试数学得了多少分?。
北师大版八年级上册数学 第六章 数据的分析 单元测试卷(Word版,含答案)

北师大版八年级上册数学第六章数据的分析单元测试卷一、选择题(每小题3分,共30分)1.一组数据2,4,3,x,4的平均数是3,则x的值为()A.1B.2C.3D.42.某市招聘老师的笔试和面试的成绩均按百分制计,并且分别按30%和70%的比例来计算综合成绩.王老师参加本次招聘考试的笔试成绩为80分,面试成绩为90分,经计算他的综合成绩是()A.85分B.87分C.87.5分D.90分3.某校八年级8个班向“希望工程”捐献图书的册数情况如下表:班级一班二班三班四班五班六班七班八班册数5096100909012050090捐献图书册数的中位数和众数分别是()A.93册,90册B.93册,500册C.90册,90册D.90册,500册4.某篮球队5名场上队员的身高(单位: cm)分别是183,185,188,190,194.现用一名身高为190 cm的队员换下场上身高为185 cm的队员,与换人前相比,场上队员身高的()A.平均数变小,方差变小B.平均数变小,方差变大C.平均数变大,方差变小D.平均数变大,方差变大5.一家鞋店在一段时间内销售了某种女鞋30双,各种尺码鞋的销售量如下表所示:鞋的尺码(cm)2222.52323.52424.525销售量(双)12511731若每双鞋的销售利润相同,则该店主最应关注的销售数据是下列统计量中的()A.平均数B.方差C.众数D.中位数6.一次数学测试,某小组5名同学的成绩统计如下表(有两个数据被遮盖):组员甲乙丙丁戊平均成绩(分)众数(分)得分(分)7781■808280■则被遮盖的两个数据依次是()A.81,80B.80,82C.81,82D.80,807.某校八年级(1)班部分学生上学路上所花的时间如图所示.设他们上学路上所花时间的平均数为a,中位数为b,众数为c,则有()A.b>a>cB.c>a>bC.a>b>cD.b>c>a8.某班级开展“好书伴成长”读书活动,统计了1至7月份该班同学每月阅读课外书的数量,绘制了如图所示的折线统计图,下列说法正确的是()A.每月阅读课外书本数的众数是45本B.每月阅读课外书本数的中位数是58本C.从2月到6月阅读课外书的本数逐月下降D.从1月到7月每月阅读课外书本数的最大值比最小值多45本9.下列说法正确的有()①样本数据7,7,6,5,4的众数是2;②如果数据x1,x2,…,x n的平均数是x̅,则(x1-x̅)+(x2-x̅)+…+(x n-x̅)=0;③样本数据1,2,3,4,5,6的中位数是3和4;④样本数据50,50,45.5,41,41的方差为16.2.A.1个B.2个C.3个D.4个10.一组数据x1,x2,…,x n的平均数为5,方差为16,其中n是正整数,则另一组数据3x1+2,3x2+2,…,3x n+2的平均数和标准差分别是()A.17,12B.17,144C.15,144D.7,16二、填空题(每小题4分,共24分)11.甲、乙、丙三人进行投飞镖比赛,已知他们每人五次投得的成绩如图所示,那么三人中成绩最稳定的是.12.某公司有10名员工,他们所在部门及相应每人所创年利润如下表所示.部门人数每人所创年利润/万元A110B28C75这个公司平均每人所创年利润是万元.13.已知一组数据:-1,0,2,x,3,它们的平均数是2,则这组数据的方差s2=.14.某公司要招聘一名职员,根据实际需要,从学历、经验和工作态度三个方面对甲、乙两名应聘者进行了测试,测试成绩如下表所示.如果将学历、经验和工作态度三项得分按2∶1∶3的比例确定两人的最终得分,并以此为依据确定录用者,那么将被录用(填“甲”或“乙”).甲乙学历98经验76工作态度5715.如果数据-1,0,3,5,x的极差为7,那么x等于.16.某校八年级随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分,共4个等级,将调查结果绘制成条形统计图(如图①)和扇形统计图(如图②).根据图中信息,这些学生的平均分是分.三、解答题(共46分)17.(6分)某公司需招聘一名部门经理,对A,B,C三名候选人进行了三项测试,包括语言表达、计算机操作、商品知识,各项成绩的权分别是3,3,4,三人的成绩如下表(单位:分):候选人语言表达计算机操作商品知识A608070B507080C608065请你通过计算分析一下谁会被录取;若想要B被录取,应如何设计各项成绩的权?18.(6分)某公司工会组织全体员工参加跳绳比赛,工会主席统计了公司50名员工一分钟跳绳成绩,列出的频数直方图如图所示.(每个小组包括左端点,不包括右端点)(1)求该公司员工一分钟跳绳的平均个数至少是多少;(2)该公司一名员工说:“我的跳绳成绩是我公司的中位数”,请你给出该员工跳绳成绩的所在范围.19.(8分)八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩(单位:分)如下表(满分为10分):甲789710109101010乙10879810109109(1)甲队成绩的中位数是分,乙队成绩的众数是分;(2)计算乙队的平均成绩和方差;(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是队.20.(8分)某中学举办“2021网络安全知识答题竞赛”,初中部七、八年级根据初赛成绩各选出5名选手代表年级参加学校决赛,两个代表队各选出的5名选手的决赛成绩如图所示.(1)根据统计图计算出下表中a,b,c的值;代表队平均数(分)中位数(分)众数(分)方差2七年级a85b s七年级八年级85c100160(2)结合两个代表队成绩的平均数和中位数进行分析,哪个代表队的决赛成绩较好?(3)计算七年级代表队决赛成绩的方差,并判断哪个代表队的选手成绩较为稳定.21.(8分)为了让青少年学生走向操场,走进自然,走到阳光下,积极参加体育锻炼.我校启动了“学生阳光体育运动”短跑活动,可以锻炼人的灵活性,增强人的爆发力,因此小明和小亮在课外活动中,报名参加了短跑训练小组.在近几次百米训练中,所测成绩(单位:秒)如图所示,请根据图中信息解答以下问题.(1)请根据图中信息,补齐下面的表格:次数12345小明13.313.413.313.3小亮13.213.113.513.3(2)分别写出他们所测成绩的中位数和众数;(3)分别计算他们所测成绩的平均数和方差,将小明与小亮的成绩比较后,你将分别给予他们怎样的建议?22.(10分)2020年是全面建成小康社会目标实现之年,是全面打赢脱贫攻坚战收官之年.为了让老师们更好地了解国家的宏观政策及具体措施,甲、乙两校组织全体教师利用“学习强国APP”对相关知识进行学习并组织定时测试(总分为100分).现从甲、乙两校中各随机抽取20名教师的测试成绩x(分)进行分析,分为五个等级:A(0≤x<60),B(60≤x<70),C(70≤x<80),D(80≤x<90),E(90≤x≤100).甲、乙两校各等级人数统计如图,其中甲校成绩在C等级的教师的具体分数(单位:分)为70,79,75,72,70,77.经过整理,得到的分析数据如下表:平均数(分)中位数(分)众数(分)甲校75a87乙校768085(1)填空:a=,并把条形统计图补充完整;(2)规定成绩在80分以上(包含80分)被评为优秀,已知甲、乙两校共有600名教师参加测试,请计算甲、乙两校共有约多少名教师被评为优秀;(3)根据以上数据,请判断哪所学校的成绩较好,并说明理由(一条即可).答案1.B[解析] 根据题意,得2+4+3+x+45=3,解得x=2.2.B[解析] 他的综合成绩为80×30%+90×70%=87(分).3.A4.C5.C6.D7.A8.B9.B10.A[解析] 因为数据x1,x2,…,x n的平均数是5,所以x1+x2+…+x n=5n,所以x'=1n [(3x1+2)+…+(3x n+2)]=1n[3×(x1+x2+…+x n)+2n]=17,s'2=1n [(3x1+2-17)2+(3x2+2-17)2+…+(3x n+2-17)2]=1n[(3x1-15)2+…+(3x n-15)2]=9×1n[(x1-5)2+(x2-5)2+…+(x n-5)2]=144.所以标准差为12.故选A.11.乙[解析] 根据图形可得乙的成绩波动最小,数据最稳定,所以三人中成绩最稳定的是乙.12.6.113.614.乙15.6或-216.2.95[解析] 总人数为12÷30%=40(人),则成绩为3分的有40×42.5%=17(人),成绩为2分的有40-17-12-3=8(人),故这些学生的平均分为1×3+2×8+3×17+4×1240=2.95(分).故答案为2.95.17.解:因为A的平均成绩=60×3+80×3+70×43+3+4=70(分),B的平均成绩=50×3+70×3+80×43+3+4=68(分),C的平均成绩=60×3+80×3+65×43+3+4=68(分),所以A的成绩最好,A会被录取.若想要B被录取,应设计语言表达、计算机操作、商品知识各项成绩的权分别是2,2,6(答案不唯一,合理即可).18.解:(1)由题意得(60×4+80×13+100×19+120×7+140×5+160×2)÷50=100.8(个).故该公司员工一分钟跳绳的平均个数至少是100.8个.(2)把50个数据从小到大排列后,处在中间位置的两个数都在100~120这个范围. 故该员工跳绳成绩的所在范围是100~120个.19.[解析] (1)将甲队的成绩从小到大排列,根据中位数的定义求出最中间两个数的平均数;根据众数的定义找出乙队成绩中出现次数最多的数即可; (2)先求出乙队的平均成绩,再根据方差公式进行计算.解:(1)把甲队的成绩(单位:分)从小到大排列为7,7,8,9,9,10,10,10,10,10,最中间两个数的平均数是(9+10)÷2=9.5,则中位数是9.5分;乙队成绩中10分出现了4次,出现的次数最多,则乙队成绩的众数是10分.故答案为9.5,10. (2)乙队的平均成绩是110×(10×4+8×2+7+9×3)=9(分), 方差是110×[4×(10-9)2+2×(8-9)2+(7-9)2+3×(9-9)2]=1.(3)因为甲队成绩的方差是1.4,乙队成绩的方差是1,所以成绩较为整齐的是乙队.故答案为乙. 20.解:(1)a=(75+80+85+85+100)÷5=85,b=85,c=80.(2)由表格及(1)可知七年级代表队成绩与八年级代表队成绩的平均数相同,七年级代表队成绩的中位数比八年级代表队高, 故七年级代表队的决赛成绩较好.(3)s 七年级2=15×[(75-85)2+(80-85)2+2×(85-85)2+(100-85)2]=70.因为70<160,所以七年级代表队的选手成绩较为稳定. 21.解:(1)补全表格如下:第 11 页 共 11 页(2)小明成绩的中位数是13.3秒,众数为13.3秒,小亮成绩的中位数是13.3秒,没有众数.(3)x ̅小明=15×(13.2+13.3×3+13.4)=13.3(秒), x ̅小亮=15×(13.1+13.2+13.3+13.4+13.5)=13.3(秒),s 小明2=15×[(13.3-13.3)2×3+(13.2-13.3)2+(13.4-13.3)2]=0.004, s 小亮2=15×[(13.1-13.3)2+(13.2-13.3)2+(13.3-13.3)2+(13.4-13.3)2+(13.5-13.3)2]=0.02. 因为x̅小明=x ̅小亮,s 小明2<s 小亮2,所以小明的成绩比较稳定,因此对小亮的建议是要加强稳定性训练,而小明应该加强爆发力训练,提高训练成绩(建议合理即可).22.解:(1)甲校20人的成绩从小到大排列后,处在中间位置的两个数的平均数为77+792=78(分),故a=78,甲校C 等级有6人,D 等级有20-2-3-6-1=8(人),补全条形统计图如图.(2)600×8+1+7+320+20=285(名).故甲、乙两校共有约285名教师被评为优秀.(3)(答案不唯一)乙校的成绩较好.理由:因为乙校的平均数、中位数均比甲校的高,所以乙校的成绩较好.。
第六章数据的分析单元测试题(附答案)详解

第六章数据的分析单元测试题(附答案)详解
S 2 1 [(23 24)2 (22 24)2 (25 24)2 (23 24)2 (27 24)2 (25 24)2 (23 24)2 7
等级
非常了解 比较了解 基本了解 不太了解
频数
40
120
36
4
频率
0.2
m
0.18
0.02
(1)本次问卷调查取样的样本容量为_______,表中的 m 值为_______.
(2)根据表中的数据计算等级为“非常了解”的频数在扇形统计图 6 所对应的扇形的圆
心角的度数,并补全扇形统计图.
(3)若该校有学生 1500 人,请根据调查结果估计这些学生中“比较了解”垃圾分类知识
B.了解宁波市居民对废电池的处理情况
C.日光灯管厂要检测一批灯管的使用寿命
D.对甲型 H1N1 流感患者的同一车厢的乘客进行医学检查
3、下列调查适合作抽样调查的是
A.了解义乌电视台“同年哥讲新闻”栏目的收视率
B.了解某甲型 H1N1 确诊病人同机乘客的健康状况
C.了解某班每个学生家庭电脑的数量
D.“神七”载人飞船发射前对重要零部件的检查
的人数约为多少?
不太了解 2%
基本了解 18%
23、经市场调查,某种优质西瓜质量为(5±0.25)kg 的最为畅销.为了控制西瓜的质量,农 科所采用 A、B 两种种植技术进行试验.现从这两种技术种植的西瓜中各随机抽取 20 颗,记 录它们的质量如下(单位:kg): A:4.1 4.8 5.4 4.9 4.7 5.0 4.9 4.8 5.8 5.2
(2)就表中专业知识、英语水平、参加社会实践与社团活动等三项的得分,分别求出三项
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数据的代表单元测试题姓名
1、评定学生的学科期末成绩由期考分数、作业分数、课堂参与分数三部分组成,并按2:3:4的比例确定,已知小明的数学期考80分,作业90分,课堂参与85分,则他的数学期末成绩为。
2、某校八年级有3个班,期中数学测验1班50人平均68分,2班48人平均70分,3班50人平均72分,则该年级期中数学测试平均为。
3、数据-2,0,2,,4,2,5的中位数是。
4、数据9,6,4,4,5,4,7,6,8,6的众数是,中位数是,平均数是。
5、某校八年级(4)班47人,身高1.70米的有10人,1.66米的有5人,1.6米的有15人,1.58米的有10人,1.55米的有5人,1.50米的有2人,则该班学生的身高的的平均数,中位数,众数为。
6、若数据4,6,x,8,12的平均数为8,则其中位数为。
7、若数据5,-3,0,x,4,6的中位数为4,则其众数为。
8.求下列各数据的方差。
(1)-2,1,4 (2)-1,1,2 (3)79,81,82 9.已知一组数据-1,x,0,1,-2的平均数是0,那么这组数据的方差是()
A、2
B、2
C、4
D、10
10.某工厂对一个生产小组的零件进行抽样调查,在10天中,这个生产小组每天出的次品数为(单位:个):0,2,0,2,3,0,2,3,1,2,在这10天中,该生产小组生产零件所出的次品数的()
A、平均数是2
B、众数是3
C、中位数是1.5
D、方差是1.25
11、某村有村同300人,其中年收入800元的有150人,1500元的有100人,2000元的有45人,还有5人收入100万元。
根据这些数据计算该村人收入的平均数、中位数、众数,你认为这个数据中哪一个代表村民年收入的“平均水平”最合适?
该班学生平均每人购买2本学习资料,求a,b的值。
13、一次科技知识竞赛,两组学生成绩统计如由表。
(1)估计甲、乙两组这的平均成绩。
(2)甲组的最高分是多少?最低分又是多少?它们相差多少?乙厂呢?
(3)请你根据所学过的统计知识,进一步判断这两个小组在这次竞赛中成绩谁更优秀?并说明理由。
①计算销售额的平均数、中位数、众数。
②商场为了完成年度的销售任务,调动售货员的积极性,在一年的最后月份采取超额有奖的办法,你认为根据上面计算结果,每个售货员统一的销售额标准是多少?。
