五年级数学思维专题训练《平面图形面积计算及等积变形》
小学五年级数学解析:几何图形的面积计算

小学五年级数学解析:几何图形的面积计算一、常见几何图形的面积公式1. 长方形的面积公式:长方形的面积 = 长×宽。
例题解析:例题1:一个长方形的长为8米,宽为5米,求其面积。
解答:面积 = 8米× 5米 = 40平方米。
2. 正方形的面积公式:正方形的面积 = 边长×边长。
例题解析:例题2:一个正方形的边长为6厘米,求其面积。
解答:面积 = 6厘米× 6厘米 = 36平方厘米。
3. 三角形的面积公式:三角形的面积 = 底×高÷ 2。
例题解析:例题3:一个三角形的底为10米,高为4米,求其面积。
解答:面积 = 10米× 4米÷ 2 = 20平方米。
4. 平行四边形的面积公式:平行四边形的面积 = 底×高。
例题解析:例题4:一个平行四边形的底为9米,高为5米,求其面积。
解答:面积 = 9米× 5米 = 45平方米。
5. 梯形的面积公式:梯形的面积 = (上底 + 下底)×高÷ 2。
例题解析:例题5:一个梯形的上底为6米,下底为10米,高为4米,求其面积。
解答:面积 = (6米 + 10米)× 4米÷ 2 = 32平方米。
6. 圆的面积公式:圆的面积 = π×半径²。
例题解析:例题6:一个圆的半径为3厘米,求其面积。
解答:面积 = π× 3²厘米²≈ 3.14 × 9厘米² = 28.26平方厘米。
二、复合图形的分割与面积计算1. 复合图形的定义与分割方法定义:复合图形是由多个简单图形组合而成的图形。
要计算复合图形的面积,可以将其分割成多个简单图形,然后分别计算面积,再将这些面积相加。
例题解析:例题1:计算一个由两个长方形组合而成的L形图形的面积。
解答:将L形图形分割为两个长方形,分别计算面积,再将两部分面积相加。
小学五年级数学思维专题训练—图形变换(含答案解析)

小学五年级数学思维专题训练—图形变换1、如下图所示,两个正方形的中心相同.其对应边成45度角,若两个阴影三角形的面积分别为36平方厘米和50平方厘米,则其中较小正方形的面积为多少平方厘米.2、下图中等腰直角三角形ABC的面积是9平方厘米,阴影正方形MNPQ的MV一边在斜边BC上,P.Q两点分别在直角边AC、AB上,求阴影正方形MNPQ的面积.3、一个长方形和一个等腰直角三角形如下图放置,图中6块的面积分别为1、1、1、1、2、长方形的面积是4、如下图所示,若将正方形ABCD各边三等分,延长等分点作出正方形MNPQ,则正方形ABCD的面积:正方形MNPQ的面积= .5、如右图所示,在长方形ABCD中.E.F.G分别是BC、CD、DA上的点,且使得四边形AEFG是直角梯形,∠GAE=45°,GF:AE=2:3。
如果梯形AEFG的面积是15平方匣米,那么长方形ABCD的面积是平方厘米6、下图中正六边形ABCDEF的面积是54. AP=2PF.CQ=2BQ,求阴影四边形CEPQ的面积·7、一张面积为7. 17平方厘米的平行四边形纸片WXYZ放在另一张平行四边形纸片EFGH上面,如下图所示,得出A、C、B、D四个交点.并且AB∥EF,CD∥WX.问纸片EFGH的面积是多少平方厘米?说明理由.8、如下图所示,涂阴影部分的小正六角星形面积是16平方厘米.问:大正六角星形面积是多少平方厘米?9、如下图所示,已知一个正八边形中最长的对角线等于a,最短的对角线等于b,这个正八边形的面积等于。
10、如右图所示,正十二边形和中心白色的正六边形的边民均为12,图中阴影部分的面积是11、一如右图所示,则四边形ABCD的面积是A.30 B.31C.32 D.3312、求下图正方形的面积,并写出思考过程13、如下图所示,点E是正方形ABCD的CD边上的一点,以BE为一条直角边作等腰直角三角形BEF,斜边BF交AD于G,已知AG=5厘米,GD=15厘米。
小学五年级数学思维专题训练—等积变形(含答案解析)
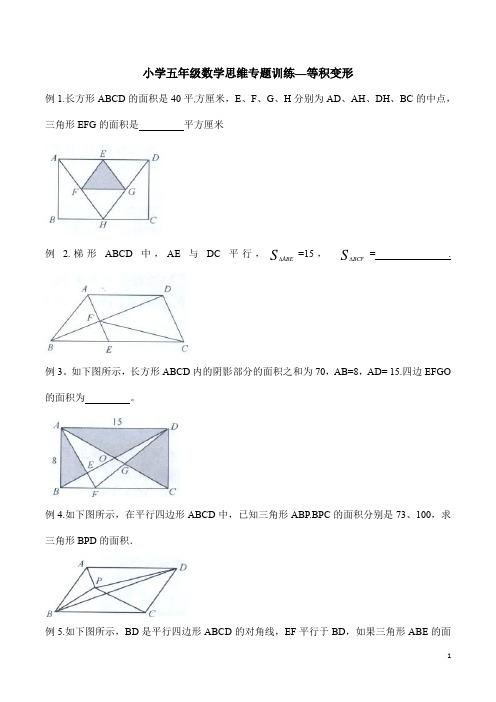
小学五年级数学思维专题训练—等积变形例1.长方形ABCD的面积是40平方厘米,E、F、G、H分别为AD、AH、DH、BC的中点,三角形EFG的面积是平方厘米例 2.梯形ABCD中,AE与DC平行,S ABE∆=15,S BCF∆= .例3。
如下图所示,长方形ABCD内的阴影部分的面积之和为70,AB=8,AD= 15.四边EFGO 的面积为。
例4.如下图所示,在平行四边形ABCD中,已知三角形ABP.BPC的面积分别是73、100,求三角形BPD的面积.例5.如下图所示,BD是平行四边形ABCD的对角线,EF平行于BD,如果三角形ABE的面积是12平方厘米,那么三角形AFD的面积是平方厘米。
例6.如下图所示,已知AE=EC,CD=DB,S ABC =60,求四边形FDCE的面积.例7.如右图所示,正方形ABC D和正方形ECGF并排放置,BF与CD相交于点H,已知AB=6厘米,则阴影部分的面积是平方厘米.例8.如下图所示,E、F、G、H分别是四边形ABCD各边的中点,EG与FH交于点O,S1、S2、S3及S4分别表示4个小四边形的面积.试比较S1+S3与S2+S4的大小.例9.将长15厘米、宽9厘米的长方形的长和宽都分成三等份,长方形内任意一点与分点及顶点连结,如右图所示,则阴影部分的面积是 平方厘米.例10.右图所示ABCD 是个直角梯形(∠DAB=∠ABC= 900),以 , AD 为一边向外作长方形ADEF ,其面积为6.36平方厘米,连接BE 交AD 于P ,再连接PC .则图中阴影部分的面积是 平方厘米。
A.6.36B.3.18C.2.12D.1.59例11.如下图所示,平行四边形内有两个大小一样的正六边形,那么阴影部分的面积占平行四边形面积的 。
A .21B .32C .52D .125例12.如下图所示,矩形ABCD 的面积是24平方厘米,三角形ADM 与三角形BCN 的面积之和是7.8平方厘米,则四边形PMON 的面积是 平方厘米.例13.一个矩形分成4个不同的三角形(如下图),绿色三角形面积占矩形面积的15%,黄色三角形的面积是21平方厘米.问:矩形的面积是多少平方厘米?例14.如下图所示,正方形每条边上的三个点(端点除外)都是这条边的四等分点,则阴影部分的面积是正方形面积的。
5年级等积变形

等积变形有一个富翁留了一块三角形的土地给两个儿子,两个儿子要求平分这块地,这可伤透了他们的脑筋,因为他们不知道怎样去测量、平分。
同学们,你们能想出多少种方法将这块土地平分成个面积相等的三角形吗?根据这个问题,你能得出什么结论?结论一:。
思维探索例1:你有什么方法将任意一个三角形分成6个面积相等的三角形?如图,把△ABC的底边BC四等分,那么甲、乙两个三角形的面积谁大,为AB的面积是多少?如果△AC的面积是,那么AAB的面积是多少?如图,已知是BC的中点,是C的中点,是AC的中点。
已知三角形的面积是平方厘米,那么三角形ABC的面积是多少平方厘米?A思维探索例:(平行线间的等积变形)如下图,△和厶夹在一组平行线之间,且有公共底边,那么△和厶的面积关系是怎样的?结论拓展:夹在平行线间的一组同底三角形面积相等例:如图,在梯形中共有个三角形,其中面积相等的三角形有哪几对?即学即练如下图,在梯形A中,梯形A的面积是,AA的面积融会贯通例:如图,在直角三角形A中,D、E分别是A、A的中点,如果△AED的面积是即学即练如下图,在AA中,D、E是所在边的中点,如果AA的面积是,那么△DE的面积是多少?例:如图,A和DE都是长方形,A的长是厘米,的长是厘米。
那么图中阴影部分的面积是多少平方厘米?即学即练在边长为厘米的正方形中有一点,将点分别和四条边的中点相连,如下图,求阴影部分的面积。
练习册知识导航一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化。
同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状。
为便于实际问题的研究,我们还会常常用到以下结论:()等底等高的两个三角形面积相等;()底在同一条直线上并且相等,该底所对的角的的顶点是同一个点或在与底平行精彩文档如图, 是直角的直线上,这两个三角形面积相等;()若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍。
五年级数学下册 思维训练

五年级数学下册思维训练(1)---复习巩固1.小芳的爸爸比小芳大27岁,当小芳爸爸的年龄是小芳年龄的2.5倍时,小芳多少岁?2.停车场客车的辆数是货车的1.5倍,客车和货车共300辆,原来客车和货车各有多少辆?3.服装厂计划做600套服装,计划每套用布2.5米,实际每套用布2.4米。
实际比计划多做多少套?4.张村、王村两地相距450千米,甲乙两车同时从张村开往王村。
甲车每小时行50千米,乙车每小时行45千米。
甲车到王村后,乙车离王村还有多少千米?5.一个直角三角形两条直角边分别是3米和4米,斜边是5米,斜边上的高是多少米6.李先生到某公司应聘,该公司前3个月是试用期,试用期每月工资600元,试用期结束后的第一个月工资800元,以后每月工资比上一个月多25元。
李先生第一个年的年收入是()元。
7.甲骑自行车追赶前面步行的乙,乙的速度是每分钟60米,甲的速度是每分钟150米。
甲出发8分钟追上了乙,那么乙比甲早出发()分钟。
8.有1克、2克、4克和8克的砝码各一个,丢了其中的一个,结果无法称出7克和12克的重量,丢了的砝码是()克。
9. 把一根钢管锯成几小段,一共花了28分钟。
已知每锯开一段需要4分钟,这根钢管被锯成了多少段?10. 甲.乙两人比赛爬楼梯,甲跑到5楼时,乙恰好跑到3楼。
照这样计划,甲跑到17楼时,乙跑到多少楼?11.盒子有红、黄、蓝三种颜色的笔,至少取出()支就一定有2支笔的颜色是一样的。
12.甲车的速度为60千米/小时,乙车的速度为40千米/小时,现在乙车先出发2小时,甲车去追赶乙车,()小时能赶上。
13. 2÷7=0.285714285714……,那么小数点后前100个数字的和是()14.把一个正方形分割成5个一样的长方形,每个长方形的周长是60厘米,那么原来的正方形的周长是()厘米。
15.一种浮萍生成非常迅速,每天生长的面积能增加一倍。
经过64天已经刚好铺满整个池塘,那么要把半个池塘铺满,需要()天?16.2010×2011-2009×2012=()五年级数学下册思维训练(2 )----新定义运算定义新运算是指用一个符号和已知运算表达式表示一种新的运算。
五年级数学思维《平面图形面积计算》专题训练

五年级数学思维《平面图形面积计算》专题训练一、选择题(每小题6分,共60分)1 平行四边形的底扩大到原来的3倍,高扩大到原来的3倍,它的面积().(A)扩大到原来的3倍(B)扩大到原来的9倍(C)扩大到原来的6倍(D)不变2 一个梯形的上、下底各扩大到原来的5倍,它的面积扩大到原来的()倍.(A)5 (B)10 (C)25 (D)不一定3 如图,梯形中两个阴影部分的大小关系是().(A)①=②(B)①>②(C)①<②(D)无法比较4 一批钢管整齐地堆放在一起,最上层有5根,最下层有16根,每两层柜差1根.这批钢管共有()根.(A)120 (B)126 (C)231 (D)2525 一个梯形,高是4m,若上底和下底不变,高增加2m后,面积增加8㎡,那么原来梯形的面积是()㎡.(A)42 (B)16 (C)21 (D)326 如图,甲、乙两点分别为长方形宽的中点,那么图中面积相等的所有三角形是().(A)A、B和C (B)D和E (C)A和B (D)B和C7 如图,两个正方形的阴影部分的面积是26cm2,那么大正方形内的空白部分面积是()cm2.(A)25 (B)15 (C)12.5 (D)108 如图,平行线间的三个图形,比较它们的面积是().(A)平行四边形大(B)三角形大(C)梯形大(D)相等9 牧羊人用15段每段长2米的篱笆,一面靠墙围成一个正方形或长方形羊圈,则羊圈的最大面积是()平方米.(A)100 (B)108 (C)112 (D)122 10 如图,每个小方格面积为1,那么△ABC面积为().(A)10(B)11(C)12(D)11.5二、解答题(每题12分,共60分)11 如图,正方形的一组对边中,一条边增加17cm,另一条边减少10cm,这样就变成梯形,这时梯形的下底长是上底长的4倍.问:这个梯形的面积是多少?12 如图,将一个长方形分成一个三角形和一个梯形,其中三角形的面积比梯形的面积小60cm2,问:梯形的面积是多少?13 如图,正方形ABCD的边长为4cm,△BCF的面积比△DEF的面积多2cm2,求DE的长度.14 如图,已知△ABC的面积等于梯形BCDE的面积,求BC的长.(单位:cm)15 如图,已知长方形ABCD的长BC=l2厘米,宽DC=8厘米,并且BF=CG,三角形EFC的面积是32平方厘米,那么线段HG的长度是多少厘米?。
等积变形题目五年级

等积变形题目五年级等积变形是指图形在形状发生改变的过程中,其面积大小保持不变的一种变形。
例如,一个四边形可以变成正方形、长方形、梯形或不规则的其他几边形,只要其面积大小保持不变,就是等积变形。
1.问题:有一个长方体,它的长、宽、高分别是a、b、c(a>b>c),现在进行等积变形,把长方体的长变成d,宽和高保持不变。
请问变形后的长方体与原长方体的体积相比,是变大还是变小?解析:因为等积变形不改变物体的体积,所以原长方体和变形后的长方体的体积是相等的。
2.问题:有一个正方体,边长为a,现在进行等积变形,把正方体的边长变成d,请问变形后的正方体与原正方体的体积相比,是变大还是变小?解析:因为等积变形不改变物体的体积,所以原正方体和变形后的正方体的体积是相等的。
3.问题:有一个三角形,它的底边为a,高为h,现在进行等积变形,把三角形的底边变成d,高保持不变。
请问变形后的三角形与原三角形的面积相比,是变大还是变小?解析:因为等积变形不改变三角形的面积,所以原三角形和变形后的三角形的面积是相等的。
4.问题:有一个正方形,边长为a,现在进行等积变形,把正方形的边长变成d,请问变形后的正方形与原正方形的面积相比,是变大还是变小?解析:因为等积变形不改变正方形的面积,所以原正方形和变形后的正方形的面积是相等的。
5.问题:有一个长方形,长为a,宽为b,现在进行等积变形,把长方形的长变成d,宽保持不变。
请问变形后的长方形与原长方形的面积相比,是变大还是变小?解析:因为等积变形不改变长方形的面积,所以原长方形和变形后的长方形的面积是相等的。
五年级下册数学思维拓展训练几何图形优秀PPT(一) 全国通用

五年级下册数学思维拓展训练几何图 形优秀P PT(一 ) 全国通用
要求△ABO面积, 必须先求出高OF
OF=EF-EO
五年级下册数学思维拓展训练几何图 形优秀P PT(一 ) 全国通用
例7:图中,梯形ABCD的面积是45平方厘米, 下底AB长10厘米,高EF长6厘米,三角形DOC的面 积为5平方厘米,求三角形ABO的面积。
例3:已知下面梯形的上底是20厘米,下底是34 厘米,其中阴影部分的面积是340平方厘米,这个梯 形的面积是多少?
阴影三角形与梯形同高 高:340×2÷34=20(厘米)
(20+34)×20÷2=540(平方厘 米)
五年级下册数学思维拓展训练几何图 形优秀P PT(一 ) 全国通用
答:这个梯形的面积是540平方厘米。
两部分的面积和=15×6.2, 利用和差公式可以求出每 部分的面积。
五年级下册数学思维拓展训练几何图 形优秀P PT(一 ) 全国通用
五年级下册数学思维拓展训练几何图 形优秀P PT(一 ) 全国通用
例8:一个平行四边形分成两部分(如图,单位: 厘米),它们的面积差是18.6平方厘米,高是6.2, 梯形的上底是多少厘米?
五年级下册数学思维拓展训练几何图 形优秀P PT(一 ) 全国通用
例3:已知下面梯形的上底是20厘米,下底是34 厘米,其中阴影部分的面积是340平方厘米,这个梯 形的面积是多少?
已知上底和下底, 只需要求出高就可以了。
五年级下册数学思维拓展训练几何图 形优秀P PT(一 ) 全国通用
五年级下册数学思维拓展训练几何图 形优秀P PT(一 ) 全国通用
你还有更简单的方法吗?
15×6.2=93(平方厘米) 梯形面积:(93+18.6)÷2=55.8(平方厘米) 梯形上底:55.8×2÷6.2-15=3(厘米)
五年级数学 平面几何图形的面积训练题 带详细答案

平面几何图形的面积板块一:基础巩固1、一个三角形的面积比与他等底等高的平行四边形的面积少12平方分米,则平行四边形的面积是()平方分米,三角形的面积是()平方分米。
2、李叔叔在院子里靠着墙边围城了一个鸡笼,围鸡笼的网子长20.5米,求这个鸡笼的占地面积是多少平方米?3、有一个长方形,如果宽减少2米,或长减少3米,则面积均减少24平方米,求这个长方形的是是多少平方米?324、如图是由边长分别为4厘米、8厘米的两个正方形组成的图形,求阴影部分面积。
5、如图是由边长分别为4、8、6厘米的三个正方形组成的图形,求阴影部分面积。
板块二:拓展提高【例题1】下图(单位:厘米)是两个相同的直角梯形重叠在一起,求阴影部分的面积.【例题2】右图中甲的面积比乙的面积大__________平方厘米.6厘米8厘米4厘米【例3】右图中,矩形ABCD 的边AB 为4厘米,BC 为6厘米,三角形ABF 比三角形EDF 的面积大9平方厘米,求ED 的长.A BC DEF【巩固】如图所示,CA=AB=4厘米,△ABE 比△CDE 的面积小2平方厘米,求CD 的长为多少厘米?A BECD【例4】一块长方形铁板,长15分米,宽12分米,如果长和宽各减少2分米,面积比原来减少多少平方分米?1215222【巩固】一个长方形,如果长减少5厘米,宽减少2厘米,那么面积就减少66平方厘米,这时剩下的部分恰好成为一个正方形,求原来长方形的面积?5×225【例5】下面图形中,长方形ABCD的面积是32平方厘米,EF都是所在边的中点,求三角形AEF的面积。
【例6】四边形ABCD是直角梯形,AD=12厘米,AB=8厘米,BC=15厘米,且三角形ADE,四边形DEBF,三角形CDF的面积相等,求阴影三角形的面积是多少平方厘米?【例7】一块长方形,用垂直于长和宽的两条线分成四块,其中三块面积分别为15、18、30平方米。
第四块面积是多少平方米?【巩固】如图有9个小长方形,其中的5个小长方形的面积分别为4、8、12、16、20平方米,其余4个长方形的面积分别是多少平方米?【例8】如下图,在一个之间三角形铁皮上剪下一个正方形,并且使正方形的面积尽可能的大,正方形的面积最大是多少?【巩固】如图,直角三角形ABC套住了一个正方形CDEF,E恰好在AB边上,直角边AC长40厘米,BC长12厘米,求正方形的边长是多少?【例9】如图,长方形ABCD 长是8厘米,宽是7厘米,点E 、F 、G 分别是长方形ABCD 边上的中点,H 为AD 边上的任意一点,求阴影部分的面积.E【巩固】如图,三角形ABC 的面积是24,D 、E 和F 分别是BC 、AC 和AD 的中点.求三角形DEF 的面积.FE DC BA【例10】如图,三角形ABC 中,DC=2BD ,CE=3AE ,三角形ADE 的面积是20平方厘米,三角形ABC 的面积是多少?ED CB A【巩固】图中三角形ABC 的面积是180平方厘米,D 是BC 的中点,AD 的长是AE 长的3倍,EF 的长是BF 长的3倍.那么三角形AEF 的面积是多少平方厘米?C B【答案】板块一:1、24 122、上底+下底=20.5-8.5=12(米)梯形面积=12×8.5÷2=51(平方米)3、原长方形的长:24÷2=12(米)原长方形的宽:24÷3=8(米)原来长方形的面积:12×8=96(平方米)4、方法一:可以分割成两个钝角三角形第一个钝角三角形的底是4,高是4,第二个钝角三角形的高是8,底是8-4=4,所以总共的面积是:4×4÷2+8×(8-4)÷2=24(平方厘米)方法二:两个正方形的面积-2处空白的面积=4×4+8×8-8×8÷2-4×(4+8)÷2=24(平方厘米)方法一:可以分割成三个钝角三角形第一个钝角三角形的底是4,高是4,面积是:4×4÷2=8(平方厘米)第二个钝角三角形的高是8,底是(8-4),面积:8×(8-4)÷2=16(平方厘米)第三个钝角三角形的高是8,底是6,面积是:6×8÷2=24(平方厘米)一共的面积:8+16+24=48(平方厘米)方法二:把右上角补起来阴影面积=三个正方形的面积+小长方形面积-两处空白的面积=4×4+8×8+6×6+6×(8-6)-(8+4)×4÷2-8×(6+8)÷2=48(平方厘米)板块二:拓展提高【例题1】、阴影部分+中间空白=中间空白+下面空白所以阴影部分=下面空白20-5=15(厘米)(15+20)×8÷2=140(平方厘米)【例题2】、利用同增同减差不变甲-乙=(甲+空白)-(乙+空白)=大三角形面积-小三角形面积=6×8÷2-4×8÷2=24-16=8(平方厘米)【例题3】、利用同增同减差不变三角形ABF-三角形EDF的面积=9平方厘米同时增加梯形BCDF的面积,则:长方形ABCD-三角形BCE=9长方形ABCD的面积=4×6=24(平方厘米)则三角形BCE的面积=24-9=15(平方厘米)EC=15×2÷6=5(厘米)ED=5-4=1(厘米)【巩固】、利用同增同减差不变三角形CDE-三角形ABE的面积=2平方厘米同时增加三角形BCE的面积,则:三角形BCD-三角形ABC=2三角形ABC的面积=4×4÷2=8(平方厘米)则三角形BCD的面积=8+2=10(平方厘米)CD=10×2÷4=5(厘米)【例题4】原来的面积=15×12=180(平方分米)现在的的面积=(15-2)×(12-2)=130(平方厘米)减少的面积:180-130=50(平方厘米)【巩固】66-2×5=56(平方厘米)设剩下的部分正方形的边长为x厘米5x+2x=56X=8原来长方形的长:8+5=13(厘米)原来长方形的宽:8+2=10(厘米)原来长方形的面积:13×10=130(平方厘米)【例题5】三角形ADF的面积:32÷2÷2=8(平方厘米)三角形ABE的面积:32÷2÷2=8(平方厘米)三角形CEF的面积:32÷2÷2÷2=4(平方厘米)三角形AEF的面积:32-8-8-4=12(平方厘米)【例题6】梯形的面积:(12+15)×8÷2=108(平方厘米)三角形ADE的面积:108÷3=36(平方厘米)AE 的长:36×2÷12=6(厘米)三角形ACF 的面积:108÷3=36(平方厘米)CF 的长:36×2÷8=9(厘米)BE 的长:8-6=2(厘米)BF 的长:15-9=6(厘米)阴影部分面积=2×6÷2=6(平方厘米)【例题7】15×30÷18=25(平方米)【巩固】A 面积:4×16÷8=8(平方米)B 面积:16×12÷8=24(平方米)D 面积:20×24÷16=30(平方米)C 面积:8×20÷16=10(平方米)【例题8】连接DB ,把大三角形分成两个小三角形,正方形的边长就是这两个三角形的高大三角形ABC 的面积是:40×10÷2=200(平方厘米)设正方形的边长为x 厘米40x÷2+10x÷2=20025x=200 X=8正方形面积=8×8=64(平方厘米)【巩固】连接CE ,把大三角形分成两个小三角形,正方形的边长就是这两个三角形的高大三角形ABC 的面积是:40×12÷2=240(平方厘米)设正方形的边长为x 厘米40x÷2+12x÷2=24026x=240X=120/13【例题9】长方形的面积:8×7=56(平方厘米) A B C D阴影部分面积:56÷2=28(平方厘米)【巩固】24÷2÷2÷2=3【例题10】三角形CDE的面积:20×3=60(平方厘米)三角形ADC的面积:20+60=80(平方厘米)三角形ABD的面积:80÷2=40(平方厘米)三角形ABC的面积:40+80=120(平方厘米)【巩固】三角形ABD的面积:180÷2=90(平方厘米)三角形ABE的面积:90÷3=30(平方厘米)三角形AEF的面积:30÷4×3=22.5(平方厘米)。
2023年五年级数学上册平面图形的面积归纳与练习

平面图形旳面积归纳与练习班级______姓名_______一、平面图形面积旳公式及其推导1、沿着平行四边形旳()将它剪成()和(),然后把剪下旳图形平移拼成一种()。
拼成旳图形旳()和平行四边形旳()相等,()和平行四边形旳()相等。
由于长方形旳面积=()×(),因此平行四边形旳面积=()×()。
用字母表达为:2、将两个()旳三角形拼成一种(),拼成旳图形旳()和三角形旳()相等,()和三角形旳()相等,每个三角形旳面积是拼成图形面积旳()。
由于平行四边形旳面积=()×(),因此一种三角形旳面积=()×()○()。
用字母表达为:3、将两个()旳梯形拼成一种(),拼成旳图形旳()和梯形旳()相等,()和梯形旳()相等,每个梯形旳面积是拼成图形面积旳()。
由于平行四边形旳面积=()×(),因此一种梯形旳面积=()×()○()。
用字母表达为:目前我们所学过旳平面图形面积公式旳推导过程,可以用如下图形来表达其中旳关系。
二、平面图形旳面积公式旳应用基础题型一、直接应用面积公式求图形旳面积。
易错点:(1)平行四边形、三角形旳面积公式中“底和高必须是想对应旳”;(2)三角形、梯形旳面积中不要忘了“除以2”。
1、求下面图形旳面积2、计算下面图形旳面积3、量出所需要旳数据,再求图形旳面积。
基础题型二、面积公式在生活中旳运用。
1、有一块平行四边形菜地,底是240m,宽是125m,在这块地里共收油菜7.38吨。
这块菜地有多少公顷?平均每公顷收油菜多少吨?2、有一块麦田旳形状是平行四边形。
它旳底是250m,高是84m,共收小麦14.7吨。
这块菜地平均每公顷收小麦多少吨?3、一块玻璃旳形状是一种三角形,它旳底是12.5dm,高是7.8dm。
每平方米玻璃旳价格是68元,买这块玻璃要用多少钱?4、小雨旳书房需要用某些同样大小旳平行四边形地砖铺地,每块砖旳第是7dm,高是4dm,每平方米地砖旳价格是0.25元,小雨带了200元钱去建材城买地砖,他最多能买多少块这样旳地砖?5、一架滑翔机模型旳尾翼是由两个完全相似旳梯形构成旳。
全国通用五年级上册数学第八周思维训练课等积变形和一半模型课件

甲乙
50×1.2= 60(平方厘米) 60+50= 110(平方厘米) 110×2= 220(平方厘米)
答:平行四边形的面积是220平方厘米。
例题2: 已知大长方形的长是6厘米,宽是4厘米,求阴影部分的面积。
4 6
思路点拨:阴影部分的面积可以分割成两个 部分,分别是两个一半模型,每个阴影部分 的面积都是是长方形形面积的一半,合起来 的面积也是长方形面积的一半。
连接长方形的对角线,长方形就被平均分成2份。 阴影三角形与空白三角形等底等高,面积相等。
知识链接:连接长方形的对角线,分成的两个三角形的面 积相等。
一半模型: 判断阴影部分是整个图形的一半吗?
连接平行四边形的对角线,平行四边形就被 平均分成2份。 □ 阴影三角形与空白三角形等底等高,面积相等。
知识链接:连接平行四边形的对角线,分成的两个三角形 的面积相等。
√
√
×
思路点拨:判断两个三角形的面积是否相等,关键是看两 个三角形的底和高是否相等。“等底等高”的三角形的形 状不一定相同,但面积一定相等。
一半模型: 判断阴影部分是整个图形的一半吗?
h
b
□
S
长=
a
ab
S 三= ah÷2
所以三角形面积是长方 形面积的一半。
空白部分面积也是长方 形面积的一半。
h
□
b
58÷2=29(平方厘米)
答:阴影部分的面积是29平方厘米。
例题4: 如图,在三角形ABC中,D、E分别是AB和BC边上的中点, 三角形ABC的面积是128平方厘米,那么,阴影部分的面积是 多少平方厘米?
甲
乙
思路点拨:因为E是BC边上的中点,所以, 三角形甲与乙等底等高,甲乙的面积相等; 三角形CAD与三角形CDB等底等高,面积相 等。
五年级数学思维《等积变形》专题训练

五年级数学思维《等积变形》专题训练一、填空题(每小题6分,共60分)1 如图,三角形ABC被ED分成甲、乙两部分,BD=DC=4,BE=3,AE=6,那么乙部分面积是甲部分而积的倍.2 如图,BD是梯形ABCD的一条对角线,线段AE与梯形的腰DC平行,AE与BD柜交于O点已知三角形BOE的面积比三角形AOD的BC,那么梯形ABCD的面积是面积大4平方厘米,并且EC=38平方厘米.3 如图,已知平行四边形ABCD中,BC=3厘米,BC边上的高AE是2厘米,那么△ACD的面积是平方厘米.4 如图,平行匹边形MNOP中,Q是OP上任意一点,则S△MRQS△NRO,S△MRN S△QRO.(填“大于”、“<”或“=”)5 如图,平行四边形ABCD中,E、F分别为AD、CD的中点,那么与△BFC面积相等的三角形有个.6 如图,△ABC中,D为BC中点,且DE=2AD,那么△ABC的面积等5于△CDE面积的倍.7 如图,AC=4AD,三角形CDE的面积是三角形ABC面积的一半,那么BE的长等于 BC.8 如图,△ABC与△BCD 中AD与BC交于点E, AE=ED,且AD⊥BC,把BC八等分,点F为第一个八等分点,E恰为第二个八等分点,各等分点分别与A、D连线,那么与△ABF面积相等的三角形个.9 如图,已知BC是5,其他数据如图所示,那么阴影部分的两个三角形的面积之和是 .10 如图,大正六边形的面积是24平方厘米,共中放了三个一样的小正六边形,那么阴影部分的面积是平方厘米.二、解答题(每小题12分,共60分)11 如图,梯形ABCD的上底AD是12厘米,高BD是18厘米,BE=2DE,那么下底BC是多少厘米?12 如图,平行四边形ABCD 的边BC是10厘米,直角三角形ECB的直角边EC是8厘米,已知阴影部分的总面积比△EFG的面积大10平方厘米,那么平行四边形ABCD的面积是多少平方厘米?13 如图,△ABC的面积是180平方厘米,D是BC的中点,AD=3AE,EF=3BF,求△AEF的面积.14 如图,正方形ABCD的边长为12,P是AB边上任意一点,M、N、I、H分别是BC 、AD的三等分点,E、F、G分别是边CD的四等分点,求图中阴影部分的面积.15 如图,BD、CF将长方形ABCD分成四块,红色三角形面积是4平方厘米,黄色三角形面积是6平方厘米,问:绿色四边形面积是多少平方厘米?。
(word完整版)小学五年级数学组合图形面积思维训练一(2021年整理)

(word完整版)小学五年级数学组合图形面积思维训练一(word版可编辑修改) (word完整版)小学五年级数学组合部内容。
图形面积思维训练一(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((word完整版)小学五年级数学组合图形面积思维训练一(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(word完整版)小学五年级数学组合图形面积思维训练一(word版可编辑修改)的全五年级数学思维秋季班方法讲义:第八讲《组合图形面积(一)》姓名【点燃思维】1、一个等腰直角三角形,最长的边是12厘米,这个三角形的面积是多少平方厘米?2、求四边形ABCD的面积.(单位:厘米)3、有一个梯形,它的上底是5厘米,下底7厘米。
如果只把上底增加3厘米,那么面积就增加4。
5平方厘米。
求原来梯形的面积。
4、下图正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点把正方形的四条边各分成两段,其中长的一段是短的2倍。
求中间长方形的面积。
5、(如下图)已知大正方形的边长是12厘米,求中间最小正方形的面积。
6、正图长方形ABCD的面积是16平方厘米,E、F都是所在边的中点,求三角形AEF的面积。
7、图中两个正方形的边长分别是6厘米和4厘米,求阴影部分的面积.8、图中三个正方形的边长分别是1厘米、2厘米和3厘米,求图中阴影部分的面积。
9、下图中两个完全一样的三角形重叠在一起,求阴影部分的面积。
(单位:厘米)10、边长分别为3厘米与5厘米的两个正方形拼在一起(如图).求阴影部分的面积。
巩固练习:1、已知正方形ABCD 的边长是7厘米,求正方形EFGH 的面积。
五年级数学思维训练组合图形的面积

组合图形的面积知识导航一,基本平面图形特点及面积公式特点①四条边都相等。
正方形②四个角都是直角。
③有四条对称轴。
①对边相等。
长方形②四个角都是直角。
③有二条对称轴。
①两组对边平行且相等。
平行四边形②对角相等,相邻两个角之和为180°③平行四边形简单变形。
①两边之和大于第三条边。
②两边之差小于第三条边。
三角形③三个角的内角和是180°。
④有三条边和三个角,拥有稳固性。
①只有一组对边平行。
梯形②中位线等于上下底和的一半。
方法将图形变为基本图形分别计算。
面积公式S=a2S=abS=ahS=ah÷2S=(a+b)h÷2二,基本解题方法:由两个或多个简单的基本几何图形组合成的组合图形,要计算这样的组合图形面积,先依据图形的基本关系,再运用分解、组合、平移、割补、添协助线等几种精典例题例1:已知平行四边表的面积是28平方厘米,求暗影部分的面积。
思路点拨此图形为平行四边形,依据S=ah,能够求出a=7厘米,则暗影部分三角形底边边长为:7-5=2厘米,面积为:4×2÷2=4平方厘米。
模拟练习假如用铁丝围成以下列图同样的平行四边形,需要用多少厘米铁丝?单位:(厘米)例2:下列图中甲和乙都是正方形,求暗影部分的面积。
(单位:厘米)思路点拨本题用分解法,先把甲、乙两个正方形以及三角形ADC的面积当作整体,可分解为三角形AGB、三角形CBF以及暗影面积三部分。
模拟练习下列图中三个正方形的边长分别是1厘米、2厘米和3厘米。
求图中暗影部分的面积。
例3:以下图,甲三角形的面积比乙三角形的面积大6平方厘米,求CE的长度。
思路点拨本题要依据已知,做出甲三角形与乙三角形的面积差。
简单看出,正方形ABCD与三角形ABC的面积差正是甲三角形与乙三角形的面积差。
模拟练习平行四边形ABCD的边长BC=10厘米,直角三角形BCE的直角边EC长8厘米,已知暗影部分的面积比三角形EFG的面积大10平方厘米。
五年级(上)数学思维美之平面图形面积问题(二)(B版)
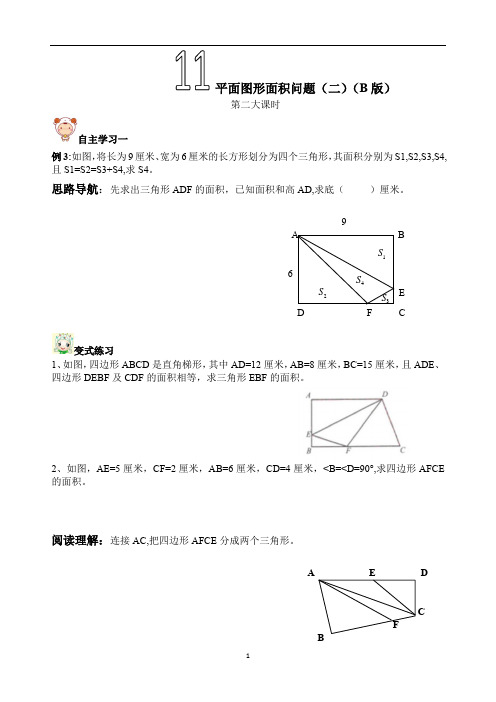
平面图形面积问题(二)(B版)第二大课时自主学习一例3:如图,将长为9厘米、宽为6厘米的长方形划分为四个三角形,其面积分别为S1,S2,S3,S4,且S1=S2=S3+S4,求S4。
思路导航:先求出三角形ADF的面积,已知面积和高AD,求底()厘米。
9A B1S62S ED F C变式练习1、如图,四边形ABCD是直角梯形,其中AD=12厘米,AB=8厘米,BC=15厘米,且ADE、四边形DEBF及CDF的面积相等,求三角形EBF的面积。
2、如图,AE=5厘米,CF=2厘米,AB=6厘米,CD=4厘米,<B=<D=90°,求四边形AFCE 的面积。
阅读理解:连接AC,把四边形AFCE分成两个三角形。
A DCFB3S4S1、如图,一个长方形被一线段分成三角形和梯形两部分,它们的面积差是28平方厘米,梯形的上底长是多少厘米。
710沟通感悟1、自主学习的主要问题与困惑点?这组材料有什么联系和区别?2、通过这组材料的学习,你获得的主要思想方法是什么?你有什么感悟?达标检测1、如图,求图示长方形中阴影部分的面积。
(单位:厘米)102、一个等腰直角三角形,最长的边为12厘米,求这个三角形的面积是多少平方厘米?3、有一个梯形,它的上底是5厘米,下底是7厘米,如果只把上底增加3厘米,那么面积就增加4.5平方厘米。
求原来梯形的面积?4、在三角形ABC中,DC=2BD,CE=3AE,阴影部分的面积是20平方厘米。
求三角形ABC的面积。
5、正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点把正方形的四条边各分成两段,其中长的一段是短的2倍。
求中间长方形的面积。
阅读理解:图中相对的两个三角形通过拼组后可以得到一个()图形。
随机应变6、右图三角形ECF中,EC=12cm,CF=8cm,并且它的面积是长方形ABCD面积的2倍,那么三角形ADF面积是多少?基本方法:1、在组合图形中计算某个图形的面积时,一定要认真观察各图形找到图形之间的联系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五年级数学思维专题练习《平面图形面积计算及等积变形》
姓名_________
知识准备:
平面图形面积计算:多边形及组合图形的面积计算,转化为求三角形、长方形、梯形、平行四边形的面积,利用相应的面积公式求解
三角形面积=底×高÷2 梯形面积=(上底+下底)×高÷2
长方形面积=长×宽平行四边形面积=底×高
等积变形问题:两个平面图形面积相等,称为这两个图形等积。
三角形等积变形技巧是各种等积变形的核心,要注意运用“等(同)底、等(同)高的两个三角形面积相等”这个基本规则
一、平面图形面积
如图,一个3×3的正方形网格,如果小正方形边长是1,那么阴影部分的面积是________
如图,在长方形ABCD中,BC=12,AB=9,F为BC上一点,且CF=4,那么三角形CEF的面积是__________
如图,正方形ABCD的面积是16,点F是BC上任意一点,点E是DF的中点,则阴影部分的面积是_______
如图,M,N分别是平行四边形ABCD两边上的中点,三角形DMN的面积是9平方厘米,那么ABCD的面积是______平方厘米
二、等积变形
如图,大正六边形的内部有7个完全一样的小正六边形,已知阴影部分的面积是180平方厘米,那么大正六边形的面积是______平方厘米
如图,正六边形ABCDEF的面积是2014平方厘米,在AB,BC,DE,EF上分别取中点G,H,I,J,四边形GHIJ的面积是______平方厘米
如图,直角边长分别为20cm,12cm的直角三角形ABC和直角边长分别为14cm,4cm的直角三角形ADE如图摆放,M为AE的中点,则三角形ACM的面积为_____cm²
5个相同的长方形放在一个正方形内,所有长方形的边都平行于正方形的对应边,正方形的边长为24厘米,求:单个长方形的面积。
