基本遗传算法的C源程序。doc
基于C语言的遗传算法应用研究

基于C语言的遗传算法应用研究介绍遗传算法是一种受生物学启发的优化算法,通过模拟进化过程来寻找最优解。
它被广泛应用于解决各种复杂问题,如组合优化、函数优化、机器学习等领域。
在本文中,我们将讨论基于C语言的遗传算法的应用研究。
遗传算法的原理遗传算法的原理是基于自然选择和遗传机制。
它模拟了生物进化过程中的选择、复制和变异等操作。
算法通过对一个种群进行迭代操作来逐步优化解的质量,直到找到全局最优解或最优近似解。
遗传算法主要包含以下几个关键步骤: 1. 初始化种群:随机生成一组个体作为初始种群。
2. 评估适应度:根据问题的定义,对每个个体计算适应度值。
3.选择操作:根据适应度值选择优秀的个体作为父代。
4. 交叉操作:通过交叉操作,将父代的基因进行混合,生成新的子代。
5. 变异操作:对子代进行变异,引入新的基因信息。
6. 更新种群:用新的个体替代原来的个体,形成新的种群。
7. 终止条件:根据预先设定的终止条件,决定算法是否结束。
C语言在遗传算法中的应用C语言作为一种通用的高级编程语言,具有高效、灵活和可移植的特点,非常适合在遗传算法中实现。
以下是C语言在遗传算法中的几个关键应用。
种群表示C语言可以使用数组或结构体等数据结构来表示遗传算法的种群。
每个个体可以用一个固定长度的二进制串或其他数据类型来表示。
C语言提供了强大的数组操作功能,使得种群的处理和操作更加简便和高效。
适应度函数C语言可以定义适应度函数来评估每个个体的适应度值。
适应度函数根据问题的特定要求来计算一个个体的适应度值,作为选择操作的依据。
C语言提供了丰富的数学函数库,使得适应度函数的计算更加方便。
选择操作C语言可以使用多种选择算法来选择优秀的个体作为父代。
例如,可以使用轮盘赌选择、锦标赛选择等方法来实现选择操作。
C语言提供了条件语句和随机数生成等功能,使得选择操作的实现简单而灵活。
交叉操作C语言可以通过交叉操作将父代的基因混合,生成新的子代。
遗传算法(GeneticAlgorithm)..

被选定的一组解 根据适应函数选择的一组解 以一定的方式由双亲产生后代的过程 编码的某些分量发生变化的过程
遗传算法的基本操作
➢选择(selection):
根据各个个体的适应值,按照一定的规则或方法,从 第t代群体P(t)中选择出一些优良的个体遗传到下一代 群体P(t+1)中。
等到达一定程度时,值0会从整个群体中那个位上消失,然而全局最 优解可能在染色体中那个位上为0。如果搜索范围缩小到实际包含全局 最优解的那部分搜索空间,在那个位上的值0就可能正好是到达全局最 优解所需要的。
2023/10/31
适应函数(Fitness Function)
➢ GA在搜索中不依靠外部信息,仅以适应函数为依据,利 用群体中每个染色体(个体)的适应值来进行搜索。以染 色体适应值的大小来确定该染色体被遗传到下一代群体 中的概率。染色体适应值越大,该染色体被遗传到下一 代的概率也越大;反之,染色体的适应值越小,该染色 体被遗传到下一代的概率也越小。因此适应函数的选取 至关重要,直接影响到GA的收敛速度以及能否找到最优 解。
2023/10/31
如何设计遗传算法
➢如何进行编码? ➢如何产生初始种群? ➢如何定义适应函数? ➢如何进行遗传操作(复制、交叉、变异)? ➢如何产生下一代种群? ➢如何定义停止准则?
2023/10/31
编码(Coding)
表现型空间
基因型空间 = {0,1}L
编码(Coding)
10010001
父代
111111111111
000000000000
交叉点位置
子代
2023/10/31
111100000000 000011111111
遗传算法的C语言程序案例
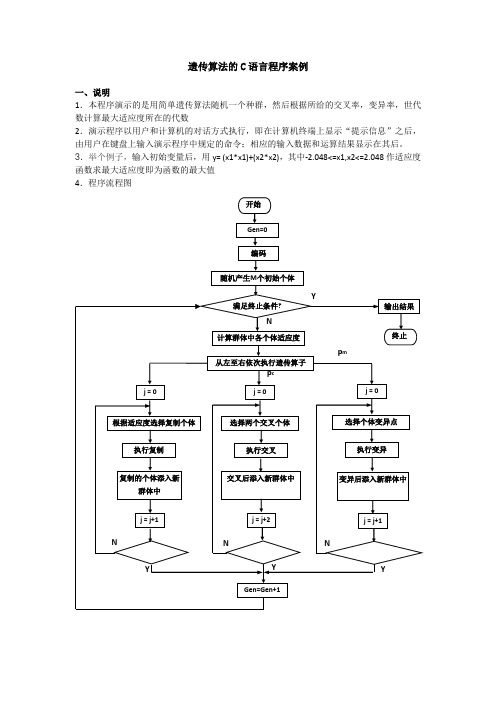
遗传算法的C语言程序案例一、说明1.本程序演示的是用简单遗传算法随机一个种群,然后根据所给的交叉率,变异率,世代数计算最大适应度所在的代数2.演示程序以用户和计算机的对话方式执行,即在计算机终端上显示“提示信息”之后,由用户在键盘上输入演示程序中规定的命令;相应的输入数据和运算结果显示在其后。
3.举个例子,输入初始变量后,用y= (x1*x1)+(x2*x2),其中-2.048<=x1,x2<=2.048作适应度函数求最大适应度即为函数的最大值4.程序流程图5.类型定义int popsize; //种群大小int maxgeneration; //最大世代数double pc; //交叉率double pm; //变异率struct individual{char chrom[chromlength+1];double value;double fitness; //适应度};int generation; //世代数int best_index;int worst_index;struct individual bestindividual; //最佳个体struct individual worstindividual; //最差个体struct individual currentbest;struct individual population[POPSIZE];3.函数声明void generateinitialpopulation();void generatenextpopulation();void evaluatepopulation();long decodechromosome(char *,int,int);void calculateobjectvalue();void calculatefitnessvalue();void findbestandworstindividual();void performevolution();void selectoperator();void crossoveroperator();void mutationoperator();void input();void outputtextreport();6.程序的各函数的简单算法说明如下:(1).void generateinitialpopulation ()和void input ()初始化种群和遗传算法参数。
遗传算法的C语言实现(二)-----以求解TSP问题为例

遗传算法的C语⾔实现(⼆)-----以求解TSP问题为例上⼀次我们使⽤遗传算法求解了⼀个较为复杂的多元⾮线性函数的极值问题,也基本了解了遗传算法的实现基本步骤。
这⼀次,我再以经典的TSP问题为例,更加深⼊地说明遗传算法中选择、交叉、变异等核⼼步骤的实现。
⽽且这⼀次解决的是离散型问题,上⼀次解决的是连续型问题,刚好形成对照。
⾸先介绍⼀下TSP问题。
TSP(traveling salesman problem,旅⾏商问题)是典型的NP完全问题,即其最坏情况下的时间复杂度随着问题规模的增⼤按指数⽅式增长,到⽬前为⽌还没有找到⼀个多项式时间的有效算法。
TSP问题可以描述为:已知n个城市之间的相互距离,某⼀旅⾏商从某⼀个城市出发,访问每个城市⼀次且仅⼀次,最后回到出发的城市,如何安排才能使其所⾛的路线最短。
换⾔之,就是寻找⼀条遍历n个城市的路径,或者说搜索⾃然⼦集X={1,2,...,n}(X的元素表⽰对n个城市的编号)的⼀个排列P(X)={V1,V2,....,Vn},使得Td=∑d(V i,V i+1)+d(V n,V1)取最⼩值,其中,d(V i,V i+1)表⽰城市V i到V i+1的距离。
TSP问题不仅仅是旅⾏商问题,其他许多NP完全问题也可以归结为TSP问题,如邮路问题,装配线上的螺母问题和产品的⽣产安排问题等等,也使得TSP问题的求解具有更加⼴泛的实际意义。
再来说针对TSP问题使⽤遗传算法的步骤。
(1)编码问题:由于这是⼀个离散型的问题,我们采⽤整数编码的⽅式,⽤1~n来表⽰n个城市,1~n的任意⼀个排列就构成了问题的⼀个解。
可以知道,对于n个城市的TSP问题,⼀共有n!种不同的路线。
(2)种群初始化:对于N个个体的种群,随机给出N个问题的解(相当于是染⾊体)作为初始种群。
这⾥具体采⽤的⽅法是:1,2,...,n作为第⼀个个体,然后2,3,..n分别与1交换位置得到n-1个解,从2开始,3,4,...,n分别与2交换位置得到n-2个解,依次类推。
遗传算法基础

比例选择法(轮盘赌)
• 基本思想
各个个体被选中的概率与其适应度大小成正比。 设群体大小为 M,个体 i 的适应度大小为F ( xi ) ,则 个体 i 被选中的概率为
Pi =
F ( xi )
∑ F (x )
i =1 i
M
比例选择法(轮盘赌)
• 具体步骤 1)计算各基因适应度值和选择概率 Pi 2)累计所有基因选择概率值,记录中间累 加值S - mid 和最后累加值 sum = ∑ Pi 3)产生一个随机数 N,0〈 N 〈 1 4)选择对应中间累加值S - mid 的基因进 入交换集 5)重复(3)和(4),直到获得足够的基 因。
t i
t i i
n
模式定理
• 选择算子的作用
f (H , t) m( H , t + 1) = m( H , t ) f (t )
若 若
f (H , t) >1,m(H,t)增加 f (t ) f ( H , t ) <1,m(H,t)减少 f (t )
在选择算子的作用下,对于平均适用度高于群体平 在选择算子的作用下, 均适应度的模式,其样本数将增长, 均适应度的模式,其样本数将增长,对于平均适用 度低于群体平均适应度的模式, 度低于群体平均适应度的模式,其样本数将减少
f ( x) f ( x) f ( x) f ( x) f ( x) f ( x)
F(x)
F(x)
F(x)
F(x)=f(x)+C
遗传算法基本要素与实现技术
• 选择算子 • 适应度较高的个体被遗传到下一代群体中 的概率较大,适应度较低的个体被遗传到 下一代群体中的概率较小。 • 选择方法 比例选择法(轮盘赌) 锦标赛选择法
遗传算法C语言源代码(一元函数和二元函数)

C语言遗传算法代码以下为遗传算法的源代码,计算一元代函数的代码和二元函数的代码以+++++++++++++++++++++++++++++++++++++为分割线分割开来,请自行选择适合的代码,使用时请略看完代码的注释,在需要更改的地方更改为自己需要的代码。
+++++++++++++++++++++++++++++++一元函数代码++++++++++++++++++++++++++++#include <>#include<>#include<>#include<>#define POPSIZE 1000#define maximization 1#define minimization 2#define cmax 100#define cmin 0#define length1 20#define chromlength length1 //染色体长度//注意,你是求最大值还是求最小值int functionmode=minimization;//变量的上下限的修改开始float min_x1=-2;//变量的下界float max_x1=-1;//变量的上界//变量的上下限的修改结束int popsize; //种群大小int maxgeneration; //最大世代数double pc; //交叉率double pm; //变异率struct individual{char chrom[chromlength+1];double value;double fitness; //适应度};int generation; //世代数int best_index;int worst_index;struct individual bestindividual; //最正确个体struct individual worstindividual; //最差个体struct individual currentbest;struct individual population[POPSIZE];//函数声明void generateinitialpopulation();void generatenextpopulation();void evaluatepopulation();long decodechromosome(char *,int,int);void calculateobjectvalue();void calculatefitnessvalue();void findbestandworstindividual();void performevolution();void selectoperator();void crossoveroperator();void mutationoperator();void input();void outputtextreport();void generateinitialpopulation( ) //种群初始化{int i,j;for (i=0;i<popsize; i++){for(j=0;j<chromlength;j++){population[i].chrom[j]=(rand()%20<10)?'0':'1';}population[i].chrom[chromlength]='\0';}}void generatenextpopulation() //生成下一代{selectoperator();crossoveroperator();mutationoperator();}void evaluatepopulation() //评价个体,求最正确个体{calculateobjectvalue();calculatefitnessvalue();findbestandworstindividual();}long decodechromosome(char *string ,int point,int length) //给染色体解码{int i;long decimal=0;char*pointer;for(i=0,pointer=string+point;i<length;i++,pointer++)if(*pointer-'0'){decimal +=(long)pow(2,i);}return (decimal);}void calculateobjectvalue() //计算函数值{int i;long temp1,temp2;double x1;for (i=0; i<popsize; i++){temp1=decodechromosome(population[i].chrom,0,length1);x1=(max_x1-min_x1)*temp1/(1024*1024-1)+min_x1;//目标函数修改开始population[i].value=(pow(x1,5)-3*x1-1)*(pow(x1,5)-3*x1-1);//目标函数修改结束}}void calculatefitnessvalue()//计算适应度{int i;double temp;for(i=0;i<popsize;i++){if(functionmode==maximization){if((population[i].value+cmin)>0.0){temp=cmin+population[i].value;}else{temp=0.0;}}else if (functionmode==minimization){if(population[i].value<cmax){temp=cmax-population[i].value;}else{ temp=0.0;}}population[i].fitness=temp;}}void findbestandworstindividual( ) //求最正确个体和最差个体{int i;double sum=0.0;bestindividual=population[0];worstindividual=population[0];for (i=1;i<popsize; i++){if (population[i].fitness>){bestindividual=population[i];best_index=i;}else if (population[i].fitness<){worstindividual=population[i];worst_index=i;}sum+=population[i].fitness;}if (generation==0){currentbest=bestindividual;}else{if(>=){currentbest=bestindividual;}}}void performevolution() //演示评价结果{if (>){currentbest=population[best_index];}else{population[worst_index]=currentbest;}}void selectoperator() //比例选择算法{int i,index;double p,sum=0.0;double cfitness[POPSIZE];struct individual newpopulation[POPSIZE];for(i=0;i<popsize;i++){sum+=population[i].fitness;}for(i=0;i<popsize; i++){cfitness[i]=population[i].fitness/sum;}for(i=1;i<popsize; i++){cfitness[i]=cfitness[i-1]+cfitness[i];}for (i=0;i<popsize;i++){p=rand()%1000/1000.0;index=0;while (p>cfitness[index]){index++;}newpopulation[i]=population[index];}for(i=0;i<popsize; i++){population[i]=newpopulation[i];}}void crossoveroperator() //交叉算法{int i,j;int index[POPSIZE];int point,temp;double p;char ch;for (i=0;i<popsize;i++){index[i]=i;}for (i=0;i<popsize;i++){point=rand()%(popsize-i);temp=index[i];index[i]=index[point+i];index[point+i]=temp;}for (i=0;i<popsize-1;i+=2){p=rand()%1000/1000.0;if (p<pc){point=rand()%(chromlength-1)+1;for (j=point; j<chromlength;j++){ch=population[index[i]].chrom[j];population[index[i]].chrom[j]=population[index[i+1]].chrom[j];population[index[i+1]].chrom[j]=ch;}}}}void mutationoperator() //变异操作{int i,j;double p;for (i=0;i<popsize;i++){for(j=0;j<chromlength;j++){p=rand()%1000/1000.0;if (p<pm){population[i].chrom[j]=(population[i].chrom[j]=='0')?'1':'0';}}}void input() //数据输入{ //printf("初始化全局变量:\n");//printf(" 种群大小(50-500):");//scanf("%d", &popsize);popsize=500;if((popsize%2) != 0){//printf( " 种群大小已设置为偶数\n");popsize++;};//printf(" 最大世代数(100-300):");//scanf("%d", &maxgeneration);maxgeneration=200;//printf(" 交叉率(0.2-0.99):");//scanf("%f", &pc);pc=0.95;//printf(" 变异率(0.001-0.1):");//scanf("%f", &pm);pm=0.03;}void outputtextreport()//数据输出{int i;double sum;double average;sum=0.0;for(i=0;i<popsize;i++){sum+=population[i].value;}average=sum/popsize;printf("当前世代=%d\n当前世代平均函数值=%f\n当前世代最优函数值=%f\n",generation,average,population[best_index].value);}void main() //主函数{ int i;long temp1,temp2;double x1,x2;generation=0;input();generateinitialpopulation();evaluatepopulation();while(generation<maxgeneration)generation++;generatenextpopulation();evaluatepopulation();performevolution();outputtextreport();}printf("\n");printf(" 统计结果: ");printf("\n");//printf("最大函数值等于:%f\n",);printf("其染色体编码为:");for (i=0;i<chromlength;i++){printf("%c",[i]);}printf("\n");temp1=decodechromosome(currentbest.chrom,0,length1);x1=(max_x1-min_x1)*temp1/(1024*1024-1)+min_x1;printf("x1=%lf\n",x1);//这是需要修改的地方printf("最优值等于:%f\n",(pow(x1,5)-3*x1-1)*(pow(x1,5)-3*x1-1));}+++++++++++++++++++++++++二元函数代码+++++++++++++++++++++++++++++++++++++++++ #include <>#include<>#include<>#include<>#define POPSIZE 500#define maximization 1#define minimization 2#define cmax 100#define cmin 0#define length1 20#define length2 20#define chromlength length1+length2 //染色体长度//-----------求最大还是最小值int functionmode=maximization;//-----------//-----------变量上下界float min_x1=0;float max_x1=3;float min_x2=1;float max_x2=5;//-----------int popsize; //种群大小int maxgeneration; //最大世代数double pc; //交叉率double pm; //变异率struct individual{char chrom[chromlength+1];double value;double fitness; //适应度};int generation; //世代数int best_index;int worst_index;struct individual bestindividual; //最正确个体struct individual worstindividual; //最差个体struct individual currentbest;struct individual population[POPSIZE];//函数声明void generateinitialpopulation();void generatenextpopulation();void evaluatepopulation();long decodechromosome(char *,int,int);void calculateobjectvalue();void calculatefitnessvalue();void findbestandworstindividual();void performevolution();void selectoperator();void crossoveroperator();void mutationoperator();void input();void outputtextreport();void generateinitialpopulation( ) //种群初始化{int i,j;for (i=0;i<popsize; i++){for(j=0;j<chromlength;j++){population[i].chrom[j]=(rand()%40<20)?'0':'1';}population[i].chrom[chromlength]='\0';}}void generatenextpopulation() //生成下一代{selectoperator();crossoveroperator();mutationoperator();}void evaluatepopulation() //评价个体,求最正确个体{calculateobjectvalue();calculatefitnessvalue();findbestandworstindividual();}long decodechromosome(char *string ,int point,int length) //给染色体解码{int i;long decimal=0;char*pointer;for(i=0,pointer=string+point;i<length;i++,pointer++)if(*pointer-'0'){decimal +=(long)pow(2,i);}return (decimal);}void calculateobjectvalue() //计算函数值{int i;long temp1,temp2;double x1,x2;for (i=0; i<popsize; i++){temp1=decodechromosome(population[i].chrom,0,length1);temp2=decodechromosome(population[i].chrom,length1,length2);x1=(max_x1-min_x1)*temp1/(1024*1024-1)+min_x1;x2=(max_x2-min_x2)*temp2/(1024*1024-1)+min_x2;//-----------函数population[i].value=x1*x1+sin(x1*x2)-x2*x2;//-----------}}void calculatefitnessvalue()//计算适应度{int i;double temp;for(i=0;i<popsize;i++){if(functionmode==maximization){if((population[i].value+cmin)>0.0){temp=cmin+population[i].value;}else{temp=0.0;}}else if (functionmode==minimization){if(population[i].value<cmax){temp=cmax-population[i].value;}else{ temp=0.0;}}population[i].fitness=temp;}}void findbestandworstindividual( ) //求最正确个体和最差个体{int i;double sum=0.0;bestindividual=population[0];worstindividual=population[0];for (i=1;i<popsize; i++){if (population[i].fitness>){bestindividual=population[i];best_index=i;}else if (population[i].fitness<){worstindividual=population[i];worst_index=i;}sum+=population[i].fitness;}if (generation==0){currentbest=bestindividual;}else{if(>=){currentbest=bestindividual;}}}void performevolution() //演示评价结果{if (>){currentbest=population[best_index];}else{population[worst_index]=currentbest;}}void selectoperator() //比例选择算法{int i,index;double p,sum=0.0;double cfitness[POPSIZE];struct individual newpopulation[POPSIZE];for(i=0;i<popsize;i++){sum+=population[i].fitness;}for(i=0;i<popsize; i++){cfitness[i]=population[i].fitness/sum;}for(i=1;i<popsize; i++){cfitness[i]=cfitness[i-1]+cfitness[i];}for (i=0;i<popsize;i++){p=rand()%1000/1000.0;index=0;while (p>cfitness[index]){index++;}newpopulation[i]=population[index];}for(i=0;i<popsize; i++){population[i]=newpopulation[i];}}void crossoveroperator() //交叉算法{int i,j;int index[POPSIZE];int point,temp;double p;char ch;for (i=0;i<popsize;i++){index[i]=i;}for (i=0;i<popsize;i++){point=rand()%(popsize-i);temp=index[i];index[i]=index[point+i];index[point+i]=temp;}for (i=0;i<popsize-1;i+=2){p=rand()%1000/1000.0;if (p<pc){point=rand()%(chromlength-1)+1;for (j=point; j<chromlength;j++){ch=population[index[i]].chrom[j];population[index[i]].chrom[j]=population[index[i+1]].chrom[j];population[index[i+1]].chrom[j]=ch;}}}}void mutationoperator() //变异操作{int i,j;double p;for (i=0;i<popsize;i++){for(j=0;j<chromlength;j++){p=rand()%1000/1000.0;if (p<pm){population[i].chrom[j]=(population[i].chrom[j]=='0')?'1':'0';}}}}void input() //数据输入{ //printf("初始化全局变量:\n");//printf(" 种群大小(50-500):");//scanf("%d", &popsize);popsize=200;if((popsize%2) != 0){//printf( " 种群大小已设置为偶数\n");popsize++;};//printf(" 最大世代数(100-300):");//scanf("%d", &maxgeneration);maxgeneration=200;//printf(" 交叉率(0.2-0.99):");//scanf("%f", &pc);pc=0.9;//printf(" 变异率(0.001-0.1):");//scanf("%f", &pm);pm=0.003;}void outputtextreport()//数据输出{int i;double sum;double average;sum=0.0;for(i=0;i<popsize;i++){sum+=population[i].value;}average=sum/popsize;printf("当前世代=%d\n当前世代平均函数值=%f\n当前世代最优函数值=%f\n",generation,average,population[best_index].value);}void main() //主函数{ int i;long temp1,temp2;double x1,x2;generation=0;input();generateinitialpopulation();evaluatepopulation();while(generation<maxgeneration){generation++;generatenextpopulation();evaluatepopulation();performevolution();outputtextreport();}printf("\n");printf(" 统计结果: ");printf("\n");//printf("最大函数值等于:%f\n",);printf("其染色体编码为:");for (i=0;i<chromlength;i++){printf("%c",[i]);}printf("\n");temp1=decodechromosome(currentbest.chrom,0,length1);temp2=decodechromosome(currentbest.chrom,length1,length2);x1=(max_x1-min_x1)*temp1/(1024*1024-1)+min_x1;x2=(max_x2-min_x2)*temp2/(1024*1024-1)+min_x2;printf("x=%lf,y=%lf\n",x1,x2);//-----------修改函数printf("最大值=%f\n",x1*x1+sin(x1*x2)-x2*x2);//-----------}。
(完整版)遗传算法的基本原理

遗传算法的基本原理和方法一、编码编码:把一个问题的可行解从其解空间转换到遗传算法的搜索空间的转换方法。
解码(译码):遗传算法解空间向问题空间的转换。
二进制编码的缺点是汉明悬崖(Hamming Cliff),就是在某些相邻整数的二进制代码之间有很大的汉明距离,使得遗传算法的交叉和突变都难以跨越。
格雷码(Gray Code):在相邻整数之间汉明距离都为1。
(较好)有意义的积木块编码规则:所定编码应当易于生成与所求问题相关的短距和低阶的积木块;最小字符集编码规则,所定编码应采用最小字符集以使问题得到自然的表示或描述。
二进制编码比十进制编码搜索能力强,但不能保持群体稳定性。
动态参数编码(Dynamic Paremeter Coding):为了得到很高的精度,让遗传算法从很粗糙的精度开始收敛,当遗传算法找到一个区域后,就将搜索现在在这个区域,重新编码,重新启动,重复这一过程,直到达到要求的精度为止。
编码方法:1、二进制编码方法缺点:存在着连续函数离散化时的映射误差。
不能直接反映出所求问题的本身结构特征,不便于开发针对问题的专门知识的遗传运算算子,很难满足积木块编码原则2、格雷码编码:连续的两个整数所对应的编码之间仅仅只有一个码位是不同的,其余码位都相同。
3、浮点数编码方法:个体的每个基因值用某一范围内的某个浮点数来表示,个体的编码长度等于其决策变量的位数。
4、各参数级联编码:对含有多个变量的个体进行编码的方法。
通常将各个参数分别以某种编码方法进行编码,然后再将他们的编码按照一定顺序连接在一起就组成了表示全部参数的个体编码。
5、多参数交叉编码:将各个参数中起主要作用的码位集中在一起,这样它们就不易于被遗传算子破坏掉。
评估编码的三个规范:完备性、健全性、非冗余性。
二、选择遗传算法中的选择操作就是用来确定如何从父代群体中按某种方法选取那些个体遗传到下一代群体中的一种遗传运算,用来确定重组或交叉个体,以及被选个体将产生多少个子代个体。
C语言人工智能算法实现神经网络和遗传算法

C语言人工智能算法实现神经网络和遗传算法人工智能(Artificial Intelligence)是当今科技领域中备受关注的热门话题,而C语言作为一种广泛应用的编程语言,也可以用于实现人工智能算法。
本文将详细介绍如何用C语言来实现神经网络和遗传算法,以展示其在人工智能领域的应用。
1. 神经网络神经网络是一种模仿人脑的学习和决策过程的计算模型。
它由多个神经元组成的层级结构构成,每个神经元接收来自上一层神经元输出的信号,并根据一定的权重和激活函数来计算输出。
下图展示了一个简单的神经网络结构:[图1:神经网络结构图]为了实现一个神经网络,我们需要在C语言中定义神经网络的结构体,并实现前馈传播和反向传播算法。
首先,我们需要定义神经网络的层级结构,可以使用数组或链表来表达。
每个神经元需要存储权重、偏差和激活函数等信息。
我们可以使用结构体来表示神经元的属性,例如:```Ctypedef struct Neuron {double* weights; // 权重数组double bias; // 偏差double output; // 输出} Neuron;```然后,定义神经网络的结构体:```Ctypedef struct NeuralNetwork {int numLayers; // 层数int* layerSizes; // 每层神经元数量的数组Neuron** layers; // 神经元层级的数组} NeuralNetwork;```接下来,我们需要实现神经网络的前馈传播算法。
前馈传播算法用于将输入数据从输入层传递到输出层,并计算网络的输出。
算法的伪代码如下所示:```Cfor each layer in network {for each neuron in layer {calculate neuron's weighted sum of inputs;apply activation function to obtain neuron's output;}}```最后,需要实现神经网络的反向传播算法,用于根据期望输出来调整网络的权重和偏差。
遗传算法程序2

种群表示和初始化函数 bs2rv: 二进制串到实值的转换Phen=bs2rv(Chrom,FieldD)FieldD=[len, lb, ub, code, scale, lbin, ubin]len是字串的长度,lb和ub是每个变量的下界和上界,lbin和ubin指明表示范围中是否包含边界,0不包括,1包括。
code(i)=1为标准的二进制编码,code(i)=0为格雷编码scale(i)=0为算术刻度,scale(i)=1为对数刻度函数 crtbp: 创建初始种群[Chrom,Lind,BaseV]=crtbp(Nind,Lind)[Chrom,Lind,BaseV]=crtbp(Nind,BaseV)[Chrom,Lind,BaseV]=crtbp(Nind,Lind,BaseV)Nind指定种群中个体的数量,Lind指定个体的长度,Basev与base是一样的,返回的是个体的各个位的进制数函数 crtrp: 创建实值原始种群Chrom=crtrp(Nind,FieldDR)适应度计算函数 ranking: 基于排序的适应度分配(此函数是从最小化方向对个体进行排序的)FitV=ranking(ObjV)FitV=ranking(ObjV, RFun)FitV=ranking(ObjV, RFun, SUBPOP)Rfun(1)线性排序标量在[1 2]间,代表的是选择压差,比如压差为2,那就限制了Objv的结果fitv在0-2之间,如果是1.5,就在0.5-1.5之间,结果的最大值与最小值加起来就是2,非线性排序在[1 length(ObjV)-2]Rfun(2)指定排序方法,0为线性排序,1为非线性排序SUBPOP指明ObjV中子种群的数量,默认为1其实我对这个函数没了解得太深刻,不过我觉得这是一种变比技术。
将原先的适应度值压缩到一定的范围,而且目标值越大,分配的适应度值越小。
例如 A=[1;2;3;4;2;3];ranking(A)= 2.0000 1.4000 0.6000 0 1.4000 0.6000,所以如果是求最大值,就得-A,求最小值就直接A就可以了,因为目标值越大分配的适应度越小,目标值越小,分配的适应度越大。
遗传算法 c语言代码

以下是一个简单的遗传算法的C语言代码示例:c#include <stdio.h>#include <stdlib.h>#include <time.h>#include <math.h>#define POPULATION_SIZE 100#define GENE_LENGTH 10#define MAX_GENERATIONS 1000#define MUTATION_RATE 0.01#define CROSSOVER_RATE 0.8typedef struct Individual {char genes[GENE_LENGTH];double fitness;} Individual;double calculate_fitness(Individual* individual) {// 计算适应度函数,这里使用简单的二进制字符串中1的个数作为适应度 int count = 0;for (int i = 0; i < GENE_LENGTH; i++) {if (individual->genes[i] == '1') {count++;}}return count;}void initialize_population(Individual* population) {// 初始化种群for (int i = 0; i < POPULATION_SIZE; i++) {for (int j = 0; j < GENE_LENGTH; j++) {population[i].genes[j] = rand() % 2 ? '0' : '1';}population[i].fitness = calculate_fitness(&population[i]); }}void selection(Individual* population, Individual* parents) {// 选择操作,采用轮盘赌算法选择两个父代个体double total_fitness = 0;for (int i = 0; i < POPULATION_SIZE; i++) {total_fitness += population[i].fitness;}double rand1 = rand() / (double)RAND_MAX * total_fitness;double rand2 = rand() / (double)RAND_MAX * total_fitness;double cumulative_fitness = 0;int parent1_index = -1, parent2_index = -1;for (int i = 0; i < POPULATION_SIZE; i++) {cumulative_fitness += population[i].fitness;if (rand1 < cumulative_fitness && parent1_index == -1) {parent1_index = i;}if (rand2 < cumulative_fitness && parent2_index == -1) {parent2_index = i;}}parents[0] = population[parent1_index];parents[1] = population[parent2_index];}void crossover(Individual* parents, Individual* offspring) {// 交叉操作,采用单点交叉算法生成两个子代个体int crossover_point = rand() % GENE_LENGTH;for (int i = 0; i < crossover_point; i++) {offspring[0].genes[i] = parents[0].genes[i];offspring[1].genes[i] = parents[1].genes[i];}for (int i = crossover_point; i < GENE_LENGTH; i++) {offspring[0].genes[i] = parents[1].genes[i];offspring[1].genes[i] = parents[0].genes[i];}offspring[0].fitness = calculate_fitness(&offspring[0]);offspring[1].fitness = calculate_fitness(&offspring[1]);}void mutation(Individual* individual) {// 变异操作,以一定概率翻转基因位上的值for (int i = 0; i < GENE_LENGTH; i++) {if (rand() / (double)RAND_MAX < MUTATION_RATE) {individual->genes[i] = individual->genes[i] == '0' ? '1' : '0'; }}individual->fitness = calculate_fitness(individual);}void replace(Individual* population, Individual* offspring) {// 替换操作,将两个子代个体中适应度更高的一个替换掉种群中适应度最低的一个个体int worst_index = -1;double worst_fitness = INFINITY;for (int i = 0; i < POPULATION_SIZE; i++) {if (population[i].fitness < worst_fitness) {worst_index = i;worst_fitness = population[i].fitness;}}if (offspring[0].fitness > worst_fitness || offspring[1].fitness > worst_fitness) {if (offspring[0].fitness > offspring[1].fitness) {population[worst_index] = offspring[0];} else {population[worst_index] = offspring[1];}}}。
一个简单实用地遗传算法c程序

一个简单实用的遗传算法c程序(转载)c++ 2009-07-28 23:09:03 阅读418 评论0 字号:大中小这是一个非常简单的遗传算法源代码,是由Denis Cormier (North Carolina State University)开发的,Sita S.Raghavan (University of North Carolina at Charlotte)修正。
代码保证尽可能少,实际上也不必查错。
对一特定的应用修正此代码,用户只需改变常数的定义并且定义“评价函数”即可。
注意代码的设计是求最大值,其中的目标函数只能取正值;且函数值和个体的适应值之间没有区别。
该系统使用比率选择、精华模型、单点杂交和均匀变异。
如果用Gaussian变异替换均匀变异,可能得到更好的效果。
代码没有任何图形,甚至也没有屏幕输出,主要是保证在平台之间的高可移植性。
读者可以从,目录 coe/evol中的文件prog.c中获得。
要求输入的文件应该命名为‘gadata.txt’;系统产生的输出文件为‘galog.txt’。
输入的文件由几行组成:数目对应于变量数。
且每一行提供次序——对应于变量的上下界。
如第一行为第一个变量提供上下界,第二行为第二个变量提供上下界,等等。
/************************************************************************** //* This is a simple genetic algorithm implementation where the *//* evaluation function takes positive values only and the *//* fitness of an individual is the same as the value of the *//* objective function *//************************************************************************** /#include <stdio.h>#include <stdlib.h>#include <math.h>/* Change any of these parameters to match your needs */#define POPSIZE 50 /* population size */#define MAXGENS 1000 /* max. number of generations */#define NVARS 3 /* no. of problem variables */#define PXOVER 0.8 /* probability of crossover */#define PMUTATION 0.15 /* probability of mutation */#define TRUE 1#define FALSE 0int generation; /* current generation no. */int cur_best; /* best individual */FILE *galog; /* an output file */struct genotype /* genotype (GT), a member of the population */{double gene[NVARS]; /* a string of variables一个变量字符串 */ double fitness; /* GT's fitness适应度 */double upper[NVARS]; /* GT's variables upper bound 变量的上限*/ double lower[NVARS]; /* GT's variables lower bound变量的下限 */ double rfitness; /* relative fitness 相对适应度*/double cfitness; /* cumulative fitness 累计适应度*/};struct genotype population[POPSIZE+1]; /* population */struct genotype newpopulation[POPSIZE+1]; /* new population; */ /* replaces the *//* old generation *//* Declaration of procedures used by this genetic algorithm */ void initialize(void);double randval(double, double);void evaluate(void);void keep_the_best(void);void elitist(void);void select(void);void crossover(void);void Xover(int,int);void swap(double *, double *);void mutate(void);void report(void);/***************************************************************/ /* Initialization function: Initializes the values of genes */ /* within the variables bounds. It also initializes (to zero) */ /* all fitness values for each member of the population. It */ /* reads upper and lower bounds of each variable from the *//* input file `gadata.txt'. It randomly generates values */ /* between these bounds for each gene of each genotype in the */ /* population. The format of the input file `gadata.txt' is */ /* var1_lower_bound var1_upper bound */ /* var2_lower_bound var2_upper bound ... */ /***************************************************************/ void initialize(void){FILE *infile;int i, j;double lbound, ubound;if ((infile = fopen("gadata.txt","r"))==NULL){fprintf(galog,"\nCannot open input file!\n");exit(1);}/* initialize variables within the bounds */for (i = 0; i < NVARS; i++){fscanf(infile, "%lf",&lbound);fscanf(infile, "%lf",&ubound);for (j = 0; j < POPSIZE; j++){population[j].fitness = 0;population[j].rfitness = 0;population[j].cfitness = 0;population[j].lower[i] = lbound;population[j].upper[i]= ubound;population[j].gene[i] = randval(population[j].lower[i], population[j].upper[i]);}}fclose(infile);}/***********************************************************//* Random value generator: Generates a value within bounds *//***********************************************************/ double randval(double low, double high){double val;val = ((double)(rand()%1000)/1000.0)*(high - low) + low;return(val);}/*************************************************************/ /* Evaluation function: This takes a user defined function. */ /* Each time this is changed, the code has to be recompiled. */ /* The current function is: x[1]^2-x[1]*x[2]+x[3] */ /*************************************************************/ void evaluate(void){int mem;int i;double x[NVARS+1];for (mem = 0; mem < POPSIZE; mem++){for (i = 0; i < NVARS; i++)x[i+1] = population[mem].gene[i];population[mem].fitness = (x[1]*x[1]) - (x[1]*x[2]) + x[3]; }}/***************************************************************/ /* Keep_the_best function: This function keeps track of the *//* best member of the population. Note that the last entry in *//* the array Population holds a copy of the best individual *//***************************************************************/ void keep_the_best(){int mem;int i;cur_best = 0; /* stores the index of the best individual */for (mem = 0; mem < POPSIZE; mem++){if (population[mem].fitness > population[POPSIZE].fitness){cur_best = mem;population[POPSIZE].fitness = population[mem].fitness;}}/* once the best member in the population is found, copy the genes */ for (i = 0; i < NVARS; i++)population[POPSIZE].gene[i] = population[cur_best].gene[i];}/****************************************************************//* Elitist function: The best member of the previous generation */ /* is stored as the last in the array. If the best member of */ /* the current generation is worse then the best member of the */ /* previous generation, the latter one would replace the worst */ /* member of the current population */ /****************************************************************/ void elitist(){int i;double best, worst; /* best and worst fitness values */ int best_mem, worst_mem; /* indexes of the best and worst member */ best = population[0].fitness;worst = population[0].fitness;for (i = 0; i < POPSIZE - 1; ++i){if(population[i].fitness > population[i+1].fitness){if (population[i].fitness >= best){best = population[i].fitness;best_mem = i;}if (population[i+1].fitness <= worst) {worst = population[i+1].fitness; worst_mem = i + 1;}}else{if (population[i].fitness <= worst){worst = population[i].fitness; worst_mem = i;}if (population[i+1].fitness >= best) {best = population[i+1].fitness; best_mem = i + 1;}}}/* if best individual from the new population is better than *//* the best individual from the previous population, then *//* copy the best from the new population; else replace the *//* worst individual from the current population with the *//* best one from the previous generation */if (best >= population[POPSIZE].fitness){for (i = 0; i < NVARS; i++)population[POPSIZE].gene[i] = population[best_mem].gene[i]; population[POPSIZE].fitness = population[best_mem].fitness;}else{for (i = 0; i < NVARS; i++)population[worst_mem].gene[i] = population[POPSIZE].gene[i]; population[worst_mem].fitness = population[POPSIZE].fitness;}}/**************************************************************//* Selection function: Standard proportional selection for *//* maximization problems incorporating elitist model - makes *//* sure that the best member survives */ /**************************************************************/ void select(void){int mem, i, j, k;double sum = 0;double p;/* find total fitness of the population */for (mem = 0; mem < POPSIZE; mem++){sum += population[mem].fitness;}/* calculate relative fitness */for (mem = 0; mem < POPSIZE; mem++){population[mem].rfitness = population[mem].fitness/sum; }population[0].cfitness = population[0].rfitness;/* calculate cumulative fitness */for (mem = 1; mem < POPSIZE; mem++){population[mem].cfitness = population[mem-1].cfitness + population[mem].rfitness;}/* finally select survivors using cumulative fitness. */for (i = 0; i < POPSIZE; i++){p = rand()%1000/1000.0;if (p < population[0].cfitness)newpopulation[i] = population[0];else{for (j = 0; j < POPSIZE;j++)if (p >= population[j].cfitness &&p<population[j+1].cfitness)newpopulation[i] = population[j+1];}}/* once a new population is created, copy it back */for (i = 0; i < POPSIZE; i++)population[i] = newpopulation[i];}/***************************************************************/ /* Crossover selection: selects two parents that take part in */ /* the crossover. Implements a single point crossover */ /***************************************************************/ void crossover(void){int i, mem, one;int first = 0; /* count of the number of members chosen */ double x;for (mem = 0; mem < POPSIZE; ++mem){x = rand()%1000/1000.0;if (x < PXOVER){++first;if (first % 2 == 0)Xover(one, mem);elseone = mem;}}}/**************************************************************/ /* Crossover: performs crossover of the two selected parents. */ /**************************************************************/ void Xover(int one, int two){int i;int point; /* crossover point *//* select crossover point */if(NVARS > 1){if(NVARS == 2)point = 1;elsepoint = (rand() % (NVARS - 1)) + 1;for (i = 0; i < point; i++)swap(&population[one].gene[i], &population[two].gene[i]); }}/*************************************************************/ /* Swap: A swap procedure that helps in swapping 2 variables *//*************************************************************/ void swap(double *x, double *y){double temp;temp = *x;*x = *y;*y = temp;}/**************************************************************/ /* Mutation: Random uniform mutation. A variable selected for */ /* mutation is replaced by a random value between lower and */ /* upper bounds of this variable */ /**************************************************************/ void mutate(void){int i, j;double lbound, hbound;double x;for (i = 0; i < POPSIZE; i++)for (j = 0; j < NVARS; j++){x = rand()%1000/1000.0;if (x < PMUTATION){/* find the bounds on the variable to be mutated */ lbound = population[i].lower[j];hbound = population[i].upper[j];population[i].gene[j] = randval(lbound, hbound);}}}/***************************************************************//* Report function: Reports progress of the simulation. Data *//* dumped into the output file are separated by commas *//***************************************************************/void report(void){int i;double best_val; /* best population fitness */double avg; /* avg population fitness */double stddev; /* std. deviation of population fitness */ double sum_square; /* sum of square for std. calc */double square_sum; /* square of sum for std. calc */ double sum; /* total population fitness */sum = 0.0;sum_square = 0.0;for (i = 0; i < POPSIZE; i++){sum += population[i].fitness;sum_square += population[i].fitness * population[i].fitness; }avg = sum/(double)POPSIZE;square_sum = avg * avg * POPSIZE;stddev = sqrt((sum_square - square_sum)/(POPSIZE - 1));best_val = population[POPSIZE].fitness;fprintf(galog, "\n%5d, %6.3f, %6.3f, %6.3f \n\n", generation, best_val, avg, stddev);}/**************************************************************/ /* Main function: Each generation involves selecting the best */ /* members, performing crossover & mutation and then */ /* evaluating the resulting population, until the terminating */ /* condition is satisfied *//**************************************************************/ void main(void){int i;if ((galog = fopen("galog.txt","w"))==NULL){exit(1);}generation = 0;fprintf(galog, "\n generation best average standard \n"); fprintf(galog, " number value fitness deviation \n"); initialize();evaluate();keep_the_best();while(generation<MAXGENS){generation++;select();crossover();mutate();report();evaluate();elitist();}fprintf(galog,"\n\n Simulation completed\n");fprintf(galog,"\n Best member: \n");for (i = 0; i < NVARS; i++){fprintf (galog,"\n var(%d) = %3.3f",i,population[POPSIZE].gene[i]);}fprintf(galog,"\n\n Best fitness = %3.3f",population[POPSIZE].fitness);fclose(galog);printf("Success\n");}/***************************************************************/链接库文件?这个简单一般的第三方库文件有2种提供方式 1.lib静态库,这样必须在工程设置里面添加。
3-遗传算法的基本实现技术-第2章

措施之二是采用罚函数方法。该方法的基本思想是对个体违背约束条 件的情况给予惩罚,并将此惩罚体现在适应度函数中,这样一个约束 优化问题就可转换为一个附带考虑惩罚的非约束优化问题。
该方法的基本思想是:各个个体的被选中的概率与其适应度大小成 正比。设群体规模为M,个体i的适应度为Fi,则i个体被选中的概率
Pis为:
Pis
Fi
M
i 1, 2, , M
Fi
i 1
显然,概率反映了个体的适应度在整个群体的个体适应度总和中所占 的比例,个体适应度越大,其被选择的概率就越高,反之亦然。
图2—4a 线性尺度变换的异常情况
2.3.3 适应度函数的设计对遗传算法的影响
1、适应度函数影响遗传算法的迭代停止条件 迭代中若发现群体中个体的进化已趋于稳定状态,换言之,若发现
占群体一定比例的个体已完全是同一个体,则终止算法迭代。 2、适应度函数与约束条件
由于许多优化问题都带约束条件,而遗传算法仅靠适应度来评估和 引导搜索,求解问题所固有的约束条件不能明确地表示出来,因而用 遗传算法求解此类问题要采取一些措施。
在不具有关于问题解空间先验知识的情况下,很难判定 最有效解的群体数量及其在可行解空间中的分布状况。因此, 我们通常在问题解空间均匀采样,随机生成一定数目的个体构 成初始群体。
2.3 适应度函数
在遗传算法中,用适应度来评估个体或解的优劣,并将 评估适应度的函数称为适应度的函数。适应度的函数值较高的 个体遗传到下一代的概率较大,反之较小。
遗传算法C语言代码

遗传算法C语言代码遗传算法C语言代码遗传算法C语言代码// GA.cpp : Defines the entry point for the console application.///*这是一个非常简单的遗传算法源代码,是由Denis Cormier (North Carolina State University)开发的,Sita S.Raghavan (University of North Carolina at Charlotte)修正。
代码保证尽可能少,实际上也不必查错。
对一特定的应用修正此代码,用户只需改变常数的定义并且定义“评价函数”即可。
注意代码的设计是求最大值,其中的目标函数只能取正值;且函数值和个体的适应值之间没有区别。
该系统使用比率选择、精华模型、单点杂交和均匀变异。
如果用 Gaussian变异替换均匀变异,可能得到更好的效果。
代码没有任何图形,甚至也没有屏幕输出,主要是保证在平台之间的高可移植性。
读者可以从, 目录 coe/evol中的文件prog.c中获得。
要求输入的文件应该命名为‘gadata.txt’;系统产生的输出文件为‘galog.txt’。
输入的文件由几行组成:数目对应于变量数。
且每一行提供次序——对应于变量的上下界。
如第一行为第一个变量提供上下界,第二行为第二个变量提供上下界,等等。
*/#include <stdio.h>#include <stdlib.h>#include <math.h>/* Change any of these parameters to match your needs *///请根据你的需要来修改以下参数#define POPSIZE 50 /* population size 种群大小*/#define MAXGENS 1000 /* max. number of generations 最大基因个数*/const int NVARS = 3; /* no. of problem variables 问题变量的个数*/#define PXOVER 0.8 /* probability of crossover 杂交概率*/#define PMUTATION 0.15 /* probability of mutation 变异概率*/#define TRUE 1#define FALSE 0int generation; /* current generation no. 当前基因个数*/int cur_best; /* best individual 最优个体*/FILE *galog; /* an output file 输出文件指针*/struct genotype /* genotype (GT), a member of the population 种群的一个基因的结构体类型*/{double gene[NVARS]; /* a string of variables 变量*/double fitness; /* GT's fitness 基因的适应度*/double upper[NVARS]; /* GT's variables upper bound 基因变量的上界*/double lower[NVARS]; /* GT's variables lower bound 基因变量的下界*/double rfitness; /* relative fitness 比较适应度*/double cfitness; /* cumulative fitness 积累适应度*/};struct genotype population[POPSIZE+1]; /* population 种群*/struct genotype newpopulation[POPSIZE+1]; /* new population; 新种群*//* replaces the old generation *///取代旧的基因/* Declaration of procedures used by this genetic algorithm *///以下是一些函数声明void initialize(void);double randval(double, double);void evaluate(void);void keep_the_best(void);void elitist(void);void select(void);void crossover(void);void Xover(int,int);void swap(double *, double *);void mutate(void);void report(void);/**************************************** ***********************//* Initialization function: Initializes the values of genes *//* within the variables bounds. It also initializes (to zero) *//* all fitness values for each member of the population. It *//* reads upper and lower bounds of each variable from the *//* input file `gadata.txt'. It randomlygenerates values *//* between these bounds for each gene of each genotype in the *//* population. The format of the input file `gadata.txt' is *//* var1_lower_bound var1_upper bound */ /* var2_lower_bound var2_upper bound ... */ /**************************************** ***********************/void initialize(void){FILE *infile;int i, j;double lbound, ubound;if ((infile = fopen("gadata.txt","r"))==NULL){fprintf(galog,"\nCannot open input file!\n");exit(1);}/* initialize variables within the bounds *///把输入文件的变量界限输入到基因结构体中for (i = 0; i < NVARS; i++){fscanf(infile, "%lf",&lbound);fscanf(infile, "%lf",&ubound);for (j = 0; j < POPSIZE; j++){population[j].fitness = 0;population[j].rfitness = 0;population[j].cfitness = 0;population[j].lower[i] = lbound;population[j].upper[i]= ubound;population[j].gene[i] = randval(population[j].lower[i],population[j].upper[i]);}}fclose(infile);}/**************************************** *******************//* Random value generator: Generates a value within bounds *//**************************************** *******************///随机数产生函数double randval(double low, double high) {double val;val = ((double)(rand()%1000)/1000.0)*(high - low) + low;return(val);}/*************************************************************//* Evaluation function: This takes a user defined function. *//* Each time this is changed, the code has to be recompiled. *//* The current function is: x[1]^2-x[1]*x[2]+x[3] *//**************************************** *********************///评价函数,可以由用户自定义,该函数取得每个基因的适应度void evaluate(void){int mem;int i;double x[NVARS+1];for (mem = 0; mem < POPSIZE; mem++){for (i = 0; i < NVARS; i++)x[i+1] = population[mem].gene[i];population[mem].fitness = (x[1]*x[1]) - (x[1]*x[2]) + x[3];}}/**************************************** ***********************//* Keep_the_best function: This function keeps track of the *//* best member of the population. Note that the last entry in *//* the array Population holds a copy of the best individual *//**************************************** ***********************///保存每次遗传后的最佳基因void keep_the_best(){int mem;int i;cur_best = 0;/* stores the index of the best individual*///保存最佳个体的索引for (mem = 0; mem < POPSIZE; mem++){if (population[mem].fitness > population[POPSIZE].fitness){cur_best = mem;population[POPSIZE].fitness = population[mem].fitness;}}/* once the best member in the population is found, copy the genes *///一旦找到种群的最佳个体,就拷贝他的基因for (i = 0; i < NVARS; i++)population[POPSIZE].gene[i] = population[cur_best].gene[i];}/**************************************** ************************//* Elitist function: The best member of the previous generation *//* is stored as the last in the array. If the best member of *//* the current generation is worse then the best member of the *//* previous generation, the latter one would replace the worst *//* member of the current population *//**************************************** ************************///搜寻杰出个体函数:找出最好和最坏的个体。
遗传算法示例

实验一、过河问题一、问题描述有三个牧师和三个野人过河,只有一条能装下两个人的船,在河的任何一方或者船上,如果野人的人数大于牧师的认输,那么牧师就会有危险.找出一种按的渡河方法。
将该问题转变为:假如有n个牧师和n个野人准备渡河,但只有一条能容纳c个人的小船,为了防止野人侵犯牧师,要求无论在何处,牧师的人数不得少于野人的人数(除非牧师人数为0),且假定两种人都会划船,试设计一个算法,确定它们能否渡过河去,若能,则给出一只小船来回次数最少的最佳方案。
二、基本要求输入:牧师人数(即野人人数)n,小船一次至多载客人数c。
输出:若问题无解,则显示“渡河失败”信息,否则,输出一组最佳方案,用三组(X1,X2,X3)表示渡河过程中的状态。
并用箭头输出这些状态之间的迁移:目的状态<- <-中间状态<- <-初始状态。
例:当n=2,c=2时,输出000<-021<-211<-110<-221上述(X1,X1,X2)表示渡河过程中各个状态。
其中:X1表示始岸上牧师人数,X2表示始岸上野人人数,X3表示小船位置,(0-在目的岸,1-在起始岸)三、算法描述(1)算法基本思想的文字描述;从初始状态S(n,n,1)出发,形成的有合法且未达状态S11、S12、……、Sli。
再分别从S11、S12、……、Sli出发形成所有合法而未达状态S111、S112、……、Sli1、Sli2、Sli ……最终达到目标(0,0,0)(有解),或者找不到合法而未达状态(无解)。
若有解,则从目标返回找前趋状态,前趋状态的前趋状态……直到初始状态。
(2)判别(X1,X2,X3)为合法状态条件:X1=0或X1=n或X1=X2。
(3)数据结构:1 栈STACK ,记下“已达”状态及踪迹,并兼作队列。
2 STATE[X1][X2]=(4)算法基本思想的具体实现:1 初始化:置STATE[N+1][N+1][2]中的有状态为“未达”置队列STACK 空,cond 为当前是否已达到目标: cond= cond 置初值 2 以S (n,n,1)为始点,置STATE 为“已达”。
遗传算法代码汇总

% 求下列函数的最小值%% y=20+x(1).^2+x(2).^2-10*(cos(2*pi.*x(1))+cos(2*pi.*x(2))) %%思路:可以转化为y=10+x.^2-10*cos(2*pi.*x),循环两次,求y值和。
%% 将x 的值用一个14位的二值形式表示为二值问题,一个14位的二值数提供的分辨率是每为(10-0)/(2^14-1)≈0.001 。
%% 将变量域[-5,5] 离散化为二值域[0,16383], x=0+10*b/16383, 其中 b 是[0, 16383] 中的一个二值数。
%% %%--------------------------------------------------------------------------------------------------------------%%--------------------------------------------------------------------------------------------------------------%% 编程%-----------------------------------------------% 2.1初始化(编码)% initpop.m函数的功能是实现群体的初始化,popsize表示群体的大小,chromlength表示染色体的长度(二值数的长度),% 长度大小取决于变量的二进制编码的长度(在本例中取10位)。
%遗传算法子程序%Name: initpop.m%初始化function pop=initpop(popsize,chromlength)pop=round(rand(popsize,chromlength)); % rand随机产生每个单元为{0,1} 行数为popsize,列数为chromlength的矩阵,% roud对矩阵的每个单元进行圆整。
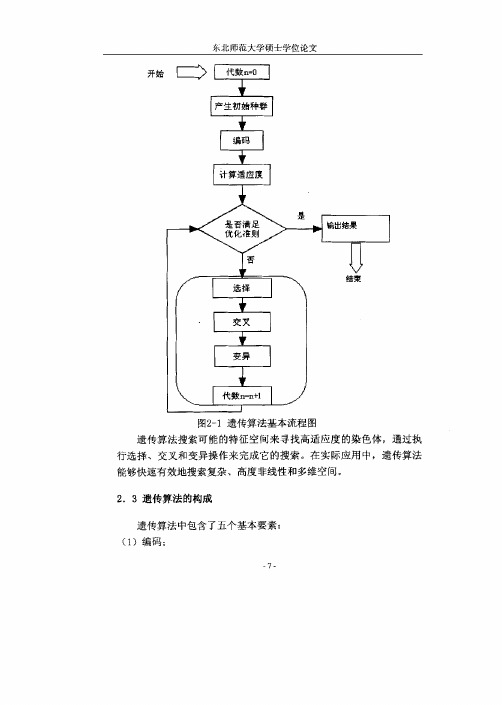
1遗传算法基本流程图
产 ( H) : 表示 在t 代种群中 存在模式x 的 个 体数目 ;
4 .遗传操作
选择 ( s e l e c t i o n )、交叉 ( c r o s s o v e r )和变异 ( m u t a t i o n )是
遗传算法中的三种基本遗传操作。下面分别加以 介绍。 1 ) 选择操作
东北师范大学硕士学位论文
选择 ( s e l e c t i o n ) ,根据染色体对应的适应度值和问题的要求, 筛选种群中的染色体,染色体的适应度越高,保存下来的概率越大, 反之则越小,甚至被淘汰。选择操作通常选用适应度比例法 ( 轮盘赌 方式) ,它是以适应度的大小为比例进行遗传过程中的父体选择,适应 度越高的个体被选中的机率就越大。也就是处于优势的个体有更多的 繁衍机会。具体做法是:首先计算群体中各个体的适应度,得相应的
东北师范大学硕士学位论文
图2 - 1遗传算法基本流程图 遗传算法搜索可能的特征空间来寻找高适应度的染色体,通过执 行选择、交叉和变异操作来完成它的搜索。在实际应用中,遗传算法 能够快速有效地搜索复杂、高度非线性和多维空间。 2 .3遗传算法的构成 遗传算法中包含了五个基本要素: ( 1 ) 编码;
. 是否到了预定算法的最大代数;
东北师范大学硕士学位论文
是否找到某个较优的染色体; 连续几次迭代后得到的解群中最好解是否变化等。
:
2 .4遗传算法的基本理论 遗传算法作为一种复杂问题的智能算法,它的理论基础是— 模 式定理和积木假说。
2 . 4 . 1模式定理
定义 1( 模式) :基于三值字符集{ 0 . 1 ,* }所产生的能描述具有某 些结构相似的 0 . 1 字符串集的字符串称作模式。 定义 2( 模式阶) :模式 H中确定位置的个数称作该模式的模式阶
《基本遗传算法》

(2) 解码
假设某一个体的编码是:
x: bl bl-1 bl-2……b2b1
则对应的解码公式为:
x = umin + (
1
i=l
bi
·2i-1
)
·Umax umin 2l 1
整理ppt
[例] 设 -3.0 ≤ x ≤ 12.1 , 精度要求 =1/10000,由公式: = Umax umin
M——群体大小; F——个体适应度评价函数; s——选择操作算于; c——交叉操作算子: m——变异操作算于; pc——交叉概率; pm——变异概率;
整理ppt
1.3 基本遗传算法描述
Procedure GA
Begin initialize P(0); t=0; while (t<=T) do for i=1 to M do Evaluate fitness of P(t); end for for i=1 to M do Select operation to P(t); end for for i=1 to M/2 do Crossover operation to P(t); end for for i=1 to M do Mutation operation to P(t); end for for i=1 to M do P(t+1) = P(t); end for t=t+1 end while
从而产生出一个新的个体。
基本位变异运算的示例如下所示:
基本位变异
A:1010 1 01010
A’:1010 0 01010
变异点
整理ppt
变异概率
变异是针对个体的某一个或某一些基因座上的基因值执行的,因此变异概率pm 也是针对基因而言,即:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
/********************************************************** ********/
/* 基于基本遗传算法的函数最优化SGA.C */
/* A Function Optimizer using Simple Genetic Algorithm */
/* developed from the Pascal SGA code presented by David E.Goldberg */
//********************************************************** ********/
#include
#include
#include
#include "graph.c"
/* 全局变量*/
struct individual /* 个体*/
{
unsigned *chrom; /* 染色体*/
double fitness; /* 个体适应度*/
double varible; /* 个体对应的变量值*/
int xsite; /* 交叉位置*/
int parent[2]; /* 父个体*/
int *utility; /* 特定数据指针变量*/
};
struct bestever /* 最佳个体*/
{
unsigned *chrom; /* 最佳个体染色体*/
double fitness; /* 最佳个体适应度*/
double varible; /* 最佳个体对应的变量值*/
int generation; /* 最佳个体生成代*/
};
struct individual *oldpop; /* 当前代种群*/ struct individual *newpop; /* 新一代种群*/ struct bestever bestfit; /* 最佳个体*/
double sumfitness; /* 种群中个体适应度累计*/ double max; /* 种群中个体最大适应度*/ double avg; /* 种群中个体平均适应度*/ double min; /* 种群中个体最小适应度*/
float pcross; /* 交叉概率*/
float pmutation; /* 变异概率*/
int popsize; /* 种群大小*/
int lchrom; /* 染色体长度*/
int chromsize; /* 存储一染色体所需字节数*/ int gen; /* 当前世代数*/
int maxgen; /* 最大世代数*/
int run; /* 当前运行次数*/
int maxruns; /* 总运行次数*/
int printstrings; /* 输出染色体编码的判断,0 -- 不输出, 1 -- 输出*/ int nmutation; /* 当前代变异发生次数*/
int ncross; /* 当前代交叉发生次数*/
/* 随机数发生器使用的静态变量*/
static double oldrand[55];
static int jrand;
static double rndx2;
static int rndcalcflag;
/* 输出文件指针*/
FILE *outfp ;
/* 函数定义*/
void advance_random();
int flip(float);rnd(int, int);
void randomize();
double randomnormaldeviate();
float randomperc(),rndreal(float,float);
void warmup_random(float);
void initialize(),initdata(),initpop();
void initreport(),generation(),initmalloc();
void freeall(),nomemory(char *),report();
void writepop(),writechrom(unsigned *);
void preselect();
void statistics(struct individual *);
void title(),repchar (FILE *,char *,int);
void skip(FILE *,int);
int select();
void objfunc(struct individual *);
int crossover (unsigned *, unsigned *, unsigned *, unsigned *); void mutation(unsigned *);
void initialize() /* 遗传算法初始化*/
{
/* 键盘输入遗传算法参数*/
initdata();
/* 确定染色体的字节长度*/
chromsize = (lchrom/(8*sizeof(unsigned)));
if(lchrom%(8*sizeof(unsigned))) chromsize++;
/*分配给全局数据结构空间*/
initmalloc();
/* 初始化随机数发生器*/
randomize();。
