遗传算法+投影寻踪程序代码
python遗传算法代码

python遗传算法代码遗传算法是一种基于生物进化原理的优化算法,适用于解决复杂问题。
在Python中,可以使用遗传算法库DEAP (Distributed Evolutionary Algorithms in Python)来实现遗传算法。
DEAP是一个灵活且易于使用的遗传算法框架,提供了用于定义和执行遗传算法的工具。
下面介绍如何使用DEAP库来实现一个简单的遗传算法。
首先,需要安装DEAP库。
可以使用以下命令来安装:```pip install deap```接下来,我们开始编写遗传算法的代码示例。
下面是一个寻找函数f(x)的最小值的例子:```pythonimport randomfrom deap import base, creator, tools# 定义目标函数def f(x):return x**2 + 4*x + 4# 创建遗传算法的环境creator.create("FitnessMin", base.Fitness, weights=(-1.0,)) creator.create("Individual", list, fitness=creator.FitnessMin)# 初始化遗传算法的参数toolbox = base.Toolbox()toolbox.register("attr_float", random.uniform, -10, 10) toolbox.register("individual", tools.initRepeat, creator.Individual, toolbox.attr_float, n=1)toolbox.register("population", tools.initRepeat, list,toolbox.individual)# 定义评估函数def evaluate(individual):x = individual[0]return f(x),# 定义遗传算法的操作toolbox.register("evaluate", evaluate)toolbox.register("select", tools.selTournament, tournsize=3) toolbox.register("mate", tools.cxTwoPoint)toolbox.register("mutate", tools.mutGaussian, mu=0, sigma=1, indpb=0.1)# 设置遗传算法的参数population_size = 100n_generations = 100cxpb = 0.5mutpb = 0.2# 创建初始种群population = toolbox.population(n=population_size)# 进化for generation in range(n_generations):offspring = toolbox.select(population, len(population))offspring = [toolbox.clone(ind) for ind in offspring]for child1, child2 in zip(offspring[::2], offspring[1::2]):if random.random() < cxpb:toolbox.mate(child1, child2)del child1.fitness.valuesdel child2.fitness.valuesfor mutant in offspring:if random.random() < mutpb:toolbox.mutate(mutant)del mutant.fitness.valuesinvalid_ind = [ind for ind in offspring if not ind.fitness.valid] fitnesses = toolbox.map(toolbox.evaluate, invalid_ind)for ind, fit in zip(invalid_ind, fitnesses):ind.fitness.values = fitpopulation[:] = offspring# 输出最优解best_individual = tools.selBest(population, k=1)[0]best_fitness = evaluate(best_individual)[0]print("Best individual:", best_individual)print("Best fitness:", best_fitness)```在上面的代码中,首先定义了目标函数f(x),然后创建了遗传算法的环境,包括创建适应度函数和个体类,以及注册遗传算法的操作。
遗传算法代码python

遗传算法代码python一、简介遗传算法是一种通过模拟自然选择和遗传学原理来寻找最优解的优化算法。
它广泛应用于各种领域,包括优化问题、搜索和机器学习等。
二、代码概述以下是一个简单的遗传算法的Python代码示例,用于解决简单的优化问题。
该算法使用一个简单的二进制编码方式,并使用适应度函数来评估每个个体的适应度。
三、代码实现```pythonimportnumpyasnp#遗传算法参数POPULATION_SIZE=100#种群规模CROSSOVER_RATE=0.8#交叉概率MUTATION_RATE=0.1#变异概率MAX_GENERATIONS=100#最大迭代次数#适应度函数deffitness(individual):#在这里定义适应度函数,评估每个个体的适应度#这里简单地返回个体值的平方,可以根据实际问题进行调整returnnp.sum(individual**2)#初始种群生成pop=np.random.randint(2,size=(POPULATION_SIZE,))#迭代过程forgenerationinrange(MAX_GENERATIONS):#评估种群中每个个体的适应度fitness_values=np.apply_along_axis(fitness,1,pop)#选择种群selected_idx=np.random.choice(np.arange(POPULATION_SIZE), size=POPULATION_SIZE,replace=True,p=fitness_values/fitness_va lues.sum())selected_pop=pop[selected_idx]#交叉操作ifCROSSOVER_RATE>np.random.rand():cross_points=np.random.rand(POPULATION_SIZE,2)<0.5#随机选择交叉点cross_pop=np.array([np.hstack((individual[cross_points[i, 0]:cross_points[i,1]]+individual[cross_points[i,1]:],other))f ori,otherinenumerate(selected_pop)]).T#合并个体并随机交叉得到新的个体cross_pop=cross_pop[cross_points]#将交叉后的个体重新排列成原始种群大小selected_pop=np.vstack((selected_pop,cross_pop))#将新个体加入种群中#变异操作ifMUTATION_RATE>np.random.rand():mutated_pop=selected_pop+np.random.randn(POPULATION_SIZE, 1)*np.sqrt(np.log(POPULATION_SIZE))*(selected_pop!=pop).astyp e(np.float)#根据变异概率对个体进行变异操作,得到新的个体种群mutated_pop=mutated_pop[mutated_pop!=0]#将二进制种群中值为0的个体去掉,因为这些个体是随机的二进制串,不是解的一部分,不应该参与变异操作selected_pop=mutated_pop[:POPULATION_SIZE]#将新种群中除最后一个以外的部分加入原始种群中(即新的种群被排除了适应度最差的个体)#选择当前最好的个体(用于更新最优解)best_idx=np.argmax(fitness_values)best_solution=selected_pop[best_idx]print(f"Generation{generation}:Bestsolution:{best_solutio n}")```四、使用示例假设要解决一个简单的优化问题:求一个一维函数的最小值。
基于加速遗传算法的投影寻踪模型代码

基于加速遗传算法的投影寻踪模型代码一些常用的遗传算法代码模板供您参考:```import random# 遗传算法参数POPULATION_SIZE = 100GENERATIONS = 50MUTATION_RATE = 0.1CROSSOVER_RATE = 0.8ELITE_SIZE = 2# 个体编码示例def create_individual():individual = []# TODO: 根据具体问题设计个体编码return individual# 适应度函数示例,fitness越小越好,用于最小化问题def fitness(individual):# TODO: 根据具体问题实现适应度函数return 0# 选择操作示例def selection(population):# TODO: 实现选择算法,返回选择的父代个体return parent1, parent2# 交叉操作示例def crossover(parent1, parent2):# TODO: 实现交叉算法,返回交叉后的子代个体return child1, child2# 变异操作示例def mutation(individual):# TODO: 实现变异算法,返回变异后的个体return mutant# 创建初始种群population = [create_individual() for _ in range(POPULATION_SIZE)]# 迭代遗传算法for generation in range(GENERATIONS):# 计算适应度fitness_list = [fitness(individual) for individual in population]# 选择最优个体elites = sorted(zip(population, fitness_list), key=lambda x: x[1])[:ELITE_SIZE]# 输出当前代数和最优个体适应度print("Generation:", generation, "Best fitness:", elites[0][1])# 选择新的父代个体parents = [selection(population) for _ in range(POPULATION_SIZE - ELITE_SIZE)]# 交叉并产生新的子代个体children = []for i in range(0, len(parents), 2):if random.random() < CROSSOVER_RATE:child1, child2 = crossover(parents[i], parents[i+1])else:child1, child2 = parents[i], parents[i+1]children.append(mutation(child1))children.append(mutation(child2))# 更新下一代种群population = [elite[0] for elite in elites] + children```需要根据具体问题进行个体编码、适应度函数、选择算法、交叉算法和变异算法的实现。
遗传算法matlab程序代码

遗传算法matlab程序代码
遗传算法(GA)是一种用于求解优化问题的算法,其主要思想是模拟
生物进化过程中的“选择、交叉、变异”操作,通过模拟这些操作,来寻
找最优解。
Matlab自带了GA算法工具箱,可以直接调用来实现遗传算法。
以下是遗传算法Matlab程序代码示例:
1.初始化
首先定义GA需要优化的目标函数f,以及GA算法的相关参数,如种
群大小、迭代次数、交叉概率、变异概率等,如下所示:
options = gaoptimset('PopulationSize',10,...
'Generations',50,...
2.运行遗传算法
运行GA算法时,需要调用MATLAB自带的ga函数,将目标函数、问
题的维度、上下界、约束条件和算法相关参数作为输入参数。
其中,上下
界和约束条件用于限制空间,防止到无效解。
代码如下:
[某,fval,reason,output,population] = ga(f,2,[],[],[],[],[-10,-10],[10,10],[],options);
3.结果分析
最后,将结果可视化并输出,可以使用Matlab的plot函数绘制出目
标函数的值随迭代次数的变化,如下所示:
plot(output.generations,output.bestf)
某label('Generation')
ylabel('Best function value')
总之,Matlab提供了方便易用的GA算法工具箱,开发者只需要根据具体问题定义好目标函数和相关参数,就能够在短时间内快速实现遗传算法。
遗传算法案例及源代码

计算智能作业三:遗传算法计算问题1.问题描述:求下述二元函数的最大值:222121),(m ax x x x x f +=S.t. }7,6,5,4,3,2,1{1∈x }7,6,5,4,3,2,1{2∈x2.程序结构:(1)变量:C :是一个1*6数组,每个数组里面是一个6位二进制数,它是遗传算法中的染色体。
new_c:每一轮的新变量c 。
first_c:初始群体矩阵。
sur_value :个体适应值的概率值,为0-1之间的数,所有概率值和为1。
survived :经过选择运算后产生的个体基因型组合。
intersect_c :经过交叉运算后产生的个体基因型组合。
mutation_c :经过变异运算后产生的个体基因型组合。
f :最后计算得到的最大值 (2)程序里面的方程function out = value_function( ci ):价值函数(自适应度函数),即222121),(x x x x f +=。
function [ sur_value ] = calc_value( c ):计算群体中每一个个体的适应度的值function survived = surviver( sur_value ):利用概率选择函数 function [ intersect_c ] = intersect( new_c ):交叉运算function [ mutation_c ,mutation_value] = mutation( intersect_c ):变异运算3.源程序(1)遗传算法的主程序主程序包括初始群体产生,最终结果展示,即各函数之间的调用关系。
个体编码遗传算法的运算对象是表示个体的符号串,所以必须把变量 x1, x2 编码为无符号二进制整数。
这个二进制整数位个体的基因型。
因为x1, x2 为 0 ~ 7之间的整数,所以分别用3位无符号二进制整数来表示,将它们连接在一起所组成的6位无符号二进制数就形成了个体的基因型,表示一个可行解。
(完整版)遗传算法c语言代码

srand((unsigned)time(NULL));
for(i=0;i<num;i++)
{
bianyip[i]=(rand()%100);
bianyip[i]/=100;
}
//确定可以变异的染色体
t=0;
for(i=0;i<num;i++)
{
if(bianyip[i]<pm)
printf("\n******************是否想再一次计算(y or n)***********************\n");
fflush(stdin);
scanf("%c",&choice);
}while(choice=='y');
return 0;
}
{
flag=0;
break;
}
}
if(flag)
{
group[i].city[j]=t;
j++;
}
}
}
printf("************初始种群如下****************\n");
for(i=0;i<num;i++)
{
for(j=0;j<cities;j++)
printf("%4d",group[i].city[j]);
{
group[i].p=1-(double)group[i].adapt/(double)biggestsum;
biggestp+=group[i].p;
遗传算法介绍并附上Matlab代码
1、遗传算法介绍遗传算法,模拟达尔文进化论的自然选择和遗产学机理的生物进化构成的计算模型,一种不断选择优良个体的算法。
谈到遗传,想想自然界动物遗传是怎么来的,自然主要过程包括染色体的选择,交叉,变异(不明白这个的可以去看看生物学),这些操作后,保证了以后的个基本上是最优的,那么以后再继续这样下去,就可以一直最优了。
2、解决的问题先说说自己要解决的问题吧,遗传算法很有名,自然能解决的问题很多了,在原理上不变的情况下,只要改变模型的应用环境和形式,基本上都可以。
但是遗传算法主要还是解决优化类问题,尤其是那种不能直接解出来的很复杂的问题,而实际情况通常也是这样的。
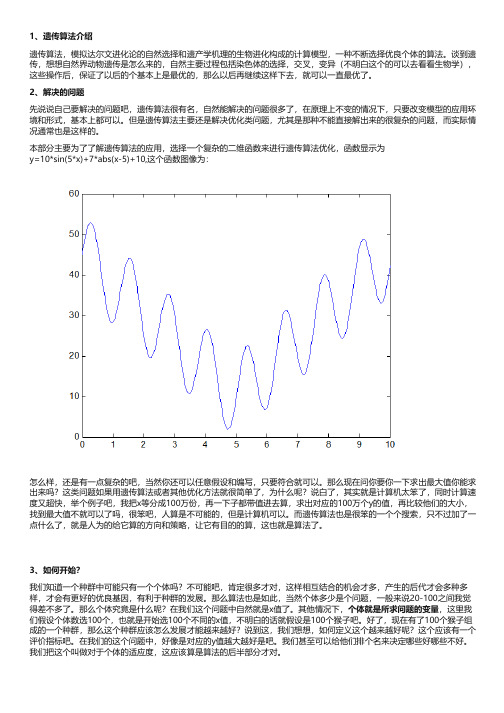
本部分主要为了了解遗传算法的应用,选择一个复杂的二维函数来进行遗传算法优化,函数显示为y=10*sin(5*x)+7*abs(x-5)+10,这个函数图像为:怎么样,还是有一点复杂的吧,当然你还可以任意假设和编写,只要符合就可以。
那么现在问你要你一下求出最大值你能求出来吗?这类问题如果用遗传算法或者其他优化方法就很简单了,为什么呢?说白了,其实就是计算机太笨了,同时计算速度又超快,举个例子吧,我把x等分成100万份,再一下子都带值进去算,求出对应的100万个y的值,再比较他们的大小,找到最大值不就可以了吗,很笨吧,人算是不可能的,但是计算机可以。
而遗传算法也是很笨的一个个搜索,只不过加了一点什么了,就是人为的给它算的方向和策略,让它有目的的算,这也就是算法了。
3、如何开始?我们知道一个种群中可能只有一个个体吗?不可能吧,肯定很多才对,这样相互结合的机会才多,产生的后代才会多种多样,才会有更好的优良基因,有利于种群的发展。
那么算法也是如此,当然个体多少是个问题,一般来说20-100之间我觉得差不多了。
那么个体究竟是什么呢?在我们这个问题中自然就是x值了。
其他情况下,个体就是所求问题的变量,这里我们假设个体数选100个,也就是开始选100个不同的x值,不明白的话就假设是100个猴子吧。
遗传算法投影寻踪模型matlab代码

遗传算法投影寻踪模型近年来,遗传算法在寻优问题中的应用越来越广泛,其中遗传算法投影寻踪模型在MATLAB代码中的实现备受关注。
本文将以此为主题,结合具体的内容,对遗传算法投影寻踪模型进行深入探讨。
一、遗传算法的原理1.1 遗传算法的基本概念遗传算法是一种基于生物进化过程的启发式优化技术,它模拟了自然选择和遗传机制,通过不断的迭代优化过程来寻找最优解。
遗传算法包括选择、交叉、变异等基本操作,其中选择过程通过适应度函数来评价个体的优劣,交叉过程通过染色体的交换来产生新的个体,变异过程通过基因的随机改变来增加种群的多样性。
1.2 遗传算法的应用领域遗传算法广泛应用于优化问题、机器学习、神经网络、信号处理、图像处理等领域,在工程、科学领域有着重要的应用价值。
二、投影寻踪模型的概念2.1 投影寻踪模型的基本原理投影寻踪模型是一种在信号处理领域中常用的算法,其基本原理是通过对信号进行投影变换来实现信号的降维和提取特征。
2.2 投影寻踪模型的应用投影寻踪模型在语音识别、图像处理、数据压缩等方面有着广泛的应用,是一种常见的信号处理技术。
三、MATLAB代码实现3.1 MATLAB环境准备在进行遗传算法投影寻踪模型的实现之前,首先需要在MATLAB环境中准备好相应的工具箱和设置参数。
3.2 遗传算法投影寻踪模型代码编写通过MATLAB的编程能力,可以实现遗传算法投影寻踪模型的代码编写,包括遗传算法的参数设置、适应度函数的定义、种群的初始化、交叉和变异操作的实现等步骤。
3.3 代码调试和优化在编写完整的遗传算法投影寻踪模型代码后,需要进行充分的调试和优化,确保代码的正确性和效率。
四、实验结果分析4.1 实验数据准备在进行实验结果分析之前,需要准备相应的实验数据集,以便进行测试和对比分析。
4.2 结果对比分析通过对遗传算法投影寻踪模型的实验结果进行对比分析,可以评估其算法性能和适用范围,与其他优化算法进行效果比较。
4.3 结果展示与解读最后需要将实验结果进行展示,并对结果进行解读和分析,从数学模型和应用角度分析遗传算法投影寻踪模型的优缺点和改进方向。
遗传算法java代码

遗传算法java代码遗传算法(Genetic Algorithm)是一种基于生物进化的启发式算法,通过模拟自然选择、交叉和突变等基因操作来优化问题的解。
以下是一个基于Java的遗传算法示例代码:```javaimport java.util.ArrayList;import java.util.List;import java.util.Random;//假设我们要求解的问题是求一个二进制序列的最大值,这个序列的长度为10public class GeneticAlgorithm//染色体长度private static final int CHROMOSOME_LENGTH = 10;//种群大小private static final int POPULATION_SIZE = 100;//迭代次数private static final int MAX_GENERATIONS = 100;//交叉概率private static final double CROSSOVER_RATE = 0.8;//变异概率private static final double MUTATION_RATE = 0.1; //随机数生成器private static final Random RANDOM = new Random(; //个体类private static class Individual//染色体private int[] chromosome;//适应度private double fitness;public Individuachromosome = new int[CHROMOSOME_LENGTH];fitness = 0.0;}//初始化染色体public void initializeChromosomfor (int i = 0; i < CHROMOSOME_LENGTH; i++) chromosome[i] = RANDOM.nextInt(2);}}//计算个体的适应度public void calculateFitnesint decimalValue = 0;for (int i = CHROMOSOME_LENGTH - 1; i >= 0; i--) decimalValue += chromosome[i] * Math.pow(2, CHROMOSOME_LENGTH - i - 1);}fitness = decimalValue;}//获取个体的适应度public double getFitnesreturn fitness;}//获取染色体public int[] getChromosomreturn chromosome;}//设置染色体public void setChromosome(int[] chromosome)this.chromosome = chromosome;}}//生成初始种群private static List<Individual> createInitialPopulatioList<Individual> population = new ArrayList<>(;for (int i = 0; i < POPULATION_SIZE; i++)Individual individual = new Individual(;individual.initializeChromosome(;population.add(individual);}return population;}//选择父母个体private static Individual selectParent(List<Individual> population)double sumFitness = 0.0;for (Individual individual : population)sumFitness += individual.getFitness(;}double randomFitness = RANDOM.nextDouble( * sumFitness;double cumulativeFitness = 0.0;for (Individual individual : population)cumulativeFitness += individual.getFitness(;if (cumulativeFitness > randomFitness)return individual;}}return population.get(0);}//交叉操作private static Individual crossover(Individual parent1, Individual parent2)Individual offspring = new Individual(;int[] parent1Chromosome = parent1.getChromosome(;int[] parent2Chromosome = parent2.getChromosome(;int crossoverPoint = RANDOM.nextInt(CHROMOSOME_LENGTH - 1) + 1;int[] offspringChromosome = new int[CHROMOSOME_LENGTH];System.arraycopy(parent1Chromosome, 0, offspringChromosome, 0, crossoverPoint);System.arraycopy(parent2Chromosome, crossoverPoint, offspringChromosome, crossoverPoint, CHROMOSOME_LENGTH - crossoverPoint);offspring.setChromosome(offspringChromosome);return offspring;}//变异操作private static void mutate(Individual individual)int[] chromosome = individual.getChromosome(;for (int i = 0; i < CHROMOSOME_LENGTH; i++)if (RANDOM.nextDouble( < MUTATION_RATE)chromosome[i] = chromosome[i] == 0 ? 1 : 0;}}individual.setChromosome(chromosome);}//遗传算法主函数public static void main(String[] args)List<Individual> population = createInitialPopulation(;for (int generation = 0; generation < MAX_GENERATIONS; generation++)for (Individual individual : population)individual.calculateFitness(;}Individual bestIndividual = population.get(0);for (Individual individual : population)if (individual.getFitness( > bestIndividual.getFitness() bestIndividual = individual;}}System.out.println("Generation: " + generation + " Best Individual: " + bestIndividual.getFitness();List<Individual> newPopulation = new ArrayList<>(;while (newPopulation.size( < POPULATION_SIZE)Individual parent1 = selectParent(population);Individual parent2 = selectParent(population);Individual offspring = crossover(parent1, parent2);mutate(offspring);newPopulation.add(offspring);}population = newPopulation;}}```以上示例代码实现了一个简单的二进制序列的最大化遗传算法。
python遗传算法代码

Python遗传算法代码概述遗传算法是一种用于解决优化问题的算法,它模拟了生物进化的过程,通过选择、交叉和变异等操作来逐步优化解的质量。
Python作为一种简单易学的编程语言,非常适合用于实现遗传算法。
在本文中,我们将介绍如何使用Python编写遗传算法的代码,并通过实例演示其应用。
具体而言,我们将通过一个二进制字符串的优化问题来讲解遗传算法的实现过程。
问题描述假设我们有一个由0和1组成的二进制字符串,长度为N。
我们的目标是找到一个最优的二进制字符串,使得其中1的个数最多。
算法思想遗传算法是基于自然进化的思想,模拟了物种进化的过程。
它通过选择、交叉和变异等操作来逐步优化解的质量。
具体而言,遗传算法包括以下几个关键步骤: 1. 初始化种群:随机生成一定数量的二进制字符串,作为初始种群。
2. 计算适应度:针对每个个体,计算其适应度值,即1的个数。
3. 选择操作:根据适应度值选取优秀的个体,用于产生下一代。
常用的选择策略有轮盘赌选择、锦标赛选择等。
4. 交叉操作:选取一对个体,按照一定的规则进行基因交叉,生成新个体。
常见的交叉方式有单点交叉、多点交叉等。
5. 变异操作:随机选取一个个体的某个基因位,进行基因突变,生成具有变异基因的个体。
6. 产生下一代:根据选择、交叉和变异的操作,生成下一代种群。
7. 重复执行:重复执行上述步骤,直到满足终止条件。
代码实现下面是使用Python编写的遗传算法代码:import random# 定义问题相关的参数N = 20 # 二进制串的长度POP_SIZE = 50 # 种群大小GENERATIONS = 100 # 迭代代数SELECT_RATE = 0.2 # 选择概率CROSS_RATE = 0.8 # 交叉概率MUTATE_RATE = 0.01 # 变异概率# 生成初始种群def generate_population(pop_size):return [random.choices([0, 1], k=N) for _ in range(pop_size)]# 计算个体的适应度def fitness(individual):return sum(individual)# 选择操作def select(population, select_rate):fitness_values = [fitness(individual) for individual in population]total_fitness = sum(fitness_values)probabilities = [fitness_value / total_fitness for fitness_value in fitnes s_values]selected_population = random.choices(population, probabilities, k=int(pop_ size * select_rate))return selected_population# 交叉操作def crossover(parent_a, parent_b):cross_point = random.randint(0, N-1)child_a = parent_a[:cross_point] + parent_b[cross_point:]child_b = parent_b[:cross_point] + parent_a[cross_point:]return child_a, child_b# 变异操作def mutate(individual, mutate_rate):mutated_individual = individual.copy()for i in range(N):if random.random() < mutate_rate:mutated_individual[i] = 1 - mutated_individual[i]return mutated_individual# 产生下一代种群def generate_next_population(population, select_rate, cross_rate, mutate_rate): selected_population = select(population, select_rate)next_population = selected_population.copy()while len(next_population) < len(population):parent_a = random.choice(selected_population)parent_b = random.choice(selected_population)if random.random() < cross_rate:child_a, child_b = crossover(parent_a, parent_b)else:child_a, child_b = parent_a, parent_bchild_a = mutate(child_a, mutate_rate)child_b = mutate(child_b, mutate_rate)next_population.append(child_a)next_population.append(child_b)return next_population# 主函数def main():population = generate_population(POP_SIZE)for generation in range(GENERATIONS):population = generate_next_population(population, SELECT_RATE, CROSS_R ATE, MUTATE_RATE)best_individual = max(population, key=fitness)print(f"Generation: {generation}, Best Individual: {best_individual}, Fitness: {fitness(best_individual)}")if __name__ == "__main__":main()实例演示假设我们将二进制串的长度设为20,种群大小为50,迭代代数为100,选择概率为0.2,交叉概率为0.8,变异概率为0.01。
遗传算法经典MATLAB代码

遗传算法经典MATLAB代码遗传算法经典学习matlab代码遗传算法实例:也就是自己请来的,原代码存有少许错误,本人都已更正了,调试运转都通过了的。
对于初学者,尤其就是还没编程经验的非常有价值的一个文件遗传算法实例%下面举例说明遗传算法%%求下列函数的最大值%%f(x)=10*sin(5x)+7*cos(4x)x∈[0,10]%%将x的值用一个10位的二值形式表示为二值问题,一个10位的二值数提供的分辨率是每为(10-0)/(2^10-1)≈0.01。
%%将变量域[0,10]线性化成二值域[0,1023],x=0+10*b/1023,其中b就是[0,1023]中的一个二值数。
%%%%--------------------------------------------------------------------------------------------------------------%%--------------------------------------------------------------------------------------------------------------%%编程%-----------------------------------------------%2.1初始化(编码)%initpop.m函数的功能就是同时实现群体的初始化,popsize则表示群体的大小,chromlength则表示染色体的长度(二值数的长度),%长度大小取决于变量的二进制编码的长度(在本例中取10位)。
%遗传算法子程序%name:initpop.m%初始化functionpop=initpop(popsize,chromlength)pop=round(rand(popsize,chromlength));%rand随机产生每个单元为{0,1}行数为popsize,列数为chromlength的矩阵,%roud对矩阵的每个单元进行圆整。
基于加速遗传算法的投影寻踪模型代码

基于加速遗传算法的投影寻踪模型代码以下是一个基于加速遗传算法的投影寻踪模型的代码示例:```pythonimport numpy as npdef fitness_function(x, y):#计算适应度函数#在此示例中,适应度函数计算点(x,y)到目标点的距离target_point = (5, 5)distance = np.sqrt((x - target_point[0])**2 + (y -target_point[1])**2)return 1 / (distance + 1)def selection(population, fitness_values, num_parents):#选择函数,选出适应度较高的个体作为父代parents = []for i in range(num_parents):max_index = np.argmax(fitness_values)parents.append(population[max_index])fitness_values[max_index] = -1 # 将已选个体的适应度设为负数,防止重复选择return parentsdef crossover(parents, num_offsprings):#交叉操作,生成新的子代个体offsprings = []for i in range(num_offsprings):parent1 = parents[i % len(parents)]parent2 = parents[(i+1) % len(parents)]offspring = (parent1[0], parent2[1])offsprings.append(offspring)return offspringsdef mutation(offsprings, mutation_rate):#变异操作for i in range(len(offsprings)):if np.random.uniform(0, 1) < mutation_rate:x = offsprings[i][0]y = offsprings[i][1]mutation_value = np.random.uniform(-1, 1) # 从[-1, 1]区间随机选择一个值来增加变异x += mutation_valuey += mutation_valueoffsprings[i] = (x, y)return offspringsdef genetic_algorithm(population, num_generations,num_parents, num_offsprings, mutation_rate):for generation in range(num_generations):fitness_values = []for i in range(len(population)):x = population[i][0]y = population[i][1]fitness = fitness_function(x, y)fitness_values.append(fitness)parents = selection(population, fitness_values, num_parents) offsprings = crossover(parents, num_offsprings)offsprings = mutation(offsprings, mutation_rate)population = parents + offspringsbest_solution_index = np.argmax(fitness_values)best_solution = population[best_solution_index]return best_solution#设置模型参数num_parents = 10num_offsprings = 100num_generations = 100mutation_rate = 0.1#生成初始种群population = []for _ in range(num_parents):x = np.random.uniform(0, 10)y = np.random.uniform(0, 10)population.append((x, y))#使用遗传算法找到最佳解best_solution = genetic_algorithm(population,num_generations, num_parents, num_offsprings, mutation_rate) print("最佳解:", best_solution)```这个代码示例实现了一个简单的投影寻踪模型,使用加速遗传算法来找到最佳解。
投影寻踪python

投影寻踪python投影寻踪是一种利用计算机视觉技术实现的目标跟踪方法。
在计算机视觉领域中,目标跟踪是指通过对视频序列中的目标进行连续观测和分析,以确定目标在不同帧中的位置和姿态变化。
投影寻踪是目标跟踪的一种常见方法,它通过将目标在图像平面上的投影与目标模型进行比较,从而实现目标的跟踪。
在使用Python进行投影寻踪时,我们可以借助一些开源的计算机视觉库,如OpenCV和Dlib等,来实现目标跟踪的功能。
首先,我们需要准备一段视频序列或者摄像头实时输入的视频流作为输入源。
接下来,我们需要选择一个合适的目标模型,可以是目标的外观特征,如颜色、纹理等,也可以是目标的形状特征,如轮廓、边缘等。
在实际应用中,我们可以使用OpenCV提供的函数来进行目标跟踪。
首先,我们需要对输入的视频序列进行初始化,即选择一个初始帧作为跟踪的起点。
然后,我们可以选择一种投影模型,如颜色直方图、灰度直方图等,将目标的模型投影到当前帧上。
通过计算投影的差异,我们可以得到目标在当前帧上的位置和姿态变化。
在进行目标跟踪时,我们还可以使用一些滤波算法来对跟踪结果进行优化,如卡尔曼滤波、粒子滤波等。
这些滤波算法可以帮助我们更准确地估计目标的位置和姿态,提高跟踪的精度和稳定性。
除了使用传统的投影寻踪方法,近年来,深度学习技术在目标跟踪中也取得了很大的进展。
通过使用卷积神经网络等深度学习模型,可以自动学习目标的外观特征和空间关系,从而实现更准确、更鲁棒的目标跟踪。
总结一下,投影寻踪是一种常见的目标跟踪方法,它通过将目标在图像平面上的投影与目标模型进行比较,实现目标的跟踪。
在Python中,我们可以借助开源计算机视觉库来实现目标跟踪的功能,通过选择合适的目标模型和使用滤波算法,可以提高跟踪的精度和稳定性。
另外,深度学习技术也为目标跟踪带来了新的突破,通过使用深度学习模型,可以实现更准确、更鲁棒的目标跟踪。
投影寻踪作为目标跟踪的一种方法,为计算机视觉领域的研究和应用提供了重要的技术支持。
多阶段生产计划问题的遗传算法代码

多阶段生产计划问题的遗传算法代码以下是一个使用遗传算法求解多阶段生产计划问题的示例代码:```pythonimport random# 定义问题参数NUM_STAGES = 3 # 阶段数NUM_TASKS = 5 # 每个阶段的任务数TIME_LIMIT = 20 # 时间限制# 随机生成任务时长task_durations = []for i in range(NUM_STAGES):stage_durations = [random.randint(1, 10) for j in range(NUM_TASKS)]task_durations.append(stage_durations)# 定义遗传算法参数POP_SIZE = 20 # 种群大小NUM_GEN = 50 # 迭代次数CROSS_RATE = 0.8 # 交叉率MUT_RATE = 0.1 # 变异率# 定义染色体编码方式(每个基因表示一个任务编号)chromosome_size = NUM_STAGES * NUM_TASKS# 初始化种群def initial_population(pop_size, chromo_size):population = []for i in range(pop_size):chromosome = [random.randint(1, NUM_TASKS) for j in range(chromo_size)] population.append(chromosome)return population# 计算染色体的适应度(代价函数为任务完成时间)def fitness(chromosome):# 将染色体解码成任务分配矩阵task_matrix = []for i in range(NUM_STAGES):stage_matrix = [chromosome[i*NUM_TASKS+j] for j in range(NUM_TASKS)] task_matrix.append(stage_matrix)# 初始化每个阶段任务的开始时间start_times = [[0] * NUM_TASKS for i in range(NUM_STAGES)]# 计算每个任务的完成时间for i in range(NUM_STAGES):for j in range(NUM_TASKS):task = task_matrix[i][j]prev_start = 0if j > 0:prev_task = task_matrix[i][j-1]prev_start = start_times[i][j-1] + task_durations[i][prev_task-1]start_times[i][j] = max(prev_start, start_times[i-1][task-1]) # max保证前驱任务全部执行完毕# 计算所有任务的完成时间end_times = []for i in range(NUM_STAGES):stage_end_times = [start_times[i][j]+task_durations[i][task_matrix[i][j]-1] for j in range(NUM_TASKS)]end_times.extend(stage_end_times)# 计算总时间total_time = max(end_times)# 返回适应度return TIME_LIMIT - total_time # 目标是使总时间尽量小# 选择算子(本例使用锦标赛选择)def selection(population, fitness_list):selected_pop = []for i in range(len(population)):competitors = random.sample(range(len(population)), 2)winner = max(competitors, key=lambda x: fitness_list[x])selected_pop.append(population[winner])return selected_pop# 交叉算子(本例使用单点交叉)def crossover(parent_1, parent_2):if random.random() < CROSS_RATE:cross_point = random.randint(1, chromosome_size-1)child_1 = parent_1[:cross_point] + parent_2[cross_point:]child_2 = parent_2[:cross_point] + parent_1[cross_point:]return child_1, child_2else:return parent_1, parent_2# 变异算子(本例使用随机重组变异)def mutation(chromosome):if random.random() < MUT_RATE:pos_1, pos_2 = random.sample(range(chromosome_size), 2)chromosome[pos_1], chromosome[pos_2] = chromosome[pos_2], chromosome[pos_1] return chromosome# 遗传算法主程序population = initial_population(POP_SIZE, chromosome_size)for i in range(NUM_GEN):# 计算种群的适应度fitness_list = [fitness(chromosome) for chromosome in population]# 输出当前最佳解best_chromosome = population[max(range(POP_SIZE), key=lambda x: fitness_list[x])]print("Generation {}: best fitness = {}".format(i, fitness(best_chromosome)))# 选择新种群new_population = selection(population, fitness_list)# 对种群进行交叉和变异for j in range(0, POP_SIZE, 2):parent_1 = new_population[j]parent_2 = new_population[j+1]child_1, child_2 = crossover(parent_1, parent_2)child_1 = mutation(child_1)child_2 = mutation(child_2)new_population[j] = child_1new_population[j+1] = child_2population = new_population# 输出最终最佳解best_chromosome = population[max(range(POP_SIZE), key=lambda x: fitness_list[x])]print("Best solution: task assignment = {}, fitness = {}".format(best_chromosome, fitness(best_chromosome)))```。
遗传算法随机森林代码

遗传算法随机森林代码以下是使用遗传算法优化随机森林模型参数的Python代码示例:```pythonimport numpy as npfrom import RandomForestClassifierfrom _selection import GridSearchCVfrom deap import base, creator, tools, algorithmsimport random创建遗传算法类class GeneticAlgorithm(object):def __init__(self, n_population, n_generations, p_crossover, p_mutation, p_elitism):_population = n_population_generations = n_generations_crossover = p_crossover_mutation = p_mutation_elitism = p_elitismdef generate_population(self):随机生成解空间return [[(0, 1) for _ in range(len(param_grid))] for _ inrange(_population)]def fitness(self, individual):计算适应度值,即交叉验证误差cv = GridSearchCV(RandomForestClassifier(), param_grid, cv=5) (X_train, y_train)return _score_, _params_def selection(self, population):选择操作,使用轮盘赌选择法fitnesses = [(ind)[0] for ind in population]total = sum(fitnesses)idxs = [i for i in range(len(population))]for i in range(len(idxs)):idxs[i] = idxs[i] if fitnesses[i] == 0 else -1selected = []count = 0for i in range(len(population)):if fitnesses[i] == 0: 精英个体直接进入下一代种群(population[i])else: 其他个体根据适应度值选择进入下一代种群的概率,使用轮盘赌选择法if () < fitnesses[i] / total:(population[i])count += 1if count == _population: 如果选择完当前种群数量,提前结束循环breakreturn selected[:_population] 返回新一代种群数量为n_population的选择结果,可能少于旧种群数量def crossover(self, parent1, parent2):交叉操作,使用单点交叉法if () < _crossover: 如果满足交叉概率,则进行交叉操作cut_point = (0, len(parent1)) 随机选择一个点作为切割点child1 = parent1[:cut_point] + parent2[cut_point:] 生成子代1 child2 = parent2[:cut_point] + parent1[cut_point:] 生成子代2 return child1, child2 返回两个子代个体else: 不满足交叉概率,则返回两个父代个体作为子代个体,保证种群数量不变return parent1, parent2def mutation(self, individual):变异操作,随机改变个体的某一位或某几位值的大小(包括增大和减小)if () < _mutation: 如果满足变异概率,则进行变异操作for i in range(len(individual)): 对个体中的每一位进行变异操作,随机改变大小(包括增大和减小)if () < : 以的概率进行增大或减小操作,保证变异后的值仍在解空间范围内(0-1之间)individual[i] = 2 将个体中的每一位乘以2,实现增大操作(若该位原本为小数,则变为整数)else: 以的概率进行减小操作,保证变异后的值仍在解空间范围内(0-1之间)individual[i] /= 2 将个体中的每一位除以2,实现减小操作(若该位原本为整数,则变为小数)return individual 返回变异后的个体作为子代个体,保证种群数量不变(若不满足交叉概率或变异概率,则返回。
遗传算法解释及代码(一看就懂)

遗传算法解释及代码(一看就懂)遗传算法( GA , Genetic Algorithm ) ,也称进化算法。
遗传算法是受达尔文的进化论的启发,借鉴生物进化过程而提出的一种启发式搜索算法。
因此在介绍遗传算法前有必要简单的介绍生物进化知识。
一.进化论知识作为遗传算法生物背景的介绍,下面内容了解即可:种群(Population):生物的进化以群体的形式进行,这样的一个群体称为种群。
个体:组成种群的单个生物。
基因 ( Gene ) :一个遗传因子。
染色体 ( Chromosome ):包含一组的基因。
生存竞争,适者生存:对环境适应度高的、牛B的个体参与繁殖的机会比较多,后代就会越来越多。
适应度低的个体参与繁殖的机会比较少,后代就会越来越少。
遗传与变异:新个体会遗传父母双方各一部分的基因,同时有一定的概率发生基因变异。
简单说来就是:繁殖过程,会发生基因交叉( Crossover ) ,基因突变( Mutation ) ,适应度( Fitness )低的个体会被逐步淘汰,而适应度高的个体会越来越多。
那么经过N代的自然选择后,保存下来的个体都是适应度很高的,其中很可能包含史上产生的适应度最高的那个个体。
二.遗传算法思想借鉴生物进化论,遗传算法将要解决的问题模拟成一个生物进化的过程,通过复制、交叉、突变等操作产生下一代的解,并逐步淘汰掉适应度函数值低的解,增加适应度函数值高的解。
这样进化N代后就很有可能会进化出适应度函数值很高的个体。
举个例子,使用遗传算法解决“0-1背包问题”的思路:0-1背包的解可以编码为一串0-1字符串(0:不取,1:取);首先,随机产生M个0-1字符串,然后评价这些0-1字符串作为0-1背包问题的解的优劣;然后,随机选择一些字符串通过交叉、突变等操作产生下一代的M个字符串,而且较优的解被选中的概率要比较高。
这样经过G代的进化后就可能会产生出0-1背包问题的一个“近似最优解”。
编码:需要将问题的解编码成字符串的形式才能使用遗传算法。
(完整版)遗传算法简介及代码详解

遗传算法简述及代码详解声明:本文内容整理自网络,认为原作者同意转载,如有冒犯请联系我。
遗传算法基本内容遗传算法为群体优化算法,也就是从多个初始解开始进行优化,每个解称为一个染色体,各染色体之间通过竞争、合作、单独变异,不断进化。
遗传学与遗传算法中的基础术语比较染色体:又可以叫做基因型个体(individuals)群体/种群(population):一定数量的个体组成,及一定数量的染色体组成,群体中个体的数量叫做群体大小。
初始群体:若干染色体的集合,即解的规模,如30,50等,认为是随机选取的数据集合。
适应度(fitness):各个个体对环境的适应程度优化时先要将实际问题转换到遗传空间,就是把实际问题的解用染色体表示,称为编码,反过程为解码/译码,因为优化后要进行评价(此时得到的解是否较之前解优越),所以要返回问题空间,故要进行解码。
SGA采用二进制编码,染色体就是二进制位串,每一位可称为一个基因;如果直接生成二进制初始种群,则不必有编码过程,但要求解码时将染色体解码到问题可行域内。
遗传算法的准备工作:1) 数据转换操作,包括表现型到基因型的转换和基因型到表现型的转换。
前者是把求解空间中的参数转化成遗传空间中的染色体或者个体(encoding),后者是它的逆操作(decoding)2) 确定适应度计算函数,可以将个体值经过该函数转换为该个体的适应度,该适应度的高低要能充分反映该个体对于解得优秀程度。
非常重要的过程。
遗传算法基本过程为:1) 编码,创建初始群体2) 群体中个体适应度计算3) 评估适应度4) 根据适应度选择个体5) 被选择个体进行交叉繁殖6) 在繁殖的过程中引入变异机制7) 繁殖出新的群体,回到第二步实例一:(建议先看实例二)求 []30,0∈x 范围内的()210-=x y 的最小值1) 编码算法选择为"将x 转化为2进制的串",串的长度为5位(串的长度根据解的精度设 定,串长度越长解得精度越高)。
slp遗传算法代码

slp遗传算法代码遗传算法(Genetic Algorithm)是通过模拟生物进化过程来解决问题的一种随机优化算法。
该算法可以应用于各种优化问题,并且具有全局优化能力、鲁棒性强等特点,被广泛应用于优化问题的解决中。
下面将介绍SLP遗传算法的代码实现。
SLP遗传算法是一种求解单目标离散组合优化问题的遗传算法。
其流程如下:1. 随机生成一个种群2. 对每个个体进行适应度计算3. 选择操作:根据轮盘赌算法等选择方法选择优秀的个体,保留至下一代。
4. 交叉操作:从选择出的优秀个体中随机选取两个进行交叉,生成子代。
5. 变异操作:对子代进行变异操作,增加遗传的多样性。
6. 重复执行第2至第5步,直到满足终止条件。
以下是SLP遗传算法的代码实现:import randomclass SLP_GA():def __init__(self, fit_func, pop_size=50,chrom_len=10, max_iter=100, p_crossover=0.8, p_mutation=0.15): """:param fit_func: 适应度函数:param pop_size: 种群大小:param chrom_len: 染色体长度:param max_iter: 最大迭代次数:param p_crossover: 交叉概率:param p_mutation: 变异概率"""self.fit_func = fit_funcself.pop_size = pop_sizeself.chrom_len = chrom_lenself.max_iter = max_iterself.p_crossover = p_crossoverself.p_mutation = p_mutationself.generation = [] # 当前种群self.best_chrom = None # 最优个体self.best_fitness = None # 最优适应度def init_population(self):"""初始化种群"""for i in range(self.pop_size):chrom = [random.randint(0, 1) for _ inrange(self.chrom_len)]fit = self.fit_func(chrom)self.generation.append((chrom, fit))def selection(self):"""选择操作"""total_fit = sum([fit for chrom, fit inself.generation])select_prob = [fit / total_fit for chrom, fit in self.generation] # 计算每个个体被选择的概率new_generation = []for i in range(self.pop_size):# 轮盘赌算法选择优秀个体choice = random.choices(self.generation, select_prob)[0]new_generation.append(choice)self.generation = new_generationdef crossover(self):"""交叉操作"""new_generation = []for i in range(self.pop_size // 2): # 随机选取两个个体进行交叉chrom1, fit1 = random.choice(self.generation) chrom2, fit2 = random.choice(self.generation) if random.random() < self.p_crossover:cross_pos = random.randint(1,self.chrom_len - 1) # 随机交叉点new_chrom1 = chrom1[:cross_pos] + chrom2[cross_pos:]new_chrom2 = chrom2[:cross_pos] + chrom1[cross_pos:]new_generation.append((new_chrom1, self.fit_func(new_chrom1)))new_generation.append((new_chrom2, self.fit_func(new_chrom2)))else:new_generation.append((chrom1, fit1)) new_generation.append((chrom2, fit2)) self.generation = new_generationdef mutation(self):"""变异操作"""for i in range(self.pop_size):chrom, fit = self.generation[i]if random.random() < self.p_mutation:mut_pos = random.randint(0,self.chrom_len - 1) # 随机变异位chrom[mut_pos] = 1 - chrom[mut_pos] # 变异操作self.generation[i] = (chrom,self.fit_func(chrom))def evolve(self):"""遗传算法进化过程"""self.init_population()for i in range(self.max_iter):self.selection()self.crossover()self.mutation()self.best_chrom, self.best_fitness = max(self.generation, key=lambda x: x[1])def run(self):"""运行函数,返回最终结果"""self.evolve()return self.best_chrom, self.best_fitness # 示例应用def knapsack(chrom):# 物品重量、价值和背包容量weights = [2, 2, 4, 6, 5, 8, 5, 11, 15]values = [4, 6, 8, 3, 5, 3, 7, 10, 13]w_limit = 30w_total = 0v_total = 0for i in range(len(chrom)):if chrom[i] == 1:w_total += weights[i]v_total += values[i]if w_total > w_limit:return 0else:return v_totalga = SLP_GA(fit_func=knapsack)print(()) # 输出最大价值及其对应的0/1序列。
投影寻踪遗传算法matlab程序

clcclearclose allAlpha=;X=load('d:\' );for k=1:21eval(sprintf( 'syms a%d',k));enda=[a1,a2,a3,a4,a5,a6,a7,a8,a9,a10,a11,a12,a13,a14,a15,a16,a17,a18,a19,a20,a21]; [n,p]=size(X);x=zeros(n,p);Xjmax=max(X);Xjmin=min(X);for i=1:nx(i,:)=(X(i,:)-Xjmin)./(Xjmax-Xjmin);end%结构投影指标for i=1:nZ(i)=sum(a.*x(i,:));end%计算投影指标函数meanZ=mean(Z);Sa=0;for k=1:nsa=(Z(i)-meanZ).^2;Sa=Sa+sa;Sa=sqrt(Sa/n);endR=Alpha*Sa;Da=0;for k=1:nrik=abs(Z(i)-Z(k));%if R>rikDa=Da+rik;%endendQa=Sa*Da;%选择操作function ret =select(individuals,sizepop)=1./;sumfitness=sum;sumf=individuals./fitness;index=[];for i =1:sizepoppick=rand;while pick==0pick=rand;endfor j =1:sizepoppick =pick-sumf(j);if pick<0index=[index j];break ;endendend=(index,:);=(index);ret=individuals;%交错操作function ret=Cross(pcross,lenchrom,chrom,sizepop,bound) for i=1:sizepoppick = rand(1,2);while prod(pick)==0pick=rand(1,2);endindex=ceil(pick.*sizepop);pick=rand;while pick==0pick=rand;endif pick>pcrosscontinue ;endflag=0;while flag==0pick=rand;while pick==0pick=rand;endpos=ceil(pick.*sum(lenchrom));pick=rand;v1=chrom(index(1),pos);v2=chrom(index(2),pos);chrom(index(1),pos)=pick*v2+(1-pick)*v1;chrom(index(2),pos)=pick*v1+(1-pick)*v2;flag1=test(lenchrom,bound,chrom(index(1),:),fcode);flag2=test(lenchrom,bound,chrom(index(2),:),fcode);if flag1*flag2==0flag=0;else flag=1;endendendret= chrom;%变异操作function ret=Mutation(pmutation,lenchrom,chrom,sizepoppop,bound) pick=rand;while pick==0pick=rand;endindex=ceil(pick*sizepop);pick=rand;if pick>pmutationcontinue ;endflag=0;while flag==0pick =rand;while pick==0pick=rand;endpos=ceil(pick*sum(lenchrom));v=chrom(i,pos);v1=v-bound(pos,1);v2=bound(pos,2)-v;pick=rand;if pick>delta=v2*(1-pick^((1-pop(1)/pop(2))^2));chrom(i,pos)=v+delta;elsedelta=v1*(1-pick^((1-pop(1)/pop(2))^2));chrom(i,pos)=v-delta;endflag=test(lenchrom,bound,chrom(1,:),fcode);endendendret=chrom;endend主函数clcclearmaxgen=200;sizepop=20;pcross=[];pmutation=[];lenchrom=[1 1 1 1 1];bound=[0 *pi;0 *pi;0 *pi;0 *pi;0 *pi;];individuals=struct( 'fitness' ,zeros(1,sizepop), 'chrom' ,[]); avgfitness=[];bestfitness=[];bestchrom=[];for i =1:sizepop(1,:)=code(lenchrom,bound);x=(i,:);individuals,fitness(i)=fun(x);end[bestfitness, bestindex]=max;bestchrom=(bestindex,:);avgfitness=sum/sizepop;trace=[];for i=1:maxgenindividuals=Select(individuals,sizepop);avggitness=sum/sizepop;=Cross(pcross,lenchrom,,sizepop,bound);=Mutation(pmutation,lenchrom,,sizepop,[i maxgen],bound);if mod(i,10)==0=nonlinear,sizepop);endfor j=1:sizepopx=(j,:);(j)=fun(x);end[newbestfitness,newbestindex]=max;if bestfitness>newbestfitness;bestfitness=newbestfitness;bestchrom=(newbestindex,:);endavgfitness=sizepop;trace=[trace;avgfitness bestfitness];end。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
for i=1:n2
d2(i,:)=(DD(i+np,:)-DDjmin)./(DDjmax-DDjmin);
end
Z2=zeros(n2,1);
for i=1:n2
Z2(i)=abs(sum(Best_a.*d2(i,:)));
end
Z2=abs(Z2);
Best_a=(BESTX{K})';%方向向量
disp('最佳投影向量为');
disp(Best_a);
d=zeros(np,p);
DDjmax=max(DD);
DDjmin=min(DD);
for i=1:np
d(i,:)=(DD(i,:)-DDjmin)./(DDjmax-DDjmin);
end
Z=zeros(np,1);
for i=1:np
Z(i)=abs(sum(Best_a.*d(i,:)));
end
Z=abs(Z);
%%
figure(2)%投影散布图
plot(year,abs(Z),'bd','LineWidth',1,'MarkerEdgeColor','k','MarkerFaceColor','b','MarkerSize',5);
plot((np+1):n,Z2,'bo','LineWidth',1,'MarkerEdgeColor','r','MarkerFaceColor','r','MarkerSize',5);
legend('训练样本投影值','预测样本投影值');
%axis([1,12,0,2.5]);%图形边界根据需要显示
grid on
xlabel('Year','FontName','Times New Roman','FontSize',12);
ylabel('Projective Value','FontName','Times New Roman','Fontsize',12);
%%
n2=n-np;
%%
figure(3)
[newZ,I]=sort(Z);
newyear=year(I);
plot(year,abs(newZ),'bd','LineWidth',1,'MarkerEdgeColor','k','MarkerFaceColor','b','MarkerSize',5);
%axis([1,12,0,2.5]);%图形边界根据需要显示
UB=ones(1,p); %决策变量的上界
Alpha=0.1; %窗口半径系数,典型取值0.1b
%% 调用遗传算法优化投影寻踪模型的程序
[BESTX,BESTY,ALLX,ALLY]=GAUCP(K,N,Pm,LB,UB,D,Alpha)
%% 以下均为整理输出结果
ቤተ መጻሕፍቲ ባይዱgrid on
xlabel('Year','FontName','Times New Roman','FontSize',12);
ylabel('Projective Value','FontName','Times New Roman','Fontsize',12);
end
year=1:np;%选择参与计算的样本,默认选择全部
Factor=1:p;%选择部分指标,默认选择全部
D=DD(year,Factor);
K=50; %迭代次数
N=14; %种群规模
Pm=0.3; %变异概率
LB=-ones(1,p); %决策变量的下界
%所有数据都在workspace里,最值得关注的三个数据是
% Z 投影指标值,和参考文献里的符号是一致的
% Best_a 最佳投影向量,参考文献里也是用的符号a,这里加了个前缀Best,表示最佳
% BESTY 投影寻踪模型中的目标函数的变化情况,文献中的模型是最大化模型,这里按照惯例,对其加了个负号成为最小化模型
%axis([1,12,0,2.5]);%图形边界根据需要显示
grid on
xlabel('Year','FontName','Times New Roman','FontSize',12);
ylabel('Projective Value','FontName','Times New Roman','Fontsize',12);
disp('预测样本的投影预测值为');
disp(Z2);
%%
figure(4)%投影散布图
plot([Z;Z2],'bd','LineWidth',1,'MarkerEdgeColor','k','MarkerFaceColor','b','MarkerSize',5);
hold on
%% “投影寻踪+遗传算法优化”的主仿真程序
% GreenSim团队原创作品,转载请注明
% Email:greensim@
% GreenSim团队主页:/greensim
% [color=red]欢迎访问GreenSim——算法仿真团队→[url=/greensim]/greensim[/url][/color]
%% 第一步:仿真参数设置
clear
clc
close all
load Q5.txt
DD=Q5;%导入D矩阵
[n,p]=size(DD);
np=8; %训练样本的个数,前面1~np个样本用于建立模型,剩下的样本用于预测
if np>=n
error('用于预测的样本个数不能大于或等于样本总数,请重新设置');
