浙教版数学九年级上册《相似三角形》习题.docx
4.3 相似三角形 浙教版九年级数学上册同步练习(含答案)

4.3 相似三角形一、选择题(共8小题)1. 如图所示,△ABC∽△CBD,CD=2,AC=3,BC=4,那么AB的值等于( )A. 5B. 6C. 7D. 42. 如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3,4及x,那么x的值为( )A. 7B. 5C. 7或5D. 无数个3. 如图所示,在平行四边形ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF∽△CDE,则BF的长是( )A. 5B. 8.2C. 6.4D. 1.84. 已知△ABC和△DEF相似,且△ABC的三边长为3,4,5,如果△DEF的周长为6,那么△DEF中某条边的边长不可能是( )A. 1.5B. 2C. 2.5D. 35. 如图所示,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )A. (6,0)B. (6,3)C. (6,5)D. (4,2)6. 如图所示,在钝角三角形ABC中,AB=6 cm,AC=12 cm,动点D从点A出发到点B止,动点E从点C出发到点A止,点D运动的速度为1 cm/s,点E运动的速度为2 cm/s.如果两点同时运动,那么当以点A,D,E为顶点的三角形与△ABC相似时,运动的时间是( )A. 3 s或4.8 sB. 3 sC. 4.5 sD. 4.5 s或4.8 s7. 已知△ABC的三边长分别为2,6,2,△AʹBʹCʹ的两边长分别为1和3,如果△ABC与△AʹBʹCʹ相似,那么△AʹBʹCʹ的第三边长应该是( )A. 2B. 22C. 62D. 338. 如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是( )A. AB2=BC⋅BDB. AB2=AC⋅BDC. AB⋅AD=BD⋅BCD. AB⋅AD=AD⋅CD二、填空题(共6小题)9. 已知△ABC的三边分别是4,5,6,与它相似的△AʹBʹCʹ的最长边为12,则△AʹBʹCʹ的周长是.10. 如图所示,在△ABC中,AB=8,AC=6,D是线段AC的中点,点E在线段AB上,且△ADE∽△ABC,则AE=.11. 如图所示,∠ACB=∠ADC=90∘,AB=5,AC=4,若△ABC∽△ACD,则AD=.12. 如图所示,在△ABC中,∠C=90∘,AC=3,BC=6,D为BC中点,E是线段AB上一动点,若△BDE∽△BAC,则BE=.13. 如图所示,在长方形ABCD中,AB=4,AD=3,E是AB边上一点(不与点A,B重合),F是BC边上一点(不与B,C重合).若△DEF和△BEF是相似三角形,则CF=.14. 如图所示,已知在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数y=k(k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若x△OCD∽△ACO,则直线OA的表达式为.三、解答题(共6小题)15. 如图所示,AD=2,AC=4,BC=6,∠B=36∘,∠D=107∘,△ABC∽△DAC.求:(1)AB 的长.(2)CD 的长.(3)∠BAD 的大小.16. 如图所示,在 △ABC 中,AD 平分 ∠BAC 交 BC 于点 D ,点 E ,F 分别在 AB ,AC 上,BE =AF ,FG ∥AB 交线段 AD 于点 G ,连接 BG ,EF .(1)求证:四边形 BGFE 是平行四边形;(2)若 △ABG ∽△AGF ,AB =10,AG =6,求线段 BE 的长.17. 如图所示,已知 △ABG ∽△FBD ,F 是 AB 的中点,求证:BD CD =AE EC .18. 如图所示,点 C ,D 在线段 AB 上,△PCD 是等边三角形,且 △ACP ∽△PDB .(1)求 ∠APB 的大小 ⋅(2)说明线段 AC ,CD ,BD 之间的数量关系.19. 如图所示,已知,在平面直角坐标系中有四点:A (―2,4),B (―2,0),C (2,―3),D (2,0),设 P 是 x 轴上的点,且 PA ,PB ,AB 所围成的三角形与 PC ,PD ,CD 所围成的三角形相似,请求出所有符合上述条件的点 P 的坐标.20. 如图,已知△ABC∽△A1B1C1,相似比为k(k>1),且△ABC的三边长分别为a,b,c(a>b>c),△A1B1C1的三边长分别为a1,b1,c1.(1)若c=a1,求证:a=kc;(2)若c=a1,试给出符合条件的一对△ABC和△A1B1C1,使得a,b,c和a1,b1,c1都是正整数,并加以说明;(3)若b=a1,c=b1,问:是否存在△ABC和△A1B1C1使得k=2 ?请说明理由.答案1. B2. C3. D4. D5. B6. A7. A8. A9. 3010. 9411. 16512. 65513. 53或3214. y=2x15. (1)∵△ABC∽△ADC,∴ABAD =BCAC,即AB2=64,∴AB=3.(2)∵△ABC∽△ADC,∴BCAC =ACDC,即64=4DC,∴CD=83.(3)∵△ABC∽△ADC,∴∠CAD=∠B=36∘,∠BAC=∠D=107∘,∴∠BAD=∠BAC+∠CAD=107∘+36∘=143∘.16. (1)∵FG∥AB,∴∠BAD=∠AGF.∵∠BAD=∠GAF,∴∠AGF=∠GAF,AF=GF.∵BE=AF,∴FG=BE.∵FG∥BE,∴四边形BGFE为平行四边形.(2)BE=3.6.17. ∵△ABG∽△FBD,∴∠G=∠BDF.∴DF∥AG.∵F是AB的中点,∴DF是△ABG的中位线.∴BD=DG.又∵DF∥AG,∴DGCD =AEEC.∴BDCD =AEEC.18. (1)因为△PCD是等边三角形,所以∠PCD=60∘.所以∠ACP=120∘.因为△ACP∽△PDB,所以∠APC=∠B.所以∠APC+∠CPB=∠B+∠CPB.所以∠APB=∠ACP=120∘.(2)因为△ACP∽△PDB,所以AC:PD=PC:BD.所以PD⋅PC=AC⋅BD.因为△PCD是等边三角形,所以PC=PD=CD.所以CD2=AC⋅BD.19. 设OP=x(x>0).(1)如图 1 所示,若点P在AB的左边,有两种可能:①若△ABP∽△PDC,则PB:CD≡AB:PD,∴(x―2):3=4:(x+2),解得x=4.∴点P的坐标为(―4,0).②若△ABP∽△CDP,则AB:CD=PB:PD,∴4:3=(x―2):(x+2),解得x=―14.不存在.(2)如图 2 所示,若点P在AB与CD之间,有两种可能:①若△ABP∽△CDP,则AB:CD=BP:PD,∴4:3=(x+2):(2―x),解得x=2.7∴点P的坐标为,0.②若△ABP∽△PDC,则AB:PD=BP:CD,∴4:(2―x)=(x+2):3,方程无解.(3)如图 3 所示,若点P在CD的右边,有两种可能:①若△ABP∽△CDP,则AB:CD=BP:PD,∴4:3=(2+x):(x―2).∴x=14.∴点P的坐标为(14,0).②若△ABP∽△PDC,则AB:PD=BP:CD,∴4:(x―2)=(x+2):3,∴x=4或x=―4(舍去).∴点P的坐标为(4,0).综止所述,点P的坐标为,0,(14,0),(4,0),(―4,0).20. (1)∵△ABC∽△A1B1C1,且相似比为k(k>1),∴aa1=k,∴a=ka1.又∵c=a1,∴a=kc.(2)取a=8,b=6,c=4,同时取a1=4,b1=3,c1=2.此时aa1=bb1=cc1=2,∴△ABC∽△A1B1C1且c=a1.(3)不存在这样的△ABC和△A1B1C1.理由如下:若k=2,则a=2a1,b=2b1,c=2c1,又∵b=a1,c=b1,∴a=2a1=2b=4b1=4c.∴b=2c.∴b+c=2c+c<4c=a,而b+c>a,故不存在这样的△ABC和△A1B1C1,使得k=2.。
浙教版九年级上册数学第4章 相似三角形含答案(配有卷)

浙教版九年级上册数学第4章相似三角形含答案一、单选题(共15题,共计45分)1、如图,在矩形ABCD中,,,将其折叠使AB落在对角线AC 上,得到折痕AE,那么BE的长度为()A. B. C. D.2、如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连结CE交AD于点F,连结BD交 CE于点G,连结BE. 下列结论中:① CE=BD;② △ADC是等腰直角三角形;③ ∠ADB=∠AEB;④ CD·AE=EF·CG;一定正确的结论有( )A.1个B.2个C.3个D.4个3、如图,在正方形中,的顶点,分别在,边上,高与正方形的边长相等,连接分别交,于点,,下列说法:① ;②连接,,则为直角三角形;③ ;④若,,则的长为,其中正确结论的个数是()A.4B.3C.2D.14、如图,在中,,则DF的长为()A.4B.C.D.35、如图的△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG 分别交DE、BC于M、N两点.若∠B=90°,AB=4,BC=3,EF=1,则BN的长度为何?()A. B. C. D.6、如图,l1∥l2∥l3,直线a,b与l1, l2, l3分别相交于点A、B、C和点D、E、F,若,DE=4,则DF的长是()A. B. C.10 D.67、如图,已知l1∥l2∥l3,直线AC分别交l1、l2、l3于点A,B,C,直线DF分别交l1、l2、l3于D,E,F,DE=4,EF=6,AB=5,则BC的长为()A. B. C. D.8、如图,直线l1∥l2∥l3 ,直线AC分别交l1 , l2 , l3于点A,B,C;直线DF分别交l1 , l2 , l3于点D,E,F.AC与DF相交于点H,且AH=2,HB=1,BC=5,则的值为()A. B.2 C. D.9、如图,在菱形ABCD中,AC=8,BD=6,DE⊥AB,垂足为E,DE与AC交于点F,则sin∠DFC的值为()A. B. C. D.10、两相似三角形的周长之比为1:4,那么他们的对应边上的高的比为()A.1∶4B.1∶2C.2∶1D. ∶211、如图,在△ABC中,∠C=90°,过重心G作AC、BC的垂线,垂足分别为D、E,则四边形GDCE的面积与△ABC的面积之比为( )A. B. C. D.12、如图,在正方形ABCD的外侧,作等边△ADE,BE、CE分别交AD于G、H,设△CDH、△GHE的面积分别为S1、S2,则()A.3S1=2S2B.2S1=3S2C.2S1= S2D. S1=2S213、如图,一组互相平行的直线a,b,c分别与直线l1, 12交于点A,B,C,D,E,F,直线11, l2交于点O,则下列各式不正确的是()A. B. C. D.14、如图,在平面直角坐标系中,矩形OABC的顶点A,B在反比例函数的图像上,纵坐标分别为1和3,则k的值为()A. B. C.2 D.315、如图,⊙O的直径为6,在⊙O上位于直径AB的异侧有定点C和动点P.已知BC:CA=4:3,P在半圆上运动,CP⊥CD交PB的延长线于D点.当点P运动到什么位置时,△PCD的面积最大为()A.36B.24C.18D.12二、填空题(共10题,共计30分)16、如图,在正方形ABCD中,E是边BC的中点,连接AE,作EF⊥AE交正方形的外角平分线于点F,连接AF,交CD于点H,连接EH.若AB=4,则EH的长为________.17、如图,平行四边形ABCD中,E为AD的中点,已知△DEF的面积为2,则平行四边形ABCD的面积是________.18、如图,a∥b∥c,直线m分别交直线a、b、c于点A、B、C,直线n分别交直线a、b、c于点D、E、F.若AB=2,CB=4,DE=3,则EF=________.19、如图所示,已知点E,F分别是△ABC的边AC,AB的中点,BE,CF相交于点G,FG=1,则CF的长为________.20、若a:b:c=3:2:5,则=________.21、如图,在平面直角坐标系中,△OAB与△OCD是以原点O为位似中心的位似图形,且位似比为1:3,已知点A的坐标为(1,2),则点C的坐标是________.22、如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O 为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则端点C 的坐标为________ .23、我国古代数学著作《九章算术》中记载:“今有方不知大小,各开中门,出北门四十步有木,出西门八百一十步见木,问:邑方几何?”译文:如图,一座正方形城池北、西边正中A、C处各开一道门,从点A往正北方向走40步刚好有一棵树位于点B处,若从点C往正西方向走810步到达点D处时正好看到此树,则正方形城池的边长为________步。
浙教版数学九年级上册 第四章 相似三角形 单元练习(含答案)

浙教版数学九年级上册第四章相似三角形一、选择题1.如果2a =5b ,那么下列比例式中正确的是( )A .a b =25B .a 5=2b C .a 2=b 5D .a 5=b 22.如图,直线l 1∥l 2∥l 3,AC =6,DE =3,EF =2,则AB 的长为( )A .3B .125C .165D .1853.如图,点P 是线段AB 的黄金分割点,且PA >PB ,若AB =2,则PA 的长度是( )A .5−1B .3−5C .25−4D .14.如图, 在▱ABCD 中, E 是边AB 上一点, 连结AC ,DE 相交于点F . 若AE EB =23,则 AF CF 等于( )A .13B .23C .25D .355.如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC 相似的是( )A .B .C.D.6.△ABC和△DEF是两个等边三角形,AB=2,DE=4,则△ABC与△DEF的面积比是( ) A.1:2B.1:4C.1:8D.1:27.如图,在△ABC中,BC=6,AC=8,∠C=90°,以B为圆心,BC长为半径画弧,与AB交于点D,再分别以点A,D为圆心,大于12AD的长为半径画弧,两弧交于点M,N,作直线MN,分别交AC,AB于点E,F,则AE的长度为( )A.52B.103C.3D.228.如图,△ABC和△A1B1C1是以点O为位似中心的位似图形,点A在线段O A1上,若OA:A A1=1:2,则△ABC和△A1B1C1的周长之比为( )A.1:2B.2:1C.1:3D.3:19.如图,在△ABC中,D为线段AC上一点,点E在AC的延长线上,过点D作DF∥AB交BC于点F,连结BE,EF,若A C2+D E2=A E2,则△BEF与△DCF的面积比为( )A.1:2B.1:3C.2:3D.2:510.如图,矩形ABCD中,AB=4,AD=2,E为边AD上一个动点,连接BE,取BE的中点G,点G绕点E逆时针旋转90°得到点F,连接CF,则△CEF面积的最小值是( )A .4B .154C .3D .114二、填空题11.如图,AC 、BD 交于点O ,连接AB 、CD ,若要使△AOB ∽△COD ,可以添加条件 .(只需写出一个条件即可)12.已知△ABC ∽△DEF ,且AB:DE =1:3,△ABC 与△DEF 的周长比是 .13.如图,在这架小提琴中,点C 是线段AB 的黄金分割点(BC >AC ).若AB =60cm ,则BC = cm .14.如图,在Rt △ABC 中,∠ABC =90°,AB =4,AC =5,AE 平分∠BAC ,点D 是AC 的中点,AE 与BD交于点O ,则的值AOOE .15.如图,矩形ABCD 中,AB =3 6 ,BC =12,E 为AD 中点,F 为AB 上一点,将△AEF 沿EF 折叠后,点A 恰好落到CF 上的点G 处,则折痕EF 的长是 .16.如图,正方形ABCD 中,BF =FG =CG ,BE =2AE ,CE 交DF 、DG 于M 、N 两点,有下列结论:①DF ⊥EC ;②S △MFC =59S 四边形MFBE ;③DM :MF =2:1;④MN NC =913.其中,正确的有 .三、解答题17.(1)已知线段a =2,b =6,求线段a ,b 的比例中项线段c 的长.(2)已知x :y =3:2,求2x−yx的值.18.如图,已知D 、E 分别是△ABC 的边AB 、AC 上的点,DE ∥BC ,AD BD =32,求DE BC 的值.19.如图,AD 、BC 相交于点P ,连接AC 、BD ,且∠1=∠2,AC =6,CP =4,DP =2,求BD 的长.20. 如图,在平行四边形ABCD 中,E 为DC 边上一点,∠EAB =∠EBC .(1)求证:△ABE∽△BEC ;(2)若AB=4,DE=3,求BE的长.21.如图,在四边形ABCD中,OA=OC,OB=OD,AB=BC,AC=12,BD=16.(1)求证:四边形ABCD时菱形;(2)延长BC至点M,连接OM交CD于点N,若∠M=12∠BAC,求MNOM.22.如图,AB∥CD,且AB=2CD,E是AB的中点,F是边BC上的动点(F不与B,C重合),EF与BD相交于点M.(1)求证:△FDM∽△FBM;(2)若F是BC的中点,BD=18,求BM的长;(3)若AD=BC,BD平分∠ABC,点P是线段BD上的动点,是否存在点P使DP⋅BP=BF⋅CD,若存在,求出∠CPF的度数;若不存在,请说明理由.23.如图,在平面直角坐标系中,已知抛物线y=12x2+bx+c与x轴交于A、B两点,与y轴交于C点,且OB=OC=4.(1)求抛物线的解析式;(2)在抛物线上是否存在点M,使∠ABC=∠BCM,如果存在,求M点的坐标,如果不存在,说明理由;(3)若D是抛物线第二象限上一动点,过点D作DF⊥x轴于点F,过点A、B、D的圆与DF交于E点,求△ABE的面积.答案解析部分1.【答案】D2.【答案】D3.【答案】A4.【答案】C5.【答案】B6.【答案】B7.【答案】A8.【答案】C9.【答案】A10.【答案】B11.【答案】∠A=∠C(答案不唯一)12.【答案】1:313.【答案】(305−30)14.【答案】9415.【答案】21516.【答案】①④17.【答案】(1)解:∵线段a=2,b=6,线段c是线段a、b的比例中项,∴c2=ab=12,∴c=23(负值舍去);(2)解:∵x:y=3:2,∴可设x=3k,y=2k(k≠0),∴2x−yx=6k−2k3k=43.18.【答案】3519.【答案】BD=320.【答案】(1)证明:∵平行四边形ABCD,∴AB//CD,∴∠EBA=∠BEC,又∵∠EAB=∠EBC,∴△ABE∽△BEC.(2)解:∵四边形ABCD 平行四边形,∴AB =DC =4,∵DE =3,∴CE =1,∵△ABE∽△BEC ,∴AB EB =EBEC,∴AB ⋅CE =B E 2=4×1=4,∴BE =2.21.【答案】(1)证明:∵ 在四边形ABCD 中,OA=OC ,OB=OD∴ 四边形ABCD 是平行四边形 ∵ AB=BC∴ 平行四边形ABCD 是菱形。
(基础题)浙教版九年级上册数学第4章 相似三角形含答案

浙教版九年级上册数学第4章相似三角形含答案一、单选题(共15题,共计45分)1、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CD=2,BD=1,则AD的长是()A.1B.C.2D.42、如图,在四边形ABCD中,BD平分∠ABC,∠BAD=∠BDC=90°,E为BC的中点,AE与BD相交于点F.若BC=4,∠CBD=30°,则DF的长为()A. B. C. D.3、如图,在平行四边形中,F为BC中点,延长AD至E,连结EF交DC 于点G,若,则()A.1:2B.1:3C.1:4D.2:94、如图,锐角△ABC的高CD和BE相交于点O,图中与△ODB相似的三角形有()A.4个B.3个C.2个D.1个5、已知线段a、b、c,其中c是a、b的比例中项,若a=9cm,b=4cm,则线段c长()A.18cmB.5cmC.6cmD.±6cm6、如图,已知点A、B分别是反比例函数y= (x>0),y= (x<0)的图象上的点,且,∠AOB=90°,则的值为()A.4B.C.2D.7、下列条件,不能判定△ABC与△DEF相似的是()A.∠C=∠F=90°,∠A=55°,∠D=35°B.∠C=∠F=90°,AB=10,BC=6,DE=15,EF=9C.∠C=∠F=90°,D.∠B=∠E=90°,=8、如图,平行四边形ABCD中,点E为AD边中点,连接AC、BE交于点,若的面积为关于的一元二次方程的解,则的面积为().A.4B.5C.6D.79、小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为30°,同一时刻,一根长为1米且垂直于地面放置的标杆在地面上的影长为2米,则树的高度为()A.(6+ )米B.12米C.(4﹣2 )米D.10米10、如图,已知△ABO与△DCO位似,且△ABO与△DCO的面积之比为1:4,点B的坐标为(﹣3,2),则点C的坐标为( )A.(3,﹣2)B.(6,﹣4)C.(4,﹣6)D.(6,4)11、如图,I是△ABC的内心,AI的延长线与△ABC的外接圆相交于点D,与BC 交于点E,连接BI、CI、BD、DC.下列说法中正确的有()①∠CAD绕点A顺时针旋转一定的角度一定能与∠DAB重合;②I到△ABC三个顶点的距离相等;③∠BIC=90°+ ∠BAC;④线段DI是线段DE与DA的比例中项;⑤点D是△BIC的外心.A.1个B.2个C.3个D.4个12、如图,已知△ABC,P是边AB上的一点,连结CP,以下条件中不能确定△ACP与△ABC相似的是()A.∠ACP=∠BB.∠APC='∠ACB'C.AC 2=AP·ABD.13、如图,△ABC是⊙O的内接三角形,把沿BC折叠后,与弦AB交于点P,恰好OP⊥AB.若OP=1,AB=4,则BC:AC等于()A. B. C. D.14、如右图所示为农村一古老的捣碎器,已知支撑柱的高为0.3米,踏板长为1.6米,支撑点到踏脚的距离为0.6米,原来捣头点着地,现在踏脚着地,则捣头点上升了()A.1.2米B.1米C.0.8米D.1.5米15、生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下a与全身b的高度比值接近0.618,可以增加视觉美感.若图中b为2米,则a约为()A.1.24米B.1.38米C.1.42米D.1.62米二、填空题(共10题,共计30分)16、如图,矩形ABCD中,AB=3cm,AD=6cm,点E为AB边上的任意一点,四边形EFGB也是矩形,且EF=2BE,则S△AFC =________cm2.17、如图,B、C、D依次为一直线上4个点,BC=3,△BCE为等边三角形,⊙O 过A、D、E三点,且∠AOD=120°.设AB=x,CD=y,则y与x的函数关系式为________.18、如图,已知Rt ABC中,AC=b,BC=a,D1是斜边AB的中点,过D1作D 1E1⊥AC于E1,连结BE1交CD1于D2;过D2作D2E2⊥AC于E2,连结BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点D4,D 5,…,Dn,分别记BD1E1,BD2E2,BD3E3,…,BDnEn的面积为S1, S2, S3,…Sn.则(1)=________,(2)Sn=________.19、如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,,则EC的长是________.20、如图,要使△ABC与△DBA相似,则只需添加一个适当的条件是________(填一个即可).21、如图,n+1个边长为2的等边三角形有一条边在同一直线上,设△B2D1C1的面积为S1,△B3D2C2的面积为S2,…,△Bn+1DnCn的面积为Sn,则Sn=________(用含n的式子表示).22、如图,在菱形中,是的中点,连接,,将沿直线翻折,使得点落在上的点处,连接并延长交于点,则的值为________.23、如果,∠C=∠F=90°,AB=5,BC=3,DE=15,则DF=________.24、若线段MN的长为1,P是MN的黄金分割点(MP<NP),则MP的长为________.25、如图,已知△ABC、△DCE、△FEG、△HGI是4个全等的等腰三角形,底边BC、CE、EG、GI在同一直线上,且AB=2,BC=1,连接AI,交FG于点Q,则QI=________三、解答题(共5题,共计25分)26、已知x:y:z=2:3:4,求的值.27、如图,AB是⊙O的直径,C,P是上两点,AB=13,AC=5.(1)如图(1),若点P是的中点,求PA的长;(2)如图(2),若点P是的中点,求PA的长.28、周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D,竖起标杆DE,使得点E与点C. A共线.已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.29、已知:= = ,x﹣y+z=6,求:代数式3x﹣2y+z的值.30、如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标;(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变化后点D的对应点D2的坐标.参考答案一、单选题(共15题,共计45分)1、D2、D3、B4、B5、C6、C7、D9、A10、B11、D12、D13、B14、C15、A二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、28、29、30、。
九年级数学上册第四章《相似三角形》练习题-浙教版(含答案)

九年级数学上册第四章《相似三角形》练习题-浙教版(含答案)一.选择题:(本题共10小题,每小题3分,共30分)温馨提示:每一题的四个答案中只有一个是正确的,请将正确的答案选择出来!1.如图,ABC △与DEF △位似,点O 为位似中心,相似比为2:3.若ABC △的周长为4,则DEF △的周长是( ) A.4B.6C.9D.162.若ABC ∆∽DEF ∆,6BC =,4EF =,则ACDF=( ) A.49B.94C.23D.323.两个相似三角形的面积之比为1:4,较小的三角形的周长为4,则另一个三角形的周长为( ) A .16 B .8C .2D .14.设32yx =,则y x y x 523+-的值为( )A .113B .199 C .193 D .167 5.如图,矩形EFGH 的四个顶点分别在菱形ABCD 的四条边上,BE BF =.将AEH △,CFG △分别沿边EH ,FG 折叠,当重叠部分为菱形且面积是菱形ABCD 面积的116时,则EB AE 为( ) A .53B .2C .25D .356.如图,△ABC 内接于⊙O ,AB 为⊙O 的直径,D 为⊙O 上一点(位于AB 下方),CD 交AB 于点E ,若∠BDC =45°,BC =62 ,CE =2DE ,则CE 的长为( ) A .22B .24C .53D .547.如图平行四边形ABCD 中,F 为BC 中点,延长AD 至E ,使4:3:=AE AD ,连结EF 交DC 于点G ,则=∆∆CPG DEG S S :( ) A .2∶3B .4∶9C .9∶4D .3∶28.如图,在四边形ABCD 中,以AB 为直径的O 恰好经过点C ,AC ,DO 交于点E ,已知AC 平分BAD ∠,90ADC ∠=︒,:25CD BC =:CE AE 的值为( )A .2:5B .4:5C .5:22D .5:89.由四个全等的直角三角形和一个小正方形组成的大正方形ABCD 如图所示.过点D 作DF 的垂线交小正方形对角线EF 的延长线于点G ,连结CG ,延长BE 交CG 于点H .若AE =2BE ,则BHCG的值为( ) A .23 B .2C .7103 D .553 10.将一张以AB 为边的矩形纸片,先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角形相似),剩下的是如图所示的四边形纸片ABCD ,其中90A ∠=︒,9AB =,7BC =,6CD =,2AD =,则剪掉的两个直角三角形的斜边长不可能是( ) A.252B.454C.10D.354二.填空题(本题共6小题,每题4分,共24分) 温馨提示:填空题必须是最简洁最正确的答案!11.如图,线段AB 两个端点的坐标分别为()12,12A ,()4,16B ,以原点O 为位似中心,在第一象限内将线段AB 缩小为原来的21后得到线段CD ,则端点D 的坐标为12.如图,在梯形ABCD 中,AD ∥EF ∥BC ,且AE :EB =2:3,CD =15,则FC = 13.如图,M 是Rt △ABC 的斜边BC 上异于B 、C 的一定点,过M 点作直线截△ABC ,使截得的三角形与△ABC 相似,这样的直线共有______________14.如图,在△ABC 中,∠ACB =90°,边BC 在x 轴上,顶点A ,B 的坐标分别为(-2,6)和(7,0).将正方形OCDE 沿x 轴向右平移,当点E 落在AB 边上时,平移的距离为_____________ 15.如图,在锐角三角形ABC 中,6cm AB =,12cm AC =,动点D 从点A 出发到点B 停止,动点E 从点C 出发到点A 停止,点D 运动的速度为1cm/s ,点E 运动的速度为2cm/s ,如果两点同时开始运动,那么以点A ,D ,E 为顶点的三角形与ABC 相似时的运动时间为_______________16.如图,四边形ABCD 是正方形,点E 在边AD 上,BEF △是以E 为直角顶点的等腰直角三角形,EF ,BF 分别交CD 于点M ,N ,过点F 作AD 的垂线交AD 的延长线于点G .连接DF ,请完成下列问题:(1)FDG ∠=_______°;(2)若1DE =,22DF =,则MN =________.三.解答题(共6题,共66分)温馨提示:解答题应将必要的解答过程呈现出来!17.(本题6分)如图,在△ABC 中,D 、E 分别是AB ,AC 上的点,∠AED =∠B ,△ABC 用平分线AF 交DE 于点G ,交BC 于点F .(1)求证:△AED ∽△ABC .(2)设23AD AC,求AG AF的值.18.(本题8分)如图,在平行四边形ABCD 中,对角线AC 、BD 交于点O .M 为AD 中点,连接CM 交BD 于点N .(1)求DN :BN 的值;(2)若△OCN 的面积为2,求四边形AONM 的面积.19(本题8分)如图,在ABC △中,点D ,E ,F 分别在边AB ,AC ,BC 上,连接DE ,EF ,已知四边形BFED 是平行四边形,14DE BC =.(1)若8AB =,求线段AD 的长.(2)若ADE △的面积为1,求平行四边形BFED 的面积.20.(本题10分)如图,锐角三角形ABC 内接于⊙O ,∠BAC 的平分线AG 交⊙O 于点G ,交BC 边于点F ,连接BG .(1)求证:△ABG ∽△AFC .(2)已知AB =a ,AC =AF =b ,求线段FG 的长(用含a ,b的代数式表示).(3)已知点E 在线段AF 上(不与点A ,点F 重合),点D 在线段AE 上(不与点A ,点E 重合),∠ABD =∠CBE ,求证:BG 2=GE •GD .21.(本题10分)如图,在平行四边形ABCD 中,点E 是AC 上一点,射线BE 与CD 的延长线交于点P ,与边AD 交于点F ,连接FC .(1)若∠ABF =∠ACF ,求证:CE 2=EF •EP ; (2)若点D 是CP 中点,BE =32,求EF 的长.22(本题12分).如图,已知△ABC 是边长为6cm 的等边三角形,动点P 、Q 同时从A 、B 两点出发,分别沿AB 、BC 匀速运动,其中点P 运动的速度是1cm /s ,点Q 运动的速度是2cm /s ,当点Q 到达点C 时,P 、Q 两点都停止运动,设运动时间为t (s ),解答下列问题:(1)当t =2时,判断△BPQ 的形状,并说明理由;(2)设△BPQ 的面积为S (cm 2),求S 与t 的函数关系式;(3)作QR ∥BA 交AC 于点R ,连接PR ,当t 为何值时,△APR ∽△PRQ .23(本题12分)如图,已知抛物线24y ax ax =-交x 轴于点A ,与直线12y x =交于点B (非原点),过点B 作BC ∥x 轴交抛物线于点C ,6BC =.(1)求a 的值.(2)若P 是线段BC 上一点,过点P 作x 轴的垂线分别交直线OB 与抛物线于E ,F .求线段EF 的最大值.(3)若P 是射线BC 上一点,作点F 关于直线BC 的对称点G ,连结PG ,BG .是否存在BPG ∆与PBE ∆相似,若不存在请说明理由,若存在请求出点G 的坐标.参考答案一、选择题:(本题共10小题,每小题3分,共30分)温馨提示:每一题的四个答案中只有一个是正确的,请将正确的答案选择出来!1.答案:B解析:由两个位似图形的周长比等于位似比可知,23ABC DEF C C =△△, 334622DEF ABC C C ∴==⨯=△△.故选B.2.答案:D解析:~ABC DEF △△, BC ACEF DF∴=, 6BC =,4EF =,6342AC DF ∴==. 故选择:D3.答案:B解析:设另一个三角形的周长为x ,则 4:x =41, 解得:x =8.故另一个三角形的周长为8, 故选:B .4.答案:C 解析:∵32y x = ∴y x 32=,∴19331953425322323523==+-=+⨯-⨯=+-y y y y y y y y yy y x y x . 故选:C .5.答案:D解析:设重叠的菱形边长为x ,BE =BF =y ,由矩形和菱形的对称性以及折叠的性质得:四边形AHME 、四边形BENF 是菱形, ∴AE =EM ,EN =BE =y ,EM =x +y ,∵当重叠部分为菱形且面积是菱形ABCD 面积的116,且两个菱形相似, ∴AB =4MN =4x , ∴AE =AB -BE =4x -y , ∴4x -y =x +y , 解得:x =23y ,∴AE =53y ,∴5533yAE EB y ==, ∴35BE AE =, 故选:D .6.答案:D解析:连接CO ,过点D 作DG ⊥AB 于点G ,连接AD ,∵∠BDC =45°, ∴∠CAO =∠CDB =45°, ∵AB 为⊙O 的直径, ∴∠ACB =∠ADB =90°, ∴∠CAB =∠CBA =45°, ∵BC =62, ∴AB = 2BC =12, ∵OA =OB , ∴CO ⊥AB ,∴∠COA =∠DGE =90°, ∵∠DEG =∠CEO , ∴△DGE ∽△COE , ∴CDDGOE GE CE DE ===21, ∵CE =2DE ,设GE =x ,则OE =2x ,DG =3, ∴AG =6﹣3x ,BG =6+3x , ∵∠ADB =∠AGD =90°, ∠DAG =∠BAD , ∴△AGD ∽△ADB , ∴DG 2=AG •BG ,∴9=(6﹣3x )(6+3x ), ∵x >0, ∴x =3, ∴OE =23 ,在Rt △OCE 中,由勾股定理得:CE =34361222=+=+OC OE ,故答案为:D .7.答案:B解析:∵4:3:=AE AD ∴设x AE x AD 4,3==, ∴x x x AD AE DE =-=-=34, ∵四边形ABCD 是平行四边形, ∴x AD BC BC AD 3,//==,∵点F 是BC 的中点,xBC CF 2321==∴BC AD //FCG EDG CFG DEG ∠=∠∠=∠∴,∴△DEG ∽△CFG,942322=⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=∴∆∆x x CF DE S S CFGDEG故答案为:B .8.答案:D解析:如图所示,连接OC ∵AB 是圆的直径, ∴∠ACB =∠ADC =90°, ∵AC 平分∠BAD ,∴∠DAC =∠CAB ,∠DAB =2∠CAB , ∴△ADC ∽△ACB , ∴5CD AC ADBC AB AC==, ∴25AC AB =, ∴225BC AB AC AB =-=,455AD AC AB == ∴255CD AB ==,又∵∠BOC =2∠CAB , ∴∠BOC =∠DAB , ∴AD ∥OC , ∴△OCE ∽△DAE ,∴152485AB CE OC AE DA AB ===,故选D .9.答案:C解析:如图,过点G 作GT ⊥CF 交CF 的延长线于T ,设BH 交CF 于M ,AE 交DF 于N .设BE =AN =CM =DF =a ,则AE =BM =CF =DN =2a , ∴EN =EM =MF =FN =a , ∵四边形ENFM 是正方形,∴∠EFH =∠TFG =45°,∠NFE =∠DFG =45°, ∵GT ⊥TF ,DF ⊥DG ,∴∠TGF =∠TFG =∠DFG =∠DGF =45°, ∴TG =FT =DF =DG =a , ∴CT =3a ,CG =()a a a 10322=+,∵MH ∥TG , ∴△CMH ∽△CTG , ∴CM :CT =MH :TG =1:3, ∴MH =a 31, ∴BH =a a a 37312=+, ∴71033710==a a BH CG ,故选:C .10.答案:A 解析:如图1所示,由已知可得,~DFE ECB △△, 则DF FE DEEC CB EB==, 设DF x =,CE y =, 则9672x yy x+==+, 解得274214x y ⎧=⎪⎪⎨⎪=⎪⎩,2145644DE CD CE ∴=+=+=,故选项B 不符合题意; 2735244EB DF AD =+=+=,故选项D 不符合题意; 如图2所示,由已知可得,DCF FEB △△, 则DC CF DF FE EB FB==, 设FC m =,FD n =, 则6927m nn m ==++, 解得810m n =⎧⎨=⎩,10FD ∴=,故选项C 不符合题意; 8614BF FC BC =+=+=,如图3所示:此时两个直角三角形的斜边长为6和7; 故选A.二、填空题(本题共6小题,每题4分,共24分)温馨提示:填空题必须是最简洁最正确的答案!11.答案:(8,2)解析:∵线段AB 端点B 的坐标分别为B (16,4),以原点O 为位似中心,在第一象限内将线段AB 缩小为原来的21后得到线段CD , ∴端点D 的横坐标和纵坐标都变为B 点的一半,∴端点D 的坐标为:(8,2).故答案是:(8,2).12.答案:9解析:∵AD ∥BC ∥EF ,AE :EB =2:3,∴32==EB AE FC DF , ∴35=FC DC , ∵CD =15,∴FC =9.故答案为:9.13.答案:三条解析:过点M 作直线与另一边相交,使所得的三角形与原三角形有一个公共角,只要再作一个直角就可以.因此,∵截得的三角形与△ABC 相似,∴过点M 作AB 的垂线,或作AC 的垂线,或作BC 的垂线,所得三角形满足题意∴过点M 作直线l 共有三条.15.答案:4解:如图,设正方形D ′C ′O ′E ′是正方形OCDE 沿x 轴向右平移后的正方形,∵顶点A ,B 的坐标分别为(-2,6)和(7,0),∴AC =6,OC =2,OB =7,∴BC =9,∵四边形OCDE 是正方形,∴DE =OC =OE =2,∴O ′E ′=O ′C ′=2,∵E ′O ′⊥BC ,∴∠BO ′E ′=∠BCA =90°,∴E ′O ′∥AC ,∴△BO ′E ′∽△BCA , ∴E O BO AC BC =''', ∴269BO '=, ∴BO ′=3,∴OO ′=7-3=4,15.答案:3s 或4.8s .解析:设以点A ,D ,E 为顶点的三角形与ABC 相似时的运动时间为s t , 根据题意得:cm AD t = ,2cm CE t = ,则()122cm AE t =- ,当ADE ABC ,即AD AE AB AC = 时, ∴122612t t -=,解得:3t = ; 当ADE ACB ,即AD AE AC AB = 时, ∴122126t t -=,解得: 4.8t = , 综上所述,以点A ,D ,E 为顶点的三角形与ABC 相似时的运动时间为3s 或4.8s .16.答案:045 1526 解析:(1)90A BEF G ∠=∠=∠=︒,BE EF =,易证ABE GEF ≅△△,EG AB AD ∴==,GF AE =,DG AE GF ∴==,DFG ∴△是等腰直角三角形,45FDG ∴∠=︒.(2)由(1)可知DFG △是等腰直角三角形.又22DF =,2DG GF ∴==,123CD BC AB EG ED DG ∴====+=+=.如图,分别延长GF ,BC ,两线交于点H ,则//CD GH ,3GH CD ==,2CH DG ==,EDM EGF ∴△△,BNC BFH △△,MD ED GF EG ∴=,NC BC FH BH=, 即123MD =,33232NC =-+, 23MD ∴=,35NC =, 232633515MN CD MD NC ∴=--=--=.三.解答题(共6题,共66分)温馨提示:解答题应将必要的解答过程呈现出来!17.解析:(1)∵∠AED =∠B ,∠BAC =∠DAE ,∴△AED ∽△ABC ;(2)∵△AED ∽△ABC ,∴∠ADE =∠ACB ,∵AF 平分∠BAC ,∴∠DAG =∠CAF ,∴△ADG ∽△ACF , ∴2=3AG AD AF AC =.18.解析:(1)∵四边形ABCD 是平行四边形,∴AD ∥BC ,且AD =BC ,∴∠MDN =∠CBN ,又∵∠BNC =∠DNM ,∴△MND ∽△CNB ,∴BNDN BC DM =, ∵M 为AD 的中点, ∴BC AD DM 2121==, ∴DN :BN =1:2;(2)连接OM ,∵△MND ∽△CNB ,DN :BN =1:2;∴MN :CN =1:2,∴MC :CN =3:2,∴S △OCM :S △OCN =3:2,∵S △OCN =2,∴S △OCM =3,∴S △ACM =2S △OCM =6,∴S 四边形AONM =S △ACM ﹣S △OCN =6﹣2=4.19.解析:(1)由题意,得//DE BC ,所以ADE ABC ∽△△, 所以14AD DE AB BC ==. 因为8AB =,所以2AD =.(2)设ABC △的面积为S ,ADE △的面积为1S ,CEF △的面积为2S . 因为14AD AB =, 所以21116S AD S AB ⎛⎫== ⎪⎝⎭. 因为11S =,所以16S =.因为34CE CA =, 所以同理可得29S =,所以平行四边形BFED 的面积126S S S =--=.20.解析:(1)证明:∵AG 平分∠BAC ,∴∠BAG =∠FAC ,又∵∠G =∠C ,∴△ABG ∽△AFC ;(2)由(1)知,△ABG ∽△AFC ,∴ACAG AF AB =, ∵AC =AF =b ,∴AB =AG =a ,∴FG =AG ﹣AF =a ﹣b ;(3)∵∠CAG =∠CBG ,∠BAG =∠CAG ,∴∠BAG =∠CBG ,∵∠ABD =∠CBE ,∴∠BDG =∠BAG +∠ABD =∠CBG +∠CBE =∠EBG ,又∵∠DGB =∠BGE ,∴△DGB ∽△BGE , ∴GE BG BG GD =, ∴GD GE BG ⨯=2.21.解析:(1)∵平行四边形ABCD ,射线BE 与CD 的延长线交于点P , ∴AB ∥CD ,∴∠ABF =∠P ,∵∠ABF =∠ACF ,∴∠ACF =∠P ,∵∠CEF =∠PEC ,∴△CEF ∽△PEC ,∴CEEF PE CE =, 即CE 2=EF •PE ;(2))∵平行四边形ABCD ,射线BE 与CD 的延长线交于点P , ∴AB ∥CD ,AB =CD ,AD ∥BC ,∴∠ABF =∠P ,∵∠AEB =∠CEP ,∴△BEA ∽△PEC ,∴CPAB PE BE =, ∵点D 是CP 的中点, ∴CP =2CD =2AB ,点F 是BP 的中点,∴2132=PE解得:34=PE ,∴PF =21BP =21(BE +PE )=33 ∴EF =PE ﹣PF =322.解析:(1)△BPQ 是等边三角形当t =2时AP =2×1=2,BQ =2×2=4∴BP =AB ﹣AP =6﹣2=4∴BQ =BP又∵∠B =60°∴△BPQ 是等边三角形;(2)过Q 作QE ⊥AB ,垂足为E在Rt △BEQ 中,∠BQE =90°﹣∠B =30°,QB =2t , ∴BE =t ,QE =3t 由AP =t ,得PB =6﹣t∴S △BPQ =21×BP ×QE =21(6﹣t )×3t =t t 33232+- ∴t t s 33232+-=; (3)∵QR ∥BA∴∠QRC =∠A =60°,∠RQC =∠B =60°∴△QRC 是等边三角形∴QR =RC =QC =6﹣2t∵BE =BQ •cos60°=21×2t =t ∴EP =AB ﹣AP ﹣BE =6﹣t ﹣t =6﹣2t∴EP ∥QR ,EP =QR∴四边形EPRQ 是平行四边形∴PR =EQ =3t又∵∠PEQ =90°,∴∠APR =∠PRQ =90°∵△APR ∽△PRQ , ∴AP PR PR QR =, ∴t t tt 3326=- 解得t =56 ∴当t =56时,△APR ∽△PRQ .23.解析:(1)抛物线24y ax ax =-,令120,0,4y x x === , 抛物线对称轴为422a x a-=-= , ∵B 点在抛物线上,且BC =6,∴B 点横坐标为6252+= , ∵B 点在直线12y x =上, ∴代入B 点横坐标求得52y =,即55,2B ⎛⎫ ⎪⎝⎭ , 将55,2B ⎛⎫ ⎪⎝⎭代入24y ax ax =-,得:525202a a =-,解得12a = ; (2)由(1)知12a =,所以抛物线为2122y x x =- , ∵P 是线段BC 上一点,PF x ⊥轴,∴E 、F 的横坐标15x -≤≤ , 设EF 的最大值为M ,E 、F 横坐标相同,则22111522222M x x x x x ⎛⎫=--=-+ ⎪⎝⎭,为开口向下的抛物线,有最大值,2215404252214842ac b M a ⎛⎫⎛⎫⨯-⨯- ⎪ ⎪-⎝⎭⎝⎭===-⨯,∴EF 的最大值为258; (3)存在, 如图:EF 交x 轴于点M∵//BC x 轴,∴OEM BEP , ∵BEP GBP , ∴OEM GBP , ∴OM EM GP BP= , ∵P 在射线BC 上且可形成△GPB ,55,2B ⎛⎫ ⎪⎝⎭, 设P 点横坐标为x ,∴P 点横坐标5x < ,∴5PB x =- ,G 点、E 点、F 点横坐标都为x , ∵E 在直线12y x =上, ∴1,2OM x EM x == , ∵G 为点F 关于直线BC 的对称点,且F 在抛物线2122y x x =-上, ∴21,22F x x x ⎛⎫- ⎪⎝⎭, 即2122MF x x =- , ∴215222PF x x =-+ , ∴215222PG x x =-+ , ∴OM EM GP BP ==212155222x x xx x =--+ 解得:123,5x x == ,∵5x <,∴取3x = , ∴2152422PG x x =-+= , ∴G 点纵坐标为513422+= ,∴133,2G ⎛⎫ ⎪⎝⎭.。
【九年级】九年级上册第4章相似三角形单元试题(浙教版带答案)

【九年级】九年级上册第4章相似三角形单元试题(浙教版带答案)M第4章相似三角形检测题(本试卷满分120分,时间:120分钟)一、(每小题3分,共30分)1.已知四条线段是成比例线段,即,下列说法错误的是()A.B.C.D.2.若,且,则的值是()A.14B.42C.7D.3.下列四组图形中,不是相似图形的是()4.已知两个相似多边形的面积比是9?16,其中较小多边形的周长为36 cm,则较大多边形的周长为( )A.48 cmB.54 cmC.56 cmD.64 cm5.如图,在△ 中,点分别是的中点,则下列结论:① ;②△ ∽△ ;③ .其中正确的有()A.3个B.2个C.1个D.0个6.如图,已知 // , // ,分别交于点,则图中共有相似三角形()A.4对B.5对C. 6对D.7对7.如图,在△ 中,∠ 的垂直平分线交的延长线于点,则的长为()A. B. C. D.8.已知△ 如图所示,则下列4个三角形中,与△ 相似的是()9.(2021•四川中考)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于点D.则△BCD与△ABC的周长之比为()A. 1?2B. 1?3C. 1?4D. 1?510.手工制作课上,小红利用一些花布的边角料,剪裁后装裱手工画.下面四个图案是她剪裁出的空心不等边三角形、等边三角形、正方形和矩形花边,其中每个图案花边的宽度都相同,那么每个图案中花边的内外边缘所围成的几何图形不相似的是()二、题(每小题3分,共24分)11.如果一个三角形的三边长为5、12、13,与其相似的三角形的最长的边为39,那么较大的三角形的周长为_______,面积为________.1 2.已知,且,则 _______.13.将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC =3,BC=4,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是.14. 若,则 .15.如图是小明设计用手电来测量某古城墙高度的示意图,点处放一水平的平面镜,光线从点出发经平面镜反射后刚好射到古城墙的顶端处,已知,,且测得,,,那么该古城墙的高度是_____ .16.已知五边形∽五边形,17.如图,在△中,分别是边上的点, , 则 _______.18.如图,△ 三个顶点的坐标分别为,以原点为位似中心,将△ 缩小,位似比为,则线段的中点变换后对应点的坐标为_________.三、解答题(共66分)19.(8分)已知:如图,是上一点,∥ ,,分别交于点,∠1=∠2,探索线段之间的关系,并说明理由.20.(8分)已知:如图所示,正方形ABCD中,E是AC上一点,EF⊥A B于点F,EG⊥AD于点G,AB=6,AE∶EC=2∶1,求S四边形AFEG.21.(8分)试判断如图所示的两个矩形是否相似.22.(8分)如图,在6×8网格图中,每个小正方形边长均为1,点O和△ABC的顶点均在小正方形的顶点.(1)以O为位似中心,在网格图中作△A′B′C′和△ABC位似,且位似比为1 2;(2)连接(1)中的AA′,求四边形AA′C′C的周长(结果保留根号).23.(8分)已知:如图,在△ 中,∥ ,点在边上,与相交于点,且∠ .求证:(1)△ ∽△ ;(2)24.(8分)如图,在正方形中,分别是边上的点,连结并延长交的延长线于点(1)求证:;(2)若正方形的边长为4,求的长.25.(8分)下面的短文,并解答下列问题:我们把相似形的概念推广到空间:如果两个几何体大小不一定相等,但形状完全相同,就把它们叫做相似体.如图,甲、乙是两个不同的正方体,正方体都是相似的,它们的一切对应线段之比都等于相似比a∶b.设S甲、S乙分别表示这两个正方体的表面积,则.又设V甲、V乙分别表示这两个正方体的体积,则.(1)下列几何体中,一定是相似体的是()A.两个球体 B.两个圆锥体C.两个圆柱体D.两个长方体(2)请归纳出相似体的三条主要性质:①相似体的一切对应线段(或弧)长的比等于______;②相似体的表面积的比等于______;③相似体的体积的比等于_______.(3)假定在完全正常发育的条件下,不同时期的同一个人的人体是相似体,一个小朋友上幼儿园时身高为1.1米,体重为18千克,到了八年级时,身高为1.65米,问他的体重是多少?(不考虑不同时期人体平均密度的变化)26.(10分)类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.原题:如图①,在 ABCD中,点E是BC边的中点,点F是线段AE上一点,BF的延长线交射线CD于点G.若 =3,求的值.(1)尝试探究在图①中,过点E作EH∥AB交BG于点H,则AB和EH的数量关系是,CG和EH的数量关系是,的值是 .(2)类比延伸如图②,在原题的条件下,若 =m(m>0),则的值是 (用含m的代数式表示),试写出解答过程.(3)拓展迁移如图③,梯形ABCD中,DC∥AB,点E是BC的延长线上一点,AE和BD相交于点F.若=a, =b (a>0,b>0),则的值是 (用含a、b的代数式表示).第4章相似三角形检测题参考答案一、1.C 解析:由比例的基本性质知A、B、D项都正确,C项不正确.2.D 解析:设,则所以所以 .3.D 解析:根据相似图形的定义知,A、B、C项都为相似图形,D项中一个是等边三角形,一个是直角三角形,不是相似图形.4.A 解析:两个相似多边形的面积比是9?16,则相似比为3?4,所以两图形的周长比为3?4,即36?48,故选A.5.A 解析:因为点分别是的中点,所以是△ 的中位线.由中位线的性质可推出①②③全部正确.6.C 解析:△ ∽△ ∽△ ∽△ .7. B 解析:在△ 中,∠ 由勾股定理得因为所以 .又因为所以△ ∽△ 所以,所以,所以 .8.C 解析:由对照四个选项知,C项中的三角形与△ 相似.9.A 解析:易证△BCD与△BAC相似,而周长比等于相似比,相似比等于对应边的比,△BCD与△BAC的相似比=,且∠BCD =∠A=30°,由30°角所对的直角边等于斜边的一半,可得= .10.D 解析:选项A中,将里面的三角形任意一条边向两边延长与外面三角形的两边相交,利用平行线的性质可以得到内、外两三角形两个角对应相等,因此两三角形相似;B中,由于任意两个等边三角形相似,因此B中两三角形相似;同理C中两正方形相似;D 中内、外两矩形对应边不成比例,故两矩形不相似.二、题11.90,270 解析:设另一三角形的其他两边长分别为由题意得,所以又因为所以三角形是直角三角形,所以周长为12.4 解析:因为,所以设,所以所以13. 或2 解析:设,由折叠的性质知,当△ ∽△ 时,,∴ ,解得 .当△ ∽△ 时, ,∴ ,解得.∴ 的长度是或2.14. 解析:设,则,,,∴ .15.8 解析:由反射角等于入射角知∠ ∠ ,所以△ ∽△ 所以,所以,所以16. 解析:因为五边形∽五边形所以 .又因为五边形的内角和为所以 .17. 解析:在△ 和△ 中,∵ , ,∴ △ ∽△ .∴ ∴ ∴ .18. 或解析:∵ (2,2),(6,4),∴ 其中点坐标为(4,3),又以原点为位似中心,将△ 缩小,位似比为,∴ 线段的中点变换后对应点的坐标为或 .三、解答题19.解: . 理由如下:∵ ∠ ∠ ,∴ .又∵ ∴ △ ∽△ ,∴ ,即 .20.分析:通过观察可以知道四边形是正方形,的值与的值相等,从而可以求出的长;根据相似多边形的面积比等于相似比的平方可以求出四边形的面积.解:已知正方形ABCD,且EF⊥AB,EG⊥AD,∴ EF∥CB,EG∥DC.∴ 四边形AFEG是平行四边形.∵ ∠1 ∠2 45°,∴ .又∵ ∠ ,∴ 四边形AFEG是正方形,∴ 正方形ABCD∽正方形AFEG,∴ S正方形ABCD∶S正方形AFEG=AB2∶AF2(相似多边形的面积比等于相似比的平方).在△ABC中,EF∥CB ,∴ AE∶EC=AF∶FB=2∶1.又,∴ .∴ S正方形ABCD∶S正方形AFEG=36∶16,∴ .21.分析:要判定两个多边形相似,必须对应角相等,对应边成比例,因矩形的四个角都是直角,符合对应角相等,只要证明对应边成比例即可.解:因为两个图形都是矩形,显然它们的四个角都分别相等.从图中数据观察可知小矩形的长为20,宽为10,于是两个矩形的长之比为 = ,宽之比为 ,符合对应边成比例,对应角相等,故这两个矩形是相似的.22.解:(1)如图.(2)四边形的周长=4+6 .23.证明:(1)∵ ,∴ ∠ .∵ ∥ ,∴ ,.∴ .∵ ,∴ △ ∽△ .(2)由△ ∽△ ,得.∴ .由△ ∽△ ,得.又∵ ∠ ∠ ,∴ △ ∽△ .∴ .∴ .∴ .24.(1)证明:在正方形中,, .∵ ∴ ,∴ ,∴ .(2)解:∵ ∴ ,由(1)得,∴ ,∴ .由∥ ,得,∴ △ ∽△ ,∴ ,∴ .25.分析:本题是相似图形的推广,理解相似正方体的概念和性质,由此类比,从而得出相似体的性质.解:(1)A(2)①相似比②相似比的平方③相似比的立方(3)可由相似体的特征,直接列方程求解.设他的体重为千克,则.解得(千克).答:他的体重为60.75千克.26.分析:(1)∵ EH∥AB,∴ ∠BAF=∠HEF,∠ABF=∠EHF,∴ △ABF∽△EHF.∴ = =3,∴ AB=3EH.∵ 四边形ABCD是平行四边形,∴ AB∥CD.又EH∥AB,∴ EH∥CD.∴ △BEH∽△BCG,∴ = =2,即CG=2EH.∴ === .(2)作EH∥AB交BG于点H,则△EFH∽△AFB,△BEH∽△BCG,∴ 可证AB=mEH,CG =2EH,从而== .(3)过点E作EH∥AB交BD的延长线于点H,则△BCD∽△BEH,△ABF∽△EHF,∴ = , = .∴ EH= , = =ab.解:(1)AB=3EH;CG=2EH; .(2) .解答过程如下:作EH∥AB交BG于点H,则△EFH∽△AFB.∴ = =m,∴ AB=mEH.∵ AB=CD,∴ CD=mEH.∵ EH∥AB∥CD,∴ △BEH∽△BCG.∴ ==2,∴ CG=2EH.∴ = = .(3)ab.5 Y感谢您的阅读,祝您生活愉快。
【浙教版】九年级数学上册 第4章《相似三角形》检测题(含答案)

九(上)第4章检测题(时间:120分钟 满分:120分)一.选择题(每小题3分,共30分)1.若互不相等的四条线段a ,b ,c ,d 满足a b =c d ,m 是任意实数,则下列各式中,一定成立的是( D ) A.a c =d b B.a +m b =c +m dC.a +m b +m =c +m d +mD.a +cm c =b +dm d2.如图,已知AB ∥CD ,AD 与BC 相交于点P ,AB =4,CD =7,AD =10,则AP 的长等于( A )A.4011B.407C.704D.7011第2题图 第3题图 第4题图 第5题图 第6题图3.如图,DE 是△ABC 的中位线,延长DE 至F 使EF =DE ,连结CF ,则S △CEF ∶S 四边形BCED 的值为( A )A.1∶3B.2∶3C.1∶4D.2∶54.如图,点A ,B ,C ,D 的坐标分别是(1,7),(1,1),(4,1),(6,1),以C ,D ,E 为顶点的三角形与△ABC 相似,则点E 的坐标不可能是( B )A.(6,0)B.(6,3)C.(6,5)D.(4,2)5.如图,直线AC ,AD 分别交⊙O 于点B ,C ,D ,E ,BD ,CE 相交于点F ,连结CD 和BE ,则图中共有相似三角形( C )A.2对B.3对C.4对D.5对6.如图,给出下列条件,其中能单独判定△ABC ∽△ACD 的个数为( C )①∠B =∠ACD ;②∠ADC =∠ACB ;③AC CD =AB BC;④AC 2=AD ·AB . A.1个 B.2个 C.3个 D.4个7.已知a 4=b 5=c 6,且a -b +c =10,则a +b -c 的值为( A ) A.6 B.5 C.4 D.38.如果线段AB =15,点C 是AB 上靠近点B 的黄金分割点,那么AC 的值约为( B )A.0.618B.9.27C.9.27或5.73D.5.739.如图,O 为矩形ABCD 的中心,将直角三角形的直角顶点与O 重合,转动三角板使两直角边始终与BC ,AB 相交,交点分别为M ,N .如果AB =4,AD =6,OM =x ,ON =y ,则y 与x 的表达式是( D )A.y =23xB.y =6xC.y =xD.y =32x 10.如图,四边形ABCD .CEFG 都是正方形,点G 在线段CD 上,连结BG ,DE ,DE 和FG 相交于点O .设AB =a ,CG =b (a >b ).下列结论:①△BCG ≌△DCE ;②BG ⊥DE ;③DG GC =GO CE;④(a -b )2·S △EFO =b 2·S △DGO .其中结论正确的个数是( B )A.4个B.3个C.2个D.1个二.填空题(每小题4分,共24分)11.已知线段a =3 cm ,b =6 cm ,若线段b 是线段a 与c 的比例中项,则c =__12__cm. 12.如图是小明设计用手电来测量某古城墙高度的示意图,点P 处放一水平的平面镜,光线从点A 出发经平面镜反射后刚好射到古城墙CD 的顶端C 处.已知AB ⊥BD ,CD ⊥BD ,测得AB =1.2米,BP =1.8米,PD =12米,那么该古城墙的高度是__8__米.第12题图 第14题图 第15题图 第16题图13.在△ABC 中,AB =8 cm ,AC =6 cm ,在AB 边上有一点D ,AD =4 cm ,在AC 边上有一动点E .试问:当AE =__3或163__cm 时,△ABC 与△ADE 相似.14.如图,△ABC 的中位线DE =5 cm ,把△ABC 沿DE 折叠,使点A 落在边BC 上的点F 处,若A ,F 两点间的距离是8 cm ,则△ABC 的面积为__40__cm 2.15.如图,在直角坐标系中有两点A (4,0),B (0,2),如果点C 在x 轴上(C 与A 不重合).当点C 的坐标为__(1,0)或(-1,0)或(-4,0)__时,使得由点B ,O ,C 组成的三角形与△AOB 相似.16.如图,△ABC 是边长为6 cm 的等边三角形,被一平行于BC 的矩形所截,被截成相同高度的三等份,则图中阴影部分的面积为__33__cm2.三.解答题(共66分)17.(7分)如图,▱ABCD中,AC,BD交于点O,BC=18,OE=2,BO=4,求AF.解:1218.(7分)如图,已知AB是⊙O的直径,点C是⊙O上一点,连结BC,AC,过点C作直线CD⊥AB于点D,点E是AB上一点,直线CE交⊙O于点F,连结BF,与直线CD交于点G.求证:BC2=BG·BF.解:证△BCG∽△BFC19.(8分)小彬星期天到郊外玩,来到一条不能到达对岸的河边,如图,他决定测量一下小河的宽度(河岸大致平行).小彬找到与河岸大致垂直的A,B两个目标,顺河岸找到点D,使C点与A,B在同一条直线上,E点与A,D在同一条直线上,并使CE∥BD,测得BC=a,BD=b,CE=c.(1)求小河的宽度AB;(用含a,b,c的代数式表示)(2)请你再设计一种利用皮尺和标杆测量河宽的方案,画出图形,用a,b,…,表示测量所得的数据,并求出小河的宽度.解:(1)AB =ab c -b(2)如图BC =a ,CD =b ,DE =c ,则AB =ac b 20.(8分)如图,在△ABC 中,∠BAC 的角平分线AD 交BC 于E 点,交△ABC 的外接圆⊙O 于D 点.(1)求证:△ABE ∽△ADC ;(2)连结BD ,OB ,OC ,OD ,且OD 交BC 于点F ,若点F 恰好是OD 的中点.求证:四边形OBDC 是菱形.解:(1)∵∠BAC 的角平分线AD ,∴∠BAE =∠CAD ,∵∠ABE =∠ADC ,∴△ABE ∽△ADC (2)∵∠BAD =∠CAD ,∴BD ︵=CD ︵,∵OD 为半径,∴DO ⊥BC ,∵F 为OD 的中点,∴OB =BD ,OC =CD ,∵OB =OC ,∴OB =BD =CD =OC ,∴四边形OBDC 是菱形21.(8分)如图,在Rt△ABC 中,∠C =90°,AC =6 cm ,BC =8 cm ,D ,E 分别是AC ,AB 的中点,连结DE ,点P 从点D 出发,沿DE 方向匀速运动,速度1 cm/s ;同时,点Q 从点B 出发,沿BA 方向匀速运动,速度为2 cm/s ,当点P 停止运动时,点Q 也停止运动,连结PQ ,设运动时间为t (s)(0<t <4),当t 为何值时,PQ ⊥AB?解:由△PEQ ∽△ABC ,则有4-t 10=2t -58,解得t =411422.(8分)如图,M 为线段AB 的中点,AE 与BD 交于点C ,∠DME =∠A =∠B =α,且DM 交AC 于F ,ME 交BC 于G ,连结FG .(1)写出图中两对相似三角形,并证明其中的一对;(2)如果α=45°,AB =42,AF =3,求FG 的长.解:(1)△AMF ∽△BGM ,△DMG ∽△DBM ,△EMF ∽△EAM (不唯一) (2)53 点拨:由△AMF ∽△BGM ,得出BG =83.∠A =∠B =45°,可推出∠FCG =90°,以及AC =BC =4.在Rt △CFG 中,FG =12+(43)2=5323.(10分)在锐角△ABC 中,AB =4,BC =5,∠ACB =45°,将△ABC 绕点B 按逆时针方向旋转,得到△A 1BC 1.(1)如图①,当点C 1在线段CA 的延长线上时,求∠CC 1A 1的度数;(2)如图②,连结AA 1,CC 1.若△ABA 1的面积为4,求△CBC 1的面积.解:(1)90° (2)证△ABA 1∽△CBC 1,由S △ABA1S △CBC 1=(AB BC )2=1625,又∵S △ABA 1=4,∴S △CBC 1=25424.(10分)如图,正方形ABCD 的边长为1,AB 边上有一动点P ,连结PD ,线段PD 绕点P 顺时针旋转90°后,得到线段PE ,且PE 交BC 于点F ,连结DF ,过点E 作EQ ⊥AB 的延长线于点Q .(1)求线段PQ 的长;(2)点P 在何处时,△PFD ∽△BFP ,并说明理由.解:(1)根据题意得:PD =PE ,∠DPE =90°,∴∠APD +∠QPE =90°.∵四边形ABCD 是正方形,∴∠A =90°,∴∠ADP +∠APD =90°,∴∠ADP =∠QPE ,∵EQ ⊥AB ,∴∠A =∠Q =90°.在△ADP 和△QPE 中,⎩⎪⎨⎪⎧∠A =∠Q ,∠ADP =∠QPE ,PD =PE ,∴△ADP ≌△QPE (AAS ),∴PQ =AD =1(2)∵△PFD ∽△BFP ,∴PB BF =PD PF.∵∠ADP =∠EPB ,∠CBP =∠A ,∴△DAP ∽△PBF ,∴PD PF =AP BF ,∴AP BF =PB BF ,∴PA =PB ,∴PA =12AB =12.∴当P 在AB 的中点时,△PFD ∽△BFP。
浙教版九年级数学上册 第四章《相似三角形》基础训练卷(含答案)

第四章《相似三角形》基础测试卷一、选择题(每题3分,共30分)1. 下列各组线段的长度成比例的为()A. 2 cm ,3 cm ,4 cm ,5 cmB. 2.5 cm ,3.5 cm ,4.5 cm ,6.5 cmC. 1.1 cm ,2.2 cm ,4.4 cm ,8.8 cmD. 1 cm ,3 cm ,4 cm ,6 cm2. 若△ABC ∽△A ′B ′C ′,相似比为1:2,则△ABC 与△A ′B ′C ′的面积的比为( )A .1:2B .2:1C .1:4D .4:13. 如图,A ,B 两地被池塘隔开,小明通过下列方法测出了A 、B 间的距离:先在AB 外选一点C ,然后测出AC ,BC 的中点M ,N ,并测量出MN 的长为12m ,由此他就知道了A 、B 间的距离.有关他这次探究活动的描述错误的是( )A. AB =24mB. MN ∥ABC. △CMN ∽△CABD. CM :MA =1:24.已知,则的值为 ( )0432≠==c b a cb a +A. B. C.2 D.5445215.用一个2倍的放大镜照一个ΔABC ,下列命题中正确的是()A.ΔABC 放大后角是原来的2倍B.ΔABC 放大后周长是原来的2倍C.ΔABC 放大后面积是原来的2倍D.以上的命题都不对3. 已知线段=9cm , =4cm , 是, 的比例中项,则等于( )a b x a b x A. 6cm B. -6cm C. ±6cm D. cm 8147. 下列叙述正确的是( )A. 任意两个等腰三角形相似;B. 任意两个等腰直角三角形相似C. 两个全等三角形不相似;D. 两个相似三角形的相似比不可能等于18.下列四个三角形,与右图中的三角形相似的是 ( )A .B .C .D .9.如图,在▱ABCD 中,点E 是边AD 的中点,EC 交对角线BD 于点F ,则EF :FC 等于( )A . 3:2B .3:1C .1:1D .1:2第9题 第10题10.如图所示,△ABC 中,AD ⊥BC 于D ,对于下列中的每一个条件①∠B +∠DAC =90° ②∠B =∠DAC ③CD :AD =AC :AB ④AB 2=BD ·BC其中一定能判定△ABC 是直角三角形的共有()A .3个 B .2个 C .1个D .0个二、填空题(每题4分,共24分)11.已知,则=_________26y x y x :12.如图,D 、E 分别是△ABC 的边AB 、AC 上的中点,则S △ADE :S △ABC = .第12题 第13题 第14题13.如图,小明用长为3m 的竹竿CD 做测量工具,测量学校旗杆AB 的高度,移动竹竿,使竹竿与旗杆的距离DB =12m ,则旗杆AB 的高为 m .14.如图,在△ABC 中,D 是AB 边上的一点,连接CD ,请添加一个适当的条件 ,使△ABC ∽△ACD .(只填一个即可)15.如图,AC ⊥CD ,垂足为点C ,BD ⊥CD ,垂足为点D ,AB 与CD 交于点O .若AC =1,BD =2,CD =4,则AB = .16.△ABC 中,D 、E 分别是边AB 与AC 的中点,BC =4,下面四个结论:①DE =2;②△ADE ∽△ABC ;③△ADE 的面积与△ABC 的面积之比为 1:4;④△ADE 的周长与△ABC 的周长之比为 1:4;其中正确的有 .(只填序号)三、简答题(共66分)17、(本题6分)已知a =3 cm ,b =6 cm ,求a ,b ,(a +b )的第四比例项.18、(本题8分)如图,在△ABC 和△DEF 中,∠A =∠D =90°,AB=DE =3,AC =2DF =4.判断这两个三角形是否相似?并说明为什么?E F19、(本题8分)如图,D是△ABC的边AC上的一点,连接BD,已知∠ABD=∠C,AB=6,AD=4,求线段CD的长.20、(本题10分)某一天,小明和小亮来到一河边,想用遮阳帽和皮尺测量这条河的大致宽度,两人在确保无安全隐患的情况下,现在河岸边选择了一点B(点B与河对岸岸边上的一棵树的底部点D所确定的直线垂直于河岸).①小明在B点面向树的方向站好,调整帽檐,使视线通过帽檐正好落在树的底部点D 处,如图所示,这时小亮测的小明眼睛距地面的距离AB=1.7米;②小明站在原地转动180°后蹲下,并保持原来的观察姿态(除身体重心下移外,其他姿态均不变),这时视线通过帽檐落在了DB延长线上的点E处,此时小亮测得BE=9.6米,小明的眼睛距地面的距离CB=1.2米.根据以上测量过程及测量数据,请你求出河宽BD是多少米?21.(本题10分)如图,在矩形ABCD中,AB=6,BC=8,沿直线MN对折,使A、C重合,直线MN交AC于O.(1)求证:△COM∽△CBA;(2)求线段OM的长度.22、(本题12分)如图,在四边形ABCD中,AB=AD,AC与BD交于点E,∠ADB=∠ACB.(1)求证:=;(2)若AB⊥AC,AE:EC=1:2,F是BC中点,求证:四边形ABFD是菱形.23、(本题12分)如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.(1)求线段CD的长;(2)设△CPQ的面积为S,求S与t之间的函数关系式,并确定在运动过程中是否存在某一时刻t,使得S△CPQ:S△ABC=9:100?若存在,求出t的值;若不存在,说明理由.参考答案一、选择题题号12345678910答案C C D B B A B B D A二、填空题三、简答题17、解:设a 、b 、(a +b )的第四比例项为x ,则有,x ba b a +=∴,x 963=x =18.18、解:(1) 不相似.在中,,;∵Rt BAC △90A ∠=°34AB AC ==,在中,,,Rt EDF △90D ∠=°32DE DF ==,..与不相似.12ABACDE DF ==∴,AB ACDE DF ≠∴Rt BAC ∴△Rt EDF △20、解:由题意得,∠BAD =∠BCE ,∵∠ABD =∠CBE =90°,∴△BAD ∽△BCE ,∴=,即=解得BD=13.6米.答:河宽BD是13.6米.21、(1)证明: A与C关于直线MN对称∴AC⊥MN∴∠COM=90°在矩形ABCD中,∠B=90°∴∠COM=∠B又 ∠ACB=∠ACB∴△COM∽△CBA(2) 在Rt△CBA中,AB=6,BC=8∴AC=10∴OC=5△COM∽△CBA∴OC OM=BC AB∴OM=15423、解:(1)∵∠ACB=90°,AC=8,BC=6,∴AB=10.∵CD⊥AB,∴S△ABC=BC•AC=AB•CD.∴CD===4.8.∴线段CD的长为4.8.(2)①过点P作PH⊥AC,垂足为H,如图2所示.由题可知DP=t,CQ=t.则CP=4.8﹣t.∵∠ACB=∠CDB=90°,∴∠HCP=90°﹣∠DCB=∠B.∵PH⊥AC,∴∠CHP=90°.∴∠CHP=∠ACB.∴△CHP∽△BCA.∴.∴.∴PH=﹣t.∴S△CPQ=CQ•PH=t(﹣t)=﹣t2+t.②存在某一时刻t,使得S△CPQ:S△ABC=9:100.∵S△ABC=×6×8=24,且S△CPQ:S△ABC=9:100,∴(﹣t2+t):24=9:100.整理得:5t2﹣24t+27=0.即(5t﹣9)(t﹣3)=0.解得:t=或t=3.∵0≤t≤4.8,∴当t=秒或t=3秒时,S△CPQ:S△ABC=9:100.。
浙教版九年级上《第四章相似三角形》期末复习试题(有答案)

期末复习:浙教版九年级数学学上册第四章相似三角形一、单选题(共10题;共30分)1.若△ABC∽△DEF,顶点A、B、C分别与D、E、F对应,且AB:DE=1:4,则这两个三角形的面积比为()A. 1:2B. 1:4C. 1:8D. 1:162.如图,在△ABC中,点D,E分AB,AC边上,DE∥BC,若AD:AB=3:4,AE=6,则AC等于()A. 3B. 4C. 6D. 83.△ABC和△DEF相似,且相似比为,那么它们的周长比是()A. B. C. D.4.如图,△ABC中,AD⊥BC于D ,下列条件:①∠B+∠DAC=90°;②∠B=∠DAC;③ = ;④AB2=BD•BC .其中一定能够判定△ABC是直角三角形的有()A. 1B. 2C. 3D. 45.若把△ABC的各边扩大到原的3倍后,得△A′B′C′,则下列结论错误的是()A. △ABC∽△A′B′C′B. △ABC与△A′B′C′的相似比为14C. △ABC与△A′B′C′的对应角相等D. △ABC与△A′B′C′的相似比为136.如果两个相似三角形对应边之比是1:4,那么它们的对应中线之比是()A. 1:2B. 1:4C. 1:8D. 1:167.如图,斜靠在墙上的梯子AB,梯脚B距墙面1.6米,梯上一点D距墙面1.4米,BD长0.55米,则梯子AB 的长为( )米A. 3.85B. 4.00C. 4.4D. 4.50.8.两个相似多边形的一组对分别是3cm和4.5cm,如果它们的面积之和是,那么较大的多边形的面积是()A. 44.8B. 42C. 52D. 549.在同一时刻,身高1.6米的小强在阳光下的影长为0.8米,一棵大树的影长为4.8米,则树的高度为()A. 10米B. 9.6米C. 6.4米D. 4.8米10.如图,正方形ABCD中,O为BD中点,以BC为边向正方形内作等边△BCE,连接并延长AE交CD于F,连接BD分别交CE、AF于G、H,下列结论:①∠CEH=45°;②GF∥DE;③2OH+DH=BD;④BG=√2DG;⑤S△BEC:S△BGC=√3+1。
浙教版数学九年级上册第四章相似三角形 单元测试(含答案)

浙教版数学九年级上册第四章相似三角形一、选择题1.已知c 是a 和b 的比例中项,a =2,b =18,则c =( )A .±6B .6C .4D .±32.如图,DE ∥BC ,在下列比例式中,不能成立的是()A .AD DB =AEECB .DE BC =AEEC C .AB AD =AC AED .DB EC =ABAC3.如果两个相似三角形的周长之比为5:7,那么这两个三角形的面积之比为( )A .5:7B .7:5C .25:49D .49:254.如图,已知AB ∥CD ∥EF ,AE =9,AC =6,BD =4,则BF 的长是( )A .5B .6C .7D .85.小明在测量楼高时,先测出楼房落在地面上的影长BA 为15米(如图),然后在A 处树立一根高2米的标杆,测得标杆的影长AC 为3米,则楼高为( )A .10米B .12米C .15米D .22.5米6.如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC 相似的是( )A .B .C.D.7.如图,△ABC与△DEF位似,点O为位似中心.已知OA:OD=1:2,则△ABC与△DEF的面积比为( ).A.1:2B.1:3C.1:4D.1:58.如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,设△OCD的面积为m,△OEB的面积为5,则下列结论中正确的是( )A.m=5B.m=45C.m=35D.m=109.如图,已知AB=AC,∠B<30°,BC上一点D满足∠BAD=120°,BDCD =73,则ADAC的值为( )A.12B.33C.13D.3210.如图,在边长为2的正方形ABCD中,对角线AC与BD相交于点O,点P是BD上的一个动点,过点P作EF∥AC,分别交正方形的两条边于点E,F,连接OE,OF,设BP=x,△OEF的面积为y,则能大致反映y与x之间的函数关系的图像为( )A .B .C .D .二、填空题11.如图,线段AC 、BD 交于点O ,请你添加一个条件: ,使△AOB ∽△COD .12.如图,点G 为△ABC 的重心,GE ∥AC ,若DE =2,则DC = .13.在某市建设规划图上,城区南北长为120cm ,该市城区南北实际长为36km ,则该规划图的比例尺是 .14.如图,在Rt △ABC 中,∠ABC =90°,AB =4,AC =5,AE 平分∠BAC ,点D 是AC 的中点,AE 与BD交于点O ,则的值AOOE .15.如图, EB 为驾驶员的盲区,驾驶员的眼睛点 P 处与地面 BE 的距离为1.6米,车头 FACD 近似看成一个矩形,且满足 3FD =2FA ,若盲区 EB 的长度是6米,则车宽 FA 的长度为 米.16.如图,在△ABC中,点D是AC边上一点,将△ABD沿BD翻折得到△EBD,BE与AC交于点F,设AF=x,EF=y.(1)当BE⊥AC,x=9,y=3时,AD的长是 ;(2)当BD=BF,2x=7y时,△DEF与△ABD的面积之比是 .三、解答题17.如图,已知D、E分别是△ABC的边AB、AC上的点,DE∥BC,ADBD =32,求DEBC的值.18.如图,在△ABC中,D为BC上一点,∠BAD=∠C.(1)求证:△ABD∽△CBA;(2)若AB=6,BD=3,求CD的长.19.在设计人体雕像时,使雕像的上部(腰以上)与下部(腰以下)的高度比,等于下部与全部的(全身)的高度比,可以增加视觉美感,按比例,如果雕像的高为2m,那么它的下部设计为多高?(结果保留小数点后两位)参考数据:2=1.414,3=1.732,5=2.23620.如图,在矩形ABCD中,AB=6,BC=4,E是边BC上的一点(不与B、C重合),DF⊥AE,垂足为F.(1)求证:△ABE∽△DFA;S△ABE,求BE的长.(2)若S△DFA=1321.如图,在△ABC中,AD是BC上的高,且BC=3,AD=2,矩形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB、AC上.(1)设EF=x(0<x<2),矩形EFGH的周长为y,求y关于x的函数解析式;(2)当EFGH为正方形时,求正方形EFGH的面积.22.如图,矩形ABCD中,点M在对角线BD上,过点A、B、M的圆与BC交于点E.(1)若AM=4,EB=EM=3,求BM.(2)若AB=6,BC=8,①求AM:ME.②若BM=7,求BE.23.如图,在矩形ABCD中,AB=6cm,BC=8cm,对角线AC,BD交于点O.点P从点A出发,沿AD方向匀速运动速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为1cm/s;当一个点停止运动时,另一个点也停止运动.连接PO并延长交BC于点E,过点Q作QF//AC,交BD于点F,设运动时间为t(s)(0<t<6),解答下列问题:(1)当t为何值时,△AOP是等腰三角形;(2)设五边形OECQF的面积为S(c m2),试确定S与t的函数关系式;(3)在运动过程中,当S五边形OECQF:S△ACD=9:16时.直接写出t的值.答案解析部分1.【答案】A2.【答案】B3.【答案】C4.【答案】B5.【答案】A6.【答案】A7.【答案】C8.【答案】B9.【答案】A10.【答案】C11.【答案】AB∥CD(答案不唯一)12.【答案】6.13.【答案】1:3000014.【答案】9415.【答案】12716.【答案】5;1417.【答案】3518.【答案】(1)证明:∵∠BAD=∠C,∠B=∠B,∴△ABD∽△CBA(2)解:设DC=x,∵△ABD∽△CBA,∴ABBD=BCAB,∴63=2+x6,解得,x=9;即CD=719.【答案】1.24米.20.【答案】(1)证明:∵四边形ABCD是矩形,AB=6,BC=4,∴∠B=90°,AD∥BC,AD=BC=4,∴∠AEB=∠DAF,∵DF⊥AE,∴∠DFA=90°,∴∠B=∠DFA,∴△ABE∽△DFA;(2)解:∵△ABE∽△DFA,S△DFA=13S△ABE,∴(AEAD )2=S△ABES△DFA=3,∴AEAD=3或AEAD=−3(负数不符合题意,舍去),∴AE=3AD=43,∴BE=AE2−AB2=(43)2−62=12=23,∴BE的长为23.21.【答案】(1)解:设AD,EH交于点M,∵矩形EFGH,∴EH∥BC,AM⊥EH,∴△ABC∼△AEH,∴EHBC=AMAD∵EF=DM=x,AD=2∴AM=2−x∴EH3=2−x2∴EH=32(2−x)∴y=2(EH+EF)=2(3−32x+x)=−x+6(0<x<2)∴y关于x的函数解析式为∴y=−x+6(0<x<2)(2)解:当EFGH为正方形时,∴EF=EH,由(1)得:EF =x ,EH =32(2−x),∵EF =EH ,∴x =3(2−x)2,∴x =65,即EF =65.正方形EFGH 的面积=65×65=3625.22.【答案】(1)245(2)①43,②17423.【答案】(1)解:在矩形ABCD 中,AB =6cm ,BC =8cm ,∴AC =10,①当AP =PO =t ,如图1,过P 作PM ⊥AO 于点M ,∴AM =12AO =52,∵∠PMA =∠ADC =90°,∠PAM =∠CAD ,∴△APM∽△ACD ,∴AP AC =AM AD,∴AP =t =258,②当AP =AO =t =5,∴当t 为258或5时,△AOP 是等腰三角形;(2)解:如图2,过点O 作OH ⊥BC 交BC 于点H ,则OH =12CD =12AB =3cm ,由矩形的性质可知∠PDO =∠EBO ,DO =BO ,又得∠DOP =∠BOE ,∴△DOP≌BOE(ASA),∴BE =PD =8−t ,则S △BOE =12BE ⋅OH =12×3(8−t)=12−32t.∵FQ//AC ,∴△DFQ∽△DOC ,相似比为DQ DC =t6,∴S △DFQ S △DOC =t 236,∵S △DOC =14S 矩形ABCD =14×6×8=12c m 2,∴S △DFQ =12×t 236=t 23,∴S 五边形OECQF =S △DBC −S △BOE −S △DFQ =12×6×8−(12−32t)−t 23=−13t 2+32t +12;∴S 与t 的函数关系式为S =−13t 2+32t +12;(3)t =3或32。
浙教版九年级数学上册第四章:相似三角形基本模型练习题(含答案)
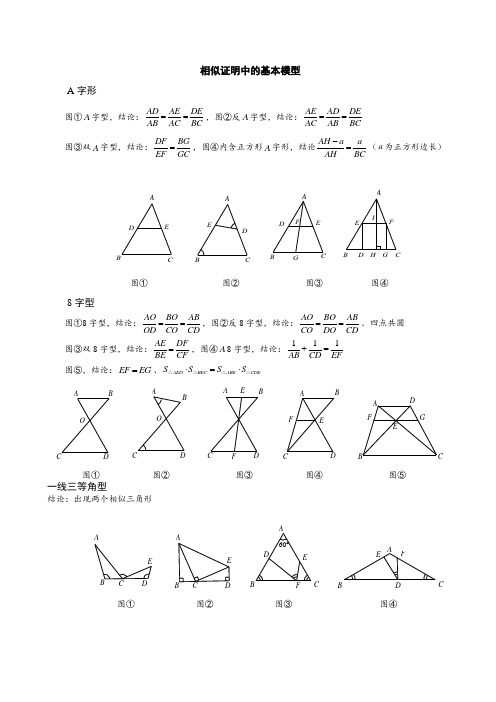
相似证明中的基本模型A 字形图①A 字型,结论:AD AE DE AB AC BC ==,图②反A 字型,结论:AE AD DEAC AB BC== 图③双A 字型,结论:DF BG EF GC =,图④内含正方形A 字形,结论AH a aAH BC-=(a 为正方形边长)IH G FED CB AGFEDC BAEDCB A ED C BA图① 图② 图③ 图④8字型图①8字型,结论:AO BO AB OD CO CD ==,图②反8字型,结论:AO BO AB CO DO CD==、四点共圆 图③双8字型,结论:AE DF BE CF=,图④A 8字型,结论:111AB CD EF += 图⑤,结论:EF EG =、AED BEC ABE CDE S S S S ⋅=⋅△△△△EFD C BA F ED C BAOD C BAODC BAGFED CB A图① 图② 图③ 图④ 图⑤一线三等角型结论:出现两个相似三角形HE DC B AE DC BAEDCBAC60°F E DCB AFED CB A图① 图② 图③ 图④角分线定理与射影定理图①内角分线型,结论:AB BD AC DC =,图②外角分线型,结论:AB BDAC CD= 图③斜射影定理型,结论:2AB BD BC =⋅,图④射影定理型,结论:1、2AC AD AB =⋅,2、2CD AD BD =⋅,3、2BC BD BA =⋅D C BD BCAEDB AD B A梅涅劳斯型常用辅助线G FEDCBAGFEDCBA G E DC B ADEFCBA四、相似证明中的面积法面积法主要是将面积的比,和线段的比进行相互转化来解决问题. 常用的面积法基本模型如下:如图:1212ABC ACDBC AHS BCS CD CD AH ⋅⋅==⋅⋅△△. 图1:“山字”型H DC B A如图:1212ABC BCDBC AHS AH AO S DG OD BC DG ⋅⋅===⋅⋅△△. 图2:“田字”型G HODCBA如图:ABD ABD AED ACE AED ACE S S S AB AD AB ADS S S AE AC AE AC⋅=⋅=⋅=⋅△△△△△△.图3:“燕尾”型CDEB A考点一:相似三角形【例1】 如图,D 、E 是ABC ∆的边AC 、AB 上的点,且AD AC ⋅=AE AB ⋅,求证:ADE B ∠=∠.EDCBA【答案】∵AD AC AE AB ⋅=⋅ ∴AD ABAE AC=∵DAE BAC ∠=∠∴DAE ∆∽BAC ∆∴ADE B ∠=∠ 【例2】 如图,在ABC ∆中,AD BC ⊥于D ,CE AB ⊥于E ,ABC ∆的面积是BDE ∆面积的4倍,6AC =,求DE 的长.ED CB A【答案】∵AD BC ⊥,CE AB ⊥,ABD CBE ∠=∠ ∴ABD ∆∽CBE ∆∴BE BCBD AB=∵EBD CBA ∠=∠ ∴BED ∆∽BCA ∆∴11322DEDE AC AC===⇒== 【例3】 如图,ABC △中,60ABC ∠=︒,点P 是ABC △内一点,使得APB BPC CPA ∠=∠=∠,86PA PC ==,,则PB =________.PCBA【解析】120APB BPC ∠=∠=︒,60BAP ABP ABC ABP CBP ∠=︒-∠=∠-∠=∠,故ABP BCP △∽△,2PB PA PC =⋅.【例4】 如图,已知三个边长相等的正方形相邻并排,求EBF EBG ∠+∠.HGFED CB A【答案】45︒ 【解析】连接DF 、CG ,则45EDF EBF DFB ∠=∠+∠=︒,若DFB EBG ∠=∠,则EBF EBG ∠+∠可求,问题的关键是证明BCG FDB △∽△.考点二:相似三角形与边的比例☞考点说明:可运用相似三角形模型,常用A 字形与8字形【例5】 在ABC ∆中,BD CE =,DE 的延长线交BC 的延长线于P , 求证:AD BP AE CP ⋅=⋅.PE D CBA MPED C BA【答案】过C 作CM AB ∥交DP 于M ,∵CM AB ∥,∴PCM PBD ∆∆∽, ∴CM PC BD PB =, ∵CM AB ∥,∴CEM AED ∆∆∽, ∴CM AD CE AE =, ∵BD CE =, ∴CM CM CE BD =, ∴PC AD PB AE=, ∴AD BP AE CP ⋅=⋅【例6】 如图,在ABC ∆的边AB 上取一点D ,在AC 取一点E ,使AD AE =,直线DE 和BC 的延长线相交于P ,求证:BP BDCP CE= PEDCBA4321MPE D CBA【答案】过C 作CM AB ∥交DP 于M ,∵CM AB ∥,∴PCM PBD ∆∆∽, ∴BP BD CP CM =, ∵CM AB ∥, ∴14∠=∠, 又∵AD AE =,∴12∠=∠,∴24∠=∠, ∵23∠=∠, ∴34∠=∠, ∴CM CE = ∴BP BD CP CE= 【例7】 如图,M 、N 为ABC △边BC 上的两点,且满足BM MN NC ==,一条平行于AC 的直线分别交AB 、AM 和AN 的延长线于点D 、E 和F .求证:3EF DE =.F NMED CBAK HF N MG ED CBA【答案】过M ,N 分别作AC 的平行线交AB 于H ,G 两点,NH 交AM 于K ,∵BM MN NC ==, ∴BG GH HA ==,易知12HK GM =,12GM HN =,∴14HK HN =,即13HK KN =,又∵DF HN ∥, ∴13DE HK EF KN ==,即3EF DE =. 考点三:相似三角形与内接矩形☞考点说明:内接矩形问题是相似三角形中比较典型的问题,考查了相似三角形对应高的比等于相似比【例1】 一块直角三角形木板的一条直角边AB 长为1.5米,面积为1.5平方米,工人师傅要把它加工成一个面积最大的正方形桌面,请甲、乙两位同学进行设计加工方案。
浙教版九年级上册数学第4章 相似三角形含答案(精品)
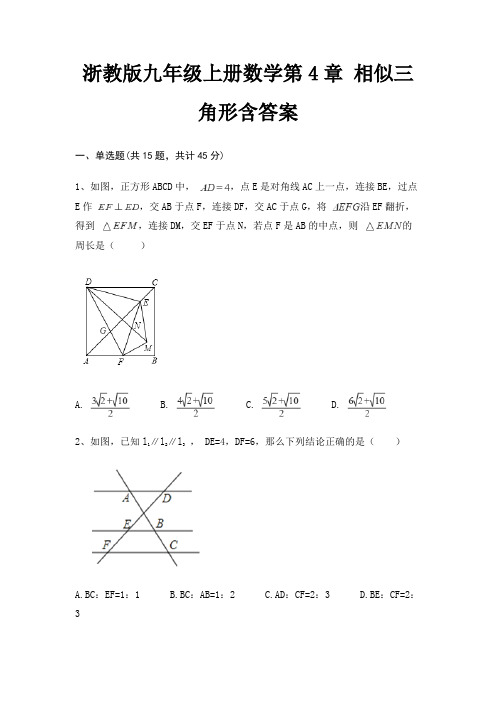
浙教版九年级上册数学第4章相似三角形含答案一、单选题(共15题,共计45分)1、如图,正方形ABCD中,,点E是对角线AC上一点,连接BE,过点E作,交AB于点F,连接DF,交AC于点G,将沿EF翻折,得到,连接DM,交EF于点N,若点F是AB的中点,则的周长是()A. B. C. D.2、如图,已知l1∥l2∥l3, DE=4,DF=6,那么下列结论正确的是()A.BC:EF=1:1B.BC:AB=1:2C.AD:CF=2:3D.BE:CF=2:33、如图,在△ABC中,E,G分别是AB,AC上的点,∠AEG=∠C,∠BAC的平分线AD交EG于点F,若,则()A. B. C. D.4、若非零实数x,y满足4y=3x,则x:y等于()A.3:4B.4:3C.2:3D.3:25、一张等腰三角形纸片,底边长15cm,底边上的高长22.5cm,现沿底边依次从下往上裁剪宽度均为3cm的矩形纸条,如图所示,已知剪得的纸条中有一张是正方形,则这张正方形纸条是()A.第4张B.第5张C.第6张D.第7张6、如图,∠APD=90°,AP=PB=BC=CD,则下列结论成立的是()A.△PAB∽△PCAB.△ABC∽△DBAC.△PAB∽△PDAD.△ABC∽△DCA7、已知如图,DE∥BC,,则=()A. B. C.2 D.38、如图,点A是反比例函数y= (x>0)上的一个动点,连接OA,过点O作OB⊥OA,并且使OB=2OA,连接AB,当点A在反比函数图象上移动时,点B也在某一反比例函数图象y= 上移动,k的值为()A.2B.﹣2C.4D.﹣49、如图,已知△AOB与△A1OB1是以点O为位似中心的位似图形,且相似比为1:2,点B的坐标为(-1,2),则点B1的坐标为()A.(2,-4)B.(1,-4)C.(-1,4)D.(-4,2)10、把一个三角形变成和它相似的三角形,若面积扩大5倍,则边长扩大;若边长扩大5倍,则面积扩大。
浙教版数学九年级上册 第四章 相似三角形 综合测试卷(原卷+答案)

第四章综合测试卷 相似三角形班级 学号 得分 姓名一、选择题(本大题有10小题,每小题3分,共30分)1.己知 ab =25,则a +b b的值为( )A 25B 35C 75D 232.如图,已知△ABC∽△DEF,AB:DE=1:2,则下列等式一定成立的是( )A.BC DF=12 B.∠A 的度数∠D 的度数=12C.△ABC的面积△def 的面积= 12 D. △ABC 的周长△def 的周长= 123.如图,在直角坐标系中,△OAB 的顶点为O(0,0),A(4,3),B(3,0).以点O 为位似中心,在第三象限内作与△OAB 的位似比 13的位似图形△OCD,则点C 坐标为( )A. (-1,-1)B.(−43,−1)C.(−1,−43) D. (-2,-1)4. 如图,四边形ABCD 是正方形,E 是CD 的中点,P 是BC 边上的一点,下列条件中,不能推出 △ABP 与△ECP 相似的是( )A.∠APB=∠EPCB. ∠APE=90°C. 点 P 是BC 的中点D. BP: BC=2:35.如图,在△ABC 中,点D 在BC 边上,连结AD,点E 在AC 边上,过点E 作EF∥BC,交 AD 于点F,过点E 作EG∥AB,交BC 于点G,则下列式子一定正确的是( ) A.AE EC=EF CDB.EF CD=EG ABC.AFFD=BG GCD.CG BC=AF AD6. 如图,小明为了测量一凉亭的高度AB(顶端A 到水平地面BD 的距离),在凉亭的旁边放置一个与凉亭台阶BC 等高的台阶DE(DE=BC=0.5m ,A ,B ,C 三点共线),把一面镜子水平放置在平台上的点 G 处,测得CG=15m ,然后沿直线CG 后退到点E 处,这时恰好在镜子里看到凉亭的顶端A ,测得 EG=3m ,小明身高EF=1.6m,则凉亭的高度AB 约为( )A. 8.5mB. 9mC. 9.5mD. 10m7. 在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”落在下列哪个位置处,能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”、“兵”所在位置的格点构成的三角形相似( )A. ①处B. ②处C. ③处D. ④处8. 如图,在△ABC 中,AD 平分∠BAC,按如下步骤作图:第一步,分别以点A ,D 为圆心,以大 12AD 的长为半径在AD 两侧作弧,交于两点M ,N第二步,连结MN 分别交AB,AC 于点E,F;第三步,连结DE,DF.若BD=6,AF=4,CD=3,则BE 的长是( )A. 2B. 4C. 6D. 89. 如图,在△ABC 中,点 D 为BC 边上的一点,且AD=AB=2,AD⊥AB,过点 D 作DE⊥AD,DE 交AC 于点E,若DE=1,则△ABC 的面积为( )A. 2B. 4C.25D. 810. 在四边形 ABCD 中,∠B=90°,AC=4,AB∥CD,DH 垂直平分 AC,点 H 为垂足.设AB=x ,AD=y ,则y 关于x 的函数关系用图象大致可以表示为( )二、填空题(本大题有6小题,每小题4分,共24分)11. 如图所示,点 E 是平行四边形ABCD 的边BC 延长线上一点,连结AE ,交 CD 于点F ,连结BF.写出图中任意一对相似三角形: .12. 已知 a6=b5=c4,且a+b-2c=6,则a 的值为 .13. 如图,在平行四边形ABCD 中,AB=10,AD=6,点E 是AD 的中点,在AB 上取一点F,使△CBF∽△CDE,则 BF 的长是 .14. 如图,在一块斜边长为30cm 的直角三角形木板(Rt△ACB)上截取一个正方形CDEF ,点D 在边BC 上,点E 在斜边AB 上,点F 在边AC 上,若AF :AC=1:3,则这块木板截取正方形 CDEF 后,剩余部分的面积为 .15.如图①,长、宽均为3,高为8的长方体容器,放置在水平桌面上,里面盛有水,水面高为6,绕底面一棱进行旋转倾斜后,水面恰好触到容器口边缘,图②是此时的示意图,则图②中水面高度为16. 如图所示,在直角坐标系中有两点A(4,0),B(0,2).如果点C 在x 轴上,且点 C 与点O 及点A 不重合,当点 C 的坐标为 时,使得由点B ,O ,C 构成的三角形与△AOB 相似(至少找出两个符合条件的点).三、解答题(本大题有8小题,共66分)17.(6分)如图,在△ABC中,DE‖BC,EF‖AB,求证:△ADEO△EFC.18. (6分)如图,一块材料的形状是锐角三角形 ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,这个正方形零件的边长是多少?19.(6分)如图,点 P 是⊙O的直径AB 延长线上一点,且AB=4,点 M为A AB上一个动点(不与A,B重合),射线 PM与⊙O交于点 N(不与M重合).(1)当M在什么位置时,△MAB的面积最大? 并求出这个最大值;(2)求证:△PAN∽△PMB.20. (8 分)如图,在△ABC中,AB=8,BC=4,CA=6,CD∥AB,BD是∠ABC的平分线,BD交AC于点E,求AE的长.21. (8分)如图,在△ABC中,点 D,E分别在边AB,AC上,且∠ABE=∠ACD,BE,CD交于点G,连结DE.(1)求证:△AEDO△ABC;(2)如果BE平分∠ABC,求证:DE=CE.22.(10分)如图,在 △ABC 中,点D,E,F 分别在AB,BC,AC 边上, DE‖AC,EF‖AB.(1)求证: △BDEO △EFC.(2)设AF FC=12,①若. BC =12,,求线段BE 的长;②若△EFC 的面积是20,求△ABC 的面积.23.(10分)在矩形ABCD 中,AE⊥BD 于点E,点 P 是边AD 上一点.(1)若BP 平分∠ABD,交 AE 于点G,PF⊥BD 于点F,如图①,证明四边形 AGFP 是菱形;(2)如图②,若PE⊥EC,求证:AE·AB=DE·AP;(3)在(2)的条件下,若AB=1,BC=2,求AP 的长.24.(12分)如图,已知 △ABC 是边长为6cm 的等边三角形,动点P ,Q 同时从A ,B 两点出发,分别沿AB,BC 匀速运动,其中点 P 运动的速度是 1cm/s,点 Q 运动的速度是2cm/s,当点 Q 到达点C 时,P ,Q 两点都停止运动.设运动时间为t(s),解答下列问题:(1) 当 t =2时,判断 △BPQ 的形状,并说明理由;(2)设 △BPQ 的面积为 S (cm²),求S 与t 的函数表达式;(3)如图,作 QR//BA 交AC 于点R,连结PR,当t 为何值时,△APR∽△PRQ?第四章综合测试卷 相似三角形1. C2. D3. B4. C5. C6. A7. B8. D9. B 10. D 11. △ADF∽△ECF(答案不唯一)12. 12 13. 1.8 14. 100cm² 15.24516. (-1,0)或(1,0)或(-4,0)(答案不唯一)17. 证明:∵DE∥BC,∴△ADE∽△ABC,∵EF∥AB,∴△EFC∽△ABC,∴△ADE∽△EFC.18. 解:设这个正方形零件的边长为 xmm ,则△AEF 的边EF 上的高AK=(80-x) mm.∵四边形EF-HG是正方形,∴EF∥GH,即 EF∥BC.∴△AEF CABC.∴EF BC=AK AD,即 x 120=80−x 80⋅∴x =48.∴这个正方形零件的边长是48mm.19. (1)解:当点 M 在 AB 的中点处时,△MAB 的面积最大,此时( OM⟂AB,∵OM =12AB =12×4=2,∴S ABM =12AB ⋅OM =12×4×2=4. (2)证明:∵∠PMB=∠PAN,∠P=∠P,∴△PAN∽△PMB.20. 解: ∵BD 为∠ABC 的平分线,∴∠ABD =∠CBD,∵AB∥CD,∴∠D=∠ABD,∴∠D=∠CBD,∴BC=CD.∵BC=4,∴CD=4.∵AB∥ CD,∴ABECDE,∴AB CD=AE CE,∴84=AE CE,∴AE=2CE,∵AC=6=AE+CE,∴AE=4.21. 证明:(1)∵∠ABE=∠ACD,且∠A 是公共角, ∴ABEACD.∴AE AD=AB AC,即AEAB =ADAC ,又∵∠A 是公共角,∴△AED∽△ABC. (2)∵∠ABE=∠ACD,∠BGD=∠CGE,∴△BGD∽ CGE.:DG EG=BG CG,即DG BG=EG CG.又∵∠DGE=∠BGC,∴△DGE∽△BGC.∴∠GBC=∠GDE,∵BE 平分∠ABC,∴∠GBC=∠ABE,∵∠ABE=∠ACD,∴∠GDE=∠ACD.∴DE=CE.22. (1)证明:∵DE∥AC,∴∠BED=∠C.∵EF∥AB,∴∠B=∠FEC,∴△BDE∽△EFC.(2)解:①∵EF//AB,∴BE EC=AF FC=12.∵BC = 12,∴BE12−BE =12,∴BE =4.②∵EF∥AB,∴△EFC∽△BAC,∴S△BC= (EC BC)2⋅∴BE EC=12,∴EC BC=23.又∵△EFC 的面积是20, ∴20SABC=(23)2,∴SABC=45,即△ABC 的面积是45.23. (1)证明:∵四边形 ABCD 是矩形,∴∠BAD=90°,∵AE⊥BD,∴∠AED=90°,∴∠BAE+∠EAD=90°,∠EAD+∠ADE=90°,∴∠BAE=∠ADE,∵BP 平分∠ABD,∴∠ABG=∠PBD.∵∠AGP=∠BAG+∠ABG,∠APB =∠ADE+∠PBD,∠ABG=∠PBD,∴∠AGP=∠APG,∴AP=AG,∵PA⊥AB,PF⊥BD,BP 平分∠ABD,∴PA=PF,∴PF=AG,∵AE⊥BD,PF⊥BD,∴PF∥AG,∴四边形AGFP 是平行四边形,∵PA=PF,∴四边形AGFP 是菱形.(2)证明:∵AE⊥BD,PE⊥EC,∴∠AED=∠PEC=90°,∴∠AEP=∠DEC,∵∠EAD+∠ADE=90°,∠ADE+∠CDE=90°,∴∠EAP=∠EDC,∴△AEP∽△DEC,∴DE·AP.(3)解:∵四边形 ABCD 是矩形,∴AD=BC=2,∠BAD=90°,∴BD=√AB²+AD² =5,∵AE ⊥BD,∴S ABD =12⋅BD ⋅AE = 12⋅AB ⋅AD,∴AE =255,∴DE =AD 2−AE 2=455,∵AE ⋅AB =DE ⋅AP,∴ AP =255×1455=12.24. 解:(1)△BPQ 是等边三角形.当t=2时,AP=21 =2( cm),BQ=2×2=4( cm),∴BP=AB-AP=6-2=4( cm),∴BQ=BP,又∵∠B = 60°,∴△BPQ 是等边三角形.(2)如图,过点 Q 作QE⊥AB,垂足为 E,由 QB=2tcm,∠B=60°,∠BEQ=90°,得 QE =3tcm,由AP= tcm,得 PB =(6−t )cm,∴S =12BP ⋅QE = 12×(6−t )×3t =−32t 2+33t.(3)∵QR‖BA,∴∠QRC=∠A=60°,∠RQC=∠B=60°,∴△QRC是等边三角形,∴QR=RC=QC=(6-2t)cm⋅:BE=12BQ=12×2t=t(cm),∴EP=AB−AP−BE=6−t−t=6−2t(cm),∵EP‖QR,EP=QR,∴四边形 EPRQ是平行四边形,∴PR=EQ3tcm.又∵∠PEQ=90°,∴∠APR∠PRQ=90°,∴△APR∽△PRQ,∴∠QPR=∠A=60∘,QRPR=6−2t3t=3,解得t=65.∴当t=65时,△APR∽△PRQ.。
【易错题】浙教版九年级数学上册《第四章相似三角形》单元测试卷含答案解析.doc

【易错题解析】浙教版九年级数学上册第四章相似三角形单元测试卷一、单选题(共10题;共30分)1•已知「夕,则?的值是()3 4 y2. 如图1, A ABC和4GAF是两个全等的等腰直角三角形,图屮相似三角形(不包括全等)共有()A. 1对B. 2对C. 3对D. 4对3. 图中的两个三角形是位似图形,它们的位似中心是()A.点PB.点OC.点MD.点N4. 在ZiABC 和△ DEF 屮,ZA=40°, ZD=60°, ZE=80°,字=器,那么ZB 的度数是()AC FEA.40°B.60°C.80°D.100°5. 如图,锐角AABC的高CD和BE相交于点0,图中与△ ODB相似的三角形有()6. 如图,在平行四边形ABCD中,AE: AD=2: 3,连接BE交AC于点F,若△ ABF和四边形CDEF的面积分别记为Si , S2 ,贝iJSi: S2% ()A. 2: 3B.4: 9C. 6: 11D. 6: 137. 如图,在AABC中,点D, E分别是AB, C的中点,则S AADE:S A ABC=()A. 1: 2B. 1: 3C. 1: 4D. 1: 58. (2017*淄惮)如图,在RtA ABC 中,ZABC=90°, AB=6, BC=8, ZBAC, ZACB 的平分线相交于点E,过点E作EF〃BC交AC于点F,则EF的长为()9.如图,点D是AABC的边AC的上一点,且ZABD=ZC;如果= |,那么譽=()CD 3 D LF八…! f►•10.如图,RtA ABC 中,BC=2V3 ,ZACB=90°, ZA=30°, 6 是斜边 AB 的中点,过 6 作 DiEi 丄AC 于 Ei二、填空题(共10题;共30分)AB=4, CD=3, OD=2,那么线段OA 的长为22.如果两个相似三角形周长的比是2:3 ,那么它们面积的比是 ____________ •13. 如图,已知直线 I] || l 2 II $,分别交直线 m 、n 于点 A^ C^ D 、E 、F, AB = 5cm, AC=15cm, DE = 3cm,则EF 的长为 ________ cm.14. ________________________________________________________________________________ 已知AABCsADEF,相似比为3:5, A ABC 的周长为6,则△ DEF 的周长为 ___________________________________ .15. ________________________________________________________________________________________________ 已知△ ABC^ADEF, △ ABC 的周长为1, △ DEF 的周长为3,则厶ABC 与氐DEF 的面积之比为 _________________ .16. 若两个相似三角形的周长之比为2:3,较小三角形的面积为8crY?,则较大三角形面积是 ____________ cm 2 . 17. 如图,在矩形ABCD 中,E 是边AB 的中点,连接DE 交对角线4C 于点F ,若AB = 4 f18. 如图,已知ZAOB=60。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《相似三角形》习题
一.填空题
1.如图,ABC ∆∽MNP ∆,则它们的对应角分别是A ∠与∠_____,∠B 与∠_____,
C ∠与∠_____;对应边成比例的是________=_________=_________;若AB =2.7cm ,cm MN 9.0=,cm MP 1=,则相似比=_________,=BC _________cm .
B
A
G
F
E
D
C
B
A
N
P
M
C (第2题)
(第1题)
2.如图,四边形ABCD 中,AD ∥EF ∥BC ,AC 交EF 于G .图中能相似的三角形共有_______对,它们分别是_________、___________,小明通过这两对相似三角形推出了比例式:AB
BE
AD FG =,对不对,为什么? 二.填空题
3.如图,ABC ∆和DEF ∆的三边长分别为7、2、6和12、4、14,且两三角形相似,则A ∠与∠_____,
∠B 与∠_____,C ∠与∠_____,)
()()(AC
DF AB ==
. (第5题)
(第4题)
(第3题)
C
G
F
E
D C
B
A
F
E
B
A
E
F
D
C
B A
4.如图,ABC ∆∽AEF ∆,写出三对对应角:_________=_________,_________=________,
________=_________,并且)
()
()()()(==AF ,若ABC ∆与AEF ∆的相似比是3:2,cm EF 8=,则________=BC .
5.如图,ABC ∆中,点D 在BC 上,EF ∥BC ,分别交AB 、AC 、AD 于点E 、F 、G ,图中共有______对相似三角形,它们是______________________________________.
6.如图,平行四边形ABCD 中,,上的一点,
是4
3
=EC BE BC E ,于点交F BD AE =BF 的值。
及,求
DF DA
BE
cm 6 F
E D
C
B
A
三.选择题
1.下列命题中不正确的是( )
A .如果两个三角形全等,那么这两个三角形相似.
B .如果两个三角形相似,且相似比为1,那么这两个三角形全等.
C .如果两个三角形与第三个三角形相似,那么这两个三角形相似.
D .如果两个三角形相似,那么这两个三角形全等.
2.给出下列四个命题,其中真命题有( )
(1)等腰三角形都是相似三角形 (2)直角三角形都是相似三角形 (3)等腰直角三角形都是相似三角形 (4)等边三角形都是相似三角形
A .1个
B .2个
C .3个
D .4个
四.综合题
如图,AD ∥AB BC ,、EF E E CD 作,过点相交于点∥,于点,交F AC AD 写出图中所有相似三角形,并说明理由.
F
E
D
C
B
A
初中数学试卷。
