2016年春西安交通大学《高等数学》(上)2 在线作业答案
2013年春西安交大高等数学在线作业题目及答案

2013年春西安交大高等数学在线作业题目及答案西交1303春《高等数学》在线作业、单选题(共25 道试题,共50 分。
)1. B.2. A3. A4. A5. D6. B7. A8. C9. c10.A11. C12. B13.B14.C15.B16.D17.C18.D19.A20.B21.B22.C23.A24.C25.C、判断题(共25 道试题,共50 分。
)1. 级数的每一项同乘一个不为零的常数后,它的收敛性改变A. 错误2. 高斯公式表达了空间闭区域上的三重积分与其边界曲面上的曲面积分之间的关系B. 正确3. 二重积分被积函数为1时积分值为积分区域的面积B. 正确4. 格林公式表明在平面闭区域D上的二重积分可以通过沿闭区域D的边界曲线L上的曲线积分来表达B. 正确5. 设区域G是一个单连通区域,函数P(x,y)、Q(x,y)在G内具有一阶连续偏导数,则P(x,y)dx+Q(x,y)dy在G内为某一函数u(x,y)的全微分的充要条件是P对y的偏导数等于Q对x的偏导数在G 恒成立。
B. 正确6. 在级数中去掉、加上或改变有限项,改变级数的收敛性A. 错误7. 多元函数的全微分等于该函数各个偏导数与对应变量微分乘积之和B. 正确8. 当积分弧段的方向改变时,对坐标的曲线积分要改变符号B. 正确9. 正项级数s的一般项不超过正项级数t的一般项,若t收敛则s 发散A. 错误10. 二重积分对于积分区域具有可加性B. 正确11. 幂级数的和函数在其收敛域上连续B. 正确12. 级数一般项趋于零是级数收敛的充分条件13. p级数当p>1时发散A. 错误14. 幂级数的和函数在其收敛域上可导B. 正确15. 函数偏导数存在是其全微分存在的充分条件A. 错误16. 等比级数的公比的绝对值小于1时发散A. 错误17. 若幂级数的相邻两项系数比值的绝对值的极限等于a,则这幂级数的收敛半径当a不等于0时是a的倒数;当a等于正无穷时是0;当a等于0时是正无穷B. 正确18. 条件收敛的级数必收敛B. 正确19. 对面积的曲面积分的计算思路是将其化为相应的二重积分B. 正确20. 对于二元函数z=f(x,y),点P(x,y)趋于点Q(a,b)的过程中,对应的函数值f(x,y)无限接近于一个确定的常数A,就说A是函数f(x,y)当(x,y)趋于(a,b)时的极限B. 正确21. 计算三重积分的基本方法是将其化为三次积分来计算B. 正确22. 计算二重积分的思路是将其化为两次单积分B. 正确23. 幂级数的和函数在其收敛域上可积B. 正确24. 函数的驻点一定是极值点A. 错误25. 各项都是正数或零的级数是正项级数。
高数上册全部答案

第1页/共8页第一章 函数、极限与连续1.1 映射与函数1. (1))(x f 与 )(x h 相同; )(x g 与)(),(x h x f 不同. (2))(x f 与 )(x ψ相同相同)(x ϕ与)(),(x x f ψ不同. (3) )(x f 与 )(x g 相同. 2. (1) [ππ)(12,2+n n ],,2,1,0 =n (2) 21≤a 时[]a a −1,;21>a 为空集. 3. (1)3arctan 213arctan 21xy y x ==;(2)xx y y y x −=−=1ln 1ln; 5.(2),224,216==−)()(πϕπϕ02=)(ϕ. 6. (1)奇 , (2)奇 , (3) 偶. 7..22332+∞<<−h r r h h hr ,)(π1.2 数列的极限1.(1)3⎯⎯→⎯∞→n n x .(2).0⎯⎯→⎯∞→n n x(3)无极限. (4) 无极限. 1.3 函数的极限2. (1) 极限不存在. (2) 极限不存在. (3),2arctan π−⎯⎯→⎯−∞→x x∞→x 时,x arctan 的极限不存在. (4),11⎯⎯→⎯++∞→−x x e ∞→x 时,x e −+1的极限不存在. (5) 极限不存在. 1.4 无穷小与无穷大3.无界,非无穷大. 1.5 极限运算法则1. 2; 2. 0; 3. -1/5; 4. -1; 5. 2x ;6. 2; 7. 0; 1.6 极限存在准则 两个重要极限1.(1) e1; (2) a ; (3) 0 ; (4) x ; (5) 1; (6)2−e ; (7) 1−e ; (8) 3; (9) e . 2. 2 ; 3. 0 1.7 无穷小的比较1. (1)x x ~arctan . (2)e a =时等价; e a ≠时同阶. (3) 同阶. (4) 同阶. 2 (1)6=n ; (2) 1=n ; (3) 8=n . 1.8 函数的连续性与间断点1.(1)2=x ,第一类可去,补充定义-4; 3=x ,第二类无穷. (2),,20ππ+==k x x 第一类可去, 分别补充定义1,0; )(0≠=k k x π为第二类无穷. (3) 0x =第一类跳跃第一类跳跃 (4)0x =第二类无穷第二类无穷2. ),),(,),(,(∞+−−∞−1122.3112∞⎯⎯→⎯−⎯⎯→⎯→−→x x x f x f )(,)(3.)()(,)(0100100f f f =−=+=−, ,0=x 第一类跳跃.4.1±=x ,第一类跳跃.1.9 连续函数的运算与初等函数的连续性1..34==b a ,2. (1)112ln ++e ; (2) 0 ; (3) 1/2 ; (4)-1/56 ; (5) 1/2 ;(6) 0 ; (7) 2−e ; (8) 0 ; (9) ;x sin − (10) 1−e . 第二章 导数与微分 2.1 导数概念1、(1)-20 (2)12、(1)(0)f ′ (2)0()f x ′−(3)02()f x ′3、2,-14、1,1y x y x −=−=−2.2 函数的求导法则1、(1)′=++y x xln ln 2222 (2)′=−+⋅y x x x x x 332155222cos sin sec () (3)2-1(1)y x x =+(4)2cos sin x x x y x −= (5)(2)(3)(1)(3)y x x x x =−−+−−(1)(2)x x +−−(6)21cos sin (1cos )x xy x ++=+ (7)()22224sin1cos (1)x x x y x x ⎡⎤++⎣⎦=+(8)x x chx shx e y x tan sec )(3−+=′ 2、(1)-2 (2)2(1)42π+ 3.(1)38(25)y x =+(2)3sin(43)y x =− (3)22xy a x−=− (4)2sin 4y x =(5)2sec (12)y x x =−−(6)()arctan 21x e y x x =+ (7)211y x=+(8)12(1)y x x =− (9)sec y x =(10)csc y x =(11)()11sin cos sin sin cos n n n n y n x x x x x x −−=+(12)211y x =−− (13)()1ln ln ln y x x x =(14)′=++−y x x x xx xx 3222212123ln ()ln cos4.22()()()()()()f x f xg x g x f x g x ′′++5.445(3),5x x −6.(1)()-241xy exx =−++(2)-24()t ty e e =+或21(ch) (3)24arctan 24xy x =+ (4)arcsin 2x y =(5)4218x x x x y x x x x x x+++=+++ 7.122.3 高阶导数1. (1)214-x (2)()23222aa x −− (3)232(1)x y x −=+2.(1)!n (2) ().xx n e +(3)-1-12sin(2).2n n y x π=+3. (1)4cos xe x −(2)21225(sin 250cos 2sin 2)2x x x x x −++5022.4隐函数及由参数方程所确定的函数的导数1 (1)22.ay x y ax −− (2)′=++−+y y x x y x x y sin cos()cos cos()2.(1)222.y x y −(2)22.e3.sin 11cot 2(1)x xx x x e e x x e ⎡⎤−+−⎢⎥−⎣⎦24.(1)cos sin 1sin cos θθθθθθ−−− (2)sin cos cos sin t t t t +−5.(1)231t t +− (2)1()f t ′′2.5函数的微分1 (1)22)sin 2).xxx e x e dx ++(((2)231(1)dx x + (3)2ln 1)1x dx x −−−((4)42.1xdx x −+2.dx3.提示:利用()(0)(0)f x f f x ′≈+第三章 微分中值定理与导数的应用3.1 微分中值定理1.提示:首先验证函数满足Lagrange 定理的条件,并可求得63(1,2)3ξ−=∈, 使(2)(1)()21f f f ξ−′=−.2.11ln()xe x x θ−=3.方程()0f x ′=有且仅有三个实根,它们分别在区间(0,1),(1,2),(2,3)内.4.提示:利用反证法.5.提示:作辅助函数()x ϕ=(1)10xx e −+>,利用Lagrange 中值定理.3.2 洛必达法则1.32 2. 12 3. 3. 11 4. 12 5. 5. 1 6. 1 6. 0 0 7. 528. 8. 1 1 9. ∞ 10. 13.3 泰勒公式 1.21()ln 2()()244f x x x ππ=−−−−− 232sec tan ()34x πξξ−− ,ξ在,4x π之间.2.2311()2!(1)!xn n xe x x x x o x n =+++++− 3.4 函数的单调性与曲线的凹凸性2. 1(,),(1,)2−∞+∞单调增加,1(,1)2上单调减少.3.2(,),(,)3a a −∞+∞单调增,2(,)3a a 上单调减.4.22[,]33−单调增, 2(,]3−∞−,2[,)3+∞单调减.7. 凸区间(,1]−∞,凹区间[1,)+∞, 拐点11(1,)9−3.5 函数的极值与最大值最小值1.2[1,]e 单调增,(0,1],2[,)e +∞单调减,极小值(1)0f =,极大值224()f e e=2.2,05x x ==3. 极大值213xy ==,极小值312.5x y ==.4. 3,0,1a b c =−==5. 0()f x 是极小值是极小值6.最大值为2,最小值为 -2.7.最小值212x y =−=8.0163x =, max 16()151.73S =9.422,33h R r R == 3.7 曲率1. 曲率2K =,曲率半径12ρ=. 2. 2x π=处曲率最大,为1.高等数学期中自测试题一、DDCDD二、1、[1,2] 2、1/2 3、-14、(1)(1)(0)(0)f f f f ′′>−>5、1t =三、1、(22)n n πππ+,(012)n =±± ,,,2lim ln sin 0x x π→=2、1/43、04、36、(]0−∞,单调减,[)0+∞,单调增单调增五、提示:利用反证法,由零点定理推出矛盾。
最新版2016年春西安交通大学《高等数学》(上)2在线作业满分答案

《高等数学》(上)2 在线作业答案一、单选题(共 40 道试题,共 80 分。
)1.求下题极限:A. AB. BC. CD. D正确答案:C 满分:2 分2.当B. BC. CD. D正确答案:D 满分:2 分3.若A. AB. BC. CD. D正确答案:B 满分:2 分4.下列极限存在的是B. BC. CD. D正确答案:B 满分:2 分5.设A. AB. BC. CD. D正确答案:A 满分:2 分6.如果:A.AB. BC. CD. D正确答案:C 满分:2 分7.若A. AB. BC. CD. D正确答案:A 满分:2 分8.在区间A. AB. BC. CD. D正确答案:B 满分:2 分9.极限:A. AB. BC. CD. D正确答案:A 满分:2 分10.当A. AB. BC. CD. D正确答案:D 满分:2 分11.已知A. AB. BC. CD. D正确答案:A 满分:2 分12.数列A.单调递增但无界的数列B.单调递减且有界的数列C.单调递增且有界的数列D.单调递减且无界的数列正确答案:C 满分:2 分13.若A. AB. BD. D正确答案:B 满分:2 分14.已知A. 17B. 170C. 18D. 180正确答案:A 满分:2 分15.若以下函数:A. AC. CD. D正确答案:D 满分:2 分16. 函数:A.偶函数B.无界函数C.周期函数D.单调函数正确答案:B 满分:2 分17.已知数列B. BC. CD. D正确答案:B 满分:2 分18.已知数列:A. 9B. 10C. 101D. 1000正确答案:B 满分:2 分19.若函数:A. AB. BC. CD. D正确答案:C 满分:2 分20.已知A. AB. BC. CD. D正确答案:C 满分:2 分21.设A. AB. BC. CD. D正确答案:C 满分:2 分22.当:A. AB. BC. CD. D正确答案:D 满分:2 分23.若A. AB. BC. CD. D正确答案:D 满分:2 分24.设A. AB. BC. CD. D正确答案:A 满分:2 分25.设对任意的A.存在且一定等于零B.一定不存在C.存在但不一定等于零D.不一定存在正确答案:D 满分:2 分26.极限A. AB. BC. CD. D正确答案:C 满分:2 分27.极限:A. AB. BC. CD. D正确答案:D 满分:2 分28.下列四个单调递增数列中,只有由()给出的数列以1为其上界A. AB. BC. CD. D正确答案:B 满分:2 分29.求值:A. AB. BC. CD. D正确答案:A 满分:2 分30.当:A. AB. BC. CD. D正确答案:B 满分:2 分31.求极限:A. AB. BC. CD. D正确答案:D 满分:2 分32.函数A. AB. BC. CD. D正确答案:C 满分:2 分33.当:A. AB. BC. CD. D正确答案:A 满分:2 分34.“对任意给定的A.充分条件但非必要条件B.必要条件但非充分条件C.充分必要条件D.既非充分条件又非必要条件正确答案:C 满分:2 分35.下列()中所给的数列是无界的A. AB. BC. CD. D正确答案:C 满分:2 分36.函数:A.不存在B. 0C. 0.5D. 1正确答案:A 满分:2 分37.当A. AB. BC. CD. D正确答案:D 满分:2 分38.设数列A. AB. BC. CD. D正确答案:D 满分:2 分39.下列极限不存在的是()A. AB. BC. CD. D正确答案:C 满分:2 分40.已知A. AB. BC. CD. D正确答案:C 满分:2 分二、判断题(共 10 道试题,共 20 分。
西安交通大学《高等数学上》作业集问题详解

文案大全第一章 函数与极限作业参考答案第一节 函数(作业一)一、1. C .2.A .3.B .4. B .5.A .6. B .7.A . B .9.B .10. D .二、填空:11.322333a a b ab b +++;12.(12)xxa +;13.sin cos cos sin x y x y +;;14.1;15.2sec x ; 16.22()()a b a ab b -++;17.(1)(21)6n n n ++.三、18.(1) (,0)-∞;(2) [4,][0,]ππ-; (3) ]0,1[-和1=x ;(4)]11,2[]2,11[ --.第一节 函数(作业二)一、1.D .2.C .3.D .4.A .5.A .6.D .7.D .8.B .9.A .10.D . 二、11.1[sin()sin()]2x y x y ++-; 12.1[cos()cos()]2x y x y ++-;13.2sin cos x x ; 14.22cos sin x x -;15...222x x ++; 18.[,]66ππ-; 19.2cos y x =;20.内点.三、计算题:21.πk x x f 2)(-=,当ππ)12()12(+<≤-k x k 时,Z k ∈.22.⎩⎨⎧><+-=.0,0,,)(22x x x x x x x f 23.(1) 3u y =,υu sin =,x v 1=;(2) u y 2=,υarcsin =u ,2x υ=;(3)u y lg =,υu lg =,ωυlg =,21xω=;(4)u y arctan =,υe u =,x cos =υ.第二节 数列的极限(作业一 )一、1. D .2.C .3.C .4.A .5.B .二、6.0;7.1;8.12; 9.0;10.1;11.0;12.0;13.1n;14.1;15.1. 三、计算题:17. (1) 0 ; (2)1;(3) 2 ;(4)13.第二节 数列的极限(作业二 )一、1.A .2.A .3.D .4.B .5.C .6.D .7. B .二、计算下列各题:8;9.1 ;10.12 ;11.32;12. e . 三、计算题:13.(1) 1; (2) ,1;31,1;1,1;1,1-=-=-<>x x x x 发散.14. (1)正确;(2)不正确,如nn a )1(-=;(3)正确;(4)正确;(5)不正确,如!1n a n =,0lim =∞→n n a ,但10lim1≠=+∞→nn n a a ;(6)正确.设A A a a n n n n =⋅=⋅=>∞→∞→ααααα1)1(lim lim ,0.119第三节 函数的极限(作业一)一、1.A .2.A .3. D .4.B .D .6. A .π- 二、计算下列各题:7.27;8; 9.1;10.32;11.3;12.13;13.0;14.1.三、计算题:15.3)(lim 3=-→x f x ,8)(lim 3=+→x f x ;16.不存在;17. 7. 第三节 函数的极限(作业二)一、单项选择题 :1.B .2.B .3.C .4.C .5.C .二、计算下列各题:6.32;7.1;8.94; 9.ln 2;10.1;11.(1)2n n +12.12;13.2;14.3;15.1;16.2e ;17.2;18.1;19.3e -.三、计算题:.第四节 无穷小量与无穷大量一、单项选择题 :1. B .2.A .3.C .4.C .5.B .6.D .7.A .8.B .9.B .二、10.0;11.1;12.29;13.1;14.ae ;15.12;16.12 ;17.1;18.cos a ;19.1;20.0. 三、22.∞→x 时是无穷小,3→x 时是无穷大.23.x ,sin x ,2tan x ,1)-是等价无穷小量.24.1x e -,ln(1)x +1-是与x 同阶的无穷小量.cos 1x -, 2sin x ,2(sin )x 是比x 更高阶的无穷小量.第五节 函数的连续性与间断点(作业一)一、单项选择题 :1.B .2.A .3.A .4.B. 二、填空:5.0;6.0;7.1;8.0;9.12e-.三、10. )(x f 在0=x 不连续;11.1=K ;12.⎪⎩⎪⎨⎧≥<≤<≤=150,6.015050,7.0500,8.0x x x x x x yy 不是x 的连续函数;13.s=332.01.第五节 函数的连续性与间断点(作业二)一、单项选择题:1. B .2.D .3.B .4.D .二、计算下列各题:5.0;6.3;7.1-;8.12e -;9.2π.三、10.(1) 2=x ,无穷型 (2) 1=x ,可去型,2=x ,无穷型 (3) 0=x ,可去型 (4)1-=x ,2-=x ,无穷型 .12.1=a ,1-=b . 13. 可去型.14.无界,非无穷大.第一章 综合练习题1.01=)(f ,02=-)(f ,224=⎪⎭⎫⎝⎛πf ,224=⎪⎭⎫ ⎝⎛-πf ;2.(1) 偶,π=T ; (2) 1=T ;文案大全(3) 偶;3.(1) ↓-∞)0,(,↓+∞),0(,无界; (2) ↑+∞-∞),(,有界; (2) ↑+∞-),1(,无界;(4) ↑-]0,[a ,↓],0(a ,有界;.4.(1))1,0(,1log 2∈-=x xx y ;(2) 0),(21≥-=-x e e y x x;5.)1arcsin()(2x x -=ϕ; 6.21)(2-=x x f ;7..4,0,0,4,,1,ln ))((2>=≠≤⎪⎩⎪⎨⎧=x x x x x x x f ϕ;8.2. 10. 求下列各极限.(1) 1;(2) 3 ;(3) 61;(4) 1;(5) 201032; (6) 0;(7) 1;(8) 0;(9) 4e ;(10)23 ;(11) 43;(12) 1;(13) 25;(14) 4; (15) 2;(16) x ;(17)16-;(18) 1-; (19) 2e -;(20) 2e ;(21) e ;(22) 3e -;(23) 2e -;(24) 16e - ;(25) 4e -(26) 2-. 11.(1) 1=x ,可去型 (2) 1=x ,跳跃型.第二章 导数与微分作业参考答案第一节 导数概念一、单项选择题 :1. B .2.B .3.D .4.C .5.B .C .6.D .7.C . 8.C .9.B .二、填空10.11ln 2xx +;11.2ln 2x xe +;12.cos sin x x -; 1321x-;14. ln x y y ;15.1x xy -;16.1-;17. 2cos a -;18.2ln 2x -;19.()()f a a ϕ'=.三、20. 连续、可导 0)0(='f ; 21. 连续、可导 1)0(='f ;22. 连续、不可导;3. 连续、不可导.第二节 导数的计算 (四则运算)一、 1.D .2.C .3.A .4.B .二、5. 23464y x x '=++;6.323(3y x '=++ 7. 566cos sin y x x x x '=- ;8. (sin cos )sin x x y e x x x xe x '=-+; 9. 2tan sec 3sec tan y x x x x x '=+-;10.1421123333341cos sin cot cos csc cos cos 33y x x x x x x x x x x x x -'=--++; 11. 52323322y x x x --'=--;12.y '=.222121x x y x +-'=+(); 14.22(sin cos )(1tan )sin sec 1tan x x x x x x xy x ++-'=+(); 15. 32322(1)sec tan 6sec 1x x x x xy x +-'=+();12116.2222(1)(2(ln )(2ln 22)2x x x x x x x x x y x x ++-++'=+)(). 17.6x y π='=213+,4x y π='=2 ;18.(0)f '=253,(2)f '=1517;19.4x y π='=8)2(2+π三、 20.切线方程02=-y x ,法线方程02=+y x . 21.ea 21=,切线方程为:022=--e y e x ,法线方程为:01222=+-+)(e y x e .第二节 导数的计算 (复合函数求导法)一、单项选择题 1. C . 2.D .3.B .4.C . 二、5.'tan y x =-;6.2'y =;7.'2sec2tan 2y x x =;8.22222sin 2cos 2sin sin 'cos x x x x x y x +=;9.2211'secy x x =- ;10.'cot y x =; 11.2'2csc 2y x =-;12.'3csc3cot 3y x x =-;13.1'ln (ln 1)x n x y a a nx x x -=+++;14.2'y =;15.'y =;16.y '=412x x+;17.y '=212arcsin xx x x -+; 18.y '=xx x 2ln 1ln arcsin 2-;19.y '=xx e x)1(2arctan+;20.y '=x arccos ;21.y '=x x x 22sec tan 3sin 1+;22.y '=211x +-; 23. y '=xx --1854; 24. y '=x x x x x xxln ln ln 1ln 1ln 22ln 2ln --⋅⋅;25.y '=211x+; 26.y '=x e xe x xx⋅⋅---2ln 2)ln 1(21;27. y '=211x +-;28.y '=22111xx -+-; 29.y '=x e x x1sin 222sin 1-;30.y '=222cos sin 2sin 2sin x x x x x +.第三节 高阶导数一、单项选择题:1.D .2.D .48.3.A .二 填空:4.sin(),1,2,2n x n π+= ; 5.1(1),1,2,n n n x --= ;6.0 ; 7.cos(),1,2,2n x n π+= ;8.,1,2,x e n = ;9.1 . 10. 2cos 2cos sin ln x y x x x x '=-⋅+ ,y ''=22cos 2sin 2ln 2cos 2x xx x x x ---;文案大全11.2y '=+,y ''=252)1(3--x x ;12.y '=,y ''=23222)(x a a --;13.221x y x -'=-,y ''=222)1()1(2x x -+-; 14.2arctan 1y x x '=+,y ''=212arctan 2xxx ++ ; 15.y '=,y ''=232)1(x x +-; 16.2323(1)x y x -'=+,y ''=333)1()12(6+-x x x ; 17. )sin (sin )sin ()cos 1(2x x f x x x f x +'⋅-+''+;18. )()]([)()(22x f x f x f x f '-'';19.322222)](1[)]()([)(1)]()()]([[)(1)()(2x f x f x f x x f x f x f x f x x f x f x f +'-+''+'++'; 20.)()(3)(32xx x x x x e f e e f e e f e ''+'+.三、 21. )(n x e x+; 22.)2(!)2()1(1≥---n x n n n ; 23.n m x n m m m m -++---1)1)(11()21)(11(1 , 24.)212sin(21π-+-n x n .第四节 其他形式下函数求导问题一、1.B .2. B .3. D .4. B .5. C .6.C . 7.A . 二、8.切线方程0222=-+y x ,法线方程0142=--y x ;9.线方程01234=-+y x ,法线方程0643=+-y x三、10.t tan - ; 11. 23-; 12.;2- ;13. π3232e -.四、 14. xy x y xy --; 15.12-y xy ;16. yx y x -+ ; 17.)sin()sin(1xy x xy y +-.第五节 函数的微分一、1.C .2.C .3. C . 4. C .5. C .6. C . 7. C .8. B .9.C . 10.A .二、11.2111sec tan dy dx x x x=-;12.22tan sec dy x xdx =;13.111(sin cos )dy dx x x x =- 14.211dy dx x =-+;15.dy = ;16.22sec ()1sec ()x y dy dx x y +=-+;17.33(2)12t t dy dx t -=-; 18.dy =;19.0t dy dx ==;20.(2sin cos )cos sin t t t t dy dx t t t+=-.三、 21.dx x x x dy )2cos 22(sin += ;22.dx x x e dy x)]3sin()3[cos(----=-;12323. ⎪⎪⎩⎪⎪⎨⎧<<--<<--=10101122x xdx x x dx dy ;24.dx x x x dy )21(sec )31tan(123222+⋅+=;25.dx x dy 232)1(-+=; 26.dx x x x dy 232)1(1)11(32++--=-.第六节 导数在经济分析中的应用1.边际成本5, 边际收入x 02.010-,边际利润x 02.05-;2. 300(单位);3.bp -;4. ⑴ 边际成本x +3,边际收入x50,边际利润x50x --3 ⑵ 1-.5.⑴ 当6190<<p 时,低弹性,当4619<<p 时,高弹性;⑵ 当30ap <<时,低弹性,当a p a<<3时,高弹性; 6. ⑴边际利润 xx 120310--;⑵ 收益的价格弹性p p --10310; 7. ⑴利润函数⎪⎩⎪⎨⎧<<-≤≤--=646402213)(2x x x x x x L ;⑵边际利润⎩⎨⎧<<-≤≤-='641403)(x x x x L . 第二章 综合练习题一、1. D .2. D . 二、3. ⑴ )(0x f '- ⑵)0(f ' ⑶)(20x f ';4. ⑴ t g gt ∆--21100; ⑵ 010gt -; 5. )(x f 在α=x 处可导,且)()(αϕα='f 6. )0(-'f 存在,且='-)0(f )0(+'f ;7.)(0x N ',当劳动力为0x 时,增加一个劳动力时该商品增加)(0x N '(劳动生产率); 8.96%,1.6%;9. 切线方程032=-+y x ,法线方程012=--y x ;10. (1) )111(ln )1(x x x x x x ++++; (2) ])2(3251[25512532+--+-x xx x x ; (3)]1534)2(21[)1()3(254+---++-+x x x x x x ;(4)])1(2sin cos 1[1sin 21x x x e e x x x e x x --+-.11.⑴ 32)2()3(y y e y -- ;⑵ )(cot )(csc 232y x y x ++-; 14.⑴3-t ; ⑵αθθ3csc sec 4;15. )/(1442s m π;文案大全16.当11181==∆=∆dy y x 时, 当0.1 1.161, 1.1x y dy ∆=∆==时,当0.010.110601,0.11x y dy ∆=∆==时.17. 21x y +;18. ⑴ 87476.0;⑵74300' ; ⑶ 9867.9; ⑷ 0052.2 ; ⑸ 96509.0-; ⑹2600'.21. )()(a f a f e '.22. 不一定成立,例⎪⎩⎪⎨⎧>≤=1132)(23x xx xx f ,⎩⎨⎧>≤≠'1212)(2x xx xx f ,⎪⎩⎪⎨⎧>=<='12112)(2x xx x x x f 不存在. 23. R a b A ∈==00;24. 12=±=b a ,.25. x x f xx f ln 1==')(,)(. 26. 0=-y x .27. 111=-=-=c b a .28. 08215=+-y x .29.122-x .30.+---)!3()1(21n n +---)!2()1(21n n )!1()1(1---n n .31. ⑴5.0 当价格4=p 时,如果价格上涨%1,收益增加%5.0⑵64.0- 当价格6=p 时,如果价格上涨%1,收益减少%636.0;如果价格下降%1,收益增加%636.0,应下调价格至16.5.第三章 微分中值定理与导数的应用作业参考答案第一节 微分中值定理一、1. D .2. B . 3. A .4. A .5. B .6.C .7. A .8.C .9.A .10. B .第二节 洛必达(L ’Hospital )法则一、 1. B . 2. B .3. C .4.A .5. B .6. C .二、7.2- ;8.13; 9.a ; 10.0;11.2(3)f '-;12.24a π-;13.12;14.16;15.216.32;17.1 ;18.1;19.31;20.0;21 ∞ ;22.61-e ;23.0;24 π2-e ;19.21;25.a ;26. 21-e;27. 1-e ;28.31e ;29. 41-;30. 21; 31. 2e- .第三节 泰勒(Taylor )公式一、⑴31,⑵ 21-. 二、⑴ ])1[()1()1()1(11332+++-+-+--=x o x x x x;⑵])4[()4(5121)4(641)4(412332-+-+---+=x o x x x x ;125⑶ )(31tan 33x o x x x ++=;⑷ )(21132sin x o x x e x +++= 三、4523)(cos 3]2)()[sin sin(31tan x x x x x x x θθθ+++=, 10<<θ.四、)()!1(!232n n x x o n x x x x xe +-++++= . 五、⑴ 10724.3303≈; 51088.1-⨯≤E ; ⑵ 1827.02.1ln ≈; 4104-⨯≤E第四节 函数性态的研究一、1. B .2. D .3.A .4. B .5. B .6.B .7.C .. B . 9.A .10. B .二、11. 4;12.2-;13.单调增加;14.'(0)0f =,"(0)0f <;15.'0y ≥;16.1p =; 四、19.1)2(=极大y ;20.4)2(-=-极大y ,0)0(=极小y ;21.205101)512(=极大y ;22.无极值. 第五节 函数作图一、1. D .2.C .3. C .4.A .5. C .6.A .7. B .8. C .9.C .10.A . 二、11.0,1y x ==;12. (,0)π; 13.(22-;14.有一个拐点;15.2π+=x y ,2π-=x y ; 16.22049x y -=;17.y x =. 第六节 最大最小值问题及在经济管理中的应用一、⑴ 0)0(=最大y , 16)4(-=最小y ⑵ 45)43(=最大y , 56)5(-=-最小y 二、设半径为32πVr =, 高为34πV h =时, 表面积最小三、产量140=x , 平均成本104=c , 边际成本104='c 四、出售3000=x 件时,收益最高.五、101=p (元), 3920=Q , 167080=最大L (元)第三章 综合练习3.(1)↓)2,0(↑∞+),2(;(2)11(,),(,)22-∞↓+∞↑; (3)↓-∞)0,(↓)21,0(↑)1,21(↓∞+),1(;(4)↑-∞)32,(a ↓),32(a a ↑∞+),(a .4.(提示: 设那条直线为b kx y +=).5. (提示: 设()()nF x x f x =) ;6.2-<a , 无根; 2-=a ,唯一根2-=x ; 2->a ,在),(a -∞和),(∞+a 内各有一根.文案大全7. ⎪⎩⎪⎨⎧=-''≠+-+'='--0,21)0(0,)()()(2x g x x e x g xe x g x x f xx , )(x f '在),(∞+-∞处处连续.9. 驻点1=x , 1)1(=极小y .10. 设)1,0(∈x ,证明:22(1)ln (1)x x x ++<. 11.2)0(=极大f , 21()e f e e--=极小.12.当n 为奇数时, 在0x 无极值,当n 为偶数时, f 在0x 有极值 13.一段为ππ+4a , 另一段为π+44a. 14.当)(0bc a cbp -<<时, 随单价p 的增加,相应的销售额也增加; 当)(bc a c bp ->时, 随单价p 的增加,相应的销售额减少; 当)(bc a c bp -=时, 销售额最大, 2max )(bc a R -=15.定价a b p 2185+=(元)时, 的最大利润: 2)45(16a b bcL -=(元).第四章 不定积分作业参考答案第一节 不定积分的概念及性质一、1. B . 2. D .3. B .4. C .5.C .6.A .7. B .8. C . 9. C .二、10.3tan x c +;11.2arctan x c +;12.ln(x c++;13.tan x x c -+;14.ln x c ++;15.31ln 3x x e c ++;16.cot tan x x c --+;17.1arctan x c x-++; 18.2sincot x x c ++;19.3arcsin x c +;20.ln(x c ++;21.cot x x c --+;22.2ln 2x xe c ++;23.sin cos x x c -+;24.sin 2x xc -+;25.sin x c +; 26.1(sin cos )2x x x c --+;27.1(tan )2x x c ++;28.tan cot x x c -+.第二节 基本积分法 (换元积分法)一、1. C .2.B .3. B .4. B . 5. C . 6.A . 7.A . 8. D .二、9.c x ++)1ln(2;10.212x e c --+;11.c u +-232)5(31; 12.c e x +-1;13.c x x +-arcsin )(arcsin 515;14.c x x +-ln 1;15.1arccos ||c x +;16.c x x +-sec sec 313;12717.c x x ++3tan 31tan ;183arcsin 2x c ++;19.c x x +-⋅9912; 20.c x a a x ++222;21.c x x ++-+2325)1(32)1(52;22.2c +; 23.11cos cos5210x x c -+;24.ln |c -+;25.arcsin x c -; 26.2ln |tan c +.第二节 基本积分法(分部积分法)一、 1.A .2.A . 3.A . 4.A . 二、5.2(22)x e x x c -++;6.c x ex+-)1(2;7.2sin 2cos 2sin x x x x x c +-+.8.ln x x x c -+;9.21arccot(2)ln(14)4x x x c -++;10.2(arccos )2x x x x c +++. 118ln(3x c -++;12.1(sin 22cos 2)5x e x x c --++; 13. 1211cos sin n n n n I x x I n n---=+.第三节 有理函数的积分一、单项选择题: 1. B .2. C .3. D .4. B . 5. A .二、6.c x x +--2)1(; 7.c x x x ++-++33)23ln(2;8.c xx x x ++++2)1(ln 1;9.c x x ++1ln2; 10.21arctan 22(1)x x c x +++;11c +. 122xc +;13.ln |1tan |2x c ++;14.cos 1ln |tan |2sin 22x x c x -++; 15.1ln |sin cos |2x x x c -++..16.1)c +;17.ln ||c +;18.1)x c -+.第四节 不定积分在经济领域的应用1.12212-+=x x y ;2.23252s t t =-+;3.()100()50100,()50C x C x x C x x x =+==+; 4.2()50100P t t t =+; 5.10000.5pQ =⋅文案大全第四章 综合练习一、单项选择题 :1. D . 2. C . 二、3.323c +;4.1ln |cos |c x+;5.c x +;6.137ln |5|ln |2|33x x c ---+; 7.13ln |1|2ln |2|ln |3}22x x x c -+++-++;8.11ln |sec tan |c x x -++;9.1x x e c ++;10.1x x xe c -+;11.12(ln |23|)923x c x++++.三、12.c x x e x +++--)22(2; 13.c x x x ++-2sin 412cos 21;14.3311()ln 39x x x x x c +--+; 15.ln(1)1x xx e c e ---+++; 16.21tan ln |cos |2x x x x c -+++; 17.11cos 2sin 248x x x c -++;18.(cosln sin ln )2x x x c ++; 19.321(ln 3ln 6ln 6)x x x c x-++++.五、23|c -++;24.2(1)arcsin 22x x c -++; 25.11ln ||x c x x ---+;26.c x x ++)ln (2122;27.c e e x x ++-ln ;28.c x++-tan 11;29.ln(1)x x e c -++;30.c x x x ++-cos 2sin ln 2; 31.1(arcsin 2x c -+;32.c x x ++-+4549)32(53)32(91;33.1c +;34.c x x++-)1(ln 1;35.c x f x xf +-)()(';36.c x x x x +-sin 2cos ;37.26ln 11x c x x ++++;38.c x x x x +-++-+312arctan 33)1()1(ln 6122;39.x x c +;40.1x x c ++.41、22(21)x x e c --++.42、()2ln(1)x dx x x c ϕ=-++⎰.43、2211,122max(1,||)0111122x c x x dx x cx x cx ⎧--+<⎪⎪=+≤≤⎨⎪⎪++>⎩⎰. 第五章 定积分及其应用作业参考答案129第一节 定积分的概念与性质一、1. B . 2. C . 3. D . 4.C . 5.A . 6.A .7.C . 二、8.3;9. 3;10.12;11.1;12. 2π;13.76;14. 4. 三、15.⎰⎰>202sin ππxdx xdx ; 16.⎰⎰<-55dx e dx e x x ;17.⎰⎰>20422sin sin ππxdx xdx ; 18.⎰⎰<-202sin sin ππxdx xdx .四、19.a dx eaeaax a 2222≤≤⎰---; 20.ππππ2)sin 1(4542≤+≤⎰dx x ;21.2ln sin 2124≤≤⎰ππdx x x; 22.2arctan 8333ππ≤≤⎰xdx x .第三节 微积分学基本定理一、1. C . 2. B . 3.A .4. B . 5. D . 6. B . 7.A . 8. B . 二、9. (())()f x x ϕϕ';10.2221x x x -++;11.()sin 2x d p x e x dx =; 12.sin cos xx e x e ---;13.1()sin 2sin(2)x x e x d p x e x e e dx--+=-.14.2e ;15.12;16.1;17.1;18.0;19.13-.20.3;21.32;22.3ln 22-;23.2021ln 21;24.23e -.第四节 定积分的换元积分法与分部积分法一、1. B . 2.A . 3.A .34.4. C . 5. C . 6. C . 二、7.0;8.0;9.1;10.8-;11.4ln 3;12.43;13.2;14.21(1)4e --;15.4π;16.51(1)5e -;17.43;18.1596π;19.32π;20.24π.第五节 反常积分初步与Γ函数一、1. D .2.A .3. B .4. D . 5. C . 6. C . 7.A . 8. C .9.A . 10.A .二、11.2;12.4π;13.2π;14.ln 2;15.2;16.0. 17. 18 ;18. π52;19.)1(1n n Γ, (0>n ) ;20.)21(21+Γn 21->n .三、21.0α≥ 发散;0α< 收敛于 1α-; 22.1α≥- 发散;1α<- 收敛于11α-+;文案大全23.1α≥- 发散;1α<- 收敛于11α-+; 24.1α≥- 发散;1α<- 收敛于2)1(1+α;25.2π; 26.发散;27.83;28.1-. 第六节 定积分的几何应用一、单项选择题 1. D .二、2.1132; 3.1132;4.1172; 5.1; 6.1; 7.1132;8.2a π;9.232a π三、10.=x V 2pa π; 11.=x V 312a π;12.=x V π; 13.=x V 24π;14.=x V e e π)52(-;15.=x V 2(1)4e π- =y V 310π; 16.=x V 1287π, =y V π8.12.第七节 定积分的经济应用1.585585058505≈⨯+-e;2.10100QR Qe-=;3.1999331666=;4.(1)9950;(2)19600;5.(1)400台(2)5000元.第五章 综合习题一、1.21;2.22π-;3.2arctan 2-;4.1;5.2ln 27+;6.105584;7.8π;8.13;9.14;10.2;11.1(1ln 2)2-;12.14π-; 14.π-4;15.122;16.154;17.2(1ln 2)-;18.ln 2;19.απsin 2;20.1718-;21.2ln 264π-;22.23;23.8π;24.23ln 211+;25.21(1)2e +;26.21ln 28-;27.21)π;28.9655;29.62ln 2-;30.2;31.2ln 32ln 3-;32.12ln 2-;33.ln 222π+-;34.214e -;35.8(2)e -;36.214e -;37.)1(10-e e .三、不一定;四、16;五、最大值为:3ln 32-;最小值为:0 .六、 1x =为极大值点,2x =为极小值点.七、 ()cos sin f x x x =-.十、在)1,(-∞单减,在),1(∞+单增,在)251,(--∞),251(∞++ 上凸,在)251,251(+-上凹。
西安交通大学网络学院《高等数学》选择题答案
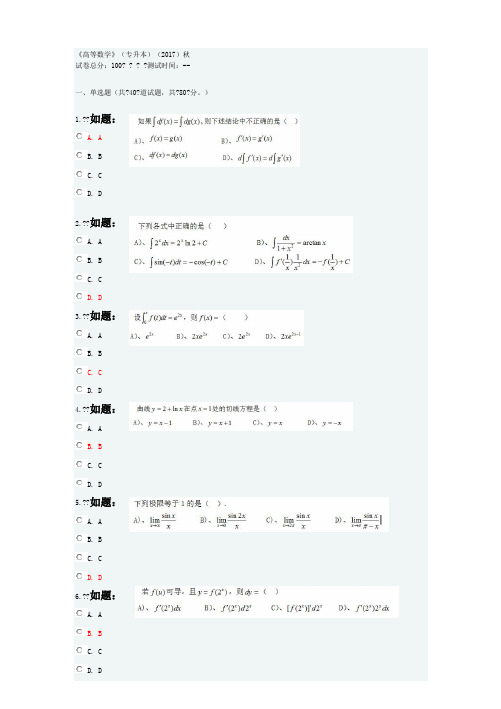
《高等数学》(专升本)(2017)秋试卷总分:100? ? ? ?测试时间:--一、单选题(共?40?道试题,共?80?分。
)1.??如题:A. AB. BC. CD. D2.??如题:A. AB. BC. CD. D3.??如题:A. AB. BC. CD. D4.??如题:A. AB. BC. CD. D5.??如题:A. AB. BC. CD. D6.??如题:A. AB. B7.??如题:A. AB. BC. CD. D8.??如题:A. AB. BC. CD. D9.??如题:A. AB. BC. CD. D10.??如题:A. AB. BC. CD. D11.??如题:A. AB. BC. CD. D12.??如题:A. AB. BC. CD. D13.??如题:A. AB. BC. CD. D14.??如题:A. AB. BC. CD. D15.??如题:A. AB. BC. CD. D16.??如题:A. AB. BC. CD. D17.??如题:A. AB. BC. CD. D18.??如题:A. AB. BC. CD. D ??????满分:2??分19.??如题:A. AB. BC. CD. D20.??如题:A. AB. BC. CD. D21.??如题:A. AB. BC. CD. D ??????满分:2??分22.??如题:A. AB. BC. CD. D ??????满分:2??分23.??如题:A. AB. BC. CD. D ??????满分:2??分24.??如题:A. AB. BC. C25.??如题:A. AB. BC. CD. D ??????满分:2??分26.??如题:A. AB. BC. CD. D ??????满分:2??分27.??如题:A. AB. BC. CD. D ??????满分:2??分28.??如题:A. AB. BC. CD. D ??????满分:2??分29.??如题:A. AB. BC. CD. D ??????满分:2??分30.??如题:A. AB. BC. C31.??如题:A. AB. BC. CD. D ??????满分:2??分32.??如题:A. AB. BC. CD. D ??????满分:2??分33.??如题:A. AB. BC. CD. D ??????满分:2??分34.??如题:A. AB. BC. CD. D ??????满分:2??分35.??如题:A. AB. BC. CD. D ??????满分:2??分36.??如题:A. AB. BC. C请同学及时保存作业,如您在20分钟内不作操作,系统将自动退出。
西安交通大学14春学期《高等数学(上)》离线作业

第一章 函数与极限本章要点:1.函数极限的概念(对极限的N -ε、δε-定义可在学习过程中逐步加深理解,对于给出ε求N 或δ不作过高要求。
)2.极限四则运算法则。
3.两个极限存在准则(夹逼准则和单调有界准则),会用两个重要极限求极限。
4.无穷小、无穷大,以及无穷小的阶的概念。
会用等价无穷小求极限。
5.函数在一点连续的概念。
6.间断点的概念,并会判别间断点的类型。
7.初等函数的连续性和闭区间上连续函数的性质(介值定理和最大、最小值定理.)本章目标:1.理解函数的概念的理解复合函数的概念,了解反函数的概念。
2.了解函数的奇偶性、单调性、周期性和有界性。
3.掌握基本初等函数的性质及其图形。
4.会建立简单实际问题中的函数关系式。
5.理解极限的概念(对于给出ε求N 或δ不作过高要求。
)6.掌握极限的四则运算法则。
7.了解极限存在准则(夹逼准则和单调有界准则),会用两个重要极限求极限。
8.了解无穷小、无穷大,以及无穷小的阶的概念。
会用等价无穷小求极限。
9.理解函数在一点连续的概念。
10.了解间断点的概念,并会判别间断点的类型。
11.了解初等函数的连续性和闭区间上连续函数的性质(介值定理和最大、最小值定理。
) 本章重点:1.函数极限的概念,会求一些简单函数的极限。
2.函数在一点连续的概念,会判断一些简单函数间断点的类型。
本章难点1.两个极限存在准则;2.判别间断点的类型。
第一章 总结本章主要介绍了极限的概念、极限存在的判定准则,极限的求法以及连续函数的定义与性质. 利用极限的定义证明函数(或数列)以某确定常数为极限,是本章的难点之一。
极限存在性问题是本章的重点,也是难点.一般地,常用以下方法判定一个极限是否存在:(1)利用单调有界准则;(2)利用夹逼准则;(3)利用柯西准则;(4)利用左右极限是否存在且相等;(5)利用子数列或部分极限。
掌握好求极限的方法是学好高等数学所必须的,这是本章的重点内容。
目前为止,我们可以(1)利用定义验证极限;(2)利用极限四则运算法则求极限;(3)利用重要极限求极限;(4)利用无穷小量等价代换求极限;(5)利用夹逼准则求极限;(6)利用单调有界数列必有极限准则求极限;(7)利用函数连续性求极限等等.在后面的章节中,我们还会陆续介绍其它一些求极限的方法。
西安交通大学《高等数学(上)》期末考试拓展学习(一)3

西交《高等数学(上)》(一)第一章函数极限与连续性一、函数定义的两个要素是什么?“如果自变量 x 在允许范围 X 内任取一个数值时,变量 y 是按一定的规则总有确定的数值和它对应,则称 y 是 x 的函数,常记为. ”我们称之为函数的“依赖关系”定义。
这个定义的关键特征为:—— x 的允许范围,即函数的定义域;——对应规则,即函数的依赖关系 .可以说函数概念有两个基本要素:定义域、对应规则。
只有当两个函数的定义域与对应规则完全相同时,才能认为它们是同一函数。
读者仔细分析教材就可以发现,“对应规则”是本章的一条知识线,它串起了许多概念。
由于函数的定义中并没有限制“对应规则”与 y的取值特点,因此可能出现:(1)当自变量 x 的值变动时,变量 y 的取值并不一定随 x 的变化而变化, y 可能总取一值。
如 y = 3 表示不论 x 取什么值,所对应的 y 的值总是 3 ,因此它符合函数的定义,可以说 y = 3 是函数。
通常称 y = c 为常量函数。
(2)函数对应规则的形式没有限制。
① 如果函数对应规则是解析表达式,可称函数为显式形式。
② 如果函数对应规则是方程,可称 y为 x的隐函数。
③ 如果函数对应规则在自变量的不同范围是由几个不同的解析表达式而表示的,例如则称为分段函数。
注意这里不可以说是三个函数,应该说是定义域为的一个函数,在不同的范围它是由三个不同解析表达式来表达而已。
④ 如果对应规则是由表格或图形表示出来,那么常称这种表示为函数的表格法或图形表示法。
⑤ 如果 x 与 y 通过第三个变量 t 而联系起来,如则称这种函数关系为参数方程表示的函数 .二、研究函数的单调性、有界性能否离开自变量的范围?不能。
如当时为单调减少函数;当时为单调增加函数;在(-1,1)内为非单调函数。
同样,在(0,1)内有界函数,在内为无界函数。
如果说函数为单调函数或有界函数,而没有指明其范围,通常要理解为是在其定义域内而言。
西交19秋《高等数学(专升本)》在线作业参考答案

西交《高等数学(专升本)》在线作业2
试卷总分:100 得分:50
一、单选题(共25 道试题,共50 分)
1.点x=0是函数y=x^4的( ).
A.驻点但非极值点
B.拐点
C.驻点且是拐点
D.驻点且是极值点
答案:D
2.函数f(x)在点x0极限存在是函数在该点连续的( )
A.必要条件
B.充分条件
C.充要条件
D.无关条件
答案:A
3.曲线y=1/∣x∣的渐近线情况是( ).
A.只有水平渐近线
B.只有垂直渐近线
C.既有水平渐近线又有垂直渐近线
D.既无水平渐近线又无垂直渐近线
答案:C
4.y=x/(x^2-1)的垂直渐近线有()条.
A.1
B.2
C.3
D.4
答案:B
5.当x→0时,下列函数不是无穷小量的是( )
A.y=x
B.y=0
C.y=ln(x+1)
D.y=e^x
答案:D
6.设f(x)=2^x-1,则当x→0时,f(x)是x的( )。
A.高阶无穷小
B.低阶无穷小
C.等价无穷小
D.同阶但不等价无穷
答案:D
7.若f(x)在处可导,则∣f(x)∣在x=x0处( )
A.可导
B.不可导。
西安交通大学高等数学(上)小抄总结

《高等数学(上)》——学习指南一、选择题1.函数lg(1)y x =-的反函数是【 】A. 1x y e =+B. 101x y =+C.101y x =-D. 101y x -=+ 参考答案:B对等式两边做e 的指数,得到101y x =-,变换一下因变量和自变量得到:101x y =-。
即:101x y =+2.极限1111lim 122334(1)n n n →∞⎡⎤++++=⎢⎥⨯⨯⨯⨯+⎣⎦【 】 A. 1 B. 0 C.23 D. 32参考答案:A由题目知通项n S 有如下的形式:()1111+12233411111111122334111111111223341111n S n n n n n n n =+++⨯⨯⨯⨯+⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++- ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭=-+-+-++-+=-+ ()11111lim +lim 1112233411n n n n n →∞→∞⎡⎤⎡⎤+++=-=⎢⎥⎢⎥⨯⨯⨯⨯++⎣⎦⎣⎦3.若33222lim 3x x x a→-=-,则a =【 】 A. 1 B. 2 C. 3 D. 4参考答案:D()()()332233222222lim 3lim 230lim 383223834x x x x x ax x a x x a a a →→→-=-⇔---=⇔-=-⇒-=-⇒=4.当1x →时,21()1f x x =-【 】 A. 极限不存在 B. 是无穷大量 C. 是无穷小量 D. 是未定式参考答案:B当x 趋向于1时,分母趋向于0,任意常数除以0都是无穷大量。
所以原式是一个无穷大量。
5.设函数2sin(2)()32x f x x x +=-+, 那么函数的所有间断点是【 】A. 0B. 1和2C.2-D.1-和3参考答案:B()()()()()2sin 2sin 23212x x f x x x x x ++==-+--,当1x =或者2时,分式的分母等于零,方程没有意义。
地大《高等数学(一)》在线作业二满分答案

地大《高等数学(一)》在线作业二满分答案1微分方程ydx+xdy=0的通解是( )A xy=CB xy=0C x+y=CD x-y=0正确答案:A2由曲线y=cosx (0=<x<=3π) 与坐标轴所围成的图形面积=()A 4B 3C 4πD 3π正确答案:B3∫{lnx/x^2}dx 等于( )A lnx/x+1/x+CB -lnx/x+1/x+CC lnx/x-1/x+CD -lnx/x-1/x+C正确答案:D4设函数f(x)=x(x-1)(x-3),则f '( 0 ) = ( )A 0B 1C 3D 2正确答案:C5设f(x)=x(x-1)(x-2)(x-3),则f’(0)=( )A -6B -2C 3D -3正确答案:A6如果函数f(x)的定义域为(0,1)则下列函数中,定义域为(-1,0)的为:()A f(1-x)B f(1+x)C f(sinx)D f(cosx)正确答案:B7微分方程dy/dx=1+y/x+y^2/x^2 是()A 一阶齐次方程,也是伯努利方程B 一阶齐次方程,不是伯努利方程C 不是一阶齐次方程,是伯努利方程D 既不是一阶齐次方程,也不是伯努利方程正确答案:B8函数y=cosx在[-1,+1]区间的拐点为A (0,0)B (1,cos1)C (-1,cos1)D 无拐点正确答案:D9f(x)是给定的连续函数,t>0,则t∫f(tx)dx , 积分区间(0->s/t)的值()A 依赖于s,不依赖于t和xB 依赖于s和t,不依赖于xC 依赖于x和t,不依赖于sD 依赖于s和x,不依赖于t正确答案:A10函数y=|sinx|在x=0处( )A 无定义B 有定义,但不连续C 连续D 无定义,但连续。
2016年陕西省专升本(高等数学)真题试卷(题后含答案及解析)

2016年陕西省专升本(高等数学)真题试卷(题后含答案及解析) 题型有:1. 选择题 2. 填空题 4. 解答题 6. 证明题选择题在每小题给出的四个选项中,只有一项是符合要求的。
1.点x=0是函数f(x)=的A.连续点B.可去间断点C.跳跃间断点D.无穷间断点正确答案:B2.设在闭区间[a,b]上,f(x)>0,f’(x)>0,f’’(x)<0,令S1=∫abf(x)dx,S2=f(a)(b一a),S3=[f(a)+f(b)],则必有A.S1<S2<S3B.S2<S1<S3C.S3<S1<S2D.S2<S3<S1正确答案:D3.曲面z=2x2+y2一3在点(1,1,0)处的切平面方程为A.4z+4y—z一8=0B.4x+4y+z一8=0C.4x+4y—z+8=0D.4x+4y+z+8=0正确答案:A4.微分方程的通解为A.xy=CB.C.x—y=CD.x2+y2=C正确答案:B5.设幂级数an(x一1)n在n=2处发散,则该幂级数在x=一1处A.绝对收敛B.条件收敛C.发散D.敛散性不确定正确答案:C填空题6.极限=______.正确答案:27.已知当x→0时,∫0sinx与xα是同阶无穷小,则常数α=______.正确答案:38.定积分∫-33(xcosx+)dx=______.正确答案:9π9.二元函数z=xy(x>0,x≠1)的全微分dz=______.正确答案:10.设曲线L为圆周x2+y2=1,则对弧长的曲线积分=______.正确答案:2π解答题解答时应写出推理、演算步骤。
11.已知函数,在x=0处可导,试确定常数a和b.正确答案:因为f(x)在x=0处可导所以f(x)在x=0处连续,从而有由f(x)在x=0处可导,且f-’(0)=f+’(0)=得a=1.12.设函数y=y(x)由参数方程所确定,求正确答案:13.求函数f(x)=x3一3x+1的极值点及其图形的拐点.正确答案:由f’(x)=3x2一3=0 得驻点x1=一1,x2=1,f’’(x)=6x,因为f’’(-1)=一6<0,f’’(1)=6>0,所以x1=—1为极大值点,x2=1为极小值点,又因为f’’(0)=0,且当x<0时,f’‘(x)<0;当x>0时,f’’(x)>0,又f(0)=1,所以函数图形的拐点为(0,1).14.求不定积分∫arctanxdx.正确答案:15.设函数z=f(x+y,exy),其中f具有二阶连续偏导数,求正确答案:=f1’+yexyf2’=f11’’+yexyf12’’+y2exyf2’+yexyf21’’+y2e2xyf22’’=f11’’+2y exyf12’’+y2e2xyf22’’+y2exyf2’’.16.求函数u=xy2z2在点P(1,1,1)处的梯度和沿该梯度方向的方向导数.正确答案:易见函数u在整个R3中可微,因为gradu=(y2z2,2xyz2,2xy2z),所以gradu|(1,1,1)=(1,2,2),函数在点(1,1,1)沿梯度方向的方向导数为该点处梯度的模:gradu|(1,1,1)|=17.将二次积分∫01dx xy2dy化为极坐标形式的二次积分,并计算积.正确答案:18.计算曲线积分I=∫L(x2+y)dx+(x+)dy,其中L为从点O(0,0)经过点A(1,0)到点B(1,1)的一段折线.正确答案:19.将函数f(x)=展开成麦克劳林级数.正确答案:20.求微分方程y’’一4y’+4y=(x+1)ex的通解.正确答案:对应齐次方程的特征方程为r2—4r+4=0,特征根为r1=2,r2=2,对应齐次方程的通解为Y=(C1+C2x)e2x,设原方程特解形式为y*=(ax+b)ex,代入原方程得a=1,b=3,得原方程的一个特解为y*=(x+3)ex,故原方程的通解为y=(C1+C2x)e2x+(x+3)ex.证明题21.设a>b>0,n>1,证明:nbn-1(a一b)<an一bn<nan-1(a一b).正确答案:设f(x)=xn,显然f(x)在闭区间[b,a]上连续,在开区间(b,a)内可导,由拉格朗日中值定理得,在(b,a)内至少存在一点ξ,使得f(a)一f(b)=f’(ξ)(a一b),即an一bn=nξn-1(a一b),因为bn-1<ξn-1<an-1,所以nbn-1(a-b)<an一bn<nan(a-b).22.求由曲线y=x2和所围成平面图形的面积S,并求此图形绕x 轴旋转一周所形成的旋转体的体积V.正确答案:V=∫01[π-π(x2)2]dx。
2016年春西安交通大学《高等数学》(上)2 在线作业答案

《高等数学》(上)2 在线作业答案一、单选题(共 40 道试题,共 80 分。
)1。
求下题极限:A。
AB. BC. CD。
D正确答案:C 满分:2 分2。
当A. AB。
BC。
CD。
D正确答案:D 满分:2 分3。
若A。
AB。
BC。
CD。
D正确答案:B 满分:2 分4.下列极限存在的是A. AB。
BC。
CD. D正确答案:B 满分:2 分5。
设A。
AB。
BC。
CD。
D正确答案:A 满分:2 分6。
如果:A.AB。
BC。
CD。
D正确答案:C 满分:2 分7。
若A。
AB. BC。
CD. D正确答案:A 满分:2 分8.在区间A。
AB. BC. CD。
D正确答案:B 满分:2 分9.极限:A. AB. BC。
CD。
D正确答案:A 满分:2 分10.当A. AB。
BC。
CD. D正确答案:D 满分:2 分11.已知A。
AB. BC。
CD。
D正确答案:A 满分:2 分12。
数列A.单调递增但无界的数列B。
单调递减且有界的数列C.单调递增且有界的数列D。
单调递减且无界的数列正确答案:C 满分:2 分13。
若A. AB。
BC。
CD. D正确答案:B 满分:2 分14。
已知A. 17B. 170C。
18D。
180正确答案:A 满分:2 分15.若以下函数:A. AB。
BC。
CD. D正确答案:D 满分:2 分16. 函数:A.偶函数B.无界函数C。
周期函数D.单调函数正确答案:B 满分:2 分17。
已知数列A。
AB. BC。
CD。
D正确答案:B 满分:2 分18。
已知数列:A. 9B. 10C。
101D. 1000正确答案:B 满分:2 分19。
若函数:A. AB. BC. CD。
D正确答案:C 满分:2 分20.已知A。
AB。
BC。
CD. D正确答案:C 满分:2 分21。
设A。
AB. BC。
CD。
D正确答案:C 满分:2 分22。
当:A. AB. BC. CD. D正确答案:D 满分:2 分23.若A。
AB。
高等数学_第2版_上册_(范周田_著)习题答案

各章习题答案第0章 预备知识综合复习题0 1.(1)62, (2)()()(){}11,4,2,4,3,4,R = ()()(){}21,5,2,5,3,5,R = ()()(){}31,4,2,4,3,5,R = ()()(){}41,4,2,5,3,4,R = ()()(){}51,5,2,4,3,4,R = ()()(){}61,4,2,5,3,5,R = ()()(){}71,5,2,5,3,4,R = ()()(){}81,5,2,4,3,5,R =2.略。
3. (1)(2)4 . (1));,(,2101+∞-∞-=-x y(2)].2,2[,2arcsin 31-=xy5. (1) 是的. (2) 积为偶函数.6. 略7. (1) 542-x (2) 2254⎪⎭⎫ ⎝⎛-x (3) 5412-x 8. (1)(2)(3)(4)9.不是.10.(1) 奇 (2) 偶 (3) 奇 (4) 奇. 11.(2)[1(2)],(2,21)(1)(),0,1,2,0(21,2)x n x n x n n f x n x n n ±⋅-±∈+⎧==±±⎨∈-⎩(2)(2)[1(2)],(2,21)(),0,1,2,0.1(21,2)x n x n x n n f x n x n n ±⋅-±∈+⎧==±±⎨-∈-⎩12.略 13. (1) 1x y +=; (2) 22x y yy e+=.14. (1)7cos r θ=; (2)r =(3)4sin r θ=; (4) 2sin 3cos r θθ=.15. 对于任意正数T ,存在(,)x ∈-∞+∞, 使()()f x T f x +≠.16. 存在(,)x ∈-∞+∞, 使()()f x f x -≠.第一章 习题1.1 4.435.1 习题1.21. (1) 1, 0, 不存在, 不存在; (2) ,,22ππ-不存在,4π; (3) 1, 8, 0,,+∞ 不存在;(4) 0, 1, lg 2, ,-∞ ,+∞(5) 2, 0, 不存在.2. (1) 0; (2) 不存在; (3) 不存在; (4) 不存在.7. (1) 错, (2) 错, (3) 正确, (4) 正确,, (5) 错, (6) 错, (7) 错, (8) 错.习题1.31. (1) 0, (2) 2, (3)2,3, (4) ,∞ (5) 0.2. (1)(2)(3) 1, (4) - 3. (1) 0, (2) 1. 4. (1)1,3 (2) 1,2(3) -1, (4) 1. 5. (1) 0, 1, 不存在, 6. (1) 2,- (2) 5.7. (1) 11,2a b ==; (2) a 任意常数, 5.3b =- 习题1.41. (1),3ω(2) 1, (3) 2, (4) x.,(5) sin18, (6) 2,π(7)12-, (8) -2. (9)12, (10) 1, (11) 12, (12) 13-. 2. (1) 1阶, (2) 1阶, (3) 2阶, (4) 1阶, (5)53阶, (6) 3阶.3.(1)1,e(2) 4e , (3) k e -, (4) 2e , (5) 2n e (6) 2e . 4. (2) 0, (3) e , 1, 不存在.6. (1) 2, (3)习题1.51. (1) 0, (2) 1, (3)1e-, (4)12e-2. (1) 1x =为第一类间断点,2x = 为第二类间断点;(2) 0x =为第一类可去间断点,2x k ππ=+为第一类间断点,(0,x k k k π=≠∈Z 为第二类间断点;(3) 0x =为第一类可去间断点; (4) 0x =为第一类间断点; (5) 0x =为第一类间断点; (6) 0x =为第二类间断点;3. (1) 0x =为第一类间断点,不可去; (2) 0x =为第一类可去间断点,补充定义使(0)ln10f =;(3) 0x =为第一类间断点,不可去; (4) 0x =为第一类可去间断点,补充定义使2(0).f e = 4. (1) 0,a = (2) ,2aπ=-(3) 32,.2a b ==- 5. ||1()0||1,||1xx f x x x x <⎧⎪==⎨⎪->⎩1x =-和1x =都为第一类间断点. 图形如右.综合练习题11. 试分析和研究0(),0x x f x x x ≥⎧=⎨-<⎩与()f x3. C 正确.4. D 正确.5. D 正确6. C 正确.7. (1)1,2 (2) 3,7 (3)- 12.1.2y x =-+1.2y x =- 第二章习题2.11. (1)22+x (2) x12. (1))(0x f '-; (2) . )(20x f ' (3) )()(000x f x f x -'.3. (1) 可导, (2)连续,不可导。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《高等数学》(上)2 在线作业答案
一、单选题(共40 道试题,共80 分。
)
1.
求下题极限:
A. A
B. B
C. C
D. D
正确答案:C 满分:2 分
2.
当
A. A
B. B
C. C
D. D
正确答案:D 满分:2 分
3.
若
A. A
B. B
C. C
D. D
正确答案:B 满分:2 分4.
下列极限存在的是
A. A
B. B
C. C
D. D
正确答案:B 满分:2 分5.
设
A. A
B. B
C. C
D. D
正确答案:A 满分:2 分6.
如果:
A.
A
B. B
C. C
D. D
正确答案:C 满分:2 分7.
若
A. A
B. B
C. C
D. D
正确答案:A 满分:2 分
8.
在区间
A. A
B. B
C. C
D. D
正确答案:B 满分:2 分9.
极限:
A. A
B. B
C. C
D. D
正确答案:A 满分:2 分10.
当
A. A
B. B
C. C
D. D
正确答案:D 满分:2 分11.
已知
A. A
B. B
C. C
D. D
正确答案:A 满分:2 分12.
数列
A.
单调递增但无界的数列
B.
单调递减且有界的数列
C.
单调递增且有界的数列
D.
单调递减且无界的数列
正确答案:C 满分:2 分13.
若
A. A
B. B
C. C
D. D
正确答案:B 满分:2 分14.
已知
A. 17
B. 170
C. 18
D. 180
正确答案:A 满分:2 分15.
若以下函数:
A. A
B. B
C. C
D. D
正确答案:D 满分:2 分
16. 函数:
A.
偶函数
B.
无界函数
C.
周期函数
D.
单调函数
正确答案:B 满分:2 分17.
已知数列
A. A
B. B
C. C
D. D
正确答案:B 满分:2 分18.
已知数列:
A. 9
B. 10
C. 101
D. 1000
正确答案:B 满分:2 分19.
若函数:
A. A
B. B
C. C
D. D
正确答案:C 满分:2 分20.
已知
A. A
B. B
C. C
D. D
正确答案:C 满分:2 分21.
设
A. A
B. B
C. C
D. D
正确答案:C 满分:2 分22.
当:
A. A
B. B
C. C
D. D
正确答案:D 满分:2 分23.
若
A. A
B. B
C. C
D. D
正确答案:D 满分:2 分24.
设
A. A
B. B
C. C
D. D
正确答案:A 满分:2 分25.
设对任意的
A.
存在且一定等于零
B.
一定不存在
C.
存在但不一定等于零
D.
不一定存在
正确答案:D 满分:2 分26.
极限
A. A
B. B
C. C
D. D
正确答案:C 满分:2 分27.
极限:
A. A
B. B
C. C
D. D
正确答案:D 满分:2 分
28.
下列四个单调递增数列中,只有由()给出的数列以1为其上界
A. A
B. B
C. C
D. D
正确答案:B 满分:2 分
29.
求值:
A. A
B. B
C. C
D. D
正确答案:A 满分:2 分30.
当:
A. A
B. B
C. C
D. D
正确答案:B 满分:2 分31.
求极限:
A. A
B. B
C. C
D. D
正确答案:D 满分:2 分32.
函数
A. A
B. B
C. C
D. D
正确答案:C 满分:2 分33.
当:
A. A
B. B
C. C
D. D
正确答案:A 满分:2 分34.
“对任意给定的
A.
充分条件但非必要条件
B.
必要条件但非充分条件
C.
充分必要条件
D.
既非充分条件又非必要条件
正确答案:C 满分:2 分35.
下列()中所给的数列是无界的
A. A
B. B
C. C
D. D
正确答案:C 满分:2 分36.
函数:
A.
不存在
B. 0
C. 0.5
D. 1
正确答案:A 满分:2 分37.
当
A. A
B. B
C. C
D. D
正确答案:D 满分:2 分38.
设数列
A. A
B. B
C. C
D. D
正确答案:D 满分:2 分39.
下列极限不存在的是()
A. A
B. B
C. C
D. D
正确答案:C 满分:2 分40.
已知
A. A
B. B
C. C
D. D
正确答案:C 满分:2 分
二、判断题(共10 道试题,共20 分。
)
1.
定义函数极限的前提是该函数需要在定义处的邻域内有意义
A. 错误
B. 正确
正确答案:B 满分:2 分
2.
等比数列的极限一定存在
A. 错误
B. 正确
正确答案:A 满分:2 分
3.
1/x的极限为0
A. 错误
B. 正确
正确答案:A 满分:2 分
4.
任何两个函数都可以构造复合函数。
A. 错误
B. 正确
正确答案:A 满分:2 分
5.
1/n的极限为0。
A. 错误
B. 正确
正确答案:A 满分:2 分
6.
数列要么收敛,要么发散
A. 错误
B. 正确
正确答案:A 满分:2 分
7.
函数极限是数列极限的特殊情况
A. 错误
B. 正确
正确答案:A 满分:2 分
8.
若定义域关于原点对称,且f(-x)=f(x),则f(x)是奇函数。
A. 错误
B. 正确
正确答案:A 满分:2 分
9.
若一个数列极限存在,则该数列不一定有界
A. 错误
B. 正确
正确答案:A 满分:2 分
10.
任何一个函数都有反函数。
A. 错误
B. 正确
正确答案:A 满分:2 分
(注:专业文档是经验性极强的领域,无法思考和涵盖全面,素材和资料部分来自网络,供参考。
可复制、编制,期待你的好评与关注)。
