最新超全的高中数学思维导图
人教版高中数学必修二章节思维导图全套
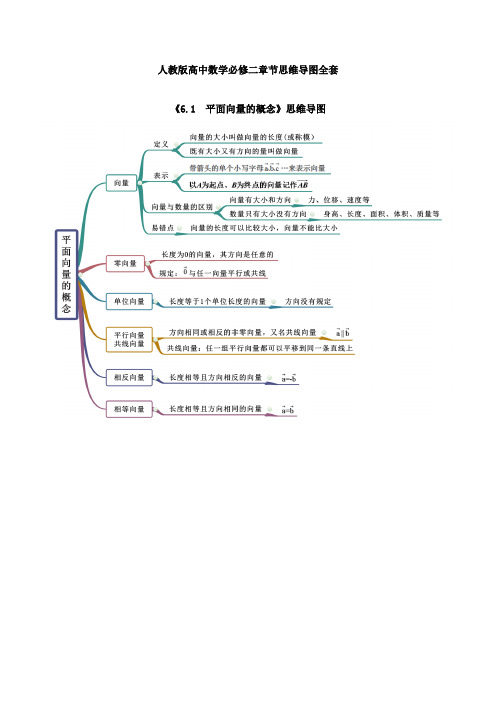
人教版高中数学必修二章节思维导图全套《6.1 平面向量的概念》思维导图
《6.3.1 平面向量的基本定理及加减数乘坐标运算》思维导图
《6.3.2 平面向量数量积的坐标表示》思维导图
《6.4.1平面向量在几何和物理中的运用》思维导图
《6.4.2 余弦定理、正弦定理》思维导图
《6.4.3 余弦定理、正弦定理的实际运用》思维导图
《7.1 复数的概念》思维导图
《7.2 复数的四则运算》思维导图
《7.3 复数的三角表示》思维导图
《8.1 基本立体图形》思维导图
《8.2 立体图形的直观图》思维导图
《8.3 简单几何体的表面积与体积》思维导图
《8.4 空间点、直线、平面之间的位置关系》思维导图
《8.5 空间直线、平面的平行》思维导图
《9.1 随机抽样》思维导图
《10.2 事件的相互独立性》思维导图
《10.3 频率与概率》思维导图。
高中数学必修全思维导图

调性不同,则 y f [g(x)] 是减函数。
4、奇函数在对称区间上的单调性相同,偶函数在对称区间上的单调性相反。 5、常用函数的单调性解答:比较大小、求值域、求最值、解不等式、证不等式、作 函数图象。 六、函数奇偶性的常用结论:
1、如果一个奇函数在 x 0 处有定义,则 f (0) 0 ,如果一个函数 y f (x) 既是
高一数学必修 1 知识网络
集合
( 1)元素与集合的关系:属于()和不属于()
集合与元素
( 2)集合中元素的特性:确定性、互异性、无序性 ( 3)集合的分类:按集合中元素的个数多少分为:有限集、无限集、空集 ( 4)集合的表示方法:列举法、描述法(自然语言描述、特征性质描述)、图示法、区间法
C.
4、空集是任何集合的(真)子集。
集合
真子集:若A
B且A
B(即至少存在x0
B但x0
A),则A是B的真子集。
集合与集合
运算集并交合集集Ca相r定定性性d等(义义质质A:::::ABAAAA)BBBC且AAaArdAAxx,(,A//BxAxA) CAAa或且rAdxx(AB,B,)BB-AACarBdB(ABBBA)A,,AABBAA,, AABB
定义
按照某个对应关系f , y都有唯一确定的值和它对应。那么y就是x的函数。记作y f ( x ).
近代定义:函数是从一个数集到另一个数集的映射。
定义域 函数及其表示 函数的三要素 值域 对应法则
解析法
函数的表示方法 列表法
函数
几类不同的增长函数模型 函数模型及其应用 用已知函数模型解决问题 建立实际问题的函数模型
高中数学全套思维导图(高清版)

23/59
请关注微信公众号“名师伴你学”获取更多精品资源
24/59
请关注微信公众号“名师伴你学”获取更多精品资源
25/59
请关注微信公众号“名师伴你学”获取更多精品资源
26/59
请关注微信公众号“名师伴你学”获取更多精品资源
27/59
请关注微信公众号“名师伴你学”获取更多精品资源
28/59
56/59
请关注微信公众号“名师伴你学”获取更多精品资源
57/59
请关注微信公众号“名师伴你学”获取更多精品资源
58/59
请关注微信公众号“名师伴你学”获取更多精品资源
59/59
请关注微信公众号“名师伴你学”获取更多精品资源
29/59
请关注微信公众号“名师伴你学”获取更多精品资源
30/59
请关注微信公众号“名师伴你学”获取更多精品资源
31/59
请关注微信公众号“名师伴你学”获取更多精品资源
32/59
请关注微信公众号“名师伴你学”获取更多精品资源
33/59
请关注微信公众号“名师伴你学”获取更多精品资源
6/59
请关注微信公众号“名师伴你学”获取更多精品资源
7/59
请关注微信公众号“名师伴你学”获取更多精品资源
8/59
请关注微信公众号“名师伴你学”获取更多精品资源
9/59
请关注微信公众号“名师伴你学”获取更多精品资源
10/59
请关注微信公众号“名师伴你学”获取更多精品资源
11/59
请关注微信公众号“名师伴你学”获取更多精品资源
请关注微信公众号“名师伴你学”获取更多精品资源
18/59
请关注微信公众号“名师伴你学”获取更多精品资源
高中数学课程内容思维导图脑图

高中数学课程内容必修课程预备知识集合(刻画一类事物的语言和工具)集合概念与表示集合的基本关系集合的基本运算常用逻辑用语必要条件、充分条件、充要条件全称量词与存在量词全称量词命题与存在量词命题的否定相等关系与不等关系等式与不等式的性质基本不等式<=ab2a+b从函数观点看一元二次方程和一元二次不等式函数函数概念与性质函数概念函数性质幂函数、指数函数、对数函数幂函数指数函数对数函数三角函数角与弧度三角函数概念与性质同角三角函数的基本不等式sinθ+2cosθ=21=cosθsinθtanθ三角恒等变换三角函数应用函数应用二分法与求解方程近似解函数与数学模型几何与代数平面向量及其应用向量概念向量运算向量基本定理及坐标表示向量应用与解三角形复数复数概念复数的运算立体几何初步基本立体图形基本图形位置关系概率与统计概率随机事件与概率随机事件的独立性统计获取数据的基本途径与相关概念抽样统计图表用样本估计总体数学建模活动与数学探究活动实际情境→提出问题→建立模型→求解模型→检验结果→实际结果选择性必修课程函数数列数列概念等差数列等比数列数学归纳法*一元函数导数及其应用导数概念及其意义导数运算导数在函数中的应用微积分的创立与发展*几何与代数空间向量与立体几何空间直角坐标系空间向量及其运算向量基本定理及坐标表示空间向量的应用平面解析几何直线与方程圆与方程圆锥曲线与方程平面解析几何的形成与发展*概率与统计计数原理两个基本计数原理排列与组合二项式定理概率随机事件的条件概率离散型随机变量及其分布列正态分布统计成对数据的统计相关性一元线性回归模型2*2列联表数学建模活动与数学探索活动选修课程A类微积分空间向量与代数概率与统计B类微积分空间向量与代数应用统计模型C类逻辑推理初步数学模型社会调查与数据分析D类美与数学音乐中的数学美术中的数学体育运动中的数学E类拓展视野的数学课程日常生活的数学课程地方特色的数学课程大学数学的先修课程。
全套高中数学思维导图(清晰打印版)

高中数学必修三目录 第一章 算法初步 算法与程序框图 基本算法语句 算法案例 第二章 统计 随机抽样 用样本估计总体 变量间的相关关系 第三章 概率 随机事件的概率 古典概型函数 任意角和弧度制 任意角的三角函数 三角函数的诱导公式 三角函数的图像与性质 函数 y=Asin(ωx+φ)的图像 三角函数模型的简单应用 第二章 平面向量 平面向量的实际背景及基本概念 平面向量的线性运算 平面向量的基本定理及坐标表示 平面向量的数量积 平面向量应用举例 第三章 三角恒等变换
高中数学必修五目录 第一章 解三角形 正弦定理和余弦定理 应用举例 实习作业 第二章 数列 数列的概念与简单表示法 等差数列 等差数列的前 n 项和 等比数列 等比数列的前 n 项和 第三章 不等式 不等关系与不等式 一元二次不等式及其解法 二元一次不等式(组)与简单的线 性规划问题 基本不等式
圆的方程 直线、圆的位置关系 空间直角坐标系
两角和与差的正弦、余弦和正切公 式
简单的三角恒等变换
高中数学选修 1-2 目录 第一章 统计案例 1.1 回归分析的基本思想及其初 步应用 1.2 独立性检验的基本思想及其 初步应用 第二章 推理与证明 2.1 合情推理与演绎推理 2.2 直接证明与间接证明 第三章 数系的扩充与复数的引 入 3.1 数系的扩充和复数的概念 3.2 复数代数形式的四则运算 第四章 框图 4.1 流程图 4.2 结构图
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
超全的高中数学思维导图
高难拉分攻坚特训(一)
1.已知椭圆M :x 2a 2+y 2
=1,圆C :x 2+y 2=6-a 2在第一象限有公共点P ,设圆C 在点P 处的切线斜率为k 1,椭圆M 在点P 处的切线斜率为k 2,则k 1
k 2
的取
值范围为( )
A .(1,6)
B .(1,5)
C .(3,6)
D .(3,5)
答案 D
解析 由于椭圆M :x 2a
2+y 2=1,圆C :x 2+y 2=6-a 2
在第一象限有公共点P ,所以⎩⎨⎧
a 2>6-a 2,6-a 2
>1,
解得3<a 2
<5.设椭圆M :x 2a 2+y 2
=1与圆C :x 2+y 2=6-a 2在
第一象限的公共点P (x 0,y 0),则椭圆M 在点P 处的切线方程为x 0x
a 2+y 0y =1,圆C 在P 处的切线方程为x 0x +y 0y =6-a 2,所以k 1=-x 0y 0,k 2=-x 0a 2y 0,k 1
k 2=a 2,所
以k 1
k 2
∈(3,5),故选D. 2.已知数列{a n }满足a 1=4,a n +1=4-4
a n
,且f (n )=(a 1-2)(a 2-2)+(a 2-2)(a 3
-2)+(a 3-2)(a 4-2)+…+(a n -1)(a n +1-2),若∀n ≥3(n ∈N *),f (n )≥m 2-2m 恒成立,则实数m 的最小值为________.
答案 -1
解析 ∵a 1=4,a n +1=4-4
a n
,∴
2a n +1-2=24a n -4a n -2
=a n a n -2=1+2
a n -2
,又
2a 1-2=1,∴数列⎩⎪⎨⎪⎧⎭
⎪⎬⎪⎫2a n -2是以1为首项,1为公差的等差数列,∴2a n -2=1+n
-1=n ,a n -2=2n ,令b n =(a n -2)(a n +1-2)=2n ·2n +1=4⎝ ⎛⎭
⎪⎫1n -1n +1,
∴f (n )=(a 1-2)(a 2-2)+(a 2-2)(a 3-2)+(a 3-2)·(a 4-2)+…+(a n -2)(a n +1-2)=b 1+b 2+…+b n =4×⎝
⎛
⎭⎪⎫1-12+12-13+…+1n -1n +1=4n n +1. 若∀n ≥3(n ∈N *),f (n )≥m 2-2m 恒成立, 则f (n )min ≥m 2-2m . 易知f (n )=
4n
n +1
在[3,+∞)上是增函数, ∴f (n )min =f (3)=3,即m 2-2m -3≤0, 解得-1≤m ≤3, ∴实数m 的最小值为-1.
3.已知椭圆C :x 2a 2+y 2
b 2=1(a >b >0)的左焦点F 和上顶点B 在直线3x -3y +3=0上,A 为椭圆上位于x 轴上方的一点且AF ⊥x 轴,M ,N 为椭圆C 上不同于A 的两点,且∠MAF =∠NAF .
(1)求椭圆C 的标准方程;
(2)设直线MN 与y 轴交于点D (0,d ),求实数d 的取值范围. 解 (1)依题意得椭圆C 的左焦点为F (-1,0),上顶点为B (0,3), 故c =1,b =3,所以a =b 2+c 2=2, 所以椭圆C 的标准方程为x 24+y 2
3=1.
(2)设直线AM 的斜率为k ,
因为∠MAF =∠NAF ,
所以AM ,AN 关于直线AF 对称,
所以直线AN 的斜率为-k ,
易知A ⎝ ⎛⎭
⎪⎫-1,32, 所以直线AM 的方程是y -32=k (x +1),
设M (x 1,y 1),N (x 2,y 2),
联立⎩⎪⎨⎪⎧ y -32=k (x +1),
x 24+y 23=1,
消去y ,得(3+4k 2)x 2+(12+8k )kx +(4k 2+12k -3)=0,
所以x 1=-4k 2-12k +33+4k 2
, 将上式中的k 换成-k ,得x 2=-4k 2+12k +33+4k 2
, 所以k MN =y 1-y 2x 1-x 2=k [(x 1+x 2)+2]x 1-x 2
=k ⎝ ⎛⎭⎪⎫-8k 2+63+4k 2+2-24k
3+4k 2
=-12, 所以直线MN 的方程是y =-12x +d ,
代入椭圆方程x 24+y 23=1,得x 2-dx +d 2-3=0,
所以Δ=(-d )2-4(d 2-3)>0,
解得-2<d <2,
又因为MN 在A 点下方,
所以-1×12+32>d ⇒d <1,
所以-2<d <1.
4.已知函数f (x )=(x -1)e x -ax 2(e 是自然对数的底数).
(1)讨论函数f (x )的极值点的个数,并说明理由;
(2)若对任意的x >0,f (x )+e x ≥x 3+x ,求实数a 的取值范围.
解 (1)f ′(x )=x e x -2ax =x (e x -2a ).
当a ≤0时,由f ′(x )<0得x <0,由f ′(x )>0得x >0,∴f (x )在(-∞,0)上单调递减,
在(0,+∞)上单调递增,
∴f (x )有1个极值点;
当0<a <12时,由f ′(x )>0得x <ln 2a 或x >0,由f ′(x )<0得0>x >ln 2a ,
∴f (x )在(-∞,ln 2a )上单调递增,在(ln 2a,0)上单调递减,在(0,+∞)上单调递增,
∴f (x )有2个极值点;
当a =12
时,f ′(x )≥0, ∴f (x )在R 上单调递增,
∴f (x )没有极值点;
当a >12时,由f ′(x )>0得x <0或x >ln 2a ,
由f ′(x )<0得0<x <ln 2a ,
∴f (x )在(-∞,0)上单调递增,在(0,ln 2a )上单调递减,在(ln 2a ,+∞)上单调递增,
∴f (x )有2个极值点.
综上,当a ≤0时,f (x )有1个极值点;当a >0且a ≠12时,f (x )有2个极值点;
当a =12时,f (x )没有极值点.
(2)由f (x )+e x ≥x 3+x 得x e x -x 3-ax 2-x ≥0.
当x >0时,e x -x 2-ax -1≥0,
即a ≤e x -x 2-1x
对任意的x >0恒成立. 设g (x )=e x -x 2-1x
, 则g ′(x )=(x -1)(e x -x -1)x 2
. 设h (x )=e x -x -1,则h ′(x )=e x -1.
∵x >0,∴h ′(x )>0,
∴h (x )在(0,+∞)上单调递增,
∴h (x )>h (0)=0,即e x >x +1,
∴g (x )在(0,1)上单调递减,在(1,+∞)上单调递增,
∴g (x )≥g (1)=e -2,∴a ≤e -2,
∴实数a的取值范围是(-∞,e-2].。
