高中数学全套知识点思维导图函数的基本性质
高一函数应用知识点总结图

高一函数应用知识点总结图一、函数及函数的基本概念1. 函数的定义:函数是一种特殊的关系,它将每个自变量映射到唯一的因变量上。
2. 自变量和因变量:自变量是函数中的输入量,因变量是函数中的输出量。
3. 定义域和值域:函数的定义域是自变量的取值范围,值域是因变量的取值范围。
二、函数的图象及性质1. 函数的图象:函数的图象是自变量和因变量之间的关系在直角坐标系中的图形表示。
2. 函数的单调性:函数在定义域内的增减情况。
3. 函数的奇偶性:函数在定义域内的对称性。
4. 函数的周期性:函数在定义域内的重复性。
三、初等函数及其性质1. 幂函数:f(x) = x^n (n为常数)。
2. 指数函数:f(x) = a^x (a>0, a≠1)。
3. 对数函数:f(x) = loga(x) (a>0, a≠1)。
4. 三角函数:sin(x), cos(x), tan(x)等。
5. 反三角函数:arcsin(x), arccos(x), arctan(x)等。
四、函数的运算1. 函数的和、差、积、商:(f+g)(x) = f(x) + g(x),(f-g)(x) = f(x) - g(x),(f*g)(x) = f(x) * g(x),(f/g)(x) = f(x) / g(x)。
2. 复合函数:(f∘g)(x) = f(g(x))。
3. 反函数:若f(x)的定义域和值域交换,则g(x)为f(x)的反函数,记作g(x) = f^(-1)(x)。
五、函数的应用1. 建立数学模型:利用函数构建实际问题的数学模型,解决现实生活中的问题。
2. 函数的最值:利用函数图象和性质求函数的最大值和最小值。
3. 函数的增长率:函数在某一点的导数即为其增长率,用以描述函数增长和减少的趋势。
4. 函数的变化率:函数的导数描述了函数在各个点的变化率,应用于相关变化的问题中。
六、导数和微分1. 导数的定义:函数在某一点的导数定义为函数在该点处的切线斜率。
2020年高中数学必修1-函数全册知识结构思维导图
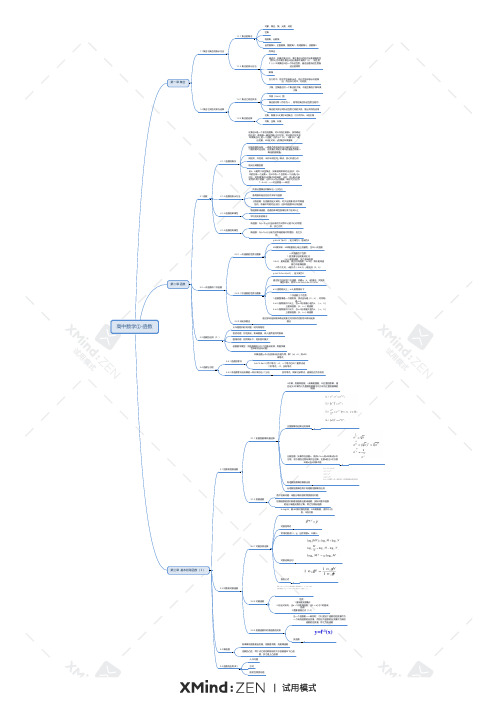
x^n=a,则x叫做a的n次根,求方根的过程叫做开方运算,正数a的正n次方根
理数指数幂适用于有理数指数幂的法则
数函数的底判断是增函数还是减函数;实际问题中函数
叫做真数,读作以a为
,自然常数e,叫做ln
性质:
1.值域是实数集R
2.在定义域内,当a>1时是增函数,当0<a小于1时是减
函数
3.图象都通过点(1,0)
指数函数和对数函数的关系当一个函数是一一映射时,可以把这个函数的因变量作为一个新的函数的自变量,而把这个函数的自变量作为新的函数的因变量,称之为反函数
反函数。
常见函数(附思维导图)

2.2常见函数一、一次函数和常函数:思维导图:(一) 、一次函数 〔二〕、常函数 定义域:〔- ∞,+ ∞〕 定义域: 〔- ∞,+ ∞〕 值 域:〔- ∞,+ ∞〕 正 k=0 反 值 域:{ b }解析式:y = kx + b ( k ≠ 0 ) 解析式:y = b ( b 为常数)图 像:一条与x 轴、y 轴相交的直线 图 像:一条与x 轴平行或重合的直线b>0 b=0 b<0 K > 0 k < 0单调性: k > 0 ,在〔- ∞,+ ∞〕↑ 单调性:在〔- ∞,+ ∞〕上不单调 k < 0 ,在〔- ∞,+ ∞〕↓奇偶性:奇函数⇔=0b 奇偶性: 偶函数 非奇非偶⇔≠0b周期性: 非周期函数 周期性:周期函数,周期为任意非零实数 反函数:在〔- ∞,+ ∞〕上有反函数 反函数:在〔- ∞,+ ∞〕上没有反函数 反函数仍是一次函数例题:二、二次函数1、定义域:〔- ∞,+ ∞〕2、值 域: ),44[,02+∞-∈>ab ac y a]44,(,02ab ac y a --∞∈<3、解析式:)0(2≠++=a c bx ax y4、图 像:一条开口向上或向下的抛物线 开口向下,开口向上;正负:增大,开口缩小绝对值:随着,00<>a a a a正半轴相交与负半轴相交与y c y c c,0,0><对称轴:ab x 2-=对称轴: ;)44,2(2ab ac ab --顶点: 轴交点个数图像与x ac b →-=∆42:与x 轴交点的个数。
两个交点,0>∆一个交点,0=∆无交点,0<∆5、单调性:↑+∞-↓--∞>),2[]2,(,0ab ab a↓+∞-↑--∞<),2[]2,(,0ab ab a6、奇偶性:偶函数⇔=0b7、周期性:非周期函数8、反函数:在〔- ∞,+ ∞〕上无反函数,上及其子集上有反函数或在),2[]2,(+∞---∞ab ab例题:三、反比例函数和重要的分式函数〔一〕、反比例函数 〔二〕、分式函数bax dcx y ++= 定义域:〔- ∞,0〕∪〔0,+ ∞〕 定义域:),(),(+∞---∞aba b 值 域:〔- ∞,0〕∪〔0,+ ∞〕 值 域: ),(),(+∞-∞a c a c解析式:)0()(≠=k xk x f 解析式:)(a bx b ax d cx y -≠++=图 像:以x 轴、y 轴为渐进线的双曲线 图 像:以abx -=和a c y =为渐近线的双曲线y y0 x 0 xk > 0 k < 0单调性: k>0,〔- ∞,0〕↓,〔0,+ ∞〕↓ 单调性:在),(a b --∞和),(+∞-ab上 k<0,〔- ∞,0〕↑,〔0,+ ∞〕↑ 单调性相同 奇偶性:奇函数 奇偶性:非奇非偶 对称性:关于原点对称 对称性:关于点),(aca b -成中心对称 周期性:非周期函数 周期性:非周期函数反函数:在定义域上有反函数, 反函数:在定义域有反函数, 反函数是其本身。
高中数学1.3函数的基本性质知识框架素材新人教必修1.ppt
函数
函数及其表示
函数的基本性质
函数图象的画法
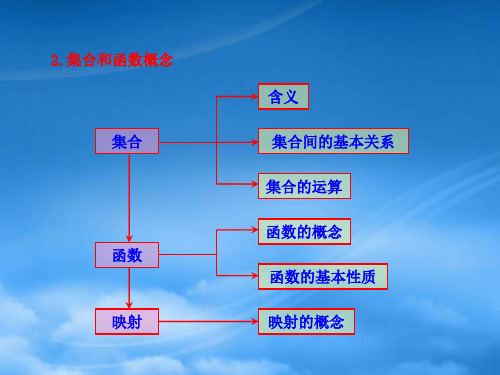
Hale Waihona Puke 2.集合和函数概念 集合
函数 映射
含义 集合间的基本关系 集合的运算 函数的概念 函数的基本性质 映射的概念
3.函数框架图 一次函数
函数 图象与性质
二次函数
定义域
值域
单调性
奇偶性
待定系数法确定解析式
4.函数及其基本性质
函数定义:设A,B是非空的数集,如果按某种确定的 对应关系f,使对于集合A中的任意一个元素x,在集 合B中都有唯一确定的元素f(x)与之对应,那么就 称对应f:A→B为从集合A到集合B的一个函数
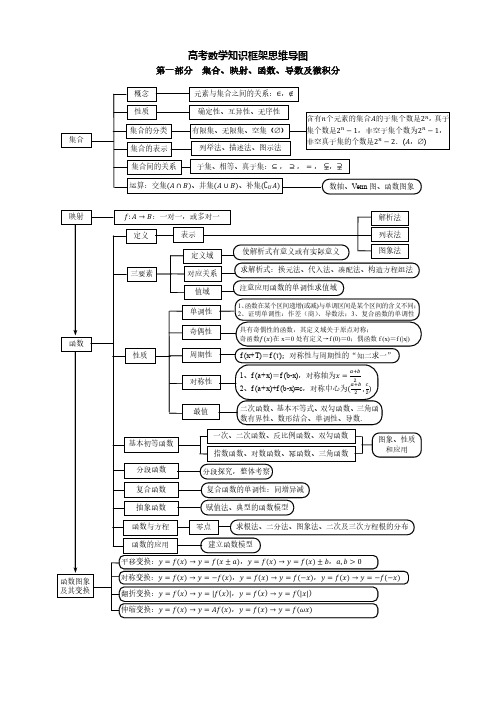
高中数学知识框架思维导图(整理版)
柯西不等式
第四部分
位置关系
截距
解析几何
斜率公式、倾斜角的变化与斜率的变化: = tan , =
倾斜角和斜率
重合
A1B2-A2B1=0,C1B2-C2B1=0
平行
A1B2-A2B1=0,C1B2-C2B1≠0
相交
A1B2-A2B1≠0
垂直
直线的方程
z 的几何意义:
过可行域内一点(, )
向直线 = , = 作
复合函数
函数与方程
2
二次函数、基本不等式、双勾函数、三角函
数有界性、数形结合、单调性、导数.
基本初等函数
分段函数
, )
零点
求根法、二分法、图象法、二次及三次方程根的分布
建立函数模型
平移变换: = () → = ( ± ), = () → = () ± ,, > 0
对称性
y=Asin(x+)+b
化简、求值、
证明(恒等变形)
)
值域
图象
对称轴(正切函数除外)经过函数图象
的最高(或低)点且垂直 x 轴的直线,
对称中心是正余弦函数图象的零点,正
切函数的对称中心为( ,0)(k∈Z).
最值
2
①图象可由正弦曲线经过平移、伸缩得到,但要注意先平移后伸缩与先伸缩后平移不同;
2.
3.
分组求和法
2
=
1
−
−1)(2+1 −1)
2 −1
+1
1 1
1
= (
2 (+2)2
(−1) ∙4
4 2
(2−1)(2+1)
1
2+1 −1
高三数学所有知识点思维导图

高三数学所有知识点思维导图数学是一门理论性较强的科学,它涉及到复杂的逻辑思维和抽象的概念。
为了更好地理解和掌握高三数学知识,在学习过程中,合理地组织知识点之间的联系和内在逻辑结构非常重要。
这篇文章将通过思维导图的方式,对高三数学的所有知识点进行概括总结。
一、函数与方程1. 函数的概念2. 常用函数的性质与图像a. 一次函数b. 二次函数c. 三次函数d. 高次函数e. 幂函数f. 指数函数g. 对数函数h. 三角函数3. 方程的基本概念a. 一元一次方程b. 一元二次方程c. 一元高次方程d. 二元一次方程e. 二元二次方程二、数与集合1. 实数与不等式a. 实数的性质b. 不等式的性质c. 一元一次不等式d. 一元二次不等式e. 二元一次不等式f. 二元二次不等式2. 复数与复数运算a. 复数的定义与性质b. 复数的运算c. 复数的共轭与模3. 集合与命题逻辑a. 集合的基本概念与运算b. 命题的概念与逻辑运算三、解析几何1. 平面坐标系a. 平面直角坐标系的建立与性质b. 向量的概念与运算c. 直线与方程d. 圆与方程2. 空间坐标系a. 空间直角坐标系的建立与性质b. 空间中的直线与平面c. 空间中的平面与方程四、三角函数与解三角形1. 三角函数的基本关系式a. 正弦函数与余弦函数b. 正切函数与余切函数c. 正割函数与余割函数2. 三角函数的性质与变换a. 周期性与奇偶性b. 幅角的增减关系c. 三角函数的和差化积3. 解三角形的基本概念a. 三角外角与内角b. 三角形的各种关系式c. 解三角形的方法与技巧五、数列与数学归纳法1. 数列的基本概念与性质a. 数列的定义b. 数列的通项公式与通项求和公式c. 数列的极限2. 等差数列与等比数列a. 等差数列的性质与公式b. 等差数列的求和公式c. 等比数列的性质与公式d. 等比数列的求和公式3. 数学归纳法的原理与应用a. 数学归纳法的基本思想b. 数学归纳法在证明问题中的应用六、概率与统计1. 随机事件与概率a. 随机事件的概念与性质b. 概率的定义与性质c. 概率计算与应用2. 统计方法与推理a. 统计调查与样本调查b. 描述性统计与统计推断c. 抽样分布与统计量的估计d. 假设检验与推断这篇文章通过思维导图的方式,对高三数学的所有知识点进行了系统的总结,有助于帮助学生快速理清思路,更好地掌握数学知识。
高中数学思维导图(新课标)

'
f x 与 f x 0 的区别
vt S , at vt
'
0 0
第 二 部 分 映 射 、 函 数 、 导 数 、 定 积 分 与 微 积 分
导 数
导数概念
运动的平均速度 曲线的割线的斜率
'
0
k f
'
'
x
0
' '
; x
n
nx 1 x
定
映
A中元素在B中都有唯一的象;可一对一 (一一映射),也可多对一,但不可一对多 定义 函数的概念 表示 定义域
列表法 解析法 图象法 使解析式有意义及实际意义
第 二 部 分 映 射 、 函 数 、 导 数 、 定 积 分 与 微 积 分
射
三要素
区间 单调性 奇偶性 周期性 对称性
对应关系 值域
常用换元法求解析式 观察法、判别式法、分离常数法、单调性法、最值法、 重要不等式、三角法、图象法、线性规划等
函数的 基本性质
函 数
函数常见的
最值
几种变换
基本初等函数 分段函数 复合函数 抽象函数 函数与方程 函数的应用
平移变换、对称变换 翻折变换、伸缩变换
三角函数 单调性:同增异减 赋值法,典型的函数 零点 建立函数模型 求根法、二分法、图象法;一元二次方程根的分布 退出 上一页
函数的平均变化率
函数的瞬时变化率 运动的瞬时速度 曲线的切线的斜率
第一部分 第二部分 第三部分 第四部分 第五部分 第六部分
集合与简易逻辑 映射、函数、导数、定积分与微积分 三角函数与平面向量 数列 不等式 立体几何与空间向量
数学高一下知识点思维导图

数学高一下知识点思维导图数学是一门理科学科,是一门需要逻辑思维的学科。
在高一下学期,学生会接触到更深入的数学知识,并需要掌握更多的数学技巧。
下面是高一下学期数学知识点的思维导图,帮助学生整理和梳理学习内容。
1. 代数- 线性方程组- 高斯消元法- 初等变换- 二次函数- 顶点坐标- 对称轴- 判别式- 不等式- 解不等式- 图像表示2. 几何- 平面几何- 平行线与垂直线 - 四边形性质- 三角形面积- 空间几何- 空间直线和平面 - 空间向量- 空间几何关系 - 三角函数- 正弦定理- 余弦定理- 向量叉乘3. 概率与统计- 随机事件- 概率的定义- 加法规则和乘法规则 - 统计分布- 频数分布- 直方图- 折线图- 抽样调查- 抽样方法- 数据分析- 推论统计4. 数列与数学归纳法- 等差数列- 公差和通项公式- 前n项和- 等比数列- 公比和通项公式- 前n项和- 数学归纳法- 原理与应用- 数学归纳证明5. 导数与微分- 导数的定义- 函数导数的定义与性质 - 高阶导数- 函数的求导法则- 乘积法则- 商法则- 链式法则- 函数的应用- 切线与法线- 最值问题- 凹凸性与拐点以上就是高一下学期数学知识点的思维导图。
通过这样的整理,学生可以更加清晰地了解数学知识点之间的联系和重点内容。
同时,思维导图也能够帮助学生在复习时更加高效地回顾相关知识。
希望这个思维导图能对学生的学习有所帮助!。
高中数学知识框架思维导图(整理版)

点斜式:y-y0=k(x-x0)
注意:截距可正、
可负,也可为 0.
2 −1
注意各种形式的转化和运用范围.
x y
截距式: + =1
a b
两直线的交点
距离
一般式:Ax+By+C=0
两点间的距离公式|1 2 | = √(1 − 2 )2 + (1 − 2 )2 .
2.
3.
分组求和法
2
=
1
−
−1)(2+1 −1)
2 −1
+1
1 1
1
= (
2 (+2)2
(−1) ∙4
4 2
(2−1)(2+1)
1ቤተ መጻሕፍቲ ባይዱ
2+1 −1
− (+2)2 )
= (−1) (
1
2−1
+
错位相加法: = ( + )−1 → = ( + ) −
复合函数
函数与方程
2
二次函数、基本不等式、双勾函数、三角函
数有界性、数形结合、单调性、导数.
基本初等函数
分段函数
, )
零点
求根法、二分法、图象法、二次及三次方程根的分布
建立函数模型
平移变换: = () → = ( ± ), = () → = () ± ,, > 0
与 的关系
1 ,
= 1,
= {
− −1 , ≥ 2.
构造等差数列
an+1 p an
= · +1 转为③
qn q qn-1
⑤an + 1=pan+qn
函数的基本性质 知识框架

函数的最大(小)值
增函数
函数的单调性减函数单调增区间单调减区间
2.集合和函数概念 含义 集合 集合间的基本关系 集合的运算
函数的概念
函数 函数的基本性质 映射 映射的概念
3.函数框架图
函数
一次函数 图象与性质 二次函数
定义域
值域
单调性
奇偶性
待定系数法确定解析式
4.函数及其基本性质
函数定义:设A,B是非空的数集,如果按某种确定的
对应关系f,使对于集合A中的任意一个元素x,在集 合B中都有唯一确定的元素f(x)与之对应,那么就
称对应f:A→B为从集合A到集合B的一个函数
函数 函数及其表示 函数的基本性质 函数图象的画法
2020年高考数学复习思维导图(人教版)02——函数
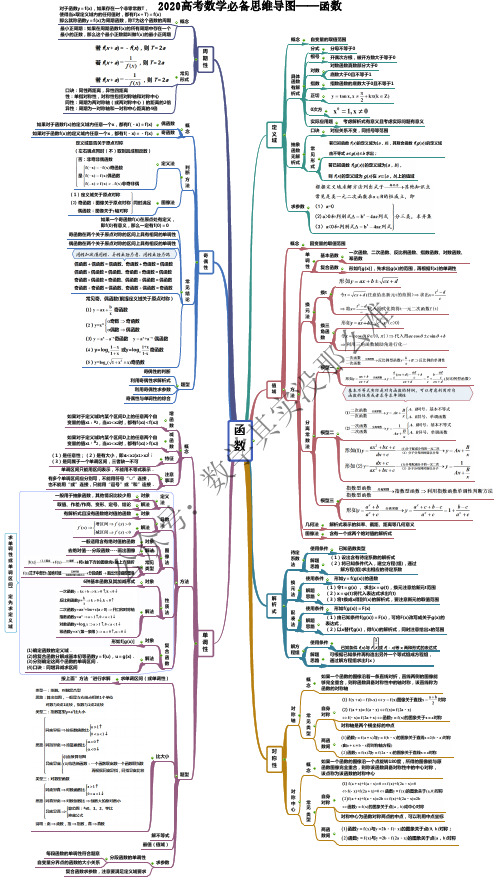
基本不等式实际是对勾函数的特例,可以考虑利用对勾实际应用题考虑解析式有意义且考虑实际问题有意义
解析式表示的斜率、截距、距离等几何意义一般适用含有绝对值的函数
6种基本函数及其加减形式
形如f[g(x)]
确定函数的定义域.
将复合函数分解成基本初等函数y =f(u),u =g(x).分别确定这两个函数的单调区间.如果一个函数的图像沿一个点旋转180度,所得的图像能与原函数图像完全重合,则称该函数具备对称性中的中心对称,对称轴是两个横坐标的中点
对称中心为函数对称两点的中点,可以利用中点坐标
如果一个奇函数f(x)在原点处有定义,即f(0)有意义,那么一定有奇偶性的判断利用奇偶性求解析式公
众
么
难。
高二数学上册知识点思维导图

高二数学上册知识点思维导图数学是一门需要系统、逻辑思维的学科,掌握数学知识点对于高中学生来说至关重要。
以下是高二数学上册的知识点思维导图,帮助学生更好地理解和掌握这些知识。
一、函数与方程1. 一次函数- 定义与性质- 斜率与截距- 函数图像与表示方法2. 二次函数- 定义与性质- 抛物线的开口方向- 顶点坐标与轴对称性- 函数图像与表示方法3. 三角函数- 弧度与角度的转换- 正弦、余弦、正切函数的定义与性质 - 三角函数的图像与周期性4. 指数与对数函数- 指数函数的性质与图像- 对数函数的性质与图像- 指数方程与对数方程的求解5. 运算与方程- 函数的四则运算- 复合函数与反函数- 一元二次方程的解法- 一元二次方程的应用二、平面几何1. 二维坐标与向量- 点的坐标与向量的表示- 向量的运算与性质- 平面向量的数量积与性质2. 三角形与四边形- 三角形的内角和定理- 三角形的外角和定理- 三角形的相似与全等- 四边形的性质与分类3. 圆的性质- 圆的定义与性质- 弧长与扇形面积- 正多边形与圆的关系4. 直线与圆的位置关系- 直线与圆的位置关系的性质与判定- 切线与切点- 弦长定理与切线定理的应用三、解析几何1. 平面与空间坐标系- 平面坐标系与直线方程- 空间坐标系与平面方程- 平面与直线的位置关系2. 点、直线、平面的位置关系- 点与直线的位置关系- 直线与平面的位置关系- 平面与平面的位置关系3. 直线与平面的交线- 直线与平面的交点与交线- 向量与平面的垂直与平行关系- 直线与平面的应用问题4. 空间几何体的性质- 球的性质与方程- 圆锥曲线的方程与图像- 空间几何体的计算问题四、统计与概率1. 数据的收集与整理- 总体与样本的定义- 数据的收集方法与调查设计 - 数据整理与展示的图表形式2. 概率与统计- 随机事件与样本空间- 概率的计算与性质- 频率与概率的关系3. 概率模型与分布- 事件的并、交、补运算- 离散型与连续型随机变量- 正态分布的性质与应用4. 统计推断与假设检验- 抽样与统计推断的基本思想- 样本均值与总体均值的估计- 假设检验的步骤与原理通过以上的思维导图,高中生可以更清晰地了解高二数学上册的知识点,并在学习中更好地进行整理与归纳。
